m ta e m a t i Q u e s ,



Notes històriques, que es corresponen amb diferents camps de les matemàtiques.
Eix cronològic, que assenyala els principals avenços en un dels camps de les matemàtiques i els situa en l’època en què es van produir.
RESOL
Activitat que pretén activar els coneixements previs de l’alumne.
Presentació de la informació de manera rigorosa i estructurada.
Fets històrics i descobriments més rellevants de cada època.

Les dues primeres pàgines de cada unitat introdueixen els continguts més importants que es tractaran.


EXERCICIS RESOLTS al llarg de la unitat que mostren com fer servir els procediments apresos.
EXERCICIS PROPOSATS al llarg de la unitat per aplicar els continguts treballats.
Emmy Noether i la seva contribució a les matemàtiques.



EXERCICIS I PROBLEMES RESOLTS al final de la unitat, classificats per continguts.
Proposta per preparar les PAU
Treball dels ODS amb l’objectiu de fomentar l’ús de l’esperit crític i de mostrar la necessitat d’actuar.
Que es plantegen a partir d’una situació real i impliquen un repte en forma de preguntes o problemes al qual cal donar resposta o sobre el qual s’ha d’intervenir. Els trobareu en l’espai personal del web www.barcanova.cat.
EXERCICIS I PROBLEMES GUIATS, amb indicacions per facilitar-ne la resolució. Inclouen la solució.
EXERCICIS I PROBLEMES PROPOSATS al final de la unitat, seqüenciats per continguts i per dificultat.
Autoavaluació de la unitat que permet, a l’alumne, comprovar l’assoliment dels continguts.
La proposta digital de Barcanova és EDUDYNAMIC, un projecte digital complet que dona una resposta global a un entorn educatiu divers i dinàmic.

A partir d’un entorn senzill i intuïtiu, EDUDYNAMIC és un projecte digital multidispositiu i multisuport que s’adapta i es visualitza a totes les plataformes i a tots els entorns d’aprenentatge virtual (Blink Learning, Moodle, Alexia, Google Classroom, Clickedu, Office 365…).
La diversitat i riquesa de recursos, des d’activitats interactives traçables a vídeos, presentacions i ludificació, fa d’EDUDYNAMIC un projecte digital actualitzat i complet pensat per canviar amb tu.
Compatibilitat i sincronització amb qualsevol dispositiu. Integració a totes les plataformes i entorns EVA. Gestió en línia de les activitats i tasques assignades als alumnes. Continguts i eines per treballar on-line i off-line Amb suport paper o sense.El projecte, adaptat a diferents enfocaments i necessitats, es pot utilitzar com a complement del llibre imprès o bé com a model autònom per a les aules més digitalitzades.



Des d’on poder accedir i treballar amb continguts digitals.
Els canvis que fa l’usuari se sincronitzen automàticament en connectar qualsevol dels dispositius amb què es treballa.
Són descarregables per poder treballar també sense connexió a la xarxa.
UNIVERSAL
Són responsive i ajusten el seu contingut a qualsevol dispositiu: mòbil, tauleta, ordinador...
Tots els projectes digitals de Barcanova s’adapten i es visualitzen a totes les plataformes i a tots els entorns virtuals d’aprenentatge (EVA).
Per millorar la comprensió dels continguts: activitats interactives traçables, vídeos, presentacions, imatges interactives, suggeriments didàctics, enllaços, ludificació i... molt més!
Una superfície cònica, tal com es mostra en la il·lustració de la dreta, és una figura formada per dos cons infinits oposats pel vèrtex.
Si una superfície cònica es talla per un pla, es poden obtenir una circumferència, una el·lipse, una paràbola o una hipèrbola, segons l’angle que formi aquest pla amb l’eix de la superfície cònica. Per això, aquestes corbes s’anomenen còniques
Al segle iii aC, el gran geòmetra grec Apol·loni de Perge va escriure un llibre dedicat a les còniques. Amb un estil polit i sistemàtic, va estudiar aquestes corbes de forma exhaustiva. D’acord amb l’esperit dels grecs, aquest tractat va ser eminentment especulatiu, sense buscar aplicacions pràctiques.
Quan Apol·loni va descriure les el·lipses, les paràboles i les hipèrboles com a còniques, estava molt lluny d’imaginar que aquestes corbes s’ajustaven als moviments dels cossos celestes. Durant molts segles es va considerar que les òrbites dels planetes eren circulars. Va ser al començament del segle xvii quan Kepler va anunciar les seves importants lleis, una de les quals assigna òrbites el·líptiques a aquests cossos.
Només un segle abans, Copèrnic havia refutat la concepció geocèntrica de l’univers i havia afirmat que era la Terra la que girava al voltant del Sol.

Les còniques són referents habituals en la tecnologia actual. Vegem-ne alguns exemples:
La paràbola té la propietat que totes les rectes paral·leles al seu eix, en «rebotar» en la corba, es reflecteixen passant pel punt anomenat focus.
Les antenes parabòliques serveixen per arreplegar un feix de «rajos» procedents del satèl·lit artificial al qual apunten i concentrar-los en el focus, on hi ha el detector que arreplega la informació.
En una el·lipse, si un raig surt d’un focus, en reflectir-se en la corba, passa per l’altre focus.
Aquesta propietat s’aplica per construir llums els rajos dels quals es concentren tots en un punt. Per exemple, en els llums dels odontòlegs, el punt de llum se situa en un dels focus de l’el·lipse (en vermell en la figura); els rajos lluminosos (en verd) es reflecteixen en la pantalla el·líptica i es troben en l’altre focus, on es col·loca l’objecte que es vol il·luminar (la boca del pacient).
On se situarà el dipòsit?
Es vol instal·lar un gran dipòsit de propà per abastir una factoria industrial i dues urbanitzacions.
S’han de complir les condicions següents: convé que el dipòsit estigui tan a prop com sigui possible de la factoria, però per raons de seguretat no pot ser a menys de 500 m d’un forn que hi ha en aquesta.
Per tant, s’haurà de situar, exactament, a 500 m del forn F. A més, ha d’estar a la mateixa distància de A que de B.
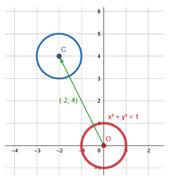
Per resoldre el problema, traslladem les dades a uns eixos cartesians (costat del quadrat = 100 m) i suposem que els punts F, A i B se situen on s’indica en el gràfic de la dreta.
• La circumferència vermella és el conjunt de punts que estan a 500 m del forn. Analíticament, són punts (x, y) la distància dels quals a F (13, 15) és 5. Expressa-ho mitjançant una equació.
• La recta verda és el conjunt de punts que equidisten de A i de B Analíticament, és una recta que passa per (6, 3) i té pendent 2. Escriu-ne l’equació.
• El punt P on hem de situar el dipòsit de propà s’obté trobant la intersecció de les dues línies que acabem de descriure. Resol el sistema que formen les seves equacions per trobar les coordenades de P
Atenció
És molt important que interpretis cada una de les línies descrites en els exemples com un conjunt de punts que compleixen una propietat:
a) Si X és un punt de la mediatriu, la distància a A és igual que la distància a B
b) Si X és un punt de la bisectriu…
c) Si X és un punt de la circumferència…
S’anomena lloc geomètric un conjunt de punts que compleixen una propietat.
Per exemple:
a) La mediatriu d’un segment AB és el lloc geomètric dels punts, X, que equidisten dels seus extrems: dist (X, A) = dist (X, B)
b) La bisectriu d’un angle de costats r1 i r2 és el lloc geomètric dels punts, X, que equidisten de r1 i de r2: dist (X, r1) = dist (X, r2)
c) La circumferència de centre O i radi r és el lloc geomètric dels punts, X, la distància a O dels quals és r : dist (X, O) = r
Per obtenir l’equació de la figura geomètrica, anomenem X (x, y) el punt genèric i hi apliquem analíticament la propietat que ha de complir.
Exercicis resolts
1 Troba l’equació de la mediatriu del segment d’extrems A(–3, 4) i B(1, 0).
Cada punt de la mediatriu, X(x, y), equidista dels extrems del segment AB. Per tant, han de complir la condició dist (X, A) = dist (X, B).
Elevem al quadrat els dos membres, desenvolupem els quadrats indicats i simplifiquem:
y + 16 = x 2 – 2x + 1 + y 2 → 8x – 8y + 24 = 0 → x – y + 3 = 0 → y = x + 3. És, en efecte, una recta.
Comprovem que la recta obtinguda és perpendicular al segment AB en el punt mitjà:
• Passa per (–1, 2), que és el punt mitjà del segment.
A (–3, 4) y = x + 3
B (1, 0)
• El seu pendent, 1, i el pendent del segment, –1, compleixen que 1 · (–1) = –1. Per tant, són perpendiculars. Per tant, efectivament, y = x + 3 és la mediatriu de AB.
Fes-ho tu. Troba l’equació de la mediatriu del segment els extrems del qual són
A(0, 0) i B(6, 4).
2 Troba l’equació de la bisectriu de l’angle format per les rectes:
r1: 4x + 3y – 5 = 0
r2: 3x + 4y – 2 = 0
Cada punt X(x, y) de la bisectriu equidista de les rectes que formen l’angle. Per tant, han de complir que dist (X, r1) = dist (X, r2):
Per interpretar aquesta equació, hem d’eliminar els valors absoluts. En fer-ho, apareix un doble signe, perquè:
El lloc geomètric buscat està compost per les dues rectes, (L1) i (L2), perpendiculars entre si i que es tallen en (2, –1), el mateix punt en què es tallen
Són les bisectrius dels angles formats per les dues rectes donades.
Fes-ho tu. Troba l’equació de la bisectriu de l’angle format per les rectes
3 Troba el lloc geomètric dels punts la diferència de quadrats de distàncies a P(4, 2) i a Q(–2, 5) dels quals és 15: [dist (X, P) ]2 – [dist (X, Q)] 2 = 15
Expressem analíticament la condició:
() () () () xy xy 42 25 15 22 2 22 2 ++ +=aakk
Operem i simplifiquem:
Per tant, la recta és perpendicular al segment, ja que 2 2 1 –1 = cm
Conclusió: El lloc geomètric buscat és una recta perpendicular al segment PQ.
Fes-ho tu. Troba el lloc geomètric dels punts la diferència de quadrats de distàncies a P(2, 5) i a Q(4, –1) dels quals és 40; és a dir, XP 2 – XQ 2 = 40.
1 Troba les equacions dels llocs geomètrics següents:
a) Mediatriu del segment d’extrems A(–5, –3) i B (7, 1). Comprova que és una recta perpendicular al segment en el seu punt mitjà.
b) Circumferència de centre O (–3, 4) i radi 5. Comprova que passa per l’origen de coordenades.
c) Bisectrius dels angles formats per aquestes rectes:
r1: 2x + y – 3 = 0
r2: x – 2y + 16 = 0
Comprova que les bisectrius són dues rectes perpendiculars que es tallen en el mateix punt en què es tallen les rectes r1 i r2.
L’equació d’una circumferència de centre O(a, b) i radi r és aquesta:
dist (X, O) = r → () () xa yb r 22+=
Per simplificar l’expressió, elevem al quadrat els dos membres i reordenem els termes:
Observem que es tracta d’un polinomi de segon grau en x i y, amb els coeficients de x 2 i y 2 iguals a 1 i sense terme en xy : x 2 + y 2 + Ax + By + C = 0
Equació d’una circumferència amb paràmetres.
Exemples
• Quina és l’equació de la circumferència de centre O(5, –3) i radi r = 7?
(
x – 5)2 + ( y + 3)2 = 49
• Correspon a una circumferència, l’equació
5x 2 + 5y 2 – 50x + 30y – 75 = 0?
I. Els termes x 2 i y 2 tenen el mateix coeficient, 5. Dividim per aquest:
x 2 + y 2 – 10x + 6y – 15 = 0
II. No té terme en xy
III. 2 10 2 6 –22 + ccmm – (–15) = 49 > 0
Per tant, és una circumferència de centre (5, –3) i radi = 49 = 7.
També podríem haver completat quadrats:
x 2 + y 2 – 10x + 6y – 15 = 0 →
x 2 – 10x + 25 + y 2 + 6y + 9 =
= 15 + 25 + 9 →
(x – 5)2 + ( y + 3)2 = 72
Comprovem de nou que el centre és (5, –3) i el radi és 7.
Exercicis resolts
Quines relacions hi ha entre els coeficients d’aquest polinomi i els elements de la circumferència (centre i radi)? Per descobrir-les, comparem aquesta equació amb l’anterior i n’igualem els termes corresponents:
Conclusions:
• Si coneixem el centre O(a, b) i el radi r d’una circumferència, l’equació serà aquesta:
(x – a)2 + ( y – b)2 = r 2
Podem desenvolupar i simplificar aquesta expressió, si convé.
• Si tenim una expressió de segon grau en x i y del tipus
x 2 + y 2 + Ax + By + C = 0
i volem saber si és una circumferència i, en cas afirmatiu, obtenir-ne el centre i el radi:
I. Observem que els coeficients de x 2 i y 2 són 1. Si tinguessin tots dos un mateix coeficient diferent d’1, dividiríem per aquest tots els termes.
II. Observem que no té terme en xy.
III Comprovem que AB 22 22 + ccmm – C > 0.
En aquest cas, és una circumferència.
El seu centre és , AB 22 cm i el seu radi és AB C 22 –22 + ccmm
1 Escriu l’equació de la circumferència de centre (3, –2) i radi 4. (x – 3)2 + ( y + 2)2 = 16. Aquesta ja és l’equació.
Podríem simplificar-la si fos necessari:
Exercicis resolts
2 Indica quines de les equacions següents corresponen a una circumferència i identifica’n el centre i el radi:
a) x 2 + y 2 – 4x + 6 = 0
b) 3x 2 + 3y 2 – 12x + 6y – 12 = 0
c) x 2 + y 2 + 4x – 6y + 13 = 0
a) Els coeficients de x 2 i y 2 són 1. No hi ha terme en xy.
Però 2 4 2cm – 6 = –2 < 0. Per tant, no és una circumferència
En completar quadrats, obtenim que:
x2 – 4x + 4 + y2 = –6 + 4 → (x – 2)2 + y2 = –2
És impossible que la suma de dos quadrats sigui –2; és a dir, el radi no pot ser negatiu; per tant, no és una circumferència.
b) Comencem dividint entre 3: x 2 + y 2 – 4x + 2y – 4 = 0.
Ara els coeficients de x 2 i y 2 són 1 i no hi ha terme en xy
2 4 2 2 22 + ccmm – (– 4) = 9 > 0
Per tant, és una circumferència de radi 9 = 3 i centre , 2 4 2 2 –cm ; és a dir, (2, –1).
Completem quadrats a partir de x
Fes-ho tu. Quines de les equacions següents corresponen a una circumferència? Determina’n el centre i el radi utilitzant la fórmula i completant quadrats:
a) 2x 2 + 2y 2 – 8x = 0
b) x 2 – y 2 + 7x – 2 = 0
c) x 2 + y 2 – 3x + 4xy – 16 = 0
d) x 2 + y 2 + 10x – 2y + 40 = 0
e) x 2 + y 2 – 6x – 8y + 25 = 0
f) x 2 + y 2 – 2x + 4y + 6 = 0
3 Troba el lloc geomètric dels punts P tals que la raó de distàncies a dos punts donats, A(0, 0) i B(6, 3), sigui igual a 2.
És a dir, (, ) (, ) dist BP distA P = 2.
Fes-ho tu. Quin és el lloc geomètric dels punts P el quocient de distàncies als punts M(6, 0) i N(–2, 0) dels quals és 3 (és a dir, / PM PN = 3)?
Quocient de distàncies: circumferència.
Exercici proposat
És clar que és una circumferència de centre (2, –1) i radi 9 = 3.
c) Els coeficients de x 2 i y 2 són 1. No hi ha terme en xy
Per tant, no és una circumferència
En completar quadrats, obtenim que:
Només el punt (–2, 3) compleix aquesta condició.
Expressem analíticament la condició:
2 Troba l’equació de la circumferència de centre (–5, 12) i radi 13.
Comprova que passa pel punt (0, 0).
B(5, 0) dels quals és 50.
1 Troba la posició relativa de la recta y = x i la circumferència següent:
x 2 + y 2 – 8x + 2y + 1 = 0
Posicions relatives d’una recta i una circumferència
Una recta, s, i una circumferència, C, poden ser exteriors (a), tangents (b) o secants (c i d). Analíticament, se’n pot identificar la posició de dues maneres:
I. Resolent el sistema format per les dues equacions, que tindrà dues solucions (són secants), una (són tangents) o cap (són exteriors).
II Comparant el radi, r, amb la distància, d, del seu centre a la recta:
• Si d > r, són exteriors.
• Si d = r, són tangents.
• Si d < r, són secants, i si, a més, d = 0, la recta passa pel centre.
• Resolent el sistema format per les equacions de la recta i la circumferència, s’obtenen els punts de tall. (Si el sistema no tingués solució, la recta seria exterior a la circumferència):
Fes-ho tu. Troba la posició relativa de les rectes
r1: y = x – 1
r2: y = x + 1
r3: y = 3
respecte de la circumferència
x 2 + y 2 – 8x + 2y + 1 = 0.
Exercicis proposats
La recta i la circumferència es tallen en els punts (0,18, 0,18) i (2,82, 2,82).
• Si només ens interessa la posició relativa, aquesta es podria esbrinar comparant el radi, r, de la circumferència amb la distància, d, del seu centre a la recta s:
Radi:
4 Estudia la posició relativa de la circumferència
C : x 2 + y 2 – 6x – 4y – 12 = 0
respecte de les rectes següents:
s1: 3x – 4y – 26 = 0
s3: 3x – 4y – 1 = 0
s2: 5x – 8y + 60 = 0
s4: x = 5
Troba’n els punts de tall i de tangència, si n’hi ha.
5 Per a quins valors de b la recta y = x + b és tangent a la circumferència x 2 + y 2 = 9?
6 Troba la posició relativa de C : x 2 + y 2 – 6x + 8y = 0 respecte de les rectes següents:
r1: x + y = 10
r3: 3x – 4y = 0
r2: 4x + 3y + 20 = 0
r4: y = –2
1 Calcula les potències del punt P(7, –4) a aquestes circumferències:
a) Té centre O(1, 4) i radi 12.
b) x2 + y2 – 8x + 3y + 12 = 0
2 Troba l’eix radical d’aquestes circumferències:
C1: x 2 + y 2 – 6x + 4y – 11 = 0
C2: x 2 + y 2 + 8x – 2y – 1 = 0
Donats un punt P(α, β) i una circumferència C de centre O(a, b) i radi r, anomenem d la distància de P a O : d = dist (O, P ).
S’anomena potència P del punt P a la circumferència C a d 2 – r 2 .
P = d 2 – r 2 = (α – a)2 + (β – b)2 – r 2
• Si el punt és exterior a la circumferència (d > r) → P > 0.
• Si el punt és de la circumferència (d = r) → P = 0.
• Si el punt és interior a la circumferència (d < r) → P < 0.
Si observem l’equació de la circumferència C, (x – a)2 + ( y – b)2 – r 2 = 0, veiem que P és el resultat de substituir x i y per les coordenades del punt P(α, β).
Eix radical de dues circumferències
S’anomena eix radical de dues circumferències el lloc geomètric dels punts del pla que tenen la mateixa potència respecte a ambdues.
L’eix radical de dues circumferències és una recta perpendicular a la línia que uneix els seus centres.
Com que P < 0, el punt és interior a la circumferència.
b) P = 72 + (– 4)2 – 8 · 7 + 3 · (– 4) + 12 = 9 > 0 Com que P > 0, el punt és exterior a la circumferència.
Expressem analíticament les potències d’un punt genèric X (x, y) respecte a les dues circumferències i les igualem:
P(X a C1) = x 2 + y 2 – 6x + 4y – 11
P(X a C2) = x 2 + y 2 + 8x – 2y – 1
Els punts que tenen la mateixa potència respecte a C1 i C2 s’obtenen igualant les dues expressions.
x
És, evidentment, una recta. Es pot comprovar que és perpendicular a la recta que uneix els centres de C1 i C2 (el seu pendent és –3/7).
7 Troba la potència de P(–3, 8) respecte a aquestes circumferències:
C1: x 2 + y 2 – 14x + 20 = 0
C2: O(4, –3), r = 20
Digues si P és interior o exterior a C1 i a C2.
8 Troba l’eix radical d’aquestes circumferències:
C1: x 2 + y 2 – 4x + 12y – 11 = 0
C2: x 2 + y 2 – 6y = 0
Comprova que és una recta perpendicular a la línia que uneix els seus centres.
Els jardiners fan servir aquest mètode per traçar un parterre en forma el·líptica: claven a terra dues estaques, lliguen una corda prou llarga entre totes dues i la tensen amb un pal, com en la fotografia. Mentre tracem la corba, la corda ha d’estar sempre tensa.

Una altra paràbola
Observa aquesta altra paràbola amb la recta fixa més allunyada del punt fix; els seus punts equidisten a tots dos.
Observa com hem fet servir aquesta trama formada per dues famílies de circumferències concèntriques per representar algunes el·lipses. Per exemple, la vermella: si sumes la distància d’un dels seus punts a F1 i a F2 obtens 28 unitats. Comprova que aquesta suma no varia en canviar de punt.
En ambdues construccions s’observa que la suma de distàncies de cada punt de l’el·lipse als dos punts fixos és sempre la mateixa.
La mateixa trama anterior serveix per representar hipèrboles.
Observa, per exemple, la vermella. Pren-ne un punt. Resta les distàncies a F1 i a F2. Comprova amb un altre punt que la diferència és la mateixa (18). És a dir, la diferència de distàncies de cada punt de la hipèrbola als dos punts fixos és sempre la mateixa
Com es dibuixa una paràbola
Aquesta altra trama servirà per representar paràboles.
Observa la vermella. Pren-ne un punt i mesura les distàncies a F i a d. Compara-les. Fes el mateix amb altres punts de la mateixa corba.
Els punts de la paràbola equidisten d’un punt fix, F, i d’una recta fixa, d
Les dues el·lipses dibuixades en la pàgina anterior tenen la mateixa distància focal: dist (F1, F2) = 24
• En la vermella, k = 28.
• En la blava, k = 42.
Les tres hipèrboles dibuixades en la pàgina anterior tenen la mateixa distància focal: dist (F1, F2) = 24
• En la blava, k = 22.
• En la vermella, k = 18.
Donats dos punts, F1 i F2, anomenats focus, i una distància k, anomenada constant de l’el·lipse [k > dist (F1, F2)], s’anomena el·lipse el lloc geomètric dels punts P la suma de distàncies a F1 i a F2 dels quals és igual a k: dist (P, F1) + dist (P, F2) = k
Donats dos punts, F1 i F2, anomenats focus, i una distància k, anomenada constant de la hipèrbola [k < dist (F1, F2)], s’anomena hipèrbola el lloc geomètric dels punts P la diferència de distàncies a F1 i a F2 dels quals és, en valor absolut, igual a k : |dist (P, F1) – dist (P, F2)| = k
• En la verda, k = 10. 1 Donats els punts F1(–2, 5), F2(7, –3) i la recta r: x – y – 1 = 0, obté les equacions següents:
Donats un punt F, anomenat focus, i una recta, d, anomenada directriu, s’anomena paràbola el lloc geomètric dels punts, P, que equidisten de F i de d: dist (P, F ) = dist (P, d )
Mitjançant aquestes definicions es poden obtenir, fàcilment, les equacions d’aquestes figures.
No obstant això, no és tan senzill reconèixer a quina figura correspon una equació determinada. Per això les estudiarem amb més detall en els pròxims apartats.
Exercici resolt
a) La de l’el·lipse de focus F1 i F2 i constant 17.
b) La de la hipèrbola de focus F1 i F2 i constant 6.
c) La de la paràbola de focus F1 i directriu r.
Fes-ho tu. Donats els punts F1(–3, 0) i F2(1, –2) i la recta r : x + 2y – 5 = 0, obté les equacions següents:
a) La de l’el·lipse de focus F1 i F2 i constant 20.
b) La de la hipèrbola de focus F1 i F2 i constant 2.
c) La de la paràbola de focus F1 i directriu r.
9 Troba l’equació de l’el·lipse de focus F1(4, 0) i F2(– 4, 0) i constant 10. Una vegada escrita l’equació inicial, passa una de les arrels al segon membre, eleva-la al quadrat (atenció amb el doble producte!), simplifica-la, aïlla l’arrel, torna-la a elevar al quadrat i simplifica-la fins a arribar a l’equació 9x 2 + 25y 2 = 225.
10 Troba l’equació de la hipèrbola de focus F1(5, 0) i F2(–5, 0) i constant 6. Simplifica-la com en l’exercici 9 fins a arribar a l’expressió 16x 2 – 9y 2 = 144.
11 Troba l’equació de la paràbola de focus F(–1, 0) i directriu r : x = 1. Simplifica-la fins a arribar a l’expressió y 2 = – 4x.
Els punts A, A', B i B' s’anomenen vèrtexs de l’el·lipse.
Si en una el·lipse de focus F i F' tracem els dos eixos de simetria, designem així els seus elements característics:
O centre de l’el·lipse
a = ' OA OA = semieix major
b = 'OOBB = semieix menor
c = 'OOFF = semidistància focal
La constant, k, de l’el·lipse és 2a, perquè:
k = FF'' AF AA AF ++ = = 2a
A més, com que B és un punt de l’el·lipse:
' BF BF + = 2a ⇒ ' BF BF = = a
Si observem el triangle rectangle BOF, veiem que es compleix que a 2 = b 2 + c 2
Resumint:
• Constant de l’el·lipse: k = 2a
• ' BF BF =
Excentricitat
Els planetes giren al voltant del Sol descrivint òrbites el·líptiques en un focus de les quals hi ha el Sol (primera llei de Kepler). Aquestes òrbites són molt poc excèntriques. Per exemple, l’excentricitat de l’òrbita de la Terra és tan petita que si la dibuixem a escala en un full de paper sembla una circumferència.
Els cometes també descriuen òrbites el·líptiques en un focus de les quals hi ha el Sol però molt més excèntriques.
Per a un mateix valor de a, com més gran sigui c més allargada serà l’el·lipse; i com més petit sigui c més s’assemblarà a una circumferència. Per mesurar fins a quin punt es diferencia la forma d’una el·lipse de la d’una circumferència, es defineix l’excentricitat d’una el·lipse.
S’anomena excentricitat d’una el·lipse el quocient entre la distància focal i l’eix major:
exc = a c
L’excentricitat d’una el·lipse és un nombre més gran que 0 i més petit que 1.
Aquestes tres el·lipses tenen el mateix eix major, 2a Com més s’allunyen els focus (2c), més gran és l’excentricitat a c a c 2 2 = .
12 Cert o fals? Si diverses el·lipses tenen la mateixa distància focal, com més gran sigui la constant k = 2a, més gran és l’excentricitat.
Exercici resolt
1 Troba els elements característics i l’equació reduïda de l’el·lipse de focus F1(4, 0) i F2(– 4, 0) i constant k = 10.
Per simplificar l’equació de l’el·lipse, triem els eixos de coordenades convenientment: prenem el seu centre com a centre de coordenades i els seus eixos de simetria com a eixos de coordenades. Les coordenades dels focus són F'(–c, 0) i
F(c, 0).
Qualsevol punt P(x, y) de l’el·lipse compleix la condició següent: dist (P, F ) + dist (P, F' ) = 2a
Aquesta igualtat, expressada analíticament, dona lloc a l’equació següent:
() () xc yx cy a2 –22 22 ++ ++ =
Es passa una arrel al segon membre: () () xc ya xc y 2 22 22 += ++
S’eleven al quadrat els dos membres:
S’eleven al quadrat els dos membres una altra vegada:
Es canvien els dos membres i s’agrupen els termes:
Exercici proposat
Semieix major:
k = 10 → 2a = 10 → a = 5
Semidistància focal:
FF12 = 8 → 2c = 8 → c = 4
Semieix menor:
b 2 = a 2 – c 2 = 25 – 16 → b = 3
Excentricitat:
c/a = 4/5 = 0,8 → exc = 0,8
Equació reduïda:
13 Troba els elements característics i l’equació reduïda d’una el·lipse de focus F(5, 0) i F'(–5, 0) i constant és k = 26. Representa-la.
4, 0)
F (4,
El·lipse amb centre en (5, 3)
En vermell: () () x y 4 5 2 3 1 ––2 2 2 2 +=
El·lipse amb els focus en l’eix Y Aquesta el·lipse és idèntica a la del marge, però amb els eixos canviats. Els seus focus són sobre l’eix Y. La seva equació és aquesta:
4) F' (0, – 4)
Per seguir utilitzant la nomenclatura habitual: eix major = 2a eix menor = 2b excentricitat = a/c en els casos en què el denominador de x 2 és més petit que el de y 2, escriurem l’equació de l’el·lipse així:
b x a y 1 2 2 2 2 += 1
El·lipse amb centre diferent de (0, 0) L’equació d’una el·lipse de semieixos a i b (en la qual a > b
eixos paral·lels als eixos de coordenades és aquesta:
Exercici resolt
a) x y 16 36 1 2 2 +=
b) () x y 25 3 1 –2 2 +=
c) () () x y 16 2 25 1 1 –2 2 + +=
d) x 2 + 4y 2 = 4
Exercici proposat
a)
exc = , 6 20 075 = F (0, 20 ) F’ (0, – 20 ) c) c = 53 4 –22 =
14 Representa i troba’n l’excentricitat i el focus:
exc = , 5 3 06 = F (–2, 4)
– 24 , 0) F’
b) Y X c = 124 5– 2 2 = exc = , 1 24 098 = d) x y 4 1 2 2 += c = 132–22 = exc = , 2 3 087 = Y X Y X Y X F (3
Si vols dibuixar una hipèrbola, comença traçant-ne les asímptotes. Després, dibuixa la corba cenyint-te a aquestes.
Si tracem els dos eixos de simetria d’una hipèrbola de focus F i F' anomenem així els elements característics:
O centre de la hipèrbola
c = ' OF OF = semidistància focal
a = 'OOAA = semieix
r i r' asímptotes
La constant de la hipèrbola és 2a, perquè:
k = ' '' '' AF AF AF AF AA 2a == =
En el cas de la hipèrbola, el segment b es representa tal com es fa en la figura del marge. Es compleix la relació:
c 2 = a 2 + b 2 (Atenció, ara c > a.)
Observem que els pendents de les asímptotes són a b i a b –.
Per a un mateix valor de a, en variar c, varia la forma de la hipèrbola:
Els llibres d’astronomia ens expliquen que, a vegades, un cometa és expulsat del sistema solar per una «empenta» de Júpiter.
El cometa descriu una trajectòria el·líptica però, en passar prop de Júpiter, aquest gran planeta en desvia la trajectòria i la converteix en hiperbòlica. En aquest cas, ja no podrà tornar al sistema solar.
Una el·lipse molt excèntrica (exc una mica més petita que 1) és molt semblant, en un cert tram, a una hipèrbola molt poc excèntrica (exc una mica més gran que 1).
Igual que en l’el·lipse, la relació entre c i a s’anomena excentricitat:
excentricitat = a c
Però, així com en l’el·lipse l’excentricitat és més petita que 1, en la hipèrbola l’excentricitat és més gran que 1.
Resumint:
• Constant de la hipèrbola: k = 2a
•
Conclusió: Com més gran sigui el pendent (b /a) de l’asímptota, més gran serà l’excentricitat (c /a) de la hipèrbola.
Observa c a a Com que en les hipèrboles equilàteres a = b:
c2 = a2 + a2 = 2a2 → c = 2 a I la seva excentricitat és, per tant, aquesta:
exc = a c = a a 2 = 2
Exercici resolt
1 Troba els elements característics i l’equació reduïda de la hipèrbola de focus F1(5, 0) i F2(–5, 0) i constant k = 8.
Per trobar una equació de la hipèrbola raonablement simplificada, cal triar convenientment els eixos de coordenades tal com s’indica en la figura del marge. D’aquesta manera, els focus són F(c, 0) i F'(–c, 0).
Un punt P(x, y) de la hipèrbola compleix la condició següent:
|dist (P, F ) – dist (P, F’ )| = 2a → () () xc yx cy 22 22 ++ + = ± 2a Operant, s’obté, finalment, l’equació reduïda:
a x b y 1 –2 2 2 2 = equació reduïda de la hipèrbola
Hipèrboles equilàteres i hipèrboles y = k /x
Si, en l’equació reduïda de la hipèrbola, considerem que a = b, llavors x 2 – y 2 = a 2 , les asímptotes, y = ±x, són perpendiculars entre si i la corba s’anomena hipèrbola equilàtera.
Les funcions de proporcionalitat inversa, y = k/x, són hipèrboles equilàteres de paràmetres a = b = k2 i c = k4 = k 2 en què les asímpotes són els eixos de coordenades, els focus són F ( k2 , k2 ) i F’(– k2 , – k2 ) i el vèrtex està situat en ( k , k ).
reduïda: x y 16 9 –2 2 = 1
15 Una hipèrbola té els focus en els punts F1(5, 0) i F2(–5, 0) i la seva constant és k = 6.
Troba’n els elements característics i l’equació reduïda. Després, representa-la.
16 Calcula la distància focal i les coordenades dels focus d’aquestes hipèrboles equilàteres:
a) y = x 1 b) y = –x 2 c) y = x 18 d) xy = 1 4
Hipèrbola amb els focus en l’eix Y
La hipèrbola (I) és idèntica a la (II), però amb els eixos intercanviats. Els seus focus estan situats sobre l’eix Y i la seva equació és aquesta:
En general, l’equació
correspon a una hipèrbola els focus de la qual són F(0, c) i F'(0, –c), amb
c = ab22 + . Les seves asímptotes són y = ± b a x .
La seva excentricitat és exc = a c
Hipèrbola amb centre diferent de (0, 0)
i eixos paral·lels als eixos de coordenades és una de les següents:
L’equació d’una hipèrbola de semieixos a i b amb el centre en (α
La forma d’una cònica queda determinada per la seva excentricitat. Dues el·lipses amb la mateixa excentricitat són semblants, tenen la mateixa forma. Passa el mateix amb les hipèrboles: com que l’excentricitat de totes les paràboles és la mateixa, 1, totes són semblants.
Anomenem V: vèrtex de la paràbola
p: distància del focus a la directriu
F: focus
d: directriu
L’excentricitat d’una paràbola és sempre 1.
Equació reduïda
Per trobar l’equació reduïda d’una paràbola de focus F i directriu d, prenem com a eix X la recta que passa per F i és perpendicular a d. El centre de coordenades el situem en el punt mitjà entre F i d:
, F p 2 0 cm i d: x = p 2 –
Qualsevol punt P(x, y) de la paràbola compleix aquesta condició: dist (P, F ) = dist (P, d ). Aquesta igualtat, expressada analíticament, és l’equació reduïda.
y 2 = 2px equació reduïda de la paràbola
Observa
Les paràboles no tenen asímptotes.
Paràboles amb vèrtex diferent de (0, 0)
L’equació d’una paràbola amb el vèrtex en V (a, b) és aquesta: ( y – b)2 = 2p (x – a)
Paràboles amb l’eix paral·lel a l’eix Y
Per trobar el focus i la directriu d’una paràbola d’equació y = kx2, l’expressem com a x2 = k 1 y i la comparem amb x2 = 2py. Així relacionem k amb p i trobem el focus i la directriu en funció de k
En la paràbola y = kx2, amb k > 0, el focus és F 0, k4 1 cm i la directriu, d: y = – k4 1
1 Troba l’equació reduïda de les paràboles següents:
a) Focus F(2, 0) i directriu x = –2.
b) Igual que l’anterior, però amb el vèrtex en el punt (3, –1).
a) Distància del focus a la directriu: p = 4
Equació reduïda: y2 = 8x
b) Equació reduïda: (y + 1)2 = 8(x – 3)
18 Troba l’equació reduïda de la paràbola de focus F(1,5, 0) i directriu x = –1,5.
19 Troba l’equació reduïda d’una paràbola com la de l’exercici
18 però amb el vèrtex en (–2, 3).
20 Troba les coordenades del focus i l’equació de la directriu de les paràboles següents. Després, dibuixa-les.
a) y = 4x2 b) y = 2 1 x2 c) y = –1 8 x2 d) y = –0,1x2
• Tangent a una el·lipse

L’activitat següent és molt interessant.
La tangent en cada punt, Q , és la bisectriu exterior dels segments QF i QF'.
Dibuixa una circumferència de centre C i radi r i, a l’interior, un punt P diferent del centre. Doblega el full fins a col·locar el punt P sobre un punt qualsevol de la circumferència. Si repeteixes el procés fins a recórrer tota la circumferència, com en la il·lustració, comprovaràs que les línies dels plecs envolten una bella el·lipse els focus de la qual són P i C.

Cada un dels plecs és una tangent a l’el·lipse, i la constant de l’el·lipse (suma de les distàncies de cada punt als focus) és el radi, r, de la circumferència.
• Tangent a una hipèrbola
Si repeteixes l’activitat però situes el punt P exterior a la circumferència, la corba tangent als plecs serà una hipèrbola.
La tangent a una hipèrbola en un punt és la bisectriu interior dels radis vectors que parteixen d’aquest punt.
El radi de la circumferència també és la constant de la hipèrbola: diferència de distàncies als focus (P i C ).
• Tangent a una paràbola


Si traces una recta d i un punt F en un full i el doblegues fent coincidir el punt F amb un punt de la recta, els plecs r són tangents a una paràbola de focus F i directriu d
Observa ara els dibuixos del marge. Les rectes paral·leles a l’eix (perpendiculars a d ) es «reflecteixen» en la paràbola i passen pel punt F. I a l’inrevés, una recta que surt de F es «reflecteix» en la paràbola i surt paral·lela a l’eix.
Aquesta propietat s’usa moltíssim per tal de construir fars de cotxes, forns solars, antenes parabòliques…

El pròxim curs estudiarem àmpliament les matrius, el seu significat, les seves propietats i les seves aplicacions. Ara, en farem un avançament breu i senzill, per poder-les utilitzar en l’estudi analític dels moviments.
Una matriu és una taula numèrica del tipus següent:
Aquesta matriu té 3 files i 4 columnes. Es diu que és una matriu 3 × 4
La matriu (1 7 4 9) té 1 fila i 4 columnes; és a dir, és una matriu 1 × 4. S’anomena vector fila de dimensió 4
Anàlogament, això és un vector columna de dimensió 3:
Les matrius quadrades tenen el mateix nombre de files que de columnes. Per exemple:
és una matriu quadrada 3 × 3 o una matriu quadrada d’ordre 3
Per a l’estudi dels moviments en el pla farem servir, exclusivament, matrius quadrades d’ordre 3 i vectors columna i fila d’ordre 3. I hem d’aprendre a multiplicar-les.
Les matrius poden sumar-se, ser multiplicades per un nombre i multiplicar-se entre elles. Amb l’objectiu de modelitzar moviments en el pla, centrarem la nostra atenció en la multiplicació.
El producte d’un vector fila d’ordre 3 per un vector columna d’ordre 3 és el nombre que s’obté multiplicant-los terme a terme i sumant els resultats:
El producte d’una matriu 3 × 3 per un vector columna d’ordre 3 és un vector columna
3 que s’obté de la manera següent:
Un exemple
Observa un exemple de multiplicació de matrius
El producte, A · B, de dues matrius 3 × 3 és una altra matriu 3 × 3 el terme cij de la qual s’obté multiplicant la fila i-èsima de A per la columna j-èsima de B. És a dir, l’element c23 (element de la 2a fila i la 3a columna) s’obté multiplicant la 2a fila de A per la 3a columna de B:
c11 = (–1) · 0 + 0 · 2 + 2 · 4 = 8
c12 = (–1) · (–1) + 0 · 1 + 2 · 0 = 1
c13 = (–1) · 3 + 0 · 3 + 2 · 1 = –1
c21 = 2 · 0 + 1 · 2 + (–1) · 4 = –2
c22 = 2 · (–1) + 1 · 1 + (–1) · 0 = –1
c23 = 2 · 3 + 1 · 3 + (–1) · 1 = 8
c31 = 3 · 0 + (–5) · 2 + 2 · 4 = –2
c32 = 3 · (–1) + (–5) · 1 + 2 · 0 = –8
c33 = 3 · 3 + (–5) · 3 + 2 · 1 = –4
En multiplicar la 2a fila de A per la 3a columna de B s’obté l’element c23
El producte de dues matrius quadrades no compleix la propietat commutativa; és a dir, en general, el producte de les matrius A · B no és igual a B · A.
Matriu unitat
21
La matriu I =
compleix que I · A = A · I = A sigui quina sigui la matriu A(3×3). Per això s’anomena matriu unitat.
Matriu inversa d’una altra
Si el producte de dues matrius 3 × 3 és la matriu unitat, I, aleshores, aquestes dues matrius són cada una inversa de l’altra. Si una l’anomenem A, l’altra l’anomenarem A–1:
· A–1 = A–1 · A = I
Per exemple:
De moment, no necessitem saber obtenir la inversa d’una matriu, però sí que hem de saber reconèixer-la veient que el seu producte és I
aquestes multiplicacions de matrius 3 × 3 pels vec-
22 Resol aquestes multiplicacions de matrius 3 ×
Fixa’t que la multiplicació de l’apartat f ) és igual que la de l’apartat e) però en l’ordre contrari. El resultat és el mateix?
A tercer d’ESO vam estudiar els moviments en el pla. Te’n recordes? Translacions, girs, simetries. I a quart, les homotècies. Ens retrobarem amb aquestes transformacions, però, ara, les matrius ens serviran per transformar punts i equacions. Com es transforma un punt P(x, y) mitjançant una transformació, T, amb l’ajuda de les matrius?
Veurem que:
• Una transformació queda caracteritzada per una matriu 3 × 3 l’última fila de la qual és 0 0 1.
• Un punt P(x, y) s’expressa mitjançant el vector columna
y
.
• La transformació es fa multiplicant la matriu quadrada 3
(a, b)
P (x, y)
P' (x', y' ) = (x + a, y + b)
Per exemple, si la matriu de la transformació és
el
(–2, 5) es transforma així:
És a dir, (–2, 5) T (1, 5)
• La composició de dues transformacions, primer T1 i després, T2, és una altra transformació la matriu de la qual s’obté multiplicant, de dreta a esquerra, T2 · T1, les matrius de T1 i de T2
Translacions
Recorda que una translació T d’un vector t (a, b) és una transformació que porta cada punt P(x, y) a un altre P l (x’, y’) tal que:
x l = x + a, y l = y + b
És a dir, P (x, y) T P l (x + a, y + b).
La matriu associada a aquesta translació és T
Vegem com es transforma un punt P (x, y):
Efectivament, (
23 Troba el resultat de transformar el punt P (5, –3) mitjançant el vector t (–4, 11).
24 Transforma el punt Q (1, 8) mitjançant la translació de vector t (4, –11).
25 Comprova que una de les matrius de les dues transformacions anteriors és la inversa de l’altra; és a dir, comprova que el seu producte és la matriu unitat.
, y +
26 Donades les matrius T
comprova que corresponen
t 2 (3, –1).
de vectors
El producte T2 · T1 és una nova matriu translació. Comprova que el seu vector és t 1 + t 2 ; és a dir, que és el resultat de compondre la translació T1 amb la T2.
Comprova-ho!
La matriu producte T · H · T–1 és la matriu de l’homotècia de centre C(a, b) i raó k
Recordem que una homotècia de centre O i raó k és una transformació que porta cada punt P a un altre P l tal que:
• O, P i P l estan alineats
• OP OP l = k
Observa com influeix el valor de k en la posició de P l respecte a O i P :
Exercicis proposats
k = –2 1 2
k = 2 k = 1 2 k = –1 2
Homotècia de centre O(0, 0) i raó k Comprova que la matriu
HO, k
transforma P (x, y)
Homotècia de centre C(a, b) i raó k
O,k P l (kx’, ky’)
Sabem transformar matricialment un punt mitjançant una homotècia de centre O i raó k. Què hem de fer quan el centre és un altre punt? Fixa-t’hi:
1. Portem el centre C a O (translació, T–1, de vector t (–a, –b)).
2. Fem una homotècia, HO, k
3. Portem el resultat al seu lloc (translació, T, de vector t (a, b)).
Componem aquestes tres transformacions, en aquest ordre, mitjançant el producte de les seves matrius:
J L K K K N P O O O , després, la del mig multiplica al resultat i, finalment, actua la tercera, la de l’esquerra. Unitat 9 P' P O P'(kx, ky) P (x,y) O
27 Transforma el punt P (4, 2) mitjançant les homotècies següents:
a) H1 de centre O i raó 3.
b) H2 de centre O i raó 2 1
c) H3 de centre O i raó –2.
28 Troba la matriu corresponent a una homotècia de centre (3, –5) i raó 2.
29 Troba el transformat del punt (–4, 7) segons l’homotècia anterior de dues maneres:
b) Multiplicant successivament per:
K K
a) Multiplicant la matriu resultant per 1
4 7 – J L
N P
O O O .
1. La matriu de la translació de vector (–3, 5).
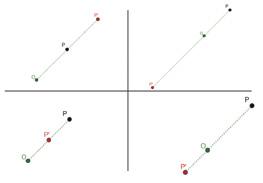
2. La matriu de l’homotècia de centre (0, 0) i raó 2.
3. La matriu de la translació de vector (3, –5).
Alguns girs
Recordem que un gir queda caracteritzat per un centre, O, i un angle α (un angle α té una mida positiva quan s’obre en sentit contrari al moviment de les agulles del rellotge).
Vegem com es caracteritza un gir de centre O(0, 0) i angle 90°:
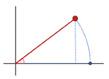
Exercicis proposats
A partir del dibuix: (, )( ,) Px yP yx–G 90 O, l
Per tant, la matriu del gir és aquesta:
Comprova-ho.
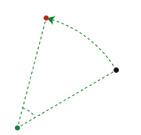
30 Troba la matriu corresponent a un gir de centre C (a, b) i angle 90°
Recorda:
• Porta C a O (translació t (–a, –b)).
• Fes el gir.
• Fes una translació mitjançant t (a, b).
31 Troba la matriu corresponent al gir de centre O i angle –90º.
32 Troba la matriu corresponent a un gir de centre C (a, b) i angle –90°
– a a a a J L N P
K K K O O O
0 0 1
correspon a un gir de centre O (0, 0) i angle α Per comprovar-ho, fes girar el punt P (1, 0) i fixa’t que les coordenades del punt corresponent són les que s’obtenen per mitjà de la matriu.
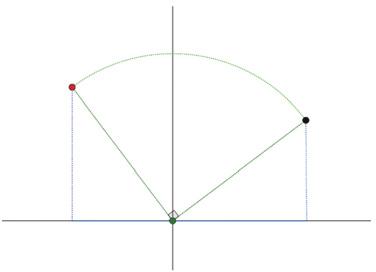
34 Gira 60° el punt (3, 5) al voltant de O.
236 P' P α O P' (–y,x) P (x,y) Y O x x –y X 90o α sin α 1
35 Gira 60° el punt (3, 5) al voltant del centre de gir C (2, 1).
Recorda: trasllada O, fes un gir al voltant de O i torna a fer una translació en sentit contrari.
Algunes simetries axials
Recordem com s’obté el simètric d’un punt respecte a una recta:
La recta, e, s’anomena eix de simetria i la transformació s’anomena simetria axial, per distingir-la de la simetria central.
Simetria central
La simetria respecte a un punt, centre, equival a un gir de 180° i, també, a una homotècia de raó –1.
Homotècia de centre O i raó –1. Gir de centre O i angle 180°.
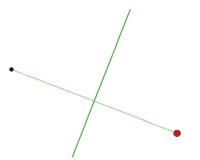
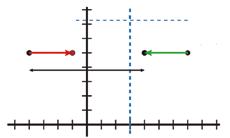
36 Comprova que la matriu corresponent a una simetria respecte a l’eix Y és aquesta:
38 Comprova que la matriu corresponent a una simetria respecte a l’eix X (y = 0) és aquesta:
37 Troba la matriu corresponent a una simetria l’eix de la qual és la recta x = 3.
39 Troba la matriu corresponent a una simetria respecte a la recta y = 5. Troba el simètric del punt (7, 0).
ff f pp p
Translació de vector (3,0) Simetr arespect de le Y Translació de vector (–3, 0) ' ie ix


40 Comprova que la matriu corresponent a la simetria d’eix y = x és aquesta:
41 Troba la matriu corresponent a la simetria d’eix y = –x
42 Troba la matriu corresponent a la simetria d’eix x + y = 8. Transforma els punts (5, 3) i (0, 0).
Troba el simètric del punt P (7, 5).
Exercici resolt
1 Troba matricialment el resultat de compondre dues simetries d’eixos:
e1: y = 0 i e2: y = x.
Els resultats següents són molt interessants, ja que permeten relacionar les simetries amb les translacions i amb els girs:
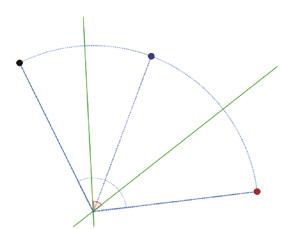
I. La composició de dues simetries els eixos de les quals formen un angle α és un gir de centre el punt de tall dels eixos i angle 2α
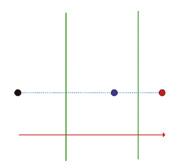
Fes-ho tu. Troba matricialment el resultat de compondre dues simetries
d’eixos:
a) e1: x = 0 i e2: x = 4.
b) e1: x = 4 i e2: y = 2.
II. La composició de dues simetries d’eixos paral·lels, e1 i e2, és una translació el vector de la qual té:
• Mòdul doble de la distància de e1 a e2.
• Direcció perpendicular a e1 i a e2.
• Sentit que va de e1 a e2.
Les matrius de simetria e1 i e2, són, respectivament, aquestes:
La composició d’aplicar primer e1 i després e2 és S2 · S1:
és un gir de 90º i centre (0, 0).
Això és el que s’esperava, ja que el punt de tall de y = 0 i y = x és el punt (0, 0) i les dues rectes formen un angle de 45º. Com s’ha dit, la composició és un gir amb el centre en el punt de tall i un angle que mesura el doble del que formen les rectes, en aquest cas 90º.
Com es transforma l’equació d’una figura
Fins ara hem vist com es transformen punts donats per les seves coordenades en sotmetre’ls a un moviment (translació, gir o simetria) o a una homotècia. A continuació, veurem com es transforma l’equació y = f (x) d’una figura:
φ1(x) = x l → Obtenim l’expressió de x en funció de x’.
φ2(x) = y l → Substituïm x per la seva expressió en funció de x l
S’obté una relació entre x l i y l . En aïllar y l , s’obté l’equació de la figura transformada: y l = F( x l ).
Això es veu molt millor amb uns exemples.
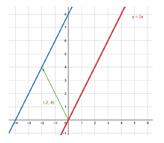
1 Com es transforma la recta y = 2x sotmesa a la translació de vector t (–2, 4)?
resolts K K K
Exercicis 1 0 0 1 2 4 – J L
y: N P
a) Gir de centre O(0, 0) i angle 90º.
b) Simetria d’eix, l’eix X
c) Simetria d’eix, l’eix Y.
d) Simetria d’eix, la recta y = x.
() ()yx 41 2 22 =+ ll
K K K
O O O · x x 1 1– 2 ! J L K K K N P O O O = x 14 –2 ! + 1
x 2 – J L
Vegem la relació que compleixen les variables transformades: x l = x – 2 → x = x l + 2 () yx x 14 12 4 22!!=+ =+ + ll ()yx 41 2 2 ! =+ ll
O O O
N P
El resultat, com calia esperar, és la circumferència de centre (–2, 4) i radi 1.
43 Aplica a la recta y = 2x les transformacions següents:
e) Homotècia de centre O(0, 0) i raó 2.
f) Homotècia de centre C(0, 2) i raó 2.
44 Aplica a la paràbola y = x – 1 les mateixes transformacions descrites en l’exercici anterior.
1. Determinació d’una circumferència coneguts tres punts pels quals passa
Obté el centre, el radi i l’equació de la circumferència que passa pels punts P(0, 0), Q(10, 0) i R(18, 12).
Anàlisi del problema La mediatriu d’un segment és el lloc geomètric dels punts que equidisten dels seus extrems. Els tres punts donats equidisten del centre. Per tant, el centre, O, pertany a les mediatrius dels segments PQ i PR i es pot trobar calculant la intersecció d’aquestes mediatrius.
• Trobem les mediatrius de PQ i PR, respectivament mPQ i mPR .
La recta mPQ passa pel punt mitjà de PQ , MPQ = (5, 0), i és perpendicular a PQ = (10, 0), és a dir, paral·lela a l’eix Y. Per tant, mPQ: x = 5.
La recta mPR passa pel punt mitjà de PR, MPR = (9, 6), i és perpendicular a PR = (18, 12) (3, 2). Per tant,
mPR : 3(x – 9) + 2(y – 6) = 0 → mPR: 3x + 2y – 39 = 0
Calculem el centre O, que és la intersecció d’aquestes mediatrius:
Fes-ho tu. Obté el centre, el radi i l’equació de la circumferència que passa per P(–1, 3), Q(2, –2) i R(3, 0).
Troba analíticament l’equació de la circumferència de radi 17 que passa per (4, –1) i el centre de la qual pertany a la recta:
= x + 2 1 2 1
Y y 1 17
(4, –1) X
= += * → ; x xy xy 5 32 39 0 512 –
x xy 5 32 39 0 –
= += == 4 → O (5, 12)
• Obtenim el radi calculant la distància de O a qualsevol dels punts donats:
r = d (O, P ) = () () 50 12 0 169 13 22+= =
• L’equació de la circumferència és (x – 5)2 + ( y – 12)2 = 169.
Un altre mètode de resolució
L’equació reduïda d’una circumferència és x 2 + y 2 + Ax + By + C = 0. Com que els punts P, Q i R pertanyen a la circumferència, compleixen la seva equació. Substituïm les coordenades i resolem el sistema d’equacions que obtenim:
2. Circumferència que passa per un punt i el centre de la qual està situat sobre una determinada recta
Anàlisi del problema Hem de trobar l’equació d’una circumferència de la qual ja coneixem el radi. Sabem que el seu centre és en una recta. Tracem una circumferència de centre (4, –1) i radi 17 . La intersecció d’aquesta circumferència amb la recta és el centre que busquem. L’equació de la circumferència de centre (4, –1) i radi 17 és (x – 4)2 + (y + 1)2 = 17.
Vegem els punts de tall de la circumferència i la recta y = x
Fes-ho tu. Obtén l’equació de la circumferència de radi 40 que passa per P(2, 11) i el centre de la qual pertany a la recta d’equació x – 3y + 11 = 0.
i (5, 3), que són els centres de les dues circumferències, C1 i C2, que compleixen les condicions:
trobat dos punts,
3. Descripció d’una cònica a partir de la seva equació
Descriu les còniques següents, obténne els elements i dibuixales:
a) x 2 + y 2 – 2x + 4y + 2 = 0
b) x 2 + 4y 2 – 8y = 0
c) y 2 – 2y – x 2 = 0
d) y 2 – 2y – 4x – 11 = 0
a) És una circumferència perquè els coeficients de x 2 i y 2 són 1.
Operem fins a obtenir-la en la forma (x – x0)2 + ( y – y0)2 = r 2
Completem quadrats: (x 2 – 2x + 1) + ( y 2 + 4y + 4) + 2 – 5 = 0 → (x – 1)2 + ( y + 2)2 = 3
Circumferència de centre O(1, –2) i radi r = 3
b) Els coeficients de x 2 i y 2 són diferents, però del mateix signe; és una el·lipse.
en l’equació fins a obtenir-la en la forma
una el·lipse de centre O(0, 1) i eix major paral·lel a l’eix X.
Semieixos: a = 2, b = 1
Semidistància focal: c 2 = a 2 – b 2 = 4 – 1 = 3 → c = 3
Excentricitat: exc = a c 2 3 =
c) És una hipèrbola perquè els coeficients de x 2 i y 2 tenen signe diferent.
en l’equació fins a obtenir-la en la forma
0 → ( y 2 – 2y
( y – 1)2 – x 2 = 1
Es tracta d’una hipèrbola equilàtera de centre O (x0, y0) = (0, 1) i focus en l’eix Y Semieixos: a = 1, b = 1 (a = b, per això és equilàtera)
Semidistància focal: c 2 = a 2 + b 2 = 12 + 12 = 2 → c = 2
Asímptotes: y = ±( ) b a xx y – 00 + → y = x + 1 i y = –x + 1
Excentricitat: exc = a c 1 2 2 ==
d) Com que té terme en y 2 i no pas en x 2, és una paràbola amb eix horitzontal. A més, O(0, 0) no compleix l’equació de la paràbola; per tant, el vèrtex de la paràbola, V(x0, y0), no està situat en l’origen de coordenades. L’equació d’una paràbola d’aquest tipus és ( y – y0)2 = 2p(x – x0), amb focus , Fx p y 2 00 + cm i directriu x = x p 2 – 0 . Operem fins a obtenir l’equació inicial d’aquesta manera. Després, completem quadrats: ( y 2 – 2y + 1) – 4x – 11 – 1 = 0 → ( y – 1)2 = 4x + 12 → ( y – 1)2 = 2 · 2(x + 3)
Vèrtex: V(x0, y0) = (–3, 1); focus: F ,( ,) x p y 2 –21 00+=cm ;
directriu: x = x0 –p 2 → x = – 4
Fes-ho tu. Descriu les còniques següents, obtén-ne els elements i dibuixa-les:
4. Equació d’una el·lipse no centrada en l’origen
Obtén l’equació de l’el·lipse de focus
F'(–1, 1) i F(5, 1) i excentricitat exc = 5 3 .
Fes-ho tu. Obtén l’equació de l’el·lipse de focus F'(3, –2) i F(3, 6), l’excentricitat de la qual és
Trobem el centre de l’el·lipse com el punt mitjà entre els focus: O = MF'F = ,( ,) 2 15 2 11 21 –+ + = cm . L’el·lipse no està centrada en (0, 0). L’equació de l’el·lipse ha de tenir la forma
Per determinar els semieixos, usarem la distància focal i l’excentricitat: dist (F', F ) = 6 = 2c → c = 3; exc =
ba c –22 2 = → ba c 25 9164 22 == == L’equació buscada és () () x y 25 2 16
5. Equació d’una hipèrbola no centrada en l’origen a partir de la seva representació gràfica
Calcula les equacions de les hipèrboles vermella i blava representades a continuació: 1 X
El centre és el punt d’intersecció d’ambdues asímptotes: C (2, 1).
Y
Hipèrbola vermella. La línia dels focus és paral·lela a
Com que a = 2 i els pendents de les asímptotes són m = ±3/4,
b 24 3 = → b 2 3 = . Per tant, l’equació buscada és
Hipèrbola blava. Com que la línia dels focus és paral·lela a
Com que les asímptotes són iguals, a i b continuen valent el mateix, i l’equació és aquesta:
6. Elements d’una paràbola d’eix vertical a partir de la seva representació gràfica
Calcula el focus i la directriu d’aquesta paràbola:
Anàlisi del problema. A partir del vèrtex i d’un altre punt de la paràbola calculem la seva equació. Amb el coeficient de la x 2 podem calcular el focus i la directriu d’una paràbola igual a aquesta centrada en l’origen. Calculem el focus i la directriu real traslladantlos amb el vector posició del vèrtex.
L’equació general d’una paràbola d’eix vertical és y = ax2 + bx + c
L’abscissa del vèrtex de la paràbola és Vx = a b 2 –→ 2= a b 2 –→ 4a + b = 0.
Com que (2, 1) pertany a la paràbola: 1 = a · 22 + b · 2 + c → 4a + 2b + c = 1. Com que (–2, 3) també hi pertany: 3 = a · (–2)2 + b · (–2) + c → 4a – 2b + c = 3.
Obtenim els coeficients a, b i c amb aquest sistema d’equacions:
Fes-ho tu. Calcula el focus i la directriu d’aquesta paràbola:
Trobem el focus i la directriu: p 8 1 2 1 = → p = 4
Paràbola amb vèrtex en (0, 0): F 0, p 2 cm → F(0, 2); d : y = –p 2 → d: y = –2
Paràbola amb vèrtex en (2, 1): F (2, 3); d: y = –1
7. Centre radical de tres circumferències
Calcula un punt que tingui la mateixa potència respecte d’aquestes tres circumferències.
C1: x2 + y2 – 6x – 6y + 9 = 0
C2: x2 + y2 + 10y = 0
C3: x2 + y2 – 12x + 11 = 0
Aquest punt s’anomena centre radical de les tres circumferències.
Anàlisi del problema Per trobar el centre radical, R, cal obtenir dos dels eixos radicals i determinar el seu punt de tall. Eix
Punt
Fes-ho tu. Troba el centre radical d’aquestes tres circumferències:
8. Equació d’una paràbola amb vèrtex diferent de (0, 0) donats el focus i la directriu
Calcula l’equació de la paràbola, amb l’eix paral·lel a l’eix X, el focus F(3, 5) i la directriu x = –1.
Si el focus d’una paràbola és F(3, 5) i la seva directriu és x = –1, la distància del focus a la directriu és p = 3 – (–1) = 4. Per tant, el vèrtex es troba a la mateixa distància del focus i de la directriu. És a dir:
V ,5 2 31 –cm = V(1, 5)
Fes-ho tu. Troba l’equació de la paràbola d’eix horitzontal amb el focus F (4, –3) i la directriu x = 2.
Com que l’equació d’una paràbola el vèrtex de la qual és (0, 0) és y2 = 2px, l’equació de la paràbola buscada serà aquesta:
(y – 5)2 = 8(x – 1)
9. Càlcul de la recta tangent a una paràbola en un punt
Troba la recta tangent a la paràbola y 2 = 8x en el punt A(8, 8).
Anàlisi del problema Com que la recta tangent no és paral·lela a l’eix Y i passa per A(8, 8), ha de ser de la forma y = m(x – 8) + 8. Per trobarne el pendent, cal tenir en compte que una recta tangent a la paràbola ha de tenir un únic punt en comú amb aquesta, A. És a dir, el sistema que formen les seves equacions ha de tenir solució única.
Si desenvolupem i operem, obtenim que:
Perquè aquesta equació de 2n grau tingui solució única, el seu discriminant ha de ser 0.
Fes-ho tu. Troba la recta tangent a la paràbola y 2 = – 4x en el punt A(– 4, 4).
Calcula la distància focal, el semieix menor i l’excentricitat d’aquesta el·lipse:
• Troba el semieix major i, a partir d’aquesta mesura i de la distància del focus a l’extrem esquerre, calcula la semidistància focal.
• Amb les dades que tens, pel teorema de Pitàgores pots calcular el semieix menor.
• Troba, a partir de les dades calculades, l’excentricitat de l’el·lipse.
Solució:
distància focal = 48 cm; semieix menor = 10 cm; excentricitat = 12/13 = 0,92
Troba l’equació de la circumferència inscrita en el triangle de costats a, b i c.
a: y = 0
b: 3x – 4y = 0
c: 4x + 3y – 50 = 0
Anàlisi del problema. Una circumferència queda determinada pel centre i el radi. El centre de la circumferència inscrita en un triangle és l’incentre; és a dir, el punt de tall de les bisectrius dels angles interiors d’aquest triangle. El radi, com que és la circumferència tangent als costats del triangle, es pot calcular com la distància del centre a qualsevol d’aquests costats.
• Troba la bisectriu de l’angle que defineixen a i b. Obtén-la com el lloc geomètric dels punts P(x, y) que equidisten d’ambdós costats: dist (P, a) = dist (P, b). Expressa en coordenades aquesta condició i resol l’equació resultant. Els valors absoluts donaran lloc a dues equacions diferents, corresponents a les dues bisectrius d’aquestes rectes. Ajuda’t d’una representació gràfica per distingir quina és la que correspon a l’angle interior del triangle.
• De manera anàloga, calcula la bisectriu corresponent als costats a i c
• Calcula l’incentre O(x0, y0) com el punt de tall d’ambdues bisectrius. Per fer-ho, resol el sistema que formen les seves equacions.
• Obtén el radi de la circumferència com la distància de O a qualsevol dels costats del triangle. Observa que, si calcules la distància al costat a, els càlculs són més simples: r = dist (O, a).
• L’equació de la circumferència és (x – x0)2 + ( y – y0)2 = r 2. Com que en les coordenades del centre i en el radi hi ha denominadors, pot ser convenient desenvolupar l’expressió obtinguda per simplificar-la.
Solució: 4x 2 + 4y 2 – 60x – 20y + 225 = 0
Les rectes tangent i normal a una circumferència en un punt P són, respectivament, aquestes:
r: x + y – 7 = 0 s: x – y – 9 = 0
Calcula l’equació de la circumferència si el radi és r = 22
• El punt de la circumferència, P, en què r és tangent és el punt d’intersecció de r i s i el pots trobar resolent el sistema que formen les equacions respectives.
• Per trobar el centre de la circumferència O(x0, y0), tingues en compte que ha de complir aquestes dues condicions: O ∈ s i dist (P, O) = 22 . Expressa analíticament aquestes condicions i resol el sistema que formen ambdues equacions. Obtindràs dues solucions, O i O'
• Troba les expressions de les circumferències solució mitjançant l’equació (x – x0)2 + ( y – y0)2 = r 2 .
Solució:
(x – 6)2 + ( y + 3)2 = 8; (x – 10)2 + ( y – 1)2 = 8
Llocs geomètrics
1 Troba, en cada cas, la mediatriu del segment AB:
a) A(5, –1) B(–3, 1) b) A(3, 6) B(–1, 6) Comprova que és una recta perpendicular a AB.
2 Troba el lloc geomètric dels punts P(x, y) la diferència de quadrats de distàncies als punts A(0, 0) i B(6, 3) dels quals és 15. Quina figura obtens?
3 Troba el lloc geomètric dels punts la distància a la recta 4x – 3y + 11 = 0 dels quals és 6.
4 Troba el lloc geomètric dels punts que equidisten de les rectes r i s. Interpreta el resultat.
r : 3x – 5y + 11 = 0 s : 3x – 5y + 3 = 0
5 Troba les equacions de les bisectrius dels angles que formen les rectes r i s:
r : 4x – 3y + 8 = 0 s : 12x + 5y – 7 = 0
Circumferències
6 Troba, en cada cas, el lloc geomètric dels punts del pla la distància al punt A dels quals és d:
a) A(0, 5) i d = 2 b) A(0, 0) i d = 1
c) A(–2, 0) i d = 2 1 d) A(–1, –5) i d = 5 3
7 Troba el lloc geomètric dels punts el quocient de distàncies als punts A(0, 6) i B(0, 3) del qual és 2, és a dir:
(, ) (, ) distP B distP A 2 =
8 Escriu, en cada cas, l’equació de la circumferència que té centre C i radi r :
a) C(0, 0) i r = 1 b) C(2, –3) i r = 2
c) C(–1, 0) i r = 3 2 d) C(0, 3) i r = 4 5
9 Esbrina quines de les expressions següents corresponen a una circumferència i troba’n el centre i el radi:
a) x 2 + y 2 – 8x + 2y + 10 = 0
b) x 2 – y 2 + 2x + 3y – 5 = 0
c) x 2 + y 2 + xy – x + 4y – 8 = 0
d) 2x 2 + 2y 2 – 16x + 24 = 0
10 Escriu l’equació de la circumferència que passa per 0, 3 1 –cm
i té centre en , 2 1 3 1 –cm
11 Troba l’equació de la circumferència que té el centre en el punt C(0, –5) i el diàmetre igual a 10.
12 Escriu l’equació de la circumferència que passa per A(1, –2) i per B(2, –1) i té radi 1.
13 Un dels diàmetres d’una circumferència té per extrems A(3, –2) i B(7, 0). Troba l’equació de la circumferència.
14 Determina l’equació de la circumferència que passa per A(2, – 4), B(8, –10) i C(4, –8).
Mira l’exercici resolt 1 de la pàgina 240.
15 Determina l’equació de la circumferència que té per centre el punt (2, –5) i és tangent a l’eix de les abscisses.
16 Obtén l’equació de la circumferència el centre de la qual està situat en el punt (3, –4) i que és tangent a l’eix de les ordenades.
17 Determina l’equació de la circumferència que té el centre en l’origen de coordenades i és tangent a la recta x + y – 3 = 0.
18 Determina les rectes tangent i normal a la circumferència (x + 4)2 + ( y + 2)2 = 13 en el punt A(–2, 1).
Posicions relatives de rectes i circumferències
19 Calcula la distància del centre de la circumferència x 2 + y 2 – 2y – 1 = 0 a la recta r : 2x – y + 3 = 0. Quina és la posició de r respecte de la circumferència?
20 Estudia la posició relativa de la circumferència d’equació x 2 + y 2 – 6x – 4y + 9 = 0 respecte de cada una de les rectes següents:
r1: x + y – 1 = 0 r2: 3x – 4y + 9 = 0
21 Estudia la posició relativa de la circumferència d’equació (x + 1)2 + ( y – 2)2 = 4 respecte a cada una de les rectes següents:
r1: x – 2 = 0 r2: y = 0 r3: y = 2x + 1 Fes servir, en cada cas, aquests dos mètodes:
a) Resol els sistemes d’equacions formats per la circumferència i cada recta.
b) Compara la mesura del radi amb la distància de cada recta al centre de la circumferència.
22 Estudia la posició relativa de la recta y = x + b i la circumferència x 2 + y 2 = 1 en funció del paràmetre b.
23 Determina la posició relativa de la recta y = 2x – 3 i la circumferència x2 + y2 = a en funció del valor del paràmetre a.
Potència d’un punt respecte a una circumferència
24 Calcula la potència dels punts P(5, 2), Q(2, 1) i R(–1, 0) respecte a la circumferència:
C: x 2 + y 2 – 6x – 4y + 9 = 0
Estudia la posició relativa de P, Q i R respecte de C
25 Troba i representa l’eix radical dels parells de circumferències següents:
a) x 2 + y 2 = 4 i x 2 + ( y – 1)2 = 9
b) (x – 3)2 + y 2 = 5 i (x – 7)2 + y 2 = 9
c) x 2 + ( y – 3)2 = 2 i (x – 5)2 + y 2 = 1
26 Calcula el centre radical d’aquestes tres circumferències:
C1: x2 + y2 – 4x + 6y = 0
C2: x2 + y2– 1 = 0
C3: x2 + y2 + 6x + 5 = 0
Mira l’exercici resolt 7.
El·lipses
27 Troba l’equació del lloc geomètric dels punts la suma de distàncies a P(– 4, 0) i Q(4, 0) dels quals és 10.
28 D’una el·lipse en coneixem els focus F(0, 1) i F' (0, –1) i la constant k = 4. Determina’n l’equació.
29 Troba l’equació de l’el·lipse de focus (–2, 0) i (2, 0) si la longitud de l’eix major és 10.
30 Escriu l’equació de l’el·lipse els focus de la qual són F(–3, 0) i F' (3, 0) i l’excentricitat, 0,5.
31 Determina l’equació de l’el·lipse que passa per (3, 1) i amb focus (4, 0) i (– 4, 0).
32 L’eix major d’una el·lipse centrada en (0, 0) és igual a 10 i està situat sobre l’eix X. A més, passa pel punt (3, 3). Obténne l’equació.
33 Determina l’equació de l’el·lipse centrada en (0, 0) que té aquestes característiques:
a) La seva excentricitat és 1/2. El seu eix major està situat sobre l’eix Y i és igual a 2.
b) Els seus vèrtexs són (–2, 0), (2, 0), (0, – 4) i (0, 4).
34 Troba els vèrtexs, els focus i l’excentricitat de les el·lipses següents. Representa-les:
a) x y 100 36 1 2 2 += b) x y 64 100 1 2 2 +=
c) 9x 2 + 25y 2 = 25 d) 9x 2 + 4y 2 = 3
35 Troba els vèrtexs, els focus i l’excentricitat d’aquestes el·lipses no centrades en l’origen de coordenades. Representa-les:
a) () x y 25 9 3 1 2 2 + + = b) () () x y 9
36 Indica l’equació d’aquestes el·lipses i calcula la seva excentricitat:
Hipèrboles
37 Troba el lloc geomètric dels punts la diferència de distàncies a F'(– 4, 0) i F (4, 0) dels quals és 6.
38 Troba l’equació de la hipèrbola de focus (– 4, 0) i (4, 0) i distància entre vèrtexs 4.
39 Obtén l’equació de la hipèrbola en què les asímptotes són y = ± 5 1 x i un dels vèrtexs és (2, 0).
40 Els focus d’una hipèrbola que passa pel punt , 85 3 ` j són (–3, 0) i (3, 0). Calcula’n l’equació.
41 Troba l’equació de la hipèrbola de focus (–3, 0) i (3, 0) i asímptotes y = ± x 5 25
42 Troba els vèrtexs, els focus, les excentricitats i les asímptotes de les hipèrboles donades per les equacions següents.
43 Indica l’equació de cada una de les hipèrboles següents i calcula la seva excentricitat: X
44 Troba el lloc geomètric dels punts que equidisten del punt (3, 0) i de la recta y = –3.
45 Troba, en cada cas, l’equació de la paràbola de focus F i directriu d:
a) F (5, 0); d: x = –5 b) F (–3, 0); d: x = 3
c) F (0, 2,5); d: y = –2,5 d) F (0, – 4); d: y = 4
46 Determina l’equació de la paràbola amb el vèrtex en l’origen de coordenades i la directriu de la qual és y = 3.
47 Troba els vèrtexs, els focus i les directrius de les paràboles següents. Representa-les:
a) y 2 = 6x b) y 2 = – 6x
c) y = x 2 d) y
e) y 2 = 4(x – 1) f) (x – 1)2 = –8( y + 1)
48 Calcula les equacions d’aquestes paràboles:
53 Determina l’equació de la circumferència de radi 10 que, en el punt (7, 2), és tangent a la recta 3x – 4y – 13 = 0.
54 Troba l’equació de la circumferència inscrita en el triangle de vèrtexs A(3, 2), , B 12 2 ` j i , C 52 2 – + ` j
55 Troba l’equació de la circumferència circumscrita al triangle determinat per la recta y = –x + 4 i els eixos de coordenades. Calcula l’equació de la recta tangent a aquesta circumferència en (0, 0).
56 Troba l’equació de la circumferència inscrita en el quadrat de vèrtexs A(–3, 3), B(–1, 3), C(–1, 1) i D(–3, 1).
57 Estudia la posició relativa del punt P(0, 3) respecte de la circumferència (x – m)2 + y 2 = 25 en funció dels valors del paràmetre m.
58 Estudia, en funció de k, la posició relativa de la recta s : 4x + 3y + k = 0 respecte a la circumferència d’equació x 2 + y 2 – 2x – 6y + 6 = 0.
Y
Y
Y a) b) c)
59 Dues circumferències es tallen en els punts (0, 0) i (0, 8). Quin n’és l’eix radical? Justifica la resposta.
*
49 Identifica les còniques següents, calcula’n els elements característics i dibuixa-les:
a) 4x 2 + 9y 2 = 36 b) 16x 2 – 9y 2 = 144
c) 9x 2 + 9y 2 = 25 d) x 2 – 4y 2 = 16
e) y 2 = 14x f) 25x 2 + 144y 2 = 900
g) () () x y 9 1 25 4 1 ––2 2 += h) () () x y 16
–2 2 + =
i) (x + 2)2 = 4( y + 5) j) x 2 + y 2 – 2x + 4y = – 4
50 a) Troba l’equació de la circumferència amb centre en C(–1, 1) que és tangent a la recta 3x – 4y – 3 = 0.
b) De totes les rectes paral·leles a la bisectriu del primer quadrant, determina les que siguin tangents a la circumferència trobada en l’apartat anterior.
51 Troba l’equació de la circumferència que passa per (–3, 2) i (4, 1) i que és tangent a l’eix X
52 La circumferència C té el centre en la recta x – 3y = 0 i passa pels punts (–1, 4) i (3, 6). Obtén l’equació de C
60 Troba els punts d’intersecció de cada parell de circumferències i digues quina n’és la posició relativa: a) xy x xy 6160 4 22 22 += += *
61 Escriu l’equació d’una el·lipse amb centre en l’origen de coordenades i focus en l’eix de les abscisses, que passa pel punt P(8, –3) i l’eix major de la qual és el doble del menor.
62 Considera les circumferències C1: (x – 1)2 + ( y + 1) 2 = 2 i C2: (x – 3)2 + ( y + 3) 2 = 10.
a) Comprova que ambdues circumferències són secants i calcula’n els punts de tall, A i B
b) Troba les potències dels punts A i B a les circumferències C1 i C2.
c) Tenint en compte el resultat obtingut en l’apartat anterior, què podries dir de l’eix radical d’ambdues circumferències?
d) Pots generalitzar aquest resultat per a un parell qualsevol de circumferències secants?
63 Troba l’equació de la hipèrbola centrada en (4, 5), de focus F (2, 5) i F'(6, 5) i semieix menor b = 1.
64 Troba les coordenades dels focus i la distància focal d’aquestes hipèrboles equilàteres:
65 Troba l’equació de la hipèrbola següent:
• Té el centre en l’origen de coordenades.
• Té els focus en l’eix de les abscisses.
• Passa pel punt P 52/, 1 ` j
• Una de les seves asímptotes és la recta y = 2x.
66 Troba l’equació de la circumferència de radi 5 que passa per P(1, 1) i el centre de la qual pertany a la recta x + 3y – 19 = 0.
Mira l’exercici resolt 2.
67 Troba l’equació de la hipèrbola equilàtera els focus de la qual són (5, 0) i (–5, 0).
68 Troba l’equació del lloc geomètric de tots els punts del pla tals que la seva distància al punt (4, 0) sigui el doble de la seva distància a la recta x = 1. Comprova que és una cònica i troba’n els focus.
69 Troba l’equació del lloc geomètric dels punts la distància al punt (4, 0) dels quals sigui igual a la meitat de la distància a la recta r : x – 16 = 0. Representa la corba que obtens.
70 Troba el lloc geomètric dels punts P(x, y) tals que el producte dels pendents de les rectes traçades des de P fins als punts A(–2, 1) i B(2, –1) sigui igual a 1. Quina figura obtens? Representa-la.
71 Troba les rectes tangents a l’el·lipse x y 94
+= que passen per A(5, 0).
72 Troba l’equació de la tangent a la hipèrbola
y
en el punt P d’abscissa x = 5. Tingues en compte que la tangent és la bisectriu dels segments PF i PF', en què F i F' són els focus de la hipèrbola (tria la bisectriu adequada).
73 Troba la tangent a la paràbola y 2 = 12x en el punt P(3, 6). Tingues en compte que la tangent és la bisectriu de l’angle format per PF (en què F és el focus) i la recta perpendicular a la directriu que passa per P.
74 El cometa Halley descriu una òrbita el·líptica d’excentricitat 0,96657, i el Sol és en un dels seus focus. Si la seva distància mínima al Sol (periheli) és de 0,6 UA, calcula quina n’és la màxima (afeli). Recorda que 1 UA (unitat astronòmica) és la distància mitjana entre la Terra i el Sol.
75 La Terra descriu una òrbita el·líptica, i el Sol és en un dels seus focus. En aquesta trajectòria, la distància mínima Terra-Sol és de 147 095 248 km i la màxima és de 152 100 492 km. Calcula l’excentricitat de l’òrbita i interpreta el resultat obtingut.
76 Associa cada una de les equacions següents amb una de les gràfiques que hi ha a continuació:
= 9
77 Determina si les equacions següents corresponen a una cònica. Si es així, indica quina cònica és en cada cas:
78 Sabem que en aquesta hipèrbola | ' PF PF – | = 4.
Quina branca correspon a ' PF PF – = 4 i quina correspon a PF' PF – = 4? F F'
79 A partir de la definició d’el·lipse i fent algunes mesures sobre el paper, digues quines d’aquestes el·lipses amb els seus focus estan mal dibuixades:
c) b) a) d)
80 Cert o fals?
a) Si la distància d’una recta al centre d’una el·lipse és més gran que el semieix major, no es tallen.
b) Totes les hipèrboles equilàteres tenen la mateixa excentricitat.
c) Les paràboles del tipus y2 = –2px tenen excentricitat –1.
d) Per tres punts alineats no pot passar una circumferència.
e) Com més s’allunyen el focus i la directriu d’una paràbola, més gran és la seva excentricitat.
Autoavaluació Resolucions d’aquests exercicis.
1 Troba l’equació de la bisectriu dels angles formats per les rectes següents:
r1: x = 3
r2: 3x – 4y + 1 = 0
2 Escriu l’equació de la circumferència amb centre en el punt C(1, –3) que passa pel punt A(5, 0).
3 Considerem la circumferència x 2 + y 2 – 2x = 0 i la recta r : 3x – 4y + k = 0. Calcula els valors que ha de prendre k perquè r sigui interior, tangent o exterior a la circumferència.
4 Descriu les còniques següents. Obtén-ne els elements i dibuixa-les:
81 a) Troba el lloc geomètric dels punts P(x, y) la suma de quadrats de distàncies als punts A(–3, 0) i B(3, 0) dels quals és 68. Pots comprovar que es tracta d’una circumferència de centre O(0, 0). Quin n’és el radi?
b) Generalitza: troba el lloc geomètric dels punts la suma de quadrats de distàncies a A(–a, 0) i B(a, 0) dels quals és k (constant) i comprova que es tracta d’una circumferència de centre O(0, 0). Determina el valor del radi en funció de a i de k. Quina relació han de complir a i k perquè realment sigui una circumferència?
82 a) Considera la circumferència C : (x – 1)2 + y 2 = 25 i el punt P(9, 6) i anomena r la recta que uneix P amb el centre de la circumferència. Troba A i B, els punts de tall de r i C Comprova que la potència de P respecte de C coincideix amb d (P, A) · d (P, B).
b) Demostra que l’apartat anterior és cert si substituïm r per qualsevol recta secant a C que passi per P. Fes un dibuix i anomena A' i B' els punts de tall de C i la nova recta. Aplica la semblança als triangles AB'P i A'PB.
83 Calcula el lloc geomètric dels punts el producte de distàncies del qual a aquestes rectes és 2:
r: 2x + 3y = 0 s: y = 3 2 x
6 Escriu l’equació de la paràbola que té per directriu la recta x = 3 i per vèrtex l’origen de coordenades.
7 Troba els focus, l’excentricitat i les asímptotes de la hipèrbola que té per equació 9y 2 – 16x 2 = 144.
Dibuixa-la.
8 Indica les equacions de les còniques següents: X
5 Obtén l’equació de l’el·lipse de focus F (– 4, 0) i F' (4, 0) i d’excentricitat 0,8.
Y a) b) c)
Y X
Y X
9 Troba l’eix radical d’aquestes circumferències:
C1: x 2 + y 2 – 4x – 2y + 1 = 0
C2: x 2 + y 2 – 4x – 18y + 21 = 0
Representa les circumferències i l’eix radical.
1 Donats els vectors , 2 1 –1 u cm i v (0, –2), calcula:
a) | u | b) –u23 v + c) 22() u– v :
2 Determina el valor de k perquè els vectors a (1, 3) i b (6, k) siguin ortogonals.
3 Donats els vectors u (–1, 0) i v (1, 2):
a) Calcula proj v u
b) Calcula l’angle que formen u i v .
c) Determina les coordenades del vector w (4, 6) en la base B ( u , v ).
4 Determina les coordenades d’un vector unitari a (x, y) si forma un angle de 60° amb el vector u (2, 0).
5 Donats a (–5, 5) i b (–1, 3), expressa a com a suma de dos vectors, un amb la mateixa direcció que b i un altre perpendicular a b .
6 Determina el valor de y perquè els punts A(0, 1), B (–1, 4) i C (3, y) estiguin alineats.
7 Troba les coordenades del vèrtex D del paral·lelogram ABCD, en què A (2, 2), B (3, 1) i C (4, 2).
8 Troba en les formes paramètrica i implícita l’equació de la recta que passa per P (0, 3) i és perpendicular a la recta s : x 1 2 + = 1 – y
9 PAU Donades les rectes r : 2x + y – 1 = 0 i s : kx – y + 5 = 0, determina k per a cada un dels casos següents:
a) r i s són paral·leles.
b) r i s es tallen en el punt P (2, –3).
c) r i s són perpendiculars.
10 Troba la distància entre les rectes r i s :
r : y = x + 2 s : xt yt 2 –= = )
11 PAU Obtén l’expressió analítica del feix de rectes al qual pertanyen r : 2x + y – 3 = 0 i s : x + y – 2 = 0. Troba la recta d’aquest feix que passa per P (2, 3).
12 Troba el simètric del punt A(0, 0) respecte a la recta r : x + y – 2 = 0.
13 PAU Troba l’equació de la recta que passa pel punt d’intersecció de les rectes r : 2x – y + 1 = 0 i s : x y
forma un angle de 45° amb la recta r.
14 Troba els punts de la recta y = 0 que disten 3 unitats de la recta 3x – 4y = 0.
15 Fixa’t en el triangle ABC de la figura i calcula:
a) L’ortocentre.
b) L’àrea del triangle.
16 Donat el triangle format per la bisectriu del primer quadrant, b, l’eix de les abscisses i la recta r : y = – x + 4, calcula:
a) La mediatriu del costat contingut en la recta r.
b) La bisectriu de l’angle que formen r i l’eix OX.
c) La mitjana relativa al costat que hi ha en b.
17 Només una d’aquestes equacions correspon a una circumferència. Justifica quina és i determina’n el centre i el radi:
C1: x 2 + y 2 – 2x + 6y + 6 = 0
C2: x 2 + y 2 – 2xy + 6y + 6 = 0
C3: x 2 + y 2 – 3x + 5x + 18 = 0
18 Escriu l’equació d’una el·lipse de centre (0, 0) i focus en l’eix de les abscisses, si saps que l’excentricitat és igual a 4/5 i que un dels focus és F (8, 0).
19 Sense resoldre el sistema format per les seves equacions, estudia la posició relativa de la circumferència d’equació
C : (x – 1)2 + ( y + 2)2 = 4 i la recta r : 3x – 4y – 1 = 0.
20 Identifica les còniques següents, calcula’n els elements característics i dibuixa-les:
a) 2y 2 – 12x = 0 b) 4x 2 + 4y 2 = 16
c) 25x 2 + 4y 2 = 100 d) () () x y 16 1 9 1 ––2 2 + = 1
21 Troba l’equació d’aquestes còniques i representa-les:
a) Circumferència de centre (2, –5) i radi 4.
b) El·lipse de centre (0, 0) i focus F1(6, 0) i F2(–6, 0), amb excentricitat 3/5.
c) Hipèrbola de focus F1(–4, 0) i F2(4, 0) i constant k = 6.
d) Paràbola de vèrtex V(–1, –1) i directriu r: x = –3.

`
Notes histOriques. EstadIstica
Es construeix el primer rellotge de
Invenció del termòmetre
Revolució científica: Copèrnic i Vesalius

1550
Introducció del tabac a Europa
Rafael
Utopia
Verdaguer: Canigó
Invenció del telèfon
Darwin: L’origen de les espècies

Guerra Civil nordamericana
1 Els primers acostaments seriosos al que més tard s’anomenaria la probabilitat van ser gràcies als esforços de personatges com Tartaglia, Luca Pacioli, Galileu i Cardano. Aquest darrer escriu el primer tractat mitjanament organitzat sobre l’atzar: Llibre dels jocs d’atzar.

2 Sembla clar que les bases en què s’assenta la teoria matemàtica de la probabilitat parteixen de les investigacions fetes per Pascal (16231662) i Fermat (16011665) amb motiu de la resolució d’una sèrie de problemes sobre jocs d’atzar que els va proposar el cavaller De Méré.
Quételet
Invenció del telègraf 1500 1900 1850





3 L’any 1662 l’anglès John Graunt va publicar un tractat amb observacions polítiques i naturals de la ciutat de Londres. Es pot considerar el primer treball estadístic seriós sobre la població. Naixia així una nova ciència: l’estadística.

4 El suís J. Bernoulli (16541705), amb l’Art de conjecturar, o el francès Laplace (17491827), amb la Teoria analítica de les probabilitats, van aprofundir en la teoria de la probabilitat.

Batalla de Waterloo Primera bicicleta de pedals
Il·luminació de gas
5 Fins al segle xviii, el terme estadística denotava les característiques més notables d’un estat. Amb l’escola alemanya d’aquest segle, el terme estadística, en la versió actual, va quedar definitivament encunyat. L’artífex va ser G. Achenwall (17191772).
• Ampliació de les notes històriques corresponents a aquest bloc.








• Lectura sobre coincidències d’aniversari.

La combinatòria té com a objecte esbrinar, a partir d’un conjunt finit d’objectes, quantes agrupacions hi ha que compleixin certes condicions. Civilitzacions antigues com la xinesa, l’índia o l’àrab ja usaven alguns conceptes bàsics sobre combinatòria. Però la primera obra impresa en la qual apareixen problemes de combinatòria és Summa, escrita per Luca Pacioli el 1494, en la qual es calcula, per exemple, de quantes formes diferents poden asseure’s al voltant d’una taula circular un nombre determinat de persones.

La combinatòria va començar a forjar-se com a ciència paral·lelament a la probabilitat i va estar lligada als jocs.
Tartaglia (segle xvi), algebrista italià, va ser un dels pioners en aquest camp. Un altre algebrista italià, contemporani seu i amb qui va tenir algunes picabaralles per l’autoria en la resolució d’algun tipus d’equacions de tercer grau, va ser Cardano, que va escriure el primer tractat mitjanament organitzat sobre aquest tema: El llibre dels jocs d’atzar. Cardano sabia del que parlava en aquest llibre, ja que era un jugador empedreït.
El 1654, el matemàtic francès Blaise Pascal va fer un viatge en companyia del seu amic el cavaller De Méré, un jugador habitual. Aquest li va proposar una sèrie de problemes d’atzar que van interessar vivament al matemàtic. Uns dies després, Pascal els va exposar al seu amic Pierre de Fermat, també matemàtic, i ambdós els van resoldre, encara que per camins diferents.
La correspondència que es va establir entre ells intercanviant idees i nous problemes va donar lloc al naixement de la teoria de la probabilitat i va proporcionar un impuls definitiu a la combinatòria.
Ni Pascal ni Fermat no van publicar les seves conclusions, però sí que ho va fer Christiaan Huygens el 1656, en un breu llibre titulat Sobre els raonaments en els jocs d’atzar.
El terme combinatòria, tal com l’utilitzem actualment, va ser introduït per l’alemany Leibniz (segle xvii).
• Jacques Bernoulli (segle xvii) va recollir l’escrit per Huygens, el va ampliar i el va completar, amb la qual cosa va publicar, de manera pòstuma, el 1713, la primera obra important sobre la teoria de les probabilitats, Art de la conjectura, que inclou la primera definició formal de probabilitat.
• Laplace (segle xviii) va publicar, un segle després, Teoria analítica de les probabilitats, on va recollir i va organitzar multitud de resultats que havia anat obtenint i difonent des de feia quaranta anys. Es tracta de l’aportació més gran de la història a aquesta teoria. És seva la frase següent:
La teoria de les probabilitats és només sentit comú expressat amb nombres.
• A mitjans del segle xix, el naturalista austríac Gregor Mendel va aplicar la probabilitat en l’estudi de l’herència.

• Al començament del segle xx, el rus Kolmogorov va establir les definicions, els axiomes i els postulats en què es basa la teoria de la probabilitat, la qual cosa va acabar de conferir-hi la precisió necessària per ser considerada una branca de les matemàtiques.

• La probabilitat moderna té multitud d’aplicacions en economia, informàtica, ciències físiques, biologia (per exemple, per desxifrar les seqüències d’ADN)…
La ciència que va néixer dels jocs avui en dia dista molt de ser un joc.
Tres ramaders porten cada un dos dels seus millors animals a la fira de bestiar. En travessar el riu, el barquer els avisa que només pot embarcar tres animals per trajecte. Cada un col·loca a la barca un dels dos que porta.
Què és més probable: que hi hagi dos animals del mateix tipus o que tots tres siguin diferents?
Si en Màrius, que portava un porc i un be, hagués portat el porc i un gall dindi, en aquest cas què seria més probable, que hi hagués tres animals diferents a la barca o que no tots fossin diferents?
Les estratègies de pensament són, com el seu nom indica, mètodes pels quals s’aconsegueix pensar eficaçment sobre un cert tipus de problemes més o menys complexos.
La combinatòria s’ocupa d’explicar agrupacions realitzades amb un determinat criteri.
El diagrama en arbre és una estratègia de pensament que permet elaborar i explicar conjunts ordenats. Vegem-ne alguns exemples.
• Exemple 1
En el torneig de Wimbledon els tenistes A, B, C i D han arribat a les semifinals. De quantes formes poden repartir-se la copa per al campió i la placa que donen al subcampió? Resolució. Hi ha quatre possibilitats per a la copa de campió. A cada una d’aquestes quatre possibilitats la poden seguir tres possibles subcampions. En total, 4 · 3 = 12 possibilitats.
• Exemple 2
Si en lloc de detallar totes les possibilitats només volem explicar-les, podrem deixar l’arbre incomplet o, fins i tot, simplement imaginar-lo: Quantes fletxes cal posar en primer lloc? Quantes en surten de cada un d’aquests resultats?
En unes olimpíades arriben a la fase final vuit saltadores d’alçada. De quantes formes es poden repartir les tres medalles? Resolució. Hi ha vuit possibles campiones. En cada un dels casos, hi ha set possibles subcampiones. I a cada parella campiona-subcampiona la pot seguir en tercer lloc qualsevol de les altres sis. En total hi ha:
8 · 7 · 6 = 336 possibilitats
El diagrama en arbre permet pensar pas a pas i veure les diferents possibilitats que es donen en cada un d’aquests passos.
1 De quantes formes es poden repartir 3 medalles entre les 12 participants d’una
Exercicis proposats
1 L’Albert, la Beatriu i la Clàudia van a veure el seu avi. Abans de marxar, aquest els mostra deu llibres diferents i els diu: «Escolliu cada un el llibre que vulgueu.»
De quantes formes poden fer la seva elecció?
2 De quantes formes diferents poden arribar a la meta els sis corredors que participen en una carrera?
• Exemple 3
Quatre amics organitzen entre ells dos tornejos: un de ping-pong i un altre d’escacs. El campió de ping-pong s’emportarà una raqueta formidable i el vencedor d’escacs guanyarà un tauler amb les seves peces. De quantes formes poden repartir-se els dos trofeus?
Resolució. És clar que el campió de ping-pong pot ser, també, campió d’escacs. Per això, a cadascun dels quatre possibles campions de ping-pong li corresponen quatre possibles campions d’escacs. El nombre total de possibilitats és aquest:
4 · 4 = 16
• Exemple 4
De quantes formes es poden repartir el primer lloc en cada una de les deu especialitats de decatló, els vuit atletes finalistes?
Resolució.
Una altra interessant aplicació del diagrama en arbre
• Exemple 5
S’ha jugat un partit de futbol de màxima rivalitat a la nostra ciutat i només sabem que el resultat ha estat un empat: 3 - 3. Ens preguntem de quantes formes es pot haver arribat a aquest resultat.
Resolució. Aquestes són totes les possibilitats que poden donar-se:
En verd: marca l’equip de casa. En vermell: marca l’equip visitant.
3 Seguint amb el partit de l’exemple 5, respon:
Aquest esquema mostra el nombre de possibles camins que arriben a cada resultat. Es pot arribar de 20 formes diferents al 3 - 3.
a) Si al descans el resultat era 2 - 1, de quantes formes possibles va poder anar variant el marcador fins a arribar al resultat final 3 - 3?
b) Repeteix el problema per a un resultat final 4 - 3 i per a un resultat 2 - 2 al descans.
Recuperem l’exemple 3 vist en la pàgina anterior:
• Quatre amics juguen un campionat de ping-pong i un altre d’escacs. De quantes formes poden repartir-se els dos trofeus?
El primer trofeu pot ser per a qualsevol dels quatre, A, B, C, D i el segon, també, sense importar qui va guanyar el primer.
Per tant, hi haurà 4 · 4 = 42 possibilitats.
• I si fossin set amics i tres trofeus?
Doncs de forma similar, 7 possibilitats per al primer, 7 per al segon i 7 per al tercer. En total, 7 · 7 · 7 = 73 possibilitats.
Variacions amb repetició
• Hi ha m elements d’inici.
• Es formen agrupacions de n d’aquests elements.
• Poden estar repetits.
• Importa l’ordre en què es col·loquen.
• Observa que pot ser n = m i, fins i tot, n > m
2n 3r 4t … n-èsim
Disposem de m elements. Formem agrupacions ordenades («tires») de n elements, repetits o no.
A aquestes agrupacions se les anomena variacions amb repetició de m elements agafats de n en n i se les designa per VRm, n (o bé VR m n ).
VRm, n = mn
Per justificar la fórmula raonem així:
En el primer lloc podem situar qualsevol dels m elements. En el segon lloc, també, sense importar quin és el que ocupa el primer. I així successivament, cada lloc pot ser ocupat per qualsevol dels m elements sense importar quins són els que ocupen els llocs anteriors. Per tant, el nombre de possibilitats és aquest:
m · m · … · m = mn (n factors)
Variacions ordinàries
• De quantes formes poden obtenir els llocs 1r i 2n els quatre participants en un torneig?
Disposem de quatre elements, A, B, C, D. Per al 1r lloc hi ha 4 opcions. Una vegada fixat el primer, per al 2n lloc queden 3 opcions (no hi ha repetició, ja que el que queda 1r no pot quedar 2n).
El nombre de possibilitats és 4 · 3 = 12.
• De quantes formes es poden repartir les 3 medalles els 8 finalistes d’una carrera?
Disposem de 8 elements. N’hem de classificar, ordenadament, 3.
Variacions ordinàries
• Hi ha m elements d’inici.
• Es formen agrupacions de n elements. Òbviament, n ≤ m
• No poden repetir-se.
• Importa l’ordre en què es col·loquen.
m – 1 m – 2 m – n + 1
2n 3r … n-èsim
Per al 1r lloc hi ha 8 possibilitats. Fixat el 1r, hi ha 7 possibles segons llocs. Fixats el 1r i el 2n, hi ha 6 possibles tercers llocs.
Nombre de possibilitats: 8 · 7 · 6 = 336.
Disposem de m elements. Formem agrupacions ordenades («tires») de n elements, sense que se’n repeteixi cap. A aquestes agrupacions se les anomena variacions ordinàries o, simplement, variacions de m elements agafats de n en n i se les designa per Vm, n (o bé V m n ).
Vm, n = () () mm m 12 ·– ·– ·…
Permutacions
• Hi ha m elements d’inici.
• Se n’agafen els m.
• No poden repetir-se.
• L’únic que importa és l’ordre.
• De quantes formes poden quedar classificats els quatre participants en un torneig?
4 · 3 · 2 · 1 = 24 formes
• I els vuit finalistes olímpics en una carrera?
8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = 40 320 formes
Les diferents formes en què es poden ordenar els m elements d’un conjunt s’anomenen permutacions, i se les designa per Pm (es llegeix «permutacions de m elements»), que és igual al nombre de variacions de m elements agafats de m en m. Pm = Vm, m = m · (m – 1) · … · 3 · 2 · 1
A aquest nombre se l’anomena m factorial, i s’escriu m !
Per exemple: 3! = 3 · 2 · 1 = 6 5! = 5 · 4 · 3 · 2 · 1 = 120
4 Quants nombres de quatre xifres es poden formar amb les xifres senars?
5 Disposem de set colors per pintar les franges següents. Quantes banderes podem obtenir?
7 En una aula hi ha sis finestres que poden estar obertes (O ) o tancades (T ), indistintament. Aquest matí la seva posició era aquesta: OTOOTO, és a dir, estaven obertes la 1a, la 3a, la 4a i la 6a i estaven tancades la 2a i la 5a. Quantes posicions diferents poden tenir les finestres?
8 L’associació de llibreters lliurarà els premis «Ploma d’Or» i «Ploma de Plata». Per a això, ha seleccionat deu llibres entre els publicats aquest any. De quantes formes poden repartir-se els dos premis entre aquests llibres?
Tingues en compte que:
• Cada franja de la bandera cal omplir-la amb un sol color.
• Dues o tres de les franges es poden pintar del mateix color.
• Dues banderes amb els mateixos colors col·locats en diferent ordre són diferents.
6 Hem de pintar aquesta diana amb tres colors diferents. Disposem de set llaunes de pintura amb colors variats. De quantes formes podrem fer-ho si no podem repetir els colors?
9 En l’alfabet morse s’utilitzen dos símbols, el punt (.) i la ratlla (–), per representar lletres i nombres. Per exemple, les vocals es representen així:
A . – E . I . . O – – – O . . –
a) Quantes tires de tres símbols (entre punts i ratlles) es poden formar?
b) Si utilitzem tires d’1, 2, 3 o 4 símbols, quantes lletres o nombres podrem representar en total?
10 Quants nombres capicua de tres xifres existeixen? I de quatre xifres? I de cinc?
11 De quantes formes poden posar-se en fila vuit amics?
12 De quantes formes poden asseure’s al voltant d’una taula circular vuit amics?
Si importés l’ordre hi hauria V4, 2:
AB BA CA DA
AC BC CB DB
AD BD CD DC
Però com que no influeix l’ordre i cada parella està comptada dues vegades, n’hi haurà V 2 , 42 .
Reflexionem sobre alguns problemes senzills.
• Quants partits han de jugar 4 amics si decideixen enfrontar-se cada un contra tots els altres?
Disposem de 4 elements, A, B, C, D. Volem agrupar-los de dos en dos, sense que importi l’ordre. El nombre de possibilitats s’obté comptant-les com si importés l’ordre (4 · 3) i, després, dividint pel nombre de vegades que està repetida cada opció.
Resultat: 2 43 = 6
• Quantes encaixades de mans faran 10 amics que es troben?
Anàlogament, comptem les salutacions com si importés l’ordre (A saluda B o B saluda A). Seran V10, 2 = 10 · 9. Després, dividim entre 2.
Resultat: 2 10 9 · = 45
• En un col·lectiu de 10 persones, de quantes formes es poden triar els 3 representants que aniran a una certa reunió?
Encara que no importa l’ordre en què surtin elegits, comencem comptant-los com si importés: V10, 3 = 10 · 9 · 8.
Però com que l’ordre no influeix, cada una de les possibles eleccions l’hem comptat 6 vegades, ABC, ACB, BAC, BCA, CAB, CBA, tantes com formes en què es poden ordenar aquests 3 elements, és a dir: P3 = 3 · 2 · 1.
Per tant, el nombre de possibles eleccions és aquest: P V 32 1 10 98 , 3 10 3 = = 120.
Generalitzem aquests resultats:
Combinacions
• Hi ha m elements d’inici.
• Es formen agrupacions de n elements.
• No poden estar repetits.
• No importa l’ordre.
Disposem de m elements. S’anomenen combinacions les diferents agrupacions que podem formar prenent n elements, sense que importi l’ordre en què apareguin i sense que puguin repetir-se, i es designen per Cm, n (o bé C m n , que es llegeix «combinacions de m elements agafats de n en n»):
mn = +
Cm, n = () () () P V nn mm mn 13 21 11 –· …· ·· – ·…· –, n
Cada combinació de n elements d’un conjunt de m és un subconjunt seu. Per això, Cm, n pot dir-se que és «el nombre de subconjunts de n elements que poden extreure’s d’un conjunt de m elements». En cada subconjunt, un element hi és o no hi és. No té sentit que hi estigui repetit.
13 En una carrera amb vuit corredores es classifiquen per a la final les tres primeres. De quantes formes pot quedar la classificació?
14 La Vera vol regalar a la Zoe tres vinils i els vol triar entre els deu que més li agraden. De quantes formes pot fer l’elecció?
15 En una muntanya hi ha cinc refugis i cada un està unit als altres per un camí. Quants camins hi ha?
16 Tenim sis punts en l’espai de manera que no n’hi ha tres d’alineats ni quatre sobre el mateix pla. Quantes rectes podem traçar unint dos d’aquests punts? I quants plans que es basin en tres d’ells?
Magnitud dels factorials
El valor de n ! creix enormement de pressa en augmentar n. Per exemple:
10! = 3 628 000
20! té 19 xifres.
Recordem dos tipus de nombres molt útils per als càlculs en combinatòria.
Factorials
Si n és un nombre natural, n ≥ 2, s’anomena factorial de n i s’escriu n ! el producte de n factors decreixents a partir de n :
Per conveniències de nomenclatura, fem extensiva la definició per a
= 1 0! = 1 (encara que resulti xocant, convé que sigui així)
Nombres combinatoris
Amb calculadora
A les calculadores científiques hi ha les tecles per a les funcions x ! i n r cm
Per exemple:
7! → 7 = {∞≠¢≠}
7 3 eo → 7 3 = {«∞}
El nombre de combinacions Cm, n es designa, també, així m n cm , es llegeix «m sobre n» i s’anomena nombre combinatori.
Fixa-t’hi:
En general, si m i n són nombres naturals, m ≥ n ≥ 2, definim:
← n factors decreixents
Fem extensiva la definició de la manera següent:
Recordem que m n cm és el nombre de subconjunts de n elements sense repetir que poden extreure’s d’un conjunt de m elements. Per exemple, de quantes formes podem seleccionar 3 vocals? Vegem-ho:
Conjunt inicial: {a, e, i, o, u}
Subconjunts de 3 elements: 3 5 eo = 32 1 54 3 = 10. N’hi haurà 10.
Comprovem-ho:
Tingues en compte
Aquesta expressió de m n cm amb factorials és útil per a desenvolupaments teòrics, però no per a càlculs. Per exemple: 7 3 eo = !! ! 34 7 = 32 14 32 1 76 54 32 1
és més feixuc que el senzill càlcul que hem fet a dalt.
Vegem com pot escriure’s un nombre combinatori utilitzant els factorials:
D’acord amb aquesta fórmula, s’entén per què definim 0! = 1, ja que així la igualtat és vàlida per a m = n i per a m = n = 0.
Un cas és cada un dels possibles resultats que poden ocórrer en fer una experiència aleatòria. També s’anomena esdeveniment elemental. L’espai mostral és el conjunt de tots els casos possibles.
Un esdeveniment, S , es diu que és el contrari de S quan entre ambdós es reparteixen els casos de l’espai mostral. És a dir, sempre ocorre l’un o l’altre, però mai no ocorren simultàniament.
La probabilitat de S (esdeveniment contrari de S ) és aquesta:
P[ S ] = 1 – P[S]
La freqüència relativa d’un esdeveniment S, fr (S ), és la proporció de vegades que ocorre S.
Esdeveniment aleatori és aquell que passarà o no depenent de l’atzar. L’estudi dels esdeveniments aleatoris pot realitzar-se experimentalment (daus, monedes, extracció de cartes...) o mitjançant l’observació sistemàtica.
S’anomena freqüència relativa d’un esdeveniment S la proporció de vegades que aquest ocorre:
fr (S ) = nombre de cops que s’esdevé S nombre d’observacions fetes = () N fS
Probabilitat. Llei
Cada esdeveniment aleatori té una certa probabilitat d’ocórrer.
S’anomena probabilitat d’un esdeveniment S el límit de la freqüència relativa de S quan el nombre N d’observacions que fem tendeix a infinit:
(S ) llei dels grans nombres
Aquesta és una definició teòrica amb la qual no podem obtenir inequívocament el valor de P [S ]. A la pràctica, se segueix un d’aquests dos processos:
• Experimentant un nombre de vegades prou gran, N, i prenent com a valor aproximat de P [S ] el de fr (S ). L’assignació serà tant més fiable com més gran sigui N.
• Si l’experiència és «regular» (un dau o una moneda correctes, una carta d’una baralla...), podem suposar que tots els «esdeveniments elementals» (cada cara del dau, cada carta de la baralla...) tenen la mateixa probabilitat (són equiprobables). En aquest cas, la probabilitat d’un esdeveniment S es troba mitjançant l’anomenada llei de Laplace:
Aquesta llei es resumeix així:
P [S ] = casospossibles casosfavorables
P [S ] = ombrecasos ombrecasos è S n totaldeelementals ndeelementalsdequconsta
Per exemple, en una baralla espanyola de 40 cartes:
P [as] = nombre d’asos nombre total de naips = 40 4 = 10 1
Hi ha experiències regulars que, perquè siguin correctament interpretades, cal que siguin considerades compostes d’unes altres (dues o més).
Per exemple, en llançar dos daus i sumar les seves puntuacions, els possibles resultats (2, 3, 4, 5..., 10, 11, 12) no són equiprobables. Per assignar-los probabilitats de forma correcta, hem de considerar els 36 parells de resultats possibles en llançar dos daus (observa la taula del marge).
D’aquesta manera, s’obté que:
«Llançar dos daus» és una experiència composta de dues experiències simples: «llançar un dau» i «llançar un altre dau». És equivalent a «llançar un dau dues vegades».
«Treure dues cartes d’una baralla» o «extreure dues boles d’una bossa» són experiències compostes de dues: «treure’n una» i «treure’n una altra».
Hi ha experiències que poden considerar-se compostes de dues o més experiències simples.
En les experiències compostes de successives extraccions (d’una baralla de cartes, d’una bossa amb boles...) poden donar-se dues modalitats que és important saber distingir:
• Extraccions amb reemplaçament
Són aquelles en les quals, després de cada extracció, l’element extret (carta, papereta, bola...) es reposa (es torna la carta a la baralla i es remena, es fica la bola a la bossa i es remou...). D’aquesta manera, cada extracció es realitza en les mateixes condicions que l’anterior.
• Extraccions sense reemplaçament
Les successives extraccions es realitzen sense tornar l’element anteriorment extret. Les condicions de cada extracció són diferents i depenen de quin o quins siguin els elements anteriorment extrets.
Extreure dues o més cartes d’una baralla sense reemplaçament és equivalent a extreure-les simultàniament.
Experiències dependents i independents
• Dues o més experiències es diuen independents quan el resultat de cada una no depèn del resultat de les altres.
Les successives extraccions amb reemplaçament són experiències independents, ja que, en reposar cada vegada l’element extret, el fet que aquest sigui un o un altre no influeix en les extraccions posteriors.
També són independents els llançaments de daus, de monedes...
• Dues o més experiències són dependents quan el resultat de cada una influeix en les probabilitats de les següents.

Per exemple, si extraiem, sense reemplaçament, dues cartes d’una baralla espanyola de 40 cartes, en la segona extracció només queden 39 cartes i, depenent de quina és la que falta, les probabilitats dels diferents esdeveniments seran unes o unes altres: si en la primera extracció s’obté un as, queden 39 cartes de les quals 3 són asos. Per tant, en la segona, P [as] = 39 3 .


Tanmateix, si la primera no és un as, en la segona P [as] = 39 4 .
Es veu, doncs, que el resultat de la primera extracció influeix en les probabilitats de la segona.
Tingues en compte
És molt més senzill calcular les probabilitats dels esdeveniments compostos descomponent-los en esdeveniments simples.
Quan diverses experiències aleatòries són independents, la probabilitat que ocorri S1 en la 1a, S2 en la 2a... és aquesta:
P [S1 en la 1a, S2 en la 2a...] = P [S1 en la 1a] · P [S2 en la 2a] · ...
Exemple 1. Llancem un dau i una moneda. Quina és la probabilitat d’obtenir 5 en el dau i cara en la moneda?
P [5 i C] = P [5] · P [C] = 5 2 · 1 2 = 1 12
Exemple 2. Llancem dos daus. Probabilitat de 5 en el 1r i parell en el 2n.
P [5 en el 1r i parell en el 2n] = P [5 en el 1r] · P [parell en el
Exemple 3. Llancem dos daus. Probabilitat d’un 5 i un parell
P [un 5 i un parell] = P [5 en el 1r] · P [parell en el 2n] + + P [parell en el 1r] · P [5 en el 2n] =
_ `
b b b b Hi ha 3 maneres d’obtenir dos 5 i un parell
Exemple 4. Llancem tres daus. Probabilitat de dos 5 i un parell
P [5 en el 1r, 5 en el 2n i parell en el 3r] =
P [dos 5 i un parell] = 3 · P [5 en el 1r, 5 en el 2n i parell en el 3r] = = 3 · 2 1 7 = 1 24
Exemple 5. Llancem tres daus. Probabilitat d’un 5, un parell i un 1.
P [5 en el 1r, parell en el 2n i 1 en el 3r] =
P [un 5, un parell i un 1] = 6 · P [5 en el 1r, parell en el 2n i 1 en el 3r] = = 6 · 2 1 7 = 1 12
Exemple 6. Llancem quatre daus. P [dos 1 i dos no 1].
P [1 en el 1r, 1 en el 2n, no 1 en el 3r i no 1 en el 4t] = = 5 2 · 5 2 · 6 5 · 6 5 = 1 296 25
P [dos 1 i dos no 1] = 6 · 1 296 25 = 216 25
Exercicis proposats
17 Llancem dues monedes. Calcula:
a) P [dues C] b) P [dues +]
c) P [una C i una +]
18 Llancem tres monedes. Calcula:
a) P [C en la 1a, + en la 2a i C en la 3a]
b) P [dues C]
19 Llancem quatre monedes. Calcula:
a) P [tres C i una +]
b) P [dues C i dues +]
20 Llancem quatre daus. Calcula:
a) P [tres parell i un 5]
b) P [un 1, un 3, un 5 i un parell]
Si els esdeveniments S1 i S2 corresponen a dues proves dependents, la probabilitat que ocorri S1 en la 1a i S2 en la 2a, és aquesta:
P [S1 en la 1a i S2 en la 2a] =
= P [S1 en la 1a] · P [S2 en la 2a/suposant que va ocórrer S1 en la 1a]
La P [S2 en la 2a/suposant que va ocórrer S1 en la 1a] es designa així:
P [S2 en la 2a/S1 en la 1a]
i s’anomena probabilitat de S2 condicionada a S1
Si són tres esdeveniments S1, S2 i S3 corresponents a proves dependents:
P [S1 en la 1a i S2 en la 2a i S3 en la 3a] =
= P [S1 en la 1a] · P [S2 en la 2a/S1 en la 1a] · P [S3 en la 3a /S1 en la 1a i S2 en la 2a]
Exemple 1. Extraiem dues cartes d’una baralla de 40. Quina és la probabilitat que siguin dos asos?
Exemple 2. Extraiem tres boles de l’urna (marge). Quina és la probabilitat que siguin vermelles?
Exemple 3. Extraiem tres boles de l’urna anterior. Troba la probabilitat que, entre aquestes, n’hi hagi alguna de vermella i alguna de verda.
Farem servir un diagrama en arbre i descriurem només els casos favorables:
21 Extraiem tres cartes d’una baralla de 40. Calcula:
a) P [tres asos] b) P [un as, un cavall i un rei]
22 Extraiem tres boles de l’urna de dalt. Calcula: a) P [alguna sigui la negra]
[la negra i alguna de vermella]
Quants nombres de set xifres es poden formar amb els dígits 3, 3, 2, 2, 2, 2, 2?
Quant sumen tots junts?
Per formar un nombre de set xifres disposem de set llocs: — — — — — — —
Hem de decidir a quins col·locarem els «3». En total hi ha · C 2 76 21 , 72 == nombres.
En cada una de les set columnes hi ha 21 dígits «2» i «3». Les 2/7 parts (6 columnes) seran «3» i les 5/7 parts (15 columnes) seran «2».
Per tant, la suma de cada columna és 6 · 3 + 15 · 2 = 48.
Fes-ho tu. Quants nombres de set xifres es poden formar amb els dígits 8, 8, 8, 1, 1, 1, 1? Quant sumen tots?
La suma total és aquesta: 48 (1 000 000 + 100 000 + ... + 10 + 1) = 48 · 1 111 111 = 53 333 328
Així doncs, la suma total és 53 333 328.
Extraiem tres boles d’una urna composta per Calcula la probabilitat d’obtenir:
a) Una bola vermella i dues de verdes.
b) Una bola vermella, una de blava i una de verda.
Fes-ho tu. Fes la mateixa activitat suposant que a l’urna hi ha aquestes boles:
a) Treure tres boles és el mateix que extreure’n primer una, després una altra i després una altra. Hi ha tres formes d’obtenir-ne una de vermella i dues de verdes, i totes tres tenen la mateixa probabilitat d’ocórrer: , ,
b) Hi ha 3! = 6 formes d’extreure’n una de vermella, una de blava i una de verda i totes sis tenen la mateixa probabilitat.
Tirem tres daus. Quina és la probabilitat d’obtenir algun 1 i algun parell ?
Considerem tres possibilitats: 1, parell = {2, 4, 6} i un altre resultat = {3, 5}.
Construïm un diagrama en arbre per seguir el procés: aconseguir algun
Fes-ho tu. Un dau té 3 cares vermelles, 2 de blanques i 1 de negra. Llancem tres daus amb aquestes característiques. Quina probabilitat hi ha d’obtenir alguna cara blanca i alguna de negra?
a) Dues jugadores, A i B, aposten uns diners que aconseguirà la que guanyi quatre partides d’un cert joc d’atzar. En un moment donat A va guanyant 2 - 1. Escriu tots els recorreguts que pot seguir la partida a partir d’aquell moment.
b) Suposem que es juguen 40 € (han apostat 20 € cada una) i que la partida s’interromp quan A va guanyant 2 - 1. Com s’hauran de repartir els 40 €?
a) Començarem amb el resultat 2 - 1 i continuarem mitjançant un diagrama en arbre. Considerem totes les ramificacions possibles. En verd, guanya A i en vermell, guanya B.
Copia en el teu quadern i completa el diagrama. No oblidis parar cada vegada que una obtingui 4 victòries.
b) En cada una de les bifurcacions la probabilitat que s’assigna a cada fletxa (cada opció) és 1 2
Si en una de les branques guanya A després de 3 ramificacions, com, per exemple,
llavors la probabilitat d’aquest final és 2 1 8 1 3 = cm .
Acaba sumant les probabilitats de tots els finals en què guanyi A i, anàlogament, B. Reparteix els 40 € proporcionalment a les probabilitats finals que venci A i que venci B.
Solució:
b) A s’hauria d’endur 27,50 € i B, 12,50 €.
2. Càlcul de probabilitats en reiterar una prova
Un jugador juvenil de bàsquet encerta el 70 % dels llançaments a cistella des de la línia de personal.
Si llança cinc vegades, calcula la probabilitat de:
a) Cinc encerts.
b) Cap encert.
c) Algun encert.
a) Encertar cinc vegades consecutives és:
⎯→ encert ⎯→ encert ⎯→ encert ⎯→ encert ⎯→ encert Quina serà la probabilitat d’aquesta experiència composta?
b) Si la probabilitat d’encert és 0,7, la d’errada és 0,3. Ara, calcula la probabilitat de:
⎯→ errada ⎯→ errada ⎯→ … (així cinc vegades)
c) Tingues en compte que algun encert (un o més) és el contrari de cap encert i que si la probabilitat d’un esdeveniment és p la del seu contrari és 1 – p.
Solució:
a) 0,75 = 0,16807; b) 0,35 = 0,00243; c) 1 – 0,35 = 0,99757
Càlcul sense fórmules
1 Quants partits de primera divisió es juguen en una temporada de la Lliga espanyola de futbol? (Són 20 equips que juguen tots contra tots dues vegades.)
2 Quants resultats possibles es poden obtenir en llançar un dau i dues monedes diferents? I si les dues monedes són iguals?
3 Un dodecàedre regular té 12 cares pentagonals. Quantes arestes té?
Les comptem així: 12 · 5 = 60 costats dels pentàgons. Cada dues cares s’ajunten en una aresta. Per tant, tindrà 2 60 = 30 arestes.
a) Esbrina quants vèrtexs té si en cada vèrtex es troben 3 cares.
Diagrama en arbre
7 Descriu en un diagrama en arbre els diferents resultats que es poden obtenir en llançar una moneda quatre vegades.
8 Utilitza un diagrama en arbre per saber quants nombres de tres xifres diferents poden formar-se amb els dígits 1, 2, 3, 4, 5 i 6 que siguin més grans que 300 i més petits que 500.
9 L’Eva i el Pere juguen un torneig d’escacs el vencedor del qual serà el primer que aconsegueixi guanyar tres partides (no es tenen en compte les partides que acaben en taules). De quantes formes possibles pot desenvolupar-se el torneig?
b) Quantes arestes i quants vèrtexs té un icosàedre regular si té 20 cares triangulars i en cada vèrtex es troben 5 cares?
10 L’Anna i la Berta juguen un torneig de tennis la vencedora del qual serà qui aconsegueixi dos sets seguits o tres d’alterns. Quins són els possibles desenvolupaments del torneig?

11 Traiem, l’una després de l’altra, tres boles d’aquesta capsa i les deixem fora en fila. Descriu tots els resultats possibles que podem obtenir.
12 Descriu mitjançant un diagrama en arbre totes les formes en què pots pagar 5 euros amb monedes de 2 €, 1 € i 0,50 €, si tens moltes monedes de 2 € i d’1 € però només quatre de 0,50 €
c) Fes el mateix amb els altres políedres regulars.
4 Al bar Coca són especialistes en combinats de sucs i en cafè. Tenen 5 tipus de sucs de fruites i 3 tipus de cafès. Quantes combinacions diferents es poden fer triant un suc i una tassa de cafè?
Si, a més, s’afegeix a cada combinació un bombó de xocolata blanc o negre, quantes se’n podran preparar?
5 Descriu totes les formes en què pots pagar un xiclet de 50 cèntims amb monedes de 20, 10 i 5 cèntims.
6 El dòmino és un joc de taula les fitxes rectangulars del qual estan formades per dos quadrats amb punts com els daus, des de 0-0, 0-1, 0-2... 0-6, 1-1, 1-2, … fins al 6-6. Quantes fitxes té un dòmino?
Quantes en tindria un dòmino gegant els valors del qual fossin des de 0-0 fins a 10-10?
13 Fa quatre minuts ha començat un partit de bàsquet i el nostre equip ha anotat cinc punts. Descriu en un diagrama en arbre totes les possibilitats que poden donar-se per assolir aquesta puntuació. Recorda que en bàsquet hi ha cistelles de tres punts, de dos punts i d’un punt.
14 Amb les lletres de la paraula tomàs volem escriure totes les paraules, tinguin o no tinguin sentit, en què les vocals i les consonants apareguin alternades. Utilitza un diagrama en arbre per veure quantes possibilitats hi ha.

15 Llancem un dau 4 vegades. Si importa l’ordre en què surten els nombres, quants resultats diferents poden donar-se?
16 Quantes possibles barreges de dos colors, en idèntiques quantitats, es poden fer amb 8 pots de pintura de diferents colors?
I quantes barreges de tres colors? I de quatre colors?
17 Si pintem de vermell tots els costats i totes les diagonals d’un pentàgon, quants segments haurem pintat?
18 A més de la locomotora, que va davant, un tren porta 5 vagons, 3 de segona classe i 2 de primera classe, que poden ordenar-se de qualsevol manera.
Un dia, la seva posició era així: 21122; un altre dia, així: 11222.
De quantes formes poden ordenar-se els vagons?
19 Cinc amigues, l’Ali, la Bea, la Carme, la Diana i l’Eva, juguen la fase final d’un campionat de pàdel en què cada una juga contra totes les altres. Es lliurarà una copa a la campiona i una medalla a la subcampiona.

a) De quantes formes poden adjudicar-se els trofeus?
b) Quantes possibles classificacions hi pot haver de les tres primeres?
Probabilitat
25 Llancem tres monedes. Calcula la probabilitat que:
a) Totes tres siguin cara.
b) S’obtinguin dues cares i una creu.
c) Hi hagi almenys una cara.
26 a) En una partida de dòmino, sobre la taula hi ha la fitxa 3-5. Quina probabilitat hi ha que una altra fitxa extreta a l’atzar pugui ajuntar-se amb aquesta?
b) I si fos la 5-5?
27 Extraiem tres boles amb reemplaçament d’aquesta urna. Calcula la probabilitat que:
a) Cada una sigui d’un color.
b) No n’hi hagi cap de blanca.
c) S’obtinguin dues boles blaves. Repeteix l’activitat suposant que l’extracció és sense reemplaçament.
28 Extraiem dues boles de l’urna següent:
a) Què és més probable, treure dues boles vermelles amb reemplaçament o sense?
b) Què és més probable, treure una bola vermella i una altra de blava amb reemplaçament o sense?
29 Es llancen dues monedes i un dau. Calcula les probabilitats següents:
a) Obtenir dues cares i un cinc.
b) Obtenir alguna creu i un sis.
c) Obtenir almenys una cara i un nombre parell.
30 Extraiem dues cartes d’una baralla de 40 cartes. Troba la probabilitat que:
20 L’Ona és la mitjana de cinc germans. Quines possibles distribucions hi pot haver en aquesta família si només la coneixem a ella? Per exemple, pot ser noi-noia-noia-noi-noi.
21 Llancem tres monedes: una de 2 €, una d’1 € i una de 0,20 €. De quantes formes diferents es poden obtenir una o dues cares?
22 A un grup de cinc amics els han regalat tres entrades per a un partit de futbol de màxima rivalitat. Quantes formes diferents tenen de repartir-se les entrades?
23 Les 28 fitxes d’un dòmino es reparteixen entre quatre jugadors. Quants jocs diferents podrà tenir cada jugador?
24 Calcula:
a) Siguin dos asos.
b) Siguin dues figures (sota, cavall i rei).
c) Siguin dues cartes d’oros.
31 Recorda les puntuacions de les 28 fitxes d’un dòmino. Anomenem S la suma dels punts de les dues meitats i D la diferència entre la puntuació més alta i la més baixa. Si extraiem una fitxa, calcula les probabilitats següents:
a) P [S = 2]
c) P [S ≠ 11]
e) P [D > 2]
b) P [S = 6]
d) P [S > 8]
f) P [obtenir algun 1]
32 En un llibre que té 4 capítols, el 5 % de les pàgines del primer capítol, el 4 % del segon i el 2 % del tercer tenen algun error. En el quart capítol no hi ha errors. Quina és la probabilitat que, en triar una pàgina a l’atzar, tingui algun error si tots els capítols tenen el mateix nombre de pàgines?
33 Quants nombres podem formar amb tres uns i dos vuits? Escriu-los i calcula la seva suma.
34 a) Forma tots els nombres de quatre xifres que es puguin fer amb els dígits 2 i 5. Quants són?
b) Quants nombres de cinc xifres es poden fer amb els dígits 0 i 2? Tingues en compte que, per exemple, el 02002 no és un nombre de cinc xifres.
35 En Ferran i la Júlia tenen dues baralles de cartes. Cada un extreu una carta de la seva baralla a l’atzar.
a) Quina probabilitat hi ha que sigui la mateixa carta?
b) Quina probabilitat hi ha que sigui el mateix nombre però de diferent coll?
c) Quina probabilitat hi ha que treguin el mateix coll?
36 S’extreu una carta d’una baralla i després es tira un dau. Si surt el 5 o el 6, es torna la carta a la baralla; si no, aquesta es retira. Es remena i es torna a extreure una carta. Quina és la probabilitat d’obtenir dos asos?
37 S’extreu una bola a l’atzar d’una urna que té 50 boles numerades així: 00, 01, …, 48, 49. Anomenem X la primera xifra del nombre extret i Y la segona. Calcula les probabilitats

següents:
a) X = 3 b) Y ≠ 5 c) X ≠ Y
d) X + Y = 9 e) X + Y ≠ 10
38 Sis amics, 3 nois i 3 noies, van al cinema. De quantes formes poden asseure’s per estar alternats?
I si es volen asseure junts els tres nois i al costat les tres noies?
39 Les probabilitats que un estudiant aprovi les tres assignatures més difícils, durant el primer any de carrera, són de 2/7, 4/9 i 1/3, respectivament.
a) Quina és la probabilitat de suspendre-les totes tres?
b) Quina és la probabilitat de suspendre només una de les tres assignatures?
c) Quina és la probabilitat d’aprovar-ne almenys una?
40 Observa com resolem aquesta equació:
Vx, 2 = 7x → x (x – 1) = 7x → x 2 – x = 7x →
→ x = 0 (no val), x = 8
Ara, resol tu aquestes altres:
a) VRx, 2 – Vx, 2 = 9
b) 2 · x 2 cm = VRx, 2 – 6
41 Una alumna ha estudiat 12 temes dels 30 que entren en un examen. Es trien 2 temes a l’atzar.
a) Quina és la probabilitat que n’hi toquin dos que no ha estudiat?
b) Quina és la probabilitat que, almenys un dels temes, sigui dels que ha estudiat?
42 Al departament d’ofertes d’uns grans magatzems es posen a la venda 100 samarretes de la marca A, 60 de la marca B i 40 de la marca C. La probabilitat que una samarreta tingui tara és de 0,01 per a la marca A, de 0,02 per a la marca B i de 0,03 per a la marca C. Triem una samarreta a l’atzar.
a) Calcula la probabilitat que tingui tara.
b) Calcula la probabilitat que sigui de la marca C i no tingui tara.
43 En una urna hi ha 4 boles blanques i 3 de negres. En una altra urna n’hi ha 3 de blanques i 5 de negres. Es treu una bola de la primera i s’introdueix en la segona. A continuació, es treu una bola de la segona. Quina és la probabilitat que aquesta segona bola sigui negra?
44 Observa aquesta quadrícula:
a) Quants camins de longitud mínima hi ha per anar de A a B?
b) Quants n’hi ha per anar de A a B, passant per C?
45 En Xavier té 10 fitxes. Jugarà, com a màxim, cinc vegades a la ruleta. En cada aposta guanya o perd 10 fitxes, i deixarà de jugar si es queda sense fitxes o si guanya 30 fitxes. Descriu en un diagrama en arbre tots els resultats possibles que poden anar-se donant.
46 Simplifica i calcula el valor de n:
47 Cert o fals?
a) Hi ha menys d’una possibilitat entre mil d’obtenir 10 cares en llançar una moneda 10 vegades.
b) Hi ha més nombres capicua de sis xifres que de cinc xifres.
c) En les VRm, n pot ser que m ≤ n o bé que m ≥ n.
d) Si Cx ,2 = 10, llavors x = –4.
e) Si P [B] = 1 – P [A], llavors A i B són esdeveniments contraris.
48 Una capsa conté quatre targetes marcades amb les lletres
A A A N. S’extreuen dues targetes a l’atzar i es col·loquen l’una al costat de l’altra.
a) Quants resultats podem obtenir?
b) Són equiprobables?
49 Si llances 5 monedes, què és més probable, treure 3 cares i 2 creus o 1 cara i 4 creus?
50 a) Extraiem tres cartes d’una baralla de 40 cartes. Quina probabilitat hi ha d’obtenir algun as i alguna figura?
b) Extraiem dues cartes d’una baralla de 40 cartes. Quina probabilitat hi ha d’obtenir alguna figura i algun oro? (figura d’oros val com a figura i com a oro.)
51 Extraiem una bola de la primera urna i la introduïm a la segona. Després, traiem una bola de la segona urna.
Quina probabilitat hi ha d’obtenir C en la segona extracció?
b) Calcula: P [1a B i 2a B]; P [1a C i 2a B]
c) Calcula: P [1a A i 2a A]; P [1a B i 2a A]; P [1a C i 2a A] i, en conseqüència, P [2a A].
52 Extraiem una bola de la primera urna i la introduïm a la segona urna. Després, traiem una bola de la segona.
1 L’Anton i la Berta estan jugant un torneig de ping-pong el guanyador del qual serà el primer que venci sis partides. La Berta va guanyant 4 a 2. Fes un diagrama en arbre que descrigui les possibles continuacions.
2 He de fer la maleta per a un viatge, i de les 6 samarretes que tinc, totes de colors diferents, vull triar-ne 4.
a) Quantes tries diferents puc fer?
b) Si vull emportar-me la blanca i la negra, quantes possibilitats em queden per a les altres dues?
3 a) Quants nombres de quatre xifres es poden formar amb els dígits 3 i 7? Calcula la seva suma.
b) Quants nombres de quatre xifres es poden formar amb els dígits 3, 3, 3, 7, 7?
4 De quantes formes podem triar els 3 representants del comitè d’esports, si es presenten 7 candidats?
5 Amb les lletres de la paraula clara, quantes ordenacions diferents poden fer-se que comencin amb la lletra A?
6 Calcula m en cada cas:
a) = () ! () ! m m 1 1 30
+ b) : mm 32 4 =
7 Tirem un dau. Si surt un 5 o un 6, extraiem una bola de l’urna A i si no, de la B. Calcula les probabilitats indicades:
a) Obtenir un 5 o un 6 i treure una bola vermella.
b) Obtenir un 4 i treure una bola verda.
8 La Loreto és saltadora de llargada, i en el 80 % dels seus salts aconsegueix superar els 6 m. Si en una competició ha de saltar quatre vegades, troba la probabilitat que:
a) En totes superi els 6 m.
b) No els superi en cap.
c) Els superi alguna de les quatre vegades.
9 Tenim tres sobres amb destinataris diferents i tres cartes personalitzades que els volem enviar. Si s’introdueix a l’atzar una carta a cada sobre, calcula la probabilitat:
a) Que totes tres arribin al destinatari correcte.
b) Que només una arribi al seu destinatari.
c) Que alguna arribi al seu destinatari.
1 Observa la representació gràfica d’aquestes dues distribucions bidimensionals: I
4 Hem de pagar una gorra de 6 € i disposem de 4 monedes de 2 €, 4 monedes d’1 € i 3 monedes de 0,50 €. De quantes formes podem fer el pagament? Completa un diagrama en arbre com el següent:
Assigna a cada una un d’aquests coeficients de correlació: 0,11; –0,11; 0,46; –0,46; 0,92; –0,92; 1; –1

2 Es vol estudiar la relació que existeix entre les variables següents:
x : la inversió, en milions d’euros per milió d’habitants, per combatre la pol·lució en una ciutat.
y : la quantitat de micrograms de corpuscles per metre cúbic en l’aire d’aquesta ciutat.
Aquests són els resultats a vuit grans ciutats:
x 25 85 130 40 110 63 50 140
y 135 32 18 79 24 40 55 22
a) Representa la distribució amb un núvol de punts.
b) Calcula els paràmetres següents: x y
x σy σxy
c) Troba la recta de regressió de Y sobre X.
d) En una altra ciutat s’invertiran 100 milions d’euros per cada milió d’habitants en mesures per acabar amb la pol·lució. Quin nivell de pol·lució es pot esperar que s’assoleixi? Com de fiable és aquesta estimació?
(impossible pagar amb monedes de 0,5 euros)
5 Per formar l’equip inicial, una entrenadora de bàsquet disposa de 9 jugadors.
a) De quantes maneres pot formar l’equip inicial?
b) I si n’hi ha tres que n’han de formar part indiscutiblement, quantes possibilitats queden?
6 En una carrera participen 8 corredores.
a) Si és una final, de quantes maneres es poden repartir les tres medalles?
b) I si és una prova classificatòria, de quantes maneres es poden seleccionar les tres corredores que passen a la ronda següent?
7 a) De quantes maneres es poden asseure 6 persones en un banc?
b) I al voltant d’una taula rodona?
8 Disposem d’un dau i de dues urnes amb boles:
Llancem el dau; si surt un 1, traiem una bola de B, i si surt una altra puntuació, la traiem de A.
Calcula:
P [ /1] P [1 i ]
P [ /1] P [1 i ]
9 Extraiem tres cartes d’una baralla espanyola, que té 40 cartes. Calcula aquestes probabilitats:
a) No obtenir cap figura (sota, cavall i rei).
b) Obtenir alguna figura.
3 El menú del dia d’un restaurant consta de 5 primers plats, 3 segons plats i 4 postres.
a) Quants menús diferents hi pot haver?
b) A quants menús augmenta l’oferta si, a més, es poden demanar dos primers plats diferents i postres o dos segons plats diferents sense postres?
c) Obtenir algun oro.
d) No obtenir ni figures ni espases.
10 Calcula el valor de m en cada una de les igualtats següents:
a) mm 12 + ccmm = 28 b) ! () ! m m 2 90 + =