Epidemiologia e Bioestatística – Fundamentos para a Leitura Crítica
2. Resposta baseada nas informações do Capítulo 17, Distribuição de Probabilidades k = 0
n = 12
p (k ) = p (k ) =
n! n−k πk (1− π) k !(n − k )!
12! 12 − 0 × 0,100 ×(1− 0,10) 0!(12 − 0)!
12 479.001.600 ×1×(0, 90) = 0, 9012 = 0, 28 ou 28% 479.001.600
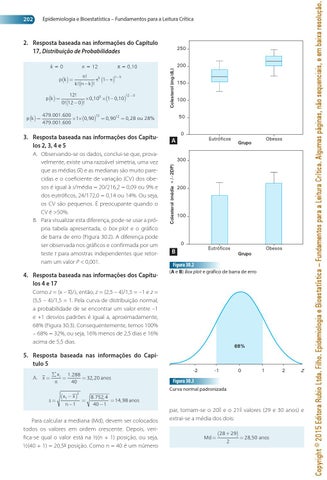
3. Resposta baseada nas informações dos Capítu los 2, 3, 4 e 5 A. Observando-se os dados, conclui-se que, provavelmente, existe uma razoável simetria, uma vez que as médias (x) e as medianas são muito parecidas e o coeficiente de variação (CV) dos obesos é igual à s/média = 20/216,2 = 0,09 ou 9% e dos eutróficos, 24/172,0 = 0,14 ou 14%. Ou seja, os CV são pequenos. É preocupante quando o CV é >50%. B. Para visualizar esta diferença, pode-se usar a própria tabela apresentada, o box plot e o gráfico de barra de erro (Figura 30.2). A diferença pode ser observada nos gráficos e confirmada por um teste t para amostras independentes que retornam um valor P < 0,001. 4. Resposta baseada nas informações dos Capítu los 4 e 17 Como z = (x – x)/s, então, z = (2,5 – 4)/1,5 = –1 e z = (5,5 – 4)/1,5 = 1. Pela curva de distribuição normal, a probabilidade de se encontrar um valor entre –1 e +1 desvios padrões é igual a, aproximadamente, 68% (Figura 30.3). Consequentemente, temos 100% – 68% = 32%, ou seja, 16% menos de 2,5 dias e 16% acima de 5,5 dias.
200 150 100 50 0
Eutróficos
A
Obesos
Grupo
300
Colesterol (média +/–2DP)
p (k ) =
π = 0,10
Colesterol (mg/dL)
250
200
100
0
Eutróficos
B
Obesos
Grupo
Figura 30.2 (A e B) Box plot e gráfico de barra de erro
68%
5. Resposta baseada nas informações do Capí tulo 5 A. x =
∑ x i 1.288 = = 32, 20 anos n 40
( x1 − x ) n −1
-2
-1
0
1
2
Z
Figura 30.3 Curva normal padronizada
2
s=
=
8.752, 4 = 14, 98 anos 40 − 1
Para calcular a mediana (Md), devem ser colocados todos os valores em ordem crescente. Depois, verifica-se qual o valor está na ½(n + 1) posição, ou seja, ½(40 + 1) = 20,5a posição. Como n = 40 é um número
30 - Epidemiologia e Bioestatistica.indd 202
par, tomam-se o 20o e o 21o valores (29 e 30 anos) e extrai-se a média dos dois: Md =
(28 + 29) 2
= 28,50 anos
C o p y r i g h t ©2 0 1 5E d i t o r aR u b i oL t d a . F i l h o . E p i d e mi o l o g i aeB i o e s t a t í s t i c a–F u n d a me n t o sp a r aaL e i t u r aC r í t i c a . Al g u ma sp á g i n a s , n ã os e q u e n c i a i s , ee mb a i x ar e s o l u ç ã o .
202
03/08/2015 11:51:03