MIJN WISKUNDE
PORTFOLIO VAARDIGHEDEN
TWEEDE JAAR
Hoe werkt dit portfolioschrift?
Basisgeletterdheid - BG
Van pagina 4 tot 17 vind je oefeningen die beantwoorden aan de doelen basisgeletterdheid (BG) van de eerste graad. In dit portfolioschriftje krijg je opdrachten rond:
• bewerkingen met getallen
• rekenen met procenten
• verhoudingen
• informatie halen uit tabellen en diagrammen
• maatgetallen en eenheden
• afronden en schatten
• omtrek en oppervlakte
Rekenvaardigheid
Van pagina 18 tot 47 vind je oefeningen waarbij vlot rekenen centraal staat. Deze volgen de onderwerpen in je boek Getallenleer.
Probleemoplossende vaardigheden
Van pagina 18 tot 47 vind je rechts onderaan een ludiek probleem dat je kan oplossen door gebruik te maken van een heuristiek. Maak op een kladblaadje aantekeningen. Herformuleer de vraag. Maak een schema, een tabel, een grafiek of een schets. Werk van achteren naar voor. Zoek naar regelmaat of gebruik een geziene formule, vergelijking of rekenregel. Zorg er steeds voor dat je kan uitleggen hoe je aan je resultaat komt.
Taalvaardigheid
Wiskundetaal en symbolen worden ingeoefend op pagina's 22, 23, 34 en 35.
Evalueer jezelf
Op de achterflap vind je een overzicht van de verschillende onderwerpen en vaardigheden. Evalueer jezelf. Dit doe je door jezelf minstens één en maximaal vijf sterren te geven. Ook je leerkracht kan je werk beoordelen. In de laatste kolom komt dan de eindbeoordeling door het correcte duimpje in te kleuren.
Auteurs
Björn Carreyn
Filip Geeurickx
Roger Van Nieuwenhuyze
Cartoons
Erwin Van Pottelberghe
ISBN
978 90 4865 1795
Bestelnummer
94 505 0299
KB D/2025/0147/117
NUR 126
Eerste editie
Verantwoordelijke uitgever die Keure
Niets uit deze uitgave mag verveelvoudigd en / of in het openbaar gemaakt worden door middel van druk, fotokopie, microfilm of op welke wijze dan ook zonder voorafgaande schriftelijke toestemming van de uitgever. No part of this book may be reproduced in any form by print, microfilm of any other means without written permission from the publisher.
MIJN WISKUNDE
PORTFOLIO VAARDIGHEDEN
TWEEDE JAAR
ook verkrijgbaar voor het tweede jaar
1
BG Bewerkingen met getallen
a Elke dag die Pierre naar zijn werk etst, ontvangt hij een etsvergoeding van 5 euro. Hoeveel dagen zal het duren voordat hij 100 euro bij elkaar heeft ge etst?
b Elke week krijgt Victor 7,50 euro zakgeld. Hoeveel euro is dit na 4 weken?
c Een bioscoopkaartje kost 11,25 euro. Als je met 5 personen naar deze bioscoop gaat, hoeveel kosten dan 5 kaartjes?
d Een zuinige elektrische wagen verbruikt 15 kWh per 100 km. Als de batterij van 60 kWh volledig opgeladen is, hoeveel km kan je dan a eggen met deze wagen?
Omdat de chau eur ook de airco aan heeft en regelmatig in de regen rijdt, daalt het bereik met 20%. Hoeveel km kan je dan a eggen met een volledig opgeladen batterij?
e Kartonnen verpakkingen.
Hoeveel appels zie je liggen in deze doos?
Hoeveel spuitbussen werden in deze doos verpakt?
Hoeveel glazen of tassen kunnen in deze doos verpakt worden?
f De prijs voor 1 kg kersen is 12 euro. Hoeveel betaal je voor 250 g kersen?
g Op een mooie zomerdag (buitentemperatuur 25 °C) stap je in een luchtballon. Per 100 m dat je stijgt, zakt de temperatuur met 1°C. Hoe hoog ben je als de temperatuur gezakt is tot 22 °C?
2
BG Rekenen met procenten
a Je huurt een at aan 850 euro per maand. Vanaf volgend jaar zal je 10% meer moeten betalen. Wat zal dan de maandelijkse huurprijs zijn?
b Je hebt bij je telefoonabonnement 50 GB dataverkeer per maand. Je hebt na 14 dagen al 20 GB verbruikt. Hoeveel procent van je maandelijkse tegoed heb je al verbruikt?
c Een digitale toets bestaat uit 20 vragen. Hiervan heb je er 80% correct opgelost. Hoeveel vragen heb je niet correct opgelost?
d 19% van de Belgische bevolking is jonger dan 18. Als België 11,8 miljoen inwoners telt, hoeveel zijn er dan jonger dan 18?
e Voor een jas van 80 euro moet je in korting 60 euro betalen. Hoeveel procent korting kreeg je?
f Als je etst in de regen, neemt je remweg toe met 60%. Je etst naar een kruispunt en remt af. Bij een droog wegdek sta je na 6,50 meter stil. Hoeveel meter wordt dit in de regen?
g Hoeveel calorieën je per dag nodig hebt, hangt af van je geslacht, je leeftijd en wat je allemaal doet. Een gemiddelde vrouw heeft per dag 2000 kcal (kilocalorieën) nodig. Hieronder zie je enkele tussendoortjes en de bijhorende kilocalorieën. Hoeveel procent van je dagelijkse caloriebehoefte krijg je als vrouw binnen als je zo'n tussendoortje eet?
dagelijkse caloriebehoefte
mandarijntjes
3 BG Verhoudingen
a Om een zomerfrisse cola mocktail te maken mix je caloriearme cola met sinaasappelsap volgens de verhouding 2 : 3.
Als je een esje cola hebt van 20 cl, hoeveel sinaasappelsap zal je dan toevoegen?
Als je 1,5 liter sinaasappelsap hebt, hoeveel cola zal je dan toevoegen?
b Je doet aan modelbouw en maakt een knappe kleinere versie van de London Bus. De gebruikte schaal is 1 : 24.
De lengte van je schaalmodel is 40 cm. Hoelang is de echte London Bus?
Als je de bus in London ziet rondrijden, zal je merken dat die echt wel hoog is, nl. 4,80 m. Hoe hoog is je schaalmodel?
c Je robot maait per uur 300 m 2. Als hij volledig is opgeladen, kan hij 3 uur lang werken. Welke oppervlakte kan je toestel maximaal aan met 1 volledige laadbeurt?
d We gaan heerlijke cinnamon rolls maken en bekijken het recept dat voorzien is voor 8 stuks. Wat hebben we per ingrediënt nodig voor 20 cinnamon rolls?
4
BG Informatie halen uit
tabellen en diagrammen
a In deze tabel vind je de campingprijzen van Panorama du Lac.
Hoeveel betaal je voor een weekend in het laagseizoen?
Hoeveel betaal je voor een week in het hoogseizoen?
In welk seizoen is er geen verschil tussen een lang weekend en een midweek?
b Tijd besteed aan verplaatsingen op een weekdag volgens leeftijd.
0u00m
12 t.e.m 17 jaar
18 t.e.m 24 jaar
25 t.e.m 39 jaar
40 t.e.m 54 jaar
55 t.e.m 64 jaar
65 t.e.m 75 jaar
76+ jaar 0u15m0u30m
0u45m1u00m1u15m1u30m tijd
Hoeveel minuten besteedt een jongere (van 12 tot en met 17) aan verplaatsingen op een weekdag?
Welke leeftijdsgroep besteedt op een weekdag het meeste tijd aan verplaatsingen?
c Medailletabel van de Olympische Spelen (Parijs 2024).
Welke landen behaalden de meeste olympische gouden medailles?
Hoeveel medailles behaalden de Britten?
Behaalden de Britten meer of minder medailles dan Nederland?
d Landen met veel inwoners halen veel medailles op de Olympische Spelen. Dat spreekt voor zich.
In deze lijst wordt het aantal inwoners per medaille berekend.
Hoeveel inwoners telt Grenada?
Hoeveel inwoners telt Dominica?
5
BG Afronden en schatten
a Onderweg naar Zuid-Frankrijk ga je ervan uit dat je met de wagen elk uur gemiddeld ongeveer 100 km a egt.
Je vertrekt om 10.00 uur en je voorziet een korte stop rond 13.00 uur voor de lunch. Hoeveel km heb je dan ongeveer afgelegd?
Je vertrekt om 10.00 uur en je voorziet om rond 20.00 uur niet meer verder te rijden en te overnachten in een hotel. Op hoeveel km van je thuis zal je een hotel zoeken?
De afstand van bij je thuis tot je locatie in Zuid-Frankrijk is 1300 km. Hoeveel uren zal je ongeveer in de wagen doorbrengen?
b Een bolletje deeg van 220 gram levert een gemiddelde pizza op. Als je 1 kg deeg hebt, hoeveel volledige pizza’s kan je dan maken?
c De schoolbibliotheek bevat 624 boeken. Per boekenkast kunnen ongeveer 80 boeken geplaatst worden. Hoeveel kasten zullen nodig zijn om alle boeken te plaatsen?
d Een getal wordt afgerond tot op de eenheid. Je bekomt 10. Welk van deze getallen is afgerond op de eenheid niet gelijk aan 10?
e Je betaalt in Japan een overnachting in een hotel. Die kost 170 000 yen. Hoeveel euro is dat afgerond als de wisselkoers 165 yen bedraagt voor 1 euro?
f Het gemiddelde van 12,24 en 18,79 ligt het dichtst tegen ...
g Het e-teken op een verpakking van 150 gram betekent dat de inhoud van de verpakking 4,5 % mag meer of minder zijn dan 150 gram. Welk gewicht voldoet niet aan deze regel?
h Het e-teken op een verpakking van 1,5 kg betekent dat de inhoud van de verpakking 1,5 % mag meer of minder zijn dan 1,5 kg.
Welk gewicht voldoet niet aan deze regel?
6
BG Maatgetallen en eenheden
a Een winkel is verplicht om de prijs per eenheid te vermelden. Zo zal je bij dranken steeds de prijs per liter kunnen terugvinden.
Noteer de prijs per liter voor elke verpakking.
b Hier zie je de weersvoorspelling voor volgende week.
Welke eenheid wordt gebruikt...
om de maximumtemperatuur weer te geven?
Het weer deze week
om de kans op neerslag weer te geven ( )?
om het aantal zonmomenten weer te geven ( )?
c Omcirkel telkens de eenheid die het best voldoet.
Een verhuisdoos heeft een inhoud van een halve ...
dm 3
m 3
De hoogte van de deur is iets meer dan 2 ... m dm
De afstand tussen twee steden is 150 ... m km
In een tasje ko e past 20 ... cl dl
Aardappelen koken? Dat duurt ongeveer 22 ... minuten
uren
De geiser Strokkur in IJsland spuit ongeveer elke 10 minuten water de lucht in tot op een hoogte van 30 ... m km
Een zeehond kan op een dag een afstand a eggen van 20 ... m
km
De oren van een olifant hebben samengeteld een oppervlakte van 4 ... dm 2
m 2
7
BG Omtrek en oppervlakte
a Rond deze visvijver wordt een schrikdraad bevestigd. Hoeveel meter draad is er minstens nodig?
b Je maakt 3 schilderijen die je achteraf ook laat inlijsten aan 15 euro per meter.
Bereken de omtrek van elk kunstwerk. Bereken nadien de prijs per inlijsting.
omtrek kostprijs inlijsting
c Een XL-tafelkleed (l = 4 m en b = 1,5 m) voor de tuintafel wordt aan de randen voorzien van een extra laagje stiksel. Hoeveel cm moet zo extra worden gestikt?
d Omtrek of oppervlakte? Wat werd hier in het oranje aangeduid?
Omtrek
Oppervlakte
Omtrek
Oppervlakte
e Bereken de oppervlakte van het werkblad van dit bureau.
Omtrek
Oppervlakte
Omtrek
Oppervlakte
f Een boer heeft een grote weide ter beschikking voor zijn koeien. Bereken de oppervlakte van deze weide als je weet dat de lengte 150 m is en de breedte 80 m.
Als je per koe 100 m 2 weiland moet voorzien, hoeveel koeien kan de boer dan plaatsen op deze weide?
8 Herhaling
Rekenen met gehele getallen
Bereken zonder gebruik te maken van ICT.
a 8 + ( –11) =
b –15 : 3 =
c ( –1)7 =
d –12 : ( –2) =
e –13 – 3 =
f 0 . ( –7) =
g –2 4 =
h –4 + ( –14) =
i –16 + 23 =
j –5 . 12 = k √196 = l 300 – ( –3) = m –114 : 3 = n ( –3)3 = o –39 + 39 = p ( –9) + ( –8) = q –34 + 16 = r –9 ( –2) =
Ook dit bereken je zonder ICT.
a –7 + ( –7) + 4 – ( –4) + ( –3) =
b 12 . ( –1) . 7 . ( –5) . ( –2) =
s 28 : ( –7) =
t 4 . ( –5) =
Reken uit volgens de volgorde der bewerkingen.
Het f lesjes-probleem
Haal een bak, gevuld met 24 kleine flesjes cola. Als de bak vol is, heb je zes rijen van vier flesjes cola. Of vier rijen van zes flesjes cola, het is maar hoe je het bekijkt.
In elk geval heeft je bak 24 flesjes met in elke horizontale en verticale rij een even aantal flesjes.
Haal uit de bak zes flesjes … maar zorg dat je in elke horizontale en verticale rij nog steeds een even aantal flesjes overhoudt.
9 Herhaling Rekenen met rationale getallen
Bereken zonder ICT. a 4 5 –2 7 =
Bereken zonder ICT.
Reken uit volgens de volgorde der bewerkingen.
Wie het hoedje past …
In een mand liggen drie zwarte hoeden en drie witte hoeden. De familie Vanpettemans (Adriaan, Beatrijs, Cornelia en Dorus) nemen geblinddoekt elk één hoed en zetten die op hun hoofd.
Als ze de blinddoek afdoen, staan ze in deze positie:
Papa (A) ziet de hoeden van mama (B) en zijn kinderen (C en D).
Mama (B) ziet de hoeden van haar kinderen (C en D).
De dochter (C) ziet de hoed van haar broertje (D).
De zoon (D) ziet geen enkele hoed.
Nu wordt de vraag gesteld wie van de vier familieleden met zekerheid kan zeggen welke kleur zijn/haar hoed heeft.
Pas na een lange stilte is er één iemand die zegt:
“Ik weet welke kleur mijn hoed heeft.”
Wie spreekt er? En … welke kleur heeft zijn/haar hoed?
10 Wiskundetaal
Symbolen
Noteer wat bedoeld wordt met het gegeven symbool.
Vul het correcte symbool in. Kies uit ∈, ∉, ⊂, ⊄ en = .
8
2, 3} del 18
Schaapjes tellen zonder in slaap te vallen
In een mooie stal zit in het midden een schaapherder die nauwlettend zijn lieve schaapjes in het oog houdt. In elke ruimte zitten vijf schapen, zoals hier in het schema voorgesteld. In de middelste ruimte zitten vier ramen, waar de herder door kan kijken. Via elk raampje ziet hij vijftien schapen (drie stallen van elk vijf schapen).
Nu komt er een nieuwe lading schapen toe. In totaal zijn er zestien nieuwe schapen, die ook in de stallen moeten worden geplaatst. Maar dat moet zo gebeuren dat de boer door elk raampje nog steeds vijftien schapen blijft zien. Hoe doet hij dit?
Het is toegestaan om de schapen van kooi te veranderen, maar er mag geen enkele stal leeg zijn. Het is niet toegestaan om de brave diertjes te slachten.
11
Herhaling Verzamelingen
Vul aan met de gepaste verzameling.
a N ∪ Z =
b Z+ ∩ Z=
c Z ∪ Q =
d Z ∩ Q =
e del 8 \ del 4 =
=
Noteer in de laatste kolom één voorbeeld van wat er in de gevraagde verzameling zit.
A is de verzameling van B is de verzameling van Gevraagd
a alle fruitsoorten aardbeien A ∩ B
b leerkrachten van mijn school wiskundeleerkrachten in Vlaanderen A \ B
c vierhoeken vierkanten A ∪ B
d namen van Belgische provincies namen van Belgische steden A ∩ B
e delers van 4 delers van 6 B \ A
In welk gebied zitten volgende getallen? Antwoord met A, B, C of D.
Herfstwandeling in het bos
In het nationale wandelpark van Mysterymathica beleeft elke bezoeker iets heel bijzonders. Dit park heeft vier ingangen die elk worden bewaakt door een boswachter. Op een dag besluit je om het park te bezoeken. “Om in het bos te komen, moet je 1,60 euro betalen”, zegt de boswachter die de eerste ingang bewaakt, “en als je het bos weer uit gaat, moet je opnieuw 1,60 euro betalen! Probeer gerust de andere drie ingangen, maar daar geldt dezelfde regel.” Dus je betaalt hem en je wandelt het bos binnen. Midden in het bos hoor je een mysterieuze stem die zegt: “Het geld dat je nu bij je hebt, wordt verdubbeld.” Nieuwsgierig voel je in je broekzak en het klopt, je hebt dubbel zoveel geld als daarnet.
Bij de tweede boswachter betaal je en wandel je buiten.
Nadien betaal je nogmaals om binnen te wandelen.
Opnieuw fluistert de stem en wordt je geld verdubbeld.
Je gaat het bos uit bij de derde wachter en ook nu wandel je terug naar binnen en wordt het geld in je broekzak verdubbeld. Bij de vierde wachter herhaalt alles zich nog eens. Je gaat terug naar buiten bij de eerste boswachter en je merkt dat er geen geld meer in je broekzak zit.
Hoeveel geld had je op zak toen je het bos binnenging?
12 Machten
Bereken zonder ICT.
Bereken zonder ICT.
Is
het resultaat positief ? Kleur dan het vakje in fluo.
Koekjesveelvraat
De papegaai Yago heeft vijftien trommels met koekjes voor zich staan.
In de trommels zitten achtereenvolgens 1, 2, 3 … 15 koekjes. Yago mag steeds een willekeurig aantal trommels uitkiezen en vervolgens uit elk van deze trommels evenveel koekjes opeten. In hoeveel rondes kan hij alle trommels snel leeg hebben? Verklaar.
13 Rekenregels machten
Werk uit door eerst een rekenregel van machten toe te passen.
Pas de rekenregels van machten toe. Je weet dat a ≠ 0. Verbind elke opgave met de oplossing.
Liegebeesten
In een klas zitten zestien leerlingen. Maar niet elke leerling is eerlijk! Sommige leerlingen zullen ALTIJD liegen, andere leerlingen zullen ALTIJD de waarheid spreken. Er komt een nieuwe leerkracht in de klas, die van deze rare situatie op de hoogte is. Daarom vraagt hij aan iedere leerling: “Hoeveel leugenaars zitten er in deze klas?”
De antwoorden lopen nogal uiteen.
Bizar!
Toch kan de leerkracht uit deze antwoorden afleiden wie de leugenaars zijn en wie de waarheid spreekt.
Ben jij ook een leugendetector?
14 Algebraïsche uitdrukkingen
optellen en aftrekken
Herleid volgende opgaven.
a 4y + 3y – 9y =
b 1 3 x + 1 2 x –1 9 x =
c 2x + 3x 2 + 2x – x 2 =
d 9x – 1 – 2 + 3x + 4x =
e 3x 2 – ( 3x 2 – x) + 1 =
Werk uit, herleid en rangschik naar dalende macht in x.
a ( 2x 2 – 4x + 2) + ( 3x 2 + 6x – 8) =
b –( 5x 3 + 3x 2 – 6x + 3) – ( 2x 2 + 6x –9) =
c ( 1 4 x 2 – 6x + 1 2 ) – ( 1 2 x 2 –5 2 x + 1 2) = d –( 0,25x + 2x 2 – 0,75) + ( 1,25 – 0,75x + x 2) =
Run with the fox
Een supersnelle vos uit Brugge was graag eens naar Luxemburg geweest. Dat is een afstand van 300 km!
De vos begint te lopen met een snelheid van 100 meter per minuut (dat is 6 km/h, maar het rekent gemakkelijker in meter per minuut).
Maar de vos heeft aan haar staart een belletje hangen dat elke minuut rinkelt, zonder aanwijsbare reden.
En wat nog vreemder is … als ze het belletje hoort, verdubbelt de vos haar snelheid.
De vos legt dus in de eerste minuut 100 m af, in de tweede 200 m, in de derde 400 m, in de vierde minuut 800 m …
Los een van de twee vragen op:
• Met welke snelheid komt ze uiteindelijk aan in Luxemburg?
• Na hoeveel minuten bereikt de vos Luxemburg?
15 Algebraïsche uitdrukkingen
vermenigvuldigen
Vermenigvuldig volgende eentermen.
a –1,5x . 6x 2 =
b 22a 3 . 5a 2 = c 5 14 x 2 . 7 10 x 4 =
d ( –1,25x 4) ( –8x 4) = e 3 4 a 3 . 5 3
Vermenigvuldig volgende algebraïsche uitdrukkingen. Herleid en rangschik naar dalende macht in x.
a ( 3x + 1) ( –3x 2) =
b ( –2x 2 + 3x – 4) . ( x + 2) =
Tijd voor een quiz
Je neemt deel aan een grote televisiequiz en je hebt gewonnen.
Proficiat!
In deze quiz heb je de mogelijkheid om een grote wereldreis te winnen. Maar … die prijs zit verscholen achter een van de drie deuren. Achter de andere twee deuren zitten twee lege vuilnisbakken.
De spelleider vraagt je om één deur te openen.
Stel dat je bv. kiest voor deur A.
Om de spanning erin te houden, doet de spelleider deur
A nog niet open! Hij maakt het een beetje spannender en doet een deur open waarvan hij weet dat er geen wereldreis achter zit. Dan stelt hij volgende vraag: “Wil je je keuze veranderen? Of blijf je bij je eerste idee om deur
A te openen?”
Wat doe je het best? Van idee veranderen … of toch je eerste idee volgen?
16 Wiskundetaal Symbolen
Noteer wat wordt bedoeld met het gegeven symbool.
AB
Hoe noem je deze ruimtefiguren?
Muizen in de kelder!
In de kelder staat een doos volledig gevuld met suikerklontjes.
De eerste avond besluiten enkele muisjes de bovenste laag suikerklontjes op te peuzelen. Ze hebben goed geteld: het waren er in totaal 88.
De tweede avond besluiten ze een volledige laag van de linkerzijkant op te peuzelen.
Ook nu hebben ze goed geteld.
Het waren er 77.
De derde avond besluiten ze om een volledige laag suikerklontjes van de voorzijde op te eten.
Hoeveel suikerklontjes eten ze die avond op?
17 Vergelijkingen oplossen
Los volgende vergelijkingen op.
a x –1 4 = 3 8
11 9 = 3 + x
b x + 0,45 = –0,25
0,5x + 0,75 = –1,75
c 1 4 x + 3 = 5
3x + 24 = –6
Omcirkel de vergelijking(en) waarbij de oplossing 2 is. Doe enkel een controle!
a –3 4 x + 2x –1 2 = 2
b 8x – 2 = 3x + 4
c ( 1 4 x + 1 2 ) . 4 = 8
Bananen à volonté
Samen met zes andere personen ben je op expeditie op een mooi eiland.
Tijdens de eerste dag verzamelen jullie met z’n zevenen een aantal bananen die de dag erna in gelijke groepjes verdeeld zullen worden.
’s Avonds gaat iedereen slapen. Maar ’s nachts wordt één expeditielid wakker. Omdat hij niet kan slapen, besluit hij de bananen in zeven gelijke groepen te verdelen. Maar hij komt er één tekort. Iets verder zit een aap in een boom. Hij heeft die banaan vast. Het expeditielid wil die ene banaan wegnemen, maar de aap slaat de man bewusteloos. Even later wordt een tweede persoon wakker. Ook hij wil de bananen verdelen. Omdat hij ziet dat één persoon is uitgeschakeld, besluit hij ze in zes gelijke groepen te verdelen. Wat blijkt? Ook hij heeft een banaan te kort en merkt op dat de aap met een banaan in de boom zit. Helaas wordt ook hij door de aap uitgeschakeld. Een derde persoon wordt wakker. Hij ziet de twee uitgeschakelde expeditieleden en besluit de bananen te verdelen in vijf gelijke groepen. Hij heeft er één te kort, ziet de aap met de banaan en jawel … Dit gebeurt met elk expeditielid. Ten slotte word jij wakker. Als laatste. Alle bananen zijn dus voor jou alleen! Laat die aap de ene banaan maar houden!
Hoeveel bananen heb je?
18 Vergelijkingen oplossen
Los volgende vergelijkingen op.
a –3 . ( 5 – 2x) = 2 . ( 4x + 3)
b –x + 5 6 = 4 3 –1 2 x
Omcirkel de vergelijking(en) waarbij de oplossing 10 is. Doe enkel een controle!
a 2x – 6 7 + x + 2 2 = 4
b 6 . ( x – 3) = 2 . ( 2x + 0,5)
c 1 5 x + 1 2 x = 7
Allemaal zessen
Vul tussen de cijfers telkens een +, –, · , : of √in zodat de gelijkheid klopt.
Ook toegelaten:
• het gebruik van haakjes;
• faculteit (symbool !).
Betekenis van faculteit:
0! = 1 1! = 1
0 0 0 = 6 1 1 1 = 6 2 2 2 = 6
3 3 3 = 6 4 4 4 = 6
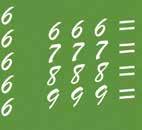
5 5 5 = 6
6 6 6 = 6
7 7 7 = 6
8 8 8 = 6
9 9 9 = 6
19 Merkwaardige producten Kwadraat
Werk uit.
a ( a + 1)
b ( m – 1)
c ( –a + 4)
d ( 2a – 1)
e ( 4 – x)
van een tweeterm
Werk uit.
a ( 2 3 x 4 –1 2 x)2 =
b ( 6x 3y + 2x y 2)2 =
c ( x 2m+ 3 – 3)2 =
d ( –xm + 2x)2 =
e ( x 2m – 4)2 =
Het
tennisprobleem
Drie meisjes (Ann-Sophie, Bandana en Charlotte) spelen graag en veel tennis.
De regels zijn de volgende.
Een van de drie is scheidsrechter.
De andere twee spelen een spelletje tennis tot er een set gewonnen is.
De winnaar wordt de nieuwe scheidsrechter.
Tot er weer een set gespeeld is, en ook hier de winnaar scheidsrechter wordt.
Na een tijdje speelde Ann-Sophie elf keer een setje tennis.
Bandana speelde zes keer een setje tennis.
Charlotte was vier keer scheidsrechter.
Wie won de vierde set?
20 Merkwaardige producten
Product van toegevoegde tweetermen
Werk uit.
a ( a – 2) . ( a + 2) =
b ( 4 – x) . ( 4 + x) =
c ( 1 2 + b) ( –1 2 + b) =
d ( y + 4) . ( y – 4) =
e ( –3 + m 3) . ( –3 – m 3) =
f ( x 4 + 1) ( 1 – x 4) =
g ( –7x + 3) ( 7x + 3) =
h ( –x 2 – 4) . ( –4 + x 2) =
i ( 3 5 + x 4) . ( x 4 –3 5 ) =
j ( 3x 3 – 2x) . ( –2x – 3x 3) =
k ( 6 – x 4) . ( – x 4 –6)=
l ( 1 2 x 2 – x) . ( 1 2 x 2 + x) =
m ( 0,3 – x 3) ( –0,3 – x 3) =
Werk uit.
a ( am – 1) . ( am + 1) =
b ( a 3b 2c + 4) ( –4 + a 3b 2c) =
c ( x 2m + 3 – 2) . ( x 2m + 3 + 2) =
d ( 9 5 x y 3 + 2 7 ) . ( 2 7 –9 5 x y 3) =
e ( 3x 9 – 5) ( 5 + 3x 9) =
In een klein stationnetje
Jij bent de machinist!
Kijk naar de opstelling en merk op dat er twee wagons zijn: wagon A en wagon B.
Nu moet jij ervoor zorgen dat de wagons netjes van plaats verwisseld worden en dat jij je locomotief op de startpositie plaatst.
Belangrijk detail: de twee wagons blijken echt hoog te zijn en kunnen niet onder de tunnel!
De locomotief kan dat wel. De locomotief kan zowel duwen als trekken en zijn motor is sterk genoeg om beide wagons aan te kunnen!
21 Merkwaardige producten Mix
Werk uit.
a ( a + 4)2 =
b ( a + 4) . ( a – 4) =
c ( 2x – 1) . ( –1 – 2x) =
d ( 1 2 a 2 –3 2 )2 =
e ( x 3 – 0,5)2 =
f ( a + 3) . ( a + 3) = g ( 3x 3 + 4x)2 =
j ( 2x – 4) . ( –4 + 2x) = k ( 3 4 x + 1 3 )2 = l ( – 7 – x) ( – 7 + x) = m ( 1 2 x 4 + 2x 2)2 =
Kleur het vak in als de inhoud van het vak gelijk is aan (4a – 2) · (4a + 2).
Kleur het vak in als de inhoud van het vak gelijk is aan (2 – x)
.
Ahmed, Boshaai en Charif eten dadels
Dit is een heel oud probleem.
Het is een Arabische puzzel die dateert van de start van de algebra, lang, heel lang geleden … Drie vrienden, laten we ze Ahmed, Boshaai en Charif noemen, eten een maaltijd in een herberg.
Als dessert is er een groot bord met dadels, maar nog voor ze één dadeltje opeten, vallen de drie vrienden in slaap.
Na een tijdje wordt Ahmed wakker.
Hij eet één derde van de dadels op en valt weer in slaap.
Even later wordt Boshaai wakker.
Hij eet één derde van de (nog overblijvende) dadels op en valt in slaap.
Niet veel later wordt ook Charif wakker.
Ook hij eet één derde van de resterende dadels op en valt in slaap.
’s Ochtends wordt Ahmed opnieuw als eerste wakker.
Hij ziet nog acht dadels liggen.
Hoeveel dadels lagen er oorspronkelijk op het grote bord?
22
Evenredigheden
Bepaal telkens de waarde van x bij volgende evenredigheden.
x 5 = 1 6
10x + 5 3 = 2
3x 16 = –5 4
3x – 1 6 = –2 5
5 2x = –15 4
16 –5 = 12 x
Tellen tot voorbij 1 googol
Bepaal
MIJN WISKUNDE
PORTFOLIO VAARDIGHEDEN
TWEEDE JAAR
Vaardigheid Mijn evaluatie
1BG Bewerkingen met getallen BG
2BG Rekenen met procenten BG
3BG Verhoudingen
4BG Informatie halen uit tabellen en diagrammen BG
5BG Afronden en schatten BG
6BG Maatgetallen en eenheden BG
7BG Omtrek en oppervlakte
8 Herhaling: rekenen met gehele getallen
9 Herhaling: rekenen met rationale getallen
10 Wiskundetaal: symbolen
11 Herhaling verzamelingen
12 Machten
Oordeel leerkracht
Gekend of niet?
- P
- P
- P
- P
- P
13 Rekenregels machten R - P
14 Algebraïsche uitdrukkingen optellen en aftrekken
15 Algebraïsche uitdrukkingen vermenigvuldigen
16 Wiskundetaal: symbolen
17 Vergelijkingen oplossen
18 Vergelijkingen oplossen
19 Merkwaardige producten: kwadraat van een tweeterm
- P
- P
- P
- P
- P
- P
20 Merkwaardige producten: product van toegevoegde tweetermen R - P
21 Merkwaardige producten: mix
22 Evenredigheden
Vaardigheden
- P
- P
BG = Basisgeletterdheid – R = Rekenvaardigheid – P = Probleemoplossende vaardigheid – T = Taalvaardigheid
Bestelnummer 94 505 0299
9 789048651795
Die Keure wil het milieu beschermen. Daarom kiezen wij bewust voor papier dat het keurmerk van de Forest Stewardship Council® (FSC®) draagt. Dit product is gemaakt van materiaal afkomstig uit goed beheerde, FSC®-gecertificeerde bossen en andere gecontroleerde bronnen.