D&A-FINALITEIT
03 Consolidatie

Inhoud (elk onderdeel behandelt de leerstof van module 01 t.e.m. 02)
blz. 02 Ken je de theorie
blz. 03 – 06Oefeningenreeks 1 peper
blz. 07 Problemen oplossen met heuristieken
blz. 08 – 13Oefeningenreeks 2 pepers
blz. 14 – 23Oefeningenreeks 3 pepers
blz. 24 Problemen oplossen met heuristieken
blz. 25 – 30Oefeningenreeks 4 pepers
blz. 31 – 32Oefeningenreeks 5 pepers
blz. 33 Problemen oplossen met heuristieken
blz. 34 - 37Wiskunde in de meteorologie
blz. 40 Overzicht oefenmateriaal

in deze consol i dat i emodule v i nd je theor i evragen en herhal i ngsvragen i n versch i llende pepercategor i eën over volgende modules:
–Module 1: Functies
–Module 2: Logaritmen
Consolidatie betekent:
• Hoe zet ik de leerstof - verspreid over vele gehelen - vast in mijn brein?
• Ik wil mijn kennis heropfrissen en beter vasthouden.
• Ik wil beter weten waar we wat gezien en geleerd hebben.
• Om dit alles nog te versterken, staan de oefeningen van alle modules kriskras door elkaar.

• Verdeel je tijd goed over de verschillende onderdelen.
• Kies wijs.
• Als je twijfelt over wat je best eerst aanpakt, vraag raad aan je leerkracht.
Net als in studentenhaver zitten in deze module naast lekkere gedroogde vruchten ook gezonde zachte en harde noten.

Ken je de theorie?
Vul aan.
a)Briggse logaritmen zijn logaritmen met grondtal .
b)De logaritme van een product is van de logaritmen.
c)De logaritme van een quotiënt is van de logaritmen.
d)Het getal van Euler (e) is tot op 2 decimalen nauwkeurig.
e)De logaritme log x geeft de orde van grootte van x aan in machten van __________________________ .
f) Om grote en uiteenlopende getallen voor te stellen, kunnen we een schaal gebruiken.
g)De grafiek van een functie f staat op een interval i als alle raaklijnen aan de grafiek op i onder de grafiek van f liggen.
h)Punten waar een grafiek van verandert noemen we buigpunten.
i)Een functie waarvan de grafiek symmetrisch is ten opzichte van de y-as noemen we een functie.
j)Een functie waarvan de grafiek symmetrisch is ten opzichte van de oorsprong noemen we een functie.
k)Een functie waarbij de functiekenmerken telkens herhaald worden, noemen we een functie.
Oefeningenreeks 1 peper
Stel de gegevens uit de rechtse grafiek voor op het logaritmisch papier.
a) x-as logaritmisch:
b) y-as logaritmisch:
3 4
Bereken zonder ICT. Vul aan.
a)log2 16 = want2 = 16
b)log3 27 = want3 = 27
c)log3 9 = want3 = 9
d)log10 100 = want10 = 100
e)log10 1000 = want10 = 1000
f)log100 100 = want100 = 100
INKIJKEXEMPLAARDIEKEURE
Gegeven: tabel met functiewaarden x 0123456
f ( x ) 1 -3 -7 -31 -3 -7
Gevraagd:
a)Wat is de periode van f ?
b)Welk van onderstaande grafieken past bij de gegeven functiewaardentabel?
Bereken met ICT tot op 3 decimalen nauwkeurig.
a)log10 70 = d)log2 20 =
b)log10 7 = e)log4 20 =
c)log10 0,7 = f)ln30 =
Annemie zet haar maandelijks aardgasverbruik uit in een staafdiagram. Ze meent hierin een patroon te herkennen en modelleert haar verbruik met een functie V( m) met V het verbruik in m3 en m de tijd in maanden sinds de start van haar metingen.
a)Wat is volgens jou de betekenis van m = 1?
INKIJKEXEMPLAARDIEKEURE
b)Van hoeveel jaar worden de gegevens getoond?
c)Wat is het maximaal gemeten verbruik?
d)Wat is het maximaal met V gemodelleerde verbruik?
e)Vul aan: dom V = ber V =
f) Wat is de periode van V?
g)Hoeveel maanden per jaar ligt het gemodelleerde verbruik boven 100 m3?
Het voorschrift van V ziet er als volgt uit:
(m)=
1 4 (1095 219m) als1 ⩽ m < 5 0 als5 ⩽ m ⩽ 10 1 3 (219m 2190) als10 < m ⩽ 13
h)Bepaal het verbruik voor:

Bepaal of onderstaande functies even, oneven of geen van beide zijn. Omkring.
EVEN / ONEVEN / GEEN VAN BEIDE EVEN / ONEVEN / GEEN VAN BEIDE b)
EVEN / ONEVEN / GEEN VAN BEIDE
EVEN / ONEVEN / GEEN VAN BEIDE

Problemen oplossen met heuristieken
Hieronder vind je twee problemen. Je moet zelf een oplossingsstrategie kiezen en nagaan welke wiskundekennis je kunt gebruiken om het probleem op te lossen.
• Raadpleeg je vademecum om een gepaste heuristiek te kiezen en denk soms out of the box.
• Schrijf jouw oplossing netjes uit zodat je die kunt presenteren voor andere leerlingen.
• Vergelijk jouw oplossing met die van een andere leerling.
• Werk samen en kom tot nieuwe inzichten bij het oplossen van problemen.
Probleem 1
Gegeven is een rechthoek en een cirkel die twee zijden van de rechthoek raakt en door het hoekpunt gaat. Eén van de raakpunten bevindt zich op een afstand 12 en 13 van de aangrenzende hoekpunten van de rechthoek.
Wat is de oppervlakte van de rechthoek?
Gekozen heuristiek:
A 13 12
Probleem 2
Janne en Lieze trainen op een ronde baan van 640 meter. Beiden lopen met een constante snelheid. Janne loopt met de klok mee en loopt een ronde in 3’45”. Lieze loopt tegen de klok in en loopt een ronde in 4’15”. Ze komen elkaar tegen ergens in de ronde. Hoeveel meter heeft Lieze dan al gelopen?
Gekozen heuristiek:
Oefeningenreeks 2 pepers
Onderstaande grafieken geven een voorstelling van het aantal besmettingen in Canada. Wat is het verschil tussen de gehanteerde logaritmische schaal in beide grafieken? Leg uit.
Influenza A (2009)
Bron: WHO + health-infobase.canada.co
COVID-19 (2020)
Een digitale kamerthermostaat kan je vaak programmeren. De vraagtemperatuur voor de ruimte werd als volgt ingesteld:

Vraagtemperatuur T (inC°)
t (inuur)
a)De gebruiker kopieert het eerste dagschema naar alle weekdagen. Vervolledig het schema voor de volgende 24 uur.
b)Op welke (vraag)temperatuur is de kamerthermostaat ingesteld? Hoe laat is het dan?
• Voor t = 25?
• Voor t = 40?
• Voor t = 46?
c)Wat is de periode van de temperatuurfunctie?
d)Wat is het bereik van de temperatuurfunctie?
e)Teken de grafiek van de temperatuur in de ruimte waar de thermostaat hangt.
De damplijn is de lijn die de dampdruk weergeeft ten opzichte van de temperatuur. Het geeft weer bij welke druk welke kooktemperatuur hoort. In onderstaande grafiek werd de damplijn van water logaritmisch weergegeven.
Druk (in bar)
INKIJKEXEMPLAARDIEKEURE
0102030405060 70 8090100 110 120130
Los op.
a)Bij welke druk is het kookpunt van water 60°?
b)Bij welke druk is het kookpunt van water 70°?
c)Bij welke druk is het kookpunt van water 80°?
d)Bij welke druk is het kookpunt van water 90°?
e)Bij welke druk is het kookpunt van water 100°?
f) Als de druk 0,4 bar is, wat is dan het kookpunt van water?
Vul de piramide aan zodat een blok telkens de som van de twee blokken eronder bevat. Gebruik hiervoor: log2 4096,log4 64,log2 128,log3 243,log7 49,log5 625
Vul aan.
a)log2 4 = log4 = log 9
b)log4 2 = log9 = log 4
Een enzymatische reactie in het spijsverteringsproces, zoals de afbraak van zetmeel door het enzym amylase dat zich bevindt in speeksel en in de dunne darm, wordt beschreven door de vergelijking:
v = 100 [S] 10 +[S] waarbij:
• v de reactiesnelheid is in μmol suiker per minuut
• [ S] de substraatconcentratie is in mmol per liter
v geeft de snelheid aan waarmee amylase zetmeel omzet in suiker in de mond of de dunne darm tijdens de spijsvertering.
Gebruik de grafiek van de reactiesnelheid v in functie van de substraatconcentratie [ S] om de volgende vragen te beantwoorden:
Substraatconcentratie [S] (inmmol/l) Reactiesnelheid v (inμmolsuiker/min)
INKIJKEXEMPLAARDIEKEURE
a)Bij welke waarde van [ S] is de reactiesnelheid v nul? Hoe kan je dit praktisch interpreteren? Maak eerst de tekentabel.
b)Voor welke waarden van [ S] stijgt de reactiesnelheid v? Teken eerst het verloop.
c) Beschrijf het verloop van de reactiesnelheid v als de substraatconcentratie [ S] toeneemt van 0 tot 50 mmol.
d)Wat is de maximale reactiesnelheid v?
Bij het KMI hanteert men normaalwaarden voor de maandelijkse zonneschijnduur. Deze waarden worden gebruikt om de metingen van een specifiek jaar te vergelijken met een vast referentiepunt.
INKIJKEXEMPLAARDIEKEURE
a)Wat is volgens de normaalwaarde het laagste aantal uren zonneschijn dat we in een maand mogen verwachten?
b)Wanneer doet dit zich voor?`
c)Wat is volgens de normaalwaarde het hoogste aantal uren zonneschijn dat we in een maand mogen verwachten?
d)Wanneer doet dit zich voor?
e)Wanneer is de daling van het aantal uren zonneschijn volgens de normaalwaarde het grootst?
f) Wanneer is de stijging van het aantal uren zonneschijn volgens de normaalwaarde het grootst?
g)Welk kenmerk vertoont de grafiek voor deze twee maanden?
h)Vul de samenvattende tabel voor het aantal uren zonneschijn aan.
tijd januarimaart juli oktoberdecember aantal uren zonneschijn
Gegeven: tabel met functiewaarden
x -1012,54567,5
f ( x ) 2 -22102 -2210
Gevraagd:
a)Wat is de periode van f?
b)Welk van onderstaande functies past bij de gegeven functiewaardentabel? Gebruik ICT om de grafieken te tekenen. Vink aan.
□ f(x)= 3sin Å 2π 5 xã + 4
□ f(x)= 6sin Å 2π 5 Åx 5 4 ãã
□ f(x)= 3sin Å 2π 5 Åx 5 4 ãã + 4
□ f(x)= 6sin Å 2π 5 Åx 5 4 ãã + 4
Los op met ICT: Van welk van de volgende functies f is het domein gelijk aan het bereik? Vink aan.
□ f(x)= x2
□ f(x)= »1 2x2
□ f(x)= 1 x2
□ f(x)= »x 4x2
□ f(x)= √x
INKIJKEXEMPLAARDIEKEURE
Bereken zonder ICT, gebruik makend van de rekenregels voor logaritmen.
a)log6 24 + log6 9 =
b)log3 12 log3 4 =
c)log2 24 log2 12 =
d)log5 25 + log5 5 =
e)log4 128 + log4 2 =
f)log25 + log4 =
Los onderstaande vragen op met behulp van ICT.
a)Wat is de limiet van f( x) = 2x + 3 als x nadert naar 5?
b)Bepaal de horizontale asymptoot van de functie f(x)= 3x + 2 x 1
INKIJKEXEMPLAARDIEKEURE
c)Wat gebeurt er met de waarde van f(x)= 1 x als x nadert naar 0?
d)Bepaal lim x → +∞
e)Bepaal de verticale asymptoten van de functie f(x)= 2x x2 4 .
Oefeningenreeks 3 pepers
Je maakt kip aan het spit in de oven. Zodra de kip een temperatuur bereikt van 80 °C haal je ze uit de oven en laat je ze afkoelen. Na een halfuur is ze nog 65 °C. In de kamer is het 23 °C.
a)Hoe warm is de kip na 50 minuten? Maak gebruik van de afkoelingswet van Newton:
k t = log Å θ S θ0 S ã

met k een constante, S de kamertemperatuur (in °C) en t de tijd (in uur) die nodig was om af te koelen van θ0 tot θ
b)Wanneer is de temperatuur van de kip 40 °C?
Een bosbrand verspreidt zich volgens de formule: A( t) = n0 ⋅ 1,13t
met A de brandende oppervlakte in hectare, n0 de initiële oppervlakte en t de tijd in uren. Dat komt neer op een groei van 13% per uur als het vuur ongecontroleerd woedt.
Hoelang duurt het voordat een brand van 10 hectare gegroeid is tot 1000 hectare?

INKIJKEXEMPLAARDIEKEURE
Wout krijgt € 1000 voor zijn communie en wil dit bedrag graag beleggen. Zijn bank stelt hem verschillende spaarplannen voor jongeren voor:
• 7% jaarlijkserente,jaarlijkssamengesteld: K1 (t)= 1000 ⋅ 1,07t
• 7% jaarlijkserente,continusamengesteld: K2 (t)= 1000 e0,07t
• 7% jaarlijkserente,elkkwartaalsamengesteld: K3 (t)= 1000 1,01754t
• 7,5% jaarlijkserente,elksemestersamengesteld: K(t)= 1000 1,03752t
a)Welk spaarplan zal het hoogste saldo opleveren voor Wout na 5 jaar?
b)Hoelang moet Wout in elk spaarplan sparen om het startbedrag te verdubbelen?
22
Een invasief woekerend onkruid groeit in oppervlakte volgens A( t) = n0 ⋅ 1,35t met A de oppervlakte in m2, n0 de initiële oppervlakte en t de tijd in jaar. Dat komt neer op een groei van 35% per jaar als het onkruid ongestoord kan verder groeien.
Hoelang duurt het voordat 5 m2 onkruid zich uitbreidt tot 50 m2?
Na het nemen van verschillende maatregelen om een duivenplaag te bestrijden, neemt het aantal duiven gestaag af volgens N( t) = n0 ⋅ 0,85t met N het aantal duiven, n0 het initiële aantal duiven en t de tijd in jaren. Dat komt neer op een afname van 15% per jaar.
Hoelang duurt het voordat de duivenpopulatie gehalveerd is?


24
Vink het juiste antwoord aan. Het domein van de functie f(x)= »√x 3 3 is …
□ [0, +∞[
□ [3, +∞[
□ [6, +∞[
□ [9, +∞[
□ [12, +∞[
Beschouw volgende drie uitspraken over de reële functie f(x)= … 1 x 1 . Vink de juiste uitspraken aan.
□ f is gedefinieerd voor alle x > 0.
□ f is gedefinieerd voor sommige negatieve waarden van x
□ f neemt alle positieve waarden aan.
VWO: eerste ronde, jaargang 1998, probleem 23

Let op het verschil tussen: “f is gedefinieerd voor ...” en “f neemt waarden aan ...”
Dauwpunt is de temperatuur waarop waterdamp in de lucht begint te condenseren. Als je bijvoorbeeld een bril draagt en je gaat van een koude naar een warme, vochtige omgeving, dan beslaat je bril. De temperatuur van de koude bril is lager dan het dauwpunt van de omringende lucht, waardoor waterdamp op je brilglazen condenseert.
Ook voor schilderwerken is het dauwpunt belangrijk. Condensatie tijdens het drogen kan leiden tot witte vlekken of glansverlies op de verf. De fabrikant van je verf adviseert een oppervlaktetemperatuur van ten minste 3 °C boven het dauwpunt.
Om het dauwpunt te berekenen, kan je de volgende formule gebruiken: Td = 237,7 γ (T, RLv ) 17,27 γ (T, RLv ) waarbij:
Td = dauwpunttemperatuur (°C)
RLv = relatieve luchtvochtigheid als een fractie (geen percentage)
T = temperatuur (°C)
γ (T, RLv ) = 17,27 T 237,7 + T + ln (RLv )
a)Je wil een kamer schilderen bij een temperatuur van 7 °C en een relatieve luchtvochtigheid van 75%. Mag dit volgens het advies?

b)Controleer je berekening met een dauwpuntcalculator, zoals bv. deze:
c)Bij welke relatieve vochtigheid bedraagt de dauwpunttemperatuur 15 °C als de omgevingstemperatuur 20 °C is?
Bekijk de info uit oefening 25 in verband met het dauwpunt.
Op een dag is de luchttemperatuur 25 °C en de luchtvochtigheid 50%.
Je schenkt jezelf een glas vruchtensap in. Het glas heeft een temperatuur van 8 °C. Zal er zichtbare condens op het glas ontstaan? Indien ja, onderzoek dan ook bij welke luchtvochtigheid het glas niet meer zal aanslaan.

INKIJKEXEMPLAARDIEKEURE
Een massa is verbonden met de muur via een veer die een natuurlijke lengte l0 van 20 cm heeft. De massa wordt 8 cm voorbij de natuurlijke lengte van de veer getrokken en losgelaten. Ze oscilleert (= heen en weer bewegen) 3 keer per seconde.
Afstandtotdemuur
a)Welke functie beschrijft de beweging van de massa?
b)Wat is de periode P van deze functie?
c)Wat is de kortste afstand van de massa tot de muur?
d)Maak een samenvattende tabel voor x ∈ [ 0, P] .
e)Hoeveel tijd tijdens elke cyclus is het object meer dan 27 cm van de muur verwijderd?
De dikte van een kabel bepaalt hoeveel elektrische stroom een draad veilig kan dragen zonder oververhit te raken. Daarom is een eenvoudige classificatie handig om de dikte te bepalen voor specifieke toepassingen.
In de Verenigde staten gebruikt men de American Wire Gauge (AWG). Het standaardiseert de dwarsdoorsnede van draden door ze een AWG-nummer toe te wijzen. Zoals je kunt zien op de figuur, heeft een draad met een lager AWG-nummer een grotere diameter en deze kan dus hogere stromen dragen. Er zijn in totaal 40 verschillende maten, met dwarsdoorsnedes van 0,013 mm2 tot 107,22 mm2.


In bovenstaande grafiek zetten we de diameter uit in functie van het AWG-nummer. Los de vragen op.
a)Bereken de dwarsdoorsnede van een draad met AWG-nummer 15. Schat eerst de diameter aan de hand van de grafiek.
b)Bereken voor elke draad uit de tabel hiernaast het geschikte AWG-nummer.
Stroombanen voor sturing, controle en signalisatie
Kookfornuis, oven, wasmachine, ... 3-fasig 4 mm2
Kookfornuis, oven, wasmachine, ... 1-fasig 6 mm2
Los onderstaande vragen op.
a)Wat weet je over lim x → 3 f(x) als f(3)= 1?
b)Wat weet je over f(x) alslim x → ∞ f(x)= 1 ?
c)Wat weet je over lim
d)Wat weet je over lim
Los op.
a)Teken de grafiek van f( x) = ln x met ICT.
b)Vul aan:
lim x → > 0 f(x)=
lim x → < 0 f(x)=
lim x → +∞ f(x)=
c)Bepaal de vergelijking van de asymptoten en geef de betekenis.
a)Teken de grafiek van f(x)= ex x met ICT.
b)Bepaal de limiet van f( x) als x nadert naar 0 van de positieve kant.
INKIJKEXEMPLAARDIEKEURE
c)Onderzoek het gedrag van f( x) voor zeer grote waarden van x en voor zeer kleine waarden van x.
d)Zijn er asymptoten? Zo ja, geef de vergelijking.

Problemen oplossen met heuristieken
Hieronder vind je twee problemen. Je moet zelf een oplossingsstrategie kiezen en nagaan welke wiskundekennis je kunt gebruiken om het probleem op te lossen.
• Raadpleeg je vademecum om een gepaste heuristiek te kiezen en denk soms out of the box.
• Schrijf jouw oplossing netjes uit zodat je die kunt presenteren voor andere leerlingen.
• Vergelijk jouw oplossing met die van een andere leerling.
• Werk samen en kom tot nieuwe inzichten bij het oplossen van problemen.
Probleem 3
INKIJKEXEMPLAARDIEKEURE
Een triatlon bestaat uit 5 km zwemmen, 40 km fietsen en 10 km lopen. Jutta wil de triatlon graag in 5 uur afwerken. Ze weet dat ze kan zwemmen aan een gemiddelde snelheid van 2,5 km/h en fietsen aan een gemiddelde snelheid van 25 km/h. Tussen het zwemmen, fietsen en lopen zit er telkens een overgang (kledij en schoenen wisselen) die ongeveer 3 minuten duurt.
Aan welke snelheid moet Jutta gemiddeld lopen om de triatlon in 5 uur te kunnen afwerken?
Gekozen heuristiek:
Probleem 4
Dit cirkeldiagram bestaat uit drie sectoren. De verhouding van de hoek die de rode cirkelsector maakt ten opzichte van het blauwe deel is 2:7, de verhouding van de hoek van de rode sector ten opzichte van de groene is 1:3. Zoek de grootte van de hoeken die elke cirkelsector maakt.
Gekozen heuristiek:
Oefeningenreeks 4 pepers
Hoe luid we een geluid ervaren hangt niet alleen af van de geluidssterkte, maar ook van de frequentie. Geluiden die we als even luid ervaren, worden aangetoond met isofonen. De eenheid voor deze maat van geluidssterkte is foon.
Geluidssterkte
gehoordrempel
Bekijk bovenstaande grafiek en los de vragen op.
a)Hoeveel decibel komt overeen met een geluid van 50 Hz en 20 foon?
b)Hoeveel decibel komt overeen met een geluid van 50 Hz en 10 foon?
Frequentie (in Hz)
c)Een geluid van 50 Hz bij 40 dB is net hoorbaar. Als we de frequentie laten toenemen tot 1000 Hz, wat gebeurt er dan met de gehoordrempel?
d)Wat is binnen het spraakgebied het effect van het verhogen van de frequentie van het geluid van 200 naar 2000 Hz bij 60 dB?
Het Gauge naaldensysteem, vaak gewoon ’de Gauge’ of G genoemd, is een internationaal gebruikte schaal om naalden te classificeren op grootte. Het werd overgenomen van bestaande maatstaven die in de industrie werden gebruikt om metalen draad te classificeren. Deze maat is eerder als een relatieve schaal. Als de maat met 1 Gauge toeneemt, dan neemt de grootte van de naald met 11% af.
De laagst en hoogst toegestane maten zijn vastgelegd in tabellen, samen met de metrische maten voor de binnendiameter, buitendiameter en wanddikte. Bij elke Gauge hoort een unieke kleur. Dat maakt het handig om de grootte direct te herkennen. Er zijn pogingen ondernomen om het naaldensysteem te vervangen door een logisch, modern systeem, maar tot nu toe hebben deze geen succes gehad.
gaugebuitendiameter
200,9081 ± 0,0064
220,7176 ± 0,0064
250,5144 ± 0,0064
260,4636 ± 0,0064
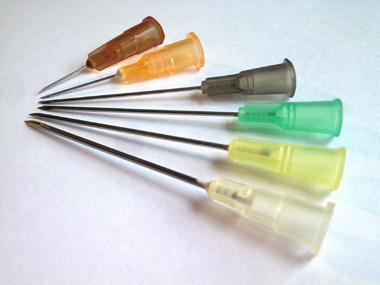
Als we een exponentiële regressie uitvoeren op de buitendiameter, dan krijgen we als model y = 9,73888e–0,11111x
a)Geef voor elk onderdeel van de formule de betekenis en indien mogelijk de eenheid: y : 9,73888: e−0,11111:
b)In de tekst is er sprake van 11% afname per Gauge. Komt dit overeen met de gegeven formule? Onderbouw je antwoord met een berekening.
c)Wat is de Gauge van de grootst en kleinst mogelijke naald? Controleer je berekening met de gegeven tabel bij het gegeven model.
I)Buitendiameter van 4,572 mm
II)Buitendiameter van 0,1842 mm
d)Wat is de groeifactor van het model als we werken met sprongen van 3 Gauge?
We vergelijken de kost van diepvriezers.
Een diepvriezer met energielabel C kost € 1200. Een diepvriezer met energielabel E kost € 550.
In onderstaande tabel vind je enkele gegevens terug over het verbruik:

a)Bereken de totale jaarlijkse kost van beide diepvriezers als we ervan uitgaan dat beide 12 jaar zullen meegaan. De kost omvat zowel de aankoop als het verbruik.
b)We kunnen het voorschrift van een functie opstellen die de totale jaarlijkse kost Kc in euro van de diepvriezer met label C weergeeft in functie van het aantal jaren n dat de diepvriezer meegaat: Kc (n)= 33 n + 1200 n
• Wat is het praktisch domein? ________________________________________________________________________
• Hoe interpreteer je de functiewaarden Kc( 1) , Kc( 10) , Kc( 0,5) en Kc( 0,25) ?
• Wat is het bereik van deze functie? __________________________________________________________________
• Maak een tabel met het waardenverloop en van de kromming van K en combineer ze tot een samenvattende tabel. Wat kan je besluiten uit het verloop?
35
• Wat is de vergelijking van de horizontale asymptoot? Hoe kan je dit interpreteren? Tip: uit welke 2 componenten bestaat de totale kost?
• Wat is de vergelijking van de verticale asymptoot? Hoe kan je dit interpreteren?
c)Stel zelf een voorschrift op van de functie die de totale jaarlijkse kost KE in euro van de diepvriezer met label E weergeeft in functie van het aantal jaren n dat de diepvriezer meegaat.
d)Na hoeveel jaar wordt de diepvriezer met label C goedkoper in verbruik? Los op met ICT.
e)Wat is volgens jou een bezwaar om dit model te gebruiken? De functie f is een tweedegraadsfunctie waarvoor geldt: als x ∈ [ -2,8] ⇔ f( x) ⩾ 0. Wat is het bereik van deze functie? Vink het juiste antwoord aan.
Bekijk onderstaande grafieken. In welke zone is de toename van het aantal nieuwe covidbesmettingen het grootst? Leg uit.
Datum
Een geheim agent heeft een kluis gevonden met een radioactieve stof erin. De kluis kan alleen geopend worden als de hoeveelheid van de radioactieve stof tot een bepaalde waarde is gedaald.
Formule voor radioactief verval: N( t) = N0 ⋅ e kt met:
N( t) de hoeveelheid materiaal op tijdstip t, N0 de initiële hoeveelheid materiaal, k de vervalconstante en t de tijd in uren.
De agent weet het volgende over de stof:
N0 = 100g
k = ln(2) 5

Hoelang moet hij wachten voordat de hoeveelheid radioactieve stof in de kluis is gedaald tot precies 12,5 gram?
Oefeningenreeks 5 pepers
Gegeven: Een functie f is even en periodiek met periode P = 2; bovendien geldt dat f( x) = x als x ∈ [ 0, 1] .
Gevraagd: Bepaal f(-3,14) met behulp van ICT. Vink aan.
□ 3,14
□ 0,86
□ 0,14
□ 0,14
□ 0,86
Vwo: eerste ronde, jaargang 1989, probleem 8
Gevraagd: x + y 38 39 logy x = 1 logx y
Gegeven:
• x, y > 1
• logy x logx y = 3 2
• x ⋅ y = 27

a) Schets zo nauwkeurig mogelijk één periode van de grafiek van een functie die voldoet aan alle onderstaande voorwaarden:
• Hetmaximumis √2enhetminimumis √2.
• Denulwaardenvan
• f(0)= 1
INKIJKEXEMPLAARDIEKEURE
b)Maak een samenvattende tabel over hetzelfde periode-interval.

Problemen oplossen met heuristieken
Hieronder vind je twee problemen. Je moet zelf een oplossingsstrategie kiezen en nagaan welke wiskundekennis je kunt gebruiken om het probleem op te lossen.
• Raadpleeg je vademecum om een gepaste heuristiek te kiezen en denk soms out of the box.
• Schrijf jouw oplossing netjes uit zodat je die kunt presenteren voor andere leerlingen.
• Vergelijk jouw oplossing met die van een andere leerling.
• Werk samen en kom tot nieuwe inzichten bij het oplossen van problemen.
Probleem 5
Onderstaande optelsom klopt niet. Kies twee verschillende cijfers en vervang op elke plek waar één van deze twee cijfers staat, het ene cijfer door het andere cijfer (en omgekeerd).
742586 + 829430 1212016
©JWO NL 2010, ronde 2
Gekozen heuristiek:
Probleem 6
Kakuro is als een kruiswoordraadsel, maar dan met cijfers in plaats van woorden. Je krijgt een leeg rooster met hokjes, net als een kruiswoordraadsel. In elk hokje moet je een cijfer invullen van 1 tot 9. Het doel is om de sommen aan de rand van het rooster te maken met de cijfers in de vakjes. Bijvoorbeeld: als er aan de bovenkant van een kolom een 6 staat, en die kolom bestaat uit drie vakjes, dan moeten de cijfers in die vakjes bij elkaar opgeteld 6 zijn. Een cijfer mag geen 2 keer voorkomen in een ‘som’. Vul onderstaande kakuro in.
Gekozen heuristiek:

Wiskunde in de meteorologie
Warmte voelt niet altijd en overal hetzelfde aan. Soms voelt 32 °C aangenaam aan, vaak ook niet.
Bij hoge temperaturen probeert ons lichaam af te koelen door middel van verdamping, wat leidt tot zweetproductie. Hoe hoger het dauwpunt, hoe moeilijker het wordt om effectief te zweten en warmte af te voeren, wat resulteert in een ongemakkelijk gevoel. Hieronder vind je de onderzoeksresultaten van Steve Horstmeyer, die de relatie tussen het dauwpunt en comfort weergeven.
DAUWPUNT
COMFORTBELEVING
meer dan 26 °C ernstig, kan zelfs dodelijk zijn voor bijvoorbeeld astmapatiënten
24 tot 26 °C erg ongemakkelijk gevoel
21 tot 24 °Czeer hoge vochtigheid, ongemakkelijk gevoel
18 tot 21 °C licht oncomfortabel gevoel
16 tot 18 °C normaal gevoel, maar men voelt wel dat de luchtvochtigheid wat hoger is
13 tot 16 °C normaal comfortabel gevoel
10 tot 13 °C zeer comfortabel gevoel
minder dan 10 °Cdroog gevoel bij sommige personen

1.De afbeeldingen hieronder tonen de gemeten luchtvochtigheid en temperatuur op 23 juni 2024 om 19u in enkele waarnemingsstations.


a)Kies 2 steden in België en vergelijk de comfortbeleving. Bereken eerst voor beide steden het dauwpunt aan de hand van onderstaande formule:
Td = 237,7 γ (T, RLv ) 17,27 γ (T, RLv )
waarbij:
Td = dauwpunttemperatuur(°C)
RLv = relatieveluchtvochtigheidalseenbreuk(geenpercentage)
T = temperatuur(°C)
γ (T, RLv ) = 17,27 T 237,7 + T + ln (RLv )
INKIJKEXEMPLAARDIEKEURE

b)Op 25 juli 2022 werd in Begijnendijk de hoogste temperatuur ooit gemeten in België. Dat was 41,8 °C. Qua comfortbeleving kreeg dit moment het label ‘licht oncomfortabel’. Wat was de minimale luchtvochtigheid?

2.Schrijf zelf een programma om het dauwpunt te berekenen waarbij je het resultaat koppelt aan een omschrijving van de comfortbeleving volgens Horstmeyer. Vertrek daarbij van onderstaande structuur:






3.Als we het dauwpunt bekijken in functie van de relatieve luchtvochtigheid, dan krijgen we de volgende grafiek:
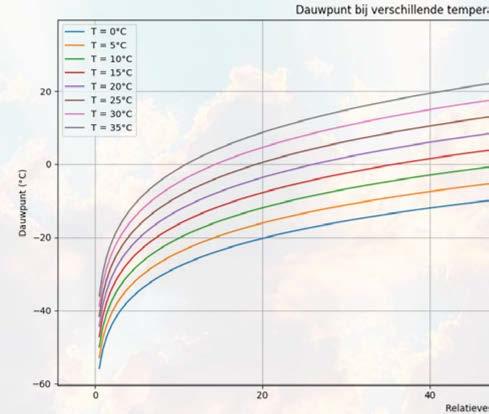
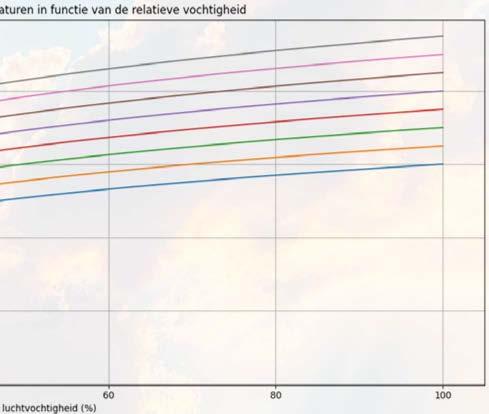
a)Wat is het praktisch domein voor deze functies?
INKIJKEXEMPLAARDIEKEURE
b)Wat is het bereik voor deze functies? Hoe kan je die praktisch interpreteren?

Het dauwpunt bij 30,0°C en 10,0% relatieve luchtvochtigheid is -4,9°C. Breng je in die omgeving een voorwerp van -5°C, dan zal er zich condens vormen op dat voorwerp. De waterdamp in de lucht, die condenseert op een oppervlak dat kouder is dan het dauwpunt, zal direct in de vorm van ijs overgaan.
c)Wat is de betekenis van de verticale asymptoot in 0?

De Pythoncode die gebruikt werd om de grafieken te tekenen kan via de QR-code terugvinden:
INKIJKEXEMPLAARDIEKEURE
d)Pas de code aan zodat je het dauwpunt te zien krijgt in functie van de temperatuur. Zorg ervoor dat je plot de grafieken bevat voor een relatieve luchtvochtigheid van 20%, 40%, 60% en 80%.


INKIJKEXEMPLAARDIEKEURE
INKIJKEXEMPLAARDIEKEURE
Overzicht oefenmateriaal
Auteurs Sarah Eeckhaudt, Kim Houben en Dries Vrijsen - Met medewerking van Björn Carreyn
Eerste druk 2024 - SO 2023/0793 - Bestelnummer 94 606 0140 (module 03 van 06)
ISBN 978 90 4864 798 9 - KB D/2024/0147/100 - NUR 128/129 - Thema YPMF
Illustrator Jona Jamart - Design en lay-out die Keure
Verantwoordelijke uitgever die Keure, Kleine Pathoekeweg 3, 8000 Brugge
RPR 0405 108 325 - © Copyright die Keure, Brugge
