D-FINALITEIT 5 UUR – DISCRETE WISKUNDE EN LOGICA
08 Grafen

wat je al kunt
–Je kan problemen oplossen met boomdiagrammen.
wat je leert in deze module
–een graaf gebruiken als model of schematische voorstelling
–in een concrete situatie die door een graaf beschreven wordt de betekenis van de knopen, de bogen en de buren van de knopen uitleggen
–een graaf die bij een concrete situatie behoort, opstellen
–het bestaan van specifieke wandelingen opsporen die alle bogen juist één keer doorlopen
–het algoritme van Kruskal of Prim toepassen om de minimaal opspannende boom in een gewogen graaf te bepalen
–het algoritme van Dijkstra toepassen om het kortste pad in een gewogen graaf te bepalen
–het handelsreizigersprobleem linken met grafen
–de betekenis van graafkleuring begrijpen en dit toepassen in concrete situaties
Inhoud
Instap
1Grafen rondom ons
2Wandelingen in een graaf
3Minimaal opspannende bomen
4Kortste paden
5Het handelsreizigersprobleem
6Graafkleuring
Signaaloefeningen
Differentiatietraject
Studiewijzer

in de kijker
Je kan met behulp van een schematische voorstelling ( graaf) en een algoritme praktische problemen uit de dagelijkse praktijk oplossen.
wiskundetaal
–graaf
–knoop van een graaf
–boog van een graaf –samenhangende graaf –orde van een graaf –grootte van een graaf –nabuurschap van een knoop
–graad van een knoop –planaire graaf
–gewogen graaf –reguliere graaf –volledige graaf –multigraaf –wandeling – pad –cykel –spoor –circuit –eulertoer –eulergraaf –hamiltoncykel –hamiltongraaf –boom –algoritme van Prim –algoritme van Kruskal –algoritme van Dijkstra –handelsreizigersprobleem –graafkleuring
Opdracht 1
Luka en Julie plannen een bezoekje aan een dierenpark. Vooraf hebben ze een plan van het dierenpark gedownload. Ze willen het volledige park bezoeken, maar wel zodanig dat ze elke weg slechts eenmaal doorlopen. Help hen een mogelijke route uit te stippelen.

INKIJKEXEMPLAARDIEKEURE
Opdracht 2
Vijf plaatsen ( A, B, C, D en E) moeten via een kabelnetwerk met elkaar verbonden worden. De kosten om twee plaatsen met elkaar te verbinden kunnen we schematisch weergeven als volgt:
a)Hoeveel bedraagt de kost om plaats A met plaats B te verbinden?
b)Wat is de goedkoopste manier om plaats B met E te verbinden?
Hiernaast vind je een mogelijke oplossing om alle plaatsen met elkaar te verbinden.
c)Wat is de totale kostprijs van deze oplossing?
Ga op zoek naar de goedkoopste oplossing.
Een mogelijke oplossing is:
1 Grafen rondom ons
1.1 Wat zijn grafen?
In het dagelijkse leven worden we met grafen geconfronteerd:
-Boomdiagrammen die je kent van bij telproblemen zijn een eenvoudig voorbeeld, maar ook stambomen of speelschema’s bij toernooien.
-Bij de uitwerking van dienstregelingen van het openbaar vervoer of het aanleggen van een nieuwe buslijn of de verbindingen tussen terminals in een luchthaven vind je grafen terug.
-Ook in de logistiek maakt men gebruik van grafen. Je kunt een app (bv. Ibi) downloaden die voor jou de snelste route bepaalt tussen een aantal ingevoerde adressen, of een app die jou een fietsroute voorstelt langs verschillende knooppunten.
Al deze voorbeelden zijn gebaseerd op de grafentheorie en de daarop voortbouwende wiskundige modellen.
STAMBOOM
INKIJKEXEMPLAARDIEKEURE
ROUTES BIJ NAVIGATIE











KNOOPPUNTEN BIJ FIETSROUTES
METROLIJNEN


















































SPEELSCHEMA'S






























































1.2Definities
In een dorpje in Oostenrijk zijn zes berghutten met elkaar verbonden door enkele pittoreske wandelpaden.
Schematisch kunnen we dit op een plan als volgt weergeven:

Zo'n schematische voorstelling door middel van punten (de berghutten) en lijnen (de wandelpaden) noemen we een graaf. Een graaf bestaat uit knopen (punten) die door middel van bogen (lijnen) met elkaar verbonden zijn. Elke boog van een graaf verbindt twee knopen. We noemen die knopen dan de de eindpunten van de boog.
definitie Een graaf G bestaat uit een eindige verzameling van knopen en een eindige verzameling van bogen.
• de knopen in deze graaf: A, B, C, D, E en F (de berghutten)
• de bogen in deze graaf: AB, AC, AD, BC, BE, CE, CF, DF, EF(de wandelpaden)

Merk op
Een graaf is een schematische voorstelling, geen weergave van de werkelijkheid op schaal. De vorm van de knopen en bogen doet er niet toe. Zo kan men de graaf uit het voorbeeld ook weergeven zoals hiernaast.
definitie De orde van de graaf is het aantal knopen in de graaf. De grootte van de graaf is het aantal bogen van de graaf.
In deze graaf G is de orde gelijk aan 6. We noteren n = 6.
In deze graaf G is de grootte gelijk aan 9. We noteren m = 9.
definitie Een knoop is een buur van een andere knoop als ze verbonden zijn door een boog.
INKIJKEXEMPLAARDIEKEURE
De graad van een knoop X, deg( X) , is het aantal bogen aan X in G.
De hoogste graad die in G voorkomt, noteren we als Δ( G) .
De laagste graad die in G voorkomt, noteren we als δ( G)
Voor deze graaf geldt:
Δ( G) = 4
δ( G) = 2
1.3Soorten grafen
definitie Een planaire graaf is een graaf die in het platte vlak kan getekend worden zonder dat de bogen elkaar snijden.
Voorbeeld
De graaf die hoort bij het voorbeeld van de berghutten is een planaire graaf.
Tegenvoorbeeld
In de graaf hieronder snijden de bogen AC en BD elkaar. Dit is geen planaire graaf.
definitie Een gewogen graaf is een graaf waarbij aan elke boog een ‘gewicht’ werd toegekend.
Afhankelijk van de context kan je bij de boog bijvoorbeeld
• de afstand (in km) tussen twee knopen noteren.
• de reistijd (in min) noteren.
• de kostprijs (in euro) om het wandelpad aan te leggen noteren.
Londen
INKIJKEXEMPLAARDIEKEURE

definitie Een multigraaf is een graaf waarbij twee knopen door meer dan één boog met elkaar verbonden zijn.
definitie Een graaf waarin alle knopen dezelfde graad hebben, is een reguliere graaf
Voorbeeld
In elke knoop is de graad 3.
We stellen vast dat bv. gr( A) = 2 en gr( E) = 4.
definitie Een graaf heet volledig als elke knoop in de graaf verbonden is met alle andere knopen in de graaf.
Voorbeeld
INKIJKEXEMPLAARDIEKEURE
De knopen A en C zijn niet met elkaar verbonden.

1.4 Grafen opstellen
Grafen kunnen helpen om problemen op te lossen. Het opstellen van de graaf die hoort bij het probleem is dus belangrijk.
Voorbeeld
Bij 5 leerlingen van het vierde jaar wordt er gekeken of ze elkaar (terug-)volgen op Instagram.
Jasleen en Zion volgen elkaar.
Jasleen en Carina volgen elkaar.
Lune en Marley volgen elkaar. Marley en Zion volgen elkaar.
Lune en Jasleen volgen elkaar.
INKIJKEXEMPLAARDIEKEURE
Op basis van deze informatie kan je nu een graaf tekenen waarbij de knopen de namen van de leerlingen zijn en waarbij de bogen aangeven of er wederzijds gevolgd wordt.
Merk op
Heel wat principes van sociale media hebben dus te maken met grafen en netwerken.
Verwerkingsopdrachten
Gegeven is de graaf G
a) Geef de knopen en bogen d.m.v. opsomming.
b) Bepaal de orde en grootte van deze graaf.
c) Bepaal de graad van elke knoop.
d) Bepaal ∆G en δG.
e) Is dit een planaire graaf?JA / NEE
Indien ja, herteken de planaire graaf zodat dit duidelijk is.
Teken de graaf G waarvoor geldt:
• knopen: P, Q, R, S, T
• bogen: PQ, PS, QS, QR, RS, RT
a) Bepaal de orde en grootte van deze graaf.
b) Bepaal de graad van elke knoop.
INKIJKEXEMPLAARDIEKEURE
c) Bepaal ∆( G) en δ( G)
Teken de planaire graaf G waarvoor geldt:
• buren van K: L, P
• buren van L: K, M, N, P
• buren van M: L, N
• buren van N: L, M, O, P
• buren van O: N, P
• buren van P: K, L, N, O
Een graaf bestaat uit 8 knopen en 17 bogen zodat elke knoop graad 4 of 5 heeft.
Hoeveel knopen hebben graad 5?
Vijf jongens ( Adrian, Bram, Cedric, Daan en Evert) zijn op sociale media onderling met elkaar via zes linken verbonden.
• Adrian is slechts met twee vrienden verbonden.
• Bram is op Daan na, met iedereen verbonden.
• Cedric heeft met iedereen een link, behalve met Evert.
a)Stel deze sociale medialinken grafisch voor d.m.v. een graaf.
b)Met wie is Daan allemaal verbonden?
Gegeven zijn grafen G1, G2 en G3.
a)Welke grafen zijn gelijk?
b)Verklaar jouw antwoord.
2 Wandelingen in een graaf
2.1 Wandelingen en paden
definitie Een wandeling tussen twee knopen X en Y van een graaf is een opeenvolging van bogen die beginnen in X en eindigen in Y.
Op een gegeven graaf G duiden we 4 verschillende wandelingen aan.
Wandeling 1: een wandeling van A naar C
W1 = ( AB – BD – DC)
INKIJKEXEMPLAARDIEKEURE
Wandeling 2: een wandeling van A naar A
W2 = ( AB – BD – DC – CB – BE – EA)
Wandeling 3: een wandeling van A naar D
W3 = ( AE – EB – BD)
Wandeling 4: een wandeling van A naar A
W4 = ( AB – BC – CD – DE – EA)
Wanneer de wandeling begint en eindigt in dezelfde knoop, spreken we van een gesloten wandeling , in het andere geval wordt de wandeling een open wandeling genoemd.
➔ W1 en W3 zijn open wandelingen.
➔ W2 en W4 zijn gesloten wandelingen.
Een graaf is samenhangend als er tussen elke twee knopen van een graaf een wandeling bestaat. De gegeven graaf G is samenhangend. Hiernaast vind je een voorbeeld van een graaf die niet samenhangend of onsamenhangend is.
Een pad tussen twee knopen X en Y is een wandeling waarbij elke knoop hoogstens één keer voorkomt (behalve eventueel begin- en eindpunt).
➔ W1, W3 en W4 zijn drie paden.
Een gesloten pad wordt een cykel genoemd.
➔ W4 is een cykel.
definitie Een gesloten wandeling in een graaf G begint en eindigt in dezelfde knoop.
Een pad in een graaf G is een wandeling waarbij elke knoop hoogstens één keer voorkomt.
Een cykel in een graaf G is een gesloten pad.
definitie
Een spoor tussen twee knopen X en Y is een wandeling waarbij elke boog hoogstens één keer voorkomt.
➔ W1, W2, W3 en W4 zijn vier sporen.
Een gesloten spoor wordt een circuit genoemd.
➔ W2 en W4 zijn circuits.
Een spoor in een graaf G is een wandeling waarbij elke boog hoogstens één keer voorkomt.
Een circuit in een graaf G is een gesloten spoor.

INKIJKEXEMPLAARDIEKEURE
Merk op
Op jouw smartphone of tablet zijn er heel wat apps die je kunt installeren die achterliggend gebruik maken van deze begrippen en principes.
Vaak is het doel om alle punten (knopen) te verbinden met elkaar in één vloeiende beweging zonder dat je twee keer gebruik maakt van dezelfde boog.

2.2De zeven bruggen van Königsberg
De stad Koningsbergen ( het huidige Kaliningrad) ligt aan de oevers van en op twee eilanden in de rivier de Pregel. De oevers en de eilanden waren in Eulers tijd verbonden door zeven bruggen. De Koningsbergers waren gewend ’s zondags een lange wandeling door de stad te maken. Euler vroeg zich af of hij een wandeling zou kunnen ontwerpen, waarbij elk van de bruggen juist eenmaal gepasseerd zou worden.
Pregel rivier
Schematisch kunnen we dit weergeven via volgende graaf waarbij de bogen de bruggen voorstellen.
We stellen ons nu de vraag : “Is het mogelijk een spoor te vinden die elke boog bevat?”
Als een wandeling een knoop passeert en je wil verder met je wandeling via een andere boog, dan heeft deze knoop altijd een even graad. Het antwoord is dus neen omdat er vier knopen zijn met een oneven graad.
De wandeling zou wel mogelijk geweest zijn mochten er slechts twee knopen van oneven graad zijn. Als de brug tussen de twee eilanden verwijderd wordt, kan de wandeling starten in punt A en eindigen in punt D ( of omgekeerd)
De graaf hieronder geeft deze situatie weer.
INKIJKEXEMPLAARDIEKEURE
2.3Eulertoeren
Een eulerwandeling in een graaf G is een spoor dat elke boog van G bevat.
Een eulertoer in een graaf G is een circuit dat elke boog van G bevat. Een graaf die een eulertoer bevat noemen we een eulergraaf .
W = ( AB – BC – CD – DB – BA – AD – DE – EA) is een eulertoer.
definitie Een eulertoer in een graaf G is een circuit dat elke boog van G bevat.
Men kan aantonen dat een graaf een eulertoer bevat als en slechts als de graad van elke knoop even is.
2.4 Hamiltoncykels
Een hamiltoncykel in een graaf G is een cykel dat elke knoop van G bevat.
Een graaf die een hamiltoncykel bevat noemen we een hamiltongraaf
INKIJKEXEMPLAARDIEKEURE
W = ( AB – BC – CD – DE – EA) is een hamiltoncykel.
definitie Een hamiltoncykel in een graaf G is een cykel die elke knoop van G bevat.
Verwerkingsopdrachten
Welke van volgende wandelingen zijn paden, welke zijn sporen, welke zijn cykels en welke zijn circuits?
a) W1 = ( AB – BD – DC – CE) :
b) W2 = ( AB – BD – DA – AG – GF) :
c) W3 =( AB – BC – CD – DG – GA) :
d) W4 = ( AB – BC – CD – DB – BC – CE) :
e) W5 = ( AG – GF – FE – ED – DA) :
f) W6 = ( AB – BD – DC – CE – ED – DC – CB – BA) :
Zoek een eulertoer in de volgende graaf.
INKIJKEXEMPLAARDIEKEURE
3 Minimaal opspannende bomen
3.1 Probleemstelling
Men wil zes plaatsen met elkaar verbinden via een netwerk. Dat kunnen rioleringswerken, telecomkabels of andere nutsvoorzieningen zijn.
De mogelijke verbindingen tussen de verschillende plaatsen kan men voorstellen met behulp van een graaf waarbij men naast elke boog de kosten van de verbinding plaatst.
Zo’n graaf noemen we een gewogen graaf . De getallen naast de bogen noemen we de gewichten van de bogen.

definitie Een boom is een graaf die alle knopen met elkaar verbindt en geen cykels bevat.
Hieronder vind je een boom die een mogelijke oplossing geeft om de zes plaatsen met elkaar te verbinden.
Met deze boom kan je berekenen wat de kostprijs is als je de verbindingswerken op die manier vastlegt: 14 + 8 + 11 + 9 + 6 = 48
Deze oplossing is niet de (economisch) beste oplossing.
Om het probleem op te lossen, moeten we dus op zoek gaan naar de boom met het kleinste totale gewicht. Zo’n boom noemen we een minimaal opspannende boom
Er bestaan algoritmes om die minimaal opspannende boom te bepalen. We bestuderen er twee: het algoritme van Prim en het algoritme van Kruskal.
methode
3.2Het algoritme van Prim
Hoe pas je het algoritme van Prim toe?
STAP 1: Kies een willekeurige knoop. Kies bijvoorbeeld A. Neem vanuit A de boog met het kleinste gewicht, de kleinste getalwaarde. Dat is de boog AF.
STAP 2:Neem vanuit de knopen A en F de boog met het kleinste gewicht. Dat is de boog FD.
STAP 3: Neem vanuit knoop A, F en D de boog met het kleinste gewicht verschillend van de reeds aanwezige bogen en zodanig dat de boog met de reeds gekozen bogen geen cykel vormt. We hebben de keuze: boog DC of boog DE. We kiezen bv. boog DC.
STAP 4: Neem vanuit knoop A, F, D en C de boog met het kleinste gewicht verschillend van de reeds aanwezige bogen en zodanig dat de boog met de reeds gekozen bogen geen cykel vormt.
Dat is boog DE.
STAP 5: Neem vanuit knoop A, F, D, C en E de boog met het kleinste gewicht verschillend van de reeds aanwezige bogen en zodanig dat de boog met de reeds gekozen bogen geen cykel vormt. Dat is boog EB. Hiermee hebben we de minimaal opspannende boom gecreëerd.

Je kan de kostprijs bepalen als de verbindingen gelegd zijn volgens deze minimaal opspannende boom: 10 + 5 + 6 + 8 + 6 = 35
Je stelt vast dat deze kostprijs (35) lager is dan de kostprijs bij de vorige oplossing (48). De gevonden kostprijs is de minimale kostprijs.
Bekijk de instructievideo die stap voor stap het algoritme uitlegt aan de hand van een concreet voorbeeld.
methode
3.3Het algoritme van Kruskal
Hoe pas je het algoritme van Kruskal toe?
STAP 1:Kies de boog met het kleinste gewicht. Hier is dat de boog DF.
STAP 2:Kies de boog op DF na met kleinste gewicht en voeg deze toe. We kunnen kiezen: DE of DC. We kiezen bv. DE.
STAP 3: Kies een volgende boog met de kleinste waarde op DF en DE na, maar wel zodanig dat er geen cykels ontstaan. Dat is de boog DC.
STAP 4:Ga volgens hetzelfde principe verder. De volgende boog is EB.
STAP 5:Als laatste boog volgt nu de boog FA. Je hebt de minimaal opspannende boom gecreëerd.

Ook met dit algoritme vind je de minimaal opspannende boom.
Bekijk de instructievideo die stap voor stap het algoritme uitlegt aan de hand van een concreet voorbeeld.
Verwerkingsopdrachten
In onderstaande graaf maken we de wandeling W = ( AB – BC – CE –
– BD –
– HG) Bepaal het gewicht van deze wandeling.
Maak gebruik van het algoritme van Prim om de minimaal opspannende boom in volgende graaf te bepalen. Bepaal ook zijn gewicht.
Maak gebruik van het algoritme van Kruskal om de minimaal opspannende boom in volgende graaf te bepalen. Bepaal ook zijn gewicht.
INKIJKEXEMPLAARDIEKEURE
4.1 Probleemstelling
Een vrachtwagenchauffeur vertrekt vanuit stad A en moet zo snel mogelijk naar stad I. Hij bekijkt de mogelijke reisroutes met naast elk traject ( de bogen van de graaf) de tijd die hij nodig heeft om dat traject af te leggen.
De chauffeur moet nu op zoek naar het kortste pad van A naar I.

Het gewicht van een boog AB is de getalwaarde die naast de boog staat.
Notatie: g( AB)
In deze graaf is g( AB) = 10.
Bestaat de boog niet, dan is het gewicht oneindig.
In deze graaf is g( AF) = ∞
De lengte van een pad met gegeven beginpunt A en eindpunt I is de som van de gewichten van de doorlopen bogen.
Notatie: l(AI)
Voorbeeld
Om ons van A naar I te begeven, volgen we het pad W:
W = ( AB - BF - FI)
l( W) = g( AB) + g( BF) + g( FI) = 10 + 8 + 17 = 35
De lengte van dit pad is een bovengrens voor de mogelijke kortste route tussen het begin- en het eindpunt van de wandeling.
l( AI) = 35

Merk op
Zolang er nog geen pad bestaat, stelt men de bovengrens op oneindig. l( AH) = ∞
Je vond nu een pad W met lengte 35. Dit is nu de bovengrens.
Bestaat er nog een ander pad met een kortere lengte?
Het algoritme van Dijkstra helpt je om hier naar op zoek te gaan. De bovengrens, de lengte van het kortste pad, stelt men voor door d( AI) .
4.2Het algoritme van Dijkstra
Hoe pas je het algoritme van Dijkstra toe?
methode
STAP 1: Geef de beginknoop ( = huidige knoop) voorlopig een afstand 0 ( l( AA) = 0) en alle andere knopen afstand ∞
Deze knopen noemen we de niet-bezochte knopen.
STAP 2:Bekijk alle buurknopen van de huidige knoop. Elke buurknoop heeft twee afstanden:
a) de voorlopige afstand die er bij staat ( = g( AX)) en b) de voorlopige afstand van de huidige knoop + de lengte van de boog vanaf de huidige knoop naar deze buurknoop ( = l( AX)) .
Kies de kortste afstand. Dat wordt de nieuwe voorlopige afstand van deze knoop.
STAP 3: Als je alle buurknopen hebt gehad, wordt de huidige knoop een bezochte knoop. Kies als nieuwe huidige knoop de knoop met de kleinste voorlopige afstand ( d( AX)) . Herhaal stap 2 en 3 tot je alle knopen hebt bezocht.
STAP 4: Je vindt het pad door in de tabel terug te redeneren. Vertrek bij het eindpunt. Telkens er zich een verandering van waarde in de kolom voordoet, ga je naar het punt dat deze verandering tot stand bracht en voeg je dit aan het pad toe. Uiteindelijk kom je bij het beginpunt terecht.
Bekijk de instructievideo die stap voor stap het algoritme uitlegt aan de hand van een concreet voorbeeld. Download de PDF die jou de volledige uitwerking toont.
Na het uitvoeren van het algoritme verkrijg je het kortste pad. Het kortste pad is W = ( AC – CG – GH – HI) met een totaal gewicht van 33.
d( AI) = 33
Bepaal in onderstaand netwerk de kortste route van A naar G.
kortste pad:
totaal gewicht:
INKIJKEXEMPLAARDIEKEURE
kortste pad:
totaal gewicht:
5 Het handelsreizigersprobleem
5.1 Probleemstelling
Een pakjesdienst gevestigd in Hasselt moet pakjes leveren in Aarschot, Beringen, Geel, Leuven, Mechelen en Turnhout. De onderlinge afstanden (in km langs de weg) vind je in onderstaand schema.
INKIJKEXEMPLAARDIEKEURE
We willen de optimale route voor de chauffeur berekenen.
schaal 1:540000
Het handelsreizigersprobleem is een complex probleem. Er bestaat nog geen algoritme dat de kortste route voor de chauffeur kan bepalen. Er bestaan wel enkele algoritmes die een “goede aanvaardbare” oplossing opleveren.

5.2Het beste-buur-algoritme
Hoe pas je het beste-buur-algoritme toe?
methode Ga naar de dichtstbijzijnde stad (knoop) die je nog niet bezocht hebt. Als alle steden zijn bezocht, ga dan vanuit deze stad terug naar het beginpunt.
starten in Hasselt
van Hasselt naar Beringen d( HB) = 22
van Beringen naar Geel d( BG) = 30
van Geel naar Turnhout d( GT) = 21
van Turnhout naar Aarschot d( TA) = 46
van Aarschot naar Leuven d( AL) = 19
van Leuven naar Mechelen d( LM) = 28
van Mechelen terug naar Hasselt d( MH) = 84
route W = ( HB – BG – GT – TA – AL – LM – MH) afstand l( W) = 250 km

schaal 1:540000

Merk op
Is dit de kortste route? Neen, maar wel een route die aanvaardbaar kort genoeg is. De kortste route is W = (HB – BG – GT – TM – ML – LA – AH) .
l( W) = 225 km
INKIJKEXEMPLAARDIEKEURE

schaal 1:540000
Een handelsreiziger moet onderstaande steden bezoeken. Wat is een mogelijke kortste route? Starten en eindigen doe je in A, de getallen naast de bogen stellen het aantal kilometers tussen de steden voor.
Deze zomer gaan we op fietsvakantie naar Noord-Nederland. We starten en eindigen in Veendam en zijn van plan om een fietstocht te maken langs de steden Assen, Drachten, Emmen, Groningen, Hoogeveen, Leeuwarden en Meppel.
Stippel een mogelijke optimale route uit.
veendamassendrachtenemmen groningenhoogeveenleeuwarden
INKIJKEXEMPLAARDIEKEURE
methode
6 Graafkleuring
6.1 Biotopen
Jorre houdt van reptielen. Hij heeft er een achttal als huisdier. Gekko’s, anolissen of iguana’s zet je echter niet zomaar in dezelfde (nagemaakte) biotoop.
Jorre heeft een lijstje gemaakt van welk reptiel niet met een ander reptiel kan samenleven.
reptielmag niet samen met
A D, G, H
B C, G
C B, E, F, G, H
D A, E, G, H
E C, D, F
F C, E
G A, B, C, D
H A, C, D
Wat is het kleinst aantal biotopen dat Jorre in elkaar moet knutselen opdat zijn reptielen vreedzaam zouden kunnen overleven?
Om het probleem van Jorre te kunnen oplossen, stellen we de lijst eerst grafisch voor d.m.v. een graaf. Reptielen die door een boog verbonden zijn, mogen niet samen zitten in eenzelfde biotoop.

6.2Algoritme
Het kleuren van een graaf is het toekennen van kleuren aan de knopen van de graaf zodat elke knoop een kleur heeft, verschillend van zijn buren.
Hoe kleur je een graaf?
STAP 1:Bepaal de graad van elke knoop uit de graaf.
STAP 2: Verwijder de knoop met de hoogste graad (want die kleuren we het laatste in) en verwijder ook alle bogen uit deze knoop. Zijn er twee knopen met dezelfde graad, dan mag je kiezen.
STAP 3: Bepaal opnieuw de graad van elke knoop. Herhaal stap 2 en 3 tot je elke knoop hebt verwijderd.
INKIJKEXEMPLAARDIEKEURE
STAP 4: Bepaal de volgorde om de knopen in te kleuren. Start met de knoop die het langste in de graaf bleef en ga verder tot je de knoop hebt die je het eerst hebt aangeduid (deze met de hoogste graad).
STAP 5: Kleur de graaf. Start met 1 kleur en ga het rijtje af. Als de volgende knoop in het rijtje een buurknoop is van een knoop die met dat kleur werd ingekleurd, neem je een ander kleur.
Voorbeeld
We bekijken de graaf die we maakten om het probleem van Jorre op te lossen.
• STAP 1: We bepalen de graad van elke knoop uit de graaf.
deg( A) = 3 deg( B) = 2 deg( C) = 5 deg( D) = 4
deg( E) = 3 deg( F) = 2 deg( G) = 4 deg( H) = 3
• STAP 2 en STAP 3: De knoop met de hoogste graad is C.
We verwijderen nu C en alle bogen vanuit C uit de graaf, en bepalen opnieuw de graad van elke knoop.
INKIJKEXEMPLAARDIEKEURE
deg( A) = 3 deg( B) = 1 deg( D) = 4 deg( E) = 2
deg( F) = 1 deg( G) = 3 deg( H) = 2
De voorlaatste knoop die we gaan kleuren, is D. We verwijderen D uit de graaf en bepalen opnieuw de graad van elke knoop.
deg( A) = 2 deg( B) = 1 deg( E) = 1
deg( F) = 1 deg( G) = 2 deg( H) = 1
Zo gaan we verder. Dit kan je ook in een tabel weergeven:
start verwijder knoop C verwijder knoop D verwijder knoop A verwijder knoop B verwijder knoop E
deg( A) 332---
deg( B) 2111--
deg( C) 5-----
deg( D) 44----
deg( E) 32111-
deg( F) 211110
deg( G) 432100
deg( H) 321000
• STAP 4: We krijgen het rijtje: H – G – F – E – B – A – D – C
• STAP 5: Graafkleuring:
•Knoop H krijgt kleur 1, bv. rood.
•Knoop G is geen buur van H en kan dus ook in het rood.
•Knoop F is geen buur van H of G en kan dus ook in het rood.
•Knoop E is een buur van F en krijgt kleur 2, bv. groen.
•Knoop B is een buur van G maar niet van E en kan ook in het groen.
•Knoop A is een buur van G en H, maar niet van E of B en kan ook in het groen.
•Knoop D is een buur van A en G en kan niet in kleur 1 of kleur 2 en krijgt dus kleur 3, bv. blauw.
•Knoop C is een buur van F en B, maar niet van D en kan ook in het blauw.
• Besluit: De graaf werd ingekleurd met 4 verschillende kleuren. Het kleinste aantal biotopen dat Jorre moet voorzien is 4.
6.3Zendmasten
In een dorp staan zeven zendmasten, elk met een bereik zoals aangegeven op onderstaand schema. Zendmasten die elkaar overlappen, moeten op een andere frequentie werken om storing te vermijden. We willen het minimaal aantal frequenties bepalen dat nodig is om deze zendmasten te laten werken op voorwaarde dat ze onderling géén storingen veroorzaken.
We stellen de zendmasten voor als knopen en verbinden ze met een boog als ze elkaar overlappen.
graafkleuring
start verwijder knoop D verwijder knoop C verwijder knoop E verwijder knoop A
deg( A) 2111-
deg( B) 32110
deg( C) 43---
deg( D) 5----
deg( E) 432--
deg( F) 22100
deg( G) 21100
volgorde inkleuren: B – F – G – A – E – C – D
Besluit: We moeten minstens 4 frequenties voorzien.

Merk op
Als we kleuren volgens het algoritme, hebben we 4 kleuren nodig. Nochtans is deze graaf kleurbaar met slechts 3 kleuren. Als we starten bij D (rood), kunnen we F ook in het rood kleuren. A, C en G worden groen en B en E kleuren we blauw in. Op die manier hebben we slechts 3 kleuren gebruikt.
6.4 Een planningsprobleem
De 18 springers en pagadders van de jeugdbeweging hebben dit weekend keuzeactiviteiten. Elk lid mag twee activiteiten kiezen uit zes keuzes. De keuzes zijn als volgt gemaakt.
keuze a keuze b keuze c keuze d keuze e keuze f Olivia Mila Emma Noah Arthur Jules Olivia Lucas Floor Finn Daan Julie Lucas Nolan Otis Lewis Daan Julie Mila Nolan Liam Lewis Jules Sofia
Emma Otis Liam Noor Liv Sofia
Hoe moet de leiding de keuzeactiviteiten organiseren zodat iedereen zijn keuze kan volgen?
Noah Floor Noor Arthur Finn Liv
We stellen de activiteiten voor door knopen en verbinden ze met een boog als een deelnemer beide activiteiten wil volgen.
graafkleuring start verwijder knoop A verwijder knoop C verwijder knoop E verwijder knoop B
deg( A) 4----
deg( B) 3211-
deg( C) 33---
deg( D) 32100
deg( E) 432-deg( F) 32210 volgorde inkleuren:
De leiding kan de activiteiten als volgt organiseren:
• tijdstip 1: activiteiten D en F
• tijdstip 2: activiteiten B en E
• tijdstip 3: activiteiten C en A
6.5Landkaarten en figuren inkleuren
Kleur volgende figuur (of landkaart) in met zo weinig mogelijk kleuren zodat aaneengrenzende vakjes (of landen) een verschillend kleur hebben.
Aaneengrenzende vakjes (landen) zijn vakjes die een lijn (grens) gemeen hebben. Vakjes die elkaar in een punt raken, zijn niet aaneengrenzend.
INKIJKEXEMPLAARDIEKEURE

Stel de vakjes voor als knopen. Hebben ze een grens gemeen, verbind ze door een boog.
graafkleuring
start verwijder knoop E verwijder knoop F verwijder knoop I verwijder knoop A verwijder knoop G verwijder knoop B verwijder knoop H
deg( A) 3222----
deg( B) 432211--
deg( C) 32111100
deg( D) 32221000
deg( E) 7-------
deg( F) 54------
deg( G) 43322---
deg( H) 5432211-
deg( I) 333-----
deg( J) 33211110
volgorde inkleuren : C
Merk op
E
Men vermoedt dat elke landkaart gekleurd kan worden met slechts vier kleuren. Deze eigenschap die men niet wiskundig sluitend kan bewijzen, noemt men het vierkleurenprobleem
Verwerkingsopdrachten
In een dierenpark wil men zoveel mogelijk dieren samenbrengen zodat de loopruimte voor elk dier groter wordt. Na overleg heeft men een schema gemaakt van welke dieren zeker niet samen mogen zitten.
diermag niet samen met
A C, E
B C, D, E
C A, B, G
D B, E, F
E A, B, D, G
F D, G
G C, E, F
INKIJKEXEMPLAARDIEKEURE

In hoeveel ruimtes kan men deze dieren minimaal plaatsen?
Kleur de volgende figuur met zo weinig mogelijk kleuren in zodat aaneengrenzende vakjes een verschillend kleur hebben. Vakjes die elkaar in een punt raken, zijn niet aangrenzend.
INKIJKEXEMPLAARDIEKEURE
Signaaloefeningen
Gegeven is de graaf G
a)Geef de knopen en bogen door opsomming.
b)Bepaal de orde en grootte van deze graaf.
c)Bepaal de graad van elke knoop.
d)Is dit een planaire graaf, m.a.w. kan je deze graaf hertekenen zodat geen twee bogen elkaar snijden? Zo ja, bewijs d.m.v. een tekening.
Zes vrienden (Ian, Jasper, Kobe, Luka, Milan en Noah) spraken gisterenavond af om nieuwtjes met elkaar uit te wisselen via sociale media. Iedereen had met exact drie vrienden contact.
• Ian had contact met Jasper, Kobe en Noah;
• Kobe had geen contact met Jasper;
• Milan had contact met Jasper, Luka en Noah. Stel deze gegevens grafisch voor d.m.v. een graaf. Met wie had Luka contact?
INKIJKEXEMPLAARDIEKEURE
Zoek een eulertoer in de volgende graaf.
INKIJKEXEMPLAARDIEKEURE
Maak gebruik van het algoritme van Prim om de minimaal opspannende boom in de volgende graaf te bepalen. Bepaal ook zijn gewicht.
Maak gebruik van het algoritme van Kruskal om de minimaal opspannende boom in de volgende graaf te bepalen. Bepaal ook zijn gewicht.
INKIJKEXEMPLAARDIEKEURE
Bepaal in onderstaand netwerk de kortste route van A naar H.
>>> Verder oefenen: D27 t.e.m. D31
INKIJKEXEMPLAARDIEKEURE
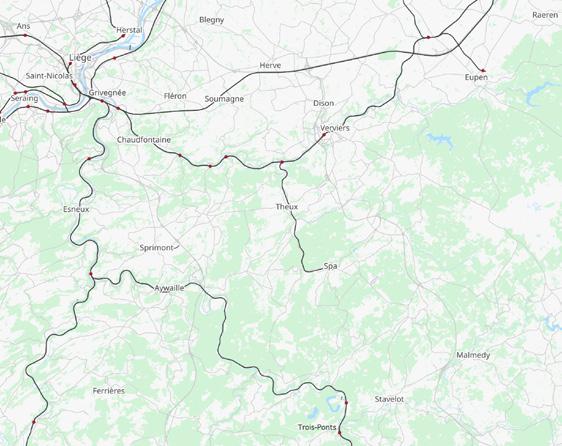
Deze zomer plannen we een rondrit in de streek van Spa. Het vertrek- en eindpunt is Spa en we willen de steden
Aywaille, Eupen, Malmedy, Stavelot, Theux, Trois-Ponts en Verviers bezoeken. Wat is een mogelijke optimale route?
Een handelsreiziger vertrekt uit stad A, moet vijf steden bezoeken en tenslotte weer huiswaarts keren naar A. Bepaal de kortst mogelijke route voor de handelsreiziger. De getallen naast de bogen stellen het aantal kilometer tussen de steden voor.
In een dorp staan acht zendmasten, elk met een bereik zoals aangegeven op onderstaand schema. Zendmasten die elkaar overlappen moeten op een andere frequentie werken om storing te vermijden. Bepaal het minimaal aantal frequenties dat nodig is om deze zendmasten te laten werken op voorwaarde dat ze onderling géén storingen veroorzaken.
INKIJKEXEMPLAARDIEKEURE
Kleur de volgende figuur met zo weinig mogelijk kleuren in zodat aaneengrenzende vakjes een verschillend kleur hebben.
Differentiatietraject
Gegeven is de graaf G
a)Geef de knopen en bogen door opsomming.
b)Bepaal de orde en grootte van deze graaf.
c)Bepaal de graad van elke knoop.
d)Is dit een planaire graaf, m.a.w. kan je deze graaf hertekenen zodat geen twee bogen elkaar snijden?
Zo ja, toon aan met behulp van een tekening.
2 3 4
a)Teken de graaf G waarvoor geldt:
• knopen: P, Q, R, S, T, U
• bogen: PQ, PS, PT, PU, QU, RS, RU, ST, SU, TU
b)Bepaal de orde en grootte van deze graaf.
c)Bepaal de graad van elke knoop.
d)Bepaal ∆( G) en δ( G)
a)Teken de graaf G waarvoor geldt:
• knopen: P, Q, R, S, T, U, V
• bogen: PT, PU, PV, QR, QS, QT, RS, RT, TU, UV
b)Bepaal de orde en grootte van deze graaf.
c)Bepaal de graad van elke knoop.
d)Bepaal ∆( G) en δ( G) .
Teken de planaire graaf G waarvoor geldt:
• buren van K: L, M, N
• buren van L: K, N, O
• buren van M: K, N, P
• buren van N: K, L, M, O, P, Q
• buren van O: L, N, Q
• buren van P: M, N, Q
• buren van Q: N, O, P
Teken een graaf G met orde 6 waarbij de graad van elke knoop gelijk is aan 4. Hoeveel bogen telt deze graaf?
6 7 8 9 10
Hoeveel bogen heeft een reguliere graaf met 12 knopen waarbij uit elke knoop 7 bogen vertrekken?
Een graaf bestaat uit 18 knopen en 21 bogen zodat elke knoop graad 2 of 3 heeft. Hoeveel knopen hebben graad 3?
Een graaf bestaat uit 20 knopen en 34 bogen zodat elke knoop graad 3 of 5 heeft. Hoeveel knopen hebben graad 5?
Zes meisjes (Anke, Britt, Charlotte, Dinah, Evy en Farah) stuurden elkaar in een sociale media app heel wat berichtjes heen en weer.
In totaal waren er negen onderlinge facebooklinken:
• Anke had met iedereen contact, behalve met Dinah.
• Dinah had met iedereen contact, behalve met Anke.
• Britt en Charlotte hadden enkel contact met Anke en Dinah.
Stel deze contacten grafisch voor d.m.v. een graaf.
Zeven dorpen zijn via een spoornet met elkaar verbonden. Vanuit elk dorp vertrekken er drie of vier spoorlijnen. In totaal zijn er twaalf spoorlijnen:
• Dorp A is verbonden met de dorpen B, E en G.
• Dorp C is verbonden met de dorpen B, D en F.
• Dorp E is verbonden met de dorpen A, B en D.
• Dorp G is verbonden met de dorpen A, D en F.
Stel dit spoornet grafisch voor d.m.v. een graaf.
INKIJKEXEMPLAARDIEKEURE
Welke van volgende wandelingen zijn paden, welke zijn sporen, welke zijn cykels en welke zijn circuits?
Wandelingen in een
INKIJKEXEMPLAARDIEKEURE
a) W1 = ( BC – CD – DE – EF – FD – DB)
b) W2 = ( EA – AB – BD – DE)
c) W3 = ( FD – DC – CB – BD – DF)
d) W4 = ( CF – FD – DE – EA – AB – BC)
Welke van volgende wandelingen zijn paden, welke zijn sporen, welke zijn cykels en welke zijn circuits?
a) W1 = ( AB – BC – CH – HD – DG)
b) W2 = ( FH – HD – DB – BC – CH – HF)
c) W3 = ( GD – DB – BC – CD – DH – HG)
d) W4 = ( CE – EF – FH – HD – DB – BC)
Zoek een eulertoer in de volgende graaf.
INKIJKEXEMPLAARDIEKEURE
Zoek een hamiltoncykel in de volgende graaf.
Zoek een eulertoer in de volgende graaf.
Zoek een hamiltoncykel in de volgende graaf.
a)Waarom is in deze graaf geen eulertoer mogelijk?
b)Hoeveel bogen moet men minimaal bijtekenen om van deze graaf een eulergraaf te maken?
c)Hoeveel bogen moet men minimaal schrappen om van deze graaf een eulergraaf te maken?
a)Is een hamiltoncykel mogelijk in deze graaf? Waarom niet?
b)Hoeveel bogen moet men minimaal bijtekenen om van deze graaf een hamiltongraaf te maken?
Minimaal opspannende
In onderstaande graaf maken we de wandeling W = ( AC – CB
Bepaal het gewicht van deze wandeling.
Maak gebruik van het algoritme van Prim om de minimaal opspannende boom in volgende graaf te bepalen. Bepaal ook zijn gewicht.
Maak gebruik van het algoritme van Kruskal om de minimaal opspannende boom in volgende graaf te bepalen. Bepaal ook zijn gewicht.
Maak gebruik van een algoritme om de minimaal opspannende boom in volgende graaf te bepalen. Bepaal ook zijn gewicht.
Maak gebruik van een algoritme om de minimaal opspannende boom in volgende graaf te bepalen. Bepaal ook zijn gewicht.
Maak gebruik van een algoritme om de minimaal opspannende boom in volgende graaf te bepalen. Bepaal ook zijn gewicht.
Maak gebruik van een algoritme om de minimaal opspannende boom in volgende graaf te bepalen. Bepaal ook zijn gewicht.
Bepaal in onderstaand netwerk de kortste route van A naar F.
Bepaal in onderstaand netwerk de kortste route van A naar H.
Bepaal in onderstaand netwerk de kortste route van A
Bepaal in onderstaand netwerk de kortste route van A naar M.
INKIJKEXEMPLAARDIEKEURE
Het
Een pizzabezorger moet pizza’s leveren op vijf plaatsen. Hij vertrekt vanuit de pizzeria (P) naar de vijf locaties en keert dan terug. Bepaal een optimale route voor de pizzabezorger. De cijfers naast de bogen stellen de tijdseenheden voor die hij nodig heeft om zich van de ene plaats naar de andere te begeven.

A 12-131219 11
B 11 13-141610
C 151214-1419
D 18191614-16
E 17 11 101916-
INKIJKEXEMPLAARDIEKEURE
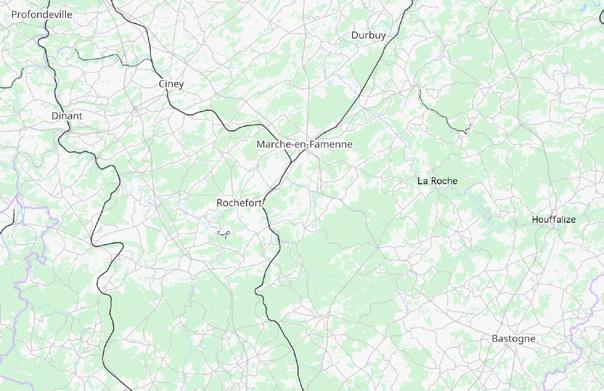
Een vervoersfirma vertrekt vanuit het centrale depot in Dinant en moet goederen ophalen in Durbuy, Houffalize, La Roche-en-Ardenne, Marche-en-Famenne en Rochefort . De onderlinge afstanden (in km langs de weg) vind je in onderstaand schema. Bereken een optimaal traject voor de chauffeur.
Een handelsreiziger moet onderstaande steden bezoeken. Wat is een mogelijke kortste route?
Vertrek- en eindpunt bevindt zich in A. De getallen naast de bogen stellen het aantal kilometer tussen de steden voor.
Om de kosten voor het zomerkamp wat te drukken, houdt de jeugdbeweging een wafelenbak.
Nolan moet met zijn fiets wafels leveren bij acht gezinnen in de buurt. De tijd tussen de adressen onderling (in minuten) vind je in volgende tabel. Hij start en eindigt in K. Stippel een optimale route voor Nolan uit.
Een handelsreiziger vertrekt uit stad A, moet zes steden bezoeken en tenslotte weer huiswaarts keren naar A.
Bepaal de kortst mogelijke route voor de handelsreiziger.
INKIJKEXEMPLAARDIEKEURE
Bepaal een zo optimaal mogelijke kleuring voor deze graaf.
Bepaal een zo optimaal mogelijke kleuring voor deze graaf.
INKIJKEXEMPLAARDIEKEURE
In een educatief centrum over het zeeleven wil men in verschillende aquaria een aantal vissen en zeedieren tentoonstellen. Omdat niet alle waterdieren vreedzaam kunnen samenleven in eenzelfde aquarium, heeft men een lijst gemaakt van welke zeedieren zeker niet samen mogen zitten.
zeediermag niet samen met
A B, F, G
B A, C, D, F
C B, F
D B, E, H
E D, F, G, H
F A, B, C, E, G
G A, E, F
H D, E

Wat is het kleinste aantal aquaria dat men moet voorzien?
In een dorp staan acht zendmasten, elk met een bereik zoals aangegeven op onderstaand schema. Zendmasten die elkaar overlappen, moeten op een andere frequentie werken om storing te vermijden. Bepaal het minimaal aantal frequenties die nodig zijn om deze zendmasten te laten werken op voorwaarde dat ze onderling géén storingen veroorzaken.
Bepaal een zo optimaal mogelijke kleuring voor volgende graaf.
Een klas gaat op driedaagse naar Parijs. Om de kosten wat te drukken, mogen de 21 leerlingen elk drie musea kiezen die ze willen bezoeken. Op de andere momenten doen ze een stadswandeling. De keuzes zijn als volgt:
keuze Akeuze Bkeuze Ckeuze Dkeuze Ekeuze Fkeuze G
Lucas
Julia Noor
Daan
Evi
Luuk
James
Lucas
Julia
Levi
Tess
Noor
Daan
Luuk
James
Sam
Levi
Finn
Zoë
Sara
Lotte
Milan
Sam
Lucas
Finn
Zoë
Adrian
Noor
Daan
Evi
Lotte
Bram
Fleur
Lars
Levi
Tess
Finn
Sara
Noah
Lotte
Bram
Olivia
Milan
Sam
Fleur
Adrian
Sara
Noah
Bram
Olivia
Fleur
Lars
Julia Tess
Zoë
Adrian
Noah
Evi
Luuk
Olivia
Milan
James
Lars

Hoe plannen de begeleidende leerkrachten de museabezoeken het best als ze de activiteiten zoveel mogelijk willen laten samenvallen?
Kleur de onderstaande figuur in met zo weinig mogelijk kleuren, zodat aaneengrenzende vakjes een verschillende kleur hebben.
INKIJKEXEMPLAARDIEKEURE
INKIJKEXEMPLAARDIEKEURE
Studiewijzer
Differentiatietraject
Doelen
Ik kan de onderdelen van een graaf correct benoemen. Ik weet wat knopen en bogen zijn en kan de graad van een knoop bepalen.
Ik weet wat een wandeling in een graaf is. Ik ken het verschil tussen een eulertoer en een hamiltoncykel.
Ik kan een minimaal opspannende boom op een gewogen graaf bepalen met behulp van de algoritmes van Prim en Kruskal.
Ik kan het kortste pad op een gewogen graaf bepalen met behulp van het algoritme van Dijkstra.
Ik ken het handelsreizigersprobleem en kan dit benaderend oplossen met behulp van het beste-buur-algoritme.
Ik weet wat graafkleuring is en kan dit in concrete situaties toepassen.
Doelstellingen
Ik kan de onderdelen van een graaf correct benoemen. Ik weet wat knopen en bogen zijn en kan de graad van een knoop bepalen. 4
Probeer de termen en afkortingen die worden gebruikt goed te memoriseren, deze heb je in deze module immers vaak nodig.
verwerking: 1, 2, 3, 4, 5, 6 signaal: 1, 2
differentiatie: 1 t.e.m. 11
Ik weet wat een wandeling in een graaf is. Ik ken het verschil tussen een eulertoer en een hamiltoncykel. 12
Maak een schema of mindmap om de verschillende soorten wandelingen te visualiseren.
verwerking: 7, 8, 9 signaal: 3, 4
INKIJKEXEMPLAARDIEKEURE
differentiatie: 12 t.e.m. 19
Ik kan een minimaal opspannende boom op een gewogen graaf bepalen met behulp van de algoritmes van Prim en Kruskal. 18
Probeer beide algoritmes onder de knie te krijgen. Bekijk, indien nodig, de instructievideo’s op POLPO.
verwerking: 10, 11, 12 signaal: 5, 6
differentiatie: 20 t.e.m. 26
Ik kan het kortste pad op een gewogen graaf bepalen met behulp van het algoritme van Dijkstra. 23
Werk heel nauwkeurig. Gebruik eventueel kleur, maar hou het overzichtelijk.
verwerking: 13, 14 signaal: 7, 8
differentiatie: 27 t.e.m. 31
Ik ken het handelsreizigersprobleem en kan dit benaderend oplossen met behulp van het beste-buur-algoritme.
Als je dit algoritme toepast, bekom je niet meteen de kortste route. Dit is enkel een benadering van een aanvaardbare (korte) route. Geef in je antwoord altijd de route W en de bijhorende afstand l( W) weer.
verwerking: 15, 16
signaal: 9, 10
differentiatie: 32 t.e.m. 36
Ik weet wat graafkleuring is en kan dit in concrete situaties toepassen.
Schenk aandacht aan het opstellen van de bijhorende graaf. Volg daarna het stappenplan.
verwerking: 17, 18
signaal: 11, 12
differentiatie: 37 t.e.m. 43
27
32
INKIJKEXEMPLAARDIEKEURE
Auteurs Philip Bogaert, Björn Carreyn en Roger Van Nieuwenhuyze
Eerste druk 2024 - SO 2024/0224 - Bestelnummer 94 606 0119 (module 08 van 18)
ISBN 978 90 4864 973 0 - KB D/2024/0147/206 - NUR 126/128/129 - Thema YPMF
Illustrator Jona Jamart - Design en lay-out die Keure
Verantwoordelijke uitgever die Keure, Kleine Pathoekeweg 3, 8000 Brugge
RPR 0405 108 325 - © Copyright die Keure, Brugge
