01 Logica en waarheidstabellen

wat je al kunt
–mondeling en schriftelijk communiceren over redeneringen
–symbolen gebruiken
–implicatie en equivalentie zinvol hanteren
–uitspraken illustreren met voorbeelden
–logische operatoren gebruiken
–een eenvoudige waarheidstabel gebruiken
–concepten van computationeel denken hanteren
wat je leert in deze module
–de waarheidswaarde van logische uitspraken bepalen met behulp van waarheidstabellen
–logische operatoren en connectieven ∧ , ∨ , ¬ , ⇒, ⇔ gebruiken
–het verschil begrijpen tussen de ‘of’ in de logica en de ‘of’ in de omgangstaal
–het verschil begrijpen tussen de ‘als … dan …’ in de logica en de ‘als … dan …’ in de omgangstaal
–het verband leggen tussen logische poorten en logica
–een wiskundige uitspraak in symbolen en logica gebruiken in bewijzen en redeneringen
Inhoud
Instap
1Logische operatoren en waarheidstabellen
2Problemen oplossen met logica
Signaaloefeningen
Differentiatietraject
Computationeel denken
Studiewijzer

in de kijker
Je reflecteert over jouw gevonden antwoord en controleert de gemaakte tussenstappen.
wiskundetaal
–proposities
–conjunctie
–disjunctie
–inclusieve of
–exclusieve of
–negatie
–implicatie
–equivalentie
–logisch equivalente uitspraken
–tautologie
–contradictie
–logische poorten
Instap
Opdracht 1
Puzzel 1
Najade en Broes spelen een partijtje tennis tegen elkaar. Bij elk spel dat ze spelen kunnen ze 1 euro winnen of 1 euro verliezen.
Broes won drie spelletjes. Najade won 5 euro.
Hoeveel spelletjes hebben ze tegen elkaar gespeeld?
Puzzel 2
Op een tafel staan drie dozen met speelgoed met daarop een label. Op het label van de eerste doos staat er 'LEGO', op het label van de tweede doos staat er 'PLAYMOBIL' en op het label van de laatste doos staat er 'LEGO & PLAYMOBIL'. Alle dozen zijn verkeerd gelabeld.

LEGO & PLAYMOBIL PLAYMOBIL
Je mag één doos kiezen waar je even in kijkt, om zo daarna de inhoud van de andere dozen (zonder kijken) met zekerheid te kunnen zeggen. Welke doos kies je? Verklaar je antwoord.
Puzzel 3
Lowie, Vicky, Jurn en Mathilde hebben elk een hond. Hier zie je de vier honden:
Zita
INKIJKEXEMPLAARDIEKEURE
Slink Milou Pongo

Zita is een Franse bulldog, Slink is een Duitse herder, Milou is een labradoodle en Pongo is een maltipoo. Wijs elke hond toe aan zijn baasje op basis van volgende uitspraken:
De hond van Vicky is geen Duitse herder of labradoodle.
Pongo’s baasje is een man die houdt van wandelingen in het bos.
Zita houdt van de zee, net zoals haar baasje ook houdt van zwemmen.
Lowie vermijdt met de hond modderpoelen en bosomgevingen.
De labradoodle nestelt zich graag in de zetel, maar is niet de hond van Mathilde.
Opdracht 2
Gegeven:P is de verzameling van de priemgetallen kleiner dan 20. R is de verzameling van de delers van 30.
a)Maak een vlinderdiagram.
b)Omkring: waar of niet waar?
1 ∈ P ∩ R
1 ∈ P ∩ R
R\P = {2,6,10,15,30} WAAR / NIET WAAR
R\P = {2,6,10,15,30} WAAR / NIET WAAR
Opdracht 3
In het spel ‘Star Battle’ zijn dit de spelregels: Op iedere rij (horizontaal en verticaal) moeten er precies twee sterren staan. Ook in elk gebied moeten er twee sterren staan. Twee sterren mogen elkaar nooit raken (ook niet diagonaal).
a)Een opwarmertje… Duid telkens aan in het blauwe gebied:
• Waar staan er mogelijks sterren?
• Waar staat er zeker geen ster?
• Waar staat er met zekerheid een ster?
c)Los nu de volledige puzzel op.
b)Duid telkens aan in het blauwe gebied:
• Waar staan er mogelijks sterren?
• Waar staan er zeker geen sterren?
• Waar staat er met zekerheid een ster?
TIP

Denk vooral aan waar er géén sterren kunnen staan.
Opdracht 4
Logische operatoren worden ook in computertaal gebruikt. Probeer telkens de geschreven code te begrijpen.
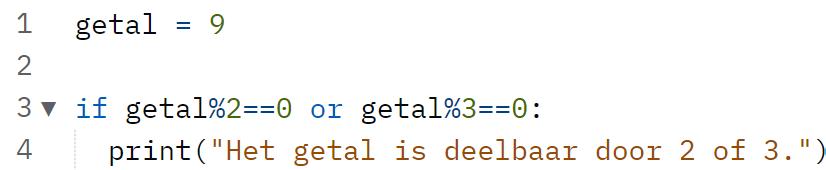
a)Omcirkel: In deze code wordt gebruik gemaakt van een conjunctie – disjunctie – negatie
b)Zal het programma uitvoer genereren? JA – NEE
Verklaar je antwoord.
INKIJKEXEMPLAARDIEKEURE

a)Omcirkel: In deze code wordt gebruik gemaakt van een conjunctie – disjunctie – negatie.
b)Zal het programma uitvoer genereren? JA – NEE
Verklaar je antwoord.


Hierboven zie je twee keer dezelfde code. Vaak wordt er gebruik gemaakt van een tweede versie.
a)Omcirkel: In deze code wordt gebruik gemaakt van een conjunctie – disjunctie – negatie.
b)Zal het programma uitvoer genereren? JA – NEE
Verklaar je antwoord.
1 Logische operatoren en waarheidstabellen
1.1 Begrippen
In de propositielogica werken we met uitspraken. Deze uitspraken zijn waar of niet waar. We noemen de logische uitspraken ook proposities . Proposities geven een feit weer. Een propositie hoeft niet waar te zijn. Het kan op dit moment nog onduidelijk zijn of een propositie waar of niet waar is.
Voorbeelden
p: Een dolfijn is een zoogdier. p is een ware uitspraak
q: Een banaan is blauw. q is een onware uitspraak
r: De thee is warm. r is een ware of onware uitspraak
Ook in de wiskunde maken we gebruik van uitspraken. Om te oordelen of een uitspraak waar of onwaar is, kunnen we onder andere beroep doen op onze wiskundekennis. Zo kunnen we met één tegenvoorbeeld een uitspraak ontkrachten en als onwaar beschouwen.
Voorbeelden
p: √2 is een irrationaal getal. p is een ware uitspraak
q: De tangens van een scherpe hoek ligt tussen -1 en 1. q is een onware uitspraak (tegenvoorbeeld: tan 50° > 1)
We kunnen uitspraken ook met elkaar verbinden door gebruik te maken van connectieven : de negatie (niet), de conjunctie (en), de disjunctie (of), de implicatie (als … dan) en de equivalentie (… als en slechts als …).
1.2De negatie
Gegeven is de uitspraak p: Amélie lust melk.
De negatie van deze uitspraak is:
¬p: Amélie lust geen melk.
notatie ¬ p (de negatie van de uitspraak p )
Het is mogelijk dat de uitspraak p waar is, dan is de negatie van deze uitspraak niet waar. Het is evengoed mogelijk dat de uitspraak p niet waar is, dan is de negatie van deze uitspraak waar.
We vatten dit samen in een waarheidstabel . In de eerste kolom staat de mogelijke waarde van p. In de tweede kolom staat de waarde van ¬p
INKIJKEXEMPLAARDIEKEURE

We kunnen hier ook een logische wet vaststellen, de wet van de dubbele negatie: ¬( ¬p) ⇔ p
Merk op
Je kan ofwel waar en niet waar gebruiken, maar je kan ook binair werken: dan gebruik je 1 voor waar en 0 voor niet waar.
1.3De conjunctie
Gegeven: twee uitspraken p en q
p: Finn draagt een zwarte broek.
q: Finn draagt een blauw T-shirt.
De nieuwe uitspraak p ∧ q wordt:
p ∧ q: Finn draagt een zwarte broek en een blauw T-shirt.
notatie p ∧ q (de conjunctie van de uitspraken p en q )
De uitspraken p en q zijn met elkaar verbonden door de logische operator ‘en’ (and).

INKIJKEXEMPLAARDIEKEURE



p is waar q is waar


p is waar q is niet waar



p is niet waar q is waar
De conjunctie van p en q is enkel waar als zowel uitspraak p als uitspraak q waar is.



p is niet waar q is niet waar
Merk op In deze context betekent p ∧¬q dat Finn een zwarte broek en géén blauw T-shirt draagt (= situatie 2).
1.4 De disjunctie
Gegeven: twee uitspraken p en q
p: In de wei staat een koe.
q: In de wei staat een paard.
De nieuwe uitspraak p ∨ q wordt:
p ∨ q : In de wei staat een koe of een paard.
notatie p ∨ q (de disjunctie van de uitspraken p en q )

INKIJKEXEMPLAARDIEKEURE
De uitspraken p en q zijn met elkaar verbonden door de logische operator ‘of’ (or). In logica wordt gebruik gemaakt van de inclusieve of. In deze context betekent dit dat er in de weide ofwel een koe moet staan, ofwel een paard moet staan, maar dat er evengoed zowel een koe als een paard mag staan.
p is waar q is waar
p is waar q is niet waar
p is niet waar q is waar
De disjunctie van twee uitspraken p en q is waar als minstens 1 van de uitspraken waar is.
p is niet waar q is niet waar
In de omgangstaal gebruiken we eerder de exlusieve of . Als je in een restaurant mag kiezen uit frietjes of rijst bij het hoofdgerecht, dan kies je slechts 1 van de 2 mogelijkheden (ofwel frietjes, ofwel rijst, maar niet beide).
Merk op Het niet waar zijn van een disjunctie zegt wel iets over de dieren, namelijk dat geen van beide in de wei staat.
We kunnen met de disjunctie ook de wet van de uitgesloten derde formuleren. Een uitspraak is waar of niet waar, er is geen derde mogelijkheid.
p ¬pp ∨¬p
WAARNIET WAARWAAR
NIET WAARWAARWAAR
formule p ∨¬p
1.5 De implicatie
Je leerde eerder al gebruik maken van implicaties in wiskunde. Ook in logica kunnen we hier dieper op ingaan.
Gegeven: twee uitspraken p en q
p: Jef neemt de trein. q: Jef beluistert muziek.
Je kan de twee uitspraken p en q verbinden met een implicatiepijl. We noemen p dan het antecedens en q het consequens .
notatie p ⇒ q (implicatie: “ Als Jef de trein neemt, dan beluistert Jef muziek.”)
De implicatie is waar als Jef effectief de trein neemt en ook muziek beluistert.
Neemt Jef de trein niet, dan kan hij al dan niet muziek beluisteren. Ook hier is de implicatie waar.
Enkel wanneer Jef de trein neemt en geen muziek beluistert, is de implicatie niet waar.

INKIJKEXEMPLAARDIEKEURE

Merk op Als het antecedens niet waar is, dan maakt het niet uit of het consequens waar of niet waar is. De implicatie is dan altijd waar.
In de omgangstaal en het dagelijkse leven, gaan we vaak uit van oorzaak en gevolg. De implicatie in de logica verschilt hiervan. Hier onderzoeken we alle gevallen, ook al lijken die in het dagelijkse leven minder relevant.
Er is een verband tussen de implicatie en de disjunctie: p ⇒ q en ¬p ∨ q zijn gelijkwaardige uitspraken.
WAARNIET WAARNIET WAARNIET WAARNIET WAAR
NIET WAARWAARWAARWAARWAAR
NIET WAARNIET WAARWAARWAARWAAR
1.6 De equivalentie
Je leerde eerder al gebruik maken van equivalenties in wiskunde. Ook in logica kunnen we hier dieper op ingaan.
Gegeven: twee uitspraken p en q
p: Dounia eet een suikerspin. q: Dounia gaat naar de kermis.
We maken een nieuwe uitspraak met behulp van een equivalentiepijl. notatie p ⇔ q (equivalentie: “Dounia eet een suikerspin als en slechts als ze naar de kermis gaat.”)

Deze uitspraak is waar als Dounia zowel een suikerspin eet als naar de kermis gaat. Het is eveneens waar als ze geen suikerspin eet en niet naar de kermis gaat.
Door gebruik te maken van de waarheidstabellen kan je eenvoudig aantonen dat p ⇔ q en ¬p ⇔¬q gelijkwaardige uitspraken zijn.
NIET WAARWAARNIET WAARWAARNIET WAARNIET WAAR
NIET WAARNIET WAARWAARWAARWAARWAAR formule
INKIJKEXEMPLAARDIEKEURE
Verwerkingsopdrachten
Gegeven:twee uitspraken p en q
p: Nona gaat naar de Scouts.
q: Selena speelt voetbal.
a)Wat betekent ¬p?
b)Verbind de uitspraken p en q met een conjunctie.
In symbolen:
Betekenis:
c)Maak een waarheidstabel om te bepalen wanneer de uitspraak p ∨ q waar is.
Gegeven:twee uitspraken p en q
p: Wiskunde is een interessant vak.
q: Het is mooi weer.
a)Wat betekent p ⇔ q?

b)Maak een waarheidstabel voor deze equivalentie.
c)Wanneer is deze equivalentie waar?
d)Beoordeel de volgende uitspraak. “Als het mooi weer is, zijn andere vakken dan wiskunde niet interessant.”
Je wilt absoluut vermijden dat je een gevaarlijk virus oploopt en raadpleegt een arts. De arts zegt: “Als je je laat vaccineren, dan krijg je het virus niet.”
a)Welke twee proposities zijn in de uitspraak van de arts met elkaar verbonden?
p:
q:
b)Schrap wat niet past:
Er werd gebruik gemaakt van een conjunctie – disjunctie – implicatie – equivalentie
c)Noteer de uitspraak in symbolen:
d)Maak een waarheidstabel die hoort bij de uitspraak van de arts.
e)Wat later zie je de arts terug en zeg je: “Ik heb het virus niet gekregen.” De arts zegt onmiddellijk: “Dan heb je je laten vaccineren.” Beoordeel de uitspraak van de arts.
4
Toon aan met een waarheidstabel dat de uitspraken logisch equivalent zijn.
a) (p ⇒ q) ⇔ (¬q ⇒¬p)
(p ⇒ q) ⇔ ¬ [p ∧ (¬q)]
b)
(p ⇒ q) ⇔ (¬q ⇒¬p)
(p ⇒ q) ⇔ ¬ [p ∧ (¬q)]
2 Problemen oplossen met logica
2.1 Tautologie en contradictie
definitie Een tautologie is een samengestelde uitspraak die voor elke waarde van de enkelvoudige proposities waar is.
Voorbeeld
Je bent voor een toets van wiskunde geslaagd of niet geslaagd.
De twee proposities zijn: p: Je bent geslaagd voor de toets wiskunde.
¬p: Je bent niet geslaagd voor de toets wiskunde.
De samengestelde uitspraak p ∨¬p is altijd waar. Bijgevolg is p ∨¬p een tautologie. Je kunt dit ook aantonen met een waarheidstabel.
p ¬pp ∨¬p
WAARNIET WAARWAAR
NIET WAARWAARWAAR
definitie Een contradictie is een samengestelde uitspraak die voor elke waarde van de enkelvoudige proposities niet waar is.
Voorbeeld
Een natuurlijk getal waarvan het laatste cijfer oneven is, is deelbaar door 2. De twee proposities zijn: p: Het laatste cijfer van het natuurlijk getal is oneven. q: Het natuurlijk getal is deelbaar door 2.
De samengestelde uitspraak p ∧ q is altijd niet waar. Bijgevolg is p ∧ q een contradictie. Je kunt dit ook aantonen met een waarheidstabel.
p qp ∧ q
WAARNIET WAARNIET WAAR
NIET WAARWAARNIET WAAR
INKIJKEXEMPLAARDIEKEURE

2.2Logische wetten
A)Wat je al kent
Logische wetten zijn logische waarheden of tautologieën. In het vorige hoofdstuk maakte je al kennis met een aantal logische wetten.
• Bij de negatie spraken we over de wet van de dubbele negatie: logische wet: ¬( ¬p) ⇔ p
Bv. “Dit is niet zonder risico” betekent: “Er is een risico.”
• Bij de disjunctie kwam de wet van de uitgesloten derde aan bod: logische wet: p ∨¬p
Bv. Je bent op tijd of je bent niet op tijd.
• Je leerde bij de implicatie dat die kan worden omgezet in een disjunctie: logische wet: ( p ⇒ q) ⇔ ( ¬p ∨ q)
Bv. “Als het woensdag is, dan padel ik.” is gelijkwaardig met “Het is niet woensdag of ik padel.” De implicatie geeft immers geen info over wat je doet als het niet woensdag is. Je kan ook padellen op donderdag.
Merk op Je kunt al deze logische wetten bewijzen door een waarheidstabel op te stellen.
B)Contrapositie van een implicatie
We bekijken twee proposities:
p: Mijn haar is te lang. q: Ik ga naar de kapper.
p ⇒ q betekent “Als mijn haar te lang is, dan ga ik naar de kapper.”
¬q ⇒¬p betekent “Als ik niet naar de kapper ga, dan is mijn haar niet te lang.”
De uitspraken p ⇒ q en ¬q ⇒¬p zijn equivalent.
formule ( p ⇒ q) ⇔ ( ¬q ⇒¬p)
INKIJKEXEMPLAARDIEKEURE

Met behulp van een waarheidstabel tonen we aan dat dit in elke situatie equivalente uitspraken zijn.
p qp ⇒ q ¬q ¬p ¬q ⇒¬p
WAARWAARWAARNIET WAARNIET WAARWAAR
WAARNIET WAARNIET WAARWAARNIET WAARNIET WAAR
NIET WAARWAARWAARNIET WAARWAARWAAR
NIET WAARNIET WAARWAARWAARWAARWAAR
C)Een equivalentie omzetten in een conjunctie
We bekijken twee proposities:
p: Vandaag is het de Vlaamse feestdag.
q: Vandaag is het 11 juli.
p ⇔ q betekent “Vandaag is het de Vlaamse feestdag als en slechts als het vandaag 11 juli is.”
p ⇔ q en (p ⇒ q) ∧ (q ⇒ p) betekent “Als het vandaag de Vlaamse feestdag is, dan is het vandaag 11 juli en als het 11 juli is, dan is het vandaag de Vlaamse feestdag.”
De uitspraken p ⇔ q en (p ⇒ q) ∧ (q ⇒ p) zijn equivalent.
Met behulp van een waarheidstabel tonen we aan dat dit in elke situatie equivalente uitspraken zijn.
WAARNIET
NIET WAARWAARNIET WAARWAARNIET WAARNIET WAAR
NIET WAARNIET WAARWAAR WAAR WAAR WAAR
D)De wetten van De Morgan (dualiteit van De Morgan)
Er zijn twee wetten van De Morgan. Zo kan de negatie van een conjunctie omgezet worden in een disjunctie.
We bekijken twee proposities: p: Ik draag een groene broek. q: Ik kijk televisie.
¬(p ∧ q) en ¬p ∨¬q betekent “Het is niet zo dat ik een groene broek draag en televisie kijk.”
¬(p ∧ q) en ¬p ∨¬q betekent “Ik draag geen groene broek of ik kijk geen televisie.”
De uitspraken ¬(p ∧ q) en ¬p ∨¬q zijn equivalent. formule
INKIJKEXEMPLAARDIEKEURE
WAARWAARWAARNIET WAARNIET WAARNIET WAARNIET WAAR
WAARNIET WAARNIET WAARWAARNIET WAARWAARWAAR
NIET WAARWAARNIET WAARWAARWAARNIET WAARWAAR
NIET WAARNIET WAARNIET WAARWAARWAARWAARWAAR
Evenzeer kan de negatie van een disjunctie omgezet worden in een conjunctie.
We hernemen de twee proposities: p: Ik draag een groene broek. q: Ik kijk televisie.
¬(p ∨ q) en ¬p ∧¬q betekent “Het is niet zo dat ik een groene broek draag of televisie kijk.”
¬(p ∨ q) en ¬p ∧¬q betekent “Ik draag geen groene broek en ik kijk geen televisie.”
De uitspraken ¬(p ∨ q) en ¬p ∧¬q zijn equivalent.
WAARNIET WAAR
NIET WAARNIET WAARNIET WAARWAARWAARWAARWAAR
Merk op dat we in de waarheidstabellen even goed gebruik hadden kunnen maken van 0 (niet waar) en 1 (waar). In de oefeningen is deze manier van werken misschien wel sneller.
2.3Bewijzen
Met behulp van de logische wetten kun je eenvoudig equivalenties aantonen. Op die manier moet je niet altijd een waarheidstabel opstellen. Zo kan je bewijzen dat ¬(p ⇒ q) ⇔ (p ∧¬q) .
Links vind je het bewijs met behulp van logische wetten, rechts de waarheidstabel. Via beide manieren toon je de equivalentie aan.
¬(p ⇒ q)
⇕ (implicatieomzettenineendisjunctie)
¬(¬p ∨ q)
⇕ (wetDeMorgan)
¬(¬p) ∧¬q
⇕ (dubbelenegatie)
p ∧¬q

Merk op Voor de conjunctie, disjunctie, implicatie, … zijn er ook eigenschappen. Zo is bijvoorbeeld de conjunctie commutatief: ( p ∧ q) ⇔ ( q ∧ p) . Je kan dit aantonen met een waarheidstabel.
De implicatie is echter niet commutatief. Ook dit kan je vaststellen met een waarheidstabel.
Voor je dus eigenschappen toepast, zal je ze moeten onderzoeken!
2.4 Logische poorten
definitie Logische poorten zijn elektronische schakelingen met één of meerdere ingangen en één uitgang.
Op basis van de invoer wordt de uitvoer bepaald. We bestuderen enkele logische poorten. Je vindt ze vaak terug in schema’s uit de elektronica.
Merk op dat deze poorten ook gebruikt worden bij het coderen.
A)De NOT-poort
Om bij een NOT-poort de uitvoer 1 te verkrijgen, moet de invoer tegengesteld zijn: 0 (niet waar). We kunnen dit schematisch voorstellen door gebruik te maken van een symbool.
input X output
Op basis van dit schema, kan je een waarheidstabel opstellen.

Merk op Andere voorstellingen van de NOT-poort zijn:
B)De AND-poort
Om bij een AND-poort de uitvoer 1 te verkrijgen, moet elke invoer 1 (waar) zijn. We kunnen dit schematisch voorstellen door gebruik te maken van een symbool.
X & XY Y
Op basis van dit schema, kan je een waarheidstabel opstellen.

Merk op Andere voorstellingen van de AND-poort zijn:
XY XY Y X AND Y

C)De OR-poort
Om bij een OR-poort de uitvoer 1 te verkrijgen, moet minstens één van de ingangen 1 (waar) zijn. We kunnen dit schematisch voorstellen door gebruik te maken van een symbool.

Merk op
• Andere voorstellingen van de OR-poort zijn:
INKIJKEXEMPLAARDIEKEURE
• Er bestaat ook een XOR-poort, dit is een exclusieve OR wat dus betekent dat je uitvoer 1 hebt als ofwel niet alle ingangen 1 zijn, ofwel als niet alle ingangen 0 zijn. Hieronder zie je een voorstelling.
D)De NAND-poort
Een NAND-poort is eigenlijk een AND-poort gevolgd door een NOT-poort. Het wil zeggen dat de uitvoer 1 is van zodra 1 van de ingangen 0 is.
Merk op
Andere voorstellingen van de NAND-poort zijn:

E)De NOR-poort
Een NOR-poort is eigenlijk een OR-poort gevolgd door een NOT-poort. Het wil zeggen dat de uitvoer 1 is als alle ingangen 0 zijn.
X ⩾ 1 Y X + Y
Op basis van dit schema, kan je een waarheidstabel opstellen.
INKIJKEXEMPLAARDIEKEURE

Merk op
• Andere voorstellingen van de NOR-poort zijn: X X + Y Y X NOR Y X + Y
• Er bestaat ook nog een XNOR-poort, dit is een exclusieve NOR wat dus betekent dat je een uitvoer 1 krijgt als ofwel alle ingangen 1 zijn ofwel als alle ingangen 0 zijn. Hieronder zie je een voorstelling.
X = 1X + Y Y
F)Toepassing
A = 0 & X
B = 0 1
• We bepalen de waarde van de uitvoer (X) aan de hand van deze schematische voorstelling. A passeert een NOTpoort → wordt 1. Daarna komen A en B samen in een AND-poort:
• We verkrijgen enkel de uitvoer 1 als A = 0 en B = 1.
Merk op
Op je smartphone (of tablet) kan je apps installeren met puzzels in verband met zo’n circuits. Erg handig om dit in te oefenen!
Verwerkingsopdrachten
Is de samengestelde uitspraak een tautologie of een contradictie? Toon aan met behulp van een waarheidstabel.
a) ( p ∧ q) ∧ ( ¬p ∨¬q)
b) ( p ⇒ q) ∨ ( p ∧¬q)
Toon volgende eigenschappen aan met een waarheidstabel.
a)In woorden: De disjunctie is commutatief.
In symbolen:
Waarheidstabel:
b)In woorden: De conjunctie is distributief ten opzichte van de disjunctie.
In symbolen:
Waarheidstabel:
Bewijs met behulp van de logische wetten.
a) [¬(¬p ∧¬q)] ⇔ (p ∨ q)
INKIJKEXEMPLAARDIEKEURE
b) ¬(p ⇔ q) ⇔ [(p ∧¬q) ∨ (¬p ∧ q)]
Bepaal bij deze schakelingen de waarde van X voor de gegeven invoer. a)
1 b)
B = 0
A = 1 & X
C = 1
B = 0
A = 1 &
C = 1
D = 1
1
1 1 X
Signaaloefeningen
Gegeven:
p: Lisse streamt een serie.
q: Seppe kijkt voetbal.
a)Noteer in symbolen: “Lisse streamt een serie en Seppe kijkt geen voetbal.”
b)Wat betekent q ⇒ p?

c)Schrijf de negatie van de implicatie q ⇒ p in symbolen en omschrijf het in woorden.
In symbolen:
In woorden:
d)Wanneer is de uitspraak p ∨ q waar?
e)Wanneer is de uitspraak p ⇔ q waar?
a)Stel een waarheidstabel op voor (f ∨ g) ∧¬(f ∧ g).
b)Verklaar waarom deze uitdrukking gebruikt kan worden voor een exclusieve of.
Toon aan met een waarheidstabel dat onderstaande uitspraken gelijkwaardig zijn.
[p ∧ (q ∨ r)] ⇔ [(p ∧ q) ∨ (p ∧ r)]
>>> Verder oefenen: D1 t.e.m. D10
Toon aan door gebruik te maken van logische wetten: ¬(p ⇒ q) ⇔ (p ∧¬q)
INKIJKEXEMPLAARDIEKEURE
Verder oefenen: D11 t.e.m. D30 5
Toon aan door gebruik te maken van logische wetten dat ¬(p ∨¬(p ∧ q)) een contradictie is.
Verder oefenen: D11 t.e.m. D30
Toon aan dat p ⇒ q
wel
Bepaal bij deze schakelingen de waarde van X voor de gegeven invoer. a)
Logische operatoren en waarheidstabellen
Differentiatietraject
Plaats het begrip, het symbool en het verwante codeerbegrip in dezelfde kleur. equivalentie
2 3
Verbind de symbolen met de juiste zin.
Gegeven:
p: Romy speelt hockey.
q: Jules eet spaghetti.
r: Fenna is blij.
p
Het is niet waar dat Jules spaghetti eet of Romy hockey speelt.
Fenna is niet blij. p
p ∧ r r
p ∧ r r ∨ q
q ¬(q ∨ p)
¬(q ∨ p)
r p ∧ q ∧ r
Fenna is blij of Jules eet spaghetti. p ∧ r r ∨ q
¬(q ∨ p) r p ∧ q ∧ r
p ∨ (¬q ∧ r)
(¬q ∧ r)
p ∨ (¬q ∧ r)
Gegeven:
p: Ik ben een smurf.
q: Ik ben blauw.
r: Ik draag een witte muts.
Gevraagd: Formuleer de uitdrukking in woorden.
a) ¬q b) p ∨ r
c) (q ∧ r) ⇔ p
d) (p ∧ q) ∨ (¬p ∧ r)
e) ¬q ⇒¬p ∨ r
f) ¬(q ∨ r) ∧¬p
Romy speelt hockey of Jules eet geen spaghetti terwijl Fenna blij is.
Romy speelt hockey, Jules eet spaghetti en Fenna is blij.
● Romy speelt hockey en Fenna is blij.

©AlenKadr - stock.adobe.com
5 6
Gegeven:
p: Pablo is fan van Club Brugge.
q: Fleur draagt een blauwzwarte sjaal.
Gevraagd: Schrijf in symbolen.
a)Fleur draagt geen blauwzwarte sjaal.
b)Pablo is fan van Club Brugge en Fleur draagt een blauwzwarte sjaal.
c)Als Fleur een blauwzwarte sjaal draagt, dan is Pablo fan van Club Brugge.
d)Pablo is fan van Club Brugge of Fleur draagt een blauwzwarte sjaal.
e)Fleur draagt een blauwzwarte sjaal als en slechts als Pablo fan is van Club Brugge.
f) Pablo is fan van Club Brugge of Fleur draagt geen blauwzwarte sjaal.
Vul de waarheidstabellen aan.
Gegeven:
p: Joni slaagt voor het examen wiskunde.
q: Lino slaagt voor het examen wiskunde.
r: Malik slaagt voor het examen wiskunde.
Noteer de volgende uitspraken in symbolen.
a)Malik is de enige die slaagt voor het examen wiskunde.
b)Er is minstens één iemand geslaagd voor het examen wiskunde.
c)Slechts één van de drie slaagt voor het examen wiskunde.
d)Er zijn er hoogstens twee van de drie geslaagd voor het examen wiskunde.
e)Er zijn er precies twee van de drie geslaagd voor het examen wiskunde.
Gegeven:
p:∆ABCisrechthoekiginA.
q: |BC| isdelangstezijde.
r: |BC|2 = |AB|2 + |AC|2
a) Maak een waarheidtabel voor p ⇒ q
b) Wanneer is q ⇒ p waar?
c) Wanneer is ( p ∧ q) ⇔ r waar?
Bepaal de gebruikte proposities en noteer de zin in symbolen.
a)Als een vlakke figuur een vierhoek is, dan is de som van de hoeken 360°.
b)Een vierhoek is een rechthoek als en slechts als het een parallellogram is met even lange diagonalen.
c)De som van de cijfers is 3 of de som van de cijfers is 9.
d) a snijdt c, b snijdt c en de verwisselende binnenhoeken zijn niet even groot of a is evenwijdig met b.
a)Stel de waarheidstabel op voor (p ⇒ q) ⇔ [(q ⇒¬r) ⇒ (¬r ⇒ p)]
b)In welke situaties is deze uitspraak waar?
Gegeven:
p: De trui heeft de maat medium.
q: De jas heeft de maat small.
r: Het T-shirt heeft de maat large.
a)Zet om in symbolen: “Het is niet zo dat als de trui geen maat medium heeft, dat dan de jas de maat small heeft of het T-shirt geen maat large heeft.”
b)Maak een waarheidstabel. Je weet met zekerheid dat de uitspraak p waar is en de uitspraak r niet waar.
INKIJKEXEMPLAARDIEKEURE
Problemen oplossen
Is dit een tautologie of een contradictie? Verklaar je antwoord.
a) p ∧¬p
b) p ⇔ ¬(¬p)
c) p ∨¬p
d) p ⇔ ¬p
Bepaal de waarde van de uitvoer X in deze logische schakelingen.
a)
Gebruik een waarheidstabel om aan te tonen dat ( p ⇒ q) ∨ ( p ⇒¬q) een tautologie is.
Noteer de eigenschap in symbolen en toon de eigenschap aan met een waarheidstabel.
a)De conjunctie is commutatief.
b)De disjunctie is associatief.
Bepaal de waarde van de uitvoer X in deze logische schakelingen.
a)
= 1 &
= 0
1
= 0
= 1
= 1
17 18 19 20
a)Bewijs met een waarheidstabel dat [(p ⇒ q) ∧ p] ⇒ q altijd waar is.
We noemen deze eigenschap Modus ponens
b)Verklaar waarom volgende redenering correct is: “Als ik schuldig ben, dan word ik gestraft, bovendien ben ik schuldig. Ik word gestraft.”
a)Bewijs met een waarheidstabel dat [(p ⇒ q) ∧¬q] ⇒¬p altijd waar is.
We noemen deze eigenschap Modus tollens.
b)Verklaar waarom volgende redenering correct is: “Als een getal deelbaar is door 10, dan is het deelbaar door 2, bovendien is het getal oneven. Het getal is niet deelbaar door 10.”
Een leraar stelt een meerkeuzevraag met precies één juist antwoord (A, B of C). Sahar, Jasper en Lucie doen elk één uitspraak om je te helpen. Slechts één van deze leerlingen doet een ware uitspraak. Geef het juiste antwoord op de meerkeuzevraag.
A of B is het juiste antwoord.
B of C is het juiste antwoord.
A is het juiste antwoord.

Toon aan dat ( p ⇔ q) ∧ ( ¬p ∧ q) een contradictie is.
Bepaal de waarde van de uitvoer X in deze logische schakeling.
= 1
= 0
= 0
a) De uitspraak p ⇒ q is waar. In welk geval kan q niet waar zijn?
b) De uitspraak p ⇔ q is niet waar. Welke waarheidswaarde heeft q als p waar is?
c) Schrijf de uitspraak p ∨ q anders door gebruik te maken van een negatie en een conjunctie.
Toon aan.
a) p ∧ (p ∨ q) ⇔ p
b) [(p ⇒ q) ∧¬q] ⇒¬p
c) (p ∧ q) ⇒ p
d) ¬(p ⇔ q) ⇔ (p ⇔ ¬q)
INKIJKEXEMPLAARDIEKEURE
Toon de eigenschap aan met een waarheidstabel.
a) De transitiviteit van de implicatie: [(p ⇒ q) ∧ (q ⇒ r)] ⇒ (p ⇒ r)
b) De commutativiteit van de equivalentie: (p ⇔ q) ⇔ (q ⇔ p)
¬(p ⇒ r) ∨ q
¬(p ⇒ r) ∨ q
q ⇒ (p ⇒ r)
q ⇒ (p ⇒ r)
¬q ⇒ (r ∨¬p)
¬(p ⇒ r) ∨ q
¬(p ⇒ r) ∨ q
¬q ⇒ (r ∨¬p)
q ⇒ (p ⇒ r)
q ⇒ (p ⇒ r)
(¬p ⇒¬r) ∨ r
¬(p ⇒ r) ∨ q
q ⇒ (p ⇒ r)
¬(p ⇒ r) ∨ q q ⇒ (p ⇒ r)
Kleur de uitspraken die equivalent zijn met ¬(p ⇒ r) ∨ q q ⇒ (p ⇒ r)
. ¬(p ⇒ q) ⇒¬r
¬(p ⇒ r) ∨ q
q ⇒ (p ⇒ r)
¬q ⇒ (r ∨¬p)
(¬p ⇒¬r) ∨ r ¬q ⇒¬(p ⇒ r)
(¬r ∧ p) ∨ q
A = 1 & B = 0
¬(p ∧¬r) ∨¬q
C = 1
¬q ⇒ (¬p ⇒¬r)
D = 0
E = 1
F = 1
¬q ⇒ (r ∨¬p)
¬q ⇒ (r ∨¬p)
(¬p ⇒¬r) ∨ r
¬q ⇒¬(p ⇒ r)
(¬p ⇒¬r) ∨ r ¬q ⇒¬(p ⇒ r)
(¬r ∧ p) ∨ q
(¬r ∧ p) ∨ q
¬(p ∧¬r) ∨¬q
¬q ⇒ (r ∨¬p) (¬p ⇒¬r) ∨ r ¬q ⇒¬(p ⇒ r) (¬r ∧ p) ∨ q
¬(p ∧¬r) ∨¬q
¬q ⇒ (¬p ⇒¬r)
¬(p ∧¬r) ∨¬q
¬q ⇒ (¬p ⇒¬r)
¬q ⇒ (¬p ⇒¬r)
¬q ⇒ (r ∨¬p)
¬q ⇒ (r ∨¬p)
(¬p ⇒¬r) ∨ r
(¬p ⇒¬r) ∨ r
¬q ⇒¬(p ⇒ r)
¬q ⇒¬(p ⇒ r)
(¬r ∧ p) ∨ q
(¬r ∧ p) ∨ q
¬(p ∧¬r) ∨¬q
¬(p ∧¬r) ∨¬q
¬q ⇒ (¬p ⇒¬r)
¬q ⇒ (¬p ⇒¬r)
Bepaal de waarde van de uitvoer X in deze logische schakeling.
G = 1 X ⩾ 1 ⩾ 1 ⩾ 1
(¬p ⇒¬r) ∨ r ¬q ⇒¬(p ⇒ r)
¬q ⇒¬(p ⇒ r)
(¬r ∧ p) ∨ q
(¬r ∧ p) ∨ q
¬(p ∧¬r) ∨¬q
¬(p ∧¬r) ∨¬q
¬q ⇒ (¬p ⇒¬r)
¬q ⇒ (¬p ⇒¬r)
Drie koppeltjes spelen samen een spelletje Uno aan een ronde tafel.
• Mathilde zegt: “Ruben zat rechts van de vrouw die rechts zat van de man die rechts zat van Vicky.”
• Daphné zat rechts van de man die rechts zat van de vrouw die rechts zat van de man die rechts zat van de vrouw die rechts zat van de man van Mathilde.
• Björn zat rechts van de vrouw die rechts zat van Robin.
• Bovendien zat Mathilde niet naast haar man.
Hoe heet de man van Mathilde?

Arshad en Hans spelen een spelletje Tic Tac Toe.
Elke speler probeert om drie kruisjes of cirkels op één lijn te krijgen (ook diagonaal).
Ze houden volgende regels aan:
- Probeer altijd te winnen.
- Probeer te voorkomen dat de andere speler wint.
De eerste regel krijgt altijd voorrang op de tweede.
Hieronder zie je de situatie waarbij al zes zetten gedaan zijn en waarbij Arshad met kruisjes speelt. Merk op, we weten niet wie er begonnen is!
Wie zal het spelletje winnen? 00 0X XX
Toon aan:
a) (p ∧ q) ⇒ (p ∨ q)
b) ¬[p ∨ (¬p ∧¬q)] ⇔ (¬p ∧ q)
c) ¬[(p ∧ q) ∧ r] ⇔ [(p ∧ q) ⇒¬r]
d) [(p ⇒¬q) ∧ (r ⇒ q)] ⇒ (p ⇒¬r)
Bepaal de waarde van de mogelijke invoer in deze logische schakeling.
Computationeel denken
Logische operatoren
Zoals je weet wordt er in programmeren ook gebruik gemaakt van logische operatoren.
Toepassing 1: Booleaanse variabelen
a)Noteer onder de code wat de uitvoer is.
b)Welke logische operator wordt er gebruikt?
c)Wijzig indien nodig de code zodat de uitvoer TRUE is.



d)Waarom wordt er in onderstaande code geen False geprint? Welk logisch begrip kan je hier eigenlijk aan koppelen?

e)Welke uitvoer verkrijg je hier? Aan welk logisch begrip doet dat je denken?

Toepassing 2: Wachtwoorden

a)Beschrijf wat er gebeurt in deze code.
b)Van welke logische operator wordt hier gebruik gemaakt?
Toepassing 3: Getallen die voldoen aan een voorwaarde

a)Hoeveel getallen (en welke) worden er uitgevoerd?
b)Pas de code aan zodat de voorwaarde wordt: niet deelbaar door 2 en deelbaar door 3.
INKIJKEXEMPLAARDIEKEURE
c) Pas de code aan zodat de getallen tussen 15 en 30 liggen. Controleer op de voorwaarde deelbaar door 3 of niet door 6.

Beschrijf wat er gebeurt in deze code.
INKIJKEXEMPLAARDIEKEURE
Studiewijzer
Differentiatietraject
Doelen
Ik kan logische operatoren gebruiken en kan de waarheidswaarde van logische uitspraken bepalen met behulp van waarheidstabellen.
Ik kan problemen oplossen met logica.
Bijvoorbeeld:
• bepalen of een uitspraak een tautologie of contradictie is
• logische wetten toepassen en gebruiken om uitspraken te bewijzen
• werken met logische poorten
INKIJKEXEMPLAARDIEKEURE
Doelstellingen pagina in module pagina in vademecum
Ik kan logische operatoren gebruiken en kan de waarheidswaarde van logische uitspraken bepalen met behulp van waarheidstabellen. 5
Om sneller te werken, kan je in de waarheidstabel gebruik maken van 0 en 1. verwerking: 1, 2, 3, 4 signaal: 1, 2, 3 differentiatie: 1 t.e.m. 10
Ik kan problemen oplossen met logica.
Met de logische wetten kan je gemakkelijk een equivalentie aantonen. Twijfel je over het gebruik van een logische wet of over een eigenschap? Dan kan je deze altijd controleren met behulp van een waarheidstabel.
verwerking: 5, 6, 7, 8 signaal: 4, 5, 6, 7 differentiatie: 11 t.e.m. 30
12
Auteurs Philip Bogaert, Björn Carreyn en Roger Van Nieuwenhuyze
Eerste druk 2024 - SO 2024/0222 - Bestelnummer 94 606 0118 (module 01 van 17)
ISBN 978 90 4864 971 6 - KB D/2024/0147/204 - NUR 126/128/129 - Thema YPMF
Illustrator Jona Jamart - Design en lay-out die Keure
Verantwoordelijke uitgever die Keure, Kleine Pathoekeweg 3, 8000 Brugge
RPR 0405 108 325 - © Copyright die Keure, Brugge
