Sinus 2P Basis (LK20) (utdrag)

Sinus 2P

Foto og grafikk: Bildene er fargemanipulert.

Omslagsfoto: Unsplash/Adam Birkett

Kapittel 1: Adobe Stock/phpetruninal14

Kapittel 2: Getty Images/BrilliantEye

Kapittel 3: Adobe Stock/Andrey Popov

Kapittel 4: Adobe Stock/Andrey Popov

Kapittel 5: Adobe Stock/Sasho Bogoev

Kapittel 6: Unsplash/Joel Filipe

Side 29: NTB, side 152 og 169: Kart, Statens kartverk. Nordeca AS, tillatelsenummer 555819-2021

©

Sinus 2P BASIS følger læreplan i matematikk fellesfag 2P fra 2020 (LK20), for vg2 studieforberedende utdanningsprogram.

Materialet i denne publikasjonen er omfattet av åndsverklovens bestemmelser. Uten særskilt avtale med Cappelen Damm AS er enhver eksemplarfremstilling og tilgjengeliggjøring bare tillatt i den utstrekning det er hjemlet i lov eller tillatt gjennom avtale med Kopinor, interesseorgan for rettighetshavere til åndsverk. Utnyttelse i strid med lov eller avtale kan medføre erstatningsansvar og inndragning, og kan straffes med bøter eller fengsel.

Kilde til alle eksamensoppgaver er Utdanningsdirektoratet. Alle disse oppgavene er merket med årstall. De er gjengitt med tillatelse.

Grafisk formgiver: BØK/Cappelen Damm AS

Omslagsdesign:

Frihåndstegninger: Per Ragnar Møkleby

Tekniske tegninger: Terje Sundby, Keops

Redaktør: Bjørn-Terje Smestad

Sats: HAVE A BOOK, Polen 2023

Trykk og innbinding: Livonia Print, Latvia 2023

Utgave nr. 1

Opplag nr. 1

ISBN 978-82-02-69638-2

www.cdu.no

sinus.cdu.no

Cappelen Damm AS, Oslo 2023

Forord

Sinus er et matematikkverk utviklet etter læreplanene fra 2020. Boka Sinus 2P BASIS er en engangsbok for elever som trenger et enklere opplegg enn andre elever. Kapittelinndelingen er den samme som i Sinus 2P.

Boka legger vekt på å gi eleven en grunnleggende forståelse av matematikken. Teoridelen er kortfattet og lett å forstå. Framstillingen er visuell, og løsningsmetodene er konkrete og presenteres med enkle eksempler. Etter eksemplene kommer det enkle oppgaver, slik at elevene kan øve på det de har lært. Disse oppgavene løser elevene direkte i boka. Elevene får mye hjelp med oppgaveløsningen til å begynne med, og lærer gradvis å arbeide mer selvstendig. Hvert kapittel avsluttes med et sammendrag av reglene og metodene som er gjennomgått i kapitlet, og repetisjonsoppgaver.

Etter hvert kapittel finner elevene oppgaver i tre kategorier: «Øv mer», «Blandede oppgaver» og «Åpne oppgaver». «Øv mer» er innlæringsoppgaver ordnet etter delkapitlene i teoridelen. «Blandede oppgaver» inneholder nettopp blandede oppgaver i form av ulike tema og vanskelighetsgrad fra hele kapitlet . Her er det også tidligere gitte eksamensoppgaver. Det er satt inn merker som viser hvor langt i kapitlet eleven må ha kommet for å kunne løse de forskjellige oppgavene. De åpne oppgavene har vanligvis ingen fast løsningsmetode eller fasit og tar ofte utgangspunkt i en praktisk problemstilling. Her må elevene bruke sin kunnskap og forståelse på en ny og ofte kreativ måte.

Helt til slutt i boka kommer fasit til oppgavene og stikkordregister.

coSinus 2P kan supplementere Sinus 2P BASIS og være en til stor hjelp for å bygge en grunnmur i forståelsen av matematikk 2P. I coSinus finner læreren også verktøy som gjør det mulig å følge med på framdriften til elevene.

I arbeidet med å utvikle læremidler er det viktig å ha god kontakt med brukerne av boka, så vi vil gjerne ha tilbakemeldinger og innspill til forbedringer.

Egil Reidar Osnes – Otto Svorstøl – Einar Gustafsson – Tore Oldervoll

1 PROSENT

Mål for opplæringen er at eleven skal kunne

•forklare og bruke prosent, prosentpoeng og vekstfaktor til modellering av praktiske situasjoner med digitalt verktøy

REGEL

1.1 Prosentregning

Prosent betyr hundredel. Det betyr at 1 % er det samme som én hundredel av noe.

Vi finner 1 % av et tall ved å dele tallet på 100. Det kan vi bruke til å finne andre prosenttall.

1 % av 350 kr 350 kr 3,50 100 kr

4 % av 350 kr 4 3,50 kr 14 kr

EKSEMPEL

LØSNING

Finn 8 % av 600 kr ved å først regne ut 1 % av 600 kr. 600 kr 6 100 kr

EKSEMPEL

LØSNING

8 6 kr 48 kr

8 % av 600 kr er 48 kr.

Når vi bruker hjelpemidler, kan vi bruke denne regelen:

p % av tallet 100 p hele tallet

Hva er 36 % av 3280 kr?

Vi kan også regne slik:

1 % av 600 kr er 6 kr. REGEL REGEL

Noen ganger skal vi finne prosenten. Da regner vi ut andelen og ganger med 100 %. Andelen finner vi ved å dele delen av tallet med hele tallet. Vi får denne regelen:

andelen i prosent delen av tallet hele tallet 100 %

EKSEMPEL

LØSNING

Hvor mange prosent utgjør 123 kr av 3500 kr?

Når vi bruker CAS, gjør vi det slik:

OPPGAVE 1.10

a) Finn 7 % av 500 kr ved først å regne ut 1 %.

b) Finn 8 % av 250 kr ved først å regne ut 1 %.

a)Jeg finner først 1 % av 500 kr.

500 kr 100 = kr

Så finner jeg 7 % ved å gange svaret med 7.

7 % av 500 kr er kr = kr.

b)

OPPGAVE 1.11

a) Hva er 3 % av 1530 kr?

b) Hva er 22 % av 9500 kr?

c) Hva er 10,2 % av 1200 kr?

a)3 % av 1530 kr = 3 100 1530 kr =

b)22 % av 9500 kr = 100 9500 kr =

c)10,2 % av 1200 kr = 1200 kr =

OPPGAVE 1.12

a) Hvor mange prosent utgjør 12 av 300?

b) Hvor mange prosent utgjør 130 kr av 5000 kr?

c) Hvor mange prosent utgjør 15 biler av 86 biler?

a)12 av 300 = 12 300

b)130 kr av 5000 kr = kr 5000 kr

c)15 biler av 86 biler =

REGEL

1.2 Prosentpoeng

I ei avis kan vi lese at oppslutningen om et politisk parti har økt fra 6 % til 9 %. Da sier vi at oppslutningen har økt med 3 prosentpoeng fordi 9 6 3.

Når vi regner ut differansen mellom to prosenttall, finner vi endringen i prosentpoeng.

Når oppslutningen øker fra 6 % til 9 %, er økningen 3 prosentpoeng, men ikke 3 %. Økningen er halvparten av den opprinnelige oppslutningen, for 3 er halvparten av 6. Halvparten er det samme som 50 %. Økningen er altså på 50 %. Vi kan regne slik:

REGEL

Når vi kjenner endringen i prosentpoeng, finner vi den prosentvise endringen ved å regne endring i prosentpoeng 100 % opprinnelig verdi

EKSEMPEL LØSNING

Oppslutningen om partiet «Motvind» synker fra 16 % til 12 %.

a) Hva er endringen i prosentpoeng?

b) Hva er endringen i prosent?

a) 16 12 4

Partiets oppslutning går ned med 4 prosentpoeng.

b) Nedgangen er på 4 prosentpoeng. Utgangspunktet var 16 %. Da finner vi den prosentvise nedgangen slik: 41 100 %100 %25 % 164

Oppslutningen til partiet synker med 25 %.

EKSEMPEL LØSNING

Oppslutningen om partiet «Medvind» øker fra 10 % til 11,5 %.

a) Hva er endringen i prosentpoeng?

b) Hva er endringen i prosent?

a) 11,5 10 1,5

Partiets oppslutning har økt med 1,5 prosentpoeng.

b) Økningen er på 1,5 prosentpoeng. Den opprinnelige oppslutningen var 10 %. Da er endringen i prosent 1,5 100 %0,15100 %15 % 10

Partiets oppslutning har økt med 15 %.

OPPGAVE 1.20

I et land settes styringsrenta opp fra 2,5 % til 2,75 %.

a) Hva er endringen i prosentpoeng?

b) Hva er endringen i prosent?

a)Endringen i prosentpoeng er 2,75 - 2,5 =

b)Endring i prosent: endring i prosentpoeng opprinnelig verdi %

OPPGAVE 1.21

Emil fikk til 75 % av oppgavene på den første matteprøven og 60 % av oppgavene på den andre matteprøven.

a) Hva var forskjellen i prosentpoeng?

b) Den første prøven inneholdt 20 oppgaver, og den andre prøven inneholdt 25. Hvor mange oppgaver fikk han til på hver prøve?

a)Endring i prosentpoeng:

b)75 % av 20:

60 % av 25:

Emil fikk til av oppgavene på den første prøven, og av oppgavene på den andre.

OPPGAVE 1.22

Et parti fikk 8 % oppslutning i en kommune ved lokalvalget i 2019. I en meningsmåling i 2022 hadde partiets oppslutning økt til 25 %.

a) Hvor stor var økningen i prosentpoeng?

b) Jonas påstår at økningen er mer enn 200 %. Har han rett i det?

a)Økningen var prosentpoeng.

b)

REGEL REGEL

1.3 Vekstfaktor

Prisen på en vare øker med 20 %. Den opprinnelige prisen svarer til 100 %. Den nye prisen er da 120 % av den opprinnelige. 120

100 %20 %120 %1,20 100

Tallet 1,20 kaller vi vekstfaktoren ved 20 % økning.

Vekstfaktoren ved p % økning er

100 % p % 1 100 p

På samme måte finner vi vekstfaktoren ved 20 % nedgang slik: 80

100 % 20 %80 %0,80 100

Vekstfaktoren ved p % nedgang er

100 % p % 1 100 p

I begge tilfeller kan vi først regne i prosent og så dele på hundre. I praksis deler vi ofte på 100 ved å flytte komma to plasser til venstre.

EKSEMPEL

a) Finn vekstfaktoren ved 7,5 % økning.

b) Finn vekstfaktoren ved 11 % nedgang.

LØSNING

a) En økning på 7,5 % gir

100 %7,5 %107,5 % 1,075 Vekstfaktoren er 1,075.

b) En nedgang på 11 % gir

100 %11 %89 % 0,89 Vekstfaktoren er 0,89.

Dersom vi kjenner den opprinnelige verdien før en endring, og den nye verdien etter endringen, kan vi regne ut vekstfaktoren med regelen nedenfor. Vekstfaktoren kan vi bruke til å bestemme den prosentvise endringen.

REGEL

ny verdi vekstfaktor opprinnelig verdi

Maya setter 6500 kr i banken. Året etter har beløpet vokst til 6695 kr.

Hvor mange prosent har hun fått i rente dette året?

Her er den opprinnelige verdien 6500 kr og den nye verdien er 6695 kr. Da blir vekstfaktoren

3 6695 kr

vekstfaktor 6500 kr 1,0

Ettersom vekstfaktoren er 1,03 103 %, har beløpet økt med 3 %.

Maya har fått 3 % rente.

OPPGAVE 1.30

Finn vekstfaktoren når en størrelse øker med a) 12 % b) 85 % c) 1,5 % d) 0,75 %

a) Vekstfaktoren er 100 % + 12 % = 112 % = 1,12

b) Vekstfaktoren er 100%+ = =

c)Vekstfaktoren er

d) Vekstfaktoren er

OPPGAVE 1.31

Finn vekstfaktoren når en størrelse minker med a) 8 % b) 55 % c) 12,5 %

a)Vekstfaktoren er 100 % - 8 % = 92 % =

b)Vekstfaktoren er 100%- = =

c)Vekstfaktoren er

OPPGAVE 1.32

Prisen på ei bukse var opprinnelig 495 kr. Da det var salg, var prisen på buksa 346,50 kr.

a) Finn vekstfaktoren.

b) Hvor mange prosent rabatt var det på buksa da den var på salg?

a)Vekstfaktoren finner jeg slik:

b)

opprinnelig verdi = kr 495 kr = 34650 ,

ny verdi

Når vi skal finne en ny verdi etter en prosentvis endring, ganger vi den opprinnelige verdien med vekstfaktoren. Dette kan vi skrive som en regel.

ny verdi opprinnelig verdi vekstfaktor

EKSEMPEL

En kafé selger kanelboller, og en bolle koster 30 kr. Det blir bestemt at prisen skal settes ned med 20 %.

a) Finn den nye prisen på en bolle.

b) Før prisen ble satt ned, solgte de 220 boller hver dag. Etter prisendringen økte salget med 15 %.

Finn hvor mange boller de selger hver dag etter prisendringen.

LØSNING

a) Prisen settes ned med 20 %. Da blir vekstfaktoren

100 % 20 % 80 % 0,80

Den opprinnelige prisen var 30 kr. Da blir den nye prisen

30 kr  0,80 24 kr

b) Salget øker med 15 %. Da blir vekstfaktoren

100 % 15 % 115 % 1,15

Det ble opprinnelig solgt 220 boller hver dag. Da blir det nye salget 220 1,15 253

Noen ganger kjenner vi verdien etter en prosentvis endring, det vil si den nye verdien. Da finner vi den opprinnelige verdien ved å regne slik:

REGEL

ny verdi opprinnelig verdi vekstfaktor

EKSEMPEL

Prisen på ei jakke ble satt opp med 10 %. Den nye prisen var 1650 kr. Hva kostet jakka før prisstigningen?

LØSNING

Prisen settes opp med 10 %. Da blir vekstfaktoren

100 % 10 % 110 % 1,10

Da finner vi den opprinnelige prisen slik:

ny verdi1650 kr opprinnelig verdi1500 kr vekstfaktor1,10

OPPGAVE 1.33

Et busselskap selger reisekort som vist i tabellen nedenfor.

Pris

I uke 45 var det 20 % rabatt på alle reisekortene. Hva kostet hvert av kortene da?

Vekstfaktoren til 20 % rabatt er 100 % - 20 % = 80 % = 0,80.

Ny pris for et ukeskort er

Ny pris for et månedskort er

OPPGAVE 1.34

I tabellen nedenfor ser du hvor mange reisekort et busselskap solgte i uke 44, og hvor stor den prosentvise endringen mellom uke 44 og uke 45 var.

Hvor mange reisekort ble det solgt av hver type i uke 45?

Vekstfaktoren for 15 % nedgang er 100 % - 15 % = 85 % =

Antall solgte dagskort blir

Vekstfaktoren for 20 % økning er 100 % + % = % =

Antall solgte ukeskort blir

Vekstfaktoren for 32 % økning er

Antall solgte månedskort blir

OPPGAVE 1.35

Katten Båtsmann veide 4,5 kg sommeren 2023. Da hadde vekta økt med 25 % siden året før.

a) Finn vek stfaktoren.

b) Hva veide Båtsmann året før?

a) Vekstfaktoren er

b) opprinnelig verdi = ny verdi vekstfaktor = kg =

3 ØKONOMI

Mål for opplæringen er at eleven skal kunne

•utforske og forklare sammenhenger mellom prisindeks, kroneverdi, reallønn, nominell lønn og brutto- og nettoinntekt

•vurdere valg knyttet til personlig økonomi og reflektere over konsekvenser av å ta opp lån og å bruke kredittkort

REGEL

3.1 Prisindekser

Statistisk sentralbyrå samler inn statistikk over prisene på varer og tjenester vi kjøper. Tall som viser en prisutvikling, regner vi om til prisindekser. Da tar vi utgangspunkt i et basisår og setter indeksen til 100 dette året. I denne boka er 2015 basisår om ikke annet er sagt.

En prisindeks er proporsjonal med prisen. Dermed er forholdet mellom indeksen og prisen det samme til enhver tid.

Det gir denne regelen:

et året annet år indeksindeks prispris

EKSEMPEL LØSNING

I 2012 var utgiftene til matvarer for en gjennomsnittsfamilie 51 429 kr. I 2022 hadde utgiftene steget til 63 115 kr. Prisindeksen for matvarer i 2012 var 93,3.

Hva var prisindeksen for matvarer i 2022?

Vi setter opplysningene inn i en tabell.

Ut fra tabellen kan vi sette opp likningen

5 429 93,3 516311 x

Denne likningen løser vi i CAS.

Prisindeksen for matvarer var 114,5 i 2022.

EKSEMPEL LØSNING

År20122022

Indeks93,3 x Pris (kr)51 42963 115

En ny leilighet i Trondheim kostet 3 700 000 kr i basisåret 2015. I 2022 var boligprisindeksen i Trondheim 136,3.

Hva var verdien av leiligheten i 2022 dersom den fulgte utviklingen til boligprisindeksen?

Vi setter opplysningene inn i en tabell. Husk at indeksen i basisåret er 100.

Ut fra tabellen kan vi sette opp likningen

100136,3 3700000 x

Denne likningen løser vi i CAS.

Verdien var 5 043 100 kr i 2022.

År20152022

Indeks100136,3

Pris (kr)3 700 000 x

OPPGAVE 3.10

I 2021 var indeksen for matvarer 107,5. I 2012 var indeksen 93,3. En handlevogn med matvarer kostet 500 kr i 2012. Hva kostet matvarene i 2021?

Jeg fyller inn i tabellen til høyre.

Det gir likningen

933 500 , = x som jeg løser i CAS.

Matvarene kostet kr i 2021.

OPPGAVE 3.11

Tabellen til høyre viser indeksen for klær og skotøy for 2000 og 2021. I 2000 betalte Jorunn 1200 kr for ei bukse. Hva ville prisen vært for buksa i 2021 om den fulgte indeksen?

Jeg fyller inn i tabellen til høyre.

Det gir likningen = x som jeg løser i CAS.

Buksa kostet kr i 2021.

OPPGAVE 3.12

Prisen på sjokoladen «Snapp» var 15 kr i 2012. Prisen har siden fulgt prisindeksen for mat. Koble sammen riktig pris med riktig årstall ved å trekke piler.

REGEL

3.2 Konsumprisindeks

Hvis vi summerer alt som norske husholdninger bruker penger på, finner vi konsumet. Det omfatter alle de vanlige utgiftene vi har, både til varer og tjenester. Prisindeksen for dette forbruket kaller vi konsumprisindeksen. Ofte forkorter vi dette til KPI. Nedenfor ser du en tabell over konsumet og konsumprisindeksen for noen år.

Også her er 2015 basisåret, og konsumprisindeksen er da 100.

I 2021 var konsumprisindeksen 116,1. Bruk tall fra tabellen ovenfor og bestem konsumet i 2021.

Vi lager tabellen til høyre. Vi velger å bruke konsumet og konsumprisindeksen i basisåret 2015. Det gir denne likningen: 100116,1

463 799 x

Nå løser vi denne likningen i CAS og runder av svaret til hele kroner.

År 20152021 KPI 100116,1 Konsum (kr)463 799 x

Konsumet til en gjennomsnittlig norsk husholdning var 538 471 kr i 2021.

Ettersom konsumprisindeksen tar med alt vi bruker penger på, er indeksen et godt mål for hvor dyrt det er å leve i Norge. Når konsumprisindeksen et år er 108,4 betyr det for eksempel at prisene har økt med 8,4 % fra basisåret 2015.

Konsumprisindeksen beskriver utviklingen i prisnivået.

I 2009 var konsumprisindeksen 89,9. I 2022 hadde den økt til 122,8.

a) Med hvor mange prosent steg prisnivået fra basisåret 2015 til 2022?

b) Med hvor mange prosent steg prisnivået fra 2009 til 2022?

a) KPI i 2022 var 122,8. Det betyr at:

Prisnivået økte med 22,8 % fra basisåret 2015.

b) I kapittel 1 lærte vi at vekstfaktor ny verdi opprinnelig verdi .

KPI for 2022 er den nye verdien. Den opprinnelige verdien svarer til KPI i 2009. Det gir

En vekstfaktor lik 1,366 tilsvarer 136,6 %. Da er økningen 136,6 % – 100 % 36,6 %.

Prisnivået økte med 36,6 % fra 2009 til 2021.

OPPGAVE 3.20

I basisåret 2015 brukte norske husholdninger i gjennomsnitt 463 799 kr.

I 2011 brukte de i gjennomsnitt 432 724 kr.

Finn konsumprisindeksen i 2011.

Jeg fyller inn i tabellen. Det gir likningen som jeg løser i CAS.

KPI i 2011 var .

OPPGAVE 3.21

År 20112015

KPI x

Forbruk (kr)

Konsumprisindeksen i 2010 var 92,1. I 2020 var den 112,2.

a) Hvor mange prosent steg prisnivået fra 2010 til basisåret 2015?

b) I hvilken periode steg konsumprisindeksen prosentvis mest, fra 2010 til 2015 eller fra 2015 til 2020?

a) vekstfaktor= ny verdi opprinnelig verdi == 100

Den prosentvise økningen er .

b) KPI i 2020 var 112,2.

Prisnivået økte med % fra basisåret 2015.

KPI steg mest i perioden fra til .

OPPGAVE 3.22

Hvilke av påstandene nedenfor er sanne? Huk av for for de riktige påstandene, og stryk ut de påstandene som er feil.

Siden prisindeksen i 2021 var 121,1 så har prisene økt mellom 2015 og 2021.

Siden prisindeksen i 2021 var 121,1 så har prisene gått ned mellom 2015 og 2021.

Siden prisindeksen i 2012 var 93,9 så har prisnivået økt mellom 2012 og 2015.

Siden prisindeksen i 2012 var 93,9 så har prisnivået gått ned mellom 2012 og 2015.

Hvis konsumprisindeksen i 2030 blir 200, så har prisene doblet seg siden 2015.

REGEL

3.3 Kroneverdi og reallønn

I 2020 var kroneverdien 0,8913. Det som kostet 1 kr i 2020, ville ha kostet 0,8913 kr i 2015. Det som kostet 1000 kr i 2020, ville ha kostet 1000 0,8913 kr 891,30 kr i 2015.

Vi finner kroneverdien i 2020 ved å regne ut 100100 0,8913 KPI112,2

Vi finner kroneverdien i andre år på samme måte.

100 kroneverdien KPI

EKSEMPEL

I 2017 var konsumprisindeksen 105,5. Finn kroneverdien dette året.

LØSNING

100100 kroneverdien 0,9479 KPI105,5

I 2017 var kroneverdien 0,9479.

Det at pengene våre blir mindre verdt, får betydning for lønna vår. Dersom vi har samme lønn fra ett år til det neste, går lønna i realiteten ned fordi pengene er mindre verdt.

For å sammenlikne lønna mellom ulike år, må vi derfor ta hensyn til endringen i konsumprisindeksen. Lønna vi får, kalles nominell lønn. Lønna korrigert for endringen i konsumprisindeksen, kalles reallønn.

REGEL

reallønn = nominell lønn · kroneverdi

Det er reallønna som må øke dersom vi skal få bedre råd. Dersom vi får bedre råd, sier vi at vi får økt kjøpekraft.

EKSEMPEL LØSNING

Den nominelle lønna til Turid var 405 000 kr i 2015 og 420 000 kr i 2020.

Konsumprisindeksen var 112,2 i 2020.

Fikk Turid økt kjøpekraft fra 2015 til 2020?

Kroneverdien i basisåret 2015 er 1. Da er også den nominelle lønna lik reallønna.

Vi regner ut kroneverdien i 2020: 100100 kroneverdien 0,8913

KPI112,2

Så regner vi ut reallønna i 2020: reallønn i 2020 nominell lønn kroneverdi 420 000 kr 0,8913 374 346 kr

Reallønna i 2020 var lavere enn reallønna i 2015. Turid fikk redusert kjøpekraft.

OPPGAVE 3.30

Konsumprisindeksen i 2011 var 93,3.

Hva var kroneverdien i 2011?

kroneverdien = KPI == 100100

OPPGAVE 3.31

Kroneverdien i 2008 var 1,1364. Hva var konsumprisindeksen dette året?

Kroneverdien gir likningen: 1,1364 = 100 x Denne likningen løser jeg i CAS.

Konsumprisindeksen i 2008 var .

OPPGAVE 3.32

Reallønna til Tomas var 470 500 kr i 2015. I 2021 tjente han 520 000 kr.

Konsumprisindeksen i 2021 var 116,1.

Fikk Tomas økt eller redusert kjøpekraften fra 2015 til 2021?

Kroneverdien i 2021 var 100 = . = Kjøpekraften ble fra 2015 til 2021.

OPPGAVE 3.33

Vi kjenner følgende formler for kroneverdi og reallønn:

100

kroneverdien KPI reallønn nominell lønn kroneverdi

Hvis vi omgjør disse formlene, hvilke av formlene nedenfor kan vi da komme fram til? Huk av for riktige formler, og stryk ut de formlene som er feil.

100

KPI kroneverdi kroneverdi KPI100

inominelllønnrealøkronlneverd n reallønn nominelllønn kroneverdi reallønn

kroneverdi nominelllønn

EKSEMPEL LØSNING

3.4 Bruttolønn og nettolønn

Alt vi tjener før skatten trekkes fra, kaller vi bruttolønn. Lønna blir beregnet på ulike måter alt etter hvilken type stilling vi har, hva slags arbeid vi gjør, og når arbeidet blir utført. For eksempel får vi høyere lønn per time for overtidsarbeid enn for arbeid vi utfører i den vanlige arbeidstiden.

Kari har 27 000 kr i fast månedslønn. En måned arbeider hun i tillegg 8 timer overtid med ei timelønn på 200 kr.

Hva blir bruttolønna til Kari?

Vi regner ut lønna til Kari i et regneark slik: Med formler:

EKSEMPEL LØSNING

Jonas jobber som avisselger. Han tjener 150 kr per time og får 15 kr i tillegg for hver avis han selger. Ei uke jobber han 10 timer og selger 52 aviser.

Hvor mye får Jonas i bruttolønn?

Vi regner ut lønna til Jonas i et regneark slik: Med formler:

EKSEMPEL LØSNING

Helle skjærer torsketunger i vintersesongen. Hun får 80 kr per kg. I løpet av sesongen skjærer hun 1200 kg tunger.

Hvor mye får Helle i bruttolønn?

Vi regner ut lønna til Helle i et regneark slik: Med formler:

OPPGAVE 3.40

Ola tjener 180 kr per time og arbeider 37,5 timer per uke. For overtidsarbeid på søndager får han 100 % tillegg. Ei uke arbeider han 5 timer overtid på søndag i tillegg til vanlig arbeidstid. Hva blir bruttolønna til Ola denne uka?

Jeg lager en tabell over lønna

og hvor mange timer han

arbeider:

Formler/utregninger i cellene: B2: B7: B8: B9: Bruttolønna til Ola denne uka blir kr.

OPPGAVE 3.41

Tove har deltidsjobb som telefonselger. Hun har ei fast timelønn på 80 kr per time. I tillegg får hun 15 kr for hvert salg. Ei uke lagde hun denne oversikten over arbeidet sitt:

a) Lag et regneark som gir en oversikt over hvor mye Tove tjente denne uka.

b) Tove får tilbud om ny lønnsavtale. Med den nye avtalen skal hun få 40 kr per time og få mer per salg. Gi Tove råd om hun bør takke ja til den nye avtalen.

ArbeidstidAntall salg

Mandag17.00–21.0012

Onsdag18.00–21.0010

Torsdag18.00–20.304

Fredag17.30–20.458

Sum12,75 timer34

a) Formler i cellene: B7: B8: B9: Bruttolønna til Tove denne uka blir kr.

b) Lønn for arbeidstimer: kr

Provisjonslønna må være kr for at hun skal tjene like mye hvis antall salg er som før. Da må lønna per salg være kr.

EKSEMPEL

En del av det vi tjener, betaler vi inn til staten og kommunen som skatt. Det vi får utbetalt etter at skatten er trukket fra, kaller vi nettolønn. Lønnsslippen vår viser både bruttolønn, nettolønn og skattetrekket. Hvor mye skatt som skal trekkes, står på skattekortet vårt. Det fins tre typer skattekort: frikort, tabellkort og prosentkort.

Dersom du tjener mindre enn et bestemt beløp i løpet av et år, kan du få frikort. I 2023 var denne grensen 70 000 kr. Da betaler du ikke skatt, men om du tjener mer enn 70 000 kr, trekker arbeidsgiver 50 % av lønna som går over frikortgrensen.

Dersom du har en fast månedslønn, har du vanligvis tabellkort. Da finner arbeidsgiver hvor mye som skal trekkes, i en tabell. Det fins ulike tabeller, og hvilke av tabellene som brukes, er blant annet avhengig av hvor stor formue og gjeld du har. Nedenfor ser du utdrag av en slik tabell:

LØSNING

Gregor tjener 33 000 kr, og Helge tjener 37 500 kr. Begge har tabellkortet ovenfor.

a) Hva er nettolønna deres?

b) Hvor mange prosent blir hver av dem trukket i skatt ifølge tabellen?

c) Sammenlikn svarene i oppgave b. Kommenter.

a) Gregor: 33 000 kr 6311 kr 26 689 kr

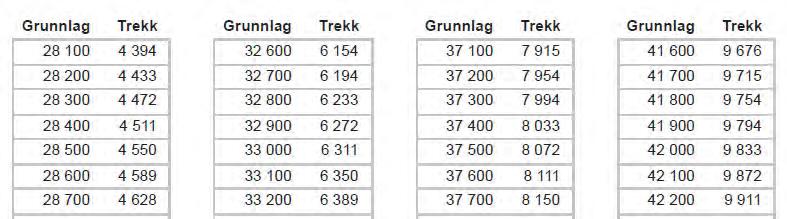
Helge: 37 500 kr 8072 kr 29 428 kr

b) Gregor: 6311 kr 0,19119,1 % 33 000 kr

Helge: 8072 kr 0,21521,5 % 37 500 kr

c) Vi ser at Helge som tjener mest, også blir trukket prosentvis mest i skatt.

Hvis lønna varierer fra måned til måned eller vi har flere arbeidsgivere, er det vanlig å bruke prosentkort. Da finner arbeidsgiveren ut hvor stort skattetrekket skal være, ved å regne ut en prosentandel av lønna. Dette beløpet rundes ned til nærmeste krone.

EKSEMPEL LØSNING

Julie har en deltidsjobb og bruker prosentkort. Prosentkortet viser at hun skal trekkes 18 % av det hun tjener. En måned tjener hun 29 000 kr. Hva er nettolønna til Julie denne måneden?

Skattetrekket er 0,18 29 000 kr 5220 kr

Da er nettolønna

29 000 kr 5220 kr 23 780 kr

OPPGAVE 3.42

Miriam har 37 300 kr i månedslønn. Det svarer til 200 kr per time. Hun får 40 % tillegg for over tidsarbeid på hverdager og 100 % tillegg for overtid på søndager. En måned arbeider hun 12 timer overtid på hverdager og 5 timer overtid på søndager i tillegg til vanlig arbeidstid. Hun bruker tabelltrekk på den faste månedslønna og trekker 35 % skatt på all annen lønn. Bruk tabellen på forrige side.

a) Hva er bruttolønna til Miriam denne måneden?

b) Hva er nettolønna?

Formler i cellene:

B2: B1 * 1,40

B3: * 2

B10:B2 *

B11: B12: B14: B15:

a) Bruttolønna til Miriam er kr.

b) Nettolønna til Miriam er kr.

OPPGAVE 3.43

Avgjør om påstandene nedenfor er riktige eller feil, og begrunn svaret.

a) Bruttolønna er alltid høyere enn nettolønna.

b) Bruttolønna kan være lik nettolønna.

c) I en skattetabell vil ei høyere lønn alltid gi et høyere trekk enn ei lavere lønn.

d) Et prosenttrekk på 35 % vil utgjøre mer enn et tabelltrekk på 8000 kr dersom månedslønna er 30 000 kr.

a)Påstanden er fordi

b)Påstanden er fordi

c)Påstanden er fordi

d)Påstanden er fordi