

Forord
Formelsamlingen for matematikkfagene 1P, 2P og 2P-Y er et praktisk oppslagsverk for både elever og lærere. Her finner du formler, tabeller, forklaringer og eksempler som gir god støtte i det daglige skolearbeidet og til eksamen.
Vi har slått sammen flere matematikkfag i én bok fordi det er stor overlapp mellom fagene. Her er en oversikt over hvilke fag de ulike kapitlene hører til. Dette er også markert på kapittelforsidene.
Matematikk 1P: kapittel 1, 2, 3 og 6
Matematikk 2P-Y: kapittel 1, 2, 3, 4 og 6
Matematikk 2P: kapittel 1, 2, 3, 4, 5 og 6
Formelsamlingen er designet slik at den skal være lett å navigere i, med stikkordsliste bakerst i boka og en innholdsfortegnelse øverst i høyre hjørne på hvert oppslag. Vi anbefaler likevel at du bruker den jevnlig og blir godt kjent med innholdet. Da finner du raskere det du trenger.
Til hvert kapittel og bakerst i boka er det også satt av plass til å skrive egne notater.
Lykke til med faget. Vi håper formelsamlingen vil være til stor hjelp.
Hilsen redaktørene, Ingrid Ertzgaard Bjørn-Terje Smestad
Innhold
Innhold
1 Tall og regning
2 Likninger, formler og geometri
Funksjoner og modellering
Tall og regning
1P | 2P | 2P-Y
1.1 Tall og tallsystemer
Plassverdisystemer
Tallmengder
Lister og intervaller
1.2 Symboler og tegn
Matematiske symboler
Geometriske symboler
Andre symboler
1.3 Grunnleggende regning
Aritmetikk
Regneregler
Negative tall
Regnerekkefølgen
1.4 Potenser og røtter
Potenser
Røtter
Standardform
Regning med potenser
1.5 Brøkregning
Brøk
Regneregler
Sum og differanse
1.6 Prosentregning
Prosent og promille
Prosentvis forskjell
Prosentpoeng
Vekstfaktor og prosentvis endring
1.7 Tallfølger og figurtall
Tallfølger
Figurtall
Sammensatte figurtall
Rekursive formler
1.5 Brøkregning
Brøk og regneregler
En brøk er et tall på formen a b
Brøkstreken er det samme som en delestrek.
Utvide
Vi utvider en brøk ved å gange med det samme tallet i teller og nevner. Verdien av brøken forblir uendret.
ac a bbc ⋅ = ⋅
Forkorte
Vi forkorter en brøk ved å dele på det samme tallet i teller og nevner. Verdien av brøken forblir uendret.
: : aac bbc =
Multiplikasjon
Når vi ganger to brøker, ganger vi teller med teller og nevner med nevner.
Hvis vi ganger en brøk med et helt tall, ganger vi det hele tallet inn i telleren.
Divisjon
Når vi har et regnestykke der divisoren er en brøk, kan vi snu brøken opp ned og bytte til multiplikasjon.
Sum og differanse
Brøker med felles nevner
Vi finner summen av to brøker med samme nevner ved å legge sammen tellerne. a bb cac b + + = a bb cac b −=
Brøker med ulik nevner
Først utvider vi brøkene slik at de får samme nevner. Så legger vi sammen. d
adcb ac cb bdbdd a bb d + +=+= ⋅⋅ d
adcb ac cb bdbdd a bb d ⋅⋅ −=−=
Eksempel: Brøk i praksis
Erik og de to søsknene hans skal dele en arv på 600 000 kr likt mellom seg. Erik fordeler sin del likt mellom de fire barna sine.
Hvor mye får hvert av barna til Erik?
Erik får
løsning
1.6 Prosentregning
Prosent og promille
Prosent
Prosent betyr «del av hundre». 100 % er lik hele.
Promille
Promille betyr «del av tusen».
Prosentandel
Finne prosenten delen prosent totalen =
24 av 30 personer stemte ved et valg.
80 % stemte ved valget. prosent = delen totalen ______ = = 0,8 = 80 % 30 24
Prosentvis forskjell
Finne delen delen = prosent totalen
35 % av 20 elever tar bussen til skolen. delen = prosent · totalen = 0,35 · 20 = 7 = 35 % · 20
7 elever tar bussen.
Vi kan regne ut den prosentvise forskjellen mellom to tall med formelen forskjell prosentvis forskjell sammenlikningsverdi =
Tallet vi deler på, gir verdien vi sammenlikner med.
Finne totalen delen totalen prosent =
12 hus er 60 % av alle husene i en gate.
Det er totalt 20 hus. totalen = delen prosent === 20 0,6 12 60
I en butikk koster en brus 20 kr. På bensinstasjonen koster den 50 kr.
50 - 20 50 =
Brusen er 60 % billigere på butikken enn på bensinstasjonen.
50 - 20 20 30 20 = = 1,5 = 150 %
Brusen er 150 % dyrere på bensinstasjonen enn på butikken. = 0,6 = 60 %
Prosentpoeng
Prosentpoeng er differansen mellom to prosenttall. Vi bruker prosentpoeng til å beskrive forskjellen mellom to prosenttall.
Vekstfaktor
Vekstfaktoren ved p % endring er gitt ved:
1 100 p ±
Vi bruker pluss ved økning og minus ved nedgang.
Prosentvis endring
Finne ny verdi
ny = gammel ⋅ vekstfaktor
Før kostet en telefon 9890 kr.
Prisen har sunket med 36,4 %. = 9890 kr 0,636 = 6290 kr = gammel vekstfaktor ny
Nå koster telefonen 6290 kr.
Prosent og promille Prosentvis forskjell Prosentpoeng Vekstfaktor og prosentvis endring
Lånerenten øker fra 4,8 % til 5,4 %. Økningen i prosentpoeng:
Vekstfaktoren ved 14 % økning:
100 = 1 + 0,14 = 1,14 14 1 +
100 = 1 - 0,35 = 0,65 35 1 -
Finne gammel verdi ny gammel vekstfaktor = I fjor kostet billetten 36 kr.
En billett koster 42 kr. Verdien har økt med 16,7 % siden i fjor. gammel = 36 kr 42 kr 1,167 = ny vekstfaktor =
Prosentvis endring over flere perioder
Ved prosentvis endring over flere perioder kan vi regne ut vekstfaktoren for hele perioden slik: vekstfaktor = v1 ⋅ v2 ⋅ … ⋅ v n der v1, v2, , v n er vekstfaktoren i hver periode. 5,4 – 4,8 = 0,6 prosentpoeng
Finne vekstfaktor ny vekstfaktor gammel =
Prisen på en pakke ost har økt fra 11 kr til 26 kr. vekstfaktor
Vekstfaktoren er 2,36. Prisen har økt med 136 %. = 2,36 = 26 kr 11 kr = ny gammel
Prisen på en vare blir satt ned med 15 %, så satt opp med 5 % og til slutt satt opp med 10 %. Vi finner vekstfaktoren for perioden.
Vekstfaktoren ved 35 % nedgang: v1 . v2 . v3 = 0,85 . 1,05 . 1,10 = 0,98
Vekstfaktoren for hele perioden er 0,98. Det tilsvarer en nedgang på 2 %.
2.4 Måleenheter
Prefikser
n nano 10–9 milliarddel h hekto 102 hundre
μ mikro 10–6 milliondel k kilo 103 tusen
m milli 10–3 tusendel M mega 106 million
c centi 10–2 hundredel G giga 109 milliard
d desi 10–1 tidel T tera 1012 billion
Vanlige måleenheter
Masse (vekt)
kg kilogram, standardenhet for masse 600 g = 0,6 kg
Strekning (lengde)
m meter, standardenhet for strekning 176 cm = 1,76 m mil mil, 1 mil = 10 km = 10 000 m 8000 m = 8 km = 0,8 mil
Tid
s sekund, standardenhet for tid 120 s = 2 min
min minutt, 1 min = 60 s 2 min og 24 s = (120 + 24) s = 144 s h time (hour), 1 time = 60 min = 3600 s 1 time og 45 min = (60 + 45) min = 105 min
Fart (hastighet)
m/s meter per sekund 10 m/s = 10 ⋅ 3,6 km/h = 36 km/h
km/h kilometer per time, 3,6 km/h = 1 m/s 72 km/h = 72 : 3,6 m/s = 20 m/s
Temperatur
K kelvin, standardenhet for temperatur
Temperaturen –273 °C = 0 K
°C celsiusgrader Temperaturen 0 °C = 273 K
Elektrisitet (spenning, strøm, motstand og effekt)
V volt, måleenhet for spenning
A ampere, måleenhet for strøm
Ω ohm, måleenhet for resistans (motstand) 1 VA = 1 W
W watt, J/s, måleenhet for effekt 230 V 7 A = 1610 W
Energi
J joule
kWh kilowattime, 1 kWh = 3 600 000 J 1000 W i 1 time = 1 kWh
kcal kilokalori, 1 kcal = 4184 J 1 kcal = 4,184 kJ
Prefikser
Vanlige måleenheter
Areal- og volummål Omgjøring mellom størrelser
Areal- og volummål
Areal (flatemål)
m2 kvadratmeter
cm2 kvadratcentimeter
km2 kvadratkilometer
Volum (hulmål)
m3 kubikkmeter
cm3 kubikkcentimeter
L liter, 1 L = 1 dm3
Omgjøring mellom ulike størrelser
Mellom m/s og km/h m/s · 3,6 : 3,6 km/h
4 m/s = 4 . 3,6 km/h
90 km/h = 90 : 3,6 m/s = 14,4 km/h = 25 m/s Fra m2 til km2 1500 m2 = 1500 : 1 000 000 km2 = 1500 : ( 1000 1000 ) km2 1,5 103 = 1,5 10-3 km2 = 0,0015 km2 106 km2 = Fra cm3 til cL
Eksempel: Regning med tid
I en gymtime krysser en elev målstreken på 3000 meter etter 12 minutter og 30 sekunder.
Eleven løper 500 meter til med samme jevne fart.
Hvor lang tid bruker eleven på 3500 m?
Vi gjør om tiden eleven bruker på 3000 meter til sekunder:
12 min + 30 s = (12 60 + 30) s = 750 s
Så finner vi tiden per 500 meter. Siden 3000 m : 500 m = 6, deler vi tiden på 6:
750 s
6
Vi legger dette til tiden for 3000 meter:
12 min 30 s + 2 min 5 s = 125 s = 2 min 5 s
= 14 min og 35 s
4.1 Begreper og tabeller
Sentrale begreper
Et datamateriale er en samling av opplysninger fra en måling som er gjort.
En observasjon er én måling i datamaterialet og består av minst én observasjonsverdi.
Frekvens
Frekvensen er hyppigheten til en observasjon. Den forteller hvor mange ganger en observasjonsverdi forekommer.
Frekvenstabell
En frekvenstabell viser frekvensen til de ulike observasjonsverdiene.
Summen av alle frekvensene er antall observasjoner, ofte kalt n
Nedenfor ser du resultatene fra en spørreundersøkelse gjennomført ved en skole.
Framkomstmiddel Antall elever
Tar buss
Sykler Går 13 7 10
30 Sum:
Frekvenstabell
Frekvensen for "Sykler" er 13. Det betyr at 13 elever sykler til skolen.
Antall observasjoner er 30. Det betyr at 30 elever deltok i spørreundersøkelsen.
Relativ frekvens
Relativ frekvens er frekvensen delt på antall observasjoner n.
= frekvens relativ frekvens n
Den relative frekvensen forteller oss hvor vanlig en observasjonsverdi er, og oppgis ofte i prosent.
Kumulativ frekvens
Kumulativ frekvens er den sammenlagte frekvensen til alle verdiene som er mindre enn eller lik den aktuelle observasjonsverdien.
13 av 30 elever sykler til skolen. Den relative frekvensen er
13
30 = 0,43 = 43 %
Det betyr at 43 % sykler til skolen.
Jens noterer hvor mange treningsøkter han har hver uke et helt år.
FrekvensKumulativ frekvens
31 11 1
49 18 2
52 3 3
Den kumulative frekvensen for 1 økt er 31. Det betyr at han hadde 1 eller færre treningsøkter 31 uker i løpet av det året. Økter 020 20
Relativ kumulativ frekvens
Relativ kumulativ frekvens er den kumulative frekvensen delt på antall observasjoner n = kumulativ frekvens relativ kumulativ frekvens n
Den relative kumulative frekvensen forteller oss hvor stor andel som har denne observasjonsverdien eller lavere.
Frekvens og frekvenstabell
Relativ frekvens
Kumulativ frekvens
Relativ kumulativ frekvens
Jens noterer hvor mange treningsøkter han har hver uke et helt år.
frekvens
Den relative kumulative frekvensen for 2 sier hvor stor andel av ukene han trente 2 eller færre ganger.
= 0,9423 = 94 %
Eksempel: Frekvens, relativ frekvens og kumulativ frekvens
Jorunn skriver ned antall dansetimer hun tar hver måned et helt år: 4, 8, 16, 8, 12, 4, 8, 4, 8, 8, 12, 0
a) Sorter dataene i en frekvenstabell. Utvid tabellen med relativ frekvens, kumulativ frekvens og relativ kumulativ frekvens.
b) Hvor mange måneder tok Jorunn nøyaktig 4 dansetimer?
c) Hvor mange måneder tok Jorunn 12 eller færre dansetimer?
d) Hvor mange prosent av året tok Jorunn mer enn 8 dansetimer?
a)
Relativ kumulativ frekvens Relativ frekvens
0,083 = 8,3 %
= 0,33 = 33 %
= 0,75 = 75 %
= 0,92 = 92 %
= 0,083 = 8,3 %
b) Frekvensen til 4 månedlige dansetimer er 3.
Jorunn tok nøyaktig 4 dansetimer 3 måneder i løpet av året.
c) Den kumulative frekvensen til 12 månedlige dansetimer er 11.
Hun tok 12 eller færre dansetimer 11 måneder i løpet av året.
= 1,0 = 100 %
d) Den relative kumulative frekvensen til 8 månedlige dansetimer er 0,75.
Det betyr at hun tok 8 eller færre dansetimer 75 % av året. Da må hun ha tatt mer enn 8 dansetimer 100 % - 75 % = 25 % av året.
5.5 Renter og lån
Begreper
Gjeld
Gjeld er det vi skylder banken. Når vi betaler avdrag, blir gjelden mindre.
Avdrag
Avdrag er det vi betaler til banken som går til nedbetaling av gjelden.
Renter
Renter er det vi må betale for å låne penger av banken. Rentene gir banken inntekter.
Terminbeløp
Nedbetalingsplan
Serielån over 5 år, med én termin per år. Fast rente 5 % per år.
Termin
Terminbeløpet er summen av renter og avdrag vi betaler til banken hver betalingsperiode (termin). Det er vanlig med 1, 4 eller 12 terminer per år.
terminbeløp = renter + avdrag
Serie- og annuitetslån
Serielån
For et serielån er avdragene like store og gitt ved lnesum avdrag antall terminer å =
Avdraget er konstant, mens rentene avtar. Terminbeløpet avtar over tid.
Annuitetslån
For et annuitetslån er alle terminbeløpene like store. Siden terminbeløpet er summen av renter og avdrag, vil rentene avta over tid, mens avdraget øker.
Gjeld Terminbeløp Avdrag Renter
Begreper Serielån
Annuitetslån Kredittkort
Kredittkort
Når vi betaler med bankkort i butikken, bruker vi enten debetkort eller kredittkort.
Debetkortet er direkte knyttet til bankkontoen, slik at et beløp vil bli trukket derfra. Ved betaling med kredittkort låner vi derimot penger, og betaler tilbake etter en viss tid.
Kredittkort har ofte veldig høy rente. Kredittkortselskapene tjener penger på folk som ikke betaler beløpet tilbake innen en frist.
Kredittkortrenten oppgis noen ganger per måned.
Vekstfaktoren til 1,8 % økning er 1,018.
Siden et år har 12 måneder, er den årlige renten gitt ved vekstfaktoren
Et kredittkort har en månedlig rente lik 1,8 %. Vi regner ut den årlige renten. 1,01812 = 1,239
Den årlige renten er 23,9 %.
Eksempel: Nedbetaling av annuitetslån
Solveig har tatt opp et boliglån på 1 750 000 kroner. Nedbetalingen er fordelt på 12 terminer i året, altså betaler hun ned på lånet én gang i måneden. Den månedlige renten er på 0,43 %. I tillegg må hun betale et gebyr på 60 kr per termin. Terminbeløpet er på 10 394 kr.
Lag en oversikt som viser hvor stort lånet vil være hver måned det første året. Hva er restlånet etter ett år?
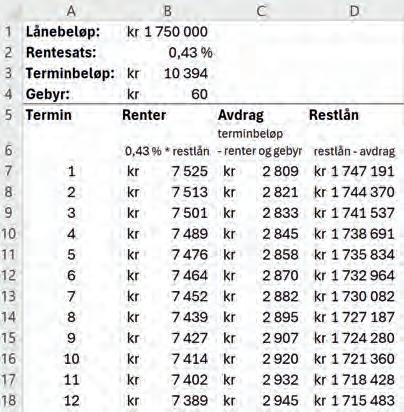

Etter ett år, eller 12 måneder, er restlånet 1 715 483 kr.
6.3 Løkker
While-løkker
While-løkker gjentar en kodeblokk så lenge en betingelse er sann.
Vi lager en while-løkke slik:
while <betingelse>: <kodeblokk som gjentas>
Vi kan tenke på en while-løkke slik: «så lenge <noe er sant>»: «<gjør dette>»
For-løkker
verdi = 300 år = 0
while verdi >= 150:
verdi = verdi*0.95 år += 1
print(år)
Programmet skriver ut antall år det går før verdien 300 er halvert til 150, når den minker med 5 % hvert år.
For-løkker gjentar kodeblokka et bestemt antall ganger. Hvis vi på forhånd vet hvor mange ganger vi vil gjenta en kodeblokk, er det ofte lettest å bruke en for-løkke.
Ved å gå gjennom en liste
Vi kan bruke en for-løkke for å utføre samme operasjon for alle elementene i en liste slik: for element in liste: <kodeblokk som gjentas>
Ved å bruke range(n)
Vi gjentar en for-løkke n ganger ved å bruke range(n). Da lager vi for-løkken slik: for i in range(n): <kodeblokk som gjentas>
Ved å bruke range(start, slutt)
Når vi ønsker en liste fra og med en startverdi til en sluttverdi, bruker vi for-løkken slik: for i in range(start, slutt):
<kodeblokk som gjentas>
Ved å bruke range(start, slutt, steg)
Hvis vi ønsker en annen steglengde enn 1, bruker vi for-løkken slik:
for i in range(start, slutt, steg):
<kodeblokk som gjentas>
navneliste = ["Ane", "Bea", "Carl", "Dave"] for navn in navneliste: print(navn)
I programmet bruker vi en for-løkke til å skrive ut navnene i lista.
for i in range(5):
print(i**2)
Koden skriver ut kvadrattallene 0, 1, 4, 9 og 16. Merk at range(5) gir oss de fem tallene fra og med 0 til, men ikke med, 5.
a = 0
for i in range(1, 11):
a = a + i
print(a)
I programmet bruker vi en for-løkke for å summere alle tallene fra 1 til 10. Programmet skriver ut summen 55.
for i in range(0, 101, 20):
print(i)
I programmet bruker vi en for-løkke med steglengde 20 for å skrive ut hvert tjuende tall fra og med 0 til og med 100. Utskriften blir 0, 20, 40, 60, 80 og 100.
While-løkker For-løkker Programmering med figurtall
Programmering med figurtall
Programmering kan være nyttig når vi jobber med figurtall, spesielt hvis vi kjenner sammenhengen mellom en figur og den neste.
Bestemme figurtall nummer n
Hvis vi skal finne det n-te figurtallet eller lage en liste over de n første figurtallene, er det enklest å bruke en for-løkke.
Finne maksimalt antall figurer
Hvis vi skal finne ut hvilket figurnummer som passer til en begrensning, som for eksempel at vi skal finne ut hvor mange figurer vi kan lage med et begrenset antall brikker, bruker vi en while-løkke. Den stopper når vi har nådd grensen.
Eksempel: Løkker og figurtall
Tenk deg at du skal lage figurer etter samme mønster som vist til høyre. Hver figur består av tre flere brikker enn den forrige figuren.
a)Lag et program som skriver ut hvor mange brikker det er i hver av de fem første figurene.
b)Du har 500 brikker og vil lage en figur i hver størrelse fra F1 og oppover. Hvor mange figurer kan du lage?
a)Vi bruker en for-løkke til å regne og skrive ut figurnummer n og figurtallet F
1 F = 7
2 n = 5
3 for n in range(1, n+1): #vi skriver n+1 for å få med fig nr. 5
4 print(n, F)
5 F = F + 3 #hver figur er 3 større enn forrige
Vi bruker en while-løkke til å summere alle figurtallene. Løkken stopper når summen overstiger 500. b)
1 n = 1
2 F = 7
3 sum = 7
4 while sum <= 500:
5 F = F + 3
6 sum = sum + F
7 n = n + 1
8 print(n, sum)
Vi kan ikke lage figur nummer 17 eller høyere. Med 500 brikker kan vi lage 16 figurer.
