HO_Algemene Economie 2025_voorbeeldhoofdstuk

3

Consumentengedrag en de afleiding van de vraag

Inleiding

In het vorige hoofdstuk bestudeerden we hoe de interactie tussen vraag en aanbod de prijzen bepaalt op competitieve markten. In dit hoofdstuk gaan we dieper in op de achtergrond van de vraag. De marktvraag naar een product komt immers tot stand als resultaat van individuele beslissingen van een zeer groot aantal consumenten. We onderzoeken in dit hoofdstuk dan ook de keuzeproblematiek waarmee het individu als consument geconfronteerd wordt, en leiden daaruit de individuele vraag van de consument af naar verschillende goederen afhankelijk van zijn preferenties, van de prijzen van diverse goederen, van het budget dat de consument beschikbaar heeft enz. Het aggregeren van al deze individuele vraagfuncties naar een bepaald product resulteert dan in de marktvraag die in het vorige hoofdstuk uitgebreid aan bod kwam.

Het keuzeprobleem van de consument wordt zeer eenvoudig benaderd. Stel dat een consument beschikt over een bepaald budget (y) dat hij kan besteden aan een gamma van n goederen, waarvan de prijzen worden voorgesteld door (p1, p2, …, pn). Hoe zal hij dit budget besteden indien hij een maximale voldoening wil realiseren uit de geconsumeerde goederenbundel? Het is dit probleem dat in dit hoofdstuk uitgebreid wordt bestudeerd. Merk op dat het hier gaat om een typevoorbeeld van een ‘economisch probleem’: het is inderdaad een keuzeprobleem waarbij schaarse middelen (in dit geval het beschikbare budget) met alternatieve aanwendingsmogelijkheden (diverse mogelijke consumptiebundels) op een optimale manier worden ingezet.

Een degelijk inzicht in de consumptiebeslissingen van individuen is essentieel om verschillende redenen. Ten eerste leidt de analyse van individueel gedrag zoals reeds gesteld tot vraagfuncties van individuele consumenten naar diverse goederen. Die vormen de onderbouw van de marktvraagcurve. De theorie van het consumentengedrag levert m.a.w. de theoretische fundering voor het verloop van de vraagcurve op een markt. Empirisch onderzoek leert bijvoorbeeld dat de gevraagde hoeveelheid van een bepaald goed doorgaans stijgt wanneer de prijs daalt. Deze ‘wet van de vraag’ werd eerder al aangeraakt, en we zullen zien dat hij theoretisch wordt onderbouwd door de analyse van het consumentengedrag.

Ten tweede biedt de micro-economische theorie van consumptie een algemeen raamwerk dat toelaat beslissingen van rationele consumenten te verklaren en te voorspellen. Wat is de precieze rol van preferenties, inkomens en prijzen in de verklaring van waargenomen

consumptiebundels van verschillende gezinstypes? Hoe reageren rationele consumenten op prijswijzigingen, op budgetveranderingen enz.? Wat is de invloed van overheidsmaatregelen zoals indirecte belastingen en subsidies, rantsoenering van goederen, of het gratis ter beschikking stellen van minimale consumptiehoeveelheden van bepaalde goederen? Wat zullen bijvoorbeeld de gevolgen zijn van het ter beschikking stellen van een gegeven hoeveelheid gratis elektriciteit, van de subsidiëring van het openbaar vervoer, van een toename van de belastingen op huisvuil, van een daling in de registratierechten op woningen, van het verhogen van de remgelden in de gezondheidszorg?

Ten derde is het aangereikte raamwerk niet alleen geschikt om te bestuderen hoe een gegeven budget optimaal kan worden besteed aan verschillende goederen. De theorie maakt het mits enkele eenvoudige aanpassingen ook mogelijk andere uiteenlopende beslissingen te analyseren, zoals de keuze tussen verschillende merken binnen een bepaald marktsegment, de keuze tussen een benzine-, diesel- of elektrische wagen, de beslissing een woning te kopen of te huren, de keuze zich al dan niet aan te bieden op de arbeidsmarkt en het bepalen van het aantal gewenste arbeidsuren, de keuze met de auto of de trein naar het werk te rijden, hoeveel men wil lenen of sparen enz.

Ten slotte is de analyse van het consumentengedrag ook een belangrijke bouwsteen voor de macro-economische analyse die verder in dit boek aan bod komt. Zo geeft de theorie van het consumentengedrag een beter inzicht in de micro-economische fundering van de macro-economische consumptie- en spaarfunctie, die een centrale rol vervullen in de macro-economische evenwichtsanalyse. Door aggregatie kan de macro-economische consumptiefunctie uit het micro-economische consumentengedrag afgeleid worden.

Een belangrijke onderliggende veronderstelling in dit hoofdstuk is dat consumenten rationele, weloverwogen beslissingen nemen. We wezen er in het inleidende hoofdstuk ‘Wat is economie?’ al op dat zowel economen als psychologen hebben aangetoond dat dit zeker niet altijd het geval is. Dat heeft geleid tot de ‘gedragseconomie’ (behavioral economics) waarin onder meer theorieën van ‘beperkte’ rationaliteit worden uitgewerkt. Ze vallen buiten het bestek van dit inleidende handboek, maar omdat ze in de recente theorievorming toch wel aan belang winnen, komen we er kort op terug in punt 9 aan het eind van dit hoofdstuk.

De opbouw van dit hoofdstuk is als volgt. We introduceren eerst enkele cruciale begrippen aan de hand van een kort, en uiteraard onvolledig, historisch overzicht rond het denken over consumptiebeslissingen. Daarna gaan we achtereenvolgens in op de wijze waarop de moderne theorie preferenties van consumenten tracht te beschrijven, en we bekijken de rol van het beschikbare budget. Vervolgens analyseren we het optimaal gedrag van de consument, en we voorspellen de reactie wanneer wijzigingen optreden in preferenties, in het beschikbaar budget, of in de prijzen van een of meer goederen. We tonen expliciet aan hoe het gedrag van de consument aanleiding geeft tot individuele vraagfuncties naar diverse goederen. Verder geven we aan hoe de marktvraagcurve de resultante is van de individuele vraagcurven van een groot aantal consumenten. Ten slotte komen we terug op de impliciete veronderstelling van rationeel gedrag.

Toepassing 1. De gemiddelde gezinsuitgaven in 2022

De huishoudbudgetenquête, een enquête waarbij een representatieve steekproef van de Belgische huishoudens uitgaven registreert binnen verschillende budgetposten, geeft een goed beeld van het consumptieprofiel van de Belgische gezinnen. Figuur 1 toont het resultaat voor 2022 voor het gemiddelde Belgische gezin. De woning (huur of fictieve huur voor eigenaars, onderhoud, verwarming, verlichting en water) vormt de belangrijkste uitgavenpost, goed voor 12 353 euro of zowat een derde van alle uitgaven. Op de tweede plaats komen voeding, dranken en tabak met gemiddelde uitgaven van nagenoeg 6 360 euro. De relatieve aandelen van deze twee categorieën waren tijdens het covidjaar 2020 licht toegenomen, en zijn in 2022 opnieuw gedaald tot het pre-covidniveau. De tegenovergestelde evolutie geldt voor de bedragen besteed aan vervoer en communicatie en cultuur, ontspanning en onderwijs. De totale uitgaven per huishouden zijn in 2022 fors toegenomen met 5 000 euro tot iets meer dan 40 000 euro.

Aangezien ook het inkomen van de gezinnen opgevraagd wordt, kunnen de consumptieprofielen eveneens vergeleken worden tussen de inkomensgroepen. Figuur 2 beschrijft de aandelen van de verschillende goederencategorieën per inkomenskwartiel. De gezinnen zijn hier gerangschikt van laagste gezinsinkomen naar hoogste gezinsinkomen; elk kwartiel bevat dan 25 % van de gezinnen. We stellen vast dat het relatief gewicht van woonuitgaven sterk varieert volgens het inkomen: in het laagste kwartiel spendeert het gezin 38 % van het consumptiebudget aan wonen en dit neemt geleidelijk af tot het hoogste kwartiel, waar men slechts 26 % spendeert. Een tegengestelde tendens ziet men voor de uitgaven voor cultuur, ontspanning en onderwijs waar het aandeel stijgt van 11 % naar 19 % van kwartiel 1 naar 4. In paragraaf 6.2 van dit hoofdstuk zullen we aantonen dat dit samenhangt met de inkomenselasticiteit van het goed.

Figuur 1 Gemiddelde uitgaven per huishouden in 2022 in euro

PERSOONLIJKE VERZORGING EN DIENSTEN ; 4 109

CULTUUR, ONTSPANNING EN ONDERWIJS ; 6 050

VERVOER EN COMMUNICATIE; 5 503

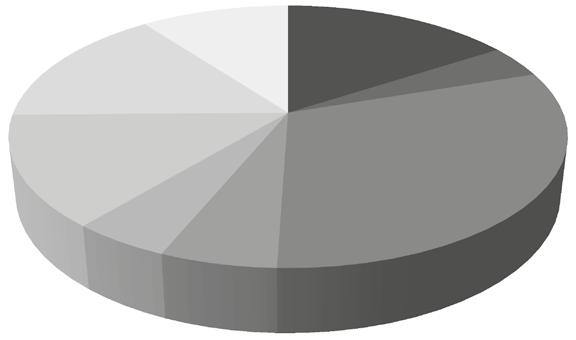
GEZONDHEID; 1 803

VOEDING, DRANKEN EN TABAK; 6 360

MEUBELEN, HUISHOUDTOESTELLEN; 2 348

Bron: Eigen verwerking op basis van de huishoudbudgetenquête1

WOONADRES OF TWEEDE WONING; 12 353

KLEDING EN SCHOEISEL; 1 611

1 http://statbel.fgov.be/nl/themas/huishoudens/huishoudbudget#figures, geraadpleegd op 24 januari 2025.

Figuur 2 Aandeel van de verschillende goederencategorieën in het gezinsbudget, naargelang inkomenskwartiel (België, 2022)

1

VOEDING, DRANKEN EN TABAK

KLEDING EN SCHOEISEL

WOONADRES OF TWEEDE WONING MEUBELEN, HUISHOUDTOES TELLEN

GEZONDHEID VERVOER EN COMMUNICATIE

CULTUUR, ONTSPANNING EN ONDERWIJS PERSOONLIJKE VERZORGING EN DIENSTEN

Bron: Eigen verwerking op basis van de huishoudbudgetenquête2

2 Nut, marginaal nut en consumptiebeslissingen

Het consumentengedrag wekte al vroeg de belangstelling van economen. De klassieke auteurs (Adam Smith, David Ricardo, John Stuart Mill) hechtten daarbij vooral belang aan het begrip nut, d.i. de voldoening die gehaald wordt uit de consumptie van een bepaalde hoeveelheid van een willekeurig goed. Omdat ze enkel oog hadden voor het totale nut als determinant van waarde, konden ze geen oplossing geven voor de zogenaamde waardeparadox: men stelt namelijk vast dat sommige goederen een zeer groot nut hebben en toch nagenoeg geen (markt)waarde (bijvoorbeeld lucht en water); andere goederen hebben dan weer weinig nut, maar een zeer grote marktwaarde (bijvoorbeeld edelstenen). Bovendien gingen deze economen ervan uit dat het nut kardinaal3 meetbaar was in een of andere vaste maatstaf. Dat is uiteraard een onaantrekkelijke veronderstelling: men is er immers nooit in geslaagd een aanvaardbaar meetinstrument van nut of voldoening te ontwerpen. Hoe kun je nagaan hoeveel voldoening Thomas exact geniet bij het eten van een stuk pizza, en of die voldoening echt hetzelfde is als de voldoening die Jolien geniet. Gelukkig is genoemde veronderstelling, zoals verder zal blijken, in de moderne microeconomische theorie niet nodig.

Onder invloed van de marginalisten (William Jevons (1835-1882), Leon Walras (18341910), Carl Menger (1840-1921)) kwam het begrip marginaal nut centraal te staan in de consumptieanalyse. Onder het marginaal nut van een goed verstaat men algemeen de toename in het totaal nut, verkregen ten gevolge van een bijkomende eenheid consumptie van dit goed. Ook genoemde auteurs hielden daarbij vast aan de idee dat nut en marginaal nut kardinaal meetbaar waren. Ze toonden aan dat het totale nut meestal een onbelangrijk

2 http://statbel.fgov.be/nl/themas/huishoudens/huishoudbudget#figures, geraadpleegd op 24 januari 2025.

3 Een maatstaf is kardinaal meetbaar als hij op een schaal ligt met een vast nulpunt en waarop de afstand tussen waarden meetbaar en vergelijkbaar is. Met andere woorden, er is een meeteenheid. Voorbeelden zijn gewicht, lengte enz.

gegeven is in het consumentengedrag en de waardeleer. Belangrijk daarentegen is het marginaal nut. Het onderscheid tussen het totaal en het marginaal nut loste ook de waardeparadox op: sommige goederen hebben een zeer groot totaal nut, maar haast geen marginaal nut; het is het marginaal nut dat de waarde bepaalt.

De Duitse econoom Hermann Gossen (1810-1858) had al vastgesteld dat het marginaal nut van een goed daalt wanneer men meer en meer van dit goed consumeert, waarbij men veronderstelt dat de hoeveelheid van alle andere goederen constant blijft (men noemt deze bevinding soms de eerste ‘wet’ van Gossen). Aanvankelijk is het mogelijk dat voor bepaalde goederen het marginaal nut eerst nog stijgt. Voor de meeste goederen bevindt men zich evenwel zeer snel in de zone van het dalend marginaal nut. Het bijkomend nut van het lezen van meer en meer boeken per maand neemt wellicht af naarmate men al zeer veel boeken gelezen heeft. Het drinken van frisdrank of de consumptie van pasta of frieten is ook, zeker vanaf een bepaald consumptieniveau, onderhevig aan afnemend marginaal nut.

Het basisidee van afnemend marginaal nut vormt de grondslag van de theorie van het consumentengedrag die door Alfred Marshall werd uitgewerkt. Hij formuleerde een theorie waarbij consumentenbeslissingen het resultaat zijn van de confrontatie van enerzijds preferenties, die beschrijven wat een consument wenst, en de budgettaire mogelijkheden van het individu. Die hangen af van de prijzen van de diverse goederen en van het beschikbare budget. Marshall slaagde erin beslissingen van consumenten te rationaliseren vanuit de veronderstelling dat consumenten wellicht hun nut willen maximaliseren, gegeven een aantal beperkingen die ze moeten respecteren, zoals bijvoorbeeld het beperkte budget dat ze ter beschikking hebben. Ook kon hij nagaan hoe een consument reageert op een verandering in de prijs van een bepaald goed of op een inkomenswijziging.

Marshall toonde formeel aan dat een consument die zijn totaal nut wil maximaliseren zijn bestedingen zodanig zal verdelen dat de laatste eurocent die aan de verschillende goederen wordt besteed eenzelfde marginaal nut oplevert (deze bevinding was al eerder intuïtief geformuleerd door Gossen; men spreekt soms van de tweede wet van Gossen). Als men er, zoals Marshall, van uitgaat dat het nut kardinaal meetbaar is, kan men dit belangrijke resultaat eenvoudig illustreren met een voorbeeld. Stel dat een individu een budget van 60 euro moet verdelen over twee goederen, bijvoorbeeld pizza’s en glazen frisdrank; stel dat een pizza 6 euro kost en een glas frisdrank 3 euro. Laten we aannemen dat het totale nut van de consumptie van opeenvolgende hoeveelheden pizza’s en frisdrank gegeven is als in tabel 1. Daarin wordt ook meteen het marginaal nut en het marginaal nut per euro van opeenvolgende hoeveelheden pizza’s en frisdrank berekend. Om het marginaal nut te berekenen, hebben we telkens de toename in het totaal nut bepaald per extra eenheid van het goed. Zo is bij een consumptie van 8 pizza’s het marginaal nut bepaald op 20: de toename van het nut voor een toename van 6 tot 8 pizza’s bedraagt 40 (nl. 290-250), dit is 20 per extra eenheid. Ook het marginaal nut per euro is aangegeven voor elke hoeveelheid van de goederen.

Tabel 1 Nut en marginaal nut

Om de combinatie pizza’s-frisdrank te bepalen die het totaal nut zo groot mogelijk maakt, is de eenvoudigste procedure eerst na te gaan welke combinaties de consument kan kopen, gegeven de prijzen en zijn budget van 60 euro. In tabel 2 worden in de eerste kolom alle mogelijke combinaties bepaald en wordt het overeenkomstig totaal nut becijferd (zie kolom 2), op basis van de informatie in voorgaande tabel. Bovendien worden voor elke combinatie de hoeveelheden pizza’s en frisdrank hernomen die ze bevatten, met het overeenkomstig marginaal nut per euro bij die hoeveelheid. We stellen vast dat, gegeven de prijzen en het budget dat beperkt is tot 60 euro, het nut maximaal is wanneer de consument 4 pizza’s combineert met 12 glazen frisdrank.

Tabel 2 Bepaling van de optimale combinatie frisdrank-pizza

Combinatie (aantal pizza’s, aantal glazen frisdrank)

Marshall bewees dat in het algemeen bij een optimale allocatie van het budget het marginaal nut van de laatste euro besteed aan elk van de goederen precies hetzelfde is. Het voorbeeld in tabellen 1 en 2 illustreert dit: wanneer de consument kiest voor 4 pizza’s en 12 glazen frisdrank is het marginaal nut per euro voor beide goederen hetzelfde.4

Marshall toonde aan dat dit geen toeval is, maar dat een optimale combinatie die het nut maximaliseert altijd de eigenschap zal hebben dat het marginaal nut per euro gelijk

4 Merk op dat de exacte gelijkheid te wijten is aan de keuze van de gegevens. In het algemeen is het marginaal nut de toename in het nut voor een oneindig kleine toename van de consumptie. Het voorbeeld werkt met discrete benaderingen, namelijk de toename in het nut voor een bijkomende eenheid.

is voor alle goederen. Want, redeneerde hij correct, stel dat een consument een bundel kiest waarvoor dit niet het geval is. Stel in ons voorbeeld dat de consument de combinatie 8 pizza’s en 4 glazen frisdrank consumeert. Dat kan nooit optimaal zijn: gegeven deze bundel bedraagt het marginaal nut per euro 10 voor frisdrank en 3,33 voor pizza’s. Dit betekent dat indien de consument minder aan pizza’s spendeerde en meer aan frisdrank, zijn nut zou toenemen. Hij wint 10 aan nut per euro die hij meer spendeert aan frisdrank, terwijl de marginale euro die hij besteedt aan pizza slechts 3,33 oplevert. Bijgevolg kan hij zijn nut nog verhogen door minder aan pizza te besteden en meer aan frisdrank. Het optimum wordt bereikt wanneer de consument zijn 60 euro verdeelt door 4 pizza’s te combineren met 12 glazen frisdrank.

Het is belangrijk voor later om erop te wijzen dat men het voorgaande ook kan interpreteren in termen van wat economen ‘kosten’ en ‘baten’ noemen. Om na te gaan of de consument zijn combinatie pizza’s en frisdrank optimaal heeft gekozen, volstaat het zich af te vragen of de voordelen van bijvoorbeeld meer uit te geven aan pizza’s (het bijkomend nut per euro) zouden opwegen tegen de nadelen (nl. het nutsverlies door een euro minder te kunnen uitgeven aan frisdrank). We kunnen immers stellen dat een consument de optimale hoeveelheid van een goed consumeert wanneer de marginale baten van een extra euro voor dit goed (de voordelen) precies gelijk zijn aan de marginale kosten (de nadelen) van deze bijkomende consumptie. Het voordeel van bijkomende consumptie wordt in het voorbeeld weergegeven door het marginaal nut per euro. De marginale kosten van meer consumptie van een bepaald goed zijn de marginale opportuniteitskosten, namelijk de waarde van wat men moet opgeven om meer van het goed te verkrijgen. In het voorbeeld zijn de marginale kosten van meer pizza gelijk aan de marginale baten van de frisdrank die men opgeeft door meer pizza te consumeren. Leren redeneren in marginale termen en in termen van ‘kosten’ en ‘baten’, waarbij deze laatste niet noodzakelijk in geld zijn uitgedrukt, is essentieel voor een goed begrip van micro-economische analyse.

Het voorgaande betreft uiteraard een erg vereenvoudigd en specifiek gekozen voorbeeld om het inzicht van Marshall en Gossen te illustreren. Het blijft echter ook in de huidige micro-economie relevant, zoals verder zal blijken. Toch hadden de hierboven vermelde theorieën allemaal een belangrijke tekortkoming. De veronderstelling was namelijk dat het nut kardinaal meetbaar was, wat uiteraard onbevredigend is. Noch economen, noch psychologen zijn erin geslaagd een manier te vinden om nut of voldoening kardinaal te meten. Gelukkig steunt de consumentenleer die onder andere ontwikkeld werd door Vilfredo Pareto (1848-1923), Francis Edgeworth (1845-1926), Eugen Slutsky (1880-1948) en John Hicks (1904-1989) niet langer op een kardinale nuttigheidsmaat. Zij gaat ervan uit dat nut enkel ordinaal meetbaar is. Dit betekent dat enkel wordt verondersteld dat consumenten alternatieve goederenbundels kunnen rangschikken afhankelijk van de voldoening die ze eruit halen. Een vaste eenheid van nut is niet vereist. Ook het begrip ‘marginaal nut’ heeft iets van zijn belang ingeboet. De moderne theorie wijst vooral op het belang van de betalingsbereidheid, die wordt uitgedrukt met het begrip marginale substitutiegraad (zie verder).

3 Preferenties, indifferentiecurven en nutsfuncties

In dit onderdeel gaan we in op de instrumenten die economen gebruiken om preferenties van mensen ten aanzien van goederen en diensten te beschrijven. Eerst introduceren we indifferentiecurven, vervolgens besteden we aandacht aan nutsfuncties. We ronden af met enkele toepassingen.

3.1 Preferenties en indifferentiecurven

Om het consumentengedrag te analyseren gaat de micro-economie uit van rationeel gedrag. Dit houdt twee essentiële veronderstellingen in. Ten eerste neemt men aan dat de consument goederenbundels kan vergelijken en ordenen. Deze eigenschap noemt men volledigheid. Met een goederenbundel bedoelt men eenvoudig een combinatie van bepaalde hoeveelheden van verschillende goederen. Stel dat een persoon wordt geconfronteerd met 2 goederenbundels, een bundel a (bijvoorbeeld 8 pizza’s en 4 glazen frisdrank) en een bundel b (bijvoorbeeld 2 pizza’s en 16 glazen frisdrank), dan wordt aangenomen dat hij in staat is zijn preferenties te uiten. Dit betekent dat hij op de vraag welke van de twee bundels hij prefereert, een van de volgende antwoorden geeft:

– ik verkies a boven b; – ik verkies b boven a; – ik ben onverschillig of indifferent tussen a en b.

Deze keuze is uiteraard subjectief, afhankelijk van de eigen individuele voorkeur. De economie doet bovendien als positieve wetenschap geen morele uitspraken over die keuze. Voor de studie van het consumentengedrag wordt de consumentenvoorkeur als gegeven beschouwd. Alleen wordt aangenomen dat de consument zijn voorkeuren kan uiten, dat hij weet wat hij wil.

Een tweede veronderstelling van rationaliteit is dat preferenties transitief zijn. Concreet betekent dit bijvoorbeeld dat een consument die bundel a prefereert boven b, en bundel b boven c, noodzakelijk bundel a zal verkiezen boven c. Dat lijkt een plausibele veronderstelling, hoewel praktische voorbeelden kunnen worden bedacht waarbij niet aan die voorwaarde is voldaan.

Hoewel dit niet strikt vereist is voor rationeel gedrag, gaat men bovendien dikwijls enkele bijkomende technische veronderstellingen over de preferenties van de consument maken, zoals niet-verzadiging en convexiteit. Met niet­verzadiging (non-saturatie) wordt bedoeld dat de consument van alle goederen liever meer heeft dan minder. Het marginaal nut, de bijkomende voldoening van een extra eenheid consumptie, wordt dus verondersteld voor geen enkel goed negatief te zijn. In dit laatste geval zou de consument immers door meer van dat goed te consumeren minder totaal nut ervaren. Saturatie is in de realiteit natuurlijk wel mogelijk (denk bv. aan roken, eten enz.), maar om de analyse te vereenvoudigen wordt hier, tenzij expliciet anders vermeld, verondersteld dat dit niet het geval is. Een

laatste eigenschap is convexiteit; dat is een technische eigenschap waaraan een duidelijke economische interpretatie kan worden gegeven. We komen er dadelijk op terug.

Laten we, om de preferenties van een willekeurige persoon te beschrijven, de analyse beperken tot twee goederen, bv. boeken en cinemabezoeken. Figuur 3 toont op de horizontale as de hoeveelheid boeken (x1) en op de verticale as de hoeveelheid cinemabezoeken (x2), beide uitgedrukt per tijdseenheid (bijvoorbeeld per maand). Hierdoor wordt het mogelijk alle combinaties van geconsumeerde hoeveelheden boeken en cinemabezoeken voor te stellen. Het punt a stelt bijvoorbeeld een goederenbundel voor bestaande uit 2 boeken en 6 filmvoorstellingen per maand. De consumptie van een dergelijke bundel geeft aan de consument een bepaald nut. Zoals gezegd is dit nut niet kardinaal te meten. Wanneer we er toch een getalwaarde aan toekennen, moeten we aan dit getal geen absolute, maar alleen een relatieve (ordinale) betekenis hechten (zie verder).

Het willekeurige punt a verdeelt het diagram in vier kwadranten, genummerd van I t.e.m. IV. In de veronderstelling van niet-verzadiging zal de consument alle mogelijke goederenbundels die in kwadrant I (dat omvat ook de stippellijnen die het kwadrant afbakenen) liggen boven de combinatie a verkiezen. Anderzijds wordt a verkozen boven alle assortimenten die zich in het derde kwadrant (inclusief de stippellijnen) bevinden. In elk punt van het eerste kwadrant beschikt de consument immers over zowel meer boeken als meer cinemabezoeken, ofwel over evenveel van het ene goed en meer van het andere, dan in a. Met bundel a corresponderen ofwel meer boeken en meer voorstellingen, ofwel meer van het ene goed en evenveel van het andere, dan met elk punt van kwadrant III.

Figuur 3 Opbouw van de indifferentiecurve

De kwadranten II en IV laten daarentegen geen algemene uitspraken toe en vereisen een nader onderzoek. Van elke bundel in deze kwadranten wordt aangenomen dat de consument kan zeggen (i) of hij bundel a verkiest, (ii) of hij de andere bundel verkiest, (iii) of hij onverschillig is tussen a en de andere bundel.

Stel nu dat we onze consument vragen zijn voorkeur voor de bundels a, b, c, en d uit te spreken, en dat uit haar antwoord blijkt dat zij: – c verkiest boven a; – a verkiest boven d; – onverschillig is tussen a en b.

Als we deze oefening herhalen en de consument confronteren met de keuze tussen combinaties van een zeer groot aantal goederenbundels, dan kan men curven construeren die alle bundels bevatten waartussen de consument indifferent is. De curve u1 bijvoorbeeld verbindt alle bundels die de consument hetzelfde totaal nut geven als de bundel a. Hij is indifferent tussen alle bundels op u1. Merk op dat het punt b op deze curve ligt. Men noemt de curve een indifferentiecurve, gedefinieerd als een verzameling van goederenbundels waartussen de consument indifferent is. Met elk nutsniveau komt een andere indifferentiecurve overeen.

Merk op dat we in het voorgaande impliciet aannemen dat de goederen deelbaar zijn. Bovendien is het nuttig erop te wijzen dat het bestaan van een exacte maat van het nut irrelevant is voor deze theorie. Het volstaat bijvoorbeeld te weten dat b hetzelfde totale nut vertegenwoordigt als a, en dat c een groter nut oplevert voor de consument dan b. Ten slotte wijzen we erop dat een indifferentiecurve slechts een instrument is dat economen gebruiken om preferenties tot uitdrukking te brengen en de vraag naar verschillende goederen formeel af te leiden; de consument is zich niet bewust van die curves bij het nemen van haar beslissingen.

3.2 Eigenschappen van de conventionele indifferentiecurve

De meeste toepassingen van de theorie van het consumptiegedrag gaan uit van de volgende eigenschappen van indifferentiecurven:

– de indifferentiecurve heeft een dalend verloop;

– de indifferentiecurve is convex ten opzichte van de oorsprong;

– indifferentiecurven geven een hoger nutsniveau weer naarmate ze verder van de oorsprong liggen;

– twee indifferentiecurven kunnen elkaar niet raken of snijden.

Er zijn goede redenen voor deze eigenschappen. We lichten ze kort toe in wat volgt. Merk echter op dat men in sommige gevallen van deze eigenschappen zal willen afwijken (zie verder onder 3.4).

3.2.1 De indifferentiecurve heeft een dalend verloop

Laten we aannemen dat de consument niet verzadigd is en dat het marginaal nut van beide goederen strikt positief is. Bekijken we figuur 4. Stel dat de consument initieel bundel a

heeft en dat men hem een zekere hoeveelheid van goed 2 ontneemt. In dat geval daalt zijn totale nut. Opdat hij hetzelfde totale nut zou behouden moet men hem ter compensatie een bepaalde hoeveelheid van goed 1 bijgeven. Dat impliceert onmiddellijk dat de indifferentiecurve dalend is. Deze eigenschap volgt rechtstreeks uit de hypothese van nietverzadiging.

Figuur 4 De indifferentiecurve is dalend en convex

3.2.2 De indifferentiecurve is convex ten opzichte van de oorsprong

Wanneer de consument de bundel gegeven door punt a (figuur 4) consumeert en men hem achtereenvolgens eenzelfde hoeveelheid van goed 1 bijgeeft, dan impliceert de convexiteit van de indifferentiecurve dat telkens minder van het goed 2 moet worden afgegeven opdat hij hetzelfde totale nut zou behouden.

De convexiteit van de indifferentiecurve betekent grafisch dat ze met de bolle zijde naar de oorsprong is gekeerd. Dat is intuïtief zeer goed aanvaardbaar en volgt ook uit empirische observaties van het consumentengedrag. In het punt a heeft deze persoon veel van goed 2 en weinig van goed 1. Vermeerdert men nu de hoeveelheid van goed 1, dan voelt de consument dat als een grote verbetering omdat hij weinig van dat goed bezit. Een grote afname van goed 2 compenseert de toename aan goed 1. In punt e is de toestand precies andersom. De consument heeft haast niets meer van goed 2 en deze hoeveelheid wordt nog verminderd. Om het nutsverlies te compenseren krijgt hij hoeveelheden bij van een goed dat hij nu al overvloedig bezit (goed 1).

Men kan de convexiteit van de indifferentiecurve eenvoudig economisch vertalen. Convexiteit betekent niets anders dan dat de betalingsbereidheid van de consument voor extra eenheden van een willekeurig goed daalt naarmate hij er meer van consumeert. Om dit te begrijpen volstaat het de maximale betalingsbereidheid van de consument voor een bijkomende eenheid van goed 1 uit te drukken in eenheden van goed 2. Hoeveel is de con-

sument maximaal bereid op te geven van goed 2 voor een extra eenheid van goed 1? Dit wordt formeel gemeten door wat men noemt de substitutieverhouding van goed 2 door goed 1. Die geeft met andere woorden de subjectieve ruilverhouding tussen beide goederen weer; anders gezegd, ze geeft de betalingsbereidheid van goed 1 in termen van eenheden van goed 2. De substitutieverhouding is gedefinieerd als:

Noteer dat men bij conventie een minteken toevoegt om een positieve uitkomst te verkrijgen. De subjectieve ruilverhouding is een maat voor de bereidheid goed 2 te substitueren door goed 1 en toch dezelfde voldoening te behouden. Convexiteit zegt dan dat de subjectieve ruilverhouding, de betalingsbereidheid van de consument voor extra eenheden van goed 1, daalt naarmate hij meer van dit goed consumeert.

In figuur 4 bedraagt de substitutieverhouding in punt a bijvoorbeeld 1,7. Met andere woorden: in punt a is deze consument bereid 1,7 eenheden van goed 2 op te geven om één eenheid van goed 1 bij te krijgen. In punt e geldt bijvoorbeeld dat de substitutieverhouding gelijk is aan 0,2.

3.2.3 Indifferentiecurven geven een hoger nutsniveau naarmate ze verder van de oorsprong liggen

Zoals de indifferentiecurve u1 alle combinaties van hoeveelheden x1 en x2 verbindt die aan de consument hetzelfde totale nut verschaffen als de combinatie a, zo is het ook mogelijk alle punten te verbinden die de consument hetzelfde nut opleveren als een willekeurige andere combinatie. Zo verkrijgt men een preferentieveld, geïllustreerd in figuur 5. De indifferentiecurve u2 bevat alle bundels die hetzelfde nut opleveren als de combinatie c. De kromme u0 geeft dan weer de verzameling van alle combinaties die de consument hetzelfde nut opleveren als de bundel d.

Aangezien de consument a boven d verkiest en c boven a geldt bijgevolg dat alle punten op de indifferentiecurve u2 verkozen zullen worden boven de combinaties van u1. Op analoge wijze worden alle bundels op u1 verkozen boven die op u0. In de veronderstelling van niet-verzadiging is het duidelijk dat de indifferentiecurven die verder van de oorsprong verwijderd zijn, geassocieerd worden met een hoger nut.

Merk op dat we convexiteit van de indifferentiecurve nu ook nog op een tweede manier kunnen begrijpen, die misschien intuïtiever is dan wat werd toegelicht onder 3.2.2. Bundels a en b leveren de consument hetzelfde nut op, maar ze zijn erg verschillend: a bevat erg veel van x2 en erg weinig van x1; voor bundel b geldt precies het omgekeerde. Stel nu dat we de consument de helft geven van bundel a en de helft van bundel b; of we geven een vierde van a en drie vierde van b. Al dergelijke lineaire combinaties liggen op de rechte die a en b verbindt. Door de veronderstelde convexiteit van de indifferentiecurven liggen al die bundels tussen a en b per definitie verder van de oorsprong; ze geven dus een hoger

nut dan a en b. Convexiteit kan dus ook als volgt geïnterpreteerd worden: het betekent dat consumenten variëteit prefereren boven extremen.

Figuur 5 Preferentieveld

3.2.4 Twee indifferentiecurven kunnen elkaar niet raken of snijden

Twee indifferentiecurven kunnen elkaar niet raken of snijden. We bekijken daarvoor figuur 6, waarop verondersteld wordt dat indifferentiecurven elkaar toch snijden. Volgens deze figuur zou de consument indifferent zijn tussen a en b en ook tussen a en q. Transitiviteit impliceert dan dat hij indifferent moet zijn tussen b en q. Merk echter op dat q meer bevat van beide goederen dan b, zodat de veronderstelling van niet-verzadiging impliceert dat de consument q moet verkiezen boven b. Dit leidt dus duidelijk tot een inconsistentie zodat het uitgangspunt, namelijk dat de indifferentiecurven elkaar snijden, verworpen moet worden.

Figuur 6 Twee indifferentiecurven kunnen elkaar niet raken of snijden

3.3 Nutsfuncties

Preferenties en indifferentiecurven kunnen op formele wijze worden beschreven door gebruik te maken van nutsfuncties. Deze leggen de relatie tussen enerzijds diverse hoeveelheden van verschillende goederen die geconsumeerd worden, en anderzijds het totale nut u dat verkregen wordt door de consumptie van deze goederenkorf: u = u (x1, x2, ..., xn).

Daarbij dient nogmaals benadrukt te worden dat het nutsniveau u enkel ordinaal geïnterpreteerd kan worden. Dit betekent concreet dat enkel de relatieve waarde van de nutsfuncties belang heeft, maar dat de absolute verschillen tussen de waarden van de nutsfunctie geen enkele betekenis hebben. Uitspraken zoals ‘de consument heeft bundel b tweemaal zo graag als bundel a’ of ‘bundel b geeft de consument een dubbele voldoening in vergelijking met bundel a’ zijn zinloos: het verschil tussen twee nutswaarden heeft geen absolute betekenis. Ook kan het nut van verschillende personen niet rechtstreeks vergeleken kan worden: het heeft geen zin te zeggen dat Michael voor een gegeven bundel een hoger nut bereikt dan Olivia. Preferenties zijn in die zin persoonlijk. Ze zijn niet ‘interpersoonlijk’ vergelijkbaar, en ze kunnen daarom ook niet worden opgeteld (‘geaggregeerd’), tenzij men specifieke bijkomende veronderstellingen maakt. In de welvaartseconomie onderzoekt men concreet onder welke speciale omstandigheden interpersoonlijke vergelijkingen en aggregatie van nut mogelijk zijn.

In het vervolg van de analyse wordt steeds aangenomen dat de nutsfunctie (i) continu en differentieerbaar is en (ii) dat de daarbij horende indifferentiekrommen strikt convex zijn. Voor een eenvoudig geval met slechts twee goederen geeft figuur 7 een grafische voorstelling van een dergelijke representatieve indifferentiecurve overeenkomstig de nutsfunctie u = u(x1, x2).

Wiskundig wordt een indifferentiecurve voor een willekeurig nutsniveau u0 beschreven door

de impliciete vergelijking u0 = u(x1, x2). Lost men deze vergelijking expliciet op voor x2 als functie van x1 en u0, dan krijgt men de wiskundige uitdrukking van de grafische voorstelling met het tweede goed op de verticale en het eerste goed op de horizontale as: x2(x1,u ).

We hebben eerder gewezen op het begrip substitutieverhouding om de subjectieve betalingsbereidheid van de consument voor goed 1 uit te drukken in termen van goed 2, namelijk de bereidheid om eenheden van goed 2 op te geven in ruil voor meer eenheden van goed 1, terwijl je toch dezelfde voldoening geniet. Om deze veranderingen aan te duiden gebruikten we het symbool ‘Δ’. Indien men zich concentreert op zeer kleine veranderingen (de toename Δ gaat in de limiet naar 0) kan men de betalingsbereidheid en bijgevolg de mate waarin de consument bereid is goederen te substitueren weergeven door het begrip marginale substitutiegraad. De marginale substitutiegraad van x2 door x1 (MSG21) wordt gedefinieerd als de substitutieverhouding voor zeer kleine (infinitesimale) veranderingen:

De marginale substitutiegraad heeft een eenvoudige grafische en intuïtieve interpretatie. Het concept wordt grafisch geïllustreerd in figuur 7. De MSG21 in punt c wordt gegeven door de absolute waarde van de richtingscoëfficiënt van de raaklijn ab aan het punt c behorende tot de indifferentiecurve u0. De MSG21 in een gegeven punt is dus niets anders dan de helling van de indifferentiecurve in dat punt. De interpretatie is eenvoudig: de marginale substitutiegraad geeft de betalingsbereidheid van goed 1 weer (uitgedrukt in eenheden van goed 2). In die zin meet het begrip het relatief belang van goed 1. Als men goed 2 beschouwt als een aggregaat goed dat alle consumptiegoederen omvat met uitzondering van goed 1 en de hoeveelheid van dit aggregaat meet in euro, dan is de marginale substitutiegraad de betalingsbereidheid voor goed 1, rechtstreeks uitgedrukt in euro.

Merk op dat naarmate de goederenbundel behorende tot u0 meer van x1 bevat, de absolute waarde van de helling kleiner wordt. Een strikt convexe indifferentiekromme geeft dus aanleiding tot een afnemende marginale substitutiegraad: de betalingsbereidheid voor goed 1 daalt naarmate men er meer van consumeert.

Figuur 7

Substitutieverhouding en marginale substitutiegraad

1

In wiskundige benadering 1 gaan we dieper in op de relatie tussen de marginale substitutiegraad en de onderliggende nutsfunctie. Men toont namelijk eenvoudig aan dat de marginale substitutiegraad uitgedrukt kan worden als de verhouding van het marginaal nut van de twee goederen: / / MSG ux ux 21 2 1 22 22 = .

Dit verband lijkt economisch plausibel: het stelt dat de betalingsbereidheid voor goed 1 (uitgedrukt in termen van goed 2) toeneemt naarmate het extra nut van een toename in dit goed groter is. Het relatief belang dat een consument aan een goed hecht neemt toe met het marginaal nut van dit goed.

Wiskundige benadering 1

Verband tussen marginale substitutiegraad en nutsfunctie

We bekijken alle combinaties van veranderingen in x1 en x2 zo dat het nut onveranderd blijft; m.a.w., we bewegen ons langs een gegeven indifferentiecurve. Dat kan wiskundig worden vertaald door de totale differentiaal van de nutsfunctie te nemen en deze differentiaal gelijk te stellen aan nul.

De totale differentiaal is gegeven door ,, du x ux x dx x ux x

waarin , x ux x 12 i

^h het marginaal nut van goed i voorstelt (i = 1, 2). Stellen we de waarde van de totale differentiaal gelijk aan nul (het nut verandert immers niet, du = 0), dan volgt daaruit onmiddellijk, na eenvoudige algebra:

Het linkerlid is de definitie van de marginale substitutiegraad, zodat we krijgen:

De marginale substitutiegraad, grafisch de absolute waarde van de helling van de indifferentiecurve, geeft dus de verhouding van het marginaal nut van de twee goederen weer. Dit is economisch zinvol: het impliceert onder meer dat wanneer het marginaal nut van het eerste goed toeneemt, de consument bereid is meer van goed 2 op te geven in ruil voor een bijkomende eenheid van goed 1. Omgekeerd zal hij minder bereid zijn eenheden van goed 2 op te geven naarmate het marginaal nut van dit goed relatief toeneemt t.a.v. goed 1.

3.4 Indifferentiecurven als weergave van preferenties: toepassingen

We zullen later in dit hoofdstuk toelichten hoe we informatie over nutsfuncties en de daarbij horende indifferentiecurven kunnen afleiden uit het gedrag van consumenten, en hoe we op die wijze iets kunnen leren over hun preferenties. Op dit ogenblik volstaat het om aan te tonen dat nutsfuncties en indifferentiecurven een elegant en nuttig instrument bieden om de preferenties van individuen te beschrijven, en dat creatief gebruik van het indifferentieraamwerk het mogelijk maakt uiteenlopende afwegingen te beschrijven die mensen in de realiteit impliciet of expliciet moeten maken.

Laten we ons er eerst van overtuigen dat indifferentiecurven van consumenten inderdaad informatie over hun preferenties bevatten en omgekeerd, dat informatie over preferenties vertaald kan worden in de vorm en de ligging van indifferentiecurven. Bekijk bijvoorbeeld figuur 8. Daar zijn voor twee verschillende consumenten indifferentiecurven getekend die hun preferenties beschrijven met betrekking tot alcoholische dranken en frisdranken. De indifferentiecurven van beide consumenten bevatten de bundel (4,5) maar hebben een verschillende helling. We leren dan uit deze figuur dat persoon a meer belang hecht aan alcoholische dranken dan persoon b. Men kan de helling van een indifferentiecurve in een gegeven punt immers vertalen naar het relatief belang (de relatieve betalingsbereidheid) van de beschouwde goederen voor een consument. De betalingsbereidheid van persoon a voor een kleine toename in de consumptie van alcohol (met andere woorden: zijn bereidheid om minder frisdrank te consumeren in ruil voor meer alcoholische dranken) is groter dan voor persoon b. Concreet voor de gegevens van figuur 8 is persoon a bereid om 1,5 eenheden frisdrank op te geven voor een extra eenheid alcohol, terwijl persoon b slechts bereid is om 0,5 eenheden frisdrank op te geven. Algemeen geldt dat hoe vlakker een indifferentiecurve door een gegeven punt, hoe kleiner het relatieve belang van het goed op de horizontale as, en hoe groter de betalingsbereidheid van de consument voor bijkomende eenheden van het goed op de verticale as.

Figuur 8 Het relatief belang van goederen Frisdranken

Enkele speciale vormen van indifferentiecurven worden voorgesteld in figuur 9. Die hebben respectievelijk te maken met perfect substitueerbare goederen (figuur (a)) en perfect complementaire goederen (figuur (b)). In het eerste geval, wanneer een consument bijvoorbeeld steeds bereid is een kop koffie op te geven voor een kop thee en omgekeerd, is de betalingsbereidheid onafhankelijk van de consumptie (de helling is constant). In het tweede geval, wanneer bijvoorbeeld iemand alleen koffie neemt met suiker, neemt het nut pas toe wanneer er meer van beide goederen samen geconsumeerd kan worden. Deze voorbeelden illustreren duidelijk dat de vorm van indifferentiecurven informatie bevat over de bereidheid van de consument om goederen te substitueren.

Figuur 9 Bijzondere vormen van indifferentiecurven

Inventieve toepassingen van het indifferentieraamwerk kunnen erg behulpzaam zijn om een aantal ideeën te vatten die enigszins buiten de gewone definitie van ‘goederen’ vallen. Denk bijvoorbeeld aan het waarderen van tijd. Iedereen is het erover eens dat tijd waardevol is, denk maar aan de uitdrukking ‘time is money’. Maar hoe zou men de afweging van tijd tegen andere goederen kunnen weergeven, of de betalingsbereidheid voor meer vrije tijd kunnen beschrijven? Laten we om dit na te gaan alle consumptiegoederen aggregeren in één samengesteld goed ‘consumptie’, waarvan we de hoeveelheid gewoon meten in euro. Bekijk dan een indifferentiecurve die de afweging beschrijft tussen dit aggregaat consumptie en vrije tijd. Die wordt voorgesteld in figuur 10. De waardering van een extra uur vrije tijd kunnen we nu onmiddellijk uit deze indifferentiecurve afleiden door de net uitgelegde theorie toe te passen. Stel bijvoorbeeld dat de consument in de initiële situatie, voorgesteld door het punt a, veertien uur vrije tijd combineert met een consumptie van 100 euro per dag. De waarde die hij hecht aan een kleine toename in vrije tijd is dan niets anders dan de helling van de indifferentiecurve: deze geeft per definitie de betalingsbereidheid voor een kleine toename in vrije tijd, m.a.w. hoeveel euro is de consument bereid op te geven van zijn consumptie in ruil voor een klein beetje meer vrije tijd? Merk overigens op dat de idee van dalende marginale substitutiegraad impliceert dat de waarde van vrije tijd toeneemt naarmate iemand minder vrije tijd heeft. Dit is een van de redenen waarom overuren meer vergoed moeten worden dan normale arbeidsprestaties.

Figuur 10 Waarde van vrije tijd

Consumptie per dag

Vrije tijd per dag

Een tweede voorbeeld betreft het meten van de betalingsbereidheid van mensen voor een schoner milieu. Hoeveel zijn mensen bereid op te geven voor een vermindering van de vervuiling? Stel dat de consument wel belang hecht aan consumptie maar ook bekommerd is om een schoon milieu. In figuur 11 stellen we zijn preferenties voor tussen consumptie en vervuiling. Dit laatste is uiteraard het omgekeerde van een goed: meer vervuiling vermindert het nut, zodat het marginaal nut van vervuiling negatief is. Merk op dat dit impliceert dat de indifferentiecurven tussen consumptie en vervuiling een positieve helling hebben: men is bereid iets op te geven aan consumptiegoederen in ruil voor een daling van de vervuiling. Indien de huidige bundel gegeven is door punt b, dan is de betalingsbereidheid gegeven door de helling van de indifferentiecurve in dit punt: deze meet hoeveel consumptie de consument bereid is op te geven voor een kleine reductie van de vervuiling.

Figuur 11 Betalingsbereidheid voor een schoner milieu

Consumptie

Vervuiling

Inventief gebruik van indifferentiecurven (en daarmee samenhangend nutsfuncties) maakt het mogelijk een heel gamma reële problemen te analyseren. Naast de al genoemde mogelijkheden kan men bijvoorbeeld analyseren hoe mensen huidige consumptie afwegen tegen toekomstige consumptie, hoe zij de afweging maken tussen kenmerken van producten (bijvoorbeeld tussen snelheid en verbruik van een auto), tussen private goederen en publieke voorzieningen enz.

4 De budgetbeperking

Bij het nemen van consumptiebeslissingen moet de consument rekening houden met een aantal beperkingen. Die kunnen bijvoorbeeld te maken hebben met het budget en de tijd die hij voor consumptieve activiteiten ter beschikking heeft. Hier besteden we uitsluitend aandacht aan de beperking op zijn budget. De budgetbeperking houdt in dat de consument slechts over een beperkt budget (bijvoorbeeld haar maandelijks inkomen) beschikt, en de betrokken goederen kunnen slechts tegen betaling van een bepaalde prijs verkregen worden.

In wat volgt gebruiken we de termen inkomen en budget als synoniem. Dat geeft twee mogelijke interpretaties. Een eerste is dat de consument een budget heeft voorbehouden om in een gegeven periode te spenderen. Een tweede interpretatie is dat de consument zijn gehele inkomen, verdiend in een gegeven periode, in diezelfde periode aan consumptie wenst uit te geven. Met andere woorden, de consument spaart niet, en hij geeft ook niet meer uit dan zijn inkomen toelaat.5

Indien we ons blijven beperken tot twee goederen, dan kan de consument zijn inkomen op verschillende wijzen over de twee goederen verdelen. In een extreem geval zou hij ervoor kunnen kiezen het volledige inkomen uit te geven aan goed 1. Een andere extreme keuze zou zijn het volledige inkomen te besteden aan goed 2. Ten slotte kan hij uiteraard zijn budget gedeeltelijk uitgeven aan goed 1 en gedeeltelijk aan goed 2.

We stellen het inkomen voor door y, en de prijzen van de goederen 1 en 2 respectievelijk door p1 en p2. Zowel het inkomen als de prijzen van de goederen worden als gegeven beschouwd. Indien de consument hypothetisch zijn volledige inkomen uitgeeft aan de consumptie van goed 2 dan kan hij y/p2 eenheden van dit goed aankopen (en niets van goed 1). Als daarentegen de consument zijn volledige inkomen uitgeeft aan de consumptie van het eerste goed, dan consumeert hij y/p1 eenheden van goed 1 en niets van het tweede goed. Uiteraard kan hij zijn budget ook verdelen over de twee goederen. De budgetrechte geeft dan alle mogelijke combinaties weer die de consument kan kopen bij de gegeven prijzen en het gegeven budget. De vergelijking van de budgetlijn is:

p1x1 + p2x2 = y.

5 Deze onrealistische veronderstelling kan zonder al te veel moeilijkheden aangepast worden als we de analyse uitbreiden in een intertemporeel kader, maar dat valt buiten het bestek van dit boek.

Deze budgetrechte wordt getekend op deel (a) van figuur 12.

We geven een eenvoudig voorbeeld. Stel dat een student een wekelijks budget van 100 euro wenst te besteden aan twee goederen, alcoholische drank (x1) en frisdrank (x2). Stel dat een alcoholische drank 4 euro kost en een frisdrank 2 euro. De budgetrechte wordt getekend in deel (b) van figuur 12.

Figuur 12 De budgetlijn

(a) (b) x 2 x 1 y / p2

Frisdrank

vergelijking p1 x 1+p2 x 2 = y y / p1

helling = - p1 / p2

50 25

vergelijking (4 alcoholische drank + 2 frisdrank) = 100

helling = - 2

Alcoholische drank

De helling van de budgetrechte heeft een duidelijke en belangrijke economische betekenis. Om de helling van de budgetrestrictie te bepalen is het nuttig de vergelijking van de budgetlijn te herschrijven als een functie met x2 aan de linkerzijde. We brengen in de budgetvergelijking eerst p1x1 naar het linkerlid:

p2x2 = y - p1x1

en delen daarna beide leden door p2 om de volgende uitdrukking te krijgen: x p y p p x 2 22 1 1 =.

Hieruit volgt dat de helling gegeven is door:

De richtingscoëfficiënt van de budgetlijn die de helling van deze budgetlijn weergeeft is gelijk aan –p1/p2. M.a.w., de helling van de budgetlijn wordt bepaald door de relatieve prijsverhouding van de twee goederen. Deze richtingscoëfficiënt is in alle punten van de lineaire budgetlijn dezelfde. In het voorbeeld geldt dat de richtingscoëfficiënt van de budgetlijn gelijk is aan -2.

Het voorgaande impliceert dat men de absolute waarde van de helling van de budgetbeperking kan interpreteren als de objectieve ruilverhouding op de markt, bepaald door de relatieve prijzen. In ons voorbeeld geeft de helling de marginale opportuniteitskosten voor de consument weer van een extra alcoholische drank, uitgedrukt in frisdrank: om een extra alcoholische drank te consumeren, moet hij 2 frisdranken opgeven. Of nog anders gezegd, de consument kan op de markt 2 frisdranken ruilen voor 1 alcoholische drank.

Wat gebeurt er met de budgetbeperking wanneer de consument een groter budget te besteden heeft, of wanneer de prijs van een willekeurig goed verandert? Beschouw eerst een toename van het beschikbare budget. Grafisch leidt dit tot een evenwijdige verschuiving van de budgetlijn naar rechts. De inkomens- of budgetverandering heeft immers geen invloed op de relatieve prijzen en beïnvloedt de helling van de budgetrechte dus niet. Wel kan de consument met een groter budget meer kopen van een goed wanneer hij het volledig budget uitgeeft aan dit goed, zodat het snijpunt met de horizontale as naar rechts verschuift en het snijpunt met de verticale as naar boven. Combinatie van voorgaande twee vaststellingen geeft een evenwijdige verschuiving naar rechts. Omgekeerd heeft men een evenwijdige verschuiving naar links wanneer het budget afneemt. Deel (a) van figuur 13 illustreert een toename van het budget van 100 tot 120 euro.

Figuur 13 Effect van inkomens- en prijswijzigingen op de budgetlijn (a)

We bekijken vervolgens een prijsverandering van een bepaald goed. Stel dat in ons hypothetisch voorbeeld de prijs van een alcoholische drank, p1, toeneemt van 4 naar 5 euro. De helling van de budgetrechte zal dan in absolute waarde stijgen. Omdat de student minder van goed 1 kan kopen wanneer hij zijn volledige budget aan dit goed besteedt, zal het snijpunt met de horizontale as bovendien dichter bij de oorsprong liggen. Het snijpunt met de verticale as blijft echter ongewijzigd, aangezien de prijs van een frisdrank, p2, niet is veranderd. Het gevolg is een rotatie van de budgetlijn naar binnen, waarbij de helling toeneemt. Dit wordt geïllustreerd in deel (b) van figuur 13.

We ronden deze paragraaf af met een belangrijke opmerking. We veronderstelden hierboven steeds dat de budgetbeperking lineair is. In de realiteit zijn er echter situaties waarbij

Frisdrank

dit niet het geval is. Dit kan zowel het gevolg zijn van overheidsbeleid op bepaalde markten als van het voeren van een bewust prijsbeleid van ondernemingen. Het automatisch gratis ter beschikking stellen van een verplichte minimale hoeveelheid E van een bepaald goed x1 door de overheid (zoals onderwijs, gezondheidszorg enz.) leidt bijvoorbeeld tot de budgetbeperking zoals voorgesteld in deel (a) van figuur 14. Wie alles uitgeeft aan andere goederen kan toch een hoeveelheid E consumeren. Wie meer van x1 wenst, betaalt de geldende marktprijs. Merk op dat het lijnstuk AB geen deel uitmaakt van de budgetbeperking. Een prijsbeleid van een bedrijf waarbij de eerste 10 eenheden van een goed x1 tegen de volle prijs betaald moeten worden, maar waarbij consumenten alle bijkomende eenheden kunnen kopen tegen een verminderde prijs, geeft aanleiding tot een budgetbeperking zoals weergegeven in deel (b) van figuur 14. De budgetbeperking is stapsgewijs lineair: de helling is kleiner in absolute waarde wanneer men meer dan 10 eenheden koopt omdat de relatieve prijs van het eerste goed is gedaald.

Figuur 14 Niet-lineaire budgetbeperkingen

5 De optimale keuze van de consument

Stel dat de consument een maximale voldoening nastreeft, maar dat hij daarbij beperkt is door het beschikbare budget. Merk op dat de veronderstelling van het nastreven van maximaal nut niet hoeft te betekenen dat de consument zich opstelt als egocentrisch en zelfzuchtig, en enkel denkt aan eigenbelang in enge zin. Preferenties kunnen immers zeer uiteenlopend zijn: sommige consumenten houden rekening met het milieu, andere met het lot van de armen of de huisvesting van daklozen enz. In wat volgt lichten we echter enkel de principes toe wanneer een consument keuzes moet maken die betrekking hebben op het toewijzen van een gegeven budget aan verschillende goederen. Veralgemeende toepassingen vallen buiten het bestek van dit inleidend boek, maar zijn perfect mogelijk. Zie hiervoor ook de kritische kanttekeningen aan het einde (punt 9) van dit hoofdstuk.

5.1 Analyse van het optimum

De oplossing van het keuzeprobleem wordt in wat volgt grafisch en intuïtief toegelicht. Een meer formele oplossing wordt uitgewerkt in wiskundige benadering 2 verder in dit hoofdstuk. Het principe voor de grafische analyse is eenvoudig: een consument die maximale voldoening nastreeft zal een bundel willen consumeren die gelegen is op een indifferentiecurve die zover mogelijk van de oorsprong is verwijderd. Maar anderzijds is hij beperkt door zijn beschikbare budget, zodat alleen bundels op de budgetlijn in aanmerking komen. We belichten de oplossing eerst voor het geval de consument in het optimum beide goederen consumeert. Uitkomsten waarbij hij ervoor kiest een van beide goederen niet te consumeren worden kort bekeken in punt 5.3.

Bekijk figuur 15. Stel dat de consument de bundel overeenkomstig het punt m consumeert. Aan de voorwaarde van totale besteding van het inkomen is dan voldaan, aangezien dit punt deel uitmaakt van de budgetlijn. Het punt m geeft echter niet de maximale voldoening gegeven zijn preferenties. De indifferentiekromme die door m gaat is immers niet degene die het verst van de oorsprong verwijderd ligt en die de consument – met zijn gegeven beperkingen – kan bereiken. De consument kan het totale nut verhogen door minder van het goed 2 te consumeren en de middelen die daardoor vrijkomen aan goed 1 te besteden. Hij zou dan bijvoorbeeld in het punt n terechtkomen. Maar ook hier kan het nut nog verhoogd worden door goed 2 verder door goed 1 te substitueren. De maximale voldoening bij het beschikbare budget wordt bereikt in het punt e. Verdere substitutie van goed 2 door goed 1 gaat dan gepaard met een vermindering van het totale nut.

Figuur 15 Het consumentenevenwicht

Het is nu duidelijk dat het evenwicht van de consument zich situeert in dat punt waar de budgetlijn raakt aan de indifferentiecurve die zo ver mogelijk van de oorsprong verwijderd is. Dit is het punt e in figuur 15. Om dit optimum economisch te interpreteren is het nuttig te vertrekken van een eenvoudige grafische vaststelling. We zien namelijk dat in punt e de raaklijn aan de indifferentiekromme precies samenvalt met de budgetlijn (noteer dat dit het enige punt is waar deze gelijkheid geldt). De absolute waarde van de helling van de raaklijn aan de indifferentiecurve is niets anders dan de marginale substitutiegraad. De absolute waarde van de helling van de budgetlijn is gelijk aan de prijsverhouding p1/p2.

In het optimum geldt dus dat de marginale substitutiegraad gelijk is aan de relatieve prijzen:

MSG p p 21 2 1 =

De economische betekenis van de voorwaarde voor optimaal keuzegedrag is duidelijk. De marginale substitutiegraad werd eerder geïnterpreteerd als de betalingsbereidheid voor meer van goed 1, uitgedrukt in termen van goed 2. Het zijn de marginale baten van een extra eenheid van goed 1, uitgedrukt in eenheden van goed 2. De relatieve prijzen daarentegen geven weer hoeveel de consument van goed 2 moet opgeven om een extra eenheid van goed 1 te kunnen kopen. Dit zijn de extra kosten van goed 1 in termen van goed 2, de marginale opportuniteitskosten van goed 1. In het optimum is dus de marginale baat van een extra eenheid van goed 1 precies gelijk aan de marginale kosten van deze bijkomende eenheid. Indien het extra voordeel van een toename in consumptie van goed 1 groter is dan de extra kosten, kan men zijn totale voldoening doen toenemen door wat van goed 2 op te geven in ruil voor meer van goed 1. Het punt m was hiervan een voorbeeld: de helling van de indifferentiecurve (baten) was groter dan de helling van de budgetrechte (kosten). Indien omgekeerd de marginale kosten van meer van goed 1 groter zijn dan de marginale baten dan kan men zijn voldoening verhogen door de consumptie van goed 2 te verhogen.

Er zijn nog verschillende varianten mogelijk om het optimum te karakteriseren. Aangezien we hebben aangetoond dat / / MSG ux ux 21 2 1 22 22 = ,

kan de voorwaarde voor optimale keuze ook geschreven worden als / / p p ux ux 2 1 2 1 22 22 = .

De interpretatie is analoog. De consument maximaliseert zijn nut als hij zijn gegeven inkomen zodanig besteedt voor de aankopen van de twee goederen dat de verhouding van de marginale nuttigheden (subjectieve ruilverhouding) gelijk is aan de verhouding van hun prijzen (objectieve ruilverhouding). Is zijn bereidheid tot ruilen van goed 2 voor goed 1 groter dan wat hij objectief, tegen de geldende marktprijzen, moet opgeven van 2 voor een bijkomende eenheid van 1, dan kan hij zijn nut nog verhogen door goed 2 verder te substitueren door goed 1.

Wiskundige benadering 2

Nutsmaximalisatie onder een budgetbeperking

Het optimale keuzegedrag van de consument kan uiteraard ook afgeleid worden met behulp van wiskundige technieken. Hoewel de wiskundige benadering zeer algemeen is, beperken we ons eenvoudigheidshalve toch tot twee goederen. Stel dat de consument maximale voldoening nastreeft voor een gegeven budget. Wiskundig kan dit vertaald worden als het maximaliseren van de nutsfunctie, die zijn preferenties beschrijft, onder de nevenvoorwaarde van zijn budgetbeperking:

, maxu xx12 x, x 12 ^h

waarbij px px y 11 22 += .

De bundel goederen die dit probleem oplost is optimaal. We herhalen dat aan de waarde van de nutsfunctie enkel een ordinale betekenis toegekend moet worden. Elke positief monotone transformatie die dezelfde rangordening oplevert, zal dus eveneens een geldige nutsindex vormen.

De meest efficiënte benadering om het probleem op te lossen bestaat erin de Lagrange-functie te vormen: , Lu xx yp xp x

waarbij m de Lagrange-multiplicator is die bij de budgetbeperking hoort. De noodzakelijke voorwaarden voor een intern optimum bestaan erin de eerste partiële afgeleiden van de Lagrange-functie naar x1, x2 en m te berekenen en die gelijk te stellen aan nul. Dat geeft:

Ten slotte leidt herschrijven van voorgaande uitdrukking tot: // p ux p ux 1 1 2 2 22 22 = .

De consument maximaliseert dus zijn nut wanneer het marginaal nut per uitgegeven euro voor alle goederen uit zijn assortiment gelijk is. Merk overigens op dat deze stelling al in paragraaf 2 van dit hoofdstuk werd aangetoond op basis van een numeriek voorbeeld; dit resultaat was immers al door Gossen intuïtief beredeneerd en door Marshall formeel aangetoond op basis van kardinale nutsfuncties. De stelling blijft dus geldig voor ordinale nutsfuncties. Is aan de gelijkheid niet voldaan, dan kan de consument het nut nog verhogen door reallocatie van zijn budget.

De derde vergelijking zegt gewoon dat de consument moet voldoen aan de budgetbeperking. De eerste twee vergelijkingen kunnen als volgt herschreven worden: , x ux x p 1 12 1 2 2 m = ^h , x ux x p 12 2 2 2 2 m = ^h en bijgevolg: , , x ux x

^ h h .

Dat geeft uiteraard dezelfde voorwaarde die we ook grafisch hadden gevonden: omdat de term in het linkerlid niets anders is dan de marginale substitutiegraad, geldt dat in het optimum de marginale substitutiegraad gelijk is aan de verhouding van de prijzen. De oplossing van die voorwaarde samen met de budgetbeperking levert dan de vraagfuncties naar de twee goederen als functie van het budget en de prijzen op.

Merk op dat er in de praktijk twee equivalente manieren zijn om de optimale keuze van twee goederen te berekenen. Uiteraard kan men de algemene Lagrange-techniek toegelicht in Wiskundige benadering 2 gebruiken. Die is algemeen toepasbaar voor een willekeurig aantal goederen. Maar in het geval van twee goederen is het dikwijls eenvoudiger rechtstreeks de gelijkheid tussen de verhouding van de prijzen en van het marginale nut van de twee goederen te exploiteren. Combineert men die gelijkheid met de budgetbeperking dan verkrijgt men een eenvoudig stelsel van twee vergelijkingen met twee onbekenden; oplossing levert onmiddellijk de gezochte waarden van de twee goederen. We illustreren beide methoden in het volgende numerieke voorbeeld.

5.2 Een numeriek voorbeeld

We illustreren de theorie hier met een eenvoudig voorbeeld. Stel dat de nutsfunctie gegeven is door

u(x1, x2) = (x1)0,2 (x2)0,8.

Dit is een functie van het Cobb-Douglas-type, genoemd naar de economen Charles Cobb (1875-1949) en Paul Douglas (1892-1976). Ze wordt veel gebruikt als eerste eenvoudige benadering omdat ze onder meer, ondanks enkele opvallende nadelen, mooi convexe indifferentiecurven impliceert. Merk op dat we hier veronderstellen dat we de nutsfunctie kennen, niet enkel de vorm maar ook de parameters. Dat is in de praktijk natuurlijk niet het geval; we leggen verder nog uit hoe economen die parameters bepalen.

Neem aan dat de prijzen van de twee goederen, bijvoorbeeld boeken en ‘alle andere goederen’, respectievelijk 20 en 1 euro bedragen.

Het beschikbare budget is 1 000 euro. De budgetbeperking is dus 20x1 + x2 = 1 000.

Er zijn verschillende manieren om het optimum te berekenen. We illustreren eerst het rechtstreekse gebruik van het resultaat dat in het optimum de verhouding van de marginale nuttigheden gelijk moet zijn aan de prijsverhouding. Berekenen van de marginale nuttigheden geeft:

De verhouding van de marginale nuttigheden is dan:

Die verhouding moet gelijk zijn aan de verhouding van de prijzen. Dat geeft de voorwaarde: x x 4 1 1 20 1 2 = .

Dat wordt dus x2 = 80x1. Combinatie van dat resultaat met de budgetbeperking levert een systeem van twee vergelijkingen in twee onbekenden:

x2 = 80x1

20x1 + x2 = 1 000.

Oplossing naar de twee onbekende hoeveelheden geeft uiteindelijk:

x1 = 10 en x2 = 800.

Een tweede techniek (die equivalent is aan de eerste) om het optimum te bepalen, maakt gebruik van de Lagrange-techniek. Om het probleem op te lossen formuleren we de Lagrange-functie

L = (x1)0,2 (x2)0,8 + m (1 000 – 20x1 – x2).

De drie eerste-ordevoorwaarden zien er als volgt uit:

0,2 (x1)-0,8 (x2)0,8 = 20m

0,8 (x1)0,2 (x2)-0,2 = m (1 000 - 20x1 - x2) = 0.

Deling van de eerste door de tweede vergelijking geeft x x xx 4 1 20 80 1 2 21 " ==

Invullen in de derde voorwaarde, die gewoon de budgetbeperking weergeeft, levert het volgende op:

1 000 – 20x1 – 80x1 = 0.

We vinden dus

x1 = 10.

We toonden eerder al aan dat x2 = 80 x1. Bijgevolg vinden we dat

x2 = 800.

De consument koopt optimaal 10 boeken per maand en geeft de rest van zijn budget, namelijk 800 euro, uit aan andere goederen.

We eindigen dit voorbeeld met een belangrijke opmerking. We kunnen de eerste-ordevoorwaarden ook gebruiken om de waarde van de multiplicator λ te berekenen. Men kan aantonen dat deze multiplicator een duidelijke economische interpretatie heeft. Hij geeft namelijk het marginale nut van het inkomen weer: met hoeveel neemt het nut toe als het inkomen met 1 euro toeneemt. Dat concept is erg belangrijk in meer geavanceerde economische analyses (bv. in de welvaartseconomie).

5.3 Hoekoplossingen

Tot slot van deze paragraaf wijzen we erop dat we impliciet veronderstelden dat het keuzeprobleem aanleiding geeft tot een oplossing waarbij de consument de twee goederen inderdaad consumeert. In dat geval spreken we van een interne oplossing waarbij in het optimum de marginale substitutiegraad en de relatieve prijzen gelijk zijn aan elkaar.

In de praktijk garandeert niets dat we in alle omstandigheden een interne oplossing zullen krijgen. Het is inderdaad best mogelijk dat iemand het optimaal vindt niets van bepaalde goederen te consumeren, bijvoorbeeld omdat hij deze producten totaal niet aantrekkelijk vindt, of omdat hij de prijs ervan te hoog vindt. In dat geval is zijn optimale bundel grafisch gegeven door een hoekoplossing; we illustreren dit in figuur 16. De consument in kwestie kiest ervoor geen vlees te consumeren. Merk op dat in het geval van een hoekoplossing niet is voldaan aan de voorwaarde van gelijkheid tussen marginale substitutiegraad en relatieve prijzen. Dat is een belangrijke aanvulling op wat eerder werd gezegd: de gelijkheid tussen marginale substitutiegraad en relatieve prijzen geldt slechts voor interne oplossingen.

Figuur 16 Hoekoplossingen

Andere goederen

Vlees

6 Veranderingen van het consumentenevenwicht

Hierboven werd aangetoond hoe de consument, rekening houdend met zijn preferenties, zijn inkomen en de gegeven marktprijzen, het nut van zijn consumptie maximaliseert. Het ligt voor de hand dat de optimale goederenbundel wijzigt telkens wanneer veranderingen optreden in de basisgegevens. Daarbij wijzigen we telkens één gegeven en laten de overige onveranderd. We redeneren met andere woorden onder de hypothese ‘ceteris paribus’.

6.1 Veranderingen in de preferentieschaal

Preferenties kunnen wel wijzigen onder invloed van vrienden, door reclame (bv. antitabaksreclame), door smaakveranderingen ten gevolge van het ouder worden (bv. meer interesse voor klassieke muziek), door ziek te worden, ze kunnen variëren naargelang de seizoenen, enz. Wel is het zo dat preferenties subjectief zijn (dus afhankelijk van persoon tot persoon); bovendien zijn smaakveranderingen moeilijk te voorspellen.

Wanneer men in figuur 17 deel (b) vergelijkt met deel (a) dan merkt men dat er een preferentiewijziging is opgetreden in het voordeel van goed 2. Het gevolg van deze preferentiewijziging is dan ook dat de consument meer van het tweede goed consumeert. Hoewel in dit geval noch het inkomen noch de prijzen veranderd zijn, wijzigt het consumptiepatroon toch.

Figuur 17 Veranderingen in de preferentieschaal

6.2 Veranderingen in het budget

Wanneer het inkomen verandert, zullen de consumptie-uitgaven eveneens wijzigen. Het is daarbij van belang te weten hoe het consumptiepatroon evolueert bij een veranderend inkomen. Zal de consument bij een toenemend inkomen van alle goederen in verhouding evenveel meer gaan consumeren? Of zullen bepaalde goederen meer of minder aan belang gaan winnen? Zijn er goederen die minder geconsumeerd worden bij een hoger inkomen?

Grafisch leidt een toename van het inkomen tot een evenwijdige verschuiving van de budgetlijn naar rechts (zie deel (a) van figuur 18). Een vermindering van het budget geeft analoog een evenwijdige verschuiving naar links, dus naar de oorsprong toe. Met elk inkomensniveau komt een ander optimum overeen. De curve die deze opeenvolgende optimale punten verbindt, noemt men de inkomensconsumptiecurve (ICC). Die geeft de verzameling weer van alle optimale goederenbundels bij verschillende inkomens, waarbij de prijzen van de goederen ongewijzigd blijven.

Figuur 18 De inkomensconsumptiecurve en de Engel-curve

Het voorgaande maakt het nu ook eenvoudig om het verband af te leiden tussen de gevraagde hoeveelheid van een goed en het inkomen, waarbij de prijzen constant worden verondersteld. Dit verband wordt samengevat door wat men noemt een Engel­curve. In deel (b) van figuur 18 wordt, vertrekkend van deel (a), de Engel-curve voor het eerste goed afgeleid.

De Engel-curven worden genoemd naar de Duitse statisticus Ernst Engel (1821-1896), die al in de negentiende eeuw empirisch onderzoek verrichtte naar de wijzigingen van het consumptiepatroon ten gevolge van inkomensvariaties. Zo werd vastgesteld dat het relatieve aandeel van noodzakelijke goederen (bv. huisvesting, voeding) afneemt wanneer het inkomen groter wordt (wet van Engel). Dit betekent concreet dat de vraag naar dit soort goederen proportioneel minder sterk toeneemt dan het inkomen, met als gevolg een afname van het budgetaandeel wanneer het inkomen stijgt. We zagen hiervan voorbeelden in figuur 2 aan het begin van dit hoofdstuk. Het budgetaandeel voor wonen in het eerste kwartiel bedroeg 38 % en nam stelselmatig af bij hogere inkomens; in het hoogste kwar-

tiel bedroeg het nog maar 26 %.6 Wanneer de vraag naar een goed meer dan proportioneel stijgt bij een inkomenstoename spreekt men soms van luxegoederen. In figuur 2 zagen we een stijging van het budgetaandeel van bv. cultuur, ontspanning en onderwijs bij hogere inkomens; het aandeel bedroeg 11 % in het eerste kwartiel en 19 % in het vierde kwartiel.

Figuur 19 bevat een grafisch voorbeeld van de Engel-curve van respectievelijk een noodzakelijk goed en een luxegoed. Panelen (a) en (b) geven de Engel-curves, nl. het verband tussen de gevraagde hoeveelheid en het inkomen. Panelen (c) en (d) illustreren voor beide gevallen de overeenkomstige relatie tussen de budgetaandelen en het inkomen.

Figuur 19 De Engel-curve van een noodzakelijk goed en een luxegoed x x

(a) (b)

Engel-curve

Engel-curve y y

px/y

budgetaandeel goed x

px/y

budgetaandeel goed x y y (c) (d)

Om op meer formele wijze de invloed van het inkomen op de vraag te meten gebruiken economen het begrip inkomenselasticiteit van de vraag. Dat begrip werd voor de marktvraag al geïntroduceerd in het hoofdstuk over het marktmechanisme. We kunnen de inkomenselasticiteit ook formuleren om de invloed van een inkomensverandering op de vraag van een individuele consument na te gaan. Ze wordt gedefinieerd als de verhouding tussen

6 Strikt genomen mag alleen het inkomen wijzigen terwijl alle andere factoren onveranderd moeten blijven (ceteris paribus). Als we de verschillende inkomensdecielen vergelijken, veranderen wellicht meer factoren dan alleen het inkomen. Toch geeft figuur 2 een goede indicatie.

de relatieve verandering van de gevraagde hoeveelheid van een goed (x) en de relatieve verandering van het inkomen (y). Formeel uitgedrukt:

/ / dy y dx x dy dx x y y v f == .

De meeste goederen hebben een positieve inkomenselasticiteit: de vraag neemt toe bij hogere inkomens. Een (positieve) inkomenselasticiteit kleiner dan 1 betekent dat een toename van het inkomen met 1 % een toename van de vraag impliceert van minder dan 1 %. De vraagtoename is dus minder dan proportioneel, zodat men noodzakelijke goederen ook eenvoudig kan definiëren als goederen met een (positieve) inkomenselasticiteit kleiner dan 1. Wat zonet luxegoederen werden genoemd zijn goederen met een inkomenselasticiteit die groter is dan 1.

Het is ook mogelijk dat de vraag naar een bepaald goed afneemt wanneer het inkomen stijgt. Dat is het geval met het goed waarvan de Engel-curve wordt weergegeven in figuur 20. Goederen waarvoor geldt dat de vraag daalt wanneer het inkomen stijgt, noemt men inferieure goederen. Als traditionele voorbeelden golden lang margarine en cichorei. Van zodra het inkomen een zeker niveau bereikt, worden deze goederen in het consumptiepakket vervangen door boter en koffie. In sommige landen gelden nu bijvoorbeeld het openbaar vervoer en veel tweedehandsproducten als inferieur (in de zin dat ze een negatieve inkomenselasticiteit hebben, niet in de zin dat ze van ondermaatse kwaliteit zijn).

Figuur 20 De Engel-curve voor een inferieur goed

Engel-curve

6.3 Veranderingen in de prijs

In deze paragraaf analyseren we ten slotte de reactie van de consument op prijsveranderingen. We bekijken eerst hoe nutsmaximerend gedrag op logische wijze leidt tot een verband tussen de gevraagde hoeveelheid en de prijs van een goed; dit verband is de individuele vraagcurve van de consument. Vervolgens geven we aan dat de invloed van een prijsverandering zowel intuïtief als formeel opgesplitst kan worden in twee componenten, namelijk een substitutie-effect en een inkomenseffect.

6.3.1 De invloed van prijsveranderingen en de individuele vraagcurve

In figuur 21 wordt het effect van een prijsdaling van x1 onderzocht. Stel bijvoorbeeld dat de prijs van het eerste goed gehalveerd wordt (p'1 = p1/2), dan zal de budgetlijn niet langer worden weergegeven door jl, maar door jw. Als gevolg van de prijsdaling van goed 1 bereikt de consument niet langer zijn maximaal nut in e0 maar wel in e1. Na de prijsdaling van goed 1 consumeert zij meer van dat goed. Dit resultaat beantwoordt aan onze a priori verwachting en het geldt dan ook voor zowat alle goederen. Er zijn nochtans uitzonderingen mogelijk (zie verder). Merk echter op dat na de prijsverandering van het eerste goed ook de consumptie van het tweede goed is veranderd. Nochtans is de prijs van dit goed ongewijzigd gebleven.

Figuur 21 Totaal prijseffect

Dit is een belangrijke vaststelling: een verandering in de prijs van één van de goederen beïnvloedt het hele consumptiepakket, dus ook de consumptie van goederen die geen prijswijziging ondergaan. De mate waarin dat gebeurt, hangt af van de kruiselingse prijselasticiteit van de vraag: is deze elasticiteit negatief, dan zal bij een prijsdaling van goed 1 de consumptie van goed 2 toenemen. Dat is het geval dat wordt voorgesteld op figuur 21.

De analyse van prijsveranderingen leidt op logische wijze tot een verband tussen de gevraagde hoeveelheid en de eigen prijs van een goed. Dat verband, de individuele vraagcurve van de consument voor het betreffende goed, wordt in deel (b) van figuur 22 afgeleid uit het

consumentenevenwicht, voorgesteld in deel (a). De prijs van goed 1 daalt van p1 tot p1 ' en vervolgens tot p1". Onder de ceteris paribus-hypothese neemt de consumptie toe van x1 naar x1 ' en vervolgens naar x1". Door in deel (b) van figuur 22 op de verticale as de prijzen aan te geven en de overeenkomstige optimale hoeveelheden van goed 1 uit deel (a) over te nemen op de horizontale as verkrijgt men onmiddellijk de individuele vraagcurve voor het eerste goed. We merken op dat de individuele vraagcurve werd afgeleid in de veronderstelling van een gegeven inkomen en voor een gegeven prijs van het tweede goed. Door herhaling van de grafische analyse voor een hoger inkomen kan men eenvoudig nagaan dat de vraagcurve in dat geval naar rechts zal verschuiven, tenminste zolang de inkomenselasticiteit positief is. Ook wijzigingen in preferenties en in de prijs van het tweede goed zullen verschuivingen in de vraagcurve veroorzaken.

22 Grafische afleiding van de individuele vraagcurve

Figuur

6.3.2 Het substitutie-effect en het inkomenseffect

Er werd al op gewezen dat een prijsverandering van een goed niet alleen de gevraagde hoeveelheid van dit goed wijzigt, maar bovendien een invloed heeft op de vraag naar andere goederen waarvan de prijs onveranderd is gebleven. Men kan die vaststelling beter begrijpen als men het dubbele effect onderkent dat voortvloeit uit een prijsdaling van goed 1:

– Enerzijds is goed 1 na de prijsdaling relatief goedkoper geworden. Ten gevolge hiervan zal de consument het relatief duurder geworden tweede goed vervangen door het relatief goedkopere goed 1. Men noemt dit het substitutie­effect van de prijsdaling van goed 1. Het substitutie-effect van een prijsdaling veroorzaakt steeds een toename in het relatief goedkoper geworden goed.

– Anderzijds is ten gevolge van de prijsdaling van goed 1 de koopkracht van het inkomen van de consument verhoogd. Intuïtief voelt men dat onmiddellijk aan: als hij dezelfde bundel zou kopen als voor de prijsdaling van goed 1, dan zou hij niet zijn volledig inkomen hebben uitgegeven en dus nog geld overhebben. Bijgevolg kan hij na de prijsdaling in principe méér kopen van alle goederen, niet alleen van goed 1 maar ook van goed 2. We zeggen dan ook dat zijn reële inkomen gestegen is en spreken daarom van het inkomenseffect van de prijsdaling van het eerste goed. Dat zal uiteraard invloed hebben op zijn consumptiepatroon. Het teken van het inkomenseffect ligt niet vast, in tegenstelling tot het teken van het substitutie-effect. Het hangt er namelijk van af of het betreffende goed een normaal goed is of een inferieur goed. Inderdaad hebben we in paragraaf 6.2 gezien dat de consument van sommige goederen proportioneel meer en van andere proportioneel minder zal gaan consumeren wanneer zijn inkomen toeneemt. Het is zelfs mogelijk dat dit effect zo sterk is dat een prijsdaling de gevraagde hoeveelheid doet afnemen (men spreekt dan van Giffen­goederen; zie de appendix bij dit hoofdstuk).

Voor veel goederen is het verrijkingseffect (bij een prijsdaling) of het verarmingseffect (bij een prijstoename) zodanig klein dat mensen het niet opmerken. Stel bijvoorbeeld dat een kilo zout, een potje kruiden, een potlood of een stuk zeep goedkoper worden. De meeste consumenten besteden een heel klein deel van hun budget aan elk van die producten. Worden ze wat goedkoper dan zullen die mensen zich niet ‘rijker’ voelen. Er is ook geen merkbaar verarmingseffect als de prijzen een beetje toenemen. Maar neem de uitgaven van gezinnen aan huisvesting of transport. Aan die goederen geven veel gezinnen wel een belangrijk deel van hun maandelijks budget uit. Als bijvoorbeeld de huurprijzen toenemen van een gezin dat 40 % van zijn budget aan huur besteedt dan zal dat wel degelijk als een verarming worden ervaren. Met andere woorden, het inkomenseffect kan echt wel belangrijk zijn voor goederen die een grote hap uit het consumentenbudget nemen.

Men kan voor elke prijsverandering de uitsplitsing naar inkomens- en substitutie-effecten grafisch illustreren. Die materie is eerder technisch en wordt toegelicht in de appendix.

6.4 Preferenties, observeerbaar gedrag en vraaganalyses

In al het voorgaande werd ervan uitgegaan dat we de preferenties van de consument kenden. Op basis van die preferenties konden we dan de invloed van prijs- en inkomensveranderingen op de keuze van consumenten analyseren. Het is echter evident dat preferenties niet observeerbaar zijn. Het is daarom voor een goed begrip nuttig aan te geven hoe economen het raamwerk dat werd besproken in de praktijk gebruiken om het probleem van niet-observeerbare preferenties te ‘omzeilen’.

Voor gegeven preferenties (samengevat door nutsfuncties met bijbehorende indifferentiecurven) leerde de theorie hoe men de vraagcurven van consumenten die het nut maximaliseren, kon afleiden. Deze preferenties zijn niet observeerbaar, maar de goederenbundels die mensen consumeren zijn dat wel. Die gekozen bundels zijn het gevolg van zowel de preferenties van de consument als van zijn budgetbeperking. Gegevens over prijzen en budgetten die consumenten ter beschikking hebben, kunnen via aangepaste technieken (door budgetenquêtes, surveys enz.) worden verkregen. Economen gebruiken dan informatie over de gekozen consumptiebundels van mensen samen met onder meer gegevens over hun beschikbare budget en de prijzen van verschillende goederen en diensten om de vraag naar verschillende goederen te bepalen, en zo indirect informatie over hun preferenties af te leiden. Dat dit mogelijk is lijkt intuïtief duidelijk. Iemand die bij gegeven prijzen en voor een bepaald beschikbaar budget zeer veel fruit eet, geeft daarmee onder meer aan dat hij een sterke preferentie heeft voor fruit.

Wat men in de praktijk doet is dus in feite het omgekeerde van wat eerder werd toegelicht. De theorie vertrok van bekende preferenties om de keuze van de consument te voorspellen en zo de vraag af te leiden. In de praktijk vertrekt men van gegevens over de geconsumeerde goederenbundels van consumenten om hun vraag naar allerlei goederen te verklaren op basis van inkomens, prijzen en een hele reeks controlevariabelen (gezinsgrootte en -samenstelling, opleidingsniveau van de gezinsleden enz.). Op die wijze leidt men dan informatie over hun preferenties af. Die persoon geeft door zijn aankoopgedrag dan zijn ‘gereveleerde preferenties’ weer. Bovendien kan men dan, vertrekkend van deze geschatte vraagfuncties, de effecten voorspellen van prijsveranderingen, budgetwijzigingen, de effecten van overheidsmaatregelen enz.

Economen gebruiken complexere nutsfuncties in praktische toepassingen, maar we illustreren het voorgaande voor een Cobb-Douglas-nutsfunctie (eenzelfde principe geldt voor meer complexe nutsfuncties):

u(x1, x2) = (x1)a(x2)(1-a)

Merk op dat de parameter ‘a’ die de preferenties van de consument beschrijft (‘a’ bepaalt de vorm van de indifferentiecurven), niet bekend is. De budgetbeperking is gegeven door:

p1 x1 + p2 x2 = y.

Optimale keuze van de consument impliceert enerzijds dat de verhouding van de marginale nuttigheden gelijk moet zijn aan de verhouding van de prijzen; anderzijds moet de budgetbeperking voldaan zijn. Dat geeft de volgende twee vergelijkingen:

(a x2)/((1-a) x1) = p1/p2

p1 x1 + p2 x2 = y

Oplossing van dat eenvoudige stelsel naar de hoeveelheden x1, x2 geeft ons de vraagfuncties naar de twee goederen:

x1=(a y)/p1

x2=((1-a) y)/p2

Economen kunnen voor verschillende gezinstypes gegevens over gekozen hoeveelheden van verschillende goederen (in het voorbeeld x1, x2) verzamelen, alsook informatie over prijzen en budgetten (inkomens). Gebruikmakend van statistische schattingstechnieken bepalen ze dan op basis daarvan de parameter ‘a’ voor een groot aantal gezinstypes (onderscheiden naar grootte, leeftijd van de kinderen, opleidingsniveau van de ouders enz.). Kennis van de vraagfuncties voor verschillende gezinstypes laat dan toe te voorspellen hoe gezinnen zullen reageren op prijs- en budgetwijzigingen. Zo voorspelt men dat een toename van het budget y met 100 euro de vraag naar het eerste goed zal doen toenemen met (100 a)/p1.

7 Consumentengedrag in actie: toepassingen

Om de relevantie van een gedegen kennis van de theorie van het consumentengedrag te benadrukken, gaan we in deze paragraaf in op enkele illustratieve toepassingen. We bekijken achtereenvolgens de invloed van belastingen op de optimale keuze van de consument, we gaan na hoe het beschreven raamwerk kan worden gebruikt om de keuze van een consument tussen een dieselauto en een benzineauto te analyseren, en we bekijken de effecten van het gratis ter beschikking stellen van een bepaalde hoeveelheid van een goed op de optimale keuze van de consument. Talloze andere voorbeelden zijn denkbaar, maar wat volgt geeft een eerste idee van de toepassingsmogelijkheden van de theorie. Een voorbeeld dat aangeeft hoe breed de toepasbaarheid van de theorie wel is, komt aan bod in toepassing 2.

We bekijken eerst de invloed van een indirecte belasting op een product. Voorbeelden zijn niet ver te zoeken. Denk aan de btw op diverse producten, aan belastingen op de verkoop van boeken via het internet, aan brandstofbelastingen, aan milieubelastingen op goederen verpakt in niet-recycleerbare materialen enz. De invloed van dergelijke belastingen wordt nagegaan aan de hand van figuur 23.

Figuur 23 Effect van een belasting

Andere goederen

Stel dat een gegeven consument met welbepaalde preferenties een budget y verdeelt over frisdranken en andere goederen, en dat er initieel geen belasting op frisdranken aan de orde is. De budgetbeperking voor de invoering van de belasting wordt voorgesteld door de rechte ab; gegeven de preferenties van de consument is de optimale bundel dan de combinatie gegeven door punt e. Stel nu dat de overheid een belasting invoert op frisdranken. Hierdoor verhoogt de prijs van frisdranken en roteert bijgevolg de budgetrechte naar ac. Het nieuwe optimum is e’. We stellen vast dat de belasting ervoor zorgt dat de vraag naar frisdranken daalt. Zo introduceerde de Deense overheid de zogenaamde vetbelasting om obesitas aan te pakken; daarbij was de idee dat de hogere belasting de consumptie van producten met een hoog vetgehalte zou afremmen.

Toepassing 2 Zijn ratten, duiven of apen rationele consumenten?

Het lijkt misschien vreemd, maar men gebruikt ook dierexperimenten om na te gaan of dierlijk gedrag in overeenstemming is met de wetten van de vraag en of ze zich met andere woorden zo gedragen als rationele consumenten. Een voorbeeld van dergelijke experimenten vinden we in Chen, M.K., Lakshminaryanan, V. & Santos, L.R. (2006). Deze auteurs werkten met capucijnapen. De apen werd het gebruik van ‘geld’ aangeleerd. Ze kregen muntjes (hun inkomen), die ze bij hun begeleiders konden ruilen voor verschillende soorten voedingsproducten. Elk voedingsproduct had een eigen prijs (aantal eenheden van het voedsel dat ze krijgen voor een muntje). Vervolgens testte men hoe het ruilgedrag van de apen wijzigde bij wijzigingen van de prijs van het voedsel en van het inkomen. De capucijnaapjes gedroegen zich in overeenstemming met de standaard nutsanalyse en prijstheorie. Ze kopen bv. meer van relatief goedkoper geworden voedsel en minder van relatief duurder geworden voedsel. Daarmee worden vroegere experimenten met ratten en duiven bevestigd. De experimenten tonen ook aan dat het gebruikelijk economisch kader niet in alle omstandigheden een goede verklaring geeft voor het gedrag. De apen gedragen zich – net als mensen trouwens – soms ook irrationeel. Dit is onder meer het geval bij beslissingen onder onzekerheid.

Bron: Chen, M.K., Lakshminaryanan, V. & Santos, L.R. (2006), The evolution of our preferences: Evidence from capuchin monkey trading behavior, Journal of Political Economy, 114(3), 517-537

De overheid hanteert niet alleen indirecte belastingen om inkomsten te verwerven, ze kan ook directe belastingen op inkomens opleggen. Dat heeft duidelijk andere effecten dan een indirecte belasting. Een belasting op het inkomen vermindert het beschikbaar budget en leidt grafisch tot een evenwijdige verschuiving van de budgetrechte naar links; een indirecte belasting daarentegen resulteerde in een rotatie naar binnen (zie hoger). Dit eenvoudige onderscheid heeft een opmerkelijk gevolg. Stel namelijk dat de overheid een gegeven totaal bedrag aan belastingen wil opleggen aan een consument en dat ze de keuze heeft tussen een belasting op het inkomen en een indirecte belasting op een bepaald product x. Men ziet dan onmiddellijk in dat vanuit het standpunt van de consument (bij een gelijkblijvend inkomen voor belasting) een belasting op het inkomen altijd leidt tot een kleinere daling van het nut dan een indirecte belasting op een goed, waarbij men er zoals gezegd van uitgaat dat de consument in beide gevallen dezelfde totale belasting betaalt. In figuur 24 illustreren we dit inzicht grafisch. Het uitgangspunt is de budgetrechte ab. De consument kan met een budget a (op de verticale as) maximaal een hoeveelheid b kopen van goed 1, aangeduid op de horizontale as. Uiteraard weerspiegelt de helling van deze budgetrechte de prijs van goed 1. De optimale hoeveelheid die deze consument wenst aan te kopen, is aangeduid met e, daar waar de indifferentiecurve u0 raakt aan de budgetrechte ab. Wanneer de overheid beslist om een (indirecte) belasting te heffen op goed 1 dan roteert de budgetrechte ab naar ac. De verandering in de helling van de budgetrechte reflecteert de hoogte van de indirecte belasting. Grafisch zien we dat de consument in het punt e’ een optimum bereikt, waar de indifferentiecurve u1 raakt aan de budgetrechte ac. Het is duidelijk dat de consument slechter af is door deze indirecte belasting, omdat u1 < u0. We zien ook dat het aantal eenheden dat de consument koopt van het goed 1 na invoering van de indirecte belasting gelijk is aan g. Het is duidelijk dat de totale uitgave van de consument voor deze g eenheden gelijk is aan ah terwijl diezelfde hoeveelheid voor de indirecte belasting te koop was tegen am, wat kleiner is dan ah. Het verschil, namelijk mh, is de belastingopbrengst voor de overheid.

De overheid kan als alternatief ook een directe inkomensbelasting heffen die evenveel opbrengt als de indirecte belasting. De budgetrechte verschuift dan parallel met de afstand mh van ab naar df (die gaat precies door de het optimale punt e’ in het geval van de indirecte belasting). Het nutsniveau is u2, wat groter is dan u1. We stellen vast dat de consument altijd een hoger nutsniveau bereikt dan met de indirecte belasting.

Dit is een relevante conclusie: het betekent vanuit individueel oogpunt dat rationele consumenten liever (gegeven een totaal bedrag aan belastingen) directe dan indirecte belastingen betalen. De reden is dat een indirecte belasting op het budget zowel een inkomenseffect heeft als een substitutie-effect; een directe belasting heeft alleen een inkomenseffect. Om soortgelijke redenen prefereren rationele consumenten een directe subsidie boven een indirecte subsidie.

Figuur 24 Directe versus indirecte belasting

andere goederen (prijs = 1)

goed 1

Als dat zo is, waarom heft de overheid dan indirecte belastingen en geeft ze indirecte subsidies? Daarvoor zijn verschillende redenen. De overheid heeft de informatie niet om voor elke consument en voor alle goederen de consumptiepatronen te kennen en op basis daarvan de correcte inkomensbelasting te bepalen. Bovendien kan de overheid andere doelstellingen hebben met het invoeren van de indirecte belasting dan alleen maar het verwerven van inkomsten: hoewel de overheid dezelfde inkomsten zou kunnen krijgen door het inkomen te belasten met een kleiner nutsverlies voor de consument, kan ze toch kiezen voor een belasting op alcoholische dranken, rookwaren, ongezonde voeding, schadelijke producten etc. als de bedoeling juist is om het verbruik daarvan tegen te gaan. Ten slotte was onze analyse gebaseerd op de veronderstelling van een gelijkblijvend inkomen voor belasting. Dit betekent dat het arbeidsaanbod gelijk blijft. Ook dit is in de realiteit niet noodzakelijk waar: inkomstenbelastingen kunnen mensen aanzetten minder te gaan werken en bijgevolg leiden tot bijkomende effecten op de budgetbeperking.

Een ander voorbeeld betreft de keuze van een individu tussen de aankoop van een benzineauto versus een elektrische auto. Stel dat de consument een jaarlijks inkomen heeft van y en dat hij een keuze moet maken tussen twee auto’s in een bepaald marktsegment, een benzineauto en een elektrische wagen. Laten we aannemen (overigens in overeenstemming met de realiteit) dat de jaarlijkse kosten van het bezit van een benzineauto kleiner zijn dan de jaarlijkse kosten voor een elektrische wagen, maar dat (wegens een lager verbruik en het gevoerde subsidiebeleid om elektrische wagens te stimuleren) de prijs per kilometer voor een elektrische auto lager ligt dan voor een benzineauto.

De keuze van de consument wordt geïllustreerd in figuur 25. We gaan ervan uit dat de consument geïnteresseerd is in autorijden (uitgedrukt in kilometers per jaar) en andere goederen; dit laatste goed is een geaggregeerd goed waarvan we de hoeveelheid meten in euro. Het jaarlijkse budget van de consument y wordt voorgesteld op de verticale as: het

punt y geeft de bundel die de consument kiest als hij geen auto koopt. Indien het individu voor een benzineauto kiest, is de budgetbeperking gegeven door ab. De afstand tussen de punten y en a geeft de jaarlijkse vaste kosten van een benzineauto weer. Analoog is de budgetbeperking cd in het geval hij een elektrische wagen kiest. We gaan ervan uit dat er voldoende snelle oplaadmogelijkheden zijn, bijvoorbeeld thuis of op het werk, zodat een elektrische wagen hogere jaarlijkse vaste kosten heeft (zie de verticale as) maar een lagere prijs per kilometer (zie de kleinere helling van cd in vergelijking met ab).

Figuur 25 Keuze tussen een benzineauto en een elektrische wagen

Andere goederen (prijs = 1)

Kilometers met de wagen

We zien dat, gegeven de preferenties van de betreffende consument, aangeduid als consument 1 in figuur 25, hij optimaal kiest voor een benzineauto. Merk echter op dat iemand met een sterkere preferentie voor autokilometers, zou kiezen voor een elektrische wagen. De consument aangeduid als consument 2 in figuur 25 kiest bijvoorbeeld voor een elektrische auto. Indien naar de toekomst toe de prijzen van elektrische wagens dalen relatief ten opzichte van benzinewagens en er bovendien nog meer snelle oplaadmogelijkheden komen, zal in termen van figuur 25 het punt c naar boven schuiven en de helling van cd vlakker worden. Het gevolg is dan dat meer consumenten zullen opteren voor een elektrische wagen. Vervallen de fiscale voordelen voor elektrische wagens dan kan het omgekeerde zich voordoen.

Toepassing 3 Gevolgen van het gratis ter beschikking stellen van een beperkte hoeveelheid van een goed

Soms stelt de overheid een beperkte hoeveelheid van een goed gratis ter beschikking van bepaalde groepen consumenten. Zo zou men om sociale redenen minimale hoeveelheden kunnen garanderen aan arme gezinnen (bijvoorbeeld een minimale hoeveelheid elektriciteit of gezondheidszorg). Ook de private sector voert echter in sommige gevallen een dergelijk beleid; denk bijvoorbeeld aan ‘frequent flyer’-tegemoetkomingen door luchtvaartmaatschappijen. Daarbij worden onder bepaalde omstandigheden gratis trips aangeboden aan goede klanten.

Neem aan dat we de keuze van een consument bestuderen tussen twee goederen en dat de overheid automatisch een hoeveelheid E van x1 gratis ter beschikking stelt. Het effect hiervan voor de budgetbeperking werd eerder in dit hoofdstuk al toegelicht. In delen (a) en (b) van figuur 26 worden de gevolgen geïllustreerd voor twee verschillende consumenten. Op het linkerdeel zien we dat de consument zonder het gevoerde beleid zeer weinig van het betreffende goed zou hebben geconsumeerd, en dat het beleid de consument ‘aanzet’ minimaal de hoeveelheid E te verbruiken. Ook het nut neemt toe. Hetzelfde geldt voor de consument van figuur (b). Toch is er een belangrijk verschil tussen beide consumenten in die zin dat voor de consument van figuur (b) de gratis hoeveelheid hetzelfde effect heeft als een toename van het inkomen ter waarde van de marktwaarde van het goed. Dat is niet het geval voor de consument van figuur (a): hij wordt, om van de gratis hoeveelheid te kunnen genieten, ‘gedwongen’ meer te verbruiken dan hij zou verbruiken als men hem de waarde van het goed als inkomenssupplement had uitbetaald.

Figuur 26 Gratis ter beschikking stellen van een hoeveelheid E

Het voorgaande gaf enkele potentiële toepassingsmogelijkheden van de theorie van de consument. Het is evident dat we het model met enige inventiviteit ook eenvoudig toepassen op uiteenlopende andere problemen: de keuze tussen huidige en toekomstige consumptie (m.a.w. op het spaargedrag van gezinnen), de keuze tussen consumptiegoederen en vrije tijd (m.a.w. op de beslissing al dan niet te werken en het optimaal aangeboden aantal arbeidsuren), op de keuze tussen gelijksoortige goederen met verschillende karakteristieken (bijvoorbeeld de keuze van een restaurant) enz. Dergelijke toepassingen vallen buiten het bestek van dit boek, maar lezers met voldoende creativiteit zien onmiddellijk in hoe dit aangepakt zou kunnen worden.

8 Afleiding van de marktvraag uit de individuele vraagcurven

We begonnen dit hoofdstuk met erop te wijzen dat de theorie van de consument een theoretische fundering is voor de wet van de vraag die in het hoofdstuk over het marktmechanisme werd besproken. Daar werd uitgegaan van een negatief verband tussen de gevraagde hoeveelheid van een bepaald product op een markt en de prijs van dit goed. De theorie van het consumentengedrag maakt het nu mogelijk het verband te leggen tussen de individuele vraagcurven van de verschillende consumenten en de geaggregeerde marktvraagcurve. In het meest eenvoudige geval kan deze laatste door horizontale sommatie van de individuele vraagcurven afgeleid worden.7 Figuur 27 geeft daarvan een voorbeeld, gemakkelijkheidshalve beperkt tot een markt met maar twee vragers. Voor elke gegeven prijs bepaalt men de marktvraag als de som van de gevraagde hoeveelheden van de twee consumenten.

Figuur 27 Grafische afleiding van de marktvraag

9 Uitbreidingen en kritische kanttekeningen

De theorie van het consumentengedrag die hierboven werd ontwikkeld is aantrekkelijk omdat ze – op basis van enkele eenvoudige hypothesen met betrekking tot het gedrag van de consument, voornamelijk met betrekking tot interne consistentie (‘rationaliteit’) – in staat is sommige fundamentele economische wetten (zoals bv. de wet van de vraag) van een theoretische onderbouw te voorzien.

De theorie kent echter ook een aantal gebreken en tekortkomingen, waarvan sommige door een aangepaste uitbreiding eenvoudig ondervangen kunnen worden. Andere vereisen een fundamenteel andere aanpak.

7 Wanneer de door een individuele consument gevraagde hoeveelheid afhangt van het aantal consumenten (wegens positieve netwerkeffecten of negatieve snobeffecten (zie het hoofdstuk over het marktmechanisme)), moet deze eenvoudige horizontale sommatie worden bijgestuurd.

9.1 Uitbreiding van de theorie

In onze uiteenzetting in dit hoofdstuk was geen plaats ingeruimd voor sparen of ontsparen: we gingen ervan uit dat consumenten in een gegeven periode precies hun volledige budget uitgeven. Met sparen en ontlenen kan evenwel eenvoudig rekening gehouden worden, aangezien sparen kan worden opgevat als afstand doen van huidige consumptie ten voordele van toekomstige consumptie, of met andere woorden door een onderscheid te maken tussen huidige en toekomstige consumptie. Het blijkt dan dat de rentevoet een belangrijke determinant vormt voor de consumptie (en het sparen), naast de beschikbare budgetten en de prijzen zowel nu als in de toekomst. Ook de vraag naar duurzame goederen kan geïncorporeerd worden zodra men consumptie analyseert in een meerperiodemodel.

We hebben aangenomen dat de consument enkel beperkt wordt door zijn gegeven budget. In de dagelijkse praktijk geldt echter ook een tijdsrestrictie (er zijn maar 24 uur in een dag) die onze keuzes beperkt. Hiermee rekening houden blijkt echter geen grote moeilijkheden te stellen. Het modelleren van optimaal gedrag waarbij men zowel met een budget- als met een tijdsbeperking rekening houdt, is een relatief eenvoudige uitbreiding van het basismodel van dit hoofdstuk.

Een verdere tekortkoming van de theorie is dat nutsfuncties klassiek op hoeveelheden goederen zijn gedefinieerd, terwijl consumenten dikwijls niet zozeer zijn geïnteresseerd in de hoeveelheden maar wel in de ‘karakteristieken’ van de geconsumeerde producten. Zo vinden consumenten niet alleen het aantal keer dat men uit eten gaat belangrijk; ze hechten bijvoorbeeld belang aan de kwaliteit van de maaltijden, of de atmosfeer in het restaurant, het gezelschap waarmee ze het restaurant bezoeken enz. Een ander voorbeeld betreft de aanschaf van auto’s: niet het aantal is de cruciale variabele, maar wel het merk, het type, het design, de kleur enz. Deze problematiek heeft aanleiding gegeven tot een vernieuwde visie op de theorie van de consument, waarbij nutsfuncties niet gedefinieerd worden op hoeveelheden goederen, maar rechtstreeks op de karakteristieken van goederen. Die zijn immers wat echt telt voor de consument. Deze benadering (ontwikkeld door de Amerikaanse econoom Kelvin Lancaster (1924-1999)) maakt het mogelijk een aantal problemen te bestuderen die de standaardtheorie van de consument niet kon aanpakken, zoals de keuze tussen verschillende merken, de vraag naar nieuwe en vroeger niet beschikbare producten enz.

Ook een andere vaak geuite kritiek kan relatief eenvoudig worden opgevangen. Dikwijls stelt men dat de theorie van het consumentengedrag flagrant in tegenspraak is met de werkelijkheid, aangezien ze niet in staat is vormen van altruïsme te verklaren. Dit is echter niet correct: indien men de argumenten van de nutsfunctie uitbreidt met het welzijn of de consumptie van anderen kan men altruïstisch gedrag gemakkelijk in de theorie opnemen. De idee is dat nutsfuncties in zekere mate interdependent kunnen zijn: zo halen ouders voldoening uit de consumptie van hun kinderen, en halen veel mensen persoonlijke voldoening uit een bijdrage tot een betere levensstandaard van de laagste inkomensklassen.

Een aantal zwakke punten in de analyse van het consumentengedrag zijn wat moeilijker –maar niet onmogelijk – op te lossen. De analyse van de consumentenvoorkeur gaat ervan uit dat het individu de relevante economische entiteit vormt. Voor vele consumptiebeslissingen blijkt het gezin echter de relevante economische entiteit te zijn. Hoe beslissingen in gezinsverband worden genomen, kan men analyseren door rekening te houden met de preferenties van de betrokken gezinsleden, en de uiteindelijke beslissingen te zien als de uitkomst van een onderhandelingsproces tussen alle betrokkenen, waarbij niet alle gezinsleden dezelfde onderhandelingsmacht hebben.

We hebben in dit hoofdstuk ook abstractie gemaakt van onzekerheid. Er werd uitgegaan van de veronderstelling dat de consument alle relevante grootheden kent: hij kent alle goederen en alle relevante prijzen met zekerheid, en ook zijn beschikbaar budget ligt vast. Dit is uiteraard niet altijd realistisch: in de praktijk zal de consument zijn keuzen moeten maken onder omstandigheden van imperfecte informatie. Voor sommige beslissingen geeft dit geen onoverkomelijke problemen. In andere gevallen (bijvoorbeeld beslissingen betreffende financiële beleggingen, aankopen van duurzame goederen enz.) is onzekerheid eerder regel dan uitzondering. Rekening houden met onzekerheid maakt de theorie wat ingewikkelder en niet geschikt voor een inleidend handboek, maar onzekerheid is geen onoverkomelijk obstakel.

Een laatste moeilijkheid die we hier vermelden bestaat erin dat men, zelfs wanneer consumenten het nut perfect maximaliseren, slechts één punt van de indifferentiecurve kent, namelijk de gekozen consumptiebundel. Een ander inkomensniveau en/of een andere prijsverhouding tussen de goederen leidt tot een andere bundel. Wel kunnen we stellen dat de consument door een bepaalde bundel te kiezen als het ware reveleert dat hij deze bundel verkiest boven alle andere die eveneens binnen zijn budgetbeperking vallen. Door het vergelijken van deze feitelijke keuzen en door het maken van enkele veronderstellingen kan men de theorie van het gedrag van de consument ‘herschrijven’ zonder een beroep te moeten doen op het begrip indifferentiecurve. Men komt dan op het domein van de theorie van de gereveleerde voorkeur (‘revealed preference theory’).

9.2 Kritiek op rationeel denken: gedragseconomie

Hoewel heel wat opiniemakers, bedrijfsleiders en beleidsmakers het onderwerp van de economische wetenschap niet in vraag stellen, bekritiseren ze economen soms sterk voor de hypothesen waarop ze hun conclusies bouwen. Vooral de veronderstelling binnen de neoklassieke economie dat consumenten (maar ook bedrijfsleiders) altijd rationeel denken en bijgevolg optimale, doordachte beslissingen nemen, ligt onder vuur. Mensen van vlees en bloed denken immers niet altijd rationeel (wegens de complexiteit van sommige problemen, door tijdsgebrek, door informatiebeperkingen) of ze laten zich bij hun beslissingen ook leiden door hun emoties. Bijgevolg nemen ze niet altijd doordachte beslissingen. Hierdoor zou er een fundamentele kloof liggen tussen enerzijds de voorspellingen van economische modellen, en anderzijds wat zich afspeelt in de werkelijkheid. De bruikbaarheid van economische inzichten op basis van modellen zou hierdoor eerder beperkt zijn. Deze

kritiek op de economische wetenschap is zeker niet nieuw en heeft opnieuw veel aandacht gekregen tijdens de financiële crisis van 2007-2008.

Door rationaliteit en optimaliserend gedrag van economische agenten te veronderstellen, verwacht de standaardtheorie wellicht te veel van consumenten. Mensen hebben niet altijd de nodige informatie en de mogelijkheden om ingewikkelde keuzeproblemen echt optimaal op te lossen, en bovendien spelen perceptie en emoties ongetwijfeld een rol bij sommige keuzeproblemen.

De economische onderzoeksgemeenschap is zich erg bewust van deze kritieken. Samen met de inzichten van sociologen, maar vooral van psychologen, hebben ze een nieuwe tak van de economische wetenschap ontwikkeld, de zogenaamde gedragseconomie (‘behavioral economics’). Die bestudeert beslissingsmodellen die rekening houden met de beperkte rationaliteit van economische agenten. Daarbij wordt aangenomen dat mensen hun nut niet altijd kunnen, en soms ook niet willen, optimaliseren. Enerzijds is de informatie en de competentie die nodig is om altijd rationele beslissingen te nemen bij complexe problemen niet bij iedereen aanwezig. Stel dat consumenten systematisch hun nut willen maximaliseren, rekening houdend met een beperkt budget, met een tijdsbeperking en met een beperking op hun eigen competentie. Dit betekent dat ze continu een reeks erg moeilijke problemen moeten oplossen, waarbij bovendien belangrijke informatie niet met zekerheid is bekend (toekomstige prijzen, beurskoersen, productkwaliteit, inkomens). Anderzijds is het zo dat mensen hun gedrag niet altijd willen optimaliseren, denk maar aan mensen die belangrijke beslissingen voor zich uit schuiven (uitstelgedrag).

Psychologen hebben in een groot aantal gepubliceerde experimenten kunnen vaststellen dat mensen beslissingen nemen die in tegenspraak zijn met de veronderstelling van rationeel gedrag.8 Ze vonden onder meer dat mensen ten onrechte bepaalde irrelevante informatie gebruikten om een beslissing op te baseren (‘anchoring’), en bijgevolg vanuit rationeel oogpunt ‘verkeerde’ beslissingen nemen. Bovendien toonden ze aan dat mensen andere beslissingen nemen afhankelijk van hoe een bepaald beslissingsprobleem wordt voorgesteld (‘framing’). Mensen zijn met andere woorden tot op zekere hoogte manipuleerbaar.

Het aanvaarden van de vaak empirisch vastgestelde beperkte rationaliteit heeft aanleiding gegeven tot een aantal nieuwe theorieën. Eén voorbeeld is de ‘prospect theory’ van Daniel Kahneman (1934-2024) en Amos Tversky (1936-1996), die rekening houdt met het psychologische proces dat economische agenten ondergaan bij het nemen van beslissingen. In het bijzonder is de focus van hun theorie op het experimenteel verklaren van zogenaamde cognitieve anomalieën, omstandigheden waarbij menselijke beslissingen significant afwijken van rationeel gedrag door o.a. perceptuele illusies en wat men noemt ‘status quo bias’. Verder vonden dezelfde auteurs empirische ondersteuning voor hun hypothese dat menselijke preferenties gedefinieerd moeten worden ten opzichte van een gegeven referentiesitu-

8 Een aantal van die experimenten worden besproken in het zeer leesbare boek van D. Kahneman (2011). Thinking: Fast and slow. London: Penguin Books.

atie. Iemand die 5 % loonsverhoging krijgt maar een toename van 10 % verwacht had, kan zich ondanks het hoger loon – en in tegenstelling tot wat de klassieke nutstheorie zou besluiten – minder goed voelen (‘een lager nut hebben’). Bovendien blijken mensen te lijden aan ‘verliesaversie’ (‘loss aversion’). Ze hechten veel meer belang aan een verlies dan aan een winst van dezelfde omvang: de (negatieve) waarde die ze hechten aan een verlies van 1 000 euro is in absolute waarde veel groter dan de waarde die ze hechten aan een winst van 1 000 euro. Tversky en Kahneman stellen daarom een alternatief voor de klassieke nutsfunctie voor die toelaat beslissingen onder beperkte rationaliteit te bestuderen en te verklaren. Ze definiëren wat ze noemen de waardefunctie, die onder meer beide genoemde empirische vaststellingen (een referentiesituatie, verliesaversie) in aanmerking neemt. Dit instrument laat toe veel schijnbaar irrationele beslissingen logisch te verklaren. De grote moeilijkheid voor empirisch onderzoek is wel dat voor veel beslissingen de referentiesituatie niet observeerbaar is.

Een andere belangrijke bevinding van de gedragseconomie is dat mensen notoir slecht zijn in het nemen van beslissingen onder onzekerheid; één belangrijke reden is dat ze het doorgaans moeilijk hebben de kansen waarmee bepaalde gebeurtenissen voorkomen correct in te schatten. In veel gevallen houden we met onzekerheid zelfs geen rekening. Zo wijst Daniel Kahneman erop dat we de ‘kwaliteit’ van beslissingen ten onrechte beoordelen op basis van de uitkomsten, zonder rekening te houden met onzekerheid. Zo gaan we ervan uit dat een succesvolle ondernemer iemand is die in het verleden de juiste beslissingen nam en om die reden succes kende. We houden daarbij geen rekening met het feit dat de ondernemer beslissingen moest nemen onder grote onzekerheid over toekomstige prijzen, voortdurend wijzigende reglementering, veranderingen in consumptiepatronen, enzovoort. Succes kan dus het gevolg zijn van verstandige beslissingen, maar de ondernemer kan ook gewoon een dosis geluk hebben gehad. Het is zelfs best mogelijk dat een succesvolle ondernemer vanuit rationeel oogpunt onverstandige beslissingen nam, maar gewoon veel geluk heeft gehad. Omgekeerd kan een bedrijf in de problemen komen als gevolg van beslissingen uit het verleden die toen rationeel verstandig waren, maar achteraf slecht bleken uit te draaien. Een voorbeeld uit de energiesector kan dat illustreren. Twintig jaar geleden waren veel specialisten ervan overtuigd dat het verstandig was te investeren in voertuigtechnologie gebaseerd op waterstof. Achteraf is gebleken dat de overheid elektrisch rijden sterk subsidieerde, en bedrijven die sterk hadden ingezet op waterstoftechnologie, kwamen in de problemen. Hoewel ook andere factoren een rol speelden, was de busbouwer Van Hool daarvan een voorbeeld.

We wezen er al op dat mensen in bepaalde mate manipuleerbaar zijn. Gedragseconoom Richard Thaler (°1945), winnaar van de Nobelprijs voor Economie in 2017, gebruikt deze (onbewuste) irrationaliteit in sommige beslissingen net om mensen via een zacht duwtje (‘nudge’) naar een betere keuze te sturen. Nudges zijn “aspects of the choice architecture that alters behavior in a predictable way, without forbidding any options or changing incentives”.9 Wellicht de meest tot de verbeelding sprekende nudge is de ‘vlieg’ in de mannentoiletten van veel hotels en luchthavens.

9 Zie R. Thaler & C.R. Sunstein (2008). Nudge. Yale University Press, p. 6.

Hoe kan men ‘nudges’ aanwenden om een aantal maatschappelijke verbeteringen te bewerkstelligen? Enkele voorbeelden kunnen dat illustreren. Om overcomsumptie van fastfood tegen te gaan zou men in principe fast food formeel kunnen verbieden, of er een hoge belasting op leggen. Een ‘nudge’ die dezelfde bedoeling heeft, is dan bijvoorbeeld gezonde voeding duidelijk zichtbaar in de supermarkt leggen en fastfood op minder in het oog springende plaatsen (of helemaal niet) aanbieden. Een ander voorbeeld: men stelt vast dat een aantal – meestal minder goed geïnformeerde – gezinnen die recht hebben op een studiebeurs voor hun kinderen, toch geen formele aanvraag indienen. Wat men dan kan doen is een systeem opzetten waarbij ieder gezin dat recht heeft op een beurs automatisch de beurs krijgt uitbetaald. Wanneer de bevolking weerstand biedt tegen een door de politiek overwogen milieubelasting, kan een nudge erin bestaan de belasting beter aanvaardbaar te maken door als overheid heel transparant aan te geven hoe men de inkomsten van de belasting zal gebruiken. Om een gezonde levensstijl te bevorderen zouden verzekeringsmaatschappijen korting kunnen geven aan wie evidentie geeft van een gezonde levensstijl. Om een massa aan onbeschofte e-mails tegen te gaan is er software die een waarschuwing geeft vooraleer een onbeleefde mail verstuurd wordt. Om mensen aan te zetten minder energie te verbruiken kan men het energieverbruik van gezinnen vergelijken met dat van de buurt waarin ze wonen, en men kan deze informatie aan de gezinnen meedelen. Om te beletten dat mensen op vergaderingen eindeloos het woord nemen en een langdradig betoog afsteken zou men kunnen vragen dat elke spreker, wanneer hij of zij het woord neemt, expliciet aangeeft na tien minuten afgestopt te willen worden. Enz.

Appendix

Uitsplitsing van prijseffecten in inkomens- en substitutie-effecten

In deze appendix gaan we in op de technische uitsplitsing van een prijswijziging in een inkomens- en een substitutie-effect. In figuur A1 wordt een veelgebruikte grafische opsplitsing voorgesteld (er zijn ook andere mogelijkheden om dit te doen). De prijsdaling wijzigt het initieel optimum e0; het nieuwe optimum is e1. Om de uitsplitsing te maken wordt er in een eerste stap hypothetisch van uitgegaan dat de prijsdaling van goed 1 gecombineerd wordt met een (nominale) inkomensdaling, zodanig dat de consument op hetzelfde nutsniveau blijft dat hij bereikte voor de prijsdaling. Deze hypothese vertaalt zich in figuur A1 door de budgetlijn jl, die geldt voor de prijsdaling van goed 1, langs de initiële indifferentiecurve te bewegen totdat de hypothetische nieuwe budgetlijn uv evenwijdig is met de budgetlijn jw, die van toepassing is na de prijsverandering. De budgetlijn uv raakt de oorspronkelijke indifferentiekromme in e1'.

De verschuiving van het evenwicht van e0 naar e1 ' is een weergave van het substitutieeffect. In deze overgang zijn de relatieve prijzen, en dus de helling van de budgetrechte, gewijzigd, maar het nutsniveau blijft onveranderd. Het substitutie-effect speelt steeds in het voordeel van het goed dat relatief goedkoper werd (hier goed 1) en in het nadeel van het goed dat relatief duurder werd (hier goed 2). Het substitutie-effect voor goed 1 is in figuur A1 gelijk aan +ab. Het substitutie-effect voor goed 2 is gelijk aan -ed.

Een tweede stap bestaat er dan in de hypothetische inkomensdaling ongedaan te maken. Het is alsof de consument, vertrekkende van het evenwicht e1', een inkomenstoename wordt toegekend. Grafisch laat men de budgetlijn uv parallel verschuiven tot ze samenvalt met de budgetrechte jw die geldt na de prijsdaling. Men merkt hoe het inkomenseffect hier positief speelt voor de beide goederen. In figuur A1 is het inkomenseffect voor goed 1 gelijk aan +bc. Voor goed 2 is het +df.

Men begrijpt nu ook waarom er na de prijsdaling van goed 1 meer van goed 2 wordt gekocht, niettegenstaande dat goed relatief duurder is geworden. In het voorbeeld is de inkomenselasticiteit van de vraag naar goed 2 van zo’n aard dat het inkomenseffect van de prijsdaling van goed 1 het substitutie-effect overtreft. Mocht dit inkomenseffect minder sterk geweest zijn, dan zou er minder van goed 2 geconsumeerd worden.

Figuur A1 Uitsplitsing van het prijseffect in een substitutie- en een inkomenseffect

Het substitutie-effect werkt, zoals reeds gezegd, altijd in het voordeel van het goed dat relatief goedkoper is geworden en in het nadeel van het goed dat relatief duurder werd. Wat het inkomenseffect betreft zijn er drie mogelijkheden: het kan het substitutie-effect versterken, afremmen of tenietdoen. De eerste mogelijkheid werd getoond in figuur A1. In figuur A2 wordt het tweede geval weergegeven: het inkomenseffect is negatief (we hebben dus te maken met een inferieur goed), maar het is minder groot in absolute waarde dan het substitutie-effect. Dit laatste wordt dus afgeremd. In het laatste geval (zie figuur A3) is het inkomenseffect niet alleen negatief, het is ook groter in absolute waarde dan het

substitutie-effect. Het eigenaardige gevolg is dat de prijsdaling van goed 1 leidt tot een verminderde vraag naar dat goed. Goederen waarvoor dit geldt noemt men Giffen-goederen, naar de Britse econoom Sir Robert Giffen (1837-1910). Deze stelde in de vorige eeuw vast dat, wanneer de prijs van het brood steeg, de arbeiders er meer van consumeerden, en dat zij er minder van consumeerden wanneer de prijs daalde. De hierboven uitgevoerde analyse geeft aan dat deze Giffen-paradox inderdaad mogelijk is: het geldt voor goederen met een negatief inkomenseffect dat het substitutie-effect in sterkte overtreft.

Figuur A2 Negatief inkomenseffect voor goed 1

Figuur A3 Substitutie- en inkomenseffect bij een Giffen-goed