GENIE Fysica 4.1 - Leerschrift (ed. 2025) by VAN IN

GENIE 4.1 Fysica

Dit leermiddel is onderdeel van de lesmethode GENIE Fysica van Uitgeverij VAN IN. Het is ontwikkeld met de intentie dat iedere leerling zich herkent en thuis voelt in beeld en tekst. Heb je op- of aanmerkingen, dan kun je contact opnemen met Uitgeverij VAN IN.

Fotokopieerapparaten zijn algemeen verspreid en vele mensen maken er haast onnadenkend gebruik van voor allerlei doeleinden. Jammer genoeg ontstaan boeken niet met hetzelfde gemak als kopieën.

Boeken samenstellen kost veel inzet, tijd en geld. De vergoeding van de auteurs en van iedereen die bij het maken en verhandelen van boeken betrokken is, komt voort uit de verkoop van die boeken.

In België beschermt de auteurswet de rechten van deze mensen. Wanneer u van boeken of van gedeelten eruit zonder toestemming kopieën maakt, buiten de uitdrukkelijk bij wet bepaalde uitzonderingen, ontneemt u hen dus een stuk van die vergoeding. Daarom vragen auteurs en uitgevers u beschermde teksten niet zonder schriftelijke toestemming te kopiëren buiten de uitdrukkelijk bij wet bepaalde uitzonderingen.

Verdere informatie over kopieerrechten en de wetgeving met betrekking tot reproductie vindt u op www.reprobel.be.

Ook voor het digitale lesmateriaal gelden deze voorwaarden. De licentie die toegang verleent tot dat materiaal is persoonlijk. Bij vermoeden van misbruik kan die gedeactiveerd worden. Meer informatie over de gebruiksvoorwaarden leest u op www.diddit.be.

Tekst- en datamining (TDM) niet toegestaan.

De uitgever heeft ernaar gestreefd de relevante auteursrechten te regelen volgens de wettelijke bepalingen.

Wie desondanks meent zekere rechten te kunnen doen gelden, wordt verzocht zich tot de uitgever te wenden.

Credits p. 6 en 9 Felix Baumgartner © Belgaimage, p. 11 Vrijevaltoren © Shutterstock/Edu Mangas, p. 57 Plopsaland © Belgaimage, p. 61 Windmolen bij attractie © Sven Popelier – Brakesection Magazine, p. 86 Chips © Wim Meijvogel, p. 96 Felix Baumgartner © Belgaimage, p. 178 Applet © CC BY PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu, p. 184 Batterij © Shutterstock/Dmitriy Prayzel

©VANIN

Eerste druk 2025

ISBN 978-94-647-0799-1

Vormgeving en ontwerp cover: Shtick

Tekeningen: Geert Verlinde, Tim Boers (Studio B) D/2025/0078/129

Art. 608545/01

NUR 126

Zetwerk: Zyncke Vanderplancke

THEMA 01: ENERGIE

` HOOFDSTUK 1: Wat is mechanische energie? 10

1 Welke vormen van mechanische energie bestaan er? 10

2 Hoe groot is de kinetische energie? 13

3 Hoe groot is de potentiële energie? 16

3.1 Potentiële zwaarte-energie 16

3.2 Potentiële elastische energie 19 Hoe groot is de mechanische energie?

` HOOFDSTUK 2: Hoe verandert de energie bij een energieomzetting? 28

1 Hoe kun je energieomzettingen omschrijven? 28

2 Hoe verandert de energie in een systeem? 31

2.1 Behoud van energie bij een geïsoleerd systeem 31

2.2 Behoud van energie bij een willekeurig systeem 34

2.3 Energiedissipatie 38

3 Wat betekent arbeid verrichten bij een constante kracht? 40

Arbeid-energietheorema Arbeid door de zwaartekracht

` HOOFDSTUK 3: Hoe kan energie gebruikt worden? 50

1 Wat betekenen energieproductie en -verbruik? 50

2 Wat is het vermogen van een energieomzetting? 53

3 Wat betekent duurzaam omgaan met energie? 57

3.1 Duurzaam energiegebruik 57

3.2 Duurzame energieproductie 60

THEMA 02: THERMODYNAMICA

` HOOFDSTUK 1: Hoe kun je het gedrag van een gas beschrijven in verschillende omstandigheden? 70

1 Wat zijn de toestandsgrootheden van een gas? 70

2 Welke verbanden bestaan er tussen de toestandsgrootheden van een vaste hoeveelheid gas? 74

2.1 Mogelijke processen

2.2 Isotherm proces

INHOUD ©VANIN

3 Welk algemeen verband bestaat er tussen de toestandsgrootheden van een gas? 87

` HOOFDSTUK 2: Welke invloed heeft warmte op de temperatuur van een systeem? 97

1 Wat is het verschil tussen warmte en temperatuur?

1.1 Warmte en temperatuur

1.2 Inwendige energie

1.3 Thermisch evenwicht

2 Hoe wordt warmte doorgegeven? 105

2.1 Vormen van warmtetransport 105 2.2 Geleiding 105

2.3 Stroming 106 2.4 Straling 107

3 Hoe verandert de temperatuur van een systeem door warmte-uitwisseling? 108

3.1 Geïsoleerd systeem 108

3.2 Warmtecapaciteit 110

3.3 Specifieke warmtecapaciteit 114

3.4 Warmtebalans 121

` HOOFDSTUK 3:

Welke invloed heeft warmte op de aggregatietoestand van een stof? 134

1 Welke faseovergangen ontstaan er bij warmte-uitwisseling? 134

2 Hoe verandert de temperatuur bij een faseovergang? 136

2.1 Smelten en stollen 136

2.2 Verdampen en condenseren 140

3 Wat is latente warmte? 146

3.1 Latente warmte bij een faseovergang 146

3.2 Grootteorde van de merkbare en latente warmte 150

4 Hoe groot is de latente warmte bij een faseovergang? 152

4.1 Specifieke smelten stolwarmte 152

4.2 Specifieke verdampings- en condensatiewarmte 157

4.3 Warmtebalans bij faseovergangen 159 Hoe wordt warmte gebruikt in technologische toepassingen?

THEMA 03: ELEKTRISCHE SYSTEMEN

` HOOFDSTUK 1:

Welke eigenschappen heeft een elektrische kring? 172

1 Wat is elektrische stroom? 172

1.1 Elektrische stroom 172

1.2 Energieomzetting in een stroomkring 175

2 Wat zijn stroomsterkte en spanning? 178

2.1 Stroomsterkte 178

2.2 Spanning 182

3 Welk verband bestaat er tussen spanning en stroomsterkte? 186

3.1 Elektrische weerstand 186

3.2 Weerstanden in de praktijk 190

4 Hoe wordt elektrische energie omgezet in elektrische toestellen? 193

4.1 Energie en vermogen van elektrische stroom 193

4.2 Warmteontwikkeling in een elektrische weerstand 195

Welke eigenschappen hebben elektrische schakelingen?

Notities

WERKEN MET GENIE

GENIE is een hybride leermiddel. Het bestaat uit een leerschrift én een digitaal aanbod op iDiddit. Dit overzicht geeft je inzicht in welke onderdelen je waar kunt terugvinden.

GENIE Fysica bestaat uit 3 thema’s. Elk thema is op dezelfde manier opgebouwd.

1 CHECK IN

2 HOOFDSTUKKEN + VERKEN

3 AAN DE SLAG

4 SYNTHESE

5 CHECK IT OUT

De CHECK IN, VERKEN en CHECK IT OUT vind je uitsluitend online.

ENERGIE

Op iDiddit vind je alle informatie die ook in je boek terug te vinden is: alle teksten, illustraties en opdrachten. Je kunt dus kiezen hoe je met GENIE aan de slag gaat.

Op iDiddit vind je ook:

• begrippenlijsten;

• instructiefilmpjes;

• vademecum;

• adaptieve oefenreeksen;

• STEM-projecten;

• kennisclips;

• labo’s.

TIP: op iDiddit kun je ook je eigen notities bijhouden.

De CHECK IN laat je kennismaken met het onderwerp en eindigt met een probleem of een vraag die je enkel op iDiddit vindt.

START HOOFDSTUK 1

AAN DE SLAG CHECK IN THEMA

Kennis vatten we samen in de rode kenniskaders. Handig zijn de verwijzingen naar de AAN DE SLAG-oefeningen waarmee je zelf kunt nagaan of je de leerinhouden begrepen hebt.

Via de AAN DE SLAG kun je individueel de leerstof van het hoofdstuk inoefenen. Je leerkracht beslist of je de oefeningen pas op het einde van het thema maakt of tijdens de lessen.

▲

wagentje wordt eerst omhooggehesen en daarna vanaf het hoogste punt losgelaten.

We duiden het laagste punt van het wagentje (m = 780 kg) aan als h = 0 m en bekijken de potentiële zwaarteenergie op drie plaatsen ten opzichte van de referentiehoogte.

• Het wagentje staat op de grond vóór vertrek: E = m ∙ g h = 0 J

• Het wagentje staat klaar om losgelaten te worden:

E pot, z, 2 = m g h = 780 kg ∙ 9,81 N kg 120,0 m = 918 216 N ∙ m = 918 10 (= 918 kJ)

• Het wagentje is tot op halve hoogte gevallen:

E pot, z, 3 = m g h = 780 kg ∙ 9,81 N kg 60,0 m = 459 108 N m = 459 10 (= 459 kJ)

Bij vertrek bezit het wagentje geen potentiële zwaarte-energie, omdat het zich op het laagste punt van de beweging bevindt. De potentiële zwaarte-energie is maximaal bovenaan de toren. Als de hoogte halveert, halveert de potentiële zwaarte-energie. Door de grote massa van het wagentje en de grote hoogte van de toren is die potentiële zwaarte-energie heel groot.

Een voorwerp op een zekere hoogte in het zwaartekrachtveld bezit potentiële zwaarte-energie (potentiële gravitatie-energie). Hoe groter de hoogte h (boven de referentiehoogte h = 0 m), de massa m van het voorwerp en de zwaarteveldsterkte g hoe groter de potentiële zwaarte-energie van het voorwerp.

Grootheid met symbool Eenheid met symbool potentiële zwaarte-energie E pot, m g h joule J (= N m) ` Maak oefening 8 t/m 10 op p. 25-26.

VOLGEND HOOFDSTUK

VERKEN

SYNTHESE

Wetenschap maakt deel uit van jouw leefwereld, al weet je het soms niet. In de verkenfase zul je merken dat je best al wat kennis hebt uit het dagelijks leven over het onderwerp dat in een hoofdstuk aan bod komt. We activeren je voorkennis bij de start van elk hoofdstuk op iDiddit.

In de thema’s:

- vind je verschillende manieren om een SYNTHESE te maken: mindmap, schema, Cornell … - vind je een checklist die je laat reﬂecteren over de leerstof. Je gaat na welke leerdoelen je al dan niet onder de knie hebt. - denk je bewust na over je leerproces, interesses en vaardigheden.

Energie

tijdsverloop); —de energie zo nuttig mogelijk te gebruiken (klein vermogen en groot rendement). • Energie duurzaam produceren door: —de beschikbare energie zo nuttig mogelijk

Grootheid met symboolEenheden met symbool energie E joule kilocalorie kilowattuur J kcal kWh Verschillende energievormen Mechanische energie: —kinetische energie: energie door snelheid E kin = 1 2 m v ² —potentiële zwaarte-energie: energie door plaats in het zwaartekrachtveld E pot, m g h —potentiële elastische energie: energie door een uitgerekte of ingedrukte veer E pot, = 2 k (∆ )² Niet-mechanische energie: stralingsenergie, chemische energie, thermische energie (warmte), vervormingsenergie, kernenergie, elektrische energie Wet van behoud van energie Energie kan niet gemaakt en niet vernietigd worden. Energie wordt: omgezet naar een andere vorm binnen het systeem (= voorwerp of aantal voorwerpen); overgedragen naar een ander systeem of naar de omgeving (= alles buiten het systeem). Geïsoleerd systeem: E mech, = E mech, Open systeem: E mech, = E

CHECK IT OUT CHECK IN VOLGEND

In elke CHECK IT OUT pas je de vergaarde kennis en vaardigheden toe om terug te koppelen naar de vraag uit de CHECK IN.

LABO

Ga zelf op onderzoek! Op iDiddit staan een aantal labo’s om experimenten uit te voeren.

Het onlineleerplatform bij GENIE Fysica 4

Mijn lesmateriaal

Hier vind je alle inhouden uit het boek, maar ook meer, zoals filmpjes, labo’s, extra oefeningen ...

Extra materiaal

Bij bepaalde stukken theorie of oefeningen kun je extra materiaal openen. Dat kan een bijkomend videofragment zijn, een extra bron of een leestekst.

Kortom, dit is materiaal dat je helpt om de leerstof onder de knie te krijgen.

Adaptieve oefeningen

In dit gedeelte kun je de leerstof inoefenen op jouw niveau. Hier kun je vrij oefenen of de oefeningen maken die de leerkracht voor je heeft klaargezet.

Opdrachten

Hier vind je de opdrachten die de leerkracht voor jou heeft klaargezet.

Evalueren

Hier kan de leerkracht toetsen voor jou klaarzetten.

Resultaten

Wil je weten hoever je al staat met oefenen, opdrachten en toetsen? Hier vind je een helder overzicht van al je resultaten.

Notities

Heb je aantekeningen gemaakt bij een bepaalde inhoud? Via je notities kun je ze makkelijk terug oproepen.

Meer weten?

Ga naar www.ididdit.be

©VANIN

Ga zelf op onderzoek! Doorheen de thema’s vind je de verwijzing naar de labo’s op iDiddit.

Dit icoon geeft aan dat er aanvullend lesmateriaal of een extra opdracht op iDiddit staat.

Soms is het handig dat je extra lesinformatie of een videofragment zelf kunt bekijken of beluisteren op je smartphone. Als je dit icoon ziet, open dan de VAN IN Plus-app en scan de pagina.

ENERGIE 01 THEMA

Stuntman Felix Baumgartner is als eerste skydiver ooit door de geluidsmuur gegaan. Hij sprong naar beneden vanuit een luchtballon op 37 kilometer hoogte en haalde een snelheid van bijna 1 350 km h . Hij kwam veilig beneden, maar heeft wel aangekondigd dat hij nooit meer zo’n stunt zal doen.

` Hoe kun je uit de energieomzetting de hoogte bepalen om een bepaalde snelheid te krijgen?

` Welke invloed heeft de omgeving op de energieomzetting?

We zoeken het uit!

Wat is mechanische energie?

©VANIN

LEERDOELEN

Je kunt al: energievormen en energieomzettingen omschrijven; de algemene betekenis van potentiële en kinetische energie omschrijven.

Je leert nu: de verschillende vormen van mechanische energie nauwkeurig omschrijven; de verschillende vormen van mechanische energie berekenen.

In een pretpark is er heel wat te beleven: de botsauto’s, de vrijevaltoren, de rollercoaster, de amusementskraampjes waar je een leuke prijs kunt verdienen … Een voor een bezorgen ze je een onvergetelijke belevenis. De meeste attracties in het pretpark zijn spectaculair door de hoogte waarop je hangt, de snelheid die je behaalt, of een combinatie van beide.

In dit hoofdstuk bestudeer je hoe de snelheid, de zwaartekracht en de veerkracht voor energie zorgen. Je leert om de verschillende mechanische energievormen te omschrijven en de grootte ervan te berekenen.

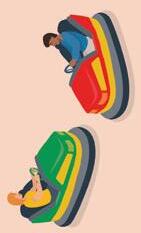
1 Welke vormen van mechanische energie bestaan er?

OPDRACHT 1

Bestudeer de mechanische energie van een voorwerp.

1 Bestudeer de drie afbeeldingen.

2 Duid de juiste uitspraken aan in de tabel.

De botsauto is in beweging.

De zwaartekracht of de veerkracht kan hier een beweging veroorzaken.

De botsauto bezit kinetische energie.

De botsauto bezit potentiële energie.

OPDRACHT 1 (VERVOLG)

▲

Het wagentje is in beweging.

De zwaartekracht of de veerkracht kan hier een beweging veroorzaken.

Het wagentje bezit kinetische energie.

Het wagentje bezit potentiële energie.

©VANIN

‘Kinetisch’ komt van het Griekse κινειν (kinein), hetgeen ‘bewegen’ betekent.

‘Potentie’ komt van het Latijnse potens, hetgeen ‘mogelijk, bekwaam’ betekent. Potentie is een synoniem voor mogelijkheid.

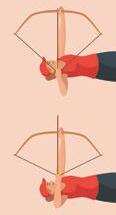
De pijl is in beweging.

De zwaartekracht of de veerkracht kan hier een beweging veroorzaken.

De pijl bezit kinetische energie.

De veer bezit potentiële energie.

Als een voorwerp mechanische energie bezit, kan dat twee dingen betekenen.

1 Het voorwerp beweegt. Het bezit kinetische energie. Om kinetische energie te bezitten, moet het voorwerp een snelheid hebben.

2 Het voorwerp heeft de mogelijkheid om zichzelf of een ander voorwerp in beweging te brengen. Het bezit potentiële energie. Om potentiële energie te bezitten, moet er een kracht inwerken op het voorwerp en moet het voorwerp zich op een bepaalde plaats bevinden. De mogelijke vormen van potentiële energie zijn: —potentiële zwaarte-energie, doordat een massa zich op een bepaalde plaats in een zwaartekrachtveld bevindt. Een andere naam voor de zwaartekracht is ‘gravitatie’. Potentiële zwaarte-energie wordt daarom ook potentiële gravitatie-energie genoemd; —potentiële elastische energie, doordat een veer opgespannen is.

VOORBEELD MECHANISCHE ENERGIE IN HET PRETPARK

We bekijken als voorbeeld de mechanische energie van enkele pretparkattracties.

• De botsauto’s zijn in beweging. Ze bezitten kinetische energie. De zwaartekracht werkt in op de botsauto’s, maar doordat ze op een horizontale ondergrond bewegen, is er geen verticale beweging mogelijk door de zwaartekracht. De potentiële zwaarte-energie is nul.

TIP

VOORBEELD MECHANISCHE ENERGIE IN HET PRETPARK (VERVOLG)

• Voordat het wagentje in een vrijevaltoren losgelaten wordt, is het in rust op het hoogste punt. De kinetische energie is nul. De zwaartekracht werkt in op het wagentje, en het wagentje bevindt zich niet op het laagste punt. Het wagentje bezit potentiële zwaarte-energie. Zodra de remmen gelost worden, zal het verticaal naar de grond (het laagste punt) bewegen door de zwaartekracht.

▲ Afb. 5 Het wagentje bezig potentiële zwaarte-energie. Het wagentje komt in beweging.

• Voordat je de elastiek tijdens het boogschieten loslaat, is het systeem pijl-elastiek in rust. De kinetische energie is nul. De veerkracht werkt in op de uitgerekte elastiek. De elastiek is opgespannen, waardoor de pijl in beweging komt zodra je de elastiek loslaat. De elastiek bezit potentiële elastische energie.

▲ Afb. 6 De elastiek bezit potentiële elastische energie. De pijl komt in beweging.

©VANIN

Er zijn twee vormen van mechanische energie:

1 kinetische energie: energie doordat een voorwerp een snelheid heeft;

2 potentiële energie: energie doordat er een kracht inwerkt op een voorwerp en het voorwerp zich op een bepaalde plaats bevindt.

` Maak oefening 1 en 2 op p. 24.

2 Hoe groot is de kinetische energie?

OPDRACHT 2

©VANIN

Bestudeer de grootte van de kinetische energie wanneer je met een bal gooit.

1 Welke energieomzetting gebeurt er wanneer je de blikjes omgooit? Vul aan.

van de bal

→ van de blikjes

2 Hoe beïnvloeden de massa en de snelheid de manier waarop de toren van gestapelde blikjes omvalt? Duid je voorspellingen aan.

Voorspelling Waarneming

• Hoe groter de massa van de bal, hoe makkelijker / moeilijker de blikjes omvallen.

• Hoe groter de snelheid van de bal, hoe makkelijker / moeilijker de blikjes omvallen.

• Als je de massa verhoogt, heeft dat minder / meer effect dan wanneer je de snelheid verhoogt.

3 Test uit.

4 Vul je waarnemingen aan.

• Hoe groter de massa van de bal, hoe makkelijker / moeilijker de blikjes omvallen.

• Hoe groter de snelheid van de bal, hoe makkelijker / moeilijker de blikjes omvallen.

• Als je de massa verhoogt, heeft dat minder / meer effect dan wanneer je de snelheid verhoogt.

De kinetische energie van een voorwerp is de energie die het voorwerp heeft doordat het in beweging is. Door de kinetische energie kan het voorwerp andere voorwerpen in beweging brengen

De grootheid kinetische energie wordt voorgesteld met het symbool Ekin

De kinetische energie hangt af van de massa (m) en de grootte van de snelheid (v):

De kinetische energie neemt recht evenredig toe met de toenemende massa.

Ekin ~ m

De kinetische energie neemt recht evenredig toe met de toenemende snelheid in het kwadraat.

Ekin ~ v2

nauwkeurig (theoretisch) onderzoek

De kinetische energie is een scalaire grootheid, met als SI-eenheid de joule.

Om de kinetische energie te berekenen, moet je de massa en de snelheid uitdrukken in de SI-eenheid:

• de massa in kilogram;

• de snelheid in meter per seconde.

▲ Afb. 7

Je kunt je eindresultaat schrijven met machten van 10 die een veelvoud zijn van 3 (10³, 106, 109 …), of gebruik de overeenkomstige voorvoegsels. Dat is de ingenieursnotatie.

Kilometer per uur ( km h ) is een andere veelgebruikte eenheid van snelheid.

1,0 m s 3,6 km h : 3,6 ∙ 3,6

Je ziet misschien niet onmiddellijk dat de eenheden kloppen. Daarvoor moet je eventjes rekenen.

• De eenheid van kinetische energie is

[Ekin] = [m] ∙ [v2] = 1 kg ∙ (1 m s )2 = 1 kg ∙ m2 s2

• De joule is een afgeleide eenheid: 1 J = 1 N ∙ m.

©VANIN

• De newton is op zijn beurt ook een afgeleide eenheid: 1 N = 1 kg ∙ m s2 .

• Samengevoegd wordt dat: 1 J = 1 kg ∙ m s2 ∙ m = 1 kg ∙ m2 s2 .

Fris je kennis over grootheden en eenheden op via .

VOORBEELD KINETISCHE ENERGIE VAN BOTSAUTO'S

De groene botsauto heeft een totale massa van 350 kg en een snelheid van 4,0 m s . De kinetische energie is:

Ekin, 1 = 1 2 ∙ m1 ∙ v2

De rode botsauto heeft een kleinere totale massa van 280 kg, maar rijdt sneller, met een snelheid van 5,0 m s . De kinetische energie is: Ekin, 2 = 1 2

= 1 2 ∙ 280 kg ∙ (5,0 m s )2 = 3 500 J

De richting en de zin van de snelheid hebben geen invloed op de grootte van de kinetische energie. Aangezien de kinetische energie van de rode auto het grootst is, is de impact van de botsing van de rode botsauto groter.

Een bewegend voorwerp bezit kinetische energie. Hoe groter de snelheid v en de massa m van dat voorwerp, hoe groter de kinetische energie.

Grootheid met symbool Eenheid met symbool kinetische energie Ekin = 1 2 m v² joule J (= kg ∙ m2 s2 )

` Maak oefening 3 t/m 7 op p. 24-25.

▲ Afb. 8 De massa en de snelheid van de botsauto’s bepalen de grootte van de kinetische energie.

OPDRACHT 3

Bestudeer de kinetische energie van de verschillende weggebruikers.

1 Vorm de formule van Ekin om, zodat je de massa en de snelheid kunt berekenen.

• m =

• v2 = , dus v =

2 Vul de tabel aan.

3 Verklaar met je berekeningen het nut van de onderstaande verkeersregels.

• zone 30 bij scholen

• strengere snelheidsbeperkingen voor bussen

OPDRACHT 4 DOORDENKER

Bestudeer de kinetische energie bij een ERB.

Welke uitspraak is correct? Duid aan.

Als een voorwerp een ERB uitvoert, is de kinetische energie constant.

Als de kinetische energie van een voorwerp constant is, voert het een ERB uit.

De kinetische energie van een voorwerp is constant als en slechts als het een ERB uitvoert.

3 Hoe groot is de potentiële energie?

3.1 Potentiële zwaarte-energie

OPDRACHT 5

Bestudeer de grootte van de potentiële zwaarte-energie bij een splash.

▲ Afb. 10

1 Welke energieomzettingen gebeuren er tijdens de afdaling van een bootje dat vertrekt vanop het hoogste punt? Vul aan.

van het bootje bovenaan

→ van het bootje onderaan de splash

→ van het water onderaan de splash

2 Wat is de correcte uitdrukking voor de potentiële zwaarte-energie (E pot, z)?

• Duid aan.

E pot, z = m ∙ g ∙ h

E pot, z = m ∙ g h

E pot, z = g ∙ h m

E pot, z = m ∙ h g

• Verklaar met je eigen ervaringen van een pretparkbezoek.

—Invloed van de massa:

—Invloed van de hoogte:

De grootheid potentiële zwaarte-energie (of potentiële gravitatie-energie) van een voorwerp is de potentiële energie die het voorwerp heeft doordat het zich op een bepaalde hoogte in het zwaartekrachtveld bevindt.

Door zijn potentiële energie als gevolg van de hoogte is het voorwerp in de mogelijkheid om zelf in beweging te komen en zo andere voorwerpen in beweging te brengen.

De grootheid potentiële zwaarte-energie wordt voorgesteld met het symbool E pot, z. De potentiële zwaarte-energie hangt af van de massa (m), de hoogte (h) en de zwaarteveldsterkte (g):

De potentiële zwaarte-energie neemt recht evenredig toe met de toenemende massa.

E pot, z ~ m

De potentiële zwaarte-energie neemt recht evenredig toe met de toenemende zwaarteveldsterkte.

E pot, z ~ g

De potentiële zwaarte-energie neemt recht evenredig toe met de toenemende hoogte.

E pot, z ~ h

©VANIN

E pot, z ~ m g h

E pot, z = m g h nauwkeurig (theoretisch) onderzoek

Daarbij is de hoogte h de afstand tot het laagste punt waar het voorwerp naartoe kan bewegen. De hoogte h = 0 m moet je vastleggen bij elke beweging die je bestudeert. Je noemt dat de referentiehoogte

De potentiële zwaarte-energie is een scalaire grootheid, met als SI-eenheid de joule. Om de potentiële zwaarte-energie te berekenen, moet je de massa en de hoogte uitdrukken in de SI-eenheid:

• de massa in kilogram;

• de hoogte in meter.

VOORBEELD POTENTIËLE ENERGIE IN EEN VRIJEVALTOREN

We bekijken het voorbeeld van de vrijevaltoren met een hoogte van 120,0 m.

h1 = 0 m

h2 = 120,0 m

h3 = 60,0 m

De hoogte van het wagentje verandert tijdens de rit op de attractie: het wagentje wordt eerst omhooggehesen en daarna vanaf het hoogste punt losgelaten.

We duiden het laagste punt van het wagentje (m = 780 kg) aan als h = 0 m en bekijken de potentiële zwaarteenergie op drie plaatsen ten opzichte van de referentiehoogte.

• Het wagentje staat op de grond vóór vertrek:

E pot, z, 1 = m ∙ g ∙ h1 = 0 J

• Het wagentje staat klaar om losgelaten te worden:

E pot, z, 2 = m ∙ g ∙ h2

9,81 N kg

• Het wagentje is tot op halve hoogte gevallen:

E pot, z, 3 = m ∙ g ∙ h3

780 kg

9,81 N kg

Een voorwerp op een zekere hoogte in het zwaartekrachtveld bezit potentiële zwaarte-energie (potentiële gravitatie-energie). Hoe groter de hoogte h (boven de referentiehoogte h = 0 m), de massa m van het voorwerp en de zwaarteveldsterkte g, hoe groter de potentiële zwaarte-energie van het voorwerp.

Grootheid met symbool Eenheid met symbool potentiële zwaarte-energie E pot, z = m ∙ g ∙ h joule J (= N ∙ m)

` Maak oefening 8, 9 en 10 op p. 25-26.

▲ Afb. 11 De massa en de hoogte van het wagentje bepalen de grootte van de potentiële zwaarte-energie.

3.2 Potentiële elastische energie

OPDRACHT 6 ONDERZOEK

Onderzoek de grootte van de potentiële elastische energie.

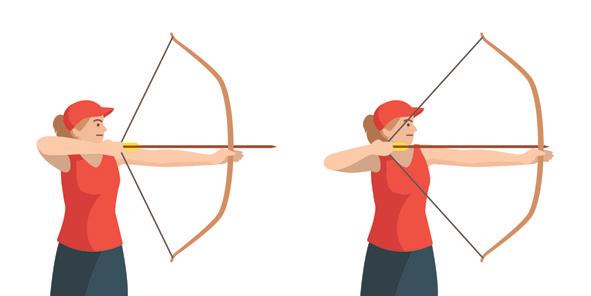
▲ Afb. 12

1 Welke energieomzetting gebeurt er tijdens het boogschieten? Vul aan. van de boog → van de pijl

2 Hoe zou jij de grootste snelheid geven aan de pijl?

©VANIN

3 Test uit met een elastiek en een propje papier.

De grootheid potentiële elastische energie van een veer is de potentiële energie die de veer bezit doordat ze over een bepaalde lengte is uitgerekt of ingedrukt. Door die potentiële energie is de veer in de mogelijkheid om andere voorwerpen in beweging te brengen.

De combinatie van de veer en het voorwerp dat de veer in beweging kan brengen, noem je een systeem. De grootheid potentiële elastische energie van een systeem wordt voorgesteld met het symbool E pot, e

De potentiële elastische energie hangt af van de veerconstante (k) en de lengteverandering (∆l):

De potentiële elastische energie neemt recht evenredig toe met de toenemende veerconstante.

E pot, e ~ k

De potentiële elastische energie neemt recht evenredig toe met de toenemende lengteverandering in het kwadraat.

E pot, e ~ (∆l)²

nauwkeurig (theoretisch) onderzoek

De potentiële elastische energie is een scalaire grootheid, met als SI-eenheid de joule. Om de potentiële elastische energie te berekenen, moet je de veerconstante en de lengteverandering uitdrukken in de SI-eenheid:

• de veerconstante in newton per meter;

• de lengteverandering in meter.

l1 ∆l2 k k ▲ Afb. 13 De uitrekking en de veerconstante van de veer bepalen de grootte van de potentiële elastische energie.

De elastiek van de boog heeft een veerconstante van 324 N m. Je rekt de veer uit om de pijl weg te schieten. De lengteverandering is de afstand tot de evenwichtstoestand van de elastiek.

We bekijken de potentiële elastische energie in twee situaties.

• De elastiek is 15,0 cm uitgerekt.

E pot, e, 1 = 1 2 ∙ k ∙ (∆l1)2 = 1 2 ∙ 324 N m ∙ (0,150 m)2 = 3,65 N ∙ m = 3,65 J

• De elastiek is 30,0 cm uitgerekt.

E pot, e, 2 = 1 2 ∙ k ∙ (∆l2)2 = 1 2 ∙ 324 N m ∙ (0,300 m)2 = 14,6 N ∙ m = 14,6 J

De veer bezit potentiële elastische energie doordat ze uitgerekt is. Die energie is klein. Ze wordt uitgedrukt in joule (tegenover kilojoule in de vorige voorbeelden). Als de uitrekking verdubbelt, wordt de potentiële elastische energie vier keer groter.

Een uitgerekte of ingedrukte veer bezit potentiële elastische energie. Hoe groter de lengteverandering ∆l en de veerconstante k, hoe groter de potentiële elastische energie van de veer.

Grootheid met symbool Eenheid met symbool potentiële elastische energie E pot, e = 1 2 ∙ k ∙ (∆l)² jouleJ (= N ∙ m)

` Maak oefening 11 t/m 14 op p. 26-27.

©VANIN

OPDRACHT 7

Los het vraagstuk op.

Je lanceert het balletje in een speelgoedgeweer door een veer in te drukken. Als je de veer indrukt over een afstand van 3,0 cm, dan krijgt de veer een potentiële elastische energie van 99 mJ.

1 Duid de lengteverandering en de veerkracht aan op de afbeelding.

2 Bereken de veerconstante en de veerkracht.

Gegeven: E pot, e = ; ∆l =

Gevraagd:a b

Oplossing:

▲ Afb. 14 Lancering van een balletje door indrukking van een veer

Controle: a Kloppen de eenheden?

• de veerconstante in

• de kracht in

b Waarom gebruik je geen absolutewaardetekens bij de potentiële elastische energie?

TIP

Gebruik het formularium achteraan het leerschrift om de formules voor de veerkracht en de potentiële elastische energie op te zoeken.

VERDIEPING

Op leer je meer over de grootte van de mechanische energie.

Het voorwerp bezit geen . Het voorwerp bezit niet-mechanische . Enkele voorbeelden:

elektrische energie

stralingsenergie

chemische energie Grootheid met symboolEenheden met symbool

joule kilocalorie kilowattuur J kcal kWh

©VANIN

Kan het voorwerp andere voorwerpen in beweging brengen?

Het voorwerp bezit . Je kunt die als volgt berekenen: =

Het voorwerp bezit . Je kunt die als volgt berekenen: = Het voorwerp bezit . Je kunt die als volgt berekenen: = nee nee

Bevindt het voorwerp zich in een van deze situaties?

• Het heeft een snelheid.

• Het bevindt zich in een zwaartekrachtveld.

Bevindt het voorwerp zich aan een uitgerekte of ingedrukte veer? nee nee ja ja ja ja

• Er werkt veerkracht op in.

Heeft het voorwerp een snelheid?

Bevindt het voorwerp zich op een bepaalde hoogte in een zwaartekrachtveld?

1 Begripskennis

• Ik kan energieomzettingen omschrijven.

• Ik kan het begrip ‘mechanische energie’ omschrijven

• Ik kan de kinetische energie van een voorwerp omschrijven.

• Ik kan de kinetische energie van een voorwerp berekenen

• Ik kan de potentiële zwaarte-energie van een voorwerp omschrijven

• Ik kan de potentiële zwaarte-energie van een voorwerp berekenen.

• Ik kan de potentiële elastische energie van een veer omschrijven

• Ik kan de potentiële elastische energie van een veer berekenen

2 Onderzoeksvaardigheden

• Ik kan kwalitatieve verbanden afleiden uit experimenten.

• Ik kan de ingenieursnotatiegebruiken.

• Ik kan formules omvormen naar de gevraagde grootheid.

• Ik kan nauwkeurig berekeningen uitvoeren.

` Je kunt deze checklist ook op invullen.

JANOG OEFENEN

Zit je vast bij een oefening?

Misschien helpt het vademecum op je weer op weg!

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’. Je kunt de oplossingsstrategie en de voorbeeldoefeningen op gebruiken als extra ondersteuning.

Bestudeer de situaties op de afbeeldingen. 1 2 3 4

a Noteer bij elke situatie het voorwerp dat de energie bezit.

b Noteer de situatie(s) waarin …

• het voorwerp kinetische energie bezit:

• het voorwerp potentiële zwaarte-energie bezit:

• het voorwerp potentiële elastische energie bezit:

• het voorwerp geen mechanische energie bezit:

Maak de onderstaande uitspraken correct door ze te vervolledigen met ‘altijd’, ‘soms’ of ‘nooit’.

• Een voorwerp in rust bezit altijd / soms / nooit kinetische energie.

• Een voorwerp in rust bezit altijd / soms / nooit potentiële zwaarte-energie.

• Een voorwerp in rust bezit altijd / soms / nooit potentiële elastische energie.

• Een voorwerp dat aan een veer hangt, bezit altijd / soms / nooit kinetische energie.

• Een voorwerp dat aan een veer hangt, bezit altijd / soms / nooit potentiële zwaarte-energie.

• Een voorwerp dat aan een veer hangt, bezit altijd / soms / nooit potentiële elastische energie.

Gwen gaat joggen met haar hond.

Welke uitspraak is correct? Duid aan.

Gwen en de hond bezitten evenveel kinetische energie.

Gwen bezit meer kinetische energie dan de hond.

Gwen bezit minder kinetische energie dan de hond.

Je hebt te weinig informatie om de kinetische energie van Gwen en de hond te kunnen vergelijken.

Bestudeer de beweging van enkele dieren.

1 een vis (m = 2,3 kg) die met een snelheid van 7,3 m s zwemt

2 een slak (m = 56,0 g) die met een snelheid van 8,0 mm s voortkruipt

3 een jachtluipaard (m = 60 kg) dat met een snelheid van 110 km h een prooi achternazit

a Bereken de kinetische energie van de dieren.

Noteer het resultaat in de ingenieursnotatie.

b Vergelijk de energie van de dieren.

Komen de verschillen overeen met je verwachtingen?

Welke snelheid heeft een marathonloper (m = 73,2 kg) die een kinetische energie van 1,10 kJ bezit?

Noteer het resultaat in m s en in km h .

Bestudeer de beweging van twee bowlingballen (mblauw = 2 ∙ mgroen).

Rangschik de situaties volgens toenemende Ekin

Een voorwerp heeft bij een snelheid v een kinetische energie Ekin.

Bij welke snelheid verdubbelt de kinetische energie? Duid aan.

2 ∙ v

4 ∙ v

Verklaar hoe een hagelbui schade kan veroorzaken aan auto’s.

In een sportclub bevinden een aantal ballen zich op verschillende hoogtes. Bestudeer de onderstaande situaties.

1 Een basketbal (m = 0,550 kg) gaat door de ring op een hoogte van 3,05 meter.

2 Een bowlingbal (m = 5,3 kg) rolt horizontaal naar de kegels.

3 Een tennisbal (m = 59,0 g) vliegt 10 cm boven het net van 1,07 m.

a Bereken de potentiële zwaarte-energie van de ballen. Noteer het resultaat in de ingenieursnotatie.

b Welke andere energievorm bezitten de ballen? Verklaar.

Na een maanmissie brachten de astronauten verschillende maanstenen (mbruin = 3 ∙ mzwart) mee naar de aarde. Rangschik de situaties volgens toenemende E pot, z van de stenen.

Welke uitspraken zijn correct? Duid alle mogelijkheden aan.

Elke ingedrukte veer bezit potentiële elastische energie.

Elke uitgerekte veer bezit potentiële elastische energie.

Elke veer bezit potentiële elastische energie.

Elke veer waarop een massa steunt, bezit potentiële elastische energie.

Bereken de potentiële elastische energie van …

a een veer in de fitness (k = 400 N m) die 0,30 m ingedrukt wordt;

b een veer van een flipperkast (k = 1,20 N cm ) die 3,5 cm uitgerekt wordt.

Na een bungeesprong bezit de elastiek 57,6 J potentiële elastische energie.

Bereken de uitrekking van de elastiek (k = 180 N m ).

Je rekt een veer uit.

a Welke grafieklijn stelt de potentiële elastische energie in functie van de uitrekking Δl voor?

b Hoe groot is de veerconstante? Duid aan.

k = 0,02 N m

k = 0,6 N m

k = 12 N m

k = 100 N m

k = 200 N m

` Verder oefenen? Ga naar .

Hoe verandert de energie bij een energieomzetting?

LEERDOELEN

Je kunt al: energieomzettingen omschrijven; de totale mechanische energie omschrijven.

Je leert nu: de veranderingen van mechanische energie omschrijven en toepassen; de veranderingen van energie omschrijven en toepassen; de arbeid die een kracht verricht bij een energieomzetting, omschrijven en berekenen.

De kick in een rollercoaster krijg je wanneer alle remmen gelost worden op het hoogste punt en je vervolgens de topsnelheid bereikt. Maar eerst moeten motoren de wagentjes omhoog slepen. Welke invloed heeft de hoogte op je snelheid? En hoe wordt de elektrische energie van de motoren omgezet in mechanische energie?

In dit hoofdstuk bestudeer je hoe de hoogte en de snelheid met elkaar verbonden zijn, en welke invloed externe factoren, zoals de motoren en de wrijving, hebben op energieomzettingen en de totale energie. Je leert hoe je energie kunt gebruiken om arbeid te verrichten, en hoe groot die arbeid is.

1 Hoe kun je energieomzettingen omschrijven?

OPDRACHT 8

Bestudeer het verschil tussen een systeem en een omgeving.

1 Bestudeer de voorwerpen en hun omgeving.

OPDRACHT 8 (VERVOLG)

2 Vul de tabel aan. A

Het wagentje valt naar beneden.

De pijl wordt weggeschoten.

Voorwerp dat je bestudeert:

Energieomzetting van dat voorwerp tijdens de val:

Omgeving van het voorwerp:

©VANIN

Voorwerp dat je bestudeert:

Energieomzetting van de voorwerpen tijdens het schieten:

Welke energie verbruikt de omgeving om het wagentje omhoog te hijsen?

Welke energie wordt er doorgegeven aan de omgeving wanneer het wagentje remt?

→ van

Omgeving van het voorwerp:

Welke energie verbruikt de omgeving om de elastiek op te spannen?

Welke energie wordt er doorgegeven aan de omgeving wanneer je raak schiet?

Energie bestaat in heel veel vormen. Er zijn voortdurend energieomzettingen. Om die te bestuderen, kies je een voorwerp of meerdere voorwerpen waarop je je aandacht zult richten. Dat noem je een systeem. Alles buiten het systeem noem je de omgeving van het systeem.

Een systeem kan open of geïsoleerd zijn:

• open systeem: Er wordt energie overgedragen tussen het systeem en zijn omgeving

• geïsoleerd systeem: Er wordt geen energie overgedragen tussen het systeem en zijn omgeving.

In werkelijkheid is elk systeem een open systeem. Er is altijd energieoverdracht naar de omgeving. Als de energieoverdracht klein is, kun je het systeem beschrijven als een geïsoleerd systeem. Dat is een model van de werkelijkheid.

VOORBEELD SYSTEEM ROLLERCOASTER

We bekijken als voorbeeld hoe een rollercoaster omhooggetrokken wordt en daarna de achtbaan afdaalt. De rit begint wanneer het wagentje (= systeem) omhooggetrokken wordt. Het krijgt dan potentiële zwaarte-energie. Dat kan nooit spontaan gebeuren.

OPEN SYSTEEM (WERKELIJKHEID)GEÏSOLEERD SYSTEEM (MODEL)

Tijdens de afdaling krijgt het wagentje snelheid en worden de baan en de wielen warm, doordat er wrijving is. Er is een energieomzetting binnen het systeem en een energieoverdracht van het systeem naar de omgeving.

potentiële zwaarte-energie van het wagentje → kinetische energie van het wagentje + warmte van de wielen en de baan

Als je de wrijving verwaarloost, is er geen energieoverdracht naar de omgeving. Het systeem is tijdens de afdaling geïsoleerd.

potentiële zwaarte-energie van het wagentje → kinetische energie van het wagentje

Een systeem is een geheel van een of meerdere voorwerpen. Alles buiten het systeem noem je de omgeving van het systeem. Bij een open systeem is er energieoverdracht tussen het systeem en zijn omgeving mogelijk. Bij een geïsoleerd systeem is er geen energieoverdracht mogelijk naar de omgeving.

2 Hoe verandert de energie in een systeem?

2.1 Behoud van energie bij een geïsoleerd systeem

OPDRACHT 9 ONDERZOEK

Onderzoek wat er met de mechanische energie gebeurt in een geïsoleerd systeem aan de hand van Labo 01 op .

Voor een geïsoleerd systeem waarop alleen de zwaartekracht en/of elastische krachten werken, is er geen wrijving. Er wordt geen energie omgezet naar warmte. Dat betekent dat de totale energie (= kinetische en potentiële energie) constant is gedurende de hele beweging.

E tot = Ekin + E pot = constant

Dat is de wet van behoud van energie voor een geïsoleerd systeem.

Als het geïsoleerde systeem overgaat van een eerste toestand naar een tweede toestand, geldt altijd:

De potentiële energie is daarbij de potentiële zwaarte-energie, de potentiële elastische energie of beide. Dat noem je de energiebalans voor een geïsoleerd systeem.

VOORBEELD BEHOUD VAN ENERGIE BIJ EEN ROLLERCOASTER

We bekijken als voorbeeld twee toestanden tijdens de afdaling van een wagentje op een rollercoaster.

Er zit geen motor in het wagentje en we verwaarlozen de wrijving.

Het systeem is geïsoleerd, dus de mechanische energie wordt behouden. Er is geen potentiële elastische energie.

Als referentiehoogte voor de potentiële zwaarte-energie kiezen we het laagste punt van de twee toestanden.

De andere hoogte is h1 = 40,0 m

We bestuderen de energieomzettingen binnen het systeem.

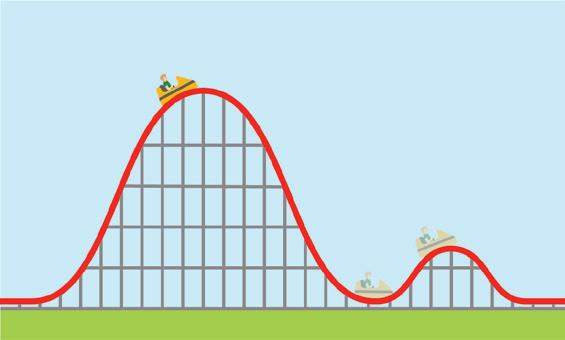
h = 0 m h1 = 40,0 m 1 2

▲ Afb. 18 Mechanische energie op verschillende hoogtes tijdens een rit van de rollercoaster

VOORBEELD BEHOUD VAN ENERGIE BIJ EEN ROLLERCOASTER (VERVOLG)

Toestand 1

Toestand 2

Omschrijving van de toestand

Het wagentje bevindt zich op het hoogste punt en heeft geen snelheid.

Het wagentje bevindt zich op het laagste punt en heeft zijn maximale snelheid. Energieomzettingen voor het systeem (wagentje)

potentiële zwaarte-energie → kinetische energie

De wet van behoud van energie is geldig.

De totale energie is in elke toestand gelijk. Met de beginhoogte kun je de totale energie van elke toestand bepalen:

tot, 1 = m ∙ g ∙ h1 = 350 kg ∙ 9,81 N kg ∙ 40,0 m = 1,37 · 105 J (= 137 kJ) = E tot, 2

De grootte van de totale energie is afhankelijk van de massa.

Als het wagentje bij de aankomst tegen het voorliggende wagentje botst, is de impact door een zwaar wagentje groter dan die door een klein wagentje.

De snelheid wordt bepaald door de hoogte van de rollercoaster. Met de hoogte van het hoogste punt (toestand 1) kun je de snelheid op elke andere hoogte (bijvoorbeeld het laagste punt, toestand 2) bepalen.

Snelheid in het laagste punt (toestand 2): m ∙ g ∙ h1 = 1 2

Je kunt de massa wegdelen, dus je hebt de massa van het wagentje niet nodig om de snelheid te bepalen. De snelheid is onafhankelijk van de massa. Het maakt niet uit met hoeveel personen je in het wagentje zit. Je gaat altijd even snel.

Om de snelheid te berekenen, vorm je het verband om naar de snelheid:

v2 2 = 2 ∙ g ∙ h1, dus

v2 = 2∙ g ∙ h1 = 2 ∙ 9,81 N kg ∙ 40,0 m = 28,0 m s = 101 km h

Je kunt ook de energie en de snelheid op een willekeurig punt bepalen. Hoe dat in zijn werk gaat, zie je in het voorbeeld op

De totale energie van een geïsoleerd systeem waarop alleen de zwaartekracht en/of elastische krachten werken, is constant

Dat betekent dat:

E tot, 1 = E tot, 2

Ekin, 1 + E pot, 1 = Ekin, 2 + E pot, 2

Dat noem je de energiebalans voor een geïsoleerd systeem.

` Maak oefening 1 t/m 5 op p. 46-47.

OPDRACHT 10

Los het vraagstuk op.

Een pijl met een massa van 56,2 gram wordt afgeschoten door een elastiek (k = 224 N m ) en krijgt daardoor een snelheid van 5,4 m s . Hoe ver is de elastiek uitgerekt?

1 Werk het vraagstuk uit op een cursusblad.

2 Controleer je antwoord via

OPLOSSINGSSTRATEGIE

Volg de algemene oplossingsstrategie om vraagstukken op te lossen. Je vindt die op . Aandachtspunten wanneer je het behoud van energie toepast:

• Omschrijf en noteer het systeem dat je kiest.

• Omschrijf en noteer de toestanden van het gekozen systeem.

• Schrijf het behoud van mechanische energie op in symbolen.

• Kijk welke vormen van energie nul zijn.

2.2 Behoud van energie bij een willekeurig systeem

OPDRACHT 11

Bestudeer de totale energie van een systeem.

1 Breng verschillende voorwerpen in beweging door ze vanop een hoogte los te laten.

Een autootje op een hellingEen balletje aan een touw

Systeem dat je bestudeert

Omgeving van het systeem

Een blokje aan een verticale, uitgerekte veer

©VANIN

2 Wat gebeurt er met de bewegingstoestand van het voorwerp een tijdje nadat je het losgelaten hebt?

• Voorspelling:

• Waarneming:

• Verklaring:

3 Vul de tabel aan met het systeem en de omgeving.

4 Boots de situaties na in de applets.

▲ Afb. 19

Afb. 20

Afb. 21

OPDRACHT 11 (VERVOLG)

5 Vul de energieomzettingen van het autootje aan met ‘mechanische energie’, ‘chemische energie’ of ‘warmte’.

• Je brengt het autootje omhoog.

• Je laat het autootje los.

van de omgeving → van het systeem

©VANIN

van het systeem → van het systeem en van het systeem en de omgeving

6 Maak de uitspraken correct.

• Er is wel / geen energieoverdracht van het systeem naar de omgeving.

• Het systeem is open / geïsoleerd.

• De totale energie wordt wel / niet behouden.

In realistische situaties bestaat een geïsoleerd systeem niet. Er zijn altijd vormen van niet-mechanische energie die uitgewisseld worden met de omgeving:

• Er is energieoverdracht van de omgeving naar het systeem: een energiebron levert elektrische, chemische of stralingsenergie die omgezet wordt in (mechanische) energie van het systeem.

• Er is altijd wrijving en luchtweerstand, waardoor er energieoverdracht is naar de omgeving. De wrijvingskrachten veroorzaken warmte

Grootheid met symbool Eenheid met symbool warmte Q joule J

Als het (open of geïsoleerde) systeem overgaat van een eerste toestand naar een tweede toestand, geldt altijd:

E tot, 1 = E tot, 2 of E tot = constant

Dat noem je de energiebalans

Dat is de wet van behoud van energie. Energie wordt niet bijgemaakt en gaat niet verloren. Energie kan omgezet worden van de ene vorm naar de andere, of kan van één systeem overgedragen worden aan een ander.

VOORBEELD BEHOUD VAN ENERGIE BIJ EEN ROLLERCOASTER

We bekijken als voorbeeld een wagentje op een rollercoaster.

• Motoren slepen het wagentje omhoog. De elektrische energie van de motoren wordt overgedragen aan het wagentje. Op het hoogste punt heeft het wagentje potentiële zwaarte-energie (in punt 1).

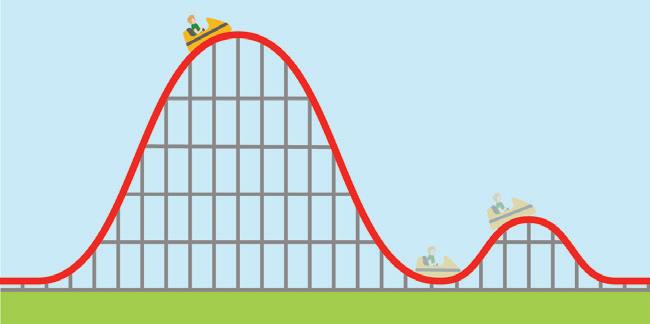
Afb. 22 Totale energie op verschillende hoogtes tijdens een rit van de rollercoaster

• Tijdens de eerste afdaling (tussen punt 1 en punt 2) werkt naast de zwaartekracht ook de wrijvingskracht in op het wagentje. Een deel van de mechanische energie wordt omgezet in warmte: de baan en het wagentje worden warm. De warmte neemt toe met de lengte van het afgelegde traject. Het systeem is open, dus de totale energie wordt behouden:

E tot = constant

Als referentiehoogte voor de potentiële zwaarte-energie kiezen we het laagste punt van de twee toestanden. We bestuderen de totale energie in de twee toestanden door de energiebalans uit te werken.

Toestand 1

Het wagentje bevindt zich op het hoogste punt en heeft geen snelheid.

©VANIN

Toestand 2

Het wagentje bevindt zich op het laagste punt en heeft zijn maximale snelheid.

potentiële zwaarte-energie → kinetische energie en warmte

E tot, 1 Emech, 1 = = E tot, 2 E

Door de energiebalans zie je dat de snelheid op het laagste punt bepaald wordt door de hoogte van de rollercoaster en de ontwikkelde warmte.

Op p. 32 heb je berekend dat de snelheid van het wagentje 101 km h is. Uit metingen blijkt dat de werkelijke snelheid 85,0 km h (= 23,6 m s ) is. Daarmee kun je de ontwikkelde warmte berekenen. De totale energie wordt behouden: m ∙ g ∙ h1 = 1 2 ∙ m ∙ v2 2 + Q

Je kunt de formule omvormen om de warmte te berekenen: Q = m ∙ g ∙ h1 –1 2 ∙ m ∙ v2 2 = 350 kg ∙ 9,81 N kg

40,0 m –1 2

350 kg

(23,6 m s )2 = 137 340 J – 97 468 J = 39 872 J = 3,39 ∙ 104 J (= 39,9 kJ)

De totale energie is voor beide toestanden gelijk: E tot, 1 = m ∙ g ∙ h1 = 350 kg ∙ 9,81 N kg ∙ 40,0 m = 1,37 · 105 J (= 137 kJ) = E tot, 2

Tussen het hoogste en het laagste punt wordt er 3,39 · 104 J van die energie omgezet naar warmte binnen het systeem (het wagentje) en overgedragen aan de omgeving (de baan en de lucht).

Energie wordt niet bijgemaakt en gaat niet verloren. Energie kan omgezet worden van de ene vorm in de andere of kan van één systeem overgedragen worden aan een ander.

De totale hoeveelheid energie is constant: E tot = constant of E tot, 1 = E tot, 2

Dat noem je de energiebalans.

OPDRACHT 12 DOORDENKER

Bestudeer de energie van vallende voorwerpen.

Je laat vier voorwerpen (① blad papier, ② prop papier, ③ tennisbal en ④ tennisbal opgevuld met water) gelijktijdig los vanop 1,5 m hoogte.

1 Voorspel de volgorde waarin de voorwerpen de grond raken.

2 Test uit.

3 Verklaar met de wet van behoud van energie.

4 Bekijk de video.

a Wat stel je vast in vacuüm?

b Verklaar met de wet van behoud van energie.

▲ Afb. 23 Voorwerpen met een verschillende massa en vorm worden gelijktijdig losgelaten.

video: vacuüm

2.3 Energiedissipatie

OPDRACHT 13

Bestudeer de energieverdeling bij de energieomzetting tijdens de afdaling in de rollercoaster van de vorige paragraaf.

1 Vul de energievormen aan in de witte vakjes.

2 Vul de getalwaarden aan in de gekleurde vakjes. Maak de nodige berekeningen.

E tot = kJ

totale energie:

van het wagentje

nuttige energie: van het wagentje

Enuttig = kJ

= % van E tot

η is de Griekse letter èta.

ongewenste vorm van energie: van het wagentje en de baan

Q = kJ

= % van E tot

Volgens de wet van behoud van energie wordt de totale energie bij elke energieomzetting behouden. Dat is een van de meest fundamentele wetten uit de fysica: energie kan niet gemaakt en niet vernietigd worden.

Bij een energieomzetting kun je slechts een deel van de energie nuttig gebruiken. De overige energie wordt omgezet in een ongewenste energievorm: warmte.

E tot = Enuttig + Q

Daarbij is E tot de startenergie en Enuttig de overgebleven eindenergie die nuttig kan worden gebruikt. De omzetting van energie naar ongewenste energie noem je energiedissipatie

De ongewenste energievorm noemt men in het dagelijks leven een energieverlies

Het rendement van een energieomzetting is de verhouding tussen de nuttige en de totale energie. Het is een onbenoemd getal dat men meestal uitdrukt met een percentage.

Grootheid met symbool

rendement

Eenheid met symbool

η = Enuttig

Etot geen eenheid (onbenoemd getal)

Bij een energieomzetting kun je slechts een deel van de energie nuttig gebruiken. Er is energiedissipatie of energieverlies in de vorm van warmte

Het rendement van een energieomzetting is de verhouding tussen de uitgaande nuttige energie en de totale energie. Daarbij is E tot de startenergie en Enuttig de overgebleven eindenergie die nuttig kan worden gebruikt.

Grootheid met symbool Eenheid met symbool

rendement

η = Enuttig Etot geen eenheid (onbenoemd getal)

Het rendement ligt altijd tussen 0 (0 %) en 1 (100 %).

` Maak oefening 6, 7 en 8 op p. 48.

OPDRACHT 14

Bestudeer het rendement van verschillende energieomzettingen.

1 Vul de tabel aan.

2 Maak de uitspraken correct door het juiste antwoord aan te duiden.

• Je kunt energie altijd / soms / nooit vernietigen.

• Warmteontwikkeling is altijd / soms / nooit een vorm van energieverlies.

• Bij een efficiënte energieomzetting is het rendement altijd / soms / nooit zo groot mogelijk.

• Het rendement van een energieomzetting is altijd / soms / nooit groter dan 1.

3 Wat betekent arbeid verrichten bij een constante kracht?

OPDRACHT 15

Bestudeer de energieomzetting wanneer je aan een kist trekt.

Hoe zwaarder de kist, hoe harder je trekt.

1 Bestudeer op de volgende pagina Tijs, die kisten voorttrekt op een gladde ondergrond (geen wrijving).

2 Noteer de energieomzetting. van Tijs → van de kist

3 Rangschik de situaties volgens toenemende inspanning van Tijs.

4 Vervolledig de afbeeldingen met …

• de krachtvector die voor de energieverandering zorgt,

• de verplaatsingsvector tussen het vertrek en de aankomst van de deelbeweging.

De verplaatsing wordt gedefinieerd als

∆x = xeind – xbegin

Je kunt dat voorstellen als een vector

∆x vanuit xbegin tot xeind x

xbegin xeind

∆x

▲ Afb. 30 De verplaatsingsvector tussen begin en eind

Als een voorwerp energie bezit, kan het een kracht uitoefenen die een verplaatsing veroorzaakt. Het voorwerp is in staat om arbeid te verrichten.

In het dagelijks leven is ‘arbeid’ een synoniem voor ‘werk’ of ‘inspanning’. Bij fysieke arbeid gebruik je je spieren om iets op te heffen, om te lopen … Bij mentale arbeid gebruik je je hersenen om na te denken. Als je hard werkt, word je moe. De arbeid (het werk) wordt verricht door een persoon.

In de fysica is arbeid de uitwerking van een kracht. Een voorwerp dat energie bezit, kan een kracht F uitoefenen die een verplaatsing ∆x veroorzaakt. De arbeid wordt verricht door een kracht. Door de arbeid wordt energie overgedragen van een systeem naar een ander systeem.

We definiëren de grootheid arbeid met het symbool W (afgeleid van het Engelse woord voor ‘arbeid’, Work) als volgt: W = F ∙ ∆x

Uit de definitie volgt dat de eenheid van arbeid joule is: [W] = [F] ∙ [∆x] = N ∙ m = J

Grootheid met symbool SI-eenheid met symbool

arbeid W = F ∙ ∆x (als F ∆x)jouleJ (= N ∙ m)

VOORBEELD ARBEID DOOR DE TREKKRACHT TIJDENS HET VOORTTREKKEN VAN EEN KIST

Tijs kan de kist vooruit trekken omdat hij chemische energie bezit. Hij trekt met een constante kracht F volgens de bewegingsrichting aan de kist. De kist verplaatst zich over een afstand ∆x. De trekkracht verricht arbeid, waardoor de kist kinetische energie krijgt.

kin, begin = 0 J

kin, eind > 0 J

• Bij dezelfde kracht geldt: hoe groter de verplaatsing, hoe groter de arbeid verricht door die kracht.

Als Tijs de kist in beweging brengt met een kracht van F = 180 N, dan neemt de arbeid recht evenredig toe met de verplaatsing:

∆x = 1,00 m: W = F ∙ ∆x = 180 N ∙ 1,00 m = 180 J

∆x = 2,00 m: W = F ∙ ∆x = 180 N ∙ 2,00 m = 360 J

• Bij dezelfde verplaatsing geldt: hoe groter de kracht, hoe groter de arbeid verricht door die kracht.

Als Tijs de kist over een vaste afstand ∆x = 1,00 m verplaatst, dan neemt de arbeid recht evenredig toe met de kracht die hij uitoefent:

F = 180 N: W = F ∙ ∆x = 180 N ∙ 1,00 m = 180 J

F = 360 N: W = F ∙ ∆x = 360 N ∙ 1,00 m = 360 J

▲ Afb. 31 De grootte van de trekkracht en de verplaatsing bepalen de verrichte arbeid.

Op een voorwerp in beweging werken verschillende krachten in, elk met hun eigen richting en zin:

• De kracht die de beweging veroorzaakt, is volgens de beweging gericht

• De wrijvingskracht is tegengesteld aan de beweging.

• De zwaartekracht is verticaal naar beneden gericht.

• De normaalkracht staat loodrecht op de bewegingsrichting met een zin weg van het oppervlak.

Voor elke kracht kun je de arbeid berekenen. De oriëntatie van de kracht ten opzichte van de verplaatsing bepaalt het teken:

• W > 0 als de kracht en de verplaatsing dezelfde zin hebben;

• W < 0 als de kracht en de verplaatsing een tegengestelde zin hebben;

• W = 0 als de kracht en de verplaatsing loodrecht op elkaar staan.

VOORBEELD ARBEID DOOR DE WRIJVINGSKRACHT, DE ZWAARTEKRACHT EN DE NORMAALKRACHT

BIJ EEN HORIZONTALE VERPLAATSING VAN EEN KIST

In de tabel zie je een overzicht van de mogelijke situaties.

F en ∆x hebben dezelfde richting en een tegengestelde zin.

Er is een wrijvingskracht tussen de kist en de ondergrond, waardoor de kist afremt nadat Tijs een duw gegeven heeft.

eind = 0

©VANIN

w = F w ∙ ∆x

De arbeid door de wrijvingskracht is negatief

Voorbeeld: als F w = 100 N en ∆x = 1,50 m dan W = –F w ∙ ∆x = –100 N ∙ 1,50 m = –150 J

F en ∆x staan loodrecht op elkaar. De zwaartekracht en de normaalkracht werken in op de kist.

Arbeid door de zwaartekracht: W z = F z ∙ ∆x = 0 J

Arbeid door de normaalkracht: W n = F n ∙ ∆x = 0 J

De arbeid door de normaalkracht en de normaalkracht is nul. ▲

▲ Afb. 32

Afb. 33

Een voorwerp dat energie bezit, kan arbeid verrichten. Als het voorwerp een kracht F uitoefent die een verplaatsing∆x bevordert of verhindert, wordt er door die kracht arbeid verricht. Die arbeid wordt bepaald door de grootte van de kracht (F), de grootte van de verplaatsing (∆x) en de hoek tussen de kracht en de verplaatsing (θ).

Grootheid met symbool

SI-eenheid met symbool

arbeid W = F ∙ ∆x (als F ∆x) joule J (= N ∙ m)

De oriëntatie van de kracht ten opzichte van de verplaatsing bepaalt het teken van de arbeid:

• W > 0 als de kracht en de verplaatsing dezelfde zin hebben;

• W = 0 als de kracht loodrecht staat op de verplaatsing;

• W < 0 als de kracht en de verplaatsing een tegengestelde zin hebben.

` Maak oefening 9 t/m 13 op p. 48-49.

VERDIEPING

• Om de snelheid te veranderen, moet er arbeid worden verricht. Het arbeid-energietheorema beschrijft het verband tussen de verrichte arbeid en de verandering van kinetische energie.

• Om de hoogte te veranderen, wordt er arbeid verricht. Tijdens de hoogteverandering verricht ook de zwaartekracht arbeid en verandert de potentiële zwaarte-energie.

Je leert er meer over op

ARBEID

bezit, is het in staat om arbeid te verrichten: het kan een uitoefenen die een bevordert of verhindert. Voor een constante kracht wordt de arbeid

Als een systeem

gegeven door: W = F ∙ = Grootheid met symbool SI-eenheid met symbool arbeid W joule J

normaalkracht: W = F ∙ ∆ x = 0

zwaartekracht: W = F ∙ ∆ x = 0

x W = 0

©VANIN

Geldig voor een systeem waar enkel de kracht en de kracht op inwerken. Er is een energieomzetting binnen het systeem van energie naar (twee soorten van) energie of omgekeerd. E mech, 1 = E kin, 1 + E

• naar een binnen het (= voorwerp of aantal voorwerpen);

• naar een ander of de (= alles buiten het systeem).

• z elfde zin: W > 0 trekkracht: W = F ∙ ∆ x

• t egengestelde zin: W < 0 wrijvingskracht: W = –F

Voorbeeld: omzetting van mechanische energie in mechanische energie en warmte E mech, 1 = + = W et van Energie kan niet gemaakt en niet vernietigd worden. Energie wordt …

ENERGIEDISSIPATIE

Bij een systeem waarop, naast de kracht en de veerkracht, ook wrijvingskracht inwerkt, wordt een deel van de energie omgezet in onnuttige . Het is de verhouding tussen de nuttige energie en de totale energie. Grootheden met symbool

Eenheden met symbool warmte Q jouleJ rendement = E nuttig E tot onbenoemd

1 Begripskennis

• Ik kan een systeem en de omgeving omschrijven.

• Ik kan het begrip ‘behoud van mechanische energie’ omschrijven

• Ik kan het behoud van mechanische energie toepassen.

• Ik kan het begrip ‘behoud van energie’ omschrijven

• Ik kan het behoud van energie toepassen bij een open systeem.

• Ik kan het begrip ‘energiedissipatie’ omschrijven.

• Ik kan het begrip ‘rendement’ omschrijven

• Ik kan het rendement berekenen

• Ik kan het begrip ‘arbeid verrichten’ omschrijven.

• Ik kan de arbeid voor een constante kracht berekenen

2 Onderzoeksvaardigheden

• Ik kan kwalitatieve verbanden afleiden uit experimenten.

• Ik kan de ingenieursnotatie gebruiken.

• Ik kan formules omvormen naar de gevraagde grootheid.

• Ik kan nauwkeurig berekeningen uitvoeren

` Je kunt deze checklist ook op invullen.

JANOG OEFENEN

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’.

Je kunt de oplossingsstrategie en de voorbeeldoefeningen op gebruiken als extra ondersteuning.

Een snowboarder glijdt een helling af via vier verschillende pistes met verschillende moeilijkheidsgraden. Elke piste heeft hetzelfde begin- en eindpunt. We verwaarlozen de wrijving. Rangschik de gevraagde grootheden van klein naar groot.

1 gemakkelijk gemiddeld moeilijk erg moeilijk 1 2 3 4

• de potentiële zwaarte-energie van de snowboarder bovenaan:

• de kinetische energie op halve hoogte:

• de eindsnelheid van de snowboarder:

• de tijd die de snowboarder nodig heeft om de helling af te glijden:

Astrid (m = 45,0 kg) glijdt van een 10,0 m hoge glijbaan.

Op halve hoogte heeft ze een snelheid van 35,6 km h

a Voorspel haar snelheid onderaan de glijbaan.

b Bereken haar snelheid onderaan de glijbaan. Verwaarloos de wrijving.

Bekijk de video.

a Waarop moet je letten om het experiment veilig uit te voeren? Verklaar.

video: experiment

b Test uit.

Eva krijgt een duwtje en schommelt met een maximale snelheid van 5,4 m s .

a Geef twee voorwaarden opdat je Eva kunt beschouwen als een geïsoleerd systeem.

b Noteer de energieomzettingen in symbolen onder de afbeelding.

c Bereken …

• de hoogte waarop Eva losgelaten is;

• de snelheid die Eva heeft op 0,50 m hoogte.

Duid de gegevens aan op de afbeelding.

Jeroen heeft zich afgestoten voor een sprong met powerskips.

Door de veer (k = 1,0 kN cm) 13 cm in te drukken, bereikt hij een hoogte van 1,7 m. Verwaarloos de luchtweerstand.

a Noteer de energieomzetting tussen de lancering en het hoogste punt in symbolen naast de afbeelding.

b Bereken …

• de potentiële elastische energie in het begin;

• de massa van Jeroen.

Je laat vier stuiterballen botsen op de grond. Ze kaatsen terug, zoals weergegeven op de afbeelding.

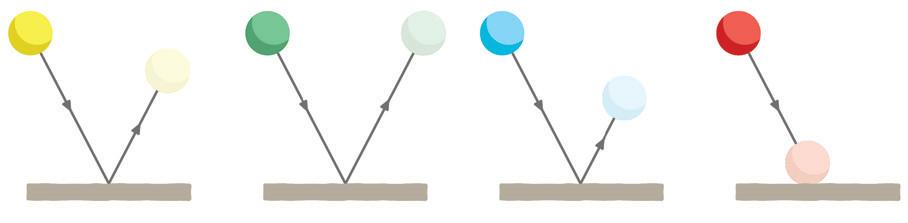
Rangschik de gevraagde grootheden van klein naar groot.

• totale energie:

• nuttige energie:

• energiedissipatie:

• rendement:

Een appel valt van de boom en heeft bij het neerkomen 10 J kinetische energie. Hoeveel potentiële zwaarte-energie bezat de appel aan de boom? Duid aan.

precies 10 J

meer dan 10 J

minder dan 10 J

onmogelijk te zeggen met deze gegevens

Na de lancering in de flipperkast met een veer (k = 120 N cm ) die 3,5 cm uitgerekt wordt, heeft het balletje (m = 80 g)

een snelheid van 0,92 m s

a Noteer de energieomzettingen in symbolen naast de afbeelding.

b Bereken de ontwikkelde warmte en het rendement.

In welke situaties verricht de spierkracht arbeid? Duid aan. 1 2 3 4

Je trapt een bal weg.Je houdt halters boven je hoofd.

Je probeert een band te verschuiven, maar het lukt niet.

Je glijdt naar beneden op een deathride.

Bas duwt tegen een winkelkar.

a Vul de energieomzetting aan.

→ arbeid verricht door → van

b Vul de tabel aan.

Een auto (m = 1 350 kg) heeft bij een remkracht van 8,0 kN een remafstand van 72 m.

a Vervolledig de afbeelding.

• Teken alle krachten in het massapunt tijdens het remmen.

• Teken de verplaatsingsvector.

b Vul de energieomzetting aan.

arbeid verricht door

c Bereken de arbeid die elke kracht verricht.

Een pakket stenen met een gewicht van 1,0 kN hangt aan een torenkraan. Vul de tabel aan.

De kraan tilt de stenen met een constante snelheid 15 m omhoog.

De kraan laat de stenen met een constante snelheid 15 m zakken.

De stenen hangen stil op 15 m hoogte.

Een astronaut verricht 30 J arbeid om een steen met een massa van 23 kg op te tillen op de maan.

Hoe hoog tilt hij de steen op?

` Verder oefenen? Ga naar .

Hoe kan energie gebruikt worden?

LEERDOELEN

Je kunt al:

het behoud van energie toepassen; de arbeid en het rendement berekenen.

Je leert nu:

de begrippen ‘energieproductie’ en ‘energieverbruik’ omschrijven; het vermogen en de verbruikte energie berekenen; hoe je duurzaam kunt omgaan met energie.

Om wagentjes omhoog te hijsen, bootjes te laten varen op woeste rivieren of lasershows te organiseren … Overal in het pretpark is er energie nodig. Ook wanneer de honderden medewerkers de attracties aanleggen en aansturen, verbruiken zij energie. Maar om hoeveel energie gaat het eigenlijk? Wat zijn de invloedsfactoren? Hoe produceert men die energie en slaat men ze op?

En hoe kan dat duurzaam gebeuren?

In dit hoofdstuk bestudeer je wat energieproductie betekent, en welke factoren het energieverbruik bepalen.

1 Wat betekenen energieproductie en -verbruik?

OPDRACHT 16

Bestudeer het verschil tussen energieproducenten en energieverbruikers.

1 Stellen de afbeeldingen energieproducenten of energieverbruikers van het pretpark voor?

Noteer onder elke afbeelding ‘producent’ of ‘verbruiker’.

▲ Afb. 34 Op de parking wekken zonnepanelen elektrische energie op.

▲ Afb. 35 In het restaurant kun je voedsel kopen om je honger te stillen.

▲ Afb. 36 De attracties worden elektrisch aangestuurd.

▲ Afb. 37 Bezoekers wandelen door het pretpark.

OPDRACHT 16 (VERVOLG)

2 Omschrijf de begrippen ‘energieproducent’ en ‘energieverbruiker’ met behulp van deze wetenschappelijke begrippen: arbeid – omgeving – systeem

• energieproducent:

©VANIN

• energieverbruiker:

Volgens de wet van behoud van energie kan energie niet gemaakt en niet vernietigd worden. Energie wordt omgezet binnen een systeem of overgedragen van de omgeving naar het systeem (of omgekeerd).

Energieproductie betekent dat energie omgezet wordt naar een energievorm die geschikt is voor gebruik. De energieproducent is de omgeving. Die levert energie aan het systeem. De energieproducent wordt vaak de energiebron genoemd.

Energieverbruik betekent dat energie omgezet wordt naar arbeid De energieverbruiker is het systeem dat de energie gebruikt.

Mensen zijn energieverbruikers. Om onze organen te laten functioneren, om te bewegen en om te denken, hebben we energie nodig. Die energie nemen we op uit voedsel. Er wordt chemische energie uit de omgeving ‘voeding’ overgedragen aan het systeem ‘mens’.

energieproducent omgeving energieverbruiker

chemische energie

orgaanfuncties, 37°C, bewegen, denken systeem

▲ Afb. 38 Mensen verbruiken chemische energie om te functioneren.

Een attractie op een pretpark is een energieverbruiker. Elektrische energie wordt omgezet naar mechanische energie.

energieproducent omgeving

energieverbruiker

elektrische energie mechanische energie systeem

▲ Afb. 39 Toestellen verbruiken elektrische energie om te functioneren.

Elektrische energie komt in de natuur niet voor in een bruikbare vorm. Ze wordt op verschillende manieren geproduceerd uit energiebronnen die wel in de natuur voorkomen. Bij de energieproductie vinden er een of meerdere energieomzettingen plaats. Hoe minder tussenstappen er nodig zijn, hoe minder energie er gedissipeerd wordt en hoe hoger het rendement zal zijn.

zon wind water geothermisch biomassa kernenergie gas energiebron

GENERATOR

©VANIN

▲ Afb. 40 Verschillende manieren om elektrische energie te produceren

omzetting naar elektrische energie

omzetting naar warme

omzetting naar bewegingsenergie

Je kunt de werking van de generator bekijken in de applet.

applet: generator

TIP

Energie wordt omgezet binnen een systeem of overgedragen tussen de omgeving en het systeem:

• De energieproducent is de omgeving. Die levert energie aan het systeem.

• De energieverbruiker is het systeem. Dat gebruikt de energie om arbeid te verrichten.

` Maak oefening 1 op p. 64.

©VANIN

2 Wat is het vermogen van een energieomzetting?

OPDRACHT 17

Bestudeer de verrichte arbeid en het tijdsverloop.

Op een bouwwerf van het pretpark moeten de bouwvakkers een pak cement naar boven brengen.

Dat kan via een ladder of met een torenkraan.

h = 6,50 m m = 25,0 kg m = 25,0 kg

▲ Afb. 41 Een bouwvakker en een torenkraan brengen een pak cement omhoog.

1 Vul de tabel aan.

a Noteer de energieomzetting. Verwaarloos de energiedissipatie. b Vul het verband aan met <, > of =.

Een bouwvakker brengt het cement naar boven.Een torenkraan brengt het cement naar boven. van de bouwvakker → van het pak cement van de torenkraan → van het pak cement

• Verrichte arbeid om alle stenen naar boven te brengen: Wbouwvakker Wtorenkraan

• Grootte van de overgedragen energie tijdens de energieomzetting: ∆Ebouwvakker ∆Etorenkraan

• Benodigde tijd om alle stenen naar boven te brengen: ∆tbouwvakker ∆ttorenkraan

2 Verklaar (aan de hand van vraag 1) waarom men op een bouwwerf kranen gebruikt.

Het vermogen geeft aan hoeveel arbeid er per tijdseenheid kan worden verricht.

We definiëren de grootheid vermogen met het symbool P (afgeleid van het Engelse Power) als volgt:

P = |W| Δt

Daarbij is |W| de hoeveelheid arbeid en Δt het tijdsverloop waarin de arbeid verricht wordt. Vermogen is een scalaire grootheid en is altijd positief

Als er arbeid verricht wordt, is er een energieomzetting. De energie wordt gebruikt om arbeid te kunnen verrichten: W = ΔE

Het vermogen is dus ook gelijk aan het tempo waarin energie wordt omgezet:

P = |W| Δt = |ΔE| Δt

Uit die definitie kun je de eenheid afleiden:

[P] = [W] [∆t] = J s

We definiëren een nieuwe eenheid: de watt (met het symbool W). Die eenheid is vernoemd naar de Schotse ingenieur James Watt.

1 watt = 1 joule 1 seconde of 1 W = 1 J s

Grootheid met symbool SI-eenheid met symbool

vermogen P = |W| Δt = |ΔE| Δt watt W (= J s )

De watt is een kleine eenheid: als je 1 kilogram in 1 seconde 0,1 meter verplaatst, produceer je een vermogen van 1 watt. Vaak gebruikt men de grotere hulpeenheden kilowatt en megawatt.

1 kW = 1 ∙ 103 W

1 MW = 1 ∙ 106 W

©VANIN

De arbeid kan negatief zijn. De hoeveelheid arbeid is echter altijd positief. Daarom voeg je absolutewaardetekens toe.

Het symbool voor de eenheid van vermogen is W. Verwar dat niet met het symbool voor de grootheid arbeid, W Je kunt de symbolen op twee manieren herkennen:

• In getypte teksten staat een grootheid altijd schuingedrukt.

• Een eenheid wordt altijd voorafgegaan door een getalwaarde.

▲ Afb. 42 Je kunt het vermogen van een microgolfoven aanpassen.

TIP

VOORBEELD VERMOGEN VAN EEN BOUWVAKKER EN EEN TORENKRAAN

We bekijken een bouwwerf op een pretpark. Als er 800 kg stenen naar boven (h = 6,50 m) moeten worden gebracht, is er verandering van potentiële zwaarte-energie:

∆E = Epot, z, eind – Epot, z, begin = m ∙ g ∙ h – 0 = 800 kg ∙ 9,81 N kg ∙ 6,50 m = 5,10 · 104 J (= 51,0 kJ)

▲ Afb. 43 Een bouwvakker en een torenkraan brengen een pak cement omhoog.

De torenkraan gebruikt elektrische energie om de stenen omhoog te heffen en heeft daarvoor 35,0 s nodig. Het vermogen van de torenkraan is:

Pkraan = |ΔE| Δtkraan = 5,10 · 104 J 35,0 s = 1,46 · 103 W (= 1,46 kW)

De bouwvakker gebruikt chemische energie om de stenen omhoog te heffen en heeft daarvoor 18,00 min nodig. Hij draagt daarvoor 32 keer een pak van 25,0 kg naar boven. Het vermogen van de bouwvakker is:

Pbouwvakker = |ΔE| Δtbouwvakker = 5,10 · 104 J 18,00 min = 5,10 · 104 J 1 080 s = 47,2 W h = 6,50 m m = 800 kg m = 25,0 kg

De eenheid kilowattuur (kWh) is de energie van een voorwerp dat gedurende 1 uur 1 000 joule per seconde produceert of verbruikt. De eenheid kWh wordt gebruikt voor elektrische toestellen omdat de elektrische energie daar heel groot is. De omzettingsfactor naar joule vind je door een omzetting naar de SI-eenheden te doen:

E = 1 kWh = 1 000 W ∙ 1 h = 1 000 J s ∙ 3 600 s = 3 600 000 J = 3,6 ∙ 106 J (= 3,6 MJ)

De grootheid vermogen is het tempo waarin arbeid wordt verricht en dus energie wordt omgezet:

Vermogen is een scalaire grootheid en is altijd positief

Grootheid met symbool SI-eenheid met symbool

vermogen P = |W| Δt = |ΔE| Δt watt W (= J s )

Veelgebruikte hulpeenheden zijn kilowatt (1 kW = 1 ∙ 103 W) en megawatt (1 MW = 1 ∙ 106 W).

De eenheid kilowattuur (kWh) is de energie van een voorwerp dat gedurende 1 uur 1 000 joule per seconde produceert of verbruikt.

Je kunt dat ook uitdrukken in J:

E = 1 kWh = 1 000 W ∙ 1 h = 1 000 J s ∙ 3 600 s = 3 600 000 J = 3,6 ∙ 106 J (= 3,6 MJ)

` Maak oefening 2 t/m 6 op p. 64-65.

OPDRACHT 18

Ga op zoek naar de betekenis van ‘kWh’.

1 Noteer ‘kWh’ in woorden.

2 Herschrijf de formule van vermogen om de verbruikte energie te berekenen.

|ΔE| =

3 Verklaar waarom kWh een eenheid van energie is.

4 Je gebruikt een verwarming met een vermogen van 1 500 W gedurende 3,0 h.

Bereken (zonder rekentoestel) de verbruikte energie.

|ΔE| =

5 Zet 1 kWh om naar joule.

E = 1 kWh = W ∙ h = 1 000 s = J = ∙ 10 J = MJ

OPDRACHT 19

Los het vraagstuk op.

De stoeltjes van de zweefmolen versnellen in een halve minuut van stilstand tot 35 km h .

De maximale massa (als alle stoeltjes bezet zijn) is 3,2 ton.

1 Noteer de energieomzetting.

2 Bereken de maximale kinetische energie, de verrichte arbeid en het vermogen van de motor.

a Werk uit op een cursusblad.

b Controleer je antwoord via

▲ Afb. 45

▲ Afb. 44 Elektrische energie wordt uitgedrukt in kWh.

3 Wat betekent duurzaam omgaan met energie?

3.1 Duurzaam energiegebruik

©VANIN

In ons dagelijks leven gebruiken we heel wat (elektrische) toestellen. Elk toestel gebruikt een hoeveelheid energie per tijdseenheid. Dat drukken we uit met de term ‘vermogen’. Duurzaam energiegebruiken betekent de beschikbareenergie zo goed mogelijk gebruiken.

Efteling bespaart veel energie door medewerkers eerder koffie te laten drinken

De Efteling heeft haar werkwijze aangepast, legt dagverantwoordelijke Lennart Stolk uit. ‘Voorheen startten we eerst de pomp van de attractie op. Vervolgens gingen we een half uurtje koffiedrinken en de dag voorbespreken. Nu drinken we éérst koffie en starten daarna pas op. Daardoor draait de Piraña twintig minuten per dag minder.’

Per uur wordt twee miljoen liter water door de betonnen geul van de attractie gepompt. Met een vermogen van driehonderd kilowatt zijn de pompen de grootste energieverbruiker van het hele park.

Bron: looopings.nl, 01/11/2019

Attractiepark Plopsaland vergroend

Attractiepark Plopsaland

De Panne zorgt voor veel plezier bij jong en oud, maar verbruikt daarbij gigantische hoeveelheden energie. Het park is daarom flink aan het verduurzamen. Dankzij de installatie van een bijzonder verwarmingssysteem stoot het park nu jaarlijks bijna 500 ton minder CO2 uit en is er een energiebesparing van 2 400 MWh.

Bron: installatieenbouw.be, 29/07/2020

Als een toestel een vermogen P heeft en gedurende een tijdsverloop ∆t gebruikt wordt, kun je met de definitie van vermogen het energieverbruik |∆E| berekenen:

P = |ΔE| Δt |∆E| = P ∙ ∆t

Daaruit volgt dat je de verbruikte energie |∆E| kunt beperken door:

• het tijdsverloop beperkt te houden;

• het totale vermogen beperkt te houden.

We bekijken wat dat betekent.

1 Het tijdsverloop beperken

De verbruikte energie neemt recht evenredig toe met het tijdsverloop

Voorbeeld: Hoe langer je werkt met je pc, hoe meer water je opwarmt, hoe verder je je verplaatst … hoe meer energie je verbruikt.

De makkelijkste manier om duurzaam om te gaan met energie, is om toestellen zo kort mogelijk te gebruiken. Bekijk via nog meer tips om minder energie te gebruiken.

2 Het totale vermogen beperken

Bij een energieomzetting wordt energie omgezet in nuttige energie en verloren energie (vaak warmte). Terwijl een toestel werkt, moet de nuttige energie zo hoog mogelijk zijn.

Met de definitie van rendement bepaal je het nuttige vermogen: η = |ΔEnuttig| |ΔEtot| = Enuttig Etot = Pnuttig

t = Pnuttig Ptot , dus Pnuttig =

Je kunt daarmee de energie bepalen:

• de nuttige energie:

nuttig = Pnuttig

• de energiedissipatie (= warmte): Q = Ponnuttig

Pnuttig)

©VANIN

Als een toestel optimaal functioneert, heeft het een hoog rendement. Om een nuttig vermogen te hebben, zijn de energiedissipatie (= ontwikkelde warmte) en het totale vermogen klein

Op toestellen vind je een energielabel dat het rendement van een toestel aangeeft.

• Een groen A-label geeft aan dat het toestel weinig energie gebruikt. Het heeft een laag vermogen en een hoog rendement

• Een rood G-label geeft aan dat het toestel veel energie verbruikt, doordat het vermogen groot is en het rendement laag.

OPDRACHT 20

Bestudeer het vermogen van verlichting.

1 Vul de tabel aan.

©VANIN

Q (kWh) na 2,0 uur (bepaald door Ponnutig)

2 De Europese Unie verbiedt (sinds 2012) het gebruik van gloeilampen. Verklaar waarom.

▲ Afb. 47

3.2 Duurzame energieproductie

OPDRACHT 21 ONDERZOEK

Bestudeer een elektriciteitscentrale.

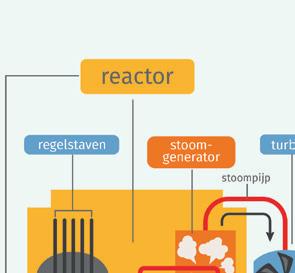
1 Bestudeer de bouw van een kerncentrale.

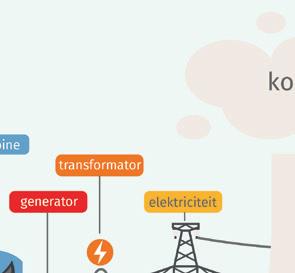
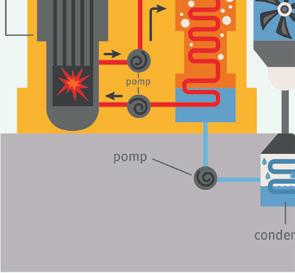
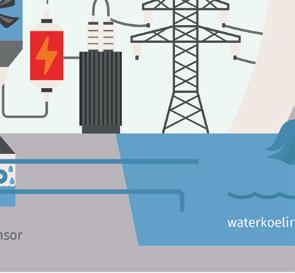
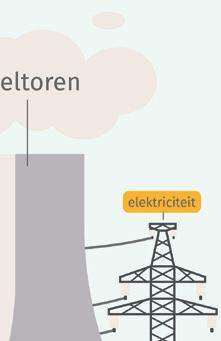
a Noteer de energieomzettingen. ① van uranium → ② van water → ③ van turbines → ④ van ladingen

b Noteer het nummer van de energie(omzetting) op de juiste plaats op de afbeelding.

c Hoe verschilt de bouw van een fossiele brandstofcentrale van die van een kerncentrale?

2 Hoe komt het dat fossiele brandstofcentrales bijdragen aan de opwarming van de aarde? Duid aan.

De koeltorens stoten onnuttige warmte uit.

De koeltorens stoten warme CO2 uit.

Er ontstaat CO2 die de warmte-uitwisseling door de atmosfeer verstoort.

▲ Afb. 48 Bouw van een elektriciteitscentrale

▲ Afb. 49

Bij de productie van elektrische energie vinden er energieomzettingen plaats. Bij elke omzetting geldt:

Pnuttig = η ∙ Ptotaal

Om elektriciteit duurzaam te produceren, moet je rekening houden met twee factoren:

1 een hoog rendement nastreven

©VANIN

De energiedissipatie in de vorm van warmte moet zo beperkt mogelijk zijn.

Dat kan door:

—het rendement van elke energieomzetting zo hoog mogelijk te maken; —het aantal energieomzettingen te beperken.

2 de afvalstoffen beperken

Bij sommige vormen van energieproductie wordt schadelijk afval geproduceerd.

—Bij de verbranding van fossiele brandstoffen komt er CO2-gas vrij. Dat broeikasgas verstoort de atmosfeer, waardoor het klimaat ontregeld wordt.

—Bij de productie van kernenergie ontstaat er radioactief afval. De afvalstoffen zenden gedurende honderden jaren straling uit die schade toebrengt aan mens en milieu.

Elektriciteitsproductie met wind, zon, water en aardwarmte levert het grootste rendement en het minste afval. Die vormen van energie worden daarom groene energie genoemd.

VOORBEELD DUURZAME ENERGIEPRODUCTIE IN HET PRETPARK

Pretparken gebruiken heel veel energie. Het reuzenrad alleen al verbruikt evenveel elektrische energie als twintig gezinnen (70 000 kWh = 70 MWh).

De meeste pretparken zetten in op duurzame elektriciteitsproductie door zonnepanelen en windmolens te installeren.

Duurzaam omgaan met energie betekent …

• energie duurzaam verbruiken door:

—de energieverbruiker zo kort mogelijk te gebruiken (kort tijdsverloop);

—de energie zo nuttig mogelijk te gebruiken (klein vermogen en groot rendement);

• energie duurzaam produceren door:

—de beschikbare energie zo nuttig mogelijk te gebruiken (groot rendement);

—de afvalstoffen zo beperkt mogelijk te houden.

` Maak oefening 7 t/m 10 op p. 66.

Kernbegrippen

energieproducent energieverbruiker vermogen

duurzaam energieverbruik

Notities

Energie wordt binnen een of tussen de omgeving en het systeem:

• De energieproducent is de omgeving. Die

©VANIN

duurzame energieproductie

• De energieverbruiker is het systeem. Dat gebruikt de energie om

De vermogen is het tempo waarin arbeid wordt verricht en dus energie wordt omgezet:

P = =

Vermogen is een grootheid en is altijd Grootheid met symbool SI-eenheid met symbool (= )

Veelgebruikte hulpeenheden zijn (1 kW = ) en (1 MW = ).

De kWh is een alternatieve van .

Duurzaam omgaan met energie betekent …

• energie duurzaam door:

—de energieverbruiker zo kort mogelijk te gebruiken (kort );

—de energie zo nuttig mogelijk te gebruiken ( vermogen en rendement);

• energie duurzaam door:

—de beschikbare energie zo nuttig mogelijk te gebruiken (groot );

—de zo beperkt mogelijk te houden.

Bespreek de verschillende voorstellingen op de afbeelding door de kernbegrippen te gebruiken.

1 Begripskennis

• Ik kan de begrippen ‘energieproductie’ en ‘energieverbruik’ omschrijven.

• Ik kan voorbeelden geven van energieproducenten en energieverbruikers.

• Ik kan de energieoverdracht tussen een energieproducent en een energieverbruiker toepassen

• Ik kan het begrip ‘vermogen’ omschrijven

• Ik kan het vermogen berekenen.

• Ik kan het begrip ‘duurzaam omgaan met energie’ omschrijven

• Ik kan de begrippen ‘energie’, ‘rendement’ en ‘vermogen’ toepassen in de context van duurzaam omgaan met energie.

• Ik kan het energieverbruik in realistische toepassingen berekenen

2 Onderzoeksvaardigheden

• Ik kan een onderzoek uitwerken

• Ik kan een onderzoek uitvoeren.

• Ik kan een STEM-project uitvoeren.

• Ik kan wetenschappelijke inzichten toepassen in een maatschappelijke context.

• Ik kan de ingenieursnotatie gebruiken.

• Ik kan formules omvormen naar de gevraagde grootheid.

• Ik kan nauwkeurig berekeningen uitvoeren

` Je kunt deze checklist ook op invullen.

JANOG OEFENEN

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’.

Je kunt de oplossingsstrategie en de voorbeeldoefeningen op gebruiken als extra ondersteuning.

Een gezonde levensstijl betekent dat er een evenwicht is tussen de opgenomen energie uit voeding en het energieverbruik via beweging.

a Hoelang moet je elke activiteit uitvoeren om een reep chocolade van 80 g (2 256 kJ 100 g ) te verbruiken? Noteer in de tabel.

Activiteit

Energieverbruik(MJ h ) Tijd nodig om chocoladereep te verbruiken t (h) t (min)

b Wat gebeurt er als je de activiteit minder lang uitoefent? Duid aan.

De overtollige energie wordt niet meer opgenomen.

De overtollige energie wordt opgeslagen als vet.

De overtollige energie wordt overgedragen aan de omgeving via de ontlasting.

Bestudeer de verschillende situaties.

Een takelwagen trekt een kapotte auto met een constante snelheid 2 km voort in 1,5 minuten.

Een man krijgt zijn kapotte auto niet in beweging. Hij trekt gedurende 2 minuten aan zijn auto.

Rangschik de situaties volgens toenemend vermogen.

Een kind trekt een vrachtwagentje 15 m vooruit in 10 seconden.

Tijdens het hoogspringen bereikt Nafi Thiam (m = 69 kg) een hoogte van 1,96 m in 0,70 s.

a Noteer de energieomzetting van Thiam. van Thiam → van Thiam

b Bereken haar vermogen.

Bestudeer het krantenartikel.

a Verbeter de fouten die de auteur gemaakt heeft tegen de grootheid en eenheid van vermogen.

b Bereken de (gemiddelde) energie die van Aert nodig had voor zijn krachtinspanning.

De ongenaakbare sprint van Wout van Aert in Tirreno-Adriatico: van ver aanzetten om beestig hoog wattage te halen

Op zo’n 200 meter van de finish zette van Aert zijn turbo aan. Gaviria werd meteen overruled en Ewan probeerde wel, maar stierf in het wiel van de oppermachtige Belg, die met gekromde rug à la Mario Cipollini in een perfect rechte lijn richting zege sprintte.

En van Aert deed dat met een onwaarschijnlijke krachtinspanning over dertien seconden met een piek van 1 445 Watt en gemiddeld 1 215 Watt. Zijn topsnelheid was … 72,6 km/u. Wie kan daar tegenop? Aan de overduidelijke finishfoto te zien, zelfs de beste sprinters niet.

Bron: nieuwsblad.be, 10/03/2021

Een Tesla S heeft een massa van 1 735 kg en een vermogen van 225 kW.

In hoeveel tijd kan hij vanuit rust optrekken tot 100 km h ?

Bestudeer de verschillende systemen die arbeid verrichten. Verbind elk systeem met het overeenkomstige vermogen. Gebruik het internet als je twijfelt.

Bestudeer de uitspraken. Wie heeft gelijk?

A B C

Het rendement stijgt als we een geschikte pot en een geschikt deksel gebruiken.

Het rendement hangt af van het vermogen van het kookvuur.

Het rendement van het kookvuur is 100 %, want de geproduceerde energie is warmte.

De elektrische motor in een lift heeft een vermogen van 11 kW en een rendement van 18 %.

In hoeveel tijd kan de motor de lift met vijf personen (m = 800 kg) drie verdiepingen hoger brengen?

Elke verdieping is 2,8 m hoog.

Een marathonloper heeft een gemiddeld vermogen van 284 W.

Tijdens zijn loop van 4,0 uur verbruikt hij 4,24 kWh energie.

a Vervolledig de energieomzetting. chemische energie van → energie + energie (bloedsomloop, ademhaling …) + van de loper

b Bereken het rendement.

Technologie gaat op zoek naar oplossingen voor de klimaatverandering. Een belangrijk onderdeel daarvan is energietransitie.

a Zoek de betekenis van het begrip ‘energietransitie’ op.

b Illustreer met een voorbeeld uit de actualiteit hoe wetenschappers en ingenieurs op zoek gaan naar vernieuwingen om die energietransitie mogelijk te maken.

` Verder oefenen? Ga naar .

Vermogen

Grootheid met symbool SI-eenheid met symbool

vermogen P watt W (= J s )

De grootheid vermogen is het tempo waarin arbeid wordt verricht en dus energie wordt omgezet : P = | W | Δ t = |Δ E | Δ t

Vermogen is een scalaire grootheid en is altijd positief. Veelgebruikte hulpeenheden zijn kilowatt

(1 kW = 1 ∙ 10 3 W) en megawatt (1 MW = 1 ∙ 10 6 W). De kWh (kilowattuur) is een alternatieve eenheid van energie .

Duurzaam omgaan met energie

• E nergie duurzaam verbruiken door: —de ener gieverbruiker zo kort mogelijk te gebruiken (kort tijdsverloop); —de ener gie zo nuttig mogelijk te gebruiken (klein vermogen en groot rendement).

• E nergie duurzaam produceren door: —de beschikb are energie zo nuttig mogelijk te gebruiken (groot rendement); —de afv alstoffen zo beperkt mogelijk te houden.

Arbeid

Als een systeem energie bezit, is het in staat om arbeid te verrichten: het kan een kracht F uitoefenen die een verplaatsing ∆ x veroorzaakt. Er wordt energie overgedragen van een systeem naar een ander systeem. Voor een constante kracht is de arbeid gegeven door: W = F ǁ ∙ ∆ x Grootheid met symbool SI-eenheid met symbool arbeid W jouleJ (= N ∙ m)

ǁ Δ x F ⊥ Δ x

Energie

Grootheid met symboolEenheden met symbool

energie E joule kilocalorie kilowattuur J kcal kWh

Verschillende energievormen

• Mechanische ener gie: —kinetische ener gie: energie door snelheid

E kin = 1 2 · m · v ² —pot entiële zwaarte-energie: energie door plaats in het zwaartekrachtveld

E pot, z = m · g · h —pot entiële elastische energie: energie door een uitgerekte of ingedrukte veer

E pot, e = 1 2 · k · (∆ l )²

• Niet -mechanische energie: stralingsenergie, chemische energie, thermische energie (warmte), vervormingsenergie, kernenergie, elektrische energie

• z elfde zin: W > 0 trekkracht: W = F ∙ ∆ x

• t egengestelde zin: W < 0 wrijvingskracht: W = –F w ∙ ∆ x W = 0 normaalkracht: W = F ∙ ∆ x = 0 zwaartekracht: W = F ∙ ∆ x = 0

Wet van behoud van energie

Energie kan niet gemaakt en niet vernietigd worden.

Energie wordt:

• o mgezet naar een andere vorm binnen het systeem (= voorwerp of aantal voorwerpen);

• ove rgedragen naar een ander systeem of naar de omgeving (= alles buiten het systeem).

Geïsoleerd systeem: E mech, 1 = E mech, 2

Open systeem: E mech, 1 = E mech, 2 + Q en = E mech, 2 E mech, 1

De wet van behoud van energie

Een fietser kan energie omzetten, krijgen en afgeven, maar niet maken of vernietigen.

De fietser bezit potentiële zwaarteenergie (= energieproducent). Hij laat zich door de zwaartekracht naar beneden rollen. Hij krijgt kinetische energie: E tot, begin = E tot, eind E pot, z, begin = E kin, eind

Een deel van de energie wordt door wrijving omgezet naar warmte (= energiedissipatie).

©VANIN

Door de berg op te rijden, krijgt de fietser potentiële zwaarte-energie: door de hoogte in het zwaartekrachtveld kan hij beweging veroorzaken.

De fietser bezit chemische energie uit voeding (= energieproducent).

Tijdens het fietsen verbruikt hij de energie door arbeid te verrichten:

• Hij krijgt kinetische energie (= energie door de snelheid).

• Een deel van de energie wordt door wrijving omgezet naar warmte (= energiedissipatie).

Het rendement van de energieomzetting is: = E nuttig E tot Het vermogen wordt bepaald door de tijd die de fietser nodig heeft: P = | W |

THERMODYNAMICA 02 THEMA

De planeet aarde is tot dusver de enige planeet waarop we leven hebben ontdekt. Daarbij speelt water een cruciale rol. De grote hoeveelheid water in vloeibare en vaste vorm (ijs) houdt de temperatuurschommelingen op onze planeet onder controle. Elke levensvorm op aarde komt voort uit organismen die in water leefden. Bij de zoektocht naar buitenaards leven gaan wetenschappers dan ook op zoek naar sporen van water.

` Hoe komt het dat de oceanen de temperatuur op aarde onder controle houden?

` Welk belang heeft het poolijs voor het klimaat?

` Hoe ontstaan wolken?

We zoeken het uit!

Hoe kun je het gedrag van een gas beschrijven in verschillende omstandigheden?

LEERDOELEN

Je kunt al: de druk in een gas omschrijven; de temperatuur uitdrukken in graden Celsius en kelvin; een gas beschrijven op deeltjesniveau.

Je leert nu: de toestandsgrootheden van een gas omschrijven; een ideaal gas omschrijven als een model voor een echt gas; de verbanden tussen de toestandsgrootheden van een gas bepalen en gebruiken; de ideale gaswet omschrijven en gebruiken.

De diepvriesdeur zit vast net nadat je ze dichtdoet; een pakje chips dat je meeneemt op een bergtocht, wordt groter; een halfvol flesje water is ingedeukt nadat het uit de koelkast komt; de verpakking van bedorven voedsel gaat bol staan … Je hebt vast al een van die fenomenen vastgesteld. Maar heb je je ook al afgevraagd hoe dat komt? En wat er gemeenschappelijk is aan die voorbeelden? Als je nauwkeurig kijkt, zul je zien dat er in elk van de voorbeelden gassen aanwezig zijn en dat de omgevingsfactoren veranderen.

In dit hoofdstuk bestudeer je hoe je gassen kunt beschrijven bij verschillende toestanden.

1 Wat zijn de toestandsgrootheden van een gas?

OPDRACHT 1

Bestudeer de toestand van het gas in een squashbal.

OPDRACHT 1 (VERVOLG)

1 Verbind de macroscopische grootheid met de juiste omschrijving en de microscopische betekenis.

Omschrijving Macroscopische grootheid Microscopische betekenis

De bal moet precies hard genoeg zijn om vlot te kunnen spelen.

Je warmt de bal voor het spelen op door hem op de grond te laten botsen.

Er zijn verschillende formaten van squashballen.

Doordat je de bal hebt opgepompt, zit er een hoeveelheid lucht in de bal.

2 Vul het symbool aan voor elke grootheid.

OPDRACHT 2

Bestudeer echte gassen.

1 Bestudeer de voorbeelden van echte gassen.

2 Vul de tabel aan.

Waterdamp condenseert op het raam tot waterdruppeltjes.

stofhoeveelheid ( ) de ruimte die de deeltjes samen innemen

volume ( ) de botsingen van de deeltjes tegen de wanden

druk ( ) maat voor de snelheid van de deeltjes

temperatuur ( ) de hoeveelheid stof, uitgedrukt in mol, die recht evenredig is met het deeltjesaantal

Om wratten te verwijderen, gebruikt de dokter vloeibare stikstof.

a Welke stof wordt beschreven?

b In welke aggregatietoestand bevindt de beschreven stof zich?

c Geef een voorbeeld waarbij de beschreven stof gasvormig is.

Droogijs (vaste CO2) wordt gebruikt als koelmiddel.

d Hoe komt het dat de gassen een faseovergang hebben ondergaan?

kelvin (K) graad Celsius (°C)

Bij –273,15 °C bewegen deeltjes niet.

De gasdruk is nul (zie ook paragraaf 2.3, p. 79). Dat is het absolutenulpunt. De kelvinschaal is een temperatuurschaal ten opzichte van het absolute nulpunt. Het verband tussen de temperatuur θ in °C en de temperatuur in K is gegeven door:

θ = ( – 273,15) °C en = (θ + 273,15) K

Kijk in de applet om de betekenis van de toestandsgrootheden op een (vertraagde) voorstelling van een gas te zien. applet: gassen

Het meest voorkomende gas rondom ons is lucht. Zowel in de atmosfeer als in dagelijkse toepassingen is lucht aanwezig. De eigenschappen van lucht verschillen naargelang de situatie.

Lucht en andere gassen bestaan uit deeltjes die snel bewegen en elkaar weinig hinderen.

De toestand van gassen kun je volledig beschrijven aan de hand van vier toestandsgrootheden

Grootheden met symbool SI-eenheden met symbool stofhoeveelheid n mol mol

volume V kubieke meter m³ druk p pascal Pa (absolute) temperatuur T kelvin K

volume: ruimte waarin de deeltjes bewegen

©VANIN

stofhoeveelheid: aantal mol van het gas

temperatuur: maat voor de snelheid van de deeltjes

druk: maat voor de botsingen tegen de wanden

▲ Afb. 56 Vier toestandsgrootheden van een ideaal gas

In deze beschrijving van gassen gebruiken we het model van een ideaal gas:

• De deeltjes hebben geen eigen volume, waardoor ze door het volledige volume kunnen bewegen

• De (cohesie)krachten tussen de deeltjes zijn nul, waardoor ze elkaar niet hinderen tijdens hun bewegingen.

Voor de meeste echte gassen is het model van een ideaal gas een goede benadering als de temperatuur hoog genoeg is (ver boven het punt waar er een overgang is naar vloeibare toestand) en de concentratie van het gas laag genoeg is (zodat de onderlinge krachten te verwaarlozen zijn). Voor metingen in de klas gebruik je lucht op kamertemperatuur. Dat kun je zonder problemen als een ideaal gas bekijken.

In echte gassen hebben de deeltjes wel een eigen volume en oefenen ze kleine krachten uit op elkaar. Daardoor treden er faseovergangen naar vloeibare toestand en vaste toestand op als je de temperatuur verlaagt

VOORBEELD CO2 ALS BEWAARMIDDEL

Om voorverpakte sla te bewaren, voegt men een hoeveelheid (n) koolstofdioxide toe, totdat er een bepaalde druk (p) is. Het gas kan bewegen in het vrije volume (V) van het zakje (daar waar er geen sla zit).

De temperatuur (T) van de sla is lager in de koelkast dan daarbuiten.

Om de toestand van de koolstofdioxide te kennen op een bepaald moment, moet je de vier toestandsgrootheden kennen.

De waterdamp die uit de sla vrijkomt, kan bij lage temperaturen vloeibaar worden. Je ziet waterdruppeltjes verschijnen op het zakje.

In een ideaal gas hebben de gasdeeltjes geen eigen volume en oefenen ze geen krachten uit op elkaar. Lucht gedraagt zich bij kamertemperatuur als een ideaal gas.

De toestand van een ideaal gas op een bepaald moment kun je beschrijven met vier toestandsgrootheden.

Toestandsgrootheden met symbool SI-eenheden met symbool stofhoeveelheid n mol mol volume V kubieke meter m³ druk p pascal Pa temperatuur T kelvin K

▲ Afb. 57 Voorverpakte groenten blijven langer vers door de toevoeging van CO2-gas.

2 Welke verbanden bestaan er tussen de toestandsgrootheden van een vaste hoeveelheid gas?

2.1 Mogelijke processen

OPDRACHT 3

Bestudeer de mogelijke verbanden tussen de toestandsgrootheden van een ideaal gas.

1 Bestudeer de afbeeldingen van verschillende situaties.

2 Vul de tabel aan.

Je gaat op een luchtzak zitten.

• Wat gebeurt er met de toestandsgrootheden?

– De hoeveelheid deeltjes is constant / verandert.

– Het volume is constant / verandert

– De temperatuur is constant / verandert

– De druk is constant / verandert.

• Welk verband kun je onderzoeken?

het verband tussen en

Je zet een duikfles in de zon.

Je legt een half opgeblazen, gesloten luchtmatras in de zon.

Wat gebeurt er met de toestandsgrootheden?

– De hoeveelheid deeltjes is constant / verandert.

– Het volume is constant / verandert

– De temperatuur is constant / verandert.

– De druk is constant / verandert

Welk verband kun je onderzoeken?

het verband tussen en

• Wat gebeurt er met de toestandsgrootheden?

– De hoeveelheid deeltjes is constant / verandert

– Het volume is constant / verandert.

– De temperatuur is constant / verandert.

– De druk is constant / verandert

• Welk verband kun je onderzoeken?

het verband tussen en

Wat gebeurt er met de toestandsgrootheden?

– De hoeveelheid deeltjes is constant / verandert

– Het volume is constant / verandert.

– De temperatuur is constant / verandert

– De druk is constant / verandert.

Welk verband kun je onderzoeken?

het verband tussen , en

Een weerballon stijgt op.

▲ Afb. 58

▲ Afb. 59

▲ Afb. 60

▲ Afb. 61

De namen van de processen zijn afgeleid uit het Grieks.

ἰσΌϚ (isos) betekent ‘gelijk’.

Als de hoeveelheid van een gas constant blijft, kunnen de andere toestandsgrootheden veranderen. Een verandering van de toestandsgrootheden bij een constante hoeveelheid gas noem je een proces Een proces is de overgang van één toestand naar een andere toestand van een systeem.

Er zijn drie processen voor een vaste hoeveelheid gas waarbij er nog één andere toestandsgrootheid constant is:

• isotherm proces: De temperatuur blijft gelijk.

Het volume beïnvloedt de druk van het gas.

• isochoor proces: Het volume blijft gelijk

De temperatuur beïnvloedt de druk van het gas.

• isobaar proces: De druk blijft gelijk

De temperatuur beïnvloedt het volume van het gas.

Bij een willekeurig proces kunnen voor een vaste hoeveelheid gas de temperatuur, het volume en de druk veranderen

We onderzoeken voor elk van die processen welk verband er tussen de toestandsgrootheden bestaat.

2.2 Isotherm proces

OPDRACHT 4

Bestudeer het volume als de druk verandert.

1 Leg enkele marshmallows en een kleine ballon in een vacuümstolp, zoals op afbeelding 62.

2 Vergelijk de druk in de twee situaties onder de stolp met de normdruk (p1). Vul de tabel aan met =, < of >.

3 Voorspel wat er gebeurt met het volume in de twee situaties onder de stolp. Vul de tabel aan met =, < of >.

Situatie

① in lucht p1

② De lucht wordt weggepompt. p2 p1

③ De lucht wordt opnieuw binnengelaten. p3 p1

4 Test uit en vul je waarneming in.

marshmallows

ballon

5 Vul het kwalitatieve verband tussen druk en volume aan.

demovideo: isotherm proces

Hoe kleiner de druk op een hoeveelheid gas bij een constante temperatuur, hoe het volume van het gas.

▲ Afb. 62 Ballon en marshmellows onder een vacuümstolp

OPDRACHT 5 ONDERZOEK

Onderzoek het verband tussen het volume en de druk in een vaste hoeveelheid gas bij een constante temperatuur.

1 Voer Labo 02 op uit.

2 Waarom is dat labo een kwantitatief onderzoek?

Als het volume V van een vaste hoeveelheid gas bij een constante temperatuur T verdubbelt, dan halveert de druk p. Als het volume halveert, dan verdubbelt de druk.

Voor een bepaalde hoeveelheid gas bij een constante temperatuur is de druk p omgekeerd evenredig met het volume : p ~ 1 V , dus ∙ = constante

De p(V)-grafiek is een hyperbool Elk punt van de hyperbool beschrijft een toestand van een bepaalde hoeveelheid gas bij een constante temperatuur (T = constant).

De hyperbool is een isotherm De overgang van één punt naar een ander punt op de hyperbool is een isotherm proces.

Bij het isotherme proces van toestand 1 naar toestand 2 geldt: p1 ∙ V1 = p2 ∙ V2

Dat is de gaswet van Boyle-Mariotte

VOORBEELD DUWEN OP EEN ZAKJE CHIPS

Een zakje chips bevat een vaste hoeveelheid lucht. In normale omstandigheden heeft de lucht een volume V1 = 150,0 cm³, zodat de druk p1 binnenin het zakje gelijk is aan de omgevingsdruk: p1 = 1 013 hPa. Als je op het zakje duwt, verlaag je het volume tot V2 = 100,0 cm³. De temperatuur is constant, dus de gaswet van BoyleMariotte is geldig.

VOORBEELD DUWEN OP EEN ZAKJE CHIPS (VERVOLG)

De overgang van toestand 1 naar toestand 2 is een isotherm proces (aangeduid met de blauwe pijl) dat een hyperbool volgt. Als je niet meer op het zakje duwt, verloopt het proces omgekeerd.

Op grafiek 2 zie je dat de druk stijgt. Je kunt de einddruk p2 als volgt berekenen:

©VANIN

Uit de lessen wiskunde weet je dat a · b c = a c · b = a · b c of, met een getalvoorbeeld, 3 · 4 2 = 3 2 · 4= 3 · 4 2 = 6.

Bij gaswetten orden je gelijke toestandsgrootheden in de breukstreep. Zo zie je snel of de eenheid klopt, en kun je het aantal berekeningen beperken.

Bekijk het deeltjesmodel van de wet van Boyle-Mariotte in de applet. applet: BoyleMariotte

Je kunt de wet van Boyle-Mariotte verklaren met het deeltjesmodel. De deeltjes bewegen bij een temperatuur T met een snelheid in een volume V1 en botsen tegen de wanden, waardoor ze een druk p1 veroorzaken. Als het volume afneemt tot V2, botsen de deeltjes meer tegen de wanden De druk neemt toe tot p2

Als je de meting herhaalt bij een constante, maar hogere temperatuur T ’ (T ’ > T), dan bekom je opnieuw een hyperbool. Hoe hoger de temperatuur, hoe hoger de isotherm ligt. Bij een hogere temperatuur (T ’) bewegen de deeltjes sneller. Bij hetzelfde volume botsen ze meer tegen de wanden. De druk is hoger en de isotherm ligt hoger.

TIP

OPDRACHT 6 VOORBEELDOEFENING

Bestudeer het uitgewerkte vraagstuk.

Een luchtzak vul je binnen een paar seconden met lucht door hem door de lucht te bewegen, zonder een pomp te gebruiken. Hij krijgt zo een volume van 600 liter. Door erin te liggen, verhoog je de druk naar 1,30 bar. Bepaal de druk voordat en het volume nadat je op de luchtzak gaat zitten.

Gegeven en gevraagd:

Begintoestand 1 p1 = ?

V1 = 600 L

Oplossing:• Je vult de luchtzak zonder pomp.

Eindtoestand 2 p2 = 1,30 bar V2 = ?

De druk in de begintoestand is hetzelfde als de omgevingsdruk.

Aangezien de druk in de eindtoestand in bar genoteerd staat, noteren we de druk in de begintoestand ook in bar.

p1 = p0 = 1,013 bar

• De temperatuur wordt niet vermeld.

Die mag je dus als constant beschouwen.

De gaswet van Boyle-Mariotte is geldig:

p2 ∙ V2 = p1 ∙ V1

Daarmee kun je het eindvolume als volgt berekenen:

V2 = p1 p2 · V1 = 1,013 bar 1,30 bar · 600 L = 468 L (= 4,68 · 102 L)

Controle:Is het volume toegenomen of afgenomen? Komt dat overeen met je verwachtingen? Het volume is afgenomen, want door op de luchtzak te gaan zitten, duw je hem samen en heeft de gevangen lucht minder plaats.

OPLOSSINGSSTRATEGIE

• Omschrijf in je eigen woorden wat er gebeurt en wat je zoekt:

– Ga na welke toestandsgrootheid constant is.

– Benoem de toestandsgrootheden die veranderen.

– Voorspel de verandering van de gevraagde toestandsgrootheden.

• Noteer de gegeven en gevraagde toestandsgrootheden in symbolen per toestand.

• Werk de oplossing uit: – Noteer de gaswet.

– Hervorm de formule indien nodig. Orden de gelijke toestandsgrootheden in de breukstreep.

– Vul gegevens in. Vergeet de eenheid niet.

– Kijk na welke eenheden je kunt schrappen.

– Reken uit en rond af.

• Sta stil bij de oplossing:

– Klopt de eenheid?

– Klopt de getalwaarde?

▲ Afb. 63

▲ Afb. 64

Voor een bepaalde constante hoeveelheid gas bij een constante temperatuur is de druk p omgekeerd evenredig met het volume V: p ~ 1 V , dus p ∙ V = constante

Bij een isotherm proces geldt: p1 · V1 = p2 · V2.

Dat is de wet van Boyle-Mariotte.

` Maak oefening 1 t/m 5 op p. 92-93.

2.3 Isochoor proces

OPDRACHT 7

Bestudeer de druk als de temperatuur verandert.

1 Vul een ballon met water, zodat de ballon juist niet door de hals van een trechtervormige fles kan. Vul de fles gedurende enkele minuten met heet water. Giet de fles leeg en leg de ballon op de hals van de fles. Wacht even.

2 Wat zal er volgens jou gebeuren? Test uit.

©VANIN

3 Vul het kwalitatieve verband tussen druk en temperatuur aan.

Hoe lager de temperatuur van een hoeveelheid gas bij een vast volume, hoe de druk in het gas.

OPDRACHT 8 ONDERZOEK

▲ Afb. 65 Een ballon sluit een volume lucht in de erlenmeyer af.

Onderzoek het verband tussen de temperatuur en de druk in een vaste hoeveelheid gas bij een constant volume aan de hand van Labo 03 op .

Als de (absolute) temperatuur T (in kelvin) van een vaste hoeveelheid gas bij een constant volume V verdubbelt, dan verdubbelt de druk p. Als de temperatuur halveert, dan halveert de druk.

Voor een bepaalde hoeveelheid gas bij een constant volume V is de druk p recht evenredig met de temperatuur T: p ~ T, dus p T = constante

Uit de definitie van de absolute temperatuur volgt: p = 0 bij T = 0.

De p(T)-grafiek is een rechte door de oorsprong. Elk punt van de rechte beschrijft een toestand van een bepaalde hoeveelheid gas bij een constant volume (V = constant).

©VANIN

De rechte is een isochoor De overgang van één punt naar een ander punt op de rechte is een isochoor proces. Bij het isochore proces van toestand 1 naar toestand 2 geldt:

p1 T1 = p2 T2

Dat is de drukwet van Gay-Lussac

VOORBEELD DIEPVRIES SLUITEN

We bekijken als voorbeeld de drukverandering als je een diepvries sluit.

Als je een diepvries sluit, is het volume lucht in de diepvries constant. De lucht koelt snel af van de omgevingstemperatuur θ = 20 °C of T 1 = 293 K bij een druk van p1 = 1 013 hPa tot een temperatuur van θ2 = –18 °C of T2 = 255 K Het volume is constant, dus de drukwet van Gay-Lussac is geldig.

De overgang van toestand 1 naar toestand 2 is een isochoor proces (aangeduid met de blauwe pijl) dat een rechte volgt.

Op de grafiek zie je dat de druk daalt. Je kunt de einddruk p2 als volgt berekenen: p1 T1 = p2 T2 p2 = T2 T1 ∙ p1 = 255 K 293 K ∙ 1 013 hPa = 882 hPa (= 8,82 · 105 Pa)

Door de temperatuurverlaging ontstaat er een drukverschil en een resulterende kracht naar de binnenkant van de diepvries. Je kunt de deur niet openen.

Op de diepvriesdeur is een afsluitrubber gemonteerd met een gaatje, zodat er geleidelijk lucht binnenstroomt in de diepvries. Na een tijdje kun je de diepvries openen. p(T)-grafiek isochoor proces

Je kunt de drukwet van Gay-Lussac verklaren met het deeltjesmodel. De deeltjes bewegen bij een temperatuur T 1 met een snelheid in het volume V en botsen tegen de wanden, waardoor ze een druk p1 veroorzaken. Als de temperatuur toeneemt tot T2, bewegen de deeltjes sneller en botsen ze meer en harder tegen de wanden. De druk neemt toe tot p2

©VANIN

Bekijk het deeltjesmodel van de drukwet van Gay-Lussac in de applet. applet: drukwet Gay-Lussac

▲ Grafiek 6

Als je de meting herhaalt bij een constant, maar groter volume V’ (V’ > V), dan bekom je opnieuw een rechte. Hoe groter het volume, hoe lager de isochoor ligt. Bij een groter volume (V’) botsen de deeltjes bij dezelfde temperatuur minder tegen de wanden. De druk is lager en de isochoor ligt lager.

Voor een bepaalde constante hoeveelheid gas bij een constant volume is de druk p recht evenredig met de absolute temperatuur T:

p ~ T, dus p T = constante

Bij een isochoor proces geldt: p1 T1 = p2 T2 .

Dat is de drukwet van Gay-Lussac.

` Maak oefening 6, 7 en 8 op p. 93.

OPDRACHT 9

Een gasfles wordt in de zon gezet, waardoor de temperatuur stijgt van 20 °C (toestand 1) naar 60 °C (toestand 2).

1 Welke uitspraken zijn correct?

n2 = n1

n2 = 3 ∙ n1

V2 = V1

V2 = 3 ∙ V1

θ2 = θ1

θ2 = 3 ∙ θ1

T2 = T 1

T2 = 3 ∙ T 1

p2 = p1

p2 = 3 ∙ p1

▲ Afb. 66 De druk in gasflessen verandert door de omgevingstemperatuur.

2 Verklaar waarom je de temperatuur altijd in kelvin moet zetten wanneer je berekeningen uitvoert met de drukwet van Gay-Lussac.

2.4 Isobaar proces

OPDRACHT 10

Bestudeer het volume als de temperatuur verandert.

1 Vul een petfles met een laagje heet water.

Sluit af met de dop en schud.

Open de fles, giet het water eruit en sluit de fles onmiddellijk weer af.

2 Wat zal er volgens jou gebeuren met de fles nadat je er het water uit gegoten hebt? Test uit.

3 Vul het kwalitatieve verband tussen temperatuur en volume aan.

Hoe hoger de temperatuur van een hoeveelheid gas bij een constante druk, hoe het volume van het gas.

OPDRACHT 11 ONDERZOEK

Onderzoek het verband tussen het volume en de temperatuur van een gas bij een constante druk in Labo 04 op .

Als de temperatuur T (in kelvin) van een vaste hoeveelheid gas bij een constante druk p verdubbelt, dan verdubbelt het volume V Als de temperatuur halveert, dan halveert het volume.

Voor een bepaalde hoeveelheid gas bij een constante druk p is het volume V recht evenredig met de temperatuur T: V ~ T, dus V T = constante

De V(T)-grafiek is een rechte door de oorsprong. Elk punt van de rechte beschrijft een toestand van een bepaalde hoeveelheid gas bij een constante druk (p = constant).

De rechte is een isobaar. De overgang van één punt naar een ander punt op de rechte is een isobaar proces

Bij het isobare proces van toestand 1 naar toestand 2 geldt:

V1 T1 = V2 T2

Dat is de volumewet van Gay-Lussac.

VOORBEELD FLESJE WATER AFKOELEN

Als je op een warme zomerdag een halfgevuld flesje water in de koelkast zet, is de druk in de fles de omgevingsdruk en blijft de druk constant.

In het begin is het volume van het gas het volume van de fles V1 = 250 mL en is de temperatuur θ1 = 30 °C of T1 = 303 K. Nadat je het flesje in de koelkast hebt gezet, krijgt het gas een temperatuur van θ2 = 6 °C of T2 = 279 K. De druk is constant, dus de volumewet van Gay-Lussac is geldig. V(T)-grafiek bij een isobaar proces

©VANIN

▲ Grafiek 8

De overgang van toestand 1 naar toestand 2 is een isobaar proces (aangeduid met de blauwe pijl) dat een rechte volgt.

Op de grafiek zie je dat het volume daalt. Je kunt het eindvolume V2 als volgt berekenen:

Door de temperatuurverlaging neemt de lucht minder plaats in om dezelfde druk te behouden. Het flesje wordt ingedeukt.

Bekijk het deeltjesmodel van de volumewet van Gay-Lussac in de applet. applet: volumewet Gay-Lussac

Je kunt de volumewet van Gay-Lussac verklaren met het deeltjesmodel. De deeltjes bewegen bij een temperatuur T 1 met een snelheid in het volume V1 en botsen tegen de wanden, waardoor ze een druk p veroorzaken die gelijk is aan de omgevingsdruk. Als de temperatuur toeneemt tot T2, bewegen de deeltjes sneller en botsen ze meer tegen de wanden. Omdat de druk constant blijft, neemt het volume toe tot V2.

©VANIN

Grafiek 9

Als je de meting herhaalt bij een constante, maar grotere druk p’ (p’ > p), dan bekom je opnieuw een rechte. Hoe groter de druk, hoe lager de isobaar ligt. Bij een grotere druk (p’) nemen de deeltjes bij dezelfde temperatuur minder plaats in. Het volume is lager en de isobaar ligt lager.

Voor een bepaalde constante hoeveelheid gas bij een constante druk is het volume V recht evenredig met de absolute temperatuur T:

V ~ T, dus V T = constante

Bij een isobaar proces geldt: V1 T1 = V2 T2

Dat is de volumewet van Gay-Lussac.

` Maak oefening 9, 10 en 11 op p. 93-94.

2.5 Willekeurig proces

Als een vaste stofhoeveelheid gas opgesloten zit in een beweegbaar systeem, kunnen de drie toestandsgrootheden druk, temperatuur en volume veranderen. Bij dat willekeurige proces is er een verband tussen die drie toestandsgrootheden. We gaan op zoek naar dat verband door een willekeurig proces op te splitsen in twee deelprocessen.

Een vaste hoeveelheid gas wordt afgesloten door een beweegbare zuiger. In de begintoestand heeft het gas een druk p1, een volume V1 en een temperatuur T1. In de eindtoestand heeft het gas een druk p2, een volume V2 en een temperatuur T2

Begintoestand 1 Tussentoestand Eindtoestand 2

©VANIN

n constant

p1 , V1 , T 1 p’ , V2 , T 1 p2 , V2 , T2

isotherm proces isochoor proces ▲ Afb. 68

Om het verband tussen de toestandsgrootheden te bepalen, splitsen we het proces op in twee deelprocessen:

1 een isotherm proces: De temperatuur blijft T 1 en het volume verandert naar V2. De druk p’ in de tussentoestand bepaal je met de gaswet van Boyle-Mariotte: p’ · V2 = p1 · V1 , dus p’ = V1 V2 · p1 (1)

2 een isochoor proces: Het volume blijft V2 en de temperatuur verandert naar T2. De druk p’ in de tussentoestand kun je met de drukwet van GayLussac schrijven als: p2 T2 = p’ T1 , dus p’ = T1 T2 · p2 (2)

Uitdrukking (1) en (2) geven een uitdrukking voor de tussendruk p’, dus je kunt ze aan elkaar gelijkstellen: p’ = p’ V1 V2 · p1 = T1 T2 · p2 (invullen uitdrukking (1) en (2))

p1 · V1 T1 = p2 · V2 T2 (herschikken volgens de begin- en eindtoestand)

OPDRACHT 12

Los het vraagstuk op.

Je neemt een zakje chips mee op een bergtocht. Het zakje heeft een volume van 340 cm³ en is voor de helft gevuld met chips. Onderaan de berg is het 24 °C en is de luchtdruk 1 015 hPa. Op de bergtop is het 7 °C bij een luchtdruk van 910 hPa.

1 Bereken het volume van het zakje chips bovenop de berg. Werk het vraagstuk uit op een cursusblad.

2 Controleer je antwoord via

Voor een bepaalde constante hoeveelheid gas geldt bij een druk p, een volume V en een temperatuur T:

p · V T = constant

Het verband tussen de toestandsgrootheden bij een willekeurig proces is gegeven door:

p1 · V1 T1 = p2 · V2 T2

` Maak oefening 12 t/m 15 op p. 94-95.

▲ Afb. 69 Zakje chips in de bergen

3 Welk algemeen verband bestaat er tussen de toestandsgrootheden van een gas?

OPDRACHT 13

Bestudeer de invloed van de stofhoeveelheid.

1 Maak de uitspraken correct en illustreer met een voorbeeld uit het dagelijks leven.

• Het volume van gas stijgt / daalt bij een constante druk als er meer gasdeeltjes zijn.

Voorbeeld:

• De druk van aan gas stijgt / daalt bij een constant volume als er minder gasdeeltjes zijn.

Voorbeeld:

• De druk van aan gas stijgt / daalt bij een constant volume als de temperatuur stijgt.

Voorbeeld:

2 Welk verbanden zijn correct?

p ~ 1 n p ∙ V ~ 1 n p ~ n p ∙ V ~ n V ~ 1 n p · V T ~ 1 n V ~ n p · V T ~ n

Het aantal deeltjes N wordt bepaald door de stofhoeveelheid n:

N = n ∙ NA, waarbij

NA = 6,022 ∙ 1023 deeltjes mol

Dat is het getal van Avogadro. Daarover leer je binnenkort meer tijdens de lessen chemie. Toch al benieuwd? Bij

GENIE Chemie 3 vind je een extra module bij het onlinelesmateriaal.

De druk in een gas wordt bij elke temperatuur bepaald door de botsingen van de deeltjes tegen de wanden. Als het aantal deeltjes N verandert, veranderen de druk en het volume.

Voor een constante hoeveelheid gas geldt bij een willekeurig proces:

p · V T = constant

Experimenten hebben aangetoond dat de constante in de gecombineerde gaswet recht evenredig is met de stofhoeveelheid n van het gas:

p · V T ~ n of p · V T = n · R

2 ▲ Afb. 70 De stofhoeveelheid bepaalt de druk in een gasfles (T = constant en V = constant).

De evenredigheidsconstante R is experimenteel bepaald en is voor alle gassen gelijk:

R = 8,31 J mol · K

Je noemt ze de universele gasconstante

Grootheid met symbool Waarde in SI-eenheid

universele gasconstante R 8,31 J mol · K

De uitdrukking p ∙ V = n ∙ R ∙ T noem je de algemene (of ideale) gaswet. Die wet is geldig voor elke hoeveelheid van een ideaal gas bij elke temperatuur, elke druk en elk volume.

VOORBEELD BOLLE VOEDSELVERPAKKINGEN

We bekijken als voorbeeld de gassen in voedselverpakkingen.

Om vlees langer te bewaren, voegt men CO2-gas toe aan een plastic verpakking. Om bij kamertemperatuur (T = 293 K) de verpakking te vullen met 200 cm³ bij atmosfeerdruk, bepaalt men de hoeveelheid CO2 met de ideale gaswet:

p ∙ V = n ∙ R ∙ T, dus n = p · V R · T

= 1,013 · 105 N m2 · 200 · 10–6 m3 8,31 N · m mol · K · 293 K = 0,00832 mol = 8,32 · 10–3 mol

Door de verdamping van water uit het vlees en door voedselbederf komen er verschillende gassen in de verpakking. De stofhoeveelheid neemt toe, waardoor het volume van het gas stijgt. Het soort gas heeft geen invloed.

Als er 1,00 ∙ 10–3 mol gas bijkomt, wordt het volume: p ∙ V = n ∙ R ∙ T, dus V = n · R · T p

= 9,32 · 10–3 mol 8,31 N · m mol · K · 293 K 1,013 · 105 N m2

= 224 · 10–6 m3 = 224 cm3 (= 2,24 · 10–4 m3)

De verpakking staat bol. Als het volume niet meer kan stijgen, neemt de druk toe. Verpakkingen die heel sterk gespannen staan en waarbij veel gas ontsnapt wanneer je ze opent, wijzen op voedselbederf.

▲ Afb. 71 De hoeveelheid gas bepaalt de druk en het volume van voedingsverpakkingen.

Voor een stofhoeveelheid n van een gas bij een druk p, een volume V en een temperatuur T geldt:

p · V T = n ∙ R of p ∙ V = n ∙ R ∙ T

R is de algemene gasconstante:

R = 8,31 J mol · K

Dat is de algemene gaswet

` Maak oefening 16 t/m 19 op p. 96.

OPDRACHT 14

Los het vraagstuk op.

Een weerballon heeft bij de normdruk en een omgevingstemperatuur van 20,3 °C een volume van 15 liter.

1 Bereken de stofhoeveelheid en de massa waterstofgas (M = 2,00 g mol ) in de ballon. Werk het vraagstuk uit op een cursusblad.

2 Controleer je antwoord via .

TIP

Wil je meer weten over hoe weerballonnen het klimaat en de klimaatverandering in kaart brengen? Kijk dan in de ontdekplaat ‘Fysica van het klimaat’.

ontdekplaat

proces

T, n zijn constant → p ∙ V = constant gaswet van

proces

V, n zijn constant → p T = constant van Gay-Lussac

Algemene gaswet

V = n

T : ruimte waarin de deeltjes bewegen (m³) : aantal mol van het gas (mol)

: maat voor de botsingen tegen de wanden (Pa) : maat voor de snelheid van de deeltjes (K)

Grootheid met symboolWaarde in SI-eenheid universele gasconstante R 8,31 J mol · K

proces

p, n zijn constant → V T = constant van Gay-Lussac

1 Begripskennis

• Ik kan de toestandsfactoren van een gas omschrijven.

• Ik kan de verschillende processen van een gas omschrijven

• Ik kan het gedrag van een gas bij een constante temperatuur omschrijven.

• Ik kan het gedrag van een gas bij een constant volume omschrijven

• Ik kan het gedrag van een gas bij een constante druk omschrijven

• Ik kan berekeningen uitvoeren met de drie aparte gaswetten voor een vaste stofhoeveelheid.

• Ik kan de drie aparte gaswetten combineren om de toestandsverandering van een vaste stofhoeveelheid van een gas te bepalen.

• Ik kan het gedrag van een gas bij een willekeurig proces omschrijven

• Ik kan berekeningen uitvoeren met de algemene gaswet.

2 Onderzoeksvaardigheden

• Ik kan eenheden omzetten.

• Ik kan formules omvormen.

• Ik kan afrondingsregels toepassen

• Ik kan informatie in symbolen noteren.

• Ik kan rekenvraagstukken gestructureerd oplossen

• Ik kan grafieken tekenen

• Ik kan een recht evenredig en omgekeerd evenredig verband aflezen op een grafiek

` Je kunt deze checklist ook op invullen.

JANOG OEFENEN

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’.

Je kunt de oplossingsstrategie en de voorbeeldoefeningen op gebruiken als extra ondersteuning.

Je verkleint het volume van een meetspuit bij een constante temperatuur.

Welke omzetting moet je doen om de einddruk te berekenen? Duid aan.

Je moet beide volumes in dezelfde eenheid noteren.

Je moet beide volumes in de SI-eenheid noteren.

Je moet de begindruk in de SI-eenheid noteren.

Een stalen gasfles is gevuld met 20,0 L zuurstofgas onder een druk van 20,3 bar.

Het gas wordt overgepompt naar een compactere gasfles van 6,00 L.

Hoe groot is de druk in de kleinere fles?

Helium zit opgesloten in een grote container met een beweegbare zuiger en bevindt zich in toestand A.

a Bestudeer de grafiek.

b In welk van de andere toestanden is de temperatuur hetzelfde? Duid aan op de grafiek.

Vier meetspuiten (a, b, c en d) bevatten dezelfde hoeveelheid gas.

De meetspuiten worden elk op een verschillende, constante temperatuur gehouden.

Voor elke meetspuit meet men het volume en de druk:

• V a = 60 cm³ en pa = 50 kPa

• Vb = 0,10 dm³ en pb = 280 kPa

• V c = 15 cm³ en pc = 2,0 bar

• Vd = 1,0 dm³ en pd = 0,35 bar

Rangschik de temperatuur van de meetspuiten van klein naar groot.

Tijdens een duikcursus zwemt Wout over de bodem van het zwembad van 3,5 m diep en stijgen er luchtbellen van 1,3 cm³ omhoog.

a Waarom stijgen de bellen?

b Hoe groot zijn de bellen als ze aan het oppervlak komen?

6 7 8 9 1 2 3

Verklaar waarom je de temperatuur altijd in kelvin moet zetten wanneer je berekeningen uitvoert met de drukwet van Gay-Lussac.

Een duikfles heeft een vuldruk van 12,4 bar bij 20,0 °C.

Liesbeth gaat duiken in de Oosterschelde bij een watertemperatuur van 3,2 °C.

Bereken de gebruikersdruk.

Bij de productie van halogeenlampen vult men de lampen met een gasmengsel bij een temperatuur van 400 °C en een druk van 1,4 ∙ 105 Pa. Als de lamp brandt, loopt de druk op tot 3,5 ∙ 105 Pa. Bereken de temperatuur in °C van de halogeenlamp wanneer ze brandt.

Wie heeft gelijk? Verklaar.

Misschien moet je hem even in de diepvries steken.

Mijn ballon is verschrompeld. Hoe krijg ik hem weer glad?

Je kunt hem opwarmen met een haardroger.

Hem opnieuw opblazen is het enige wat je kunt doen.

Een bepaalde hoeveelheid gas bevindt zich in een toestand zoals weergegeven door het punt A op de V(T)-grafiek.

De druk in A is 2,0 bar.

a Welke gaswet is geldig bij de toestandsverandering van A naar B en van A naar C?

b Bereken de toestandsgrootheden van toestand B en C.

c Bepaal voor beide isobaren de temperatuur in °C waarbij het gas een volume van 120 mL heeft.

Op de grafieken staat een toestand van een vaste hoeveelheid gas weergeven.

Duid aan op elke grafiek:

• een isotherm proces 1 → 2 in het blauw;

• een isochoor proces 1 → 3 in het groen;

• een isobaar proces 1 → 4 in het rood.

Je blaast een soepele ballon (met verwaarloosbare elasticiteit) bij 21,0 °C op tot een volume van 0,80 L.

Je legt de ballon op de verwarming, waardoor de temperatuur toeneemt met 15 °C.

Bepaal de drie toestandsgrootheden van de warme ballon.

Zijn de volgende beweringen juist of fout?

Verbeter indien nodig.

a Als je bij een constante temperatuur het volume van een gas in een meetspuit verdubbelt van 20 mL naar 40 mL, dan zal de druk veranderen van 1,0 bar naar 2,0 bar.

b Als je bij een constant volume de temperatuur van het gas in een meetspuit verdubbelt van 20 °C naar 40 °C, dan zal de druk veranderen van 1,0 bar naar 2,0 bar.

c Als je bij een constante druk de temperatuur van het gas in een meetspuit verdubbelt van 20 °C naar 40 °C, dan zal het volume veranderen van 20 mL naar 40 mL.

d Als je bij een constant volume de hoeveelheid gas in een meetspuit verdubbelt van 1 mol naar 2 mol, dan zal de druk veranderen van 1,0 bar naar 2,0 bar.

Een gas bevindt zich in toestand A en ondergaat toestandsveranderingen zoals weergegeven in de tabel.

a Duid de toestandsveranderingen aan op de grafiek.

b Vul de tabel aan. (Betekenis symbolen: = blijft gelijk; ↘ daalt; ↗ stijgt.)

(bar)

Naam proces

Geldige gaswet

Verklaar de volgende fenomenen.

a Plastic flacons lekken tijdens een vliegtuigreis.

b Als je een rietje met een vloeistof bovenaan sluit met je vinger, stroomt het water er niet uit.

Hoe groot is je fietsband, als je er 0,12 mol lucht in moet pompen om een druk van 2,6 bar te bekomen bij een temperatuur van 20,0 °C?

Felix Baumgartner skydivede op 14 oktober 2012 als eerste man door de geluidsmuur. Daarvoor sprong hij vanuit de stratosfeer (p = 0,45 kPa, θ = –5,0 °C) naar de aarde. Zijn capsule zweefde op een hoogte van 36,6 km door een heliumballon met een volume van 850 miljoen liter.

a Welk volume had de ballon bij het vertrek (standaardomstandigheden)?

De temperatuur aan de grond bedroeg die dag 20,0 °C. b Hoeveel mol helium bevatte de ballon?

Een vat bevat heliumgas. Een ander identiek vat bevat dezelfde massa stikstofgas. Welke uitspraak is correct? Duid aan.

pHe = pN2

pHe > pN2

pHe < pN2

Je kunt geen uitspraak doen, want je hebt geen informatie over de temperatuur.

Een vaste hoeveelheid van een ideaal gas zit opgesloten in een container en ondergaat twee processen.

Bestudeer de grafiek.

a Vul in de tabel het verband tussen de verschillende grootheden aan met een getal.

Kies uit: 1, 2, 4, 1 2 en 1 4

b Benoem de verschillende processen.

Verder oefenen?

Welke invloed heeft warmte op de temperatuur van een systeem?

LEERDOELEN

Je kunt al: de temperatuur linken aan de (tril)snelheid van deeltjes; de aggregatietoestand van een stof toelichten met behulp van het deeltjesmodel; de transportmogelijkheden van thermische energie uitleggen.

Je leert nu: de begrippen ‘warmte’, ‘temperatuur’, ‘thermisch evenwicht’ en ‘inwendige energie’ omschrijven; warmtetransport via geleiding, stroming en straling omschrijven; de grootte van de merkbare warmte bepalen; een warmtebalans opstellen en gebruiken.

Om voedsel op te warmen, gebruik je een gasvuur of een microgolfoven. Om het af te koelen, laat je het eventjes staan of zet je het in de koelkast. Hoe komt het dat de temperatuur verandert? Hoe bekom je de gewenste temperatuur? Welke invloed heeft de samenstelling van het voedsel? En wat betekenen warmte en temperatuur?

In dit hoofdstuk bestudeer je de grootheden warmte en temperatuur, en het verband tussen beide.

Wat is het verschil tussen warmte en temperatuur?

1.1 Warmte en temperatuur

OPDRACHT 15

Bestudeer het verschil tussen warmte en temperatuur.

1 Maak de uitspraken correct door het juiste antwoord aan te duiden.

• Water met een temperatuur van 90 °C (bijvoorbeeld thee) zal je huid wel / niet beschadigen bij contact. Het geeft veel / weinig warmte aan je lichaam, waardoor de temperatuur van je huid veel / weinig toeneemt.

• Lucht met een temperatuur van 90 °C (bijvoorbeeld in een sauna) zal je huid wel / niet beschadigen bij contact. Het geeft veel / weinig warmte aan je lichaam, waardoor de temperatuur van je huid veel / weinig toeneemt.

OPDRACHT 15 (VERVOLG)

2 Bestudeer de onderstaande begrippen en symbolen.

Kleur alles wat met warmte te maken heeft, rood en alles wat met temperatuur te maken heeft, groen.

joule

θ T J Q

deeltjessnelheid

toestandsgrootheid

energie

graden Celsius kelvin

©VANIN

opnemen afgeven

In het dagelijks leven worden de begrippen ‘warmte’ en ‘temperatuur’ door elkaar gebruikt.

In de fysica zijn warmte en temperatuur twee verschillende grootheden

1 Temperatuur

Deeltjes van een stof bezitten een (tril)snelheid zodra hun temperatuur groter is dan 0 kelvin, het absolute nulpunt. Niet alle deeltjes in de stof hebben dezelfde ogenblikkelijke snelheid, maar bij een constante temperatuur is de gemiddelde snelheid van de deeltjes constant. Hoe hoger de temperatuur van de stof, hoe groter de snelheid van de deeltjes.

Aangezien de deeltjes een massa en een snelheid hebben, bezitten ze kinetische energie. (Absolute) temperatuur is een maat voor de gemiddelde kinetische energie van de deeltjes.

Grootheid met symbool Eenheden met symbool temperatuur θ graden Celsius°C absolute temperatuur T kelvin K

2 Warmte

Als er een temperatuurverschil is tussen twee systemen, wordt er energie uitgewisseld. Die energie noem je warmte. Warmte is, net zoals arbeid, een energievorm die overgedragen wordt van één systeem naar een ander systeem.

Er wordt arbeid verricht door de trekkracht. De chemische energie van de man wordt omgezet naar kinetische energie van de reiskoffer.

Er wordt warmte overgedragen. De chemische energie van de houtblokken wordt omgezet naar thermische energie van het water.

Het symbool voor warmte is Q. De eenheid is joule.

Grootheid met symbool SI-eenheden met symbool warmte Q joule J

Op afbeelding 77 zie je een systeem dat bestaat uit een beker gevuld met een vloeistof. De omringende lucht is de omgeving

• In de eerste situatie is de temperatuur van het systeem lager dan de temperatuur van de omgeving. Het systeem neemt warmte op. De warmte is positief: Q > 0

• In de tweede situatie is de temperatuur van het systeem hoger dan de temperatuur van de omgeving. Het systeem geeft warmte af De warmte is negatief: Q < 0

Q > 0

Q < 0

▲ Afb. 75

▲ Afb. 76

▲ Afb. 77 Warmte kan worden opgenomen of afgestaan.

Door de energie-uitwisseling is er een temperatuurverandering (als er geen faseovergang optreedt). De warmte die toegevoegd of afgestaan wordt en waardoor de temperatuur van een systeem verandert, noem je merkbare warmte.

• (Absolute) temperatuur is een maat voor de trilling en dus de gemiddelde kinetische energie van de deeltjes.

• Warmte is een vorm van energieoverdracht die uitgewisseld wordt als gevolg van een temperatuurverschil

Grootheden met symbool Eenheden met symbool warmte Q joule J temperatuur θ graden Celsius°C absolute temperatuur T kelvin K

` Maak oefening 1 en 2 op p. 128.

1.2 Inwendige energie

OPDRACHT 16

Bestudeer de temperatuur op deeltjesniveau.

1 Vul een beker met koud water en een met warm water.

Meet hun temperatuur en noteer die.

Temperatuur beker 1 θ1 =

©VANIN

Temperatuur beker 2 θ2 =

2 Laat een druppel kleurstof vallen in beide bekers water.

Voorspel wat er zal gebeuren.

De verspreiding van de kleurstof bij een lage temperatuur verloopt trager / even snel / sneller dan bij een hoge temperatuur.

3 Voer de proef uit en neem waar wat er gebeurt.

4 Verklaar je waarneming.

Maak de uitspraken correct door het juiste antwoord aan te duiden.

• Bij een hoge temperatuur is de snelheid van de deeltjes groot / klein

Ze bezitten veel / weinig kinetische energie.

• Bij een lage temperatuur is de snelheid van de deeltjes groot / klein. Ze bezitten veel / weinig kinetische energie.

Deeltjes zijn in beweging en oefenen krachten uit op elkaar. Daardoor bezitten ze mechanische energie. Je noemt de mechanische energie van deeltjes de inwendige energie. Er zijn twee vormen van inwendige energie.

1 Inwendige kinetische energie

Een deeltje bezit inwendige kinetische energie Ekin, i doordat het een snelheid en een massa heeft. Hoe groter de (tril)snelheid of de massa, hoe groter de inwendige kinetische energie. De gemiddelde inwendige kinetische energie van een systeem noem je de thermische energie. Die energie is constant als de temperatuur constant is.

• Bij gassen heeft een deeltje een grote snelheid

Het bezit veel thermische energie.

• Bij vloeistoffen hebben de deeltjes een beperkte snelheid

De thermische energie is kleiner dan bij gassen.

• Bij vaste stoffen kan een deeltje enkel trillen rond een vaste positie.

Het bezit weinig thermische energie

2 Inwendige potentiële energie

Een deeltje bezit inwendige potentiële energie Epot, i door de krachten die inwerken op de deeltjes. Vanwege de elektrische krachtwerking ontstaat er een kracht tussen de deeltjes (van dezelfde soort), de cohesiekracht De grootte van die cohesiekracht is afhankelijk van de stofsoort en de aggregatietoestand.

• Voor gassen is de cohesiekracht verwaarloosbaar, waardoor de inwendige potentiële energie Epot, i verwaarloosbaar is.

• Voor vaste stoffen en vloeistoffen zijn er grotere cohesiekrachten

De inwendige potentiële energie Epot, i van een deeltje wordt bepaald door de plaats waar het zich bevindt ten opzichte van de andere deeltjes in een systeem.

©VANIN

▲ Afb. 78 ▲ Afb. 79 ▲ Afb. 80 vast vloeibaar gas

Snelheid van de deeltjes kleine trilsnelheid redelijk grootheel groot Krachten tussen de deeltjes (cohesiekrachten) heel grootredelijk grootklein

De totale inwendige energie Einw van een systeem is gelijk aan de som van de kinetische en de potentiële energie van alle deeltjes van dat systeem. Ze is afhankelijk van de aggregatietoestand, de temperatuur, het totale aantal deeltjes en de stofsoort.

VOORBEELD INWENDIGE ENERGIE BIJ WATER EN KOFFIE

Als voorbeeld bekijken we de inwendige energie van water en koffie op verschillende temperaturen.

m = 0,1 kg

= 20 °C m = 0,1 kg

= 80 °C m = 1 kg

thermische energie neemt toe inwendige energie neemt toe

▲ Afb. 81 De thermische energie hangt (binnen een fase) af van de massa en de temperatuur.

= 80 °C

• Een glas water op kamertemperatuur bezit minder inwendige energie dan een kop hete koffie, omdat de temperatuur lager is.

• Een kop koffie bezit minder inwendige energie dan de koffie in een pot van 1 liter, omdat er minder deeltjes zitten in de kop koffie dan in de koffiepot.

De inwendige energie Einw van een systeem is de som van de kinetische energie van de deeltjes (thermische energie) en de potentiële energie van de deeltjes. Ze is afhankelijk van de aggregatietoestand, de temperatuur, het totale aantal deeltjes en de stofsoort.

1.3 Thermisch evenwicht

OPDRACHT 17

Bestudeer de verandering van temperaturen bij warmte-uitwisseling.

1 Vul een beker met koud water en een met warm water.

Gebruik twee afzonderlijke thermometers om hun temperatuur te bepalen, en noteer die.

Temperatuur beker 1 θ1 =

Temperatuur beker 2 θ2 =

Meng de twee hoeveelheden water en steek beide thermometers mee in het mengsel.

Zodra de twee thermometers een gelijke temperatuur aangeven, is het thermisch evenwicht bereikt.

Noteer de waarde op de thermometers.

Eindtemperatuur θeind =

3 Wat gebeurt er met de onderstaande grootheden?

Duid aan.

Water uit beker 1

Water uit beker 2

θ stijgt / daalt / blijft gelijkstijgt / daalt / blijft gelijk

Ekin, i stijgt / daalt / blijft gelijkstijgt / daalt / blijft gelijk

Q neemt op / staat af neemt op / staat af

4 Vervolledig de omschrijving van thermisch evenwicht.

Voorwerpen met een verschillende temperatuur wisselen warmte uit totdat ze een eindtemperatuur hebben. Bij thermisch evenwicht is de gemiddelde kinetische energie van alle deeltjes .

Voorwerpen en hun omgeving hebben vaak een verschillende temperatuur.

Twee systemen met een verschillende temperatuur wisselen warmte uit tot ze een evenwicht bereiken bij dezelfde temperatuur θeind. Op dat moment ontstaat er thermisch evenwicht

Dat kun je verklaren met het deeltjesmodel. De deeltjes met een hoge kinetische energie (θhoog) staan energie af aan de deeltjes met minder kinetische energie (θlaag), waardoor de kinetische energie van de snelle deeltjes daalt en de kinetische energie van de trage deeltjes stijgt.

De warmte-uitwisseling blijft optreden tot er een gelijke verdeling is van de kinetische energie over alle deeltjes. De temperatuur (θeind) van alle deeltjes is op dat moment gelijk. Hoe groot die eindtemperatuur is, hangt af van de begintemperaturen, de stofsoort en hun massa.

warmte-uitwisseling

©VANIN

▲ Afb. 83 Koffie koelt af tot de omgevingstemperatuur.

Wanneer je koffie inschenkt, heeft die een temperatuur van 90 °C.

De kop heeft een temperatuur van 20 °C.

Een deeltje van de koffie bezit gemiddeld gezien meer kinetische energie dan een deeltje van de kop. Na een tijdje bereiken de systemen een thermisch evenwicht, op 75 °C.

De gemiddelde kinetische energie per deeltje van de koffie en de kop is nu gelijk.

Als je roert in de kop, bereik je het thermisch evenwicht sneller, doordat er meer deeltjes met elkaar in contact komen om onderling warmte uit te wisselen. Voeg je koude melk toe, dan zal er een nieuw thermisch evenwicht ontstaan bij een lagere temperatuur. Laat je de kop een lange tijd staan, dan zal zowel de koffie als de kop een thermisch evenwicht bereiken met de lucht in de kamer.

Wanneer stoffen een thermisch evenwicht bereiken, hebben ze allemaal dezelfde temperatuur.

Hoe groot die eindtemperatuur is, hangt af van de begintemperaturen, de stofsoort en hun massa

thermisch evenwicht

warmte afstaan warmte opnemen hoog laag eind

Evolutie van twee systemen naar thermisch evenwicht (boven: macroscopisch, onder: microscopisch)

2 Hoe wordt warmte doorgegeven?

2.1 Vormen van warmtetransport

OPDRACHT 18

Bestudeer de vormen van warmtetransport.

1 Kijk naar de experimenten in de demovideo.

Plaats ze bij de juiste vorm van warmtetransport.

Geleiding Stroming Straling

Voorbeeld

2 Duid in de tabel de juiste antwoorden aan.

Geleiding Stroming Straling

Bij welke aggregatietoestand komt de vorm van warmtetransport vooral voor?

vaste stoffen

vloeistoffen

gassen

geen middenstof nodig

blijven op hun plaats

bewegen door elkaar

zijn niet nodig

vaste stoffen

vloeistoffen

gassen

geen middenstof nodig

Wat gebeurt er met de deeltjes?

blijven op hun plaats

bewegen door elkaar

zijn niet nodig

vaste stoffen

vloeistoffen

gassen

geen middenstof nodig

blijven op hun plaats

bewegen door elkaar

zijn niet nodig

Om een thermisch evenwicht te bereiken, wordt er warmte uitgewisseld.

Dat kan op drie manieren gebeuren.

2.2 Geleiding

Deeltjes op een vaste positie met een hogere temperatuur hebben meer kinetische energie dan hun omringende deeltjes met een lagere temperatuur en zullen heviger trillen (zie afbeelding 84). Door botsingen met de naburige deeltjes wordt de energie doorgegeven. Die vorm van warmtetransport heet geleiding (conductie). De atomen blijven ter plekke trillen. Er is bij geleiding geen transport van deeltjes.

In de lessen chemie bestudeerde je de structuur van metalen. Je vindt daarover meer informatie via .

De snelheid waarmee de warmte wordt doorgegeven, is afhankelijk van de atoomstructuur en het temperatuurverschil tussen de deeltjes. Door de grote orde in hun roosterstructuur zullen vaste stoffen het best warmte geleiden.

Metalen zijn heel goede warmtegeleiders door de aanwezigheid van vrije elektronen. Die vrije elektronen bewegen over grote afstanden door het metaalrooster en geven bij botsingen met de verschillende ionen energie door. De warmte verspreidt zich makkelijker doorheen het hele materiaal.

©VANIN

De wanorde van de deeltjes en de afstand tussen de deeltjes zorgen ervoor dat vloeistoffen en gassen slechte warmtegeleiders zijn. Stoffen die de warmte slecht geleiden, noem je warmte-isolatoren

VOORBEELD KOOKPOT VERPLAATSEN

Kookpotten bestaan uit metalen die de warmte goed geleiden, zodat het voedsel gemakkelijk opgewarmd wordt.

De temperatuur van de metalen pot is te hoog om hem zonder bescherming aan te raken. De handvaten van een kookpot bestaan vaak uit een ander materiaal (bakeliet), dat slechter warmte geleidt. Dankzij die warmte-isolatoren kun je de warme kookpot toch verplaatsen zonder je vingers te verbranden.

Om het deksel op te tillen, gebruik je een pannenlap. De lucht tussen de stofdeeltjes is een goede warmte-isolator.

2.3 Stroming

Als een gas of een vloeistof wordt opgewarmd, stijgt de snelheid van de deeltjes en neemt hun kinetische energie toe, waardoor ze zich verplaatsen Er ontstaat een stroming (convectie). Bij vaste stoffen trillen de deeltjes op een vaste positie. Er kan geen warmtetransport zijn door stroming.

Spontane stroming is het gevolg van de verandering in massadichtheid Omdat de deeltjes heviger bewegen, nemen ze meer plaats in beslag en zet de stof uit. Daardoor daalt de massadichtheid. De verhouding tussen de zwaartekracht en de opwaartse stuwkracht (archimedeskracht) verandert daardoor. De opgewarmde stof stijgt omhoog. Je kunt de spontane stroming versterken door te roeren. Samen met de deeltjes verplaatst de warmte zich doorheen heel de vloeistof.

▲ Afb. 85 Niet alle materiaalsoorten geleiden de warmte even snel.

VOORBEELD FRIETKETEL

Het elektrische verwarmingselement in een frietketel is een aantal centimeter boven de bodem gemonteerd. De olie die verwarmd wordt, stijgt omhoog door convectie. Je kunt de frietjes bakken op 190 °C. De olie onder het verwarmingselement blijft op een veel lagere temperatuur. De restjes van vorige bakbeurten liggen op de bodem en zullen daardoor niet verder doorbakken. De olie waarmee je bakt, blijft dankzij die koudezone langer bruikbaar.

2.4 Straling

Elk voorwerp met een temperatuur boven 0 kelvin zendt warmte uit in de vorm van infraroodstraling. De warmte wordt doorgegeven via straling. Straling heeft geen deeltjes nodig om zich voort te planten, en kan dus ook door het vacuüm heen.

VOORBEELD WARMTESTRALING VAN EEN KOOKPOT

Als je in de buurt komt van een kookpot op het vuur, voel je zonder contact dat de pot warm is. Je voelt de warmtestraling. Infraroodthermometers registreren die warmtestraling en zetten ze om naar de temperatuur van het voorwerp.

Er zijn drie vormen van warmtetransport:

• geleiding: De deeltjes verplaatsen zich niet. De energie van de trillende deeltjes wordt door botsingen doorgegeven. Geleiding treedt gemakkelijk op bij vaste stoffen (deeltjes dicht bij elkaar), matig bij vloeistoffen en moeilijk bij gassen.

• stroming: De trillende deeltjes verplaatsen zich (door een verschil in massadichtheid met hun omgeving). Stroming treedt op bij vloeistoffen en gassen

• straling: Deeltjes met een hogere temperatuur dan 0 kelvin zenden (infrarood)straling uit. Er is geen middenstof nodig om de warmte door straling door te geven.

` Maak oefening 3 t/m 6 op p. 128-129.

Door temperatuurverschillen door zonneschijn ontstaat er wind. Wil je meer weten?

Kijk dan zeker eens naar de ontdekplaat ‘Fysica van het klimaat’.

▲ Afb. 86 Stijgende en dalende deeltjes bij stroming

▲ Afb. 87 Een infraroodsensor meet de straling die vrijkomt uit een systeem.

▲ Afb. 88 Warmte kan op drie manieren worden doorgegeven: via geleiding, stroming en straling.

WEETJE

3 Hoe verandert de temperatuur van een systeem door warmte-uitwisseling?

3.1 Geïsoleerd systeem

OPDRACHT 19

Bestudeer de warmte- en materie-uitwisseling in systemen.

1 Vul de tabel aan.

a Benoem het systeem.

b Maak de uitspraken correct.

Systeem:

• De deeltjes kunnen wel / niet vrij in of uit het systeem.

• De warmte kan wel / niet vrij in of uit het systeem.

• Dit is een voorbeeld van een open / gesloten / geïsoleerd systeem.

• De deeltjes kunnen wel / niet vrij in of uit het systeem.

• De warmte kan wel / niet vrij in of uit het systeem.

• Dit is een voorbeeld van een open / gesloten / geïsoleerd systeem.

2 Geef nog een voorbeeld van een open, gesloten en geïsoleerd systeem.

• open systeem:

• gesloten systeem:

• geïsoleerd systeem:

• De deeltjes kunnen wel / niet vrij in of uit het systeem.

• De warmte kan wel / niet vrij in of uit het systeem.

• Dit is een voorbeeld van een open / gesloten / geïsoleerd systeem.

▲ Afb. 89

▲ Afb. 90

▲ Afb. 91

Een systeem staat in contact met de omgeving. Daardoor kunnen er deeltjes en/of warmte uitgewisseld worden.

Er zijn drie soorten thermodynamische systemen:

1 open systeem: Er worden deeltjes en warmte uitgewisseld met de omgeving.

2 gesloten systeem: Er worden geen deeltjes uitgewisseld met de omgeving, maar er wordt wel warmte uitgewisseld

3 geïsoleerd systeem: Er worden geen deeltjes en geen warmte uitgewisseld met de omgeving.

thermodynamische systemen

©VANIN

GEÏSOLEERD SYSTEEM geen warmtetransport geen massatransport

▲ Afb. 92 Verschillende soorten thermodynamische systemen

Om warmte en temperatuur te onderzoeken, gebruik je een geïsoleerd systeem. De massa van het systeem is constant en er is enkel warmteuitwisseling binnen het systeem. Een geïsoleerd systeem is een model. In werkelijkheid zal ook een thermos na verloop van tijd een thermisch evenwicht bereiken met de omgeving, hoe goed de isolatie ook gebouwd is.

In een wetenschappelijke context gebruikt men als geïsoleerd systeem een calorimeter of joulevat.

Dat is een geïsoleerde beker (te vergelijken met een thermos) waarbij in het deksel openingen zijn voorzien voor een elektrisch verwarmingselement een roerstaaf en een thermometer

De naam ‘calorimeter’ is wat misleidend, want een calorimeter meet niets.

WEETJE

▲ Afb. 93 Een calorimeter wordt gebruikt als geïsoleerd systeem voor experimenten.

De naam calorimeter komt van het Latijnse woord calor, dat ‘warmte’ betekent.

OPEN

GESLOTEN

3.2 Warmtecapaciteit

OPDRACHT 20 ONDERZOEK

Onderzoek de temperatuurverandering van een systeem aan de hand van Labo 05 op .

Om een voorwerp op te warmen, moet je warmte toevoegen. Om een voorwerp af te koelen, moet je warmte afvoeren. De hoeveelheid warmte hangt af van het voorwerp en de temperatuurverandering.

Een systeem met een constante massa en een begintemperatuur θbegin zal door de opgenomen warmte Qop opwarmen tot een eindtemperatuur θeind.

De warmte in een calorimeter wordt toegevoegd met een elektrisch verwarmingselement

Je kunt de toegevoegde warmte bepalen aan de hand van het vermogen en het tijdsverloop:

Verschillende warmtetoevoer bij dezelfde hoeveelheid water met een begintemperatuur θbegin = 20 °C

▲ Afb. 94 Invloed van de warmte op de temperatuur

Als de warmte gelijkmatig toegevoegd wordt, stijgt de temperatuur gelijkmatig

De θ(Q)-grafiek is een rechte die de verticale as snijdt bij de begintemperatuur. Er is een lineair verband tussen de temperatuur en de warmte.

(Q)-grafiek van een vaste hoeveelheid water

De temperatuurverandering tijdens de opwarming bereken je als volgt: Δθ = θeind – θbegin

Grootheid met symbool Eenheid met symbool temperatuurverandering Δ

= θeind – θbegin graden Celsius °C

De temperatuurschalen van Celsius en Kelvin delen dezelfde schaalverdeling.

Daardoor hebben de temperatuurveranderingen Δθ en ΔT dezelfde waarde en is het niet nodig om de temperaturen om te zetten naar kelvin.

De Δθ(Q)-grafiek is een rechte door de oorsprong. Er is een recht evenredig verband tussen de temperatuurverandering en de warmte: Δθ ~ Q. Als de toegevoegde warmte verdubbelt, dan verdubbelt de temperatuurverandering.

Uit de helling van de grafiek kun je aflezen hoeveel de temperatuur verandert als je een bepaalde hoeveelheid warmte toevoegt. Dat is een constante waarde die gegeven is door Δθ Q en die afhankelijk is van het systeem.

θ (Q)-grafiek van een vaste hoeveelheid water

In de thermodynamica gebruikt men om de helling te beschrijven, de grootheid warmtecapaciteit met als symbool C. Die grootheid wordt gedefinieerd als de mogelijkheid om warmte op te nemen of af te staan. Ze geeft aan hoeveel energie er nodig is om bij een systeem een temperatuurverandering van 1 graad Celsius te veroorzaken. Dat is een voorwerpseigenschap

In symbolen: C = Q Δθ

Grootheid met symbool Eenheid met symbool warmtecapaciteit C = Q Δθ joule per graad Celsius J °C

Uit de definitie van warmtecapaciteit blijkt dat de helling van de Δθ(Q)-grafiek gegeven is door 1 C : Δθ Q = ( Q Δθ )–1 = 1 C

Dat betekent dat voor een systeem met een grote warmtecapaciteit er een kleine temperatuurverandering is als er warmte toegevoegd wordt. Hoe kleiner de helling van de Δθ(Q)-grafiek, hoe groter de warmtecapaciteit.

Uit de definitie van warmtecapaciteit volgt: Q = C ∙ Δθ

Δθ (°C)

Δθ (Q)-grafiek voor twee verschillende systemen

©VANIN

▲ Grafiek 12

Q (J) grote C kleine C

Die formule is toepasbaar op een systeem dat warmte opneemt en warmte afgeeft:

• warmte opnemen, waardoor de temperatuur stijgt:

Δθ = θeind – θbegin > 0, dus Q = C ∙ Δθ > 0

• warmte afstaan, waardoor de temperatuur daalt:

Δθ = θeind – θbegin < 0, dus Q = C ∙ Δθ < 0

VOORBEELD KOM SOEP DIE WARMTE OPNEEMT EN AFGEEFT

De warmtecapaciteit van een kom soep is bijvoorbeeld 1 800 J °C

• Om een kom soep uit de koelkast van 6,0 °C tot 80,0 °C op te warmen, moet je warmte toevoegen:

Q = Ckom + soep

Δθ = 1 800 J °C · (80,0 °C – 6,0 °C) = 1 800 J °C · 74,0 °C = 133 kJ (= 1,33 · 105 J)

• Als de kom soep blijft staan, koelt ze af van 80,0 °C tot kamertemperatuur, 20,0 °C. Er wordt warmte afgevoerd:

Q = Ckom + soep

Δθ = 1 800 J °C

(20,0 °C – 80,0 °C) = 1 800 J °C · (–60,0 °C) = –108 kJ (= –1,08 · 105 J)

©VANIN

OPDRACHT 21

Los het vraagstuk op.

Een kom soep heeft een temperatuur van 20 °C.

Na 60 seconden in de microgolfoven met een vermogen van 900 W is de temperatuur 60 °C.

1 Bereken op een cursusblad:

a de opgenomen warmte na 1,0 minuten; b de warmtecapaciteit van de kom soep; c de totale tijd die nodig is om het systeem op te warmen tot 80,0 °C.

2 Controleer je antwoord via .

De temperatuurverandering Δθ van een systeem is recht evenredig met de hoeveelheid warmte Q die opgenomen (of afgestaan) wordt:

Q = C ∙ Δθ

De grootheid warmtecapaciteit C is de warmte(overdracht) die nodig is om bij het systeem een temperatuurtoename of -afname van 1 °C te veroorzaken.

Grootheid met symbool Eenheid met symbool temperatuurverandering Δθ = θeind – θbegin graden Celsius °C warmtecapaciteit C joule per graad Celsius J °C

` Maak oefening 7 t/m 11 op p. 129-130.

3.3 Specifieke warmtecapaciteit

OPDRACHT 22

Bestudeer de invloed van de temperatuurverandering in dit voorbeeld.

Een glas water en een zwembad bevinden zich allebei een uur lang in de zon.

1 Welke uitspraak is correct?

De temperatuur van het glas water en het zwembad stijgt evenveel.

De temperatuur van glas water stijgt het meest.

De temperatuur van het zwembad stijgt het meest.

2 Kleur de invloedsfactoren die constant blijven, groen.

Kleur de invloedsfactoren die veranderen, rood.

©VANIN

massa soort stof warmtehoeveelheid

3 Geef een voorbeeld uit het dagelijks leven waarbij een factor een invloed heeft op de temperatuursverandering. Bespreek met je buur en je leerkracht.

OPDRACHT 23 ONDERZOEK

Onderzoek de invloedsfactoren op de temperatuurverandering van een systeem aan de hand van Labo 06 via .

Hoeveel een voorwerp opwarmt of afkoelt, hangt af van de warmtehoeveelheid die eraan toegevoegd/onttrokken wordt, maar ook van de massa en de samenstelling van het voorwerp.

Als er warmte uitgewisseld wordt met een systeem, is er een temperatuurverandering.

De hoeveelheid warmte die nodig is voor een temperatuurverandering, wordt bepaald door de warmtecapaciteit van het systeem:

Q = C ∙ ∆θ

De warmtecapaciteit van een systeem is afhankelijk van de massa en de stofsoort

▲ Afb. 97 De zon schijnt evenveel op een glas water als op een zwembad.

1 Invloed van de massa

Om de invloed van de massa te bepalen, onderzoek je de temperatuurverandering Δθ voor verschillende massa’s van dezelfde stof waar je dezelfde warmtehoeveelheid aan toevoegt.

Gelijke warmtetoevoer aan een toenemende hoeveelheid water met een begintemperatuur θbegin = 20 °C

©VANIN

massa m na 2 minuten

massa 2 · m na 2 minuten

massa 3 · m na 2 minuten

▲ Afb. 98 Invloed van de massa op de temperatuurverandering

massa 4 · m na 2 minuten

De Δθ(m)-grafiek is een hyperbool. Als de massa verdubbelt, dan halveert de temperatuurverandering. Er is een omgekeerd evenredig verband tussen de temperatuurverandering en de warmte:

θ (°C)

θ (m)-grafiek bij gelijke warmtetoevoer

2 Invloed van de stofsoort

Om de invloed van de stofsoort te bepalen, onderzoek je de temperatuurverandering Δθ voor dezelfde massa van verschillende stoffen waar je dezelfde warmtehoeveelheid aan toevoegt.

De massa van een stof wordt bepaald door het volume en door de massadichtheid (ρ = m V ).

Bij een gelijke massa van verschillende stoffen kan het volume verschillen: m = ρ ∙ V

Gelijke warmtetoevoer aan een gelijke massa water, olie en alcohol met een begintemperatuur θbegin = 20 °C

©VANIN

massa m na 2 minuten

massa m na 2 minuten alcohol massa m na 2 minuten

▲ Afb. 99 Invloed van de stofsoort op de temperatuurverandering

De Δθ(Q)-grafiek is voor elke stof een rechte door de oorsprong. Er is een recht evenredig verband tussen de temperatuurverandering en de warmte: Δθ ~ Q

De temperatuurverandering bij dezelfde warmtetoevoer is groter voor olie dan voor water. Olie warmt makkelijker op.

De helling van de grafiek wordt bepaald door de soort stof.

Δθ (°C) olie alcohol water

Δθ (Q)-grafiek voor drie verschillende stoffen

Q (J)

▲ Grafiek 14

Uit het voorgaande blijkt:

De temperatuurverandering neemt recht evenredig toe met de toenemende warmtehoeveelheid.

Δθ ~ Q

©VANIN

De temperatuurverandering neemt omgekeerd evenredig af met de toenemende massa. Δθ ~ 1 m

Dat betekent: Q

= constante

Die constante grootheid, die afhangt van de specifieke stof die wordt opgewarmd, noem je de specifieke warmtecapaciteit c Q m · Δθ = c

Dat is een stofeigenschap. De specifieke warmtecapaciteit is de hoeveelheid energie die nodig is om 1 kg van een stof een temperatuurtoename of -afname van 1 °C te geven.

De eenheid van specifieke warmtecapaciteit is J kg · °C

Grootheid met symbool Eenheid met symbool specifieke warmtecapaciteit c joule per kilogram graad Celsius J kg · °C

Uit de definitie van specifieke warmtecapaciteit volgt:

Q = c ∙ m ∙ Δθ

Aangezien voor het systeem Q = C ∙ Δθ geldt, wordt het verband tussen de warmtecapaciteit en de specifieke warmtecapaciteit van een systeem dat bestaat uit één stof, gegeven door: C = c ∙ m

VOORBEELD FRITUUROLIE OPWARMEN

Voor olie is de specifieke warmtecapaciteit:

colie = 2 000 J kg · °C

Dat betekent dat je aan olie 2 000 joule energie moet toevoegen om 1 kg van die stof een temperatuurtoename van 1 °C te geven.

Om 2,0 kg frituurolie van 20 °C op te warmen tot 100 °C, heb je warmte nodig: Q = colie ∙ m

Vaste stoffen: metalen

)

Vaste stoffen: niet-metalen c ( J kg · °C ) diamant 490 glas 837 ijs 2 090 keukenzout 880 paraffine 290 porselein 1 085

▲ Tabel 1 Specifieke warmtecapaciteit van een aantal stoffen

▲ Afb. 100 Olie warmt sneller op dan water.

OPDRACHT 24

Bestudeer de tabel met de verschillende specifieke warmtecapaciteiten van veelvoorkomende stoffen op p. 118.

1 In welke eenheid staan de waarden uitgedrukt?

©VANIN

2 Welke stof in de tabel heeft de hoogste specifieke warmtecapaciteit?

3 Leg de betekenis van de grootheid warmtecapaciteit uit in één zin.

Gebruik water als voorbeeld.

4 Maak de uitspraken correct.

• Metalen hebben een kleine / grote specifieke warmtecapaciteit. Daardoor zal hun temperatuur traag / snel stijgen of dalen bij warmteoverdracht.

• IJs heeft wel / niet dezelfde specifieke warmtecapaciteit als water.

De waarde is wel / niet afhankelijk van de aggregatietoestand.

• Gassen hebben een specifieke warmtecapaciteit die afhankelijk is van of ze gebruikt worden bij een constante druk cp / c v of bij een constant volume cp / c v

WEETJE

De grote specifieke warmtecapaciteit van water heeft een impact op het leven op aarde.

• De mens en andere organismen bevatten 55-60 % water. Daardoor is hun lichaamstemperatuur constant bij variaties in de omgevingstemperatuur. Kinderen zijn gevoeliger voor onderkoeling of koorts vanwege hun kleinere massa.

• De aarde is voor 70 % bedekt met water. De grote warmtecapaciteit van water verhindert grote temperatuurschommelingen bij dag/nacht- en seizoenswisselingen, waardoor er leven mogelijk is.

• Het klimaat van gebieden die grenzen aan een zee, is beduidend zachter dan het klimaat in het binnenland.

Wil je meer weten? Kijk dan zeker eens naar de ontdekplaat ‘Fysica van het klimaat’.

▲ Afb. 101 Je drinkt het best twee liter water per dag.

▲ Afb. 102 Oceanen bedekken het grootste deel van de aarde.

De meeste systemen bestaan uit verschillende stoffen. De warmte die uitgewisseld wordt met het systeem Qsys, kun je als volgt noteren:

Qsys = Qstof 1 + Qstof 2 + …

Via de definitie van warmtecapaciteit en specifieke warmtecapaciteit wordt dat:

De temperatuurverandering Δθ is voor alle stoffen gelijk vanwege het thermisch evenwicht tussen de stoffen. Dat betekent:

VOORBEELD WARMTECAPACITEIT VAN EEN KOM SOEP

We bekijken het voorbeeld van een kom soep.

Een kom die gemaakt is van 500 g porselein, heeft samen met 343 g soep (c soep = 3 670 J kg · °C ) een warmtecapaciteit die je als volgt kunt vinden:

C sys = cporselein ∙ mporselein + c soep ∙ m soep = 1 085 J kg · °C ∙ 0,500

Om de temperatuur van een massa m van een stof te veranderen met Δθ, heb je een warmtehoeveelheid Q nodig die gelijk is aan: Q = c ∙ m ∙ Δθ

Daarbij is c de specifieke warmtecapaciteit van de stof. Dat is een stofeigenschap.

Grootheid met symbool SI-eenheid met symbool specifieke warmtecapaciteit c joule per kilogram graad Celsius J kg · °C

Het verband tussen de warmtecapaciteit C van een systeem en de specifieke warmtecapaciteit van een stof is gegeven door:

• systeem dat bestaat uit één stof: C = c ∙ m

• systeem dat bestaat uit meerdere stoffen: C sys = cstof 1

` Maak oefening 12 t/m 21 op p. 131-132.

OPDRACHT 25

Los het vraagstuk op.

Je vult een roestvaststalen (RVS) kookpot van 3,00 kilogram met 4,00 liter water om spaghetti te koken. Bereken de hoeveelheid warmte om de kookpot met het water op te warmen van 20,0 °C tot 100,0 °C.

1 Bereken op een cursusblad.

2 Controleer je antwoord via .

3.4 Warmtebalans

OPDRACHT 26

Bestudeer de afbeelding en de uitspraken.

Nora: De eindtemperatuur van de koffie met melk is de som van beide begintemperaturen.

Wie heeft er volgens jou gelijk?

OPDRACHT 27 ONDERZOEK

Lily: De eindtemperatuur ligt tussen beide begintemperaturen.

Dario: De eindtemperatuur is het gemiddelde van beide begintemperaturen.

Onderzoek een warmtebalans aan de hand van Labo 07 op .

Als je twee systemen met een verschillende temperatuur met elkaar in contact brengt, vindt er een warmte-uitwisseling plaats totdat er een thermisch evenwicht is. De eindtemperatuur van het samengestelde systeem wordt bepaald door de begintemperatuur en de warmtecapaciteit van elk systeem.

Qop

Om de eindtemperatuur te bepalen, gebruik je de wet van behoud van energie.

Volgens de wet van behoud van energie kan energie niet gemaakt of vernietigd worden, maar wordt ze overgedragen van één systeem naar een ander. Als er geen warmte-uitwisseling gebeurt met de omgeving, is de hoeveelheid afgestane warmte (Qaf ) door het systeem met de hoge temperatuur even groot als de hoeveelheid opgenomen warmte Qop door het systeem met de lage temperatuur.

Voor systemen met verschillende begintemperaturen die geïsoleerd zijn van de omgeving, kun je zo een warmtebalans opstellen. Dat is een wiskundige vergelijking waarbij de opgenomen warmtehoeveelheid Qop en de afgestane warmtehoeveelheid Qaf in grootte gelijk zijn:

Qop = |Qaf|

Aangezien de afgestane warmte negatief is, bereken je de hoeveelheid afgestane warmte als de absolute waarde |Qaf|.

De warmtehoeveelheden bereken je aan de hand van de (specifieke) warmtecapaciteit.

• Voor zuivere stoffen gebruik je Q = c ∙ m ∙ Δθ

• Voor voorwerpen gebruik je Q = C ∙ Δθ.

Aangezien c, C en m altijd positief zijn, geldt:

Je kunt de warmtebalans voorstellen op een θ(t)-grafiek. Daarop schets je de temperatuurveranderingen van alle systemen tot ze een thermisch evenwicht bereikt hebben.

• Je schat de eindtemperatuur. Die is niet noodzakelijk het gemiddelde van de begintemperaturen.

• De temperatuurverandering is in het begin het grootst, omdat het temperatuurverschil tussen beide systemen dan het grootst is. Daardoor is de warmte-uitwisseling per tijdseenheid groot. Je ziet dat op de grafiek door de sterke helling van de curves in het begin.

(°C)

θ (t)-grafiek bij een thermisch evenwicht

systeem met hoge begintemperatuur staat warmte af Qaf < 0

systeem met lage begintemperatuur neemt warmte op Qop > 0

OPDRACHT 28 VOORBEELDOEFENING

Bestudeer het uitgewerkte vraagstuk.

In een thermosfles met een warmtecapaciteit C sys van 250 J °C zit 800 g koffie (ckoffie = 4 200 J kg · °C ) met een temperatuur van 80,0 °C. De koffie en de thermos zijn al in thermisch evenwicht. Wanneer je 100 g melk met een temperatuur van 6,0 °C toevoegt, wordt er een nieuw thermisch evenwicht bereikt op 72,8 °C. Hoe groot is de specifieke warmtecapaciteit van melk?

Gegeven en gevraagd:

θbegin, koffie = 80,0 °C

mkoffie = 800 g

C sys = 250 J °C

ckoffie = 4 200 J kg · °C

θbegin, melk = 6,0 °C

mmelk = 100 g

cmelk = ? θeind = 72,8 °C

▲ Afb. 105

Oplossing:Je past de warmtebalans toe:

Qop = |Qaf|

In deze toepassing staat zowel de thermos als de koffie warmte af, omdat de temperatuur daalt.

De melk neemt warmte op, omdat de temperatuur stijgt.

Qmelk = |Qthermos + Qkoffie|

+ koffie: staan warmte af melk: neem warmte op

Je past de uitdrukking voor de warmte toe voor elke Q:

Je vormt de uitdrukking om, om de specifieke warmtecapaciteit cmelk te berekenen:

cmelk = Cthermos · |Δθthermos| + ckoffie · mkoffie · |Δ

Daarbij geldt:

OPDRACHT 28 (VERVOLG) VOORBEELDOEFENING

Je vult de gegevens in:

cmelk = 250 J °C · |–7,2 °C| + 4 200 J kg · °C · 0,800

· |–7,2 °C| 0,100 kg · 66,8 °C = 1,8 · 103 J + 24 · 103 J 6,68 kg · °C = 26 · 103 J 6,68 kg · °C = 3,9 ∙ 10³ J kg · °C

Controle:• Klopt de gevonden eenheid?

Ja, J kg · °C is de eenheid van de specifieke warmtecapaciteit.

• Klopt de grootte van de getalwaarde?

Ja, de specifieke warmtecapaciteit van de verschillende vloeistoffen schommelt

tussen 2 000 J kg · °C en 4 000 J kg · °C .

OPLOSSINGSSTRATEGIE

• Beschrijf in je eigen woorden wat er gebeurt.

• Stel de situatie schematisch voor:

– Maak een schets van de begin- en eindsituatie.

– Noteer de gegevens en het gevraagde bij je tekeningen.

Let op de verwijzingen in subscript.

– Maak een θ(t)-grafiek met de gegevens en het gevraagde.

• Gebruik de warmtebalans Qop = |Qaf| om het gevraagde te berekenen:

– Ga na welke systemen en stoffen warmte opnemen of afgeven.

– Bereken de warmtehoeveelheden.

• Voor zuivere stoffen gebruik je Q = c ∙ m ∙ Δθ.

• Voor voorwerpen gebruik je Q = C ∙ Δθ

– Vul de gegevens in en werk wiskundig uit naar de onbekende.

TIP

Het is belangrijk dat je de warmtebalans kunt opstellen.

Voor het rekenwerk kun je gebruikmaken van de ICT-tool op

• Controleer je antwoord:

– Komt de berekende waarde overeen met je schematische voorstelling?

– Kloppen de eenheid en de grootteorde van de massa’s en de warmtecapaciteiten?

Als je voorwerpen met een verschillende begintemperatuur bij elkaar brengt in een geïsoleerd systeem, is (volgens de wet van behoud van energie) de warmtehoeveelheid Qop even groot als de warmtehoeveelheid |Qaf| die afgestaan wordt: Qop = |Qaf|

Dat noem je een warmtebalans

` Maak oefening 22 t/m 26 op p. 133.

Kernbegrippen

Notities (absolute) temperatuur warmte

Temperatuur is een maat van deeltjes: hoe hoger de temperatuur, hoe de gemiddelde kinetische energie van de deeltjes.

©VANIN

inwendige energie

Warmte is een vorm van energie die uitgewisseld wordt als gevolg van een .

• warmte opnemen: Q 0

• warmte afstaan: Q 0

Grootheden met symbool

Eenheden met symbool temperatuur warmte

De inwendige energie van een systeem Einw:

1 inwendige kinetische energie Ekin, i of thermische energie door gelinkt aan de temperatuur

2 inwendige potentiële energie Epot, i door de tussen naburige deeltjes

thermisch evenwicht

warmtetransport

Thermisch evenwicht is een toestand waarbij twee systemen met een verschillende

temperatuur warmte uitgewisseld hebben tot ze hebben. De eindtemperatuur is afhankelijk van de , de en hun

Warmte wordt bij een temperatuurverschil op drie manieren doorgegeven:

1 : door de botsing van deeltjes tegen elkaar (vooral bij vaste stoffen);

2 : door de verplaatsing van deeltjes (bij gassen en vloeistoffen);

3 : door infraroodstraling, geen deeltjes nodig

warmtecapaciteit

De warmtecapaciteit van een systeem geeft de energie weer die nodig is om een systeem . Het is een voorwerpseigenschap

Kernbegrippen

Notities specifieke warmtecapaciteit

De specifieke warmtecapaciteit van een stof geeft de energie weer die nodig is om

©VANIN

Het is een stofeigenschap warmtebalans

Grootheden met symbool

Eenheden met symbool temperatuurverandering warmtecapaciteit (van een systeem) specifieke warmtecapaciteit (van een stof)

Benodigde warmte voor een temperatuurverandering Δθ:

• voor zuivere stoffen: Q =

• voor voorwerpen: Q =

Als meerdere systemen met een verschillende temperatuur warmte uitwisselen om een thermisch evenwicht te bereiken, is

Dat is de wet van voor warmte. Qop = |Qaf|

Dat noem je een warmtebalans

JANOG OEFENEN

1 Begripskennis

• Ik kan het verband tussen de temperatuur en de kinetische energie van deeltjes omschrijven

• Ik kan warmte omschrijven.

• Ik kan de inwendige energie van een stof omschrijven

• Ik kan een thermisch evenwicht omschrijven

• Ik kan de verschillende vormen van warmtetransport omschrijven aan de hand van het deeltjesmodel.

• Ik kan de verschillende soorten systemen omschrijven

• Ik kan de warmtecapaciteit van een systeem omschrijven.

• Ik kan de warmte die een systeem opneemt of afgeeft, berekenen

• Ik kan de specifieke warmtecapaciteit van een stof omschrijven.

• Ik kan de warmte die een stof opneemt of afgeeft, berekenen.

• Ik kan een warmtebalans omschrijven en opstellen.

2 Onderzoeksvaardigheden

• Ik kan een onderzoek uitvoeren volgens een gegeven stappenplan.

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan nauwkeurig berekeningen uitvoeren

• Ik kan een thermometer aflezen

• Ik kan het verband tussen grootheden onderzoeken.

` Je kunt deze checklist ook op invullen.

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’.

Je kunt de oplossingsstrategie en de voorbeeldoefeningen op gebruiken als extra ondersteuning.

Wie heeft gelijk? Verklaar.

Lena: De temperatuur van de spijker is hoger dan die van de koffie. De warmte die de spijker afgeeft, is hoger dan de warmte die de koffie afgeeft.

Soufian: De temperatuur van de koffie is lager dan die van de spijker. Toch is de warmte die de koffie afgeeft, hoger dan de warmte die de spijker afgeeft.

20°C20°C 400°C90°C

Wat is er fout aan de volgende uitspraken?

a Doe een warme jas aan.

b Sluit het raam, zodat de koude niet binnenkomt.

De aarde wordt voortdurend door de zon bestraald. Waarom neemt de temperatuur van de aarde dan niet voortdurend toe?

Kies de correcte uitspraak.

Alleen een voorwerp met een temperatuur hoger dan de kamertemperatuur zendt straling uit.

Alleen een roodgloeiend voorwerp zendt straling uit.

Alle voorwerpen zenden straling uit.

Wanneer je in de winter het klaslokaal binnenkomt, voelt het vaak koud aan. Na de les is het een stuk warmer. a Hoe komt dat?

b Wat gebeurt er als je na de les het raam openzet? Verklaar.

Als je met je ene hand een metalen stoelpoot aanraakt en met je andere hand de houten rugleuning, dan lijken ze een verschillende temperatuur te hebben. Klopt dat?

Elisabeth warmt een beker water voor thee op tot het kookpunt in de microgolfoven. Jef maakt de thee klaar door in een identieke beker die op de keukentafel staat, kokend water te gieten. Welke uitspraak is correct? Verklaar waarom.

De thee van Elisabeth en Jef heeft dezelfde temperatuur.

De thee van Jef heeft een hogere temperatuur.

De thee van Elisabeth heeft een hogere temperatuur.

Je kunt niet voorspellen welke thee de hoogste temperatuur heeft, omdat je het vermogen van het kookvuur en de microgolfoven niet kent.

Op de grafiek zie je het temperatuurverloop van drie gelijke porties kokende soep die uitgeschonken zijn in een beker, een soepbord en een isomobekertje.

a Welke curve hoort bij elke situatie? Vul aan in de legende.

b Verklaar:

• de vorm van de curves:

• de lage temperatuur van de oranje curve na 30 s:

• de sterkere daling van de oranje curve:

• het bijna evenwijdige verloop van de grijze en de blauwe curve:

Een verwarmingselement met een vermogen van 300 W wordt gedurende exact 2,00 min ingeschakeld.

Hoeveel warmte wordt er geproduceerd?

Om de juiste temperatuur van je mok chocomelk te bekomen, moet je op een microgolfoven zowel de geschikte tijd als het geschikte vermogen kiezen.

Rangschik de eindtemperaturen in de volgende situaties van klein naar groot.

a 2 min op 750 W

b 2 min op 250 W

c 1 min op 500 W

d 1 min op 1 000 W

Laptops verwerken niet alleen informatie, maar produceren ook warmte.

In moderne toestellen is die warmteontwikkeling beperkt en is er een rendement van 90 % mogelijk.

a Bereken de hoeveelheid warmte die ontwikkeld wordt als je laptop (P = 75 W) aanstaat van 19.30 u tot 21.45 u.

b Hoeveel lucht warm je daarmee 1,0 °C op, als er 800 J nodig is om de temperatuur van 1,0 m³ lucht met 1,0 °C te laten stijgen?

Zijn de volgende uitspraken juist of fout? Verbeter indien nodig.

a Hoe groter de specifieke warmtecapaciteit van een stof, hoe makkelijker de stof opwarmt.

b Om een ijzeren spijker op te warmen van 0 tot 10 °C, heb je evenveel warmte nodig als om hem op te warmen van 100 tot 110 °C.

c Om 1 L olie 1 °C op te warmen, heb je 2 000 kJ warmte nodig.

d Je kunt de specifieke warmtecapaciteit uitdrukken in J kg · K

e De specifieke warmtecapaciteit van aluminium is 899 J kg · °C . Dat betekent dat de temperatuur van 2 kg aluminium met 2 °C zal stijgen als je 1 800 J toevoegt.

f De warmtecapaciteit van een voorwerp geeft de hoeveelheid warmte aan die het voorwerp afgeeft als de temperatuur ervan 1 °C stijgt.

Verklaar de volgende fenomenen.

a Kersenpittenkussentjes zijn uiterst geschikt als bed-, nek- en voetverwarmers. Is de warmtecapaciteit van een kersenpittenkussen volgens jou groot of klein? Verklaar je antwoord.

b Elektriciteitscentrales zijn meestal aan een rivier gevestigd.

Een zwembad van 20,0 m lang, 12,0 m breed en 1,80 m diep is volledig gevuld met water op een temperatuur van 12,0 °C. Hoeveel warmte is er nodig om het water te verwarmen tot 25,0 °C ?

Op de grafiek zie je de temperatuurstijging van twee bekers met verschillende vloeistoffen.

Welke vloeistof heeft de grootste specifieke warmtecapaciteit? Duid aan.

vloeistof 1

vloeistof 2

Je kunt daarover geen uitspraak doen. Er is niets gegeven over de hoeveelheid vloeistof.

Een glas met een warmtecapaciteit van 172 J °C bevat 210 g water.

Bereken de warmtecapaciteit van het geheel.

Een visboer gebruikt ijs om zijn vis koel te houden.

Hoeveel warmte neemt 2,50 kg ijs op terwijl het opwarmt van –8,0 °C tot –3,0 °C ?

Els meet met een glazen alcoholthermometer (m = 61,8 g) een buitentemperatuur van –3 °C.

De thermometer bevat 15,3 g alcohol.

Hoeveel warmte staat de thermometer (glas en alcohol) af, als hij daarvoor binnen lag, waar het 22 °C was ?

Rick wil spaghetti koken en zet een pan (m = 560 g) uit roestvast staal die gevuld is met 2,3 L water (allebei op 18 °C), op een kookplaat met een nettovermogen van 8,0 kW.

a Hoelang duurt het tot hij de spaghetti in het kokende water kan leggen?

b Hoeveel procent van de warmte gaat naar de pot? Bespreek.

De warmtecapaciteit van de trommel van een wasmachine is 950 J °C

Het duurt 5 min 8 s om 5,00 L water in de machine te verwarmen van 12,0 °C tot 50,0 °C.

Bereken het nuttige vermogen van het verwarmingselement.

De energie van voedingsmiddelen wordt vaak in een andere eenheid dan joule uitgedrukt.

a Welke eenheid?

b Bereken de omzettingsfactor van die eenheid naar joule aan de hand van voedingsetiketten.

c Met welke waarde komt dat overeen?

d Formuleer een definitie voor die alternatieve eenheid.

Terwijl je je huiswerk maakt, drink je een kop koffie. Welk van volgende grafieken geeft het juiste temperatuurverloop van de koffie (oranje curve) en de mok (blauwe curve) weer net nadat je de koffie hebt ingeschonken? Duid aan.

In twee identieke thermossen die gevuld zijn met dezelfde hoeveelheid water, worden twee verwarmde blokjes gelegd. Na enige tijd wordt het thermisch evenwicht in beide bekers op dezelfde eindtemperatuur bereikt.

Wat kun je met zekerheid zeggen? (meerdere antwoorden mogelijk)

De blokjes zijn identiek.

De blokjes hebben dezelfde begintemperatuur.

De blokjes geven evenveel warmte af.

Het water in beide thermossen neemt evenveel warmte op.

De blokjes bezitten dezelfde hoeveelheid inwendige energie.

De eindtemperatuur ligt tussen de begintemperatuur van het water en elk blokje.

Vanuit een boiler stroomt 60 L warm water met een temperatuur van 45 °C naar een lege badkuip.

De warmteafgifte aan de leiding en de omgeving is 750 kJ.

De lege badkuip heeft een warmtecapaciteit van 1,5 ∙ 104 J °C en een (begin)temperatuur van 17 °C.

a Welke temperatuur heeft het water als het de badkuip instroomt?

b Welke temperatuur heeft het badwater nadat de badkuip gevuld is?

Een smid koelt een hoefijzer met een massa van 950 g en een temperatuur van 1 100 °C af door het in een vat met 10,0 kg water op 18,0 °C te dompelen.

Bepaal de temperatuurstijging van het water in het vat.

In een thermos met een warmtecapaciteit van 80 J °C zit 400 g water met een temperatuur van 20 °C.

Er wordt een blokje roestvast staal (RVS) aan toegevoegd met een massa van 200 g en een temperatuur van 100 °C. De eindtemperatuur bedraagt 24 °C.

Bereken de specifieke warmtecapaciteit van RVS.

` Verder oefenen? Ga naar .

Welke invloed heeft warmte op de aggregatietoestand van een stof?

LEERDOELEN

Je kunt al:

een faseovergang door de toe- of afvoer van energie verklaren met behulp van het deeltjesmodel; een warmtebalans opstellen.

Je leert nu:

de verandering van de temperatuur tijdens een faseovergang beschrijven; de verandering van de inwendige energie bij een faseovergang beschrijven; de grootte van de latente warmte bepalen; een warmtebalans opstellen bij een thermisch evenwicht met faseovergangen.

Het ijsblokje in je frisdrank, water om te spoelen, en stoom om groenten te garen: het zijn voorbeelden van water in allerlei vormen. Hoe kun je van de ene (aggregatie)toestand naar de andere gaan? Wat gebeurt er met de temperatuur tijdens de overgang? Is er een vergelijkbaar verschijnsel bij andere stoffen?

In dit hoofdstuk bestudeer je de verschillende faseovergangen en de invloed die warmte erop heeft.

1 Welke faseovergangen ontstaan er bij warmte-uitwisseling?

OPDRACHT 29

Bestudeer de verschillende faseovergangen.

1 Bestudeer de afbeeldingen.

2 Vul de tabel aan.

Uitgelopen kaarsvet verhardt op de fles.

Benoem de faseovergang. 1 2 3

Gedroogde bloemblaadjes geven een aroma af.

Na het douchen zijn er waterdruppels op de spiegel.

OPDRACHT 29 (VERVOLG)

Benoem de omgekeerde faseovergang.

Geef een voorbeeld van een stof die de omgekeerde faseovergang ondergaat.

©VANIN

3 Markeer:

a de faseovergangen waarbij warmte wordt opgenomen, in het rood; b de faseovergangen waarbij warmte wordt afgestaan, in het blauw.

Een stof kan voorkomen in verschillende aggregatietoestanden of fasen: vast, vloeibaar en gasvormig. In welke fase de stof zich bevindt, hangt af van de omgevingsdruk en de temperatuur van de stof.

Als een systeem een andere temperatuur heeft dan de omgeving, neemt het warmte op of staat het warmte af om een thermisch evenwicht te bereiken. Daarbij kan de temperatuur van het systeem zodanig veranderen dat de stof verandert van aggregatietoestand. Er is een faseovergang

Als een stof warmte opneemt (Qop > 0), zijn er drie faseovergangen mogelijk:

• smelten: de faseovergang van vast naar vloeibaar;

• verdampen: de faseovergang van vloeibaar naar gasvormig;

• sublimeren: de faseovergang van vast naar gasvormig.

Als een stof warmte afgeeft (Qaf < 0), zijn er drie faseovergangen mogelijk:

• stollen: de faseovergang van vloeibaar naar vast;

• condenseren: de faseovergang van gasvormig naar vloeibaar;

• desublimeren: de faseovergang van gasvormig naar vast.

Een faseovergang is een fysisch proces: de samenstelling van de stof verandert niet en de faseovergang is omkeerbaar. In de volgende paragrafen leer je meer over de verschillende faseovergangen. Omdat bij faseovergangen de omgevingsdruk een rol speelt, bestuderen we ze bij constante normdruk (1 013 hPa).

Door warmte-uitwisseling kan een stof van aggregatietoestand veranderen

Er is een faseovergang. Dat is een fysisch proces: de samenstelling van de stof verandert niet en de faseovergang is omkeerbaar.

Er zijn zes faseovergangen mogelijk.

` Maak oefening 1 t/m 5 op p. 165.

2 Hoe verandert de temperatuur bij een faseovergang?

2.1 Smelten en stollen

©VANIN

A Smeltproces

OPDRACHT 30 DEMO

Bestudeer hoe de temperatuur verandert tijdens het smeltproces.

1 Maak samen met je leerkracht de opstelling zoals op de afbeelding. Warm de stof op en stel de sensor in om de temperatuur om de dertig seconden te meten.

thermometer of temperatuursensor

water vaste stof

dompelkoker

▲ Afb. 110 Je meet de temperatuur op tijdens het smeltproces.

2 Hoe zal het temperatuurverloop eruitzien volgens jou? Schets je hypothese van de θ(t)-grafiek.

Hypothese van de θ(t)-grafiek

3 Voer de proef uit.

4 Teken de opgemeten θ(t)-grafiek.

5 Vergelijk met je hypothese en omschrijf de eventuele verschillen.

Opgemeten θ(t)-grafiek

6 Maak de volgende zinnen correct.

• Het smeltproces is uitgevoerd bij een heel lage druk / de normdruk / een heel hoge druk.

• Bij een vaste omgevingsdruk smelt een stof altijd op een andere / dezelfde temperatuur.

• De smelttemperatuur is afhankelijk / onafhankelijk van de stofsoort.

• De smelttemperatuur is afhankelijk / onafhankelijk van de massa.

demovideo: smeltproces

Smelten is de overgang van de vaste naar de vloeibare fase. Wanneer een stof smelt, neemt ze warmte op uit de omgeving.

Stollen is de overgang van de vloeibare naar de vaste fase. Wanneer een stof stolt, staat ze warmte af aan de omgeving.

Om een stof in de vaste fase te smelten, moet je er warmte aan toevoegen uit de omgeving. De verandering van de temperatuur in functie van de warmte noem je de smeltgrafiek (θ(Q)-grafiek).

In de praktijk meet men de smeltgrafiek op in functie van de tijd: een θ(t)-grafiek. De omzetting naar de θ(Q)-grafiek gebeurt voor een verwarmingselement aan de hand van het vermogen: Q

Als een zuivere vaste stof warmte opneemt, gaat de stof bij een specifieke temperatuur over naar de vloeibare toestand. Die temperatuur noem je de smelttemperatuur θ sm of het smeltpunt van de stof. Dat smeltpunt is afhankelijk van de soort stof. Het is een stofeigenschap. In tabel 2 zie je enkele voorbeelden.

Uit experimenten blijkt dat de smeltgrafiek voor zuivere stoffen tijdens de toevoer van warmte altijd hetzelfde verloop heeft. De smeltgrafiek is voorgesteld in het onderstaande schema.

Stof θsm/st (°C) bij 1 013 hPa alcohol –114 aluminium 660 glycerol 19 goud 1 064 ijzer 1 538 koper 1 084 kwik –39 lood 327 tin 232 water 0 zilver 962 zuurstof –219 zwavel 113

▲ Tabel 2 Smelt- en stoltemperaturen bij normdruk

Grafiek 17 op p. 138 is een geïdealiseerde voorstelling. In de praktijk zullen de delen dicht bij het verwarmingselement na het smelten al verder opwarmen, terwijl het binnenste nog vast is. Als je de stof traag opwarmt en genoeg mengt, wordt de geïdealiseerde smeltgrafiek het best benaderd.

thermometer

De vaste stof bevindt zich op een begintemperatuur θbegin

Smeltproces: warmtetoevoer aan een zuivere vaste stof

dompelkoker

©VANIN

Bij de smelttemperatuur θ sm start de faseovergang van vast naar vloeibaar. De stof komt in beide fasen voor.

Zodra de volledige stof vloeibaar is, stijgt de temperatuur opnieuw, tot de eindtemperatuur θeind bereikt is.

▲ Grafiek 17 Smeltgrafiek van een vaste stof (een andere stof dan water)

De temperatuur van de vaste stof stijgt lineair, tot de stof begint te smelten.

De temperatuur blijft constant, zolang niet al de vaste stof gesmolten is.

VOORBEELD SMELTPROCES VAN IJS EN CHOCOLADE

Qop (J)

De temperatuur van de vloeistof stijgt lineair.

Als je een blok ijs van 0,5 kg uit de diepvries (–18 °C) haalt en het op kamertemperatuur (20 °C) laat ontdooien, volgt de temperatuur het verloop van grafiek 18. Er zijn drie zones:

• zone ①: Eerst stijgt de temperatuur van het ijsblok tot θsm, ijs = 0 °C.

• zone ②: Vanaf θsm, ijs = 0 °C smelt het ijs. De temperatuur verandert niet. Het water en het ijs hebben een temperatuur van 0 °C.

• zone ③: Als al het ijs gesmolten is, warmt het water op tot kamertemperatuur.

VOORBEELD SMELTPROCES VAN IJS EN CHOCOLADE (VERVOLG)

De smeltgrafiek van evenveel chocolade op kamertemperatuur (20 °C) heeft een gelijkaardig verloop. Zone ② begint bij θsm, chocolade = 30 °C.

De grafiek van chocolade stopt vroeger. Een massa van 0,5 kg chocolade heeft minder warmte nodig om te smelten, dan dezelfde massa water.

B Stolproces

Als een stof in de vloeibare fase stolt, staat ze warmte af aan de omgeving. De verandering van de temperatuur in functie van de warmte noem je de stolgrafiek (θ(Q)-grafiek).

Als een zuivere vloeistof warmte afstaat, gaat ze op een specifieke temperatuur over naar de vaste fase. Die temperatuur noem je de stoltemperatuur θst of het stolpunt van de stof.

De stoltemperatuur θst heeft dezelfde waarde als de smelttemperatuur θ sm .

Uit experimenten blijkt dat het verloop van de stolgrafiek voor zuivere stoffen tijdens de afvoer van warmte altijd omgekeerd verloopt ten opzichte van de smeltgrafiek. Tijdens het stollen blijft de temperatuur in de stolgrafiek constant zolang de vloeistof overgaat naar een vaste stof.

▲ Grafiek 19 Stolgrafiek van een vloeistof

Tijdens het smeltproces zijn er drie zones in de smeltgrafiek (θ(Q)-grafiek):

① De stof blijft vast en stijgt in temperatuur, terwijl ze warmte opneemt.

② De stof verandert van vast naar vloeibaar. Beide aggregatietoestanden komen tegelijk voor.

De smelttemperatuur blijft constant, terwijl de stof warmte opneemt

③ De stof blijft vloeibaar en stijgt in temperatuur, terwijl ze warmte opneemt.

De stolgrafiek verloopt omgekeerd in vergelijking met de smeltgrafiek. De stof staat warmte af aan de omgeving. De smelttemperatuur en stoltemperatuur hebben dezelfde waarde.

Grootheid met symbool

Si-eenheid met symbool smelt-/stoltemperatuur θsm/st graden Celsius °C

▲ Grafiek 18 Smeltgrafiek voor chocolade en water

2.2 Verdampen en condenseren

A Vrije verdamping en condensatie

OPDRACHT 31 DOORDENKER

ONDERZOEK

Werk een onderzoek uit om de invloedsfactoren op de verdampingssnelheid te onderzoeken. Gebruik het stappenplan op .

Verdampen is de overgang van de vloeibare naar de gasvormige fase

Wanneer een stof verdampt, neemt ze warmte op uit de omgeving.

Condenseren is de overgang van de gasvormige naar de vloeibare fase

Wanneer een stof condenseert, staat ze warmte af aan de omgeving.

Vrije verdamping gebeurt aan het oppervlak van een vloeistof en kan bij elke temperatuur gebeuren.

De verdampingssnelheid bij vrije verdamping:

• stijgt als de temperatuur hoger wordt;

• stijgt als de ventilatie toeneemt;

• stijgt als het vloeistofoppervlak groter wordt;

• is afhankelijk van de soort stof.

VOORBEELD WAS DROGEN

Door de was uit te hangen aan een wasdraad, vergroot je het oppervlak waar water kan verdampen. Als bovendien de zon schijnt en er een beetje wind staat, zal het water in een mum van tijd verdampt zijn.

VOORBEELD ONTSMETTINGSALCOHOL

Je kunt handzeep op basis van alcohol kopen. De alcohol heeft niet alleen een ontsmettende functie, maar is ook vluchtiger (heeft minder energie nodig) dan water. Dat zorgt ervoor dat de stof snel verdampt en je handen sneller droog zijn, zonder dat je een handdoek hoeft te gebruiken.

▲ Afb. 111 Verschillende factoren bepalen hoe snel de was droogt.

▲ Afb. 112 Ontsmettingsalcohol verdampt sneller dan water.

Condenseren kan bij elke temperatuur gebeuren, als de stof in de gasvormige toestand warmte afstaat. Als de omgeving de atmosfeer is, noem je dat vrije condensatie

VOORBEELD WATERDAMP

Als je soep kookt, verdampt er water. Je ziet de waterdamp (als een wolkje) doordat hij onmiddellijk condenseert tot kleine waterdruppeltjes.

©VANIN

Je gebruikt een dampkap om te vermijden dat de waterdamp condenseert tot waterdruppels op de ramen.

VOORBEELD FRITUUROLIE

Als je frietjes bakt, verdampt de vloeibare frituurolie uit de warme frietketel. Dat merk je door de geur.

Op het rooster van de dampkap vormen zich oliedruppels. De frituurolie condenseert bij kamertemperatuur.

▲ Afb. 113 Waterdamp condenseert tot waterdruppeltjes.

▲ Afb. 114 Frituurolie verdampt uit de warme frietketel en condenseert op de koudere dampkap.

B Kook- en condensatieproces

OPDRACHT 32 DEMO

Bestudeer het verloop van de temperatuur tijdens het koken.

1 Maak samen met je leerkracht de opstelling zoals op de afbeelding.

Warm de stof op en stel de sensor in om de temperatuur om de dertig seconden te meten.

thermometer of temperatuursensor

water

dompelkoker

▲ Afb. 115 Je meet de temperatuur op tijdens het kookproces.

2 Hoe zal het temperatuurverloop eruitzien volgens jou?

Schets je hypothese van de θ(Q)-grafiek.

Hypothese van de θ(Q)-grafiek

3 Voer de proef uit.

4 Teken de opgemeten θ(Q)-grafiek.

5 Vergelijk met je hypothese en omschrijf de eventuele verschillen.

Opgemeten θ(Q)-grafiek

6 Maak de volgende zinnen correct.

• Het kookproces is uitgevoerd bij een heel lage druk / de normdruk / een heel hoge druk

• Bij een vaste omgevingsdruk kookt een stof altijd op een andere / dezelfde temperatuur.

• De kooktemperatuur is voor elke zuivere stof anders / hetzelfde.

7 In dit experiment kun je moeilijk een derde zone realiseren waarin je de stof verder verwarmt. Hoe komt dat?

demovideo: kookproces

Koken is een speciale vorm van verdampen. Tijdens het koken ontstaan er binnen de vloeistof gasbellen. Die gasbellen zijn deeltjes van de vloeistof die zijn overgegaan naar de gasvormige fase. Dat gebeurt bij een specifieke temperatuur.

(Vrij) verdampen Koken (inwendige verdamping) ▲ Afb. 116

©VANIN

Plaats aan het vloeistofoppervlakoveral in de vloeistof

Temperatuur op elke temperatuur op een specifieke temperatuur

Tijdens het koken neemt de stof warmte op. De grafiek die de verandering van de temperatuur toont in functie van de warmte, noem je de kookgrafiek (θ(Q)-grafiek).

Als je warmte toevoegt aan een vloeibare zuivere stof, beginnen er zich gasbellen te vormen in de vloeistof (= koken) op een specifieke temperatuur. Die kooktemperatuur θk (het kookpunt) is afhankelijk van de soort stof. Het is een stofeigenschap. In tabel 3 zie je enkele voorbeelden.

Stof θk/c (°C) bij 1 013 hPa ethanol 78 ether 35

ijzer 3 023

stikstof –196 terpentijn 180 water 100 zilver 2 193 zuurstof –183

▲ Tabel 3 Kook- en condensatietemperaturen bij normdruk

Uit experimenten blijkt dat de kookgrafiek voor zuivere stoffen tijdens de toevoer van warmte altijd hetzelfde verloop heeft. Dat wordt voorgesteld in het schema op de volgende pagina.

Je kunt de temperatuur in de derde zone enkel opmeten als je het gas opvangt.

117

thermometer

Koken: warmtetoevoer aan een zuivere vloeistof

dompelkoker

De vloeistof bevindt zich op een begintemperatuur θbegin

▲ Grafiek 20 Kookgrafiek van een vloeistof

De temperatuur van de vloeistof stijgt lineair, tot de stof begint te koken.

Bij de kooktemperatuur θk start de faseovergang van vloeibaar naar gas. De stof komt in beide fasen voor.

+ gasvormig

De temperatuur blijft constant, zolang niet al de vloeistof verdampt is.

Zodra de volledige stof gasvormig is, stijgt de temperatuur opnieuw, tot de eindtemperatuur θeind bereikt is.

Qop (J)

De temperatuur van het gas stijgt lineair

De condenseergrafiek verloopt omgekeerd aan de kookgrafiek. Het gas zal eerst afkoelen tot de condensatietemperatuur θ c, waarbij de gasvormige fase overgaat naar de vloeibare. De temperatuur is constant tijdens het condenseren. Eenmaal de stof volledig gecondenseerd is, zal de temperatuur verder afnemen tot het thermisch evenwicht met de omgeving bereikt is.

VOORBEELD TEMPERATUURVERLOOP BIJ HET CONDENSEREN VAN STOOM

Om melk op te schuimen, gebruikt men vaak een stoommachine. De stoom staat warmte af aan de melk. Op de bijbehorende θ(Q)-grafiek zijn er drie zones.

©VANIN

▲ Grafiek 21 Condenseergrafiek van stoom

① gasfase: De stoom start op een temperatuur van 115 °C en koelt af tot 100 °C.

② faseovergang: De stoom condenseert tot water van 100 °C.

③ vloeibare fase: Het water koelt af tot 65 °C.

De melk neemt de warmte op. De temperatuur stijgt gelijkmatig van 6 °C tot 65 °C. Er is geen faseovergang.

Vrije verdamping en vrije condensatie kunnen aan het oppervlak en bij elke temperatuur gebeuren.

Tijdens het kookproces zijn er drie zones in de kookgrafiek (θ(Q)-grafiek).

① De stof blijft vloeibaar en stijgt in temperatuur, terwijl ze warmte opneemt

② De stof verandert van vloeibaar naar gas. Beide aggregatietoestanden komen tegelijk voor. De kooktemperatuur blijft constant, terwijl de stof warmte opneemt

③ De stof is gasvormig en stijgt in temperatuur, terwijl ze warmte opneemt

De condenseergrafiek verloopt omgekeerd in vergelijking met de kookgrafiek. De stof staat warmte af aan de omgeving.

De condensatietemperatuur en kooktemperatuur hebben dezelfde waarde.

Grootheid met symbool SI-eenheid met symbool kook-/condensatietemperatuur θk/c graden Celsius °C

` Maak oefening 6 en 7 op p. 166.

vloeibaar

▲ Afb. 118 Melk opstomen

OPDRACHT 33

Bestudeer de onderstaande grafieken.

©VANIN

Faseovergang

Temperatuur faseovergang

1 Noteer in de tabel om welke faseovergang het gaat. Kies uit: condenseergrafiek ethanol – kookgrafiek stikstof – smeltgrafiek kwik – stolgrafiek goud

2 Zoek in tabel 2 op p. 137 en tabel 3 op p. 143 de exacte temperatuur van elke faseovergang op en vul ze aan in de tabel hierboven.

3 Wat is latente warmte?

3.1 Latente warmte bij een faseovergang

Een systeem neemt warmte op van of staat warmte af aan de omgeving om een thermisch evenwicht te bereiken.

Als de opgenomen warmte Qop of de afgestane warmte |Qaf| zorgt voor de temperatuurverandering Δθ van een stof, noem je die warmte merkbare warmte. Door de warmte verandert de thermische energie (= inwendige kinetische energie) van de deeltjes. In de θ(Q)-grafieken die je in het begin van dit hoofdstuk zag (grafiek 17, 19 en 20), zijn de gebieden met merkbare warmte benoemd als zone ① en zone ③.

Als de opgenomen warmte Qop of de afgestane warmte |Qaf| zorgt voor een faseovergang, blijft de temperatuur constant. De warmte die wordt opgenomen of afgestaan, noem je latente warmte In de θ(Q)-grafieken uit het vorige deel (grafiek 17, 19 en 20) zijn de gebieden met latente warmte benoemd als zone ②

De latente warmte heeft zes verschillende benamingen, naargelang de faseovergang.

Dat wordt voorgesteld op de onderstaande afbeelding.

©VANIN

sublimatiewarmte

▲ Afb. 119 De verschillende soorten latente warmte

Je kunt de latente warmte verklaren door de inwendige energie van de stof te bestuderen. Een faseovergang betekent dat de inwendige potentiële energie van de stof verandert

• Om bij warmtetoevoer een faseovergang in gang te zetten, moet de inwendige kinetische energie groot genoeg zijn om de cohesiekrachten te overwinnen. De opgenomen warmte wordt gebruikt om de deeltjes verder van elkaar te brengen. De inwendige potentiële energie stijgt (naar een minder grote negatieve inwendige potentiële energie, zie Weetje op p. 148).

• Om bij warmteafvoer een faseovergang in gang te zetten, moet de inwendige kinetische energie klein genoeg zijn om de cohesiekrachten te laten inwerken. De inwendige potentiële energie daalt (naar een grotere negatieve inwendige potentiële energie).

De inwendige kinetische energie van de stof blijft constant tijdens latente warmteoverdracht, omdat de snelheid van de deeltjes niet verandert tijdens de faseovergang. De totale inwendige energie is toe- of afgenomen met de warmte die werd opgenomen of afgestaan tijdens de faseovergang.

Cohesiekrachten zijn het resultaat van de elektrische aantrekking en afstoting tussen atomen als gevolg van de positieve protonen in de kern en de negatieve elektronen op de schil. Op een bepaalde afstand tussen atomen is er een evenwicht tussen afstoting en aantrekking. De deeltjes hebben er een vaste positie. Die afstand (r0) wordt bepaald door de temperatuur en de stofsoort.

De inwerkende krachten veroorzaken een inwendige potentiële energie die afhankelijk is van de afstand. De grafiek toont het verloop van de inwendige potentiële energie.

©VANIN

Grafiek 22 Inwendige potentiële energie tussen deeltjes

In de vaste fase bevinden de deeltjes zich op een afstand r0 De inwendige potentiële energie is het kleinst (een sterk negatieve waarde).

Als de afstand toeneemt (vloeistoffen), stijgt de inwendige potentiële energie. Op een grote afstand (gassen) wordt ze nul.

We bespreken de verandering van inwendige potentiële energie voor de verschillende faseovergangen.

1 Smelt- en stolwarmte

Op grafiek 17 op p. 138 zie je het temperatuurverloop tijdens het smelten van een stof. Smelten begint bij de smelttemperatuur. Tijdens het smelten (zone 2 op de grafiek) wordt er warmte toegevoegd (de smeltwarmte), zonder dat de temperatuur stijgt. Er zijn sterke cohesiekrachten bij een vaste stof. Door warmtetoevoer worden de verbindingen verbroken De deeltjes kunnen na het smelten vrij bewegen ten opzichte van elkaar in de vloeistof. De cohesiekrachten zijn kleiner geworden en de deeltjes bevinden zich iets verder uit elkaar. De inwendige potentiële energie is toegenomen.

Stollen is het omgekeerde proces: de warmte die afgestaan wordt, resulteert in een afname van de inwendige potentiële energie en een versterking van de cohesiekrachten.

smelten: inwendige potentiële energie neemt toe door warmtetoevoer stollen: inwendige potentiële energie neemt af door warmteafvoer

2 Verdampings- en condensatiewarmte

Op grafiek 20 op p. 144 zie je het temperatuurverloop tijdens het koken van een stof. Tijdens het koken (zone 2 op de grafiek) wordt er warmte toegevoegd (de verdampingswarmte), zonder dat de temperatuur stijgt. Bij een vloeistof zijn er matige cohesiekrachten. Door warmtetoevoer worden de verbindingen verbroken: de stof wordt gasvormig en de deeltjes kunnen helemaal vrij bewegen ten opzichte van elkaar. De cohesiekrachten worden verwaarloosbaar klein. De inwendige potentiële energie is toegenomen tot (bijna) nul.

Verdampen treedt op bij elke temperatuur. De verdampingssnelheid neemt toe met de temperatuur, omdat deeltjes met een hoge kinetische energie makkelijker de cohesiekrachten overwinnen als er warmte wordt toegevoegd. Bij koken treedt de verdamping niet enkel op aan het oppervlak, maar ook in de vloeistof. Als de kooktemperatuur wordt bereikt, is de kinetische energie zo groot dat alle deeltjes de cohesiekrachten kunnen overwinnen.

Condenseren is het omgekeerde proces: de warmte die afgestaan wordt, resulteert in een afname van de inwendige potentiële energie

k constant → Ekin, inw = constant

vloeibaar

vloeibaar + gasvormig gasvormig

©VANIN

verdampen: inwendige potentiële energie neemt toe door warmtetoevoer condenseren: inwendige potentiële energie neemt af door warmteafvoer

Bij warmte-uitwisseling kun je twee types warmte onderscheiden.

Merkbare warmte Latente warmte binnen een fase bij een faseovergang:• smelten stolwarmte • verdampings- en condensatiewarmte temperatuur van de stof verandert temperatuur van de stof is constant inwendige kinetische energie verandertinwendige potentiële energie verandert

Het leven op aarde is mogelijk door de aanwezigheid van water. Niet enkel de hoeveelheid water (de aarde is voor 70 % bedekt met water), maar ook de aanwezigheid van ijs is cruciaal om de temperatuur onder controle te houden.

Wil je meer weten over het belang van ijs voor het klimaat en over de volumeverandering wanneer stoffen smelten en stollen? Kijk dan zeker in de ontdekplaat ‘Fysica van het klimaat’.

ontdekplaat

WEETJE

3.2 Grootteorde van de merkbare en latente warmte

OPDRACHT 34

Bestudeer de ernst van brandwonden door warm water.

1 Duid in de onderstaande zin je voorspelling aan.

Brandwonden door stoom op 100 °C zijn altijd / soms / nooit schadelijker dan brandwonden door kokend water op 100 °C (voor een gelijke massa water en stoom).

2 Bestudeer de grafiek en vul de tabel aan.

▲ Grafiek 23

Condenseergrafiek voor 300 g water

a Hoe groot is de temperatuurverandering van het water?

b Hoeveel warmte is er afgestaan aan de omgeving?

Zone 1Zone 2Zone 3

3 Vergelijk de grootte van de latente warmte met die van de merkbare warmte. Wat valt je op?

4 Bekijk opnieuw je hypothese uit stap 1. Hoe kun je aantonen wat het schadelijkst is?

Wanneer je warmte toevoert aan of afvoert van een stof, kunnen de temperatuur en de fase van die stof veranderen. De grootte van de merkbare warmte en latente warmte hangt af van de stofsoort, de hoeveelheid stof en het type faseovergang

We bekijken de grootteorde van de merkbare en latente warmte aan de hand van een aantal toepassingen.

▲ Afb. 122 Stoom kan ernstige brandwonden veroorzaken.

VOORBEELD ZWETEN BIJ MENSEN EN HONDEN

Als onze lichaamstemperatuur te hoog wordt, beginnen we te zweten. De zweetdruppels nemen lichaamswarmte op om te verdampen, waardoor ons lichaam afkoelt.

Om 10 gram zweet te laten verdampen, is er Qaf = 25 kJ warmte nodig.

Dat is evenveel als de energie die je nodig hebt om 6 kg water 1 °C op te warmen. De mens kan tot 10 L zweten op een dag, naargelang de inspanningen.

Honden hebben geen zweetklieren op hun huid. Enkel via hun poten en hun bek kunnen ze warmte afstaan. Dat verklaart waarom honden hijgen bij de inspanning.

VOORBEELD BLOESEMS BESCHERMEN TEGEN NACHTVORST

In het voorjaar kunnen bloesems kapotgaan door (nacht)vorst. Als die kans bestaat, sproeit men water. Dat water stolt en geeft daarbij warmte af. Zolang er nieuw water bijkomt om te stollen, zal de temperatuur van de takken niet onder het stolpunt (0 °C) dalen.

20 g water met een temperatuur van 5 °C staat een grote hoeveelheid warmte af om volledig te bevriezen:

Qaf = Qkoelen + Qst = 0,42 kJ + 6,68 kJ = 7,10 kJ. Er wordt ongeveer zestien keer meer warmte afgestaan tijdens het stolproces dan tijdens het koelproces.

VOORBEELD HEATPIPE

Bij de koeling van computerelementen kan men heatpipes gebruiken. Dat zijn dunne buisjes met een vloeistof die warmte opneemt van de processor en daardoor verdampt. Het gas stroomt verder naar de koelvinnen, waar het opnieuw condenseert door de warmte af te geven aan de omgeving. Een ventilator versnelt de warmteafvoer naar de omgeving.

De vloeistof blijft in een gesloten circuit en ondergaat voortdurend die faseovergangen. De grote verdampingswarmte en condensatiewarmte zorgen voor een efficiënt transport van warmte.

©VANIN

De grootte van de latente warmte hangt af van de stofsoort, de hoeveelheid stof en het type faseovergang De latente warmte heeft een grote waarde in vergelijking met de merkbare warmte.

` Maak oefening 8 en 9 op p. 166-167.

▲ Afb. 123 Honden koelen hoofdzakelijk af via hun mond.

▲ Afb. 124 Stollingswarmte beschermt bloesems tegen vrieskoude.

▲ Afb. 125 Vloeistof in de buizen zorgt voor koeling door faseovergangen.

4 Hoe groot is de latente warmte bij een faseovergang?

4.1 Specifieke smelt- en stolwarmte

OPDRACHT 35

Bestudeer de invloedsfactoren op de smeltwarmte.

1 Bestudeer de voorbeelden met waarnemingen.

2 Duid de stelling aan die hoort bij de afbeelding en de bewering, en maak ze vervolgens correct.

Hoe meer ijsblokjes je in een glas water legt, hoe meer het water afkoelt.

Om een hoeveelheid zilver te smelten, is er meer warmte nodig dan om dezelfde hoeveelheid goud te smelten.

De hoeveelheid warmte die het ijs kan opnemen om volledig te smelten, neemt toe met / neemt af met / is onafhankelijk van de massa.

De smelttemperatuur van het ijs neemt toe met / neemt af met / is onafhankelijk van de massa.

De hoeveelheid warmte die het ijs kan opnemen, is afhankelijk / onafhankelijk van de stofsoort.

De hoeveelheid warmte die het metaal kan opnemen om volledig te smelten, neemt toe met / neemt af met / is onafhankelijk van de massa.

De smelttemperatuur van het metaal neemt toe met / neemt af met / is onafhankelijk van de massa.

De hoeveelheid warmte die het metaal kan opnemen, is afhankelijk / onafhankelijk van de stofsoort.

De hoeveelheid warmte die nodig is om een stof volledig te laten smelten of stollen, hangt af van de massa van het systeem en de stofsoort.

De warmte in een calorimeter wordt toegevoegd met een elektrisch verwarmingselement. Je kunt de toegevoegde warmte bepalen aan de hand van het vermogen en het tijdsverloop:

Smeltwarmte bij verschillende massa’s van een stof op smelttemperatuur θ sm

©VANIN

▲ Afb. 128

De smeltwarmte Qsm is de warmte die wordt opgenomen om een hoeveelheid van een stof volledig te laten smelten. Het volledige proces gebeurt bij de smelttemperatuur θ sm van de stof.

sm (J)

(kg)

▲ Grafiek 24 Smeltwarmte in functie van de massa

De Qsm(m)-grafiek is een rechte door de oorsprong. Er is een recht evenredig verband tussen de smeltwarmte en de massa: Qsm ~ m. Als de massa verdubbelt, verdubbelt de smeltwarmte.

Uit de helling van de grafiek kun je aflezen hoeveel smeltwarmte er nodig is om een bepaalde massa te smelten. Dat is een constante waarde, gegeven is door Qsm m .

Die evenredigheidsconstante noem je de specifieke smeltwarmte ℓ sm .

ℓ sm = Qsm m

De specifieke smeltwarmte ℓ sm geeft aan hoeveel energie je moet toevoegen om een systeem van 1 kg volledig te smelten op de smelttemperatuur.

De SI-eenheid van de specifieke smeltwarmte is J kg . De specifieke smeltwarmte is afhankelijk van de soort stof. Het is een stofeigenschap. In tabel 4 zie je enkele voorbeelden.

Specifieke smeltwarmte ℓ sm Stof ℓ sm ( kJ kg )

Tabel 4 Specifieke smeltwarmte bij normdruk (1 013 hPa)

VOORBEELD IJS EN CHOCOLADE SMELTEN

▲ Afb. 129 IJs en chocolade smelten

Voor water bedraagt de specifieke smeltwarmte:

ℓsm, water = 334 kJ kg

Om 2,0 kg ijs (van 0 °C) volledig om te zetten naar water, heb je warmte nodig:

Qsm = ℓ sm ∙ m = 334 kJ kg ∙ 2,0 kg = 6,7 ∙ 105 J

Voor chocolade bedraagt de specifieke smeltwarmte:

ℓsm, chocolade = 150 kJ kg

Om 2,0 kg chocolade volledig om te zetten naar de vloeibare toestand, heb je minder warmte nodig:

Qsm = ℓ sm ∙ m = 150 kJ kg ∙ 2,0 kg = 3,0 ∙ 105 J

De stolwarmte Qst is de latente warmte die vrijkomt als de vloeistof volledig stolt. Die warmte is negatief, omdat de stof warmte afstaat aan de omgeving. Je kunt de stolwarmte als volgt berekenen:

Qst = –ℓ sm ∙ m

De specifieke stolwarmte ℓst is even groot als de specifieke smeltwarmte. De grootte van de stolwarmte kun je als volgt berekenen:

|Qst| = ℓst ∙ m

OPDRACHT 36

Los het vraagstuk op.

Een chocolatier laat 100 g chocolade met een temperatuur van 40 °C afkoelen tot een paasei op kamertemperatuur (20 °C).

1 Hoe groot is de warmte die wordt afgestaan tijdens het koelproces?

2 Stel het proces voor op een stolgrafiek.

Chocolade stolt bij 30 °C. De specifieke warmtecapaciteit voor vaste chocolade bedraagt 1,8 kJ kg ∙ °C , die voor de vloeibare toestand 1,6 kJ kg ∙ °C . De specifieke stolwarmte is –150 kJ kg

Gegeven:

Gevraagd: Qaf = ?

Oplossing: Chocolade stolt bij 30 °C.

Terwijl de chocolade afkoelt van 40 °C tot 20 °C, is er een faseovergang.

Je kunt de totale warmte berekenen door de warmte te berekenen in elke zone.

Neem de absolute waarde om de grootteorde van de warmte te bekomen.

|Qch, vl|

|Qch, st|

|Qch, v|

▲ Afb. 130 Chocolade laten stollen in een vorm

OPDRACHT 36 (VERVOLG)

De totale warmte die afgestaan wordt, is de som van de merkbare warmte (zone ① en ③) en de latente warmte (zone ②).

De θ(Q)-grafiek is de stolgrafiek. Chocolade heeft een stoltemperatuur van 30 °C.

▲ Grafiek 25 Stolgrafiek van chocolade

Controle: • Bestudeer de berekende waarden. Klopt de eenheid?

• Vergelijk de merkbare en de latente warmte. Wat stel je vast?

Om volledig te smelten bij de smelttemperatuur, neemt een hoeveelheid vaste stof met massa m en specifieke smeltwarmte ℓ sm een hoeveelheid smeltwarmte Qsm op die gelijk is aan:

Qsm = ℓ sm ∙ m

De stolwarmte is negatief:

Qst = –ℓ sm ∙ m = ℓst ∙ m

Grootheid met symbool

SI-eenheid met symbool specifieke smelt-/ stolwarmte ℓsm/st joule per kilogram J kg

4.2 Specifieke verdampings- en condensatiewarmte

OPDRACHT 37 ONDERZOEK

Onderzoek de grootte van de specifieke verdampingswarmte van water aan de hand van Labo 08 op .

©VANIN

De hoeveelheid warmte die nodig is om een stof volledig te laten verdampen of condenseren, hangt af van de massa van het systeem en de stof

Qv (J)

m (kg)

▲ Grafiek 26 Verdampingswarmte in functie van de massa

De verdampingswarmte Qv is de warmte die een stof opneemt om een hoeveelheid van die stof volledig te laten verdampen. Het volledige proces gebeurt bij de kooktemperatuur θk van de stof.

Net zoals bij het smelten, is de Qv(m)-grafiek een rechte door de oorsprong. Er is een recht evenredig verband tussen de smeltwarmte en de massa: Qv ~ m. Als de massa verdubbelt, verdubbelt de verdampingswarmte.

Uit de helling van de grafiek kun je aflezen hoeveel smeltwarmte er nodig is om een bepaalde massa te verdampen. Dat is een constante waarde, gegeven door Qv m , die afhankelijk is van de stof. Die evenredigheidsconstante noem je de specifieke verdampingswarmte ℓ v ℓ v = Qv m

De specifieke verdampingswarmte ℓ v geeft aan hoeveel energie een systeem van 1 kg moet opnemen om volledig te verdampen op de kooktemperatuur.

De SI-eenheid van de specifieke verdampingswarmte is J kg .

De specifieke verdampingswarmte is afhankelijk van de soort stof. Het is een stofeigenschap. In tabel 5 zie je enkele voorbeelden.

Specifieke verdampingswarmte ℓ v

ℓ v ( kJ

)

©VANIN

▲ Tabel 5 Specifieke verdampingswarmte bij normdruk (1 013 hPa)

De condensatiewarmte Qc is de latente warmte die vrijkomt als het gas volledig condenseert. De specifieke condensatiewarmte ℓ c is even groot als de specifieke verdampingswarmte.

De condensatiewarmte is negatief, omdat de stof warmte afstaat aan de omgeving. Je kunt die warmte als volgt berekenen:

Qc = –ℓ v ∙ m

De grootte van de condensatiewarmte kun je als volgt berekenen: |Qc| = ℓ c ∙ m

Om volledig te verdampen bij de kooktemperatuur, neemt een hoeveelheid vaste stof met massa m en specifieke verdampingswarmte ℓ v een hoeveelheid verdampingswarmte Qv op die gelijk is aan:

Qv = ℓ v ∙ m

De condensatiewarmte is negatief: Qc = –ℓ v

Grootheid met symbool SI-eenheid met symbool specifieke verdampings-/ condensatiewarmte ℓc/v joule per kilogram J kg

` Maak oefening 10 t/m 13 op p. 167-168.

OPDRACHT 38

Los het vraagstuk op.

In een theeketel met warmtecapaciteit Cketel = 400 J °C zit 1,000 kg water met een begintemperatuur θbegin = 23,0 °C.

Door onoplettendheid laat je de ketel te lang op het vuur staan en verdampt de helft van het water voordat je de ketel verzet.

1 Schets de θ(Q)-grafiek.

2 Bereken de totale warmte die het water en de ketel hebben opgenomen.

▲ Afb. 131 Waterdamp ontsnapt tijdens het koken.

3 Controleer je antwoord via

4.3 Warmtebalans bij faseovergangen

OPDRACHT 39

Bestudeer de onderstaande opgave en stel de warmtebalans op. In een sauna doet men vaak een scheut water op de hete stenen of kachel. Het water wordt fel opgewarmd en er ontstaat stoom. De warmte die uitgewisseld wordt, kun je voorstellen met een warmtebalans.

1 Noteer welk systeem er warmte opneemt en welk systeem warmte afgeeft.

• systeem dat warmte opneemt:

• systeem dat warmte afgeeft:

2 De stenen hebben een starttemperatuur van 400 °C. Het water begint op 30 °C. Beide bereiken een thermisch evenwicht op 130 °C. Welk van de onderstaande θ(t)-grafieken hoort bij die beschrijving?

3 Schrijf bij de gekozen grafiek de symbolen voor merkbare/latente warmte (bv. Qstenen) bij de lijnen die ze vertegenwoordigen.

4 Een warmtebalans steunt op de wet van behoud van energie: Qop = |Qaf|. Schrijf alle symbolen die je op de grafiek hebt aangeduid, aan de juiste kant van de balans.

▲ Afb. 132 Het water verdampt op de lavastenen in de sauna.

Een paar ijsblokjes in een glas frisdrank zijn welkom op een warme zomerdag. Het ijs zal warmte opnemen uit zijn omgeving (de frisdrank) om te smelten. Uiteindelijk wordt er een eindtemperatuur bereikt die lager ligt dan de begintemperatuur van de frisdrank. Een faseovergang van een stof kan gepaard gaan met een streven naar een thermisch evenwicht met de omgeving.

Als je twee systemen met een verschillende temperatuur met elkaar in contact brengt, is er warmte-uitwisseling totdat er een thermisch evenwicht is. Daarbij kan er ook een faseovergang gebeuren, die samen met de begintemperatuur en de warmtecapaciteit van elk systeem een invloed zal hebben op de eindtemperatuur.

Volgens de wet van behoud van energie kan energie niet gemaakt of vernietigd worden, maar wordt ze overgedragen van één systeem naar een ander. Als er geen warmte-uitwisseling is met de omgeving, is de hoeveelheid afgestane warmte (Qaf ) door het systeem met de hoge temperatuur even groot als de hoeveelheid opgenomen warmte (Qop) door het systeem met de lage temperatuur. Dat kun je noteren met een warmtebalans:

Qop = |Qaf|

De warmte die wordt opgenomen of afgestaan door een systeem, kan zowel merkbare als latente warmte zijn.

Merkbare warmte Latente warmte binnen een fase bij een faseovergang temperatuur van het systeem verandert temperatuur van het systeem is constant

• voor een systeem: Q = C sys ∙ Δθ

• voor een stof: Q = cstof ∙ m ∙ Δθ

(c is afhankelijk van de fase en de stof.)

©VANIN

• opnemen: Q = ℓ ∙ m

• afstaan: Q = –ℓ ∙ m

(ℓ is afhankelijk van de faseovergang en de stof.)

Het uitwerken van het behoud van energie voor systemen die warmte uitwisselen, noem je de warmtebalans: als je voorwerpen met een verschillende begintemperatuur bij elkaar brengt in een geïsoleerd systeem, is (volgens de wet van behoud van energie) de warmtehoeveelheid Qop die opgenomen wordt, even groot als de warmtehoeveelheid Qaf die afgestaan wordt: Qop = |Qaf|. Tijdens de warmte-uitwisseling kan een stof van aggregatietoestand veranderen.

` Maak oefening 14 t/m 17 op p. 168.

OPDRACHT 40 VOORBEELDOEFENING

Bestudeer het uitgewerkte vraagstuk.

Lana wil haar beker (Cbeker = 250 J °C ) met 200 g frisdrank met een temperatuur van 20,0 °C koelen. Ze legt er ijsblokjes van –15,0 °C in. De eindtemperatuur van de frisdrank is 12,0 °C.

Welke massa hebben de ijsblokjes?

(Gebruik voor de frisdrank de specifieke warmtecapaciteit en de latente warmte van water.)

Gegeven en gevraagd:

θb, frisdrank = θb, glas = 20,0 °C

mfrisdrank = 200 g

cfrisdrank = 4 186 J kg ∙ °C

Cbeker = 250 J °C

▲ Afb. 134

©VANIN

θb, ijs = –15,0 °C

cijs = 2 100 J kg ∙ °C

ℓsm, ijs = 334 kJ kg

mijs = ?

θeind = 12,0 °C

Oplossing:De θ(Q)-grafiek stelt het verwachte verloop voor.

θ (°C)

beker en frisdrank: staan warmte af ijsblokje: neemt warmte op

▲ Grafiek 27 Temperatuurverloop van de beker en de frisdrank (afkoeling zonder faseovergang) en het ijsblokje (smeltproces)

Om de massa van de ijsblokjes te vinden, moet je de warmtebalans opstellen:

Qop = |Qaf|

• Systeem dat warmte opneemt: ijsblokjes

Het ijs warmt op tot 0 °C en smelt tot water.

Het water warmt verder op tot de eindtemperatuur.

De massa van het ijs verandert niet tijdens dat proces.

Qop = Qijs + Qsm + Qwater

Daarbij geldt:

Qijs = cijs ∙ mijs ∙ Δθijs (merkbare warmte ijs van –18,0 °C tot 0,0 °C)

Qsm = ℓsm, ijs ∙ mijs (smeltwarmte ijs bij 0 °C)

Qwater = cwater ∙ mwater ∙ Δθwater (merkbare warmte water van 0,0 °C tot 12,0 °C)

▲ Afb. 133 IJsblokjes koelen de frisdrank.

OPDRACHT 40 (VERVOLG) VOORBEELDOEFENING

• Systeem dat warmte afstaat: frisdrank en beker

De beker met frisdrank koelt af.

Er is geen faseovergang.

|Qaf| = |Qfrisdrank + Qbeker|

Daarbij geldt:

|Qfrisdrank| = cfrisdrank ∙ mfrisdrank

|Δθfrisdrank|

(merkbare warmte frisdrank van 20,0 °C tot 12,0 °C)

|Qbeker| = Cbeker ∙ |Δθbeker|

(merkbare warmte beker van 20,0 °C tot 12,0 °C)

Als je die uitdrukkingen combineert, vind je de warmtebalans:

frisdrank| + Cbeker

|Δθbeker|

Je kunt de warmtebalans oplossen door de vergelijking met onbekende mijs op te lossen.

De oplossing vind je op .

Je vindt als oplossing: mijs = 21 g.

Controle:• Bestudeer de berekende waarden. Klopt de eenheid?

Ja, g is een eenheid van massa.

• Is de grootteorde realistisch?

Ja, 21 g water is 21 cm³ groot, ongeveer het volume van vijf ijsblokjes.

OPLOSSINGSSTRATEGIE

• Beschrijf in je eigen woorden wat er gebeurt.

• Stel de situatie schematisch voor:

– Maak een schets van de begin- en eindsituatie.

– Noteer de gegevens en het gevraagde bij je tekeningen.

Let op de verwijzingen in subscript.

– Maak een θ(t)- of θ(Q)-grafiek met de gegevens en het gevraagde.

• Gebruik de warmtebalans Qop = |Qaf| om het gevraagde te berekenen:

– Ga na welke systemen en stoffen warmte opnemen of afgeven.

– Bereken de warmtehoeveelheden met de formules voor merkbare en/of latente warmte.

– Vul de gegevens in en werk wiskundig uit naar de onbekende.

• Controleer je antwoord:

– Komt de berekende waarde overeen met je schematische voorstelling?

– Kloppen de eenheid en de grootteorde van de massa’s en de warmtecapaciteiten?

Tot nu toe bestudeerde je de faseovergangen bij atmosferische druk.

Als je de druk verandert, zijn er verschuivingen in de temperatuur van de faseovergang.

Dat leidt tot interessante technologische toepassingen.

Je leert er meer over op

De warmte die nodig is om een stof te laten veranderen van aggregatietoestand, is vernoemd naar de faseovergang.

• Bij een faseovergang in een rode pijl het systeem warmte van de omgeving.

• Bij een faseovergang in een blauwe pijl het systeem warmte aan de omgeving.

Smeltof kookgrafiek:

• zone ① : De vaste stof / vloeistof neemt warmte op. De E kin, inw . • zone ② : De stof smelt / verdampt op een constante smelttemperatuur θ sm / kooktemperatuur θ k .

Ze neemt smeltwarmte / verdampingswarmte op om de te verzwakken, waardoor de E pot, inw . • zone ③ : De vloeistof / het gas neemt warmte op. De E kin, inw . Bij het stollen / condenseren wordt warmte afgestaan. De grafiek verloopt omgekeerd, waarbij de stoltemperatuur θ st = θ sm / condensatietemperatuur θ c = θ v .

Qsub desublimatie-warmteQdesub

• De latente warmte die wordt opgenomen of afgestaan voor een faseovergang, is afhankelijk van de en de .

• Wanneer er een thermisch evenwicht gevormd wordt tussen systemen, kan er een faseovergang ontstaan. De geeft aan dat de opgenomen warmte is als de afgestane warmte: Q op = | Q af |.

• Je kunt de grootte van de atente warmte vinden met de formule Q = , waarbij ℓ afhankelijk is van de stof en de faseovergang.

• De opgenomen of afgestane warmte kan bestaan uit merkbare warmte, waarbij de stof , of latente warmte, waarbij de stof een ondergaat.

1 Begripskennis

• Ik kan de verschillende vormen van faseovergangen bij warmte opnemen of afgeven omschrijven

• Ik kan het temperatuurverloop van een stof die een faseovergang ondergaat, omschrijven

• Ik kan latente warmte omschrijven

• Ik kan de invloed van latente warmte op de inwendige energie van een systeem omschrijven

• Ik kan de specifieke smelten stol-, verdampings- en condensatiewarmte van een stof omschrijven.

• Ik kan de latente warmte die een stof opneemt of afgeeft, berekenen

• Ik kan verdampen, condenseren, smelten en/of stollen omschrijven en een warmtebalans opstellen.

• Ik kan een warmtebalans met een faseovergang berekenen

2 Onderzoeksvaardigheden

• Ik kan een onderzoek uitvoeren volgens een gegeven stappenplan.

• Ik kan samenwerken om tot onderzoeksresultaten te komen.

• Ik kan nauwkeurig berekeningen uitvoeren met afgelezen waarde.

• Ik kan een thermometer aflezen

• Ik kan het verband tussen grootheden onderzoeken en benoemen.

` Je kunt deze checklist ook op invullen.

JANOG OEFENEN

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’.

Je kunt de oplossingsstrategie en de voorbeeldoefeningen op gebruiken als extra ondersteuning.

Welke faseovergang(en) treden op in de onderstaande voorbeelden?

a Een ijssalon maakt zijn eigen ijs.

b Bij koud weer komen er wolkjes uit je mond.

c Op een koud glas frisdrank vormen zich druppels aan de buitenkant.

d Er vormen zich ijskristallen op de producten in de diepvries.

e Mist klaart op in de loop van de ochtend.

Wie heeft gelijk? Verklaar.

Halina: Deze jas zal ervoor zorgen dat de sneeuwman trager smelt wanneer de dooi begint. 3 4 5

Idris: Je mag een sneeuwman geen jas aandoen. Hij zal smelten.

Vince: Ik denk dat het geen verschil uitmaakt of de sneeuwman een jas draagt of niet.

Water bevriest. Welke faseovergang bedoelt men daarmee?

Is het stollen van een ei een faseovergang? Beargumenteer je antwoord.

Als je in het zwembad stapt, voelt dat koud aan. Als je eruit komt, voelt dat ook koud aan. Verklaar dat fenomeen.

Maak de onderstaande uitspraken correct.

a De smelttemperatuur ligt altijd / soms / nooit onder 0 °C.

b De kooktemperatuur is altijd / soms / nooit hoger dan de smelttemperatuur.

c De nodige warmte voor een faseovergang hangt altijd / soms / nooit af van de hoeveelheid stof.

d Wanneer een stof verdampt, staat ze altijd / soms / nooit warmte af aan de omgeving.

e De temperatuur van kokend water stijgt altijd / soms / nooit als de bellen groter worden.

f Zuurstof is altijd / soms / nooit vloeibaar.

Wie heeft gelijk? Verklaar.

Leg via het deeltjesmodel de verschillende invloedsfactoren op de vrije verdamping uit.

Helena: Je kunt hete bellen zien

het kokende water.

Yara: Dat zijn onzuiverheden in het water.

Imran: Nee, het zijn hete luchtbellen.

Simon: Ik denk dat het in gas veranderde waterbellen zijn.

Kato: Volgens mij zijn het bellen van zuurstof en waterstof.

Maak de uitspraken correct en verklaar.

a IJs is een goed koelmiddel omdat het een grote / kleine smeltwarmte heeft.

b Nomaden maken hun veldfles uit dierenhuid nat omdat water een grote / kleine verdampingswarmte heeft.

c Je verbrandt jezelf meer / minder aan kaarsvet van 70 °C dan aan water van 70 °C.

d Een druppel ether verdampt makkelijker / moeilijker dan een druppel water.

e Het is makkelijker / moeilijker om een hoeveelheid ijs met een temperatuur van 0 °C volledig te smelten, dan om dezelfde hoeveelheid water met een temperatuur van 100 °C volledig te laten verdampen.

Leg de volgende uitspraken uit in je eigen woorden.

a De specifieke stolwarmte van ijzer is –247 kJ kg .

b De specifieke verdampingswarmte van ether is 377 J g

William blaast een theelichtje uit. In het aluminium omhulsel bevindt zich nu 5,0 g paraffine op smelttemperatuur. De specifieke smeltwarmte bedraagt 190 kJ kg . Bereken hoeveel warmte er vrijkomt tijdens het stollen.

Je stopt 1,00 kg soep (c = 3 851 J kg ∙ °C ) met een temperatuur van 20 °C in een diepvries met een nuttig vermogen van 15 W. Hoelang duurt het (in uren) vooraleer de soep volledig bevroren is? (Gebruik als stoltemperatuur 0 °C.)

14 15 16 17

Destillatie is een techniek om twee of meer stoffen in een oplossing te scheiden door middel van verdamping. Die techniek is gebaseerd op het verschil in kookpunt van de stoffen. De verschillende componenten van het mengsel condenseren tegen de wanden van de destillatiekolf.

a Tot welke temperatuur moet je een mengsel van water en ethanol verwarmen om het in fracties te scheiden? Verklaar je antwoord.

θmengsel < 78 °C

78 °C < θmengsel

78 °C < θmengsel < 100 °C

θmengsel > 100 °C

b Bereken de hoeveelheid warmte die vrijkomt als 22,5 cL ethanol op kooktemperatuur condenseert en afkoelt tot 16 °C.

Een calorimeter met een warmtecapaciteit van 110 J °C bevat 250 g water met een temperatuur van 5,0 °C. Daaraan voeg je 720 g ijs toe. Bij het thermisch evenwicht blijkt er 30 g ijs meer te zijn. Bepaal: a de temperatuur bij thermisch evenwicht; b de begintemperatuur van het ijs.

Je legt een onbekende hoeveelheid ijsblokjes met een temperatuur van –18,0 °C in 300 g water met een temperatuur van 25,0 °C. Het thermisch evenwicht wordt bereikt op 8,0 °C. Bereken de massa van het ijs.

Aan 100 g ijs met een temperatuur van 0 °C wordt 100 g kokend water met een temperatuur van 100 °C toegevoegd. Welke grafiek beschrijft het best de temperatuur van het water en het ijs in functie van de tijd? Verwaarloos de invloed van het vat.

Bestudeer deze smeltgrafiek van een stof.

a Welk deel is de latente warmte?

b Welk verband bestaat er tussen de specifieke warmtecapaciteit van deze stof in de vaste fase en in de vloeibare fase?

cvast = cvloeibaar

2 ∙ cvast = cvloeibaar

cvast = 2 ∙ cvloeibaar

Je kunt daarover geen uitspraak doen.

` Verder oefenen? Ga naar

Thermodynamica: onderdeel van de fysica dat de toestandsveranderingen (druk, temperatuur, volume, aggregatietoestand) tijdens processen van een systeem bestudeert

Temperatuurverandering Faseovergang van een systeem voor een systeem

Als een systeem warmte opneemt of afgeeft, treden er faseovergangen op waarbij de temperatuur niet verandert. De latente warmte is afhankelijk van de soort stof en de massa, waarbij Q = ℓ ∙ m .

De temperatuurverandering ∆ θ is afhankelijk van de warmte Q , de massa m en de specifieke warmtecapaciteit c , waarbij Q = c ∙ m

De temperatuurverande ring ∆ θ is afhankelijk van de warmte Q en de warmtecapaciteit C , waarbij Q = C ∙ ∆ θ . voor een stof

Deeltjes die warmte opnemen tijdens een faseovergang, verzwakken de cohesiekrachten en nemen meer afstand ten opzichte van andere deeltjes. De inwendige potentiële energie E p, inw stijgt. Als de deeltjes warmte afstaan, versterken ze de cohesiekrachten. De inwendige potentiële energie daalt.

Deeltjes die warmte opnemen , bewegen/trillen sneller . De inwendige kinetische energie E kin, inw stijgt . Als de deeltjes warmte afstaan, daalt hun bewegingssnelheid en daalt dus de inwendige kinetische energie. Er is merkbare warmte .

Systemen met een onderling temperatuurverschil zullen warmte uitwisselen tot ze het thermisch evenwicht bereikt hebben. In een geïsoleerd systeem geldt de wet van behoud van energie: Q op = | Q

©VANIN

Toestand van een gas

= constant gaswet van Boyle-Mariotte isochoor proces , zijn constant → = constant drukwet van Gay-Lussac isobaar proces , zijn constant → = constant volumewet van Gay-Lussac

isotherm proces , zijn constant

Notities

ELEKTRISCHE SYSTEMEN 03 THEMA

Acht vleugels met daarop gigantische zonnepanelen zorgen voor de energievoorziening van het internationaal ruimtestation (ISS). Dat beschrijft in 90 minuten een baan rond de aarde, waarbij de zonnepanelen het telkens 35 minuten zonder invallend zonlicht moeten stellen. Om die periodes van ‘zonsverduistering’ op te vangen, gebruikt men Li-ionbatterijen, die de nodige energie kunnen opslaan.

` Hoe bepaalt het aantal zonnepanelen het aantal toestellen dat men kan gebruiken?

` Hoe moet men de toestellen in het ISS schakelen om ze optimaal te laten functioneren?

We zoeken het uit!

Welke eigenschappen heeft een elektrische kring?

LEERDOELEN

Je kunt al:

een eenvoudige elektrische stroomkring bouwen en een lampje laten branden; energieverschil en druk begrijpen als de oorzaak van een waterstroom; energieomzettingen omschrijven; vermogen omschrijven als de energieomzetting in een tijdsverloop.

Je leert nu: de begrippen ‘lading’, ‘stroomsterkte’ en ‘spanning’ omschrijven; het verband tussen de spanning over en de stroomsterkte door een elektrische weerstand omschrijven en berekenen; de energie en het vermogen in een elektrische stroomkring berekenen.

1 Wat is elektrische stroom?

1.1 Elektrische stroom

OPDRACHT 1

Bestudeer de kenmerken van elektrische stroom.

1 Vul de tabel aan.

’s Morgens word je waarschijnlijk gewekt door je smartphone. Na een passage door de badkamer, nog snel een toast en misschien een kop koffie stap je op je fiets om naar school te vertrekken. In een uur tijd maak je gebruik van je smartphone, een elektrische tandborstel, een broodrooster en een koffiezet: allemaal toestellen die werken op elektriciteit. Maar wat is elektriciteit precies en wat is er nodig opdat de toestellen kunnen werken?

In dit hoofdstuk bestudeer je de grootheden lading, stroomsterkte, spanning en weerstand, en leer je de onderlinge verbanden ertussen kennen. Je leert hoe het vermogen dat in een toestel wordt opgewekt, gelinkt is aan die grootheden.

stromen? b Wat is de oorzaak van de stroom?

OPDRACHT 1 (VERVOLG)

2 Welke uitspraken zijn correct?

Duid aan.

Als er ladingen zijn, is er een elektrische stroom.

Als er bewegende ladingen zijn, is er een elektrische stroom.

Als er bewegende ladingen zijn in dezelfde richting en zin, is er een elektrische stroom.

Er kan een elektrische stroom zijn zonder bron.

Er kan geen elektrische stroom zijn zonder bron.

De beweging van voorwerpen en deeltjes kan chaotisch of geordend verlopen. De geordendebeweging van deeltjes in dezelfde richting en zin noem je een stroom. De stroom ontstaat door een externe oorzaak in de omgeving, de bron

Elektrische stroom is de beweging van ladingen in dezelfde richting en zin. Er zijn twee voorwaarden voor elektrische stroom:

1 Er moeten ladingen zijn die kunnen bewegen.

2 Er moet een oorzaak zijn die de ladingen in een ordelijke beweging brengt.

Het woord ‘elektriciteit’ is afgeleid van het Griekse ἠλεκτρον (èlektron), hetgeen ‘gele amber’ betekent. Amber heeft de bijzondere eigenschap om andere stoffen aan te trekken.

In een elektrische stroomkring gebruikt men metalen om de elektrische stroom te geleiden.

Die metalen noem je geleiders. In de metalen kunnen vrije elektronen vrij bewegen tussen de roosterionen.

In de lessen chemie leerde je over ladingen, de metaalbinding en de elektrische eigenschappen van metalen. Je kunt die leerstof opfrissen via en de video.

video: lading

WEETJE TIP

Als de geleider niet verbonden is met een bron in een stroomkring, is de beweging van de elektronen chaotisch. De elektronen bewegen kriskras door de geleider. Er is geen elektrische stroom. Dat kun je vergelijken met het water in een meer (afbeelding 138 en 139).

▲ Afb. 138 De elektronen bewegen kriskras door elkaar in een geleider.

▲ Afb. 139 De waterdeeltjes kunnen zich onderling verplaatsen.

Als in een werkende stroomkring de geleider verbonden is met een bron, verloopt de beweging van de elektronen in dezelfde richting en zin. Er is een elektrische stroom. Dat kun je vergelijken met het water in een rivier, waar de waterdeeltjes in beweging komen door een hoogteverschil.

▲ Afb. 140 De elektronen bewegen in dezelfde

Een elektrische stroom is de beweging van ladingen in dezelfde richting en zin Die wordt veroorzaakt door een bron.

Bij een onweer ontstaat door wrijving een ophoping van ladingen in de wolken. Als de ophoping te groot wordt, ontladen de wolken zich. Ladingen verplaatsen zich van de wolken naar de aarde. Er is een elektrische stroom, die we waarnemen als bliksem.

Signalen van en naar de hersenen zijn elektrische stromen. Geladen ionen verplaatsen zich doorheen het zenuwstelsel.

elektron

richting en zin door de geleider. Er is een elektrische stroom.

▲ Afb. 141 De waterdeeltjes bewegen in dezelfde richting en zin in de rivier. Er is een waterstroom.

▲ Afb. 142

▲ Afb. 143

WEETJE

1.2 Energieomzetting in een stroomkring

OPDRACHT 2

Bestudeer de energieomzetting in een stroomkring.

1 Noteer de energieverbruiker.

2 Noteer de energiebron.

3 Vul de energieomzettingen aan.

van de ladingen → van de elektronen

van de broodrooster

©VANIN

Waterkringloop

van het water

van de turbine

De bouw van en de energieomzetting in een elektrische stroomkring kun je vergelijken met een waterkringloop. Dat wordt voorgesteld op afbeelding 146 en 147. We bekijken de energieomzettingen in beide kringen.

Elektrische stroomkring

▲ Afb. 144

▲ Afb. 145

▲ Afb. 146 Een pomp zorgt ervoor dat het water potentiële zwaarte-energie krijgt, waardoor het water het rad kan doen draaien.

▲ Afb. 147 Een batterij geeft ladingen potentiële elektrische energie, waardoor de lamp kan branden.

1 Energieomzetting in een waterkringloop

In een waterkringloop stroomt het water door het hoogteverschil, dat voor potentiële zwaarte-energie zorgt. De potentiële energie van het water wordt omgezet in kinetische energie van het water. In de verbruiker wordt de kinetische energie van het water overgedragen naar energie van de verbruiker.

potentiële zwaarte-energie van het water → kinetische energie van het water → energie van de verbruiker

Om het water blijvend te laten stromen, moet de kring gesloten zijn en is er een energiebron nodig. De energiebron brengt het water omhoog. Die

energiebron

▲ Afb. 148 De warmte van de zon wordt omgezet in potentiële zwaarte-energie van het water.

VOORBEELD WATERTURBINE

In een stuwmeer wordt de potentiële zwaarte-energie omgezet in elektrische energie. De zon is de energiebron en de waterturbine is de verbruiker.

potentiële zwaarte-energie van het water → kinetische energie van het water → kinetische energie van de turbine → elektrische energie

De chemische energie in batterijen wordt omgezet in elektrische energie.

TIP

2 Energieomzetting in een elektrische stroomkring

In een elektrische stroomkring bezit de bron elektrische energie. Dat is een vorm van potentiële energie. De potentiële elektrische energie van de ladingen wordt omgezet in kinetische energie van de ladingen. In de verbruiker wordt de kinetische energie van de ladingen overgedragen naar energie van de verbruiker.

(potentiële) elektrische energie van de ladingen → kinetische energie van de ladingen → energie van de verbruiker

Om de ladingen blijvend te laten stromen, moet de kring gesloten zijn en is er een energiebron nodig. Die geeft de ladingen elektrische energie.

In de energiebron (batterij, waterkrachtcentrale, kerncentrale …) wordt een andere vorm van energie omgezet in elektrische energie.

De potentiële zwaarte-energie uit het hoger gelegen stuwmeer wordt omgezet in elektrische energie.

Door de splitsing van kernen wordt in de kerncentrale van Doel kernenergie omgezet in elektrische energie.

De animatie toont de rol van de energiebron in een watercircuit en een elektrische stroomkring, en de analogie daartussen.

VOORBEELD BUREAULAMP

©VANIN

animatie: analogie waterkringloop –elektrische stoomkring

Door de stekker van een bureaulamp in het stopcontact te steken, zorg je ervoor dat er ladingen met veel (potentiële) elektrische energie door de lamp kunnen lopen. Vervolgens gebeuren er deze energieomzettingen:

elektrische energie van de ladingen → kinetische energie van de ladingen → licht en warmte van de lamp

De bron levert potentiële elektrische energie aan de ladingen.

In de verbruiker wordt de energie omgezet in een andere energievorm.

elektrische energie van de ladingen → kinetische energie van de ladingen → energie van de verbruiker

` Maak oefening 1 en 2 op p. 200.

2 Wat zijn stroomsterkte en spanning?

2.1 Stroomsterkte

A Betekenis

OPDRACHT 3

Bestudeer de zin en de grootte van de stroom.

1 Open de applet.

2 Bouw de weergegeven kring na.

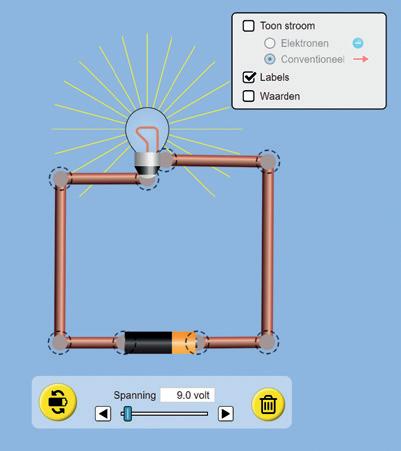
▲ Afb. 152 Elektrische stroom in een eenvoudige kring

3 Bestudeer de stroomzin.

a Vervolledig de afbeelding.

• Benoem de plus- en minpool van de batterij.

• Duid de bewegingszin van de elektronen aan met een blauwe pijl.

(Kies in de applet voor ‘Toon stroom – elektronen’.)

• Duid de conventionele stroomzin aan met een rode pijl.

(Kies in de applet voor ‘Toon stroom – conventioneel’.)

b Bestudeer wat er gebeurt als je de polen van de batterij omwisselt.

c Maak de uitspraken over de stroomzin correct.

• De elektronen bewegen van de plus- naar de minpool / van de min- naar de pluspool

• De conventionele stroomzin gaat van de plus- naar de minpool / van de min- naar de pluspool.

4 Bestudeer de stroomsterkte.

a Verander de instelling van de batterij, zodat de elektronen sneller bewegen.

b Welke omschrijving geeft de stroomsterkte correct weer?

Duid aan.

het aantal elektronen

het aantal elektronen die per tijdseenheid door een oppervlak gaan

de energie die de batterij aan de elektronen geeft

Hoeveel deeltjes zich per tijdseenheid verplaatsen, hangt af van verschillende factoren en kan dus verschillen. Om de grootte van de stroom te bepalen, bestudeer je de hoeveelheid deeltjes die er per tijdseenheid door een oppervlak passeren. e –A ▲ Afb. 153 Het water van de rivier stroomt door een oppervlak

Bij een waterkringloop is het debiet de hoeveelheid water die zich per tijdseenheid door een oppervlak (A) verplaatst (in m3 s ).

©VANIN

Afb. 154 De elektronen stromen door een oppervlak

Bij een elektrische stroomkring verplaatsen de elektronen zich. Elk elektron heeft een bepaalde lading. De stroomsterkte is de hoeveelheid ladingen die zich per tijdseenheid door een oppervlak (A) van het elektrische snoer verplaatsen.

Lading is een grootheid met als symbool q en als eenheid coulomb (met het symbool C).

WEETJE

Elke lading bestaat uit een veelvoud van een eenheidslading.

• Voor positieve ladingen is dat het aantal keer de lading van een proton e (1,6 · 10–19 C).

• Voor negatieve ladingen is het een veelvoud van de lading van een elektron –e (–1,6 · 10–19 C).

We definiëren de grootheid stroomsterkte met het symbool als volgt:

I = |Δq| Δt

Daarbij is |Δq| de hoeveelheid verplaatste lading en Δt het tijdsverloop waarin de lading zich verplaatst. Stroomsterkte is een scalaire grootheid en is altijd positief. Omdat ladingen zowel positief als negatief kunnen zijn, voeg je het absolutewaardeteken toe.

Uit de definitie kun je de eenheid van stroomsterkte afleiden:

[I] = [Δq] [Δt] = C s

We definiëren een nieuwe eenheid: de ampère (met het symbool A).

1 ampère = 1 coulomb 1 seconde of 1 A = 1 C s

Conventioneel betekent ‘volgens afspraak’.

Grootheden met symbool SI-eenheden met symbool lading q coulomb C

verplaatste lading|Δq| coulomb C tijdsverloop Δt seconde s

stroomsterkte I = |Δq| Δt ampère C s = A

In een schakelschema stel je de elektrische stroom voor met een stroompijl. De stroompijl geeft de zin aan waarin de positieve ladingen bewegen (of zouden bewegen): van de pluspool naar de minpool. Dat noem je de conventionele stroomzin. In een metalen geleider bewegen de elektronen van de minpool naar de pluspool. De elektronenstroom is tegengesteld aan de stroompijl.

conventionele stroomzin

elektronenstroom lamp

batterij

OPDRACHT 4

Los het vraagstuk op.

Je steekt de stekker van een bureaulamp in het stopcontact. Op het typeplaatje van de bureaulamp staat ‘300 mA’.

Wanneer je het toestel verbindt met het stopcontact, zal er in de stroomkring per seconde een hoeveelheid ladingen van in totaal 0,300 C worden verplaatst.

1 Teken het schakelschema met de conventionele stroomzin en geef de zin van de elektronenstroom aan.

2 Bereken hoeveel ladingen door de lamp lopen. Werk het vraagstuk uit op een cursusblad.

3 Controleer je antwoord via .

▲ Afb. 155 Conventionele stroomzin (rode pijl) en elektronenstroom (blauwe pijlen) in een stroomkring

▲ Afb. 156 Typeplaatje van een bureaulamp

B Stroomsterkte meten

OPDRACHT

5 ONDERZOEK

Onderzoek de eigenschappen van de stroomsterkte in een stroomkring met één verbruiker aan de hand van Labo 09 op .

©VANIN

De stroomsterkte meet je met een ampèremeter. Die stel je in een schakelschema voor met dit symbool:

Aangezien je de stroomsterkte door een lampje meet, plaats je de ampèremeter in de kring. De ampèremeter staat in serie met de verbruiker. De animatie toont hoe je de ampèremeter opneemt in de kring.

Een digitale multimeter die op de juiste manier is ingesteld, kun je gebruiken als ampèremeter. In de video kun je zien hoe je te werk gaat.

Uit experimenten blijkt dat de stroomsterkte voor en na de verbruiker even groot is. Dat betekent dat er evenveel ladingen passeren per tijdseenheid. De verbruiker verbruikt geen stroom

◀ Afb. 157 Multimeter die je kunt gebruiken als ampèremeter

▲ Afb. 158 Schakeling van ampèremeters in serie om de stroomsterkte voor en na een verbruiker op te meten.

▲ Afb. 159 De stroomsterkte verandert niet ter hoogte van de verbruiker.

animatie: ampèremeter in de stroomkring plaatsen

video: stroom meten met een multimeter

Je kunt dat vergelijken met een waterkringloop. Het debiet van een rivier is op de verschillende plaatsen in de rivier hetzelfde, ook al zijn er hindernissen zoals stenen of een turbine.

De grootheid lading wordt voorgesteld door het symbool en uitgedrukt in coulomb (C).

De grootheid stroomsterkte met het symbool wordt gedefinieerd als de hoeveelheid verplaatste lading (|Δq|) per tijdsverloop.

©VANIN

Grootheden met symbool SI-eenheden met symbool lading q coulombC verplaatste lading Δq coulombC

stroomsterkte I = |Δq| Δt ampère C s = A

De stroomsterkte wordt opgemeten met een ampèremeter, die in serie wordt geschakeld met de verbruiker. De stroomsterkte voor en na een verbruiker is even groot. De verbruiker verbruikt geen stroom

2.2 Spanning

A Betekenis

OPDRACHT 6

Bestudeer de batterijen in een zaklamp.

1 Open de batterijhouder van een zaklamp.

2 Hoeveel batterijen zitten er in de zaklamp?

3 Maak de uitspraken correct.

a De batterijen in een zaklamp produceren ladingen / geven ladingen energie.

b Als je meer batterijen gebruikt, is er evenveel / meer / minder energie per lading beschikbaar.

c De beschikbare energie per lading staat op een batterij weergegeven in joule / volt.

Een bron levert elektrische energie aan de ladingen. In een stroomkring gebeuren energieomzettingen:

potentiële elektrische energie van de ladingen → kinetische energie van de ladingen → energie van de verbruiker

De grootheid spanning wordt gedefinieerd als de hoeveelheid elektrische energie die wordt omgezet wanneer een lading van +1 C de stroomkring doorloopt Spanning is een scalaire grootheid met als symbool U

▲ Afb. 160 Zaklamp

De eenheid van spanning is volt (met als symbool V).

Grootheid met symbool SI-eenheid met symbool spanning U volt V

Een bron houdt de elektrische stroom in stand en levert elektrische energie aan elke lading. Je noemt de bron een spanningsbron.

VOORBEELD BLOKBATTERIJ

Een blokbatterij levert een spanning van 9 V. Wanneer je die batterij opneemt in een stroomkring, verplaatsen er zich elektronen tussen de polen van de bron. De spanning geeft aan hoeveel elektrische energie er daarbij wordt omgezet wanneer er in totaal 1 C aan ladingen tussen de polen wordt verplaatst. Bij dit type batterij is de hoeveelheid omgezette energie daarbij 9 J.

Er zijn verschillende types spanningsbronnen.

©VANIN

• Bij een gelijkspanningsbron is de waarde van de spanning constant. De stroomzin verandert niet in de tijd. Er ontstaat gelijkstroom. Bij een regelbare gelijkspanningsbron kun je de constante waarde instellen. Bij een batterij kan dat niet.

In een schakelschema stel je zulke spanningsbronnen voor met de volgende symbolen:

: gelijkspanningsbron

: regelbare gelijkspanningsbron

▲ Grafiek 28 Constante gelijkspanning van een gelijkspanningsbron

▲ Afb. 161 Een 9 V-batterij

• Bij een wisselspanningsbron wisselen de polen voortdurend van teken. De spanning neemt voortdurend toe en af. Dat type spanning wordt geleverd door de stopcontacten in huis.

In een schakelschema stel je zo’n spanningsbron voor met het volgende symbool:

: wisselspanningsbron

: regelbare wisselspanningsbron

©VANIN

▲ Grafiek 29 Wisselspanning van een wisselspanningsbron

In het dagelijks leven gebruiken we zowel gelijkspanning als wisselspanning. Over de eigenschappen ervan en de verschillen ertussen leer je meer in de derde graad. Tijdens experimenten in de klas gebruik je voornamelijk een regelbare gelijkspanningsbron.

Een batterij levert een vaste gelijkspanning. Bij deze AA-batterij is dat 1,5 V.

Het elektriciteitsnet levert een wisselspanning van 230 V.

WEETJE

Heel wat apparaten in huis werken rechtstreeks met de netspanning van 230 V. Andere toestellen werken bij een veel kleinere spanning. De adapter van je smartphone zet de netspanning om naar een spanning van 5 V om je smartphone op te laden.

Je kunt de constante spanning van een regelbare gelijkspanningsbron aanpassen.

Afb. 165

Afb. 162

Afb. 163

Afb. 164

B Spanning meten

OPDRACHT 7 ONDERZOEK

Onderzoek de eigenschappen van de spanning in een stroomkring met één verbruiker aan de hand van Labo 10 op .

©VANIN

De spanning meet je met een voltmeter. Die stel je in een schakelschema voor met dit symbool:

Omdat je het verschil in elektrische energie meet voor en na een verbruiker, staat de voltmeter parallel met de verbruiker. De animatie toont hoe je de voltmeter opneemt in de kring.

Een digitale multimeter die op de juiste manier is ingesteld, kun je gebruiken als voltmeter. In de video kun je zien hoe je te werk gaat.

voltmeter in de stroomkring plaatsen video: spanning meten met een multimeter

Uit metingen blijkt dat de spanning over de bron gelijk is aan de spanning over het lampje. Concreet betekent dat dat de energie die in de kring wordt omgezet, ‘verbruikt’ wordt inhetlampje zelf.

▲ Afb. 166 Schakeling van voltmeters in parallel om de spanning over de bron en een verbruiker op te meten.

elektronen met veel elektrische energie elektronen met weinig elektrische energie

▲ Afb. 167 De spanning over de verbruiker is hetzelfde als de bronspanning.

animatie:

Spanning wordt gedefinieerd als de hoeveelheid elektrische energie die wordt omgezet wanneer een lading van +1 C de stroomkring doorloopt.

Grootheid met symbool SI-eenheid met symbool spanning U volt V

Een spanningsbron kan gelijkspanning of wisselspanning leveren. Afhankelijk van de bron is die spanning vast of regelbaar

De spanning wordt opgemeten met een voltmeter, die parallel geschakeld wordt met de verbruiker. De spanning overdebron is gelijk aan de spanning over de verbruiker. In de kring wordt de elektrische energie omgezet in de verbruiker.

` Maak oefening 3 en 4 op p. 200.

3 Welk verband bestaat er tussen spanning en stroomsterkte?

3.1 Elektrische weerstand

A Betekenis

©VANIN

In snoeren gebruikt men een recht stuk geleider (meestal koper). Dat wordt in een wetenschappelijke context ‘een metallische geleider’ genoemd.

Wanneer je spanning aanlegt over een rechte metallische geleider, veroorzaakt die spanning een verplaatsing van de elektronen in dezelfde richting en zin. De bewegende elektronen botsen daarbij tegen de ionen in het metaalrooster en ondervinden hinder

▲ Afb. 168

Stenen in een rivier verhinderen de vlotte doorgang van het water en bepalen mee hoe het water stroomt.

elektronion

▲ Afb. 169

De vrije doorgang van elektronen in een geleider wordt gehinderd door de aanwezige roosterionen.

De elektronen kunnen zich niet ongehinderd verplaatsen door de geleider. De stroomsterkte door de geleider is beperkt. Een rechte geleider noem je daarom ook een weerstand.

In een schakelschema wordt een weerstand op twee manieren voorgesteld: of

B Wet van Ohm

OPDRACHT 8 ONDERZOEK

Onderzoek het kwantitatieve verband tussen de spanning en de stroomsterkte door een rechte metallische geleider aan de hand van Labo 11 op .

De spanning en de grootte van de weerstand bepalen de grootte van de stroomsterkte door de verbruiker. Dat kun je vergelijken met een waterkringloop.

Elke lamp heeft een bepaalde maximale lichtsterkte, die bepaald is door de weerstand. Wanneer een dimmer de spanning over de spots verlaagt, branden ze minder hard.

Hoogteverschillen in het landschap en de hinder door de structuur van de rivier bepalen het debiet van een rivier.

Het precieze verband tussen de spanning over en de stroomsterkte door een weerstand meet je op door een voltmeter parallel en een ampèremeter in serie met de weerstand te schakelen.

Stroomsterkte door een weerstand bij verschillende aangelegde spanningen

spanningsbron weerstand

▲ Afb. 170 ▲ Afb. 171

Als de spanning U aangelegd over een geleider verdubbelt, verdubbelt de stroomsterkte I. Als de spanning halveert, halveert de stroomsterkte. De I(U)-grafiek is een rechte door de oorsprong ▲ Grafiek 30 ( )-grafiek van een metallische geleider

Er is een recht evenredig verband tussen de stroomsterkte door een geleider en de spanning over de geleider:

I ~ U, dus I U = constante (1)

Die verhouding is gelinkt aan twee verschillende grootheden uit de fysica.

Grootheid geleidbaarheid weerstand

Definitie

©VANIN

Ω is de Griekse hoofdletter omega.

In woorden

Betekenis

G = I U R = U I

G = 1 R

De geleidbaarheid is de verhouding tussen de stroomsterkte door een geleider en de spanning die erover is aangelegd. De weerstand is de verhouding tussen de aangelegde spanning en de stroomsterkte die daarvan het gevolg is.

mate waarin ladingen doorgelaten worden

mate waarin ladingen gehinderd worden

SI-eenheid met symbool [G] = [I] [U] = A V = S, siemens[R] = [U] [I] = V A = Ω, ohm

S= 1 Ω

Met die definitie kun je de verkregen constante (1) als volgt herschrijven:

constante = I U = G = 1 R

Voor een metallische geleider geldt dat = constante, ongeacht de spanning die je aanlegt.

Dat is de wet van Ohm:

R = U I = constante

Een geleider die daaraan voldoet, noem je een ohmse weerstand

Bouw in de applet een stroomkring met een bron, een weerstand, een voltmeter en een ampèremeter. Ga vervolgens na of de wet van Ohm effectief geldt voor de metallische geleider.

©VANIN

Uit de helling van de ( )-grafiek kun je aflezen hoeveel de stroomsterkte verandert als je een bepaalde spanning aanlegt. Die helling is een constante waarde, gegeven door I U , die afhankelijk is van de gebruikte geleider.

Voor een geleider met een grote weerstandswaarde is de toename van de stroomsterkte beperkt wanneer je de spanning verhoogt. Hoe kleiner de helling van de ( )-grafiek, hoe kleiner de geleidbaarheid en hoe groter de weerstand.

kleine R,

G grote R, kleine G

De mate waarin een stof elektrische stroom goed geleidt, wordt uitgedrukt door de grootheden weerstand en geleidbaarheid: • weerstand: mate waarin ladingen gehinderd worden;

• geleidbaarheid: mate waarin ladingen doorgelaten worden.

De weerstand van een voorwerp is de verhouding van de spanning die je erover aanlegt, ten opzichte van de stroomsterkte die daardoor ontstaat.

De geleidbaarheid wordt gedefinieerd als de verhouding van de stroomsterkte die door een voorwerp vloeit, ten opzichte van de spanning die je erover aanlegt.

Grootheden met symbool SI-eenheden met symbool

weerstand R = U I ohm Ω = V A

geleidbaarheid G = I U siemens S = A V

Voor een metallische geleider geldt de wet van Ohm: de weerstand is constant bij elke spanning.

` Maak oefening 5, 6 en 7 op p. 201.

▲ Grafiek 31 ( )-grafiek voor twee metallische geleiders

grote

OPDRACHT 9

Los het vraagstuk op.

Door de weerstandsdraad in een broodrooster loopt bij een spanning van 230 V een stroomsterkte van 4,00 A.

1 Bepaal de weerstandswaarde en de geleidbaarheidswaarde van de gebruikte draad. Werk het vraagstuk uit op een apart blad.

2 Controleer je antwoord via .

OPDRACHT 10 DOORDENKER

Bestudeer de ( )-grafiek van een ledlampje.

Welke uitspraken zijn correct? Duid aan.

De grafiek kan niet juist zijn.

De weerstand is niet gedefinieerd bij een ledlampje.

De weerstand is afhankelijk van de spanning bij een ledlampje.

De wet van Ohm is niet geldig bij een ledlampje.

3.2 Weerstanden in de praktijk

OPDRACHT 11

Grafiek 32 ( )-grafiek van een ledlampje

Bestudeer de verschillende betekenissen van het woord ‘weerstand’.

1 Bekijk de voorbeelden.

De draden zijn eenweerstand voor de elektrische stroom.

2 Markeer het woord ‘weerstand’ …

Op het moederbord van een pc zijn verschillendweerstanden gemonteerd.

• groen als het een elektronische component is;

• blauw als het een metallische geleider is;

• rood als het de weerstandswaarde van een toestel is.

De laptop heeft eenweerstand van 700 Ω.

OPDRACHT 11 (VERVOLG)

3 Zoek de betekenis van deze Engelse woorden op in de context van elektriciteit.

• resistor: • resistance:

De meeste weerstanden in elektronische schakelingen bestaan niet uit een metallische draad. Het zijn componenten die uit een specifiek materiaal bestaan en zo de gewenste weerstandswaarde (R) hebben. Zo’n elektronische component wordt, net als de grootheid en de weerstandswaarde, weerstand genoemd.

Elk voorwerp heeft een bepaalde weerstand. De stofsoort bepaalt het elektrisch gedrag van het voorwerp.

Op basis van hun elektrische eigenschappen kun je stoffen onderverdelen in twee groepen:

• geleiders: Stoffen waarin een lading zich makkelijk verplaatst, hebben een lage weerstand en een hoge geleidbaarheid.

• isolatoren: Stoffen waarin een lading zich moeilijk verplaatst, hebben een hoge weerstand en een lage geleidbaarheid

De weerstandswaarde hangt af van het soort materiaal en de afmetingen van de weerstand.

Op de afbeelding zie je enkele gerangschikte voorbeelden voor draden met identieke afmetingen die zouden bestaan uit de verschillende getoonde stoffen.

geleidbaarheid grote geleidbaarheid grote weerstand

VOORBEELD KOPERDRAAD VERSUS RUBBERDRAAD

Draden met dezelfde afmetingen kunnen, afhankelijk van het materiaal waaruit ze zijn gemaakt, erg verschillende weerstandswaarden hebben.

• Een koperdraad met een lengte van 1 m heeft een typische weerstandswaarde van RCu = 10 mΩ = 1,0 ∙ 10–2 Ω.

• Een pvc-draad met dezelfde afmetingen heeft een typische weerstandswaarde van R pvc = 10 EΩ = 1,0 ∙ 1019 Ω, zowat 1021 keer groter.

De term weerstand verwijst in de praktijk naar een metallische geleider, een elektronische component of de grootheid met een bepaalde waarde (in ohm).

Je kunt stoffen opdelen op basis van hun weerstand of geleidbaarheid:

• Geleiders hinderen de beweging van ladingen weinig (grote G, kleine R).

• Isolatoren hinderen de beweging van ladingen sterk (kleine G, grote R).

OPDRACHT 12

Verklaar de volgende fenomenen aan de hand van elektrische stofeigenschappen.

• Het omhulsel van een laptop is gemaakt uit kunststof.

• Het is gevaarlijk om elektrische toestellen te gebruiken in de badkamer.

▲ Afb. 177 De combinatie van water en elektriciteit is gevaarlijk.

4 Hoe wordt elektrische energie omgezet in elektrische toestellen?

4.1 Energie en vermogen van elektrische stroom

OPDRACHT 13

Bestudeer het vermogen van een oplader voor een smartphone.

1 Duid het vermogen, de uitgaande spanning en de uitgaande stroomsterkte aan op het typeplaatje.

2 Omschrijf in je eigen woorden wat het vermogen van de adapter betekent.

©VANIN

3 Gebruik de gegevens op het typeplaatje om de uitdrukking voor elektrisch vermogen te bepalen met de spanning en de stroomsterkte. a Duid aan. P = U I P = U ∙ I P = I U ander verband

b Bewijs met de gegevens.

4 Bereken het energieverbruik in kilowattuur als je de oplader 2,0 h gebruikt.

∆E =

In elektrische toestellen wordt elektrische potentiële energie omgezet in een andere energievorm. Elk toestel heeft daarbij een bepaald vermogen.

Het elektrisch vermogen dat een toestel ontwikkelt, is de verhouding van de hoeveelheid elektrische energie die in een toestel wordt omgezet, ten opzichte van het tijdsverloop waarin dat gebeurt:

P = |ΔEel| Δt

Experimenten tonen aan dat het elektrisch vermogen bepaald wordt door de spanning over het toestel en de stroomsterkte erdoor:

P = U ∙ I

▲ Afb. 178 Typeplaatje van een oplader

Op basis van de definitie van weerstand (R = U I ) wordt dat:

P = U ∙ I

= I ∙ R ∙ I

= I2 ∙ R

Grootheid met symbool

P = U ∙ I

= U ∙ U R

= U 2 R

SI-eenheid met symbool elektrisch vermogen P = U ∙ I watt W

VOORBEELD WATERKOKER

Op het typeplaatje van een waterkoker staat zowel het vermogen van het toestel (P = 2 300 W) aangegeven als de spanning waarbij het werkt (230 V). Met de definitie van vermogen kun je de stroomsterkte door de waterkoker berekenen:

P = U ∙ I, dus I = P U

Bij een normale werking van het toestel loopt er een stroomsterkte I = 2 300 W 230 V = 10,0 A.

In elektrische toestellen wordt elektrische energie omgezet in een andere energievorm.

Het vermogen van een toestel hangt af van de spanning en de stroomsterkte.

Je berekent het als volgt: P = U ∙ I

Grootheid met symbool

SI-eenheid met symbool elektrisch vermogen P = U ∙ I watt W

Het elektrisch vermogen dat wordt omgezet in een geleider met weerstandswaarde R, kun je als volgt berekenen: P = U 2 I of P = I2 ∙ R

` Maak oefening 8, 9 en 10 op p. 201-202.

WEETJE

In Coo, in de provincie Luik, bevindt zich een waterkrachtcentrale.

Water dat op grote hoogte wordt opgeslagen in bassins, werkt als ‘energiebatterij’.

Bij een tijdelijk energietekort stroomt het water uit de hoger gelegen bassins naar beneden, waar het terechtkomt in een afgesloten meander van de Amblève. Daarbij drijft het water turbines aan.

Het vermogen dat tijdelijk kan worden ontwikkeld, bedraagt ongeveer 1 000 MW, evenveel als bij een volwaardige kernreactor. Tijdens periodes waarin het elektriciteitsverbuik lager ligt, pompt men het water opnieuw in de bassins.

Bekijk de informatiepagina over de spaarbekkencentrale van Coo.

▲ Afb. 179 Hoger gelegen bassins van de spaarbekkencentrale van Coo

website: spaarbekkencentrale Coo

4.2 Warmteontwikkeling in een elektrische weerstand

OPDRACHT 14

Bestudeer de warmteontwikkeling.

1 Maak de uitspraken onder de afbeeldingen correct.

• De warmteontwikkeling hangt wel / niet af van de gebruiksduur.

• Het vermogen hangt wel / niet af van de gebruiksduur.

• De geproduceerde warmte is nuttige / onnuttige energie.

2 Welke uitspraak is correct?

Duid aan.

• De warmteontwikkeling hangt wel / niet af van de gebruiksduur.

• Het vermogen hangt wel / niet af van de gebruiksduur.

• De geproduceerde warmte is nuttige / onnuttige energie.

In verwarmingstoestellen wordt een weerstand gebruikt die warmte produceert.

In verwarmingstoestellen wordt een speciale component gebruikt die warmte produceert.

Je kunt elektrische toestellen ontwikkelen die geen warmte produceren.

In alle elektrische toestellen wordt er warmte ontwikkeld. In sommige toestellen is dat de gewenste energievorm en in andere is het een vorm van energieverlies (energiedissipatie).

• In verwarmingstoestellen is warmte nuttige energie. Het percentage ontwikkelde warmte is het best zo hoog mogelijk.

• In andere toestellen is warmte onnuttige energie. Het percentage ontwikkelde warmte is het best zo laag mogelijk, om energiedissipatie te beperken.

In een elektrische weerstand is het rendement van de warmteomzetting erg hoog. Nagenoeg alle elektrische energie wordt omgezet in warmte. Dat effect noem je het Joule-effect

Aan de hand van de definities van weerstand (R = U I ) en vermogen (P = U · I) wordt de hoeveelheid ontwikkelde warmte in een weerstand R:

Je kunt dat effect verklaren door de beweging van de elektronen. De bewegende elektronen van het metaal botsen voortdurend met de trillende roosterionen van het metaal.

Bij die botsingen wordt de kinetische energie omgezet in warmte.

©VANIN

▲ Afb. 182 Warmteontwikkeling door botsingen tussen elektronen en roosterionen

VOORBEELD WARMTE ALS NUTTIGE EN NIET-NUTTIGE ENERGIE

In een waterkoker (P = 1,0 kW) verloopt de omzetting naar warmte efficiënt. De ontwikkelde warmte is de nuttige energie.

Het rendement bedraagt meer dan 80 %:

Pnuttig = P warmte = 0,80 ∙ P = 0,80 ∙ 1,0 kW = 0,80 kW

▲ Afb. 183 Warmte is de gewenste energievorm bij een waterkoker, maar een vorm van energieverlies bij een computer.

Bij een computer (P = 400 W) wordt in de processor bij intensief gebruik tot 15 % warmte ontwikkeld. Verschillende koelingssystemen, waaronder een ventilator, proberen die warmte af te voeren.

Pnuttig = 0,85 ∙ P = 0,85 ∙ 400 W = 340 W

P warmte = 0,15 ∙ P = 0,15 ∙ 400 W = 60 W

Ook in een broodrooster wordt de elektrische energie hoofdzakelijk omgezet in warmte. De video licht de werking van een broodrooster toe.

video: werking broodrooster

Het rendement van een warmteomzetting η bepaalt welk percentage van de elektrische energie wordt omgezet in warmte.

In een elektrische weerstand wordt een groot deel van de elektrische energie omgezet in warmte. Dat is het Joule-effect

De hoeveelheid ontwikkelde warmte in een weerstand bereken je als volgt:

Q = P warmte ∙ Δt (waarbij P warmte = η ∙ P; P = U ∙ I en R = U I )

` Maak oefening 11 op p. 202.

OPDRACHT 15

Bestudeer sluimerverbruik.

Het sluimerverbruik van je pc en randapparatuur heeft een gemiddeld vermogen van 6,5 W.

Veronderstel dat je je computer dagelijks 16,0 h in stand-bymodus zet.

1 Wat betekent ‘sluimerverbruik’?

©VANIN

2 Bereken hoeveel energie en geld je kunt besparen op jaarbasis door je computer uit te schakelen na gebruik. Gebruik een schatting van de actuele elektriciteitsprijs.

3 Geef twee voorbeelden van hoe jij nog energie kunt besparen door sluimerverbruik te beperken.

UITBREIDING

Op vind je het uitbreidingshoofdstuk ‘Welke eigenschappen hebben elektrische schakelingen?’.

• Je ontdekt hoe spanning en stroom zich gedragen in eenvoudige schakelingen, en maakt kennis met de kenmerken van serie- en parallelschakelingen.

• Daarna leer je hoe je de spanning, de stroomsterkte en de (totale) weerstand berekent in serie-, parallelen gemengde schakelingen.

• Tot slot sta je stil bij de risico’s van elektriciteit en de veiligheidsmaatregelen die nodig zijn om er veilig mee te werken.

▲ Afb. 184 Een pc verbruikt energie in stand-bystand.

stroomsterkte meten: ampèremeter met verbruiker elektrische stroom wordt niet verbruikt

• conventionele stroomzin : van pool naar pool

• zin elektronenstroom : tegengesteld spanning meten: voltmeter met verbruiker elektrische energie wordt omgezet in de verbruiker

elektrische energie ladingen → energie verbruiker ontwikkeld

P = in een geleider met weerstand : = 2 = 2 ·

Joule-effect : In een weerstand wordt elektrische energie deels omgezet in . Q = P warmte · Δ t wet van Ohm : metallische geleider: = constante bij elke aangelegde spanning batterij weerstand lamp ampèremeter voltmeter

©VANIN

• spanningsbron : oorzaak verschil in (elektrische) energie tussen de polen

• spanning : hoeveelheid elektrische energie die wordt omgezet wanneer een lading van +1 C tussen twee punten wordt verplaatst

• : beweging van ladingen in dezelfde richting en zin

• stroomsterkte (A) = waarbij |∆ q |: verplaatste lading (C) en ∆ t : tijdsverloop (s)

Weerstand en geleidbaarheid

GrootheidSI-eenheid

Weerstand R = Geleidbaarheid G = GeleiderIsolator

Weerstand groot / kleingroot / klein

Geleidbaarheid groot / kleingroot / klein

1 Begripskennis

• Ik kan een elektrische stroomkring omschrijven.

• Ik kan het begrip ‘elektrische stroom’ omschrijven

• Ik kan een elektrische stroomkring vergelijken met een waterkringloop.

• Ik kan het begrip ‘elektrische stroomsterkte’ omschrijven

• Ik kan de elektrische stroomsterkte berekenen

• Ik kan de begrippen ‘spanning’ en ‘spanningsbronnen’ omschrijven.

• Ik kan het verschil tussen gelijkspanning en wisselspanning omschrijven

• Ik kan voorbeelden geven van gelijk- en wisselspanningsbronnen.

• Ik kan de begrippen ‘weerstand’ en ‘geleiding’ omschrijven.

• Ik kan de wet van Ohm omschrijven

• Ik kan de weerstand en de geleiding berekenen.

• Ik kan het elektrisch vermogen en het energieverbruik van toestellen berekenen.

• Ik kan het Joule-effect omschrijven

• Ik kan de warmteontwikkeling in weerstanden berekenen.

2 Onderzoeksvaardigheden

• Ik kan eenheden omzetten.

• Ik kan formules omvormen

• Ik kan afrondingsregels toepassen

• Ik kan informatie in symbolen noteren.

• Ik kan rekenvraagstukken gestructureerd oplossen

• Ik kan grafieken tekenen.

• Ik kan een recht evenredig en een omgekeerd evenredig verband aflezen op een grafiek

` Je kunt deze checklist ook op invullen.

JANOG OEFENEN

Werk alle vraagstukken uit op een cursusblad met ‘gegeven’, ‘gevraagd’ en ‘oplossing’.

Je kunt de oplossingsstrategie en de voorbeeldoefeningen op gebruiken als extra ondersteuning.

Benoem de energiebron en de verbruiker op de afbeeldingen.

Welke energievorm wordt er omgezet in elektrische energie?

Welke uitspraak over punt A en B is correct?

De elektronen in A hebben meer elektrische potentiële energie dan die in B.

De elektronen in B hebben meer elektrische potentiële energie dan die in A.

De stroomsterkte in A is groter dan die in B.

De stroomsterkte in B is groter dan die in A.

Verbeter de fouten in de krantenkoppen door de correcte terminologie te gebruiken.

Arbeider (55) overleeft stroomstoot van 10 000 volt bij werken in station

Bron: hln.be, 23/10/2019

Stroomverbruik spreiden loont vanaf 2022

Bron: tijd.be, 05/05/2020

Vul de uitspraken aan door ‘altijd’, ‘soms’ of ‘nooit’ aan te duiden.

a Bewegende ladingen veroorzaken altijd / soms / nooit een elektrische stroom.

b Elektrische stroom wordt altijd / soms / nooit veroorzaakt door positieve ladingen.

c De conventionele stroomzin is altijd / soms / nooit gelijk aan de zin van de elektronenstroom.

d De elektrische energie van een elektron is na de verbruiker altijd / soms / nooit lager dan voor de verbruiker.

e De weerstand van een metallische geleider neemt altijd / soms / nooit toe wanneer je de spanning erover vergroot.

Er vloeit een stroom van 4,75 A door je laptop (R = 4,3 Ω).

a Welke spanning levert de adapter?

b Hoeveel ladingen stromen er gedurende 1,00 h door de laptop?

c Bepaal het aantal elektronen dat daarbij wordt verplaatst.

Milena maakt een I(U)-grafiek van twee weerstandsdraden. I (mA)

a Welke uitspraak is correct?

G1 = 2 ∙ G2

R1 = 2 ∙ R2

G1 = 4 ∙ G2

R1 = 4 ∙ R2

b Bepaal de weerstand en de geleidbaarheid voor beide weerstandsdraden.

In de tabel staan meetresultaten van verschillende verbruikers.

a Vul de tabel aan.

b Welke verbruiker is een verwarmingstoestel? Verklaar.

Wie heeft er gelijk? Bespreek.

Aron: Om in een weerstand een groot vermogen te ontwikkelen, moet de weerstandswaarde groot zijn, want = 2 ∙

Fabian: Om in een weerstand een groot vermogen te onwikkelen, moet de weerstandswaarde klein zijn, want = 2

Malika: De weerstandswaarde heeft geen invloed op het in een weerstand ontwikkelde vermogen, want = ∙ .

Rangschik van kleine naar grote stroomsterkte.

a Je sluit een waterkoker met een vermogen van 2 400 W aan op de netspanning.

b Je sluit een draad met een geleidbaarheid van 300 mS aan op een spanning van 230 V.

c Een broodrooster met een rendement van 80,0 % waarin een weerstand van 60 Ω zit, produceert in 5,00 min 220 kJ aan warmte.

d Door de doorsnede van een geleider passeert in 30,0 s tijd een hoeveelheid ladingen van 600 C.

Het vermogen dat ontwikkeld wordt in een kernreactor, bedraagt 1 000 MW. Voor het transport gebruikt men hoogspanningen tot 380 kV. Vanuit de kerncentrale van Doel loopt een kabel waarvan de weerstand, ondanks de kabelengte van 23 km, beperkt is tot 7,00 Ω.

a Hoe groot is het warmtevermogen dat in de draad wordt ontwikkeld?

b Hoeveel procent van het vermogen van de centrale is dat?

c Hoeveel keer groter is het energieverlies wanneer de hoogspanning maar 110 kV bedraagt?

` Verder oefenen? Ga naar

Stromen: potentiële energie wordt omgezet in de gewenste energievorm

Een spanningsbron (een batterij, een elektriciteitsnetwerk …) levert potentiële energie aan de elektronen.

Grootheden met symbool

Eenheden met symbool stroomsterkte aantal ladingen per tijdsverloop I = |Δq| Δt ampèreA spanning maat voor de energieomzetting U voltV weerstand mate van hinder R = U I ohmΩ geleidbaarheid mate van doorlaten G = 1 R = I U siemensS

wet van Ohm: metallische geleider: R = constante bij elke aangelegde spanning

• energiebron: Een pomp of de zon levert potentiële energie aan het water.

• debiet: de hoeveelheid water per tijdsverloop door een doorsnede

• hoogteverschil: Door het hoogteverschil bezit het water potentiële energie.

• weerstand: Stenen, de breedte van de paden … bepalen de hinder voor het water.

Mogelijke schakelingen van weerstanden