IM_TM_G06_MA_MB_Text_AY25-26_eBook by Uolo

6 Master Mathematical Thinking MATHEMATICS

Teacher Manual

MATHEMATICS

Master Mathematical Thinking

Acknowledgements

Academic Authors: Muskan Panjwani, Anjana AR, Anuj Gupta, Simran Singh

Creative Directors: Bhavna Tripathi, Mangal Singh Rana, Satish

Book Production: Sanjay Kumar Goel, Vishesh Agarwal

Project Lead: Neena Aul

VP, Learning: Abhishek Bhatnagar

All products and brand names used in this book are trademarks, registered trademarks or trade names of their respective owners.

First impression 2024

Second impression 2025

This book is sold subject to the condition that it shall not by way of trade or otherwise, be lent, resold, hired out, or otherwise circulated without the publisher’s prior written consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser and without limiting the rights under copyright reserved above, no part of this publication may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of both the copyright owner and the above-mentioned publisher of this book.

Book Title: Imagine Mathematics Teacher Manual 6

ISBN: 978-81-984519-1-0

Published by Uolo EdTech Private Limited

Corporate Office Address:

85, Sector 44, Gurugram, Haryana 122003

CIN: U74999DL2017PTC322986

Illustrations and images: www.shutterstock.com, www.stock.adobe.com and www.freepik.com

All suggested use of the internet should be under adult supervision.

Preface

Mathematics is an essential tool for understanding the world around us. It is not just another subject, but an integral part of our lives. It shapes the very foundation of our understanding, personality and interaction with the world around us. Studies from across the globe have shown that proficiency in mathematics significantly influences career prospects and lifelong learning.

According to the NEP 2020, mathematics and mathematical thinking are crucial for empowering individuals in their everyday interactions and affairs. It focuses on competencies-based education, which essentially means actively and effectively applying mathematical concepts in real life. It also encourages innovative approaches for teaching maths, including regular use of puzzles, games and relatable real-world examples to make the subject engaging and enjoyable.

It is in this spirit that Uolo has introduced the Imagine Mathematics product for elementary grades (1 to 8). This product’s key objective is to eliminate the fear of mathematics by making math exciting, relatable and meaningful for children.

Imagine Mathematics positions itself on the curricular and pedagogical approach of the Gradual Release of Responsibility (GRR), which has been highly recommended by the NEP 2020, the NCF 2023 and other literature in learning and educational pedagogies. Subsequent pages elaborate further on this approach and its actualisation in this book.

This book incorporates highly acclaimed, learner-friendly teaching strategies. Each chapter introduces concepts through real-life situations and storytelling, connecting to children’s experiences and transitioning smoothly from concrete to abstract. These teacher manuals are designed to be indispensable companions for educators, providing well-structured guidance to make teaching mathematics both effective and enjoyable. With a focus on interactive and hands-on learning, the manuals include a variety of activities, games, and quizzes tailored to enhance conceptual understanding. By integrating these engaging strategies into the classroom, teachers can foster critical thinking and problem-solving skills among students. Moreover, the resources emphasise creating an enriched and enjoyable learning environment, ensuring that students not only grasp mathematical concepts but also develop a genuine interest in the subject.

In addition, the book is technologically empowered and works in sync with a parallel digital world, which contains immersive gamified experiences, video solutions and practice worksheets, among other things. Interactive exercises on the digital platform make learning experiential and help in concrete visualisation of abstract mathematical concepts. We invite educators, parents and students to embrace Imagine Mathematics and join us in nurturing the next generation of thinkers, innovators and problem-solvers. Embark on this exciting journey with us and let Imagine Mathematics be a valuable resource in your educational adventure.

Numbers up to 8 Digits 1

Imagine Mathematics Headings: Clear and concise lessons, aligned with the topics in the Imagine Mathematics book, designed for a seamless implementation.

Alignment

C-1.1:

C-4.3:

Numbers up to 8 Digits 1

Imagine Mathematics Headings

Place Value, Face Value and Expanded Form

Indian and International Number Systems

Comparing and Ordering Numbers

Numbers up to 8 Digits 1

Learning Outcomes: Clear, specific and measurable learning outcomes that show what students should know, understand, or do by the end of the lesson.

Learning Outcomes

Students will be able to:

Rounding–off Numbers

Learning Outcomes

Students will be able to: write the place value, face value, expanded form and number names for numbers up to write numbers up to 8 digits in the Indian and International number system. compare numbers up to 8 digits and arrange them in ascending and descending order. round off numbers up to 8 digits to the nearest 10, 100 and 1000.

Alignment to NCF

Numbers up to 8 Digits 1

C-1.1: Represents numbers using the place value structure of the Indian number system, numbers, and knows and can read the names of very large numbers

C-4.3: Selects appropriate methods and tools for computing with whole numbers, such as computation, estimation, or paper pencil calculation, in accordance with the context

C-5.1: Understands the development of zero in India and the Indian place value system for the history of its transmission to the world, and its modern impact on our lives and in all technology

Let’s Recall

write the place value, face value, expanded form and number names for numbers up to 8 digits. write numbers up to 8 digits in the Indian and International number system. compare numbers up to 8 digits and arrange them in ascending and descending order. round off numbers up to 8 digits to the nearest 10, 100 and 1000.

Alignment to NCF

Place Value, Face Value and Expanded Form

Recap to check if students know how to write the place value, expanded form and number 6-digit numbers.

Indian and International Number Systems

Ask students to solve the questions given in the Let’s Warm-up section.

Comparing and Ordering Numbers

C-1.1: Represents numbers using the place value structure of the Indian number system, compares whole numbers, and knows and can read the names of very large numbers

Alignment to NCF: Learning Outcomes as recommended by NCF 2023.

Vocabulary

Rounding–off Numbers

C-4.3: Selects appropriate methods and tools for computing with whole numbers, such as mental computation, estimation, or paper pencil calculation, in accordance with the context

Learning Outcomes

C-5.1: Understands the development of zero in India and the Indian place value system for writing numerals, the history of its transmission to the world, and its modern impact on our lives and in all technology

Let’s Recall

expanded form: writing a number as the sum of the values of all its digits order: the way numbers are arranged estimating: guessing an answer that is close to the actual answer rounding off: approximating a number to a certain place value for easier calculation

Teaching Aids

Recap to check if students know how to write the place value, expanded form and number names for 6-digit numbers.

Students will be able to: write the place value, face value, expanded form and number names for numbers up to 8 digits. write numbers up to 8 digits in the Indian and International number system. compare numbers up to 8 digits and arrange them in ascending and descending order. round off numbers up to 8 digits to the nearest 10, 100 and 1000.

Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

Chart papers with empty place value chart drawn; Buttons; Beads; Bowls; Digit

Alignment to NCF

5 number cards with a 7-digit or 8-digit number written on them; Two bowls with number 8-digit numbers in one bowl and rounded-off places in another bowl

Teaching Aids

Let’s Recall: Recap exercises to check the understanding of prerequisite concepts before starting a topic.

C-1.1: Represents numbers using the place value structure of the Indian number system, compares whole numbers, and knows and can read the names of very large numbers

C-4.3: Selects appropriate methods and tools for computing with whole numbers, such as mental computation, estimation, or paper pencil calculation, in accordance with the context

Let’s Recall

Chart papers with empty place value chart drawn; Buttons; Beads; Bowls; Digit cards; Bowls with 5 number cards with a 7-digit or 8-digit number written on them; Two bowls with number cards having 8-digit numbers in one bowl and rounded-off places in another bowl

Recap to check if students know how to write the place value, expanded form and number names for 6-digit numbers. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

Teaching Aids

Chart papers with empty place value chart drawn; Buttons; Beads; Bowls;

cards; Bowls

Learning Outcomes

Numbers up to 8 Digits 1

Numbers up to

Alignment to NCF

C-1.1: Represents numbers using the place value structure of the Indian number system, compares whole numbers, and knows and can read the names of very large numbers

C-4.3: Selects appropriate methods and tools for computing with whole numbers, such as mental computation, estimation, or paper pencil calculation, in accordance with the context

QR Code: Provides access to digital solutions and other interactive resources.

Learning Outcomes

Let’s Recall

Recap to check if students know how to write the place value, expanded form and number names for 6-digit numbers.

Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

Alignment to NCF

Teaching Aids

Vocabulary: Helps to know the important terms that are introduced, defined or emphasised in the chapter.

C-1.1: Represents numbers using the place value structure of the Indian number system, compares whole numbers, and knows and can read the names of very large numbers

C-4.3: Selects appropriate methods and tools for computing with whole numbers, such as mental computation, estimation, or paper pencil calculation, in accordance with the context

Let’s Recall

expanded form and number names for numbers up to 8 digits. Indian and International number system. arrange them in ascending and descending order. nearest 10, 100 and 1000.

place value structure of the Indian number system, compares whole names of very large numbers and tools for computing with whole numbers, such as mental pencil calculation, in accordance with the context zero in India and the Indian place value system for writing numerals, world, and its modern impact on our lives and in all technology

Teaching Aids: Aids and resources that the teachers can use to significantly improve the teaching and learning process for the students.

Chapter: Numbers up to 8 Digits

Recap to check if students know how to write the place value, expanded form and number names for 6-digit numbers.

Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

Teaching Aids

Place Value, Face Value and Expanded Form Imagine Maths Page 2 Learning Outcomes

write the place value, expanded form and number names for given in the Let’s Warm-up section.

the sum of the values of all its digits close to the actual answer to a certain place value for easier calculation

Place Value, Face Value and Expanded Form

Learning Outcomes

Teaching Aids

Imagine Maths Page 2

Students will be able to write the place value, face value, expanded form and number names for numbers up to 8 digits.

Chart papers with empty place value chart drawn; Buttons; Bowls; Digit cards

Activity

Teaching Aids

Chart papers with empty place value chart drawn; Buttons; Bowls; Digit cards

Activity

Instruct the students to work in small groups. Distribute the teaching aids among the groups. Keep number cards (0–9) in a bowl. Pick a card from the bowl and say the digit aloud along with a place, for example “3 in the thousands place.” Instruct the groups to place as many buttons as the digit in that place on the place value chart. Repeat this to form a 7-digit or 8-digit number. You can repeat digits in more than 1 place. Once the 7-digit or 8-digit number is formed, have each group record the expanded form and number names in their notebooks. Discuss the face value and place value of a few digits in the class. Ask the students to say the number names aloud.

Extension Idea

Activity: A concise and organised lesson plan that outlines the activities and extension ideas that are to be used to facilitate learning.

Ask: In a number 1,67,48,950, if we interchange the digit in the ten thousands place with the digit in the crores place, then what is the difference in the place values of the digits in the ten thousands place?

Extension Idea

Say: On interchanging the digits, the new number is 4,67,18,950. Difference in the place values = 40,000 – 10,000 = 30,000.

Extension Idea: A quick mathematical-thinking question to enhance the critical thinking skill.

Indian and International Number Systems Imagine Maths Page 5

Say: On interchanging the digits, the new number is 4,67,18,950. Difference in the place values = 40,000 – 10,000 = 30,000.

chart drawn; Buttons; Beads; Bowls; Digit cards; Bowls with number written on them; Two bowls with number cards having rounded-off places in another bowl

Learning Outcomes

Students will be able to write numbers up to 8 digits in the Indian and International number system.

Indian and International Number Systems Imagine Maths Page 5

Teaching Aids

Learning Outcomes

Chart papers with empty place value chart drawn; Buttons; Beads

Students will be able to write numbers up to 8 digits in the Indian and International number system.

Activity

Teaching Aids

Chart papers with empty place value chart drawn; Buttons; Beads

Activity

Arrange the class in groups of 4, with each group split into teams of 2 students. Distribute the teaching aids among the groups. Guide the students to form 7-digit or 8-digit numbers on the chart using buttons and beads as in the previous lesson. Ask them to place buttons for the Indian number system on one chart and beads for the International number system on the other. The two teams should record the expanded form of the numbers using commas in their notebooks and number names. Ask the groups to find the similarities and differences between the two systems. Discuss the answers with the class.

Extension Idea

Ask: How many lakhs are there in 10 million?

Answers: Answers, provided at the end of each chapter, for the questions given in Do It Together and Think and Tell sections of the Imagine Mathematics book.

Answers

Say: To find out, we divide 10,000,000 by 100,000. So, there are 100 lakhs in ten million.

Extension Idea

Ask: How many lakhs are there in 10 million?

Say: To find out, we divide 10,000,000 by 100,000. So, there are 100 lakhs in ten million.

Period Plan

The teacher manuals corresponding to Imagine Mathematics books for Grades 1 to 8 align with the recently updated syllabus outlined by the National Curriculum Framework for School Education, 2023. These manuals have been carefully designed to support teachers in various ways. They provide recommendations for hands-on and interactive activities, games, and quizzes that aim to effectively teach diverse concepts, fostering an enriched learning experience for students. Additionally, these resources aim to reinforce critical thinking and problem-solving skills while ensuring that the learning process remains enjoyable.

In a typical school setting, there are approximately 180 school days encompassing teaching sessions, exams, tests, events, and more. Consequently, there is an average of around 120 teaching periods throughout the academic year.

The breakdown of topics and the suggested period plan for each chapter is detailed below.

Chapters No. of Periods

1. Large Numbers and Operations 13

2. Patterns in Whole Numbers 7

3. Playing with Numbers: Factors and Multiples 12

Break-up of Topics

Indian Number System

International Number System

Comparing and Ordering Numbers

Roman Numerals

Rounding Off

Estimation in Operations

Addition and Subtraction

Multiplication and Division

Parentheses and Order of Operations

Revision

Predecessor and Successor; Representing Numbers on the Number Line

Operations on a Number Line

Properties of Whole Numbers

Patterns in Numbers; Patterns in Shapes

Revision

Reviewing Factors and Multiples

Even and Odd Numbers; Perfect Numbers

Prime and Composite Numbers

Divisibility Rules

Prime Factorisation

Common Factors and Common Multiples

Highest Common Factor

Lowest Common Multiple

Word Problems on LCM and HCF

Revision

Key Geometrical Concepts

Measuring and Drawing Line Segments

Basics of Angles; Types of Angles

Measuring and Drawing Angles

Triangles and Their Features

4. Line, Angles and Shapes 13

5. 3-D Shapes 4

6. Integers 7

7. Fractions 10

Classification of Quadrilaterals

Polygons and Their Features

Types of Curves

Parts of a Circle; Circumference of the Circle

Constructing Circles

Revision

Features of 3-D Shapes

Nets of 3-D Shape

Revision

Representing Integers; Comparing and Ordering Integers

Addition of Integers

Subtraction of Integers

Revision

Representing Fractions

Comparing Fractions; Ordering Fractions

Conversion Between Mixed Numbers and Improper Fractions

Equivalent Fractions and Simplest Form

Addition and Subtraction of Fractions

Multiplying Fractions or Mixed Numbers

Dividing Fractions or Mixed Numbers

Revision

Representing Decimals on Number Line

Place Values in Decimals

Conversion Between Fractions and Decimals

Equivalent Decimals; Comparing Decimal

8. Decimals 10

9. Data Handling 6

Addition and Subtraction of Decimals

Multiplication of Decimals

Division of Decimals

Revision

Organising Data as Tally Marks

Pictographs

Bar Graphs

Revision

10. Mensuration 10

11. Introduction to Algebra 8

12. Introduction to Ratio and Proportion 8

13. Symmetry 6

14. Construction of Line Segments and Angles 9

Perimeter of Plane Figures

Perimeter of Regular Shapes

Area on Graph Paper

Area of Squares and Rectangles

Area of Triangles

Area and Perimeter of Combined Shapes

Word Problems on Perimeter and Area

Revision

Number Patterns

Rules in Patterns

Algebraic Expressions

Forming Algebraic Equations

Solving Linear Equations in One Variable

Revision

Introducing Ratios

Ratio in Simplest Form

Equivalent Ratios

Proportion abd Their Applications

Unitary Method

Revision

Lines of Symmetry

Reflection and Symmetry

Rotational Symmetry

Revision

Constructing Line Segments; Constructing a Copy of a Line Segment

Construction of Shapes and Figures

Constructing a Perpendicular Using a Compass

Constructing Angles of Given Measures

Constructing an Angle Bisector

Constructing 60°, 120° and 30° Angles

Revision

Total Number of Periods 123

Large Numbers and Operations 1

Learning Outcomes

Students will be able to:

read and write 9-digit numbers in the Indian number system. read and write 9-digit numbers in the international number system. compare and order 9-digit numbers and form numbers using the given digits. read and write Roman numerals. round off large numbers to the nearest 10, 100 or 1000. estimate the sum, difference, product or quotient in large numbers. add or subtract numbers up to 9 digits. multiply or divide large numbers up to 9 digits by numbers up to 3 digits. use parentheses to show the order of operations.

Alignment to NCF

C-1.1: Develops a sense for and an ability to manipulate (e.g., read, write, form, compare, estimate, and apply operations) and name (in words) large whole numbers of up to 20 digits, and expresses them in scientific notation using exponents and powers

Let’s Recall

Recap to check if students know how to read and write 7-digit numbers. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

9-digit numbers: numbers that have place values ranging from ones to crores, that is, from 10,00,00,000 to 99,99,99,999

roman numbers: a system where letters were used by ancient Romans to represent numbers, which is still used today

estimation: the process of guessing an answer that is close to the actual answer

DMAS: the order of operations (division, multiplication, addition, subtraction) that makes it easy to solve a mathematical problem with multiple operations

Teaching Aids

Number cards (0–9); Bowl; Indian place value chart; International place value chart; Blank cards; Clock with Roman numerals; Place value blocks of 10s, 100s and 1000s; Bingo cards with Roman numerals; Sticky notes; Cards with sets of numbers with operations; Puzzle cards; Bingo cards; Problem cards; Crayons; Puzzle interlocking cards

Chapter: Large Numbers and Operations

Indian

Number System

Learning Outcomes

Students will be able to read and write 9-digit numbers in the Indian number system.

Teaching Aids

Number cards (0–9); Bowl; Indian place value chart

Activity

Prepare a bowl of number cards (0–9) and keep it on your table for the activity.

Ask the students to work in groups of 4 and distribute one blank Indian place value chart to each group. Instruct one student from each group to come forward and pick 9 numbers from the bowl. Once they have selected the cards, they should return to their group and display the digits. Ask the groups to form the largest and the smallest 9-digit numbers on the place value chart using those digits. Instruct the students to write the expanded form of both the numbers, as well as their number names in the Indian number system in their notebooks. Repeat the activity with more number cards.

Ask questions like, “What are periods? What are all the places in the number? Does the face value of the digit change with its place value? Why and where do we put commas in the number?”

International Number System Imagine Maths Page 5

Learning Outcomes

Students will be able to read and write 9-digit numbers in the international number system.

Teaching Aids

Number cards (0–9); Bowl; International place value chart

Activity

Ask the students to work in groups of 4 and distribute one blank international place value chart to each group. Reuse the number cards (0–9) from the previous lesson. Repeat the activity to get groups to form the largest and smallest 9-digit numbers on the place value chart. Instruct the students to record the expanded form and number name in the international system in their notebooks.

Ask questions like, “How is the placement of commas different in the Indian and the international number systems? How does it impact the place value of each digit and the number name in the two systems?” Repeat the activity with more number cards.

Extension Idea

Ask: How many millions are there in 16,89,04,231?

Say: 16,87,04,231 is written in the Indian number system. In the international number system, it will be written as 168,704,231. So, there are 168 millions in this number.

Learning Outcomes

Students will be able to compare and order 9-digit numbers and form numbers using the given digits.

Teaching Aids

Blank cards

Activity

Tell the students that today they will create their own numbers. Ask the class to work in groups of 4. Distribute 4 empty cards to each group. Instruct them to create their own 9-digit numbers using different digits and write them on the blank card given to them. Everyone will place the card in the centre and then compare and order them as a group. If any two numbers are same in the group, one of them will change it, so that 4 different numbers are there to compare. Instruct the students to compare and arrange the numbers in ascending and descending order in their notebooks. Ask questions like, “How are the two orders different from each other? How many places have the same digits and different digits? What points should be kept in mind while comparing and ordering numbers?”

Extension Idea

Ask: Take the 9-digit number 87,06,98,543. If you add 1 to ones place then 1 to the tens place and so on (starting with the lowest) and form a new number each time, what numbers will you get? List the first four numbers and arrange them in descending order.

Say: The first four numbers would be 87,06,98,544 (87,06,98,543 + 1); 87,06,98,553 (87,06,98,543 + 10); 87,06,98,643 (87,06,98,543 + 100); 87,06,99,543 (87,06,98,543 + 1000). So, the descending order is 87,06,99,543 > 87,06,98,643 > 87,06,98,553 > 87,06,98,544. Roman Numerals Imagine Maths Page 10

Learning Outcomes

Students will be able to read and write Roman numerals.

Teaching Aids

Clock with Roman numeralsl; Place value blocks of 10s, 100s and 1000s; Bingo cards with Roman numerals

Activity

Begin by showing the students a clock with Roman numerals. Explain the 7 basic symbols used to form Roman numbers. Tell them about the Roman numerals that can be repeated, added or subtracted. Elaborate on the rules used to form these numerals.

Ask the class to work in groups of 4. Distribute bingo cards with a 5 × 5 grid of random Roman numbers up to 2000 to each group.

Use the place value blocks to form a 2-digit, 3-digit or 4-digit number (up to 2000). Ask one student from each group to come up and read the number, then go back and tell their group the number. Instruct the group to find its corresponding Roman number and cross it off from their bingo card. Repeat this process until all the Roman numbers in a line—horizontally, vertically or diagonally—are crossed off. The group to cross off the Roman numbers in all three directions first wins the game.

Learning Outcomes

Students will be able to round off large numbers to the nearest 10, 100 or 1000.

Teaching Aids

Sticky notes

Activity

Begin the class by asking the students where they might use rounding off numbers in real life. Use these scenarios to review the concept of rounding off large numbers to the nearest 10, 100 and 1000.

Write various large numbers on sticky notes and paste them on the board.

Divide the class into small groups and call a student from each group up to the board to select a number. Instruct group members to work together to round off the selected number to the nearest 10, 100 and 1000, and write their answers on another sticky note to be pasted on the board next to the original number. If their answers are correct, then the group gets a point; otherwise no points. Repeat this process until all the members of the group are covered. The group with the maximum points wins.

Extension Idea

Ask: I am thinking of a number. When I round off the number to the nearest 100, it is 2,43,26,500. When I round off the same number to the nearest 10, it is 2,43,26,450. What could my number be?

Say: Considering the possible numbers before rounding off to the nearest 10, the number may lie between 2,43,26,445 and 2,43,26,454. But to meet the condition for rounding off to the nearest 100, the number would be between 2,43,26,450 and 2,43,26,549. To satisfy both conditions, the numbers should be between 2,43,26,450 and 2,43,26,454

Estimation in Operations

Learning Outcomes

Imagine Maths Page 13

Students will be able to estimate the sum, difference, product or quotient in large numbers.

Teaching Aids

Cards with sets of numbers with operations; Bowls

Activity

Prepare some cards with sets of numbers and operations written on them, such as, Sum to the nearest 100: 1,24,37,548 + 3,25,43,768 and Difference to the nearest 1000s: 98,78,563 − 45,47,658, and keep them in a bowl. Divide the board into 4 columns for sum, difference, product and quotient. Then, divide the class into teams of equal sizes.

Start the activity by calling one student from each team to the front of the class. They should pick a card from the bowl, read the expression, quickly find the estimated answer and write it in the relevant column on the board. If the result is correct, award the team 1 point. Continue in this manner until all the students in each team have had a turn. The team with the highest total score wins the game.

Learning Outcomes

Students will be able to add or subtract numbers up to 9 digits.

Teaching Aids

Puzzle cards

Activity

Prepare puzzle cards involving addition and subtraction of numbers up to 9 digits. Divide the class into groups of equal sizes. Distribute the puzzle cards (9 individual cards) to each group.

Instruct the students to solve the calculations on the puzzle cards and arrange the cards to form a 3 × 3 puzzle matrix.

The group which forms the matrix in the least time wins.

Review the matrix formed by each group and discuss the answers. Also ask the students to write the answers in their notebook.

Extension Idea

Ask: Tripti is keeping track of how far she walks each week. On Monday, she walks 1780 m and on Tuesday she walks 50 m farther than on Monday. If her target is to walk 2000 m each day, then by how much is she short of her target over the two days?

Say: Tripti walks 1780 m on Monday. She walks 1780 m + 50 m = 1830 m on Tuesday. Her target distance for two days is 4000 m. So, she is short of the target by 4000 – (1780 + 1830) m = 390 m.

Learning Outcomes

Students will be able to multiply or divide large numbers up to 9 digits by numbers up to 3 digits.

Teaching Aids

Bingo cards; Problem cards; Crayons

Activity

Prepare a set of cards or small pieces of paper with multiplication and division problems, like 56 × 21 or 18,240 ÷ 5, written on them with their corresponding answers. Shuffle the cards and place them face down in a pile. Write the answers to the problems on bingo cards.

Ask the students to work in groups.

Distribute a bingo card to each group. Play the game by drawing cards, one by one, from the pile and reading the questions aloud. Ask the groups to calculate the answers (they may use their notebooks for rough work) and cross out/colour the corresponding square on their bingo card if the answer matches. The game will continue until a group successfully completes a row, column or diagonal on their bingo card and shouts “BINGO!” to indicate their win. Verify all the answers on the winning bingo card.

Parentheses and Order of Operations

Learning Outcomes

Students will be able to use parentheses to show the order of operations.

Teaching Aids

Puzzle interlocking cards; Bowls

Activity

Make sets of puzzle interlocking cards where one card (red) has an expression involving DMAS and brackets and its interlocking card (green) has the answer. Put the red cards in one bowl and the green cards in another bowl.

Maths Page 19

Divide the class into groups and distribute bowls with both types of cards to each group. Instruct each group to pick a red card, solve the expression, and match it with its corresponding green card. Instruct them to match all the cards in the two bowls. The group which completes all the pairs first wins. Verify all the answers and ask the students to write them in their notebooks.

Extension Idea

Ask: What operations would you fill in these blanks to make the given statement true? (20 8) 2 9 = 5

Say: If we add 20 and 8, we get 28. Then, we divide it by 2 to get 14. Next, if we subtract 9 from 14, we get 5. So, the correct order of operations is: (20 + 8) ÷ 2 − 9 = 5.

Answers

1. Face Value and Place Value

Do It Together

3 is in the crores place.

The place value of 3 is 3,00,00,000.

The face value of 3 is 3

2. Expanded Form and Number Names

Think and Tell

Yes. Population of U.S.—33,99,96,563: thirty-three crore ninety-nine lakh ninety-six thousand five hundred sixty-three. Population of Russia—14,44,44,359: fourteen crore forty-four lakh forty-four thousand three hundred fifty-nine. Population of Japan—12,32,94,513: twelve crore thirty-two lakh ninety-four thousand five hundred thirteen.

Do It Together

56,70,34,219 = 500000000 + 60000000 + 7000000 + 30000 + 4000 + 200 + 10 + 9

Number name: fifty-six crore seventy lakh thirty-four thousand two hundred nineteen

3. Face Value and Place Value

Do It Together

4 is in the millions place.

So, the place value of 4 is 4,000,000. The face value of 4 is 4

4. Expanded Form and Number Names

Do It Together

902,564,875 = 900,000,000 + 2,000,000 + 500,000 + 60,000 + 4000 + 800 + 70 + 5

Number name: nine hundred two million five hundred sixty-four thousand eight hundred seventy-five.

5. Comparing and Ordering Numbers

Think and Tell

Population of Russia = 14,44,44,359

Population of Indonesia = 27,75,34,122

1 < 2, so 14,44,44,359 < 27,75,34,122. So, the population of Russia is less.

Think and Tell

Yes. Descending order: 33,99,96,563 > 27,75,43,122 > 14,44,44,359 > 12,32,94,513

Think and Tell

Yes, more such numbers can be formed. Some examples are 517860932, 783096521 and 602983571.

Think and Tell

The greatest 9-digit number can be formed by using the two greatest 1-digit numbers i.e. 8 and 9: 99,99,99,998. The smallest 9-digit number can be formed by using the two smallest 1-digit numbers i.e. 1 and 0: 10,00,00,000.

Do It Together

Ascending Order: 126,856,384 < 165,121,349 < 400,897,234 < 860,778,653

Descending Order: 860,778,653 > 400,897,234 > 165,121,349 > 126,856,384

6. Understanding Roman Numerals

Do It Together

1. 45 MCCCXC

2. 98 CX

3. 110 XLV

4. 185 XCVIII

5. 1390 CLXXXV

7. Rounding Off

Think and Tell

To round off an 8-digit number to the largest place, that is, the crores place, we look at the digit to its right (that is the ten lakhs place). If the digit is greater than or equal to 5, the number rounds off to the next crores, else the number rounds off to the same crores.

Do It Together

So, the number 73,26,63,547 rounded off to the nearest 10 is 73,26,63,550

So, the number 73,26,63,547 rounded off to the nearest 100 is 73,26,63,500

So, the number 73,26,63,547 rounded off to the nearest 1000 is 73,26,64,000

8. Estimation in Operations

Do It Together

1. 765 + 213 (to the nearest hundred)

765 rounded off to 100 800

213 rounded off to 100 200

So, the estimated sum of 765 and 213 = 800 + 200 = 1000.

2. 984 − 356 (to the nearest ten)

984 rounded off to 10 980

356 rounded off to 10 360

So, the estimated difference of 984 and 356 = 980 360 = 620.

3. 758 × 510 (to the nearest hundred)

758 rounded off to 100 800

510 rounded off to 100 500

800 × 500 = 4,00,000

So, the estimated product of 758 and 510 is 4,00,000

4. 332 ÷ 25 (to the nearest ten)

332 rounded off to 10 300

25 rounded off to 10 30

300 ÷ 30 = 10

So, the estimated quotient of 332 ÷ 25 is 10

9. Addition and Subtraction

Think and Tell

30 kg 100 g and 14 kg 500 g are written as 30.100 kg and 14.500 kg because 1 kg = 1000 g, so 1 g = 1 1000 kg = 0.001 kg.

Do It Together

Number of children in the city = 37,65,392 – (18,90,898 + 16,54,976)

So, the number of children in the city was 2,19,518

10. Multiplication and Division

Do It Together

Total fee collected by the school = 5678 × 16,000

So, the total fee collected by the school is 9,08,48,000

11. Parentheses and Order of Operations

Do It Together

8 × 105 = 8 × (100 + 5) = (8 × 100) + (8 × 5) = 800 + 40 = 840

Patterns in Whole Numbers

Learning Outcomes

Students will be able to: show whole numbers on a number line and identify the predecessor and the successor of a whole number. perform operations on whole numbers on a number line. identify and apply the closure, commutative, associative and distributive properties of whole numbers. identify patterns in whole numbers and shapes, and extend them.

Alignment to NCF

C-1.2: Discovers, identifies, and explores patterns in numbers and describes rules for their formation (e.g., multiples of 7, powers of 3, prime numbers), and explains relations between different patterns

C-1.4: Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line

Let’s Recall

Recap to check if students know how to recognise natural numbers and perform skip counting by various intervals on a number line.

Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

consecutive numbers: numbers one after another property: rules defining the relationship between numbers

Teaching Aids

Number cards per the number of students; Operation cards (including addition, subtraction, multiplication and division) per the number of students; Paper cups; Marbles; Beads; Shape cutouts; Chart paper

Chapter: Patterns in Whole Numbers

Predecessor and Successor; Representing

Numbers on the Number Line

Learning Outcomes

Imagine Maths Page 27

Students will be able to show whole numbers on a number line and identify the predecessor and successor of a whole number.

Teaching Aids

Number cards per the number of students

Activity

Prepare stacks of number cards per the number of students in the class.

Take the students out to the playground.

Shuffle the stack and distribute one card to each student.

Instruct the students to move around and find the student with the predecessor of their number and stand behind them, forming a line.

Once students have found their predecessors, they will naturally form a line based on the numerical order of their cards.

Repeat the activity by shuffling and distributing the cards again and asking the students to stand in front of the student that has the successor of their number.

Ask questions like, “What do you think is the importance of understanding the predecessor and successor of a number?”

Extension Idea

Ask: B is positioned 2 places behind A and 3 places in front of the number 26. What is A’s position?

Say: As B is 3 places in front of the number 26, B’s position is 23. As B is positioned 2 places behind A, A’s position is 21.

Operations on a Number Line

Learning Outcomes

perform operations on whole numbers on a number line.

Teaching Aids

Imagine Maths Page 28

Operation cards (including addition, subtraction, multiplication and division) per the number of students

Activity

Ask the students to form groups of 4. Distribute the operation cards to the groups. 4 + 6 12 – 3

Take the students out to the playground. Instruct each group to draw a large horizontal number line of range 0–20 on the ground. Instruct the students to show each operation on the number line.

For example to show addition of numbers, start from the first number and jump forward as many unit distance as in second number and arrive at the answer. Similarly, show subtraction, multiplication and division on the number line.

Back in the classroom, instruct the students to draw a number line in their notebooks and show the answers. Give them a few more questions to perform operations on whole numbers on a number line in their notebooks.

Extension Idea

Ask: Ria bought 5 pencils for ₹20. How much did one pencil cost? Show your answer on the number line. Say:

Cost of 5 pencils = ₹20

Cost of 1 pencil = 20 ÷ 5 = 4

Therefore, the cost of 1 pencil is ₹4.

Properties of Whole Numbers Imagine Maths Page 29

Learning Outcomes

identify and apply the closure, commutative, associative and distributive properties of whole numbers.

Teaching Aids

Paper cups; Marbles; Beads

Activity

Ask the students to work in groups. Distribute paper cups and marbles to each group. Instruct the groups to show 3 + 5 using the marbles and cups and write the result in their notebooks. Verify if the obtained number is a whole number. Explain that this is the closure property. Ask them to now show 5 + 3 using the marbles and cups and note down the answer. Discuss the commutative property.

Instruct them to show 8 – 3 and then 3 – 8 using the cups and marbles and record the results in their notebooks. Discuss whether they get a whole number or the same answer in both cases and explain that subtraction of whole numbers does not satisfy the closure and commutative properties. Distribute beads to each group.

Instruct the groups to show 6 × 3 using beads and make 2 groups of 6 × 3. Help them understand that this can be shown as (6 × 3) × 2. Ask them to show 6 × (3 × 2) and check the result. Discuss the associative property and ask the groups to record the results in their notebooks. Instruct the groups to show 6 × 3; 6 × 2; 6 × 5; and 6 × 1; and record the results in their notebooks. Discuss how (6 × 3) + (6 × 2) = 6 × 5 and (6 × 3) – (6 × 2) = 6 × 1. Discuss the distributive property of multiplication and subtraction.

Instruct the students to show 10 ÷ 5 by threading a total of 10 beads with 5 beads in each group. Instruct the groups to show (10 ÷ 5) ÷ 2 and 10 ÷ (5 ÷ 2) using beads and discuss the associative property.

Extension Idea

Ask: Suppose you have one group of 13 red and 17 blue beads. How many beads are there in total if there are 10 such groups?

Say: 10 × (13 + 17) = 130 + 170 = 300. So, there are 300 beads in total.

Patterns in Numbers; Patterns in Shapes Imagine Maths Page 33

Learning Outcomes

Students will be able to identify patterns in whole numbers and shapes and extend them.

Teaching

Aids

Shape cutouts; Chart paper

Activity

Ask the students to form groups. Distribute the shape cutouts and chart paper to the students. Instruct each group to create 2 patterns one with whole numbers by drawing the dots and the other with shapes, by pasting shapes. Ask them to write the numbers below the dots in the number pattern.

They will then pass the chart paper to the group sitting next to them. Each group will then identify the rules and extend the patterns made by other groups.

Discuss the patterns in the class.

Extension Idea

Ask: A number is multiplied by 1. The product is multiplied by the next whole number, which is 2. The pattern continues 5 times. What is the original number if the final product is 1200?

Say: 1200 ÷ 5 = 240 → 240

So, the original number was 10.

Answers

1.

Whole Numbers on a Number Line

Think and Tell

Yes. Whole numbers are numbers starting from 0 like 0, 1, 2, 3,... Natural numbers are numbers starting from 1 like 1, 2, 3,... So, all natural numbers are whole numbers.

Do It Together

The predecessor of 87,452 = 87,452 – 1 = 87,451

The predecessor of 87,451 = 87,451 – 1 = 87,450

Therefore, the three consecutive numbers before 87,453 are 87,452, 87,451 and 87,450

2. Representing Numbers on the Number Line

Think and Tell

The largest whole number is infinite because every whole number must have a successor.

Do It Together

1. If you are standing in section 3, the whole number that represents the section just before the one you’re in is section 2

2. If you take a step to the right and move to section 5, the whole number that represents the section you were previously in is section 4

3. Operations on a Number Line

Do It Together

–4 –4 –4 –4

Cost of 4 candies = ₹20 Cost of 1 candy = ₹20 ÷ 4

Therefore, the cost of 1 candy is ₹5

4. Properties of Whole Numbers

1. 6579 × 0 = 0

2. 56 + 45 = 45 + 56

3. 108 × 1 = 108

4. 29 + (12 + 16) = (29 + 12) + 16

5. 83 ÷ 1 = 83

6. 64 ÷ 64 = 1

5. Patterns in Numbers

a. 3, 9, 27, 81, 243

b. 5, 16, 49, 148, 445

c. 1, 2, 6, 24, 120, 720

6. Patterns in Shapes

Rule followed by the sequence: Number of triangles in each shape is 1, 4, 9, 16, 25.

The number of triangles in the next shape in the sequence is 36.

Playing with Numbers: Factors and Multiples

Learning Outcomes

Students will be able to: list the factors and multiples of a number. identify perfect, odd and even numbers. identify prime and composite numbers and understand how to find co-prime numbers. identify and apply the divisibility rule for 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11. use the factor tree and repeated division to express a number as a product of its prime factors. find the common factors and multiples of two or more numbers. find the HCF of 2 or more numbers using prime factorisation and repeated division. find the LCM of 2 or more numbers by prime factorisation and the division method. solve word problems on LCM and HCF.

Alignment to NCF

Let’s Recall

Recap to check if students know how to find the factors of any number. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

factor: any one of two or more numbers that are multiplied together to give a product multiples: number obtained when a number is multiplied by an integer prime factorisation: a way of expressing a number as a product of its prime factors lowest common multiple: the smallest multiple that two or more numbers have in common

Teaching Aids

Squared paper; Number cards; Slips with divisibility rules; Square and circle cutouts; Blank cards; Number cards (with numbers 6, 28, 56, 3, 11, 55 written on them); Orange ribbons/colour paper strips (24 cm, 18 cm); Yellow ribbons/colour paper strips (36 cm, 30 cm); Scissors; Glue; Ruler; Sheets of paper; Word problem cards

Chapter: Playing with Numbers: Factors and Multiples

Reviewing Factors and Multiples

Learning Outcomes

Students will be able to list the factors and multiples of a number.

Teaching Aids

Squared paper

Activity

Provide each student with a sheet of squared paper. Ask them to draw as many different rectangles as possible, each with an area of 8 square units. Ask them to explore all the different lengths and widths possible for such rectangles. When they are done drawing, ask them to label the side lengths of each rectangle.

Discuss the side lengths and how they are related to the number 8. Summarise by saying that the side lengths 1, 2, 4, and 8 are the factors of 8.

Next, instruct the students to shade squares to show a 1 × 12 rectangle with an area of 12 sq. units, and then show stacks of up to 4 rectangles of 1 × 12 each. Ask them to write the area of each new rectangle formed and how the areas are related to the number 12. Summarise by saying that the areas of 12, 24, 36 and so on are multiples of 12.

Repeat the activity for a rectangle with an area of 15 square units.

Ask questions like, “How are the number of factors of a number different from the number of multiples of the same number?”

Extension Idea

Ask: What type of numbers have an odd number of factors?

Say: Only square numbers have an odd number of factors. For example, five numbers which have an odd number of factors are 1, 4, 9, 16, and 25.

Even and Odd Numbers; Perfect Numbers

Learning Outcomes

Students will be able to identify perfect, odd and even numbers.

Teaching Aids

Squared paper; Number cards

Activity

Ask the students to form groups of 6. Instruct each member of a group to take one number card (out of 6, 28, 56, 3, 11, 55).

Ask them to check if the number is exactly divisible by 2 or not. Explain the odd and even numbers.

Distribute a sheet of squared paper to each student and ask them to shade squares to form as many rectangles as possible with an area equal to that number. Ask them to list the factors of each number in their notebooks and then add all the factors except the number itself. Ask them to discuss in their groups what they notice about the factors and their sum.

Discuss how the sum of the factors decides if a number is a perfect number or not

Extension Idea

Ask: Check whether 28 perfect number or not.

Say: Factors of 28 = 1, 2, 4, 7, 14, 28

Sum of factors (excluding itself) = 1 + 2 + 4 + 7 + 14 = 28

Therefore, 28 is a perfect number.

Prime and Composite Numbers

Learning Outcomes

Imagine Maths Page 46

Students will be able to identify prime and composite numbers and understand how to find co-prime numbers.

Teaching Aids

Squared paper

Activity

Provide each student with a sheet of squared paper. Ask them to draw as many different rectangles as possible, each with an area of 7 and 9 square units. Ask them to write all the factors of 7 and 9.

Discuss that the number 7 has two factors 1 and 7, and number 9 has three factors 1, 3 and 9.

Explain, a number greater than 1 that has exactly two factors is called prime number and if it has more than two factors it is called the composite number.

Next, instruct the students to write all the prime numbers between 10 to 20 in their notebooks.

Ask the students list the factors which are common to both 7 and 9 and explain the co-prime numbers.

Ask questions like, “Which even number is the prime number? ”

Extension Idea

Ask: Write any 3 pairs of twin prime numbers.

Say: Twin prime numbers are a pair of prime numbers with a difference of 2. Three pairs of twin prime numbers are (3, 5), (5, 7), (11, 13).

Divisibility Rules

Learning Outcomes

Imagine Maths Page 48

Students will be able to identify and apply the divisibility rule for 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11.

Teaching Aids

Number cards; Slips with divisibility rules

Activity

Prepare cards with numbers written on them, including some that are divisible by 2, 3, 4, 5, 6, 8, 9, 10 and 11 and some that are not.

Divide the class into 4 groups and assign each group with numbers. For example, Group 1 gets 2, 3 and 6, Group 2 gets 4 and 8, Group 3 gets 5, 9 and 10 and Group 4 gets 11.

Take the students out to the playground and distribute the slips with the divisibility rules of those numbers written on them.

Scatter the number cards all around the playground facing down.

Divisibility rule of 2: The digit in the ones place of the number is 0, 2, 4, 6 or 8.

Divisibility rule of 3: The sum of the digits of the number should be divisible by 3.

Instruct one student from each group to run around to find the number divisible by the number on their slip and bring it back. The group that collects the maximum number of cards wins.

If any of the cards have a number that is divisible by two numbers, then the student who finds it first should bring it back to their group.

Prime Factorisation

Learning Outcomes

Imagine Maths Page 50

Students will be able to use the factor tree and repeated division to express a number as a product of its prime factors.

Teaching Aids

Square and circle cutouts

Activity

Start by discussing what a factor pair of a number is.

Instruct the students to write any one factor pair of 24. Show the factor pairs of 24 using a factor tree as given.

Ask the students to work in pairs. Distribute square and circle cutouts to each pair.

Instruct them to create a factor tree on their desks for the number 48 using circle cutouts for the prime factors and square cutouts for the composite factors. Ask them to then write all the prime factors in their notebooks with multiplication signs in between and multiply to check if they get the same number.

Next, instruct the students to find the factors using the repeated division method. Let them write 48 inside the division house and ask them which prime number divides 48. Instruct them to write the prime number outside the division house and write the quotient below 48 and then continue dividing in this way until the quotient is 1. Finally, ask them to compare the answers that they got using both methods.

Common Factors and Common Multiples

Learning Outcomes

Imagine Maths Page 53

Students will be able to find the common factors and multiples of two or more numbers.

Teaching Aids

Number cards; Blank cards

Activity

Prepare cards with numbers 8 and 12 written on them.

Ask the students to work in pairs. Distribute 2 number cards and few blank cards to each pair.

Ask one student to write factors of the numbers shown in the cards and other multiples. Say that the common factors of 8 and 12 are 1, 2, 4 and common multiples are 24, 48, 72, …

Instruct them to observe common factors and common multiples of the given numbers.

Next, summarise saying them that 8 and 12 have limited number of factors but have infinite number of multiples. Discuss that for any 2 given number there are finite number of common factors but there are infinite number of common multiples.

Repeat the activity for a number 15, 20 and 30. Ask the students to find the common factors and common multiples of the given numbers, in their notebooks.

Extension Idea

Ask: What are the common factors of 2 prime numbers?

Say: The common factor of two prime numbers is 1. For example,

Factors of 7 are 1 and 7.

Factors of 11 are 1 and 11.

Common factors of 7 and 11 is 1.

Highest

Common Factor

Learning Outcomes

Imagine Maths Page 54

Students will be able to find the HCF of 2 or more numbers using prime factorisation and repeated division.

Teaching Aids

Orange ribbons/colour paper strips (24 cm, 18cm); Yellow ribbons/colour paper strips (36 cm, 30 cm); A pair of scissors; Glue; Ruler

Activity

Divide the class into groups and distribute ribbons of length 24 cm (orange) and 36 cm (yellow) to each group. Ask the students what is the maximum length of ribbon possible if they want to cut the ribbons into equal pieces without having any left.

Ask them to place the orange ribbon along the yellow ribbon as shown. Instruct them to cut the additional part of the yellow ribbon and place it along the orange ribbon. They should repeat this process until both ribbons are equal in length. Ask them to measure the length of the equal ribbons using a ruler.

Explain that 12 cm (length of the last part cut) is the HCF of 36 cm and 24 cm.

Next, instruct the students to find the HCF of 24 and 36 using prime factorisation and the long division method in their notebooks. If time permits, give them 2 more ribbons of different lengths and ask them to find the highest common factor.

If time permits, distribute next set of ribbons of length 18 cm and 30 cm. Ask them to repeat the activity. If ribbons are unavailable, give them strips of coloured paper for the activity.

Extension Idea

Ask: What is the HCF of any 5 consecutive numbers?

Say: The HCF of any 5 consecutive numbers is 1.

Lowest Common Multiple

Learning

Outcomes

Students will be able to find the LCM of 2 or more numbers by prime factorisation and the division method.

Teaching Aids

Sheets of paper

Activity

Ask the students to work in pairs. Distribute sheets of paper to each pair.

Instruct them to draw the factor pairs of 16 and 24. Instruct the students to list the prime factors of both numbers and write each number as the multiplication of its prime factors. Ask them to identify the prime factors common to both 16 and 24, and circle the prime factors. Ask them to write the all the circled common factors once and multiply it with non-common factors to find the LCM.

Ask questions like, “Is there any method to find the LCM quickly?”

Instruct the students to draw a division house and write the two numbers inside it. Ask them which prime number divides both numbers. Collect the responses and instruct the students to write the prime number outside the division house and write the quotients below 16 and 24. They should follow these steps to continue the process of dividing by prime numbers, when the quotients are no longer be divided by a common prime number, divide each quotient individually until both reach 1. Instruct the students to multiply the prime numbers to find the LCM.

Ask the students to compare the answers that they got using both methods.

Extension Idea

Instruct: Find the smallest number that is divisible by all the numbers from 1 to 10.

Say: To find the smallest number that is divisible by all the numbers from 1 to 10, we will find the LCM of all the numbers from 1 to 10. So, LCM = 2 × 2 × 2 × 3 × 3 × 5 × 7 = 2520.

Word Problems on LCM and HCF

Learning

Outcomes

Students will be able to solve word problems on LCM and HCF.

Teaching Aids

Word problem cards

Activity

Begin the class by discussing the concepts of LCM and HCF.

Divide the class into groups and distribute the word problem cards to each group.

Kushal has a book stare. He has 15 comic books and 24 history books in each cupboard.

(a) He wants to arrange the books in such a way that each shelf has the same number of comic books and the same number of history books. What is the maximum number of shelves he can fill in this way?

(b) Kushal packed the books into cartons. He packed sets of 15 comic books and sets of 24 history books such that the total number of each type of book was the same. What is the least possible number of each type of book he packed in the carton?

Instruct the groups to read the word problem on their card and determine whether it requires finding the LCM or the HCF. Discuss the reasoning for the answers and ask the students to write the answers in their notebooks.

Extension Idea

Instruct: Create an LCM word problem using the numbers 10, 24 and 30.

Say: “A water pump fills a tank in 10 hours, a second pump in 24 hours, and a third pump in 30 hours. The pumps are switched on to fill tanks at the same time. Find the least amount of time after which all three pumps will complete filling a tank at the same time.”

Answers

1.

Reviewing Factors and Multiples

Do It Together

2. 21

Factors = 1, 3, 7, 21

Multiples = 21, 42, 63

3. 27

Factors = 1, 3, 9, 27

Multiples = 27, 54, 81

4. 39

Factors = 1, 3, 13, 39

Multiples = 39, 78, 117

2. Even and Odd Numbers

Do It Together

1. 91—Odd

2. 61—Odd

3. 79—Odd

4. 7—Odd 5. 45—Odd 6. 82—Even

3. Perfect Number

Do It Together

7. 39—Odd 8. 19—Odd

The factors of 8128 are 1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064, 8128.

Sum of factors (excluding itself) = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064 = 8128

Therefore, 8128 is a perfect number.

4. Prime and Composite Numbers

Think and Tell

There is only 1 even prime number which is 2.

Do It Together

1. Hence, 15 and 28 are co-prime numbers

2. Factors of 21: 1, 3, 7, 21

Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40

Only 1 is the common factor Hence, 21 and 40 are co-prime numbers.

5. Divisibility Rules

Do It Together

1. 5628

Divisibility by 4: 28 is divisible by 4.

So, 5628 is divisible by 4.

Divisibility by 6: Digits at ones place is 8 which is divisible by 2.

5 + 6 + 2 + 8 = 21, which is divisible by 3

So, 5628 is divisible by both 2 and 3, hence it is divisible by 6.

Divisibility by 9: 5 + 6 + 2 + 8 = 21, which is not divisible by 9

So, 5628 is not divisible by 9.

Divisibility by 11: (6 + 8) – (5 + 2) = 7, which is not divisible by 11.

So, 5628 is not divisible by 11.

So, 5628 is divisible by 4 and 6.

2. 4356

Divisibility by 4: 56 is divisible by 4. So, 4356 is divisible by 4.

Divisibility by 6: Digits at ones place is 6 which is divisible by 2

4 + 3 + 5 + 6 = 18, which is divisible by 3

So, 4356 is divisible by both 2 and 3, hence it is divisible by 6

Divisibility by 9: 4 + 3 + 5 + 6 = 18, which is divisible by 9.

So, 4356 is divisible by 9

Divisibility by 11: (6 + 3) – (5 + 4) = 0.

So, 4356 is divisible by 11.

So, 4356 is divisible by 4, 6, 9 and 11.

6. Prime Factorisation

Do It Together

1. Prime factors of 76 2 76 2 38 19 19 1

2. Factor tree of 99 3 3 33 99 11

99 = 3 × 3 × 11

7. Common Factors and Common Multiples

Do It Together

1. 12, 18, 24: 6, 3, 2, 1 9, 18 4, 12 1, 3, 6 2 8, 24

Factors of 12

Factors of 18

Factors of 24

2. 18, 27, 36: 1, 3, 9 27 2, 6, 18 1, 9, 3, 4, 8, 12, 36

Factors of 18 Factors of 36 Factors of 27

8. Highest Common Factor

Do It Together

72 = 2 × 2 × 2 × 3 × 3 108 = 2 × 2

Hence, HCF of 72, 108 and 96 = 2 × 2 × 3 = 12

9. Lowest Common Multiple

Do It Together

1. 60, 84: 2 × 2 × 3 × 5 × 7 = 420

2. 126, 154, 189: 2 × 3 × 3 × 3 × 7 × 11 = 4158

10. Word Problems on LCM and HCF

Do It Together

Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24

Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36

Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48

So, the HCF of the numbers is 12. Emily will make 2 packs of chocolate chip cookies + 3 packs of oatmeal cookies + 4 packs of peanut butter cookies.

Hence, Emily will make 9 packs.

Lines, Angles and Shapes

Learning Outcomes

Students will be able to: identify a plane, point, line segment, ray and line. measure and draw line segments.

identify the parts of angle and classify the different types of angles. measure and draw angles using a protractor. identify the parts of a triangle and classify them on the basis of their sides and angles. identify parts of a quadrilateral and classify quadrilaterals on the basis of their types. identify parts of a polygon and classify polygons on the basis of their sides, angles and diagonals. classify curves as open or closed, simple or non-simple. identify parts of circles and find the circumference of a circle using the formula. construct a circle for the given radius.

Alignment to NCF

C-3.1: Describes, classifies, and understands relationships among different types of two– and three–dimensional shapes using their defining properties/attributes

C-3.2: Outlines the properties of lines, angles, triangles, quadrilaterals, and polygons and applies them to solve related problems

C-3.4: Draws and constructs geometric shapes, such as lines, parallel lines, perpendicular lines, angles, and simple triangles, with specified properties using a compass and straightedge

Let’s Recall

Recap to check if students know about various types of lines, angles and shapes. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

line segment: a part of a line that has two definite end points angle: the space between two rays emerging from the same point vertices: points where the sides of a polygon meet sides: line segments that form a polygon quadrilateral: a polygon with four sides loop: a shape formed by a curve when it crosses itself line segment: a part of a straight line with two end points equidistant: at equal distances from a common point intersect: meet at a point

Teaching Aids

Set of cards showing points, lines, line segments, rays and planes; Pieces of string; Scissors; Ruler; Glue stick; Rectangular origami sheets in different colours (15 cm × 4 cm); Ice-cream sticks; Tape; Chart paper; Blue and orange buttons; Circular cutouts of radius 10 cm; Protractor; Sheets of coloured paper; Markers; Thermocol sheets; Quadrilateral cutouts; Geoboards; Rubber bands of different colours; Sheet of paper; Compass; Drawing sheets; Crayons; Pin; Pencil

Chapter: Lines, Angles and Shapes

Key Geometrical Concepts

Learning Outcomes

Students will be able to identify a plane, point, line segment, ray and line.

Teaching Aids

Set of cards showing points, lines, line segments, rays and planes

Activity

Ask the students to work in groups of 3. Distribute a shuffled set of cards showing points, lines, line segments, rays and planes to each group.

Instruct the groups to look at the cards and sort them according to their features. Once they are done, have a discussion around the features of all the elements.

Instruct the students to draw a table in their notebooks with columns for each element. Ask them to draw and label the elements and list the features discussed so far. Also ask them to add 2 examples for each element that they see in everyday life.

Measuring and Drawing Line

Segments

Imagine Maths Page 67

Learning Outcomes

Students will be able to measure and draw line segments.

Teaching Aids

Pieces of string; Scissors; Ruler; Glue stick

Activity

Begin by discussing the various units of length. Discuss the meaning of the big and small markings on the ruler. Ask the students to show various lengths such as 5 cm 3 mm in decimals.

Ask the students to work in pairs. Distribute a piece of string, a ruler, glue stick and a pair of scissors to each pair.

Instruct the students to measure 5.3 cm of the string, cut the string of that length and paste it in their notebooks. Ask them to draw a line of the same length using a ruler below the pasted thread and label it. Repeat the activity for various lengths of thread.

Extension Idea

Ask: What would be the total length of the line drawn below three pieces of string of lengths 2 cm 5 mm, 52 mm and 6.7 cm pasted end to end without any gaps?

Say: The length of the line will be the sum of the lengths of the three threads = 2.5 cm + 5.2 cm + 6.7 cm = 14.4 cm.

Basics of Angles; Types of Angles

Learning Outcomes

Imagine Maths Page 71

Students will be able to identify the parts of angles and classify the different types of angles.

Teaching Aids

Rectangular origami sheets in different colours (15 cm × 4 cm); Ice-cream sticks; Glue stick; Tape; Chart paper; Blue and orange buttons

Activity

Discuss an angle and the different parts of an angle, with the students.

Ask the students to work in groups of 6. Distribute origami sheets, ice cream sticks and glue sticks to each group.

Ask each student in a group to take one origami sheet, start from the smaller side and make accordion-style folds along the horizontal edge such that each fold is about 1 cm wide. Then, ask them to paste ice-cream sticks at both ends of the folded sheet and join the sticks together at one end using tape. Instruct the groups to take the first folded sheet and stick the ice-cream sticks on the chart paper so as to make an angle less than 90° .

Explain that angles less than 90° are called acute angles. Ask them to take the next sheet and stick it on the chart paper forming a 90° angle. Explain that a 90° angle is also known as a right angle. Instruct the groups in the same way so that they paste all six types of angles.

Instruct the groups to label the arms and vertex of the acute angle. Ask them to stick blue buttons outside and orange buttons inside the figure.

Explain that the blue buttons represent points on the exterior and orange buttons represent points on the interior of the angle.

Extension Idea

Ask: Can a point be on the exterior of an angle but on the interior of its adjacent angle? Draw and label such a figure.

Say: Point P is exterior to angle CAB but on the interior of its adjacent angle DAC.

Measuring and Drawing Angles

Learning Outcomes

Students will be able to measure and draw angles using protractor.

Teaching Aids

Circular cutouts of radius 10 cm; Ruler; Scissors; Protractor

Imagine Maths Page 73

Activity

Recall the steps of measuring an angle using a protractor.

Ask the students to work in pairs. Distribute circular cutouts, a ruler, a pair of scissors and protractor to each pair. Ask the students to fold the circular cutout in half and then open it. Ask them to cut it along the fold using scissors to get 2 semicircles. Ask each student to take a semicircle cutout and fold it in half, then into a tri-fold twice to get a fan. Ask them to draw lines along the creases obtained starting from the centre of the semicircle. Then, ask them to measure each of the angles drawn on the semicircle using a protractor and mark them.

Ask questions like, “What have you noticed about the angles so formed in the semicircle?”

Triangles and Their Features

Learning Outcomes

Imagine Maths Page 76

Students will be able to identify the parts of triangle and classify them on the basis of their sides and angles.

Teaching Aids

Sheets of coloured paper; Scissors; Tape; Markers; Thermocol sheets

Activity

Begin by discussing different parts of a triangle and how triangles can be classified.

Ask the students to work in groups of 3. Distribute the craft materials and a Thermocol sheet to each group.

Instruct each group to create 3 triangles on the Thermocol sheet using a ruler and different coloured paper. Ask them to label each type of triangle it represents. Encourage creativity in designing the triangles. Instruct each group to create triangles of all three types in varying shapes and sizes.

Instruct the students to create 3 more triangles each with different angle like aciute angled, right-angled and obtuse-angled on the Thermocol sheet using ruler and different coloured paper. Ask them to measure the angles and label the triangles.

Ask the students to collaborate to create aesthetic patterns using triangles they have created. Ask them to paste the pattern on a Thermocol sheet.

Ask question such as, “What were the measure of the angles? Were all the angles equal or different?”

Extension Idea

Ask: Can all the sides of a triangle be unequal, but the angles be equal?

Say: No, this is not possible. If the sides of a triangle are equal, its angles will be equal too and vice-versa.

Classification of Quadrilaterals

Learning

Outcomes

Imagine Maths Page 79

Students will be able to identify parts of quadrilateral and classify quadrilaterals on the basis of their types.

Teaching Aids

Quadrilateral cutouts; Protractor; Ruler; Chart paper

Activity

Start by explaining the fundamental concepts of a quadrilateral, including the presence of 4 sides, 4 vertices, and 4 angles.

Ask the students to work in groups. Distribute cutouts of different types of quadrilaterals (convex, concave, square, rectangle, trapezium, and kite), a protractor, a ruler and chart paper to each group.

Instruct the groups to paste these cutouts on the chart paper and measure the angles, sides and diagonals of each quadrilateral using a protractor and ruler. Also instruct the students to mark the vertices, sides and diagonals of the quadrilaterals.

Ask the groups to record their observations about the angles, sides and diagonals of the cutouts on the chart paper.

Discuss the types of quadrilaterals based on their features. Ask the groups to classify and label the pasted quadrilaterals based on the discussion.

Extension Idea

Ask: Name a quadrilateral that shares characteristics with both a rhombus and a rectangle.

Say: A square shares characteristics with a rectangle as all its angles are right angles. Also, all the sides of a square are equal, so it shares characteristics with a rhombus too.

Polygons

and Their Features

Learning Outcomes

Imagine Maths Page 83

Students will be able to identify parts of polygon and classify polygons on the basis of their sides, angles and diagonals.

Teaching Aids

Geoboards; Rubber bands of different colours; Markers

Activity

Start by introducing the concept of polygons and their basic parts: vertices, sides, and angles.

Ask the students to work in groups of 6. Distribute geoboards, rubber bands and coloured markers to each group.

Instruct the groups to create two different polygons on the geoboards using the rubber bands. Ask them to use different colours of rubber bands to show the diagonals. Encourage them to experiment with varying the number of sides and vertices. As they create each polygon, ask the students to count the vertices, sides, diagonals and angles. Finally, ask them to recreate the shapes using coloured markers in their notebooks.

Instruct the students to discuss the various polygon that they formed based on their features like number of sides. Ask the students to discuss and classify different type of polygons.

Teacher Tip: In case of unavailability of geoboards, you can stick notice board push pins on a Thermocol sheet as a substitute.

Extension Idea

Ask: Can you name a polygon that does not have any diagonals?

Say: Triangles are polygons that do not have any diagonals.

Types of Curves

Learning

Outcomes

Students will be able to classify curves as open or closed, simple or non-simple.

Teaching Aids

Pieces of string; Sheets of paper; Glue stick

Activity

Ask the students to work in groups of 4. Distribute the teaching aids.

Imagine Maths Page 86

Guide the groups to create a curved pattern of their choice using their pieces of string and paste them on the sheet of paper. Allow time for the glue to dry.

Collect all the sheets and mix them up. Redistribute the sheets, one to each group.

Instruct the groups to identify the type of curve on the sheet as simple or non-simple and open or closed. Ask each student in a group to write a reason for their answer in their notebook. Discuss the reasons and types of curves.

Ask questions like, “How did you know that a curve was a non-simple curve?”

Extension Idea

Draw a curve that is non-simple and open on the board.

Ask: What do you notice about this figure?

Say: The shape is an open non-simple curve because the starting point and the end point of the curve are different.

Parts of a Circle; Circumference of a Circle

Learning

Outcomes

Students will be able to identify parts of a circle.

Teaching Aids

Compass; Ruler; Pieces of string; Circular cutouts; Drawing sheets; Crayons; Ruler

Activity

Imagine Maths Page 87

Ask the students to work in groups of 3. Distribute a compass, ruler and a piece of string to each group.

Distribute a circular cutout and drawing sheet to each pair.

Instruct them to identify the centre, radius, diameter and chord, and to mark and label the specified parts on the cutout using crayons. Allow them to use different ways like folding the cutout in half to identify the diameter. They will then shade the major and minor arcs in the circle.

Ask questions like, “How did you find the centre, radius and diameter of the circle?”

Draw a table as shown on the board. Ask the students to copy it into their notebooks.

Instruct each student in a group to construct one of the three circles of radius 4 cm, 5 cm and 6 cm using a compass and then measure the distance around the boundary (circumference) of that circle. Ask the students to write the circumference (C), the diameter (D) and the value of C ÷ D in the table. Then, they should discuss in their groups how they can form the formula for C if the value of R or D is given. Discuss how the circumference of a circle is pi (π) or around 3.14 times the diameter of the circle and how to find the circumference when the radius or diameter is given. Ask the students to find the circumference of a circle with a radius of 7 cm.

Extension Idea

Ask: What is the diameter of a circle with a circumference of 88 cm?

Say: We know that the circumference = 2πr. So, r = 14 cm and diameter = 28 cm.

Constructing Circles Imagine Maths Page 88

Learning Outcomes

Students will be able to identify parts of a circle and find the circumference of a circle using the formula.

Teaching Aids

Drawing sheet; Pin; Pieces of string; Pencil; Compass Activity

Distribute the teaching aids to each student.

Instruct them to tie a pencil to one end of the string and a pin to the other end. Ask them to place the pin on the drawing sheet and then turn the string with the pencil end all the way around so that a circle is drawn. Then, ask them to measure the radius of the circle.

Next, ask the students to use the compass to construct a circle with the same radius as the circle drawn using the string on the drawing sheet. Explain that without moving the compass needle, they should rotate the compass around it in a way that the pencil draws a circle. Instruct them to keep turning until the pencil goes all the way around. Then, ask them to mark and label the centre, radius and diameter.

Ask questions like, “How can you identify the centre and the diameter in the circle?”

Answers

1. Key Geometrical Concepts

Think and Tell

No, the surface of a volleyball is not the part of a plane. The volleyball court is a part of a plane.

Do It Together

Real‐life Example Football Field Stars in the Sky Straw Pipe Light Emitted by the Sun

Geometry Plane Point Line segment Ray Figure

2. Measuring and Drawing Line Segments

Do It Together

3. Comparison of Line Segments

Do It Together

Measures

4. Basics of Angles

Do It Together

5. Types of Angles

6. Measuring and Drawing Angles

Do It Together

The smallest angles are

7. Triangles and Their Features

Do It Together

1. Students will measure the lengths of the sides.

Equilateral Scalene Isoceles

2. Students will measure the angles of the triangles.

8. Parts of a Quadrilateral

Do It Together

9. Types of Quadrilaterals

Do It Together

10. Polygons and Their Features

Think and Tell

All the sides in a right-angled triangle are not equal therefore it is not a regular polygon.

Do It Together

Vertices:

Diagonals:

11. Types of Curves

Think and Tell

Yes curves that are simple and closed can be drawn. One example is a circle.

Do It Together

Figures may vary. Sample figures.

Simple Open Curve Simple Closed Curve

Non-simple Open Curve Non-simple Closed Curve

12. Circles: Parts and Construction

Think and Tell

No. The diameter of a circle is the longest chord.

13. Constructing Circles

Do It Together

3-D Shapes 5

Learning Outcomes

Students will be able to: list the features of 3-D shapes, and differentiate between prisms and pyramids. identify and draw the nets of a 3-D shape.

Alignment to NCF

C-3.1: Describes, classifies, and understands relationships among different types of two- and threedimensional shapes using their defining properties/attributes

C-3.3: Identifies attributes of three-dimensional shapes (cubes, parallelepipeds, cylinders, cones), works hands-on with material to construct these shapes, and also uses two-dimensional representations of three-dimensional objects to visualise and solve problems

Let’s Recall

Recap to check if students know how to identify the faces of a 3-D shape. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

polygon: a 2-D shape made up of 3 or more line segments

prism: a 3-D shape with identical and parallel opposite bases, and square or rectangular lateral faces pyramid: a 3-D shape in which the base is a polygon and all the other faces are triangles tapered to a vertex

net: a 2-D figure that can be folded to form a 3-D shape

Teaching Aids

Plastic prisms and pyramids; Boxes shaped like a pyramid and a prism; A pair of scissors; Thick chart paper; Sellotape

Chapter: 3-D Shapes

Features of 3-D Shapes

Learning

Outcomes

Imagine Maths Page 96

Students will be able to list the features of 3-D shapes, and differentiate between prisms and pyramids.

Teaching Aids

Plastic prisms and pyramids

Activity

Ask the students to work in groups. Distribute the plastic prisms and pyramids to each group. Instruct them to sort the shapes into 2 groups and then ask them what the similarities and differences between the two groups are. Ask the students to name the type of prisms and pyramids, and list their features. Let them discuss in their groups, the similarities and differences between a prism and a pyramid.

Note: In case the shapes are unavailable, ask the students to look at the picture of the shapes in their Imagine Mathematics books.

Ask questions like, “What is one major difference between a prism and a pyramid?”

Extension Idea

Ask: If you cut a cuboid diagonally, what other 3-D shape do you get?

Say: If a cuboid is cut diagonally, we get a triangular prism.

Nets of 3-D Shapes

Learning

Outcomes

Students will be able to identify and draw the nets of a 3-D shape.

Teaching Aids

Boxes shaped like a pyramid and a prism; Scissors; Thick chart papers; Sellotape

Activity

Imagine Maths Page 99

Show the students a pyramid-shaped paper box and ask them which and how many 2-D shapes do they see in its faces. Then, lay out flat the faces of the box to show them the faces in the net of the box. Ask the students to try and describe how 3-D objects are different from their 2-D representations.

Ask the students to work in pairs. Distribute the teaching aids to each pair. Allow the students to imagine what the nets of the prism and pyramid might look like, and ask them to draw the nets on the thick chart paper. Finally, instruct them to cut out the nets, fold them, stick the edges together using Sellotape to see if the shapes look the same as the given boxes.

Extension Idea

Ask: In how many ways can we create the net of a tetrahedron?

Say: A tetrahedron is also called a triangular pyramid. There are two different nets of a tetrahedron.

1. Features of 3-D Shapes

Think and Tell

No. A decagonal prism has 12 faces, and a decagonal pyramid has 11 faces. Do It Together

Answers

3. Nets of Cones and Cylinders Do It Together

2. Nets of Cubes and Cuboids Do It Together

There are 2 ways of placing rectangles to form the net of a closed cuboid.

4. Nets of Pyramids and Prisms Do It Together

Name of the shape: Hexagonal pyramid

Integers

Learning Outcomes

Students will be able to: represent integers on a number line and compare them. add integers using the rules. subtract integers using the rules.

Alignment to NCF

C-1.4: Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line

Let’s Recall

Recap to check if students know how to find the predecessor and successor of a given number. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

predecessor: the number that comes before a number successor: the number that comes after a number integer: a positive or negative whole number or zero absolute value: distance of an integer from zero

Teaching Aids

Chart paper; Index cards; Integer tiles made using red and yellow paper square cutouts to show negative and positive integers, respectively

Chapter: Integers

Representing Integers; Comparing and

Ordering

Integers

Learning Outcomes

Students will be able to represent integers on a number line and compare them.

Teaching Aids

Chart paper; Index cards

Activity

Imagine Maths Page 107

Begin the class with a discussion on how to write a number for the second floor and Basement 2, to bring out the uses of integers. Discuss more examples with the students. Ask the students to work in groups. Distribute a sheet of chart paper to each group and one index card to each student in the group. Each index card should describe a different situation involving integers.

Spending `5 4 kg decrease in weight

Predecessor of 3

Successor of 6 Absolute value of –7

Instruct the groups to draw a number line from −10 to +10 on the chart paper, ensuring that it is clearly labelled. Ask the groups to read and discuss the situation on their index card, and represent the corresponding integer on the number line pasting the index card above or below the number line at that mark. They will then compare the integers marked on the number line to say which is biggest and which is the smallest.

Have a discussion around how to compare integers.

For practice, give them some more integers and ask them to arrange them in ascending and descending order.

Addition of Integers

Learning Outcomes

Students will be able to add integers using the rules.

Teaching Aids

Imagine Maths Page 111

Integer tiles made using red and yellow square paper cutouts to show negative and positive integers, respectively

Activity

Ask the students to work in pairs. Distribute the integer tiles to each pair. Instruct them to add 3 and −4 using the tiles. Ask them to first show the positive integer using the yellow tiles and then the negative integer using the red tiles. Explain that one positive tile and one negative tile cancel each other out because they make 0, so they should be removed. Explain that the remaining number of integer tiles (−1 in this case) is the answer. So, 3 + (−4) = −1.

Give the students more problems to solve using the integer tiles. Ask questions like, “What is the sign of the sum of two negative integers? Discuss the rules of adding integers. Give students some addition problems to solve in their notebooks. Instruct them to add the integers using addition rules.”

Extension Idea

Instruct: Find three integers whose sum is −25.

Say: There are multiple sets of three integers whose sum is −25. One such set could be −10, −8 and −7.

Subtraction of Integers

Learning Outcomes

Students will be able to subtract integers using the rules.

Teaching Aids

Imagine Maths Page 116

Integer tiles made using red and yellow square paper cutouts to show negative and positive integers, respectively

Activity

Begin the class by asking the students the difference between the two floors of a building: Floor 5 and Basement 2. Discuss the answers.

Ask the students to work in groups. Distribute the integer tiles to each group.

Instruct them to subtract –6 from 3. Ask them to use yellow tiles to show the integer 3.

Ask questions like, “Can you take away 6 negative tiles from the 3 positive tiles?”

Explain that they can do so only if they have 6 negative tiles, which they don’t. To take away 6 negative tiles, they need to add 0 tiles, that is, pairs of positive and negative tiles. So, to take away 6 red tiles, they need to first add 6 red and 6 yellow tiles. Ask the students to add the required zero tiles, show the subtraction and find the answer. They will then show the subtraction in their notebooks by drawing the tiles and writing the subtraction sentence in their notebooks. Discuss the answer in class.

Instruct the students to next subtract −7 from 4 using the integer tiles and note down the result in their notebooks as a subtraction sentence.

Ask questions like, “What is the sign of the answer when you subtract one negative integer from another? What is it when you subtract one negative from one positive integer? What does the sign depend on?”

Discuss the rules of subtracting integers. Give the students more subtraction problems to practise solving using the rules.

Extension Idea

Ask: Find the missing integer: − (19) = −34.

Say: We can find the missing integer by adding 19 to −34.

−34 + 19 = −15.

−15 − (19) = −34. So, the missing integer is −15.

Answers

1. Representing Integers

Think and Tell

The largest negative integer is –1, as it is the closest to zero on the negative side of the number line. Negative integers go infinitely in the negative direction. So, we cannot find the smallest negative or the largest positive integer.

Do It Together

2. Comparing and Ordering Integers

Do It Together

Rudra’s flat

Suhani’s flat

Rudra’s car parking

Suhani’s car parking

3. Addition of Integers Using Tokens

Do It Together

+3 + (–8) = –5

4. Rules for Addition of Integers

Do It Together

1200 feet beneath the surface = –1200

Rise of 635 feet = +635

Descend again 455 feet = –455

Current location of vessel = (–1200) + (635) + (–455) = –1020

Hence, the vessel is 1020 feet below the surface of the water.

5. Properties of Addition of Integers

Do It Together

1. –25 + 0 = –25 Existence of additive identity

2. –15 + 35 = 35 +(–15) Commutative property

3. 39+ (−12) = +27 Closure property

4. 26 + (–13 + 9) = (26 + (–13)) + 9 Associative property

6. Subtraction of Integers Using Tokens

Do It Together

7. Rules for Subtraction of Integers

Do It Together

1. –36 from 58

= 58 – (–36)

= 58 + 36 = 94

3. –247 from 354

= 354 – (–247)

= 354 + 247 = 601

2. –145 from –365

= –365 – (–145) = –365 + 145 = –220

4. 3654 from –5214

= –5214 – 3654

= –5214 + (−3654)

= −8868

8. Properties of Subtraction of Integers

Do It Together

1. Property Used: Commutative Property

523 – 365 = 158

365 – 523 = − 158

Thus, 523 − 365 ≠ 365 – 523

2. Property used: Associative property

(125 – 523) − 363 = −761

125 – (523 – 363) = −35

Thus, (125 – 523) − 363 ≠ 125 − (523 – 363)

Fractions 7

Learning Outcomes

Students will be able to: represent fractions and classify them as proper, improper and mixed. compare and order unlike fractions. convert improper fractions to mixed numbers and vice versa. find equivalent fractions and the simplest form of fractions. add and subtract unlike fractions. multiply fractions and mixed numbers. divide fractions and mixed numbers.

Alignment to NCF

C-1.2: Represents and compares commonly used fractions in daily life (such as 1 2 , 1 4 ) as parts of unit wholes, as locations on number lines and as divisions of whole numbers

C-1.4: Explores and understands sets of numbers, such as whole numbers, fractions, integers, rational numbers, and real numbers, and their properties, and visualises them on the number line

Let’s Recall

Recap to check if students know how to identify and write fractions. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

fractions: numbers of the form a b , where a and b are whole numbers and b ≠ 0 like fractions: fractions with the same denominator reciprocal: fraction obtained by interchanging the numerator and denominator

Teaching Aids

Fraction cards (including 2 proper, 2 improper and 2 mixed fractions); Circle cutouts; Chart paper; Scissors; Glue stick; Rectangular strips; Colour pencils; Fraction circles; Fraction strips

Chapter: Fractions

Representing Fractions

Learning

Outcomes

Imagine Maths Page 125

Students will be able to represent fractions and classify them as proper, improper and mixed.

Teaching Aids

Fraction cards (including 2 proper, 2 improper and 2 mixed fractions); Circle cutouts; Chart paper; Scissors; Glue stick

Activity

Begin with a discussion on proper, improper and mixed fractions. Give some examples for each type of fraction. Ask the students to work in groups. Distribute the fraction cards and other teaching aids to each group.

Explain that the fraction cards represent the fraction of pizza left after a party. Ask them to consider each circle cutout as a whole pizza. Instruct them to divide and cut the circular cutouts as per the fraction on the fraction cards and paste them on the chart paper. When they are done, ask them to exchange charts with other groups for peer review.

Ask questions like, “How is an improper fraction different from a mixed number?”

Comparing Fractions; Ordering Fractions

Learning

Outcomes

Students will be able to compare and order unlike fractions.

Teaching Aids

Rectangular strips; Colour pencils

Activity

Ask the students to work in pairs. Distribute the rectangular strips and colour pencils to each pair.

Imagine Maths Page 125

Instruct them to show 1 3 and 3 4 on two rectangular strips and compare them. Discuss how to divide the strips such that both show the same total number of equal parts, either by finding the LCM of the denominators or by multiplying the denominators.

Instruct the pairs to divide each strip into the same number of parts as the LCM of the denominators and then compare the shaded parts.

Then, ask them to compare the two fractions by first converting them to like fractions and then comparing the numerators in their notebooks.

Give the students some practise questions on ordering unlike fractions.

Extension Idea

Ask: Which is bigger: 6 1 2 or 5 1 4 ?

Say: We convert the mixed numbers into improper fractions as 13 2 and 21 4 . We know that 13 2 = 26 4 and as 26 > 21, 6 1 2 > 5 1 4 .

Conversion

Learning Outcomes

Students will be able to convert improper fractions to mixed numbers and vice versa.

Teaching Aids

Fraction circles

Activity

Ask the students to work in pairs. Distribute the fraction circles showing improper fractions to each pair.

Instruct one student in each pair to look at the circles and write the fraction as an improper fraction and the other student to look at the same circles and write the fraction as a mixed number. Ask them to look at the fractions written by both partners and discuss how they are related and how to convert one form to the other without using fraction circles.

Discuss the answers with the whole class along with the method used for converting between improper fractions and mixed numbers without using fraction circles.

Extension Idea

Ask: My dog is 5 1 2 years old. My cat is 9 4 years old. Which is older?

Say: Here, we have a mixed number and an improper fraction. On converting the improper fraction 9 4 into a mixed number, we get 2 1 4 . As 5 1 2 > 2 1 4 , the dog is older than the cat.

Equivalent Fractions and Simplest Form

Learning Outcomes

Students will be able to find equivalent fractions and the simplest form of fractions.

Teaching Aids

Fraction strips

Activity

Imagine Maths Page 131

Ask the students to work in groups of 4. Distribute 4 fraction strips to each group. Instruct them to show 1 2 , 2 4 , 3 6 and 4 8 on the fraction strips. Once they have done so, ask them to place the number strips one below the other and discuss what they notice about the strips. Encourage them to share their observations with the rest of the class. Bring out the fact that the given fractions are equivalent.

Guide the discussion to help the students deduce the way to find equivalent fractions without using fraction strips.

Ask them to find 3 more equivalent fractions for the given fraction and write these in their notebooks. Give them 2 more fractions to find equivalent fractions in their notebooks.

Extension Idea

Ask: Molly baked 14 cookies. Her mother ate 2 cookies, and her father ate 4 cookies. What fraction of the cookies was left? Write it in its simplest form.

Say: We know that Molly’s parents ate 6 14 of the cookies, so 8 14 was left. The simplest form of 8 14 is 4 7

Addition and Subtraction of Fractions

Learning Outcomes

Students will be able to add and subtract unlike fractions.

Teaching Aids

Rectangular strips; Colour pencils

Activity

Ask the students to work in pairs. Distribute the rectangular strips and colour pencils to each pair.

Instruct them to show 1 2 and 1 3 on two rectangular strips and add the two fractions.

Ask them to find the LCM of the denominators of the fractions and then divide each strip into the same number of equal parts as the LCM; in this case, each strip will have a total of 6 equal parts. Instruct them to then count the total number of shaded parts.

Next, instruct the students to add the two fractions in their notebooks by first converting them to like fractions and then adding the numerators.

Repeat the activity for subtraction of unlike fractions.

Extension Idea

Ask: How do we solve 5 1 4 − 2 2 3 ?

Say: We change the mixed numbers to improper fractions, convert them into like fractions and then subtract.

Learning Outcomes

Students will be able to multiply fractions and mixed numbers.

Teaching Aids

Rectangular strips; Colour pencils

Activity

Ask the students to work in pairs. Distribute rectangular strips and colour pencils to each pair.

Instruct the pairs to multiply 3 8 and 4 5 using the strips. Ask them to first show 3 8 by dividing the strip horizontally into 8 parts and shading 3 parts using a colour pencil. Ask them to then show 4 5 on the same strip by dividing it vertically into 5 equal parts and crossing out 4 vertical parts. Ask them to now count the total number of equal parts and number of parts that have both shading and crosses. Explain that the fraction obtained is the answer of the multiplication. Then, ask them to solve the problem in their notebooks by multiplying the numerators and then the denominators.

Give the students a few problems on multiplication of fractions to solve in their notebooks.

Extension Idea

Ask: Jen is preparing a dish that calls for 3 4 of a cup of oil per serving. If Jen needs to prepare 2 2 3 servings, how many cups of oil will she need?

Say: We need to multiply the two fractions. 3 4 × 2 2 3 = 3 4 × 8 3 = 2. Hence, she needs 2 cups of oil for 2 2 3 servings.

Dividing Fractions or Mixed Numbers

Learning Outcomes

Students will be able to divide fractions and mixed numbers.

Teaching Aids

Rectangular strips; Colour pencils

Activity

Ask the students to work in pairs. Distribute rectangular strips and colour pencils to each pair.

Explain that if there is a division sign between the two fractions, we replace it with a multiplication sign and write the reciprocal of the divisor and then follow the steps of multiplication.

Imagine Maths Page 139

Instruct the pairs to divide 4 5 and 3 2 . Ask them write the reciprocal of the divisor 3 2 as 2 3 and then follow the steps of multiplication.

Ask them to first show 4 5 by dividing the strip horizontally into 5 parts and shading 4 parts using a colour pencil.

Ask them to then show 2 3 on the same strip by dividing it vertically into 3 equal parts and crossing out 2 vertical parts. Ask them to now count the total number of equal parts and number of parts that have both shading and crosses. Explain that the fraction obtained 8 15 , is the answer of the division.

Next, instruct the students to divide two fractions in their notebooks by first writing the reciprocal of the divisor and then multiplying the numerators and then the denominators. Give the students a few problems on division of fractions to solve in their notebooks.

Extension Idea

Ask: How many pieces, each measuring 7 3 of a foot, can be cut from a rope that is 9 1 3 feet long?

Say: We need to divide the two fractions. 9 1 3 ÷ 7 3 = 28 3 × 3 7 = 4 Hence, 4 pieces of 7 3 of a foot can be cut from the rope of length 9 1 3 feet.

Answers

1. Representing Fractions

Do It Together

A = 5 8 B = 12 8 or 1 4 8 C= 21 8 or 2 5 8

2. Comparing Fractions

Do It Together

LCM of 7 and 6 = 42

5 7 = 30 42 ; 3 6 = 21 42

As 30 > 21. Thus, the larger fraction is 30 42 or 5 7

3. Ordering Fractions

Do It Together

LCM of 4, 5, 2, 8 = 40

4 = 30 40; 4 5 = 32 40

1 2 = 20 40; 7 8 = 35 40

35 > 32 > 30 > 20

Thus, 7 8 > 4 5 > 3 4 > 1 2

4. Conversion Between Mixed Numbers and Improper Fractions

Do It Together

1. 10 4 5 = (5 × 10) + 4 5 = 54 5

2. 31 6 = 5 1 6

5. Equivalent Fractions and Simplest Form

Do It Together

Answers may vary. Sample answers.

Using multiplication:

8 10 × 3 3 = 24 30

Using division:

8 10 ÷ 2 2 = 4 5

6. Addition and Subtraction of Unlike Fractions

Do It Together

Fraction of the cake eaten by Radha = 1 9 ; Fraction of the cake eaten by Riya = 2 3

LCM of 9 and 3 = 9

Fraction of cake eaten by Radha and Riya

As the whole cake is 1.

So, the fraction of cake remaining = 1 –7 9 = 2 9

7. Addition and Subtraction of Mixed Numbers

Do It Together

LCM of 4, 6 = 12

On converting to improper fractions, we get:

5 2 6 = 32 6 7

8. Multiplying Fractions or Mixed Numbers

Think and Tell

The product of any number and its reciprocal is always 1. Hence, 5 8 × 8 5 = 1.

Do It Together

5 13 14 = 83 14 and 2 1 2 = 5 2

83 14 × 5 2 = 415 28 = 14 23 28

9. Dividing Fractions or Mixed Numbers

Do It Together

2 3 11 ÷ 15 11 = 25 11 × 11 5 = 5 1

Decimals 8

Learning Outcomes

Students will be able to: represent decimals on a number line. identify the place value of digits in a decimal number and write the decimal number in its expanded form and as a number name. convert fractions to decimals and vice versa. find equivalent decimals and compare decimals. add and subtract decimals up to 3 decimal places. multiply decimals up to 2 decimal places by whole numbers or decimals up to 1 decimal place. divide decimals up to 2 decimal places by whole numbers or decimals up to 1 decimal place.

Alignment to NCF

C-1.6: Explores and applies fractions (both as ratios and in decimal form) in daily-life situations

Let’s Recall

Recap to check if students know about decimal numbers, their parts and how to rearrange them in increasing or decreasing order.

Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

equivalent decimals: decimal numbers that have the same value

Teaching Aids

Decimal cards; Blank decimal place value chart (up to thousandths); Bowl of decimal number cards; Coloured counters; Shaded grids showing 0.8 and 1.05; 10 × 10 grid; Coloured pencils; Two decks of cards (one with decimal numbers and the other with their decimal equivalents); Grids to represent decimal numbers up to 2 decimal places

Chapter: Decimals

Representing Decimals on Number Line

Learning Outcomes

Students will be able to represent decimals on a number line.

Teaching Aids

Decimal cards

Activity

Briefly explain the concept of decimals and their relation to the number line. Explain that tenths can be further divided into hundredths.

Take students out to the playground and ask them to form groups of equal sizes. Give each student a decimal card.

Draw a large horizontal number line of range 1–5 on the ground. Ask students to read the decimal number on the card and to go and stand at the correct place on the number line with the card. The group with all its members to stand at the correct places first, wins the game.

Back in the classroom, instruct students to draw a number line in their notebooks and write the answers. Give them a few more decimal numbers to represent on a number line in their notebooks.

Place Values in Decimals Imagine Maths Page 145

Learning Outcomes

Students will be able to identify the place value of digits in a decimal number and write the decimal number in its expanded form and as a number name.

Teaching Aids

Blank decimal place value chart (up to thousandths); Bowl of decimal number cards; Coloured counters

Activity

Briefly explain the concept of decimals and their relation to tenths and hundredths. Prepare some decimal number cards and put them in a bowl.

Ask students to work in groups. Distribute a sheet of paper with a blank decimal place value chart (up to thousandths) to each group. Assign a colour to each place and distribute counters of the same colours to each group. Pick a decimal number card from the bowl. Ask the groups to place as many counters as the digit in the correct place on the place value chart. Help them identify the place value of each digit of the number.

Instruct them to interchange the counters at the tenths place and the tens place. Ask them to identify the new number and the place value of each of its digits. Discuss the importance of the placement of the digits in a number. Ask questions like: How does the value of a digit change depending on its place in the number?

Extension Idea

Ask: What is the decimal number for 50 + 4 + 2 10 + 8 1000 ?

Say: 50 + 4 + 2 10 + 8 1000 = 50 + 4 + 0.2 + 0.008 = 54.208.

Conversion Between Fractions and Decimals

Learning

Outcomes

Students will be able to convert fractions to decimals and vice versa.

Teaching Aids

Shaded grids showing 0.8 and 1.05

Activity

Imagine Maths Page 146

Begin the class by reviewing the concept of fractions and decimals. Give students some examples on conversion to emphasise that the numbers represent the same value even though they are expressed in different forms. Divide the class into groups of 4. Distribute the shaded grids to each group.

Ask 2 students from each group to write the fractions representing the given grids and 2 students to write the decimals representing the same grids. Then, have them compare their answers to see how one can be converted to the other.

Discuss the answers and the reasons for conversion. Give them a few more grids and ask them to write the corresponding fractions and decimals in their notebooks.

Equivalent Decimals; Comparing Decimals

Learning

Outcomes

Students will be able to find equivalent decimals and compare decimals.

Teaching Aids

Imagine Maths Page 148

10 × 10 grid; Coloured pencils; Two decks of cards (one with decimal numbers and the other with their decimal equivalents)

Activity

Begin the class by reviewing the concept of like and unlike decimals. Give a few examples to emphasise how they are different from each other. Explain that we can convert unlike decimals to like decimals by adding zeroes to form equivalent decimals and then compare them.

Ask students to work in pairs. Distribute the teaching aids to each pair.

Instruct them to shuffle each deck of cards. Each student should draw 2 cards each from the decks and represent the numbers on the empty grids using coloured pencils. Then, ask them to match the grids with their partners and find out if their representations are equivalent decimals. If they are not equivalent, ask them to form equivalent decimals. Then, instruct them to compare the 2 representations. Explain that the student with the largest decimal number wins the round and keeps both cards.

Extension Idea

Ask: A chef is baking cookies and needs to add exactly 1.75 cups of flour. She only has measuring cups in sizes of 0.25 cups, 0.5 cups and 1 cup. Find all the possible combinations she can use to achieve the measurement. Which combination requires the minimum number of cups?

Say: The possible combinations are: 3 × 0.5 cups + 1 × 0.25 cup; 1 × 1 cup + 1 × 0.5 cup + 1 × 0.25 cup; and 1 × 1 cup + 3 × 0.25 cups. The second option requires the minimum number of cups, that is, 3.

Addition and Subtraction of Decimals

Learning Outcomes

Students will be able to add and subtract decimals up to 3 decimal places.

Teaching Aids

Grids to represent decimal numbers up to 2 decimal places; Coloured pencils

Activity

Begin the class by reviewing the concept of adding and subtracting decimals. Give examples to emphasise the placement of digits of decimal numbers one below the other in the column method.

Ask students to work in pairs. Distribute the teaching aids and write an addition problem and a subtraction problem of decimals on the board.

Ask the pairs to represent the decimal numbers on the grid provided using coloured pencils. Explain that they may need more than one grid to represent the numbers. Ask them to add or subtract using the grid and by writing the decimals one below the other.

0.5 + 0.25

– 0.25 = 0.23

Repeat this for 5 rounds with different addition and subtraction problems of decimal numbers written on the board. The pair to get the maximum number of correct sums or differences wins the game.

Extension Idea

Ask: A theme park has 3 rides: a roller coaster costing ₹7.99, a water flume costing ₹6.50, and a mystery ride costing x rupees. You have ₹20.00 and want to go on 2 rides. What are the possible prices of the mystery ride if you spend exactly ₹20.00?

Say: Cost of the mystery ride if the roller coaster is included: ₹20 − ₹7.99 = ₹12.01. Cost of the mystery ride if the water flume is included: ₹20 − ₹6.50 = ₹13.50. So, the cost of the mystery ride is ₹13.50 or ₹12.01.

Multiplication of Decimals

Learning Outcomes

Students will be able to multiply decimals up to 2 decimal places by whole numbers or decimals up to 1 decimal place.

Teaching Aids

Grids to represent decimal numbers up to 2 decimal places; Coloured pencils

Activity

Begin the class by reviewing the concept of multiplying 2 decimals. Give examples to emphasise the placement of the digits of a decimal number at the appropriate places in the column method.

Ask students to work in pairs. Distribute the teaching aids and write a multiplication problem of decimals, say 0.2 × 0.7, on the board.

Instruct the pairs to represent the decimal numbers on the grid using coloured pencils and multiply them. Ask them to shade the first number (0.2) vertically on the grid and shade the second number (0.7) horizontally on the same grid. Explain that the portion of the grid shaded with 2 colours (merged portion) is the product of the 2 numbers.

Now, ask students to solve the problem in their notebooks by writing the decimals one below the other. Repeat the activity for 5 rounds and instruct students to write the answers in their notebooks. The pair to get the maximum correct products wins!

Extension Idea

Ask: Rubal hired a car costing ₹1500 plus 85 p for each km she travels. The car’s odometer showed 28361 km when she returned the car. How much would Rubal pay if the odometer showed 27612 km when she hired the car?

Say: Total distance travelled by Rubal = 28361 – 27612 = 749 km. So, she will pay 749 × ₹0.85 + ₹1500 = ₹2136.65.

Division of Decimals

Learning Outcomes

Students will be able to divide decimals up to 2 decimal places by whole numbers or decimals up to 1 decimal place.

Teaching Aids

Grids to represent decimal numbers up to 2 decimal places; Coloured pencils

Activity

Begin the class by reviewing the concept of dividing decimals. Give examples to emphasise the placement of the digits of a decimal number in the long division method.

Ask students to work in pairs. Distribute the teaching aids and write a division problem of decimals on the board.

Instruct the pairs to represent the decimal numbers on the grid using coloured pencils and divide. Explain that they will need more than one grid for the division. To divide, ask them to take as many empty grids as the divisor and then shade the dividend equally in the empty grids. Explain that the number of squares coloured in each group/grid is the quotient of the 2 numbers.

÷ 3 = 0.18 0.54

Instruct students to solve the problem in their notebooks using the column method. Repeat the activity for 5 rounds and instruct students to write the answers in their notebooks. The pair to get the maximum number of correct answers wins!

Extension Idea

Ask: A log is 17.60 m long. It is to be cut into fence posts which must be 80 cm long. What is the largest number of fence posts that can possibly be cut from this log?

Say: Length of the log = 17.60 m = 1760 cm, length of each fence post = 80 cm. So, the largest number of fence posts that can possibly be cut from this log = 1760 ÷ 80 = 22.

1. Representing Decimals on a Number Line

Do It Together

Answers

6. Comparing Decimals

Do It Together

2. Place Values in Decimals

Do It Together

Expanded form = 200 + 50 + 6 + 0.003 or 200 + 50 + 6 + 3 1000

Number name = two hundred fifty-six point zero zero three

3. Conversion Between Fractions and Decimals

Do It Together

1. 3.25 = 3.25 ×

2. 4.14 = 4.14 ×

4. Like and Unlike Decimals

Do It Together

Number of digits after the decimal point in 15.45 = 2

Number of digits after the decimal point in 814.012 = 3

So, the number of digits after the decimal point are not equal.

Thus, 15.45 and 814.012 are unlike decimals.

5. Equivalent Decimals

Do It Together

18.3 = 18.30, 18.300

On comparing, the descending order of the numbers is: 48.100 > 48.023 > 48.020 > 48

7. Addition and Subtraction of Decimals

Think and Tell

Weight he carries = 53.25 kg + 5.2 kg = 58.45 kg

Xavier can carry 65 kg – 58.45 kg = 6.55 kg more weight.

Do It Together

Thus, the difference of the heights of Aman and Rajneesh is 0.17 m

8. Multiplication of Decimals

Do It Together

Total cost of 18 books = ₹156.56 × 18 = ₹2818.08

9. Division of Decimals

Do It Together

Cost of each packet of paint = ₹3547.5 ÷ 15 = ₹236.5

Data Handling

Learning Outcomes

Students will be able to: organise data in a table using tally marks. read and draw pictographs. read and draw bar graphs.

Alignment to NCF

C-5.2: Selects, creates, and uses appropriate graphical representations (e.g., pictographs, bar graphs, histograms, line graphs, and pie charts) of data to make interpretations

Let’s Recall

Recap to check if students know how to draw and interpret the data in a table. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

tally marks: a system of counting using vertical strokes, often in groups of five, to keep track of quantities pictograph: a table that shows the given data using pictures or symbols bar graph: a graph that shows information in the form of bars of different lengths

Teaching Aids

Ice-cream sticks; Buttons of 5 colours; Chart papers; Smiley stickers; Building blocks

Chapter: Data Handling

Organising Data as Tally Marks

Learning Outcomes

Students will be able to organise data in a table using tally marks.

Teaching Aids

Ice-cream sticks; Buttons of 5 colours; Chart papers

Activity

Demonstrate how to show tally marks to the students.

Ask the students to work in groups. Distribute the resources to each group.

Imagine Maths Page 162

Instruct the groups to make a tally marks table to show the number of each colour of the buttons.

Ask them to pick one button at a time and place an ice-cream stick as a tally mark under the column of that colour. Keep the button on the other side. Then, pick the next button, see its colour and place the ice-cream stick as a tally mark. Repeat till all buttons are used. Ask them to remember to place every fifth ice-cream stick across the previous 4 ice-cream sticks. The total tally marks tells us the number of buttons for each colour. Then, instruct the students to create a tally marks table in their notebooks.

Extension Idea

Ask: If each ice-cream stick stands for 5 items instead of just 1 item, how would this change the tally marks drawn for each colour?

Say: Suppose there are 10 red buttons and 20 blue buttons. The red buttons will be represented by 2 ice-cream sticks and the blue buttons will be represented by 4 ice-cream sticks.

Pictographs

Learning Outcomes

Students will be able to read and draw pictographs.

Teaching Aids

Chart papers; Smiley stickers

Activity

Imagine Maths Page 164

Begin by asking what mode of transport students use to get to school. As each student responds, write the name of the mode of transport on the board as bus, car, bicycle, and so on.

Ask the students to work in groups. Distribute the smiley stickers and chart paper to each group. Instruct the group to create a table on the chart paper and ask them to paste the smiley sticker to show the data as 1 smiley sticker = 5 students.

Ask the students to arrange the mode of transport used in increasing order.

Learning Outcomes

Students will be able to read and draw bar graphs.

Teaching Aids

Chart papers; Building blocks

Activity

Ask each student to tell you the number of hours he/she spends playing outside every day. Draw a table on the board as given to show this data.

No. of Students

Ask the students to work in groups. Distribute building blocks and chart paper to each group.

Instruct the groups to draw the axes and write the title, label and scale on the chart paper. Next, ask them to create a bar graph to show the data by stacking the blocks, where each colour represents a specific time frame, like 1 hour, 2 hours, 3 hours or 4 hours and each block represents 5 students. Explain that the height of each stack corresponds to the number of students that spend that many hours playing outside.

Instruct the students to draw the bar graph in their notebooks. Ask questions like, “How many students spend 3 hours playing outside? What is the maximum number of hours spent playing outside in a day? If student A spends x hours in a day, how many hours will he spend playing outside in a week?”

Extension Idea

Ask: How will the number of blocks you stack change if you take the key as 1 block = 20 students?

Say: If you take 1 block = 20 students as the key, the number of blocks that you stack will reduce to one-fourth.

1. Organising Data as Tally Marks

Do It Together

Answers

3. Drawing Bar Graphs

Do It Together

2. Pictographs

Do It Together

1. 480

2. Saturday, 800

3. Tuesday, 320

4. 41 × 80 = 3280

4. Interpreting Bar Graphs

Do It Together

1. March, 50 cm

2. 130 cm

3. 140 cm – 90 cm = 50 cm

Mensuration 10

Learning Outcomes

Students will be able to: find the perimeter of plane shapes by adding the lengths of sides. find the perimeter of regular shapes by using formulas. find the area of regular and irregular shapes on graph or squared paper. find the area of squares and rectangles using the formula. find the area of triangles using the formula. find the area and perimeter of combined shapes. solve word problems on finding the perimeter and area of shapes and figures.

Alignment to NCF

C-3.4: Understands the definition and formula for the area of a square or rectangle as length times breadth

C-3.5: Devises strategies for estimating the distance, length, time, perimeter (for regular and irregular shapes), area (for regular and irregular shapes), weight, and volume and verifies the same using standard units

C-3.6: Deduces that shapes having equal areas can have different perimeters and shapes having equal perimeters can have different areas

Let’s Recall

Recap to check if students know how to find the perimeter of a shape using a grid. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

plane figures: shapes that can be drawn on paper regular shapes: plane figures in which all the sides are equal combined shapes: combinations of more than one plane figure

Teaching Aids

Cutouts of polygons; Ribbon; Cutouts of regular polygons; Cutouts of rectangles; String; Marker; Ruler; Shape drawn on squared paper; Sheets of squared paper; Crayons; Leaves; Square and rectangle paper cutouts; Small square stickers; Rectangle paper cutouts with one diagonal marked with a dotted line; Scissors; Squared paper cutouts; Word problem sheets

Chapter: Mensuration

Perimeter of Plane Figures

Learning Outcomes

Imagine Maths Page 178

Students will be able to find the perimeter of plane shapes by adding the lengths of sides.

Teaching Aids

Cutouts of polygons; Ribbons

Activity

Show the students an object with a border, such as a photo frame, and ask them how to determine how much ribbon would be required to cover its border. Explain to them that we would have to measure the lengths of all the sides and add them.

Ask the students to work in pairs. Provide each pair with some ribbon and a cutout of a polygon.

Instruct them to design a card using the cutout by adding a ribbon border. Ask them to determine the total length of ribbon that will be required for the border by first measuring the length of each side of the polygon cutout and noting down the measures in their notebooks; and then adding the lengths to find the perimeter of their cutouts.

Extension Idea

Instruct: The perimeter of a pentagon is 84 cm. Three sides measure 12 cm, 15 cm and 25 cm. The remaining two sides are equal. Determine the length of these two equal sides.

Say: The total length of the two remaining sides is 84 – (12 + 15 + 25), which equals 32. Therefore, each of the remaining sides measures 16 cm.

Perimeter of Regular Shapes

Learning Outcomes

Students will be able to find the perimeter of regular shapes by using formulas.

Teaching Aids

Cutouts of regular polygons; Cutout of rectangles; String; Marker; Ruler Activity

Imagine Maths Page 179

Ask the students to work in groups. Distribute 3 cutouts of regular polygons, 1 cutout of a rectangle and string to each group.

Instruct each student in the group to take one shape. Using the string and ruler, have them measure the length of the boundary of each shape. Ask them to record the measure in their notebooks. Next, instruct the students to try forming a rule or formula that will help them find the perimeter of each shape quickly. Ask them to discuss in their groups the differences between the perimeter of polygons with equal sides and the perimeter of a rectangle. For example, in a regular polygon that has 5 sides, each measuring 10 cm, the perimeter will be 10 + 10 + 10 + 10 + 10 = 5 × 10 = 50 cm, whereas in case of a rectangle with sides measuring 5 cm and 10 cm, the perimeter will be 10 + 5 + 10 + 5 = 2 × (10 + 5) = 2 × 15 = 30 cm. Give them the length of the sides of 2–3 regular polygons and ask them to find the perimeter in their notebooks.

Extension Idea

Ask: If a regular shape with 17 sides has a perimeter of 357 cm, what is the measure of each side?

Say: The measure of each side is 357 ÷ 17 = 21 cm.

Area on Graph Paper

Learning Outcomes

Imagine Maths Page 182

Students will be able to find the area of regular and irregular shapes on graph or squared paper.

Teaching Aids

Shape drawn on squared paper; Sheets of squared paper; Crayons; Leaves

Activity

Begin by showing the students a shape drawn on squared paper. Explain that since 5 squares are fully shaded or filled, the area of the shape is 5 sq. units.

Ask the students to work in pairs. Distribute a sheet of squared paper, a leaf and crayons to each pair. Instruct the pairs to place a leaf on the squared paper and draw its outline. Ask them to colour their drawing using crayons, assigning different colours for fully filled, half-filled, more than half-filled, and less than half-filled squares. Instruct them to count each square that is more than half-filled as 1 square, count two half-filled squares as 1 square and do not count the less than half squares. Ask them to record the number of squares for each category in their notebooks. Then, instruct them to find the total area of the shape using the information obtained about the squares corresponding to each category.

Ask questions like, “Why do you think we do not consider the less than half-filled squares while finding the area?”

Area of Squares and Rectangles

Learning Outcomes

Students will be able to find the area of squares and rectangles using the formula.

Teaching Aids

Square and rectangle paper cutouts; Small square stickers

Activity

Imagine Maths Page 184

Distribute the square and rectangle paper cutouts to the students along with some stickers. Ask the students to work in pairs. Instruct them to fill the shapes using the stickers. Then, ask them to count the total number of stickers used for each shape and record it in their notebooks.

Next, ask the students to count the stickers in a row for the length and in a column for the breadth of the shape and record these in their notebooks. They should then multiply the number of stickers along the length and breadth. Guide them to verify how are the areas obtained by both methods related. Ask them to write a formula for the area of both shapes based on their finding.

Ask question like, “Why do you think we multiply the same length by itself for a square but multiply different lengths for a rectangle?”

Give the students more problems to solve using the formula.

Extension Idea

Ask: The area of a square field is 100 sq. m. The owner wants to fence this field. The cost of fencing for 10 m is ₹500. How much would it cost to fence the entire field?

Say: As the area is 100 sq. m., the measure of each side is 10 m. So, the cost to fence the entire field would be ₹500 × 4 = ₹2000.

Area of Triangles

Learning Outcomes

Find the area of triangles using the formula.

Teaching Aids

Rectangle paper cutouts with one diagonal marked with a dotted line; Scissors

Activity

Imagine Maths Page 185

Ask the students to work in pairs. Distribute the rectangle paper cutouts and scissors to each pair. Instruct the students to measure the length of the sides of the rectangle and find the area. They will then cut the rectangles along the dotted lines to get 2 triangles. Ask them to place one triangle over the other to ensure that they overlap. Discuss with them that the area of each triangle is half the area of the rectangle. Ask them to write the formula for the area of a triangle using the formula for the area of a rectangle.

Ask questions like, “Which lengths in a rectangle and a triangle equal? What are the lengths needed in a triangle to find its area?”

Extension Idea

Ask: The area of a triangle doubles when the height of the triangle is doubled? Justify the statement with an example.

Say: The statement is true. Area of a triangle = 1 2 � Height � Base. When height is doubled, Area of the triangle = 1 2 � 2 � Height � Base = B � H.

For example, H = 25 cm, B = 20 cm. A = 250 sq. cm. H = 50 cm, B = 20 cm, A = 500 sq. cm.

Area and Perimeter of Combined Shapes

Learning Outcomes

Students will be able to find the area and perimeter of combined shapes.

Teaching Aids

Squared paper cutouts

Activity

Imagine Maths Page 186

Ask the students to work in pairs. Distribute squared paper cutouts to each student. Instruct each pair to cut out the squared cutouts into smaller squares or rectangles and put them together to form a combined shape. Ask them to work together to find the perimeter of their combined shape by counting the number of squares along each side and adding the lengths of all the sides.

When they are done, ask the students to count the total number of squares inside their combined shapes (representing the area) and record the counts in their notebooks. Then, instruct them to find the areas of the individual shapes in the combined shapes and write the total area in their notebooks. Ask them to verify the value with the area obtained earlier and check whether they are the same.

Word Problems on Perimeter and Area

Learning Outcomes

Imagine Maths Page 188

Students will be able to solve word problems on finding the perimeter and area of shapes and figures.

Teaching Aids

Word problem sheets

Activity

Give each student a sheet of squared paper and a sheet with a word problem, such as: A playground is divided into two rectangular areas. The first section measures 25 metres by 20 metres, and the second section has dimensions of 15 metres by 10 metres. If the cost of planting grass is ₹50 per m2, what is the total cost of planting grass in the playground? How much fencing is needed for the two sections?

Instruct the students to use the CUBES strategy by circling the numbers, underlining the question, boxing the key words, evaluating and solving the problem. Ask them to solve the problem in their notebooks.

Extension Idea

Instruct: Create a problem that requires finding the combined area of a triangle and a square sharing the same base. Say: A sample problem is: Aman is planning a garden area. He wants to have a square patch of grass with an equilateral triangular flower bed next to it. The side of the square patch is 5 metres, and the height of the triangle is 4.3 cm. Find the total area

Answers

1. Perimeter of Plane Figures

Do It Together

1. Perimeter

= 7 cm + 5 cm + 6 cm + 2 cm

= 20 cm

2. Perimeter

= 6 m + 2 m + 2 m + 6 m + 3 m

= 19 m

3. Perimeter

= 9 cm + 5 cm + 5 cm + 11 cm + 6 cm

= 36 cm

2. Perimeter of Regular Shapes

Think and Tell

The perimeter of a regular octagon with sides of 7 cm will be 8 × 7 cm = 56 cm.

Do It Together

1. Regular Hexagon

Number of sides = 6

Perimeter = 6 × 6 cm = 36 cm

2. Equilateral Triangle

Number of sides = 3

Perimeter = 3 × 6 cm = 18 cm

3. Perimeter of Rectangles

Do It Together

Length of the side of heptagon = 8 m

Perimeter of heptagon = 7 × 8 m = 56 m

Length of rectangle = 15 m

Perimeter of rectangle = Perimeter of heptagon

2 × (L + B) = 56

B = 56 2 – L; B = 28 – 15 = 13 m

Hence, the breadth of the rectangle is 13 m.

4. Area on Graph Paper

Do It Together

1. Fully filled squares = 33

Half-filled squares = 5

More than half-filled squares = 10

Less than half-filled squares = 3

Area = 33 + 5 × 1 2 + 10 = 45 1 2 sq. units

2. Fully filled squares = 30

Half-filled squares = 0

More than half-filled squares = 14

Less than half-filled squares = 10

Area = 44 sq. units

3. Fully filled squares = 5

Half-filled squares = 2

More than half-filled squares = 12

Less than half-filled squares = 8

Area = 18 sq. units

5 Area of Squares and Rectangles

Think and Tell

Yes.

Do It Together

Width of the room = 5 m; Length of the room = 6 m

Area of the room = Length × Breadth = 6 × 5 = 30 sq. m

Width of the rectangular tile = 0.2 m

Length of the rectangular tile = 0.3 m

Area of one tile = Length × Breadth = 0.3 × 0.2 = 0.06 sq. m

Number of tiles required = Area of the room Area of one tile = 500

Thus, the number of tiles required is 500

6. Area of Triangles

Do It Together

Height of the triangle = 6 cm

Length of base = 11 cm

Area = 1 2 × 6 × 11 = 33 square cm

7. Area and Perimeter of Combined Shapes

Do It Together

We split the shape into parts. Name them and find the missing dimensions.

Area of part A = l × b = 5 × 3 = 15 sq. cm

Area of part B = l × b = 2 × 6 = 12 sq. cm

Area of the figure = 15 + 12 = 27 sq. cm

Perimeter of the figure = 5 + 3 + 2 + 6 + 7 + 3 = 26 cm.

8. Word Problems on Perimeter and Area

Do It Together

Cost of installing a border around the rectangular crop field = ₹5200

Width = 8 m; Rate of installing the border = ₹130 per metre

Total cost of installing the border = Perimeter × Rate of installing the border per metre

Perimeter = Total cost of installing the border ÷ Rate of installing the border per metre

Perimeter = ₹5200 ÷ ₹130 = 40 metres

Perimeter = 2 × (Length + Breadth)

Length + Breadth = Perimeter ÷ 2

Length = (Perimeter ÷ 2) − Breadth

Length = 20 − 8 = 12 metres

Area = Length × Breadth = 12 × 8 = 96 square metres

Introduction to Algebra

Learning Outcomes

Students will be able to: identify or form the rule of a pattern using variables and use it to find the nth term. use variables to write rules to deduce formulas for finding the perimeter or area of shapes. form algebraic expressions for given statements and solve them for the given value of variables. form algebraic equations for given statements. solve linear equations in one variable to find the value of the variable.

Alignment to NCF

C-2.1: Understands equality between numerical expressions and learns to check arithmetical equations

C-2.2: Extends the representation of a number in the form of a variable or an algebraic expression using a variable

C-2.3: Forms algebraic expressions using variables, coefficients, and constants and manipulates them through basic operations

C-2.4: Poses and solves linear equations to find the value of an unknown, including to solve puzzles and word problems

C-2.5: Develops own methods to solve puzzles and problems using algebraic thinking

Let’s Recall

Recap to check if students know how to recognise and extend patterns. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

pattern: an arrangement of shapes, lines, letters, numbers or colours that keep repeating polygon: a 2-D shape made up of 3 or more line segments

algebraic expression: a statement formed by meaningful combinations of variables, constants and operators linear equation: an equation in which the highest power of each variable is 1

Teaching Aids

Matchsticks; Sheet of paper with a table drawn on it; Toothpicks; Slips of paper with statements written on them; Two sets of index cards (one set with statements and the other set with the corresponding algebraic equations); Index cards (with a linear equation in one variable)

Chapter: Introduction to Algebra

Number Patterns

Learning Outcomes

Imagine Maths Page 196

Students will be able to identify or form the rule of a pattern using variables and use it to find the nth term.

Teaching Aids

Matchsticks; Sheet of paper with a table drawn on it

Activity

Begin with a discussion about patterns in everyday life. Write a simple pattern on the board, for example, 5, 7, 9, 11 …

Ask the students to find the rule of the pattern. Discuss how to find the rule. Explain that the rule is 2 times the term number added to 3 and that this rule will help find any term of the pattern. So, the nth term is 2n + 3.

Ask the students to work in groups.

Distribute matchsticks and the sheets with the following table drawn on them.

Shape Number 1 2 3 4 5

Number of Sticks Required 5 9 13 Rule

Number of sticks required =

Instruct each group to use matchsticks to form the pattern as shown in the table. Let them form at least 5 terms of the pattern. After forming the shapes, ask each group to discuss among themselves to identify the rule of the pattern and write the rule on the sheet.

Allow the students to show one more pattern with matchsticks and identify the rule.

Extension Idea

Instruct: Consider (3, 6), (5, 10), (7, 14). Identify the rule that describes how to get the second number from the first number in every ordered pair.

Say: In each pair, the pattern is: [2 × 1 + 1, 2 × (2 × 1 + 1)] = (3, 6); [2 × 2 + 1, 2 × (2 × 2 + 1) = (5, 10) and [2 × 3 + 1, 2 × (2 × 3 + 1)] = (7, 14). So, the rule is [2n + 1, 2 × (2n + 1)].

Rules in Patterns

Learning Outcomes

Imagine Maths Page 197

Students will be able to use variables to write rules to deduce formulas for finding the perimeter or area of shapes.

Teaching Aids

Toothpicks

Activity

Say: Consider a square with sides measuring x. To find the perimeter, we just multiply the number of sides by the length, i.e., 4 × x, and for the area, we multiply the lengths of two sides, i.e., x × x.

Ask the students to work in pairs. Distribute a set of toothpicks to each pair.

Instruct them to form polygons using toothpicks and write down the number of sides (which are all equal) for each polygon in their notebooks. Then, ask them to assign a variable, let us say x, as the length of one toothpick, calculate the perimeter of each polygon and write the results in their notebooks. Guide them to use the toothpicks to create squares and rectangles, using x as the length of one toothpick. Instruct them to calculate the area of each square and rectangle.

Ask questions like, “Is there a connection between the side length and the number of toothpicks?”

Algebraic Expressions

Learning Outcomes

Imagine Maths Page 200

Students will be able to form algebraic expressions for given statements and solve them for the given value of variables.

Teaching Aids

Slips of paper with statements written on them

Activity

Write a statement on the board, such as, “3 less than the perimeter of a square of side ‘a’”. Discuss the algebraic expression for this statement, which is 4a – 3. Write the expression on the board. Explain to the students that 4 is the coefficient of a, a is the variable, 3 is a constant and 4a and 3 are the terms of the expression.

Divide the class into groups. Distribute the slips of paper with statements written on them.

2 more than 4 times m 7 less than 5 times a number 8 times a number decreased by 32

Instruct the students to write the algebraic expressions for the statements written on their slips, for example, 4m + 2.

Ask the students to find the value of the algebraic expressions for any given values of the variables.

Extension Idea

Ask: For the statement, “3 less than 4 times a number is equal to 13”, a student wrote the equation 3a – 4 = 13. Was his response accurate? If not, what is the correct equation for the statement?

Say: His response was not correct. The correct equation is 4a – 3 = 13.

Forming Algebraic Equations

Imagine Maths Page 203 Learning Outcomes

Students will be able to form algebraic equations for given statements.

Teaching Aids

Two sets of index cards (one set with statements and the other set with the corresponding algebraic equations) Activity

Write a statement on the board, such as, “4 more than 4 times ‘a’ is twice of 8”. Discuss the algebraic equation for this statement, which is 4 + 4a = 16.

Explain that 4 + 4a is the LHS and 16 is the RHS and the highest power of a in the equation is 1, so this is a linear equation.

Divide the class into 2 equal groups.

Give one group the set of index cards containing written statements, such as “5 times m less than 10 is 5”.

Give the other group the set of index cards containing the corresponding algebraic expressions for the statements, such as 10 – 5m = 5. Ensure that both sets of cards are thoroughly shuffled.

Instruct the first group to write the algebraic equations for their statements and the second group to write the possible statements for their equations.

Instruct the student look for a student from the other group who has a card that matches their work.

Solving Linear Equations in One Variable

Learning Outcomes

Imagine Maths Page 205

Students will be able to solve linear equations in one variable to find the value of the variable.

Teaching Aids

Index cards (with a linear equation in one variable)

Activity

Write a statement on the board, such as, “If a number is tripled, its result is 30.”

Discuss with the class how, if the number is n, then 3n = 30 ⇒ n = 30 ÷ 3 ⇒ n = 10.

Ask the students to work in pairs. Give each pair an index card with a linear equation in one variable written on it. Instruct one student in each pair to use the trial and error method to find a solution and the other student to use the transposition method to solve the equation. Ask them to write the solutions in their notebooks.

When they are done, ask the pairs to compare and cross-verify their solutions. Ask, “Which do you think is easier: the trial and error method or the transposition method?”

Extension Idea

Instruct: Find the number if 15 added to three times the number results in 45.

Say: Let the number be x. As 15 + 3x = 45, using the transposition method, we get

⇒ x = 10.

Answers

1. Number Patterns

Think and Tell

There will be 10 × 3 = 30 seats in the tenth row.

Do It Together

Number of Sticks Required 5 10 15 20 25 75

Rule Number of sticks required = n × 5

2. Rules in Patterns

Do It Together

Perimeter of a regular pentagon = sum of the lengths of all its sides

So, P = a + a + a + a + a = 5 × a = 5a

Thus, we get the rule for the perimeter of a regular pentagon as 5a.

3. Forming Algebraic Expressions

Do It Together

Let Anil’s age be x years.

So, the age of Anil’s mother = 3x – 2 years.

4. Solving Algebraic Expressions

Do It Together

1. 4a(b + c)

= (4 × 6) (1 + 3)

= 24 × 4 = 96

5. Forming Algebraic Equations

Do It Together

Let the number be z.

Adding 3 to 4 times this number can be written algebraically as 4z + 3

So, the required equation is 4z + 3 = 21.

6. Solving Linear Equations in One Variable

Do It Together

Let Sonal have x number of friends.

Number of balloons distributed among friends = 5x.

She has 3 balloons left. But the total number of balloons is 33. So, the equation that satisfies the condition is 5

Therefore, Sonal has 6 friends.

Introduction to Ratio and Proportion

Learning Outcomes

Students will be able to: represent a ratio in the form a:b, a b or a to b. reduce a given ratio to its simplest form. find equivalent ratios for a given ratio. check whether 4 terms are in proportion. solve word problems on the unitary method.

Alignment to NCF

C-1.6: Explores and applies fractions (both as ratios and in decimal form) in daily-life situations

Let’s Recall

Recap to check if students know about fractions and their types. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

ratio: a relation or comparison between numbers equivalent: equal in value

Teaching Aids

Colour buttons (red, blue, green and yellow); Index cards (with ratios written on them); Marbles in two different colours; Cotton balls; Ice cream sticks; Chart paper; Red and blue ribbons; Ruler; Scissors; Crayon box; Pencil box, Tiffin box; Water bottle; Price tags

Chapter: Introduction to Ratio and Proportion

Introducing Ratios

Learning Outcomes

Students will be able to represent a ratio in the form a:b, a b or a to b.

Teaching Aids

Colour buttons (red, blue, green and yellow)

Activity

Begin by explaining what a ratio is and give an example. Place some number cards on the table. Distribute coloured buttons to each pair.

Ask the students to pick one colour button and find the ratio of that colour button to the total number of buttons. Instruct the students to write down the ratio in their notebook.

Then, ask the students to find the ratio of red colour button to blue button. Ask, “How will the ratio change when the number of red buttons is increased?”

Extension Idea

Ask: A wall has a width of 5 m. The ratio of the width of a window on the wall to that of the wall is 2:5. What is the width of the window?

Say: As the ratio is 2:5, the width of the window is 2 m.

Ratio in Simplest Form

Learning Outcomes

Students will be able to reduce a given ratio to its simplest form.

Teaching Aids

Index cards (with ratios written on them); Marbles in two different colours

Activity

Ask the students to work in groups. Distribute index cards with a ratio written (example: 12:15) and marbles to each group.

Instruct them to use marbles of two different colours to represent the ratio (example: 12 red marbles and 15 blue marbles to show 12:15). Next, ask them to divide each set of marbles into the same number of groups. For example: The 12 red and 15 blue marbles can be divided into 3 groups each to get 4 red marbles in each group and 5 blue marbles in each group. Ask them to count the number of marbles in each group and write the new ratio. Explain that the number of marbles in each group for each colour gives the simplest form, 4:5, of the given ratio, which can be written as 4/5. Ask the students to write the ratio in the simplest form in their notebooks. Discuss how to divide the numerator and denominator by their HCF to find the simplest form. Ask questions like, “Why do you think it is important to simplify a ratio?”

Extension Idea

Ask: Can you divide 50 marbles into two cups in the ratio 3:7? How many marbles will there be in each cup? Say: Yes, we can divide 50 marbles into two cups in the ratio 3:7. There will be 15 marbles in one cup and 35 in the other.

Learning Outcomes

Students will be able to find equivalent ratios for a given ratio.

Teaching Aids

Cotton balls; Ice cream sticks; Chart paper

Activity

Ask the students to work in groups. Distribute the cotton balls, ice cream sticks to each group. Instruct them to place 4 ice cream sticks and 8 cotton balls together. Then place 3 ice cream sticks and 6 cotton balls together. Finally they write the ratios for both groups. Instruct them to bring down the ratios to their simplest form. Explain that when the simplest form of two or more ratios is the same, they are known as equivalent ratios. Ask them to take away 1 ice-cream stick and 2 cotton balls for each ice-cream stick taken away, from the 2 sets.

Ask: What do you notice about the ice cream sticks and cotton balls left in both sets?

Proportion and Their Applications

Learning Outcomes

Students will be able to check whether 4 terms are in proportion.

Teaching Aids

Red and blue ribbons; Ruler; Scissors

Activity

Imagine Maths Page 219

Ask the students to work in groups. Distribute red and blue ribbons, a ruler and a scissors to each group. Instruct the groups to cut red ribbons of lengths 2 cm and 6 cm, and then to cut a blue ribbon of length 3 cm. Then, ask them to think and cut another length of blue ribbon such that the ratio of the 2 cm red ribbon to the 3 cm blue ribbon is equivalent to the ratio of the 6 cm red ribbon to the length of blue ribbon they cut. Once they cut the blue ribbon, ask them to note down the ratios in their notebooks. Discuss the sign of proportion and the terms. Instruct the students to use the formula and find the correct length of the blue ribbon in their notebooks.

Then, ask them to find the length of the red ribbon if a third blue ribbon is 15 cm long and write the answer in their notebooks.

Extension Idea

Ask: Do the ratios 25 cm to 1 m 50 cm and 30 seconds to 2 minutes 30 seconds form a proportion?

Say: The ratio of 25 cm to 1 m 50 cm is 25:150 = 1:6. The ratio of 30 seconds to 2 minutes 30 seconds is 30:150 = 1:5. So, the ratios are not in proportion.

Learning Outcomes

Students will be able to solve word problems on the unitary method.

Teaching Aids

Crayon box; Pencil box, Tiffin box; Water bottle; Price tags

Activity

Box of 6 crayons with price tag of ₹60; Pencil box with price tag of ₹80; Tiffin box with price tag of ₹250; Water bottle with price tag of ₹100

Set up the things with the price tag on the table. Divide the class into groups. Ask each group to come forward and buy any 2 items in any quantity.

Ask the students to find the cost of the items and also the total cost of items in the notebook.

Ask all the groups to come forward and share the cost of the items that they chose and the total cost of the items that they had bought.

Ask, “What is the cost of 1 crayon? What is the cost of 6 water bottles?”

Extension Idea

Instruct: Create your own word problem based on unitary method. Say: There can be many such problems. One could be: Rahul purchased 15 kg of oranges for ₹600. How much will 4 kg of oranges cost?

1. Introducing Ratios

Do It Together

1. Number of red balls = 4; Number of white balls = 9

Answers

The ratio of the number of red balls to the number of white balls = 4:9

2. Number of black balls = 5; Total number of balls = 20

The ratio of the number of black balls to the total number of balls = 5:20

2. Ratio in Simplest Form

Do It Together

1 year 8 months = 12 months + 8 months = 20 months

The required ratio = 20 months : 5 months = 20 5 = 4 1

The ratio of 1 year 8 months to 5 months is 20:5 or 4:1.

3. Equivalent Ratios

Think and Tell

A ratio can have infinite equivalent ratios.

Do It Together

Number of parts given to group A = 5 out of 9 parts = 5 9

Number of parts given to group B = 4 out of 9 parts = 4 9

Number of chocolates given to group A = 5 9 × 90 = 50 chocolates

Number of chocolates given to group B = 4 9 × 90 = 40 chocolates

4. Introducing Proportion

Do It Together

Mansi’s weight = 25 kg; Mother’s weight = 60 kg

Ratio of Mansi’s weight to mother’s weight = 25:60 = 25 60 = 5 12

Ramesh’s weight = 30 kg; Father’s weight = 75 kg

Ratio of Ramesh’s weight to father’s weight = 30:75 = 30 75 = 2 5

Hence, the given weights are not proportion.

5. Proportional Terms

Do It Together

Let the number of cups of flour required be x.

Using proportion, 3:x::2:16

Therefore, x × 2 = 3 × 16 ⇒ 2x = 48 ⇒ x = 48 2 = 24

Hence, 24 cups of flour are required to make 16 dozen cookies.

6. Continued Proportion

Do It Together

7:14::14:x 7 × x = 14 × 14 ⇒ 7x = 196 ⇒ x = 28

So, the third term is 28

7. Unitary Method

Do It Together

Cost of 15 litres of paint A = ₹750

Cost of 1 litre of paint A = 750 15 = ₹50

Cost of 20 litres of paint B = ₹900

Cost of 1 litre of paint B = 900 20 = ₹45

Hence, paint B will be cheaper than paint A.

Symmetry 13

Learning Outcomes

Students will be able to: draw lines of symmetry in given shapes or figures. draw the reflection of a shape or figure on squared paper. determine the angle through which a shape or figure rotates to show rotational symmetry.

Alignment to NCF

C-2.3: Recognises and creates symmetry (reflection, rotation) in familiar 2D and 3D shapes

Let’s Recall

Recap to check if students know what symmetrical and non-symmetrical shapes are. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

line of symmetry: a line that divides a shape into equal and identical halves reflection: an image of the original formed in the mirror rotational symmetry: property of a shape where the shape appears unchanged when rotated by a specific angle

order of symmetry: number of positions in which a figure can be rotated and still appears exactly as it did before the rotation

Teaching Aids

Picture cards with figures having 0, 1 or more lines of symmetry; Sheets of paper; Shape cards with shapes/designs having 1 line of symmetry; Mirror; Squared paper with half shapes drawn; Shape cards with shapes/designs having 2/3/4 angles of rotation

Chapter: Symmetry

Lines of Symmetry

Learning Outcomes

Students will be able to draw lines of symmetry in given shapes or figures.

Teaching Aids

Picture cards with figures having 0, 1 or more lines of symmetry; Sheets of paper

Activity

Ask the students to work in groups of 3. Distribute picture cards and sheets of paper to each group.

Instruct the groups to fold the picture cards to identify the lines of symmetry in them and then draw lines of symmetry on each card for the shapes/designs drawn. Ask them about the similarities and differences in these shapes/designs.

Ask if there can be designs that have no lines of symmetry or infinite lines of symmetry. Instruct them to verify their answers by creating designs on a sheet of paper that have 0, 1 or more than 1 line of symmetry. Instruct them to exchange their designs with another group and compare the lines of symmetry.

Extension Idea

Ask: How many lines of symmetry does the cross section of a lemon have?

Say: The cross section of a lemon is a circle, so it has infinite lines of symmetry.

Reflection and Symmetry

Learning Outcomes

Students will be able to draw the reflection of a shape or figure on squared paper.

Teaching Aids

Shape cards with shapes/designs having 1 line of symmetry; Mirror; Squared paper with half shapes drawn

Activity

Instruct each student the day before to bring a plane mirror to the class.

Ask the students to work in groups. Distribute 2–3 cards with different shapes/designs having 1 line of symmetry to each group.

Instruct the groups to place the shape cards on a piece of paper one by one and draw a vertical line on the right for each card. Guide them to place the mirror along the line such that the given shape is reflected in it.

Ask them to observe and draw the reflected shape in their notebooks and compare the two shapes to tell if they are symmetrical.

Ask questions like, “Is the image in the mirror the same shape and size as the original figure? Is it at an equal distance from the mirror line as the original?”

Distribute a sheet of squared paper with half a shape drawn on it to each group. Ask the students to complete the shape by drawing its other half on the squared paper itself. Ask them to exchange sheets with other groups for peer review. Help them generalise that in all cases of mirror symmetry, there is a line of symmetry along which the mirror symmetry is shown.

Extension Idea

Ask: What are the first 5 letters of the English alphabet that appear to be the same as their reflections in the mirror?

Say: A, H, I, M and O are the first 5 letters of the English alphabet that appear to be the same as their reflections.

Rotational Symmetry

Learning Outcomes

Imagine Maths Page 234

Students will be able to determine the angle through which a shape or figure rotates to show rotational symmetry.

Teaching Aids

Shape cards with shapes/designs having 2/3/4 angles of rotation

Activity

Ask the students to work in groups. Distribute 2–3 cards with different shapes/designs having 2/3/4 angles of rotation to each group.

Instruct the groups to rotate the shape cards around the fixed point, so that the rotated figure should look exactly same as the figure before rotation. Ask them to observe that different shapes have different number of rotations.

Ask the students to count the number of positions through which the figure can be rotated and appear the same as before the rotation. Discuss in class the centre of rotation and the angle of rotational symmetry in different shapes/designs.

Instruct them to exchange their designs with another group and find angle of symmetry and order of symmetry.

Extension Idea

Ask: What is the relationship between angle of symmetry and rotational symmetry?

Say: Angle of symmetry × Order of symmetry = 360°

Answers

1. Symmetry in Shapes

Think and Tell

We can draw a line of symmetry exactly at the centre of a line segment.

Think and Tell

A parallelogram is asymmetrical since it cannot be divided into two identical halves by a straight line.

Do It Together Lines of symmetry = 5 Lines of symmetry = Lines of symmetry = Lines of symmetry =

2. Symmetry in Designs or Figures

Do It Together

3. Reflection and Symmetry

Think and Tell

The word “AMBULANCE” is written in the form of its mirror image so that drivers in vehicle ahead can view it in their mirror and instantly identify the word as “AMBULANCE” giving way in an emergency.

Do It Together

4. Rotational Symmetry

Think and Tell

The angles of symmetry of a wheel are infinite. Do It Together

Number of angles of symmetry = 6

Angles

Construction of Line Segments and Angles

Learning Outcomes

Students will be able to:

construct a line segment and the copy of a given line segment using a compass.

construct 2-D shapes and figures using a compass. construct a perpendicular using a compass.

draw angles of given measures using a protractor.

construct an angle bisector using a compass.

construct angles of 60°, 120° and 30° using a compass.

Alignment to NCF

C-3.4: Draws and constructs geometric shapes, such as lines, parallel lines, perpendicular lines, angles, and simple triangles, with specified properties using a compass and a straightedge

Let’s Recall

Recap to check if students know the basics of line segments and angles. Ask students to solve the questions given in the Let’s Warm-up section.

Vocabulary

perpendicular: two lines that intersect at a right angle, forming a 90° angle perpendicular bisector: a perpendicular that divides a line segment into two equal parts angle bisector: a line or ray that divides an angle into two equal angles

Teaching Aids

Straws; String; Ruler; Compass; Pencil; Picture cards figures made with 2 shapes like a house or a tree; Chart paper; Colour pencils; Sheets of paper; Protractor

Chapter: Construction of Line Segments and Angles

Constructing Line Segments;

Constructing a Copy of a Line Segment

Learning Outcomes

Students will be able to construct a line segment and the copy of a given line segment using a compass.

Teaching Aids

Straws; String; Ruler; Compass; Pencil

Activity

Ask the students to work in pairs. Distribute a straw and a length of string to each pair.

Instruct the pairs to cut the straw such that it has a length of 6.3 cm. Ask them to use the string to check the length. Then ask them to make a copy of the straw by placing it on paper and drawing a line along it.

Instruct the students to read the steps of construction of a line segment and its copy from the Imagine Mathematics book. Ask each student to draw a line segment of any length in their partner’s notebook and then use a compass to construct a copy of the line segment drawn by their partner below it.

Ask questions like, “How do you know that the line segment and its copy have the same length?”

Extension Idea

Ask: How will you construct a line segment equal to the sum of two lengths?

Say: First, you will copy the length of the first line segment. Then, from the end point of this line segment, you will draw a line segment of the second length.

Construction of Shapes and Figures

Learning Outcomes

Student will be able to construct 2-D shapes and figures using a compass.

Teaching Aids

Imagine Maths Page 245

Picture cards figures made with 2 shapes like a house or a tree; Chart paper; Pencil; Compass; Colour pencils

Activity

Ask the students to work in pairs. Distribute one picture card to each pair. Ask the students to identify the shapes in the picture card. Ask them to start making a copy of shapes one by one. For example, if the picture is a house made of a triangle and a square, ask the students to first copy the line segments of the square and then the triangle.

Ask the students to colour the picture on the chart paper.

Ask questions like, “What type of shapes/figures cannot be constructed using compass?”

Extension Idea

Ask: How will you construct a curve or an arc in a figure?

Say: Draw a line segment and mark the centre points above or below the line segment. Taking the points as centre, draw an arc.

Constructing a Perpendicular Using a Compass

Learning

Outcomes

Students will be able to construct a perpendicular using a compass.

Teaching Aids

Straws; Ruler; Compass; Pencil; String; Sheets of paper Activity

Introduce the concept of a perpendicular.

Imagine Maths Page 249

Ask the students to work in pairs. Provide each pair with 2 straws, some string, a pencil, and a sheet of paper. Give them a specific length, say 4.3 cm. Ask them to cut one straw to the given length and affix it to the sheet of paper horizontally. They should tie one end of a length of string to a pencil. Then, with the other end fixed to any point on the straw, they should stretch the string and move the pencil to draw arcs cutting the straw at 2 points, marking the two points. Next, ask them to take a longer piece of string, tie one end to the pencil, place the other end on one of the two points marked on the straw and draw an arc above the straw. They should repeat this by holding one end of the string on the other point marked on the straw. The two arcs will intersect at a point. Instruct the students to connect the initial arc’s centre to the intersection point and paste the second straw vertically along this line. This will help students understand the concept of constructing a perpendicular.

Ask the students to read the steps of construction of a perpendicular in their Imagine Maths books and then use a compass to construct a perpendicular in their notebooks.

Drawing Angles of Given Measures

Learning

Outcomes

Students will be able to draw angles of given measures using a protractor.

Teaching Aids

Protractor; Ruler

Activity

Begin the class by discussing angles and how to measure them using a protractor. Ask the students to form pairs. Provide each student with a protractor and ruler.

Imagine Maths Page 251

Instruct the students to draw a line segment in their notebooks and label it as PQ. Ask them to use the protractor to draw angles of 45° and 57° from points P and Q, respectively, and extend them to meet at a point. Then, ask them to measure the third angle of the triangle formed. Finally, ask them to exchange notebooks to measure the angles drawn by their partners and check if the angle measure is correct.

Extension Idea

Ask: Using a protractor that measures up to 180°, how can you draw an angle of 200°?

Say: To begin drawing 200°, we will first subtract 180 from 200. 200° − 180° = 20°. Then, we will draw a 20° angle and mark the reflex angle.

Constructing an Angle Bisector

Learning Outcomes

Students will be able to construct an angle bisector using a compass.

Teaching Aids

String; Sheets of paper; Compass; Ruler; Protractor; Pencil

Activity

Begin the class by discussing examples of using angle bisectors in real life such as to divide a slice of pizza to share equally with a friend. Explain that the imaginary line from the edge of the slice to the centre dividing it into 2 equal parts is like an angle bisector.

Ask the students to work in pairs. Distribute the teaching aids.

Instruct the students to use the protractor to draw an angle of 80° on the sheet of paper. Ask them to tie a pencil to one end of the string and place the other end on the vertex of the angle drawn; then, stretch the string and draw an arc cutting the arms of the angle. From the points where the arcs cut the arms, instruct them to draw two more arcs cutting each other and draw a line segment joining the intersection point to the vertex of the angle. Ask them to measure the angles formed.

Instruct the students to use the same method of constructing an angle bisector using a compass.

Extension Idea

Draw a triangle and angle bisectors to the three angles in the triangle on the board.

Ask: What do you notice about the angle bisectors drawn to the three angles in the triangle?

Say: The angle bisectors meet at one point in the centre of the triangle.

Constructing 60°, 120° and 30° Angles

Learning Outcomes

Students will be able to construct angles of 60°, 120° and 30° using a compass.

Teaching Aids

Protractor; Compass; Ruler

Activity

Ask the students to form pairs. Provide each student with a ruler, compass and protractor.

Instruct the students to use the protractor to draw a line segment AB of length 8 cm in their notebooks.

Ask them to read the steps of constructing 60°, 30° and 120° angles in their Imagine Maths books and use these steps to construct angles of 60° using a compass on points A and B (ensuring that the rays do not meet). Then, ask them to construct an angle bisector to the 60° angle created on point A to get the 30° angle.

Instruct them to use the 60° angle constructed on point B as the base to draw another 60° to get a 120° angle at point B.

Ask the students to exchange notebooks with their partners to check each other’s work.

Answers

1. Constructing a Copy of a Line Segment

Do It Together

2. Constructions of Shapes and Figures Do It Together

3. Constructing a Perpendicular Using a Compass Do It Together

4. Drawing Angles of Given Measures Do It Together

5. Constructing an Angle Bisector Do It Together

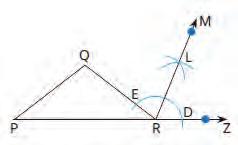
6. Constructing 60°, 120° and 30° Angles Do It Together

SolutionsAnswers

Chapter 1 Let’s Warm-up

1. The number 586592 can be rewritten using commas as 5,865,952. False

2. The place value and face value of 0 in 9,80,564 is 0 in each case. True

3. The expanded form of 3,83,452 is 300000 + 80000 + 3000 + 400 + 50 + 2. True

4. The number name of 7,03,478 is seven lakh three hundred four thousand seventy-eight. False

5. Between 40,73,548 and 40,72,187, 40,73,548 is greater. True

Do It Yourself 1A

1. a. 38,57,64,999 = 7 is in the lakhs place, so the face value of 7 is 7 and the place value of 7 is 7,00,000

b. 27,89,73,653 = 7 is in the ten thousands place, so the face value of 7 is 7 and the place value of 7 is 70,000

c. 18,90,37,890 = 9 is in the ten lakhs place, so the face value of 9 is 9 and the place value of 9 is 90,00,000

d. 81,87,50,658 = 1 is in the crores place, so the face value of 1 is 1 and the place value of 1 is 1,00,00,000

e. 58,76,03,653 = 8 is in the crores place, so the face value of 8 is 8 and the place value of 8 is 8,00,00,000

f. 20,56,78,450 = 2 is in the ten crores place, so the face value of 2 is 2 and the place value of 2 is 20,00,00,000

2. a. 24,85,67,835 = 20,00,00,000 + 4,00,00,000 + 80,00,000 + 5,00,000 + 60,000 + 7000 + 800 + 30 + 5

b. 56,42,86,604 = 50,00,00,000 + 6,00,00,000 + 40,00,000 + 2,00,000 + 80,000 + 6000 + 600 + 4

c. 93,27,59,191 = 90,00,00,000 + 3,00,00,000 + 20,00,000 + 7,00,000 + 50,000 + 9000 + 100 + 90 + 1

3. a. 23,34,26,578 = Twenty-three crore thirty-four lakh twentysix thousand five hundred seventy-eight

b. 74,36,54,679 = Seventy-four crore thirty-six lakh fifty-four thousand six hundred seventy-nine

c. 46,57,68,979 = Forty-six crore fifty-seven lakh sixty-eight thousand nine hundred seventy-nine

4. a. Sixteen crore twenty-six lakh ninety-two thousand one hundred forty-three = 16,26,92,143

b. Sixty-five crore twenty-two lakh forty-four thousand nine hundred = 65,22,44,900

c. Eighty crore ninety-nine lakh forty thousand two hundred one = 80,99,40,201

5. On interchanging digits 5 and 4 in 76,47,56,229, we get 76,57,46,229.

a. No, the face values will remain the same.

b. The place value of 5 in new number = 50,00,000 The place value of 4 in new number = 40,000

c. The place value of 5 in old number = 50,000

The difference of place values of 5 in old and new number = 50,00,000 – 50,000 = 49,50,000

6. Number using commas = 27,25,45,619

Number in expanded form = 20,00,00,000 + 7,00,00,000 + 20,00,000 + 5,00,000 + 40,000 + 5000 + 600 + 10 + 9

Number name: Twenty-seven crore twenty-five lakh forty-five thousand six hundred nineteen

7. Distance from Jupiter to Saturn = 64,62,70,000 km

Distance in words: Sixty-four crore sixty-two lakh seventy thousand

Challenge

1. The smallest 9-digit number using all odd digits at least once = 11,11,13,579

Number name: Eleven crore eleven lakh thirteen thousand five hundred seventy-nine

Do It Yourself 1B

1. a. 179,043,456 = 9 is in the millions place, so the face value of 9 is 9 and the place value of 9 is 9,000,000

b. 205,145,450 = 2 is in the hundred millions place, so the face value of 2 is 2 and the place value of 2 is 200,000,000

c. 385,876,243 = 8 is in the hundred thousands place, so the face value of 8 is 8 and the place value of 8 is 800,000

d. 580,398,653 = 8 is in the ten millions place, so the face value of 8 is 8 and the place value of 8 is 80,000,000

e. 754,750,213 = 0 is in the thousands place, so the face value and the place value of both is 0

f. 807,973,436 = 7 is in the ten thousands place, so the face value of 7 is 7 and the place value of 7 is 70,000

2. a. 248,567,465 = 200,000,000 + 40,000,000 + 8,000,000 + 500,000 + 60,000 + 7000 + 400 + 60 + 5

b. 787,135,436 = 700,000,000 + 80,000,000 + 7,000,000 + 100,000 + 30,000 + 5000 + 400 + 30 + 6

c. 932,542,191 = 900,000,000 + 30,000,000 + 2,000,000 + 500,000 + 40,000 + 2000 + 100 + 90 + 1

3. a. 345,768,979 = three hundred forty-five million, seven hundred sixty-eight thousand nine hundred seventy-nine

b. 575,123,389 = five hundred seventy-five million one hundred twenty-three thousand three hundred eighty-nine

c. 978,764,224 = nine hundred seventy-eight million seven hundred sixty-four thousand two hundred twenty-four

4. a. Eight hundred twenty-six million one hundred twenty thousand sixty-six = 826,120,066

b. One hundred ninety-two million five hundred four thousand sixteen = 192,504,016

c. Seven hundred eighteen million seven hundred ten thousand one hundred fifty-six = 718,710,156

5. Number of teachers = 4,824,238

Number name: Four million eight hundred twenty-four thousand two hundred thirty-eight

6. The speed of light is 299,792,458 metres per second.

The light of speed in words is two hundred ninety-nine million seven-hundred ninety-two thousand four-hundred forty-eight metres per second.

Challenge

1. 9-digit number, so

The ones digit is four times the tens digit. ___ ____ ___ ___ ___ ___ ___ 1 4

The sum of the ones and tens digit is equal to the sum of the hundred thousand and million digits.

So, 1 + 4 = 2 + 3 = 5 ___ ____ 3 2 ___ ___ 1 4

The sum of the ten thousands and thousands digit is equal to the double of the hundreds digit.

___ ____ 3 2 86 7 1 4

The millions digit is greater than the hundred thousands digit, and the ten thousands digit is 2 more than the thousands digit. ___ ____ 3 2 8 6 7 1 4

The digit at hundred million place is the largest digit.

9 ____ 3 2 867 1 4

The digit at the ten million place is the remaining digit.

9 5 3 2 86 71 4

So, the number is 953,286,714.

Do It Yourself 1C

1. a. 99 = 90 + 9 = XC + IX = XCIX

b. 184 = 100 + 80 + 4 = C + LXXX + IV = CLXXXIV

c. 285 = 200 + 80 + 5 = CC + LXXX + V = CCLXXXV

d. 438 = 400 + 30 + 8 = CD + XXX + VIII = CDXXXVIII

e. 1564 = 1000 + 500 + 60 + 4 = M + D + LX + IV = MDLXIV

f. 1287 = 1000 + 200 + 80 + 7 = M + CC + LXXX + VII = MCCLXXXVII

2. a. CDLXVI = CD + LX + VI = (500 – 100) + (50 + 10) + (5 + 1) = 400 + 60 + 6 = 466

b. XCVI = XC + VI = (100 – 10) + (5 + 1) = 90 + 6 = 96

c. CXV = C + XV = 100 + (10 + 5) = 100 + 15 = 115

d. CCCLXV = CCC + L + XV = (100 + 100 + 100) + 50 + (10 + 5) = 300 + 50 + 15 = 365

e. MDCCCLXIV = M + DCCC + LX + IV = 1000 + (500 + 100 + 100 + 100) + (50 + 10) + (5 – 1) = 1000 + 800 + 60 + 4 = 1864

f. CMXCIX = CM + XC + IX = (1000 – 100) + (100 – 10) + (10 – 1) = 900 + 90 + 9 = 999

3. a. Compare the digits in the hundred millions place 1 < 5 < 8 < 9

100,356,782 < 500,040,367 < 887,210,460 < 931,124,820

b. Compare the digits in the hundred millions place 3 < 6 < 8 < 9

360,841,910 < 692,180,350 < 826,020,031 < 927,516,890

c. Compare the digits in the hundred millions place 5 < 6 < 9

The digits in hundred millions place are the same in 604,503,821 and 650,241,567.

Compare the digits in ten millions place 0 < 5

500,216,138 < 604,503,821 < 650,241,567 < 945,241,823

4. a. Compare the digits in the ten crores place 8 > 6 > 4

The digits in hundred millions place are the same in 826,374,510 and 871,926,345.

Compare the digits in ten millions place 7 > 2

871,926,345 > 826,374,510 > 670,814,256 > 450,070,921

b. Compare the digits in the hundred millions place 9 > 8 > 6 > 4

962,115,108 > 801,210,450 > 678,203,001 > 423,516,789

c. Compare the digits in the ten crores place 9 > 7 > 5

The digits in hundred millions place are the same in 543,343,867 and 578,206,010.

Compare the digits in ten millions place 7 > 4

967,208,891 > 788,216,134 > 578,206,010 > 543,343,867

5. To form the greatest number, arrange the digits in the descending order from ten crores place to ones place.

To form the smallest number, arrange the digits in the ascending order from ten crores place to ones place.

a. Greatest 9-digit number = 98,75,43,210

Smallest 9-digit number = 10,23,45,789

b. Greatest 9-digit number = 87,65,43,210

Smallest 9-digit number = 10,23,45,678

c. Greatest 9-digit number =98,76,54,321

Smallest 9-digit number = 12,34,56,789

6. To form the greatest number, arrange the digits in the descending order from ten crores place to ones place.

To form the smallest number, arrange the digits in the ascending order from ten crores place to ones place.

a. Greatest 9-digit number = 88,76,54,210

Smallest 9-digit number = 10,24,56,788

b. Greatest 9-digit number = 99,87,65,431

Smallest 9-digit number = 13,45,67,899

c. Greatest 9-digit number = 99,75,43,210

Smallest 9-digit number= 10,23,45,799

7. a. Two digits that will be used here are 9 and 8.

So, the greatest 9-digit number = 99,99,98,888

b. Five digits that will be used here are 9, 8, 7, 6, and 5.

So, the greatest 9-digit number = 99,99,98,765

c. Four digits that will be used here are 9, 8, 7, and 6.

So, the greatest 9-digit number = 99,99,99,876

8. Cotton produced by US = 3,180,410 tonnes

Cotton produced by India = 6,131,050 tonnes

Cotton produced by China = 5,910,500 tonnes

Cotton produced by Brazil = 2,757,353 tonnes

Compare the digits at the ten crores place, 2 < 3 < 5 < 6

So, the increasing order of cotton produced by the countries is Brazil < US < China < India

Challenge

1. Sana’ year of birth = MMXII = 1000 + 1000 + 10 + 1 + 1 = 2012

Yana’s year of birth = MCMXCIV = 1000 + 900 + 90 + 4 = 1994

Yana is born earlier so she is older than Sana.

Difference between the ages = 2012 – 1994 = 18 years

Thus, Yana is older than Sana by 18 years.

Do It Yourself 1D

1. a. i. Digit at ones place = 6 (> 5)

Hence, 40,536 will be rounded off to 40,540.

ii. Digit at ones place = 7 (> 5)

Hence, 94,267 will be rounded off to 94,270.

iii. Digit at ones place = 5 (= 5)

Hence, 2,54,765 will be rounded off to 2,54,770.

iv. Digit at ones place = 2 (> 5)

Hence, 20,45,542 will be rounded off to 20,45,540.

b. i. Digit at tens place = 5 (= 5) Hence, 8,09,757 will be rounded off to 8,09,800.

ii. Digit at tens place = 9 (> 5) Hence, 23,98,790 will be rounded off to 23,98,800.

iii. Digit at tens place = 2 (< 5)

Hence, 3,80,08,023 will be rounded off to 3,80,08,000.

iv. Digit at tens place = 4 (< 5) Hence, 89,74,53,542 will be rounded off to 89,74,53,500.

c. i. Digit at hundreds place = 7 (> 5)

Hence, 4,89,779 will be rounded off to 4,90,000.

ii. Digit at hundreds place = 4 (< 5) Hence, 31,41,457 will be rounded off to 31,41,000.

iii. Digit at hundreds place = 0 (< 5) Hence, 1,03,09,095 will be rounded off to 1,03,09,000.

iv. Digit at hundreds place = 6 (> 5) Hence, 30,47,57,698 will be rounded off to 30,47,58,000.

2. All the numbers between 4250 and 4349 can be rounded off to the nearest hundred as 4300.

3. Greatest number that can be rounded off to the nearest thousand to give 7000 = 7499

Smallest number than can be rounded off to the nearest thousand to give 7000 = 6500

4. a. 4356 rounded off to the nearest 100 = 4400 9120 rounded off to the nearest 100 = 9100 Estimated sum: 4400 + 9100 = 13,500

TTh Th H T O

4 4 0 0

+ 9 1 0 0

1 3 5 0 0

b. 89,174 rounded off to the nearest 100 = 89,200 23,589 rounded off to the nearest 100 = 23,600

Estimated sum: 89,200 + 23,600 = 1,12,800

L TTh Th H T O

8 9 2 0 0

+ 2 3 6 0 0

1 1 2 8 0 0

c. 8900 rounded off to the nearest 100 = 8900 5220 rounded off to the nearest 100 = 5200

Estimated difference: 8900 – 5200 = 3700

Th H T O

8 9 0 0

– 5 2 0 0

3 7 0 0

d. 79,174 rounded off to the nearest 100 = 79,200 23,543 rounded off to the nearest 100 = 23,500

Estimated difference: 79,200 – 23,500 = 55,700

TTh Th H T O

8 12

7 9 2 0 0 –

2 3 5 0 0

5 5 7 0 0

e. 215 rounded off to the nearest hundreds = 200 956 rounded off to the nearest hundreds = 1000

Estimated product: 200 × 1000 = 2,00,000

f. 6786 rounded off to the nearest 100 = 6800

9123 rounded off to the nearest 100 = 9100

Estimated product: 6800 × 9100 = 6,18,80,000

C TL L TTh Th H T O

6 1 8 8 0 0 0 0

g. 715 rounded off to the nearest 100 = 700 115 rounded off to the nearest 100 = 100

700 ÷ 100 = 700 100 = 7

Hence, the estimated quotient is 7.

h. 4356 rounded off to the nearest 100 = 4400 1025 rounded off to the nearest 100 = 1000

4400 ÷ 1000 = 4400 1000 = 4

Hence, the estimated quotient is 4.4.

Cost of suit = ₹3659

Cost of suit rounded off to the nearest thousand = ₹4000

Cost of saree = ₹6342

Cost of suit rounded off to the nearest thousand = ₹6000

Total money paid rounded off to nearest thousand = ₹12,000

Total cost of suit and saree = ₹6000 + ₹4000 = ₹10,000

Cost of a bedsheet = Total money paid by Rita – Total cost of the suit and saree = ₹12,000 – ₹10,000 = ₹2000

Thus, Reeti paid about ₹2000 for the bedsheet.

6. Number of apple trees in the orchard = 8869

8869 rounded off to the nearest thousand = 9000

Number of rows in the orchard = 303

303 rounded off to the nearest hundred = 300

Number of rows = 9000 ÷ 300

There are approximately 30 rows in the orchard.

7. Cost of calculators = ₹595

₹595 rounded off to the nearest hundred = ₹600

Number of calculators bought = 45

45 rounded off to the nearest tens = 50

Estimated cost of calculators = ₹600 × 50 = ₹30,000

Challenge

1. New number = 415276

415276 rounded off to the nearest tens = 415280

465271 rounded off to the nearest hundreds = 465300

Required difference = 465300 – 415280 = 50020

2 10 4 6 5 3 0 0 – 4 1 5 2 8 0

0 5 0 0 2 0

2. Number estimated to the nearest 10 = 5,67,790

Smallest possible number that can be rounded off to 5,67,790 = 5,67,785

Greatest possible number that can be rounded off to 5,67,790 = 5,67,794

c. 1 1 1 1 1 4 3 7 5 4 8 2 3 4 5 + 7 6 5 6 7 5 1 2 0 5 5 6 8

3. a. 402 – 118 + 180 ÷ 45 × 162 = 402 − 118 + 4 × 162 = 402 − 118 + 648 = 1050 – 118 = 932

b. 168 ÷ 14 × 22 – 210 + 185 = 12 × 22 − 210 + 185 = 264 − 210 + 185 = 449 − 210 = 239

c. 15 × 35 ÷ 3 7 + 20 = 525 ÷ 3 7 + 20 = 525 × 7 3 + 20 = 175 × 7 + 20 = 1245

d. 35 ÷ 5 × 9 + 7 × 30 ÷ 3 = 7 × 9 + 7 × 10

= 63 + 70 = 133

e. 250 + [24 – {4 × 3 + (8 – 5)}] = 250 + [24 – {4 × 3 + 3}] = 250 + [24 – {12 + 3}]

= 250 + [24 – 15]

= 250 + 9

= 259

f. (70 − 42) ÷ 14 + 15 × 3 – 7 × 5

= 28 ÷ 14 + 15 × 3 – 7 × 5

= 2 + 45 – 35 = 47 – 35 = 12

4. 14 12 13 15 14

8 4 2 3 5 4 17

9 5 3 4 6 5 7 – 4 6 9 8 7 9 9

4 8 3 5 8 5 8

5 0 3 9 7 8 2

Hence, 48,35,858, when added to 46,98,799, gives 95,34,657.

9. Distance between Mercury and Earth = 9,63,77,000 km

Distance between Earth and Jupiter = 6,56,96,000 km

Distance between Mercury and Jupiter = Distance between Mercury and Earth + Distance between Earth and Jupiter = 9,63,77,000 km + 6,56,96,000 km = 16,20,73,000 km 1 1 1 1 9 6 3 7 7 0 0 0 + 6 5 6 9 6 0 0 0 1 6 2 0 7 3 0 0 0

10. Amount of water in the vessel = 8 L 650 mL = 8000 + 650 mL = 8650 mL (1 L = 1000 mL)

Capacity of one glass = 500 mL

Number of glasses that can be fully filled = Quotient of 8650 mL ÷ 500 ml = 17 glasses

11. Scholarship received per year = ₹3408

Number of years over which the scholarship was received = 5 years

Total scholarship received = ₹3408 × 5 = ₹17,040 3 4 0 8 × 5 1 7 0 4 0

12. Number of sets of gloves = 78

Total number of gloves = 546

Total number of gloves in each set = 546 ÷ 78 = 7

Thus, there are 7 gloves in each set.

13. Number of sets bought by Megha = 8 sets

Number of flowers in each set = 5

Total number of flowers = 8 × 5 = 40

Number of sets bought by Megha = 12

Total number of flowers = 12 × 5 = 60

Total number of flowers bought by Megha = 40 + 60 = 100

7. Quotient = 9,04,35,460

Other number = 1,80,87,09,200

8. Distance travelled by Ajay = 18 km 685 m = 18,000 m + 685 m = 18,685 m (1 km = 1000 m)

Ajay travels twice the distance in a day = 2 × 18,685 m = 37,370 m

TTh Th H T O

1 1 1 1

1 8 6 8 5 × 2 3 7 3 7 0

Distance travelled in 5 days = 37,370 × 5 = 1,86,850 m

So, Ajay travels a distance of 1,86,850 m in 5 days.

Thus, Megha bought 100 carnations.

14 Answer may vary. Sample answer:

The number of men in a town is 2,13,765 and number of women is 3,98,761. How many more women than men are there in the town?

Challenge

1. The pattern is decrease by 1000 and then increase by 500 and repeat.

4,02,304, decrease the number by 1000

4,01,804, decrease the number by 1000

2. a. (6 + 5) × 3 – 1 = 32

b. 3 + {4 × (8 – 4)} = 19

c. 10 × (8 – 4) + 1 + 5 = 46

Chapter Checkup

1. a. 350427681

Indian system: 35,04,27,681 = Thirty-five crore four lakh twenty-seven thousand six hundred eighty-one

Expanded form = 30,00,00,000 + 5,00,00,000 + 4,00,000 + 20,000 + 7000 + 600 + 80 + 1

International system: 350,427,681 = Three hundred fifty million four hundred twenty-seven thousand six hundred eighty-one

Expanded form = 300,000,000 + 50,000,000 + 400,000 + 20,000 + 7000 + 600 + 80 + 1

b. 420879502

Indian system: 42,08,79,502 = Forty-two crore eight lakh

seventy-nine thousand five hundred two

Expanded form = 40,00,00,000 + 2,00,00,000 + 8,00,000 + 70,000 + 9000 + 500 + 2

International system: 420,879,502 = four hundred twenty million eight hundred seventy-nine thousand five hundred two

Expanded form = 400,000,000 + 20,000,000 + 800,000 + 70,000 + 9000 + 500 + 2

c. 635658421

Indian system: 63,56,58,421 = Sixty-three crore fifty-six lakh fifty-eight thousand four hundred twenty-one

Expanded form = 60,00,00,000 + 3,00,00,000 + 50,00,000 + 6,00,000 + 50,000 + 8000 + 400 + 20 + 1

International system: 635,658,421 = Six hundred thirty-five million six hundred fifty-eight thousand four hundred twenty-one

Expanded form = 600,000,000 + 30,000,000 + 5,000,000 + 600,000 + 50,000 + 8000 + 400 + 20 + 1

d. 901500084

Indian system: 90,15,00,084 = Ninety crore fifteen lakh eighty-four

Expanded form = 90,00,00,000 + 10,00,000 + 5,00,000 + 80 + 4

International system: 901,500,084 = Nine hundred one million five hundred thousand eighty-four

Expanded form = 900,000,000 + 1,000,000 + 500,000 + 80 + 4

2. a. Four hundred sixty million seven hundred twenty-two thousand two hundred thirty-nine = 460,722,239

b. Sixty-three crore twelve lakhs fifty-eight thousand one hundred forty-three = 63,12,58,143

c. Eighty crore nine lakh fifty thousand sixty-two = 80,09,50,062

d. One hundred million one hundred thousand thirty-nine = 100,100,039

3. a. Since the digit in hundred million place is the same, compare the digits in ten millions place, 5 > 4

So, 656,502,567 > 648,900,650

b. The numbers are equal So, 314,572,879 > 314,527,879

c. The digits in hundred millions, ten millions, millions and hundred thousands place are same, so compare the digits in thousands place 0 < 8 So, 900,760,518 < 900,768,757

d. The digits are same in both the numbers So, 113,005,885 = 113,005,885

4. a. Compare the digits in ten crores place, 1 < 6 < 7

The digits in ten crores place in 67,23,56,475 and 68,91,63,896 is same, compare the digits in crores place, 7 < 8

So, 19,08,04,365 < 67,23,56,475 < 68,91,63,896 < 76,90,87,687

b. Compare the digits in hundred millions place, 3 < 4 < 6

The digits in hundred millions, ten million, millions place of 676,162,895 and 676,817,980 are same. Compare digits at hundred thousands 1 < 8

So, 324,335,678 < 435,406,576 < 676,162,895 < 676,817,980

c. Compare the digits in ten crores place, 6 < 8 < 9

The digits in ten crores place in 65,45,12,845 and 65,78,15,325 is same, compare the digits in ten lakhs place, 4 < 7

So, 65,45,12,845 < 65,78,15,325 < 87,12,63,256 < 97,12,36,125

5. a. 635 = 600 + 30 + 5 = DC + XXX + V = DCXXXV

b. 2015 = 2000 + 10 + 5 = MM + X + V = MMXV

c. 2087 = 2000 + 80 + 7 = MM + LXXX + VII = MMLXXXVII

d. 2750 = 2000 + 700 + 50 = MM + DCC + L = MMDCCL

6. a. CCXVII = CC + XVII = (100 + 100 + 100) + (10 + 7) = 300 + 17 = 317

b. MCDIX = M + CD + IX = 1000 + (500 – 100) + (10 – 1) = 1000 + 400 + 9 = 1409

c. DCCXCVII = DCC + XC + VII = (500 + 100 + 100) + (100 –10) + (5 + 1 + 1) = 700 + 90 + 7 = 797

d. CCXVIII = CC + X + VIII = (100 + 100) + 10 + (5 + 1 + 1 + 1)

= 200 + 10 + 8 = 218

7. Ten 7,65,380 65,410 57,67,880

Hundred 2,34,600 43,300 1,23,35,000

Thousand 9,03,000 83,000 47,70,000

8. a. [72 – 36 ÷ 6 of 2] + (30 – 22) + 5

= [72 – 6 × 2] + 8 + 5

= 60 + 8 + 5 = 68 + 5 = 73

b. 9 [8{12 – 7 + 5}] of 8

= 9 [8{17 – 7}] × 8

= 9 [8 × 10] × 8

= 9 × 80 × 8 = 5760

c. 888 × [370 ÷ {65 + (18 ÷ 2)}]

= 888 × [370 ÷ {65 + 9}]

= 888 × [370 ÷ 74]

= 888 × 5 = 4440

d. 60 + 13 – {(5 × 1/2 of 10) – 75 ÷ (17 – 2)}

= 73 – {(5 × 1/2 × 10) – 75 ÷ 15}

= 73 – {(5 × 5) – 5}

= 73 – {25 – 5}

= 73 – 20 = 53

9. a. TL L TTh Th H T O 1 1 1 1 1 9 8 7 6 5 4 + 8 2 3 9 0 1 2 8 1 1 5 5 5

b. TL L TTh Th H T O 1 10 9 8 7 4 3 2 0 – 4 3 7 1 0 0 1 5 5 0 3 3 1 9

c. TC C TL L TTh Th H T O 5 1 3 2 4

e. 67,589 – 23,543 + 13,678 = 57,724

1 1 1 1 6 7 5 8 9

1 3 6 7 8 8 1 2 6 7

f. 90,800 + 32,552 – 45,765 = 77,587

10. 444,777,888

International number system: 444,777,888 = Four hundred forty-four million seven hundred seventy-seven thousand eight hundred eighty-eight

Indian number system: 44,47,77,888 = Forty-four crore forty-seven lakh seventy-seven thousand eight hundred eighty-eight

11. 750635389

Indian number system: 75,06,35,389 = Seventy-five crore six lakh thirty-five thousand three hundred eighty-nine

International number system: 750,635,389 = Seven hundred fifty million six hundred thirty-five thousand three hundred eighty-nine

12. Number of books sold each month = 76,578

Number of books sold each month rounded off to the nearest thousand = 77,000

Number of months in a year = 12

Estimated number of books sold each year = 76,578 × 12 = 9,24,000

13. Toys manufactured on Monday = 7,65,875

7,65,875 rounded off to the nearest thousand = 7,66,000

Toys manufactured on Tuesday = 4,36,586 4,36,586 rounded off to the nearest thousand = 4,37,000

Estimated number of more toys manufactured on Monday = 7,66,000 – 4,37,000 = 3,29,000

5 16

7 6 6 0 0

14. Answers may vary. Sample answers: (30 + 3) × 3 – 6 ÷ 3 + 3 = 100 (20 + 5) × 3 – 25 ÷ 5 + 5 × 6 = 100

15. Greatest 9-digit number: 98,65,43,210, smallest 9-digit number: 10,23,45,689

Greatest 9-digit number (except 0): 99,86,54,321, smallest 9-digit number (except 0): 11,23,45,689

Ascending order: 10,23,45,689 < 11,23,45,689 < 98,65,43,210 < 99,86,54,321

Descending order: 99,86,54,321 > 98,65,43,210 > 11,23,45,689 >10,23,45,689

16. Total number of ships = 35

Capacity of each ship = 27,850 tons

Number of ships in fleet A = 9 ships

Number of ships in fleet B = 12 ships

Number of ships in fleet C = 35 – (9 + 12) = 35 – 21 = 14

a. Cargo capacity of fleet A and fleet B combined = (9 + 12) × 27,850 tonnes = 5,84,850 tonnes

2 7 8 5 0 × 2 1 + 2 7 8 5 0

+ 5 5 7 0 0 5 8 4 8 5 0

b. Capacity of fleet C = 14 × 27,850 tonnes = 3,89,900 tonnes

2 7 8 5 0

× 1 4

+ 1 1 1 4 0 0

+ 2 7 8 5 0

3 8 9 9 0 0

c. Total cargo capacity of all the three fleets = 5,84,850 tonnes + 3,89,900 tonnes = 9,74,750 tonnes

L TTh Th H T O

Challenge

1. Place value of 5 in the crores place = 5,00,00,000 = 5 × 1,00,00,000 = 1,00,00,000 times 5

Place value of 5 in the hundreds place = 500 = 5 × 100 = 100 times 5

1,00,00,000 is 1,00,000 times 100.

So, the place value of 5 in 5,00,00,000 is 1,00,000 times more than 500.

2. Assertion (A): The number 6468 rounded off to the nearest hundred is 6500.

Reason (R): To round off a number, if the digit at the tens place is 5 or more, then the number is rounded off to the nearest 100 by increasing the hundreds digit by 1 and replacing each digit on its right by 0.

The number 6468 rounded off to the nearest hundred is 6500. The digits in tens place is 6, which is greater than 5, so the number is rounded off to 6500.

So, the assertion is true.

The given reason is true and explains how 6468 is rounded off to 6500.

So, A is true and R is the correct explanation of A.

Thus, option c is correct.

Case Study

1. Quantity of grapes produced in Italy = 84,37,970 94,37,970 rounded off to the nearest thousand is 84,38,000.

2. a. True

Total quantity of grapes produced in India = 34,01,000 34,01,000 rounded off to the nearest ten thousands = 34,00,000

Total quantity of grapes produced in Chile = 24,02,686 24,02,686 rounded off to the nearest ten thousands = 24,00,000

Total quantity produced = 34,00,000 + 24,00,000 = 58,00,000

b. False

Total quantity of grapes produced in Turkey = 41,65,000 41,65,000 rounded off to nearest ten thousands = 41,60,000

Total quantity of grapes produced in France = 61,99,950 61,99,950 rounded off to the nearest ten thousands = 62,00,000

Difference = 62,00,000 − 41,60,000 = 20,40,000

L TTh Th H T O

3. 65,67,686 tonnes is produced by Turkey and Chile together.

TL L TTh Th H T O

4 1 6 5 0 0 0 + 2 4 0 2 6 8 6 6 5 6 7 6 8 6

4. France has produced 27,98,950 tonnes more than India.

TL L TTh Th H T O

6 1 9 9 9 5 0 –

3 4 0 1 0 0 0

2 7 9 8 9 5 0

5. Quantity of grapes produced in Turkey = 4,165,000 Number name in international number system = four-million one-hundred sixty-five thousand

Chapter 2

Let’s Warm-up

1. By 3

2. By 4

3. By 5

4. By 6

1. 13,214

13,214 + 1 = 13,215

13,215 + 1 = 13,216 13,216 + 1 = 13,217 13,217 + 1 = 13,218 13,218 + 1 = 13,219

2. a. Predecessor = 66,778 − 1 = 66,777

Successor = 66,778 + 1 = 66,779

b. Predecessor = 54,557 − 1 = 54,556

Successor = 54,557 + 1 = 54,558

c. Predecessor = 86,457 − 1 = 86,456

Successor = 86,457 + 1 = 86,458

d. Predecessor = 89,665 − 1 = 89,664

Successor = 89,665 + 1 = 89,666

e. Predecessor = 97,564 − 1 = 97,563

Successor = 97,564 + 1 = 97,565

3. Area of New Delhi = 1484 sq. km

Predecessor of 1484 = 1484 − 1 = 1483

Successor of 1484 = 1484 + 1 = 1485

4. a. 452 × 0 = 0

Multiplicative property of zero.

b. 6567 × 1 = 6567

Existence of multiplicative identity.

c. (4 × 7) × 10 = 4 × (7 × 10)

Associative property of multiplication.

d. 785 × 45 = 785 × (50 5)

Distributive property of multiplication.

e. 14 × (10 + 12) = (14 × 10) + (14 × 12)

Distributive property of multiplication.

f. 9875 ÷ 1 = 9875

Division by 1, the quotient is the whole number itself.

g. 0 ÷ 789 = 0

Zero divided by a whole number, so the quotient is 0.

h. 448 × (224 + 28) = (448 × 224) + (448 × 28)

Distributive property of multiplication over addition.

i. 999 + (45 ÷ 45) = 999 + 1 = 1000

A number divided by the same number, so the quotient is 1.

j. (14,500 ÷ 50) − (99 ÷ 3) = 257

14,500 ÷ 50 = 290

99 ÷ 3 = 33

290 − 33 = 257

5. a. On the given number line: 0 + 10 = 10; 10 + 10 = 20; 20 + 10 = 30 and so on,

So, 40 + 10 = 50; 60 + 10 = 70; 80 + 10 = 90

0 60 10 20 30 50 70 90 80 40 100

b. On the given number line: 0 + 25 = 25; 25 + 25 = 50; 50 + 25 = 75 and so on,

So, 75 + 25 = 100; 125 + 25 = 150; 175 + 25 = 200; 200 + 25 = 225; 225 + 25 = 250

6. a. 20 + 10 + 10 + 10 + 10 = 60

b. 18 − 3 − 3 − 3 − 3 − 3 = 3

7. a.

15 + 7 = 22

14 − 9 = 5

7 + 5 = 12

0 11 1 12 2 3

18 ÷ 3 = 6

2 × 5 =10

f. 0

20 ÷ 5 = 4

8. a. 41 ÷ 41 = x x = 1

b. 0 ÷ y = 0

y can be any non-zero whole number (e.g., y = 1)

c. (36 − 25) ÷ p = 11 (36 − 25) = 11

So, 11 ÷ p = 11 p = 1

d. (144 ÷ 12) × r = 12

144 ÷ 12 = 12

So, 12 × r = 12 r = 1

9. Total surface area of the Earth = 510 million square km

Area covered by water = 357 million square km

So, area covered by land 510 − 357 = (510 − 350) − 7 = 160 − 7 = 153 million square km

Thus, the total area covered by land is 153 million square km.

10. a.

0 11

15 − 7 = 8

So, 8 cookies were not burnt. 12. 0

Total amount =

13. The smallest whole number is 0.

Whole numbers between 67 and 75 = 68, 69, 70, 71, 72, 73, 74 = 7

Hence, there are 7 whole numbers between 67 and 75.

Challenge

1. The largest six-digit number is 9,99,999. The successor of 9,99,999 is 10,00,000. The predecessor of 9,99,999 is 9,99,998.

The product of the successor and predecessor = 10,00,000 × 9,99,998 = 9,99,99,80,00,000

Therefore, the product of the successor and predecessor of the largest two-digit number is 9,99,99,80,00,000.

2. Answers may vary. Sample answer: Divisor = 5

Let the quotient = 1, and the remainder = 1

The whole number is 6. 5 6 1 − 5 1

Do It Yourself 2B

1. Number of circles in the first figure = 4

Number of circles in the second figure = 8

Number of circles in the third figure = 12

So, 4 circles are increasing each time in the pattern. Number of circles in the next figure = 12 + 4 = 16

2. a. 5 + 2 = 7

7 + 5 = 12

12 + 2 = 14

14 + 5 = 19

19 + 2 = 21

21 + 5 = 26

5 ,7, 12, 14, 19, 21, 26

b. 2 × 3 = 6

3 × 6 = 18

6 × 18 = 108

18 × 108 = 1944

2, 3, 6, 18, 108, 1944

c. 1 × 1 × 1 = 1

2 × 2 × 2 = 8

3 × 3 × 3 = 27

4 × 4 × 4 = 64

5 × 5 × 5 = 125

1, 8, 27, 64, 125

3. We will add 2 rectangles. 4. 1 × 1 = 1 11 × 11 = 121

111 × 111 = 12321

1111 × 1111 = 1234321

11111 × 11111 = 123454321

5. 1 × 11 + 1 = 12 1 × 12 + 1 = 13 1 × 13 + 1 = 14 2 × 8 + 1 = 17 2 × 10 + 1 = 21 2 × 12 + 1 = 25 12 × 11 + 2 = 134 12 × 12 + 2 = 146 12 × 13 + 2 = 158 123 × 11 + 3 = 1356 123 × 12 + 3 = 1479 123 × 13 + 3 = 1602

6. Amount Aman gets for:

1 task = ₹99 3 tasks = ₹999

5 tasks = ₹9999 7 tasks = ₹99,999

9 tasks = ₹9,99,999 11 tasks = ₹99,99,999

13 tasks = ₹9,99,99,999

So, Aman gets ₹9,99,99,999 for 13 tasks.

7. The first shape has 6 rectangles; the next shape has 11 rectangles and the next shape has 16 rectangles.

So, the rule followed by the pattern is to add 5 rectangles every time.

The third shape has 16 rectangles.

The fourth shape will have, 16 + 5 = 21 rectangles

The fifth shape will have, 21 + 5 = 26 rectangles

So, the fifth shape will have 26 rectangles.

8. a. 45 × 9 = 45 × (10 − 1) = 45 × 10 − 45 × 1 = 450 − 45 = 405

b. 45 × 99 = 45 × (100 − 1) = 45 × 100 − 45 × 1 = 4500 − 45 = 4455

c. 45 × 999 = 45 × (1000 − 1) = 45 × 1000 − 45 × 1 = 45,000 − 45 = 44955

d. 45 × 9999 = 45 × (10000 − 1) = 45 × 10000 − 45 × 1 = 4,50,000 − 45 = 449955

So, the pattern is: 405, 4455, 44955, 449955, 4499955, 44999955, ...

9. Given the sequence: 1, 1, 2, 3, 5, 8

The next number in the sequence will be 5 + 8 = 13

Following that, the next number will be 13 + 8 = 21

So, the Fibonacci series are: 1, 1, 2, 3, 5, 8, 13, 21

10. Answer may vary. Sample answer:

Challenge

1. Number of students in a line = 7

Number of pencils with:

1st student = 1 2nd student = 2 × 1 = 2

3rd student = 2 × 2 = 4 4th student = 2 × 4 = 8

5th student = 2 × 8 = 16 6th student = 2 × 16 = 32

7th student = 2 × 32 = 64

So, the 7th student has 64 pencils.

Chapter Checkup

1. a. Predecessor: 1,54,698 − 1 = 1,54,697

Successor: 1,54,698 + 1 = 1,54,699

b. Predecessor: 2,54,895 − 1 = 2,54,894

Successor: 2,54,895 + 1= 2,54,896

c. Predecessor: 5,45,977 − 1 = 5,45,976

Successor: 5,45,977 + 1 = 5,45,978

d. Predecessor: 6,45,712 − 1 = 6,45,711

Successor: 6,45,712 + 1 = 6,45,713

5. The first shape has 6 dots, the second shape has 9 dots and the third shape has 12 dots.

6, 6 + 3 = 9, 9 + 3 = 12

So, the rule is to add 3 more dots in the next shape in the sequence.

The fourth shape in the pattern will have 12 + 3 = 15 dots

6. The first shape has 5 + 3 + 1 = 9 dots

The second shape has 7 + 5 + 3 + 1 = 16 dots

The third shape has 9 + 7 + 5 + 3 + 1 = 25 dots

The fourth shape will have 11 + 9 + 7 + 5 + 3 + 1 = 36 dots

The fifth shape will have 13 + 11 + 9 + 7 + 5 + 3 + 1 = 49 dots

So, the fifth shape will have 49 dots.

7. Answer may vary. Sample answer:

8. Number of languages in India = 780

Number of languages in Papua New Guinea = 840

Difference = 840 − 740 = 60

Thus, there are 60 more languages in Papua New Guinea than in India.

9. Number of gifts collected = 1245 gifts

Number of gifts added = 999 gifts

Total number of gifts = 1245 gifts + 999 gifts = 1245 + 1000 − 1 = 2245 − 1 = 2244 gifts. So, the total number of gifts is 2244.

10. Budget for the event = ₹82,360

Amount spent on:

Decorations = ₹15,500

Music = ₹10,000

Refreshments = ₹6500

Total money left = ₹15,500 + ₹10,000 + ₹6500 = ₹32,000

Money left after the expenses = ₹82,360 − ₹32,000 = ₹50,360

So, ₹50,360 is left after the expenses.

11. Divisor = 65; Quotient = 9; Remainder = 5

(Divisor × Quotient) + Remainder = Dividend

(65 × 9) + 5 = 585 + 5 = 590

Dividend = 590

Property: Multiplication by 9

12. Number of English books = 45

Cost of each English book = ₹100

Total cost of the English books = ₹100 × 45

Number of Hindi books = 45

Cost of each Hindi book = ₹75

Total cost of the books = ₹75 × 45

Total cost = ₹[100 × 45 + 75 × 45] = ₹(100 + 75) × 45 = ₹175 × 45 = ₹7875

So, the total amount the librarian has to pay is ₹7875.

13. Number of chairs = 96

Cost of each chair = ₹200

Total cost of the chairs = ₹200 × 96 = ₹19,200

Number of tables = 48

Cost of each table = ₹150

Total cost of the tables = ₹150 × 48 = ₹7200

Total cost = ₹19,200 + ₹7200 = ₹26,400

Amount given in advance = ₹3500

Amount to be given = ₹26,400 − ₹3500 = ₹22,900

So, the amount given is ₹22,900.

14. a. 550 × 45 − 550 × 15 = 550 × (45 − 15) = 550 × 30 = 16,500

b. 865 × 12 + 865 × 45 = 865 × (12 + 45) = 865 × 57 = 49,305

c. 420 × 36 − 420 × 23 = 420 × (36 − 23) = 420 × 13 = 5460

d. 630 × 25 − 630 × 15 = 630 × (25 − 12) = 630 × 10 = 6300

15. Length of the playground = 324 m

Width of the playground = 220 m

Perimeter = 2 × (length + width)

= 2 × (324 + 220)

= 2 × 324 + 2 × 220

= 648 + 440 = 1088 m

Distance Vicky covers going 4 times around it = 4 × 1088 m = 4352 m

So, Vicky will cover 4352 m. The distributive property was used in calculating the perimeter.

Challenge

1. Assertion (A): The sum of 100, 150 and 100 is 15,00,000. Reason (R): If a, b and c are three whole numbers then, (a + b) + c = a + (b + c).

The sum of 100 + 150 + 100 = 350. So, the assertion is false. (100 + 150) + 100 = 100 + (150 + 100) = 350. So, the reason is true.

Since the assertion is false and the reason is true, option d is correct.

Hence, the answer is option d.

2. The first figure has 1 dot. In the second term, 4 more dots are added. In the third term, 7 more dots are added.

The pattern is 1, 1 + 4, 1 + 4 + 7, 1 + 4 + 7 + 10

The rule is to add 3 to the previous term. So, the fifth term will have 1 + 4 + 7 + 10 + 13

Case Study

1. Triangle and circle.

2. The first figure of the pattern has 2 triangles and 1 circle.

Hence, option c is correct.

3. The pattern is one man, one woman, one man, one woman, ... So, the rule is to repeat man and woman alternatively.

4. The next term will have 1 man and 1 woman.

5. Answer may vary. Sample answer:

Chapter 3

Let’s Warm-up

Answers may vary. Sample answers:

1. 10: 2, 5

2. 15: 3, 5

3. 17: 1, 17

4. 20: 4, 5

5. 32: 4, 8

Do It Yourself 3A

1. a. 20

1 × 20 = 20

2 × 10 = 20

4 × 5 = 20

5 × 4 = 20 (We stop here as 5 and 4 are already covered.)

So, the factors of 20 are 1, 2, 4, 5, 10 and 20.

b. 26

1 × 26 = 26

2 × 13 = 26

So, the factors of 26 are 1, 2, 13 and 26.

c. 36

1 × 36 = 36

2 × 18 = 36

3 × 12 = 36

4 × 9 = 36

6 × 6 = 36

9 × 4 = 36 (We stop here as 9 and 4 are already covered.)

So, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36.

a. 37 × 1 = 37

37 × 2 = 74

37 × 3 = 111

37 × 4 = 148

37 × 5 = 185

37 × 6 = 222

So, the first six multiples of 37 are 37, 74, 111, 148, 185 and 222.

c. 84 × 1 = 84

84 × 2 = 168

84 × 3 = 252

84 × 4 = 336

84 × 5 = 420

84 × 6 = 504

So, the first six multiples of 84 are 84, 168, 252, 336, 420 and 504.

d. 88

1 × 88 = 88

2 × 44 = 88

4 × 22 = 88

8 × 11 = 88

11 × 8 = 88 (We stop here as 11 and 8 are already covered.)

So, the factors of 88 are 1, 2, 4, 8, 11, 22, 44 and 88.

b. 62 × 1 = 62

62 × 2 = 124

62 × 3 = 186

62 × 4 = 248

62 × 5 = 310

62 × 6 = 372

So, the first six multiples of 62 are 62, 124, 186, 248, 310 and 372.

d. 99

99 × 1 = 99

99 × 2 = 198

99 × 3 = 297

99 × 4 = 396

99 × 5 = 495

99 × 6 = 594

So, the first six multiples of 99 are 99, 198, 297, 396, 495 and 594.

3. The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.

Clearly, 2 and 12 are the required numbers as their sum is 14 and the product is 24.

4. The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72.

Clearly, 9 and 8 are the required numbers as their difference is 1 and the product is 72.

5. a.

Challenge

1. Amount with Raj = ₹100

Factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, 100

So, 2 is a factor of 100.

So, Raj can have 100 rupees, all in 2-rupee coins.

Amount with Roy = ₹67

Factors of 67 are 1 and 67

So, 5 is not a factor of 67.

So, Roy cannot have 67 rupees, all in 5-rupee coins.

Thus, Roy’s claim is wrong, as 67 is not a multiple of 5.

Do It Yourself 3B

1. Even numbers end with 0, 2, 4, 6 or 8.

Odd numbers end with 1, 3, 5, 7 or 9.

a. 42 – E

b. 57 – O

c. 64 – E

d. 89 – O

2. a. Factors of 57 = 1, 3, 19, 57

Sum of factors (excluding itself) = 1 + 3 + 19 = 23

Since 57 does not meet the criterion (23 ≠ 57), it is not considered a perfect number.

b. Factors of 63 = 1, 3, 7, 9, 21, 63

Sum of factors (excluding itself) = 1 + 3 + 7 + 9 + 21 = 41

Since 63 does not meet the criterion (41 ≠ 63), it is not considered a perfect number.

c. Factors of 28 = 1, 2, 4, 7, 14

Sum of factors (excluding itself) = 1 + 2 + 4 + 7 + 14 = 28

Since 28 meet the criterion (28 = 28), it is considered a perfect number.

d. Factors of 83 = 1, 83

Sum of factors (excluding itself) = 1

Since 83 does not meet the criterion (1 ≠ 83), it is not considered a perfect number.

3. a. 25 is an even number. False

b. 17 is a prime number. True

c. 6 is a composite number. True

d. 13 and 17 are twin prime numbers. False

4. a. The prime numbers between 40 and 50 are 41, 43 and 47.

Co-prime numbers sample answer: 41 and 43

b. The prime numbers between 60 and 70 are 61 and 67.

Co-prime numbers sample answer: 61 and 67

c. 11, 13, 17, 19, 23 and 29 are prime numbers between 10 and 30.

Co-prime numbers sample answer: 11 and 13

d. 2, 3, 5 and 7 are prime numbers between 0 and 10.

Co-prime numbers sample answer: 2 and 3

5. Prime numbers between 60 and 90 are 61, 67, 71, 73, 79, 83 and 89.

From the list of prime numbers, we can say only one twin prime pair exists between 60 and 90, that is (71, 73).

6. A number is divisible by 2 if the digit at the ones place of the number is 0, 2, 4, 6 or 8.

So, the numbers 990, 2484, 41,870 and 9,12,048 are divisible by 2.

A number is divisible by 3 if the sum of its digits is divisible by 3. Let us calculate the sums:

For 990: 9 + 9 + 0 = 18 (divisible by 3)

For 2484: 2 + 4 + 8 + 4 = 18 (divisible by 3)

For 41,870: 4 + 1 + 8 + 7 + 0 = 20 (not divisible by 3)

For 9,12,048: 9 + 1 + 2 + 0 + 4 + 8 = 24 (divisible by 3)

So, the numbers 990, 2484 and 9,12,048 are divisible by 3.

A number is divisible by 4 if its last two digits form a number that is divisible by 4.

For 990: The last two digits are 90, which is not divisible by 4. For 2484: The last two digits are 84, which is divisible by 4.

Therefore, the number 2484 is divisible by 4.

For 41,870: The last two digits are 70, which is not divisible by 4.

For 9,12,048: The last two digits are 48, which is divisible by 4.

Therefore, the number 9,12,048 is divisible by 4.

So, the numbers 2484 and 9,12,048 are divisible by 4.

A number is divisible by 5 if the digit at the ones place of the number is 0 or 5.

So, the numbers 990 and 41,870 are divisible by 5.

A number is divisible by 6 if the number is divisible by both 2 and 3.

We already found that 990, 2484 and 9,12,048 are divisible by both 2 and 3.

So, the numbers 990, 2484 and 9,12,048 are divisible by 6.

A number is divisible by 8 if its last three digits form a number that is divisible by 8.

For 990: The last three digits are 990, which is not divisible by 8. For 2484: The last three digits are 484, which is not divisible by 8.

For 41870: The last three digits are 870, which is not divisible by 8.

For 9,12,048: The last three digits are 048, which is divisible by 8.

So, only the number 912048 is divisible by 8.

A number is divisible by 9 if the sum of its digits is divisible by 9.

Let us calculate the sums:

For 990: 9 + 9 + 0 = 18 (divisible by 9)

For 2484: 2 + 4 + 8 + 4 = 18 (divisible by 9)

For 41,870: 4 + 1 + 8 + 7 + 0 = 20 (not divisible by 9)

For 9,12,048: 9 + 1 + 2 + 0 + 4 + 8 = 24 (not divisible by 9)

So, the numbers 990 and 2484 are divisible by 9.

A number is divisible by 10 if the digit at the ones place of the number is 0.

So, the numbers 990 and 41,870 are divisible by 10. 7. Answers may vary. Sample answers:

a. 14 is 7 times 2, so it is divisible only by 2 and not 6.

b. 6 times 8 is 48. So 48 is divisible by 6 and 8.

c. 9 times 11 is 99 which is divisible by both 9 and 11.

d. 9 is divisible by 3 and not 2. 8.

× 1 = 14

× 2 = 14 1 × 14 = 14

× 7 = 14

14 has more than 4 factors. So, 14 is a composite number.

9. Total number of students in the class = 36

Roll numbers up to 36 that are prime = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 and 31

Roll numbers up to 36 that are composite = 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35 and 36

Roll number 1 does not belong to either of the two groups. Number of students having roll numbers that are prime = 11 Number of students having roll numbers that are composite = 24

10. Answers may vary. Sample answer: Is 1331 divisible by 11?

11. No, 20 and 8 are not co-primes.

20 and 8 are not co-prime numbers because they share a common factor greater than 1, they both have 2 as a factor.

Challenge

1. Answers may vary. Sample answer:

Prime numbers: 2, 3, 5, 7, 9, 11, 17, 19, 23

To get sum as prime numbers, add 4 different prime numbers and check, 17 = 2 + 3 + 5 + 7 23 = 2 + 3 + 5 + 13

Do It Yourself 3C

2. a. 189 = 3 × 3 × 21 is not the correct prime factorisation of 189, as 21 can be further factorised as 3 × 7.

So, 189 = 3 × 3 × 3 × 7

b. 252 = 2 × 6 × 3 × 7 is not the correct prime factorisation of 252, as 6 can be further factorised as 2 × 3.

So, 2 × 2 × 3 × 3 × 7

3. 3 345

5 115 23 23 1

345 = 3 × 5 × 23

The prime factors of 345 in ascending order are 3, 5 and 23.

4. a. 210 2 105 35 7 3 5

b. 293 is a prime number.

210 = 2 × 3 × 5 × 7

c. 816 2 408 204 102 51 17 2 2 2 3

816 = 2 × 2 × 2 × 2 × 3 × 17

d. 952

2 476 238 119 17 2 2 7

952 = 2 × 2 × 2 × 7 × 17

5. 560 = 2 × 2 × 2 × 2 × 5 × 7

The prime factors of 560 in ascending order are 2, 5 and 7.

The product of the two smallest prime factors = 2 × 5 = 10

6. The smallest 5-digit number is 10,000.

10,000 = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5

2 10000 2 5000 2 2500 2 1250 5 625 5 125 5 25 5 5 1

7. For 56 samples

Prime factorisation of 56 = 2 × 2 × 2 × 7

Possible rectangular arrays = 1 × 56 or 56 × 1, 2 × 28 or 28 × 2, 4 × 14 or 14 × 4, 7 × 8 or 8 × 7 For 63 samples

Prime factorisation of 63 = 3 × 3 × 7

Possible rectangular arrays = 1 × 63 or 63 × 1, 3 × 21 or 21 × 3, 7 × 9 or 9 × 7

Since the samples are to be arranged into 4 rows, then the biologist can have 56 samples and not 63 samples as 56 can

be grouped into equal groups of 4 while 53 cannot be. Thus, the biologist should have 56 samples.

Challenge

1. The four smallest prime numbers are 2, 3, 5, 7

The product of 2, 3, 5, 7 = 2 × 3 × 5 × 7 = 210

210 is more than 100

Thus, 210 is the smallest number positive integer that can be expressed as the product of four distinct prime numbers and is greater than 100.

Do It Yourself 3D

1. a. i. The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.

The factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84.

Common factors of 48 and 84 are 1, 2, 3, 4, 6 and 12.

The largest common factor is 12.

So, the HCF of 48 and 84 is 12.

ii. The factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.

The factors of 45 are 1, 3, 5, 9, 15 and 45.

Common factors of 30 and 45 are 1, 3, 5 and 15.

The largest common factor is 15.

So, the HCF of 30 and 45 is 15.

iii. The factors of 18 are 1, 2, 3, 6, 9 and 18.

The factors of 27 are 1, 3, 9 and 27.

Common factors of 18 and 27 are 1, 3 and 9.

The largest common factor is 9.

So, the HCF of 18 and 27 is 9.

iv. The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36.

The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72.

The factors of 108 are 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54 and 108.

Common factors of 36, 72 and 108 are 1, 2, 3, 4, 6, 9, 12, 18 and 36.

The largest common factor is 36.

So, the HCF of 36, 72 and 108 is 36. b. i. 2 20

So, the HCF of 20 and 30 = 2 × 5 = 10 ii. 2 30 3 15 5 5 1 3 45 3 15 5 5 1

30 = 2 × 3 × 5 45 = 3 × 3 × 5

So, the HCF of 30 and 45 = 3 × 5 = 15 iii. 3 45 3 15 5 5 1 3 75 5 25 5 5 1

45 = 3 × 3 × 5 75 = 3 × 5 × 5

So, the HCF of 45 and 75 = 3 × 5 = 15

54 = 2 × 3 × 3 × 3 90 = 2 × 3 × 3 × 5 126 = 2 × 3 × 3 × 7

So, the HCF of 54, 90 and 126 = 2 × 3 × 3 = 18

c. i. 48 60 1 – 48 12 48 4 – 48 0

So, the HCF of 48 and 60 is 12.

ii. 63 105 1 – 63 42 63 1 – 42 21 42 2

So, the HCF of 63 and 105 is 21.

iii. 96 120 1 – 96 24 96 4 – 96 0 24 72 3 – 72 0

The HCF of 96 and 120 is 24.

So, the HCF of 72, 96 and 120 is 24.

iv. 65 132 2 – 130 2 65 32 – 64 1 2 2 – 2 0

So, the HCF of 65 and 132 is 1.

2. a. i. Multiples of 60 are 60, 120, 180, 240, 300, 360, …

Multiples of 20 are 20, 40, 60, 80, 100, 120, …

The common multiples of 60 and 20 are 60, 120, …

The least common multiple of 60 and 20 is 60.

So, the LCM of 60 and 20 is 60.

ii. Multiples of 15 are 15, 30, 45, 60, 75, 90, 105, 120, …

Multiples of 35 are 35, 70, 105, 140, 175, 210, …

The first common multiple of 15 and 35 is 105.

So, the LCM of 15 and 35 is 105.

iii. Multiples of 4 are 4, 8, 12, 16, 20, 24, …

Multiples of 8 are 8, 16, 24, 32, 40, 48, …

Multiples of 12 are 12, 24, 36, 48, 60, 72, …

The common multiples of 4, 8 and 12 are 24, 48, …

The least common multiple of 4, 8 and 12 is 24.

So, the LCM of 4, 8 and 12 is 24.

iv. Multiples of 12 are 12, 24, 36, 48, 60, 72, …

Multiples of 16 are 16, 32, 48, 64, 80, 96, …

The first common multiple of 12 and 16 is 48.

So, the LCM of 12 and 16 is 48.

= 2 × 2 × 2 × 2

= 2 × 2 × 7

= 2 × 2 × 2 × 5

= 7 × 11 LCM = 2 × 2 × 2 × 2 × 5 × 7 × 11 = 6160 iv. 2 20 2 10 5 5 1

20 = 2 × 2 × 5

25 = 5 × 5

30 = 2 × 3 × 5

50 = 2 × 5 × 5

LCM = 2 × 2 × 3 × 5 × 5 = 300

c. i. 2 11, 22, 36

2 11, 11, 18

3 11, 11, 9

3 11, 11, 3

11 11, 11, 1 1, 1, 1

Hence, LCM of 11, 22 and 36 = 2 × 2 × 3 × 3 × 11 = 396

ii. 2 96, 128, 240

2 48, 64, 120

2 24, 32, 60

2 12, 16, 30

2 6, 8, 15

2 3, 4, 15

2 3, 2, 15

3 3, 1, 15

5 1, 1, 5 1, 1, 1

Hence, LCM of 96, 128 and 240 = 2 × 2 × 2 × 2 × 2 × 2

× 2 × 3 × 5 = 1920

2 9, 12, 36, 54

2 9, 6, 18, 27

3 9, 3, 9, 27

3 3, 1, 3, 9

3 1, 1, 1, 3 1, 1, 1, 1

Hence, LCM of 9, 12, 36 and 54 = 2 × 2 × 3 × 3 × 3 = 108 iv.

2 102, 170, 136

2 51, 85, 68

2 51, 85, 34

3 51, 85, 17

5 17, 85, 17 17 17, 17, 17 1, 1, 1

Hence, LCM of 102, 170 and 136 = 2 × 2 × 2 × 3 × 5 × 17 = 2040

3. Let us denote the two numbers as A and B.

Given: HCF = 18; LCM = 126

Let us say one of the numbers A = 54

We can use the relationship between HCF, LCM and the numbers: HCF × LCM = A × B

Substitute the values:

18 × 126 = 54 × B

B = 18 × 126 54 = 42

So, the other number (B) is 42.

4. The HCF of the given numbers is always a factor of their LCM. Since 780 is not divisible by 25, it is not possible to have two numbers whose LCM and HCF are 780 and 25, respectively.

5. In 57 days, there are 57 7 = 8 weeks and 1 day.

So, there are 8 complete weeks and 1 extra day. Each week has exactly 1 Sunday. Therefore, in 8 weeks, there are 8 Sundays. The extra day can be any day of the week. If it happens to be a Sunday, you get one more Sunday. So, the maximum number of Sundays in the first 57 days is 8 + 1 = 9.

6. Subtract the remainder from each number: 655 − 7 = 648; 889 − 7 = 882; The HCF of 655 and 889 is 18.

The greatest number that can divide these numbers leaving a remainder of 7 is 18.

7. Subtract the remainders from each number: 77 − 5 = 72; 263 − 7 = 256; 462 − 6 = 456

The HCF of 72, 256, 456 is 8.

The greatest number that can divide these numbers leaving the given remainders is 8.

Challenge

1. Given that the HCF of the numbers is 13 and the product is 2028.

Let the numbers be 13a and 13b

Then, 13a × 13b = 2028

ab = 2028 ÷ 169 ab = 12

Now, the co-primes with product 12 are (1, 12), (12, 1), (4, 3) and (3, 4). Hence, there are only 4 pairs of numbers possible.

Do It Yourself 3E

1. Number of toy cars = 64

Number of action figures = 80

Greatest number of possible gift bags = HCF of 64 and 80

HCF of 64 and 80 = 16

So, Shaini can prepare 16 bags with no items left.

2. Time taken by machine X to produce the toys = 25 minutes

Time taken by machine Y to produce the toys = 35 minutes

Time taken by machine Z to produce the toys = 40 minutes

To find the time taken by all three machines to complete their work simultaneously, we need to find the LCM of 25, 35 and 40.

25 = 5 × 5

35 = 5 × 7

40 = 2 × 2 × 2 × 5

LCM of 25, 35 and 40 = 2 × 2 × 2 × 5 × 5 × 7 = 1400

All three machines will complete their work simultaneously after 1400 minutes.

3. Number of cows with the farmer = 72

Number of bales of grass with farmer = 36

To find the maximum number of identical groups such that each group has an equal number of cows and an equal number of bales of grass, we need to find the HCF of 72 and 36. 2 72 2 36 2 18 3 9 3 3 1 2 36

72 = 2 × 2 × 2 × 3 × 3

36 = 2 × 2 × 3 × 3

HCF of 72 and 36 = 2 × 2 × 3 × 3 = 36

Thus, the maximum number of groups are 36.

4. Sansevieria needs watering every 18 days. Euphorbia milii needs watering every 12 days.

To find number of days we will find the LCM of 18 and 12 2 18 3 9 3 3 1 2 12 2 6 3 3 1

18 = 2 × 3 × 3

12 = 2 × 2 × 3

LCM = 2 × 2 × 3 × 3 = 36

So, Sansevieria and Euphorbia milii will be watered together after 36 days.

5. To find the maximum length of the wooden planks, we need to find the HCF of 54, 72 and 90.

Chapter Checkup

1. a. 1 × 24 = 24

2 × 12 = 24

3 × 8 = 24

4 × 6 = 24

6 × 4 = 24 (We stop here as 6 and 4 are already covered)

So, the factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.

b. 1 × 30 = 30

2 × 15 = 30

54 = 2 × 3 × 3 × 3

72 = 2 × 2 × 2 × 3 × 3

90 = 2 × 3 × 3 × 5

HCF of 54, 72 and 90 = 2 × 3 × 3 = 18

So, the maximum length of the wooden planks can be 18 cm.

6. We need to find the least common multiple of 8, 12 and 16.

8 = 2 × 2 × 2

12 = 2 × 2 × 3

16 = 2 × 2 × 2 × 2

LCM of 8, 12 and 16 = 2 × 2 × 2 × 2 × 3 = 48

So, the buses depart simultaneously after every 48 minutes. The buses leave the station at 8:00 a.m.

The next time all three buses leave the station at the same time is at 8:48 a.m.

7. Simran visits every 6th day, so she visits on days divisible by 6. Shiva visits every 7th day, so he visits on days divisible by 7. For them to meet, the day must be divisible by both 6 and 7, meaning itʼs divisible by their least common multiple (LCM).

LCM of 6 and 7 is 42. So, they meet every 42nd day. December has 31 days; January has 31 days. Total days = 62

Dividing 62 by 42 gives a quotient of 1 and a remainder. This means they meet once in December and January.

8. Prime factorisation of 365: 5 × 73 5 365 73 73 1 3 687 229 229 1

LCM = 5 × 73 × 3 × 229 = 250,755 days

Therefore, Earth and Mars will align with the Sun again in approximately 250,755 days.

Challenge

1. If three cyclists start at the same point and ride around a circular track with different lap times, they will all meet at the starting point together after the LCM of their lap times. The assertion is true.

The LCM of the lap times represents the first time all events will coincide. The reason is also true and it explains the statement in the assertion.

Thus, option a is correct.

3 × 10 = 30

5 × 6 = 30

6 × 5 = 30 (We stop here as 6 and 5 are already covered)

So, the factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.

c. 1 × 48 = 48

2 × 24 = 48

3 × 16 = 48

4 × 12 = 48

6 × 8 = 48

8 × 6 = 48 (We stop here as 8 and 6 are already covered)

So, the factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.

d. 1 × 76 = 76

2 × 38 = 76

4 × 19 = 76

So, the factors of 76 are 1, 2, 4, 19, 38 and 76.

2. a. 267 3 89 267 = 3 × 89 b. 315 3 105 35 7 3 5

315 = 3 × 3 × 5 × 7 c. 539 7 77 11 7

539 = 7 × 7 × 11 d. 714 2 357 119 17 3 7

714 = 2 × 3 × 7 × 17

3. a. 54 and 36 are divisible by 9.

Their sum = 54 + 36 = 90 is also divisible by 9 (as 9 + 0 = 9 is divisible by 9)

Their difference = 54 – 36 = 18 is also divisible by 9 (as 1 + 8 = 9 is divisible by 9)

b. 546 and 364 are divisible by 13.

Their sum = 546 + 364 = 910 is also divisible by 13 (as 910 ÷ 13 = 70)

Their difference = 546 – 364 = 182 is also divisible by 13 (as 182 ÷ 13 = 14)

4. The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36. Clearly, 4 and 9 are the required numbers as their sum is 13 and the product is 36. Yes, they are co-primes since their factor is 1.

9 8 7 6 5 4 3 2 1

5. a. i. 2 36

2 18

3 9 3 3 1 2 48 2 24 2 12 2 6 3 3 1

36 = 2 × 2 × 3 × 3

48 = 2 × 2 × 2 × 2 × 3

HCF of 36 and 48 = 2 × 2 × 3 = 12

ii. 2 42

3 21 7 7 1 2 56 2 28 2 14 7 7 1

42 = 2 × 3 × 7

56 = 2 × 2 × 2 × 7

HCF of 42 and 56 = 2 × 7 = 14

b. i. 54 72 1 – 54 18 54 3 – 54 0

HCF of 54 and 72 is 18. ii. 77 121 1 – 77 44 77 1 – 44 33 44 1 – 33 11 33 3 – 33 0

HCF of 77 and 121 is 11.

6. a. i. 2 18

3 9 3 3 1 5 35 7 7 1 7 49 7 7 1

18 = 2 × 3 × 3

35 = 5 × 7

49 = 7 × 7

LCM of 18, 35 and 49 = 2 × 3 × 3 × 5 × 7 × 7 = 4410

ii. 2 24 2 12 2 6 3 3 1 2 36 2 18 3 9 3 3 1 2

2 60 2 30 3 15 5 5 1

24 = 2 × 2 × 2 × 3

36 = 2 × 2 × 3 × 3

120 = 2 × 2 × 2 × 3 × 5

LCM of 24, 36 and 120 = 2 × 2 × 2 × 3 × 3 × 5 = 360

b. i. 2 14, 28, 42 2 7, 14, 21

3 7, 7, 21 7 7, 7, 7 1, 1, 1

LCM of 14, 28 and 42 = 2 × 2 × 3 × 7 = 84

ii. 2 80, 112, 200

2 40, 56, 100

2 20, 28, 50

2 10, 14, 25

5 5, 7, 25 5 1, 7, 5

7 1, 7, 1 1, 1, 1

LCM of 80, 112 and 200 = 2 × 2 × 2 × 2 × 5 × 5 × 7 = 2800

7. First, we find the LCM of 7, 14, 21, 28 and 35.

2 7, 14, 21, 28, 35

2 7, 7, 21, 14, 35

3 7, 7, 21, 7, 35

5 7, 7, 7, 7, 35

7 7, 7, 7, 7, 7 1, 1, 1, 1, 1

LCM of 7, 14, 21, 28 and 35 = 2 × 2 × 3 × 5 × 7 = 420

Greatest 5-digit number = 99,999

We will divide 99,999 by 420 and find the remainder. 99,999 ÷ 420

Quotient = 238

Remainder = 39

As per the question, we need the greatest 5-digit number divisible by 420.

Therefore, the required number is 99,999 – 39 = 99,960

8. To determine the greatest 3-digit number exactly divisible by 8, 12, 18, 24 and 32, we need to find the LCM of the given numbers.

2 8, 12, 18, 24, 32

2 4, 6, 9, 12, 16

2 2, 3, 9, 6, 8

2 1, 3, 9, 3, 4

2 1, 3, 9, 3, 2

3 1, 3, 9, 3, 1

3 1, 1, 3, 1, 1 1, 1, 1, 1, 1

LCM of 8, 12, 18, 24 and 32 = 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288

As we know that the greatest 3-digit number is 999, we will now divide 999 by the LCM obtained. 999 ÷ 28 gives 3 as the quotient and 135 as the remainder. Since the remainder is not zero, we subtract 135 from 999. 999 – 135 = 864 which is a multiple of 288 and exactly divisible by the given numbers.

Hence, the greatest 3-digit number exactly divisible by 8, 12, 18, 24 and 32 is 864.

9. Number of history books = 30

Number of science books = 45

Number of literature books = 60

We need to find the maximum number of books that can be placed on each shelf, such that each shelf contains an equal number of each type of book.

For this, we need to find the HCF of 30, 45 and 60.

2 30 3 15 5 5

30 = 2 × 3 × 5

45 = 3 × 3 × 5

60 = 2 × 2 × 3 × 5

HCF of 30, 45 and 60 = 3 × 5 = 15

Hence, the maximum number of books that can be placed on each shelf is 15.

10. The traffic lights at three different road crossings change every 40 seconds, 60 seconds and 80 seconds, respectively. We will take the LCM of 40, 60 and 80.

2 40, 60, 80

2 20, 30, 40

2 10, 15, 20

2 5, 15, 10

3 5, 15, 5

5 5, 5, 5 1, 1, 1

LCM of 40, 60 and 80 = 2 × 2 × 2 × 2 × 3 × 5 = 240 seconds or 4 minutes

Therefore, after 240 seconds, the traffic lights will change simultaneously.

So, the traffic lights will change again at 4 minutes past 7 or 7:04 a.m.

11. Number of erasers with Sarah = 18

Number of pencils with Sarah = 24

Number of pens with Sarah = 30

To find the largest number of friends among whom Sarah can distribute these supplies, we need to find the HCF of 18, 24 and 30.

2 18 3 9 3 3 1 2 24 2

30 = 2 × 3 × 5

HCF of 18, 24 and 30 = 2 × 3 = 6

So, Sarah can distribute the supplies among 6 of her friends.

12. Answer may vary. Sample answer:

A number divisible by 6 must be divisible by both 2 and 3. For divisibility by 2, the last digit must be even (2 or 4). For divisibility by 3, the sum of the digits must be divisible by 3.

Let us take 23154:

Sum of the digits: 2 + 3 + 1 + 5 + 4 = 15 (divisible by 3)

Last digit is 4 (even)

Therefore, 23154 is divisible by 6.

13. To find the minimum amount of time one would have to wait for all three sprinklers to operate simultaneously, we need to find the LCM of 20, 25 and 30.

2 20, 25, 30

2 10, 25, 15

3 5, 25, 15

5 5, 25, 5 5 1, 5, 1 1, 1, 1

LCM of 20, 25 and 30 = 2 × 2 × 3 × 5 × 5 = 300 minutes

Hence, a person would have to wait for 300 minutes or 5 hours to watch all sprinklers operate at the same time.

14. Rita can memorise 2 national park names each day.

This is because 106 divided by 2 equals 53, which means she would memorise 53 names in 2 days.

106 divided by 3 equals 35 with a remainder 1.

106 divided by 4 equals 26 with a remainder 2.

106 divided by 5 equals 21 with a remainder 1.

So, Rita cannot memorise the same number of words each day since there are remainders.

Challenge

1. To find the smallest number from which if 15 is subtracted, the result is exactly divisible by 9, 12, 18, 21, 27 and 36, we need to determine the least common multiple (LCM) of these numbers.

9 = 3 × 3

12 = 2 × 2 × 3

18 = 2 × 3 × 3

21 = 3 × 7

27 = 3 × 3 × 3

LCM = 2 × 2 × 3 × 3 × 3 × 7 = 756

Smallest number = 756 + 15 = 771

So, 771 is the smallest number from which if 15 is subtracted, the result is exactly divisible by 9, 12, 18, 21, 27 and 36.

2. The LCM and HCF of two numbers are 360 and 18, respectively.

Statement 1: The first number is 72.

We know that, LCM × HCF = Product of the two numbers.

So, we can find the second number.

Thus, Statement 1 alone is sufficient to find the second number.

Statement 2: The second number is 72 more than the HCF. The second number is 18 + 72 = 90

Again, we can use LCM × HCF = Product of the two numbers to find the other number.

So, we can find the second number. Thus, Statement 2 alone is sufficient to find the second number.

In this case, either of the statement is sufficient to find the answer.

Thus, option c is correct.

Case Study

1. Number of stations = Total distance Distance between stations + 1 = 150 25 + 1 = 6 + 1 = 7

(There is 1 starting station for which 1 is added)

So, 7 stations will be required along the route. Hence, option d is correct.

2. Cargo depart from city A every 30 minutes. Parcel ship from city A departs every 40 minutes.

To find the next departure at the same time, we will have to find the LCM of 30 and 40.

2 30 3 15 5 5 1 2 40 2 20 2 10 5 5 1

30 = 2 × 3 × 5

40 = 2 × 2 × 2 × 5

LCM = 2 × 2 × 2 × 3 × 5 = 120

This means both shipments will next depart at the same time 120 minutes or 2 hours after 10 a.m.

So, the next time both shipments will depart together at 12 p.m. (noon).

3. The distance between the cities is not provided. Hence, the information is incomplete. So, option c is correct.

4. Answers may vary.

1. a. H is a point.

b. GH is a line segment.

c. OP is a line.

d. KL is a ray.

So, option c represents a line.

2. A ray is obtained by extending a line segment indefinitely in one direction.

So, option c is correct.

3. a. A line extends in two directions. True

b. A plane has a definite size. False

c. A line segment is part of a ray. True

d. A ray has more endpoints than a line. False

4. a. OP = 2.7 cm b. QR = 3.9 cm c. ST = 5.7 cm

5. a. 5.2 cm

b. 7.7 cm

c. 61 mm = 6.1 cm 6.1 mm

d. 35 mm = 3.5 cm 35 mm

6. Convert each measure into mm.

a. 2000 mm = 2000 mm

b. 150 cm = 1500 mm

c. 100 dm = 10,000 mm

d. 10 m = 10,000 mm

1500 mm < 2000 mm < 10,000 mm = 10,000 m

150 cm < 2000 mm < 100 dm = 10 m

Here, 150 cm is the shortest length.

So, option b is correct.

7. a. 1 km = 1000 m

Hence, 23 km = 23 × 1000 m = 23,000 m

b. 1 km = 1,00,000 cm

Hence, 23 km = 23 × 1,00,000 cm = 23,00,000 cm

c. 1 km = 100 dam

Hence, 23 km = 23 × 100 dam = 2300 dam

d. 1 km = 10 hm

Hence, 23 km = 23 × 10 hm = 230 hm

8. There are 9 stars in the Leo constellation.

9. Length of the Great Wall of China = 20,000 km

Scale 5000 km = 1 cm

For 20,000 km, the length will be = 20,000 5000 = 4 cm

The length of the Great Wall of China will be 4 cm on the map with scale 1 cm = 5000 km

Challenge 1.

routes.

2. No. While all perpendicular lines are intersecting, not all intersecting lines are perpendicular.

Perpendicular lines intersect at 90º, while intersecting lines can meet at any angle.

Do It Yourself 4B

1. ∠BQB is the incorrect representation of the angle. This is incorrect because it suggests that an angle has the same initial and final points, which doesn’t define an angle. An angle is formed by two distinct rays with a common endpoint.

So, option c is an incorrect representation of an angle.

2. a. Since 36° is less than 90°, the angle is an acute angle.

b. Since 93° is more than 90°, the angle is an obtuse angle.

c. Since 192° is more than 180°, the angle is a reflex angle.

d. Since 89° is less than 90°, the angle is an acute angle.

3. a. A bat kept on the floor is close to the ground and not at right angles to the ground.

Hence it is not perpendicular to the ground.

b. A clock hand at 3:00 forms a right angle and hence they are perpendicular lines.

c. A boy leaning against the wall is closer to the wall and is parallel, hence does not form a perpendicular line.

d. A book kept on the table is parallel to the ground. Hence, the book is not perpendicular to the ground.

Hence, option b is correct.

4. ∠P = 34°; ∠Q = 66° ; ∠R = 67°

5. ∠QON and ∠QOR have a common vertex Q and a common arm QO.

Hence, ∠QON and ∠QOR are adjacent angles.

6. Blue Angle Red Angle Difference

a. 60° 35° 25°

b. 62° 17° 45°

c. 48° 29° 19°

d. 129° 22° 107°

7. Each hour on the clock represents = 360° 12 = 30°

a. The hour hand from 5 to 8 moves 3 numbers.

It moves = 3 × 30° = 90°

One full turn = 360°

So moving 90° = 90° 360° = 1 4 of the full rotation.

b. The hour hand from 3 to 7 moves 4 numbers.

It moves = 4 × 30° = 120°

One full turn = 360°

So, moving 120° = 120° 360° = 1 3 of the full rotation.

c. The hour hand from 11 to 5 moves 6 numbers.

It moves = 6 × 30° = 180°

One full turn = 360°

So, moving 180° = 180° 360° = 1 2 of the full rotation.

d. The hour hand from 9 to 6 moves 9 numbers.

It moves = 9 × 30° = 270°

One full turn = 360°

So, moving 270° = 270° 360° = 3 4 of the full rotation.

9. Angle made by the body is estimated to be around 85 degrees. It is closer to a right angle.

10. a. South b. West c. North

12. One full turn of the bicycle wheel = 360° A right angle = 90°

Each full turn consists of 4 right angles

° = ° 360 4

4 full turns = 4 × 4 = 16 right angles

Half a turn = 0.5 × 4 = 2 right angles

Total right angles = 16 + 2 = 18 right angles

Hence, Reena’s bicycle makes 18 right angles.

13. You would be facing the west direction by turning anti-clockwise by three right angles when you were initially facing the south direction.

Challenge

1. Alphabets E, F and K have adjacent angles.

2. Angle between any two consecutive directions

= =   360 45 8

Hence, the angle between any two consecutive directions at the centre of the compass is 45°.

3. Rohit’s interview is at 3:00 p.m.

If he wants to leave 2 hours before 3:00 p.m., he should leave at 1:00 p.m.

Hour hand position: At 1:00 p.m., the hour hand is on the 1. Minute hand position: At 1:00 p.m., the minute hand will be on 12.

Each hour on the clock represents ° =° 360 30 12 = 30°

So, the angle between 1 and 12 = 1 × 30° = 30°

Do It Yourself 4C

1. Triangle TRS

Vertices: T, R, S Sides: TR or RT, TS or ST, RS or SR

Angles: ∠T or ∠RTS or ∠STR, ∠R or ∠TRS or ∠SRT, ∠S or ∠TSR or ∠RST

2. a. 6 cm, 7 cm, 9 cm – Length of all sides are unequal, so the triangle is scalene.

b. 15 cm, 15 cm, 15 cm – Length of all sides are equal, so the triangle is equilateral.

c. 19 cm, 23 cm, 29 cm – Length of all sides are unequal, so the triangle is scalene.

d. 9 cm, 11 cm, 9 cm – Length of the two sides are equal, so the triangle is isosceles.

e. 18 cm, 31 cm, 27 cm – Length of all sides are unequal, so the triangle is scalene.

f. 3 mm, 3 mm, 3 mm – Length of all sides are equal, so the triangle is equilateral.

3. a. 60°, 40°, 80° – Since all angles measure less than a right angle, the triangle is acute-angled.

b. 65°, 85°, 30° – Since all angles measure less than a right angle, the triangle is acute-angled.

c. 130°, 20°, 20° – Since one of the angles measures more than a right angle, the triangle is obtuse-angled.

d. 90°, 40°, 50° – Since one of the angles measures equal to a right angle, the triangle is right-angled.

e. 110°, 25°, 45° – Since one of the angles measures more than a right angle, the triangle is obtuse-angled.

f. 60°, 60°, 60° – Since all angles measure less than a right angle, the triangle is acute-angled.

5. Measure of the first garden = 7 m, 7 m and 10 m

Measure of the second garden = 5 m, 6 m and 7 m

Since two sides of the first garden have equal measures, an isosceles triangle is formed.

All three sides of the second garden are unequal, so the triangle formed is scalene.

Challenge

1. a. Every equilateral triangle is necessarily an isosceles triangle.

b. Every right-angled triangle is necessarily an isosceles triangle.

Statement a: An equilateral triangle, having all three sides equal, indeed has at least two sides equal, making it an isosceles triangle. Thus, statement a is correct.

Statement b: A right-angled triangle does not necessarily have two sides equal; it can have all three sides of different lengths (scalene).

Therefore, a right-angled triangle is not necessarily an isosceles triangle. Thus, statement b is incorrect.

So, option (i) is correct.

Do It Yourself 4D

1. a. Square PQRS

Sides (PQ, QR, RS, SP); Vertices (P, Q, R, S); Adjacent sides: (PS, SR), (RQ, QP), (SR, RQ), (QP, PS)

Opposite sides: (PS, QR), (SR, PQ)

b. Rectangle ABCD

Sides (AB, BC, CD, DA); Vertices (A, B, C, D); Adjacent sides: (AB, BC), (BC, CD), (CD, AD), (AD, AB)

Opposite sides: (AB, CD), (AD, BC)

c. Kite JKLM

Sides (JK, KL, LM, MJ); Vertices (J, K, L, M); Adjacent sides: (JM, ML), (ML, LK), (LK, KJ), (KJ, JM)

Opposite sides: (JM, KL), (ML, JK) 2.

Diagonals: BD, AC Diagonals: SU, VT

Diagonals: MK, JL

3. a. All sides of equal length and all angles measure 90° – Square

b. Opposite sides are parallel and opposite angles are equal – Parallelogram

c. Two pairs of adjacent sides are of equal length, and one pair of opposite angles is equal. – Kite

4. Figures may vary. Sample figures:

4. Maharashtra Karnataka

Telangana Odisha

Madhya Pradesh

5. a. The angles of the quadrilateral are ∠ABC = 80°, ∠BCD = 100°, ∠CDA = 75°, and ∠DAB = 105°

The measure of all the angles is less than 180°, so the quadrilateral is a convex quadrilateral.

So, the patch of land is a convex quadrilateral.

b. For a quadrilateral to be a rectangle or a square, all interior angles must be 90°.

None of the given angles are 90°, so the quadrilateral cannot be a rectangle or square.

So, the patch of land cannot be a rectangle or a square.

c. For a quadrilateral to be a parallelogram, opposite angles must be equal and the sum of adjacent angle must be 180°.

∠ABC (80°) ≠ ∠CDA (75°)

∠BCD (100°) ≠ ∠DAB (105°)

Since the opposite sides are not equal, the quadrilateral cannot be a parallelogram.

So, the patch of land cannot be a parallelogram.

Challenge

1. The quadrilateral formed by joining the midpoints of the sides of any quadrilateral is always a parallelogram. So, the correct answer is option c—a parallelogram.

Challenge

1. Let us put D in one corner. E is two seats to the left of D. E

B must be next to D and C, Then A is two seats to the left of F. After arranging everyone, we see who is directly across from D. E

Sitting opposite D is A. So, the person sitting directly across from D is A.

Do It Yourself 4F

Closed curve Open curve Open curve Open curve Closed curve

a. b. c. d.

Do It Yourself 4E

1. A square is a regular polygon since it has all its sides equal.

2. Vertices: A, B, C, D, E, F, G, H

Sides: AB or BA, BC or CB, CD or DC, DE or ED, EF or FE, FG or GF, GH or HG, HA or AH.

3. Figures may vary. Sample figures:

4. Since all the sides and angles in this polygon are equal, this is a regular polygon.

The logo has 9 diagonals; hence the shape is a hexagon.

5. Sarah planted two sunflower plants on each side of the hexagonal garden.

A hexagon has 6 sides.

So, the total number of sunflower plants = 2 × 6 = 12

Alex planted one sunflower plant on each side of the octagonal garden.

An octagon has 8 sides.

So, the total number of sunflower plants = 1 × 8 = 8

Sarah planted 4 sunflower plants more than Alex.

Two circles are inside the bigger circle. Hence, these are not concentric circles.

b. One circle is inside the bigger circle and other circle is lying on the circumference of the bigger circle. Hence, these are not concentric circles.

Both the circles are lying on the circumference of the bigger circle. Hence, these are not concentric circles.

The circles do not intersect each other as they have the same centre. Hence, these are concentric circles. Hence, option d is the correct answer.

5. A chord is a line segment that connects two points on the circle. So, a chord has a finite length.

An arc is a part of the circumference of the circle, so it has finite length.

A diameter is line that connect 2 points on the circle through the centre, so the diameter has a finite length.

A secant is a line. Hence, it does not have a finite length. Hence, option d is the correct answer.

Boundary of the curve Q P R

Interior of the curve

Exterior of the curve

7. Figures may vary. Sample figures: a. b. c. d.

8. a. 3 cm b. 3.8 cm c. 4 cm d. 3.6 cm

9. Answer may vary. Sample answer:

Simple curves Non-simple curves

10. a. Radius = 7 cm

Circumference = 2πr = 2 × 22 7 × 7 cm = 44 cm

b. Radius = 8.4 cm

Circumference = 2πr = 2 × 22 7 × 8.4 cm = 52.8 cm

c. Radius = 21 cm

Circumference = 2πr = 2 × 22 7 × 21 cm = 132 cm

d. Radius = 49 cm

Circumference = 2πr = 2 × 22 7 × 49 cm = 308 cm

11. a. Circumference = 66 cm

Radius = Circumference 2p = 66 2 × 22 7 = 66 × 7 2 × 22 = 10.5 cm

b. Circumference = 88 cm

Radius = Circumference 2p = 88 2 × 22 7 = 88 × 7 2 × 22 = 14 cm

c. Circumference = 110 cm

Radius = Circumference 2p = 110 2 × 22 7 = 100 × 7 2 × 22 = 17.5 cm

d. Circumference = 154 cm

Radius = Circumference 2p = 154 2 × 22 7 = 154 × 7 2 × 22 = 24.5 cm

12. Circumference of the Ashoka Chakra on a replica flag = 3.14 m

Circumference = 2πr

Radius = Circumference 2p = × 3.14 2 3.14 = 0.5 m

So, the radius of Ashoka Chakra in the replica flag is 0.5 m.

Challenge

1. Assertion (A): Chord, secant, sector, segment and radius are the parts of a circle.

Reason (R): The centre of the circle is always in the interior of the circle.

The assertion is true. These are all elements used to describe different parts of a circle.

The reason is also true. By definition, all points on the circle are the same distance away from the centre.

The centre itself cannot be on the circle or outside of it.

However, the truth of Reason (R) does not explain why the listed elements are all parts of a circle.

Therefore, the answer is option (b). Both Assertion (A) and Reason (R) are true, but Reason (R) is not a correct explanation of Assertion (A).

Chapter Checkup

1. a. 9 b. 8 c. 5 d. 7

2. a. 4: A polygon with 4 sides is a quadrilateral.

b. 8: A polygon with 8 sides is a octagon.

c. 5: A polygon with 5 sides is a pentagon.

d. 7: A polygon with 7 sides is a heptagon.

3. a. F G 4.6 cm

b. B 77 mm = 7.7 cm C

c. X 6.9 cm Y

d. D 2.2 cm E

4. Figures may vary. Sample figures:

Y P O Q X

6. a. Since 26° is less than 90°, so it is an acute angle.

b. Since 256° is more than 180°, so it is a reflex angle.

c. Since 79° is less than 90°, so it is an acute angle.

d. Since 129° is more than 90°, so it is an obtuse angle.

e. Since 165° is more than 90°, so it is an obtuse angle.

f. Since 189° is more than 180°, so it is a reflex angle.

g. Since 270° is more than 180°, so it is a reflex angle.

h. Since 179° is more than 180°, so it is a reflex angle.

7. a. b. c.

Number of sides = 3

Number of sides = 6

d. Number of sides = 10

Number of sides = 8

12. a. One full rotation = 360°

Going from 12 to 3 = 1 4 of full rotation = 1 4 × 360° = 90°

b. One full rotation = 360°

Going from 12 to 6 = 1 2 of full rotation = 1 2 × 360° = 180°

c. One full rotation = 360°

Going from 12 to 12 = one full rotation = 360°

d. One full rotation = 360°

Going from 12 to 9 = 3 4 of full rotation = 3 4 × 360° = 270°

13. a. East b. West E N W S N E W S

14. R S U Q T

a. RT and SU

b. Answers may vary: ∠RST, ∠STU, ∠TUR, ∠URS

c. Yes, UQ = TQ because the diagonals in a square are equal and bisect each other at right angles.

d. Pair of parallel sides: (RU || ST), (UT || RS)

15. secant

Closed curve Closed curve Open curve Open curve

10. a. 7 cm, 7 cm, 10 cm

Since two sides of the triangle are equal, the triangle is an isosceles triangle.

b. 14 cm, 15 cm, 16 cm

Since all three sides of the triangles are different, the triangle is a scalene triangle.

c. 29 cm, 29 cm, 29 cm

Since all three sides of triangle are equal, the triangle is an equilateral triangle.

11. a. 70°, 30°, 80°

All the measures of the angles are less than 90°, the triangle is an acute-angled triangle.

b. 45°, 85°, 50°

All the measures of the angles are less than 90°, the triangle is an acute-angled triangle.

c. 120°, 20°, 40°

Measure of one of the angles is greater than 90°, the triangle is an obtuse-angled triangle.

Challenge

chord 3 cm 4 cm diameter

16. Scalene triangles: ΔAEF, ΔBFC, ΔABF

Equilateral triangle: ΔDEC

Isosceles triangle: ΔFEC

17. a. Both ΔDEF and ΔPQR: Points 6, 7, 8

b. Both ΔABC and ΔDEF: Point 2

c. Only ΔDEF: Points 1, 4, 5

d. Only ΔPQR: Points 9, 10, 11, 12, 13

18. a. Yes, MN = PM. Pair of adjacent sides of a kite are equal.

b. Yes, ∠MNQ is equal to ∠MPQ because in the isosceles triangle MNP, the angles opposite to equal sides are equal in measure.

c. Yes, ∠ONQ is equal to ∠OPQ because in the isosceles triangle NOP, the angles opposite to equal sides are equal in measure.

1. By counting all the four-sided shapes, we found 15 quadrilaterals.

2. Assertion (A): In an isosceles trapezium, the non-parallel sides are equal in length.

Reason (R): A trapezium is a quadrilateral with exactly one pair of parallel sides.

The assertion correctly states that in an isosceles trapezium, the length of the non-parallel sides are equal.

The reason is also correct, the trapezium has exactly only one pair of parallel sides.

Both assertion and reason are true, however the reason does not explain the assertion.

Hence, A and R are true, but R does not explain A.

So, option (b) is correct.

Case Study

1. The shadow of the gnomon in the morning forms an acute angle.

So, option a is correct.

2. The shadow of the gnomon forms a right angle with the dial at noon.

So, option b is correct.

3. In the morning the shadow of the gnomon forms an acute angle.

4. In the afternoon, the shadow of the gnomon forms an obtuse angle.

5. The angle of the gnomon affects the types of angles formed by the shadow throughout the day. True

Chapter 5

Let’s Warm-up

Do It Yourself 5A

1. a. A circle is not a solid figure.

Option ii is correct.

b. A triangular pyramid has 4 faces.

Option ii is correct.

c. The shape of a playing dice is a cube. Option i is correct.

d. A heptagonal pyramid has 8 vertices. Option ii is correct.

2. a. Cuboid b. Cylinder c. Cone d. Cube

3. a. A cylinder has 2 circular edges.

b. All the faces of a cube are identical.

c. A pentagonal prism has 5 more edges than vertices.

d. A cube and a square pyramid have square bases.

4. The Pyramids of Giza is in the shape of square pyramid. A square pyramid has 5 faces, 8 edges and 5 vertices.

The shape formed is a cuboid. It has 6 faces, 12 edges and 8 vertices.

6. a. 6 faces

b. 12 edges and 7 vertices

c. 1 vertex and 2 faces

d. 16 edges

e. 7 faces and 10 vertices

Octagonal pyramid

Cone

Cuboid

Pentagonal prism

Hexagonal pyramid

Octagonal Prism Octagonal Pyramid

Differences:

a. Number of bases: An octagonal pyramid has one base, while an octagonal prism has two bases.

b. Shape of the lateral faces: An octagonal pyramid has triangular lateral faces, while an octagonal prism has rectangular lateral faces.

Similarities:

a. Number of edges in the base: Both an octagonal pyramid and an octagonal prism have 8 edges in the base.

b. Three-dimensional shape: Both an octagonal pyramid and an octagonal prism are three-dimensional shapes.

Hexagonal Pyramid Nonagonal Pyramid

Differences: A nonagonal pyramid has a base with 9 edges, while a hexagonal pyramid has a base with 6 edges. Also, a nonagonal pyramid has 10 vertices and 9 lateral faces, while a hexagonal pyramid has 7 vertices and 6 lateral faces.

Similarity: Both nonagonal and hexagonal pyramids are 3D shapes with a polygonal base and triangular lateral faces.

Challenge

1. The number of faces = 8

So, the number of vertices = 8

Number of edges = 2 × 8 − 2 = 14

Since, a heptagonal pyramid has 8 faces, 14 edges and 8 vertices, the solid is a heptagonal pyramid.

Do It Yourself 5B

1. a. The base of the shape is a hexagon and the lateral faces of the shape are triangles. Thus, this is the net of a hexagonal pyramid.

b. The base of the shape is a triangle. This is the net of a triangular pyramid.

c. The base of the shape is a square. This is the net of a cube.

d. The base of the net is a circle and the lateral face is in the shape of rectangle. This is the net of a cylinder.

2. a. A sphere has no net.

b. The net of a cylinder has 3 faces.

c. A cubical box is open from the top. The net of the box has 5 faces.

d. A square pyramid has 1 square and 4 triangles in its net.

4. Answers may vary. Sample answer:

5. Answers may vary. Sample answer:

6. The shape belongs to the net of a triangular pyramid.

7. A kaleidescope has two triangular mirrors opposite to each other and 3 rectangular mirrors at the sides. So, the shape of a kaleidoscope is triangular prism.

TRIANGULAR PRISM

Shape Net

Challenge

1. An open cube has 5 faces, 12 edges and 8 vertices. A square pyramid has 5 faces, 8 edges and 5 vertices.

So, the combination of figure:

Faces = 5 + 5 – 1 = 9 (the base of the pyramid)

Edges = 12 + 8 – 4 = 16 (4 are common edges)

Vertices = 8 + 5 – 4 = 9 (4 are common vertices)

So, the combination of an open cube and a triangular pyramid has 9 faces, 16 edges and 9 vertices.

Chapter Checkup

1. a. This is a pentagonal pyramid. It has 10 edges, 6 vertices and 6 faces.

b. This is a cuboid. It has 12 edges, 8 vertices and 6 faces.

c. This is a cone. It has 1 edge, 1 vertex and 2 faces.

d. This is an octagonal prism.

It has 24 edges, 16 vertices and 10 faces.

2. a. A pentagonal pyramid has 10 edges and 6 vertices.

b. The difference between the number of vertices and the number of faces of a decagonal prism is 8

c. The number of edges in a heptagonal prism is 21

3. A cone has a curved lateral face and an apex. So, it is not a prism. A cone is not a prism.

4. a. Square prism

Total number of faces = 6

Type – 4 rectangular, 2 square shaped

b. Heptagonal pyramid

Total number of faces = 8

Type: 7 triangular, 1 heptagon shaped

c. Hexagonal prism

Total number of faces = 8

Type: 6 parallelograms, 2 hexagons

5. When the net of the cube is folded, the face opposite to the:

a. Red face will be opposite to the blue face.

b. Grey face will be opposite to the orange face.

6. Jenna creates a paper model of a triangular prism, using a net.

A triangular prism has 2 triangular faces and 3 rectangular faces.

Answer may vary. Sample answer:

7. David creates a unique gift box in the shape of a rectangular prism. A rectangular prism has 6 rectangular faces.

Answer may vary. Sample answer:

9. a. The given net has an octagonal shapes base and 8 triangular faces. Thus, it is the net of an octagonal pyramid.

b. The base and the faces of the shape are square. Thus, it is the net of a cube.

c. The given net has pentagon shape base and triangular faces. Thus, it is the net of a pentagonal pyramid.

d. The given net has a hexagonal shape base and square faces. Thus, it is the net of a hexagonal prism.

10. The base of a nonagonal pyramid is nonagon. It has 9 triangular faces. The base of the hexagonal pyramid is hexagon and it has 6 triangular faces.

a. b.

11. Answers may vary. Sample answer: a. b.

c. d.

Challenge

1. Assertion (A): A cube and a cuboid are both examples of rectangular prisms.

Reason (R): A cube has all its faces as squares, whereas a cuboid has faces that are all rectangles but not necessarily squares.

Both a cube and a cuboid are types of rectangular prisms. So, the assertion is true. A cube is a special case of a cuboid where all faces are squares, while a cuboid’s faces are rectangles, which may not all be squares. So, the reason is true. Both the assertion and the reason are true and the reason explains the assertion. So, option a is correct.

8. Triangular pyramid Cone Cylinder Square pyramid

2. Since the sum of the numbers on opposite faces of a die always equals 7, we have:

1 + 6 = 7

2 + 5 = 7

3 + 4 = 7

Thus, the missing dots are 4, 5 and 6, respectively.

Case Study

1. A rectangular prism has 6 faces, 12 edges and 8 vertices. Since the shed consists only of walls and a ceiling, it will have 5 faces. Therefore, only 5 tin sheets will be needed. So, option a is correct.

2. The four walls will be pink and the ceiling at the top will be red.

A = −6, B = −9, C = −2, D = 3, E = 6, F = 1

4. a. Predecessor of 17 is 16, Successor of 17 is 18

b. Predecessor of –12 is −13, Successor of –12 is −11

c. Predecessor of 25 is 24, Successor of 25 is 26

d. Predecessor of –88 is −89, Successor of –88 is −87

e. Predecessor of 125 is 124, Successor of 125 is 126

5. Numbers to the left of 1 is 0, −1, −2, −3.

So, if we move 4 numbers to the left of 1, we will go to 0, −1, −2 and −3. We will land on −3.

3. A rectangular pyramid has 5 faces, 8 edges and 5 vertices. So, option d is correct.

4. A rectangular prism has all 6 rectangular faces, while a rectangular pyramid has 1 rectangular and 4 triangular faces.

5. Answer may vary.

Chapter 6

Let’s Warm-up

1. S. No.

Do It Yourself 6A

1. a. +10 km; opposite = −10 km

b. −₹1000; opposite = +₹1000

c. +5 apples; opposite = −5 apples

d. −3 kg; opposite = +3 kg

e. +3 runs; opposite = −3 runs

f. −10 minutes; opposite = +10 minutes

10. a. −10 < −8 < −2 < 5 < 9

6. a. Integers between −3 and 4 are: −2, −1, 0, 1, 2, 3

b. Integers between −5 and 0 are: −4, −3, −2, −1

c. Integers between 1 and 6 are: 2, 3, 4, 5

d. Integers between −9 and –4 are: −8, −7, −6, −5

e. Integers between −15 and –8 are: −14, −13, −12, −11, −10, −9

a. The absolute value of 8 can be written as:|8| = 8

b. The absolute value of −10 can be written as:|−10| = 10

c. The absolute value of 25 can be written as:|25| = 25

d. The absolute value of −35 can be written as:|−35| = 35

e. The absolute value of −65 can be written as:|−65| = 65

8. a. Rule: add by 3: −13, −16, −19, −22, −25

b. Rule: subtract by 6: 18, 12, 6, 0

c. Rule: Subtract by 2: −30, −32, −34, −36

9. a. −26 is to the right of −33. So, −26 > −33

b. –15 is to the left of –12. So, −15 < −12

c. 47 is to the right of –47. So, 47 > −47

d. 14 is to the left of 18. So, 14 < 18

e. –51 is to the left of –15. So, −51 < −15

12. +35 Parachute

+10 Helium Balloon

0 Sea level

–15 Submarine

The helium balloon is in between the submarine and the parachute. Challenge 1. |–10| + |9 –7| – |___| = 6

10 + 2 = 12

12 – 6 = 6

So, the number 6 will replace the box.

1. a. +5 + (+6)

Total number of tokens = 11 positive tokens

+5 + (+6) = 11

b. −1 + (+7)

Number of tokens left = 6

−1 + (+7) = +6

c. −5 + (−9)

Total number of tokens = 14 negative tokens

−5 + (−9) = −14

2. a. 6 + 4 = 10

b. −6 + (−4) = −10

c. −9 + 3 + 5 = −1

3. a. −4 + 6 = +2 b. −3 + (−4) = −7

4. a. 12 + (−14) = −2 b. −16 + (−18) = −34

c. −25 + 63 = 38 d. 52 + (−45) = 7

e. 125 + (−256) = −131 f. −365 + (−145) = −510

5. a. (–9) + 12 + (–15) = –9 + 12 – 15 = −12

b. 18 + (–25) + 28 = 18 – 25 + 28 = 21

c. –32 + (–14) + (–35) = – 32 – 14 – 35 = −81

d. 36 + (–78) + (–14) + 63 = 36 – 78 – 14 + 63 = 7

e. –175+ (–48) + 259 + 88 = –175 – 48 + 259 + 88 = 124

f. –148 + 32 – 238 + 54 = –300

6. Successor of –1025 = –1024; Predecessor of 923 = 922 – 1024 + 922 = −102

7. a. Additive inverse of −8 = 8

b. Additive inverse of 12 = −12

c. Additive inverse of −14 = 14

8. a. 5 + a = 5

⇒ a = 5 − 5

⇒ a = 0

b. 7 + a = 0

⇒ a = 0 − 7

⇒ a = −7

c. 6 + a = 3 + 6

⇒ a = 9 − 6

⇒ a = 3

9. Temperature on Monday = 42°C

Temperature falls on Tuesday = 42°C – 15°C = 27°C

Temperature falls on Wednesday = 27°C – 7°C = 20°C

So, the temperature recorded on Wednesday is 20°C.

Challenge

1. a. 1 + 3 + 6 + 7 + 9 – 2 – 4 – 5 – 8

26 – 19 = 7

b. 1 + 2 + 3 – 4 – 5 + 6 + 7 – 8 + 9

6 – 9 + 13 – 8 + 9

6 + 13 – 8 = 19 – 8 = 11

2. Answers may vary. Sample answer: Since, (–59) + 36 + (–135) = –158

The three integers could be −59, 36 and −135.

Do It Yourself 6C

1. a. +11 − (+5) + + + + + + + + + + + + +

Number of tokens left = 6 +11 − (+5) = +6

b. −9 − (−5)

Number of tokens left = 4 negative tokens −9 − (−5) = −9 + 5 = −4

−6 − (+7)

+ + + + + +

Number of tokens left = 1 positive token −6 − (+7) = +1

2. a. −3 – (−4) = −3 + 4 = +1

–7 –8 –9

−10 – (5) = −10 + (−5) = −15

c. 15 – (−8) = 15 + (+8) = +23

d. −2 − (−6) = −2 + 6 = +4

3. a. −36 – 15 = −51

b. −42 – (−48) = −42 + 48 = 6

c. 69 – (−52) = 69 + 52 = 121

4. a. –125 – (–253)

b. 236 – (–541)

c. –365 – (425) –157

d. –414 – (–257) 128

5. a. Using additive identity property –90 + 1 = –89

b. Using subtraction property of zero 25 – 0 = 25

c. Using additive identity property

–35 + 0 = –35

d. Using closure property

32 – 15 = 17

6. Sum of 623 and –584 = 623 + (–584) = 39

Sum of –795 and 475 = –795 + 475 = −320

Subtracting 39 from −320 = −320 – 39 = −359

7. Let the two integers be 89 and x

Given, 89 + x = –423

⇒ x = –423 – 89 ⇒ x = –512

8. The distance driven on Monday in the north = +125 km

The distance driven on Tuesday in the south = −182 km

Distance from the initial point = 125 + (–182) = –57

Dev is 57 km south of his initial point.

9. The melting point of mercury = –38.9°C; The boiling point of mercury = 356.7°C

Difference between the melting and boiling points = 356.7°C – (–38.9°C)

= 356.7°C + 38.9°C = 395.6°C

10. The lowest point in Africa = 153 m below sea level

The highest point in Africa = 5895 m above sea level 5895 m

0 Sea Level

153 m

Difference = 5895 – (–153) = 5895 + 153 = 6048 m

11. Initial balance in Pooja’s account = ₹(–1250)

Amount she is willing to have in her account = ₹5000

Let the amount deposited be x

₹(−1250) + x = ₹5000

x = 5000 + 1250 = 6250

Hence, the money she needs to deposit is ₹6250.

12. 10,500 feet

0 2514 feet

13.

Challenge

Distance between the submarine and the aeroplane = 10,500 – (–2514) = 10,500 + 2514 = 13,014 feet

1. Anu goes up 4 steps and then comes down 2 steps.

Anu takes 17 rounds to reach the top.

Piya goes up 3 steps and then comes down 1 step.

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Piya takes 19 rounds to reach the top.

Both Anu and Piya move at the same pace.

Anu will reach faster since she takes 17 steps to cover 20 steps while Priya takes 19 steps to cover 20 steps. So, Anu reaches the top first.

Chapter Checkup

1. a. +3 + (+8)

Total number of tokens = +3 + (+8) = +11

−2 + (+7)

Number of tokens left = 5 positive tokens

−5 − (−7)

Number of tokens left = 2 positive tokens

−5 − (−7) = −5 + 7 = +2 d. −4 − (+9)

Number of tokens left = 13 negative tokens

−4 − (+9) = −4 – 9 = −13

2. a. –2 is on the left of 5 on the number line.

b. 13 is on the left of 18 on the number line.

c. –8 is on the left of 8 on the number line.

d. –17 is on the left of –13 on the number line.

e. 25 is on the left of 36 on the number line.

3. a. The temperatures in the form of integers can be written as: Chennai = 31° above 0° = +31°; Pune = 18° above 0° = +18°; Ladakh = 5° below 0° = –5°; Sonamarg = 8° below 0° = –8°

b. Since Sonamarg has the lowest temperature, it is the coldest place, and Chennai has the highest temperature, it is the hottest place.

4. The point E will be marked as −2. 0 –2 –1 1 2 3

A B C D E

5. Absolute value does not have a sign with it. Hence, the integers 9 and 57 are given in their absolute values. So, a and d are the correct answers.

6. a. Predecessor of −8 = −9; Successor of −8 = −7

b. Predecessor of −26 = −27; Successor of −26 = −25

c. Predecessor of −38 = −39; Successor of −38 = −37

d. Predecessor of 45 = 44; Successor of 45 = 46

7. a. +8 is larger than –16. True

b. +16 is smaller than +8. False

c. –8 is larger than +16. False

d. +16 is smaller than –8. False

8. The integers between −5 and 0 are … So, no positive integers lie between −5 and 0.

9. a. Ascending order of –25, –65, 28, 63, 100 = –65, –25, 28, 63, 100

b. Ascending order of –22, –18, –15, 16, 36 is already arranged in ascending order.

c. Ascending order of 29, 15, –9, –16, –32 = −32, −16, −9, 15, 29

d. Ascending order of –32, –17, –19, 42, 48 = –32, –19, –17, 42, 48. So, the set of integers written in ascending order is b) –22, –18, –15, 16, 36.

10. a. –25 + 36 = 11

b. –142 + (–48) = −190

c. –157 + 96 = −61

d. 452 + –152 = 300

11. Predecessor of −526 = −527, successor of 658 = 659 659 – (−527) = 659 + 527 = 1186

12. Answers may vary. Sample answer:

Three integers with different signs whose difference is –48 can be: −25, +42 and −65

13. Numbers smaller than −858 but greater than −861 = −859, −860 −859 is the odd number smaller than −858 but greater than −861.

14. The temperature of liquid = 78°C

Dropped temperature = –114°C

Difference in temperatures = 78°C – (–114°C) = 78°C + 114°C = 192°C

15. Calories burnt after working out on a treadmill = −480

Calories burnt after skipping = −260

Total calories burnt = −480 + (−260) = −740

Calories indulged with sweet = 500

Calories lost or gained = −740 + 500 = −240

As the answer has a negative sign, she lost 240 calories.

16. Initial temperature = 132℉

Temperature after drop = –250°F

Difference between the temperatures = 132℉ – (−250℉) = 132℉ + 250℉ = 382℉

17. Initial balance in the account = ₹−125

Balance after adding ₹1500 = ₹−125 + ₹1500 = ₹1375

Balance after purchasing a dress worth ₹1000 = ₹1375 − ₹1000 = ₹375

18. Number of correct answers = 40

Marks for correct answer = 40 × 6 = 240

Number of incorrect answers = 6

Marks for incorrect answer = 6 × −1 = −6

Total marks obtained = 240 + (−6) = 240 – 6 = 234

So, Manoj obtained 234 marks in the test.

Challenge

1. A – D = −1400 − 306 = −1706

C – B = 125 – (−300) = 125 + 300 = 425

D – E = 306 – 782 = −476

C – D = 125 – 306 = −181

A – E = − 1400 – 782 = −2182

Descending order = (C – B), (C – D), (D – E), (A – D), (A – E)

2. Assertion: On a number line, 3 and −3 are equidistant from 0.

Conclusion: While both statements are true, the reason does not explain the assertion. Therefore, option b is correct.

Case Study

1. The average temperature of Qatar = 28.02°C The average temperature of Russia = –3.79°C Since, 28.02°C > –3.79°C

The average temperature of Qatar is greater than the average temperature in Russia. Thus, option c is correct.

2. Since, −18.68°C < −3.79°C < 7.44°C < 25.44°C < 28.02°C

So, arranging the countries in ascending order of the average temperature: Greenland, Russia, Austria, Brazil, Qatar

3. Russia is warmer than Greenland by 22.47°C −3.79°C – (−18.68°C) = −3.79°C + 18.68°C = 14.89°C

4. It gets warmer as the temperature rises because the energy and heat in the environment increases.

Chapter 7

Let's Warm-up

This is true because both numbers are the same distance from 0, but in opposite directions.

Reason: The absolute value of both 4 and −4 is the same. Since, |4| = 4 and |–4| = 4

This is also true.

Do It Yourself 7A

1. a. Total parts = 4

Shaded parts = 3 Fraction = 3 4 b. Total parts = 16 Shaded parts = 6 Fraction = 6 16

c. Total parts = 20

Shaded parts = 10 Fraction = 10 20 d. Total parts = 9 Shaded parts = 5 Fraction = 5 9

2. Answers may vary. Sample answer: a. b. c. d.

3. Proper fractions: 4 5 , 1 22 , 51 89 , 4 9

Improper fractions: 6 4 , 47 14 , 16 3 , 15 14

Mixed fractions: 3 1 5 , 4 2 5 , 6 7 8 , 1 1 3

c. 3 4 6 = 3 2 3

The whole part is the same, so we can directly compare the proper fraction.

4 × 3 = 12 and 6 × 2 = 12

b. 14 11

c. 23 7

d. 11 8 0 1 2 1 8 1

5. a. 5 7 and 3 7

0 1 2 3 7 5 7

b. 2 8 and 6 8 0 1 2 2 8 6 8

c. 7 8 and 11 14

d. 11 12 > 12 15 11 × 15 = 165 and 12 × 12 = 144

165 > 144

Thus, 11 12 > 12 15

12 = 12

Thus, 3 4 6 = 3 2 3

7. a. 4 19 , 6 19 , 8 19 , 7 19

Since 4 < 6 < 7 < 8

Thus, 4 19 < 6 19 < 8 19 < 7 19

b. 15 28 , 4 14 , 3 7 , 18 28

Converting all the fractions into like fractionsLCM of 28, 14, 7, 28 is 28.

4 14 × 2 2 = 8 28

3 7 × 4 4 = 12 28

Since the denominators are same, compare the numerators and order the fractions.

8 < 12 < 14 < 15

So, 8 28 < 12 28 < 14 28 < 15 28

Thus, 4 14 < 3 7 < 14 28 < 15 28

c. 1 3 , 4 18 , 6 9 , 21 27

Converting all the fractions into like fractionsLCM of 3, 18, 9, 27 is 54.

LCM of 8 and 14 is 56.

So, 77 749 88756

114 11 44 1414456 × == × × == × 77 749 88756 114 11 44 1414456 × == × × == ×

d. 4 5 and 12 20

Since, 49 > 44 , then, 77 749 88756 114 11 44 1414456 × == × × == × > 77 749 88756 114 11 44 1414456 × == × × == ×

LCM of 5 and 20 is 20.

So, × == × 44416 55420

Since, 16 > 12 , then, × == × 44416 55420 > 12 20

6. a. 2 1 2 < 2 4 7

The whole part is the same, so we can directly compare the proper fraction.

1 × 7 = 7 and 2 × 4 = 8

7 < 8

Thus, 2 1 2 < 2 4 7 b. 8 7 > 7 8 8 × 8 = 64 and 7 × 7 = 49 64 > 49

Thus, 8 7 > 7 8

1 3 = 1 3 × 18 18 = 18 54

4 18 = 4 18 × 3 3 = 12 54

6 9 = 6 9 × 6 6 = 36 54

21 27 = 21 27 × 2 2 = 42 54

Since the denominators are same, compare the numerators and order the fractions.

12 < 18 < 36 < 42

So, 12 54 < 18 54 < 36 54 < 42 54

Thus, 4 18 < 1 3 < 6 9 < 21 27

d. 7 8 , 1 2 , 3 4 , 21 16

Converting all the fractions into like fractionsLCM of 8, 2, 4, 16 is 16.

7 8 × 2 2 = 14 16

1 2 × 8 8 = 8 16

3 4 × 4 4 = 12 16

Since the denominators are same, compare the numerators and order the fractions.

8 < 12 < 14 < 21

So, 8 16 < 12 16 < 14 16 < 21 16

Thus, 1 2 < 3 4 < 7 8 < 21 16

8. Fraction of students passed in School A = 480 500

Fraction of students passed in School B = 550 600

LCM of 500 and 600 is 3000.

480 500 × 6 6 = 2880 3000

550 600 × 5 5 = 2750 3000

Since, 2880 3000 > 2750 3000

Thus, 480 500 > 550 600

In School A, a greater fraction of students passed.

9. Answers may vary. Sample answer:

10. Lengths of clothes purchased by Sana = 2 1 4 , 2 1 3 , 2 3 4 , 2 1 8

Since the whole part is the same, we will compare the proper fractions.

LCM of 4, 3, and 8 is 24.

1 4 × 6 6 = 6 24

1 3 × 8 8 = 8 24

3 4 × 6 6 = 18 24 1 8 × 3 3 = 3 24

Thus, 18 24 > 8 24 > 6 24 > 3 24

2 3 4 > 2 1 3 > 2 1 4 > 2 1 8

11. Rounds covered by Jacky = 5 8

Rounds covered by Pritam = 7 12

LCM of 8 and 12 is 24.

5 8 × 3 3 = 15 24

7 12 × 2 2 = 14 24

Since 15 > 14

Thus, 5 8 > 7 12

Hence, Jacky covers a longer distance than Pritam.

Challenge

Answer may vary. Sample answer:

Make the first cut by slicing the brownie in half width wise, then cut the brownie into quarters (4 pieces) using the remaining 2 cuts – one horizontally down the centre of the brownie and the

other vertically down the centre of the brownie. This will leave you with 8 pieces (or slices) of brownie.

2nd cut

Do It Yourself 7B

1. a. 15 4 b. 38 7 3 4 1 5 – 1 2 3 5 7 3 8 – 3 5 3

Thus, 15 4 = 3 3 4 Thus, 38 7 = 5 3 7

c. 11 1 8 = (11 × 8) + 1 8 = 89 8 d.

2. a. HCF of 12 and 15 is 3.

Divide the numerator and the denominator by 3. 12 15 ÷ 3 3 = 4 5

b. HCF of 14 and 28 is 14.

Divide the numerator and the denominator by 14. 14 28 ÷ 14 14 = 1 2

c. HCF of 6 and 28 is 2.

Divide the numerator and the denominator by 2. 6 28 ÷ 2 2 = 3 14

d. HCF of 16 and 144 is 16.

Divide the numerator and the denominator by 16. 16 144 ÷ 16 16 = 1 9

3. a. 4 5 and 12 15

4 × 15 = 60; 5 × 12 = 60

So, 4 × 15 = 5 × 12 Thus, 4 5 and 12 15 are equivalent.

b. 1 3 and 5 21

1 × 21 = 21; 3 × 5 = 15

1 × 21 ≠ 3 × 5

Thus, 1 3 and 5 21 are not equivalent.

c. 7 8 and 14 24

7 × 24 = 168; 8 × 14 = 112

7 × 24 ≠ 8 × 14

Thus, 7 8 and 14 24 are not equivalent.

d. 2 9 and 12 54

2 × 54 = 108; 9 × 12 = 108

2 × 54 = 9 × 12

Thus, 2 9 and 12 54 are equivalent

4. Answers may vary. Sample answers:

a. 4 5 × 2 2 = 8 10 4 5 × 3 3 = 12 15

b. 3 7 × 2 2 = 6 14 3 7 × 3 3 = 9 21

c. 36 48 ÷ 2 2 = 18 24 36 48 ÷ 3 3 = 12 16 d. 228 144 ÷ 2 2 = 114 72 228 144 ÷ 3 3 = 76 48

5. a. 5 9 × 9 9 = 45 81 b. 17 19 × 5 5 = 85 95

c. 18 24 ÷ 6 6 = 3 4 d. 36 72 ÷ 12 12 = 3 6

6. Length of the small intestine = 38 5 m 7

5 3 38 35

Length as a mixed number = 3 7 5 m

7. Total number of cookies baked = 100

Number of siblings = 3

Share of each sibling = 100 3 3 3

3 1 0 0 – 9 1 0 – 9 1

Thus, 100 3 = 33 1 3

Share of each sibling expressed as a mixed number = 33 1 3

8. Number of fruits Riya has = 24

Number of fruits she gave to her friend = 10

Number of fruits she gave to her sister = 10

Number of fruits left with Riya = (24 − (10 + 10)) = 4

Fraction of fruits left with Riya = 4 24 = 1 6

Riya is left with 1 6 fraction of fruits.

9. Number of slices of the cake baked by Eva = 8

Number of slices given away by Eva = 3

Number of slices left with Eva = 5

Fraction of cake left with Eva = 5 8

Number of slices of the cake baked by Sarah = 12

Number of slices given away by Sarah = 5

Number of slices left with Sarah = 7

Fraction of cake left with Sarah = 7 12

LCM of 8 and 12 is 24.

5 8 × 3 3 = 15 24

7 12 × 2 2 = 14 24

Since 15 > 14, thus, 15 24 > 14 24

Therefore, 5 8 > 7 12

Hence, Eva had the greater fraction of her cake left.

Challenge

1. a. The numerator is 3 less than twice the denominator. Let us call the denominator x and the numerator y So, y = 2x − 3

b. When you add 1 to both the numerator and the denominator, the fraction becomes 2 3

So, if we add 1 to the numerator and denominator, the new fraction is: (1)2 13 y x + = +

Now, cross-multiply to solve for y and x:

3 � (y + 1) = 2 � (x + 1)

3y + 3 = 2x + 2

3y − 2x = 2 − 3 = −1

We know y = 2x − 3

So, ×−−=−

6921

621910

= 3(23)21

48 xx xx xx x

Dividing by 4: x = 2

Now that we know x = 2, we can find y using y = 2x − 3: y = 2 � 2 − 3 = 4 − 3 = 1

Therefore, the fraction is 1 2

2. Since = 305 549 and = 455 819

Fraction shown in the figure = 4 9

Hence, to make the picture equivalent to these fractions, we would need to shade one more box.

Do It Yourself 7C

1. a. 1 7 + 2 7 = 1 + 2 7 = 3 7 b. 2 1 3 + 4 2 3 = 6 + 3 3 = 7 c. 3 7 + 2 14

LCM of 7 and 14 is 14. 3 7 × 2 2 = 6 14 6 14 + 2 14 = 8 14 = 4 7

d. 2 9 10 + 3 11

2 9 10 = (2 × 10) + 9 10 = 29 10

LCM of 10 and 11 is 110. 29 10 × 11 11 = 319 110

3 11 × 10 10 = 30 110

319 110 + 30 110 = 349 110 = 3 19 110

e. 5 2 3 + 2 1 3

Adding the wholes = 5 + 2 = 7

Adding the proper fraction = 2 3 + 1 3 = 3 3 = 1

7 + 1 = 8

f. 9

3 5 + 6 2 5

Adding the wholes = 9 + 6 = 15

Adding the proper fraction

= 3 5 + 2 5 = 5 5 = 1

15 + 1 = 16

2. a. 5 17 –2 17 = 5 – 2 17 = 3 17

b. 3 11 15 – 1 2 15 113151156 3 151515 2115217 1 151515 561739393133 =2 15151515355 ×+ = = ×+ =−= ÷

c. 9 13 –1 2

LCM of 2 and 13 is 26.

9 13 × 2 2 = 18 26

1 2 × 13 13 = 13 26

18 26 –13 26 = 5 26

d. 2 5 7 – 1 3 14

2 5 7 = (2 × 7) + 5 7 = 19 7

1 3 14 = (1 × 14) + 3 14 = 17 14

LCM of 7 and 14 is 14.

19 7 × 2 2 = 38 14

38 14 –17 14 = 21 14 = 3 2

e. 7 4 9 – 4 7 12

= (7 × 9) + 4 9 = 67 9

= (12 × 4) + 7 12 = 55 12

LCM of 9 and 12 is 36. 67 9 × 4 4 = 268 36

55 12 × 3 3 = 165 36

268 36 –165 36 = 103 36 = 2 31 36

f. 4 3 11 –11 22

4 3 11 = (4 × 11) + 3 11 = 47 11

LCM of 11 and 22 is 22.

47 11 × 2 2 = 94 22

32 9 –21 10 = 320 90 –189 90 = 131 90 = 1 41 90

We get 1 41 90

4. Fraction of conifers = 1 4

94 22 –11 22 = 83 22 = 3 17 22 3. 4 1 5 – 2 1 10 = 21 5 –21 10 = 42 10 –21 10 = 21 10 8 2 3 – 5 1 9 = 26 3 –46 9 = 78 9 –46 9 = 32 9

Fraction of deciduous = 1 4

Total population that are either conifers or deciduous = +== 1121 4442

Hence, 1 2 of the trees are either conifers or deciduous.

5. Weight of the empty box = 2 6 7

Weight of the iron pan inside the box = 5 2 3

2 6 7 + 5 2 3 = 20 7 + 17 3

= 60 21 + 119 21 = 179 21

Total weight = 8 11 21 kg

The total weight of the box is 8 11 21 kg.

6. Amount of sugar used in the first batch = 3 5 cups

Amount of sugar used in the second batch = 1 5 cups

Total sugar used for both the batches = 3 5 + 1 5 = 4 5 cups

The total sugar used for both the batches together = 4 5 cups

7. Fraction of cookies given to Priya’s sister = 3 5

Fraction of cookies given to the neighbours = 1 4

a. Fraction of cookies given away = 3 5 + 1 4 = 12 20 + 5 20 = 17 20

b. Fraction of cookies left with Priya = 1 – 17 20 = 3 20

Challenge

1. Fraction of:

Oxygen atoms = 1 12 ; Nitrogen atoms = 1 6 ; Hydrogen atoms = 5 12

Sum = ++=++= 1151258 1261212121212 ++=++= 1151258 1261212121212

Carbon atoms = −=−== 812841 1 121212123 −=−== 812841 1 121212123

Fraction of atoms of caffeine that are oxygen, nitrogen or carbon = ++ 111 1263 1247 = 12121212 ++=

Do It Yourself 7D

1. a. 3 15 × 2 15

= 3 × 2 15 × 15 = 6 225 = 2 75

b. 3 5 × 2 9

= 6 45 = 2 15

c. 9 12 × 3 9 = 27 108 = 1 4

d. 1 1 2 × 2 1 2

= 3 2 × 5 2 = 15 4 = 3 3 4

e. 5 1 3 × 4 2 3

= 16 3 × 14 3 = 224 9 = 24 8 9

f. 1 1 3 × 2 1 9

= 4 3 × 19 9 = 76 27 = 2 22 27

2. a. The reciprocal of 17 6 is 6 17

b. The reciprocal of 8 15 is 15 8

c. The reciprocal of 11 18 is 18 11

d. The reciprocal of 5 is 1 5

e. The reciprocal of 1 9 is 9.

f. The reciprocal of 3 7 is 7 3

3. a. 10 15 ÷ 12 15

= 10 15 × 15 12

= 150 180 = 5 6

b. 14 12 ÷ 10 22

= 14 12 × 22 10

= 77 30 = 2 17 30

c. 3 9 10 ÷ 1 1 2 = 39 10 ÷ 3 2 = 39 10 × 2 3

= 13 5 = 2 3 5

d. 1 1 2 ÷ 2 1 2

= 3 2 ÷ 5 2

= 3 2 × 2 5 = 3 5

e. 5 1 3 ÷ 4 2 3

= 16 3 ÷ 14 3 = 16 3 × 3 14

= 8 7 = 1 1 7

f. 3 4 5 ÷ 1 3 10

= 19 5 ÷ 13 10 = 19 5 × 10 13

= 38 13 = 2 12 13

4. Fraction of field ploughed by Ananya = 9 12

Fraction of field ploughed by Atif = 1 3 × 9 12 = 3 12 = 1 4

Thus, Atif ploughed 1 4 of the total field.

5. Total raisins Maya has = 75 g

Fraction of raisins used by her = 1 5

The amount of raisins used by Maya = 1 5 × 75 = 15 g

6. Total flour Emma has = 4 1 2 cups = 9 2 cups

Flour needed for one batch of cream rolls = 2 3 cups

Number of batches Emma can make = 9 2 ÷ 2 3

= 9 2 × 3 2 = 27 4 = 6 3 4

Emma can make 6 batches of cream rolls and 3 4 cup will be left over.

7. Perimeter = 2 3 4 cubits

So, 3 � side = 2 3 4 cubits = 11 4 cubits

Side = 11 4 � 3 = 11 4 � 1 3 = 11 12

Length of each side = 11 12 cubits

Challenge

1. Answers may vary. Sample answer:

A rectangular grid represents a garden divided into 24 equal sections. 4 6 of the garden is planted with sunflowers, and onethird of the garden is planted with roses. What fraction of the garden is planted with both sunflowers and roses?

4 6 � 1 3 = 4 18

Chapter Checkup

1. a. 10 1 2 = (10 × 2) + 1 2 = 21 2

b. 5 2 3 = (5 × 3) + 2 3 = 17 3

c. 4 8 23 = (23 × 4) + 8 23 = 100 23

d. 1 7 8 = (1 × 8) + 7 8 = 15 8

2. a. 15 4

b. 43 5 3

4 1 5 – 1 2 3 8 5 4 3 – 4 0 3

Thus, 15 4 = 3 3 4 Thus, 43 5 = 8 3 5

c. 146 7 d. 87 17 2 0 7 1 4 6 – 1 4 0 0 6 5 1 7 8 7 – 8 5 2

Thus, 146 7 = 20 6 7 Thus, 87 17 = 5 2 17

3. Answers may vary. Sample answers:

a. 5 7 × 3 3 = 15 21

5 7 × 2 2 = 10 14

5 7 × 4 4 = 20 28

b. 2 9 × 3 3 = 6 27 2 9 × 2 2 = 4 18 2 9 × 4 4 = 8 36 c. 11 121 × 3 3 = 33 363 11 121 × 2 2 = 22 242 11 121 × 4 4 = 44 484 d. 4 5 × 3 3 = 12 15 4 5 × 2 2 = 8 10 4 5 × 4 4 = 16 20

4. a. HCF of 32 and 56 is 8.

Divide the numerator and the denominator by 8

32 56 ÷ 8 8 = 4 7

b. HCF of 45 and 125 is 5.

Divide the numerator and the denominator by 5

45 125 ÷ 5 5 = 9 25

c. HCF of 66 and 94 is 2.

Divide the numerator and the denominator by 2

66 94 ÷ 2 2 = 33 47

d. HCF of 66 and 94 is 2.

Divide the numerator and the denominator by 2

62 134 ÷ 2 2 = 31 67

5. a. 21 3 and 8 1 21 × 1 =21; 3 × 8 = 24 21 ≠ 24

Thus, the fractions are not equivalent.

b. 54 9 and 2 1 3

2 1 3 = 7 3

54 × 3 = 162; 9 × 7 = 63

162 ≠ 63

Thus, the fractions are not equivalent.

c. 3 1 2 and 13 5

3 1 2 = 7 2;

7 × 5 = 35; 2 × 13 = 26

35 ≠ 26

Thus, the fractions are not equivalent.

d. 5 4 5 and 35 4

5 4 5 = 29 5

29 × 4 = 116; 35 × 5 = 175

116 ≠ 175

Thus, the fractions are not equivalent.

6. a. 3 5 × 10 15 = 3 × 10 5 × 15 = 30 75 = 2 5

b. 50 33 ÷ 10 22

= 50 33 × 22 10

= 1100 330 = 10 3 = 3 1 3

c. 1 1 9 × 18 36

= 10 9 × 18 36

= 10 × 18

9 × 36 = 180 324 = 5 9

d. 2 9 27 ÷ 1 1 157

= 63 27 ÷ 58 57

= 63 27 × 57 58 = 3591 1566 = 2 17 58

7. a. Difference: 8 3 8 – 3 1 4

= 67 8 –13 4 = 67 8 –26 8 = 41 8

Sum: 2 1 4 + 1 2 15 = 9 4 + 17 15

= 135 60 + 68 60 = 203 60

To compare, find a common denominator. LCM of 8 and 60 is 240.

41 8 × 30 30 = 1230 240

203 60 × 4 4 = 812 240

Since 1230 > 812, hence, the difference of 8 3 8 and 3 1 4 is more than the sum of 2 1 4 and 1 2 15 .

b. The product of 1 2 3 and 4 5 = 5 3 × 4 5 = 20 15 = 4 3

Sum of 1 4 and 2 4 5 = 1 4 + 14 5 = 5 20 + 56 20 = 61 20

LCM of 3 and 20 is 60.

4 3 × 20 20 = 80 60 ; 61 20 × 3 3 = 183 60

Since 183 > 61, sum of 1 4 and 2 4 5 is greater than the product of 1 2 3 and 4 5

c. The product of 3 and 4 5 = 12 5

The sum of 1 3 and 1 4 = 7 12

12 5 + 7 12 = 144 60 + 35 60 = 179 60

d. 1 5 of a dozen = 1 5 × 12 = 12 5

10 dozen = 10 × 12 = 120

8. Vitamin C in one tablet = 1 4 grams

Vitamin C in 1 2 2 grams = ×=×= 11155 2 42428 grams

Hence, Sunny took 5 8 grams of vitamin C today.

9. Amount of sugar Shweta has = 4 5 kg

Sugar used to make sweet dish = 3 4 kg

Sugar left = 4 5 –3 4 = 16 20 –15 20 = 1 20 kg

Shweta is left with 1 20 kg of sugar.

10. Total length of the cloth = 40 m

Cloth used for curtains = 2 5 m

Cloth used for bedsheet = 3 3 4 m

Total cloth used = 2 5 + 3 3 4

= 2 5 + 15 4

= 8 20 + 75 20 = 83 20 m

Total cloth left = 40 – 83 20 = 800 20 –83 20 = 717 20 m = 35 17 20 m

Radha is left with 35 17 20 m of cloth.

11. Answer may vary. Sample answer:

2. Assertion: 21 84 and 12 56 are equivalent fractions.

÷= 21211 84214

12 56 ÷ 4 4 = 3 14

The fractions are not equivalent.

Reason: Two fractions a b and c d , (b, d = 0) are equivalent if their simplest form is the same. This statement is true as it correctly describes the condition for two fractions to be equivalent.

Hence, option d. Assertion is false, but the Reason is true.

Case Study

1. Total training time = 5 12

Time spent on martial arts = ×= 155 41248 So, option b is correct.

2. Time spent on dance = ×= 155 31236 So, option c is correct.

3. Time spent on yoga = −−=−−= == 55560152025 251 of 24 hourshours4 124836144144144144 6

55560152025 251 of 24 hourshours4 hours. 124836144144144144 6 6

== 55560152025 251 of 24 hourshours4 hours. 124836144144144144 6 6 of the day. Since a full day is 24 hours, the number of hours Ravi spends on yoga is: 25 144 × 24 = 600 144 = 25 6 = 4 1 6 hours.

1 5 of a chocolate is eaten by Rahul. He gives 1 2 of the remaining chocolate to his sister. How much chocolate is left with Rahul?

Challenge

1. For every 4 tote bags of type X sold, they would donate 5 12 of the proceeds.

Price of each tote bag of type X = ₹400

Price of 4 tote bag of type X = ₹400 × 4 = ₹1600

Donation made per 4 tote bags = ×=×=  552000 1600400 123 3

×=×=  552000 1600400 123 3 = ₹ ×=  242000 43

Number of tote bags sold = 24

Donation made on 24 bags = ×=  242000 43 ₹4000

For every 2 tote bags of type Y sold, they would donate 2 5 of proceeds.

Price of each tote bag of type Y = ₹600

Price of 2 tote bag of type Y = ₹600 × 2 = ₹1200

Donation made per 2 tote bags = ×=  2 1200480 5 ₹480

Number of tote bags sold = 18

Donation made on 18 bags = ×=  18 480 2 ₹4320

Total donation = ₹4000 + ₹4320 = ₹8320

4. Time spent on martial arts = 5 48 × 5 48 × 3 3 = 15 144

Time spent on dance = = 5

Time spent on yoga = 25 144

Ascending order: Martial arts < Dance < Yoga 5. Answers may vary.

Chapter 8

Let’s Warm-up

1. 15.61 > 15.6 2. 14.5 = 14.500 3. 15.33 < 15.4 4. 17.32 > 17.3 5. 16.5 > 16.45

Do It Yourself 8A

4. a. 0.24 = 24 100 = 6 25

b. 0.59 = 59 100

c. 0.65 = 65 100 = 13 20

d. 0.125 = 125 1000 = 1 8

e. 0.225 = 225 1000 = 9 40

f. 0.512 = 512 1000 = 64 125

5. There are 5 divisions between any two whole numbers. So, each division here between two whole numbers is 0.2.

A represents 0.8

B represents 1.4

C represents 3.4

D represents 4.6

6. a. 3

8 has 8 as the denominator.

8 × 125 = 1000

Multiply the denominator by 125 to convert 3 8 into a decimal number. The decimal equivalent is 0.375.

b. 7 4 has 4 as the denominator.

4 × 25 = 100

Multiply the denominator by 25 to convert 7 4 into a decimal number. The decimal equivalent is 1.75.

c. 13 2 has 2 as the denominator.

2 × 5 = 10

Multiply the denominator by 5 to convert 13 2 into a decimal number. The decimal equivalent is 6.5.

d. 37 25 has 25 as the denominator.

25 × 4 = 100

Multiply the denominator by 4 to convert 37 25 into a decimal number. The decimal equivalent is 1.48.

e. 12 5 has 5 as the denominator.

5 × 2 = 10

Multiply the denominator by 2 to convert 12 5 into a decimal number. The decimal equivalent is 2.4.

f. 89

40 has 40 as the denominator.

40 × 25 = 1000

Multiply the denominator by 25 to convert 89 40 into a decimal number. The decimal equivalent is 2.225.

f. 25.06 = 25 + 0.06 = 25 + 6 100 = 25 + 3 50 = 25 3 50

8. a. 1.54 = 1.540

So, 1.540 and 15.021 are like decimals.

b. 54 = 54.000

So, 54.000 and 48.021 are like decimals.

c. 1.1 = 1.10

So, 1.10 and 4.65 are like decimals.

d. 97 = 97.000

18.054 and 97.000 are like decimals.

9. a. 15.4, 15, 15.14, 15.41

The tens and the ones place are the same.

Compare the tenths place.

4 > 1

Compare the hundredths place in 15.4 and 15.41

1 > 0

Thus, 15.41 is the greatest number.

b. 178.1, 178.2, 1.78, 178.15

The hundreds, tens and ones place are the same in three numbers.

Compare the tenths place.

2 > 1

Thus, 178.2 is the greatest number.

c. 12.810, 12.82, 12.815, 12.825

The tens, ones and tenths place are the same in all the numbers.

Compare the hundredths place.

2 > 1

Compare the thousandths place in 12.82 and 12.825

5 > 2

Thus, 12.825 is the greatest number.

d. 15.151, 15.015, 15.51, 15.5

The tens and ones place are the same in all.

Compare the tenths place.

5 > 1 > 0

Compare the hundredth place in 15.51 and 15.5

1 > 0

Thus, 15.51 is the greatest number.

10. a. 7.3, 8.37, 7.23, 8.32

Compare the ones place.

8 > 7

Compare the tenths place in 7.23, 7.3 and 8.37, 8.32

2 < 3

So, 7.23 < 7.3

3 = 3

Compare the hundredths place in 8.37 and 8.32

2 < 7

So, 8.32 < 8.37

Thus, 7.23 < 7.3 < 8.32 < 8.37.

b. 58.37, 58.73, 58.45, 58.54

The tens and ones place is the same in all the numbers.

Compare the tenths place.

3 < 4 < 5 < 7

Thus, 58.37 < 58.45 < 58.54 < 58.73.

c. 97.08, 97.18, 97.2, 97.8

The tens and ones place is the same in all the numbers.

Compare the tenths place.

0 < 1 < 2 < 8

Thus, 97.08 < 97.18 < 97.2 < 97.8.

d. 18.1, 18.101, 18, 18.11

The tens and ones place are the same in all the numbers.

Compare the tenths place.

1 > 0

Compare the hundredths place in 18.1, 18.101 and 18.11

1 > 0

Thus, 18 < 18.1 < 18.101 < 18.11.

11. a. 3 kg 68 g = 3 kg + 68 1000 kg

= 3 kg + 0.068 kg = 3.068 kg

14 kg 50 g = 14 kg + 50 1000 kg

= 14 kg + 0.05 kg = 14.05 kg

5 kg 5 g = 5 kg + 5 1000 kg

= 5 kg + 0.005 kg = 5.005 kg

725 g = 725 1000 kg = 0.725 kg

45 g = 45 1000 kg = 0.045 kg

b. 4 km 15 m = 4 km + 15 1000 km

= 4 km + 0.015 km = 4.015 km

8 km 40 m = 8 km + 40 1000 km

= 8 km + 0.04 km = 8.04 km

3 km 4 m = 3 km + 4 1000 km

= 3 km + 0.004 km = 3.004 km

750 m = 750 1000 km = 0.75 km

15 m = 15 1000 km = 0.015 km

12. The length of the cloth bought from the first shop

= 5 m 15 cm = 5 m + 15 100 m = 5 m + 0.15 m = 5.15 m

The length of the cloth bought from the second shop = 5.25 m 5.15 < 5.25

Thus, Reena bought less cloth from the first shop.

13. 33

14. The lengths of the three pieces of cloth = 1.56 m, 21.5 m and 14.5 m

In words, 1.56 = one point five six or one and fifty-six hundredths

21.5 = twenty-one point five or twenty-one and five tenths

14.5 = fourteen point five or fourteen and five tenths

In expanded form,

1.56 = 1 + 0.5 + 0.06 or 1 + 5 10 + 6 100

21.5 = 20 + 1 + 0.5 or 20 + 1 + 5 10

14.5 = 10 + 4 + 0.5 or 10 + 4 + 5 10

15. The fraction of students that participated in the discussion = 2 5

The fraction of students who did not participate = 1 − 2 5 = 5 5 − 2 5 = 3 5

3 5 as a decimal = 3 5 × 2 2 = 6 10 = 0.6

16. The distance Kunal swam on day 1 = 1.58 km

The distance Kunal swam on day 2 = 2.53 km

The distance Kunal swam on day 3 = 2.39 km

The distance Kunal swam on day 4 = 3.13 km

1.58 < 2.39 < 2.53 < 3.13

Thus, Kunal swam the most on day 4.

17. 2.54 L, 1.75 L, 2.45 L, 2.3 L

Compare the ones digit, 2 > 1, so, 1.75 L is the smallest.

Compare the tenths place in 2.54, 2.45, 2.3

5 > 4 > 3

So, 2.54 > 2.45 > 2.3

Thus, 2.54 L > 2.45 L > 2.3 L > 1.75 L

Challenge

1. Tablet Screen Size (inches) A 12.1 B 10.3 C 8.7 D 7.8

Arranging the screen size in descending order:

12.1 > 10.3 > 8.7 > 7.8

A > B > C > D

Vidhi’s tablet has the greatest display size.

So, Vidhi's tablet is A (12.1 inches).

Given that Ansh’s tablet’s display size is greater than Sejal’s but less than Shiva’s.

From the remaining sizes, we have 10.3, 8.7 and 7.8 inches.

Ansh must have tablet C (8.7 inches) because it is larger than Sejal’s tablet D (7.8 inches) and smaller than Shiva’s tablet B (10.3 inches).

So, Ansh’s tablet screen size is 8.7 inches.

Do It Yourself 8B

1. a. 5.7 + 4.6 + 8.97 + 5.35 b. 14.2 + 15.3 + 14.51 + 18.33

c. 1.1 + 2.22 + 3.333 + 4.444

T O . t h th 1 1

1 . 1 0 0 2 . 2 2 0 3 . 3 3 3 + 4 4 4 4 1 1 0 9 7

2. a. 15.4 − 12.9 b. 14.51 − 12.79 T O t 4 14 1 5 4 1 2 9

2 5

c. 1.215 − 0.986

O t h th 11 10

0 1 0 15

1 . 2 1 5

0 . 9 8 6 0 2 2 9

3. a. 96.321 + 53.412 = 149.733 149.733 > 147.733

b. 148 − 20.35 = 127.65 127.65 = 127.65

c. 851.02 + 25.999 = 877.019 877.019 < 879.019

4. a. 53.64 + 18.3 + 51.97

H T O t h 1 1 1 1

5 3 . 6 4 1 8 3 0

+ 5 1 9 7 1 2 3 9 1

Thus, 53.64 + 18.3 + 51.97 = 123.91

b. 17.9 + 97.74 + 56.47

H T O . t h 1 2 2 1 1 7 9 0

9 7 . 7 4

+ 5 6 . 4 7

1 7 2 . 1 1

Thus, 17.9 + 97.74 + 56.47 = 172.11

c. 814.64 − 15.903 + 12.17

Let us first find 814.64 − 15.903

H T O . t h th 10 13

7 0 3 16 3 10

8 1 4 . 6 4 0

1 5 9 0 3

7 9 8 7 3 7

Let us add 798.737 and 12.17

H T O t h th 1 1

7 9 8 7 3 7

+ 1 2 1 7 0

8 1 0 9 0 7

Thus, 814.64 − 15.903 + 12.17 = 810.907

d. 71.023 + 41.846 − 12.998

Let us first add 71.023 and 41.846

H T O . t h th

7 1 0 2 3

+ 4 1 8 4 6

1 1 2 8 6 9

Let us subtract 12.998 from 112.869

H T O . t h th 10 11 17

0 1 7 16

1 1 2 8 6 9

1 2 9 9 8

0 9 9 8 7 1

Thus, 71.023 + 41.846 − 12.998 = 99.871

e. 51.97 + 87.2 − 97.807

Let us add 51.97 and 87.2

H T O . t h 1 1

5 1 . 9 7 + 8 7 . 2 0

1 3 9 1 7

Let us subtract 97.807 from 139.17

H T O . t h th 13 8 11 6 10

1 3 9 1 7 0 + 9 7 . 8 0 7

4 1 . 3 6 3

Thus, 51.97 + 87.2 − 97.807 = 41.363

f. 35.143 − 23.5 + 64.52

Let us subtract 23.5 from 35.143

H T O t h th 8 11

3 5 . 1 4 3

2 3 5 0 0 1 1 6 4 3

Let us add 11.643 and 64.52

T O . t h th 1

1 1 . 6 4 3

+ 6 4 . 5 2 0

7 6 . 1 6 3

Thus, 35.143 − 23.5 + 64.52 = 76.163

5. The amount of rainfall on Tuesday = 3.5 mm

The amount of rainfall on Wednesday = 3.75 mm

The amount of rainfall on Thursday = 4.2 mm

The total amount of rainfall = 4 mm + 3.5 mm + 3.75 mm + 4.2 mm = 15.45 mm

6. The weight of the gold chain = 20 g 45 mg = 20 g + 45 1000 g = 20.045 g

The weight of the ring = 12.5 g

The total weight of the jewellery = 20.045 g + 12.5 g = 32.545 g

7. The distance between Ruhi’s home and school = 6.98 km

The distance between Ruhi’s new home and school = 9 km

The distance between Ruhi’s old home and new home = 9 km − 6.98 km = 2.02 km

8. The amount of money in Rajul’s bank account = ₹587.2

The amount of money deposited in his bank account = ₹300 and ₹950

The total money deposited = ₹300 + ₹950 = ₹1250

The total money in the bank account = ₹587.2 + ₹1250 = ₹1837.2

The amount of money withdrawn from the bank account = ₹450.5

The amount of money left in the bank account = ₹1837.2 − ₹450.5 = ₹1386.7

9. The amount of money spent on stationery = ₹148.6

The amount of money spent on clothes = ₹1500.5

The amount of money spent on transport = ₹238.6

The total money spent = ₹148.6 + ₹1500.5 + ₹238.6 = ₹1887.7

The total amount of money with Monica = ₹2000

The amount of money left with Monica = ₹2000 − ₹1887.7 = ₹112.3 H T O t 9 9 9

1 10 10 10 10

2 0 0 0 . 0

+ 1 8 8 7 . 7 0 1 1 2 3

10. The mass of one hydrogen atom = 1.0079 amu

The mass of two hydrogen atoms = 2 × 1.0079 = 2.0158 amu

The mass of one oxygen atom = 15.999 amu

The mass of one molecular of water = 2.0158 + 15.999 = 18.0148 amu

Challenge

1. Weight of citric acid = 32.89 grams

Weight of boric acid = 11.889 grams

Total weight = 32.89 + 11.889 = 44.779 grams

Weight on the scale = 123.03 grams; 44.779 < 123.03

Items on the scale = citric acid, boric acid and the container

Hence, the extra weight was the weight of the container.

Do It Yourself 8C

1. a. 51.2 × 4

512 × 4 = 2048

51.2 × 4 = 204.8 5 1 2 × 4

2 0 4 8

b. 12.6 × 9

126 × 9 = 1134

c. 81.7 × 11 817 × 11 = 8987

× 11 = 898.7

1 7

1 1

1 7

8 1 7 0

9 8 7 d. 123.5 × 14 1235 × 14 = 17,290 123.5 × 14 = 1729 1 2 3 5 × 1 4 4 9 4 0 + 1 2 3 5 0 1 7 2 9 0

2. a. 1.2 × 5.3 12 × 53 = 636 1.2 × 5.3 = 6.36 1 2 × 5 3 3 6 + 6 0 0 6 3 6 b. 2.6 × 23.5 26 × 235 = 6110 2.6 × 23.5 = 61.1 2 3 5 × 2 6 1 4 1 0 + 4 7 0 0 6 1 1 0

c. 12.3 × 51.31

12.6 × 9 = 113.4 1 2 6 × 9 1 1 3 4

123 × 5131 = 631113 12.3 × 51.31 = 631.113 5 1 3 1 × 1 2 3 1 5 3 9 3 1 0 2 6 2 0 + 5 1 3 1 0 0 6 3 1 1 1 3

d. 2.36 × 1.24

236 × 124 = 29264 2.36 × 1.24 = 2.9264 2 3 6

b. 191.2 ÷ 8 = 23.9 2 3 9 8 1 9 1 . 2 1 6 3 1 2 4 7 2 7 2 0 0

c. 495.6 ÷ 12 = 41.3 4 1 3 1 2 4 9 5 6 4 8 1 5 1 2 3 6 3 6 0 0

5. a. Quotient = 12.36 0 1 2 . 3 6 0 9 1 1 1 . 2 4 0

2.76

b. Quotient = 89.7

6. a. Product of 15.3 and 81.36 = 15.3 × 81.36

153 × 8136 = 1244808

15.3 × 81.36 = 1244.808 8 1 3 6 × 1 5 3 2 4 4 0 8 4 0 6 8 0 0

+ 8 1 3 6 0 0

1 2 4 4 8 0 8

b. Product of 87.64 and 23.6 = 87.64 × 23.6

8764 × 236 = 2068304

87.64 × 23.6 = 2068.304

8 7 6 4 × 2 3 6

5 2 5 8 4

2 6 2 9 2 0

+ 1 7 5 2 8 0 0

2 0 6 8 3 0 4

7. The length of the rectangular garden = 5.8 feet

The width of the rectangular garden = 3.6 feet

The area of the rectangular garden = Length × Width = 5.8 feet × 3.6 feet

58 × 36 = 2088

Area = 20.88 sq. feet

8. The quantity of milk purchased by Anuj = 3.6 gallons

1 gallons = 4 quarts

The amount of milk purchased by Anuj in quarts = 3.6 × 4 = 14.4 quarts

9. The special sauce required for 10 servings = 0.75 cups

The special sauce required for 1 serving = 0.75 ÷ 10 = 0.075

The special sauce required for 35 servings = 0.075 × 35 = 2.625 cups

Thus, 35 servings required 2.625 cups of special sauce.

10. The cost of one pencil = ₹2.5

The cost of fifty pencils = ₹2.5 × 50 = ₹125

The cost of one eraser = ₹5.6

The cost of twenty erasers = ₹5.6 × 20 = ₹112

The cost of one notebook = ₹34.55

The cost of thirty notebooks = ₹34.55 × 30 = ₹1036.5

Total money Vikas paid to the shopkeeper = ₹125 + ₹112 + ₹1036.5 = ₹1273.5

11. Answer may vary. Sample answer: Rani is preparing for a bake sale. She has 6.75 kg of flour, and each batch of cookies she makes requires 0.45 kg of flour. How many batches of cookies can Rani make with the amount of flour she has?

Challenge

1. Statement 1: Doctors recommend that sixth graders should eat about 5 ounces of protein each day. One serving of yogurt has 0.6 ounces of protein.

Statement 2: Suvarna, a sixth grader, eats 2.5 servings of yogurt each day.

Statement 1 alone tells us the recommended protein intake and the protein content of one serving of yogurt, but it does not tell us how much Suvarna eats.

Statement 2 alone tells us how many servings Suvarna eats, but it does not provide the recommended daily intake or the protein content per serving.

Together, the statements allow us to calculate that Suvarna consumes 2.5 × 0.6 = 1.5 ounces of protein per day, which is less than the recommended 5 ounces. Hence, option c is correct.

Chapter Checkup

The shaded part is 0.5.

The shaded part is 1.8.

c. The shaded part is 1.51. 1.5 1.6 1.51

3. a. 40 + 3 + 1 10 = 40 + 3 + 0.1 = 43.1

b. 900 + 50 + 4 10 + 3 100 = 900 + 50 + 0.4 + 0.03 = 950.43

c. 600 + 40 + 9 + 8 10 + 9 100 + 1 1000 = 600 + 40 + 9 + 0.8 + 0.09 + 0.001 = 649.891

4. a. 5.3 = 5 + 0.2 + 0.3 or 5 + 2 10 + 3 100

b. 12.056 = 10 + 2 + 0.05 + 0.006 or 10 + 2 + 5 100 + 6 1000

c. 507.633 = 500 + 7 + 0.6 + 0.03 + 0.003 or 500 + 7 + 6 10 + 3 100 + 3 1000

5. a. 45 1 2 = 45

Compare 1.23 with 1.2 and 1.331 with 1.303 by comparing the digit at the hundredths place.

0 < 3 0 < 3

So, 1.2 < 1.23 So, 1.303 < 1.331

Thus, 1.331 > 1.303 > 1.23 > 1.2

c. 153.32, 153.23, 152.1, 153.233

The digits at the hundreds place and tens place is the same.

Compare the digit at the ones place.

2 < 3

So, 152.1 is the smallest.

Compare the tenths digit in rest of the numbers.

2 < 3

So, 153.32 is the largest number.

Compare 153.23 and 153.233 by comparing the hundredths digit.

0 < 3

So, 153.23 < 153.233

Thus, 153.32 > 153.233 > 153.23 > 152.1

1 2 × 5 5 = 45

5 10 = 45.5

b. 145 8 = 145 8 × 125 125 = 18125 1000 = 18.125

c. 12 3 5 = 12

3 5 × 2 2 = 12

 6 10 = 12.6

6. a. 51.26 = 5126 100 = 2563 50

b. 6.814 = 6814 1000 = 3407 500

c. 12.508 = 12508 1000 = 3127 250

7. a. 15.1, 15, 15.05, 14.95

The tens place in all the numbers is the same.

Compare the digit at ones place.

4 < 5

So, 14.95 is the smallest.

Compare the tenths digit in rest of the numbers.

0 < 1.

15.1 is the largest.

Compare the hundredths digit in 15 and 15.05

0 < 5

Thus, 15.1 > 15.05 > 15 > 14.95

b. 1.23, 1.2, 1.331, 1.303

The ones place is the same in all the numbers.

Compare the digit at the tenths place.

2 < 3

c. 1.2 × 6.7

12 × 67 = 804

Thus, 1.2 × 6.7 = 8.04 1 2 × 6 7 8 4 + 7 2 0 8 0 4

d. 492.36 ÷ 6 = 82.06 0 8 2 0 6 0 6

e. 5.9 × 47.6

59 × 476 =28084

Thus, 5.9 × 47.6 = 280.84

4 7 6

× 5 9

4 2 8 4

+ 2 3 8 0 0

2 8 0 8 4

f. 14.65 × 165.7

1465 × 1657 = 2427505

Thus, 14.65 × 165.7 = 2427.505

1 4 6 5

× 1 6 5 7

1 0 2 5 5

7 3 2 5 0

8 7 9 0 0 0

+ 1 4 6 5 0 0 0

2 4 2 7 5 0 5

9. The distance jumped by Rachna = 3.6 m

The distance jumped by Nina = 3.65 m

The distance jumped by Rohini = 3.55 m

The digit at the ones place is the same.

Compare the tenths digit.

6 > 5

Compare the hundredths digit in 3.6 and 3.65

5 > 0

So, 3.65 > 3.6

Thus, Nina jumped the farthest.

10. The distance covered in the morning = 15.486 km

The distance covered in the afternoon = 8.75 km

The total distance covered = 15.486 km + 8.75 km = 24.236 km

T O t h th 1 1

1 5 4 8 6

+ 8 7 5 0

2 4 2 3 6

Thus, the cyclist covers a total distance of 24.236 km.

Water needed for 10 kilometre = 0.75 litres

Water needed per kilometre= 0.75 10 = 0.075

Water needed for 24.236 kilometre = 0.075 × 24.236 = 1.8177 litres

0 0 7 5

× 2 4 2 3 6

4 5 0 0

11. The cost of the laptop = ₹62,542.50

The amount of money saved by Bhoomi = ₹42,765.75

The total amount of money required by Bhoomi to buy the laptop = ₹62,542.50 − ₹42,765.75 = ₹19,776.75

Thus, Bhoomi needs ₹ 19,776.75 more to buy the laptop.

TT T H

12. The cost of the shirt = ₹1998.50

The cost of the pair of shoes = ₹6545.75

The total amount of money spent on shopping = ₹1998.50 + ₹6545.75.50 = ₹8544.25

The total amount of money paid = ₹10,000

The amount of money left with Himani = ₹10,000 − ₹8544.25 = ₹1455.75

13. The weight of the apples initially = 65.75 kg

The weight of the apples sold = 42.5 kg

The weight of the apples left at the store = 66.75 kg − 42.5 kg = 23.25 kg

T O t h

5 7 5

The weight of apples that is restocked at the store = 28.325 kg

The total weight of the apples at the store = 23.25 kg + 28.325 kg = 51.575 kg

Thus, the total weight of the apples at the store is 51.575 kg.

14. The total amount of money earned each hour by Sarah = ₹400.50

The number of hours worked in a week = 25.50 hours

The total amount of money earned = 25.50 × ₹400.50 = ₹10,212.75

Thus, the total money earned by Sarah over the week is ₹10,212.75.

4 0 0 5

× 2 5 5

+ 2 0 0 2 5

+ 8 0 1 0

= 1 0 2 1 2 7 5

Challenge

1. The initial cost of 100 text messages = ₹45

The cost of each message of first 100 messages = ₹0.10 per message

The total cost of 275 messages = Cost of first 100 messages + Cost of (275 − 100) messages

= Cost of first 100 messages + Cost of 175 messages

= ₹45 + (175 × ₹0.10)

= ₹45 + ₹17.5

= ₹62.5

Thus, the cost of 275 messages is ₹62.5.

2. The cost of type A toys = ₹129.90

The cost of type B toys = ₹97.50

The total toys sold = 60

The total amount of money earned = ₹7567.20

Let us say, the number of toys sold for type A are x, then the number of toys sold for type B are (60 − x).

The total revenue = Revenue from selling type A toys + Revenue from selling type B toys

7567.20 = (129.90 × x) + (97.50 × (60 − x))

7567.20 = 129.90x + 5850 − 97.50x

7567.20 − 5850 = 129.90x − 97.50x 1717.20 = 32.4x

x = 53

Number of toys of type B sold = 60 − 53 = 7

Thus, 53 type A toys were sold and 7 type B toys were sold.

3. Assertion (A): The sum of 23.56 and 78.4 is 101.96. T O . t h 1

2 3 5 6

+ 7 8 4 0

1 0 1 . 9 6

So, the assertion is correct.

Reason (R): When adding decimal numbers, the decimal points do not need to be aligned; you simply add the numbers as if they were whole numbers. No, when adding decimal numbers, the decimal points need to be aligned in such a way that they are placed in the correct place according to their place values. Thus, the assertion is true, and the reason is false. Hence, option c is correct.

Case Study

1. b. 1.52 AU

2. Distance of Mercury and Earth from the Sun = 1.000 + 0.39 = 1.39 AU O t h

0 . 3 9 + 1 0 0 1 3 9

b. 1.39 AU

3. Distance of Jupiter from the Earth = 5.20 − 1.000 = 4.20 AU O . t h 5 2 0 1 0 0 4 2 0

4. Venus (0.72 AU) < Mars (1.52 AU) < Uranus (19.22 AU) < Neptune (30.05 AU)

Chapter 9

Let’s Warm-up

1. 7 students like to have milk for breakfast.

2. Fruit is liked the least

3. Juice is liked the most

4. The total number of students who took the survey is 31. 5. 2 more students like to have poha for breakfast than fruit.

Do It Yourself 9A

1. a. Raw data is the organised form of data. False b. Arranging the numerical numbers in ascending or descending order is called an array. True

c. Five as tally marks is represented as False d. Frequency is always the same for every observation in data. False

2. a. 20 |||| |||| |||| |||| b. 27 |||| |||| |||| |||| |||| || c. 31 |||| |||| |||| |||| |||| |||| | d. 42 |||| |||| |||| |||| |||| |||| |||| |||| ||

3. Name of Mughal Emperor Number of Wars Won Babur |||

Humayun ||| Akbar ||||

Jahangir ||| Shah Jahan ||||

Aurangzeb |||||

4. Fruit Number Tally Marks Orange 7 |||| ||

a. 7 students are 12 years old.

b. 6 students are 14 years old.

c. Students that are less than 13 years old = 7 + 3 + 7 = 17

d. Students that are more than 11 years old but less than 14 years old = 7 + 7 = 14

Challenge

a. If the scale of the tally marks is changed from one tally mark representing one animal to one tally mark representing two animals, the new tally marks for oranges will be: ‘Pet Rescue Centre’: 8 animals will be represented by 4 tally marks, i.e. ||||

b. If the number of animals in ‘Animal Haven’ increases to 15 and one tally mark represents five animals, the tally marks for animals in ‘Animal Haven’ will change to 3 tally marks representing 15 animals, i.e. | = 5 animals

||| = 3 × 5 = 15 animals

Do It Yourself 9B

1. Brand A Brand B Brand C Brand D Brand E Key: = 500 soaps

2. Key: = 300 bulbs

a. The number for symbols on Tuesday = 5

The number of bulbs sold on Tuesday = 5 × 300 = 1500 bulbs

b. The number of symbols on Wednesday = 11

The number of symbols on Thursday = 10

Difference between the number of symbols on Wednesday and Thursday = 1

The number of bulbs that were sold more on Wednesday than that on Thursday = 1 × 300 = 300 bulbs.

c. The number of bulbs sold on Monday = 8 × 300 = 2400 bulbs

The number of bulbs sold on Tuesday = 5 × 300 = 1500 bulbs

Total number of bulbs sold on Monday and Tuesday together = 2400 + 1500 = 3900 bulbs

d. Day on which there are least number of symbols = Tuesday

The number of bulbs sold on Tuesday = 5 × 300 = 1500 bulbs.

e. Total number of bulbs sold in the week = (8 × 300) + (5 × 300) + (11 × 300) + (10 × 300) + (15 × 300) = 2400 + 1500 + 3300 + 3000 + 4500 = 14,700 bulbs

3. Name Population of Tigers

Ranthambore National Park

Jim Corbett National Park

Bandhavgarh National Park

Kanha National Park

Sundarbans National Park

Scale: = 20 tigers

4. = 1000 fans and = 500 fans

a. The number of symbols in May = 4 and a half

The number of fans manufactured in May = (4 × 1000) + 500 = 4000 + 500 = 4500 fans

b. The number of symbols in January = 5 and a half

The number of fans manufactured in January = (5 × 1000) + 500 = 5000 + 500 = 5500 fans

c. The month in which there are maximum number of symbols = June

The number of symbols in June = 8

The number of fans manufactured in June = 8 × 1000 = 8000 fans

d. The number of fans manufactured in April = 7 × 1000 = 7000

The number of fans manufactured in February = (6 × 1000) + 500 = 6000 + 500 = 6500

The number of fans that were manufactured more in April than in February = 7000 − 6500 = 500 fans

5. Year

2013–2014

2015–2016

2017–2018

2019–2020

2021–2022

Key: = 10 earthquake

Number of Earthquakes

6. Answer may vary Sample answer: How many more earthquakes occured in 2015–2016 than that in 2013–2014?

7. Number of shirts sold on Wednesday = 50

Number of shirts sold on Tuesday = 10 more than the number of shirts sold on Wednesday = 50 + 10 = 60

Number of shirts sold on Monday = Half of that sold on Tuesday = 60 ÷ 2 = 30

Number of shirts sold on Thursday = 10 less than the number of shirts sold on Wednesday = 50 − 10 = 40

Number of shirts sold on Friday = Two times of that the number of shirts sold on Thursday = 2 × 40 = 80

Let us draw the pictograph for the given data now.

Day Number of Shirts Sold

Monday 30

Tuesday 60

Wednesday 50

Thursday 40

Friday 80

Key: = 10 shirts

Challenge

1. The number of flowers in week 1 when 1 picture = 30 flowers are 9 × 30 = 270 flowers

The number of flowers in week 2 when 1 picture = 45 flowers are 7 × 45 = 315 flowers

The number of flowers in week 3 when 1 picture = 45 flowers are 5 × 45 = 225 flowers

The number of flowers in week 4 when 1 picture = 40 flowers are 12 × 40 = 480 flowers

The number of pictures used to represent flowers in week 1 when 1 picture = 60 flowers are 270 ÷ 60 = 4.5 pictures

The number of pictures used to represent flowers in week 2 when 1 picture = 60 flowers are 315 ÷ 60 = 5.25 pictures

The number of pictures used to represent flowers in week 3 when 1 picture = 60 flowers are 225 ÷ 60 = 3.75 pictures

The number of pictures used to represent flowers in week 4 when 1 picture = 60 flowers are 5400 ÷ 60 = 8 pictures

Do It Yourself 9C

1. a. The power supply from the generators was at its highest during the time 09:00–10:00.

b. The power supply from the generators was at its lowest during the time 08:00–09:00

Scale: 1 division = 10 families

3. Scale: 1 division = ₹1000

a. Expenditure on food = ₹7000

b. The family spends the least on clothes. Money spent on clothes = ₹6000

c. The family spends the most on rent. Money spent on rent = ₹9000

d. Total money spent by the family = ₹7000 + ₹6000 + ₹7500 + ₹9000 + ₹7750 = ₹37,250

4. a. Total number of COVID-19 vaccine doses administered in India as of June 1st = 210 million doses

b. Number of COVID-19 vaccine doses administered in India as of March 1st = 10 million doses

Number of COVID-19 vaccine doses administered in India as of April 1st = 60 million doses

The number of vaccine doses administered increased from March to April = 60 – 10 = 50 million doses

c. The number of vaccine doses administered increased from March to April = 60 – 10 = 50 million doses

The number of vaccine doses administered increased from April to May = 150 – 60 = 90 million doses

The number of vaccine doses administered increased from May to June = 210 – 150 = 60 million doses

Therefore, in May month there was the highest increase in the number of vaccine doses administered compared to the previous month

5. Answers may vary. Sample answer:

a. How many families have more than 2 members in their family?

b. How many families have less than 5 members in their family?

Challenge

1. Assertion (A): Arsenal had the smaller increase in population from 1975 to 2015 compared to Cottage and Britannia.

Increase in population of Arsenal town from 1975 to 2015 = 10,000 – 1000 = 9000

Increase in population of Cottage town from 1975 to 2015 = 18,000 – 4000 = 13,000

Increase in population of Britannia town from 1975 to 2015 = 20,000 – 5000 = 15,000

Therefore, Arsenal had the smaller increase in population from 1975 to 2015 compared to Cottage and Britannia.

So, the assertion is true.

Reason (R): The graph shows that Arsenal’s population bar increased by only one division between 1975 and 2015

The scale division used to represent Arsenal’s population in 1975 is 1 division = 1000 people whereas the Scale division used to represent Arsenal’s population in 2015 is 1 division = 5000 people. Since the scale divisions are different, we cannot compare the two divisions.

So, the reason is false.

Hence, the correct answer is option c.

Chapter Checkup

1. Transportation Tally Marks Number of People

3. Number of students whose favourite subject is Science = 10

Number of students whose favourite subject is Maths = 17

Number of students whose favourite subject is Technology = 13

Number of students whose favourite subject is English = 14

a. Maths is the most favourite subjects among the students.

b. Number of students who look like English = 10 + 4 = 14

c. Science is the least favourite subjects among the students.

d. The number of students who like Maths = 17

Total number of students = 10 + 17 + 13 + 14 = 54

Fraction of students who like Maths = 17 54

4. Scale: 1 division = 5 saplings

Number of saplings planted in Block A = 35

Number of saplings planted in Block B = 40

Number of saplings planted in Block C = 30

Number of saplings planted in Block D = 33

Number of saplings planted in Block E = 35

a. Saplings planted in block C = 30

b. Saplings planted in block D = 33

c. The maximum number of saplings are placed in block B.

d. Total number of saplings planted 35 + 40 + 30 + 33 + 35 = 173

5. Scale: 1 division = 200 sq. km

Area of Chandigarh = 100 sq. km

Area of Dadra and Nagar Haveli and Daman and Diu = 600 sq. km

Area of Lakshadweep = 50 sq. km

Area of Delhi = 1500 sq. km

Area of Puducherry = 500 sq. km

a. Delhi has the largest area.

b. Lakshadweep has the smallest area.

c. The National Capital Territory of India is Delhi. The area covered by Delhi = 1500 sq. km

d. 100 + 600 + 50 + 1500 + 500 = 2750 sq. km

6. Answers may vary. Sample answers. What is the area of Chandigarh?

7. Key: = 150 ice creams

Number of ice creams sold in January = (3 × 150) = 450

Number of ice creams sold in February = (4 × 150) = 600

Number of ice creams sold in March = (4 × 150 + 1 2 × 150) = 675

Number of ice creams sold in April = (6 × 150 + 1 2 × 150) = 975

Number of ice creams sold in May = (8 × 150) = 1200

Number of ice creams sold in June = (2 × 150 + 1 2 × 150) = 375

a. The number of ice creams sold in the month of March = 675

b. The month for which there are the maximum number of symbols = May

The number of ice creams sold in the month of May = 8 × 150 = 1200 ice creams

c. Number of ice creams sold in the month of January = 3 × 150 = 450 ice creams

Number of ice creams sold in the month of May = 8 × 150 = 1200 ice creams

Difference between the number of ice creams sold in the month of January and May = 1200 – 450 = 750 ice creams

d. Total number of ice creams sold = (3 × 150) + (4 × 150)

+ (4 × 150 + 1 2 × 150) + (6 × 150 + 1 2 × 150) + (8 × 150)

+ (2 × 150 + 1 2 × 150)

= 450 + 600 + 675 + 975 + 1200 + 375 = 4275 ice creams

8. Scale: 1 division = 5000 books

The number of books sold in the year 2017 = 35,000

The number of books sold in the year 2018 = 40,000

The number of books sold in the year 2019 = 30,000

The number of books sold in the year 2020 = 33,000

The number of books sold in the year 2021 = 36,000

a. The number of books sold in the year 2019 = 30,000

b. The number of books sold in the year 2018 = 40,000

c. The number of books sold in the year 2020 = 33,000

Total number of books over the years = 35,000 + 40,000

+ 30,000 + 33,000 + 36,000 = 1,74,000

Fraction of total books that were sold in the year 2020

= 33000 174000 = 33 174 = 11 58

d. The number of books sold in the year 2017 = 35,000

The number of books sold in the year 2021 = 36,000

The ratio of the number of books sold in years 2017 and 2021 = 35000:36000 = 35:36

9. a. June has the highest temperature.

The temperature in the month of June = 40°C

b. Yes, January and December have the same temperatures.

The temperature in the months of December and January = 5°C

c. The temperature in the month of September = 27°C

Months which are warmer than the month of September are June, July and August.

Thus, 3 months are warmer than the month of September.

d. The month which is colder than July but warmer than September is August.

10.

Number of Bedsheets

Scale: 1 division = 100 bedsheets

11.

Sohail Ashraf Mahmood Raju Vivek

Key: = 1000 mangoes

Challenge

1. Number of cars sold by Dealership 1 = 30

Number of cars sold by Dealership 2 = 45

Number of cars sold by Dealership 3 = 25

Number of cars sold by Dealership 4 = 40

Statement 1: Dealership 4 sold more cars than Dealership 1 but fewer than Dealership 2. This is true.

Statement 2: The total number of cars sold by the 4 dealerships is 140.

The total number of cars sold by the 4 dealerships

= 30 + 45 + 25 + 40 = 140

So, Statement 2 is also true.

Thus, the correct answer is option c.

2. a. Key: = 10 students

Then 60 students will be represented by 6 symbols.

b. The number of students participating in chess = 5 × 10 = 50 students

When each face represents 5 students, 10 faces will represent 50 students.

The number of students participating in music = 2 × 10 = 20

When each face represents 5 students, 4 faces will represent 20 students.

Thus, the students participating in chess will be shown by 10 faces and the students participating in music will be represented by 4 faces.

c. The number of symbols used for drama = 5

Total number of students participating in drama as per the question = 35 students

Key: 1 symbol = 35 ÷ 5 = 7 students

Thus, each symbol will represent 7 students

Case Study

1. We can see that the number of sunflowers is the maximum in the month of March.

So, the greatest number of sunflowers were planted in March.

Thus, the correct answer is option b.

2. The number of symbols of marigold in the month of February = 6

1 symbol = 10 flowers

The number of marigolds planted in February = 6 × 10 = 60 marigolds

Thus, the correct answer is option c.

3. We can see that the number of tulips is the maximum in the month of April.

So, the greatest number of tulips were planted in April.

1 symbol = 10 flowers

The number of tulips planted in April = 4 × 10 = 40 tulips

4. 1 symbol = 10 flowers

The number of daisies planted in the month of February = 3 × 10

= 30 daisies

The number of daisies planted in the month of May = 4 × 10 = 40 daisies

Since, 30 < 40 and 40 − 30 = 10

So, May month had 10 more daisies than February month.

5. Answers may vary.

Chapter 10

Let’s Warm-up 1.

Do It Yourself 10A

1. a. 4 cm + 13 cm + 3.5 cm + 3.5 cm + 13 cm = 37

c. 2

= 64 cm

2. Length = 30 cm; Breadth = 12 cm

Perimeter = 2 × (Length + Breadth)

= 2 × (30 + 12)

= 2 × 42 = 84 cm

3. Perimeter of the square = 164 cm

Perimeter of the square = 4 × Side of the square 164 = 4 × Side of the square

Side of the square = 164 ÷ 4 = 41 cm

4. Perimeter of the isosceles triangle = 57 cm

Measure of the unequal side = 17 cm

Two sides of the isosceles triangle are equal. Let the equal side of the triangle be x.

x + x + 17 cm = 57 cm

2x = 57 cm – 17 cm

2x = 40 cm

x = 20 cm

5. Length of the string = 42 cm

a. An equilateral triangle has 3 equal sides

Perimeter of the equilateral triangle = Length of the string

3 × Length of side = 42

⇒ Length of side = 42 3 = 14 cm

b. Perimeter of the regular heptagon = Length of the string

7 × Length of side = 42

⇒ Length of side = 42 7 = 6 cm

6. Length = 3 m 25 cm = 3.25 m; Breadth = 1 m 42 cm = 1.42 m

Perimeter = 2 × (Length + Breadth)

= 2 × (3.25 + 1.42)

= 2 × 4.67 = 9.34 m

7. Answers may vary. Sample answers: 4 cm

3 cm

Perimeter = 2 × (4 + 3) = 14 cm 2 cm

5 cm

Perimeter = 2 × (5 + 2) = 14 cm

8. Length of the football field = 77 m; Breadth of the field = 52 m

Distance covered in one round = Perimeter of football field

= 2 × (Length + Breadth)

= 2 × (77 + 52)

= 2 × 129 = 258 m

Distance covered in 2 and a half round = 258 × 2.5 = 645 m

9. Length of the side of the square with perimeter 40 cm = 40 ÷ 4 = 4 cm

Length of the side of the square with perimeter 60 cm = 60 ÷ 4 = 15 cm

Length of the side of the new square = 10 cm + 15 cm = 25 cm

Perimeter of the new square = 2 × 25 = 50 cm

10. Length of each side of the given figure = 4 cm

Number of sides in the given figure = 12

Perimeter of the given figure = 4 × 12 = 48 cm

Let the length of the side of decagon = x;

Perimeter of decagon = 10 × x

Perimeter of decagon = 48 cm

10 × x = 48 ⇒ x = 48 10 = 4.8 cm

Hence, the length of each side of the decagon = 4.8 cm

11. Length = 25 m; Breadth = 17 m

Perimeter = 2 × (Length + Breadth)

= 2 × (25 + 17) = 2 × 42 = 84 cm

Cost of fencing at ₹28/m = 84 × 28 = ₹2352

Challenge

1. The perimeter will remain the same. For example, if a square with a side length of Perimeter = 164 cm

5 cm is cut from a bigger square with a side length of 10 cm, the perimeter, which was originally 40 cm, is still 40 cm.

Do It Yourself 10B

1. Area of a square = Side × Side

Side of the given square = 7 cm

Area of the given square = 7 cm × 7 cm = 49 sq. cm

2. Area of the rectangle = 375 sq. cm

Breadth of the rectangle = 25 cm

Area of rectangle = Length × Breadth

375 = Length × 25

Length = 375 25 = 15 cm

Thus, the length of the rectangle is 15 cm.

3. a. Fully-filled squares = 30

Area = 30 sq. cm

b. Fully-filled squares = 8

Half-filled squares = 7

Area = 8 + 1 2 × 7 = 11.5 sq. cm

c. Fully-filled squares = 34

More than half-filled squares = 13

Less than half-filled squares = 5

Area = 34 + 13 = 47 sq. cm

4. Area of the triangular frame = 1125 sq. cm

Height of the triangular frame = 25 cm

Area of a triangle = 1 2 × Base × Height

1125 sq. cm = 1 2 × Base × 25

2250 = Base × 25

Base = 2250 25 cm

Base = 90 cm

Thus, the base of the triangular frame is 90 cm.

5. To find the number of tiny squares created, we need to find the area of both the big and the tiny square.

Length of the side of the bigger square = 10 cm

Area of the bigger square = 10 × 10 = 100 sq. cm

Length of the tiny square = 2 cm

Area of tiny square = 2 × 2 = 4 sq. cm

Number of tiny squares that can be created = 100 4 = 25

6. To find the tiling cost, find the area of the plots.

Length of sides of the square plot = 15 cm

Area of the square plot = 15 m × 15 m = 225 sq. cm

Cost of tiling at the rate of ₹15 per sq. m = 225 × ₹15 = ₹3375

Length of the rectangular plot = 45 m

Breadth of the rectangular plot = 37 m

Area of the rectangular plot = 45 m × 37 m = 1665 sq. m

Cost of tiling at the rate of ₹15 per sq. m = 1665 × ₹15 = ₹24,975

7. Perimeter of the square = 12 cm

Perimeter = 12 cm

Side of the square = 12 cm ÷ 4 = 3 cm

Area of the square = 3 × 3 = 9 sq. cm

Length of the rectangle = 4 cm

Perimeter of the rectangle = Perimeter of the square = 12 cm

2 × (4 + Breadth) = 12

4 + Breadth = 6

Breadth = 2 cm

Area of the rectangle = 4 cm × 2 cm = 8 sq. cm

Thus, the square has larger area than the rectangle.

8. a. Perimeter = 20 cm + 4 cm + 8 cm + 8 cm + 8 cm + 4 cm + 20 cm + 4 cm + 8 cm + 8 cm + 8 cm + 4 cm = 104 cm

Area = Area of part A + Area of part B + Area of part C

Area of part A = 20 × 4 = 80 sq. cm

Area of part B = 8 × 4 = 32 sq. cm

Area of part C = 20 × 4 = 80 sq. cm

Total Area = 80 + 32 + 80 = 192 sq. cm

b. Perimeter = 3 + 3 + 3 + 3 + 6 + 3 +

3 + 3 + 3 + 3 + 3 + 3 + 3 + 6 = 48 units

Area = Area of part A + Area of part B

+ Area of part C + Area of part D

Area of part A = 3 × 3 = 9 sq. units

Area of part B = 12 × 3 = 36 sq. units

Area of part C = 3 × 3 = 9 sq. units

Area of part D = 3 × 3 = 9 sq. units

Total Area = 9 + 36 + 9 + 9 = 63 sq. units

9. Size of the rectangular plot = 140 m by 30 m

Area of the rectangular plot = 140 × 30 = 4200 sq. m

Size of the square plot = 6400 cm = 64 m

Area of the square plot = 64 × 64 = 4096 sq. m

As the area of the rectangular plot > Area of the square plot, Kunal should purchase the rectangular plot.

Challenge

1. Initial area of a square = (side × side)

Perimeter of a square = (4 × side)

Double the perimeter = 2 × (4 × side) = 4 × (2 × side)

So, new side = (2 × side)

New area = (2 × side) × (2 × side) = 4 × (side × side)

So, the area will increase 4 times.

Do It Yourself 10C

1. Given that the length of the kitchen = 10 m

10 × breadth = 130 sq. m × breadth

= 130 10 = 13 m

Perimeter of the kitchen = 2 × (10 + 13) = 2 × 23 = 46 m

2. Length of the strip light needed = 84 m

Shape of the ceiling = Square

Perimeter of the square = 4 × Side

84 m = 4 × Side

Side = 84 4 m = 21 m

Area of the square = 21 × 21 = 441 sq. m

Thus, Yash has to paint 441 sq. m of the area.

3. Length of two sides of the triangle = 15 m and 20 m

Total perimeter of the triangle = 60 m

Length of all three sides of the triangle

= Perimeter of the triangle

15 m + 20 m + Length of the third side = 60 m

35 m + Length of the third side = 60 m

Length of the third side = 60 m – 35 m = 25 m

Thus, the length of the third side of the triangle is 25 m.

4. Dimension of stickers to be pasted = 8 cm and 13 cm

Perimeter of the region on which the stickers need to be pasted = 552 cm;

Length of the region = 120 cm

Perimeter of the region = 2 × (120 + breadth) = 552 cm

Breadth of the region = 552 120 – 120 = 276 – 120 = 156 cm

To find the number of stickers to be pasted, we first need to find the area of the region,

Area of the region = length × breadth = 120 × 156 = 18,720 sq. cm

Area of sticker = 8 × 13 = 104

Number of stickers to be pasted = Area of region Area of stickers

= 18,720 104

= 180

5. Length of sides of squares kept side by side = 10.5 cm

Length of new figure formed = (10.5 + 10.5) = 21 cm

Breadth of new figure (rectangle) formed = 10.5 cm

10.5 cm 10.5 cm

Perimeter of figure formed = 2 × (length + breadth) = 2 × (21 + 10.5) = 2 × 31.5 = 63 cm

Area of figure formed = length × breadth = 21 × 10.5 = 220.5 sq. cm

6. Perimeter = 32 m

Length of each side of the square room = 32 ÷ 4 = 8 m

7 Area of the rectangular park = 3150 sq. m

Length of the park = 90 m

To find the number of rounds, we first need to find the perimeter of the park.

Area = Length × Breadth = 90 × Breadth = 3150

Breadth = 3150 90 = 35 m

Perimeter of park = 2 × (length + breadth)

= 2 × (90 + 35)

= 2 × 125 = 250 m

Distance covered by Rahul = 6 km = 6000 m

Number of rounds taken by Rahul

= Total distance covered

Distance covered in one round

= 6000 250 = 24 rounds

8. Shape of the base of the pyramid = Square

Perimeter of the square = 920 m

Side of the square = 920 m ÷ 4

= 230 m

Thus, Riya walked 230 m.

9. Answers may vary. Sample answer: Maria has a rectangular garden. She knows the perimeter of the garden is 40 metres, and one of the sides measures 12 metres. To find out how much area she needs to plant flowers, calculate the area of the garden.

Challenge

1. Perimeter of the square = 4 × 10 m = 40 m

Length of equal sides of the triangle = 10 ÷ 2 = 5 m

So, perimeter of triangle = 10 m + 5 m + 5 m = 20 m

Removing the common sides, total perimeter of the community hall = 40 m + 20 m − (10 m + 10 m) = 40 m

Chapter Checkup

1. a. Perimeter = 10 cm + 3 cm + 2 cm + 1 cm + 3 cm + 4 cm + 2 cm + 6 cm + 9 cm + 6 cm + 2 cm = 48 cm

b. Perimeter = 4 cm + 2.5

= 22 cm

c. Perimeter = 5 cm + 10 cm + 2 cm + 3

+ 1

+ 2

+ 2 cm + 2 cm + 3 cm + 10 cm = 40 cm

2. a. Fully-filled squares = 15

Half-filled squares = 7

Area = 15 + 1 2 × 7

= 18.5 sq. units

b. Fully-filled squares = 18

Half-filled squares = 0

More than half-filled squares = 13

Less than half-filled squares = 7

Area = 18 + 13 = 31 sq. units

c. Fully-filled squares = 20

Half-filled squares = 5

More than half-filled squares = 5

Less than half-filled squares = 4

Area = 20 + 1 2 × 5 + 5 = 27.5 sq. units

3. Length of the tabletop = 21 cm

Breadth of the tabletop = 19 cm

Area of the tabletop = Length × Breadth = 21 cm × 19 cm

= 399 sq. cm

4. To find the number of squares tiles needed, we need to find the area of both squares.

Length of the side of the square = 3 m = 300 cm

Area of the square = 300 × 300

= 90,000 sq. cm

Length of the square tile = 12 cm

Area of the square tile = 12 × 12 = 144 sq. cm

Number of square tiles needed = Area of square Area of square tile

= 90,000 144 = 625

5. Perimeter of the rectangular sheet = 50 cm

Length of the rectangular sheet = 10 cm

Perimeter = 2 × (Length + Breadth)

50 = 2 × (10 + Breadth)

25 = 10 + Breadth

Breadth = 15 cm

Given that, the triangle is cut into two triangles along the diagonal.

The area of each triangle will be equal.

So, the area of the triangle = 1 2 × Area of the rectangle

Area of the triangle = 1 2 × 10 × 15 = 75 sq. cm

Thus, the area of each triangle is 75 sq. cm.

6. Total length of the thread = 72 cm

Perimeter of the square = Length of the thread

4 × Side = 72 cm

Side = 18 cm

Thus, the length of each side of the square is 18 cm.

7. Perimeter of Sunita’s plot = 2 m + 10 m + 8 m + 4 m + 6 m +

6 m = 36 m

Area of Sunita’s plot

= Area of part A + Area of part B

Area of part A = 6 × 2 = 12 sq. m

Area of part B = 8 × 4 = 32 sq. m

Total Area = 12 + 32 = 44 sq. m

Perimeter of Ramesh’s plot

= 10 m + 7 m + 5 m + 7 m + 5 m

+ 14 m = 48 m

Rectangle A

Area of Ramesh’s plot = Area of part A + Area of part B

Area of part A = 10 × 7 = 70 sq. m

Area of part B = 7 × 5 = 35 sq. m

Total Area = 70 + 35 = 105 sq. m

Thus, Ramesh’s plot has greater area and perimeter.

8. Area of square = 144 m

Rectangle A

Area of rectangles = 2 m × 1 m = 2 sq. m

Number of rectangles = 144 2 = 72 rectangles

9. To find the cost of painting, we first need to find the area of the cardboard.

Length = 80 cm; Breadth = 1 4 m = 25 cm

Area = Length × Breadth = 80 × 25

= 2000 sq. cm

Cost of painting = 25 paise/sq. cm = ₹0.25/sq. cm

Cost of painting 2000 sq. cm = 2000 × ₹0.25 = ₹500

10. Length of square plot = 25 m

Area of the plot = side × side = 25 m × 25 m = 625 sq. m

Area used for farming = 1 4

Area vacant = 1 – 1 4 = 3 4

Area vacant = 3 4 of total area = 3 4 × 625 = 468.75 sq. m

11. Length of each side of the base of square shaped monument = 10 m

Area of the base of square shaped monument = 10 m × 10 m = 100 sq. m

12. Length of the square park = 88 m

Perimeter of the square park = 4 × side = 4 × 88 = 352 m

Distance while running 3 times a day = 3 × 352 = 1056 m

Length of the rectangular park = 30 m; Breadth of the rectangular park = 70 m

Perimeter of the rectangular park = 2 × (length + breadth) = 2 × (30 + 70) = 200 m

Distance covered while running 5 times a day = 5 × 200 = 1000 m

Sailesh runs the longer distance every day.

13. To find the area of shaded portion, we need to subtract the area of the smaller rectangle from the area of the bigger rectangle.

Length of the bigger rectangle = 6 m; Width = 10 m

Area of the bigger rectangle = 6 × 10 = 60 sq. m

Length of the smaller rectangle = 10 – (4 + 1) = 5 m;

Width = 6 – (2 + 2) = 2 m

Area of the smaller rectangle = 5 × 2 = 10 sq. m

Area of the shaded portion = 60 sq. m – 10 sq. m = 50 sq. m.

Therefore, Kanika needs 50 sq. m of carpet for her room.

14. Length of the wire = Perimeter of the rectangle = Perimeter of the square = 42 cm

Perimeter of the rectangle formed = 2 × (length + breadth) = 42 cm

Breadth = 5 cm; 2 × (length + 5) = 42 cm

⇒ length = 42 2 – 5

= 21 – 5 = 16 cm

Area of rectangle = length × breadth = 16 × 5 = 80 sq. cm

Perimeter of square formed = 4 × side = 42 cm

Length of side of square = 42 4 = 10.5 cm

Area of square = side × side = 10.5 × 10.5 = 110.25 sq. cm.

Difference in the area = (110.25 – 80) = 30.25 sq. cm

The square formed has a greater area. The difference in the area is 30.25 sq. cm.

Area = 9 × 4 = 36 sq.m

Perimeter = 2 × (4 + 9) = 26 cm

Area = 12 × 3 = 36 sq.m

Perimeter = 2 × (12 + 3) = 30 cm

Rectangle A and B have the same area but different perimeters.

Challenge

1. Assertion: 1500 bricks of 40 cm by 40 cm can be used to construct a particular wall, whose length and breadth are 16 m and 15 m, respectively.

Total area of the wall = 16 m × 15 m

= 1600 cm × 1500 cm

= 24,00,000 sq. cm

Area of each bricks = 40 cm × 40 cm = 1600 sq. cm

Number of bricks required = 24,00,000 1600 = 1500 bricks

So, the assertion is true.

Reason: Area of a rectangle is given as the product of its length and breadth.

The reason is also true and it helps us find the total number of bricks.

Thus, both assertion and reason are true, and the reason correctly explains the assertion. Hence, option a is correct.

2. Areas of the two rectangles = 20 sq. cm and 12 sq. cm

Area of the new rectangle = Sum of the areas of the two rectangles

Sum of areas = 20 + 12 = 32 square cm

Length = 2 × breadth

So, length × breadth = 32

l × b = 32

2b × b = 32

b × b = 32 4 = 16

b = 4 × 4

b = 4

So, l = 2b = 2 × 4 = 8

Perimeter = 2 × (8 + 4) = 24 cm

Case Study

1. Length of the flat = 50 ft

Breadth of the flat = 30 ft

Area of the flat = 50 ft × 30 ft = 1500 sq. ft

Thus, option d is correct.

2. Area of the hall = 480 sq. feet

Length of the hall = 40 feet

Breadth of the hall = 480 ÷ 40 = 12 feet

Perimeter of the hall = 2 × (40 + 12) = 2 × 52 feet = 104 feet

3. Width of bedroom 1 = 16 feet

Total width of the flat = 30 feet

Width of the flat = Width of bedroom 1 + Width of kitchen

30 feet = 16 feet + Width of the kitchen

Width of the kitchen = 14 feet

4. Total length of the kitchen = 10 feet

Breadth of the kitchen = 14 feet

Area of the kitchen = 10 × 14 = 140 sq. feet

Cost of tiling = ₹120 per sq. feet

Total cost of tiling = 120 × 140 = ₹16,800

5. Answers may vary.

Chapter 11

Let’s Warm-up

1. 1, 2, 3, 4… 9

2. 3, 6, 9… 16

3. 1, 3, 5, 7… 10

4. 2, 4, 6, 8… 12

5. 4, 8, 12… 5

Do It Yourself 11A

1. a. 2, 4, 6, 8, 10, ...

The first term of the sequence = (2 × 1) = 2

The second term of the sequence = (2 × 2) = 4

The nth term of the sequence = (2 × n) = 2n

So, the general rule = (2n)

18th term = (2 × 18) = 36

b. 3, 6, 9, 12, 15, ...

The first term of the sequence = (3 × 1) = 3

The second term of the sequence = (3 × 2) = 6

The nth term of the sequence = (3 × n) = 3n

So, the general rule = 3n 18th term = (3 × 18) = 54

c. 6, 11, 16, 21, ...

The first term of the sequence = (5 × 1 + 1) = 6

The second term of the sequence = (5 × 2 + 1) = 11

The nth term of the sequence = (5 × n + 1) = 5n + 1

So, the general rule = 5n + 1

18th term = (5 × 18 + 1) = 91

d. 3, 8, 13, 18, 23, …

The first term of the sequence = (5 × 1) – 2 = 3

The second term of the sequence = (5 × 2) – 2 = 8

The nth term of the sequence = (5 × n) – 2 = 5n − 2

So, the general rule = 5n − 2 18th term = (5 × 18) – 2 = 90 – 2 = 88

2. a. Shape Number of Matchsticks Rule

Shape 1 3 = 3 × 1

Shape 2 6 = 3 × 2

Shape 3 9 = 3 × 3

Shape 4 12 = 3 × 4

Number of sticks required = (3 × n) = 3n

Number of matchsticks used in the 50th shape = (3n)

= 3 × 350 = 150

b. Shape Number of Matchsticks Rule

Shape 1 7 = 7 × 1

Shape 2 14 = 7 × 2

Shape 3 21 = 7 × 3

Do It Yourself 11B

Number of sticks required = (7 × n) = 7n

Number of matchsticks used in the 50th shape = (7n) = 7 × 50 = 350

3. a.

3, 5, 7, 9, ...

The first term of the sequence = (2 × 1) + 1 = 3

The second term of the sequence = (2 × 2) + 1 = 5

The nth term of the sequence = (2 × 3) + 1 = (2 × n) + 1 = 2n + 1

So, the general rule = 2n + 1

b. 5, 8, 11, 14, ...

The first term of the sequence = (3 × 1) + 2 = 5

The second term of the sequence = (3 × 2) + 2 = 8

The nth term of the sequence = (3 × n) + 2 = 3n + 2

So, the general rule = 3n + 2

4. The first term of the sequence = 10 × 1 = 10

The second term of the sequence = 10 × 2 = 20

The nth term of the sequence = 10 × n = 10n

So, the general rule = 10n

Cupcakes

Number of hours in a day = 24 hours

Number of cupcakes made in 24 hours = 10 × 24 = 240

5. A = l × b

Where A is the area, l is the length of the rectangle and b is the breadth of the rectangle.

6. a. As the length of the sides of a regular hexagon are equal and it has 6 sides, the perimeter can be given as: 6 × a = 6a; where a is the length of each side.

b. As the opposite the sides of a parallelogram are equal and it has 4 sides, the perimeter can be given as: 2(l + b); where l is the length and b is the breadth.

c. As the length of the sides of a regular nonagon are equal and it has 9 sides, the perimeter can be given as: 9 × a = 9a, where a is the length of each side.

d. As the length of the sides of a regular octagon are equal and it has 8 sides, the perimeter can be given as: 8 × a = 8a, where a is the length of each side.

7. Diameter = 2 × Radius

D = 2 × r = 2r

8. Shape—Heptagon, General rule to find the perimeter—7a

Challenge

1. A polygon with a perimeter 4a is a square. A polygon with a perimeter 5a is a pentagon. The perimeter of the new shape formed when they are joined on one side = 7a

1. a. 7 × 2 + 3 – 2 = 14 + 1 = 15; as the expression has only numerical terms, it is an arithmetic expression.

b. 7x + 5; as the expression has variables, it is an algebraic expression.

c. 12y; as the expression has variables, it is an algebraic expression.

d. 10y – 6x; as the expression has variables, it is an algebraic expression.

2. a. x and y b. 2a, 3b, –c c. x, y, 2z d. x, –6z

e. 2x, 5 f. 4 3 x, 2 g. 5abc, –2ab, 7ac h. 2ab, 4ac, –6c

3. a. 3 + 6m b. n – 10 c. 15 × x = 15x

d. 2 × (x × y) = 2xy e. (9 × y) + 1 = 9

4. Given that, x = 2, y = 4 and z = 9

a. x(y + 8)

Substituting the values, 2(4 + 8) = 2 × 12 = 24

b. (x + z)(xy – z)

Substituting the values, (2 + 9) (2 × 4 – 9) = 11 × − 1 = − 11

c. xy – 9zx

2 × 4 – (9 × 9 × 2) = 8 – 162 = −154

d. 10x – 3y

3xy + 8

10 × 2 − 3 × 4

3 × 2 × 4 + 8 = 8 32 = 1 4

5. Number of months in a year = 12 months

Number of months in u years = 12 × u = 12u

Algebraic expression = 12u

Value of the expression = 12 × 13 = 156 months

6. Number of pencils shared = x

Number of pencils left = 7

So, the total number of pencils = x + 7

7. Number of apples in one small box = x

Total number of apples in 3 small boxes = 3 × x = 3x

Number of apples left = 5

So, the total number of apples in the large box = 3x + 5

8. Total number of students = y

Number of students who are performing in the group dance = x

Number of students who are performing in solo = 6

then, y = x – 6

9. Let Rima’s age be x.

Mala is five years younger than Rima.

Malas’s age = x – 5

10. Number of chocolates with Karan = m

Number of chocolates given to his younger brother = 5

Number of chocolates left = m – 5

Number of chocolates each his friend and him got = m – 5

11. Amount spent daily = ₹y

Amount spent weekly = ₹7 × y = ₹7y

Weekly expenditure = ₹7y

Amount saved weekly = Weekly Savings = ₹z

Income for one week = Expenditure + Savings = ₹ (7y + z)

Income for three weeks = 3 × Income for one week = 3 × ₹(7y + z) = ₹(3 × 7y + 3 × z) = ₹(21y + 3z)

12. Cost of tomatoes = ₹29 per kg

Cost of cucumbers = ₹38 per kg

Weight of tomatoes = x kg

Weight of cucumbers = (x – 4) kg

Total purchase = ₹[29 × x + 38 × (x – 4)] = ₹29 x + 38x – 152 = ₹67x – 152

13.

14. Answer may vary. Sample answer:

On a birthday party, Rahul distributed 3 candies to all his friends and he was still left with 5 candies. How many total candies Rahul had initially if the total number of friends were x

Challenge

1. a. k 10 k + 10

Do It Yourself 11C

1. a. Let the number be x

When we add 3 to the number: x + 3

We get 12: x + 3 = 12

b. Let the number be x. When 7 is taken away from a number: x – 7 It leaves 2: x – 7 = 2

c. Let the number be x. Twice of the number = 2x

When 7 is taken away from twice a number, it leaves 3: 2x – 7 = 3

We get 2x – 7 = 3

d. Let the number be x.

The product of a number and 4: 4 × x = 4x

2 added to the product of a number and 4 gives 26: 4x + 2 = 26

2. Let the numerator of the fraction be x

Then, the denominator = x + 5

Thus, the fraction: x x + 5

When 3 is added to both, the fraction becomes 3 4 x + 3

x + 5 + 3 = 3 4

x + 3

x + 8 = 3 4

3. Number of people that signed up for the soccer league = 72

Number of teams = 6

Number of people in each team = x

→ 6x = 72

4. Let the number Tina thought of was x

When tripled = 3x

Subtracting 7 from the result = 3x – 7

Multiplying by 2 we get: 2 × (3x – 7) = 52

5. Answers may vary. Sample answers:

a. When we add 5 to the product of 4 and a number, we get 9.

b. When we add 1 to twice a number, we get 5.

c. When 7 is taken away from the product of 12 and a number, we get 5.

d. Three times the sum of a number and 1 gives 12.

6. a. If x = 1

LHS = 3x + 5 = 3(1) + 5 = 8 RHS = 8

LHS = RHS

Hence, x = 1 is the solution of the given expression.

c. If x = 1

LHS = 32 – 5x = 32 – 5(1) = 32 – 5 = 27

RHS = 12

LHS ≠ RHS If x = 2

LHS = 32 – 5x = 32 – 5(2) = 32 – 10 = 22

RHS = 12

LHS ≠ RHS If x = 4

LHS = 32 – 5x = 32 – 5(4) = 32 – 20 = 12

RHS = 12

LHS = RHS

Hence, x = 4 is the solution of the given expression.

e. If y = 1

LHS = 8y = 8(1) = 8

RHS = 48

LHS ≠ RHS

If y = 3

LHS = 8y = 8(3) = 24

RHS = 48

LHS ≠ RHS

If y = 6

b. If x = 0

LHS = 2(3x + 1) = 2(3(0) + 1)

= 2(0 + 1) = 2(1) = 2

RHS = 8

LHS ≠ RHS

If x = 1

LHS = 2(3x + 1) = 2(3(1) + 1)

= 2(3 + 1) = 2(4) = 8

RHS = 8

LHS = RHS

Hence, x = 1 is the solution of the given expression.

d. If x = 1

LHS = 5x – 8 = 5(1) – 8 = 5 – 8 = –3

RHS = 7

LHS ≠ RHS

If x = 2

LHS = 5x – 8 = 5(2) – 8 = 10 – 8 = 2

RHS = 7

LHS ≠ RHS If x = 3

LHS = 5x – 8 = 5(3) – 8 = 15 – 8 = 7

RHS = 7

LHS = RHS

Hence, x = 3 is the solution of the given expression.

f. If x = 1

LHS = 1 3 x – 3 = 1 3 – 3 = 1 – 9 3 = –8 3

RHS = 0

LHS ≠ RHS

If x = 3

LHS = 1 3 x – 3 = 1 3 (3) – 3 = 1 – 3 = –2

LHS = 8y = 8(6) = 48

RHS = 48

LHS = RHS

Hence, y = 6 is the solution of the given expression.

7. a. If a = 10

LHS = 6 a = 6 × 10 = 60

RHS = 48

LHS ≠ RHS

If a = 8

LHS = 6a = 6 × 8 = 48

RHS = 48

LHS = RHS

8. a. If x = 2

LHS = 4x + 2 = 4 × 2 + 2

= 8 + 2 = 10

RHS = 10

LHS = RHS

Hence, x = 2 is the solution of the given expression.

c. If x = 10

LHS = 5 2 x = 5 2 × 10 = 50 2 = 25

RHS = 25

LHS = RHS

Hence, x = 10 is the solution of the given expression.

e. If z = 1

LHS = 5z – 6 = 5 × 1 – 6

= 5 – 6 = –1

RHS = 0

LHS ≠ RHS

⇒ 5z – 6 = 0

⇒ 5z = 6

⇒ z = 6 5

Hence, z = 6 5 is the solution of the given expression.

RHS = 0

LHS ≠ RHS

If x = 9

LHS = 1 3 x – 3 = 1 3 (9) – 3

= 9 3 – 3 = 3 – 3 = 0

RHS = 0

LHS = RHS

Hence, x = 9 is the solution of the given expression.

b. If x = 7

LHS = 3x + 2 = 3(7) + 2

= 21 + 2 = 23

RHS = 23

c. If y = 3

LHS = y 4 = 3 4

RHS =3

LHS ≠ RHS

If y = 7

LHS = y 4 = 7 4

RHS = 3

LHS ≠ RHS

If y = 12

LHS = y 4 = 12 4 = 3

RHS = 3

LHS = RHS

b. If y = 3

LHS = 9y – 8 = 9 × 3 – 8

= 27 – 8 = 19

RHS = 1

LHS ≠ RHS

⇒ 9y – 8 = 1

⇒ 9y = 1 + 8

⇒ 9y = 9

⇒ y = 9 9

⇒ y = 1

Hence, y = 1 is the solution of the given expression.

d. If n = 12

LHS = 2n 3 – 6 = 2 × 12 3 – 6

= 24 3 – 6 = 8 – 6 = 2

RHS = 2

LHS = RHS

Hence, n = 12 is the solution of the given expression.

f. If x = 1

LHS = 3x + 2 = 3 × 1 + 2

= 3 + 2 = 5

RHS = 5

LHS = RHS

Hence, x = 1 is the solution of the given expression.

9. a. x + 6 = 10

x = 10 – 6

x = 4

Hence, x = 4 is the solution of the given expression.

b. 5 = a + 2

a + 2 = 5

a = 5 – 2

a = 3

Hence, a = 3 is the solution of the given expression.

c. m – 12 = 3

m = 3 + 12

m = 15

Hence, m = 15 is the solution of the given expression.

e. 4 + k – 7 = 2

k + 4 – 7 = 2

k – 3 = 2

k = 2 + 3

k = 5

Hence, k = 5 is the solution of the given expression.

d. –7 = x + 4

x + 4 = –7

x = –4 –7

x = –11

Hence, x = –11 is the solution of the given expression.

f. 3 – 4x = –13

3 + 13 – 4x = 0

16 = 4x

x = 16 4

x = 4

Hence, x = 4 is the solution of the given expression.

10. Let one number be x, then the other number will be x + 1.

Sum = 25

x + x + 1 = 25

⇒ 2x = 25 − 1

⇒ 2x = 24

⇒ x = 24 2

⇒ x = 12

⇒ x + 1 = 12 + 1 = 13

Hence, the numbers are 12 and 13.

11. Let the breadth of the slide = x mm

Length of the slide = x + 50 mm

Perimeter of the slide = 200 mm

→ 2(length + breadth) = 200

→ 2(x + 50 + x) = 200

→ 2(2x + 50) = 200

→ 2x + 50 = 200 2

→ 2x + 50 = 100

→ 2x = 100 − 50

→ 2x = 50

→ x = 50 2

→ x = 25

Thus, breadth of the slide = 25 mm and length of the slide

= 25 + 50 = 75 mm

12. Let Ishita’s present age be x Rekha’s present age = x + 24

After 8 years:

Ishita’s age = x + 8

Rekha’s age = x + 24 + 8 = x + 32

Also, 2 × (x + 8) = x + 32

→ 2 × x + 2 × 8 = x + 32

→ 2x + 16 = x + 32

→ 2x − x = 32 − 16

→ x = 16

→ x + 24 = 16 + 24 = 40

Thus, Ishita’s present age is 16 and Rekha’s present age is 40.

13. Let the marks scored in English = x

Marks scored in mathematics = 2x

Marks scored in science = 70

Total marks = 220

Then, x + 2x + 70 = 220

x + 2x = 220 – 70

3x = 150

x = 150 3

⇒ x = 50

⇒ 2x = 2 × 50

⇒ 2x = 100

So, Sreeja scored 100 marks in mathematics and 50 marks in English.

14. Let the amount in Meenal’s purse be ₹x

If she adds ₹51 to it, it becomes four times the original amount:

x + 51 = 4x

51 = 4x – x

51 = 3x

3 = x

x = 17

So, the original amount in her purse is ₹17.

Challenge

1. Let the number be x

Three consecutive multiples of 8 x, x + 8, x + 16

x + (x + 8) + (x + 16) = 192

x + x + 8 + x + 16 = 192

3x + 24 = 192

3x = 192 – 24

3x = 168

x = 168 3

x = 56

x + 8 = 56 + 8 = 64

x + 16 = 56 + 16 = 72

So, the numbers are 56, 64 and 72

Chapter Checkup

1. a. Number of Matchsticks Rule

4 = 4 × 1

8 = 4 × 2

12 = 4 × 3

Number of sticks required

= (4 × n) = 4n

b. Number of Matchsticks Rule

6 = 4 × 1 + 2

10 = 4 × 2 + 2

14 = 4 × 3 + 2

Number of sticks required = (4 × n + 2) = 4n + 2

c. Number of Matchsticks Rule

5 = (4 × 1 + 1)

9 = (4 × 2 + 1)

13 = (4 × 3 + 1)

2. Let the number be x

Then, 0 + x = x And x + 0 = x

So, 0 + x = x = x + 0

3. a. 3 times x = 3x

Adding 4 we get 3x + 4

c. Quotient of x by 3 = x 3

Subtracting 4 we get x 3 – 4

4. a. 2x + 5 = 9

b. 2 times y = 2y

Subtracting 2 we get 2y – 2

d. y is divided by 5 = y 5

Quotient is added to 6 we get 6 + y 5

The highest power of x in the equation is 1.

9 = 2x + 5

The equation remains the same if its LHS and RHS are interchanged.

Hence, it is a linear equation.

b. 9x + 4 > 5

The highest power of x in the equation is 1.

5 < 9x + 4

The equation does not remain the same if its LHS and RHS are interchanged.

Hence, it is not a linear equation.

c. 2y + 7 = 9

The highest power of y in the equation is 1.

9 = 2y + 7

The equation remains the same if its LHS and RHS are interchanged.

Hence, it is a linear equation.

5. a. 5x + 9y

= 5 × 3 + 9 × 7

= 15 + 63 = 78

b. 6xy – 2yz + 10

= 6 × 3 × 7 – 2 × 7 × 5 + 10

= 126 – 70 + 10 = 66

c. 9xz –1 5 yz

= 9 × 3 × 5 – 1 5 × 7 × 5

= 135 – 7 = 128

d. 11yz + x + 4y

= 11 × 5 × 7 + 3 + 4 × 7

= 385 + 3 + 28

= 388 + 28 = 416

6. Lengths of the sides of the triangle are 3x – 5, 2x – 1 and x + 1.

a. Perimeter = 3x – 5 + 2x

– 1 + x + 1

= 3x + 2x + x – 5 – 1 + 1

= 6x – 5

Number of sticks required

= (4 × n + 1) = 4n + 1

b. If perimeter = 31 cm, then

⇒ 6x – 5 = 31

⇒ 6x = 31+5

⇒ 6x = 36

⇒ x = 36 6

⇒ x = 6

Hence, x = 6 cm is the solution of the given expression.

7. Statements may vary. Sample statements:

a. Raj has some money and after receiving ₹30, he has a total of ₹50. How much money does he originally have?

When 30 is added to a number, we get 50.

⇒ x + 30 = 50

⇒ x = 50 – 30

⇒ x = 20

Hence, x = 20 is the solution of the given expression.

b. When 3 is taken away from 6 times a number we get 9.

⇒ 6x – 3 = 9

⇒ 6x = 9 + 3

⇒ 6x = 12

⇒ x = 12 6

⇒ x = 2

Hence, x = 2 is the solution of the given expression.

c. Ravi distributes 24 pieces of candy equally among some friends, and each friend gets 4 pieces. How many friends were there?

Total number of candies = 24

Let number of friends be x Number of candies each friend get = 4

⇒ 24 x = 4

⇒ 24 = 4x

⇒ 24 4 = x

⇒ 6 = x or x = 6

So, there are 6 friends.

d. Four times the sum of three times a number and 7 equals 40. What is the number?

Let the number be x

According to the question,

4 (3x + 7) = 40

⇒ 3x + 7 = 40 4

⇒ 3x + 7 = 10

⇒ 3x = 10 − 7

⇒ 3x = 3

⇒ x = 3 3

⇒ x = 1

So, the number is 1.

8. Let the number of marbles with Ajit = x

Number of marbles with Badri = 2x

Number of marbles with Charu = 2x + 5

Total number of marbles = x + 2x + 2x + 5 = 5x + 5 = 55

Then, 5x = 55 – 5

⇒ x = 50 5 = 10

⇒ x = 10

⇒ 2x = 20

⇒ 2x + 5 = 25

So, Charu has 25 marbles.

9. The length of the rink is l.

The width of the rink is w.

The perimeter of the rink is 2(l + w).

10. Present age of Rohit = z

a. Age after 8 years = z + 8

b. Grandmother’s age = 5z + 9

11. Number of drawing sheets with Sahil = x

Number of drawing sheets with Rahul = x – 2

Number of drawing sheets with Aryan = x + 6

Number of sheets Rahul and Aryan have in total = x – 2 + x + 6

= 2x + 4

Total number of sheets that the three of them have in total

= x + x – 2 + x + 6 = 3x + 4

12. Height of cuboidal box = x

Breadth of cuboidal box = 2x

Length of cuboidal box = 2x – 4

13. Number of tennis balls ordered = 42

Number of tennis balls in one package = 3

Number of packages = x

Then, 3 × x = 42

So, option b is correct.

14. Price of the bracelet = P = ₹115

2.5m + 35 = 115

2.5m = 115 – 35

2.5m = 80

m = 80 2.5 = 800 25 = 32

m = 32

So, the cost of materials is ₹32.

15. Let Akash’s age be x. Lakhan’s age = 3x

Mala’s age = 3x – 7

Sum of their ages = x + 3x + 3

7x – 7 = 126

7x = 126 + 7 = 133

x = 133 7 = 19

So, the age of Akash is 19 years old.

Challenge

126

1. Assertion (A): The equation for '3 subtracted from t to equal to 5’ is written as t – 3 = 5.

t − 3 = 5 is the correct expression for '3 subtracted from t to equal to 5.

So, the assertion is true.

Reason (R): Any equation like the above, is a condition on a variable. It is satisfied only for a definite value of the variable.

The above expression t – 3 = 5 uses one variable and has only one solution.

So, the reason is also true and it correctly explains the assertion.

Hence, option a is correct.

2. Initial price = ₹90,000

Half the price = ₹45,000

Let the number of years be n

₹90,000 − ₹3,000n = ₹45,000

₹90,000 − ₹45,000 = ₹3,000n

₹45,000 = ₹3,000n

n = ₹ 45,000 ÷ ₹3,000 = 15

Thus, after 15 years the price of the refrigerator will be half its original price.

Case Study

1. Delivery charge = ₹300

Cost of making each piece = ₹30

Price for supplying the product (P)

= Delivery charge (C) + cost of making Q pieces

P = ₹300 + ₹30Q

2. Delivery charge = ₹300

Cost of making each piece = ₹30

Q = 4

Price for supplying the product (P) = Delivery charge (C)

+ Cost of making Q pieces

P = ₹300 + ₹30 × 4 = ₹300 + ₹120 = ₹420

3. Demand of the product (D) = Cost of product 2

Expression when the cost rises 4 times

D = 4c 2 = 2C

4. Delivery charge = ₹300

Cost of making each piece = ₹30

If the cost has to be equal to the delivery charge, 30Q = 300

Q = 10

So, the quantity has to be 10.

Chapter 12

Let’s Warm-up

1. Number of apple slices = 6

Slices eaten = 3

Fraction of apple eaten = 3 6 = 1 2

2. 8 12 = 8 ÷ 4 12 ÷ 4 = 2 3

8 12 in its simplest form is 2 3

3. 2 5 = 2 × 2

5 × 2 = 4 10

An equivalent for 2 5 is 4 10

4. As the denominator is the same, 4 7 and 6 7 are like fractions.

4 7 and 6 7 are a pair of like fractions.

5. Fraction of cake left = 1 − 4 16 = 12 16 = 3 4

The fraction of cake left is 3 4

Do It Yourself 12A

1. a. A ratio can have units, depending on the types of quantities being compared. False

b. In 3:5, the consequent is 5. True

c. The terms of a ratio a:b are called the antecedent and consequent, respectively. True

d. 10:2 is the same as 2:10. False

e. 10 litres of water can be compared with 10 km. False

2. a. HCF of 48 and 72 = 24

48 72 = 48 ÷ 24

72 ÷ 24 = 2 3

Thus, 48:72 in its simplest form is 2:3

b. 6 m = 6 × 100 = 600 cm

HCF of 400 and 600 = 200

400

600 = 400 ÷ 200

600 ÷ 200 = 2 3

Thus, 400 cm:6 m in its simplest form is 2:3

c. 1.5 kg = 1500 g

HCF of 1500 and 750 = 750

1500

750 = 1500 ÷ 750

750 ÷ 750 = 2 1

Thus, 1.5 kg:750 g in its simplest form is 2:1

d. 25 L = 25000 mL

HCF of 25000 and 750 = 250

25000

750 = 25000 ÷ 250 750 ÷ 250 = 100 3

Thus, 25 L:750 mL in its simplest form is 100:3

e. 9 hours = 9 × 60 = 540 minutes

9 hours:540 minutes = 540 minutes:540 minutes

= 540:540 = 1:1

Thus 9 hours:540 min in its simplest form is 1:1

f. 10000 paise = 10000 100 = ₹100

₹100 :10000 paise = ₹100:₹100 = 1:1

Thus, ₹100 :10000 paise in its simplest form is 1:1

3. Answers may vary. Sample answer:

a. 5:7 = 5 × 2 7 × 2 = 10 14 ; 5 × 3 7 × 3 = 15 21 ; 5 × 4 7 × 4 = 20 28

Three equivalent ratios to 5:7 = 10:14, 15:21, 20:28

b. 4:9 = 4 × 2 9 × 2 = 8 18 ; 4 × 3 9 × 3 = 12 27 ; 4 × 4 9 × 4 = 16 36

Three equivalent ratios to 4:9 = 8:18, 12:27, 16:36

c. 12:16 = 12 × 2 16 × 2 = 24 32 ; 12 × 3 16 × 3 = 36 48 ; 12 × 4 16 × 4 = 48 64

Three equivalent ratios to 12:16 = 24:32, 36:48, 48:64

d. 6:15 = 6 × 2 15 × 2 = 12 30 ; 6 × 3 15 × 3 = 18 45 ; 6 × 4 15 × 4 = 24 60

Three equivalent ratios to 6:15 = 12:30, 18:45, 24:60

e. 8:11 = 8 × 2 11 × 2 = 16 22 ; 8 × 3 11 × 3 = 24 33 ; 8 × 4 11 × 4 = 32 44

Three equivalent ratios to 8:11 = 16:22, 24:33, 32:44

f. 9:17 = 9 × 2 17 × 2 = 18 34 ; 9 × 3 17 × 3 = 27 51 ; 9 × 4 17 × 4 = 36 68

Three equivalent ratios to 9:17 = 18:34, 27:51, 36:68

4. a. 5:3 = 5 3 ; 3:4 = 3 4

LCM of 3 and 4 = 12

5 3 = 5 × 4 3 × 4 = 20 12 ; 3 4 = 3 × 3 4 × 3 = 9 12

As 20 12 > 9 12 ⇒ 5 3 > 3 4 or 5:3 > 3:4

b. 3:5 = 3 5 ; 2:9 = 2 9

LCM of 5 and 9 = 45

3 5 = 3 × 9 5 × 9 = 27 45 ; 2 9 = 2 × 5 9 × 5 = 10 45

As 27 45 > 10 45 ⇒ 3 5 > 2 9 or 3:5 > 2:9

c. 4:7 = 4 7 ; 5:8 = 5 8

LCM of 7 and 8 = 56

4 7 = 4 × 8 7 × 8 = 32 56 ; 5 8 = 5 × 7 8 × 7 = 35 56

As 32 56 < 35 56 ⇒ 4 7 < 5 8 or 4:7 < 5:8

d. 3:5 = 3 5 ; 5:6 = 5 6

LCM of 5 and 6 = 30

3 5 = 3 × 6

5 × 6 = 18 30 ; 5 6 = 5 × 5 6 × 5 = 25 30

As 18 30 < 25 30 ⇒ 3 5 < 5 6 or 3:5 < 5:6

e. 3:7 = 3 7 ; 7:9 = 7 9

LCM of 7 and 9 = 63

3 7 = 3 × 9

7 × 9 = 27 63 ; 7 9 = 7 × 7 9 × 7 = 49 63

As 27 63 < 49 63

⇒ 3 7 < 7 9 or 3:7 < 7:9

f. 2:7 = 2 7 ; 4:14 = 4 14 = 2 7

Hence, 2 7 = 4 14 or 2:7 = 4:14

5. a. 480 : 32 46 : 37

b. 378 : 105 3 : 20

c. 138 : 111 18 : 5

d. 42 : 280 15 : 1

6. Number of red apples = 16

Number of green apples = 24

Ratio of red apples to green apples = 16:24

7. Number of cats = 20

Total number of animals = 30 + 20 + 10 = 60

Ratio of cats to total animals = 20:60

8. Number of roses = 15

Number of tulips = 10

Number of lilies = 5

a. Ratio of number of roses to tulips = 15:10

b. Ratio of number of lilies to roses = 5:15

c. Ratio of number of tulips to roses and lilies = 10:(15 + 5) = 10:20

9. Weight of a male tiger = 220 kg

Weight of a male rhino = 2200 kg

Ratio of the weight of tiger to rhino = 220: 2200

220:2200 can be simplified as 1:10.

10. 24 hours = 1 day

Ratio of 24 hours to 2 days = Ratio of 1 day to 2 days = 1:2

11. Amount of water = 18 litres

Amount of juice = 12 litres

Ratio of water to juice = 18:12 = 3:2

12. Length of rectangular field = 80 m

Width of field = 60 m

Perimeter of field = 2 × (l + b) = 2 × (80 + 60) = 280 m

Ratio of length to perimeter = 80:280 = 2:7

13. HCF of two numbers = 5

The simplest form of the ratio = 3:4

The given numbers are, 3 × 5 = 15 and 3 × 4 = 20

14. The scale of the floor plan is 1:300, meaning 1 cm on the plan represents 300 cm (or 3 metres) in reality.

If the room measures 3 cm by 2 cm on the plan, its actual dimensions are calculated as follows:

Length: 3 cm × 300 = 900 cm = 9 metres

Width: 2 cm × 300 = 600 cm = 6 metres

Therefore, the actual dimensions of the room are 9 metres by 6 metres.

15. The ratio of the tree’s height to the pole’s height should equal the ratio of their shadow lengths.

Height of the tree (H) is found using: 18 = 2025 H

Solving this gives: H = × 20 18 25 = 14.4

Thus, the height of the tree is 14.4 metres.

16. Ratio in which the colours are mixed = 1:2

Quantity of the first colour = 3 litres

Quantity of the second colour = 3 × 2 = 6 litres

17. Ratio in which spending and saving is split = 2:3

Amount saved each month = 3x = ₹6000 x = 6000 3 = 2000

Amount spent = 2x = 2 × 2000 = ₹4000

Hence, Sneha spends ₹4000 each month.

18. The baker’s grandma uses a ratio of 3:6 milk to flour, which can be simplified to 1:2.

Since the baker only has 2 cups of milk (which is considered 1 part), they should use 2 parts flour which is 2 × 2 = 4 cups of flour.

Thus, 4 cups of flour should be used.

Challenge

1. Ratio of the rafting rentals to bungee rentals at a store = 10:7

If the number of bungee rentals doubles while the number of rafting rentals stays the same, the ratio changes from 10:7 to 10:14.

14 = 10 × 1.4

Thus, the number of bungee rentals becomes 1.4 times the number of rafting rentals.

Do It Yourself 12B

1. a. 4:5 = 4 5 ; 12:15 = 12 15 = 12 ÷ 3 15 ÷ 3 = 4 5

Hence, the ratios are in proportion.

b. 8:5 = 8 5 ; 9:6 = 9 6 = 9 ÷ 3 6 ÷ 3 = 3 2

Hence, the ratios are not in proportion.

c. 15:5 = 15 5 = 15 ÷ 5 5 ÷ 5 = 3:1 ; 12:4 = 12 4 = 12 ÷ 4 4 ÷ 4 = 3:1

Hence, the ratios are in proportion.

d. 9:5 = 9 5 ; 18:10 = 18 10 = 18 ÷ 2 10 ÷ 2 = 9:5

Hence, the ratios are in proportion.

2. a. 17:8 ≠ 1:3 = False

b. 5:15 = 5 ÷ 5 15 ÷ 5 = 1:3; 3:9 = 3 ÷ 3 9 ÷ 3 = 1:3

As 5:15 = 3:9 = True

c. 21:4; 84:16 = 84 ÷ 4 16 ÷ 4 = 21 4

As 21:4 = 84:16 = True

d. 7:12; 21:36 = 21 ÷ 3 36 ÷ 3 = 7:12

As 7:12 = 21:36 = True

3. Answer may vary. Sample answer:

a. 9:13::3:39 3 13 is in simplest form

÷ ÷ 99 33 = = 3939 313

So, 9:13::3:39

b. 7:42::3:18 71 = 426 31 = 186

So, 7:42::3:18

c. 7:21::4:12 71 = 213 4 12 = 1 3

So, 7:21::4:12

d. 2:14::8:56 2 14 = 1 7

8 56 = 1 7

So, 2:14::8:56

4. a. 2:x :: 5:10

x × 5 = 2 × 10

⇒ x = 20 5 = 4

c. x:16 :: 12:24

x × 24 = 16 × 12

⇒ x = 192 24 = 8

5. a. 12:4 :: 9:x

12 × x = 4 × 9

⇒ x = 36 12 = 3

c. 9:3 :: 6:x

9 × x = 3 × 6

⇒ x = 18 9 = 2

6. a. 9:3 :: 3:x

9 × x = 3 × 3

⇒ x = 9 9 = 1

c. 16:36 :: 36:x

16 × x = 36 × 36

⇒ x = 1296 16 = 81

7. x:21 :: 45:63

x × 63 = 21 × 45

⇒ x = 945 63 = 15

9. Ratio of length to width = 5:3

Length = 5x = 15 ⇒ x = 15 5 = 3

Width = 3 × x = 3 × 3 = 9 m

10. The proportion of a person’s weight to protein can be given as 55:132 :: x:156

132 × x = 55 × 156

⇒ x = 8580

132 = 65

Hence, 156 mg of protein will be given to a person weighing 65 kg.

11. The proportion of miles to gasoline require can be given as:

126:18 :: 175:x

126 × x = 18 × 175

⇒ x = 3150

126 = 25

Hence, 25 gallons of gasoline is required to travel 175 miles.

12. The proportion for the chemical reaction can be given as: 3 mole of hydrogen: 1 mole of nitrogen :: 9 moles of hydrogen: x

9 × 1 = 3 × x

x = 9 =3 3

So, 3 moles of nitrogen are required.

Challenge

1. Riya’s time = 300 metres =4 75 metres/minute minutes

Opponent’s pace: 15 metres in 12 seconds = 1 15 minutes

Or 75 metres in 1 minutes.

Let us check the distance covered by opponent in 4 minutes. 75 m × 4 = 300 metres

b. 3:6 :: 9:x

3 × x = 6 × 9

⇒ x = 54 3 = 18

d. 1:3 :: x:12

3 × x = 1 × 12

⇒ x = 12 3 = 4

b. 2:6 :: 1:x

2 × x = 6 × 1

⇒ x = 6 2 = 3

d. 32:8 :: 24:x

32 × x = 8 × 24

⇒ x = 192 32 = 6

b. 2:4 :: 4:x

2 × x = 4 × 4

⇒ x = 16 2 = 8

d. 36:42 :: 42:x

36 × x = 42 × 42

⇒ x = 1764 36 = 49

8. x:9 :: 9:3

3 × x = 9 × 9

⇒ x = 81 3 = 27

According to the question, Riya had to cover 300 metres before the opponent covers 280 metres but in the same time, the opponent has covered 300 metres.

Thus, opponent wins the race.

Do It Yourself 12C

1. Cost of 12 pens = ₹108

Cost of 1 pen = ₹ 108 12 = ₹9

Cost of 20 pens = 20 × ₹9 = ₹180

Hence, 20 pens will cost ₹180.

2. 2 km are covered in 1 hour

1 km will be covered in 1 2 hour

8 km will be covered in 1 2 × 8 = 4 hours

Hence, he will cover 8 km in 4 hours.

3. Number of post cards purchased in ₹375 = 125

Number of post cards purchased in ₹1 = 125 375

Number of postcards purchased for ₹180 = 125 375 × 180 = 60

Hence, 60 postcards can be purchased for ₹180.

4. Months to earn ₹1350 = 1 month

Months to earn ₹1 = 1 1350

Months to earn ₹12,150 = 1 1350 × 12,150 = 9 months

Hence, it will take 9 months to Amit to earn ₹12,150.

5. Temperature increases in 100 days = 25℃

Temperature increases in 1 day = 25 100 ℃

Temperature increases in 16 days = 25 100 × 16 = 4℃

Hence, the temperature will increase by 4℃ in 16 days.

6. Number of school buses require to carry 120 students = 3

Number of buses require to carry 1 student = 3 120

Number of school buses require to carry 1000 students = 3 120 × 1000 = 25

Hence, 25 school buses are required to carry 1000 students.

7. Interest paid in 1 year or 12 months = ₹18,000

Interest paid in 1 month = 18,000 12 = ₹1500

Interest paid in 7 months = ₹1500 × 7 = ₹10,500

Hence, the interest paid by Manya in 7 months = ₹10,500

8. Cost of 24 oranges bought by Raju = ₹336

Cost of 1 orange bought by Raju = ₹ 336 24 = ₹14

Cost of 21 oranges bought by Kiran = ₹273

Cost of 1 orange bought by Kiran = ₹ 273 21 = ₹13

Hence, Kiran bought the oranges at cheaper price.

9. Number of words typed in half an hour or 30 minutes = 660

Number of words typed in 1 minute = 660 30 = 22

Number of words type in 10 minutes = 22 × 10 = 220

Hence, Shreya can type 220 words in 10 minutes.

Challenge

1. The original recipe uses 3 cups of flour for 10 cookies. To make 30 cookies, we need 3 times the amount of flour. (30 cookies is 3 times 10 cookies)

3 cups � 3 = 9 cups

10% of 9 cups is:

0.1 � 9 cups = 0.9 cups

Add extra 0.9 cups to the 9 cups to find the total flour

9 cups + 0.9 cups = 9.9 cups

9.9 cups of flour is required to make 30 cookies with the extra 10% adjustment.

Chapter Checkup

1. Number of packets of potato chips = 45; Number of packets of banana chips = 66; Number of packets of corn chips = 32

a. Ratio of potato to corn chips = 45:32

b. Ratio of banana to total chips = 66:143

2. a. 8 m = 800 cm

HCF of 800 and 700 = 100

800

700 = 800 ÷ 100 700 ÷ 100 = 8 7

Thus, 8 m:700 cm in its simplest form is 8:7.

b. 360 sec = 360 60 = 6 min

Thus, 360 sec:7 min in its simplest form is 6:7.

c. 5 L = 5 × 1000 = 5000 mL

HCF of 5000 and 750 = 250

5000

750 = 5000 ÷ 250 750 ÷ 250 = 20 3

Thus, 5 L:750 mL in its simplest form is 20:3.

3. Answers may vary. Sample answers:

a. 3:8 = 3 × 2

8 × 2 = 6 16 ;

3 × 3

8 × 3 = 9 24 ;

3 × 4

8 × 4 = 12 32 ;

3 × 5

8 × 5 = 15 40

Four equivalent ratios to 3:8 = 6:16, 9:24, 12:32, and 15:40

b. 5:9 = 5 × 2 9 × 2 = 10 18 ; 5 × 3 9 × 3 = 15 27 ; 5 × 4 9 × 4 = 20 36 ; 5 × 5 9 × 5 = 25 45

Four equivalent ratios to 5:9 = 10:18, 15:27, 20:36, and 25:45

c. 11:15 = 11 × 2 15 × 2 = 22 30 ; 11 × 3 15 × 3 = 33 45 ; 11 × 4 15 × 4 = 44 60 ; 11 × 5 15 × 5 = 55 75

Four equivalent ratios to 11:15 = 22:30, 33:45, 44:60, and 55:75

4. a. 8:11 = 8 11 ; 7:9 = 7 9

LCM of 11 and 9 = 99

8 11 = 8 × 9 11 × 9 = 72 99 ;

7 9 = 7 × 11 9 × 11 = 77 99

As 72 99 < 77 99

⇒ 8 11 < 7 9 or 8:11 < 7:9

b. 9:12 = 9 ÷ 3 12 ÷ 3 = 3 4 ; 10:13 = 10 13

LCM of 4 and 13 = 52

3 4 = 3 × 13 4 × 13 = 39 52 ; 10 13 = 10 × 4 13 × 4 = 40 52

As 39 52 < 40 52

⇒ 9 12 < 10 13 or 9:12 < 10:13

c. 5:12 = 5 12 ; 9:14 = 9 14

LCM of 12 and 14 = 84

5 12 = 5 × 7 12 × 7 = 35 84 ;

9 14 = 9 × 6 14 × 6 = 54 84

As 35 84 < 54 84

⇒ 5 12 < 9 14 or 5:12 < 9:14

5. a. 14:20 = 14 20 = 14 ÷ 2 20 ÷ 2 = 7 10 ;

28:40 = 28 40 = 28 ÷ 4 40 ÷ 4 = 7 10

Hence the ratios are in proportion.

b. 16:17 = 16 17 ;

20:25 = 20 25 = 20 ÷ 5 25 ÷ 5 = 4 5

Hence the ratios are not in proportion.

c. 21:19 = 21 19 ; 21:34 = 21 34

Hence the ratios are not in proportion.

6. Number of red stamps = 24; Number of blue stamps = 36

Ratio of red stamps to blue stamps = 24 36 = 24 ÷ 12 3612

= 2 3 = 2:3

Hence, the ratio of red stamps to blue stamps is 2:3.

7. 12:x :: 6:36

x × 6 = 12 × 36

⇒ x = 432 6 = 72

8. 9:12 :: 12:x

x × 9 = 12 × 12

⇒ x = 144 9 = 16

9. Cost of 4 dozen or 48 eggs = ₹288

Cost of 1 egg = ₹ 288 48

Cost of 15 eggs = ₹ 288 48 × 15 = ₹90

Hence, 15 eggs will cost ₹90.

10. Ratio of pencils to pens = 4:5

Number of pencils = 4x = 36; x = 36 4 = 9

Number of pens = 5x = 5 × 9 = 45

11. Given that the numbers are in the ratio 3:5 So, 3x + 5x = 30

8x = 30

⇒ x = 30 8 = 3.75

Hence, the numbers are 3 × 3.75 = 11.25 and 5 × 3.75 = 18.75

12. Time taken to cover 60 miles = 1 hour

Rime taken to cover 1 mile = 1 60 hour

Time taken to cover 180 miles = 1 60 × 180 = 3 hours

Hence, the time taken to cover 180 miles is 3 hours.

13. Number of bottles filled in 5 hours = 750

Number of bottles filled in 1 hour = 750 5 = 150

Number of bottles filled in next 3 hours = 150 × 3 = 450

Hence, the machine will fill 450 bottles in the next 3 hours.

14. Number of painters required for painting the building in 6 days = 18

Number of painters required to paint the building in 1 day = 18 × 6 = 108 (less days, more painters)

Number of painters required to paint the building in days = 180 4 = 27

Hence, 27 painters are required to paint the building in 4 days.

15. Ratio of John’s age to Mary’s age = 2:3

John’s age = 2x = 24 years; x = 24 2 = 12

Mary’s age = 3x = 3 × 12 = 36 years

16. Number of hours taken to cover 1200 km = 6 hours

Number of hours taken to cover 1 km = 6 1200 hours

Number of hours taken to cover 800 km = 6 1200 × 800 = 4 hours = 4 × 60 minutes = 240 minutes

17. Present age of mother = 36 years; Age of mother after 12 years = 36 + 12 = 48 years

Present age of daughter = 36 – 20 = 16 years; Age of daughter 10 years ago = 16 – 10 = 6 years

Required ratio = 48:6 = 8:1

18. Answers may vary. Sample answer:

A factory produces 120 toys in 5 hours. How many toys can the factory produce in 8 hours at the same rate?

Challenge

1. Ratio of 1st class and 2nd class fares = 3:2

Ratio of passengers travelling in 1st and 2nd class = 1:15

Ratio of amounts collected from 1st and 2nd class = (3 × 1): (2 × 15) = 3:30 = 1:10

Fraction of the 1st class passengers to total passengers

= + 11 = 11011

Total money collected as fare = ₹26,400

Amount collected from the first class passengers

= 1 11 × 26,400

= ₹2400

2. Assertion (A): If the ratio of the mass of zinc to copper in an alloy is 7:5 and the total mass of the alloy is 120 kg, then the mass of zinc in the alloy is 70 kg.

To find the mass of zinc in the alloy, we will first determine the total parts of the ratio.

The ratio of zinc to copper is 7:5.

Total parts = 7 + 5 = 12

Now, we will use the formula given in the reason to find the mass of zinc:

Mass of zinc = × 7 120 12 = 70 kg

So, the assertion is true.

Reason (R): The mass of zinc in the alloy can be calculated using the formula part of zinc × part mass total parts

This is also true and helps us find the mass of zinc. Therefore, the correct answer is option a:

Both A and R are true, and R is the correct explanation of A.

Case Study

1. Ranthambore National Park has 60 tigers and 200 deer.

So, ×= 60 10030 200 tigers per deer

Therefore, the answer is 30 tigers per 100 deer. Hence, option a is correct.

2. Ranthambore National Park has 20 leopards, and Bandhavgarh National Park has 15 leopards.

The difference is 20 − 15 = 5

So, there are 5 more leopards in Ranthambore National Park than Bandhavgarh National Park. Hence, option a is correct.

3. Ratio of tigers to leopards in Ranthambore National Park is 60 : 20 = 3:1.

4. Ranthambore National Park has 280 total animals (60 tigers + 20 leopards + 200 deer), and Bandhavgarh National Park has 345 total animals (80 tigers + 15 leopards + 250 deer). So, Ranthambore National Park has ≈ 200 0.714 280 deer per total animals, and Bandhavgarh National Park has ≈ 250 0.724 345 deer per total animals. Therefore, Bandhavgarh National Park has a higher proportion of deer to total animals compared to Ranthambore National Park. So, the statement is true.

5. Answer may vary. Sample answer: We should observe wildlife from a distance, avoid disturbing their natural habitats, follow park rules and regulations, and learn about conservation efforts to protect these animals and their environments.

Chapter 13

Let’s Warm-up

1. Symmetrical 2. Non-symmetrical

3. Symmetrical 4. Symmetrical 5. Non-symmetrical

Do It Yourself 13A

1. Isosceles triangle has two opposite sides equal. It has a vertical line of symmetry.

One line of symmetry.

3. Pihu is right. The chessboard has two (diagonals) lines symmetry. The horizontal and vertical lines will not divide the chessboard symmetrically.

4. a. l2 l1

Both l1 and l2 show the line of symmetry in the given figure.

Neither l1 or l2 show the line of symmetry in the given figure.

6. The 4 letter that have 2 or more lines of symmetry are H, I, O and X.

H = 2 lines of symmetry

I = 2 lines of symmetry

O = Infinite lines of symmetry

X = 2 lines of symmetry

7. Answers may vary. Sample answers:

Challenge

1. The lower right portion is missing a black dot towards the centre. We can make it symmetrical by drawing another black dot.

1. a. Option b b. The arrows are mirror images of each other. 2. a.

3. The reflected word is WOW so the original word was MOM.

7. a. 180° 360°

Order of rotational symmetry = 2

b. 60° 120° 180° 240° 300° 360°

Order of rotational symmetry = 6

c. 120° 240° 360°

Order of rotational symmetry = 3

d. 360°

Order of rotational symmetry = 1

e. The logo has 3 angles of symmetry. The angles of symmetry are 120°, 240° and 360°. 120° 240° 360°

4. The actual word is GOVERNMENT OF INDIA. GOVERNMENT OF INDIA GOVERNMENT OF INDIA

5. a. MIRROR MIRROR

b. SYMMETRY SYMMETRY

c. REFLECTION REFLECTION

d. MATHEMATICS MATHEMATICS

6. a. b.

Challenge

1. The correct mirror image of the given image is shown below.

Blue and yellow colour at the bottom of the figure are incorrectly coloured in the mirror image.

Chapter Checkup

1. Yes, the figure has 1 line of symmetry.

2. Z S 3 D 8 U

3. no line of symmetry 1 line of symmetry more than 1 line of symmetry

4. a. There is 1 line of symmetry in the letter T. True

b. A regular pentagon has 5 lines of symmetry. True

c. All the quadrilaterals have 4 lines of symmetry. False

d. A semicircle has 1 line of symmetry. True

5. No, Rahul is not correct because a rainbow has a semi-circular shape; hence, it has only 1 line of symmetry (vertical).

6. a. Number of all possible lines of symmetry = 4

b. Number of all possible lines of symmetry = 2

c. Number of all possible lines of symmetry = 4

d. Number of all possible lines of symmetry = 4

a. ; Yes the lines of symmetry marked on the given figure. b. ; Yes the lines of symmetry marked on the given figure.

No; the lines of symmetry does not marked on the given figure.

11. The smallest angle of symmetry is 90°.

So the other angles of symmetry are: 180°, 270°, 360°.

12. The outline of the sign board is in the shape of a rhombus.

Order of symmetry of a rhombus = 4 Angle of symmetry = 90°

Challenge

1. Assertion: A regular hexagon has six lines of symmetry. This is true.

Reason: A line of symmetry divides a shape into two identical shapes. The reason is also true and it explains the assertion. Thus, option a is correct.

2. The girl walks 3 blocks north, then 4 blocks west, then 3 blocks south and finally 4 blocks east.

This way, she reaches her original position and the shape formed by the path is a rectangle.

A rectangle has 2 lines of symmetry.

Case Study

1. The butterfly has only one line of symmetry. Thus, option b is correct.

4 blocks 3 blocks 3 blocks

4 blocks

2. Only the leaf in option b has a line of symmetry.

Thus, option b is correct.

12 lines of symmetry.

Chapter 14

Let’s Warm-up

1. Line segments = 5 Angles = 5

2. Line segments = 5 Angles = 6

Do It Yourself 14A

1. Not drawn to scale. Sample figures:

a. 5.4 cm A B 5.4 cm

b. 6.7 cm P Q 6.7 cm

c. 6.1 cm L M 6.1 cm

d. 7.2 cm X Y 7.2 cm

2. Not drawn to scale. Sample figures:

a. AB = 4.3 cm b. DE = 5.6 cm

B 4.3 cm D E 5.6 cm c. GH = 3.9 cm d. PQ = 2.7 cm G H 3.9 cm P Q 2.7 cm

3. Students will construct line segments of the same length as AB, PQ and MN.

4. a. BC = 4RS – 3PQ = 4 × 3.6 − 3 × 2.3 cm = 14.4 − 6.9 = 7.5 cm B C 7.5 cm

b. XY = RS + 2PQ = 3.6 + 2 × 2.3 cm = 3.6 + 4.6 = 8.2 cm X Y 8.2 cm 5. 5 cm 5 cm 5 cm 5 cm S H J I

6. Figure may vary. Sample figure:

Challenge

1. Yes, we can construct a square by drawing a perpendicular to the diagonal.

Do It Yourself 14B

Each angle measures 60°. b. 75°

Each angle measures 75°. c. 22.5°

Each angle measures 22.5°.

Challenge

1. Statement 1: There can be more than one angle bisector to any given angle.

Statement 2: The angle bisector of an angle is also its line of symmetry.

The angle bisector is a geometric line or ray that divides an angle into two congruent or equal angles.

So, Statement 1 is incorrect as for any given angle, there is exactly one angle bisector. Hence, there cannot be more than one angle bisector for the same angle.

Statement 2 is correct as when we reflect one side of the angle across the bisector, we obtain the other side of the angle, which shows symmetry, making it the line of symmetry for that angle.

Here only Statement 2 is correct. So, the correct option is b.

Chapter Checkup

1. a. PQ = 3.6 cm P 3.6 cm Q

b. AB = 8.2 cm A 8.2 cm B

2. Given EF = 10.2 cm and EG = 3.8 cm EF − EG = FG

FG = 10.2 − 3.8 = 6.4 cm E G 3.8

4. a. Given, UV = 6.2 cm and ST = 4.7 cm WX = 3UV – 2ST

= 3 × 6.2 – 2 × 4.7 cm

= 19.6 – 9.4 = 9.2 cm

Not drawn to scale. Sample figures:

Using a ruler: W X 9.2 cm

Using a ruler and a compass: W X 9.2 cm l

b. Given, UV = 6.2 cm and ST = 4.7 cm AB = 3ST + 2UV = 3 × 4.7 + 2 × 6.2 cm = 14.1 + 12.4 = 26.5 cm

Not drawn to scale. Sample figures:

Using a ruler: A B 26.5 cm

Using a ruler and a compass: A B 26.5 cm l

5. The outline of the new parliament building in India is shown: A O B

A single line segment that equals the total length of any two sides in the given shape using a ruler and compass is shown:

10. The angle of release of a javelin = 30°

12. No, all the angle bisectors didn’t intersect at a given point.

1. Assertion(A): Two lines intersecting at a point at 90° can look like alphabet ‘L’.

Reason(R): Both lines are perpendicular to each other. Assertion is true as when two lines intersect at a right angle (90°), the resulting shape resembles the letter ‘L�. This is a common representation of two perpendicular lines.

Reason is true as two lines that intersect at 90° are indeed perpendicular to each other by definition.

Thus, both A and R are true, and R is the correct explanation of A.

Hence, option d is correct.

2. Yes, the bisecting rays are perpendicular to each other.

A linear pair of angles is formed when two adjacent angles add up to 180°.

Let us denote the two angles as ∠A and ∠B.

Let ∠A = x and ∠B = 180° − x

The bisector of ∠A = 2 x and the bisector of ∠B = 180 2 x °−

Sum of angles formed by the bisectors = 2 x + 180 2 x °− = +°− 180 2 xx = 180 2 ° = 90°

Since the sum of two angles formed by the bisectors is 90°, the bisecting rays are perpendicular to each other.

Case Study

1. The length of the rod in a sundial = 45 cm

If the scale is 5 cm = 1 mm

⇒ 1 cm = 1 5 mm

⇒ The length of the rod in the sundial when drawn on paper = 45 5 = 9 mm

Hence, option b is correct.

2. Not drawn to scale. Sample figure: A 9 mm B

3. Angle formed by the shadow = 120°

Measure of angle bisector = 120° ÷ 2 = 60°

2° = 1 unit

1° = 1 2 unit

60° = 60° 2° = 30 units

So, 30 units will be equal to 60°.

4. A P B D Q C 60°

About the Book

The Imagine Mathematics teacher manuals bridge the gap between abstract mathematics and real-world relevance, offering engaging activities, games and quizzes that inspire young minds to explore the beauty and power of mathematical thinking. These teacher manuals are designed to be indispensable companions for educators, providing well-structured guidance to make teaching mathematics both effective and enjoyable. With a focus on interactive and hands-on learning, the lessons in the manuals include teaching strategies that will ensure engaging lessons and foster critical thinking and problem-solving skills. The teaching aids and resources emphasise creating an enriched and enjoyable learning environment, ensuring that students not only grasp mathematical concepts but also develop a genuine interest in the subject.

Key Features

• Alignment with Imagine Mathematics Content Book: Lesson plans and the topics in the learners’ books are in sync

• Learning Outcomes: Lessons designed as per clear, specific and measurable learning outcomes

• Alignment to NCF 2022-23: Lessons designed in accordance with NCF recommendations

• Built-in Recaps: Quick recall of pre-requisite concepts covered in each lesson

• Supporting Vocabulary: Systematic development of mathematical vocabulary and terminology

• Teaching Aids: Resources that the teachers may need to facilitate the lesson

• Activity: Concise and organised lesson plans that outline each activity

• Extension Ideas: Analytical opportunities upon delivery of each lesson

• Detailed Solutions: Solutions to all types of questions in the Imagine Mathematics Content Book

• Digital Assets: Access to supplementary interactive resources

About Uolo

Uolo partners with K-12 schools to provide technology-enabled learning programs. We believe that pedagogy and technology must come together to deliver scalable learning experiences that generate measurable outcomes. Uolo is trusted by over 15,000+ schools across India, Southeast Asia and the Middle East.

ISBN 978-81-984519-1-0