Sbírka úloh z matematiky 7

7 SBÍRKA ÚLOH Z MATEMATIKY

pro základní školy

I. ÚVODNÍ OPAKOVÁNÍ

ARITMETIKA OBSAH

1 Uspořádání přirozených čísel Číselná osa

2. Dělitelnost .

3. Uspořádání desetinných čísel .

4 Počítáme pomocí závorek

5. Jednotky délky, hmotnosti, obsahu a objemu

6 Sčítání, odčítání, násobení a

1 Dělení celku, zlomek

2. Rozšiřování a krácení zlomků

3. Porovnávání zlomků

4

5. Násobení a dělení zlomků

6 Složené zlomky

7.

III. CELÁ ČÍSLA

1. Porovnávání celých čísel .

2

3 Sčítání a odčítání celých čísel

4. Násobení a dělení celých čísel

IV. RACIONÁLNÍ ČÍSLA

1. Kladná a záporná desetinná čísla, kladné a záporné zlomky

2 Porovnávání racionálních čísel

3. Sčítání a odčítání racionálních čísel

V. POMĚR, PŘÍMÁ A NEPŘÍMÁ ÚMĚRNOST

1. Určení poměru. Krácení a rozšiřování poměru. Porovnávání poměrem

Postupný pomě

6. Jednoduché úrokování

7. Promile .

VII. ZÁVĚREČNÉ OPAKOVÁNÍ

1 Zlomky a celá a racionální čísla

2. Poměr, přímá a nepřímá úměrnost

GEOMETRIE

I. ÚVODNÍ OPAKOVÁNÍ

1 Úhly a některé jiné geometrické rovinné a prostorové útvary

2. Trojúhelník a další učivo o úhlech

3 Osová souměrnost

4. Krychle a kvádr

II. SHODNOST

1. Základní útvary a jejich shodnost

2. Shodnost trojúhelníků

III. STŘEDOVÁ SOUMĚRNOST

1. Opakování osové souměrnosti

2 Středová

3. Středově souměrné útvary

IV. ČTYŘÚHELNÍKY

1. Základní pojmy

2. Rozdělení čtyřúhelníků

Rovnoběžníky

4. Lichoběžníky

5 Úlohy na závěr

V. HRANOLY

1 Opakování a doplnění učiva o krychli a kvádru

2. Kolmé hranoly, jejich povrch a objem

VI. ZÁVĚREČNÉ

Shodnost

7. Čtyřúhelníky

Hranoly

VÝSLEDKY

3. Uspořádejte sestupně: a) (pomocí číselné osy) b) c) d)

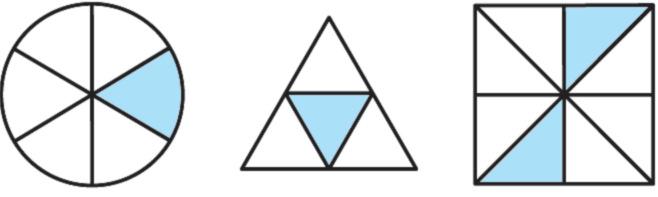
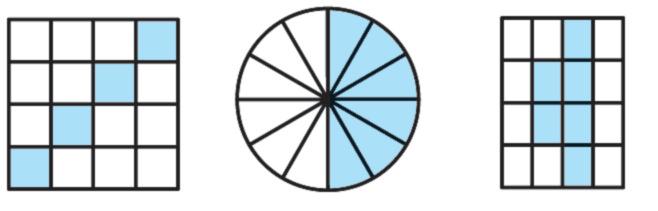
4. II. Ve kterých dvou obrázcích z a), b), c) jsou zvýrazněny jejich stejné části?

II. Ve kterém z obrázků d), e), f) je zvýrazněna jeho a) největší část, b) nejmenší část?

5 8 , 7 8 , 9 8 3, 20 17 , 2, 17 17 5, 9 3 , 8 2 , 5 6 1, 6 7 , 7 6 , 19 21 , 2 3 5 3 3

5. Ze 120stránkové knihy přečetl Dan již 54 stránek Jeho mladší sestra Jitka přečetla z 80stránkové knihy prozatím 44 stránek. Který ze sourozenců přečetl větší část své rozečtené knihy?

6. Trať přespolního běhu překonal Petr za h, Standa za h a Olda za 95 minut. Který z těchto tří chlapců běžel: a) nejrychleji, b) nejpomaleji?

7. Milan a Jirka jezdí do školy na kole. Milanovi trvá jízda h, Jirkovi h. Kdo z nich bydlí dále od školy za předpokladu, že jezdí stejnou rychlostí?

8. V Jihlavě bylo naměřeno centimetru dešťových srážek, v Táboře centimetru srážek a v Českých Budějovicích 8 mm srážek. Ve kterém městě byly tyto srážky nejvydatnější?

9. V pátek přišlo do prodejny se sportovními potřebami 180 návštěvníků a 117 z nich uskutečnilo nákup. V sobotu jich přišlo 240 a 170 z nich uskutečnilo nákup. Ve kterém z těchto dvou dnů nakoupila větší část návštěvníků?

10. Paní Zámečníková nakupovala v obchodním domě. V nákupním košíku s hmotností 800 g měla kg hovězího masa, kg vepřového sádla, 100 g salámu a kávy V košíku téže hmotnosti měla paní Kafková nákup s hmotností 1 kg. Která z nich měla: a) lehčí košík i s nákupem, b) lehčí nákup?

11. Manželé Nestlerovi si hodlají v Německu koupit nový automobil za 90 000 €. Tři pětiny této částky mají našetřeno, prodejní ceny získají prodejem svého starého auta a zbytek této prodejní ceny jim uhradí banka. Jak vysoký úvěr jim banka musí poskytnout?

1. Sečtěte:

2. Odečtěte:

3. Vypočítejte:

4. Odečtěte. Před odčítáním vyjádřete každý zlomek v základním tvaru:

5. Menšenec je , menšitel . Vypočítejte rozdíl.

6. Napište zlomek, který je o menší než:

20. Autobazaru bylo v letošním jarním období nabídnuto k prodeji 96 „ojetin“ osobních automobilů. Z tohoto počtu jich měla metalízu, z nich měly tuto povrchovou úpravu viditelně poškozenou. Kolik nabízených „ojetin“ mělo poškozenou metalízu?

21. Monika dostala od babičky tabulku čokolády rozdělenou na 15 dílků. Třetinu jí snědla a polovinu zbytku dala bratrovi. Kolik dílků čokolády a) Monika snědla, b) dala bratrovi?

22. Plnotučné kravské mléko obsahuje v 1 kg tuku. Kolik kilogramů tuku obsahuje 50 kg tohoto mléka?

23. Natálčina babička peče buchty ze kg mouky Dvě třetiny této hmotnosti tvoří polohrubá mouka a zbytek hladká mouka. Vyjádřete hmotnost obou druhů mouky v gramech

24. V Plzni se hrálo ligové fotbalové utkání s Jabloncem. V průběhu utkání bylo oznámeno, že počet přihlížejících platících diváků je 6 240 Dodejme, že pětinu těchto diváků tvořili jablonečtí fanoušci a šestina z nich přijela do Plzně autobusy. Kolik jabloneckých fanoušků přijelo do Plzně autobusy?

25. V 7. třídě je 30 žáků. Z nich hraje fotbal, se věnují jiným sportovním odvětvím. Zbytek žáků nesportuje Kolik žáků a) hraje fotbal, b) věnuje se jiným sportům, c) nesportuje?

26. V minulém školním roce měla Jana ve středu 5 vyučovacích hodin po 45 minutách. Mezi nimi byly 3 desetiminutové přestávky a 1 čtvrthodinová přestávka. Jak dlouho trvalo ve středu Janě vyučování (včetně přestávek)? Délku vyučování vyjádřete a) v minutách, b) v hodinách

27. V Pardubicích musel pan Janda přestoupit z rychlíku do osobního vlaku do Letohradu. Čekací doba byla poměrně dlouhá, proto si šel koupit před nádraží do trafiky noviny. Po návratu měl ještě čekat 30 minut, což představovalo tři čtvrtiny celkové čekací doby Jak dlouhá byla celková čekací doba na přestup?

28. Machačovi si koupili stavební parcelu s výměrou 6 a (600 m2). Na její výměry si postavili rodinný domek s garáží, zaujaly přístupová cesta ke garáži a chodník Jaká část této parcely zbyla na zahrádku? Výsledek vyjádřete a) ve tvaru zlomku, b) v počtu čtverečných metrů.

III. CELÁ ČÍSLA

1. Porovnávání celých čísel

1. Následující dvojice celých čísel porovnejte podle velikosti [obdélníčky nahraďte správnými znaky nerovnosti (>, <), případně rovnosti (=)]: a) –5  3 b) +9  –10 c) –7  0 d) 6  –6 e) 0  1 f) –26  –27 g) –205  –206 h) 1 300  +1 300

2. Napište aspoň tři celá čísla, jejichž obrazy leží na číselné ose mezi obrazy čísel: a) 6; 2 c) –9; 0 d) +23; +29 e) –302; –295

3. V roce 52 př. n. l. dobyl římský vojevůdce Gaius Iulius Caesar [cézar] Galii (část dnešní Francie). V roce 30 př. n. l. obsadil římský císař Octavianus [oktaviánus] Augustus (Vznešený) severoafrický Egypt. Která z těchto dobyvačných válečných událostí starověkého Říma se stala dříve?

Octavianus Augustus Gaius Iulius Caesar

4. Upořádejte podle velikosti bankovní konta zahraničních klientů (zákazníků) u téhož peněžního ústavu. Jako první v tomto uspořádání napište nejvyšší konto: +1 200 €, –2 600 €, +17 200 €, – 620 €, –150 €, +23 800 €, 61 120 €.

8. Pravoúhlá soustava souřadnic v rovině

1. Podle dvou obrázků pravoúhlých soustav souřadnic zapište souřadnice vyznačených

bodů A, B, C, D, E, F, G, H, I

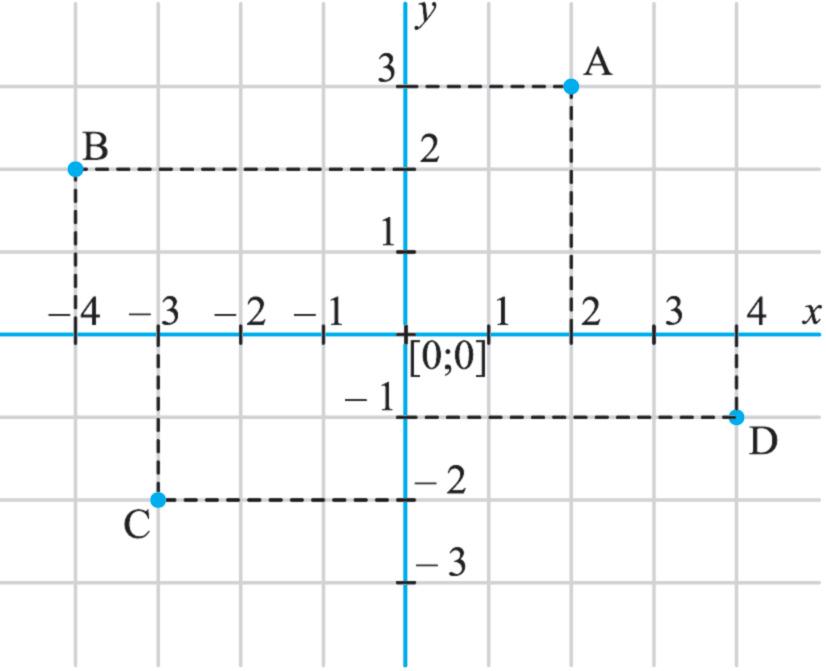
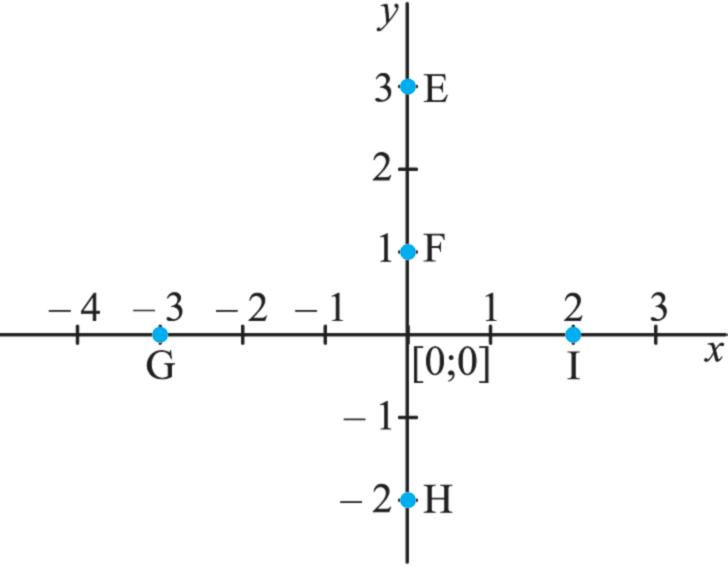
2. a) V pravoúhlé soustavě souřadnic s jednotkovou úsečkou délky 1 cm narýsujte

čtyřúhelník ABCD s vrcholy A [ –1; –2 ] , B [ 5; –2 ] , C [ 5; 4 ] , D [ –1; 4 ] Jak se tento čtyřúhelník nazývá?

b) Vypočítejte jeho obvod a obsah.

c) Vyznačte dvě jeho osy souměrnosti o1, o2, pro které platí: o1 || x, o2 || y O ∈ o1 ∩ o2

d) Zapište souřadnice bodu O.

3. a) V pravoúhlé soustavě souřadnic s jednotkovou úsečkou délky 1 cm narýsujte

čtyřúhelník EFGH s vrcholy E [–2; –1], F[4; –1], G[4; 4], H[–2; 4] Jak se tento čtyřúhelník nazývá?

b) Vypočítejte jeho obvod a obsah.

c) Určete souřadnice průsečíku P jeho os souměrnosti.

4. V pravoúhlé soustavě souřadnic narýsujte trojúhelník ABC s vrcholy A[3; 3], B[0; 0], C[3; 0]. Na straně AB vyznačte aspoň jeden bod X, na straně BC aspoň jeden bod Y a na straně AC aspoň jeden bod Z (různé od bodů A, B, C) a zapište jejich souřadnice.

5. V pravoúhlé soustavě souřadnic Oxy s počátkem O[0; 0] vyznačte bod M[–3; –2].

Sestrojte obraz

a) M1 bodu M v osové souměrnosti podle osy souřadnic x a zapište jeho souřadnice,

b) M2 bodu M v osové souměrnosti podle osy souřadnic y a zapište jeho souřadnice.

1. V následující tabulce je proměnná y přímo úměrná proměnné x.

a) Určete koeficient k přímé úměrnosti a napište její rovnici.

9. Přímá úměrnost x 13 0,4 1 2 5 8 y 20 32 52

b) Překreslete si tabulku do sešitu a její prázdná políčka doplňte

2. Za 7 autobusových jízdenek pro jízdu z města A do města B vybral řidič 294 Kč.

a) Vypočítejte a zapište do tabulky dvojice hodnot [x (počet jízdenek); y (jejich celková cena v Kč)] pro x {0; 3; 5; 9; 11; 13; 40}.

b) Vztah mezi počtem jízdenek z města A do města B vyjádřete rovnicí

3. Podlahová krytina na obdélníkovou podlahu s rozměry 4 m a 3 m stála paní Konečnou 3 600 Kč. Kolik korun by stála paní Milanovou krytina na pokrytí čtvercové podlahy kuchyně se stranou délky 3,6 m (za předpokladu stejné ceny za 1 m2)?

4. III. Tři natěrači natřeli za 2 hodiny část plechové ohrady s obsahem 24 m2. Za předpokladu, že každý z nich má tentýž pracovní výkon, vypočítejte obsah části ohrady ve čtverečných metrech, kterou natře: a) 1 natěrač za 2 h b) 1 natěrač za 1 h c) 3 natěrači za 1 h d) 4 natěrači za 1 h e) 6 natěračů za 1 h f) 6 natěračů za h

4. III. Natěrači Zezulkovi se podařilo během 2 h natřít plechové střechy nad garáží pro nákladní automobil Jak dlouho při stejném pracovním výkonu mu trvalo natření celé střechy?

4. III. Plechovka se 2 kg barvy vystačí k natření podlahy s obsahem 16 m2. Kolik kilogramů barvy se spotřebuje k natření obdélníkové podlahy s rozměry 5 m a 4 m?

5. Stavební mistr věděl, že 6 kopáčů při stejných výkonech vyhloubí příkop dlouhý 30 m za 4 hodiny Položil si otázku: „Jak dlouhý příkop vyhloubí 5 kopáčů za 5 hodin?“ Jak si na tuto otázku správně odpověděl?

6. K výrobě 250 školních sešitů se spotřebovalo 1 500 dvojlistů.

a) Kolik dvojlistů bylo spotřebováno při výrobě 800 stejných sešitů?

b) Kolik dvojlistů obsahoval 1 školní sešit?

7. Ocelový „prut“ k výrobě železobetonových panelů dlouhý 2,4 m má hmotnost 18 kg. Určete hmotnost těchto prutů v 10 panelech, víte­li, že v každém z nich jich je osm.

8. V televizním pořadu s názvem KLUCI v AKCI spotřebovali mladí kuchaři na přípravu 5 plněných závitků 0,9 kg hovězího masa. Kuchař Zilvar připravil podle jejich receptu 24 závitků. Kolik kilogramů hovězího masa k jejich přípravě spotřeboval? 1 2 3 4

II. SHODNOST

1. Základní útvary a jejich shodnost

1. Nejdříve si uvědomte definici shodnosti geometrických útvarů v rovině. K ní nyní připojme důležitý doplněk:

Řekneme­li například, že trojúhelník ABC je shodný s trojúhelníkem A´B´C´, pak to znamená, že trojúhelník ABC vznikl přemístěním trojúhelníku A´B´C´ (nebo naopak), viz obrázek Říkáme, že

● vrcholu A´přísluší vrchol A,

● vrcholu B´přísluší vrchol B,

● vrcholu C´ přísluší vrchol C.

Tuto příslušnost vrcholů obou

trojúhelníků zapíšeme:

A´ → A, B´ → B, C´ → C.

Z toho plyne

a) příslušnost stran ∆ A´B´C´a ∆ ABC:

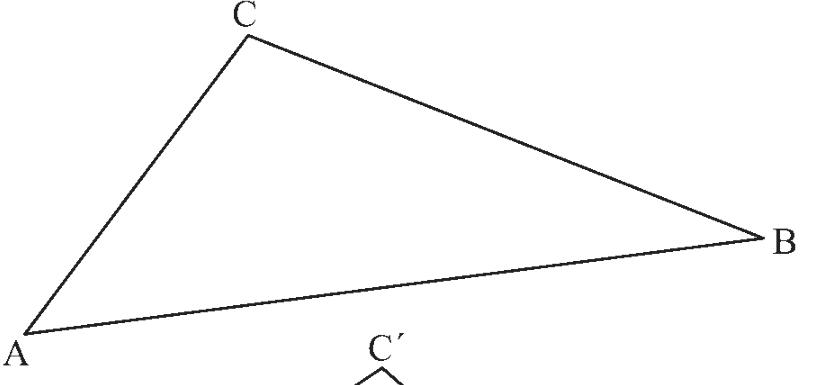
A´B´ → AB, B´C´ → BC, A´C´ → AC. O nich prohlásíme, že jsou shodné, a jejich shodnost zapíšeme:

A´B´ ≅ AB, B´C´ ≅ BC, A´C´ ≅ AC

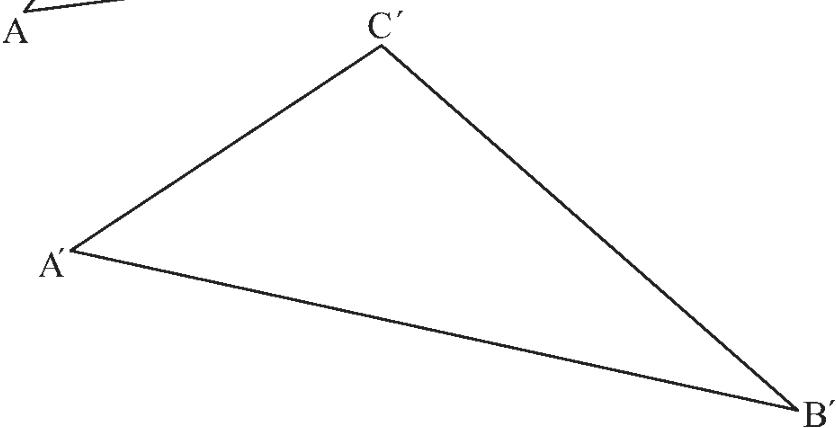
Rovnost jejich délek vyjádříme zápisy: |A´B´| = |AB|, |B´C´| = |BC|, |A´C´| = |AC|,

b) příslušnost vnitřních úhlů ∆ A´B´C´a ∆ ABC:

∢A´B´C´ → ∢ABC, ∢B´A´C´ → ∢BAC, ∢C´A´B´ → ∢CAB. Také o nich prohlásíme, že jsou shodné, a jejich shodnost zapíšeme:

∢A´B´C´ ≅∢ABC, ∢B´A´C´ ≅∢BAC, ∢C´A´B´ ≅∢CAB.

Úkol: Doplňte následující neúplné zápisy shodnosti trojúhelníků ABC a A´B´C´, které jsou na obrázku: a) ∆ ABC … ∆ A´B´C´ b) ∆ B´A´C´ ≅ … c) … ≅ ∆ CAB

2. Vztah: ∆ KLM ≅ ∆ EFG je pravdivý. Zapište všechny dvojice k sobě příslušných a) vrcholů, b) stran, c) úhlů.

3. Úhly α, β jsou vnitřní úhly trojúhelníku ABC, pro které platí: α = β = 38° Přepište si následující zápis a doplňte ho: γ = …

4. Velký trojúhelník KLM po přemístění zcela zakryl malý trojúhelník PQR. Můžeme o těchto dvou trojúhelnících prohlásit, že jsou shodné? Své odpovědi zdůvodněte

5. Na obrázku je ukázka dekoračního papíru prodejny s obojživelníky. Co můžeme prohlásit o stejných motivech tohoto papíru?

6. V tabulce jsou uvedeny rozměry pěti obdélníků. Které z nich jsou shodné?

obdélník ABCD EFGH PQRS MNOP UVXY

délka a 12 m 40 cm 1 200 mm 0,4 m 120 dm šířka b 8m 26,5 cm 800 mm 0,265 m 80 dm

7. Na obrázku jsou fotografie téhož kamionu. Jsou tyto fotografie přímo, nebo nepřímo shodné?

8. II. Na následujícím obrázku je několik geometrických obrazců rozdělených dvěma různými přímkami. Pomocí písmen popište části jednotlivých útvarů, které jsou shodné.

8. II. U každého z těchto útvarů vyhledejte a zapište aspoň dvě dvojice a) shodných úseček včetně rovnosti jejich délek, b) shodných úhlů.

a) Společnou část vzoru (úsečky QR) a obrazu (úsečky Q´R´) zvýrazněte silnou nebo barevnou čarou.

b) Pro společnou část obou geometrických útvarů (čili pro průnik úseček QR a Q´R´) použijte znak ∩ a proveďte příslušný zápis.

4. a) Sestrojte trojúhelník ABC, je­li dáno: |AB| = 70 mm, |BC| = 65 mm, β = |∢ABC| = 60°.

b) Uvnitř tohoto trojúhelníku vyznačte bod E tak, aby platilo: |AE| = 23 mm, |CE| = 49 mm. Potom sestrojte obraz A´B´C´trojúhelníku ABC ve středové souměrnosti určené středem E. Společnou část vzoru (∆ABC) a obrazu (∆A´B´C´) barevně odlište od ostatních částí požadované konstrukce Jak se společná část trojúhelníků ABC a A´B´C´nazývá?

5. Sestrojte obraz K´L´M´ trojúhelníku KLM (|KL| = 7,6 cm, |∢MKL| = 58°, |∢KLM| = 46°) ve středové souměrnosti se středem V, který je průsečíkem jeho výšek vk, vl, vm. Společnou část obou trojúhelníků opět zvýrazněte a určete její název

6. Sestrojte obraz E´F´G´ trojúhelníku EFG (|EF| = 8 cm, |FG| = 6 cm, φ = |∢EFG| = 50°) ve středové souměrnosti určené středem T, který je průsečíkem těžnic te, tf, tg čili těžištěm trojúhelníku EFG. Je možné společnou část trojúhelníků EFG a E´F´G´nazvat šestiúhelník?

7. Narýsujte kružnici k(S; 2,8 cm). Sestrojte obraz k´ kružnice k ve středové souměrnosti se středem O, jestliže: a) |SO| = 2,8 cm b) |SO| = 2 cm c) |SO| = 3,5 cm d) O = S

8. Kružnice k1(S1; r = 3 cm), k2(S2; r = 3 cm) mají vnější dotyk v bodě A (A ∈ k1 ∩ k2). a) Jsou obě kružnice středově souměrné podle bodu A? b) Sestrojte přímku, která prochází bodem A a na obou kružnicích vytíná shodné tětivy dlouhé 4 cm

3. Středově souměrné útvary

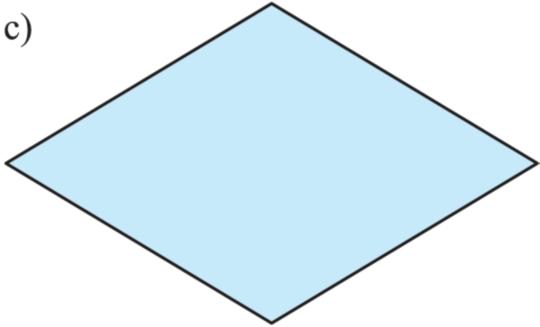
1. Nejdříve se zaměřme na pojem obrazec, který v základní škole běžně používáme Připomeňme si, že za obrazec považujeme rovinný útvar, jehož hranice je nám natolik dobře známá, že nám umožňuje vypočítat jeho obvod o a obsah S Tři obrazce jsou na obrázcích a) – c). Prohlédněte si je a pak rozhodněte, který z nich je a který není

středově souměrný

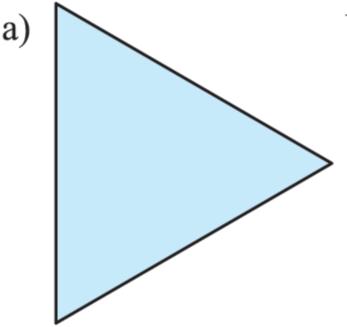
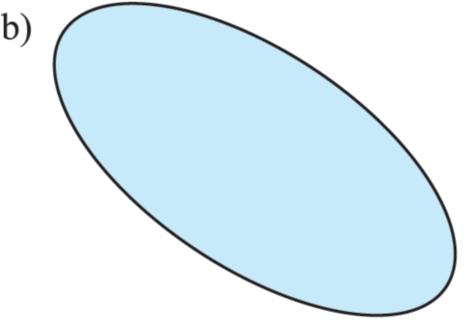
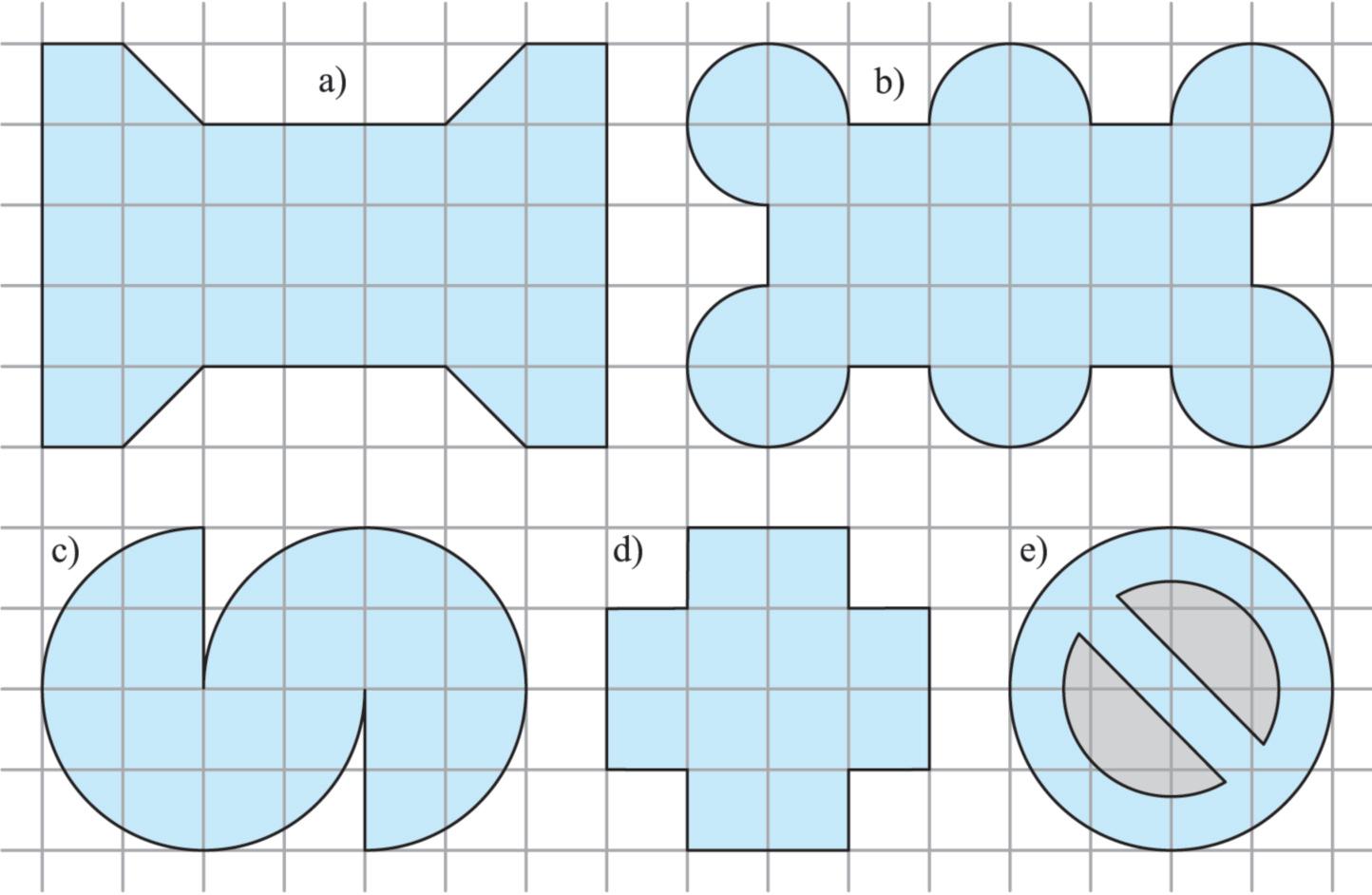
2. II. Na obrázcích a), b), c), d) jsou ve čtvercové síti zobrazeny obrazce různých tvarů Jsou všechny středově souměrné? V kladném případě ukažte polohy jejich středů.

2. II. Na obrázku e) není obrazec, ale obraz dopravní značky

a) Co řidičům zakazuje?

b) Máte­li možnost, přineste si do školy publikaci s dopravními značkami a vyberte z ní značky středově i osově souměrné. Co řidičům přikazují, nebo zakazují?

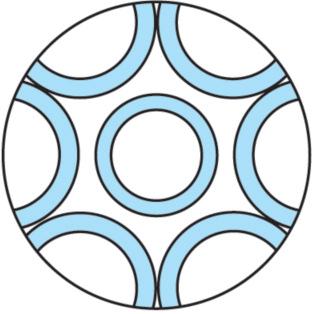
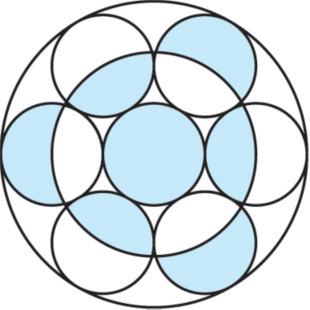
3. Který z útvarů a), b), c), d), e), f) je:

3. III. středově i osově souměrný,

3. III. jen středově souměrný podle jednoho středu,

3. III. středově souměrný podle více středů,

3 . IV. jen osově souměrný?

Upozornění: Zvláštní pozornost věnujte též souměrnosti ploch téže barevnosti, zejména u obrázků c) a e).

3. Vypočítejte obsah kosodélníku EFGH ve čtverečných metrech, znáte­li: |GH| = 17 dm, ve = vEF = 12 dm.

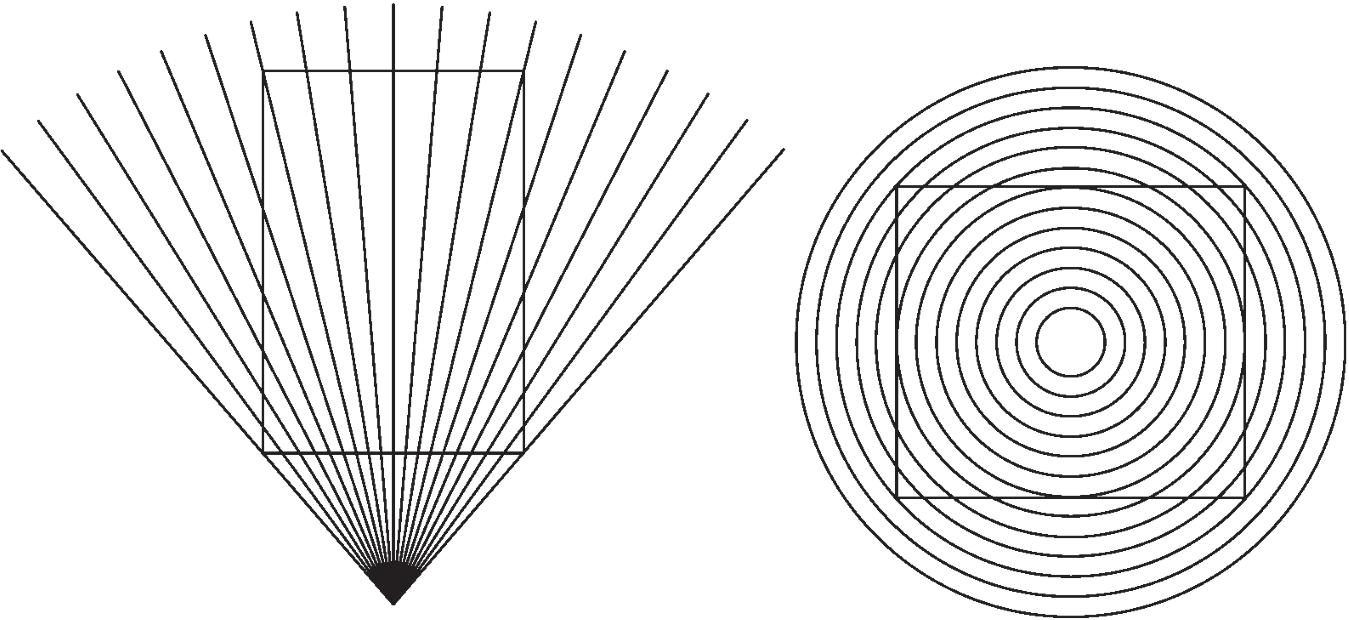
4. Pomocí dvou trojúhelníkových pravítek rozhodněte, zda útvary v množině polopřímek či kružnic na obrázku jsou rovnoběžníky V kladném případě uveďte jejich názvy

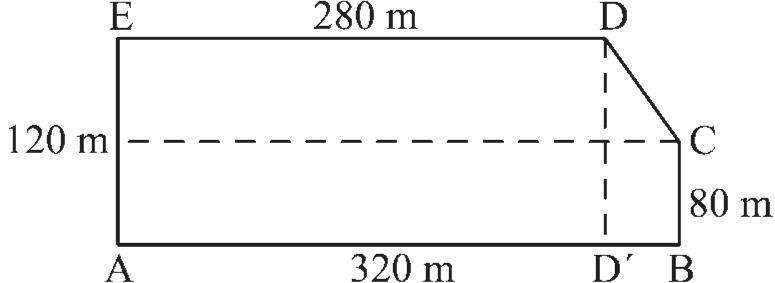
5. Zemědělský pozemek na obrázku byl převzat z katastrální mapy obce Sloveč V minulém roce byl oset žitem. Tento pozemek má tvar pětiúhelníku ABCDE, pro který platí: AB || DE, AE || BC, |∢EAB| = |∢ABC| = 90°, |AB| = 320 m, |AE| = 120 m, |BC| = 80 m, |DE| = 280 m. Na 1 ha tohoto pozemku se urodilo průměrně 2,6 t žita. Kolik tun mouky bylo možné z celkové sklizně žita z tohoto pozemku namlet, víte­li, že žitná mouka tvoří 85 % jeho hmotnosti?

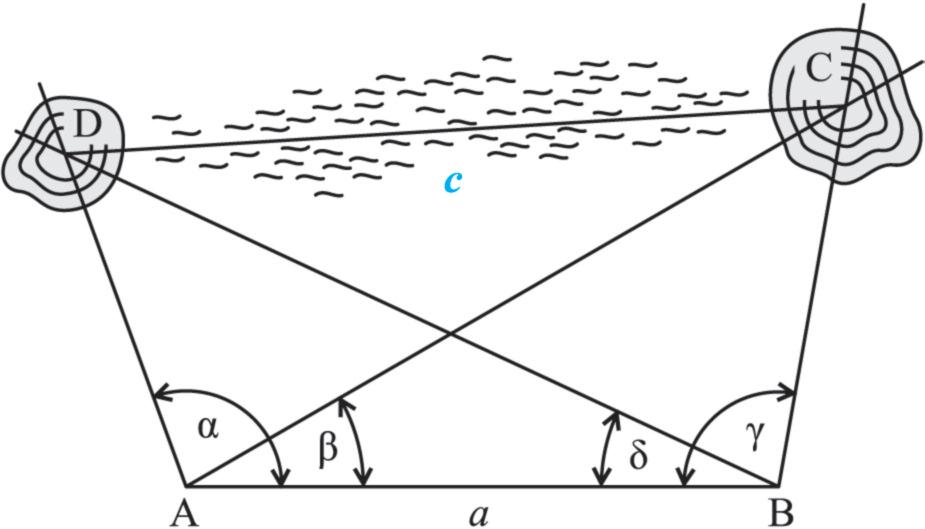
6. Zeměměřiči měli za úkol zjistit a zakreslit do plánu daného území s měřítkem 1 : 3 000 vzdálenost c vrcholků C, D dvou kopců, mezi nimiž byl nepřístupný močálovitý terén porostlý rákosem. K tomuto účelu si zjistili potřebné údaje, které si zakreslili do následujícího plánku. (Vzdálenost a terénních bodů A, B byla přístupná měření pomocí měřičského pásma, velikosti úhlů α, β, γ, δ určili zeměměřiči pomocí přístroje zvaného teodolit )

Zjistili: |AB| = 150 m, α = |∢DAB| = 110°, β = |∢CAB| = 30°, γ = |∢ABC| = 100°, s = |∢ABD| = 25°

Podle obrázku si narýsujte co nejpřesněji plánek této terénní situace do svých sešitů a určete, jaká je vzdálenost vrcholků C, D uvedených kopců ve skutečnosti

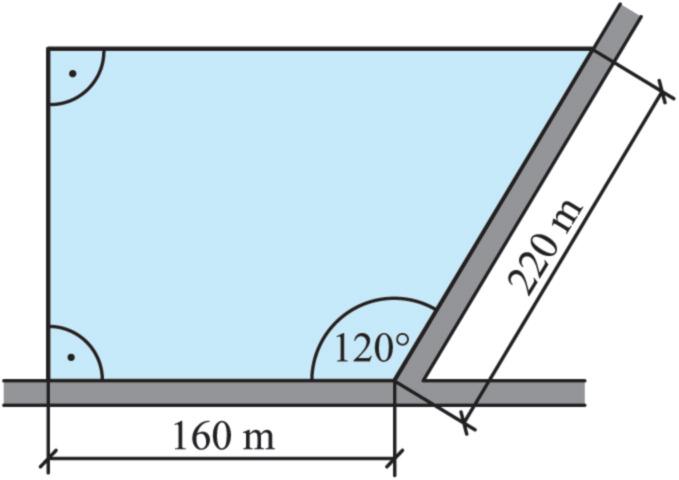
7. Pozemek pana Kafky má tvar pravoúhlého lichoběžníku.

Leží u křižovatky dvou cest, které svírají úhel 120° (viz obr.).

Narýsujte tento pozemek v měřítku 1 : 2 000

8. Lišta kolem čtvercové parketové podlahy má délku 19,6 m. Vypočítejte celkový počet obdélníkových parket s rozměry 30 cm a 10 cm, který spotřeboval parketář na zhotovení podlahy, víte­li, že v důsledku jejich tvarové úpravy na krajích podlahy jich spotřeboval o 5 % víc

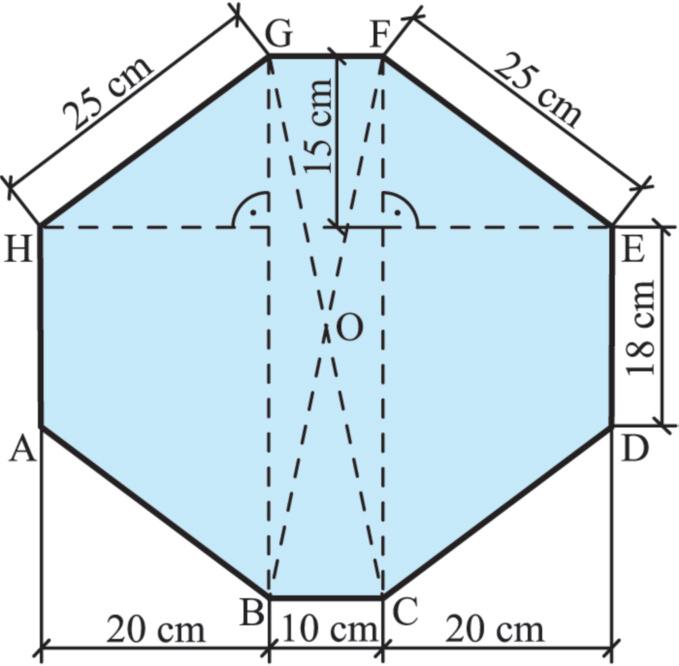
9. Geometrický útvar na obrázku je středově souměrný podle průsečíku O úhlopříček BF a CG. Je možné ho rozdělit na obdélník BCFG a dva shodné rovnoramenné lichoběžníky BGHA a FCDE. Vypočítejte: a) obvod, b) obsah tohoto útvaru

10. Sestrojte kosodélník KLMN Jestliže platí: |KL| = 3,2 cm, |∢KLM| = 120° a proveďte zápis konstrukce

11. Sestrojte lichoběžník ABCD, víte­li, že AB || CD, |AB| = 75 mm, |CD| = 30 mm, vzdálenost obou podstav – výška lichoběžníku v = 4 cm, |∢ABX| = 75°, a proveďte zápis konstrukce

12. Sestrojte kosočtverec EFGH, je­li: |EF| = 6,8 cm, |∢HEF| = 45°. Konstrukční postup zapište.

13. a) Sestrojte čtyřúhelník ABCD, víte­li, že pro délku jeho úhlopříčky AC platí: |AC| = 8,3 cm, pro délky jeho stran AB, BC platí: |AB| = 8 cm, |BC| = 7 cm a pro velkosti úhlů DAB, ACD platí: |∢DAB| = 30°, |∢ACD| = 60°.

b) Které věty o shodnosti trojúhelníků jste při konstrukci uplatnili? Ve smyslu těchto vět proveďte i zápis postupu konstrukce

Tato sbírka slouží učitelům k rozšíření námětů procvičovacích úloh využitelných přímo při vyučování, nebo za domácí úkol. Je rozdělena na část aritmetickou a geometrickou. V závěru sbírky najdete klíč k řešení všech úloh. Řazení tematických celků odpovídá struktuře učebnic matematiky pro 7. ročník (aritmetika a geometrie) vydaných naším nakladatelstvím. Univerzálnost sbírky však zajišťuje její využití nezávisle na těchto učebnicích.

Ve zmíněné řadě učebnic jsou pro každý ročník určeny dvě učebnice, z nichž jedna je věnována aritmetice, druhá geometrii. Praktickým a užitečným doplňkem učebnic jsou pracovní sešity ke každé z nich.

Koncepce učebnic vychází z osvědčené praxe škol, vyhovuje však i záměrům

Rámcového vzdělávacího programu pro základní vzdělávání. O tom svědčí mimo jiné i udělená schvalovací doložka MŠMT.

Celou řadu učebnic matematiky pro 6.–9. ročník ZŠ tvoří:

Matematika pro 6. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 6. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 6. ročník ZŠ

Matematika pro 7. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 7. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 7. ročník ZŠ

Matematika pro 8. ročník ZŠ – algebra (učebnice a pracovní sešit)

Matematika pro 8. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 8. ročník ZŠ

Matematika pro 9. ročník ZŠ – algebra (učebnice a pracovní sešit)

Matematika pro 9. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Sbírka úloh z matematiky pro 9. ročník ZŠ

Pro výuku matematiky na 1. stupni ZŠ je určena obdobná ucelená řada učebnic. (blíže viz www.spn.cz)