





PR O
ŠKOL Y 5. RPZ A COVÁNO V SOULAD U S RVP PRO ZÁKLADNÍ VZDĚLÁVÁNÍ
ROČNÍK ZÁKLADNÍ
Zpracovaly: Mgr. Ivana Vacková, Mgr. Ludmila Fajfrlíková, Mgr. Zdeňka Uzlová
Lektorovaly: RNDr. Marie Ausbergerová, RNDr. Růžena Blažková, Mgr. Dagmar Sejkorová
Schválilo MŠMT č. j. MSMT-2127/2022-4 ze dne 15. 6. 2022 k zařazení do seznamu učebnic pro základní vzdělávání jako součást ucelené řady učebnic pro vzdělávací
obor Matematika a její aplikace s dobou platnosti šest let.
Vydalo roku 2024 SPN – pedagogické nakladatelství, a. s.,
Ostrovní 126/30, 110 00 Praha
Ilustrace Antonín Šplíchal
Technické obrázky Kateřina Samková
Odpovědná redaktorka RNDr. Soňa Samková
Technické zpracování obálky Michal Špatz
Tisk a vazba Tiskárny Havlíčův Brod, a. s.,
Husova 1881, 580 01 Havlíčkův Brod
Počet stran 152
Třetí vydání
5950
© Ivana Vacková za kolektiv, 2010, 2016, 2024
Illustrations © Antonín Šplíchal, 2010, 2016, 2024
© SPN – pedagogické nakladatelství, a. s., 2010, 2016, 2024
ISBN 978-80-7235-680-5
OBSAH

I. OPAKOVÁNÍ – čísla do milionu
II. NOVÉ UČIVO
3
Číselná řada a porovnání čísel 5 Sčítání .............................................................................................................................8 Odčítání 10 Násobení 13 Převody jednotek délky .................................................................................................14 Dělení 15 Převody jednotek času ..................................................................................................16 Převody jednotek hmotnosti .........................................................................................18 Převody jednotek objemu 19 Zlomky .........................................................................................................................21 Záporná a kladná čísla 22 Souhrnné opakování učiva 4. ročníku ...........................................................................23 Chytrost nejsou žádné čáry (pro zvídavé žáky) – 1. část .......................................26
Čísla větší než milion Číselná řada ..................................................................................................................27 Rozvinutý zápis čísel 30 Porovnávání čísel 31 Zaokrouhlování čísel .....................................................................................................34 Pamětné sčítání a odčítání 37 Písemné sčítání ............................................................................................................40 Písemné odčítání ..........................................................................................................43 Římské číslice – rozšiřující učivo 46 Pamětné násobení a dělení ..........................................................................................50 Písemné násobení jednociferným činitelem 54 Písemné násobení dvojciferným činitelem ....................................................................57 Písemné násobení trojciferným činitelem .....................................................................60 Písemné dělení jednociferným dělitelem 63 Písemné dělení dvojciferným dělitelem ........................................................................66 Chytrost nejsou žádné čáry – 2. část 73 Převody jednotek – prohloubení ......................................................................................74 Jednotky délky ..............................................................................................................74 Jednotky času 77 Jednotky hmotnosti .......................................................................................................80 Jednotky objemu – rozšiřující učivo 83 Jednotky obsahu – rozšiřující učivo ..............................................................................86 Chytrost nejsou žádné čáry – 3. část ..............................................................................89 Aritmetický průměr 90 Práce s daty .......................................................................................................................91 Zlomky 92 Desetinná čísla 99 Závěrečné opakování aritmetiky ....................................................................................105 Chytrost nejsou žádné čáry – 4. část 118 ARITMETIKA
OBSAH

GEOMETRIE
I. OPAKOVÁNÍ
úsečka, přímka, rovina
II. NOVÉ UČIVO
Konstrukce
Závěrečné opakování geometrie ....................................................................................149
pro rozvoj digitální kompetence
Základní přehled převodů jednotek









– náročnější (nebo problémové) úlohy, pro jejichž vyřešení se vám musí „rozsvítit“ v hlavě – k této úloze najdete na s.151–152 doplňující úlohu na rozvoj digitální kompetence – nové učivo, které byste si měli zapamatovat – připomeňte si učivo, které byste měli znát již z předcházejících ročníků – zodpovězte danou otázku, řešte daný problém – skupinová práce – použijte kalkulačku – zamyslete se – řešte úlohu s důvtipem



4
Bod,
119 Vzájemná
............................................................................................121 Rovinné geometrické útvary 123 Kružnice a kruh ...........................................................................................................124
poloha přímek
trojúhelníku .................................................................................................125 Trojúhelníky 127 Čtverec a obdélník...........................................................................................................128 Konstrukce čtverce a obdélníku – prohloubení 129 Osově souměrné útvary..................................................................................................131 Obvody geometrických útvarů .......................................................................................133 Obvod čtverce 134 Obvod obdélníku .........................................................................................................135 Obvod obdélníku a čtverce – procvičování 136 Obsah obdélníku 137 Obsah čtverce ..................................................................................................................138 Obsah čtverce a obdélníku – procvičování 139 Tělesa ...............................................................................................................................140 Povrch krychle, síť krychle 141 Povrch kvádru, síť kvádru 143 Stavby z krychlí ...........................................................................................................145 Soustava souřadnic 146
151
Úlohy
Číselná řada a porovnání čísel


1. Pracuj s čísly v rámečku:
a) Najdi a přečti nejmenší a největší číslo.
b) Najdi a přečti všechna čísla sudá.
c) Najdi a přečti čísla menší než tisíc.
Prohlédni si čísla tiketů vylosovaných v loterii.
d) Seřaď čísla od nejmenšího k největšímu a přečti je.
e) Najdi a přečti čísla, která mají na řádu jednotek číslo 7.
f) Najdi a přečti všechna pěticiferná čísla.
g) Všechna čísla zmenši o pět.
h) Všechna čísla zvětši o 30.

2. Přirozená čísla z 1. cvičení použij ve větách odpovídajících skutečnosti.
Vzor: V Praze žije přibližně 1 000 000 obyvatel. (správně)
U stolu je 1 000 000 židlí. (nesprávně)
3. Pokračuj v číselných řadách:
a) 2, 4, 6, 8, ……………………………………………………………………
b) 2 447, ………, ………, ………, 2 451, ………, ………, ………, ………
c) 5 324, 5 314, ………, ………, ………, ………, ………, ………, ………
d) 800 000, 799 000, 798 000, ………, ………, ………, ………, ………
4. Zapiš číslo, které má:
a) 3 tisíce, 5 stovek, 7 jednotek
8 desetitisíců, 4 stovky, 2 desítky
6 stovek, 2 desítky, 4 jednotky
5 tisíců, 1 stovku, 7 desítek, 9 jednotek
16 desítek, 4 jednotky

b) Zapsaná čísla seřaď od největšího k nejmenšímu a podtrhni čísla sudá.
5. V létě byl Honzík na cyklistickém táboře. První den ujel 46 km. Druhý den ujel o 7 km více než první den. Kolik kilometrů ujel za oba dny dohromady?
5 ČÍSLA DO MILIONU – opakování

8. Převeď
a) na litry: 24 hl, 312 hl, 500 hl, 5 hl 24 l, 78 hl 32 l, 120 hl 63 l
b) na hektolitry: 1 000 l, 700 l, 9 600 l, 320 000 l, 5 400 l, 63 000 l
9. Hnojivo na trávník je třeba před použitím naředit vodou. Ke 2 l hnojiva je třeba přilít 12 litrů vody. Kolik litrů vody se musí přidat k 1 litru, 7 litrům a 14 litrům hnojiva?
10. V cestovní kanceláři ŠLÁPOTA prodávají pobyty v letní sezoně za tyto ceny:
Řím
Londýn
Paříž
Berlín
Atény
Benátky
Brusel
a) Vypočítej, kolik stojí týdenní pobyt s dopravou a snídaní v Římě, kolik v Berlíně a kolik v Bruselu. Který zájezd je nejlevnější?
b) Manželé Dvořákovi ušetřili 18 000 Kč na dovolenou. Vyber jim dovolenou.


c) Rodina Svobodova chce jet se dvěma dětmi do Atén.
Chtějí pobyt s dopravou a polopenzí. Kolik za zájezd zaplatí, když cena zájezdu pro dítě je 1 2 ze základní ceny?
d) Zahrajte si ve třídě na cestovní kancelář.
11. Sdružuj sčítance a výhodně sčítej:
125 + 54 + 75 + 46
913 + 68 + 97 + 122
560 + 74 + 96 + 50
410 + 78 + 1 090 + 12
12. Převáděj:

730 + 450 + 270 + 650
320 + 826 + 154 + 80
170 + 930 + 1 250 + 250
61 + 483 + 57 + 489


20 ČÍSLA
opakování
DO MILIONU –
7 dní pobytu 4 500 4 800 3 900 3 500 5 000 5 300 3 700 doprava 3 500 5 100 3 600 2 500 4 300 2 900 3 700 snídaně 120 120 120 120 130 130 110 polopenze 360 360 400 320 450 430 340 78 hl = l 130 hl = l 5 hl = l 920 hl = l 600 l = hl 9 000 l = hl 77 000 l = hl 10 000 l = hl 9 854 l = hl l 8 003 l = hl l 68 950 l = hl l 90 502 l = hl l
ZLOMKY – opakování

1. Zopakuj si zápis a čtení zlomků:

Připomeň si:




2. Čti zlomky:


Ve jmenovateli zlomku nesmí být nikdy nula.
3. Zapiš zlomkem, jakou část koláče Katka snědla:
4. Zapiš zlomkem a přečti: tři čtvrtiny pět osmin dvě šestiny dvě třetiny čtyři šestiny šest desetin jedna polovina jedna sedmina pět devítin
5. Graficky znázorni zlomky, např. jako části kruhu:

21
1 2 2 2 1 4 3 4 2 3 3 5
1 _ 2 čitatel zlomková čára jmenovatel 3 6 3 6 2 3 1 8 4 5 1 2 1 2 2 4 2 _ 4 2 5 6 9 1 3 4 4 4 _ 8 6 12 3 10 5 10 27 100 99 1000 11 23

6. Z daných čísel vyber číslo, které je největší, a číslo, které je nejmenší. Pak čísla seřaď od největšího k nejmenšímu:
a) 15 235 465, 15 285 465, 1 523 465, 15 465 135
b) 584 434, 5 434 584, 4 434 584, 58 000
c) 291 146 222, 146 291 222, 222 291 146, 292 146 222
d) 232 322, 322 232, 323 223, 333 222
7. NA CESTÁCH

Babička navštívila své vzdálené příbuzné. Během dovolené poznala téměř celý svět a dozvěděla se, jak velké jsou jednotlivé kontinenty.
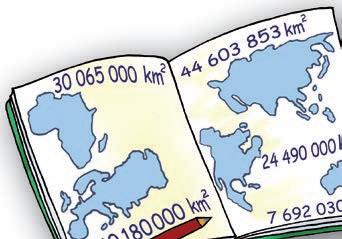

Porovnej rozlohy jednotlivých

8. Zopakuj si:

















kontinentů a seřaď je vzestupně podle velikosti. Navštívila babička skutečně všechny kontinenty? Uhodneš, kde všude žijí babiččini příbuzní?


5 · 7 72 : 8 13 · 4 93 : 3
9 · 6 42 : 7 17 · 2 48 : 2
8 · 4 36 : 4 19 · 6 132 : 6
8 · 9 21 : 3 15 · 5 1 000 : 5
9. Doplň čísla: 4 327 526 > , , 2 478 967 < , , 3 845 258 < < 4 321 000
896 501 < < 3 000 000 < 5 259 847 < > 8 526 203 >
10. Zapiš pod sebe a vypočítej: 4 327 – 3 472 526 487 – 363 921 27 843 – 14 359 847 520 – 739 435 437 256 – 72 037 284 062 – 96 261

32 ČÍSLA VĚTŠÍ NEŽ MILION
2
Francie
USA Egypt
Čína Austrálie

11. V továrně na sladkosti vyrobí za jednu směnu 271 380 lízátek. V jednom balení je 6 lízátek. Kolik balení vyrobí za jednu směnu?
12. Doplň do tabulky čísla:
hned před
dané číslo 4 527 6 000 23 471 46 999 321 002 500 999 hned za
13. VE VELKOMĚSTĚ
Lucie během své prázdninové cesty navštívila 5 světových metropolí. Jako správná cestovatelka si o nich zjistila co nejvíce informací. Ty si zapsala do tabulky:
město počet obyvatel rozloha města (km2) vzdálenost od Prahy (m)
Paříž 2 162 000 105 km2 884 000
New York 8 468 000 1 215 km2 6 551 000
Sydney 5 313 000 12 145 km2 16 123 000
Káhira 10 230 350 214 km2 2 636 000
Peking 21 540 000 16 808 km2 7 455 000
a) Vyber města s nejmenším a největším počtem obyvatel.
b) Seřaď města vzestupně podle počtu obyvatel.

c) Které město je nejdále od Prahy?
d) Seřaď města sestupně podle jejich rozlohy.
Tvořte ve dvojicích podobné otázky.
14. Vypočítej a proveď zkoušku:
6 921 : 3

506 002 : 6
47 855 : 5 123 456 : 7
603 968 : 2
858 524 : 6
349 368 : 7 923 001 : 3
15. Porovnej:



33 ČÍSLA VĚTŠÍ NEŽ MILION
243 · 1000 24 300 42 025 + 100 42 125 183 000
10 13 800 11 400 6 · 19 · 10 92 540 + 100 92 550 620 360 + 20 + 140 82
1000 72 009 1 007 560
80
1000
:
009 –
:
+

Připomeň si: 95 899 : 17 = 5 641 zb. 2



Dělíme:
dělenec dělitel podíl zbytek
1. krok – zaokrouhlíme 95 = . 100 , 17 = . 20
2. krok – 100 : 20 = 5
Zkrácený zápis: 95 899 : 17 = 5 641
Podíl v jednotlivých krocích dělení musí být menší než 10.
Nezapomeň! Zbytek nesmí nikdy zůstat větší než dělitel. 5 2


899 : 17 = 5 641 – 85 3. krok – 5 · 17 = 85 10 8 10 8 69 – 10 2 19 69 – 68 19 – 17 Při dělení provádíme zkoušku násobením: 2 5 641 · 17 = 95 897 95 897 + 2 = 95 899 10 8
1. Počítej hbitě:
: 8
:
: 7
: 6
:
:
:
: 4
2. Vypočítej a proveď zkoušku:
:
:
:
:
:
:
:

74 675 : 25 312 382 : 53 3 027 180 : 65
91 728 : 36 466 754 : 71 1 017 576 : 14
63 826 : 47 197 450 : 22 1 346 399 : 41
3. Pan Novák prováděl rekonstrukci domu. Za 13 nových oken zaplatil 88 140 Kč, za 14 nových dveří zaplatil 222 180 Kč a za novou vanu 16 850 Kč.
a) Kolik stálo jedno okno?
b) Kolik stály jedny dveře?
c) Kolik zaplatil pan Novák za okna, dveře a vanu dohromady?




66 PÍSEMNÉ DĚLENÍ DVOJCIFERNÝM DĚLITELEM
95
72
250
50 73
7 350
70 91
100
25 54
8 410
50 63
300
93
3 293
10 48
280
42
9 157
30
9
:
6

4. Vypočítej a proveď zkoušku:
66 497 : 18
320 022 : 46 1 354 712 : 14
91 362 : 34 517 393 : 24 2 576 889 : 14
96 247 : 13 634 004 : 15 4 914 873 : 51
5. V realitní kanceláři prodávají bytový dům s jedenácti stejnými byty za 21 454 400 Kč. Kolik stojí jeden byt? Kolik bytů si může koupit pan Rybář, má-li nyní k dispozici 4 000 000 Kč?
6. Zjisti:
a) kolikrát je číslo 172 764 větší než číslo 36, b) kolikrát je číslo 72 menší než číslo 1 316 088, c) jaký je podíl čísel 543 015 a 55, d) o kolik je číslo 943 531 větší než 524 003, e) jaký je součet čísel 435 241, 16 353 a 723 941.
7. Doplň chybějící činitele:

375 243 + = 520 000 : 16 = 93 147
9 438 + 4 359 + = 130 000 : 76 = 37 794
983 745 – = 560 430 . 21 = 43 512 1 357 400 – = 500 000 . 34 = 39 100
8. Farmář Motyčka vypěstoval 184 200 kg brambor. Pro svoji rodinu si nechal 3 150 kg brambor a zbytek připravil k prodeji. Brambory určené k prodeji rozdělil do pytlů po 25 kg. Kolik pytlů celkem naplnil? Kolik si farmář Motyčka může celkem vydělat, bude-li pytel brambor prodávat za 243 Kč?
9. Vypočítej a proveď zkoušku:
99 736 : 15
34 205 : 29
68 440 : 73
158 435 : 22

1 354 222 : 11
372 926 : 85 23 437 572 : 19
432 192 : 16 3 530 143 : 46
10. Pan Hladký vypouští vždy na konci léta svůj bazén. Nyní v něm má 10 500 litrů vody. Za jednu minutu odteče 25 litrů vody. Jak dlouho bude trvat, než se bazén vyprázdní? Výsledek uveď v hodinách.
11. Vypočítej a výsledky seřaď sestupně:
926 805 – 423 509
35 263 · 9
873 052 : 4
450 850 : 50


372 153 + 94 124
9 356 · 17
67 PÍSEMNÉ DĚLENÍ DVOJCIFERNÝM DĚLITELEM
PŘEVODY JEDNOTEK – prohloubení

Připomeň si:

Jednotky hmotnosti






Jednotky hmotnosti jsou 1 tuna (1 t), 1 kilogram (1 kg) a 1 gram (1 g). gramy kilogramy tuny 1 kg = 1 000 g 1 t = 1 000 kg
1. Zvažte ve třídě aktovku, učebnici, penál, některé žáky atd. Jednotlivé hmotnosti si zapiš.
2. Zahradník sklidil ze sadu 185 kg jablek, 95 kg hrušek a 30 kg švestek. Kolik kilogramů ovoce sklidil celkem?
3. Převáděj
a) na gramy: 4 kg, 2 kg 350 g, 5 kg 64 g, 12 kg 781 g, 25 kg
b) na kilogramy: 6 000 g, 7 t, 3 t 24 kg, 17 000 g, 10 t 632 kg c) na tuny: 3 000 kg, 15 000 kg, 45 000 kg, 0 kg, 74 000 kg
4. V krabici je 20 ks čokolád. Každá čokoláda má hmotnost 300 g. Jakou hmotnost v kg má celá krabice? Jakou hmotnost by mělo 5, 7, 10 takových krabic?
5. Převáděj jednotky hmotnosti:
2 t = kg 1 282 g = kg g 2000 g = kg
5 kg = g 13 004 g = kg g 4 t = kg
8 000 kg = t 4 072 kg = t kg 35 kg = g
1 t 75 kg = kg 3 kg 200 g = g 7 kg = g
6. Na nákladní auto naložili 20 přepravek s ovocem po patnácti kg, 30 krabic s kompoty po dvanácti kg a 15 balení sirupu po deseti kg. Jaká je celková hmotnost naloženého zboží?
7. Maminka nakoupila 5 000 g mandarinek, 400 g salámu, 600 g kuřecího masa, 1 000 g cukru a 2 kg brambor. Kolik vážil celý nákup? Výsledek vyjádři v kilogramech.
Další jednotky hmotnosti, se kterými se můžeš setkat v praktickém životě, jsou: 1 metrický cent (1 q) 1 dekagram (1 dag)
1 t = 10 q
1 kg = 1 000 g
1 q = 100 kg 1 kg = 100 dag
1 dag = 10 g

80
PŘEVODY JEDNOTEK –

8. Doplň jednotky hmotnosti:
4 t = 4 000
12 kg = 12 000
6 000 g = 6
51 000 kg = 51
47 000 g = 47
120 kg = 120 000
7 kg 300 g = 7 300
2 450 g = 2 450
5 470 kg = 5 470
1 005 g = 1 5
12 t 42 kg = 12 042
50 203 kg = 50 203
9. Ve školní jídelně se stravuje 450 žáků a 30 dospělých. Každý dostal po obědě 1 pomeranč o průměrné hmotnosti 250 g. Kolik kg pomerančů musela jídelna objednat?
10. Sestav pořadí zvířat podle jejich hmotnosti od nejlehčího po nejtěžší:




hmotnost pořadí gorila 200 kg slon 5 t medvěd 1 000 kg nosorožec 2 t tygr 300 kg hroch 4 t








11. Pan Holý chová papoušky. Každý den jim míchá krmnou směs, která se skládá ze 100 g prosa, 250 g sezamu, 200 g slunečnice, 100 g vajec natvrdo vařených a 250 g strouhanky. Kolik kg směsi spotřebují papoušci za den, kolik za týden, kolik za měsíc a kolik za rok?
12. Doplň magické čtverce: 6 750 16 200 ?

81
prohloubení
2 500 3 250 3 000 3 600 5 400 4 200 4 340 3 920 3 500 3 080
ZLOMKY

2. Petra dostala k narozeninám dort. Rozdělila ho na 8 stejných kousků, 2 8 dortu snědla
sama a 1 8 dortu dala kamarádce. Kolik kousků jí zbylo? Řeš graficky a pak výpočtem.



Připomeň si: 3 _ 8
Základní informace o zlomcích:
čitatel (vyjadřuje počet částí)

zlomková čára

jmenovatel (informuje, na kolik stejných částí byl celek rozdělen)

2. Zapiš zlomkem: a) zelenou část obrazce b) žlutou část obrazce
3. Přečti zlomky:
4. Zapiš zlomky:
a) čtyři devítiny f) sedm setin b) osm patnáctin g) jedna tisícina c) čtyři poloviny h) dvacet desetin d) devatenáct dvacetin i) čtyři čtvrtiny e) jedna pětina j) nula polovin
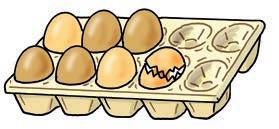
5. Zapiš zlomkem, kolik je v krabičce celých vajec, kolik se jich rozbilo a kolik jich chybí.



92
2 3 1 2 4 5 0 9 3 4 3 7 7 2 6 10 27 100 58 100 19 100 123 1000 8 12 22 8 12 8 17 50
ZLOMKY

6. Zapiš zlomky:
a) čitatel je 13 a jmenovatel je 18
b) jmenovatel je 23 a čitatel je 42
c) jmenovatel je 8 a čitatel je o 5 větší než jmenovatel
d) čitatel je 7 a jmenovatel je o 2 menší než čitatel
e) čitatel je 11 a jmenovatel je 2krát větší než čitatel
f) jmenovatel je 32 a čitatel je 4krát menší než jmenovatel
g) čitatel je roven jmenovateli
h) čitatel je 9 a jmenovatel je jeho trojnásobek
7. Počítej zpaměti:

8. Ve třídě je 24 žáků. Z toho 1 3 je chlapců. Kolik je ve třídě chlapců a kolik dívek?


Připomeň si: z 15 vypočítáme tak, že číslo 15 vydělíme 3 (jmenovatelem) z 15 je 5 15 : 3 = 5 z 12 vypočítáme tak, že číslo 12 vydělíme jmenovatelem zlomku (12 : 4 = 3) a výsledek vynásobíme čitatelem (3 · 2 = 6) z 12 je 6 (12 : 4) · 2 = 3 · 2 = 6 1 3 2 4
9. Vypočítej: ze 30 ze 60 z 28 ze 160 ze 40 ze 30 ze 46 z 56 z 99 z 210 z 1 000 ze 480
93
14
36
4 48
6 88
8 16
8
29 54 : 3 210
3 19 · 8 13 · 20 64 : 4 390 : 10 11 · 5 9 · 19 666 : 3 640 : 80 13 · 6 45 · 8 96 : 6 84 : 4 21
7 10 · 63 124 : 4 165
3
· 4
·
:
:
· 3
·
:
·
:
9 1 5 1 6 3 3 1 7 1 2 4 5 3 4 2 8 2 10
2 4 1 3 1 5 1 5 7
KONSTRUKCE TROJÚHELNÍKU

Zopakuj si postup při konstrukci trojúhelníku:



Sestroj trojúhelník ABC, jestliže a = 4 cm, b = 3 cm, c = 6 cm.
Nejprve pomocí trojúhelníkové nerovnosti ověříme, zda lze trojúhelník sestrojit: 3 + 4 > 6
Náčrt:
7 > 6 Trojúhelník lze sestrojit.
Konstrukce: 4
● Nejprve provedeme náčrt trojúhelníku.
● Vyznačíme jednotlivé vrcholy a zapíšeme délky zadaných stran.
● Vybereme stranu, která bude vhodná pro začátek konstrukce.
4. Rýsuj trojúhelníky:
1. Sestrojíme úsečku AB, |AB| = 6 cm.
2. Opíšeme oblouk kružnice se středem v bodě A a poloměrem r = 3 cm.
3. Opíšeme oblouk kružnice se středem v bodě B a poloměrem r = 4 cm.
4. Průsečík oblouků kružnic označíme C.
5. Sestrojíme trojúhelník ABC.
a) trojúhelník ABC, jestliže |AB| = 7 cm, |BC| = 4 cm, |AC| = 5 cm
b) trojúhelník KLM, jestliže |KL| = 42 mm, |LM| = 50 mm, |KM| = 10 mm
c) trojúhelník RST, jestliže r = 8 cm, s = 8 cm, t = 5 cm
d) trojúhelník EFG, jestliže e = 55 mm, f = 36 mm, g = 43 mm
5. Narýsuj trojúhelník ABC, jehož strany mají délky |AB| = 5 cm, |BC| = 4 cm, |AC| = 3 cm. Zapiš název trojúhelníku.
6. Zjisti, můžeš-li sestrojit trojúhelník s danými délkami stran. Ty, které jdou sestrojit, narýsuj do sešitu:
a) Všechny strany trojúhelníku mají délku 70 mm.
b) Strana a = 3 cm, b = 7 cm, strana c je o 1 cm delší než strana b
c) Strana a = 42 mm, b = 6 cm, strana c je 2krát delší než strana a.
7. Změř a zapiš délky stran jednotlivých trojúhelníků. Trojúhelníky pak narýsuj do sešitu:
126
A a
cm B b
cm C c = 6 cm A B C
= 4
= 3
A b a f e l k m g c B C G E F M K L





rovnostranný
Má všechny strany stejně dlouhé. a = b = c
rovnoramenný
Má dvě strany stejně dlouhé.
různostranný
Má každou stranu jinak dlouhou.
1. Na obrázcích najdi trojúhelníky a urči, jak se nazývají:



2. Vypiš, kde ve svém okolí můžeš najít příklady jednotlivých druhů trojúhelníků.



Trojúhelník, který má jeden pravý úhel, se nazývá pravoúhlý. Pravoúhlý trojúhelník má dvě strany k sobě kolmé. Tyto strany se nazývají odvěsny. Třetí strana se nazývá přepona. Je nejdelší a leží vždy proti pravému úhlu. A B c b a C
3. Sestroj pravoúhlý trojúhelník ABC, je-li dáno:
a) |AB| = 3 cm, |BC| = 4 cm, |AC| = 5 cm
b) a = 55 mm, b = 60 mm, c = 75 mm
c) a = 43 mm, c = 61 mm a zároveň platí a b b
4. Sestroj:


Vždy si nejdříve ověř, zda lze trojúhelník sestrojit, proveď náčrtek a potom trojúhelník narýsuj.
a) rovnostranný trojúhelník XYZ, jehož strana má délku 7 cm, b) rovmoramenný trojúhelník KLM, jehož základna má délku 6 cm a ramena mají délku 4 cm.
5. Sestroj rovnostranný trojúhelník DEF se stranou d = 6 cm. Najdi středúsečky DE a pojmenuj ho S. Sestroj úsečku FS. Jak se nazývají geometrické útvary, které vznikly rozdělením rovnostranného trojúhelníku DEF?
127
TROJÚHELNÍKY
A b a c B C A b a c základna rameno rameno B C A b a c B C
Tato učebnice je součástí ucelené řady učebnic matematiky pro výuku na 1. stupni ZŠ. Je zpracována v souladu se záměry a doporučeními RVP pro základní vzdělávání. Odpovídá požadavkům a názorům učitelů, neboť především z jejich praxe vznikla.
Pro výuku v 5. ročníku je určena tato učebnice, kterou doplňují dva pracovní sešity k procvičení učiva v 1. a 2. pololetí školního roku. Učebnice i pracovní sešity mají schvalovací doložku MŠMT.
Celou řadu matematik pro 1.–5. ročník ZŠ tvoří:
Matematika pro 1. ročník ZŠ, 1. a 2. díl – pracovní učebnice
Matematika pro 1. ročník ZŠ, 3. díl (volitelný) – pracovní učebnice
Matematika pro 2. ročník ZŠ, 1. a 2. díl – pracovní učebnice
Matematika pro 3. ročník ZŠ, učebnice a pracovní sešity
Matematika pro 4. ročník ZŠ, učebnice a pracovní sešity
Matematika pro 5. ročník ZŠ, učebnice a pracovní sešity
Učebnice pro každý ročník provází metodická příručka pro učitele.







ISBN 978-80-7235-680-5
5950




















































































































