RIK MATEMATIK 3A
Lärarpaket – Tryckt + Digitalt


LÄS OCH PROVA
LÄRARPAKETETS
SAMTLIGA DELAR



LÄS OCH PROVA
LÄRARPAKETETS
SAMTLIGA DELAR
Rik matematik är utvecklat för en undervisning där både elever och lärare är aktiva. Eleverna får resonera, diskutera och lösa problem, och utveckla en djupare förståelse för matematik.

I lärarhandledningen får du det stöd och de resurser du behöver för att planera och genomföra din undervisning. Det finns mer än 100 detaljerade lektionsförslag per läsår, som ger konkret stöd och tips på saker att betona, frågor att ställa och exempel att visa. Bildspelen, som hör till varje lektion, fungerar som ett stöd genom hela lektionen, både visuellt för att fånga elevernas uppmärksamhet och för att tydliggöra matematiken med pedagogiska animeringar och bilder. I lärarhandledningen finns även avslutslappar, diagnoser, extra övningsblad m.m.

Det digitala lärarmaterialet är ett komplement till den trycka lärarhandledningen. Här finns alla digitala resurser samlade, samt kom igång-hjälp och annat stöd som du kan behöva.
Interaktiv version av lärarmaterialet, i vilken det går att söka, stryka under, anteckna och länka.

Fungerar på dator, surfplatta och mobiltelefon.

3A Lärarhandledning


Andreas Ryve
Manuel Tenser
Patrik Gustafsson
Jannika Lindvall
Hillevi Gavel
Daniel Brehmer
Fredrik Blomqvist
Välkommen till Rik matematik!
Ikoner i lärarhandledningen
Kapitel 1 – Mer om addition och subtraktion ........................................
1.0 Introduktion
1.1 Stora addition och subtraktion ...........................................................
1.2 Positionssystemet – Talen 0–9999 .....................................................
1.3 Uppskatta vid addition och subtraktion
1.4 Skriftliga räknemetoder för
1.5 Skriftliga räknemetoder för
1.6 Addition med uppställning
1.7 Subtraktion med uppställning ...........................................................
1.8 Sorteringsprogrammet
2.2 Dra olika färger
2.3 Slå tärning
2.4 Hur stor är sannolikheten?
2.5 Kombinatorik
2.6 Undersökningar i klassen .................................................................
2.7 Organisera data
2.8 Repetition
2.9 Diagnos ...........................................................................................
Kapitel 3 – Mer om multiplikation och division ....................................
3.0 Introduktion
3.2 Dela upp en faktor
3.4 Multiplikation

3.5 De sista
3.6 Division
3.7
3.8 Räknehändelser
3.9
3.10
3.11
Kapitel
4.0
4.1
4.2
4.3
4.6
4.7
4.8
4.9
4.10
5.2 Funktionsmaskinens
5.3 Talföljder ..........................................................................................
5.4 Skapa talföljder med funktionsmaskinen
5.5 Hagelföljden
5.6 Textproblem och generaliseringar
5.7
5.8 Ekvationer
5.9 Räknehändelser och ekvationer
5.10
Med Rik matematik får du stöd att varje lektion bedriva en strukturerad undervisning där eleverna får resonera, lösa problem, diskutera, tänka och räkna matematik.
Rik matematikundervisning kännetecknas också av att både läraren och eleverna är aktiva – en elevaktiv och lärarledd undervisning. För att genomföra detta har lärarhandledningen mer än 100 detaljerade lektionsförslag per läsår, med bildspel till varje lektion, medan elevboken är full av forskningsbaserade uppgifter och problem. Bildspelen hjälper dig att visualisera och förklara den matematik som ni arbetar med och blir en utgångspunkt för resonemangen.
I din digitala lärarresurs finns lektionernas alla bildspel men där finns också fler resurser, såsom färdighetsträning, avslutslappar, diagnoser och kopieringsunderlag. Lärarresursen når du via licensen som du får när du köper lärarhandledningen. Inloggning sker på sidan "Min bokhylla" som du hittar på Studentlitteratur.se.
Kapitelstrukturen
Alla kapitel här i lärarhandledningen inleds med en kort matematisk och didaktisk genomgång: Vad är det för matematik, vad vet vi från forskning om hur barn lär sig den och hur har vi därför lagt upp undervisningen? Varje lektion har en översiktssida där du bland annat hittar lektionsmålen och en sammanfattning av lektionen. Är du erfaren räcker det kanske att läsa sammanfattningen och klicka igenom bildspelet innan lektionen.
Lektionerna
Vill du ha mer stöd så ger lektionsförslaget också en detaljerad bild av hur du med bildspelet kan genomföra lektionen. Här får du konkret stöd och tips på saker att betona, frågor att ställa, exempel att visa. På lektionens sista sida får du tips på vanliga missuppfattningar och fel, hur du kan agera då, och hur du kan ge elever extra stöd och mer utmaning vid behov.
Lektionerna inleds alltid med en uppstartsfas. Här repeterar ni det viktigaste i föregående lektion,
och här får eleverna möta innehållet i den nya lektionen, ofta genom en lärarledd genomgång med stöd av bildspelet. I aktivitetsfasen diskuterar, tänker, räknar och löser eleverna problem, ofta i grupp eller par. Läraren har en viktig roll under aktivitetsfasen i att utmana elever, ställa frågor för att uppmana tänkande och diskussion, samla information inför avslutningen av lektionen, etc. Naturligtvis finns det också tid för enskild färdighetsträning. I avslutsfasen sammanfattar du lektionen tillsammans med eleverna och lyfter upp den centrala matematiken. Ofta gör eleverna en avslutslapp där de får visa vad de lärt sig och samtidigt tänka igenom det mest centrala i lektionen.
Var beredd att anpassa
Se lektionsplaneringen som ett förslag, inte som ett strikt manus. Följ inte alltid lektionsplaneringen till punkt och pricka utan utgå ifrån vad eleverna säger och tänker, och styr mot den matematik som de ska lära sig. Om du inte tror att grupparbete kommer att funka, kör par eller enskilt. Förstod de inte? Förklara på ett annat sätt. Och hoppa över delar som eleverna redan förstått.
Avslutslappar
Många lektioner avslutas med en avslutslapp. Det är ett effektivt sätt för dig att ta reda på vad eleverna kan:
• Har eleverna nått målen?
• Är det något som många har missat?
• Finns det enskilda elever som behöver arbeta mer med något?
Nästan varje kapitel avslutas också med att eleverna gör en diagnos. Svaren matar du enkelt in i diagnosverktyget som visar en sammanställning på klass- och elevnivå. Då kan du svara på frågor som:
• Vad kan eleverna bra, vad är svårare?
• Vilka behöver extra anpassningar eller särskilt stöd?
• Vilka behöver utmanas mer?
När du har koll på det kan du fundera på hur din undervisning påverkat resultaten:
• Vad gick bra och varför?
• Vad gick mindre bra och varför?
• Vad tar du med dig?
Lärarhandledningen ger dig stöd vid analysen, inte bara av hur elevernas resultat är på individ- och klassrumsnivå utan också hur du kan planera och genomföra framtida undervisning.
Både avslutslappar och diagnoser finns att ladda ner och skriva ut från din digitala lärarresurs.
Förstå läromedlets grundtankar
Forskning visar att det kan vara lätt att missförstå grundtanken med ett läromedel – och att normer, rutiner och gamla vanor ibland kan vara ett hinder för förbättring av undervisningen. I Sverige är det t.ex. väldigt vanligt att lärare låter eleverna sitta och räkna själva i boken större delen av lektionerna, i tron att de utvecklas matematiskt på det sättet. I rik matematikundervisning ligger tyngdpunkten på att eleverna lär och utvecklas i samspel med läraren och med varandra. När de arbetar i boken färdighetstränar de oftast för att befästa kunskaper. Vi vet också att allt för få lektioner har en avslutning där den centrala matematiken och lärandet lyfts fram, diskuteras och repeteras. Vi lyfter därför här några viktiga grundtankar i den undervisning som Rik matematik stödjer.
Lärarens viktiga roll
Läraren har en central roll i klassrummet. Du planerar undervisningen, diskuterar mål, utmanar elever, förklarar matematik, ställer frågor för att få igång diskussioner, summerar och pekar ut viktiga samband, bedömer, uppmuntrar, skapar struktur, etc. Rik matematik är utvecklat för en undervisning där både elever och lärare är aktiva.
Stöd för diskussion och interaktion
Att som lärare låta eleverna komma till matematisk förståelse genom att resonera, argumentera och lyssna i matematiska diskussioner är ett arbetssätt som är utmanande för alla lärare, men det är också roligt och stimulerande.
Läromedlet tillhandahåller strukturer och resurser som ger stöd för att du ska lyckas med detta. Utöver lektionsförlag med tydliga mål och bildspel, tillhandahåller läromedlet en ”verktygslåda” med en uppsättning diskussionstyper, lärartaktiker och en repertoar av frågetyper som du kan använda för att styra diskussion och interaktion mot avsett mål.
Ramverk för diskussion och interaktion
Målfokus istället för sidfokus
Ha fokus på mål och lärande istället för ett fokus på hur långt eleverna kommit i elevboken. Alla ska inte göra alla uppgifter. När eleverna nått målen ska ni gå vidare till nästa lektion, och nästa mål. Det viktiga är elevernas lärande och större delen av lärandet sker under aktiviteter där de inte sitter själva och löser uppgifter i boken. Det är också viktigt att eleverna inte tror att matematik handlar om att räkna många uppgifter så snabbt som möjligt. Matematiker tänker, funderar och försöker förstå begrepp och samband. Matematiker löser problem.
Elevbok
Det är en vanlig missuppfattning att alla elever måste göra alla uppgifter i elevboken, under eller efter lektionen. Det är inte tanken. Det viktiga är att eleverna når lektionsmålen.
Om du har elever som är snabba eller behöver utmanas kan de arbeta med de mer utmanande uppgifterna, vilka markeras med en eller två cirklar innan instruktionen.
När snabba elever räcker upp handen och anser sig klara med alla uppgifterna, måste du kontrollera om de verkligen löst uppgifterna med tillräcklig noggrannhet och kvalité. Utmana dem i att vara noggranna istället för snabba, genom att låta dem göra om slarvigt eller felaktigt utförda uppgifter, och uppmana dem att i fortsättningen vara noggranna från början.
Korta pass med färdighetsträning
Lägg in färdighetsträningspass mellan lektionerna. Det är bra att kunna saker utantill eftersom det frigör utrymme för tänkande och problemlösning. Lägg in pass på 5–20 minuter emellanåt då eleverna får träna för att befästa delar av matematiken, exempelvis genom arbete i elevboken eller träning med winnetkakort.
Winnetkakort är små papperskort med ett räkneuttryck på ena sidan, till exempel en addition, där summan av additionen framgår av kortets baksida. Korten är lämpliga för färdighetsträning som syftar till att eleverna ska bli mer förtrogna med olika räknestrategier och automatisera grundläggande talkombinationer. Winnetkakort finns för utskrift i den digitala lärarresursen.
Tomoyo
Tomoyo är ett spelifierat, digitalt läromedel där arbetet med de matematiska momenten varvas med fantasifulla berättelser. Tomoyo ingår i elevpaketet.
Elevens motivation och engagemang höjs när hen får snabb återkoppling och samlar poäng och märken.
Svårighetsnivån regleras automatiskt. Övningarna anpassas så att eleven får dem på samma, enklare eller svårare nivå, beroende på hens tidigare svar.
I Tomoyo är all text inläst och till varje övning finns det skräddarsydd hjälp i form av filmer, tips och begreppsförklaringar.
Som lärare kan du skapa ett digitalt klassrum och på så sätt följa dina elevers arbete och skicka uppdrag.
Här hittar du även förberedda uppdrag som är kopplade till lektionerna i Rik matematik
Klassrumsnormer och Professor Uggla
För att kunna bedriva en rik matematikundervisning är det viktigt med ett tillåtande och respektfullt klassrumsklimat där eleverna vågar berätta vad de tänker, vågar göra fel och är tysta och lyssnar när någon annan har ordet. Strukturer och resurser som stödjer detta arbetssätt finns inbyggt i materialet. Till din hjälp har du även karaktären Professor Uggla som dyker upp i bildspelen och hjälper till att etablera de viktigaste klassrumsnormerna.
Ramverk för Rika klassrumsnormer
Arbeta långsiktigt!
Arbeta med tålamod och långsiktighet! Rik matematikundervisning är mer utmanande än att låta eleverna sitta ensamma och räkna i boken. Stressa inte upp dig om det inte fungerar perfekt direkt. Kapitel och lektioner kan ta längre tid i början.
I takt med att ni – du och eleverna – lär er hur Rik matematik fungerar och kommer in i arbetssättet, kommer det att gå allt lättare och bättre. Låt det ta den tid det tar! Tänk på att du ska ha eleverna i tre läsår.
Ta hjälp av det stöd som finns i den digitala lärarresursen och hos Rik-matematikkollegor för att snabbare komma in i läromedlet. Skriv till oss på Rik matematik-sidan på Facebook om du behöver råd och stöd.
Det digitala stöd som hör till lärarhandledningen finns i din digitala lärarresurs. Lärarresursen når du via licensen som du får när du köper lärarhandledningen. Inloggning sker på sidan "Min bokhylla" som finns på studentlitteratur.se.
För att visa bildspelen (ppt) som inleder varje lektion, laddar du först ner dem till din dator och öppnar sedan upp dem med Powerpoint.
Bildspelen är ofta animerade. Se till att starta bildspelen så att du får en verklig bild av hur de ser ut.
Om din skola inte har en installerad version av Powerpoint kan du använda den webbaserade gratisversionen av Powerpoint.
Om du arbetar med en Chromebook kan du se filmen nedan för att lära dig om hur du då startar upp bildspelen.
Så här fungerar bildspelen i Rik matematik
Så här fungerar de webbaserade bildspelen i Rik matematik
Så här fungerar Rik matematiks bildspel med Chromebook
Ikonerna visar vilken/vilka förmågor som lektionen direkt utvecklar.
Begreppsförmåga
Kommunikationsförmåga
Metodförmåga
Problemlösningsförmåga
Resonemangsförmåga
Dessa ikoner visar i vilken konstellation en aktivitet är tänkt att genomföras i.
Undervisning under lärarens ledning
Enskilt arbete
Enskilt arbete i elevboken
Arbete i par
Arbete/diskussioner i grupp
Här kommer du direkt till bildspelet.
Ljudfil i bildspelet
Visar att det finns en särskild funktion i bildspelet och att läraren måste klicka på ett särskilt sätt för att använda funktionen.
Nästa bild
Stanna upp innan du klickar fram svaret. Fråga hur ni kan göra.
BETÄNKETID
Film
Dokumentet kan laddas ner.
Referat av det som sägs av berättarrösten
Extra information

Guldkantslektion

Syftet med kapitel 1 är att fortsätta utveckla elevernas begreppsliga förståelse för positionssystemet samt deras förståelse för och färdighet i centrala skriftliga räknemetoder för addition och inom talområdet 0–9999.
I det här kapitlet fortsätter vi att utveckla elevernas förståelse för positionssystemet samt olika skriftliga räknemetoder för addition och subtraktion. Kapitlet kan i det avseendet ses som en fortsättning på kapitel 7 och 8 i åk 2, nu med ett talområde som utökats till 0–9999.
Fokus ligger på att eleverna ska förstå de olika räknemetoderna, det räcker inte med att de kan använda dem. Det är också viktigt att de förstår och kan hantera minnessiffror vid uppställning samt förstår vad det innebär att växla vid uppställning för subtraktion. Detta kräver en god förståelse för platsvärde och hur siffrorna i ett tal, beroende på siffrornas position i talet, visar ett antal talsorter.
I kapitlet kommer eleverna också att få arbeta med textuppgifter och träna på att använda professor Ugglas metod för problemlösning: ALP.
Lektionerna 1–7 fördjupar och breddar vi det som behandlades i kapitel 7 och 8 i åk 2. Det handlar framför allt om addition och subtraktion med skriftliga räknemetoder. I lektion 9 får eleverna träna på att välja lämplig metod beroende på situation. I lektion 10 och 11 arbetar vi med huvudräkningsstrategier, och i lektion 12 får eleverna träna på att lösa textuppgifter med hjälp av professor Ugglas metod för problemlösning, ALP. Kapitlet avslutas med repetition och en diagnos.
Pedagogisk planering – Mer om addition och subtraktion
Uppgifternas koppling till förmågorna, kunskapskrav, centralt innehåll och mätområden
1.0.1 Kapitelintroduktionens innehåll
Detta kapitel är en fortsättning på kapitel 7 och 8 i åk 2. Kapitelintroduktionen nedan behandlar därför till stor del samma sak som dessa kapitel, men på ett något mer sammanfattande sätt. Utöver det som tas upp i nämnda kapitel omfattar följande text även momentet problemlösning.
1.0.2 Positionssystemet, tiobas och uppskattningar
Vårt skrivsystem för tal är ett positionssystem med basen 10. Positionssystem innebär att en siffras betydelse beror av siffran och dess position i talet. Detta gör det möjligt att beteckna tal av vilken storlek som helst med ett begränsat antal symboler.
Tiobassystemet är konstruerat så att siffran längst till höger i ett heltal är entalssiffran, vilken står för antalet ental. Varje steg till vänster innebär en ökning med en faktor 10. Andra siffran från höger visar därför antalet tiotal och kallas då tiotalssiffran. Tredje siffran från höger visar antal hundratal, etc. Med matematisk notation kan man skriva att talet abcd ska tolkas som
a · 1000 + b · 100 + c · 10 + d · 1
eller, om man använder potenser, som
a · 103 + b · 102 + c · 101 + d · 100
Man använder ibland ordet platsvärde för en siffra i talet; platsen där a står har i det här fallet platsvärdet tusen.
Systemet kan också vidareutvecklas med siffror till höger om entalssiffran. Dessa kallas decimaler. Decimaler kommer vi in på i senare årskurser.
Förstå och använda tiobassystemet
För att kunna förstå och använda tiobassystemet har vi arbetat systematiskt för att utveckla en adekvat förståelse. En sådan förståelse för tiobassystemet bygger på:
1) förståelse för tiobasidén och en färdighet i att gruppera i grupper om tio;
Förståelse för tiobassystemet är avhängigt en tillräckligt god taluppfattning för att eleven ska kunna förstå samma tal på flera olika sätt, t.ex. 32 som tre tiotal och två ental samtidigt som ett tiotal och 22 ental. Detta kallas för ekvivalent gruppering: oavsett hur ett visst antal grupperas så är det alltid samma antal. När elever förstår detta kan de gruppera i, och operera med, 10-grupper och 100-grupper på ett flexibelt sätt.
2) förståelse för och färdighet i att läsa av och skriva tal med siffror;
Eleverna ska redan ha förstått det upprepade mönstret i hur tresiffriga tal kontureras med siffrorna 0–9. Nu ska detta utvidgas till fyrsiffriga tal. De behöver kunna koppla ihop uttalade tal och tal skrivna med bokstäver med tal skrivna med siffror.
3) förståelse för platsvärde;
Eleverna behöver koppla ihop tiobasidén och hur man läser och skriver tal med en förståelse för platsvärde. Det räcker inte att eleverna t.ex. kan säga ”siffran 3 i talet 35 står för tre tiotal”. De behöver också ha en djupare förståelse för vad det betyder: eftersom siffran 3 står på tiotalsplatsen talar den om att det finns tre grupper av tio i talet 35, vilket är detsamma som 30 ental, vilket motsvarar talet 30.
Utöver detta samband behöver eleverna förstå siffran 0 och dess funktion som platshållare. I t.ex. talet 302 visar nollan att talet saknar tiotal, samtidigt som den gör att trean representerar tre hundratal eftersom den står två steg till vänster om entalspositionen.
Eftersom ni nu arbetar med en ny talsort behöver du återigen vara nästan övertydligt noggrann när du pratar om talen. Uttolka siffrornas betydelse istället för att bara säga talen. För talet 4302 skulle det innebära att till en början säga ”fyratusentrehundratvå, alltså fyra 1000-grupper (eller tusental), tre 100-grupper (eller hundratal), ingen 10-grupp (alltså noll tiotal), och två ental”.
Vid arbete med tiobasmaterial är det extra viktigt att tänka på ovanstående då det är möjligt att elever kan namnge tusental, hundratal, tiotal och ental korrekt, men ändå sakna en taluppfattningsbaserad förståelse för vad detta innebär. Det finns alltså en risk att eleverna kan ha lärt sig benämningarna på både material och symboler utan att förstå vad de representerar Därför är det viktigt att göra aktiviteter och ställa frågor som leder till dialoger där eleverna får sätta ord på sambandet mellan tiobasidén, grupper av tio, och platsvärde.
4) sambandet mellan allt detta;
Konkret material är till stor hjälp när eleverna ska förstå tiobasidén och positionssystemet. Detta kan antingen vara förgrupperade material som t.ex. tiobasmaterial vars delar man inte kan plocka isär, eller grupperade som t.ex. stickor som kan buntas ihop.
Material som är fysiskt proportionerliga, där tio ental motsvarar storleken av ett tiotal och ett hundratal storleken av tio tiotal, är bäst att börja med. Material som inte är fysiskt proportionerliga, t.ex. mynt, bör användas först när den nya tusentalsplatsen i positionssystemet är befäst.
För att eleverna ska ges möjlighet att utveckla en djupare förståelse kommer de att få många och olika typer av erfarenheter av de här idéerna, och få utveckla färdigheterna genom flera olika typer av aktiviteter.
Uppskattningar
Uppskattningar, också kallat överslag eller överslagsräkning, har länge haft en undanskymd roll i matematikundervisningen, trots att det av flera orsaker visat sig vara en mycket viktig färdighet. Ibland gör man snabba och ungefärliga beräkningar utan hjälpmedel, och då är uppskattning ett sätt att bedöma rimligheten i en slutsats. Att arbeta med uppskattningar är också ett bra sätt att utveckla taluppfattning och förståelse för platsvärde. Av dessa anledningar fokuserar vi i lektion 3 på uppskattningar. En viss färdighet i att göra uppskattningar kommer dessutom vara nödvändig för eleverna i kommande kapitel.
Uppskattningar kan göras mer eller mindre noga och mer eller mindre snabbt, beroende på vad syftet med uppskattningen är. En mer noggrann uppskattning tar ofta längre tid, men ger ett uppskattat värde som ligger närmare det exakta värdet. Därför finns det sällan ett rätt svar på uppskattningsuppgifter. Snarare handlar sådana uppgifter om att behärska en hållbar strategi för uppskattning så att man kan uppskatta på ett effektivt sätt och få uppskattningen inom ett rimligt intervall kring det exakta värdet.
Det finns många olika strategier för uppskattning. I Rik matematik fokuserar vi på avrundning, kompensering och kompatibla tal.
Avrundning
Avrundning kan ske på olika sätt. Ett sätt är att avrunda termer till närmaste tiotal eller hundratal, till exempel 93 + 29 ≈ 90 + 30 = 120. Notera att det vid addition är lämpligt att avrunda en term uppåt och en term nedåt för att utjämna, istället för att avrunda båda termerna uppåt/nedåt. Vid subtraktion bör, av samma anledning, båda termerna avrundas antingen uppåt eller nedåt.
Ett annat sätt att avrunda vid beräkningar med två termer är att enbart avrunda det tal som adderas eller subtraheras, t.ex. 98 – 37 ≈ 98 – 40.
Observera att vi i detta kapitel inte går in på avrundningsregler. Vårt fokus ligger istället på elevernas begreppsliga förståelse för uppskattningar och färdighet i att använda en fungerande uppskattningsstrategi. Avrundningsregler tas upp i högre årskurser, och då i förhållande till ett större talområde.
Kompensering
Denna strategi är en utveckling av avrundning, där eleven avrundar en term eller båda termerna och därefter kompenserar för detta genom att addera eller subtrahera. Ett exempel är
178 + 207 ≈ 200 + 200 – 20 + 10 = 390.
I exemplet har 178 avrundats till 200, 207 avrundats till 200 och dessa har sedan adderats. Därefter har 20 subtraherats eftersom det är cirka 20 upp till 200 från 178. Slutligen har 10 adderats eftersom det är cirka 10 ned till 200 från 207.
Talkamrater eller Samma ental
I vissa fall kan man försöka hitta talkamrater till riktvärden som 10, 100 och 500 och avrunda termerna så att de blir sådana talkamrater. Det kallas att göra talen kompatibla. Ett exempel är 24 + 77 ≈ 25 + 75 där första och andra termen har avrundats så att de är kompatibla på så sätt att de är 100-kamrater.
Vid subtraktion kan det ibland vara värt att enbart avrunda det tal som subtraheras så det blir kompatibelt, t.ex. genom att se till att båda termerna har samma ental 123 – 26 ≈ 123 – 23.
Vanliga svårigheter och missuppfattningar
Det finns några vanliga missuppfattningar när det gäller uppskattningar. En sådan missuppfattning är att en uppskattning är samma sak som en ”slumpartad gissning”. Till skillnad från en gissning bygger en uppskattning på resonemang, förståelse och faktiska beräkningar, men förenklade sådana. Det är därför mycket viktigt att undvika ord som ”gissa” när man arbetar med uppskattningar. Säg alltid ”uppskatta” istället för ”gissa” och förklara skillnaden vid behov. Begrepp som är lämpliga att använda är: ungefär, nästan, drygt, lite mer än, lite mindre än, mellan x och y.
Ett annat tänkbart problem är att elever inte förstår syftet med att göra uppskattningar och istället ser det som ett onödigt krångligt sätt att göra beräkningar. Som lärare är det därför viktigt att poängtera varför man gör uppskattningar och när man kan ha nytta utav det.
En annan missuppfattning är att elever tror att de måste göra en exakt beräkning innan en uppskattning. Detta kan bero på att hen inte förstår syftet med uppskattning eller tror att det är samma sak som en gissning.
Undervisa om uppskattningar
I Rik matematik fokuserar vi på strategin bakom uppskattningarna och inte på själva svaren. Detta är viktigt av två anledningar. För det första ligger vårt fokus på elevens flexibla användning av strategier för uppskattningar. Helklassdiskussioner kring olika strategier är en mycket viktig del i undervisningen för att uppnå flexibilitet och för att uppmuntra eleven att använda sin taluppfattning istället för att förlita sig på generella regler. För det andra ligger rätt svar till uppskattningsuppgifter i ett intervall (mellan X och Y). Genom att diskutera de svar som olika uppskattningar ger gör man eleven uppmärksam på att svaren ligger inom ett intervall runt det exakta svaret. Tänk på att den strategi som ger det mest exakta svaret till en uppgift inte alltid är den mest lämpliga/effektiva: vad som är den lämpligaste strategin måste avgöras i det enskilda fallet sett till syftet med uppskattningen och hur noggrann den behöver vara. Fokusera istället på om svaren som ges är rimliga för den aktuella uppgiften.
Viktigt att nämna är att uppskattning är något som eleven behöver träna på kontinuerligt och inte enbart i enstaka lektioner. Framöver, t.ex. i de kapitel som följer efter kapitlet som är dedikerat till just uppskattningar, uppmuntrar vi eleven att vid exakta beräkningar först göra en uppskattning för att se ungefär vad svaret bör bli.
1.0.3
I åk 2 arbetade vi med addition och subtraktion i talområdet 0–200. Nu utökar vi talområdet till att omfatta 0–9999 och arbetar med beräkningar som nu är mer utmanande och komplexa.
Skriftliga räknemetoder är ett samlingsnamn för olika sätt att stegvis genomföra en beräkning enligt ett mönster som är givet på förhand. Ofta kallas detta också algoritmer. När man använder en skriftlig räknemetod utför man en beräkning i enlighet med metoden, steg för steg. Det kanske mest kända exemplet på en skriftlig räknemetod är uppställning, även kallad standardalgoritmen. Vi kommer att benämna den som uppställning.
Räknemetoderna i detta kapitel bygger på tillämpningar av den teori för addition och subtraktion som gåtts igenom i åk 2. Vid behov kan du gå tillbaka och läsa valda delar av kapitelintroduktionerna i relevanta kapitel, främst kapitel 8 i åk 2.
I kursplanen för matematik talar man om centrala metoder för beräkningar. Med detta avses metoder som fungerar i alla tänkbara situationer, men som kan vara mer eller mindre effektiva i olika situationer beroende på uttrycket och de tal som ingår. Vid undervisning om skriftliga räknemetoder betonas därför vikten av ett flex-
ibelt användande av olika metoder. Med detta menas att målet är att eleverna ska kunna välja en lämplig metod givet situationen, beroende på vilka tal som ingår i beräkningen och hur det påverkar själva beräkningen.
Skriftliga räknemetoder för addition
Det finns många olika skriftliga räknemetoder för addition. Nedan beskriver vi tre av de vanligaste metoderna kort och ger sedan mer information inklusive visualiseringar i informationen för enskilda lektioner. Den skriftliga räknemetoden Uppställning behandlas i ett eget avsnitt under rubriken Uppställning.
Talsorterna för sig I metoden Talsorterna för sig delas de ingående termerna upp i talsorter varpå talsorterna adderas var för sig. I denna metod skapar man en ny term för varje talsort som motsvarar båda de ursprungliga termernas antal av respektive talsort, varpå de nya termerna adderas. Ett exempel är 122 + 34 = 100 + 50 + 6 = 156. Metoden är särskilt lämplig om beräkningarna inte kräver växling över talsorterna.
Hopp på tallinjen
Metoden Hopp på tallinjen innebär att en av termerna delas upp i talsorter varpå dessa adderas till den andra termen en i taget. Ett exempel är 57 + 22 = 77 + 2 = 79. Även denna metod är lämplig om beräkningarna inte kräver några växlingar över talsorterna. En fördel med metoden är att den är lätt att förstå och illustrera med hjälp av tallinjen.
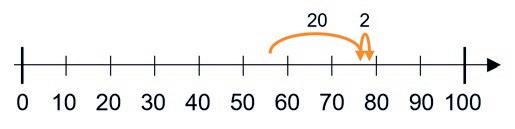
Kompatibla tal
I metoden Kompatibla tal flyttar man ental från den ena termen för att skapa ett jämnt tiotal i den andra. Ett exempel är 46 + 39 = 50 + 35 = 85 där man flyttar fyra ental från 39 till 46 för att skapa ett jämnt tiotal i den ena termen. Metoden är särskilt lämplig vid addition med växling över tiotalet. I metoden Kompatibla tal underlättas växlingen genom att eleven kan använda sina tidigare kunskaper om 10-kamrater.
Skriftliga räknemetoder för subtraktion
Precis som för addition finns det många olika skriftliga räknemetoder för subtraktion. Vi fokuserar på fyra av dem, utöver Uppställning. Samtliga fungerar för alla subtraktioner, även om de är mer eller mindre effektiva beroende på vilka termer uttrycken har. Nedan beskriver vi metoderna kort. För mer information om respektive metod, inklusive visualiseringar, hänvisar vi till informationen för enskilda lektioner.
Talsorterna för sig
I denna metod delas de ingående termerna upp i talsorter varpå talsorterna subtraheras var för sig. Ett exempel är 88 – 32 = 50 + 6 = 56 där man först subtraherat tre tiotal ifrån den första termens åtta tiotal, och sedan subtraherat två ental ifrån den första termens åtta ental. Därefter summeras de tiotal och de ental som blev kvar, i det här fallet fem tiotal och sex ental. Metoden är lämplig vid subtraktion utan växling. Vid växlingar är det vanligt att eleverna gör misstag då de glömmer att tal måste omgrupperas. Uppmuntra därför eleverna att i dessa fall använda en annan räknemetod.
Hopp på tallinjen
Metoden innebär att den andra termen, den som ska subtraheras ifrån den första termen, delas upp i talsorter som sedan subtraheras från den första termen. Ett exempel är 72 – 25 = 52 – 5 = 47. En fördel med metoden är att den är lätt att illustrera med visuellt stöd.
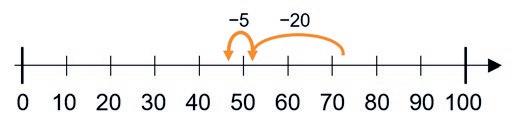
Kompatibla tal
Metoden går ut på att omgruppera den andra termen för att skapa en enklare subtraktion. Ett exempel är 72 – 25 = 72 – 22 – 3 = 50 – 3 = 47. Metoden passar extra bra om beräkningen kräver växling över tiotalet. Denna metod innebär då färre steg än de två tidigare metoderna och är lättare att göra i huvudet.
Tänk addition (Jämföra på tallinjen)
Metoden Tänk addition passar bra när de ingående termerna ligger mycket nära varandra. Ett exempel är subtraktionen 151 –149, där det endast är två steg på tallinjen från 151 till 149 och 149 + 2 = 151. Då tallinjen är ett kraftfullt verktyg för att illustrera metoden kallas den också Jämföra på tallinjen.
Undervisa om skriftliga räknemetoder
Liksom i kap 8 åk 2 kommer vi här att börja med olika skriftliga räknemetoder och diskutera deras lämplighet i olika situationer utifrån vilka tal som ingår i uttrycken. Först efter detta kommer metoden Uppställning för addition respektive subtraktion. Syftet med denna ordning är att främja elevernas utveckling av taluppfattning och flexibla användning av skriftliga räknemetoder. Forskning har visat att särskilt elever med matematiksvårigheter missgynnas av att introduceras för uppställning innan de fått arbeta med andra typer av skriftliga räknemetoder. Dessa elever löper hög risk att då enbart mekaniskt lära sig stegen i räknemetoden och inte utveckla en förståelse för hur den fungerar.
För att eleverna ska fortsätta utveckla förståelse för olika
skriftliga räknemetoder, och inte bara memorera stegen, fortsätter vi undervisningen från kap 8 åk 2 med direkt modellering. Detta innebär att eleverna använder konkret material eller bilder för att beskriva innebörden av en operation eller uttryck. Det är här viktigt att eleverna kan gruppera i 10-grupper istället för att räkna en i taget. Efter att eleverna modellerat operationen med det konkreta materialet går man vidare till att uttrycka detta med matematisk notation.
Nästa steg är att eleverna själva får beräkna uppgifter på valfritt sätt. Många elever har en intuitiv känsla för hur beräkningarna kan göras, och det kan vara gynnsamt om de själva får upptäcka en effektiv metod.
Det är viktigt att påpeka att du som lärare har en viktig roll i att strukturera undervisningen och leda eleverna till att själva upptäcka olika strategier för olika situationer. Detta får inte dras för långt och det kanske heller inte fungerar för alla elever. Men så långt det är möjligt och rimligt bör du sträva efter att låta elevernas upptäckta strategier leda till metoder som du sedan mer formellt introducerar, kopplat till elevernas egna erfarenheter. I de fall ingen elev upptäcker den metod du ska introducera behöver du introducera den själv och sedan låta eleverna lösa en ny uppgift med den introducerade metoden.
För att ytterligare utveckla elevernas färdighet i att flexibelt använda olika skriftliga räknemetoder behöver de få diskutera och resonera kring olika metoders för- och nackdelar.
Vanliga problem och missuppfattningar
Ett vanligt problem är att elever lär sig stegen i de olika räknemetoderna utantill, utan att utveckla en förståelse för vad man faktiskt gör när metoderna används. Det kan i många fall bero på att de fått undervisning som inte varit förståelseorienterad. Att utveckla elevernas förståelse för vad de håller på med är centralt i Rik matematik. I det här fallet är det viktigt av den anledningen att om eleverna har förståelse för en metod och dess ingående steg kan de återkonstruera metoden när den behövs istället för att hänga upp den på att behöva minnas utantill hur den rent mekaniskt går till. Risken är då också mindre att eleven gör fel utan att förstå det. Därför börjar vi med att utveckla elevernas förståelse för de ingående stegen när vi introducerar skriftliga räknemetoder. Det sker bland annat genom visualiseringar med tiobasmaterial och på tallinjen. Först när eleverna har en viss förståelse för metoderna kan de gå vidare till färdighetsträning.
Ett annat problem kopplas till att många vuxna har uppfattningen att räknemetoden Uppställning är det ”rätta sättet” att beräkna på, och kan överföra denna uppfatt-
ning till barnen. Detta kan orsaka förvirring för elever när de i skolan istället uppmuntras att använda olika metoder flexibelt, eller åtminstone själva välja en hållbar metod som de känner sig bekväma med. En del elever som kommer till skolan kan även ha blivit introducerade för Uppställning hemma, och kan då motsätta sig att lära sig ytterligare räknemetoder. I dessa fall är det viktigt att resonera med eleverna om olika skriftliga räknemetoders lämplighet beroende på de ingående talen. Det är t.ex. onödigt tidskrävande att beräkna 151 – 149 med Uppställning när man kan beräkna med Tänk addition Observera att detta också kan gälla andra räknemetoder, även om uppställning kanske är den vanligaste.
Uppställning
Precis som med de andra skriftliga räknemetoderna fokuserar vi i början på att utveckla elevernas förståelse för stegen i uppställning, istället för att eleverna ska memorera dem.
Addition med uppställning
Den skriftliga räknemetoden Uppställning går ut på talsortsuppdelning. Formen för uppställningen kan beskrivas som en tabell där termerna står på rader och där kolumnerna utgör talsortskolumner, se exemplet nedan.
Den nedersta raden kan ses som summeringsraden. Termerna placeras på raderna ovanför summeringsraden så att entalssiffrorna hamnar i entalskolumnen, tiotalssiffrorna i tiotalskolumnen, o.s.v. Om termerna har olika antal siffror placeras de överskjutande positionerna i nya kolumner åt vänster.
Här illustreras hur 975 + 864 beräknas med uppställning:
01 01
9 7 5 9 7 5 9 7 5 9 7 5
+ 8 6 4 + 8 6 4 + 8 6 4 + 8 6 4
1 4 4 3 4 4 9 1 4 3 9 1 8 3 9
Först adderas antalet ental, vilka ges av entalssiffrorna. Här ger det additionen 5 + 4 = 9. Resultat ger antalet ental i summan, vilket noteras på summeringsraden i entalskolumnen. Därefter adderas antalet tiotal på motsvarande sätt. Tänk på att det är antalet tiotal som adderas. Det spelar här ingen roll att det är just tiotal. Här ger det additionen 7 + 6 = 13. Det är alltså sammanlagt ett antal om 13 tiotal. I talet 13 anger siffran 3 hur många tiotal som ska noteras på summeringsraden i tiotalskolumnen och siffran 1 hur många hundratal som ska noteras i hundratalskolumnen ovanför den översta termen. Tio stycken tiotal är som bekant ett hundratal. Därefter adderas antalet hundratal enligt samma princip: 1 + 9 + 8 = 18. Det är alltså sammanlagt ett antal om 18 hundratal. I talet 18 anger då siffran 8 hur många hundratal som ska noteras på summeringsraden i hund-
ratalskolumnen och siffran 1 hur många tusental som ska noteras i tusentalskolumnen men på summeringsraden Att den noteras där beror på att det inte är några termer som ska adderas i tusentalskolumnen. Uppställningen är klar, additionen är genomförd.
Uppställning kan även användas för addition med tal med fler siffror än tre, och för fler termer än två. Man startar alltid med minst signifikanta talsorten, vilket är ental så länge man bara arbetar med heltal, och adderar sedan en talsort i taget. Om summan av antalet av en viss talsort blir flersiffrig, t.ex. 13, så noteras siffrorna till vänster om nämnda summas entalssiffra, i det här fallet siffran 1, som en minnessiffra överst i nästa talsortskolumn. Detta fungerar eftersom positionen ett steg till vänster i vårt positionssystem alltid är värd tio gånger mer än positionen till höger. Tio ental motsvarar ett tiotal, tio tiotal motsvarar ett hundratal, etc.
Uppställning fungerar även för decimaltal. Eftersom olika termer kan ha olika antal decimaler är det då avgörande att förstå principen om att de positioner i termerna som representerar samma talsort ska stå i samma talsortskolumn. Man bör därför aldrig säga att det är ”sista siffran” man går efter, utan istället uttrycka det som ”entalssiffra över entalssiffra”, etc.
Subtraktion med uppställning
Även subtraktion med uppställning bygger på talsortsuppdelning, och formen är i stort sett densamma som för addition (se exemplet nedan). Det finns dock en avgörande skillnad. Skillnaden är att subtraktionens första term måste skrivas i den översta raden, eftersom subtraktion till skillnad från addition inte är kommutativt. I övrigt noteras termerna på samma sätt så att siffrorna hamnar i rätt talsortskolumn. Den nedersta raden är differensraden där differensen kommer att noteras.
Här visas subtraktionen 1839 – 864: 10 10 10
Det är den andra termen som ska subtraheras ifrån den första, och den andra termen står alltså alltid under den första termen. Man börjar med den minst signifikanta talsorten, i det här fallet ental. Först subtraheras alltså fyra ental ifrån nio ental, vilket ger subtraktionen 9 – 4 = 5. Differensen av den uppställda subtraktionen kommer alltså att ha fem ental, och siffran 5 noteras därför i entalskolumnen på differensraden.
Av tiotalskolumnen framgår att sex tiotal ska subtraheras ifrån tre tiotal, vilket inte går: man kan inte ta bort sex tio-
tal om man bara har tre att ta bort ifrån. Svaret är därför odefinierat. Därför får man ta ett av de åtta hundratalen och växla till tio stycken tiotal som läggs till överst i tiotalskolumnen. Detta markeras genom att man noterar 10 överst i tiotalskolumnen och drar ett streck över 8:an. Nu har man istället 13 tiotal ifrån vilka sex tiotal ska subtraheras, vilket ger en subtraktion som går att lösa med naturliga tal: 13 – 6 = 7. Differensen av den uppställda subtraktionen kommer alltså att ha sju tiotal, och siffran 7 noteras i på differensraden i tiotalskolumnen.
Vi har tidigare starkt avrått ifrån att lära eleverna minnesregeln ”störst går först”. Här är ett bra exempel på varför. Elever som arbetar efter ”störst går först” kommer vilja dra det minsta talet från det största och därför beräkna 6 – 3 = 3. När eleven då noterar siffran 3 i tiotalskolumnen blir differensen felaktig.
Slutligen ska hundratalen subtraheras. Av de sju hundratalen i första termen – observera att det är just sju hundratal eftersom siffran 8 i hundratalskolumnen sedan tidigare är överstruken då ett hundratal tidigare har växlats mot tio stycken tiotal – ska åtta subtraheras eftersom det är åtta hundratal i den andra termen. Detta går inte med enbart naturliga tal och man får därför göra på samma sätt som med tiotalen: man växlar första termens enda tusental mot tio hundratal. Detta visas genom att 1:an i tusentalskolumnen på första termens rad stryks över och 10 noteras överst i hundratalskolumnen. Nu har man istället 17 hundratal, från vilka åtta hundratal ska subtraheras, vilket ger 17 –8 = 9. Differensen av den uppställda subtraktionen kommer alltså att ha nio hundratal, och siffran 9 noteras på differensraden i hundratalskolumnen.
Efter detta är den uppställda subtraktionen genomförd eftersom det inte finns några talsorter kvar att subtrahera.
Vanliga problem och missuppfattningar
En vanlig missuppfattning avseende uppställning är att eleven vill räkna från vänster till höger, d.v.s. i läsriktningen, istället för att börja med entalen.
Ett vanligt problem vid uppställning, precis som med andra skriftliga räknemetoder, är att elever memorerar hur stegen i metoden rent mekaniskt går till utan utveckla förståelse för vad som sker när de använder metoden. Detta kan i många fall bero på att de fått undervisning som inte varit förståelseorienterad. Elever som har förståelse för stegen i en räknemetod kan återkonstruera metoden när den behövs istället för att behöva minnas utantill hur den rent mekaniskt går till. Förståelse för stegen minskar också risken att göra fel utan att man upptäcker det.
När det gäller addition med uppställning är ett vanligt problem att elever efter att ha beräknat talsorterna var för sig tappar kopplingen till positionssystemet och t.ex. kommer fram till att 57 + 69 = 1116. Eleven har då först adderat entalen, 7 + 9 = 16, och noterat 16 på summeringsraden istället för att bara notera siffran 6 i entalskolumnen på summeringsraden och siffran 1 överst i tiotalskolumnen. Därpå har eleven adderat tiotalen, 5 + 6 = 11, och noterat 11 till vänster om 16 på summeringsraden. På så sätt ges att summan av 57 + 69 är lika med 1116. Här har eleven inte memorerat exakt hur stegen i räknemetoden går till och har inte förstått metoden.
Om du märker att elever har det här problemet kan du ställa frågor för att försöka få dem att se orimligheten i den typen av felsvar. Ett sätt är att låta dem lösa uppgiften med en annan räknemetod och/eller använda tiobasmaterial, samt låta dem uppskatta svaren i förväg för att bedöma rimligheten i sina svar. Du kan också låta dem skriva upp de partiala summorna och sedan addera. Hjälp dem förstå vad de gör kopplat till positionssystemet och i termer av talsorter.
När det gäller subtraktion med uppställning är det vanligt att elever flyttar siffror mellan termer för att få lättare beräkningar och t.ex. byter plats på sjuan och nian så att 57 – 29 blir 59 –27. Denna missuppfattning avstyrs bäst i modelleringsstadiet med konkret material. Modellera uppgiften med 10-rutor och tiobasmaterial för att visa orimligheten i bytet för eleven.
Arbeta vidare med skriftliga räknemetoder För att eleverna ska bli säkra på skriftliga räknemetoder måste de kontinuerligt få färdighetsträna dessa. Skriv gärna upp en eller ett par additioner eller subtraktioner med och utan växling som eleverna får lösa på egen hand med en skriftlig räknemetod. Detta är utmärkt att göra på färdighetsträningspass eller i väntan på att alla elever kommer in från rast eller liknande. I kommande kapitel finns dessutom flera övningsblad som tränar just detta. Använd dem gärna även om det inte passar med det matematiska innehållet i kapitlet ni arbetar med för tillfället.
Att utveckla elevers problemlösningsförmåga är något som betonas i läroplaner från förskolan upp till gymnasiet. I den här delen går vi igenom vad problemlösning är och hur det definieras och kan förstås ur en didaktisk synvinkel. Vi beskriver även den systematiska metod för problemlösning som vi använder i Rik matematik
Definitionen av problem
I dagligt tal brukar problem vara något som man skulle
vilja lösa, men där man inte är säker på hur detta ska gå till (vet man hur man ska göra är det inget problem). Ofta är frasen ”detta är ett problem” en omskrivning för ”detta går faktiskt inte att göra”.
I skolämnet matematik används ordet problem ofta i bemärkelsen större räkneuppgift, ofta framskrivet som en textuppgift. I matematikdidaktiken används och definieras ordet i betydelsen ”uppgift som den lösande saknar en färdig strategi för”.
Vi kommer i det här läromedlet använda beteckningen problem i betydelsen ”uppgift som kräver inledande tanke- och planeringsarbete innan man kan starta med själva beräkningarna”. Alltså, en anpassad formulering av definitionen ”uppgift som den lösande saknar en färdig strategi för”, eftersom man utifrån att man inte har någon färdig strategi tvingas att genomföra ett inledande tanke- och planeringsarbete. Ett sådant förarbete innefattar modellering.
Modellering
De flesta matematiska problem som startar med en problembeskrivning i ord, både sådana i läroböcker och sådana som uppstår i verkliga livet, innefattar ett moment av matematisk modellering. En modell kan beskrivas som en förenklad version av verkligheten, och en matematisk modell är en beskrivning av verkligheten i matematiska termer. ”Skriv på mattespråk” är matematisk modellering.
Vid modelleringen försöker man skala bort allt som är oväsentligt för resultatet. Ibland tar man även bort sådant som har inverkan, men där inverkan är så pass liten att man får ett tillräckligt bra svar även om man struntar i det. Poängen med förenklingarna är att ta ner svårighetsgraden på matematiken, så att man får något som över huvud taget går att lösa. Ett exempel på en sådan förenkling kan vara ”vi antar att löparen håller samma hastighet hela loppet”. Alltför stora förenklingar leder dock till svar som inte har något med verkligheten att göra, så ett viktigt moment är att granska både modeller och resultat kritiskt.
Så länge man arbetar med heltalsproblem brukar förenklingarna inte påverka resultaten. Då man sammanfattar ”två äpplen och tre bananer är fem frukter” som 2 + 3 = 5 förenklar man bort informationen om vilken sorts objekt det handlade om, men svaret, 5, är helt korrekt.
Att undervisa problemlösning
Problemlösning betraktas som en förmåga som eleverna ska ges möjlighet att utveckla. När du som lärare undervisar problemlösning är det mycket viktigt att uppgiften som eleverna ska lösa är just ett problem. Ett
vanligt misstag vid problemlösningsundervisning är att läraren lotsar eleven genom lösningen med hjälp av frågor eller förslag på hur man skulle kunna göra. Ofta är orsaken till denna lotsning en vilja hos läraren att hjälpa eleverna genom svårigheter de stöter på under problemlösningsprocessen.
Lotsandet sänker den kognitiva nivån problemet initialt hade, och därmed blir uppgiften inte längre ett problem. Det viktiga lärmomentet för eleven vid problemlösning sker just när eleverna får kämpa, inte när allt är lätt och lösningen/strategin presenteras ”på silverfat”. Med andra ord kan (och bör) arbetet med problemlösning i matematik inte bara förväntas ge positiva känslor hos eleverna till en början, utan det kan också skapa en känsla av frustration.
Det är mycket viktigt att du som lärare hjälper eleverna att förstå att denna initiala förvirring och strukturerande av tankar utifrån den, är det som leder till att man lär sig något nytt och utvecklar sin problemlösningsförmåga. I Sverige är ett sådant ”kämpande med uppgifter som initialt ter sig förvirrande” ofta något ovant för både elever och lärare och kan skapa frustration. I andra länder, t.ex. Japan, är lösandet av uppgifter som man från början inte har någon direkt metod för att lösa (alltså ett problem) något helt självklart för elever och lärare. Där genererar det inte frustration på samma sätt som här, eftersom tillvägagångssättet betraktas som självklart vid arbete med matematik och alla är vana vid det.
Problemlösningsmetoden ALP
Det finns olika metoder för problemlösning. Vi har valt att designa en metod som vi kallar ALP, vilket är en förkortning för Analysera, Lösa och Presentera.
1) Analysera: Vad är egentligen problemet?
• Förstå problemet. Vad handlar det om? Vad frågar man efter?
• Tänk på svaret. Vad kommer svaret att säga oss? Vad kan vara ett rimligt svar?
2) Lösa: Hur kan man lösa det?
• Tänk ut en plan. Vad vet vi? Vad vet vi inte som vi behöver veta? Hur tar vi reda på det?
• Genomför planen.
• Värdera. Verkar detta rätt?
3) Presentera: Visa lösningen och svara på frågan.
• Presentera lösningen så att andra kan förstå den. Det kan göras med bilder och/eller matematikspråk.
• Besvara frågan.
Vid undervisning av problemlösning med ALP är det viktigt att tänka på följande;
Analysera. Det är viktigt att från början lägga stort fokus på att hjälpa eleverna att förstå problemet. Här behöver eleven initialt mycket hjälp av läraren. Det kan handla om vilka fakta i uppgiften som är relevanta (och inte), att förstå vissa ord i uppgiften korrekt och att förstå vad som faktiskt frågas efter i uppgiften. Notera att det i denna fas alltså är viktigt att stötta elever med öppna frågor – och mer vägledande frågor efterhand om det behövs.
Lösa. Det är vid denna del, att lösa uppgiften, som eleverna måste få utrymme att tänka själva utan lotsning från läraren. Självklart behöver eleverna hjälp med att följa själva ALP-metoden – med att tänka ut en plan, genomföra planen och värdera det genomförda. Det är vid själva planeringen som eleverna behöver kämpa själva, utan lotsning från läraren, för att utveckla sin problemlösningsförmåga. När planen sedan genomförs och svaret ska avgöras som rimligt eller inte är det också viktigt att initialt inte tillrättavisa eleven om man som lärare ser att det blir fel. Att göra fel är något man lär sig mycket av om det hanteras väl i efterhand.
Presentera. Det är mycket viktigt att inte bara presentera, utan även diskutera vad man kommit fram till för svar och hur man kom fram till det. Har eleven gjort något fel i sina beräkningar eller i sin plan så är det viktigt att lokalisera dessa fel, vad i tankeprocessen som ledde till felet och adressera vad som är korrekt och varför. Därmed blir presentationsfasen mycket viktig som lärtillfälle och inte bara som en summering av vad man gjort. En sådan presentationsfas kan med fördel genomföras i helklass där eleverna presenterar sina lösningar för klassen, lösningarna diskuteras och läraren summerar diskussionen och lyfter fram de viktiga matematiska idéerna.
1.0.5
Till det här kapitlet finns övningsblad att dela ut efter lektion 1, 2, 6, och 7. Övningsbladen kan användas som extra färdighetsträning eller som extrauppgifter/utmaningar till elever som snabbt blir klara.
Generellt om övningsblad
Till alla kapitel finns övningsblad som du kan skriva ut och ge elever som extra färdighetsträning – under lektioner, mellan två lärarledda lektioner eller som läxa. Det finns alltid ett övningsblad på grundläggande nivå och ett mer utmanande blad, och det framgår av lektionsförslagen när det är lämpligt att dela ut dem.
Övningsbladen möjliggör extra färdighetsträning på sådant som eleverna lärt sig under den lärarledda undervisningen i syfte att de ska befästa kunskaperna. Poängen
med övningsbladen, oavsett hur du väljer att arbeta med dem, är att förlänga lärandet som skett i klassrummet så att eleverna i högre grad befäster kunskaperna. Om du väljer att skicka hem övningsbladet som läxa måste du därför försäkra dig om att eleven inte behöver hjälp av en vuxen för att förstå uppgiften. Detta gäller särskilt de övningsblad som testar eleven på en högre nivå.
Mer generell information om hur du kan arbeta med övningsbladen finns i den digitala lärarresursen.
Baroody, A. J., & Purpura, D. J. (2017). Early number and operations: Whole numbers. I C. J. (Red ), Compendium for research in mathematics education (s. 308–354). Reston, VA: National Council of Teachers of Mathematics.
Foegen A., & Dougherty, B. (2017). Instruction that meets the needs of students with mathematical disabilities and difficulties I C. J. (Red.), Compendium for research in mathematics education (s. 893–907). Reston, VA: National Council of Teachers of Mathematics.
Lemaire, P., LeCacheur, M., & Farioli, F. (2000). Children’s strategy use in computational estimation. Canadian Journal of Experimental Psychology, 54(2), 141–148.
McIntosh, A. (2020). Förstå och använda tal: En handbok. Göteborg: Nationellt centrum för matematikutbildning.
Selter, C. (2001). Addition and subtraction of three-digit numbers: German elementary children’s success, methods and strategies. Educational Studies in Mathematics, 47(2), 145–173.
Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2020). Elementary and middle school mathematics: Teaching developmentally, global edition (uppl. 10). New York, NY: Pearson Education.
Woodward, J. (2006). Developing automaticity in multiplication facts: Integrating strategy instruction with timed practice drills. Learning Disability Quarterly, 29(4), 269–289.
Lektionens huvudsyfte är att eleverna ska befästa och slutligen automatisera talkombinationerna i stora additions- och subtraktionstabellen genom att repetera och använda olika räknestrategier. Detta är kunskap eleverna måste ha för att senare effektivt kunna göra beräkningar i ett större talområde. Ett annat syfte är att motivera eleverna inför åk 3 genom att introducera det nya läsårets matematik, bland annat genom att visa ett spännande problem som eleverna kommer kunna lösa i slutet åk 3 med hjälp av den matematik de ska lära sig.
Lektionsmål
• Eleven förstår flera olika räknestrategier för beräkning av kombinationer inom stora addition och subtraktion, och visar det genom att förklara sina lösningar.
• Eleven har automatiserat stora additions- och subtraktionstabellen och visar det genom att direkt veta resultatet på talkombinationerna.
Matematiska begrepp: Addition, subtraktion, term, summa, differens, talkamrat, tiokamrat
SvA: Inget särskilt.
Material: Kopieringsunderlagen Först till mål, Winnetkakort 14 – Addition tiotalsväxling, Winnetkakort 15 – Subtraktion tiotalsväxling, sexsidiga tärningar och spelpjäser.
Uggla: Årskurs 3
Professor Uggla berättar om vad som komma skall i åk 3.
Övning: Stora plus
Eleverna SURRA r om hur man kan beräkna additioner i stora plus.
Repetition: Strategier för addition
Du spelar de animerade genomgångarna av strategier för addition.
Övning: Stora minus
Eleverna SURRAR om hur man kan beräkna subtraktioner i stora minus.
Repetition: Tänk addition
Du spelar vid behov den animerade genomgången av strategin.
Repetition: Skapa 10 vid subtraktion
Du spelar vid behov den animerade genomgången av strategin.
Förberedelser
• Skriv ut Först till mål i A3 så att varje grupp får varsitt exemplar.
• Skriv ut avslutslappar.
• Skriv ut Winnetkakort 14 och Winnetkakort 15. Låt eleverna klippa ut de kort de behöver träna extra på.
• Övningsblad finns. Skriv ut vid behov (se kapitelintrot).
Först till mål Winnetkakort 14 – Addition tiotalsväxling Winnetkakort 15 – Subtraktion tiotalsväxling Avslutslapp Övningsblad grundläggande Övningsblad utmanande
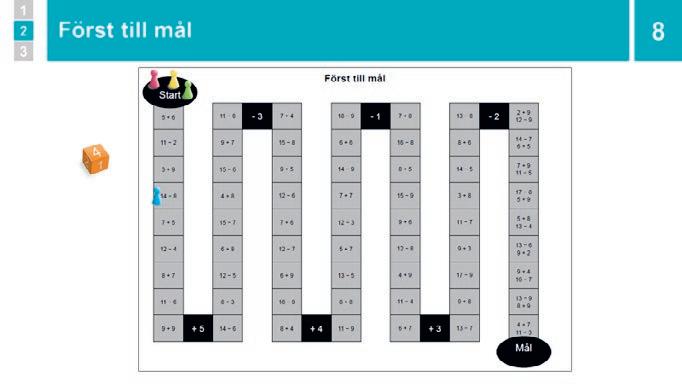
Gruppövning: Först till mål Grupperna spelar Först till mål
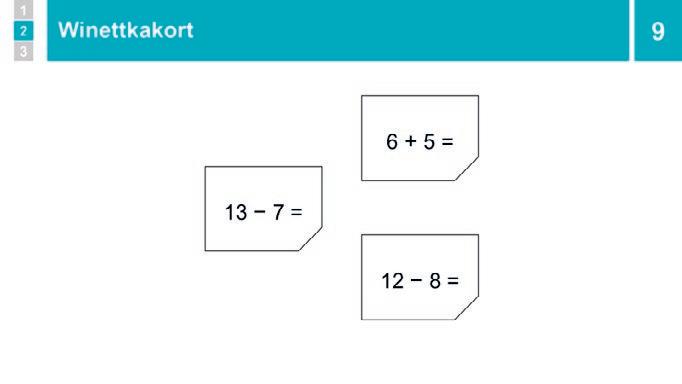
Winnetkakort
Eleverna tränar enskilt eller i par med sina winnetkakort.
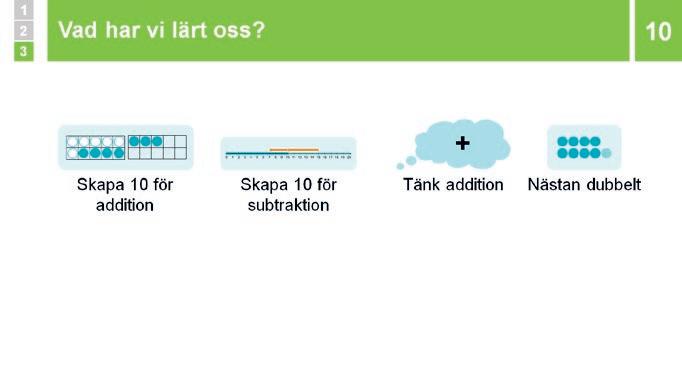
Sammanfattning: Vad har vi lärt oss?
Du sammanfattar: När man ska beräkna en addition eller en subtraktion där man måste växla mellan talsorter kan man använda strategierna Skapa 10, Tänk addition eller Nästan dubbelt
Avslutslapp



2 Uggla: Årskurs 3 15 min
Hälsa alla matematiker välkomna till det första kapitlet i årskurs 3 och låt sedan professor Uggla berätta om åk 3.
3 Övning: Stora plus
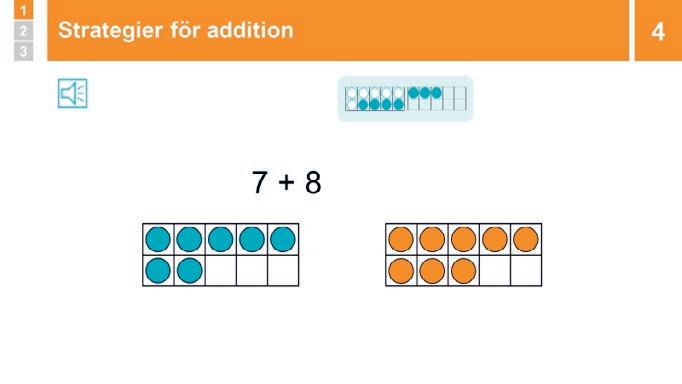
Visa 7 + 8 samt 6 + 7. Låt eleverna SURRA om hur man kan tänka för att beräkna additionerna. Fördela ordet. Om elever använder hållbara strategier, t.ex. Skapa 10 eller Nästan dubbelt (t.ex. 6 + 6 + 1), så låter du andra ÅTERGE
Förklara strategin Skapa 10 noggrant eller spela den animerade genomgången av strategin på bild 4 i bildspelet.
4 Repetition: Strategier för addition
Om man ska addera två tal där entalen i termerna tillsammans har en summa över 10 och man inte direkt vet svaret kan man använda strategin ”Skapa 10”. T.ex. om man ska addera 7 + 8. Vi tar 2 från 7 och skapar 10 tillsammans med 8 eftersom 8 och 2 är 10-kamrater. 10 och de 5 som är över är tillsammans 15. Alltså är 7 + 8 också lika med 15. Man kan även tänka ”nästan dubbelt”: Om man vet att 7 + 7 = 14 så måste 7 + 8 vara 1 mer, alltså 15.
5 Övning: Stora minus
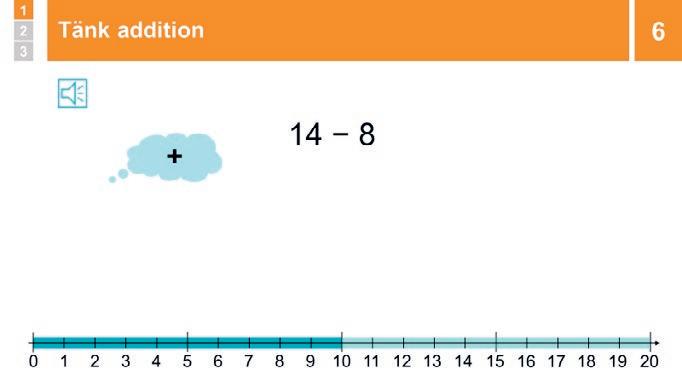
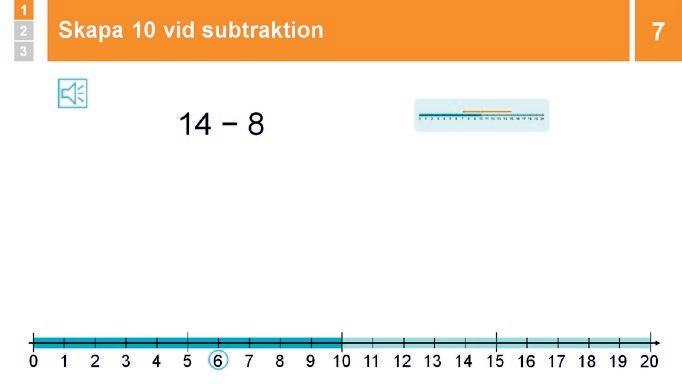
Låt eleverna SURRA om hur man kan tänka för att beräkna 14 – 8. Fördela ordet. Om elever använder hållbara strategier, t.ex. Tänk addition eller Skapa 10 vid subtraktion, så låter du andra ÅTERGE
Vid behov förklarar du strategierna Tänk addition och Skapa 10 vid subtraktion, eller spelar de animerade genomgångarna på bild 6 och 7 i bildspelet.
Om någon räknat ned åtta steg från 14 säger du att det kan fungera, men att det är lätt att tappa bort sig och att det tar lång tid. Därför är de andra strategierna lämpligare i denna situation.
6 Repetition: Tänk addition
Om man ska lösa subtraktionen 14 8 kan man använda sig av strategin ”Tänk addition”, eftersom addition och subtraktion är varandras motsatser. Vad tillsammans med 8 är lika med 14?
Om man inte direkt vet svaret kan man ta vägen över 10. Från talet 8 till 10 är det 2 eftersom 8 och 2 är 10-kamrater.
Från 10 till 14 är det 4. Man adderar sedan 2 + 4 vilket är lika med 6, vilket innebär att skillnaden mellan talen 8 och 14 också är 6. Alltså är 14 8 = 6.
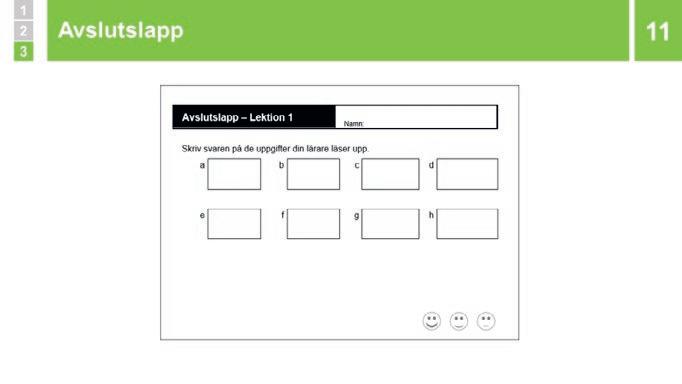
7 Repetition: Skapa 10 vid subtraktion
Subtraktion går också att lösa med hjälp av strategin ”Skapa 10”. Om man ska lösa subtraktionen 14 8 tar man först bort 4 så att man får 10 kvar, då 10 är lättare att räkna med. Det betyder att man ska ta bort 4 till, eftersom talet 8 kan delas upp i 4 och 4. Tar man bort 4 från 10 är det 6 kvar. Alltså är 14 8 = 6.
8 Gruppövning: Först till mål
25 min
Dela in eleverna i smågrupper (tre–fyra elever) eller i par om du tycker att det är mer lämpligt. Förklara hur spelet går till:
• Eleverna slår i tur och ordning en sexsidig tärning, går lika många steg framåt och beräknar den addition/subtraktion som hen hamnar på. Om rutan är svart går hen bakåt/framåt så många steg som anges.
• När hen beräknat färdigt säger hen summan/differensen och förklarar hur hen kom fram till svaret.
• Övriga kontrollräknar med lämplig strategi.
• Om eleven har räknat rätt står hen kvar, annars får hen backa ett steg. Därefter går turen över till nästa spelare.
9 Winnetkakort
Dela ut winnetkakorten och låt eleverna färdighetsträna med dem i 5–10 minuter.
10 Sammanfattning: Vad har vi lärt oss?
10 min
Sammanfatta att när man ska beräkna en addition eller en subtraktion där man måste växla mellan talsorter så kan man använda strategierna Skapa 10, Tänk addition eller Nästan dubbelt.
För att bli en duktig matematiker behöver man förstå och kunna använda några bra räknestrategier för huvudräkning. Då kommer man alltid kunna ta reda på svaret. Och ju mer man tränar, desto fler talkombinationer kommer man lära sig utantill. Om man sedan skulle glömma en talkombination, men har en strategi, så kan man alltid använda strategin för att tänka ut resultatet.
11 Avslutslapp
Du läser additionerna och subtraktionerna högt, en i taget. Eleverna beräknar och skriver svaret i rätt ruta. Säg exempelvis: ”Vad är 9 + 2 lika med? Skriv summan i ruta a.” Ge eleverna cirka 10 sekunders BETÄNKETID per uppgift.
Uppgifterna är:
Lektionen ger möjlighet att utveckla och befästa elevernas färdigheter i att använda hållbara strategier för beräkningar med tiotalsövergång. Uppmärksamma om elever uppenbarligen inte använder hållbara strategier och t.ex. räknar på fingrarna eller använder sig av upp- eller nedräkning. Det tyder på att de antingen inte behärskar någon mer hållbar strategi eller inte litar på strategierna. Undersök vad detta beror på och försök hjälpa eleven vidare till hållbara strategier.
Det fortsatta arbetet bör individualiseras utifrån elevernas eventuella specifika svårigheter. Du kan t.ex. individanpassa de winnetkakort som eleverna arbetar med så att elever arbetar med de talkombinationer som de behöver träna mer på. Undersök utifrån uppgifter som eleven inte klarar av om hen använder sig av en hållbar strategi eller inte. Om eleven saknar en effektiv strategi undervisar du hen i hur hen ska använda sig av strategin och låter sedan hen öva tills hen behärskar den. Låt gärna eleven öva på särskilt svåra talkombinationer i korta pass på ca 5 minuter. Gör gärna detta dagligen, t.ex. med winnetkakort. Det är viktigt eleverna inte tränar med winnetkakorten innan de har hållbara strategier.
Om du har elever som egentligen kan hållbara strategier men ändå faller tillbaka på mindre hållbara strategier som de upplever som mer säkra, t.ex. fingerräkning, så behöver du hjälpa dem att lita på sig själva och på att strategierna fungerar. Låt dem beräkna några liknande uppgifter enbart med den hållbara strategin, och påpeka för eleven att det fungerar. Låt dem sedan träna med t.ex. winnetkakort och uppmana dem att då fortsätta med de hållbara strategierna.
Elever som säger att de ”bara vet” om du frågar hur de kom fram till det korrekta svaret kan ha automatiserat tabellerna. Säg att detta är bra, men att det också är viktigt att förstå och kunna använda strategierna om man i framtiden skulle glömma det man nu automatiserat.
Förenkla
Du kan förenkla för elever genom att låta dem arbeta med dubbla 10-rutor och markörer i början av lektionen. Vid addition läggs termerna i varsin 10-ruta, så att eleven ser hur hen ska skapa 10. Om eleven ska beräkna 8 + 6 kan hen se att man behöver flytta 2 från 6 till 8 för att skapa 10. Det är då 10 i den ena och 4 i den andra 10-rutan. Summan är alltså 14.
Vid subtraktion läggs den första termen genom att den första 10-rutan fylls, vilket motsvarar tiotalet, varpå
entalen läggs i den andra. Om eleven ska beräkna 13 – 5 så ser eleven att man först tar bort 3 för att skapa 10, innan man tar bort resterande 2. Alltså är 13 – 5 lika med 8. Var noga med att eleven inte tar bort en i taget, då det inte är en hållbar strategi.
Även om dessa förenklingar görs i början av lektionen är det viktigt att poängtera att eleven i slutändan förväntas genomföra beräkningarna utan konkret material.
Utmana mer
Elever som blivit skickliga på huvudräkning inom stora plus och minus kan utmanas med huvudräkning med tvåsiffriga tal, t.ex. med den skriftliga räknemetoden Kompatibla tal. Skriv t.ex. 28 + 43 och be dem att, i huvudet, flytta 2 från 43 till 28, för att på så sätt skapa ett jämnt tiotal i första termen, och sedan beräkna 30 + 41.
Utmana elever att även arbeta med räknemetoden vid subtraktion. Om de ska beräkna t.ex. 53 – 25 tar de först bort 23, för att skapa ett jämnt tiotal i första termen, varpå de tar bort återstående 2:
53 – 25 = 53 – 23 – 2 = 30 – 2 = 28
Avslutslappen
Avslutslappen ger dig möjlighet att observera elever som uppenbarligen inte använder hållbara strategier. Du kan till exempel se att de räknar på fingrarna, nickar rytmiskt eller använder upp- och nedräkning. Elever som verkar använda hållbara strategier, men som inte kommer fram till de rätta svaren, upptäcker du när du rättar avslutslappen. Undersök vad det beror på.
10 sekunder bör vara tillräcklig tid för respektive uppgift om eleven behärskar en hållbar strategi. Vänta därför inte mer än 10 sekunder innan du läser nästa uppgift. Om eleven redan har automatiserat talkombinationerna märker du det genom att hen svarar direkt och korrekt. Om eleven har automatiserat kombinationen tar det max 5 sekunder för hen att få fram ett korrekt svar.
Om elever inte klarar uppgifterna inom 10 sekunder måste du undersöka vad det beror på. Elever som inte behärskar hållbara strategier måste öva mer, då detta är förkunskaper som krävs för att klara kommande lektioner i kapitlet. Läs mer under Uppmärksamma och stötta samt Förenkla om hur du kan stödja dessa elever. Du kan även gå tillbaka till lektion 6 i kapitel 1 i åk 2 för mer stöd. Vi rekommenderar inte att särskild undervisning ersätter den ordinarie undervisningen. Den bör pågå parallellt i korta pass utöver den ordinarie undervisningen.
Syftet med lektionen är att utveckla elevernas förståelse för positionssystemet och platsvärde genom att introducera tusental. Syftet är också att befästa deras befintliga kunskaper kopplat till positionssystemet genom repetition.
Lektionsmål
• Eleven kan tolka, läsa och skriva talen 0–9999 och visar det genom att beskriva och skriva fyrsiffriga tal utifrån representationer av tal med tiobasmaterial, samt genom att lägga fyrsiffriga tal med tiobasmaterial.
• Eleven förstår platsvärde inom talområdet 0–9999 och visar det genom att skriva tal i utvecklad form samt genom att storleksordna tal.
Matematiska begrepp: Tusental, hundratal, tiotal, ental, platsvärde, utvecklad form
SvA: Grupp, plats, position, storleksordna
Repetition: Positionssystemet
Du repeterar talsorterna ental, tiotal och hundratal, och hur de visas med siffror på olika platser i talen.
Genomgång: Tusental
Du introducerar tusental som en grupp med tio hundratal.
Övning: Tusental
Du visar fyrsiffriga tal och låter elever säga talen.
Genomgång och övning: Platsvärde
Du går igenom hur siffror på tusentalsplatsen anger hur många tusental ett tal har och låter sedan eleverna SURRA om hur några fyrsiffriga tal skrivs i utvecklad form.
Genomgång och övning: Storleksordna tal
Du går igenom hur man storleksordnar fyrsiffriga tal och låter eleverna storleksordna några tal.
Material: Kopieringsunderlaget Positionsspelet, tiosidig tärning numrerad 0–9, tiobasmaterial som stöd vid behov
Förberedelser
• Skriv ut Positionsspelet så att varje elev kan få varsitt exemplar.
• Skriv ut avslutslappar.
• Övningsblad finns. Skriv ut vid behov.
Positionsspelet
Avslutslapp Övningsblad grundläggande Övningsblad utmanande
Övning: Positionsspelet
Ni spelar Positionsspelet med fyrsiffriga tal.
Elevboken s. 4−7
Sammanfattning: Vad har vi lärt oss?
Du sammanfattar att ett tusental är en grupp med tio hundratal, och att siffran på tusentalsplatsen i ett tal visar hur många tusental talet har.
Du sammanfattar hur man skriver fyrsiffriga tal i utvecklad form och hur man storleksordnar fyrsiffriga tal.
Avslutslapp
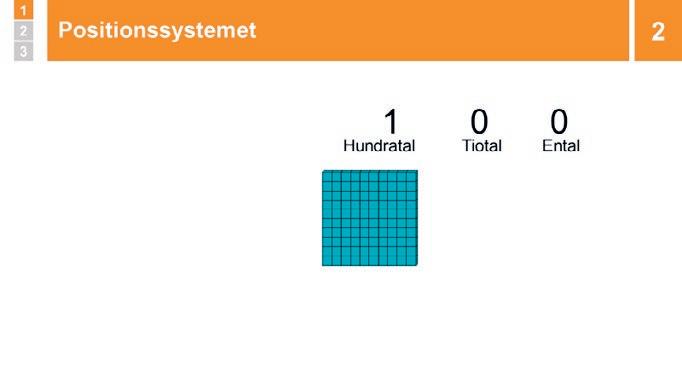
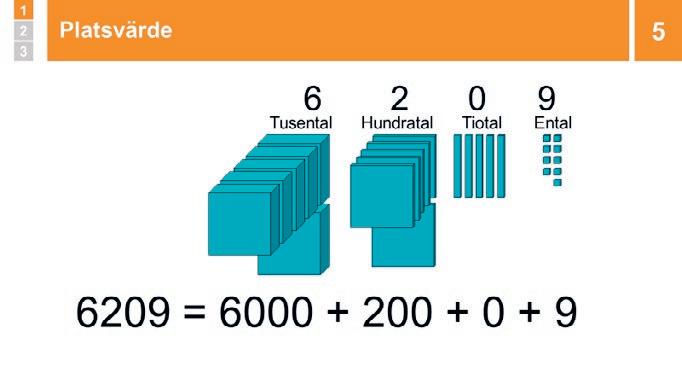
2 Repetition: Positionssystemet 10 min
Visa och repetera: Ett ental motsvarar talet 1, vilket visas med att siffran 1 står på entalsplatsen. Tio ental är ett tiotal, en grupp av tio ental, vilket visas med siffran 1 på tiotalsplatsen och 0 på entalsplatsen. Tio stycken tiotal är ett hundratal, en grupp med tio stycken tiotal, vilket visas med siffran 1 på hundratalsplatsen och siffran 0 på tiotalsplatsen och entalsplatsen.
3 Genomgång: Tusental
Visa hur tio hundratal grupperas till en stor kub. Fråga: ”Vilket tal är tio hundratal?” BETÄNKETID. Fördela ordet. När någon svarar 1000 förklarar du att en grupp med tio hundratal är ett tusental, vilket motsvarar talet 1000.
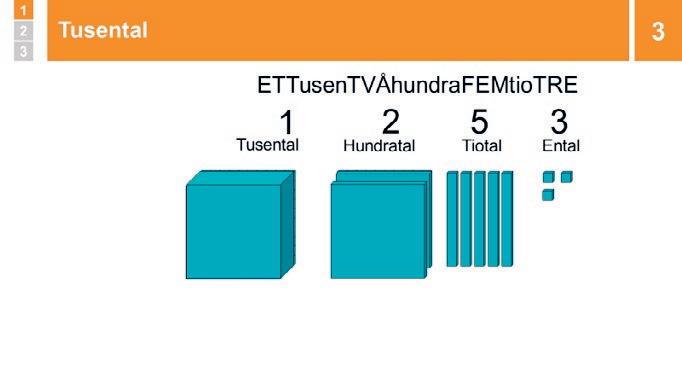
Visa talet 1253 med siffror och tiobasmaterial. Visa hur tiobasmaterialet ändras till förenklade bilder, och konstatera att det fortfarande är samma tal: en liten kub är ett ental, en stav är ett tiotal, en platta är ett hundratal och en stor kub är ett tusental. Säg: ”Det är ett tusental, två hundratal, fem tiotal och tre ental”. Repetera att man läser talen från vänster till höger: ”ETTtusenTVÅhundraFEMtioTRE.”
4 Övning: Tusental
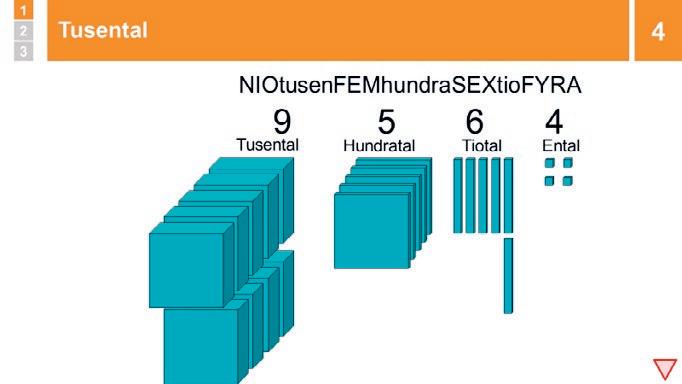
Visa fyrsiffriga tal med siffror och tiobasmaterial, låt någon förklara vad det är för tal och hur det sägs, eller förklara själv.
5 Genomgång och övning: Platsvärde
Visa talet 2431 med siffror och tiobasmaterial. Förklara: Siffran 2 står på tusentalsplatsen, alltså är det två tusental, vilket motsvarar 2000. Siffran 4 står på hundratalsplatsen, alltså är det fyra hundratal, vilket motsvarar 400. Siffran 3 står på tiotalsplatsen, alltså är det tre tiotal, vilket motsvarar 30. Siffran 1 på entalsplatsen, alltså är det ett ental, vilket motsvarar talet 1.
Visa hur talet skrivs i utvecklad form och förklara: Utvecklad form betyder att man skriver ett uttryck där man visar vad varje siffra i talet står för med en term för varje siffra. Förklara varför 2431 i utvecklad form är 2000 + 400 + 30 + 1.
Visa 1625. Låt eleverna SURRA om hur man skriver talet i utvecklad form. Fördela ordet. När någon svarar rätt ber du hen redogöra för hur det hänger ihop med det ursprungliga talet. Om hen ger en bra förklaring låter du någon annan ÅTERGE . Annars förklarar du själv. Gör samma sak med talen 4052 och 6209.
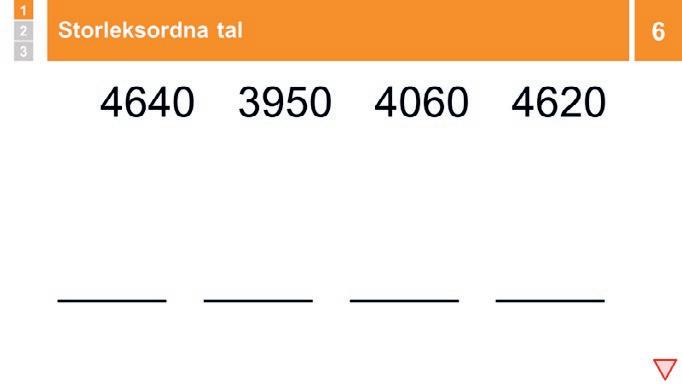
6 Genomgång och övning: Storleksordna tal
Säg att talen 1540, 2310 och 2280 ska storleksordnas från minst till störst. Repetera att när man jämför tal som har lika många siffror så börjar man med den största talsorten. Här är det tusental. Visa och förklara: 1540 har ett tusental medan de andra talen har två, alltså är talet 1540 minst. 2310 och 2280 har lika många tusental, men 2310 har tre hundratal och 2280 har bara två. 2310 är störst.

Låt eleverna SURRA för att storleksordna 4640, 3950, 4060 och 4620. Låt sedan någon redogöra för hur de storleksordnat. Förstärk om de storleksordnat genom att jämföra den största talsorten först.
7 Övning: Positionsspelet
30 min
Förse alla elever med underlaget Positionsspelet. Spelet går ut på att få ett tal som är så stort som möjligt och ett som är så litet som möjligt. För varje omgång har man två spelplaner med fyra fält. Förklara spelet med exemplet:
• Du slår en tiosidig tärning och skriver talet på tavlan. Eleverna placerar talet i något av fälten på spelplanen. Sedan får man inte flytta talet.
• Du slår igen och upprepar tills alla fält är fyllda och talen bildade.
• Någon får berätta vilket hens största tal är. Fråga om någon har ett tal som är större, och låt hen berätta vilket tal det är och hur hen vet att det är större. Fortsätt tills det största talet som bildats i klassen är hittat.
• Gör på samma sätt för att hitta det minsta talet.
Börja spela när alla förstått. Spela en eller två omgångar.
8 Elevboken s. 4−7
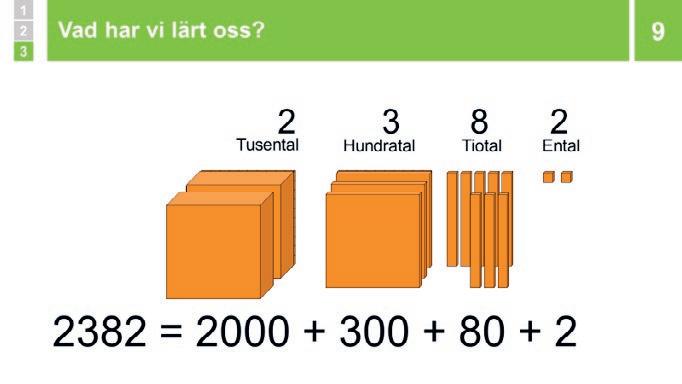
9 Sammanfattning: Vad har vi lärt oss? 10 min
Visa talet 100 med siffror och tiobasmaterial. Visa hur nio hundratal läggs till, hur ett tusental bildas och hur siffran 1 flyttas till tusentalsplatsen. Konstatera att siffran 1 står på tusentalsplatsen och visar att det är ett tusental. Siffran noll står på övriga positioner och visar att talet inte har några hundratal, tiotal eller ental.
Visa talet 2382 med tiobasmaterial och i utvecklad form. Berätta att i utvecklad form visar man varje siffra i ett tals värde. Säg att siffan 2 i talet står på tusentalsplatsen och visar att det är två tusental. Två tusental motsvarar talet 2000. Gör sedan likadant med de andra siffrorna i talet.
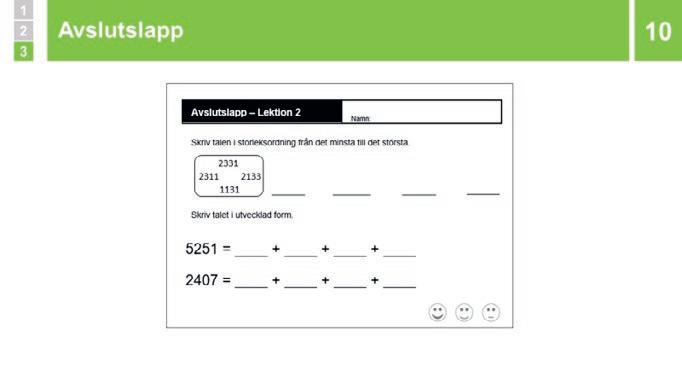
Visa talen 1347, 2229 och 2051, och säg att om man ska storleksordna dem så börjar man med att titta på den största talsorten. Talet 1347 har bara ett tusental medan de andra talen har två. 1347 är alltså det minsta talet. Talen 2229 och 2051 har lika många tusental, men 2229 har två hundratal och talet 2051 har inget hundratal. Alltså är 2229 större än 2051.
10 Avslutslapp
Det räcker inte att eleverna kan säga hur många av varje talsort ett tal har, t.ex. att talet 2451 har två tusental, etc.
De måste även förstå att två tusental motsvarar talet 2000 eftersom siffran 2 står på tusentalsplatsen. Eleverna behöver alltså förstå att de olika positionerna i ett tal har olika platsvärde, i form av talsorter, och att siffran visar hur många av respektive talsort ett tal har beroende på siffrans plats i talet. När eleverna arbetar med tiobasmaterial så synliggörs detta samband. Det kan vara enklare att förstå positionssystemet om man t.ex. lägger talet 432 med tiobasmaterial och kan se att siffran 4 visar fyra hundratal, vilket motsvarar fyra hundraplattor, alltså 400, etc.
Eleverna behöver också förstå att platsvärdet är tio gånger större för varje steg till vänster och en tiondel så stort för varje steg till höger. Detta samband gäller då också mellan talsorterna som positionerna hänger ihop med: ett tiotal är tio gånger större än ett ental, ett hundratal är tio gånger större än ett tiotal, etc. Det är viktigt att eleverna förstår att ett hundratal motsvarar talet 100, ett tiotal motsvarar talet 10 och ett ental motsvarar talet 1. De behöver på samma sätt förstå att tio ental är ett tiotal, att tio stycken tiotal är ett hundratal och att tio hundratal är ett tusental.
Uppmärksamma elever som skriver tal i utvecklad form i omvänd ordning, t.ex. 1231 = 1 + 30 + 200 + 1000. Utsagan är förvisso sann, men poängen med att skriva termerna i samma ordning som de positioner de motsvarar i det ursprungliga talet är att det ska utveckla förståelsen för platsvärde och positionssystemet.
För att snabbt kunna storleksordna tal behöver eleverna lära sig att först jämföra hur många av den största talsorten som talen har genom att först titta på platsen längst till vänster i talen.
Uppmärksamma elever som verkar ramsräkna för att avgöra talens storleksordning. Det kan tyda på att de inte har utvecklat en mental bild av talraden eller tallinjen 0–1000, eller inte förstår platsvärde och talens uppbyggnad tillräckligt väl. Låt dessa elever till att börja med använda tiobasmaterial och arbeta med tal i talområdet 0–99. Visa hur de kan börja med att jämföra tiotalen för att storleksordna. Om talen har samma antal tiotal visar du hur de fortsätter med att titta på entalen.
Förenkla
Du kan förenkla Positionsspelet genom att eleverna först skapar ett så stort tal som möjligt med de fyra första siffrorna som slagits. När detta är gjort diskuterar ni de olika talen i klassen. Sedan går ni över till att slå fyra nya slag för att skapa ett så litet tal som möjligt.
Vid behov kan elever arbeta med tiobasmaterial under arbetet i elevboken.
Utmana mer
Introducera tiotusental och utmana elever att skriva femsiffriga tal i utvecklad form. Du kan också utmana elever att storleksordna femsiffriga tal.
Avslutslappen
Avslutslappens första uppgift visar om eleven kan storleksordna flera fyrsiffriga tal. Om eleven inte klarar detta behöver du undersöka vad det beror på. Gå igenom platsvärde på nytt om det behövs och låt eleven färdighetsträna. Om elever behöver kan du låta dem använda tiobasmaterial som konkret stöd. När de verkar ha förstått kan de testa igen med nya tal, utan tiotalsmaterial.
Den andra uppgiften hjälper dig att se om eleven förstår platsvärde för fyrsiffriga tal genom att testa om de kan skriva fyrsiffriga tal i utvecklad form. Elever som inte klarar att skriva båda talen i utvecklad form kan försöka igen med stöd av tiobasmaterial. Uppmuntra dem då att först lägga talen med materialet och sedan skriva talen i utvecklad form.
Elever som inte förstår positionssystemet och platsvärde måste öva mer på det omedelbart och parallellt med den fortsatta undervisningen, eftersom det är nödvändiga förkunskaper för kommande lektioner. Läs mer direkt under rubriken Uppmärksamma och stötta samt under Förenkla om hur du kan stötta dessa elever. Du kan även gå tillbaka till kapitel 7, lektion 1–3 samt lektion 5, i åk 2 för mer information och stöd. Dessa elever behöver repetera och arbeta med innehållet dagligen i korta pass utöver den ordinarie undervisningen.
Syftet med lektionen är att eleverna ska befästa sina färdigheter i uppskattning vid addition och subtraktion inom talområdet 0–9999 med fokus på olika strategiers lämplighet för specifika uppgifter. Detta är en färdighet vi började utveckla i åk 2 och som eleverna har nytta av bland annat för att bedöma vad som kan vara rimliga svar vid addition och subtraktion med skriftliga räknemetoder.
Lektionsmål
• Eleven behärskar hållbara strategier för uppskattning vid addition och subtraktion inom talområdet 0–9999 och visar det genom att beskriva hur hen använt strategin för att komma fram till en viss uppskattning.
• Eleven kan resonera kring olika strategiers lämplighet vid uppskattning och visar det genom att framföra argument för och/eller mot en specifik strategi kopplat till en specifik addition/subtraktion.
Matematiska begrepp: Uppskatta, avrunda, ungefär lika med, rimligt.
SvA: Ungefär
Material: Miniräknare (en per par), miniwhiteboards med penna och sudd
Förberedelser
• Skriv ut avslutslappar.
• Förbered miniwhiteboards.
Avslutslapp
Repetition: Fyrsiffriga tal
Du repeterar platsvärdena i fyrsiffriga tal, samt utvecklad form och hur man storleksordnar fyrsiffriga tal.
Repetition: Varför uppskatta?
Du repeterar poängen med att göra uppskattningar.
Övning: Uppskattning vid addition
Eleverna uppskattar summan av en addition. Du repeterar de vanligaste strategierna. Eleverna funderar på om någon strategi alltid är bäst.
Övning: Uppskattning vid subtraktion
Eleverna uppskattar differensen av en subtraktion. Du repeterar de vanligaste strategierna.
Parövning och diskussion:
Värdera uppskattningar
Du visar en addition/subtraktion och hur två fiktiva barn har uppskattat summan/differensen med olika strategier. Paren diskuterar hur de två barnen kan ha tänkt, vilken strategi de tycker är bäst för uppgiften och varför. Du leder en kort diskussion om vilket sätt som var bäst och varför. Poängen är att strategier kan ha olika för- och nackdelar i olika situationer.
Elevboken s. 8−10
Sammanfattning:
Vad har vi lärt oss?
Sammanfatta: Ibland är det bra att snabbt uppskatta vad summan eller differensen blir, t.ex. för att man bara behöver veta på ett ungefär eller för att kunna se om svaret till en beräkning är rimligt. Det finns många olika strategier för uppskattning som har olika för- och nackdelar i olika situationer.
Avslutslapp
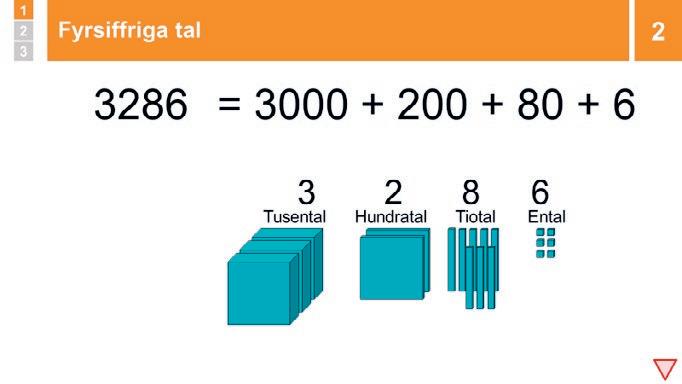




2 Repetition: Fyrsiffriga tal 15 min
Visa talet 3286. Konstatera att siffran 3 står på tusentalsplatsen och visar att talet har tre tusental, vilket motsvarar talet 3000. Upprepa med övriga positioner. Visa sedan talet i utvecklad form och repetera hur termerna till höger om likhetstecknet hänger ihop med siffrorna i talet till vänster om likhetstecknet.
Visa talen 3286 och 3256 bredvid varandra. Fråga vilket tal som är störst. BETÄNKETID. Fördela ordet. När någon svarar rätt ber du hen förklara hur hen jämförde. Förstärk om hen först jämförde tusentalen, därefter hundratalen och slutligen konstaterade att 3286 hade fler tiotal.
3 Repetition: Varför uppskatta?
Repetera att det ibland räcker att veta ungefär vad summan eller differensen är, och att det då är bra att kunna göra en enkel uppskattning. Man vill t.ex. kanske veta om pengarna kommer att räcka när man ska handla utan att man behöver veta exakt vad det kommer att kosta. Det kan också vara bra att göra en uppskattning när man ska göra en beräkning, så att man vet vad som är ett rimligt svar.
4 Övning: Uppskattning vid addition
Förse alla elever med en miniwhiteboard eller dela in dem i par och ge varje par en miniwhiteboard. Visa additionen 154 + 79 ≈ och repetera att ≈ betyder ungefär lika med. Be eleverna uppskatta summan och skriva den på sin miniwhiteboard.
Be dem hålla upp tavlorna när alla börjar bli klara. Påminn om JAG MED, ge ordet till en elev som har gjort en korrekt uppskattning och låt hen redogöra för hur hen tänkte. Ge sedan ordet till någon som inte gör JAG MED och fråga hur hen tänkt istället.
Repetera de vanligaste strategierna i bildspelet och visa sedan den exakta summan av additionen. Låt eleverna SURRA om vilken uppskattning som kom närmast. Fördela sedan ordet och konstatera att i det här fallet kom man närmast om man endast avrundande den andra termen. Säg: ”Är det alltid så tror ni?
Det ska vi fundera mer på senare.”
5 Övning: Uppskattning vid subtraktion
Visa 324 67 och låt eleverna uppskatta differensen. Gör sedan på samma sätt som i steg 4. Här kommer alla uppskattningar lika nära den exakta differensen.
Aktivitet
6 Parövning och diskussion: Värdera uppskattningar 25 min
Dela in eleverna i par. Förse dem med miniräknare. Gör så här:
• Visa 64 + 324 ≈ samt hur två fiktiva barn har uppskattat summan med två olika strategier.
• Be paren diskutera vilken strategi barnen använt, samt vilken strategi de tycker är bäst för uppgiften och varför. Vilket sätt verkar vara snabbast och enklast? Vilket sätt verkar komma


närmast det exakta resultatet? Finns den någon annan strategi som kan fungera bättre? De kan använda miniräknaren för att beräkna det exakta svaret.
• Led en kort helklassdiskussion om vilket sätt som var bäst och varför. En strategi kan vara snabbare men mindre exakt, en annan kan komma närmare det exakta resultatet men vara krångligare, beroende på additionen. Förstärk när elever delger resonemang om för- och nackdelar och låt andra elever ÅTERGE viktiga saker som sägs.
• Kom överens om vilken strategi som var mest lämplig för additionen 269 + 58. I additionen är strategin att göra om entalen till 10-kamrater överlägset mest exakt, men kan vara krångligare. Låt paren prova att uppskatta två nya additioner med dessa strategier: 269 + 58 ≈ och 154 + 63 ≈.
• Led en ny kort helklassdiskussion om huruvida den strategin som eleverna provat alltid är den som kommer närmast det exakta resultatet. Låt eleverna komma fram till att i additionen 269 + 58 är det mest exakt att avrunda båda termerna upp, medan i additionen 154 + 63 är det mest exakt att avrunda entalen till 10-kamrater.
7 Parövning och diskussion: Värdera uppskattningar
Gör samma parövning och diskussion som ovan fast för subtraktion med den skillnaden att fokus i diskussionen ska vara på vilken strategi som är enklast. Båda strategierna ger uppskattningar som kommer lika nära den exakta differensen, men komplexiteten i strategin kan upplevas olika.
Vid strategin Samma ental behöver endast en avrundning göras, men det kan vara svårare att beräkna. Vid strategin Avrunda båda termerna uppåt måste två avrundningar göras, men beräkningen kan vara enklare.
8 Elevboken s. 8–10
Låt eleverna arbeta i elevboken om ni hinner.
9 Sammanfattning: Vad har vi lärt oss? 10 min
Sammanfatta: Ibland är det bra att snabbt uppskatta vad summan eller differensen blir, t.ex. för att man bara behöver veta på ett ungefär eller för att kunna se om svaret på en beräkning är rimligt.
Det finns många olika strategier för att uppskatta additioner. Vilken strategi som kommer närmast det exakta resultatet beror på vilka tal som ingår i beräkningen. För additionen 124 + 54 kommer uppskattningen närmast om man gör om entalen till 10-kamrater, men så är det inte i t.ex. 129 + 59. Vilken strategi som är mest exakt beror alltså på termerna.
När det gäller strategier för uppskattning vid subtraktion så kommer alla strategierna lika nära den exakta differensen. Därför kan man välja den man tycker bäst om.
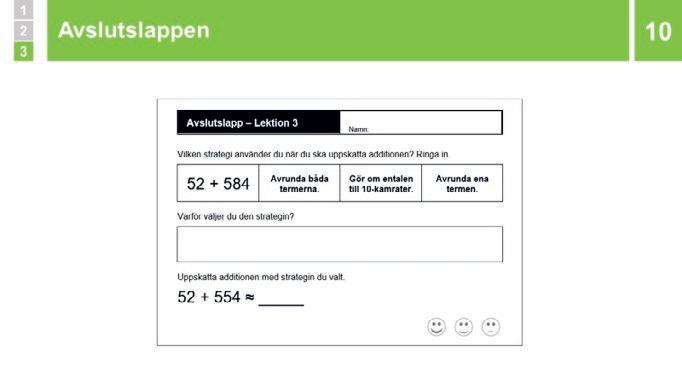
1.3.1 Uppmärksamma och stötta
Uppmärksamma elever som har svårt med uppskattningar. Dessa elever kan behöva repetera strategierna som presenteras i kapitel 7 i åk 2.
Lyft inte fram en enda strategi som den i alla lägen bästa, utan hjälp istället eleverna att förstå de olika strategiernas för- och nackdelar i olika situationer. Här spelar det bland annat roll varför man gör uppskattningen och hur nära den exakta summan/differensen man behöver komma. Ofta får man välja mellan snabbhet och exakthet, och då måste man ha den förståelsen så att man kan välja den strategi som passar i den aktuella situationen.
I vissa fall, t.ex. i subtraktionen 191 – 78, är det mer exakt att avrunda till närmaste 10-tal i subtraktion än att avrunda båda termerna upp eller ned. Dessa fall är ganska få, men om elever upptäcker dem kan du bekräfta att så är fallet.
Ta vara på tillfällen som dyker upp då det är lämpligt att uppskatta och låt eleverna göra det. Att kunna göra bra uppskattningar har eleverna nytta av i många sammanhang i livet.
Förenkla
Låt elever ha tillgång till tallinjen för att underlätta avrundning till närmaste tiotal. Om det behövs kan du sänka talområdet så att de enbart fokuserar på tal där termer och summa/differens är inom talområdet 0–100.
Utmana mer
Utmana eleverna att med olika strategier uppskatta summan/differensen där termerna är tresiffriga tal. Du kan t.ex. låta eleverna uppskatta 284 + 352 genom att först beräkna 300 + 400 och sedan beräkna 700 – 20 – 50 = 630. Alltså är 284 + 352 ≈ 630. Denna strategi kallas Kompensering. Den kan vara lite mer komplicerad för eleverna, men ger å andra sidan uppskattningar som kommer ganska nära det exakta resultatet.
Avslutslappen
Avslutslappen visar om eleven kan titta på de ingående talen i en addition och välja en strategi som passar, motivera varför hen gjort valet, samt göra uppskattningen med vald strategi. Den strategi som är mest exakt är att avrunda den första termen.
Elever kan mycket väl ha valt en annan strategi, och det okej om de kan motivera varför. T.ex. tycker de kanske att den strategi de valt är enklare.
Uppmärksamma elever som tar väldig lång tid på sig att göra avslutslappen. Det kan bero på att de inte förstår vad uppskattning är eller inte behärskar någon hållbar strategi för uppskattning. Det kan också vara så att de beräknar det exakta resultatet, kanske för att de inte behärskar någon strategi för uppskattning. I så fall behöver de träna mer på någon strategi.
Syftet med lektionen är att utveckla elevernas metodförmåga och problemlösningsförmåga där kontexten är tidsskillnader mellan klockslag. I åk 4–6 fortsätter vi att fördjupa detta.
Lektionsmål
• Eleven kan beräkna tidsskillnader med hela timmar.
• Eleven kan lösa enklare problem som har med tidsskillnad att göra och visar det genom att göra en lämplig analys av uppgiften och utifrån den göra nödvändiga beräkningar.
• Eleven kan beräkna tidsskillnader med växling mellan timmar och visar det genom att t.ex. svara på hur lång tid som har gått från 09:45 till 10:10.
Matematiska begrepp: Timvisare, minutvisare, tidsskillnad, digital tid, timme, minut
SvA: Skillnad, sedan, dykare, dyk, påbörjar, dammsuga, våttorka, klockslag
Material: Analoga och digitala elevklockor.
Förberedelser
• Skriv ut avslutslappar.
• Övningsblad finns. Skriv ut vid behov.
Avslutslapp Övningsblad grundläggande Övningsblad utmanande
Repetition: Tidsskillnader
Du repeterar med hjälp av den analoga och digitala klockan hur man kan beräkna tidsskillnader.
Genomgång och övning: Vad är klockan då?
Du visar klockslag och läser räknehändelser, och paren beräknar vad klockan kommer att vara om en viss tid. För varje uppgift sammanfattar du hur man kan göra.
Genomgång och övning: Tidsskillnad mellan klockslag
Du läser en räknehändelse och paren beräknar vad tidsskillnaden är mellan två klockslag.
Parövning: Räkna med tidsskillnader
Du visar klockslag till textuppgifter som paren löser med hjälp av en analog och en digital klocka. Du låter par redogöra för hur de har löst uppgiften.
Elevboken s. 4–7
Sammanfattning: Vad har vi lärt oss?
Du visar och sammanfattar: Ibland behöver man beräkna hur lång tid som har gått sedan ett visst klockslag, vad klockan är om en viss tid eller vad klockan var för en viss tid sedan. Det kan man göra genom att göra ett 5-hopp för varje 5 minuter. Man kan också göra det genom fram- eller tillbakaräkning med hel- eller halvtimme.
Avslutslapp
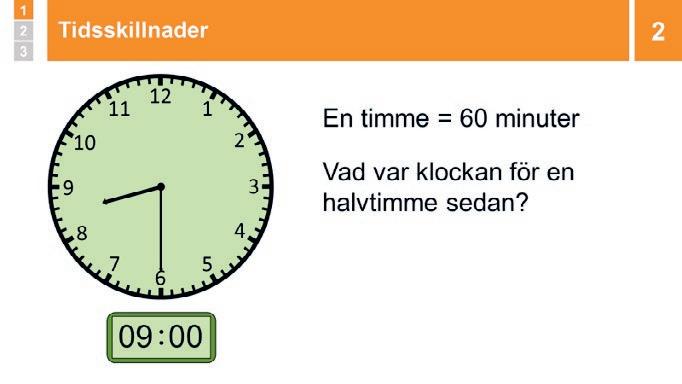


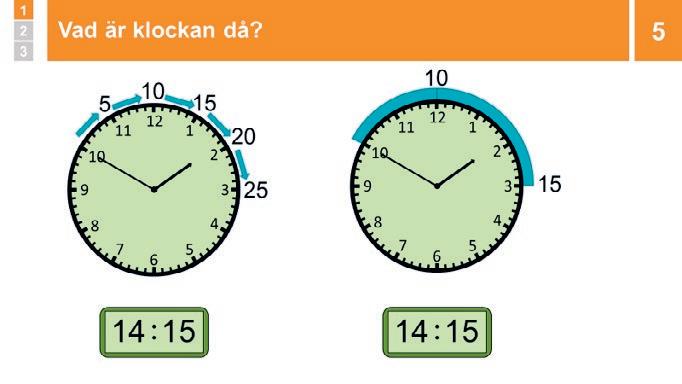
2 Repetition: Tidsskillnader 10 min
Konstatera att både den analoga och den digitala klockan visar halv 9 på förmiddagen. Repetera att 1 timme är 60 minuter. Säg att om en timme kommer minutvisaren att ha gått ett helt varv och peka på samma plats som den gör nu medan timvisaren kommer att peka mitt emellan 9 och 10 på urtavlan. Den digitala klockan kommer att visa 09:30, eftersom det gått en timme sedan den visade 08:30.
Klicka så att klockan blir halv tio/09:30. Fråga: ”Vad var klockan för en halvtimme sedan?” BETÄNKETID. Fördela ordet. När någon svarar ”prick 9” frågar du hur hen kom fram till det. FÖRSTÄRK om eleven kan förklara att man med ordet ”sedan” menar tidigare. Om eleven istället svarar 10 hjälper du hen förstå skillnaden mellan att säga ”om” eller ”sedan”, och påminner om att MATEMATIKER GÖR MISSTAG OCH LÄR SIG AV FEL.
3 – 5 Genomgång och övning: Vad är klockan då?
Dela in eleverna i par. Förse dem med elevklockor om de behöver. Visa 10 över 10 och läs räknehändelsen: ”Ellen spelar spel. Hon börjar spela klockan 10 över 10. Hon spelar i 35 minuter. Vad är klockan när hon slutar?”
Låt paren lösa uppgiften. CIRKULERA och VÄLJ UT ett par som gör ett 30-hopp från 10:10 till 10:40 och sedan ett 5-hopp 10:45, samt ett par som gör sju stycken 5-hopp från 10:10 till 10:45.
Låt de par du valt ut svara på frågan och förklara hur de kom fram till svaret. Visa och förklara själv om inget par resonerat på något av sätten.
Visa 10 i 2 och läs nästa räknehändelse: ”Lite senare på dagen spelar Ellen spel igen. Hon börjar spela klockan 10 i 2 på eftermiddagen och slutar spela 25 minuter senare. Vad är klockan då?”
Innan du låter paren börja ställer du upp 50 + 25 och berättar att ett vanligt misstag är att räkna så här och sedan säga ”klockan 13:75”. Det kan så klart inte stämma, eftersom en 1 timme bara har 60 minuter. Sedan börjar ju nästa timme.
Låt paren lösa uppgiften. CIRKULERA och VÄLJ UT ett par som beräknar tidsskillnaden med 5-hopp och/eller ett par som gör ett 10-hopp till 14:00 och sedan ett 15-hopp till 14:15. Låt paren redogöra.
Visa och förklara hur man kan beräkna tidsskillnaden både med 5-hopp och genom att göra ett 10-hopp följt av ett 15-hopp.
FÖRSTÄRK att dessa metoder är hållbara när man ska beräkna en tidsskillnad som passerar hel timme.
6 Genomgång och övning: Tidsskillnad mellan klockslag
Läs räknehändelsen: ”En dykare påbörjar sitt dyk klockan kvart i 8 på morgonen. När dykaren kommer upp till ytan igen är klockan 5 över 8. Hur lång tid har hen varit under vattenytan?”



Visa båda klockslagen och låt paren beräkna hur länge dyket pågått. Om det finns tid låter du ett par som beräknat tidsskillnaden korrekt förklara hur de har gjort. Annars visar och förklarar du själv: Man kan t.ex. räkna 5-minutershopp från kvart i 8 till 5 över 8. Eftersom 5 + 5 + 5 + 5 = 20 har dykaren dykt i 20 minuter. Man kan också tänka att det är 15 minuter till 8 och sedan 5 minuter till, alltså 15 + 5 = 20 minuter.
7 – 12 Parövning: Räkna med tidsskillnader 30 min
Gör så här:
• Visa ett klockslag till en textuppgift . Låt paren läsa, tolka och lösa uppgiften på egen hand. Stötta vid behov.
• CIRKULERA och VÄLJ UT ett par som löser uppgiften korrekt med 5-hopp eller andra lämpliga metoder, t.ex. fram- eller tillbakaräkning med hel- eller halvtimme.
• Påminn om JAG MED och låt det utvalda paret redogöra för hur de gjort. Om det passar ber du ett par som löst uppgiften på ett annat sätt redogöra. Diskutera då kort hur metoderna är lika och olika.
Den sista av de sex räknehändelserna är mer utmanande. Du kan hoppa över den om du vill genom att trycka på triangeln i övre högra hörnet.
13 Elevboken s. 4–7
14 Sammanfattning: Vad har vi lärt oss? 10 min
Sammanfatta att man ibland behöver beräkna hur lång tid som har gått sedan ett visst klockslag, vad klockan är om en viss tid eller vad klockan var för en viss tid sedan. Det kan man göra genom att göra ett 5-hopp för varje 5 minuter. Man kan också göra det genom fram- eller tillbakaräkning över hel- eller halvtimme.
Visa klockslagen 15:35 och 16:15. Peka och säg: ”Om klockan är kvart över 4 nu, hur lång tid har det då gått sedan klockan var 5 över halv 4?”
Visa och förklarar hur man kan beräkna tidsskillnaden med 5-hopp, och konstatera att det gått 40 minuter sedan klockan var 5 över halv 4. Visa och förklara sedan hur tidsskillnaden kan beräknas genom att först tänka hur många minuter det är från 15:35 till 16:00 och sedan addera 15 minuter till, alltså 25 + 15 = 40 minuter.
15 Avslutslapp
4.1.1 Uppmärksamma och stötta
För att kunna beräkna tidsskillnader med en analog klocka måste eleverna förstå klockans uppbyggnad, hur den visar tid och hur man läser av tiden på den. Om klockslagen är inom samma timme är det sällan några problem, eftersom det räcker med att titta på minutvisaren. Om klockslagen däremot är på olika timmar, t.ex. 15:35 och 16:15, är det mer utmanande att beräkna tidsskillnaden. Det är då vanligt att eleverna avläser och jämför visarna var för sig istället för att föreställa sig hur visarna måste ha rört sig från det ena klockslaget till det andra.
En hållbar strategi för att beräkna tidsskillnader utifrån den analoga klockan är att göra lika många 5-hopp som det antal 5-minutare som gått. Om frågan är hur lång tid som gått från klockan 4 till klockan 5 i halv 5 så kan eleven göra 5-hopp från klockan 4 tills klockan visar 5 i halv 5. Det är fem stycken hopp, och eftersom 5 multiplicerat med 5 är lika med 25 måste det ha gått 25 minuter.
En annan hållbar strategi är fram- eller tillbakaräkning med hel- eller halvtimme eller kombinationer av det. Man kan t.ex. först göra ett 30-hopp, motsvarande en halvtimme, och sedan ett 5-hopp, motsvarande 5 minuter, för att beräkna vad tiden är om 35 minuter eller vad den var för 35 minuter sedan. Uppmärksamma elever som räknar fram eller tillbaka med enskilda minuter, alltså gör ett hopp per minut. Det är vanligt att det leder till onödiga fel eftersom det är lätt att tappa bort sig.
En annan hållbar strategi är att beräkna fram till hel timme och sedan resten. Om eleverna t.ex. ska beräkna tidsskillnaden mellan kvart i 12 och 10 över 12 kan de först beräkna tidsskillnaden till prick 12 och sedan till 10 över.
Uppmärksamma elever som endast adderar antalet minuter som gått till vad minutvisaren visar. Detta fungerar när de två klockslagen är på samma timme, men leder ofta till svårigheter när man ska beräkna tidsskillnaden mellan t.ex. 15:45 och 16:30, eftersom klockan har 60 som bas till skillnad från vårt positionssystem som har 10 som bas. Elever kan även försöka sig på uppställningar med både timmar och minuter, vilket kommer att leda till svårigheter av samma anledning: 60 minuter ska växlas mot 1 timme medan eleverna är vana vid att växla tio ental på ett tiotal, etc. Elever bör därför inte använda skriftliga räknemetoder i det här sammanhanget.
En metod som kommer introduceras i mellanstadiet är att använda sig av en tom tallinje. Om eleven exempelvis ska beräkna hur lång tid det är mellan 14:40 och 15:25 kan eleven rita en tom tallinje och skriva talet 15 i mitten. Eleven kan då beräkna hur lång tid det är mellan 14:40 och 15:00 och sedan från 15:00 till 15:25 och slutligen beräkna 20 + 25 = 45 minuter. Vi introducerar inte den metoden i åk 3, men om du tycker att det är lämpligt kan du göra det redan nu.
Förenkla
Du kan förenkla genom att låta eleverna enbart använda en analog klocka för att beräkna tidsskillnader. Visa hur de ska använda metoden att räkna intervall på 5-minuter. Låt dem gärna använda en elevklocka med synkrona visare, så att de kan se visarnas rörelse under tidsskillnaden.
Det kan också underlätta för vissa elever att använda två analoga klockor. De kan då ställa klockorna på respektive klockslag och jämföra dem för att beräkna tidsskillnaden. Först läser de av den ena klockan och sedan den andra innan de slutligen beräknar tidsskillnaden. När de genomfört beräkningen kan de skruva fram (eller tillbaka) tiden på den första klockan och samtidigt räkna 5-minutersintervall för att kontrollera att beräkningen stämmer.
Utmana mer
Utmana elever att arbeta med större tidsskillnader, gärna tidsskillnader som överskrider 1 timme. Du kan också arbeta med textuppgifter som innebär flera tidsskillnader. Till exempel: Marwa tar tåget från Södertälje klockan 09:50. Hon är framme i Eskilstuna 10:20. En kvart senare går ett annat tåg från Eskilstuna till Västerås. Den resan tar 40 minuter. Vad är klockan när tåget är framme?
Avslutslappen
Avslutslappen visar om eleverna kan beräkna tidsskillnader utifrån en kontextuppgift samt beräkna tidsskillnaden mellan två klockslag. Elever som inte klarar detta behöver träna mer, gärna i vardagskontext. Du kan t.ex. säga vad klockan är när en lektion startar och hur länge den kommer att pågå, och sedan låta eleverna beräkna vilken tid det är rast. Uppmuntra eleverna att räkna 5-minutersintervall för att komma fram till svaret.
Syftet med lektionen är att befästa och utveckla elevernas förståelse för storheterna längd och volym. Syftet är också att utveckla deras färdighet i att välja, hantera och omvandla mellan olika enheter vid mätning.
Lektionsmål
• Eleven känner till några samband mellan enheter för längd och volym (litersystemet) och visar det genom att hantera uppgifter med olika enheter eller omvandla enhet.
Matematiska begrepp: Längd, volym, liter, deciliter, centiliter, meter, decimeter, centimeter
SvA: Vattendunk, dunk
Repetition: Tidsskillnad
Du repeterar hur man kan beräkna tidsskillnader.
Övning: Längd eller volym
Du låter eleverna sortera in ord under rubrikerna Längd respektive Volym
Genomgång: Längdenheterna m, cm och dm
Du repeterar att 10 dm är 1 m, att 100 cm är 1 m och att 10 cm är 1 dm.
Övning: Byta mellan längdenheter
Du ställer frågor som ”Hur många centimeter är 2 meter?”, och eleverna övar på att byta mellan enheter.
Genomgång och övning:
Volymenheter
Du går igenom volymenheterna liter, deciliter och centiliter, och eleverna övar på att byta mellan dem.
Material: Miniwhiteboards med penna och sudd.
Förberedelser
• Skriv ut avslutslappar.
• Övningsblad finns. Skriv ut vid behov.
Avslutslapp
Övningsblad grundläggande
Övningsblad utmanande
Parövning: Textuppgifter
Du läser textuppgifter som kräver omvandling mellan längdenheter. Paren diskuterar hur de kan lösa uppgifterna och svarar genom att hålla upp sina miniwhiteboards. Du låter par som svarat korrekt förklara hur de tänkte, och lyfter vid behov andra sätt att tänka.
Elevboken s. 8–11
Sammanfattning: Vad har vi lärt oss?
Du sammanfattar: 1 m är 100 cm eller 10 dm. Ordet centi betyder just hundradel och ordet deci betyder tiondel. Vi mäter volym i volymenheterna liter, deciliter och centiliter. 1 l är 10 dl och samtidigt 100 cl. Ibland behöver man byta mellan enheter för att kunna säga på ett enklare sätt hur långt något är. Om en flaggstång är 6 m hög kan det upplevas krångligare om man istället säger att den är 60 dm eller 600 cm hög, även om det är helt korrekt.
Avslutslapp

2 Repetition: Tidsskillnad 15 min
Peka och säg: ”När Saga gick och lade sig var klockan prick 9. När hon vaknade var klockan prick 7. Hur länge sov Saga?”
Låt eleverna SURRA en stund. Fördela sedan ordet. När någon svarar ”10 timmar” frågar du hur hen kom fram till det. FÖRSTÄRK om hen använt en hållbar strategi för att komma fram till svaret. Visa på två olika sätt hur man kan beräkna hur många timmar det är mellan 21:00 och 07:00 genom att göra hopp med timmar på urtavlan.
3 Övning: Längd eller volym
Dela in eleverna i par och förse dem med miniwhiteboards. Be dem skriva rubrikerna Längd och Volym på sina tavlor. Peka på orden i bildspelet och säg att paren ska diskutera vilka ord som passar under vilken rubrik. Berätta att några ord inte passar under någon av rubrikerna, och att de orden ska de inte skriva någonstans.
Låt dem sätta igång när alla förstått. CIRKULERA
Bryt när alla börjar bli klara. Peka och säg: ”Meter, under vilken rubrik ska det stå?” Låt paren ropa ut sina svar. Om du klickar på ordet placeras det under rätt rubrik. Fortsätt på samma sätt tills alla ord är placerade. Gram och sekund skulle passa under Massa och Tid, men dessa rubriker finns inte.



4 Repetition: Längdenheterna m, cm och dm
Repetera att när man mäter längd kan man mäta i längdenheterna meter och centimeter. 1 m kan delas i 100 cm. Ordet centi betyder hundradel, så ordet centimeter betyder just hundradels meter. Berätta att man även kan mäta i decimeter, vilket är detsamma som 10 centimeter och en tiondels meter. Ordet deci betyder just tiondel. Det är ovanligt att man mäter i dm.
5 Övning: Byta mellan längdenheter
Fråga paren: ”Hur många centimeter är 2 meter?” Låt paren diskutera och skriva sitt svar på tavlan. Säg till när alla ska visa sina tavlor. Ge ordet till ett par som skrivit 200 cm, och låt dem förklara hur de tänkt. Förstärk om de kan förklara att om 100 cm är 1 meter så måste 2 meter vara 200 cm. Gör på samma sätt med de två följande frågorna.
6 – 7 Genomgång och övning: Volymenheter
Berätta att volymen hos t.ex. en hink kan mätas i liter och deciliter. Påminn om att ordet deci betyder tiondel, alltså är 1 dl en tiondels liter. 10 dl är alltså 1 l.
Om man ska mäta volymen på något mindre, t.ex. ett litet dricksglas, kan man mäta i centiliter istället. Eftersom ordet centi betyder hundradel så är 1 cl en hundradels liter.
Lektion 2 | Samband mellan enheter




Visa och förklara att 1 l är lika mycket som 10 dl, att 1 dl är en tiondels liter, att 1 dl är lika mycket som 10 cl, samt att 1 cl är en hundradels liter eftersom 100 cl är 1 l Förklara även hur enheterna förkortas.
Fråga paren: ”Hur många centiliter är 3 deciliter?” Låt eleverna SURRA och skriva svaret på sin miniwhiteboard. När de är klara visar alla samtidigt. Ge ordet till något par som skrivit 30 cl och låt dem förklara hur de har tänkt. FÖRSTÄRK om de kan säga att om 10 cl är 1 dl så måste 30 cl motsvara 3 dl. Gör på samma sätt med de två följande frågorna.
8 – 12 Parövning: Textuppgifter 25 min
Säg att ni ska öva på att omvandla mellan enheter. Gör så här:
• Visa textuppgift 1 och läs den högt.
• Låt paren diskutera hur de kan lösa uppgiften. Sedan försöker de lösa den och skriver svaret på sin miniwhiteboard.
• När alla börjar bli klara ber du dem hålla upp sina svar. Påminn om JAG MED och låt ett par som svarat korrekt förklara hur de tänkt. Aktivera andra, särskilt par som svarat fel genom att de låta dem ÅTERGE Be även elever som inte gör JAG MED förklara hur de tänker annorlunda.
Gör på samma sätt med nästa textuppgift.
I vissa uppgifter är det möjligt att svara i olika enheter. Lyft gärna detta om det är så att elever har gett olika svar.
I elevboken finns det på sida 7 en omvandlingstabell för längd och på sida 9 en för volym.
Det finns fem uppgifter. Den femte är mer utmanande, och vid behov kan du hoppa över den genom att trycka på triangeln i övre högra hörnet.
13 Elevboken s. 8–11
Avslut
14 Sammanfattning: Vad har vi lärt oss? 10 min
Sammanfatta att i Sverige och många andra länder mäter man längd i längdenheterna meter, decimeter och centimeter. 1 m är 100 cm, men också 10 dm. Ordet centi betyder hundradel och ordet deci betyder tiondel.
Vi mäter volym i volymenheterna liter, deciliter och centiliter 1 l är 10 dl, men också 100 cl.
Berätta att man ibland behöver byta enhet för att på ett enklare sätt kunna säga hur långt något är. Om en flaggstång är 6 m hög kan det upplevas krångligare om man istället säger att den är 60 dm eller 600 cm hög, även om det är helt korrekt.
4.2.1 Uppmärksamma och stötta
För att kunna göra tillräckligt noggranna mätningar behöver eleverna bli väl förtrogna med enheterna de mäter i och deras samband med varandra. De måste också ha en uppfattning om enheternas storlek för att kunna välja en lämplig enhet att mäta i, givet den aktuella kontexten.
Enheternas prefix kan hjälpa eleverna att förstå sambandet mellan några av de vanliga längd- och volymenheterna. Om eleverna vet att centi betyder en hundradel kan de förstå att 1 centiliter är en hundradels liter och att 1 centimeter är en hundradels meter. Detta underlättar förståelsen för att 100 cm är 1 m och att 200 cm är 2 m.
Om du märker att elever har svårt att förstå sambandet mellan enheterna bör du avbryta lektionen och arbeta med volym och/eller längd praktiskt. Du kan t.ex. låta elever laborera med konkret material för att förstå hur enheterna hör ihop. De kan t.ex. undersöka hur många fyllda decilitermått som motsvarar en liter, hur många centikuber på rad som motsvarar längden på en meterlinjal eller hur många centikuber som motsvarar den längsta av cuisenairestavarna (den orangefärgade, som är 1 dm lång).
Förenkla
Du kan förenkla genom att låta eleverna hålla sig till endast två enheter för volym och två för längd. Låt dem
översätta hela meter eller liter till centimeter och deciliter. När de är förtrogna med detta kan de göra andra, mer utmanande enhetsbyten.
Utmana mer
Utmana elever genom att introducera enheterna milliliter och millimeter. Förklara att prefixet milli betyder tusendel, vilket innebär att 1000 millimeter är 1 meter. Låt sedan elever som behöver utmanas lösa uppgifter genom att svara i så många olika enheter som möjligt.
De kan då t.ex. svara:
18 dl
180 cl
1800 ml
1 l och 8 dl
Avslutslappen
Avslutslappen visar om eleven vet att 1 l är 10 dl och att en 1 m är 100 cm, samt om hen kan generalisera den kunskapen till att 3 m är 300 cm.
Avslutslappen testar även om eleven kan göra enhetsväxlingar i en kontextuppgift. För att kunna lösa uppgiften måste eleven förstå att 2 l är 20 dl, och att om det redan finns 4 dl saft i flaskan så måste 16 dl vatten hällas i för att flaskan ska bli full.
Syfte med lektionen är att utveckla elevernas förståelse för kongruenta objekt och förmåga att föra geometriska resonemang om dessa. Detta är en förutsättning för att eleverna ska kunna förstå area. I nästa lektion introducerar vi area genom att jämföra storleken på olika geometriska objekt från ett tangrampussel.
Lektionsmål
• Eleven kan föra enkla geometriska resonemang och visar det genom att förklara varför två objekt har eller inte har samma form och storlek.
• Eleven har en grundläggande förståelse för kongruens och visar det genom att känna igen eller skapa figurer med samma storlek och form.
Matematiska begrepp: Storlek, form, vrids, läge, fyrhörning, figur, spegelsymmetrisk, lika, olika.
SvA: Rutnät
Repetition: Samband mellan enheter
Du repeterar sambanden mellan m, dm och cm samt l, dl och cl.
Genomgång: Samma storlek och form
Du visar att figurer som har samma storlek och form har det även om de flyttas och vrids.
Övning: Vilka har samma storlek och form?
Du visar ett antal figurer. Eleverna försöker para ihop de figurer som har samma storlek och form. Du konstatera att två figurer som har samma storlek och form fortsätter att ha det även om figurerna vrids, flyttas eller spegelvänds.
Material: Kopieringsunderlaget Figurer, saxar
Förberedelser
• Skriv ut kopieringsunderlaget Figurer i storlek A3 så att varje par kan få varsitt exemplar.
• Skriv ut avslutslappar.
Figurer Avslutslapp Elevbok s. 13
Pararbete: Vilka har samma storlek och form?
Paren arbetar med underlaget Figurer och parar ihop figurer med samma storlek och form. Sedan låter du olika par redogöra och argumentera för vilka figurer som har samma storlek och form.
Övning: Avbilda så att det är lika
Du visar en figur i ett rutnät. Eleverna får säga vilka rutor i ett tomt rutnät bredvid som ska färgläggas för att en identisk figur ska skapas.
Övning: Är det samma figur om man vrider den?
En av två identiska figurer vrids varv. Du påstår att de inte längre har samma storlek och form, och eleverna får förklara för dig varför det inte stämmer.
Elevboken s. 12–15
Sammanfattning: Vad har vi lärt oss?
Du visar och sammanfattar att figurers storlek och form inte ändras bara för att de flyttas, vrids eller spegelvänds.
Du visar figurer. Eleverna funderar över vilka av figurerna som har samma form och storlek.
Avslutslapp

2 Repetition: Samband mellan enheter 10 min
Repetera att man kan mäta längd i enheterna meter, decimeter och centimeter. Ordet deci betyder tiondel, och 1 dm är en tiondels meter. Alltså är 10 dm lika med 1 m. Ordet centi betyder hundradel, och 1 cm är en hundradels meter. Alltså är 100 cm lika med 1 m.
Volym kan mätas i enheterna liter, deciliter och centiliter. 10 dl är 1 l och 100 cl är också 1 l.
3 Genomgång: Samma storlek och form
Fråga: ”Har de här två fyrhörningarna samma storlek och form?” Låt eleverna SURRA en kort stund. Visa att figurerna har det genom att lägga den ena fyrhörningen på den andra.
Visa sedan hur den ena fyrhörningen vrids och flyttas. Fråga återigen om de har samma storlek och form, och låt eleverna SURRA . Fördela ordet, och när någon svarar ”Ja” ber du hen utveckla varför hen anser det. Om eleven säger något i stil med att figurers storlek och form inte ändras bara för att man flyttar eller vrider på dem så ber du hen SÄGA DET IGEN . FÖRSTÄRK och poängtera att detta är viktigt.
Visa att figurerna fortfarande har samma storlek och form.
4 Övning: Vilka har samma storlek och form?
Konstatera att ni ser ett antal figurer som antingen har en bokstav eller en siffra. Be eleverna para ihop de figurer som har samma storlek och form genom att titta och jämföra. Ge BETÄNKETID. När eleverna fått tänka en stund låter du dem SURRA om vilka figurer som har samma storlek och form.
Påminn om JAG MED, och låt elever i tur och ordning säga ett par figurer och argumentera för att de har samma storlek och form. Låt elever som inte håller med förklara hur de tänker.
När ni kommit fram till att ett givet par figurer har samma storlek och form klickar du på den av figurerna som betecknas med en bokstav. Då visas vilken figur som har samma storlek och form, och figurerna läggs ovanpå varandra. Om ingen figur har samma storlek och form kryssas den.
Om ingen elev har argumenterat för att figurerna C och 1 har samma storlek och form så visar du att de har det och förklarar att de är spegelvända.
När ni gått igenom alla figurer konstaterar du att två figurer som har samma storlek och form fortsätter att ha det även om figurerna vrids, flyttas eller spegelvänds. Genom att lägga figurerna ovanpå varandra kan man se om de har samma form och storlek.

5 Pararbete: Vilka har samma storlek och form? 30 min
Dela in eleverna i par. Förse dem med underlaget Figurer. Säg att de ska para ihop figurer som har samma storlek och form. Påminn om att vissa figurer kan vara spegelvända, men ändå ha samma storlek och form.
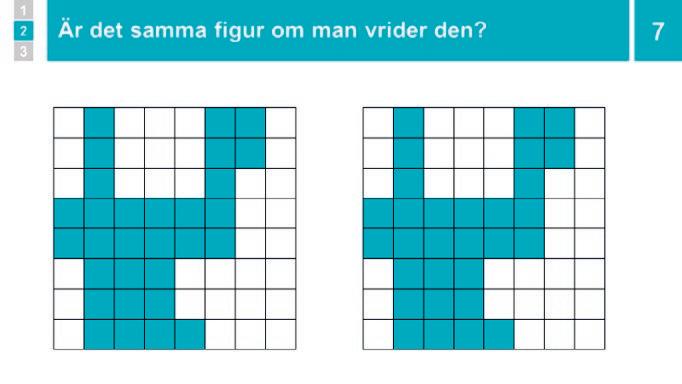

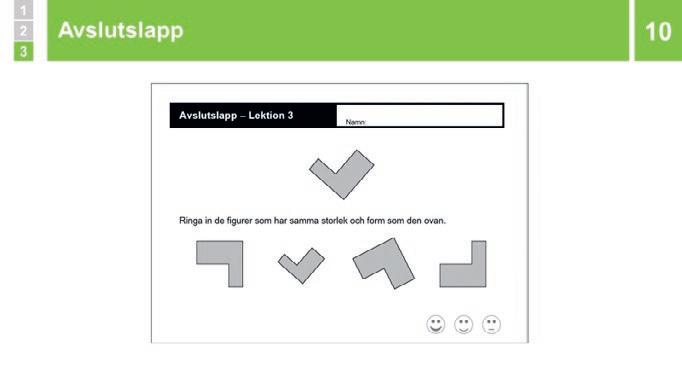
Lektion 3 | Figurer med samma storlek och form
Låt dem börja när alla förstått. CIRKULERA . Notera om elever vrider på pappret när de föreställer sig vridningar eller om de verkar kunna göra det mentalt.
Om någon frågar om man får klippa ut figurerna så FÖRSTÄRKER du och uppmuntrar idén. Tipsa vid behov par som har svårt med uppgiften att göra så.
Ingen figur har samma storlek och form som D, F, K, N, P och R.
Bryt när alla börjar bli klara. Påminn om JAG MED, och låt olika par redogöra och argumentera för vilka figurer de hittat som har samma storlek och form. Visa att man kan klippa ut figurer och lägga dem på varandra, och säg att man istället kan försöka tänka sig detta i sitt eget huvud för att se om figurerna har samma storlek och form.
6 Övning: Avbilda så att det är lika
Peka på figuren till vänster. Peka på rutnätet till höger och fråga: ”Vilka rutor ska vi färglägga för att det ska bli en exakt likadan figur här?”
Fördela ordet och låt elever komma fram till tavlan och peka. Visa och förklara hur man t.ex. kan säga ”den andra rutan från vänster i översta raden”. Klicka på rutan för att färglägga den (klickar du igen så försvinner färgen). Fortsätt på samma sätt tills figuren är klar.
När eleverna förstått kan du snabba på genom att fylla i själv, eller gå till nästa steg där den färdiga figuren visas.
7 Övning: Är det samma figur om man vrider den?
Visa hur den högra figuren vrids ett kvarts varv. Påminn om JAG MED och påstå felaktigt: ”Nu är figurerna inte lika längre.” Ge ordet till elever som inte gör JAG MED. Ställ frågor för att hjälpa dem förklara att figurer inte ändras bara för att man vrider på dem. Låt elever ÅTERGE viktiga poänger som görs.
8 Elevboken s. 12–15
9 Sammanfattning: Vad har vi lärt oss? 10 min
Visa hur en figur dubbleras och flyttas. Konstatera genom att lägga den ena figuren ovanpå den andra att figuren är oförändrad. Sammanfatta att figurers storlek och form inte ändras bara för att de flyttas, vrids eller spegelvänds.
Visa fler figurer. Be eleverna fundera över vilken av figurerna som har samma form. Konstatera att en figur kan vara spegelvänd, men ändå ha samma storlek och form. Visa att trianglarna och sexhörningen har samma form även om den första är vriden och den andra är spegelvänd. Fyrhörningarna har däremot inte samma form.
10 Avslutslapp
4.3.1 Uppmärksamma och stötta
Var uppmärksam på om elever tror att figurer förändras när de flyttas eller vrids. Stötta dem att komma tillrätta med den här missuppfattningen genom att låta dem titta på en figur som ligger på ett bord. Låt dem flytta sig så att de tittar på figuren från ett annat håll. Fråga om det fortfarande är samma figur. När de förstått det kan du flytta och/eller vrida samt spegelvända figuren och fråga om det är samma figur. När de förstår att figuren inte ändras bara för att den flyttas, vrids eller spegelvänds kan de fortsätta med aktiviteten eller elevboken.
Det kan särskilt vara svårt för elever att förstå att två spegelvända figur har samma form och storlek. Om du låter dem klippa ut figurerna kan de undersöka saken genom att spegelvända en och samma figur och konstatera att det dels är samma figur, dels att den har samma form oavsett vilken sida den har uppåt.
I bildspelet finns en enkel animation som visar detta, men att se det med fysiska objekt är mer kraftfullt. Du kan t.ex. ta två tangrambitar med formen av en parallellogram och visa det här för eleverna.
Förenkla
Du kan förenkla för elever genom att låta dem klippa ut figurerna i aktiviteten i steg 5.
Om det behövs kan du skriva ut sidan från elevboken så att eleven kan klippa ut även dessa figurer när hen gör de uppgifterna.
Utmana mer
Utmana elever att konstruera egna figurer på rutat papper. Låt dem sedan sitta i par och beskriva för partnern som ska rita en identisk figur på ett tomt rutat papper.
Avslutslappen
Figuren längst till vänster och längst till höger har samma storlek och form som den översta figuren.
Avslutslappen visar om eleven kan identifiera figurer som har samma storlek och form. Figuren längst till höger har samma storlek och form som den övre, men är spegelvänd. Om elever missar den så kan det bero på att de ännu inte förstått att spegelvända figurer har samma form.
Om eleven har särskilt svårt med uppgiften kan du låta hen klippa ut den övre figuren och fysiskt lägga den på de andra figurerna för att jämföra storlek och form.
Studentlitteratur AB
Box 141
221 00 LUND
Besöksadress: Åkergränden 1
Telefon 046-31 20 00 studentlitteratur.se
Kopieringsförbud
Detta verk är skyddat av upphovsrättslagen. Kopiering, utöver lärares begränsade rätt att kopiera för undervisningsbruk enligt Bonus Copyright Access skolkopieringsavtal, är förbjuden. Kopieringsunderlag får dock kopieras under förutsättning att kopiorna delas ut endast i den egna undervisningsgruppen. För information om avtalet hänvisas till utbildningsanordnarens huvudman eller Bonus Copyright Access.
Vid utgivning av detta verk som e-bok, är e-boken kopieringsskyddad.
Användning av detta verk för text- och datautvinningsändamål medges ej.
Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig att erlägga ersättning till upphovsman eller rättsinnehavare.
Studentlitteraturs trycksaker är miljöanpassade, både när det gäller papper och tryckprocess.
Art.nr 46123
ISBN 978-91-44-18230-8
Upplaga 3:1
© Andreas Ryve, Rik matematik AB och Studentlitteratur 2024
© Andreas Ryve, Rik matematik AB och Bonnierförlagen Lära 2022
Formgivning: Marit Messing – Go Form AB, Frangkle
Illustrationer: Jessica Svendeborn (uggla och barn), Sinnebild (alla saker och ting, förutom kanna, skål med bär: Manuel Tenser)
Foto: registreringsskylt: magr80/Shutterstock, fotbollsstadium: Paolo Bona/ Shutterstock, jordgubbar: Manuel tenser, bullar: Manuel Tenser, rep: Manuel Tenser, ägg: BlueRingMedia/Shutterstock, glas: mollicart/Shutterstock, Julius Ceasar: Jacopo Giangiulio/Shutterstock, ENIAC (dator): Everett Collection/ Shutterstock, dykare: Manuel Tenser
Printed by Eurographic Group, Denmark 2024
Rik matematik ger lärare stöd att planera, genomföra och utvärdera rik matematikundervisning. Rik matematikundervisning kännetecknas av aktiva elever och en aktiv lärare där begrepp, resonemang och problemlösning står i fokus. Varje årskurs innehåller mer än 100 strukturerade lektioner med bildspel. Lektionerna har tydliga inledningar och avslutningar där central matematik betonas. Med Rik matematik får läraren stöd att varje lektion bedriva en undervisning som engagerar och utvecklar elevernas matematiska tänkande.
Rik matematik är utvecklat i ett nära samarbete mellan lärare och forskare och noggrant utprovat i klass.
I Rik matematik 3A Lärarpaket ingår utöver det tryckta lärarmaterialet, även en digital lärarresurs samt tillgång till förberedda uppdrag i Tomoyo, en digital spelifierad färdighetsträning. De digitala delarna nås via Min bokhylla på Studentlitteratur.se

Rik matematik 3A omfattar 5 områden:
Kapitel 1 – Mer om addition och subtraktion
Kapitel 2 – Sannolikhet och statistik
Kapitel 3 – Mer om multiplikation och division
Kapitel 4 – Mätning, area och skala
Kapitel 5 – Algebra