L ÄRARHANDLEDNING med lärarwebb
Sofie Bellman
Janna Malmgren
Kurt Rosenlund
Karin Nygårds
Introduktion
INNEHÅLL
OLA HELENIUS Få eleverna att resonera matematiskt 12 KENNY SKAGERLUND
Välkommen till Flex!
VI SOM ÄR FÖRFATTARE till Flex matematik lärde känna varandra på Södermalmsskolan i Stockholm.
Idén till Flex matematik föddes av Kurt Rosenlund, som tidigare skrivit läromedel i matematik. Kurt ville skapa ett klimat där alla elever var delaktiga och när datorerna gjorde intåg i klassrummen började han experimentera. Med hjälp av genomgångar som stöddes av bildspel blev fler elever engagerade. Men det var först när de fick var sin liten skrivtavla för att snabbt kunna anteckna lösningar och funderingar, som alla blev riktigt delaktiga.
Mycket av vår undervisning går ut på att vi gör saker gemensamt. Det är inte läraren som avgör om en lösning är rätt, utan det resonerar vi om tillsammans och i stället för att avfärda något som ”fel” säger eleverna ”jag har tänkt annorlunda” eller ”jag håller inte med”. Det skapar ett öppet klassrumsklimat.
Vi svarar sällan på frågan ”Är det rätt?” , i stället bollar vi tillbaka med ”Hur kan vi ta
reda på det?” Och vid korrekta lösningar utmanar vi med frågor som ”Hur kan du säkert veta att det stämmer?” Allt för att främja meningsfulla samtal om matematik.
En annan viktig aspekt av läromedlet är att det är anpassat efter den enskilde elevens behov. Ingen behöver göra 15 uppgifter om sådant de redan kan och heller inte möta något som är alldeles för svårt.
Det vi uppskattar mest med Flex matematik är att det tydligt skapar engagemang hos eleverna. Alla deltar i genomgångarna, funderar, skriver på sina skrivtavlor, samtalar och argumenterar. Eventuella missuppfattningar blir då lätta att upptäcka och skapar bra utgångspunkter för matematiska resonemang, i en miljö där man vågar ha fel.
Det känns också tryggt att undervisningen vilar på en stabil grund och att den blir likvärdig i alla klasser på skolan. Mycket goda resultat på de nationella proven talar också sitt tydliga språk.
Vi hoppas att du ska uppskatta Flex matematik lika mycket som vi gör!
KURT ROSENLUND
SOFIE BELLMAN
JANNA MALMGREN
Undervisa med Flex matematik
Med Flex matematik undervisar du i 3 steg:
1. BILDSPEL
Varje lektion inleds med ett bildspel. Du leder genomgången med hjälp av frågorna som finns i handledningen. Eleverna funderar först enskilt och skriver ned sina svar. Sedan kan de parvis eller i grupp komma överens om ett svar och på så sätt få träning i att argumentera. Låt eleverna visa svaren. Du får snabbt en överblick över klassens kunskaper och kan använda elevernas skrivtavlor för att visa exempel på olika lösningsstrategier. Genom att undvika handuppräckning och själv fördela ordet får du eleverna aktiva under lektionen. Ställ frågor som:
– Vilka olika svar hade ni från början?
– Vilka argument använde ni när ni enades om det ena svaret och inte det andra?
– Håller ni andra med om deras argument?
Lektionen avslutas alltid med en minicheck (exit ticket) som visar hur eleverna har förstått lektionens innehåll.
2. LEKTIONSBOK
Efter bildspelet är det dags för eleverna att lösa liknande uppgifter på egen hand i lektionsboken. Den första uppgiften är kopplad till bildspelet medan efterföljande uppgifter är kopplade till arbetsområdet i stort.
Lektionsboken redovisas gemensamt genom att du tar fram uppgifterna på helskärm (finns i bildspelen) och elever kommer fram till tavlan där de skriver och berättar om sina lösningar. Använd handuppräckning eller annat sätt att fördela turen på, så att många elever får möjlighet att redovisa sina svar. Blyga elever kan gå fram i par. Tänk på att i detta skede inte låta någon kommentera det som skrivs. När alla uppgifter är besvarade kan du fråga vilka elever som har tänkt annorlunda och vilka som håller med. Passa gärna på att ställa frågor som lyfter vanliga missuppfattningar.
När eleverna är färdiga med lektionsboken loggar de in på elevwebben. Här finns blandade övningar på flera olika nivåer. Med hjälp av ledtrådar blir ingen uppgift för svår och medaljerna triggar eleverna att räkna vidare. Uppgifterna är adaptiva, de anpassas efter elevernas svar och utmanar eleverna på den nivå de befinner sig.
3. FLEX WEBB
Grovplanering
Flex matematik årskurs 6 är fördelat på sju kapitel. Det finns möjlighet att förlänga eller förkorta undervisningen utifrån dina elevers behov. Förslag på läsårsfördelning:
Problemlösning
Kluringarna är problemlösningsuppgifter som finns i lektionsboken och på lärarwebben. I Flex finns det en kluring per vecka. Du kan inleda med att visa kluringen på helskärm och samtidigt låta eleverna ha motsvarande kluring i lektionsboken framför sig. Gå tillsammans igenom svåra ord och be eleverna att stryka under viktig information i kluringen. Ni kan med fördel arbeta enligt metoden EPA (Ensam, Par, Alla). Välj ut två till tre lösningar där olika metoder och strategier har använts och låt eleverna gå fram och redovisa på tavlan.
Efter varje redovisning får övriga elever ställa frågor om sådant de inte förstått eller ge tips om andra metoder. Låt inte eleverna kommentera lösningarna genom att bara säga ”det är fel” utan uppmuntra formuleringar som ”jag håller inte med” , ”jag har gjort annorlunda” , ”jag har en annan lösning”. Det skapar ett tryggare klassrumsklimat. Diskuera inte rätt svar förrän alla som redovisat på tavlan är klara. Om redovisningarna leder till olika svar, så samtala gemensamt om hur ni kan bevisa vilket svar som är korrekt. Avsluta genomgången med att lyfta vanliga missuppfattningar och effektiva strategier.
KAP 1 Tal 6 v.
KAP 2 Bråk och procent 5 v. KAP 3 Statistik 4 v.
KAP 4 Geometri 5 v.
KAP 5 Räknesätt och algebra 6 v. KAP 6 Enheter 5 v.
KAP 7 Programmering 2 v.
TRÄNA INFÖR NP 0 – 2 v.
Procent betyder hundradel B
Vecka 5 Lektion 3 34 Beräkna med miniräknare. a)
I en skål ligger röda och gula tomater. En fjärdedel av tomaterna är gula. Awa äter upp hälften av de röda tomaterna. Sedan är det sammanlagt tio tomater kvar skålen. Hur många tomater låg det skålen från början?
Svar: Bråk i enklaste form A
En full syltburk väger 0,75 kg. När 60 % av sylten är uppäten väger den 390 g. Hur mycket väger själva burken?
Svar:
Formativ bedömning
I Flex matematik finns flera olika stöd för att synliggöra elevers lärande genom formativ bedömning. Förutom att du på lärarwebben kan följa elevernas individuella arbete på elevwebben finns följande stöd för formativ bedömning:
CHECK IN
Check in är det första bildspelet i varje kapitel och motsvarande uppgifter ligger även först i varje kapitel i elevboken. Tanken är att eleverna ska få pröva och reflektera över olika uppgifter som de kommer att möta i kapitlet. Samtidigt som du klickar fram en uppgift i taget i bildspelet, så testar eleverna att svara i lektionsboken. De gör även individuella skattningar av uppgifterna på en skala från ”aldrig sett” till ”löser lätt” .
MINICHECK
Till varje lektion finns en avslutande uppgift i form av en Minicheck, som testar hur väl eleverna hängt med. Denna uppgift har ofta fyra svarsalternativ och är tänkt att kunna lösas förhållandevis snabbt, som en ”exit ticket” på att eleven förstått. Eleverna kan använda sina skrivtavlor eller något digitalt alternativ med mentometerfunktion för att svara. Uppgiften Minicheck ligger sist i varje bildspel.
CHECK OUT
När ett kapitel är klart gör eleverna en Check out (prov) med uppgifter som testar det som tränats i det aktuella kapitlet. Efter att uppgifterna är rättade får eleverna reflektera över sitt lärande genom att jämföra sin Check in med sin Check out. Du hittar Check out i pdf:format på lärarwebben. Det finns två versioner till varje kapitel.
CHECK OUT Bråk och procent del 1:A åk
Namn: Poäng: /42
1 Starta vid den röda pricken i figuren och följ pilens 1 p riktning längs sidorna. Markera med ett kryss när du har kommit 3 4 av vägen runt figuren.
2 Vilka bråk visar de färgade rutorna? 4 p Svara med ett bråk i enklaste form.
Flex matematik och kursplanens centrala innehåll
Taluppfattning och tals användning
Rationella tal, däribland negativa tal, och deras egenskaper samt hur talen kan delas upp och användas.
Positionssystemet och hur det används för att beskriva hela tal och tal i decimalform.
Olika talsystem och några talsystem som använts i olika kulturer genom historien.
Tal i procentform och deras samband med tal i bråk- och decimalform.
Hur tal i bråk- och decimalform kan användas i vardagliga situationer.
De fyra räknesätten och regler för deras användning vid beräkningar med naturliga tal.
Metoder för beräkningar med naturliga tal och enkla tal i bråk- och decimalform vid överslagsräkning, huvudräkning och skriftlig beräkning.
Användning av digitala verktyg vid beräkningar.
2 Bråk och procent
2 Bråk och procent ? Kluringar
Flex matematik stämmer överens med läroplanen Lgr22. För att ge en överblick visas här vilka delar av det centrala innehållet i matematik som behandlas i respektive kapitel och årskurs.
2 Bråk och procent 2 Bråk och procent
2 Bråk och procent 6 Enheter ? Kluringar
2 Bråk och procent 6 Enheter ? Kluringar
5 Räknesätt och algebra 5 Räknesätt och algebra 5 Räknesätt och algebra
1 Tal 5 Räknesätt och algebra
1 Tal 5 Räknesätt och algebra
1 Tal ? Kluringar ? Kluringar
Rimlighetsbedömning vid uppskattningar och beräkningar. 1 Tal 1 Tal
4
Matematiska likheter och hur likhetstecknet används för att teckna enkla ekvationer.
Variabler och deras användning i enkla algebraiska uttryck och ekvationer.
Metoder, däribland algebraiska, för att lösa enkla ekvationer.
Mönster i talföljder och geometriska mönster samt hur de konstrueras, beskrivs och uttrycks.
Programmering i visuella Programmeringsmiljöer. Hur algoritmer skapas och används vid programmering.
1 Tal
1 Tal 5 Räknesätt och algebra
5
1 Tal 5 Räknesätt och algebra
1 Tal 5 Räknesätt och algebra
4 Geometri 5 Räknesätt och algebra ? Kluringar
1 Tal 5 Räknesätt och algebra
6
1 Tal 5 Räknesätt och algebra
1 Tal 5 Räknesätt och algebra 1 Tal 5 Räknesätt och algebra
5 Räknesätt och algebra 5 Räknesätt och algebra 5 Räknesätt och algebra
1 Tal 4 Geometri
1 Tal 5 Räknesätt och algebra
1 Tal 5 Räknesätt och algebra
7 Programmering 7 Programmering
Algebra
Grundläggande geometriska två- och tredimensionella objekt samt deras egenskaper och inbördes relationer. Konstruktion av geometriska objekt, såväl med som utan digitala verktyg.
Jämförelse, uppskattning och mätning av längd, area, massa, volym, tid och vinkel med standardiserade måttenheter samt enhetsbyten i samband med detta.
Metoder för hur omkrets och area hos olika tvådimensionella geometriska figurer kan bestämmas och uppskattas.
Skala vid förminskning och förstoring samt användning av skala i elevnära situationer.
Symmetri i planet och hur symmetri kan konstrueras.
Slumpmässiga händelser, chans och risk med utgångspunkt i observationer, simuleringar och statistiskt material. Jämförelse av sannolikhet vid olika slumpmässiga försök.
Enkel kombinatorik i konkreta situationer.
Tabeller och diagram för att beskriva resultat från undersökningar, såväl med som utan digitala verktyg. Tolkning av data i tabeller och diagram.
Lägesmåtten medelvärde, typvärde och median samt hur de används i statistiska undersökningar.
Samband och förändring
Proportionalitet samt hur proportionella samband uttrycks i bråk-, decimal- och procentform.
Koordinatsystem och gradering av koordinataxlar.
Grafer för att uttrycka proportionella samband.
Problemlösning
Strategier för att lösa matematiska problem i elevnära situationer.
Formulering av matematiska frågeställningar utifrån vardagliga situationer.
Statistik
KAPITEL 3 Statistik
• Bestämma medelvärde, median och typvärde.
• Använda kombinatorik.
• Bestämma sannolikhet för att något ska inträffa.
Mål för kapitlet
• Tolka och skapa tabeller och diagram.
• Tolka proportionella samband och rita grafer.
• Använda koordinatsystem.
• Lösa matematiska problem inom området.
Kapitel 3
S TATISTIK
Centralt innehåll Lgr22
Sannolikhet och statistik
• Slumpmässiga händelser, chans och risk med utgångspunkt i observationer, simuleringar och statistiskt material. Jämförelse av sannolikhet vid olika slumpmässiga försök.
• Enkel kombinatorik i konkreta situationer.
• Tabeller och diagram för att beskriva resultat från undersökningar, såväl med som utan digitala verktyg. Tolkning av data i tabeller och diagram.
• Lägesmåtten medelvärde, typvärde och median samt hur de används i statistiska undersökningar.
Problemlösning
• Strategier för att lösa matematiska problem i elevnära situationer.
Innehåll i kapitel Statistik
Det här kapitlet handlar om statistik, kombinatorik och sannolikhet. Eleverna undersöker olika diagram, grafer och tabeller, samt tolkar och avläser information utifrån dessa. De skapar även egna diagram, grafer och tabeller.
Eleverna tränar också på att bestämma sannolikhet och använda lägesmåtten typvärde, medelvärde och median. De arbetar även med kombinatorik, undersöker proportionella samband och löser problem med fokus på statistik.
Förväntade förkunskaper
Vi utgår från att eleverna har förkunskaper (enligt Lgr22) om att avläsa och skapa enkla tabeller och diagram för att sortera och redovisa resultat.
Begrepp
medelvärde genomsnitt median typvärde kombinatorik sannolikhet stapeldiagram cirkeldiagram punktdiagram graf proportionalitet koordinatsystem
VECKA 1
Översikt veckoplanering
LEKTION 1
Bildspel
Lektionsbok s. 59–61
LEKTION 2
Bildspel
Lektionsbok s. 62
Sammanfattning
Medelvärde A
1 Skriv talen som fattas. a) Medelvärdet är 4. b) Medelvärdet är 5. c) Medelvärdet är 6. 3 4 4 4 3 7 6 10 5 d) Medelvärdet är 20. e) Medelvärdet är 3. 25 30 10 7 3 4
2 I genomsnitt ska fem rutor vara färgade i var och en av de här figurerna. Rita ett förslag på hur många rutor som kan vara färgade i varje figur.
3 Vilket är medelvärdet? a) Medelvärdet av b) Medelvärdet av antalet syskon: antalet prickar:
Antal syskon Namn 8 4 0 Alva Carl Frans Freja Haddad 6 2 –2
c) Medelvärdet av talen:
S TATISTIK 62
1 Lektion 2
Minicheck Bildspel
VECKA 1
Översikt veckoplanering
LEKTION 3
Bildspel
Lektionsbok s. 63
Kombinatorik
4 Varje ring på kodlåset består av siffrorna 0 –5. Hur många kombinationer är möjliga?
5 På hur många olika sätt kan de här personerna vara placerade i kön?
VECKANS KLURING
6 a) Hur många tresiffriga tal kan du bilda av talkorten om talen får bestå av likadana siffror? 1 3 5 7 9
b) Hur många tresiffriga tal kan du bilda av talkorten om alla siffror ska vara olika? 1 3 5 7 9 Visa hur du löser uppgifterna. Beräkna med miniräknare om du vill.
? KLURING 1 Den här etiketten finns på ett paket med lammracks. Vilket pris ska stå i den tomma rutan? Lammracks Vikt (kg) Kilopris (kr/kg) Pris (kr) 0,800 240
Minicheck Bildspel
LEKTION 1
DU BEHÖVER:
• Bildspel – CHECK IN Statistik
• Lektionsboken s. 59–61
• Skrivtavlor
Bildspel CHECK IN Statistik
SÅ HÄR KAN DU GÖRA
1
Öppna bildspelet och ta fram det på helskärm. Se till att alla elever är beredda med sina skrivtavlor.
Berätta att arbetsområdet är Statistik och skriv begreppen koordinater och sannolikhet på tavlan.
Ställ sedan frågor:
– När kan vi använda koordinater?
– Hur skrivs koordinater?
– När använder vi oss av sannolikhet?
– Finns det andra ord för sannolikhet?
Samtala om elevernas tankar kring begreppen och sammanfatta till exempel i en tankekarta på din whiteboard.
2
Visa kapitlets introduktionsbild i bildspelet och samtala om vilken matematik eleverna tänker på när de ser bilden. Det kan vara att resultaten i bowling visas i en tabell, hur stor andel av sakerna som har en viss färg, hur stor sannolikhet det är att få en strike.
3
Visa Check in i bildspelet och berätta att uppgifterna här ger en översikt av vad eleverna kommer att möta i kapitlet Statistik. Betona att det inte är ett test, utan är till för att eleverna ska få chans att bekanta sig med innehållet.
Klicka fram en uppgift i taget i bildspelet och låt eleverna svara i lektionsboken.
Flex webb
Efter genomgången av Check in påbörjar eleverna arbetet med kapitel Statistik på Flex webb.
DU BEHÖVER:
LEKTION 2
• Bildspel – Medelvärde A
• Lektionsboken s. 62
• Skrivtavlor
Bildspel Medelvärde A
Träna på att bestämma medelvärde.
SÅ HÄR KAN DU GÖRA
1
Öppna bildspelet och ta fram det på helskärm. Se till att alla elever är beredda med sina skrivtavlor.
2
Bilden visar tre gula kvadrater. Varje kvadrat är indelad i 9 små rutor. Klicka fram de röda rutorna och fråga eleverna hur många röda rutor det är sammanlagt. Konstatera tillsammans att det är 6 stycken. Klicka vidare och fråga hur många röda rutor det skulle vara i varje figur om de vore jämnt fördelade. Låt eleverna skriva förslag på sina skrivtavlor, sedan jämföra parvis, enas om ett svar och argument för det svaret. Lyft fram argument för att det måste vara lika många i varje.
Klicka vidare och fråga om man kan räkna ut hur många röda rutor det måste vara i varje om de ska vara jämnt fördelade.
Låt dem samtala parvis en stund och sedan presentera sina förslag på beräkningar. Fokusera på argument om det totala antalet röda rutor och antalet stora gula kvadrater, eftersom detta leder oss fram till medelvärdet. Enas om att ” = jämnt fördelat” och att ”jämnt fördelat 3 = summan”
Konstatera tillsammans att en jämn fördelning av de 6 röda rutorna måste vara 2 röda rutor i varje och klicka vidare i bildspelet för att visa svaret. Uppmuntra eleverna att skriva uträkningen som ett uttryck, det vill säga . Det är bra att vänja sig vid att skriva beräkningar på detta sätt i stället för i flera led.
3
Bilden visar tre gula kvadrater. Varje kvadrat är indelad i 9 små rutor, varav några är blå. Fråga eleverna om de utan att ställa upp en beräkning kan fördela de blå rutorna jämnt mellan kvadraterna. Låt dem presentera sina strategier och fråga sedan vilken summan av antalet blå kvadrater är. Klicka vidare och fråga om de kan visa en beräkning som visar hur många blå rutor det måste vara i varje om de ska vara jämnt fördelade. Arbeta på motsvarande sätt som med bild 2 och upprepa att ” = jämnt fördelat” och att ”jämnt fördelat · 3 = summan”
Konstatera tillsammans att en jämn fördelning av de 9 blå rutorna måste vara 3 blå rutor i varje och klicka vidare i bildspelet för att visa svaret.
4
Bilden visar fyra gula kvadrater. Varje kvadrat är indelad i 16 små rutor, varav några är gröna. Arbeta på motsvarande sätt som med bild 2.
Konstatera tillsammans att en jämn fördelning av de 24 gröna rutorna måste vara 6 gröna rutor i varje och klicka vidare i bildspelet för att visa svaret.
5
Bilden visar texten ”att något är jämnt fördelat kan uttryckas på olika sätt”. Fråga eleverna om de minns några av dessa begrepp. Klicka vidare i bildspelet och visa begreppen ”medelvärde” och ”genomsnitt”. Konstatera att båda begreppen går bra att använda eftersom de har samma innebörd. Klicka fram stjärnorna och fråga hur många stjärnor det skulle vara i varje ruta om man inte ändrar det totala antalet stjärnor, men fördelar dem så att det är lika många i varje ruta. Berätta att en sådan jämn fördelning kallas just medel-
värde och att det alltså är medelvärdet vi har räknat ut i föregående bilder. Samtala om att det är ett sätt att se hur det skulle vara om ”alla hade lika” och att medelvärde används inom statistiken för att analysera data och resultat.
Be eleverna att beräkna medelvärdet av antal stjärnor per ruta. Låt dem skriva förslag på sina skrivtavlor och presentera sina beräkningar.
Samtala om att ” = medelvärdet” vilket ger = = 4. Påminn även om att ”medelvärdet 4 = summan”, 4 4 = 16. Enas om att medelvärdet måste vara 4 och klicka vidare i bildspelet för att visa svaret.
6
Bilden visar fem tärningar med olika antal prickar. Be eleverna att räkna ut medelvärdet av antalet prickar på sina skrivtavlor och visa upp. Observera om eleverna har delat upp uträkningarna och uppmuntra dem i så fall att i stället skriva uträkningarna som en enda likhet så här:
6 + 3 + 6 + 1 + 4 5 20 5
= = 4
Enas om att medelvärdet måste vara 4 och klicka vidare i bildspelet för att visa svaret.
7
Bilden visar fem personer. Berätta att de här personerna i genomsnitt har ätit 7 köttbullar var och fråga hur många köttbullar de då har ätit sammanlagt. Be var och en av eleverna att skriva ett uttryck för hur medelvärdet 7 kan ha räknats fram på sina tavlor. Låt dem sedan jämföra sina uttryck parvis och enas om ett som de argumenterar för. Samtala om deras olika förslag och om ingen grupp skrivit det, så presentera = 7. Ställ frågor, exempelvis:
alla uppätna köttbullar 5 alla uppätna köttbullar 5
– Om vi vet att = 7, hur kan vi då beräkna hur många de åt tillsammans?
Om alla åt 7 köttbullar i genomsnitt betyder det att om de hade ätit exakt lika många var, så skulle de ha ätit 7 stycken var. Eftersom det är 5 personer som skulle ätit 7 var, så går det att tänka 5 7 = 35 köttbullar tillsammans.
– Betyder det att alla åt 7 köttbullar var? Nej, men i genomsnitt åt de 7 var. – Kan ni ge exempel på hur många köttbullar de olika personerna kan ha ätit? Låt eleverna skriva förslag på sina skrivtavlor.
Enas om att om vi vet medelvärdet och antalet personer, så kan vi räkna ut summan genom att multiplicera medelvärdet med antalet personer.
8
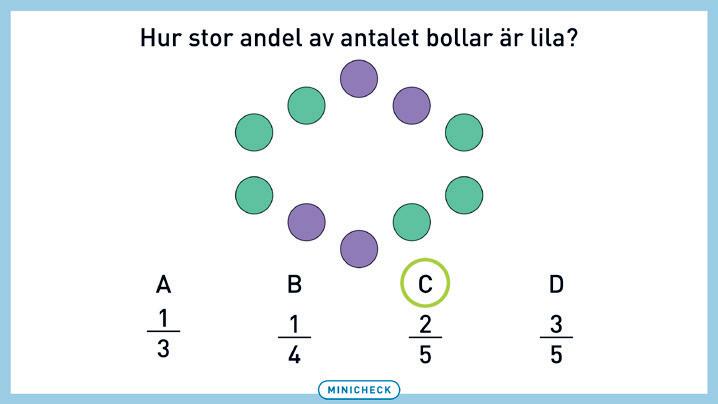
ELEVUPPGIFT: Eleverna ritar en bild med olika antal bollar i tre hinkar. De beräknar sedan medelvärdet för antalet bollar per hink.
Lektionsboken
s. 62
Medelvärde A
1 Skriv talen som fattas. a) Medelvärdet är 4. b) Medelvärdet är 5. c) Medelvärdet är 6. 3 4 4 4 3 7 6 10 5 d) Medelvärdet är 20. e) Medelvärdet är 3. 25 30 10 7 3 4
2 I genomsnitt ska fem rutor vara färgade i var och en av de här figurerna. Rita ett förslag på hur många rutor som kan vara färgade i varje figur.
3 Vilket är medelvärdet?
a) Medelvärdet av b) Medelvärdet av antalet syskon: antalet prickar:
c) Medelvärdet av talen: Antal syskon Namn 8 4 0 Alva Carl Frans Freja Haddad 6 2 –2
UPPGIFT 1: Eleverna fyller i det tal som saknas för att medelvärdet ska stämma.
TIPS:
Uppmuntra eleverna att räkna ut vilken summan av talen i cirklarna är genom att multiplicera medelvärdet med antalet cirklar.
UPPGIFT 2: Eleverna fyller i kvadraterna så att medelvärdet av de färgade rutorna blir 5.
UPPGIFT 3: Eleverna räknar ut medelvärdet.
TIPS:
Påminn eleverna om att medelvärdet är när vi ”fördelar lika” och det gör vi genom att beräkna summan av olika värden och sedan dividera den summan med antalet värden.
Flex webb
Eleverna arbetar vidare med uppgifter på Flex webb fram till redovisning. Efter redovisning av lektionsboken arbetar samtliga elever med Flex webb.
Redovisning av lektionsboken
Ta fram lektionsboken på helskärm. När eleverna har redovisat sina lösningar går ni gemensamt igenom och diskuterar dem. Uppmärksamma till exempel vanliga missförstånd.
Minicheck
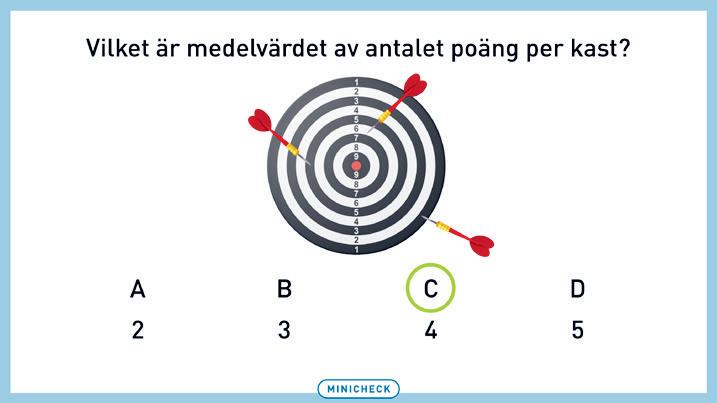
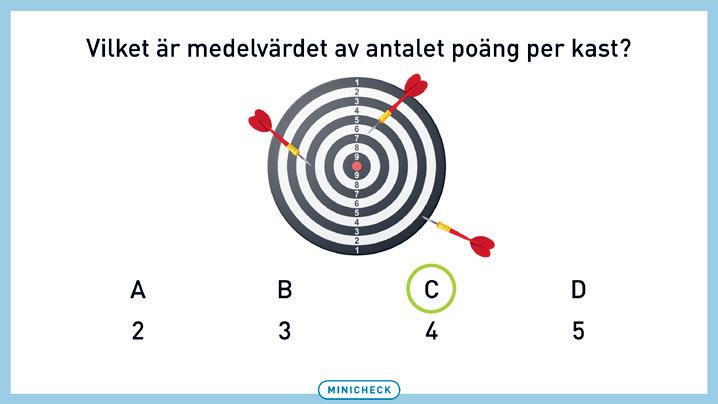
MEDELVÄRDE: Eleverna räknar ut medelvärdet av kasten.
LEKTION 3
DU BEHÖVER:
• Bildspel – Kombinatorik
• Lektionsboken s. 63
• Skrivtavlor
• Miniräknare
• Klossar
Bildspel Kombinatorik
Träna på att bestämma på hur många olika sätt vi kan kombinera saker med varandra.
SÅ HÄR KAN DU GÖRA 1
Öppna bildspelet och ta fram det på helskärm. Se till att alla elever är beredda med sina skrivtavlor. Börja med att fråga om eleverna minns vad ordet kombinatorik betyder och enas om att det handlar om på hur många olika sätt vi kan kombinera saker med varandra.
2
Bilden visar tre frukter. Fråga eleverna om de kan rita och visa på sina skrivtavlor på hur många sätt de kan välja i vilken ordning frukterna ska ätas. Förtydliga att du med ordning menar vilken de äter först, vilken de äter därefter och så vidare.
Påpeka även att de bara har en av varje frukt, så de kan inte ta ”banan, banan, äpple”. Låt gärna eleverna arbeta med olikfärgade klossar som kan symbolisera frukterna och med hjälp av dem visa alla kombinationer som är möjliga. Om du väljer att låta eleverna rita, så låt dem jämföra sina förslag parvis och enas om ett som de argumenterar för.
Samtala om de olika förslagen och visa några om är hållbara på tavlan. Många har säkert valt att använda någon sorts tabell eller att rita frukterna och visa genom att dra streck mellan dem. Ställ frågor, exempelvis:
– Hur gjorde ni för att lösa uppgiften?
– Hur många kombinationer hittade ni?
– Kan vi räkna fram antalet kombinationer i stället för att rita eller använda en tabell?
Klicka vidare i bildspelet och visa träddiagrammet. Förklara att oavsett hur de löst uppgifterna är det i första steget alltid tre frukter att välja på. I andra steget är det alltid två frukter att välja på, oavsett vilken de valde först. Till sist har de bara en frukt kvar att ta. Förklara att i slutet har vi sex stycken grenar, där varje gren symboliserar en specifik ordning att välja frukterna i, en specifik kombination av val.
Klicka fram multiplikationen 3 2 1 = 6. Fråga eleverna vad de tror att 3, 2 och 1 står för i multiplikationen och låt dem samtala parvis. Enas om att de står för antalet möjliga val. I första steget kan man välja mellan tre frukter, i andra steget mellan två frukter och i tredje steget finns bara en frukt att välja.
Enas om att det finns sex olika kombinationer och klicka fram svaret.
3
Bilden visar fyra lådor på rad och fyra bollar, en grön, en röd, en gul och en blå. Fråga eleverna på hur många olika sätt vi kan ordna bollarna i fyra lådor, om det bara får ligga en boll i varje låda. Alla sätt måste ha olika ordning på bollarna. Låt dem rita på sina tavlor om de vill och sedan jämföra med en klasskompis. Ställ frågor, exempelvis:
– Hur gjorde ni för att lösa uppgiften?
– Vilken multiplikation visar antalet kombinationer? Först kan vi välja mellan fyra bollar, i nästa steg har vi tre att välja mellan, sedan två och till sist en boll, det blir 4 3 2 1 = 24.
Om eleverna inte har ritat ett träddiagram eller en tabell för att lösa uppgiften, så kan du be dem att göra det. Samtala sedan om vilket sätt att lösa
uppgiften som är enklast, att utföra multiplikationen eller att rita. I det här läget tycker kanske några elever att det fortfarande är enklare att rita. Enas om att det finns 24 olika kombinationer och klicka fram svaret.
Klicka vidare i bildspelet och fråga på hur många olika sätt vi kan placera 5 bollar i olika ordning i fem lådor och arbeta på motsvarande sätt som ovan. Enas om att det finns 120 kombinationer och klicka fram svaret. Fråga eleverna varför det här är mer praktiskt att använda sig av multiplikationen. Antagligen inser de snabbt att det är svårt att få det tydligt när man ska rita ett diagram eller en tabell som mynnar ut i 120 olika grenar.
4
Bilden visar siffrorna 2, 4, 6 och 8. Fråga eleverna på hur många olika sätt de kan skapa ett tvåsiffrigt tal av siffrorna, om de får använda samma tal flera gånger. Låt dem fundera enskilt, skriva förslag på skrivtavlorna, jämföra parvis och enas om ett förslag som de presenterar. Ställ frågor, exempelvis:
– Hur många val har vi till tiotalssiffran? Vi har fyra val, eftersom vi har fyra siffror att välja mellan.
– Hur många val har vi till entalssiffran? Vi har fyra val här också, eftersom vi har fyra siffror att välja mellan.
Klicka fram förklaringen och be eleverna att skriva en multiplikation som passar till om de inte redan har gjort det. Samtala sedan om att 4 · 4 symboliserar att vi har fyra val till entalssiffran och fyra val till tiotalssiffran. Enas om att det går att bilda 16 olika tal och klicka fram svaret.
Klicka fram nästa fråga och be eleverna att skriva ned hur många tvåsiffriga tal de kan bilda av talen om de bara får använda varje siffra en gång. Arbeta på motsvarande sätt som tidigare. Ställ frågor, exempelvis:
– Vad skiljer den här uppgiften från uppgiften ovan? I den första har vi fyra val till båda siffrorna, men i den här uppgiften har vi fyra val till en av siffrorna och tre val till den andra.
Klicka vidare i bildspelet och visa hjälptexten. Be eleverna att skriva en multiplikation som passar
6
till om de inte redan har gjort det. Samtala sedan om att 4 · 3 symboliserar att vi har fyra val till en av siffrorna och tre val till den andra. Enas om att det går att bilda 4 3 = 12 olika tal och klicka fram svaret.
Ställ gärna fler frågor, exempelvis: –
Hur många kombinationer skulle det finnas om vi skulle skapa ett fyrsiffrigt tal där alla siffror måste vara olika? Det skulle vara som med bollarna, 4 3 2 1 = 24 sätt.
5
Bilden visar ett kodlås. Förklara för eleverna att vi låser upp med hjälp av en kod som består av två bokstäver och fyra siffror och att vi får använda samma siffra och bokstav fler gånger. Fråga hur många olika kombinationer det finns. Arbeta på motsvarande sätt som med bild 4. Ställ frågor, exempelvis:
Hur gjorde ni för att lista ut antalet möjliga kombinationer? Det finns 2 bokstäver och de kan kombineras på 4 sätt, eftersom varje plats kan väljas på två sätt, alltså 2 2. Det finns 10 siffror och de kan kombineras på 100 sätt, eftersom varje plats kan väljas på två sätt, alltså 10 · 10.
– Hur vet vi hur många kombinationer det blir sammanlagt? Eftersom vi har 2 2 10 10 är det 400 kombinationer att välja på. Eller så kan vi tänka 4 · 100.
Enas om att det finns 400 sätt och klicka fram svaret.
Ställ gärna fler frågor som kan utmana och väcka intresse, exempelvis:
– Kan ni lista ut hur många kombinationer det finns på ett vanligt cykellås med en kod som består av 4 siffror? Där kan vi välja samma siffra flera gånger, så det finns 10 · 10 · 10 · 10 = 10 000 kombinationer.
– Tänk er att vi har samma typ av kodlås fast med fler siffror i koden, hur många siffror består koden av om det finns 1 000 000 kombinationer?
Då består koden av 6 siffror eftersom 10 · 10 · 10 · 10 · 10 · 10 = 1 000 000.
Bilden visar sju personer som står i kö. Fråga eleverna på hur många olika sätt personerna kan vara placerade i kön. Låt dem fundera enskilt, skriva ned sina svar och sedan jämföra parvis. Lyssna på elevernas argument och samtala om deras förslag. Ställ frågor, exempelvis:
– Varför ska vi multiplicera 7 · 6 · 5 · 4 · 3 · 2 · 1 här och inte 7 7 7 7 7 7 7? Här kan vi ju inte använda samma person flera gånger, så det vi använder oss av ”tar slut”. Första positionen kan väljas på 7 sätt, andra positionen på 6 sätt, tredje positionen på 5 sätt och så vidare.
– Finns det något knep för att veta när vi ska använda vilken metod? Om det vi använder oss av ”tar slut” ska vi använda oss av multiplikationen där antalet positioner minskar. Om det vi använder oss av ”finns kvar att välja av” ska vi använda oss av multiplikationen där antalet positioner är samma.
Enas om att det finns
7 · 6 · 5 · 4 · 3 · 2 · 1 = 5 040 olika sätt och klicka fram svaret.
Låt eleverna föreställa sig ett scenario där sju personer ska ställa sig i ett led, men där bara fyra personer kan stå. Hur många kombinationer finns det då? Låt dem samtala parvis och konstatera sedan gemensamt att det då finns 7 6 5 4 kombinationer. Det är 7 val till första platsen, 6 val till andra platsen, 5 val till tredje platsen och 4 val till fjärde platsen. Återkoppla till uppgiften med det tvåsiffriga talet.
7
ELEVUPPGIFT: Eleverna hittar på ett eget kodlås, som består av siffor och minst en typ av symboler till. De räknar sedan ut hur många kombinationer det finns på kodlåset.
Lektionsboken s. 63
Kombinatorik
4 Varje ring på kodlåset består av siffrorna 0 –5. Hur många kombinationer är möjliga?
5 På hur många olika sätt kan de här personerna vara placerade i kön?
6 a) Hur många tresiffriga tal kan du bilda av talkorten om talen får bestå av likadana siffror?
b) Hur många tresiffriga tal kan du bilda av talkorten om alla siffror ska vara olika?
1 Den här etiketten finns på ett paket med lammracks. Vilket pris ska stå i den tomma rutan?
UPPGIFT 4–6: Eleverna räknar ut antalet kombinationer i de olika uppgifterna.
Svar:
TIPS:
• Uppmuntra eleverna att använda metoden med multiplikation från bildspelet.
• Låt eleverna pröva att rita träddiagram, men konstatera att modellen med multiplikation är bra när det finns många kombinationer.
• Påminn eleverna om att vi räknar på olika sätt beroende på om vi får använda samma sak (siffra, person) flera gånger eller inte.
Flex webb
Eleverna arbetar vidare med uppgifter på Flex webb fram till redovisning. Efter redovisning av lektionsboken arbetar samtliga elever med Flex webb.
Redovisning av lektionsboken
Ta fram lektionsboken på helskärm. När eleverna har redovisat sina lösningar går ni gemensamt igenom och diskuterar dem. Uppmärksamma till exempel vanliga missförstånd.
Minicheck
KOMBINATORIK: Eleverna räknar ut på hur många olika sätt det går att ta två kulor ur skålen.
Kombinatorik
4 Varje ring på kodlåset består av siffrorna 0 –5. Hur många kombinationer är möjliga?
VECKANS KLURING
5 På hur många olika sätt kan de här personerna vara placerade i kön?
DU BEHÖVER:
• Bildspel – Kluring 1
• Lektionsboken s. 63
• Skrivtavlor
6 a) Hur många tresiffriga tal kan du bilda av talkorten om talen får bestå av likadana siffror?
Kluring 1 s. 63
b) Hur många tresiffriga tal kan du bilda av talkorten om alla siffror ska vara olika?
Träna problemlösning och proportionalitet.
KLURING 1
Den här etiketten finns på ett paket med lammracks.
Vilket pris ska stå i den tomma rutan?
Vikt (kg) Kilopris (kr/kg) Pris (kr)
SÅ HÄR KAN DU GÖRA
• Visa kluringen på helskärm.
• Läs problemet högt för eleverna.
• Fråga vilken viktig information som finns i texten.
Eleverna arbetar med problemet enligt metoden EPA (Ensam, Par, Alla).
TIPS:
• Uppmuntra eleverna att göra en tabell.
• Hjälp eleverna att omvandla till hekto.
• Låt eleverna räkna ut vad 1 hg kostar.
• Förtydliga att kr/kg betyder kronor per kilo.
ELEVLÖSNING 1 = 30 kr/hg
30 10 = 300 kr/kg
Svar: Det kostar 300 kr/kg.
Eleven har använt division för att räkna ut vad priset per hekto är. Här kan man uppmuntra att även visa enhetsomvandling.
ELEVLÖSNING 2
0,800 kg = 8 hg
Vikt Pris 8 hg 240 kr 4 hg 120 kr 2 hg 60 kr 1 hg 30 kr 10 hg 300 kr
Svar: 300 kr/kg
Den här eleven har omvandlat till hekto och sedan gjort en tabell för att kunna räkna fram priset för 10 hg som motsvarar 1 kg.
ELEVLÖSNING 3 Vikt (hg) Pris (kr) 8 240 4 120 2 60 8 + 2 = 10 240 + 60 = 300 10 hg 300 kr
Svar: 300 kr/kg
Den här eleven har gjort en tabell och i den adderat stegvis upp till 10 hg och motsvarande pris i kronor.
Flex webb
När arbetet med kluringen är avslutat loggar eleverna in på Flex webb och arbetar på egen hand med uppgifter.
Träna inför NP
Här kan eleverna träna mer på uppgifter från alla kapitel inför det nationella provet.
TRÄNA INFÖR NP
Träna inför NP i lektionsboken
Det här kapitlet innehåller blandade uppgifter som förbereder eleverna inför de nationella proven i matematik. Uppgifterna 1–25 och 40 bör eleverna lösa utan miniräknare. Till uppgifterna 26–39 kan de använda miniräknaren som stöd.
Kapitlet avslutas med ett uppslag med undersökande uppgifter kopplade till geometri och algebra. Även dessa uppgifter bör eleverna lösa utan hjälp av miniräknare.
Till det här kapitlet finns inga bildspel, utan inled i stället med att visa uppgifterna i lektionsboken på helskärm. Gå gemensamt igenom de uppgifter som ni har tänkt arbeta med under lektionen och låt sedan eleverna lösa uppgifterna i sina lektionsböcker.
Avsluta lektionen med att åter visa uppgifterna på helskärm och låt eleverna redovisa sina lösningar. Diskutera lösningarna och svaren tillsammans i helklass och uppmärksamma till exempel vanliga missförstånd.
Träna inför NP på Flex webb
På Flex webb kan eleverna arbeta vidare med blandade uppgifter till lektionsbokens kapitelområden.
Lektionsboken s. 167
1 a) Rita en rektangel med omkretsen 14 cm. b) Vilken area har din rektangel? Visa hur du löser uppgiften.
Svar:
2 Marko, Saga, Helga och Carl är alla 13 år. Om hur många år är de 100 år tillsammans? Visa hur du löser uppgiften.
UPPGIFT 1: Eleverna ritar en rektangel med omkretsen 14 cm och beräknar sedan arean av rektangeln.
TIPS:
• Uppmuntra eleverna att ta reda på hur lång en långsida och en kortsida på rektangeln är vara sammanlagt.
• Påminn eleverna om att arean är storleken av ytan och omkretsen är längden av sträckan runtomkring.
UPPGIFT 2: Eleverna räknar ut hur många år det är kvar tills barnen är 100 år tillsammans.
TIPS:
• Uppmana eleverna att först beräkna den nuvarande sammanlagda åldern.
• Uppmärksamma att barnen ska vara 100 år tillsammans, vilket innebär att det antal år som är kvar ska divideras med 4.
Lektionsboken s. 168
3 När klassen gör en utflykt i maj är det 17 °C ute.
På klassens utflykt i vintras var det –6 °C. Hur stor är temperaturskillnaden?
Visa hur du löser uppgiften.
Svar:
4 Skriv talen som fattas så att likheterna stämmer.
a) 0,7 + = 1,05 b) 9 5 = + 35
c) 100 = 20 d) + 2,8 = 4
5 Martina snurrar en gång på ett lyckohjul.
a) Hur stor är sannolikheten att hjulet stannar på blått?
Svara med ett tal i procentform.
Svar:
b) Hur stor är sannolikheten att hjulet stannar på rött?
Svara med ett tal i bråkform.
Svar:
c) Hur stor är sannolikheten att hjulet stannar på gult?
Svara med ett tal i procentform.
Svar:
UPPGIFT 3: Eleverna räknar ut skillnaden i temperatur.
TIPS:
Uppmuntra eleverna att rita en tallinje och se hur långt från 0 temperaturerna ligger.
UPPGIFT 4: Eleverna tar reda på talen som fattas.
TIPS:
Påminn eleverna om att använda det motsatta räknesättet.
UPPGIFT 5: Eleverna beräknar hur stor sannolikhet det är att hjulet stannar på en viss färg.
TIPS:
Påminn eleverna om att uttrycka sannolikheten som till exempel P(gul) = .
Svar:
Lektionsboken s. 169
6 Vi stoppar in olika tal i en räknemaskin. Räknemaskinen gör samma beräkning varje gång innan den matar ut resultatet. a) Skriv talen som fattas i rutorna.
b) Välj ett eget tal att stoppa in. Vilket tal matar maskinen ut? Skriv talen i rutorna.
UPPGIFT 7: Eleverna använder överslagsräkning och ringar in uttrycket med störst värde.
TIPS:
TIPS:
c) Vi stoppar bara in hela tal. Vilket av talen kan inte matas ut ur maskinen? Ringa in.
7 Vilket av uttrycken har störst värde? Ringa in. Använd överslagsräkning.
8 Vilken av ekvationerna har lösningen x = 12? Ringa in.
• Påminn eleverna om ”att göra överslag” motsvarar ”att räkna ungefär” .
• Uppmuntra eleverna att avrunda till närmaste hundratal.
UPPGIFT 8: Eleverna undersöker vilken av ekvationerna som har lösningen x = 12.
TIPS:
Uppmuntra eleverna att byta ut x mot 12 och se om det då blir en likhet. De kan också lösa varje ekvation direkt för att ta reda på vad x är.
UPPGIFT 6: Eleverna tar reda på mönstret och skriver de tal som fattas.
• Påminn i uppgift c) om att mönstret är ”multiplicera med 3” .
• Uppmuntra eleverna att dividera talen med 3.
L ÄRARHANDLEDNING
Flex matematik är ett läromedel för dig som vill ha ett elevaktivt klassrum. Med hjälp av färdiga veckoplaneringar och bildspel blir undervisningen både rolig och varierad. Eleverna är delaktiga genom att diskutera strategier och lösningar som de visar på sina skrivtavlor. Färdighetsträningen sker först i lektionsboken och sedan på elevwebben, där var och en arbetar vidare på sin nivå.
Lärarhandledningen vägleder dig under genomgångarna med bildspelen och veckoöversikten underlättar din planering. På lärarwebben finns alla bildspel och här kan du följa dina elevers utveckling.
består av lärarhandledning med lärarwebb samt lektionsbok med elevwebb.
Läs mer på nok.se/flexmatematik