9780141999869

Leonard Susskind & André Cabannes

General Relativity

The Theoretical Minimum

General Relativity

Leonard Susskind has been the Felix Bloch Professor in Theoretical Physics at Stanford University since 1978, and his online lectures are viewed all around the world. One of the fathers of string theory, he is the author of The Black Hole War and The Cosmic Landscape.

André Cabannes taught mathematics at the Massachusetts Institute of Technology and translated the Theoretical Minimum series into French. He lives in France.

This book is the fourth volume of The Theoretical Minimum series. The first volume, The Theoretical Minimum: What You Need to Know to Start Doing Physics, covered classical mechanics, which is the core of any physics education. We will refer to it from time to time simply as volume 1. The second book, volume 2, explains quantum mechanics and its relationship to classical mechanics. Volume 3 covers special relativity and classical field theory. This fourth volume expands on that to explore general relativity.

PENGUIN BOOKS

UK | USA | Canada | Ireland | Australia India | New Zealand | South Africa

Penguin Books is part of the Penguin Random House group of companies whose addresses can be found at global.penguinrandomhouse.com.

First published in the United States of America by Basic Books, Hachette Book Group 2023

First published in Great Britain by Allen Lane 2023 Published in Penguin Books 2024 001

Copyright © Leonard Susskind and André Cabannes, 2023

The moral right of the authors has been asserted

Printed and bound in Great Britain by Clays Ltd, Elcograf S.p.A.

The authorized representative in the EEA is Penguin Random House Ireland, Morrison Chambers, 32 Nassau Street, Dublin D 02 YH 68

A CIP catalogue record for this book is available from the British Library

ISBN : 978–0–141–99986–9 www.greenpenguin.co.uk

Penguin Random Hous e is committed to a sustainable future for our business , our readers and our planet. is book is made from Forest Stewardship Council® certified paper

To my family —LS

To my parents, who taught me work and tenacity —AC

Preface

ThisfourthvolumeinTheTheoreticalMinimum(TTM)serieson generalrelativityisthenaturalcontinuationofthethirdvolume onspecialrelativity.

Inspecialrelativity,Einstein,startingfromaverysimpleprinciple–thelawsofphysicsshouldbethesameinindistinguishable Galileanreferentials–deeplyclarifiedinacoupleofpaperspublishedin1905thevariousdisturbingobservationsphysicistshad madeandtheequationstheyhadwritteninthelastyearsofthe nineteenthandthefirstyearsofthetwentiethcenturyconcerning lightandotherphenomena.

Specialrelativityledtoastrangedescriptionofspace-timewhere timeandspacewereinextricablymingled.Forinstance,itexplainedhowparticleswhoselifetimeismeasuredinfractionsofa secondcanhave,inourreferential,atraveltimefromtheSunto Earthofmorethaneightminutes.

Then,from1907until1915,essentiallyalone,Einsteinreproduced hisfeatstartingnowfromanotherverysimpleprinciple–accelerationanduniformgravityareequivalent.Hegeneralizedspecial relativitytoaspace-timecontainingmassivebodies.Thetheoryis called generalrelativity (GR).Itledtoanevenstrangerdescriptionofspace-timewheremassesbendlightandmoregenerally warpspaceandtime.

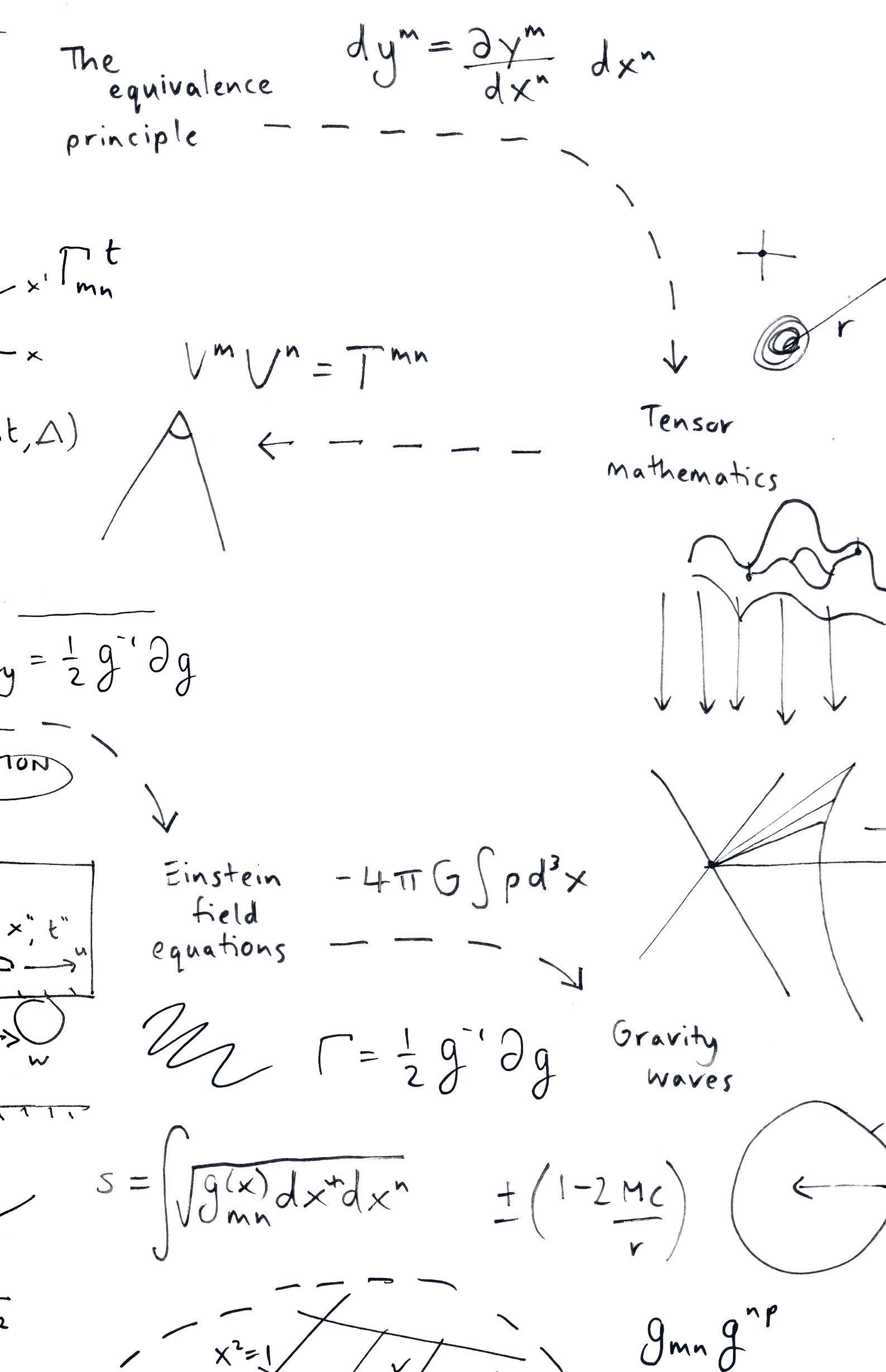
Inlecture1,wepreparethegroundwork.Weshowhowtheequivalenceprincipleinescapablyleadstothebendingoflightraysby massivebodies.

Lecture2isdevotedtotensormathematicsbecauseinGRwe mustfrequentlychangereferentialsandtheequationsrelatingcoordinatesinonereferentialtocoordinatesinanotheraretensor equations.

GeneralRelativity

Thenalargepartofthetheoryisexpressedusingtensorequationsbecausetheyhavethegreatqualitythatiftheyholdinone referential,theyholdinallofthem.

Lectures3,4,and5aredevotedtothegeometryofRiemannian spaceandMinkowskianspace-timebecauseitcanbesaid,very summarily,thatgravityisgeometryinaMinkowskianspace-time.

Inlectures6,7,and8,weexploreblackholes,notsomuchbecause theyareinterestingastronomicalphenomenaperse,thanbecause theyaretheequivalentinMinkowskianspace-timeofpointmasses inNewtonianmechanics.Space-timehoweverpresentsastranger behaviorinthevicinityofablackholethanNewtonianspacein thevicinityofapointmass.Understandingwellblackholes,the metric theycreate,theirhorizon,timeandgravityinthevicinity oftheirhorizon,thewaypeopleinandoutofablackholecan communicate,etc.isaprerequisitetounderstandingGR.

Inlecture9wesketchthederivationofEinsteinfieldequations. Andinlecture10wepresentasimpleapplicationpredictinggravitywaves.

Thisbook,astheprecedingonesintheseries,isadaptedfroma courseIgaveforseveralyears,withmuchpleasure,atStanfordin theContinuingStudiesprogramtoanaudienceofadults.

MycoauthorthistimeisAndr´eCabannes.Eventhoughheisnot aprofessionalscientist,hisscientifictraining,includingaStanford doctorateandacoupleofyearsofteachingappliedmathematics attheMassachusettsInstituteofTechnology(MIT),helpedhim assistme.

MayEinstein’swayofdoingphysics–startingfromthesimplestprinciplesandpursuingdauntlesslythemathematicsand thephysicstotheirultimateconsequences,howeverunsettling theymaybe–asIhavestrivedtoshowinthisbook,beasource ofinspirationtoyoungandfuturephysicists.

Tenyearsago,whentwoofmychildren,thenintheirlateteens, werestudyingsciencestoentertheFrenchsystemofgrandes ´ecoles,IdecidedtobrushupwhatIhadlearnedintheseventies inordertoaccompanythemintheirstudies.Idiscoveredthat theInternethadprofoundlychangedthelearninglandscape.Besidereadingbooks,onecouldnowalsotakeexcellentfreecourses ontheNet.Ileisurelyattendedcoursesinmathematics,physics, computerscience,etc.fromMIT,Stanford,andotherplaces. Thesubjectmattersoftenwerebetterexplained,thecoursesmore livelyandeasiertounderstand,thanwhatIhadexperiencedin thepast.Onecouldchoosecoursesbytheworld’sbestteachers.

AmongthesecourseswasTheTheoreticalMinimumseriesby LeonardSusskind,famousamongotherreasonsforhispioneeringworkonstringtheory.IlikedthemsomuchthatwhenI discoveredthattwoofhisfilmedphysicscourseshadalreadybeen transformedintobooks,IdecidedtotranslatetheminFrench. LaterIalsotranslatedthethirdbook.Then,sincethenextvolumedidn’texistinEnglishyet,ItookupwritingtheEnglish notesaswell,havinginmindthatthisworkmightturnoutto beuseful.AfteralotmoreworkwithProfessorSusskindandBasicBooksteam,volume4inTheTheoreticalMinimumseries,on generalrelativity,thatyouholdinyourhandsistheresult.

Ibelongtothegroupofpeopletowhomtheseso-calledContinuingStudiescourseswereintended:individualswhostudied physicsattheundergraduateandsometimesgraduatelevelwhen theywerestudents,thendidotherthingsinlife,butkeptaninterestinsciencesandwouldliketohavesomeexposuretowhere physicsstandstodayatalevelaboveplainvulgarization.Indeed, personally,Ihavealwaysfoundvulgarizationmoreconfusingand hardertounderstandthanrealexplanationswithsomeequations.

Leonard’scoursesgavemeaccesstoLagrangianclassicalmechanics,quantummechanics,andclassicalfieldtheorywithaclarity thatIhadneverknownbefore.Withhispedagogyandpresentationitbecomesapleasuretolearn.Ofcourse,itisallthemore truewhenthereisnoexaminationofanysortattheend.Butthe coursesandbooksturnedouttobeusefulforstudentsaswell,to prepareformoreadvancedandacademicstudies.

Sowhetheryouaresomeonewhoonlywantstohavesomereal understandingofwhatgeneralrelativityisabout–thestuffon gravitationthatisgeometry,massesthatbendspace,light,and time,blackholesouttherethatyoushouldavoidfallinginto,gravitywavesthatwebegintodetect,etc.–oryouareastudentin physicswhowantstohaveafirstpresentationofgeneralrelativity, thisbookisforyou.

Andr´eCabannes Saint-Cyr-sur-mer, FrenchRiviera

Fall2022

Lecture1:EquivalencePrinciple andTensorAnalysis

Andy: SoifIaminanelevatorandIfeelreallyheavy,Ican’t knowwhethertheelevatorisacceleratingoryoumischievouslyput meonJupiter?

Lenny: That’sright,youcan’t.

Andy: But,atleastonJupiter,ifIkeepstill,lightrayswon’t bend.

Lenny: Ohyestheywill.

Andy: Hmm,Isee.

Lenny: Andifyouarefallingintoablackhole,beware,thingswill getreallystrange.But,don’tworry,I’llshedsomelightonthis.

Andy: Er,bentorstraight?

Introduction

Equivalenceprinciple

Acceleratedreferenceframes

Curvilinearcoordinatetransformations

Effectofgravityonlight

Tidalforces

Non-Euclideangeometry

Riemanniangeometry

Metrictensor

Mathematicalinterlude:Dummyvariables

Mathematicalinterlude:Einsteinsummationconvention

Firsttensorrule:Contravariantcomponentsofvectors

Mathematicalinterlude:Vectorsandtensors

Secondtensorrule:Covariantcomponentsofvectors

Covariantandcontravariantcomponentsofvectorsandtensors

Introduction

GeneralRelativity isthefourthvolumeinTheTheoreticalMinimum(TTM)series.Thefirstthreeweredevotedrespectively toclassicalmechanics,quantummechanics,andspecialrelativity andclassicalfieldtheory.ThefirstvolumelaidouttheLagrangian andHamiltoniandescriptionofphysicalphenomenaandtheprincipleofleastaction,whichisoneofthefundamentalprinciples underlyingallofphysics(seevolume3,lecture7onfundamental principlesandgaugeinvariance).Theywereusedinthefirstthree volumesandwillcontinueinthisandsubsequentones.

Physicsextensivelyusesmathematicsasitstoolboxtoconstruct formal,quantifiable,workabletheoriesofnaturalphenomena.The maintoolsweusedsofararetrigonometry,vectorspaces,and calculus,thatis,differentiationandintegration.Theyhavebeen explainedinvolume1aswellasinbriefrefreshersectionsinthe othervolumes.Weassumethatthereaderisfamiliarwiththese mathematicaltoolsandwiththephysicalideaspresentedinvolumes1and3.Thepresentvolume4,likevolumes1and3(but unlikevolume2),dealswithclassicalphysicsinthesensethatno quantumuncertaintyisinvolved.

Wealsobegantomakelightuseoftensorsinvolume3onspecial relativityandclassicalfieldtheory.Nowwithgeneralrelativity wearegoingtousethemextensively.Weshallstudythemindetail.Asthereaderremembers,tensorsgeneralizevectors.Justas vectorshavedifferentrepresentations,withdifferentsetsofnumbers(componentsofthevector)dependingonthebasisusedto chartthevectorspacetheyform,thisistrueoftensorsaswell. Thesametensorwillhavedifferentcomponentsindifferentcoordinatesystems.Therulestogofromonesetofcomponents toanotherwillplayafundamentalrole.Moreover,wewillwork mostlywith tensorfields ,whicharesetsoftensors,adifferent tensorattachedtoeachpointofaspace.Tensorswereinvented byRicci-CurbastroandLevi-Civita1 todevelopworkofGauss2

1 GregorioRicci-Curbastro(1853–1925)andhisstudentTullioLevi-Civita (1873–1941)wereItalianmathematicians.Theirmostimportantjointpaper is“M´ethodesdecalculdiff´erentielabsoluetleursapplications,”in MathematischeAnnalen 54(1900),pp.125–201.Theydidnotusetheword tensor, whichwasintroducedlaterbyotherpeople.

2 CarlFriedrichGauss(1777–1855),Germanmathematician.

oncurvatureofsurfacesandRiemann3 onnon-Euclideangeometry.Einstein4 madeextensiveuseoftensorstobuildhistheoryof generalrelativity.Healsomadeimportantcontributionstotheir usage:thestandardnotationforindicesandtheEinsteinsummationconvention.

In Savantset´ecrivains (1910),Poincar´e5 writesthat“inmathematicalsciences,agoodnotationhasthesamephilosophicalimportanceasagoodclassificationinnaturalsciences.”Inthisbook wewilltakecaretoalwaysusetheclearestandlightestnotation possible.

EquivalencePrinciple

Einstein’srevolutionarypapersof1905onspecialrelativitydeeply clarifiedandextendedideasthatseveralotherphysicistsandmathematicians–Lorentz,6 Poincar´e,andothers–hadbeenworking onforafewyears.Einsteininvestigatedtheconsequencesofthe factthatthelawsofphysics,inparticularthebehavioroflight, arethesameindifferentinertialreferenceframes.Hededuced fromthatanewexplanationoftheLorentztransformations,of therelativityoftime,oftheequivalenceofmassandenergy,etc.

After1905,Einsteinbegantothinkaboutextendingtheprinciple ofrelativitytoanykindofreferenceframes,framesthatmaybe acceleratingwithrespecttooneanother,notjustinertialframes. An inertialframe isonewhereNewton’slaws,relatingforcesand motions,havesimpleexpressions.Or,ifyoupreferamorevivid image,andyouknowhowtojuggle,itisaframeofreferencein whichyoucanjugglewithnoproblem–forinstanceinarailwaycarmovinguniformly,withoutjerksoraccelerationsofany sort.Aftertenyearsofeffortstobuildatheoryextendingthe principleofrelativitytoframeswithaccelerationandtakinginto accountgravitationinanovelway,Einsteinpublishedhiswork inNovember1915.Unlikespecialrelativity,whichtoppedoffthe workofmany,generalrelativityisessentiallytheworkofoneman.

3 BernhardRiemann(1826–1866),Germanmathematician.

4 AlbertEinstein(1879–1955),German,Swiss,Germanagain,andfinally Americanphysicist.

5 HenriPoincar´e(1854–1912),Frenchmathematician.

6 HendrikAntoonLorentz(1853–1928),Dutchphysicist.

Weshallstartourstudyofgeneralrelativityprettymuchwhere Einsteinstarted.ItwasapatterninEinstein’sthinkingtostart withareallysimpleelementaryfact,whichalmostachildcould understand,anddeducetheseincrediblyfar-reachingconsequences. Wethinkthatitisalsothebestwaytoteachit,tostartwiththe simplestthingsanddeducetheconsequences.

Soweshallbeginwiththe equivalenceprinciple.Whatisthe equivalenceprinciple?Itistheprinciplethatsaysthat gravity isinsomesensethesamethingasacceleration.Weshallexplain preciselywhatismeantbythat,andgiveexamplesofhowEinstein usedit.Fromthere,weshallaskourselves:whatkindofmathematicalstructuremustatheoryhavefortheequivalenceprinciple tobetrue?Whatkindofmathematicsmustweusetodescribeit?

Mostreadershaveprobablyheardthatgeneralrelativityisatheorynotonlyaboutgravitybutalsoaboutgeometry.Soitis interestingtostartatthebeginningandaskwhatisitthatled Einsteintosaythatgravityhassomethingtodowithgeometry. Whatdoesitmeantosaythat“gravityequalsacceleration”?You allknowthatifyouareinanacceleratedframeofreference,say, anelevatoracceleratingupwardordownward,youfeelaneffective gravitationalfield.Childrenknowthisbecausetheyfeelit.

Whatfollowsmaybeoverkill,butmakingsomemathematicsout ofthemotionofanelevatorisusefultoseeinaverysimpleexamplehowphysiciststransformanaturalphenomenonintomathematics,andthentoseehowthemathematicsisusedtomake predictionsaboutthephenomenon.

Beforeproceeding,let’sstressthatthefollowingstudyonanelevator,andthelawsofphysicsasperceivedinsideit,issimple.Yet itisafirstpresentationofveryimportantconcepts.Itisfundamentaltounderstanditverywell.Indeed,wewilloftenrefertoit. Inlectures4to9,itwillstronglyhelpusunderstandacceleration, gravitation,andhowgravitation“warps”space-time.

Solet’simaginetheEinsteinthoughtexperimentwheresomebody isinanelevator;seefigure1.Inlatertextbooks,itgotpromoted toarocketship.ButIhaveneverbeeninarocketship,whereas

1.EquivalencePrincipleandTensorAnalysis5

Ihavebeeninanelevator.SoIknowwhatitfeelslikewhenit acceleratesordecelerates.Let’ssaythattheelevatorismoving upwardwithavelocity v .

Sofartheproblemisone-dimensional.Weareonlyinterestedin theverticaldirection.Therearetworeferenceframes:oneisfixed withrespecttoEarth.Itusesthecoordinate z .Theotherisfixed withrespecttotheelevator.Itusesthecoordinate z ′ .Apoint P anywherealongtheverticalaxishastwocoordinates:coordinate z inthestationaryframe,andcoordinate z ′ intheelevatorframe. Forinstance,theflooroftheelevatorhascoordinate z ′ =0.Its z -coordinateisthedistance L,whichisobviouslyafunctionof time.Sowecanwriteforanypoint P

Wearegoingtobeinterestedinthefollowingquestion:ifweknow thelawsofphysicsintheframe z ,whataretheyintheframe z ′

Onewarningaboutthislecture:atleastatthestart,wearegoing toignorespecialrelativity.Thisistantamounttosayingthat wearepretendingthatthespeedoflightisinfinite,orthatwe aretalkingaboutmotionssoslowthatthespeedoflightcanbe regardedasinfinitelyfast.Youmightwonder:ifgeneralrelativity isthegeneralizationofspecialrelativity,howdidEinsteinmanage tostartthinkingaboutgeneralrelativitywithoutincludingspecial relativity?

Figure1:Elevatorandtworeferenceframes.

Theansweristhatspecialrelativityhastodowithveryhighvelocities,whilegravityhastodowithheavymasses.Thereisa rangeofsituationswheregravityisimportantbuthighvelocities arenot.SoEinsteinstartedoutthinkingaboutgravityforslow velocities,andonlylatercombineditwithspecialrelativityto thinkaboutthecombinationoffastvelocitiesandgravity.And thatbecamethegeneraltheory.

Let’sseewhatweknowforslowvelocities.Supposethat z ′ and z arebothinertialreferenceframes.Thatmeans,amongother things,thattheyarerelatedbyuniformvelocity:

Wehavechosenthecoordinatessuchthatwhen t =0,theyline up.At t =0,foranypoint, z and z ′ areequal.Forinstance,at t =0theelevator’sfloorhascoordinate0inbothframes.Then thefloorstartsrising,itsheight z equaling vt.Soforanypoint wecanwriteequation(1).Inviewofequation(2),itbecomes

Noticethatthisisa coordinatetransformation involvingspace andtime.Forreaderswhoarefamiliarwithvolume3ofTTMon specialrelativity,thisnaturallyraisesthequestion:whatabout timeinthereferenceframeoftheelevator?Ifwearegoingto forgetspecialrelativity,thenwecanjustsaythat t′ and t arethe samething.Wedon’thavetothinkaboutLorentztransformationsandtheirconsequences.Sotheotherhalfofthecoordinate transformationwouldbe t′ = t.

Wecouldalsoaddtothestationaryframeacoordinate x going horizontallyandacoordinate y juttingoutofthepage.Correspondingly,coordinates x′ and y ′ couldbeattachedtotheelevator;seefigure2.The x-coordinatewillplayaroleinamoment withalightbeam.Aslongastheelevatorisnotslidinghorizontally, x′ and x canbetakentobeequal.Samefor y ′ and y .

Forthesakeofclarityofthedrawinginfigure2,weoffsetabitthe elevatortotherightofthe z -axis.Butthinkofthetwovertical axesasactuallyslidingoneachother,andat t =0thetwoorigins O and O ′ coincide.Onceagain,theelevatormovesonlyvertically.

1.EquivalencePrincipleandTensorAnalysis7

Finallyourcompletecoordinatetransformationis

(4)

Itisacoordinatetransformationofspace-timecoordinates.For anypoint P inspace-time,itexpressesitscoordinatesinthemovingreferenceframeoftheelevatorasfunctionsofitscoordinates inthestationaryframe.Itisrathertrivial.Onlyonecoordinate, namely z ,isinvolvedinaninterestingway.

Letuslookatalawofphysicsexpressedinthestationaryframe. TakeNewton’slawofmotion F = ma appliedtoanobjectora particle.Theacceleration a is¨ z ,where z istheverticalcoordinate oftheparticle.Sowecanwrite

(5)

Asweknow,¨ z isthesecondtimederivativeof z withrespectto time–itiscalledtheverticalacceleration–and F ofcourseis theverticalcomponentofforce.Theothercomponentswewill taketobezero.Whateverforceisexerted,itisexertedvertically.Whatcouldthisforcebedueto?Itcouldberelatedto theelevatorornot.Therecouldbesomechargeintheelevator pushingontheparticle.Oritcouldjustbeaforceduetoarope

Figure2:Elevatorandtworeferenceframes,threeaxesineachcase.

attachedtotheceilingandtotheparticlethatpullsonit.There couldbeafieldforcealongtheverticalaxis.Anykindofforce couldbeactingontheparticle.Whateverthecauses,weknow fromNewton’slawthattheequationofmotionoftheparticle,expressedintheoriginalframeofreference,isgivenbyequation(5).

Whatistheequationofmotionexpressedintheprimedframe? Thisisveryeasy.Allwehavetodoisfigureoutwhattheoriginal accelerationisintermsoftheprimedacceleration.Whatisthe primedacceleration?Itisthesecondderivativewithrespectto timeof z ′ .Usingthefirstequationinequations(4)

onedifferentiationgives

andasecondonegives

Theaccelerationsinthetwoframesofreferencearethesame.

Allthisshouldbefamiliar.ButIwanttoformalizeittobringout somepoints.Inparticular,Iwanttostressthat wearedoinga coordinatetransformation.Weareaskinghowthelawsofphysics changeingoingfromoneframetoanother.Whatcanwenow sayaboutNewton’slawintheprimedframeofreference?We substitute z ′ for¨ z inequation(5).Astheyareequal,weget

WefoundthatNewton’slawintheprimedframeisexactlythe sameasNewton’slawintheunprimedframe.Thatisnotsurprising.Thetwoframesofreferencearemovingwithuniform velocityrelativetoeachother.Ifoneofthemisaninertialframe, theotherisaninertialframe.Newtontaughtusthatthelawsof physicsarethesameinallinertialframes.Itissometimescalled the Galileanprincipleofrelativity .Wejustformalizedit.

Let’sturntoanacceleratedreferenceframe.

1.EquivalencePrincipleandTensorAnalysis9

AcceleratedReferenceFrames

Supposethat L(t)fromfigure1isincreasinginanaccelerated way.Theheightoftheelevator’sfloorisnowgivenby

Weusetheletter g fortheaccelerationbecausewewilldiscover thattheaccelerationmimicsagravitationalfield–aswefeelwhen wetakeanelevatoranditaccelerates.Weknowfromvolume1 ofTTMonclassicalmechanicsorfromhighschool,thatthisisa uniformacceleration.Indeed,ifwedifferentiate L(t)withrespect totime,afteronedifferentiationweget

whichmeansthatthevelocityoftheelevatorincreaseslinearly withtime.Afteraseconddifferentiationwithrespecttotime, weget

Thismeansthattheaccelerationoftheelevatorisconstant.The elevatorisuniformlyacceleratedupward.Theequationsconnectingtheprimedandunprimedcoordinatesaredifferentfromequations(4).Thetransformationfortheverticalcoordinatesisnow

Theotherequationsinequations(4)don’tchange:

Thesefourequationsareournewcoordinatetransformationto representtherelationshipbetweencoordinatesthatareacceleratedrelativetoeachother.

Wewillcontinuetoassumethatinthe z ,orunprimed,coordinate system,thelawsofphysicsareexactlywhatNewtontaughtus. Inotherwords,thestationaryreferenceframeisinertial,andwe

have F = m ¨ z .Buttheprimedframeisnolongerinertial.Itis inuniformaccelerationrelativetotheunprimedframe.Let’sask whatthelawsofphysicsarenowintheprimedframeofreference. Wehavetodotheoperationofdifferentiatingtwiceoveragainon equation(8).Weknowtheanswer:

Ahha!Nowtheprimedaccelerationandtheunprimedaccelerationdifferbyanamount g .TowriteNewton’sequationsinthe primedframeofreference,wemultiplybothsidesofequation(9) by m,theparticlemass,andwereplace mz by F .Weget

Wehavearrivedatwhatwewanted.Equation(10)lookslikea Newtonequation,thatis,masstimesaccelerationisequaltosome term.Thatterm, F mg ,wecalltheforceintheprimedframe ofreference.Younotice,asexpected,thattheforceintheprimed frameofreferencehasanextraterm:themassoftheparticle timestheaccelerationoftheelevator,withaminussign.

Whatisinterestingaboutthe“fictitiousforce” mg ,inequation(10),isthatitlooksexactlyliketheforceexertedonthe particlebygravityonthesurfaceoftheEarthorthesurfaceof anykindoflargemassivebody.Thatiswhywecalledtheacceleration g .Theletter g stoodforgravity.Itlookslikeauniform gravitationalfield.Letmespelloutinwhatsenseitlookslike gravity.Thespecialfeatureofgravityisthatgravitationalforces areproportionaltomass–thesamemassthatappearsinNewton’sequationofmotion.Wesometimessaythat thegravitational massisthesameastheinertialmass.Thathasdeepimplications. Iftheequationofmotionis

andtheforceitselfisproportionaltomass,thenthemasscancels inequation(11).Thatisacharacteristicofgravitationalforces: forasmallobjectmovinginagravitationalforcefield,itsmotiondoesn’tdependonitsmass.Anexampleisthemotionof theEarthabouttheSun.Itisindependentofthemassofthe Earth.IfyouknowwheretheEarthisattime t,andyouknow

itsvelocityatthattime,thenyoucanpredictitstrajectory.You don’tneedtoknowwhattheEarth’smassis.

Equation(10)isanexampleof fictitiousforce –ifyouwantto callitthat–mimickingtheeffectofgravity.Mostpeoplebefore Einsteinconsideredthislargelyanaccident.Theycertainlyknew thattheeffectofaccelerationmimicstheeffectofgravity,butthey didn’tpaymuchattentiontoit.ItwasEinsteinwhosaid:look, thisisadeepprincipleofnaturethatgravitationalforcescannot bedistinguishedfromtheeffectofanacceleratedreferenceframe.

Ifyouareinanelevatorwithoutwindowsandyoufeelthatyour bodyhassomeweight,youcannotsaywhethertheelevator,with youinside,isrestingonthesurfaceofaplanetor,farawayfrom anymassivebodyintheuniverse,someimpishdevilisacceleratingyourelevator.Thatisthe equivalenceprinciple.Itextends therelativityprinciple,whichsaidyoucanjuggleinthesameway atrestorinarailwaycarinuniformmotion.Withasimpleexample,wehaveequatedacceleratedmotionandgravity.Wehave beguntoexplainwhatismeantbythesentence:“gravityisin somesensethesamethingasacceleration.”

Wehavetodiscussthisresultabit,though.Dowereallybelieve ittotallyordoesithavetobequalified?Beforewedothat,let’s drawsomepicturesofwhatthesevariouscoordinatetransformationslooklike.

CurvilinearCoordinateTransformations

Let’sfirstconsiderthecasewhere L(t)isproportionalto t.That iswhenwehave

Infigure3,everypoint–alsocalled event –inspace-timehasa pairofcoordinates z and t inthestationaryframeandalsoapair ofcoordinates z ′ and t′ intheelevatorframe.Ofcourse, t′ = t andweleftoutthetwootherspatialcoordinates x and y ,which don’tchangebetweenthestationaryframeandtheelevator.We representedthetimetrajectoriesoffixed z withdottedlinesand offixed z ′ withsolidlines.

GeneralRelativity

Afundamentalideatograspisthateventsinspace-timeexistirrespectiveoftheircoordinates,justaspointsinspacedon’tdepend onthemapweuse.Coordinatesarejustsomesortofconvenient tags.Wecanusewhicheverwelike.We’llstressitagainafterwe havelookedatfigures3and4.

Figure3:Linearcoordinatetransformation.Thecoordinates(z ′ ,t′ ) arerepresentedinthebasiccoordinates(z,t).Aneventisapointon thepage.Ithasonesetofcoordinatesinthe(z,t)frameandanother setinthe(z ′ ,t′ )frame.Herethetransformationissimpleandlinear.

Thatiscalleda linearcoordinatetransformation betweenthetwo framesofreference.Straightlinesgotostraightlines,notsurprisinglysinceNewtontellsusthatfreeparticlesmoveinstraight linesinaninertialframeofreference.Whatisastraightline inoneframehadthereforebetterbeastraightlineintheother frame.Notonlydofreeparticlesmoveinstraightlinesinspace, whenweadd x and y ,buttheirtrajectoriesarestraightlinesin space-time–straightinspaceandwithuniformvelocity.

Let’sdothesamethingfortheacceleratedcoordinatesystem.The transformationequationisnowequation(8)linking z ′ and z .The othercoordinatesdon’tchange.Again,infigure4,everypointin space-timehastwopairsofcoordinates(z,t)and(z ′ ,t′ ).The timetrajectoriesoffixed z ,representedwithdottedlines,don’t change.Butnowthetimetrajectoriesoffixed z ′ areparabolas lyingontheirside.Wecanevenrepresentnegativetimesinthe past.Thinkoftheelevatorthatwasinitiallymovingdownward withanegativevelocitybutapositiveacceleration g (inother words,slowingdown).Thentheelevatorbouncesbackupward

1.EquivalencePrincipleandTensorAnalysis13

withthesameacceleration g .Eachparabolaisjustshiftedrelative tothepreviousonebyoneunittotheright.

Whatfigure4illustratesis,notsurprisingly,thatstraightlinesin oneframearenotstraightlinesintheotherframe.Theybecome curvedlines.Asregardsthelinesoffixed t orfixed t′ ,theyare ofcoursethesamehorizontalstraightlinesinbothframes.We haven’trepresentedthem.

Weshouldviewfigure4asjusttwosetsofcoordinatestolocate eachpointinspace-time.Onesetofcoordinateshasstraightaxes, whilethesecond–representedinthefirstframe–iscurvilinear. Itslines z ′ =constantareactuallycurves,whileitslines t′ =constantarehorizontalstraightlines.Soitisa curvilinearcoordinate transformation.

Let’sinsistonthewaytointerpretandusefigure4becauseitis fundamentaltounderstanditverywellifwewanttounderstand thetheoryofrelativity–specialrelativityandevenmoreimportantlygeneralrelativity.Thepagerepresentsspace-time–here, onespatialdimensionandonetemporaldimension.

Points(=events)inspace-timearepointsonthepage.Anevent doesnothavetwopositions onthepage,i.e.,inspace-time. Ithas

Figure4:Curvilinearcoordinatetransformation.

onlyoneposition onthepage.Butthispositioncanbelocated, mapped,“charted”onealsosays,usingseveraldifferentsystemsofreference.Asystemofreference,alsocalledaframeofreference,is nothingmorethanacompletesetof“labels,”ifyouwill,attachingonelabel(consistingoftwonumbers,becauseourspace-time hereistwo-dimensional)toeachpoint,i.e.,toeachevent.

Inatwo-dimensionalspace,thesystemofreferencecanbegeometricallysimple,likeorthogonalCartesianaxesintheplane. Howeverthisisnotanecessity.Foronething,onEarth,whichis notaplane,theaxesarenotstraightlines.Theusualaxesused bycartographersandmarinersaremeridiansandparallels.But ona2Dsurface,beitaplaneornot,wecanimaginequitefancyor intricatecurvilinearlinestoserveasaframeofreference–solong asitattachesunequivocallytwonumberstoeach(bydefinition, fixed)point.Thisiswhatfigure4doesinthespace-timemadeof onetemporalandonespatialdimensionrepresentedonthepage. Wewillseemanymoreinlecture2.

SomethingEinsteinunderstoodveryearlyisthis:

Thereisaconnectionbetweengravityandcurvilinearcoordinate transformationsofspace-time.

Specialrelativitywasonlyaboutlineartransformations–transformationsthattakeuniformvelocitytouniformvelocity.Lorentz transformationsareofthatnature.Theytakestraightlinesin space-timetostraightlinesinspace-time.However,ifwewantto mockupgravitationalfieldswiththeeffectofacceleration,weare reallytalkingabouttransformationsofcoordinatesofspace-time thatarecurvilinear.Thatsoundsextremelytrivial.WhenEinsteinsaidit,probablyeveryphysicistknewitandthought:“Oh yeah,nobigdeal.”ButEinsteinwasverycleverandverypersistent.Herealizedthatifhefollowedveryfartheconsequences ofthis,hecouldthenanswerquestionsthatnobodyknewhowto answer.

Let’slookatasimpleexampleofaquestionthatEinsteinansweredusingthecurvedcoordinatesofspace-timerepresenting acceleration,andconsequently,ifthetwoarethesame,gravity. Thequestionis:whatistheinfluenceofgravityonlight?

1.EquivalencePrincipleandTensorAnalysis15

EffectofGravityonLight

WhenEinsteinfirstaskedhimselfthequestion“whatistheinfluenceofgravityonlight”?around1907,mostphysicistswould haveanswered:“Thereisnoeffectofgravityonlight.Lightis light.Gravityisgravity.Alightwavemovingnearamassive objectmovesinastraightline.Itisalawoflightthatitmoves instraightlines.Andthereisnoreasontothinkthatgravityhas anyeffectonit.”

ButEinsteinsaid:“No,ifthisequivalenceprinciplebetweenaccelerationandgravityistrue,thengravitymustaffectlight.Why? Becauseaccelerationaffectslight.”Itwasagainoneoftheseargumentsthatyoucouldexplaintoacleverchild.

Let’simaginethat,at t =0,aflashlight(todaywemightusea laserpointer)emitsapulseoflightinahorizontaldirectionfrom theleftsideoftheelevator;seefigure5.Thelightthentravels acrosstotherightsidewiththeusualspeedoflight c.Since thestationaryframeisassumedtobeaninertialframe,thelight movesinastraightlineinthestationaryframe.

Thefirstoftheseequationsjustsaysthatthelightmovesacross theelevatorwiththespeedoflight–nosurprisehere.

Figure5:Trajectoryofalightbeaminthe stationary referenceframe.

Thesecondsaysthatinthestationaryframethetrajectoryofthe lightbeamishorizontal.

Let’sexpressthesameequationsintermsoftheprimedcoordinates.Thefirstequationbecomes

Andthesecondtakesthemoreinterestingform

Itsaysthatasthelightraymovesacrosstheelevator,atthesame timethelightrayacceleratesdownward–towardthefloor–just asifgravitywerepullingit.

Wecaneveneliminate t fromthetwoequationsandgetanequationforthecurvedtrajectoryofthelightray:

Thus,thetrajectory,intheprimedframeofreference,isaparabola, notastraightline.

But,saidEinstein,iftheeffectofaccelerationistobendthetrajectoryofalightray,thensomustbetheeffectofgravity.

Andy: GeeLenny,that’sreallysimple.Isthatallthereistoit?

Lenny: YupAndy,that’sallthereistoit.Andyoucanbetthata lotofphysicistswerekickingthemselvesfornotthinkingofit.

Tosummarize,inthestationaryframe,thephotontrajectory(figure5)isastraightline,whileintheelevatorreferenceframe,it isaparabola(figure6).

Let’simaginethreepeoplearguing.Iamintheelevator,andI say:“Gravityispullingthelightbeamdown.”Youareinthe stationaryframe,andyousay:“No,it’sjustthattheelevatoris acceleratingupward;thatmakesitlooklikethelightbeammoves onacurvedtrajectory.”AndEinsteinsays:“Theyarethesame thing!”

Thisprovedtohimthatagravitationalfieldmustbendalight ray.AsfarasIknow,nootherphysicistunderstoodthisatthe time.

Inconclusion,wehavelearnedthatitisusefultothinkabout curvilinearcoordinatetransformationsinspace-time.

Whenwedothinkaboutcurvilinearcoordinatestransformations, theformofNewton’slawschanges.Oneofthethingsthathappen isthatapparentgravitationalfieldsmaterialize,whicharephysicallyindistinguishablefromordinarygravitationalfields.

Well,aretheyreallyphysicallyindistinguishable?Forsomepurposesyes,butnotforall.Solet’sturnnowtorealgravitational fields,namelygravitationalfieldsofgravitatingobjectslikethe SunortheEarth.

TidalForces

Figure7representstheEarth,ortheSun,oranymassivebody. Thegravitationalaccelerationdoesn’tpointverticallyonthepage. Itpointstowardthecenterofthebody.

Itisprettyobviousthatthereisnowaythatyoucoulddoa coordinatetransformationlikewedidintheprecedingsection thatwouldremovetheeffectofthegravitationalfield.Yet,ifyou

Figure6:Trajectoryofalightbeaminthe elevator referenceframe.

areinasmalllaboratoryinspaceandthatlaboratoryisallowed tosimplyfalltowardEarth,ortowardwhatevermassiveobject youareconsidering,thenyouwillthinkthatinthatlaboratory thereisnogravitationalfield.

Figure7:Gravitationalfieldofamassiveobject,andsmalllaboratory fallingtowardtheobject,experiencinginsideitselfnogravitation.

Exercise1:Ifwearefallingfreelyinauniformgravitationalfield,provethatwefeelnogravityandthatthings floatarounduslikeintheInternationalSpaceStation.

But,again,thereisnoway globally tointroduceacoordinate transformationthatisgoingtogetridofthefactthatthereis agravitationalfieldpointingtowardthecenter.Forinstance,a verysimpletransformationsimilartoequations(12)mightgetrid ofthegravityinasmallportionononesideoftheEarth,butthe sametransformationwillincreasethegravitationalfieldonthe otherside.Evenmorecomplextransformationswouldnotsolve theproblem.

Onewaytounderstandwhywecan’tgetridofgravityistothink ofanobjectthatisnotsmallcomparedtothegravitationalfield. Myfavoriteexampleisa2000-milemanwhoisfallinginthe Earth’sgravitationalfield;seefigure8.Becauseheissobig,differentpartsofhisbodyfeeldifferentgravitationalfields.Remember thatthefartherawayyouare,theweakeristhegravitationalfield.

1.EquivalencePrincipleandTensorAnalysis19

Hisheadfeelsaweakergravitythanhisfeet.Hisfeetarebeing pulledharderthanhishead.Hefeelslikeheisbeingstretched, andthatstretchingsensationtellshimthatthereisagravitating objectnearby.Thesenseofdiscomfortthathefeels,duetothe nonuniformgravitationalfield,cannotberemovedbyswitchingto afree-fallingreferenceframe.Indeed,nochangeofmathematical descriptionwhatsoevercanchangethisphysicalphenomenon.

Theforceshefeelsarecalled tidalforces,becausetheyplayan importantroleinthephenomenonoftides,too.Theycannot beremovedbyacoordinatetransformation.Let’salsoseewhat happensifheisfallingnotverticallybutsideways,stayingperpendiculartoaradius.Inthatcasehisheadandhisfeetwillbe atthesamedistancefromEarth.Bothwillbesubjectedtothe sameforceinmagnitudepointingtoEarth.Butsincetheforce directionsareradial,theyarenotparallel.Theforceonhishead andtheforceonhisfeetwillbothhaveacomponentalonghis body.Amoment’sthoughtwillconvinceusthatthetidalforces willcompresshim,hisfeetandheadbeingpushedtowardeach other.Thissenseofcompressionisagainnotsomethingthatwe canremovebyacoordinatetransformation.Beingstretchedor shrunk,orboth,bytheEarth’sgravitationalfield–ifyouarebig enough–isaninvariantfact.

Insummary,itisnotquitetruethatgravityisequivalenttogoing toanacceleratedreferenceframe.

Figure8:A2000-milemanfallingtowardEarth.

2 000 -m ile ma

Andy: Aha!SoEinsteinwaswrongafterall.

Lenny: Well,Einsteinwaswrongattimes,butno,Andy,thiswas notoneofthosetimes.Hejusthadtoqualifyhisstatementand makeitabitmoreprecise.

WhatEinsteinreallymeantwasthatsmallobjects,forasmall lengthoftime,cannottellthedifferencebetweenagravitational fieldandanacceleratedframeofreference.

Itraisesthefollowingquestion:ifIpresentyouwithaforcefield, doesthereexistacoordinatetransformationthatwillmakeit vanish?Forexample,theforcefieldinsidetheelevator,associatedwithitsuniformaccelerationwithrespecttoaninertial referenceframe,wasjustaverticalforcefieldpointingdownward anduniformeverywhere.Therewasatransformationcanceling it:simplyuse z -insteadof z ′ -coordinates.Itisanonlinearcoordinatetransformation.Nevertheless,itgetsridoftheforcefield.

Withotherkindsofcoordinatetransformations,youcanmake thegravitationalfieldlookmorecomplicated,forexampletransformationsthataffectalsothe x-coordinate.Theycanmakethe gravitationalfieldbendtowardthe x-axis.Youmightsimultaneouslyacceleratealongthe z -axiswhileoscillatingbackandforth onthe x-axis.Whatkindofgravitationalfielddoyousee?A verycomplicatedone:ithasaverticalcomponentandithasa time-dependentoscillatingcomponentalongthe x-axis.

Ifinsteadoftheelevatoryouuseamerry-go-round,thatis,a carousel,andinsteadofthe(x′ ,z ′ ,t)coordinatesoftheelevator, youusepolarcoordinates(r,θ,t),anobjectthatinthestationaryframewasfixed,orhadasimplemotionlikethelightbeam, mayhaveaweirdmotionintheframemovingwiththemerry-goround.Youmaythinkthatyouhavediscoveredsomerepulsive gravitationalfieldphenomenon.Butnomatterwhat,thereverse coordinatechangewillrevealthatyourapparentlymessyfieldis onlytheconsequenceofacoordinatechange.Bychoosingfunny coordinatetransformations,youcancreatesomeprettycomplicatedfictitious,apparent,alsocalled effective,gravitationalfields. Nonethelesstheyarenotgenuine,inthesensethattheydon’tresultfromthepresenceofmassiveobjects.

IfIgiveyouthefieldeverywhere,howdoyoudeterminewhether itisfictitiousorgenuine,i.e.,whetheritisjustthesortoffake gravitationalfieldresultingfromacoordinatetransformationto aframewithallkindsofaccelerationswithrespecttoasimple inertialone,oritisarealgravitationalfield?

IfwearetalkingaboutNewtoniangravity,thereisaneasyway. Youjustcalculatethetidalforces.Youdeterminewhetherthat gravitationalfieldwillhaveaneffectonanobjectthatwillcause ittosqueezeandstretch.Ifcalculationsarenotpractical,you takeanobject,amass,acrystal.Youletitfallfreelyandsee whethertherewerestressesandstrainsonit.Ifthecrystalisbig enough,thesewillbedetectablephenomena.Ifsuchstressesand strainsaredetected,thenitisarealgravitationalfieldasopposed toonlyafictitiousone.

Ontheotherhand,ifyoudiscoverthatthegravitationalfield hasnosucheffect,thatanyobject,whereveritislocatedandlet freelytomove,experiencesnotidalforce–inotherwords,that thefieldhasnotendencytodistortafree-fallingsystem–then itisafieldthatcanbeeliminatedbyacoordinatetransformation.

Einsteinaskedhimselfthequestion:whatkindofmathematics goesintotryingtoanswerthequestionofwhetherafieldisa genuinegravitationaloneornot?

Non-EuclideanGeometry

Afterhisworkonspecialrelativity,andafterlearningofthemathematicalstructureinwhichMinkowski7 hadrecastit,Einstein knewthatspecialrelativityhadageometryassociatedwithit.So let’stakeabriefrestfromgravitytoremindourselvesofthisimportantideainspecialrelativity.Specialrelativitywasthemain subjectofthethirdvolumeofTTM.Here,however,theonlything wearegoingtouseaboutspecialrelativityisthatspace-timehas ageometry.

7 HermannMinkowski(1864–1909),Polish-Germanmathematicianand theoreticalphysicist.

IntheMinkowskigeometryofspecialrelativity,thereexistsa kindofdistancebetweentwopoints,thatis,betweentwoevents inspace-time;seefigure9.

Thedistancebetween P and Q isnottheusualEuclideandistance thatwecouldbetemptedtothinkof.Itisdefinedasfollows.Let’s call∆X the4-vectorgoingfrom P to Q.Tothepairofpoints P and Q weassignaquantitydenoted∆τ ,definedby

Noticethat∆τ doesnotsatisfytheusualpropertiesofadistance. Inparticular,∆τ 2 canbepositiveornegative;anditcanbezero fortwoeventsthatarenotidentical.Thereaderisreferredto volume3ofTTMfordetails.Hereweonlygiveabriefrefresher.

Thequantity∆τ iscalledthe propertime between P and Q.Itis aninvariantunderLorentztransformations.Thatiswhyitqualifiesasasortofdistance,justasinthree-dimensional(3D)Euclideanspacethedistancebetweentwopoints,∆x2 +∆y 2 +∆z 2 , isinvariantunderisometries.

Wealsodefineaquantity∆

Wecall∆s the properdistance between P and Q.Ofcourse,∆τ and∆s arenottwodifferentconcepts.Theyarethesame–just differingbyanimaginaryfactor i.Theyarejusttwowaystotalk

Figure9:Minkowskigeometry:a4-vectorgoingfrom P to Q.

1.EquivalencePrincipleandTensorAnalysis23

abouttheMinkowski“distance”between P and Q.Dependingon whichphysicistiswritingtheequations,theywillratheruse∆τ or∆s asthedistancebetween P and Q.

Einsteinknewaboutthisnon-Euclideangeometryofspecialrelativity.Inhisworktoincludegravity,andtoinvestigatetheconsequencesoftheequivalenceprinciple,healsorealizedthatthe questionweaskedattheendoftheprevioussection–arethere coordinatetransformationsthatcanremovetheeffectofforces?–wasverysimilartoacertainmathematicsproblemthathadbeen studiedatgreatlengthbyRiemann.Itisthequestionofdeciding whetherageometryisflatornot.

RiemannianGeometry

Whatisaflatgeometry?Intuitively,itisthefollowingidea:the geometryofapageisflat.Thegeometryofthesurfaceofasphere orasectionofasphereisnotflat.The intrinsicgeometry ofthe pageremainsflatevenifwefurlthepagelikeinfigure10.We willexpoundmathematicallyontheideainamoment.

Fornow,let’sjustsaythattheintrinsicgeometryofasurfaceis thegeometrythatatwo-dimensionalbugroamingonit,equipped withtinysurveyingtools,wouldseeifitweretryingtoestablish anordnancesurveymapofthesurface.

Ifthebugworkedcarefully,itmightseehillsandvalleys,bumps andtroughs,iftherewereany,butitwouldnotnoticethatthe

Figure10:Theintrinsicgeometryofapageremainsflat.

pageisfurled.Weseeitbecause forus thepageisembeddedin the3DEuclideanspacewelivein.Byunfurlingthepage,wecan makeitsflatnessobviousagain.

Einsteinrealizedthattherewasagreatdealofsimilarityinthetwo questionsofwhetherageometryisnon-flatandwhetheraspacetimehasarealgravitationalfieldinit.Riemannhadstudiedthe firstquestion.ButRiemannhadneverdreamtaboutgeometries thathaveaminussigninthedefinitionofthesquareofthedistance.Hewasthinkingaboutgeometriesthatwerenon-Euclidean butweresimilartoEuclideangeometry–notMinkowskigeometry.

Let’sstartwiththemathematicsofRiemanniangeometry,that is,ofspaceswherethedistancebetweentwopointsmaynotbe theEuclideandistance,butinwhichthesquareofthedistanceis alwayspositive.8

Welookattwopointsinaspace;seefigure11.Inourexample therearethreedimensions,thereforethreeaxes, X 1 , X 2 ,and X 3 . Therecouldbemore.Thusapointhasthreecoordinates,which wecanwriteas X m ,where m isunderstoodtorunfrom1to3 ortowhatevernumberofaxesthereis.Andalittleshiftbetween onepointandanothernearbyhasthreecomponents,whichcan bedenoted∆X m or,ifitistobecomeaninfinitesimal, dX m

Figure11:Smalldisplacementbetweentwopointsinaspace.

8 Inmathematics,theyarecalled positivedefinitedistances.

1.EquivalencePrincipleandTensorAnalysis25

IfthisspacehastheusualEuclideangeometry,thesquareofthe lengthof dX m isgivenbyPythagorastheorem

Ifweareinthreedimensions,thentherearethreetermsinthe sum.Ifweareintwodimensions,therearetwoterms.Ifthespace is26-dimensional,thereare26ofthemandsoforth.Thatisthe formulaforEuclideandistancebetweentwopointsinEuclidean space.

Forsimplicityandeaseofvisualization,let’sfocusonatwodimensionalspace.Itcanbetheordinaryplane,oritcanbe atwo-dimensionalsurfacethatwemayvisualizeembeddedin3D Euclideanspace,asinfigure12.

Figure12:Two-dimensionalmanifold(i.e.,2Dsurface)anditscurvilinearcoordinatesviewedembeddedinordinary3Deuclideanspace.

Thereisnothingspecialabouttwodimensionsforsuchasurface, exceptthatitiseasytovisualize.Mathematiciansthinkof“surfaces”evenwhentheyhavemoredimensions.Usuallytheydon’t callthemsurfacesbut manifolds orsometimes varieties

Gausshadalreadyunderstoodthatoncurvedsurfacestheformula forthedistancebetweentwopointswasmorecomplicatedingeneralthanequation(14).Indeed,wemustnotbeconfusedbythe factthatinfigure12thesurfaceisshownembeddedintheusual three-dimensionalEuclideanspace.Thisisjustforconvenience