RELAZIONI E FUNZIONI
12 Quando Paolo va in bicicletta parte da casa, arriva fino al circuito, fa un certo numero di giri e poi torna a casa seguendo lo stesso percorso dell’andata. Sapendo che il circuito è lungo 400 m e che la casa di Paolo dista 700 m dal circuito, qual è la formula che permette di stabilire quanti metri ha percorso Paolo (d) in funzione del numero di giri (n) del circuito?
A d = 400 + 700 $ n
B d = 700 + 400 n
C d = 1300 $ n
XD d = 1400 + 400 n
COSA RICORDARE Interpretare e cos truire for mule che contengono let tere per esprimere rel azioni tra due grandezze.
COSA CONSIDERARE La distanza che dipende dal numero di gir i del circuito; la dis tanza tot ale percorsa per raggiungere il circuito e tornare a casa.
COME PROCEDERE Il circuito ha una lunghezza di 400 m e se Paolo fa n giri, percorre 40 0 $ n metri. Inoltre Paolo percorre due volte la str ada da cas a al circuito (una volta all’andata e una al ritorno): il doppio di 700 m è 140 0 m. Sommando i due valori si ottiene la for mula che esprime la dis tanza percorsa da Paolo in funzione del numero di gir i: d = 1400 + 400 n La risposta esatta è quindi la D.
13 Jury costruisce una serie di quadrati sempre più grandi con i fiammiferi:
Ha usato 4 fiammiferi per il primo quadrato, 12 per il secondo, 24 per il terzo, 40 per il quarto. Quanti fiammiferi userà per il decimo quadrato?
220
Risposta: fiammiferi.
COSA RICORDARE Riconoscere regolarità in una sequenza di numeri o di figure.
COSA CONSIDERARE Come sarà for mata la decima figura; espressioni che per mettono di calcolare il numero di fiammiferi senza cont arli uno a uno; quanti fiammiferi avrà per fil a; su quante file saranno disposti.
COME PROCEDERE Osserva come è costruito il ter zo quadrato: è formato da file di 3 fiammiferi, 4 file verticali e 4 orizzontali per un totale di 8 file. Il quarto quadrato è formato invece da 5 file orizzontali e 5 verticali di 4 fiammiferi ciascuna. Il decimo quadrato avrà dunque 10 fiammiferi per fila e sarà composto da 11 file verticali e 11 orizzontali per un totale di 22 file. Da cui n = 22 $ 10 = 220 fiammiferi.
27 ALLENAMENTO GUIDATO
14 Karima e Nicola corrono spesso lungo la spiaggia. Sotto è riportato il grafico che rappresenta la distanza percorsa dai due amici lo scorso venerdì in funzione del tempo.
In base al grafico riportato indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Karima è più veloce di Nicola.
b. Per percorrere 3 km Nicola ha impiegato 25 minuti.
c. Alle 16:15 i due amici avevano percorso la stessa distanza.
d. Nicola è partito quando Karima aveva già percorso 1,5 km.
COSA RICORDARE Interpretare e rappresentare relazioni e funzioni nel piano cartesiano.
F
F
COSA CONSIDERARE Cosa rappresenta la pendenza della ret ta; come calcolare il tempo trascorso e lo spazio percorso tra due diversi punti di una stessa retta.
COME PROCEDERE
a. La pendenza della ret ta azzurra (Kar ima) è minore di quella ros sa (Nicola): inf atti in 10 minuti Karima percorre 1 km, mentre sempre in 10 minuti Nicola percorre 1,5 km.
b. Alle 16:25 Nicola ha percorso 3 km, ma è partito alle 16:05, quindi ha impiegato solo 20 minuti.
c. Alle 16:15 entrambi hanno percorso 1,5 km.
d. Nicola è partito alle 16:05 e in quel momento Karima aveva percorso solo 0,5 km.
28
ALLENAMENTO GUIDATO
V F
V
V F
V
0 0,5 1 1,5 Distanza (km) Karima Tempo (min) 2 2,5 3 3,5 4 4,5 5 Nicola 16:0016:0516:1016:1516:2016:2516:3016:3516:40 X X X X
15 Nella figura seguente è mostrato un trapezio in cui l’altezza e la base minore misurano x, mentre la proiezione del lato obliquo sulla base maggiore vale 10.
Qual è la formula che esprime l’area in funzione di x?
Risposta: A =
x 2 + 5x
COSA RICORDARE Costruire for mule che contengono let tere per esprimere rel azioni e proprietà; calcolare l’area di figure piane.
COSA CONSIDERARE Calcolare l’area di un trapezio; come esprimere, usando i dati dell’esercizio, le lunghezze dei segmenti che consentono di trovare l’area.
COME PROCEDERE
L’area del trapezio è data dalla formula 2 ABbh = + Dai dati del testo ricaviamo: B = x + 10
Andando a sos tituire nella for mula generale, si ha: x 10 A x = + 2 $ x + `j che già è una espressione elementare della formula, ma semplificando con le regole del calcolo letterale diventa:
In alternativa pos so considerare il trapezio come for mato da un quadrato e un triangolo ret tangolo.
L’area del quadrato è x2 , mentre quella del triangolo rettangolo è 5x 2 10 x = $ , da cui A = x2 + 5 x.
29 ALLENAMENTO GUIDATO
b
x h = x
=
2 210 x + xxxxxx 2 10 2 55 A x = + == += + $$
x + ` ` j j
$
x 10
x
SPAZIO E FIGURE
16 Una scala a libretto lunga 2,5 m viene aperta in modo che le due basi distino tra loro di 1,4 m. Di quanti centimetri si abbassa il vertice della scala?
Risposta: cm.
COSA RICORDARE Teorema di Pitagora; risolvere problemi con le figure geometriche.
COSA CONSIDERARE Quale figura si for ma avendo la scal a a libretto; come applicare il teorema di Pitagora alla figura per calcolare l’altezza; la differenza tra le altezze nelle due figure.
COME PROCEDERE Puoi schematizzare la scala aperta come un triangolo isoscele: calcola l’altezza del triangolo applicando il teorema di Pitagora (ricordati di dividere per due la base, per trovare il cateto minore):
HB = 1,4 | 2 = 0,7m
CH = 525497674 22 , 2,0,6, 05,2,== = m
La differenza tra l'altezza della scal a chiusa e aper ta è dunque h – CH = 2,5 – 2,4 = 0,1m = 10 cm
17 Sapendo che ogni quadretto misura 1 cm, qual è l’area della figura?
Risposta: cm2
COSA RICORDARE Principio di equiscomponibilità; calcolare l’area di figure piane anche scomponendole in altre figure più semplici.
COSA CONSIDERARE Se è necessario calcolare l’area delle parti cur vilinee; se la figura può essere ritagliata in figure più semplici e ricomposta in altro modo.
COME PROCEDERE Per risolvere ques to problema conviene scomporre la figura come mos trato di seguito.
Troverai che la figura è equivalente a un quadrato di lato 4 cm: A = l2 = 4 2 = 16 cm2 .
30 ALLENAMENTO GUIDATO
AB A H 1,4 m B C 2,5 m
10
16
Calcola il perimetro della figura sapendo che ogni segmento è lungo 20 cm.
A 120 cm.
B Circa 154 cm.
X
C Circa 248 cm.
D Circa 283 cm
COSA RICORDARE Calcolare il per imetro delle figure piane; calcolare le lunghezze della circonferenza e di parti della circonferenza.
COSA CONSIDERARE Se è possibile scomporre la figura in parti lineari e cur vilinee; come è pos sibile sommare le lunghezze lineari con quelle curvilinee.
COME PROCEDERE La figura è composta da tre segmenti lineari e tre linee cur ve che sono delle semicirconferenze. La lunghezza complessiva dei tre segmenti è 3 $ 20 cm = 60 cm
La lunghezza di ogni semicirconferenza è uguale alla met à della lunghezza della circonferenza corrispondente: C = d $ r = 20 r cm
Quindi C1/2 = 20 r | 2 = 10 r cm
La lunghezza complessiva delle tre semicirconferenze è: 3 10 r cm = 30 r cm
Il perimetro della figura è: 60 + 30 r c 60 + 94,2 = 154,2 cm, pertanto la risposta è B.
È errato invece: 60 + 30 r = 90 r c 282,6 cm poiché bisogna prima trasformare la scr ittura esatta con r nella scrittura approssimata per poter sommare le misure curvilinee con quelle lineari.
31 ALLENAMENTO GUIDATO 18
19 Un cubo viene tagliato lungo i punti medi di sei dei suoi lati, come mostrato in figura.
Sapendo che lo spigolo del cubo è lungo 8 cm, qual è il perimetro dell’esagono formato nella sezione di taglio?
A 24 cm.
X
B Circa 34 cm.
C Circa 42 cm.
D 48 cm.
COSA RICORDARE Conoscere le for me del piano e dello spazio; applicare il teorema di Pit agora; calcolare il perimetro di figure geometriche piane.
COSA CONSIDERARE A cosa corrisponde il lato dell’esagono; come calcolare la sua lunghezza.
COME PROCEDERE La lunghezza del lato dell’esagono equi vale all’ipotenusa di un triangolo ret tangolo isoscele i cui cateti corrispondono a metà dello spigolo del cubo.
c = 8 | 2 = 4 cm
l = 4 $ 2
Per calcolare il perimetro dell’esagono basta moltiplicare la lunghezza del suo lato per 6:
cm
32
ALLENAMENTO GUIDATO
2 p = 6 $ l = 6 $ 4 $ 2 = 24 $ 2 c 33,94
20 Osserva il seguente solido:
Le seguenti figure rappresentano lo stesso solido visto da angolazioni differenti, tranne una che rappresenta un solido simmetrico a quello dato, quale?
COSA RICORDARE Rappresentare figure solide.
COSA CONSIDERARE Ruotare la figura di 90° attorno a una delle tre direzioni ortogonali dello spazio. COME PROCEDERE Questi esercizi necessitano dell’abilità di visualizzare e rappresentare ment almente oggetti tridimensionali. Provando a ruotare le varie figure puoi osservare che la 2 non può essere trasformata nella figura originale, ma è la sua simmetrica. È consigliabile esercitarsi su carta puntata per rappresentare i solidi.
33 ALLENAMENTO GUIDATO
A Figura 1
B Figura 2
C Figura 3
D Figura 4
X
1 Andrea costruisce delle figure utilizzando tessere bianche e verdi come quella in figura. Quale delle seguenti figure non è possibile costruire?
tessera
A Figura A
B Figura B
C Figura C
D Figura D
2 Se il numero naturale n è pari, come sarà il prodotto di ] n + 1g $ ] n 1g?
A Pari, perché se aggiungo 1 e sottraggo 1 il risultato sarà sempre pari
B Pari, perché la differenza tr a n + 1 e n 1 è sempre 2
C Dispari, perché il prodotto di due numeri dispari è dispari
D Non ci sono dati sufficienti per dare la risposta
3 Quale frazione corrisponde alla parte colorata del disegno?
34 ALLENAMENTO 1
A 4 3 B 10 6 C 6 16 D 3 8
X
B A C D
X X
4 Il punteggio delle prove INVALSI di Matematica viene assegnato sulla base della seguente tabella:
35 ALLENAMENTO 1
Blocco A Punti 0 domande o item ai quali è stato risposto correttamente 0 Da 1 a 3 domande o item ai quali è stato risposto correttamente 10 Da 4 a 8 domande o item ai quali è stato risposto correttamente 15 Da 9 a 13 domande o item ai quali è stato risposto correttamente 20 Da 14 a 17 domande o item ai quali è stato risposto correttamente 25 Da 18 a 19 domande o item ai quali è stato risposto correttamente 30 Blocco B 0 domande o item ai quali è stato risposto correttamente 0 Da 1 a 2 domande o item ai quali è stato risposto correttamente 2 Da 3 a 7 domande o item ai quali è stato risposto correttamente 5 Da 8 a 10 domande o item ai quali è stato risposto correttamente 10 Da 11 a 12 domande o item ai quali è stato risposto correttamente 14 Blocco C 0 domande o item ai quali è stato risposto correttamente 0 Da 1 a 2 domande o item ai quali è stato risposto correttamente 2 Da 3 a 4 domande o item ai quali è stato risposto correttamente 4 Da 5 a 6 domande o item ai quali è stato risposto correttamente 6 Totale blocchi A, B e C 50 Se Silvia ha risposto correttamente a 12 domande del Blocco A, 9 domande del blocco B e 3 domande del blocco C, quale sarà il suo punteggio? Risposta: 34
5 Nella figura a sinistra è rappresentata la pianta di tre edifici. Se un osservatore vede i tre edifici come nella figura a destra, da quale posizione li sta osservando?
A Posizione A
B Posizione B
C Posizione C
D Posizione D
6 Il seguente grafico rappresenta la distribuzione dei voti in un compito in classe di Grammatica:
a. Quanti alunni hanno preso almeno la sufficienza?
Risposta:
b. Qual è la media dei voti degli alunni della classe?
Risposta: …................…
36 ALLENAMENTO 1
C A B D 0 1 2 3 4 5 6 7 8 45678910 alunni voto X 20 6,8
7 Osserva la seguente figura che rappresenta il triangolo inscritto nella circonferenza di centro O:
Se l’angolo AB ˆ C misura 27°, quanto misura l’angolo CÂB?
Risposta: °
8 Indica se ciascuna delle seguenti uguaglianze è vera (V) o falsa (F).
a. | 361006 10 = | V F
b. 22 ––41404140 = V F
c. 131384 = V F
d. 12225125 +=+ V F
9 Osserva il seguente solido costituito dal cubo di lato a, a cui è stata tolta una sezione a forma di prisma quadrangolare regolare con lato di base pari a b:
Qual è la formula che esprime il volume del solido?
37 ALLENAMENTO 1
A V = a3 B V = a3 − b3 C V = a3 − ab2 D V = a3 − b2 A C B O a b
X
X 63
X
X X
10
Un’automobile viaggia per 120 km a 60 km/h e per altri 120 km a 100 km/h. Qual è la sua velocità media?
A 65 km/h
B 70 km/h
C 75 km/h
D 80 km/h
11 Zia Ada va dal fioraio e compra una begonia da € 8,50 e tre sanseverie da € 18,00. Se paga con due banconote da € 50,00 come può essere calcolato il resto?
A 2 $ 50 – ]8,50 + 18 g $ 3
B 2 $ 50 – ]8,50 + 18 $ 3g
C 2 $ 50 – ]8,50 – 18 $ 3g
D 8,50 + 18 $ 3 – 50 $ 2
12 Osserva le seguenti lettere maiuscole:
13
Quale delle quattro ha il maggior numero di assi di simmetria interni?
A Lettera R
B Lettera A
C Lettera D
D Lettera I
Vincenzo ha la passione per le rose. Coltiva cespugli di rose rosse, bianche, rosa e gialle. Il seguente grafico rappresenta la distribuzione delle rose nei diversi colori:
Che percentuale rappresentano le rose bianche rispetto al totale?
Risposta: %
X X X 12,5
38 ALLENAMENTO 1
Rosse Gialle Rosa Bianche
14 Di seguito sono elencati i prezzi della benzina senza piombo di quattro diversi distributori:
a. Qual è la massima differenza di prezzo al litro tra i vari distributori scegliendo il «servito»?
A 0,142 centesimi/litro
B 1,42 centesimi/litro
C 14,2 centesimi/litro
D 142 centesimi/litro
b. Quanti euro risparmia il papà di Veronica facendo il pieno di 40 litri al self-service invece che al servito presso il distributore ZetaBenz?
Risposta: …………………… €
15 Il rettangolo ABCD ha un’area di 30 cm2. Se i punti E, F, G, H sono i punti medi dei lati, qual è l’area dell’esagono EBFGDH?
A 20 cm2
B 22,5 cm2
C 24 cm2
D 25 cm2
39 ALLENAMENTO 1
Servito (€ /litro) Self-service (€ /litro) InquinaMen 1,618 1,578 TuttoGas 1,492 1,472 ViaggiaPiù 1,526 1,481 ZetaBenz 1,634 1,569
D H A C F B G E X
2,6
X
16 Di seguito è rappresentata schematicamente una gru meccanica. Le macchine di questo tipo si comportano come leve di primo genere in cui vale la relazione P $ bP = R $ bR.
a. Sapendo che il prodotto della resistenza per il braccio della resistenza, R $ bR, non può superare il prodotto della potenza per il braccio della potenza, P $ bP, quale sarà la portata massima (ovvero la resistenza massima, R) al termine del braccio della gru?
A 750 kg
B 3000 kg
C 12 000 kg
D 24 000 kg
b. Qual è la distanza massima dal fulcro per un carico di 1000 kg?
Risposta: m
17
Osserva la seguente moltiplicazione:
216 $ 35 = 7560
Indica quali delle seguenti operazioni sono corrette (C) e quali sono errate (E).
a. 2,16 $ 350 = 756 C E
b. 21,6 $ 35 = 75,6 C E
c. 0,216 $ 3,5 = 0,0756 C E
d. 2,16 $ 0,35 = 0,756 C E
40 ALLENAMENTO 1
P
R? fulcro bP 2m bR 16m X X X X X
6000kg
12
18
In un sacchetto ci sono 4 caramelle alla menta e 2 alla fragola.
a. Qual è la probabilità di estrarre casualmente una caramella alla menta?
A 2 1 C 4 1
B 3 1 D 3 2
b. Come calcoleresti invece la probabilità che estraendo due caramelle siano entrambe alla fragola?
19 Un biologo ha a disposizione una bottiglia da 25 cl di un certo liquido da suddividere in una serie di provette da 15 cm3 ciascuna. Quante provette riuscirà a riempire completamente?
Risposta: provette
X 16
20 Nella seguente immagine sono rappresentati due contenitori cilindrici:
Sapendo che il secondo ha altezza doppia, ma diametro la metà rispetto a quelli del primo, indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Il volume del primo è doppio di quello del secondo
b. L’area di base del primo è quattro volte quella del secondo
c. I due solidi sono equivalenti
d. L’area laterale del primo è doppia rispetto a quella del secondo
X X X X X
F
41 ALLENAMENTO 1
A 6 2 6 2 + C 6 2 6 1 + B 6 2 6 2 $ D 6 2 5 1 $
V
F
V
F
V
F
V
1 Carlo, che è pasticciere, quando prepara delle torte usa una quantità di impasto (in grammi) pari a:
q = 2,5 $ d2
dove d è il diametro (in cm) della tortiera utilizzata.
In genere usa tortiere da 24 cm, ma l’altro giorno ha dovuto utilizzarne una da 36 cm. Poiché il diametro della tortiera è aumentato di 1,5 volte, di quante volte sarà aumentata in proporzione la quantità di impasto?
A 1,5 volte
B 2 volte
C 2,25 volte
D 3 volte
2 La seguente tabella rappresenta la distribuzione delle altezze tra gli alunni di una classe.
Quale tra i seguenti grafici rappresenta la distribuzione della tabella?
42 ALLENAMENTO 2
Altezza (cm) Alunni 100 - 110 0 110 - 120 1 120 - 130 3 130 - 140 8 140 - 150 6 150 - 160 5 160 - 170 2
A C B D 0 2 4 alunni 6 8 10 100110120130140 altezza (cm) 150160170 0 2 4 alunni 6 8 10 100110120130140 altezza (cm) 150160170 0 2 4 alunni 6 8 10 100110120130140 altezza (cm) 150160170 0 2 4 alunni 6 8 10 100110120130140 altezza (cm) 150160170 X X
3 Di seguito sono riportate la pianta del sito archeologico di Stonehenge e una sua foto dall’alto.

Quale numero riportato sulla pianta corrisponde alla pietra indicata con la freccia rossa?
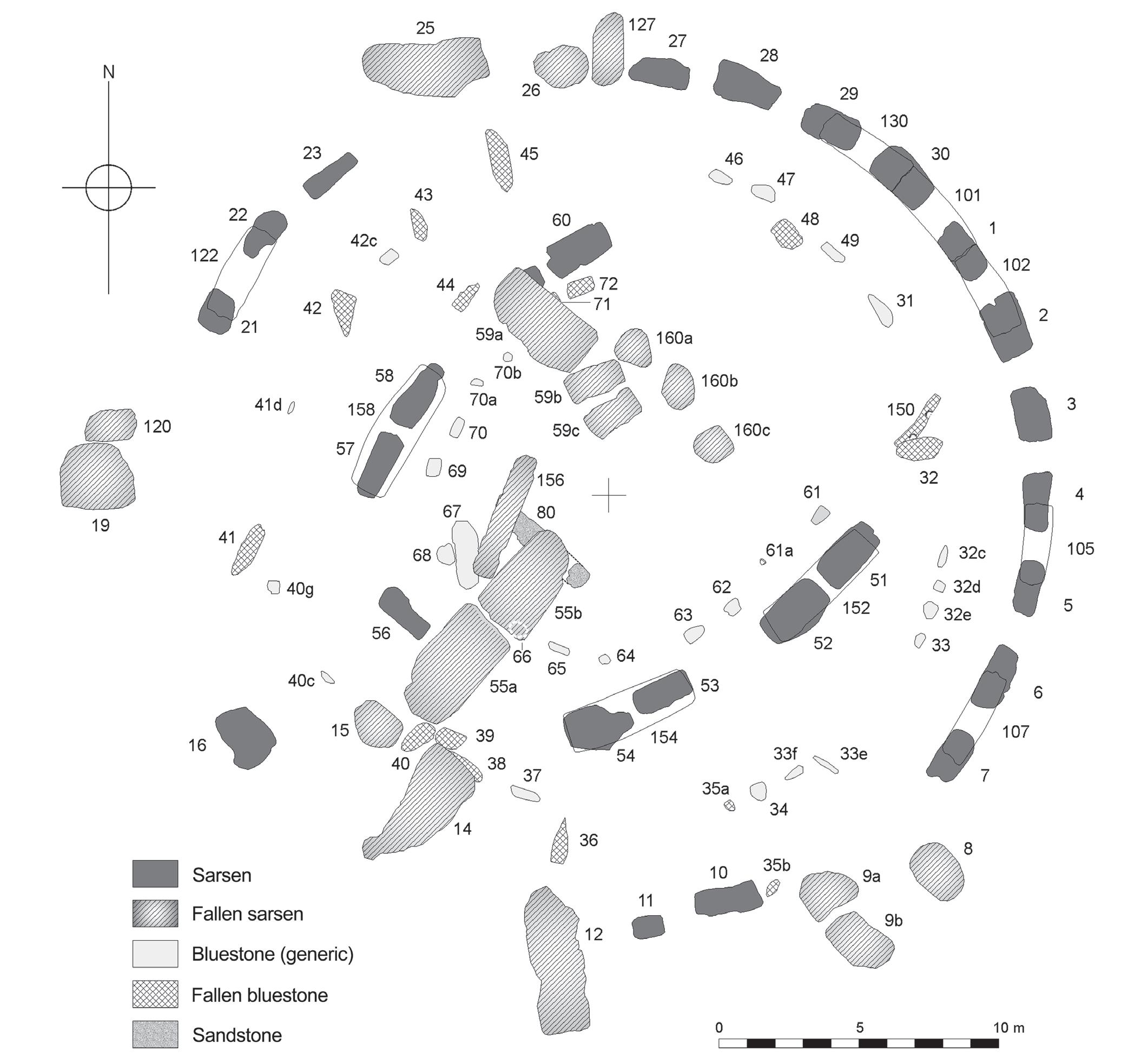
43 ALLENAMENTO 2
A 8 B 12 C 19 D 25 X
4 Collega ogni numero razionale con una scrittura equivalente:
5 Osserva la seguente uguaglianza, ad ogni simbolo uguale corrisponde uno stesso valore.
Sapendo che = , quanto vale ?
A Zero
B
C
D
6 Osserva il seguente solido.
Tra le seguenti figure, quale potrebbe rappresentare il suo sviluppo piano?
A Figura 1
B Figura 2
C Figura 3
D Figura 4
44 ALLENAMENTO 2
a.
b.
c. 0,03 d. 3,0 1. 3% 2.
3. –1 3 1 c m 4. 3 1
0,3
0,3
10 3
=
1 2 3 4 X
X
7 Un commerciante decide di liberarsi dei modelli di televisione dello scorso anno e li mette in vendita con il 30% di sconto. Visto che non è riuscito a vendere l’ultimo televisore che a prezzo intero costava € 800, decide di fare un ulteriore sconto del 20% sul prezzo già scontato. Qual è il prezzo finale del televisore?
Risposta: €
8 Il recipiente conico mostrato in figura è riempito con 1 litro d’acqua fino a un’altezza h che è la metà di quella massima, 2h. L’area A della superfice dell’acqua è un quarto rispetto a quella sul recipiente completamente pieno 4A.
Ricordando che il volume di un cono è 3 V Ah = , quanti altri litri d’acqua servono per riempire completamente il recipiente?
a è 2 3 e b è i suoi 5 2 , quanto vale b?
45 ALLENAMENTO 2
A 1 l B 3 l C 5 l D 7 l 9 Se
A 5 2 B 7 5 C 5 3 D 15 4 2 h 4 A A h 1l 448 X X
10 Dati quattro numeri consecutivi, indica quale delle seguenti affermazioni è falsa.
A La loro somma è sempre pari, infatti 2 + 3 + 4 + 5 = 14
B Il loro prodotto è multiplo di tre, infatti 2 $ 3 $ 4 $ 5 = 120
C La differenza tra la somma degli ultimi due e la somma dei primi due è sempre uguale a uno stesso numero, inf atti ]4 + 5g – ]2 + 3g = 9 – 5 = 4, ma anche ]8 + 9g – ]6 + 7g = 17 – 13 = 4
D Il loro prodotto è sempre multiplo di cinque, infatti 2 $ 3 $ 4 $ 5 = 120
11 Antonio, Lara e Carlo giocano a testa o croce lanciando due monete. Antonio vince se escono due teste, Lara vince se escono due croci e Carlo vince se esce una testa e una croce.
Chi ha più probabilità di vincere?
A Antonio
B Lara
C Carlo
D Nessuno, hanno tutti la stessa probabilità
12 Osserva la seguente figura costruita in modo tale che ogni triangolo inscritto ha i vertici sui punti medi del triangolo circoscritto:
Sapendo che l’area azzurra è 156 cm2 calcola l’area verde della figura.
Risposta: cm2
X X 36
46 ALLENAMENTO 2
13 Enrico vorrebbe costruire una compostiera come quella disegnata in figura, utilizzando dei pannelli di legno larghi 80 cm.
a. Quale dovrà essere la lunghezza x del coperchio?
A 80 cm B 100 cm C 120 cm D 140 cm
b. Qual è la superficie totale dei pannelli che dovrà usare in tutto?
Risposta: m2
14 Secondo Esopo, la volpe e la cicogna si invitano spesso a pranzo. Quando la volpe va a casa della cicogna percorre il tragitto ABCD, mentre la cicogna vola direttamente dalla propria casa a quella della volpe secondo il tragitto DA.
Sapendo che AB = 528 m; BC = 850 m; CD = 792 m, quanta strada percorre in più la volpe rispetto alla cicogna?
A 600 m
B 850 m
C 1570 m
D Non si può sapere, perché non si hanno le misure di BH e HC
47 ALLENAMENTO 2
140cm 80cm80cm 80cm x AB H CD X X 4,96
15 Nella notazione musicale ogni nota ha una sua durata corrispondente a una certa frazione secondo lo schema seguente:
La durata delle note può però essere aumentata ad esempio dalla legatura di valore, per cui il valore della nota è data dalla somma dei valori delle singole note. Ad es.:
2/4 + 1/4 = 3/4
Qual è il valore complessivo della seguente scrittura?
48 ALLENAMENTO 2
Figura musicale Valore semibreve 4/4 minima 2/4 semiminima 1/4 croma 1/8 semicroma 1/16 biscroma 1/32 semibiscroma 1/64
A 4 3 B 4 7 C 8 5 D 16 7 X
16 Il pianeta Marte dista da noi mediamente 225 milioni di km.
a. Come si può esprimere la distanza in metri?
A 2,25 $ 106 m
B 2,25 $ 10 8 m
C 2,25 $ 1011 m
D 2,25 $ 1014 m
b. Se i segnali radio viaggiano alla velocità di 300 000 km/s, quanto impiega un segnale inviato da quel pianeta a raggiungere la Terra?
A Meno di 1 secondo
B Circa 2 minuti
X
C Circa 12 minuti
D Circa 2 ore
c. Sapendo che in un’ora ci sono 3600 secondi, se riceviamo i segnali di una sonda spaziale circa 4 ore dopo che sono stati emessi, a che distanza si trova la sonda?
A Circa 1,2 milioni di km
B Circa 72 milioni di km
C Circa 144 milioni di km
X
D Circa 4,3 miliardi di km
17 È Halloween, quattro bambini vestiti da Fantasma, Mummia, Strega e Zombie sono intenti a fare «dolcetto o scherzetto», ma poiché litigano sempre su chi deve essere il primo o il secondo decidono di seguire questa semplice regola: a ogni casa a cui suonano il campanello per chiedere i dolcetti dovranno utilizzare un ordine differente da ognuno dei precedenti ed, entro la serata, dovranno aver esaurito tutte le possibili combinazioni.
a. In quanti modi si possono disporre in ordine Fantasma, Mummia, Strega e Zombie?
A 4
B 8
C 16
X
D 24
b. Ipotizzando che impieghino 5 minuti per ogni casa, dopo quante ore avranno terminato?
X 2
Risposta: ore
49 ALLENAMENTO 2
Quali sono le coordinate del punto B' simmetrico del punto B rispetto alla retta r?
Risposta:
50 ALLENAMENTO 2
18 Nel seguente piano cartesiano è rappresentato il quadrilatero ABCD, Nicoletta deve disegnare il simmetrico della figura rispetto alla retta r.
B' ] ; g
A
B
C
D 4 39 −202 −2 −4 −6 −10−8−6−446810 2 4 6 8 10 D A B C X – 2 – 7
19 Un quarto di 440 è:
140
220
410
20 Il seguente profilo altimetrico rappresenta una delle quattro sezioni della successiva carta in rilievo di una zona appenninica:
A quale delle sezioni corrisponde il profilo altimetrico?

51 ALLENAMENTO 2
A Sezione A B Sezione B C Sezione C D Sezione D 1900 1950 2000 Quota (m) 2050 2100 2150 2200
A B C D X
Distanza
1 La radice quadrata di 1000 è circa pari a:
A 10 B 30 C 100 D 500
2 Il seguente grafico rappresenta l’andamento climatico di una località sciistica italiana:
Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Il mese più piovoso è luglio V F
b. I mesi più freddi sono febbraio e marzo V F
c. Il mese meno piovoso è dicembre V F
d. Nel mese più piovoso cadono più di 100 mm di pioggia V F
3 Di seguito sono riportate la pianta del castello di Chenonceau in Francia e una sua fotografia.

52 ALLENAMENTO 3
20 40 60 0 20 40 60 80 100 120 140 2 4 6 0 2 Temperature(°C) Precipitazioni(mm) 4 6 8 10 12 14 Precipitazioni (mm) Temperature (°C)
A quale numero sulla piantina corrisponde la stanza contrassegnata con la freccia? A 1 B 2 C 4 D 9 1 2 3 54 6 7 8 9 10 X X X X X X
GennaioFebbraioMarzoAprileMaggioGiugnoLuglioAgostoSettembreOttobreNovembreDicembre
4 Una ditta che vende prodotti on line applica le spese di spedizione solo sugli ordini inferiori a € 50. Il seguente grafico rappresenta il costo complessivo per l’acquisto di DVD (che hanno tutti lo stesso prezzo) in funzione del numero di DVD acquistati.




















a. Quanto è più alta Martina di Laura?
b. Quanto è alta realmente Laura?
53 ALLENAMENTO 3
Osserva il grafico e completa la frase. Ogni DV D costa € e le spese di spedizione per ordini inferiori a € 50 ammontano a €
5 Laura e Martina misurano la loro altezza. Laura misura 148,5 cm e Martina 156 cm, però si accorgono che al metro da loro usato mancano i primi 2,5 centimetri.
A
D
5 cm B 7,5 cm C 8,5 cm
10 cm
Risposta: cm 0 16 8 24 32 40 80 72 64 56 48 96 88 012345678910111213 Spesa complessiva ( € ) Numero DVD X 12 146 8
6 Disponi i seguenti poligoni in ordine da quello di area minore a quello di area maggiore.
7 In un Istituto Comprensivo nel 2019 si sono avute 200 nuove iscrizioni, nel 2020 si è registrato un calo del 20% rispetto al 2019 e nel 2021 si è avuto un aumento del 20% rispetto al 2020.
Qual è la variazione percentuale del numero di nuove iscrizioni del 2021 rispetto a quelle del 2019?
A Nessuna var iazione (0%)
B Un decremento del 4%
C Un decremento dell’8%
D Un incremento del 4%
8 Osserva la seguente figura ABCDEF, ottenuta ritagliando il quadrato DCKE dal quadrato ABKF:
Sapendo che il lato AB è lungo 8 cm, mentre il lato CK è lungo x, quale delle seguenti affermazioni è falsa?
A L’area della figura ABCDEF è A = 64 – x2
B La lunghezza del lato DC è x
C Il perimetro della figura ABCDEF è pari a 2 p = 32 – 4 x
D Il segmento FE è lungo 8 – x
54 ALLENAMENTO 3
< < <
AB C EK D 8 F A B C D X X D A C B
9 Matteo in questo quadrimestre ha avuto come valutazioni di Scienze tre 6 e un 8.
a. Qual è la media dei voti?
6,5
Risposta: ................…
b. Quale altro voto dovrebbe prendere per avere la media esatta del 7?
A Sette
B Otto
C Nove
D Dieci
10 La famiglia Schmidt, composta da padre, madre e due bambini, in estate va in vacanza in una località balneare della Puglia. L’albergo da loro scelto applica le seguenti tariffe a persona:
31/5
a. Quanto spende la famiglia Schmidt se arrivano il pomeriggio del 15/6 e ripartono la mattina del 22/6, alloggiando a mezza pensione? Risposta: €
b. Quanto avrebbe speso di meno al giorno la famiglia Schmidt se avesse alloggiato in camera con la sola colazione?
1596,00 74,00
Risposta: € 11 Un’automobile viaggia per due ore a 80 km/h e per un’ora a 110 km/h. Qual è la sua velocità media?
A 85 km/h
X
B 90 km/h
C 95 km/h
D 100 km/h
55 ALLENAMENTO 3
Dal
al
Dal 16/9 al 31/12 Dal 1/6 al 30/6 Dal 1/9 al 15/9 Dal 1/7 al 31/8 Dal 25/8 al 31/8 Dal 1/8 al 24/8 Camera e colazione Camera singola 60,00 € 70,00 € 80,00 € 90,00 € Camera doppia 40,00 € 48,00 € 58,00 € 70,00 € 3°/4° letto in camera doppia 20,00 € 29,00 € 35,00 € 42,00 € Mezza pensione Camera singola 72,00 € 82,00 € 90,00 € 100,00 € Camera doppia 50,00 € 65,00 € 75,00 € 92,00 € 3°/4° letto in camera doppia 35,00 € 49,00 € 60,00 € 60,00 €
1/1
X
12
Quanti sono i cubi nascosti, cioè quelli che non è proprio possibile vedere, nemmeno osservando la struttura dall’altro lato?

Risposta:
13 Cinque cuginetti decidono di misurare la loro statura e la segnano su un foglio:
Michele 1,55 m
Nadia 1,37 m
Aida 1,45 m
Ludovico 1,25 m
Rebecca 1,38 m
Quale valore rappresenta la mediana?
A 1,37 m
B 1,38 m
C 1,40 m
D 1,45 m
56 ALLENAMENTO 3
Osserva la seguente immagine, è una «piramide» formata da cubi tutti uguali.
30
X
14 Determina il valore dell’espressione:
15
Il marchese di Falcobolzo sta assaltando il castello del conte di Roccataccola. Le sue truppe hanno delle scale alte 15 m e il castello ha le mura alte 14 m, ma è protetto da un fossato largo 9 m disposto come nella figura.
a. A quanti metri dalla cima delle mura poggerà la scala?
Risposta: m
b. Quanti metri dovrà essere lunga come minimo la scala per riuscire a raggiungere la cima delle mura?
57 ALLENAMENTO 3
1 1 2 2 1 4 1 8 1 4 1 ++ ++ = A 2 B 2 1 C 32 49 D 7 8
A 16 m B 17 m C 20 m D 23 m 15 m 9 m 14 m X X 2
16 Osserva la mappa di una zona centrale di Milano. Corso Sempione si estende da piazza Firenze (punto A) a piazza Sempione (punto B).
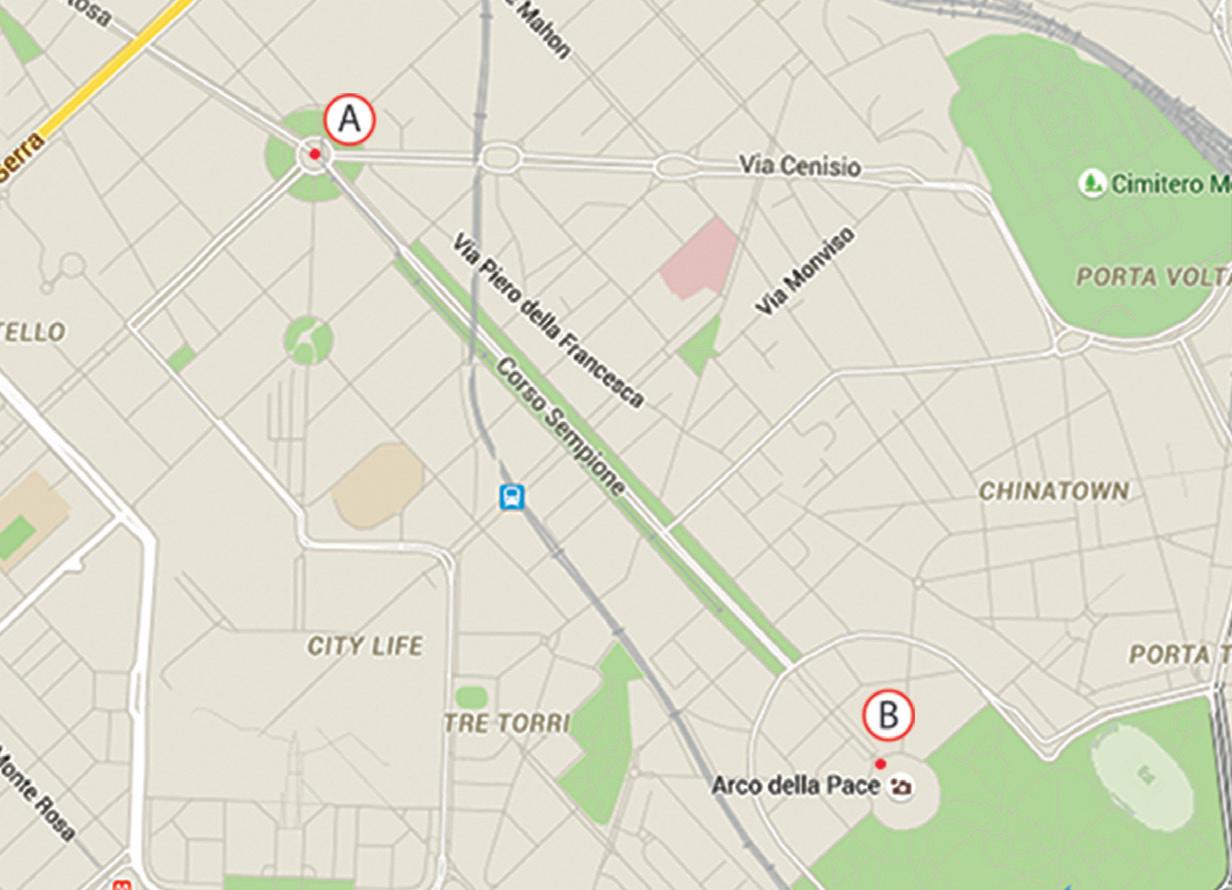
a. Considerando che la scala della cartina è 1 : 25 000, quanto è lungo corso Sempione?
A Circa 180 m
B Circa 300 m
C Circa 1,8 km
D Circa 3 km
b. Se la scala fosse 1 : 10 000 quanto sarebbe la lunghezza di corso Sempione sulla carta?
A Circa 3 cm
B Circa 10 cm
C Circa 18 cm
D Circa 30 cm
17 L’Adansonia grandidieri è un baobab del Madagascar dal tronco pressoché cilindrico.

Se il tronco di un albero adulto è alto 20 m e ha un diametro di 4 m quale potrebbe essere il suo volume?
A 40 r m3
B 80 r m3
X X X
C 160 r m3
D 320 r m3
58 ALLENAMENTO 3
18
In alcuni giochi, oltre al comune dado a 6 facce, si usano dei dadi a 4 facce; in quest’ultimo caso il risultato è il numero che si legge sul vertice in alto.


Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. La probabilità che esca 1 nel dado a quattro facce è maggiore di quella che esca 1 in quello a 6 facce V F
b. La probabilità che esca un numero pari è uguale in entrambi i dadi V F
c. La probabilità che esca il numero 4 nel dado a quattro facce è uguale all a probabilità che esca 4 nel dado a sei facce V F
19 Osserva la seguente figura:
X
d. La probabilità che esca un numero primo è uguale in entrambi i dadi V F
Sapendo che OH = HB, e che ED è perpendicolare al diametro AB, indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Il segmento EB (non rappresentato) è congruente al raggio OA V F
b. L’angolo ODE (non rappresentato) è di 45° V F
c. Il segmento OH è la metà del segmento DH V F
d. Il segmento AE (non rappresentato) è il doppio del segmento DH V F
20 In un uomo di 78 kg circolano circa 6 litri di sangue. Se in 1 millimetro cubo ci sono mediamente 5 000 000 di globuli rossi, quanti globuli rossi saranno presenti in tutto?
A 30 milioni
B 30 miliardi
C 300 miliardi
D 30 bilioni (= 30 000 miliardi)
X X X X X X X X
59 ALLENAMENTO 3
AH D E OB c
1 In una scuola viene fatto un sondaggio per valutare quali corsi pomeridiani attivare. Il risultato viene riportato nella seguente tabella:
Attività Preferenze (n) Attività sportive 30 Laboratorio teatrale 10 Strumento musicale 15
Laboratorio di informatica 25
Quale dei seguenti grafici può rappresentare la distribuzione delle preferenze?
2 Osserva il seguente solido composto da un cubo con due piramidi aventi le basi coincidenti a due delle sue facce opposte:
Completa la seguente tabella.
a. Numero facce quadrate
b. Numero facce triangolari ..............................
c. Totale facce ..............................
3 Se n è un numero pari qualsiasi, quale delle seguenti operazioni dà sempre come risultato un numero dispari?
60 ALLENAMENTO 4
A n | 2 B 5 $ n C n2 | 2 + 1 D 3 $ n + 2
X 4 12 8
A B C D X
4 Tra i pianeti nani del sistema solare, Eris ha una massa quattro volte maggiore a quella di Haumea. Sapendo che la massa di Haumea è di 4,2 $ 1021 kg, qual è la massa di Eris?
A 4,2 $ 10 84 kg
B 16,8 $ 4021 kg
C 1,68 $ 1022 kg
D 4,2 $ 1025 kg
5 La professoressa di Scienze ha scritto su un foglio il numero di relazioni che gli alunni le hanno consegnato nel quadrimestre, in ordine crescente. Purtroppo una macchia di caffè ha coperto tre valori, tuttavia la professoressa pensa di poter calcolare almeno uno dei seguenti indicatori statistici: media, moda e mediana.
Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. La media dei valori è sicuramente 4
b. Non è possibile calcolare la moda perché non si può determinare quale dei valori è il più frequente
c. La mediana è 3,5
d. È possibile calcolare la mediana perché non sono stati coperti i valori centrali
61 ALLENAMENTO 4
Alunno Relazioni Olimpia 0 Davide * Dario * Elisa * Alice 2 Matteo 3 Nadia 3 Francesco 4 Giacomo 4 Ilaria 4 Helen 5 Luca 5 Barbara 5 Catia 6 Paride 6 Emanuele 6 Simone 6 Tea 6
V F
V F
V F
V F
X
X
X X X
6 Per svolgere la moltiplicazione 57 · 990 si possono utilizzare diversi modi. Quale tra i seguenti NON è corretto?
A 50 $ 990 + 7 $ 990
B 57 $ 900 + 57 $ 90
C 50 $ 900 + 7 $ 90
D 57 $ 1000 57 $ 10
7 Osserva il seguente grafico che rappresenta l’andamento della raccolta differenziata e dei rifiuti urbani residui nella Regione Veneto a partire dal 2000. Le percentuali indicano la parte di raccolta differenziata rispetto al totale.
Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Dal 2007 la raccolta differenziata supera i rifiuti urbani residui
b. Nel 2010 sono stati raccolti 1 000 000 000 di kg di rifiuti ur bani residui
c. Dal 2010 la raccolta differenziata è di circa 1400 tonnellate per anno
X X X X
d. Dal 2010 al 2012 la percentuale della raccolta differenziata sul totale V F è aumentata
62 ALLENAMENTO 4
V F
V F
V F
20002001200220032004200520062007200820092010201120122013 1600000 raccoltadifferenziata 1400000 1200000 1000000 800000 600000 400000 200000 0 tonnellate anno 28,4% 34,5% 39,5% 43,1% 45,1% 47,5% 49,0%51,0% 53,9%56,3% 58,3%60,5%62,5%63,6% residuo
X
8 Una struttura a base quadrata è composta da elementi verticali e orizzontali di metallo, uniti da tiranti in acciaio che decorrono lungo tutte le diagonali delle facce laterali.
Se tutta la struttura è alta 12 m e larga 4 m, quanti metri di tiranti in acciaio serviranno come minimo per sostenere la struttura?
A 80 m
B 160 m
C 250 m
D 320 m
9 Di seguito è rappresentata la tabella di conversione delle misure delle scarpe da donna.
Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Chi ha in Europa il 38 in Brasile indosserà il 36,5
b. La taglia 8 degli Stati Uniti corrisponde alla taglia 6 nel Regno Unito
c. Chi ha la taglia 40 in Europa ha il piede più lungo di chi ha la taglia 40 in Brasile
d. Per passare dalle taglie degli Stati Uniti a quelle del Brasile è sufficiente
moltiplicarle per 5
63 ALLENAMENTO 4
Paese Taglia Brasile 35 35,5 36 36,5 37 37,5 38 38,5 39 39,5 40 40,5 Europa 36 36,5 37,5 38 38,5 39 40 40,5 41 42 42,5 43 Giappone 22 22,5 23 23,5 24 24,5 25 25,5 26 26,5 27 27,5 Regno Unito 3 3,5 4 4,5 5 5,5 6 6,5 7 7,5 8 8,5 Stati Uniti 5 5,5 6 6,5 7 7,5 8 8,5 9 9,5 10 10,5
V F
V F
V F
V F
X
X X X X
10 Quanto vale la metà di 16 2 1 c m ?
A 17 2 1 c m
B 16 4 1 c m
C 15 2 1 c m
D 8 2 1 c m
11 Osserva la seguente figura mistilinea:
Quale delle seguenti figure ha il perimetro diverso da quella sopra rappresentata?
Secondo Marco, il suo compagno di banco, c’è un errore in un passaggio, ma Luca è convinto di averla svolta correttamente. Chi dei due ha ragione?
Luca, perché ef fettivamente l’equazione è corretta.
Marco, perché Luca ha commesso un errore nel passaggio.
64
ALLENAMENTO 4
A Figura 1 B Figura 2 C Figura 3 D Figura
Luca risolve l’equazione 3]x – 4g = 2]9 – xg + 5 nel seguente modo: testo: 3 ] x – 4g = 2]9 – xg + 5 primo passaggio 3x – 12 = 18 – 2 x + 5 secondo passaggio 3x – 2 x = 18 – 12 + 5 terzo passaggio x =
4 12
11
1 2 3 4 X X X
secondo
13 La seguente figura rappresenta un cubo. La relazione che lega la lunghezza del lato l al volume V è V = l 3 .
Un secondo cubo avente il lato pari alla metà del primo avrà il volume pari:
A a un ottavo rispetto a quella del primo cubo
B a un sesto rispetto a quella del primo cubo
C a un quarto rispetto a quella del primo cubo
D alla metà rispetto a quella del primo cubo
14 In un poster appare la scritta seguente:
Osservando il poster da uno specchio, come apparirà la scritta?
15 Nel sistema di misurazione anglosassone 16 once corrispondono a 1 libbra, mentre 14 libbre corrispondono a 1 stone. Se 1 oncia corrisponde a circa 28 grammi, a quanti chilogrammi corrisponde il peso di 1 stone?
A 0,45 kg
B 1,8 kg
C 3,6 kg
D 6,4 kg
X X X
65 ALLENAMENTO 4
A B
D
C
16 Per una ricerca di Scienze, Rachele, Simone e Tania raccolgono fiori di Pisum sativum. Nella seguente tabella riassumono i dati ottenuti:
Alunno Fiori viola Fiori bianchi Percentuale di fiori bianchi Rachele 24 16
Tania 24
Gli studenti decidono poi di mettere insieme i risultati. Quale sarà la percentuale di fiori bianchi tra tutti i fiori raccolti?
A Circa il 23%
B 25%
C Circa il 27%
D 30%
17 La seguente figura è formata da quadrati di diverse dimensioni:
18
Se il lato del quadrato azzurro è lungo 1 cm, quanto vale l’area dell’intera figura?
Risposta: cm2
40
Quale delle seguenti quantità è la più piccola?
A 10 2 di 250
B 6 7 di 42
C 16% di 300
X X
D 9 16 di 30
66 ALLENAMENTO 4
40%
3 10%
Simone 27
6 20%
19 Osserva la seguente figura che rappresenta il rettangolo ADEF inscritto nel triangolo isoscele rettangolo ABC:
Sapendo che i lati AB e AC del triangolo misurano 10 cm e il lato AD del rettangolo misura x, qual è la formula che permette di trovare l’area del rettangolo?
A A = 10 $ x
B A = x $ ] 10 – xg
C A = 100 – x2
D Non è possibile con i dati a disposizione calcolare l’area del rettangolo
20 Osserva il seguente quadrilatero inscritto in una circonferenza.
Sapendo che la lunghezza del lato AD è uguale a quella del raggio AO e che l’angolo AÔB è retto, quale sarà l’ampiezza dell’angolo DÂB?
67 ALLENAMENTO 4
A
B
C 105° D 120° A x 10FE 45° C DB A D OC B X X
85°
100°
1 Se il numero naturale n è dispari come sarà il prodotto n $ ] n + 3g?
A Dispari perché il prodotto di due numeri dispari è dispari
2

B Pari, perché il fattore n + 3 è pari
C Pari, perché la somma di due numeri dispari è sempre pari
D Non ci sono dati sufficienti per dare la risposta
In quale delle seguenti serie i numeri sono disposti in ordine crescente?
A – 2; –2 3 ; –2 1 ; –2 2
B –2 3 ; – 2; –2 1 ; –2 2
C –2 1 ; –2 2 ; –2 3 ; – 2
D – 2; –2 3 ; –2 2 ; –2 1
3 Un contenitore cilindrico in plastica, vuoto e chiuso, ha un volume esterno di 3 dm3, pesa 750 g e galleggia in acqua.
a. Considerando che il peso specifico è il rapporto del peso rispetto al volume P3 = V P , qual è il peso specifico del contenitore espresso in kg/dm3?
Risposta: kg/dm3
b. Per affondare il contenitore è possibile riempirlo anche parzialmente di sabbia fino a fargli superare il peso specifico dell’acqua che è di 1 kg/dm3. Quanti grammi di sabbia si dovranno aggiungere come minimo per fare affondare il contenitore?
A Non è possibile determinarlo
B 750 g
C 1250 g
D 2250 g
X X 0,25 X
68 ALLENAMENTO 5
4 Di seguito è rappresentato un solido e quattro possibili sviluppi piani:
Quale dei quattro sviluppi piani genera il solido rappresentato nella figura in alto?
X
A Figura 1 B Figura 2 C Figura 3 D Figura 4
5 Osserva il seguente triangolo ABC, in cui è inscritto il quadrato CDEF:
a. Calcola l’area del triangolo EBF.
Risposta: cm2
b. Qual è il rapporto tra l’area del triangolo EBF e l’area del triangolo AED?
69 ALLENAMENTO 5
A 4 | 1 B 5 | 1 C 16 | 1 D 25 | 1 1 2 3 4 AB C1cm 4cm F E D 2
X
6 Francesca, Giulio, Ilaria e Luca risolvono la seguente espressione:
Chi dei quattro la svolge correttamente?
7 Roberto e Simona sono nel laboratorio di fisica: Roberto fa muovere un oggetto lungo un percorso e Simona prende i dati della posizione dell’oggetto per un minuto. Simona ha prodotto poi il seguente grafico:
8
Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. A 10 secondi l’oggetto sta accelerando
b. Tra 20 e 40 secondi l’oggetto è fermo
c. A 50 secondi l’oggetto è tornato nella posizione di partenza
d. A 45 secondi la velocità è maggiore che a 15 secondi
F
F
F
Carla, durante i saldi di fine stagione, decide di comprarsi una certa borsa venduta in due diversi negozi, A e B. Nel negozio A la borsa costa € 250 ed è scontata del 20%; nel negozio B la stessa borsa costa € 270 ed è scontata del 30%.
Completa la frase:
A Carla conviene acquistare la bor sa nel negozio , dove la pagherà € in meno rispetto all’altro negozio.
70 ALLENAMENTO 5
8422+=
6416=+ = 8040== 6416=+ = 80 9 = . = 8422=+ = 8 + 4 = 12 = 8422=+ = 2,82 + 2 . 4,82 A Francesca B
C Ilaria D Luca
Giulio
V
V
V
V F
0 20 40 60 80 100 120 140 0102030405060 Distanza (cm) Tempo (secondi) B 11 X X X X X
9 Tommaso e Daryl giocano con i dadi. Tommaso lancia due dadi a 6 facce e somma il punteggio ottenuto, Daryl lancia un solo dado a dodici facce.
Chi ha la maggiore probabilità di fare come punteggio 12?
10 Osserva le seguenti figure:
a. Se si continua allo stesso modo la sequenza delle figure da quanti quadretti sarebbe composta la figura 9?
Risposta:
81
b. Una figura con 210 quadretti potrebbe appartenere alla sequenza?
A Sì, perché è pari a 21 $ 20 | 2
B Sì, perché è uguale alla somma di tutti i numeri da 1 a 20

C No, perché il numero non è un quadrato perfetto

X X
D No, perché è un numero pari
71 ALLENAMENTO 5 1 2 3 4 5 ..... 6 ..... 7 ..... 8 ..... 9 .....
A Tommaso perché la sua probabilità di fare 12 è 66 1 6 12+= , mentre per Daryl è 1 12 B Tommaso perché la sua probabilità di fare 12 è –6 1 6 1 36 1 36 11 += , mentre per Daryl è 1 12 C Nessuno, infatti hanno entrambi 1 12 di probabilità che il punteggio sia 12 D Daryl perché la sua probabilità di fare 12 è 1 12 , mentre per Tommaso è 6 1 6 1 36 1 = $
11 Il quadrilatero ABDC è formato da due triangoli rettangoli ABC e BCD e ha tre dei quattro lati lunghi 1 dm. Quanto è lungo il lato BD?
2 dm
3 dm
2 dm
5 dm
12 Agnese, Beatrice, Christian e Dario risolvono la seguente espressione:
13 Quale delle seguenti figure ha il volume maggiore delle altre?
72 ALLENAMENTO 5 1 2 3 4
A
B
C
D
2 + 2 $ 22 = Chi l’ha
= 4 $ 22 = = 82 = = 64 = 2 $ 4 2 = = 2 + 16 = = 18 = 2 + 2 $ 4 = = 2 + 8 = = 10 = 2 + 2 $ 4 = = 4 $ 4 = = 16 A Agnese B
C Christian D Dario
risolta correttamente?
Beatrice
A Figura 1 B Figura 2 C Figura 3 D Figura 4 1dm D AB C ? 1dm 1dm X X X
14 Luca, Masha e Giorgio giocano al tiro al bersaglio. Luca che è meno bravo fa più tiri di Masha, Giorgio che è il più bravo ne fa meno di tutti. La seguente tabella riassume il numero dei tiri e la media dei punteggi ottenuta:
Qual è la media complessiva dei punteggi di tutti i tiri effettuati dai tre giocatori?
X
A 5 B 6 C 7 D 13,3
15 Sul triangolo ABC sono stati costruiti dei semicerchi aventi il diametro coincidente con ciascuno dei lati del triangolo.
Sapendo che AB = 4 cm e BC = 6 cm, determina l’area del semicerchio costruito sul lato
73 ALLENAMENTO 5
Giocatore N° tiri Punteggio totale Media dei punteggi Luca 25 100 4 Masha 10 60 6 Giorgio 5 40 8
AC. A 4 r cm2 B 2 13 r cm2 C 8 r cm2 D 2 25 r cm2 2 3 4 5 6 7 8 9 1 8 7 6 5 4 3 2 1 9 A BC
X
16 Nella figura è riportato un quadrato inscritto in un cerchio.
Sapendo che il raggio vale 10 cm, quanto vale l’area della figura colorata?
A 314 cm2
B 264 cm2
C 214 cm2
D 114 cm2
17 Alice e Omar giocano a dadi, lanciando ad ogni tiro due dadi blu e uno rosso. Il punteggio viene calcolato sommando il punteggio dei due dadi blu e sottraendo il punteggio del dado rosso.
18
Completa la frase:
Il punteggio minimo che è pos sibile ottenere è , il punteggio mas simo è invece
In Italia ogni abitante consuma mediamente 10 kg di spaghetti all’anno. Considerando che in Italia ci sono 60 000 000 di abitanti, che ogni spaghetto è lungo circa 25 cm e che pesa circa 1 grammo, mettendo in fila tutti gli spaghetti mangiati in un anno in Italia quale lunghezza si raggiungerebbe?
A Una volta e mezzo la lunghezza dell’equatore (60 000 km)
B Poco meno della metà della distanza tr a la Terra e la Luna (150 000 km)
C La distanza tr a la Terra e il Sole (150 000 000 di km)
D Quasi la distanza percorsa dalla sonda Voyager 2 (15 000 000 000 di km)
74 ALLENAMENTO 5
O – 4 11 X X
a. La velocità massima è raggiunta:
A dal corpo A all’istante t = 21 s
B dal corpo A tr a i tempi di 10 s e 21 s
C dal corpo B dopo i 17 s
D dal corpo B tr a il tempo di 10 s e 17 s
b. Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Nei primi 10 s il corpo A è più veloce del corpo B V F
b. Tra 10 s e 17 s il corpo B è fermo V F
c. Il corpo A si muove di moto rettilineo uniforme V F
d. All’istante t = 10 s i due corpi hanno la stessa velocità V F
75 ALLENAMENTO 5
19 Il seguente grafico rappresenta il moto dei corpi A (linea blu) e B (linea rossa) su una traiettoria rettilinea.
0 0 20 40 60 80 100 120 510152025 tempo (s) spazio (cm) X
X X X X
20 La seguente carta altimetrica riporta alcuni sentieri di montagna:
Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Il dislivello tra A e C è di circa 200 m V F
b. Per andare da E a C prima si sale poi si scende di quota V F
c. Il tratto più ripido è il sentiero che va da B a C V F
d. Il tratto col maggiore dislivello è quello che va da A a D V F
76 ALLENAMENTO 5
A E C B 2100m 2100m 2200 m 2100m 2000 m 2100 m D X X X
X
1 Per svolgere la moltiplicazione 17 $ ] 42g si possono utilizzare diversi modi. Quale tra i seguenti NON è corretto?
A 17 $ 8 17 $ 50
B 17 $ 40 17 · 2
C 17 $ ] 6g + 17 $ ] + 7g
D 17 $ ] 40g + 17 $ ] 2g
2 Di seguito è riportata la mappa di un giardino, qual è la sua superficie?
A 20 m
B 23 m
C 19 m2
D 21 m2
3 Durante una gita, una guida turistica informa che l’obelisco di Montecitorio è alto circa 34 m, compreso il basamento e il globo. In quel momento un palo alto 1,8 m piantato verticalmente rispetto al terreno proietta un’ombra di 2,7 m, quanto sarà lunga l’ombra proiettata dall’obelisco?
77 ALLENAMENTO 6
A 48 m B 51 m C 54 m D 68 m 4m 2m 3m 2m 3m 3m 34m 1,8m ?2,7m X X X
4 Osserva la seguente tabella che rappresenta i dati meteorologici rilevati in una località balneare nel giugno 2021.
Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. La più alta temperatura massima è stata registrata il giorno 13 V F
b. I giorni in cui non è piovuto sono stati i due terzi del totale V F
c. La minore temperatura massima è stata registrata il giorno 19 V F
78 ALLENAMENTO 6
Giorno T min T max Umidità Fenomeni 1 12 °C 21 °C 63% pioggia 2 11 °C 22 °C 65% –3 11 °C 23 °C 65% –4 13 °C 24 °C 65% –5 18 °C 25 °C 55% –6 16 °C 25 °C 56% –7 16 °C 26 °C 61% –8 16 °C 27 °C 65% –9 17 °C 27 °C 68% –10 18 °C 28 °C 70% –11 18 °C 30 °C 60% –12 18 °C 29 °C 69% –13 21 °C 28 °C 68% –14 19 °C 24 °C 78% temporale 15 17 °C 23 °C 67% pioggia 16 17 °C 19 °C 91% temporale 17 16 °C 22 °C 84% temporale 18 16 °C 23 °C 82% temporale 19 15 °C 24 °C 70% –20 15 °C 27 °C 62% temporale 21 17 °C 26 °C 64% –22 17 °C 29 °C 65% –23 21 °C 30 °C 54% –24 20 °C 30 °C 58% –25 20 °C 30 °C 69% temporale 26 18 °C 26 °C 73% temporale 27 16 °C 24 °C 78% –28 16 °C 28 °C 71% –29 17 °C 31 °C 66% –30 17 °C 24 °C 77% temporale
è
5 V F
d. La giornata meno umida
stata il giorno
X X X X
5 Di seguito è riportato il certificato delle competenze di Letizia. I livelli di competenza degli alunni sono indicati con livelli da D (iniziale) ad A (avanzato):
Competenze chiave europee Livello
1. Comunicazione nella madrelingua o lingua di istruzione A
2. Comunicazione nelle lingue straniere B
3. Competenza matematica e competenze di base in scienza e tecnologia D
4. Competenze digitali B
5. Imparare ad imparare B
6. Competenze sociali e civiche A
7. Spirito di iniziativa e imprenditorialità B
8. Consapevolezza ed espressione culturale C
a. Qual è la moda dei livelli di competenza?
A A B B C C D D
b. È possibile calcolare la media dei livelli di competenza?
A Sì
B Sì, ma solamente as segnando un valore numerico a ogni lettera
C Sì, perché ai livelli è già as segnato un valore numerico
D No, poiché i livelli sono dati qualitativi e non quantitativi
6 Osserva il seguente grafico cartesiano. Tracciando la retta r passante per AB e la retta s passante per CD quali sono le coordinate del punto di intersezione E delle rette r ed s?
79 ALLENAMENTO 6
Risposta: E ] ; g 02 -4 -6 -4-64681012141618 2 4 6 8 10 12 D A B C 9,5 2,5 X X
7 Una ditta etichetta i suoi prodotti con un codice alfanumerico costituito da una lettera dell’alfabeto internazionale a 26 lettere, esclusa la O, e da due cifre. Sapendo che la seconda cifra deve essere pari, quante combinazioni del codice si possono ottenere? A 3 4
A 1250
B 1300
C 2500
D 3500
8 Collega ogni figura con quella equivalente.
80 ALLENAMENTO 6
1234 ABCD X
9 Tra i protisti (organismi eucarioti unicellulari) l’Amoeba proteus, ha un diametro circa 10 volte più grande della lunghezza di una Euglena gracilis. Sapendo che l’Euglena gracilis è lunga circa 5 $ 10 5 m, qual è il diametro di un’Amoeba proteus? Indica la potenza. 5 $ 10...
10 Nella figura a sinistra sono rappresentati due solidi visti dall’alto. Se vedi i due solidi nella prospettiva della figura a destra, da quale posizione li stai osservando?
A Punto A
B Punto B
C Punto C
D Punto D
11 Se n è un qualsiasi numero naturale, come sarà la differenza n $ ] n + 1g – n $ ] n – 1g?
A Dispari se n è pari e pari se n è dispari
B Pari se n è pari e dispari se n è dispari
C Sempre dispari
D Sempre pari
X X
81 ALLENAMENTO 6
A
D C
– 4
B
12 Osserva la seguente carta topografica in scala 1 : 25 000.
a. Qual è la distanza in linea d’aria tra i punti A e B segnati sulla carta?
Risposta: km
(accettato da 1,7 a 1,8)
b. Se la stessa distanza fosse riportata in una scala 1 : 10 000, di quanto sarebbe la distanza rispetto alla scala 1 : 25 000?
A 4 volte minore
B 2,5 volte minore
C 2,5 volte maggiore
D 4 volte maggiore
13 Sapendo che la formula per trasformare i gradi Fahrenheit in gradi Celsius è:
C = ] F – 32g $ 9 5
A quanti gradi Celsius corrispondono 14 °F?
1,75 – 10
Risposta: °C
82 ALLENAMENTO 6
A B
X
14 Lo studio dei ghiacci polari fornisce numerose informazioni sull’atmosfera e sul clima del passato. Per ottenerle si effettuano delle perforazioni in profondità e vengono estratte delle «carote di ghiaccio» come quella in figura, del diametro di circa 10 cm e lunghe fino a qualche metro.

a. Qual è il volume della carota di ghiaccio rappresentata in figura?
A r dm3
B 2,5 r dm3
C 4r dm3
D 10 r dm3
b. A volte le perforazioni sono molto lunghe. Sapendo che il peso specifico del ghiaccio è 0,9 kg/dm3, quale potrebbe essere l’operazione da svolgere per calcolare il peso del ghiaccio, espresso in kg, complessivamente estratto in una perforazione di 1000 m?
A r $ 0,52 $ 10 000 | 0,9
X
B r $ 0,52 $ 10 000 $ 0,9
C r $ 12 $ 10 000 | 0,9
D 2r $ 5 $ 1000 $ 0,9
15 Indica se ciascuna delle seguenti uguaglianze è vera (V) o falsa (F).
a. 14 8 = 74 $ 2 4 V F
b. ] − 3g9 | ] − 3g6 = ] + 3g3 V F






c. 1111 = 1110 $ 11 V F
d. ] − 5g6 = − ] + 5g6 V F
X X X X X

16 Un elefante pesa circa 6 tonnellate ovvero 6 $ 103 kg. Sapendo che il peso della Grande Piramide di Giza è di 6 $ 109 kg sapresti dire quanti elefanti ci vorrebbero per eguagliare il suo peso?
Risposta: elefanti
1 000 000 di
83 ALLENAMENTO 6
1m 10cm
17 Sul retro di una confezione di cornflakes sono riportati i seguenti valori nutrizionali:
Valori nutrizionali ed energetici (100 g)
Alimenti Cornflakes
Proteine 6,6 g
Lipidi 0,8 g
Carboidrati 87,4 g
Zuccheri solubili 10,4 g
Fibra totale 3,8 g
Energia 361 kcal - 1512 kj
Qual è il valore energetico di una porzione di cornflakes da 30 g?
A circa 108 kcal
B circa 120 kcal
C circa 450 kcal
D oltre 10 000 kcal
18 Il seguente grafico rappresenta la distribuzione delle attività pomeridiane degli alunni di terza di un istituto:
Qual è la probabilità in percentuale che un alunno scelto a caso non pratichi alcuno sport?
84 ALLENAMENTO 6
Risposta: % 0 2 1 3 5 6 7 8 4 numero alunni CalcioBasketNuotoAltrisportNessuna 24
X
19 Osserva la seguente figura.
32cm
Sapendo che l’area dei due triangoli isosceli rettangoli è rispettivamente di 32 cm2 e 8 cm2, qual è l’area della parte bianca della figura?
A 104 cm2
B 112 cm2
C 128 cm2
D 144 cm2
20
In quale delle seguenti serie i numeri sono scritti dal più piccolo al più grande?
A 100 29 ; 3 7 ; 9 ; r
B r; 9 ; 3 7 ; 100 29
C 9 ; r; 3 7 ; 100 29
D 3 7 ; 100 29 ; 9 ; r
85 ALLENAMENTO 6
2 8cm2 X X
1 Scrivi in ordine crescente i seguenti numeri:

2 Il triangolo ABC è inscritto nella circonferenza di centro O. Sapendo che il raggio CO = 5 cm e che la corda BC = 8 cm, calcola la lunghezza del perimetro del triangolo.
Risposta: cm
3 I satelliti geostazionari ruotano alla stessa velocità della Terra compiendo un giro attorno a essa in 24 ore esatte. Sapendo che il raggio della Terra è di 6378 km e che i satelliti geostazionari orbitano a una altitudine di 36 000 km, quale potrebbe essere la formula che permette di calcolare la velocità del satellite?

A 24 6378 km/h V =
B 637836000 km/h V = + 224 r
h
C 637836 000 km/h
V = + 24 2r $ `j
D 236000 km/h V r = $ 24
86
PROVA SIMULATA
0,2
– 2 –
1 a. b. c. d.
– 2
2
AB C O
24
– 2 0,2 –2 1 – 2
X
4 Quando la luce bianca attraversa un prisma, si ha il fenomeno della dispersione nelle componenti con diverse lunghezze d’onda e quindi nei diversi colori dell’arcobaleno. Alla lunghezza d’onda ( m ) di 6 $ 10 7 m corrisponde il colore arancione. La relazione tra frequenza e lunghezza d’onda è la seguente:

f m c =
Sapendo che la velocità della luce (c) equivale a 3 $108 m/s, indica quanto vale la frequenza della luce arancione.
A 8 $ 101 Hz
B 0,5 $ 10 –1 Hz
C 2 $ 10 –15 Hz
D 0,5 $ 1015 Hz
5 Su ogni lato del triangolo equilatero ABC mostrato in figura viene disegnato un triangolo rettangolo isoscele. Quanto misura l’ampiezza dell’angolo DA ˆ F?
150
Risposta: °
87 PROVA SIMULATA
AB C D FE
X
6 Uno stabilimento balneare, nella terza settimana di agosto, ha 25 ombrelloni tutti prenotati. Per migliorare il servizio, il titolare segna ogni giorno se il cliente è presente o meno. Al termine della settimana riepiloga i dati nella seguente tabella:
a. In media quanti giorni è venuto nello stabilimento ogni cliente?
Risposta: giorni
b. Qual è la percentuale di clienti che è stata presente almeno 4 giorni?
Risposta: %
7 Un pallone da calcio viene realizzato cucendo tra loro 12 pentagoni e 20 esagoni, usando come modello geometrico l’icosaedro troncato.
Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Il lato dell’esagono è più lungo di quello del pentagono V F
X
b. Il numero di vertici complessivi è 60 V F
c. Il numero di spigoli complessivi è 180 V F
X X X
d. L’area complessiva degli esagoni bianchi è poco meno del V F doppio dell’area complessiva dei pentagoni neri
(valida con almeno 3 risposte corrette su 4)
88 PROVA
SIMULATA
N° di giorni N° clienti 0 0 1 1 2 5 3 4 4 7 5 5 6 2 7 1
3,8 60
8 Kevin costruisce le mura di un castello con dei cubetti colorati.
a. Il primo giorno ne usa 8, il secondo ne usa 24 e ogni giorno aumenta di un cubetto sia la lunghezza del lato del castello sia la sua altezza. Il settimo giorno quanti cubetti dovrà utilizzare per costruire le mura del suo castello?
Risposta: cubetti
b. Considerando n = numero dei cubetti e g = numero del giorno, quale delle seguenti relazioni NON è corretta.
A n = 4 g $ ] g + 1g
B n = 4 g2 + 4 g
C n = 4 g $ ] g + 2g
D n = 4 $ Q g $ ] g + 2g – gU
Qual è il rapporto (espresso come frazione) tra l’area della parte bianca e quella della parte colorata della figura?
Risposta:
89 PROVA SIMULATA
9 Osserva la seguente figura:
Giorno 1
Giorno 2
224 X
Giorno 3
9 5
10 Osserva la seguente figura, rappresenta due circonferenze, rispettivamente di diametro AB e CD. La corda BD unisce i due punti di intersezione delle circonferenze.
Indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. La distanza OO’ è minore della somma dei raggi V F
b. La retta che congiunge i due centri OO’ è perpendicolare alla corda BD V F
c. Il quadrilatero ABCD è un trapezio V F
d. Il quadrilatero OBCO’ è un parallelogramma V F
(valida con almeno 3 risposte corrette su 4) X X X X
11 La legge di Moore è nota tra gli addetti dell’informatica perché stima la velocità di sviluppo delle prestazioni dei microprocessori.
«La complessità di un microcircuito, misurata ad esempio tr amite il numero di transistor per chip, raddoppia ogni 18 mesi (cioè un anno e mezzo)»

Se un’azienda in un certo anno avesse prodotto un processore con un milione di transistor, dopo un anno e mezzo ne produrrebbe uno con 2 milioni di transistor e dopo tre anni con 4 milioni di transistor.
Quanti milioni di transistor avrebbe un processore prodotto da quell’azienda dopo 12 anni?
Risposta: milioni
256
90 PROVA SIMULATA
C O' D AOB
12 La professoressa di italiano fa svolgere un esercizio alla classe: usare dei cartoncini colorati per comporre differenti frasi disponendo in ordine un cartoncino giallo, uno rosso e uno azzurro, tra quelli di seguito mostrati.
Poiché gli alunni e le alunne sono 21, è possibile per ciascuno di loro comporre una frase diversa dagli altri?
Sì, perché il numero di combinazioni è
No, perché il numero di combinazioni è
13 Norman taglia un triangolo (come quello mostrato sotto) lungo le linee tratteggiate a e b, che sono parallele alla base e poste rispettivamente a 1 3 e a 3 2 dell’altezza.
Frammento 1
Frammento 2
Frammento 3
Se l’area del frammento 2 è di 12 cm2, quanto misura l’area del frammento 3?
A 13,5 cm2
B 20 cm2
C 16 cm2
D 18 cm2
91 PROVA SIMULATA
Zio
una mela il pesce un gelato ha mangiato ha comprato
La mamma
Peppe Arianna Joshua
a b
24 X X
14 Uno, nessuno e centomila, ovvero 1, 0 e 100 000. Quale delle seguenti serie di potenze corrisponde ai numeri citati nel titolo del famoso romanzo di Pirandello?
A 15 , 05 , 105
B 11, 0 0 , 105
C 10 0 , 10 –1 , 106
D 101, 10 0 , 106
15
Osservando la scala presente in figura, a quanto potrebbe corrispondere la superficie del Wyoming?
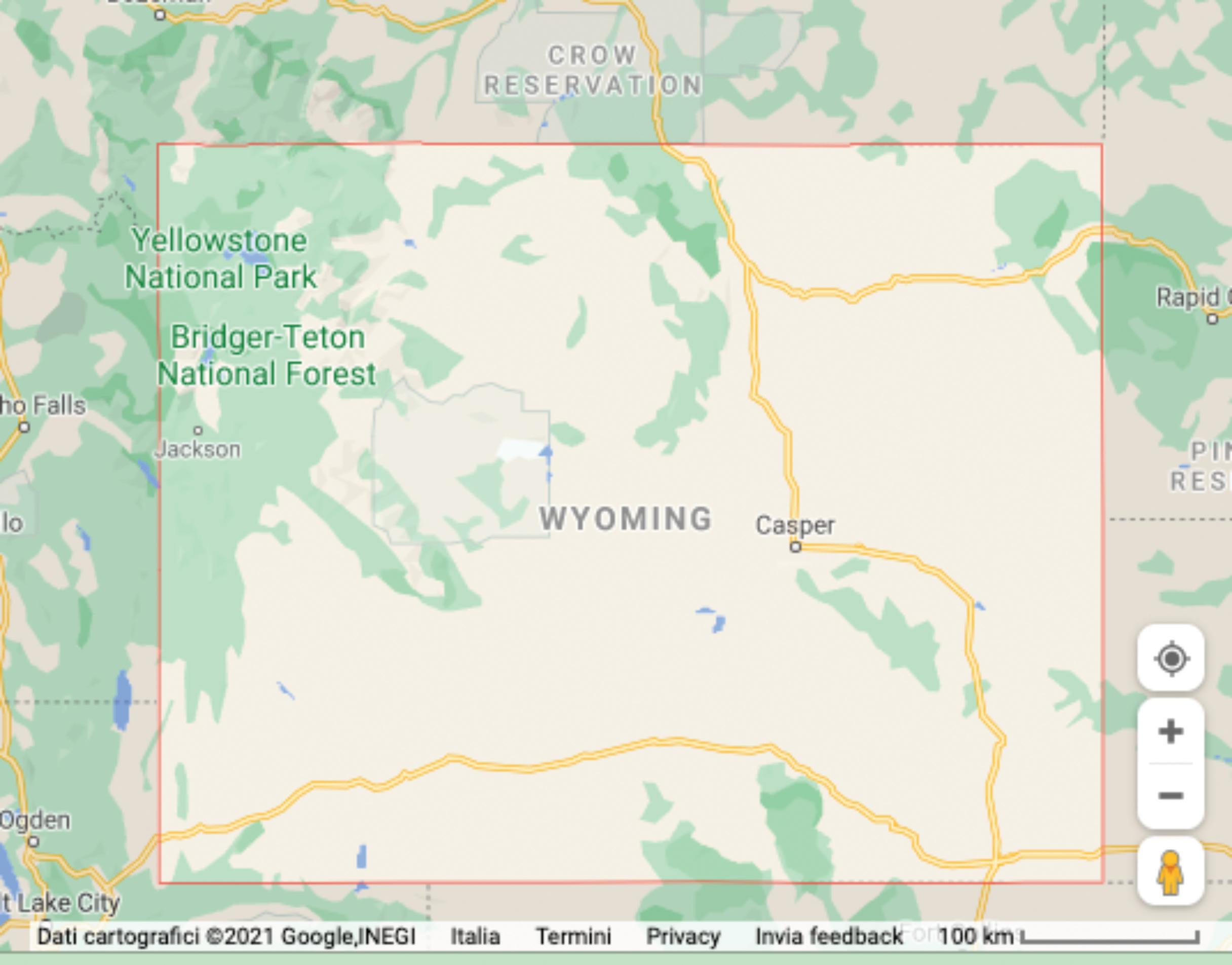
A Meno di 50 000 km2
B Tra 50 000 e 20 0 000 km2
C Tra 200 000 e 40 0 000 km2
D Più di 400 000 km2
92 PROVA SIMULATA
Nella carta geografica di seguito mostrata è rappresentato lo Stato del Wyoming, negli Stati Uniti d’America.
X X
16 Osserva la seguente figura.
Sapendo che l’area della sua superficie è 125 cm2, calcola il perimetro della figura.
A 50 cm
X
B 60 cm
C 80 cm
D 100 cm
17 Il seguente grafico mostra il numero di eventi estremi connessi con i cambiamenti climatici avvenuti in Italia tra il 2008 e il 2019.
In base al grafico, indica se ciascuna delle seguenti affermazioni è vera (V) o falsa (F).
a. Nel 2013 ci sono state sicuramente meno di 600 piogge intense
b. Il numero totale di eventi estremi del 2014 è stato più alto degli anni precedenti
c. Nel 2019 ci sono stati più di 1600 tornadi
d. Il numero complessivo di eventi estremi è aumentato ogni anno
X X X (valida con almeno 3 risposte corrette su 4)
93 PROVA SIMULATA
V F
V
F
V F
V F 1800 1600 1400 1200 1000 800 600 400 200 20082009201120122013201420152016201720182019 2010 RaffichediventoGrandinePioggeintenseTornado Fonte:elaborazioneFondazioneperlosvilupposostenibilesudatiEuropeanSevereWeatherDatabase 0
X
18 Eric vuole imparare a suonare un brano rock di 4 minuti. Il brano nella versione originale viene eseguito a 120 bpm (battiti per minuto). All’inizio per esercitarsi Eric lo suona più lentamente a soli 80 bpm. Quanto impiegherebbe a suonare l’intero brano a questa velocità?
Risposta: minuti
19 Gli Egizi non avevano il nostro sistema di notazione delle frazioni, ma usavano soltanto le frazioni unitarie n 1 . Per cui se dovevano scrivere qualsiasi altra frazione propria lo facevano come somma di frazioni unitarie. Quali delle seguenti frazioni NON corrisponde alla frazione 7 3 ?
20 Per entrare in un parco giochi ci sono le seguenti opzioni:
Opzione 1 Tessera A: € 100 annuale con ingressi illimitati
Opzione 2 Tessera B: € 25 annuale + sconto del 25% a ingresso
Opzione 3 Ingresso singolo: € 12
a. Natasha vorrebbe andare al parco giochi 9 volte nella stagione. Qual è l'opzione più conveniente?
Risposta: Opzione
b. Quanto risparmia rispetto all’opzione meno conveniente?
€
94 PROVA SIMULATA
A 3 1 + 1 14 + 42 1 B 3 1 + 5 1 1 + 1 35 C 1 4 + 1 12 + 1 84 D 1 4 + 1 7 + 1 28
Risposta:
1 2 1 4 1 16 1 64 1 32 1 8 6 1 8 X
21 In una scuola viene svolto un sondaggio per conoscere il tipo di dispositivi utilizzati durante la didattica a distanza. I risultati in quattro delle classi sono i seguenti:
Per una delle classi viene costruito il seguente grafico:
A quale delle classi corrisponde il grafico?
A Prima C B Seconda B C Terza A D Terza C
22 La legge di Keplero afferma che «I quadrati dei tempi (T) che i pianeti impiegano a percorrere le loro orbite sono proporzionali al cubo del semiasse maggiore (a)».
T 2 = a3
Considerando per la Terra T = 1 anno e a = 1 unità astronomica, 12 = 13.
Quanto durerebbe l’anno in un pianeta in cui il semiasse maggiore dell’orbita a fosse pari a 4 unità astronomiche?
A Un anno B 4 anni C 8 anni D 64 anni
X
95 PROVA SIMULATA
Prima C Seconda B Terza A Terza C Computer fisso 12 8 7 6 Portatile 6 7 3 6 Tablet 3 5 5 4 Smartphone 3 5 5 2
Computer fisso Portatile Tablet Smartphone 32% 20% 20% 28% a = 4u.a. X
23
Enrico pensa a un numero n, poi calcola il suo quadrato n2 e il suo cubo n3, infine li dispone sulla seguente linea dei numeri:
Quale potrebbe essere il numero pensato da Enrico?
A + 1 3
B – 2
C –1 2
D Nessuno dei precedenti
24 Giacomo gioca a memory con i suoi amici. Il mazzo di carte che usano è composto da 40 carte, uguali a due a due. Già sono state trovate 7 coppie di carte.
Ha girato la carta con la mela. Giacomo si ricorda che l’altra carta con la mela sicuramente non è né nella stessa riga né nella stessa colonna di quella appena girata.
Qual è la probabilità che Giacomo possa trovare al primo tentativo l’altra carta con la mela?

























96 PROVA SIMULATA
A 1 10 B 1 1 9 C 0 1 2 D 1 25 nn3 n2 x
X
X
Quanto
Risposta:
97 PROVA SIMULATA 25 Qual è il valore della seguente espressione? $ 22 2 10 20 1 31 22 22 22 22 ++ = ccmm A 1 B 2 C 4 D 6 26 Osserva la seguente figura, in cui quattro rette si intersecano tra loro.
misura l’angolo c?
° B A C D d = 50° b = 45° a = 60° c 205 X
27 Frida controlla tutti i mesi il proprio conto corrente. Il grafico seguente è relativo ai primi sei mesi dell’anno.
a. In quale mese ha risparmiato maggiormente?
Risposta:



b. Quanto ha risparmiato complessivamente nei primi sei mesi dell’anno?

98 PROVA SIMULATA
A 1150 € B 1500 € C 1750 € D 1850 € 0 200 400 600 800 1000 1200 1400 1600 1800 2000 aprile 850 € 1550 € 1500 € 1150 1550 € 1750 € gennaiofebbraiomarzomaggiogiugno EntrateUscite 1200 € giugno X





































































