Matematica e Scienze
nella Scuola Primaria
Guida didattica mista con CD-Rom
Claudia Riccardi, Eva Pigliapoco e Ivan Sciapeconi
Il progetto
Insegnare.LIM presenta un percorso integrato che coinvolge sia Matematica sia Scienze. I materiali presenti in Insegnare.LIM sono stati organizzati su base mensile, per consentire ai docenti il pieno controllo dell’andamento della programmazione didattica.
Le novità introdotte dal legislatore con l’ultima riforma, infatti, hanno accentuato il concetto di “docente prevalente” della classe. Una prevalenza che può disorientare, se non opportunamente organizzata. Per quanto scandito mese per mese, il percorso si compone di schede che possono essere utilizzate indipendentemente dalla collocazione pensata dagli autori.
I materiali (le schede e gli oggetti digitali presentati nelle prossime pagine) vengono forniti anche su CD-Rom in modo da poter sfruttare la massima flessibilità del digitale.
Ciascun mese è introdotto da una breve descrizione delle attività proposte e degli obiettivi da raggiungere. Anche se può sembrare ridondante presentare le attività mensili, è però importante che il docente condivida l’impostazione di fondo del lavoro. Potrà poi, se lo ritiene necessario, operare su questo sfondo con scelte personali e integrazione di materiali. Le pagine introduttive hanno lo scopo di fornire una mappa con la quale orientarsi tra le schede e le indicazioni operative.
Il curricolo di terza
La prima parte dell’anno sarà dedicata alla scrittura, scomposizione-composizione e rappresentazione dei numeri sull’abaco. Si introdurranno l’addizione e la sottrazione, il calcolo mentale e le operazioni in colonna, la moltiplicazione e la divisione con le loro proprietà, e la risoluzione dei problemi. In Geometria si affronteranno i poliedri, i solidi di rotazione, i concetti di linea e di punto. In Scienze si affronterà il metodo scientifico-sperimentale e si introdurranno i materiali, i fenomeni atmosferici e la materia. Nel secondo quadrimestre si affronteranno le frazioni e le unità di misura. In Geometria si lavorerà sui diversi tipi di linea, sugli angoli e sulle figure geometriche piane, per concludere con i concetti di perimetro e di area. In Scienze si lavorerà sul concetto di ecosistema e di catena alimentare, si affronteranno gli elementi viventi e non viventi dei vari ecosistemi, per concludere con la classificazione dei mammiferi.
Le vacanze e i compiti
I periodi di vacanza sono assolutamente necessari, ma è indubbio che possano avere delle ricadute negative sugli apprendimenti dei bambini. Normalmente, al ritorno a scuola dopo un periodo più o meno lungo di assenza, i docenti rilevano la necessità di recuperare una parte degli apprendimenti. All’interno di Insegnare.LIM, sono previste due diverse sezioni, relative ai compiti di Natale e Pasqua, che il docente potrà fotocopiare in tutto o in parte e distribuire ai bambini. I compiti ricalcano il percorso didattico della Guida, quindi gli alunni potranno contare su una sostanziale unitarietà di percorso didattico.
I materiali per la verifica e la valutazione
Un altro importante materiale di lavoro, presente in Insegnare.LIM, è rappresentato dalle schede per la verifica e la valutazione delle competenze.
Al termine del primo e del secondo quadrimestre, vengono fornite:
• pagine per la verifica delle attività svolte;
• pagine per la registrazione e la sintesi dei dati. Il docente potrà decidere se avvalersi in tutto o in parte dei materiali proposti. È anche possibile partire da essi per personalizzarli sulle esigenze e sulle caratteristiche della classe.
Il materiale digitale
Negli ultimi anni, i materiali didattici tradizionali sono stati accompagnati da prodotti digitali: principalmente CD-Rom e risorse online. Nel caso di Insegnare.LIM, la scelta è stata quella di pensare a un percorso integrato. Nel CD-Rom non sono stati inseriti materiali digitali genericamente aggiuntivi rispetto al percorso didattico delineato nella Guida. Il Web è pieno di risorse digitali che, in questo senso, possono supportare il lavoro del docente. I materiali messi a disposizione sono, invece, funzionali alla conduzione di vere e proprie lezioni con la Lavagna Interattiva Multimediale o con un normale videoproiettore. Le lezioni sono scandite secondo una metodologia precisa e una presentazione “step by step”, che ha lo scopo di facilitare i docenti meno esperti.
Una descrizione più accurata di questa distinzione, tutt’altro che sottile, viene articolata nelle pagine seguenti.
Gli strumenti digitali
Negli ultimi tempi, le proposte di strumenti didattici digitali sono aumentate notevolmente. È importante, però, saper riconoscere che cosa realmente è utile alla didattica.
L’inserimento delle Lavagne Interattive Multimediali nelle aule della Scuola Primaria ha segnato un importante segno di svolta.
Dopo aver inserito l’Informatica nei laboratori, limitando in modo sostanziale il suo apporto alla didattica, finalmente le nuove tecnologie entrano nelle discipline e nel fare scuola di tutti i giorni.
Anche per questo motivo, sul versante delle opportunità metodologiche, Insegnare.LIM propone una soluzione integrata tra materiale cartaceo e digitale. A supporto di questa scelta, c’è la convinzione che le risorse per la LIM, da sole, non possano innovare la didattica o fornire aiuti di rilievo agli apprendimenti dei bambini.
In questa Guida non verranno proposti giochi animati o prodotti multimediali caratterizzati da una forte incidenza di “effetti speciali”. Ai docenti verrà fornito qualcosa di tecnologicamente molto più semplice, ma enormemente più interessante e produttivo sotto il profilo del rapporto fra insegnamento e apprendimento: idee e strategie didattiche. È utile ricordare che tutte le soluzioni proposte possono essere utilizzate, rinunciando a una pur significativa interattività, con un videoproiettore collegato a un computer.
Che cosa aspettarsi dalla LIM
Indubbiamente, la Lavagna Interattiva Multimediale rappresenta una innovazione significativa nel panorama delle tecnologie per la didattica. Essa si basa su un’idea sostanzialmente semplice: espandere le funzioni della lavagna collegandola al computer. O, volendo, espandere le caratteristiche del computer portandolo ad assumere l’aspetto di una lavagna.
Al di là dei giochi di parole, però, è fondamentale che i docenti sappiano che cosa aspettarsi da questa come da qualsiasi altra innovazione.
Appiattire la didattica su un versante tutto incentrato sugli aspetti ludici e multimediali potrebbe non essere una prospettiva condivisibile, per molti docenti.
Gran parte dei prodotti software attualmente in circolazione e destinati alla LIM si possono dividere in due grandi categorie:
• gli Edutainment, ovvero i programmi che coniugano insegnamento e intrattenimento (Education e Entertainment). Sono i software che, sotto una impostazione molto simile a quella dei videogiochi, nascondono degli intenti didattici;
• i Learning Object, che sono percorsi di apprendimento strutturati, un insieme di istruzioni e verifiche che dovrebbero consentire agli alunni, autonomamente, di costruire i propri apprendimenti.
I materiali contenuti in Insegnare.LIM partono da tutt’altro punto di vista e hanno ambizioni ben diverse.
I materiali di Insegnare.LIM:
i Teaching Object
Insegnare.LIM è un progetto che si basa in modo sostanziale sul potenziamento della relazione di insegnamento-apprendimento. Le risorse didattiche non sono pensate per intrattenere i bambini o per catturare genericamente la loro attenzione. Esse sono costruite, piuttosto, intorno alla necessità del docente di strutturare una lezione completa ed efficace.
Volendo anticipare la loro descrizione con un nome, si potrebbero definire Teaching Object: oggetti utili al docente per fare lezione.
Contrariamente ai Learning Object, espressamente pensati per far lavorare gli alunni in modo autonomo (con il rischio di perdere i più deboli o i meno motivati), i Teaching Object di Insegnare.LIM sono pensati come risorse per condurre la lezione, per attivare tutti gli alunni, per scandire le tappe del lavoro.
Per questo, prima di utilizzare i materiali digitali contenuti nel CD-Rom, si consiglia un’attenta lettura delle indicazioni metodologiche.
Le risorse abbinate alla Guida possono essere utilizzate solo in abbinamento alle schede e alle procedure descritte nelle pagine seguenti. Diversamente, non avrebbero alcuna utilità.
L’organizzazione
Per una maggior chiarezza espositiva, le lezioni con la LIM sono state raggruppate alla fine di ogni quadrimestre. Questa scansione non è l’unica possibile, tanto più che il docente potrà proporre le attività con gli strumenti digitali in qualsiasi periodo dell’anno e gestirle con la dovuta flessibilità. In realtà, la scansione quadrimestrale serve solo per consentire una facile consultazione in base alla programmazione mensile delle attività.
Da un punto di vista tecnico, le attività digitali richiedono competenze informatiche minime. Tutte le risorse multimediali (immagini, suoni, animazioni) sono già contenute nei singoli file. Sarà sufficiente lanciare lo strumento digitale desiderato per essere immediatamente operativi.
Le risorse digitali presenti nel CD-Rom
Il CD-Rom allegato a Insegnare.LIM contiene una serie di risorse digitali facilmente identificabili nella schermata principale.
• Prove nazionali: prove INVALSI in formato PDF.
• Librosfogliabile: è un vero e proprio libro digitale, sfogliabile tramite l’apposito player.
• Materiale per la LIM. Sono i materiali digitali sicuramente più interessanti. I materiali interattivi consentono di integrare le normali attività di classe con strumenti digitali di approfondimento o consolidamento. All’interno del menu, sono presenti:
– le schede in formato PDF. Le pagine operative di Insegnare.LIM sono presentate anche in forma digitale, per essere proiettate sulla LIM. In questo modo risulterà agevolata, per esempio, la spiegazione dell’esercizio o la correzione collettiva dei lavori. Le schede in formato PDF possono essere gestite con il software caratteristico del modello di LIM in dotazione (per esempio, per sottolineare, scrivere o cancellare);
– attivitàdigitalidivise tra I e II quadrimestre. Si tratta di attività che possono essere condotte con l’aiuto di risorse presenti nel CD-Rom allegato, pensate in stretto collegamento con le attività del primo e del secondo quadrimestre, utilizzabili con la LIM o con un videoproiettore.
Anche nel
CD-Rom, i materiali interattivi sono organizzati con la stessa scansione della Guida.
Come già accennato nelle pagine precedenti, tutte le attività con la LIM fanno riferimento e si integrano alle soluzioni proposte in cartaceo. Per questo motivo, le descrizioni delle attività digitali faranno costante riferimento al contenuto della Guida e alle schede operative. Tutte le schede operative, inoltre, sono accompagnate da un sistema di icone che segnala la presenza di risorse aggiuntive sul CD-Rom.
Icona digitale: la scheda fa parte di uno dei percorsi legati alla LIM ed è accompagnata da risorse digitali. Per sapere come utilizzare la scheda in abbinamento all’attività per la LIM, si può fare riferimento alle pagine di descrizione dell’attività, raccolte al termine di ogni quadrimestre.
Programmazione Matematica
Classe terza
Competenze alla fine della classe terza
L’alunno:
• sviluppa un atteggiamento positivo rispetto alla matematica, anche grazie a molte esperienze in contesti significativi, che gli hanno fatto intuire come gli strumenti matematici che ha imparato siano utili per operare nella realtà;
• si muove con sicurezza in semplici calcoli con i numeri naturali, sia nel calcolo scritto sia in quello mentale;
• opera con i numeri decimali, facendo anche riferimento alle monete o ai risultati di semplici misurazioni;
• riesce a risolvere semplici problemi, mantenendo un certo controllo sia sul processo risolutivo sia sui calcoli;
• riconosce, denomina e descrive figure geometriche solide e piane;
• rappresenta relazioni e dati con tabelle, schemi e diagrammi.
SETTEMBRE – OTTOBRE
Conoscenze Obiettivi Schede operative di riferimento
Il nostro sistema di numerazione: decimale e posizionale
L’addizione
L’ordinamento e il confronto dei numeri
Lo spazio e le figure: le figure solide
Le relazioni
Comporre e scomporre i numeri naturali entro il 1 000. Pag. 17
Rappresentare i numeri sull’abaco. Pag. 18
Leggere e scrivere i numeri entro il 1 000. Pagg. 24-32
Completare la tabella dell’addizione. Pag. 19
Eseguire addizioni sulla linea dei numeri. Pag. 20
Conoscere e applicare la proprietà associativa dell’addizione. Pag. 21
Risolvere problemi di tipo additivo. Pagg. 22-23
Saper applicare strategie di calcolo mentale. Pag. 25
Eseguire addizioni con macchine per contare. Pag. 26
Eseguire addizioni in colonna e scoprire la proprietà commutativa. Pag. 27
Eseguire addizioni in colonna sull’abaco con il cambio. Pagg. 28-29
Ordinare i numeri naturali. Pag. 30
Confrontare i numeri naturali. Pag. 31
Consolidare il riconoscimento delle figure solide. Pagg. 32-34
Denominare le figure solide. Pag. 35
Rappresentare utilizzando i connettivi “e” e “non” Pag. 36
Classificare in base a uno o più attributi. Pag. 37
Scoprire la proprietà di un insieme. Pag. 38
La statistica Saper realizzare un istogramma. Pagg. 39-40
Conoscenze
Il nostro sistema di numerazione: posizionale e decimale
NOVEMBRE
Obiettivi
Schede operative di riferimento
Costruire e rappresentare con vari strumenti il 1 000. Pag. 45
Leggere e scrivere numeri oltre il 1 000, mediante sequenze numeriche. Pag. 52
L’addizione Comporre numeri con coppie di addendi. Pag. 46
L’ordinamento e il confronto dei numeri
La sottrazione
Lo spazio e le figure
Confrontare numeri naturali. Pagg. 47-48
Completare la tabella del maggiore o uguale. Pag. 49
Completare la tabella della sottrazione. Pag. 50
Completare sequenze numeriche mediante calcolo mentale. Pag. 51
Eseguire sottrazioni in colonna. Pag. 53
Eseguire sottrazioni con l’abaco. Pag. 54
Eseguire sottrazioni con il prestito, con l’abaco. Pagg. 55-56
Eseguire sottrazioni in colonna con il doppio prestito. Pag. 57
Eseguire sottrazioni in colonna, con la prova. Pag. 58
Risolvere problemi di tipo sottrattivo. Pagg. 59-60
Osservare e descrivere cubo e parallelepipedo. Pag. 61
Osservare e descrivere prismi. Pag. 62
La misura Effettuare misure di oggetti della classe. Pag. 63
Le relazioni Classificare in base a uno o più attributi. Pag. 64
La statistica Rilevare la moda. Pag. 65
DICEMBRE
Conoscenze
La moltiplicazione
Obiettivi Schede operative di riferimento
Conoscere la moltiplicazione. Pag. 74
Completare la tabella della moltiplicazione. Pag. 73
Eseguire moltiplicazioni in tabella sulla linea dei numeri. Pagg. 75-76
Eseguire moltiplicazioni con gli incroci. Pag. 77
Conoscere e applicare la proprietà associativa della moltiplicazione. Pag. 78
Moltiplicare per 10. Pag. 79
Moltiplicare per 100. Pag. 80
Moltiplicare per 1 000. Pag. 81
Conoscere e applicare la proprietà distributiva della moltiplicazione. Pagg. 82-83
Eseguire moltiplicazioni in colonna senza cambio. Pag. 84
La moltiplicazione
Lo spazio e le figure:
le figure solide
La misura
Le relazioni
La statistica
Conoscenze
La moltiplicazione
La divisione
Lo spazio e le figure
La misura
Le relazioni
Applicare la proprietà distributiva nella moltiplicazione. Pag. 85
Eseguire moltiplicazioni in colonna con entrambi i fattori di due cifre. Pag. 86
Risolvere problemi di tipo moltiplicativo. Pag. 87
Osservare e descrivere piramidi. Pag. 88
Descrivere poliedri. Pag. 89
Distinguere strumenti di misura arbitrari da strumenti convenzionali. Pagg. 90-91
Scoprire la proprietà di un insieme. Pag. 92
Rilevare la moda. Pag. 93
GENNAIO
Obiettivi Schede operative di riferimento
Applicare la proprietà distributiva nella moltiplicazione. Pag. 103
Eseguire moltiplicazioni in colonna con entrambi i fattori di due cifre.
Conoscere la tecnica della moltiplicazione araba.
Pag. 104
Pag. 105
Avviare all’intuizione di problemi con la divisione di contenenza. Pagg. 106-107
Avviare alla differenza tra divisioni di contenenza e di ripartizione.
Pag. 108
Risolvere problemi rappresentando la situazione sulla linea dei numeri. Pag. 109
Risolvere problemi utilizzando tabelle. Pagg. 110-111
Eseguire divisioni sulla linea dei numeri. Pagg. 112-113
Costruire poliedri. Pagg. 114-115
Descrivere i solidi di rotazione. Pag. 116
Intuire il concetto di linea e di punto. Pag. 117
Effettuare misurazioni di oggetti con il righello. Pagg. 118-119
Conoscere le fasi di risoluzione di un problema. Pag. 120
Rappresentare con tabelle le combinazioni possibili in una situazione. Pag. 121
VERIFICHE QUADRIMESTRALI
Conoscenze Obiettivi
Il nostro sistema di numerazione: decimale e posizionale
L’addizione e la sottrazione
La moltiplicazione
Comporre e scomporre i numeri naturali oltre il 1 000.
Conoscere e saper operare con addizione e sottrazione.
Conoscere e saper operare con la moltiplicazione.
Schede operative di riferimento
Pag. 126
Pag. 127
Pag. 128
L’ordinamento dei numeri
Lo spazio e le figure
Conoscenze
La divisione
Le frazioni
Lo spazio e le figure
La misura
Le relazioni
Conoscenze
Le frazioni
Confrontare e ordinare i numeri naturali oltre il 1 000. Pag. 129
Riconoscere le figure geometriche soide Pag. 130
FEBBRAIO
Obiettivi
Schede operative di riferimento
Comprendere la divisione in relazione alle altre operazioni. Pag. 145
Completare la tabella della divisione. Pag. 146
Eseguire divisioni in riga. Pag. 147-148
Eseguire divisioni con l’abaco. Pag. 149-153
Eseguire divisioni con l’abaco, con dividendo a tre cifre. Pag. 150
Eseguire divisioni per 10, 100, 1 000. Pag. 151
Eseguire divisioni con l’abaco, con il cambio. Pag. 152
Risolvere problemi con la divisione. Pag. 154-155
Introdurre il concetto di frazione. Pag. 156
Consolidare il concetto di metà. Pag. 157
Conoscere e denominare diversi tipi di linea. Pag. 158
Ordinare punti su una linea orientata. Pag. 159
Intuire il concetto di retta. Pag. 160
Conoscere il metro e i suoi sottomultipli. Pag. 161
Comporre e scomporre misure di lunghezza e completare equivalenze. Pag. 162-163
Saper individuare i dati che mancano per la risoluzione di un problema. Pag. 164
Risolvere problemi con due domande e due operazioni. Pag. 165
MARZO
Obiettivi Schede operative di riferimento
Consolidare il concetto di metà. Pag. 175
Leggere e scrivere frazioni. Pag. 176
Rappresentare su figure la frazione data. Pag. 177
Risolvere semplici problemi con il calcolo dell’unità frazionaria. Pagg. 178-179
Calcolare l’unità frazionaria in un gruppo di elementi. Pag. 180
Individuare e scrivere la frazione che rappresenta parti di figure. Pag. 181
Calcolare il valore di una frazione. Pag. 182
Risolvere problemi con il calcolo della frazione. Pag. 183
Lo spazio e le figure
La misura
Le relazioni
Conoscenze
Le frazioni e i numeri decimali
Disegnare segmenti e comprenderne il concetto. Pag. 184
Disegnare rette e comprenderne il concetto. Pag. 185
Intuire il concetto di semiretta. Pag. 186
Intuire il concetto di rette incidenti. Pag. 187
Intuire il concetto di rette perpendicolari. Pag. 188
Risolvere problemi con le unità di misura di lunghezza. Pagg. 189-190-193
Conoscere i multipli del metro. Pagg. 191-192
Conoscere le unità di misura di peso/massa. Pagg. 194-195
Formulare la domanda implicita in un testo problematico. Pag. 196
Risolvere problemi individuando i dati nascosti. Pag. 197
Individuare e saper rappresentare relazioni. Pag. 198
APRILE
Obiettivi Schede operative di riferimento
Comprendere il concetto di frazione decimale. Pag. 209
Trasformare una frazione decimale in numero decimale. Pag. 210
Leggere e scrivere numeri decimali. Pagg. 211-212-213-214
Collocare i numeri decimali sulla linea dei numeri. Pag. 215
Intuire il concetto di rette perpendicolari. Pag. 216
Intuire il concetto di rette parallele. Pag. 217
Lo spazio e le figure
La misura
Le relazioni
Intuire il concetto di angolo. Pag. 218
Osservare e descrivere figure geometriche piane. Pagg. 219-220
Conoscere e operare con i sottomultipli del chilogrammo. Pag. 221
Conoscere le unità di misura di peso/massa e completare equivalenze. Pag. 222-223
Risolvere problemi con le unità di misura di peso/massa. Pag. 224
Conoscere e operare con i sottomultipli del grammo. Pag. 225
Comprendere i concetti di peso netto, peso lordo e tara. Pag. 226
Conoscere le misure di valore (euro e i suoi sottomultipli). Pag. 227
Individuare i dati superflui in un testo problematico. Pag. 228
Risolvere problemi con diagramma a blocchi. Pag. 229
Dati e previsioni
Conoscenze
I numeri decimali
Lo spazio e le figure
La misura
Le relazioni
Dati e previsioni
Conoscenze
La divisione
Le frazioni
Rappresentare con grafici e tabelle le combinazioni possibili in una situazione data. Pag. 290
MAGGIO - GIUGNO
Obiettivi
Schede operative di riferimento
Confrontare numeri decimali. Pag. 247
Ordinare in senso crescente e decrescente numeri decimali. Pag. 248
Conoscere il valore posizionale delle cifre dei numeri decimali. Pag. 249
Eseguire addizioni in colonna con i numeri decimali. Pag. 250
Eseguire sottrazioni in colonna con i numeri decimali. Pagg. 251-252-253
Osservare e descrivere figure geometriche piane. Pag. 254
Riconoscere e denominare poligoni. Pagg. 255-256
Avviare al concetto di perimetro. Pagg. 257-258
Avviare al concetto di area. Pag. 259
Comprendere la necessità di utilizzare unità di misura convenzionali. Pag. 260
Conoscere il litro e i suoi sottomultipli. Pagg. 261-262-263
Operare con il litro e i suoi sottomultipli. Pag. 264
Conoscere i multipli del litro. Pag. 265
Risolvere problemi con le unità di misura di capacità. Pag. 266
Operare con i multipli e i sottomultipli del litro. Pag. 267
Conoscere le banconote dell’euro. Pag. 268
Saper operare con l’euro. Pag. 269
Conoscere le misure di tempo. Pag. 270
Saper calcolare il valore unitario e il valore totale. Pag. 271
Intuire la probabilità in una situazione. Pagg. 272-273
VERIFICHE QUADRIMESTRALI
Obiettivi
Schede operative di riferimento
Conoscere e saper operare con la divisione. Pag. 284
Comprendere il valore di una frazione in una figura. Pag. 285
Lo spazio e le figure
La misura
I numeri decimali
I problemi e le quattro operazioni
La statistica
Conoscere e classificare le linee e i poligoni. Pag. 286
Operare con le unità di misura. Pag. 287
Operare con i numeri decimali. Pag. 288-289
Risolvere problemi con le quattro operazioni. Pag. 290
Individuare la moda e la probabilità. Pag. 291
Programmazione Scienze
Classe terza
Competenze alla fine della classe terza
L’alunno:
• ha capacità operative e manuali che utilizza in contesti di esperienza-conoscenza per un primo approccio scientifico ai fenomeni;
• fa riferimento in modo pertinente alla realtà e, in particolare, all’esperienza che fa in classe, sul campo, nel gioco, in famiglia, per dare supporto alle proprie considerazioni e motivazione alle proprie esigenze di chiarimenti;
• con la guida dell’insegnante e in collaborazione con i compagni, ma anche da solo, formula ipotesi e previsioni, osserva, registra, classifica, identifica relazioni spazio-temporali, misura, prospetta soluzioni; racconta in forma chiara ciò che ha fatto e sperimentato.
Conoscenze
Gli oggetti e i materiali
Conoscenze
Il metodo scientificosperimentale
Gli animali e l’ambiente
SETTEMBRE – OTTOBRE
Obiettivi
Schede operative di riferimento
Osservare oggetti dell’aula per individuare i materiali con i quali sono realizzati. Pag. 41
Individuare le proprietà dei materiali. Pag. 42
NOVEMBRE
Obiettivi
Schede operative di riferimento
Conoscere le fasi del metodo scientificosperimentale e la funzione dello scienziato. Pag. 66-67
Conoscere forme di adattamento all’ambiente. Pag. 68-69
Classificare gli animali in vertebrati e invertebrati. Pag. 70
Conoscenze
I fenomeni atmosferici
Conoscenze
Gli aspetti della materia
Conoscenze
Gli oggetti e i materiali
Conoscenze
Gli aspetti della materia
Il rapporto uomo-natura e la tutela dell’ambiente
DICEMBRE
Obiettivi
Individuare simboli che rappresentano i fenomeni atmosferici per realizzare semplici grafici.
Conoscere e utilizzare il termometro per effettuare rilevazioni.
GENNAIO
Obiettivi
Schede operative di riferimento
Pag. 94
Pagg. 95-96
Schede operative di riferimento
Conoscere i passaggi di stato dell’acqua. Pag. 122
Analizzare e comprendere il ciclo dell’acqua. Pag. 123
Conoscere le caratteristiche dell’acqua. Pag. 124-125
VERIFICHE QUADRIMESTRALI
Obiettivi
Schede operative di riferimento
Riconoscere i diversi materiali degli oggetti. Pag. 131
FEBBRAIO
Obiettivi
Schede operative di riferimento
Conoscere la composizione dell’aria. Pag. 166
Conoscere le caratteristiche dell’aria. Pag. 167-172
Individuare situazioni che indicano la presenza di vento. Pag. 171
Intuire le cause dell’inquinamento dell’aria. Pag. 168
Conoscere i comportamenti dannosi per la salute dei polmoni. Pag. 169
Comprendere le cause e gli effetti delle piogge acide. Pag. 170
MARZO
Conoscenze Obiettivi
L’ambiente e gli esseri viventi
Schede operative di riferimento
Comprendere il significato di ecosistema. Pag. 199
Comprendere il significato di catena alimentare. Pag. 200
Descrivere una catena alimentare in un albero. Pag. 201
Conoscere la funzione dei decompositori in una catena alimentare Pag. 202
Conoscere le caratteristiche dei funghi. Pag. 203
Conoscere diversi tipi di funghi e le loro caratteristiche. Pag. 204
Conoscere forme di vita animale del bosco. Pag. 205
Individuare e descrivere una semplice catena alimentare del bosco. Pag. 206
APRILE
Conoscenze Obiettivi
Il regno vegetale
Il rapporto uomo-natura e la tutela dell’ambiente
L’ambiente e gli esseri viventi
Schede operative di riferimento
Comprendere la funzione della fotosintesi clorofilliana. Pag. 231
Comprendere la respirazione delle piante. Pag. 232
Conoscere le cause degli incendi e attuare comportamenti di prevenzione. Pag. 233
Identificare forme di vita animale e vegetale nel prato. Pag. 234
Conoscere alcuni aspetti della società delle api. Pag. 235
Identificare forme di vita animale e vegetale nello stagno. Pag. 236
Descrivere una catena alimentare dello stagno. Pag. 237
Descrivere la metamorfosi di un girino. Pag. 238
MAGGIO - GIUGNO
Conoscenze Obiettivi
Identificare gli organismi viventi dell’ambiente marino.
Conoscere gli elementi viventi e non viventi dell’ambiente marino.
L’ambiente e gli esseri viventi
Il rapporto uomo-natura e la tutela dell’ambiente
Il regno animale
L’alimentazione come bisogno fondamentale dell’uomo
Descrivere le caratteristiche morfologiche dei pesci.
Schede operative di riferimento
Pag. 274
Pag. 275
Pag. 276
Individuare le caratteristiche dei mammiferi marini. Pag. 277
Descrivere una catena alimentare dell’ambiente marino. Pag. 278
Intuire le cause dell’inquinamento dell’acqua. Pag. 279
Conoscere e saper classificare i mammiferi. Pag. 280
Classificare gli alimenti in base alla loro funzione. Pag. 281
Comprendere l’importanza di una alimentazione equilibrata. Pag. 282
Comprendere il rapporto tra nutrizione e attività fisica. Pag. 283
VERIFICHE QUADRIMESTRALI
Conoscenze Obiettivi
L’ambiente e gli esseri viventi
Schede operative di riferimento
Conoscere gli organismi che compongono un ecosistema. Pag. 292
Conoscere l’ambiente marino. Pag. 293
Settembre Ottobre
Le prime proposte didattiche si riferiscono al nostro sistema di numerazione. In Scienze, il percorso didattico inizia con la conoscenza dei Pianeti del Sistema Solare. Si affrontano quindi i materiali.
Presentazione
I primi mesi scolastici saranno dedicati alla conoscenza del nostro sistema di numerazione, decimale e posizionale, mediante attività di scomposizione-composizione e rappresentazione dei numeri con l’abaco (figura 1). Verrà introdotta l’addizione con la relativa tabella (figura 2), la cui osservazione sarà fondamentale per consolidare l’acquisizione di questa operazione.
In Scienze, si proporranno esperienze di osservazione di oggetti per individuarne i materiali (figura 3).
Fig. 1
Fig. 2
Fig. 3
SCOMPONI E RICOMPONI I NUMERI
Collega ogni smartphone al bambino con il numero corrispondente.
320 109 68 503 104 160 152 222
Scomponi i numeri, come nell’esempio.
Ora ricomponi i numeri, come nell’esempio.
• 5 h; 7 da; 4 u = 500 + 70 + 4 = 574
• 1 h; 6 da; 5 u = =
• 2 h; 4 da; 2 u = =
• 8 h; 8 da; 6 u = ...................................... = ...................
Scomponi i numeri, come nell’esempio. 473
3 u = 3
da = 70
NUMERI SULL’ABACO
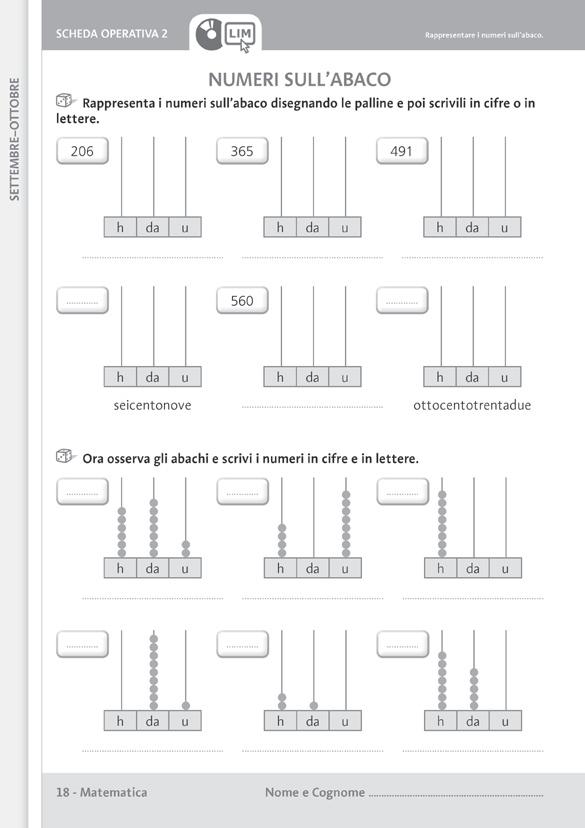
Rappresenta i numeri sull’abaco disegnando le palline e poi scrivili in cifre o in lettere. h da u
Ora osserva gli abachi e scrivi i numeri in cifre e in lettere. h da u h da u
ADDIZIONI IN TABELLA
Completa la tabella dell’addizione, poi rispondi alle domande e completa le affermazioni sottostanti.
• Da quali numeri è formata la prima riga?
• Perché? .................................................................
• Da quali numeri è formata la prima colonna? .................................................................
• Perché? .................................................................
• I numeri scritti lungo la diagonale si ottengono sommando due numeri ........................, sono i numeri ...........................................
• Osserva le somme agli incroci e i loro addendi; puoi notare: – numero P (pari) + numero P (pari) = numero P (pari) – numero D (dispari) + numero D (dispari) = numero P (pari) – P + D = ; D + P =
• Se colori dello stesso colore alcune coppie di addendi, per esempio (3; 1) e (1; 3) e la loro somma 4, (4; 2) e (2; 4) e la loro somma 6, puoi scoprire una proprietà dell’addizione: se si cambia l’ordine degli addendi la somma .................................................. Questa è la proprietà commutativa
• A destra e sotto a ogni numero vi è il suo (+ 1).
• A sinistra e sopra a ogni numero vi è il suo ......................................................... (– 1).
ADDIZIONI SULLA LINEA DEI NUMERI
Alessandro e i suoi compagni giocano in palestra con la linea dei numeri. Esegui con loro le addizioni, come nell’esempio.
Ora osserva l’addizione rappresentata sulla linea dei numeri, ricava l’operazione ed eseguila.
LA PROPRIETÀ ASSOCIATIVA DELL’ADDIZIONE
Leggi, osserva e completa.
• Oggi nella pasticceria “Crema e cioccolato” sono stati venduti questi pasticcini.
Quanti sono in tutto?
Per contarli puoi usare diversi modi:
a) 8 + 7 + 2 = 17 15 + 2 = 17
c) 8 + 7 + 2 = 17 10 + 7 = 17
b) 8 + 7 + 2 = 17 8 + 9 = 17 Ricorda
proprietà associativa
Ora esegui le seguenti addizioni associando nel modo più conveniente, come nell’esempio, e poi calcola.
• 30 + 70 + 420 = (30 + 70) + 420 = 100 + 420 = 520
• 28 + 250 + 50 =
• 80 + 600 + 20 = ..............................................................................................................................................
• 65 + 400 + 35 = ..............................................................................................................................................
• 10 + 90 + 700 =
• 24 + 160 + 40 =
PROBLEMI CON L’ADDIZIONE
Leggi e risolvi i seguenti problemi.
1 Simone ha 36 pastelli nuovi. Matteo ne ha 12 in più. Quanti pastelli ha Matteo?
• Operazione: ............................................... .............................................................................
• Risposta: .............................................................................
2 Eleonora conta le pagine del suo sussidiario: le pagine di Matematica sono 72, quelle di Scienze sono 40, quelle di Storia 64 e quelle di Geografia 48. Quante pagine ha in tutto il sussidiario?
• Operazione: ...............................................
• Risposta: .......................................................
3 Giulia ha 123 perline gialle. La mamma gliene regala 15 blu, 19 rosse e 33 bianche. Quante perline ha adesso Giulia?
• Operazione:
• Risposta: .......................................................
SUPERPROBLEMI CON L’ADDIZIONE
Leggi e risolvi i seguenti problemi.
1 Su un treno in partenza da Milano sono salite 165 persone. Alla prima fermata salgono altre 24 persone. Quante persone viaggiano su quel treno?
• Operazione: ...............................................
• Risposta: .......................................................
2 La zia di Anna ha acquistato un televisore ultrapiatto a € 250 e un tablet a € 325. Quanto ha speso in tutto?
• Operazione: ...............................................
• Risposta: .......................................................
3 Il giardiniere del parco ha piantato 40 rose bianche, 35 rose rosse e 24 rose gialle. Quante rose ha piantato in tutto?
• Operazione:
• Risposta: .......................................................
QUADRI DI NUMERI
Completa le tabelle che vedi in ogni quadro, poi colora secondo le indicazioni.
• Colora le caselle che seguono l’operatore + 10. Che cosa osservi?
Colora le
+ 5
CALCOLA A MENTE!
Completa le tabelle calcolando a mente.
Ricorda
Per aggiungere 10 a un numero, basta aggiungere 1 alla cifra delle decine!
Se devi aggiungere 20 o 30, allora aggiungi 2 o 3 alla cifra delle decine.
Ricorda
Per aggiungere 100 a un numero, basta aggiungere 1 alla cifra delle centinaia!
Se devi aggiungere 200 o 300, allora aggiungi 2 o 3 alla cifra delle centinaia.
MACCHINE PER CONTARE
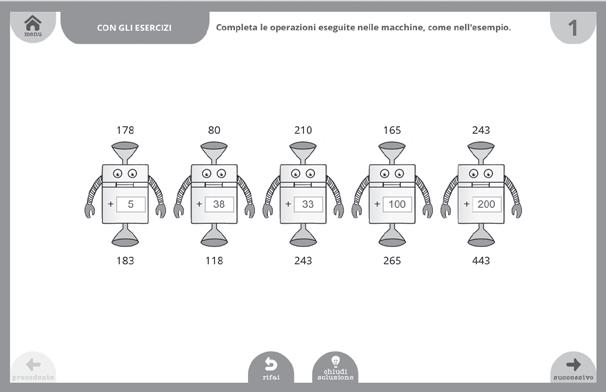
Completa le operazioni eseguite con le macchine, come nell’esempio.
Ora scrivi tu l’addendo di entrata.
Adesso scrivi i numeri di entrata e di uscita.
ADDIZIONI CON LA PROVA
Esegui le addizioni in colonna, poi verificane l’esattezza con la prova, applicando la proprietà commutativa.
ADDIZIONI SULL’ABACO
Esegui le addizioni con l’aiuto dell’abaco, come nell’esempio.
ADDIZIONI CON DOPPIO CAMBIO
Esegui le addizioni con l’aiuto dell’abaco, come nell’esempio.
ORDINA I NUMERI
Completa i “pezzi” di linea dei numeri.
Ordina in senso crescente i numeri sui succhi di frutta.
Ordina in senso decrescente i numeri sui sacchetti di patatine.
Scrivi il precedente e il successivo di ogni numero dato.
TABELLE E CONFRONTI
Completa le tabelle colorando le caselle corrispondenti alle relazioni corrette. < 583 12 2 015
Completa le tabelle inserendo i numeri adatti a rendere corrette le relazioni.
Inserisci tutti i numeri possibili e poi completa.
7 > ...................................................... ...................................................................................... • Quanti numeri hai scritto? ....... 12 < ..................................................... • Quanti numeri puoi scrivere? ............................................................... 15 < ................................................
• Quanti numeri puoi scrivere? 9 > ......................................................
• Quanti numeri hai scritto? .......
ANCORA QUADRI DI NUMERI
Completa le tabelle, poi colora secondo le indicazioni.
• Colora le caselle che seguono l’operatore – 10 partendo da 799. Che cosa osservi?
• Colora le caselle che seguono l’operatore – 5 partendo da 899. Che cosa osservi?
