

Representación gráficadeecuacioneseinecuacionesendos variables.
¿Qué es una ecuación en dos variables?
Es una igualdad algebraica que involucra dos variables, típicamente $x$ y $y$, cuya solución general es un conjunto de pares ordenados $(x, y)$ que satisfacen la relación.
La representación gráfica de una ecuación lineal en dos variables es una recta.
Ejemplo:
�� = 2�� + 1
Es una recta con pendiente 2 y ordenada al origen 1.
¿Cómo graficarla con herramientas digitales?
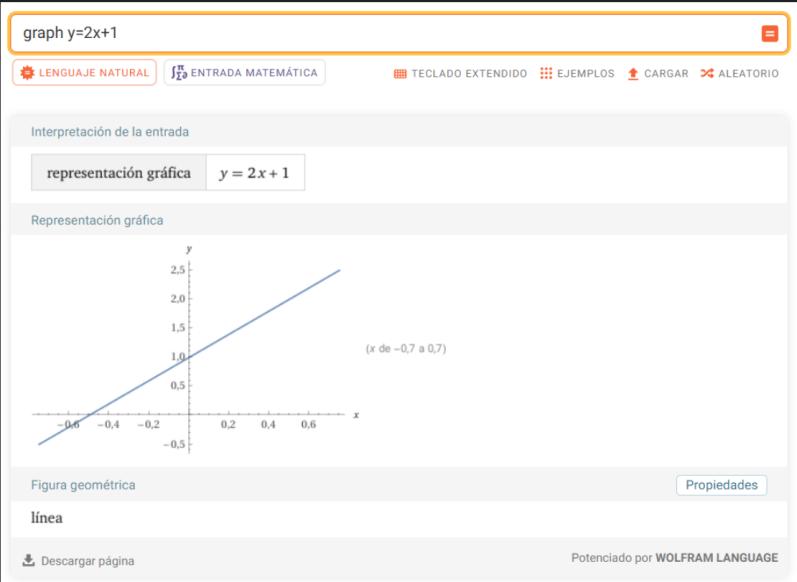
En WolframAlpha:
Escribe en el buscador:
`graph y = 2x + 1`
Esto genera automáticamente una gráfica interactiva.
En GeoGebra:
Abre GeoGebra (modo gráfico) y escribe en la barra de entrada:
`y = 2x + 1`

¿Cómo resolver un sistema de ecuaciones gráficamente?
Cuando tienes dos ecuaciones, su solución gráfica corresponde al punto de intersección entre las dos rectas.
Ejemplo:
= �� + 2 ��= −��+4
La solución es el punto donde ambas gráficas se cruzan: (1,3).
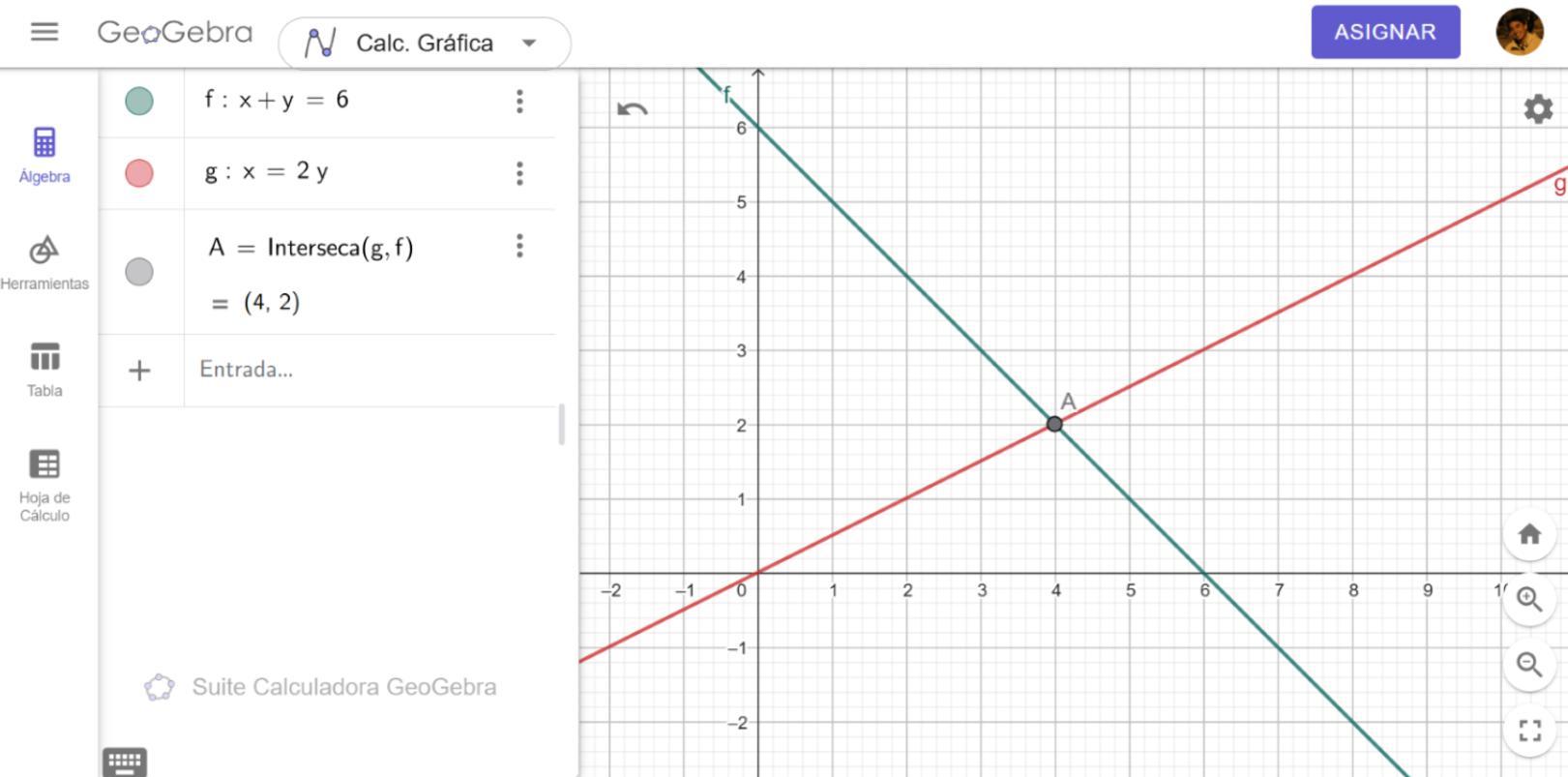
En GeoGebra:
1. Escribe ambas ecuaciones en la barra de entrada.
2. Usa el comando:
`Interseca[recta1, recta2]`
Esto marcará automáticamente el punto de intersección.
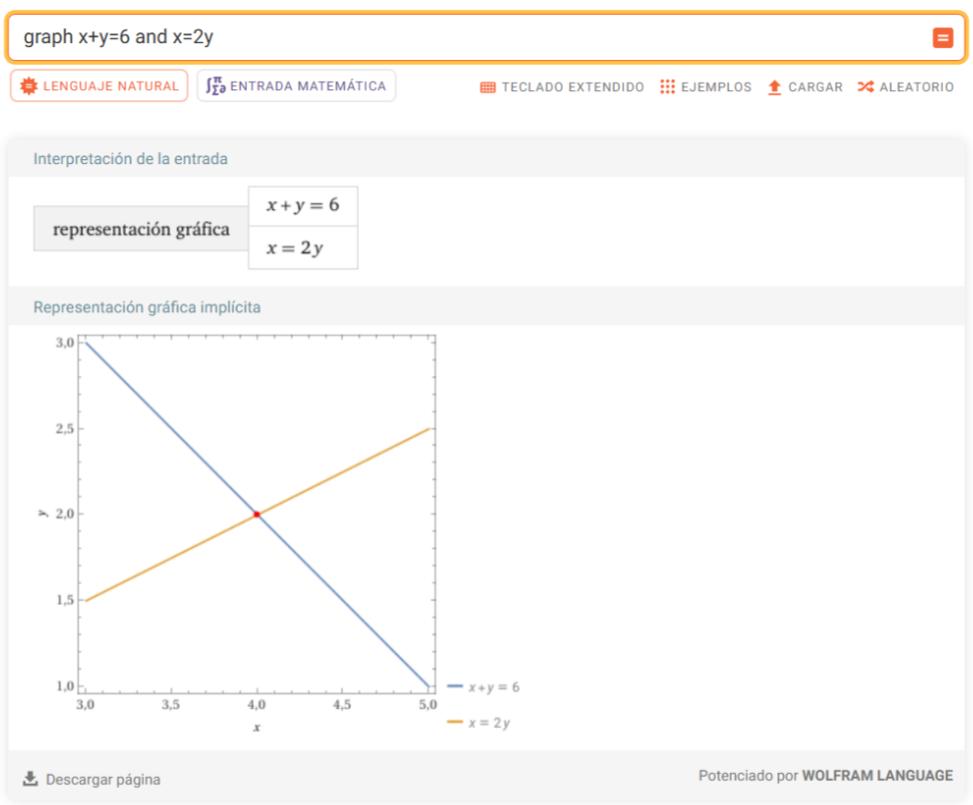
En WolframAlpha:
Escribe en el buscador (usando el símbolo `and` para combinar): `solve y = x + 2 and y = -x + 4`
¿Qué es una inecuación en dos variables?
Es una desigualdad que involucra �� y �� y representa una región del plano cartesiano, no solo una línea.
Ejemplo: �� < 2�� + 1
Representa todos los puntos por debajo de la recta �� = 2�� + 1, sin incluirla.
Símbolos clave:
<, >: línea punteada (frontera no incluida)
≤, ≥: línea continua (frontera incluida)
�� ¿Cómo graficarla en GeoGebra y WolframAlpha?
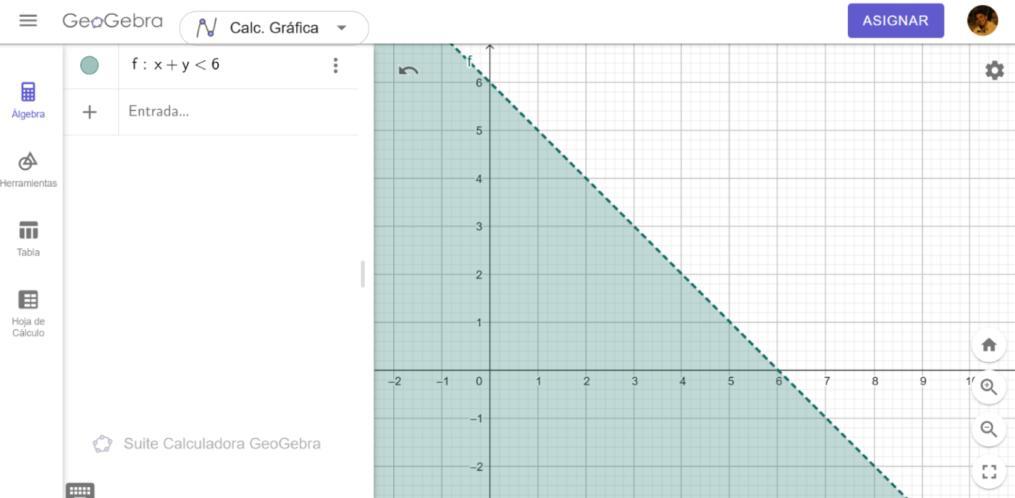
En GeoGebra:
1. Escribe directamente la inecuación:
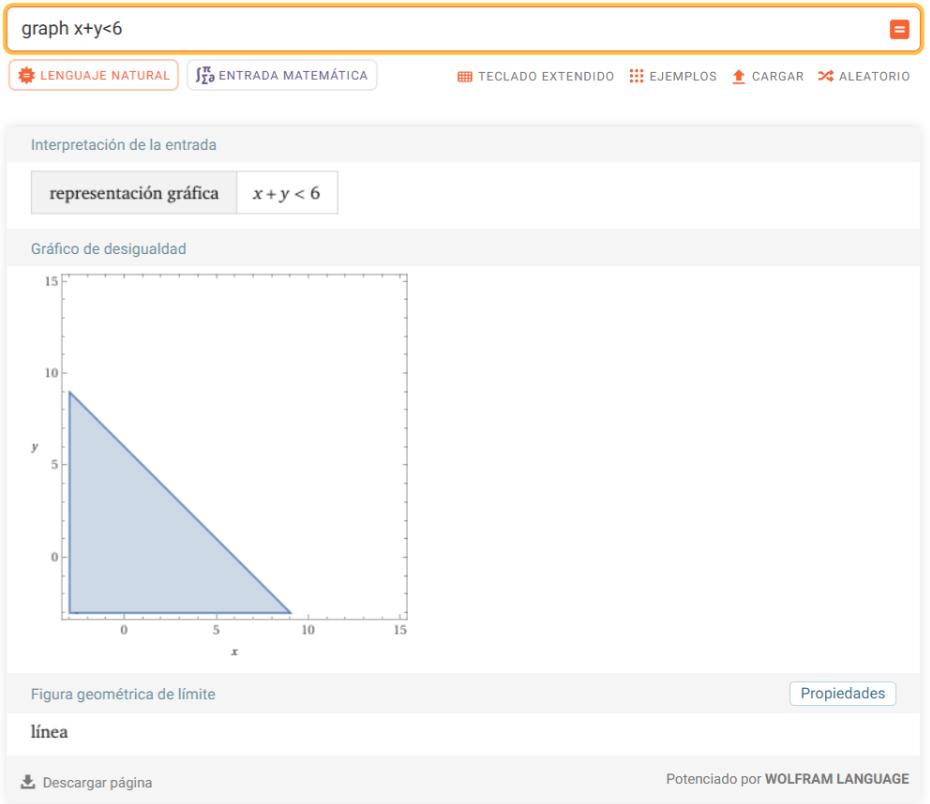
`x+y<6`
El área bajo la línea aparecerá sombreada.
En WolframAlpha:
Escribe:
`plot x+y<6`
Genera la región válida con un sombreado visual.
¿Qué pasa con un sistema de inecuaciones?
Un sistema de inecuaciones representa la intersección de varias regiones. Es decir, la solución es el área donde se superponen las zonas pintadas por cada desigualdad.
Ejemplo:
La solución es el área entre las dos líneas.
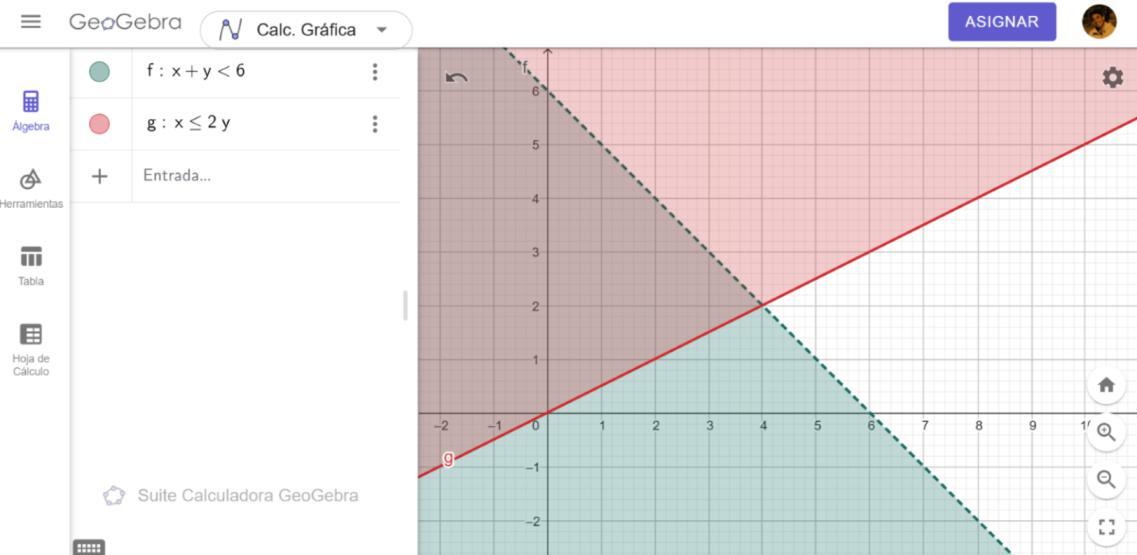
En GeoGebra:
Escribe ambas inecuaciones una por una. El área común quedará sombreada automáticamente.
En WolframAlpha:
Escribe:
`plot y > x and y <= -x + 4`
Se mostrará solo la intersección de ambas regiones.

