




1. Predicados
La lógica de predicados analiza cómo las proposiciones describen relaciones internas. En este contexto, un predicado es lo que se afirma o niega de un argumento
Por ejemplo, en la oración “Raúl canta”, el argumento es “Raúl” y el predicado es “canta”.
Otro ejemplo: en “Elena es cuñada de Rosa”, los argumentos son “Elena” y “Rosa” y el predicado es “es cuñada de”.
También en “El número 5 es impar”, el argumento es “5” y el predicado es “es impar”.
Cuando se usan cuantificadores, los predicados se extienden a varios individuos o elementos.
• Ejemplo con cuantificador universal: “Todos los estudiantes estudian”. Aquí, el argumento es “los estudiantes” y el predicado es “estudian”.
• Ejemplo con cuantificador existencial: “Algún número es primo”. El argumento es “número” y el predicado es “es primo”. Los predicados, junto con los cuantificadores, permiten describir propiedades o relaciones de forma más general y analizar inferencias que la lógica proposicional no puede resolver.
Las proposiciones en lógica de predicados se clasifican en cinco tipos, según cómo se relacionan argumentos y predicados y el uso de cuantificadores:
Afirman que todos los elementos de un conjunto tienen una propiedad.
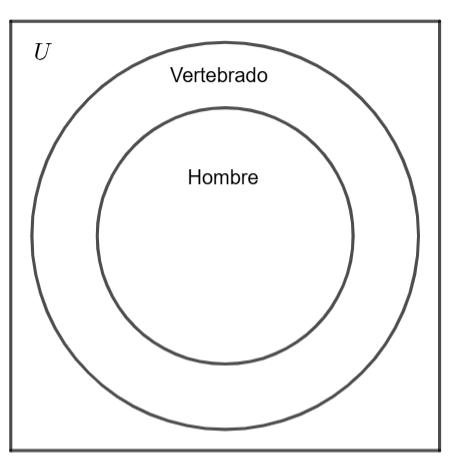
Ejemplo: “Todos los hombres son vertebrados.”
• Argumento: “los hombres”
• Predicado: “son vertebrados”
• Cuantificador: “todos”
Representación gráfica: Diagrama de Venn donde el conjunto “hombres” está completamente contenido dentro del conjunto “vertebrados”.
2) Proposiciones singulares
Estas hablan de un solo individuo. Aunque tratan de un caso particular, lógicamente pueden verse como una proposición universal que afirma algo de un solo elemento.
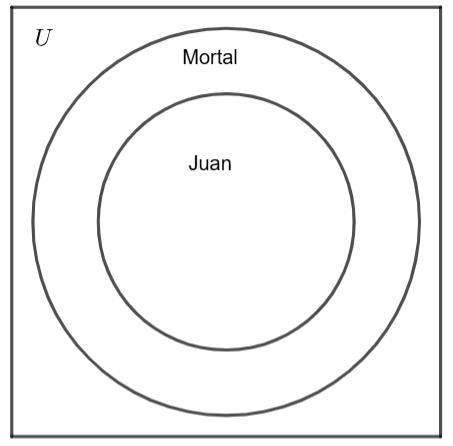
Ejemplo: “Juan es mortal.”
• Argumento: “Juan”
• Predicado: “es mortal”
• Cuantificador implícito: “todos los Juan (solo uno)”
Descripción de imagen sugerida: Diagrama de Venn donde el conjunto “Juan” está completamente dentro del conjunto “seres mortales”.
3) Universales negativas
Niegan que cualquier elemento de un conjunto tenga cierta propiedad; afirman que ningún elemento la tiene.
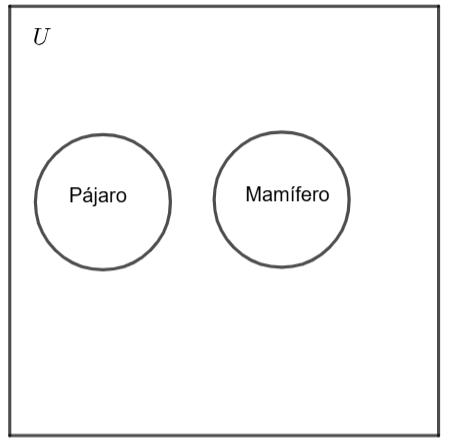
Ejemplo: “Ningún pájaro es mamífero.”
• Argumento: “los pájaros”
• Predicado: “es mamífero”
• Cuantificador: “ningún”
Representación gráfica: Diagrama de Venn donde los conjuntos “pájaros” y “mamíferos” no tienen intersección.
4) Particulares afirmativas
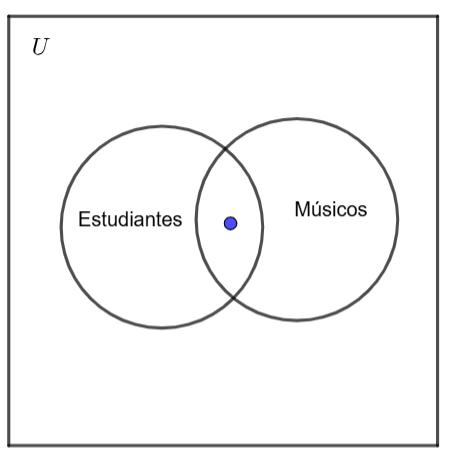
Afirman que al menos un elemento de un conjunto tiene cierta propiedad. Ejemplo: “Algunos estudiantes son músicos.”
• Argumento: “los estudiantes”
• Predicado: “son músicos”
• Cuantificador: “algunos”
Representación gráfica: Diagrama de Venn mostrando una intersección parcial entre “estudiantes” y “músicos”.
5) Particulares negativas
Niegan que al menos un elemento de un conjunto tenga cierta propiedad.
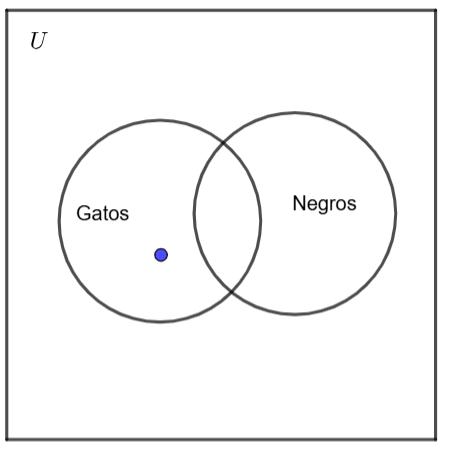
Ejemplo: “Algunos gatos no son negros.”
• Argumento: “los gatos”
• Predicado: “son negros”
• Cuantificador: “algunos”
Representación gráfica: Diagrama de Venn donde algunos elementos de “gatos” están fuera del conjunto “negros”
3. Validez, invalidez y contraejemplo
Un argumento es válido si, cuando las premisas son verdaderas, la conclusión también lo es necesariamente. Esto significa que la conclusión está completamente contenida en la información de las premisas.
Un argumento es inválido si existe al menos un caso en que las premisas sean verdaderas y la conclusión falsa. Un contraejemplo es ese caso específico que demuestra la invalidez.
Para comprobar la validez o invalidez de un argumento, se utilizan diagramas de Venn, los cuales representan gráficamente cómo se relacionan las regiones de las premisas y la conclusión.
Procedimiento para verificar validez mediante diagramas de Venn:
1️) Graficamos cada una de las premisas y la conclusión.
• Se dibujan los diagramas de Venn de las premisas, mostrando las relaciones entre los conjuntos involucrados.
• Se representa la conclusión de la misma forma, destacando la región que se afirma.
2)Verificamos si la conclusión se produce a partir de la información de las premisas en todos los casos posibles.
• Si la región de la conclusión está completamente incluida en la intersección de las premisas, el argumento es válido.
• Si no está completamente incluida, el argumento es inválido.
Ejemplo concreto de argumento válido:
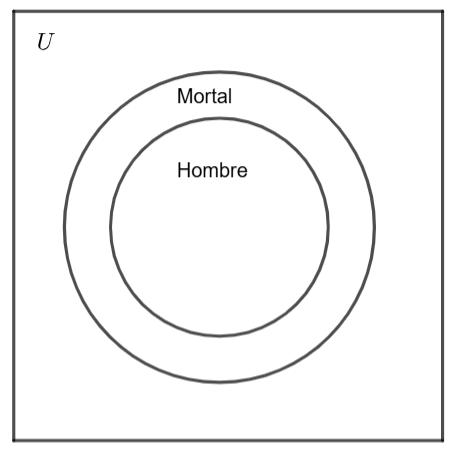
• Premisa 1️: “Todos los hombres son mortales.”
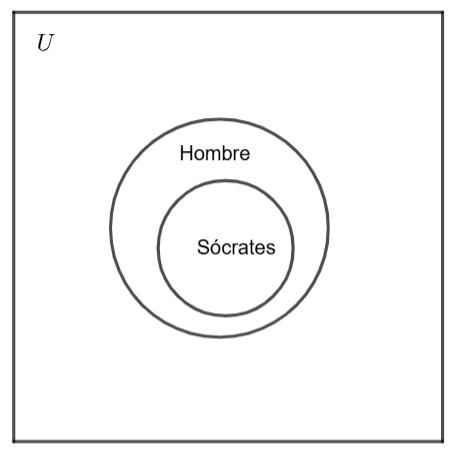
• Premisa 2: “Sócrates es un hombre.”
• Conclusión: “Sócrates es mortal.”
Aplicación del procedimiento:
1️)Graficamos las premisas y la conclusión
• Premisa 1️: “Todos los hombres son mortales” Se dibuja un diagrama de Venn con el conjunto de los “hombres” completamente contenido dentro del conjunto de los “mortales”.
• Premisa 2: “Sócrates es un hombre”
En el diagrama, “Sócrates” es representado como un punto dentro del conjunto de los “hombres”.
• Conclusión: “Sócrates es mortal”
La conclusión gráfica es que el punto “Sócrates” también está dentro del conjunto de los “mortales”.

2) Verificamos la relación en todos los casos posibles Empezamos graficando la premisa 1️

Sobre la base de esta imagen construimos la premisa 2. Como puedes ver en la imagen anterior, la única manera de graficar la premisa 2, es poner a Sócrates dentro del conjunto hombres
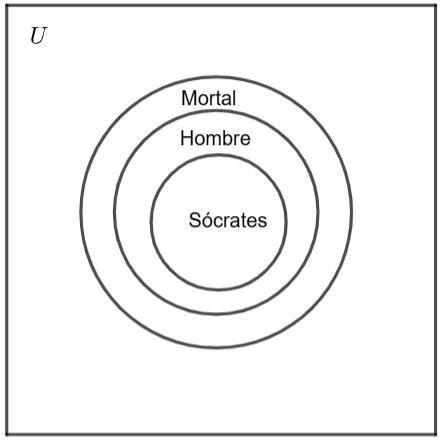
Como no tenemos otras maneras de disponer las premisas y la conclusión sí está representada a través de las premisas, concluimos que el razonamiento es válido.
Como la premisa 1️ asegura que todo hombre está dentro de “mortales” y la premisa 2 pone a Sócrates dentro de “hombres”, en todos los casos posibles
Sócrates estará dentro de “mortales”. Por tanto, la conclusión se sigue necesariamente de las premisas.
Resultado: El argumento es válido.
Ejemplo de argumento inválido
Argumento:
• Premisa 1️: “Todo el que estudia, aprueba.”
• Premisa 2: “Pepito no estudia.”
• Conclusión: “Pepito no aprueba.”
Aplicación del procedimiento:
1️)Graficamos las premisas y la conclusión
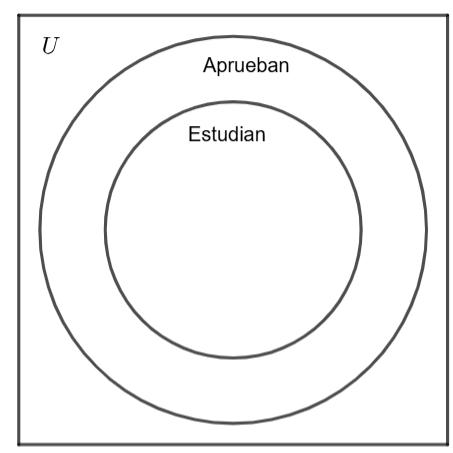
• Premisa 1️: “Todo el que estudia, aprueba.”
Se dibuja un diagrama de Venn con el conjunto de los “estudian” completamente contenido dentro del conjunto de los “aprueban”.
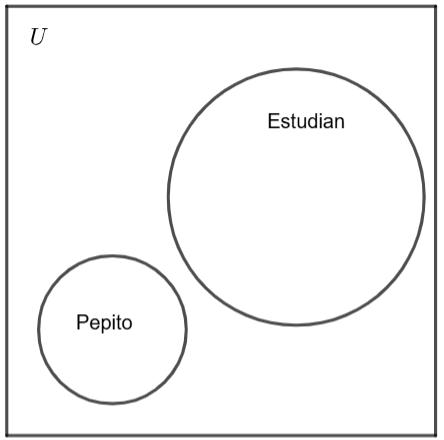
• Premisa 2: “Pepito no estudia”
En el diagrama, “Pepito” es representado como un conjunto separado del conjunto “estudia”.
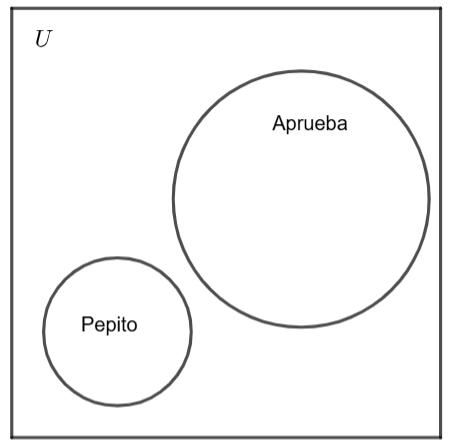
• Conclusión: “Pepito no aprueba” La conclusión gráfica es que el conjunto “Pepito” es un conjunto separado del conjunto de los que “aprueban”.
2) Verificamos la relación en todos los casos posibles Empezamos graficando la premisa 1️
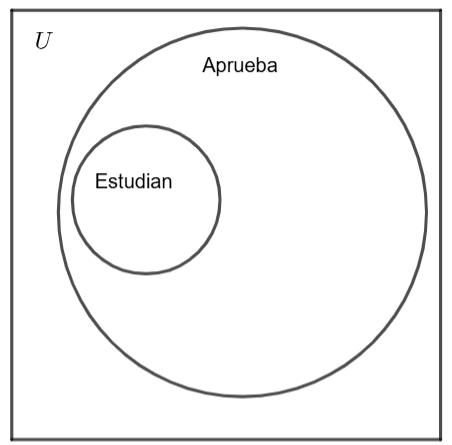
Sobre la base de esta imagen construimos la premisa 2. Como te puedes dar cuenta, para graficar la premisa 2 en base a la premisa 1️, tenemos las siguientes 3 posibilidades:
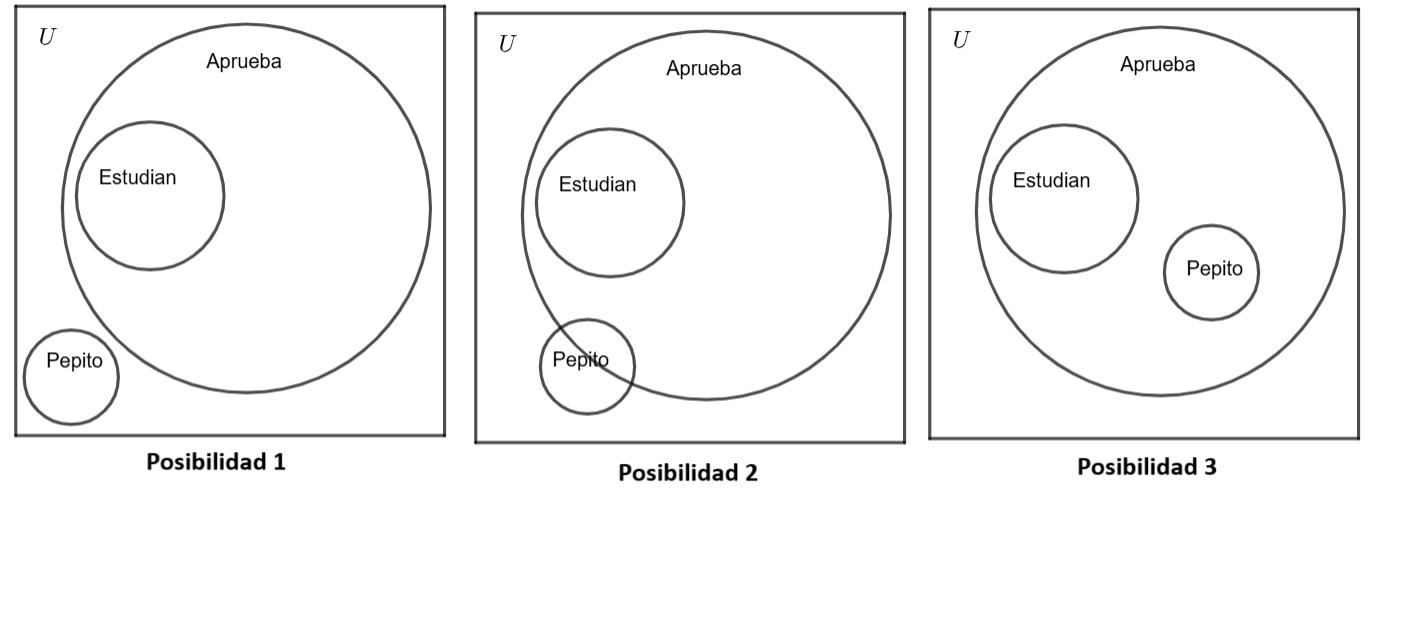
En la primera posibilidad, se cumple la conclusión “Pepito no aprueba”, pero en las dos siguientes posibilidades, no se cumple. En la segunda posibilidad, una parte de Pepito aprueba y otra no, esto es absurdo y en la tercera posibilidad a pesar de que Pepito no estudia, aprueba. Por la inconsistencia de las dos posibilidades, se concluye que el razonamiento es inválido, aunque es suficiente que si en una de las posibilidades no cumple la conclusión, el razonamiento es inválido. Cuando un razonamiento es inválido, podemos construir un contraejemplo, para esto, debemos mantener la estructura del razonamiento y cambiar las premisas y la conclusión
• Premisa 1️: “Todo el que estudia, aprueba.”
• Premisa 2: “Pepito no estudia.”
• Conclusión: “Pepito no aprueba.”
• Premisa 1️ nueva: “Todo ser que es animal es ser vivo”
• Premisa 2 nueva: “La rosa no es animal”
• Conclusión nueva: “La rosa no es ser vivo
Como puedes ver, a pesar de mantener la estructura del razonamiento, las premisas son verdaderas y la conclusión falsa, esto revela que el razonamiento es inválido.
Resultado: El argumento es inválido
