POUR LA SCIENCE • SEPTEMBRE 2025 by Pour la Science

Cancérologie DE NOUVELLES

CIBLES CONTRE LA DOULEUR

Informatique

Paléoanthropologie DES HUMAINS EN ASIE IL Y A 3 MILLIONS D’ANNÉES ? 09/25

GÉOMÉTRIE ALÉATOIRE

La science expliquée par ceux qui la font

MENSUEL POUR LA SCIENCE

Rédacteur en chef : François Lassagne

Rédacteurs en chef adjoints : Loïc Mangin, Marie-Neige Cordonnier

Rédacteurs : François Savatier, Sean Bailly

Stagiaires : Louise Le Ridant et Simon Vionnet

HORS-SÉRIE POUR LA SCIENCE

Rédacteur en chef adjoint : Loïc Mangin

Développement numérique : Philippe Ribeau-Gésippe

Directeur marketing et développement : Frédéric-Alexandre Talec

Chef de produit marketing : Ferdinand Moncaut

Directrice artistique : Céline Lapert

Maquette : Pauline Bilbault, Raphaël Queruel, Ingrid Leroy, Ingrid Lhande

Réviseuses : Anne-Rozenn Jouble, Maud Bruguière, Isabelle Bouchery et Marie-Louise Desfray

Directrice des ressources humaines : Olivia Le Prévost

Fabrication : Marianne Sigogne et Stéphanie Ho

Directeur de la publication et gérant : Nicolas Bréon

Ont également participé à ce numéro : Olivier Arnaez, Julien Baglio Yannick Chancerelle, Anna Degioanni, Alain Doressoundiram, Nicolas Giuseppone, Alice Guyon, Clémentine Laurens, Serge Luquet, Claire Martin, Thomas Matreux, Sophie Roman

PUBLICITÉ France stephanie.jullien@pourlascience.fr

ABONNEMENTS

https ://www.pourlascience.fr/abonnements/ Courriel : serviceclients@groupepourlascience.fr

Tél. : 01 86 70 01 76

Du lundi au vendredi de 8 h 30 à 12 h 30 et de 13 h 30 à 16 h 30

Adresse postale : Service abonnement Groupe Pour la Science c/o opper Services - CS 60003 31242 L’Union

Tarif d’abonnement Formule Intégrale 1 an (12 numéros du magazine + 4 numéros Hors-Série + accès au site) : 99 euros Europe / Reste du monde : consulter https ://www pourlascience fr/abonnements/

DIFFUSION

Contact réservé aux dépositaires et diﬀuseurs de presse Société OPPER

1 montée de Saint-Menet – « Espace La Valentine » Bât B 13011 Marseille 01 40 94 22 23 – aabadie@opper.io

DISTRIBUTION

MLP

ISSN 0 153-4092

Commission paritaire n° 0927K82079 Dépôt légal : 5636 – Septembre 2025 N° d’édition : M0770575-01 www.pourlascience.fr

170 bis boulevard du Montparnasse – 75 014 Paris Tél. 01 55 42 84 00

SCIENTIFIC AMERICAN

Editor in chief : David M. Ewalt

President : Kimberly Lau 2025. Scientific American, une division de Springer Nature America, Inc. Soumis aux lois et traités nationaux et internationaux sur la propriété intellectuelle. Tous droits réservés. Utilisé sous licence. Aucune partie de ce numéro ne peut être reproduite par un procédé mécanique, photographique ou électronique, ou sous la forme d’un enregistrement audio, ni stockée dans un système d’extraction, transmise ou copiée d’une autre manière pour un usage public ou privé sans l’autorisation écrite de l’éditeur. La marque et le nom commercial « Scientific American » sont la propriété de Scientific American, Inc. Licence accordée à «Pour la Science SARL ». © Pour la Science SARL, 170 bis bd du Montparnasse, 75014 Paris. En application de la loi du 11 mars 1957, il est interdit de reproduire intégralement ou partiellement la présente revue sans autorisation de l’éditeur ou du Centre français de l’exploitation du droit de copie (20 rue des Grands-Augustins, 75006 Paris).

Origine du papier : Autriche

Taux de ﬁbres recyclées : 30 %

« Eutrophisation » ou « Impact sur l’eau » : Ptot 0,007 kg/tonne

Imprimé en France

Maury Imprimeur SA Malesherbes N° d’imprimeur : 285 998

François Lassagne

Rédacteur en chef

FRUCTUEUX HASARD

Imaginez une feuille, placez-y quelques points, sans ordre apparent. Reliez certains de ces points entre eux, sans règle particulière. Vous venez de construire un graphe aléatoire, et d’entrer dans le foisonnant domaine de la géométrie aléatoire, où la construction des objets géométriques est laissée aux bons soins du hasard. Pourquoi s’en remettre à ce maître aveugle ? Parce que, comme l’explique avec simplicité Nalini Anantharaman, « on fait ainsi apparaître des objets moins symétriques que ceux que notre cerveau se plaît naturellement à créer. […] Parfois, le résultat choque l’intuition, mais parfois, à l’inverse, on espère voir se révéler des objets dont l’existence est conjecturée ou désirée, mais que personne n’arrive à trouver ».

Cette mathématicienne occupe la chaire de géométrie spectrale au Collège de France – « spectrale », car il s’agit là de faire le lien entre la géométrie d’un objet et son spectre de vibration. Et c’est à la frontière de deux géométries, aléatoire et spectrale, que progressent aujourd’hui ses recherches : pour comprendre les productions géométriques du hasard, elle mesure leur spectre de vibration, en les soumettant mathématiquement au passage d’ondes.

Sans doute, à l’avenir, ces travaux irrigueront-ils de nombreux domaines. Comme le souligne Nalini Anantharaman, « les géométries aléatoires sont aussi au cœur des tentatives de construction de la gravité quantique, en physique, et sont aussi très utilisées pour produire des images, des textures, modéliser des réseaux de communication, etc. ».

Mais nul besoin d’attendre de telles traductions pour être saisi par la richesse de la rencontre entre la chaotique productivité du hasard et l’intelligence mathématique, que démontre le précieux témoignage de la chercheuse, qui nous emmène au ﬁl de ses explorations, et rapporte hauts, bas, révélations, belles rencontres… et fructueuses découvertes. n

ACTUALITÉS GRANDS FORMATS

P. 6

ÉCHOS DES LABOS

• Les lymphocytes T, messagers vers le cerveau

• Un tatouage contre le GHB, quelle eﬃcacité ?

• L’adaptation progressive de sapiens en Afrique

OMMAIRE

575 / Septembre 2025

LETTRE D’INFORMATION

NE MANQUEZ PAS

LA PARUTION DE

VOTRE MAGAZINE

GRÂCE À LA NEWSLETTER

• Notre sélection d’articles

• Des offres préférentielles

• Nos autres magazines en kiosque

Inscrivez-vous www.pourlascience.fr

• Combien faut-il d’électrons pour faire un « liquide » ?

• Protocellule sans membrane

• Ces ﬂeurs qui empestent

• Un arc-en-ciel sonore

P. 18

LES LIVRES DU MOIS

P. 20

DISPUTES

ENVIRONNEMENTALES

Le mirage de l’avion vert Catherine Aubertin

P. 22

LES SCIENCES À LA LOUPE

Qui accepte les données probantes ?

Yves Gingras

P.

PHYSIQUE

DES PARTICULES

DÉSINTÉGRATION

DU VIDE : UNE MENACE POUR L’UNIVERS ?

Matthew von Hippel

Le célèbre boson de Higgs pourrait être lié à un phénomène d’instabilité qui aurait le potentiel pour anéantir toutes les galaxies et la vie, mais ce scénario est extrêmement improbable.

P. 40

MÉDECINE

En couverture : © Bruno Vacaro

Les portraits des contributeurs sont de Seb Jarnot

Ce numéro comporte un courrier de réabonnement posé sur le magazine sur une sélection d’abonnés.

DOULEUR DU CANCER : CIBLER L’INTERFACE TUMEUR-SYSTÈME NERVEUX

Bernard Calvino

L’étude de l’interaction des tumeurs solides et du système nerveux sensoriel a révélé une forme spéciﬁque de douleur cancéreuse, qui ouvre la voie à de nouvelles thérapies ciblant des messagers impliqués dans cette interaction.

P. 48

PHYSIQUE

« LES GAZ D’ATOMES FROIDS ONT DES APPLICATIONS CONCRÈTES »

Entretien avec Jean Dalibard

Le physicien raconte comment les gaz d’atomes à très basse température ont ouvert une fenêtre sur les lois fondamentales de la matière et sont au cœur de certaines technologies quantiques

P. 54

PRÉHISTOIRE

IL Y A 3 MILLIONS D’ANNÉES : DES HUMAINS EN ASIE ?

Anne Dambricourt-Malassé et François Savatier

Un site du piémont himalayen révèle qu’il y a quelque 3 millions d’années, des hominines sont passés d’Afrique en Asie. S’agissait-il déjà d’humains ?

P. 64

HISTOIRE DES SCIENCES

LACEPÈDE : UN TRANSFORMISME

PRUDENT AUTOUR DE 1800

Stéphane Schmitt

Au tout début du XIXe siècle, alors que Lamarck élaborait la première grande théorie transformiste, le naturaliste Lacepède, dont on célèbre cette année le bicentenaire de la mort, défendit des conceptions plus modérées, mais aussi plus acceptables pour l’époque

P. 24

MATHÉMATIQUES

L’ART DE FAIRE VIBRER LES SURFACES HYPERBOLIQUES

Nalini Anantharaman

À quoi ressemble une surface « typique », en géométrie ? Comment vibre-t-elle quand des ondes s’y propagent ? Est-il facile de s’y déplacer d’un point à un autre ? Une approche probabiliste donne des outils pour calculer le « trou spectral » des surfaces hyperboliques, un précieux paramètre qui renseigne sur leurs propriétés.

RENDEZ-VOUS

P. 72

LOGIQUE & CALCUL

IA CONNEXIONNISTE ET IA SYMBOLIQUE : L’INÉVITABLE

ASSOCIATION ?

Jean-Paul Delahaye

L’essentiel des progrès récents en IA reposent sur une approche appelée « connexionnisme » Mais l’IA symbolique, qui a dominé le domaine pendant des décennies, conserve des atouts qui la font revenir dans la course.

P. 78

ART & SCIENCE

Le dragon des mers… fantôme

Loïc Mangin

P. 80

IDÉES DE PHYSIQUE

Le secret de l’incroyable

Lulu !

Jean-Michel Courty et Édouard Kierlik

P. 84

CHRONIQUES DE L’ÉVOLUTION

Adorables, les marmottes ?

Hervé Le Guyader

P. 88

SCIENCE & GASTRONOMIE

La levure ne fait pas le croustillant

Hervé This

P. 90

À PICORER

PALÉOANTHROPOLOGIE

L’EXPANSION PROGRESSIVE DE SAPIENS EN AFRIQUE

Une nouvelle étude suggère qu’Homo sapiens a occupé de plus en plus de niches écologiques africaines avant d’entrer en expansion en Eurasie. Une « maturation écologique » a-t-elle eu lieu avant la dispersion de la principale population ancestrale des Eurasiens ?

D’où viennent les gènes des Eurasiens, c’est-à-dire des habitants de l’Europe et de l’Asie ? On sait que des membres de notre espèce sont entrés en Eurasie très tôt. Pour ne donner qu’un exemple, le fossile d’Apidima 1 suggère qu’il y a environ 210 000 ans, des Homo sapiens archaïques ont foulé ce qui est devenu plus tard la Grèce continentale… D’autres cas à travers le monde – en Chine et en Europe –suggèrent que des pionniers sapiens ont quitté l’Afrique à des dates très anciennes. Pour autant, c’est une population sapiens fondatrice, partie d’Afrique entre 60 000 et 50 000 avant le présent (AP), qui nous a légué la plupart de nos gènes après s’être hybridée avec les Néandertaliens. Pourquoi est-ce elle qui a « réussi », alors que les pionniers qui l’ont précédée n’ont pas eu le même impact ? C’est cette question qu’une équipe de chercheurs, dirigée par Eleanor Scerri de l’institut Max-Planck pour la géoanthropologie à Iéna, en Allemagne, s’eﬀorce de faire progresser en analysant un vaste ensemble de données issues de sites archéologiques africains à l’aide de méthodes statistiques complexes.

Qu’ont fait les chercheurs ? Tout d’abord, ils ont utilisé 479 sites habités à un moment donné entre 120 000 et 14 000 AP pour déﬁnir l’« écologie » de l’espèce sapiens pendant cette même période En d’autres termes , ils ont reconstruit pour chaque site les valeurs de cinq variables environnementales dans le passé (couverture végétale, plage de températures, température moyenne pendant la saison chaude, température moyenne pendant la saison des pluies et précipitations pendant cette même saison) et, par là, mis en évidence une relation entre conditions climatiques et occupations humaines.

Ensuite, ils ont utilisé ce lien pour calculer la probabilité de présence humaine dans n’importe quelle zone en dehors des sites étudiés Ils ont testé à la fois un modèle dans lequel la probabilité dépend uniquement des cinq variables, et un autre où la relation entre l’occupation humaine et le climat évolue au ﬁl du temps C’est leur second modèle qui capture

Entre 120 000 et 14 000 avant le présent, Homo sapiens a investi un nombre croissant de niches écologiques africaines, là où les conditions climatiques lui étaient favorables.

le mieux les données, c’est-à-dire la présence humaine à travers l’Afrique et au ﬁl du temps Il ressort de cette modélisation statistique que les H sapiens africains ont progressivement habité de plus en plus de niches écologiques à travers l’Afrique depuis 70 000 ans, tendance qui aurait culminé il y a quelque 50 000 ans Or on pense, d’après l’horloge génétique, que c’est pendant cette période de 20 000 ans que la vague sapiens principale, celle qui a produit l’appareil génétique des Eurasiens actuels, s’est largement répandue en Eurasie, notamment en Europe Ainsi , l’exploration statistique des chercheurs accrédite l’idée qu’une augmentation de la plasticité écologique de la population fondatrice sapiens, sensible d’abord en Afrique, puis produisant ses e ﬀ ets en Eurasie , aurait précédé la dispersion de la population sapiens ancestrale à l’origine de la plus grande part de l’appareil génétique eurasien actuel . n François Savatier

E. Hallett et al., Nature, 2025. W. Banks, Nature, 2025.

© Volodymyr Burdiak/Shuttetstock

Le premier roi de Caracol

Caracol, au Bélize, a été l’une des plus importantes cités mayas. Selon une inscription, Te’ K’ab Chaak aurait accédé au trône en l’an 331 de notre ère et aurait été le premier souverain de la cité. L’équipe d’Arlen et Diane Chase, de l’université de Houston, vient de découvrir trois tombes dont la sienne, dotée d’un riche mobilier funéraire. Certains indices révèlent des liens naissants à cette époque avec l’inﬂuente cité de Teotihuacán, à 1 200 kilomètres, l’actuelle Mexico.

Université de Houston, 10 juillet 2025.

Un trajet en « S » Lorsqu’ils reviennent d’expédition en mer, les manchots de Magellan n’optent pas pour le chemin le plus direct. Si les courants de marée sont forts, les oiseaux se laissent dériver et corrigent leur trajectoire juste sur la ﬁn, lui donnant une forme de « S ». C’est ce que Richard Gunner, de l’institut Max-Planck, et ses collègues ont observé. Cela rallonge le temps du trajet, mais coûte moins en énergie et o re davantage d’occasions de trouver de la nourriture.

Plos Biology, 17 juillet 2025.

Exposition évaluée à la hausse

Les microplastiques transportés dans l’air sont une source de préoccupation pour la santé. L’équipe de l’université de Toulouse, autour de Nadiia Yakovenko, s’est intéressée aux particules entre 1 et 10 micromètres (capables de pénétrer profondément dans les poumons) présentes dans les domiciles et les voitures. Les chercheurs ont calculé qu’en moyenne un individu respire 68 000 de ces microparticules par jour. Une valeur 100 fois supérieure aux précédentes estimations.

Plos One, 30 juillet 2025.

GÉNÉTIQUE

UNE HISTOIRE DE TAILLE

Alors que le concombre domestique a une peau lisse et peut atteindre 30 centimètres de long, son cousin sauvage a une forme bien plus petite, ronde et épineuse. Comment expliquer cette diﬀérence ? L’équipe de Xueyong Yang, de l’Académie chinoise des sciences agricoles, a montré qu’une mutation dite « synonyme » en serait à l’origine.

Dans le concombre sauvage , les gènes ACS2 et YTH1 contribuent au façonnement des traits phénotypiques du fruit L’ARN messager ( ARNm ) issu de la transcription du gène ACS 2 subit des modifications : des enzymes procèdent à des méthylations La lecture de ces modiﬁcations par l’enzyme codée par le gène YTH1 favorise alors la traduction de l’ARNm altéré en protéine. Résultat : le fruit a une taille réduite

Cependant, au cours de la domestication du concombre , une mutation synonyme est apparue sur le gène ACS 2 . Les mutations synonymes , anciennement qualifiées de « silencieuses », se caractérisent par la modiﬁcation d’un gène sans que change la séquence de la protéine qui en découle. Ces mutations ont longtemps été considérées comme sans eﬀet, mais diverses équipes ont mis en doute cette conclusion

GÉOSCIENCES

COMMENT LA

DENDRITE SE FORME

Une centrale géothermique injecte en profondeur dans le sol un fluide caloporteur pour produire de l’énergie. Mais des particules (d’argile, notamment) peuvent obstruer progressivement les pores de la roche, limitant la circulation du fluide. Dans ce contexte, Walid Okaybi et ses collègues, de l’institut des sciences de la Terre d’Orléans, ont étudié la formation de dendrites. En partant d’un grain solide, la matière en suspension dans l’écoulement peut adhérer à ce grain, et progressivement former une excroissance, la dendrite, qui finit par rejoindre un autre grain, bloquant ainsi le mouvement du fluide. Grâce à des expériences sur des puces microfluidiques et des simulations numériques, les chercheurs ont mis en évidence que la compétition entre l’adhésion des particules et leur détachement (avec remise en circulation dans le milieu)

Les concombres domestiques, très allongés avec une peau lisse, se distinguent de leurs cousins sauvages, petits, ronds et épineux.

Dans le cas du concombre, la mutation synonyme sur le gène ACS2 limite la méthylation de son ARNm, et, par répercussion, son interaction avec YTH 1 « L’ARN messager adopte une structure tridimensionnelle plus complexe et plus compacte, ce qui a un eﬀet négatif sur la traduction », explique Guillaume Moissiard, chercheur au CNRS À cause de la mutation synonyme , la protéine ACS 2 est moins présente Cela se manifeste par la forme plus allongée du concombre domestique. n Sarah Boulvard

T. Xin et al., Cell, 2025.

Entre les grains de roche, l’accumulation de matière forme des dendrites qui bouchent les pores du milieu.

dépend de façon cruciale de la vitesse d’écoulement du ﬂuide. Une vitesse modérée favorise la formation de la dendrite tandis qu’une vitesse élevée l’entrave. n

Sean Bailly

W. Okaybi et al., Soft Matter, 2025.

EN BREF

ASTROPHYSIQUE

L’EXPLOSION EN DEUX TEMPS D’UNE SUPERNOVA DE TYPE Ia

Une fois arrivées au terme de leur vie, dans une sorte de baroud d’honneur, certaines étoiles explosent en supernovæ. La manière dont se déroulent ces événements extrêmes garde une part de mystère. En particulier, les supernovæ de type Ia se déroulent-elles toutes suivant le même schéma ? Pour ce type de supernovæ, le mécanisme reposait jusqu’alors sur un unique scénario : une naine blanche dans un système binaire accrète de la matière de son compagnon et explose une fois qu’elle dépasse 1,44 masse solaire, la masse dite « de Chandrasekhar ». On pensait que les supernovæ de type Ia devraient donc toutes avoir la même signature. Mais certaines observations récentes mettaient en doute cette idée et s’expliqueraient mieux, en théorie, si ces explosions s’étaient produites sous la masse critique et en deux temps. Dans cette approche, la couche extérieure de matière accrétée explose d’abord sous sa propre pression gravitationnelle. L’onde de choc vient ensuite comprimer la matière au cœur de la naine blanche, déclenchant une explosion encore plus puissante. Il manquait cependant une preuve visuelle pour corroborer ce scénario alternatif.

Grâce à de nouvelles images du VLT (Very Large Telescope), au Chili, Priyam Das, de l’université de Nouvelle-Galles du Sud, en Australie, et ses collègues viennent de conﬁrmer cette possibilité. Les chercheurs ont scruté les vestiges de la supernova de type Ia SNR 0509-67.5, située à presque 160 000 années-lumière, dans le Grand Nuage de Magellan. Les astronomes ont identiﬁé deux couches de calcium (en bleu, la couleur orange indique la présence d’hydrogène) séparées par du soufre et du silicium. Cette structure est la signature d’une explosion en deux temps n

S. V.

P. Das et al., Nature Astronomy, 2025.

© ESO/P. Das et al. ; fond d’étoiles (Hubble) : K. Noll et al.

L’art de faire vibrer les surfaces hyperboliques

L’ESSENTIEL

> En théorie des graphes, les méthodes probabilistes se sont révélées un outil puissant. On cherche aujourd’hui à appliquer ces méthodes en géométrie.

> Déﬁnir une bonne méthode pour construire « au hasard et équitablement » des surfaces hyperboliques est un déﬁ.

> Le « trou spectral » est un paramètre important, lié à la manière dont les surfaces « vibrent » et à leur caractère « bien connecté ». Les résultats les plus récents permettent de mettre la main sur ce paramètre pour des surfaces aléatoires.

L’AUTRICE

NALINI ANANTHARAMAN

titulaire de la chaire de géométrie spectrale au Collège de France et chercheuse à l’Institut de recherche mathématique avancée, à Strasbourg

Mars 2018. Laura Monk vient d’arriver à Strasbourg Elle a quelques rudiments de théorie des probabilités, et une vague idée de ce qu’est la géométrie hyperbolique. Elle cherche un sujet de mémoire pour son master, une collègue l’a envoyée me voir et, m’avouera-t-elle bien plus tard, elle ne voit pas trop pourquoi elle quitterait Paris pour l’Alsace

De mon côté, je m’intéresse depuis ma thèse aux surfaces hyperboliques, c’est-à-dire aux surfaces de courbure négative , qui ressemblent localement à un col ( voir la ﬁgure page 26) Je viens d’écrire une série d’articles décrivant le comportement des ondes dans divers types de géométries. Cela m’a conduite à fréquenter des communautés de chercheurs et chercheuses qui étudient les mêmes questions que moi , mais pour des graphes , dont des graphes « aléatoires » . Je suis intriguée par cette démarche probabiliste, et il me démange d’essayer de manipuler, de mon côté, des surfaces aléatoires Avec Laura, nous décidons que son sujet de mémoire consistera, dans un premier temps, à comprendre ce que peut être une surface hyperbolique aléatoire, puis, peut-être dans un deuxième temps, à essayer de décrire leur « spectre » – une des propriétés les plus importantes pour caractériser les surfaces Ce projet , commencé en 2018, vient tout juste

de s’achever en 2025. Il aura produit une belle thèse, soutenue en 2021, et trois années supplémentaires de collaboration pour terminer les recherches… non sans diﬃcultés

La géométrie aléatoire consiste à étudier des objets géométriques construits au hasard Il y a plusieurs raisons de vouloir faire cela. En construisant au hasard, on fait apparaître des objets moins symétriques que ceux que notre cerveau se plaît naturellement à créer Des objets diﬃciles à se représenter, mais qui pourtant existent Parfois, le résultat choque l’intuition, mais parfois, à l’inverse, on espère voir se révéler des objets dont l’existence est conjecturée ou désirée, mais que personne n’arrive à trouver (voir l’encadré La méthode probabiliste, page 26) On peut aussi envisager la géométrie aléatoire comme une manière de faire des mathématiques expérimentales : on laisse les objets se construire indépendamment de notre volonté, puis on essaie de décrire le produit de l’expérience. Les géométries aléatoires sont aussi au cœur des tentatives de construction de la gravité quantique, en physique (voir l’encadré Gravité quantique, page 29), et elles sont par ailleurs très utilisées pour produire des images, des textures, modéliser des réseaux de communication, etc. La géométrie différentielle « traditionnelle » étudie des courbes, des surfaces et leurs analogues en dimension 3 ou plus, appelées « variétés » Sur une « variété riemannienne »,

Sauf mention contraire, toutes les illustrations sont de © Bruno Vacaro

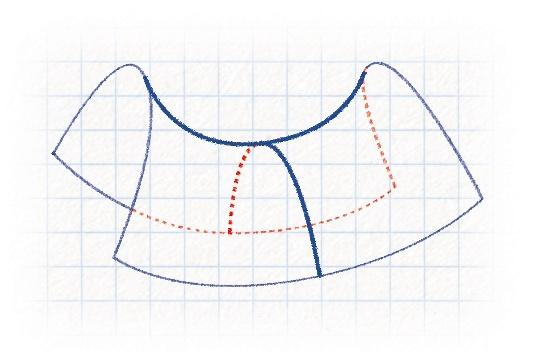
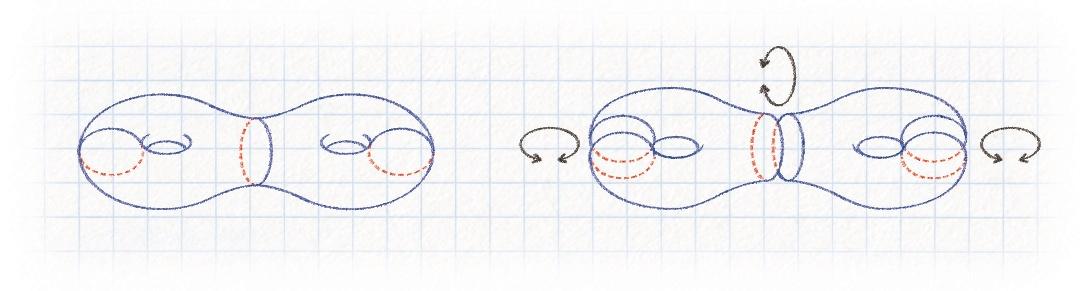
En tout point, une surface hyperbolique ressemble à un col, avec deux courbes orthogonales qui ont des courbures de signes opposés, et inverses l’une de l’autre (en gras) . On représente ici un petit morceau de surface hyperbolique, mais il est impossible de visualiser, dans l’espace euclidien de dimension 3, une surface hyperbolique inﬁnie ou une surface hyperbolique fermée (c’est-à-dire sans bord et de diamètre ﬁni).

on peut en outre mesurer des longueurs, des vitesses ou encore des courbures Le calcul diﬀérentiel puis la géométrie riemannienne se sont développés depuis plusieurs siècles pour les besoins de la physique, et sont toujours considérés comme de bons outils pour modéliser le monde qui nous entoure . Les objets de cette géométrie traditionnelle sont continus et lisses : espace euclidien, cylindre, sphère, tore, … Ceux qui attirent naturellement les mathématiciens ont, de plus, beaucoup de symétries La géométrie aléatoire, au contraire, mène rapidement vers des objets très irréguliers (voir l’encadré Hasard et irrégularité, page 30).

LEGOS ALÉATOIRES

Comme dans un jeu de construction , beaucoup de modèles géométriques aléatoires reposent sur l’assemblage de pièces de base, suivant une méthode de tirage au sort qui détermine la façon de combiner les pièces entre elles – on parle de « modèle probabiliste » Selon le modèle choisi, les pièces élémentaires auront des formes diﬀérentes, et il peut y avoir diverses techniques d’assemblage. Imaginons un jeu de Lego dans lequel on laisserait le hasard décider à notre place la construction à réaliser, par exemple en eﬀectuant des lancers de dés dont le résultat indiquerait quelle forme de pièce choisir, de quelle couleur, où et comment les associer…

Un exemple simple de géométrie aléatoire provient de la théorie des graphes. Un graphe est constitué de sommets reliés par des arêtes On dit que deux sommets sont voisins s’ils sont reliés par une arête Les graphes sont au cœur de la combinatoire et de l’informatique théorique, et sont omniprésents dans les mathématiques actuelles, des plus abstraites (théorie des groupes, algèbre…) aux plus appliquées (chaînes de Markov, modélisation des réseaux

de communication… ). Pour construire un graphe aléatoire, on assemble au hasard des sommets et des arêtes, souvent en se ﬁxant un certain nombre de contraintes – par exemple, on peut imposer de construire un graphe aléatoire « régulier », c’est-à-dire dont tous les sommets ont le même nombre de voisins L’étude des graphes aléatoires connaît actuellement un âge d’or, et les nouvelles perspectives qui en découlent s’immiscent petit à petit dans d’autres champs mathématiques – dont la géométrie traditionnelle. Cela alimente l’idée qu’étudier non plus des graphes, mais des surfaces aléatoires pourrait se révéler fécond : peut-être est-il possible de construire, pour ces surfaces, des techniques et outils analogues à ceux qui sont développés pour les graphes aléatoires ?

Avec Laura Monk , nous nous sommes intéressées au cas des surfaces hyperboliques aléatoires Nous les avons étudiées en nous inspirant des avancées réalisées autour des années 2010 par Maryam Mirzakhani , grande mathématicienne iranienne, disparue en 2017, dont les travaux lui ont valu de recevoir la médaille Fields en 2014. Les blocs élémentaires couramment utilisés en géométrie hyperbolique sont les « triangles idéaux » (voir la figure page ci-contre) et les « pantalons hyperboliques » (voir la figure page 28). Un premier type de surface hyperbolique aléatoire, assez simple, est obtenu grâce au modèle probabiliste de Brooks-Makover Ce dernier consiste à se donner un certain nombre N de triangles idéaux et à coller aléatoirement leurs côtés Il s’agit d’un modèle probabiliste discret, car il n’y a qu’un nombre fini de recollements possibles Les surfaces hyperboliques ainsi créées sont lisses et possèdent des pointes infinies, appelées « cusps hyperboliques » Mais le théorème d’uniformisation de Poincaré-Koebe assure qu’il est possible de « compactifier » ces pointes infinies : on produit alors des surfaces hyperboliques fermées et lisses Ce modèle a beaucoup

LA MÉTHODE PROBABILISTE

L’expression « modèle probabiliste » remonte aux travaux de Paul Erdös sur les graphes aléatoires dans les années 1960. À l’époque, beaucoup de spécialistes pensaient que si un graphe n’avait pas de circuits trop courts, alors on pouvait le colorier avec peu de couleurs en s’assurant que deux voisins aient toujours des couleurs di érentes. Paul Erdös a détruit cette croyance à l’aide d’un modèle de graphes aléatoires : la probabilité qu’un graphe tiré au hasard satisfasse les propriétés attendues peut se calculer de manière assez simple, et cette probabilité est très faible. Cela signiﬁe qu’il y a beaucoup de graphes qui vont à l’encontre de ce qu’attendaient les mathématiciens ! C’est un exemple frappant où la méthode probabiliste a servi à contredire l’intuition. Dans d’autres cas, comme dans le théorème d’AnantharamanMonk, dont l’histoire est racontée dans cet article, la méthode probabiliste sert au contraire à trouver des objets « rêvés » mais qu’on n’arrivait pas à dénicher autrement.

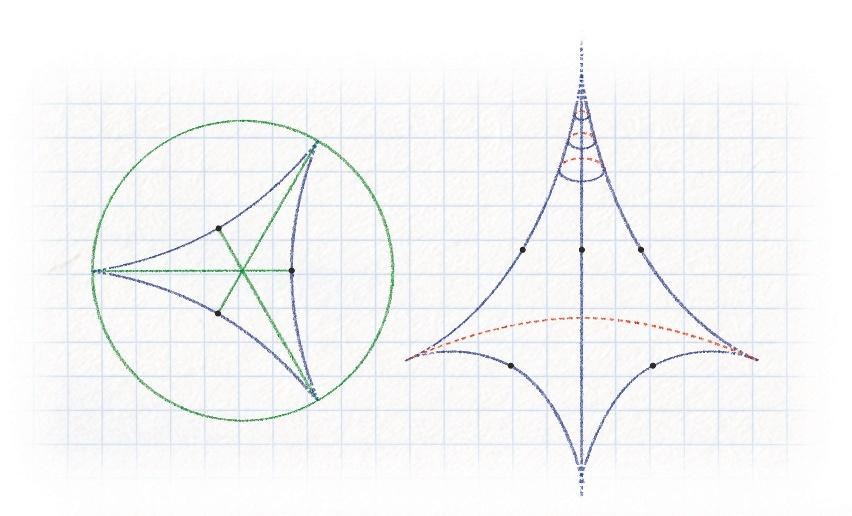
Les « triangles hyperboliques idéaux » sont des triangles dont les côtés sont infinis, et dont les sommets sont donc localisés sur un horizon situé à l’infini. Malgré tout, du fait de la courbure négative en géométrie hyperbolique, leur aire est finie et vaut π. On peut représenter un triangle hyperbolique idéal sur le « disque de Poincaré » (figure de gauche) : un disque euclidien sur lequel les distances ont été modifiées par un facteur de grossissement, de plus en plus grand à mesure qu’on approche du bord du disque. Pour effectuer le plus court chemin entre deux points du disque, il faut se rapprocher du centre : les géodésiques du disque de Poincaré sont des arcs de cercles, perpendiculaires au bord. Si on les parcourt à vitesse constante, on n’atteint jamais le bord du disque : celui-ci est un horizon « idéal », situé à l’infini. En recollant entre eux des triangles hyperboliques idéaux (figure de droite), on obtient des surfaces hyperboliques d’aire finie et qui ont des cusps (« pointes infinies »).

été étudié depuis 2004, avec de grandes valeurs de N, pour rechercher des surfaces hyperboliques avec des propriétés inattendues ou difficiles à mettre en évidence. Laura et moi commençons donc par consulter les travaux de Robert Brooks et Eran Makover, ainsi que ceux d’Alexander Gamburd Il y est démontré, entre autres, que les surfaces construites au hasard selon ce modèle sont des bouées avec environ N/2 anses (on dit que leur « genre » vaut environ N/2) et qu’à l’instar de beaucoup de graphes aléatoires, elles ont la propriété dite small world, « petit monde » Cela signifie que ces surfaces sont très « connectées » : même quand N est très grand, deux points sur la surface ne sont jamais très éloignés Plus précisément, on peut marcher d’un point de la surface à l’autre avec un nombre de pas de l’ordre de log(N). Ainsi, pour N = 1 000, la distance entre deux points est de l’ordre de 3 pas, pour N = 1 000 000, elle est de l’ordre de 6 pas. Une autre manière de mesurer la propension d’une surface à être « bien connectée » consiste à regarder sa constante isopérimétrique, aussi appelée « constante de Cheeger » : elle mesure la longueur du coup de ciseau qu’il faudrait donner pour séparer la surface en deux morceaux disjoints. Nos surfaces aléatoires ont une grande constante de Cheeger : elles sont difficiles à disconnecter.

Le modèle de Brooks-Makover a l’inconvénient de ne pas être « équitable » : certaines surfaces hyperboliques n’ont aucune chance d’être produites avec ce modèle probabiliste En eﬀet,

l’ensemble des surfaces hyperboliques fermées de genre g = N/2 est non seulement infini, mais infini non dénombrable Or, si nous fixons le nombre de triangles N à assembler, nous n’obtenons qu’un nombre fini de surfaces hyperboliques, et même si nous autorisons N à varier nous n’obtiendrons au mieux qu’une infinité dénombrable de surfaces. C’est ennuyeux, car en travaillant avec des surfaces hyperboliques aléatoires, Laura et moi espérons récolter des informations sur le plus de surfaces possibles Cependant, si notre modèle n’est capable de reproduire qu’une petite partie des surfaces hyperboliques existantes, il ne nous renseignera pas beaucoup sur ce à quoi ressemble une surface « typique » C’est un peu comme si, dans un sondage destiné à connaître l’opinion des Français, on n’interrogeait que des personnes issues d’une certaine classe sociale !

TIRAGE ÉQUITABLE

La mesure de probabilité de Weil-Petersson, avec laquelle Maryam Mirzakhani est parvenue à des avancées considérables, est au contraire considérée comme une méthode équitable pour construire au hasard une surface hyperbolique Nous nous tournons donc vers cette méthode. Il faut souligner le côté iconoclaste de l’expression « mesure de probabilité de Weil-Petersson ». Hans Petersson puis André Weil, travaillant dans le domaine de la géométrie algébrique complexe, ont élaboré un outil de mesure nommé « structure symplectique sur l’espace des surfaces de

Riemann » : une structure symplectique permet de mesurer des aires et des volumes, c’est la structure mathématique qui sous-tend toute la mécanique classique. Cela peut être quelque chose d’assez concret en physique, ou de très abstrait en mathématiques , et la construction de Hans Petersson et André Weil est un exemple particulièrement abstrait. Elle n’était pas du tout pensée, au départ, pour faire des probabilités ! Il faut avoir en tête la sociologie des mathématiques dans la seconde moitié du XXe siècle (encore vivace aujourd’hui) : les branches des mathématiques les plus abstraites, telles la géométrie algébrique ou l’algèbre, étaient à la fois considérées comme les plus diﬃciles et les plus nobles Au contraire, les mathématiques appliquées étaient (et sont encore parfois) tenues pour plus « faciles » et moins respectables La théorie des probabilités peut être extrêmement abstraite, mais comme elle est née de spéculations sur la chance et emprunte souvent ses exemples à l’étude des jeux de hasard, elle a longtemps été regardée comme une discipline « appliquée » et peu sérieuse. Mélanger la théorie des probabilités avec la géométrie algébrique, ou toute autre forme de « mathématiques pures », aurait été impensable à l’époque ! Heureusement, cette hiérarchie sociologique entre domaines des mathématiques est en train de s’estomper, et de nombreux grands mathématiciens actuels mêlent joyeusement algèbre, géométrie, probabilités et statistiques.

Pour comprendre comment on construit une surface hyperbolique aléatoire suivant la loi de probabilité de Weil-Petersson, commençons par décrire les surfaces hyperboliques de genre g – autrement dit des « bouées » avec g anses Une telle surface est décomposable sous la forme d’un assemblage de pièces élémentaires appelées « pantalons hyperboliques » (voir la figure ci-dessous), recollés le long de leurs trois courbes de bord (voir les figures page ci-contre). Dans la suite, nous fixons une telle décomposition pour chaque surface La forme

de chaque pantalon du découpage est déterminée par la longueur des bords, et d’autres paramètres nommés twists indiquent comment on a fait tourner deux pantalons adjacents avant de les coller, dans l’assemblage On sait depuis les années 1930 environ que ces paramètres de longueurs et de twists, qualifiés de « paramètres de Fenchel-Nielsen », suffisent à décrire exactement une surface hyperbolique Choisir au hasard une surface hyperbolique de genre g fixé revient donc à tirer au sort les longueurs et les twists qui la définissent.

Mais comment opérer un tel tirage en garantissant un choix « équitable » parmi l’ensemble des surfaces ? On peut imaginer tirer au sort uniformément des longueurs et

Mélanger théorie des probabilités et géométrie algébrique était impensable £

Outre les triangles idéaux, une autre pièce élémentaire couramment utilisée pour construire des surfaces hyperboliques est le « pantalon hyperbolique ». Les bords de ces pantalons sont des courbes, dont on peut faire varier les longueurs. L’aire d’un pantalon vaut toujours 2π, même quand on fait varier les longueurs des bords.

des twists. Un piège réside toutefois dans le fait qu’une même surface hyperbolique peut être découpée en pantalons de plusieurs manières différentes (voir l’encadré Paramètres de Fenchel-Nielsen, page 31). En fixant, comme on l’a fait, un découpage pour chaque surface, on a donc introduit une part d’arbitraire dans notre méthode, ce qui n’est pas satisfaisant Imaginons, en effet, qu’on doive tirer au sort un des 27 pays de l’Union européenne pour organiser une certaine manifestation : serait-il équitable d’attribuer une chance identique à chaque pays ? Ou faudrait-il pondérer le tirage au sort par le choix d’un autre critère (population, superficie, PIB…) ? Cet exemple illustre bien qu’un tirage juste ne peut pas reposer sur des choix arbitraires De même, dans le cas des surfaces hyperboliques, faire dépendre notre méthode de tirage au sort d’un choix préalable de découpage pour chaque surface ne semble pas équitable Heureusement, un théorème difficile (même pour les spécialistes), démontré dans les années 1980 par Scott Wolpert, assure que les calculs qu’on mène avec cette méthode donnent le même résultat quelle que soit la manière dont on a découpé les surfaces au départ, et que cette méthode redonne bien la mesure de Weil-Petersson telle qu’elle avait été définie en géométrie algébrique complexe Cela sauve notre approche !

Un autre problème persiste toutefois : les twists et les longueurs des géodésiques

(l’analogue, dans un espace hyperbolique, de la notion de droite) peuvent être arbitrairement grands Par conséquent, si nous voulons les tirer au sort de manière équiprobable, nous aboutissons à une « probabilité » totale égale à l’inﬁni au lieu de 1 (voir l’encadré Loi uniforme, page 33) La mesure de Weil-Petersson telle que nous venons de la décrire ne déﬁnit pas une loi de probabilité !

SURFACES INDISTINGUABLES

Une manière de le comprendre est de se rendre compte qu’il existe une infinité de découpages possibles d’une même surface (voir la figure page 31). Une fois que nous choisissons un découpage (cela s’appelle « marquer » la surface), nous sommes conduits à distinguer des surfaces qui, sans le marquage, seraient indistinguables. Par exemple, dans la figure page 31, les deux surfaces S1 et S2 peuvent avoir les mêmes longueurs et les mêmes twists, mais pour deux marquages différents Avec notre méthode, elles seront comptées comme deux surfaces différentes, puisque produites par des jeux de paramètres différents… alors qu’elles sont indistinguables (on dit « isométriques », en mathématiques) : quitte à les regarder sous le bon angle, l’œil ne fera pas de différence entre les deux Cela crée donc des redondances dans notre tirage au sort, d’où ce problème de probabilité totale infinie

On peut introduire ici un peu de jargon : « l’espace de Teichmüller » désigne l’ensemble des surfaces hyperboliques où on a marqué un découpage en pantalons Notons que la référence à Oswald Teichmüller est amère en raison de son implication enthousiaste dans la politique nationale-socialiste. Elle n’a cependant pas été gommée et reste universellement utilisée « L’espace des modules » désigne au contraire l’ensemble des surfaces hyperboliques où on ne distingue pas deux surfaces isométriques. Considérons un cas élémentaire : celui d’un lancer de dés, où on jette simultanément deux dés identiques Dans l’espace de Teichmüller, les dés seraient marqués et le résultat « dé nº 1 = 5 ; dé nº 2 = 3 » serait considéré comme diﬀérent de « dé nº 1 = 3 ; dé nº 2 = 5 », alors que dans l’espace des modules (où les dés ne sont pas marqués), ces deux résultats seraient estimés

comme identiques Dans le cas des surfaces aléatoires, décider de ne pas compter plusieurs fois des surfaces indistinguables, permet de lever ce problème de probabilité inﬁnie

Nous voici donc, enﬁn, avec un modèle probabiliste qui permet de construire au hasard des surfaces hyperboliques en les tirant au sort de manière équitable. Convenons que le chemin pour y parvenir a été un peu tortueux ! On peut légitimement se demander si on peut calculer quoi que ce soit avec cette description alambiquée. Par exemple, quelle est la probabilité que le diamètre d’une surface de genre 2 soit compris entre 5 et 5,8 ? La vérité, c’est qu’à l’heure actuelle on ne sait encore presque rien calculer Une des explications est qu’il est impossible de savoir si deux surfaces sont indistinguables (isométriques) juste à partir des paramètres de FenchelNielsen Une autre raison, c’est que la plupart des quantités intéressantes (par exemple, le diamètre) ne peuvent pas être calculées de manière simple à partir de ces paramètres. Le peu que nous sachions est essentiellement dû aux travaux révolutionnaires de Maryam Mirzakhani En utilisant des formules

GRAVITÉ QUANTIQUE

LPour construire une surface hyperbolique, on peut recoller bord à bord des pantalons à condition que les longueurs des bords soient les mêmes. Ce faisant, on a la liberté de faire tourner un pantalon par rapport à l’autre : c’est ce qu’on appelle un twist. En recollant N pantalons, si N est pair, on obtient une surface hyperbolique fermée de genre (N/2) + 1, c’est-à-dire une bouée avec (N/2) + 1 trous.

’un des problèmes majeurs de la physique contemporaine consiste à essayer d’uniﬁer la relativité générale – qui est, depuis Einstein, la grande théorie de l’espace-temps, au cœur de laquelle se trouve la notion de gravité – et la mécanique quantique, laquelle régit le « modèle standard de la physique », la grande théorie de la matière. Dans cette quête d’une « théorie quantique de la gravitation », qui réconcilierait ces deux théories di ciles à faire fonctionner ensemble, certains spécialistes font appel aux géométries aléatoires. En mécanique newtonienne, le principe de moindre action stipule que le mouvement d’une particule suit les trajectoires qui minimisent une forme d’énergie appelée « action » : il n’y a qu’un mouvement possible. Au contraire, en mécanique quantique, d’après la vision de Richard Feynman, toutes les trajectoires sont a priori possibles : il est attribué à chacune une « amplitude de probabilité », et les trajectoires de moindre action sont les plus probables. En relativité générale, la géométrie de l’espace elle-même est incluse dans les inconnues du problème. L’espace y est courbé par le champ de gravitation, selon les équations d’Einstein accompagnées elles aussi d’un principe de moindre action. Une manière d’essayer d’uniﬁer la relativité générale et la mécanique quantique serait donc de construire une théorie où toutes les géométries seraient possibles, chacune venant avec une certaine amplitude de probabilité : c’est le domaine des géométries aléatoires !

HASARD ET IRRÉGULARITÉ

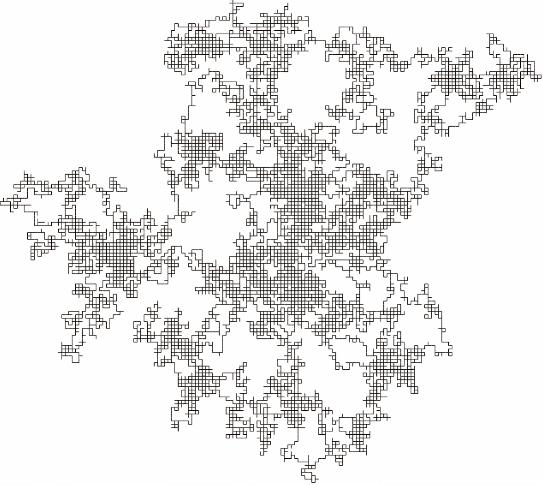
En règle générale, les objets géométriques construits au hasard sont très irréguliers. Prenons l’exemple des trajectoires browniennes (voir la figure ci-dessous) : une manière classique de les définir est de les approximer par des trajectoires de marches aléatoires simples. Le dessin représente la trajectoire d’un marcheur qui, à chaque pas, a une probabilité 1/4 d’aller vers l’est, l’ouest, le nord ou le sud. Après un grand nombre N de pas, si on dézoome d’un facteur √N, ces trajectoires s’approchent des trajectoires browniennes, qui sont très irrégulières : elles n’ont pas de vecteur tangent, et bien qu’étant des courbes, elles sont de dimension 2. Voici un bel exemple où un modèle probabiliste contredit ce qu’on se représente intuitivement : rappelons qu’au XIXe siècle, les courbes sans vecteur tangent étaient considérées comme pathologiques – Henri Poincaré les qualifiait carrément de « monstres » ! On sait maintenant qu’elles sont partout, en mathématiques comme en physique.

géométriques appelées « identités de McShane » (dues à l’origine à Gregory McShane, professeur à l’université de Grenoble), la mathématicienne obtient une manière originale de ne pas compter plusieurs fois des surfaces indistinguables. Pour ce faire, elle s’autorise dans un premier temps à les compter plusieurs fois, mais elle adopte ensuite la formule de McShane pour supprimer le poids des comptages redondants. Maryam Mirzakhani trouve ainsi une formule de récurrence qui permet, théoriquement, de calculer le volume total de l’« espace des modules » en fonction du genre g C’est très important, puisque la probabilité d’un événement est donnée par la division du « volume de l’événement » par le « volume total de l’espace des modules » Ce calcul du volume total se fait par récurrence sur le genre de la surface : on parle de « récursion topologique » Connaissant le volume total de l’espace des modules pour des surfaces de petit genre, on peut donc théoriquement calculer ce volume pour des surfaces de plus grand genre En pratique, cependant, les calculs deviennent vite trop lourds pour

pouvoir être effectués de la sorte Dans des travaux communs avec le mathématicien russe Peter Zograf , Maryam Mirzakhani parvient toutefois à calculer les volumes des espaces de modules pour les petites valeurs de g, mais aussi à les estimer de manière approchée quand g devient très grand Enfin, la chercheuse iranienne exploite la récursion topologique pour démontrer une famille d’équations conjecturées par le physicien Edward Witten en lien avec la gravité quantique – équations qui avaient été préalablement démontrées par Maxim Kontsevich, mais avec une méthode complètement différente

SURFACES TRÈS CONNECTÉES

Au bout de quelques mois, Laura et moi commençons à être familières des techniques introduites par Maryam Mirzakhani, et je souhaite alors comprendre jusqu’à quel point les nouvelles idées qui foisonnent dans le domaine des graphes aléatoires vont pouvoir s’appliquer aux surfaces. Depuis mes travaux sur le chaos quantique, je m’intéresse particulièrement au « spectre » des surfaces hyperboliques. Pour comprendre cette notion, imaginons que la surface soit un gong parcouru de vibrations : son spectre de fréquences correspondrait aux harmoniques produites par cet instrument bizarre On parle aussi de « fréquences propres » pour désigner les harmoniques. En dehors de cette métaphore musicale, le spectre intéresse de près les géomètres : la fréquence propre la plus basse de la surface est en eﬀet directement reliée à la manière dont cette surface est bien connectée Les musiciens appellent cette fréquence la plus basse « fréquence fondamentale », les mathématiciens, « trou spectral » C’est un nombre réel positif, dont on démontre qu’il est inversement proportionnel au temps que mettrait un marcheur se déplaçant au hasard sur la surface pour la visiter en entier Un « grand » trou spectral signiﬁe donc que la surface est bien connectée, car un tel marcheur la visitera entièrement en un temps réduit. Depuis le début du XXIe siècle, la connaissance du trou spectral des graphes aléatoires – une notion parfaitement analogue à celle de trou spectral d’une surface – a fait des avancées spectaculaires. Je propose donc à Laura d’essayer de comprendre les basses fréquences des surfaces hyperboliques aléatoires, sans plan très précis en tête Il est connu depuis un article de Heinz Huber de 1974 que, pour des surfaces de grand genre g, le trou spectral ne peut pas excéder une valeur seuil de 1/4 + ε, avec ε une erreur qui devient de plus en plus petite à mesure que g croît Ce résultat coïncide avec l’intuition physique qu’on peut avoir : on s’intéresse, ici, à des objets de plus en plus grands, et on s’attend donc à ce que les notes qu’ils émettraient si

on les faisait vibrer soient de plus en plus graves . Leur fréquence fondamentale – i . e . leur trou spectral – devrait donc, en principe, rester petite . Mais peut- on trouver des surfaces de grand genre dont le trou spectral est proche de cette valeur seuil – autrement dit , des surfaces aussi bien connectées que possible ? Le cas échéant, de telles surfaces sont-elles rares, ou au contraire abondantes ? L’approche de ces questions par l’intermédiaire des surfaces hyperboliques aléatoires est particulièrement pertinente : en étudiant les propriétés de surfaces tirées au sort, on voit à quel point une propriété est susceptible ou non d’être observée, à quel point un phénomène est fréquent Maryam Mirzakhani elle-même a adopté cette approche, et démontré qu’une surface hyperbolique de grand genre tirée au hasard est toujours très bien connectée. Pour mesurer cela, elle a travaillé sur la constante isopérimétrique des surfaces : elle est parvenue à estimer cette constante pour une surface hyperbolique de grand genre prise au hasard. Son résultat implique que le trou spectral d’une telle surface est plus grand que 0,02. Autrement dit, même en regardant de très grands « instruments hyperboliques aléatoires », leur note fondamentale ne descend pas en dessous d’un certain plancher. Ce premier plancher est certes très éloigné du seuil convoité de 1/4, mais il s’agit, historiquement, de la première information dans cette direction !

GÉODÉSIQUES

Pendant son master, Laura aﬃne certains calculs de Maryam Mirzakhani concernant le nombre de fréquences propres inférieures à 1/4 que peut avoir une surface aléatoire Ses résultats donnent de premières informations semblant indiquer que les surfaces dont le trou spectral est très inférieur à 1/4 sont bel et bien rares Son approche part d’un double constat D’une part, quand des ondes se propagent dans un espace plat, les fronts d’ondes ont tendance à se déplacer en « ligne droite » Or, dans un espace courbe, les géodésiques remplacent la notion de ligne droite D’autre part, en physique, les fréquences propres correspondent à des manières de vibrer très particulières, appelées « vibrations stationnaires ». On peut donc penser que les fronts d’ondes qui produisent des fréquences propres sur une surface hyperbolique vont épouser des chemins géodésiques « fermés » – c’est-à-dire qui reviennent à leur point de départ, à la manière des ondes stationnaires. Comprendre les basses fréquences émises par une surface hyperbolique passerait ainsi par la compréhension des géodésiques fermées de grande longueur Laura a donc utilisé la célèbre formule des traces de Selberg, démontrée en 1956, qui donne une relation entre le spectre de fréquences d’une

surface hyperbolique et les longueurs des chemins géodésiques fermés de la surface . Malheureusement , tout cela relève plus de l’intuition que d’un raisonnement précis, et la formule des traces de Selberg, tout en énonçant clairement un lien entre ondes stationnaires et géodésiques fermées, se heurte à la malédiction du principe d’incertitude : une onde ne se déplacera jamais exactement en ligne droite, elle se disperse. Une onde stationnaire ne va donc jamais épouser une seule géodésique : elle va toutes les emprunter à la fois, et la superposition de tous ces chemins est un casse-tête auquel de nombreux mathématiciens et physiciens se sont trouvés confrontés

PARAMÈTRES DE FENCHEL-NIELSEN

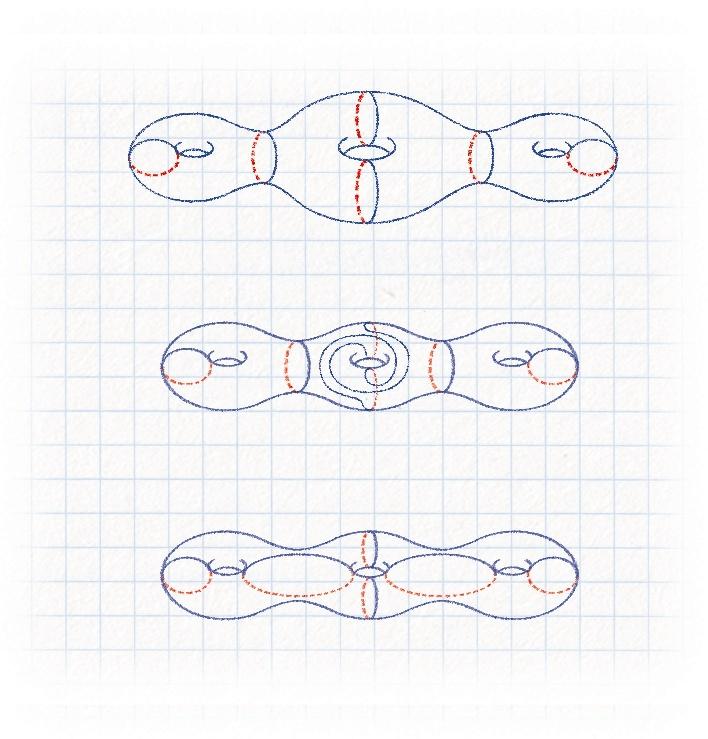
Toute surface fermée de genre g peut être découpée en 2g – 2 pantalons. Les longueurs des courbes géodésiques qui séparent ces pantalons, ainsi que les twists le long de ces courbes, sont des paramètres qui caractérisent entièrement la géométrie d’une surface hyperbolique. Ils s’appellent « paramètres de Fenchel-Nielsen ». Il y a une inﬁnité de manières di érentes de découper une surface, et selon la manière dont on découpe, on obtient des paramètres di érents. Dans le dessin ci-dessous, on montre trois découpages possibles d’une surface de genre 3, qui donne donc 4 pantalons hyperboliques. On constate que les deux premiers découpages ont la même topologie : deux des courbes le long desquelles on découpe disconnectent la surface, et les quatre autres la laissent connexe. À l’inverse, dans le troisième découpage, aucune courbe ne disconnecte la surface. Avec les deux premiers découpages, si les longueurs des bords sont les mêmes et si les twists sont identiques, alors les deux surfaces sont indistinguables.

Une des formules de Maryam Mirzakhani permet de calculer la contribution des géodésiques « simples » (i e les géodésiques fermées qui ne s’intersectent pas) dans la formule des traces lorsqu’on moyenne cette formule sur toutes les surfaces. Un jour, je fais un calcul au brouillon et je découvre une identité remarquable dans cette formule de Maryam Mirzakhani, qui rend possible de simpliﬁer tous les termes provenant des géodésiques simples Je soupçonne que cette identité devrait permettre de faire de grands progrès dans l’estimation du trou spectral de nos surfaces aléatoires ! Reste cependant qu’il faudrait aussi comprendre toutes les géodésiques qu’on a négligées (celles qui se recoupent), pour voir si on retrouve la même identité remarquable dans leur contribution à la formule des traces De la sorte, après avoir moyenné sur toutes les surfaces, la formule des traces se simpliﬁerait dans son ensemble, et on aurait accès au trou spectral Laura accroche tout de suite à cette idée. Nous rêvons de démontrer que le trou

Je soupçonne qu’une identité remarquable nous aiderait à estimer

le trou spectral £

spectral d’une surface prise au hasard est supérieur à 1/4 – ε, avec de nouveau ε une erreur qui devient de plus en plus petite à mesure que le genre de la surface croît. Autrement dit, nous souhaitons montrer que les surfaces hyperboliques aussi bien connectées que possible sont très abondantes Je retrouve un e-mail de Maryam Mirzakhani, daté de 2015, dans lequel elle m’écrivait avoir passé du temps à « jouer avec la formule des traces ». Peut-être avait-elle le même rêve que nous ?

Au départ , nous progressons bien . En mars 2020, quand un conﬁnement d’un ou deux mois est annoncé pour faire face au Covid-19, je pense : « C’est exactement le temps qu’il nous faut pour ﬁnir notre démonstration » Au bout de deux mois, je déchante, mais pas Laura, qui a trouvé de nouvelles formules pour calculer la longueur des géodésiques non simples. Mais début 2022, nous sommes à la peine Je commence à me demander si nous serons plus vite débarrassés du Covid ou de notre démonstration. L’année précédente, en 2021, deux autres équipes ont réalisé des avancées remarquables en démontrant que le trou spectral d’une surface aléatoire de grand genre est supérieur à 3/16. Ce n’est pas tout à fait 1/4, mais c’est déjà très bien ! Nous nous disons que nous avons été aveugles, que le résultat nous regardait droit dans les yeux car il était accessible grâce à notre méthode, et que nous n’avons pas su le voir. Nous nous demandons combien de temps nous devons encore nous entêter dans ce projet. C’est dans cet état d’esprit plutôt pessimiste que nous rencontrons, en mai 2022, Joel Friedman, la personne la plus à même de nous

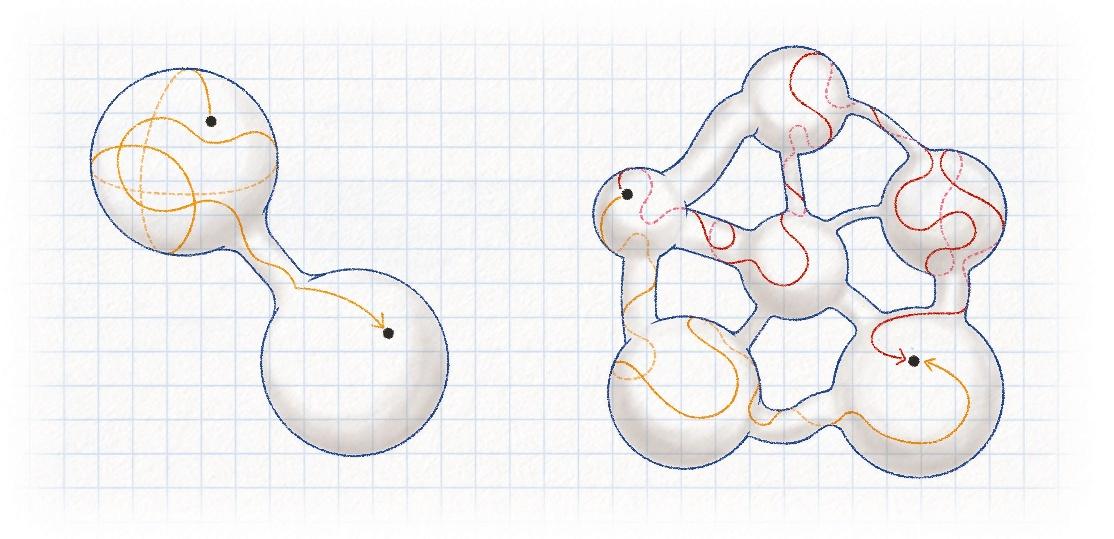
Une surface faiblement connectée (figure de gauche) et une surface bien connectée (figure de droite). En se déplaçant aléatoirement, on mettra du temps à visiter l’entièreté de la surface de gauche en raison de la présence d’un goulot d’étranglement. À l’inverse, on visitera rapidement la surface de droite, car il est facile d’y passer d’une zone à une autre. Cela signifie que le trou spectral de la surface de gauche est plus petit que celui de la surface de droite.

© Bruno Vacaro, d’après

Quanta Magazine

sortir de cette ornière Il a su estimer le trou spectral des graphes réguliers aléatoires, et nous savons qu’il s’est acharné là-dessus pendant une vingtaine d’années, en surmontant des diﬃcultés inimaginables Au début, nous ne comprenions absolument rien à ses travaux, mais depuis quelque temps nous commençons à voir qu’il a suivi un cheminement semblable au nôtre Peut-être arrivera-t-il à nous débloquer ? Sinon, il appréciera peut-être de savoir que nous sommes de ferventes admiratrices de son travail, et cela fera du bien de discuter. Le premier contact est bon, et Joel, qui travaille au Canada, propose de venir nous voir en France dès l’automne 2022. Il nous explique l’idée ﬁnale qui l’a amené à conclure son travail sur le trou spectral des graphes aléatoires

Comme nous, il avait trouvé une identité remarquable lui permettant de simplifier la formule des traces après en avoir pris la moyenne sur tous les graphes. Il était cependant resté bloqué par l’existence de « mauvais » graphes, rares mais suffisamment présents pour faire échouer toute sa tactique Ces graphes contiennent des motifs géométriques qu’il appelle tangles (« enchevêtrements »), qui obligent les géodésiques à s’enrouler pendant très longtemps dans de petites régions — ce qui confère aux graphes concernés un petit trou spectral. Ces mauvais graphes sont un obstacle majeur à toute l’entreprise d’utiliser la formule des traces : il fallait donc s’en débarrasser Joel Friedman a, pour ce faire, inventé une formule, qu’il nomme « formule d’inversion de Moebius » (par analogie avec une célèbre formule de théorie des nombres), capable de filtrer tous les graphes contenant des tangles C’est cette formule qu’il nous explique lors de son passage en France

Les deux années suivantes sont pour Laura et moi une époque de dur labeur, pendant laquelle nous travaillons à adapter la formule d’inversion de Moebius au cas des surfaces, non sans faire face à de nombreuses difficultés Dans ce laps de temps, Laura donne naissance à une petite fille : c’est une période fatigante mais heureuse pour elle. En février 2025, nous y voilà enfin : notre démonstration complète est en ligne ! La rédaction de cet article m’a fait revivre six années éprouvantes et riches en émotions, et il me semble pertinent de le conclure en rendant hommage à mon ami Nicolas Bergeron Le 1er décembre 2023, je le vois pour la dernière fois Il est malade et nous sommes écrasés par la perspective de sa disparition prochaine. Pour parler d’autre chose, je lui raconte que le trou spectral d’une surface prise au hasard est proche de 1/4, à epsilon près Il est content, mais très vite arrive la question à laquelle je m’attends : peut-on démontrer que le trou spectral d’une surface aléatoire est en fait supérieur à 1/4, au lieu du 1/4 – ε que nous avons obtenu ? En effet, en théorie des nombres, une conjecture

LOI UNIFORME

Tirer au sort de manière équitable un nombre dans un ensemble ﬁni ne pose pas de problème : au loto, un tirage aléatoire d’une boule parmi 49 sera équitable si chaque boule a la probabilité 1/49 de sortir. Mais comment tirer au hasard de manière équitable un nombre parmi tous les nombres réels compris entre 1 et 49 ? Il paraît logique de requérir que la probabilité de choisir un nombre dans l’intervalle [1, 25] soit égale à la probabilité de choisir un nombre dans l’intervalle [25, 49], puisque ces deux intervalles ont la même longueur. Comme ces probabilités doivent s’additionner à 1, elles doivent donc toutes les deux valoir 1/2. Pour la même raison, la probabilité de choisir un nombre dans l’intervalle [1, 17] doit être la même que dans l’intervalle [17, 33] et que dans l’intervalle [33, 49], et cette probabilité doit valoir 1/3 = 16/48. Plus généralement, pour être équitable, la probabilité de choisir un nombre entre deux nombres a et b doit valoir (b a)/48. Cette formule, « longueur de l’intervalle [a, b] divisée par longueur totale » s’appelle la « loi de probabilité uniforme » : c’est la manière équitable de tirer au sort un réel entre 1 et 49. Maintenant, comment choisir au hasard et de manière équitable un nombre parmi tous les nombres réels ? Eh bien, ce n’est pas possible au sens du calcul des probabilités, car nous souhaiterions alors que la probabilité de choisir un nombre entre deux nombres a et b soit proportionnelle à la longueur (b a) de l’intervalle [a, b]… mais nous ne pouvons pas diviser par la longueur totale (maintenant inﬁnie) pour faire en sorte que la probabilité totale vaille 1.

énoncée par Atle Selberg en 1956 veut que certaines surfaces hyperboliques, appelées « revêtements de congruence », aient un trou spectral supérieur à 1/4. Atle Selberg avait prouvé que ces surfaces avaient un trou spectral supérieur à 3/16, et les théoriciens des nombres ont progressivement réussi à montrer qu’il était supérieur à 975/4 096 = 0,238... Je demande à Nicolas s’ils ne seraient pas déjà contents de ce résultat les rapprochant de 1/4, même « à epsilon près » Non, me dit-il : si pour les analystes, ce petit chouïa n’a pas d’importance, c’est une montagne pour les théoriciens des nombres À titre personnel, j’ai peu d’espoir de progresser dans cette direction Il a été démontré ﬁn 2024 que 69 % des graphes réguliers sont des « graphes de Ramanujan », c’est-à-dire qu’ils ont le meilleur trou spectral possible. Par analogie, on pourrait conjecturer que 69 % des surfaces hyperboliques ont un trou spectral plus grand que 1/4, et cela répondrait peut-être à la question posée par Nicolas. Je ne sais pas du tout démontrer cela Même si c’était le cas, cela ne dirait rien sur les revêtements de congruence qui intéressent les théoriciens des nombres ! En eﬀet, notre résultat ne nous apprend rien à leur sujet, car ces surfaces sont trop rares pour que notre énoncé statistique puisse les éclairer Ce qui me ferait rêver serait de donner une tournure probabiliste à l’étude des revêtements de congruence : peut-on trouver une manière de tirer au sort une surface parmi cette famille très restreinte, et évaluer la probabilité d’avoir tel ou tel trou spectral ? Voilà, peut-être, une question à laquelle se consacrer dans les années à venir n

BIBLIOGRAPHIE

N. Anantharaman et L. Monk, FriedmanRamanujan functions in random hyperbolic geometry and application to spectral gaps (I et II), arXiV preprints, 2025.

J. Huang et al., Ramanujan property and edge universality of random regular graphs, arXiv preprint, 2025.

L. Monk, Geometry and Spectrum of Typical Hyperbolic Surfaces, thèse de l’université de Strasbourg, 2021.

M. Mirzakhani, Growth of Weil-Petersson volumes and random hyperbolic surface of large genus, Journal of Di erential Geometry, 2013.

V. Rivasseau, Quantum gravity as random geometry, conférence à l’université Paris-Saclay, 2013.

N. Bergeron, Le Spectre des surfaces hyperboliques, CNRS éditions, 2011.

JEAN DALIBARD est professeur de physique au Collège de France. Il est spécialiste de l’interaction matière-rayonnement et plus particulièrement de la manipulation d’atomes par laser. Il dirige l’équipe Condensats de Bose-Einstein au sein du laboratoire Kastler-Brossel, à Paris. Il a reçu la médaille d’or du CNRS en 2021 pour l’ensemble de ses travaux. Il a publié récemment Piéger les atomes (CNRS Éditions, 2025).

Les gaz d’atomes froids ont des applications concrètes

Article réalisé en partenariat avec le Collège de France

Un gaz d’atomes refroidis à très basse température présente des comportements quantiques étonnants. Le physicien Jean Dalibard, un pionnier dans ce domaine de recherche, nous raconte comment ces systèmes ont ouvert une fenêtre sur les lois fondamentales de la matière et sont au cœur de certaines technologies, des horloges atomiques aux simulateurs quantiques.

Qu’est-ce qu’un gaz d’atomes froids ?

Il s’agit d’un ensemble d’atomes que l’on refroidit à une température proche du zéro absolu, vers – 273 °C. Pour y parvenir, les physiciens ont dû développer des techniques de refroidissement reposant sur des lasers et des méthodes pour conﬁner le système dans un petit volume.

L’intérêt de ces gaz est avant tout fondamental, car ils permettent de matérialiser des phénomènes ondulatoires et de sonder les lois de la physique quantique. Mais de façon surprenante, ces expériences ont également nourri de nombreuses idées pour exploiter les gaz d’atomes froids, qui sont aujourd’hui au cœur de diverses applications

Pourquoi ces systèmes sont-ils intéressants pour étudier les fondements de la mécanique quantique ?

Pour le comprendre , il faut remonter en 1900, aux premiers pas d’une théorie qui allait révolutionner tout le XXe siècle : la mécanique quantique À cette époque, Max Planck s’intéressait au problème du corps noir. Quand on chauffe fortement un matériau, le filament d’une ampoule électrique , par exemple , il émet de la lumière Or les physiciens du tournant du siècle ne réussissaient pas à décrire théoriquement la distribution d’énergie de ce rayonnement en fonction de la fréquence. Les expériences indiquaient que cette distribution était « universelle », car elle ne dépendait que de la température du matériau, mais cette universalité restait inexplicable. Max Planck a fourni une première solution en ayant recours à une astuce mathématique qui se traduit physiquement par une hypothèse audacieuse : la paroi du corps noir serait couverte d’oscillateurs qui n’émettent pas la lumière de façon continue, mais par paquets discrets, l’énergie d’un paquet étant égale à la fréquence lumineuse multipliée par une constante, la « constante de Planck » (h = 6,626 07 015 × 10 – 34 m2 kg/s). L’hypothèse de Planck était perturbante, car elle allait à l’encontre de la physique classique dont les principes reposent sur des grandeurs continues, c’est-à-dire où n’importe quelle valeur d’énergie est autorisée. En 1905, Albert Einstein a généralisé et amélioré l’idée de Planck. Jusque-là, la lumière était décrite comme une onde classique, à l’aide d’un champ électromagnétique obéissant aux équations de Maxwell En combinant les résultats connus sur le rayonnement du corps noir et sur l’effet photoélectrique, Einstein a compris que la lumière elle-même est quantique : elle est formée de corpuscules, les photons, dont l’énergie est donnée par la formule de Planck. Presque vingt ans plus tard , en 1924, Louis de Broglie a soutenu à la Sorbonne sa

À ÉCOUTER

Découvrez la version complète de cet entretien en audio, avec le podcast

« À l’écoute de la science ».

https ://s.42l.fr/PodcastPourLaScience

thèse intitulée Recherches sur la physique des quanta. Il a fait le chemin inverse d’Einstein, qui était parti d’un phénomène ondulatoire, la lumière, pour postuler qu’elle avait aussi une description corpusculaire Louis de Broglie a fait l’hypothèse que toute particule de matière n’est pas uniquement corpusculaire, mais peut aussi avoir un comportement ondulatoire. Il suggère donc une complète dualité « onde-corpuscule ». Cette idée de de Broglie a ensuite été mise à proﬁt par Schrödinger, qui a proposé une équation d’évolution pour cette onde de matière [dite « onde de de Broglie », ndlr].

Et dans les quelques années qui ont suivi, la physique quantique a pris la forme que nous utilisons désormais

Quel est le lien avec les gaz d’atomes froids ?

Un vide poussé règne dans la cellule en verre. En son centre, la boule rouge est un gaz de plusieurs millions d’atomes de rubidium, refroidis à une température de quelques microkelvins et conﬁnés dans un piège magnéto-optique. Les atomes sont visibles, car ils diffusent la lumière utilisée pour les manipuler.

L’onde associée à une particule a une longueur d’onde λ = h/(mv), où m est la masse de la particule et v sa vitesse. Pour observer expérimentalement ce caractère ondulatoire, il faut une longueur d’onde assez grande pour être mesurable En d’autres termes, il faut exacerber cette propriété ondulatoire. La formule nous indique deux façons de le faire Plus la masse est faible, plus la longueur d’onde est grande. Ainsi, à vitesse donnée, les phénomènes ondulatoires sont plus facilement observables avec des particules légères comme des électrons

L’autre solution pour avoir une grande longueur d’onde consiste à diminuer fortement la vitesse des particules. Cela peut sembler paradoxal, car si les vitesses deviennent faibles, plus rien ne paraît bouger et ça ne s’avère pas très intéressant, du moins d’un point de vue classique. Mais comme de Broglie l’indiquait,

il y a une onde associée à chaque particule Et c’est là qu’intervient l’idée de refroidir un gaz d’atomes : la vitesse moyenne des atomes est proportionnelle à la racine carrée de la température Dans un gaz froid, les atomes sont lents, leurs propriétés ondulatoires dominent, et l’assemblée d’atomes devient quantique

En dessous de quelle température parle-t-on de « matière quantique » ?

Pour donner une idée du chemin à parcourir, à température ambiante, les vitesses des atomes sont de plusieurs centaines de mètres par seconde, ce qui correspond à une longueur d’onde de l’ordre de 10 –11 mètre , soit une faible fraction du diamètre d’un atome C’est très insuffisant pour que les effets quantiques soient significatifs

Dès le début du XXe siècle, les physiciens ont développé des techniques de cryogénie qui permettent de refroidir des matériaux à quelques degrés au-dessus du zéro absolu Grâce à ces dispositifs, Heike Kamerlingh Onnes a observé, en 1911, que le mercure devenait supraconducteur en dessous de 4,2 kelvins, c’est-à-dire que le courant électrique y circulait avec une résistance nulle. Ce phénomène se retrouve dans de nombreux métaux et alliages refroidis à une température proche du zéro absolu. Aujourd’hui, on l’exploite dans de nombreuses applications, par exemple pour produire des champs magnétiques intenses comme dans les dispositifs d’IRM (imagerie par résonance magnétique). Dans les années 1930, la superﬂuidité de l’hélium liquide a été découverte : cette possibilité pour le liquide de s’écouler sans viscosité est un autre exemple de « matière quantique »

La supraconductivité et la superfluidité reposent donc sur la nature ondulatoire de la matière Mais leur compréhension fine n’est arrivée que plus tard. En effet, aux débuts de la mécanique quantique, les physiciens se sont concentrés sur le cas de particules individuelles ou de systèmes simples, comme l’atome d’hydrogène, pour en étudier les raies d’émission, par exemple À partir de la deuxième moitié du XXe siècle, les scientifiques ont voulu comprendre les propriétés des matériaux supraconducteurs ou superfluides, puis généraliser leurs travaux à tout système quantique doté de nombreux composants, tel un gaz d’atomes. Mais pour cela, il allait être nécessaire de diminuer davantage la température pour l’amener dans la gamme du microkelvin, soit un millionième de kelvin. Un système 300 millions de fois plus froid que l’air que l’on respire !

Comment refroidir d’autant un gaz d’atomes ? Par une approche qui semble paradoxale au premier abord : on éclaire le gaz avec des lasers. On pourrait penser qu’un laser conduit

systématiquement à un réchauffement du matériau illuminé, mais ce n’est pas toujours le cas. Pour refroidir, il faut bien choisir la fréquence du laser et on exploite alors l’e ff et Doppler Celui-ci est bien connu, car on l’expérimente dans la vie quotidienne quand une moto passe à côté de nous à grande vitesse Le son est d’abord aigu quand le véhicule s’approche , puis devient plus grave quand il s’éloigne. L’effet Doppler est précisément cette variation de la fréquence perçue lorsque l’émetteur et le receveur sont en mouvement l’un par rapport à l’autre La fréquence augmente quand ils se rapprochent et elle diminue lorsqu’ils s’écartent Et cela fonctionne avec tout type d’onde : acoustique, lumineuse, etc

C’est ce qu’on met à proﬁt dans un gaz éclairé par un laser Les atomes absorbent des photons du laser et subissent une pression de radiation, une force qui les pousse Or, quand les atomes bougent par rapport à un faisceau lumineux, l’eﬀet Doppler fait que la fréquence du rayonnement varie. Supposons que la fréquence de la lumière soit choisie légèrement plus basse que celle nécessaire pour exciter l’atome, c’est-à-dire lui faire absorber des photons de manière optimale. Quand un atome se déplace dans la direction de la source du faisceau lumineux, il le voit avec une fréquence plus élevée, donc plus proche de la fréquence

optimale , ce qui veut dire une pression de radiation plus forte . En revanche , quand il s’éloigne de la source laser, il voit la lumière avec une fréquence plus basse, et subit donc une pression plus faible

Prenons maintenant deux lasers identiques pour éclairer le gaz, un venant de la gauche, l’autre venant de la droite. Si l’atome est immobile, la pression de radiation exercée par les deux ondes est la même, le bilan des forces est nul et l’atome reste à sa place, comme s’il n’y avait pas de lumière. Si l’atome bouge vers la gauche, la pression de radiation créée par le laser de gauche est plus forte et donc freine l’atome dans son mouvement Ce dernier va progressivement s’arrêter Le résultat est identique si l’atome va dans l’autre sens Il suﬃt alors d’ajouter une deuxième paire de lasers pour le mouvement haut-bas et une troisième pour celui dans l’axe devant-derrière et le tour est joué : le gaz est quasiment immobilisé. La décélération est entre 10 000 et 100 000 fois plus grande que l’accélération de pesanteur. Un atome qui se déplaçait à 100 mètres par seconde est arrêté sur une distance de quelques centimètres. Les physiciens ont baptisé « mélasse optique » leur gaz ainsi refroidi, car les atomes y subissent le sort d’une cuillère engluée dans un pot de miel. Si la cuillère est au repos, elle ne ressent aucune force Mais dès que vous

Pour refroidir et contrôler le gaz d’atomes, il faut utiliser divers dispositifs optiques qui mettent en forme les faisceaux lumineux. Les cubes en verre (à gauche) sélectionnent la polarisation de la lumière, les lentilles focalisent les faisceaux sur les atomes et les caméras détectent la lumière émise par le gaz.

essayez de la bouger, elle est soumise à une force de friction considérable.

Quand la technologie est-elle devenue disponible pour appliquer cette méthode de refroidissement ?

Les premiers lasers datent des années 1960, mais ils étaient d’abord à fréquence ﬁxe. Pour mettre en œuvre cette technique , il a fallu attendre les années 1970 pour avoir des lasers dont on pouvait régler la longueur d’onde Et les physiciens ont ensuite adopté ces dispositifs pour refroidir leurs gaz En 1985, Steve Chu et son équipe, à l’époque aux Bell Labs, ont créé les premières mélasses optiques Ils ont mesuré des températures qui semblaient compatibles avec les prédictions théoriques du refroidissement Doppler Mais quand William Phillips a réalisé une expérience plus précise en 1988, il a trouvé que ces températures étaient en fait dix fois plus faibles que les 100 microkelvins attendus

Comment mesure-t-on la température d’un gaz d’atomes froids ?

Rappelons que la température est liée à l’agitation thermique. Dans la mélasse optique qui occupe un volume bien défini, les atomes refroidis se déplacent à une vitesse très faible. Si vous coupez les faisceaux laser, les atomes tombent sous l’effet de la pesanteur et sans frottement (l’expérience est faite dans une enceinte sous vide). Du fait de la vitesse initiale résiduelle des atomes, qui est de l’ordre de quelques millimètres par seconde , le volume qu’ils occupent s’étale peu à peu lors de la chute. Si vous laissez le gaz tomber sur une hauteur suffisante, typiquement quelques centimètres , et si vous disposez en bas un capteur qui détecte les atomes et mesure leur étalement, cette mesure vous donne la répartition des vitesses initiales des atomes dans la mélasse et, donc, la température du gaz

Comment expliquer le résultat de William Phillips ?

Une expérience qui fonctionne moins bien que la théorie , c’est le quotidien des expérimentateurs, mais une expérience qui fonctionne mieux que ce qui est prévu, c’est beaucoup plus rare Pour trouver une explication , William Phillips nous a contactés , Claude Cohen-Tannoudji et moi Nous avons commencé à travailler sur cette énigme et nous avons trouvé la solution, que nous avons nommée l’« eﬀet Sisyphe ».

Les atomes de sodium que William Phillips étudiait sont plus compliqués que le modèle simple d’une particule à deux niveaux d’énergie, avec un niveau fondamental et un niveau excité, qu’on utilisait pour décrire le refroidissement par eﬀet Doppler Le niveau

fondamental d’un atome de sodium possède plusieurs sous-niveaux, qui correspondent à différentes orientations du moment magnétique de l’atome. Ces sous-niveaux ne se comportent pas tous de la même façon lors d’une interaction avec de la lumière. Dans la mélasse optique, l’atome se retrouve dans un champ de potentiel périodique comparable à une alternance de collines et de vallées Quand l’atome dans un sous-niveau donné se retrouve à gravir une colline, il perd en énergie cinétique (donc en vitesse) mais, une fois au sommet, il interagit avec la lumière qui le fait retomber au creux d’une vallée pour un autre sous-niveau, sans pour autant regagner sa vitesse initiale Et l’histoire se répète, comme pour Sisyphe dans la mythologie grecque, l’atome recommence à gravir une colline, retombe, remonte, etc L’atome dissipe son énergie cinétique très vite, très efficacement Et finalement, il termine sa course, piégé au fond d’une vallée quand il n’a plus assez d’énergie pour remonter Et cela explique très bien les températures anormalement basses que mesurait William Phillips

Il manquait encore une petite touche pour faire des expériences avec des gaz d’atomes froids. Vous avez imaginé le piège magnéto-optique, de quoi s’agit-il ?

Dans la mélasse optique, les atomes sont freinés et s’immobilisent en diﬀérents points de l’espace Or, pour de nombreuses expériences de physique quantique , il faut une densité d’atomes assez grande Il faut donc rassembler les atomes froids dans un petit volume au centre de la mélasse

Dans les années 1980, les physiciens ont exploré différentes solutions , mais aucune n’était vraiment viable En 1986, lors d’un congrès à Helsinki, j’ai proposé une technique que j’avais imaginée pour autre chose, mais

Images d’un condensat de Bose-Einstein mis en rotation à l’aide d’un agitateur lumineux. La fréquence de rotation de l’agitateur augmente de gauche à droite. Si cette vitesse est trop faible, le condensat reste au repos (image de gauche). Quand cette vitesse dépasse un certain seuil, un, puis plusieurs tourbillons quantiques apparaissent.

Dans cette vue d’artiste, les atomes (sphères rouges) forment un réseau dans un potentiel périodique créé par une onde lumineuse stationnaire (surface bleue). Quand les interactions répulsives entre les atomes sont assez fortes, on arrive à un état où chaque puits du réseau est occupé par un seul atome. Ce système permet de simuler l’état des électrons évoluant dans le potentiel périodique d’un cristal.

qui avait des chances d’être efficace pour ce problème L’idée combinait des lasers de polarisation bien choisie et un gradient de champ magnétique La pression de radiation est nulle au centre du piège où le champ magnétique est nul et augmente dès qu’on s’en écarte Ainsi, les atomes ressentent une force de rappel vers ce centre, comme un ressort que l’on déplace de sa position d’équilibre. David Pritchard, du MIT, et Steve Chu ont testé mon idée avec succès. Dans leur article, ils me remercient de leur avoir soufflé la solution Aujourd’hui, ce système est employé dans toutes les expériences d’atomes froids (voir la figure page 49)

À partir de ce moment, tous les ingrédients sont réunis pour explorer les lois de la physique quantique ?

Oui, on savait refroidir et concentrer le gaz d’atomes froids Une des premières étapes a consisté à vériﬁer le caractère ondulatoire de ces systèmes Le physicien japonais Fujio Shimizu a ainsi mené l’expérience des fentes de Young avec un gaz d’atomes froids C’est une expérience bien connue pour la lumière : lorsqu’on éclaire une plaque percée de deux fentes très proches, on obtient un phénomène d’interférence sur un écran placé derrière . En certains points de l’écran, les ondes de lumière sont en phase et les interférences sont « constructives », mais en d’autres les ondes sont déphasées et les interférences sont « destructives » On obtient ainsi une alternance de franges lumineuses et de franges sombres. Fujio Shimizu a adapté cette expérience à des atomes froids , qu’il a laissés tomber (comme pour une mesure de température) en mettant sur leur chemin des fentes de Young. Et il a obtenu une ﬁgure d’interférence sur une caméra placée quelques dizaines de centimètres en dessous

On peut exploiter cette idée pour créer des interféromètres atomiques d’une très grande sensibilité, capables de mesurer un déphasage induit par des perturbations très faibles On peut, par exemple, évaluer l’intensité de la

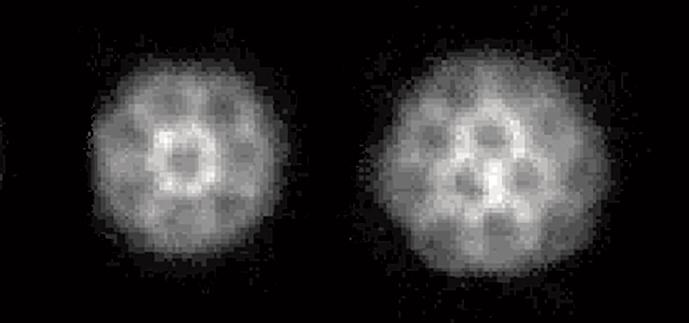
gravité terrestre avec une grande précision Des entreprises développent actuellement des dispositifs reposant sur des interféromètres de gaz d’atomes froids pour estimer localement l’accélération de pesanteur. Les objectifs vont de la prospection du sous-sol à la détection anticipée des séismes. Un autre exemple est celui des horloges atomiques, qui sont constituées d’un gaz d’atomes que l’on excite avec un laser On atteint désormais avec ces horloges une précision relative meilleure que 10 – 18 Avec une telle horloge qui utilise un nuage d’atomes froids de quelques centaines de micromètres de hauteur, Jun Ye, de l’université du Colorado à Boulder, est capable d’observer une prédiction de la relativité générale d’Einstein : le temps s’écoule plus lentement quand on se rapproche d’une source de gravitation, par exemple quand on passe d’une zone en altitude à un endroit situé au niveau de la mer. L’équipe de Jun Ye a réussi à détecter cette diﬀérence dans l’écoulement du temps entre le bas et le haut de son gaz d’atomes froids, distants de moins d’un millimètre !

Avec les gaz d’atomes froids, on peut tester une autre prédiction d’Einstein… En eﬀet, il faut encore une fois remonter en 1924 ! Cette année-là, un jeune physicien indien, Satyendra Nath Bose, a découvert une nouvelle méthode pour dénombrer les états possibles dans un gaz de photons. Sa technique lui permettait notamment de retrouver de façon élégante les résultats de Planck sur le corps noir Mais il n’arrivait pas à faire publier son article et a fini par l’envoyer à Albert Einstein Ce dernier, enthousiaste, a traduit l’article et l’a fait publier dans une revue prestigieuse Il ne s’est pas arrêté là Il a généralisé la méthode de Bose à des gaz d’atomes.

L’approche développée par Einstein s’applique à toutes les particules ayant un spin entier ( on parle d’ailleurs de « bosons » en l’honneur de Bose), ce qui est le cas de nombreux isotopes des atomes existants Elle prédit un phénomène étonnant : quand on refroidit

BIBLIOGRAPHIE

J. Dalibard, Piéger les atomes, CNRS Éditions, 2025.

I. Bloch et al., Quantum simulations with ultracold quantum gases, Nature Physics, 2012.

K. W. Madison et al., Vortex formation in a stirred Bose-Einstein condensate, Physical Review Letters, 2000.

J. Dalibard et C. CohenTannoudji, Laser cooling below the Doppler limit by polarization gradients : simple theoretical models, Journal of the Optical Society of America B, 1989.

suﬃsamment un gaz de bosons, il subit une transition de phase dans laquelle une fraction des atomes voient leur onde de de Broglie se mettre en phase avec celle de leurs voisins. On parle de « condensation de Bose-Einstein » Les premiers condensats ont été observés en 1995 avec des gaz d’atomes de sodium et de rubidium. Ces systèmes ont de nombreuses propriétés fascinantes

Par exemple ?

Avec mon équipe, nous avons regardé ce qui se passe quand on met un condensat en rotation. Pour cela, on manipule (encore) un laser qui sert d’agitateur Mais ce qui se passe est très différent d’une tasse de café où la vitesse croît linéairement avec la distance au centre Dans le condensat, on s’attend à ce que se forment des tourbillons quantiques Chaque tourbillon est un microcyclone, avec une densité centrale très faible associée à une vitesse très élevée proche du centre et qui diminue quand on s’en écarte Après plusieurs tentatives, nous avons finalement réussi à produire ces tourbillons, dont les propriétés sont une preuve que nos systèmes sont bien des condensats de Bose - Einstein (voir la figure ci-contre).

Autre domaine d’application qui gagne en importance : les simulateurs quantiques. Comment les gaz d’atomes froids interviennent-ils dans de tels systèmes ? Quand on cherche à modéliser de manière quantitative un système qui contient N particules qui interagissent et ont un comportement quantique, on a rapidement un problème Au-delà de quelques dizaines de particules, les calculs deviennent vite trop diﬃciles, même avec des supercalculateurs Au début des années 1980, Richard Feynman a proposé une solution pour contourner le problème Au lieu de faire le calcul, il faudrait simuler le système Et quoi de mieux qu’un système quantique pour en simuler un autre ? Et c’est là que les gaz d’atomes froids entrent en jeu Par exemple, si on s’intéresse au comportement des électrons dans un cristal pour comprendre les propriétés électriques ou magnétiques du matériau, on peut simuler ce dernier en remplaçant les électrons par les atomes de notre gaz froid On utilise des lasers pour créer un potentiel (les collines et les vallées) qui modélise celui dans lequel baignent les électrons (voir la ﬁgure page ci-contre, en bas). On mesure ensuite les propriétés du gaz et, en ajustant les paramètres, il est possible de tester les modèles qui décrivent le matériau initial Mon équipe et moi travaillons activement sur ces dispositifs, car les gaz d’atomes froids sont un outil précieux pour reproduire et émuler une grande variété de systèmes physiques n Propos recueillis par Sean Bailly

IL Y A 3 MILLIONS D’ANNÉES

Des humains en Asie ?

Un site du piémont himalayen révèle qu’il y a quelque 3 millions d’années, des hominines sont passés d’Afrique en Asie. S’agissait-il déjà d’humains ?

चं

डीगढ – c’est - à - dire Chandigarh en hindi –, est la capitale du Pendjab et du Haryana En 2009, quatre spécialistes de la préhistoire indienne, Claire Gaillard , du Muséum national d’histoire naturelle (MNHN), Mukesh Singh, qui y ﬁt sa thèse en préhistoire, l’une de nous (Anne Dambricourt-Malassé , paléoanthropologue au CNRS), et un étudiant, Manjil Hazarika, se sont rejoints près de cette grande agglomération Leur excursion n’avait pas pour but d’admirer l’architecture moderniste de cette ville nouvelle, mondialement connue, imaginée dans les années 1950 par Le Corbusier (18871965). Non, les chercheurs étaient attirés par l’anticlinal de Chandigarh, situé au nord de la ville près du village de Masol, parce que, revenu après leur première visite en 2008, Mukesh y était tombé sur un chopper c’est-à-dire un galet que des mains avaient fracturé et aﬀûté sur un bord – bref, ce que les préhistoriens francophones nomment un « galet aménagé ». Expliquons Les anticlinaux intéressent les paléontologues, car la compression tectonique

L’ESSENTIEL

> À Masol, au pied de l’Himalaya, des préhistoriens ont découvert des galets taillés et des marques de découpes sur de très vieux ossements.

> La géologie et le géomagnétisme locaux

conduisent à la conclusion qu’ils datent de presque 3 millions d’années.

> S’agissait-il d’humains ou d’une forme hominine proche ?

LES AUTEURS

ANNE DAMBRICOURTMALASSÉ paléoanthropologue (CNRS, Institut de paléontologie humaine et Muséum national d’histoire naturelle)

FRANÇOIS SAVATIER journaliste à Pour la Science

Il y a 3 millions d’années, le long d’une rivière sortant de l’Himalaya, des mains ont fracturé et affûté des galets pour mieux exploiter les carcasses d’animaux noyés par une crue. Des mains humaines ?

des strates géologiques qui a produit ces plissements convexes fait remonter des couches profondes (voir la ﬁgure ci-dessous) Quand ces strates sont fossilifères, leur érosion par les éléments met en surface des témoins de la vie du passé lointain, qui, sinon, resteraient des centaines voire des milliers de mètres en profondeur. Résultat : sur l’anticlinal érodé de Chandigarh, la petite équipe a trouvé les fossiles qu’elle était venue chercher. Sur une cinquantaine de mètres carrés, elle est tombée sur des choppers dispersés au milieu de vestiges osseux d’animaux morts il y a très longtemps Toutefois, les chercheurs ont découvert bien davantage, car, alors que la collecte des vestiges commençait à peine, Manjil Hazarika s’écria : « Traces de découpe ! »

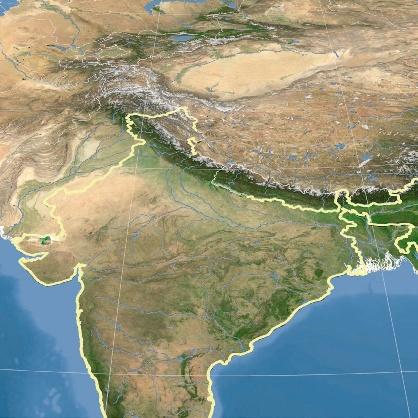
Chandigarh ouvre une fenêtre sur un passé vieux de plus de 2,6

millions d’années £

Le gisement paléontologique de Masol résulte du froncement de la plaque indienne glissant sous l’Himalaya à grande vitesse (4 à 5 centimètres par an). L’érosion due à la mousson a transformé ce froncement – on parle d’« anticlinal » –en deux vallées séparées par un dôme dans lequel se trouve la zone archéologique. Cette conﬁguration est une chance, car, exposant les strates de l’anticlinal, elle a grandement facilité la datation du site.

A priori, la découverte de marques de tranchants sur les restes d’une vieille carcasse peut sembler anodine Après tout, un tiers des Indiens actuels mangent de la viande, de sorte que certains de leurs ancêtres vivant sous les Gupta (fin du IIIe siècle – milieu du VIe siècle) ou sous les Moghols (1526-1858), ont peutêtre équarri une carcasse dans les collines de Chandigarh ? L’équipe, toutefois, savait cela très improbable tant l’os trouvé était minéralisé Et, du reste, il avait été ramassé au milieu d’une quarantaine d’autres fossiles, ceux d’animaux morts depuis très longtemps à l’évidence En fait, le plus fascinant n’était pas le fossile en lui-même, mais son âge, car l’anticlinal de Chandigarh ouvre une fenêtre sur un passé vieux de plus de… 2,6 millions d’années ! Situé dans les Siwaliks, des collines étroites coincées entre les piémonts himalayens vers le nord et la grande plaine indusienne vers le sud, cet anticlinal intéresse particulièrement les paléontologues à cause de l’immense gisement de fossiles datant de la fin du Pliocène (3,6 millions à 2,6 millions d’années ) qu’il contient le long de sa bordure nord : la zone Quranwala (voir la figure page ci-contre) C’est donc pour s’y rendre qu’en 2009 l’équipe a remonté le Patiali Rao, un torrent saisonnier passant au milieu du village de Masol . Elle espérait découvrir d’autres de ces vestiges culturels que sont les galets aménagés, mais

Masol

Himalaya

Inde

aussi – espoir fou – des fossiles de ceux qui les ont taillés. Les galets aménagés, en eﬀet, ont avant tout l’apparence de pierres cassées, de sorte que même si leur « aménagement » ne laisse guère de doute au spécialiste, ils constituent des preuves de présence moins fortes que les fossiles d’hominines

En ce jour de 2009, aucun fossile de… tailleur ne fut trouvé, mais avec cette sortie, les chercheurs avaient tout de même rapporté une preuve indiscutable que des mains avaient taillé des outils tranchants dans la zone Quranwala il y avait plus de 2,6 millions d’années La découverte était sensationnelle !

En effet, après les années 1970, à force de ne presque rien trouver en Asie, les préhistoriens y ont largement abandonné la quête de vestiges de plus de 2 millions d’années pour aller les chercher en Afrique. Or voilà qu’une scène de boucherie apparaissait en Inde, avec ses os marqués et ses outils de découpe façonnés à la main ; plus impressionnant encore, du moins pour les chercheurs, elle datait d’avant la fin du Pléistocène, cette période géologique s’étendant de 2,588 millions d’années à 11 700 avant le présent, définie, rappelons-le, dans le but de marquer l’apparition du genre Homo. Alors, oui, c’était sensationnel, mais l’accueil des collègues indiens fut prudent, car, en Inde, les plus anciens outils remontent à 1,7 million d’années… seulement ; et le plus ancien fossile humain du sous-continent – le crâne de l’homme de la Narmada, découvert en Inde centrale – n’a guère que… 200 000 ans Dès lors, la découverte semblait à la limite du croyable, de sorte que les chercheurs ont immédiatement entrepris de renforcer les évidences en multipliant les données Le programme « Siwaliks » fut lancé afin de rassembler dans une grande équipe pluridisciplinaire les nombreuses compétences nécessaires afin de mener une étude systématique des 80 hectares du site de Masol et des vestiges de la zone Quranwala. En plus de dix ans de travail, les membres du projet ont analysé une énorme moisson de données, puis publié leurs résultats par le moyen d’une dizaine d’articles dans la revue de l’Académie des sciences Palévol et, récemment dans la revue L’Anthropologie

UN INTÉRESSANT BESTIAIRE

Les collectes ont ainsi rassemblé plus de 1 600 fossiles, ce qui a révélé un assemblage faunique comprenant deux éléphantidés , le stégodon et l’éléphant, le Sivatherium (un girafﬁdé), l’Hipparion (un équidé), des bovidés, des cervidés, des sangliers, des tortues terrestres géantes, l’hippopotame et un proche parent Merycopotamus ; les carnivores, telles la hyène et la panthère, sont rares ; le milieu aquatique est représenté par des tortues , des crocodiles et des gavials. Trouvaille remarquable,

Anne - Marie Moigne , archéozoologue au MNHN, a identiﬁé les plus anciens fossiles de chevaux (Equus) hors d’Amérique Ces carcasses , manifestement , intéressaient les charognards de Masol, puisque sur les 13 localités inventoriées, ce ne sont pas moins de 330 outils qui ont été ramassés, ainsi que 4 ossements portant des traces de découpe, dont un portant d’évidentes marques de fracture par percussion visant à la consommation de moelle Le fossile qu’avait brandi Manjil Hazarika en 2009 est un fût (la partie centrale d’un os long) tibial de bovidé minéralisé, dont la cavité médullaire est tapissée de cristaux de calcite À les examiner de près, les incisions qu’il portait l’étaient aussi Elles résultaient incontestablement du contact sur l’os d’un tranchant lithique alors que le cadavre était encore frais Manifestement, l’auteur des gestes était un familier de l’anatomie, puisqu’il avait su trouver les insertions des tendons et les sectionner pour libérer la masse de viande recherchée (voir la photo page 60). Tout indiquait que les outils en matériau dur capable d’entailler l’os frais consistaient en galets de quartzite aménagés pour obtenir des arêtes coupantes

LES FOSSILES DES PLUS ANCIENS CHEVAUX HORS D’AMÉRIQUE

Anne Dambricourt-Malassé, qui s’est spécialisée dans l’étude de la boucherie préhistorique, a étudié ces traces et celles des trois autres ossements marqués avec Anne-Marie Moigne Les deux préhistoriennes ont pu examiner les os au microscope numérique 3D et faire effectuer des microtomographies par rayons X . Pour confirmer les interprétations, elles ont aussi taillé des choppers et des éclats à partir de galets ramassés à Masol, puis mené des expériences de découpe sur des os frais, notamment un pied de cochon Il s’avère que dans les deux cas, on observe les mêmes marques fines, rectilignes, comportant des barbelures typiques, ordonnées d’après les zones d’insertion de tendons qu’il s’agissait de détacher pour atteindre l’os afin de le briser pour accéder enfin à la moelle (voir pages 60 et 61) À toute époque, les Préhistoriques ont en effet raffolé de cette succulente et « substantifique » moelle riche en graisse ultraénergétique. Manifestement , c’était déjà le cas il y a plus de 2,6 millions d’années, et pour ne rien manquer on savait déjà se tailler les outils nécessaires. Collectés à côté des fossiles, ces derniers consistaient pour leur part en galets d’abord fendus en deux puis retouchés sur un bord ou en quelques éclats , percuteurs , nucléus et enclumes. Tous étaient dans un très bon état de conservation, leurs arêtes encore vives et tranchantes. Or les pluies de mousson et la gravitation ont tendance à entraîner rapidement les pierres dans les torrents où

Épaisseur des strates (en mètres)

Galets

–2,95 millions d’années

Os avec traces de découpe

Galets aménagés

De très nombreuses strates érodées composent l’anticlinal de Masol. Le sol en surface correspond en réalité à une longue accumulation de sédiments souvent ﬂuviatiles. Au bout de 600 000 ans, la tectonique a ﬁni par provoquer son plissement et l’émergence en surface des plus anciennes strates de cette pile sédimentaire. Par chance, elles étaient fossilifères !

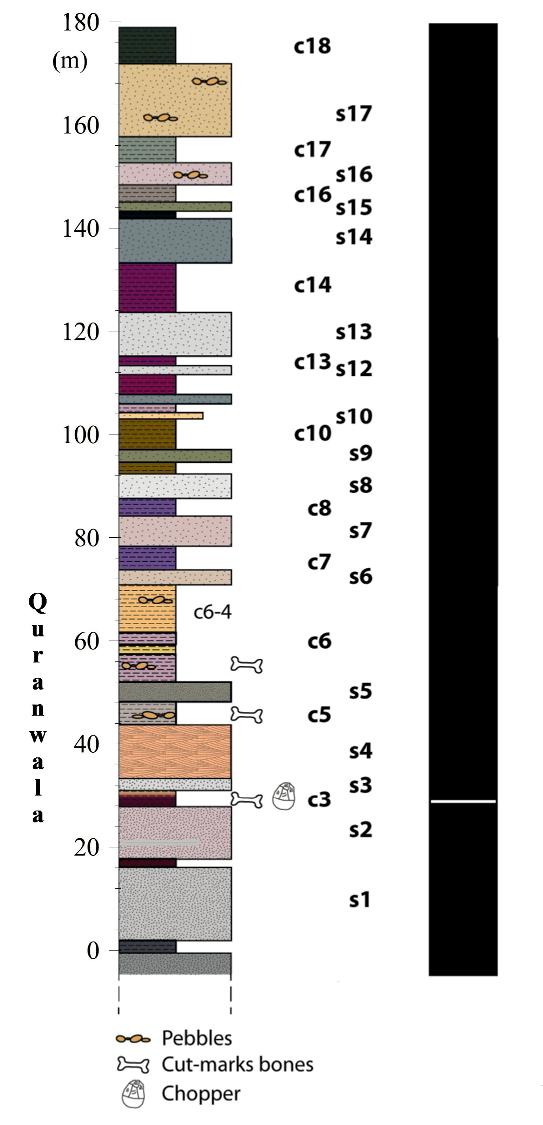
Ci-dessous, une chercheuse est en train de prospecter la zone Quranwala. À droite, une strate fossilifère dans laquelle l’intercalation d’un lit de gravier signale qu’une ancienne crue turbulente a déplacé et rassemblé des galets provenant de l’Himalaya. C’est après de telles crues et en taillant des outils dans les galets que les hominines sont venus exploiter une carcasse de gros herbivore dans la zone Quranwala. Sur la page de droite, le galet trouvé in situ, une fois en main et alors qu’il était encore pris dans sa gangue de limon (tout à fait à droite).

ils s’émoussent en roulant Cela signiﬁe que les galets aménagés de Masol n’ont pas été déplacés, mais plutôt dégagés récemment des limons par la pluie. Depuis quelles strates ? La réponse est venue d’un galet aménagé dont, en 2017, Mukesh Singh a eu la bonne fortune de remarquer l’extrémité que l’érosion commençait à faire ressortir des limons , alors qu’en 2015, il était encore complètement invisible (voir photos page ci-contre).

L’APPUI PRÉCIEUX DE LA GÉOCHRONOLOGIE

Cette trouvaille a suscité l’enthousiasme, car la strate contenant le galet se trouvait tout en bas de la pile sédimentaire de la zone Quranwala, ce qui suggérait qu’elle datait probablement d’au-delà de 2,8 millions d’années… Situer un site correctement dans le temps implique de réunir le plus grand nombre possible de dates. La tâche, souvent, n’est pas facile, mais, dans cette zone, elle s’est avérée relativement aisée, car la stratigraphie et la morphologie du terrain parlaient d’ellesmêmes. L’endroit est une sorte de haute combe de forme ovale où des couches géologiques plissées formaient autrefois comme une voûte que les fortes averses de la mousson ont fini par défaire en grande partie tout en creusant deux ravins de part et d’autre du pli tectonique (voir la figure page 56). C’est au fond de ces ravins qu’apparaissent les strates fossilifères sur une épaisseur de 50 mètres, ainsi qu’au sommet du dôme central, où il n’en reste qu’une épaisseur de 5 mètres correspondant à la base de la séquence fossilifère de Quranwala (voir la figure page 57). Les fossiles et les os marqués se trouvent uniquement dans ces strates paléontologiques Pour le géomorphologue

Baldev Karir et son ancien élève Surinder Pal, de l’université du Pendjab à Chandigarh, qui sont familiers des prospections dans l’anticlinal, aucun doute n’était possible : ces fossiles se trouvaient bien sur le lieu de leur extraction naturelle, de sorte que le chopper trouvé sur place avait donc la même ancienneté que lui Il restait à déterminer cet âge de façon sûre. Pour cela, une méthode s’imposait : localiser l’inversion du champ magnétique terrestre dite « de Gauss-Matuyama », datée de 2,588 millions d’années. Dans les années 1990, des géochronologues indiens l’avaient déjà repérée le long du Patiali Rao, à une hauteur qui conﬁrmait que la zone Quranwala se trouve nettement sous cette inversion Toutefois, son emplacement restait imprécis Des échantillons furent donc prélevés dans les limons intercalés entre les bancs de sable en voie de transformation en grès constituant la pile sédimentaire locale, en allant aussi haut que possible, c’est-à-dire à 150 mètres au-dessus de la base de Quranwala Jusque-là, les mesures n’indiquent aucun changement d’orientation du champ magnétique, de sorte que l’inversion Gauss-Matuyama ne pouvait que se trouver plus haut encore dans la stratigraphie. En clair : la couche où se trouvait le chopper est bien plus ancienne que l’inversion de Gauss-Matuyama. Mais de combien ? C’est la découverte inattendue de Cécile ChaponSao, géochronologue au CNRS, qui a apporté la réponse : ses mesures ont révélé l’enregistrement magnétique d’une excursion, c’est-à-dire d’une brève variation du champ magnétique terrestre. Cette excursion se trouvait à la base de la zone Quranwala De quelle excursion située à la ﬁn du Pliocène pouvait-il s’agir ? Ce sont les évaluations des vitesses de sédimentation qui allaient permettre de le déterminer :

après les avoir soigneusement prises en considération les géologues de l’équipe de terrain

Alina Tudryn, Julien Gargani de l’université Paris-Saclay, et Salah Abdessadok, du Muséum national d’histoire naturelle, sont parvenus à la conclusion qu’il ne pouvait s’agir que de l’excursion Huahine Or les géochronologues s’accordent sur son âge : 2,95 millions d’années. Les repas de charognards de Masol ont donc eu lieu il y a quelque 3 millions d’années…

Jusqu’à présent, n’ont été évoqués ici que des « mains » de « charognards » , mais rien n’a été avancé sur leurs propriétaires d’il y a quelque 3 millions d’années. Cette date est si ancienne, qu’il est diﬃcile d’avancer ou d’exclure qu’il s’agissait d’humains Expliquons pourquoi : nous avons tous appris que le genre Homo est apparu en Afrique Mais où et quand ? Ce genre appartient à la sous-famille Homininae – hominines en français –, des primates bipèdes exclusifs au sol (mais encore arboricoles) portant leur tête au-dessus du bassin, avec lequel elle est reliée par une colonne vertébrale verticale

La lignée hominine est apparue bien après la divergence il y a quelque 8 millions d’années, d’avec Pan, le genre dont fait partie notre plus proche cousin non humain, le chimpanzé, dont la lignée est pour sa part restée quadrupède. Les hominines comprennent, entre autres, les genres Australopithecus (4,2-1,9 millions d’années), Kenyanthropus (3,5-3,3 millions

d’années) et Paranthropus (2,9-1,2 millions d’années). Longtemps, les spécialistes ont cru que ce qui distinguait les humains des autres hominines était leur capacité à façonner des outils, mais ce critère d’humanité, séduisant parce que simple , s’est révélé insuffisant. Depuis 2015, en eﬀet, la plus ancienne attestation de façonnage manuel d’outils en pierre date de 3,3 millions d’années, et provient du Kenya Dans ce pays d’Afrique de l’Est, à Lomekwi 3 sur les rives occidentales du lac Turkana, Sonia Harmand, du CNRS et des collègues de l’université de Stony Brook, à New York, ont montré que des mains fabriquaient déjà des éclats tranchants Deux méthodes étaient utilisées pour les obtenir : les frapper contre de grosses pierres (percussion unipolaire sur enclume), ou les maintenir sur une grosse pierre aﬁn de les frapper avec un « percuteur » (percussion bipolaire sur enclume). On ignore qui a « taillé » à Lomekwi, mais le Kenyanthrope vivait alors sur les rives du lac Turkana La culture lithique de Lomekwi, la plus ancienne connue, est nommée le Lomekwien

LE PLUS ANCIEN OUTIL DE PIERRE PROVIENT DU KENYA

Puis, en 2023, une autre localité kényane, Nyayanga, sur la rive orientale du lac Victoria, a livré – au milieu de carcasses aux os portant des traces de découpe datées d’environ 2,8 millions d’années (2,58 à 3,03 millions d’années) – des pierres taillées par une autre technique : l’Oldowayen Celle-ci permet en particulier de débiter des éclats dans un galet nommé « nucléus » Il semble qu’un autre hominine que le Kenyanthrope l’ait pratiquée à Nyayanga : l’équipe de Thomas Plummer, de l’université de New York, y a ramassé dans

des niveaux sédimentaires proches un fragment de grosse molaire inférieure et une énorme molaire supérieure très usée Elles ne sont pas humaines, mais ont appartenu à des paranthropes Or Paranthropus boisei, l’une des espèces de paranthrope, a laissé son crâne dans le nord du Kenya L’interprétation la plus parcimonieuse de ces constatations est d’attribuer les outils de Nyayanga à cet hominine

Or l’Oldowayen, la technique de taille de Nyayanga, est connu depuis les années 1960. À l’époque, les préhistoriens l’ont pensé inventé par Homo habilis, la plus vieille espèce humaine découverte par Louis et Mary Leakey dans les gorges de l’Olduvaï, en Tanzanie Soulignons que l’Oldowayen est diﬀérent du Lomekwien parce qu’il s’agit d’une technique de taille à mains libres : une main tient une pierre, que vient frapper une autre pierre, le percuteur, tenu dans l’autre main L’objectif poursuivi par les tailleurs oldowayens est soit de produire des galets retouchés sur un bord pour les rendre coupants, soit de débiter des éclats. À l’origine, l’Oldowayen est donc la taille datée d’environ 1,8 million d’années associée à Homo habilis en 1962, date à laquelle elle était la plus ancienne technique de taille connue. Depuis, d’un site oldowayen à l’autre, l’âge de cette technique de taille n’a cessé de remonter le temps, jusqu’à atteindre en 2023 l’âge impressionnant de 2,8 millions d’années à Nyayanga, où le seul hominine connu est Paranthropus boisei

OÙ PLACER LA CULTURE LITHIQUE DE LA ZONE QURANWALA ?

Tout cela place donc les galets aménagés de Masol de presque 3 millions d’années dans un contexte paléoanthropologique impressionnant

Les chercheuses ont taillé des choppers et des éclats à partir de galets ramassés à Masol, et mené des expériences de découpe sur des os frais. Dans les deux cas, on observe des marques ﬁnes, rectilignes, comportant des barbelures typiques.

par son ancienneté Cela oblige aussi à la réflexion avant d’assigner un genre taxonomique aux artisans de Masol Dominique Cauche, de l’Institut de paléontologie humaine, à Paris, qui a collaboré à l’extraction du galet fendu engoncé dans sa strate à Masol, a démontré qu’il s’agit d’un chopper obtenu par percussion bipolaire sur enclume. Pour lui, le but des tailleurs de Masol n’était pas la production d’éclats : le bord tranchant d’un galet fendu en deux suﬃsait à leur activité de boucherie, consistant à détacher de la viande, mais aussi à briser les os à moelle En ce sens, leur taille sur enclume fait bien plus penser au Lomekwien qu’à l’Oldowayen

La technique de taille masolienne une fois située, il faut pour avancer vers une détermination des auteurs de Masol se demander quel est le plus ancien fossile considéré comme humain ? À ce jour, il s’agit de LD 350-1, une demi-mandibule de 2,8 millions d’années découverte à Ledi Geraru, en Éthiopie Elle atteste une avancée de la face inférieure vers l’avant – ce que l’on nomme « prognathisme sous-nasal » – plutôt caractéristique des australopithèques, mais la dernière molaire est partiellement cachée par la partie verticale restante de la branche qui l’attache au crâne, ce qui constitue un trait signiﬁcatif de l’évolution vers la forme humaine. Pour cette raison, nombre de paléoanthropologues se sont laissé convaincre que LD 350-1 est humain, même si le fossile garde des traits australopithèques. Dès lors, faisons de LD 350-1 un marqueur, et acceptons cette demi-mandibule comme le plus ancien relevant du genre Homo Il y a 2,8 millions d’années, ce dernier aurait donc été déjà assez caractérisé Or une espèce n’apparaît pas en un jour, mais au cours du temps : l’examen des calculs menés à cet égard par les paléontologues et par les paléogénéticiens suggère que les durées de spéciations des primates africains – c’est-à-dire les durées d’émergence de leurs espèces – excèdent toutes 1 demi-million d’années. Dès lors, se dit-on, l’hominisation a sans doute commencé nettement avant 3 millions d’années…

PAR OÙ SONT PASSÉS LES HOMININES DE MASOL ?

Toutefois, étant donné que les hominines de plus de 3 millions d’années sont tous africains, le point de vue le plus parcimonieux qu’impose la datation des outils de Masol est de considérer qu’une dispersion hors d’Afrique de cette sous-famille s’est produite bien plus tôt que les préhistoriens n’étaient préparés à le penser jusqu’à présent Dès lors, se demande-t-on, par où sont passés les ancêtres des hominines de Masol en venant d’Afrique ? La réponse passe par l’explication de deux faits majeurs : la présence du cheval à Masol et l’occurrence d’inondations catastrophiques dans la plaine

sous - himalayenne à partir de 2,95 millions d’années. S’agissant du cheval, rappelons pour commencer que Equus, son genre, est apparu en Amérique du Nord pendant le Pliocène il y a 4 à 4,5 millions d’années Sa dispersion en Asie n’étant dès lors possible que si le détroit de Béring était hors d’eau, cela implique la survenue d’un épisode glaciaire. Cette déduction surprend puisque la température moyenne planétaire de toute la période entourant 3 millions d’années excédait de 2 à 3 degrés l’actuelle Cependant, les sédiments d’un lac du nord-est sibérien donnent l’explication : ils ont enregistré un pic glaciaire entre 3,043 et 3,025 millions d’années , la fenêtre climatique par laquelle des chevaux ont gagné l’Asie. Second fait majeur : juste après l’ouverture de cette fenêtre, entre 2,97 et 2,96 millions d’années, un bref mais important réchauﬀement climatique s’est produit, qui a ramené la mousson loin vers le nord, typiquement jusqu’à la latitude du Levant Cela implique donc qu’un même climat de type tropical a recouvert alors l’Afrique du Nord-Est, le Levant, les plateaux iraniens, le bassin du Séistan (Afghanistan) et le bassin de l’Indus Au sein de cette ceinture écosystémique commençant sur le lac Tchad et s’étendant jusqu’à la plaine indienne, de très nombreux cours d’eau ont créé de vastes écosystèmes pleins de réseaux hydrographiques favorables à la vie des herbivores, et, partant, à l’arrivée d’hominines les suivant à la recherche de carcasses. En particulier, pendant la saison des pluies, ils pouvaient compter sur celles des animaux noyés par les inondations, ce qui fut le cas à Masol selon l’équipe rassemblée autour d’Anne Dambricourt-Malassé.

Ainsi, Masol se serait trouvé au sein des couloirs de circulation formés de l’Afrique à l’Asie peu après 3 millions d’années, lesquels – et cela a été aperçu par les paléontologues – ont été parcourus par de nombreuses grandes espèces herbivores, donc aussi par leurs charognards,

Pour vériﬁer que ces marques de découpe sur l’un des fossiles de Masol résultent bien de l’application d’une arête de quartzite, les chercheuses qui les ont étudiées les ont imagées de très près, constatant leur répétition au même endroit aﬁn de détacher un tendon.

dont – c’est l’hypothèse défendue ici – des hominines. Toute la logique géoclimatique expliquant les découvertes sur le site de Masol tient ainsi dans un « mouchoir de poche paléoclimatique » de 80 000 ans seulement, qui va de 3,04 à 2,96 millions d’années. Résumons cet épisode : un pic glaciaire rapidement suivi par un pic de chaleur a provoqué la formation puis la fonte des glaciers himalayens, formés il y a environ 3 millions d’années, et des inondations catastrophiques dans la zone Quranwala, avant une nouvelle glaciation annonçant le Pléistocène. À l’appui de ce scénario, il faut noter que ce gisement de fossiles illustre un phénomène qui a toujours cours dans l’Himalaya : lors des moussons, les rivières qui arrivent des hautes vallées grossissent énormément, arrachent les

La logique géoclimatique expliquant la découverte tient dans un épisode de 80 000 ans £

terrasses avec leurs galets et provoquent de grandes inondations dans la plaine, si brusques et si violentes qu’elles emportent et noient des herbivores en train de pâturer sur leurs rives Les carcasses s’échouent sur les berges et les carnivores viennent les consommer Voilà de quoi convaincre les préhistoriens indiens, d’autant plus dubitatifs que la ﬁn du Pliocène se distingue par ses régimes hydrauliques calmes, entraînant le dépôt très lent des particules de vase en suspension dans les eaux Or l’une des

découvertes de Masol montre qu’à l’époque de la formation de la zone Quranwala, juste après la fin du Pliocène, le régime des eaux était bien plus violent. À Masol, les chercheurs ont observé des amas de galets dans les limons de la zone Quranwala, et seulement dans ces limons-là, pour la même raison qu’il y a de très nombreux fossiles de carcasses désarticulées dans ces mêmes sédiments Ce sont des inondations catastrophiques qui les ont apportés depuis les terrasses himalayennes lors du pic de réchauffement climatique provoquant la fonte des énormes glaciers constitués pendant le pic glaciaire. Les hominines du piémont himalayen se seraient dispersés depuis des écosystèmes africains similaires très irrigués et régulièrement inondés Comme on dispose de très peu de fossiles pour les identifier, la paléoanthropologue a travaillé à partir des souches hominines les plus proches des systèmes hydrographiques africains orientés vers le nord. Cela converge avec l’hypothèse de Michel Brunet, du Collège de France, selon qui Homo aurait émergé dans ces environnements de forêts - galeries bordant des rivières, telles celles qui se déversent dans l’immense paléo-lac Tchad Comme ces écosystèmes africains auraient été connectés à des écosystèmes comparables jusqu’au Levant, des hominines s’y seraient introduits de proche en proche en suivant les faunes , qui, elles aussi, se sont répandues d’Afrique en Asie vers 3 millions d’années

HOMO OU HOMININAE ?

Alors qui à Masol ? Un Homo ou un autre hominine ? Tout dépend de la définition paléontologique d’Homo. Les définitions qui s’appliquent aujourd’hui à des fossiles de 100 000 ans d’époque néandertalienne, voire à ceux de 1,5 million d’années d’époque erectus, ne sont pas les mêmes Elles ne s’appliquent certainement pas à des spécimens plus anciens que Ledi Geraru (LD 350-1) et ne permettent pas de remonter jusqu’à il y a 3 millions d’années Si l’on pouvait rencontrer aujourd’hui des membres d’Australopithecus, de Paranthropus et d’Homo archaïques de cette période (à supposer leur existence), leurs différences anatomiques extérieures pourraient sans doute sembler minces… de sorte qu’il peut se révéler à ce stade difficile de se forger une préférence entre Homo et d’autres hominines, s’agissant des espèces pionnières en Asie, notamment de celle qui a œuvré à Masol. Anne Dambricourt-Malassé rappelle que la spéciation d’une espèce africaine de primate demande au moins 500 000 ans, ce qui place Masol dans le demi-million d’années qui précède LD 350-1, le plus ancien fossile humain admis. En outre, elle souligne que, étant donné à quel point la fossilisation est un processus exceptionnel , il faut , pour en obtenir des

spécimens, qu’une population soit déjà assez dense et assez dispersée. Dès lors, pour elle, c’est clair, des formes archaïques d’Homo ont pu exister nettement avant 3 millions d’années, à temps pour se retrouver à Masol et elle préfère ainsi l’hypothèse selon laquelle il s’agirait d’humains Force est de constater, en eﬀet, que les hominines de Masol étaient des pionniers en Eurasie, qui, comme tous les pionniers,

Les hominines de Masol étaient des pionniers en Eurasie, susceptibles de s’adapter à l’inconnu £

BIBLIOGRAPHIE

A. Dambricourt-Malassé et al., Masol (India, Punjab) : horses (Equus) and hominins in the sub-Himalayan ﬂoodplain as early as 2,95 Ma, L’Anthropologie, 2025.

C. Chapon-Sao et al., Magnetostratigraphy of the Pliocene Masol Formation, Siwalik Frontal Range, India : Implications for the age of intentional cut-marked fossil bones, Journal of Asian Earth Sciences, 2024.

A. Dambricourt-Malassé et D. Cauche, Des traces de boucherie aux outils lithiques de Masol (Pliocène supérieur, Inde du Nord). Une approche psychomotrice de l’origine et de l’identité des hominiens, L’Anthropologie, 2022.

D. Cauche et al., Pre-Quaternary hominin settlements in Asia : archaeology, biolithostratigraphy and magnetostratigraphy evidences at Masol, Siwaliks, Northwestern India, L’Anthropologie, 2021.

étaient plus généralistes , dotés d’une plus grande plasticité cognitive, et davantage susceptibles, grâce à la créativité qui y est associée, de s’adapter à l’inconnu. Or, souligne-t-elle, la plasticité cognitive des hominines dépendait du dialogue entre le cerveau – centre de planification – et le cervelet – centre de contrôle de la posture et de la motricité, mais également intégré dans les réponses réfléchies Selon ses observations , Homo se caractérisait par un développement du dialogue cerveau-cervelet plus long et donc par des capacités cognitives plus réfléchies, plus inventives, moins dépendantes des modes de vie arboricoles et donc plus volontiers exploratrices de l’environnement Pour le dire autrement, les paranthropes de Nyayanga taillaient, certes, des outils pour pouvoir charogner plus efficacement , mais étaient arboricoles, vraisemblablement moins omnivores et plus dépendants d’une locomotion arboricole. Cela se voit, par exemple, à leurs énormes dents de mâchouilleurs de plantes coriaces. Plus graciles, comme le suggère déjà LD 350-1, les humains archaïques auraient aussi eu une appétence plus grande pour la viande et, surtout, pour la moelle, dont la consommation favorisait l’intensification énergétique du dialogue planification-contrôle, c’est-à-dire cerveau-cervelet. Selon nombre de résultats en neuroscience, ces échanges accrus entre les deux organes favorisaient aussi le développement langagier, l’attention, la mémoire de travail et la dextérité. Quoi qu’il en soit , il est clair que Masol illustre le phénomène récurrent de l’expansion hominine hors d’Afrique, et qu’il est une étape sur le chemin de l’Orient, lequel semble avoir été parcouru pour la première fois vers 3 millions d’années n

LA REVUE DES SCIENCES

DE LA VIE ET DE LA TERRE

DANS LES FORÊTS DE NOUVELLE-GUINÉE,

UN DANGER SE CACHE DANS

LES PLUMES DES OISEAUX !

SOUS NOS LATITUDES, C’EST UNE ÉTRANGE

SUBSTANCE GLUANTE QUI FAIT FANTASMER.

AUSSI DANS CE NUMÉRO : LES “PUCES D’EAU” ET LEURS

PARASITES, DES LOUPS

TRACÉS PAR LEUR ADN ET LES NOMS D’ESPÈCES LES PLUS FARFELUS !

n° 57 : septembre 2025

100 pages - 9,50 €

Espèces est une revue à comité de lecture associative et indépendante.

SOUTENEZ-NOUS

ABONNEZ-VOUS !

1 an 34 €

Inscrivez-vous sur notre site pour bénéﬁcier d’avantages exclusifs et consulter nos articles en ligne

Bathysphaera intacta and bathysphere, d’Else Bostelmann, peint en 1934

Wildlife Conservation Society.

Reproduit avec la permission des archives WCS.

L’AUTEUR

LOÏC MANGIN

rédacteur en chef adjoint à Pour la Science

CLE DRAGON DES MERS… FANTÔME

Une exposition rend hommage à deux siècles d’exploration des océans et à la fascination que les fonds marins ont exercée, et exercent encore, sur les artistes.

e fut une décennie décisive, marquée par la publication de trois ouvrages fondateurs : en 1861 La Mer, de Jules Michelet ; en 1866, Les Travailleurs de la mer, de Victor Hugo ; et en 1869, Vingt Mille Lieues sous les mers, de Jules Verne Ensemble, ils illustrent l’engouement qui a saisi à la ﬁn du XIXe siècle le grand public pour ce qui se passe sous la surface de la mer. Les artistes et les scientiﬁques ne sont pas en reste, et beaucoup ont entrepris de donner à voir le fond des océans Cette fascination, jamais démentie depuis, est au cœur de la nouvelle exposition des Franciscaines, à Deauville

On y découvre notamment comment des peintres, après avoir fréquenté assidûment les aquariums, dont beaucoup sont inaugurés à cette époque, ont eu le désir d’aller au plus près de leur nouveau sujet de prédilection. Mais comment peindre sous l’eau ?

Eugen Von Ransonnet-Villez, baron autrichien, conçoit en 1864, lors d’un séjour à Ceylan (aujourd’hui le Sri Lanka), une cloche de plongée équipée de hublots pour peindre au sec. Il utilise pour ce faire un papier verni de son invention qui résiste à l’humidité. Avec ses œuvres très réalistes, l’objectif est d’emmener les spectateurs sous l’eau et de leur faire admirer la beauté mais aussi le mystère qui entoure les fonds marins. Il rejoint en cela, et son style lui est comparable, l’école de Barbizon, dont les membres ont à cœur de travailler « en plein air et d’après nature », mais sur le plancher des vaches.

Au tournant du XXe siècle, le Britannique

Walter « Zarh » Pritchard choisira quant à

lui le scaphandre – les premiers sont fabriqués au milieu du XIXe siècle – pour rendre sensible les perspectives, les couleurs et les ambiances sous-marines perçues lors de ses plongées, au large de l’Écosse ou bien à Tahiti.

L’Américaine d’origine allemande Else Bostelmann a suivi un autre chemin. En 1929, elle rejoignit en tant qu’artiste l’expédition de William Beebe, aux Bermudes, financée par la National Geographic Society. Le naturaliste avait fait construire par l’ingénieur Otis Barton un submersible sphérique afin d’étudier la faune sous-marine : la bathysphère. Avec cet engin, suspendu à un câble, les records de plongée se succédèrent, jusqu’à ce 923 mètres, atteint le 15 août 1934. Mais le plus spectaculaire fut ce que les deux individus qui pouvaient prendre place dans l’habitacle observèrent. Ils purent pour la première fois contempler les innombrables créatures improbables qui peuplent les profondeurs. William Beebe les décrivait in situ à son assistante Gloria Hollister, restée sur le bateau, par la ligne téléphonique qui reliait la bathysphère à la surface, tandis qu’Else Bostelmann s’empressait de traduire les mots en esquisses, que, plus tard, le plongeur amenderait pour coller au plus près à la réalité (voir la reproduction, page ci-contre). Au total, l’artiste dessina plus de trois cents planches, dont beaucoup firent sensation lors de leur publication.

Les poissons que l’on distingue sur l’œuvre d’Else Bostelmann seraient des Bathysphaera intacta, ainsi nommés en l’honneur du submersible, intacta

signifiant « intouchable », et feraient, selon William Beebe, près de 2 mètres de longueur. Ils appartiendraient à la famille des Stomiidæ , ( dragonfish , en anglais, c’est-à-dire les « poissons dragons »). Cependant, ni cette espèce de poisson ni les quatre autres prétendument nouvelles décrites par l’explorateur n’ont été conﬁrmées depuis. Le dragon à écaille le plus long connu, un Opostomias micripnus, mesure seulement 55 centimètres… Sur une autre toile serait ﬁguré un Bathysidus pentagrammus, un poisson constellé de cinq lignes de points lumineux dans lequel l’ichtyologiste Carl Hubbs reconnaît à l’époque plutôt un cténophore, un organisme planctonique à l’allure de méduse.

En revanche, d’autres existent bel et bien, comme le Stomiidæ Photostomias guernei, la crevette Acanthephyra purpurea… Quoi qu’il en soit, Else Bostelmann et William Beebe furent bien les premiers à révéler l’existence de poissons luminescents.

Ensemble, les œuvres présentées à Deauville conﬁrment la beauté du monde du silence tout autant que sa vulnérabilité. Si seulement les mesures de protection pouvaient être à la hauteur de la fascination exercée… n

« Bleu profond. L’océan révélé », aux Franciscaines, à Deauville, jusqu’au 21 septembre 2025. lesfranciscaines.fr

L’auteur a publié : Pollock, Turner, Van Gogh, Vermeer et la science… (Belin, 2018)

Simulez

réels

Innovez plus vite.

Testez davantage votre design avant le prototypage.

Innovez mieux.

Analysez les prototypes virtuels et développez un prototype physique à partir du design le plus performant.

Innovez

grâce à la simulation multiphysique.

Basez vos choix de conception sur des résultats précis grâce à un logiciel qui vous permet d’étudier sans limitation de multiples eﬀets physiques en un seul modèle.