Behavioral Biomimicry & Defense Mechanisms

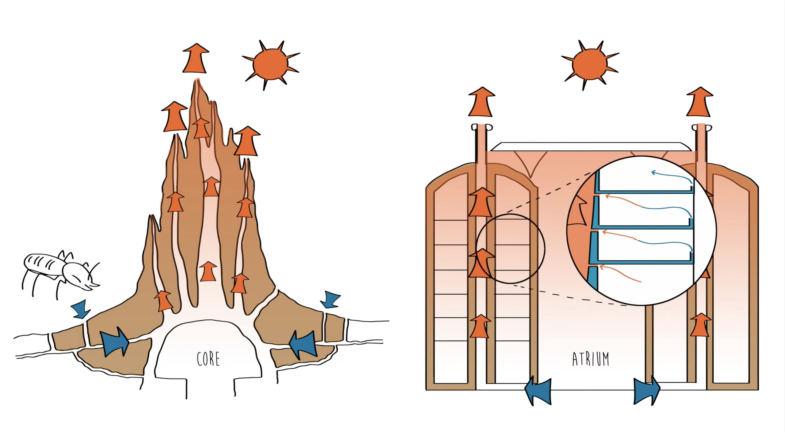
Animals similarly develop adaptive protection mechanicsontheirbodies,buttheyalsotendtoperform active behaviors to prolong their survival. A prime example of this is how termites build their dirt towers in a structure that promotes passive cooling and thermal regulation. A termite mound internally resembles the structure of a lung, it features inhalation opening from the sides where the cool air falls, spreads it through the smaller pathways on the interior, and releases the hot air through a wide chimney in the center with an exhalation opening at the top (Turner and Soar 2008).

3.2

Ecosystem Level Biomimicry - Urban Level

Biomimicry can be used as a regenerative process for the urban fabric, using organic methods that use the ecosystem as a model to solve urban problems. Architects have been exploring ecological concepts as design solutions for the past couple of decades, suggesting an artificial recreation and reincorporation of natural processes in the ecosystem, such as energy conversion, water treatment, nutrient recycling, and thermal and wind control.

The ecological system can be broken down into two parts, the biophysical structures in the ecosystem, the biotic and abiotic parts of an ecosystem and their patterns, and the processes and functions in the ecosystem that occur through the interactions within it, which serve the organisms that exist in the ecosystem.

The Lavasa Hill Project in Maharashtra, India is a case that has applied ecological methods of biomimicry at an ecosystem level to solve urban design issues sustainably. They took inspiration from the local monsoon ecosystems and simulated the organic functions to create design solutions that would boost aspects of the city that needed improvement: being water collection, solar gain, carbon sequestriation, water filtration, evapotransportation, and nitrogen and phosphorus cycling. This was achieved through many creative biomimetic technical designs, and “among the technical solutions applied were: rooflines designed to create wind turbulence to facilitate evaporation; green roofs to slow water flows; infiltration swales; massive revegetation using hydro-seeding; and dams to store rainwater,” (Blanco et al. 2021).

Mathematics in Art & Architecture

Geometry & Proportions

4.0 - History of Mathematics in Art & Architecture

4.1 - Human Proportions in Architecture

4.2 - Golden Ratio in Art & Architecture

History of Mathematics in Architecture 4.0

Historically, architecture was a branch of mathematics, and at various points in time, there was no distinction betweenthetwofieldsofstudy.Thepyramids,ziggurats, temples, stadia, and irrigation projects that we admire today were built by mathematicians in the ancient past. Architects had to be mathematicians in Classical Greece and Ancient Rome. Isidoros and Anthemius, two mathematics (geometry) professors, were chosen by Justinian the Byzantine emperor to design the Hagia Sophia, a structure that outperformed all buildings ever constructed. In the Islamic civilisation, this practice was even more prevalent. Before western mathematicians provided a comprehensive categorization, Islamic architects produced a vast array of two-dimensional tiling patterns (Sagdiç 2000).

One of the first examples in history of mathematics and geometry being used in architecture is the Great Pyramids of Egypt. This structure has sparked many disagreements between theorists about whether or not mathematics and number theory were used in its design and construction. There have been at least nine theories that attempt to explain the Pyramid’s shape, and at least half of them are accurate to one decimal place in their predictions of the measured measurements. This is a challenging topic because it is undeniable that the pyramid was built in accordance with specific astronomical alignments (O’Connor and Robertson 2002).

Additionally, Egyptians considered regular geometric shapestobesacredandonlyusedtheminthedesignof ceremonialandofficialstructures.Itisstillunknowntothis day whether the mathematics involved in the design of theKhufuPyramidiscoincidentalornot,asconnections with numerical ratios were found in the analysis of the structure. An angle based on the golden ratio (1 + √5)/2 will have a dimension of arcsec(1.618033989) = 51° 50’. The Great Pyramid’s sides currently rise at an angle of 51° 52’, landing close to the golden ratio. It has been suggested that the closeness to the golden ratio has to do with the construction methods used to build the pyramid rather than an intentional mathematical calculation.

Chapter 4: History of Mathematics in Art & Architecture: Geometry & Proportions

Pythagorasalsorecognizedthegeometricalqualitiesof numbers. The Pythagoreans discussed square, oblong, triangular,andotherformsofnumerals.Shapeswerethe subject of geometry, which was the study of shapes. In addition to this, the Pythagoreans created proportionbased aesthetics. Symmetry was used in architecture to portray geometric regularity’s expression of beauty and harmony, and thus, it is important to realize that the word “symmetry” originates from the ancient Greek architectural term “symmetria,” which denoted the repetition of shapes and ratios from the smallest parts of a building to the entire structure. To a mathematician today, symmetry suggests an underlying action of a group on a basic configuration. Now that this has been established,itshouldbeevidentwhatthePythagoreans meant when they said that “all things are numbers” and how this would affect ancient Greek architecture (O’Connor and Robertson 2002).

Chapter 4: History of Mathematics in Art & Architecture: Geometry & Proportions

The Parthenon can be taken as an example to analyse the proportions and dimensions of Greek architecture to see how the lengths follow the Pythagorean mathematical laws of proportion. A study by Berger elaborated on how the Pythagorean concepts of tiny number ratios were applied during the building of the Temple of Athena Parthenos. The foundation of the building was the ratio 2: 3 and its square, 4: 9. Three rectangles with sides 3 and 4 and a diagonal of 5 were combined to create a basic rectangle with sides 4: 9. Because of this method of building, it was also possible to properly establish the right angles in the structure by using the 3: 4: 5 Pythagorean triangle (Berger and Basel 1980).

Chapter 4: History of Mathematics in Art & Architecture: Geometry & Proportions

Human Proportions in Architecture 4.1

We owe much of our knowledge of mathematical methods of building historical architecture to Vitruvius, as he analysed the elements of roman architecture deeply in ten books, each targeted at a specific aspect of the architecture of the city. Vitruvius believed that the human body’s proportions are critical for creating beauty, and he proposes that the temple’s proportions should mimic these human proportions.

He argues that because they closely resemble the geometry of the splayed human form, the circle and square are ideal shapes for developing architectural designs. Given that Vitruvius thought the human body was flawless because it was created in the likeness of a god, there is theological importance to this. In fact, many have claimed that the golden number may be found in the proportions of the human body, therefore it’s possible that the connection between the golden number and human proportions explains the modern evidence for the number discovered in Greek temples (Essley 2019a).

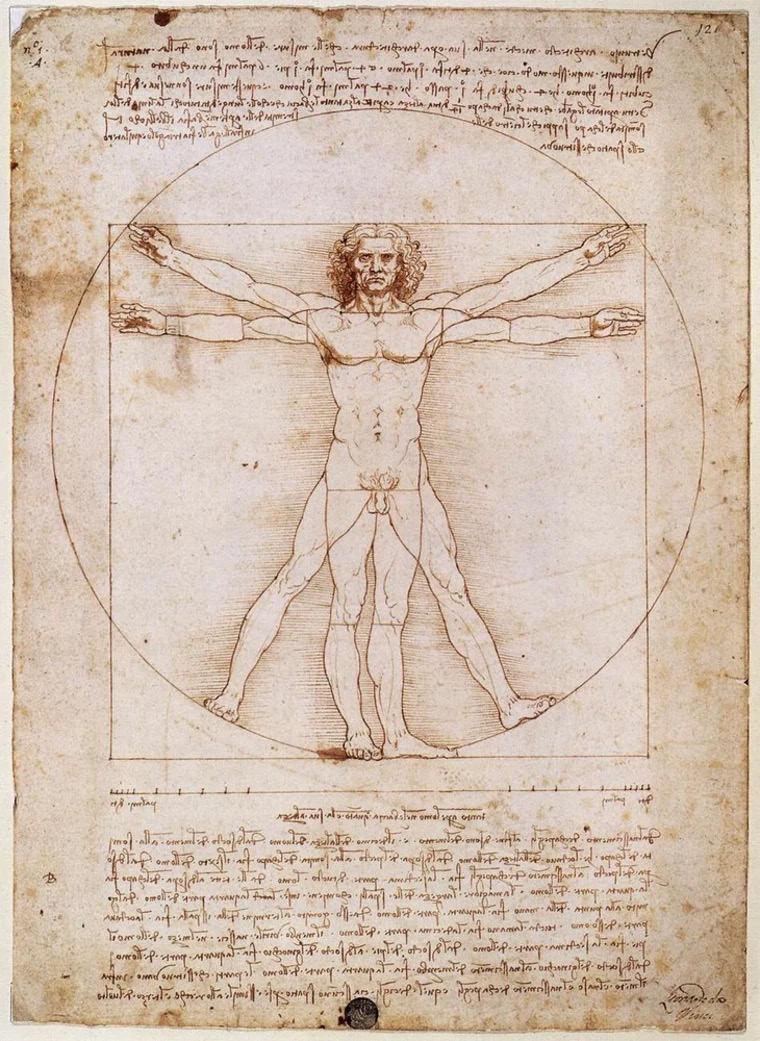
It wasn’t until Leonardo Da Vinci studied the work of Vitruvius that the correlation of human proportion with architecture was explicitly stated and described in architectural history. Da Vinci studied the dimensions of the Vitruvian man to note the proportions of the human body’s parts, and he noted the following proportions (Essley 2019b).

In the face he found:

• 1/3 of the face’s width is between the chin and the nostrils.

• 1/3 of the face extends from under the nose to the brows.

• 1/3 of the face is also measured from the eyebrow to the hairline.

In the body he found:

• The entire face, from chin to hairline, makes up 1/10 of the human body.

• The head is 1/8 of the size of the human body from chin to crown.

• 1/6 of the human body extends from the breast to the hairline.

• 1/4 of the human body extends from the breast to the crown.

• 1/6 of a person’s height is represented by the length of a foot.

• 1/10 of a human’s height is measured from the wrist to the tips of the fingers.

• 1/4 of a human’s height is equal to their forearm and breast width

Chapter 4: History of Mathematics in Art & Architecture: Geometry & Proportions

As such, the primary proportions used in developing the proportions of architectural elements are 1:3, 1:4, 1:6, 1:8, and 1:10, although they could not be applied to every architectural element, and some have developed through different concepts.

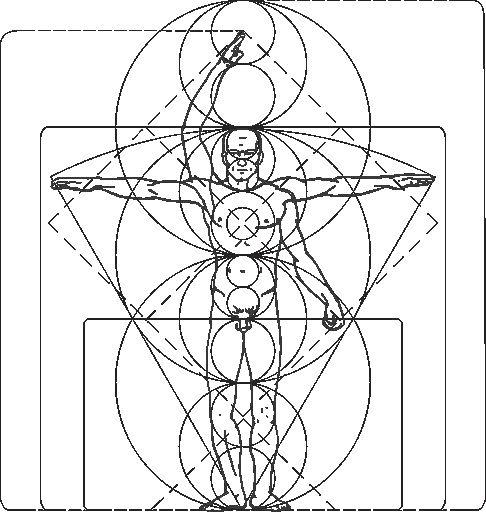
If we carefully examine the diagram, we can see that Vitruvius starts with the navel as its central point. From this point, all the elements in this diagram are measured, forming circles and squares. A game of symmetry governs both architecture and the human body. The ideas of architecture were developed using the Vitruvian Man. Both the artists Vitrivuis and Da Vinci gained an understanding of the significance of proportions and symmetry in design by examining the human body, and modern architectural design adheres to the same philosophy (Dewani 2020a).

Chapter 4: History of Mathematics in Art & Architecture: Geometry & Proportions

Golden Ratio in Art & Architecture 4.2

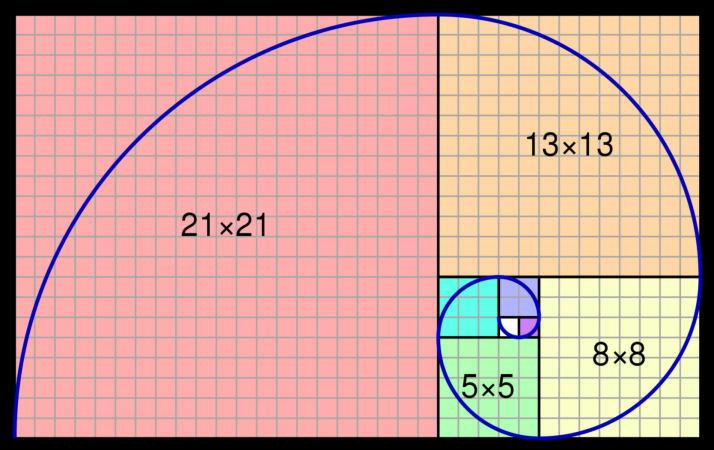
A more recent important figure in the study of mathematical proportions in architecture is the architect, artist, and writer Le Corbusier. Le Corbusier developed the study of the golden ratio and the Fibonacci sequence in the context of architecture with his books “The Modulor” and “The Modular 2,” and to understand the work of Le Corbusier on this topic, a fundamental understanding of the golden ratio must be present.

Thegoldenratioisessentiallythegeometricrepresentation of the Fibonacci sequence to develop proportions. The Fibonacci sequence is a numeric pattern in which every number in the pattern is added to the one before it, ie. the following sequence of numbers: {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …}. The golden ratio takes the numbers of this sequence and applies them as the length of the sides of a square, and adds the next square in the sequence to the longer side of the resulting rectangle (Obara 2000).

Chapter 4: History of Mathematics in Art & Architecture: Geometry & Proportions

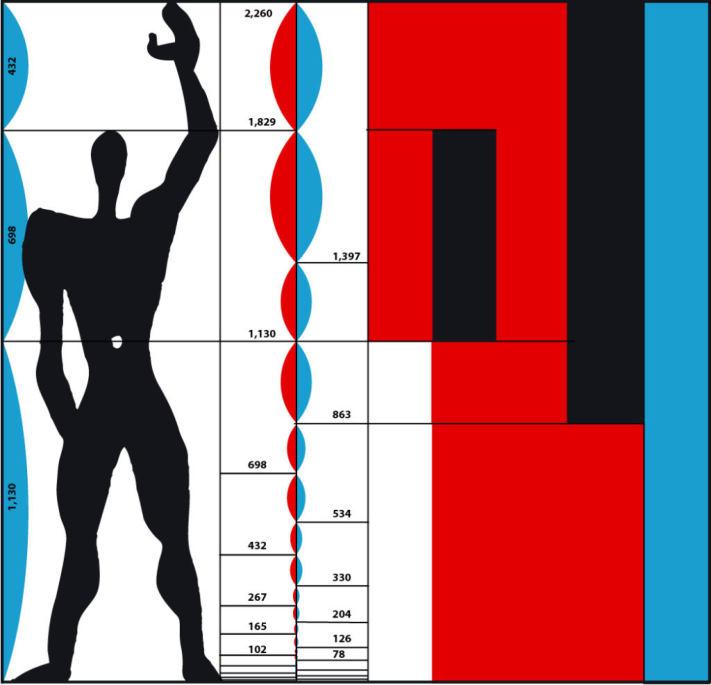
Going back to Le Corbusier, he created “The Modulor” as a scale with a universal use. It was designed with a grand ambition: to integrate mathematics, the human form, architecture, and aesthetics into one system. Corbusier thought that this approach might be extended to industry and mechanics and utilized to offer measurements for all parts of design, from door knobs to urban design. The scales and measures used in the modulor system were organized into a modulor rule. A six-foot man is the primary “module” of the Modulor, supposedly modelled by the average height of the detectives in the English crime novels Corbusier loved (Icon Eye 2009).

Chapter 4: History of Mathematics in Art & Architecture: Geometry & Proportions

Le Corbusier’s goal was to research proportions to explain the design of the Parthenon and other Greek temples and cathedrals, as they were peculiarly built accurately to exact measurements that follow standard mathematical rules of proportion. The first step towards finding how they came to the essence of these proportions is to find their instruments of measurement, and it is not unlikely that the Greeks used their fingers, palms, hands, arms, feet, and legs as instruments of measurement. This is the most likely answer as to how they ended up with golden ratio proportions in their structures.

It is important to note that the reason behind the disconnection of the current system of measurement from human proportions is the movement of standardizing the “meter” unit that represents a ten millionth part square of the earth’s meridian as the primary unit of measurement in most fields during the French Revolution. This gave way to many scientific advances, but prioritized order rather than representing the human body in proportion.

The Modulor serves a crucial role in the field of architectural mathematics as it connected the metric system back to the human body’s proportions, and draws attention to the disconnection of the industry from the body’s natural proportions with the industry’s persistent efforts towards standardization (Arellano 2018).

Chapter 4: History of Mathematics in Art & Architecture: Geometry & Proportions

Throughout history, the study of proportion has been extensively investigated in the field of architectural mathematics, and several systems, such the Fibonacci sequence, the Golden Ratio, the double unit, and the Vitruvian Man, have been developed. It has been established that these methods that have been around for centuries are the secret to perfection in proportionate design. It is now evident why it is crucial to research human proportions in architecture and design since the structures are made for humans and should follow human proportions (Dewani 2020b).

Chapter 4: History of Mathematics in Art & Architecture: Geometry & Proportions

5

Organic Mathematical Patterns & Morphology

5.0 - Categorisation & Analysis of Patterns

5.1 - Simple Geometric Patterns & Tessellations

5.2 - Fibonacci Patterns

5.3 - Branching Patterns

5.4 - Fractal Patterns

Categorisation & Analysis of Patterns 5.0

The mathematician Pythagoras found that patterns are to mathematics and geometry what harmonies are to music and that they are the fundamental constitution of all life on earth. Patterns in nature come in almost every shape and form that mathematics suggests at radically different scales, from galaxies to the tiniest molecule, the “known” Hubble-length universe is made of similar repeating patterns that create micro- and super-structures that have a commonly structured symmetry.

A pattern repeats itself in a predictable way down to its fundamental components, whether it be repeated numbers, occasions, or objects. To create larger objects that originate from an underlying pattern, the pattern itself serves as a template to the object, and so, it may be inferred that the “known” Hubble-length universe is likewise in orbit as all of these objects have similar orbital patterns, including elementary particles, stars, and planets (Joseph 2010).

To clearly analyse the massive plethora of patterns in nature, they must be split into categories, and the major ones that will be discussed in this case will be the following:

• Simple Geometric Patterns & Tessellations

• Fibonacci Patterns

• Branching Patterns

• Fractal Patterns

Branching Patterns

Fra

Patterns

Simple Geometric Patterns & Tessellations 5.1

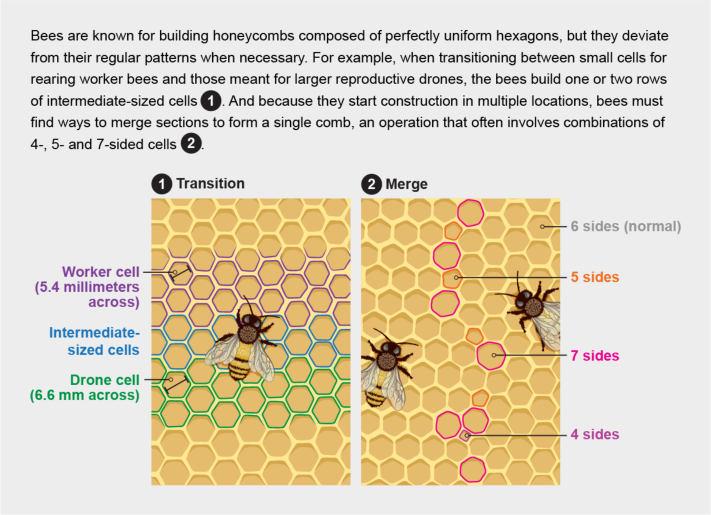
The most basic geometries in mathematics can be found in nature in abundance, and the first and most obvious case is the hexagonal pattern of beehives. The question to ask when analysing every pattern in nature is why did this pattern form? Nature works towards efficiency, survivability, and adaptability, so why would beehives adopt the hexagonal structure as the geometry of choice for their habitat?

Whythehoneycombcellsarenotcircularisanintriguing subject, since for a given perimeter, a circle has a greater ratio of perimeter to area than a hexagon. One explanation for this is that there would be a lot of waste withcircles,asopposedtonormalhexagons,whichcan be placed side by side to fill space without any gaps. In the hexagonal arrangement, each wall serves as a wall for two distinct chambers, to put it another way. This would still be the case with circles, but the spaces between the circles would be tiny, weirdly shaped, and likely, non-functional (Illustrative Mathematics 2016).

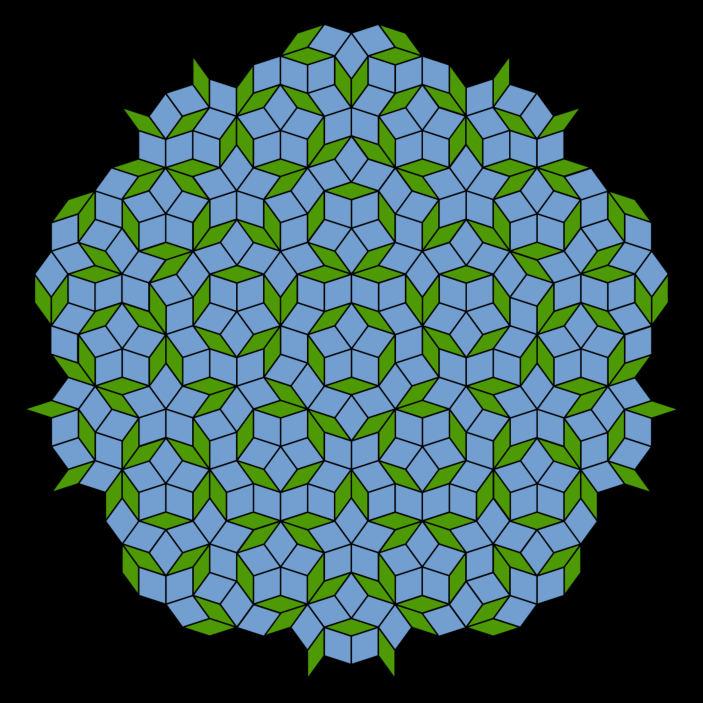
Thepatternfoundinmathematicsthatisformedwithsimple geometry, covering a plane of tiles, and does not leave any gaps or overlaps in between is called a tessellation. These patterns have proved to have aesthetic beauty and their mosaic decorative potential has mesmerized designers for as long as art and architecture have existed.

Tessellation’s beginnings may be found in the Sumerians, who utilized clay tiles to create decorative elements for their dwellings and temples roughly 4,000 years ago. Tessellation then made its way into the art of several civilizations, including the Egyptians, Persians, Romans, and Greeks, as well as the Byzantines, Arabs, Japanese, Chinese, and Moors. Naturally, tiling took on many forms and designs as it grew and adjusted to fit each of these civilizations and customs. A group of thinkers started investigating tessellation in nature throughout the Middle Ages and continued to do so into the 19th century in an effort to understand its geometric patterns. This gave rise to various major mathematical research to further understand nature’s beauty and its applications in art and design (Widewalls Editorial 2016).

It is required to define a few technical terminologies used by geometry in order to discuss tessellation, also known as tiling, in mathematics. A shape that is repeatedly used to create a tessellation is referred to as a basic area. The tile is another name for it. An edge is the junction of two adjacent tiles, which is frequently a straight line. The intersection of three or more adjacent tiles is known as a vertex. A polygon is a planar shape that has five or more sides and angles that are all straight.

Afterunderstandingtheterminologyandmathematical background, it is now easier to study the nature of tessellations and their different types. A prototile is one typeoftilefoundinatessellation.Thetilingusingjustone prototile is known as monohedral tiling, mono referring to the number of prototiles employed. Every tile used in this kind of tiling has the same form, therefore they are all complementary to one another (Widewalls Editorial 2016).

Tilingintessellationscancomeinclosetoinfinitenumber of prototiles. Dihedral tiling refers to two distinct shapes in the pattern, and similar to this, trihedral, tetrahedral, and n-hedral tilings denote the presence of three, four, or ‘n’ prototiles, respectively.

Tessellation patterns can be further categorized into their arrangement and the nature of their repetition. If the pattern repeats its tiles in a regular manner in two separate directions infinitely, then the tessellation is periodic. On the other hand, if the pattern becomes asymmetrical and almost random without the ability to be repeated periodically, then the pattern is categorized as aperiodic. Clear and famous examples of this type of pattern are the Penrose and Pinwheel Tiling patterns (Widewalls Editorial 2016).

Fibonacci Patterns 5.2

When calculating the optimal expansion pairs of rabbits over the period of a year, Leonardo Fibonacci came up with his revolutionary Fibonacci sequence. Today, its emerging patterns and ratios (phi = 1.61803) may be observed at all scales, both in inanimate things and living systems. The Golden Ratio is going to be observed inalmosteveryexampleofFibonaccipatterns,itcannot explain every structure or pattern in the cosmos, but it is undoubtedly a common occurrence within nature (Obara 2000).

ThereisamassiveplethoraofexamplesoftheFibonacci geometries appearing in nature, but a select few will be enough for analysis and understanding their function in thenaturalorder.Forexample,theFibonaccisequence is regularly reflected in the number of petals of a flower. Famous examples include the daisy’s 34 petals, the chicory’s 21, the lily’s three petals, buttercups’ five, and so on. Due to the perfect packing configuration chosen by Darwinian processes, where each petal is positioned at 0.618034 per turn (out of a 360° circle), allowing for the best possible exposure to sunlight and other variables, phi occurs in petals.

The Golden Rectangle intrinsically has the special characteristic where its sides have an aspect ratio of a/b equal to the golden ratio (phi), and they can lead to a spiral-shaped nesting process that can continue on infinitely, and this logarithmic spiral can be seen commonly in nature. The inner ear’s cochlea, along with snail and nautilus shells, follow the logarithmic spiral. Likewise, it may be observed in the form of some spider webs and the horns of particular goats (Dvorsky 2013).

Spiral galaxies naturally depict the Fibonacci pattern as well, and an example of this can be seen in our own Milky Way’s spiral arms, as they are roughly 12-degree logarithmic spirals. Astronomers discovered in 1925 that the radial arms of galaxies should curve as they spin because the angular speed of the galactic disk’s rotation changes with distance from the center. Spiral arms should then start to coil around a galaxy after a few rotations, but they evidently do not behave according to this prediction, hence the “winding problem.” The stars outside appear to move faster than anticipated, which is an unusual feature of the universe that contributes to the preservation of its structure (Pflugerville 2017).

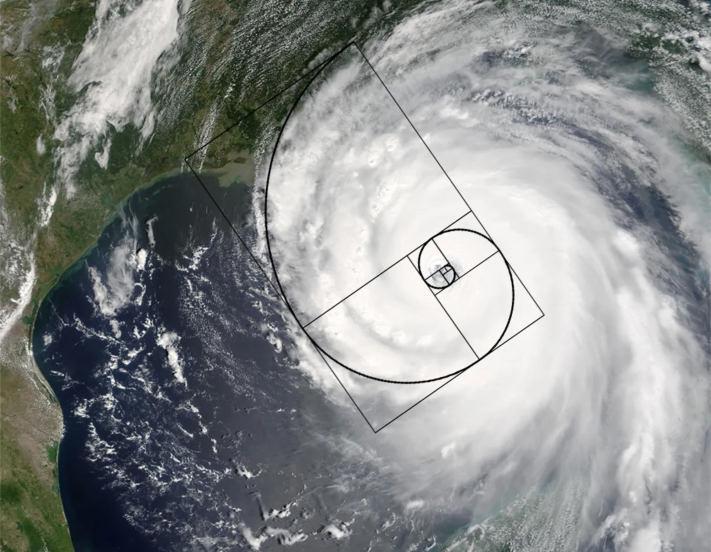
Even hurricanes can be observed following the golden ratio and the Fibonacci pattern. The Coriolis Effect is the name given to the structure when the center circle is produced by variations in pressure. The creation of the first spiral shape was caused by variations in wind pressure and speed both below and above the formation. The shape of the Fibonacci spiral was so prevalent to observation that a student at California State University performed a research project to investigate whether the tightness or looseness of the spiral can predict the intensity of the storm. Her results, unfortunately, did not yield supporting data, however, she did discover that “the variance from the Golden Spiral became greater as the distance of the spiral from the eye of the hurricane became greater,” (Hillebrandt 2013).

Branching Patterns 5.3

Branching patterns are seen in all of nature, including trees, ferns, and coral, but they also occur at much smallerscales,wheretheyarecrucialformaximizingthe surfaceareaavailable sothatorganismsmayefficiently exchange gases and fluids with their surroundings. One component of the comparable branching patterns in various systems has been attributed to the “principle of least work,” which has been proposed as an explanation. The idea is that branches grow in a way that uses the least amount of energy to keep fluids moving. The ratio of the trunk’s size to the branch’s diameter is thought to determine where a branch grows. The branch would typically be higher up and closer to a 90-degree angle if it were tiny in relation to the trunk since it is more efficient to keep the fluid in the bigger artery for as long as possible (Rhyne 2012).

During development, stem-like cells that control ductal growth and division, or “bifurcation,” regulate the creation of branching structures. After then, each new branch will either stop growing or start growing again. The finding that development occurs pretty much randomly suggested that there may be a very basic rule underlying it, even if there is a communal decisionmaking process taking place involving several distinct stem cell types. At the Hubrecht Institute in Utrecht, ProfessorSimonsandhiscolleagueDr.EdouardHannezo noticed that there was very little branch crossing - the ducts appeared to extend to cover the area but did not overlap. They made the assumption that the ducts were expanding and branching, but would halt when a tip hit another branch (Hannezo et al. 2017).

In this manner, the simplest local instruction such as branching and stopping when you encounter a mature duct generates a completely space-filling network with precisely the observed statistical organization. The ramifications for fundamental biology are enormous in this case, as It informs that rather than following a strict, predetermined sequence of genetically programmed events, complex branching epithelium structures grow by a self-organized process that is based on a very straightforward yet general rule (Harris et al. 2017).

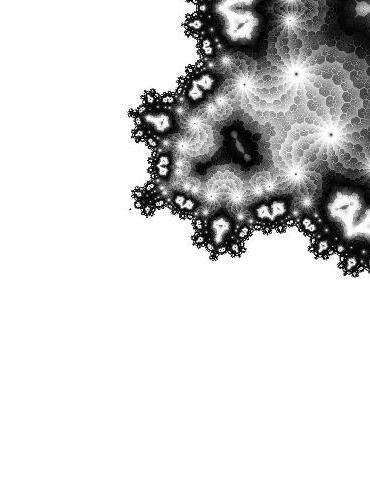
Fractal Patterns 5.4

Fractals are never-ending infinitely intricate patterns that resemble one another at various scales. They are made by repeatedly performing a straightforward technique in a never-ending feedback loop. Fractals, which are driven by recursion, are representations of chaotic dynamical systems. They lie between the recognizable dimensions of our world in terms of geometry. Since fractals occur often in nature, fractal patterns are easily recognised among even laymen. Consider the following examples: trees, rivers, beaches, mountains, clouds, seashells, etc (Hand 2019).

The mathematician Benoit Mandelbrot first used the term“fractal”in1975.Hedescribesafractalas“arough or fractured geometric shape that may be broken into parts, each of which is (at least roughly) a reduced-size replica of the whole” in his landmark book The Fractal Geometry of Nature. The Mandelbrot Set can be used to program few lines of code to generate an unlimited stream of changing, self-similar patterns, and this is Mandelbrot’s most famous mathematical discovery. The Mandelbrot set’s representation demonstrates how relatively simple mathematical principles may lead to extremely complex, completely unexpected structures. Modeling weather patterns and financial markets are just a few examples of how this insight might be put to use (Mandelbrot 1978).

A fascinating example of a fractal pattern that one only gets to experience for only a blink at a time is the pattern of lightning strikes. Lightning does not move in straight lines, as Benoit Mandelbrot pointed out in his opening passage. Instead, a disordered, jagged path is generated as a result of the unexpected breakdown of the enormous charge separation that had been building up in the sky (Pearce 2018).

“Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line”

Similar to how an iceberg conceals itself beneath the water, the bulk of a lightning bolt is often obscured in a cloud. Although lightning may reach distances of many kilometres, it forms in a matter of microseconds. The sound of thunder is fractal in itself, and it is created by the superheating of the air around the lightning. The time it takes a lightning bolt to reach your ear varies because its course is a jagged fractal in 3D space, and the thunder rumbles in a similar fractal pattern to its parent.

A famous recreation of a lightning strike in a smaller scale is the Lichtenberg Figure, which shows the fractal nature of lightning in a clearer representation. A lightning-like discharge channel is produced and left as a trace in the acrylic substance by utilizing a particle accelerator to charge up a section of the material’s electronsbeforeabruptlydischargingthem,thiscreates a pattern inside the acrylic that appears like a frozen lightning strike (Fractal Foundation 2003).

The Koch snowflake is another iconic fractal structure, and it classifies as a fractal because the pattern consists of cutting a side into three equal pieces and drawing an equilateral triangle in the central section, and repeating infinitely. The physical morphogenesis of the snowflake is the spontaneous production of pattern and form by its inanimate material, water, and it is the process by which order emerges from chaos. This process can be shown by the transition of a faceted ice prism into an elaborately branching star dendrite, forming a fractal-like snowflake (Weisstein 1999).

When you take a microscopic look at either side of the snowflake, the fractal pattern remains consistent, but the Koch snowflake, however, is not a genuine snowflake.Eachofthebranchesinagenuinesnowflake has some self-similarity, but the pattern does not continue infinitely, so it is not technically a true fractal. (Future Science Leaders 2019)As shown in this fernlike starry dendrite, the production of side branches can be chaotic. When the ice grows quickly, the side branches are haphazardly placed, with no symmetry between the branches or even between the two sides of a single branch (Snow Crystals 1999).

Detachment from Biology & Injection into Architecture

6.0 - Biomimetic Architecture

6.1 - Computational Design & Form Generation

6.2 - Evolutionary Efficiency Studies

6.3 - Artificial Intelligence & Robotics for Digital Fabrication

Biomimetic Architecture 6.0

After studying the background of mathematics and patterns in history and analysing their relevance to natureandtheirclearprevalenceineverythingorganic, how can it be applied into architecture to improve our design philosophies? It has been concluded that the proportions of the elements in modern day architecture have been derived from human proportions, so the research suggests that current architectural methods are being optimized for human use.

Interior spaces being designed for human proportions is logical,butthequestionseemstorisehere,isitnecessary to design the exterior form of our buildings based on human proportions too? The interior is designed to be occupied by humans, but the exterior occupies nature, and should therefore be designed to be more alike to nature, and moreover, this justifies the use of biomimicry as a design principle for the morphology of building design.

Itisnotenoughtojustusenatureasaninspirationforform development though, as it would create construction methodissuesandmoreinefficientbuildings.Biomimetic architecture is a multidisciplinary scientific approach to sustainable design that goes beyond using nature for aesthetic inspiration to understanding and using construction principles found in natural settings and species (Ghisleni 2020).

It is imperative to the biomimetic method that the designer focuses on looking at nature for inspiration in technology to reduce the carbon footprint associated with the construction industry. Buildings that are created and developed as living structures, or even as environments that interact with their inhabitants and the world around them, can have a lower carbon footprint and maintain more living ecosystems, resulting in a net positive influence on natural resources (GarciaHolguera et al. 2016).

Computational Design & Form Generation 6.1

The tool that makes the most sense to use in creating biomimeticdesignsisatoolthatcansimulatethegrowth patterns of the natural morphogenesis of organisms to generate forms that follow evolutionary methods, and the tool that fits this bill is computational design. Computational architectures are computationally based processes of form origination and change, and thisconceptisgenerallyknownasdigitalmorphogenesis. Based on the fundamental concepts of computational design,severalarchitecturescanbedistinguished,such as topological architecture, isomorphic architecture, animate architecture, metamorphic architecture, parametric architecture, and evolutionary architecture (Kolarevic 2000).

It is important to understand first what Euclidean and Non-Euclidean geometries refer to and what their relevance in architecture is before diving into the different types of computational morphogenesis. The term “Non-Euclidean” literally means that which is not Euclidean. Non-Euclidean geometry refers to the various forms of geometry that stray from plane and solid geometry, and the first five postulates of Euclidean geometry should be stated to fully understand the changes that are done to make a geometry nonEuclidean. These axioms must be present in a geometry to be Euclidean (Encyclopedia.com 2018):

1. Any point-to-point straight line can be drawn.

2. A continuous straight line can yield a finite straight line.

3. A circle can have any location as its center and any distance as its radius.

4. Every right angle is equal to every other right angle.

5. If a transversal falls on two lines in such a way that the interior angles on one side of the transversal are fewer than two right angles, the lines meet on the side with the lesser angles.

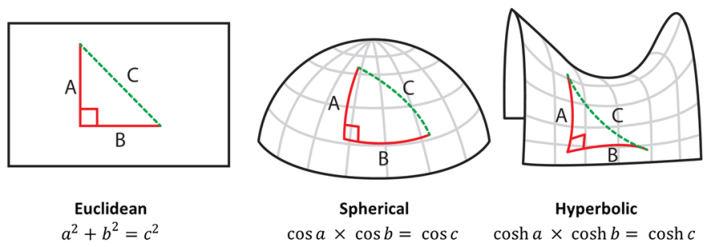
Non-Euclidean geometry is now being used in architectureasameansofproducingoptimalstructural shapes and searching for practical engineering solutions,andisimperativetothefieldofcomputational design to produce biomimetic forms. (Gawell 2013)

The primary type of digital surface used in the modelling of Non-Euclidean geometries in the field of computational design is Non-Uniform Rational B-Splines, also popularly known as NURBS. These surfaces can be easily controlled by shifting control points, weights or knots (İçmeli 2008).

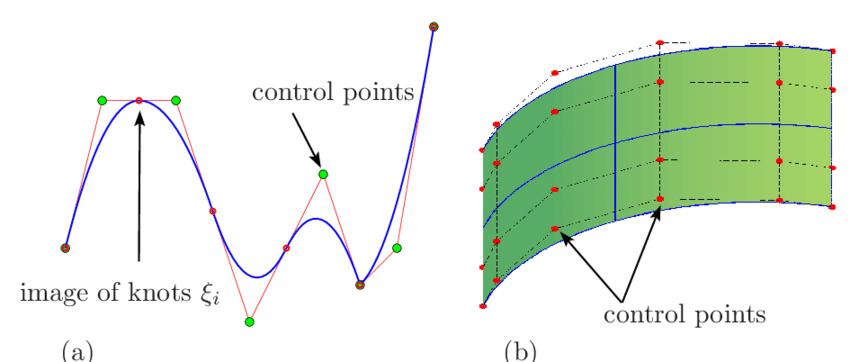
Now that a fundamental understanding of the nature of the surfaces used in computational design has been established, a definition can be given to every computational architecture that has been listed.

The topological architecture is distinguished by its departurefromEuclideangeometryofdiscretevolumes represented in Cartesian space and significant use of topological, “rubber-sheet” geometry of NURBS curves and surfaces. Geometry is represented in topological space by parametric functions rather than implicit equations, which explain a spectrum of possibilities.

Isomorphic surfaces are another divergence from Euclidean geometry and Cartesian space. Blobs or metaballs, as isomorphic surfaces are frequently referenced in this design method, are amorphous structures composed of mutually inflecting parametric objects with intrinsic forces of mass and attraction. They have impact fields or areas that can be additive or subtractive. The geometry is built by computing a surface where the intensity of the composite field is the same - hence the name isomorphic surfaces (Kolarevic 2000).

Greg Lynn was one of the first architects to use animation software for form development rather than depiction. The popular “cinematic model” of motion in architecture, according to Lynn, removes force and motion from form articulation and reintroduces them subsequently, after the fact of design, using notions and practices of “optical procession.” According to Lynn in contrast, “animate design is defined by the copresence of motion and force at the time of formal conception.” As an initial condition, force becomes “the source of both motion and certain inflections of a shape.” “While motion indicates movement and action, animation suggests the growth of a shape and its shaping forces,” writes Lynn (Lynn 1999).

Some instances of metamorphic form generation techniques are key shape animation, deformations of themodelingspacearoundthemodelusingabounding box, a spline curve, or one of the coordinate system axis or planes, and path animation, which deforms an object as it moves along a selected path, are instances of metamorphic form generation techniques. Changes in geometry are stored as keyframes (key forms) in key shape animation, and the program subsequently computes the in-between states. Object forms adhere to changes in geometry of the modeling space in deformations of the modeling space.

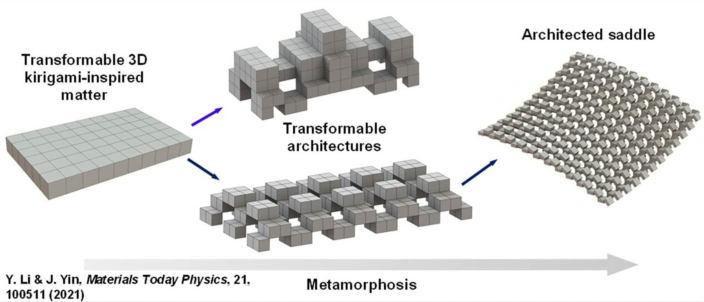
The characteristics of a specific design, rather than its shape,aredefinedin parametricdesign.Variousobjects or configurations may be effortlessly built by providing different values to the parameters. Equations can be used to define an associative geometry by describing the connections between objects. Interdependencies between items may be formed this manner, and the behavior of objects under transformations can be described. Parametric design benefits greatly from the capacity to specify, determine, and modify geometrical relationships.

The evolutionary model of nature is proposed as the producing mechanism for architectural form in evolutionary architecture. Architectural concepts are articulated as generative rules in this design technique so that their emergence and development may be expedited and verified using computer models. Concepts are defined in a genetic language, which generates a coding script of form-generation instructions. Computer models are used to mimic the evolution of prototype shapes, which are then assessed basedontheirperformanceinasimulatedenvironment. In a short period of time, a huge number of evolutionary steps may be formed, and the emergent forms are frequently surprising (Kolarevic 2000).

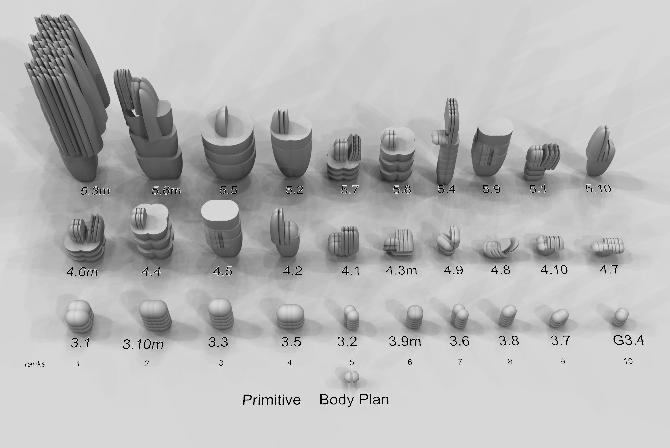
Evolutionary Efficiency 6.2

In the same way that organisms have evolved over centuries to their current form as mentioned earlier, computational design methods can be used to mimic the evolutionary adaptation of organisms to achieve maximum efficiency in multiple aspects that can advance the sustainability of architecture.

The objective of energy-efficient design is to provide a comfortable indoor climate, effective use of space and materials, and a high degree of architectural quality, all while minimizing energy consumption and producing energy efficiently, and this can be boosted using evolutionary computing. Many architectural features, such as geometry or transparency, have a direct impact on the building’s ability to generate energy, even little alterations, such as increasing the wall thickness by insulating material will have an impact on the building’s efficiency.

The CAM Software Rhinoceros provided a graphical algorithm editor, Grasshopper, that enables the direct integration of all mathematical processes into an architecturalmodel.Galapagos,anevolutionarysolver, is included with Grasshopper, and allows designers to input the parameters relevant to the project that need to be optimized to achieve maximum efficiency for whatever result is specified. Automatically, the software goes through the process of evolution from the starting model by altering all the parameters through a number of generations specified by the designer, and the end result provides multiple altered forms that have proved to be the most optimized through all the generations simulated (Sommer Bernhard and Pont 2014).

Artificial Intelligence & Robotics for Digital Fabrication 6.3

In the same way that organisms have evolved over centuries to their current form as mentioned earlier, computational design methods can be used to mimic the evolutionary adaptation of organisms to achieve maximum efficiency in multiple aspects that can advance the sustainability of architecture.

The objective of energy-efficient design is to provide a comfortable indoor climate, effective use of space and materials, and a high degree of architectural quality, all while minimizing energy consumption and producing energy efficiently, and this can be boosted using evolutionary computing. Many architectural features, such as geometry or transparency, have a direct impact on the building’s ability to generate energy, even little alterations, such as increasing the wall thickness by insulating material will have an impact on the building’s efficiency.

Another benefit of using biomimetic computational methods is that it becomes easier to implement artificial intelligence and robotics into the construction process for more efficient digital fabrication. Morphogenetic robotics’ fundamental idea is to apply evolutionary developmentalprinciplestoroboticsinordertoconstruct self-organizing, self-reconfigurable, and self-repairable single or multi-robot systems. This methodology can be used in the construction process to construct a building’s components in a similar evolutionary pattern to how it was designed (Jin and Meng 2011).

AI allows for the transferring of smart data and Machine Leaning datasets to physical robots that can construct entire structures on their own. The NVIDIA program named Ai-Build is currently capable of 3D printing building components and saving a massive amount of constructionmaterials,butthemainadvancementhere isintheirdevelopmentoftheirAiSync,whichautomates the creation of advanced toolpaths and construction methods to a simple and intuitive user interface. The softwareallowsforstreamingmanufacturinginstructions directly to the machines and provide real-time additive control over the construction process (NVIDIA 2022).

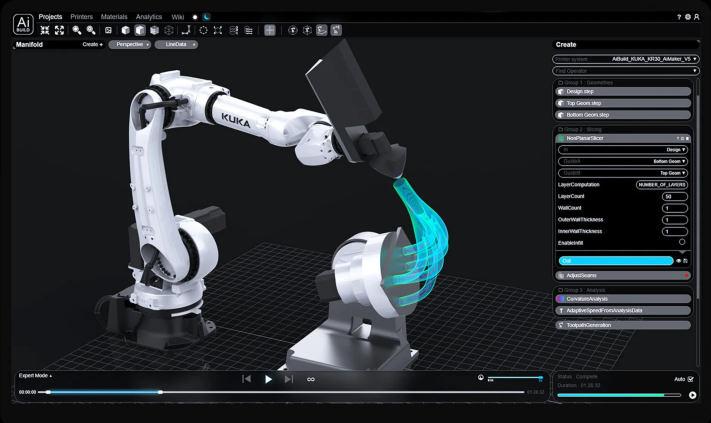
This technology revolution is expected to benefit all parties involved in an architectural project, including contractors, owners, and service suppliers. The application of statistical machine learning techniques in construction makes it much easier and less timeconsuming to evaluate data relevant to modified orders, information requests, and so on. This will aid in proactively alerting project leaders to issues that require immediate attention and can allow for safety monitoring to be done more efficiently (Srivastava 2022).

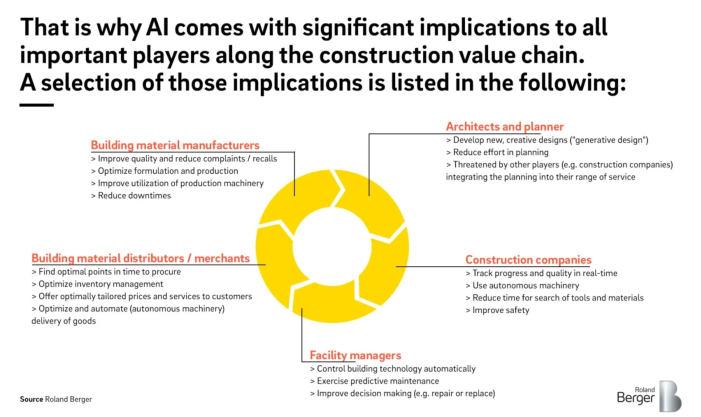
7

7.0 - Potential Solutions & Case Studies

7.1 - Case Study 1: Research / BEEAH Headquarters

7.2 - Case Study 2: Exhibition / Exhibition Center of Otog

7.3 - Case Study 3: Campus / Nucleus: Hyperloop Desert Campus

7.4 - Case Study 4: Office Building / Semaphore: Soprema HQ

7.5 - Inspiring Projects & Relevant Architecture

7.0 Potential Solutions & Case Studies

To choose appropriate case studies, a solution must first be stated clearly to be able to develop functions for the project that will solve the issue discussed.

A few solutions can be proposed in this case, the first being a research center that is dedicated to study the principles of genetics and biology and their applications into art and design. The second solution is an urban infill that serves to inject organic architecture and parametrism into the rigid urban fabric to inspire change in the morphology of the city, functioning as an exhibtion center and a public pavilion that displays the most representative works of this theory, while also setting an example through its form and design.

The case studies chosen will study different aspects required for both solutions, such as research building requirements, exhibition spaces, public spaces, landscaping, and biomimicry.

Case Study 1: Research Center / BEEAH Headquarters

Research Center / BEEAH Headquarters 7.1

Architect: Zaha Hadid Architects

Location: Sharjah, United Arab Emirates

Function: Office Building

Year: 2022

Status: Built

Area: 9,000 sqm

Project Brief

In 2013, BEEAH launched a design competition for designing their headquarters that requires the design to net zero emissions and feature new technologies to embody futuristic design and achieve excellence in sustainbablity, tackling the environmental issues in Sharjah, UAE.

Architect’s Concept

“With their twin-pillared strategy of sustainability and digitalisation, BEEAH Group works across six key industries that include waste management and recycling, clean energy, environmental consulting, education and green mobility.

The headquarters is the latest milestone for BEEAH Group as it continues to pioneer innovations for Sharjah and across the globe, establishing a base of operations for the group to diversify into new, future-critical industries. With their new headquarters, BEEAH demonstrates how technology can scale sustainable impact and ultimately serve as a blueprint for tomorrow’s smart, sustainable cities.

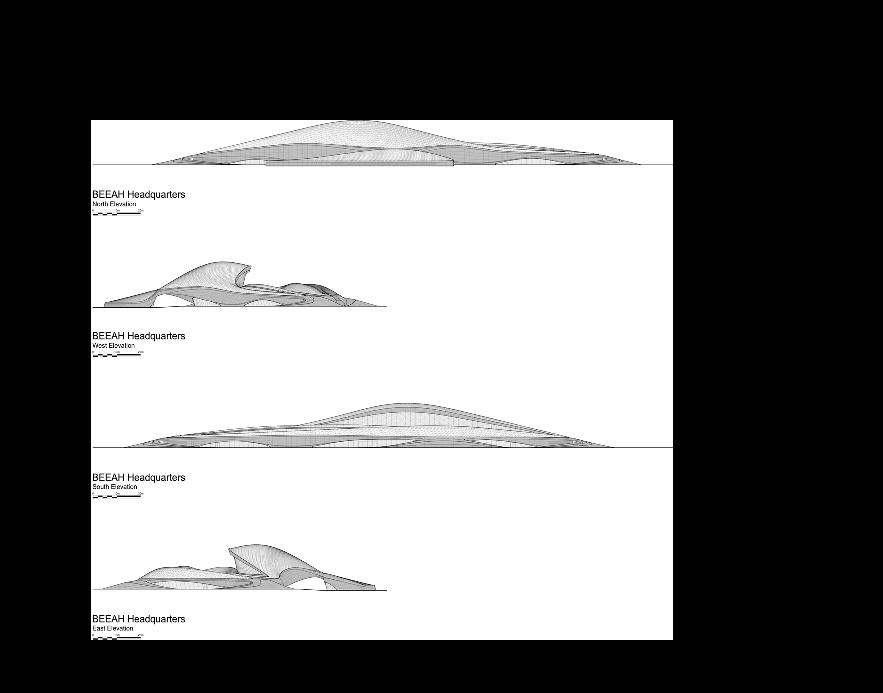
Embodying these principles, the headquarters’ design responds to its environment as a series of interconnecting ‘dunes’ orientated and shaped to optimize local climatic conditions. Embedded within its context of Sharjah’s Al Sajaadesert,thedesignechoesthesurroundinglandscape shaped by prevailing winds into concave sand dunes and ridges that become convex when they intersect,” (Pintos, 2022).

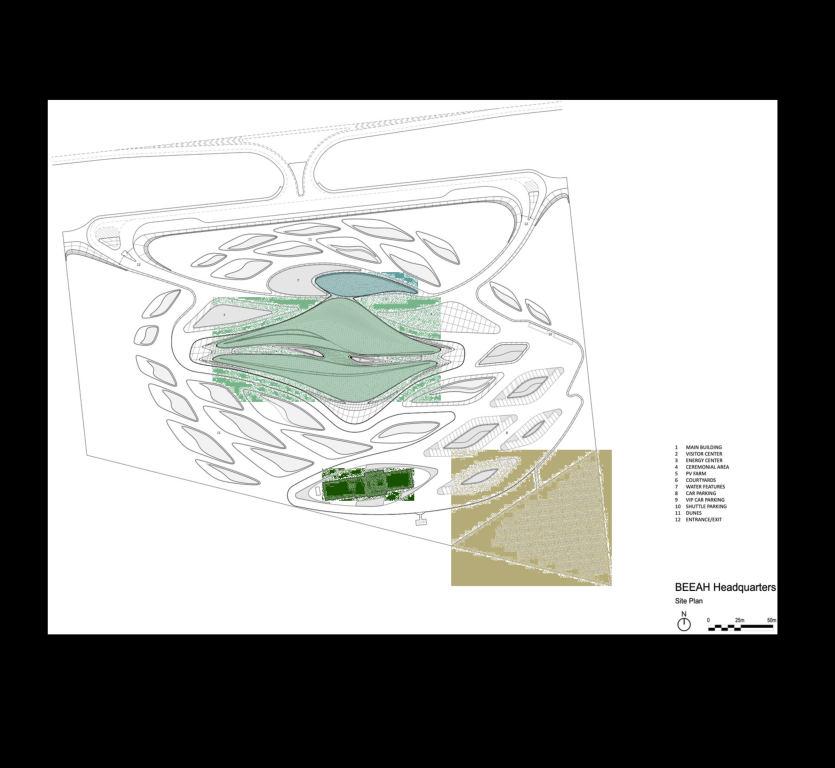
Site & Context

Thesiteoftheprojectislocatedintheindustrialareaofsharjah,surrounded by government institutions, mainly the BEEAH Waste Management Complex. There is barely any context to work with near the site, as it is mostly barren desert land, sand dunes, and asphalt roads with low rise governmental buildings built with basic sand blasted concrete finish. Since the project was to be designed in such a secluded site, it had to blend with the natural desert topography of the Al Dhaid desert. This inspired the organic dune-like form of the building and further supported by environmental studies for energy efficiency and sustainability.

Relation to Topic

This project is a prime example of the use of biomimicry for form creation, as it truly mimics nature’s sand dunes in its context to create a more energy efficient form with influence from environemental studies to further its practicalyity as a building that is designed the same way that nature is designed.

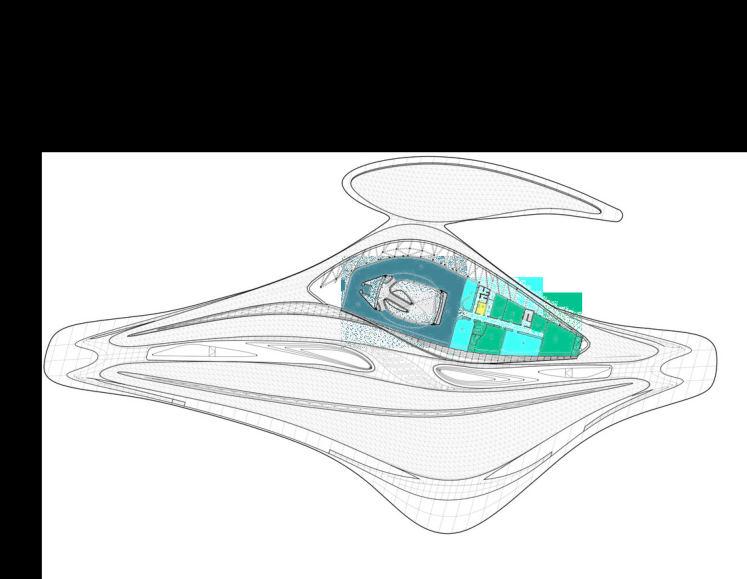
Program Investigation (1st Floor)

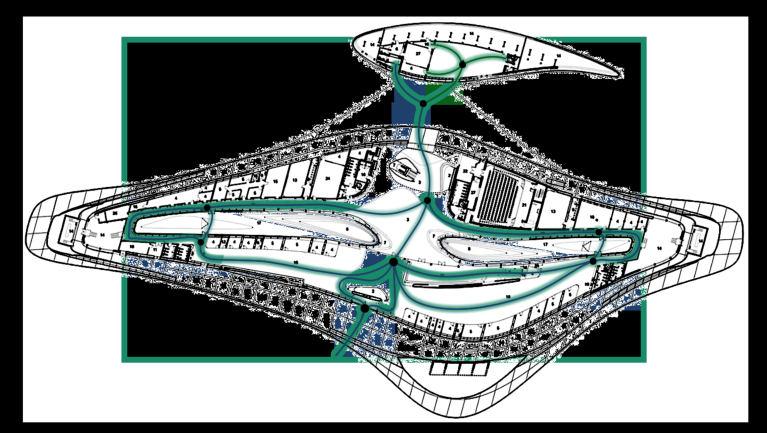
Circulation Diagram