Spistreści
1.Jaksiecizawładnęłyświatem..................................11
2.Własnościsiecirzeczywistych..................................17
2.1.Pojęciapodstawowe,elementyteoriigrafów....................17
2.2.Rozkładstopniwęzłów....................................27
2.3.Współczynnikgronowania..................................29
2.4.Siecimałychświatów......................................36
2.5.Miarycentralności........................................38
2.5.1.Średniaodległość...................................38
2.5.2.Wydajność.........................................40
2.5.3.Pośrednictwo.......................................41
2.6.Korelacje...............................................44
2.6.1.Korelacjedwuwęzłowe................................44
2.6.2.Motywy...........................................50
2.7.Skalowanieodległościwsieciachzłożonych.....................52
2.8.Modularnośćwsieciachzłożonych............................53
2.8.1.Analizaspołecznościlokalnych........................53
2.8.2.Podziałspektralnysieci...............................61
2.8.3.Hierarchicznośćwsieciachzłożonych....................68
3.Prawapotęgowewprzyrodzieifizyce............................73
3.1.Wprowadzenie–cooznaczatermin„bezskalowość”idlaczegorozkłady potęgowesąważne........................................74
3.2.Matematykaprawpotęgowych..............................81
3.2.1.Jaksprawdzić,czydanyrozkładjestpotęgowy............82
3.2.2.Metodywyznaczaniawykładnikówcharakterystycznych......87
3.2.3.Ciągłeidyskretnezmiennelosoweorazwarunek unormowaniarozkładówpotęgowych....................89
3.2.4.Wartośćoczekiwana,odchyleniestandardowe izdarzeniaekstremalnewukładachbezskalowych..........91
3.2.5.Rozkładyztłustymiogonamiireguła80/20..............94
3.2.6.Rozkładbezskalowy,rozkładParetoirozkładZipfa.Reguła kolejności-wielkości..................................98
3.2.7.Czybezskalowośćmożeistniećbezprawpotęgowych?.......101
3.3.Rzeczywisteukładyizjawiskamającecechębezskalowości.........103
3.4.Mechanizmypowstawaniarozkładówpotęgowych................107
3.4.1.Składaniezależnościwykładniczych.....................108
3.4.2.Potęgowezależnościmiędzyzmiennymilosowymi...........110
3.4.3.Modelbłądzeniaprzypadkowego........................112
3.4.4.ProcesYule’a......................................117
3.4.5.Procesymultiplikatywne..............................121
3.5.Przemianyfazoweizjawiskakrytyczne........................125
3.5.1.Klasyfikacjeprzemianfazowych........................127
3.5.2.ModelIsinga–modelprostegomagnetyka................133
3.5.3.Perkolacja–strukturalnaprzemianafazowa...............139
3.6.Skalowanie,fraktaleifraktalnesiecizłożone....................142
3.6.1.Wymiar,podobieństwo,samopodobieństwoiskalowanie.....143
3.6.2.Skalowanieallometryczne,fraktalnesiecidystrybucyjne iczwartywymiarżycia...............................150
3.6.3.Średniadrogawsieciach.Fraktalnesiecizłożone...........154
4.Modelesieci................................................162
4.1.Klasyfikacjasiecizłożonych.Siecideterministyczneiprzypadkowe, statyczneiewoluujące.....................................162
4.2.Sieciewoluujące..........................................166
4.2.1.ModelBarabásiego–Albert(BA)........................166
4.2.2.ModyfikacjemodeluBAiregułypreferencyjnegodołączania węzłów...........................................180
4.2.3.Innemechanizmyprowadzącedopotęgowychrozkładówstopni węzłów...........................................185
4.2.4.Ważonesiecibezskalowe..............................191
4.3.Konstrukcjestatyczne.....................................195
4.3.1.KlasycznegrafyprzypadkoweErdösa–Rényi(ER)..........195
4.3.2.Modelkonfiguracyjny................................201
4.3.3.Sieciprzypadkoweozadanymhamiltonianie.Wykładniczegrafy przypadkowe.......................................217
5.Zastosowaniasiecizłożonych...................................228
5.1.Strukturasiecispołecznych.................................228
5.1.1.Ideapołączeńdalekozasięgowych.......................228
5.1.2.Sieciprzestępcze....................................234
5.2.Dynamikasiecispołecznych–jakpowstająkoalicje..............239
5.2.1.Sojuszewpolityce–teoriakrajobrazowaAxelrodaiBennetta.239
5.2.2.Formowaniesięopiniiwspołeczeństwie..................242
5.2.3.ModelIsinga.......................................245
5.3.Przypadkoweuszkodzeniaiceloweatakiwsieciachzłożonych......248
5.3.1.Przykładyusterekiatakówwsieciachrzeczywistych........249
5.3.2.Modelowanieusterekiataków.........................254
5.4.Epidemiewsieciachzłożonych..............................262
5.4.1.Oepidemiach–fakty,mity,przykłady...................262
5.4.2.Modelowanieepidemii................................267
5.5.Ewolucjajęzyka..........................................278
5.6.Siecibiologiczne..........................................281
5.6.1.Sieciprotein.......................................281
5.6.2.ModelKauffmana...................................283
5.7.Wyszukiwanieinformacjiwsieci.PageRank....................289
DodatekA.Własnościmacierzysąsiedztwagrafówprostych.............294
DodatekB.Generowanieliczblosowych.............................296
B.1.Ciągłezmiennelosowezrozkładupotęgowego.................296
B.2.Dyskretnezmiennelosowezrozkładupotęgowego..............297
B.3.Zmiennelosowezinnychrozkładówprawdopodobieństwa........298
B.4.Przybliżonemetodygenerowaniadyskretnychzmiennychlosowych.298
DodatekC.Wyznaczaniewykładnikówcharakterystycznychrozkładów potęgowych................................................301
DodatekD.Zdarzeniaekstremalnewrozkładachpotęgowych............304
DodatekE.SymulacjeMonteCarlo................................306
DodatekF.Korelacjestrukturalnewsieciachzłożonych................309
DodatekG.Stabilnośćpunktustałego..............................312 Literatura....................................................314
Skorowidz....................................................329
EdwikBendyk
Rozdział1
Jaksiecizawładnęłyświatem
Czytegochcemy,czynie,sieciczęstokojarząnamsięnegatywnie.Wpadająwnie niewinnezłoterybki,pająkchwytaswojeofiary.Filmy,takiejak TheNet (System) zSandrąBullock,wyrażająnaszeobawyprzedwszechogarniającązależnościąod siecikomputerowych.Ostatniewielkieawarieenergetyczneczylawinybankructw bankówwywołaneprzezsiećwzajemnychniespłaconychpożyczekutwierdzająnas wprzekonaniu,żesieciniosązesobązagrożenia,wobecktórychpojedynczyczłowiekjestbezsilny.
Niepowinniśmyjednakzapominać,żesieciniosąteżzesobąwieledobrego.Już kilkadziesiąttysięcylattemu,dziękiistnieniupoczątkowosporadycznych,apóźniejtrwałychkontaktówmiędzyplemionamirozrzuconymipocałymświecie,dochodziłodopropagowaniaidei,transferuwiedzy(naprzykładowykorzystaniu ognia)itechnologii,anawetdowymianycennegoprzezswąodmiennośćmateriału genetycznego.
Żadnezwierzęniewykształciłotakzłożonychsiecispołecznychjakczłowiek. Todziękinimmożliwabyłaspecjalizacjafunkcjipełnionychwgrupie,pozwalająca stworzyćzgranyiwszechstronnyzespółzdolnydoskutecznejwalkioprzetrwanie. Doskonaleniesięwpolowaniubyłomożliwedziękiświadomości,żejestktoś,kto zajmujesięwychowaniemdzieci,iktoś,ktoznakogośświetnieumiejącegoleczyć rany.Wobecnychczasachkontaktyznajomychnaszychznajomychumożliwiają namznalezienieatrakcyjnejpracylubchociażbyzdobyciewymarzonegoautografu idola.
RównieżInternetniejestjedynieźródłemwszelkiegozła.Umożliwiaprzecież zbliżenieludzinaniespotykanądotądskalę.Łagodziwyobcowanieisamotnośćpowodowaneprzeztechnokratyzacjęwspółczesnegoświata.Anonimowaznajomość przezsiećtoczęstojedynykontakt,najakipotrafiąodważyćsiędziśtysiącewyalienowanychpracoholików.
Sieciotaczająnas,aleistniejątakżewnassamych.Dziękisieciomoddziaływańmiędzygenaminaszekomórkipotrafiąróżnicowaćsięipełnićodmienne
funkcje,tworząckości,mięśnieczyukładkrwionośny.Samkrwioobiegrównieżjest siecią,któranawzórsiecirzecznych,służącychdotransportusurowców,zaopatrujewcenneskładnikiodżywczecałyorganizm.Niemożemyrównieżzapomnieć onajwiększejwnaszymorganizmie,złożonejzokoło100miliardówelementówsieci neuronowej,czylimózgu.
Jakwidzimy,siecisąwszędzie,choćniezawszezdajemysobieztegosprawę. Historyczniepierwszyrazstałysięobiektembadańw1736roku,gdyszwajcarski matematykifizykLeonhardEulerrozwiązałzaichpomocązagadnieniemostów królewieckich.Popularnywówczasproblem,którymzainteresowałsięEuler,sformułowanybyłnastępująco(patrzrysunek1.1):czymożnaprzejśćkolejnoprzez wszystkiesiedemmostówwKrólewcutak,żebykażdyprzekroczyćtylkoraziwrócićdomiejsca,zktóregosięwyruszyło?Eulerwykazał,żejesttoniemożliwe,ajego pracanatentematbyłapierwsząpublikacjązteoriigrafów,rodzącejsięwłaśnie gałęzimatematyki.
Rysunek1.1. Zagadnieniemostówkrólewieckich.A.Czymożnaprzejśćkolejnoprzez wszystkiesiedemmostówwKrólewcutak,żebykażdyprzekroczyćtylkoraziwrócić domiejsca,zktóregosięwyruszyło?B.W1736r.Eulerjakopierwszypokazał,że jesttoniemożliwe.Problemmostówkrólewieckichzobrazowałzapomocąprostego grafu,anastępnieudowodniłogólnetwierdzenie,żejeślistopieńkażdegowierzchołka dowolnegografuspójnegojestliczbąparzystą,towgrafiemusibyćprzynajmniejjedna zamkniętaścieżkazawierającakażdąkrawędźtegografu
Dwieścielatpóźniejsieciamizainteresowalisięsocjologowie.Początkisocjologicznejanalizysiecispołecznychsięgająlattrzydziestychubiegłegowiekuiprac JacobaMoreno.Starałsięonzrozumieć,jakrelacjeinterpersonalnewpływająna psychologicznefunkcjonowaniejednostki.Wtymceluwprowadziłpojęciesocjogramu,będącegograficznąprezentacjąstosunkówmiędzyludźmi,więzispołecznych,relacjisympatii-antypatiiczyuznaniawgrupiespołecznej,orazzwiązaną ztympojęciemmetodę.Należypodkreślić,żeanalizasiecispołecznychrozwijała siępoczątkowozupełnieniezależnieodpracmatematyków.Dopierozbiegiemlat metodywypracowanewnaukachścisłychzaczęłyprzenikaćdośrodowiskasocjologów,tworzącnowoczesneiefektywnenarzędziepozwalającebadaćskomplikowane strukturyrelacjimiędzyróżnegorodzajupodmiotamispołecznymi.
Wieloelementowośćiwielopoziomowośćtychrelacjiuzasadniatraktowaniesieci jakotakzwanychukładówzłożonych.Pojęciezłożonościugruntowałosięwdrugiejpołowieubiegłegowieku,gdyzaczętobadaćsystemy,którychwłaściwościnie możnabyłowywieśćzwłaściwościelementówskładowych.Trudnośćopisutakich układówmetodamiklasycznejfizykiimatematykisprawiła,żeukładzłożonyjawił sięjakoniemalżywyorganizmrządzącysiętajemniczymiiniezrozumiałymiprawami.Zlicznychprzykładówtakichukładówizachodzącychwnichprocesówwarto wymienićmiędzyinnymikoloniemrówek,klimat,mózg,korkiuliczne,lawiny,jak równieżsieci.
Złożonośćsiecinieulegawątpliwości.Sieci,zbudowanezsetek,tysięcy,anawetmilionówelementówpełniącychzazwyczajróżnorakiefunkcje,powiązanych wskomplikowany,ajednakprecyzyjnysposób,rosną,dopasowująsiędozmian otoczenia,optymalizująswojedziałanie,tworzącprzydatneiusuwajączbędnepowiązania,prawiejakżyweistoty.
Siecizłożonebardzodługobroniłysięprzedujarzmieniemzapomocąteorii sprowadzającychichfunkcjonowaniedoparuprostychwzorówireguł.Właściwie nawetdzisiajwielokrotniejedynymnarzędziemdoichanalizypozostająsymulacje komputerowe.Tymwiększeznaczeniewrozwojunaukiosieciachnależyprzypisać pracomPaulaErdősaiAlfredaRényiegozpoczątkówlatsześćdziesiątychubiegłego wieku.Tychdwóchwęgierskichmatematyków,przyjąwszy,żesiecipowstająwsposóblosowy,wprowadziłodoichanalizyrachunekprawdopodobieństwa.Zamiast badaćjedenprzypadek,utworzylicałyzbiórsieci(zespółstatystyczny,ansambl). Podejścietopozwoliłowprowadzićdoopisusiecinieuniknionyprzecieżwnaturze elementprzypadkowościijednocześnieprzenieśćanalizęnawyższypoziomabstrakcji.NajważniejszymosiągnięciemprobabilistycznejteoriiErdősaiRényiegobyło odkryciewsieciachperkolacyjnegoprzejściafazowego.
Abyzrozumieć,czymowoprzejściejest,wyobraźmysobiegrupęnieznanych sobieosób,naprzykładnowoprzyjętychuczniówpierwszejklasyszkołypodstawowej.Zczasemwklasiezawiązująsięnoweznajomości,powodującpowstanie małychsieciprzyjaźni.Dowcip,opowiedzianyprzezczłonkajednejztakichsieci, nieupowszechnisięwcałejklasiezpowodubrakukontaktówmiędzyróżnymipodgrupami.Poznagojedyniedwójkaczytrójkaprzyjaciół.Okazujesię,żewpewnym momencienawiązaniejeszczezaledwiekilkuprzyjaźnispowodujerozprzestrzenieniesiędowcipunacałąklasę.Mówiącjęzykiembardziejformalnym,istniejepewna krytycznagęstośćpowiązańwklasie,takażenawetdrobnajejzmianaumożliwi wsieciniemożliwydotychczasnieograniczonytransferinformacji.
ProbabilistycznametodaanalizyzaproponowanaprzezErdősaiRényiegoutorowaładrogędobadańnadpropagacjąinformacjiwsieci.Pozwoliłamiędzyinnymi zrozumiećmechanizmyrozprzestrzenianiasięinfekcjilubplotkiorazwybuchu epidemiiczypaniki.
NiewątpliwiepięknamatematycznieteoriadwóchwybitnychWęgrówkrólowała wdziedziniesiecizłożonychprzezponadtrzydekady.Ironiąlosudojejdetronizacji przyczyniłasięinnasieć–Internet.Podkoniecubiegłegowiekugwałtownywzrost
1.Jaksiecizawładnęłyświatem mocyobliczeniowejkomputerówumożliwiłgromadzenie,wymianęianalizowanie naniespotykanądotądskalędanychnatematróżnychsiecirzeczywistych.Należy przytymwspomnieć,żesiećErdősaiRényiegowyróżniałasiętym,żekażdyjej elementmiałpodobnąliczbępołączeńzinnymielementami.Byłoparęelementów omniejszej,aparęowiększejliczbiepołączeń,aleśredniabyładobrzeokreślona.
Pierwszyzwróciłuwagęnanienaturalnośćtejcechywsieciachrzeczywistych, zarównostworzonychprzeznaturę,jakizbudowanychprzezczłowieka,innywęgierskifizykAlbert-LászlóBarabási.Dostrzegłonmianowicie,żechociażwotaczającychnassieciachogromnawiększośćelementówmaniewielepołączeń,toistnieją wnichrównieżniezwykleusieciowionewęzły,tzw.huby.Przeciętnymieszkaniec Polskiwciągumiesiącaspotykasięnaprzyjęciachzaledwiezkilkomainnymiosobami.Bywająjednaktakzwanisalonowibywalcy,dlaktórychdzieńbezbalu,imprezyczyuroczystościtodzieństracony.Ichmiesięcznesalonowekontaktymożna liczyćwsetkach,anawetwtysiącach.Choćjestichjedyniegarstka,topełniąoni istotnąfunkcjęwspołeczeństwie,wyznaczająctrendy,rozpowszechniającplotkiczy choćbyzapoznajączesobądwojeobcychludzi.Mówienieośredniejliczbiepołączeń elementuwtakiejsiecispołecznejniedostarczynaminformacjiojejstrukturze.
Podobnącechęmająrównieżsiecikomputerowe,genetyczne,neuronoweiwiele, wieleinnych,októrychbędziemymówićwdalszychrozdziałach.ObserwacjadokonanaprzezBarabásiego,niczymmałeziarenkorozpoczynającelawinę,spowodowałagwałtownąeksplozjępracnaukowychpoświęconychsieciom.Jeszczepod koniecubiegłegowiekukażdegorokupowstawałokilkadziesiątpracpoświęconych sieciomzłożonym.Obecnietaliczbaprzekraczatrzytysiąceiwciążrośnie(patrz rysunek1.2).
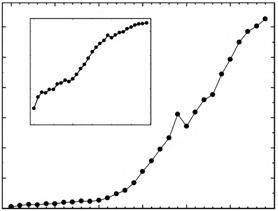
Rysunek1.2. Liczbapublikacjizawierającychwtytulelubwstreszczeniufrazę complexnetwork (siećzłożona)wdanymroku(napodstawiebazyScienceCitationIndex). Podkoniecubiegłegowiekunastąpiłwyraźnywzrostpublikacjipoświęconychsieciom złożonym.Mniejszywykresprzedstawiatęsamązależnośćwskalilogarytmicznej
Każdemubowiem,ktoma,będziedodane... Ewangeliaśw.Mateusza[13, 12]
Rozdział4
