Función exponencial
Forma general ��=��(�� ��) +��
�� es la variable independiente
�� es la base de la función exponencial, si 0<�� <1 decrece, si �� >1 crece
�� es el desplazamiento horizontal
�� es el desplazamiento vertical
Ejemplo:


La base de la exponencial es �� >1 por lo tanto, la función es creciente, la asíntota horizontal está en �� = ��, y hay un desplazamiento a derecha de la función.
Ejemplo:



��=��

La base de la exponencial es (1/��) < 1 por lo tanto, la función es decreciente, la asíntota horizontal está en �� =1 , y hay un desplazamiento a izquierda de la función.
Se sugiere utilizar el aplicativo GeoGebra Clásico 5 para la simulación de funciones.
https://www.geogebra.org/download?lang=es

Función logaritmo
��(��)=�� log��(�� ��+��)+��
�� es la variable independiente �� es un factor de amplificación si �� >1 , o atenuación si 0<�� <1 (��.��+��)>0 el argumento del logaritmo debe ser positivo �� es la base del logaritmo. Si �� =�� → ���� (logaritmo neperiano) Si �� >1 la función es creciente, si 0<�� <1 la función es decreciente �� es el desplazamiento horizontal �� es el desplazamiento vertical
El argumento puede tomar la forma de cualquier expresión, la citada es sólo un ejemplo.
Ejemplo:
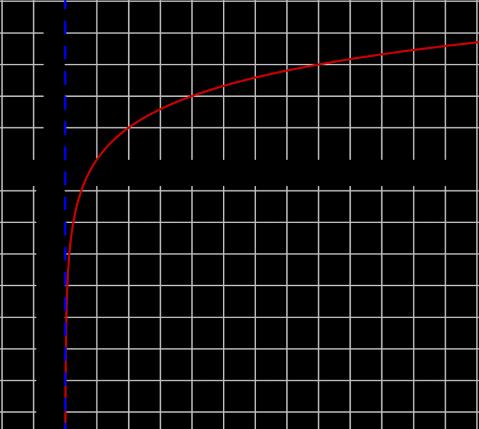
�� �� ��(��)=log2��


Se observa una asíntota vertical, en �� =0 , sin desplazamientos. Analizar en clase.
Ejemplo:
�� >1 creciente �� <1 decreciente �� �� �� ��
��= 3 2 ln(�� 3) 1 ��=��



En este caso, el logaritmo es neperiano �� =2,71…, hay un factor de amplificacion (�� = 3 2), un desplazamiento horizontal a derecha, un desplazamiento vertical hacia abajo, la asíntota vertical está ubicada en �� =3 Analizar en clase y ensayar con GeoGebra diferentes casos.
Utilizamos el logaritmo neperiano, debido a que es el que más utilizaremos en el curso.

Propiedades de los logaritmos
Definición de logaritmo logb�� =�� ⟺ ���� =��
Propiedad log�� �� =1 ⟺ ��1 =��
Logaritmo de un producto log��(��.��)=log�� ��+log�� ��
Logaritmo de un cociente log�� ቀ�� ��ቁ =log�� �� log�� ��
Logaritmo de una potencia log��(��)�� =��. log�� ��
Cambio de base log�� �� = log���� log����
Función polinómica
Su forma general: ��(��) =���� .���� +���� 1 .���� 1 +���� 2 .���� 2+. . . .+��2 .��2 + ��1 .��+��0
Donde ���� ∈ ℝ siendo ���� ≠0 y �� ∈ ℕ
���� es el coeficiente del término principal y ��0 el término independiente.
Ejemplos:





El polinomio �� es de grado cuatro, con cuatro raíces reales, mientras que el polinomio �� es de grado tres, con tres raíces reales. Analizar los mismos para mayor comprensión de la función polinómica.
Forma factorizada ��(��)=���� (�� ��1) (�� ��2) (�� ���� 2) (�� ���� 1) (�� ����)
Siendo
1
Herramientas para hallar las raíces de los polinomios
Teorema de Gauss �������������������������
del polinomio

Teorema del resto
Consiste en asignar un valor a la variable �� y reemplazarlo en el polinomio que estamos estudiando, si el resultado es cero, entonces hemos hallado una raíz del mismo.
Regla de Ruffini
El polinomio a analizar, debe estar completo y cada división le baja un grado
Cuando se halle una raíz, el resto valdrá cero y se procede a reescribir el polinomio en forma factorizada.
Divisor
Ejemplo:
��(��)=��4 2��2 +1
Coeficientes del nuevo polinomio
Divisores de p: p=1 → ±1
Divisores de q: q=1 → ±1
Posibles raíces p q : p q =±1
El polinomio es: ��(��)=��4 2��2 +1
Probamos con �� = 1 ��( 1)=( 1)4 2. ( 1)2 +1=1 2+1=0

Polinomio a factorizar
Como el resto es cero, decimos que �� = 1 es una raíz del polinomio, ahora aplicamos Ruffini
Completamos la función polinómica ��(��)=��4 +0��3 2��2 +0��+1
Podemos ahora reescribir el polinomio sabiendo que la raíz hallada es (��+1)
��(��)=1 (��+1) (��3 ��2 ��+1) es el resultado de la primera factorización
Analizamos el nuevo polinomio, que podemos llamarlo ��(��)=��3 ��2 ��+1
Probamos otra posible raíz, por ejemplo �� = 1
��( 1)=( 1)3 ( 1)2 ( 1)+1= 1 1+1+1=0 hay una raíz en �� = 1

Surge una nueva raíz (��+1) que ahora por haberse repetido, es una raíz multiplicidad par.
El cociente nos entrega un nuevo polinomio de un grado menor al anterior
��(��)=��2 2 ��+1 el cual deberemos factorizar
El polinomio principal se puede reescribir como: ��(��)=1.(��+1).(��+1).(��2 2��+1)
Analizamos ��(��) en �� =1
��(1)=(1)2 2 (1)+1=1 2+1=0
Aplicamos Ruffini para �� =1
Obtuvimos otra raíz (�� 1) y el polinomio que queda como resto de la división también nos deja la última raíz (x-1). Podemos reescribir el polinomio así: ��(��)=1(��+1) (��+1) (�� 1) (��+1)
O de una forma más reducida ��(��)=1(��+1)2 (�� 1)2
Poniéndose en evidencia la multiplicidad de las raíces.
En estas condiciones podemos graficar el polinomio
��


��(��)=��4 2��2 +1


Análisis de la función
Dom ℝ Img [0; +∞) ��+ ( ∞; 1)∪( 1;1) ∪(1; +∞) �� ∅ ��0 { 1;1}
Ordenada al origen ��(0) ��(0)=(0)4 2 (0)2 +1=1
Las raíces halladas son de multiplicidad par, y por eso rebotan en el eje x.
Función Homográfica
Es de la forma ��(��)= �� �� �� +��
Si �� >0 la función es decreciente y viceversa.
En �� =�� la función no está definida, en �� =�� hay una asíntota vertical
�� es la asíntota horizontal
Ejemplo:


��������:( ∞;3) ∪ (3; +∞) o también ��������: ℝ {3} �� �� ���� ��=1

Se observan las dos asíntotas, la función no está definida en �� =3 y es decreciente en todo su dominio.

