Issuu

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

A Study on Funicular Shell Structure with various rise and thickness

Saravanan. M1 , Dr. D. Shoba Rajkumar2

1PG Student, Department of Civil Engineering, Government College of Engineering, Salem, Tamil Nadu, India

2Professor & HOD, Department of Civil Engineering, Government College of Engineering, Salem, Tamil Nadu, India

Abstract - Shell structures are characterized as stressed skin systems due to their geometric form and minimalflexural rigidity, which enable them to primarily carry loads through in-plane direct stresses. In their ideal membrane state, concrete shells sustain external forces predominantlythrough compressive stresses, eliminating the need for reinforcement except for secondary effects such as bending or shrinkage. In most shell roof structures, the self-weight isthedominantload and selecting a shell geometry that facilitates compressive loading without inducing bending is beneficial. This study explores how the thickness and rise of funicular shells constructed on a square base affect their ultimate load capacity. Using ABAQUS Finite Element Analysis software,the impact of rise and thickness on displacements, maximum absolute stresses and membrane stresses are examined. Results indicate that increasingtherisereduces displacements and stress levels. The influence of thickness on membrane stress becomes less significant at higher rises, confirming the importance of shell rise in minimizing stress concentrations.

Key Words: FunicularShell,Rise,Thickness,Displacement, Stresses

1. INTRODUCTION

Shell structures area category of load-bearing systems that primarily depend on direct in-plane stresses for structural integrity, made possible by their curved geometries and low bending stiffness. These thin, curved elements,typicallyconstructedfromconcretereinforcedwith asteelmesh,resistappliedloadsviacombinationsoftensile, compressive and shear stresses distributed across their surface.Thegoalinshelldesignistomakethestructureas thin as practical constraints allow, thereby reducing dead loadandallowing itto behave likea membrane,free from significantbendingeffects.Thisstrategypromotesmaterial efficiencywhileenablingstrongandelegantstructuralforms. Natural shell forms are mostly doubly curved, offering advantagesinbothaestheticsandstructuralperformance.

Particularly,funicularshellsexhibithigherultimateload capacitycomparedtosinglycurvedshellssuchascylindrical ones.Instructuralanalysis,shellelementsareoftenassumed tobeisotropicandhomogeneous.However,whendesigning reinforcement,concreteistypicallytreatedascrackedand steelisintroducedtoresistdirectanddiagonaltensileforces. Thisdistinctionremainsnecessaryaslongaselastictheory governs shell stress analysis. The analytical modeling of

complexshellroofscanbedifficult,leadingtothecontinued useofphysicalmodelsasdesigntools.

Certain secondary effects, like those caused by temperaturefluctuationsormaterialshrinkage,aredifficult tocalculateaccurately,especiallyintropicalclimateswhere temperature-inducedstressescanexceedthosefromloading. Fine, closely spaced reinforcement is crucial in such situations to prevent cracking and increase ductility. This principle is applied in ferrocement, which involves embeddingmultiplelayersoffinewiremeshinrichmortarto achievethedesiredthicknessandductility.

Althoughnumerousshellgeometriesarepossible,onlya fewstandardformsarecommonlyusedinconstruction,often individually or in combination. These combinations are referred to as composite shells. Shell surfaces can be categorized based on curvature (single or double) or generation method (translational or rotational). However, theseclassificationsarenotalwayspreciseandmayoverlap.

Additionally,shell like structuresmadefromflatplates connectedalongstraightedgesoftentermedfoldedplatesare widely used due to ease of construction. Finite element methods are a standard approach for analyzing such structures.PlateandshellelementsinFEMcanbetriangular orquadrilateralandtheirthicknesscanvaryacrossnodes. Whenquadrilateralelementsarenotplanar,itisadvisableto modelthemastrianglesforbetteraccuracy.

Software tools such as ABAQUS, ANSYS, STAAD.Pro, SAP2000andSTRAPofferstrongcapabilitiesforanalyzing shell behavior under varied support conditions. In this investigation, ABAQUS is utilized for the modeling and analysisoffunicularshellstructures.

2. OBJECTIVES AND SCOPE

This study investigates the structural response of funicular concrete shells with a square base, focusing on variationsinshellriseandthickness.Usingthefiniteelement platformABAQUS,theanalysisevaluates displacement(y), maximumabsolutestressandmembranestresses(S11&S22) using the Finite Element Software ABAQUS. The Funicular shellswithfivedifferentrisesandthreedifferentthicknesses (40mm,50mmand65mm)areconsideredforthisstudyand aredesignatedasfollows,

1. FS-I-Funicularshellwithrise,r1 (125mm)

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

2. FS-II-Funicularshellwithrise,r2 (143mm)

3. FS-III-Funicularshellwithrise,r3 (167mm)

4. FS-IV-Funicularshellwithrise,r4 (200mm)

5. FS-V-Funicularshellwithrise,r5 (250mm)

Due to their lightweight nature, aesthetically pleasing geometryandhighload-bearingcapacity,shellstructuresare widelyusedinconstruction.Particularly,funicularshellsare suitableforlarge-scaleroofingapplications,offeringgreater strength with minimal use of materials making them a sustainablealternativetoconventionalstructuralsystems.

3. LITERATURE REVIEW

 S. Elangovan (1990) developedacomputerprogramme to analyze the funicular shell on a rectangular ground plan, witha uniformly distributed load. The eight-node iso-parametricelementsareusedtoanalyzeshells.

 K. N. Lakshmikandhan et al. (2014) investigatedboth material and geometrical nonlinearities in the finite element analysis of concrete shells and the results are comparablewiththeexperimentalresults.Theresultalso infersthatthereinforcementsarenotrequiredattheshell surface.

 Siddesh T M et al. (2016) observed that with the increase in rise and thickness of funicular shell the deflectionisreduced.Themembranestressesdecrease with the increase in rise and thickness of concrete funicularshell.

 Vidya Vijay K. et al. (2023) explains the use of lightweightmaterialtocreatelightweightstructureswith larger spaces by optimizing the structural frame. The analysis of shell structures reveals a fascinating intersectionofarchitecturalingenuityandengineering precision.

 Gloria Rita Argento et al. (2024) discussed MATLAB based tool named R-Fun Optimization and used to optimize the shape of a bi-parabolic shell roof with respecttosixobjectivefunctionssomehowdependingon thegeneralizedeccentricity.

4. ANALYTICAL SIMULATION USING ABAQUS

ABAQUSisafiniteelementbasedstructuralprogramfor the analysis and design of structural elements. It offers an intuitive,yetpowerfuluserinterfacewithmanytoolstoaidin thequickandaccurateconstructionmodels,alongwiththe sophisticated analytical techniques needed to do the most complexprojects.

ABAQUSisacontrolledbase,meaningthatthemodelsare created with member that represents the physical reality. Results for analysis and design of reported for the overall object,andnotforeachsubelementthatmakesuptheobject, providinginformationthatitisbotheasiertointerpretand moreconsistencywiththephysicalstructure.

The theoretical Finite Element Analysis and the computation of maximum absolute stresses, membrane stresses and displacements corresponding to the applied loads on funicular shells are carried using the standard program ABAQUS. Shell elements are a special class of elements that are designed to efficiently model thin structures.TheFunicularShellswithvariousrisesandthree different thicknesses (40mm, 50mm and 65mm) are modelledbytakingthex,yandzcoordinatesoftheshells

MaterialpropertiesoftheFunicularshellsaredefinedand the values are assigned to the elements. The values of the material propertiesassignedtotheelementsareshownin table-1.

Table -1: PhysicalPropertiesofFunicularShell

Physical Property Value (mm)

LengthoftheShell, l 1000 BreadthoftheShell, b 1000 Shellthickness, t1, t2 & t3 40,50&65

Rise, r1, r2, r3, r4, & r5 125,143,167,200&250

Table -2: MaterialPropertiesofFunicularShell

YieldStress(N/m2) 25x106 500x106

FunicularShellwithvariousrisesismodeledwithfournodedquadrilateralshellelements.Theshellisdiscretized intosmall elementsandthesupportsarerestrainedatthe certain boundaries. To determine the displacements, membranestressesandshearstressesan arbitraryloadis appliedallovertheshellelements.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

5. RESULTS AND DISCUSSION

Fromtheresultsoftheanalysis,displacements,maximum absolutestressandmembranestressesareobtained.

Table -3: ResultsofFunicularShellofThickness-40mm

Table -5: ResultsofFunicularShellofThickness-65mm

Stress, S11 (N/mm2)

MembraneStress, S22 (N/mm2)

Displacement, y (mm)

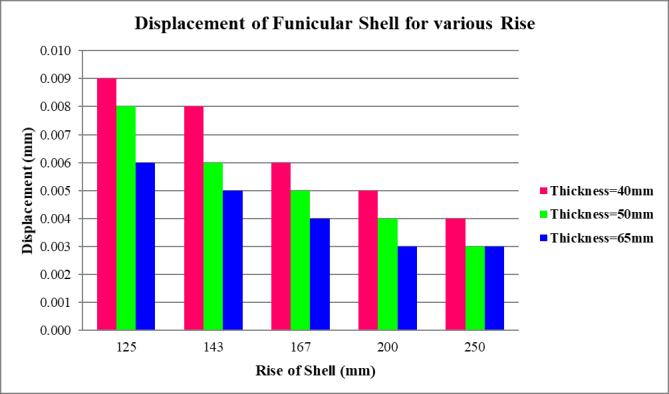
Chart -1:Displacement(y)forvariousrise&thickness

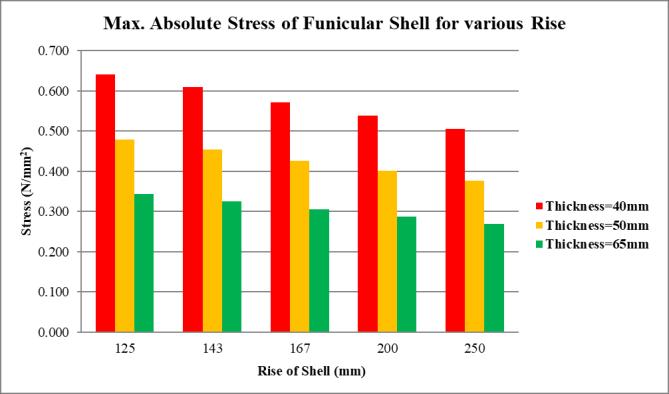
Chart -2:Max.AbsoluteStressforvariousrise&thickness

Table -4: ResultsofFunicularShellofThickness-50mm

(N/mm2)

Stress, S

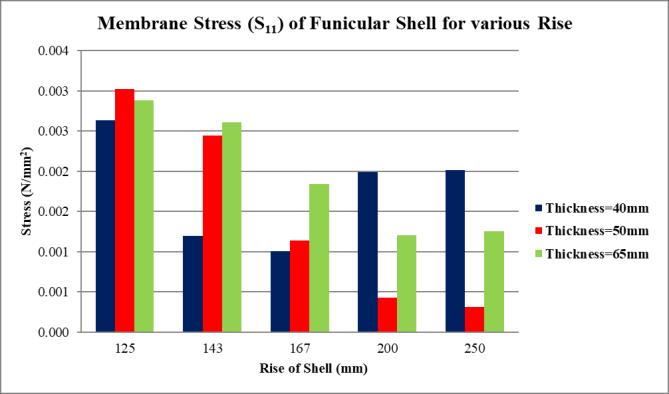
Chart -3:MembraneStress(S11)forvariousrise& thickness

Fig -1:PartModule-FunicularShell

Fig -2:AssigningBoundaryConditions

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 12 Issue: 07 | Jul 2025 www.irjet.net p-ISSN: 2395-0072

6. CONCLUSIONS

Basedonthefiniteelementanalysisoffunicularshellswith varying rises and three different thickness configurations, thefollowingkeyobservationshavebeenmade:

 Astheriseoftheshellincreases,themaximumabsolute stress experienced by the structure consistently decreasesacrossallthicknesscategories(40mm,50mm and 65mm). This trend suggests that greater shell curvaturecontributessignificantlytoloweringinternal stress.

 Foranyfixedshellrise,increasingthethicknessresultsin reducedstresslevels.Specifically,the65mmthickshells demonstratesuperiorstressresistancecomparedtotheir thinner counterparts, implying that a thicker shell improvesstructuralperformanceunderloading.

 Themembranestresses(S11 andS22)decreasewhenthe rise increases from 125mm to 167mm, but a reverse trendisobservedbeyondthispoint.Thisindicatesanonlinear relationship between shell rise and membrane stress,highlightingtheexistenceofanoptimalrisethat minimizesstressconcentrations.

 As the rise becomes more significant, the effect of thicknessonmembranestressbecomeslesspronounced. Thisemphasizesthedominantroleofrisegeometryin influencingthestressbehavioroftheshell.

 Displacementvaluesdeclinewithincreasingriseforall considered thicknesses. This suggests that shells with greater rise exhibit improved stiffness and reduced deformation,particularlybenefitingthinnershellprofiles byenhancingtheiroverallstructuralstability.

 Thicker shells show less deformation under load, with 65mmshellsexhibitingtheleastdisplacement,followed by50mmand40mm.Thisconfirmsthatincreasingshell

thickness directly contributes to greater rigidity and reducedstructuraldeflection.

REFERENCES

[1] Bhattacharya and G. S Ramaswamy, “Analysis of funicularshellsbythefiniteelementmethod,”Journal ofStructuralEngineering,October,pp158-164,1978.

[2] S. V Chaudhari, “Modeling of concrete for nonlinear analysis Using Finite Element Code ABAQUS,” InternationalJournalofComputerApplications,Vol.44, No.7,2012.

[3] K.N.Lakshmikandhan,P.Sivakumar,R.Ravichandran and R. Manisekar, “Mathematical Modelling of ReinforcedConcreteBeamsandRepairedRCBeams,” ResearchReport,RR17,2012,CSIR-SERC,India.

[4] Indian Standard (IS). (1995). “Code of practice for construction of reinforced concrete shell roof”. IS: 2204-1962,NewDelhi,India.

[5] Indian Standard (IS). (1998). “Criteria for design of Reinforcedshellconcretestructureandfoldedplates”. IS:2210_1988NewDelhi,India.

[6] IS6332-1984,“Indianstandardcodeforconstructionof floors and roofs using precast doubly curved shell units”.

[7] S. Rajasekaran and P. Sujatha, “Configuration of deep funicularshellsbyboundaryintegralelementmethod,” JournalofStructuralEngineering,Vol9,No1,pp37-46, April1992.

[8] G.S.Ramaswany,“InnovativeApplicationsofFunicular Shells,” Shells, Membranes and Space Frames, Proceedings IASS Symposium, Osaka, Vol 1, pp 313320,1986.

[9] Ramaswamy,G.S,“Designandconstructionofconcrete shell roofs”. CBS Publishers and Distributors 11, Daryaganj,NewDelhi-110002(India).

[10] G.S.Ramaswamy,N.V.RamanandZachariaGeorge,“A doubly-curvedfunicularshellroofforacementstore,” IndianConcreteJournal,pp20-23,January1961.

[11] G.R.Suresh,C.S.DesaiandG.SRamaswamy.,“Shape generationofthin,shallow,funicularconcreteshellsby thefiniteelementtechnique”,IndianConcreteJournal, pp334-336,Dec1985.

[12] Vafai and M. Mofid, “Experimental study of prefabricated funicular shell units”, Engineering Structures,Vol.19,No.9,pp.748-759,1997.

Chart -4:MembraneStress(S22)forvariousrise& thickness

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

[13] W. Weber, ‘Ultimate Loads for Shallow Funicular ConcreteShells’,Northwest,Vol.(58),No.3,187–19, 1984.

[14] P. Sachithanantham, S. Sankaran, S. Elavenil (2015) “Deflection Characteristics of Shallow Funicular Concrete Shells over Rectangular Ground Plan Ratio 1:0.5”.InternationalJournalonRecentandInnovation Trends in Computing and Communication, Volume3, Issue7.

[15] S.ElangovanandA.R.Santhakumar(1988)“Parametric StudyofFunicularShells”.InternationalSymposiumon Innovative Application of Shells and Spatial Forms, pp.193-203.