AJUSTE DE DATOS
REGRESIÓN LINEAL SERIES CRONOLÓGICAS
PRESENTADO POR:
WENDY LORAINE SERRANO ARENAS - 222286
ANDRES JULIÁN ARENIZ CASTRO - 222280
DOCENTE: AURA ESMIR NAVARRO CARRASCAL
DUSHSPORT S.A.S
ESTRATEGIA PEDAGÓGICA DOSSIER FORMATIVO INTEGRADOR
UNIVERSIDAD FRANCISCO DE PAULA SANTANDER SECCIONAL OCAÑA
FACULTAD DE CIENCIAS ADMINISTRATIVAS Y ECONÓMICAS
CONTADURÍA PÚBLICA
OCAÑA N. S
2023
1
2 TABLA DE CONTENIDO INTRODUCCIÓN..........................................................................................................................5 OBJETIVO GENERAL..................................................................................................................6 Objetivos Específicos 6 JUSTIFICACIÓN 7 ALCANCEDE LA INVESTIGACION.........................................................................................8 Planteamiento Del Problema.......................................................................................................8 TABLA DE DATOS 1 9 TABLA DE DATOS 2 9 ACTIVIDAD DOSSIER...............................................................................................................10 SOLUCIÓN..................................................................................................................................11 1. ¿Cuál es la variable independiente y dependiente? 11 2. Representar la información en un diagrama de dispersión. ..............................................11 3. Calcule la media, la varianza, la desviación estándar y la covarianza...............................11 TABLA DE DATOS 3 .................................................................................................................12 Media Aritmética 12 Varianza................................................................................................................................12 Desviación Estándar..............................................................................................................13 Coeficiente deVariación 13 Error estándar de estimación 13
3 Error estándar de estimación.................................................................................................14 Media Aritmética..................................................................................................................14 Varianza 14 Desviación Estándar..............................................................................................................15 Coeficiente deVariación.......................................................................................................15 Error estándar de estimación.................................................................................................15 Error estándar de estimación 16 Covarianza Simple de X e Y.................................................................................................16 4. Calcula los parámetros y establecer las ecuaciones de la estimación mediante la regresión tanto para y como par x.............................................................................................................16 Los parámetros b y c en la recta de regresión “2 en 1”.........................................................16 Hallamos C 17 Recta Ajustada Para Y..........................................................................................................17 Los parámetros b y c en la recta de regresión “1 en 2”.........................................................18 Hallamos C............................................................................................................................18 Recta Ajustada Para X 19 5. Los valores estimados para ���� represéntelo en un plano cartesiano................................19 Gráfica de ajustede datos con respecto a Y estimada..........................................................19 Gráfica de ajustede datos con respecto a X estimada 20 6. ¿Cuál es el coeficiente de correlación y determinación? ......................................................21
4 Coeficiente De Correlación...................................................................................................21 Coeficiente De Determinación..................................................................................................22 7. MétodoDe Semipromedio 22 Hallamos B............................................................................................................................23 Hallamos C............................................................................................................................23 CONCLUSIONES........................................................................................................................24
INTRODUCCIÓN
En el contexto actual, el manejo y análisis de datos se ha convertido en un aspecto fundamentalendiversas áreas delconocimiento. Desdelaciencia yla tecnologíahastala economía y la investigación, la capacidad deextraer información valiosa deconjuntos de datosse ha vuelto esencial para la toma de decisiones informadas y el avance en diferentes campos.
En este trabajo, abordaremos específicamente los datos bidimensionales; creando una relación entre dos empresas usando precios de diferentes productos, para así entender la dependencia intrínseca que contiene estos datos.
Para lograr esto se usarán las técnicas estadísticas que nos permiten lograr su cálculo y obtener el conocimiento de la relación investigada; además se implementaran deducciones como el funcionamiento de las empresas y con respecto a su comparación.
Usaremos una base teórica y práctica en este tema, dondese espera obtener la experiencia estadística, contribuir al avance del conocimiento estadístico y brindar herramientas útiles para analizar y comprender las relaciones entre variables en diversas disciplinas.
5
OBJETIVO GENERAL
Describir el comportamiento de la relación entre las variables impuestas por las dos empresas “Dushsport S.A.S” y “Damiansport S.A.S”, para lograr su entendimiento funcional e implementar las correctas deducciones. Tales deduccionesson creadas directamente por las técnicas empleadas para la aplicación de la estadística, donde podemos entender de plano cómo funciona la relación investigada.
Objetivos Específicos
1. Construir tablas de datos.
2. Construir grafica de dispersión de los datos.
3. Responderemos las preguntas propuestas.
4. Con base a las preguntas propuestas, calcularemos la regresión implícita en las variables. Posteriormente, se calcularán las medias aritméticas, varianzas, desviaciones, covarianzas y correlación, para el efectivo ajuste de los datos, obteniendo así la ecuación de la recta.
6
JUSTIFICACIÓN
La regresión lineal es un tema de gran importancia, donde se observa gran variedad de aplicaciones, por eso en el ámbito Económico Empresarial es de carácter necesario, pues es una herramienta fundamentaly crucial en la toma dedecisiones, predicción deventas,perdidas,etc.A groso modo es obligatorio si queremos optimizar la empresa en general.
La estadística inferencial es una herramienta poderosa, pero también puede presentar desafíosysupuestos quedebenser comprendidosy gestionadosadecuadamente;como estudiantes de la Ciencia Estadística, tenemos el deber desiempre dar aplicación a los conceptos aprendidos para conocer su método, y de tal manera obtener la experiencia y el conocimiento.
Por lo tanto,el presente trabajo desarrolla la técnica del estudiante,al igual que mejora su conocimiento, así mismo el lector será consciente de la gran utilidad y funcionalidad de la regresión por medio de este ejercicio práctico brindando a los investigadores y profesionales las habilidades necesarias para utilizarla de manera efectiva.
7
ALCANCE DE LA INVESTIGACION
Planteamiento Del Problema
Con el propósito de potenciar nuestra empresa DUSHSPORT S.A.S, líder en ventas de artículos deportivos,se haoptadoporllevar acabo unainvestigación conel findeadecuarnuestros precios a los dela competencia. Para ello, hemos realizado un análisis exhaustivo delas empresas circundantes a nuestra ciudad,centrándonosen la comparación con la empresa DAMIANSPORT
S.A.S. Hemos evaluado los precios de 15 productos similares a los nuestros, y los resultados obtenidos se presentan en las siguientes tablas de regresión y correlación lineal simple.
8
TABLA DE DATOS 1
En la siguiente tabla se encuentran reflejados los productoscon sus respectivos precios de cada una de las empresas de venta de artículos deportivos existentes en nuestra ciudad.
A continuación, mostramos y analizamos el gráfico de dispersión de la tasa de variación diaria del precio de la Empresa DUSHSPORT S.A.S contra el índice DAMIANSPORT S.A.S, para observar si existe una relación entre las dosempresas, desarrollaremos una serie defórmulas de regresión y correlación lineal.

TABLA

DE DATOS 2
9
ACTIVIDAD DOSSIER
1. ¿Cuál es la variable independiente y dependiente?
2. Representar la información en un diagrama de dispersión.
3. Calcule la media, la varianza, la desviación estándar y la covarianza.
4. Calcula los parámetros yestablecer las ecuaciones dela estimación mediantela regresión tanto para y como par x.
5. Los valores estimados para represéntelo en un plano cartesiano.
6. ¿Cuál es el coeficiente de correlación y determinación?
7. ¿Cuál es la ecuación de la recta por ajuste de semipromedio?

10
SOLUCIÓN
1. ¿Cuál es la variable independiente y dependiente?
La variable X será DUSHSPORT S.A.S y la variable Y será DAMIANSPORT S.A.S
2. Representar la información en un diagrama de dispersión.

3. Calcule la media, la varianza, la desviación estándar y la covarianza.
Para calcular la media, la varianza, la desviación estándaryla covarianza debemosrealizar una tabla primero.
11
TABLA DE DATOS 3

Ahora procedemos a calcular la media, la varianza, la desviación estándar y la covarianza
Respecto a x:
Media Aritmética



= 1.415.000
Varianza

12
���� ² = 6.232.169.750.000 - 2.002.225.000.000




���� ² = 4.229.944.750.000
Desviación Estándar
���� = √4.229.944.750.000
���� = 2.056.682,94
Coeficiente de Variación
����=14534,861767% El grado de dispersión se podrá obtener a través con una medida conocida con varianza residual o varianza no explicada.
(������)2=172.693.809,68
Error estándar de estimación
������= 13141,30167
13
2= 172.725.335




Error estándar de estimación
������= 13142,50109
Ahora procedemos a calcular la media, la varianza, la desviación estándar y la covarianza
Respecto a Y: Media Aritmética = 1.407.029
14 (������
)
² ���� ² = 6.225.582.405.612,5 - 1.979.730.606.841 ���� ² = 4.245.851.798.771,5
Varianza
Desviación Estándar
Coeficiente de Variación
����= 146,4466248%
El grado de dispersión se podrá obtener a través con una medida conocida con varianza residual o varianza no explicada. o (������)
2= 173.343.240






Error estándar de estimación ��
= 13165,988
15
����
(������)2= 29.308.035.849,88
Error estándar de estimación
������= 171195,899
Covarianza Simple de X e Y
����������=4.237.804.282.500
4. Calcula los parámetros y establecer las ecuaciones de la estimación mediante la regresión
tanto para y como par x.
Los parámetros b y c en la recta de regresión “2 en 1”
1) ∑ ���� = ������ ∑ ���� + ��������



2) ∑ �������� = ������ ∑ ���� ² + ∑ ����������
2) 49.830.002.540.000=������ (49.857.358.000.000)+����(11.320.000)
16
1)
2) 49.830.002.540.000=������


1)
+������(11.320.000)
17
11.256.230=������(11.320.000)+������ (8) (-1.415.000)
(49.857.358.000.000)
________________________________________________________________
(36.895.958.000.000)
Hallamos
(10.401.561,81495003)
(8)
10.401.561,81495003
(8)
15.927.565.450.000=����(−12.961.400.000.000)+������ (−11.320.000)
33.902.437.090.000=����
0,9188658847129=������
C 11.256.230=����(11.320.000)+������ (8) 11.256.230=(0,9188658847129)(11.320.000)+ ������ (8) 11.256.230=
+ ������
11.256.230−
= ������
854.668,18504997=������ (8)
106.833,5231312463=������
����=
Recta Ajustada Para Y
(106.833,5231312463) + (0,9188658847129)��
Los parámetros b y c en la recta de regresión “1 en 2”
1)
2)

18
∑ X�� = ��xy ∑ Y�� + ����xy
∑
��
��
��xy ∑ Y�� ² + ∑
����xy
49.830.002.540.000=������ (49.804.659.244.900)+����(11.256.230)
11.320.000=������(11.256.230)+������ (8) (-1.407.029) 2) 49.830.002.540.000=������ (49.804.659.244.900)+������(11.256.230)
15.927.568.280.000=����(−15.837.842.040.670)+������ (−11.256.230) ___ 33.902.434.260.000=����(33.966.817.204.230) 0,99810453408563749154624217810903= ������ Hallamos C 11.320.000=(0,99810453408563749154624217810903)(11.256.230)+ ������ (8) 11.320.000=(11.234.894,199710775301467557592496)+ ������ (8) 11.320.000−(11.234.894,199710775301467557592496)+ ������ (8) 85.105,800289224698532442407504= ������ (8) 10.638,225036153087316555300938= ������
X
Y
=
Y
2)
1)
1)
5. Los valores estimados para �� �� represéntelo en un plano cartesiano.
Ahora procederemos a estimar los valores de ���� e ���� para lo cual realizamos una tabla de datos donde se represente los cálculos:
Gráfica de ajuste de datos con respecto a Y estimada
19 Recta Ajustada Para X ����=(10.638,225036153087316555300938) +(0,99810453408563749154624217810903)��
TABLA DE DATOS Xi Y estimada 5.915.000 5.541.925 3.780.000 3.580.147 215.000 304.390 510.000 575.455 440.000 511.135 220.000 308.984 72.000 172.992 168.000 261.203 11.320.000 11.256.230

20
de ajuste de datos con respecto a X estimada TABLA DE DATOS Yi X estimada 5.932.500 5.931.893 3.750.000 3.753.530 200.000 210.259 492.000 501.706 435.150 444.963 205.000 215.250 70.900 81.404 170.680 180.995 11.256.230 11.320.000
Gráfica
6. ¿Cuál es el coeficiente de correlación y determinación?

Procederemos a calcular la correlación para determinar cuanta relación existen entre las dos variables y determinar si la estimación o predicción es fiable.
Coeficiente De Correlación

21





22 r=R=0,9999891820653181 Coeficiente De Determinación ��2=1−0,00690274469828976056509490316684 ��2=0,99309725530171023943490509683316 ��2=0,84115115734652309619937296504959
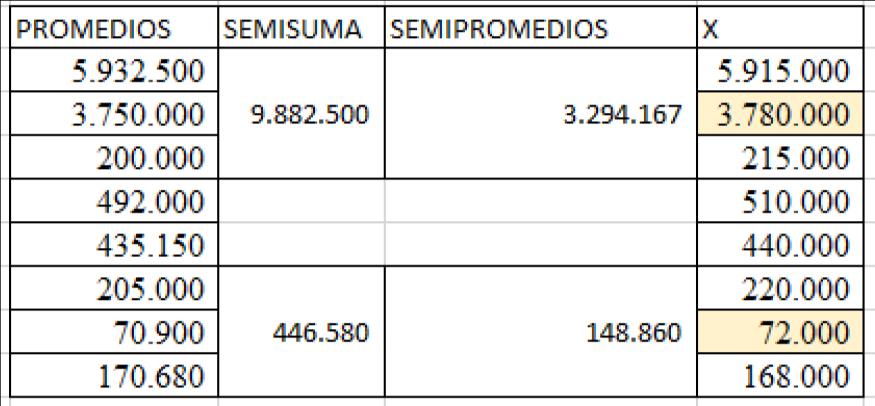
Método De Semipromedio .
7.
Hallamos B
3.294.167 = 3.780.000�� + C (-1)
148.860 = 72.000��+ C
-3.294.167 = −3.780.000�� - C
148.860 = 72.000��+ C
-3.145.307 = 3.708.000 B
Hallamos C
3.294.167 = + C
3.294.167 = -3.145.307 + C





23 ����= ���� + C
B
c Xi
CONCLUSIONES
Con base a los datos obtenidos, y gracias a las gráficas trazado observamos que las variables son muy cercanas, de tal modo podemos estimar que los coeficientes son beneficiosos, brindándonos una posible confianza para el pronóstico; A posteriori, la gráfica ajustada nos permite entender la relación exacta de las variables, y con base a los cálculos de los coeficientes dedeterminación ycorrelación, nos demuestra que la predicción si es confiable, brindándonos así la posibilidad de tener una alta certeza de estimación.
Del mismo modo, observamos que las sumas de cuadrados de regresión (SCR = 28.571.229.969.764), comparado, con la suma decuadradosde errores (CSE = 234.464.286.799), nos hace entender que el ajuste es lo suficientemente correcto para poder estimar, demostrando una disminución del -120,85...%, conforme a los cálculos.
Para nuestra empresa DushSport S.A.Ses beneficiosa esta predicción para la comparación defuturasvariables, lo cual nos ha permitido entenderquelas empresas en comparación tienen un comportamiento muy similar a los precios, dándonoscoeficientes altos como prueba deello; a su veznos demuestraquela capacidadparaestablecer precios dela empresa en comparación (Damian Sport S.A.S), puedeestimarse la similitud conforme a los cálculos, y establecer series de tiempo sobre las mismas para saber cuáles serán sus posibles ventas.
En conclusión, el comportamiento es muy similar y se soporta o se defineconforme a los cálculos realizados anteriormente, donde se demuestra altos coeficientes, gran reducción de la variabilidad en la regresión y por ello nos brinda firmeza; entonces se deduce que los comportamientos de las empresas son similares con base a los precios, al igual se puede afirmar que otrasvariables uotros comportamientos son pronosticables, dándonosasíla certeza para crear estrategias en la empresa DushSport S.A.S en su libre competencia.
24









































