4
DUAL FOCUS
SECONDARY EDUCATION PHYSICS AND CHEMISTRY ANDALUSIA
CONTENTS
1. The atom 7
1 The atom and chemical changes • 2 Early atomic models and other discoveries • 3 Bohr’s atomic model • 4 Quantum mechanical model
• 5 The periodic table • 6 Atomic masses • The final challenge
2. Chemical bonding 15
1 Chemical bonding • 2 Ionic substances
• 3 Covalent bond • 4 Covalent substances
• 5 Intermolecular forces • 6 Metallic substances
• The final challenge
3. Carbon chemistry 23
1 Carbon • 2 Formulas and three-dimensional models • 3 Nomenclature • 4 Compounds of carbon and hydrogen • 5 Carbon compounds with heteroatoms • 6 Relevant carbon compounds and allotropes • The final challenge
4. Chemical reactions 31
1 Atomic theory of chemical change • 2 Energy and chemical reactions • 3 Chemical equations and amount of substance • 4 Stoichiometric calculations • 5 Acids and bases • 6 Useful reactions • The final challenge
5. Kinematics ................................................ 39
1 Rest and movement • 2 Study of motion
• 3 Types of movements • 4 Rectilinear movements
• 5 Circular motions • 6 Interpretation of graphical representations • The final challenge
6. Dynamics ................................................... 49
1 Forces • 2 Everyday forces • 3 Newton’s laws
• 4 Newton’s laws of everyday motion • The final challenge
7. Universal gravitation 57
1 Models of the universe • 2 Kepler and his three laws • 3 Law of universal gravitation
• 4 Consequences of the law of universal gravitation • The final challenge
8. Force in fluids. Pressure 67
1 Pressure • 2 Fundamental law of hydrostatics
• 3 Archimedes’ principle • 4 Pascal’s principle
• 5 Atmospheric pressure • 6 Meteorological concepts • The final challenge
9. Work and mechanical energy 75
1 Energy • 2 Physical work • 3 Mechanical power • 4 Conservation of mechanical energy • 5 Waves
• The final challenge
10. Thermal energy and heat 83
1 Thermal energy. Temperature • 2 Heat transfer
• 3 Electromagnetic radiation • 4 Effects of heat
• 5 Thermal engine and energy degradation
• 6 Energy and society • The final challenge
6 DYNAMICS
What is the static coefficient of friction? Does it depend on the contact surface?
SCAN THE CODE TO FIND OUT ABOUT THE CHALLENGE
FORCES
• Definition
• Effects
• Characteristics YES are the in NO
Contact forces Forces at a distance
Property of the related matter Weight Normal
Friction Tension
• Gravitational
• Electromagnetic
• Nuclear
• Law of inertia
• Fundamental law of dynamics
• Law of action and reaction
• Movement in a horizontal plane
• Movement in an inclined plane
• Uniform circular motion
FOCUS O N ENGLISH
Listening and Speaking
Listen and repeat the most important terms of this unit, paying attention to their pronunciation.
Reading and Writing
Read the outline on the dynamics and write a sentence in your notebook that summarises the content of each branch.
Forces 1
1.1 Characteristics and classification of forces
Force is the quantity that measures the interaction of objects with each other. It is anything whose effect is a change in the state of motion, a deformation or both.
Force is a vectorial magnitude, so its effect depends on the direction in which it is applied, and on its modulus, or intensity. Its SI unit is the newton, N.
How are forces defined? How do you operate with forces?
1 Reading and writing. Hooke's law describes elastic deformations: ‘The modulus of the elastic force is directly proportional to the deformation of the system’. Look for information about Hooke´s law and:
a) Express this law in mathematical and graphical language.
b) Derive the dimensions of Hooke’s constant, k.
c) Suggest two units in which this constant can be expressed, including IS.
2 Writing. Someone tells you that they can move an object at a distance by pulling on it with a rope. Are they really talking about forces at a distance? In the following processes, is energy transferred by heat or work?
1.2 Composition and decomposition of forces
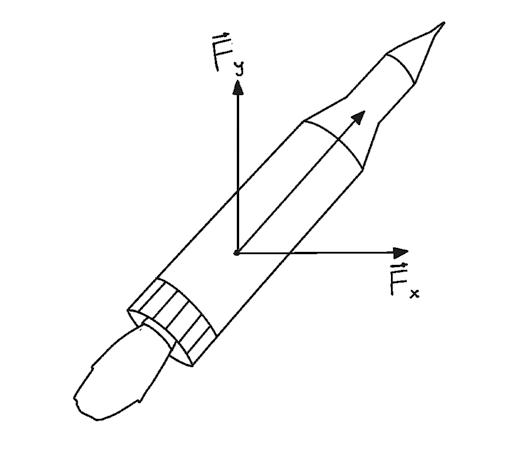
Normally more than one force acts on an object, so the principle of superposition of forces states that the net or resultant force is the vector sum of them all. The force can also be decomposed along the axes to obtain its two components.
Problem solved
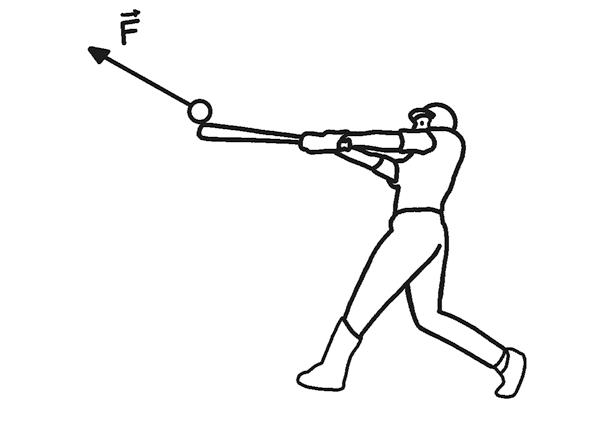
1 The motors of a drone exert on it the force shown in the figure. Obtain the components in the horizontal and vertical directions.
Vocabulary
Force – Vectorial magnitude –State of movement –Deformation – Gravitational force – Electromagnetic force –Nuclear force – Resultant force
Plot the requested axes to obtain the components of the force.
Everyday forces 2
What forces do we live with?
What is the coefficient of friction?
Weight Normal
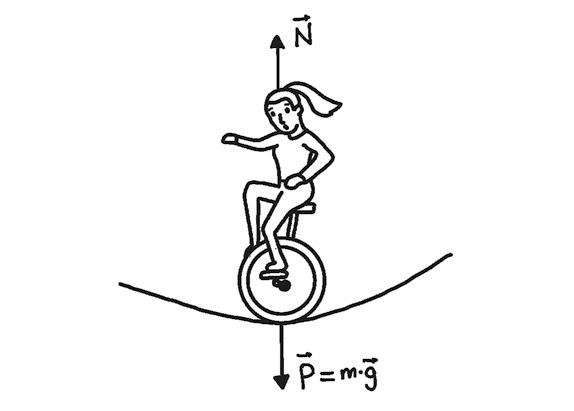
Weight, P " , is due to the gravitational pull of the Earth. It is a force that acts at a distance and always points towards the centre of the planet.
On the Earth's surface, the weight force always has a vertical direction and downward direction.
When two objects are in contact, the normal force acts, N " , perpendicular to the contact surface.
When an object slides over a surface or when we move in a fluid such as a liquid or gas, it experiences resistance to motion. This gives rise to
The frictional force , R, is an electromagnetic contact force acting in the opposite direction to the motion. Its modulus is directly proportional to that of the normal force:
The constant µ is the friction coefficient, (it is dimensionless and its value is between 0 and 1). This coefficient can be static, µe, or dynamic or kinetic, µd 2
When a rope is under tension, its particles tend to separate and, at the same time, oppose this separation, thus creating tension, which is transmitted throughout.
Vocabulariy
Weight – Gravitatory attraction – Normal – Friction – Fluid – Resistance – Friction force – Fluid – Drag force – Coefficient of Friction
If the force exerted is very large, it can overcome the interaction between particles and break the rope.
Newton's laws 3
Newton's laws, published in 1687, are three laws that describe how forces act in motion.
3.1 Law of inertia
This law states that all objects maintain their state of rest or uniform rectilinear motion, unless they are forced to change this state by externally applied forces.
As long as a vehicle is moving at a constant speed, passengers stay in their seats. However, if it brakes, passengers tend to move forward. If it accelerates passengers move backward, or sideways if the vehicle takes a curve.
Inertia is responsible.
3.2 Fundamental law of dynamics
The change in the state of rest or motion of an object is proportional to the force acting on it and acts in the direction of the force. The constant of proportionality is related to the mass of the object. Mathematically:
== " " " F " is the net force acting on the object.
Mass is the quantity that measures the inertia of an object.
Fundamental law of dynamics
The second law states that the acceleration has the same direction as the force.
An object at rest in a reference frame will remain at rest if the net force is zero due to the law of inertia. An object at rest may not be in equilibrium if the forces applied cause the object to rotate about itself.
Rotation, if it occurs, is due to the moment of force: M = F · d
Its IS unit is N · m
How are movements studied in terms of forces?
What do Newton's laws say?
The law of inertia contains important aspects:
• It is a qualitative definition of force as an agent capable of modifying velocity.
• Rest and uniform rectilinear motion are equivalent states.
• Introduces the concept of inertia, or opposition to changes in motion.
This law makes it possible to define the newton, the IS unit of force, as the force which can accelerate an object of 1 kg mass at 1 m/s2
In this case, the momentum produces a counterclockwise rotation; if the force were directed upwards, it would be clockwise. F M = F · d d
Thus, an object is in equilibrium if it fulfils these two conditions:
(rot
Pair of forces
A case in which only rotation occurs is a pair of forces. These are two parallel forces of the same modulus and opposite directions. The sum of the forces is zero (rest), but both contribute the same type of momentum.
3.3 Law of action and reaction
Forces always act in pairs and no force can ever be found in isolation. For every action there is always a reaction in the opposite direction and equal in modulus. Both act simultaneously, each on one of the interacting objects, so they do not cancel each other out.
If F is the modulus of the forces and d is the diameter of the flywheel, the torque moment: M = F · d.
The acceleration of each object depends on the force acting on it and its mass.
3 Writing. We find that the acceleration with which an object slides down an inclined plane at an angle α and with a coefficient of friction µ is: a x = (sen α – µ · cos α ) · g
Interpret the result obtained for the case where α = 90°.
4 We want to make a 60 kg box slide by pushing it with a horizontal force on a horizontal floor.
a) What minimum force should we apply if the static coefficient of friction is µ e = 0,15?
b) If we exert a double force, what will the acceleration be if the dynamic coefficient is µ d = 0,1?
Vocabulary
Law of inertia – Fundamental law of dynamics –Law of action and reaction – Newton – Equilibrium –Torque – Acceleration – Rotation – Traslation
If two objects, 1 and 2, interact, and we call " F12 the force exerted by 1 on 2 and " F21 the force exerted by 2 on 1, then the mathematical expression of the law of action and reaction is: " F12 = –" F21
5 Writing. Reason at which point on this bar is the least amount of force required to keep it horizontal.
6 Represent the Earth and the Moon in a picture and draw on it the pair of forces with which they interact.
7 Reading and writing. Read aloud and complete: «According to the law of .... all objects maintain their state of .... or uniform rectilinear motion, unless an outside… changes that state.»
8 Speaking. Explain in your own words what happens (from a physical point of view) when you push on a wall. Think about and answer questions such as: What forces are involved, what law applies, why doesn't the wall move?
Newton's laws of everyday motion
To apply Newton's laws in the study of motion it is recommended to follow three steps:
1. Identify the forces acting on the object and represent them in a diagram using the material point model.
2. Establish a reference system with the components of each force on the axes.
3. Apply the second law to the resultant on each axis.
4.1 Horizontal plane
To study motion in a horizontal plane, use a reference frame whose positive X-axis coincides with the direction and direction of motion.
• The resultant on the X-axis is the cause of the changes in motion.
• The resultant on the Y-axis is zero (if the object does not leave the ground, there is no displacement in the vertical direction).
Study of motion in a horizontal plane
The following forces act on an object sliding along a horizontal plane:
• Its weight, P " , vertical downwards.
• The normal force, N " , vertical upwards, perpendicular to the contact surface.
• Friction, R " , which opposes motion.
• The applied force, F " , which forms an angle, α, with the plane.
The force diagram, with vectors applied at the centre of mass and in the described reference frame, is as follows:
How are motions described by Newton's laws?
Apply the fundamental law of dynamics to each axis:
X-axis : FRma xx += "" " → Fx – R = m · a
Y-axis : NFP 0 y ++ = "" " N + Fy – P = 0 → N = P – Fy
Since the frictional force is R = µ · N, the X-axis expression gives the following formula: Fx – µ · (P – Fy ) = m · a
Therefore,
() µ am FPF xy =
If we substitute the value of the weight and the components: () µ cossin a m Fm gF aa =
Note. In the Y-axis expression, if we increase F it comes a point where Fy = P, so that N = 0; at this point there is no longer contact between the surfaces.
4.2 Inclined plane
In this case use a reference system in which the positive X-axis coincides with the direction of motion parallel to the inclined plane.
• The resultant on the X-axis is the cause of the changes in motion.
• The resultant on the Y-axis is zero; the object neither separates from the plane nor sinks through it.
Vocabulary
Horizontal plane – Inclined plane –Axis – Trajectory – Centripetal force
Study of inclined plane motion at α
We will assume that the object slides downwards due to its own weight. The forces acting on the object are:
• Its weight, P " , downwards.
• The normal force, N " , perpendicular to the contact surface.
• Friction, R " , which resists motion.
The force diagram, applied at the centre of mass in the reference frame, is as follows:
4.3 Dynamics of uniform circular motion
Newton'ssecondlawappliedtothetwoaxes:
Therefore:
Note. If, instead of going down, the object goes up, the force diagram is the same, but with the frictional force in the opposite direction, since it always opposes the motion. It is easy to see that, in this case, the acceleration is:
In addition, other forces could be applied to the object, the components of which we would have to consider.
In uniform circular motion the acceleration has only a normal, or centripetal, component.
At each point on the trajectory, the acceleration, " an , points towards the centre of the circle. 1
If the moving object describes a circle of radius R with speed v, the modulus of the acceleration is constant, of value: aR v n 2 = 2
9 A 35 kg crate is pulled along with a force of 200 N at 30° to the horizontal. What is its acceleration if the coefficient of friction is µ = 0,25?
10 Calculate the coefficient of friction of a 35 kg object sliding down an inclined plane at 25° with acceleration a = 1,5 m/s 2 .
According to the fundamental law of dynamics, this acceleration, " an , is due to a force acting in the same direction, called the normal, or centripetal, force:
11 A 300 g drone travels with a constant speed of 70 km/h around a circumference of radius 50 metres. Calculate the acceleration and the forces acting on it.
12 What force does the Earth exert on the Moon, whose mass is M L = 7,35 · 10 22 kg, if the average distance between them is R = 348 000 km? Consider that the Moon is in uniform circular motion around the Earth.
Take action! The final challenge
STATIC COEFFICIENT OF FRICTION
Determine whether the static coefficient of friction depends on surface area.
Group work. Organise the class into small groups to work on this challenge with your classmates.
Proposal
Before proceeding, consider how you would determine weather the static coefficient of friction depends on surface area. To do this, design an experiment and put it into practice, drawing conclusions. Afterwards, review our proposals, carry out one of them and compare the results with those you obtained with your own.
Procedure
Experiment A
Place a parallelepiped-shaped on a board and tilt the board until it moves. Measure the angle of the board and determine the coefficient of friction. Repeat with the object resting on each of its faces.
Experiment B
Place the object on the surface and pull it with a dynamometer until it moves. Calculate the coefficient of friction from the force indicated by the dynamometer. Repeat with the different faces of the parallepiped.
Tips
In the first experiment, the board must be lifted very slowly and care must be taken not to move it before measuring the angle (it is easier to work in pairs).
In the second experiment, the object must be pulled very slowly with the dynamometer, and the scale must be kept in sight. In both cases, make at least three measurements for each side, and calculate the average.
Materials
• Parallelepiped-shaped object
•Wooden board
•Protractor
•Balance
•Dynamometer
When the object starts to move, the frictional force coincides with the component of the weight parallel to the motion:
Therefore, we can say that:
When the object starts the applied force coincides with the force of friction: the frictional force:
1 Write a short scientific report on the experiment.
2 Compare your results with those of other colleagues who may have used a different procedure than yours. If there are differences, what might they be due to?
DYNAMICS 6
Forces and their characteristics
In physics, force is defined as any cause whose effect is either a deformation or a change in the state of motion.
Force measures the interaction between bodies, is a vector magnitude, and its unit of measurement is the newton, N.
1 What are the properties of forces?
Classification of forces
2 What differentiates contact forces from forces at a distance?
Composition and decomposition
The principle of superposition of forces states that the effect of each force is independent of the others, and the total force is the sum of the individual ones. Therefore, this force is called the total, or net, force.
Forces can be decomposed into their components along the axes. These are calculated by multiplying their modulus by the sine or cosine of the angle that the force makes with the coordinate axis.
3 What do we call net force?
Forces can be classified into:
• Contact forces (require direct contact, such as kicking a ball).
• Forces at a distance (between magnets, or the weight of bodies).
On the other hand, depending on the matter to which the force is related, this can be:
• Gravitational forces (mass).
• Electromagnetic forces (electric charge).
• Nuclear forces (atomic nuclei and radioactivity).
Normal force and weight
Weight is due to the gravitational pull of the Earth. It is a force at a distance, directed towards the centre of the planet. Its modulus is directly proportional to the acceleration due to gravity, g = 9.8 m/s2:
P=m·g
The normal force is due to the impenetrability of matter. When two bodies come into contact, a force is exerted perpendicular to the contact surface. This is the normal force, N $
4 Why do objects have weight?
Newton’s laws
Newton’s laws, or the laws of dynamics, are three laws by which the movements of our environment can be interpreted. They are:
1. Law of inertia
2. Fundamental law of dynamics
3. Law of action and reaction
Newton´s laws were published by Isaac Newton in 1687, and are still used in many fields today.
Friction forces
When we slide an object over a surface or move through a fluid (like liquids or gases), we notice resistance to the movement. This is due to a contact force that acts in the direction of motion in an orientation opposite to the motion. Its modulus is directly proportional to that of the normal force:
Fr = µ ·N
where µ is the coefficient of friction.
6 What are Newton’s three laws?
Law of inertia
The law of inertia was first formulated by Galileo Galilei. It states that all bodies will remain in their state of rest or continue moving in a straight line at a constant speed, unless they are forced to change that state by forces applied from outside.
7 What do we call inertia?
Fundamental law of dynamics
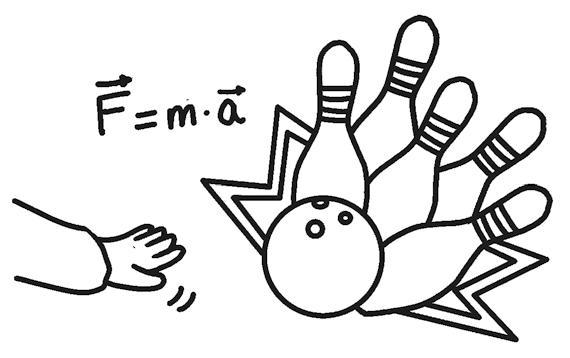
The fundamental law of dynamics states that the change in the state of motion of a body is proportional to the force acting on it, and takes place in the direction of the force. Its formula is: Fma = " "
8 What is the fundamental law of dynamics?
Law of action and reaction
The law of action and reaction indicates that for every action there is always a reaction, the two forces being of opposite direction and equal in modulus.
FF – = ABBA ""
From the law of action and reaction, we can deduce that an isolated force can never be found.
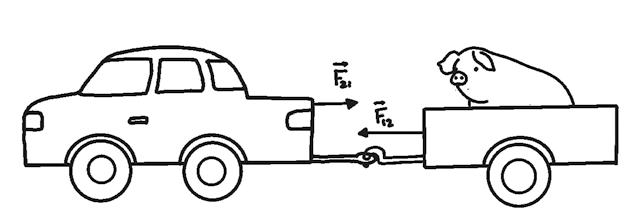
9 What does the law of action and reaction indicate?
Everyday motion: horizontal plane
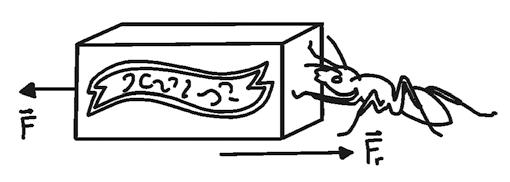
10 What forces influence horizontal motion?
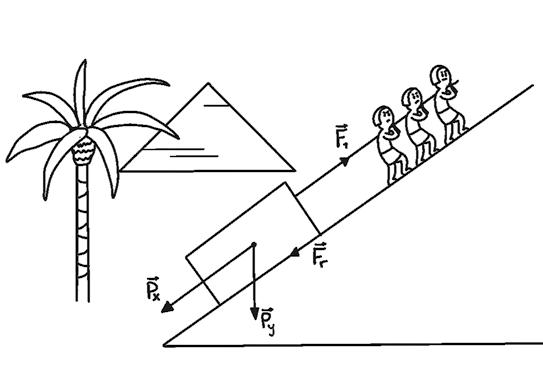
Everyday motion: inclined plane
In this case, the body will tend to fall down the plane due to its weight. However, there may be forces that cause it to move upwards or hinder its movement.
It is important to decompose the forces in this system properly.
11 Why does an object fall when left on an inclined plane?
In horizontal motion, the relevant forces will generally be the force applied and the opposing frictional force, which depends on the weight.
For this type of motion, the positive X-axis should be defined in the same direction and orientation as the motion of the body.
Everyday motion: uniform circular motion (UCM)
In uniform circular motion, if the moving body describes a circle of radius R, with velocity v " , then the modulus of the centripetal acceleration is: aR v c 2 = and this acceleration is due to the centripetal force, in the same direction and orientation, so that:
v c 2 == " " "
12 What do we call the net force in uniform circular motion? In uniform circular motion, the net force has a centripetal nature.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior permission of the publishers.
© GRUPO ANAYA, S.A., 2025 - C/ Valentín Beato, 21 - 28037 Madrid.