Operación mundo: Física y Química 4º ESO (demo)

E S O ESO F ÍSICA Y QUÍMICA

J. M. Vílchez, A. M.ª Morales, G. Villalobos, P. Tonda, L. Garrido

Índice Los saberes básicos del curso

La actividad científica 10

Una historia para conocer cómo es la actividad científica

1. Investigación científica

2. Magnitudes físicas y unidades

3. Medida de magnitudes físicas. Errores

4. Análisis de datos experimentales

Orientaciones para la resolución de problemas

Proyecto de investigación

Ciencia recreativa. Experimentos mentales

Trabajo práctico. «Densidad» de la plastilina

Para terminar

1 E l átomo y el sistema periódico 38

Una historia para conocer la complejidad del átomo

1. Discontinuidad de la materia

2. Descubrimientos que hicieron evolucionar la idea del átomo

3. Los primeros modelos atómicos

4. Los espectros atómicos y el modelo de Bohr

5. Modelo cuántico del átomo

6. El sistema periódico de los elementos químicos

7. Masas atómicas

Orientaciones para la resolución de problemas

TIC. Modelos atómicos

Ciencia recreativa. Las petites Curie

Trabajo práctico. Rayos catódicos y tubos de descarga

Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

Apéndice. Formulación y nomenclatura química

2 E nlace químico y fuerzas

Una historia sobre el enlace químico

1. El enlace químico

2. El enlace iónico

3. El enlace covalente

4. Fuerzas intermoleculares

5. El enlace metálico

6. Propiedades de los compuestos químicos

Orientaciones para la resolución de problemas

TIC. Hojas de cálculo y recursos web

Ciencia recreativa. Tipos de sustancias

Trabajo práctico. Determinación del tipo de enlace Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

3 C ompuestos del carbono

Carbono, con «C» de conveniente

1. El átomo de carbono

2. Formas alotrópicas del carbono

3. Fórmulas y modelos moleculares

4. Hidrocarburos

5. Compuestos de carbono oxigenados y nitrogenados

6. Moléculas de especial interés

7. Masas atómicas

TIC. Las TIC te ayudan a fijar conocimientos Ciencia recreativa. Modelos moleculares

del corcho blanco

4 Reacciones químicas: fundamentos

Cuando el milagro pasó a ser ciencia

1. Cambios químicos

2. Velocidad de reacción

3. Cantidad de sustancia

4. Cálculos estequiométricos

5. La energía en las reacciones químicas

Orientaciones para la resolución de problemas

TIC. Simulaciones sobre reacciones químicas

130

74

Ciencia recreativa. Reacciones de oxidación del hierro Trabajo práctico. Velocidad de reacción Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

5 Algunas reacciones

químicas de interés

Una reacción química, dos posturas y el nacimiento de la química moderna

1. Ácidos y bases

2. Reacciones de combustión

3. Importancia de las reacciones de combustión

4. Reacciones de oxidación

5. Importancia de las reacciones de oxidación

6. Reacciones de síntesis

Orientaciones para la resolución de problemas

TIC. Representaciones gráficas

Ciencia recreativa. Indicadores caseros de pH

Trabajo práctico. Identificación del CO2

Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

154

Situación de aprendizaje. Porfolio 178

6 C inemática

Caída libre, pero libre de verdad

1. Sistema de referencia

2. Magnitudes del movimiento

3. Tipos de movimiento

4. Movimientos rectilíneos

5. Movimientos circulares

6. Interpretación de representación de gráficas Orientaciones para la resolución de problemas

TIC. Hojas de cálculo para el estudio de movimientos Ciencia recreativa. El factor tiempo en las fuerzas Trabajo práctico. ¿Es movimiento uniformemente acelerado?

Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

7 L eyes de Newton

Una manzana que cayó por su peso

1. Fuerzas

2. Fuerzas cotidianas

3. Leyes de Newton

4. Leyes de Newton en movimientos cotidianos Orientaciones para la resolución de problemas TIC. Simuladores de fenómenos físicos Ciencia recreativa. El rozamiento Trabajo práctico. Coeficiente de rozamiento por deslizamiento Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

8 F uerzas en el universo

El universo, un gran desconocido

1. Evolución histórica del estudio del universo

2. Fuerzas gravitatorias

3. Aplicaciones de la ley de gravitación universal

4. Satélites artificiales en órbita

Orientaciones para la resolución de problemas

TIC. Stellarium Ciencia recreativa. Simulación de la teoría de la gravitación de Einstein Trabajo práctico. Localización de los astros

Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

182

9 F uerzas en fluidos.

Presión

Bílbilis, evidencias del conocimiento del concepto de presión

1. Presión

2. Ley fundamental de la hidrostática

3. Principio de Arquímedes

4. Ley de Pascal

5. Presión atmosférica

6. Conceptos meteorológicos

Orientaciones para la resolución de problemas

TIC. Aplicación interactiva online Ciencia recreativa. La presión atmosférica Trabajo práctico. El tonel de Pascal Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

10 E nergía mecánica y trabajo

De la vis viva al concepto actual de energía

1. Energía

216

2. Trabajo

3. Potencia

4. Energía cinética

5. Energía potencial

6. Conservación de la energía mecánica

7. Transporte de energía mediante ondas mecánicas

Orientaciones para la resolución de problemas TIC. Trabajo con la hoja de cálculo Ciencia recreativa. El sol como fuente de energía renovable Trabajo práctico. Conservación de la energía mecánica Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

11 E nergía térmica y calor

Calor, ¿una materia invisible o transferencia de energía?

1. Energía térmica. Temperatura

246

2. Equilibrio térmico. Calor y propagación

3. Efectos del calor

4. Motor térmico

5. Degradación de la energía

6. Energía y sociedad

Orientaciones para la resolución de problemas

TIC. Geogebra Ciencia recreativa. Espectroscopio

Trabajo práctico. Calor latente de fusión del agua Situación de aprendizaje. Comprende, reflexiona y pon a prueba tus competencias

302

334

Situación de aprendizaje. Porfolio 364

4

Reacciones químicas: fundamentos

La evidencia más antigua de la producción y el consumo del vino es una vasija de cerámica hallada en los montes Zagros (actuales Irán e Irak), datada en el 5400 a. C. Tradicionalmente, el vino y su proceso de producción se han relacionado con el misterio y lo divino. Tanto es así que, primero, la cultura griega y, después, la romana disponían de un dios del vino y de los viñedos: Dionisos y Baco, respectiva-

Estas creencias se han ido modificando y desapareciendo debido a la lógica y la curiosidad. Así, en el Medievo se afirmaba que el vino se producía debido a la descomposición de la materia (zumo de uva o mosto), mientras que en el siglo xix se descubrió que el vino se producía gracias a una reacción química: la fermentación. El químico francés Louis Pasteur fue quien explicó la fermentación y, en consecuencia, dotó de una base científica al proceso de producción del vino. Este cambio químico consiste en la transformación del azúcar del mosto (glucosa) en alcohol etílico y dióxido de carbono. Esta reacción química puede llevarse a cabo gracias a la actividad de levaduras (hongos) tales como candida,pichia,zygosaccharomyces o la popular saccharomycescerevisiae. Actualmente, existe una ciencia especializada en el estudio de estos procesos químicos; ¿sabes de cuál se trata?

COMPROMISO ODS

El año 2020 fue un año desastroso para los viñedos de Galicia, Cataluña, Castilla-La Mancha y Andalucía, por una plaga del hongo plasmoparaviticola, causante del mildiu, que suele conllevar tratamientos con fungicidas por parte de los agricultores para salvar la cosecha.

1. Rompecabezas. Busca información sobre la enfermedad mildiu y las consecuencias de la utilización de fungicidas en la agricultura.

2. Realiza una infografía para los agricultores en la que:

– Se expongan las metas de los ODS relacionados con este problema y se justifique la necesidad de cumplirlos.

– Se explique, al menos, un tratamiento natural alternativo para combatir la enfermedad mildiu.

En esta unidad

Cuando el milagro pasó a ser ciencia

1. Cambios químicos

2. Velocidad de reacción

3. Cantidad de sustancia

4. Cálculos estequiométricos

5. La energía en las reacciones químicas

Orientaciones para la resolución de problemas

• Cómo resolver un ejercicio de estequiometría

TIC

• Simulaciones sobre reacciones químicas

Taller de ciencias

• Ciencia recreativa: Reacciones de oxidación del hierro

• Trabajo práctico: Factores que afectan a la velocidad de reacción

En anayaeducacion.es

Para motivarte:

• Vídeo: «Antes de empezar».

• Documento: «Grados superiores relacionados con el desarrollo de energías renovables».

Para detección previa de ideas:

• Actividad interactiva: Autoevaluación inicial.

• Presentación: «Qué necesitas saber».

Para estudiar:

• Simulaciones: «Ajuste de ecuaciones químicas».

• Presentación: «La cantidad de sustancia» y «Para estudiar».

• Vídeo: «Evidencias de una reacción química».

Para evaluarte:

• Actividad interactiva: Autoevaluación final.

• Soluciones de las actividades numéricas.

Y, además, toda la documentación necesaria para aplicar las claves del proyecto.

SITUACIÓN DE APRENDIZAJE

SECUENCIA DE APRENDIZAJE

VÍDEO. EXPERIMENTO SENCILLO SOBRE LA FERMENTACIÓN.

1.1 Responded a las siguientes preguntas: ¿qué tipo de reacción es la fermentación?, ¿quién fue la primera persona que estudió su mecanismo?, ¿cómo lo hizo? Sitúala en el momento histórico correspondiente.

1.2 A partir del artículo sobre la fermentación de la leche con yogur que encontraréis en anayaeducacion.es, pensad la manera en que podéis hacer esta reacción en el laboratorio. Después, grabaos en vídeo mostrando el proceso y explicando cómo lo habéis hecho.

EXPERIMENTACIÓN. VELOCIDAD DE REACCIÓN.

2.1 Leed el guion de la práctica de laboratorio propuesta en anayaeducacion.es, y, con ayuda de vuestro profesor o profesora, llevadla a cabo en el laboratorio del centro. ¿Cómo influyen el grado de división de reactivo y la temperatura en la velocidad de reacción? ¿Se conserva la masa en todas las reacciones? ¿Es diferente el volumen de los diferentes globos? ¿Por qué?

EXPERIMENTACIÓN. ENERGÍA EN LAS REACCIONES.

3.1 En el laboratorio, en dos vasos de precipitados, verted 50 mL de agua en uno y 50 mL de vinagre en otro. Medid sus temperaturas. A continuación, añadid 1 g de hidróxido de sodio en el primer vaso y dos cucharas de bicarbonato de sodio en el segundo. Cuando acabe la reacción, medid la temperatura de cada vaso. ¿Son reacciones exotérmicas o endotérmicas?

3.2 En la Feria de Ciencias del centro, repetid estas experiencias y explicad a vuestros compañeros y compañeras el fundamento químico que habéis aprendido.

+ orientaciones en anayaeducacion.es

¿Qué vas a descubrir?

Cambios químicos 1

1.1 Conceptos básicos

En una reacción química se parte de unas sustancias denominadas reactivos, presentes antes del cambio, y se obtienen otras nuevas como consecuencia del cambio, denominadas productos de la reacción.

Para que se produzca el cambio químico, los reactivos han de estar en contacto entre sí. Durante el proceso también se producen cambios físicos que los evidencian, como se muestra a continuación.

1.2 Teoría atómica de las reacciones químicas

La aparición de sustancias nuevas como resultado de una reacción química se basa en un reordenamiento de los átomos de los reactivos. Para que este tenga lugar, las entidades elementales que forman los reactivos deben colisionar entre sí. Como resultado de estas colisiones se rompen enlaces y se forman enlaces nuevos, teniendo así nuevas sustancias. Al tratarse de una reordenación de átomos, la masa total de las sustancias antes y después del cambio químico no varía; por tanto, podemos decir que:

Evidencias físicas de un cambio químico +

Durante un cambio químico, la masa se conserva; es decir, la suma de las masas de los reactivos es igual a la suma de las masas de los productos. Este enunciado se conoce como ley de conservación de la masa.

energía.

Teoría atómica y conservación de la masa

Cambio de color.

En la ilustración se representa la reacción de oxidación del monóxido de nitrógeno para dar dióxido de nitrógeno.

Como podemos observar, durante la reacción se produce una reordenación de los átomos y la masa se conserva durante todo el proceso.

COMPRENDE, PIENSA, INVESTIGA…

1 A partir de la información de la ilustración, deduce qué enlaces se han roto y cuáles se han formado en el cambio químico que se representa.

2 1-2-4. Dibuja un esquema como el anterior para la siguiente reacción:

CH4 + 2 O2 → CO2 + 2 H2O

Cambio de estado.

¿Cuántos y cuáles son los enlaces que se han roto y cuántos y cuáles son los que se han formado?

Intercambio de

2 NO O2 +

2 NO2

1.3 Expresión de una reacción química: la ecuación química

Para expresar cuantitativamente los cambios químicos, utilizamos ecuaciones químicas.

Las ecuaciones químicas expresan la relación entre los reactivos y los productos durante una reacción química, y la proporción que guardan entre sí sus entidades elementales mediante coeficientes estequiométricos.

En ocasiones, también informan de los estados de agregación de las sustancias, de la temperatura o de la presión a la que tienen lugar. Ajustar una ecuación química consiste en elegir los valores de los coeficientes, de modo que el número de átomos de cada elemento sea el mismo en los reactivos que en los productos.

Expresión y ajuste de ecuaciones químicas

Utilizaremos como ejemplo la reacción entre el amoníaco y el oxígeno molecular, que tiene como productos el nitrógeno molecular y el agua.

1 Escribimos las fórmulas de los reactivos y de los productos, separándolos por una flecha que marca el sentido de la reacción:

NH3 + O2 → N2 + H2O

2 Elegimos los valores de los coeficientes estequiométricos para hacer que el número de átomos de cada elemento sea el mismo en los reactivos y en los productos. Para ello:

2.1 Ajustamos, primero, los coeficientes de las sustancias no elementales:

2 NH3 + O2 → N2 + 3 H2O

2.2 A continuación, los de las sustancias elementales. Si es preciso, corregiremos los coeficientes ya elegidos, tanteando. Es posible utilizar números fraccionarios:

2 NH3 + 3/2 O2 → N2 + 3 H2O

Observa que el coeficiente estequiométrico del nitrógeno molecular es 1, por lo que no se escribe.

También, podemos multiplicar por dos la ecuación química para que no haya coeficientes fraccionarios:

2 NH3 + 3/2 O2 → N2 + 3 H2O 4 3 2 6

3 Por último, comprobamos, elemento a elemento, que el número de átomos que aparece en los reactivos es el mismo que el que aparece en los productos:

COMPRENDE, PIENSA, INVESTIGA…

3 Indica qué significan los coeficientes estequiométricos en la reacción del ejercicio anterior.

4 Comprobamos. Ajusta las siguientes reacciones químicas:

a) CO2 + H2O → H2CO3

b) NO + O2 → NO2

c) Cr2O3 + Al → Al2O3 + Cr

d) NO2 + H2O → HNO3 + NO

e) C2H2 + O2 → CO2 + H2O

2

Velocidad de reacción

La velocidad a la que transcurre una reacción química se define en función del tiempo que tarda en desaparecer un reactivo o en aparecer un producto.

En ocasiones, también se puede determinar por la variación de otra propiedad en el lugar donde ocurre la reacción química.

2.1 Teoría de colisiones

Como hemos visto, en una reacción química se rompen y se forman enlaces como resultado de las colisiones que tienen lugar entre las entidades elementales de los reactivos.

No todas las colisiones dan lugar a la ruptura o a la formación de enlaces; no todas las colisiones son efectivas. Solo lo son las que tienen energía suficiente y en las que las partículas tienen una orientación adecuada.

2.2 Factores que influyen en la velocidad de reacción

Diversos factores influyen en la velocidad de reacción en mayor o menor medida según el estado de agregación de los reactivos. Estos son:

■ Temperatura

En las reacciones en las que intervienen sustancias en estado líquido o gaseoso, un incremento de la temperatura hace que aumente la velocidad de las entidades elementales de los reactivos. Esto causa un mayor número de colisiones con suficiente energía para que la reacción progrese.

■ Concentración de reactivos

Superficie de reacción

Supón que el lado del cuadrado de la figura mide 1 cm. Calcula cuánto valdría la superficie disponible en los tres casos. Obtén una regla general en función del número de divisiones.

En reacciones que ocurren en disolución acuosa, un aumento de la concentración de los reactivos implica una mayor probabilidad de que se produzcan colisiones, aumentando así la velocidad de reacción.

■ Grado de división de los reactivos

En el caso de que uno de los reactivos se encuentre en estado sólido, el tamaño de las porciones de este es determinante en la velocidad del cambio químico (figura inferior).

Teoría atómica y conservación de la masa

La figura explica el porqué del incremento de la velocidad de reacción que se produce en función del tamaño de las porciones del reactivo sólido.

Observa que según aumenta el grado de división del reactivo sólido, aumenta la superficie de contacto entre él y el otro reactivo (que puede ser gaseoso o líquido). El número de choques efectivos entre las moléculas de ambos reactivos será mayor y, por tanto, aumentará la velocidad de reacción.

2.3 Catalizadores

En muchas ocasiones, para poder modificar la velocidad de una reacción química debemos variar tanto ciertos factores que no resulta rentable. En ese caso, se suelen utilizar catalizadores.

Los catalizadores son sustancias químicas que modifican la velocidad de una reacción química sin alterar la naturaleza de los reactivos ni de los productos.

Además de esta característica, presentan otras dos propiedades:

• Son extremadamente específicos. Generalmente, para cada reacción química existe un catalizador determinado. Su presencia provoca que ocurra una reacción química en concreto, y no otra que fuera posible.

• Participan en la reacción química sin sufrir cambios permanentes. La mayoría de los catalizadores se recuperan al finalizar la reacción; por ello, no se incluyen en la ecuación química como reactivos o productos.

Enzimas como catalizadores

Formadas por Determinan su

Características

Aminoácidos (combinaciones de H, C, O, N, S)

• Varían la velocidad de reacción.

• Son muy específicas.

• Actúan a pH y T determinadas.

Biológicas

Estructura y su función

• Sistema digestivo.

• Degradación de moléculas.

• Respiración celular.

• Transporte de energía y señales.

Aplicaciones

Industriales

COMPRENDE, PIENSA, INVESTIGA…

• Fármacos.

• Producción de alimentos.

• Desarrollo de biocombustibles.

5 Al mezclar una disolución de ácido sulfúrico concentrado con agua, siempre se ha de añadir, gota a gota, el ácido sobre el agua, y no al revés. Dado que entre ellos reaccionan violentamente, explica por qué tomamos esta precaución. ¿Con qué factor físico que afecta a la velocidad de reacción lo relacionarías?

6 Busca información sobre la lactasa y por qué algunas personas no digieren bien la leche. ¿Conoces otra enzima que si no funciona repercute en la no digestión de alimentos? ¿Cómo pueden remediarse estos hechos?

Las enzimas son moléculas que actúan como catalizadores dentro de los organismos. Su acción es muy específica; existe prácticamente una enzima para cada reacción química que se produce en el interior de un ser vivo.

En el caso de los seres humanos, su presencia es vital, pues si su efecto catalítico no se desarrolla adecuadamente, la termorregulación, la presión arterial o la formación del ADN podrían verse afectadas. La imagen muestra la estructura tridimensional de una enzima. Hay enzimas de muchos tamaños y formas.

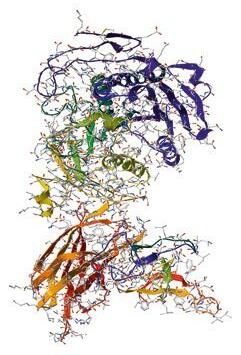
7 Folio giratorio. ¿Qué crees que ocurriría si las reacciones químicas que se producen en el interior de nuestro cuerpo no se llevaran a cabo con enzimas catalíticas?

8 Busca imágenes de enzimas de nuestro organismo. Dibújalas en tu cuaderno y explica diferencias y semejanzas en sus formas y tamaños. ¿A qué crees que se deben?

9 ¿Por qué la carne picada se estropea antes que un trozo de carne de las mismas características que no se haya picado? ¿Con qué factor físico lo relacionas?

3

Cantidad de sustancia

3.1 Cantidad de sustancia

En una reacción química conviene conocer cuántas entidades elementales, N, de cada sustancia intervienen. Para ello, utilizamos una magnitud denominada cantidad de sustancia.

La cantidad de sustancia, n, es una medida del número de entidades elementales que contiene una determinada porción de una sustancia. Su unidad en el SI es el mol.

Al ser la masa de los átomos del orden de 10–27 kg, el número de entidades elementales de 1 kg de cualquier sustancia es muy grande. Tomando como referencia la masa del isótopo de carbono-12, se establece que en un mol de sustancia hay 6,022 · 1023 entidades elementales. Este valor es constante y se conoce como número de Avogadro, NA.

Análisis de 1 mol de H 2 O

contiene

18 g

6,022 · 1023 moléculas cada una tiene una masa de 18 u

Un mol de una sustancia contiene el número de Avogadro de entidades elementales (NA = 6,022 · 1023 entidades elementales/mol), y es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como átomos hay en 0,012 kg de carbono-12.

Así, la cantidad de sustancia, n, queda determinada por la expresión: nN N A =

■ Masa y volumen molares

soluto ó = de los cuales de las cuales

La cantidad de sustancia se cuantifica de forma indirecta midiendo la masa o el volumen de una sustancia y estableciendo relaciones:

• La masa molar, M, de una sustancia es la masa, m, expresada en gramos, de un mol de sustancia. Su unidad es g · mol–1, y su valor coincide con la masa molecular o de la unidad fórmula de la sustancia.

() () () mol g mol g n M m –1 =

• El volumen molar es el que ocupa un mol en ciertas condiciones de presión y temperatura. En condiciones normales, c. n. (273 K y 1 atm), el volumen molar de cualquier gas es, aproximadamente, de 22,4 L/mol.

3.2 Concentración molar o molaridad

Muchas reacciones químicas tienen lugar en disolución acuosa, por lo que resulta conveniente expresar la concentración de reactivos y productos en concentración molar, o molaridad.

La molaridad, M, de una disolución es la cantidad de sustancia de soluto que contiene un litro de disolución. Su unidad en el SI es mol/L.

Conocer este parámetro es útil para relacionar directamente el volumen de la disolución con la cantidad de sustancia que contiene, lo que nos permitirá realizar cálculos de las sustancias reaccionantes de forma rápida. Así, la relación matemática es:

()

EJERCICIOS RESUELTOS

1 Obtén el valor de la constante de Avogadro, NA.

Un mol es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como átomos hay en 0,012 kg de C-12, y este número coincide con el NA: NA = 6,022 · 1023 entidades elementales/mol

Dado que el isótopo de C-12 tiene una masa de 12 u, esto es, de 1,9932 · 10–26 kg (1 u = 1,661 · 10–27 kg), la cantidad de isótopos de C-12 presentes en una muestra de 0,012 kg de C-12 será:

,/ , kg is topo C kg N 1 99321012 0012 ó –26 =→ , NN 6022 10 entidades A 23 - =

2 Calcula el número de moléculas y de átomos que contiene una muestra de 77 g de dióxido de carbono. ¿Qué volumen ocupa en condiciones normales? Datos: M (C) = 12 g/mol; M (O) = 16 g/mol.

Primero, calculamos la masa molar del CO2:

gmol M 12 1162 44 CO –1 2 =+ =

Así, la cantidad de sustancia que corresponde a los 77 g de CO2 es: g/mol g ,mol nM m 44 77 175 == =

Por tanto, el número de moléculas de CO2 es:

En cada molécula de CO2 hay dos átomos de oxígeno y uno de carbono, luego:

Así, si 1 mol de cualquier gas en c. n. ocupa 22,4 L: ,mol mol ,L ,L V 175 1 22 4 39 2 m ==

3 Calcula la molaridad de una disolución de hidróxido de sodio sabiendo que 500 mL contienen 120 g de NaOH.

Datos: M (Na) = 23 g/mol; M (O) = 16 g/mol; M (H) = 1 g/mol. En primer lugar, determinamos cuál es la masa molar del NaOH: gmol M 23 1161 11 40 NaOH –1 =+ +=

A partir de la masa molar, calculamos la cantidad de sustancia presente:

gmol g mol nM m 40 120 3 –1 == =

Expresamos el volumen de la disolución en las unidades adecuadas: mL ,L V 500 05 disolución ==

Así, podemos calcular la molaridad de la disolución de hidróxido de sodio como: ,L mol M M 05 3 6 ==

Observa que expresamos la molaridad como su valor seguido de la letra M.

COMPRENDE, PIENSA, INVESTIGA…

10 Calcula la masa molar del amoníaco, el cloruro de hidrógeno y el hidróxido de calcio.

11 Piensa y comparte en pareja. ¿Cuál de las sustancias de la actividad anterior contendrá mayor cantidad de sustancia en un kilogramo de masa?

12 Busca información acerca de la determinación del número de Avogadro y elabora un pequeño informe.

13 Calcula la cantidad de sustancia que hay en 250 mL de una disolución 2 M de NaOH. ¿Variará el resultado si la disolución es de Ca (OH)2?

4

Cálculos estequiométricos

Para poder realizar cálculos estequiométricos en una ecuación química, debemos ajustarla primero. Para ello, utilizamos los coeficientes estequiométricos, que relacionan la cantidad de sustancia, tanto de reactivos como de productos, que intervienen en ella. Observa que si multiplicamos estos coeficientes por el NA, podemos conocer el número de entidades elementales de las sustancias que intervienen.

4.1 Cálculos estequiométricos masa-masa

Con ellos, se calcula la masa de una de las sustancias (sustancia incógnita) que interviene en la reacción, a partir de la masa de otra de ellas (sustancia dato). Los pasos que debemos seguir se recogen en el siguiente ejemplo.

EJERCICIO RESUELTO

4 El clorato de potasio, KClO3, se descompone en cloruro de potasio y oxígeno. Calcula la masa de oxígeno obtenida al descomponerse 86,8 g de clorato de potasio por la acción del calor.

Datos: M (K) = 39,1 g/mol; M (Cl) = 35,5 g/mol; M (O) = 16,0 g/mol.

1 Para relacionar la cantidad de sustancia que reacciona y que se forma de cada especie, ajustamos estequiométricamente la reacción:

() KClO s 2 3 → () () KClOsg23 2 +

2 Identificamos la sustancia dato y la sustancia incógnita:

() KClO s 2 3 → () () KClOsg23 2 + , g m 86 8 KClO3 =

3 Calculamos las masas molares de las sustancias dato e incógnita:

,; , g/molg/molMM 1226 32 0 KClO O 32 ==

4 Calculamos la cantidad de la sustancia dato con su masa molar: ,

, , gmol g mol n 1226 86 8 0 708 KClO –1 3 - =

5 Calculamos la cantidad de sustancia incógnita con los coeficientes estequiométricos:

, molKClO molKClO molO n 0708 2 3 O3 3

2 2 = → , molO n 1062 O2 2 =

6 Hallamos la masa de la sustancia incógnita con su masa molar:

,, mol32, 0g molg m 1062 33 984 O –1 2 ==

COMPRENDE, PIENSA, INVESTIGA…

14 Calcula la masa de cloruro de potasio que se obtiene en la reacción del ejemplo.

15 Calcula la cantidad de sustancia de PCl3 que se obtiene si reaccionan 426 g de Cl2 según la reacción: Cl2 + P4 → PCl3

16 Calcula la cantidad de sustancia de P4 que es necesaria en la reacción de la actividad anterior.

17 Comprobamos. Se hace reaccionar carbonato de calcio con ácido clorhídrico según la siguiente reacción.

CaCO3 + 2 HCl → CaCl2 + H2O + CO2

Calcula la masa de cloruro de calcio que se obtiene a partir de 350 g de carbonato de calcio.

18 ¿Qué volumen de ácido clorhídrico se necesita en la reacción anterior suponiendo condiciones normales?

4.2 Cálculos con reactivos en disolución

Como ya hemos indicado, muchas reacciones químicas tienen lugar en disolución acuosa en las que el agua actúa como disolvente. Para aquellas sustancias, tanto reactivos como productos, que intervienen en la reacción y que están en disolución, este hecho se indica haciendo acompañar en la ecuación química a las sustancias de la abreviatura (aq).

Sin embargo, el agua, en ocasiones, participa en la reacción como reactivo o como producto. Veamos un ejemplo en el siguiente ejercicio resuelto para entenderlo mejor.

EJERCICIO RESUELTO

5 Calcula el volumen de una disolución de ácido clorhídrico 0,2 M necesario para que reaccionen completamente 250 mL de una disolución de hidróxido de calcio 0,1 M. Los productos de esta reacción química son cloruro de calcio y agua.

Igual que en el ejercicio resuelto de la página anterior, seguiremos esta secuencia de pasos:

1 Partiremos de la ecuación química ajustada e identificamos la sustancia dato y la sustancia incógnita:

() () HClCa(OH)aqaq 2 2 + →

() HO CaCl aq 2 22 +

En este caso, la sustancia dato es el hidróxido de calcio, Ca(OH)2, y la sustancia incógnita, el ácido clorhídrico, HCl.

Observa que el agua es, además del disolvente, un producto de la reacción.

2 Escribimos los datos del enunciado junto con la ecuación química:

() () HClCa(OH)aqaq 2 2 + →

() HO CaCl aq 2 22 +

? V¿ HCl ; , mL L V 2500 250 Ca (OH) 2 ==

3 Calculamos la cantidad de sustancia dato a partir de la definición de molaridad:

() () L mol MV n = → () ()molLnMV =

COMPRENDE, PIENSA, INVESTIGA…

19 Calcula el volumen necesario de una disolución de ácido clorhídrico 2,5 M para que reaccionen 0,2 mol de zinc según esta reacción:

2 HCl + Zn → ZnCl2 + H2

20 Infórmate sobre otras formas de expresar la concentración de una disolución. ¿Qué ventaja tiene usar la molaridad frente a otras para realizar cálculos estequiométricos?

En nuestro caso:

,, , ML mol n 01 0250 0025 () Ca OH 2 ==

4 A continuación, calculamos la cantidad de sustancia incógnita correspondiente a partir de los coeficientes estequiométricos:

molCa(OH) molCa(OH) HCl n n

= =

0025 1 2 0050 ml de HCl o

, ,

HCl2 2 HCl

5 Por último, calculamos el volumen de la disolución incógnita a partir de la definición de molaridad: () () L mol MV n = → () () L mol VM n =

En nuestro caso, los datos de que disponemos son los siguientes:

nHCl = 0,050 mol ; M = 0,2 mol/L Por tanto, el volumen necesario de ácido clorhídrico para que reaccionen completamente los 250 mL de la disolución del enunciado será:

(L) ,mol L ,(mol) ,L mL V 02 0 050 0 250 250 –1 == =

Recuerda que estos pasos los hemos seguido para este tipo de ejercicios en concreto, pero debemos tener en cuenta los datos que nos facilita el enunciado para obtener la solución pedida.

21 ¿Qué volumen de una disolución 2 M de una sustancia A será necesario para hacer reaccionar completamente 3 mL de otra disolución 2 M de una sustancia B si los coeficientes estequiométricos de A y B son iguales?

22 Calcula el volumen de disolución de ácido clorhídrico del ejercicio resuelto de esta página si la concentración de este reactivo fuera 0,1 M. ¿Cuál es la relación entre ambos resultados?

EJERCICIO RESUELTO

4.3 Cálculos de reacciones entre gases

La cantidad de sustancia de un gas se puede relacionar con el volumen que ocupa si conocemos sus condiciones de presión y temperatura. La ecuación que relaciona estas magnitudes, considerando el gas ideal, es:

pVnRT =

donde p es la presión; V, el volumen; n, la cantidad de sustancia; T, la temperatura, y R, la constante de los gases ideales, cuyo valor depende de las unidades en que esté expresada. Habitualmente, utilizamos este valor:

, Kmol atmL R 0082 =

Según la ley de Avogadro, dos sustancias gaseosas en las mismas condiciones de presión y temperatura ocupan el mismo volumen. Por tanto:

Las relaciones entre los coeficientes estequiométricos, en reacciones entre gases, son las mismas que entre los volúmenes de gas, medidos en las mismas condiciones de presión y temperatura.

6 Demuestra que la relación entre los volúmenes de los gases de esta reacción química es la misma que la que obtenemos entre los coeficientes estequiométricos, si se miden en las mismas condiciones de presión y temperatura.

2 N2 (g) + 3 H2 (g) → 2 NH3 (g)

La relación entre los coeficientes estequiométricos es:

2 mol de N2 reaccionan con 3 mol de H2 para obtener 2 mol de NH3. Supongamos que las condiciones de presión y temperatura son p y T.

COMPRENDE, PIENSA, INVESTIGA…

23 Calcula la cantidad de gas metano que hay en un recipiente de 3 litros si p = 1,2 atm y T = 27 °C. Si enfriamos el recipiente hasta los 10 °C, ¿cuál será el nuevo valor de la presión?

24 Calcula el volumen de hidrógeno (H2), medido a 25 °C y 0,98 atm, que se desprende cuando una muestra de 41,4 g de sodio reacciona con agua, como se representa en la ecuación química siguiente:

2 Na (s) + 2 H2O → 2 NaOH (aq) + H2 (g)

25 Comprueba que el valor de la constante de los gases ideales, expresado en unidades del SI, es de 8,31 J · K–1 · mol–1.

26 Comprueba que un mol de cualquier gas medido en c. n. (273 K y 1 atm) ocupa un volumen aproximadamente igual a 22,4 L.

Los volúmenes se calcularían con la ecuación:

Utilizando la relación estequiométrica tenemos:

RT 23 2 NH NH 22 3 == =

Como (R ·  T/p) no varía, se puede concluir que 2 L de N2 reaccionan con 3 L de H2 para producir 2 L de NH3, observándose la misma relación que entre los coeficientes estequiométricos.

27 Calcula el volumen de CO2 desprendido en c. n. en cada caso, al quemarse:

a) 5 mol de propano.

b) 3 mol de butano.

c) 2 mol de metano.

28 Intuyo y deduzco. A partir de las reacciones de combustión de los cuatro primeros alcanos, indica el volumen y la masa de CO2 que se desprende al quemarse un litro de cada uno de ellos, medido en c. n. CH4 + 2 O2 → CO2 + 2 H2O

C2H6 +  2 7 O4 → 2 CO2 + 3 H4O

C3H8 + 5 O2 → 3 CO2 + 4 H2O

C4H10 +  2 13 O2 → 4 CO2 + 5 H2O

La energía en las reacciones químicas

5.1 Reacciones endotérmicas y exotérmicas

Cuando tiene lugar una reacción química, al igual que sucede en otros procesos, se intercambia energía entre el sistema sobre el que se está produciendo el cambio y sus alrededores.

Este tipo de energía que se transforma durante una reacción química se denomina energía química.

La energía química es la que está asociada con los enlaces químicos y las atracciones intermoleculares.

La energía química del conjunto de las sustancias que reaccionan se modifica, pues se rompen unos enlaces para formar otros nuevos, dando lugar a los productos.

Podemos tener dos situaciones diferentes, una en la que a los reactivos les corresponda mayor energía que a los productos de la reacción, y la contraria.

En el primer caso se tratará de una reacción exotérmica y en el segundo de una reacción endotérmica.

Podemos cuantificar la energía química de un cambio químico a partir de la variación de la energía de los reactivos y de los productos:

∆E = Eproductos – Ereactivos

El signo de la variación de energía para una reacción endotérmica será positivo, mientras que, por el contrario, para una reacción exotérmica el signo de la variación de energía será negativo.

Existen reacciones químicas muy exotérmicas; por ejemplo, las combustiones. En ellas se libera energía química mediante calor.

Por el contrario, algunas reacciones químicas absorben energía del ambiente, enfriándolo; son las reacciones endotérmicas.

Tipos de reacciones

Reacciones exotérmicas

REACTIVOS

PRODUCTOS

AVANCE DE LA REACCIÓN

En una reacción exotérmica, la energía de los reactivos es mayor que la de los productos, siendo por este motivo negativa la variación de energía de la reacción.

Reacciones endotérmicas

PRODUCTOS

REACTIVOS

AVANCE DE LA REACCIÓN

Sin embargo, en una reacción endotérmica, la energía de los reactivos es menor que la de los productos, haciendo que la variación de la energía de la reacción sea positiva.

5.2 Intercambio de energía. Calores de reacción

Un intercambio de energía entre un sistema y sus alrededores, o entre dos sistemas, se puede producir mediante calor o trabajo. Al ocurrir una reacción química, se produce una variación de la energía del sistema que reacciona. La medimos con la energía de reacción, o calor de reacción.

El calor de reacción, Qr , es la energía intercambiada en forma de calor entre un sistema en el que ocurre una reacción química y sus alrededores.

El calor de reacción nos permitirá diferenciar entre una reacción endotérmica y una exotérmica. Para ello, definimos previamente un criterio de signos:

• Reacciones endotérmicas. Al producirse estas reacciones, la energía del sistema aumenta. El intercambio de energía mediante calor ocurre desde los alrededores hacia el sistema; el calor de reacción es positivo.

• Reacciones exotérmicas. Al darse estas reacciones, la energía del sistema disminuye. El intercambio de energía mediante calor ocurre desde el sistema hacia los alrededores; el calor de reacción es negativo.

5.3 Diagramas de energía y catalizadores

En los diagramas de energía que mostramos en la página anterior, solo se informa sobre la energía de los estados inicial y final de una reacción química. Sin embargo, la evolución del sistema durante la reacción es más compleja. Recuerda que no todos los choques entre las partículas de reactivos son efectivos, pues no todos tienen la orientación adecuada y la energía suficiente.

Durante el transcurso de una reacción química se alcanza un estado de transición energético entre los reactivos y los productos con una energía mayor que la de ambos. En este punto se forma el complejo activado. Independientemente de si la reacción es endotérmica o exotérmica, en toda reacción química se pasa por este estado de energía.

Energía de activación. Catalizadores

Reacción sin catalizar

Energía de activación sin catalizador, Ea

REACTIVOS

Reacción catalizada

AVANCE DE LA REACCIÓN

Energía de activación con catalizador, Ea '

La diferencia de energía entre los reactivos y la del estado de transición se denomina energía de activación.

Esta energía supone una barrera que solo será rebasada por las partículas de reactivo que tengan suficiente energía y choquen de forma efectiva.

PRODUCTOS

Cuando esta energía es muy alta, y los reactivos no pueden superarla, se utilizan catalizadores. Estas sustancias disminuyen la energía de activación y proporcionan una ruta energética más favorable, haciendo, de este modo, que los reactivos puedan transformarse en los productos.

5.4 Ecuaciones termoquímicas

Llamamos ecuación termoquímica a aquella que nos informa no solo de cuáles son las sustancias que intervienen en una reacción química, sino también de sus estados de agregación y de qué cantidad de energía se pone en juego. El valor del calor de reacción que aparece en una ecuación termoquímica depende de:

• El estado de agregación de reactivos y productos, pues un cambio de estado implica una variación de energía.

• La cantidad de sustancia que reaccione, por lo que hay que fijarse en los valores de los coeficientes estequiométricos que se hayan utilizado. Por ejemplo, la siguiente ecuación termoquímica nos informa de que en la combustión de un mol de butano gaseoso, C4H10, se liberan 2 877 kJ si obtenemos CO2 en estado gaseoso y agua líquida:

() ()gg 2 13 CH O 4102 + → () ()gl Q kJ 45 2 877 CO HO –r 22+=

Para las reacciones de combustión, como la del ejemplo, el calor de reacción se denomina calor de combustión y está referido a un mol del combustible.

En ocasiones, podemos encontrar el calor de reacción integrado dentro de la ecuación química; estará sumado a los reactivos, si se trata de una reacción endotérmica, o a los productos si es exotérmica.

EJERCICIO RESUELTO

7 Calcula la cantidad de energía que se libera al hacer reaccionar 1 kg de butano y la que se desprende cuando reacciona 1 kg de metano. Datos:

Qr (CH4) = –890 kJ/mol; Qr (C4H10) = –2 877 kJ/mol; M (C) = 12 g/mol, M (H) = 1 g/mol.

Los calores de combustión vienen referidos a un mol de combustible. Por tanto, debemos calcular la cantidad de sustancia de cada uno de ellos sumado a los reactivos.

Previamente, necesitamos conocer las masas molares, que calcularemos a partir de las fórmulas moleculares:

/ gmol M 12 11 416 CH4 =+ =

/ gmol M 12 41 10 58 CH410 =+ =

Calculamos la cantidad de sustancia de cada uno de los combustibles:

/ , gmol g mol n 16 1000 62 5 CH4 ==

/ , gmol g mol n 58 1000 17 2 CH410 - =

Y por último, el calor desprendido por cada uno de ellos en su combustión:

COMPRENDE, PIENSA, INVESTIGA…

29 Si tocamos un vaso en el que está ocurriendo una reacción endotérmica, ¿qué sensación tendremos?

30 Busca ejemplos de reacciones exotérmicas y endotérmicas y cita sus aplicaciones en productos cotidianos.

31 ¿Qué puedes decir de una reacción química, si Qr = –287,9 kJ/mol? ¿Y si fuera de signo contrario?

32 Folio giratorio. La presencia de un catalizador, ¿altera el valor de Qr?

33 Dibuja un esquema en el que representes las situaciones de intercambio de energía tanto en reacciones endotérmicas como exotérmicas.

34 Razona si una reacción es endotérmica o exotérmica si el calor de reacción en su ecuación termoquímica es de signo positivo sumado en los reactivos.

35 Calcula la energía necesaria para la formación de 75 g de monóxido de nitrógeno según la reacción:

N2 (g) + O2 (g) + 181 kJ → 2 NO (g)

36 Mesa redonda. El calor de combustión del ácido benzoico es –26,42 kJ/g:

a) ¿Es una reacción endotérmica o exotérmica?

b) ¿Qué cantidad de energía en forma de calor se desprende en la combustión de 3 mol de ácido benzoico (C7H6O2)?

Cómo resolver un ejercicio de estequiometría

EJEMPLO 1

Una muestra de aluminio puro se hace reaccionar con 150 mL de una disolución de ácido clorhídrico (HCl) de concentración 5 M. Se forma cloruro de aluminio (AlCl3) y se desprende hidrógeno gaseoso (H2). ¿Qué masa tenía la muestra de aluminio? ¿Qué volumen de hidrógeno se ha desprendido si se mide en c. n.? Datos: M (Al) = 27g/mol.

PASOS

ENTIENDE EL ENUNCIADO Y EXTRAE DATOS

Busca el significado de los términos que no entiendas y que consideres relevantes. Tras una segunda lectura, extrae los datos que se proporcionan e identifica qué se pide. Recuerda expresar las magnitudes con su símbolo e intenta utilizar subíndices para las distintas sustancias.

REALIZA UN DIBUJO DE LA SITUACIÓN

Se trata de un problema de estequiometría, pues nos dan datos de sustancias que reaccionan. Debemos escribir la ecuación química ajustada, junto con los datos y las masas molares de las sustancias.

IDENTIFICA LAS LEYES QUÍMICAS

QUE INTERVIENEN

• Masa molar, cantidad de sustancia y masa:

() mol g nM m =

()

• Ley de los gases ideales, P · V = n · R · T, si hay reactivos o productos gaseosos.

• Definición de molaridad:

() () L mol MV n =

• Definición de calor de reacción.

OBTÉN EL RESULTADO Y ANALIZA SU VALIDEZ

• Realiza los cálculos que sean necesarios para llevar a cabo tu estrategia de resolución del problema y recuerda mantener coherencia en las unidades de las magnitudes implicadas.

• Analiza el resultado y coméntalo si es necesario.

RESOLUCIÓN

• El enunciado describe una reacción química.

• Diferenciamos entre los tipos de datos:

– Sustancia dato: ácido clorhídrico:

VHCl = 150 mL; 5 M = 5 mol/L

– Sustancias incógnita: mAl y VH2 en c. n.

La ecuación química ajustada es:

2 Al (s) +  6 HCl (aq) → 2 AlCl3 (aq)  +  3 H2 (g) mAl V = 150 mL VH2 , c. n.

MAl = 27 g/mol 5 M

Por tanto, 2 mol de Al se combinan con 6 mol de HCl y dan 2 mol de AlCl3 y 3 mol de H2

En este caso, debemos seguir esta secuencia:

1. Calcular la cantidad de sustancia dato:

n (mol) = M · V (L)

2. A partir de la relación estequiométrica, se calcula la cantidad de sustancia de cada compuesto incógnita.

3. Calcular la masa y el volumen de las sustancias incógnita a partir de la masa molar y de la ecuación de los gases, respectivamente.

Calculamos la cantidad de HCl: ,, L mol Lmol n 50 15 075 HCl $ ==

Con este valor, hallamos la cantidad de Al y H2:

molHCl 6mol HCl 2mol Al mol n 0750 25 Al ==

0750 375

molHCl 6mol HCl 3 mol H mol

Calculamos la masa de Al y el volumen de H2:

, , mol g/mol g m 02527 675 Al ==

EJEMPLO 2

Calcula la energía que se desprende en forma de calor cuando reaccionan 440 g de propano con la cantidad suficiente de oxígeno. Dato: Qr = –2 218,8 kJ/mol.

RESOLUCIÓN

• El enunciado describe una reacción exotérmica y la energía que se libera en forma de calor.

• Datos que extraemos:

– Sustancia dato: propano, C3H8: mg 440 CH38 =

– Calor de reacción: Qr = –2 218,8 kJ/mol

La ecuación química ajustada es:

C3H8 + 5 O2 → 3 CO2 + 4 H2O Qr = –2 218,8 kJ /g mol M 44 CH38 =

Lo que significa que en la combustión de un mol de propano se liberan 2 218,8 kJ.

COMPRENDE, PIENSA, INVESTIGA…

37 Calcula la masa de cloruro de aluminio que se ha formado a partir de la reacción química del primer ejemplo resuelto. Dato: M (Cl) = 35,5 g/mol.

38 Calcula el volumen de hidrógeno desprendido del primer ejemplo resuelto si se mide a 25 °C. ¿Será mayor o menor que el del ejemplo?

39 Calcula la cantidad de oxígeno necesaria para la combustión completa de la cantidad de propano del segundo ejemplo.

40 Lápices al centro. El hidruro de calcio reacciona con agua según la siguiente reacción química:

CaH2 (s) + H20 (l ) → Ca(OH)2 (s) + H2 (g)

a) Ajusta la ecuación química.

b) Calcula la cantidad de hidruro de calcio que reaccionará con 3,6 mol de agua.

c) Calcula la masa de hidróxido de calcio que se forma con la misma cantidad de agua.

d) ¿Qué volumen de hidrógeno, medido a 300 K y 1,2 atm, se desprende a partir del agua que reacciona?

En este caso, debemos seguir esta secuencia:

1. Calcular la cantidad de sustancia dato:

() () mol g nM m =

2. Calcular la energía liberada en forma de calor a partir de la ecuación termoquímica.

Calculamos la cantidad de C3H8, dividiendo entre la masa molar (M ), que podemos expresar como: 44 g/mol g mol n 440 10 CH38 ==

Datos: M (Ca) = 40 g/mol; M (O) = 16 g/mol; M (H) = 1 g/mol.

41 ¿Qué energía se desprende cuando reaccionan 330 g de C2H4O2 con la cantidad suficiente de oxígeno? Si la reacción se diera en c. n., ¿qué volumen de CO2 se formaría? ¿Y de agua? Qc = –875,4 kJ/mol.

Datos: M (C) = 12 g/mol; M (O) = 16 g/mol; M (H) = 1 g/mol.

42 Una muestra de hierro se mezcla con 200 mL de ácido sulfúrico, H2SO4, de concentración 3,5 M. En esta reacción se forman: hidrógeno en estado gaseoso y sulfato de hierro (II). ¿Qué masa tenía la muestra de hierro? ¿Qué volumen de hidrógeno se desprende medido a 30 °C y 0,95 atm?

Datos: M (Fe) = 55,8 g/mol; M (S) = 32 g/mol; M (O) = 16 g/mol; M (H) = 1 g/mol.

43 Una de las formas de obtener hidrógeno es el reformado del metano:

Energía–38 38 ==

Calculamos la energía liberada: molC H 1mol CH (–2 218,8 kJ) kJ 10 22 188

Expresamos el resultado con signo negativo para indicar que se trata de energía liberada.

CH4 + H2O → CO + H2

a) Ajusta la ecuación química.

b) Calcula el volumen de metano, medido a 100 ºC y 1 atm, necesario para producir 150 m3 de hidrógeno medido en las mismas condiciones.

c) ¿Qué cantidad de CO (en mol) se produciría?

Simulaciones sobre reacciones químicas

INTERPRETAMOS ECUACIONES QUÍMICAS

En esta unidad trabajaremos con simulaciones que nos permitirán estudiar la información que nos proporciona una ecuación química; la cantidad de reactivo que

desaparece y se transforma en producto, el equilibrio y la reversibilidad en una reacción química, y los efectos de algunos factores en las reacciones químicas.

AJUSTANDO REACCIONES QUÍMICAS

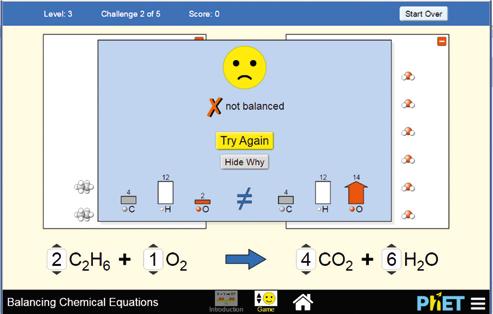
Utilizaremos una aplicación disponible en la web de Anaya: Balanceo de ecuaciones químicas. Esta aplicación tiene dos partes: Introducción y Juego.

• En esta aplicación se trata de una forma visual e intuitiva el ajuste de reacciones químicas llevando la cuenta de forma inmediata del número de átomos de cada elemento presentes en los reactivos y en los productos. Para empezar, utiliza la parte Introducción; activa en la esquina superior derecha la herramienta que te permite visualizar la balanza de elementos.

• Observa que el número de moléculas, o entidades elementales, que permite usar esta aplicación debe ser un número entero.

• Utiliza ahora el Juego para ajustar ecuaciones en nivel de dificultad creciente. Si no realizas bien alguno de los ejercicios, la aplicación te da la opción de averiguar por qué y hacer un nuevo intento, como mostramos en la figura siguiente.

VELOCIDADES DE REACCIÓN

En esta ocasión, utilizaremos una aplicación disponible en: https://phet.colorado.edu/es/simulations/reactions-and-rates

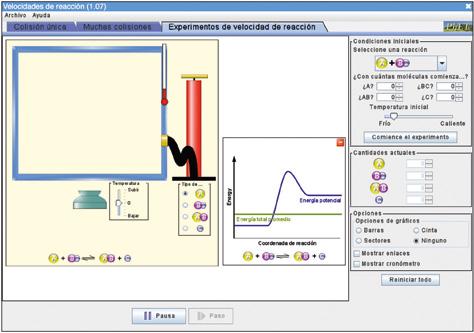
La simulación tiene tres partes: Colisión única, Muchas colisiones y Experimentos de velocidad de reacción. En los tres casos se trata de una reacción reversible, es decir, que una vez que se forman los productos de reacción, estos interaccionan entre sí dando lugar de nuevo a los reactivos. Decimos, entonces, que se ha alcanzado el equilibrio químico. Existen muchas reacciones químicas en las que esta situación tiene lugar.

Reacciones reversibles

Empezaremos por la pestaña de Experimentos de velocidad de reacción. Aquí, la aplicación permite variar el número de moléculas de los reactivos. En la parte derecha tenemos las opciones para controlar el experimento:

Por tanto, podríamos interpretar que los coeficientes estequiométricos indican el número de entidades de reactivo que hay al iniciar la reacción y el número de entidades de producto que habrá al finalizarla. Pero esto no siempre es así, pues dependerá de si la reacción es reversible o no, es decir, de si se alcanza una situación de equilibrio químico.

• Selección de la reacción. Podemos utilizar una de las reacciones, o bien diseñar una, basándonos en el diagrama de energía. Son editables los valores de energía de reactivos y productos, para tener reacciones endotérmicas o exotérmicas, y el valor de la energía de activación, que nos permitirá simular la presencia de un catalizador.

• Número de moléculas al inicio. Nos permite variar el número de moléculas de reactivos y productos al inicio de la reacción.

• Temperatura inicial.

• Opciones de gráficos. El gráfico de barras da una idea de las cantidades de reactivos y productos presentes y el denominado gráfico de cinta, sobre el avance de la reacción.

Haremos la práctica con diez moléculas de cada uno de los reactivos y un valor de temperatura suficientemente elevado. Además, marcaremos que se muestre el gráfico de barras.

Colisión única

En esta parte de la simulación puedes observar el efecto que tienen la orientación relativa de las dos moléculas de reactivo y la energía de la colisión. Para observar cómo la orientación relativa hace que la colisión sea, o no, efectiva, debes seleccionar en las opciones del lanzador (esquina superior derecha) tiro oblicuo y lanzar la molécula de reactivo con energía suficiente.

Durante la reacción, observamos la variación de altura de las barras en el gráfico; al principio, la cantidad de reactivos va disminuyendo y la de productos aumentando. Después, ocurre lo contrario. Y, finalmente, cuando dejamos que transcurra el tiempo, las cantidades permanecen constantes y las alturas prácticamente se igualan. En este punto se alcanza el equilibrio químico.

La reacción que ha tenido lugar es reversible, pues, de forma simultánea, ocurren dos reacciones: la directa, donde los reactivos dan lugar a los productos, y la inversa, donde los productos reaccionan y dan los reactivos.

COMPRENDE, PIENSA, INVESTIGA…

1 Realiza experimentos con una sola colisión variando la energía y el ángulo de lanzamiento. Extrae conclusiones de la probabilidad de que se produzca una colisión efectiva y los factores de los que depende.

2 Haz un experimento de velocidad de reacción con la primera reacción ofrecida variando la cantidad de moléculas de los reactivos. Activa el cronómetro y el diagrama de

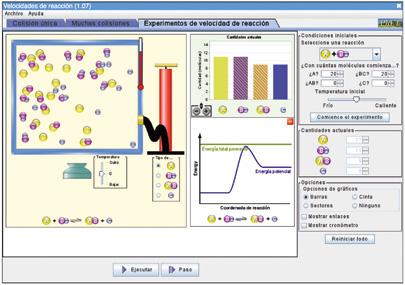
El efecto de la energía de colisión se puede observar haciendo tiros, ampliando más o menos el ángulo del lanzador. Si la energía del tiro es inferior a la energía de activación de la reacción no obtendrás una colisión efectiva. Para visualizar el diagrama de energía de la reacción, debes activar la opción gráfico de energía. Para poder ver el diagrama de energía de la reacción, activa la opción ver gráfico de energía. En este gráfico, el eje de abscisas representa la «coordenada de reacción», es decir, el avance de la reacción con el tiempo. Esta coordenada está relacionada con la distancia entre las dos moléculas de reactivo: si están próximas entre sí, la distancia disminuye y el valor de la coordenada aumenta, pues cuanto más cerca estén, más avanzada está la reacción, más próxima la colisión entre ambas y más probable que se obtenga el producto de la reacción.

evolución de la reacción para ver el tiempo que tarda esta en estabilizarse. Recoge tus resultados en una tabla y extrae conclusiones sobre la influencia de la concentración de reactivos. ¿Por qué decimos que el equilibrio químico es dinámico?

3 Realiza la misma experiencia variando ahora la temperatura. Extrae conclusiones.

Reacción de oxidación del hierro Ciencia recreativa

Introducción

Una de las reacciones químicas que más se emplea como ejemplo es la oxidación del hierro, puesto que en circunstancias de pH neutro se forma un precipitado de óxido de hierro(III) hidratado (herrumbre), de llamativo color pardo rojizo, lo que permite observar el cambio químico por cambio de color.

Te proponemos una experiencia en la que se actúe sobre algunos de los factores que influyen en la velocidad del proceso de oxidación. Para llevarla a cabo, necesitas: clavos de hierro, agua fuerte (o salfumán, que es una disolución de ácido clorhídrico de venta en droguerías), agua, cloruro de sodio (sal común), vinagre, aceite, hidróxido de sodio, cuatro recipientes de gran superficie y poca profundidad.

Vamos a realizar una serie de experimentos para observar de forma cualitativa cómo el ambiente químico (pH y presencia de sales) afecta a la oxidación de los clavos de hierro. Clavos de hierro oxidados.

Experimento

Para poder comparar los resultados, necesitamos un experimento de referencia, blanco, que haremos con agua hervida, para eliminar parte del oxígeno disuelto.

Preparación de los recipientes

Agua hervida (BLANCO)

Disolución de NaCl (Ambiente marino)

Disolución de HCl o vinagre (pH ácido) Agua y aceite (Ambiente aislado)

• Recipiente 1: un clavo + agua hervida.

• Recipiente 2: un clavo + una disolución de cloruro de sodio.

• Recipiente 3: un clavo + una disolución de ácido clorhídrico.

• Recipiente 4: un clavo + vinagre.

• Recipiente 5: un clavo + agua y aceite.

Con estos experimentos reproducimos en parte el ambiente químico que hay en las zonas costeras, en situaciones de pH ácido y en lugares más secos.

Observación tras 24 horas

La oxidación en el recipiente 2 da como resultado la formación de óxido de hierro(III) que queda suspendido en el agua en forma de precipitado coloidal. ¿Observas ese precipitado pardo rojizo en el resto de los recipientes? Si no es así, no tiene por qué indicar que no se ha oxidado el hierro, sino que el óxido de hierro(III) ha quedado disuelto, pues en medio ácido no precipita.

Para comprobar si hay o no oxidación, añade unas gotas de disolución de hidróxido de sodio; si se forma el precipitado es que se había producido antes la oxidación.

Después de haber terminado esta actividad, ¿cuál es tu opinión acerca de limpiar los restos de herrumbre con ácido clorhídrico?

Trabajo práctico

Procedimiento

Medidas de seguridad

En ambas reacciones se observará el desprendimiento de gases. Utiliza gafas de seguridad para evitar proyecciones.

Experiencia 1.

Grado de división de un reactivo sólido

• Coloca en un tubo de ensayo una masa conocida de caliza pulverizada, y en otro la misma masa de mármol troceado. Añade agua a cada tubo hasta sumergir el trozo de mármol, y obtener una suspensión, en el caso de la caliza pulverizada.

• Coloca en otros dos tubos de ensayo una cantidad de la disolución de ácido clorhídrico, la misma en los dos.

• Con cuidado, añade las disoluciones de ácido clorhídrico sobre los tubos de ensayo con los trozos de mármol y con la caliza pulverizada. Anota lo que ocurre.

Experiencia 2.

Concentración de un reactivo

Factores que afectan a la velocidad de reacción

Planteamiento del problema

Analizar el efecto que tienen el grado de división de un reactivo sólido, la concentración y la presencia de catalizadores sobre la velocidad de reacción.

Para ello, te proponemos que desarrolles experimentos con estas dos reacciones químicas:

Reacción 1: CaCO3 (s) + 2 HCl (aq) → CaCl2 + CO2 (g) + H2O

Reacción 2: Zn (s) + H2SO4 (aq) → ZnSO4 + H2 (g)

Tu propuesta

Diseña una práctica para comprobar cualitativamente cómo afectan la concentración y el grado de división del reactivo sólido a la velocidad de reacción de la primera, y la presencia de un catalizador en la segunda.

Nuestra propuesta

En ambas reacciones se desprende un gas. Por tanto, la velocidad de burbujeo del gas puede dar una idea de la velocidad de reacción. Solo debe variar el factor estudiado en cada caso.

Material

• Caliza pulverizada • Trozos de mármol • Disolución de ácido clorhídrico • Virutas de cobre y de zinc • Disolución de ácido sulfúrico diluido • Tubos de ensayo • Gradilla • Matraz aforado • Agua destilada.

• A partir de la disolución de ácido clorhídrico de partida, prepara otras dos más diluidas hasta que su concentración sea la mitad que la inicial.

• Procede de modo análogo a lo realizado en la experiencia 1, pero solo con la muestra de mármol en agua destilada. Realiza tres veces la experiencia, una para la disolución de ácido clorhídrico inicial, y las otras dos para las diluidas.

Experiencia 3.

Presencia de un catalizador

• En un tubo de ensayo pon unas virutas de zinc y cúbrelas con una disolución de ácido sulfúrico diluida. Observa y anota lo que ocurre.

• En otro tubo de ensayo pon, junto con las virutas de zinc, otras de cobre y añade la misma cantidad de ácido sulfúrico diluido. Observa y anota lo que sucede.

EXTRAE CONCLUSIONES…

1 Elabora una tabla en la que recojas las condiciones de cada experiencia junto con las observaciones que hayas obtenido y extrae conclusiones.

2 A partir de la experiencia 3, experimenta añadiendo solo el catalizador, el cobre y el ácido. ¿Qué observas?

3 ¿Tendríamos resultados análogos a la experiencia 3 si en vez de utilizar cobre usáramos un compuesto como el sulfato de cobre? ¿Podríamos decir que el sulfato de cobre cataliza la reacción? Explica tu respuesta.

Para terminar

COMPRENDE

Organiza tus ideas Mapa conceptual sistémico

1 Explica, rotulando tus propios dibujos, los factores que afectan a la velocidad de reacción y la diferencia entre una reacción endotérmica y una exotérmica.

2 Completa el esquema conceptual inferior con los contenidos que has estudiado en esta unidad, además de los señalados con las letras A, B, C, D y E.

está formada por se expresa mediante su que nos informa sobre

cuyos enlaces se

energía B rompen

de reacción Una reacción química

Recuerda que dispones de las soluciones de todas las actividades numéricas en anayaeducacion.es

Los cambios químicos

1 Asamblea de ideas. Enumera cinco cambios químicos que ocurren en tu día a día, de los que seas consciente.

2 Comprobamos. Ajusta estas ecuaciones:

a) MgCl2 + Li2CO3 → MgCO3 + LiCl

b) P4 + O2 → P2O3

c) MgI2 + Mn(SO3)2 → MgSO3 + MnI4

d) C3H6O + O2 → CO2 + H2O

e) SeCl6 + O2 → SeO2 + Cl2

3 Comprueba que se cumple la ley de conservación de la masa en las reacciones químicas anteriores considerando la masa de los átomos que forman las sustancias presentes en estas.

4 1-2-4. ¿Qué enlaces se rompen y se forman en estos cambios químicos?

Velocidad de reacción

5 Explica cómo afecta la concentración de los reactivos a la velocidad de reacción, utilizando para ello la teoría de las colisiones.

6 Explica cómo afecta la temperatura a la velocidad de una reacción química según la teoría cinética.

7 Explica cuáles son las ventajas de utilizar catalizadores en reacciones que requieran de condiciones extremas de presión y/o temperatura.

8 Medimos la concentración de una sustancia en una reacción química y obtenemos estos datos:

13 Escribe la fórmula y calcula las masas molares de estas sustancias:

a) Cloruro de calcio. e) Dicloro.

b) Plata. f) Tricloruro de aluminio.

c) Trióxido de dihierro. g) Ácido sulfhídrico.

d) Ozono. h) Ácido sulfúrico.

14 Calcula la molaridad de estas disoluciones:

a) Una masa de 200 g de hidróxido de sodio en un volumen total de 500 mL.

b) Una masa de 20 g de nitrato de sodio en agua hasta completar un volumen de 250 mL.

c) Una disolución de ácido nítrico en agua cuya densidad es 1,12 g/cm3 y riqueza (% en masa) del 80 %.

a) ¿Se trata de un reactivo o de un producto?

b) Representa los datos de concentración frente al tiempo. La pendiente del gráfico en cada punto es una medida de la velocidad de reacción. ¿Aumenta o disminuye la velocidad de reacción según avanza la reacción? Explica tu observación.

Cantidad de sustancia

9 Indica si estas afirmaciones son verdaderas o falsas:

a) En un mol de agua hay el mismo número de moléculas que en un mol de butano.

b) En un mol de agua hay el mismo número de átomos de hidrógeno que en un mol de butano.

c) En un mol de agua hay un mol de átomos de oxígeno y dos mol de átomos de hidrógeno.

d) En un mol de agua hay 1,8066 · 1024 átomos.

e) En un mol de agua hay 1,8066 · 1024 moléculas.

10 Indica cuántos átomos hay en 360 g de cobre.

11 Calcula el número de átomos de hidrógeno que contienen unas muestras de un gramo de amoníaco, cloruro de hidrógeno e hidróxido de calcio. ¿Qué masa de hidrógeno contiene cada una de las muestras?

12 Completa la tabla para 20 mol de agua:

d) Una disolución preparada a partir de 200 mL de una disolución 2 M de ácido clorhídrico y agua hasta completar un volumen de 500 mL.

15 Calcula la cantidad de sustancia de ácido clorhídrico que presenta la disolución del apartado (d) del ejercicio anterior y la que había antes de que se llevara a cabo el proceso de dilución; ¿qué observas?

16 Calcula la molaridad de una disolución de 70 g de cloruro de amonio en 500 mL de disolución. ¿Cuántos átomos de H contiene?

Cálculos estequiométricos

17 El carbonato de calcio se descompone por la acción del calor en óxido de calcio y dióxido de carbono.

a) Escribe la ecuación química ajustada.

b) Calcula cuánto dióxido de carbono se forma si reaccionan 150 g de carbonato de calcio.

18 El hidróxido de litio reacciona con bromuro de hidrógeno para dar bromuro de litio y agua.

a) Escribe la ecuación química ajustada.

b) Calcula la cantidad de bromuro de hidrógeno que es necesaria para que reaccionen 5 mol de hidróxido de litio.

c) ¿A qué masa corresponden los resultados obtenidos en el apartado anterior?

d) Calcula la masa de productos que se obtiene a partir de los 5 mol de hidróxido de litio.

e) Verifica, con los datos del ejercicio, que se cumple la ley de conservación de la masa.

19 Se tienen 250 mL de una disolución de ácido sulfúrico 3 M. Calcula el volumen de disolución de hidróxido de sodio 1,5 M necesario para que reaccione por completo la disolución de ácido sulfúrico.

Para terminar

20 El blanco litopón o blanco de bario (ZnS + BaSO4) es un pigmento que se utiliza en acuarelas y que se prepara por precipitación de sales solubles a partir de sus disoluciones, según esta reacción química:

BaS (aq) + ZnSO4 (aq) → ZnS (s) + BaSO4 (s)

a) Nombra todos los compuestos que aparecen en esta reacción química. ¿Cuáles son los reactivos y cuáles los productos?

b) Calcula la masa de litopón que se obtiene cuando se hacen reaccionar 300 mL de una disolución de sulfato de zinc 0,2 M con la cantidad suficiente de una disolución 0,3 M de sulfuro de bario.

c) Calcula el volumen de la disolución de sulfuro de bario que ha sido necesario.

21 Calcula el volumen de amoníaco, medido a 68 °C y 704 mmHg, que se obtiene si reaccionan 27,4 L de nitrógeno, medidos en las mismas condiciones, con el suficiente hidrógeno según la reacción:

() () NHgg 3 22 + → () NH l 2 3

¿Qué cantidad de hidrógeno sería necesaria para que se produjera la reacción?

22 Los metales reaccionan con los ácidos liberando hidrógeno.

a) Escribe la reacción del zinc y el ácido clorhídrico.

b) ¿Qué volumen de ácido clorhídrico 3 M es necesario para que reaccionen 60 g de Zn?

c) Calcula el volumen de hidrógeno que se desprenderá si lo medimos a 1 atm y 298 K.

d) Calcula las masas de todas las sustancias implicadas en esta reacción y verifica que se cumple la ley de conservación de la masa.

La energía en las reacciones químicas

23 Indica en el diagrama cuál es la representación de la reacción catalizada. ¿Se trata de una reacción endotérmica o exotérmica?

Estado de transición

24 ¿Qué te hace decir eso? Explica por qué las siguientes afirmaciones son verdaderas o falsas:

a) La energía asociada a los enlaces químicos y a las fuerzas intermoleculares es energía cinética.

b) La variación de energía que se produce en una reacción endotérmica es positiva.

c) La energía de activación es la diferencia de energía entre los reactivos y los productos de una reacción química.

d) El calor de reacción siempre es positivo.

e) Todas las reacciones necesitan superar una barrera de energía para iniciarse.

f) La energía del complejo activado es mayor que la energía de los reactivos y que la de los productos.

25 Piensa y comparte en pareja. Escribe el calor de reacción a partir de esta información:

a) N2 (g) + O2 (g) + 181 kJ → 2 NO (g)

b) C (s) + O2 (g) → CO2 (g) + 393,5 kJ

¿Son reacciones endotérmicas o exotérmicas?

26 Se ha medido el calor de combustión de un combustible y se han obtenido los siguientes datos:

Calcula el calor de combustión y su error absoluto.

27 A partir de estas ecuaciones termoquímicas:

a) CH3OH (g) → CH2O (g) + H2 (g)

Qr = 54,5 kJ

b) C2H6 (g) + 7/2 O2 (g) → 2 CO2 + 3 H2O (l)

Qr = –3 119,6 kJ

c) CO (g) + H2 (g) → CH2O (g)

Qr = 21,3 kJ/mol

d) HCl (g) + NH3 (g) → NH4Cl (g)

Qr = –1 75,9 kJ

¿Cuáles son endotérmicas y cuáles exotérmicas?

28 A partir de los datos de la actividad anterior, calcula el calor que se desprende al reaccionar 71 g de HCl (g) según la reacción del apartado (d).

Progreso de reacción

29 El calor de combustión de algunos hidrocarburos saturados es el que se muestra en la tabla:

SITUACIÓN DE APRENDIZAJE

a) Calcula la cantidad de dióxido de carbono desprendido en la combustión de un mol de cada hidrocarburo.

b) Calcula la energía en forma de calor que se libera en la combustión de un mol de cada hidrocarburo y realiza un gráfico en el que compares la cantidad de dióxido de carbono emitido con la energía liberada. ¿Qué observas?

c) Busca el significado de las siglas PC y explica por qué podemos considerar su valor como el calor de combustión de estas sustancias.

Química cotidiana: calor portátil

Hoy en día, el consumo de comidas y bebidas en cualquier lugar y momento es un hecho cotidiano. Nos hemos acostumbrado a disponer de forma casi inmediata de productos listos para tomar. Incluso podemos calentarlos o enfriarlos antes de ingerirlos. Es el caso de las bedidas autoenfriables o autocalentables.

En una bebida autocalentable, el envase está provisto de un depósito que, sin estar en contacto directo con la bebida, es donde tiene lugar la reacción exotérmica.

El punto clave del diseño del envase es hacer que la reacción comience cuando se vaya a consumir la bebida, y que el intercambio de calor entre el compartimento donde tiene lugar la reacción y el que contiene la bebida que se ha de calentar sea suficiente para poder consumir la bebida a la temperatura óptima.

En el momento de tomar la bebida, el consumidor ha de romper la separación que existe entre los compartimentos que contienen los reactivos, haciendo que comience la reacción exotérmica que calentará su bebida y permitirá que esta esté lista para su consumo.

REFLEXIONA

En esta unidad, has reproducido prácticas de laboratorio para estudiar su velocidad. Descarga el cuestionario disponible en anayaeducacion.es y reflexiona sobre el nivel que has alcanzado en cada aspecto.

Aspectos Totalmente conseguido Bastante conseguido Conseguido Casi conseguido Comprende el concepto de velocidad de reacción y los factores que pueden modificarla.

PON A PRUEBA TUS COMPETENCIAS

Realiza la autoevaluación competencial incluida en anayaeducacion.es

CHOCOLATE

En la web

• ¿Podríamos utilizar una reacción endotérmica para tener frío instantáneo? Busca información sobre la reacción entre el nitrato de amonio y el agua. Escribe su reacción y di si este proceso se utiliza a nivel comercial. Pon algún ejemlo.

Actividad

• Organizad, en grupos, una exposición de carteles en la que informéis al resto de las clases del centro educativo sobre el fundamento del enfriamiento y el calentamiento instantáneos en productos como compresas de frío o bebidas autocalentables.

Fuerzas en fluidos. Presión

Bílbilis, una antigua ciudad romana situada cerca de la actual Calatayud (Zaragoza), constituye una de las evidencias de que la cultura romana conocía el concepto de presión. Esta ciudad contaba con una amplia red de cisternas muy próximas y conectadas entre sí. Su finalidad no era almacenar agua, sino que cubrían otros menesteres. Ello se debe a que el orificio de salida del agua se localizaba ligeramente más bajo que el orificio de entrada, por lo que estas cisternas no podían vaciarse por completo.

Los ingenieros romanos diseñaron esta red de cisternas para disminuir la presión en las tuberías de plomo y, así, evitar roturas en sus acueductos. ¿Serías capaz de pensar una alternativa distinta para aliviar la presión de las tuberías?

Como ya sabemos, los romanos conocían los efectos de la presión. Sin embargo, no fue hasta mediados del siglo xvii cuando se le dio una explicación física a este concepto, relacionando diferentes factores. El responsable de este avance científico fue el francés Blaise Pascal.

COMPROMISO ODS

Un estudio médico, que ha sido llevado a cabo desde el año 2000 en la Universidad de Duisburgo-Essen (Alemania), ha revelado que los niveles de contaminación en el aire incrementan la presión arterial de manera notable. Este hecho aumenta a su vez las probabilidades de que la población sufra infartos y derrames cerebrales.

1. Preparar la tarea. Busca información sobre el concepto de «presión arterial», los factores que podrían incrementarla o disminuirla y las consecuencias de sufrir una elevada presión en nuestro sistema circulatorio.

2. CTF. Relaciona el hallazgo descrito por este estudio médico alemán con las metas 3.4 , 3.9 , 13.3 y 13.a de los ODS. Puedes consultar los vídeos en anayaeducacion.es .

¿Qué vas a descubrir?

En esta unidad

• Bílbilis, evidencias del conocimiento del concepto de presión

1. Presión

2. Ley fundamental de la hidrostática

3. Principio de Arquímedes

4. Ley de Pascal

5. Presión atmosférica

6. Conceptos meteorológicos

Orientaciones para la resolución de problemas

• Ejercicios relacionados con la presión y el empuje

TIC

• Aplicación interactiva online

Taller de ciencias

• Ciencia recreativa. La presión atmosférica

• Trabajo práctico. El tonel de Pascal

En anayaeducacion.es

Para motivarte:

• Vídeo: «Antes de empezar».

Para detección previa de ideas:

• Actividad interactiva: Autoevaluación inicial.

• Presentación: «Qué necesitas saber».

Para estudiar:

• Vídeo: «Principio de Arquímedes».

• Simulación: «Bajo presión».

• Presentación: «Para estudiar».

Para evaluarte:

• Actividad interactiva: Autoevaluación final.

• Soluciones de las actividades numéricas.

Y, además, toda la documentación necesaria para aplicar las claves del proyecto.

SITUACIÓN DE APRENDIZAJE

SECUENCIA DE APRENDIZAJE

BAJO PRESIÓN.

4.1 Buscamos información sobre los límites de presión que puede aguantar el ser humano, identificando situaciones extremas que relacionaremos con las fuerzas en fluidos. También reflexionamos sobre la diferencia que existe entre la presión y la gravedad, utilizando ejemplos de astronautas en condiciones de ingravidez.

4.2 Elaboramos un informe para explicar los resultados obtenidos. Debe incluir imágenes representativas, que después usaremos para la elaboración de un vídeo en la actividad 5.

BUSCANDO LIMITES.

5.1 Aplicamos los conceptos de presión atmosférica a las condiciones de Marte, que compararemos con la presión en la Tierra y la Luna. Explicamos cómo afectarían a nuestro día a día esos cambios de presión, buscando ejemplos concretos como la práctica del buceo en apnea.

5.2 Elaboramos un breve vídeo donde expliquemos como nos afectaría los cambios de presión. En este vídeo podemos incluir material generado a lo largo de la situación de aprendizaje.

+ orientaciones en anayaeducacion.es

Comprende la presión

En las imágenes se observa como se deforma la arcilla al aplicar la fuerza con la palma de la mano o con un dedo. ¿Y si se aplicara la fuerza utilizando un clavo?

1.1 Presión en la superficie de contacto

Uno de los efectos que producen las fuerzas es la deformación de los cuerpos sobre los que actúan; el otro efecto es el cambio en su estado de movimiento. Estudiaremos aquí el primero de ellos.

Como sabes, las fuerzas de contacto son las que se ejercen los cuerpos al interactuar mediante contacto físico; tocándose entre ellos. Por ejemplo, son fuerzas de contacto las que se aplican dos cuerpos al chocar, o la fuerza normal que el suelo ejerce sobre un objeto apoyado en él, impidiendo que lo atraviese.

Si aplicamos una fuerza con la palma de la mano a un trozo de arcilla, comprobaremos que se deforma. Pero si lo hacemos aplicando la misma fuerza pero tocando solamente con un dedo, veremos que el dedo se hunde en la arcilla; es decir, la deforma aún más. Comprobamos, pues, que la deformación que sufren los objetos ante la acción de una fuerza de contacto no depende únicamente del valor de la fuerza aplicada, sino también de la superficie de contacto (fotografías inferiores).

Cuanto menor sea la superficie de contacto, más «concentrada» se encuentra la fuerza aplicada en esa superficie, y por lo tanto mayor es la deformación que dicha fuerza produce. De ello se desprende la necesidad de definir una magnitud que nos informe precisamente de esto; esta magnitud es la presión.

Se define la presión que ejerce una fuerza de contacto que actúa perpendicularmente sobre una superficie como la fuerza ejercida por unidad de dicha superficie.

Matemáticamente, la presión se expresa como:

pS F =

Su unidad en el SI es el Pascal (Pa), y equivale a N/m2.

Deformación de la arcilla mediante una fuerza

EJERCICIO RESUELTO

1 Un objeto con forma paralelepípeda de dimensiones

2 · 3 · 4 centímetros, cuya densidad es de 2 g/cm3, se encuentra en reposo sobre el suelo. Determina la presión que ejerce sobre el suelo cuando se apoya sobre:

a) Su cara mayor.

b) Su cara más pequeña.

El volumen del objeto, expresado en cm3, es:

23 424cm V 3 = =

Ahora veamos qué masa tiene; para ello, aplicamos la definición de densidad; de acuerdo con los datos que proporciona el enunciado:

dVm = → mdV = →

→ 2 cm g 24 cm 48 g0,048 kg m 3 3 == =

El peso de este objeto es:

0, 048kg9,8 s m Pmg 2 == ≃ 0,47 N

Sobre este cuerpo en equilibrio solamente se ejercen dos fuerzas, el peso, P, y la normal, N, y, por tanto, se anulan mutuamente:

N = P ≃ 0,47 N

La fuerza normal es la fuerza que el suelo ejerce sobre el cuerpo. Por el principio de acción y reacción, el cuerpo ejerce una fuerza contraria sobre el suelo, que representamos por F:

F = N = P ≃ 0,47 N

COMPRENDE, PIENSA, INVESTIGA…

1 ¿Qué resultará más doloroso, que te pisen el pie con un zapato plano o con un zapato de tacón? Explícate.

2 Asamblea de ideas. Da una explicación de por qué es mejor que un cuchillo esté bien afilado para cortar bien.

3 Determina la dimensión de la presión.

4 Una moneda de un euro tiene un diámetro de 23,25 mm y una masa de 7,5 g. Determina la presión que ejerce un euro apoyado sobre la mesa.

5 ¿Qué fuerza se estará aplicando sobre una superficie de 50 cm2 si la presión que ejerce es de 10 000 Pa?

6 Si un folio de papel mide 21,0 × 29,7 cm, y tiene una masa de 5,0 g, ¿qué presión ejerce sobre una mesa?

7 Comprobamos. Una persona de 80 kg tiene una superficie de apoyo en cada pie de 170 cm2. ¿Qué presión ejerce sobre el suelo?

De esta manera, hemos obtenido este resultado general: la fuerza que todo objeto ejerce sobre el suelo es igual a su peso.

Para determinar la presión que ejerce el cuerpo sobre el suelo, aplicamos la expresión: pS F =

a) La superficie de la cara mayor es: 34 12 cm 12 10 m S 2–42 1 == =

La presión ejercida sobre ella es: 12 10 m 0, 47 N pS F –4 2 1 1 == ≃ 392 Pa

b) La superficie más pequeña es: 23 6cm6 10 m S 2–42 2 == =

La presión sobre esta cara es:

8 Un dado de densidad 1,2 g/cm3 ejerce una presión debido a su peso de 1 470 Pa. Determina las dimensiones del cubo.

9 Una memoria USB de 12 g tiene forma aproximada de paralelepípedo, cuya superficie mayor es de 1,6 × 5,4 cm. ¿Qué presión ejercerá sobre tu mano cuando lo sostengas apoyado sobre esa cara?

P N F

Ley fundamental de la hidrostática

2.1 Fluidos

Un fluido es toda sustancia que pueda fluir, no mantiene su forma propia bajo la atracción gravitatoria, y fluye hasta adaptarse a la forma del recipiente que lo contiene. En definitiva, un fluido es cualquier sustancia que se encuentre en estado líquido o gaseoso.

La diferencia empírica fundamental entre un líquido y un gas es que los líquidos son prácticamente incompresibles, manteniendo su volumen constante. Sin embargo, los gases se pueden comprimir y, por tanto, no tienen un volumen propio: depende del recipiente que los contenga.

Unos líquidos fluyen con más facilidad que otros; ello depende de su naturaleza. Esta propiedad es medible con la magnitud viscosidad. Cuanto más viscoso es un líquido, más le «cuesta» fluir, como sucede con la miel. Por último, hay que dejar claro que un fluido no lo es para siempre. Denominamos fluido a una sustancia cuando se encuentra en estado líquido o gaseoso, pero, por supuesto, dejaría de ser fluido cuando se enfriara por debajo de su temperatura de fusión y se solidificara.

2.2 Equilibrio en un fluido

Investiga los fluidos

Busca en Internet vídeos de líquidos en ingravidez, ¿qué forma adquieren?

Fluidos

Gravedad cero Con gravedad

La hidrostática es la parte de la física que centra su estudio en el equilibrio de líquidos.

Un líquido en equilibrio es aquel en el que la suma de todas las fuerzas en cualquiera de sus partes que se quiera considerar es nula; por tanto, no existirán corrientes en su interior.

Experimentalmente, un líquido se caracteriza por tener volumen propio, pero no forma propia; adopta la del recipiente que lo contiene cuando está sujeto a la gravedad, y forma esférica en gravedad cero.

Los líquidos son prácticamente incompresibles; sin embargo, los gases sí se pueden comprimir. Por eso, la primera jeringa, llena de aire, se puede comprimir, mientras que la tercera, llena de líquido, no.

2.3 Presión hidrostática

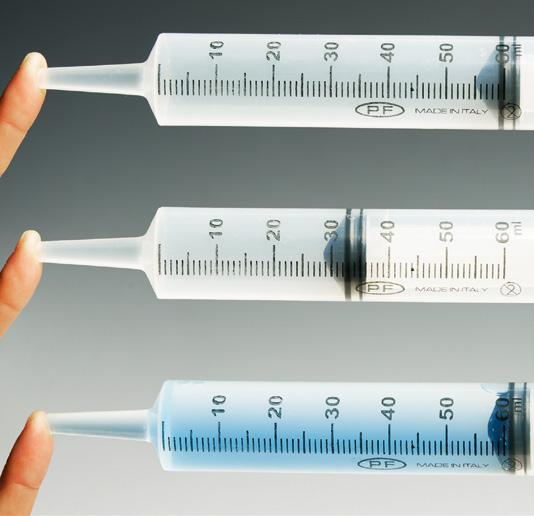
Supongamos que tenemos un líquido en equilibrio que, por simplicidad, consideraremos con forma de paralelepípedo, como puede ser el agua de una piscina. Calculemos la presión que ejerce el líquido sobre el fondo de la piscina debido a su peso.

La fuerza, F, que ejerce el líquido, de masa mF y volumen V, sobre la superficie, S, del fondo, es su propio peso, PF Si la densidad es dF y la profundidad h, la expresión de la presión del líquido es:

Este resultado es generalizable a cualquier forma que tuviera el líquido, y también es válido para encontrar la presión que ejerce a cualquier otra profundidad, h, en la capa de líquido inferior sobre la que descansa.

De esta manera, hemos encontrado una expresión matemática que permite calcular la presión que hay a una determinada profundidad en un líquido.

Esta expresión es la ley fundamental de la hidrostática:

La presión en un líquido en equilibrio de densidad dF a una profundidad h viene dada por la expresión:

Para cada punto del interior de un líquido se puede encontrar su presión hidrostática. Esta presión se manifiesta como una fuerza cuando se introduce un objeto sumergido. La fuerza que aparece debida a la presión es perpendicular a la superficie del objeto en todo punto de ella y, en consecuencia, tiende a comprimirlo.

Presión hidrostática

COMPRENDE, PIENSA, INVESTIGA…

10 CTF. Desde el punto de vista de las partículas constituyentes de la materia, ¿sabes explicar por qué los gases se pueden comprimir y los líquidos no? Repasa la teoría cinético-molecular, estudiada en cursos anteriores.

11 Piensa y comparte en pareja. El estado de un cuerpo libre de fuerzas es el reposo o el movimiento rectilíneo uniforme. ¿Por qué en un líquido en equilibrio no pueden existir corrientes con MRU?

12 Determina cuál será la presión que tendrá que soportar un buzo que se encuentra a 20 m de profundidad en agua de mar. Dato: d = 1,025 g/cm3.

Debido al peso del fluido, se aplica una fuerza sobre el fondo del fluido. Pero también ejerce una fuerza a distintas profundidades, medidas desde la superficie, sobre la capa de líquido sobre la que descansa.

En cada punto del interior del fluido hay una presión. Al colocar un objeto en el interior de un líquido, la presión en cada punto de su superficie se transforma en una fuerza perpendicular que comprime el objeto.

13 Si la presión máxima que puede soportar un submarino es 3 000 000 Pa, ¿cuál será la profundidad máxima a la que podrá sumergirse en agua de mar? Dato: d = 1,025 g/cm3

14 En el fondo de un aljibe de 1,8 m de profundidad lleno de agua hay losas cuadradas cuyos lados miden 15 cm. ¿Qué fuerza soporta cada una de las losas? Dato: d = 1 g/cm3

15 ¿Qué fuerza actuará sobre cada una de las dos caras de una moneda de 3 cm de diámetro que se encuentra en el fondo de una piscina de 2,5 m de profundidad? Dato: d = 1 g/cm3.

Infórmate sobre los acueductos romanos

¿Para qué construían los romanos sus acueductos? ¿Por qué no construían tubos en forma de U? Busca esta información en Internet.

Infórmate también acerca de la paradoja hidrostática; para ello, observa la primera ilustración de la izquierda.

2.4 Vasos comunicantes

Del principio fundamental de la hidrostática se desprende que dos puntos del interior de un líquido en equilibrio que estén a la misma profundidad se encuentran a la misma presión. De no ser así, aparecería una fuerza neta que empujaría el volumen de líquido a mayor presión hasta el de menor. Es decir, surgiría una corriente de líquido que tendería equilibrar las presiones, y el líquido no estaría en equilibrio.

Este hecho nos permite deducir el fenómeno conocido como principio de vasos comunicantes.

Dos o más recipientes que contengan un mismo líquido y que estén conectados tienen necesariamente la superficie libre a la misma altura.

Gracias a este fenómeno, se puede deducir que dos lagos vecinos no pueden estar comunicados subterráneamente si sus superficies están a distinta altura. Sin embargo, si estuvieran a la misma altura, tendríamos serios indicios para sospechar que los dos lagos están conectados. Un líquido vertido en un tubo en forma de U quedará con los niveles de las superficies de cada rama a la misma altura. En esto consiste un sifón. En las cañerías de desagüe de nuestros hogares, después del sumidero, hay un sifón lleno de agua. Así se aisla el interior de las tuberías de desagüe, que suelen oler mal, del sumidero del lavabo y del resto de la casa. Igualmente, se utilizan tuberías en forma de U para salvar obstáculos en el abastecimiento de agua corriente. La única condición es que el embalse que provee de agua esté en una de las ramas del tubo a mayor altitud que los lugares a donde se quiere llevar el agua.

Los recipientes conectados tienen su superficie libre a la misma altura, independientemente del volumen de líquido.

Si los dos lagos estuviesen conectados, sus superficies estarían a la misma altura.

El mal olor del interior de las tuberías no puede salir, ya que hay un tapón formado por el propio líquido.

El depósito de agua debe estar más alto que los lugares de consumo.

2.5 Medición de la densidad de un líquido

La densidad de un líquido se puede medir utilizando un tubo de vidrio en U. Para ello, se utiliza un líquido de densidad conocida que sea inmiscible con el líquido problema, que se verterá en una de las ramas. Por ejemplo, es muy útil para medir la densidad de distintos tipos de aceites, utilizando para ello agua, ya que el agua y el aceite no se mezclan.

En la imagen, los puntos E y F, aunque están a la misma altura, no están a la misma presión, porque pertenecen a líquidos de distinta densidad. Los puntos A y B sí están a la misma presión, puesto que pertenecen al mismo líquido. El caso límite está en los puntos C y D, que también están a la misma presión; podemos utilizar estos puntos para determinar la densidad del aceite, dF l , imponiendo esta condición:

ppCD = → dghdgh F F = ll → dhhd FF = l l

EJERCICIO RESUELTO

2 En un tubo en forma de U se vierte agua pura y, seguidamente, en una de las ramas se echa un líquido cuya densidad queremos determinar. En el equilibrio, queda tal y como se muestra en la imagen. Determina la densidad de este aceite.

Recordemos que la densidad del agua es de 1 g/cm3 Como la presión en los puntos A y B es la misma:

ppAB = → dghdgh FF = ll → dhhd FF = l l 8cm (8 –2)cm 1 cm g 0, 75 g/cm

COMPRENDE, PIENSA, INVESTIGA…

16 El depósito de agua de un pueblo está situado a una altitud de 450 m. ¿Con qué presión llegará el agua al ayuntamiento, si está a una altitud de 426 m?

17 En el tubo en forma de U de la imagen hay dos líquidos inmiscibles en equilibrio. Si el líquido 1 tiene una densidad de 1,05 g/cm3, determina cuál será la densidad del líquido 2.

La presión en los puntos C y D es igual. Por ello, midiendo las distintas profundidades, y conociendo la densidad del agua, en nuestro caso, podemos calcular la densidad del aceite.

18 La presión a la que llega el agua a la planta baja de un edificio es de 140 000 Pa. ¿A qué presión llega el agua al cuarto piso? Ten en cuenta que cada planta tiene una altura de 3 m.

19 Comprobamos. Si la presión del agua en la planta baja de un edificio es de 300 000 Pa, ¿cuántas plantas puede tener dicho edificio para que le llegue el agua con presión, si cada planta tiene una altura de 3 m? En el caso de que se quisiera construir un edificio de mayor altura aún, ¿qué solución se te ocurre que se podría tomar?

Principio de Arquímedes

Empuje de Arquímedes

3.1 Determinación de la ley

Imaginemos un cuerpo con forma de paralelepípedo sumergido en un líquido (imagen de la izquierda). Sobre cada cara del objeto se está aplicando una fuerza debido a la presión hidrostática. Las fuerzas sobre las caras laterales se anulan dos a dos, pero la fuerza sobre la cara superior, FS, no puede anularse con la inferior, FI, ya que está a menor profundidad, y la presión ejercida sobre ella es menor. Como consecuencia, aparece una fuerza neta debida a la diferencia de presión que empuja al objeto hacia arriba. Esta fuerza se denomina empuje:

EFFpSpSdghSdghS –F lS lS lF S == ==

() dShhgdVg –FF lS == → Ed Vg F =

El resultado obtenido representa el peso del fluido desalojado por el objeto al sumergirlo, pues dF · V =  mF, y mF · g =  PF. O, lo que es lo mismo, representa el peso del objeto si estuviera hecho del líquido en el que se sumerge. Además, se ha tenido en cuenta que V =  S · (hI – hs) es el volumen del cuerpo sumergido.

La fuerza en la cara inferior () F I " no es compensada con la fuerza de la cara superior () F S " . El resultado es una fuerza neta, denominada empuje, que tira del objeto hacia arriba igual a EFF –lS =

Este resultado es totalmente generalizable para cualquier forma que tenga el objeto sólido, e incluso si el fluido se trata de un gas. Así, podemos enunciar el principio de Arquímedes diciendo que:

Todo cuerpo sumergido en un fluido experimenta una fuerza vertical hacia arriba, denominada empuje, E, cuyo módulo es igual al peso del fluido desalojado.

EJERCICIO RESUELTO

3 Determina el empuje sobre un dado de 1 cm de lado que está sumergido en agua.

Simplemente debemos calcular el peso de un dado de 1 cm de lado si estuviera hecho de agua o, lo que es lo mismo:

EdVg F =

Aproxima las formas

1-2-4. Si el objeto de la imagen superior tuviera una forma irregular, ¿crees que podríamos aproximar su forma a base de juntar pequeños cubos como si fuera una figura de construcción? Si los cubos son muy pequeños, ¿se ajustará la construcción mejor a la forma del objeto real? ¿Para qué generalización se puede usar este hecho?

COMPRENDE, PIENSA, INVESTIGA…

La densidad del agua en el SI es: 1 cm g 1000 m kg d 33 F = =

Y el volumen del dado: 1cm10m V 3–63 = =

Por tanto: 1000 m kg 10 m9,8 m/s E 3 –6 32 = ≃ 0,01 N

Como puedes observar, el resultado es totalmente independiente del material del que esté fabricado el dado.

20 Mesa redonda. ¿Por qué crees que nos cuesta menos esfuerzo sostener una piedra que se encuentra dentro del agua que cuando está fuera?

21 El empuje de un cuerpo que se encuentra sumergido en agua es de 2 N. Determina cuál es el volumen que tiene dicho cuerpo.

3.2 Peso aparente

Un cuerpo sobre la superficie terrestre es atraído verticalmente hacia el suelo por la fuerza de la gravedad; es la fuerza que llamamos peso. Además, si se encuentra sumergido en un fluido, también actúa sobre él una fuerza vertical hacia arriba, denominada empuje.

Todo objeto en la Tierra está sumergido en aire; como este es muy poco denso, su empuje suele ser muy pequeño comparado con el peso. Así, aunque sea poco, el cuerpo parece pesar ligeramente menos; este efecto está muy agudizado cuando el objeto se halla sumergido en un líquido, como el agua; en este caso, el empuje ya no es nada despreciable, y parece pesar bastante menos.

Por ello, tendremos que ejercer menos fuerza para sujetarlo (figura inferior derecha), pues parte del peso se compensa con el empuje del líquido. Se habla, en este caso, del peso aparente, Pap, cuyo módulo es: PPE –ap =

Cuando un objeto se pesa en una báscula, el valor que nos indica esta es la fuerza que realiza para sostener el objeto, es decir, la fuerza normal. Si no estuviera sumergido en un fluido la normal sería igual al peso, pero cuando consideramos el empuje, porque esté sumergido en un fluido, la medida de la báscula sería el peso aparente.

Peso aparente

La medida de una báscula es la fuerza normal que sostiene el cuerpo, y es distinta si se realiza haciendo el vacío, o con aire; en este último caso mide el peso aparente.

COMPRENDE, PIENSA, INVESTIGA…

22 Determina el peso y el peso aparente de una roca de 2,7 g/cm3 y 2,00 kg de masa que se encuentra en agua.

EJERCICIO RESUELTO

4 Determina la fuerza normal que ejerce el suelo sobre una persona de 75,0 kg cuyo volumen es de 79,0 litros. Dato: densidad del aire, 1,19 g/L. Si no estuviera sumergido en aire, la normal sería igual al peso. Pero debemos considerar el empuje, que se opone al peso. Para calcularlo, primero escribimos la densidad en kg/L: 1, 19

Como P = m · g = 75 · 9,8 = 735 N: 735– 0, 9734,1 N PPE –ap = ==

La fuerza normal que sostendría esta persona, esto es, la que mediría una báscula, sería de 734,1 N. Como las básculas no tienen su escala calibrada en N, sino en kg, indican la masa cuyo peso está midiendo. Así, considerando el empuje:

Pmg ap = → 9, 8 734, 1 mg Pap == ≃ 74,9 kg

Por tanto, aunque la masa real de la persona es de 75,0 kg, la báscula nos «engañaría» con 74,9 kg.

El niño tiene que realizar una fuerza mayor con sus brazos (F ) para sostener la roca fuera del agua que dentro, puesto que el empuje del agua es mucho mayor que el del aire.

23 Intuyo y deduzco. ¿Cuándo crees que marcaría más una báscula, con 1 kg de plomo o con 1 kg de paja?

¿Es correcto decir que el kilogramo de plomo pesa más?

Deduce y comprende

Sumamos. ¿Hasta dónde subirá el globo de la imagen inferior? Para razonar tu respuesta, necesitas saber que la densidad del aire va disminuyendo con la altitud.

Flotac ión

De un globo en el aire

3.3 Flotación

Si el empuje que actúa sobre un objeto sumergido en aire es mayor que su peso, este cuerpo se elevará. Es lo que ocurre con los globos aerostáticos o los globos de feria. La manera de conseguirlo es hacer que su densidad media sea menor que la del aire, y para ello se rellenan con gases menos densos que el aire que los envuelve. Si la densidad del gas que rellena el globo es dC , y la del aire, dF , siendo V el volumen del globo:

PE < → dVgdVg < CF → dd < CF Igualmente podemos razonar para un cuerpo sumergido en un líquido, como el agua. Este flotará si su peso es menor que su empuje o, lo que es lo mismo, si su densidad media es menor que la del líquido. En ese caso, el cuerpo ascenderá hasta la superficie y, cuando empiece a salir de ella, el volumen de líquido que desaloja empezará a disminuir y, con ello, el empuje. Se alcanzará el equilibrio de flotación cuando el nuevo empuje (E' ) se haga igual de intenso que el peso del cuerpo:

El nuevo empuje, E’, se calcula únicamente con el volumen de líquido desalojado, V’, que es menor que el volumen total del cuerpo, V.

El globo asciende, puesto que el empuje es mayor que el peso.

EJERCICIO RESUELTO

5 ¿Qué porcentaje del volumen de un cuerpo de densidad 0,78 g/cm3 que flota en agua está emergido?

En el equilibrio, el empuje es igual al peso:

1 078 078

,

Ya tenemos el volumen sumergido. El volumen que queda emergido, Ve , es el restante:

VVVV 0780 12

e ==

Ve es el 12 % del volumen total, V, del cuerpo.

Cuando el objeto está totalmente sumergido, si el empuje es mayor que el peso, asciende. Cuando queda flotando en la superficie, el nuevo empuje, E’, se hace igual al peso, P.

COMPRENDE, PIENSA, INVESTIGA…

24 Determina la densidad de un iceberg que, flotando en agua de mar, emerge 1/9 de su volumen.

Dato: d (agua de mar) = 1,025 g/cm3

25 Determina el volumen de agua de mar, de densidad 1,025 g/cm3, que desaloja un transatlántico de 200 000 toneladas. Expresa el resultado en litros.

26 Un globo esférico de 8 m de radio flota en el aire soportando su propio peso, que consiste en la lona, 90 kg, y una canasta con personas y equipaje, 500 kg. Determina la densidad del aire interior si la del exterior es de 1,23 kg/m3.

Ley de Pascal 4

Principio de Pascal

4.1 Transmisión de cambios de presión

La ley de Pascal se refiere a cómo se transmite la presión en el interior de un líquido cuando, por el motivo que sea, aumenta en un punto de este.

La presión ejercida en un punto de un líquido se transmite al resto de puntos de este, manteniendo la misma intensidad.

La velocidad a la que esta transmisión ocurre es a la velocidad del sonido en el líquido. En el agua es de unos 1 500 m/s.

Gracias a esta ley se consiguen transmitir fuerzas de un punto a otro e incluso multiplicarlas, como veremos.

En los gases, la presión también se transmite, pero, debido a la compresibilidad del gas, no lo hace con la misma intensidad, y se debilita rápidamente según se propaga.

Al aplicar una fuerza sobre la superficie del tapón A, se transforma en una presión en los puntos del líquido en contacto con el tapón. Este aumento de presión se transmite a todos los puntos del fluido y, en particular, a los que están en contacto con el tapón B.

Prensa hidráulica

4.2 Prensa hidráulica

Una prensa hidráulica es un mecanismo que consiste en un depósito en el que hay un líquido, normalmente un aceite, con dos émbolos; uno de ellos, el de menor tamaño, es sobre el que se aplica una fuerza; al otro, de mayor sección, es al que se transmite la fuerza multiplicada, como puedes observar en la imagen izquierda inferior.

Según la ley de Pascal, la presión que ejercemos en el émbolo 1 se transmite en igual intensidad al émbolo 2. Así, podemos establecer las siguientes relaciones:

Al aplicar una fuerza en el émbolo pequeño, se obtiene una fuerza mayor en el émbolo grande.

COMPRENDE, PIENSA, INVESTIGA…

Como puedes observar, la relación que hay entre las fuerzas es la misma que existe entre las superficies de los émbolos.

Las aplicaciones que presenta la prensa hidráulica son muy diversas. Se utiliza en la fabricación de los elevadores de los talleres de automoción, gatos hidráulicos, frenos hidráulicos, direcciones asistidas, etc.

27 Si con una prensa hidráulica queremos multiplicar la fuerza por 16, ¿cuál será la relación que deberán cumplir sus radios?

28 Una prensa hidráulica que es utilizada como elevador de vehículos tiene un émbolo pequeño de 2 cm de diámetro, y otro grande, de 20 cm. Determina cuál será la fuerza que habrá que ejercer en el émbolo pequeño para conseguir elevar un vehículo cuya masa es de 1 000 kg.

29 Comprobamos. El pedal de freno de un coche tiene un émbolo de 0,3 cm de diámetro. Para frenar el vehículo hay dos émbolos por rueda para pinzar el disco de freno de 4 cm de diámetro. Si pisamos el freno con una fuerza de 10 N, ¿cuánto será la fuerza total de frenado entre los ocho cilindros?

30 La superficie del émbolo pequeño de una prensa hidráulica es de 2 cm2. Si al aplicar 2 N se transforman en 90 N, ¿qué radio tiene el otro émbolo?

5

Presión atmosférica

5.1 Experimento de Torricelli

Vivimos sumergidos en aire, y aunque su densidad es muy pequeña, veremos que la presión que ejerce sobre la superficie de la Tierra, debido al propio peso, no es nada despreciable.

Para medirla, podríamos pensar en aplicar la ley fundamental de la hidrostática a la profundidad a la que nos encontramos sumergidos en el aire, pero esta ley no es aplicable en este caso, puesto que la densidad del aire no es constante en toda la atmósfera, sino que va disminuyendo con la altura.

El primero en determinar el valor de la presión atmosférica en la superficie del planeta fue Evangelista Torricelli en 1643. Su experimento consistió en llenar un tubo de vidrio largo con mercurio; tapando la boca del tubo, lo invirtió y sumergió la boca en un recipiente que también contenía mercurio.

Al quitar el dedo de la boca del tubo, observó que este no se vaciaba por completo, sino que quedaba en él una columna de mercurio de 760 mm. Para dar explicación al fenómeno, propuso que la presión de la atmósfera igualaba la presión que ejercía la columna de mercurio, así que, calculando la presión del mercurio a una profundidad de 760 mm, obtendríamos la presión que ejerce el aire.

Sabiendo que la densidad del mercurio es de 13,6 g/cm3, encontramos:

Imagina y razona

¿Qué te hace decir eso? Si el experimento de Torricelli se hubiera hecho con agua, ¿qué longitud de tubo habría sido necesaria?

,, Pa pdgh 13 600 98 0 760 101300 Hg atm - ==

Este resultado es aproximado. Si utilizamos una medida más precisa de la densidad del mercurio y de la gravedad terrestre, se obtiene un valor más preciso para la presión atmosférica: 101 325 Pa. Esta es la presión atmosférica en un día de condiciones meteorológicas normales y a nivel del mar.

Variación de la presión con la altura

La presión de la atmósfera mantiene la columna de mercurio. Por tanto, la columna de mercurio ejerce una presión igual a la columna de aire que la mantiene. A partir de esto se puede calcular la presión de la atmósfera.

Una persona en una montaña está sometida a una presión atmosférica menor (tiene menos aire encima). La variación aproximada es de 1 milímetro de mercurio menos por cada 10 m que ascendamos en las capas bajas de la atmósfera.

Experimento de Torricelli

Columna de aire

Columna de aire

5.2 Unidades de presión

Son muchas las unidades que se utilizan para medir la presión. Hasta ahora solo hemos visto la del SI, el Pascal, Pa. Se define una nueva unidad de presión, denominada atmósfera, atm, de tal modo que:

1 atm = 101 325 Pa

Recuerda que se asigna el valor 1 atm a la presión que hay debida a la atmósfera a nivel del mar un día de condiciones meteorológicas normales.

El milímetro de mercurio, mmHg, es otra unidad de presión. Es la presión que hay a un milímetro de profundidad sumergido en mercurio. Del experimento de Torricelli deducimos la siguiente equivalencia:

1 atm = 760 mmHg

En meteorología se utiliza el milibar, mb, que es la milésima parte de un bar, que es la unidad de presión cuando se trabaja en centímetros, gramos y segundos. Su equivalencia con la atmósfera es:

1 atm ≃ 1 013 mb

EJERCICIOS RESUELTOS

6 La presión que medimos en la rueda de una bicicleta es de 2,5 kg/cm2. Expresa esta presión en las distintas unidades estudiadas.

Este es un ejercicio simple de cambios de unidades. Utilizando factores de conversión, resulta:

Una unidad muy utilizada por los países anglosajones es el psi (libras por pulgada cuadrada). Vale la pena que veamos su equivalencia, ya que son muchos los dispositivos de medida de presiones que nos encontramos con esta escala:

1 atm ≈ 14,7 psi

La última unidad de presión que vamos a exponer es la atmósfera técnica. Es una unidad en desuso, pero que todavía solemos usar al hinchar las ruedas de la bicicleta o del coche. La unidad es kg/cm2, y representa la presión que ejerce un kilogramo debido a su peso apoyado en un centímetro cuadrado. Su equivalencia con la atmósfera es:

1 atm ≃ 1,034 kg/cm2

Esta última equivalencia puede que te llame la atención, puesto que nos da una idea más clara de la intensidad de la presión atmosférica a la que estamos sometidos. Una presión de 1 atm supone algo más de un kilogramo en cada centímetro cuadrado de nuestra piel, presionando debido al peso de la atmósfera.

7 Demuestra la equivalencia entre la atmósfera, atm, y el kg/cm2.

La presión de 1 kg apoyado en 1 cm2 es:

= == ==

De acuerdo con la definición de kg/cm2, como la presión que ejerce una masa de 1 kg debido a su peso, podemos escribir que:

98 000Pa1 cm kg 2 =

Esta relación es equivalente a:

101 325 Pa 1, 034 cm kg 2 =

De donde se deduce que:

1atm 1, 034 cm kg 2 =

COMPRENDE, PIENSA, INVESTIGA…

31 En la base de un cerro, la presión que se mide es de 1 014 mb, y en la cima, de 947 mb. ¿Qué altura tiene, aproximadamente, el cerro?

32 Si al sumergirnos en agua de mar medimos una presión de 30 psi, ¿a qué profundidad estamos? Dato: d = 1,025 g/cm3

5.3 Aparatos de medida de la presión

Disponemos de dos aparatos de medida de presión: el barómetro, que mide la presión atmosférica, y el manómetro, que mide la presión de gases encerrados en un recipiente o a una determinada profundidad en un líquido. La lectura de la medida de un manómetro no incluye la atmosférica; es decir, la presión que se mide es a partir de la atmosférica.

El propio experimento de Torricelli es un ejemplo de cómo se construye un barómetro de mercurio. Consiste en una columna de mercurio graduada que es sostenida por la presión atmosférica. Además, se han construido barómetros mecánicos, aunque con menos precisión.

Los manómetros que vemos en las gasolineras para medir la presión de las ruedas, o los que utilizan los buzos, son mecánicos. Tienen un lámina sujeta a un resorte que, al ser presionada, mueve una aguja sobre una escala graduada. A nosotros nos interesa el funcionamiento de un manómetro elemental, que se puede utilizar para medir la presión de un gas encerrado en un recipiente. Consiste en un tubo con forma de U donde una de las ramas se conecta a un depósito con gas y la otra queda abierta a la atmósfera. Estudiando el desequilibrio de las superficies libres de cada rama se puede determinar la presión relativa del gas.

Manómetro

EJERCICIO RESUELTO

8 Si el manómetro de la imagen de arriba está hecho con mercurio, y la diferencia de niveles es de 420 mm, ¿a qué presión está el gas? Exprésalo en milibares.

El manómetro de la figura proporciona la presión relativa del gas; para hallar la absoluta tendríamos que sumar al resultado la presion atmosférica exterior.

La densidad del mercurio es:

13,6 cm g 13 600 m kg d 33 = =

La presión en el punto A es igual a la presión en el punto . La presión en el punto A’ es igual a la presión del gas encerrado, y la presión en A la podemos calcular por la ley fundamental de la hidrostática.

Y la altura de la columna de mercurio es: h = 420 mm = 0,420 m

Por tanto, la presión relativa del gas vale: p = dHg · g · h = 13 600 · 9,8 · 0,420 ≃ 55 978 Pa

Esta cantidad, expresada en milibares, mb, resulta:

5.4 Intensidad de la presión atmosférica

Torricelli fue capaz de medir la intensidad de la presión atmosférica, descubriendo que es igual a la ejercida por el mercurio a una profundidad de 76 cm. Si lo hubiera hecho con agua, habría obtenido una columna de, aproximadamente, 10,34 m, y hubiera tenido que utilizar como mínimo un tubo de esa longitud. Seguramente, al principio lo intentara con agua, pero ¿qué le debió de ocurrir cuando lo intentó con agua y con un tubo de un metro?

El agua no caería, y se sostendría completamente bajo la acción de la presión atmosférica. O podría incluso sustituirse el depósito de agua por un papel plastificado, como muestra la imagen de la derecha.

Imaginemos un tubo de unos 11 m con el que hacemos el experimento de Torricelli. El agua descendería hasta mantener una columna de 10,34 m. En el espacio superior se tendría espacio vacío a presión cero. Si abrimos el extremo superior del tubo, como si fuese una pajita muy larga, e intentáramos succionar para beber el agua, veríamos que sería totalmente imposible. Cuando se succiona lo máximo posible (presión cero), el agua solo sube 10,34 m.

De este resultado deducimos que no es posible extraer agua de un pozo con el agua a más de 10,34 m de profundidad haciendo uso de una bomba de succión a ras del suelo.

Para hacer visible la gran presión atmosférica a la que estamos sometidos, el científico alemán Otto von Guericke hizo una exhibición pública en la ciudad alemana de Magdeburgo en 1656. Su experimento consistía en dos semiesferas de cobre de unos 50 cm de diámetro. Las dos semiesferas se juntaban formando una única esfera, y mediante una válvula, se extraía el aire haciendo el vacío en su interior. Las esferas quedaban fuertemente unidas, debido a la presión externa de la presión atmosférica. Se cuenta que ni siquiera podían separar las semiesferas tirando de cada una de ellas con un tiro de ocho caballos a cada lado.

Efectos de la presión atmosférica

Vaso con agua

COMPRENDE, PIENSA, INVESTIGA…

33 Deseamos medir la presión de un gas encerrado en un depósito a 1,15 atm. Si el líquido utilizado es mercurio, ¿cuánto se desnivelarán las superficies?

34 ¿Qué fuerza hace falta para separar las semiesferas?

Dato: R = 50 cm. Considera que la fuerza se ejerce sobre una superficie circular de radio R.

La presión atmosférica es capaz de sostener la columna de agua. El vaso podría tener una longitud de hasta 10,34 m.

El agua no cae

Se puede sustituir el depósito de agua por un papel plastificado, puesto que la fuerza de la presión es perpendicular a la superficie y puede empujar hacia arriba en el papel.

Las semiesferas de Magdeburgo

La presión atmosférica mantiene unidas las dos semiesferas con una fuerza muy intensa.

6

Conceptos meteorológicos

6.1 Centros de acción

La atmósfera terrestre no es una masa de aire en equilibrio. Debido a la acción desigual del Sol sobre las distintas zonas de la atmósfera, se originan masas de aire caliente y masas de aire frío que provocan el desequilibrio y, con ello, el movimiento de estas, dando lugar a los vientos.

Los centros de acción son las zonas en la atmósfera en las que la presión es más alta de lo normal (anticiclones), o más baja de lo normal, (borrascas).

En un anticiclón hay masas de aire de las capas altas que descienden, bien porque son empujadas por otras masas de aire, o bien porque se trata de aire a baja temperatura, que es más denso y por eso baja. Este aire descendente produce altas presiones. Al ser aire frío, lleva poco vapor de agua; es aire poco húmedo. Esta situación suele provocar cielos claros con ausencia de lluvias; esto es, tiempo estable.

Por el contrario, una borrasca consiste en una zona de la atmósfera en la que se producen corrientes de aire ascendente, normalmente a mayor temperatura y humedad, que al subir se enfría, condensando el vapor de agua y formando nubes. Esta situación conlleva vientos fuertes, lluvias y bajadas de temperatura.

Investiga el sentido de giro

Busca en Internet cómo se llama a las fuerzas ficticias que desvían las trayectorias hacia la derecha en el hemisferio norte y hacia la izquierda en el sur.

Investiga el sentido de giro

Anticiclón y borrasca

Los centros de acción son las zonas en las que se impulsa el movimiento del aire a lo largo de la superficie terrestre. En un mapa meteorológico, se representa el anticiclón mediante la letra A, y la borrasca, mediante la letra B. El aire de la atmósfera se expande desde los anticiclones, debido a sus altas presiones, y converge en las borrascas, ya que se trata de bajas presiones. Como consecuencia del movimiento de rotación de la Tierra, ni la expansión de aire procedente del anticiclón, ni la convergencia de aire en la borrasca se producen radialmente, sino que lo hacen girando en torno al centro de acción. En el hemisferio norte, el aire de los anticiclones gira en el sentido de las agujas del reloj, mientras que, en las borrascas, el aire gira en el sentido contrario a las agujas del reloj. En el hemisferio sur ocurre al contrario.

y borrasca en el mapa del tiempo

En la borrasca, el aire caliente con humedad asciende, enfriándose y formando nubes. En el anticiclón, el aire frío y seco desciende, dejando días despejados.

En este mapa se encuentran localizados un anticiclón y una borrasca. También se indica el sentido de giro del aire en ellos (fíjate en que ese es el sentido en el hemisferio norte).

6.2 Masas de aire y frentes

En los mapas meteorológicos se representan las isobaras, líneas que unen todos los puntos de igual presión atmosférica sobre la superficie terrestre, prorrateados a altura del nivel del mar. Se suele expresar la presión en milibares (igual a hectopascales, hPa), de cuatro en cuatro unidades.

Si están muy juntas, indican gran cambio de presión en poca distancia (fenómenos meteorológicos violentos con fuertes vientos) y si están muy separadas, poco cambio. Las masas de aire siguen las isobaras en su movimiento.

Se denomina frente a la franja de separación entre dos masas de aire a distinta temperatura. Los frentes pueden ser fríos, cálidos u ocluidos.

El hecho de que el aire frío sea más denso que el cálido, y que este último pueda contener mayor cantidad de agua disuelta que el frío, puesto que la solubilidad del agua en el aire aumenta con la temperatura, son conceptos clave para entender el comportamiento de los frentes.

COMPRENDE, PIENSA, INVESTIGA…

35 Busca en Internet el significado de humedad relativa del aire y cómo su valor depende de la temperatura.

36 Justifica el hecho de que cuando el aire caliente y cargado de humedad se enfría, se formen nubes.

El frente cálido se representa con semicírculos en la dirección en la que se desplaza, y el frente frío, con triángulos en el lado hacia donde se desplaza.

El aire frío, más denso, desplaza al aire caliente, empujándolo y haciendo que se eleve y enfríe, formando nubes al condensar el vapor de agua que contenía y originando precipitaciones.

Frente

El aire caliente empuja al aire frío, subiéndose por encima de este y elevándose. Se forman nubes y precipitaciones, pero menos intensas que con el frente frío.

Un frente ocluido se produce cuando un frente frío alcanza a uno cálido. Dependiendo de la temperatura del frente frío, hay dos posibilidades; ambas producen precipitaciones.

Ejercicios relacionados con la presión y el empuje

EJEMPLO 1

Determina la presión a 200 m de profundidad en agua de mar, en atm, kg/cm2 y psi. ¿Qué fuerza sentirá un pez plano, si la superficie de cada lado es de 100 cm2? Dato: dF = 1,025 g/cm3.

RESOLUCIÓN

3

ENTIENDE EL ENUNCIADO Y EXTRAE DATOS

• Si no entiendes algún concepto del enunciado, realiza la consulta apropiada.

• A cada dato asígnale el símbolo adecuado.

• Realiza los cambios de unidades que necesites; en general vas a necesitar los datos en el SI.

REALIZA UN DIBUJO DE LA SITUACIÓN

Hay ejercicios en los que un buen dibujo es fundamental para resolverlo. Otras veces, puede parecernos que no es necesario, como puede ser este ejercicio.

Aunque creas que es una pérdida de tiempo, te acon sejamos que realices un pequeño croquis del proble ma; alguna vez puede salvarte de cometer un error en el que no habías reparado.

Tomamos los datos y los expresamos en el SI:

IDENTIFICA LAS LEYES FÍSICAS QUE INTERVIENEN

En este punto tienes que recordar lo que has estudiado en relación con el ejercicio. Escribe las ecuaciones que intervienen.

La presión a una profundidad h en el mar se transforma en fuerza al colocar una superficie a esa profundidad. Esta fuerza siempre es perpendicular a la superficie. Si el pez tiene dos superficies, se ejercerá una fuerza en cada una de ellas.

4

OBTÉN EL RESULTADO Y ANALIZA SU VALIDEZ

Realizamos el cálculo de la presión a la profundidad indicada en el SI.

A continuación, hacemos los cambios de unidades necesarios para expresar la presión en las unidades que se nos indica.

Con la ley fundamental de la hidrostática hallamos la presión a cierta profundidad en un líquido.

p = dF gh

Y para calcular la fuerza en cada superficie debida a la presión, utilizamos la definición de presión.

1025

EJEMPLO 2

Una embarcación cuadrada de 100 kg, con 2 m de lado y de 15 cm de espesor transporta rocas flotando en el agua del río. ¿Qué masa de rocas se puede cargar como máximo?

RESOLUCIÓN

ENTIENDE EL ENUNCIADO Y EXTRAE DATOS

• Anota los datos que nos proporciona el enunciado del ejercicio; puede que algún dato esté oculto como, por ejemplo, en este caso, la densidad del agua, 1 g/cm3, dato que debemos tener en cuenta.

• Asigna a cada dato el símbolo adecuado.

• Expresa los datos en el SI.

REALIZA UN DIBUJO DE LA SITUACIÓN

En un dibujo de un cuerpo flotando es fundamental dibujar las dos fuerzas que intervienen. Debe quedar claro que hay un volumen sumergido y otro emergido.

Tomamos los datos y los expresamos en el SI:

• Cada lado de la embarcación cuadrada: a = 2 m.

• Espesor de la embarcación: b = 15 cm = 0,15 m.

• Masa de la embarcación: m = 100 kg.

• Densidad del fluido (agua): dF = 1 g/cm3

Sobre la embarcación en equilibrio actúan dos fuerzas; el peso total hacia abajo, y el empuje hacia arriba. Ambos son iguales en módulo.

3

IDENTIFICA LAS LEYES FÍSICAS

QUE INTERVIENEN

La ley fundamental para un ejercicio de este tipo es la de Arquímedes. Además, debemos recordar cómo se calcula el peso de un cuerpo.

Es imprescindible reconocer que, puesto que el cuerpo está en equilibrio, el empuje es igual de intenso que el peso total.

OBTÉN EL RESULTADO Y ANALIZA SU VALIDEZ

En cualquier ejercicio de un cuerpo flotando tendremos que resolver la ecuación: EP = l

En este caso, habrá que desarrollarla con los datos que tenemos. Debemos tener en cuenta que el peso es el debido a la barcaza y al de las rocas. Y que para determinar el peso máximo que la barcaza puede cargar, habrá que suponerla lo máximo posible hundida, para desalojar el mayor volumen posible, y hacer que el empuje tenga el máximo valor posible.

Necesitamos la expresión de Arquímedes:

EdVg F = ll

El peso de un cuerpo se calcula con la expresión: Pmg =

Recordemos que un cuerpo al flotar cumple que: EP = l

El empuje máximo que puede realizar la barcaza se dará cuando esta se hunda 15 cm. En ese caso:

1000 20,159,8 5 880 N

Así, el peso máximo será de 5880 N y será el de la embarcación más el de las rocas:

100 9, 8m 9, 85 880 N

APLICACIÓN VIRTUAL INTERACTIVA SOBRE LÍQUIDOS

Existen multitud de páginas web que contienen aplicaciones virtuales que nos permiten visualizar distintos fenómenos naturales y observar la evolución de las magnitudes que intervienen en ellos; hay, incluso, aplicaciones interactivas, en las que el usuario puede manipular: cambiar parámetros, medir, etc.

En esta unidad te proponemos que visites PhetInteractiveSimulations, que está patrocinada, entre otros, por la Universidad de Colorado Boulder. La página se encuentra traducida a una gran cantidad de idiomas. Es muy fácil encontrar la página; escribe Phet en cualquier buscador.

DESCARGANDO «BAJO PRESIÓN»

Una vez que te encuentres en la web, escribe en su buscador «hidrostática», y te aparecerán dos aplicaciones. Nosotros haremos clic sobre la primera: Bajo Presión.

FAMILIARIZÁNDONOS CON EL ENTORNO

Una vez que ejecutes la aplicación se mostrará un depósito con un líquido. Además del depósito inicial, dispondrás de otros dos que se encuentran en la esquina superior izquierda. Quédate por ahora con el primer recipiente simple.

La llave del grifo sirve para echar más líquido, y la del sumidero, para vaciar. Tienes la posibilidad de cambiar la densidad del líquido, y la gravedad del planeta en la parte inferior derecha.

Como instrumentos de medida, es posible activar una cuadrícula, para ver la profundidad del líquido; también disponemos de una regla de cuatro metros para colocarla donde queramos y medir diferentes alturas.

A continuación, entraremos en la página de la aplicación, y veremos un botón que pulsaremos para visualizarla en nuestro dispositivo.

Hay también un barómetro, cuya unidad de medida es configurable entre kilopascales (kPa), atmósferas (atm) o libras por pulgada cuadrada (psi). Haciendo clic sobre el barómetro y tirando, sin soltar el botón del ratón, podemos colocar tantos barómetros como queramos en las posiciones que deseemos.

MANIPULANDO LA APLICACIÓN

Presión atmosférica

En primer lugar, arrastra un barómetro hasta colocarlo en el aire. Observa que, si lo colocas más arriba o más abajo, la presión cambia ligeramente. En esta unidad indicamos que varía, aproximadamente, 1 mmHg por cada 10 m de desnivel. Utiliza la regla y dos barómetros para comprobarlo. Como no podemos medir 10 m, habrá que hacerlo con una altura más pequeña, y tampoco podemos utilizar mmHg, sino otra unidad. Anota los cálculos en tu libreta.

Si ahora quitas la atmósfera activando la opción de Apagado, verás cómo los barómetros marcan cero, independientemente de cuál sea su altura.

Presión hidrostática

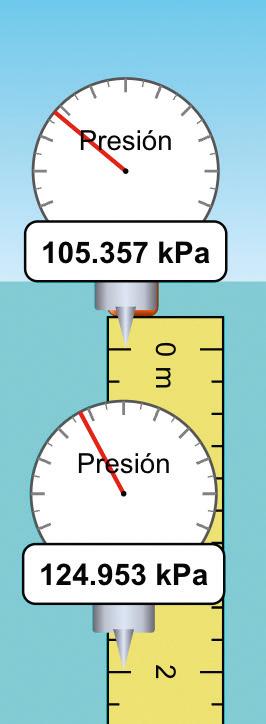
Pulsa ResetAll para empezar una nueva experiencia. Si arrastras un barómetro hasta el interior del líquido, podrás observar cómo la presión modifica mucho más rápido al variar la profundidad. Fíjate en que la presión que está midiendo el barómetro es la presión atmosférica más la hidrostática. Si quisieras medir únicamente la presión hidrostática, tendrías que eliminar la atmosférica, como ya sabes.

Vas a diseñar un montaje simple como hiciste antes en el aire, pero ahora en esta ocasión será dentro del líquido. Cuando lo hagas, date cuenta de que la diferencia de presión entre los dos barómetros permanece fija cuando cambias el nivel del depósito.

Lo que importa es la diferencia de profundidad; aunque elimines la atmósfera, la diferencia de presiones permanece constante.

Realiza tú mismo los cálculos y comprueba que la diferencia de presión en las dos profundidades que hayas escogido es la que la aplicación indica. Hazlo varias veces con distintos valores de densidad y de gravedad. Anota los cálculos en tu libreta.

Vasos comunicantes

Si cambias al segundo tipo de depósito, tendrás disponible un ejemplo de vasos comunicantes. Llenando y vaciando los recipientes, verás que los niveles de la superficie libre se mantienen a la misma altura. Incluso puedes colocar en ambos recipientes a la misma altura un barómetro y comprobar que marcan la misma presión al llenar y vaciar los recipientes. Observa que si colocas un barómetro en el tubo que comunica los dos recipientes, hay presión, aunque encima de ese punto no haya una columna de líquido hasta la superficie.

Prensa hidráulica

En el tercer tipo de depósito dispones nuevamente de dos depósitos comunicados pero, además, se puede observar la ley de Pascal, o el principio por el cual funcionan las prensas hidráulicas.

Colocando las pesas en el émbolo pequeño, vemos cómo el nivel del líquido en el émbolo grande sube. Si tuviera una plataforma, se podría aprovechar para elevar un objeto muy pesado, puesto que, como sabemos, la fuerza se multiplica.

Te proponemos que te las ingenies con la aplicación para que calcules la superficie del émbolo pequeño. Quizás la imagen de abajo te dé una pista de una manera de hacerlo. Anota los cálculos en tu libreta.

La presión atmosférica Ciencia recreativa

Vivimos bajo una presión atmosférica de aproximadamente 1 atm, que equivale al peso de 1,034 kg en cada cm2 de nuestra piel. Esta presión varía ligeramente dependiendo de las condiciones meteorológicas y de los cambios de altitud. Seguramente hayas experimentado alguna vez la variación de presión cuando has viajado, perdiendo altitud o ganándola, y se te hayan taponado los oídos.

El tímpano es la membrana que recoge las vibraciones del aire y que separa el oído externo del oído medio. Para poder oír correctamente, la presión del interior del oído medio tiene que ser igual a la presión externa, que es la que hay en el oído externo. La presión del oído medio se iguala a la externa mediante la trompa de Eustaquio, que comunica el oído medio con el interior de la nariz. Este conducto tiene mucosidades para protegernos de la entrada de patógenos. Cuando cambiamos de altitud y este conducto tiene demasiadas mucosidades, no puede salir o entrar aire para igualar la presión, el tímpano queda tenso y sentimos los oídos taponados.

oído interno oído externo

Experimento

En tu próximo viaje a la montaña o a la costa

Prepara una bolsa de patatas para tu próximo viaje. Si, por ejemplo, subes a una montaña, donde la presión se hace menor a la del interior de la bolsa, observarás cómo esta se hincha.

Si por el contrario, desciendes hasta la costa desde una localidad del interior, verás que ocurre todo lo contrario: la bolsa se queda arrugada.

• ¿Cómo crees que pueden afectar los cambios de altitud a la presión de los neumáticos de un vehículo?

• Los aviones de pasajeros vuelan en torno a los 10 000 m de altitud. La presión a esa altura es demasiado baja para que la podamos soportar. Por este motivo, la cabina del avión va presurizada a mayores presiones que las de la superficie. Averigua a qué altitud equivale la presión interior y por qué no se presuriza a 1 atm.

Trabajo práctico

El tonel de Pascal

Planteamiento del problema

Pretendemos realizar el experimento del tonel de Pascal, pero a escala más pequeña.

Tu propuesta

Necesitas revisar la ley fundamental de la hidrostática y el principio de Pascal para comprender plenamente el experimento. Una vez hecho esto, intenta idear una forma de llevar a cabo la experiencia.

Nuestra propuesta

En lugar de reventar un tonel, vamos a hacerlo con un vaso de refresco con tapón y pajita, como los que sirven en muchos lugares de comida rápida.

Material

• Un vaso de refresco con tapón lleno de agua.

• Una manguera o tubo que tenga un metro y medio o dos de longitud.

• Cinta adhesiva o silicona caliente.

• Un embudo.

• Una botella con agua.

• Rotulador y cinta métrica.

Cuando hayas revisado los conocimientos requeridos y comprendas adecuadamente la experiencia a realizar, nos pondremos manos a la obra, de acuerdo con los siguientes pasos:

• Debemos acoplar el tubo o la manguera al orificio de la tapadera que tiene para la pajita. Para ello, utilizaremos la cinta adhesiva o la silicona. Debe quedar herméticamente sellado.

• Llenamos totalmente el vaso con agua.

• Acoplamos el tapón con el tubo pegado al vaso lleno de agua.

EXTRAE CONCLUSIONES…

1 Explica cómo es posible que con el peso de tan poca agua vertida se haya reventado el vaso. Para ello, utiliza el lenguaje científico apropiado y enuncia las leyes o principios adecuados.

2 Calcula la presión que se le ha aplicado al vaso debido a esa columna de agua, utilizando la ley fundamental de la hidrostática.

• Sellamos el tapón al vaso con la cinta adhesiva o con la silicona caliente.

• Ya solo queda llenar poco a poco el tubo con agua. Para ello, utilizaremos la botella con agua y el embudo. Si se trata de la manguera, debemos colocarla verticalmente mientras se llena.

• Cuando el vaso reviente, realiza una marca con un rotulador en el punto hasta donde habías llenado de agua.

• Mide la altura de la columna de agua desde la tapa del vaso hasta la marca.

3 Expresa el resultado en atmósferas y en libras por pulgada cuadrada, y anótalo en tu cuaderno.

4 Si hiciéramos el mismo experimento con mercurio, ¿qué altura habríamos necesitado?

5 ¿Qué crees que ocurriría si hiciéramos el experimento con agua, pero en la cima de una montaña?

COMPRENDE

Organiza tus ideas Mapa conceptual sistémico

1 Dibuja un cuerpo flotando en un líquido, incluyendo las fuerzas que intervienen sobre él. Realiza la misma representación, para un cuerpo que está apoyado en el fondo de un depósito con líquido.

2 Completa en tu cuaderno el esquema siguiente. A partir de este, elabora un mapa conceptual completo en el que se recojan los diferentes contenidos que has estudiado en esta unidad.

P

ap =

su expresión matemática es ................ ?

consecuencias

Recuerda que dispones de las soluciones de todas las actividades numéricas en anayaeducacion.es

Presión

1 Se aplica una fuerza de 100 N a una superficie circular de 5 cm de diámetro. ¿Qué presión se está ejerciendo?

2 Una columna de granito de 2,71 g/cm3 de densidad tiene un diámetro de 50 cm y una altura de 4 m. Determina la presión que ejerce sobre su base debido a su propio peso.

3 Una persona de 75 kg lleva unas botas de 200 cm2 de superficie de apoyo cada una. Determina la presión que ejercerá sobre la nieve cuando esté de pie. ¿Y cuando lo haga con sus esquís, de superficie 1 800 cm2 cada uno? ¿Puedes explicar por qué se hunde menos en la nieve cuando lleva los esquís?

4 Una mesa de 20 kg tiene un tablero rectangular de 100 × 70 cm. Las cuatro patas son de sección cuadrada de 4 × 4 cm. Determina la presión que ejerce la mesa debido a su propio peso cuando está apoyada sobre sus cuatro patas, y también, cuando se le da la vuelta y se apoya sobre el tablero.

5 Determina la densidad de un cubo de 7,5 cm de arista que aplica una presión bajo su peso de 1 102,5 Pa.

6 Cuando estudies más adelante la energía, verás que su dimensión es [E ] = M · L2 · T–2. Comprueba que la presión es una energía por unidad de volumen.

Flotación

Ley fundamental de la hidrostática

7 Sumamos. ¿Eres capaz de dar una explicación científica al hecho de que los líquidos en gravedad cero adopten una forma esférica y no otra?

8 Determina la presión que habrá en el fondo de la fosa de las Marianas, que es el punto conocido más profundo del planeta, con 11 012 m. Supongamos una densidad de 1,025 g/cm3.

d = 1 g/cm3

a = 8,5 cm

b = 4,2 cm

9 Determina la presión que hay en el punto A. a

c = 2,0 cm

bc A

R = 10 cm

a = 2 cm

b = 9 cm

10 ¿Con qué fuerza estará presionando el agua del recipiente el tapón de la rama más corta? a

11 En el fondo de una piscina de 2,6 m de profundidad está puesto el tapón del sumidero, circular, de 12 cm de diámetro y 1,5 cm de espesor, y su densidad es de 7,9 g/cm3. ¿Cuánto pesa el tapón? ¿Qué fuerza tendremos que hacer para quitar el tapón?

d = 1 g/cm3

12 Determina la fuerza que ejerce el agua sobre el fondo del depósito y di si es mayor o menor que el peso del agua que contiene. Ten en cuenta que el volumen de agua se calcula a partir de la expresión:

V = 1/3 π · R 2 · a – 1/3 π · r 2 · b

a = 10 cm

b = 4 cm

R = 6 cm

r = 3 cm

r

R

b a

13 El depósito de la imagen contiene 1 000 litros de agua. En el fondo tiene un orificio de 0,5 cm de diámetro. ¿Podría una persona aplicar fuerza suficiente con el dedo y taponar el depósito para que no se vacíe?

Dato: h = 1 m.

14 Rueda lógica. Si dos lagos cercanos tienen sus superficies a la misma altura, ¿podremos asegurar que están comunicados subterráneamente?

15 En una calle inclinada hay una tapia en la que queremos dibujar una línea horizontal; para ello, disponemos de una manguera translúcida. Explica claramente cómo procederías para hacerlo y en qué principio te basarías.

16 ¿Para qué crees que en ciertas zonas urbanas hay una torre alta con un depósito de agua en la parte superior?

17 Círculo de puntos de vista. Los romanos construían grandes acueductos para salvar obstáculos y llevar el agua de un punto a otro. ¿Por qué nosotros no necesitamos construirlos?

18 ¿Crees que el líquido de la imagen de abajo está en equilibrio? Justifica tu respuesta.

19 Si el agua llega a un sexto piso a una presión de 20 000 Pa, ¿qué presión habrá en la planta baja? Dato: hay 3 m por planta.

20 El líquido de menor cantidad de la imagen es un aceite de 0,8 g/cm3. Determina la densidad del líquido desconocido.

a = 5 cm

b = 12 cm

21 En un tubo con forma de U hay tres líquidos inmiscibles. El líquido 1 es agua, y el 2 es un líquido de densidad 1,2 g/cm3. Determina cuál será la densidad del líquido 3.

a = 3,1 cm

b = 1,3 cm

c = 0,6 cm

Principio de Arquímedes

22 Un cuerpo de 350 cm3 de volumen está sumergido en agua pura. Determina el empuje que experimenta.

23 Determina el empuje que experimenta una esfera de 3 cm de diámetro que se encuentra sumergida en alcohol etílico, cuya densidad es: d = 0,79 g/cm3 Dato: VEsfera = 4/3 · π · R3

24 Determina el peso y el peso aparente de un cubo de 1,6 g/cm3 de densidad y de 5 cm de arista cuando lo sumergimos en agua.

25 El peso aparente de una roca de 150 cm3 cuando está sumergida en agua es de 1,76 N. Determina la densidad de la roca.

26 Un cilindro metálico de 6 cm de altura y cuya base tiene 2 cm de radio se sumerge en un recipiente con agua, tal y como se muestra en la imagen. Si el dinamómetro marca 1,40 N, determina cuál es la densidad del cilindro. Dato: VCilindro = π · R2  · h

31 Realizamos el siguiente montaje. En el lado A se han colocado pesas hasta equilibrar la varilla, lo que sucede cuando la masa es de 4 911 g. En el otro del montaje, el lado B, hemos situado una esfera de 8 cm de diámetro y de densidad desconocida sumergida en agua. Determina cuál es la densidad de la esfera. Dato: VEsfera = 4/3

27 Si la densidad media de una persona es de 1,04 g/cm3, ¿se hundirá o flotará en agua?

28 Un cuerpo de 80 cm3 de volumen y 0,49 g/cm3 de densidad está flotando en gasolina, cuya densidad es: dF = 0,68 g/cm3. ¿Qué volumen del cuerpo está emergido?

29 Si un barco que está cargado al máximo va navegando por agua de mar, ¿podrá entrar por la desembocadura de un río, navegando río arriba? Razona la respuesta.

30 Mesa redonda. ¿Cuál crees que puede ser la razón por la que los buzos se cuelgan pesas? Razona y justifica tu respuesta.

32 CTF. ¿Dónde crees que cansará menos nadar, en agua dulce o salada? Justifica tu respuesta.

33 La densidad del agua del mar Muerto tiene un valor de 1,240 g/cm3. ¿Puedes explicar por qué las personas pueden flotar en ella?

34 Un densímetro es un pequeño dispositivo que, al flotar en un líquido, marca el volumen que queda emergido. Con este valor, se determina la densidad del líquido en el que flota. Si un densímetro de 0,65 g/cm3 de densidad flota en un líquido, y emerge un 35 % de su volumen, ¿qué densidad tiene el líquido?

Ley de Pascal

35 Explica el fundamento del funcionamiento de la prensa hidráulica.

36 Una prensa hidráulica tiene una superficie pequeña de 0,3 cm2, y la grande, de 40 cm2. ¿Qué fuerza se obtendrá en el émbolo mayor al aplicar una fuerza de 100 N sobre el émbolo pequeño?

37 El diámetro del émbolo pequeño de una prensa hidráulica es de 1,5 cm, y el del grande, de 30,0 cm. Si se tiene elevado un coche de 900 kg, ¿qué fuerza se está aplicando sobre el émbolo pequeño?

Presión atmosférica

38 Folio giratorio. Si la presión atmosférica se debe al peso del aire que tenemos encima, ¿por qué cuando nos ponemos bajo techo no notamos disminución de presión?

39 Expresa un valor de presión de 990 mb en el resto de unidades estudiadas.

40 Una persona succionando agua con una pajita muy larga es capaz de hacer en su boca un vacío igual a la décima parte de la presión atmosférica. ¿Hasta qué altura subirá el agua?

41 Si tapamos con una cartulina plastificada un vaso a rebosar de agua y le damos la vuelta, veremos que el agua no se cae. ¿Cómo empuja la presión atmosférica la cartulina hacia arriba?

42 ¿Estarán los líquidos de las imágenes en equilibrio? Justifica la respuesta.

SITUACIÓN DE APRENDIZAJE

Conceptos meteorológicos

43 Busca en Internet el mapa meteorológico de hoy, y justifica el tiempo de hoy y el de mañana.

REFLEXIONA

En las actividades de esta unidad has obtenido información sobre los límites de presión del cuerpo humano y has aplicado conceptos de presión atmosférica al estudio de las condiciones de Marte.

Descarga el cuestionario que te ofrecemos en anayaeducacion.es para reflexionar sobre este proceso.

Aspectos Totalmente conseguido Bastante conseguido Conseguido Casi conseguido Investiga, selecciona e interpreta información en diferentes formatos (tablas, gráficos, esquemas, pósteres, etc.).

PON A PRUEBA TUS COMPETENCIAS

Realiza la autoevaluación competencial incluida en anayaeducacion.es

Vivimos sumergidos en aire, y, aunque este «pesa» poco, es mucha la cantidad que tenemos encima, que ejerce sobre nosotros una presión nada despreciable.

Recuerda: es, aproximadamente, el peso de un kilogramo en cada centímetro cuadrado. A nuestro alrededor podemos encontrar pruebas de la existencia de esta presión del aire.

¿Te has preguntado alguna vez por qué pegan las ventosas? Si tiramos fuerte, no las despegamos; sin embargo, si levantamos un borde, se despegan fácilmente.

O, ¿te has fijado cómo es el bebedero que hay en la jaula del canario? ¿Por qué no se derrama el agua?

Te proponemos un experimento muy fácil de hacer. Coloca en el filo de la mesa una hoja de periódico. Por debajo introduce una regla, tal y como se ve en la imagen.

Si empujas suavemente el extremo de la regla hacia abajo, verás que la hoja se levanta. ¿Pero qué le ocurre cuando le das un golpe seco hacia abajo?

La próxima vez que vayas de viaje llévate una botella de plástico vacía, es decir, con aire. Ciérrale bien el tapón y observa qué le ocurre cuando cambies de altitud.

Física cotidiana: evidencias de la presión atmosférica

© GRUPO ANAYA, S.A., 2023 - C/ Valentín Beato, 21 - 28037 Madrid.

Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.