Operación mundo: Mathematics 3. Secondary DF (muestra)

3 DUAL FOCUS

ANDALUSIA

INDEX

1. Numbers for counting, numbers for meansuring .......................... 7

1 Natural numbers • 2 Other ways of counting

• 3 Integers • 4 Fractions • 5 Operations with fractions • 6 Decimal numbers • 7 Fractions and decimals with the calculator • The final challenge

2. Powers and roots 21

1 Powers • 2 Scientific notation • Exact roots

• 4 Radicals • The final challenge

3. Arithmetic problems ............................... 29

1 Approximations and errors • 2 Calculating with percentages • 3 Compound interest

• 4 Common problems • 5 Compound proportion and arithmetic problems • The final challenge

4. Progressions ................................................. 41

1 Sequencues • 2 Arithmetic progressions

• 3 Geometric progressions • The final challenge

5. Algebraic language 49

1 Algebraic expressions • 2 Monomials

• 3 Polynomials • Identities • 5 Dividing polynomials

• The final challenge

6. Equations ..................................................... 57

1 Equations. Solving an equation • 2 First-degree equations • 3 Second-degree equations • 4 Solving problems with equations • The final challenge

7. Systems of equaions 65

1 Linear equations with two unknowns • 2 Systems of linear equations • 3 Equivalent systems

• 4 Types of systems by number of solutions

• 5 Methods for solving systems • 6 Solving problems through systems • The final Challenge

8. Functions. Characteristics 73

1 Functions and their graphs • 2 Function aspects

• 3 Analytic expression of a function • The final challenge

9. Linear and quadratic functions 81

1 Proportionality function y = mx • 2 Linear function y = mx + n • 3 Applications of linear functions. Movement problems • 4 Studying two linear functions together • 5 Parabolas and quadratic functions • The final challenge

10. Metric Problems in plane geometry ................................... 91

1 Angle relationships • 2 Similiar triangles. Thales´s theorem • 3 Similar shapes. Scales • 4 Pythagorean theorem • 5 Algebraic applications of the Pytagorean theorem • 6 Areas of polygons • 7 Areas of curved shapes • The final challenge

11. Geometric solids ......................................

99

1 Regular and semiregular polyhedra • 2 Truncating regular polyhedra • 3 Planes of symmetry of a shape • 4 Axes of symmetry of a shape • 5 Surface area of geometric shapes • 6 Volume of geometric shapes • 7 Geographic coordinates • The final challenge

12. Geometric transformations ............

109

1 Geometric transformations • 2 Motions in the plane • 3 Translations • 4 Rotations. Shapes with a centre of rotation • 5 Axial symmetries. Shapes with axes of symmetry • 6 Composition of movements • 7 Mosaics, friezes and rosettes • The final challenge

13. Statistical graphs and tables

121

1 The statistical process • 2 Statistical variables • 3 Population and sample • 4 Making a frequency table • 5 Using the rigth graph • The final challenge

14. Statistical parameters

129

1 Two types of statistical parameters • 2 Calculating x and σ in frequency tables • 3 Joint interpretation of x and σ • 4 Position parameters, median and quartiles • 5 Using a calculator to get x and σ • The final challenge

15. Chance and probability

137

1  Random events • 2 Probability of an event • 3 Probability in regular experiments. Laplace’s law • 4 Probability in irregular experiments. Law of large numbers • 5 Probabilities in compound experiments • The final challenge

1 NUMBERS FOR COUNTING, NUMBERS FOR MEASURING

Fractions

Natural numbers

operations

ACTION!

How does your family spend on its grocery shop?

Take on the ‘Final Challenge’ and draw a chart of the distribution.

operations simplifying fractions equivalent fractions comparing fractions

• mixed

• pure

• adding and subtracting

• simplified

• irreducible

Decimal numbers

• multiplying and dividing

• combined operations

• fraction of an amount

Integers

operations counting solving problems

transforming the quotient can be types from fractions into decimals decimals into fractions

• an integer

absolute value solving problems terminating decimals with a calculator recurring decimals irrational numbers

• terminating decimal

• pure recurring decimal

• mixed recurring decimal

• a terminating decimal

• a recurring decimal

Listening

Listen and repeat. The vocabulary is at anayaeducacion.es

Discover

FOCUS ON ENGLISH

Today, we use fractions and decimals with ease, but it was a long journey to get here. In ancient Mesopotamia, the Babylonians used the sexagesimal system to write numbers. They also used sexagesimal fractions to write parts of the unit. These fractions have denominators that are powers with a base of 60.

Reading

Read the text ‘In Mesopotamia’ at anayaeducacion.es and answer the questions.

Natural numbers 1

The numbers we use to count objects are called natural numbers. We count using natural numbers. The natural numbers are, as you know, 0, 1, 2, 3, …, 10, 11, …, 100, 101, … There is an infinite amount of them. We call the set of these numbers N. They have an order, which means we can represent them on a line:

The natural numbers can also be used to indicate the position that different elements occupy in an ordered set: October is the second month of autumn and the tenth of the year.

1 Reading. A farmer buys 45 cows for €475 each. Unfortunately, two of them are injured on the journey home so he has to have them put down. Six months later he sells the remaining cows for €1 690 each. Taking into account that the costs of maintenance and feed were €34 680, what profit did he make on each of the cows he bought?

2 Reading. At a bakery, they take 7 trays of cupcakes out of the oven. Each tray has 65 cupcakes on it. They then package the cupcakes in bags of 8 and sell them for € 2 per bag.

How much money do they make, bearing in mind that 13 cakes were spoiled during the handling process?

Other ways of counting 2

successively (1, 2, 3, 4, …) from first to last. However, there are other more complex ways of counting using basic arithmetic. For example:

How many boxes are in a stack that is 45 boxes long, 30 wide and 40 high? Clearly, 45 · 30 · 40 = 54 000 boxes.

There are also more sophisticated ways of counting which require a systematic approach and the use of specific strategies. Let’s look at some examples:

How many different starting lineups of 5 players can we select from a basketball team with 7 players?

There are 7 players (a, b, c, d, e, f, g) and we have to select 5. However, it is easier to think about the two players who are not in the starting lineup.

ab ac ad ae af ag bc bd be bf bg cd

As you can see on the left, there are 21 ways of selecting 2 from 7 (the 2 that do not start). Therefore, there will be 21 ways of selecting the 5 players in the sarting lineup.

3

In a championship with five participants, there are three different prizes for the top three. How many ways can these prizes be awarded?

We can use a tree diagram to analyse all the possibilities.

We see that player A is the first in 4 · 3 of the possible cases. The same will occur with the other players.

Therefore, the total number of possibilities is: 5 · 4 · 3 = 60.

1 Speaking. How many ways are there of sharing out 3 different books among 6 students?

2 How many ways can we get from A to B? And from B to C?

And from A to C via B?

3 How many ways can we share 6 tickets between 7 people? And between 8 people?

4 Writing. A table tennis tournament is organised between six players. How many matches have to be played? Describe them.

5 Writing. How many ways can five friends arrange themselves in five adjacent seats in the cinema? Describe the possibilities.

6 Calculate the sum of the first 50 prime natural numbers. Do this without adding them together one by one. To do so, remember that 1 + 50 = 2 + 49 = 3 + 48 = …

Integers 3

The set Z

Negative integers, together with natural numbers, form the set of integers, which is represented by the letter by Z.

Integers can be shown in order on a line: –7 – 6 –5 – 4 –3 –2 –1 0 1 2 3 4

The absolute value of an integer

The absolute value of a number is its magnitude without its sign. | x | 8 value absolute of x

Operations with integers

When we add, subtract and multiply integers, the result will always be another integer. However, when dividing two integers, the result is not always an integer.

a) 7 – |5 – 8| – (4 – 12 + 6 – 11) = 7 – |–3| – (10 – 23) = 7 – |–3| – (–13) = = 7 – 3 + 13 = 20 – 3 = 17

b) |2 · (–9)| – [–16 – 5 · (11 – 17)] : (7 – 8) = |–18| – [–16 · 5 – (–6)] : (–1) = = 18 – [–16 + 30] : (–1) = 18 – [14] : (–1) = 18 + 14 = 32

c) |–4 + (–3) · 2 + 5| – 2 · |3 – |4 – 5|| = |– 4 + (–6) + 5| – 2 · |3 – 1| = = |–10 + 5| – 2 · 2 = |–5| – 4 = 5 – 4 = 1

1 Put the following in order from smallest to largest: |–4|, 19, 7, 0, –6, |–5|, – 2

2 Calculate.

a) [(1 – 4) – (5 – 3) – (–6)] · [–3 + (–7)]

b) |3 – 3 · (–7) – |5 · (–8)||

c) –3(4 – 2) – 4(3 – 8) – [4 · (–5)] · [(–3) · 11]

3 Perform the operations in the following expressions:

a) [(1 – 7) – (8 – 3) – 2] · (15 – 11)

b) (7 – 3) · 12 + (5 – 1) · [6 – 3 · 2]

c) –3) – 2 · (–1) + 5 · (–2) – [2 – 4 · (–7)]

d) 17 – 4 · (–3 + 6) – 2[4 – 5(2 – 3) · (–2)]

e) |26 – (– 4) · (–3) · (–3 + 2)| – |–2 + 7| · (–4)

Observe

Graphically, the absolute value of a number is its distance from zero: |– 4| = 4

4 0 3 |+3| = 3

4 Reading. The temperature of a freezer drops 2 °C every 3 minutes until it reaches –18 °C. How long would it take to get to –12 °C if it was at 16 °C when we turned it on?

5 Aristotle died in the year 322 BCE and lived for 62 years. What year was he born in?

6 Reading. Find the temperature difference (in °C) between the melting point, MP (solid to liquid), and the boiling point, BP (liquid to gas), of each of these chemical elements:

a) Chlorine. MP: –101; BP: –35

b) Phosphorus. MP: 44; BP: 280

c) Mercury. MP: –39; BP: 357

Fractions 4

A fraction is a quotient of two integers. This quotient can be an integer , 2 6 3 3 12 4 –– == dn or a fraction , 2 17 8 2 1 5 13 2 5 3 –=+ =

The set of all the integers and all the fractions is called the set of rational numbers and is represented by the letter à.

Rational numbers are numbers that can be written as a fraction.

Simplifying fractions

If the numerator and denominator of a fraction can be divided by the same number (other than 1 and –1), when we divide them by that number we say that we have simplified or reduced the fraction. Look at figure ❶.

When a fraction with a positive denominator cannot be reduced further, we say that it is irreducible.

Equivalent fractions

We say that two fractions are equivalent when they can be simplified to the same irreducible fraction. This irreducible fraction is the common expression of that rational number.

and 35 21 are

Comparing fractions

It is very easy to compare two fractions with the same denominator just by looking at their numerators. To compare two fractions with different denominators, we ‘reduce to a common denominator’. In other words, we find two fractions with the same denominator that are equivalent to the ones we have.

Remember

If the numerator is a multiple of the denominator, the fraction is an integer. If not, it is a fraction.

1 What fractions do these points on the number line represent?

Observe

Cross-multiplication is a method that we use to check if two fractions are equivalent.

b

For example, 30 18 and 35 21 are equivalent because: 18 · 35 = 630 = 21 · 30

2 Simplify and use cross-multiplication to determine whether or not these fractions are equivalent:

a) 20 12 and 35 21 b) 102 36 and 221 78 3 Reading. True or false?

a) 5 2 > – 4 7 because the first is positive and the second is negative. b) 3 7 > 5 2 because the first is greater than 1 and the second is less than 1. c) 3 8 > 4 7 because the first is greater than 2 and the second is less than 2.

Operations with fractions 5

Adding and subtracting fractions

To add (or subtract) fractions with the same denominator, we add (or subtract) their numerators and leave the same denominator.

To add (or subtract) fractions with different denominators, first transform them into equivalent fractions with the same denominator, then add (or subtract) their numerators. Look at example ❶

Multiplying and dividing fractions

The product of two fractions is a fraction in which the numerator is the product of the numerators and the denominator is the product of the denominators.

Look at example ❷.

The quotient of two fractions is the product of the first fraction multiplied by the inverse of the second fraction. : b a d c b a c d =

Look at example ❸.

Combined operations with fractions

To do combined operations, solve the expressions in brackets first and then do the rest of the operations, solving products and quotients before additions and subtractions. Look at example ❹.

Fraction of an amount

To find a fraction, b a , of an amount, C, we multiply b a · C.

To find 5 3 of €1 200, divide by 5 and then multiply the result by 3. Look at example ❺.

1 Do these operations and simplify the results:

2 Find the portion of the total represented by each fraction. a) 2 1 of €520 000 b) 10 7 of 500 buildings.

3 Speaking. A cyclist has completed 5/9 of today’s 216 km stage. How many kilometres has he gone? Answer and discuss with your classmates.

Problems with fractions

In a class of 36 pupils, 2/3 are boys. 3/4 of the girls do music. What fraction of the class are girls who do music? How many girls is that?

3 2 are boys → 3 1 are girls

Fraction that are girls who do music: 4 3 of 3 1 = 4 3 3 1 12 3 4 1 ·= = of the total class

Number of girls who do music: 4 1 of 36 = 36 : 4 = 9 2

Three friends share a prize. The first one gets 2/5 of the total; the second 5/9 of the remainder, and the third, €92. How much was the prize?

The first gets 5 2 of the prize; the remainder is 5 3

The second gets 9 5 of 5 3 = 9 5 · 3 5 = 9 3 = 3 1 of the prize.

The first and the second friend get 5 2 3 1 15 65 15 11 += + = of the prize between them.

The third gets 15 15 15 11 15 4 –= of the prize. 15 4 of the prize is €92; 15 1 is

:

Therefore, the prize was (92 : 4) · 15 = €345.

4 Express the following as an integer and a fraction. a) 9 40 b) 5 86 c) 10 127 d) 12 127 e) 8 43 –

5 Find the irreducible fraction. a) 21 18 b) 35 14 c) 36 42 d) 56 14 e) 200 75

6 Calculate. a) 5 1 of 275 b) 7 3 of 581 c) 20 11 of 580

7 Find the resulting fraction. a) 2 1 of 3 1 b) 3 2 of 4 1 c) 9 5 of 5 3

8 Calculate. a) · 1

9 A greengrocer sells 3/5 of its fruit in the morning and, in the afternoon, half of what was left.

a) What fraction is left to sell?

b) If there were 750 kg of fruit at the beginning of the day, how many kilos were sold?

10 Reading. A dentist spends 1 and 3/4 hours in his practice. If he sees 15 patients in that time, what fraction of an hour can he spend with each one? How many minutes is that?

Decimal numbers 6

Writing numbers in decimal form gives us a very easy and effective way to assess them, compare them and use them for mathematical calculations.

Types of decimal numbers

Terminating decimals: have a limited number of decimal places.

• Terminating decimals: have a limited number of decimal places.

5.4; 0.97; 8; –0.0725

• Pure recurring decimals: all the figures after the decimal point are repeated.

7.81818181... = 81 7 $

• Mixed recurring decimals: at least one of the figures after the decimal point is not repeated. 18.35222222... = . 2 18 35 !

• Decimals that are neither terminating nor recurring: These decimals have an infinite number of figures that do not repeat regularly. Unlike terminating decimals and recurring decimals, these numbers are not rational. We call them irrational numbers.

2 = 1.4142135…; π = 3.14159265…

1 Writing. Indicate which type of decimal each of these are:

3.52 . 28 ! . 154 # 3 = 1.7320508…

2.7 3.5222… π – 2 = 1.1415926…

2 Order the following from smallest to largest:

a) 3.56; 356 ! ; 35 ! ; 356 #

b) –1.32; – . 132 ! ; – . 132 # ; – . 13 !

c) .; ;. ;; 23 3 8 234 15 32 10 21 !

Remember

In a number, the group of decimal places that repeats again and again is called the period. We draw an arc over the repeating figures to indicate the period:

. 568 # 16.14 7 !

Using the calculator

On calculators we use a full stop for the decimal point. 1 437.54 → {∫∫‘¢«|…∞¢}

3 Writing. Order the following from largest to smallest: . 25 ! 2.5 . 235 ! 2.505005…

Explain your answer in your notebook.

4 Write three numbers that fall between:

a) 2.5 and . 25 !

b) 0.345 and 0.346

c) 23 ! and 2.4

d) – 4.5 and – 4.4

Transforming

fractions into decimals

To write a fraction in decimal form, divide the numerator by the denominator. The quotient can be:

• An integer: the numerator is a multiple of the denominator. 9 72 = 8; 15 –240 = –16

• A terminating decimal: the only prime factors of the denominator of the simplified fraction are 2 and 5 (or either of them).

123 = 3.075; 25 42 = 1.68

• A recurring decimal: the denominator of the simplified fraction has a prime factor other than 2 or 5.

The quotients and remainders repeat from here on.

All irreducible fractions can be written in decimal form:

• As a terminating decimal if the only prime factors of the denominator are 2 and 5.

• As a recurring decimal if the denominator has prime factors other than 2 and 5.

Therefore, they are both rational numbers. However, decimals with infinite decimal places that do not repeat are irrational numbers.

5 Speaking . Discuss as a group: True or false?

a) 3 1 = 0.333… = . 03 ! 3 3 = 3 · 0.333… = 0.999… = . 09 ! Because 3 3 = 1, then . 09 ! = 1

b) . 54 ! = . 544 #

c) . 372 # = 3.7272727… = 3. 727 #

d) . 03 ! + . 06 ! = 1

6 Without doing the division and looking only at the denominator of the simplified fraction, say whether these fractions transform into terminating decimals or recurring decimals:

7 Write a value of k that makes the fraction k 84 :

a) An integer.

b) A terminating decimal.

c) A recurring decimal.

TAKE ACTION!

The final challenge

MAKE THE CHART

Alone or in a team, role play, carry out the activities and, at the end, make a chart showing your family’s monthly expenditure in the supermarket.

This week Manuel didn’t have time to go to the supermarket and did his shopping via an app.

After payment, the application shows you the summary of his purchase in a pie chart.

1 Manuel paid € 254.95 for the purchase.

a) How much did he pay for fresh food?

b) Half of the amount he spent on fresh food was on fruit and vegetables, two-sixths on fish and the rest on meat. How much money did he spend on each product?

2 Manuel bought 9 bags of blueberries in the freezer section. When he received the groceries, he saw that 3 of them were broken.

a) What fraction of the bags were broken?

b) If he has been reimbursed for these 3 bags, how much money has he been reimbursed?

3 This week Manuel is looking after Fibi, his sister’s pet. He has run out of dog food and has included it in the shopping, as well as a couple of toy bones to keep Fibi entertained.

If the amount of dog food represents three quarters of what Manuel spent in the pet section, what is the price of each product?

4 Manuel has spent one eighth of his monthly budget on shopping. What is this budget?

Final product

Collect your family’s shopping receipts for one month. Divide the products into different departments, calculate the fractions and draw the corresponding pie chart. To do this, you can organise the data in a spreadsheet and create the charts by choosing the option in the ‘Insert’ tab.

2 POWERS AND ROOTS

Do you want to raise money in solidarity?

Take on the ‘Final Challenge’ and organise a crowdfunding on your birthday. TAKE ACTION!

Powers and roots exact roots

exponentiation radicals scientific notation

integer part

integer power of base 10

operating with radicals index

radicand

decimal part

powers with positive exponents

powers with zero exponents

powers with negative exponents

• square roots

• cube roots

• other roots

FOCUS ON ENGLISH

Listening

Listen and repeat. The vocabulary is at anayaeducacion.es

Discover

The Greek mathematician Archimedes (3rd century BCE) took the decision of writing a number greater than the number of grains of sand in the universe to show that the number of grains of sand that would fit ‘was not infinite’. He invented a new way of writing extremely large numbers using powers of base 10. Archimedes is therefore considered to be the father of scientific notation.

Reading

Read the text ‘The Sand Reckoner’ at anayaeducacion.es and answer the questions.

Powers 1

Powers with positive exponents

Powers with positive integer exponents (1, 2, 3, etc.) are easy to interpret:

Properties:

1 Product of powers with the same base.

2 Power of a product.

3 Power of a power.

4 Quotient of powers.

5 Power of a quotient.

1 Reduce to just one power.

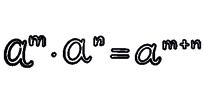
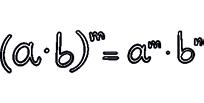
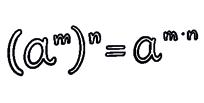
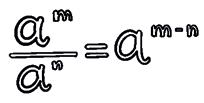
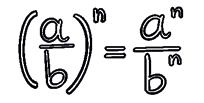
2 Use the properties of powers to calculate.

Powers

with zero or negative exponents

The property 4 on the previous page is only valid for m > n. Let’s see what happens if m = n or m < n :

a a 3 3 = a 3 – 3 = a 0. But a a 3 3 = 1. Therefore, it must be true that a 0 = 1. a a 5 3 = a 3 – 5 = a –2. But

These equalities give us the following definition:

If a is a rational number other than zero and n is an integer:

Therefore:

The properties for powers with positive exponents are also valid for powers with any integer exponents.

Simplify.

3 Calculate.

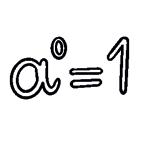
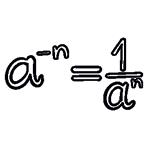
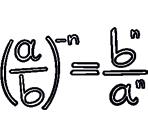
Using the calculator

We use these keys to calculate powers with a calculator:

• For squares: x 5 x= 25

• For cubes: 2 = 8

• For any power: á 3 á 4 = 81

4 Simplify and find the result when possible.

Scientific notation 2

Scientific notation is useful for expressing very small or very large numbers. N = a · b c d … · 10n Integer power of base 10

Integer part (one figure only)

A number in scientific notation is written like this:

Decimal part

• An integer part that is a one-figure number other than zero.

• The rest of the significant figures, if there are any, after the decimal point.

• A power of base 10 showing the order of magnitude of the number.

Look at the example on the right.

Operations with numbers in scientific notation

Remember that every number has two parts: the decimal and the power of base 10.

Multiplying and dividing is done in the usual way. But when we add and subtract, we first have to rewrite the addends with the same power of base 10 to be able to remove the common factor.

• (4.73 · 107) · (7.5 ·

+

·

• 1.7 · 108 – 2.5 · 107 = 17 · 107 – 2.5 · 107

1 Calculate:

a) (3.25 · 107) · (9.35 · 10–15) b) (5.73 · 104) + (–3.2 · 105) c) (4.8 · 1012) : (2.5 · 103)

2 Writing. True or false? Correct the ones that are false and justify your answer.

a) (0.001)–3 = 109 b) (0.001)4 = 1012 c) (0.01)3 = 10–6 d) (10–2)5 = (0.1)10

3 Complete these equalities:

a) 5.25 · 107 = … 106 b) 2 · 103 = … 104

c) 4.7 · 10–3 = … 10–2 d) 234 · 104 = … 103

·

·

These numbers are written in scientific notation: 3.65 · 1011 = = 365 000 000 000 11 digits 9.207 · 10–14 = = 0.00000000000009207 14 digits

4 Express as a power of base 10.

a) (0.01)–5 b) 0.001 1 4dn c) 10 1 3 –3dn

5 Speaking . Discuss as a group: What is the value of n in each case?

a) 0.001 = 10n b) (10 000)2 = 10n c) 0.0000001 = 10n d) 0.00013 = 10n

6 Calculate and write the results in full:

a) 5.3 · 1011 – 1.2 · 1012 + 7.2 · 1010 b) 4.2 · 10– 6 – 8.2 · 10–7 + 1.8 · 10–5

c) (2.25 · 1022) · (4 · 10–15) : (3 · 10–3)

d) (1.4 · 10–7)2 : (5 · 10–5)

Exact roots 3

In general, if a = bn then a n = b. ab n = n is the index a is the radicand

In general, if a = bn then a n = b.

If a n is a rational number (integer or fraction), then we say it is an exact root.

➜ square roots

As you know, 25 = 5, because 52 = 25. However, –25 does not exist because (–5)2 = 25.

Similarly, 4 25 = 2 5 , because 2 5 2dn = 2 5 2 2 = 4 25

➜ cube roots

Cube roots behave similarly to square roots:

8 3 = 2, because 23 = 8; and –8 3 = –2, because (–2)3 = –8.

1 000 8 3 = 10 2 , because 10 2 3dn = 10 2 3 3 = 1 000 8 .

➜ other roots

We interpret roots with an index larger than 3 in the same way: Given that 25 = 32, 32 5 = 2. 10 000 4 = 10, because 104 = 10 000.

Let’s calculate these roots:

a) 16 49 b) 4 356 c) 64 1 000 3 d) 243 –1 5 a) 4 7 4 7 16 49 2 2 2 == dn . Therefore, 16 49 4 7 = .

b) Given that they ask for 4 356 , we will assume that 4 356 is a perfect square.

To check it, we decompose it into prime factors: 4 356 = 22 · 32 · 112

This means that 4 356 = (2 · 3 · 11)2 = 66 2. Therefore, 4 356 = 66.

c) 1 000 = 103, 64 = 43. Therefore, 64 1 000 4 10 3 = .

d) 243 = 35 and –1 = (–1)5. Therefore, 243 3 1 3 1 1– 5 5 5 == dn .

Using the calculator

We use these keys to calculate roots with a calculator:

• For the square root: í í16 = 4

• For the cube root: g8 = –2

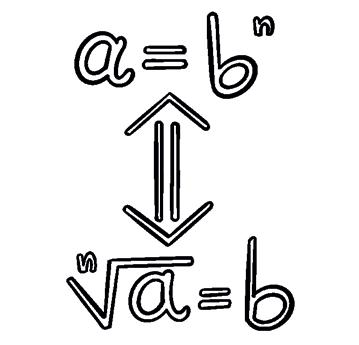
1 Calculate the following roots:

2 Speaking Discuss with a classmate if these statements are true or false:

a) (–5)2 = 25, so 25 = –5.

b) –5 is a square root of 25.

c) 81 has two square roots: 3 and –3.

d) 27 has two cube roots: 3 and –3.

Radicals 4

Expressions that contain root symbols are called radicals.

Rules for operating with radicals

Product of radicals with the same index

The product of two radicals with the same index can be put under a single radical. • 3322 6 == • 55 15 15 75 ·· 33 33 ==

Simplifying radicals

If the factorised radicand has powers with an exponent greater than or equal to the index of the root, some can be removed from under the radical.

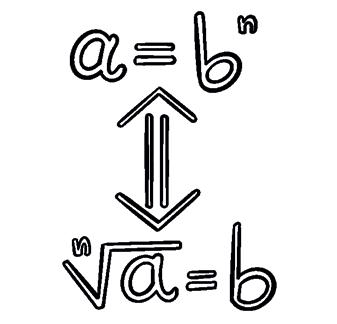
Adding and subtracting radicals

Only identical radicals can be added and subtracted.

Two different radicals can only be added by using their decimal approximations.

• • 32 77 –3 + 4 They can only be calculated as approximations or left with the root symbol in the expression.

1 Reading. Read these statements and answer. True or false?

a) (–5)2 = 25, so 25 = –5.

b) –5 is a square root of 25.

c) 81 has two square roots: 3 and –3.

d) 27 has two cube roots: 3 and –3.

e) 7 has two fourth roots: 7 4 and – 7 4

f) 4 – = –2 and 4 = 2.

2 Operate.

3 Simplify any expressions you can

4 Speaking . Simplify when possible . For the others, explain to your classmate why they cannot be simplified.

Sometimes we can do sums that seem impossible:

Irrational numbers

Using the calculator

We use these keys to calculate roots with a calculator:

• For the square root: í í16 = 4

Irrational numbers are all decimals that are not terminating or recurring. These include all approximate roots and the number π = 3.14159265… Look at the example on the right.

There are infinite irrational numbers and the set of all irrational numbers is designated with the letter ·5 55 55 5 20 45 180 45 9362 36 += += +=

When we add these numbers to the table, we notice that each one can go in more than one row:

24; 0.71; . 07 1 ! ; –5; 5 3 ; 7 ; – 9 ; 7 28 ; π – 1

natural numbers, N 24; 28/7 = 4

integers, Z 24; –5; – 2 = –3; 28/7 = 4

fractions 0.71; . 07 1 ! ; 3/5

rational numbers, Q 24; 0.71; 07 1 ! ; –5; 3/5; – 2 = –3; 28/7 = 4

irrational numbers, 7 ; π – 1

5 Simplify any expressions you can. a) 85 63 – b) 35 45 + c) 25 8 –3

6 Calculate:

a) 50 72 10 2 – + b) 80 45 20 c) 48 375 108 + d) 175 28 563 – + e) 250 128 2 –33 3 + f) 81 73 24 –33 3 +

• For the cube root: g8 = –2

7 Writing. Simplify any expressions you can. For the others, explain why they cannot be simplified. a) 72 42 – b) 32 – c) 43 53 –d) 63 2 –

8 Calculate and simplify.

9 Simplify. a) 10 1 000 33 b) 55216 c) 33981 2 = 1.41421256… 4 3 = 1.58740105…

TAKE ACTION!

The final challenge

ORGANISE A CROWDFUNDING

Alone or in a team, role play, carry out the activities and, at the end, come up with a plan to raise money through crowdfunding on your birthday.

Marta is the director of an NGO that carries out humanitarian work. She wants to calculate how much income she will get this year to be able to distribute it among different objectives.

1 The NGO receives different types of donations:

a) Marta knows that there are about 700 000 members and the membership fee for each member is €30. How much money will they get over the year, approximately?

b) The NGO receives occasional donations from different companies and individuals. Last year they received €3.5 – 106 and this year they expect to get a tenth more. How much money do you think they will get from one-off donations?

c) Through the NGO’s website you can organise solidarity crowdfunding. Last year they raised €1.1 – 105 with such donations, but this year they hope to double this amount. How much money will they raise through solidarity crowdfunding?

d) Organise the data you have calculated in a table like this one, expressed in scientific notation. Then calculate how much money you expect to raise this year.

2 11% of the donations are used to pay the NGO’s employees.

a) How much money will be spent this year on staff salaries? How much will be left for humanitarian action?

b) Marta, the director of the NGO, receives one twentieth of the amount allocated to salaries. What is her annual salary?

c) The rest of the money is divided equally among the remaining employees. If their salary cannot exceed €20 000 per year, how many people can they employ?

product

Organise a crowdfunding on your birthday. How much money do you want to raise? Where do you want to donate it? How many friends will you invite? What is the least amount of money per person everyone must contribute to meet your goal?

Numbers for counting, numbers for measuring 1

Natural numbers

The numbers we use to count objects are called natural numbers.

N= {0, 1, 2, 3, …, 10, 11, …, 100, 101, …}

Negative integers, together with natural numbers, form the set of integers.

Z= {…, –11, –10, …, –3, –2, –1, 0, 1, 2, 3, …, 10, 11, …} –7 – 6 –5 – 4 –3 –2 –1 0 1 2 3

The absolute value of a number is its magnitude without its sign. |x | → absolute value of x.

1 In how many ways can 3 prizes be allocated among 7 candidates?

Integers

2 · (–9) – [–16 – 5 · (11 – 17)] : (7 – 8) = –18 – [–16 – 5 . (– 6)] : (–1) = –18 –

2 To the operation.

12 – 5 · (–4 + 8) – 3[2 – 2(5 – 7) · (–2)]

To simplify a fraction divide its numerator and denominator by the same number (other than 1 and –1).

Fractions

A fraction is irreducible when we can’t reduce it any more and its denominator is positive.

Two fractions are equivalent when we can simplify them to the same irreducible fraction.

We use cross-multiplication to check if two fractions are equivalent:

Operations with fractions

Addition and subtraction Operations

Different denominator:

3 Find the irreducible fraction.

Decimal numbers

Limited number of decimal places.

5.4; 0.97; 8; –0.0725

There are other decimal places before the period.

The period begins after the decimal point.

They have an infinite number of decimal places that do not repeat periodically.

Transforming decimals into fractions

• From terminating decimals to fractions

• From pure recurring decimals to fractions o Period with one figure: o Period with more than one figure:

• From

The decimal part disappears when we subtract: The decimal part disappears when we subtract:

Powers and roots 2

Powers with positive exponents

a1 = 1

Powers with zero or negative exponents

If a is a rational number other than zero and n is an integer:

Properties:

1 Reduce these expressions:

Scientific notation

N = a, b c d ... . 10ⁿ integer part ≠ 0 decimal part power of base 10 showing the order of magnitude of the number.

Operations:

We multiply and divide in the usual way, but when we add and subtract, we first have to rewrite the addends with the same power of base 10 to take out the common factor.

2 Calculate and express each result in scientific notation:

We cannot operate, we must convert the first addend

Roots and radicals

If is a rational number (integer or fraction), then it is an exact root.

Expressions that contain root symbols are called radicals.

• Square roots: √25 = 5 because 52 = 25

• Cube roots: √8 = 2 because 23 = 8

• Other roots: √32 = 2 because 25 = 32 3 5

• Product of radicals with the same index:

• Simplifying radicals: If the factorised radicand has powers with an exponent greater than or equal to the index of the root, some can be removed from under the radical.

• Adding and subtracting radicals: We can only add/subtract radicals with the same index and same radicand.

Radicand

© This edition: GRUPO ANAYA, S.A., 2024 - Valentín Beato, 21 - 28037 Madrid - Printed in Spain.

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior permission of the publishers.