Operación mundo: Matemáticas 6º (demo)

Matemáticas

LICENCIA 12 MESES

vamos a aprender?

1 5 9

2 6 10

3 7 11

4 8 12

Números y operaciones

SITUACIÓN DE APRENDIZAJE OBJETIVO EN ACCIÓN ODS

¿Por qué es necesario cuidar los árboles? Creemos juntos un árbol de la vida con mensajes para fomentar el cuidado de la naturaleza.

¿Por qué es necesario trabajar para conseguir la paz? Construye la paz con abrazos: diseña una campaña para fomentar los abrazos de 8 segundos.

Potencias Conectados

Números decimales y operaciones Únete al consumo responsable

¿Por qué es importante que todos tengamos acceso a internet? Diseña una camiseta para reivindicar el derecho de todos al acceso de la información.

¿Qué podemos recomendar a nuestras compañeras y compañeros para que realicen un consumo responsable? Debatimos sobre si se debe dar paga o no y cómo usarla de manera responsable.

REPASO TRIMESTRE 1 STEAM: Clara Grima

¿Cómo podemos establecer alianzas entre nosotros? Crea un espacio para generar alianzas entre personas.

¿Qué podemos hacer para dar a conocer que no todos tenemos las mismas oportunidades de aprender?

Realizamos un concurso literario con el título: «Quiero ser científico».

¿Cómo puede afectar el uso de los dispositivos electrónicos al bienestar de los adolescentes?

Elabora un plan de ocio alternativo a la tecnología para chicas y chicos de tu edad.

Los ángulos y su medida Dibujar para cuidar

¿Cómo podemos concienciar a todos de la necesidad de cuidar el agua? Dibujamos un logo para fomentar el cuidado del agua.

REPASO TRIMESTRE 2 STEAM: Sophie Germain

¿Qué otras mujeres han aportado al campo de las matemáticas? Elabora una línea del tiempo indicando datos personales y sus aportaciones.

Figuras circulares Innovo, innovas, innovamos

Cuerpos geométricos Premio al

del mar

Azar y probabilidad Predecir el futuro

¿Cómo podemos entrenar la creatividad para dar respuestas innovadoras a los problemas actuales?

¡Mide tu creatividad!

¿Qué podemos hacer para cuidar nuestros mares? Elabora un trofeo con figuras geométricas para premiar las buenas prácticas de cuidado del mar.

Vida de ecosistemas terrestres

Paz, justicia e instituciones sólidas

Industria, innovación e infraestructura

Producción y consumo responsables

Alianzas para lograr objetivos

Educación de calidad

Salud y bienestar

Agua limpia y saneamiento

Igualdad de género

Industria, innovación e infraestructura

Vida submarina

¿Qué podemos hacer para frenar el cambio climático? Elabora una infografía con recomendaciones de acciones para frenar el cambio climático.

REPASO TRIMESTRE 3 STEAM: Grace Hopper

Acción por el clima

SABERES BÁSICOS LO RESUELVO SIN PROBLEMA

• El sistema de numeración decimal. Técnicas de conteo.

• Operaciones básicas con números naturales. Propiedades.

• Operaciones combinadas.

Múltiplos de un número. Mínimo común múltiplo.

• Divisores de un número. Máximo común divisor.

• Potencia de un número natural.

• Cuadrados y cubos.

• Raíz cuadrada.

• Décimas, centésimas y milésimas. Números: lectura, escritura y valor de posición. Precios.

• Comparación y ordenación de números decimales.

• Números positivos y negativos.

• Comparación y ordenación.

• Coordenadas cartesianas.

• Problemas aritméticos: de cambio, de igualación, de comparación.

• Criterios de divisibilidad.

• Números primos y compuestos.

• Potencias de base 10.

• Descomposición polinómica.

• Redondeo de números decimales. Suma, resta, multiplicación y división de números.

• Problemas aritméticos: de comparación, de grupos iguales, de reparto, de agrupación.

• Estrategia heurística: Descifro códigos

• Cálculo mental: Multiplicar por 4

• Pensamiento computacional: Descomposición

• Estrategia heurística: Busco todas las respuestas posibles

• Cálculo mental: Multiplicar por 20

• Pensamiento computacional: Generalización

• Estrategia heurística: Busco regularidades

• Cálculo mental: Multiplicar por 50

• Pensamiento computacional: Codificación

• Estrategia heurística: Estimo la solución

• Cálculo mental: Dividir entre 4

• Pensamiento computacional: Descomposición

PROYECTO INTERDISCIPLINAR · La caja mágica y su cuidado: Misterios de la caja mágica

• Fracción. Fracción y unidad. Fracciones propias e impropias.

• Fracción de una cantidad.

• Fracciones equivalentes. Fracción irreducible.

• Comparación de fracciones.

• Unidades de medida de longitud, capacidad, masa, superficie y volumen.

• Transformación de unidades.

• Magnitudes proporcionales.

• Reducción a la unidad. La regla de tres.

• Porcentajes. Porcentaje de una cantidad.

• Clasificación de ángulos según su amplitud y su posición.

• Medida de ángulos: grados, minutos y segundos.

• Suma, resta, multiplicación y división de fracciones.

• Problemas aritméticos: de combinación, de comparación multiplicativa, de cambio, de grupos iguales, de agrupación.

• Expresiones complejas e incomplejas.

• Problemas aritméticos: de combinación, de cambio, de agrupación.

Aumentos y descuentos.

• La escala: gráfica y numérica.

• Estrategia heurística: Planteo preguntas intermedias

• Cálculo mental: Dividir entre 20

• Pensamiento computacional: Generalización

• Estrategia heurística: Empiezo por casos más sencillos

• Cálculo mental: Multiplicar por una fracción

• Pensamiento computacional: Generalización

• Estrategia heurística: Hago un esquema

• Cálculo mental: 1 4 de una cantidad

• Pensamiento computacional: Funciones

• Estrategia heurística: Hago un dibujo

• Suma y resta de ángulos.

• Problemas aritméticos: de igualación.

• Cálculo mental: 10 % de una cantidad

• Pensamiento computacional: Algoritmo

PROYECTO INTERDISCIPLINAR · Ahora o nunca: Salud planetaria

• Polígonos: elementos y clasificación.

• Polígonos cóncavos y convexos.

• Perímetro de polígonos.

• La circunferencia. El círculo y las figuras circulares.

• Posición de puntos, rectas y circunferencias.

• Poliedros y cuerpos redondos.

• Poliedros regulares. Cuerpos de revolución.

• Experiencias de azar. Suceso seguro, posible e imposible.

• Área de paralelogramos y triángulos.

• Área de polígonos regulares.

• Área de figuras compuestas.

• El número π. Longitud de la circunferencia.

• Área del círculo.

• Área y volumen de prismas.

• Área y volumen de pirámides. Área y volumen de figuras compuestas.

• Probabilidad de un suceso. Regla de Laplace. Técnicas de conteo.

• Estrategia heurística: Empiezo por casos más sencillos

• Cálculo mental: 50 % de una cantidad

• Pensamiento computacional: Generalización

• Estrategia heurística: Hago un dibujo

• Cálculo mental: 20 % de una cantidad

• Pensamiento computacional: Generalización

• Estrategia heurística: Elimino posibles respuestas

• Cálculo mental: Multiplicar por 0,1

• Pensamiento computacional: Generalización

• Estrategia heurística: Analizo una muestra de datos

• Cálculo mental: Multiplicar por 0,5

• Pensamiento computacional: Datos

PROYECTO INTERDISCIPLINAR · Pulmón verde: Por extinguir

El sistema de numeración decimal

En nuestro sistema de numeración, la posición de las cifras determina su valor.

¿Cómo sumarías los números del 1 al 100?

¿Cómo cuentas cuántos hay?

LOS

NÚMEROS NATURALES

Imagina que no existieran los números.

Reescribe esta noticia.

Descarga la noticia en anayaeducacion.es

Indica varios ejemplos.

PARES IMPARES

1 Copia la tabla y escribe estos números en ella. Indica el valor de la cifra 5 en cada caso.

CMM DMM UMM CM DM UM C D U ? ? ? ? ? ? ? ? ?

a) Siete millones trescientos ocho mil quinientos veintiuno.

b) Ciento cuarenta millones ciento treinta y cinco mil seiscientos.

2 Lee y escribe este número de izquierda a derecha y de derecha a izquierda.

Di números entre 10 000 y 1 000 000.

¡Cien millones!

¿Qué observas? ¿Qué tipo de número es? Escribe otros ejemplos.

¿Conoces algo que se pueda contar por millones?

UMM unidades de millón

DMM decenas de millón

CMM centenas de millón

3 Observa el ejemplo y descompón estos números.

87 604 021

8 0 000 000 +  7  000 000 +  6 00 000 +  4  000 +  2 0 +  1  8 × 10 000 000 +  7 × 1 000 000 +  6 × 100 000 +  4 × 1 000 +  2 × 10 +  1  a) 125 386 090 b) 9 999 999 c) 31 402 578

4 Un billón es un millón de millones. Pero en otros países, como Inglaterra, significa mil millones. Escribe un billón de las dos formas posibles.

UN BILLÓN ONE BILLION

5 Sigue las pistas y descubre cuál es el documento nacional de identidad, o DNI, de Coque.

PISTA 1: Es un número de 8 cifras, pero la cifra de las decenas de millón no tiene valor.

PISTA 2: La cifra de las unidades de millar es igual que la cifra de las centenas de millar.

Una hectárea es un hectómetro cuadrado.

6 Tal y como hemos leído al comienzo de la unidad: «El mundo ha perdido una superficie de 178 millones de hectáreas de bosque desde 1990». ¿Cuántas centenas de millón son aproximadamente?

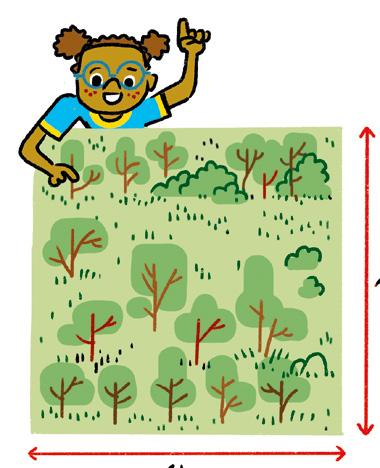
Si no recuerdas cómo se aproximan números, «Te lo cuento en un momento» en anayaeducacion.es

¿Cómo cuentas cuántos hay?

Observa la imagen y explica cómo cuentas cuántos hay.

¡Hay muchas formas de hacerlo y todas estupendas!

¿Y si…

… cada elemento vale 1 D?

… cada elemento vale 1 C?

… cada elemento vale 1 UM?

¿Contarías de la misma manera? Explica tus razones.

Con números grandes puedes contar la cantidad de árboles que se pierden o se ganan anualmente en la Tierra.

Operaciones básicas

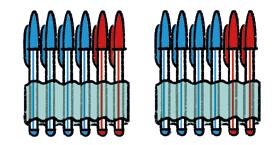
1 Lápices al centro Lee y resuelve.

a) ¿Cuántos puntos tienen entre el equipo rojo y el azul?

b) ¿Cuántos tiene el equipo rojo más que el verde?

sencillas. 1

c) Si los puntos del equipo amarillo son 5 veces los del azul, ¿cuántos puntos son?

d) ¿Cuál es el equipo ganador? ¿Hay algún empate?

2 El documento nacional de identidad está formado por un número de 8 cifras y una letra.

a) En pareja, buscad información sobre los pasos que hay que seguir para el cálculo de la letra del DNI.

b) Juega a descubrir la letra de cualquier DNI en anayaeducacion.es

3 Piensa y contesta.

¿Cuál es la propiedad del resto?

4 Esquema Haz un esquema en tu cuaderno con estos conceptos, añadiendo un ejemplo en cada caso.

TÉRMINOS PROPIEDADES

5 Un fotógrafo de espacios naturales tiene 125 320 fotografías de bosques de hoja caduca y 93 008 de bosques de hoja perenne. ¿Cuántas fotografías tiene aproximadamente? Primero redondea cada dato a las unidades de millar.

Si no lo recuerdas, «Te lo cuento en un momento» en anayaeducacion.es

Si lo necesitas, puedes descargar la información en anayaeducacion.es

?

La suma, la resta, la multiplicación y la división son las operaciones básicas que utilizamos para resolver situaciones matemáticas

6 En un bosque han plantado 2 585 árboles. Si ahora hay 24 310 árboles, ¿cuántos había al principio?

2 585 ? 24 310

7 En la ciudad de Málaga vivían 571 026 habitantes en el año 2018. Si la ciudad de Sevilla hubiese tenido 117 685 habitantes menos, las dos ciudades habrían tenido la misma población. ¿Cuántos habitantes tenía Sevilla?

571 026 117 685 ?

Si plantan árboles, entonces al principio había menos que ahora.

Son datos del año 2018.

Resuelve paso a paso en anayaeducacion.es

2 139 705

8 En la feria del libro más importante del año, se han vendido 2 139 705 novelas. Son 1 850 329 más que los cuentos infantiles que se han vendido. ¿Cuántos cuentos son? ?

1 850 329

9 Emma cambia su vehículo por una furgoneta más sostenible. Ha pagado 6 000 � de entrada y el resto lo pagará en 40 cuotas iguales. Si la furgoneta cuesta 40 000 � , ¿cuánto dinero le queda por pagar? ¿Cuánto tendrá que pagar en cada cuota?

Descomponer para operar

Resuelve paso a paso en anayaeducacion.es

Pagar 40 cuotas significa pagar 40 veces.

Existen otras formas de resolver operaciones, como la descomposición de los términos. Practica para encontrar la manera que te resulte más rápida o sencilla.

SUMA o RESTA: 16 489 5 226

MULTIPLICACIÓN: 257 × 25

1 6 4 8 9 =  10 000 + 6 000 + 400 + 80 + 9

5 2 2 6 = − 5 000 − 200 − 20 − 6

10 000 +  1  000  + 200 + 60 + 3 = 11 263

«Te lo cuento en un momento» en anayaeducacion.es

• Calcula descomponiendo los términos. Prepara bien la resta con llevadas.

a) 25 730 + 500

b) 8 423 − 2 980

c) 125 × 15

Málaga Sevilla

Málaga Cádiz

Sevilla

Córdoba Jaén Granada Almería

Huelva

Operaciones combinadas

A veces es útil escribir varias operaciones en una sola expresión, pero es importante saber el orden en el que se resuelve.

1 Observa y relaciona cada número con la letra que corresponde.

Para resolver expresiones con varias operaciones, calculamos:

1.o Operaciones entre paréntesis.

A Dos paquetes de cuatro bolis azules, y dos bolis rojos.

2 × 4 + 2

2 Resuelve en tu cuaderno.

a) 5 + 4 × 3

b) 10 − 2 × (3 + 1) + 5

B Dos paquetes de: cuatro bolis azules y dos bolis rojos.

2 × (4 + 2)

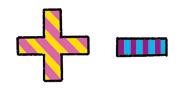
c) 4 × 7 − 24 : 2

d) 5 × (3 + 18) − (20 − 4)

Si necesitas ayuda, «Te lo cuento en un momento» en anayaeducacion.es

3 Convierte estas oraciones en expresiones numéricas y calcula los resultados.

a) Multiplica por 3 la suma de 8 y 4.

b) Al doble de 3 suma el producto de 5 y 8.

c) Multiplica por 6 la suma de 4 y 3, y resta 9.

d) Suma a 20 el producto de 4 por la diferencia de 10 menos 6.

4 1–2–4 Copia y escribe paréntesis, o no, para obtener el mayor y el menor resultado en cada caso.

90 + 10 × 5 90 – 10 × 5

5 Escribe una expresión con paréntesis que contenga una suma y una multiplicación y que dé como resultado 100. 100

2.o Multiplicaciones y divisiones de izquierda a derecha.

3.o Sumas y restas de izquierda a derecha.

No pasa nada si te equivocas. ¡El error es parte del aprendizaje!

Si no escribes paréntesis, el signo de la resta afecta al resultado de la multiplicación.

1.

2.

6 Copia y escribe paréntesis donde lo necesites para conseguir las soluciones que se indican.

a) 5 × 3 + 2 × 4

Posibles soluciones: 68 55 23 100

b) 2 × 5 + 100 : 5

Posibles soluciones: 42 30 22 50

c) 10 + 2 × 5 5 : 5

Posibles soluciones: 19 18 3 59

7 En la cesta de la compra de Bruno hay 2 cajas de bombones de 28 � cada una, pescado por valor de 32 � y 4 mallas de naranjas de 4 � cada una. Pero... ¡le faltan 4 � para pagar su compra!

a) ¿Cuánto cuesta la compra? Escribe con una expresión.

b) ¿Cuánto dinero tenía Bruno?

c) Si una amiga le presta 20 � , ¿cuánto dinero le sobra?

Paréntesis y corchetes

Trabajamos en parejas para compartir puntos de vista diferentes.

• Existen expresiones matemáticas con paréntesis y corchetes. ¿Cómo se resuelven?

250 + (100 + 50) × [10 − (3 + 2)] [ ] corchetes ( ) paréntesis

• ¡Muy fácil! Solo tienes que seguir estos pasos:

1. o Resuelve la expresión entre corchetes.

250 + (100 + 50) × [10 − (3 + 2)] = 250 + (100 + 50) × [10 − 5] = 250 + (100 + 50) × 5 Aplica la jerarquía de operaciones.

2. o Resuelve los paréntesis.

250 + (100 + 50) × 5 = 250 + 150 × 5

3. o Resuelve el resto de las operaciones aplicando la jerarquía de operaciones.

250 + 150 × 5 = 250 + 750 = 1000

• Ahora, resuelve en tu cuaderno estas expresiones.

a) (2 + 3) × [100 : (1 + 4)]

b) [100 : (7 + 3)] × [150 − (20 + 30)]

Números positivos y negativos

Con estos números podemos medir temperaturas, ubicarnos en las plantas de un edificio o conocer la profundidad a la que se encuentra un tesoro en el mar.

• Los números +1, +2, +3, +4… son números positivos.

• Los números −1, −2, −3, −4… son números negativos.

1 ¿Con qué números representas estas expresiones: positivos o negativos? Clasifica en una tabla.

a) Subir – Bajar c) Deber – Recibir

b) Ganar – Perder d) Bajo cero – Sobre cero

2 Comprobamos Copia las oraciones y escribe el número positivo o negativo que corresponde en cada caso.

a) c)

Negativos Positivos ? ?

Bajo 3 plantas.

−3

He perdido 10 puntos.

b) d)

El conjunto de números enteros está formado por los números negativos, el número 0 y los números positivos. ? ? ?

Tengo 20 � Está a 1 200 m sobre el nivel del mar.

Voy a la planta –2.

El congelador está a –18 °C.

El tesoro se encuentra a 75 m bajo el mar.

3 ¿Qué temperatura marca cada termómetro?

Cuando un número no lleva signo, es positivo.

5 = + 5

4 Dibuja y marca los números que corresponden.

a) Un edificio con 6 plantas y 3 sótanos.

b) Un submarino a 150 m bajo el nivel del mar.

c) Un avión volando a 2 100 m de altura.

5 Ana coge el ascensor en el tercer piso. Baja 5 plantas para tirar la basura y sube una planta para coger su bicicleta.

a) ¿En qué planta está el cuarto de la basura?

b) ¿Y el cuarto de bicicletas?

Representar números enteros en la recta numérica

• ¿Cuál de estas temperaturas es la máxima? ¿Y la mínima?

• Para comparar los números, los situamos en la recta numérica.

Los números negativos se sitúan a la izquierda del 0.

Cualquier número es menor que los que están situados a su derecha en la recta numérica.

Los números positivos se sitúan a la derecha del 0.

Cualquier número es mayor que los que están situados a su izquierda en la recta numérica.

¡Toma nota!

• Un termómetro marca −4  ° C y llega hasta los +5  ° C. ¿Qué temperatura marca el termómetro en ese recorrido? Indícalo de manera ordenada.

Si necesitas ayuda, «Te lo cuento en un momento» en anayaeducacion.es

Utiliza los números positivos y negativos para expresar si se ganan o se pierden árboles en la Tierra.

Coordenadas cartesianas

Para representar puntos en el plano, utilizamos las coordenadas cartesianas.

Los ejes cartesianos son dos rectas con estas características.

• Son dos ejes perpendiculares.

• Se numeran de la misma manera que en la recta numérica.

• Se cortan en el punto 0 de ambos ejes.

• Dividen a la cuadrícula en cuatro partes que se llaman cuadrantes.

Un punto se representa en un plano mediante dos coordenadas.

• La primera coordenada se lee en el eje horizontal.

• La segunda coordenad a se lee en el eje vertical.

2.

1 Observa la imagen y contesta.

a) Indica en tu cuaderno cuáles son las coordenadas de los puntos señalados.

b) ¿Cuál es la primera coordenada del punto que está sobre el eje vertical?

c) ¿Cuál es la segunda coordenada del punto que está sobre el eje horizontal?

2 Sitúa estos puntos en un eje de coordenadas. Dibújalo en tu cuaderno.

A = (+3, −1) B = (0, 0) C = (−5, +2)

El camino más corto

Tomás está repoblando una zona de un bosque en el punto (+4, +4). Necesita comprobar si en otras dos zonas, (−3, −2) y (−7, +4) es necesaria la repoblación.

Si Tomás va primero a la zona más cercana, ¿qué zona será?

1. o Situamos los datos en un eje de coordenadas.

– Tomás está en el punto (+4, +4).

– Tiene que ir a las zonas (−3, −2) y (−7, +4).

2. o Unimos el punto donde está Tomás con los otros dos puntos.

3. o Medimos los segmentos con una regla y comparamos las longitudes.

La longitud más corta nos indica cuál es la zona más cercana a Tomás.

a) En parejas, elegid otra posición para Tomás y otros dos puntos. Buscad cuál es el punto más cercano.

b) Marta está justamente en el punto (−3, −2). ¿En qué cuadrante está Tomás? ¿Y Marta?

• Elige un punto del segundo cuadrante que esté más cerca de Tomás que de Marta.

Recuerda que la distancia más corta entre dos puntos es una línea recta.

• Elige un punto del cuarto cuadrante que esté más cerca de Marta que de Tomás.

Descifro códigos

Olivia sabe que los antiguos romanos utilizaban un sistema de numeración diferente al nuestro. Ha visto números romanos en algunos edificios de su ciudad. Si su edificio se construyó en 1953, ¿cómo se escribiría el año en el que se construyó su casa en números romanos?

Los antiguos romanos utilizaban 7 letras mayúsculas para representar los números. Cada letra tenía un valor diferente.

I V X L C D M

1 5 10 50 100 500 1 000

REGLAS PARA ESCRIBIR NÚMEROS ROMANOS

1. a Descomponemos el número en unidades y sustituimos los números por las letras de su valor.

2. a Las letras I, X, C y M se pueden repetir hasta tres veces seguidas.

3. a Si colocamos las letras I, X o C a la izquierda de otra de mayor valor, se restan sus valores.

Con esta información, escribimos en romano el número 1 953:

1. o Descomponemos el número en unidades.

1 953 = 1 000 + 900 + 50 + 3

2. o Sustituimos los números por letras, aplicando las reglas anteriores.

1 000 + 900 + 50 + 3

M CM L III

Como el valor de C es menor que el de M:

CM = 1 000 − 100 = 900

La letra I repetida tres veces es:

1 + 1 + 1 = 3

El año de construcción se escribe MCMLIII.

¿La solución tiene sentido?

Sumamos los valores de las letras y comprobamos que el resultado es 1 953.

MCMLIII → 1 000 + (1 000 − 100) + 50 + 1 + 1 + 1 = 1 953

1 Escribe algunos números importantes para ti en el sistema de numeración romano.

1953

Es muy importante descomponer el número en unidades.

Trabaja con el sistema de numeración romano en anayaeducacion.es

2 Inventa tu propio sistema de numeración y escribe algunos números con él.

Problemas exprés

2 1

¿Cuál es el mayor número de 9 cifras? ¿Y el menor?

¿Cuántas unidades de millar tiene 1 000 000?

Cálculo mental

Resuelve 12 × 4.

4 = 2 × 2

3 5

Si repartimos una cantidad entre 25, ¿pueden sobrar 25 unidades? Explica por qué.

El termómetro marcaba −1 °C, pero ahora hace más frío. ¿Qué temperatura puede hacer ahora?

Mira cómo pienso

Cuenta una historia a partir de la expresión:

10 : 5 – 2

4 6

Di las coordenadas de un punto de cada cuadrante.

Divide y vencerás

24 12

× 2 × 2 48

En anayaeducacion.es puedes ver cómo se hace.

Ahora, hazlo tú.

6 ×  4

8 ×  4

9 ×  4

7 ×  4

14 ×  4

15 ×  4

35 ×  4

45 ×  4

21 ×  4

13 ×  4

Imagina que quieres buscar el significado de una palabra en el diccionario y, al abrirlo, las palabras están desordenadas. ¡Menudo lío!

Ordenar es importante. Ayuda a comprender la información fácilmente. Existe un método para ordenar rápidamente los elementos de un conjunto llamado quicksort. Observa cómo se hace:

1. o Elegimos un número cualquiera que llamamos pívot.

2. o Comparamos uno a uno el resto de los elementos con el pívot.

– Si el elemento es menor que el pívot, lo escribimos a la izquierda.

– Si el elemento es mayor que el pívot, lo escribimos a la derecha.

Practica el método quicksort en anayaeducacion.es

¿Q ué he aprendido?

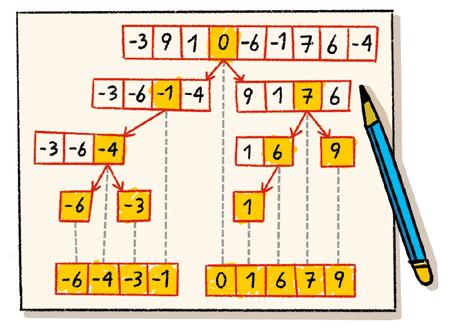
1 ¿Qué número corresponde a cada descomposición?

a) 3 UMM + 2 CM + 6 UM + 7 D + 2 U

b) 2 000 000 + 100 000 + 20 000 + 3

2 Indica el valor de la cifra 4 en estos números.

a) 649 d) 240 012

b) 4 e) 4 830 000

c) 4 913 f) 24 120 948

3 ¿Cuántos años tiene Lara? Sigues los pasos.

6 Dibuja sobre una hoja de papel un eje de coordenadas.

a) Sitúa estos puntos.

A = (+3, +5) C = (−3, −5)

B = (+3, −5) D = (−3, +5)

b) Une los puntos. ¿Qué figura has dibujado?

7 Dibuja un cuadrilátero que tenga los cuatro vértices sobre los ejes de coordenadas. Escribe las coordenadas de cada vértice.

8 En una granja ecológica hay 57 000 huevos. Si se venden 3 542 docenas, ¿cuántos huevos quedan?

1 . o Fíjate en la cifra de las decenas de millar del número 527 341.

2. o Calcula el triple de esa cifra.

2. o Súmale la cifra de las decenas.

4. o ¡El resultado es la edad de Lara!

9 Un centro médico tiene 5 250 vacunas. La primera semana se han puesto 2 296 vacunas, y la segunda, 1 985. Si hay 1 200 personas en lista de espera, ¿habrá suficientes vacunas?

10 En una estación de esquí el termómetro marcaba 3  ° C a las 8 de la mañana. Al mediodía la temperatura subió 8  ° C y, a las 20:00 bajó 4  ° C respecto al mediodía. ¿Cuál era la temperatura a las 20:00?

5 Escribe la expresión numérica que corresponde a estos textos. Después, calcula los resultados.

a) A 25 le sumo 75 y el resultado lo multiplico por 2.

b) Multiplico 8 por la diferencia de 25 y 5.

c) Al cociente de dividir 16 entre 4 le sumo el resultado de restar 5 de 9 y multiplicarlo por 3.

El semáforo. Junto a cada actividad, colorea así en tu cuaderno:

si has sabido la respuesta

si has necesitado ayuda

si no has sabido responder

OBJETIVO EN ACCIÓN

Crea un árbol de la vida

Observa los siguientes datos aproximados sobre la pérdida de millones de hectáreas de bosques en los distintos continentes.

Entre 1990 y 2000 Entre 2000 y 2010 Entre 2010 y 2020

África Perdió 3 millones. Perdió 3 millones. Perdió 4 millones.

América del Sur Perdió 5 millones. Perdió 6 millones. Perdió 3 millones.

Europa Ganó 1 millón. Ganó 2 millones. Ganó 1 millón.

Oceanía Perdió 1 millón. Perdió 1 millón. Ganó 1 millón.

a) Copia la tabla y expresa la ganancia o pérdida al año de cada continente mediante números positivos o negativos.

b) ¿Cuánto ganó o perdió cada continente al final de las tres décadas?

c) ¿Cuánto se ganó o perdió en total entre los cuatro continentes en las tres décadas? Expresa esta cantidad en unidades.

d) ¿Qué continente ganó más? ¿Qué continente perdió más?

Nos planteamos

Utilizamos la estrategia Consecuencias y resultados para analizar por qué es bueno trabajar en equipo.

a) Copia y completa el organizador.

b) Investiga qué es la imagen del árbol de la vida y qué representa.

c) En equipo, creamos un árbol de la vida gigante para nuestro colegio colgando en él mensajes para defender la naturaleza. Invitamos a participar a todo el colegio.

¿C ómo he aprendido?

Completa en tu cuaderno.

¿Qué

ocurrirá

si desaparecen los árboles?

A largo plazo ¿Qué puede pasar? ¿Qué consecuencias producirá?

¿Qué resultados tendrá?

A corto plazo ¿Qué puede pasar? ¿Qué consecuencias producirá?

¿Qué resultados tendrá?

Identifica tres fortalezas que tengas para trabajar en el área de Matematicas.

Identifica tres aspectos que puedas mejorar en el trabajo de matemáticas.

¿Qué puedes hacer para mejorarlos?

Múltiplos de un número

Calculamos los múltiplos de un número para saber cuántos hay en total en varios grupos iguales.

En el patio del colegio han pintado manos blancas como símbolo de la paz. Entre todos han decidido que en cada dedo van a escribir el nombre de un niño o niña del colegio.

• Si no hay manos pintadas, no hay espacios para escribir nombres.

5  × 0 = 0

• En una mano hay 5 espacios para escribir nombres.

5  × 1 = 5

¿Cuántos habrá en dos, tres, cuatro… manos?

5  × 2  = 5 + 5 = 10

5  × 3 = 5 + 5 + 5 = 15

5  × 4 = 5 + 5 + 5 + 5 = 20

Cuando multiplicamos un número por

estamos calculando los múltiplos de un número.

1 Lee el ejemplo y completa en tu cuaderno.

20 es múltiplo de 5 porque 5 × 4 = 20.

a) 24 es múltiplo de 8 porque ?  ×  ? =   ?

b) 30 es múltiplo de 2 porque ?  ×  ? =   ?

c) 100 es múltiplo de 10 porque ?  ×  ? =   ?

2 Busca estos números en la tabla 100.

Múltiplos de 5. Múltiplos de 10.

¡Los pares se pueden agrupar de 2 en 2!

3 Piensa y contesta en tu cuaderno.

a) Escribe los diez primeros múltiplos de 2.

b) Encuentra un múltiplo de 2 que sea mayor que 100.

2 ×  ?  = ¡mayor que 100!

c) ¿Qué tipo de números son los múltiplos de 2?

d) ¿Son estos números múltiplos de 2? Explica por qué.

14 50 21 158 3 726

e) Escribe otros números que sean múltiplos de 2.

f) ¿Es posible escribir todos los múltiplos de 2? ¿Por qué?

4 En la tienda de Pablo venden packs de 4 yogures. Lee y contesta razonadamente.

a) ¿Cuántos yogures hay en 3 packs ?

b) ¿Es posible comprar 15 yogures exactamente?

c) ¿Cuántos packs comprarías si necesitas 15 yogures?

5 ¿Qué te hace decir eso? Piensa y explica por qué estas oraciones son verdaderas.

El 0 es múltiplo de cualquier número.

Todo número es múltiplo de sí mismo. No es posible escribir todos los múltiplos de un número.

Múltiplos comunes

¿Cuáles son los múltiplos de 2? ¿Y de 3? ¿Tienen alguno en común?

Los números pares terminan en 0, 2, 4, 6 u 8.

Los números impares terminan en 1, 3, 5, 7 o 9.

Así represento los múltiplos de 2 y de 3 en el diagrama.

a) Dibuja en tu cuaderno los diagramas con:

– Múltiplos de 2 y de 5.

– Múltiplos de 5 y de 10.

Múltiplos de 2 Múltiplos de 5 Múltiplos de 5 Múltiplos de 10

b) ¿Qué observas en el último diagrama? Explícalo con tus palabras.

¡Toma nota!

Utiliza los múltiplos para analizar cuántos abrazos puedes dar en un tiempo fijado.

Mínimo común múltiplo

Calculamos el mínimo común múltiplo para saber cuál es el menor de los múltiplos iguales.

Para calcular el mínimo común múltiplo de dos números, hacemos lo siguiente:

Mínimo común múltiplo de 4 y de 6.

1. o Calculamos los primeros múltiplos de cada número.

Múltiplos de 4: 0, 4, 8, 12, 16, 20...

Múltiplos de 6: 0, 6, 12, 18, 24, 30...

2.o Buscamos los múltiplos comunes y elegimos el menor, sin tener en cuenta el 0.

Múltiplos de 4: 0, 4, 8, 12 , 16, 20, 24

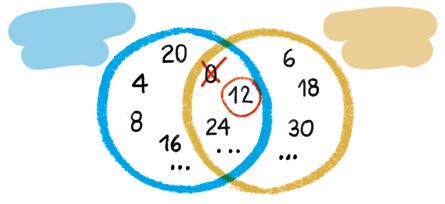
Múltiplos de 6: 0, 6, 12 , 18, 24 , 30...

Si necesitas ayuda, «Te lo cuento en un momento» en anayaeducacion.es

1 Calcula el mínimo común múltiplo de estos números. Exprésalo con un diagrama como el del ejemplo.

a) 4 y 10

b) 3 y 7 c) 8 y 6 d) 4 y 5

2 Diego va al cine de su barrio cada 14 días y María va al mismo cine cada 21. Si han coincidido en el cine el 1 de octubre, ¿qué día volverán a coincidir? Sigue estos pasos.

Paso 1: Calcula varios múltiplos de 14 y de 21, hasta que encuentres el primero que sea común. × 1 × 2 × 3 × 4 14 ? ? ? ? 21 ? ? ? ?

Paso 2: Haz un esquema que represente la situación y busca la fecha en un calendario. 14 14 14 21 21

3 El autobús A pasa por la parada junto a la casa de Lucas cada 3 minutos y el autobús B pasa cada 5 minutos. Si ambos pasan a las 8 de la mañana…

a) ¿Cuándo vuelven a coincidir?

b) De 8 a 9 de la mañana, ¿a qué horas coinciden en la parada?

De los múltiplos comunes, el menor es el 12. m.c.m. (4, 6) = 12

Múltiplos de 4 Múltiplos de 6

4 Parada de 5 minutos Por la mañana, el despertador de Nico suena cada 15 minutos; el de Gabriel, cada 5 minutos y el de Martina, cada 10 minutos. Los tres despertadores suenan por primera vez a las 07:30.

a) ¿Cuándo volverán a sonar los tres despertadores a la vez?

Cada 15 min. Cada 5 min. Cada 10 min.

b) Se levantan la segunda vez que suenan los despertadores a la vez, y tardan media hora en desayunar y asearse. ¿A qué hora terminan?

c) Recogen el desayuno y hacen la cama en 10 minutos. Entonces, salen para el colegio y tardan 15 minutos en llegar caminando. ¿Llegarán a tiempo si entran a las 9 en punto?

Relaciones especiales: ¿Cuál es el m.c.m. de dos números, uno múltiplo de otro?

¿Cuál es el mínimo común múltiplo de 5 y 100? ¡En un nanosegundo lo puedes saber!

Cuando un número es múltiplo de otro, el mínimo común múltiplo de estos números es el mayor de los dos.

m.c.m. (5, 100) = 100

100 es múltiplo de 5.

• Halla el mínimo común múltiplo de estos pares de números.

Un nanosegundo es una milmillonésima parte de un segundo, es decir, 0,000000001 segundos.

Puedes comprobar tu resultado con regletas y una cuadrícula que puedes descargar en anayaeducacion.es

N ico G abriel M artina

Divisores de un número

Calculamos los divisores de un número para saber cuántas veces cabe otro número de manera exacta.

¿De cuántas formas se pueden agrupar 10 personas en grupos iguales sin que sobre ninguno?

Pueden hacer grupos de 1, de 2, de 5 y de 10 personas.

Los divisores del número 10 son 1, 2, 5 y 10.

Un número es divisor de otro si al hacer la división, el resto es 0.

Dividendo divisor 0 cociente

Los divisores de un número son menores o iguales que ese número.

1 Calcula los divisores de estos números.

5 7 6 8 9

2 Lee el ejemplo y completa en tu cuaderno.

5 es divisor de 20 porque 20 : 5 = 4 (resto 0).

a) 8 es divisor de 24 porque ? : ? = ? (resto 0).

b) 2 es divisor de 30 porque ? : ? = ? (resto 0).

c) 10 es divisor de 100 porque ? : ? = ? (resto 0).

3 Calcula de esta manera los divisores de 18.

Si necesitas ayuda, «Te lo cuento en un momento» en anayaeducacion.es

4 Las variaciones ¿De cuántas formas se pueden colocar 12 sillas en varias filas iguales?

5 Celia tiene 24 m de cuerda. Quiere cortarla en trozos para hacer varias combas del mismo tamaño. ¿De cuántas formas puede hacerlo? ¿Cuál crees que habrá elegido? Explica por qué.

Divisores comunes

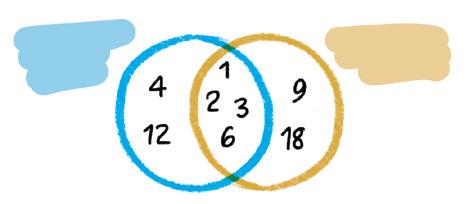
¿Cuáles son los divisores de 12? ¿Y de 18? ¿Tienen alguno en común?

Divisores de 12

Así represento los divisores de 12 y 18 en el diagrama.

a) Dibuja en tu cuaderno los diagramas con: – Divisores de 2 y 15. – Divisores de 5 y 10.

Divisores de 2 Divisores de 5

Divisores de 18 Divisores de 15

b) ¿Qué observas en el último diagrama? Explícalo con tus palabras.

Divisores de 10

Utiliza el concepto de divisor de un número para calcular el número de abrazos que puedes dar.

Máximo común divisor

Calculamos el máximo común divisor para saber cuál es el mayor de los divisores iguales.

Para calcular el máximo común divisor de dos números, hacemos lo siguiente:

Máximo común divisor de 12 y de 18.

1. o Calculamos los divisores de cada número.

Divisores de 12: 1, 2, 3, 4, 6, 12

Divisores de 18: 1, 2, 3, 6, 9, 18

2.o Buscamos los divisores comunes y elegimos el mayor. Divisores de 12: 1 , 2 , 3 , 4, 6 , 12

Divisores de 18: 1 , 2 , 3 , 6 , 9, 18

Si necesitas ayuda, «Te lo cuento en un momento» en anayaeducacion.es

1 Calcula el máximo común divisor de estos números. Exprésalo con un diagrama como el del ejemplo.

a) 8 y 10 b) 15 y 18 c) 24 y 36 d) 9 y 21

2 Piensa y comparte en pareja Olivia tiene una cuerda azul de 12 m y una cuerda amarilla de 8 m. Corta ambas cuerdas en trozos del mismo tamaño sin que sobre cuerda.

a) ¿De cuántas formas puede cortar las cuerdas?

b) ¿Cuál será la longitud máxima de cada trozo?

Una ayuda: Haz un esquema como este. Observa los divisores comunes y cuál es el mayor.

De los divisores comunes, el mayor es el 6. m.c.d. (12, 18) = 6 Divisores de 12 Divisores de 18

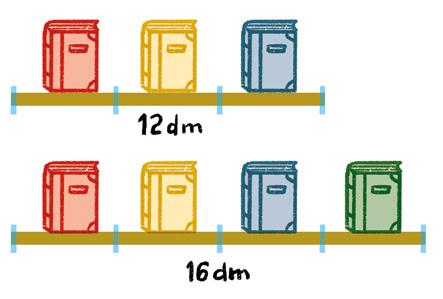
3 En una librería exponen las novedades en dos estanterías, a igual distancia unos libros de otros.

a) Si las estanterías miden 12 dm y 16 dm, respectivamente, ¿cada cuántos decímetros pueden colocar los libros? Indica todos los casos posibles.

b) ¿Crees que todas las opciones se pueden llevar a cabo? Explica por qué.

c) Si colocan los libros respetando el mayor espacio posible entre ellos, ¿cada cuántos decímetros lo harán?

dm

dm

4 En 6.o A hay 20 estudiantes y en 6.o B, 16. La próxima semana irán de excursión al Teatro Real de la Ópera.

a) Si forman equipos iguales sin mezclar estudiantes de las dos clases, ¿de cuántas personas pueden ser los equipos? 20 16

b) Si quieren ir a la excursión con el máximo número de personas en cada equipo, ¿cuántas personas lo formarán?

c) ¿Cuántos equipos se forman en 6. o A? ¿Y en 6. o B?

d) A la excursión van también 6 profesores y profesoras. Contratan un microbús de 16 plazas y otro de 26. ¿Cómo pueden distribuirse si los estudiantes de un mismo equipo no se pueden separar y deben ir profes en cada autobús?

Relaciones especiales. ¿Cuál es el m.c.d. de dos números, uno divisor de otro?

¿Cuál es el máximo común divisor de 5 y de 100? Un instante y… ¡lo tienes!

Cuando un número es divisor de otro, el máximo común divisor de estos números es el menor de los dos.

m.c.d. (5, 100) = 5

5 es divisor de 100.

Halla el máximo común divisor de estos pares de números.

Una ayuda: busca los divisores de 20 y de 16, y encuentra los comunes.

Puedes comprobar tu resultado con regletas y una cuadrícula que puedes descargar en anayaeducacion.es

Criterios de divisibilidad

Utilizamos los criterios de divisibilidad para saber cuáles son algunos de los divisores de un número.

1 Encuentra en la tabla 100 los números que son divisibles por 2, 4, 3, 9, 5 y 10. Comprueba que lo has hecho bien con los criterios de divisibilidad.

Divisibles por 2

Divisibles por 4

14 es divisible por 2 porque al dividir 14 : 2 el resto es 0.

Un número es divisible por 2 si termina en 0 o en cifra par.

Divisibles por 3

Un número es divisible por 4 si el número que forman sus dos últimas cifras es múltiplo de 4, o acaba en 00.

Divisibles por 9

Un número es divisible por 3 si la suma de sus cifras es un múltiplo de 3.

Divisibles por 5

Un número es divisible por 9 si la suma de sus cifras es un múltiplo de 9.

Divisibles por 10

Un número es divisible por 5 si termina en 0 o en 5.

Un número es divisible por 10 si termina en 0.

Puedes descargar la plantilla de la tabla 100 en anayaeducacion.es

2 Copia y completa las tablas con los números que se indican.

3 Observa los resultados de la actividad anterior y contesta.

a) ¿Todos los números divisibles por 2 lo son por 4?

¿Todos los números divisibles por 4 lo son por 2?

b) ¿Todos los números divisibles por 3 lo son por 9?

¿Todos los números divisibles por 9 lo son por 3?

c) ¿Todos los números divisibles por 5 lo son por 10?

¿Todos los números divisibles por 10 lo son por 5?

4 En el colegio de Isabel hay 116 estudiantes de 6.o de Primaria. Quieren organizarse en grupos de 2, de 3 o de 4 para vender papeletas del viaje de fin de curso. ¿Pueden hacerlo?

5 Petición del oyente Investiga con tu calculadora. ¿Qué tiene que ocurrir para que un número sea divisible por 6?

¿Trabalenguas?

Parecen trabalenguas, pero son, simplemente, enunciados equivalentes. Es decir, enunciados distintos que significan lo mismo. Por ejemplo:

2 es DIVISOR de 10

10 es DIVISIBLE por 2

10 es MÚLTIPLO de 2

• Haz lo mismo con estos pares de números. ¡Es sencillo si lo piensas bien!

a) 3 y 60 b) 9 y 45 c) 50 y 200 d) 10 y 1 000

Piensa que: 6 = 2  × 3

Con los criterios de divisibilidad podrás calcular el número exacto de abrazos que puedes dar.

Números primos y compuestos

Distinguimos números primos y compuestos para saber si tienen 2 o más divisores.

Si en una hoja cuadriculada dibujas los números del 2 al 10 y sus divisores… ¿qué observas?

¡Efectivamente!

• Hay números que solo tienen dos divisores: el 1 y él mismo. Son números primos. Por ejemplo: 2, 3, 5 y 7.

• Otros números tienen más de dos divisores: el 1, él mismo y otros divisores. Son números compuestos. Por ejemplo: 4, 6, 8, 9 y 10.

Un número es primo si solo tiene dos divisores: el 1 y él mismo. Un número es compuesto si tiene más de dos divisores.

Para descubrir algunos divisores, puedes utilizar los criterios de divisibilidad.

1 Clasifica estos números en primos y compuestos.

2 Demuestra que estos números no son primos.

Utiliza la calculadora si lo necesitas.

3 ¿Qué números primos hay del 1 al 100? Sigue estos pasos con la tabla 100.

Paso 1: Tacha el número 1, no se considera primo.

Paso 2: Tacha los múltiplos de 2 (son divisibles por 2).

Paso 3: Tacha los múltiplos del siguiente número que no aparece tachado (3).

Paso 4: Sigue así hasta que termines la tabla.

También puedes hacerlo en anayaeducacion.es.

4 ¡Menudo problema! Hay 31 personas para la visita guiada al museo, pero tienen que ir en varios grupos del mismo número de personas. ¿Pueden hacerlo? ¿Y si se unen 2 personas más a la visita?

5 Katia quiere colocar las 23 mesas del aula en varias filas con el mismo número de mesas.

a) ¿Crees que puede hacerlo? Explica por qué.

b) ¿Podría si fuesen 24 mesas? Describe todas las formas posibles.

Descomponer en factores primos

Puedes descomponer cualquier número en factores primos. Para hacerlo, sigue estos pasos:

Descompón 280

1 o . Busca dos factores cualesquiera de 280.

280 = 28 × 10

2 o . Busca dos factores de esos factores.

28 = 4 × 7 10 = 2 × 5

3 o . Haz lo mismo hasta que todos los factores sean números primos.

4 = 2 × 2

4 o . ¡Ya lo tienes! Expresa el número con todos sus factores primos.

280 = 2 × 2 × 7 × 2 × 5 = = 2 x 2 x 2 x 5 x 7

Ordena los factores para dar una solución más elegante.

Este método se llama Criba de Eratóstenes.

Busco todas las respuestas posibles

En 6.o de Primaria hay menos de 100 estudiantes. Esta semana tienen que formar grupos iguales para participar en la realización de un gran mural sobre la paz. Han comprobado que, para que todos participen, pueden colocarse en grupos de 7 o de 3, pero no por parejas.

¿Cuántos estudiantes hay en 6. o de Primaria?

Para averiguarlo, buscamos todas las respuestas posibles con ayuda de la tabla 100.

1.° Elegimos los múltiplos de 7 menores que 100.

2.° De la selección anterior, seleccionamos los múltiplos de 3.

3.° Eliminamos los múltiplos de 2.

En 6. o de Primaria puede haber 21 o 63 estudiantes.

¿La solución tiene sentido?

Comprobamos que los resultados cumplen las condiciones.

- Son números menores que 100.

- Son múltiplos de 7 y de 3.

- No son múltiplos de 2.

1 En una yincana han participado entre 40 y 70 personas. Para realizar las diferentes pruebas, se han colocado en grupos de 2 o de 9 sin que sobrara ninguno. ¿Cuántas personas participaron en la yincana?

2 Carlos tiene una baraja con menos de 100 cartas. Se ha dado cuenta de que, si son 3, 4 o 7 jugadores, cada uno recibe el mismo número de cartas y no sobra ninguna. ¿Cuántas cartas tiene la baraja?

Problemas exprés

Cálculo mental

¿Podrías escribir todos los múltiplos del número 5? Explica tu respuesta.

Como mínimo, ¿cuántos divisores tiene cualquier número?

1 3 5

¡Rápido! Di cinco números primos.

Mira cómo pienso

Di todos los divisores del número 10.

¿Cómo se llama el conjunto de números naturales que no son divisibles por 2?

2 4 6

¿Es 123 456 789 un número primo? Explica por qué.

Descifrando códigos

Escribe un poema sobre algo que te guste. Sigue el mismo patrón que tiene el poema de Sophie Germain:

- Estrofas de 4 versos.

- Versos de 8 sílabas, en la mayoría de los casos.

¡Libertad, Igualdad, Fraternidad!

¡Respetemos los derechos de toda la Humanidad!

Sophie oía aquellos gritos asomada a la ventana. Era una niña pequeña y era revolucionaria.

Ella quería ser libre igual que los otros niños, aunque pronto descubrió que ser niña era distinto.

No podía ir al colegio. No dejaban que estudiara. Ni siquiera que leyera los libros que había en casa.

Pero Sophie no aceptaba esa forma de pensar. A escondidas, por las noches, se dedicaba a estudiar.

De mayor, siempre firmaba sus cartas y sus trabajos como si ella fuera un hombre para que le hiciesen caso.

A pesar de haber luchado con tantas dificultades Sophie tuvo una carrera llena de genialidades.

Puedes descargar el poema en anayaeducacion.es.

Resuelve 14 × 20.

20 = 2 × 10

28 14

× 2 × 10 280

En anayaeducacion.es puedes ver cómo se hace.

Ahora, hazlo tú.

8 ×  20

12 ×  20

15 ×  20

24 ×  20

25 ×  20

7 ×  20

11 ×  20

13 ×  20

21 ×  20

41 ×  20

Los poemas parecen canciones porque siguen una estructura ordenada.

Estudió, entre muchas cosas, los raros números primos, que son los que no se dejan dividir por sus vecinos.

Y así Sophie puso en marcha su propia revolución, pues sus cálculos cambiaron el mundo para mejor.

¿Q ué he aprendido?

1 Lee y escribe en tu cuaderno.

a) Los cinco primeros múltiplos de los siguientes números.

6 12 100

b) Todos los divisores de estos números. 10 20 50

2 Piensa y contesta sin hacer operaciones.

a) ¿Por qué estos números no son múltiplos de 10? 7 3 4 9

b) ¿Por qué estos números no son divisores de 10? 33 15 20 100

3 Calcula el mínimo común múltiplo de estos pares de números. 4 y 7 6 y 9

4 Calcula el máximo común divisor de estos pares de números. 10 y 15 8 y 16

5 ¡Sin hacer cálculos! Piensa y contesta.

a) m.c.m. (5, 10) y m.c.d. (5, 10)

b) m.c.m. (2, 12) y m.c.d. (2, 12)

8 Indica cuáles de estos números son primos y cuáles son compuestos. Explica por qué. 3 12 31 35 17 20

9 ¡En 1 minuto! Con ayuda de la tabla 100, señala los números primos que ves.

Descarga la tabla en anayaeducacion.es.

10 Sole tiene 80 € en monedas de 2 € .

a) ¿Podrá hacer 2 paquetes con la misma cantidad de monedas?

b) ¿Podrá hacer 3 paquetes? ¿Y 4?

c) ¿Podrá hacer 5 o 10 paquetes?

d) En los casos que sí pueda, indica cuántas monedas tendrá cada paquete.

11 Ana sale a correr cada 2 días y Berta sale cada 5 días. Si coinciden este lunes, ¿qué día de la semana volverán a coincidir?

12

6 Utiliza los criterios de divisibilidad para averiguar si estos números son divisibles por 2, 3, 4, 5, 9 o 10. 900 150 123 40

7 Copia y completa la cifra de las unidades de estos números para que sean divisibles por 3. 2_ 13_ 28_ 104_

12 Un bizcocho rectangular mide 24 cm de largo y otro con la misma forma mide 30 cm. Si Pedro quiere cortarlos en porciones iguales, ¿de cuántas formas puede hacerlo? ¿Cuál elegirías tú?

El semáforo. Junto a cada actividad, colorea así en tu cuaderno:

si has sabido la respuesta

si has necesitado ayuda

si no has sabido responder

OBJETIVO EN ACCIÓN

Diseña una campaña para fomentar los abrazos

Esta mañana hemos probado si había diferencia entre un abrazo de 3 segundos y otro de 8 segundos. ¡Ha sido muy divertido porque nos hemos abrazado realmente!

a) Si he estado dando abrazos ininterrumpidamente durante 15 segundos…

– ¿Cuántos abrazos he dado si eran de 3 segundos?

– ¿Podría haber dado solo abrazos de 8 segundos? ¿Por qué?

– ¿Podría haber dado abrazos de 8 segundos y de 3 segundos? ¿Cuántos de cada?

b) Responde a las mismas preguntas si hubiese dado abrazos durante 24 segundos.

c) Si en mi clase hay 20 personas, ¿cuánto tiempo como mínimo necesito para poder abrazarlos a todos con abrazos de 3 segundos? ¿Y de 8? Justifica tu respuesta.

Nos planteamos

Utilizamos la estrategia Puntos cardinales para analizar por qué es necesario construir la paz.

¿Qué obstáculos ves en la construcción de la paz?

a) Copia y completa el organizador en tu cuaderno.

b) En equipo diseñad una campaña para fomentar los abrazos de 8 segundos. Ponedla en marcha en el colegio, en vuestro entorno, en vuestras reuniones familiares…

¿C ómo he aprendido?

Completa en tu cuaderno.

No tengas en cuenta el tiempo que tardas entre abrazo y abrazo.

¿Qué información necesitarías para responder a la pregunta de por qué es necesario construir la paz?

Necesidad

Obstáculo preOcupación

Entusiasmo Emociones

Sugerencias poSiciones

¿Cuál es tu opinión personal sobre el tema? ¿Qué sugerencias harías para la construcción de la paz?

¿Qué te entusiasma de esta idea?

¿Crees que la paz se construye?

Escribe tres emociones positivas que sientas cuando estás trabajando las actividades de matemáticas.

Escribe tres emociones negativas que surjan cuando trabajas esta área. ¿Qué podrías hacer para cambiarlas?

Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.

© GRUPO ANAYA, S.A., 2023 - C/ Valentín Beato, 21 - 28037 Madrid.