Operació món: Matemàtiques 4º. Illes Balears (demo)

Matemàtiques PRIMÀRIA

Els nombres Nombres al barri

La suma i la resta Junts sumam

La multiplicació Cuida l’aigua

SITUACIÓ D’APRENENTATGE OBJECTIU EN ACCIÓ ODS PÀG.

La divisió Residus zero

Les fraccions T’apuntes a l’estalvi d’energia?

Els nombres decimals Matemàticament som iguals

Unitats de longitud Quilòmetres d’exercici

Unitats de capacitat i massa Mesures universals

La mesura del temps És hora d’inventar!

Moviments i transformacions Paisatges matemàtics

Figures planes i cossos geomètrics Geometria marina

L’atzar Que plogui, que plogui!

8 80 148

24 96 162

40 114 180

58 128 202

Per què la vida d’una persona pot ser diferent segons el lloc on viu? Fes un llistat de 10 coses bones que tens per viure al teu barri.

Per què és important treballar en equip? Dissenya un cartell per mostrar els beneficis de treballar en equip.

Què podem fer per gastar menys aigua? Crea una campanya amb recomanacions per cuidar l’aigua.

Com podem reciclar bé els residus al pati? Elabora un collage amb paper reciclat per indicar què va a cada contenidor.

REPÀS TRIMESTRE 1 STEAM: Dorothy Vaughan

Què podem fer per estalviar energia?

Inventa una cançó curta per a un anunci que animi tothom a estalviar energia. T’atreveixes a cantar-la?

Com podem mostrar que el pensament matemàtic no depèn de si ets ninao nin?

Crea jocs numèrics amb decimals per jugar tots plegats a classe.

Què podem fer per donar a conèixer la importància de fer esport entre els més petits?

Escriu un conte que mostri per què és important fer esport.

Com podem defensar la importància de tenir mesures universals?

Inventa una unitat de mesura de capacitat o de massa.

REPÀS TRIMESTRE 2 STEAM: Emma Castelnuovo

Com podem conservar neta la localitat on vivim?

Crea un nou mètode per mantenir els carrers nets.

Què podem fer perquè les persones vegin la bellesa de la naturalesa i vulguin cuidar-la?

Fes un dibuix d’un paisatge utilitzant rectes, angles i simetries, que mostri la bellesa de la naturalesa.

Com podem conèixer els animals que estan a les nostres costes per cuidarlos millor?

Elabora un dibuix d’un animal marí real que visqui a Espanya utilitzant figures geomètriques.

Aliances per aconseguir objectius

Aigua neta i sanejament

Producció i

Pau,

Indústria, innovació i infraestructura

Vida d’ecosistemes terrestres

Vida submarina

Què passarà al nostre voltant si plou molt menys?

Fes un pòster que mostri què passarà si no plou prou.

REPÀS TRIMESTRE 3 STEAM: Graciela Salicrup

Acció pel clima

Reducció de les desigualtats

Energia assequible i no contaminant

Igualtat de gènere

Salut i benestar

justícia i institucions sòlides

SABERS BÀSICS

• Per a què serveixen els nombres?

• Els nombres de quatre xifres

• Els nombres de fins a sis xifres

La suma en vertical

• Propietats de la suma

• La resta en vertical

• La multiplicació

• Propietats commutativa i associativa

• L’ordre de les operacions. Propietat distributiva

• La multiplicació per desenes, centenes i milers

Repartiments i agrupaments

• La divisió

• Descompondre nombres per dividir

• La divisió entre la unitat seguida de zeros

• Comparació de nombres

• Arrodoniment de nombres

Sumes i restes combinades

• Problemes de sumes i restess

• Problemes aritmètics: de combinació i de canvi

La multiplicació en vertical

• La multiplicació per diverses xifres

• Problemes aritmètics: de grups iguals

• Operacions combinades

• La divisió entre un nombre de dues xifres

• Problemes aritmètics: de repartiment

• Anomenar les fraccions

• Mig, terç i quart

• La fracció i la unitat

• Fraccions pròpies i impròpies

• Unitats, dècims i centèsims

• Els nombres decimals Els preus

• Comparació de nombres decimals

• Unitats de mesura no convencionals

Unitats menors que el metre

• Unitats majors que el metre

• Unitats menors que el litre

• Unitats majors que el litre

• Unitats menors que el gram

• Unitats majors que el gram

• Comparació de fraccions

• La fracció com a repartiment

• La fracció d’una quantitat

• Representació de nombres decimals en la recta

• Arrodoniment de nombres decimals

La suma i la resta de nombres decimals

• Problemes aritmètics: de comparació

HO RESOLC SENSE PROBLEMA

• Estratègia heurística: Desxifr codis

• Càlcul mental: Sumar completant al 10

• Pensament computacional: Abstracció

• Estratègia heurística: Planteig preguntes intermèdies

• Càlcul mental: Sumar completant al 10

• Pensament computacional: Funcions

• Estratègia heurística: Començ per casos més senzills

• Càlcul mental: Sumar completant a les desenes

• Pensament computacional: Generalització

• Estratègia heurística: Estim la solució

• Càlcul mental: Restar completant al 10

• Pensament computacional: Generalització

• Unitats menors que l’any

• Unitats majors que l’any

• Dies, hores, minuts i segons

• Expressions complexes i incomplexes

• Problemes aritmètics: de comparació

• Expressions complexes i incomplexes

• Problemes aritmètics: de repartiment, de combinació i de comparació

• Estratègia heurística: Faig un dibuix

• Càlcul mental: Restar completant a les desenes

• Pensament computacional: Algoritme

• Estratègia heurística: Cerc tots els casos possibles

• Càlcul mental: Sumar completant al 100

• Pensament computacional: Generalització

• Estratègia heurística: Assaig i error

• Càlcul mental: Multiplicar per 2

• Pensament computacional: Funcions

• Estratègia heurística: Organitz les dades en una taula

• Càlcul mental: Sumar fraccions

• Pensament computacional: Simulació

• Punts, rectes, semirectes, segments

• Tipus de rectes: paral·leles, secants i perpendiculars

• Els polígons

• Classes de triangles

• Classes de quadrilàters Àrea de polígons

• El rellotge de busques i el rellotge digital

• Problemes aritmètics: de grups iguals i de comparació

• Mesurar i dibuixar angles

• Gir, translació i simetria

• Coordenades en el pla. Situació i moviment

• Circumferència i cercle

• Cossos geomètrics

• Poliedres: prismes i piràmides Cossos rodons

• Experiències d’atzar

• Esdeveniment segur, possible i impossible

• Probabilitat d’un esdeveniment

• Estratègia heurística: Elimin possibles respostes

• Càlcul mental: Dividir entre 2

• Pensament computacional: Simulació

• Estratègia heurística: Seguesc un patró

• Càlcul mental: Dividir entre 2

• Pensament computacional: Algoritme

• Estratègia heurística: Cerc el camí més senzill

• Càlcul mental: Un mig d’una quantitat

• Pensament computacional: Dades

• Estratègia heurística: Organitz les dades en un diagrama d’arbre

• Càlcul mental: Multiplicar per 5

• Pensament computacional: Generalització

PROJECTE

Els nombres

1 Nombres al barri

Els nombres estan presents en la nostra vida. Hi ha nombres al nostre voltant, pertot arreu.

Alguns nombres serveixen per donar informació sobre el nostre barri: quantes persones hi viuen, quants de restaurants hi ha, o on està situat...

Com? On està situat? Sí, hi ha un nombre que indica on està situat el teu barri. Es diu codi postal.

A Espanya, el codi postal es construïx amb cinc xifres. Les dues primeres indiquen la província a la qual pertany. Saps quin és el codi postal de la població on vius?

Com ho veus?

Què diries a algú que vol venir al teu barri?

Per què? Quins nombres són importants per determinar com és un barri?

Per a aquesta unitat...

Objectiu en acció

Per què la vida d’una persona pot ser diferent segons el lloc on viu?

Elabora un llistat de 10 coses bones que tens per viure al teu barri.

La dada

Els pobles i les ciutats es divideixen en barris, que són zones més petites. Només a Palma hi ha més de 80 barris.

1

Per a què serveixen els nombres? Els nombres de quatre xifres

Per a què serveixen els nombres?

Escrivim amb una sola paraula:

• els nombres del 0 al 30: 17 desset

• les desenes completes: 50 cinquanta

• les centenes completes: 400 quatre-cents

• el nombre 1 000: 1 000 mil

5 Compt en veu alta.

a) D’1 en 1, des del 80 al 130.

b) De 3 en 3, des del 0 fins al 30. c) De 4 en 4, des del 0 fins al 40. d) De 5 en 5, des del 125 fins al 225.

6 Amb l’ajuda de la teva parella, compta en veu alta.

a) De 10 en 10, des del 50 fins al 200. b) De 25 en 25, des del 25 fins al 150.

c) De 50 en 50, des del 100 fins al 500. d) De 100 en 100, des del 0 fins al 1 000.

7 Pensa i contesta: Quin és el nombre següent al 99?

Quin és el nombre següent al 999?

Pots descarregar les taules de nombres a anayaeducacion.es

Quin és el nombre següent al 9 999?

Nombres ordinals

8 Observa i completa la taula al quadern. anterior 3r ? ? ? posició 4t 10è 21è 39è posterior 5è ? ? ?

9 Llegeix i completa les frases amb paraules. La carrera de Sant Silvestre se celebra el 31 de desembre.

• Si el tercer avança el segon, queda en posició ? .

• Si al quinzè l’avancen dues persones, queda en la posició ?

• Si al primer l’avancen tres persones, queda en la posició ?

A partir del vintè, els nombres ordinals es llegeixen: 20è vintè 21è vint-i-unè 22è vint-i-dosè 30è trentè 31è trenta-unè 32è trenta-dosè

Nombres ordinals fins al 99è a anayaeducacion.es .

Pren nota!

Els nombres ens permeten conèixer millor el nostre barri.

Els nombres de quatre xifres

Per llegir les matrícules dels cotxes elèctrics del barri, utilitzam els nombres de quatre xifres.

Quants de punts hi ha?

1 1 1 1

1 10 10 10 100 100 200 5 30 1 235 1 000

1 unitat de miler = 1 000 unitats

UM C D U 1 2 3 5

2 centenes = 200 unitats 3 desenes = 30 unitats 5 unitats = 5 unitats

1 0 0 0 2 0 0 3 0 + 5 1 2 3 5

Els nombres de quatre xifres estan formats per unitats, desenes, centenes i unitats de miler.

1 Completa el text al quadern.

1 unitat de miler = ? centenes = ? desenes = ? unitats Si necessites ajuda, «T’ho explic en un moment» a anayaeducacion.es

2 Escriu amb xifres: a) b)

Pots dibuixar els blocs així.

3 Representa aquests nombres amb blocs.

1 283 5 210 1 001

4 Descompon els nombres com en l’exemple.

2 UM, 5 C, 1 D, 3 U

2 513

2 000 + 500 + 10 + 3

a) 25 c) 124 e) 6 184 b) 78 d) 893 f) 1 500

5 Quin és el valor de la xifra 5 en aquests nombres?

UM C D U 5 8 2 3

5 unitats de miler són 5 000 unitats.

El valor de la xifra 5 és 5 000.

a) 57 c) 125 e) 5 007

b) 35 d) 502 f) 2 950

6 Pensa i comparteix en parella En equip, anotau les vostres dates de naixement.

a) Quantes xifres pot tenir el dia en una data? I el mes?

b) Quantes xifres té l’any de naixement?

c) Pensa en algú que coneguis. Creus que el seu any de naixement pot tenir més o menys de quatre xifres? Explica per què.

Jugam amb les xifres

Utilitzam nombres de quatre xifres per expressar dades personals com l’any de naixement.

Escriu aquestes xifres en trossos de paper. Col·loca-les a damunt la taula formant els nombres següents:

a) Un nombre amb 5 UM.

b) Un nombre amb 0 C. c) Un nombre capicua de tres xifres. Es llegeix igual d’esquerra a dreta que de dreta a esquerra!

Els nombres de fins a sis xifres

De vegades necessitam utilitzar nombres grans per indicar quantes persones viuen al barri o quants barris celebren les festes.

Un habitant més al barri. És el 153 296!

miler

miler (DM)

miler (UM)

lloc

ocupen.

3 Escriu amb xifres i amb lletres el nombre que conté cada requadre.

5 CM 7 D 1 U 3 UM 6 DM 2 DM 8 C 5 D 4 UM 7 U

4 Copia i completa la taula al quadern.

1 524 1 UM + 5 C + 2 D + 4 U 1 000 + 500 + 20 + 4 ? ? 40 000 + 600 + 60 + 2 ? 2 CM + 5 DM + 3 UM + 7 U ?

5 Copia la taula i escriu-hi aquests nombres. Indica el valor del 8 en cada cas.

a) vuit mil tres-cents quaranta b) vint-i-vuit mil quatre-cents vint-i-cinc c) vuit-cents vint-i-tres mil sis-cents vint-i-tres

Un barri diferent

En algun lloc de Kenya viuen en Jackson i la seva germana, na Salomé. En Jackson té 11 anys i na Salomé en té 6. Al dematí s’aixequen molt prest per anar a escola perquè des de ca seva hi ha una distància de 15 000 metres. No hi van amb cotxe, ni amb bicicleta ni amb patinet. Cada dia en Jackson i na Salomé recorren a peu aquesta distancia. Tarden 2 hores a anar-hi i unes altres 2 hores a tornar.

CM DM

U ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

Com que el trajecte és llarg, duen una garrafa amb 2 litres d’aigua per beure si tenen set. A més a més, s’han d’amagar dels elefants que pesen milers de quilos (entre 2 000 i 7 000 quilos!) i altres animals salvatges que es troben al seu pas.

Però a en Jackson i a na Salomé no els importa la distància, el temps que tarden o quant pesen les garrafes i motxilles. Caminen somrient perquè saben que, en arribar a l’escola, els esperen coses meravelloses a aprendre.

1-2-4 Quines diferències observes entre com vas tu a l’escola i com van en Jackson i na Salomé a la seva? Compartiu-ho amb la classe.

Pren nota!

Els nombres ens indiquen quantes persones viuen al barri.

UM C D

Text basat en una de les històries del documental «Camí a l’escola».

Compar nombres

Per saber quantes persones hi ha en un barri més que en un altre, comparam nombres.

Per comparar dos nombres, ens fixam en les seves xifres.

Si tenen diferent quantitat de xifres, el nombre menor és el que té menys xifres.

DM UM C D U 5 8 2 3 1 4 1 0 5

5 823 és menor que 14 105 5 823 < 14 105

Si tenen la mateixa quantitat de xifres, els comparam xifra a xifra, començant per l’esquerra, fins a trobar dues xifres diferents.

DM UM C D U 6 2 7 1 9 6 2 7 1 7 9 > 7

62 719 és major que 62 717 62 719 > 62 717

Per entendre-ho millor, «T’ho explic en un moment» a anayaeducacion.es

1 Compara aquests nombres. Utilitza els signes >, < o =. 1 250 i 2 051 9 099 i 999

16 343 i 6 343 105 444 i 150 444

2 Pensa i comparteix en parella Juga amb els nombres i contesta les preguntes.

a) Quin és el menor nombre de quatre xifres?

b) I el major de quatre xifres?

c) Quin és el menor nombre de sis xifres? d) I el major de sis xifres?

3 Digues en veu alta:

a) Un nombre entre 1 000 i 10 000.

b) Un nombre entre 6 515 i 6 900. c) Un nombre entre 20 000 i 20 005. d) Un nombre entre 1 CM i 2 CM.

e) Un nombre entre 2 D i 2 DM.

Un nombre entre 2 i 8 és major que 2 i menor que 8.

Recorda-ho > major < menor = igual

Un nombre a la dreta d’un altre en la recta numèrica és sempre

4 Ordena els nombres de cada grup. Pensa on estan situats a la recta.

1 001 1 100 1 010 1 000 100 000 10 000 25 500 55 000 2 500

5 Dibuixa aquesta recta numèrica al quadern. 10 000 10 500 11 000

Pots utilitzar la recta numèrica per comparar nombres.

a) Tria tres nombres que estiguin entre el 10 000 i el 11 000. Situa’ls a la recta.

b) Quin és el major dels nombres que has triat?

c) I el menor?

6 Tots els bitllets d’una tómbola tenen un nombre major que 1 000 però menor que 1 300. Quins no són bitllets d’aquesta tómbola?

1 000 2 200

Una pista d’altura

1 500 1 111

250 1 080

1 299

Tens dificultats per recordar què signifiquen els signes > o <?

Dibuixa en un full quadriculat barres de diferents altures i traça-hi línies com les de la imatge. Això et donarà la pista!

Major que Menor que

Pren nota!

Comparar el nombre de persones o de parcs de diversos barris t’ajuda a conèixer-los millor.

Arredonesc nombres

De vegades ens interessa substituir un nombre de moltes xifres per un altre que tengui un valor aproximat, perquè sigui més fàcil de recordar.

1 Copia i completa la taula.

Nombre Està entre… Punt mitjà Arrodoniment

5 757 5 000 i 6 000 5 500 6 000

8 400 ? ? ?

1 800 ? ? ?

2 Na Marta viu al barri de la Ciència. Aproxima la longitud de cada carrer.

Carrer dels Nombres Carrerd’Hipàcia

Pitàgores

PasseigdelPensament

Jardí de la Geometria Carrer de

• Carrer dels Nombres: 892 m

• Carrer d’Hipàcia: 1 209 m

• Passeig del Pensament: 1 990 m

• Carrer de Pitàgores: 2 005 m

3 Pensa i completa les frases amb les dades de l’activitat 2.

a) El carrer més curt és ? . La longitud és ? m aproximadament.

b) El carrer més llarg és ? . La longitud és ? m aproximadament.

c) El carrer més llarg i el més curt es diferencien en ? km aproximadament.

Arrodonir a les unitats de miler

Cercam la unitat de miler més pròxima a 2 638:

• Marca entre quines unitats de miler està el 2 638.

2 000 3 000

• Senyala’n el punt mitjà.

2 000 2 500 3 000

• Col·loca el nombre en la recta.

2 638

2 000 2 500 3 000

Com que 2 638 > 2 500, triem la unitat de miler major.

La unitat de miler més pròxima a 2 638 és 3 000.

Per entendre-ho millor, «T’ho explic en un moment» a anayaeducacion.es

Per comparar he de restar. Recorda que 1 km són 1 000 m.

4 Arrodoneix el nombre 4 088 a l’ordre que s’indica.

a) A les unitats de miler.

UM C D U 4 0 8 8

Arrodonit a les unitats de miler és ? b) A les centenes.

UM C D U 4 0 8 8

Arrodonit a les centenes és ? c) A les desenes.

UM C D U 4 0 8 8

Arrodonit a les desenes és ?

Arrodonir a qualsevol ordre de unitat

Per arrodonir 7 549 a les centenes:

• Marca entre quins nombres està el 7 549, tenint en compte l’ordre al qual aproximes.

7 500 7 600

• Senyala’n el punt mitjà.

7 500 7 550 7 600

• Col·loca el nombre a la recta.

7 549

7 500 7 550 7 600

Com que 7 549 < 7 550, triem la centena menor.

7 549 arrodonit a les centenes és 7 500.

5 Arrodoneix les dades a la unitat de miler. Indica si les oracions són vertaderes (V) o falses (F), i corregeix les falses.

a) Al barri de la Ciència hi ha uns 2 000 habitants.

b) També n’hi ha gairebé 2 000 al barri de les Lletres. c) A la Pau no viuen tantes persones, només unes 1 000.

6 Assemblea d’idees En grups, pensau dos nombres de quatre xifres que, arrodonits a les centenes, siguin 2 800.

I si estic a la meitat?

Què et fa dir això?

Com arrodoneixes un nombre que es troba a la mateixa distància dels dos extrems als quals s’aproxima? Escriu-ne algun exemple.

La Ciència 1 989 hab. La Pau 919 hab. Les Lletres 2 580 hab.

En aquests casos sempre es tria l’extrem major.

Pren nota!

Arrodonir nombres ens ajuda a comparar amb més facilitat la població de diversos barris.

Desxifr codis

A l’església de la ciutat d’en Roderic està inscrit l’any en què se’n va acabar de construir la façana. Saps quin any és? L’any està escrit en xifres romanes.

MCMXXX

Els romans utilitzaven 7 lletres majúscules per representar els nombres. Cada lletra tenia un valor diferent.

1 5 10 50 100 500   1 000

Per llegir una xifra romana:

• Sumam els valors de les lletres d’esquerra a dreta.

MCCXIII → 1 000 + 100 + 100 + 10 + 1 + 1 + 1 = 1 213

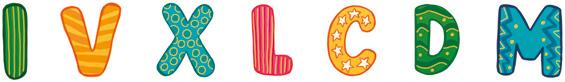
• Si una xifra de menor valor està a l’esquerra d’una de major valor, en restam els valors.

IV → 5 – 1 = 4

Desxifrem el nombre MCMXXX?

1r Ens fixam en les lletres i comprovam si estan ordenades de major a menor valor. Si no, aplicam la regla de la resta.

M CM XXX 900

2n Sumam els seus valors.

1 000 + 900 + 10 + 10 + 10 = 1 930 La façana es va acabar de construir l’any 1930.

Església de Santo Domingo, Jerez de la Frontera (Cadis).

Si necessites ajuda, «T’ho explic en un moment» a anayaeducacion.es

1 Na Paula ha agafat el tom xvii d’una enciclopèdia de la biblioteca. Quin número de tom és?

2 Enguany se celebra el xlv aniversari de l’escola. Quants anys duu oberta?

Problemes exprés

1

Quin és el major nombre de 3 xifres? I de 4 xifres? I de 5? I de 6?

2

Quin és el menor nombre de 3 xifres? I de 4 xifres? I de 5? I de 6?

Càlcul mental

Resol 6 + 8.

6 + 8 = 6 + 10 – 2 = 14 2 10

3 5

El 5 de juny a la nit varen regar el meu carrer. Si en aquest mes ho varen fer cada 5 dies, quins dies varen regar el carrer?

Els números de les cases del meu carrer comencen en la plaça. Quin està més a prop de la plaça, el 48 o el 84?

Mira com pens

Qui som?

Hi ha més estudiants a l’escola que a l’institut. Quants n’hi pot haver a cada lloc? Inventa la resposta.

4 6

Al meu carrer hi ha 8 289 veïnats i veïnades. Quants són aproximadament?

A anayaeducacion.es pots veure com es fa.

Ara, fes-ho tu: 9 + 6 7 + 5 4 + 7 8 + 6 6 + 9 9 + 4 5 + 6 5 + 8 8 + 4 6 + 7

La teva parella et donarà un nombre escrit en una targeta o paper. Sense mirar el nombre, fes preguntes per endevinar quin és.

Som una xifra romana?

Som major que mil?

Som capicua?

Quantes xifres tenc?

D’APRENENTATGE

DOSSIER

Q uè he aprés?

1 Copia i substituei els nombres ordinals pel seu nom.

• Na Lara va guanyar la carrera perquè va arribar la 1a.

• Em vaig equivocar en el 6è pas.

• Avui és el 50è aniversari de noces dels meus tiets. Cinquanta anys!

• El 13 en ordinal es diu 13è.

2 N’Alfons viu a l’onzè pis. Si baixa 4 pisos i després en puja 7, en quin pis es troba ara? 3 Quin nombre és? 4 Escriu al quadern com es llegeixen aquests nombres. Observa l’exemple. 2 DM, 5 UM, 3 D → 25 030 vint-i-cinc mil trenta a) 6 CM, 4 UM, 2 C, 7 U b) 1 DM, 7 C, 3 D, 4 U c) 8 UM, 1 U

6 Descompon com en l’exemple: 1 UM, 9 C, 3 D, 5 U 1 935 1 000 + 900 + 30 + 5 a) 27 358 c) 400 032 b) 37 125 d) 840 724

7 Utilitza aquestes xifres per escriure els nombres que s’indiquen. 5 3 2 0 4 a) El major nombre. b) El major nombre imparell. c) El menor nombre. d) El menor nombre parell.

8 Al meu poble, hi ha més passos de vianants que semàfors. Quants n’hi pot haver? Inventa la resposta. 9 Copia i arrodoneix: Nombre A les unitats de miler A les desenes 2 425 ? ? 13 542 ? ? 243 782 ? ? 10 A la meva localitat hi ha 4 567 habitants. Quants són aproximadament?

El semàfor. Al costat de cada activitat, pinta-ho així al quadern: si has sabut la resposta si has necessitat ajuda si no has sabut respondre-la

OBJECTIU EN ACCIÓ

Llegeix les dades dels tres barris d’una localitat.

a) Quantes persones viuen a cada barri de manera aproximada?

b) Ordena els barris de menor a major segons la població.

c) On hi ha més parcs? I més centres culturals?

d) En quin barri voldries viure i per què?

Ens ho plantejam

Utilitzam l’estratègia Pens, m’interessa, investig per analitzar per què la vida d’una persona pot ser diferent depenent del lloc on visqui. Utilitza informació de barris que coneguis.

a) Copia i completa l’organitzador al quadern.

b) Elabora un llistat de 10 coses bones que tens per viure al teu barri.

C om ho he après?

Copia les frases al quadern i pinta al costat de cada oració.

• Em sent bé treballant amb nombres.

• Sé utilitzar les matemàtiques en la vida diària.

• M’esforç per millorar el meu treball.

Què pots fer per millorar el teu treball en matemàtiques?

J unts sumam

De vegades, organitzam jocs al pati en els quals és necessari que col·laborem en equip. També quan feim feina, necessitam els companys i companyes per aconseguir acabar algunes tasques de grup o perquè ens ajudin.

Jugar o fer feina en equip no sempre és fàcil perquè som diferents i pensam de manera diferent, però val la pena! Amb els altres aprenem, junts i juntes vencem les dificultats i ens aliam per aconseguir els objectius. L’alegria compartida és més alegria.

Com ho veus?

Quines recomanacions donaries a un equip en un treball o en un joc perquè sumin totes les seves forces?

Quan fas feina en equip, quines coses fan més difícil el treball i resten energia al grup?

La dada

Aprendre a fer feina en equip fa que ens relacionem millor amb els altres i guanyem confiança.

Per a aquesta unitat…

Objectiu en acció

Per què és important fer feina en equip?

Dissenya un cartell per mostrar els beneficis de fer feina en equip.

Practic la suma

Sumam per unir diverses quantitats en una sola.

Feim la suma 2 056 + 3 874.

1r Col·locam els nombres, l’un davall de l’altre.

UM C D U 2 0 5 6 + 3 8 7 4

El resultat de 2 056 + 3 874 és 5 930.

2n Sumam les unitats, les desenes, les centenes i els milers.

UM C D U 1 1 2 0 5 6 + 3 8 7 4 5 9 3 0

Per sumar dos nombres, els col·locam l’un davall de l’altre fent coincidir els ordres d’unitats i feim la suma.

1 Copia i suma. Després, indica els termes de cada operació. 7 2 6 8 + 1 4 0 9 2 2 7 5 + 5 3 3 5

9 2 0 4 1 + 1 8 5 7 6 6 7 8 4 3 + 7 2 5 4

2 Caps numerats Fes aquestes sumes i contesta la pregunta. a) 1 238 + 4 507 + 121 b) 41 790 + 72 796 En una suma, quin és el terme major?

3 Aquest és el camí que uneix la casa de na Maria amb l’escola.

Termes de la suma 2 4 5 7 + 1 3 9 2 5 9 6

sumands suma o total

Propietat commutativa

Hi ha la mateixa distància de la casa a l’escola que de l’escola a la casa? Per què? Comprova-ho.

En una suma, si canviam l’ordre dels sumands, el resultat és el mateix. 2 + 5 = 7 5 + 2 = 7

4 Fixa’t bé en les operacions i esbrina els nombres que falten en cada cas. Quina propietat hi has aplicat?

a) 2 450 + ? = 743 + 2 450 = ? b) ? + 6 705 = 6 705 + 132 = ? c) 405 + 1 250 + 300 = ? + 300 = ? d) 3 075 + 125 + 800 = 3 075 + ? = ?

Propietat associativa

En una suma de diversos sumands, si canviam l’ordre en què els agrupam, el resultat és el mateix.

7 + 3 + 5 = 10 + 5 = 15

7 + 3 + 5 = 7 + 8 = 15

5 Quants de punts ha aconseguit l’equip blau? Calcula-ho de dues formes diferents i comprova que el resultat és el mateix. 125 107 174 199 156 92

6 A la fira del llibre d’una ciutat s’han venut 1 245 exemplars divendres, 2 456 dissabte i 983 diumenge. Quants de llibres s’han venut en total durant aquests dies?

7 La pregunta Inventa un problema amb aquestes dades que es resolgui amb una suma. 925 2 575

Sumam d’una altra forma

Saps que pots sumar descomponent els sumands? Observa-ho.

Pren nota!

Ara, fes-ho tu. Resol descomponent els sumands.

a) 3 118 + 4 720 b) 5 426 + 527 c) 945 + 7 736

Quan fas sumes, pots ordenar les quantitats de diferents maneres i el resultat no canvia.

Practic la resta

Restam quan comparam dues quantitats o calculam el que sobra o el que falta.

9 716 cm 5 432 cm

Quina és la diferència entre la longitud d’aquestes cordes? Feim la resta 9 716 − 5 432.

1r Col·locam els nombres, l’un davall de l’altre.

UM C D U 9 7 1 6 5 4 3 2

El resultat de 9 716 5 432 és 4 284.

2n Restam les unitats, les desenes, les centenes i els milers.

UM C D U 11 9 7 1 6 5 5 4 3 2 4 2 8 4

Per restar dos nombres, els col·locam l’un davall de l’altre fent coincidir els ordres d’unitats i feim la resta.

1 Ho comprovam Copia i resta. Després, indica els termes de cada operació. 5 3 7 3 2 0 6 4 7 8 4 7 4 1 9 3

4 6 0 2 8 1 6 5 0 6 8 5 3 7 5 3 8 9 3

2 Caps numerats Resol aquestes restes i contesta la pregunta. a) 6 407 1 352 b) 72 274 18 330 En una resta, quin és el terme major? 3 Fes els càlculs i comprova-ho amb la prova de la resta. Resta 3 7 2 0 1 5 9 4 2 1 2 6

Termes de la resta 1 7 6 3 3 0 2 1 4 6 1

minuend diferència subtrahend Comprova els resultats amb la calculadora.

minuend diferència subtrahend

Prova de la resta 1 5 9 4 + 2 1 2 6 3 7 2 0

subtrahend minuend diferència a) 3 703 1 481 b) 50 429 3 132

4 Observa la relació entre tres nombres i completa-ho.

2 525

890 1 635

890 + 1 635 = ?

1 635 + 890 = ?

2 525 890 = ? 2 525 1 635 = ?

775

4 000

5 Escriu totes les sumes i les restes que pots formar en cada cas. 350 425

2 150 1 850

6 Llegeix i resol aquesta història contada de tres formes.

– A la plaça hi ha 1 104 banderoles verdes i 836 blaves. Quantes banderoles hi ha en total?

– A la plaça hi ha 1 940 banderoles verdes i blaves. Si 1 104 són verdes, quantes són blaves?

– A la plaça hi ha 1 940 banderoles verdes i blaves. Si 836 són blaves, quantes no ho són?

Ara inventa una altra història amb els nombres 750 i 1 245. Comparteix la teva resposta amb la resta de companys i companyes.

Restam d’una altra forma

Saps que pots restar descomponent el minuend i el subtrahend? Observa-ho.

A 2 no li puc llevar 9.

Ara, fes-ho tu. Resol descomponent el minuend i el subtrahend.

a) 783 − 162 b) 5 671 − 1 022 c) 6 903 − 4 872

Pren nota!

Recorda col.locar bé les quantitats per fer restes correctament.

Faig sumes i restes combinades

A vegades, per resoldre un problema, és molt útil escriure diverses operacions en una sola expressió.

Si pagam els dos jocs amb un bitllet de 10 €, quants de doblers ens tornen? Plantejam l’expressió que resol el problema i seguim els passos per resoldre-la. 10 (3 + 4)

1r Realitzam l’operació que està entre parèntesi. 10 (3 + 4) = 10 7

Per resoldre expressions amb sumes i restes:

3 € 4 €

2n Resolem la resta. 10 − (3 + 4) = 10 − 7 = 3

1r Calculam les operacions que estan dins del parèntesi. 2n Resolem les sumes i les restes d’esquerra a dreta.

1 Observa aquestes expressions i indica l’ordre en el qual has de resoldre les operacions. a) 18 (9 + 4) b) 20 (15 5) c) 15 12 + 10

2 Ho comprovam Calcula el resultat d’aquestes expressions. Fixa’t si hi ha o no parèntesi! a) 25 + 10 18 c) 132 (44 14) b) 70 (31 + 19) d) 18 + 22 15 7

3 Què et fa dir això? Observa les expressions i contesta les preguntes.. 69 (13 + 26) 69 13 + 26

a) En què s’assemblen? En què es diferencien? b) Resol-les. Has obtengut resultats iguals o diferents? Explica per què.

4 Observa la torre del marge. Si hi afegesc 14 policubs i després en llev 8, quants formen la torre ara? A. 20 14 + 8 B. 20 + 14 8 C. 20 (14 8)

5 Llegeix i tria l’expressió que resol cada problema. Després, calcula’n la solució.

a) Si la massa d’aquests tres cans és de 42 kg en total, quina és la massa del petit? 22 kg 13 kg ? kg

A. 42 (22 + 13) B. 42 22 + 13

b) En un forn hi ha 45 barres blanques i 32 d’integrals. Si venen 40 barres, quantes en queden per vendre?

A. 45 + 32 40 B. 45 (32 + 40)

c) Una taula de surf costava 179 € . En les primeres rebaixes el preu va baixar 18 € i en les segones rebaixes, 16 € més. Quant costa ara?

A. 179 (18 16) B. 179 18 16

6 Avui, les gallines d’una granja han post 1 052 ous. Si se n’han romput 30 i els grangers se n’han menjat una dotzena, quants d’ous poden vendre?

En una dotzena hi ha 12 ous.

7 Les alternatives Inventa una pregunta per a aquest enunciat i resol el problema.

Na Virgínia té un bitllet de 50 € . Compra una caixa d’aquarel·les per 19 € , un estoig de pinzells per 12 € i un bloc de dibuix per 4 €

179 €

Intenta resoldre el problema escrivint les operacions en una sola expressió.

Pren nota! 19 € 12 € 4 €

Quan inventes sumes i restes, les pots combinar.

Resolc problemes de suma i resta

Per resoldre un problema, primer és necessari comprendre’l .

1 Hem retallat 154 banderoles grogues i 246 de verdes per fer garlandes per a la festa de l’escola. Quantes banderoles hem retallat en total?

1r El total de banderoles és major que el nombre de banderoles de cada color.

Passos per resoldre un problema

1r  Comprenc el problema.

2n Organitz les dades.

3r Resolc el problema.

4t Comprov que la solució té sentit.

?

2n Dibuix un diagrama parts-tot. 154 246

3r He de… sumar o restar? ?

4t El total de banderoles és el nombre major. Resol-ho pas a pas en anayaeducacion.es

2 En una fàbrica de ceràmica hi ha 2 615 pitxers, uns grans i altres petits. Si 1 720 són grans, quants són petits?

1r  El nombre de pitxers petits és menor que el total.

2n Dibuix un diagrama parts-tot. 1 720 2 615 ?

3r He de… sumar o restar? ?

4t La solució és menor que el total de pitxers. Resol-ho pas a pas en anayaeducacion.es

3 En Robert té una pàgina web amb 3 840 receptes de cuina. Si aquest mes ha publicat 162 receptes noves, quantes receptes hi ha ara a la web?

1r Si publica receptes, ara n’hi ha més que al principi. 2n Dibuix una recta numèrica. 3 840

162 ?

3r He de… sumar o restar? ?

4t Ara hi ha més receptes que al principi. Resol-ho pas a pas en anayaeducacion.es

4 Avui la nova biblioteca ha obert les portes. A les estanteries podem trobar 15 315 llibres. Si aquest dematí se n’han prestat 628, quants llibres hi ha ara?

1r  Si es presten llibres, ara hi ha menys que al principi. 2n Dibuix una recta numèrica. 15 315

628 ?

3r He de… sumar o restar? ?

4t Ara hi ha menys llibres que al principi. Resol-ho pas a pas en anayaeducacion.es

Resolc problemes de suma i resta

5 En un parc natural hi havia 23 740 flamencs. Alguns se n’han anat i ara n’hi queden 5 260. Quants de flamencs se n’han anat?

1r Pregunten per la diferència entre els que hi havia i els que hi queden.

Passos per resoldre un problema

1r  Comprenc el problema.

2n Organitz les dades.

3r Resolc el problema.

?

2n Dibuix una recta numèrica. 23 740 5 260

3r He de… sumar o restar? ?

4t La diferència és menor que el nombre de flamencs que hi havia al principi.

Resol-ho pas a pas en anayaeducacion.es

6 En una carrera de relleus es varen apuntar 270 persones. A última hora, s’hi varen inscriure algunes persones més i ara són 346 participants. Quantes persones s’hi varen apuntar a última hora?

1r Pregunten per la diferència entre els participants que hi ha ara i els que hi havia.

4t Comprov que la solució té sentit.

?

2n Dibuix una recta numèrica. 346 270

3r He de… sumar o restar? ?

4t La diferència és menor que el total de participants. Resol-ho pas a pas en anayaeducacion.es

7 L’estiu passat hi va haver un incendi a la pineda. Per repoblar-la s’han plantat 2 750 pins. Si ara hi ha uns 10 500 pins, quants n’hi havia al principi?

1r Si s’hi planten pins, al principi n’hi havia menys que ara.

2n Dibuix una recta numèrica. 10 500

2 750 ?

3r He de… sumar o restar? ?

4t Al principi hi havia menys pins que ara. Resol-ho pas a pas en anayaeducacion.es

8 Na Clara té doblers estalviats. S’ha comprat un parell de sabatilles per fer esport per 59 € . Si li queden 94 € , quants de doblers tenia al principi?

1r  Si gasta doblers, al principi en tenia més que ara.

2n Dibuix una recta numèrica. 94

59 ?

3r He de… sumar o restar? ?

4t Al principi na Clara tenia més doblers que ara. Resol-ho pas a pas en anayaeducacion.es

Pren nota!

Utilitza el que saps sobre la suma i la resta per inventar problemes.

Planteig preguntes intermèdies

En Carles té 11 anys més que na Núria. Na Beatriu té 13 anys menys que en Carles. Quants d’anys té na Beatriu?

Som na Núria. 25 anys ? ?

Per esbrinar-ho, primer necessitam saber: Quants d’anys té en Carles?

Calculam l’edat d’en Carles sabent que és 11 anys major que na Núria, que té 25 anys.

25 + 11 = 36

En Carles té 36 anys. Amb aquesta dada ja podem solucionar el problema, perquè sabem que na Beatriu té 13 anys menys que en Carles.

36 13 = 23

Na Beatriu té 23 anys.

La solució té sentit? Comprova que na Beatriu és menor que en Carles i que en Carles és major que na Núria.

1 Na Marta ha tardat 9 segons menys que en Joan a fer una prova d’atletisme. En Nico ha tardat 4 segons menys que na Marta. Quant de temps ha tardat en Nico?

2 La massa d’un plàtan és 70 g menys que la d’una taronja, i la d’una poma és 165 g més que la d’un plàtan. Quina és la massa d’una poma?

JOAN

Problemes exprés

1

Hi ha dos nombres que sumen 1 000. Quins nombres poden ser?

2

Si 25 + 75 són 100, quant és 100 − 75? I 100 − 25?

Càlcul mental

Resol 18 + 7.

18 + 7 = 18 + 10 – 3 = 25 3 10

3 5

Digues en veu alta el resultat de 10 − (2 + 4) en menys de 5 segons.

4 6

Si compres una barra de pa de 80 ct. i dones un euro, quants de cèntims et tornen?

1 € = 100 ct.

Mira com pens

Com funciona?

De les 5 000 entrades d’un concert, s’han venut 2 500. Quantes en falten per vendre En un parc hi ha uns 1 500 arbres. La tempesta n’ha arrabassat 200. Quants d'arbres queden drets?

A anayaeducacion.es pots veure com es fa.

Ara, fes-ho tu: 15 + 6 17 + 5 24 + 7 29 + 6 18 + 4 25 + 9 27 + 5 18 + 6 14 + 8 25 + 8

Perquè un cub sigui un dau, els punts de les seves cares oposades han de sumar 7. Quina d’aquestes imatges correspon al desenvolupament d’un dau?

Si necessites muntar els cubs per a comprovar-ho, descarrega els desenvolupaments d' anayaeducacion.es

Q uè he aprés?

1 Calcula aquestes sumes i comprova’n el resultat amb la calculadora.

a) 567 + 3 480 b) 62 034 + 8 827 c) 48 + 5 248 + 12 409 d) 53 729 + 903 + 7 722

7 Inventa un problema que es resolgui amb aquesta expressió, i calcula’n la solució. 60 (24 + 10)

8 En Jordi ha recorregut 1 704 km amb cotxe en tres dies. El primer dia va recórrer 796 km, i el segon, 671 km. Quants de quilòmetres va recórrer el tercer dia?

minuend

2 Tria les paraules relacionades amb la suma. commutativa associativa

menys subtrahend

més sumand

3 Resol i comprova’n la solució realitzant la prova de la resta.

a) 7 439 1 608 b) 3 814 872 c) 12 782 2 723 d) 37 002 985

4 Qui és l’intrús? Explica per què. diferència resta total

5 Completa la taula al quadern. minuend ? 13 606 subtrahend 489 ? diferència 11 204 5 992

6 Calcula el resultat d’aquestes expressions.

a) 35 (5 + 10) b) 50 25 + 30 c) 63 (18 5) d) 87 12 4

796km 671 km ?

9 En una localitat viuen 102 872 habitants. Si 18 305 són majors de 65 anys, quants no ho són? 102 872

18 305 ?

10 Una empresa d’automòbils ha fabricat 105 810 cotxes elèctrics. Si en venen 75 430, quants de cotxes falten per vendre? 105 810

75 430 ?

El semàfor. Al costat de cada activitat, pinta-ho així al quadern: si has sabut la resposta si has necessitat ajuda si no has sabut respondre-la

OBJECTIU EN ACCIÓ

Dissenya un cartell

Farem feina en equip!

• Formam equips de 4 persones per inventar operacions (sumes, restes o expressions combinades) i problemes.

• A cada equip s’estableixen dos responsables d’operacions i dos responsables de problemes.

• L’objectiu del joc és intercanviar les operacions i els problemes amb un altre equip perquè els resolguin, sense errors, en el menor temps possible.

• Per finalitzar, els responsables comproven els resultats i ajuden els altres si han tengut dificultats o errors.

Ens ho plantejam Utilitzam l’estratègia Considerar tots els factors per analitzar per què és important fer feina en equip.

a) Copia i completa l’organitzador al quadern.

b) Dissenya un cartell per mostrar a tots i a totes els beneficis de fer feina junts.

C om ho he aprés?

Copia les frases al quadern i pinta al costat de cada oració.

• Puc explicar amb les meves paraules com resolc un problema.

• Mantenc la calma quan no estam d’acord en l’equip.

• M’esforç per fer bé la tasca.

Què pots fer per millorar la teva feina en equip?

Per què és important fer feina en equip?

© GRUPO ANAYA, S.A., 2022 - C/ Valentín Beato, 21 - 28037 Madrid.

Reservats tots els drets. El contingut d’aquesta obra està protegit per la llei, que estableix penes de presó, multes o ambdues ensems, ultra les indemnitzacions corresponents per danys i perjudicis, per a aquells qui reproduïssin, plagiassin, distribuïssin o comunicassin públicament, en tot o en part, una obra literària, artística o científica, o la seva transformació, interpretació o execució artística fixada en qualsevol tipus de suport o comunicada per qualsevol mitjà sense autorització prèvia.