Muestra de Matemáticas 2 Bachillerato. Nueva etapa Bruño.

MATE MÁTI CAS

José María Arias Cabezas Ildefonso Maza Sáez

MATE MÁTI CAS

José María Arias Cabezas Ildefonso Maza Sáez

Integral definida

¿Para qué sirve la integral definida?

Hemos estudiado que la integral indefinida es la operación inversa a la derivada. Esto lo podemos ver en una aplicación muy interesante de la Física en el movimiento, si la velocidad es la derivada del espacio con respecto al tiempo, entonces el espacio es la integral de la velocidad con respecto al tiempo y, de igual modo, si la aceleración es la derivada de la velocidad con respecto al tiempo, entonces la velocidad es la integral de la aceleración con respeto al tiempo. Esto es de gran utilidad en todos los movimientos, como, por ejemplo, cuando enviamos una nave al espacio.

en tu cuaderno una imagen y un breve texto de una aplicación de las integrales definidas.

INTEGRAL DEFINIDA 1

EXPLORA

Halla, contando, el área de la 2.a figura del margen, la que tiene un signo + en su interior. Cada cuadradito es una unidad cuadrada.

El símbolo ∫es una s alargada y representa la palabra suma de las áreas de los rectángulos para hallar el área bajo la curva. En el resultado del cálculo de una integral por la regla de Barrow no se pone u 2 porque, como veremos en el apartado 3 de esta unidad, no solo tiene aplicación al cálculo de áreas y pueden ser m, m/s, m/s², hectolitros, personas...

132

INTEGRAL DEFINIDA DE RIEMANN

a

b f (x) dx = F(b) – F(a) siendo F(x) una primitiva de f (x)

a

b f (x) dx se lee «integral de f (x) entre a y b»; el número a es el límite inferior y b es el límite superior.

La interpretación gráfica de la regla de Barrow es que calcula el área comprendida entre el eje X y la función f (x) en el intervalo [a, b]; pero considerando que si el área está en la parte superior es positiva, y si está en la parte inferior, es negativa.

1.1 1.2

PROCEDIMIENTO PARA APLICAR LA REGLA DE BARROW

a) Dada la función f (x), se halla una primitiva F (x) sin constante.

b) Se calcula F (a) y F (b)

c) Se halla la diferencia F (b) – F (a)

EJERCICIOS RESUELTOS

1 Calcula aplicando la regla de Barrow: ∫2

x

5 (x – 1) dx

1 4 (x 2 – 6x + 4) dx a)

F

(1)

PROPIEDADES DE LA INTEGRAL DEFINIDA

Las propiedades más importantes de la integral definida son:

1. Si f (x) es continua en el intervalo [a, c] y a < b < c, entonces se verifica que:

2. Si f (x) y g (x) son funciones continuas en el intervalo [a, b] y además se cumple que para x ∈ [a, b], f (x) ≤ g (x) se verifica que:

Estos resultados se desprenden de la interpretación gráfica de la integral definida.

4 |x | dx 0 (–x) dx = F (0) – F (– 4) = 8 ∫0

b) 4 |x| dx = ∫– 4

las propiedades de la integral definida, se tiene: 4 x dx = G(4) – G(0) = 8 ∫– 4

– 8, 0 (– x) dx + ∫0

4 x dx = 8 + 8 = 16

DERIVADA DE UNA INTEGRAL

La derivada de una integral con límites variables F(x) =

Calcula la derivada de la función F (x) = ∫x 2 x 3 ln t dt F ′(x) = (ln x 3) 3x 2 – (ln x 2) 2x = 9x 2 ln x – 4x ln x = (9x 2 – 4x) ln x 1.3 1.4

∫ g (x) h(x) f (t) dt viene dada por: F ′(x) = f [h(x)] · h ′(x) – f [ g (x)] · g ′(x) EJERCICIO RESUELTO

2 Calcula ∫

CÁLCULO DE ÁREAS

EXPLORA

Halla por aproximación el área de las dos regiones, la amarilla y la verde, del dibujo del margen. Cada cuadradito es una unidad cuadrada.

ÁREA COMPRENDIDA ENTRE EL EJE X Y LA FUNCIÓN f ( x ) EN EL INTERVALO DE INTEGRACIÓN [ a, b ]

a) Se calculan las raíces de la ecuación f (x) = 0 y se toman aquellas que están en el intervalo de integración [a, b], por ejemplo, c y d

b) Se descompone el intervalo [a, b] en los intervalos necesarios: [a, c], [c, d ], [d, b]

c) Dada la función f (x), se halla la primitiva F(x) sin constante.

d) Se calculan F(a), F(c), F(d ) y F(b)

e) Se calcula cada una de las áreas aplicando la regla de Barrow y tomando el valor absoluto.

f) Se suman todas las áreas obtenidas.

EJERCICIO RESUELTO

5 Calcula el área del recinto limitado por el eje X y la función

en el intervalo de integración [1, 4]

que está en el intervalo de integración [1, 4]

b) Se descompone el intervalo de integración [1, 4] en los intervalos [1, 3] y [3, 4]

f) El área es A = A1 + A2 = 16 3 + 7 3 = 23 3 = 7,67 u2

Diferencia de funciones

Es lo mismo tomar

Si se toma como primera función la que está arriba, el valor de la regla de Barrow es positivo; si no, es negativo. Como se toma el valor absoluto, no importa el orden.

ÁREA COMPRENDIDA ENTRE DOS FUNCIONES

a) Se calculan las abscisas de los puntos de corte de las dos funciones resolviendo la ecuación f (x) = g(x)

b) Se halla la función diferencia de las dos funciones: f (x) – g(x)

c) Dada la función f (x) – g(x) se halla la primitiva F(x) sin constante.

d) Se calculan F(a), F(b), F(c), siendo a, b, c... las abscisas de los puntos de corte de las dos funciones f (x) con g (x)

e) Se calcula cada una de las áreas aplicando la regla de Barrow y tomando el valor absoluto.

EJERCICIO RESUELTO

6 Calcula el área comprendida entre las siguientes funciones:

a) Se calculan las abscisas de los puntos de corte resolviendo la ecuación:

ÁREA COMPRENDIDA ENTRE EL EJE X Y UNA CURVA f ( x )

Este problema es un caso particular del área comprendida entre dos curvas. En este caso, se calculan los puntos de corte de la curva f(x) con el eje X resolviendo la ecuación f(x) = 0, y se aplica la regla de Barrow a los intervalos que se obtienen con dos raíces consecutivas y se toma el valor absoluto. EJERCICIO

7 Calcula el área comprendida entre el eje X y la siguiente función:

a) Se calculan los puntos de corte de f (x) con el eje X

+ 3, el eje de abscisas y las rectas

7 Halla el área de la región plana limitada por la gráfica de f (x

8 Halla el área del recinto limitado por la recta y = 3 – 2x y la parábola y = 2x – x 2

9 Halla el área de la región plana limitada por la gráfica de y = x 3 – 4x y el eje X

10 Calcula el área de la región limitada por la curva y = x

y las rectas y = 0, x = 2, x = 3

11 Resuelve las siguientes cuestiones:

a) Dibuja el recinto limitado por las curvas: y = e x + 2 , y = e – x , y = 0, x = – 2, x = 0

b) Halla el área del recinto considerado en el apartado anterior.

12 Dada la función, definida en los números reales salvo en x = 0 f

calcula el área de la región plana limitada por la gráfica de f (x) y el semieje positivo X

EXPLORA

Escribe las fórmulas del espacio y de la velocidad de un movimiento rectilíneo uniformemente acelerado (m.r.u.a.).

APLICACIONES A LA FÍSICA

a) El espacio es la integral de la velocidad.

b) La velocidad es la integral de la aceleración.

EJERCICIOS RESUELTOS

8 Deduce las fórmulas del movimiento rectilíneo uniformemente acelerado (m.r.u.a.).

se caracteriza porque tiene aceleración constante, a

9 Se deja caer un objeto en el vacío. Suponiendo que la gravedad es de 9,8 m/s2, ¿cuál es la velocidad, v, y el espacio, e, recorrido al cabo de 4 s?

APLICACIONES AL MEDIOAMBIENTE

Se llama caudal a la velocidad que lleva el agua de un río. Por lo general, el caudal es en función de los meses del año; en invierno llevan más agua, y en verano, menos.

La cantidad de agua que pasa por un río durante un periodo de tiempo es igual al área encerrada por el eje X y la curva del caudal en el intervalo de tiempo correspondiente.

EJERCICIO RESUELTO

10 La función que mide el caudal de un río en función de los meses del año viene dada por:

f (x) = 3 + 2 cos πx 6

donde f (x) está dado en miles de hectolitros por mes y x en meses.

¿Qué cantidad de agua pasa por el río en un año? a)

APLICACIONES A LA ECONOMÍA

Si los ingresos, los costes y los beneficios de una empresa, en función de x unidades de producto fabricadas y vendidas, se llaman I(x), C(x) y B(x), se tiene:

• Ingreso marginal: es el ingreso adicional que se consigue al vender una unidad más de un producto, y es la derivada de los ingresos: i(x) = I ′(x)

• Coste marginal: es el coste adicional necesario para producir una unidad más de producto, y es la derivada de los costes: c(x) = C ′(x)

• Beneficio marginal: es el beneficio que se consigue al producir y vender una unidad más de un producto, y es la derivada del beneficio: b(x) = B ′(x)

Si se da una función de ingresos, costes o beneficios marginales, el área que hay bajo estas funciones es el ingreso, el coste o el beneficio.

EJERCICIO RESUELTO

11 Una fábrica produce chips para ordenadores. La función de ingreso marginal viene dada por:

donde x es el número de chips vendidos e i(x) viene dado en euros. Si vende 10 000 unidades, ¿cuáles son los ingresos obtenidos?

ELABORA

13 Un móvil lleva una velocidad en m/s, en función del tiempo, según la función: v(t) = 2t + 1

donde t se mide en segundos. Calcula el espacio que recorre el móvil entre los segundos 2 y 5 del movimiento.

14 Una fábrica produce objetos de decoración. La función de ingreso marginal viene dada por:

i (x) = 5 + 3 x + 2

donde x es el número de objetos vendidos e i (x) viene dado en euros.

¿Cuál es el incremento de los ingresos obtenidos cuando se pasa de vender 100 a vender 200 objetos?

15 La función que mide el caudal que sale de un depósito es:

f (x) = 10 – x

donde f (x) está dado en litros por segundo, y x, en segundos.

¿Qué cantidad de agua sale del depósito entre el segundo 4 y el segundo 8?

16 Una moto cuando arranca lleva un movimiento uniformemente acelerado, en el que la aceleración es de 2 m/s2

a) Calcula la velocidad al cabo de 30 segundos.

b) Calcula el espacio que habrá recorrido en esos 30 segundos.

EXPLORA

Escribe las fórmulas del volumen de un prisma, de una pirámide, de un cilindro, de un cono y de una esfera.

VOLUMEN DE UN CUERPO POR SECCIONES

Para hallar el volumen de un cuerpo por secciones de área A(x) perpendiculares al eje X en el intervalo [a, b], se aplica la fórmula:

EJERCICIO RESUELTO

12 Deduce la fórmula del volumen de una pirámide.

Se dibuja una pirámide que tenga el vértice en el origen de coordenadas y la altura sobre el eje X. El intervalo de integración es [0, H ], siendo H la altura de la pirámide.

La sección A(x) es paralela a la base B; por tanto, se tiene:

VOLUMEN DE UN CUERPO DE REVOLUCIÓN

Para hallar el volumen de un cuerpo de revolución, que se obtiene al girar la función f(x) sobre el eje X en el intervalo [a, b], se aplica la fórmula:

13 Calcula el volumen generado por la función f (x) = x 3 cuando gira alrededor del eje X en el intervalo [3, 9]

Cuando el trapecio gira alrededor del eje X genera un tronco de cono.

VOLUMEN GENERADO ENTRE DOS CURVAS

Para hallar el volumen del cuerpo de revolución que se obtiene al girar la superficie comprendida entre dos curvas sobre el eje X en el intervalo [a, b], se sigue el procedimiento:

a) Se calculan las abscisas de los puntos de corte de las dos funciones, resolviendo la ecuación f (x) = g (x)

b) En cada uno de los intervalos resultantes [a, b] se aplica la fórmula:

EJERCICIO RESUELTO

14 Calcula el volumen generado por la superficie comprendida entre las siguientes funciones cuando giran alrededor del eje X:

la superficie comprendida entre una hipérbola y una recta.

Se calculan las abscisas de los puntos de corte de

17 Deduce la fórmula del volumen del prisma.

19 Calcula el volumen generado por la superficie comprendida entre las siguientes funciones cuando giran alrededor del eje X:

20 Deduce la fórmula del volumen de un cono.

18 Calcula el volumen generado por la función:

cuando

alrededor del eje X en el intervalo [0, 4]

INTEGRAL DEFINIDA DE RIEMANN

Dada una función f (x) continua en [a, b] y positiva, se puede hacer una aproximación del área comprendida entre el eje X y la gráfica de la función en el intervalo [a, b] del siguiente modo:

a) Se divide el intervalo [a, b] en n partes iguales:

b) La función f (x) es continua en los intervalos [xi , xi + 1], ya que lo es en [a, b]. Por el teorema de Weierstrass, se puede garantizar que la función alcanza un valor máximo, Mi , y un valor mínimo, mi , en cada intervalo [xi, xi + 1]

c) Se dibujan los rectángulos inferiores de base xi + 1 – xi y de altura mi

d) Se dibujan los rectángulos superiores de base xi + 1 – xi y de altura Mi

2+83x 1+54)20

e) Se suma el área de los rectángulos inferiores y se obtiene una aproximación del área por defecto:

Se llaman sumas inferiores a las distintas aproximaciones del área por defecto que se pueden calcular del recinto según el número de intervalos que se tomen. Se representan por:

+ 1(xi + 1 – xi)

f ) Se suma el área de los rectángulos superiores y se obtiene una aproximación del área por exceso. Área por exceso = (x1 – x0)M

Se llaman sumas superiores a las distintas aproximaciones del área por exceso que se puede calcular del recinto según el número de intervalos que se tomen. Se representan por: Sn = n ∑ i = 0 Mi + 1(xi + 1 – xi)

Las sumas inferiores y superiores dependen de n, es decir, del número de intervalos que se tomen en [a, b], y se tiene entonces que:

g) Las sumas inferiores son una sucesión s1, s2, s3…, sn…, que corresponderán a las distintas divisiones que se hagan del intervalo [a, b]

h) Las sumas superiores son una sucesión S1, S2, S3…, Sn…, que corresponderán a las distintas divisiones que se hagan del intervalo [a, b]

Se puede asegurar que el área del recinto está comprendida entre estas dos aproximaciones:

sn = n ∑

= 0 mi + 1(xi + 1 – xi) ≤ Área del recinto ≤ Sn = n ∑

Si se hacen cada vez más intervalos en [a, b], es decir, que n tienda a infinito, entonces los valores Mi y mi de cada intervalo se aproximarán y tendremos que:

n → ∞ (Sn – sn) = 0 y entonces tendremos que el área será: Área = lím

Se define la integral definida en el intervalo [a, b] como el límite, cuando n tiende a infinito, de las sumas inferiores o superiores, y se representa por:

TEOREMA DEL VALOR MEDIO DEL CÁLCULO INTEGRAL

Si f (x) es una función continua en el intervalo [a, b], existe un punto c ∈ [a, b] tal que:

●●● Demostración

Como f (x) es continua en el intervalo cerrado [a, b], se puede garantizar, por el teorema de Weierstrass, que la función alcanza su valor máximo, M, y su valor mínimo, m, en dicho intervalo cerrado [a, b]

Por tanto, la integral:

estará comprendida entre las áreas de los rectángulos de base b – a y alturas m y M, respectivamente:

Dividiendo por b – a se tiene:

Por el teorema de los valores intermedios, existirá un

∈ (a, b) tal que:

De donde se deduce que:

PROFUNDIZACIÓN: DEMOSTRACIONES

●●● Interpretación gráfica

El área del recinto limitado por el eje X y la gráfica de f (x) en el intervalo cerrado [a, b] es igual al área del rectángulo de base b – a y altura f (c)

LA FUNCIÓN ÁREA

Sea f (x) una función continua en el intervalo cerrado [a, b]. Se llama función área o función integral a la función

F(x) = ∫ a

x f (t ) dt que está definida en el intervalo cerrado [a, b]

●●● Interpretación gráfica

Esta función calcula el área del recinto limitado por la función f (x) en todo intervalo cerrado [a, x], siendo x ∈ [a, b]

Si en la función F(x) aparece la x en el límite de integración, no se puede poner en el integrando. Por esta razón, aparece otra variable, que es la t y que recorre los valores desde a hasta x

TEOREMA FUNDAMENTAL DEL CÁLCULO INTEGRAL

Si f es una función continua en el intervalo cerrado [a, b] entonces la función

x f (t ) dt para todo x ∈ [a, b] es derivable y su derivada es F ′(x) = f (x)

●●● Demostración

F(x) = ∫ a

Por el teorema del valor medio del cálculo integral existe un

[

+ h] tal que:

,

Por tanto, se tiene:

Como c ∈ [x, x + h] y f (t ) es función continua, cuando h → 0, f (c) tiende a f (x)

De donde se deduce que:

VOLUMEN DE UN CUERPO DE REVOLUCIÓN

●●● Demostración

Un cuerpo de revolución es el que se obtiene al girar un recinto plano alrededor de una recta. Se considera una función continua y = f (x) en el intervalo [a, b]. La gráfica de esta función determina con las rectas x = a y x = b un recinto que se llama R

Si se hace girar el recinto R alrededor del eje X, se obtiene un cuerpo de revolución.

●●● Cálculo del volumen

Una aproximación del volumen del cuerpo de revolución que se obtiene al hacer girar sobre el eje X el recinto R engendrado por la función f (x) y las rectas x = a y x = b, se puede obtener siguiendo el procedimiento:

a) Se hace una partición del intervalo [a, b]:

a = x0 < x1 < x2 < < xi < xi + 1 < < xn = b

b) Tomamos un punto ci ∈ [xi, xi + 1] y se calcula f (ci)

c) Se construyen los cilindros con altura xi + 1 – xi, y radio de la base f (ci), cuyo volumen es:

Vi = π(xi + 1 – xi) f 2(ci)

d) Se suman todos los volúmenes así conseguidos y se tiene una aproximación del volumen total: Volumen

Si se hace que el número de intervalos tienda a infinito, se puede definir el volumen como el límite de una suma de volúmenes cuya altura tiende a cero:

Se define:

Regla de Barrow

15 Dada la función:

16 Calcula la integral definida:

La siguiente integral se calcula por partes (véase el ejemplo del apartado 2.5 de la unidad anterior) y el resultado es:

Derivada de una integral

17 Sea la función F : [0, +3) → R, definida por:

Halla la ecuación de la recta tangente a la gráfica de

(x) en el punto de abscisa x = 1

Área comprendida entre el eje X y la función f ( x ) en el intervalo [ a, b ]

18 Se considera la función:

Para x

[0, 5] calcula el área comprendida entre ella y el eje X

Área comprendida entre dos funciones

19 Sean:

g : ℝ → ℝ

las funciones definidas por:

f (x) = x 2 – 1

g(x) = 2x + 2

Calcula el área del recinto limitado por dichas gráficas.

a) Se calculan las abscisas de los puntos de corte resolviendo la ecuación:

b) Representamos las dos funciones y el área que encierran:

c) Hallamos la función diferencia:

d)

f

Área comprendida entre una función y el eje X

20 Sea: f : ℝ → ℝ

la función definida por:

f (x) = x|x – 2|

Calcula el área del recinto limitado por la gráfica de f (x) y el eje de abscisas.

a) Se calculan las abscisas de los puntos de corte de f (x) con el eje X: x|x – 2| ⇒ x = 0, x = 2

b) Representamos la función y el área: Y X

c) La función en el intervalo de integración [0, 2] está definida por: g (x) = – x 2 + 2x

d) G(x) =∫(– x 2 + 2x) dx = –1 3 x 3 + x 2

e) G(0) = 0, G(2) = 4 3

f ) Área = |G(2) – G(0)| = 4 3 – 0 = 4 3 = 1,33 u2

Cálculo de áreas con parámetros

21 Calcula el valor de a para que el área de la región plana encerrada entre la parábola: y = x 2 y la recta: y = a sea el doble del área de la región limitada por dicha parábola y la recta y = 1

Representamos la función, las rectas horizontales y el área:

1. Como la parábola es simétrica respecto del eje Y consideramos solo el área en la que x ≥ 0

2. Cálculo del área de la región positiva limitada por la parábola y la recta y = 1

a) Abscisas de los puntos de corte de las funciones y = x 2 , y = 1 x 2 = 1, x = – 1, x = 1

b) Función diferencia:

f (x) = 1 – x 2

c) F(x) = ∫(1 – x 2) dx = x –1 3 x 3

d) F(0) = 0

F(1) = 1 – 1 3 = 2 3

e) Área = |F(1) – F(0)| = 2 3 – 0 = 2 3 u 2

3. Cálculo del área de la región positiva limitada por la parábola y la recta y = a

a) Abscisas de los puntos de corte de las funciones y = x 2 , y = a x 2 = a, x = –√a , x = √a

b) Función diferencia:

g (x) = a – x 2

c) G(x) = ∫(a – x 2) dx = ax –1 3 x 3

d) G(0) = 0

G(√a ) = a √a –a √a 3 = 2a √a 3

e) Área = |G(√a ) – G(0)| = 2a √a 3 – 0 = 2a √a 3 u 2

Y como esta área tiene que ser el doble de la anterior:

E L J B S E P R O C R I M C S I A O E Y E L J B S E P R O C R I M C S I A O E Y

CONTESTA EN TU CUADERNO

1 Dada la función:

calcula: ∫0

a) 7/2

b) 3/2

c) 5

d) 6

2 f (x) dx

2 Dada la función:

calcula: ∫1

x + 1 f (t) dt

a) 2ax 2 + bx

b) ax 2 + (2a + b)x

c) (2a + b)x – x 2

d) ax 3 + 2ax 2 + bx

f (t) = 2at + b

3 Calcula el área del recinto limitado por la función y = ln x, el eje X y las rectas x = 1, x = 2

a) 2,33 u2

b) 5,26 u2

c) 0,05 u2

d) 0,39 u2

4 Sean las funciones:

Obtén el área del recinto limitado por f y g entre x = 0,

x = 1

a) 1/4 u2

b) 2,5 u2

c) 0,15 u2

d) 1/2 u2

5 Calcula el área encerrada por las funciones:

f (x) = 1 + ln x, g (x) = 1/x

y las rectas x = 1, x = 2

a) 0,50 u2

b) 1/e u2

c) 0,69 u2

d) e u 2

6 Calcula el área encerrada por las funciones: f (x) = x 3 + x 2 + 1, g (x) = 2x + 1

a) 5 u2

b) 3 u2

c) 37/12 u2

d) 35/12 u2

7 Calcula el área encerrada por las funciones: f

a) 8 u2

b) 4 u2

c) 15 u2

d) 25/3 u2

8 Dada la función:

Calcula el área de la región acotada por su gráfica y el eje X

a) 10 u2

b) 9,83 u2

c) e 3 u 2

d) 16π/3 u2

9 Calcula el área encerrada por la función:

f

1

y los ejes X e Y

a) e 2 u 2

b) 23 u2

c) e/5 u2

d) 0,63 u2

10 Se considera, en el primer cuadrante, la región R del plano limitada por el eje X, el eje Y, la recta x = 2 y la curva:

y = 1 4 + x 2

Calcula el área de la región R. Halla el valor de c para que la recta x = c divida a la región R en dos partes, A (izquierda) y B (derecha), tales que el área de A sea el doble que la de B

a) 2 √3 3

b) 2 √3

c) 3 √2 3 d) 3 √2

Elabora actividades de las secciones

1 INTEGRAL DEFINIDA

21 Calcula ∫2

22 Calcula ∫1

5 x 2 + 1 dx

3 (x 2 – 2x – 4) dx

23 Sea f : ℝ → ℝ la función definida por f (x) = |x 2 – 1|

a) Esboza la gráfica de f

b) Calcula ∫0

2 f (x) dx

24 Calcula la derivada de F(x) = ∫2

25 Calcula ∫1

x 2 + 1 ln t dt

e x 2 ln x dx

3 A PLICACIONES DE LA INTEGRAL DEFINIDA

33 La recta de ecuación y = – 4x + 2 representa la trayectoria de un móvil A. Otro móvil B se desplaza según la trayectoria dada por la curva de ecuación y  =  g ( x ), donde g : ℝ → ℝ es la función definida por:

a) Halla el valor de c sabiendo que ambas trayectorias coinciden en el punto en el que la función g (x) tiene un máximo local.

b) ¿Coinciden ambas trayectorias en algún otro punto? En tal caso, dibuja la región limitada por ambas trayectorias y calcula su área.

34 La velocidad de un móvil que parte del origen viene dada, en m/s, por la gráfica siguiente:

X

6 f (x) dx

26 Considera la función f (x) definida para x ≠ – 2 por la relación: f (x) = 4x 2 + 3x – 9 x + 2 Calcula ∫2

2 C ÁLCULO DE ÁREAS

27 Halla el área de la región plana limitada por la gráfica de f (x) = x 3 – 4x, el eje de abscisas y las rectas x = – 1, x = 2

28 Halla el área del recinto limitado por las gráficas de las funciones: y = 2 – x 4 y = x 2

29 Dada la función f (x) = 4 – x 2, calcula el área encerrada entre la gráfica f (x) y el eje de abscisas.

30 Calcula el área de la región limitada por la gráfica de la función f (x) = – 4x 3 + 5, el eje de abscisas, la recta x = – 1 y la recta x = 1

31 Calcula el área de la región limitada por las curvas: y = x 2 2 , y = 1 x 2 + 1

32 Dada la función f (x) = x √5 – x 2, calcula el área encerrada entre la gráfica f (x) y el eje de abscisas.

a) Calcula la función espacio recorrido.

b) Dibuja la gráfica de la función espacio recorrido.

c) Prueba que el área bajo la curva que da la velocidad coincide con el espacio total recorrido.

35 Dos hermanos heredan una parcela que han de repartirse. La parcela es la región plana limitada por la curva y = √x – 1 y la recta y = 1 2 (x – 1)

Calcula el área de la parcela.

4 C ÁLCULO DE VOLÚMENES

36 Deduce la fórmula del volumen de un cilindro.

38 Calcula el volumen generado por la función: f (x) = x 2 + 1

cuando gira alrededor del eje X en el intervalo [2, 6]

37 Calcula el volumen generado por la función: f (x) = √3x cuando gira alrededor del eje X en el intervalo [0, 3]

39 Deduce la fórmula del volumen de una esfera.

Elabora actividades para reforzar

40 Calcula

41 Sea la función f (x) = 2x 3 + bx 2 + ax – 5

a) Halla los valores de a y b, de forma que f (x) tenga un máximo en x = 1 y un mínimo en x = 2

b) Halla el área de la región limitada por la gráfica f (x) y el eje X entre x = 0 y x = 3

42 Sea la función f (x) = 3x – x 3

Halla el área de la región limitada por el eje X y dicha función.

43 Considera las funciones f , g : ℝ → ℝ definidas por:

f (x) = 6 – x 2 , g(x) = |x|, x ∈ ℝ

a) Dibuja el recinto limitado por las gráficas f y g

b) Calcula el área del recinto descrito en el apartado anterior.

44 Sea f : ℝ → ℝ la función definida por:

f (x) = 5x + 10 si x ≤ – 1

x 2 – 2x + 2 si x > – 1

a) Esboza la gráfica de f (x)

b) Calcula el área de la región limitada por la gráfica f (x), el eje de abscisas y la recta x = 3

45 Halla el volumen de un cuerpo de revolución obtenido al hacer girar alrededor del eje X el recinto acotado por la gráfica de f (x) = 9 – x 2 y el eje X Y

y =9– x 2 X

46 Considera la función f : [0, 4] → ℝ definida por:

f (x) = 4x si 0 ≤ x ≤ 1 16 (x + 1)2 si 1 < x < 3

4 – x si 3 ≤ x ≤ 4

a) Esboza la gráfica f (x)

b) Halla el área del recinto limitado por la gráfica de f (x) y el eje de abscisas.

47 Calcula el valor de a, positivo, para que el área encerrada entre la curva y = ax – x 2 y el eje de abscisas sea 36. Representa la curva que se obtiene para dicho valor de a

48 Resuelve las siguientes cuestiones:

a) Dibuja la región limitada por la curva de ecuación y = x(3 – x) y la recta de ecuación y = 2x – 2

b) Halla el área de la región descrita en el apartado anterior.

49 Resuelve las siguientes cuestiones:

a) Esboza la gráfica de la función f : ℝ → ℝ dada por:

f (x) = 2x + 2 si x ≤ – 1 x 3 – 2 si x > – 1

b) Calcula el área del recinto limitado por la gráfica f (x), el eje X y las rectas de ecuaciones x + 2 = 0 y 2x – 1 = 0

50 Halla los valores de m para que el área de la región limitada por la parábola y 2 = x y la recta y = mx sea 1

51 Sea la función f (x) = x cos x. Calcula la integral de f entre x = 0 y el primer cero positivo que tiene la función.

Nota: se llaman ceros de una función a los valores para los que esta se anula.

52 Se tiene la función f (x) definida para todo número real no negativo y dada por:

53 Calcula el área de la región limitada por la curva y = ln x y las rectas y = 0, y = ln 3, x = 0

54 Halla el valor del parámetro a sabiendo que el área limitada por la gráfica de la parábola y = x 2 – ax y el eje X es 32 3

55 Dibuja la figura limitada por las curvas cuyas ecuaciones son: y = 2 – x 2 y = |x| y halla el área de la misma.

56 Si f es una función continua en [a, b], ¿puede ser la integral ∫a

b f (x) dx = 0? Razona la respuesta con un ejemplo.

57 Sea la función f (x) = ∫1

x 1 t dt, y sean a, b ∈ ℝ+. Demuestra que f (a · b) = f (a) · f (b)

58 Mediante argumentos geométricos, demuestra que si f (x) y g (x) son funciones positivas en el intervalo [a , b] y f (x) ≤ g (x) para todo x de dicho intervalo, entonces se cumple que: ∫a

b f (x) dx ≤∫a

b g (x) dx

59 Si f (x) es una función continua positiva en el intervalo [a, b], justifica, mediante argumentos geométricos, si la siguiente afirmación es cierta.

=

()fx x x x

10 1 1 1 si ≤≤ si > 2

3 f (x) dx Interpreta gráficamente el resultado.

Halla ∫0

61 Se considera la función real de variable real definida por:

f (x) = 1 x 2 + 3

a) Halla la ecuación cartesiana de la recta tangente en el punto de inflexión de abscisa positiva de la gráfica f (x)

b) Calcula el área del recinto plano acotado por la gráfica f (x), la recta anterior y el eje x = 0

62 Se considera la función real de variable real definida por:

f (x) = x x 2 + 1

Calcula el valor de a > 0 para el cual se verifica la siguiente igualdad:

= 1

b f (x) dx ≥ 0 Si es falsa, pon un contraejemplo.

a

60 Encuentra el área de la región determinada por la curva y = x 2 4 – x 2 , el eje X y las rectas x = 1 y x = – 1

Elabora problemas

63 Calcula el valor de a > 0 para que:

a 1 x + 1 dx = 3

0

64 Sea la función f (x) = sen x. Calcula a > 0 tal que el área encerrada por la gráfica f ( x ), el eje y = 0 y la recta x = a sea 1 2

65 Sea la función real de variable real definida por:

f (x) = (2 – x)3 si x ≤ 1

x 2 si x > 1

Determina el área encerrada por la gráfica f (x) y por las rectas y = 8, x = 0, x = 2

Se consideran las funciones:

f (x) = x 2 – 2x + 3

g(x) = ax 2 + b

a) Calcula a y b para que las gráficas f (x) y g (x) sean tangentes en el punto de abscisa x = 2

b) Para los mismos valores de a y b, halla el área limitada por las gráficas de las funciones y el eje vertical Y

67 Sean las funciones:

f (x) = x 2 + ax + b

g (x) = – x 2 + c

a) Determínense a, b y c sabiendo que las gráficas de ambas funciones se cortan en los puntos (– 2, – 3) y (1, 0)

b) Calcula el área de la región limitada por las gráficas f (x) y g (x)

68 Halla el área del recinto delimitado por la siguiente curva y = x 2  + 4x + 5 y la recta y = 5

69 Sea la función f (x) = – 2x si x ≤ 0 x – 1 si 0 < x ≤ 2 3x – 5 si x > 2

Halla el área de la región plana limitada por la gráfica de la función, el eje de abscisas y las rectas x = – 1 y x = 3

70 Sea la función f (x) = x 4 – 4x 3 + x 2 + 6x

Calcula el área determinada por la gráfica f (x), el eje horizontal y las rectas x = – 1 y x = 2

71 Calcula el valor de la integral ∫

72 Calcula el valor de la integral ∫

2 + 5) e– x dx

73 Se quiere dividir la región plana encerrada entre la parábola y = x 2 y la recta y = 1 en dos regiones de igual área mediante una recta y = a. Halla el valor de a

76 Sea f : ℝ → ℝ la función definida por: f (x) = – 2x 3 – 9x 2 – 12x

Determina los extremos relativos α y β de la función f (x) con α < β y calcula ∫α

β f (x) dx

77 Considera la función f : ℝ → ℝ definida por: f (x) = xe 2x

Determina el valor de la integral: ∫0

1/2 (1 + f (x)) dx

78 Sea f : ℝ → ℝ la función definida por:

f (x) = 1 1 – x si x < 0 1 – mx – x 2 si x ≥ 0

a) Determina m sabiendo que f (x) es derivable.

b) Calcula ∫– 1

1 f (x) dx

79 Resuelve las siguientes cuestiones:

a) Dibuja el recinto limitado por los semiejes positivos de coordenadas y las curvas:

y = x 2 + 1, y = 2 x e y = x – 1

b) Halla el área del recinto considerado en el apartado anterior.

80 Resuelve las siguientes cuestiones:

a) Dibuja el recinto limitado por la siguiente curva y = 9 – x 2 4 , la recta tangente a esta curva en el punto de abscisa x = 1 y el eje de abscisas.

b) Calcula el área del recinto considerado en el apartado anterior.

81 De la función f : ℝ → ℝ definida por: f (x) = ax 3 + bx 2 + cx + d se sabe que tiene un máximo relativo en x = 1, un punto de inflexión en (0, 0) y que: ∫0

1 f (x) dx = 5 4 Calcula a, b, c y d

82 La recta de ecuación 3x – y + 2 = 0 es tangente a la parábola de ecuación y = ax 2 + c en el punto P(1, 5)

2

Y X

74 Halla el área del recinto coloreado que aparece en la figura adjunta sabiendo que la parte curva tiene como ecuación y = 2x + 2 1 – x 2 03 –1 –1

75 Sabiendo que ln x es el logaritmo neperiano de x, considera la función f : (– 1, +∞) → ℝ definida por f (x) = a(x – 1) si – 1 < x ≤ 1

x ln x si x > 1

a) Determina el valor de a sabiendo que f (x) es derivable.

b) Calcula ∫0

2 f (x) dx

a) Calcula las constantes a y c de la ecuación de la parábola describiendo el procedimiento que sigas.

b) Dibuja la región plana limitada por el eje Y, la parábola y la recta tangente.

c) Calcula el área de la región descrita en el apartado anterior.

83 Calcula el área de la región coloreada en la figura y justifica el procedimiento empleado (ln x es el logaritmo neperiano de x).

84 Dibuja el recinto limitado por las curvas de ecuaciones y = sen x, y = cos x, x = 0, x = π/3

Calcula el área del recinto descrito en el apartado anterior.

85 La figura siguiente representa la gráfica de una función f : [0, 7] → ℝ

Sea F : [0, 7] → ℝ la función definida por: F(x) = ∫0

x f (t) dt

a) Calcula F(4) y F(7)

b) Dibuja la gráfica F(x) explicando cómo lo haces.

86 Halla la recta tangente a la curva de ecuación y = x 3 – 3x en el punto de abscisa x = – 1

Dibuja el recinto limitado por dicha recta tangente y la curva dada y calcula su área.

87 Calcula el área de la región limitada por las curvas y = e x , y = e –x y la recta x = 1

88 En la figura aparece una curva que representa una función polinómica de grado 2. Los puntos de intersección de la curva con el eje X son el A(1, 0) y el B(3, 0). Además, el área limitada por la curva y los dos ejes coordenados vale 4/3. Halla la expresión de dicha función.

89 Dibuja con la mayor exactitud posible las gráficas de las funciones f (x) = 3x 2 – 6x y g (x) = –x 2 + 6x – 8. Representa el recinto limitado por ambas funciones y obtén su área.

90 Calcula una primitiva de la función: f (x) = x ln (1 + x 2)

Determina el área encerrada por la gráfica de la función anterior, el eje X y la recta x = 1

91 Representa gráficamente el recinto plano limitado por la curva y = x 3 – x y su recta tangente en el punto de abscisa x = 1. Calcula su área.

92 Calcula ∫0

√3 x √1 + x 2 dx

93 Calcula el área determinada por la curva y = tg x, el eje X y la recta x = π 3

94 Sin hacer ningún cálculo, di cuál de las siguientes integrales es mayor: ∫0

1 x 2 sen 2 x dx ∫0

1 x sen 2 x dx

95 Calcula el área determinada por la curva y = ln x, el eje  X y la recta x = e

96 Calcula el área determinada por la curva y = 1 1 – x 2 , el eje X y las rectas x = –1 2 , x = 1 2

97 Encuentra el área del recinto determinado por las curvas: y = |x – 2| y = – x 2 + 4x – 2

98 Demuestra que 0 ≤∫0

π/2 sen x 1 + x 2 dx ≤ 1

99 Calcula el área del recinto determinado por la curva y = 1 1 + x 2 , las rectas x = 2, x = – 2 y el eje de abscisas.

100 Si f (x) y g (x) son dos funciones continuas positivas en el intervalo [a, b], justifica, mediante argumentos geométricos, si la siguiente afirmación es cierta.

∫a

b ( f (x) + g (x)) dx = ∫a

b f (x) dx + ∫a

b g (x) dx Si es falsa, pon un contraejemplo.

101 Determina el área comprendida entre las curvas y  =  x 2 , y = √x y la recta que pasa por los puntos A(2, 4) y B(4, 2)

102 Demuestra que si m es un número cualquiera mayor que 1, y k un número natural cualquiera mayor que uno, se cumple que:

m x k + 1 x k + 1 + 1 dx < m

n

103 Dada la función f (x) = x ln x si x > 0 0 si x = 0

calcula el área de la región limitada por la gráfica de la función y el eje X, desde x = 0 hasta x = b, siendo b la abscisa del mínimo de la función.

104 Calcula la integral definida:

π/2 x sen x dx

π/4

105 Resuelve las siguientes cuestiones:

a) Obtén el área de la superficie S, limitada por el eje X, la curva y = x 2, con 0 ≤ x ≤ 2, y la recta x = 2

b) Calcula el volumen generado por la superficie S al dar una vuelta completa alrededor del eje X

106 Al girar la elipse x 2 25 + y 2 9 = 1 alrededor del eje X, esta genera una superficie parecida a un huevo, que se llama elipsoide. Halla el volumen de dicho elipsoide.

Elabora problemas de más nivel

107 Calcula el valor de a > 0 para que:

3 1 x + a dx = 5

0

108 Sea la función f (x) = sen x

a) Calcula la ecuación de la tangente a la gráfica f (x) en el punto de abscisa x = π 4

b) Calcula el área de la superficie encerrada por la tangente anterior, la gráfica de la función f (x) y las rectas x = π 4 , x = 3π 4

109 Sea la función f (t) = 1 1 + et . Se define: g (x) =∫0

Calcula lím x → 0 g ′(x) x

x f (t) dt

110 Se consideran las curvas y = x 2 e y = a, donde a es un número real comprendido entre 0 y 1(0 < a < 1). Ambas curvas se cortan en el punto (x 0, y0) con abscisa positiva. Halla a sabiendo que el área encerrada entre ambas curvas desde x = 0 hasta x = x0 es igual a la encerrada entre ellas desde x = x0 hasta x = 1

111 Sea la función f (x) = – x – 2 si x < – 1

a – 2x 2 si – 1 ≤ x ≤ 1

b/x si x > 1

a) Determina los valores de a y b para que f (x) sea continua en toda la recta real.

b) Con los valores de a y b determinados en el apartado anterior, calcula el área del recinto limitado por la gráfica de f (x) y el eje de abscisas, en el intervalo [0, 2]

112 Resuelve las siguientes cuestiones:

a) Dibuja el recinto limitado por y = 1 2 + cos x, los ejes de coordenadas y la recta x = π

b) Calcula el área del recinto descrito en el apartado anterior.

113 Halla el volumen de un cuerpo de revolución obtenido al hacer girar alrededor del eje X el recinto acotado por la gráfica de f (x) = –sen x entre las abscisas x = 0 y x = 2π

115 Halla el volumen de un cuerpo de revolución obtenido al hacer girar alrededor del eje X el recinto acotado por la gráfica de f (x) = ln x entre las abscisas x = 1/e y x = e

114 Determina una constante positiva a sabiendo que la figura plana limitada por la parábola y = 3ax 2 + 2x, la recta y = 0 y la recta x = a tienen un área (a2 – 1)2

116 Considera la siguiente función f : ℝ → ℝ definida por f (x) = 2 + x – x 2. Calcula a, a < 2, de forma que

117 Calcula la siguiente integral definida:

¿Qué representa gráficamente?

Representa el área comprendida entre el eje X y la curva en el intervalo [0, 2]

118 Considera la siguiente función f : ℝ → ℝ definida en la forma f (x) = 1 + x |x|

Calcula ∫– 1

2 f (x) dx

119 De la gráfica de la función polinómica f : ℝ → ℝ dada por: f (x) = x 3 + ax 2 + bx + c se conocen los siguientes datos: que pasa por el origen de coordenadas y que en los puntos de abscisas 1 y – 3 tiene tangentes paralelas a la bisectriz del segundo y cuarto cuadrantes.

a) Calcula a, b y c

b) Dibuja el recinto limitado por la gráfica de la función f (x) y el eje de abscisas, y calcula su área.

120 Justifica gráficamente que si f (x) es una función positiva definida en el intervalo [a, b] y c ∈ [a,  b], entonces se cumple: ∫a

c f (x) dx +∫ c

b f (x) dx =∫a

b f (x) dx

121 Halla el área del recinto limitado por la curva y =  xe x, el eje X y la recta paralela al eje Y que pasa por el punto donde la curva tiene un mínimo relativo.

COMPETENCIA digital con

GeoGebra y CalcMe en Moodle

1. Ejercicio (Calificación: 2,5 puntos)

Dibuja el recinto correspondiente y calcula la siguiente integral definida: ∫2

Observa y justifica el signo del valor obtenido.

SOLUCIÓN:

6 (1 – x) dx

En GeoGebra elige el applet: Procedimiento para aplicar la regla de Barrow.

6 (1 – x) dx = – 12 El signo es negativo porque está debajo del eje X

2

2. Ejercicio (Calificación: 2,5 puntos)

Calcula el área comprendida entre las funciones: f (x) = 5 – x 2 , g (x) = x 2 – 4x – 1

SOLUCIÓN:

En GeoGebra elige el applet: Área comprendida entre dos funciones f y g

Área = 21,33 u 2

3. Problema (Calificación: 2,5 puntos)

Calcula el volumen generado por la superficie comprendida entre las siguientes funciones cuando giran alrededor del eje X: () ,( ) f x x gx x 6 2 4 – == +

SOLUCIÓN:

En GeoGebra elige el applet: Volumen de un cuerpo de revolución.

Volumen = 16,76 m 2

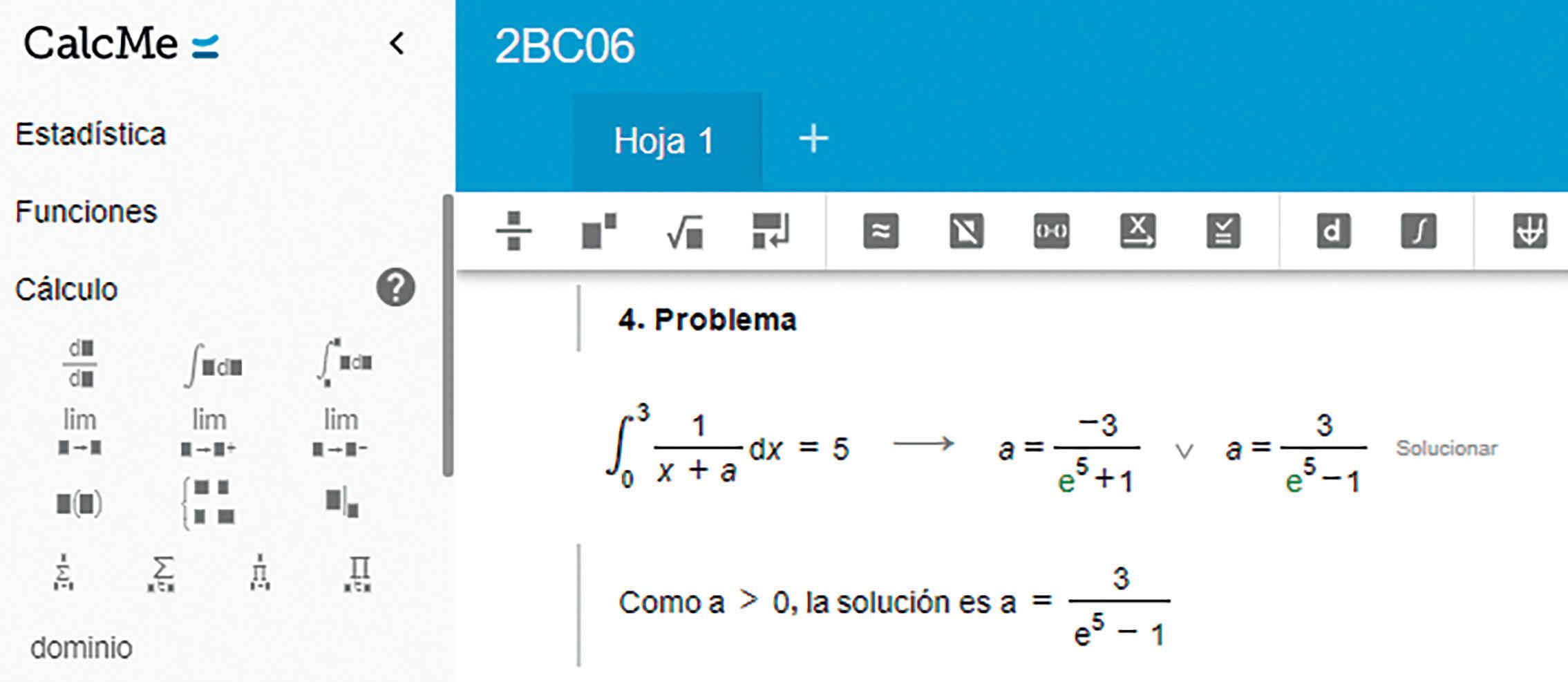
4. Problema (Calificación: 2,5 puntos)

Calcula el valor de a > 0 para que: ∫0

SOLUCIÓN:

a = 3/(e5 – 1)

3 1 x + a dx = 5

PONTE PRUEBA A

PROBLEMAS RESUELTOS

1 Calcula el siguiente límite:

2 Calcula el siguiente límite:

3 Dada la función:

a) Determina su dominio.

b) Determina sus intervalos de crecimiento y decrecimiento.

a) Como es una función irracional, existe cuando el radicando es mayor o igual que cero: 4

) = [– 2, 2]

b) Calculamos la 1.a derivada, cuando sea positiva es creciente, y cuando sea negativa, decreciente.

Las raíces del numerador son

4 Dada la función: f (x)= * ln x si x ∈ (0, e] ax + b si x ∈ (e, + ∞)

Halla los valores a y b para que la función sea derivable.

Las funciones y = ln (x), y = ax + b son continuas y derivables en todo su dominio de definición, así que el único problema lo tendremos en x = e

a) Para que sea derivable tiene que ser continua, por tanto, el valor de la función para x = e y los límites laterales en x = e tienen que ser iguales.

f (e) = ln e = 1

lím x → e –f (x) = lím

→ e –ln x = ln e = 1

lím

+ b = 1 (I)

b) Las derivadas laterales también tienen que ser iguales.

Sustituyendo el valor de a = 1

Solución: a = 1/e, b = 0

en la ecuación (I) obtenemos b = 0

PONTE PRUEBA A

5 Sean las funciones:

f (x) = ln (x + 2)

g (x) = 1 2 (x – 3)

a) Esboza el recinto que determinan las gráficas

f, g, y las rectas x = 1, x = 3

b) Determina el área del recinto anterior.

a) La función f (x) = ln (x + 2) es una función logarítmica cuyo dominio es (– 2, + ∞), para x = 2 tiene una asíntota vertical y corta al eje X en el punto A(– 1, 0)

La función g (x) = 1 2 (x – 3) es una recta de pendiente m = 1/2, la ordenada en el origen es – 3/2 y corta a los ejes en los puntos B (3, 0) y

– 3/2)

6 Dada la función:

Halla un punto de la curva en el que la recta tangente sea horizontal y analiza si dicho punto es un extremo relativo.

b)

Calculamos

Si la recta tangente es horizontal tiene de pendiente cero y por tanto la 1.a derivada tiene que valer cero.

7 Sea f la función definida, para x ≠ 0, por:

Determina las asíntotas de la gráfica de f

Asíntotas verticales: x = 0 Asíntotas horizontales: no tiene.

8

a) Calcula los máximos y los mínimos absolutos de

b) Estudia si f (x) es una función simétrica respecto al eje

a) Hallamos los máximos y los mínimos relativos:

A(– 1/2, 2), máximo relativo; B(1/2, 0), mínimo relativo.

La función f (x) tiene una asíntota horizontal y = 1

Por tanto, los máximos y mínimos relativos son también absolutos.

c)

PONTE

9 Se dispone de una chapa de acero que puede representarse por la región del plano determinada por la parábola:

= – x 2 + 4 y la recta y = 1

a) Representa gráficamente la chapa y calcula su área.

a)

cálculo del

una

calculan las abscisas de los puntos de corte resolviendo la ecuación:

10 Dada la función: f (x) = ax 3 + bx 2 + cx + d

determina los valores a, b, c y d para que se cumplan las siguientes condiciones:

1.a Que la recta tangente a la gráfica de f en el punto (0, 2) sea paralela a la recta y + 1 = 0

Área

Planteamiento: Área(x, y) = 2x( y – 1)

(x) = – 2x 3 + 6x A ′(x) = – 6x 2 + 6 ⇒ – 6x 2 + 6 = 0 ⇒ x 2 = 1 ⇒

La solución negativa no tiene sentido.

A ″(x) = – 12x ⇒ A ″(1) = – 12 < 0 ⇒ el área es máxima.

Altura del rectángulo – 1 + 4 – 1 = 2

El rectángulo mide de base 2 y de altura 2 unidades.

Si pasa por (0, 2) ⇒ f (0) = 2 ⇒ d = 2

Pendiente de la recta y + 1 = 0, m1 = 0 ⇒ f ′(0) = 0

f ′(x) = 3ax 2 + 2bx + c ⇒ f ′(0) = 0 ⇒ c = 0

Para x = 1 en x – y – 2 = 0 ⇒ y = – 1 ⇒ f (1) = – 1 ⇒ a + b + c + d = – 1

Pendiente de la recta x – y – 2 = 0, m2 = 1 ⇒ f ′(1) = 1 ⇒ 3a + 2b + c = 1

Como d = 2 y c = 0, resolviendo el sistema:

2.a Que la recta x – y – 2 = 0 sea tangente a la gráfica de f en el punto de abscisa x = 1

a + b + 2 = – 1

3a + 2b = 1

se obtiene:

a = 7, b = – 10

Los valores pedidos son:

Y X 158

11 Define la primitiva de una función. Sabiendo que:

F(x) = ex 2 es una primitiva de la función f (x):

a) Comprueba que f (x) es una función creciente en ℝ

b) Calcula el área determinada por la gráfica de f (x), el eje de abscisas y las rectas x = – 1, x = 1

Una primitiva de la función f (x) es una función F(x) tal que F ′(x) = f (x)

a) Para probar que f (x) es creciente en todo ℝ vamos a estudiar su derivada:

Si F(x) = ex 2 es una primitiva de f (x), entonces f (x) = F ′(x) = 2xe x 2 f

12 Sea: f (x) = 2 – x + ln(x), con x ∈ (0, +∞)

a) Determina los intervalos de crecimiento y decrecimiento, los extremos relativos, los intervalos de concavidad y convexidad y las asíntotas de f . Esboza la gráfica de f

b) Prueba que existe un punto c ∈ [1/e2, 1] tal que f (c) = 0

+ 2) > 0 y ex 2 > 0; por tanto, f (x) es creciente.

(4x

b) Hallamos los puntos de corte de f (x) con el eje X

2xe x 2 = 0 ⇒ x = 0

Hay que integrar en los intervalos [– 1, 0] y [0, 1]

Como la función es impar, es simétrica respecto del eje Y, solo hallaremos el área en el intervalo [0, 1]

F(x) = ex 2 ; F(0) = e0 = 1; F(1) = e1 = e

Área parcial = |e – 1| = e – 1

Área total: 2(e – 1) unidades cuadradas

a) Características de la curva:

Dom( f ) = ℝ+ = (0, +∞)

Máximos y mínimos relativos:

Crecimiento: f ′(2) = – 1 + 1/2 = – 1/2 < 0 (–), decreciente.

f ′(x) + –

x 0 1

Creciente (): (0, 1)

Decreciente (): (1, +∞)

Puntos de inflexión y curvatura:

f ″(x) ≠ 0 siempre, no tiene puntos de inflexión, f ″(1) = – 1 < 0 (–)

Convexa (∪): ∅

Cóncava (∩): (0, +∞)

Asíntotas: solo tiene una vertical, x = 0

b) Veamos si verifica las hipótesis del teorema de Bolzano: continua en el intervalo cerrado [1/e2, 1] y que tome valores de signo opuesto en los extremos.

f (x) es continua en [1/e2, 1] por ser suma y resta de funciones continuas.

f (1/e2) = – 1/e2

f (1) = 1

Como verifica las hipótesis del teorema de Bolzano, existe un punto

c ∈ [1/e2, 1] tal que f (c) = 0

PONTE PRUEBA A

13 Resuelve las cuestiones:

a) Calcula el siguiente límite: lím x →

1) x

b) Indica, razonadamente, el valor que debe tomar a para que la siguiente función sea continua:

f (x) = a si x = 0

ln (x 2 + 1) x si x ≠ 0

a) Aplicamos la regla de L’Hôpital:

Aplicamos L’Hôpital

b) Si x ≠ 0, f (x) es continua por ser cociente de funciones continuas; en el numerador hay una función logarítmica en la que x 2 + 1 > 0 siempre, lo que garantiza que es continua.

Si x = 0, para que sea continua se tiene que verificar:

f (0) = lím x → 0 f (x)

Por la definición de la función f , f (0) = a

En el apartado a) hemos hallado que lím x → 0 f (x) = 0

Por tanto, se tiene que verificar que a = 0

14 Resuelve las cuestiones:

a) Para cada valor de c > 0, calcula el área de la región comprendida entre la gráfica de la función: f

+ 1 el eje X y las rectas x = 0, x = 1

b) Halla el valor de c para el cual el área obtenida en el apartado a) es mínima.

a) Área: si c > 0, f (x) no tiene raíces en el intervalo [0, 1], por ser las potencias pares y los signos positivos.

b) Calculamos el mínimo derivando:

Para que el área sea mínima:

15 Se desea vallar un terreno rectangular usando 100 m de una tela metálica. Se ha decidido dejar una abertura de 20 m sin vallar en uno de los lados de la parcela para colocar una puerta. Calcula las dimensiones de la parcela rectangular de área máxima que puedan vallarse de esa manera. Calcula el valor de dicha área máxima.

a) Dibujo, datos e incógnita. y

Perímetro = 100 m

b) Función que hay que maximizar.

A(x, y) = xy

2x + 2y – 20 = 100 ⇒ y = 60 – x

c) Se escribe la función con una sola variable.

A(x) = x(60 – x) = 60x – x 2

d) Se calculan los máximos y mínimos derivando.

A ′(x) = 60 – 2x ⇒ 60 – 2x = 0 ⇒ x = 30 ⇒ y = 30

e) Se comprueba en la segunda derivada.

A ″(x) = – 2 < 0 ⇒ máximo relativo

f) La parcela medirá 30 m de largo y 30 m de ancho, será cuadrangular. Es un rectángulo porque todo cuadrado es un rectángulo.

g) Área máxima = 30 · 30 = 900 m2

16 Halla el volumen de un cuerpo de revolución obtenido al hacer girar alrededor del eje X el recinto acotado por la gráfica de

PROBLEMAS PROPUESTOS

1 Sea f : ℝ → ℝ la función definida por f (x) = e– 2x

a) Justifica que la recta de ecuación y = – 2ex es la recta tangente a la gráfica de f en el punto de abscisa x = – 1/2

b) Calcula el área del recinto limitado por la gráfica de f , el eje de ordenadas y la recta tangente del apartado anterior.

2 Una empresa ha decidido mejorar su seguridad instalando 9 alarmas. Un especialista señala que, dada la estructura de la empresa, solo puede optar a dos tipos, A o B; además, afirma que la seguridad de la empresa se puede expresar como la décima parte del producto entre el número de alarmas del tipo A instaladas y el cuadrado del número de alarmas instaladas del tipo B . Estudia cuántas alarmas de cada tipo deben instalar en la empresa para maximizar la seguridad.

3 Se considera la función:

f (x) = 1 x – 1 si x < 2 x 2 – 3 si x ≥ 2

a) Determina su dominio de definición, estudia su continuidad y halla las asíntotas.

b) Esboza una gráfica de la función.

c) Halla los puntos donde la recta tangente es paralela a la recta x + 4y = 0

4 Considera el recinto limitado por la curva y = x 2 y la recta y = 3: Y

6 Estudia la continuidad en ℝ de la función: f (x) = 1 – cos x x si x ≠ 0 0 si x = 0

7 Calcula la función f (x) cuya gráfica pasa por el punto (0, 1) (es decir, f (0) = 1) y que tiene como derivada la función:

f ′(x) = 2x x 2 + 1

8 Resuelve las siguientes cuestiones:

a) Halla los máximos y los mínimos relativos y los puntos de inflexión de la función:

b) Determina una función F(x) tal que su derivada sea f (x) y además F(0) = 4

9 Dada la función

se pide:

a) Dominio y cortes con el eje X

b) Asíntotas verticales (calculando los límites laterales).

c) Asíntotas horizontales y oblicuas.

y =3 (x, y)

X (– x, y)

De entre todos los rectángulos situados como el de la figura anterior, determina el que tiene área máxima.

5 Determina los valores de los parámetros a, b ∈ ℝ para que la función:

f (x) = (ax 2 + bx)e– x tenga un extremo relativo en el punto de abscisa x = 3 y además pase por el punto (1, – 1/e). Halla la ecuación de la recta tangente a f (x) en el punto de abscisa x = 0

d) Intervalos de crecimiento y decrecimiento. Extremos.

e) Representación gráfica aproximada.

10 En un terreno con forma de semicírculo de radio √50 metros, se dibuja un rectángulo que tiene dos vértices sobre la semicircunferencia del perímetro del terreno. Los otros dos vértices del rectángulo están sobre el segmento rectilíneo de dicho perímetro y distan x metros. Obtén razonadamente:

a) El área del rectángulo en función de x

b) El valor de x para el que el área del rectángulo es máxima.

© de esta edición: Grupo Editorial Bruño, S. L., 2023 Valentín Beato, 21 28037 Madrid