Volum 6A Elevbok BM (9788211039569)

ELEVBOK BM

Audun Rojahn Olafsen

Morten Johannessen

Åse Marie Bugten

Illustrert av Solveig Lid Ball

Copyright © 2021 by Vigmostad & Bjørke AS

All Rights Reserved

1. utgave / 1. opplag 2021

ISBN: 978-82-11-03956-9

Grafisk produksjon: John Grieg, Bergen

Grafisk design og ombrekking: Dimitri Kayiambakis / Concorde Design AS

Omslagsdesign: Dimitri Kayiambakis / Concorde Design AS

Omslagsillustrasjon: Solveig Lid Ball

Illustrasjoner og design: Solveig Lid Ball

Digital fargelegging: Liz Minton

Det faglitterære fond har gitt forfatterstøtte.

Spørsmål om denne boken kan rettes til: Fagbokforlaget

Kanalveien 51

5068 Bergen

Tlf.: 55 38 88 00

e-post: fagbokforlaget@fagbokforlaget.no www.fagbokforlaget.no

Materialet er vernet etter åndsverkloven. Uten uttrykkelig samtykke er eksemplarfremstilling bare tillatt når det er hjemlet i lov eller avtale med Kopinor.

VELKOMMEN TIL VOLUM 6A!

Hvordan lærer elevene matematikk?

Elevene lærer ved å løse problemer. Viktige forutsetninger for å oppnå læring er å gi elevene ro og tid til selvstendig tankearbeid. Ideer kan utveksles og drøftes gjennom samarbeid med andre elever.

Volum legger til rette for dette arbeidet i et motiverende læringsmiljø, der oppgaver og aktiviteter skal gi elevene lyst til å regne og glede ved mestring.

Tilpasset opplæring

Hver økt inneholder fire sider med varierte oppgaver av ulik vanskelighetsgrad.

Elevene skal arbeide med et utvalg oppgaver som gir passe utfordring, og kan velge oppgavetyper som de ønsker å bryne seg på.

Kjennetegn for VOLUM:

• Lærebok og oppgavebok i ett.

• Elevbok og lærerveiledning utgjør en fullstendig enhet.

• Fast ukentlig økt for undring og utforsking.

• Fast ukentlig økt med spill, lek eller aktiviteter.

• Oppgaver og gjøremål ivaretar kjerneelementene.

• Elevene lærer kjente problemløsingsstrategier.

• Den matematiske samtalen inngår som en naturlig del av matematikktimene.

• Tilrettelagt opplæring gjennom oppgaver som er tilpasset nivået til den enkelte elev.

Dette er VOLUM:

V ariasjon

O pplæring tilpasset den enkelte elev

L æringsmiljø og læringsmetoder

U ndring og utforsking

M otivasjon og mestring

LEKSJONENE

Hver hovedleksjon er bygd opp av én lilla økt med utforsking, to gule økter der nytt stoff presenteres, og én rød økt med aktiviteter. Hver tredje/fjerde leksjon er oppsummering med anvendelse av det elevene har lært. Elevene skal kunne velge blant oppgaver i hver økt, som gir utfordring på deres eget nivå. ØKT

I utforskende økter oppfordres elevene til å undre seg og undersøke ulike problemstillinger. De skal finne løsningsmetoder og forklare og begrunne løsningene sine.

Nytt lærestoff presenteres. De innledende oppgavene er grunnleggende og ofte konkrete med visuell støtte. Oppgavene øker i vanskelighetsgrad og er gjerne åpne, utforskende eller problemløsende.

Økta har samme oppbygging som økt 2.

De røde aktivitetssidene er basert på lærestoffet fra de to første øktene. Elevene samarbeider i praktiske oppgaver og spill.

Disse leksjonene inneholder oppsummering og anvendelse av emner fra de foregående leksjonene. Oppgavene øker i vanskelighetsgrad fra grunnleggende til mer sammensatte, utforskende eller problemløsende.

1

ØKT 2

ØKT 3

ØKT 4

ANVEND OG REPETER

INNHOLD

LEKSJON 1

LEKSJON 2

LEKSJON 3

LEKSJON 4

LEKSJON 5

LEKSJON 6

LEKSJON 7

LEKSJON 8

LEKSJON 9

LEKSJON 10

LEKSJON 11

LEKSJON 12

LEKSJON 13

LEKSJON 14

LEKSJON 15

LEKSJON 16

LEKSJON 17

LEKSJON 18

Kvadrat, rektangel og parallelle linjer - s.6

Vinkelstørrelser - s.16

Konstruksjon - s.26

Anvend og repeter leksjon 1, 2 og 3 - s.36

Vinkelsum i trekanter og firkanter - s.40

Trekanter - s.50

Firkanter - s.60

Anvend og repeter leksjon 5, 6 og 7 - s.70

Regneartene - s.74

Desimaltall - s.84

Desimaltall - addisjon og subtraksjon - s.94

Anvend og repeter leksjon 9, 10 og 11 - s.104

Desimaltall - multiplikasjon og divisjon - s.108

Brøk, desimaltall og prosent - s.118

Anvend og repeter leksjon 13 og 14 - s.128

Firkanter - areal og omkrets - s.132

Trekanter - areal og omkrets - s.142

Anvend og repeter leksjon 16 og 17 - s.152

LEKSJON 19

Trapes - s.156

LEKSJON 20

Mangekanter - s.166

LEKSJON 21

Anvend og repeter leksjon 19 og 20 - s.176

KVADRAT, REKTANGEL OG PARALLELLE LINJER

1.1 samtalebilde.

Kan dere finne eksempler på geometriske former i illustrasjonen?

Med geometriske former begrenser vi oss her til todimensjonale figurer som er avgrenset av linjer eller linjestykker.

1.2 Mangekanter.

a) Hvilke mangekanter finner dere i illustrasjonen?

b) Hvor skjuler disse formene seg: rektangel – kvadrat – parallellogram – trapes – drake – sekskant –likesidet trekant – likebeint trekant – rettvinklet trekant – sirkel.

c) Studer mangekantene under som er merket med bokstaver. Sammenlikn figurene og finn likheter og forskjeller. Se etter parallelle sider, like vinkler, lengder av sidekanter, og så videre.

DEFINISJON AV REKTANGEL

REkTAnGEl er en firkant der alle vinklene er 90 grader, (90°).

Rektangelet over er bestemt av punktene ABCD.

Sidekant AB kalles a. Lengden av a = 5 cm.

Sidekant BC, b = 3 cm.

Vinkelen i B kan vi skrive som ∠ ABC = ∠ B = 90°.

I rektangler og kvadrater er diagonalene like lange.

kVADRAT er en firkant der alle vinklene er 90 grader, (90°), og alle sidene er like lange. Kvadratet er bestemt av punktene EFGH.

Sidekantene s = 3 cm.

1.3 Hvor lange er sidekantene i firkantene over?

BC = ■ CD = ■ EF = ■ GH = ■ EH = ■

1.4 Hvilke av vinklene er like i firkantene over?

1.5 Hvilke figurer er

a) firkanter

b) kvadrater

c) rektangler

1.6 Del mangekantene med én strek, og lag

a) to like rektangler b) to kvadrater

c) et kvadrat og et rektangel d) to kvadrater

1.7 skriv koordinatene.

Tegn de to kvadratene ABCD og EFGH. Hvilke koordinater har D og H?

Den loddrette linja har verdi lik 4, x = 4. Den vannrette linja har verdi lik 2, y = 2. Skjæringspunktet mellom de to linjene har koordinatene (4, 2).

1.8 Tegn punkter i koordinatsystemet.

Sidelengden i hver rute er 1 cm.

a) Tegn punktene A (3, 2) og B (7, 2).

b) Hvor langt er linjestykket AB?

I rektangelet ABCD er lengden BC = 3 cm.

c) Tegn punktene C og D.

1.9 kvadrater.

Tegn kvadrater slik at hjørnene ligger på punkter.

Hvor mange kvadrater

klarer du å lage?

1.10 Rektangler.

Tegn rektangler slik at hjørnene ligger på punkter.

Hvor mange rektangler

klarer du å lage?

Drøft om arealene av rektanglene o og B er like store.

Figur 1

Figur 2

Figur 1

Figur 2

De rette linjene l og m har lik avstand fra hverandre. De er parallelle, og vi skriver l ∥ m. Linje m og l vil aldri krysse hverandre siden de er parallelle.

Er linje l og m parallelle?

Velg et punkt på linje l. Gå 1 cm til høyre og 3 cm loddrett ned for å treffe et nytt punkt på linja.

Dersom vi kan gjenta det samme på linje m, er linjene parallelle: l ∥ m.

1.12 Er linjene parallelle? Svar for eksempel f ∥ g eller f ∦ g.

Tegnet betyr ikke parallell.

1.13 Hvilke av linjene er parallelle?

1.14 Hvilke sider i firkantene er parallelle?

1.15 Parallelle sidekanter.

a) AB ∥ DE betyr at AB er parallell med DE. Hvilke andre sider er parallelle i sekskanten?

b) Hvilke sider er parallelle i denne sekskanten?

1.16 Foreslå et punkt D som gjør at linjestykkene AB og CD blir parallelle. Skriv koordinatene.

1.17 Bruk brikkene du har i konvolutten.

a) Lag begge pilene med brikkene. De illustrerer to hytter.

b) Lag en tegning av hyttene med markering av hvilke brikker som ble brukt.

c) Hva er likt og ulikt på hyttene?

d) Lag dine egne hytter. Tegn hyttene med markering av hvilke brikker du bruker.

1.18 Blir bordet kvadratisk?

Jeg måler sidene. Dersom alle sidene er like lange, får bordet riktig form.

Jeg måler vinklene. Dersom de er 90o, får bordet riktig form.

Jeg måler diagonalene. Hvis de er like lange, er bordet kvadratisk.

a) Er påstandene riktige?

b) Hvordan vil du sjekke om et bord har kvadratisk form?

snekkerens triks.

Dere trenger

• 8 m hyssing

• metermål

• saks

1.19 lag rektangler og kvadrater med hyssing.

a) Finn et område inne eller ute hvor dere kan lage rektangler og kvadrater med hyssing.

Hyssingen er 8 meter lang. Knyt den sammen. Lag et rektangel.

1) Hvordan kan dere være sikre på at det er et rektangel?

2) Hva er omkretsen og arealet av rektangelet?

b) Lag et annet rektangel der langsiden er ca. 2 meter lengre enn kortsiden. Hva er omkretsen og arealet av rektangelet?

c) Lag et kvadrat med hyssingen.

1) Hvordan vet dere at det er et kvadrat?

2) Hva er omkretsen og arealet av kvadratet?

d) Hvordan kontrollere om en vinkel er 90°?

1: Marker et punkt på sidekanten, 60 cm fra hjørnet.

2: Marker et punkt på den andre sidekanten, 80 cm fra hjørnet.

3: Avstanden mellom de to merkene skal være 100 cm.

1.20

Hva er felles egenskaper for tre av figurene, som den fjerde ikke har?

1.21 studer klasserommet ditt.

Hvor finner du

– rektangler

– kvadrater

– parallelle linjer

– linjer som ikke har en parallell linje

– mangekanter uten parallelle linjer

1.22 Finn ut!

– Er det mulig å tegne en trekant med to parallelle sider?

– Er det mulig å tegne en femkant med to og to parallelle sider?

– Er det mulig å tegne en sekskant der ingen sider er parallelle?

Hvilken skal ut?

LEKSJON 2 VINKELSTØRRELSER

2.1 Vurder vinkelstørrelsene.

a) Beskriv ulike vinkler i tegningen fra Fløien.

b) Tegn seks forskjellige vinkler, og kall dem vinkel A, B, C, D, E og F.

c) Lag denne tabellen. Gjett størrelsen på vinklene som du har tegnet.

d) Vent med å måle vinklene. Bytt bok med en annen elev, og gjett vinkelstørrelsene. Skriv dem inn i tabellen.

e) Bytt tilbake. Mål vinklene dine med vinkelmåleren, og skriv resultatet inn i tabellen.

f) Regn ut differansene mellom hva dere gjettet og de målte vinklene.

g) Samarbeid om å regne ut poeng og summere. Vurder resultatene.

2.2 Vinkler i sirkler.

Vinkelsummen i en sirkel er 360°. Hvor mange grader er vinklene?

Vinkel Jeg gjetter Nabo gjetter Målt vinkel Min differanse Mine poeng Nabo differanse Nabo poeng

En vinkel avgrenses av to vinkelbein. Vinkelbeina møtes i vinkelens toppunkt. Vinkelstørrelsen måles i grader, og skrives med gradtegnet °.

Vinkelen ABC er markert med et blått felt.

Vi kan skrive ∠ ABC eller ∠ B.

∠ ABC er 90° og kalles en rett

En vinkel som er større enn 0º og mindre enn 90°, er en spiss vinkel.

En vinkel som er større enn 90°, men mindre enn 180°, er en stump vinkel.

< spiss vinkel < 90°

2.3 Er vinkelen spiss, rett eller stump?

2.4 sett sammen begrepene med rett figur og gradtall.

2.5 Hvilke av vinklene er størst?

2.6 Toppunkt og vinkelbein.

Tegn en spiss, en rett og en stump vinkel der vinkelbeina er linjestykker på 6 cm. Merk toppunktet med A.

2.7 kassiopeia.

a) Hvilke vinkler er spisse, stumpe og rette i stjernebildet Kassiopeia?

b) Hva mangler i teksten under? ∠

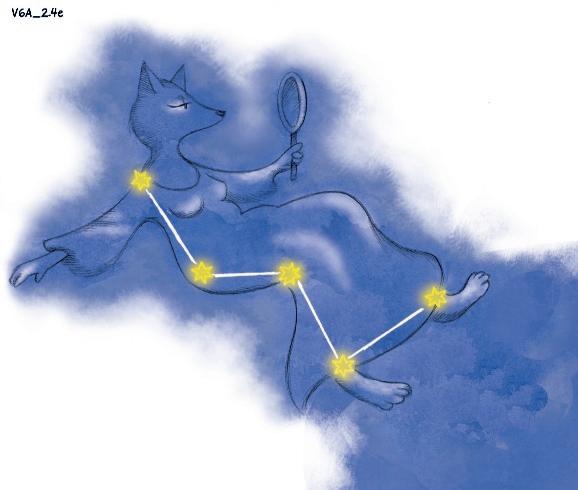
c) Hvilket vinkelbein er felles i disse vinklene?

C

Vinkelbein AC

Vinkelbein AB AB

Toppunkt A

2.8 Hvilket gradtall er riktig?

2.9 Bestem vinkelen mellom den store og den lille viseren på klokka. Er vinkelen mellom viserne spiss, stump eller rett når klokka er

a) 12.30 b) 18.15 c) 21.20

2.10 Vinduer.

På tur i gamlebyen la Ida merke til disse fire vindusformene.

I hvilke av vinduene finner du

a) rette vinkler

b) spisse vinkler

c) stumpe vinkler

d) flere størrelser på vinklene i samme vindu

MÅLING MED VINKELMÅLER

1. Sjekk om vinkelen er spiss eller stump.

2. Plasser vinkelmåleren med nullpunktet i vinkelens toppunkt og vinkelmålerens langside langs det ene vinkelbeinet.

3. Les av gradtallet.

Vinkel ABC er stump, og gradtallet er 110°.

∠ ABC er 110°.

Vinkel BAC er spiss, og gradtallet er 40°.

∠ BAC er 40°.

2.11 Hvor store er vinklene? lag en tabell som beskriver hver vinkel, antall grader og type vinkel.

Vinkel Grader Egenskap

AHB 20° Spiss

AHC …

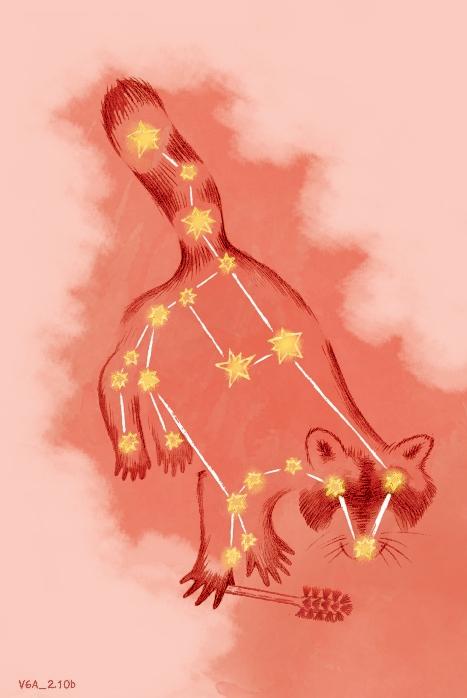
2.12 stjernebildet til jomfruen.

Hvor stor er ∠ ABC

og ∠ BCD?

∠ CDE?

∠ DGH?

∠ HGI?

∠ IGD?

2.13 Hvilken vinkel er …

2.14 Mål vinklene.

a) Hvor stor er ∠ ASB og ∠ DSC? b) Hvor stor er ∠ ASB og ∠ CSB?

c) Hva er summen av vinklene i a)?

d) Hva er summen av vinklene i b)?

e) Kan du angi begge vinklene i b) ved å måle kun én vinkel?

2.15 Mål vinklene.

a) Hvor stor er hver av vinklene i firkant ABCD?

b) Hva er summen av vinklene i firkant ABCD?

2.16 Mål vinklene.

a) Hvor store er vinklene i firkant ABCD?

b) Hva er summen av vinklene i firkant ABCD?

c) Hvor store er vinklene i firkant EFGH?

d) Hva er summen av vinklene i firkant EFGH?

AB

DC E

HG

2.17 Hva viser klokka når minuttviseren har beveget seg

a) 90° d) 30° b) 180° c) 60°

2.18 GH er parallell med EF, GH ∥ EF, i begge firkantene.

Hvor store er de to vinklene som mangler? Du kan kontrollere ved å måle etterpå.

2.19 Hvilket ord kan du lage av bokstavene i løsningen?

Hva er vinkelen? Bokstav

1. 35° mer enn en rett vinkel. 12° = l ■

2. Det dobbelte av en rett vinkel. 45° = R ■

3. Halvparten av en rett vinkel. 125° = H ■

4. En tidel av en stump vinkel på 120°. 30° = I ■

5. 1 3 av en rett vinkel. 180° = E ■

6. En kvart sirkel. 90° = G ■

2.20 Hvilken mangekant er dette?

Bruk brikkene i konvolutten med konkreter.

En rett vinkel og ingen parallelle sider.

Enrettvinkel.Allesidenehar uliklengde.

ingenIngenvinklererlike,og sidererparallelle.

Ingenavvinkleneerrette, menallesideneerlikelange.

To stumpe og to spisse vinkler. To og to sider er parallelle. Alle vinklene er rette, og to og to sider er like lange.

Alle vinklene er rette, og alle sidene er like lange.

Tosidererparallelle,og tosidererikkeparallelle.

ToIngensidererparallelle. sidererlikelange.

Stjernebildene Storebjørn og Lillebjørn var en gang en mor og hennes unge datter. De skrøt så mye av hvor pene de var, at gudene skapte dem om til bjørner. Til trøst fikk de plass på stjernehimmelen.

2.21 Tegn firkanten til høyre.

Dere trenger linjal og gradskive.

a) Hjørnene i firkanten er ABCD.

∠ DAB tilsvarer ∠ A. AB = 4 cm

b) Tegn en ny firkant med disse målene. La punktet A starte omtrent midt på et ark. AB er vannrett.

1. Side AB = 7,5 cm

2. ∠ DAB = 103°

3. Side AD = 3,5 cm

4. ∠ ABC = 99°

5. Side BC = 4 cm

6. Tegn linjestykket DC og sjekk om det er ca. 9 cm.

c) Tegningen fortsetter:

7. Mot nordvest: ∠ ADE = 128°

8. DE = 4 cm

9. ∠ DEF = 180°

10. EF = 3 cm

11. Vest: ∠ EFG = 140°

12. FG = 4 cm

Hvilket kjent stjernemønster er dette?

Svaret er en del av stjernebildet Storebjørn.

3.1 Tegn banemarkeringene.

Banenes rette linjer er tegnet inn på kopioriginalen, men buene mangler.

Bruk passer for å tegne sirkler, halvsirkler og kvartsirkler. Bruk kopioriginal 3.1.

3.2 Tegn figurer.

• Bruk en hyssing på ca. 30 cm, og knyt endene sammen.

• Fest hyssingen med to stifter som vist i figuren. La stiftene stå ca. 4 cm fra hverandre.

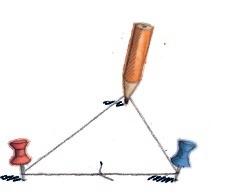
• Sett blyanten innenfor hyssingen, og tegn en runde mens hyssingen holdes stram.

• Tegn flere figurer med ulike avstander mellom stiftene.

• Hva kalles figurene som tegnes?

• Hvordan kan du lage en sirkel?

ca. 12 cm

ca. 4 cm

Dere trenger passer.

Du kan også lage sirkler og former med andre hjelpemidler.

3.3

a) Lag denne figuren med passer.

b) Lag flere like figurer, og fargelegg dem på ulike måter.

Eksempel på fargelegging.

konstruksjon.

3.4 konstruer figuren. Fargelegg speilsymmetriske mønstre.

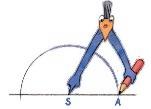
KONSTRUKSJON AV 60 ° VINKEL

En sirkel er 360° Lag en halvsirkel ved å halvere 360° :

360° 2 = 180°

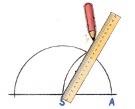
Konstruer en halvsirkel (180°) med sentrum i punktet S og radius lik SA.

Sett passerspissen i A og konstruer en bue med samme radius. SA = SB

Tegn linja som går igjennom punktene S og B.

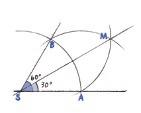
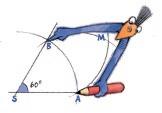
KONSTRUKSJON AV 30 °

VED Å HALVERE 60

∠ ASB = 60°

°

Konstruer en vinkel på 60°. Slå en bue med sentrum i toppunktet, S. Buen skal krysse begge vinkelbeina. Kall skjæringspunktene A og B.

Konstruer en bue med radius AB og sentrum i A.

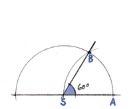
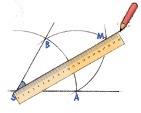
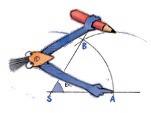
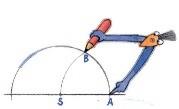
Konstruer en bue med radius AB og sentrum i B. De to buene krysser hverandre i M.

Tegn ei linje mellom S og M.

Vinkelen på 60° er halvert.

∠ ASM = 30°