Parkinson, Carlsson, Möbius

Parkinson, Carlsson, Möbius ¿te suenan? ciencia

Parkinson

1923 – 2018 (Inglaterra)

Carlsson

1923 – 2018 (Suecia)

Möbius

1790 – 1868 (Alemania)

De Parkinson (hijo de Parkin) no hace falta que demos muchas explicaciones. No sabemos que cara tenía Parkinson porque hay muchos retratos que han circulado como suyos siendo todos falsos. Carlsson (hijo de Carl) tal vez les suene a algunos; es el padre de la levodopa, por la cual recibió el premio Nobel. ¿Y qué tienen que ver con un tal Möbius? Es una especie de acertijo matemático; voy a dar unas pistas. levo - en español no dice nada, salvo a los que sepan algo de latín (laevus). Un cierto parecido con el inglés (left) y con el alemán (links): eso es, izquierda. ¿Alguien de izquierdas que se dopa? No exactamente, pero sí podemos decir que nuestro medicamento estrella es de izquierdas. Si fuera de derechas, se llamaría... de - dex - dextrodopa. Las moléculas pueden ser de izquierdas o de derechas como también, por ejemplo, las conchas marinas. Estas dos giran cada una hacia un lado. L-Glucosa y D-Glucosa

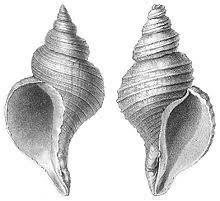
La dextrodopa no existe (o no nos sirve), pero sí existe y se consume la dextrosa, que es una glucosa de derechas, Dglucosa. Estos dos ejemplos, de conchas marinas y de moléculas, son en tres dimensiones, pero en el plano, en una superficie de dos dimensiones, una hoja de papel, también hay izquierda y derecha: podemos escribir una palabra “Möbius”, y podemos escribirla de tal manera que tengamos que reflejarla en el espejo para verla bien.

En realidad, una hoja de papel tiene tres dimensiones: largo, ancho y grosor, aunque el grosor sea de menos de un milímetro. Pero vamos a jugar a que es una auténtica superficie de dos dimensiones y no tiene grosor. Simplemente, usando un rotulador de esos que sueltan bastante tinta y pintan gordo, como el que he utilizado más arriba. Entonces, como la tinta se ve por el revés de la hoja, tenemos por un lado la palabra bien escrita y por el otro, en plan espejo. Nada que objetar, ¿verdad? Podemos distinguir claramente entre las palabras escritas bien y las escritas en plan espejo.

Pues bien, ¿y si un matemático te dijera que hay una hoja de papel en la que no se puede distinguir entre “normal” y “espejo”, es decir, entre las dos orientaciones? Al no poderse distinguir la orientación, esa hoja, o mejor dicho, esa superficie, se llama, en lenguaje matemático, superficie no orientable. Eso se le ocurrió a un tal Möbius. Es verdad que se trata de una hoja de papel un poco especial, pero tampoco demasiado; te la fabricas tú en un santiamén con unas tijeras y pegamento o celo o incluso una grapadora. Tiene una sola cara y un solo borde. Esta cinta o banda, como la llaman algunos, es la cinta de Möbius (o Moebius para quien no sepa poner la diéresis).. Brinda muchas sorpresas. Propongo al lector o lectora que corte la cinta a lo largo por la mitad, con unas tijeras, para obtener dos cintas más estrechas. Y que siga experimentando, si le apetece. O averiguando más cosas sobre este ente que ha inspirado a muchos artistas. Como habéis visto, este ente un poco misterioso existe. Es decir, existe en el mundo real (tiene incluso aplicaciones prácticas). Hay otro ente parecido que viene a ser como una cinta de Möbius en tres dimensiones. Si en la cinta coinciden el anverso y el reverso: se convierten en una misma cosa, en este otro objeto se confunde el dentro y el afuera. Sí, es muy misterioso. En el mundo real, existe y se llama botella de Klein, pero no es una buena representación porque intersecta consigo misma, pero sí se representa sin problemas en el mundo de las matemáticas. No por ello deja de ser fascinante. No digo más.

Anahí Seri Murciano

anahiseri@gmail.com