PREFACE 1.SPECIALRELATIVITYWITHAMISSION
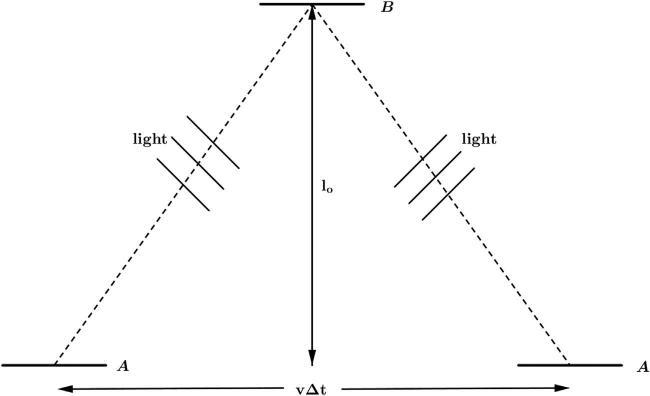
Thisbookisarevisionandextensionof “IntroductiontoRelativity.” That bookpresentsanapproachtorelativityinwhichthetheoryisdeveloped through “thoughtexperiments” thatillustratetheconceptsinsimple fashions.Forexample,toderivetimedilationandLorentzcontraction,a clockisconstructedoutofmirrorsandalightbeam,andwelearnhowit worksinitsrestframeandinaframeinwhichitmoveswithvelocity v Thisanalysisissimpleanddirectbecauselightbeamsandrodsare governedbythepostulatesofspecialrelativity:
1. Thelawsofphysicsarethesameinallinertialframesofreference.
2. Thereisacommon finitespeedlimitcinallinertialframes.
Throughoutthebooktherulesofnonrelativisticphysics(Newton’ s world)arecontrastedwithrelativisticphysics(Einstein’sworld).Itisthe secondpostulatethatdistinguishesNewtonianrulesfromEinstein’s.In Newton’sworld,velocitiesareunboundedbutinEinstein’sworld,the speedoflightcisanupperbound.Theexistenceofaspeedlimitcombined withPostulate1,thatallinertialframesareequivalent,producesrelativistic space time.
Thebookshowsthattimedilation,Lorentzcontraction,andthe relativityofsimultaneity,thatclockswhichareseparatedinspaceand synchronizedinoneframeare not synchronizedinaframeinrelative motion,areintimatelyrelated.
Thebookbuildsthesubjectfromthegroundup.ItusesMinkowski space timediagrams,whichshowthespatialandtemporalcoordinatesof twoframesinrelativemotion v.Timedilation,Lorenzcontraction,and therelativityofsimultaneitycanbeunderstoodthroughsimplepictures (cartoons,really),bothqualitativelyandquantitatively.Fromthisperspective, westudythetwinparadoxandseethatthereisnothingreallyparadoxical aboutit whenonetwinleavestheotherandtakesaroundtrip,shereturns youngerthanhersibling.Itisfuntoseehowitworksout!
Oncewehavemasteredkinematics themeasurementofspaceand timeintervals wemovetodynamics,thestudyofenergy,momentum, interactionsandequationsofmotion.InNewtonianmechanicsthereis momentumconservation,ontheonehand,andmassconservation,onthe
other.Inrelativity,however,oncewehave figuredouthowspatialand temporalmeasurementsarerelatedininertialframes,thepropertiesof momentum,energy,andmassaredetermined.Wepresentanotherof Einstein’sfamousthoughtexperimentsthatshowthatenergyandinertia (mass)aretwoaspectsofoneconcept,relativisticenergy,and find E ¼ mc 2 . Thepropertiesofrelativisticmomentumthenfollowfromthepropertiesof spatialandtemporalmeasurementsandwelearnthatmomentumand energyconservationmustgohandinhand.
SinceNewton’ssecondlaw,forceequalsmasstimeacceleration,isnot consistentwiththeexistenceofaspeedlimit,wemustmodifyitandinvent anewforcelawthatisrelativistic.Wedothisaided,again,bytheoriginal thoughtexperimentsofthemasters,EinsteinandMaxBorn.Inthiscase,a closelookataninelasticcollisioninseveralframesofreferenceleadsusto relativisticmomentaandenergy.Fromthereweobtaintherelativistic versionofNewton’ssecondlaw.Wethenconsiderhigh-energycollisions betweenparticlesandillustratehowenergycanbeconvertedintomassand howmasscanbeconvertedintoenergy.Theseillustrationsshowthat Newton’sconceptoftheintegrityofaparticleisviolatedinrelativity. Thereisnowayinrelativitytorestrictone’sattentiontothe “singleparticle sector.” Thefundamentalsofrelativitysimplydonotallowit.Thisfacthas consequencesbeyondthescopeofthisbookand findsitsfruitionin relativistic fieldtheoriesofparticlephysics.
Inthe firsteditionofthisbookweweresatisfiedwithintroductory workonrelativisticdynamics.Inthisextendedbookwehavegreater ambitions.Wewillstartwithelectrostatics,thatthereisastaticforcewhich fallsoffasthesquareofthedistancebetweencharges.Wewillusethisfact coupledwithspecialrelativitytodeduce:
1. Theexistenceofmagnetism,a fieldthatisgeneratedbyelectric currents,
2. TheLorentzforcelaw,whichstatesthatparticlesaredeflectedby electric fieldsandalsobymagnetic fieldsinwhichcasetheforceis proportionaltotheparticle’svelocity,
3. Maxwell’sequations:theAmpere Maxwellequationpredictinghow currentsproducemagnetic fieldsandFaraday’slaw,whichpredicts howchangingmagnetic fieldsproduceelectricforces(electromotive forces),
4. Thewaveequationforelectromagnetismandthedemonstrationthat lighttravelsatthespeedlimitcofspecialrelativityinallinertial referenceframes.
Thebookemphasizesthatmagnetismisaconsequenceofrelativity thatNewton’sworld,aworldwithoutaspeedlimit,hasnoplaceforthis phenomenon.Inaddition,magnetismproducesvelocity-dependentforces onchargedparticlesthatdonotsatisfyNewton’sthirdlaw,thataction equalsreaction.OnceweunderstandthatNewton’sthirdlawfails,wemust lookelsewhereforanunderstandingofmomentumconservationin dynamicalinteractions.
OncewehavederivedtheLorentzforcelaw,weareabletodeduce howelectricandmagnetic fieldstransformunderboosts.Welearnfrom carryingoutthisexercisethatelectricandmagnetic fieldsmixunder transformationsbetweenframesofreference.Theseeffectsareconsequencesofthefactthatspaceandtimemixundersuchtransformations. TheseresultsillustrateoneofEinstein’sfamousremarksthat “electricforces inoneframecanbeinterpretedasmagneticeffectsinanother.” The problemsetsinthispartofthebookconsidermoretraditionalwaysof obtainingthesameresults,consideringcapacitorsandsolenoidsinvarious referenceframes.
Theseargumentselucidatethenatureofmagnetism,buttheydonot quitegettotheheartofthematter.Electrostaticsstatesthatchargesarethe sourcesofelectric fields.ThisisstatedquantitativelythroughGauss’ law. Ontheotherhand,welearnthatelectriccurrentsarethesourcesof magnetic fields.Sinceelectriccurrentsareproducedfromchargedensities byLorentztransformations(“boosts”),itmustbethattheequationthat predictsthatmagnetic fieldsareproducedfromelectriccurrentscanbe obtainedbyboostingGauss’ law.Wecarryoutthisexerciseanddiscover Ampere Maxwell’sequation.ThisisAmpere’slawcorrectedfornonstationarycurrentsbyMaxwell’sdisplacementcurrent.Similarly,weobtain Faraday’slawfromthedivergence-freecharacterofmagnetic fields.
Thisbookshowsthestudentthatascientistcan build thetheoryof electromagnetismfromelectrostaticsandspecialrelativity.Unlikeconventionaltextbooks,welearntomanipulatedifferentialequationsand accomplishourgoalsingeneralfundamentaltermsratherthanworking throughmyriadillustrationsofdevices.OncewehaveMaxwell’sequations, itisaneasytasktoshowthatrelativityelevateselectromagnetic fieldsto independentdynamicaldegreesoffreedom,whichpropagateatthespeed limitc.
Inthisjourneywe finditnecessarytoforsakeNewtonianideasand replacethemwithmodernconcepts:forcesleadto fields,whichbecome dynamicalobjectsthatpropagatenonlocalconservationlawssuchas
Newton’slawofaction reactionarethrownoverandarereplacedbylocal conservationlaws,whicharecompatiblewiththerelativisticnotionofcausality andthe finitenessofthespeedofpropagationofinformation.Inaddition,the integrityofparticlenumber,socrucialinNewton’sworld,isreplacedby particlecreationanddestruction, whichisforceduponusbytheenergy mass relationship,causalityandlocalityofrelativisticinteractionsofrelativity,etc.
Thusourintroductiontoelectrodynamicsisanalternativetothe traditionalapproachpopularizedbythetextbooksofJ.D.Jackson [1] and hismanyfollowers.Ourbookstartswithpostulates1and2ofspecial relativityandtheprimitivenotionthatchargesarethelocalsourcesof electric fields,anddevelopsthefundamentalsofelectromagnetism:unified magneticandelectric fields,theLorentzforcelaw,Maxwell’sequations, andthewaveequation.Aftermasteringthesefundamentals,thestudentis inapositiontodomorecomplexapplicationsofrelativityandelectrodynamics.Theapproachinthisbookissimpleandstraightforward.The derivationofMaxwell’sequations,havingcomefromsuchhumble beginningsinChapter1,shouldbeanepiphanyforthestudent.
2.GENERALRELATIVITY
Ourlasttopicinthisbookisthegeneraltheoryofrelativity,wherewe consideracceleratedreferenceframesinEinstein’sworld.Thekeyinsight hereisEinstein’sversionoftheequivalenceprinciple:thereisnolocal, physicalmeanstodistinguishauniformgravitational fieldfromanacceleratedreferenceframe.
Thisprinciplehasmanyinterestingformsandapplications.Supposeyou areonthesurfaceofEarthandwanttounderstandtheinfluenceofthe gravitational fieldonyourmeasuringsticksandclockscomparedtothoseof yourassistantwhoisatagreaterheightintheEmpireStateBuilding. Einsteinsuggeststhattheassistantjumpoutthewindow,becauseinafreely fallingframealleffectsofgravityareeliminatedandwehaveaperfectly inertialenvironmentwherespecialrelativityholdstoarbitraryprecision! Duringhisdescent,yourassistantcanmakemeasurementsofclocksand metersticks fixedatvariousheightsalongthebuildingandmeasurehow theiroperationdependsontheirgravitationalpotential.Wepursueideas likethisoneinthebooktoderivethegravitationalredshift,thefactthat clocksclosetostarsrunmoreslowlythanthosefarawayfromstars;the resolutionofthetwinparadoxasaprobleminacceleratingreference frames;andthebendingoflightbygravitational fields.
Preface xv
Afascinatingaspectoftheequivalenceprincipleisitsuniversality,which becomesparticularlyclearwhenwecalculatethebendingoflightasaray glancesbytheSun.Whydoesthelightrayfeelthepresenceofthemassof theSun?Theequivalenceprinciplestatesthatanenvironmentwitha uniformgravitational fieldisequivalenttoanenvironmentinanacceleratingreferenceframe explicitaccelerationclearlyaffectsthetrajectoryof lightandanyotherphysicalphenomena.Sogravitybecomesaproblemin acceleratedreferenceframes,whichisjustaproblemincoordinatetransformations,whichisanaspectofgeometry!Weshowthatthisproblemin geometrymustbedoneinthecontextoffour-dimensionalspace time, ourworldofMinkowskidiagrams.Einstein’stheoryofgravitybrought moderngeometry,thestudyofcurvedspaces,intophysicsforever.
Aslongasweconcentrateonuniformgravitational fieldsofordinary strength,weareabletousetheequivalenceprincipletomakereliable,accurate predictions.Theequivalenceprinciplereducesgravitytoanapparentforce, muchlikethecentrifugalorCoriolisforcesthatwefeelwhenridingona carousel.Infact,weuserelativisticturntablesandrotatingreferenceframes asanaidetostudyingandderivingrelativisticgravitationaleffects.
However,wearealsointerestedinstrongnon-uniformgravity,situationswheretheequivalenceprincipleisnotsufficienttodescribethe physics.Wediscusstidalforces,whichareattheheartofthedynamicsof generalrelativity.ThisisdonebothwithinNewton’sworldandgeneral relativitywherewelearnthattidalforcesandthecurvatureofspace time aretwosidesofthesamecoin.Sincecurvatureistheessenceofthedynamicsofgeneralrelativity,wereviewclassicaldifferentialgeometryand learnaboutthecurvatureofcurvesandthecurvatureoftwo-dimensional surfaces.Gaussiancurvatureisintroducedandthefundamentaltheorems ofclassicaldifferentialgeometryarederivedanddiscussed.
Thesedevelopmentsleadtoadiscussionofmoderngeneralrelativity. ThecriticalsymmetriesofspecialrelativitywereLorentztransformations (boosts)andingeneralrelativitythesesymmetriesareelevatedtolocal symmetries,generalcoordinatetransformations.TheRiemanntensoris introducedasameasureofthelocal,intrinsiccurvatureofspace time. Theseideasleadtothecentralideaofgeneralrelativity,thatlocalenergy momentumproducelocalspace timecurvature.Thisideaisexpressed quantitativelythroughEinstein’ s fieldequation,whichisintroducedasa grandextensionofNewton’sequationforthegravitationalpotential.We solvetheseequationsinthecaseofastatic,symmetricmassdistribution, whichgivesrisetotheSchwarzschildmetric.Thismetriccontainsablack
hole,whichwestudyinconsiderabledetail.We findthatthereisan “event horizon,” theSchwarzschildradius,insideofwhichthereisnoescape.We alsoconsidertheproductionandpropagationofgravitationalwaves.We seethatgravitywavesaredescribedby fluctuationsofthespace time metricthattravelatthespeedlimitofspecialrelativityandaregeneratedby oscillatingquadrupolemomentsofmassdistributions.Wereviewthe “AdvancedLIGO” experimentthatdiscoveredgravitywavesgenerated fromtheviolentmergeroftwoblackholesoveronebillionlight-years awayfromearth.
Weendourdiscussionofgeneralrelativitybycomparingitsfundamentalswithmoderntheoriesofelementaryparticles,whicharealsobased onlocalsymmetrygroups,aswellasalookatcurrentpuzzlesandunsolved problems,suchasdarkenergy.
3.BACKGROUNDREADINGANDRECOMMENDATIONSFOR FUTUREREADING
Althoughtheperspectiveofthisbookisitsown,itowesmuchtoother presentations.Theinfl uenceofA.P.French’s1968book [2] Special Relativity isconsiderable,andreferencesthroughoutthetextindicate wheremydiscussionsfollowhis.Tomyknowledge,thisisthe fi nest textbookwrittenonthesubjectbecauseitbalancestheoryandexperiment perfectly.Thereaderwill fi nddiscussionsoftheMichelson Morley experimentandearlytestsofrelativitythere.French’sdiscussionsof energyandmomentumarere fl ectedinmylaterchapters,andhisproblem setsareasigni fi cantin fl uenceonthoseincludedhere.Thepresentbook goesbeyondFrench’swhenwederivetheLorentztransformationlawsfor theelectricandmagnetic fi eldandthendeduceallofMaxwell’sequations byboostingGauss’ law.WeincludeashortenedversionofFrench’ s demonstrationthatthemagneticattractionbetweenparallelcurrent carryingwiresisduetoaminusculeLorentzcontractioneffect.Weshow thattheforcebetweensuchwiresisstrongenoughtobendtypicalcopper wiresbecausethehugenumberofelectronsinthewiremultipliesthetiny Lorentzcontractiontheyexperienceduetotheirtinyvelocitiesrelativeto thewire’sstationaryCuþ ions.Thisobservationexplainswhymagnetic forcescanbesubstantialunderordinarylabconditionseventhough magnetismisapurerelativisticeffect.Thesenumbersunderliehowrelativitywasdiscoveredattheturnofthe20thcentury,longbeforethe
moderneraofparticleacceleratorswhereparticlevelocitiesclosetothe speedlimitwerepossible.
Anotherinfluentialbookis TheClassicalTheoryofFields byL.D.Landau andE.M.Lifshitz [3].Unlikemostbooksonelectromagnetism,which followthehistoricaldevelopmentofthe fieldandintroducerelativitytoward theend,LandauandLifshitzstartwithrelativityandbuildthetheoryof relativisticparticlesandlight.Theemphasisisonfundamentalprinciples ratherthanapplications.Unfortunately,thebookisaimedatadvanced studentsandmosteditionsare flushwithtypographicalerrors.Nonetheless, thebookisveryinspiringandhasuniqueinsightsintothesubject.Severalof themorechallengingproblemsinchapters7 10inthisvolumewere inspiredbyLandauandLifshitz.Thisbookalsointroducesgeneralrelativity andincludesderivationsoftheSchwarzschildmetric,gravitationalwaves,the bendingoflightraysinagravitational field,etc.Thediscussionsarebriefand powerful,theessenceofLandau’sbrilliantapproachtophysics.
TheexpositionbyN.D.Mermin [4] influencedseveraldiscussionsof theparadoxesofspecialrelativity.Thisbookisalsorecommendedtothe studentbecauseitshowsacondensedmatterphysicistlearningthesubject and findingacomfortlevelinitthroughthought-provokinganalysesthat avoidlengthyalgebraicdevelopments.ThehugebookbyJ.A.Wheeler andE.F.Taylor [5] titled SpacetimePhysics inspiredseveralofourdiscussions andproblemsets.Thisbook,aworkthatonlytheunique,creativesoulof JohnArchibaldWheelercouldproduce,isrecommendedforitsleisurely, interactive,thought-provokingcharacter.Finally,thebooksbyW.Rindler [6,7],apioneerinmoderngeneralrelativity,arealsorecommended.His book EssentialRelativity [7] isasolidintroductiontogeneralrelativity rootedintheeraofEinsteinandthepioneers.Afterthestudenthas masteredelectricityandmagnetismandLagrangianmechanics,heorshe couldtackle TheClassicalTheoryofFields byL.D.LandauandE.M.Lifshitz [3] and EssentialRelativity [7].
Thefutureofresearchinrelativityand fieldtheoryisbright.Hopefully thisbookwillsparksomeinterestinitsfuturepractitioners.
“Timetravelsindiversepaceswithdiversepersons,” Rosalind,fromAct3, Scene2, “AsYouLikeIt” byWilliamShakespeare.
“Mathematicsallowsyoutoexceedyourimagination,” LevLandau, Moscow,1952.
“Magic!”,student,anonymous,2018.
REFERENCES
[1]J.D.Jackson,ClassicalElectrodynamics,JohnWiley&Sons,NewYork,1962.
[2]A.P.French,SpecialRelativity,W.W.Norton,NewYork,1968.
[3]L.D.Landau,E.M.Lifshitz,TheClassicalTheoryofFields,PergamonPress,Oxford, 1962.
[4]N.D.Mermin,SpaceTimeinSpecialRelativity,WavelandPress,ProspectHeights,IL, 1968.
[5]E.F.Taylor,J.A.Wheeler,SpacetimePhysics,W.H.Freeman,NewYork,1992.
[6]W.Rindler,IntroductiontoSpecialRelativity,OxfordUniversityPress,Oxford,1991.
[7]W.Rindler,EssentialRelativity,Springer-Verlag,Berlin,1971.
Contents
1.1 Newton’sWorld:LawsandMeasurements1 1.2 Newton’sWorld:NoPlaceforMagnetism 8
1.1NEWTON’SWORLD:LAWSANDMEASUREMENTS
WhenyousetupaprobleminNewtonianmechanics,youchoosea referenceframe.Thismeansthatyousetupathree-dimensionalcoordinate system,forexample,soanypoint r canbelabeledwithan x measurement oflength,a y measurement,anda z measurement, r ¼ (x,y,z).Inaddition, youplaceclocksatconvenientpointsinthecoordinatesystemsoyoucan makemeasurementsandrecordwhenandwheretheyoccurred.
Newtonimaginedcarryingoutexperimentsonamasspoint m inthis coordinatesystem.Heimaginedthatthecoordinatesystemwasfarfrom anyexternalinfluences,andunderthoseconditionsheclaimed,onthebasis oftheexperimentsofGalileoandothers,thatthemasspointwouldmove inastraightlineataconstantvelocity.Newtonlabeledsuchaframeof reference “inertial.” ThisideaiscodifiedinNewton’ s firstlaw: Law1.Abodyinaninertialreferenceframeremainsatrestorinuniformmotionunlessactedonbyaforce.
Newtonandothersrealizedthattheremustbeawideclassofinertial frames.Ifwediscoveredoneframethatwasinertial,thenNewton arguedthatotherinertialreferenceframescouldbegeneratedby
1. Translation movethecoordinatesystemtoaneworiginandusethat system.
2. Rotation rotatethecoordinatesystemaboutsomeaxistoa fixed,new orientation.
3. Boosts consideraframemovingatvelocity v withrespecttothe first. Properties1and2arereferredtoastheuniformityandisotropyof space.Property3isreferredtoasGalileaninvariance:theGalileanboost
SpecialRelativity,Electrodynamics,andGeneralRelativity
ISBN978-0-12-813720-8
https://doi.org/10.1016/B978-0-12-813720-8.00001-5
isasymmetry itmapsthephysicalsystemtoanotherinertialreference frame,andthisprocesshasnophysicalimpactonthesystem.
Newton’sconceptofrelativitycannowbestated:Allinertialframesare physicallyequivalent.Thismeansthatthelawsofphysicsarethesameinall ofthem.
ThereadershouldbeawarethatNewtonandhiscolleaguesargued constantlyaboutthesepoints.Whatistheoriginofinertia?Whyareinertial framessospecial?Can’twegeneralizetheProperties1 3toawiderclassof referenceframes?Wewillnotdiscussthesehistoricalissueshere,butthe readermightwanttopursuethemforagreaterinterestingperspective.Our approachiscomplementarytothetraditionaloneandisforwardlooking ratherthanhistorical.
UnderlyingNewtonianmechanicsarehisera’sconceptsofspaceand time.Tomeasurethedistancebetweenpoints,weimagineameasuring rod.Startingfromanorigin(0,0,0),welaydownmarkersinthe x and y and z directionssowecanmeasureaparticle’sposition r ¼ (x, y, z)inthis inertialframe.Nextweneedaclock.Asimpledevicesuchasasimple harmonicoscillatorwilldo.Takeamasspoint m ontheendofaspring,and letitexecuteperiodicmotionbackandforth.Makeaconventionthatone unitoftimepasseswhenthemasspointgoesthroughonecycleofmotion. Inthiswayweconstructaclockandmeasurespeedsofothermassesby notinghowfartheymoveinseveralunitsoftime inotherwords,we comparethemotionofour “standard” simpleharmonicoscillatorwiththe motionofexperimentalparticles.Notethatthisisjustwhatwemeanby timeinday-to-daysituations.Tomakeanaccurateclock,weneedone withasufficientlyshortunitoftime,orperiod.Clocksbasedontheinner workingsoftheatomcanbeusedindemanding,moderncircumstances. Justasitwasconvenienttoplacedistancemarkersalongthethreespatial axes r ¼ (x, y, z),itisconvenienttoplaceclocksonthespatialgridwork. Thiswillmakeiteasytomeasurevelocitiesofmovingparticles wejust recordthepositionsandtimesofthemovingparticleonourgridof measuringrodsandclocks.Whenthemovingparticleisattheposition r andtheclocktherereadsatime t,werecordtheevent.Measuringtwosuch eventsallowsustocalculatetheparticle’svelocityinthisframeatandnear thatspatialposition.Insettingupthegridofclocks,wemustsynchronize themsowecanobtainmeaningfultimedifferences.Thisiseasytodo.Place aclockattheoriginandoneat r ¼ (1,0,0).Then,atthehalfwaypoint betweenthem,placeabeaconthatsendsoutasignalinalldirections. Becausespaceishomogeneousandisotropic,thesignaltravelsatthesame
speedtowardbothclocks.Settheclockstozero,say,whentheyboth receivethesignal.Thetwoclocksaresynchronized,andwedidnoteven needtoknowthespeedofthesignalemittedfromthebeacon.Clearly,we couldusethismethodtosynchronizealltheclocksonthegrid.
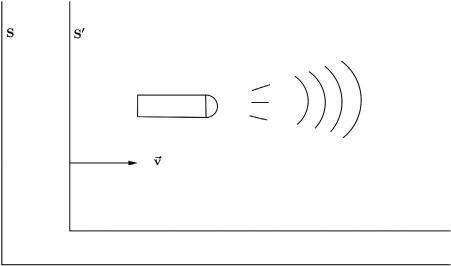
Nowwearereadytodoexperimentsinvolvingspace timemeasurementsinthisframeofreference.Callthisframe S.Itconsistsofthegridworkofmeasuringrodsandclocks,allatrest,withrespecttoeachother. Now,supposewewanttocompareourexperimentalresultswiththose obtainedbyafriendofoursatrestinanotherframethatmovesatconstant velocity v ¼ (vx,0,0)withrespecttous.Accordingtoourpostulates,hisor hermeasurementsareasgoodasoursandallourphysicallawscanbe writteninhisorherframeofreference S0 withoutanychange(Fig.1.1).
Themeasuringrodsin S0 areidenticaltothosein S;theclocksin S0 are alsoidenticaltothosein S.Supposethattheoriginof S and S0 coincide whentheclockattheoriginin S readstime t ¼ 0andtheclockatthe originin S0 reads t0 ¼ 0.Nowforthecrucialquestion:Dotheothergrid markingsandclocksatthosemarkingsalsoagreeinthetwoframes S and S0 ? Therearetwodistinctphysicsissuestoconsiderhere.The firstisthe operationoftheclocksandrodsineachframe.FollowingNewton’ s principleofrelativity,thatallinertialreferenceframesareequivalent,allthe clocksandrodsin S workexactlythesameasthoseatrestin S0 .Weneed onlyknowthatbothframesareinertial therelativevelocitybetweenthe framesisphysicallyirrelevanttothedynamicswithineach.Thesecondissue isthephysicalmechanismbywhichwecantransmittheinformationinone gridofrodsandclockstotheotheratrelativevelocity v.InNewton’ s world,objectscanmovewithunboundedrelativevelocitiesrelativetoone another,asweshalldiscussfurtherin Eq.(1.2).Accordingly,signalsand informationcanbetransmittedatunboundedvelocities,essentially
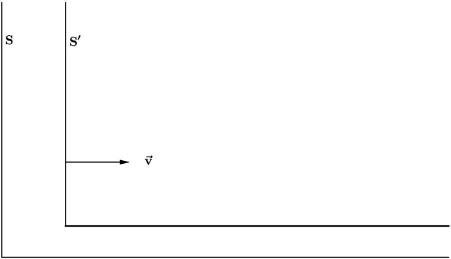
Figure1.1 Twoinertialframesofreferenceinrelativemotion.
instantaneously.Therefore,thespatialgridworkandthetimesoneachclock in S0 canbeinstantaneouslybroadcasttothecorrespondingrodsandclocks intheframe S.Therefore,thegridworkofcoordinatesandtimesinboth framesmustbeidentical,eventhoughtheyareinrelativemotion.So,the lengthsofmeasuringrodsandtheratesofclocksareindependentoftheir relativevelocities.Wethereforeneedonlyonemeasuringrodandone clockatonepointinoneinertialframe,andweknowthepositionsand timesofallmeasuringrodsandclocksinanyotherinertialframe.Forthe purposesofthisbook,thisservesasthemeaningof “absolutespace” and “absolutetime” inNewtonianmechanics.Weneednothypothesizeabout thesenotionsfromaphilosophicalbasis,aswasdonehistorically,butcan deducethemfromthefactthatinNewtonianmechanicsthereisnospeed limit informationcanbetransmittedinstantaneously.
Nowconsidertherulebywhichtimesandpositionmeasurementsare comparedbetweenthetwoframes, S and S0 ,inrelativemotionin Newton’sworld,
where x, y, z,and t aremeasurementsin S and x 0 , y 0 , z 0 ,and t0 arethecorrespondingmeasurementsin S0 .Forexample,ifwemeasurethepositionof aparticlein S0 tobe x 0 , y 0 ,and z 0 ,attime t0 ,thenthecoordinatesofthis event(measurement)inframe S aregivenby Eq.(1.1).Theserelations, whicharesofamiliarand “obvious,” arecalledGalileantransformations. Notethatthe firstofthem, x ¼ x 0 þ vt,statesthatthepositionoftheparticleattime t consistsoftwopieces:(1)thedistance vt betweentheorigins ofthetwoframesattime t and(2)thedistance x 0 fromtheorigintothe particleintheframe S0 .Thisrulecontainsthenotion “absolute” space it usesthefactthatinaNewtonianworldthedistance x 0 intheframe S0 isalso measuredas x 0 intheframe S.Thelastequationin Eq.(1.1) isthestatement of “absolute” time.Notealsothatiftheparticlehasavelocity v 0 p with respecttotheframe S0 inthe x 0 direction,then x 0 ¼ v 0 p t 0 ¼ v 0 p t ; andits positioninframe S is x ¼ v 0 p þ v t ; soitsvelocityrelativetotheorigin offrame S is vp,
whichisthefamiliarrulecalled “additionofvelocities.” Itrestson Newton’sideasofabsolutespaceandtime.Itwillbeinterestingindeed toseehowtheresultsfrom Eqs.(1.1)and(1.2) aredifferentinEinstein’ s world!
Wecangoslightlyfurtherthan Eq.(1.2) byconsideringasequenceof frames.Let S1 moveatvelocity v10 alongthex-axiswithrespectto S,let S2 moveatvelocity v21 alongthex-axiswithrespectto S1.Thenthevelocity ofaparticlein S, vp,0,isrelatedtoitsvelocitymeasuredinframe S2 by addinguptherelativevelocities,
Thereisnothingstoppingusfromgeneralizingthisprocessagainand againto Sn framesuntil vp,0 isavelocityaslargeasonewishes.Inother words,velocitiesinNewton’sworldareunboundedbecauseoftheaddition lawforvelocities.
Perhaps,ithasnotoccurredtothereaderbeforethatinformationcould betransmittedinstantaneouslyinaNewtonianworld.Actually,ifthereader recallssomeelementaryproblemsindynamics,theassumptionwaslurking justunderthesurface.
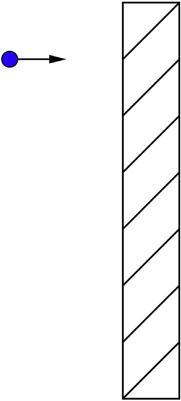
Supposeyouconsiderthecollisionofapointparticleandarod,as shownin Fig.1.2.
Figure1.2 Collisionbetweenaparticleandtheupperedgeofarod.
WhenyousolvethisproblemusingNewtonianmechanicsusingconservationoflinearandangularmomentum,youimplicitlyassumethatthe impactattheupperedgeoftherigidrodinstantaneouslyacceleratesthe centerofmassoftherodandbeginsrotatingthebottomendoftherodto theleft.Ifinformationwastransmittedata finitevelocity,callit c,thelower edgeoftherodcouldnotknowaboutthecollisionuntilalatertime, t ¼ [/c where [ isthelengthoftherod.Itisclearthattheverynotionofrigid bodiesrequiresatheoreticalbasiswhereinformationistransmittedinstantaneously.RigidbodiescannotexistinEinstein’sworld.Ofcourse,in practicalproblemswhere [ isafewmeters,say,and c isenormous, c z 3.0$108 m/s,thetimedelayencounteredhereisusuallyconsidered negligible.(Butitcertainlywouldbesignificantif [ werethediameterofa star.)Nonetheless,thematterofprincipleisourmajorconcerninthese discussions.
Anotherplacewhereinstantaneoustransmissionofinformationoccurs inNewtonianmechanicsproblemsisintheuseofpotentials.Whenwe havetwobodiesinteractingthroughamutualforcethatisdescribed throughapotentialthatdependsonthedistancebetweentheparticles,we areassumingthattheforceoneachparticleisdeterminedbytherelative positionoftheotherparticleatthatexactmoment.Noaccountisgivenof thetransmissionofthatinformationbetweentheseparateparticles.This Newtoniannotioniscalled “actionatadistance,” anditunderliessomeof thegreatestsuccessesofnonrelativisticmechanics.Wewillseethatitis absolutelyimpossibleinEinstein’sworld.
NowletusmoveontodiscussionsofNewton’ssecondandthirdlaws.
Thesecondlawintroducesdynamics:
Law2.Ifaparticleofmass m issubjecttoaforce f,thenitexperiences anacceleration a givenby,
Inslightlymoregenerality,
where p istheparticle’smomentum, p ¼ mv.Beforediscussingthe secondlawfurther,ithelpstointroduceNewton’sthirdlaw:
Law3.Whenoneparticleexertsaforceonasecondparticle,the secondoneexertsanequalandoppositeforceonthe first.
Thislawisthebasisofaconservationlaw:theconservationof momentum.Considertwointeractingparticles.Denotetheforceof particle1onparticle2 F12 andtheforce2on1 F21.Thethirdlawstates that,
Noticethatthisisavectorequation:theforcesareequalinmagnitudebut oppositeindirection.Wecanseethatthetotalmomentumofthesystem, p1 þ p2 isconstantintime,
Conservationlawsarefundamentaltoallsubfieldsofphysics.Newton’ s thirdlawisanessentialingredientinmechanics.Butitisimportanttonote somethingveryperplexingaboutthethirdlaw:itisa nonlocal conservation law.Theforcesofactionandreactioncancelasstatedin Eq.(1.7),butthe actionandreactionforcesacton different particles,whichcouldbeveryfar fromeachotheriftheforceactsoverlongdistancessuchaselectrostaticsor gravity. Eq.(1.7) makestheremarkablestatementthatateveryinstantof time t,particle1respondstothemotionofparticle2justsothesumoftheir momentaisaconstanteveniftheparticlesarethousandsofmetersapart. Thisispossibleinacausalworldonlyifinformationtravelsinstantaneously. ClearlythethirdlawwillnotsurviveinthisforminEinstein’sworldwhere informationcannottravelfasterthanc,thespeedoflight.Theimplications ofthefailureofthethirdlawwillbemoreprofoundthanwecanimagineat thispointinourstudies.
Themass m in Eq.(1.4) isclarifiedinpartbythethirdlaw,thelawof action reaction,whichimpliesinthecaseoftwointeractingparticlesthat
So,ifthe fi rstbodyischosentosetthescaleforinertia,inotherwords,if wede fi ne m 1 h 1,then m 2 isdeterminedfrom Eq.(1.8) .Thethirdlaw providesanoperationalmeaningtothe “ mass ” or “ inertia ” ofaparticle.
Arethelawsofdynamics,Newton’ssecondandthirdlaws,compatible withNewton’sprincipleofrelativity,thatallinertialreferenceframesare physicallyequivalent?Thekeyobservationisthataccelerationisa “Galilean invariant,” whichmeansthatanacceleration a isthesameinallinertial
referenceframes.Thisfollowsfrom Eq.(1.2).Differentiateitwithrespect totime,usethefactthat v isaconstantandlearnthat,
WelearnthatforcesareGalileaninvariants.Weareusingthefactthat massesareGalileaninvariantinNewton’sworldtomakethisobservation. ThispropertywasassumedinNewton’seraandwasverifiedexperimentally toreasonableprecisionatmodestvelocities.Weshallseethatmassesarenot invariantinEinstein’sworld,andtheimplicationsofthisfactwillproveto beverysignificant.
Wehavedealtwiththeseissuesveryexplicitlybecausetheywillhelpus appreciatespecialrelativity,wherethereisaspeedlimit,thespeedoflight. InalltherulesofNewtonianmechanics,therulesofhowthingswork,the secondandthirdlaws,donotdistinguishbetweeninertialframes.The dynamicsdosatisfyaprincipleofrelativity.Thedifferencebetweenthetwo theoriescomesfromthefactthatonehasaspeedlimitandtheotherdoes not.Thisaffectshowinformationissharedbetweenframes.Italsoaffects thedynamicswithineachframe Einstein’sformofNewton’ s “force equalsmasstimesacceleration” isdifferentbecauseitmustnotpermit velocitiesgreaterthanthespeedlimit.Buteachtheoryisconsistentwithin itsownrules.
1.2NEWTON’SWORLD:NOPLACEFORMAGNETISM
Itisinstructivetoreturntoourexampleofelectrostaticsandconsider Newtoniandynamicsinmoredetail.Thegoaltothisdiscussionisto demonstratethatifyouacceptNewton’slaws1 3andyouknow Coulomb’slaw,thenyoucanruleouttheveryexistenceofmagnetism!
Whatdowemeanbymagnetisminthiscontext?Weacceptthe experimentalfactthatelectricchargesproduceelectrostaticforces.Wewill writedownCoulomb’slawandwillmanipulateitandstudyit.Magnetic forcesare,bydefinition,thoseforcesproducedbyelectriccurrents.For example,ifathinwirecarriesacurrentI,thismeansthatelectronsare flowinginthewireatarateofICoulomb’spersecondpassinga fixedpoint alongthewire.Thewireisunchargedbutelectrons flowalongit.We knowfromourexperiencesinthelab,perhapsmakinganelectromagnet andbendingchargedparticletrajectorieswithit,thatthereisamagnetic fieldinthelabanditsstrengthisproportionaltothecurrentI.Inaddition,if
asinglechargesuchasafreeelectron,whosechargewelabel q andmeasure inunitsofcoulombs,hasa fixedposition r inareferenceframe S thenit producesaCoulomb fieldemanatingfrom r.Iftheelectronisviewedfrom theperspectiveofaframe S0 ,whichmoveswithvelocity v alongthexaxis, thentheelectronhasavelocity v inthisframesoitalsohasacurrent, qv, in S0 .Fromourexperiencesinthelab,weknowthattherewillbea magnetic fieldin S0 whosestrengthisproportionalto qv
LetusseewhereNewtongetsintotroublewiththesesimpleobservations.Letusreturntoourexampleofelectrostatics.Letparticle1beat restattheorigin r ¼ (0,0,0)inaframe S.Theelectric fieldgeneratedbythe charge q1 is,
where k isconstantdeterminedexperimentally.Theelectric fieldisintroducedsotheforceoncharge q2 atposition r ¼ r2 canbewrittenas,
Aswewillmotivateinlaterchapters,theseequationsmeanthatthecharge q1 attheorigingeneratesastaticelectric field E(r)arounditthatproducesa forceonotherchargedparticles.Nowsupposethatthecharge q2 hasa velocity v2(t)inframe S.Attime tq2 isatposition r2(t)andexperiencesthe electric fieldthere.So,theforceitexperiencesbecomestimedependent,
AccordingtoNewton’sthirdlaw,thecharge q1 experiencesaforce F(t). Wecanviewtheforceinthefollowingway:themovingcharge q2 generatesanelectric fieldofmagnitude kq2 =jr r 2 ðt Þj2 inthedirection r r2(t). Multiplyingthis fieldby q1 givestheforceonparticle1.
Welearnfromallthisthattheforcebetweenparticle1andparticle2is independentofthevelocitiesofeitherparticleanddependsonlyonthe instantaneouspositionsofeachparticle.
So,inNewton’sworld,theforcebetweencharge q1 and q2 dependsonly ontheparticles’ instantaneouspositionsandnotontheirvelocities.Thisisa veryperplexingresultbecause,aspromised,itrulesouttheexistenceof
magnetisminNewton’sworld.Thisvital flawwillbecuredbyspecial relativity.SpecialrelativityandCoulomb’slawwillbeshowntoimply magneticforcesofjustthesortobservedinthelabandwill,infact,produce allofMaxwell’sequations,andthewaveequationforelectromagnetic wavesthattravelatthespeedlimitofrelativity, c.
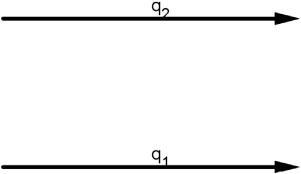
ToemphasizethefailureofNewton’slawstoaccommodatemagnetism, consideranevensimplerexamplethatdoesnotusethethirdlaw.Imagine twocharges q1 and q2 movingparalleltooneanotherwithacommon velocity v asshownin Fig.1.3.Wewanttocalculatetheforcebetween them.Todothis,weviewthechargesfromtheperspectiveoftheirrest frame.Inthisframe,weknowtheanswerimmediately:Coulomb’slaw appliesandtheparticlesexperienceaforcethatactsonthelinebetween themandthatfallsoffasthesquareofthedistancebetweenthem.This producesaformulaforeachparticle’sacceleration.ButinNewton’sworld, accelerationsareindependentoftheinertialframeinwhichtheyare calculated.Therefore,theparticlesexperiencethesameacceleration a in theframe S wheretheyaremovingandareproducingcurrents.This demonstratesthatthesecurrentsdonoteffecttheaccelerationofthe charges,andmagneticforcesareruledoutyetagain.
InChapter9,wewillseethattheoriginofmagneticforcesandthe magnetic field B isthespace timeofspecialrelativity.Wewillgofurther andderiveallofelectromagnetism(Maxwell’slaws,includingAmpere’slaw ofmagnetic fieldsandthedisplacementcurrentandFaraday’slawof electromagneticinduction)fromspecialrelativityandCoulomb’slawof electrostatics.Fromthereweshallseethatelectromagneticwavesexistand travelwithauniversalspeedlimit,c.Butbeforeweheadoffinthat directionletuslearnthebasicsofthephysicsofspace timemeasurements accordingtoEinstein.
Figure1.3 Twochargesmovingparalleltooneanotheratacommonvelocityin thelab.