EM2_G6_M2_UTE_Teach_24SPAA_910850_Updated 06.24

Una historia de razones

Razones y tasas

ENSEÑAR ▸ Operaciones con fracciones y números de varios dígitos

¿Qué tiene que ver esta pintura con las matemáticas?

El tema de esta pintura impresionista de perspectiva aérea es una intersección en París durante un día gris y lluvioso. En esta escena, Gustave Caillebotte crea una sensación de profundidad al usar la perspectiva y la proporción de diversas formas, por ejemplo, ubicando figuras grandes en primer plano y figuras más pequeñas a lo lejos. Imagina que hay un plano de coordenadas en el edificio del fondo. ¿Cómo podrías determinar la distancia desde el frente del edificio hasta el fondo usando el plano de coordenadas?

En la portada

Paris Street; Rainy Day, 1877 Gustave Caillebotte, French, 1848–1894 Oil on canvas

The Art Institute of Chicago, Chicago, IL, USA

Gustave Caillebotte (1848–1894).

Paris Street; Rainy Day, 1877. Oil on canvas, 212.2 x 276.2 cm (83 1/2 x 108 3/4 in).

Charles H. and Mary F. S. Worcester Collection (1964.336). The Art Institute of Chicago, Chicago, IL, USA. Photo Credit: The Art Institute of Chicago/Art Resource, NY

Great Minds® is the creator of Eureka Math® , Wit & Wisdom® , Alexandria Plan™, and PhD Science®

Published by Great Minds PBC. greatminds.org

© 2024 Great Minds PBC. All rights reserved. No part of this work may be reproduced or used in any form or by any means—graphic, electronic, or mechanical, including photocopying or information storage and retrieval systems—without written permission from the copyright holder. Where expressly indicated, teachers may copy pages solely for use by students in their classrooms.

979-8-89191-085-0

Una historia de razones

ENSEÑAR

Módulo

1

2

Razones, tasas y porcentajes

3

Operaciones con fracciones y números de varios dígitos

4

Números racionales

5

Expresiones y ecuaciones de un paso

6

Área, área de la superficie y volumen

Estadística

Antes de este módulo

Módulo 2 de 4.o grado

En 4.o grado, la clase identifica pares de factores de un número dado y múltiplos de un número dado. Además, la clase determina si un número es primo o compuesto identificando sus factores.

Módulos 2 y 5 de 5.o grado

En 5.o grado, la clase divide números enteros usando estrategias que se basan en el valor posicional, las propiedades de las operaciones y la relación entre la multiplicación y la división. La clase aplica este razonamiento para dividir números enteros entre fracciones unitarias y fracciones unitarias entre números enteros.

Además, la clase suma, resta y multiplica números decimales usando estrategias y modelos concretos que se basan en el valor posicional, las propiedades de las operaciones y la relación entre las operaciones.

Contenido general

Operaciones con fracciones y números de varios dígitos

Tema A

Factores, múltiplos y divisibilidad

En el tema A, sus estudiantes exploran al principio modelos visuales que contienen fichas cuadradas y rectangulares para determinar factores comunes y múltiplos comunes de pares de números. Aprenden estrategias para determinar la divisibilidad entre 3 y 6, usan el sentido numérico para razonar sobre la divisibilidad de un número dado y exploran la relación entre la divisibilidad y los factores. Asimismo, aprenden las definiciones de máximo común divisor (MCD) y mínimo común múltiplo (mcm) y usan distintas estrategias para hallar el MCD y el mcm, entre las que se incluyen las listas organizadas de factores y múltiplos, la factorización prima y los diagramas de Venn. En una lección opcional, la clase aprende y aplica el algoritmo de Euclides para hallar el MCD de dos números y usa el MCD para hallar el mcm.

Tema B

Dividir fracciones

En el tema B, sus estudiantes dividen fracciones entre números enteros y números enteros entre fracciones. Representan la división de fracciones usando diagramas de cinta y rectas numéricas, razonan sobre la relación entre la multiplicación y la división e interpretan problemas de división con fracciones como un número de grupos desconocido o un tamaño del grupo desconocido. Al final del tema, crean denominadores comunes para dividir fracciones entre fracciones.

Tema C

Dividir fracciones con fluidez

En el tema C, se presenta la estrategia de invertir y multiplicar para dividir fracciones. Sus estudiantes usan diagramas de cinta para razonar acerca de por qué sirve la estrategia. Luego, aplican la estrategia para dividir fracciones y números mixtos con fluidez. Asimismo, usan la división de fracciones para resolver problemas del mundo real y hacen comparaciones multiplicativas. Al final

del tema, sus estudiantes suman, restan, multiplican y dividen fracciones en tareas del mundo real en las que diseñan carritos de carrera de madera.

Tema D

Suma, resta y multiplicación de números decimales

En el tema D, sus estudiantes suman, restan y multiplican números decimales de varios dígitos con fluidez. Primero, usan el sentido numérico y el razonamiento de valor posicional para sumar y restar números decimales y determinan la ubicación del punto decimal en sumas y restas. Luego, razonan acerca de los productos de factores decimales y usan el algoritmo estándar para la multiplicación a fin de multiplicar números decimales de forma eficiente. Al final del tema, aplican estas destrezas en una tarea del mundo real al calcular los costos e ingresos de un proyecto de construcción y al ajustar el modelo de su construcción para aumentar las ganancias.

Tema E

División de números de varios dígitos

En el tema E, sus estudiantes amplían su comprensión de la división y usan el algoritmo estándar para dividir números enteros con fluidez. Razonan sobre el tamaño del cociente y la ubicación del punto decimal usando el razonamiento del valor posicional y estiman para determinar si sus respuestas son razonables. Además, aprenden a expresar cocientes como números decimales y a redondear cocientes cuando es necesario.

Tema F

División con números decimales

En el tema F, sus estudiantes amplían su comprensión del algoritmo estándar para la división con el fin de dividir números decimales con fluidez. Comienzan dividiendo números decimales entre números enteros y, luego, avanzan hacia la división de números decimales entre números decimales y aplican la división con números decimales para resolver problemas del mundo real de varios pasos. Al final de este tema, practican la división con números decimales en una tarea de varios pasos que incluye cálculos sobre los recursos necesarios para sobrevivir en Marte.

Después de este módulo

Módulo 4 de 6.o grado

En el módulo 4, la clase repasa el máximo común divisor cuando usa la propiedad distributiva y aplica su comprensión de los factores para generar expresiones equivalentes.

Más adelante en el módulo, la clase aplica su comprensión de la división de fracciones, la división de números de varios dígitos y las operaciones con fracciones y números decimales cuando resuelve ecuaciones de un paso que incluyen constantes y coeficientes de números racionales.

Contenido

Operaciones con fracciones y números de varios dígitos

¿Por qué?

Criterios de logro académico: Contenido general �

Tema A

Factores, múltiplos y divisibilidad

Lección 1

Factores y múltiplos

• Usar modelos visuales para determinar factores comunes y múltiplos comunes de pares de números

Lección 2

Divisibilidad

• Determinar si los números son divisibles entre otros números

Lección 3

El máximo común divisor

• Determinar el máximo común divisor de dos números enteros menores que o iguales a 100

Lección 4

El mínimo común múltiplo

6

10

12

14

Lección 7

Dividir una fracción entre un número entero

• Dividir una fracción entre un número entero

• Dividir un número mixto entre un número entero

Lección 8

Dividir fracciones formando denominadores comunes

• Dividir una fracción entre otra fracción usando un denominador común

• Dividir un número mixto entre una fracción usando un denominador común

Tema C

26

Dividir fracciones con fluidez

Lección 9

48

70

• Hallar el mínimo común múltiplo de dos números enteros menores que o iguales a 12

Lección 5

El algoritmo de Euclides (opcional)

90

• Hallar el máximo común divisor de números grandes usando el algoritmo de Euclides

• Hallar el mínimo común múltiplo de números grandes usando el máximo común divisor

Tema B

Dividir fracciones

Lección 6

Dividir un número entero entre una fracción

• Dividir un número entero entre una fracción usando diagramas de cinta y el razonamiento sobre la división

112

Dividir fracciones usando diagramas de cinta

• Usar un diagrama de cinta para dividir una fracción entre otra fracción

• Relacionar la división de una fracción entre otra fracción con un problema de factor desconocido

Lección 10

Dividir fracciones usando la estrategia de invertir y multiplicar

• Usar la estrategia de invertir y multiplicar para dividir una fracción entre otra fracción

Lección 11

Aplicaciones de la división con fracciones

• Resolver problemas del mundo real dividiendo fracciones y números mixtos

Lección 12

Operaciones con fracciones en una situación del mundo real

• Sumar, restar, multiplicar y dividir fracciones y números mixtos para resolver problemas del mundo real

186

204

224

114

Tema D

Suma, resta y multiplicación de números decimales

Lección 13

Suma y resta de números decimales

• Sumar y restar números decimales usando los algoritmos estándares para cada operación

Lección 14

Patrones en la multiplicación de números decimales

• Reconocer y aplicar patrones en los factores al multiplicar números enteros y números decimales

Lección 15

Multiplicación con números decimales

• Multiplicar números decimales usando el algoritmo estándar

Lección 16

Aplicaciones de las operaciones con números decimales

236

Tema F

División con números decimales

238

Lección 21

Dividir un número decimal entre un número entero

• Dividir un número decimal entre un número entero de varios dígitos usando el algoritmo estándar para la división

Lección 22

256

268

286

• Crear un modelo de un edificio y usar operaciones con números decimales para calcular el costo, los ingresos, y las ganancias o las pérdidas

Tema E

División de números de varios dígitos

Lección 17

Cocientes parciales

• Dividir números enteros de varios dígitos usando el método de los cocientes parciales, y expresar cocientes como números mixtos

Lección 18

El algoritmo estándar para la división

• Dividir números enteros de varios dígitos usando el algoritmo estándar

Lección 19

Expresar cocientes como números decimales

304

Dividir un número decimal entre otro número decimal mayor que 1

• Dividir un número decimal entre otro número decimal mayor que 1 usando el algoritmo estándar

Lección 23

Dividir un número decimal entre otro número decimal menor que 1

• Dividir un número decimal entre otro número decimal menor que 1 usando el algoritmo estándar

• Resolver problemas del mundo real dividiendo un número decimal entre otro número decimal

Lección 24

Vivir en Marte

320

428

• Resolver problemas del mundo real usando operaciones con números decimales

Recursos

Criterios de logro académico: Indicadores de competencias

Vocabulario

Las matemáticas en el pasado

Materiales

340

• Dividir números enteros de varios dígitos usando el algoritmo estándar, y expresar cocientes como números decimales

Lección 20

Problemas de división del mundo real

• Crear y resolver problemas de división del mundo real

Ejemplos de soluciones

Obras citadas

Créditos

Agradecimientos

438

¿Por

qué?

Operaciones con fracciones y números de varios dígitos

¿Por qué el tema sobre factores y múltiplos se encuentra al principio del módulo y no al final?

El trabajo de la clase con factores, múltiplos y divisibilidad en el tema A sirve como preparación para calcular con precisión y eficiencia en temas posteriores del módulo. Sus estudiantes aplican su comprensión de los factores, los múltiplos y la divisibilidad al usar el algoritmo de la división larga, determinar los denominadores comunes, escribir fracciones con la unidad más grande posible y razonar acerca del tamaño de los cocientes.

La clase aprende las reglas de divisibilidad en la lección 2. ¿Qué reglas de divisibilidad ya deberían saber sus estudiantes?

La clase ya debería saber cómo determinar la divisibilidad entre 2, 5 y 10 basándose en su trabajo con la multiplicación de un número de un solo dígito y el sistema en base diez en los grados anteriores. También pueden usarse las palabras número par e impar para comentar la divisibilidad entre 2. Además, parte de sus estudiantes pueden darse cuenta de manera intuitiva de otras reglas de divisibilidad informales, como determinar si un número es divisible entre 4 dividiendo el número a la mitad dos veces.

Esperaba ver a la clase usar el máximo común divisor y la propiedad distributiva para factorizar expresiones numéricas en este módulo. ¿Cuándo se trabaja eso?

En este módulo, la clase solo halla el máximo común divisor y mínimo común múltiplo de un par de números. Sus estudiantes repasan estos conceptos en el módulo 4, cuando trabajan con expresiones algebraicas y numéricas y con ecuaciones. En dicho módulo, escriben expresiones tales como 36 + 8 como el producto de dos factores, 4(9 + 2), como preparación para usar las propiedades de las operaciones a fin de generar expresiones algebraicas equivalentes, por ejemplo, 36x + 8 y 4(9x + 2). Escribir expresiones numéricas equivalentes con la propiedad distributiva ofrece a sus estudiantes una comprensión más concreta antes de escribir expresiones algebraicas más abstractas.

Factores primos de 6 Factores primos de 10

32 5

Esperaba ver a la clase escribir la factorización prima de un número usando exponentes. ¿Cuándo se trabaja eso?

La clase expresa la factorización prima de un número al usar exponentes después de que se presenta la notación exponencial en el módulo 4. En grados anteriores, sus estudiantes solo expresaron potencias de 10 con exponentes. Todavía no se familiarizaron con la escritura de exponentes como números enteros para números que tienen bases diferentes de 10.

¿Por qué no se presenta el método de invertir y multiplicar en el tema B?

Los temas B y C guían con intención a la clase a través de una serie de representaciones concretas y pictóricas de la división de fracciones, pero en estos temas no se presenta directamente el método abstracto de invertir y multiplicar fracciones para dividir fracciones. Primero, sus estudiantes aprenden a interpretar, representar y razonar sobre problemas de división con fracciones al crear diagramas de cinta, aplicar interpretaciones de tamaño del grupo desconocido o número de grupos desconocido y razonar sobre denominadores comunes. Luego, una vez que se han sentado estas bases, usan diagramas de cinta para descubrir que dividir entre cualquier fracción tiene el mismo resultado que multiplicar por el recíproco de esa fracción.

¿Por qué hay aplicaciones del mundo real y tareas para representar en temas que abordan los conceptos de fluidez?

La clase tiene la oportunidad de adquirir fluidez con las operaciones con números decimales y la división de fracciones y números enteros a través de una amplia práctica a lo largo del módulo. Además, sus estudiantes aplican estas destrezas cuando participan de distintas tareas enriquecedoras de representación matemática que requieren de cálculos eficientes y precisos, como el diseño de un carrito de carrera de madera, el cálculo de costos e ingresos de un edificio residencial o la exploración de la logística para la supervivencia en Marte.

¿Por qué hay una lección opcional en este módulo?

En la lección 5, la clase tiene la oportunidad de estudiar un método histórico para dividir dos números, el algoritmo de Euclides, y aplicar este método para hallar el máximo común divisor de dos números. En esta lección, se resume el trabajo de sus estudiantes con los acertijos matemáticos de la lección 1, que incluían fichas cuadradas y rectangulares, y su comprensión del máximo común divisor de la lección 3. El algoritmo de Euclides es un método eficiente para determinar el máximo común divisor de números grandes y tiene aplicaciones en el mundo real en el cifrado de datos.

La lección está identificada como opcional dado que los estudiantes deben ir más allá de solo calcular el máximo común divisor de dos números menores que o iguales a 100. Sin embargo, el algoritmo de Euclides es un tema de estudio útil para sus estudiantes debido a su relevancia histórica, su conexión con distintos temas dentro del módulo, su eficiencia en el cálculo del máximo común divisor de grandes números y su potencial para despertar la curiosidad y construir un sentido numérico.

¿Por qué el trabajo de la clase en este módulo muestra una estimación antes de cada cálculo?

Desde 3.er grado, la clase usa la estimación para evaluar si las respuestas a los problemas de cálculo son razonables. En 6.o grado, sus estudiantes ya tienen una comprensión de distintas estrategias de estimación como el redondeo, el cálculo mental y el uso del valor posicional. Debido a que tienen bases sólidas sobre la estimación, el trabajo de la clase en este módulo no exige que sus estudiantes estimen sistemáticamente sus respuestas antes de realizar una operación. En cambio, la guía del maestro o la maestra ofrece sugerencias sobre cuándo pedir a sus estudiantes que estimen y cómo considerar con criterio si su respuesta es razonable. Cada maestro o maestra puede decidir incorporar la estimación con mayor frecuencia según sea necesario para reforzar la comprensión de sus estudiantes.

100 unidades

60 unidades 60 unidades

40 unidades

Pasos del algoritmo de Euclides

Par de números Diferencia

y 60

y 40

y 20

20 y 20

− 60 = 40

− 40 = 20

− 20 = 20

Criterios de logro académico: Contenido general

Operaciones con fracciones y números de varios dígitos

Los Criterios de logro académico (CLA) son descripciones alineadas con los estándares que detallan lo que cada estudiante debe saber y poder hacer. Los criterios se escribieron usando secciones de distintos estándares para formar una descripción clara y precisa del trabajo que se abarca en cada módulo.

Cada módulo tiene su propio conjunto de criterios y el número de criterios varía según el módulo. En conjunto, los grupos de criterios por módulo/ nivel describen lo que cada estudiante debe haber aprendido al terminar el año escolar.

Los criterios y sus indicadores de competencias ayudan a las maestras y los maestros a interpretar el trabajo de cada estudiante a través de:

• observaciones informales en el salón de clases;

• datos acumulados en evaluaciones formativas de otras lecciones;

• Boletos de salida;

• Pruebas cortas de los temas y

• Evaluaciones de los módulos.

Este módulo contiene los 13 CLA que se indican.

6.Mód2.CLA1 Resuelven problemas verbales dividiendo números de varios dígitos con el algoritmo estándar.

6.Mód2.CLA2 Resuelven problemas verbales realizando operaciones con números decimales de varios dígitos.

6.Mód2.CLA3 Razonan acerca del tamaño de los cocientes de fracciones y números mixtos.

6.Mód2.CLA4 Dividen dos fracciones o números mixtos.

6.Mód2.CLA5 Resuelven e interpretan problemas verbales que incluyen la división de fracciones y de números mixtos.

6.Mód2.CLA6 Interpretan la división de fracciones y de números mixtos usando modelos.

6.Mód2.CLA7 Razonan acerca del tamaño de los cocientes de dos números de varios dígitos.

6.Mód2.CLA8 Dividen números enteros de varios dígitos usando el algoritmo estándar.

6.Mód2.CLA9 Suman y restan números decimales de varios dígitos.

6.Mód2.CLA10 Multiplican números decimales de varios dígitos.

6.Mód2.CLA11 Dividen números decimales de varios dígitos.

6.Mód2.CLA12 Determinan el máximo común divisor de dos números enteros menores que o iguales a 100.

6.Mód2.CLA13 Determinan el mínimo común múltiplo de dos números enteros menores que o iguales a 12.

La primera página de cada lección identifica los Criterios de logro académico (CLA) alineados con esa lección. Cada criterio puede tener hasta tres indicadores, cada uno de estos alineado con una categoría de competencia (es decir, Parcialmente competente, Competente, Altamente competente). Cada criterio tiene un indicador para describir el rendimiento Competente, pero solo algunos criterios tienen un indicador para Parcialmente competente o Altamente competente.

Un ejemplo de uno de estos criterios, incluyendo sus indicadores de competencias, se muestra a continuación como referencia. El grupo completo de criterios de este módulo con los indicadores de competencias puede encontrarse en el recurso Criterios de logro académico: Indicadores de competencias.

Código del CLA: Grado.Mód#.CLA#

Los Criterios de logro académico contienen las siguientes partes:

• Código del CLA: El código indica el grado y el número del módulo y, luego, presenta los criterios sin un orden específico. Por ejemplo, el primer criterio para el módulo 2 de 6.o grado se codifica como 6.Mód2.CLA1.

• Texto del CLA: El texto se ha escrito a partir de los estándares y describe de manera concisa lo que se evaluará.

• Indicadores del CLA: Los indicadores describen las expectativas precisas del criterio para la categoría de competencia dada..

Texto del CLA

6.Mód2.CLA5 Resuelven e interpretan problemas verbales que incluyen la división de fracciones y de números mixtos.

Parcialmente competente Competente Altamente competente

Relacionan contextos con expresiones de división de fracciones y de números mixtos.

Una receta lleva 3 4 de taza de azúcar. Adesh tiene 4 1 2 tazas de azúcar. ¿Cuántas veces puede hacer

Adesh la receta con esa cantidad de azúcar?

Encierra en un círculo la expresión que coincida con la situación del problema verbal. 3 4 ÷ 4 1 2 4 1 2 ÷ 3 4

Resuelven problemas verbales que incluyen la división de fracciones y de números mixtos

Jada tiene una cinta que mide 30 pulgadas de largo.

Corta la cinta en trozos que miden 4 1 2 pulgadas de largo cada uno. ¿Cuántos trozos de cinta tiene

Jada al final?

Interpretan la división de fracciones y de números mixtos creando problemas verbales que aplican conceptos partitivos y de medidas.

Escribe un problema verbal que coincida con la oración numérica.

3 1 8 ÷ 2 1 2 = 1 1 4

Indicadores del CLA

Tema A Factores, múltiplos y divisibilidad

En 4.o y 5.o grado, sus estudiantes identifican factores y múltiplos dentro del rango de 1 a 100 y determinan si los números son primos o compuestos. Reconocen que un número entero es un múltiplo de cada uno de sus factores. Con base en esta comprensión, determinan si un número entero es múltiplo de un número de un dígito dado. En el tema A de 6.o grado, amplían su comprensión sobre factores, múltiplos y divisibilidad, y aplican lo aprendido a la resolución de problemas que incluyen el máximo común divisor y el mínimo común múltiplo.

En la lección 1, sus estudiantes exploran, en formato digital, una serie de acertijos matemáticos con figuras geométricas. Primero, determinan la longitud del lado del cuadrado más grande que puede cubrir de forma completa un rectángulo de dimensiones dadas. Luego, para determinar la longitud de los lados de los cuadrados más pequeños que se pueden crear, cubren con fichas rectángulos de dimensiones dadas. Resuelven varios acertijos matemáticos con rectángulos de diferentes tamaños para reconocer el papel que juegan los factores comunes y los múltiplos comunes para hallar soluciones.

En la lección 2, sus estudiantes aprenden estrategias para poner a prueba la divisibilidad y examinan la relación entre divisibilidad, factores y múltiplos. Aplican los conocimientos previos sobre la divisibilidad entre números como 2 y 5, y hacen conjeturas acerca de la divisibilidad entre otros números como 3 y 6. Justifican sus conjeturas y dan contraejemplos para refutar una conjetura que saben que es falsa.

En las lecciones 3 y 4, sus estudiantes usan distintas estrategias para hallar el máximo común divisor y el mínimo común múltiplo de dos números. A partir de lo hecho en grados anteriores, enumeran pares de factores de dos números para identificar el máximo común divisor y enumeran múltiplos

de dos números para hallar el mínimo común múltiplo. Determinan las factorizaciones primas de dos números y organizan factores primos mediante el uso de tablas, listas y diagramas de Venn para determinar el máximo común divisor o el mínimo común múltiplo de un par de números. Aplican estos conocimientos para resolver problemas del mundo real e interpretar el significado de máximo común divisor y mínimo común múltiplo en contexto.

El tema finaliza con una lección opcional en la que sus estudiantes usan el algoritmo de Euclides para hallar el máximo común divisor de dos números, cada uno de los cuales es mayor que 100. Luego, usan el máximo común divisor y el producto de dos números para hallar el mínimo común múltiplo de los dos números.

Sus estudiantes aplican lo que saben acerca de factores, múltiplos y divisibilidad a lo largo del módulo cuando escriben fracciones equivalentes, hallan denominadores comunes y dividen números usando el algoritmo estándar. En módulos posteriores, aplican sus conocimientos sobre el máximo común divisor cuando usan la propiedad distributiva.

Progresión de las lecciones

Lección 1 Factores y múltiplos

Lección 2 Divisibilidad

Lección 3 El máximo común divisor

Lección 4

Lección 5

Factores y múltiplos

Usar modelos visuales para determinar factores comunes y múltiplos comunes de pares de números

Vistazo a la lección

1. ¿Cuál es la longitud del lado, en pies, de la ficha cuadrada más grande que puede cubrir un rectángulo de 6 pies por 9 pies de forma completa?

La longitud del lado de la ficha cuadrada más grande que puede cubrir un rectángulo de forma completa es 3 pies.

2. ¿Cuál es la longitud del lado, en pulgadas, del cuadrado más pequeño que se puede crear con fichas rectangulares de 6 pulgadas por 9 pulgadas? 6 in 9 in

La longitud del lado del cuadrado más pequeño que se puede crear es 18 pulgadas.

En esta lección digital, sus estudiantes identifican las diferencias entre factores y múltiplos. Primero, participan en un juego y desarrollan estrategias para hallar factores y múltiplos de números. Luego, exploran dos modelos visuales interactivos para descubrir los factores comunes y los múltiplos comunes de dos números.

Use la plataforma digital para preparar y enseñar esta lección. Sus estudiantes también explorarán el contenido de la lección y las actividades a través de la plataforma digital.

Preguntas clave

• ¿Qué es un factor común de dos números?

• ¿Qué es un múltiplo común de dos números?

Criterios de logro académico

6.Mód2.CLA12 Determinan el máximo común divisor de dos números enteros menores que o iguales a 100.

6.Mód2.CLA13 Determinan el mínimo común múltiplo de dos números enteros menores que o iguales a 12.

Agenda

Fluidez

Presentar 10 min D

Aprender 25 min D

• Cubrir con fichas cuadradas

• Cubrir con fichas rectangulares

Concluir 10 min

Materiales

Maestro o maestra

• computadora o dispositivo*

• proyector*

• libro Enseñar*

Estudiantes

• marcador de borrado en seco*

• lápiz*

• pizarra blanca individual*

• borrador para la pizarra blanca individual*

• libro Aprender*

Preparación de la lección

• No se necesita.

*Estos materiales solo se mencionan en la lección 1. Prepare estos materiales para cada una de las lecciones de este módulo.

Fluidez

Identificar factores

La clase identifica los factores de un número como preparación para hallar factores comunes.

Instrucciones: Elige todos los números que sean factores del número dado.

Nota para la enseñanza

Las actividades de fluidez son sets breves de problemas de práctica secuenciados que sus estudiantes resuelven durante los primeros 3 a 5 minutos de clase. Administre una actividad de fluidez como una actividad para iniciar la clase o conviértala en una actividad guiada de Intercambio con la pizarra blanca o de Respuesta a coro. Puede encontrar instrucciones para administrar estas actividades en el recurso de la sección Fluidez.

Nota para la enseñanza

En lugar de administrar la actividad de Fluidez de esta lección, considere usar la Práctica veloz de Encerrar en un círculo los factores. Puede encontrar instrucciones para administrar estas actividades en el recurso de la sección Fluidez.

Presentar

La clase participa en un juego para identificar factores y múltiplos de un solo número.

Sus estudiantes participan en un juego de factores varias veces. En este juego, se requiere que apliquen lo que saben sobre factores y múltiplos. Cuanta mayor facilidad tengan sus estudiantes para hallar factores y múltiplos, más éxito tendrán en el juego. Después del juego, la clase repasa los términos factor, primo y múltiplo.

Participarán en un juego que se llama Búsqueda de factores. Den un ejemplo de un factor.

Por ejemplo, 2 y 4 son factores de 8 porque 2 × 4 = 8.

La primera persona participante elige un número del tablero. El número que elige es el número de puntos que gana en esa ronda. La segunda persona que participa gana puntos por cualquiera de los otros factores del número que eligió la primera persona. Entonces, el número elegido y todos sus factores se eliminan del juego. Deben turnarse para elegir el número. El juego continúa hasta que no queden más números para elegir. Quien tenga el mayor número de puntos, gana.

¿Cuáles son los factores de 37? ¿Cómo lo saben?

Los factores de 37 son 37 y 1 porque 37 es un número primo.

Si sus estudiantes no mencionan el término número primo, brinde el ejemplo y la definición que siguen:

37 es un ejemplo de un número primo. Un número primo tiene solo dos factores que son números enteros: 1 y el propio número. Den algunos ejemplos de otros números primos.

31, 29, 23

¿Cómo se relaciona el número 38 con el número 19?

38 es un múltiplo de 19.

DUA: Representación

Las actividades digitales están alineadas con el principio de Participación de DUA, dado que incluyen lo siguiente:

• Varios formatos y modos de representación: la clase observa los factores y los múltiplos de un par de números en un modelo visual de cuadrados y rectángulos y en una lista organizada.

• Oportunidades para aplicar el aprendizaje a nuevas situaciones: la clase observa patrones en el tamaño de las fichas que cubrirán un área dada y generaliza la idea de factores comunes y múltiplos comunes.

Nota para la enseñanza

El diálogo que se muestra proporciona sugerencias de preguntas y ejemplos de respuesta. Para maximizar la participación de cada estudiante, guíe conversaciones usando herramientas y estrategias que incentiven el intercambio entre estudiantes. Por ejemplo, use con flexibilidad la Herramienta para la conversación y las rutinas Reunirse y conversar en parejas, Pensar-Trabajar en parejas-Compartir y Siempre, a veces, nunca.

Si sus estudiantes no mencionan el término múltiplo, brinde la siguiente definición:

Un múltiplo de un número entero es el producto de ese número y otro número entero.

Aprender

Cubrir con fichas cuadradas

La clase usa un modelo visual para hallar los factores comunes de dos números.

En una actividad interactiva, sus estudiantes exploran los posibles tamaños de las fichas cuadradas que pueden cubrir un rectángulo de dimensiones dadas. Hallan que la longitud del lado de la ficha cuadrada debe ser factor común tanto de la longitud como del ancho del rectángulo para cubrir de forma completa el rectángulo.

¿Qué observan acerca de la longitud de los lados de las fichas cuadradas y la longitud y el ancho del rectángulo?

La longitud de los lados de las fichas cuadradas que cubren el rectángulo son todos los factores tanto de la longitud como del ancho del rectángulo. Los cuadrados con una longitud del lado de 1 pie sirven para todos los rectángulos porque 1 es un factor de todos los números.

¿Cómo piensan que llamamos a los números que son factores de dos números?

Podemos llamarlos factores comunes porque la palabra común puede significar que algo es compartido, o que es lo mismo.

¿Qué observan acerca de la longitud del lado de la ficha más grande?

La longitud del lado de la ficha más grande es el factor más grande tanto de la longitud como del ancho del rectángulo.

Promoción de la práctica de las matemáticas

Cada estudiante reconoce y expresa regularidad en la lógica de la repetición cuando halla repetidamente las longitudes de los lados de las fichas cuadradas que cubren un rectángulo y observa que las longitudes de los lados de las fichas cuadradas son factores tanto de la longitud como del ancho del rectángulo.

Considere hacer las siguientes preguntas:

• ¿Qué patrones observan cuando hallan cuadrados para cubrir el rectángulo?

• ¿Qué hay de igual en la forma en que trabajan con cada ejemplo?

• Cuando buscan cuadrados con los que se puede cubrir un rectángulo, ¿se repite algo?

¿Cómo les ayuda eso a hallar las longitudes de los lados de los cuadrados con los que se puede cubrir un rectángulo de forma más eficiente?

Cubrir con fichas rectangulares

La clase usa un modelo visual para hallar los múltiplos comunes de dos números.

En una actividad interactiva, sus estudiantes exploran los posibles tamaños de los cuadrados que se pueden crear con fichas rectangulares de dimensiones dadas. Observan que las fichas rectangulares forman un cuadrado cuando la longitud del lado del cuadrado es un múltiplo común de la longitud y el ancho del rectángulo.

En esta actividad, ¿cómo se relacionan las longitudes de los lados de los cuadrados que podemos crear con la longitud y el ancho del rectángulo?

Las longitudes de los lados de los cuadrados son múltiplos tanto de la longitud como del ancho del rectángulo.

¿Cómo piensan que llamamos a un número que es múltiplo de dos números dados?

Podemos llamarlos múltiplos comunes porque la palabra común significa que algo es compartido, o que es lo mismo.

En un rectángulo de 2 pies por 3 pies, ¿cuál es la longitud del lado del cuadrado más grande que pueden crear? ¿Por qué?

No puedo crear el cuadrado más grande porque puedo seguir sumando más y más rectángulos para crear cuadrados más y más grandes.

Apoyo para la comprensión del lenguaje

Considere formar grupos de manera estratégica y flexible a lo largo del módulo.

• Forme parejas de estudiantes que tengan distintos niveles de competencia en matemáticas.

• Forme parejas de estudiantes que tengan distintos niveles de competencia en el idioma.

• Forme grupos pequeños de cuatro uniendo dos parejas de estudiantes.

De ser posible, intente formar las parejas con estudiantes que tengan la misma lengua materna.

Concluir

Reflexión final 5 min

Objetivo: Usar modelos visuales para determinar factores comunes y múltiplos comunes de pares de números

Use los planteamientos y las preguntas que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a complementar las respuestas de sus pares.

¿Qué es un factor común de dos números? Den un ejemplo.

Un factor común es un factor compartido por dos números. Por ejemplo, 2 es un factor de 6 y 2 es un factor de 10. Entonces, 2 es un factor común de 6 y 10.

¿Qué es un múltiplo común de dos números? Den un ejemplo.

Un múltiplo común es un múltiplo compartido por dos números. Por ejemplo, 12 es un múltiplo de 4 y 12 es un múltiplo de 6. Entonces, 12 es un múltiplo común de 4 y 6.

Describan cómo usaron los factores comunes para cubrir rectángulos con fichas cuadradas.

Las longitudes de los lados de las fichas cuadradas son factores comunes de la longitud y el ancho de los rectángulos.

Describan cómo usaron los múltiplos comunes para crear cuadrados con fichas rectangulares.

Las longitudes de los lados de los cuadrados son múltiplos comunes de la longitud y el ancho de las fichas rectangulares.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Factores y múltiplos

En esta lección:

• hallamos factores comunes de dos números;

• hallamos múltiplos comunes de dos números.

Ejemplos

1. Las dimensiones de una habitación rectangular son 18 pies por 12 pies.

18 ft

12 ft

Dos números enteros que se multiplican para formar un número dado se denominan par de factores de ese número. Un número es un factor del número dado si es un número entero en un par de factores. Por ejemplo, 5 y 2 son factores de 10 porque 5 × 2 = 10

Un múltiplo de un número dado es el producto cuando el número dado se multiplica por otro número. Por ejemplo, 30 es múltiplo de 10 porque 10 × 3 = 30

Al responder preguntas como las de las partes (a) y (b), considera dibujar los cuadrados en el rectángulo.

a. ¿Cuál es la longitud del lado, en pies, de la ficha cuadrada más grande que puede cubrir la habitación de forma completa?

18 ft 12 ft

La longitud del lado de la ficha cuadrada más grande que puede cubrir la habitación de forma completa es 6 pies porque 6 es el factor más grande que es común a ambas dimensiones de la habitación, 18 pies y 12 pies.

La longitud del lado de la ficha cuadrada más grande que puede cubrir la habitación de forma completa es 6 pies.

b. ¿Cuál es la longitud del lado, en pies, de otra ficha cuadrada que puede cubrir la habitación de forma completa?

La longitud del lado de otra ficha cuadrada que puede cubrir la habitación de forma completa es 3 pies.

2. Una ficha rectangular mide 15 pulgadas por 6 pulgadas.

Otros factores comunes de 18 y 12 son 1 2 y 3 Esto significa que, en este caso, las longitudes de los lados de las fichas cuadradas que pueden cubrir esta habitación de forma completa pueden ser 1 pie, 2 pies o 3 pies.

a. ¿Cuál es la longitud del lado, en pulgadas, del cuadrado más pequeño que se puede crear con fichas rectangulares de este tamaño? Traza un diagrama para respaldar tu respuesta.

30 in

6 in 6 in 6 in 6 in 6 in 15 in 15 in

30 in

Todas las posibles longitudes de los lados de un cuadrado que se puede crear deben ser múltiplos de 15 y de 6 porque el cuadrado se forma con fichas de 15 pulgadas por 6 pulgadas. La longitud del lado del cuadrado más pequeño que se puede crear con fichas de este tamaño es 30 pulgadas porque 30 es el número más pequeño que es múltiplo común de 15 y 6

La longitud del lado del cuadrado más pequeño que se puede crear es 30 pulgadas.

b. ¿Cuál es la longitud del lado, en pulgadas, de otro cuadrado que se puede crear con fichas rectangulares de este tamaño?

Ejemplo: La longitud del lado de otro cuadrado que se puede crear es 60 pulgadas.

Otra posible longitud del lado de un cuadrado que se puede crear es 60 pulgadas porque 60 es múltiplo tanto de 15 como de 6. Para hacer este cuadrado, se necesitan 4 filas de 10 fichas.

EUREKA MATH

Nombre

Fecha

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

En los problemas 6 a 8, enumera todos los factores comunes de los números dados.

1. Un rectángulo mide 12 pulgadas por 20 pulgadas. ¿De qué tamaño deben ser los cuadrados para cubrir el rectángulo de forma completa? Elige todas las opciones que correspondan.

12 in 20 in

A. 12 pulgadas por 12 pulgadas

B. 6 pulgadas por 6 pulgadas

C. 5 pulgadas por 5 pulgadas

D. 4 pulgadas por 4 pulgadas

E. 2 pulgadas por 2 pulgadas

En los problemas 2 a 5, enumera todos los factores del número. 2. 12 1, 2, 3, 4, 6, 12 3. 25 1, 5, 25 4. 30

, 2, 3, 5, 6, 10 15, 30 5. 37 1, 37

En los problemas 9 a 12, enumera seis múltiplos del número. 9. 3

Ejemplo: 3, 6, 9 12, 15, 18 10. 6

Ejemplo: 6, 12 18, 24, 30, 36

8

Ejemplo: 8, 16 24, 32, 40, 48

12

Ejemplo: 12 24, 36, 48, 60 72

En los problemas 13 a 15, enumera dos múltiplos comunes de los números dados.

13. 8 y 12

Ejemplo: 24 y 48

14. 6 y 12

Ejemplo: 12 y 24

15. 12 y 10

Ejemplo: 60 y 120

16. Un pasillo mide 3 pies por 9 pies. 3 ft 9 ft

a. ¿Cuál es la longitud del lado, en pies, de la ficha cuadrada más grande que puede cubrir el pasillo de forma completa?

La longitud del lado de la ficha cuadrada más grande que puede cubrir el pasillo de forma completa es 3 pies.

b. ¿Cuál es la longitud del lado, en pies, de otra ficha cuadrada que puede cubrir el pasillo de forma completa?

Ejemplo: La longitud del lado de otra ficha cuadrada que puede cubrir el pasillo de forma completa es 1 pie.

17. Un rectángulo mide 14 centímetros por 25 centímetros. Sara dice que el cuadrado más grande que puede cubrir el rectángulo de forma completa mide 1 centímetro por 1 centímetro. ¿Estás de acuerdo con Sara? Explica tu razonamiento.

Sí, estoy de acuerdo con Sara. El único factor común de 14 y 25 es 1

18. ¿De qué medida es el cuadrado que puedes crear con rectángulos que miden 12 pulgadas por 6 pulgadas? Elige todas las opciones que correspondan.

A. 12 pulgadas por 12 pulgadas

B. 24 pulgadas por 24 pulgadas

C. 36 pulgadas por 36 pulgadas

D. 6 pulgadas por 6 pulgadas

E. 2 pulgadas por 2 pulgadas

19. Para hacer una obra de arte, Ryan usa fichas rectangulares que miden 2 pulgadas por 7 pulgadas cada una. ¿Cuál es la longitud del lado, en pulgadas, del cuadrado más pequeño que Ryan puede crear con estas fichas rectangulares?

2 in 7 in

La longitud del lado del cuadrado más pequeño que Ryan puede crear es 14 pulgadas.

20. Un rectángulo mide 10 metros por 6 metros.

a. ¿Cuál es la longitud del lado, en metros, del cuadrado más pequeño que se puede crear con rectángulos de este tamaño?

La longitud del lado del cuadrado más pequeño que se puede crear es 30 metros.

b. ¿Cuál es la longitud del lado, en metros, de otro cuadrado que se puede crear con rectángulos de este tamaño?

Ejemplo: La longitud del lado de otro cuadrado que se puede crear es 60 metros.

c. Toby dice que no se puede determinar cuál es el cuadrado más grande que se puede crear con rectángulos de este tamaño. ¿Estás de acuerdo con Toby? Explica.

Sí, estoy de acuerdo con Toby. Podría seguir sumando más y más rectángulos para formar cuadrados más y más grandes.

Recuerda

En los problemas 21 a 24, multiplica. 21. 3 × 1

25. Una ballena azul pesa aproximadamente 200 toneladas. Solo se alimenta de pequeñas criaturas marinas llamadas kril. La ballena azul come todos los días el 2 % de su peso corporal. ¿Cuántas toneladas de kril come la ballena azul cada día? Explica tu razonamiento.

El 1 % de 200 toneladas es 2 toneladas.

El 2 % de 200 toneladas es 4 toneladas.

La ballena azul come aproximadamente 4 toneladas de kril cada día.

26. Empareja las expresiones con la potencia correcta de 10

10 × 10 × 10 104

10 × 10 × 10 × 10 103

10 × 10 102

Divisibilidad

Determinar si los números son divisibles entre otros números

¿Entre cuáles de los siguientes números es divisible el número 96? Elige todas las opciones que correspondan. Explica tu razonamiento para todas las opciones de respuesta.

A. 3

B. 4

C. 5

D. 6

E. 9

Ejemplo:

A. El número 96 es divisible entre 3 porque la suma de sus dígitos es 15, que es divisible entre 3

B. El número 96 es divisible entre 4. El número 80 es divisible entre 4 porque 4 × 20 = 80 Si contamos salteado de 4 en 4, llegamos a 84, 88, 92, 96

C. El número 96 no es divisible entre 5 porque no tiene un 0 o un 5 en la posición de las unidades.

D. El número 96 es divisible entre 6 porque es divisible tanto entre 2 como entre 3

E. El número 96 no es divisible entre 9. El número 90 es divisible entre 9 porque 9 × 10 = 90 El siguiente múltiplo de 9 es 99.

Vistazo a la lección

En esta lección, la clase trabaja en grupos para hacer conjeturas sobre la divisibilidad. Sus estudiantes defienden su razonamiento, expresan acuerdo o desacuerdo acerca de las conjeturas de sus pares y dan contraejemplos según sea necesario. Repasan las reglas de divisibilidad para 2, 5 y 10 y establecen reglas de divisibilidad para 3 y 6. Aprenden que pueden contar salteado como método general para determinar la divisibilidad entre otros números como 4, 7, 8 y 9.

Pregunta clave

• ¿Cómo podemos saber si un número es divisible entre otro número sin dividir los números?

Criterios de logro académico

6.Mód2.CLA12 Determinan el máximo común divisor de dos números enteros menores que o iguales a 100.

6.Mód2.CLA13 Determinan el mínimo común múltiplo de dos números enteros menores que o iguales a 12.

Nombre

Fecha

BOLETO DE SALIDA

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Divisibilidad entre 3

• Divisibilidad entre 6

• Divisibilidad entre otros números

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• No se necesita.

Fluidez

Conteo salteado

La clase cuenta salteado para hallar números desconocidos como preparación para determinar la divisibilidad.

Instrucciones: Cuenta salteado y completa los espacios.

Presentar

La clase analiza grupos de números y hace conjeturas sobre la divisibilidad.

Divida a sus estudiantes en grupos de 3. Muestre los diagramas A, B y C del problema 1. Indique a los grupos que asignen un diagrama a cada estudiante del grupo.

Cada diagrama representa una regla diferente. Los números dentro del círculo siguen la regla. Los números fuera del círculo no siguen la regla.

Reflexionen sobre las conclusiones que pueden sacar respecto de la ubicación de los números. Hagan una conjetura sobre la regla para el diagrama que les tocó y compártanla con el resto del grupo.

Si no están de acuerdo con una conjetura, proporcionen como contraejemplo un número que no siga la regla. Luego, trabajen en equipo para hacer otra conjetura sobre la regla.

Recorra el salón de clases y escuche las conjeturas de sus estudiantes. Preste atención al vocabulario que usan y a los contraejemplos que proporcionan si están en desacuerdo con una conjetura.

Apoyo para la comprensión del lenguaje

Para apoyar la comprensión de sus estudiantes de la palabra conjetura, dígales que una conjetura es una conclusión que se saca basándose en un patrón o en evidencias y razonamientos. Por ejemplo, pregunte qué conclusiones podrían sacar si se les mostrara la lista de números 2, 4, 6, y se les pidiera completar el espacio en blanco. Puede haber estudiantes que formulen la conjetura de que con 8 se completa el espacio en blanco porque hay un patrón de sumar 2.

Para apoyar la comprensión de sus estudiantes de la palabra contraejemplo, diga un enunciado como “el producto de cualquier número y 7 siempre es impar”. Luego, pregunte a sus estudiantes si están de acuerdo o en desacuerdo con el enunciado. Si están en desacuerdo, pídales que proporcionen un contraejemplo para demostrar que el enunciado es falso, tal como “el producto de 2 y 7 es par”.

1. Haz una conjetura sobre la regla de cada diagrama. Los números dentro del círculo siguen la regla.

Los números fuera del círculo no siguen la regla.

Diagrama A

Diagrama B

Diagrama C

Conjetura: Divisible entre 2

Conjetura: Divisible entre 5

Conjetura: Divisible entre 10

Cuando la mayoría de los grupos se haya puesto de acuerdo sobre una conjetura para cada diagrama, seleccione a diferentes estudiantes para que compartan sus conjeturas con la clase. Considere pedir a quienes hicieron variaciones de la misma conjetura que también las compartan. Por ejemplo, algunas variaciones de conjeturas para el diagrama A incluyen las siguientes:

• Los números dentro del círculo son pares.

• Los números dentro del círculo son divisibles entre 2.

• Los números dentro del círculo son múltiplos de 2.

• Los números dentro del círculo tienen un factor común de 2.

Si sus estudiantes no usan distintos términos de vocabulario cuando enuncian sus conjeturas, ofrezca variaciones que considere apropiadas. Luego, use los planteamientos y las preguntas que siguen para enfocar la conversación en la divisibilidad:

El número 150 está dentro de los círculos en los tres diagramas. ¿Realmente hace falta dividir el número 150 entre 2, 5 y 10 para saber si es divisible entre 2, 5 y 10? Expliquen.

No. El número 150 es par, entonces es divisible entre 2. El número 150 tiene el dígito 0 en la posición de las unidades, entonces es divisible entre 5 y 10.

Promoción de la práctica de las matemáticas

Cada estudiante construye argumentos viables y ofrece valoraciones sobre el razonamiento de otros y otras cuando determina si cierta afirmación, posiblemente una conjetura propia, es verdadera, cuando ofrece contraejemplos y cuando crea un argumento para justificar su afirmación.

Considere hacer las siguientes preguntas:

• ¿Qué preguntas pueden hacer al grupo para asegurarse de que comprendan las conjeturas de cada integrante?

• ¿La conjetura es verdadera? ¿Cómo lo saben?

• ¿Qué cambios le harían a su propia conjetura para que sea más precisa?

¿Qué dígito debe tener un número en la posición de las unidades para ser divisible entre 2 y 5?

Para ser divisible tanto entre 2 como entre 5, un número debe tener el dígito 0 en la posición de las unidades.

Si un número tiene el dígito 0 en la posición de las unidades, ¿entre qué otro número es divisible?

Si un número tiene el dígito 0 en la posición de las unidades, es divisible entre 10.

Los números que son divisibles tanto entre 2 como entre 5 son múltiplos comunes de 2 y 5. Los múltiplos comunes de 2 y 5 son múltiplos de 10. Entonces, todos los números que son divisibles tanto entre 2 como entre 5 también son divisibles entre 10.

Muestre los diagramas D, E y F.

Diagrama D

Diagrama E

Diagrama F

Invite a la clase a que se reúna y converse en parejas acerca de la siguiente pregunta:

Dado que los números dentro del círculo del diagrama D son divisibles entre 2, el número 432 está dentro del círculo del diagrama D. ¿Por qué el número 432 está dentro de los círculos de los diagramas E y F?

Hoy, determinaremos las reglas para los diagramas E y F. Aprenderemos estrategias para determinar si un número, como 432, es divisible entre otros números, sin usar la división.

Aprender

Divisibilidad entre 3

La clase establece y usa la regla de divisibilidad para 3.

Pida a sus estudiantes que vayan al problema 2. Muestre los bloques en base diez que representan el número 432.

¿Qué número representan los bloques? ¿Cómo lo saben?

Los bloques representan el número 432 porque hay 4 centenas, 3 decenas y 2 unidades.

Invite a la clase a trabajar en parejas para agrupar los bloques con el fin de determinar si 432 es divisible entre 3. Recorra el salón de clases mientras sus estudiantes trabajan. Observe las distintas formas en que eligen agrupar los bloques.

2. Agrupa los bloques para determinar si 432 es divisible entre 3. Dibuja y rotula tu trabajo para explicar tu razonamiento.

Ejemplo:

El número 432 es divisible entre 3.

Cuando la mayoría haya terminado, invite a diferentes estudiantes a compartir sus estrategias para agrupar los bloques, a fin de mostrar que 432 es divisible entre 3. Luego, muestre la imagen de los 432 bloques con las unidades separadas de las centenas y de las decenas.

Haga la siguiente pregunta para guiar la conversación:

¿Qué observan?

Hay una unidad separada de las centenas y de las decenas.

Dirija la atención de sus estudiantes a las 9 unidades. Considere usar diferentes colores para encerrar en un círculo las 4 unidades separadas de las centenas, las 3 unidades separadas de las decenas y las 2 unidades para hacer énfasis en la relación con los dígitos del número 432. Trace flechas desde cada dígito del número 432 hacia las unidades encerradas en un círculo, como se muestra. Reagrupe las 9 unidades y muestre que pueden dividirse en grupos de 3.

Nota para la enseñanza

La regla de divisibilidad para 9 es semejante a la regla de divisibilidad para 3. Un número es divisible entre 9 si y solo si la suma de sus dígitos es divisible entre 9. Si hay suficiente tiempo, pregunte a sus estudiantes si tener grupos de 99, grupos de 9 y 9 unidades ayuda a mostrar que 432 es divisible entre 9.

Luego, pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta:

Tenemos 4 grupos de 99, 3 grupos de 9 y 9 unidades. ¿De qué forma nos ayuda eso a mostrar que 432 es divisible entre 3?

Podemos dividir los grupos de 99, los grupos de 9 y las 9 unidades en grupos de 3 porque los números 99 y 9 son divisibles entre 3.

Use las preguntas que siguen como guía para que sus estudiantes determinen si otros números son divisibles entre 3:

Consideren el número 431, que tiene 4 grupos de 100, 3 grupos de 10 y 1 unidad. Si separáramos 1 unidad de cada una de las centenas y de cada una de las decenas, ¿qué tendríamos?

Tendríamos 4 grupos de 99, 3 grupos de 9 y 8 unidades.

¿431 es divisible entre 3? Expliquen.

No. El número 431 no es divisible entre 3. Los grupos de 99 y los grupos de 9 pueden dividirse en grupos de 3, pero las 8 unidades no pueden dividirse en grupos de 3.

Determinamos que 432 es divisible entre 3. Si contamos salteado de 3 en 3, el siguiente número divisible entre 3 es 435. ¿De qué forma separar 1 unidad de cada una de las centenas y de cada una de las decenas muestra que el número 435 es divisible entre 3?

Seguiríamos teniendo 4 grupos de 99 y 3 grupos de 9, pero tendríamos 12 unidades en lugar de 9 unidades. Como el número 12 puede dividirse en grupos de 3, 435 es divisible entre 3.

Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta:

¿Cómo podemos determinar si un número es divisible entre 3 sin tener que dividir el número entre 3? Hagan una conjetura.

Podemos sumar el número de unidades separadas de las centenas y de las decenas al número de unidades con el que comenzamos. Si la suma es divisible entre 3, entonces el número es divisible entre 3. Si la suma no es divisible entre 3, entonces el número no es divisible entre 3.

Luego, muestre la tabla de 100.

Dé tiempo a sus estudiantes para que analicen la tabla. Luego, pídales que se reúnan y conversen en parejas sobre lo que observan. Reúna a la clase y haga la siguiente pregunta:

¿Qué observan acerca de la tabla de 100?

Observo que los números en los cuadrados resaltados son múltiplos de 3. Observo que los números en los cuadrados que no están resaltados no son múltiplos de 3. Observo que las sumas de los dígitos de los números se muestran en azul. Observo que las sumas de los dígitos de los múltiplos de 3 también son múltiplos de 3.

Si la clase no observa que los números azules representan las sumas de los dígitos de los números o que los cuadrados resaltados muestran números y sumas de dígitos que son múltiplos de 3, señálelo.

¿De qué forma lo que vemos con las sumas de los dígitos de los números en la tabla de 100 se relaciona con lo que vimos cuando separamos y sumamos unidades con los bloques?

El dígito en la posición de las unidades nos indica con cuántas unidades comenzamos. Los dígitos restantes nos indican el número de unidades que se separan de cada una de las decenas, de las centenas y así sucesivamente. Sumar el número de unidades con las que comenzamos al número de unidades separadas de las decenas y de las centenas es como sumar los dígitos de un número.

Piensen en un número en la posición de los millares, las decenas de millar, las centenas de millar o incluso mayor. Si separamos unidades de los millares, de las decenas de millar y de las centenas de millar, tendríamos grupos de 999, grupos de 9,999 y grupos de 99,999. Todos esos grupos pueden dividirse en grupos de 3. Entonces, ¿cómo podrían determinar si un número grande es divisible entre 3?

Podemos simplemente sumar los dígitos y determinar si la suma es divisible entre 3.

¿Cómo podemos mejorar nuestra conjetura anterior sobre la manera de determinar si un número es divisible entre 3? Reúnanse y conversen en parejas.

Si la suma de los dígitos de un número es divisible entre 3, entonces el número es divisible entre 3. Si la suma de los dígitos de un número no es divisible entre 3, entonces el número no es divisible entre 3.

Divisibilidad entre 6

La clase establece la regla de divisibilidad para 6.

Pida a sus estudiantes que vuelvan a los grupos de 3. Muestre los diagramas D, E y F del problema 3.

Los números dentro del círculo del diagrama D son divisibles entre 2. ¿Entre qué números son divisibles los números dentro de los círculos de los diagramas E y F? ¿Cómo lo saben?

Todos los números dentro de los círculos de los diagramas E y F son divisibles entre 3 porque las sumas de sus dígitos son divisibles entre 3.

El número 432 está dentro de los círculos en los tres diagramas. ¿Los tres diagramas siguen la misma regla? ¿Cómo lo saben?

No. Los mismos números están fuera del círculo en un diagrama y dentro del círculo en otro diagrama; entonces, la regla para cada diagrama es diferente.

Diferenciación: Apoyo

Con el fin de brindar apoyo a quienes necesiten más práctica para determinar si un número es divisible entre 3, proporcione otro número, como 5,109, y pida a sus estudiantes que determinen si es divisible entre 3.

El número 5,109 es divisible entre 3

La suma de los dígitos de 5,109 es 15 y 15 es divisible entre 3

Diferenciación: Desafío

Como desafío, pida a sus estudiantes que escriban un número que cumpla con las siguientes condiciones, si es posible:

• Un número de 4 dígitos que sea divisible entre 3

Ejemplo: 2,070

• Un número de 3 dígitos que sea divisible entre 3 pero que no sea divisible entre 2

Ejemplo: 207

• Un número de 3 dígitos que no sea divisible entre 2 y que no sea divisible entre 3

Ejemplo: 209

Invite a sus estudiantes a trabajar en grupos para hacer conjeturas sobre las reglas para los diagramas E y F. Pídales que se preparen para justificar su razonamiento.

3. Haz una conjetura sobre la regla de cada diagrama. Los números dentro del círculo siguen la regla. Los números fuera del círculo no siguen la regla.

Diagrama D

E

F

Conjetura: Divisible entre 2

Conjetura: Divisible entre 3

Conjetura: Divisible entre 6

Cuando la mayoría de los grupos se haya puesto de acuerdo sobre una conjetura para cada diagrama, seleccione a diferentes estudiantes para que compartan sus conjeturas. Para poner a prueba las conjeturas de sus estudiantes, considere decirles números que correspondan a los siguientes lugares:

• Dentro de los círculos de los diagramas E y F, como 66 y 180

• Dentro del círculo del diagrama E pero fuera del círculo del diagrama F, como 63 y 183

• Fuera de los círculos de los diagramas E y F, como 62 y 184

Permita que sus estudiantes repasen las conjeturas que hicieron, si es necesario. Luego, use las preguntas y los planteamientos que siguen:

Anteriormente, razonamos que los números que son divisibles tanto entre 2 como entre 5 son divisibles entre 10. Los números dentro del círculo del diagrama F son divisibles entre 2 y 3.

¿Entre qué otros números son divisibles los números dentro del círculo del diagrama F?

Son divisibles entre 6.

¿Cómo podemos determinar si un número es divisible entre 6 sin tener que dividir el número entre 6? Hagan una conjetura.

Podemos determinar si el número es divisible tanto entre 2 como entre 3. Los números que son divisibles tanto entre 2 como entre 3 son divisibles entre 6.

Los números que son divisibles tanto entre 2 como entre 3 son múltiplos comunes de 2 y 3. Los múltiplos comunes de 2 y 3 son múltiplos de 6. Entonces, todos los números que son divisibles tanto entre 2 como entre 3 también son divisibles entre 6. Los números que son divisibles entre 2 pero no entre 3, o los números que son divisibles entre 3 pero no entre 2, no son divisibles entre 6.

Divisibilidad entre otros números

La clase aprende métodos para determinar la divisibilidad entre otros números.

Muestre la tabla donde se ven los métodos de Kayla y Blake para determinar si 134 es divisible entre 4.

Método de Kayla

Método

de Blake

120 es divisible entre 4 porque 4 × 30 = 120

120, 124, 128, 132, 136

Entonces, 134 no es divisible entre 4.

134 = 100 + 34

100 puede dividirse en grupos de 4, pero 34 no puede dividirse en grupos de 4

Entonces, 134 no es divisible entre 4

Kayla y Blake determinaron que 134 no es divisible entre 4. Expliquen de qué forma Kayla determinó que 134 no es divisible entre 4.

Kayla separó 134 en 100 y 34 y, luego, trató de dividir cada número en grupos de 4. Ella sabía que 100 puede dividirse en grupos de 4, pero descubrió que 34 no se puede dividir en grupos de 4.

Nota para la enseñanza

El método de Kayla se basa en la idea de la descomposición, que sus estudiantes aprendieron en grados anteriores. Kayla descompone 134 en la suma 100 + 34 y, luego, determina si cada número de la suma es divisible entre 4. Sus estudiantes continuarán trabajando con esta estrategia en el módulo 4 de 6.o grado cuando usen la propiedad distributiva para expresar una suma de dos números enteros con un factor común como un múltiplo de una suma de dos números enteros sin factor común. Por ejemplo, escribirán 100 + 36 como 4(25 + 9).

¿Pueden usar el método de Kayla para determinar si un número como 1,234 es divisible entre 4? ¿Por qué?

Sí. Podemos usar el método de Kayla. Sabemos que 1,234 = 1,200 + 34. El número 1,200 puede dividirse en grupos de 4, pero el número 34 no puede dividirse en grupos de 4. Entonces, 1,234 no es divisible entre 4.

Expliquen de qué manera Blake determinó que 134 no es divisible entre 4.

Primero, Blake mostró que 120 es múltiplo de 4. Luego, comenzó en 120, contó salteado de 4 en 4 y halló que 134 no es múltiplo de 4.

Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Podemos usar el método de conteo salteado de Blake para determinar si 134 es divisible entre 7? De ser así, ¿cómo?

Sí. Podemos hallar un número cercano a 134 que sepamos que es múltiplo de 7, como 140, y contar salteado para ver si llegamos a 134. Si empezamos en 140 y contamos salteado hacia atrás de 7 en 7, llegamos a 133. Entonces, 134 no es divisible entre 7.

Anime a sus estudiantes a compartir si comenzaron contando salteado desde otro número.

Podemos usar el conteo salteado para comprobar la divisibilidad entre 7. Primero, pensamos en algún número que sepamos que es múltiplo de 7. Luego, contamos salteado de 7 en 7 hasta llegar al número o pasarnos del número. Este método también funciona para determinar la divisibilidad entre otros números.

Pida a sus estudiantes que cuenten salteado para determinar si 134 es divisible entre otros números, como 8 y 9.

Luego, pida a sus estudiantes que vayan a los problemas 4 a 6 y que los completen en parejas. Recorra el salón de clases mientras sus estudiantes trabajan y brinde apoyo, según sea necesario.

4. Determina si el número 272 es divisible entre los siguientes números. Explica tu razonamiento.

a. 2

Sí. El número 272 es divisible entre 2 porque 272 es par.

b. 3

No. El número 272 no es divisible entre 3 porque la suma de sus dígitos es 11, que no es divisible entre 3.

c. 4

Sí. El número 272 es divisible entre 4. El número 280 es divisible entre 4 porque

4 × 70 = 280. Si contamos salteado hacia atrás de 4 en 4, llegamos a 272.

d. 6

No. El número 272 no es divisible entre 6 porque 272 no es divisible entre 3.

e. 8

Sí. El número 272 es divisible entre 8. El número 240 es divisible entre 8 porque

8 × 30 = 240. Si contamos salteado de 8 en 8, llegamos a 272

f. 9

No. El número 272 no es divisible entre 9. El número 270 es divisible entre 9 porque

9 × 30 = 270. Si contamos salteado de 9 en 9, el siguiente número divisible entre 9 es 279.

5. El Anciano ha estado contando desde el inicio de los tiempos. Recientemente, ha alcanzado el número 1,000,000,000,000,010.

¿Cuál es el siguiente número que contará el Anciano que es

a. divisible entre 2?

El siguiente número que es divisible entre 2 es 1,000,000,000,000,012.

b. divisible entre 5?

El siguiente número que es divisible entre 5 es 1,000,000,000,000,015

c. divisible entre 3?

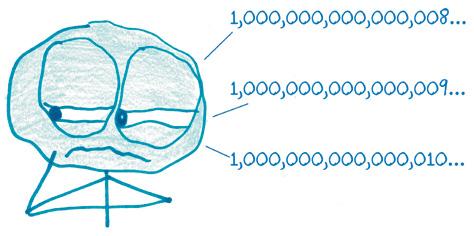
El siguiente número que es divisible entre 3 es 1,000,000,000,000,011.

d. divisible entre 6?

El siguiente número que es divisible entre 6 es 1,000,000,000,000,014.

Diferenciación: Apoyo

En el problema 5, considere pedir a sus estudiantes que primero respondan la pregunta para números más pequeños, como 110, 1,010 y 1,000,010.

Diferenciación: Desafío

En el problema 5, desafíe a sus estudiantes a determinar el siguiente número después de 1,000,000,000,000,010 que sea divisible entre más de un número, como los siguientes:

• Divisible entre 2 y 5

• Divisible entre 3 y 5

• Divisible entre 2, 3 y 5

6. Determina si los enunciados son verdaderos o falsos. Si son verdaderos, justifica tu razonamiento. Si son falsos, da un contraejemplo.

a. Si un número es divisible entre 9, entonces es divisible entre 3

El enunciado es verdadero. Si un número es divisible entre 9, entonces es múltiplo de 9. Como 9 es múltiplo de 3, todos los múltiplos de 9 también son múltiplos de 3, lo que significa que son divisibles entre 3.

b. Si un número es divisible entre 3, entonces es divisible entre 9.

El enunciado es falso. Un contraejemplo es el número 15, que es divisible entre 3, pero no es divisible entre 9.

Cuando la mayoría haya terminado, pida a diferentes estudiantes que compartan sus respuestas y razonamiento.

Concluir

Reflexión final 5 min

Objetivo: Determinar si los números son divisibles entre otros números

Use las preguntas que siguen para guiar una conversación acerca de la divisibilidad, los factores y los múltiplos. Anime a sus estudiantes a complementar las respuestas de sus pares.

¿Qué conjeturas hicieron hoy?

Hice la conjetura de que todos los números dentro del círculo del diagrama A son divisibles entre 2 porque todos son pares.

¿Cómo podemos saber si un número es divisible entre otro número sin tener que dividir?

Den algunos ejemplos.

Los dígitos del número pueden ayudarnos a determinar si el número es divisible entre otro número. Por ejemplo, si el último dígito es par, entonces el número es divisible entre 2. Si el último dígito es 0 o 5, entonces el número es divisible entre 5. Si el último dígito es 0, entonces el número es divisible entre 2, 5 y 10.

Si la suma de los dígitos de un número es divisible entre 3, entonces el número es divisible entre 3.

Además, si un número es divisible tanto entre 2 como entre 3, entonces es divisible entre 6.

También podemos contar salteado para hallar otros múltiplos de los números. Los múltiplos de un número son divisibles entre ese número.

¿El siguiente enunciado es verdadero o falso? Todos los números son divisibles entre sus múltiplos. Expliquen su razonamiento o den un contraejemplo.

Este enunciado es falso. No todos los números son divisibles entre sus múltiplos.

Ejemplo: El número 12 es un múltiplo de 4, pero 4 no es divisible entre 12.

¿El siguiente enunciado es verdadero o falso? Todos los números son divisibles entre sus factores. Expliquen su razonamiento o den un contraejemplo.

Este enunciado es verdadero. Todos los números son divisibles entre sus factores. Por ejemplo, 3 y 4 son un par de factores de 12. Entonces, 3 y 4 son factores de 12 y 12 ÷ 3 = 4 y 12 ÷ 4 = 3.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Divisibilidad

En esta lección:

• determinamos si un número es divisible entre otro número sin usar la división;

• hicimos conjeturas según patrones y evidencias, y buscamos contraejemplos para demostrar que las conjeturas son falsas.

Ejemplos

1. ¿352 es divisible entre 3? Explica cómo lo sabes.

Ejemplo: No. La suma de los dígitos de 352 es 10 porque 3 + 5 + 2 = 10. Como 10 no es divisible entre 3, 352 tampoco es divisible entre 3

2. ¿192 es divisible entre 6? Explica cómo lo sabes. Un número es divisible entre 6 si es divisible entre 2 y entre 3 Si un número no es divisible entre 2 y entre 3, entonces no es divisible entre 6

Ejemplo: Sí. La suma de los dígitos de 192 es 12 porque 1 + 9 + 2 = 12. Como 12 es divisible entre 3 192 también es divisible entre 3. Como 192 es par, es divisible entre 2. Como 192 es divisible entre 2 y entre 3, es divisible entre 6

3. ¿418 es divisible entre 4? Explica cómo lo sabes.

Ejemplo: No. Sé que 400 es divisible entre 4 Si cuento salteado de 4 en 4 desde 400, llego a 404, 408 412, 416 y 420. Como 418 está entre 416 y 420, no es divisible entre 4 El conteo salteado se puede usar para comprobar la divisibilidad de cualquier número. Piensa en un número que sea múltiplo de un número dado. En este caso, el múltiplo de 4 que está cerca de 418 es 400. Desde 400, cuenta salteado de 4 en 4 para comprobar si 418 también es divisible entre 4

4. ¿Cuáles de los siguientes números son divisibles entre 3 y entre 5? Elige todas las opciones que correspondan.

A. 30

B. 25

C. 215

D. 105 Los números 30, 105 y 510 son todos divisibles entre 3 y entre 5 Para confirmarlo, suma los dígitos del número. Si la suma es divisible entre 3, entonces el número es divisible entre 3 Si el número termina en 0 o en 5, entonces es divisible entre 5

E. 545

F. 510

5. Scott dice que si un número es divisible entre 3 y entre 6, entonces es divisible entre 9. ¿Estás o no estás de acuerdo con la conjetura de Scott? Si estás de acuerdo, explica tu razonamiento. Si no estás de acuerdo, da un contraejemplo.

Ejemplo: No estoy de acuerdo con la conjetura de Scott. Un contraejemplo es el número 24, que es divisible entre 3 y entre 6 pero no entre 9

Un contraejemplo muestra que un enunciado es falso. El número 24 es un contraejemplo del enunciado de Scott porque 24 es divisible entre 3 y entre 6 pero no es divisible entre 9

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. Ryan dice que si un número es divisible tanto entre 2 como entre 5, entonces también es divisible entre 10. ¿Estás de acuerdo con Ryan? Explica.

Sí. Si un número es divisible entre 5, entonces el dígito de las unidades es 0 o 5. Si el número también es divisible entre 2, entonces el dígito de las unidades debe ser 0. Si el dígito de las unidades es 0, entonces es divisible entre 10.

2. ¿5,652 es divisible entre 3? ¿Por qué?

Sí. El número 5,652 es divisible entre 3 porque la suma de los dígitos es 18, que es divisible entre 3

3. ¿5,652 es divisible entre 6? ¿Por qué?

Sí. El número 5,652 es divisible entre 6. El número es par, entonces es divisible entre 2. La suma de los dígitos es 18, entonces el número es divisible entre 3. Los números que son divisibles tanto entre 2 como entre 3 también son divisibles entre 6

4. ¿Entre cuáles de los siguientes números es divisible el número 132? Elige todas las opciones que correspondan.

5. ¿Entre cuáles de los siguientes números es divisible el número 132,850? Elige todas las opciones que correspondan.

A. 2

B. 3

C. 4

D. 5

E. 6

F. 10

6. Considera el número 2,353

a. Halla el siguiente número que sea divisible entre 2 2,354

b. Halla el siguiente número que sea divisible entre 3 2,355

c. Halla el siguiente número que sea divisible entre 6 2,358

En los problemas 7 a 11, determina si el número es divisible entre 2, si es divisible entre 3, si es divisible tanto entre 2 como entre 3 o si no es divisible ni entre 2 ni entre 3

7. 186

El número es divisible tanto entre 2 como entre 3.

8. 243

El número es divisible entre 3

9. 340

El número es divisible entre 2

10. 451

El número no es divisible ni entre 2 ni entre 3

11. 588

El número es divisible tanto entre 2 como entre 3

En los problemas 12 a 15, determina si el número es múltiplo de 4, múltiplo de 6 o múltiplo tanto de 4 como de 6

12. 168

El número es múltiplo tanto de 4 como de 6

13. 200

El número es múltiplo de 4

14. 300

El número es múltiplo tanto de 4 como de 6.

15. 450

El número es múltiplo de 6.

16. Escribe un número de 3 dígitos mayor que 700 que sea divisible tanto entre 2 como entre 3

Explica cómo sabes que este número es divisible tanto entre 2 como entre 3

Ejemplo: El número 720 es divisible tanto entre 2 como entre 3. El número es par, entonces es divisible entre 2. La suma de los dígitos es 9, que es divisible entre 3. Entonces, el número es divisible entre 3

17. ¿El número 714 es divisible entre 7? Explica tu razonamiento.

Sí. El número 714 es divisible entre 7 porque 714 es múltiplo de 7 Sé que 700 es múltiplo de 7

Si cuento salteado de 7 en 7 desde 700, llego a 714

18. Sasha dice que si un número es divisible tanto entre 2 como entre 4, entonces es divisible entre 8. ¿Estás o no estás de acuerdo con la conjetura de Sasha? Si estás de acuerdo, explica tu razonamiento. Si no estás de acuerdo, da un contraejemplo.

No estoy de acuerdo. Un contraejemplo es el número 20, que es divisible tanto entre 2 como entre 4, pero no es divisible entre 8

19. Ryan dice que si un número es divisible entre 12, entonces es divisible tanto entre 2 como entre 3. ¿Estás o no estás de acuerdo con la conjetura de Ryan? Si estás de acuerdo, explica tu razonamiento. Si no estás de acuerdo, da un contraejemplo.

Estoy de acuerdo. Un número que es divisible entre 12 es múltiplo de 12. Como 12 = 2 × 6, un múltiplo de 12 es múltiplo de 6. Como 6 = 2 × 3, un múltiplo de 6 es múltiplo tanto de 2 como de 3. Los múltiplos tanto de 2 como de 3 son divisibles tanto entre 2 como entre 3

Recuerda

En los problemas 20 a 23, multiplica.

24. Riley ahorró $60 para comprar un monopatín. Esta cantidad es el 30 % de lo que necesita ahorrar. ¿Cuál es la cantidad total de dinero que necesita ahorrar Riley para comprar un monopatín nuevo?

Ahorro de Riley (dólares)

Porcentaje

Riley necesita ahorrar un total de $200 para comprar un monopatín nuevo.

EUREKA MATH

En los problemas 25 a 27, describe el cambio en el valor posicional en la ecuación que se muestra.

25. 0.25 × 10 = 2.5

En 0.25 × 10, los dígitos 2 y 5 se desplazan una posición decimal hacia la izquierda. El producto es 2 unidades y 5 décimos.

26. 0.25 × 100 = 25

En 0.25 × 100, los dígitos 2 y 5 se desplazan dos posiciones decimales hacia la izquierda.

El producto es 2 decenas y 5 unidades.

27. 0.25 × 1,000 = 250

En 0.25 × 1,000, los dígitos 2 y 5 se desplazan tres posiciones decimales hacia la izquierda.

El producto es 2 centenas y 5 decenas.

3

El máximo común divisor

Determinar el máximo común divisor de dos números enteros menores que o iguales a 100

1. ¿Cuál es la factorización prima de 24?

24 = 2 × 2 × 2 × 3

2. ¿Cuál es la factorización prima de 60?

60 = 2 × 2 × 3 × 5

3. ¿Cuál es el máximo común divisor de 24 y 60? Explica.

24 = 2 × 2 × 2 × 3

60 = 2 × 2 × 3 × 5

El máximo común divisor de 24 y 60 es 12 porque 2 × 2 × 3 = 12

4. ¿Cuál es el máximo común divisor de 24 y 35? Explica.

24 = 2 × 2 × 2 × 3

35 = 5 × 7

El máximo común divisor de 24 y 35 es 1 porque 1 es su único factor común.

Vistazo a la lección

En esta lección, la clase enumera pares de factores de dos números para hallar su máximo común divisor. Mediante el trabajo en grupos, sus estudiantes escriben factorizaciones primas de números y reconocen que cada número tiene una factorización prima única. Usan las factorizaciones primas de dos números para hallar su máximo común divisor. En parejas, hallan el máximo común divisor en contextos del mundo real. En esta lección, se presentan los términos máximo común divisor y factorización prima.

Preguntas clave

• ¿Qué significa que un número sea el máximo común divisor de dos números?

• ¿Cómo se relacionan la factorización prima de un número y un par de factores de un número?

Criterio de logro académico

6.Mód2.CLA12 Determinan el máximo común divisor de dos números enteros menores que o iguales a 100.

Nombre

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Factores comunes

• Factorización prima y el máximo común divisor

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• tarjetas de Pares de factores (1 tarjeta por grupo de 3)

Preparación de la lección

• Haga copias de las tarjetas de Pares de factores y recórtelas.

Fluidez

Fracciones equivalentes

La clase escribe fracciones equivalentes como preparación para hallar el máximo común divisor.

Instrucciones: Escribe una fracción equivalente con la mayor unidad posible.

Nota para la enseñanza

Incentive el razonamiento flexible al momento de escribir fracciones equivalentes. Habrá quienes dividan el numerador y el denominador entre el máximo común divisor y quienes dividan entre varios factores comunes. Por ejemplo, en el problema 3, puede haber estudiantes que dividan el numerador y el denominador entre 30 y quienes dividan primero entre 10 y, luego, entre 3. Pida a sus estudiantes que compartan distintas estrategias.

Presentar

La clase busca patrones en un diagrama de números con figuras que representan las factorizaciones primas de los números.

Muestre el diagrama con el acertijo matemático con números.

Dé tiempo a sus estudiantes para que estudien el acertijo. Luego, reúna a la clase y haga las siguientes preguntas:

¿Qué observan?

Ejemplo:

Observo que hay muchas figuras de diferentes colores alrededor de los números. Observo los números 2 al 18. Observo que los números pares tienen círculos rojos. Observo que todos los números de la primera y la quinta columna tienen solo una figura. Observo que los números primos tienen solo una figura. Observo que todos los múltiplos de 3 tienen cuadrados azules.

¿Qué se preguntan?

Ejemplo:

Me pregunto por qué el número 1 no se muestra en el acertijo matemático. Me pregunto por qué algunos números tienen más de una figura. Me pregunto qué significan los diferentes colores. Me pregunto qué significan las diferentes figuras. Me pregunto por qué algunos números tienen varias figuras. Me pregunto por qué algunos números tienen la misma figura varias veces.

¿Qué patrones observan en las figuras? ¿Observan algunos números con figuras que tienen algo en común? Den algunos ejemplos.

Ejemplo:

Sí. Los números pares tienen al menos un círculo rojo. Cada múltiplo de 5 tiene un diamante rojo. Los números primos tienen solo una figura. Los números 2, 4, 8 y 16 solo tienen círculos rojos. Los números que son divisibles entre 3 tienen al menos un cuadrado azul.

¿Qué tienen en común los números 12 y 18?

Ambos números tienen al menos un círculo rojo y un cuadrado azul. Ambos números tienen tres figuras.

Pida a sus estudiantes que se reúnan y conversen en parejas acerca de la siguiente pregunta:

Si el patrón continúa, ¿qué tendrán en común los números 20 y 24?

Hoy, vamos a usar lo que sabemos sobre factores para hallar factores que sean comunes a un par de números.

Aprender

Factores comunes

La clase enumera pares de factores para identificar el máximo común divisor de dos números.

Pida a sus estudiantes que completen el problema 1 en parejas. Si necesitan ayuda para comenzar, recuérdeles los problemas de cubrir con fichas que resolvieron en las actividades interactivas en la lección 1. Pídales que repasen los problemas de la lección 1, según sea necesario.

1. ¿Cuál es la longitud del lado del cuadrado más grande que puede cubrir un rectángulo de 20 unidades por 24 unidades?

24 unidades

20 unidades

La longitud del lado del cuadrado más grande que puede cubrir el rectángulo es 4 unidades.

Cuando la mayoría haya terminado, confirme la respuesta. Pida a diferentes estudiantes que compartan su razonamiento. Destaque a quienes digan que 4 es el número entero más grande que es un factor común de 20 y 24. Luego, haga las siguientes preguntas:

¿Cómo saben que 3 no es factor de 20?

Sé que 3 no es factor de 20 porque 20 no es divisible entre 3.

¿Qué números enteros son factores de 20? ¿Cómo lo saben?

Los números enteros 1, 2, 4, 5, 10 y 20 son factores de 20 porque 1 × 20, 2 × 10 y 4 × 5 dan como resultado 20.

Diferenciación: Apoyo

Con el fin de brindar apoyo a sus estudiantes para hallar todos los pares de factores de un número, pídales que dibujen todas las matrices posibles, como lo hacían en 4.o grado. Luego, pídales que enumeren los factores y tracen una flecha desde un factor en un par hacia el otro factor del par, como se muestra para el número 18:

1 x 18 = 18

2 x 9 = 18

3 x 6 = 18

1, 2 3 6 9, 18 ,, ,

Cree una tabla para organizar los factores en pares de factores. Pida a sus estudiantes que copien la tabla debajo del problema 1 en sus libros. Comience enumerando el par de factores 1 y 20. Luego, use las preguntas que siguen y enumere los pares de factores restantes en orden:

Los factores 1 y 20 forman un par de factores de 20 porque 1 × 20 = 20. ¿Qué significa que dos números sean un par de factores?

Un par de factores es un par de números enteros con un número dado como producto.

¿Cuáles son los otros pares de factores de 20?

Los otros pares de factores son 2 y 10, y 4 y 5.

Si un factor entre 5 y 10 estuviera en la columna derecha de la tabla de pares de factores, entonces el otro factor de ese par tendría que estar entre 2 y 4. ¿Hay un factor de número entero de 20 que esté entre 5 y 10?

No. No hay factores de 20 entre 5 y 10. El único número entero entre 2 y 4 es 3, pero 3 no es un factor de 20.

¿Hay un factor de número entero de 20 que esté entre 10 y 20?

No. No hay factores de 20 entre 10 y 20 porque no hay factores de número entero entre 1 y 2.

Pida a sus estudiantes que trabajen en parejas para enumerar los pares de factores de 24 debajo del problema 1, como lo hicieron para el número 20. Anime a sus estudiantes a comenzar con el par de factores 1 y 24 y a enumerar los pares de factores restantes en orden.

Cuando la mayoría considere haber hallado todos los pares de factores, pida a sus estudiantes que compartan los pares de factores que enumeraron. Luego, use las preguntas y los planteamientos que siguen para continuar la conversación:

¿Cómo supieron que habían hallado todos los pares de factores de 24?

Supe que los había hallado todos cuando enumeré los pares de factores en orden y llegué al par de factores 4 y 6. El único número entero entre 4 y 6 es 5 y el número 5 no es factor de 24 porque 24 no es divisible entre 5.

Anteriormente, dijimos que el número 4 es el número más grande que es factor común de 20 y 24. ¿Cómo podríamos decir que se llama el número 4 para distinguirlo de los demás factores comunes de 20 y 24?

Podríamos decir que el número 4 es el mayor factor común de 20 y 24.

El número 4 es el máximo común divisor de 20 y 24. El máximo común divisor de dos números enteros que no sean ambos cero es el número entero mayor diferente de cero que es un factor de ambos números. El máximo común divisor suele abreviarse como MCD.

Apoyo para la comprensión del lenguaje

Con el fin de apoyar a sus estudiantes en la comprensión del nuevo término máximo común divisor, relaciónelo con lo que aprendieron sobre los factores comunes en lecciones anteriores. Dígales que la palabra máximo colocada antes de común divisor simplemente les indica que deben hallar el factor mayor que dos números tienen en común.

Para reforzar la comprensión del término, pida a sus estudiantes que resalten todos los factores comunes de 20 y 24. Pídales que encierren en un círculo y rotulen el número 4 como el máximo común divisor de 20 y 24.

¿Cómo podemos hallar el máximo común divisor, o MCD, de dos números?

Podemos enumerar los pares de factores de ambos números y hallar el número más grande que aparezca en ambas listas.

Sabemos que los números son divisibles entre sus factores. Entonces, ¿qué pueden concluir sobre dos números y su máximo común divisor?

El máximo común divisor de dos números es el número más grande entre el que se pueden dividir ambos números.

Invite a sus estudiantes a completar los problemas 2 a 4 en parejas. Recorra el salón de clases mientras sus estudiantes trabajan. Sugiera que hagan tablas para organizar los factores, según sea necesario.

2. ¿Cuál es el máximo común divisor de 36 y 48?

factores de 36: 1, 2, 3, 4, 6, 9, 12, 18, 36

factores de 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48

El máximo común divisor de 36 y 48 es 12.

3. ¿Cuál es el máximo común divisor de 36 y 55?

factores de 36: 1, 2, 3, 4, 6, 9, 12, 18, 36

factores de 55: 1, 5, 11, 55

El máximo común divisor de 36 y 55 es 1.

4. Riley tiene 28 bolígrafos y 14 libretas. Usa todos los bolígrafos y las libretas para hacer bolsitas de regalo iguales para las maestras y los maestros.

a. ¿Cuál es el mayor número de bolsitas de regalo iguales que puede hacer Riley?

factores de 28: 1, 2, 4, 7, 14, 28

factores de 14: 1, 2, 7, 14

El mayor número de bolsitas de regalo iguales que puede hacer Riley es 14

b. ¿Cuántos bolígrafos hay en cada bolsita? ¿Cuántas libretas?

28 ÷ 14 = 2

14 ÷ 14 = 1

En cada bolsita, hay 2 bolígrafos y 1 libreta.

Nota para la enseñanza

Pronunciar el término completo máximo común divisor, en lugar de usar el acrónimo MCD, constituye un apoyo para la comprensión de este término nuevo. Cuando solo se usa el acrónimo para referirse a este concepto nuevo, sus estudiantes pueden incurrir en un concepto erróneo común: confundir el máximo común divisor con el mínimo común múltiplo (mcm).

Diferenciación: Desafío

Como desafío, pida a sus estudiantes que hallen el máximo común divisor de tres números como 30, 42 y 72.

El máximo común divisor de 30, 42 y 72 es 6.

Cuando la mayoría haya terminado, pida a diferentes estudiantes que compartan sus respuestas y razonamiento. Luego, haga las siguientes preguntas para continuar la conversación:

En el problema 2, el máximo común divisor es menor que los dos números dados. ¿Puede ocurrir que el máximo común divisor de dos números sea mayor que alguno de los dos números? Expliquen.

No. El máximo común divisor nunca puede ser mayor que alguno de los dos números porque los factores de un número son menores que o iguales al número.

Lacy hace la conjetura de que algunos pares de números no tienen ningún factor común.

¿Están o no están de acuerdo con la conjetura de Lacy? Si están de acuerdo, expliquen su razonamiento. Si no están de acuerdo, den un contraejemplo.

No estoy de acuerdo. El número 1 es un factor común de todos los pares de números porque todo número es el producto de 1 y de sí mismo.

¿Todos los pares de números que no sean ambos cero tienen un máximo común divisor? Expliquen.

Sí. Todos los pares de números tienen 1 como factor común. Si un par de números no tienen otros factores comunes, el número 1 es el máximo común divisor.

¿Cómo hicieron para hallar el máximo común divisor y responder la pregunta del problema 4?

En el problema 4, se pregunta cuál es el mayor número de bolsitas de regalo iguales que podría hacer Riley. Como el problema decía que las bolsitas eran iguales, yo sabía que necesitaba hallar un número que fuera factor de 28 y 14 para que el número de bolígrafos y libretas fuera el mismo en cada bolsita de regalo. Como en el problema se pedía el mayor número de bolsitas iguales, sabía que necesitaba hallar el máximo común divisor.

Hallaron el máximo común divisor de cada par de números en los problemas 2 a 4. ¿Cuál es el mínimo común divisor de cada par de números en los problemas 2 a 4? ¿Cuál es el mínimo común divisor de todo par de números?

El mínimo común divisor de cada par de números en los problemas 2 a 4 es 1. El mínimo común divisor de todo par de números es 1.

Nota para la enseñanza

Un concepto erróneo común en que pueden incurrir sus estudiantes es usar las palabras mínimo común divisor cuando en realidad se refieren al máximo común divisor. Permítales reflexionar sobre cuál es el mínimo común divisor de dos números. Se darán cuenta de que el mínimo común divisor de todo par de números es 1. Esto puede ayudar a la clase a consolidar su comprensión acerca de la razón por la que enumeramos factores para hallar el máximo común divisor, en lugar del mínimo común divisor, de dos números.

Factorización prima y el máximo común divisor

La clase escribe la factorización prima de los números y usa un diagrama de Venn para hallar el máximo común divisor.

Muestre el diagrama de la sección Presentar con las figuras de números. Luego, haga las siguientes preguntas:

Describan los números primos que se muestran en el acertijo.

Cada número primo tiene solo una figura, que es una figura diferente a la de otros números primos. Cada una de las figuras de un número primo es de un color diferente.

¿Cómo se llaman los números del acertijo que tienen más de una figura?

Los números que tienen más de una figura se llaman números compuestos.

Si sus estudiantes no mencionan el término número compuesto, brinde la siguiente definición:

El número 14 es un ejemplo de un número compuesto. Un número compuesto es un número entero con factores distintos de 1 y el número en sí. Den algunos ejemplos de otros números compuestos.

Algunos ejemplos de otros números compuestos son 4, 6, 15, 16.

Un número primo tiene exactamente dos factores: 1 y sí mismo. ¿El número 1 es un número primo? ¿Por qué?

El número 1 no es un número primo porque no tiene dos factores.

Muestre todas las expresiones que tienen un producto de 14.

1 × 14

2 × 7

¿Qué expresión tiene solo números primos como factores?

2 × 7 solo tiene números primos como factores.

2 × 7 es la factorización prima de 14. La factorización prima de un número es el número escrito como un producto de números primos.

El número 14 tiene un par de factores que solo tiene números primos como factores, o factores primos. Hay números que no tienen un par de factores que tenga solo factores primos.

Nota para la enseñanza

El teorema fundamental de la aritmética sostiene que todo número entero a excepción de 1 tiene una factorización prima única, lo que significa que tiene exactamente una factorización prima.

El teorema proporciona una explicación de por qué el número 1 no es primo. Si el número 1 fuera primo, entonces los números ya no tendrían factorizaciones primas únicas. Por ejemplo:

10 = 2 × 5

10 = 2 × 5 × 1

10 = 2 × 5 × 1 × 1

Entonces, para que los números tengan una factorización prima única, el número 1 no puede ser primo.

Apoyo para la comprensión del lenguaje

Con el fin de dar apoyo a sus estudiantes en la comprensión del término factorización prima, considere pedirles que escriban la definición cerca de las tablas de los problemas 5 y 6.

Muestre todas las expresiones que tienen un producto de 28. 2 × 14 4 × 7

Consideren el número 28. ¿Cuál es la factorización prima de 28, 2 × 14 o 4 × 7? ¿Por qué?

Ninguna expresión es la factorización prima de 28 porque 14 y 4 no son números primos.

Para hallar la factorización prima de números como 28, podemos reescribir factores compuestos, como 14 y 4, como productos de factores primos.

Pida a la mitad de la clase que escriba 2 × 14 en una pizarra blanca individual. Pida a la otra mitad de la clase que escriba 4 × 7 en una pizarra blanca individual. Pida a sus estudiantes que trabajen en parejas para hallar la factorización prima de 28 reescribiendo el producto en sus pizarras blancas como un producto de números primos.

Cuando tengan una respuesta, pida a sus estudiantes que muestren sus pizarras blancas y compruebe las respuestas. Brinde retroalimentación para que puedan corregir sus errores. Cuando la totalidad de sus estudiantes tenga la misma factorización prima de 28, pídales que den una mirada a las pizarras blancas de sus pares para comprobar que la factorización prima de toda la clase, 28, es el producto de 2, 2 y 7.

Si un número tiene un par de factores que son solamente factores primos, entonces el par de factores es la factorización prima del número. Por ejemplo, 2 × 7 es la factorización prima de 14.

Si un número no tiene un par de factores que son solamente factores primos, podemos elegir uno de sus pares de factores y escribir todos los factores compuestos como producto de factores primos. Por ejemplo, 4 × 7 = 28, pero 4 no es primo. Podemos escribir 4 como 2 × 2 para obtener 2 × 2 × 7, la factorización prima de 28.

Invite a la clase a que se reúna y converse en parejas acerca de la siguiente pregunta:

¿Cuál es la factorización prima de un número primo como 7?

Permita que sus estudiantes compartan sus ideas. Luego, explíqueles que la factorización prima de un número primo es el número en sí mismo.

Después, divida a la clase en grupos de tres y distribuya una tarjeta de Pares de factores a cada grupo. Dé las siguientes instrucciones:

Con su grupo, reescriban el producto que se muestra en la tarjeta como un producto de números primos para determinar la factorización prima. Recuerden que 1 no es un número primo, por lo que deben usar factores que no sean 1.

Diferenciación: Apoyo

Como apoyo para que sus estudiantes identifiquen la factorización prima de un número, coloque en el salón de clases un ejemplo de problema con los pasos escritos, para que les sirva de referencia.

28 = 4 × 7

28 = 2 × 2 × 7

Elige cualquier par de factores para el número dado.

Escribe cada factor compuesto como un producto de uno de sus pares de factores.

28 = 2 × 2 × 7

Continúa hasta que solo queden los factores primos.

Recorra el salón de clases mientras sus estudiantes trabajan para asegurarse de que escriban la factorización prima correcta del número en la tarjeta de Pares de factores asignada.

Después de unos minutos, o cuando la mayoría de los grupos haya terminado, pida a alguien de cada grupo que tenga el número 36 que comparta el par de factores de sus tarjetas y la factorización prima de 36. Repita la actividad con los grupos que tengan el número 48. Mientras los grupos comparten, pida a la clase que escriba todos los pares de factores y la factorización prima en las tablas de los problemas 5 y 6.

5. Completa la tabla para el número 36.

Ejemplo:

Producto de par de factores Factorización prima

Promoción de la práctica de las matemáticas

Cada estudiante utiliza estructuras cuando aplica su comprensión de los pares de factores para determinar las factorizaciones primas de los números.

Considere hacer las siguientes preguntas:

• ¿De qué manera sus conocimientos sobre los pares de factores les ayudan a hallar la factorización prima de un número?

• ¿Pueden separar 2 × 18 en un producto de números primos para hallar la factorización prima?

• ¿De qué manera sus conocimientos sobre la propiedad conmutativa de la multiplicación les ayudan a determinar que la factorización prima de un número es la misma independientemente del par de factores inicial que se usó?

6. Completa la tabla para el número 48.

Ejemplo:

Producto de par de factores

Factorización prima

Resalte que, sin importar cuál sea el par de factores de un número con el que hayan comenzado, hay solo una factorización prima del número. Puede haber estudiantes que se pregunten si factorizaciones primas como 2 × 3 × 2 × 3 y 2 × 2 × 3 × 3 son equivalentes. Considérelo como una oportunidad para repasar la propiedad conmutativa de la multiplicación aprendida en grados anteriores. Si es necesario, pida a sus estudiantes que calculen los productos de los factores primos para confirmar que las factorizaciones primas son equivalentes.

Muestre las factorizaciones primas de 36 y 48.

¿Cuántos 2 tienen en común las factorizaciones primas? ¿Cuántos 3 tienen en común las factorizaciones primas?

Ambas factorizaciones primas tienen dos 2 y un 3.

Muestre las factorizaciones primas de 36 y 48 con los factores primos comunes resaltados en diferentes colores.

36 = 2 × 2 × 3 × 3

48 = 2 × 2 × 2 × 2 × 3

En el problema 2, hallamos que el máximo común divisor de 36 y 48 es 12. ¿Cuál es el producto de 2, 2 y 3?

El producto de 2, 2 y 3 es 12.

Muestre las factorizaciones primas de 36 y 48 junto a su máximo común divisor.

36 = 2 × 2 × 3 × 3

48 = 2 × 2 × 2 × 2 × 3

El máximo común divisor de 36 y 48: 2 × 2 × 3 = 12

Para hallar el máximo común divisor de dos números podemos escribir la factorización prima de cada número y multiplicar todos los factores primos que sean comunes a ambas factorizaciones primas.

DUA: Representación

Considere presentar la información en otro formato, como mostrar los factores primos de la factorización prima de cada número organizados en un diagrama de Venn. Pida a sus estudiantes que multipliquen los factores primos de cada círculo para verificar que los productos son 36 y 48. Pídales que confirmen que el producto de los factores primos en el sector donde los círculos se superponen es el máximo común divisor. 3 2 2 2 2 3

Factores primos de 36 Factores primos de 48

En la próxima lección, sus estudiantes usarán los diagramas de Venn como ayuda para identificar el mínimo común múltiplo de dos números.

Pida a sus estudiantes que vayan a los problemas 7 a 9 y que los completen en parejas. Permítales elegir el método que quieran usar para hallar el máximo común divisor. Recorra el salón de clases mientras sus estudiantes trabajan y brinde apoyo, según sea necesario.

7. ¿Cuál es el máximo común divisor de 26 y 39?

26 = 2 × 13

39 = 3 × 13

El máximo común divisor de 26 y 39 es 13

8. ¿Cuál es el máximo común divisor de 13 y 14?

13 = 13

14 = 2 × 7

El máximo común divisor de 13 y 14 es 1.

9. Un grupo de 18 estudiantes de sexto grado y 24 estudiantes de quinto grado participan en un juego de preguntas y respuestas. Se dividen en equipos.

a. La razón entre el número de estudiantes de sexto grado y el número de estudiantes de quinto grado debe ser igual en cada equipo. ¿Cuál es el mayor número de equipos que pueden participar en el juego de preguntas y respuestas?

El mayor número de equipos que pueden participar en el juego de preguntas y respuestas es 6.

b. ¿Cuál es el número de estudiantes de sexto grado que hay en cada equipo? ¿Y de quinto grado?

En cada equipo, hay 3 estudiantes de sexto grado y 4 estudiantes de quinto grado.

Cuando la mayoría haya terminado, confirme las respuestas. Luego, pida a sus estudiantes que respondan la siguiente pregunta:

Anteriormente, cuando enumeramos los pares de factores para identificar el máximo común divisor, llegamos a la conclusión de que el número 1 es un factor común de todo par de números. También llegamos a la conclusión de que si un par de números tienen 1 como el único factor común, entonces 1 es el máximo común divisor de los dos números.

Entonces, ¿por qué no escribimos el número 1 en las factorizaciones primas de los números?

El número 1 no es un número primo, entonces no lo escribimos como factor en una factorización prima.

Diferenciación: Apoyo

Puede haber estudiantes que incurran en el concepto erróneo de que números como 13 y 14 no tienen factores comunes porque no hay factores comunes en las factorizaciones primas de 13 y 14. Como apoyo, anime a ese grupo de estudiantes a enumerar todos los pares de factores de los números. Esto debería permitirles recordar que todos los pares de números tienen 1 como factor común.

Diferenciación: Desafío

Como desafío, pida a sus estudiantes que hallen el máximo común divisor de dos números más grandes, como 144 y 200

El máximo común divisor de 144 y 200 es 8.

Nota para la enseñanza

Los métodos que se muestran en esta lección son formas eficientes de hallar el máximo común divisor de dos números enteros diferentes de cero menores que o iguales a 100. Sin embargo, a veces, es necesario hallar el máximo común divisor de números más grandes. El algoritmo de Euclides es muy antiguo, data del 300 a. e. c. Ofrece un método más eficiente de calcular el máximo común divisor de números más grandes. Consulte la lección 5 o el recurso Las matemáticas en el pasado para aprender más acerca del algoritmo de Euclides.

Concluir

Reflexión final 5 min

Objetivo: Determinar el máximo común divisor de dos números enteros menores que o iguales a 100

Use las preguntas y los planteamientos que siguen para guiar una conversación acerca del máximo común divisor:

En el problema 1 de la lección 1, hallamos la longitud del lado de la ficha cuadrada más grande que puede cubrir un rectángulo. ¿Qué es lo que hallamos en realidad?

Hallamos el máximo común divisor de la longitud y el ancho del rectángulo.

¿Qué significa que un número sea el máximo común divisor de dos números?

El máximo común divisor de dos números es el número más grande que es un factor de ambos números. El máximo común divisor es el número más grande entre el que se pueden dividir dos números.

¿Cómo se relacionan la factorización prima de un número dado y un par de factores de ese número?

La factorización prima de un número dado es ese número representado como un producto de números primos. El par de factores de un número dado tiene un producto que es igual a ese número, pero los números del par de factores pueden ser o no ser primos.

Los números de todo par de factores de un número dado pueden escribirse como factores primos para hallar la factorización prima del número dado.

Piensen en los métodos que aprendieron para determinar el máximo común divisor. ¿Prefieren alguno de los métodos? Expliquen.

Ejemplo: Prefiero enumerar los pares de factores de ambos números porque puedo observar ambas listas para hallar el máximo común divisor. Puedo observar ambas listas y también hallar otros factores comunes, no solo el máximo común divisor.

Ejemplo: Prefiero escribir la factorización prima de cada número y multiplicar los factores primos comunes. Me gusta este método porque no tengo que enumerar todos los pares de factores para cada número. Solo necesito un par de factores para poder comenzar. Puedo seguir reescribiendo factores hasta que el producto solo tenga números primos como factores.

Boleto de salida

5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

El máximo común divisor

En esta lección:

• hallamos el máximo común divisor de dos números enteros;

• escribimos números como productos de sus números primos como factores.

Ejemplos

1. Enumera los pares de factores de cada número y halla el máximo común divisor de 45 y 75.

El máximo común divisor de 45 y 75 es 15. 45

Vocabulario

El máximo común divisor de dos números enteros que no sean ambos cero es el número entero mayor diferente de cero que es un factor de ambos números. El máximo común divisor suele abreviarse como MCD.

La factorización prima de un número es el número escrito como un producto de números primos como factores.

2. Escribe la factorización prima de cada número y halla el máximo común divisor de 48 y 60

48 = 2 × 2 × 2 × 2 × 3

60 = 2 × 2 × 3 × 5

El máximo común divisor de 48 y 60 es 12

48 = 2 × 2 × 2 × 2 × 3

60 = 2 × 2 × 3 × 5

Como 2, 2 y 3 son los factores primos comunes a ambas listas, multiplícalos para hallar el máximo común divisor, 12

Usa la factorización prima para hallar el máximo común divisor de dos números. Por ejemplo:

48 = 4 × 12 Elige cualquier par de factores para el número dado.

48 = 2 × 2 × 3 × 4 Escribe cada factor compuesto como una multiplicación de uno de sus pares de factores.

48 = 2 × 2 × 3 × 2 × 2 Continúa hasta que solo queden factores primos.

3. Escribe la factorización prima de cada número y halla el máximo común divisor de 27 y 32

27 = 3 × 3 × 3

32 = 2 × 2 × 2 × 2 × 2

El máximo común divisor de 27 y 32 es 1.

No hay números primos que sean factores comunes de 27 y 32 Entonces, 1 es el máximo común divisor porque es el único factor común.

Después de enumerar todos los pares de factores de ambos números, identifica los factores que aparecen en ambas listas. El factor mayor que aparece en ambas listas es el máximo común divisor. El número 15 es el máximo común divisor de 45 y 75

© Great Minds

4. En una clase de Matemáticas, hay 24 estudiantes. En una clase de Ciencias Sociales, hay 30 estudiantes. Las clases se juntaron y, luego, se dividieron en grupos para hacer una actividad.

a. La razón entre el número de estudiantes de Matemáticas y el número de estudiantes de Ciencias Sociales debe ser igual en cada grupo. ¿Cuál es el mayor número de grupos que se puede formar?

24 = 2 × 2 × 2 × 3

30 = 2 × 3 × 5

2 × 3 = 6

El mayor número de grupos que se puede formar es 6 Halla el máximo común divisor de 24 y 30 para determinar el mayor número de grupos que se puede formar con estudiantes de ambas clases.

b. ¿Cuál es el número de estudiantes de Matemáticas que hay en cada grupo? ¿Cuál es el número de estudiantes de Ciencias Sociales?

En cada grupo, hay 4 estudiantes de Matemáticas y 5 estudiantes de Ciencias Sociales.

En cada grupo, hay 4 estudiantes de Matemáticas, porque 24 ÷ 6 = 4. En cada grupo, hay 5 estudiantes de Ciencias Sociales, porque 30 ÷ 6 = 5 En cada grupo, hay un total de 9 estudiantes.

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

En los problemas 2 a 6, halla el máximo común divisor del par de números.

35 y 75

1. Considera los números 45 y 30

a. Completa las tablas para mostrar los pares de factores de 45 y 30.

b. Enumera todos los factores comunes de 45 y 30

1 3 5, 15

c. ¿Cuál es el máximo común divisor de 45 y 30? 15

d. Halla la factorización prima de 45 45 = 3 × 3 × 5

e. Halla la factorización prima de 30. 30 = 2 × 3 × 5

f. Explica cómo usar las factorizaciones primas para hallar el máximo común divisor de 45 y 30

El máximo común divisor de 45 y 30 es el producto de cada uno de sus factores primos comunes. Los números 45 y 30 tienen factores primos comunes de 3 y 5, entonces su máximo común divisor es 3 × 5 o 15 45 30

7. Toby ata cintas a los regalos. Tiene una cinta roja que mide 44 pulgadas de largo. Tiene una cinta azul que mide 33 pulgadas de largo. Quiere cortar ambas cintas en trozos que sean todos iguales en longitud y lo más largos posible. ¿De qué longitud debería cortar Toby cada trozo de cinta?

Toby debería cortar ambas cintas en trozos que midan 11 pulgadas de largo.

8. Un grupo de 20 estudiantes de séptimo grado y 24 estudiantes de sexto grado participan en un torneo de kickball. Se dividen en equipos.

a. La razón entre el número de estudiantes de séptimo grado y el número de estudiantes de sexto grado debe ser igual en cada equipo. ¿Cuál es el mayor número de equipos que se puede formar?

El mayor número de equipos que se puede formar es 4.

b. ¿Cuál es el número de estudiantes de séptimo grado que hay en cada equipo?

¿Y de sexto grado?

En cada equipo, hay 5 estudiantes de séptimo grado y 6 estudiantes de sexto grado.

9. La administradora de un hotel tiene 63 chocolates y 42 mentas. Usa todos los chocolates y las mentas con el fin de hacer bolsitas de bienvenida iguales para quienes se hospeden en el hotel.

a. ¿Cuál es el mayor número de bolsitas de bienvenida iguales que puede hacer la administradora?

El mayor número de bolsitas de bienvenida iguales que puede hacer es 21.

b. ¿Cuántos chocolates tiene cada bolsita de bienvenida? ¿Cuántas mentas?

Cada bolsita de bienvenida tiene 3 chocolates y 2 mentas.

10. Escribe dos números que sean mayores que 5 y tengan un máximo común divisor de 5.

Ejemplo: 10 y 15

Recuerda

En los problemas 11 a 14, multiplica.

15. Kelly tiene $80 Usa un cupón de 40 % de descuento para comprar una chaqueta que cuesta $75. Después de usar el cupón para comprar la chaqueta, ¿cuánto dinero le queda a Kelly?

A Kelly le quedan $35

16. Halla el cociente. Traza un modelo para respaldar tu respuesta.

de par de factores Factorización

Producto de par de factores Factorización prima

de par de factores

Producto de par de factores Factorización prima

de par de factores Factorización prima

Factorización prima

Producto de par de factores

Factorización prima

Producto de par de factores

Factorización prima

Producto de par de factores

Factorización prima

Producto de par de factores

Factorización prima

Producto de par de factores

Factorización prima

Producto de par de factores

= 4 × 9

Factorización prima

Producto de par de factores

Factorización prima

Producto de par de factores

El mínimo común múltiplo

Hallar el mínimo común múltiplo de dos números enteros menores que o iguales a 12

1. ¿Cuál es el mínimo común múltiplo de 3 y 7?

múltiplos de 3 3 6, 9, 12, 15, 18, 21

múltiplos de 7 7 14, 21

El mínimo común múltiplo de 3 y 7 es 21

2. ¿Cuál es el mínimo común múltiplo de 8 y 12?

múltiplos de 8 8 16, 24…

múltiplos de 12: 12, 24

El mínimo común múltiplo de 8 y 12 es 24.

3. ¿Cuál es el mínimo común múltiplo de 2 y 10?

múltiplos de 2 2 4, 6, 8, 10…

múltiplos de 10: 10, 20

El mínimo común múltiplo de 2 y 10 es 10.

Vistazo a la lección

Para comenzar la lección, sus estudiantes miran un video acerca de una situación que les lleva a hacer preguntas cuyas respuestas obtendrán tras hallar múltiplos comunes. Enumeran los múltiplos de dos números para identificar el mínimo común múltiplo. En parejas, sus estudiantes crean un diagrama de Venn con los factores primos de dos números. Se dan cuenta de que el mínimo común múltiplo de dos números es el producto de todos los factores primos que se muestran en el diagrama de Venn. En esta lección, se presenta el término mínimo común múltiplo.

Pregunta clave

• ¿Qué significa que un número sea el mínimo común múltiplo de dos números?

Criterio de logro académico

6.Mód2.CLA13 Determinan el mínimo común múltiplo de dos números enteros menores que o iguales a 12.

Nombre

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Múltiplos comunes

• Factorización prima y el mínimo común múltiplo

• Diagramas de Venn

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• dado de seis caras (dos por pareja de estudiantes)

Preparación de la lección

• No se necesita.

Fluidez

Identificar múltiplos

La clase identifica múltiplos de un número como preparación para hallar el mínimo común múltiplo.

Nota para la enseñanza

En lugar de administrar la actividad de Fluidez de esta lección, considere usar la Práctica veloz de Encerrar en un círculo los múltiplos. Puede encontrar instrucciones para administrar estas actividades en el recurso de la sección Fluidez.

Presentar

La clase explora un problema del mundo real que incluye múltiplos comunes.

Reproduzca el video El dilema de los perritos calientes para la clase. Anime a sus estudiantes a tomar notas en sus libros para el problema 1 mientras miran el video. Si es necesario, reproduzca el video varias veces. Pregunte quiénes quieren compartir con la clase las notas que tomaron sobre el video. Luego, guíe una conversación de toda la clase para incentivar la comprensión del problema.

¿De qué trataba el video?

El video trataba sobre una persona que compra perritos calientes y panes.

¿Por qué piensan que la persona fue y volvió varias veces en busca de más y más paquetes de perritos calientes y de panes?

El número de perritos calientes que hay en un paquete es diferente del número de panes que hay en un paquete. Ella quería un número igual, pero cada vez que tomaba más paquetes de un producto, tenía que tomar más paquetes del otro.

¿Qué preguntas de matemáticas podríamos hacer basándonos en el video?

¿Cuántas veces irá y vendrá en busca de perritos calientes y de panes?

¿Cuántos paquetes de perritos calientes y cuántos paquetes de panes puede comprar para obtener un número igual de perritos calientes y de panes?

¿Cuántos perritos calientes y panes necesita?

¿Cuánto tiene para gastar en perritos calientes y en panes?

¿Tendrá que comprar más perritos calientes y panes de los que necesita? De ser así, ¿cuántos más?

Si sus estudiantes no preguntan cuántos paquetes de perritos calientes y cuántos paquetes de panes puede comprar una persona para obtener un número igual de perritos calientes y de panes, plantéelo en forma de pregunta. Pida a sus estudiantes que escriban en sus libros la pregunta para el problema 2 y que trabajen en parejas para responderla. Recorra el salón de clases mientras trabajan y busque a quienes razonen acerca de los múltiplos comunes de 8 y 10. Si hay estudiantes que hallan una respuesta de forma rápida, pregúnteles si hay más números que podrían ser la respuesta a la pregunta.

Registra la información recopilada del video.

1. Notas del video:

Hay 10 perritos calientes en un paquete.

Hay 8 panes para perritos calientes en un paquete.

Tiene muchos paquetes de perritos calientes y de panes en su carrito de las compras al final del video.

2. Preguntas de matemáticas del video:

¿Cuántos paquetes de perritos calientes y cuántos paquetes de panes puede comprar para obtener un número igual de perritos calientes y de panes?

Ejemplo:

Perritos calientes: 10 × 4 = 40, 10 × 8 = 80, 10 × 12 = 120

Panes: 8 × 5 = 40, 8 × 10 = 80, 8 × 15 = 120

Puede comprar 4 paquetes de perritos calientes y 5 paquetes de panes para obtener 40 perritos calientes y 40 panes.

Puede comprar 8 paquetes de perritos calientes y 10 paquetes de panes para obtener 80 perritos calientes y 80 panes.

Puede comprar 12 paquetes de perritos calientes y 15 paquetes de panes para obtener 120 perritos calientes y 120 panes.

Después de varios minutos, vuelva a reunir a la clase. Seleccione a un grupo de estudiantes para que compartan sus respuestas y describan sus estrategias. Destaque a quienes hayan usado múltiplos comunes para hallar sus respuestas.

¿Ustedes querrían tener un número igual de perritos calientes y de panes? ¿Por qué?

Ejemplo: Sí. Yo querría tener un número igual de perritos calientes y de panes, para no desperdiciar nada.

¿Por qué querríamos saber cuál es el número menor de paquetes de perritos calientes y de paquetes de panes que podemos comprar para obtener un número igual de perritos calientes y de panes?

Podríamos querer saber el número menor de cada producto porque cuantos más perritos calientes y panes compremos, más dinero vamos a gastar.

Hoy, aprenderemos más sobre múltiplos comunes, diferentes maneras de hallarlos y cómo aplicarlos en contextos del mundo real.

Aprender

Múltiplos comunes

La clase enumera múltiplos para identificar el mínimo común múltiplo de dos números.

Empiece pidiendo a sus estudiantes que enumeren diez múltiplos de 8, comenzando desde 8 y contando salteado de 8 en 8. Luego, pídales que enumeren diez múltiplos de 10, comenzando en 10 y contando salteado de 10 en 10. Escriba los múltiplos en el pizarrón a medida que sus estudiantes los dicen, como se muestra:

• Múltiplos de 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80…

• Múltiplos de 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100…

¿Cuáles son dos múltiplos comunes de 8 y 10?

Dos múltiplos comunes de 8 y 10 son 40 y 80.

¿El número 800 es un múltiplo común de 8 y 10? ¿Cómo lo saben?

Sí. El número 800 es un múltiplo común de 8 y 10 porque 800 es divisible tanto entre 8 como entre 10.

¿Cuál es el número más pequeño de las listas de múltiplos que es múltiplo común de 8 y 10?

El número más pequeño que es múltiplo común de 8 y 10 es 40.

Apoyo para la comprensión del lenguaje

Con el fin de apoyar a sus estudiantes en la comprensión del nuevo término mínimo común múltiplo, relaciónelo con lo que aprendieron sobre los múltiplos comunes en lecciones anteriores. Dígales que la palabra mínimo colocada antes de común múltiplo simplemente les indica que deben hallar el múltiplo menor que dos números tienen en común.

A modo de refuerzo, pida a sus estudiantes que escriban múltiplos de 8 y 10, como se muestra. Pídales que resalten los múltiplos comunes y que encierren en un círculo y rotulen 40 como el mínimo común múltiplo.

Múltiplos de 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80... Mínimo común múltiplo

Múltiplos de 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100...

¿Cómo podríamos decir que se llama el número 40 para distinguirlo de los demás múltiplos comunes de 8 y 10?

Podríamos decir que es el menor múltiplo común de 8 y 10.

Decimos que el número 40 es el mínimo común múltiplo de 8 y 10. El mínimo común múltiplo de dos números enteros es el número entero más pequeño que es mayor que cero y que es un múltiplo de ambos números. El mínimo común múltiplo suele abreviarse como mcm.

¿Cómo podemos hallar el mínimo común múltiplo de dos números?

Podemos comenzar con los números dados y enumerar múltiplos de ambos números hasta hallar un número que aparezca en ambas listas.

Pida a sus estudiantes que completen los problemas 3 a 5 en parejas. Si necesitan ayuda para comenzar con el problema 5, recuérdeles los problemas de cubrir con fichas que resolvieron en la actividad interactiva en la lección 1. Pídales que repasen los problemas de la lección 1 si necesitan apoyo con el problema 5.

3. ¿Cuál es el mínimo común múltiplo de 3 y 5?

múltiplos de 3: 3, 6, 9, 12, 15…

múltiplos de 5: 5, 10, 15…

El mínimo común múltiplo de 3 y 5 es 15.

4. ¿Cuál es el mínimo común múltiplo de 4 y 8?

múltiplos de 4: 4, 8, 12…

múltiplos de 8: 8, 16, 24…

El mínimo común múltiplo de 4 y 8 es 8.

5. ¿Cuál es la longitud del lado del cuadrado más pequeño que puedes crear con fichas rectangulares que miden 6 unidades por 10 unidades cada una?

múltiplos de 6: 6, 12, 18, 24, 30…

múltiplos de 10: 10, 20, 30…

La longitud del lado del cuadrado más pequeño que puedo crear con fichas rectangulares que miden 6 unidades por 10 unidades cada una es 30 unidades.

Nota para la enseñanza

Pronunciar el término completo mínimo común múltiplo, en lugar de usar el acrónimo mcm, constituye un apoyo para la comprensión de este concepto nuevo. Cuando solo se usa el acrónimo para referirse a este concepto nuevo, sus estudiantes pueden incurrir en un concepto erróneo común: confundir el mínimo común múltiplo con el máximo común divisor.

Diferenciación: Desafío

Considere presentar a sus estudiantes los siguientes problemas a modo de desafío:

• Completen la tabla con números que cumplan las condiciones dadas en los encabezamientos de las filas y las columnas.

Múltiplo de 5 Divisible entre 3 Factor de 36

Múltiplo de 6

Primo

Factor de 60

• Como desafío adicional, pídales que rotulen los encabezamientos de las filas y las columnas de una tabla ya completada.

7 24 18 11 48 27 13 12 9

Cuando la mayoría haya terminado, confirme las respuestas. Luego, haga las siguientes preguntas:

¿Hay un número determinado de múltiplos que debemos enumerar para hallar el mínimo común múltiplo?

No. Podemos detenernos en cuanto aparece un múltiplo en ambas listas.

En el problema 3, ¿cuál es la relación entre 3 y 5 y su mínimo común múltiplo?

El mínimo común múltiplo de 3 y 5 es el producto de 3 y 5.

En el problema 4, ¿cómo se relacionan los números 8 y 4? ¿Qué observan acerca del mínimo común múltiplo de 8 y 4?

El número 8 es múltiplo de 4. El mínimo común múltiplo de 8 y 4 es 8, que es el mayor de los dos números.

Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para responder las preguntas y los planteamientos que siguen:

En los problemas 3 y 5, el mínimo común múltiplo de dos números es mayor que ambos números. En el problema 4, el mínimo común múltiplo de dos números es igual al mayor de los dos números.

¿Es posible que el mínimo común múltiplo de dos números sea menor que uno de los números? ¿Por qué?

No. El mínimo común múltiplo de dos números debe ser un múltiplo de ambos números. El múltiplo de un número dado debe ser mayor que o igual a ese número. Entonces, el mínimo común múltiplo de dos números debe ser mayor que o igual al mayor de los dos números.

¿Es posible determinar el máximo común múltiplo de dos números? ¿Por qué?

No. Es imposible determinar el máximo común múltiplo de dos números porque podemos seguir enumerando más y más múltiplos de cada número y hallar múltiplos comunes cada vez mayores.

Nota para la enseñanza

Un concepto erróneo común en que pueden incurrir sus estudiantes es usar las palabras máximo común múltiplo en lugar de mínimo común múltiplo. Permítales reflexionar sobre el máximo común múltiplo. Deberían darse cuenta de que es imposible determinar el máximo común múltiplo. Esto puede ayudar a la clase a consolidar su comprensión acerca de la razón por la que hallamos el mínimo común múltiplo, en lugar del máximo común múltiplo.

Factorización prima y el mínimo común múltiplo

La clase usa la factorización prima para identificar el mínimo común múltiplo de dos números.

Pida a sus estudiantes que completen el problema 6 en parejas.

6. Considera los números 11 y 12

a. ¿Cuál es el mínimo común múltiplo de 11 y 12?

múltiplos de 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132…

múltiplos de 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132…

El mínimo común múltiplo de 11 y 12 es 132.

b. Escribe las factorizaciones primas de 11 y 12

11 = 11

12 = 2 × 2 × 3

Cuando la mayoría haya terminado, confirme las respuestas.

¿Cuál es la relación entre 11 y 12 y su mínimo común múltiplo?

El mínimo común múltiplo de 11 y 12 es el producto de 11 y 12.

Muestre la factorización prima de 132.

132 = 2 × 2 × 3 × 11

¿Qué observan acerca de las factorizaciones primas de 11 y 12 y su mínimo común múltiplo?

Los factores del mínimo común múltiplo de 11 y 12 son los mismos que los factores de las factorizaciones primas de 11 y 12.

A continuación, muestre las factorizaciones primas de 6, 10 y 30.

6 = 2 × 3

10 = 2 × 5

30 = 2 × 3 × 5

En el problema 5, hallamos que el mínimo común múltiplo de 6 y 10 es 30. ¿Qué observan acerca de las factorizaciones primas de 6 y 10 y la factorización prima de su mínimo común múltiplo?

La factorización prima del mínimo común múltiplo de 6 y 10 tiene los mismos factores primos que 6 y 10, pero solo tiene uno de los 2.

Muestre las factorizaciones primas de 132 y 30.

Factor pr imo de 11

132 = 2 × 2 × 3 × 11

Factores primos de 12

Factores primos de 6

30 = 2 × 3 × 5

Factores primos de 10

La factorización prima de 132 incluye los números primos de las factorizaciones primas tanto de 11 como de 12. La factorización prima de 30 incluye los números primos de las factorizaciones primas tanto de 6 como de 10.

En la última lección, usamos la factorización prima para hallar el máximo común divisor de dos números. ¿Cuál es el máximo común divisor de 6 y 10? ¿Cómo lo saben?

El máximo común divisor de 6 y 10 es 2 porque tanto 6 como 10 tienen al número 2 como factor primo.

¿Cuál es el máximo común divisor de 11 y 12? ¿Cómo lo saben?

El máximo común divisor de 11 y 12 es 1 porque 11 y 12 no tienen factores primos en común.

¿Por qué 2 × 2 × 3 × 5 no es la factorización prima del mínimo común múltiplo de 6 y 10? 6 y 10 tienen 2 como factor común, entonces no necesitamos a 2 como factor adicional en la factorización prima del mínimo común múltiplo.

Promoción de la práctica de las matemáticas

Cada estudiante pone atención a la precisión cuando escribe las factorizaciones primas de dos números para determinar el mínimo común múltiplo.

Considere hacer las siguientes preguntas:

• Cuando usan las factorizaciones primas de dos números para hallar el mínimo común múltiplo, ¿en qué pasos deben prestar mayor atención? ¿Por qué?

• ¿Por qué es fácil cometer errores al momento de hallar el mínimo común múltiplo?

¿Por qué 2 × 3 × 11 no es la factorización prima del mínimo común múltiplo de 11 y 12?

2 × 3 × 11 no es múltiplo de 12. Entonces, 2 × 3 × 11 no es el mínimo común múltiplo de 11 y 12.

Para escribir la factorización prima del mínimo común múltiplo de dos números, como 6 y 10, comenzamos escribiendo la factorización prima de uno de los dos números.

Si comienzan con 2 × 3, ya tienen 2. ¿Qué factor necesitan todavía?

5

Si comienzan con 2 × 5, ya tienen 2. ¿Qué factor necesitan todavía?

3

Invite a sus estudiantes a completar el problema 7 en parejas. Recorra el salón de clases mientras trabajan y brinde apoyo, según sea necesario. Invite a quienes terminen primero a que lancen los dos dados de 6 caras nuevamente y repitan el problema 7 con números diferentes.

7. Lanza los dos dados de 6 caras dos veces. Si obtienes la misma suma la segunda vez, vuelve a lanzar los dados hasta obtener una suma diferente.

a. Enumera las dos sumas.

Ejemplo: 4, 11

b. ¿Cuál es el mínimo común múltiplo de los dos números que aparecen en la parte (a)?

4 = 2 × 2

11 = 11

2 × 2 × 11 = 44

El mínimo común múltiplo de 4 y 11 es 44.

Cuando la mayoría haya terminado, vuelva a reunir a la clase y, como parte de una reflexión final, pida a un grupo pequeño de estudiantes que compartan las sumas que sacaron y los mínimos comunes múltiplos de esas sumas.

Diagramas de Venn

La clase identifica el mínimo común múltiplo y el máximo común divisor de dos números usando un diagrama de Venn.

Muestre el diagrama donde aparecen los círculos separados para los factores primos de 6 y 10.

Nota para la enseñanza

Para el problema 7, si no tiene dos dados de 6 caras para que cada pareja de estudiantes pueda lanzarlos, considere usar un lanzador de dados en línea. Como alternativa, haga una lista de los números del 2 al 12 en tiras de papel y asigne números a cada pareja de estudiantes o pídales que elijan dos números al azar.

Diferenciación: Desafío

Como desafío adicional, pida a sus estudiantes que lancen los dados tres veces y que enumeren las tres sumas. Explique que deben lanzar los dados las veces que sean necesarias hasta tener tres sumas diferentes. Luego, pídales que hallen el mínimo común múltiplo de los tres números de su lista.

Ejemplo:

Lista de sumas: 6, 8, 5

El mínimo común múltiplo de 6, 8 y 5 es 120.

Factores primos de 6

Factores primos de 10

2 3 25

¿Qué representan los números dentro de los círculos?

Los números dentro de los círculos representan los factores primos de 6 y 10.

¿Cuál es el producto de los números dentro del círculo rojo? ¿Cuál es el producto de los números dentro del círculo azul?

El producto de los números dentro del círculo rojo es 6. El producto de los números dentro del círculo azul es 10.

Muestre el diagrama que ilustra la transición de los círculos separados para los factores primos de 6 y 10 al diagrama de Venn.

Factores primos de 6 Factores primos de 10

Factores primos de 6 Factores primos de 10

2 3 25

Rojo Azul

Rojo Azul Azul Rojo

Si sus estudiantes no están familiarizados con los diagramas de Venn, explique que el diagrama de Venn se puede usar para organizar factores. Señale que la parte más extrema del lado izquierdo y del derecho se usa para enumerar diferentes factores, y que la intersección de los círculos es para enumerar factores en común. Luego, use las preguntas y los planteamientos que siguen para que sus estudiantes ayuden a ubicar los factores en el diagrama de Venn, como se muestra:

Factores primos de 6 Factores primos de 10

5

Rojo

Azul

Necesitamos que el producto de los factores dentro del círculo rojo sea 6. Necesitamos que el producto de los factores dentro del círculo azul sea 10.

Comencemos con factores comunes. Los factores comunes van en la intersección de los dos círculos. ¿Qué factores tienen en común las factorizaciones primas de 6 y 10?

Tienen en común el factor 2.

Escriba el número 2 en la intersección de los círculos del diagrama de Venn.

El círculo rojo de los factores primos de 6 tiene el factor 2. ¿Qué necesita el círculo rojo para que el producto de los factores dentro del círculo rojo sea 6?

El círculo rojo necesita el factor 3.

¿Dónde va el factor 3? ¿Por qué?

El factor 3 va dentro del círculo rojo y no en la intersección de los círculos porque 3 no es factor de 10.

Escriba el número 3 dentro del círculo rojo pero fuera de la intersección de los círculos.

Nota para la enseñanza

Los círculos en los diagramas de Venn incluyen todos los factores primos de la factorización prima de cada número, como se muestra en el diagrama de Venn para 36 y 48. Esto incluye los factores primos que se repiten.

Factores primos de 36

Factores primos de 48

Rojo Azul

• El producto de los factores primos dentro del círculo rojo es 36

• El producto de los factores primos dentro del círculo azul es 48.

• El producto de los factores primos en la intersección es el máximo común divisor de 36 y 48.

• El producto de todos los factores primos en el diagrama de Venn es el mínimo común múltiplo.

El círculo azul de los factores primos de 10 tiene el factor 2. ¿Qué necesita el círculo azul para que el producto de los factores dentro del círculo azul sea 10?

El círculo azul necesita el factor 5.

¿Dónde va el factor 5? ¿Por qué?

El factor 5 va dentro del círculo azul y no en la intersección de los círculos porque 5 no es factor de 6.

Escriba el número 5 dentro del círculo azul pero fuera de la intersección de los círculos.

Hallamos que el mínimo común múltiplo de 6 y 10 es 30 y la factorización prima de 30 es 2 × 3 × 5. ¿Cómo se representa eso en el diagrama de Venn?

El diagrama de Venn muestra todos los factores primos de la factorización prima del mínimo común múltiplo.

Usamos las factorizaciones primas para mostrar que 2 es el máximo común divisor de 6 y 10. ¿Dónde ven el máximo común divisor en el diagrama de Venn?

El máximo común divisor está en la intersección de los círculos.

El producto de todos los factores en el diagrama de Venn es el mínimo común múltiplo. El producto de los números en la intersección de los círculos es el máximo común divisor.

Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para analizar las preguntas y los planteamientos que siguen:

Dividan el producto de 6 y 10 entre el máximo común divisor de 6 y 10. ¿Qué observan?

60 ÷ 2 = 30

Cuando dividimos el producto de 6 y 10, 60, entre el máximo común divisor de 6 y 10, 2, obtenemos el mínimo común múltiplo de 6 y 10, 30.

Podemos multiplicar los factores que están en los círculos separados para obtener los productos de 6 y 10. Cuando los círculos se trazan con una intersección para formar un diagrama de Venn, el número 2 se enumera solo una vez y no dos veces. Es como dividir el producto de los dos números entre el máximo común divisor.

Invite a sus estudiantes a completar los problemas 8 y 9 en parejas. Recorra el salón de clases mientras sus estudiantes trabajan. Observe los métodos que eligen para determinar el mínimo común múltiplo y brinde ayuda, según sea necesario.

8. El diagrama de Venn muestra los factores primos en las factorizaciones primas de 8 y 12.

Factores primos de 8 Factores primos de 12

a. Escribe las factorizaciones primas de 8 y 12.

8 = 2 × 2 × 2

12 = 2 × 2 × 3

b. ¿Cuál es el mínimo común múltiplo de 8 y 12?

2 × 2 × 2 × 3 = 24

El mínimo común múltiplo de 8 y 12 es 24

c. ¿Cuál es el máximo común divisor de 8 y 12?

2 × 2 = 4

El máximo común divisor de 8 y 12 es 4.

9. Cada paquete de perritos calientes trae 10 perritos calientes. Cada paquete de panes trae 8 panes.

a. Una persona quiere comprar un número igual de perritos calientes y de panes. ¿Cuál es el menor número de paquetes de perritos calientes y el menor número de paquetes de panes que debe comprar? ¿Cuántos perritos calientes y cuántos panes tendrá? Explica.

8 = 2 × 2 × 2

10 = 2 × 5

2 × 2 × 2 × 5 = 40

DUA: Acción y expresión

Ofrezca retroalimentación mientras sus estudiantes trabajan. Ofrezca a sus estudiantes un reconocimiento por los métodos que apliquen para determinar los mínimos comunes múltiplos. Haga las siguientes preguntas para brindar apoyo, según sea necesario:

• ¿Pueden escribir las factorizaciones primas de los números?

• ¿Pueden trazar un diagrama de Venn para organizar los factores primos de cada número?

• ¿Pueden enumerar los múltiplos de cada número?

El mínimo común múltiplo de 8 y 10 es 40.

40 ÷ 10 = 4

40 ÷ 8 = 5

Debe comprar 4 paquetes de perritos calientes y 5 paquetes de panes para obtener el mismo número de 40 perritos calientes y 40 panes.

b. El personal del comedor necesita comprar un número igual de perritos calientes y de panes para alimentar a 60 estudiantes. ¿Es posible comprar paquetes de perritos calientes y paquetes de panes para obtener exactamente 60 perritos calientes y 60 panes? Explica.

No. Si el personal compra 6 paquetes de perritos calientes, tendrá exactamente 60 perritos calientes. Si compran 7 paquetes de panes, solo tendrán 56 panes. Si compran 8 paquetes de panes, les sobrarán 4 panes.

c. Cada paquete de perritos calientes cuesta $3.50. Cada paquete de panes cuesta $2.00.

El personal del comedor gasta $48.00 cuando compra un número igual de perritos calientes y de panes. ¿Cuántos paquetes de perritos calientes y cuántos paquetes de panes compran?

40 perritos calientes: 3.5 × 4 = 14

40 panes: 2 × 5 = 10

Costo total de 40 perritos calientes y 40 panes: $24.00

48 ÷ 24 = 2

El costo total de 40 perritos calientes y 40 panes es $24.00. Como el personal del comedor gasta $48.00, compra el doble del número de perritos calientes y de panes. Entonces, el personal compra 8 paquetes de perritos calientes y 10 paquetes de panes para obtener el mismo número de 80 perritos calientes y 80 panes.

Cuando la mayoría haya terminado, elija a un grupo pequeño de estudiantes para que compartan sus respuestas y estrategias.

Diferenciación: Apoyo

Para apoyar a sus estudiantes en problemas con contexto, como el problema 9, considere proporcionar otro ejemplo de práctica:

• Leo corta el césped del jardín de dos de sus vecinos. Corta el césped de un jardín cada 10 días. Corta el césped del otro jardín cada 6 días. Hoy, Leo corta el césped de ambos jardines. ¿En cuántos días a partir de hoy Leo cortará el césped de ambos jardines el mismo día?

Leo cortará el césped de ambos jardines el mismo día en 30 días a partir de hoy.

Concluir

Reflexión final 5 min

Objetivo: Hallar el mínimo común múltiplo de dos números enteros menores que o iguales a 12

Use las siguientes preguntas para guiar una conversación acerca del mínimo común múltiplo de dos números. Anime a sus estudiantes a reformular o desarrollar las respuestas de sus pares.

¿Qué significa que un número sea el mínimo común múltiplo de dos números?

El mínimo común múltiplo de dos números es el número más pequeño que es un múltiplo de ambos números.

Aprendimos más de un método para determinar el mínimo común múltiplo de dos números. ¿Prefieren un método a otro? ¿Por qué?

Ejemplo: Me gustó enumerar múltiplos porque con solo mirar pude hallar el mínimo común múltiplo en ambas listas. También podría hallar otros múltiplos si lo necesitara.

Me gustó usar la factorización prima porque no tuve que escribir una lista larga de múltiplos. También podría hallar el máximo común divisor si lo necesitara.

¿Qué número es mayor: el máximo común divisor de dos números diferentes o el mínimo común múltiplo de los dos números? ¿Cómo lo saben?

El mínimo común múltiplo de dos números es mayor que el máximo común divisor de dos números.

Los múltiplos de los números son mayores que o iguales a los números. Los factores de los números son menores que o iguales a los números.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

El mínimo común múltiplo

En esta lección:

• hallamos el mínimo común múltiplo de dos números enteros.

Ejemplos

1. Enumera los múltiplos y halla el mínimo común múltiplo de 3 y 12

múltiplos de 3: 3 6 9 12…

múltiplos de 12 12, 24, 36, 48

El mínimo común múltiplo de 3 y 12 es 12

2. Usa la factorización prima para hallar el mínimo común múltiplo de 12 y 9.

12 = 2 × 2 × 3

9 = 3 × 3

36 = 2 × 2 × 3 × 3

Factores primos de 12

Factores primos de 9

2 2 3 3

Vocabulario

El mínimo común múltiplo de dos números enteros es el número entero más pequeño que es mayor que cero y que es un múltiplo de ambos números.

El mínimo común múltiplo suele abreviarse como mcm.

Enumera múltiplos de cada número, comenzando con los propios números. El múltiplo más pequeño de ambas listas es el mínimo común múltiplo.

La factorización prima de 36 incluye todos los factores primos de 12 y 9

Factores primos de 12

36 = 2 × 2 × 3 × 3

Factores primos de 9

El producto de todos los factores primos en el diagrama de Venn es el mínimo común múltiplo. El producto de los números en la intersección de los círculos es el máximo común divisor. El mínimo común múltiplo de 12 y 9 es 36

3. Toby anda en bicicleta cada 2 días. Sale a trotar cada 3 días. Si Toby anda en bicicleta y trota el 1 de enero, ¿cuál es la siguiente fecha en que andará en bicicleta y trotará en el mismo día?

Muestra tu trabajo.

múltiplos de 2: 2, 4, 6

múltiplos de 3: 3, 6

La siguiente fecha en que Toby andará en bicicleta y trotará es el 7 de enero.

Halla el mínimo común múltiplo de 2 y 3 para determinar cuántos días después Toby vuelve a andar en bicicleta y a trotar en el mismo día. El mínimo común múltiplo de 2 y 3 es 6 y 6 días después del 1 de enero es el 7 de enero.

EUREKA MATH

Great Minds

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

En los problemas 3 a 5, halla el mínimo común múltiplo de los números dados.

1. Considera los números 2 y 3

a. Escribe los siguientes 10 múltiplos de 2.

2 4 6 , 8 , 10 , 12 , 14 16 , 18 , 20 , 22 , 24

b. Escribe los siguientes 10 múltiplos de 3

3 6 9 , 12 , 15 , 18 , 21 24 , 27 , 30 , 33 , 36

c. Enumera cinco múltiplos comunes de 2 y 3

Ejemplo: 6, 12, 18 24, 30

d. Explica por qué el número 84 es un múltiplo común de 2 y 3

El número 84 es un múltiplo común de 2 y 3 porque es divisible tanto entre 2 como entre 3

e. ¿Cuál es el mínimo común múltiplo de 2 y 3?

6

2. Considera los números 12 y 10

a. Escribe la factorización prima de 12 12 = 2 × 2 × 3

b. Escribe la factorización prima de 10 10 = 2 × 5

c. ¿Cuál es el mínimo común múltiplo de 12 y 10? 60

6. Considera los números 9 y 12

a. ¿Cuál es el mínimo común múltiplo de 9 y 12?

b. ¿Cuál es el máximo común divisor de 9 y 12?

c. ¿Cuál es el producto de 9 y 12? 108

d. Divide el producto de 9 y 12 entre el máximo común divisor de 9 y 12. ¿Qué observas?

Observo que el cociente, 36, es el mínimo común múltiplo de 9 y 12

e. Divide el producto de 9 y 12 entre el mínimo común múltiplo de 9 y 12. ¿Qué observas?

Observo que el cociente, 3, es el máximo común divisor de 9 y 12.

f. Multiplica el mínimo común múltiplo de 9 y 12 por el máximo común divisor de 9 y 12 ¿Qué observas?

Observo que el producto, 108, es el producto de 9 y 12. © Great Minds

7. Tanto Riley como Tyler fueron al gimnasio el 1 de junio. Durante el mes de junio, Riley va al gimnasio cada 2 días y Tyler va cada 3 días. Si es necesario, usa el calendario para responder las partes (a) y (b).

c. Si cada paquete de vasos cuesta $1.50, ¿cuál es el costo de cada vaso?

El costo de cada vaso es $0.15

d. Ryan compra el menor número de paquetes para obtener un número igual de platos y vasos. ¿Cuál es la cantidad total que gasta Ryan?

Ryan gasta un total de $21 para comprar el menor número de paquetes y obtener el mismo número de platos y vasos.

10. Escribe dos números que tengan un máximo común divisor de 2 y un mínimo común múltiplo de 30

Ejemplo: 6 y 10

Recuerda

En los problemas 11 a 14, multiplica.

a. ¿Cuál es la siguiente fecha en que ambos van al gimnasio el mismo día?

La siguiente fecha en que ambos van al gimnasio es el 7 de junio.

b. Durante el mes de junio, ¿cuántos días fueron al gimnasio el mismo día?

Fueron al gimnasio el mismo día 5 días durante el mes de junio.

8. Un semáforo se pone en verde cada 3 minutos. Otro semáforo se pone en verde cada 4 minutos. Si ambos semáforos se ponen en verde a las 8:00 a. m., ¿cuál es la siguiente hora en que ambos se pondrán en verde?

Ambos se pondrán en verde a las 8:12 a. m.

9. Ryan compra platos y vasos para una fiesta. Hay 12 platos en un paquete y 10 vasos en un paquete.

a. Ryan quiere tener igual número de platos y vasos. ¿Cuál es el menor número de paquetes de platos y el menor número de paquetes de vasos que debe comprar Ryan?

Ryan debe comprar 5 paquetes de platos y 6 paquetes de vasos.

b. Si cada paquete de platos cuesta $2.40, ¿cuál es el costo de cada plato?

El costo de cada plato es $0.20

15. Un periódico encuesta a 325 personas. El periódico dice que el 76 % de las personas encuestadas usa redes sociales. ¿Cuál es el número de personas encuestadas que usa redes sociales?

247 personas encuestadas usan redes sociales.

16. El real es la moneda oficial de Brasil. En su viaje a Brasil, Lacy cambió sus 40 dólares estadounidenses por 120 reales brasileños. ¿Cuál es la tasa de cambio entre los dólares estadounidenses y los reales brasileños? Elige todas las opciones que correspondan.

A. 3 dólares por real

B. 3 reales por dólar

C. 1 3 de real por dólar

D. 1 3 de dólar por real

El algoritmo de Euclides (opcional)

Hallar el máximo común divisor de números grandes usando el algoritmo de Euclides

Hallar el mínimo común múltiplo de números grandes usando el máximo común divisor

Vistazo a la lección

Usa el algoritmo de Euclides para hallar el máximo común divisor de 48 y 128 Traza un diagrama o haz una tabla para respaldar tu respuesta.

Ejemplo:

de números Diferencia

En esta lección opcional, la clase trabaja en parejas para resolver un nuevo acertijo matemático. Sus estudiantes hallan la longitud del lado del cuadrado que queda tras retirar repetidamente los cuadrados más grandes de unos rectángulos. Usan el algoritmo de Euclides para calcular el máximo común divisor de dos números grandes y comparan ese método con la forma en que resolvieron el acertijo matemático. Luego, usan el máximo común divisor y un diagrama de Venn para calcular el mínimo común múltiplo de dos números grandes.

Preguntas clave

• ¿Por qué nos ayuda el algoritmo de Euclides a calcular el máximo común divisor de números grandes de manera más eficiente?

• ¿Por qué saber el máximo común divisor de dos números nos ayuda a hallar el mínimo común múltiplo de los dos números?

Criterios de logro académico

6.Mód2.CLA12 Determinan el máximo común divisor de dos números enteros menores que o iguales a 100.

6.Mód2.CLA13 Determinan el mínimo común múltiplo de dos números enteros menores que o iguales a 12.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Otro acertijo matemático con cuadrados

• El algoritmo de Euclides

• Conexión común

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• Repase el recurso Las matemáticas en el pasado como apoyo para la enseñanza de la sección Aprender.

Fluidez

Máximo común divisor y mínimo común múltiplo

La clase halla el máximo común divisor y el mínimo común múltiplo de pares de números como preparación para el uso del algoritmo de Euclides.

Instrucciones: Responde cada pregunta.

1. ¿Cuál es el máximo común divisor de 6 y 9?

2. ¿Cuál es el mínimo común múltiplo de 6 y 9?

3. ¿Cuál es el máximo común divisor de 6 y 12?

4. ¿Cuál es el mínimo común múltiplo de 6 y 12?

5. ¿Cuál es el máximo común divisor de 8 y 9?

6. ¿Cuál es el mínimo común múltiplo de 8 y 9?

Presentar

La clase determina el máximo común divisor y el mínimo común múltiplo de dos números.

Para comenzar, pida a sus estudiantes que completen el problema 1 de manera individual o en parejas. Recorra el salón de clases mientras trabajan y observe las estrategias que eligen para hallar el máximo común divisor y el mínimo común múltiplo.

1. Considera los números 60 y 100.

a. ¿Cuál es el máximo común divisor de 60 y 100?

60 = 2 × 2 × 3 × 5 100 = 2 × 2 × 5 × 5

Factores primos de 60

Factores primos de 10 0

El máximo común divisor de 60 y 100 es 20

El mínimo común múltiplo de 60 y 100 es 300. 5

2 × 2 × 5 = 20

b. ¿Cuál es el mínimo común múltiplo de 60 y 100?

3 × 2 × 2 × 5 × 5 = 300

Cuando la mayoría haya terminado, seleccione a diferentes estudiantes que hayan usado distintas estrategias para que compartan sus respuestas y estrategias. Luego, haga la siguiente pregunta:

¿Cuál es el máximo común divisor y el mínimo común múltiplo de 544 y 238?

Luego de aproximadamente 1 minuto, pida a sus estudiantes que dejen de trabajar, aun cuando la mayor parte de la clase no haya hallado todavía las respuestas. Pregúnteles si es posible determinar el máximo común divisor y el mínimo común múltiplo de números tan grandes. La mayoría de sus estudiantes deberían decir que es posible, pero que les llevaría más tiempo porque los números son muy grandes.

Lleva mucho tiempo hallar el máximo común divisor y el mínimo común múltiplo de dos números de 3 dígitos como 544 y 238. Piensen cuánto tiempo llevaría hallar el máximo común divisor y el mínimo común múltiplo de números grandes que tienen cientos de dígitos. Ni siquiera las computadoras pueden hallar rápidamente el máximo común divisor de números grandes con métodos de factorización. Es por esto que los números grandes, y sus productos, se usan con frecuencia como claves de seguridad para ayudar a los navegadores de Internet a mantener los datos seguros.

Hoy, aprenderemos cómo podemos hallar de forma más eficiente el máximo común divisor y el mínimo común múltiplo de números grandes, tales como 544 y 238.

Aprender

Otro acertijo matemático con cuadrados

La clase resuelve un acertijo matemático con cuadrados para determinar el máximo común divisor.

Muestre el rectángulo que mide 100 unidades por 60 unidades del problema 2. Use la pregunta que sigue para guiar a la clase durante la primera parte de la actividad:

Si el rectángulo mide 100 unidades por 60 unidades, ¿cuál es la longitud del lado de cada cuadrado de la cuadrícula?

La longitud del lado de cada cuadrado de la cuadrícula es 10 unidades.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta:

¿Cuál es el cuadrado más grande que podemos retirar de este rectángulo?

El cuadrado más grande que podemos retirar mide 60 unidades por 60 unidades.

Muestre el rectángulo con un cuadrado de 60 unidades por 60 unidades sombreado en azul.

60 unidades

100 unidades

Pida a sus estudiantes que sombreen un cuadrado que mida 60 unidades por 60 unidades en el rectángulo del problema 2, como se muestra.

¿Cuál es el tamaño del rectángulo que queda después de retirar un cuadrado que mide 60 unidades por 60 unidades?

Queda un rectángulo que mide 40 unidades por 60 unidades.

Muestre el diagrama donde se ve el rectángulo de 40 unidades por 60 unidades que queda después de retirar un cuadrado que mide 60 unidades por 60 unidades.

100 unidades 60 unidades 60 unidades

40 unidades

Pida a sus estudiantes que trabajen en parejas con el fin de completar los pasos que quedan para resolver el acertijo matemático del problema 2 y hallar la longitud del lado del cuadrado que queda.

2. Considera el rectángulo que mide 100 unidades por 60 unidades. Retira el cuadrado más grande. Luego, retira el cuadrado más grande posible del rectángulo que queda. Continúa retirando el cuadrado más grande posible de cada rectángulo que va quedando hasta que solo quede un cuadrado. ¿Cuál es la longitud del lado del cuadrado que queda?

60 unidades

100 unidades

La longitud del lado del cuadrado que queda es 20 unidades.

Cuando la mayoría haya terminado, use las preguntas que siguen para conversar sobre el problema 2:

¿Cuál es el tamaño del cuadrado que retiraron del rectángulo que medía 40 unidades por 60 unidades? ¿Cuál es el tamaño del rectángulo que quedó?

Retiramos un cuadrado que medía 40 unidades por 40 unidades. Quedó un rectángulo que medía 40 unidades por 20 unidades.

Muestre el diagrama donde se ve el rectángulo de 40 unidades por 20 unidades que queda después de retirar un cuadrado que mide 40 unidades por 40 unidades.

40 unidades 60 unidades 20 unidades

40 unidades

¿Cuál es el tamaño del cuadrado que retiraron del rectángulo que medía 40 unidades por 20 unidades? ¿Cuál es el tamaño del cuadrado que quedó?

Retiramos un cuadrado que medía 20 unidades por 20 unidades. Quedó un cuadrado que medía 20 unidades por 20 unidades.

Muestre el diagrama donde se ve el cuadrado de 20 unidades por 20 unidades que queda después de retirar un cuadrado que mide 20 unidades por 20 unidades.

20 unidades

40 unidades

20 unidades

20 unidades

La longitud del lado del cuadrado que queda después de que retiraron el cuadrado más grande es 20 unidades. ¿Cómo se relaciona el número 20 con los números 100 y 60?

20 es el máximo común divisor de 100 y 60.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Pueden hallar un cuadrado que mida más de 20 unidades por 20 unidades y pueda cubrir completamente un rectángulo de 100 unidades por 60 unidades? ¿Por qué?

No. Un cuadrado que mide 20 unidades por 20 unidades es el cuadrado más grande que puede cubrir un rectángulo de 100 unidades por 60 unidades porque 20 es el máximo común divisor de 100 y 60.

Muestre la tabla donde se ven los tamaños de los cuadrados retirados y los tamaños de los rectángulos que quedaron para el rectángulo de 100 unidades por 60 unidades.

Tamaño del rectángulo que queda

Tamaño del cuadrado retirado

Pida a sus estudiantes que analicen los números de la columna Tamaño del rectángulo que queda. Después de aproximadamente 1 minuto, pídales que se reúnan y conversen en parejas sobre lo que observan. Luego, haga las preguntas y los planteamientos que siguen:

¿Cuál de las dos longitudes de los lados de cada rectángulo será la longitud del lado del próximo rectángulo?

La longitud del lado más corta de cada rectángulo será la longitud del lado del próximo rectángulo.

Describan la medida de la otra longitud del lado del próximo rectángulo.

La medida de la otra longitud del lado del próximo rectángulo es la diferencia entre las medidas de las longitudes de los lados del rectángulo anterior.

Haga referencia a números específicos de la tabla para resumir el patrón.

La medida de una longitud del lado del próximo rectángulo es la diferencia entre las medidas de las longitudes de los lados del rectángulo anterior. La medida de la otra longitud del lado del próximo rectángulo es la longitud del lado más corta del rectángulo anterior.

Pida a sus estudiantes que completen el problema 3 en parejas.

3. Considera el rectángulo.

240 unidades

180 unidades

a. Retira el cuadrado más grande. Continúa retirando el cuadrado más grande posible de cada rectángulo que va quedando hasta que solo quede un cuadrado. Completa la tabla para mostrar el tamaño de los cuadrados retirados, el tamaño de los rectángulos que fueron quedando y el tamaño del cuadrado final que queda.

Tamaño del rectángulo que queda

Tamaño del cuadrado retirado

240 por 180 180 por 180

180 por 60

120 por 60

60 por 60

por 60

por 60

b. ¿Cuál es la longitud del lado del cuadrado que queda? ¿Cuál es el máximo común divisor de 240 y 180?

La longitud del lado del cuadrado que queda es 60 unidades. El máximo común divisor de 240 y 180 es 60.

Diferenciación: Apoyo

Para apoyar a sus estudiantes a determinar el tamaño del cuadrado que se debe retirar o el tamaño del rectángulo que queda, considere pedirles que dibujen el rectángulo en papel cuadriculado. Pídales que determinen la longitud del lado de cada cuadrado en la cuadrícula, como 10 unidades, para que puedan dibujar el rectángulo con más precisión.

Diferenciación: Desafío

Desafíe a sus estudiantes pidiéndoles que consideren un rectángulo que mide 660 unidades por 840 unidades, pero no proporcione el rectángulo. Pídales que determinen el máximo común divisor de 660 y 840 completando una tabla como la del problema 3 que muestra el tamaño de los cuadrados retirados, el tamaño de los rectángulos que fueron quedando y el tamaño del último cuadrado que queda.

El máximo común divisor de 660 y 840 es 60.

Cuando la mayoría haya completado los problemas, reúna a la clase y seleccione a algunas parejas para que compartan sus respuestas.

El algoritmo de Euclides

La clase usa el algoritmo de Euclides para calcular el máximo común divisor de dos números.

Para comenzar, comparta algo de la historia del algoritmo de Euclides. El proceso que usamos para resolver los acertijos matemáticos con cuadrados de los problemas 2 y 3 es una de las formas en que se puede aplicar del algoritmo de Euclides. El algoritmo de Euclides es un proceso que da como resultado el máximo común divisor de dos números grandes. Data de alrededor del año 300 a. e. c., mucho antes de que aparecieran las calculadoras o las computadoras. El algoritmo de Euclides se llama así por el experto en matemáticas griego Euclides, aunque también fue descubierto por las expertas y los expertos en matemáticas de China aproximadamente en la misma época.

Muestre las tablas donde se ven los pasos del acertijo matemático con cuadrados y del algoritmo de Euclides. Diga a sus estudiantes que en una de las tablas se muestran los pasos del acertijo matemático con cuadrados que comienzan con un rectángulo cuyas medidas son 100 unidades por 60 unidades, y en la otra tabla se muestran los pasos del algoritmo de Euclides, que comienzan con los números 100 y 60.

Pasos del acertijo matemático con cuadrados

Tamaño del rectángulo que queda Tamaño del cuadrado retirado

100 por 60 60 por 60

60 por 40 40 por 40

40 por 20 20 por 20

20 por 20

Las

matemáticas en el pasado

El recurso Las matemáticas en el pasado incluye más información sobre el algoritmo de Euclides, sus aplicaciones y su historia. En el recurso Las matemáticas en el pasado, el algoritmo de Euclides se aplica a dos segmentos de recta, de forma similar a la manera en que se aplica al acertijo matemático con cuadrados en esta lección.

238 238238 68 × ×

Si hay estudiantes que muestran interés en saber más sobre el algoritmo de Euclides y su origen, incorpore otras actividades del recurso Las matemáticas en el pasado.

Pasos del algoritmo de Euclides

de números

y 20

Promoción de la práctica de las matemáticas

Cada estudiante reconoce y utiliza estructuras cuando aplica su comprensión sobre retirar cuadrados de un rectángulo para desarrollar y entender el algoritmo de Euclides.

Considere hacer las siguientes preguntas:

• ¿Cómo se relacionan el acertijo matemático con cuadrados y el algoritmo de Euclides?

¿De qué manera eso puede ser de ayuda para hallar el máximo común divisor de dos números?

• ¿En qué se parece el problema a los acertijos matemáticos con cuadrados que resolvieron antes?

Dé 1 minuto a sus estudiantes para que comparen los pasos de cada proceso. Pídales que conversen en parejas sobre lo que observan. Luego, haga la siguiente pregunta:

¿Qué observan acerca de los pasos en el acertijo matemático con cuadrados y en el algoritmo de Euclides?

Ejemplo: Ambos comienzan con los números 100 y 60. Ambos terminan con los números 20 y 20, y el número 20 es el máximo común divisor de 100 y 60. Los números del próximo paso incluyen el número más pequeño del paso anterior y la diferencia entre el número más grande y el más pequeño del paso anterior.

Pida a sus estudiantes que vayan al problema 4 y que lo completen en parejas. Si es necesario, continúe mostrando las dos tablas a modo de ayuda.

4. Usa el algoritmo de Euclides para hallar el máximo común divisor de 396 y 540. Escribe los pares de números y sus diferencias en cada paso restante del algoritmo para completar la tabla.

Par de números

El máximo común divisor de 396 y 540 es 36

DUA: Acción y expresión

Según sea necesario, considere exhibir los pasos del algoritmo de Euclides en el salón de clases para que sus estudiantes los tengan de referencia.

1. Ordena los dos números de mayor a menor.

2. Para hallar su diferencia, resta el número menor del número mayor.

3. Quédate con el menor de los dos números. Descarta el mayor de los dos números.

4. Usa el menor de los dos números y la diferencia para formar un nuevo par de números.

5. Repite hasta que los dos números sean el mismo.

Diferenciación: Apoyo

Para apoyar a sus estudiantes en el uso del algoritmo de Euclides en el problema 4, pídales que dibujen un rectángulo rotulado con las dimensiones 396 unidades y 540 unidades. Anime a sus estudiantes a usar primero el mismo proceso que usaron para los acertijos matemáticos con cuadrados de los problemas 2 y 3 y, luego, a completar la tabla del problema 4.

Diferenciación: Desafío

Desafíe a sus estudiantes pidiéndoles que usen uno de los métodos que aprendieron en lecciones anteriores para confirmar que el máximo común divisor de 396 y 540 es 36.

Cuando la mayoría haya completado el problema, confirme que 36 es el máximo común divisor de 396 y 540.

Conexión común

La clase usa el máximo común divisor para hallar el mínimo común múltiplo de dos números.

Muestre los círculos separados para los factores de 396 y los factores de 540. Factores de 396 Factores de 540

Señale que los rótulos de los círculos indican que cualquier factor de los números dados podría ir en los círculos, no solo factores primos; sin embargo, el producto de los factores en cada círculo debe ser igual a cada número dado. Escriba el número 36 en cada círculo y haga la siguiente pregunta:

¿Cómo sabemos que 36 es un factor de cada número?

Sabemos que 36 es un factor de cada número porque es el máximo común divisor de los dos números.

Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para analizar las preguntas y los planteamientos que siguen:

Como 36 es el máximo común divisor de 396 y 540, el número 36 es uno de los factores en un par de factores de 396 y uno de los factores en un par de factores de 540.

¿Podemos hallar el otro factor en cada uno de estos dos pares de factores? ¿Por qué?

Sí. Podemos dividir 396 entre 36 y podemos dividir 540 entre 36.

Nota para la enseñanza

En 5.o grado, la clase multiplicó con fluidez números enteros de varios dígitos usando el algoritmo estándar. Sus estudiantes también hallaron cocientes de números enteros para números enteros con dividendos de hasta cuatro dígitos y divisores de dos dígitos. En los temas D a F del módulo 2 de 6.o grado, adquieren fluidez para hallar los productos y los cocientes de números de varios dígitos usando el algoritmo estándar para cada operación.

Según sea necesario, permita que sus estudiantes usen calculadoras para dividir tanto 396 como 540 entre 36. Escriba los cocientes en los círculos correctos. Luego, muestre la transición entre los círculos separados y el diagrama de Venn.

DUA: Acción y expresión

Cuando sus estudiantes deban multiplicar y dividir números grandes, y para facilitar la flexibilidad en la expresión del aprendizaje, permítales usar calculadoras a modo de apoyo según sea necesario.

En la última lección, ¿dónde hallamos el máximo común divisor de dos números en un diagrama de Venn?

El producto de los factores en la intersección es el máximo común divisor de los dos números.

En este caso, hay solo un número en la intersección de los dos círculos, entonces el máximo común divisor de 396 y 540 es 36.

¿Cómo podemos usar los factores del diagrama de Venn para hallar el mínimo común múltiplo de 396 y 540? ¿Cuál es el mínimo común múltiplo de 396 y 540?

Podemos multiplicar todos los factores del diagrama de Venn para hallar el mínimo común múltiplo. Sabemos que 11 × 36 = 396. Entonces, podemos multiplicar 396 por 15 y hallamos que el mínimo común múltiplo de 396 y 540 es 5,940. También sabemos que 15 × 36 = 540. Entonces, podemos multiplicar 540 por 11 y hallamos que el mínimo común múltiplo de 396 y 540 es 5,940.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta. Anime a sus estudiantes a complementar las respuestas de sus pares.

En la última lección, vimos que podemos dividir el producto de dos números entre su máximo común divisor para obtener su mínimo común múltiplo. ¿De qué forma la transición entre los círculos separados y el diagrama de Venn nos muestra por qué funciona esto?

Nota para la enseñanza

En la lección anterior, sus estudiantes aprendieron que pueden hallar el mínimo común múltiplo de dos números al dividir su producto entre su máximo común divisor. En esta lección, habrá quienes prefieran usar ese método para hallar el mínimo común múltiplo para los números 396 y 540, como se muestra:

396 × 540 = 213,840

213,840 ÷ 36 = 5,940

El mínimo común múltiplo de 396 y 540 es 5,940.

El producto de todos los factores en los círculos separados es igual al producto de 396 y 540. Como todos los factores en la intersección de los círculos del diagrama de Venn son factores de ambos números, escribimos el máximo común divisor, 36, una sola vez en la parte superpuesta en lugar de escribirlo dos veces. Es como dividir el producto entre el máximo común divisor. El producto de todos los factores en el diagrama de Venn es el mínimo común múltiplo de 396 y 540.

Pida a sus estudiantes que completen los problemas 5 y 6 en parejas. Recorra el salón de clases mientras sus estudiantes trabajan y haga las siguientes preguntas para apoyar su razonamiento:

• ¿Dónde pueden hallar el máximo común divisor de dos números en un diagrama de Venn completo?

• Cuando multiplican los números dentro de un círculo de un diagrama de Venn, ¿qué deberían obtener?

• Si conocen uno de los números de un par de factores, ¿cómo pueden hallar el otro número del par de factores?

• ¿Cómo hallan el mínimo común múltiplo usando los factores en un diagrama de Venn?

5. Halla el mínimo común múltiplo de 180 y 240. Usa el diagrama de Venn y el máximo común divisor de 180 y 240 del problema 3. 4 60 3

Factores de 180 Factores de 240

3 × 60 × 4 = 720

El mínimo común múltiplo de 180 y 240 es 720

6. Considera los números 544 y 238.

a. Usa el algoritmo de Euclides para hallar el máximo común divisor de 544 y 238. Par de números Diferencia

El máximo común divisor de 544 y 238 es 34.

b. Halla el mínimo común múltiplo de 544 y 238. Usa el máximo común divisor de 544 y 238.

Factores de 544

Factores de 23 8

16 34 7

16 × 34 × 7 = 3,808

El mínimo común múltiplo de 544 y 238 es 3,808.

Cuando la mayoría haya completado los problemas, seleccione a un grupo pequeño de estudiantes y pídales que compartan sus respuestas y razonamiento.

Concluir

Reflexión final 5 min

Objetivos: Hallar el máximo común divisor de números grandes usando el algoritmo de Euclides

Hallar el mínimo común múltiplo de números grandes usando el máximo común divisor

Use las preguntas que siguen para guiar la conversación. Anime a sus estudiantes a complementar las respuestas de sus pares.

¿De qué forma la actividad del acertijo matemático con cuadrados que hicimos hoy representa el algoritmo de Euclides?

En el acertijo matemático con cuadrados, retiramos el cuadrado más grande de un rectángulo dado y continuamos hasta que quedó un cuadrado. La longitud y el ancho del rectángulo dado son como los números dados cuando se usa el algoritmo de Euclides para hallar el máximo común divisor. Cuando usamos el algoritmo, continuamos restando hasta que los números fueran iguales, que fue como retirar los cuadrados hasta que quedara uno solo.

¿El algoritmo de Euclides les permite calcular el máximo común divisor de números grandes de manera más eficiente que otros métodos? ¿Por qué?

Sí. El algoritmo de Euclides parece más eficiente que otros métodos, como hallar pares de factores o usar la factorización prima. Con los otros métodos tardaríamos mucho para números más grandes.

¿Saber cuál es el máximo común divisor de dos números les ayuda a hallar el mínimo común múltiplo de los dos números? ¿Por qué?

Sí. Podemos dividir cada uno de los dos números entre el máximo común divisor para hallar el otro factor del par de factores de cada número. Luego, una vez que ponemos todos los números en el diagrama de Venn, podemos multiplicarlos para calcular el mínimo común múltiplo.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

El algoritmo de Euclides

En esta lección:

• usamos el algoritmo de Euclides para hallar el máximo común divisor de dos números grandes;

• usamos el máximo común divisor para hallar el mínimo común múltiplo de dos números grandes.

Ejemplos

1. Usa el algoritmo de Euclides para hallar el máximo común divisor de 186 y 66.

a. Completa la tabla. ¿Cuál es el máximo común divisor de 186 y 66?

Par de números Diferencia

186 y 66 186 − 66 = 120

120 y 66 120 − 66 = 54

66 y 54 66 − 54 = 12

54 y 12 54 − 12 = 42

42 y 12 42 − 12 = 30

30 y 12 30 − 12 = 18

18 y 12 18 − 12 = 6

12 y 6 12 − 6 = 6 6 y 6

El máximo común divisor de 186 y 66 es 6

Pasos del algoritmo de Euclides

1. Ordena los dos números de mayor a menor.

2. Para hallar su diferencia, resta el número menor del número mayor.

3. Quédate con el menor de los dos números. Descarta el mayor de los dos números.

4. Usa el menor de los dos números y la diferencia para formar un nuevo par de números.

5. Repite hasta que los dos números sean el mismo.

¿Cuál es el mínimo común múltiplo de 186 y 66?

186 × 66 = 12,276

12,276 ÷ 6 = 2,046

El mínimo común múltiplo de 186 y 66 es 2,046

Una forma de hallar el mínimo común múltiplo de dos números es primero hallar el producto de dos números. Luego, dividir entre el máximo común divisor. El resultado es el mínimo común múltiplo. 11 3 31 2 Factores primos de 186 Factores primos de 66

Considera organizar los factores primos de 186 y 66 en un diagrama de Venn. Multiplica todos los factores primos para hallar el mínimo común múltiplo de 186 y 66

31 × 2 × 3 × 11 = 2,046

EUREKA MATH

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. Considera el rectángulo de 120 unidades por 80 unidades.

a. ¿Cuál es la longitud del lado del cuadrado más grande que se puede retirar del rectángulo?

80 unidades

b. ¿Cuál es el tamaño del rectángulo que queda?

40 unidades por 80 unidades

c. Continúa retirando el cuadrado más grande posible de cada rectángulo que va quedando hasta que solo quede un cuadrado. ¿Cuál es la longitud del lado del cuadrado que queda?

40 unidades

d. ¿Cuál es el máximo común divisor de 120 y 80?

40

2. Considera el rectángulo con dimensiones de 108 unidades por 168 unidades.

a. ¿Cuál es la longitud del lado del cuadrado más grande que se puede retirar del rectángulo?

108 unidades

b. ¿Cuáles son las dimensiones del rectángulo que queda?

108 unidades por 60 unidades

c. Continúa retirando el cuadrado más grande posible de cada rectángulo que va quedando hasta que solo quede un cuadrado. ¿Cuál es la longitud del lado del cuadrado que queda?

12 unidades

d. ¿Cuál es el máximo común divisor de 108 y 168?

12

3. Usa el algoritmo de Euclides para hallar el máximo común divisor de 136 y 96

Par de números Diferencia

y 8 El máximo común divisor de 136 y 96 es 8

Usa el algoritmo de Euclides para hallar el máximo común divisor de 264 y 360. Completa la tabla.

Par de números Diferencia

El máximo común divisor de 264 y 360 es 24

EUREKA MATH

. Completa la tabla.

5. Considera los números 90 y 12

a. ¿Cuál es el máximo común divisor de 90 y 12?

6

b. ¿Cuál es el mínimo común múltiplo de 90 y 12?

180

6. Considera los números 144 y 252

a. ¿Cuál es el máximo común divisor de 144 y 252?

36

b. ¿Cuál es el mínimo común múltiplo de 144 y 252?

1,008

7. Considera los números 495 y 345

a. ¿Cuál es el máximo común divisor de 495 y 345?

15

b. ¿Cuál es el mínimo común múltiplo de 495 y 345?

11,385

8. Halla dos números que tengan un máximo común divisor de 20 y un mínimo común múltiplo de 2,400

Ejemplo: 300 y 160

9. Jada hace una pizza rectangular que mide 21 pulgadas por 36 pulgadas. Quiere cortar la pizza completa en cuadrados del mismo tamaño y que no sobre pizza

a. ¿Cuál es la longitud del lado, en pulgadas, de los cuadrados más grandes en que puede cortar la pizza Jada?

La longitud del lado de los cuadrados más grandes en que puede cortar la pizza Jada es 3 pulgadas.

b. ¿Cuántos trozos de este tamaño puede cortar Jada?

Puede cortar 84 trozos.

10. Leo está haciendo una colcha. Tiene un trozo de tela que mide 48 pulgadas por 168 pulgadas. Quiere cortar la tela completa en cuadrados del mismo tamaño y que no sobre tela.

a. ¿Cuál es la longitud del lado, en pulgadas, de los cuadrados más grandes en que puede cortar la tela Leo?

La longitud del lado de los cuadrados más grandes en que puede cortar la tela Leo es 24 pulgadas.

b. ¿Cuántos trozos de este tamaño puede cortar Leo?

Leo puede cortar 14 trozos.

Recuerda

En los problemas 11 a 14, escribe las fracciones como números mixtos y escribe los números mixtos como fracciones.

15. ¿Cuál es la longitud del lado, en pulgadas, del cuadrado más pequeño que

puede crear con rectángulos que miden 4 pulgadas por 6 pulgadas cada uno?

La longitud del lado del cuadrado más pequeño que se puede crear es 12 pulgadas.

16. Completa la tabla de razones.

Número de galones de pintura amarilla 3

Número de galones de pintura azul

9 1 3 2

EUREKA MATH2

Tema B

Dividir fracciones

En 5.o grado, sus estudiantes aprenden a dividir un número entero entre una fracción unitaria y una fracción unitaria entre un número entero. En el tema B del módulo 2 de 6.o grado, amplían su comprensión de la división para dividir un número entero entre una fracción no unitaria, una fracción no unitaria entre un número entero y una fracción entre una fracción. A lo largo del tema, hacen conexiones entre la multiplicación y la división, y escriben expresiones de división como ecuaciones de factor desconocido. Además, adquieren flexibilidad en su razonamiento a medida que aprenden distintos métodos para dividir fracciones. En cada lección, dividen con números mixtos y con fracciones.

En la lección 6, sus estudiantes usan actividades interactivas para observar y generalizar patrones cuando se dividen números enteros entre fracciones. Usan diagramas de cinta digitales para apoyar su razonamiento. Por ejemplo, razonan que 4 ÷

debe ser la mitad de 4

Concluyen la lección resolviendo problemas del mundo real en los que un número entero se divide entre una fracción o entre un número mixto.

En la lección 7, sus estudiantes exploran diferentes interpretaciones de la división cuando dividen fracciones unitarias entre números enteros. Escriben la división entre un número entero como la multiplicación por una fracción unitaria, y escriben e interpretan ecuaciones de factor desconocido. Desarrollan el sentido numérico al razonar acerca del tamaño de un cociente basándose en el tamaño del dividendo y el divisor.

En la lección 8, sus estudiantes desarrollan su experiencia previa con el lenguaje de unidades de valor posicional al dividir fracciones con denominadores comunes. Por ejemplo, hacen una transición de razonar una expresión como 8 novenos ÷ 2 novenos a 8 9 ÷ 2 9 y, luego, 8 9 ÷ 3 9 . Sus estudiantes usan la aritmética para reescribir 2 3 1

fracciones con denominadores comunes y, luego, dividir los numeradores. Usan diagramas de cinta y rectas numéricas para apoyar su comprensión. Usan ecuaciones de multiplicación relacionadas para comprobar sus respuestas.

Sus estudiantes continúan trabajando con la división de fracciones en el tema C. Aplican su comprensión de las ecuaciones de factor desconocido y su experiencia con los diagramas de cinta para desarrollar y aplicar el método de invertir y multiplicar para dividir fracciones.

Progresión de las lecciones

Lección 6 Dividir un número entero entre una fracción

Lección 7 Dividir una fracción entre un número entero

Lección 8 Dividir fracciones formando denominadores comunes

Dividir un número entero entre una fracción

Dividir un número entero entre una fracción usando diagramas de cinta y el razonamiento sobre la división

Vistazo a la lección

Un grupo de personas comparte 4 sándwiches. Cada persona recibe 2 5 de sándwich.

¿Cuántas personas comparten los sándwiches? Muestra cómo lo sabes.

10 personas comparten los sándwiches.

Como 4 ÷ 1 5 = 20 sé que 4 ÷ 2 5 es 20 ÷ 2, o 10

En esta lección digital, sus estudiantes exploran la división de un número entero entre una fracción. Usan una jarra interactiva que vierte partes fraccionarias en un cilindro y predicen el número de veces que hay que verter agua para llenar el cilindro. Luego, usan un diagrama de cinta como ayuda para dividir un número entero entre una fracción o entre un número mixto y desarrollan métodos para dividir sin un modelo.

Use la plataforma digital para preparar y enseñar esta lección. Sus estudiantes también explorarán el contenido de la lección y las actividades a través de la plataforma digital.

Preguntas clave

• ¿Por qué son útiles los modelos para dividir un número entero entre una fracción?

• ¿Qué patrones observaron al dividir un número entero entre una fracción?

Criterios de logro académico

6.Mód2.CLA4 Dividen dos fracciones o números mixtos.

6.Mód2.CLA5 Resuelven e interpretan problemas verbales que incluyen la división de fracciones y de números mixtos.

6.Mód2.CLA6 Interpretan la división de fracciones y de números mixtos usando modelos.

EUREKA

Nombre

Fecha

Agenda

Fluidez

Presentar 5 min D

Aprender 30 min D

• Verter agua

• Diagramas de cinta

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• computadoras o dispositivos (1 por pareja de estudiantes)

Preparación de la lección

• No se necesita.

Fluidez

Fracciones y números mixtos

La clase escribe números mixtos como fracciones mayores que 1 y escribe fracciones mayores que 1 como números mixtos como preparación para dividir números enteros entre fracciones.

Instrucciones: Escribe las fracciones de la columna izquierda como números mixtos.

Escribe los números mixtos de la columna derecha como fracciones mayores que 1.

Presentar

La clase razona para comprender cómo al verter jarras de agua en un cilindro se representa la división de un número entero entre una fracción.

Sus estudiantes usan una actividad interactiva para cambiar el tamaño de una jarra que se usa para llenar un cilindro. Eligen el denominador para crear tamaños posibles de jarras que sean fracciones unitarias: 1 2  , 1 3  , 1 4  , 1 5  , 1 6 o 1 7   .

Sus estudiantes eligen un cilindro con capacidad para 1, 2, 3 o 4 litros y predicen el número de veces que hay que verter el agua de la jarra elegida para llenar el cilindro elegido.

Escriban una oración numérica que represente la situación.

Ejemplo: 2 ÷ 1 _ 3 = 6 1 3 × 6 = 2

Expliquen cómo la actividad interactiva representa la oración numérica.

Ejemplo: La actividad interactiva muestra que hay 6 grupos de 1 3 de litro en 2 litros.

La actividad interactiva muestra que verter 1 3 de litro 6 veces llena un cilindro de 2 litros.

¿Qué pregunta se responde con 2 ÷ 1 _ 3 ?

Ejemplo: ¿Cuántos grupos de 1 3 hay en 2      ?

Apoyo para la comprensión del lenguaje

Si es necesario, recuerde a sus estudiantes los términos dividendo, divisor y cociente. Considere crear un afiche de referencia similar al que se muestra junto a sus estudiantes y colocarlo en el salón de clases durante el resto de este módulo. Sus estudiantes pueden consultar el afiche de referencia cuando dividen fracciones, números enteros y números decimales.

20 4 5 ÷

÷ = = dividendo cociente divisor

Es posible que también necesiten repasar los términos numerador, denominador, fracción unitaria y fracción no unitaria. Según sea necesario, cree un afiche de referencia similar que sirva de apoyo de esos términos a lo largo del módulo y exhíbalo en el salón de clases.

Aprender

Verter agua

La clase explora la división de un número entero entre una fracción.

Sus estudiantes continúan usando la actividad interactiva para cambiar el tamaño de una jarra que se usa para llenar un cilindro. En esta actividad, exploran cómo tanto el numerador como el denominador del número de litros que hay en una jarra afectan el número de veces que hay que verter el contenido de la jarra para llenar un cilindro. Dividen números enteros entre fracciones no unitarias al hacer conexiones con la división entre fracciones unitarias. Usan el factor desconocido para determinar el número de veces que hay que verter el agua de una jarra que tiene capacidad para un número fraccionario de litros.

¿De qué manera hallar el número de veces que hay que verter 1 _ 4 de litro les ayuda a hallar el número de veces que hay que verter 3 _ 4 de litro?

Sé que el número de veces que hay que verter 3 _ 4 de litro es el número de veces que hay que verter 1 _ 4 de litro dividido entre 3 porque 3 _ 4 de litro es 3 veces 1 _ 4 de litro.

¿Cómo pueden determinar el número de veces que hay que verter agua usando solo los números?

Puedo usar fracciones unitarias para hallar el número de veces que hay que verter agua para llenar el cilindro si multiplico el denominador por el número de litros. Para las fracciones no unitarias, puedo dividir entre el numerador.

Por ejemplo, sé que hay que verter 15 veces 1 5 de litro para llenar 3 litros. Entonces, hay que verter 5 veces 3 5 de litro para llenar el cilindro de 3 litros.

Diagramas de cinta

La clase divide un número entero entre una fracción usando diagramas de cinta.

Sus estudiantes trabajan con un diagrama de cinta para dividir un número entero entre una fracción. Usan el diagrama de cinta para determinar el número de grupos del divisor que hay en el dividendo.

DUA: Representación

Las actividades digitales están alineadas con el principio de Representación de DUA, dado que incluyen lo siguiente:

• Varios formatos y modos de representación: una jarra interactiva que vierte agua en un cilindro ilustra la división de un número entero entre una fracción. Sus estudiantes también representan la división usando diagramas de cinta y oraciones de multiplicación y división.

• Soportes que relacionan la información nueva con los conocimientos previos: sus estudiantes relacionan sus conocimientos previos de la división de un número entero entre una fracción unitaria para razonar acerca de la división de un número entero entre una fracción no unitaria. También relacionan la división de fracciones con su experiencia previa con ecuaciones de factor desconocido y la interpretación de la división.

• Estrategias que hacen énfasis en patrones, relaciones e ideas clave fundamentales: sus estudiantes observan patrones en los cocientes de expresiones cuyos divisores tienen fracciones unitarias y en los cocientes de expresiones cuyos divisores tienen fracciones no unitarias relacionadas y usan estos patrones para resolver problemas.

¿Cómo pueden hallar el número de grupos de 3 _ 4 que hay en 5?

Hay 20 grupos de 1 4 en 5. Puedo dividir 20 entre 3 para hallar el número de grupos de 3 4 que hay en 5, porque 3 4 es 3 veces 1 4 .

¿Cómo les ayuda el diagrama de cinta a hallar el número de grupos de 3 _ 4 que hay en 5?

Hay 20 3 de grupo , o 6 2 3 grupos, de 3 4 en 5. El diagrama de cinta muestra 6 grupos de 3 4 en 5 junto con 2 de 3 partes de un grupo más, lo que da como resultado 6 2 _ 3 .

Luego, sus estudiantes escriben expresiones de división basándose en diferentes contextos, usan el diagrama de cinta para representar y evaluar las expresiones de división e interpretan los cocientes. El siguiente es un ejemplo de un problema de división con contexto:

• El maestro Evans compra 6 sándwiches para una fiesta de la clase. Cada estudiante come exactamente 3 5 de sándwich. La clase come todos los sándwiches. ¿Qué número de estudiantes comen sándwiches?

¿Cómo muestra el diagrama de cinta el número de estudiantes que comen 3 _ 5 de sándwich?

En el diagrama de cinta, 10 rectángulos con un tamaño de 3 5 llenan 6 cuadrados. Esto quiere decir que 10 estudiantes comen 6 sándwiches si cada estudiante come exactamente 3 5 de sándwich.

Traza el diagrama de cinta que usaste para evaluar 4 ÷ 2 3 . Luego, responde las preguntas.

1. ¿Cuántos grupos de 1 3 hay en 4?

12

2. ¿Cuántos grupos de 2 3 hay en 4?

6

Traza el diagrama de cinta que usaste para evaluar 5 ÷ 3 4 . Luego, responde las preguntas.

3. ¿Cuántos grupos de 1 4 hay en 5?

20

4. ¿Cuántos grupos de 3 4 hay en 5?

6 2 _ 3

Promoción de la práctica de las matemáticas

Cada estudiante razona de forma abstracta y cuantitativa cuando escribe una ecuación de división a partir de un contexto.

Considere hacer las siguientes preguntas:

• ¿Cómo representa esta situación la división de un número entero entre una fracción?

• ¿Qué situaciones del mundo real se representan con la división de un número entero entre una fracción?

• ¿Tienen sentido sus respuestas en esta situación?

Traza el diagrama de cinta que usaste para responder los siguientes problemas del mundo real.

5. El maestro Evans compra 6 sándwiches para una fiesta de la clase. Cada estudiante come exactamente 3 _ 5 de sándwich. La clase come todos los sándwiches. ¿Qué número de estudiantes comen sándwiches?

10 estudiantes comen sándwiches.

6. La Sra. Song quiere preparar limonada con 8 libras de limones. Necesita 3 4 de libra de limones para preparar 1 litro de limonada. ¿Cuántos litros de limonada puede preparar la Sra. Song?

La Sra. Song puede preparar 10 2 3 litros de limonada.

7. La Sra. Baker compra 6 libras de arándanos. Quiere colocarlos en bolsas. En cada bolsa caben 1 1 3 libras de arándanos. ¿Cuántas bolsas puede llenar la Sra. Baker con arándanos?

Sra. Baker puede llenar 4 1 2 bolsas con arándanos.

Concluir

Reflexión final 5 min

Objetivo: Dividir un número entero entre una fracción usando diagramas de cinta y el razonamiento sobre la división

Use las preguntas y los planteamientos que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a complementar las respuestas de sus pares.

¿Son útiles los modelos de esta lección para dividir un número entero entre una fracción? ¿Por qué?

Sí. Los modelos son útiles para dividir un número entero entre una fracción. Nos permiten ver cuántas veces cabe una fracción en un número entero dado.

¿Qué patrones observaron al dividir un número entero entre una fracción?

Observé que el cociente de un número entero y una fracción a veces es un número entero. Observé que, a veces, el cociente es una fracción o un número mixto si el divisor no cabe en el dividendo un número entero de veces.

Observé que puedo usar lo que sé sobre el número entero dividido entre la fracción unitaria para hallar el cociente de un número entero y una fracción no unitaria con el mismo denominador.

Por ejemplo, sé que 2 ÷ 1 _ 3 es 6, y 2 ÷ 2 _ 3 es la mitad de 6, porque 2 _ 3 es el doble de 1 _ 3 . Puedo dividir el cociente del número entero y la fracción unitaria entre el numerador de la fracción no unitaria porque la fracción no unitaria será ese número de veces la fracción unitaria.

Den un ejemplo de un problema de división que incluya un número entero dividido entre una fracción cuyo resultado sea un número entero. ¿Cómo saben que el cociente es un número entero?

Ejemplo: 7 ÷ 7 8 = 8. Sé que el cociente es un número entero porque el numerador es un factor del número entero, es decir, 8 veces 7 _ 8 es 7.

Boleto de salida 5

min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Dividir un número entero entre una fracción

En esta lección:

• dividimos un número entero entre una fracción con un diagrama de cinta;

• dividimos un número entero entre una fracción unitaria;

• razonamos acerca del cociente de un número entero y una fracción no unitaria.

Ejemplos

1. Considera 4 ÷ 3 5

Piensa en 4 ÷ 3 5 como una pregunta. ¿Cuántos grupos de 3 5 hay en 4?

Traza un diagrama de cinta con 4 unidades. Divide cada unidad en quintos. Luego, cuenta el número de grupos de 3 5 que hay en 4 unidades.

a. Traza un diagrama de cinta para representar 4 ÷ 3 5 3 5 4 3 5 3 5 3 5 3 5 3 5

Hay 6 grupos de 3 5 en 4 unidades completas, más 2 3 adicionales de un grupo. El cociente es 6 2 3

b. Usa cualquier método para evaluar 4 ÷ 3 5 . Muestra cómo lo sabes.

Como 4 ÷ 1 5 = 20 sé que 4 ÷ 3 5 es 20 ÷ 3 o 6 2 3

2. Una caja de cereales contiene 13 onzas de cereales. Una porción de cereales es 1 1 4 onzas. ¿Cuántas porciones contiene la caja de cereales? Muestra cómo lo sabes.

La caja de cereales contiene 10 2 5 porciones.

Como 13 ÷ 1 4 = 52, sé que 13 ÷ 5 4 es 52 ÷ 5, o 10 2 5 .

El número mixto 10 2 5 es equivalente a la fracción 52 5

Hay 52 grupos de 1 4 en 13 Dado que 5 4 es 5 veces 1 4 el número de grupos de 5 4 que hay en 13 es igual a 1 5 del número de grupos de 1 4 que hay en 13. Entonces, el número de grupos de 5 4 que hay en 13 es 52 5

Al dividir, escribe los números mixtos como fracciones mayores que 1 1 1 4 = 4 4 + 1 4 = 5 4

EUREKA MATH2

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. Considera

a. Traza un diagrama de cinta que represente

Considera 6 ÷ 3 5 a. ¿Cuánto es 6 ÷ 1 5 ?

b. Usa tu respuesta de la parte (a) para evaluar 6 ÷ 3 5 . Muestra cómo lo sabes.

Como 6 ÷ 1 5 = 30, sé que 6 ÷ 3 5 es 30 ÷ 3, o 10

En los problemas 4 a 7, divide.

b. Usa el diagrama de cinta de la parte (a) para evaluar 3

2. Considera 5 ÷ 2 3

a. Traza un diagrama de cinta que represente

b. Usa el diagrama de cinta de la parte (a) para evaluar

8. El techo de una oficina escolar mide 9 pies de alto. Cada caja de archivo mide 3 4 de pie de alto.

¿Cuántas de estas cajas se pueden apilar en la oficina escolar como máximo? Muestra cómo lo sabes.

En la oficina escolar se pueden apilar 12 de estas cajas de archivo.

Como 9 ÷ 1 4 = 36, sé que 9 ÷ 3 4 es 36 ÷ 3, o 12

9. La empleada de una tienda de comestibles corta 11 libras de queso en porciones. Cada porción pesa 2 3 de libra. ¿Cuántas porciones de queso corta la empleada? Muestra cómo lo sabes.

La empleada corta 16 1 2 porciones de queso.

Como 11 ÷ 1 3 = 33, sé que 11 ÷ 2 3 es 33 ÷ 2, o 16 1 2

Recuerda

En los problemas 10 a 12, multiplica. 10. 1 1 2 × 2 1 3 3 1 2

13. Determina el máximo común divisor de 36 y 56. Muestra cómo lo sabes. 36 = 2 × 2 × 3 × 3

56 = 2 × 2 × 2 × 7

El máximo común divisor de 36 y 56 es 4 porque 2 × 2 = 4

14. Resuelve usando el algoritmo estándar. 24,165 − 9,059

15,106

EUREKA MATH2

Dividir una fracción entre un número entero

Dividir una fracción entre un número entero

Dividir un número mixto entre un número entero

Jada tiene 3 4 de litro de mezcla para hacer burbujas. Vierte la misma cantidad de la mezcla en 5 botellas. ¿Qué cantidad de mezcla para hacer burbujas, en litros, hay en cada botella? Muestra cómo lo sabes.

3 4 ÷ 5 = 3 4 × 1 5 = 3 20

En cada botella hay 3 20 de litro de mezcla para hacer burbujas.

Vistazo a la lección

Al inicio de la lección, la clase mira un video y determina cómo un grupo de personas puede repartir dos pizzas y media. Sus estudiantes usan diagramas de cinta y estrategias de multiplicación para ampliar su comprensión sobre la división de una fracción unitaria entre un número entero a la división de una fracción no unitaria entre un número entero.

Trabajan en parejas para resolver problemas del mundo real y de manera independiente para escribir un problema que incluya una expresión en la que un número mixto se divide entre un número entero.

Preguntas clave

• ¿Qué estrategias podemos usar para dividir una fracción o un número mixto entre un número entero?

• ¿Cómo se relacionan la división entre un número entero y la multiplicación?

Criterios de logro académico

6.Mód2.CLA4 Dividen dos fracciones o números mixtos.

6.Mód2.CLA5 Resuelven e interpretan problemas verbales que incluyen la división de fracciones y de números mixtos.

6.Mód2.CLA6 Interpretan la división de fracciones y de números mixtos usando modelos.

Agenda

Fluidez

Presentar 10 min

Aprender 25 min

• Dividir una fracción entre un número entero

• Preparar lasaña

• Escribir un problema

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• No se necesita.

Fluidez

Dividir una fracción unitaria entre un número entero

La clase divide fracciones unitarias entre números enteros como preparación para dividir fracciones no unitarias entre números enteros.

Instrucciones: Divide.

Presentar

La clase divide un número mixto entre un número entero para resolver un problema del mundo real.

Reproduzca el video Repartir la pizza. En el video, tres personas intentan determinar cómo repartir en partes iguales 2 1 2 pizzas sobrantes.

Después de reproducir el video, pida a sus estudiantes que trabajen en parejas o en grupos pequeños para calcular cómo dividir las pizzas de manera que cada persona reciba la misma cantidad. Pida a quienes terminen antes que determinen otro método para resolver el problema.

Cuando la mayoría haya terminado, pida a sus estudiantes que compartan sus soluciones y estrategias con la clase.

En este problema, debíamos dividir 2 1 _ 2 entre 3. Hoy, vamos a dividir fracciones no unitarias y números mixtos entre números enteros.

Aprender

Dividir una

fracción entre un número entero

La clase divide una fracción entre un número entero.

Dirija la atención de sus estudiantes al problema 1. Dé unos minutos para que completen el problema en parejas.

1. Kayla llena un vaso con agua. Vierte el agua en una jarra con capacidad para 1 _ 5 de galón.

Si 4 vasos de agua llenan la jarra, ¿cuántos galones de agua caben en el vaso de Kayla?

En el vaso de Kayla cabe 1 20 de galón de agua. 1 5 ÷ 4 = 1 5 × 1 4 = 1 20

DUA: Representación

Presentar el problema de repartir la pizza mediante un video elimina las barreras asociadas con el lenguaje escrito y hablado y ayuda a sus estudiantes a comprender el contexto del problema.

Diferenciación: Apoyo

Si sus estudiantes necesitan apoyo adicional, use el siguiente ejemplo alternativo para brindar apoyo visual:

Si 2 vasos de agua llenan la jarra, ¿cuánta agua cabe en 1 vaso?

1 5 de galón

1 vaso = ? de galón / ga lones

Cuando la mayoría haya terminado, invite a un par de estudiantes a compartir sus estrategias. Resalte todas las estrategias que generen una respuesta correcta. Resalte también los siguientes ejemplos del razonamiento de sus estudiantes:

• Evaluar

1 5 ÷ 4

• Calcular 1 5 de 1 4

• Preguntar cuántos grupos de 4 hay en 1 5

¿Cómo sabemos que 1 _ 5 ÷ 4 es menor que 1 _ 5 ?

Ejemplo: Dividir 1 5 en 4 grupos creará grupos menores que 1 5 .

¿Dividir entre 4 es equivalente a multiplicar por qué número?

1 4

A medida que hace las siguientes preguntas, muestre la expresión de división y la ecuación de factor desconocido relacionada: 1 5 ÷ 4 1 5 = 4 × ?

Podemos escribir la ecuación de factor desconocido 1 _ 5 = 4 × ? para representar la expresión de división 1 _ 5 ÷ 4. ¿Cómo podemos interpretar esta ecuación de factor desconocido?

Podemos interpretar la ecuación como una pregunta: ¿ 1 _ 5 es 4 grupos de qué número?

Podemos usar la multiplicación para comprobar la solución. Si pensamos que 1 _ 5 ÷ 4 = 1 __ 20 ; entonces, 1 _ 5 debe ser igual a 4 × 1 __ 20 . ¿Es 1 _ 5 igual a 4 × 1 __ 20 ?

Sí.

Si 1 _ 5 ÷ 4 = 1 __ 20 , ¿cuánto es 2 _ 5 ÷ 4? ¿Por qué?

2 20

Ejemplo:

2 _ 5 es el doble de 1 _ 5 ; entonces, 2 _ 5 ÷ 4 debe ser el doble de 1 _ 5 ÷ 4.

2 5 × 1 4 = 2 20

Nota para la enseñanza

En 5.o grado, sus estudiantes usan la interpretación de la división que incluye el tamaño de un grupo desconocido para escribir ecuaciones de factor desconocido y representar expresiones de división. Por ejemplo, interpretan 1 3 ÷ 4 como “¿ 1 3 es 4 grupos de qué número?” y escriben la ecuación de factor desconocido 1 3 = 4 × ? para representar la expresión de división.

En 6.o grado, sus estudiantes continúan usando esta estrategia para interpretar expresiones de división con fracciones y entender diagramas de cinta. También usan ecuaciones de factor desconocido para comprobar sus soluciones una vez que han determinado el factor desconocido.

Nota para la enseñanza

A medida que resuelven los problemas de esta lección, anime a sus estudiantes a comprobar sus respuestas con la ecuación de multiplicación relacionada. Según sea necesario, recuérdeles cómo comprobar sus respuestas y por qué pueden usar la multiplicación para comprobar la solución a un problema de división.

Muestre el diagrama de cinta que representa 2 _ 5 ÷ 4. Describa la manera en que el diagrama de cinta muestra cómo 2 5 se divide entre 4 para formar 2 20 . 1 2 5

¿Cuál es la ecuación de factor desconocido para 2 5 ÷ 4?

2 5 = 4 × ?

Podemos interpretar la ecuación de factor desconocido para 2 5 ÷ 4 como una pregunta:

¿ 2 _ 5 es 4 grupos de qué número?

Si observamos el diagrama, podemos ver que 2 _ 5 es 4 grupos de 2 __ 20 . Podemos usar la ecuación de factor desconocido para comprobar el valor de 2 _ 5 ÷ 4.

Presente los siguientes pasos para mostrar cómo comprobar el valor de 2 5 ÷ 4. En el último paso, resalte que 2 5 es equivalente a 8 20 . 2 5 = 4 × ?

2 5 = 4 × 2 20

2 5 = 8 20

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las preguntas y los planteamientos que siguen. Resalte las respuestas de la clase que se refieran al tamaño del grupo, al número de grupos o a la relación entre la multiplicación y la división.

Indiquen una expresión de división que sea mayor que 4 _ 5 ÷ 3. Expliquen.

Ejemplo:

4 _ 5 ÷ 2

Dividir 4 5 en 2 grupos creará grupos de tamaño más grande que dividir 4 5 en 3 grupos.

Nota para la enseñanza

Mire el video para el desarrollo profesional en la enseñanza Usar un diagrama de cinta para dividir una fracción entre un número entero para ver cómo representar este problema de división con un diagrama de cinta.

Diferenciación: Apoyo

Puede haber estudiantes que necesiten apoyo adicional para razonar sobre el valor de una expresión de división basándose en el dividendo y el divisor. Considere repasar los planteamientos y las preguntas ofreciendo expresiones para que sus estudiantes comparen.

• ¿Es 4 5 ÷ 2 mayor o menor que 4 5 ÷ 3?

¿Cómo lo saben?

• ¿Es 2 5 ÷ 3 mayor o menor que 4 5 ÷ 3?

¿Cómo lo saben?

4 _ 5 ÷ 2

4 _ 5 ÷ 2 es equivalente a 4 _ 5 × 1 _ 2 y 4 _ 5 ÷ 3 es equivalente a 4 _ 5 × 1 _ 3 . La mitad de cualquier número positivo es mayor que 1 3 de ese número.

Indiquen una expresión de división que sea menor que 4 _ 5 ÷ 3. Expliquen.

Ejemplo:

2 5 ÷ 3

Como 2 5 es menor que 4 5 , sabemos que 2 5 ÷ 3 será menor que 4 5 ÷ 3.

4 _ 5 ÷ 10

4 5 ÷ 10 es equivalente a 4 5 × 1 10 y 4 5 ÷ 3 es equivalente a 4 5 × 1 3 . Un décimo de cualquier número

positivo es menor que 1 3 de ese número.

¿Cómo podríamos evaluar 4 _ 5 ÷ 3 sin un diagrama de cinta?

Podríamos multiplicar 4 5 por 1 3 .

¿Cómo podríamos evaluar 1 4 _ 5 ÷ 3 sin un diagrama de cinta?

Podríamos escribir 1 4 5 como una fracción mayor que 1 y, luego, multiplicar por 1 3 .

Preparar lasaña

La clase divide una fracción o un número mixto entre un número entero para resolver un problema del mundo real.

Dé unos minutos para que sus estudiantes completen los problemas 2 y 3 de manera independiente o en parejas. Recorra el salón de clases mientras sus estudiantes trabajan y vaya haciendo las siguientes preguntas para apoyar el razonamiento de sus estudiantes:

• ¿Qué expresión matemática están evaluando?

• Antes de poder dividir 3 1 2 entre 4, ¿cómo deberíamos reescribir la expresión de división?

• ¿Dividir entre 4 es equivalente a multiplicar por qué número?

DUA: Acción y expresión

Agregue un ejemplo al afiche de la lección 6 que muestre la división de una fracción entre un número entero.

Ejemplo: 4 5 ÷ 3

¿ 4 5 es 3 grupos de qué número?

2. Kelly usa 3 1 2 tazas de albahaca fresca para preparar 4 bandejas de lasaña.

a. Kelly usa la misma cantidad de albahaca en cada bandeja de lasaña. ¿Cuántas tazas de albahaca usa Kelly en cada bandeja de lasaña? Muestra cómo lo sabes.

Ejemplo:

Kelly usa 7 8 de taza de albahaca en cada bandeja de lasaña.

b. Comprueba tu solución a la parte (a).

3. Seis personas reparten 2 _ 3 de una bandeja de lasaña en partes iguales. ¿Qué fracción de la bandeja de lasaña recibe cada persona? Muestra cómo lo sabes.

Ejemplo:

Cada persona recibe 2 18 de la bandeja de lasaña.

Promoción de la práctica de las matemáticas

Cada estudiante da sentido a los problemas y persevera en su resolución cuando resuelve problemas de división del mundo real escribiendo números mixtos como fracciones mayores que 1, determinando qué cantidad es el dividendo y qué cantidad es el divisor, y preguntándose si los valores que calcula tienen sentido.

Considere hacer las siguientes preguntas:

• ¿Cómo pueden explicar este problema con sus palabras?

• ¿Qué pasos pueden seguir para comenzar a resolver este problema?

• ¿Tienen sentido sus respuestas? ¿Por qué?

Cuando la mayoría haya terminado, pida a sus estudiantes que compartan sus respuestas y estrategias para los problemas 2 y 3. Comente las semejanzas y diferencias en el razonamiento de sus estudiantes. Resalte las estrategias que incluyan escribir un número mixto como una fracción mayor que 1 e interpretar la división de un número entero como la multiplicación por una fracción unitaria.

Haga las siguientes preguntas para ampliar el razonamiento de la clase sobre los problemas de la sección Preparar lasaña:

En el problema 3, cada persona recibe 2 __ 18 de una bandeja de lasaña. ¿De qué otra manera podemos pensar en 2 __ 18 ?

Ejemplo: Puedo pensar en 2 18 como 1 9 .

¿Por qué elegirían no usar diagramas de cinta para resolver estos problemas?

Ejemplo: Trazar un diagrama de cinta es más complicado que multiplicar por una fracción unitaria.

Escribir un problema

La clase escribe un problema que se pueda representar con una expresión de división.

Dirija la atención de sus estudiantes al problema 4. Dé uno o dos minutos para que completen la tarea de manera independiente.

4. Escribe un problema que se pueda representar con 4 1 3 ÷ 5.

Ejemplo: Un carpintero corta un trozo de madera de 4 1 3 pies de largo en 5 trozos de la misma longitud. ¿Cuál es la longitud, en pies, de cada trozo de madera?

Cuando la mayoría haya terminado, pida a sus estudiantes que compartan su problema en parejas.

Concluir

Reflexión final 5 min

Objetivos: Dividir una fracción entre un número entero

Dividir un número mixto entre un número entero

Use las preguntas que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a reformular o desarrollar las respuestas de sus pares.

En la lección anterior, dividimos números enteros entre fracciones. En esta lección, dividimos fracciones entre números enteros. ¿Cómo interpretarían 4 ÷ 2 _ 5 y 2 _ 5 ÷ 4 de manera diferente?

Ejemplo: Puedo interpretar 4 ÷ 2 5 como la pregunta “¿Cuántos grupos de 2 5 hay en 4?”. Puedo interpretar 2 5 ÷ 4 como la pregunta “¿Cuánto es 1 4 de 2 5 ?” o “¿  2 5 es 4 grupos de qué número?”.

¿Qué estrategias pueden usar para dividir una fracción entre un número entero?

Puedo trazar un diagrama de cinta. Puedo reescribir la división como una multiplicación por una fracción unitaria.

¿Cómo se relacionan la división de una fracción entre un número entero y la multiplicación?

Den un ejemplo.

Ejemplo:

Podemos pensar en la división de una fracción entre un número entero como la multiplicación por una fracción unitaria. Si quiero dividir una fracción entre 3, puedo multiplicar esa fracción por 1 _ 3 .

Podemos pensar en la división de una fracción entre un número entero como una ecuación de multiplicación con un factor desconocido. Por ejemplo, puedo escribir 2 5 = 4 × ? para representar 2 5 ÷ 4. Sé que el cociente de la expresión de división es el factor desconocido en la ecuación.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

RESUMEN 7

Dividir una fracción entre un número entero

En esta lección:

• dividimos una fracción entre un número entero;

• dividimos un número mixto entre un número entero.

Ejemplos

1. Kelly tiene 3 4 de libra de granola. Divide la granola entre 4 personas, de manera que cada una reciba la misma cantidad.

a. Escribe una expresión de división que represente esta situación.

3 4 ÷ 4

b. Traza un diagrama de cinta para representar la expresión de división de la parte (a).

3 4 1

c. ¿Cuántas libras de granola recibe cada persona?

3 4 ÷ 4 = 3 16

Cada persona recibe 3 16 de libra de granola.

Comienza con un diagrama de cinta que represente 3 4 Divide el diagrama de cinta de manera horizontal en 4 partes iguales para representar 3 4 ÷ 4 Al dividir entre 4, se obtiene el mismo resultado que al multiplicar por 1 4 La sección más oscura del diagrama de cinta muestra

3 4 ÷ 4 o 3 4 × 1 4

Para comprobar la respuesta, usa la ecuación de factor desconocido relacionada. Dado que 3 16 × 4 = 3 4 , el cociente 3 16 es correcto.

2. Una maestra de Ciencias tiene una bolsa con 7 1 2 libras de gravilla. Quiere colocar la misma cantidad de gravilla en 4 peceras. ¿Cuántas libras de gravilla puede colocar la maestra en cada pecera? Muestra tu trabajo. 7 1 2 ÷ 4 = 15 2 ÷ 4 = 15 2 × 1 4 = 15 8 = 1 7 8 Al dividir 15 2 entre 4 se obtiene el mismo resultado que al multiplicar 15 2 por 1 4 Al dividir, escribe los números mixtos como fracciones mayores que 1 7 1 2 = 14 2 + 1 2 = 15 2

La maestra puede colocar 1 7 8 libras de gravilla en cada pecera.

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. Considera 3 8 ÷ 4

a. Traza un diagrama de cinta para representar 3 8 3 8 1 3 8 1

b. Usa el diagrama de cinta de la parte (a) para evaluar 3 8 ÷ 4 3 32

(Nota: La respuesta de cada estudiante se muestra en el diagrama de cinta de la parte (a)).

2. ¿Qué preguntas pueden responderse al evaluar 2 3 ÷ 5? Elige todas las opciones que correspondan.

A. ¿Cuánto es 2 3 de 5?

B. ¿ 2 3 es 5 veces qué número?

C. ¿Cuántos grupos de 5 hay en 2 3 ?

D. ¿Cuántos grupos de 2 3 hay en 5?

E. ¿Cuánto es 2 3 × 1 5 ?

3. Considera 5 6 ÷ 2

a. Escribe 5 6 ÷ 2 como una ecuación de factor desconocido.

5 6 = 2 × ?

b. Evalúa 5 6 ÷ 2 5 12

c. Comprueba tu respuesta de la parte (b).

5 6 = 2 × 5 12

5 6 = 10 12

En los problemas 4 y 5, divide.

4. 5 7 ÷2 5 14 5. 1 2 9 ÷ 5 11 45

6. Indica una expresión de división que sea mayor que 2 3 ÷ 5. Explica tu razonamiento.

Ejemplo: 2 3 ÷ 4.

2 3 ÷ 4 es mayor que 2 5 ÷ 5 porque, al repartir 2 3 en menos grupos, se crean grupos de mayor tamaño.

7. Indica una expresión de división que sea menor que 3 4 ÷ 7. Explica tu razonamiento.

Ejemplo: 3 4 ÷ 8

3 4 ÷ 8 es menor que 3 4 ÷ 7 porque, al repartir 3 4 en más grupos, se crean grupos de menor tamaño.

8. Mara vierte 5 8 de cuarto de galón de mezcla en 10 moldes para pastelitos. Vierte la misma cantidad en cada molde. ¿Qué cantidad de mezcla, en cuartos de galón, vierte Mara en cada molde para pastelitos?

Mara vierte 5 80 de cuarto de galón de mezcla en cada molde para pastelitos.

9. Leo tiene una cuerda de 4 5 de metro de largo. Corta la cuerda en 3 trozos de la misma longitud. ¿Cuál es la longitud, en metros, de cada trozo de cuerda?

La longitud de cada trozo de cuerda es 4 15 de metro.

10. Si 7 cargas de piedra pesan 2 3 de tonelada, ¿cuál es el peso, en toneladas, de 1 carga de piedra?

El peso de 1 carga de piedra es 2 21 de tonelada.

11. Considera 2 5 ÷ 4

a. ¿Cuál es el cociente?

2 20

b. Escribe un problema verbal que pueda representarse con 2 5 ÷ 4

Ejemplo: A Lacy le quedaron 2 5 de pastel. Quiere dividirlo en 4 porciones del mismo tamaño. ¿Qué fracción del pastel representa cada porción?

Recuerda

En los problemas 12 a 15, suma o resta. Escribe tu respuesta en la misma forma que el problema.

12. Un tercio más un tercio

Dos tercios 13. 1 quinto más 3 quintos 4 quintos

14. Cinco novenos menos dos novenos Tres novenos 15. 8 décimos menos 4 décimos 4 décimos

Halla el mínimo común múltiplo de 10 y 12

17. Halla el mínimo común múltiplo de 6 y 10

18. Multiplica.

3,529 × 46

Dividir fracciones formando denominadores comunes

Dividir una fracción entre otra fracción usando un denominador común

Dividir un número mixto entre una fracción usando un denominador común

Vistazo a la lección

En esta lección, el lenguaje de unidades sirve como punto de partida para dividir fracciones usando denominadores comunes. Sus estudiantes analizan diagramas de cinta y miran una actividad interactiva para aprender por qué es útil usar un denominador común al dividir fracciones. Mediante la conversación guiada y el trabajo en parejas, la clase usa distintas estrategias, como formar denominadores comunes e interpretar rectas numéricas, para dividir una fracción entre otra fracción.

Pregunta clave

• ¿Son útiles los denominadores comunes para dividir fracciones? ¿Por qué?

Criterios de logro académico

6.Mód2.CLA3 Razonan acerca del tamaño de los cocientes de fracciones y números mixtos.

6.Mód2.CLA4 Dividen dos fracciones o números mixtos.

6.Mód2.CLA6 Interpretan la división de fracciones y de números mixtos usando modelos.

Nombre

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Dividir fracciones con una unidad común

• Formar denominadores comunes para dividir fracciones

• Usar rectas numéricas para dividir fracciones

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• No se necesita.

Fluidez

¿Cuántas fracciones hay?

La clase determina cuántas fracciones hay en una fracción o en un número mixto como preparación para dividir una fracción entre otra fracción.

Instrucciones: Responde las preguntas.

¿Cuántos

4. ¿Cuántos 2 5 hay en 4 5 ? 2 5. ¿Cuántos 2 5 hay en 8 5 ? 4 6. ¿Cuántos 2 _ 5 hay en 3 1 _ 5 ?

Presentar

La clase resuelve un problema del mundo real usando la división de fracciones con denominadores comunes.

Dirija la atención de sus estudiantes al problema 1. Permita que trabajen en grupos para responder tantas de las tres preguntas como puedan en 2 minutos.

1. Tres estudiantes usan alambre para hacer pulseras. ¿Cuántas pulseras puede hacer cada estudiante? Muestra cómo lo sabes.

a. Eddie necesita 11 12 de pie de alambre para cada pulsera que hace. Tiene un trozo de alambre de 33 __ 12 de pie de largo. ¿Cuántas pulseras puede hacer Eddie?

Eddie puede hacer 3 pulseras.

b. Noah necesita 2 3 de pie de alambre para cada pulsera que hace. Tiene un trozo de alambre de 5 1 3 pies de largo. ¿Cuántas pulseras puede hacer Noah?

5 1 3 = 16 3 2 3 × 8 = 16 3

Noah puede hacer 8 pulseras.

c. Julie necesita 1 1 _ 4 pies de alambre para cada pulsera que hace. Tiene un trozo de alambre de 7 1 _ 2 pies de largo. ¿Cuántas pulseras puede hacer Julie?

Julie puede hacer 6 pulseras. 5

Apoyo para la comprensión del lenguaje

Se pueden hacer diferentes clases de pulseras con alambre. Si sus estudiantes se preguntan por qué alguien podría necesitar tanto alambre como se indica en el problema 1, considere mostrar una imagen de una pulsera hecha con alambre entrelazado.

Diferenciación: Apoyo

Considere mostrar a quienes necesiten apoyo adicional cómo contar salteado en una recta numérica.

Cuando se acabe el tiempo, invite a sus estudiantes a compartir sus respuestas y estrategias para las tres situaciones en este orden: Eddie, Noah y Julie. Habrá quienes usen la división y los denominadores comunes, y habrá quienes usen la suma repetida o la multiplicación. A medida que sus estudiantes compartan, haga las siguientes preguntas para comprobar su razonamiento:

¿En qué se diferencian los cálculos para las pulseras de Eddie de los cálculos para las pulseras de las otras personas?

Para las pulseras de Eddie, debo determinar cuántos grupos de 11 12 hay en 33 12 , que es 3. Para las pulseras de las otras personas, debo trabajar con números mixtos.

Escribir cada número mixto como una fracción mayor que 1, ¿hace que los cálculos para las pulseras de Noah y de Julie sean más fáciles? Expliquen.

Sí. Es más fácil ver cuántas de las partes más pequeñas caben en el total. Escribir cada número mixto como una fracción mayor que 1 hace que estos cálculos se parezcan a los cálculos de Eddie.

¿En qué se diferencian los cálculos para las pulseras de Julie de los cálculos para las pulseras de las otras personas?

Ambos números son números mixtos; entonces, debemos escribir los dos números como fracciones mayores que 1 antes de hacer los cálculos.

¿Cómo pueden expresar con otro nombre los números de Julie para que sea más fácil trabajar con ellos?

Puedo expresarlos como fracciones mayores que 1 con el mismo denominador.

Hoy, aplicaremos lo que sabemos sobre los denominadores comunes para dividir una fracción entre otra fracción.

Diferenciación: Desafío

Si hay estudiantes que necesitan un desafío, pídales que determinen el número de pulseras que puede hacer Toby dada la siguiente situación:

Toby necesita 7 8 de pie de alambre para cada pulsera que hace. Tiene un trozo de alambre de 4 3 4 pies de largo. ¿Cuántas pulseras puede hacer Toby?

Toby puede hacer 5 pulseras.

Aprender

Dividir fracciones con una unidad común

La clase divide fracciones con un denominador común.

Dirija la atención de sus estudiantes al problema 2. Dé alrededor de un minuto para que completen el problema de manera independiente.

2. Calcula los cocientes.

a. 8 ÷ 2

4

b. 8 unidades ÷ 2 unidades

4

c. 8 decenas ÷ 2 decenas

4

d. 8 millares ÷ 2 millares

4

e. 8 décimos ÷ 2 = décimos

4

f. 8 tercios ÷ 2 tercios

4

Use las preguntas que siguen para guiar una conversación sobre el problema 2:

¿Por qué tenemos el cociente 4 en cada parte del problema 2?

En cada parte, dividimos 8 unidades entre 2 de las mismas unidades y 8 unidades ÷ 2 unidades = 4.

Hay 4 grupos de 2 unidades en 8 unidades. ¿Cuáles son algunos ejemplos de unidades en el problema 2?

Ejemplo: unidades, decenas, tercios

Nota para la enseñanza

No se espera que sus estudiantes escriban respuestas fraccionarias de ninguna manera particular en 6.o grado. En este tema, hay varios tipos de respuesta. Todas las formas de una respuesta son aceptables siempre y cuando sean equivalentes.

Si el dividendo y el divisor tienen las mismas unidades, las llamamos unidades comunes.

En el problema 8 tercios ÷ 2 tercios, tercios es una unidad común. ¿Usamos unidades comunes en el problema de las pulseras? De ser así, ¿cómo?

Sí, usamos unidades comunes en el problema de las pulseras.

Ejemplo:

Determinamos cuántas pulseras podía hacer Eddie calculando cuántos grupos de 11 doceavos se necesitan para formar 33 doceavos mediante la suma o la resta repetida.

Determinamos cuántas pulseras podía hacer Julie escribiendo fracciones con un denominador común.

Dividimos 33 doceavos entre 11 doceavos, así que doceavos es la unidad común.

¿Por qué funciona siempre dividir con unidades comunes?

Ejemplo: Podemos pensar en la división con unidades comunes como una resta repetida con unidades comunes. La división nos indica cuántas veces restamos; entonces, la unidad no importa mientras sea común.

Pida a sus estudiantes que completen los problemas 3 y 4 en sus libros mientras usted usa las preguntas y los planteamientos que siguen para comentar los dos problemas con toda la clase.

Muestre 8 9 ÷ 2 9 .

Vamos a trazar un diagrama de cinta para representar 8 _ 9 ÷ 2 _ 9 . Podemos comenzar por trazar 8 _ 9 y,

luego, dividir los 8 _ 9 en grupos de 2 _ 9 . Podemos ver que hay exactamente 4 grupos de 2 _ 9 en 8 _ 9 .

¿Cuánto es 8 _ 9 ÷ 2 _ 9 ? Expliquen.

4. Hay exactamente 4 grupos de  2 _ 9 en 8 _ 9 ; entonces, 8 _ 9 ÷ 2 _ 9 = 4.

Muestre 8 9 ÷ 3 9 .

Vamos a trazar un diagrama de cinta para representar 8 _ 9 ÷ 3 _ 9 . Podemos comenzar por trazar 8 _ 9 y, luego, dividir los 8 _ 9 en grupos de 3 _ 9 . 8 9 8 9 3 9 3 9 3 9 de grupo 2 3 1 grupo 1 grupo

¿En qué se diferencia el diagrama de cinta que representa 8 _ 9 ÷ 3 _ 9 del que trazamos recién para representar 8 9 ÷ 2 9 ?

El número de grupos de 3 9 que hay en 8 9 no es un número entero.

Sabemos que el número de grupos de  3 _ 9 que hay en 8 _ 9 no es un número entero porque 2 grupos de 3 _ 9 son muy pocos y 3 grupos de 3 _ 9 son demasiados. En el diagrama de cinta hay 2 grupos de  3 _ 9 y una parte adicional. ¿Qué fracción de un grupo de 3 _ 9 representa esta parte adicional? 2 3

Podemos ver que hay 2 2 _ 3 grupos de  3 _ 9 en 8 _ 9 . ¿Cuánto es 8 _ 9 ÷ 3 _ 9 ?

2 2 3 o 8 3

Nota para la enseñanza

A medida que resuelven los problemas de esta lección, anime a sus estudiantes a comprobar sus respuestas con la ecuación de multiplicación relacionada. Según sea necesario, recuérdeles cómo comprobar sus respuestas y por qué pueden usar la multiplicación para comprobar la solución a un problema de división.

¿Qué observan acerca del cociente 2 2 _ 3 ?

2 2 _ 3 es el cociente de los numeradores de las dos fracciones que estamos dividiendo: 8 ÷ 3 = 2 2 _ 3 .

8 9 y 3 9 tienen las mismas unidades, así que 2 2 3 tiene el mismo cociente que 8 ÷ 3.

¿Son correctas nuestras respuestas? ¿Cómo podemos comprobar nuestro trabajo para asegurarnos de que 8 _ 9 ÷ 3 _ 9 = 2 2 _ 3 ?

Sí. Cuando multiplicamos 2 2 3 por 3 9 , obtenemos 8 3 × 3 9 = 24 27 , y 24 27 es equivalente a 8 9 .

3. Considera 8 9 ÷ 2 9 .

a. Traza un diagrama de cinta para representar

Diferenciación: Apoyo

Para apoyar el razonamiento de sus estudiantes acerca de las expresiones de división y el tamaño de los cocientes, proporcione una sucesión de expresiones de división y pídales que estimen si el cociente estará cerca del 0, cerca del 1 o si será mucho mayor que 1

b. ¿Cuánto es 8 9 ÷ 2 9 ? 4

4. Considera 8 9 ÷ 3 9 . a. Traza un diagrama de cinta para representar

Luego, pida a sus estudiantes que expliquen cómo usaron el tamaño del dividendo y el divisor para estimar el tamaño del cociente. Recuérdeles este razonamiento a lo largo de la lección.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta:

¿Cómo determinamos el cociente de dos fracciones cuando tienen un denominador común?

Dividimos el numerador de la primera fracción entre el numerador de la segunda fracción.

Dé alrededor de un minuto para que sus estudiantes completen el problema 5 de manera independiente.

5. Yuna dice que 5 8 ÷ 3 8 es menor que 1. ¿Está en lo correcto? Explica. No.

Ejemplo: 5 8 es mayor que 3 8 ; entonces, 5 8 ÷ 3 8 es mayor que 1.

Pida a diferentes estudiantes que compartan su solución y su razonamiento acerca del problema 5. Resalte las diferentes maneras en que sus estudiantes razonan sobre este problema. Los ejemplos de respuesta incluyen los siguientes:

• 5 8 es mayor que 3 8 ; entonces, 5 8 ÷ 3 8 es mayor que 1.

• 3 8 es menor que 5 8 ; entonces, 5 8 ÷ 3 8 es mayor que 1.

• Dado que las fracciones tienen un denominador común, 5 8 ÷ 3 8 es 5 3 , que es mayor que 1.

Dé unos minutos para que sus estudiantes completen los problemas 6 a 8 de manera independiente o en parejas. Recorra el salón de clases mientras sus estudiantes trabajan y, si es necesario, anime a la clase a trazar diagramas.

En los problemas 6 a 8, divide. Comprueba cada solución.

6. 6 7 ÷ 2 7 3

6 7 = 2 7 × 3

6 _ 7 = 6 _ 7

Diferenciación: Desafío

Después del problema 5, plantee las siguientes situaciones para ampliar el razonamiento de sus estudiantes sobre los cocientes:

• El euro es la moneda oficial de muchos países de Europa. Una moneda de 1 euro tiene un espesor de 2 1 3 milímetros. Una moneda de 2 euros tiene un espesor de 2 1 __ 5 milímetros. Mara forma una pila de monedas de 1 euro y una pila de monedas de 2 euros. Ambas pilas se elevan desde el piso hasta el techo. ¿Qué pila tiene más monedas? Expliquen.

La pila de monedas de 2 euros tiene más monedas. Las monedas de 2 euros no son tan gruesas como las de 1 euro; entonces, caben más monedas en la pila.

• Tyler dice que 3 4 ÷ 1 5 es mayor que 3 4 . Julie dice 3 4 ÷ 1 5 es menor que 3 4 . ¿Quién está en lo correcto? Expliquen.

Tyler está en lo correcto. El divisor, 1 5 , es menor que 1. Cuando divides un número entre un número menor que 1, el cociente será mayor que el número que estás dividiendo; entonces, 3 __ 4 ÷ 1 __ 5 es mayor que 3 __ 4

Lea en voz alta las soluciones a los problemas 6 a 8 y responda preguntas. Considere hacer las siguientes preguntas:

• En el problema 7, cuando usamos una ecuación de multiplicación relacionada para comprobar nuestra respuesta, obtenemos 5 _ 9 = 20 __ 36 . ¿Estas fracciones son equivalentes? ¿Cómo lo saben?

• ¿En qué se diferencia el problema 8 de los problemas 6 y 7?

Formar

denominadores comunes para dividir fracciones

La clase forma denominadores comunes para dividir fracciones.

Escriba 3 4 ÷ 2 3 en el pizarrón. Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejasCompartir para responder las siguientes dos preguntas:

¿Cómo podemos escribir 3 _ 4 ÷ 2 _ 3 como una ecuación de factor desconocido?

3 _ 4 = 2 _ 3 × ?

Promoción de la práctica de las matemáticas

Cada estudiante reconoce y utiliza estructuras cuando halla un denominador común para dividir una fracción entre otra fracción.

Considere hacer las siguientes preguntas:

• ¿Cómo puede ayudarles lo que saben sobre los problemas de división con unidades semejantes a dividir una fracción entre otra fracción?

• ¿De qué otra manera pueden escribir 3 __ 4 ÷ 2 __ 3 que les ayudaría a resolver el problema?

• ¿Cómo pueden usar lo que tienen en común dos fracciones como ayuda para dividir una fracción entre otra fracción?

¿Cómo podemos interpretar 3 _ 4 ÷ 2 _ 3 ?

Ejemplo:

¿ 3 4 es 2 3 de qué número?

¿Cuántos grupos de 2 3 hay en 3 4 ?

Si sus estudiantes no proporcionan las dos interpretaciones de  3 4 ÷ 2 3 , considere compartirlas con la clase.

¿En qué se diferencia 3 _ 4 ÷ 2 _ 3 de las expresiones de división que ya vimos en esta lección?

Las fracciones no tienen denominadores comunes.

Usaremos un diagrama de cinta interactivo para representar cómo dividir fracciones que tienen denominadores que no son iguales. Vamos a dividir 3 _ 4 entre 1 _ 3 .

Presente la actividad interactiva para demostrar la división de fracciones.

Verde Morado

¿Es 3 _ 4 ÷ 1 _ 3 mayor que 1 o menor que 1? ¿Cómo lo saben?

3 4 ÷ 1 3 es mayor que 1 porque 1 3 es menor que 3 4 .

¿Aproximadamente cuántos grupos de 1 3 hay en 3 4 ? ¿Cómo lo saben?

Hay aproximadamente 2 1 2 grupos de 1 3 en 3 4 . La porción de color verde oscuro del diagrama de cinta que representa 3 4 es aproximadamente 2 1 2 veces tan larga como la sección de color morado oscuro del diagrama de cinta que representa 1 3 .

Nota para la enseñanza

Mire el video para el desarrollo profesional en la enseñanza Usar un diagrama de cinta para dividir fracciones con denominadores comunes para ver cómo representar este problema de división con un diagrama de cinta.

Nota para la enseñanza

El objetivo de la actividad interactiva es mostrar a la clase cómo usar diagramas de cinta para dividir dos fracciones con denominadores distintos.

Si hay suficiente tiempo, muestre dos ejemplos diferentes: uno en el que el dividendo sea mayor que el divisor y uno en el que el divisor sea mayor que el dividendo. Por ejemplo, demuestre 3 4 ÷ 1 3 y 1 3 ÷ 3 4 .

¿Por qué no podemos determinar exactamente cuántos grupos de 1 _ 3 hay en 3 _ 4 con solo mirar este diagrama de cinta?

Los dos diagramas no están divididos en unidades del mismo tamaño; entonces, no podemos

decir exactamente cuántos grupos de 1 3 hay en 3 4 .

Intentemos dividir cada diagrama de cinta en unidades del mismo tamaño.

Use la barra deslizadora para dividir cada diagrama de cinta en unidades más pequeñas. A medida que la mueve, haga una pausa en tamaños de unidades específicos para preguntar a sus estudiantes si esas unidades les ayudan a resolver el problema. Por ejemplo, comente que las unidades como sextos u octavos no nos ayudan a resolver el problema porque 1 3 no se puede escribir como una fracción equivalente con un 8 en el denominador y 3 _ 4 no se puede escribir como una fracción equivalente con un 6 en el denominador.

Verde Morado

Verde

Morado

Los doceavos son el tamaño de unidad más grande que funciona porque tanto 1 _ 3 como 3 _ 4 se pueden escribir con el denominador común de 12. Observen que todas las unidades verdes y moradas tienen el mismo tamaño de 1 __ 12 y que el denominador común de 1 _ 3 y 3 _ 4 es 12.

¿Cuántas unidades verdes hay en 3 _ 4 ?

9

¿Cuántas unidades moradas hay en 1 _ 3 ?

4

Arrastre el diagrama de cinta morado de manera que quede arriba del diagrama de cinta verde.

Verde Morado

Verde

Morado

¿Cuántos grupos de 1 _ 3 hay en 3 _ 4 ? ¿Cómo lo saben?

2 1 _ 4 . Puedo ver 2 1 _ 4 grupos de 4 __ 12 en 9 __ 12 .

Si es necesario, use la herramienta de dibujo para mostrar que 2 1 4 de las secciones de color morado oscuro caben en la sección de color verde oscuro.

Verde Morado

Verde

Morado

2 1 _ 4 grupos de las secciones de color morado oscuro caben en la sección de color verde oscuro.

Por lo tanto, 3 _ 4 ÷ 1 _ 3 = 2 1 _ 4 .

¿Cómo podemos escribir las fracciones 3 _ 4 y 1 _ 3 con un denominador común?

9 12 y 4 12

¿Cuánto es 9 __ 12 ÷ 4 __ 12 ?

9 4 o 2 1 4

Podemos comprobar nuestra respuesta con una ecuación de multiplicación relacionada.

¿Cuál es una ecuación de multiplicación relacionada para 3 _ 4 ÷ 1 _ 3 = 9 _ 4 ?

3 _ 4 = 9 _ 4 × 1 _ 3

¿Es la ecuación de multiplicación relacionada verdadera? ¿Es 3 _ 4 igual al producto de  9 _ 4 y 1 _ 3 ?

Expliquen.

Sí. 9 4 × 1 3 = 9 12 y 9 12 es equivalente a 3 4 .

Dirija la atención de sus estudiantes a los problemas 9 y 10. Brinde varios minutos para que sus estudiantes completen los problemas de manera individual o en parejas. Recorra el salón de clases mientras sus estudiantes trabajan y vaya tomando notas de las estrategias que usan. Mientras recorre el salón de clases, considere hacer las siguientes preguntas:

• ¿Cómo saben si un cociente será mayor que 1 o menor que 1 con solo mirar la expresión de división?

• ¿Pueden usar más de un denominador común? De ser así, indiquen algunos.

• ¿Por qué usan la multiplicación para comprobar la solución?

• ¿Cómo saben que 18 30 es equivalente a 3 5 ?

9. Considera 3 _ 5 ÷ 2 _ 3 .

a. ¿El cociente es mayor que 1 o menor que 1? Explica. El cociente es menor que 1 porque 2 3 es mayor que 3 5

b. ¿Cómo podemos reescribir 3 5 ÷ 2 3 de manera que las fracciones tengan un denominador común? 9 15 ÷ 10 15

DUA: Acción y expresión

Considere exhibir preguntas que sirvan como referencia a sus estudiantes mientras completan estos problemas. Demuestre cómo podrían hacerse preguntas mientras crean e interpretan el modelo.

• ¿Expresé las fracciones con un denominador común?

• ¿Creé un diagrama de cinta que represente el dividendo?

• ¿Me pregunté cuántas veces cabe el divisor en el dividendo? (La respuesta a esta pregunta es el cociente).

• ¿Escribí el problema de multiplicación relacionado para comprobar mi respuesta?

c. Traza un diagrama de cinta para representar 3 5 ÷ 2 3 . 9 15 10 15

d. Evalúa 3 5 ÷ 2 3 . 9 10

e. Escribe una ecuación de multiplicación relacionada para mostrar que la respuesta a la parte (d) es correcta.

3 5 = 9 10 × 2 3

9 10 es correcto porque 9 10 × 2 3 = 18 30 , y 18 30 es equivalente a 3 5 .

10. Divide. Muestra tu trabajo.

a. 5 6 ÷ 2 3 5 6 ÷ 2 3 = 15 18 ÷ 12 18 = 15 12 = 5 4 5 4 b. 4 _ 5 ÷ 3 _ 7 4 5 ÷ 3 7 = 28 35 ÷ 15 35 = 28 15 28 15

Cuando la mayoría haya terminado, haga las siguientes preguntas para comprobar la comprensión:

¿Qué denominador usaron en la parte (a) del problema 10? ¿Por qué?

Ejemplo: Usé el 18 porque sé que tanto el 3 como el 6 son factores de 18.

Ejemplo: Usé el 6 porque sé que tanto el 3 como el 6 son factores de 6.

¿Qué hicieron con el número mixto en la parte (c) del problema 10 antes de dividir?

Reescribí el número mixto como una fracción mayor que 1.

Usar rectas numéricas para dividir fracciones

La clase usa una recta numérica con un diagrama de cinta para dividir una fracción entre otra fracción.

Muestre la recta numérica y el diagrama de cinta.

¿Qué expresión de división representa el diagrama? Expliquen.

2 2 _ 4 ÷ 3 _ 4 . La porción sombreada del diagrama de cinta es 2 2 _ 4 y los tamaños de las unidades del grupo son 3 4 .

DUA: Representación

Considere crear un organizador gráfico de red que incluya las estrategias de división de fracciones para mostrar y completar con toda la clase a medida que se avanza en el tema. Rotule el centro de la red Estrategias de división de fracciones y agregue una burbuja cada vez que se presente una estrategia nueva. Por ejemplo, rotule una burbuja

Denominadores comunes e incluya un ejemplo de la estrategia.

Denominadores comunes

8 3 = ÷÷ = Estrategias de división de fracciones

¿Cuánto es 2 2 _ 4 ÷ 3 _ 4 ? ¿Cómo lo saben?

3 1 3 . Hay 3 1 3 grupos de 3 4 en 2 2 4 .

¿En qué se diferencia esta representación de la división de otras representaciones de la división que hemos visto?

Ejemplo: Esta representación usa una recta numérica para mostrar el tamaño del dividendo.

Dé unos minutos para que sus estudiantes completen los problemas 11 y 12 de manera independiente o en parejas.

11. Escribe una ecuación de división que se pueda representar con el diagrama que se muestra.

123

Ejemplo:

a. Usa una recta numérica y un diagrama de cinta

b. Usa la recta numérica para evaluar

Cuando la mayoría haya terminado, pida a diferentes estudiantes que compartan sus respuestas al problema 11. Resalte que pueden interpretar el diagrama como 3 1 3

Muestre la solución a la parte (a) del problema 12. Pida a alguien de la clase que comparta cómo usar el diagrama de cinta para evaluar 3 4 ÷ 5 12 .

Concluir

Reflexión final 5 min

Objetivos: Dividir una fracción entre otra fracción usando un denominador común

Dividir un número mixto entre una fracción usando un denominador común

Use las preguntas que siguen para guiar una conversación acerca de dividir una fracción entre otra fracción usando un denominador común. Anime a sus estudiantes a reformular o desarrollar las respuestas de sus pares.

¿En qué se parece dividir una fracción entre otra fracción a otros problemas de división que hemos explorado, como dividir un número entero entre una fracción? ¿En qué se diferencia?

Dividir una fracción entre otra fracción se parece a los problemas de división que hemos completado antes porque también podemos escribir el problema como una ecuación de factor desconocido y también podemos representar el problema usando diagramas. Dividir una fracción entre otra fracción se diferencia de los problemas de división que hemos completado antes porque es la primera vez que tenemos que hallar un denominador común para dividir.

¿Cómo podemos usar un diagrama de cinta para dividir una fracción entre otra fracción?

Ejemplo: Podemos determinar cuántos grupos del divisor hay en el dividendo.

¿Son útiles los denominadores comunes para dividir fracciones? ¿Por qué?

Sí. Los denominadores comunes son unidades semejantes, y hacen que la división sea más fácil. Cuando dividimos cantidades con unidades semejantes, podemos simplemente dividir los números de cada cantidad.

Boleto de salida

5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

b. Usa el diagrama para evaluar la expresión de división de la parte (a).

Dividir fracciones formando denominadores comunes

En esta lección:

• usamos el lenguaje de unidades de valor posicional y diagramas para comprender cómo dividir fracciones con denominadores comunes;

• usamos denominadores comunes para dividir una fracción entre otra fracción;

• usamos denominadores comunes para dividir un número mixto entre una fracción.

Ejemplos

1. Kayla y Lacy escriben una expresión que es equivalente a 15 quintos ÷ 3 quintos. Kayla escribe 15 décimos ÷ 3 décimos. Lacy escribe 1,500 300 . ¿Quién está en lo correcto? Explica.

Tanto Kayla como Lacy están en lo correcto.

Las expresiones 15 quintos ÷ 3 quintos, 15 décimos ÷ 3 décimos y 1,500 300 equivalen a 5

En cada expresión, 15 de una unidad se divide entre 3 de la misma unidad.

2. Considera el diagrama.

Observa que 1 3 es equivalente a 4

a. Escribe una expresión de división que pueda representarse con el diagrama.

Ejemplo: 5 12 ÷ 1 3

La fracción 1,500 300 se puede pensar como 15 centenas ÷ 3 centenas Dado que 15 y 3 tienen unidades semejantes, el cociente es 5

Cada grupo de 1 3 está representado con 4 unidades en el diagrama de cinta porque 1 3 es equivalente a 4 12 . Hay 1 grupo completo de 1 3 en 5 12 , y hay 1 unidad restante. Esa unidad restante es 1 4 de un grupo de 1 3 Entonces, el cociente es 1 1 4

3. Evalúa 1 3 8 ÷ 1 3

5 de las 12 unidades están sombreadas. Las unidades sombreadas representan el dividendo. Cuatro de las unidades sombreadas están rotuladas 1 3 , que representa el divisor.

Al dividir, escribe los números mixtos como fracciones mayores que 1 1 3 8 = 8 8 + 3 8 = 11 8

Forma denominadores comunes. 11 8 × 3 3 = 33 24 1 3 × 8 8 = 8 24

Luego, divide los numeradores. Si el dividendo y el divisor tienen denominadores comunes, el cociente de las fracciones es el cociente de sus numeradores.

EUREKA MATH

Nombre

Fecha

© Great Minds PBC

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

6. ¿Qué expresión tiene el mismo valor que 5 7 ÷ 3 4 ?

1. ¿En qué se parecen las siguientes expresiones? ¿En qué se diferencian? Explica.

6 decenas ÷ 4 decenas 6 5 ÷ 4 5

Ejemplo: Las expresiones se parecen en que el valor de cada expresión se puede hallar al dividir 6 entre 4. Las expresiones se diferencian en que tienen unidades diferentes.

2. Mara y Adesh escriben una expresión que es equivalente a 12 décimos ÷ 4 décimos

Mara escribe 12 tercios ÷ 4 tercios. Adesh escribe 1,200 400 . ¿Quién está en lo correcto? Explica.

Tanto Mara como Adesh están en lo correcto. Las expresiones 12 décimos ÷ 4 décimos, 12 tercios ÷ 4 tercios y 1,200 400 equivalen a 3. En cada expresión, 12 de una unidad se divide entre 4 de la misma unidad.

En los problemas 3 y 4, divide.

3. 9

÷ 3

5. Considera el diagrama.

En los problemas 7 a 10, divide.

11. Elige un problema de los problemas 7 a 10 y comprueba tu solución.

Ejemplo:

a. Escribe una expresión de división que pueda representarse con el diagrama.

Ejemplo: 1 3 4 ÷ 1 2

b. Usa el diagrama para evaluar la expresión de división de la parte (a).

Ejemplo: 3 1 2

Recuerda

En los problemas 12 a 15, suma o resta.

12. 1 4 + 1 4

16. Un libro tiene 5 8 de pulgada de espesor. ¿Cuántas copias del libro caben en un estante que tiene 20 pulgadas de largo?

En el estante caben 32 copias del libro.

17. ¿Cuál es mayor, el 5 % de 90 o el 90 % de 5? Explica.

Ninguno es mayor. Tanto el 5 % de 90 como el 90 % de 5 es 4.5

EUREKA MATH2

Tema C

Dividir fracciones con fluidez

En el tema B, sus estudiantes dividen fracciones entre números enteros y números enteros entre fracciones. Además, escriben fracciones con denominadores comunes para dividirlas. Relacionan la multiplicación y la división cuando escriben expresiones de división como ecuaciones de factor desconocido. En el tema C, aplican todas estas destrezas al desarrollar y usar la estrategia de invertir y multiplicar. A lo largo del tema, sus estudiantes adquieren fluidez con la división de fracciones y dividen fracciones para resolver problemas del mundo real.

En las primeras dos lecciones, sus estudiantes desarrollan y formalizan la estrategia de invertir y multiplicar. Primero, examinan expresiones de división en las que una fracción se divide entre una fracción unitaria. Crean ecuaciones de factor desconocido y trazan diagramas de cinta para calcular los cocientes. Luego, aplican estas mismas estrategias para dividir una fracción entre una fracción no unitaria. Observan y generalizan patrones en sus trabajos y usan esos patrones para desarrollar y comprender la estrategia de invertir y multiplicar. Luego, dividen números mixtos y fracciones para adquirir fluidez con esta estrategia.

En la tercera lección, sus estudiantes aplican su comprensión de la división de fracciones para resolver distintos problemas del mundo real. Para comenzar, emparejan situaciones de multiplicación y división con expresiones matemáticas, y justifican cómo saben que deben usar una operación en lugar de otra y cómo determinan el dividendo y el divisor. Luego, aplican su comprensión de la división de fracciones a medida que resuelven problemas del mundo real y hacen comparaciones multiplicativas. Por ejemplo, sus estudiantes pueden determinar que un objeto es 1 1 3 veces tan largo como otro objeto.

El tema concluye con una lección digital en la que sus estudiantes diseñan sus propios carritos de madera y los hacen correr carreras. Suman, restan, multiplican y dividen fracciones y números mixtos para determinar el peso y la velocidad de los carritos. Sus estudiantes aplican su comprensión de la división de fracciones nuevamente en este módulo cuando dividen números decimales. Además, usan la división de fracciones cuando simplifican expresiones y resuelven ecuaciones de un paso en el módulo 4, y cuando resuelven problemas que incluyen área y volumen en el módulo 5.

Progresión

de las lecciones

Lección 9 Dividir fracciones usando diagramas de cinta

Lección 10 Dividir fracciones usando la estrategia de invertir y multiplicar

Lección 11 Aplicaciones de la división con fracciones

Lección 12 Operaciones con fracciones en una situación del mundo real

a. Escribe

Dividir fracciones usando diagramas de cinta

Usar un diagrama de cinta para dividir una fracción entre otra fracción

Relacionar la división de una fracción entre otra fracción con un problema de factor desconocido

Vistazo a la lección

En esta lección, la clase desarrolla las estrategias de división de fracciones de la lección anterior al usar diagramas de cinta y ecuaciones de factor desconocido para determinar los cocientes. Primero, sus estudiantes realizan una tarea de clasificación para razonar sobre las expresiones de división y comparar los cocientes. En parejas, evalúan las expresiones de división, analizan los cocientes y buscan patrones. Por último, aplican su comprensión de la división de fracciones para resolver problemas del mundo real.

Pregunta clave

b. Traza un diagrama de cinta que represente la ecuación de factor desconocido de la parte (a).

c. ¿Cuál es el valor de una unidad en el diagrama de cinta de la parte (b)?

¿Cuánto es

• ¿Por qué escribiríamos una expresión de división con fracciones como una ecuación de factor desconocido?

Criterios de logro académico

6.Mód2.CLA4 Dividen dos fracciones o números mixtos.

6.Mód2.CLA5 Resuelven e interpretan problemas verbales que incluyen la división de fracciones y de números mixtos.

6.Mód2.CLA6 Interpretan la división de fracciones y de números mixtos usando modelos.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Dividir una fracción entre una fracción unitaria

• Dividir una fracción entre una fracción no unitaria

• Situaciones de división

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• tarjetas de Clasificar: División con fracciones (1 set por pareja de estudiantes)

Preparación de la lección

• Haga suficientes copias de las tarjetas de Clasificar: División con fracciones de manera que cada pareja de estudiantes tenga 1 set.

• Recorte las tarjetas y organícelas en sets de manera que cada set contenga 1 copia de cada tarjeta.

• Cree 2 o 3 hojas de respuestas para los problemas 4 a 6 y cuélguelas en distintos lugares del salón de clases.

Fluidez

Dividir un número entero entre una fracción unitaria

La clase divide un número entero entre una fracción unitaria como preparación para dividir fracciones.

Instrucciones: Divide.

Presentar

Sus estudiantes clasifican tarjetas para razonar sobre el tamaño del cociente al dividir fracciones.

Agrupe a sus estudiantes en parejas y dé a cada pareja un set de tarjetas de Clasificar: División con fracciones. Dé algunos minutos para que sus estudiantes clasifiquen las tarjetas en tres pilas:

• La pila A tiene tarjetas con expresiones cuyos cocientes son menores que 1.

• La pila B tiene tarjetas con expresiones cuyos cocientes son iguales a 1.

• La pila C tiene tarjetas con expresiones cuyos cocientes son mayores que 1.

Recorra el salón de clases mientras sus estudiantes trabajan y preste atención a las estrategias que usan para clasificar las tarjetas. Si sus estudiantes necesitan apoyo para determinar dónde ubicar una tarjeta, haga preguntas sobre expresiones de división que les resulten conocidas. Por ejemplo, pregunte si 4 ÷ 5 es menor que 1 o mayor que 1 y cómo lo saben.

Cuando la mayoría haya terminado, pida a sus estudiantes que ayuden a clasificar las expresiones. Muestre las tarjetas de cada pila a medida que las comentan.

Pila A: 5 6 ÷ 5, 5

Pila B: 5 6 ÷ 5 6

Pila C: 5 6 ÷ 1 6 , 6 5 ÷ 5 6 , 6 5 ÷ 3 4 , 5 6 ÷ 4 6 , 6 ÷ 1 5

Use las preguntas que siguen para hacer una reflexión final sobre la actividad. Anime a sus estudiantes a usar los términos dividendo y divisor al explicar su razonamiento.

¿Cómo supieron qué tarjetas iban en la pila A?

Miré los dos números de la expresión de división. Si el divisor era mayor que el dividendo, entonces sabía que el valor de la expresión sería menor que 1.

¿Cómo supieron qué tarjetas iban en la pila B?

Miré los dos números de la expresión de división. Si el divisor y el dividendo eran iguales, entonces sabía que el valor de la expresión sería igual a 1.

¿Cómo supieron qué tarjetas iban en la pila C?

Miré los dos números de la expresión de división. Si el divisor era menor que el dividendo, entonces sabía que el valor de la expresión sería mayor que 1. 5

Tanto la expresión 6 _ 5 ÷ 4 _ 3 como 5 _ 6 ÷ 4 _ 3 están en la pila A. ¿Qué expresión tiene un valor mayor? Expliquen.

6 5 ÷ 4 3 tiene un valor mayor que 5 6 ÷ 4 3 . En los dos casos, el divisor es 4 3 , y 6 5 es mayor que 5 6 .

Entonces, 6 _ 5 ÷ 4 _ 3 debe ser mayor que 5 _ 6 ÷ 4 _ 3 .

Tanto la expresión 6 _ 5 ÷ 5 _ 6 como 6 _ 5 ÷ 3 _ 4 están en la pila C. ¿Qué expresión tiene un valor mayor?

Expliquen.

6 5 ÷ 3 4 tiene un valor mayor que 6 5 ÷ 5 6 . Hay más grupos de 3 4 en 6 5 que grupos de 5 6 en 6 5 porque 3 4

es menor que 5 6 .

Podemos clasificar estas expresiones en estas pilas si razonamos sobre el tamaño del cociente.

Hoy, usaremos diagramas de cinta de una nueva manera para determinar el cociente de una fracción y otra fracción.

Aprender

Dividir una fracción entre una fracción unitaria

La clase divide una fracción entre una fracción unitaria.

Muestre el diagrama de cinta que representa 2 _ 3

Nota para la enseñanza

En esta lección, se sientan las bases de la estrategia de invertir y multiplicar para dividir fracciones, que sus estudiantes aprenderán formalmente en la próxima lección. Si hay estudiantes que sacan conclusiones sobre la estrategia de invertir y multiplicar en esta lección en función de los patrones que ven, anime a esas personas a compartir lo que piensan. Sin embargo, considere esperar hasta la próxima lección para formalizar esta estrategia.

¿Qué expresión de división representa el diagrama?

2 3 ÷ 1 4

¿Cuánto es 2 _ 3 ÷ 1 _ 4  ? Expliquen.

2 3 ÷ 1 4 es más que 2, pero menos que 3. Lo sé porque veo más que 2, pero menos que 3, grupos de 1 4 .

2 _ 3 ÷ 1 _ 4 es 2 2 _ 3 porque veo 2 2 _ 3 grupos de 1 _ 4 en 2 _ 3 .

Considere encerrar en un círculo los grupos en el diagrama a medida que dice el siguiente enunciado:

Podemos ver que hay más que 2, pero menos que 3, grupos de 1 _ 4 en 2 _ 3 . Hay exactamente 2 2 _ 3 grupos de 1 _ 4 en 2 _ 3 .

En la lección anterior, aprendimos que podemos determinar el cociente de dos fracciones si reescribimos las fracciones con denominadores comunes.

Muestre el siguiente trabajo. Recuerde a sus estudiantes que 8 _ 3 es equivalente a 2 2 _ 3 .

2 _ 3 ÷ 1 _ 4 = 8 __ 12 ÷ 3 __ 12 = 8 _ 3

¿Por qué resulta útil hallar denominadores comunes para dividir fracciones?

Si tenemos denominadores comunes, entonces dividimos unidades semejantes. Si los denominadores son iguales, el cociente de las dos fracciones es el cociente de los dos numeradores.

Una manera de pensar en 2 3 ÷ 1 4 es como el número de grupos de 1 4 que hay en 2 3  . O, después de hallar los denominadores comunes, podemos hacernos la pregunta “¿Cuántos grupos de 3 __ 12 hay en 8 __ 12  ?”.

Muestre 2 3 ÷ 1 4 = ?.

Otra manera de pensar en 2 _ 3 ÷ 1 _ 4 es con la multiplicación. ¿Cuál es la ecuación de factor desconocido para esta expresión de división?

2 3 = 1 4 × ?

Muestre la ecuación de factor desconocido 2 3 = 1 4 × ?.

Podemos interpretar la ecuación de factor desconocido como la pregunta “¿2 _ 3 es 1 _ 4 de qué número?”. Tracemos un diagrama de cinta para representar esa ecuación de factor desconocido.

Sabemos que 2 _ 3 representa 1 _ 4 de un número. Entonces, podemos trazar un diagrama de cinta con 4 unidades y rotular una unidad 2 _ 3 .

Pida a sus estudiantes que escriban la ecuación de factor desconocido y su interpretación en la primera fila de la tabla del problema 1.

Muestre el diagrama de cinta que representa 2 3 = 1 4 × ?. ? 2 3

¿Cómo saben que el diagrama de cinta representa la pregunta “¿2 _ 3 es 1 _ 4 de qué número?”.

Hay 4 unidades en el diagrama de cinta y el valor de una unidad es 2 3 .

¿Cuál es el total? Expliquen.

Hay 4 unidades de 2 _ 3, así que es 8 _ 3 porque 4 × 2 _ 3 = 8 _ 3 .

Pida a sus estudiantes que terminen de completar la primera fila de la tabla del problema 1.

Sin importar la manera en que pensemos en la división, determinamos que

Apliquemos nuestra comprensión de las ecuaciones de factor desconocido para dividir fracciones entre fracciones.

Dirija la atención de sus estudiantes al problema 1. Lea las instrucciones en voz alta y pida a sus estudiantes que sigan la lectura. Señale que la primera fila de la tabla es un resumen del problema que acaban de completar en grupo. Dé varios minutos para que sus estudiantes completen el problema en parejas. Se espera que completen al menos las primeras tres filas. El resto de la sucesión de problemas se brinda como práctica adicional, si fuera necesario. Recorra el salón de clases mientras sus estudiantes trabajan y, según sea necesario, haga las siguientes preguntas como ayuda para crear ecuaciones de factor desconocido y diagramas de cinta:

• ¿Qué ecuación de factor desconocido se relaciona con esta expresión de división?

• ¿Qué representa todo el diagrama de cinta en esa ecuación de factor desconocido?

¿Qué representa cada unidad?

DUA: Acción y expresión

Para brindar apoyo con la escritura de ecuaciones de factor desconocido a partir de expresiones de división, escriba y cuelgue en el salón de clases el comienzo de oración y el ejemplo que siguen para que sus estudiantes puedan acceder a ellos a lo largo del tema:

¿ es de qué número?

número?

1. Para cada expresión de división:

• escribe la expresión de división como una ecuación de factor desconocido;

• escribe la interpretación de la ecuación de factor desconocido;

• traza un diagrama de cinta para representar la ecuación de factor desconocido;

• determina el valor de una unidad en el diagrama de cinta;

• calcula el cociente.

Expresión de división

Ecuación de factor desconocido

Interpretación de la ecuación de factor desconocido

Diagrama de cinta Valor de una unidad

Expresión de división

Ecuación de factor desconocido

Interpretación de la ecuación de factor desconocido

Diagrama de cinta

Después de varios minutos, reúna a la clase. Pida a las parejas que comparen sus cocientes con otra pareja. Permita que sus estudiantes hagan preguntas si lo desean.

¿Cómo saben cuál es el número de unidades en el diagrama de cinta?

El número de unidades en el diagrama de cinta es el denominador del divisor.

Valor de una unidad Cociente

¿Cómo están representados el dividendo y el divisor en el diagrama de cinta?

El denominador del divisor nos indica el número de unidades en el diagrama de cinta. En todos los casos, el divisor es una fracción unitaria, así que el dividendo está representado por una unidad en el diagrama de cinta.

¿Cómo hallaron el cociente para cada expresión?

Multipliqué el valor de una unidad por el número de unidades en el diagrama de cinta.

¿Es correcto decir que 2 _ 3 ÷ 1 _ 4 es equivalente a 2 _ 3 × 4 ?

Sí.

En el problema 2, sus estudiantes generalizarán los patrones que descubrieron en el problema 1 y escribirán las expresiones de multiplicación relacionadas para las fracciones divididas entre una fracción unitaria. Como preparación para el problema 2, pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder el siguiente planteamiento:

Expliquen a su pareja cómo evaluar 4 _ 7 ÷ 1 _ 5 .

Sabemos que 4 _ 7 es 1 _ 5 de un número, así que 4 _ 7 es el valor de una unidad en un diagrama de cinta que tiene 5 unidades. Multiplicamos 4 _ 7 por 5 para evaluar 4 _ 7 ÷ 1 _ 5 .

Dé, como máximo, un minuto para que sus estudiantes completen el problema 2 de manera independiente.

2. Determina el número desconocido que hace que cada oración numérica sea verdadera.

a. 3 4 ÷ 1 2 = 3 4 × 2

b. 4 7 ÷ 1 5 = 4 7 × 5

c. 2 _ 5 ÷ 1 _ 3 = 2 _ 5 × 3

Cuando la mayoría haya terminado, comparta las respuestas del problema 2. Invite a sus estudiantes a hacer preguntas.

Promoción de la práctica de las matemáticas

Cada estudiante reconoce y expresa regularidad en la lógica de la repetición cuando usa repetidamente un diagrama de cinta para dividir entre una fracción unitaria a fin de reconocer el patrón que muestra que dividir entre una fracción unitaria es equivalente a multiplicar por el denominador de la fracción unitaria.

Considere hacer las siguientes preguntas:

• ¿Qué tiene en común su razonamiento en todos estos ejemplos?

• ¿Qué patrón observan cuando usan un diagrama de cinta para dividir entre una fracción unitaria?

• ¿Funcionará siempre este patrón? Expliquen.

Dividir una fracción entre una fracción no unitaria

La clase divide una fracción entre una fracción no unitaria.

Hasta ahora, en esta lección, dividimos entre fracciones unitarias. Ahora, vamos a dividir fracciones entre fracciones no unitarias. ¿Creen que verán un patrón similar cuando dividan fracciones entre fracciones no unitarias? Expliquen.

Ejemplo: Sí. Creo que veré un patrón similar porque sigo dividiendo entre una fracción.

Pensemos en el ejemplo de problema 1 _ 4 ÷ 3 _ 5 . Al trazar el diagrama de cinta para el problema

1 _ 4 ÷ 3 _ 5 , ¿cuántas unidades representará el valor 1 _ 4 ? ¿Cuál es el número total de unidades en el diagrama de cinta? Expliquen.

1 4 representará 3 unidades de un total de 5 unidades.

Si 1 _ 4 representa 3 unidades en el diagrama de cinta, ¿qué representa una unidad en el diagrama de cinta? Reúnanse y conversen en parejas.

Después de que sus estudiantes conversen en parejas, dirija su atención al problema 3. Lea las instrucciones en voz alta y pídales que sigan la lectura. Sus estudiantes repetirán el mismo proceso que siguieron anteriormente en la lección, pero esta vez los divisores serán fracciones no unitarias.

Dé varios minutos para que completen el problema en parejas. Es posible que no completen las seis filas en el tiempo dado. Recorra el salón de clases mientras sus estudiantes trabajan y, según sea necesario, haga las siguientes preguntas como ayuda para crear ecuaciones de factor desconocido y diagramas de cinta:

• ¿Qué ecuación de factor desconocido se relaciona con esta expresión de división?

• ¿Qué representa todo el diagrama de cinta en esa ecuación de factor desconocido? ¿Qué representa cada unidad?

3. Completa la tabla.

Expresión de división

Ecuación de factor desconocido

Interpretación de la ecuación de factor desconocido

Diagrama de cinta Valor de una unidad Cociente

Expresión de división

Ecuación de factor desconocido

Interpretación de la ecuación de factor desconocido

Diagrama de cinta

Después de varios minutos, reúna a la clase. Pida a las parejas que comparen sus cocientes con otra pareja. Permita que sus estudiantes hagan preguntas según sea necesario.

En estas expresiones, los divisores son fracciones no unitarias. ¿Cómo cambia el diagrama de cinta al tener un divisor que es una fracción no unitaria?

El valor de una unidad en el diagrama de cinta no es el dividendo.

Escriba 1 3 ÷ 4 5 en el pizarrón. Trace el diagrama de cinta a medida que comentan las siguientes preguntas:

¿Cómo determinan el valor de una unidad en el diagrama de cinta en la cuarta

expresión, 1 _ 3 ÷ 4 _ 5   ?

Sé que 1 3 es 4 5 de algún número. Entonces, 1 3 representa 4 de 5 unidades en un diagrama de cinta.

Por lo tanto, una unidad debe ser 1 4 de 1 3 , o 1 12 .

Nota para la enseñanza

Mire el video para el desarrollo profesional en la enseñanza Usar un diagrama de cinta para dividir fracciones con ecuaciones de factor desconocido para ver cómo representar este problema de división con un diagrama de cinta.

En este problema, hallamos que una unidad en el diagrama de cinta tiene un valor de 1 __ 12 . ¿Cómo usamos el valor de una unidad para determinar el cociente?

Como el diagrama tiene 5 unidades, multiplicamos el valor de una unidad por 5. El cociente es 5 12 .

La penúltima expresión de la tabla es 6 _ 5 ÷ 3 _ 4 . Clasificamos esta expresión al comienzo de la lección. ¿En qué pila la colocamos? ¿Estábamos en lo correcto?

Colocamos la expresión en la pila C. Estábamos en lo correcto porque 6 5 ÷ 3 4 = 8 5 .

Situaciones de división

La clase divide fracciones para resolver problemas del mundo real.

Dirija la atención de sus estudiantes a los problemas 4 a 6. La complejidad de los problemas aumenta. Sus estudiantes deben intentar completar al menos dos problemas en el tiempo asignado. Permita que trabajen de manera independiente o en parejas. Pídales que comprueben sus respuestas con una de las hojas de respuestas colgadas en el salón de clases. Recorra el salón de clases mientras sus estudiantes trabajan y asegúrese de que estén interpretando la pregunta correctamente.

En los problemas 4 a 6, responde la pregunta y traza un diagrama para justificar tu razonamiento.

4. Leo vierte 1 4 de galón de limonada en una jarra. La limonada llena 1 8 de la jarra. ¿Cuántos galones de limonada debe verter Leo para llenar toda la jarra?

Diferenciación: Desafío

Para quienes necesiten un desafío adicional, presente las siguientes preguntas:

• Si 4 1 2 ÷ 1 4 = 18, ¿cuánto es 4 1 2 ÷ 3 4 ? 6

Leo debe verter 2 galones de limonada para llenar toda la jarra.

Diferenciación: Apoyo

Para quienes necesiten apoyo adicional, considere brindar diagramas de cinta parcialmente completados. En su defecto, considere cambiar el contexto para que haya una fracción y un número entero.

• Leo vierte 2 galones de limonada en una jarra. La limonada llena 1 __ 8 de la jarra. ¿Cuántos galones de limonada debe verter Leo para llenar toda la jarra?

• Un grifo llena una cubeta a una tasa de 2 galones por minuto. ¿Cuántos minutos se tarda en llenar una cubeta en la que caben 7 8 de galón?

5. Un grifo llena una cubeta a una tasa de 1 5 de galón por minuto. ¿Cuántos minutos se tarda en llenar una cubeta en la que caben 7 8 de galón? Escribe tu respuesta como un número mixto.

8

8 × 5 = 35 8 = 4 3 8

Se tarda 4 3 8 minutos en llenar la cubeta.

6. Ryan recoge arándanos y congela 3 4 de ellos. Congela 2 1 2 libras de arándanos. ¿Cuántas libras de arándanos recogió Ryan? Escribe tu respuesta como un número mixto.

Ryan recogió 3 2 6 libras de arándanos.

Después de que la mayoría haya completado uno o dos problemas y comprobado sus respuestas, reúna a la clase para hacer una reflexión final sobre la lección.

Concluir

Reflexión final 5 min

Objetivos: Usar un diagrama de cinta para dividir una fracción entre otra fracción

Relacionar la división de una fracción entre otra fracción con un problema de factor desconocido

Use las preguntas que siguen para guiar una conversación acerca de escribir expresiones de división como ecuaciones de factor desconocido. Invite a sus estudiantes a complementar las respuestas de sus pares.

Muestre las dos preguntas y los diagramas de cinta que representan 2 3 ÷ 3

¿Cuántos grupos de 3 _

hay en

Usamos dos tipos diferentes de diagramas de cinta para dividir fracciones. Los dos diagramas de cinta representan

¿Qué método muestra cada diagrama de cinta?

El método de la izquierda muestra cómo usar denominadores comunes para dividir fracciones.

El método de la derecha muestra cómo interpretar la división de fracciones como una ecuación de factor desconocido.

¿Qué método prefieren? ¿Por qué?

Ejemplo: Prefiero el método de la ecuación de factor desconocido porque creo que el diagrama de cinta es más fácil para trabajar.

DUA: Representación

Agregue una segunda burbuja al organizador gráfico de red de estrategias de división de fracciones que se presentó en la lección 8 para la estrategia de ecuación de factor desconocido. Incluya un ejemplo con el diagrama de cinta.

¿Por qué escribiríamos una expresión de división con fracciones como una ecuación de factor desconocido?

Escribir una ecuación de factor desconocido nos permite interpretar la división de otra manera. Escribir una ecuación de factor desconocido nos permite crear un diagrama de cinta que sea más eficiente para trabajar.

Boleto de salida

5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Dividir fracciones usando diagramas de cinta

En esta lección:

• relacionamos la división de una fracción entre otra fracción con una ecuación de factor desconocido;

• usamos un diagrama de cinta para dividir una fracción entre otra fracción.

Ejemplos

1. Considera 2 3 ÷ 3 5 .

a. Escribe 2 3 ÷ 3 5 como una ecuación de factor desconocido.

2 3 = 3 5 × ?

Piensa en esta ecuación de factor desconocido como la pregunta “¿ 2 3 es 3 5 de qué número?”.

b. Traza un diagrama de cinta que represente la ecuación de factor desconocido de la parte (a).

? 2 3

Traza un diagrama de cinta con 5 unidades. Dado que 2 3 es 3 5 de un número desconocido, 3 de las 5 unidades, o 3 5 , están rotuladas 2 3

c. ¿Cuánto es 2 3 ÷ 3 5 ?

10 9 Una unidad del diagrama de cinta representa 2 9 porque 2 9 + 2 9 + 2 9 = 6 9 o 2 3 Dado que hay 5 unidades en todo el diagrama de cinta y cada unidad representa 2 9 , el cociente es 10 9

2. Leo vierte 3 4 de litro de un líquido en un recipiente. El líquido llena 1 4 del recipiente. ¿Cuántos litros de líquido debe verter Leo para llenar todo el recipiente? Traza un diagrama de cinta para justificar tu solución.

El diagrama de cinta representa el recipiente, y 3 4 de litro llenan 1 4 del recipiente.

Dado que cada unidad representa 3 4 de litro, todo el diagrama de cinta representa 3 litros.

Leo debe verter 3 litros de líquido para llenar todo el recipiente.

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

En los problemas 5 a 10, divide. Muestra tu trabajo.

1. Julie y Sasha evalúan 4 5 ÷ 1 2 .

• Julie piensa en 4 5 ÷ 1 2 como la pregunta “¿Cuántos grupos de 1 2 hay en 4 5 ?”.

• Sasha piensa en 4 5 ÷ 1 2 como la pregunta “¿ 4 5 es 1 2 de qué número?”.

¿Quién está en lo correcto?

A. Solo Julie está en lo correcto.

B. Solo Sasha está en lo correcto.

C. Tanto Julie como Sasha están en lo correcto.

D. Ni Julie ni Sasha están en lo correcto.

En los problemas 2 a 4, considera el diagrama de cinta. Escribe una expresión de división y la ecuación de factor desconocido relacionada. Luego, calcula el cociente.

Diagrama de cinta Expresión de división Ecuación de factor desconocido

11. Un maestro de educación física divide 3 4 de un campo en secciones para juegos. Cada sección es 1 8 de todo el campo. ¿Cuántas secciones forma el maestro? Muestra tu trabajo.

3 4 ÷ 1 8 = 3 4 × 8 = 24 4 = 6

El maestro forma 6 secciones.

12. Se necesitan 5 6 de galón de agua para llenar 1 3 de una cubeta. ¿Cuántos galones de agua llenarán toda la cubeta? Traza un diagrama de cinta para justificar tu solución. 15 6 5 6

15 6 de galón, o 2 3 6 galones, de agua llenarán toda la cubeta.

Recuerda

En los problemas 13 a 16, escribe la fracción como un número mixto o escribe el número mixto como una fracción.

17. Eddie comparte 4 pasteles con amigas. Cada amiga recibe exactamente 2 5 de pastel. ¿Con cuántas amigas comparte Eddie los pasteles? Muestra tu trabajo.

4 ÷ 2 5 = 10

Eddie comparte los pasteles con 10 amigas.

18. ¿Cuál de los siguientes enunciados es verdadero?

A. El valor de 6 en 620 es 100 veces el valor de 6 en 62

B. El valor de 6 en 62 es 10 veces el valor de 6 en 6.2

C. El valor de 6 en 6.2 es 1 100 del valor de 6 en 0.62

D. El valor de 6 en 0.62 es 1 10 del valor de 6 en 0.062

EUREKA MATH2

Dividir fracciones usando la estrategia de invertir y multiplicar

Usar la estrategia de invertir y multiplicar para dividir una fracción entre otra fracción

Vistazo a la lección

En esta lección, la clase desarrolla una comprensión conceptual de por qué sirve la estrategia de invertir y multiplicar para dividir fracciones. Sus estudiantes basan su comprensión tanto en la ecuación de factor desconocido como en el diagrama de cinta. Mediante la rutina Intercambio con la pizarra blanca, usan la estrategia de invertir y multiplicar para dividir fracciones y números mixtos de manera independiente. Además, examinan un trabajo que incluye la división de fracciones en busca de errores comunes. En esta lección, se presenta el término recíproco.

Pregunta clave

• ¿Por qué sirve la estrategia de invertir y multiplicar para dividir una fracción entre otra fracción?

Criterios de logro académico

6.Mód2.CLA4 Dividen dos fracciones o números mixtos.

6.Mód2.CLA6 Interpretan la división de fracciones y de números mixtos usando modelos.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• La estrategia de invertir y multiplicar

• Intercambio con la pizarra blanca: División con fracciones

• Análisis de errores en la división con fracciones

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• No se necesita.

Fluidez

Multiplicar fracciones

La clase multiplica fracciones como preparación para usar la estrategia de invertir y multiplicar.

Instrucciones: Multiplica.

Nota para la enseñanza

Las soluciones en la sección Fluidez están expresadas como fracciones con la unidad más grande posible, pero no es necesario que sus estudiantes escriban las respuestas de esta manera. Acepte todas las respuestas correctas.

Presentar

La clase determina si determinadas oraciones numéricas que incluyen la multiplicación y la división son verdaderas o falsas.

Guíe un Intercambio con la pizarra blanca en el que sus estudiantes trabajen en parejas. Considere usar solo algunas de las oraciones numéricas dadas.

Mostraré una oración numérica. En parejas, determinen si la oración numérica es verdadera o falsa. Escriban verdadera o falsa en sus pizarras blancas y levántenlas para que pueda verlas. Prepárense para defender su respuesta.

Pida a las parejas que compartan lo que escribieron en sus pizarras blancas con el resto de la clase. Invite a un grupo o dos a explicar su razonamiento y permita que los grupos comenten las respuestas.

Aborde los conceptos erróneos según sea necesario.

A continuación, se muestran las oraciones numéricas y los ejemplos de razonamiento que justifican por qué cada oración es verdadera o falsa:

• 4 ÷ 1 _ 3 = 4 × 3

Esta oración numérica es verdadera porque, al dividir entre 1 3 , se obtiene el mismo resultado que al multiplicar por 3.

• 4 × 1 3 = 4 ÷ 3

Esta oración numérica es verdadera porque, al multiplicar por 1 3 , se obtiene el mismo resultado que al dividir entre 3.

• 3 ÷ 4 = 1 3 × 4

Esta oración numérica es falsa porque 3 ÷ 4 = 3 _ 4 y 1 _ 3 × 4 = 4 _ 3 .

• 3 × 4 = 3 ÷ 1 _ 4

Esta oración numérica es verdadera porque, al multiplicar por 4, se obtiene el mismo resultado que al dividir entre 1 4 .

• 1 3 ÷ 4 = 1 3 × 1 4

Esta oración numérica es verdadera porque, al dividir entre 4, se obtiene el mismo resultado que al multiplicar por 1 4 .

Esta oración numérica es falsa porque 3 4 ÷ 2 es equivalente a 3 4 × 1 2 , pero 3 4 × 1 2 no es equivalente a 4 3 × 2.

3 _ 4 ÷ 1 _ 2 = 3 _ 4 × 2

Esta oración numérica es verdadera porque, al dividir entre 1 _ 2 , se obtiene el mismo resultado que al multiplicar por 2.

Esta oración numérica es verdadera porque 1 2 ÷ 3 4 =

¿Por qué es posible que razonar sobre la última oración numérica sea más difícil que razonar sobre las otras?

Estamos dividiendo una fracción entre otra fracción.

Hoy, aprenderemos una estrategia eficiente para dividir fracciones que no requiere el uso de denominadores comunes o diagramas de cinta.

Aprender

La estrategia de invertir y multiplicar

La clase explora y explica la estrategia de invertir y multiplicar para la división de fracciones con diagramas de cinta.

Use las preguntas que siguen para guiar una conversación de toda la clase que muestre de qué manera el trabajo con diagramas de cinta de la lección anterior lleva a la estrategia de invertir y multiplicar:

Observemos en detalle el problema 1 _ 3 ÷ 4 _ 5 de la lección anterior. ¿Cuál es la ecuación de factor desconocido para 1 _ 3 ÷ 4 _ 5 ? ¿Cómo podemos interpretar esa ecuación?

La ecuación de factor desconocido es 1 3 = 4 5 × ? y significa “¿ 1 3 es 4 5 de qué número?”.

Pida a sus estudiantes que le ayuden a trazar el diagrama de cinta que representa la ecuación de factor desconocido 1 3 = 4 5 × ?. ? 1

¿Cómo determinamos el valor de una unidad del diagrama de cinta? Expliquen.

Hallamos 1 _ 4 de 1 _ 3 porque 1 _ 3 representa 4 unidades en nuestro diagrama de cinta.

¿Cuál es el valor de una unidad?

1 12

Escriba el valor de cada unidad, 1 12 , en el diagrama de cinta. ?

Sabemos que el valor de una unidad es 1 __ 12 . ¿Cómo determinamos el valor del total, o de todo el diagrama de cinta?

Multiplicamos 1 12 por 5.

¿Por qué multiplicamos 1 __ 12 por 5?

Hay 5 unidades en el diagrama de cinta.

¿Cuánto es 1 _ 3 ÷ 4 _ 5 ?

5 12

Para dividir 1 3 entre 4 5 , primero multiplicamos 1 3 por 1 4 para determinar el valor de una unidad del diagrama de cinta. Luego, multiplicamos por 5 porque tenemos 5 unidades.

Al lado del diagrama de cinta, muestre los pasos que se usaron para evaluar 1 _ 3 ÷ 4 _ 5 . 1 _ 3 ÷ 4 _ 5

4 unidades = 1 3

1 unidad = 1 3 × 1 4 = 1 12

5 unidades = 1 __ 12 × 5 = 5 __ 12

1 3 ÷ 4 5 = 1 3 × 5 4 = 5 12

Pida a sus estudiantes que resuman lo que sucede en cada paso del trabajo que se muestra y cómo se relaciona con el trabajo del diagrama de cinta.

El trabajo que se muestra es parecido a lo que hicimos para evaluar 1 _ 3 ÷ 4 _ 5 con un diagrama de cinta. Primero, en los pasos se muestra cómo calcular 1 _ 4 de 1 _ 3 para determinar el valor de una unidad del diagrama de cinta. Luego, se muestra cómo multiplicar el valor de una unidad, 1 __ 12 , por 5 para calcular el cociente, 5 __ 12 .

Muestre la ecuación y haga la siguiente pregunta:

1 _ 3 × 1 _ 4 × 5 = 5 __ 12

Para evaluar 1 _ 3 ÷ 4 _ 5 , multiplicamos 1 _ 3 por 1 _ 4 y, luego, multiplicamos por 5. Con esos dos pasos, se obtiene el mismo resultado que al multiplicar 1 _ 3 por 5 _ 4 . Observen que en el último paso del trabajo, se muestra 1 _ 3 ÷ 4 _ 5 reescrito como 1 _ 3 × 5 _ 4 .

¿Es verdadero que 1 _ 3 ÷ 4 _ 5 = 1 _ 3 × 5 _ 4 ?

Sí.

Acepte todas las respuestas a las siguientes preguntas. Sus estudiantes tendrán la oportunidad de razonar sobre esas preguntas en los próximos minutos.

¿Creen que esta estrategia de escribir una expresión de división como una expresión de multiplicación equivalente siempre funciona? En otras palabras, ¿creen que podemos usar esta estrategia para cualquier expresión de división? Reúnanse y conversen en parejas.

Promoción de la práctica de las matemáticas

Cada estudiante reconoce y utiliza estructuras cuando razona sobre por qué sirve la estrategia de invertir y multiplicar.

Considere hacer las siguientes preguntas:

• ¿Cómo se relaciona una ecuación de factor desconocido con la estrategia de invertir y multiplicar?

• ¿Pueden separar la división de una fracción entre otra fracción en otros cálculos?

Use las siguientes preguntas para ayudar a sus estudiantes a darse cuenta de que la estrategia de invertir y multiplicar sirve para muchos tipos de expresiones de división:

Consideremos un cociente que ya calculamos en una lección anterior. ¿Es verdadero que

3 ÷ 1 _ 4 = 3 × 4 _ 1 ? Expliquen.

Sí. Sé que 3 ÷ 1 4 = 12 y 3 × 4 1 = 12, así que la oración numérica es verdadera.

Consideremos otro cociente conocido. Sabemos que 1 1 _ 2 ÷ 3 es 1 _ 2 . ¿Cómo podemos escribir

1 1 _ 2 ÷ 3 sin usar ningún número mixto?

3 _ 2 ÷ 3

¿Es verdadero que 3 _ 2 ÷ 3 = 3 _ 2 × 1 _ 3 ? Expliquen.

Sí. Sé que al dividir entre 3, se obtiene el mismo resultado que al multiplicar por 1 3 .

¿Cómo le describirían este método a una amiga o un amigo?

Ejemplo: Al dividir fracciones, puedo dar vuelta la segunda fracción y multiplicarla por la primera fracción.

A este método para dividir fracciones lo llamamos estrategia de invertir y multiplicar. Podemos invertir el numerador y el denominador del divisor y, luego, multiplicar por el dividendo.

Dé unos minutos para que sus estudiantes completen los problemas 1 y 2 de manera independiente o en parejas.

1. Considera 2 3 ÷ 3 4 . a. Usa un diagrama de cinta para calcular el cociente.

Apoyo para la comprensión del lenguaje

Considere relacionar el término invertir con “voltear y quedar bocabajo”. Por ejemplo, cuando sus estudiantes se cuelgan del pasamanos (monkey bars) con las rodillas, hay una inversión. Del mismo modo, cuando hacen una parada de manos, también hay una inversión y quedan al revés.

b. Usa la estrategia de invertir y multiplicar para calcular el cociente.

2 _ 3 ÷ 3 _ 4 = 2 _ 3 × 4 _ 3 = 8 _ 9 8 9

2. Considera 5 ÷ 6 7 . ¿Qué oraciones numéricas son verdaderas? Elige todas las opciones que correspondan.

A. 5 ÷ 6 _ 7 = 5 × 6 ÷ 7

B. 5 ÷ 6 _ 7 = 5 × 7 ÷ 6

C. 5 ÷ 6 7 = 5 × 7 × 1 6

D. 5 ÷ 6 7 = 5 × 6 7

E. 5 ÷ 6 7 = 5 × 7 6

Cuando la mayoría haya terminado, pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

Sus dos respuestas a los problemas 1(a) y 1(b) deberían ser 8 _ 9 . ¿Qué método prefieren?

¿Por qué?

Ejemplo: Prefiero la estrategia de invertir y multiplicar porque me toma menos tiempo que trazar un diagrama de cinta.

¿Cómo usaron la estrategia de invertir y multiplicar para hallar las oraciones numéricas verdaderas en el problema 2?

Ejemplo: Sabía que 5 ÷ 6 7 es equivalente a 5 × 7 6 , y, a partir de allí, busqué expresiones que fueran equivalentes a 5 × 7 6 .

Sabemos que 5 ÷ 6 _ 7 es equivalente a 5 × 7 _ 6 . Entonces, también podemos pensar en esta expresión como 5 × 7 ÷ 6 o 5 × 7 × 1 _ 6 .

Cuando invertimos una fracción, el nuevo número es el recíproco del número original.

Un recíproco es el número que se obtiene al invertir una fracción. El recíproco de 3 _ 4 es 4 _ 3 .

El recíproco de 5 _ 2 es 2 _ 5 .

Nota para la enseñanza

Al comentar el problema 2, no se debe mencionar el orden de las operaciones, que sus estudiantes aprenderán en el módulo 4. En cambio, recuerde a sus estudiantes, según sea necesario, otros conceptos sobre fracciones que hayan aprendido en grados anteriores:

• En 5.o grado, la clase interpreta una fracción como 7 6 como la expresión de división 7 ÷ 6.

• En 4.o grado, la clase comprende una fracción como 7 6 como el producto 7 × 1 6   .

Para resolver el problema 2, sus estudiantes deberían combinar esos conocimientos previos con los nuevos conocimientos que adquirieron sobre la estrategia de invertir y multiplicar.

Apoyo para la comprensión del lenguaje

Considere colocar en el salón de clases una tabla como la siguiente para mostrar cómo invertir una fracción a fin de obtener su recíproco:

Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para analizar las siguientes preguntas:

¿Creen que podemos determinar el recíproco de un número entero como 4? ¿Por qué?

Sí. El número entero 4 puede escribirse como la fracción 4 1 . Podemos invertir esa fracción para formar su recíproco, 1 4 .

Los números mixtos no tienen recíprocos. Cuando dividimos entre un número mixto, primero debemos escribir el número mixto como una fracción mayor que 1. ¿Cómo escribimos el número

como una fracción mayor que 1?

Intercambio

con la pizarra blanca: División con fracciones

La clase divide fracciones y números mixtos.

Guíe un Intercambio con la pizarra blanca.

Vamos a practicar cómo dividir fracciones usando la estrategia de invertir y multiplicar. Les daré una expresión de división y tendrán que evaluarla de manera independiente. Muestren su trabajo y el cociente en sus pizarras blancas. Cuando hayan escrito su respuesta, levanten la pizarra blanca para que pueda verla.

Las expresiones de división están ordenadas de menor a mayor complejidad. Puede elegir no usar todas las expresiones. Muestre una expresión a la vez y compruebe las respuestas de la clase antes de mostrar las siguientes expresiones. Brinde retroalimentación inmediata a cada estudiante.

Expresiones de división:

Nota para la enseñanza

La intención de que sus estudiantes usen la estrategia de invertir y multiplicar en el Intercambio con la pizarra blanca es que demuestren su comprensión de esta estrategia. Al avanzar, podrán elegir un método para la división.

Durante la actividad, considere formar parejas de estudiantes de manera que quienes necesiten apoyo adicional puedan recibirlo de su pareja.

Hacia el final del Intercambio con la pizarra blanca, considere recordar a sus estudiantes que, al dividir entre un número mixto, primero deben escribirlo como una fracción mayor que 1.

Diferenciación: Desafío

Para quienes necesiten un desafío adicional, considere hacer las siguientes preguntas:

• ¿Cuál es el producto de 4 5 y su recíproco?

• ¿Cuál es el producto de 5 1 y su recíproco?

• ¿Cuál es el número desconocido? 2 3 × = 1

• ¿Qué conclusiones pueden sacar sobre el producto de una fracción y su recíproco?

Análisis de errores en la división con fracciones

La clase analiza un trabajo en busca de errores en la división de fracciones.

Dirija la atención de sus estudiantes a los problemas 3 y 4. Cada integrante de la pareja debe elegir un problema para completar. Cuando las dos personas hayan terminado, deben turnarse para explicar el error y comprobar si la otra persona está de acuerdo. Recorra el salón de clases mientras sus estudiantes trabajan y vaya haciendo las siguientes preguntas:

• ¿Cómo calcularían el cociente?

• ¿En qué se diferencia el trabajo que se muestra del trabajo que realizaron ustedes?

• ¿Qué es lo que está mal en el cociente del trabajo que se muestra?

3. Riley le explica a un amigo que 5 _ 6 ÷ 3 _ 4 = 15 __ 24 , porque 5 _ 6 × 3 = 15 __ 6 y 15 __ 6 × 1 _ 4 = 15 __ 24 . Explica cualquier error que haya cometido Riley.

Ejemplo: Riley multiplica por 3 y, luego, por 1 4 en lugar de multiplicar por 1 3 y, luego, por 4.

4. Leo dice que 2 5 ÷ 7 9 = 35 18 , porque 2 5 ÷

9 = 5 2 × 7 9 . Explica cualquier error que haya cometido Leo.

Ejemplo: Al usar la estrategia de invertir y multiplicar, Leo invierte la primera fracción en lugar de la segunda fracción.

Cuando la mayoría haya terminado, reúna a la clase.

Concluir

Reflexión final 5 min

Objetivo: Usar la estrategia de invertir y multiplicar para dividir una fracción entre otra fracción

Use las preguntas y los planteamientos que siguen para guiar una conversación de toda la clase acerca de la división de fracciones. Anime a sus estudiantes a volver a expresar o desarrollar las respuestas de sus pares.

¿Qué estrategia suele ser más eficiente para dividir una fracción entre otra fracción: la estrategia de denominador común o la estrategia de invertir y multiplicar? Expliquen.

La estrategia de invertir y multiplicar suele ser más eficiente, ya que no se necesita el paso de hallar los denominadores comunes.

Expliquen cómo usar la estrategia de invertir y multiplicar para evaluar 2 _ 5 ÷ 3 _ 4 .

Invertimos 3 4 para hallar su recíproco, 4 3 . Luego, multiplicamos 2 5 por 4 3 . El producto de esas fracciones es 8 15 , que es equivalente a 2 5 ÷ 3 4 .

Expliquen por qué sirve usar la estrategia de invertir y multiplicar para evaluar 2 _ 5 ÷ 3 _ 4 .

Podemos pensar en 2 5 ÷ 3 4 como “ ¿ 2 5 es 3 4 de qué número?”. Como 2 5 es 3 4 de un número, primero dividimos 2 5 en 3 grupos, donde cada uno represente 1 4 del número desconocido. Luego, multiplicamos uno de esos grupos por 4 para hallar 4 4 , o el número desconocido entero. El resultado de dividir entre 3 y multiplicar por 4 es el mismo que el de multiplicar 2 5 por la fracción 4 3 , y esa es la estrategia de invertir y multiplicar.

Podemos pensar en el problema como un diagrama de cinta. Como 2 _ 5 representa 3 _ 4 de un número, el número entero representa 4 3 de 2 5 , o 2 5 × 4 3 . El total es 4 3 de 3 4 .

Considere pedir a sus estudiantes ejemplos de distintos tipos de expresiones de división, por ejemplo, un número entero dividido entre otro número entero, una fracción dividida entre un número entero, un número entero dividido entre una fracción, y una fracción dividida entre otra fracción.

DUA: Representación

Agregue una tercera burbuja para la estrategia de invertir y multiplicar en el organizador gráfico de red de estrategias de división de fracciones de las lecciones 8 y 9. Incluya un ejemplo. Consulte el organizador gráfico a medida que compara las estrategias durante la conversación.

1 3 ÷ 4 5

4 5 → 5 4 (Invertir)

1 3 × 5 4 (Multiplicar)

¿Podemos usar la estrategia de invertir y multiplicar para resolver todos estos tipos de problemas de división? ¿Por qué?

Sí. Podemos invertir y multiplicar por cualquier divisor, incluso si no es una fracción. Por ejemplo, podemos escribir el número entero 3 como la fracción 3 1 y, luego, invertirla para formar su recíproco, 1 _ 3 . Dividir entre el número entero 3 es lo mismo que multiplicar por 1 _ 3 .

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Dividir fracciones usando la estrategia de invertir y multiplicar

En esta lección:

• usamos la estrategia de invertir y multiplicar para dividir una fracción entre otra fracción.

Ejemplos

En los problemas 1 a 3, divide. Muestra tu trabajo.

1. 7 8 ÷ 10

Vocabulario

Un recíproco es el número que se obtiene al invertir una fracción. El recíproco de 3 4 es 4 3

El recíproco de 5 2 es 2 5

Para dividir una fracción entre otra fracción, multiplica el dividendo por el recíproco del divisor. Escribe 10 como la fracción 10 1 . Su recíproco es 1 10

Escribe 5 1 2 como una fracción mayor que 1 antes de usar la estrategia de invertir y multiplicar.

Escribe un divisor con número mixto como una fracción mayor que 1 antes de determinar su recíproco. 5 1 6 = 31 6

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

En los problemas 6 a 11, divide.

1. Considera 3

a. Traza un diagrama de cinta de 3 5 ÷ 2 3 Úsalo para calcular el cociente. 9 10

Ejemplo:

b. Usa la estrategia de invertir y multiplicar para confirmar tu solución a la parte (a).

En los problemas 2 a 4, determina el número desconocido que hace que la oración numérica sea verdadera.

Considera

4 7 . ¿Qué oraciones numéricas son verdaderas? Elige todas las opciones que correspondan. A.

12. Elige uno de los problemas 6 a 11. Explica qué estrategia usaste en ese problema y por qué. Ejemplo: En el problema 8, elegí la estrategia de invertir y multiplicar. El recíproco de 1 7 es 7 1 entonces, fue fácil reescribir la expresión como 3 4 × 7 1 y, luego, evaluarla.

EUREKA

En los problemas 13 a 15, escribe el recíproco. 13. 4 9 9 4 14. 6 5 5 6 15. 3 1 3

16. Para evaluar 3 5 ÷ 2 7 , Lisa calcula 5 3 × 7 2 . Explica el error de Lisa.

Lisa invirtió las dos fracciones en lugar de solo invertir 2 7

Recuerda

En los problemas 17 a 20, suma o resta.

21. Julie tiene 2 1 2 bolsas de granola. Una receta lleva 1 4 de bolsa de granola para preparar un refrigerio. ¿Cuántos refrigerios puede preparar Julie?

Julie puede preparar 10 refrigerios.

22. Empareja cada expresión con el producto correcto.

Aplicaciones de la división con fracciones

Resolver

problemas del mundo real dividiendo fracciones y números mixtos

Lisa tiene una cuerda que mide 2 1 4 yardas de largo. Blake tiene una cuerda que mide 5 1 2 yardas de largo. ¿Cuántas veces tan larga como la cuerda de Lisa es la cuerda de Blake?

Vistazo a la lección

En esta lección, la clase trabaja en grupos pequeños para determinar si determinadas piezas de cerámica con longitudes y anchos fraccionarios pueden cubrir el tablero de una mesa sin cortar ninguna pieza. Sus estudiantes examinan varias situaciones con contexto que usan los mismos números fraccionarios para determinar qué operación aritmética se podría usar para resolver cada problema. Asimismo, trazan diagramas para apoyar su razonamiento. En una actividad en grupos pequeños, resuelven problemas del mundo real que incluyen la multiplicación y división de fracciones y números mixtos. Aplican su comprensión de la división de fracciones para hacer comparaciones multiplicativas sobre las medidas de objetos.

cuerda

Pregunta clave

• ¿Qué estrategias podemos usar para resolver problemas de división con fracciones del mundo real?

Criterio de logro académico

6.Mód2.CLA5 Resuelven e interpretan problemas verbales que incluyen la división de fracciones y de números mixtos.

Nombre

La

de Blake es 2 4 9 veces tan larga como la cuerda de Lisa.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Interpretar situaciones de multiplicación y de división

• Resuelve y busca: División con fracciones

Concluir 10 min

Materiales

Maestro o maestra

• tarjetas de Resuelve y busca

Estudiantes

• ninguno

Preparación de la lección

• Imprima, recorte y exponga las tarjetas de Resuelve y busca en diferentes partes del salón de clases. Si sus estudiantes forman más de cinco grupos, entonces imprima, recorte y exponga dos sets de tarjetas. No deben colocarse dos tarjetas iguales juntas.

Fluidez

Usar el razonamiento multiplicativo

La clase usa el razonamiento multiplicativo como preparación para resolver problemas del mundo real que incluyen la división de fracciones.

Instrucciones: Determina el número que hace que cada oración sea verdadera.

Presentar

La clase determina si se pueden usar piezas de cerámica rectangulares con longitudes y anchos fraccionarios para cubrir el tablero de una mesa.

Dirija la atención de sus estudiantes al problema 1. Dé unos minutos para que completen el problema en parejas o en grupos pequeños. Tenga en cuenta que sus estudiantes podrían no terminar el problema, pero sí razonar sobre cómo usar la división para comenzar a resolverlo.

1. El tablero de la mesa de Ryan mide 4 1 _ 2 pies por 1 1 _ 4 pies. Ryan quiere cubrir el tablero con copias de la pieza de cerámica coloreada sin cortar ninguna pieza. ¿Puede cubrir el tablero? De ser así, ¿cuántas piezas de cerámica necesita? De no ser así, ¿por qué?

DUA: Acción y expresión

Para brindar apoyo a sus estudiantes, haga preguntas que guíen una planificación estratégica:

• ¿Qué pregunta el problema?

• ¿Qué información conocemos?

• ¿Qué estrategias podemos usar para resolver este problema?

Diferenciación: Desafío

Considere hacer las siguientes preguntas a quienes primero terminen la sección Presentar:

• ¿Qué otros tamaños de piezas de cerámica podrían cubrir el tablero?

• ¿Hay alguna pieza cuadrada de cerámica que podría cubrir el tablero? De ser así, ¿cuál es su longitud del lado?

Caben 10 piezas de cerámica a lo ancho del tablero.

4 1 2 pies = 54 pulgadas

54 ÷ 7 8 = 54 × 8 7

Sé que 54 × 8 7 no es un número entero; entonces, Ryan no puede cubrir su tablero con piezas de cerámica como esta sin cortar ninguna pieza.

Cuando la mayoría haya terminado, invite a algunos grupos a compartir sus soluciones y estrategias. Anime a sus estudiantes a participar en la conversación, incluso a quienes no hayan terminado el problema. Resalte aquellas estrategias que incluyan la conversión de unidades y la división de fracciones. Dirija la atención de sus estudiantes a las diferentes maneras en que completan los cálculos: diagramas de cinta, rectas numéricas, denominadores comunes, la estrategia de invertir y multiplicar, etc. Además, haga énfasis en el hecho de que con todas estas estrategias se llega a la misma respuesta.

Podemos usar el razonamiento multiplicativo como ayuda para razonar sobre este problema. Si la longitud del tablero es un múltiplo de la longitud de la pieza de cerámica y el ancho del tablero es un múltiplo del ancho de la pieza de cerámica, entonces las piezas de cerámica pueden cubrir todo el tablero sin que se deba cortar ninguna de ellas.

¿Cómo pueden determinar de forma eficiente si una pieza de cerámica de determinado tamaño cubrirá el tablero?

Puedo dividir la longitud del tablero entre la longitud de la pieza de cerámica y el ancho del tablero entre el ancho de la pieza de cerámica. Si las dos respuestas son números enteros, la pieza de cerámica cubrirá el tablero.

¿Por qué usaríamos la división para resolver este problema?

Queremos saber cuántos 7 8 de pulgada hay en 4 1 2 pies y cuántas 1 1 2 pulgadas hay en 1 1 4 pies.

La longitud del tablero es 4 1 _ 2 pies, o 54 pulgadas. Para determinar el número de piezas de cerámica que caben a lo largo del tablero, podemos dividir 54 entre 7 _ 8    .

Muestre 54 ÷ 7 8   .

Para evaluar 54 ÷ 7 8  , ¿por qué la estrategia de invertir y multiplicar es más eficiente que la estrategia de usar denominadores comunes?

Ejemplo: Al usar la estrategia de invertir y multiplicar, podemos saltearnos el paso de escribir las cantidades como fracciones con denominadores comunes.

Sin calcular 54 ÷ 7 _ 8  , ¿cómo sabemos que el cociente no es un número entero?

54 ÷ 7 8 es equivalente a 54 × 8 7

54 no es divisible entre 7, así que 54 × 8 no es divisible entre 7.

Hoy, resolveremos problemas del mundo real dividiendo fracciones y números mixtos y aplicando el razonamiento multiplicativo.

Aprender

Interpretar situaciones de multiplicación y de división

La clase usa varias estrategias para interpretar problemas del mundo real que incluyen fracciones.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta. Después de hacer la pregunta, muestre las tres opciones de respuesta para que sus estudiantes elijan. Tenga en cuenta que sus estudiantes podrían usar diferentes estrategias para responder esta pregunta.

Mara y su equipo de mantenimiento de senderos construyeron 7 __ 10 de milla de un sendero.

La distancia es 2 3 de la distancia total que planean construir. ¿Qué expresión representa la distancia total del sendero, en millas, que Mara y su equipo planean construir? Expliquen su razonamiento.

Apoyo para la comprensión del lenguaje

Para brindar apoyo con los distintos contextos de los problemas de esta lección, considere comentar cada contexto antes de que sus estudiantes trabajen con las matemáticas del problema. Haga preguntas amplias para que la clase use la rutina Pensar-Trabajar en parejas-Compartir:

• ¿De qué trata este problema?

• ¿Qué significan todas las palabras de este problema?

Los 7 __ 10 del sendero que construyeron son 2 _ 3 de la distancia total del sendero. Por lo tanto, puedo representar este problema con la ecuación de factor desconocido 7 10 = 2 3 × ?. El factor desconocido es equivalente al valor de 7 10 ÷ 2 3        .

Según sea necesario, para brindar apoyo con el contexto, haga dibujos o muestre imágenes de los contextos y las palabras específicas que se usan en cada problema.

Distancia total de sendero por constr uir de m illa de sendero constr uido

Si sus estudiantes no usan un diagrama para responder esta pregunta, considere mostrar el diagrama de cinta que representa 7 10 ÷ 2 3         . 7 10

Mara y su equipo de mantenimiento de senderos construyeron 7 __ 10 de milla de un sendero.

La distancia es 2 _ 3 de la distancia total que planean construir. ¿Creen que la distancia total del sendero que planean construir es menor que 1 milla o mayor que 1 milla? ¿O tienen dudas? Expliquen.

Ejemplo: Creo que mi respuesta debe ser mayor que 1 porque, si 7 10 es 2 3 del total, creo que el total será mayor que 1. Pero tengo dudas porque los números 2 3 y 7 10 están cerca.

¿Cuál es la distancia total del sendero, en millas, que Mara y su equipo planean construir?

21 20 de milla

Dé algunos minutos para que sus estudiantes completen el problema 2 en parejas o en grupos pequeños. Anime a sus estudiantes a crear algún tipo de diagrama que les ayude a razonar sobre el problema. Recorra el salón de clases mientras sus estudiantes trabajan y vaya haciendo las siguientes preguntas para comprobar el razonamiento de la clase:

• ¿Qué tipo de diagrama podrían trazar?

• Si tienen dudas sobre cómo representar la situación con un diagrama de cinta, ¿podrían hacer un dibujo del recipiente y los cuartos de galón?

• ¿Cómo pueden determinar si deben multiplicar o dividir?

2. Empareja cada situación con la expresión que representa. Justifica tu razonamiento.

a. Si 2 3 de cuarto de galón de agua llenan 3 4 de un recipiente, ¿cuántos recipientes llenará 1 cuarto de galón de agua?

1 cuarto de galón

3 4 de un recipiente 3 8 de un recipiente 3 8 de un recipiente 3 8 de un recipiente

b. Si 2 3 de cuarto de galón de agua llenan 3 4 de un recipiente, ¿cuántos cuartos de galón de agua hay en 1 recipiente?

1 recipiente

2 3 de cuarto de galón 2 9 de cuarto de galón 2 9 de cuarto de galón 2 9 de cuarto de galón 2 9 de cuarto de galón

c. Si Jada saca 2 3 de 3 4 de cuarto de galón de agua de un recipiente, ¿cuánta agua saca Jada?

3 4 2 3 de cuarto de galón 3 4 de cuarto de galón de

Diferenciación: Apoyo

Para quienes necesiten apoyo adicional, elija números diferentes para el problema 2. Por ejemplo, en cada situación, 1 2 cuarto de galón de agua podría llenar 1 4 de un recipiente. O 3 cuartos de galón de agua podrían llenar 1 2 recipiente.

Nota para la enseñanza

Tenga en cuenta que sus estudiantes podrían usar una amplia variedad de estrategias y diagramas para razonar sobre las tres situaciones en el problema 2:

2 9 de cuarto de galón

1 recipiente

2 3 de cuarto de galón

Cuando la mayoría haya terminado, invite a sus estudiantes a compartir sus soluciones y estrategias. Resalte el hecho de que hay muchas maneras diferentes de representar las tres situaciones en el problema 2. Pida a quienes hayan hecho diagramas claros que los compartan con el resto de la clase. Considere hacer las siguientes preguntas durante la conversación:

• ¿Por qué eligieron esa estrategia?

• ¿Cómo les ayudó su interpretación a emparejar la situación con la expresión?

• ¿Cómo les ayudó esa estrategia a interpretar ese problema en particular?

Resuelve y busca: División con fracciones

La clase resuelve problemas del mundo real multiplicando y dividiendo fracciones y números mixtos.

Divida a la clase en parejas o en grupos pequeños. Indique a cada grupo que se dirija a una de las tarjetas de Resuelve y busca expuesta en diferentes partes del salón de clases. Cada tarjeta de Resuelve y busca muestra uno de los problemas 3 a 9 y una respuesta a otro de los problemas 3 a 9. Comparta las siguientes instrucciones antes de que sus estudiantes comiencen a trabajar:

Resuelvan el problema de la tarjeta. Registren su trabajo en sus libros. Si la solución es mayor que 1, escriban la solución como un número mixto. Recorran el salón de clases en busca de la tarjeta que muestra la respuesta a su problema. Por ejemplo, si la solución al problema de su tarjeta es 15 onzas, deben hallar la tarjeta que muestra la respuesta 15. Cuando hallen la tarjeta que muestra su respuesta, resuelvan el problema de esa tarjeta. Luego, recorran el salón de clases en busca de la tarjeta que muestra la respuesta a ese problema.

Continúen hasta que el tiempo se acabe o hasta que regresen a una tarjeta que tenga el primer problema que resolvieron.

Pida a sus estudiantes que completen tantos problemas como puedan en 15 minutos. Tenga en cuenta que sus estudiantes podrían resolver al menos cuatro de los problemas. Recorra el salón de clases mientras sus estudiantes trabajan y haga las siguientes preguntas para brindar apoyo según sea necesario:

• ¿Les ayudaría trazar un diagrama a resolver este problema? ¿Qué tipo de diagrama podrían trazar?

• ¿Debería su respuesta ser menor que 1 o mayor que 1? Expliquen cómo lo saben.

• ¿Cómo saben que su expresión representa correctamente el problema?

Promoción de la práctica de las matemáticas

Cada estudiante da sentido a los problemas y persevera en su resolución cuando resuelve problemas del mundo real que incluyen fracciones trazando diagramas para representar una situación, determinando la expresión de división o multiplicación adecuada y evaluando si las soluciones son razonables.

Considere hacer las siguientes preguntas:

• ¿Qué información o datos necesitan para escribir una ecuación que represente esta situación?

• ¿Qué pueden saber sobre esta situación con solo observar el diagrama de cinta?

• ¿Tienen sentido sus respuestas? ¿Por qué?

3. Kayla tiene 8 tazas de avena. La receta para preparar una tanda de panecillos lleva 1 2 3 tazas de avena. ¿Cuántas tandas de panecillos puede preparar Kayla?

Kayla puede preparar 4 4 _ 5 tandas de panecillos.

4. El agua circula por un grifo de cocina a una tasa de 7 8 de galón por minuto. A esa tasa, ¿cuántos minutos se tarda en llenar una jarra que contiene 2 1 4 galones?

Nota para la enseñanza

Las respuestas a la actividad de Resuelve y busca: División con fracciones se muestran con la unidad más grande posible. Además, las fracciones mayores que 1 se expresan como números mixtos. En 6.o grado, no se espera que sus estudiantes escriban respuestas fraccionarias con la unidad más grande posible. Acepte todas las respuestas correctas. Sin embargo, en algunos problemas con contexto, escribir respuestas con la unidad más grande posible y escribir fracciones como números mixtos permite a sus estudiantes comprender el significado de la solución con mayor facilidad.

Se tarda 2 4 7 minutos en llenar la jarra.

5. Una persona planea correr 7 1 2 millas. Solo corre 2 1 4 millas. ¿Qué fracción de la distancia planeada corre?

2

Corre 3 10 de la distancia planeada.

6. Cuando se colocan 6 1 2 piezas de cerámica extremo con extremo, la longitud total de las piezas es 4 pies y 4 pulgadas. ¿Cuál es la longitud de cada pieza de cerámica en pies?

4 pies 4 pulgadas = 4 1 3 pies

Cada pieza de cerámica mide 2 3 de pie de largo.

7. Una porción de yogur es 3 4 de taza. Tyler come 1 taza de yogur. ¿Cuántas porciones de yogur come Tyler?

Tyler come 1 1 3 porciones de yogur.

8. Lacy mide 3 1 2 pies de alto. Su hermano Leo mide 5 1 4 pies de alto. ¿Cuántas veces tan alto como Lacy es Leo?

Leo es 1 1 _ 2 veces tan alto como Lacy.

9. Las tijeras naranjas miden 8 1 4 pulgadas de largo. La longitud de las tijeras rosas es 2 3 de la longitud de las tijeras naranjas. ¿Cuánto miden de largo las tijeras rosas en pulgadas?

Tijeras rosas

Tijeras naranjas

Las tijeras rosas miden 5 1 2 pulgadas de largo.

Cuando se acabe el tiempo, seleccione dos de los problemas para comentar. Invite a algunos grupos a compartir sus soluciones. Elija a algunos grupos que hayan usado diferentes métodos para dividir las fracciones. Registre las estrategias de sus estudiantes para que las ideas estén a la vista de toda la clase. Según sea necesario, use las siguientes preguntas para guiar la conversación sobre la reflexión final y ayude a sus estudiantes a resumir las estrategias de división de fracciones:

• ¿En qué se parecen y en qué se diferencian estas estrategias?

• ¿Qué conexiones ven entre estas estrategias?

• ¿Por qué elegirían usar esta estrategia?

Dirija la atención de sus estudiantes a los problemas 8 y 9. Según sea necesario, use las siguientes preguntas para conversar como ayuda a fin de que sus estudiantes relacionen el lenguaje de los problemas de comparación multiplicativa con lo que saben de la división de fracciones:

• ¿En qué se parecen los problemas 8 y 9? ¿En qué se diferencian?

• ¿Cómo supieron que debían multiplicar en lugar de dividir para responder la pregunta del problema 9?

• ¿Es posible que en un problema en el que hay que dividir se usen las frases tanto de una cantidad o tantas veces una cantidad? ¿Por qué?

Luego, guíe la transición al problema 10. Dé alrededor de 1 minuto para que sus estudiantes trabajen en el problema 10 de manera independiente.

10. Escribe un problema verbal que pueda resolverse con la expresión 4 1 4 ÷ 2 3 .

Ejemplo: La receta de Julie para preparar una tanda de panecillos de frambuesa lleva 2 3 de taza de frambuesas. ¿Cuántas tandas de panecillos puede preparar Julie si tiene 4 1 _ 4 tazas de frambuesas?

Pida a diferentes estudiantes que compartan sus problemas verbales con la clase.

¿En qué se parecen los problemas?

Ejemplo: En todos los casos, 4 1 4 representa la cantidad total de algo.

Apoyo para la comprensión del lenguaje

Para ayudar a quienes estén aprendiendo el idioma a elegir un contexto para escribir un problema verbal en el problema 10, considere formar parejas de estudiantes y guiarlas para que usen un contexto que hayan comprendido de los problemas 3 a 9.

Concluir

Reflexión final 5 min

Objetivo: Resolver problemas del mundo real dividiendo fracciones y números mixtos

Use las preguntas y los planteamientos que siguen para guiar una conversación acerca de comprender y resolver problemas del mundo real con fracciones y números mixtos. Anime a sus estudiantes a reformular o desarrollar las respuestas de sus pares.

¿Qué estrategias podemos usar para resolver problemas de división con fracciones del mundo real? Expliquen.

Ejemplo: Podemos trazar diagramas de cinta o hacer dibujos que representen la situación. Podemos pensar si nuestra respuesta debe ser menor que 1 o mayor que 1. Podemos usar denominadores comunes o la estrategia de invertir y multiplicar para dividir fracciones. Podemos reescribir números mixtos como fracciones.

¿Por qué usamos el lenguaje multiplicativo en el mundo real?

Usamos el lenguaje multiplicativo para hacer comparaciones. Cuando tenemos una cantidad de algo, el lenguaje multiplicativo describe cuánto de otra cantidad o cuántas veces otra cantidad es lo que tenemos.

Usen el lenguaje multiplicativo para comparar el tamaño de dos objetos que haya en este salón de clases.

Ejemplo: La longitud del escritorio es aproximadamente 1 3 de la longitud de la mesa.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección.

Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Aplicaciones de la división con fracciones

En esta lección:

• dividimos fracciones y números mixtos para resolver problemas del mundo real.

Ejemplos

1. Noah vierte 8 galones de agua en un tanque. El agua llena 2 5 del tanque.

a. ¿Cuántos galones debe verter Noah para llenar todo el tanque? ? 8

Este diagrama de cinta representa la pregunta “¿8 es 2 5 de qué número?”.

8 ÷ 2 5 = 8 1 × 5 2 = 40 2 = 20 Noah debe verter 20 galones de agua para llenar todo el tanque. Invierte el divisor, 2 5  , y multiplica por el dividendo, 8 1

b. Cuando el tanque está lleno, ¿cuántas botellas de 1 4 de galón pueden llenarse con el agua del tanque?

20 ÷ 1 4 = 20 × 4 = 80

Se pueden llenar ochenta botellas de 1 4 de galón con el agua del tanque.

Piensa en esta situación como la pregunta “¿Cuántos grupos de 1 4 hay en 20?”.

2. Adesh coloca piezas de cerámica cuadradas extremo con extremo a lo largo del borde de una mesa que mide 24 3 4 pulgadas de largo. Cada pieza de cerámica mide 5 8 de pulgada de largo.

a. ¿Cuántas piezas de cerámica puede colocar Adesh a lo largo del borde de la mesa?

24 3 4 ÷ 5 8 = 99 4 ÷ 5 8 = 198 8 ÷ 5 8 = 198 5 = 39 3 5

Considera usar denominadores comunes para resolver este problema de división.

99 4 × 2 2 = 198 8 Luego, divide los numeradores.

Adesh puede colocar 39 piezas de cerámica a lo largo del borde de la mesa.

b. Adesh dice: “Redondeé mi solución hacia arriba, a 40. Puedo colocar 40 piezas de cerámica a lo largo del borde de la mesa”. ¿Está en lo correcto Adesh? Explica.

No, Adesh no está en lo correcto. Solo hay espacio suficiente para 39 3 5 , o 39 piezas de cerámica a lo largo del borde de la mesa.

Al redondear, considera la situación. El cociente 39 3 5 está más cerca de 40 que de 39 Sin embargo, en este caso, no cabría otra pieza de cerámica completa. Entonces, la respuesta debe ser 39

EUREKA

EUREKA MATH

Nombre

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. Riley vierte 12 galones de agua en un tanque. El agua llena 3 4 del tanque.

a. ¿Cuántos galones caben en todo el tanque?

En todo el tanque caben 16 galones.

b. Riley llena todo el tanque con agua. Llena botellas de 1 2 galón con el agua del tanque.

¿Cuántas de estas botellas puede llenar Riley?

Riley puede llenar 32 botellas con el agua del tanque.

2. Scott completa 1 6 de los niveles de un videojuego en 3 1 2 meses. ¿Qué expresión puede usarse para determinar el número de meses que tardará Scott en completar todos los niveles a esta tasa?

A. 3 1 2 × 1 6

B. 3 1 2 ÷ 1 6

C. 1 6 ÷ 3 1 2

D. 6 ÷ 3 1 2

3. Para preparar una tanda de panqueques, se necesitan 1 1 4 tazas de mezcla para panqueques. Una caja contiene 9 tazas de mezcla para panqueques. ¿Cuántas tandas de panqueques se pueden preparar con una caja de mezcla para panqueques?

Se pueden preparar 7 1 5 tandas de panqueques con una caja.

4. Sara come 2 1 2 porciones de cereales. Come 1 2 3 tazas de cereales. ¿Cuántas tazas de cereales hay en una porción?

Hay 2 3 de taza de cereales en una porción.

5. Eddie apila cajas en el estacionamiento. Cada caja mide 1 3 4 pies de alto. La distancia desde el piso del estacionamiento hasta el techo es 8 1 2 pies.

a. ¿Cuál es el mayor número de cajas que Eddie puede apilar en el estacionamiento?

Eddie puede apilar 4 cajas.

b. Explica cómo decidiste de qué manera redondear tu respuesta en la parte (a). Como no es posible apilar 4 6 7 cajas, tuve que decidir si la respuesta era 4 o 5 cajas.

Ya que 5 cajas no cabrían, el mayor número de cajas que Eddie puede apilar en el estacionamiento es 4

EUREKA MATH2

EUREKA MATH2

Nombre

Fecha

6. En la práctica de carrera a campo traviesa, Yuna corre 2 1 4 millas. Ryan corre 5 1 2 millas.

¿Cuántas veces la distancia de Ryan corre Yuna?

Yuna corre 9 22 de la distancia que corre Ryan.

7. Escribe un problema verbal que pueda resolverse con la expresión 3 4 ÷ 1 3

Ejemplo: Lacy nada 3 4 de milla. Blake nada 1 3 de milla. ¿Cuántas veces la distancia de Blake nada Lacy?

8. Tyler cultiva un tomate que pesa 3 4 de libra. Lisa cultiva un tomate que pesa 1 1 5 libras.

¿Qué fracción del peso del tomate de Lisa es el peso del tomate de Tyler?

El peso del tomate de Tyler es 5 8 del peso del tomate de Lisa.

Recuerda

En los problemas 9 a 12, suma o resta.

9. 2 5 + 3 7 29

3 8 +

13. Sasha usa 3 5 de los duraznos para hacer una ensalada de frutas. Si usa 3 4 de libra de duraznos, ¿cuántas libras de duraznos tiene Sasha al principio?

Sasha tiene 1 1 4 libras de duraznos al principio.

14. Empareja cada producto con la expresión correcta. A. 2 15 1 2 × 1 2 B. 1 4 1 3 × 2 5

5 8 5 6 × 3 4

1 1 2

3. Kayla tiene 8 tazas de avena. La receta para preparar una tanda de panecillos lleva 1 2 3 tazas de avena. ¿Cuántas tandas de panecillos puede preparar Kayla?

2 3

4. El agua circula por un grifo de cocina a una tasa de 7 8 de galón por minuto. A esa tasa, ¿cuántos minutos se tarda en llenar una jarra que contiene 2 1 4 galones?

4 4 5 5. Una persona planea correr 7 1 2 millas. Solo corre 2 1 4 millas. ¿Qué fracción de la distancia planeada corre?

5 1 2

6. Cuando se colocan 6 1 2 piezas de cerámica extremo con extremo, la longitud total de las piezas es 4 pies y 4 pulgadas. ¿Cuál es la longitud de cada pieza de cerámica en pies?

2 4 7

7. Una porción de yogur es 3 4 de taza. Tyler come 1 taza de yogur. ¿Cuántas porciones de yogur come Tyler? 1 1 3

8. Lacy mide 3 1 2 pies de alto. Su hermano Leo mide 5 1 4 pies de alto. ¿Cuántas veces tan alto como Lacy es Leo?

3 10 9. Las tijeras naranjas miden 8 1 4 pulgadas de largo. La longitud de las tijeras rosas es 2 _ 3 de la longitud de las tijeras naranjas. ¿Cuánto miden de largo las tijeras rosas en pulgadas?

Tijeras rosas

Tijeras naranjas

be

Operaciones con fracciones en una situación del mundo real

Sumar, restar, multiplicar y dividir fracciones y números mixtos para resolver problemas del mundo real

Vistazo a la lección

Leo tiene 2 3 de taza de harina. Esta cantidad es 4 5 de la cantidad de harina que necesita para preparar 1 tanda de panecillos.

¿Cuántas tazas de harina necesita Leo para preparar 2 tandas de panecillos?

2 3 de taza de harina es 4 5 de la cantidad de harina que necesita Leo para preparar 1 tanda de panecillos.

2

Leo necesita 5 6 de taza de harina para preparar 1 tanda de panecillos.

2

Leo necesita 1 2 3 tazas de harina para preparar 2 tandas de panecillos.

En esta lección digital, sus estudiantes miran un video de presentación sobre una carrera de carritos de madera. Deben predecir qué características del carrito de madera afectan su velocidad. En la actividad interactiva, se les dan opciones para que decidan cómo quieren construir un carrito de carrera. Después de tomar cada decisión, usan operaciones con fracciones para hallar el peso total del carrito. Una vez que han terminado de construir sus carritos, usan la división de fracciones para hallar la velocidad de los carritos. Luego, hacen una carrera entre sus carritos y los del resto de la clase. Por último, sus estudiantes observan las características de los carritos más veloces y las comparan con las predicciones que hicieron al comienzo. Después de hacer esto, miran un video que les muestra cómo aumentar la velocidad del carrito.

Use la plataforma digital para preparar y enseñar esta lección. Sus estudiantes también explorarán el contenido de la lección y las actividades a través de la plataforma digital.

Pregunta clave

• ¿En qué tipos de situaciones del mundo real se usan la suma, la resta, la multiplicación o la división de fracciones y de números mixtos?

Criterio de logro académico

6.Mód2.CLA5 Resuelven e interpretan problemas verbales que incluyen la división de fracciones y de números mixtos.

Agenda

Fluidez

Presentar 5 min D

Aprender 30 min D

• Construir un carrito de carrera

• Carreras de carritos

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• computadoras o dispositivos (1 por pareja de estudiantes)

Preparación de la lección

• No se necesita.

Fluidez

Sumar, restar y multiplicar números mixtos

La clase suma, resta y multiplica números mixtos como preparación para resolver problemas del mundo real de varios pasos que incluyen fracciones.

Instrucciones: Evalúa cada expresión.

Presentar

Se presenta una carrera de carritos de madera y sus requisitos a la clase.

La clase mira un video que presenta una carrera de carritos de madera y los pasos para construirlos. Después de mirar el video, sus estudiantes comentan las características que harán que un carrito de carrera de madera sea más veloz que el resto.

Describan el proceso para construir un carrito de carrera de madera.

Primero, debo cortar un bloque de madera y darle la forma del carrito. Luego, debo agregarle las ruedas y los ejes. Debo pintar el carrito y agregarle calcomanías. Por último, debo agregarle carga para hacer que el carrito tenga un peso que esté lo más cerca posible de 6 onzas.

¿Qué creen que hace que un carrito de carrera de madera sea más veloz que el resto? ¿Por qué?

Creo que el peso afecta la velocidad, cuanto más pesado sea el carrito, más velozmente se moverá por la pista. Creo que la forma del carrito también afecta su velocidad. Creo que el tipo de ruedas también puede influir en su velocidad.

DUA: Participación

Las actividades digitales están alineadas con el principio de Participación de DUA, dado que incluyen lo siguiente:

• Temas interesantes y atractivos: sus estudiantes crean sus propios carritos de carrera de madera y los hacen correr una carrera virtual de la clase.

• Opciones que promueven la flexibilidad y la capacidad para elegir: sus estudiantes eligen entre diferentes opciones de carritos para construir el suyo.

• Retroalimentación formativa inmediata: después de cada decisión, sus estudiantes calculan el peso total del carrito e intentan que el peso final esté por debajo, pero lo más cerca posible, de 6 onzas.

Aprender

Construir un carrito de carrera

La clase realiza operaciones con fracciones para hallar el peso acumulado de sus carritos de carrera de madera personalizados.

Sus estudiantes toman una serie de decisiones para construir un carrito de carrera de madera y predicen qué elementos tendrán un mayor efecto en la velocidad. Dichas decisiones incluyen la forma del carrito, el tipo de

ruedas, el color de la pintura, las calcomanías y la carga adicional. Sus estudiantes calculan el peso acumulado del carrito y sus partes a medida que lo construyen. Para cada elección, usan operaciones con fracciones para evaluar una expresión. La clase intenta lograr el objetivo de construir un carrito cuyo peso esté lo más cerca posible de 6 onzas, sin superarlo.

Después de que sus estudiantes hayan terminado de construir, se les brinda información sobre una carrera de prueba y calculan la velocidad de sus carritos.

¿Cuál es el peso total en onzas de sus carritos con 4 ruedas y 2 ejes?

Ejemplo: 91 25 de onza

¿Cuál es la velocidad de sus carritos en pies por segundo?

Ejemplo: 15 pies por segundo

¿Qué cálculo fue más desafiante? ¿Por qué?

Ejemplo: Hallar el peso de las ruedas y los ejes fue desafiante. Primero, tuvimos que dividir para hallar el peso de 1 rueda y 1 eje. Luego, tuvimos que multiplicar el peso de 1 rueda por 4 y multiplicar el peso de 1 eje por 2 para hallar el peso total de las 4 ruedas y los 2 ejes. Por último, tuvimos que sumar los totales al peso total del carrito.

1. Muestra los cálculos que usaste para hallar los cambios en el peso del carrito de carrera.

Cambios en el peso del carrito de carrera

Peso del bloque de madera dado Ejemplo:

Cálculos

Peso total: 3 2 5 onzas

Bloque de madera luego de cortarlo Ejemplo: 3 2 5 − 3 5 = 14 5

Peso total del carrito: 14 5 de onza

Promoción de la práctica de las matemáticas

Cada estudiante razona de forma abstracta y cuantitativa cuando escribe y resuelve expresiones matemáticas que incluyen fracciones para determinar el peso y la velocidad de un carrito de carrera de madera.

Considere hacer las siguientes preguntas:

• ¿Qué les pide hacer el problema?

• ¿Qué significa su expresión en esta situación?

• ¿Cómo les ayudan las unidades que se usan para hallar la velocidad del carrito a reflexionar sobre el problema?

Cambios en el peso del carrito de carrera

Después de agregar las ruedas y los ejes

Cálculos

Después de pintarlo

Cambios en el peso del carrito de carrera Cálculos

Después de colocar las calcomanías Ejemplo:

1 25 × 2 = 2 25

Peso de las calcomanías: 2 25 de onza

2 25 + 203 50 = 207 50

Peso total del carrito: 207 50 de onza

Después de agregarle carga Ejemplo:

Peso de la carga agregada: 3 2 de onza

3 _ 2 + 207 _ 50 = 141 _ 25

Peso total del carrito: 141 25 de onza

2. ¿Cuál es la velocidad de tu carrito en pies por segundo?

Ejemplo:

Velocidad del carrito: 15 pies por segundo

Carreras de carritos

La clase observa la simulación de una carrera y comenta las características de los carritos de carrera más veloces.

Sus estudiantes miran una carrera virtual entre los carritos construidos por la clase. Después de la carrera, identifican los carritos más veloces y comparan sus características para determinar si algunas de las elecciones hicieron que sus carritos sean más veloces. La clase mira un video que revela las características que afectan la velocidad de los carritos de carrera de madera.

¿Qué tienen en común los carritos más veloces? ¿Qué características hacen que algunos carritos sean más veloces que otros?

Ejemplo: Los carritos 1, 5 y 14 tienen una estructura similar. Los carritos más veloces parecen tener su carga en la parte de atrás y su peso total está muy cerca de las 6 onzas.

¿Las características que eligieron hicieron que su carrito fuera el más veloz? ¿Por qué?

Ejemplo: No. Pensé que el carrito tenía que pesar lo máximo posible y que la forma tenía algún tipo de relación con la velocidad. No pensé que importaría el peso de las ruedas y dónde colocaba la carga.

Concluir

Reflexión final 5 min

Objetivo: Sumar, restar, multiplicar y dividir fracciones y números mixtos para resolver problemas del mundo real

Use las preguntas que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a reformular o complementar las respuestas de sus pares.

En la lección de hoy, ¿cómo usaron las operaciones con fracciones y números mixtos?

Usamos la suma cada vez que debíamos hallar un nuevo peso total del carrito. Para hallar el peso después de elegir la forma del carrito, tuvimos que restar el peso de la madera cortada del peso total del bloque. Usamos la división para hallar el peso de 1 rueda y para hallar cuánta pintura se necesita para pintar 1 carrito.

¿Qué otros tipos de situaciones del mundo real incluyen operaciones con fracciones y números mixtos?

Ejemplo: Las situaciones del mundo real que incluyen medidas de peso o de longitud suelen incluir operaciones con fracciones. Por ejemplo, en la lección anterior, resolvimos un problema sobre la longitud fraccionaria de una pieza de cerámica que incluía la división, o la suma repetida, para calcular la respuesta. Otras situaciones incluyen, por ejemplo, cuando dividimos cantidades fraccionarias en partes iguales o cuando dividimos un total en partes iguales, como porciones de una pizza o de un pastel.

¿Cuándo usaron varias operaciones para calcular el nuevo peso del carrito en la lección de hoy? ¿Cómo supieron qué operación hacer primero?

Cuando calculamos el peso del carrito con las ruedas y los ejes, usamos la división, la multiplicación y la suma.

Sabíamos que teníamos que dividir primero, ya que el peso correspondía a 5 ruedas y teníamos que hallar el peso de 1 sola rueda. Una vez que hallamos el peso de 1 rueda, lo multiplicamos por 4 y lo sumamos al peso total del carrito.

Boleto de salida

5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Operaciones con fracciones en una situación del mundo real

En esta lección:

• sumamos, restamos, multiplicamos y dividimos fracciones y números mixtos para resolver problemas del mundo real.

Ejemplos

1. El libro de Matemáticas de Kelly pesa 3 1 2 libras. El libro de Historia de Riley pesa 2 1 4 libras. Halla el número que hace que cada enunciado sea verdadero.

a. Juntos, los libros de Kelly y Riley pesan libras.

3 1 2 + 2 1 4 = 3 2 4 + 2 1 4 = 5 3 4

b. El libro de Kelly pesa libras más que el libro de Riley.

3 1 2 − 2 1 4 = 3 2 4 − 2 1 4 = 1 1 4

Suma para hallar el peso combinado de los libros de Kelly y Riley.

Resta para hallar cuántas libras más pesado es el libro de Kelly que el de Riley.

c. El libro de Kelly pesa veces la cantidad de libras que pesa el libro de Riley.

2 1 4 × ? = 3 1 2 3 1 2 ÷ 2 1 4 = 7 2 ÷ 9 4 = 7 2 × 4 9

= 28 18 = 1 5 9

Primero, piensa en una ecuación de factor desconocido. ¿Cuántas veces el peso del libro de Riley es el peso del libro de Kelly? Luego, evalúa la expresión de división relacionada.

2. Noah tiene una jarra de 1 3 4 litros de limonada. Vierte la misma cantidad de limonada en 4 vasos.

Luego, todavía queda 1 3 de litro de limonada en la jarra. ¿Cuántos litros de limonada hay en cada vaso?

Primero, resta 1 3 de 1 3 4 para determinar cuántos litros de limonada vierte Noah en los 4 vasos. Luego, divide la diferencia entre 4 para determinar cuántos litros de limonada hay en cada vaso.

Hay 17 48 de litro de limonada en cada vaso.

EUREKA MATH

Nombre

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. Dos clases de escuela intermedia trabajan en equipo para pintar un mural en la escuela. Empareja cada situación con la expresión que podría usarse para responder la pregunta.

La clase del maestro Pérez pinta 1 5 del mural completo, lo que es 2 3 de la sección que deben pintar. ¿Qué porción del mural completo le corresponde a la clase del maestro Pérez?

La clase de la maestra Chan debe pintar 1 5 del mural. La clase pinta 2 3 de su sección. ¿Qué porción del mural completo pinta la clase de la maestra Chan?

La clase de la maestra Chan usa 2 3 de un galón de pintura blanca. La clase del maestro Pérez usa 1 5 del galón de pintura blanca. ¿Cuánta más pintura usa la clase de la maestra Chan que la clase del maestro Pérez? 1 5 × 2 3

La clase de la maestra Chan usa 2 3 de un galón de pintura blanca. La clase del maestro Pérez usa 1 5 del galón de pintura blanca. ¿Qué porción del galón de pintura blanca usan las dos clases en total?

5 ÷ 2 3

2. La mochila de Leo pesa 12 3 4 libras. La mochila de Sara pesa 8 1 2 libras. Completa cada enunciado.

a. En total, las mochilas de Leo y Sara pesan 21 1 4 libras.

b. La mochila de Leo pesa 4 1 4 libras más que la mochila de Sara.

c. La mochila de Leo pesa 1 1 2 veces la cantidad de libras que pesa la mochila de Sara.

3. Mara gasta 2 3 de su dinero en un videojuego. Gasta la mitad del dinero restante en el almuerzo.

Si el almuerzo cuesta $10, ¿cuánto dinero tenía Mara al principio?

Mara tenía $60 al principio.

4. El Sr. Pérez recibe dinero por su cumpleaños. Gasta 1 5 del dinero en zapatos nuevos. Dona el resto del dinero a 3 organizaciones benéficas diferentes. Dona la misma cantidad de dinero a cada organización benéfica.

a. ¿Qué fracción de su dinero dona el Sr. Pérez a cada organización benéfica?

El Sr. Pérez dona 4 15 de su dinero a cada organización benéfica.

b. Si el Sr. Pérez da $60 a cada organización benéfica, ¿cuánto dinero recibió por su cumpleaños?

Recibió $225 por su cumpleaños.

5. Leo usa tres bolsas de harina para preparar galletas. La cantidad de harina en cada bolsa es la siguiente:

• 2 3 de taza de harina

• 1 1 2 tazas de harina

• 1 1 3 tazas de harina

Para cada tanda de galletas, se necesitan 1 3 4 tazas de harina. ¿Cuántas tandas de galletas puede preparar Leo?

Leo puede preparar 2 tandas de galletas.

6. Tyler tiene una jarra de 1 3 4 litros de limonada. Vierte la misma cantidad de limonada en 3 vasos.

Luego, todavía queda 1 3 de litro de limonada en la jarra. ¿Cuántos litros de limonada hay en cada vaso?

Hay 17 36 de litro de limonada en cada vaso.

Recuerda

En los problemas 7 a 10, suma o resta.

En los problemas 11 y 12, divide.

13. Kayla tiene 3 cintas rojas. Cada cinta mide 1 2 5 metros de largo. ¿Cuál es la longitud total de todas las cintas de Kayla en metros?

La longitud total de todas las cintas de Kayla es 4 1 5 metros.

Tema D

Suma, resta y multiplicación de números decimales

En grados anteriores, sus estudiantes suman, restan y multiplican con fluidez números enteros de varios dígitos usando el algoritmo estándar para cada operación. Usan estrategias basadas en el valor posicional y en las propiedades de las operaciones para sumar, restar y multiplicar números decimales hasta la posición de los centésimos. En el tema A de 6.o grado, aprenden sobre los factores comunes, los múltiplos comunes y la divisibilidad. En los temas B y C, dividen fracciones usando varias estrategias. En el tema D, continúan su trabajo con operaciones mientras suman, restan y multiplican con fluidez números decimales de varios dígitos usando el algoritmo estándar para cada operación.

En la primera lección del tema D, sus estudiantes razonan acerca de la posición del punto decimal en sumas y diferencias de números decimales usando estrategias de estimación y el sentido numérico. Luego, continúan sumando y restando números decimales de varios dígitos usando los algoritmos estándares para adquirir fluidez en cada operación.

3475

Al comparar la suma y resta de fracciones decimales, como 1 6 ____ 1,000 − 2 __ 10 , con la suma y resta de números decimales, como 1.006 − 0.2, reconocen la importancia del valor posicional en sus cálculos.

En la lección 14, una lección digital, sus estudiantes identifican patrones en los factores y los productos de números decimales a través de una serie de actividades interactivas. También exploran cómo cambia un producto cuando uno de los factores cambia, y cómo cambia un factor cuando el producto cambia y el otro factor es fijo. Comparan la multiplicación de números decimales y fracciones usando una cuadrícula de 10 × 10. Cuando usan una tabla de valor posicional, reconocen cómo el valor posicional de los factores afecta su producto. En la lección 15, hacen una transición al uso del algoritmo estándar para multiplicar números decimales de varios dígitos. Razonan acerca de la posición del punto decimal en productos usando estrategias de estimación y el sentido numérico. Para resolver problemas del mundo real, aplican estas destrezas al usar la multiplicación con números decimales.

En la última lección del tema, sus estudiantes adquieren fluidez con la suma, resta y multiplicación de números decimales al completar una tarea abierta del mundo real. Teniendo en cuenta las pautas de diseño inspiradas en el hito arquitectónico Hábitat 67, construyen modelos de sus propios hábitats con cubos. Asimismo, usan tasas para calcular el costo y los ingresos, y ajustan sus modelos para aumentar la ganancia de las ventas de sus hábitats.

En los temas E y F, sus estudiantes continúan su trabajo con operaciones al dividir números enteros de varios dígitos y números decimales usando el algoritmo estándar. En módulos posteriores, aplicarán su comprensión de la suma, resta y multiplicación de números decimales cuando trabajen con coeficientes decimales y variables en expresiones y ecuaciones, cuando resuelvan problemas de área y volumen que incluyan medidas decimales y cuando calculen medidas de tendencia central y analicen conjuntos de datos que incluyan valores decimales.

Progresión de las lecciones

Lección 13 Suma y resta de números decimales

Lección 14 Patrones en la multiplicación de números decimales

Lección 15 Multiplicación con números decimales

Lección 16 Aplicaciones de las operaciones con números decimales

Suma y resta de números decimales

Sumar y restar números decimales usando los algoritmos estándares para cada operación

Vistazo a la lección

En esta lección, la clase adquiere fluidez con la suma y resta de números decimales de varios dígitos. Sus estudiantes estiman las sumas y diferencias para predecir o confirmar la razonabilidad de sus respuestas. Luego de resolver un acertijo matemático donde tienen que colocar puntos decimales en sumandos, trabajan en parejas para crear sus propios acertijos matemáticos. Después, intercambian acertijos matemáticos con sus pares como práctica para colocar números decimales en sumandos. Analizan y comentan dos estrategias para restar números decimales y comparan la resta de fracciones decimales con la resta de números decimales. Mediante una conversación, se dan cuenta de la importancia del valor posicional al sumar y restar números decimales.

Pregunta clave

• ¿Por qué es importante el valor posicional al sumar y restar números decimales?

Criterios de logro académico

6.Mód2.CLA2 Resuelven problemas verbales realizando operaciones con números decimales de varios dígitos.

6.Mód2.CLA9 Suman y restan números decimales de varios dígitos.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• El acertijo matemático del punto decimal

• El valor posicional en la suma y la resta

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• tarjeta de índice (1 por estudiante)

Preparación de la lección

• No se necesita.

Fluidez

Sumar

y restar números en forma unitaria

La clase suma y resta números en forma unitaria como preparación para sumar y restar números decimales.

Instrucciones: Suma o resta. Escribe la respuesta en forma unitaria.

1. 3 decenas y 5 unidades + 4 decenas y 3 unidades 7 decenas y 8 unidades

2. 3 décimos y 5 centésimos + 4 décimos y 5 centésimos 8 décimos y 0 centésimos

3. 4 decenas, 6 unidades y 7 décimos + 2 decenas, 3 unidades y 5 décimos

4. 4 centenas, 6 decenas y 7 unidades − 2 centenas, 3 decenas y 5 unidades

7 decenas, 0 unidades y 2 décimos

2 centenas, 3 decenas y 2 unidades

5. 7 décimos y 2 centésimos + 4 décimos y 3 centésimos 2 décimos y 9 centésimos

6. 5 decenas y 6 unidades − 2 unidades y 8 décimos

5 decenas, 3 unidades y 2 décimos

Presentar

La clase razona acerca de la suma de números enteros de varios dígitos y números decimales.

Muestre la ecuación que tiene sumandos formados por números enteros y una suma de número enteros.

205 + 457 + 91 = 753

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

Sin sumar, ¿pueden determinar si 753 es una respuesta razonable para la suma de los tres números? De ser así, ¿cómo lo hacen?

Sí. Podemos estimar la suma redondeando los números que estamos sumando como 200, 500 y 100. La suma estimada es 800 porque 200 + 500 + 100 = 800.

Pida a sus estudiantes que sumen los números en una pizarra blanca individual y que comprueben que la suma 753 sea correcta.

Luego, muestre la ecuación que tiene sumandos formados por números decimales y una suma de número entero.

20.5 + 45.7 + 9.1 = 753

La ecuación 20.5 + 45.7 + 9.1 = 753 no es correcta. ¿Qué podríamos hacer para corregirla?

Podríamos cambiar la suma. Podríamos cambiar los números que estamos sumando.

Podemos cambiar los sumandos o cambiar la suma. En este problema, los sumandos son correctos y la suma tiene dígitos correctos, pero falta algo. Trabajen en parejas para determinar dónde colocar el punto decimal en la suma de manera que la ecuación sea correcta.

Cuando la mayoría haya concluido que la suma es 75.3, pida a sus estudiantes que compartan sus estrategias para saber cómo determinaron la posición correcta del punto decimal. Luego, haga las siguientes preguntas para resumir la actividad:

¿Cómo puede ayudar la estimación a resolver un problema de suma o resta con números decimales?

La estimación nos brinda una forma de predecir una respuesta o comprobar si una respuesta es razonable.

Apoyo para la comprensión del lenguaje

Anime a sus estudiantes a usar el vocabulario correcto a la hora de describir partes de un problema de suma o resta. Considere brindar apoyo para la comprensión de los términos de grados anteriores como sumando, suma y diferencia. Señale los términos o rotúlelos en un ejemplo. Para recordarles el vocabulario de los números decimales, muéstreles una tabla de valor posicional y repasen los nombres de cada valor posicional para relacionarlo con las fracciones decimales. Por ejemplo, 20.5 es 20 5 10 , o veinte y cinco décimos, y 30.057 es 30 57 1,000 , o treinta y cincuenta y siete milésimos.

¿Cómo se relaciona la suma y resta de números decimales y la suma y resta de números enteros?

La suma y resta de números decimales es lo mismo que la suma y resta de números enteros. Sumamos y restamos unidades semejantes como decenas y decenas, unidades y unidades, décimos y décimos, y así sucesivamente.

Pida a sus estudiantes que se reúnan y conversen en parejas acerca de la siguiente pregunta:

Recién resolvimos nuestro primer acertijo matemático del punto decimal. ¿Cómo podría ser más desafiante el acertijo matemático si la suma fuera correcta, pero a los sumandos les faltaran puntos decimales?

Hoy, vamos a sumar y restar números decimales. Usaremos la estimación para comprobar que nuestras respuestas sean razonables.

Aprender

El acertijo matemático del punto decimal

La clase suma números decimales y razona acerca de la posición del punto decimal.

Muestre la ecuación que tiene sumandos formados por números enteros y una suma decimal.

205 + 457 + 91 = 30.057

La suma en esta ecuación es correcta, pero los sumandos no son correctos. Los sumandos tienen los dígitos correctos, pero a cada sumando le falta un punto decimal. Trabajen en parejas para determinar dónde colocar un punto decimal en cada uno de los tres sumandos para que la ecuación sea correcta.

Recorra el salón de clases mientras sus estudiantes trabajan y observe las estrategias que usan para colocar el punto decimal en los sumandos. Habrá quienes estimen usando el valor posicional y quienes usen una tabla de valor posicional o el algoritmo estándar para la suma.

Nota para la enseñanza

Evite usar lenguaje como “alinear los puntos decimales” para describir la suma y la resta. Más bien, represente y anime a sus estudiantes a usar enunciados sobre el razonamiento del valor posicional, como “sumar y restar unidades semejantes”.

Diferenciación: Apoyo

Como preparación para crear sus propios acertijos matemáticos del punto decimal, considere pedir a sus estudiantes que determinen dónde colocar los puntos decimales en varias ecuaciones con menos sumandos que tengan los mismos dígitos.

• 325 + 18 = 0.505

0.325 + 0.18 = 0.505

• 325 + 18 = 5.05

3.25 + 1.8 = 5.05

• 325 + 18 = 34.3

32.5 + 1.8 = 34.3

Cuando la mayoría haya concluido que los tres números son 20.5, 0.457 y 9.1, seleccione a estudiantes para que compartan sus estrategias para determinar la posición correcta de los puntos decimales.

Muestre la expresión con los sumandos decimales.

20.5 + 0.457 + 9.1

El primer paso para crear un acertijo matemático del punto decimal como este es elegir tres números decimales que tengan por lo menos un número que no sea 0 a la derecha del punto decimal. Luego, sumamos los tres números decimales. En este caso, los tres números decimales que elegimos eran 20.5, 0.457 y 9.1.

¿Cómo podemos redondear los sumandos al número entero más cercano y hallar la suma estimada?

Podemos redondear 20.5 a 21, 0.457 a 0 y 9.1 a 9. La suma estimada es 30 porque 21 + 0 + 9 = 30.

Muestre los sumandos que se organizan apropiadamente por valor posicional. Luego, haga la siguiente pregunta:

¿Por qué organizamos los sumandos de esta forma?

Organizamos los sumandos de esta forma para que podamos sumar unidades semejantes. Todas las unidades se suman a las unidades, todos los décimos se suman a los décimos, y así sucesivamente.

Alinear los sumandos según el valor posicional de cada dígito y sumar unidades semejantes de forma vertical se denomina algoritmo estándar para la suma.

DUA: Acción y expresión

Ayude a sus estudiantes a organizar los números en problemas de suma y resta con un papel cuadriculado. Pídales que escriban un dígito en cada cuadrado como ayuda para alinear los dígitos según el valor posicional.

0.5 9. 1

0. 45 7

Permita que sus estudiantes le guíen al momento de sumar números decimales con el algoritmo estándar. Mientras suma, considere hacer preguntas como las siguientes para ayudar a sus estudiantes:

• ¿Qué dígitos están en la posición de los centésimos y en la posición de los milésimos en los números 20.5 y 9.1?

• ¿Cuál es la suma de los dígitos en la posición de los décimos?

• Como tenemos 10 décimos, ¿qué dígito escribimos en la posición de los décimos de la suma?

• ¿Cuántas unidades tenemos? ¿Cuántas decenas tenemos?

• La suma es 30.057. ¿Está cerca de nuestra estimación?

Pida a sus estudiantes que vayan al problema 1. Brinde varios minutos para que completen el problema en parejas. Dado que sus estudiantes van a usar sus sumas para crear sus propios acertijos matemáticos del punto decimal, considere pedirles que hagan una señal cuando hayan terminado para que usted pueda comprobar si sus sumas son correctas. Invite a quienes terminen primero a repetir el problema 1 con diferentes números.

1. Elige dos o tres números decimales menores que 1,000. Los números decimales pueden extenderse hasta la posición de los milésimos. Asegúrate de que los números decimales tengan al menos un número que no sea 0 a la derecha del punto decimal.

a. Enumera los números decimales elegidos.

Ejemplo: 864.61, 15.3, 33.115

b. Usa el algoritmo estándar para calcular la suma de los números decimales de la parte (a).

Ejemplo:

025 11 1

Diga a la clase que el último paso en la creación de un acertijo matemático del punto decimal es escribir la ecuación de suma de forma horizontal sin puntos decimales en los sumandos. Si es necesario, muestre la ecuación que tiene sumandos formados por números enteros y una suma decimal, 205 + 457 + 91 = 30.057.

Proporcione a cada pareja de estudiantes una tarjeta de índice y pídales que creen su propio acertijo matemático del punto decimal con los números que eligieron en el problema 1.

DUA: Participación

Durante la actividad del acertijo matemático del punto decimal, sus estudiantes eligen la cantidad de números decimales y la cantidad de dígitos después del punto decimal. Esto les brinda autonomía para determinar el nivel de dificultad en sus problemas.

Escriban su ecuación de suma de forma horizontal en la tarjeta de índice con la suma correcta de la parte (b) pero sin puntos decimales en los sumandos. Luego, escriban sus nombres en la tarjeta de índice.

Pida a sus estudiantes que hagan una señal cuando terminen de escribir sus acertijos matemáticos y sus nombres en sus tarjetas. Recoja las tarjetas de índice, mézclelas y repártalas entre las parejas de estudiantes para que resuelvan los acertijos. Considere pedirles que escriban los sumandos correctos en el reverso de la tarjeta. Luego, devuélvalas a cada estudiante cuyo nombre aparezca en la tarjeta para que haga la comprobación.

El valor posicional en la suma y la resta

La clase suma y resta números decimales y compara el proceso de sumar y restar fracciones.

Muestre la ecuación de suma incorrecta.

1.6 + 0.02 = 1.8

Sumaron los dos números de forma incorrecta. ¿Por qué la suma es incorrecta?

La suma es incorrecta porque sumaron el 2 en la posición de los centésimos al 6 en la posición de los décimos, en vez de sumar los dígitos según su valor posicional.

Sumamos dígitos según su valor posicional. ¿Qué deberían haber hecho? ¿Cuál es la suma correcta?

Deberían haber sumado unidades semejantes: centésimos con centésimos, décimos con décimos, unidades con unidades. La suma correcta es 1.62.

Muestre la ecuación de resta incorrecta.

1.006 − 0.2 = 1.004

Restaron el segundo número del primer número de forma incorrecta. ¿Por qué la diferencia es incorrecta?

La diferencia es incorrecta porque restaron el 2 en la posición de los décimos del 6 en la posición de los milésimos, en vez de restar los dígitos según su valor posicional.

Miremos el trabajo de otras personas que evaluaron 1.006 − 0.2.

Diferenciación: Desafío

Pregunte a sus estudiantes qué creen que podría hacer que un acertijo matemático del punto decimal sea más o menos desafiante para resolver. Invite a sus estudiantes a crear acertijos matemáticos del punto decimal que sean, intencionalmente, más o menos desafiantes para resolver.

Muestre el trabajo de Ryan y el trabajo de Tyler.

Trabajo de Ryan Trabajo de Tyler

1.006 − 0.2 = 1 6 _____ 1,000 − 2 __ 10 =

En estos ejemplos, Ryan y Tyler usan una estrategia diferente para restar números decimales. Vamos a analizar cada una de sus estrategias para determinar si la estrategia funciona y por qué.

Use la rutina Cinco preguntas estructuradas para invitar a sus estudiantes a analizar el trabajo de Ryan y el trabajo de Tyler.

Observar y preguntarse

¿Qué observan acerca de este trabajo?

Observo que Ryan cambió los números decimales por fracciones decimales. Observo que el trabajo de Ryan tiene más pasos. Observo que Tyler escribió un problema de forma vertical y organizó los dígitos según el valor posicional. Observo que Tyler escribió ceros en la posición de los centésimos y milésimos de 0.2. Observo que Ryan y Tyler obtuvieron la misma respuesta.

A partir de sus observaciones, ¿qué se preguntan?

Me pregunto por qué Ryan escribió los números decimales como fracciones decimales en lugar de solo restar los números decimales. Me pregunto por qué Tyler escribió ceros en la posición de los centésimos y los milésimos de 0.2.

Organizar

¿Qué pasos siguió Ryan? ¿Cómo lo saben? Reúnanse y conversen en parejas.

¿Qué pasos siguió Tyler? ¿Cómo lo saben? Reúnanse y conversen en parejas.

Guíe la conversación para enfocarse en las unidades semejantes y el valor posicional. Incentive el razonamiento de sus estudiantes para que hagan conexiones entre escribir fracciones decimales con denominadores comunes y alinear sumandos según el valor posicional.

Mostrar

Enfoquémonos en la idea de unidades semejantes, como décimos y décimos o milésimos y milésimos, en los problemas de suma y resta. ¿Dónde ven eso en el trabajo de Ryan?

Ryan escribió 2 10 como 200 1,000 de manera que tenga el mismo denominador que 1,006 1,000 . Como las fracciones tienen denominadores comunes, Ryan puede restar unidades semejantes.

¿Dónde ven la idea de unidades semejantes en el trabajo de Tyler?

Tyler alineó los sumandos según el valor posicional de los dígitos. Colocó un cero en la posición de los centésimos y en la posición de los milésimos de 0.200. Como los dígitos están alineados según el valor posicional, puede restar unidades semejantes.

Sintetizar

¿Por qué es útil escribir fracciones con un denominador común como vemos en el trabajo de Ryan?

Escribir fracciones con un denominador común nos permite sumar o restar porque las fracciones tienen unidades semejantes.

¿Por qué es útil alinear los dígitos según el valor posicional como vemos en el trabajo de Tyler?

Alinear los dígitos según el valor posicional nos permite sumar o restar porque los dígitos que están alineados tienen unidades semejantes.

Promoción de la práctica de las matemáticas

Cada estudiante utiliza las herramientas apropiadas estratégicamente cuando compara dos métodos para restar números decimales, detecta errores por medio del conocimiento sobre el valor posicional y, luego, resta números decimales con un método de su elección.

Considere hacer las siguientes preguntas:

• ¿Cómo pueden estimar la solución? ¿Les parece razonable su estimación?

• ¿Por qué eligieron organizar los dígitos según el valor posicional para restar?

• ¿Por qué eligieron escribir los números como fracciones decimales para restar?

Comprender

¿Por qué la idea de unidades semejantes es útil para sumar y restar números decimales, fracciones o números enteros?

A la hora de sumar y restar números decimales, fracciones o números enteros, sumamos y restamos unidades semejantes, como decenas y decenas, unidades y unidades, décimos y décimos, y así sucesivamente.

Haga una encuesta para ver si sus estudiantes piensan que el método de Ryan o el método de Tyler es más eficiente en este caso. Invite a un grupo pequeño de estudiantes a compartir su razonamiento.

Pida a sus estudiantes que vayan a los problemas 2 a 6 y que trabajen en parejas o de manera individual para resolverlos. Anime a sus estudiantes a estimar para confirmar que sus respuestas sean razonables. Recorra el salón de clases mientras sus estudiantes trabajan y haga las siguientes preguntas para incentivar su razonamiento:

• ¿Por qué deben considerar el valor posicional al sumar o restar números decimales?

• ¿Es razonable su respuesta? ¿Cómo lo saben?

• ¿Cómo pueden hacer para comprobar que su respuesta es correcta?

Para ayudar a sus estudiantes a entender la situación del mundo real del problema 4, haga las siguientes preguntas:

• ¿Qué significan los números en este problema?

• ¿Creen que en este problema hay que sumar o restar? ¿Por qué?

• ¿Qué significa su respuesta en esta situación?

2. Resta.

5107

60 8. 050

608.05 − 51.308 5 1. 308

55 6. 742

Diferenciación: Apoyo

Si sus estudiantes necesitan más práctica con el algoritmo estándar, pídales que completen los siguientes problemas antes de completar los problemas 2 a 6:

• 3.45 + 1.24

4.69

• 3.45 − 1.24

2.21

• Lacy compra alimento para perros por $4.99 y alimento para gatos por $3.78. ¿Cuál es la cantidad total de dinero que Lacy gasta en el alimento para perros y el alimento para gatos? Si Lacy paga con un billete de $10.00, ¿cuánto cambio debería recibir?

Lacy gasta un total de $8.77 en el alimento para perros y el alimento para gatos. Lacy debería recibir $1.23 de cambio.

3. Considera la lista de números. ¿Qué número es la suma de otros dos números de la lista?

1 2 , 1 331 1,000 , 0.701, 1.218, 63 100

0.5, 1.331, 0.701, 1.218, 0.63 + 0.6 3

0. 701 1. 331 1

1.331 es la suma de 0.701 y 0.63.

4. Una lanzadora de beisbol arroja una pelota. La pelota alcanza la base de bateo en aproximadamente 0.458 segundos. Una lanzadora de softbol arroja una pelota. La pelota alcanza la base de bateo en aproximadamente 0.419 segundos. ¿Cuántos segundos menos tarda la pelota de softbol en llegar a la base de bateo en comparación con la pelota de beisbol?

0. 458 0. 039 18 4

0. 419

La pelota de softbol tarda 0.039 segundos menos en llegar a la base de bateo en comparación con la pelota de beisbol.

En los problemas 5 y 6, escribe los dígitos desconocidos para que la suma o la diferencia sea correcta.

5. + 4. 6525 5. 3475

1 0. 0000

6. 1. 369 2.4 1. 031

Diferenciación: Desafío

Elija un número entre 5 y 25 para representar la suma deseada. Como desafío, pida a sus estudiantes que usen los dígitos de 0 a 9 solo una vez para completar los espacios para que la suma sea lo más cercana a la suma deseada. . + . + .

Cuando la mayoría haya terminado, confirme las respuestas. Elija a diferentes estudiantes para que compartan sus estrategias, en particular las que usaron en los problemas 3, 5 y 6. Luego, pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Pueden pensar en un problema que pueda resolverse de forma más eficiente sumando o restando fracciones o números mixtos en lugar de números decimales? De ser así, den un ejemplo.

Ejemplo: Sería más eficiente sumar fracciones que tengan un denominador común o denominadores que sean fáciles de igualar, como 1 4 y 3

porque tienen un denominador común.

Den un ejemplo de un problema que incluya la suma o resta de fracciones o números mixtos que creen que pueda resolverse de forma más eficiente si primero se escriben los números como números decimales.

Ejemplo: Si restamos números mixtos con diferente denominador, como 57 1 4 y 5 53 100

sería

más eficiente convertirlos primero en números decimales para que no tengamos que hallar un denominador común.

Concluir

Reflexión final 5 min

Objetivo: Sumar y restar números decimales usando los algoritmos estándares para cada operación

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas. Anime a sus estudiantes a desarrollar las respuestas de sus pares.

¿Por qué es útil estimar una suma o diferencia al sumar o restar?

Estimar una suma o diferencia al sumar o restar nos ayuda a confirmar si la respuesta es razonable.

¿Por qué es importante el valor posicional al sumar y restar números decimales?

El valor posicional es importante porque solo se pueden sumar dígitos que tengan unidades semejantes, como centésimos y centésimos. Si no sumamos o restamos según el valor posicional, no vamos a obtener la suma o diferencia correcta.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Suma y resta de números decimales

En esta lección:

• sumamos números decimales usando el algoritmo estándar;

• restamos números decimales usando el algoritmo estándar.

Ejemplos

1. Considera 3.458 + 32.63

a. Estima la suma. Muestra cómo estimaste.

3 + 33 = 36

b. Halla la suma.

36.088

2. Halla la diferencia. 86 − 15.47 70.53

3. Las camisetas cuestan $8.99 cada una. Un paquete de calcetines cuesta $5.50. Toby compra 2 camisetas y 1 paquete de calcetines. Paga con $40.00. ¿Cuánto cambio debería recibir Toby?

8.99 + 8.99 + 5.50 = 23.48

40 − 23.48 = 16.52

Toby debería recibir $16.52 de cambio.

Redondea a los números enteros más cercanos para estimar la suma.

Cuando sumes números decimales, asegúrate de sumar las unidades semejantes.

Compara la suma con la estimación para determinar si la suma es razonable.

Cuando restes números decimales, asegúrate de restar las unidades semejantes.

Resta el costo total de los productos de los $40.00 que paga Toby para hallar cuánto cambio debe recibir.

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

6. 15.003 − 0.03 = 15 Falsa 14.973

1. Estima la suma. Muestra cómo estimaste. 15.236 + 24.901 15 + 25 = 40 40

2. Estima la diferencia. Muestra cómo estimaste. 91.887 − 61.4

Ejemplo: 90 − 60 = 30 30

3. Coloca un punto decimal en cada sumando para que la oración numérica sea verdadera. 154 + 31 + 8 = 5.44

1.54 + 3.1 + 0.8 = 5.44

En los problemas 4 a 7, determina si la oración numérica es verdadera o falsa. Si es falsa, calcula la respuesta correcta.

4. 2,300 + 40 = 2,700

Falsa

2,340

5. 2.3 + 0.04 = 2.34

Verdadera

7. 15,003 − 30 = 14,973 Verdadera

En los problemas 8 a 11, calcula la suma o la diferencia. 8. 517.97 + 312.03 830 9. 32 − 16.21 15.79

12. Un restaurante vende tacos a $0.99 cada uno y bebidas a $1.19 cada una. Kelly pide 2 tacos y 1 bebida. Paga con un billete de $5.00. ¿Cuánto cambio debería recibir Kelly? Muestra tu trabajo. 0.99 + 0.99 + 1.19 = 3.17 5 − 3.17 = 1.83

Kelly debería recibir $1.83 de cambio.

EUREKA

EUREKA MATH2

13. El precio del yogur helado se basa en el peso del yogur. La tabla muestra los precios para distintos pesos de yogur.

Peso de yogur (en onzas) Precio (en dólares)

Menor que 5.0 2.99

5.001 a 10.0 3.89 10.001 a 15.0 5.29 15.001 a 20.0 6.79

Mayor que 20.0 7.59

El yogur de Riley pesa 8.641 onzas. El yogur de Sasha pesa 5.77 onzas. Para pagar un precio menor, ¿Riley y Sasha deberían pagar sus yogures en conjunto o por separado? Justifica tu respuesta.

Riley y Sasha deberían pagar en conjunto sus yogures para pagar un precio menor de $5.29 Si pagan por separado, cada persona pagaría $3.89, que en total sería $7.78

14. Escribe los dígitos desconocidos para que la suma sea correcta.

+ 0. 204

000 1 0. 796

15. Escribe los dígitos desconocidos para que la diferencia sea correcta.

843

Recuerda

En los problemas 16 a 19, suma o resta.

20. Lisa corre 3 1 2 millas. Noah corre 5 1 2 millas. ¿Cuántas veces la distancia de Lisa corre Noah?

Noah corre 1 4 7 veces la distancia de Lisa.

21. ¿Cuál de las siguientes situaciones puede representarse por 1 4 ÷ 3? Elige todas las opciones que correspondan.

A. La cantidad de jarabe en cada plato si 1 4 de taza de jarabe se divide entre 3 platos de panqueques

B. La cantidad que nada Yuna si nada 1 4 de milla 3 veces

C. El tiempo transcurrido mirando 1 4 de una película de 3 horas

D. La cantidad de avena que se necesita para una receta si 1 4 de libra es 3 veces la cantidad que Eddie necesita.

Patrones en la multiplicación de números decimales

Reconocer y aplicar patrones en los factores al multiplicar números enteros y números decimales

Vistazo a la lección

1. ¿Qué expresiones son equivalentes a 0.15? Elige todas las opciones que correspondan.

A. 5 × 3 10

B. 5 × 0.03

C. 5 10 × 3 10

D. 0.05 × 3

E. 0.05 × 0.03

2. Completa los espacios con el factor correcto para que las ecuaciones sean verdaderas. Usa la ecuación dada. 24 × 314 = 7,536

a. 240 × 31.4 = 7,536

b. 2.4 × 3,140 = 7,536

En esta lección digital, la clase usa varias actividades interactivas para reconocer la relación entre factores y productos en expresiones de multiplicación con números decimales. Al crear diferentes rectángulos con un área o un ancho fijos, sus estudiantes descubren patrones en la relación entre las medidas de la longitud y el área. Luego, usan una tabla de valor posicional para multiplicar números decimales que se extiendan más allá de la posición de los centésimos. Observan patrones en el valor posicional de factores y productos y crean estrategias que les ayuden a multiplicar números decimales de forma eficiente.

Use la plataforma digital para preparar y enseñar esta lección. Sus estudiantes también explorarán el contenido de la lección y las actividades a través de la plataforma digital.

Pregunta clave

• ¿Por qué nos ayuda la relación entre factores decimales y productos a multiplicar números decimales de manera eficiente?

Criterio de logro académico

6.Mód2.CLA10 Multiplican números decimales de varios dígitos.

Agenda

Fluidez

Presentar 5 min D

Aprender 30 min D

• Modelo de área

• Patrones en el valor posicional

• ¿Cuál es mayor?

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• computadoras o dispositivos (1 por pareja de estudiantes)

Preparación de la lección

• No se necesita.

Fluidez

Multiplicar fracciones decimales

La clase multiplica fracciones decimales como preparación para multiplicar números decimales.

Instrucciones: Multiplica.

Presentar

La clase descubre patrones en la multiplicación de números decimales cuando un factor o un producto es fijo.

Sus estudiantes usan una actividad interactiva de modelo de área para observar patrones en la longitud y el ancho de un rectángulo cuando el área es fija. Ven los efectos de multiplicar la longitud del rectángulo por 10 o 0.1 mientras el ancho sigue fijo. Observan que el área del rectángulo cambia por un factor equivalente.

¿Qué observan y qué se preguntan acerca del rectángulo cuando se hacen cambios en su longitud?

Observo que el ancho del rectángulo no cambia.

Observo que cuando la longitud del rectángulo se multiplica por 0.1, el área del rectángulo cambia por un factor de 0.1. Lo mismo ocurre cuando la longitud del rectángulo se multiplica por 10: el área cambia por un factor de 10. Me pregunto qué pasaría si el ancho del rectángulo también cambiara.

¿Cuál creen que sería la longitud si el área fuera 0.0024 pulgadas cuadradas? ¿Por qué?

La longitud sería 0.0004 pulgadas cuadradas porque cada vez que el área se multiplica por 0.1, la longitud también se multiplica por 0.1. 5

in cuad.

Aprender

Modelo de área

La clase multiplica por múltiplos de décimos, centésimos y milésimos.

La clase usa su conocimiento sobre los números decimales y las fracciones junto con una cuadrícula interactiva de 10 × 10 con un área total de 1 unidad cuadrada para hallar el área de los rectángulos dentro de la cuadrícula. Para representar el área de los rectángulos, sus estudiantes crean oraciones de multiplicación y relacionan patrones en fracciones decimales con patrones en números decimales.

Escriban una oración de multiplicación que represente el área del rectángulo. Expliquen.

0.7 × 0.6 = 0.42

El área del rectángulo es 42 ___ 100 unidades cuadradas o 0.42 unidades cuadradas porque hay 42 cuadrados que se superponen de un total de 100 cuadrados. 7 10 del rectángulo está sombreado de morado. 6 __ 10 del rectángulo está sombreado de azul. La parte que se superpone entre lo morado y lo azul representa 7 10 × 6 10 = 42 100   .

Colores superpuestos

Usen 4 __ 10 × 8 __ 10 = 32 ___ 100 como ayuda para hallar 4 __ 10 × 8 ___ 100     . Expliquen cómo les ayudó. El producto es 32 1,000 o 0.032. Como 8 10 se multiplica por 1 10 para igualar a 8 100 , sé que 32 100 también debe multiplicarse por 1 10 .

DUA: Representación

Las actividades digitales están alineadas con el principio de Representación de DUA, dado que incluyen lo siguiente:

• Varios formatos y modos de representación: los rectángulos, la cuadrícula de 10 × 10, la tabla de valor posicional y las oraciones de multiplicación representan la multiplicación con números decimales a través de la actividad interactiva.

• Soportes que relacionan la información nueva con los conocimientos previos: sus estudiantes usan sus conocimientos previos de fracciones y modelos de área para hacer conexiones con la multiplicación con números decimales.

• Estrategias que hacen énfasis en patrones, relaciones e ideas clave fundamentales: las pistas de colores, los planteamientos, las preguntas y varios ejemplos ayudan a descubrir patrones y mostrar la relación entre factores y productos en la multiplicación con números decimales.

Azul

Morado

Patrones en el valor posicional

La clase razona acerca del valor posicional de los dígitos en el producto de dos números decimales.

La clase descubre cómo los valores posicionales de los dígitos en cada factor afectan los valores posicionales de los dígitos en el producto. Al usar una tabla de valor posicional para examinar factores y productos, sus estudiantes ven que si un factor se multiplica por 10, entonces el producto también se multiplica por 10. Si un factor se multiplica por 0.1, entonces el producto también se multiplica por 0.1.

¿Qué patrones hallaron al usar la tabla de valor posicional?

Cuando un factor se multiplica por 10, el producto también. Cuando un factor se multiplica por 0.1, el producto también. Multiplicar un factor por 10 mueve el valor posicional de cada dígito en el producto hacia la izquierda. Multiplicar un factor por 0.1 mueve el valor posicional de cada dígito en el producto hacia la derecha. Cuando un factor se multiplica por 10 y el otro se multiplica por 0.1, el producto se mantiene igual.

¿Cuál es el producto de 0.23 y 0.56? ¿Por qué?

El producto es 0.1288. Sé que el producto de 23 y 56 es 1,288. Multiplico 23 por 0.1 dos veces para obtener 0.23, y multiplico 56 por 0.1 dos veces para obtener 0.56. Esto significa que el producto de 0.23 y 0.56 debe ser 1,288 multiplicado por 0.1 cuatro veces, que es 0.1288.

Luego, sus estudiantes usan los patrones que observaron para colocar un punto decimal en cada factor, 17 y 348. Sus estudiantes determinan cómo sus elecciones afectan los valores posicionales de los dígitos en el producto.

17 × 348 = 5,916

1.7 × 348 = 591.6

1.7 × 3.48 = 5.916

0.17 × 34.8 = 5.916

Promoción de la práctica de las matemáticas

Cada estudiante reconoce y expresa regularidad en la lógica de la repetición cuando multiplica factores por potencias de 10 repetidamente para observar el patrón de que multiplicar un factor por una potencia de 10 hace que el producto se multiplique por la misma potencia de 10

Considere hacer las siguientes preguntas:

• ¿Qué patrones observaron al multiplicar un factor por 0.1? ¿Cómo puede ayudarles eso a multiplicar números decimales de forma más eficiente?

• ¿Este patrón funcionará siempre? Expliquen.

¿Cuál es mayor?

La clase ordena expresiones de multiplicación de menor a mayor usando patrones en los factores.

Sus estudiantes usan patrones que descubrieron en actividades anteriores para ordenar expresiones de menor a mayor. Primero, ordenan grupos de cuatro expresiones donde los primeros factores son el mismo número y los segundos factores son fracciones decimales o números decimales diferentes. Luego, examinan cuatro expresiones donde ambos factores se multiplicaron por 10 o por 0.1.

Expliquen cómo ordenaron las expresiones.

Me enfoqué en el valor del número decimal porque todas las expresiones tienen un 16 como factor. Escribí cada número decimal en la posición de los milésimos y, luego, ordené las expresiones por el valor de los números decimales.

¿Cómo les ayudan los valores posicionales de los dígitos en cada factor a ordenar las expresiones?

Observé los valores posicionales de los dígitos en cada factor y determiné en qué eran diferentes a los valores posicionales de los dígitos en los factores de otras expresiones.

Por ejemplo, sé que 0.16 × 0.5 es mayor que 0.16 × 0.05, porque el primer factor es el mismo y el segundo factor es 10 veces 0.05.

Menor Mayor

Concluir

Reflexión final 5 min

Objetivo: Reconocer y aplicar patrones en los factores al multiplicar números enteros y números decimales

Use las preguntas que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a complementar las respuestas de sus pares.

¿Qué patrones son útiles cuando se multiplican números decimales?

Un patrón útil es que los valores posicionales de los dígitos en el producto pueden determinarse por los valores posicionales de los dígitos en los factores. Multiplicar uno de los factores por 10 significa que el producto también se multiplica por 10. Multiplicar uno de los factores por 0.1 significa que el producto también se multiplica por 0.1. Otro patrón útil es que podemos obtener el mismo producto con dos pares de números diferentes si multiplicamos un factor por 10 y el otro por 0.1, o si multiplicamos un factor por 10 y dividimos el otro factor entre 10.

¿Por qué nos ayuda la relación entre factores decimales y productos a multiplicar números decimales de manera eficiente? Den un ejemplo.

Si conozco el producto de dos números enteros, puedo usar los patrones para determinar los productos de números decimales. Por ejemplo, como sé que 7 × 6 = 42, puedo calcular también 0.7 × 6 o 0.7 × 0.06 al determinar la potencia de 10 por la que se multiplican los factores y aplicar esa multiplicación al producto original, 42.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Patrones

en la multiplicación de números decimales

En esta lección:

• reconocimos patrones en los factores al multiplicar números enteros y números decimales.

Ejemplos

1. Completa los espacios con el factor correcto para que las ecuaciones sean verdaderas.

a. 0.036 × 100 = 3.6

b. 0.36 × 10 = 3.6

c. 3.6 × 1 = 3.6

d. 36 × 0.1 = 3.6

e. 360 × 0.01 = 3.6

Observa cómo cambia el valor posicional de cada dígito en los factores cuando se multiplica por potencias de 10 Cada ecuación da como resultado el mismo producto.

2. Completa los espacios con el factor correcto para que las ecuaciones sean verdaderas. Usa la ecuación dada.

4.3 × 6.04 = 25.972

a. 0.43 × 60.4 = 25.972

b. 0.43 × 6.04 = 2.5972

c. 43 × 0.604 = 25.972

d. 4.3 × 0.604 = 2.5972

3. ¿Qué expresiones son equivalentes a 0.48? Elige todas las opciones que correspondan.

A. 8 × 6 10

B. 8 × 0.06

C. 8 10 × 6 10

D. 0.08 × 0.06

E. 0.08 × 6

8 grupos de 6 centésimos equivalen a 48 centésimos.

8 décimos multiplicados por 6 décimos equivalen a 48 centésimos.

6 grupos de 8 centésimos equivalen a 48 centésimos.

4. ¿Qué expresiones son equivalentes a 0.4 × 0.8? Elige todas las opciones que correspondan.

A. 4 × 0.01 × 8 × 0.01

B. 4 × 0.1 × 8 × 0.1

C. 4 × 1 1,000 × 8 × 1 100

D. 4 × 0.001 × 8 × 0.1

E. 4 × 10 × 8 × 0.001

F. 4 × 8 × 1 10 × 1 10

G. 4 10 × 8 10

Cuando un factor se divide entre una potencia de 10 y el otro factor se multiplica por la misma potencia de 10, el producto permanece igual.

Cuando un factor se divide entre una potencia de 10 y el otro factor permanece igual, el producto se divide entre la misma potencia de 10

4 10 es equivalente a 0.4 y 8 10 es equivalente a 0.8. Por lo tanto, esta expresión es equivalente a 0.4 × 0.8

4 × 0.1 = 0.4 y 8 × 0.1 = 0.8

Por lo tanto, esta expresión es equivalente a 0.4 × 0.8

(4 × 10) × (8 × 0.001) = 40 × 0.008 Multiplicar el factor 40 por 0.01 y el factor 0.008 por 100 no cambia el producto. Por lo tanto, esta expresión es equivalente a 0.4 × 0.8

La expresión es equivalente a (4 × 1 10 ) × (8 × 1 10 )

4 × 1 10 = 4 10 y 8 × 1 10 = 8 10

Por lo tanto, esta expresión es equivalente a 0.4 × 0.8

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

4. Completa los espacios para que las ecuaciones sean verdaderas. Usa cada número de la columna Factor solo una vez.

1. Ordena las expresiones de menor a mayor.

A. 5 × 0.22

B. 5 × 0.201

C. 5 × 0.21

D. 5 × 0.2

D, B, C, A

2. Ordena las expresiones de menor a mayor.

A. 18 × 303 1,000

B. 18 × 3 10

C. 18 × 39 100

D. 18 × 37 100

B, A, D, C

3. Ordena las expresiones de menor a mayor.

A. 350 × 0.03

B. 35 × 3.1

C. 3.5 × 0.32

D. 0.35 × 0.33

D, C, A, B

5. Completa los espacios con el factor correcto para que las ecuaciones sean verdaderas.

a. 0.024 × 100 = 2.4

b. 0.24 × 10 = 2.4

c. 2.4 × 1 = 2.4

d. 24 × 0.1 = 2.4

e. 240 × 0.01 = 2.4

6. Completa los espacios con el factor correcto para que las ecuaciones sean verdaderas. Usa la ecuación dada.

3.7 × 5.02 = 18.574

a. 0.37 × 50.2 = 18.574

b. 0.37 × 5.02 = 1.8574

c. 37 × 0.502 = 18.574

d. 3.7 × 0.502 = 1.8574

EUREKA MATH

7. Empareja cada expresión de la columna A con una expresión de la columna B que tenga el mismo valor.

Columna A Columna B

1 10 de 5 1,000 0.1 × 0.05

1 100 de 5 10 0.01 × 5

1 10 de 5 10 1 × 0.5

1 10 de 5 0.01 × 0.05

8. ¿Qué expresiones son equivalentes a 0.24? Elige todas las opciones que correspondan.

A. 8 × 3 10

B. 8 × 0.03

C. 8 10 × 3 10

D. 0.08 × 0.03

E. 0.08 × 3

9. ¿Qué expresiones son equivalentes a 0.7 × 0.3? Elige todas las opciones que correspondan.

A. 7 × 0.01 × 3 × 0.01

B. 7 × 0.1 × 3 × 0.1

C. 7 × 1 1,000 × 3 × 1 100

D. 7 × 0.001 × 3 × 0.1

E. 7 × 10 × 3 × 0.001

F. 7 × 3 × 1 10 × 1 10

G. 7 10 × 3 10

10. Lacy dice que 54 × 2.37 es menor que 54 porque 54 se multiplica por un número decimal. ¿Estás de acuerdo o en desacuerdo con Lacy? Explica. No estoy de acuerdo con Lacy. 2.37 es mayor que 1; entonces, 54 × 2.37 es mayor que 54

11. Scott dice que 5.4 × 0.237 es menor que 5.4. Eddie dice que 5.4 × 0.237 es mayor que 5.4 ¿Estás de acuerdo con Scott o con Eddie? ¿Por qué?

Estoy de acuerdo con Scott. 0.237 es menor que 1 y multiplicar 5.4 por un número decimal menor que 1 da como resultado un producto menor que 5.4

12. Completa los espacios con el producto correcto para que las ecuaciones sean verdaderas. Usa la ecuación dada.

21 × 13 = 273

a. 21 × 1.3 = 27.3

b. 210 × 13 = 2,730

c. 21 × 1,300 = 27,300

d. 2.1 × 1.3 = 2.73

e. 2.1 × 0.13 = 0.273

f. 0.21 × 0.13 = 0.0273

Recuerda

En los problemas 13 a 16, suma o resta.

17. Ryan corre 3 4 de milla. La distancia es 2 3 de su objetivo diario. ¿Cuál es el total del objetivo de Ryan en millas durante 3 días?

El total del objetivo de Ryan durante 3 días es 3 3 8 millas.

18. ¿Qué situaciones se pueden representar por 6 ÷ 1 2 ? Elige todas las opciones que correspondan.

A. El número de horas que un avión estuvo en el aire si voló 1 2 de su vuelo de 6 horas

B. El número de hamburguesas de 1 2 libra que se pueden hacer con 6 libras de carne

C. El número de trozos de chocolate si 6 barras de chocolate se dividen por la mitad

D. El peso de la mochila de Kelly si tiene 6 carpetas que pesan 1 2 libra cada una

E. El número total de huevos que Blake necesita para hacer una tortilla si 6 huevos es 1 2 del número total de huevos que necesita

F. La cantidad de mezcla de frutos secos en cada bolsita si Ryan reparte 1 2 libra de mezcla en partes iguales entre 6 bolsitas

Multiplicación con números decimales

Multiplicar números decimales usando el algoritmo estándar

Vistazo a la lección

En esta lección, sus estudiantes examinan una obra de arte hecha con pennies y determinan qué información necesitan y qué operaciones podrían usar para responder una serie de preguntas sobre el retrato. En la rutina Intercambio con la pizarra blanca, estiman productos y usan sus estimaciones para determinar dónde colocar puntos decimales en los productos. En grupos pequeños, reconocen la importancia de la precisión y el valor posicional cuando usan el algoritmo estándar para multiplicar números decimales. Aplican estas destrezas para multiplicar números decimales en contextos del mundo real.

Preguntas clave

• ¿Por qué estimar un producto nos ayuda a determinar dónde colocar el punto decimal en el producto?

• ¿Cómo usamos el valor posicional al multiplicar números decimales con el algoritmo estándar?

Criterios de logro académico

6.Mód2.CLA2 Resuelven problemas verbales realizando operaciones con números decimales de varios dígitos.

6.Mód2.CLA10 Multiplican números decimales de varios dígitos.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Estimar productos

• Multiplicar números decimales

• Aplicaciones de la multiplicación con números decimales

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• No se necesita.

Fluidez

Multiplicar números decimales

La clase multiplica números decimales como preparación para multiplicar números decimales usando el algoritmo estándar.

Instrucciones: Multiplica.

1. 7 × 0.5 3.5

2. 7 × 0.6 4.2

3. 8 × 0.6 4.8

4. 0.8 × 0.6 0.48

5. 0.9 × 0.7 0.63 6. 10 × 0.7 7

Nota para la enseñanza

En lugar de administrar la actividad de Fluidez de esta lección, considere usar la Práctica veloz de Multiplicar números decimales. Puede encontrar instrucciones para administrar estas actividades en el recurso de la sección Fluidez.

Presentar

La clase determina cómo podría responder preguntas sobre una obra de arte hecha con monedas.

Muestre la obra de arte.

Diga a sus estudiantes que la obra de arte está hecha completamente con pennies. Pídales que compartan lo que observan y que se hagan preguntas acerca de la obra de arte. Luego, divida a sus estudiantes en grupos de 3 o 4 y pídales que vayan al problema 1. Pídales que elijan tres partes del problema 1 y determinen qué información necesitan y qué operaciones pueden usar para responder las preguntas.

1. Determina la información que necesitas y las operaciones que puedes usar para responder cada pregunta.

a. ¿Cuál es el número total de pennies que se usaron para hacer la obra de arte?

Podríamos contar el número de pennies a lo largo y el número de pennies a lo ancho. Después, podríamos multiplicar los números.

b. ¿Cuál es la longitud de la obra de arte en pulgadas? ¿Cuál es el ancho de la obra de arte en pulgadas?

Podríamos hallar el ancho de un penny en pulgadas. Para hallar la longitud de la obra de arte, podríamos multiplicar el ancho de un penny por el número de pennies que hay a lo largo. Para hallar el ancho de la obra de arte, podríamos multiplicar el ancho de un penny por el número de pennies que hay a lo ancho.

c. ¿Cuál es el valor total en dólares de los pennies que se usaron para hacer la obra de arte?

Podríamos multiplicar el número total de pennies por 0.01.

d. ¿Cuál es el peso total en gramos de los pennies que se usaron para hacer la obra de arte?

Podríamos hallar el peso de un penny y multiplicarlo por el número total de pennies.

e. Si todos los pennies que se usaron para la obra de arte estuvieran apilados, ¿cuál sería la altura de la pila?

Podríamos hallar el grosor de un penny y multiplicarlo por el número total de pennies.

Cuando la mayoría haya terminado, pida a sus estudiantes que compartan sus respuestas. Si eligen no responder una de las preguntas, considere responder la pregunta con toda la clase.

Una forma eficiente de hallar la respuesta a cada pregunta es usar la multiplicación.

Hoy, vamos a multiplicar números decimales y usar la estimación para comprobar que el producto sea razonable.

Aprender

Estimar productos

La clase estima para determinar dónde colocar el punto decimal en los productos.

Comience una conversación acerca de la estimación usando la siguiente pregunta:

El ancho de un penny es 19.05 milímetros. Si se ordenan 46 pennies en una fila, ¿cómo podemos hallar la longitud de la fila de pennies en milímetros?

Podemos multiplicar 19.05 por 46.

Si sus estudiantes sugieren sumar 19.05 cuarenta y seis veces, pregúnteles si se les ocurre una forma más eficiente. Luego, muestre la tabla donde se observa el método de Julie y el método de Scott para estimar 19.05 × 46.

DUA: Representación

El método de Scott muestra el algoritmo estándar para la multiplicación. Sus estudiantes analizan el trabajo de Scott y repasan su comprensión previa del algoritmo. Esto les permite hacer conexiones cuando usan el algoritmo estándar para multiplicar números decimales.

Dé tiempo a sus estudiantes para que analicen cada método. Luego, haga las preguntas y los planteamientos que siguen:

Expliquen cómo estima el producto Julie.

Julie redondea 19.05 a 20 y redondea 46 a 50, luego, multiplica 20 por 50. Estima que la longitud de la fila de pennies es 1,000 milímetros.

Expliquen cómo estima el producto Scott.

Scott redondea 19.05 a 19 y multiplica 19 por 46 usando el algoritmo estándar. Estima que la longitud de la fila de pennies es 874 milímetros.

¿Cuál es el método que da una estimación más precisa, el de Julie o el de Scott? ¿Por qué?

Creo que el método de Scott da una estimación más precisa porque redondea solo uno de los números y lo redondea al número entero más cercano. Entonces, la estimación debería ser más cercana al producto real.

¿Cuál es el método que da una estimación más eficiente, el de Julie o el de Scott? ¿Por qué?

Creo que el método de Julie es más eficiente porque 20 y 50 se pueden multiplicar mentalmente.

Muestre la expresión de multiplicación.

4.9 × 2.8

Probemos con otro problema. ¿Cómo pueden estimar el producto de 4.9 y 2.8? ¿Cuál es su estimación?

Podemos redondear 4.9 a 5 y redondear 2.8 a 3. Una estimación del producto es 15.

Guíe un Intercambio con la pizarra blanca.

Vamos a practicar la estimación de productos. Voy a mostrar una ecuación de multiplicación. Al producto de la ecuación le falta un punto decimal. Van a estimar el producto. Luego, van a escribir el producto correcto en sus pizarras blancas con el punto decimal colocado de forma correcta según su estimación. Cuando hayan escrito su respuesta, levanten la pizarra blanca para que pueda verla.

Nota para la enseñanza

En la notación que se muestra en el método de Scott, se colocan las nuevas unidades compuestas de un producto parcial, como 54, que resulta de 9 × 6, en la columna correcta, con el 4 en la posición de las unidades y 5 en la posición de las decenas. Luego, se suman las nuevas unidades compuestas al próximo producto parcial, como se hizo con 6 multiplicado por 1 decena más 5 decenas para obtener 11 decenas.

Este método de registro evita mostrar las nuevas unidades compuestas sobre el factor de arriba, 19, ya que hacer eso mostraría de forma incorrecta, por ejemplo, que las 3 centenas de 360 de 40 × 9 se suman a las decenas. También, colocar las nuevas unidades compuestas sobre los productos parciales ayuda a sus estudiantes a evitar errores comunes en la suma y la reagrupación.

Muestre la ecuación de multiplicación donde se observa el producto de 4.9 y 2.8 al que le falta el punto decimal.

4.9 × 2.8 = 1372

Cuando la mayoría haya colocado el punto decimal y le haya mostrado las pizarras blancas, use el siguiente planteamiento antes de continuar con el resto de la sucesión:

Expliquen cómo determinaron dónde colocar el punto decimal para que los dígitos del producto tengan el valor posicional correcto.

Coloqué el punto decimal entre 3 y 7 de manera que el producto sea 13.72. La estimación de 15 significa que el producto debería ser aproximadamente 15 unidades, o que el producto tiene aproximadamente 1 decena. Si hubiese colocado el punto decimal entre 1 y 3, eso significaría que el producto tiene aproximadamente 1 unidad. Si hubiese colocado el punto decimal entre 7 y 2, eso significaría que el producto tiene aproximadamente 137 unidades.

Continúe con la siguiente secuencia. Muestre una ecuación a la vez y compruebe las respuestas de sus estudiantes después de cada problema. Proporcione retroalimentación inmediata a cada estudiante. Si un gran número de estudiantes necesita ayuda con un problema en particular, comente la solución con toda la clase antes de seguir con el próximo problema de la sucesión.

• 9.1 × 5.5 = 5005

50.05

• 9.31 × 3.7 = 34447

34.447

• 10.011 × 6.4 = 640704

64.0704

• 4.4 × 0.25 = 1100 1.1

¿Por qué creen que es una buena idea estimar el producto?

Es una buena idea estimar el producto para que podamos colocar el punto decimal de forma apropiada y comprobar si nuestro producto es razonable.

Multiplicar números decimales

La clase estima productos y multiplica números decimales.

Pida a sus estudiantes que vayan a los problemas 2 y 3 y que completen los problemas en grupos de 3 con un método de su elección. Habrá quienes elijan comenzar con el algoritmo estándar y quienes elijan usar productos parciales, un modelo de área o multiplicación de fracciones. Dígales que se preparen para compartir sus estrategias para determinar dónde colocar el punto decimal en cada producto.

Recorra el salón de clases mientras sus estudiantes trabajan. Observe los métodos que usan los grupos para multiplicar. Brinde apoyo a sus estudiantes haciendo las siguientes preguntas, según sea necesario:

• ¿Qué métodos usaron en el pasado para multiplicar números decimales?

• ¿Cómo pueden multiplicar con el algoritmo estándar como hizo Scott?

• ¿Cómo pueden usar una estimación como ayuda para colocar el punto decimal en su respuesta?

• ¿Cómo pueden usar la multiplicación de fracciones como ayuda para colocar el punto decimal en su respuesta?

En los problemas 2 y 3, multiplica. Justifica tu razonamiento para la ubicación del punto decimal en el producto.

2. 17.125 × 6

Ejemplo:

Estimé redondeando 17.125 a 20 y multiplicando 20 por 6 para obtener 120. Ubiqué el punto decimal entre 2 y 7 para hacer el producto 102.750, que está más cerca de mi estimación de 120.

Si el punto decimal estuviera en una ubicación distinta, el producto no estaría cerca de 120.

Multipliqué 17,125 _____ 1,000 por 6, que es 102,750 ______ 1,000 . Como el denominador es 1,000, el último dígito debería estar en la posición de los milésimos, y el producto sería 102.750.

Diferenciación: Apoyo

Para activar los conocimientos previos, considere pedir a sus estudiantes que determinen los siguientes productos de números enteros antes de completar los problemas 2 y 3:

• 17,125 × 6

102,750

• 115 × 235

27,025

Después de que sus estudiantes hayan completado los problemas 2 y 3, pídales que comparen los productos de los problemas 2 y 3 con estos productos.

Nota para la enseñanza

Según sea necesario, permita que sus estudiantes usen métodos para multiplicar, como productos parciales o el modelo de área para 19 × 46, como se muestra. Ayude a la clase a relacionar estos métodos con el algoritmo estándar.

6

3. 11.5 × 23.5

Ejemplo:

Estimé redondeando 11.5 a 10 y 23.5 a 24 y multiplicando 10 por 24 para obtener 240. Ubiqué el punto decimal entre 0 y 2 para hacer el producto 270.25, que está más cerca de mi estimación de 240. Si el punto decimal estuviera en una ubicación distinta, el producto no estaría cerca de 240.

Multipliqué 115 10 por 235 10 , que es 27,025 100 . Como el denominador es 100, el último dígito debería estar en la posición de los centésimos, y el producto sería 270.25.

Cuando la mayoría haya terminado, elija a diferentes grupos para que compartan sus respuestas y justificación para la ubicación del punto decimal. Si observa que un gran número de estudiantes no usó el algoritmo estándar para multiplicar o necesitó apoyo para usarlo, considere usar el algoritmo estándar para multiplicar los números decimales del problema 3 con toda la clase.

Promoción de la práctica de las matemáticas

Cada estudiante pone atención a la precisión cuando multiplica números decimales y determina dónde colocar el punto decimal en el producto.

Considere hacer las siguientes preguntas:

• ¿Qué tan precisa debe ser la estimación del producto?

• Al multiplicar números decimales, ¿con qué pasos deben tener mucho cuidado? ¿Por qué?

• ¿En qué parte es más común cometer errores a la hora de determinar dónde colocar el punto decimal en el producto?

Luego, muestre la tabla donde se observan algunas de las ecuaciones de multiplicación que la clase ha visto hasta el momento en la lección, incluidas las de los problemas 1 y 2.

Ecuaciones de multiplicación

9.1 × 5.5 = 50.05

9.31 × 3.7 = 34.447

10.011 × 6.4 = 64.0704

17.125 × 6 = 102.750

11.5 × 23.5 = 270.25

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Ven una conexión entre el número de dígitos a la derecha del punto decimal en los factores y el número de dígitos a la derecha del punto decimal en el producto? De ser así, ¿cuál?

Si se cuenta el número de dígitos a la derecha del punto decimal en cada factor y se suman, se obtiene el número de dígitos a la derecha del punto decimal en el producto.

Elijan una ecuación de la lista y escríbanla en su pizarra blanca como un problema de multiplicación con fracciones.

Luego, compartan su problema en parejas. Reúnanse y conversen en parejas acerca de lo que observan sobre los denominadores en el problema de multiplicación de fracciones y el número de dígitos a la derecha del punto decimal en el producto.

Cuando el algoritmo estándar se usa para multiplicar números decimales, pueden ver que el número de dígitos a la derecha del punto decimal en el producto es igual a la suma del número de dígitos a la derecha del punto decimal en cada factor.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta:

¿Cómo se relaciona esto con los patrones que observaron en la lección anterior sobre la relación entre factores decimales y productos? Den un ejemplo. Es el mismo que el patrón que observamos en la lección anterior. Si multiplicamos uno de los factores en una expresión de multiplicación por 0.1, entonces el producto también se multiplica por 0.1 y los dígitos en el producto se desplazan un valor posicional hacia la derecha. Por ejemplo, si 0.4 × 0.8 = 0.32, entonces 0.4 × 0.08 = 0.032.

Si la clase recuerda esta estrategia de la lección anterior, reitere que la estrategia es útil para determinar dónde colocar el punto decimal en el producto. Use la ecuación 17.125 × 6 = 102.750 para mostrar a sus estudiantes que deben colocar el punto decimal antes de eliminar cualquier cero innecesario de su respuesta final.

Luego, pida a sus estudiantes que continúen trabajando en grupos de 3 y vayan a los problemas 4 a 7. Asigne un problema a cada grupo, y asigne las partes (a), (b) o (c) a cada estudiante del grupo. Indíqueles que hallen el producto de sus partes asignadas. Una vez que todas las personas de cada grupo hallen el producto de sus partes asignadas, pídales que sumen sus productos. Si la suma no es igual a la suma deseada que se muestra para ese problema, indique a quienes integran el grupo que trabajen en equipo para hallar y corregir cualquier error en su trabajo. Si los grupos terminan antes, pídales que completen todos los problemas que puedan si hay tiempo suficiente.

En los problemas 4 a 7, suma los productos de las partes (a) a (c) para calcular la suma.

4. Suma: 5.3508

5. Suma: 20.8148

6. Suma: 12.5888

Nota para la enseñanza

Para apoyar la comprensión de sus estudiantes, pídales que consideren la última ecuación del Intercambio con la pizarra blanca.

4.4 × 0.25 = 1.1

Pregunte a sus estudiantes por qué los factores tienen un total de tres dígitos a la derecha del punto decimal, pero 1.1 tiene solo un dígito a la derecha del punto decimal. Pídales que multipliquen las fracciones decimales o que multipliquen usando el algoritmo estándar para mostrar por qué debería haber habido ceros en la posición de los centésimos y la posición de los milésimos que se eliminaron de la respuesta final.

DUA: Acción y expresión

Considere pedir a sus estudiantes que repitan y confirmen las instrucciones antes de comenzar con la tarea de la suma deseada. Esto les ayuda a planear y elaborar estrategias para que puedan entender completamente la tarea que deben completar. Muestre las siguientes indicaciones escritas para que los grupos puedan usarlas como referencia:

• De manera individual, hallen el producto de su parte asignada.

• En grupo, sumen los productos y comprueben si la suma coincide con la suma deseada de su grupo.

• Hallen y corrijan los errores, si es necesario.

• Repitan el proceso.

7. Suma: 18.5489 a. 7.8 × 1.81

9.03 × 0.03

6.5 × 0.64

Cuando sus estudiantes hayan calculado la suma deseada de al menos un problema, reúna a la clase y pida a sus estudiantes que compartan las estrategias que usaron para colocar el punto decimal en cada producto. Pregúnteles si estimaron, contaron dígitos a la derecha del punto decimal o usaron una combinación de estrategias.

Aplicaciones de la multiplicación con números decimales

La clase aplica el algoritmo estándar para multiplicar números decimales en contextos del mundo real.

Pida a sus estudiantes que vayan a los problemas 8 y 9 y que luego los completen en parejas. Recorra el salón de clases mientras las parejas trabajan. Haga las siguientes preguntas para incentivar el razonamiento de la clase:

• ¿Cómo hallaron el área de un rectángulo?

• ¿Cómo pueden usar la tasa unitaria dada para calcular el costo?

• ¿Cómo escriben 85 % como un decimal?

• ¿Cómo pueden comprobar que sus respuestas sean razonables?

8. El ancho de un salón de clases rectangular es 29.25 pies. La longitud del salón de clases es 31.5 pies.

a. ¿Cuál es el área del salón de clases en pies cuadrados?

El área del salón de clases es 921.375 pies cuadrados.

Diferenciación: Desafío

Pida a sus estudiantes que consideren el siguiente trabajo, determinen el error y hallen el producto correcto:

El producto solo muestra un dígito a la derecha del punto decimal. Como los factores tienen un total de dos dígitos a la derecha del punto decimal, el producto debería tener dos dígitos a la derecha del punto decimal.

Nota para la enseñanza

Un método que sus estudiantes usaron en el módulo 1 para calcular el porcentaje de un número fue la multiplicación de fracciones. Por ejemplo, para hallar el 35 % de 74, sus estudiantes multiplicaron la fracción decimal 35 100 por 74 para obtener 2,590 100 o 25 90 ___ 100 . Ahora, sus estudiantes pueden usar el algoritmo estándar para multiplicar 0.35 por 74 para obtener 25.90 o 25.9.

b. Una compañía cobra $0.40 por pie cuadrado para encerar un piso. ¿Cuál es el costo para encerar el piso del salón de clases?

El costo para encerar el piso del salón de clases es $368.55.

9. La Sra. Song quiere beber 2.2 litros de agua por día. Para la hora del almuerzo, ha bebido el 85 % de su cantidad diaria de agua.

a. ¿Cuál es la cantidad total de agua en litros que ha bebido la Sra. Song para la hora del almuerzo?

Diferenciación: Desafío

Como desafío, pida a sus estudiantes que hallen el factor desconocido.

3. 375 × 8.0 250

El factor desconocido es 0.6.

La Sra. Song ha bebido un total de 1.87 litros de agua para la hora del almuerzo.

b. ¿Cuántos litros más de agua necesita beber la Sra. Song para alcanzar su cantidad de agua diaria?

2.2 − 1.87 = 0.33

La Sra. Song necesita beber 0.33 litros más de agua.

Cuando la mayoría haya terminado, pida a diferentes estudiantes que compartan sus respuestas y el razonamiento para cada problema.

Concluir

Reflexión final 5 min

Objetivo: Multiplicar números decimales usando el algoritmo estándar

Use las preguntas que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a complementar las respuestas de sus pares.

¿En qué situaciones podrían necesitar multiplicar números decimales? ¿Cuándo podrían elegir multiplicar números decimales en vez de usar otra operación?

Multiplicamos números decimales cuando queremos hallar el área de un rectángulo que tiene una longitud o un ancho que es un número decimal. Multiplicamos números decimales cuando queremos hallar el porcentaje de un número. Multiplicamos números decimales cuando queremos usar la tasa unitaria para calcular un número. Elegimos multiplicar números decimales en vez de sumar números decimales una y otra vez.

¿Por qué estimar un producto nos ayuda a determinar dónde colocar el punto decimal en el producto?

La estimación nos ayuda a determinar cuán grande es el producto y qué valores posicionales deberían tener los dígitos del producto. Colocamos el punto decimal en la respuesta para que el producto esté lo más cerca posible de nuestra estimación. Por ejemplo, en el problema 8, estimamos el área del salón de clases en aproximadamente 900 pies cuadrados. La estimación nos ayudó a saber que el punto decimal debería colocarse en el producto para que el número esté más cerca de 900, no de 90 ni de 9,000.

¿Cómo usamos el valor posicional al multiplicar números decimales con el algoritmo estándar?

Podemos usar la información sobre los factores para determinar los valores posicionales de los dígitos en el producto. La suma del número de dígitos a la derecha del punto decimal en cada factor indica el número de dígitos que debería haber a la derecha del punto decimal en el producto.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Multiplicación con números decimales

En esta lección:

• multiplicamos números decimales usando el algoritmo estándar.

Ejemplos

1. Coloca un punto decimal en el producto para que la ecuación sea verdadera.

18.6 × 3.07 = 57102

57.102

2. Multiplica.

162.868

21.43 × 7.6

Usa la estimación para determinar dónde colocar el punto decimal en el producto. Una forma de estimar es redondear los factores a 20 y 3, porque estos números son simples para multiplicar mentalmente. El punto decimal debería colocarse a la derecha de 57 porque 20 × 3 = 60 y 57 está cerca de 60

Cuando el algoritmo estándar se usa para multiplicar números decimales, el número de dígitos a la derecha del punto decimal en el producto es igual a la suma del número de dígitos a la derecha del punto decimal en cada factor. Observa que 21.43 tiene dos dígitos a la derecha del punto decimal, mientras que 7.6 tiene uno. Por lo tanto, el producto debería tener tres dígitos a la derecha del punto decimal. × 7.6 2 1.4 3 + 12858 150010

3. Blake gana $1,025.75 todos los meses en su trabajo. Gana un adicional de $13.50 cada vez que corta el césped de un jardín. El mes pasado, Blake cortó el césped de 4 jardines.

a. ¿Cuánto dinero ganó Blake el mes pasado cortando el césped de los jardines?

13.50 × 4 = 54

Blake ganó $54 el mes pasado cortando el césped de los jardines.

b. ¿Cuál es la cantidad total de dinero que ganó Blake el mes pasado?

1,025.75 + 54 = 1,079.75

Blake ganó un total de $1,079.75 el mes pasado.

No es necesario incluir ceros al final de un número decimal cuando se usa el algoritmo estándar. La expresión 13.50 × 4 es equivalente a 13.5 × 4. Los productos 54.00, 54.0 y 54 son todos equivalentes.

Al sumar números decimales, asegúrate de alinear los sumandos de manera que sean unidades semejantes las que sumas. + 5 4.0 0 1, 02 5.7 5 1, 07 9.7 5

4. Lacy quiere comprar una bicicleta que cuesta $65.50 Lacy ahorró el 70 % de la cantidad que necesita para comprar la bicicleta. ¿Cuánto dinero ahorró Lacy?

65.5 × 0.7 = 45.85

Lacy ahorró $45.85

Recuerda que el 70 % es 70 100, o 0.7. Multiplica 0.7 por 65.5 para determinar el 70 % de $65.50

Nombre

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

En los problemas 1 a 4, estima el producto.

1. 15 × 3.8

Ejemplo: 60

3. 9.71 × 0.494

2. 7 × 4.22

Ejemplo: 28

Ejemplo: 5 4. 211.3 × 8.429

Ejemplo: 1,688

En los problemas 5 a 8, coloca un punto decimal en cada producto para que las ecuaciones sean verdaderas.

5. 6.7 × 4.1 =

7. 7.5 × 0.61 = 4575 4.575

En los problemas 9 a 14, multiplica. 9. 20 × 3.73

492.6 × 3.22 = 1586172 1,586.172

15. ¿Qué expresión tiene un producto mayor: 8.2 × 4.19 u 8.28 × 4.09? Explica cómo lo sabes. 8.2 × 4.19 tiene un

68.5 × 101.2

26.994

Una carrera tiene 6.21 millas de largo. Adesh corre a un ritmo constante de 1 milla cada 9.5 minutos. A ese ritmo, ¿puede Adesh correr la carrera en menos de 1 hora? Justifica tu respuesta.

Número de millas Número de minutos

Sí. Adesh puede correr la carrera en 58.995 minutos, que es menos que 1 hora.

17. La entrenadora de un gimnasio gana $2,456.75 todos los meses. Gana un adicional de $4.75 cada vez que vende una membresía del gimnasio. El mes pasado, vendió 32 membresías. ¿Cuál es la cantidad total de dinero que ganó la entrenadora el mes pasado?

La entrenadora ganó un total de $2,608.75 el mes pasado.

18. Kayla quiere comprar un juego de arte que cuesta $58.50 Kayla ahorró el 80 % de la cantidad que necesita para comprar el juego de arte. ¿Cuánto dinero ahorró Kayla? Kayla ahorró $46.80

25. Considera el diagrama.

Recuerda

En los problemas 19 a 22, calcula la suma o la diferencia.

19. 5 4 + 5 12

23. Halla la suma. 554.99 + 951.287 1,506.277

24. Halla la diferencia. 45 12.19

a. Usa el diagrama para emparejar cada descripción con su razón.

La razón del número de estrellas al número de triángulos

La razón del número total de figuras al número de círculos

La razón del número de círculos al número de estrellas

La razón del número de cuadrados al número total de figuras

La razón del número de triángulos al número de círculos

b. Usa el diagrama para escribir una razón diferente a las de la parte (a). Usa el lenguaje de las razones para describir la razón que escribiste.

Ejemplo:

1 : 4

Por cada 1 cuadrado, hay 4 círculos.

EUREKA MATH

Aplicaciones de las operaciones con números decimales

Crear un modelo de un edificio y usar operaciones con números decimales para calcular el costo, los ingresos, y las ganancias o las pérdidas

Vistazo a la lección

En la lección de hoy, ¿cómo calculaste el costo total, el ingreso total y la ganancia o pérdida de tu hábitat? Explica cómo las características de tu diseño dieron como resultado una ganancia o una pérdida para tu hábitat.

Ejemplo:

Calculamos los costos de construir nuestro hábitat al multiplicar el costo por elemento, como los jardines en la azotea y las ventanas, por el número de cada elemento que teníamos en nuestro diseño. Luego, calculamos el impuesto sobre bienes inmuebles y les sumamos todos los costos para determinar el costo total.

Para calcular el ingreso, multiplicamos el número de cada tipo de cubo de nuestro diseño por el precio de venta de ese tipo de cubo. Luego, sumamos todos estos precios para determinar el ingreso total.

Como nuestro ingreso total fue mayor que nuestro costo total, dio como resultado una ganancia. Restamos el costo total del ingreso total para determinar la ganancia. Nuestro diseño tenía 12 jardines en la azotea pero solo 11 plantas, lo que contribuyó a mantener el costo total menor que el ingreso total.

En esta lección, la clase practica y adquiere fluidez con operaciones con números decimales al completar una tarea abierta del mundo real. Teniendo en cuenta las pautas de construcción inspiradas en el hito arquitectónico Hábitat 67, sus estudiantes trabajan en grupos para construir estructuras con cubos para representar sus propios hábitats. Usan las tasas dadas para calcular el costo total y el ingreso total y determinan si su hábitat dio como resultado una ganancia o una pérdida. Luego, ajustan sus modelos para aumentar las ganancias de sus hábitats.

Pregunta clave

• ¿Cómo usamos sumas, diferencias y productos de números decimales en el mundo real?

Criterio de logro académico

6.Mód2.CLA2 Resuelven problemas verbales realizando operaciones con números decimales de varios dígitos.

Nombre

Fecha

BOLETO DE SALIDA

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Construir un hábitat

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• cubos interconectables de 1 cm (20 por grupo de 3 o 4 estudiantes)

Preparación de la lección

• No se necesita.

Fluidez

Sumar, restar y multiplicar números decimales

La clase suma, resta y multiplica números decimales como preparación para calcular con números decimales de varios dígitos.

Instrucciones: Suma, resta o multiplica.

1.

6. 78.05 × 4.67

Presentar

La clase observa y se pregunta acerca de la arquitectura, el costo y los ingresos de Hábitat 67.

Muestre la imagen de Hábitat 67.

¿Qué observan?

Ejemplo: Observo un edificio hecho de cubos. Observo árboles en partes del edificio. Observo que algunos cubos cuelgan del costado. Observo que parece como si el edificio tuviera agujeros. Observo muchas ventanas.

¿Qué se preguntan?

Ejemplo: Me pregunto qué es este edificio. Me pregunto dónde está este edificio. Me pregunto cómo hicieron para que crezcan árboles en partes del edificio. Me pregunto cómo se mantienen algunos de los cubos. Me pregunto cuánto cuesta vivir allí.

Invite a la clase a leer el fragmento en silencio mientras usted lo lee en voz alta.

Hábitat 67 es un edificio de apartamentos ubicado en Montreal, Quebec, en Canadá. En 1967, el arquitecto Moshe Safdie diseñó este edificio único que, hasta el día de hoy, se mantiene como monumento histórico. La visión de Safdie era reinventar el edificio de apartamentos mediante la creación de hogares accesibles en la ciudad que tuvieran atributos propios de los hogares fuera de la ciudad. Su lema era “Jardines para todos”.1 Hábitat 67 está formado por 354 bloques de hormigón agrupados. Su diseño geométrico brinda a quienes residen en los apartamentos jardines en la azotea, aire fresco, privacidad y luz natural. Cada apartamento tiene acceso a por lo menos un jardín en la azotea, muchos de ellos construidos en el techo de un apartamento vecino.

Según sea necesario, repase los términos costo, ingresos, ganancia y pérdida.

El dinero que los constructores gastan para construir una estructura como Hábitat 67 se denomina costo. El dinero que los constructores ganan por vender unidades de apartamentos se denomina ingresos. Si los ingresos son mayores que el costo, los constructores obtuvieron una ganancia. Si los ingresos son menores que el costo, los constructores obtuvieron una pérdida.

Pida a sus estudiantes que se reúnan y conversen en parejas acerca de las siguientes preguntas. Se espera que sus estudiantes no tengan las respuestas precisas. Sin embargo, pídales que usen un razonamiento válido para hacer sus estimaciones. Por ejemplo, “Si cada apartamento se vende a $100,000 y hay aproximadamente 100 apartamentos en el edificio, eso representaría ingresos de $10,000,000”.

¿Cuánto creen que costaría construir una estructura como Hábitat 67?

Imaginen que los constructores quieren obtener una ganancia de al menos $500,000 con la construcción y venta de apartamentos en una estructura como Hábitat 67. Teniendo en cuenta su estimación de costo, ¿a qué precio creen que es necesario vender cada apartamento para alcanzar esa ganancia?

1 Andrew McIntosh y Jennifer Carter,

“Habitat 67”, The Canadian Encyclopedia.

Apoyo para la comprensión del lenguaje

Para apoyar la comprensión de los términos costo, ingresos, ganancia y pérdida, active los conocimientos previos y use un contexto conocido. Por ejemplo, pida a sus estudiantes que consideren hacer y vender vasos de limonada. Use las siguientes preguntas para promover la comprensión de la clase:

• ¿Qué materiales necesitarían para una venta de limonadas? ¿Cuánto costarían esos materiales?

• ¿A qué precio venderían cada vaso de limonada? Si vendieran 25 vasos de limonada a $1.00 por vaso, ¿cuántos ingresos obtendrían?

• ¿Qué número querrían que fuese mayor: la cantidad que gastan en materiales o la cantidad que obtienen de las ventas?

• La diferencia entre la cantidad que ganan, o los ingresos, y la cantidad que gastan, o el costo, podría ser una ganancia o una pérdida. Cuando sus ingresos totales son mayores que su costo total, obtienen una ganancia. Por otro lado, cuando su costo total es mayor que sus ingresos totales, obtienen una pérdida.

Invite a sus estudiantes a compartir sus ideas sobre el costo, los ingresos y la ganancia asociados a Hábitat 67.

El costo para construir Hábitat 67 fue mucho más alto de lo esperado, lo que dio como resultado un aumento de los precios de los apartamentos. Hoy, trabajarán en grupos para diseñar y construir un modelo de su propio hábitat teniendo en cuenta las pautas que inspiraron a Hábitat 67. Van a calcular el costo y los ingresos de su hábitat y ajustar su hábitat para aumentar su ganancia.

Aprender

Construir un hábitat

La clase construye un hábitat y calcula el costo y los ingresos para determinar si su hábitat da como resultado una ganancia o una pérdida.

Divida a la clase en grupos de 3 o 4. Dé tiempo a los grupos para que lean la tarea, las pautas y la información de costo e ingresos.

Pautas para el hábitat

Usa 20 cubos para construir un modelo de tu propio hábitat. Debes usar los 20 cubos.

• Cada cubo representa un hogar de tu hábitat. El hábitat entero debe ser una pieza.

• Tu hábitat debe tener al menos 3 plantas. La primera planta debe tener de 2 a 8 cubos. La cara inferior de cada cubo de la primera planta debe estar de forma horizontal.

• Las caras de los costados visibles de los cubos representan las paredes con ventanas. Las caras superiores visibles de los cubos representan los jardines en la azotea.

• Debes construir tu modelo inspirándote en Hábitat 67. Cada cubo debe tener por lo menos 2 caras de los costados visibles para que el apartamento tenga más ventanas y entre luz natural. Cada cubo debe tener una cara superior visible o estar conectado a un cubo con una cara superior visible para que cada apartamento tenga acceso a un jardín en la azotea.

Nota para la enseñanza

Más adelante en la lección, sus estudiantes determinan si su modelo da como resultado una ganancia o una pérdida. Como los números negativos se presentan recién en el módulo 3, sus estudiantes deben determinar si sus ingresos totales o el costo total es mayor y, luego, restar el número más pequeño del número más grande. Si los ingresos totales de un grupo son mayores que su costo total, sus estudiantes calculan su ganancia cuando restan su costo total de sus ingresos totales. Si el costo total de un grupo es mayor que sus ingresos totales, sus estudiantes calculan su pérdida cuando restan sus ingresos totales de su costo total.

Costo

• El costo por planta es $5,467.16.

• Hay 1 jardín en la azotea por cada cara superior visible. El costo por jardín en la azotea es $5,648.40.

• Hay 2 ventanas por cada cara de los costados visibles. El costo por ventana es $546.42.

• Una unidad de tierra es un cuadrado o un cuadrado cerrado visible desde la vista superior del edificio. Considera la vista superior del hábitat A y la vista superior del hábitat B.

Hábitat AHábitat B

El hábitat A tiene 10 unidades de tierra porque hay 10 cuadrados visibles desde la vista superior del edificio. El hábitat B tiene 12 unidades de tierra porque hay 10 cuadrados y 2 cuadrados cerrados visibles desde la vista superior del edificio. El costo por unidad de tierra es $4,260.90.

• El impuesto sobre bienes inmuebles es el 3 % del costo total de las unidades de tierra. La cantidad de impuesto se suma al costo total del hábitat.

Ingresos

• Un apartamento representado por un cubo con 4 caras de los costados visibles y una cara superior visible se vende por $16,249.99.

• Un apartamento representado por un cubo con 4 caras de los costados visibles y sin una cara superior visible se vende por $14,889.99.

• Un apartamento representado por un cubo con 3 caras de los costados visibles y una cara superior visible se vende por $11,249.99.

DUA: Acción y expresión

Ayude a sus estudiantes a planear y divida la tarea en los siguientes segmentos:

• Primero, pídales que construyan su hábitat según las pautas dadas.

• Para organizar su trabajo, pídales que creen una tabla con 4 columnas con estos encabezamientos: Cubo, Planta, Caras de los costados visibles y Caras superiores visibles. En la columna Cubo, pídales que hagan una lista de los números de 1 a 20 y que registren la planta, el número de caras de los costados visibles y el número de caras superiores visibles para cada cubo en su modelo.

• Por último, pídales que hagan los cálculos necesarios para determinar el costo total, los ingresos totales y la ganancia o pérdida de su hábitat.

Recuerde a sus estudiantes la cantidad de tiempo aproximada que tienen y compruebe su trabajo de forma periódica.

• Un apartamento representado por un cubo con 3 caras de los costados visibles y sin una cara superior visible se vende por $9,889.99.

• Un apartamento representado por un cubo con 2 caras de los costados visibles y una cara superior visible se vende por $7,249.99.

• Un apartamento representado por un cubo con 2 caras de los costados visibles y sin una cara superior visible se vende por $5,889.99.

Use las siguientes preguntas para facilitar la comprensión de la tarea:

¿Qué tipos de elementos tendrán un mayor impacto en el costo total para construir su hábitat?

El número de plantas, el número de jardines en la azotea y el número de unidades de tierra tendrán el mayor impacto en el costo total para construir nuestro hábitat.

¿Qué tipos de elementos generarán mayores ingresos?

Los jardines en la azotea y las ventanas generarán los mayores ingresos.

Dé 20 cubos a cada grupo.

Compartan ideas con su grupo antes de comenzar a construir su hábitat. Comenten cómo quieren diseñar su edificio para que puedan tener el menor costo total y los mayores ingresos totales.

Recorra el salón de clases mientras sus estudiantes construyen sus hábitats y hacen sus cálculos. Anime a sus estudiantes a volver a comprobar que cada cubo tenga por lo menos dos caras de los costados visibles y una cara superior visible o que esté conectado a un cubo con una cara superior visible. Si observa que un grupo no cumple con una pauta, muéstreles qué cubo o cubos no cumplen con la pauta para que puedan hacer los ajustes necesarios para su modelo.

Cuando ya hayan construido su hábitat, pida a sus estudiantes que continúen con los problemas 1 a 6. Con el fin de practicar las operaciones con números decimales, pídales que hagan todos los cálculos necesarios a mano para determinar si su hábitat da como resultado una ganancia o una pérdida. Si los grupos tienen tiempo después de completar el problema 6, permítales que modifiquen sus modelos para aumentar su ganancia y que usen una calculadora para volver a calcular el costo, los ingresos y la ganancia nuevos de su hábitat modificado.

Diferenciación: Apoyo

Si sus estudiantes necesitan apoyo para construir un modelo, considere permitirles usar menos de 20 cubos o brindarles las siguientes instrucciones para construir un modelo de 20 cubos:

• Para la primera planta, unan 8 cubos en una fila.

• Para la segunda planta, unan 1 cubo a la cara superior de cada uno de los otros cubos de la primera planta.

• Para la tercera planta, unan 1 cubo a la cara superior de cada cubo de la segunda planta. Unan los 4 cubos restantes a una cara de los costados de los cubos de la tercera planta.

Considere hacer las siguientes preguntas para ayudar a sus estudiantes mientras trabajan:

• ¿Cómo pueden hallar el número de ventanas una vez que sepan el número de caras de los costados visibles?

• ¿Cómo es 3 % como fracción? ¿Cómo es 3 % como un número decimal?

• ¿Cómo calculan el porcentaje de un número?

• En el problema 4, ¿cuál debería ser la suma del número de cubos?

• ¿A qué valor posicional deberían redondear sus respuestas? ¿Por qué?

• ¿Cómo pueden reducir su costo total para aumentar su ganancia?

• ¿Cómo pueden aumentar sus ingresos totales para aumentar su ganancia?

• ¿Qué suposiciones hacen cuando calculan el costo total y los ingresos totales?

1. Ingresa el número de plantas de tu hábitat, el número de jardines en la azotea, el número de ventanas y el número de unidades de tierra. Usa las tasas dadas para calcular el costo total de cada tipo de elemento.

Ejemplo: Tipo de elemento

Promoción de la práctica de las matemáticas

Cada estudiante representa a través de las matemáticas cuando usa cubos interconectables para representar un edificio de apartamentos, cuando desarrolla e implementa un plan para reducir el costo y aumentar los ingresos, y cuando ajusta su modelo para aumentar la ganancia del edificio.

Considere hacer las siguientes preguntas:

• ¿Qué ideas clave de las pautas para el hábitat deben asegurarse de incluir en su hábitat?

• ¿Cómo pueden mejorar su modelo para reflejar mejor Hábitat 67?

• ¿Cómo pueden mejorar su modelo para aumentar la ganancia de su edificio?

2. Calcula el impuesto sobre bienes inmuebles de tu hábitat.

Ejemplo: El impuesto sobre bienes inmuebles de nuestro hábitat es $1,406.10.

3. Calcula el costo total de tu hábitat.

Ejemplo: El costo total de nuestro hábitat es $195,843

4. Ingresa el número de cada tipo de cubo de tu hábitat. Usa las tasas dadas para calcular el ingreso total por cada tipo de cubo.

Ejemplo: Tipo de cubo

4 caras de los costados visibles, 1 cara superior visible

4

3 caras de los costados visibles, 1 cara superior visible

3 caras de los

2 caras de los costados

Nota para la enseñanza

Cuando sus estudiantes calculan el impuesto sobre bienes inmuebles de sus hábitats, es posible que obtengan un número decimal que se extienda más allá de los centésimos. De ser así, pídales que redondeen al centésimo más cercano porque el impuesto sobre bienes inmuebles es una cantidad en dólares.

Diferenciación: Desafío

Como desafío, considere pedir a sus estudiantes que intercambien hábitats con otro grupo. Pídales que comprueben la precisión de los hábitats y los cálculos de los demás. Según sus cálculos, sus estudiantes pueden modificar la ganancia del grupo de la siguiente forma:

• Si los cálculos de un grupo son correctos, sumen $1,000.00 a la ganancia.

• Si los cálculos de un grupo son incorrectos, resten $1,000.00 de la ganancia.

5. Calcula el ingreso total de tu hábitat.

Ejemplo: El ingreso total de nuestro hábitat es $210,119.80.

6. Si tu costo total del problema 3 es menor que tu ingreso total del problema 5, completa la parte (a).

En caso contrario, completa la parte (b).

a. Resta tu costo total de tu ingreso total. Completa el espacio con la diferencia.

Ejemplo:

Mi hábitat da como resultado una ganancia de $14,276.80 .

b. Resta tu ingreso total de tu costo total. Completa el espacio con la diferencia.

Mi hábitat da como resultado una pérdida de .

Cuando la mayoría haya terminado, invite a los grupos a compartir sus ganancias o pérdidas.

Considere registrar las cantidades en el pizarrón para que puedan compararlas.

Concluir

Reflexión final 5 min

Objetivo: Crear un modelo de un edificio y usar operaciones con números decimales para calcular el costo, los ingresos, y las ganancias o las pérdidas

Use las preguntas que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a complementar las respuestas de sus pares.

¿Cómo influyó su conocimiento sobre el costo de diferentes elementos y los ingresos de distintos tipos de apartamentos en el diseño de su hábitat?

Cuando diseñamos nuestro hábitat, tratamos de usar el número más pequeño posible de unidades de tierra para disminuir el costo. Tratamos de que la mayor cantidad de cubos tenga caras de los costados visibles para ventanas y caras superiores para jardines en la azotea.

¿Cómo usaron las sumas, diferencias y productos de números decimales cuando calcularon la ganancia o pérdida de su hábitat?

Para hallar nuestro costo total e ingresos totales, hallamos la suma de los números individuales de costo e ingresos.

Para hallar nuestra ganancia o pérdida, hallamos la diferencia entre nuestro costo total y nuestros ingresos totales.

Para hallar nuestros números individuales de costo e ingresos, hallamos el producto del número de cada tipo de material, o cubo, y el costo del elemento.

¿Cómo podrían haber modificado el modelo de su hábitat para aumentar la ganancia de su hábitat?

Podríamos haber reducido el número de plantas o unidades de tierra para reducir nuestros costos, lo que aumentaría nuestra ganancia. Podríamos haber aumentado el número de cubos con mayor número de caras de los costados visibles y caras superiores visibles para aumentar nuestros ingresos, lo que aumentaría nuestra ganancia.

¿En qué otras situaciones del mundo real usamos sumas, diferencias y productos de números decimales? Den ejemplos.

Ejemplo: Vemos algunos ejemplos de otras situaciones donde usamos sumas, diferencias y productos de números decimales cuando calculamos los precios de las cosas que compramos, cuando trabajamos con diferentes medidas y cuando calculamos estadísticas sobre deportes.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

©

Aplicaciones de las operaciones con números decimales

En esta lección:

• usamos operaciones con números decimales para calcular el costo, los ingresos y las ganancias o las pérdidas.

Ejemplos

Yuna compra materiales para hacer pulseras y venderlas en una feria de artesanías.

a. Yuna compra 4 cajas de cuentas de colores que cuestan $13.49 cada una. Compra 4 cajas de cuentas de cristal que cuestan $12.00 cada una. Compra 1 paquete de elásticos a $2.50 ¿Cuál es el costo total de Yuna por la compra de estos materiales?

4 × 13.49 = 53.96

3 × 12.00 = 36 53.96 + 36 + 2.50 = 92.46

El costo total de Yuna por la compra de todos estos materiales es $92.46.

La cantidad total que Yuna gasta en materiales para hacer pulseras es el costo total.

b. En la mañana de la feria de artesanías, Yuna vende 12 pulseras a $4.50 cada una. Luego, vende 18 pulseras a $3.75 cada una. ¿Cuál es el ingreso total de Yuna?

12 × 4.50 = 54

18 × 3.75 = 67.5

54 + 67.5 = 121.5

El ingreso total de Yuna es $121.50

La cantidad total que Yuna gana por la venta de pulseras es el ingreso total.

c. ¿La venta de pulseras dio como resultado una ganancia o una pérdida para Yuna? Determina la ganancia o la pérdida.

121.5 − 92.46 = 29.04

La venta de pulseras dio como resultado una ganancia de $29.04 para Yuna.

Yuna obtuvo una ganancia porque el ingreso total es mayor que el costo total. La ganancia se calcula restando el costo total del ingreso total.

Nombre Fecha

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. Describe las diferentes operaciones matemáticas que usaste en la lección de hoy para diseñar tu hábitat y determinar tu ganancia o pérdida. Multipliqué y sumé números decimales para determinar el costo y el ingreso de mi hábitat. Resté números decimales para determinar la cantidad de ganancia o pérdida.

En los problemas 2 a 7, calcula.

8. Lisa abre un puesto de limonada.

a. Para comenzar con el puesto de limonada, Lisa necesita comprar vasos, limones y azúcar. Compra 4 paquetes de vasos que cuestan $2.89 cada uno. Compra 12 limones que cuestan $0.39 cada uno y 1 bolsa de azúcar que cuesta $1.25. ¿Cuál es el costo total de Lisa para abrir el puesto de limonada?

El costo total de Lisa para abrir el puesto de limonada es $17.49

b. El primer día de venta, Lisa vende 22 vasos de limonada a $1.00 cada uno. El segundo día, Lisa vende 18 vasos de limonada a $0.75 cada uno. ¿Cuál es el ingreso total de Lisa?

El ingreso total de Lisa es $35.50.

c. Después de vender limonada durante esos dos días, ¿obtuvo Lisa una ganancia o una pérdida? Determina la ganancia o la pérdida.

Lisa obtuvo una ganancia de $18.01 después de vender limonada durante esos dos días.

9. Noah hace 20 collares para perros para vender en una feria de artesanías. Le cuesta $29.80 comprar todos los materiales que necesita para los collares. Noah vende 11 collares para perros a $2.25 cada uno. ¿Obtuvo Noah una ganancia o una pérdida en la feria de artesanías?

Determina la ganancia o la pérdida.

Noah obtuvo una pérdida de $5.05 en la feria de artesanías.

EUREKA MATH

EUREKA MATH

Recuerda

En los problemas 10 a 13, suma las fracciones. Escribe la respuesta como un número mixto. 10.

14. ¿Qué expresiones son equivalentes a 0.18? Elige todas las opciones que correspondan.

A. 6 × 3 10

B. 6 × 0.03

C. 6 10 × 3 10

D. 0.06 × 3

E. 0.06 × 0.03

15. Cada recta numérica está dividida en partes iguales. Escribe una fracción en cada recuadro para rotular las marcas de graduación.

Tema E

División de números de varios dígitos

En el tema D, sus estudiantes desarrollan fluidez con los algoritmos estándar para la suma, resta y multiplicación de números decimales al ampliar el trabajo sobre cálculos con números decimales que hicieron en 5.o grado y generalizarlo a todos los números, sin importar cuántos dígitos haya después del punto decimal. Esto prepara a sus estudiantes para el trabajo en el tema E sobre la estimación y los cocientes parciales. Sus estudiantes establecen conexiones con estas destrezas a medida que aprenden a usar el algoritmo estándar para dividir números enteros que dan como resultado un cociente decimal.

La primera lección del tema, la lección 17, comienza con una actividad interactiva en la que sus estudiantes deben dividir números en grupos de igual tamaño. Luego, aprenden el método más eficiente de cocientes parciales para dividir números de 3 dígitos entre números de 1 dígito y 2 dígitos. Interpretan residuos y los escriben como fracciones. Por último, determinan la razonabilidad de sus respuestas mediante la estimación.

En las lecciones 18 y 19, sus estudiantes continúan desarrollando el trabajo realizado en la lección 17 con los cocientes parciales para dividir usando el algoritmo estándar. Adquieren fluidez y comienzan a representar cocientes como números decimales. En la lección 18, amplían el trabajo con cocientes parciales y desarrollan el algoritmo estándar para la división. Luego, aplican el algoritmo estándar para la división al algoritmo de Euclides para hallar el máximo común divisor de dos números. En la lección 19, aprenden a escribir cocientes como números decimales reagrupándolos como décimos, centésimos y milésimos.

En la lección 20, sus estudiantes aplican su comprensión de la división al usar el algoritmo estándar para la división a fin de analizar problemas de división del mundo real. Interpretan el significado del cociente en situaciones contextuales dadas. También reconocen el significado del residuo en cada contexto y determinan si deben redondear hacia arriba o hacia abajo según la situación. Aplican esta comprensión mientras crean problemas verbales para que resuelvan sus pares.

Sus estudiantes ponen en uso las destrezas de estimación y el algoritmo estándar para la división en el tema F, cuando aprenden a dividir números decimales entre números decimales. En módulos posteriores, aplican sus conocimientos sobre la división a distintas disciplinas, como ecuaciones, geometría y estadística.

Progresión de las lecciones

Lección 17 Cocientes parciales

Lección 18 El algoritmo estándar para la división

Lección 19 Expresar cocientes como números decimales

Lección 20 Problemas de división del mundo real

Cocientes parciales

Dividir números enteros de varios dígitos usando el método de los cocientes parciales, y expresar cocientes como números mixtos

Vistazo a la lección

Considera

a. Estima el cociente. Justifica tu estimación.

Ejemplo:

15 El cociente es aproximadamente 15

En esta lección, sus estudiantes usan la plataforma digital para visualizar las conexiones entre un contexto dado y la división en grupos de igual tamaño. Después de esta experiencia, pasan a escribir la división de números de 3 dígitos entre números de 1 dígito y 2 dígitos usando cocientes parciales. Mediante la conversación guiada, sus estudiantes hacen una transición hacia el uso de un algoritmo similar al algoritmo estándar para la división.

Use la plataforma digital para preparar y enseñar esta lección. Sus estudiantes también explorarán el contenido de la lección y las actividades a través de la plataforma digital.

Preguntas clave

• ¿Qué estrategias podemos usar para estimar un cociente?

• Al dividir, ¿cómo sabemos si hay un residuo? ¿Qué hacemos con el residuo?

Criterios de logro académico

6.Mód2.CLA7 Razonan acerca del tamaño de los cocientes de dos números de varios dígitos.

6.Mód2.CLA8 Dividen números enteros de varios dígitos usando el algoritmo estándar.

Agenda

Fluidez

Presentar 5 min D

Aprender 30 min D

• Repartir lápices

• División de arriba abajo

• Método de los cocientes parciales

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• computadora o dispositivo (1 por pareja de estudiantes)

Preparación de la lección

• No se necesita.

Fluidez

Expresar cocientes como números mixtos

La clase expresa cocientes como números mixtos como preparación para hallar cocientes con residuos fraccionarios.

Instrucciones: Expresa cada cociente como un número mixto.

Presentar

La clase resuelve un problema de aplicación en el que se deben dividir objetos en grupos de igual tamaño.

Apoyo para la comprensión del lenguaje

Cajas Estuches Lápices

En el problema que se les plantea, sus estudiantes deben distribuir igual número de lápices a 4 maestros. Deciden que la situación se puede representar con la división. Tienen la libertad de reagrupar los lápices, como ayuda para distribuirlos en grupos de igual tamaño. Sus estudiantes analizan otro método y deciden qué método es el más eficiente para distribuir los lápices en grupos de igual tamaño. Escriben oraciones numéricas para describir la situación y explican de qué manera esas oraciones numéricas la describen.

¿Qué oración numérica describe mejor el problema original? ¿Por qué?

La oración de división describe mejor el problema original porque se nos da el número total de lápices que tenemos que repartir en partes iguales entre 4 maestros. No sabemos que cada maestro recibe 134 lápices hasta que hacemos la división en la actividad.

Aprender

Repartir lápices

La clase divide números de 3 dígitos entre números de 1 dígito y razona sobre los cocientes parciales.

Sus estudiantes dividen números descomponiéndolos en partes iguales y restando del total hasta que el residuo es 0. En otra actividad, ingresan el número de lápices que deben distribuir a cada maestro en un modelo de cocientes parciales. Luego, comparan sus cocientes parciales con los

Si es necesario, consulte el afiche de referencia de la lección 6 del tema B, o un afiche similar, para que sus estudiantes recuerden los términos dividendo, divisor y cociente. Considere ofrecer un ejemplo adicional que tenga un residuo, y muestre el residuo y su rótulo en un cuarto color.

4 5 ÷ = = dividendo ÷ divisor cociente

cocientes parciales que usó el resto de la clase. Sus estudiantes concluyen que es más eficiente usar números grandes. Frente a un residuo, exploran cómo dividir ese residuo en partes fraccionarias para distribuir un número igual de lápices a cada maestro.

788 ÷ 5 = 157 3

En la primera fila, ¿es más eficiente usar un número grande o uno pequeño?

Es más eficiente comenzar usando un número grande, para no tener que restar tantas veces como cuando usamos un número pequeño.

¿Por qué sobra un 3?

No hay ningún número entero que se pueda multiplicar por 5 y dé como resultado 3.

¿Qué fracción va en cada columna para dividir el residuo?

3 _ 5

División de arriba abajo

La clase razona sobre cocientes parciales y divide números de 3 dígitos entre números de 1 dígito.

Muestre el modelo vertical donde se ve 788 ÷ 5.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta:

¿Qué semejanzas y diferencias observan en la manera en que está escrito este modelo en comparación con el modelo con el que trabajaron en la actividad interactiva?

Observo que este modelo muestra el número de lápices que recibe cada maestro y el residuo, pero es vertical en lugar de ser horizontal.

Observo que la resta está al lado, como hicimos antes.

Luego, use las preguntas que siguen para guiar una conversación:

Los números 500, 250 y 35 no están escritos del lado izquierdo del modelo como el número de lápices que recibe cada maestro. ¿Por qué estos números están restados del lado derecho?

Se entregan 100 lápices a cada uno de los 5 maestros y 100 × 5 = 500; entonces, restamos 500 de 788 y hallamos que quedan 288 lápices. Se entregan 50 lápices a cada uno de los 5 maestros y 50 × 5 = 250; entonces, restamos 250 de 288 y hallamos que quedan 38 lápices . Se entregan 7 lápices a cada uno de los 5 maestros y 7 × 5 = 35; entonces, restamos 35 de 38 y hallamos que quedan 3 lápices.

Nota para la enseñanza

Mientras trabajan con los problemas de esta lección, anime a sus estudiantes a comprobar las respuestas mediante la oración de multiplicación relacionada. Según sea necesario, recuérdeles cómo comprobar las respuestas y por qué pueden usar la multiplicación para comprobar la solución de un problema de división.

¿Por qué creen que este método de división se llama cocientes parciales?

Se llama cocientes parciales porque seguimos hallando partes del cociente hasta hallar todo el cociente.

Pida a sus estudiantes que vayan al problema 1. Pídales que completen el problema de manera individual o en parejas. Continúe mostrando el modelo vertical de 788 ÷ 5 para que lo usen como guía.

1. Divide.

DUA: Acción y expresión

Considere ofrecer a sus estudiantes papel cuadriculado como apoyo para organizar los números en los problemas de división. Pueden escribir un dígito en cada cuadrado como ayuda para mantener los dígitos alineados por su valor posicional al restar.

Nota para la enseñanza

En 6.o grado, no se espera que sus estudiantes escriban respuestas fraccionarias con la unidad más grande posible. En este tema, hay distintos tipos de respuestas. Son aceptables todas las formas equivalentes de una respuesta.

Después de varios minutos, o cuando la mayoría haya terminado, considere hacer las siguientes preguntas:

• ¿Cuántos grupos se necesitan para los cocientes parciales?

• ¿Cómo saben cuándo terminaron de dividir?

• ¿Cómo saben si hay un residuo?

• Si hay un residuo, ¿qué hacen con él?

• ¿Cómo saben si su respuesta es razonable?

• ¿Cómo pueden comprobar si el cociente que hallaron es correcto?

Confirme que 946 ÷ 8 es el número mixto 118 2 8    , o 118 1 4    . Luego, pida a sus estudiantes que conversen en parejas acerca de la siguiente pregunta:

¿Qué podemos hacer en lugar de escribir los cocientes parciales una y otra vez?

Elija a diferentes estudiantes para que compartan sus ideas.

Método de los cocientes parciales

La clase razona sobre cocientes parciales y divide números de 3 dígitos entre números de 1 dígito y 2 dígitos.

Pida a sus estudiantes que vayan al problema 2.

Intentemos hacer un modelo para registrar los cocientes parciales solo una vez.

Muestre el modelo revisado.

885

Diferenciación: Apoyo

Para ofrecer más práctica a sus estudiantes, considere pedirles que usen un modelo vertical para dividir 567 entre 9.

En los ejemplos anteriores, escribimos los cocientes parciales en cada grupo. ¿Qué representa el número 7 en este modelo?

El número 7 es el divisor y representa el número de grupos de cocientes parciales.

Complete el problema con toda la clase. Guíe a sus estudiantes para que dividan 885 entre 7 como se muestra en la solución para el problema 2. Mientras dividen, considere hacer las siguientes preguntas para promover el razonamiento de sus estudiantes:

• ¿Debemos comenzar restando grupos de centenas, decenas o unidades?

• ¿Podemos distribuir 100 a cada uno de los 7 grupos? ¿Y 200? ¿Por qué?

• ¿Qué número restamos de 885? ¿Cómo lo saben?

• ¿Podemos distribuir 10 a cada uno de los 7 grupos? ¿Y 20? ¿Y 30? ¿Por qué?

• ¿Qué número restamos de 185? ¿Cómo lo saben?

• ¿Cuántos 7 hay en 45? ¿Cómo lo saben?

Promoción de la práctica de las matemáticas

Cada estudiante reconoce y expresa regularidad en la lógica de la repetición cuando resta repetidamente distribuyendo centenas, decenas y unidades y determina que puede dividir de forma más eficiente hallando los números más grandes de centenas, decenas y unidades.

Considere hacer las siguientes preguntas:

• Cuando distribuyen centenas, decenas y unidades, ¿hay algo que se repite? ¿Cómo puede ayudarles eso a dividir de forma más eficiente?

• ¿Qué tienen en común sus razonamientos en estos ejemplos?

2. Divide.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Qué pasa si el divisor es 5 en lugar de 7? ¿Esperan que 885 ÷ 5 sea mayor o menor que 885 ÷ 7? ¿Por qué?

Espero que 885 ÷ 5 sea mayor que 885 ÷ 7 porque el divisor 5 es menor que 7. Cuando hay menos grupos, hay más en cada grupo.

¿Qué pasa si el divisor es 15 en lugar de 7? ¿Esperan que 885 ÷ 15 sea mayor o menor que 885 ÷ 7? ¿Por qué?

Espero que 885 ÷ 15 sea menor que 885 ÷ 7 porque el divisor 15 es mayor que 7. Cuando hay más grupos, hay menos en cada grupo.

Pida a sus estudiantes que vayan al problema 3. Muestre la tabla que incluye dos estimaciones de 885 ÷ 15.

Estimación A

885 ÷ 15

900 ÷ 20 = 90 ÷ 2 = 45

Estimación B

885 ÷ 15

900 ÷ 15 = 60

¿Cuál de las dos estimaciones creen que es más precisa? ¿Por qué?

Creo que la estimación B es más precisa. En ambas estimaciones se redondeó 885 a 900, pero en la estimación B se usó el divisor real en lugar de un divisor redondeado.

Muestre el problema de división 885 ÷ 15. 15 885

Permita que sus estudiantes se reúnan y conversen en parejas acerca de las semejanzas y diferencias que ven en el modelo que se usó en el problema 2. Luego, complete el problema con toda la clase. Guíe a sus estudiantes para que dividan 885 entre 15 como se muestra en la solución para el problema 3. Mientras dividen, considere hacer las siguientes preguntas para promover el razonamiento de sus estudiantes:

Diferenciación: Apoyo

Para dar a sus estudiantes más práctica con la división, pídales que completen los siguientes problemas:

• 960 ÷ 4

240

• 960 ÷ 45

21 1 3

• ¿Podemos distribuir 100 a cada uno de los 15 grupos? ¿Cómo lo saben?

• ¿Podemos distribuir 10 a cada uno de los 15 grupos? ¿Y 20? ¿Y 30? ¿Y 40? ¿Y 50? ¿Y 60? ¿Por qué?

• ¿Qué número restamos de 885? ¿Por qué?

• ¿Cuántos 15 hay en 135? ¿Cómo lo saben?

Compare el cociente con las dos estimaciones. Luego, pida a sus estudiantes que completen el problema 4 de manera individual o en parejas de la misma manera que completaron el problema 3. Recorra el salón de clases mientras trabajan. Según sea necesario, haga preguntas similares a las del problema 3 para brindar apoyo a la clase.

3. Divide. 885 ÷ 15 –135 –750 15 885 13 5 0 50 9 59

4. Considera 3,184 ÷ 24.

a. Estima el cociente. Justifica tu estimación.

Ejemplo:

3,184 ÷ 24 ≈ 3,000 ÷ 20

3,000 ÷ 20 = 300 ÷ 2 = 150

El cociente es aproximadamente 150.

Diferenciación: Desafío

Para dar a sus estudiantes más práctica con la división, pídales que completen los siguientes problemas:

• 952 ÷ 112

8 1 __ 2

• 4,032 ÷ 112 36

b. Divide.

Cuando la mayoría haya terminado, confirme la respuesta al problema 4. Invite a diferentes estudiantes a compartir las estrategias de estimación que usaron.

Concluir

Reflexión final 5 min

Objetivo: Dividir números enteros de varios dígitos usando el método de los cocientes parciales, y expresar cocientes como números mixtos

Use las preguntas que siguen para guiar una conversación acerca de la división. Anime a sus estudiantes a reformular o desarrollar las respuestas de sus pares.

¿Qué estrategias podemos usar para estimar un cociente?

Podemos redondear el dividendo y el divisor a números que podemos dividir mentalmente.

Al dividir, ¿cómo sabemos si hay un residuo? Si hay un residuo, ¿qué hacemos con él?

Distribuimos todo lo que podemos en partes iguales a cada grupo. Si queda 0, entonces no hay residuo. Si queda un número entero menor que el divisor, entonces hay un residuo. Cuando hay un residuo, expresamos el cociente como un número mixto. En la fracción, el residuo es el numerador y el divisor es el denominador.

¿Qué sucede con el cociente a medida que el divisor aumenta si el dividendo se mantiene igual? ¿Qué sucede con el cociente a medida que el divisor disminuye si el dividendo se mantiene igual?

Para el mismo dividendo, el cociente disminuye a medida que el divisor aumenta, y el cociente aumenta a medida que el divisor disminuye.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

RESUMEN 17

Cocientes parciales

En esta lección:

• estimamos cocientes;

• escribimos cocientes como números mixtos;

• dividimos números enteros de varios dígitos usando el método de los cocientes parciales.

Ejemplos

1. Considera 475 ÷ 6

a. Estima el cociente.

80

b. Traza un diagrama o usa el método de los cocientes parciales para hallar el cociente.

Para estimar el cociente, redondea el dividendo y el divisor a números que se puedan dividir mentalmente.

480 ÷ 6 = 80

Distribuimos 75 en cada uno de los 6 grupos, y 6 × 75 = 450

Restamos 450 de 475 y hallamos que quedan 25

Distribuimos 4 en cada uno de los 6 grupos, y 6 × 4 = 24

Restamos 24 de 25 y hallamos que queda 1

Dado que el residuo es menor que el divisor, se puede escribir como la fracción 1 6 , donde el residuo es el numerador y el divisor es el denominador.

2. Considera 3,565 ÷ 65

a. Estima el cociente. 50

b. Traza un diagrama o usa el método de los cocientes parciales para hallar el cociente. –260 – 3, 250 65 3, 565 31 5

Estimar el cociente puede ayudar a confirmar si la respuesta después de dividir es razonable.

3,500 ÷ 70 = 50

50 es el mayor múltiplo de 10 que se puede distribuir en cada uno de los grupos de 65 porque 50 × 65 = 3,250 y 60 × 65 = 3,900

4 es el mayor número entero que se puede distribuir en cada uno de los 65 grupos porque 4 × 65 = 260 y 5 × 65 = 325

Los dos cocientes parciales, 50 y 4, se suman para obtener 54. Dado que el residuo de 55 es menor que el divisor, se puede escribir como la fracción 55 65

Nombre Fecha

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

3. Considera 4,812 ÷ 75

a. Estima el cociente.

1. Considera 590 ÷ 6

a. Estima el cociente.

b. Traza un diagrama o usa el método de los cocientes parciales para hallar el cociente.

2. Considera 254 ÷ 21

a. Estima el cociente.

b. Traza un diagrama o usa los cocientes parciales para hallar el cociente.

b. Traza un diagrama o usa los cocientes parciales para hallar el cociente.

17. La factorización prima de un número es 2 × 2 × 5. La factorización prima de otro número es 2 × 3 × 5.

a. ¿Cuál es el máximo común divisor de estos dos números?

El máximo común divisor de los dos números es 10

b. ¿Cuál es el mínimo común múltiplo de estos dos números?

El mínimo común múltiplo de los dos números es 60

c. ¿Cuáles son los dos números?

Los dos números son 20 y 30

Recuerda

En los problemas 12 a 15, suma.

Multiplica.

EUREKA MATH

El algoritmo estándar para la división

Dividir números enteros de varios dígitos usando el algoritmo estándar

Divide usando el algoritmo estándar para la división. Expresa el cociente como un número mixto.

Vistazo a la lección

En esta lección, sus estudiantes comparan el método de los cocientes parciales con el algoritmo estándar para la división. Mediante la enseñanza guiada, aprenden a dividir números enteros de varios dígitos usando el algoritmo estándar para la división. Asimismo, trabajan con una secuencia de problemas de división para adquirir fluidez. En parejas, aplican el algoritmo estándar para la división con el fin de hallar el máximo común divisor de dos números usando el algoritmo de Euclides.

Pregunta clave

• ¿Qué ventajas tiene el algoritmo estándar para la división respecto del método de los cocientes parciales?

Criterio de logro académico

6.Mód2.CLA8 Dividen números enteros de varios dígitos usando el algoritmo estándar.

Nombre

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• El algoritmo estándar para la división

• El algoritmo de Euclides

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• No se necesita.

Fluidez

Multiplicar números enteros

La clase multiplica números enteros como preparación para trabajar con la multiplicación en el algoritmo estándar para la división.

Instrucciones: Multiplica.

Presentar

La clase compara el método de los cocientes parciales de la división con el algoritmo estándar para la división.

Muestre los trabajos de Sasha y Toby.

Trabajo de Sasha

Trabajo de Toby

Dé tiempo para que sus estudiantes analicen las estrategias de división de Sasha y Toby. Luego, use las preguntas y los planteamientos que siguen para comparar las dos estrategias de división:

¿Qué pasos sigue Sasha? Reúnanse y conversen en parejas.

Sasha distribuye 60 a cada uno de los 5 grupos y, luego, distribuye 10 a cada uno de los 5 grupos. En lugar de eso, ¿podría haber distribuido 70 a cada uno de los 5 grupos?

¿Cuántas decenas es 70?

Sí. Podría haber distribuido 70 a cada uno de los 5 grupos. 70 es 7 decenas.

Nota para la enseñanza

Otra forma de referirse al algoritmo estándar para la división es llamarlo división larga. Considere exponer a sus estudiantes a ambos términos.

Toby distribuye 7 decenas a cada uno de los 5 grupos. ¿Dónde ven eso en su trabajo?

Toby escribe 7 en la posición de las decenas del cociente y distribuye las 7 decenas a cada uno de los 5 grupos, lo que forma 35 decenas.

¿Podrían Sasha o Toby haber distribuido más de 7 decenas? ¿Por qué?

No. No podrían haber distribuido más de 7 decenas. Si intentaran distribuir 8 decenas a cada uno de los 5 grupos, tendrían 400, que es mayor que 365.

Hay 3 centenas, 6 decenas y 5 unidades en 365. Entonces, cuando dividimos 365 entre 5, debemos dividir las 3 centenas, las 6 decenas y las 5 unidades entre 5. Toby separa el problema de división en varios problemas más simples.

Resalte el 3 en el dividendo del trabajo de Toby y luego resalte el 6 en el dividendo cuando haga la siguiente pregunta:

Comenzando con el 3 en la posición de las centenas, no hay ningún múltiplo de 5 que esté cerca de 3 pero que no sea mayor que 3. Entonces, Toby reagrupa las 3 centenas y las 6 decenas.

¿Cuántas decenas es 3 centenas y 6 decenas?

3 centenas y 6 decenas es 36 decenas.

Toby divide 36 decenas entre 5 y obtiene 7 decenas en el cociente. Al igual que Sasha, Toby resta para ver lo que queda. Cuando Toby resta 35 decenas de 36 decenas, queda 1 decena.

¿Qué hace Toby con 1 decena?

Toby reagrupa 1 decena y 5 unidades y obtiene 15 unidades.

Toby divide usando el algoritmo estándar para la división. El algoritmo estándar para la división nos permite dividir números más grandes mediante la reagrupación y haciendo una serie de problemas de división más simples. En este algoritmo, solo registramos un dígito de cada cociente parcial para representar su valor posicional.

¿Qué problemas de división más simples hace Toby en el algoritmo estándar para la división?

Toby divide 36 entre 5 y divide 15 entre 5.

Pida a sus estudiantes que se reúnan y conversen en parejas acerca de la siguiente pregunta:

¿Qué método creen que sería más eficiente para dividir 6,194 entre 19: el método de Sasha de los cocientes parciales o el de Toby de usar el algoritmo estándar para la división?

Hoy, usaremos el algoritmo estándar para la división con el fin de dividir de forma eficiente números enteros de varios dígitos.

Aprender

El algoritmo estándar para la división

La clase divide dos números usando el algoritmo estándar para la división.

Pida a sus estudiantes que vayan al problema 1. Muestre el problema de división.

19 6,1 94

Pida a sus estudiantes que estimen el cociente. Dígales que escriban su estimación en una pizarra blanca individual y se la muestren. Se espera que la mayoría redondee 19 a 20. Puede haber estudiantes que redondeen 6,194 a 6,200 y dividan entre 20, y habrá quienes redondeen 6,194 a 6,000 y dividan entre 20.

Elija a diferentes estudiantes para que compartan sus estimaciones y estrategias. Una vez establecida una estimación, complete el problema 1 con toda la clase. Use la pregunta que sigue para guiar la conversación:

Una estrategia que ayuda al dividir entre un número como 19 es crear una tabla que muestre los múltiplos de 19. ¿Cuáles son los múltiplos de 19?

Nota para la enseñanza

Si sus estudiantes no ofrecen distintas estrategias de estimación, considere ofrecer otras ideas. Por ejemplo, redondear 6,194 a 6,200 y 19 a 20. Luego, haga un problema más simple para estimar el cociente.

6,200 ÷ 20 = 620 ÷ 2 = 310

A partir de las respuestas de sus estudiantes, complete una tabla en la que se enumeren los múltiplos de 19, como se muestra. Exhíbala en el salón de clases para que sus estudiantes la usen como referencia, según sea necesario.

Múltiplos de 19

1 × 19 = 19

2 × 19 = 38

3 × 19 = 57

4 × 19 = 76

5 × 19 = 95

6 × 19 = 114

7 × 19 = 133

8 × 19 = 152

9 × 19 = 171

Considere resaltar el número 6 en el dividendo, como se muestra: 19 6,1 94

Hay un 6 en la posición de los millares que debemos dividir entre 19. ¿Qué múltiplo de 19 está cerca de 6 pero no es mayor que 6?

No hay ningún múltiplo de 19 que esté cerca de 6 pero que no sea mayor que 6.

Promoción de la práctica de las matemáticas

Cada estudiante reconoce y utiliza estructuras cuando aplica su comprensión de los cocientes parciales para desarrollar y usar el algoritmo estándar para la división.

Considere hacer las siguientes preguntas:

• ¿En qué se parece el algoritmo estándar para la división al método de los cocientes parciales que han usado antes?

• ¿Cómo pueden separar 6,194 ÷ 19 en problemas de división más simples?

Considere resaltar el número 1 en el dividendo, como se muestra:

19 6,1 94

Debemos reagrupar los 6 millares y combinarlos con 1 centena para obtener 61 centenas. ¿Podemos dividir 61 entre 19?

Sí.

¿Cómo podemos estimar 61 ÷ 19?

Podemos redondear 61 a 60 y 19 a 20. Podemos dividir 60 entre 20 para obtener 3.

En la tabla de múltiplos, vemos que 3 × 19 es 57, que está cerca de 61 pero no es mayor que 61. ¿En qué nos ayuda conocer ese múltiplo?

Sabemos que 61 ÷ 19 es 3 con un residuo de 4 porque 61 − 57 = 4.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Dónde escribimos 3? ¿Dónde escribimos 57? ¿Dónde escribimos 4? Expliquen.

Escribimos 3 en la posición de las centenas del cociente porque dividimos 61 centenas entre 19 y obtuvimos 3 centenas.

Escribimos 57 debajo de 61 porque multiplicamos 3 centenas por 19 y obtuvimos 57 centenas.

Escribimos el residuo 4 directamente debajo de la resta de 61 centenas menos 57 centenas.

Registre 3 y 57 como se muestra. Señale que se restan 57 centenas de 61 centenas para obtener 4 centenas como residuo.

Nota para la enseñanza

Al usar el algoritmo estándar para la división, puede haber estudiantes que necesiten crear una tabla de múltiplos del divisor, como la tabla de múltiplos de 19 del problema 1, por cada problema de división. También puede haber quienes sean capaces de aplicar la estimación para razonar sobre los cocientes parciales. En este caso, haga preguntas para guiar el razonamiento de sus estudiantes, como por ejemplo: “¿Cuál es una estimación de 61 ÷ 19?”.

Debemos dividir el residuo de 4 en la posición de las centenas entre 19. ¿Qué múltiplo de 19 está cerca de 4 pero no es mayor que 4?

No hay ningún múltiplo de 19 que esté cerca de 4 pero que no sea mayor que 4. Entonces, debemos reagrupar.

Debemos reagrupar las 4 centenas y combinarlas con las 9 decenas. ¿Cuántas decenas es 4 centenas y 9 decenas?

4 centenas y 9 decenas es 49 decenas.

Registre 9 en la posición de las decenas para mostrar que hay 49 decenas. Considere resaltar 49, como se muestra:

Ahora, debemos dividir 49 entre 19. ¿Qué múltiplo de 19 está más cerca de 49 pero no es mayor que 49? ¿En qué nos ayuda conocer ese múltiplo?

En la tabla de múltiplos, vemos que 2 × 19 = 38, y 38 está más cerca de 49 pero no es mayor que 49. Ese múltiplo nos ayuda a comprender que el cociente de 49 y 19 es 2 con un residuo de 11 porque 49 − 38 = 11.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Dónde escribimos 2? ¿Dónde escribimos 38? ¿Dónde escribimos 11? Expliquen.

Escribimos 2 en la posición de las decenas del cociente porque dividimos 49 decenas entre 19 y obtuvimos 2 decenas.

Escribimos 38 debajo de 49 porque multiplicamos 2 decenas por 19 y obtuvimos 38 decenas.

Escribimos el residuo 11 directamente debajo de la resta de 49 decenas menos 38 decenas. Esto equivale a 11 decenas.

Registre 2 y 38 como se muestra. Señale que se restan 38 decenas de 49 decenas para obtener 11 decenas como residuo.

Debemos dividir 11 decenas entre 19. ¿Qué múltiplo de 19 está cerca de 11 pero no es mayor que 11?

No hay ningún múltiplo de 19 que esté cerca de 11 pero que no sea mayor que 11. Entonces, debemos reagrupar.

Debemos reagrupar las 11 decenas y combinarlas con las 4 unidades. ¿Cuántas unidades es 11 decenas y 4 unidades?

11 decenas y 4 unidades es 114 unidades.

Registre 4 en la posición de las unidades para mostrar que hay 114 unidades. Considere resaltar 114, como se muestra:

¿Qué múltiplo de 19 está más cerca de 114 pero no es mayor que 114? ¿En qué nos ayuda conocer ese múltiplo?

En la tabla de múltiplos, vemos que 6 × 19 = 114. Ese múltiplo nos ayuda a comprender que el cociente de 114 y 19 es 6.

¿Dónde escribimos 6? ¿Dónde escribimos 114? Expliquen.

Escribimos 6 en la posición de las unidades del cociente porque 114 unidades dividido entre 19 es 6 unidades. Escribimos 114 debajo de 114 porque 6 unidades multiplicado por 19 es 114 unidades.

Registre 6 y 114 como se muestra. Señale que se resta 114 de 114 para obtener 0 como residuo.

Nota para la enseñanza

Considere preguntar a sus estudiantes cómo pueden comprobar que sus respuestas sean correctas. Pídales que describan cómo multiplicarían para comprobar si el cociente fuera un número mixto.

¿Cómo podemos escribir un cociente si hay un residuo?

Podemos escribir el cociente como un número mixto. En la fracción, el residuo sería el numerador y el divisor sería el denominador.

Pida a sus estudiantes que vayan a los problemas 2 a 5 y que trabajen de manera individual o en parejas. Recorra el salón de clases mientras trabajan y brinde apoyo según sea necesario. Pida a sus estudiantes que estimen el cociente antes de dividir.

En los problemas 1 a 5, divide. Según sea necesario, expresa los cocientes como números mixtos.

1. 6,194 ÷ 19

DUA: Participación

En los problemas 2 a 5, permita que sus estudiantes elijan al menos dos de los cuatro problemas para completar. Anime a sus estudiantes a elegir lo que les resulte desafiante.

5. 55,233 ÷ 51

Cuando la mayoría haya completado al menos dos problemas, invite a sus estudiantes a compartir sus respuestas. Considere hacer las siguientes preguntas a medida que sus estudiantes compartan:

• ¿Creen que uno de los problemas fue más difícil de resolver que los otros? ¿Por qué?

• En el problema 2, ¿por qué podemos expresar el cociente como 25 2 32 o como 25 1 16 ?

• En el problema 3, ¿cómo supieron que tenían que registrar un 0 en la posición de las decenas del cociente?

• En el problema 4, ¿cómo reagruparon los millares, las centenas y las decenas?

• En el problema 5, ¿cómo supieron que tenían que registrar un 0 en la posición de las centenas del cociente?

• ¿Cómo pueden comprobar sus respuestas? ¿Funciona el método si el cociente es un número mixto? ¿Por qué?

Si sus estudiantes dicen que un problema en particular es más difícil que otros o si todas las parejas eligen no completar uno de los problemas, y hay suficiente tiempo, considere completar ese problema con toda la clase.

Diferenciación: Apoyo

Si sus estudiantes necesitan práctica adicional con el algoritmo estándar para la división, considere pedirles que resuelvan problemas de división como los de la siguiente secuencia, en lugar de explorar el algoritmo de Euclides en la siguiente actividad. •

El algoritmo de Euclides

La clase aplica el algoritmo estándar para la división cuando usa el algoritmo de Euclides para hallar el máximo común divisor de dos números.

Considere hacer las siguientes preguntas para refrescar la comprensión de sus estudiantes sobre el máximo común divisor de dos números que vieron en el tema A:

• ¿Cómo saben si un número es un factor de otro número?

• ¿Qué significa que un número sea el máximo común divisor de dos números?

• ¿Cuáles son algunas maneras de hallar el máximo común divisor de dos números?

Si sus estudiantes aún no aprendieron sobre el algoritmo de Euclides en la lección 5, comparta la siguiente información:

Si debemos hallar el máximo común divisor de números pequeños, como 36 y 48, los métodos que aprendimos anteriormente en el módulo funcionan bien. Pero, a veces, es necesario hallar el máximo común divisor de números más grandes, como 840 y 660. Según el método usado, puede llevar mucho tiempo hallar el máximo común divisor y el mínimo común múltiplo de dos números de 3 dígitos.

Piensen cuánto tiempo llevaría hallar el máximo común divisor y el mínimo común múltiplo de números grandes que tienen cientos de dígitos. Ni siquiera las computadoras pueden hallar rápidamente el máximo común divisor de números grandes con métodos de factorización. Es por esto que los números grandes, y sus productos, se usan con frecuencia como claves de seguridad para ayudar a los navegadores de Internet a mantener sus datos seguros.

El algoritmo de Euclides es un proceso que da como resultado el máximo común divisor de dos números grandes. Data de alrededor del año 300 a. e. c., mucho antes de que aparecieran las calculadoras o las computadoras. El algoritmo de Euclides se llama así por el experto en matemáticas griego Euclides, aunque también fue descubierto en China aproximadamente en la misma época histórica.

Las matemáticas en el pasado

Esta lección es el momento ideal para incorporar el material del recurso Las matemáticas en el pasado. Este recurso incluye más información sobre el algoritmo de Euclides, sus aplicaciones y su historia. En el recurso, el algoritmo de Euclides se aplica a dos números de 3 dígitos, de manera similar a como se lo aplica en esta lección.

Dividendo Divisor Cociente Residuo

Si hay estudiantes que muestran interés en saber más sobre el algoritmo de Euclides y su origen, incorpore otras actividades del recurso Las matemáticas en el pasado.

Si sus estudiantes aprendieron sobre el algoritmo de Euclides en la lección 5, comience la conversación con el siguiente planteamiento:

Podemos calcular el máximo común divisor de números grandes de forma más eficiente usando el algoritmo de Euclides, que se basa en la división.

Pida a sus estudiantes que vayan al problema 6. Muestre la tabla donde se ven los números 840 y 660.

Dividendo Divisor Algoritmo estándar para la división Cociente Residuo

840 660

Pida a sus estudiantes que creen sus propias tablas y escriban el más grande de los dos números en la columna Dividendo y el más pequeño de los dos números en la columna Divisor. Luego, pídales que trabajen en parejas para dividir 840 entre 660 usando el algoritmo estándar para la división. Pídales que escriban el cociente y el residuo en la tabla.

Indique a sus estudiantes que escriban en la siguiente fila de la tabla el divisor anterior, 660, como el nuevo dividendo y que escriban el residuo como el nuevo divisor. Luego, pídales que trabajen en parejas para dividir y escribir el cociente y el residuo en las tablas. Pídales que repitan el proceso hasta obtener un residuo de 0. Diga a sus estudiantes que el divisor final, o el último residuo diferente de cero, es el máximo común divisor de los dos números originales.

Recorra el salón de clases para brindar apoyo, según sea necesario, y confirme las respuestas.

DUA: Acción y expresión

Considere exhibir el proceso del algoritmo de Euclides para que sus estudiantes lo consulten mientras completan el problema 6. En el algoritmo presentado en el tema A se usa la resta repetida. Ahora que sus estudiantes tienen experiencia con la división de números de varios dígitos, en el algoritmo que se presenta aquí se usa la división.

1. Dividir el número más grande entre el número más pequeño.

2. Dividir el divisor entre el residuo.

3. Seguir dividiendo el divisor anterior entre el residuo anterior hasta que el residuo sea 0.

4. El divisor final es el máximo común divisor de los dos números originales.

6. Usa el algoritmo de Euclides para hallar el máximo común divisor de 840 y 660.

Dividendo Divisor

para la división

El máximo común divisor de 840 y 660 es 60.

Diferenciación: Apoyo

Considere permitir que sus estudiantes usen una calculadora para comprobar los múltiplos de los divisores si todavía no tienen fluidez con el uso del algoritmo estándar para la división o si tienen dificultades para hacer estimaciones.

Diferenciación: Desafío

Como desafío, pida a sus estudiantes que usen el algoritmo de Euclides para hallar el máximo común divisor de números incluso más grandes, como 3,132 y 2,196.

El máximo común divisor de 3,132 y 2,196 es 36.

Concluir

Reflexión final 5 min

Objetivo: Dividir números enteros de varios dígitos usando el algoritmo estándar

Use las preguntas y los planteamientos que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a reformular o desarrollar las respuestas de sus pares.

Den un ejemplo que muestre por qué deben reagrupar cuando usan el algoritmo estándar para la división.

Ejemplo: El número 230 es 2 centenas y 3 decenas. Si dividimos 230 entre 6, debemos dividir las 2 centenas y las 3 decenas entre 6. No hay ningún múltiplo de 6 que esté cerca de 2 pero que no sea mayor que 2. Podemos reagrupar las 2 centenas y las 3 decenas para obtener 23 decenas. Ahora, 18 es un múltiplo de 6 que no es mayor que 23.

¿Qué ventajas tiene el algoritmo estándar para la división respecto del método de los cocientes parciales?

El algoritmo estándar para la división puede ser más eficiente que el método de los cocientes parciales. Con el algoritmo estándar para la división, se separa un problema grande de división en varios problemas más simples al descomponer el dividendo por valor posicional. Cuando dividimos usando el algoritmo estándar para la división, registramos cada cociente parcial una vez y registramos un dígito por cada valor posicional del cociente.

¿Cómo aplicaron el algoritmo estándar para la división cuando usaron el algoritmo de Euclides para hallar el máximo común divisor de dos números?

Dividimos el número más grande entre el número más pequeño para hallar un cociente y un residuo. Luego, dividimos el divisor original entre el residuo para hallar un nuevo cociente y un nuevo residuo. Seguimos haciendo esto hasta que obtuvimos 0 como residuo. El último divisor diferente de cero es el máximo común divisor.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

3. Usa el algoritmo de Euclides para hallar el máximo común divisor de 480 y 396

Dividendo Divisor Algoritmo estándar para la

El algoritmo estándar para la división

En esta lección:

• dividimos números enteros de varios dígitos usando el algoritmo estándar;

• usamos el algoritmo de Euclides para hallar el máximo común divisor de dos números.

Ejemplos

En los problemas 1 y 2, divide usando el algoritmo estándar para la división. Según sea necesario, expresa los cocientes como números mixtos. 1.

Una estrategia que ayuda al dividir entre un número como 18 es crear una tabla que muestre los múltiplos de 18

Múltiplos de 18 1 × 18 = 18 2 × 18 = 36 3 × 18 = 54

× 18 = 72

Comienza mirando la posición de las centenas en el dividendo. No hay ningún múltiplo del divisor, 18, que esté cerca de 7, pero que no sea mayor que 7 Reagrupa 7 centenas y combina con 5 decenas para obtener 75 decenas. Dado que 4 × 18 = 72, que está cerca de 75, pero no es mayor que 75 registra un 4 en la posición de las decenas del cociente.

Resta 72 decenas de 75 decenas para obtener 3 decenas. Reagrupa las 3 decenas con las 6 unidades para obtener 36 unidades. Luego, divide 36 entre 18 Dado que 2 × 18 = 36, no sobra nada, es decir, no hay residuo.

Dado que el residuo es menor que el divisor, escríbelo como la fracción 2 38 donde el residuo es el numerador y el divisor es el denominador.

El máximo común divisor de 480 y 396 es 12.

1. Escribe el número más grande en la columna Dividendo y el número más pequeño en la columna Divisor.

2. Divide y registra el cociente y el residuo.

3. El divisor anterior es el nuevo dividendo.

4. El residuo es el nuevo divisor.

5. Repite el proceso hasta obtener un residuo de 0 El último divisor usado es el máximo común divisor.

Podemos usar la división en lugar de la resta repetida en el algoritmo de Euclides, un método para hallar el máximo común divisor de dos números.

Nombre Fecha

© Great Minds PBC

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

En los problemas 1 a 10, divide. Según sea necesario, expresa los cocientes como números mixtos.

11. Elige dos problemas de los problemas 1 a 10. Luego, usa la estimación para mostrar que tu cociente es razonable.

Ejemplo:

En el problema 1, sé que 320 ÷ 80 = 4. Por lo tanto, el cociente que hallé es razonable, porque 320 está cerca de 328 y 80 está cerca de 82

En el problema 9, sé que 5,400 ÷ 60 = 90. Como 5,420 está cerca de 5,400 y 61 está cerca de 60, sé que mi respuesta de 88 52 61 es razonable, porque está cerca de 90.

12. Noah comete un error cuando divide 1,004 entre 20 100 20 1,0 04 04

5 4 20 = 5 5

a. ¿De qué número debe estar cerca el cociente? Usa la estimación. El cociente debe estar cerca de 50 porque 1,000 ÷ 20 = 50

b. Describe el error de Noah.

Cuando Noah divide 100 decenas entre 20, no escribe el 5 en la posición de las decenas del cociente. Luego, Noah se olvida de escribir un 0 en la posición de las unidades del cociente, lo que es necesario hacer porque no hay ningún múltiplo de 20 que no sea mayor que 4

c. ¿Cuánto es 1,004 ÷ 20?

50 1 5

Recuerda

En los problemas 13 a 16, suma.

En los problemas 17 a 19, ¿el cociente es mayor que 17.2 o menor que 17.2? Explica tu razonamiento.

17. 17.2 ÷ 3.3

El cociente es menor que 17.2 porque el divisor es mayor que 1

18. 17.2 ÷ 0.33

El cociente es mayor que 17.2 porque el divisor es menor que 1

19. 17.2 ÷ 33

El cociente es menor que 17.2 porque el divisor es mayor que 1

20. ¿Qué par de fracciones y números decimales son equivalentes? Elige todas las opciones que correspondan.

A. 3 10 y 0.03

B. 5 10 y 0.5

C. 2 6 10 y 0.26

D. 8 100 y 0.08

E. 90 100 y 0.9

Expresar cocientes como números decimales

Dividir números enteros de varios dígitos usando el algoritmo estándar, y expresar cocientes como números decimales

Vistazo a la lección

En esta lección, sus estudiantes continúan adquiriendo fluidez para dividir números enteros de varios dígitos usando el algoritmo estándar para la división. Amplían su comprensión de cocientes y residuos cuando reagrupan residuos y continúan dividiendo hasta la posición de los décimos, centésimos y milésimos. Se dan cuenta de que no queda nada para dividir cuando en el dividendo no quedan dígitos y el residuo es 0. En parejas, sus estudiantes completan una secuencia de problemas de división y redondean cocientes a la posición de los décimos y centésimos, según sea necesario.

Pregunta clave

• ¿Por qué expresamos un cociente como un número decimal?

Criterio de logro académico

6.Mód2.CLA8 Dividen números enteros de varios dígitos usando el algoritmo estándar.

Nombre

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Cocientes como números decimales

• Resolución de problemas de división

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• No se necesita.

Fluidez

Expresar fracciones como números decimales

La clase expresa fracciones como números decimales como preparación para expresar cocientes como números decimales.

Instrucciones: Expresa cada fracción como un número decimal.

Presentar

La clase resuelve un problema de aplicación de división en el que el cociente es un número decimal.

Presente el siguiente problema y siga la rutina Charla matemática para que toda la clase participe de una conversación matemática:

• Un grupo de 4 personas organizan una venta de limonada. Obtienen 23 billetes de $1.00 como ganancia de la venta. ¿Pueden distribuir el dinero de manera que cada persona reciba la misma cantidad? De ser así, ¿cómo?

Dé 2 minutos para que sus estudiantes tengan tiempo para pensar en silencio y resolver el problema. Pídales que hagan una señal silenciosa para indicar que terminaron y, luego, pídales que comenten su razonamiento en parejas. Recorra el salón de clases y escuche las conversaciones. Habrá quienes piensen que una de las personas recibe $1.00 menos que las otras tres. Y habrá quienes se den cuenta de que deben reagrupar tres de los dólares como quarters de manera que cada persona reciba 5 3 4 dólares, o $5.75. Identifique a un grupo pequeño de estudiantes para que compartan su razonamiento. Elija a quienes hayan abordado el problema de manera diferente, con el objetivo de dar lugar a una conversación enriquecedora acerca de las relaciones entre los residuos, los cocientes expresados como números decimales y la reagrupación.

Guíe una conversación de toda la clase. Invite a sus estudiantes a compartir su razonamiento con todo el grupo y regístrelo.

Luego, pídales que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta:

Estas personas descubren que ganaron dos quarters adicionales que no habían contado antes. ¿Cómo pueden distribuir los $0.50 adicionales de manera que cada persona reciba la misma cantidad?

Deben reagrupar o cambiar los quarters por dimes, por nickels o por pennies. Pero incluso así sobrarán 2 pennies y no hay una moneda de un valor menor que un penny.

Si hubiera una moneda que tuviera la mitad del valor de un penny, podríamos dividir los 2 centavos restantes entre las 4 personas.

Hoy, usaremos el algoritmo estándar para la división con el fin de dividir números de varios dígitos y expresar cocientes como números decimales.

Aprender

Cocientes como números decimales

La clase divide usando el algoritmo estándar para la división y expresa cocientes como números decimales.

Muestre el trabajo con el algoritmo estándar para la división de 612 ÷ 8.

Nota para la enseñanza

Considere pedir a sus estudiantes que compartan ideas sobre números decimales conocidos y escriban diferentes fracciones equivalentes para cada uno.

Dé tiempo a sus estudiantes para analizar el trabajo. Luego, haga la siguiente pregunta:

Un estudiante dice que el cociente es 76 4 _ 8 y otra estudiante dice que es 76.5. ¿Qué estudiante está en lo correcto y por qué?

Tanto uno como otra están en lo correcto. La fracción 4 8 es equivalente al número decimal 0.5; entonces, 76 4 8 es equivalente a 76.5.

Muestre el trabajo con el algoritmo estándar para la división de 610 ÷ 8.

Diferenciación: Apoyo

Considere pedir a sus estudiantes que completen los siguientes problemas de división como preparación para trabajar con problemas de división tales como 610 ÷ 8. • 610,000 ÷ 8

÷ 8

÷ 8

Dé tiempo a sus estudiantes para analizar el trabajo. Luego, haga la siguiente pregunta:

¿Cómo podemos expresar 76 2 _ 8 como un número decimal?

La fracción 2 8 es equivalente al número decimal 0.25; entonces, podemos expresar 76 2 8 como el número decimal 76.25.

Pida a sus estudiantes que se reúnan y conversen en parejas acerca de la siguiente pregunta:

¿Creen que podemos expresar todos los cocientes como números decimales?

Muestre el trabajo del problema 1 con el algoritmo estándar para la división de 611 ÷ 8.

Dé tiempo a sus estudiantes para analizar el trabajo. Luego, pídales que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta:

El cociente es 76 3 _ 8  . ¿Cómo podemos estimar el valor del número decimal de este cociente?

El cociente debe estar entre 76.25 y 76.5 porque 76 3 8 es mayor que 76 2 8 y menor que 76 4 8   .

Invite a sus estudiantes a compartir las ideas que tengan sobre cómo hallar el valor del número decimal del cociente. Luego, haga las siguientes preguntas:

El dividendo 611 tiene 6 centenas. El único múltiplo de 8 que está cerca de 6 es 8, pero 8 es mayor que 6. Entonces, debemos reagrupar. ¿Cómo se reagruparon las 6 centenas?

Las 6 centenas se reagruparon y se combinaron con 1 decena para formar 61 decenas.

Al restar las 56 decenas de las 61 decenas, quedaron 5 decenas. ¿Cómo se reagruparon las 5 decenas?

Las 5 decenas se reagruparon y se combinaron con 1 unidad para formar 51 unidades.

Al restar las 48 unidades de las 51 unidades, quedaron 3 unidades. ¿Cuántos décimos es 3 unidades?

3 unidades es 30 décimos.

¿Cuántos de los décimos que se muestran en el dividendo 611 podríamos combinar con los 30 décimos?

No podemos combinar ningún décimo con los 30 décimos porque hay 0 décimos en el dividendo.

¿Cómo podemos escribir 611 para mostrar que hay 0 décimos para combinar con los 30 décimos?

Podemos escribir 611 como 611.0.

Registre un punto decimal y un 0 en la posición de los décimos, como se muestra. Señale que el residuo es 30 décimos.

Promoción de la práctica de las matemáticas

Cada estudiante pone atención a la precisión cuando divide usando el algoritmo estándar para la división y pone atención al valor posicional y a la ubicación del punto decimal.

Considere hacer las siguientes preguntas:

• Al dividir, ¿con qué pasos deben tener mucho cuidado? ¿Por qué?

• ¿Dónde es fácil cometer errores al reagrupar?

Haga las siguientes preguntas para continuar la conversación:

¿Cuál es el cociente cuando se divide 30 décimos entre 8? ¿Cuál es el residuo? ¿Cómo lo saben?

El cociente es 3 décimos porque 3 × 8 = 24. El residuo es 6 décimos porque 30 décimos menos 24 décimos es 6 décimos.

¿Cómo podemos representar 3 décimos en el cociente?

Escribimos un 3 después de 76 y colocamos un punto decimal entre 6 y 3.

¿Dónde escribimos 24?

Escribimos 24 debajo de 30.

DUA: Representación

Considere rotular el valor posicional de cada dígito del cociente. Resalte los décimos, centésimos y milésimos en el dividendo y el cociente cuando guíe a sus estudiantes en el uso del algoritmo estándar para dividir 611 entre 8. Por ejemplo, pregunte: “Cuando restaron 48 unidades de 51 unidades, quedaron 3 unidades. ¿Cuántos décimos es 3 unidades?”. Luego, resalte los décimos cuando sus estudiantes respondan: “3 unidades es 30 décimos”.

Decenas Centenas Unidades DécimosCentésimosMilésimos

86

76 37 5 1 1 00 0 .

Registre 3 y 24, como se muestra. Señale que se restan 24 décimos de 30 décimos para obtener 6 décimos como residuo.

Haga las siguientes preguntas para continuar la conversación:

Ahora, tenemos un residuo de 6 décimos. ¿Cuántos centésimos es 6 décimos?

6 décimos es 60 centésimos.

¿Cuántos de los centésimos que se muestran en el dividendo 611.0 podríamos combinar con los 60 centésimos?

No podemos combinar ningún centésimo con los 60 centésimos porque hay 0 centésimos en el dividendo.

¿Cómo podemos escribir 611.0 para mostrar que hay 0 centésimos para combinar con los 60 centésimos?

Podemos escribir 611.0 como 611.00.

Registre un 0 en la posición de los centésimos, como se muestra. Señale que el residuo es 60 centésimos.

¿Podemos continuar dividiendo? ¿Cómo lo saben?

Sí. Podemos continuar dividiendo porque quedan 60 centésimos.

Invite a sus estudiantes a terminar el problema 1 en parejas. Recorra el salón de clases para apoyar a sus estudiantes mientras continúan con la reagrupación, escriben más números 0 después del punto decimal y dividen hasta obtener 0 como residuo.

1. Divide. Expresa el cociente como un número decimal.

Nota para la enseñanza

En esta lección, sus estudiantes no dividen más allá de la posición de los milésimos. Sin embargo, al final de la lección, la clase comenta cómo continuar usando el algoritmo estándar para la división a fin de dividir valores posicionales más pequeños.

Cuando la mayoría haya terminado de dividir, confirme las respuestas. Pida a sus estudiantes que verifiquen que el valor del número decimal del cociente esté entre 76.25 y 76.5, como lo estimaron antes. Luego, haga las siguientes preguntas:

¿Cuánto es 76.375 redondeado al centésimo más cercano?

76.38

¿Cuánto es 76.375 redondeado al décimo más cercano?

76.4

Muestre las siguientes ecuaciones para resumir las diferentes maneras de redondear el cociente de 611 y 8:

Apoyo para la comprensión del lenguaje

En grados anteriores, la clase redondeó un número hallando el mínimo y el máximo del número en función del valor posicional y hallando el punto medio del mínimo y el máximo. Los números mayores que o iguales al punto medio se redondean hacia arriba. Los números menores que el punto medio se redondean hacia abajo.

• 76.375 está entre 76.37 y 76.38 y es igual al punto medio de 76.37 y 76.38. Entonces, 76.375 se redondea hacia arriba, a 76.38

• 76.375 está entre 76.3 y 76.4 y es mayor que 76.35, el punto medio de 76.3 y 76.4. Entonces, 76.375 se redondea hacia arriba, a 76.4.

Sabemos que tenemos el cociente exacto y que no queda nada para dividir cuando el residuo es 0 y no quedan dígitos en el dividendo.

Si nos piden redondear un cociente al centésimo más cercano, ¿cuándo podemos dejar de dividir? Expliquen.

Debemos dividir hasta que el cociente esté en los milésimos. El dígito en la posición de los milésimos nos indica cómo redondear el dígito en la posición de los centésimos.

Si nos piden redondear un cociente al décimo más cercano, ¿tenemos que dividir hasta que el cociente esté en los milésimos? ¿Por qué?

No. Debemos dividir hasta que el cociente esté en los centésimos. El dígito en la posición de los centésimos nos indica cómo redondear el dígito en la posición de los décimos.

¿Cuándo podemos dejar de dividir si nos piden redondear un cociente al número entero más cercano? Expliquen.

Debemos dividir hasta que el cociente esté en los décimos. El dígito en la posición de los décimos nos indica cómo redondear el dígito en la posición de las unidades.

• 76.375 está entre 76 y 77 y es menor que 76.5, el punto medio de 76 y 77. Entonces, 76.375 se redondea hacia abajo, a 76.

Recuerde a la clase que el símbolo ≈ significa aproximadamente igual a. Anime a sus estudiantes a usar este símbolo cuando haya respuestas que no sean exactas, como cocientes redondeados.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

Hasta ahora, el dividendo ha sido mayor que el divisor. ¿Qué saben sobre un cociente cuando el dividendo es menor que el divisor, como 7 ÷ 9?

Si el dividendo es menor que el divisor, entonces el cociente es menor que 1.

¿Podemos usar el algoritmo estándar para la división con el fin de dividir cuando el dividendo es menor que el divisor, como 7 ÷ 9? De ser así, ¿cómo?

Sí. Podemos escribir un punto decimal después de 7 y escribir números 0 después del punto decimal. Luego, podemos reagrupar las 7 unidades en 70 décimos y dividir.

Pida a sus estudiantes que vayan a los problemas 2 a 4. Recorra el salón de clases mientras trabajan y brinde apoyo, según sea necesario. Anime a sus estudiantes a estimar el cociente antes o después de dividir, para verificar que su respuesta es razonable.

2. Divide. Expresa el cociente como un número decimal.

Nota para la enseñanza

En 5.o grado, sus estudiantes interpretaron una fracción como la división del numerador entre el denominador. Considere establecer la siguiente relación: si un dividendo es menor que el divisor, entonces el cociente es menor que 1, igual que cuando en una fracción el numerador es menor que el denominador, la fracción es menor que 1

3. Divide. Redondea tu respuesta al décimo más cercano.

4. Divide. Redondea tu respuesta al centésimo más cercano.

Cuando la mayoría haya terminado, confirme las respuestas. Luego, haga las siguientes preguntas:

En el problema 2, ¿cómo supieron cuándo dejar de dividir?

Supe que había que dejar de dividir cuando hubo un residuo de 0 y no quedaban dígitos en el dividendo.

Nota para la enseñanza

Sus estudiantes aprenden el vocabulario decimales periódicos y decimales finitos en 7.o grado. A esta altura, no es necesario hacer observaciones sobre patrones en los cocientes o los residuos. Más bien, sus estudiantes deben saber hasta dónde calcular el cociente para redondear a la posición decimal dada.

¿Cómo reagrupamos cuando un dividendo es menor que el divisor, como vimos en el problema 3?

Cuando el dividendo es menor que el divisor, las unidades se deben reagrupar en décimos para que podamos dividir.

En el problema 3, ¿cuántos dígitos debieron hallar después del punto decimal para redondear el cociente al décimo más cercano? ¿Por qué?

Dividí hasta que el cociente tuvo dos dígitos después del punto decimal. El dígito en la posición de los centésimos nos indica cómo redondear un número decimal a la posición de los décimos.

En el problema 4, ¿cuántos dígitos tuvieron que hallar después del punto decimal para redondear el cociente al centésimo más cercano? ¿Por qué?

Dividí hasta que el cociente tuvo tres dígitos después del punto decimal. El dígito en la posición de los milésimos nos indica cómo redondear un número decimal a la posición de los centésimos.

Resolución de problemas de división

La clase usa el algoritmo estándar para la división a fin de resolver problemas.

Pida a sus estudiantes que completen los problemas 5 y 6 en parejas. En el problema 6, considere pedir a cada estudiante de la pareja que determine solo uno de los dos promedios de bateo y, luego, lo compare con el promedio de bateo determinado por su pareja. Recorra el salón de clases mientras sus estudiantes trabajan. Haga las siguientes preguntas para apoyar el razonamiento de sus estudiantes:

• ¿Cuál es el dividendo? ¿Cuál es el divisor?

• ¿Pueden estimar el cociente? ¿Cómo?

• ¿Cuál es el residuo?

• ¿Pueden reagrupar el residuo? ¿Cómo?

• ¿Cuántos dígitos necesitan después del punto decimal para responder la pregunta?

5. Riley divide 11,586 entre 24, como se muestra. Llega a la conclusión de que el cociente es 482.18.

a. ¿Por qué el cociente que halló Riley, 482.18, es incorrecto?

El cociente que halló Riley es incorrecto porque 482.18 no es equivalente a 482 18 24 .

b. Halla el cociente correcto expresado como un número decimal.

482 18 24 = 482 3 4 = 482.75

El cociente correcto es 482.75

6. Durante su carrera en las Grandes Ligas de Beisbol, Hank Aaron jugó para los Milwaukee Braves y los Atlanta Braves.

• El primer año en que Hank Aaron jugó para los Milwaukee Braves fue 1954. Ese año, bateó 131 hits en 468 turnos al bate.

• El primer año en que Hank Aaron jugó para los Atlanta Braves fue 1966. Ese año, bateó 168 hits en 603 turnos al bate.

El promedio de bateo de un jugador se calcula dividiendo el número de hits entre el número de turnos al bate. Los promedios de bateo se expresan en milésimos. ¿En qué año Hank Aaron tuvo el promedio más alto de bateo? Divide hasta tres posiciones después del punto decimal.

Diferenciación: Desafío

Como desafío adicional, considere pedir a sus estudiantes que resuelvan el siguiente problema:

• Una lanzadora de beisbol lanza una pelota a una velocidad de 8,360 pies por minuto, o 95 millas por hora. La pelota tarda aproximadamente 0.007 minutos en recorrer 60.5 pies, la distancia desde la lanzadora hasta la base de bateo. Una lanzadora de softbol lanza una pelota a 6,160 pies por minuto, o 70 millas por hora. ¿Cuántos minutos tarda la pelota en recorrer 43 pies, la distancia desde la lanzadora hasta la base de bateo?

La pelota tarda aproximadamente 0.007 minutos en recorrer 43 pies.

Apoyo para la comprensión del lenguaje

Para brindar apoyo con el contexto del problema 6 y desarrollar los conocimientos previos de sus estudiantes, muéstreles imágenes o un video de un jugador de beisbol en un turno al bate. Explique que el término turnos al bate indica el número de veces que un jugador batea a lo largo de una temporada.

Hank Aaron tuvo el promedio más alto de bateo en 1954.

Cuando la mayoría haya terminado, elija a diferentes estudiantes para que compartan sus respuestas y su razonamiento. Luego, haga la siguiente pregunta:

En el problema 6, vimos que Hank Aaron tuvo menos hits en 1954 que en 1966. ¿De qué manera la división nos mostró que su promedio de bateo fue en realidad más alto en 1954 que en 1966?

Al dividir hasta tres posiciones después del punto decimal, pudimos ver que su promedio de bateo fue más alto en 1954 porque teníamos unidades semejantes de milésimos, lo que hizo que fuera más fácil comparar.

Nota para la enseñanza

Observe que, en el problema 6, se pide a sus estudiantes que dividan hasta tres posiciones después del punto decimal, no que redondeen. Dividir y detenerse en la posición de los milésimos alcanza para que sus estudiantes comparen los promedios de bateo de manera suficiente.

Para calcular los promedios de bateo con precisión, tendrían que dividir hasta la posición de los diezmilésimos y redondear a la posición de los milésimos. Además, los promedios de bateo por lo general se muestran sin el cero a la izquierda, por ejemplo .280. No se espera que sus estudiantes tengan tanta precisión en este problema.

Si en el problema 6 se les pidiera redondear el promedio de bateo de Hank Aaron a la posición de los milésimos, ¿cuántos dígitos deberían hallar después del punto decimal? ¿Por qué?

Deberíamos hallar cuatro dígitos después del punto decimal o dividir hasta la posición de los diezmilésimos, de manera que pudiéramos determinar cómo redondear el dígito en la posición de los milésimos.

Para determinar el cociente hasta la posición de los diezmilésimos, podemos continuar usando el algoritmo estándar para la división. Para calcular el promedio de bateo de Hank Aaron en 1966, podemos escribir el dividendo como 168.0000 y, luego, dividir los 3,660 diezmilésimos restantes entre 603.

Podemos continuar usando el algoritmo estándar para la división a fin de hallar el cociente en cualquier valor posicional después del punto decimal. Sin embargo, en muchas situaciones del mundo real será suficiente con hallar el cociente hasta la posición de los milésimos.

Concluir

Reflexión final 5 min

Objetivo: Dividir números enteros de varios dígitos usando el algoritmo estándar, y expresar cocientes como números decimales

Use las preguntas que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a complementar las respuestas de sus pares.

Cuando el cociente no es un número entero, ¿cómo podemos expresar el cociente como un número decimal?

Cuando el cociente no es un número entero, hay un residuo. Podemos reagruparlo como décimos y seguir dividiendo. Si hay otro residuo, podemos reagruparlo como centésimos y seguir dividiendo. Si hay otro residuo, podemos reagruparlo como milésimos y seguir dividiendo.

¿Cómo sabemos cuándo terminamos de dividir?

Cuando el residuo es 0 y no quedan dígitos en el dividendo, no queda nada para dividir y terminamos la división. Terminamos de dividir si dividimos al número de dígitos necesarios para redondear una respuesta a un valor posicional dado.

¿A qué valor posicional debemos calcular el cociente si queremos redondear nuestra respuesta al centésimo más cercano? ¿Y al décimo más cercano?

Si queremos redondear nuestra respuesta al centésimo más cercano, debemos calcular el cociente a la posición de los milésimos. Si queremos redondear nuestra respuesta al décimo más cercano, debemos calcular el cociente a la posición de los centésimos.

¿Por qué expresamos un cociente como un número decimal?

Cuando expresamos dos cocientes como fracciones o números mixtos, a veces puede ser difícil hacer comparaciones, a menos que tengan denominadores comunes. Cuando expresamos dos cocientes como números decimales, es más fácil comparar los números, como los promedios de bateo de Hank Aaron, porque tenemos denominadores comunes de décimos, centésimos, milésimos, y así sucesivamente. También tiene sentido expresar cocientes como números decimales cuando el cociente representa una cantidad de dinero, como la cantidad que recibió cada persona en el problema de la limonada.

Boleto

de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Expresar cocientes como números decimales

En esta lección:

• dividimos números enteros de varios dígitos usando el algoritmo estándar;

• expresamos cocientes como números decimales.

Ejemplos

En los problemas 1 a 3, divide. 1. 645 ÷ 6

Registra un 0 en la posición de los centésimos si todavía hay un residuo. Continúa con estos pasos hasta que el residuo sea 0 o hasta que haya suficientes dígitos después del punto decimal para redondear a un valor posicional dado.

Registra un punto decimal y un 0 en la posición de los décimos. El residuo ahora es 30 décimos. Luego, calcula 30 ÷ 6

Cuando el dividendo sea menor que el divisor, las unidades se deben reagrupar como décimos. Comienza registrando un punto decimal y un 0 en la posición de los décimos. Luego, calcula 360 ÷ 80

Nombre Fecha

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. Coloca un punto decimal en el cociente donde creas que corresponda. Justifica tu respuesta.

6,450 ÷ 16 = 403125

403.125

Sé que 6,400 ÷ 16 = 400; entonces, la respuesta debe estar cerca de 400

En los problemas 2 a 11, divide. Cuando sea necesario, redondea tu respuesta al décimo más cercano.

12. Sasha divide 1,449 entre 18 y obtiene un cociente de 8.5

a. ¿Es razonable la respuesta de Sasha? ¿Por qué?

No. La respuesta de Sasha no es razonable porque no está cerca de una estimación de 1,449 ÷ 18. Podemos redondear 1,449 a 1,400 y 18 a 20 para obtener 1,400 ÷ 20 = 70 La respuesta de Sasha, 8.5, no está cerca de la estimación de 70

b. Considera el trabajo de Sasha. Describe el error de Sasha. – 144

18 1, 44 9.0

09 0 .5 90 –0 8

El 8 debería estar escrito arriba de la posición de las decenas en el dividendo. Sasha se saltea el paso en el que debería escribir un 0 para representar que hay 0 grupos de 18 en 9 unidades. La respuesta debería ser 80.5

13. Un ejemplo del promedio de bateo de un jugador de beisbol es 0.279. El promedio de bateo de un jugador se calcula dividiendo el número de hits entre el número de turnos al bate. Los promedios más altos de bateo son los mejores promedios de bateo.

Jugador Hits Turnos al bate

Jugador 1 155 580

Jugador 2 198 660

Jugador 3 140 500

a. Elige un jugador con un promedio de bateo que sea mejor que el del ejemplo, 0.279. Explica.

Ejemplo: El jugador 2 tiene un promedio de bateo de 0.300. Como 0.300 es mayor que 0.279, el promedio de bateo del jugador 2 es mejor que el del ejemplo.

17. Considera 453 ÷ 32

a. Estima el cociente. Explica cómo hiciste la estimación. 15

Redondeé 453 a 450 y 32 a 30. Como 450 ÷ 30 = 15, sé que el cociente debe estar cerca de 15

b. Calcula el cociente. Expresa el residuo como una fracción. Muestra tu trabajo.

b. Elige un jugador con un promedio de bateo que sea peor que el del ejemplo, 0.279. Explica. El jugador 1 tiene un promedio de bateo de aproximadamente 0.267. Como 0.267 es menor que 0.279, el promedio de bateo del jugador 1 es peor que el del ejemplo.

Recuerda

En los problemas 14 a 16, suma.

18. Blake y Leo asisten a la misma escuela intermedia. Blake vive a 5 4 de milla de la escuela. Leo vive a 1 3 5 millas de la escuela. ¿En cuál de las siguientes opciones se comparan correctamente las dos distancias?

A. 5 4 de milla < 1 3 5 millas

B. 5 4 de milla > 1 3 5 millas

C. 5 4 de milla = 1 3 5 millas

D. 1 3 5 millas < 5 4 de milla

Problemas de división del mundo real

Crear y resolver problemas de división del mundo real

Un estadio de futbol tiene 4,608 asientos. Cada sección del estadio tiene 144 asientos. ¿Cuántas secciones de asientos hay en el estadio? Explica.

Hay 32 secciones de asientos porque 4,608 ÷ 144 = 32

Vistazo a la lección

En esta lección, sus estudiantes trabajan en parejas para interpretar y resolver problemas de división del mundo real. Identifican distintas características de los problemas verbales de división, como un número de grupos desconocido, un tamaño del grupo desconocido, un problema de tasas o un problema de comparación multiplicativa. Reconocen que puede ser necesario redondear los cocientes decimales para responder la pregunta. En grupos pequeños, sus estudiantes crean un problema verbal propio y resuelven un problema verbal creado por otro grupo.

Pregunta clave

• ¿En qué tipos de situaciones del mundo real usamos la división?

Criterio de logro académico

6.Mód2.CLA1 Resuelven problemas verbales dividiendo números de varios dígitos con el algoritmo estándar.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• El acertijo de los $179.00

• Lo desconocido

• Narrar historias

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• tarjeta de índice (1 por grupo de 2 o 3 estudiantes)

Preparación de la lección

• No se necesita.

Fluidez

Redondear números decimales

La clase redondea números decimales como preparación para expresar cocientes como números decimales.

Instrucciones: Redondea cada número decimal como se indica.

3.25 redondeado al décimo más cercano

8.742 redondeado al décimo más cercano

9.009 redondeado al décimo más cercano 9.0

10.299 redondeado al centésimo más cercano

1.

2.

3. 8.742 redondeado al centésimo más cercano 8.74

4. 9.009 redondeado al centésimo más cercano 9.01

5.

6.

Presentar

La clase escribe un contexto para una ecuación de división dada.

Presente el problema 1 a la clase. Forme parejas de estudiantes y use la rutina Construcción colaborativa para que las parejas escriban un contexto que se pueda representar con la ecuación.

1. Escribe un problema verbal para esta ecuación.

40 ÷ 10 = 4

Ejemplo:

Número de grupos desconocido: Hay 40 personas en una cena. A cada mesa se sientan diez personas. ¿Cuántas mesas hay?

Tamaño del grupo desconocido: Hay 40 personas en una cena. Hay 10 mesas. A cada mesa se sienta el mismo número de personas. ¿Cuántas personas se sientan a cada mesa?

Tasa: Noah anota 40 puntos en 10 juegos. Si Noah anota el mismo número de puntos en cada juego, ¿cuántos puntos anota Noah por juego?

Comparación multiplicativa: Noah anota 40 puntos. Este número es 10 veces la cantidad de puntos que anota Scott. ¿Cuántos puntos anota Scott?

Dé a las parejas 2 minutos para comparar con otras parejas los contextos que construyen. Invite a sus estudiantes a compartir sus ideas con la clase y a explicar la relación entre el contexto y la ecuación.

A medida que sus estudiantes compartan los contextos, señale los diferentes tipos de características de estos contextos, como un número de grupos desconocido, un tamaño del grupo desconocido, una tasa o una comparación multiplicativa. Considere usar los ejemplos de problema proporcionados en la solución del problema 1 para cualquier tipo de problema que sus estudiantes no compartan. Hoy, identificaremos diferentes tipos de situaciones para las que se necesita la división. Crearemos nuestros propios problemas verbales y los resolveremos usando la división.

Nota para la enseñanza

En grados anteriores, sus estudiantes diferencian problemas verbales de división en dos tipos: número de grupos desconocido y tamaño del grupo desconocido. Active los conocimientos previos señalando estas características cuando sus estudiantes creen problemas propios.

DUA: Representación

Considere crear un afiche rotulado Situaciones de división. Mientras sus estudiantes comparten diferentes contextos, enumere los diversos tipos, como número de grupos desconocido, tamaño del grupo desconocido, tasa y comparación multiplicativa. A lo largo de la lección, agregue en el afiche ejemplos de cada tipo para que sus estudiantes tengan como referencia.

Aprender

El acertijo de los $179.00

La clase interpreta el cociente en problemas verbales de división para determinar cómo redondear la respuesta.

Comience con el planteamiento y las preguntas que siguen:

En el problema 1, vimos que pueden existir muchas situaciones diferentes para la misma ecuación de división. Imaginen que tenemos tres problemas y que cada uno se puede representar con 179 ÷ 18. ¿Creen que eso significa que los tres problemas tienen la misma respuesta? ¿Por qué?

Ejemplo: Sí. Todos tienen el mismo cociente; entonces, todos deben tener la misma respuesta.

Pida a sus estudiantes que vayan a los problemas 2 a 4. Pídales que completen los problemas en parejas.

Los problemas 2 a 4 se pueden representar con 179 ÷ 18. Considera si esto significa que todos los problemas tienen la misma respuesta.

179 ÷ 18 ≈ 9.944

2. Tienes $179.00 para comprar libros. Cada libro cuesta $18.00. ¿Cuál es el mayor número de libros que puedes comprar?

Puedo comprar 9 libros. No tengo suficiente dinero para comprar 10 libros porque 10 × 18 = 180. Entonces, redondeo 9.944 hacia abajo, a 9.

3. Quieres ganar $179.00. Puedes ganar $179.00 si vendes libros a $18.00 cada uno. ¿Cuántos libros debes vender para ganar $179.00?

Debo vender 10 libros. Si vendo solo 9 libros, ganaré menos de $179.00. Entonces, redondeo 9.944 hacia arriba, a 10.

4. Tienes $179.00. Divides los $179.00 en partes iguales entre 18 personas. ¿Cuánto dinero obtiene cada persona?

Cada persona obtiene $9.94, pero sobrará dinero. Como se trata de dinero, redondeo 9.944 hacia abajo, a la posición de los centésimos.

Cuando la mayoría haya terminado, invite a sus estudiantes a compartir las respuestas y el razonamiento para cada problema.

Pida a sus estudiantes que consideren la pregunta planteada arriba de los problemas. A medida que compartan su razonamiento, guíe la conversación para dar lugar a la noción de que diferentes situaciones del mundo real pueden requerir diferentes formas de redondeo, según el significado del cociente en el contexto.

Lo desconocido

La clase resuelve problemas verbales usando la división.

Pida a sus estudiantes que vayan a los problemas 5 a 10. Asigne a cada pareja de estudiantes uno de los siguientes pares de problemas para resolver:

• Problemas 5 y 6

• Problemas 7 y 8

• Problemas 9 y 10

Recorra el salón de clases y haga las siguientes preguntas para apoyar el razonamiento de sus estudiantes:

• ¿Qué información conocen? ¿Qué intentan hallar?

• ¿Cuál es el dividendo? ¿Cuál es el divisor?

• ¿Deben redondear el cociente para responder la pregunta? ¿Cómo?

Invite a quienes terminen primero a elegir otros problemas para resolver.

5. Kayla prepara 175 onzas de limonada para una venta de limonada. Quiere llenar cada vaso con 8 onzas de limonada. ¿Cuál es el mayor número de vasos de 8 onzas que puede llenar Kayla?

175 ÷ 8 = 21.875

Kayla puede llenar 21 vasos.

6. En un día, un hotel alquila 56 habitaciones y gana $6,678. El costo del alquiler es el mismo para todas las habitaciones. ¿Cuál es el costo por habitación?

6,678 ÷ 56 = 119.25

El costo por habitación es $119.25.

7. Una familia hace un viaje por carretera. Conducen 475 millas por día. ¿En qué día la familia habrá conducido 1,615 millas?

1,615 ÷ 475 = 3.4

Habrán conducido 1,615 millas el 4. o día.

8. Una escuela compra 228 computadoras portátiles nuevas. Este número es 6 veces la cantidad de computadoras portátiles que la escuela compró el año pasado. ¿Cuántas computadoras portátiles compró la escuela el año pasado?

228 ÷ 6 = 38

La escuela compró 38 computadoras portátiles el año pasado.

9. La longitud de un tablero de madera es 3 pies. El tablero se divide en 8 trozos iguales de madera. ¿Cuál es la longitud, en pies, de cada trozo de madera?

3 ÷ 8 = 0.375

La longitud de cada trozo de madera es 0.375 pies.

10. Toby tiene 493 nickels con los que quiere armar rollos. Cada rollo lleva 40 nickels. ¿Cuál es el número más grande de rollos de nickels que puede armar Toby?

493 ÷ 40 = 12.325

Toby puede armar 12 rollos de nickels.

Diferenciación: Desafío

Como desafío adicional, pida a sus estudiantes que resuelvan los siguientes problemas de porcentajes. Comente cómo se aplica la división de números enteros para calcular porcentajes.

• El libro de Yuna tiene 220 páginas. Lee 187 páginas el fin de semana. ¿Qué porcentaje del libro ha leído Yuna hasta ahora?

Yuna ha leído 85 % del libro hasta ahora.

• Eddie debe escribir un ensayo con un total de 750 palabras. Hasta ahora, ha escrito 345 palabras. ¿Qué porcentaje del número total de palabras le falta escribir a Eddie?

A Eddie le falta escribir 54 % del número total de palabras.

Cuando la mayoría haya resuelto los dos problemas asignados, reúna a la clase para revisar las respuestas. Por cada problema, elija a una pareja de estudiantes para que compartan sus respuestas a las siguientes preguntas:

• ¿Qué información conocen y qué desconocen en el problema?

• ¿Cuáles son el dividendo, el divisor y el cociente del problema?

• ¿Cuál es la respuesta a la pregunta del problema?

• ¿Por qué redondearon como lo hicieron? Si no redondearon, ¿por qué no lo hicieron?

Guíe a sus estudiantes para que expresen la idea de que los cocientes se pueden redondear de diferentes maneras, de acuerdo con el contexto. Por ejemplo, en el problema 5, deben redondear el cociente hacia abajo para responder la pregunta. Sin embargo, en el problema 6, deben mantener el cociente decimal para responder la pregunta.

Luego, use las siguientes preguntas para resaltar diferentes características de los problemas:

¿Qué problemas incluían un número de grupos desconocido?

En el problema 5, el número de vasos de 8 onzas que puede llenar Kayla es un número de grupos desconocido. En el problema 10, el número de rollos de nickels que puede armar Toby es un número de grupos desconocido.

¿Qué problema incluía un tamaño del grupo desconocido?

En el problema 9, la longitud de los trozos de madera es un tamaño del grupo desconocido.

¿Qué problemas incluían una tasa?

En el problema 6, el costo por habitación es una tasa. En el problema 7, las millas por día son una tasa.

¿Qué problema incluía una comparación multiplicativa?

En el problema 8, hay una comparación multiplicativa entre el número de computadoras portátiles que la escuela compra este año y el número de computadoras portátiles que compró el año pasado.

Promoción de la práctica de las matemáticas

Cada estudiante razona de forma abstracta y cuantitativa cuando representa una situación del mundo real con una expresión de división, evalúa la expresión y la vuelve a contextualizar considerando las cantidades en la situación del mundo real.

Considere hacer las siguientes preguntas:

• ¿Qué les dice este problema verbal sobre el número de grupos y el tamaño del grupo?

• ¿Qué situaciones del mundo real se representan con la división?

• ¿Cómo les ayudan las unidades de la situación a pensar en este problema?

Narrar historias

La clase crea y resuelve problemas verbales de división.

Use la rutina Cabezas numeradas. Organice a sus estudiantes en un número de grupos par con 2 o 3 estudiantes por grupo. Asigne un número del 1 al 3 a cada estudiante.

Muestre las siguientes restricciones:

A. Dividendo de 3 o 4 dígitos, divisor de 2 dígitos con un cociente entero

B. Dividendo de 3 o 4 dígitos, divisor de 1 dígito con un cociente decimal

Asigne una de las restricciones a cada grupo. Dé a sus estudiantes de 5 a 7 minutos para crear un problema verbal de división que cumpla con las restricciones y para resolver el problema. Pídales que registren el problema verbal y la solución del problema 11 en sus libros.

Luego, entregue a cada grupo una tarjeta de índice.

Escriban la letra que les fue asignada en el frente de la tarjeta de índice. Escriban el problema verbal que creó su grupo en el reverso de la tarjeta de índice.

Coloquen la tarjeta completada en la pila correcta: A o B.

Una vez que los grupos hayan entregado una tarjeta, pídales que elijan una de la pila opuesta y que resuelvan el problema. Pídales que registren el problema y la solución del problema 12 en sus libros. Recuerde a sus estudiantes que cualquiera podría responder por el grupo, por lo que cada estudiante debe prepararse para compartir.

Cuando los grupos hayan terminado, diga un número del 1 al 3. Pida a quienes tengan asignado ese número que lean el problema que resolvieron; deben indicar cuáles son el dividendo, el divisor y el cociente del problema y dar la respuesta a la pregunta del problema.

11. Escribe el problema que creó tu grupo. Escribe la solución del problema.

Ejemplo:

La banda ha recaudado $6,432.00 en lo que va del año. Esa cantidad es 12 veces la cantidad que la banda recaudó el año pasado. ¿Cuánto dinero recaudó la banda el año pasado?

6,432 ÷ 12 = 536

La banda recaudó $536.00 el año pasado.

DUA: Representación

A medida que sus estudiantes compartan las respuestas, agregue los ejemplos al afiche de situaciones de división que comenzó en la sección Presentar.

Situación de división Ejemplos

Número de grupos desconocido

El número de rollos de nickels que puede armar Toby

Tamaño del grupo desconocido La longitud de cada trozo de madera

Tasa

Comparación multiplicativa

El costo por habitación

El número de computadoras portátiles que se compraron este año en comparación con el año pasado

12. Escribe el problema que creó el otro grupo. Escribe la solución del problema.

Ejemplo:

La banda prepara 425 galletas para una venta de pasteles. Planean hacer bolsitas que tengan 3 galletas por bolsita. ¿Cuál es el mayor número de bolsitas de galletas que puede hacer la banda?

425 ÷ 3 ≈ 141.7

La banda puede hacer 141 bolsitas de galletas.

Concluir

Reflexión final 5 min

Objetivo: Crear y resolver problemas de división del mundo real

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las preguntas y los planteamientos que siguen. Anime a sus estudiantes a desarrollar las respuestas de sus pares.

Piensen en los problemas 5 a 10. ¿Les resultó útil identificar las características de esos problemas antes de crear sus propios problemas? Expliquen.

Ejemplo: Sí. Identificar características como el número de grupos desconocido y los problemas de tasas me mostró diferentes tipos de situaciones en las que necesitamos dividir números. Eso me dio ideas cuando escribimos nuestro propio problema verbal en grupos.

¿En qué tipos de situaciones del mundo real usamos la división? Den un ejemplo.

Ejemplo: Usamos la división cuando hay un número de grupos desconocido, como el número de rollos de nickels que podía armar Toby. Usamos la división cuando el tamaño del grupo es desconocido, como la longitud de cada trozo de madera. Usamos la división en problemas de tasas, como el costo por habitación en el hotel. Usamos la división en problemas de comparación multiplicativa, como el número de computadoras portátiles que se compraron este año en comparación con el año pasado.

Den un ejemplo de cuándo podríamos necesitar un cociente preciso. Den un ejemplo de cuándo es suficiente una estimación del cociente.

Ejemplo:

Si necesito repartir dinero en partes iguales entre algunas personas, entonces divido para determinar la cantidad de dinero que recibe cada una. Necesito un cociente preciso, de manera que cada persona reciba la misma cantidad.

Si quiero saber cuántos días dura una bolsa de alimento para perros, entonces divido el número de onzas de la bolsa entre el número de onzas que come por día mi perro. Es suficiente una estimación del cociente.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota

para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

RESUMEN 20

Problemas de división del mundo real

En esta lección:

• resolvimos problemas de división del mundo real;

• creamos problemas de división del mundo real.

Ejemplos

1. Una florería tiene 284 margaritas para armar 15 ramos. El encargado de la florería pone el mismo número de margaritas en cada ramo. ¿Cuántas margaritas pone en cada ramo?

Presta atención al redondear en determinadas situaciones.

4 4

El encargado de la florería pone 18 margaritas en cada ramo.

No hay suficientes margaritas para que cada ramo tenga 19 porque 19 × 15 = 285 Entonces, hay que redondear 18.9 hacia abajo, a 18

2. El centro de estudiantes establece el objetivo de recaudar $400 con la venta de latas de palomitas de maíz. Vende cada lata de palomitas de maíz a $7.

a. ¿Cuántas latas de palomitas de maíz debe vender el centro de estudiantes para alcanzar el objetivo?

El centro de estudiantes no puede vender una parte de una lata de palomitas de maíz. Vender 57 latas no será suficiente para alcanzar el objetivo de $400 porque 57 × 7 = 399. Por lo tanto, el centro de estudiantes debe vender 58 latas de palomitas de maíz.

El centro de estudiantes debe vender 58 latas de palomitas de maíz para alcanzar el objetivo.

b. Leo dice que el centro de estudiantes debe vender 57 latas de palomitas de maíz. Dice: “El cociente es aproximadamente 57.1. Redondeé hacia abajo, a 57, porque 57.1 está más cerca de 57 que de 58”. ¿Estás de acuerdo con Leo? Explica.

No estoy de acuerdo con Leo. Si el centro de estudiantes vende 57 latas de palomitas de maíz, no alcanza el objetivo de $400. En este caso, tenemos que redondear hacia arriba, a 58 latas de palomitas de maíz, porque el centro de estudiantes no puede vender 0.1 de una lata de palomitas de maíz.

Nombre

Fecha

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. En una clase de educación física hay 50 estudiantes. El maestro quiere organizar equipos de 8 estudiantes para un juego.

a. ¿Pueden dividirse 50 estudiantes en equipos de 8 estudiantes? Explica.

No. No hay ningún número entero que se pueda multiplicar por 8 para obtener 50

b. Sugiere el número de estudiantes que puede haber en cada equipo. Todos los equipos deben tener el mismo número de estudiantes. Explica tu respuesta.

Ejemplo:

El maestro puede formar 5 equipos de 10 estudiantes o 10 equipos de 5 estudiantes, porque 5 × 10 = 50

2. Hay 368 estudiantes que van a ir de excursión. Un autobús escolar puede transportar a 64 estudiantes. ¿Cuántos autobuses se necesitan para transportar a 368 estudiantes? Explica.

Se necesitan seis autobuses para transportar a 368 estudiantes, porque 5.75 no es un número posible de autobuses. 5.75 se debe redondear hacia arriba, a 6, porque 5 autobuses no serán suficientes.

3. Una senderista tiene 93 onzas de granola. Quiere armar bolsitas de 6 onzas de granola. ¿Cuál es el mayor número de bolsitas de 6 onzas que puede armar? Explica.

La senderista puede armar 15 bolsitas. No hay suficiente granola para armar 16 bolsitas.

4. Un club escolar recauda $1,230 en una actividad para recaudar fondos. El club quiere usar todo el dinero para comprar mochilas y donarlas a sus estudiantes. Una mochila cuesta $12 ¿Cuál es el mayor número de mochilas que puede comprar el club? Explica.

El club escolar puede comprar 102 mochilas. Al club le sobrará un poco de dinero, pero no lo suficiente para comprar 103 mochilas.

5. La maestra Baker prepara estaciones de ciencias para sus estudiantes. Para cada estación se necesitan exactamente 250 mililitros de vinagre. ¿Cuál es el mayor número de estaciones que puede preparar la maestra Baker con 1,890 mililitros de vinagre? Explica.

La maestra Baker puede preparar 7 estaciones porque 7.56 no es un número posible de estaciones. No hay suficiente vinagre para 8 estaciones.

6. La maestra Song tiene 300 tarjetas para repartir entre sus 32 estudiantes. Quiere entregar el mismo número de tarjetas a cada estudiante. ¿Cuál es el mayor número de tarjetas que puede entregar a cada estudiante? Explica.

La maestra Song puede entregar 9 tarjetas a cada estudiante porque 9.375 no es un número posible de tarjetas. Si redondea hacia arriba, a 10, no tendrá tarjetas suficientes para entregar a cada estudiante el mismo número de tarjetas.

7. Yuna tiene 3 paquetes de chicle. En cada paquete hay 5 barras de chicle. Yuna quiere darles todos los chicles a 4 amigos y repartirlos en partes iguales entre los 4 amigos. ¿Cuántas barras de chicle recibirá cada amigo? Explica.

Cada amigo recibirá 3 barras de chicle. Sobrarán 3 barras, y esa cantidad no es suficiente para que cada amigo reciba 4 barras.

8. El objetivo de Ryan es recaudar $250 por la venta de velas. Vende cada vela a $13.

a. ¿Cuántas velas debe vender Ryan para alcanzar su objetivo?

Ryan debe vender 20 velas para alcanzar su objetivo.

b. Julie dice que Ryan debe vender 19 velas. Dice: “El cociente es aproximadamente 19.23

Redondeé hacia abajo, a 19 porque 19.23 está más cerca de 19 que de 20”. ¿Estás de acuerdo con Julie? Explica.

No estoy de acuerdo con Julie. Si Ryan vende 19 velas, solo recauda $247 porque 13 × 19 = 247 En este caso, tenemos que redondear hacia arriba, a 20 velas, porque 19 no es suficiente para que Ryan alcance su objetivo de $250

Nombre Fecha

Recuerda

En los problemas 9 a 11, suma. 9. 2 3 4 +

12. Estima el cociente. Luego, calcula el cociente usando el algoritmo estándar. Expresa el cociente como un número mixto.

7,226 ÷ 23

Estimación: 300

Cociente: 314 4 23

13. Usa <, > o = para hacer que cada oración numérica sea verdadera.

a. 0.756 > 0.736

b. 0.110 = 0.11

c. 0.0883 < 0.83

d. 1.03 < 1.035

Tema F

División con números decimales

En el tema D, sus estudiantes desarrollan fluidez con la suma, la resta y la multiplicación de números decimales. En el tema E, dividen números enteros de varios dígitos usando el algoritmo estándar. En el tema F, se valen de estas destrezas al desarrollar fluidez con el uso del algoritmo estándar para la división cuando dividen números decimales y al desarrollar la flexibilidad en su razonamiento sobre la división.

Al comienzo del tema, sus estudiantes dividen números decimales entre números enteros usando estrategias de multiplicación, la estimación, la descomposición y las potencias de 10. Practican cómo hallar mentalmente cocientes como 9.3 ÷ 300 y, luego, hacen una transición hacia el uso del algoritmo estándar para la división. Usan la estimación y, luego, el razonamiento del valor posicional para determinar la ubicación del punto decimal en un cociente.

Más adelante en el tema, en las lecciones 22 y 23, sus estudiantes usan cálculos mentales y el algoritmo estándar para la división a fin de dividir números decimales entre otros números decimales. Identifican y escriben expresiones de división equivalentes. Por ejemplo, reconocen que 48.5 ÷ 1.2 y 485 ÷ 12 tienen el mismo cociente. Aplican esta comprensión para escribir expresiones de división con números decimales con divisores que son números enteros antes de dividir. Para profundizar su comprensión del algoritmo, analizan errores como expresiones de división que están escritas incorrectamente y cocientes y dividendos que no están alineados.

El tema concluye con una exploración digital que incluye la planificación de un viaje a Marte. Sus estudiantes aplican su comprensión de las razones, las tasas y la conversión de unidades del módulo 1 al hacer cálculos con números decimales. A lo largo de esta actividad, determinan qué operaciones usar para resolver un problema.

Sus estudiantes aplican su comprensión de la división con números decimales en los módulos posteriores al trabajar con expresiones y ecuaciones, al resolver problemas de área y volumen, y al calcular la media y la desviación media absoluta.

Progresión de las lecciones

Lección 21 Dividir un número decimal entre un número entero

Lección 22 Dividir un número decimal entre otro número decimal mayor que 1

Lección 23 Dividir un número decimal entre otro número decimal menor que 1

Lección 24 Vivir en Marte

Dividir un número decimal entre un número entero

Dividir un número decimal entre un número entero de varios dígitos usando el algoritmo estándar para la división

Vistazo a la lección

Al comienzo de esta lección, sus estudiantes trabajan en parejas para resolver un acertijo matemático de división. Usan la descomposición y las potencias de 10 para dividir un número decimal entre un número entero. Participan en un Intercambio con la pizarra blanca para desarrollar fluidez con estas destrezas de división, que no requieren el uso del algoritmo estándar para la división. Asimismo, hacen una transición hacia el uso del algoritmo estándar para dividir un número decimal entre un número entero razonando acerca de por qué se alinean los puntos decimales del dividendo y del cociente.

Preguntas clave

• ¿Qué estrategias podemos usar para dividir un número decimal entre un número entero?

• Cuando usamos el algoritmo estándar para dividir un número decimal entre un número entero, ¿por qué se alinean los puntos decimales del dividendo y del cociente?

Criterio de logro académico

6.Mód2.CLA11 Dividen números decimales de varios dígitos.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Razonar sobre la división con números decimales

• Usar el algoritmo estándar con un número decimal como dividendo

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• No se necesita.

Fluidez

Dividir entre potencias de 10

La clase divide entre potencias de 10 como preparación para dividir números decimales entre números enteros.

Instrucciones: Divide. Expresa tu respuesta como un número decimal.

Presentar

La clase resuelve un acertijo matemático de división que incluye dividir un número decimal entre un número entero.

Muestre el problema 1. Dé a sus estudiantes unos minutos para que completen el problema en parejas.

1. Completa los espacios con cinco dígitos diferentes para hacer una oración numérica verdadera.

Ejemplo: 3.4 ÷ 2 = 1.7

Reúna las respuestas de la clase y muéstrelas a sus estudiantes. Pídales que compartan sus estrategias. Comente qué soluciones son correctas y cómo usar la multiplicación para comprobar que las soluciones son correctas. Considere usar las preguntas que siguen para guiar una conversación de toda la clase acerca del problema:

• ¿Podría el primer dígito ser un 0? Expliquen.

• ¿Podríamos interpretar esta oración numérica como ÷ =   ? Expliquen.

• ¿Podemos usar siempre la multiplicación para comprobar nuestra solución a un problema de división?

Hoy, aprenderemos distintas estrategias para dividir números decimales entre números enteros.

DUA: Participación

Considere pedir a sus estudiantes que piensen en un motivo por el que podrían tener que dividir un número decimal entre un número entero. Por ejemplo, si 5 personas necesitan dividir el costo de una comida que costó $46.80, necesitan dividir $46.80 entre 5 para determinar la cantidad que debe pagar cada persona.

Aprender

Razonar sobre la división con números decimales

La clase usa la estimación, la descomposición y las potencias de 10 para razonar acerca de los cocientes con números decimales como dividendo.

Muestre la siguiente expresión de división:

73.8 ÷ 5

¿Cuál es una estimación para 73.8 ÷ 5? Expliquen.

15, porque 75 ÷ 5 = 15

Pida a la clase que use la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta. Anime a sus estudiantes a hacer cálculos en una pizarra blanca individual.

Si 5 personas dividen de manera uniforme la cuenta de una cena que cuesta $73.80, ¿cuánto debe pagar cada persona?

$14.76

Muestre el cociente. Pida a diferentes estudiantes que compartan su trabajo con la división. Resalte las distintas estrategias, que probablemente incluyan la descomposición, los cocientes parciales y la división larga.

Si debo a alguien $73.80 y solo tengo billetes de $5, ¿cuántos billetes de $5 necesito dar a esa persona para pagar la totalidad de la deuda? Expliquen.

15. Sé que 73.80 ÷ 5 = 14.76, así que es necesario dar a la persona quince billetes de $5 para pagar la totalidad de la deuda.

¿Cuántas revistas de $5 se pueden comprar con $73.80? Expliquen.

14. Sé que 73.80 ÷ 5 = 14.76, así que se pueden comprar solo 14 revistas.

Cuando resolvemos problemas del mundo real que incluyen la división, es posible que necesitemos redondear hacia arriba o hacia abajo una respuesta para responder correctamente una pregunta.

Una manera de evaluar 73.8 ÷ 5 es usar la descomposición. Veamos un ejemplo de esta estrategia.

DUA: Representación

Considere crear un afiche de referencia de las estrategias de división y agregar un ejemplo de cada una de ellas a medida que avanza la lección.

Potencias de 10 porque 75 ÷ 5 = 15.

Estimación

Estrategias para dividir un número decimal entre un número entero

Descomposición

Algoritmo estándar

Muestre las siguientes ecuaciones. Pida a sus estudiantes que usen cálculos mentales para determinar los cocientes. Muestre los cocientes a medida que sus estudiantes se los dicen.

600 ÷ 3 = 200

90 ÷ 3 = 30 27 ÷ 3 = 9 2.7 ÷ 3 = 0.9

¿Cómo pueden usar 27 ÷ 3 = 9 para evaluar 2.7 ÷ 3?

Como 2.7 es 1 10 de 27, el cociente es 1 10 de 27 ÷ 3.

¿Cuánto es 692.7 ÷ 3? Expliquen.

230.9

600 ÷ 3 = 200, 90 ÷ 3 = 30 y 2.7 ÷ 3 = 0.9, así que 692.7 ÷ 3 debe ser igual a 200 + 30 + 0.9

o 230.9.

Una estrategia para dividir un número decimal entre un número entero es pensar en el dividendo en su forma desarrollada y, luego, dividir cada parte de la expresión desarrollada por separado. En este caso, pensamos en 692.7 como 600 + 90 + 2.7, dado que 600, 90 y 2.7 son divisibles entre 3. ¿Pueden pensar en una expresión de división en la que la descomposición no funcionaría bien?

Ejemplo: 692.7 ÷ 4

A veces, podemos usar potencias de 10, tales como 10, 100 y 1,000, como ayuda para dividir.

Muestre las siguientes ecuaciones. Anime a sus estudiantes a usar las pizarras blancas individuales si lo necesitan para responder sus preguntas. Muestre las soluciones a medida que se las dicen.

2.4 ÷ 20 = 0.12

0.24 ÷ 20 = 0.012

¿Cuánto es 2.4 ÷ 20? Expliquen.

0.12

Dividí 2.4 entre 2 para obtener 1.2 y, luego, dividí 1.2 entre 10 para obtener 0.12.

¿Cuánto es 0.24 ÷ 20? ¿Cómo se relacionan este cociente y 2.4 ÷ 20?

0.012

El cociente es 1 10 de 2.4 ÷ 20.

¿Qué sucede con el cociente si el dividendo se divide entre un factor de 10?

El cociente también se divide entre un factor de 10.

Muestre las siguientes ecuaciones. Anime a sus estudiantes a usar las pizarras blancas individuales si lo necesitan para responder sus preguntas. Muestre las soluciones a medida que se las dicen.

2.4 ÷ 400 = 0.006

2.4 ÷ 4,000 = 0.0006

0.24 ÷ 400 = 0.0006

¿Cuánto es 2.4 ÷ 400? Expliquen.

0.006

Dividí 2.4 entre 4 para obtener 0.6 y, luego, dividí 0.6 entre 100 para obtener 0.006.

¿Cuánto es 2.4 ÷ 4,000? ¿Cómo se relacionan este cociente y 2.4 ÷ 400?

0.0006

El cociente es 1 10 de 2.4 ÷ 400.

¿Cuánto es 0.24 ÷ 400? ¿Cómo se relacionan este cociente y 2.4 ÷ 4,000?

0.0006

Los cocientes son iguales.

Las expresiones 2.4 ÷ 4,000 y 0.24 ÷ 400 tienen el mismo cociente. ¿Por qué?

El divisor y el dividendo en la primera expresión son 10 veces el divisor y el dividendo en la segunda expresión.

Resumamos lo que hemos visto en estos patrones. Si se multiplica el dividendo por un factor de 10 y el divisor queda igual, ¿qué sucede con el cociente?

El cociente se multiplica por el mismo factor de 10 que el dividendo.

Si se multiplica el divisor por un factor de 10 y el dividendo queda igual, ¿qué sucede con el cociente?

El cociente se divide entre ese factor de 10.

Si se multiplican el divisor y el dividendo por el mismo factor de 10, ¿qué sucede con el cociente?

El cociente queda igual.

Guíe un Intercambio con la pizarra blanca.

Vamos a dividir números decimales entre potencias de 10 y sus múltiplos. Les mostraré una expresión de división y deberán evaluarla en parejas. Cuando hayan escrito su respuesta, levanten la pizarra blanca para que pueda verla.

Dé una expresión a la vez y compruebe las respuestas de la clase después de cada expresión. Brinde retroalimentación inmediata a cada pareja. Anime a sus estudiantes a usar las mismas estrategias de cálculo mental que ya usaron anteriormente en esta lección. Las expresiones de división están ordenadas de menor a mayor dificultad.

Expresiones de división:

• 1.5 ÷ 50 0.03

• 0.36 ÷ 90 0.004

• 1.28 ÷ 20 0.064

• 4.22 ÷ 200 0.0211

• 96.9 ÷ 300 0.323

• 0.56 ÷ 8,000

Diferenciación: Desafío

Si sus estudiantes calculan las respuestas con rapidez durante el Intercambio con la pizarra blanca, propóngales el desafío de usar cálculos mentales para evaluar las siguientes expresiones:

Dirija la atención de sus estudiantes al problema 2.

En los problemas 2 a 5, aplicarán su comprensión de la estimación, la descomposición y las potencias de 10. A medida que trabajen con los problemas, consideren de qué manera cambiar el dividendo, el divisor o ambos por una potencia de 10 impacta en el cociente.

Brinde varios minutos para que sus estudiantes completen los problemas 2 a 5 en parejas.

2. ¿Es 168.3 ÷ 3 igual a 561, 56.1, 5.61 o 0.561? Explica.

56.1

Ejemplo: 150 ÷ 3 = 50, así que el cociente debe estar cerca de 50.

3. Usa las operaciones de división para completar los espacios y hacer que cada oración numérica sea verdadera.

a. 144 ÷ 12 = 12

b. 14.4 ÷ 12 = 1.2

c. 1.44 ÷ 12 = 0.12

d. 1.44 ÷ 120 = 0.012

e. 14.4 ÷ 1,200 = 0.012

4. Sin dividir, escribe tres expresiones de división que sean equivalentes a 42.68 ÷ 9

Ejemplo: 426.8 ÷ 90, 4.268 ÷ 0.9, 4,268 ÷ 900

5. Tyler determina que 82.4 ÷ 8 es igual a 10.3 porque 80 ÷ 8 = 10 y 2.4 ÷ 8 = 0.3 y 10 + 0.3 = 10.3. ¿Es correcto el razonamiento de Tyler? Explica.

Sí. Su razonamiento es correcto. 8 × 10.3 = 8 × (10 + 0.3) = 8 × 10 + 8 × 0.3

= 80 + 2.4

= 82.4

Diferenciación: Apoyo

Para quienes necesiten apoyo adicional, considere proporcionar números más pequeños y menos partes en cada problema de la siguiente manera:

• En el problema 2, ¿es 17.5 ÷ 5 igual a 3.5 o 0.35?

• En el problema 4, escribe tres expresiones de división que sean equivalentes a 2.4 ÷ 6

• En el problema 5, Tyler determina que 26.5 ÷ 5 es igual a 5.3 porque 25 ÷ 5 = 5 y 1.5 ÷ 5 = 0.3 y 5 + 0.3 = 5.3.

Nota para la enseñanza

Aunque es posible que no conozcan la propiedad distributiva por su nombre, sus estudiantes desarrollan estrategias de multiplicación y división en grados anteriores cuando componen y descomponen números usando las propiedades distributiva y asociativa.

Cuando la mayoría haya terminado, invite a sus estudiantes a compartir las soluciones y el razonamiento del problema 2.

Dirija la atención de sus estudiantes al problema 3.

¿Por qué los cocientes en las partes (d) y (e) del problema 3 son iguales?

Las dos expresiones son equivalentes. El dividendo y el divisor en la parte (e) son 10 veces el dividendo y el divisor de la expresión en la parte (d).

Pida a diferentes estudiantes que compartan sus soluciones del problema 4. Escriba todas las soluciones correctas en el pizarrón.

¿Cómo podemos crear expresiones de división equivalentes?

El divisor y el dividendo se pueden multiplicar por o dividir entre la misma potencia de 10. Por ejemplo, cuando multiplicamos tanto el divisor como el dividendo por 10, el cociente no cambia.

Pida a alguien que explique cómo sabe que el razonamiento de Tyler en el problema 5 es correcto.

Usar el algoritmo estándar con un número decimal como dividendo

La clase usa el algoritmo estándar para la división a fin de dividir un número decimal entre un número entero.

Dirija la atención de sus estudiantes al problema 6.

A veces, necesitaremos usar el algoritmo estándar para la división a fin de dividir un número decimal entre otro número. ¿Cuál es una estimación para 61.65 ÷ 5? Expliquen. 60 ÷ 5 = 12, así que 61.65 ÷ 5 debe ser aproximadamente 12.

¿Cómo usarían el algoritmo estándar para dividir 6,165 entre 5? ¿Cómo pueden usar 6,165 ÷ 5 como ayuda para hallar 61.65 ÷ 5? Reúnanse y conversen en parejas.

Después de que sus estudiantes hayan tenido la oportunidad de comentar las preguntas anteriores, dé uno o dos minutos para que completen el problema 6 en parejas.

En los problemas 6 a 9, estima el cociente. Luego, usa el algoritmo estándar para dividir.

6. 61.65 ÷ 5

Estimación: 12

Pida a alguien que comparta su respuesta del problema 6.

¿Cómo saben dónde ubicar el punto decimal? Por ejemplo, ¿cómo saben que la respuesta es 12.33 en lugar de 1.233 o 123.3?

Como estimé que la respuesta es 12, sabía que debía haber 2 dígitos antes del punto decimal en el cociente. 12.33 está más cerca de la estimación de 12 que 1.233 o 123.3.

Muestre la solución del problema 6.

¿Por qué se alinean los puntos decimales del dividendo y del cociente? ¿Creen que esto siempre será así?

Los puntos decimales se alinean porque el dividendo y el cociente se alinean según el valor posicional. Sí, creo que esto siempre será así.

Nota para la enseñanza

En la lección 13 del tema D se aconseja no usar lenguaje como alinear los puntos decimales cuando la clase suma y resta números decimales. En esta lección, se señala intencionalmente que los puntos decimales en el dividendo y el cociente se alinean. Esta conversación tiene como objetivo hacer que sus estudiantes comprendan cómo funciona el algoritmo con un número decimal como dividendo.

Al dividir números enteros usando el algoritmo estándar, el dividendo y el cociente se alinean según el valor posicional. Esto es así porque el algoritmo nos ayuda a organizar las respuestas a partir de una serie de problemas de división más simples con cada valor posicional del dividendo, comenzando con 6 decenas ÷ 5. Cuando alineamos el dividendo y el cociente según el valor posicional, los puntos decimales también se alinean.

Brinde varios minutos para que sus estudiantes completen los problemas 7 a 9 de manera individual o en parejas. Anime a sus estudiantes a estimar los cocientes para comprobar sus respuestas.

Recorra el salón de clases mientras trabajan y brinde apoyo según sea necesario. Considere hacer las siguientes preguntas:

• ¿Qué expresión de división con un número entero como dividendo tiene el mismo cociente que 316.2 ÷ 12?

• ¿Cómo pueden usar el algoritmo estándar como ayuda para determinar este cociente?

• ¿Cuál es su estimación del cociente?

• ¿Cómo pueden usar su estimación para determinar dónde ubicar el punto decimal en el cociente?

7. 316.2 ÷ 12

Estimación: 30

8. 15.17 ÷ 37

Estimación: 1 2

9. 0.294 ÷ 14

Estimación: 3 ___ 100

0.021

Cuando la mayoría haya terminado, reúna a la clase para comentar los problemas 7 a 9.

Es posible que la estimación resulte más desafiante en el problema 9 que en los problemas 7 y 8. ¿Cómo podemos usar la estimación en el problema 9?

Ejemplo: Podemos pensar en el dividendo como una fracción y evaluar 3 10 ÷ 10 como 3 100 .

Promoción de la práctica de las matemáticas

Cada estudiante pone atención a la precisión cuando divide un número decimal entre un número entero y pone atención al valor posicional y a la ubicación del punto decimal.

Considere hacer las siguientes preguntas:

• Cuando usan el algoritmo estándar para la división, ¿con qué pasos deben tener mucho cuidado? ¿Por qué?

• ¿En qué parte es fácil cometer errores al usar el algoritmo estándar para dividir un número decimal entre un número entero?

Concluir

Reflexión final 5 min

Objetivo: Dividir un número decimal entre un número entero de varios dígitos usando el algoritmo estándar para la división

Use las preguntas que siguen para guiar una conversación acerca de la división de un número decimal entre un número entero. Anime a sus estudiantes a reformular o desarrollar las respuestas de sus pares.

¿Qué estrategias podemos usar para dividir un número decimal entre un número entero?

Podemos usar los cálculos mentales, las potencias de 10 y sus múltiplos, la descomposición, el algoritmo estándar con la estimación y el algoritmo estándar con la ubicación del punto decimal según el valor posicional.

Cuando usamos el algoritmo estándar para dividir un número decimal entre un número entero, ¿por qué se alinean los puntos decimales del dividendo y del cociente?

Los dígitos del dividendo y del cociente se alinean según el valor posicional, así que los puntos decimales se alinean.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Estimación: 0.03

Dividir un número decimal entre un número entero

En esta lección:

• estimamos cocientes usando el razonamiento del valor posicional;

• dividimos un número decimal entre un número entero de varios dígitos usando el algoritmo estándar para la división.

Ejemplos

En los problemas 1 y 2, estima el cociente. Luego, usa el algoritmo estándar para dividir.

1. 582.61 ÷ 41

Estimación: 15

4.2

Para estimar el cociente, primero redondea 582.61 a 600 y 41 a 40 60 decenas ÷ 4 decenas = 15

Por lo tanto, 15 es una estimación razonable para 582.61 ÷ 41

Observa que el punto decimal del dividendo y del cociente se alinean, ya que el dividendo y el cociente se alinean según el valor posicional. 14.21

Estimar un cociente antes de dividir puede ayudar a confirmar si la respuesta es razonable.

3. Las libretas cuestan $4 cada una. ¿Cuál es el mayor número de libretas que Tyler puede comprar con $50.50?

Divide 50.5 entre 4 para determinar el mayor número de libretas de $4 que Tyler puede comprar con $50.50

El cociente es 12.625. Tyler tiene dinero suficiente para comprar 12 libretas. No tiene dinero suficiente para comprar 13 libretas porque 13 × 4 = 52

Tyler puede comprar 12 libretas.

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

En los problemas 4 a 7, calcula el cociente.

÷ 50

÷ 8

1. Usa la estimación para evaluar 8,627.5 ÷ 35

A. 2,465

B. 246.5

C. 24.65

D. 2.465

2. Sin dividir, usa potencias de 10 para escribir tres expresiones de división que sean equivalentes a 35.78 ÷ 6

Ejemplo:

3.578 ÷ 0.6

357.8 ÷ 60

3,578 ÷ 600

3. ¿Qué expresiones son equivalentes a 486 ÷ 30? Elige todas las opciones que correspondan.

A. 486 ÷ 10 ÷ 3

B. 4,860 ÷ 3,000

C. 48.6 ÷ 3

D. 4.86 ÷ 0.03

E. 0.0486 ÷ 0.003

195.52 ÷ 32 6.11

0.495 ÷ 15

8. Toby compra camisas nuevas. Las camisas cuestan $8 cada una. ¿Cuál es el mayor número de camisas que Toby puede comprar con $107.60?

Toby puede comprar 13 camisas.

9. Adesh tiene 4.65 libras de fruta seca. Coloca la fruta seca en 5 bolsitas. Coloca una cantidad igual de fruta seca en cada bolsita. ¿Cuántas libras de fruta seca coloca Adesh en cada bolsita?

Adesh coloca 0.93 libras de fruta seca en cada bolsita.

EUREKA MATH

EUREKA MATH

Recuerda

En los problemas 10 a 13, resta.

14. Divide. Expresa el cociente como un número decimal. Si es necesario, redondea al milésimo más cercano.

15. Usa <, > o = para hacer que cada oración numérica sea verdadera.

a. 0.456 < 0.546

b. 0.010 = 0.01

c. 0.083 < 0.83 d. 2.04 > 2.035

Dividir un número decimal entre otro número decimal mayor que 1

Dividir un número decimal entre otro número decimal mayor que 1 usando el algoritmo estándar

Vistazo a la lección

En esta lección, la clase aprende a dividir un número decimal entre otro número decimal. Sus estudiantes comienzan usando la estimación para razonar acerca del cociente de dos números decimales. Examinan de qué manera multiplicar el dividendo y el divisor por una potencia de 10 cambia el cociente. En parejas, usan operaciones matemáticas y estrategias de cálculo mental para dividir números decimales entre otros números decimales mayores que 1. Aprenden por qué se escriben las expresiones de división con números enteros como divisores al usar el algoritmo estándar. Trabajan en parejas para dividir números decimales con el algoritmo estándar y para analizar trabajos con divisiones en busca de errores.

Pregunta clave

• ¿Cómo usamos el algoritmo estándar para dividir un número decimal entre otro número decimal? ¿Por qué funciona?

Criterio de logro académico

6.Mód2.CLA11 Dividen números decimales de varios dígitos.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• Números decimales como divisores

• Dividir números decimales con el algoritmo estándar

• Análisis de errores en la división con números decimales

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• ninguno

Preparación de la lección

• No se necesita.

Fluidez

Dividir con el algoritmo estándar

La clase usa el algoritmo estándar a fin de dividir números enteros como preparación para dividir números decimales entre otros números decimales.

Instrucciones: Divide usando el algoritmo estándar.

Presentar

La clase determina si el cociente de dos números decimales es correcto.

Muestre 17.4 ÷ 1.2. Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta:

Ryan divide 17.4 entre 1.2 y obtiene 1.45. ¿Tiene sentido la respuesta de Ryan? Expliquen.

La respuesta de Ryan no tiene sentido porque 1.2 multiplicado por 1.45 no es igual a 17.4. El producto de 1.2 y 1.45 debe estar cerca de 1.

Después de que diferentes estudiantes compartan sus respuestas, confirme que la respuesta de Ryan es incorrecta. 5

Muestre el trabajo de Ryan que usa el algoritmo estándar para la división.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

Consideren el trabajo de Ryan que usa el algoritmo estándar para calcular 17.4 ÷ 1.2. ¿Qué observan? ¿Qué se preguntan?

Observo que los puntos decimales del dividendo y del cociente se alinean. Observo que el divisor tiene un punto decimal. Me pregunto dónde está el error de Ryan.

¿Cómo saben que la respuesta de Ryan es incorrecta?

La respuesta de Ryan es incorrecta porque el cociente de 17.4 y 1.2 debe estar cerca de 17. Para estimar el cociente, redondeé 17.4 hacia abajo a 17 y redondeé 1.2 hacia abajo a 1, y el cociente de 17 y 1 es 17.

Sabemos que el trabajo de Ryan es incorrecto porque su respuesta no tiene sentido. Cuando estimamos, sabemos que la respuesta será aproximadamente 17.

Hoy, aprenderemos acerca del error que cometió Ryan y cómo dividir números decimales entre otros números decimales mayores que 1.

Aprender

Números decimales como divisores

La clase razona acerca del valor posicional para dividir un número decimal entre otro número decimal.

Muestre las expresiones que son equivalentes a 485 ÷ 12.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Cuál de estas expresiones de división tiene el mismo cociente que 485 ÷ 12?

Todas

¿Cómo sabemos que todas estas expresiones de división tienen el mismo cociente que 485 ÷ 12?

Si tanto el dividendo como el divisor se multiplican por o se dividen entre la misma potencia de 10, entonces la expresión de división tiene el mismo cociente.

En el tema B, comentamos por qué 8 décimos ÷ 4 décimos y 8 centenas ÷ 4 centenas tienen el mismo cociente. Podemos aplicar esa misma lógica cuando dividimos entre números decimales: 485 milésimos ÷ 12 milésimos tiene el mismo cociente que 485 ÷ 12.

Cuando se nos da alguna de estas expresiones de división, podemos reescribirla como 485 ÷ 12, lo que transforma la expresión de división en una división de dos números enteros. Para evaluar esa expresión, podemos usar el algoritmo estándar para la división como hicimos en el tema anterior.

Brinde varios minutos para que sus estudiantes completen los problemas 1 a 3.

En los problemas 1 a 3, escribe la expresión de división como la división de dos números enteros. Luego, divide.

1. 6 ÷ 1.2

Ejemplo: 60 ÷ 12

5

2. 4.5 ÷ 1.5

Ejemplo: 45 ÷ 15

3

3. 5.25 ÷ 2.5

Ejemplo: 525 ÷ 250 2.1

Cuando la mayoría haya terminado, invite a sus estudiantes a compartir sus soluciones y los números enteros que eligieron usar para la división. Luego, use las preguntas que siguen para guiar una conversación:

Cada una de estas expresiones puede escribirse como una expresión equivalente con un número entero como divisor. ¿Por qué queremos dividir entre un número entero?

Ejemplo: Cuando dividimos entre un número entero, podemos alinear el dividendo y el cociente según el valor posicional y sabemos que el punto decimal estará en la posición correcta.

En el problema 3, parte de la clase escribió la expresión de división equivalente 52.5 ÷ 25, que tiene un número decimal como dividendo. ¿El dividendo en la expresión equivalente también tiene que ser un número entero para que el cociente y el dividendo se puedan alinear según el valor posicional? ¿Por qué?

No, solo el divisor tiene que ser un número entero. La expresión 52.5 ÷ 25 es equivalente a 525 ÷ 250.

¿Cuál es la ventaja de multiplicar tanto el dividendo como el divisor por 10 o por otra potencia de 10?

Multiplicar los dos números por una potencia de 10 hace una expresión equivalente con un número entero como divisor, lo que hace que sea más fácil dividir.

Diferenciación: Desafío

Anime a quienes completen de manera rápida los problemas 1 a 3 a usar otro método para calcular los cocientes.

Además, considere pedir a sus estudiantes que evalúen la siguiente expresión:

DUA: Representación

Considere escribir comentarios en los ejemplos para dirigir la atención de sus estudiantes hacia la relación entre las expresiones con números decimales y sus expresiones equivalentes sin números decimales. 4.5÷ 1.5

¿Podríamos multiplicar tanto el dividendo como el divisor por un número que no sea 10?

Expliquen o den un ejemplo.

Sí. Podríamos usar cualquier número. Por ejemplo, 12 ÷ 4 = 3. Si multiplico tanto el dividendo como el divisor por 2, obtengo 24 ÷ 8, que también es igual a 3.

Siempre que multipliquemos el dividendo y el divisor por el mismo número, podemos multiplicar por cualquier número que haga que el divisor sea un número entero. Por ejemplo, 3 ÷ 1.5 es equivalente a 6 ÷ 3. En este caso, multiplicamos tanto el dividendo como el divisor por 2. Las dos expresiones de división son equivalentes.

Dividir números decimales con el algoritmo estándar

La clase divide un número decimal entre otro número decimal mayor que 1 usando el algoritmo estándar.

Muestre el trabajo de Ryan.

Repasemos el trabajo de Ryan del comienzo de la lección. ¿Qué error cometió Ryan en su trabajo?

Ryan ignoró el punto decimal en el divisor y dividió 17.4 entre 12 en lugar de hacerlo entre 1.2.

¿Cómo podría Ryan escribir correctamente este trabajo de división?

Ryan podría multiplicar tanto el dividendo como el divisor por 10 para dividir 174 entre 12.

Antes de usar el algoritmo estándar para la división, ¿qué deben hacer con cualquier expresión de división que tenga un número decimal como divisor?

Debo multiplicar el dividendo y el divisor por la misma potencia de 10 para escribir la expresión de división como una expresión de división equivalente con un número entero como divisor.

Brinde a sus estudiantes varios minutos para que completen los problemas 4 a 7 de manera individual o en parejas. Recorra el salón de clases mientras trabajan y pídales que escriban las expresiones de división con un número entero como divisor según sea necesario.

En los problemas 4 a 7, escribe la expresión de división con números decimales como una expresión equivalente con un número entero como divisor. Luego, estima el cociente y usa el algoritmo estándar para dividir.

4. 39.2 ÷ 4.9

Expresión de división equivalente: Estimación: 8

5. 34.84 ÷ 6.7

Expresión de división equivalente: Estimación: 5

Diferenciación: Apoyo

A fin de brindar apoyo adicional a sus estudiantes, considere proporcionar una secuencia alternativa de expresiones de división con menos dígitos en lugar de los problemas 4 a 7.

• 8.2 ÷ 2.1

• 53.6 ÷ 6.7

• 8.67 ÷ 3.4

• 0.91 ÷ 1.3

6. 11.61 ÷ 8.6

Expresión de división equivalente: Estimación: 1.5

7. 0.3808 ÷ 1.12

Cuando la mayoría haya terminado, reúna a la clase para comentar los problemas 4 a 7. Comparta las soluciones con la clase. Pregunte a sus estudiantes qué expresión de división usaron para cada problema. Luego, haga las siguientes preguntas:

¿Por qué debemos escribir una expresión de división equivalente para cada problema?

Debemos escribir una expresión de división equivalente para tener un número entero como divisor que dé el mismo cociente que la expresión original.

¿Hay más de una expresión que podrían usar para cada problema? Expliquen.

Sí. Podríamos usar cualquier expresión que sea equivalente a la expresión dada.

¿Qué hace que el problema 7 sea diferente de los otros problemas?

Estamos dividiendo un número más pequeño entre un número más grande.

Aunque estamos dividiendo un número más pequeño entre un número más grande en el problema 7, ¿podemos usar el mismo proceso para calcular el cociente?

Sí.

¿Por qué el cociente del problema 7 tiene un 0 en la posición de las unidades?

Como el divisor es mayor que el dividendo, el cociente será menor que 1.

Análisis de errores en la división con números decimales

La clase analiza los errores en diferentes trabajos de división.

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

Para calcular 3.69 ÷ 1.2, Noah divide 3,690 entre 1,200. ¿Funciona su método? ¿Harían algo de otra manera?

Su método funciona, pero no es muy eficiente. Dividiría 36.9 entre 12.

Podemos multiplicar los dos números en una expresión de división por cualquier potencia de 10, pero elegir intencionalmente por qué potencia de 10 multiplicamos nos permite ser más eficientes.

Dirija la atención de sus estudiantes a los problemas 8 a 11. Brinde varios minutos para que completen los problemas en parejas.

Apoyo para la comprensión del lenguaje

Pida a quienes estén aprendiendo el idioma que usen la sección Estar de acuerdo o en desacuerdo de la Herramienta para la conversación cuando trabajen en parejas en los problemas de la actividad de Análisis de errores en la división con números decimales.

8. Para calcular 3.69 ÷ 1.2, Lacy escribe la expresión de división como 369 ÷ 12. Explica el error de Lacy.

Ejemplo: Lacy multiplica 3.69 por 100 y multiplica 1.2 por 10 antes de dividir. Debe multiplicar los dos números por la misma potencia de 10.

9. Para calcular 45.8 ÷ 4.16, Leo escribe su división de la siguiente manera. Explica el error de Leo.

416 4 5.8

Ejemplo: Leo escribe 4.16 como 416, pero no escribe 45.8 como 4,580.

10. Jada calcula 8.65 ÷ 2.5 como 34.6 de la siguiente manera. Explica el error de Jada.

Ejemplo: Jada no alinea el cociente y el dividendo según el valor posicional. El cociente debe ser 3.46 en lugar de 34.6

11. Toby calcula 0.084 ÷ 2.4 como 0.35 de la siguiente manera. Explica el error de Toby.

Ejemplo: Toby no alinea el cociente y el dividendo según el valor posicional. El cociente debe ser 0.035 en lugar de 0.35.

Promoción de la práctica de las matemáticas

Cada estudiante ofrece valoraciones sobre el razonamiento de otros y otras cuando, al analizar trabajos con división de números decimales, considera la efectividad de los argumentos y halla errores en el razonamiento.

Considere hacer las siguientes preguntas:

• ¿Qué cambios le harían al trabajo para que sea más preciso?

• ¿Con qué partes del trabajo de Leo están en desacuerdo? ¿Por qué?

Cuando la mayoría haya terminado, elija un problema e invite a diferentes estudiantes a compartir sus respuestas y explicaciones. Permita que conversen acerca del error y cómo se podría corregir. Muestre la división correcta según sea necesario para complementar la comprensión de la clase.

Concluir

Reflexión final 5 min

Objetivo: Dividir un número decimal entre otro número decimal mayor que 1 usando el algoritmo estándar

Use las preguntas que siguen para guiar una conversación acerca de la división de un número decimal entre otro número decimal. Anime a sus estudiantes a desarrollar las respuestas de sus pares.

¿Cómo usamos el algoritmo estándar para dividir un número decimal entre otro número decimal? ¿Por qué funciona?

Escribimos una expresión de división equivalente con un número entero como divisor antes de usar el algoritmo estándar para la división. Funciona porque estamos usando el algoritmo para la división de la misma manera que lo hacemos con los números enteros.

¿En qué se parece dividir números decimales a dividir números enteros?

Para dividir números decimales, podemos usar las mismas estrategias que usamos para dividir números enteros, como la estimación, el cálculo mental, la descomposición y el algoritmo estándar.

¿En qué se diferencia la división de números decimales de la división de números enteros?

Es posible que tengamos que escribir una expresión de división con números decimales como una expresión equivalente con un número entero como divisor antes de dividir.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección.

Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Dividir un número decimal entre otro número decimal mayor que 1

En esta lección:

• dividimos un número decimal entre otro número decimal mayor que 1 usando el algoritmo estándar.

Ejemplos

1. Jada dice que puede hallar 64.28 ÷ 2.5 si calcula 642.8 ÷ 25 ¿Está Jada en lo correcto? Explica.

Sí. Jada multiplica tanto el dividendo como el divisor de 64.28 ÷ 2.5 por 10 para crear la expresión de división equivalente 642.8 ÷ 25

Multiplicar el dividendo y el divisor por el mismo valor no cambia el cociente.

En los problemas 2 a 4, escribe la expresión de división con números decimales como una expresión equivalente con un número entero como divisor. Luego, usa el algoritmo estándar para dividir.

2. 149.1 ÷ 3.55

Expresión equivalente: 14,910 ÷ 355 –7 10 35 51 4,9 10 0

Multiplica tanto el dividendo como el divisor por 100 para crear una expresión de división equivalente con un número entero como divisor. La expresión 14,910 ÷ 355 es equivalente a 149.1 ÷ 3.55.

Multiplica el dividendo y el divisor por la misma potencia de 10 para crear una expresión de división equivalente con un número entero como divisor. Observa que no es necesario que el dividendo sea un número entero.

El residuo no es 0 al restar 390 de 468. Para continuar dividiendo, coloca un punto decimal a la derecha del 8 en la posición de las unidades en el dividendo de manera que se pueda escribir un 0 en la posición de las decenas.

© Great Minds PBC

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. ¿Qué expresiones son equivalentes a 634.7 ÷ 1.23? Elige todas las opciones que correspondan.

A. 6,347 ÷ 12.3

B. 63,470 ÷ 123

C. 634.7 ÷ 12.3

D. 634.7 ÷ 123

E. 63.47 ÷ 12.3

F. 63.47 ÷ 123

2. Jada dice que puede hallar 38.4 ÷ 1.6 si calcula 384 ÷ 16. ¿Está Jada en lo correcto? Explica. Sí. Jada está en lo correcto. Multiplica tanto el dividendo como el divisor por 10 para crear una expresión de división equivalente.

En los problemas 3 a 10, calcula el cociente.

multiplicó el divisor por 100 pero multiplicó el dividendo solo por 10.

EUREKA MATH

Recuerda

En los problemas 12 a 15, resta. 12. 4 3

16. Un criador de gallinas recoge huevos y los coloca en envases de cartón. Recoge 384 huevos y coloca 12 huevos en cada envase. ¿Cuántos envases de cartón llena el criador?

Llena 32 envases de cartón.

17. El maestro Pérez organiza una fiesta con pizzas para su clase. Quiere saber cuántas pizzas debería pedir para 30 estudiantes. Hay 8 porciones por pizza. ¿Cuál es el menor número de pizzas que puede pedir para que cada estudiante reciba 3 porciones?

A. 8 pizzas

B. 10 pizzas

C. 11 pizzas

D. 12 pizzas

Dividir un número decimal entre otro número decimal menor que 1

Dividir un número decimal entre otro número decimal menor que 1 usando el algoritmo estándar

Resolver problemas del mundo real dividiendo un número decimal entre otro número decimal

Vistazo a la lección

En esta lección, la clase adquiere fluidez con la división de números decimales entre otros números decimales. Sus estudiantes usan cálculos mentales para razonar sobre la división con números decimales y para expresar números decimales como fracciones o para convertir números decimales en números enteros antes de dividir. En un Intercambio con la pizarra blanca, usan operaciones matemáticas para dividir un número decimal entre otro número decimal menor que 1. Estiman cocientes y usan el algoritmo estándar para dividir números decimales. En estaciones, trabajan en parejas para resolver problemas del mundo real que incluyen cálculos con números decimales.

Preguntas clave

• ¿Cuál es la importancia del valor posicional al dividir números decimales?

• ¿Qué situaciones del mundo real pueden representarse mediante expresiones de división con números decimales?

Criterio de logro académico

6.Mód2.CLA11 Dividen números decimales de varios dígitos.

Agenda

Fluidez

Presentar 5 min

Aprender 30 min

• División con números decimales en la pizarra blanca

• División con números decimales usando el algoritmo estándar

• Estaciones de división con números decimales

Concluir 10 min

Materiales

Maestro o maestra

• ninguno

Estudiantes

• tarjetas de las Estaciones de división con números decimales

Preparación de la lección

• Haga cuatro copias de cada tarjeta de las Estaciones de división con números decimales y recórtelas. Organice cuatro estaciones. Coloque un grupo de tarjetas en cada estación.

Fluidez

Dividir números enteros entre fracciones

La clase divide números enteros entre fracciones como preparación para dividir números decimales entre otros números decimales.

Instrucciones: Divide.

Presentar

La clase ordena expresiones en las que se divide un número decimal entre otro número decimal.

Divida a sus estudiantes en grupos de 3 o 4. Muestre la imagen y la tabla de Banquete para hormigas.

En cada banquete para hormigas, se divide una cantidad de azúcar en porciones de un determinado tamaño. Cada hormiga recibe una porción.

1,201 gramos de azúcar

Banquete A

Banquete B

Cada hormiga recibe 0.31 gramos de azúcar.

12,002 gramos de azúcar

Cada hormiga recibe 3.1 gramos de azúcar.

120.2 gramos de azúcar

Banquete C

Banquete D

Cada hormiga recibe 0.031 gramos de azúcar.

120,007 gramos de azúcar

Cada hormiga recibe 31 gramos de azúcar.

Use los siguientes planteamientos para explicar la tarea:

En la tabla, se muestra el número total de gramos de azúcar que se sirve en cada banquete y el número de gramos de azúcar que recibe cada hormiga en cada banquete.

Queremos determinar en qué banquete puede comer el mayor número de hormigas y en cuál puede comer el menor número de hormigas. En sus grupos, ordenen los banquetes del menor número de hormigas que pueden comer al mayor número de hormigas que pueden comer. Prepárense para explicar su razonamiento.

Banquete D, banquete B, banquete A, banquete C

Apoyo para la comprensión del lenguaje

Diga a la clase que un banquete es una comida para un grupo grande de personas. Considere mostrar imágenes de banquetes o hacer las siguientes preguntas:

• ¿Alguna vez estuvieron en un banquete?

• ¿Por qué estuvieron en el banquete?

• ¿Pueden describir cómo era el banquete?

Cuando la mayoría haya terminado, invite a los grupos a compartir sus respuestas y su razonamiento. Resalte las respuestas en las que se escriban expresiones de división equivalentes.

¿Cómo podemos ordenar los banquetes sin hacer ninguna división?

Podemos escribir una expresión de división para cada banquete que tenga 31 como divisor. Luego, podemos comparar los dividendos.

¿Cómo podemos escribir una expresión de división para cada banquete que tenga 31 como divisor?

Para escribir una expresión de división para cada banquete que tenga 31 como divisor, podemos multiplicar el dividendo y el divisor en cada expresión de división por una potencia de 10.

¿Cuáles son las expresiones de división para cada banquete escritas con 31 como divisor?

Banquete A: 120,100 ÷ 31

Banquete B: 120,020 ÷ 31

Banquete C: 120,200 ÷ 31

Banquete D: 120,007 ÷ 31

¿Cómo sabemos que en el banquete C pueden comer más hormigas que en el banquete B?

Ejemplo: En el banquete C hay más azúcar que en el banquete B para dividir en porciones del mismo tamaño. Entonces, en el banquete C pueden comer más hormigas.

En el problema del Banquete para hormigas, podemos razonar acerca de los cocientes de números decimales sin hacer ninguna división. Hoy, aprenderemos a dividir un número decimal entre otro número decimal menor que 1 como ayuda para resolver problemas y responder preguntas como “¿Cuántas hormigas pueden comer en el banquete A?”.

Aprender

División con números decimales en la pizarra blanca

La clase hace cálculos mentales para dividir números decimales entre otros números decimales.

Muestre 0.6 ÷ 0.2. Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Cuál es el valor de la expresión? Expliquen.

3. Hay 3 grupos de 2 décimos en 6 décimos.

¿Por qué 0.6 ÷ 0.2 no es igual a 0.3?

0.3 × 0.2 es igual a 0.06 y no a 0.6.

¿Cuáles son algunas expresiones de división que son equivalentes a 0.6 ÷ 0.2?

Ejemplo: 6 10 ÷ 2 10 , 6 ÷ 2, 60 ÷ 20, 60 100 ÷ 20 100 , 0.6 0.2 , 6 2

Podemos usar lo que sabemos sobre valor posicional para dividir números decimales. Por ejemplo, pensar en 6 décimos dividido entre 2 décimos como 6 ÷ 2 o escribir la división con números decimales como una división de fracciones puede ser útil.

En el siguiente Intercambio con la pizarra blanca, permita que sus estudiantes trabajen de manera individual o en parejas:

Pensemos en la división con números decimales como una división con números enteros para practicar cómo dividir números decimales entre otros números decimales. Escribiré una expresión de división en el pizarrón. Calculen su valor y levanten la pizarra blanca para que pueda verla.

Dé una expresión a la vez y compruebe las respuestas de la clase después de cada expresión. Brinde retroalimentación inmediata. Anime a sus estudiantes a usar estrategias de cálculo mental y el razonamiento sobre el valor posicional para calcular los cocientes, pero también permita un razonamiento flexible. Haga una pausa ocasionalmente para abordar los conceptos erróneos

DUA: Representación

Cree y muestre un afiche con el título “Expresiones de división equivalentes” para mostrar distintas expresiones de división que sean equivalentes a 0.6 ÷ 0.2.

Brinde otro ejemplo, como expresiones de división que sean equivalentes a 0.44 ÷ 1.1.

o para invitar a sus estudiantes a compartir el razonamiento. Las expresiones de división están ordenadas de menor a mayor dificultad. Puede elegir no usar todas las expresiones.

Diferenciación: Apoyo

Para brindar apoyo adicional a sus estudiantes, considere usar las siguientes modificaciones:

• Anime a sus estudiantes a expresar los números decimales como fracciones. Por ejemplo, 0.63 ÷ 0.07 se puede escribir como 63 100 ÷ 7 100 .

• Proporcione expresiones adicionales semejantes a las primeras siete y no use las últimas cinco.

Diferenciación: Desafío

Para ofrecer un desafío adicional a sus estudiantes, considere proporcionar expresiones en las que el divisor sea mayor que el dividendo. Pídales que expresen sus respuestas como números decimales o como fracciones con la unidad más grande posible.

• 0.05 ÷ 0.1

• 0.04 ÷ 0.024

• 0.12 ÷ 9.6

¿En qué se diferencia la última expresión de división, 3 ÷ 0.08, de las expresiones anteriores?

El cociente no es un número entero.

¿Qué estrategia prefirieron usar para resolver la mayoría de estos problemas de división con números decimales?

Ejemplo: Pensé en los números decimales como fracciones. Convertí los números decimales a números enteros antes de dividir.

¿Cuáles son los beneficios de usar estrategias de cálculo mental al dividir números decimales?

Ejemplo: A veces, usar el cálculo mental nos permite dividir sin tener que usar el algoritmo estándar.

División con números decimales usando el algoritmo estándar

La clase divide números decimales entre otros números decimales usando el algoritmo estándar.

Dirija la atención de sus estudiantes al problema 1.

En los ejemplos anteriores, no necesitamos usar el algoritmo estándar para dividir. En los siguientes tres problemas, escribirán expresiones de división con números enteros como divisores antes de usar el algoritmo estándar para la división.

Pida a la clase que estime el cociente. Invite a un par de estudiantes a compartir sus estimaciones y estrategias. Resalte las estrategias en las que se escriba una expresión de división equivalente con un número entero como divisor, como 14.72 ÷ 3.2 escrito como 147.2 ÷ 32.

Brinde varios minutos para que sus estudiantes completen los problemas 1 a 3 de manera individual.

En los problemas 1 a 3, escribe la expresión de división con números decimales como una expresión equivalente con un número entero como divisor. Luego, estima el cociente y usa el algoritmo estándar para dividir. Si es necesario, redondea las respuestas al centésimo más cercano.

1. 1.472 ÷ 0.32

Expresión de división equivalente: 147.2 ÷ 32

Estimación: 5

Diferenciación: Apoyo

Si es necesario, considere proporcionar expresiones de división que tengan números con menos valores posicionales.

• 2.24 ÷ 0.32

• 4.35 ÷ 0.02

• 0.15 ÷ 0.6

2. 4.714 ÷ 0.021

Expresión de división equivalente: 4,714 ÷ 21

Estimación: 225

3. 0.128 ÷ 0.15

Expresión de división equivalente: 12.8 ÷ 15

Estimación: 1

Cuando la mayoría haya terminado, reúna a la clase y use las siguientes preguntas para hacer una reflexión final sobre el trabajo:

¿Qué paso siguieron antes de usar el algoritmo estándar para la división?

Reescribí la expresión de división con un número entero como divisor.

¿Cómo saben dónde ubicar el punto decimal en el cociente?

El punto decimal del cociente se alinea con el punto decimal del dividendo. Lo sé porque el cociente y el dividendo se alinean según el valor posicional.

Estaciones de división con números decimales

La clase divide números decimales entre otros números decimales para resolver problemas del mundo real.

Lea en voz alta con sus estudiantes las instrucciones para la actividad de Estaciones de división con números decimales. Permítales que trabajen en parejas. Deben completar tantos problemas como puedan. Tenga en cuenta que parte de la clase podría no completar las cuatro estaciones.

Mientras sus estudiantes trabajan, recorra el salón de clases y escuche sus estrategias. Preste atención al uso eficiente del cálculo mental y las operaciones matemáticas.

Apoyo para la comprensión del lenguaje

Anime a sus estudiantes a usar la sección Compartir tu razonamiento de la Herramienta para la conversación a fin de que comuniquen sus ideas mientras trabajan en la actividad de Estaciones de división con números decimales.

Instrucciones: Trabaja en pareja para completar tantas estaciones como puedan en el tiempo asignado. Después de completar una estación, comprueben su solución con su maestra o maestro antes de pasar a una nueva estación. Pueden completar las estaciones en cualquier orden. Justifiquen sus soluciones.

Estación 1

Estación 2

Estación 3

Estación 4

Cuando la mayoría haya terminado, seleccione una estación e invite a sus estudiantes a compartir sus soluciones.

DUA: Representación

Como preparación para las estaciones 2 y 3, repase la conversión de unidades y las estrategias de porcentaje a fin de activar los conocimientos previos de sus estudiantes. Por ejemplo, comente lo siguiente:

• Cómo convertir entre onzas y libras

• Cómo interpretar problemas de porcentaje del mundo real

• Cómo resolver distintos tipos de problemas de porcentaje Promoción de la práctica de las matemáticas

Cada estudiante da sentido a los problemas y persevera en su resolución cuando resuelve problemas de división con números decimales al hallar puntos de partida, observar su propio progreso y analizar si los valores que calculan tienen sentido.

Considere hacer las siguientes preguntas:

• ¿Cuáles son algunas estrategias que podrían probar para comenzar a resolver el problema?

• ¿Cómo pueden simplificar el problema?

• ¿Tiene sentido su respuesta?

Concluir

Reflexión final 5 min

Objetivos: Dividir un número decimal entre otro número decimal menor que 1 usando el algoritmo estándar

Resolver problemas del mundo real dividiendo un número decimal entre otro número decimal

Pida a sus estudiantes que usen la rutina Pensar-Trabajar en parejas-Compartir para responder las siguientes preguntas:

¿Cuál es la importancia del valor posicional en la división con números decimales?

Alinear el dividendo y el cociente según el valor posicional al usar el algoritmo estándar nos permite determinar dónde insertar el punto decimal.

¿Qué situaciones del mundo real pueden representarse mediante expresiones de división con números decimales?

Ejemplo: Una situación que requiere calcular una tasa puede representarse con una expresión de división con números decimales.

Al resolver problemas del mundo real que incluyen la división con números decimales, ¿cómo saben qué número es el dividendo y qué número es el divisor?

Si sé qué número representa el total, entonces sé qué número es el dividendo. Si sé qué número representa el número de grupos o el tamaño de los grupos, entonces sé qué número es el divisor.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Dividir un número decimal entre otro número decimal menor que 1

En esta lección:

• dividimos un número decimal entre otro número decimal menor que 1 usando el algoritmo estándar;

• resolvimos problemas del mundo real dividiendo un número decimal entre otro número decimal.

Ejemplos

1. ¿Qué expresiones de división son equivalentes a 5.2 ÷ 0.045? Elige todas las opciones que correspondan.

A. 52 ÷ 0.45

B. 252 ÷ 0.45

C. 520 ÷ 4.5

D. 0.52 ÷ 0.045

E. 5,200 ÷ 45

Multiplica tanto el dividendo como el divisor por 10 para crear esta expresión equivalente.

Multiplica tanto el dividendo como el divisor por 100 para crear esta expresión equivalente.

Multiplica tanto el dividendo como el divisor por 1,000 para crear esta expresión equivalente. 2. Divide.

40.5 ÷ 0.54

40.5 ÷ 0.54 = 4,050 ÷ 54

4,0

Multiplica tanto el dividendo como el divisor por 100 para crear una expresión equivalente que no tenga un punto decimal en el divisor.

3. Divide. Si es necesario, redondea al centésimo más cercano. 0.136 ÷ 0.54

Para redondear al centésimo más cercano, primero calcula el cociente a la posición de los centésimos.

0.251 ≈ 0.25

El punto decimal del cociente se alinea con el punto decimal del dividendo, ya que el cociente y el dividendo se alinean según el valor posicional.

4. Una carretera mide 12.8 millas de largo. Hay una farola a 0.8 millas del inicio de la carretera. Hay una farola cada 0.8 millas a partir de allí. ¿Cuántas farolas hay a lo largo de la carretera? 12.8 ÷ 0.8 = 128 ÷ 8

Divide 12.8 entre 0.8 para determinar el número de farolas a lo largo de la carretera de 12.8 millas. – 8 81 28 48 16 –4 8 0

Hay 16 farolas a lo largo de la carretera.

© Great Minds PBC

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

Soluciones de las Tarjetas de las Estaciones de división con números decimales

Estación 1

Scott lleva una bolsita con nickels al banco. Quiere cambiar los nickels por dólares. Recibe

$8.85 por los nickels. ¿Cuántos nickels lleva Scott al banco?

Scott lleva 177 nickels al banco.

Estación 2

Un grupo de canicas pesa 1.35 libras. Cada canica pesa 0.15 onzas. ¿Cuántas canicas hay en el grupo?

El grupo de canicas

onzas.

Hay 144 canicas en el grupo.

Estación 3

Yuna ahorra $161.25. Esta cantidad representa el 15 % de la cantidad que quiere ahorrar. ¿Cuánto dinero quiere ahorrar Yuna?

Yuna quiere ahorrar $1,075.

Estación 4

Se considera que la lluvia es intensa si cae a una tasa de más de 0.76 centímetros por hora. En una ciudad, caen 5.68 pulgadas de lluvia en 7.5 horas. ¿Se considera lluvia intensa? Expliquen.

Usen 1 pulgada = 2.54 centímetros –5 2 5 75 5 6. 800 4 30 0. 757 –3 75

La lluvia cayó a una tasa de aproximadamente 0.76 pulgadas por hora. 0.76 × 2.54 = 1.9304

Sí. La lluvia cayó a una tasa de aproximadamente 1.9304 centímetros por hora, que es más que 0.76 centímetros por hora. Entonces, se considera lluvia intensa.

ÁCTICA 23

1. ¿Cuánto es 0.21 ÷ 0.07 ? Explica. 3 21 ÷ 7 es equivalente a 0.21 ÷ 0.07 y 21 ÷ 7 = 3

2. ¿Qué expresiones de división son equivalentes a 2.3 ÷ 0.056? Elige todas las opciones que correspondan.

A. 23 ÷ 0.56

B. 2.3 ÷ 0.56

C. 230 ÷ 5.6

D. 0.23 ÷ 0.056

E. 2,300 ÷ 56

En los problemas 3 a 10, divide.

3.

11. Un club de atletismo dispone estaciones de hidratación cada 0.8 millas en una carrera de 6.2 millas. ¿Cuántas estaciones de hidratación dispone el club?

El club de atletismo dispone 7 estaciones de hidratación.

12. Una farmacéutica tiene 18.5 gramos de una determinada medicación. La farmacéutica llena cápsulas con la medicación. Cada cápsula debe contener 0.735 gramos de la medicación. ¿Cuántas cápsulas puede llenar la farmacéutica?

La farmacéutica puede llenar 25 cápsulas.

Recuerda

En los problemas 13 a 16, resta.

17. Divide usando el algoritmo estándar. Expresa el cociente como un número decimal.

Si es necesario, redondea al centésimo más cercano. 15.535 ÷ 12

1.29

18. ¿Qué valores son mayores que 409.806? Elige todas las opciones que correspondan.

A. 409.186

B. 409.81

C. 490.806

D. 409.086

E. 409.805

Estación 1

Scott lleva una bolsita con nickels al banco. Quiere cambiar los nickels por dólares.

Recibe $8.85 por los nickels . ¿Cuántos nickels lleva Scott al banco?

Estación 2

Un grupo de canicas pesa 1.35 libras. Cada canica pesa 0.15 onzas. ¿Cuántas canicas hay en el grupo?

Estación 3

Yuna ahorra $161.25 . Esta cantidad representa el 15 % de la cantidad que quiere ahorrar. ¿Cuánto dinero quiere ahorrar Yuna?

Estación 4

Se considera que la lluvia es intensa si cae a una tasa de más de 0.76 centímetros por hora.

En una ciudad, caen 5.68 pulgadas de lluvia en 7.5 horas. ¿Se considera lluvia intensa?

Expliquen.

Usen 1 pulgada = 2.54 centímetros

Vivir en Marte

Resolver problemas del mundo real usando operaciones con números decimales

La Estación Espacial Internacional (ISS, por sus siglas en inglés) orbita la Tierra a una velocidad de aproximadamente 4.76 millas por segundo. Supón que orbita a una velocidad constante.

¿Aproximadamente cuántos minutos tarda la ISS en recorrer 1,000 millas? Redondea tu respuesta al décimo más cercano.

Vistazo a la lección

En esta lección digital, sus estudiantes realizan operaciones con números decimales para resolver problemas en el contexto de la vida en Marte. Miran un video que les presenta la idea de cómo podría ser la vida en Marte. Luego, trabajan en distintos problemas contextuales y usan actividades interactivas para confirmar sus respuestas.

Use la plataforma digital para preparar y enseñar esta lección. Sus estudiantes también explorarán el contenido de la lección y las actividades a través de la plataforma digital.

Pregunta clave

• ¿En qué situaciones del mundo real se usa la multiplicación o la división de números decimales?

Criterios de logro académico

6.Mód2.CLA2 Resuelven problemas verbales realizando operaciones con números decimales de varios dígitos.

6.Mód2.CLA11 Dividen números digitales de varios dígitos.

Agenda

Fluidez

Presentar 5 min D

Aprender 30 min D

• La vida en Marte

Concluir 10 min

Materiales

Maestra o maestro

• ninguno

Estudiantes

• computadoras o dispositivos (1 por pareja de estudiantes)

Preparación de la lección

• No se necesita.

Fluidez

Sumar y restar números decimales

La clase suma o resta números decimales como preparación para resolver problemas del mundo real que incluyen números decimales.

Instrucciones: Suma o resta.

Presentar

La clase se familiariza con la idea de la vida en Marte.

Sus estudiantes miran un video sobre un viaje a Marte y la vida allí. Luego, consideran y planifican qué provisiones llevar para sobrevivir en Marte.

¿Qué recursos naturales tenemos en la Tierra que necesitaremos llevar a Marte?

Necesitaremos llevar agua, alimento y oxígeno a Marte porque no podemos conseguir esos recursos allí.

¿Qué información sobre estos recursos necesitan saber a fin de prepararse para el viaje?

Tenemos que saber qué cantidad de alimento, agua y oxígeno necesitamos para el tiempo que estaremos allí. Debemos saber cuánto necesitamos que duren las provisiones.

Necesitamos saber el costo y la cantidad de espacio que se requiere para transportar las provisiones a Marte.

¿Qué otra información creen que necesitan para viajar a Marte?

Ejemplo: Creo que necesitamos saber cómo viajar a Marte y cómo construir una casa en el medioambiente de Marte.

Aprender

La vida en Marte

La clase usa operaciones con números decimales para resolver problemas relacionados con la supervivencia en Marte.

Se presentan a la clase diferentes situaciones relacionadas con las provisiones necesarias para vivir en Marte. En todas las situaciones, es necesario que sus estudiantes usen operaciones con números decimales. Se les brinda una lista con información que deben usar durante toda la lección. Antes de cada actividad, sus estudiantes deciden qué información de la lista sirve para hallar la respuesta. En la primera actividad, deciden qué información se necesita para responder la pregunta acerca de cuánto tarda un mensaje en llegar a la Tierra desde Marte. Luego, calculan cuántos mensajes podrían enviar y recibir cuando Marte se encuentra a la distancia más lejana a la Tierra.

¿Cómo hallaron el tiempo que tarda su mensaje en llegar de Marte a la Tierra cuando los planetas se encuentran a la distancia más lejana entre sí?

Como la velocidad de la luz no está dada en millones de millas por segundo, tuvimos que dividir 186,000 millas entre 1,000,000 primero para que los números tuvieran las mismas unidades. Luego, dividimos la distancia más lejana entre Marte y la Tierra, 250 millones de millas, entre la velocidad de la luz, 0.186 millones de millas por segundo. La respuesta está expresada en segundos, así que dividimos entre 60 para hallar el número de minutos.

Promoción de la práctica de las matemáticas

Cada estudiante da sentido a los problemas y persevera en su resolución cuando halla puntos de partida, analiza la relación entre valores dados, presta atención a las unidades y determina si su respuesta es razonable para resolver problemas de varios pasos.

Considere hacer las siguientes preguntas:

• ¿Cuáles son algunas estrategias que pueden probar para comenzar a resolver el problema?

• ¿Tiene sentido su respuesta?

• ¿Qué información u operaciones necesitan para resolver el problema?

Imaginen que Marte se encuentra a la distancia más lejana a la Tierra y que envían un mensaje a una persona que está en la Tierra. ¿Cuántos minutos tardarán en recibir una respuesta si la persona responde inmediatamente? Expliquen.

El mensaje tarda 22.4 minutos en llegar a la Tierra y 22.4 minutos en volver si la persona responde inmediatamente. Eso da un total de 44.8 minutos.

A continuación, sus estudiantes determinan qué cantidad de alimento, agua y oxígeno necesita una persona para sobrevivir en Marte durante un periodo de dos años. Descubren que la cantidad que se necesita excede lo que es posible llevar a Marte. Comentan opciones que podrían haber en Marte para conseguir más alimento, agua y oxígeno.

¿Qué problemas creen que podrían surgir al planificar una cantidad exacta de alimento, agua y oxígeno para dos años?

Ejemplo: La misión que lleva las provisiones podría no llegar exactamente en dos años. Podríamos necesitar provisiones adicionales si se demora. Las provisiones podrían ocupar mucho espacio en la nave y eso haría que fuera necesario más combustible.

Registra tus notas y cálculos para cada sección. Si es necesario, redondea las respuestas al centésimo más cercano.

1. Mensaje de radio

Distancia más cercana:

34.8 ÷ 0.186 = 187.097

187.097 ÷ 60 = 3.118

3.12 minutos

Distancia más lejana:

250 ÷ 0.186 = 1,344.086

1,344.086 ÷ 60 = 22.401

22.40 minutos

DUA: Participación

Las actividades digitales están alineadas con el principio de Participación de DUA, dado que incluyen lo siguiente:

• Temas interesantes y atractivos: la situación de la planificación del viaje y los aspectos detallados en el video de la vida en Marte captan el interés y despiertan la curiosidad de sus estudiantes y, al mismo tiempo, brindan un propósito general para la actividad.

• Retroalimentación formativa inmediata: sus estudiantes calculan la cantidad de oxígeno necesaria para la supervivencia de una persona en Marte durante dos años y confirman su respuesta por medio de una actividad interactiva sobre un medidor en un tanque de oxígeno. De esa manera, pueden ajustar su respuesta basándose en la información de la actividad interactiva.

2. Oxígeno

0.84 kilogramos

613.2 ÷ 730 = 0.84

3. Agua 25.9 × 104 = 2,693.6

2,693.6 litros

4. Alimento 1.27 × 3 = 3.81 3.81 × 730 = 2,781.3

2,781.3 libras

5. Total

Alimento: 2,781.3 × 0.45 = 1,251.585

1,251.59 kilogramos

Agua:

2,693.6 kilogramos

Oxígeno:

613.2 kilogramos

Total: 1,251.59 + 2,693.6 + 613.2 = 4,558.39

4,558.39 kilogramos

6. Costo 4,558.39 × 20,000 = 91,167,800

$91,167,800

Concluir

Reflexión final 5 min

Objetivo: Resolver problemas del mundo real usando operaciones con números decimales

Use las preguntas que siguen para guiar una conversación de toda la clase. Anime a sus estudiantes a complementar las respuestas de sus pares.

¿Cuáles son algunos ejemplos de la lección de hoy en los que usamos la multiplicación o la división de números decimales?

Usamos la multiplicación para hallar qué cantidad de alimento, agua y oxígeno necesitamos llevar a Marte. Usamos la división cuando determinamos cuánto tardan las señales de radio en llegar a la Tierra.

¿Cómo saben cuándo usar la división y cuándo la multiplicación? Den un ejemplo.

Usamos la división cuando se separa una cantidad total en grupos iguales o cuando la cantidad total se separó en grupos y estamos hallando cuántas unidades hay en cada uno. Se nos dio la cantidad de oxígeno necesaria para un periodo de dos años y tuvimos que dividir a fin de hallar la cantidad de oxígeno necesaria por día. Usamos la multiplicación cuando necesitamos sumar el mismo número un número dado de veces. Se nos dio una tasa y tuvimos que multiplicar esa tasa por una determinada cantidad de tiempo para hallar la cantidad total de alimento, agua y oxígeno necesaria.

¿Por qué creen que es importante que los cálculos y los modelos sean precisos al planificar un viaje a Marte?

Ejemplo: Es importante que sean precisos porque un pequeño error podría impedir que una nave espacial llegue a destino. Si un modelo o un cálculo no son precisos, las personas que viajan al espacio podrían quedarse sin las provisiones esenciales como el alimento, el agua o el oxígeno.

Boleto de salida 5 min

Proporcione hasta 5 minutos para que cada estudiante complete el Boleto de salida. Es posible recopilar datos formativos incluso si hay estudiantes que no completan todos los problemas.

Nota para la enseñanza

Asigne los problemas de la sección Práctica para que sus estudiantes los completen fuera del horario de clase o los usen durante la clase si sobra tiempo después de la lección. Pídales que consulten la sección Resumen si necesitan ayuda.

Resumen

Vivir en Marte

En esta lección:

• resolvimos problemas del mundo real usando operaciones con números decimales.

Ejemplos

1. Marte tiene menos gravedad que la Tierra. Entonces, la altura del salto de una persona en la Tierra es alrededor de 0.38 veces la altura que tendría el salto de la persona en Marte. La altura del salto de Ryan en la Tierra es 13.5 pulgadas. ¿Cuál sería la altura del salto de Ryan en Marte? Redondea tu respuesta al décimo más cercano.

13.5 ÷ 0.38 = 1,350 ÷ 38

38 1,3 50 .0 0 21 0 20 0 3 5.5 2 – 19 0 1 00 4 2 4 – 76 1 24

–190 –1 14

La altura del salto de una persona en la Tierra es alrededor de 0.38 veces la altura del salto en Marte. Por lo tanto, 13.5 = 0.38 × ?. Para hallar el factor desconocido, divide 13.5 entre 0.38

La altura del salto de Ryan en Marte sería alrededor de 35.5 pulgadas.

Un astronauta respira alrededor de 613.2 kilogramos de oxígeno en 2 años.

a. ¿Cuál es la cantidad total de oxígeno que necesitan 3 astronautas para sobrevivir en una estación espacial durante 2 años?

× 3 61 3.2 1, 83 9.6

Multiplica la cantidad de oxígeno que 1 astronauta respira en 2 años por 3 para hallar la cantidad total de oxígeno que necesitan 3 astronautas.

Se necesitan aproximadamente 1,839.6 kilogramos de oxígeno para que 3 astronautas sobrevivan en una estación espacial durante 2 años.

b. ¿Qué cantidad de oxígeno se necesita por día para que 1 astronauta sobreviva en la estación espacial durante 2 años?

365 × 2 = 730

73 06 13 .2 0

– 58 4 0

29 20 0.8 4

– 29 20 0 1 2

Multiplica el número de días en 1 año por 2 para hallar el número de días en 2 años.

Divide la cantidad de oxígeno necesaria para 2 años entre el número de días en 2 años para determinar la cantidad de oxígeno que 1 astronauta necesita por día.

Se necesitan alrededor de 0.84 kilogramos de oxígeno por día para que 1 astronauta sobreviva en una estación espacial durante 2 años.

c. Un sistema de reciclaje de aire en la estación espacial produce solo aproximadamente 2 kilogramos de oxígeno por día. El resto del oxígeno que se necesita se provee a la estación espacial. ¿Qué cantidad de oxígeno debe proveerse a la estación espacial para que 3 astronautas sobrevivan durante 2 años?

2 × 365 × 2 = 1,460

37 9.6 713

– 1, 46 0.0 1, 83 9.6

El sistema de reciclaje de aire produce un total de 1,460 kilogramos de oxígeno en 2 años.

Deben proveerse aproximadamente 379.6 kilogramos de oxígeno a la estación espacial para que 3 astronautas sobrevivan durante 2 años.

© Great Minds PBC

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

1. Durante el despegue, un cohete tiene una masa de 2.3 millones de kilogramos. Después de haber usado suficiente combustible para alcanzar una altura de 61 kilómetros, su masa es 0.131 millones de kilogramos. ¿Cuánto combustible usa el cohete para alcanzar la altura de 61 kilómetros?

El cohete usa 2.169 millones de kilogramos de combustible.

2. El número de días que tarda la Tierra en orbitar el Sol es aproximadamente 0.531 veces el número de días que tarda Marte en orbitar el Sol. La Tierra tarda 365 días en orbitar el Sol. ¿Cuántos días tarda Marte? Redondea tu respuesta al día más cercano. Marte tarda aproximadamente 687 días en orbitar el Sol.

4. La distancia del Sol a la Tierra es 92.96 millones de millas. La luz viaja a aproximadamente 11 millones de millas por minuto. ¿Aproximadamente cuántos minutos tarda la luz en llegar del Sol a la Tierra? Redondea tu respuesta al centésimo más cercano.

La luz tarda aproximadamente 8.45 minutos en llegar del Sol a la Tierra.

5. La distancia más cercana de la Tierra a la Luna es alrededor de 225 mil millas. La distancia más cercana de la Tierra a Marte es alrededor de 34 millones de millas. ¿Aproximadamente cuántas veces la distancia más cercana de la Tierra a la Luna es la distancia más cercana de la Tierra a Marte? Redondea tu respuesta al décimo más cercano.

La distancia más cercana de la Tierra a Marte es alrededor de 151.1 veces la distancia más cercana de la Tierra a la Luna.

Recuerda

En los problemas 6 a 9, suma o resta.

6.

3. La fuerza de gravedad en Marte es alrededor del 38 % de la fuerza de gravedad en la Tierra. Por lo tanto, el peso de un objeto en Marte es aproximadamente el 38 % del peso del objeto en la Tierra. Una bolsa de manzanas pesa 3 libras en la Tierra. ¿Cuántas libras pesará aproximadamente la bolsa de manzanas en Marte?

La bolsa de manzanas pesará aproximadamente 1.14 libras en Marte.

10. Divide usando el algoritmo estándar. Redondea tu respuesta al milésimo más cercano. 46.41 ÷ 4.5

10.313

11. Usa >, < o = para hacer que cada oración numérica sea verdadera.

a. 1.238 < 1.5

b. 6.736 > 6 × 1 + 7 × 0.1

c. 7 unidades + 8 décimos + 9 centésimos = 7.890

EUREKA

Criterios de logro académico: Indicadores de competencias

6.Mód2.CLA1 Resuelven problemas verbales dividiendo números de varios dígitos con el algoritmo estándar.

Parcialmente competente Competente

Resuelven problemas verbales dividiendo dos números de varios dígitos.

Un estuche con 24 cartuchos de tinta cuesta $498. ¿Cuánto cuesta cada cartucho de tinta?

Altamente competente

Resuelven problemas verbales de varios pasos dividiendo números de varios dígitos.

La compañía A vende 24 cartuchos de tinta por $498. La compañía B vende 50 cartuchos de tinta por $995. ¿Qué compañía ofrece un precio mejor por cartucho de tinta? Explica tu razonamiento.

6.Mód2.CLA2 Resuelven problemas verbales realizando operaciones con números decimales de varios dígitos.

Parcialmente competente

Competente

Resuelven problemas verbales sumando, restando, multiplicando o dividiendo números decimales de varios dígitos.

Un caracol se arrastra 0.78 metros en 60 segundos.

¿Cuál es la velocidad del caracol en metros por segundo?

Altamente competente

Resuelven problemas verbales de varios pasos sumando, restando, multiplicando o dividiendo números decimales de varios dígitos.

Un caracol se arrastra 0.78 metros en 60 segundos. Un perezoso trepa 4.5 metros en 140.6 segundos.

Parte A

¿Qué animal tiene mayor velocidad en metros por segundo?

Parte B

¿Cuánto más rápido se mueve el animal con mayor velocidad en metros por segundo?

6.Mód2.CLA3 Razonan acerca del tamaño de los cocientes de fracciones y números mixtos.

Parcialmente competente

Estiman los cocientes de fracciones y números mixtos.

Escribe <, > o = para hacer que cada oración numérica sea verdadera.

Competente

Justifican estimaciones para los cocientes de fracciones y números mixtos.

Eddie dice que 2 __ 3 ÷ 1 4 es mayor que 2 __ 3 . Mara dice que 2 3 ÷ 1 4 es menor que 2 3 . ¿Quién está en lo correcto? Explica tu razonamiento.

6.Mód2.CLA4 Dividen dos fracciones o números mixtos.

Parcialmente competente

Competente

Dividen dos fracciones o números mixtos. Divide. 1 4 ÷ 2 7

Altamente competente

Altamente competente

6.Mód2.CLA5 Resuelven e interpretan problemas verbales que incluyen la división de fracciones y de números mixtos.

Parcialmente competente

Relacionan contextos con expresiones de división de fracciones y de números mixtos.

Una receta lleva 3 4 de taza de azúcar. Adesh tiene 4 1 2 tazas de azúcar. ¿Cuántas veces puede hacer

Adesh la receta con esa cantidad de azúcar?

Encierra en un círculo la expresión que coincida con la situación del problema verbal.

3 __ 4 ÷ 4 1 __ 2 4 1 __ 2 ÷ 3 __ 4

Competente

Resuelven problemas verbales que incluyen la división de fracciones y de números mixtos.

Jada tiene una cinta que mide 30 pulgadas de largo.

Corta la cinta en trozos que miden 4 1 2 pulgadas de largo cada uno. ¿Cuántos trozos de cinta tiene

Jada al final?

Altamente competente

Interpretan la división de fracciones y de números mixtos creando problemas verbales que aplican conceptos partitivos y de medidas.

Escribe un problema verbal que coincida con la oración numérica.

6.Mód2.CLA6 Interpretan la división de fracciones y de números mixtos usando modelos.

Parcialmente competente

Interpretan la división de fracciones y de números mixtos relacionando modelos con expresiones.

¿Qué expresión representa el diagrama de cinta?

Competente

Interpretan la división de fracciones y de números mixtos creando modelos para las expresiones dadas.

Usa la expresión para responder la parte A y la parte B.

Parte A

Dibuja un modelo para representar la expresión.

Parte B

Usa el modelo para hallar el cociente.

Altamente competente

6.Mód2.CLA7 Razonan acerca del tamaño de los cocientes de dos números de varios dígitos.

Parcialmente competente

Estiman los cocientes de dos números de varios dígitos.

Estima el cociente.

261.9 ÷ 0.2

Competente

Justifican estimaciones para los cocientes de dos números de varios dígitos.

Leo dice que 261.9 ÷ 0.2 es aproximadamente 1,000. Sara dice que 261.9 ÷ 0.2 es aproximadamente 100. ¿Quién está en lo correcto? Explica tu razonamiento.

6.Mód2.CLA8 Dividen números enteros de varios dígitos usando el algoritmo estándar.

Parcialmente competente

Competente

Dividen números enteros de varios dígitos usando el algoritmo estándar.

Divide.

8,466 ÷ 68

6.Mód2.CLA9 Suman y restan números decimales de varios dígitos.

Parcialmente competente

Competente

Suman y restan números decimales de varios dígitos.

Resta.

9.241 − 0.078

Altamente competente

Altamente competente

Altamente competente

6.Mód2.CLA10 Multiplican números decimales de varios dígitos.

Parcialmente competente Competente Altamente competente

Multiplican números decimales de varios dígitos. Multiplica.

30.46 × 2.1

6.Mód2.CLA11 Dividen números decimales de varios dígitos.

Parcialmente competente

Competente

Dividen números decimales de varios dígitos.

Divide.

69.43 ÷ 5.4

Altamente competente

6.Mód2.CLA12 Determinan el máximo común divisor de dos números enteros menores que o iguales a 100.

Parcialmente competente

Identifican factores comunes de dos números enteros menores que o iguales a 100.

¿Qué números son factores comunes de 18 y 64?

Elige todas las opciones que correspondan.

Competente

Determinan factores comunes, incluido el máximo común divisor, de dos números enteros menores que o iguales a 100.

¿Cuál es el máximo común divisor de 16 y 56?

Altamente competente

Resuelven problemas verbales usando factores comunes.

El Sr. Sharma tiene 35 manzanas y 56 naranjas. Quiere usar todas las manzanas y las naranjas para hacer cestas de regalos iguales.

Parte A

¿Cuántas cestas puede hacer el Sr. Sharma?

Parte B

¿Cuántas manzanas habrá en cada cesta?

Parte C

¿Cuántas naranjas habrá en cada cesta?

6.Mód2.CLA13 Determinan el mínimo común múltiplo de dos números enteros menores que o iguales a 12.

Parcialmente competente

Identifican los múltiplos comunes de dos números enteros menores que o iguales a 12.

¿Qué números son múltiplos comunes de 3 y 8?

Elige todas las opciones que correspondan.

A. 18

B. 36

C. 48

D. 64

E. 72

F. 96

Competente

Determinan los múltiplos comunes, incluido el mínimo común múltiplo, de dos números enteros menores que o iguales a 12.

¿Cuál es el mínimo común múltiplo de 8 y 12?

Altamente competente

Resuelven problemas verbales usando múltiplos comunes. Los lápices se venden en paquetes de  8. Los borradores se venden en paquetes de   12. Ryan quiere comprar un número igual de lápices y borradores. Dice que el número más pequeño de lápices y borradores que puede comprar es 96 lápices y 96 borradores, porque 8 multiplicado por 12 es 96. ¿Está Ryan en lo correcto? Explica.

Vocabulario

Los siguientes términos son sumamente importantes para el trabajo en el módulo 2 de 6.o grado. Este recurso agrupa el vocabulario en las siguientes categorías: Nuevo, Conocido y Verbos académicos. Las lecciones del módulo incorporan el vocabulario con la expectativa de que la clase use el vocabulario durante las discusiones y en sus escritos.

Los elementos en la categoría Nuevo son palabras específicas de la disciplina que se presentan a la clase en este módulo. Estos elementos incluyen la definición, la descripción o una ilustración como aparece en la lección. En ocasiones, este recurso incluye también explicaciones en cursiva para las maestras y los maestros destinadas a ampliar la terminología usada con la clase.

Los elementos de la categoría Conocido son palabras específicas de la disciplina que se han presentado en módulos o en grados anteriores.

Los elementos de la categoría Verbos académicos son términos de gran utilidad que pueden usarse en otras disciplinas. Los términos provienen de una lista de verbos académicos que se presentan estratégicamente en el currículo para este grado.

Nuevo

factorización prima

La factorización prima de un número es el número escrito como un producto de números primos como factores. (Lección 3)

máximo común divisor (MCD)

El máximo común divisor de dos números enteros que no sean ambos cero es el número entero mayor diferente de cero que es un factor de ambos números. (Lección 3)

mínimo común múltiplo (mcm)

El mínimo común múltiplo de dos números enteros es el número entero más pequeño que es mayor que cero y que es un múltiplo de ambos números. (Lección 4)

recíproco

Número que se obtiene al invertir una fracción (Lección 10)

Conocido

algoritmo

cociente denominador dividendo divisible divisor estimación estimar factor fracción decimal múltiplo

numerador

número compuesto número decimal número primo par de factores punto decimal residuo sumando

Verbos académicos

En el módulo 2 no se presenta ningún verbo académico de la lista de 6.o grado.

Las matemáticas en el pasado

El algoritmo de Euclides

¿Fue Euclides el primero en describir el algoritmo que lleva su nombre?

¿Es más simple aplicar el algoritmo de Euclides que factorizar para hallar el MCD?

¿Qué aplicaciones modernas existen para el algoritmo de Euclides?

¿Cómo calculamos el máximo común divisor (MCD) de dos números?

Podemos factorizar cada número en números primos, identificar los números primos que aparecen en ambas listas de factorización y, luego, multiplicarlos, ¿verdad?

Hagamos uno. Pida a sus estudiantes que hallen el MCD de 96 y 60. Podrá ver un trabajo similar a este:

96 = 2 × 2 × 2 × 2 × 2 × 3

60 = 2 × 2 × 3 × 5

Es probable que sus estudiantes le digan que el número primo 2 está dos veces en ambas listas y que el número primo 3 está una vez en ambas listas. Entonces, el MCD de 96 y 60 es 2 × 2 × 3, o 12.

Si solo debemos hallar el MCD de números pequeños; entonces, el método de factorización funciona bien. Pero, a veces, es necesario hallar el MCD de números muy grandes. Eso es un desafío mucho mayor. Por ejemplo, la capacidad de un sitio web seguro para encriptar datos se basa realmente en hallar el MCD de números muy grandes: ¡cientos de dígitos! Factorizar números de ese tamaño y, luego, multiplicar los números primos es poco práctico, incluso para las computadoras.

Afortunadamente, los griegos y los chinos descubrieron otro método para calcular el MCD que es mucho más simple que factorizar. Ambas civilizaciones hicieron los descubrimientos aproximadamente en el mismo momento de la historia. No hay prueba de contacto entre las dos culturas que sugiera la comunicación de conocimiento matemático, así que damos crédito por el descubrimiento a los griegos y a los chinos por igual.

Por un lado, el libro chino Nueve capítulos sobre el arte matemático (Nine Chapters on the Mathematical Art) (alrededor del año 100 a. e. c. o antes) describe el método como la manera de simplificar una fracción (es decir, escribirla con la unidad más grande posible). Por otro lado, el matemático griego Euclides explora el método en su libro Elementos (Elements) (alrededor del año 300 a. e. c.) como la manera de hallar el segmento de recta más largo que mida dos segmentos de recta dados (es decir, que esté contenido en cada segmento un número entero de veces).

Hoy, el método se conoce como el algoritmo de Euclides. Las versiones china y griega del algoritmo de Euclides son esencialmente idénticas y usan la resta repetida. A continuación, parafraseamos la descripción que hace Euclides del método.

El algoritmo de Euclides

• Comenzando con dos números, resta repetidamente el menor del mayor hasta que ambos números sean iguales. Ese número es el MCD.

Aunque Euclides escribe sobre números, traza segmentos de recta y representa la resta cortando un trozo de un segmento de recta. Intentemos ilustrar también el algoritmo de Euclides de esta manera.

Ayude a sus estudiantes a usar el algoritmo de Euclides para hallar que el MCD de 544 y 238 es 34.

• Cree los segmentos de recta.

238 54 4

• Reste el menor del mayor una vez y, luego, una segunda vez.

238 238238 68 × ×

• Reorganice los segmentos que quedan.

• Reste el menor del mayor, pero esta vez hágalo tres veces.

68 68 ×× × 68 68 34

• Reorganice los segmentos que quedan.

34 68

• Reste el menor del mayor.

34 34 34 ×

• Quedan dos segmentos de la misma longitud. ¡Ese es el MCD! 34 34

Sus estudiantes también deben verificar la respuesta usando el método ya comprobado de factorización.

544 = 2 × 2 × 2 × 2 × 2 × 17

238 = 2 × 7 × 17

Los números primos en ambas listas son 2 y 17, y al multiplicarlos da 34. ¡Verificado!

Llevemos el algoritmo de Euclides un paso más adelante y usemos la división en lugar de la resta. Después de todo, ¡la división no es más que la resta repetida! Este es el mismo problema anterior, pero con los números en formato de tabla.

Los números iniciales van en la fila superior de la tabla.

Dividendo Divisor Cociente Residuo

544 238

Pida a sus estudiantes que resuelvan este problema de división.

Dividendo Divisor Cociente Residuo

544 238 2 68

El cociente 2 corresponde a restar 238 dos veces en el problema anterior para obtener el residuo de 68.

Baje una línea. El divisor anterior se convierte en el nuevo dividendo, y el residuo anterior, en el nuevo divisor.

Dividendo Divisor Cociente

544 238 2 68 238 68

Haga la división. Baje una línea. Copie el divisor y el residuo anteriores en sus nuevas posiciones.

Repita una vez más.

El último residuo diferente de cero (que se muestra en color rojo) es el MCD. Ayude a sus estudiantes a comprender que la división es simplemente una forma más eficiente de hacer la resta repetida en el algoritmo de Euclides.

¿Por qué funciona el algoritmo de Euclides? ¿Cómo puede la resta obtener el factor más grande que divide dos números? Esta es una manera de guiar el razonamiento de sus estudiantes:

Cada número primo que divide 544 y 238 también debe dividir 544 − 238. Esto se deriva de la propiedad distributiva. Por ejemplo, nos concentramos en el número primo 17.

544 = 17 × 32

238 = 17 × 14 544 − 238 = 17 × (32 − 14)

Cada número primo que divide ambos números originales continuará dividiendo el resultado después de restarlos, hasta el final del algoritmo. Dado que esto es verdadero para cada número primo, es verdadero para su producto, el MCD.

Este razonamiento también funciona a la inversa. Si un número primo divide el último número que queda en el algoritmo de Euclides; entonces, divide todos los números en la cadena y, por lo tanto, divide ambos números originales.

Entonces, solo aquellos números primos que componen el MCD llegan al final del algoritmo de Euclides. ¡Por eso este método funciona!

Considere dar a la clase un ejemplo final para reforzar que no es necesario factorizar números cuando usamos el algoritmo de Euclides. ¡Aquí, factorizar los números dados “a mano” llevaría mucho tiempo!

Pida a sus estudiantes que muestren que el MCD de 412,163 y 404,471 es 641. Su tabla final debe ser similar a esta.

¿Pueden dos números tener un MCD de 1? ¡Por supuesto! Decimos que esos números son relativamente primos. Por ejemplo, dos números primos diferentes son relativamente primos. Pida a sus estudiantes que expliquen por qué. Si hay estudiantes que tienen dificultades, pídales que consideren cómo aplicarían el algoritmo de Euclides a dos números primos.

Por último, pídales que piensen por qué dos números enteros consecutivos deben ser relativamente primos. ¿Pueden ver que esto es verdadero al pensar en los factores primos de los números? Parece un poco complicado. Pero, ¿qué sucede cuando sus estudiantes realizan el algoritmo de Euclides en dos números consecutivos? La primera línea de la tabla mostrará un residuo de 1. Esto significa que ya terminaron. El MCD es 1 y los números son relativamente primos.

¡Tal es el poder del algoritmo de Euclides!

Materiales

Se necesitan los siguientes materiales para implementar este módulo. Las cantidades sugeridas se basan en una clase de 24 estudiantes y una maestra o un maestro.

24 borradores

24 borradores para las pizarras blancas individuales

1 computadora o dispositivo para la enseñanza

12 computadoras o dispositivos para estudiantes

160 cubos interconectables de 1 cm

25 lápices

1 libro Enseñar

24 libros Aprender

24 marcadores de borrado en seco

24 pizarras blancas individuales

1 proyector

1 set de 12 dados

24 tarjetas de índice

Fluidez

Las actividades de fluidez permiten que sus estudiantes desarrollen y practiquen la automaticidad con las destrezas fundamentales, de modo que puedan dedicar su capacidad cognitiva a resolver problemas más desafiantes. Las destrezas se incorporan a las actividades de fluidez solo después de haber sido presentadas conceptualmente dentro del módulo.

Cada lección de Una historia de razones comienza con un segmento de Fluidez, diseñado para que sus estudiantes se preparen para la lección del día. Este segmento diario proporciona problemas de práctica secuenciados que sus estudiantes pueden resolver de manera independiente, por lo general, durante los primeros minutos de clase. Sus estudiantes pueden usar sus pizarras blancas individuales para completar la actividad, o bien puede darles una versión impresa que se encuentra disponible en línea. Cada rutina de fluidez está diseñada para que pueda completarse en entre 3 y 5 minutos y no forma parte de los 45 minutos destinados a la lección. Adminístrela como una actividad para iniciar la clase o conviértala en una actividad guiada de Intercambio con la pizarra blanca o de Respuesta a coro.

Actividad para iniciar la clase

En esta rutina, sus estudiantes cuentan con determinado tiempo para trabajar de manera independiente y determinar las respuestas a un grupo de problemas.

1. Muestre todos los problemas a la vez.

2. Anime a sus estudiantes a trabajar de manera independiente y a su propio ritmo.

3. Lea o muestre las respuestas.

Intercambio con la pizarra blanca

En esta rutina, sus estudiantes adquieren fluidez mediante la práctica repetida y la retroalimentación inmediata. Un Intercambio con la pizarra blanca maximiza la participación, ya que cada estudiante debe registrar soluciones o estrategias para una secuencia de problemas. Gracias a estos registros escritos, usted puede llevar a cabo diferenciaciones: según las respuestas que observe, puede ajustar la secuencia de problemas al instante de acuerdo a las necesidades de la clase. Para esta rutina, cada estudiante necesita una pizarra blanca individual y un marcador para pizarra con borrador.

1. Muestre un problema de la secuencia.

2. Dé tiempo a sus estudiantes para que trabajen. Espere hasta que casi toda la clase haya terminado.

3. Dé una señal para que sus estudiantes muestren las pizarras blancas. Ofrezca retroalimentación inmediata y específica a cada estudiante. Si necesitan corregir su trabajo, regrese brevemente para validarlo una vez que sus estudiantes lo hayan corregido.

4. Continúe con el siguiente problema de la secuencia y repita el proceso.

Respuesta a coro

En esta rutina, sus estudiantes participan de forma activa para familiarizarse con las destrezas aprendidas previamente, lo que refuerza el conocimiento fundamental necesario para ampliar y aplicar los conceptos de matemáticas. La respuesta a coro permite que toda la clase participe, a la vez que disminuye el riesgo para quienes puedan dar una respuesta incorrecta.

1. Establezca una señal para que sus estudiantes respondan al unísono.

2. Muestre un problema. Pida a sus estudiantes que levanten la mano cuando sepan la respuesta.

3. Cuando casi todas las manos estén levantadas, dé la señal para que respondan.

4. Muestre la respuesta y continúe con el siguiente problema.

Conteo salteado

En esta rutina, sus estudiantes participan de forma activa en la memorización de secuencias de conteo, lo que refuerza el conocimiento fundamental necesario para ampliar y aplicar los conceptos de matemáticas.

1. Establezca una señal para contar hacia arriba y contar hacia abajo, y otra señal para dejar de contar.

2. Diga a sus estudiantes qué unidad van a usar para contar. Establezca el número inicial y final para el conteo.

3. Dé comienzo al conteo salteado brindando las señales. Mientras sus estudiantes cuentan, tenga cuidado de no hacer gestos con la boca que indiquen la respuesta.

Prácticas veloces

Las Prácticas veloces son actividades que desarrollan la fluidez con las matemáticas mediante una variedad de operaciones y destrezas. Uno de los objetivos principales de cada Práctica veloz es que sus estudiantes puedan apreciar su propio progreso en un lapso muy breve de tiempo. La rutina Práctica veloz es una experiencia divertida, de ritmo rápido y llena de adrenalina que genera energía y entusiasmo de forma intencional. Esta estimulante rutina motiva a sus estudiantes para que hagan su mejor esfuerzo y les da tiempo para celebrar sus logros.

Cada Práctica veloz incluye dos partes, A y B, que contienen problemas muy relacionados. Sus estudiantes completan la Práctica veloz A, seguida de dos rutinas de conteo salteado (una de ritmo rápido y otra de ritmo lento) que incluyen estiramientos u otros movimientos físicos.

Luego, sus estudiantes completan la Práctica veloz B con el objetivo de mejorar la puntuación que obtuvieron en la Práctica veloz A. Se calcula la puntuación de cada parte, pero no se asigna una calificación.

Las Prácticas veloces se pueden administrar en cualquier momento después de que el contenido de la Práctica veloz se haya desarrollado conceptualmente y se haya practicado. La misma Práctica veloz se puede repetir más de una vez a lo largo del año o de los niveles de grado. Con la práctica, la rutina se completa en aproximadamente 10 minutos.

Instrucciones

1. Pida a sus estudiantes que lean las instrucciones y los ejemplos de problema. Presente la tarea animando a sus estudiantes a completar tantos problemas como puedan y a que hagan su mejor esfuerzo.

2. Dé 1 minuto para completar la Práctica veloz A, pero no espere que sus estudiantes la terminen en ese tiempo. Cuando se acabe el tiempo, pídales que hagan una línea debajo del último problema que hayan completado.

3. Lea las respuestas de la Práctica veloz A de forma rápida y enérgica. Pida a sus estudiantes que digan “¡Sí!” si pusieron la respuesta correcta, o que encierren en un círculo su respuesta si es incorrecta.

4. Pida a sus estudiantes que cuenten las respuestas correctas y que registren ese número en la parte superior de la hoja. Ese número es su objetivo personal para la Práctica veloz B.

5. Celebre el esfuerzo de sus estudiantes y el éxito logrado en la Práctica veloz A.

6. Para generar mayor éxito con la Práctica veloz B, dé tiempo adicional para que sus estudiantes completen más problemas de la Práctica veloz A o haga preguntas para comentar y analizar los patrones de la Práctica veloz A.

7. Guíe a sus estudiantes para que completen las rutinas de conteo salteado de ritmo rápido y lento. Incluya un estiramiento u otro movimiento físico durante el conteo.

8. Pida a sus estudiantes que tengan en mente el objetivo personal que establecieron en la Práctica veloz A.

9. Pida a sus estudiantes que vayan a la Práctica veloz B.

10. Dé 1 minuto para completar la Práctica veloz B. Cuando se acabe el tiempo, pida a sus estudiantes que hagan una línea debajo del último problema que hayan completado.

11. Lea las respuestas de la Práctica veloz B de forma rápida y enérgica. Pida a sus estudiantes que digan “¡Sí!” si pusieron la respuesta correcta, o que encierren en un círculo su respuesta si es incorrecta.

12. Pida a sus estudiantes que cuenten las respuestas correctas y que registren ese número en la parte superior de la hoja.

13. Pida a sus estudiantes que hallen la diferencia entre el número de respuestas correctas de la Práctica veloz A y de la Práctica veloz B para calcular cuánto mejoraron. Dígales que registren el número en la parte superior de la hoja.

14. Celebre el progreso que hayan logrado de la Práctica veloz A a la Práctica veloz B.

Ejemplo de diálogo

Pida a sus estudiantes que lean las instrucciones y que completen los ejemplos de problema. Presente la tarea:

• Quizás no terminen, y eso está bien. Completen tantos problemas como puedan; hagan su mejor esfuerzo.

• En sus marcas, prepárense, ¡a pensar!

Dé 1 minuto para completar la Práctica veloz A.

• ¡Alto! Hagan una línea debajo del último problema que completaron.

• Voy a leer las respuestas rápidamente. A medida que las lea, digan “¡Sí!” si pusieron la respuesta correcta. Si se equivocaron, encierren en un círculo la respuesta.

Lea las respuestas de la Práctica veloz A de forma rápida y enérgica.

• Cuenten el número de respuestas correctas que obtuvieron y registren ese número en la parte superior de la hoja. Ese es su objetivo personal para la Práctica veloz B.

Celebre el esfuerzo y el éxito de sus estudiantes.

Dé 2 minutos para que sus estudiantes completen más problemas o haga preguntas para que comenten y analicen los patrones en la Práctica veloz A.

Guíe a sus estudiantes para que completen las rutinas de conteo salteado de ritmo rápido y lento. Incluya un estiramiento u otro movimiento físico durante el conteo.

• Señalen el número de respuestas correctas que obtuvieron en la Práctica veloz A. Recuerden que este es su objetivo personal para la Práctica veloz B.

Pida a sus estudiantes que vayan a la Práctica veloz B.

• En sus marcas, prepárense, ¡a mejorar!

Dé 1 minuto para completar la Práctica veloz B.

• ¡Alto! Hagan una línea debajo del último problema que completaron.

• Voy a leer las respuestas rápidamente. A medida que las lea, digan “¡Sí!” si pusieron la respuesta correcta. Si se equivocaron, encierren en un círculo la respuesta.

Lea las respuestas de la Práctica veloz B de forma rápida y enérgica.

• Cuenten el número de respuestas correctas que obtuvieron y registren ese número en la parte superior de la hoja.

• Calculen cuánto mejoraron y regístrenlo en la parte superior de la hoja.

Celebre el progreso de sus estudiantes.

En esta tabla encontrará una guía de implementación para las Prácticas veloces que se recomiendan en este módulo.

Práctica veloz Pautas de administración Preguntas para conversar Rutinas de conteo salteado

Sumar números decimales

Encerrar en un círculo los factores

La clase suma números decimales.

Administrar después de la lección 14 del módulo 2.

La clase encierra en un círculo los factores como preparación para hallar el máximo común divisor (MCD).

Administrar después de la lección 1 del módulo 2 o en lugar de la actividad de Fluidez de la lección 1 del módulo 2.

Encerrar en un círculo los múltiplos

La clase encierra en un círculo los múltiplos como preparación para hallar el mínimo común múltiplo (mcm).

Administrar después de la lección 1 del módulo 2 o en lugar de la actividad de Fluidez de la lección 4 del módulo 2.

Dividir números decimales

La clase usa operaciones de división para dividir números decimales.

Administrar después de la lección 18 del módulo 2.

Dividir números enteros entre fracciones y fracciones entre números enteros

Multiplicar números decimales

La clase divide números enteros entre fracciones y fracciones entre números enteros.

Administrar después de la lección 8 del módulo 2.

La clase multiplica números decimales.

Administrar después de la lección 16 del módulo 2.

¿En qué se parecen y en qué se diferencian los problemas 16 a 20?

¿Qué observan acerca de los problemas 12 y 13 y 28 y 29?

¿Cómo pueden usar los problemas 5 a 8 como ayuda para resolver el problema 9?

¿En qué se parecen los problemas 9, 13 y 18?

¿En qué se parecen los problemas 5, 9 y 16?

¿Qué observan acerca del problema 18?

Ritmo rápido: Contar de cuatro en cuatro desde 0 hasta 60.

Ritmo lento: Contar de tres en tres desde 21 hasta 60.

Ritmo rápido: Contar de seis en seis desde 0 hasta 60.

Ritmo lento: Contar de seis en seis desde 60 hasta 0.

Ritmo rápido: Contar de decena en decena desde 0 hasta 120.

Ritmo lento: Contar de un cuarto en un cuarto desde 0 cuartos hasta 10 cuartos.

¿Cómo pueden usar el problema 1 como ayuda para resolver los problemas 2 a 5?

¿Cómo pueden usar el problema 23 como ayuda para resolver los problemas 24 a 27?

¿En qué se parecen y en qué se diferencian los problemas 1 a 4?

¿Qué observan acerca de los problemas 28 y 30?

¿En qué se parecen y en qué se diferencian los problemas 19 a 22?

¿En qué se parecen los problemas 15 a 18 a los problemas 31, 33 y 35?

Ritmo rápido: Contar de decena en decena desde 0 hasta 200.

Ritmo lento: Contar de seis en seis desde 42 hasta 0.

Ritmo rápido: Contar de tres en tres desde 0 hasta 48.

Ritmo lento: Contar de un tercio en un tercio desde 9 tercios hasta 30 tercios.

Ritmo rápido: Contar de un quinto en un quinto desde 0 quintos hasta 40 quintos.

Ritmo lento: Contar de un quinto en un quinto desde 30 quintos hasta 0 quintos. Restar números decimales

La clase resta números decimales.

Administrar después de la lección 14 del módulo 2.

¿Cómo los ayuda el problema 1 a resolver el problema 2?

¿En qué se parecen y en qué se diferencian los problemas 10 a 13?

Ritmo rápido: Contar de un tercio en un tercio desde 0 tercios hasta 10 tercios, cambiando a números mixtos cuando sea apropiado.

Ritmo lento: Contar de siete en siete desde 0 hasta 70.

números decimales

Sumar números decimales

Práctica veloz

M2

números decimales

Sumar números decimales

Práctica veloz

Número de respuestas correctas: Progreso:

Número de respuestas correctas:

▸ Encerrar en un círculo los factores

▸ Práctica veloz

Encerrar en un círculo los factores 6 ▸ M2

AEncierra en un círculo cada número que sea un factor del número dado.

Encerrar en un círculo los factores

EUREKA MATH 2

M2 ▸ Práctica veloz ▸ Encerrar en un círculo los factores

Número de respuestas correctas: Progreso:

Encierra en un círculo cada número que sea un factor del número dado.

Número de respuestas correctas:

Encerrar en un círculo los múltiplos

Encerrar en un círculo los múltiplos

Práctica veloz

M2

AEncierra en un círculo cada número que sea un múltiplo del número dado.

Encerrar en un círculo los múltiplos

EUREKA MATH 2

6 ▸ M2 ▸ Práctica veloz ▸ Encerrar en un círculo los múltiplos

Número de respuestas correctas: Progreso:

Encierra en un círculo cada número que sea un múltiplo del número dado.

Práctica veloz ▸ Dividir números decimales

Dividir números decimales 6 ▸ M2

Dividir números decimales

Número de respuestas correctas: Progreso:

Práctica veloz

Dividir números enteros entre fracciones y fracciones entre números enteros 6 ▸ M2 ▸ Práctica veloz ▸ Dividir números enteros entre fracciones y fracciones entre números enteros

Número de respuestas correctas:

Práctica veloz ▸ Dividir números enteros entre fracciones y fracciones entre números enteros

M2

Dividir números enteros entre fracciones y fracciones entre números enteros 6

Número de respuestas correctas: Progreso:

Multiplicar números decimales

▸ Multiplicar números decimales

▸ Práctica veloz

6 ▸ M2

ANúmero de respuestas correctas: Multiplica.

Multiplicar números decimales 6 ▸ M2 ▸ Práctica veloz ▸ Multiplicar números decimales EUREKA MATH 2

Número de respuestas correctas: Progreso: Multiplica.

números decimales

Restar números decimales

Práctica veloz

M2

Número de respuestas correctas:

números decimales

Restar números decimales

Práctica veloz

Número de respuestas correctas: Progreso:

Ejemplos de soluciones

Espere ver diferentes estrategias para hallar la solución. Acepte respuestas precisas, explicaciones razonables y respuestas equivalentes en todo el trabajo de la clase.

Práctica mixta

1. El área del rectángulo que se muestra es 91 yardas cuadradas. ?

a. ¿Cuál es la longitud del rectángulo?

La longitud del rectángulo es 13 yardas.

b. ¿Cuál es el perímetro del rectángulo?

El perímetro del rectángulo es 40 yardas.

2. La tabla muestra el número de tazas de harina en ocho recetas diferentes de pan.

Receta de pan

de tazas de harina

a. Usa los datos de la tabla y la recta numérica que se muestra para crear un diagrama de puntos. Marca una × en el diagrama de puntos para el número de tazas de harina de cada receta.

Cantidad de harina (tazas)

b. ¿Cuántas recetas necesitan 1 1 2 tazas de harina?

3 recetas necesitan 1 1 2 tazas de harina.

c. ¿Cuántas recetas necesitan menos de 1 1 2 tazas de harina?

4 recetas necesitan menos de 1 1 2 tazas de harina.

3. Una figura se forma apilando cubos de 1 pulgada en tres capas, como se muestra. ¿Cuál es el volumen de la figura en pulgadas cúbicas?

El volumen de la figura es 15 pulgadas cúbicas.

4. 10 de los 25 cubos de una torre son amarillos. Eddie dice: “La razón del número de cubos amarillos al número total de cubos es 10 : 25”. Sara dice: “La razón del número de cubos amarillos al número total de cubos es 25 : 10”. ¿Qué estudiante está en lo correcto? Explica tu razonamiento.

Eddie está en lo correcto. El orden de los números en la razón coincide con el orden de las palabras que describe la razón.

5. En la tienda Food Mart, el precio de una bolsita de 3 libras de papas es $3.75. En la tienda Save More, el precio de una bolsita de 5 libras de papas es $6.50. ¿Qué tienda cobra menos por libra de papas?

Food Mart cobra menos por libra de papas que Save More. El precio de las papas en Food Mart es $1.25 por libra. El precio de las papas en Save More es $1.30 por libra.

6. Blake recoge manzanas y las coloca en cestos. Blake trabaja a una tasa constante y llena 12 cestos con manzanas cada 8 horas.

a. ¿Cuántos cestos llena Blake con manzanas en 30 horas?

Blake llena 45 cestos con manzanas en 30 horas.

b. En cada cesto, caben 1,000 libras de manzanas. ¿Cuántas horas tarda Blake en llenar cestos con 15,000 libras de manzanas?

Blake tarda 10 horas en llenar cestos con 15,000 libras de manzanas.

7. En una escuela, 180 estudiantes comen sándwiches en el almuerzo. Este número es el 45 % del número total de estudiantes de la escuela. ¿Cuál es el número total de estudiantes de la escuela?

A. 81

B. 99

C. 327

D. 400

En los problemas 8 a 10, escribe una expresión numérica para representar el enunciado.

8. Resta 1 2 de 3 4 Luego, multiplica por 3 3 (3 4 − 1 2 )

9. Suma 8 y 6. Luego, divide entre 2 (8 + 6) ÷ 2

10. Resta 8 del producto de 7 y 4 7 × 4 − 8

6 ▸ M2 ▸ Práctica mixta 1

EUREKA MATH2

Indica el punto que representa cada par ordenado.

1. Completa la tabla.

Nombre en palabras Dibujo

Punto D D

Segmento de recta OE 0 E Recta AB

3. Determina si cada enunciado es verdadero o falso.

2) D (2, 5) B (3, 6) C

a. El valor de 9 en el número decimal 2.19 es 1 10 del valor de 9 en 49.45. Falso

b. El valor de 9 en el número decimal 3.95 es 1 100 del valor de 9 en 96.31

Verdadero

c. El valor de 9 en el número decimal 9.82 es 100 veces el valor de 9 en 8.193

Verdadero

4. ¿Qué expresiones tienen un valor de 105 ? Elige todas las opciones que correspondan.

A. 10 × 5

B. 10 + 5

C. 10,000

D. 100,000

E. 10 × 10 × 10 × 10 × 10

F. 10 + 10 + 10 + 10 + 10

5. Redondeado al décimo más cercano, ¿cuál de los siguientes números se convierte en 12.4? Elige todas las opciones que correspondan.

A. 12.45

B. 12.35

C. 12.445

D. 12.349

E. 12.371

6. Usa >, < o = para comparar los números.

a. 1.8 > 1.08

b. 3.6 = 3.60

c. 0.48 < 0.5

7. Kelly quiere preparar ponche de frutas en un recipiente de 5 galones. La receta de ponche lleva 1 2 3 galones de jugo de piña, 1 3 4 galones de jugo de arándanos rojos y 2 galones de jugo de naranja. ¿Puede caber en el recipiente de 5 galones de Kelly la cantidad total del ponche de frutas? Explica.

No. En el recipiente de Kelly, no puede caber la cantidad total del ponche de frutas. La suma de las cantidades del jugo de piña y el jugo de arándanos rojos es mayor que 3 galones, porque 1 2 3 galones y 1 3 4  galones son, cada uno, mayores que 1 1 2 galones. Cuando esos jugos se combinan con los 2 galones de jugo de naranja, la suma de las cantidades de los tres jugos es mayor que 5 galones.

8. Escribe una fracción en la línea para que el enunciado sea verdadero.

5 7 × 3 4 < 5 7 × Ejemplo: 4 5

Obras citadas

Burns, Marilyn. “Teaching Adding Decimals: What If You Give the Answer First?” Marilyn Burns Math Blog (blog), January 14, 2018. https://marilynburnsmath.com/decimals /teaching-adding-decimals-what-if-you-gave-the-answer-first/

CAST. Universal Design for Learning Guidelines version 2.2. Retrieved from http://udlguidelines.cast.org, 2018.

Heath, Thomas L., trans. The Thirteen Books of Euclid’s Elements. New York: Dover Publications, 1956.

Liu Hui. The Nine Chapters on the Mathematical Art: Companion and Commentary. Translated and edited by Shen Kangshen, John N. Crossley, and Anthony W. C. Lun. New York: Oxford University Press, 1999.

McIntosh, Andrew and Jennifer Carter. “Habitat 67.” In The Canadian Encyclopedia. Historica Canada. Article published October 30, 2008. Last edited October 3, 2018. https://www .thecanadianencyclopedia.ca/en/article/habitat-67.

Rober, Mark, n.d. “Use Science to Build the Fastest Pinewood Derby Car.” Boys’ Life. Accessed May 7, 2020. https://boyslife.org/hobbies -projects/projects/138909/use-science-to-make-a-fast -pinewood-derby-car/.

Zwiers, Jeffrey, Jack Dieckmann, Sara Rutherford-Quach, Vinci Daro, Renae Skarin, Steven Weiss, and James Malamut. Principles for the Design of Mathematics Curricula: Promoting Language and Content Development. Retrieved from Stanford University, UL/SCALE website: http://ell.stanford.edu/content/mathematics -resources-additional-resources, 2017.

Créditos

Great Minds® has made every effort to obtain permission for the reprinting of all copyrighted material. If any owner of copyrighted material is not acknowledged herein, please contact Great Minds for proper acknowledgment in all future editions and reprints of this module.

For a complete list of credits, visit http://eurmath.link/media-credits.

Cover, Gustave Caillebotte (1848–1894). Paris Street; Rainy Day, 1877. Oil on canvas, 212.2 x 276.2 cm (83 1/2 x 108 3/4 in.). Charles H. and Mary F. S. Worcester Collection. (1964.336). The Art Institute of Chicago, Chicago, IL, USA. Photo Credit: The Art Institute of Chicago/Art Resource, NY; page 143, Jim Whitney/Shutterstock.com; pages 237, 289, Pinkcandy/Shutterstock.com; page 271, Amanda.Reynolds/Shutterstock. com; All other images are the property of Great Minds.

Agradecimientos

Agnes P. Bannigan, Erik Brandon, Joseph T. Brennan, Beth Brown, Amanda H. Carter, Mary Christensen-Cooper, David Choukalas, Cheri DeBusk, Jill Diniz, Mary Drayer, Dane Ehlert, Scott Farrar, Kelli Ferko, Levi Fletcher, Krysta Gibbs, Winnie Gilbert, Julie Grove, Marvin E. Harrell, Stefanie Hassan, Robert Hollister, Rachel Hylton, Travis Jones, Raena King, Emily Koesters, Liz Krisher, Robin Kubasiak, Connie Laughlin, Alonso Llerena, Gabrielle Mathiesen, Maureen McNamara Jones, Bruce Myers, Marya Myers, Kati O’Neill, Ben Orlin, Darion Pack, Brian Petras, DesLey V. Plaisance, Lora Podgorny, Janae Pritchett, Bonnie Sanders, Deborah Schluben, Andrew Senkowski, Erika Silva, Ashley Spencer, Hester Sofranko, Danielle Stantoznik, Tara Stewart, Heidi Strate, James Tanton, Carla Van Winkle, Jessica Vialva, Caroline Yang

Ana Alvarez, Lynne Askin-Roush, Stephanie Bandrowsky, Mariel Bard, Rebeca Barroso, Brianna Bemel, Rebecca Blaho, Charles Blake, Carolyn Buck, Lisa Buckley, Shanice Burton, Adam Cardais, Cindy Carlone, Gina Castillo, Ming Chan, Tatyana Chapin, Christina Cooper, Kim Cotter,

Gary Crespo, Lisa Crowe, David Cummings, Brandon Dawley, Cherry dela Victoria, Timothy Delaney, Delsena Draper, Erin DuRant, Sandy Engelman, Tamara Estrada, Ubaldo Feliciano-Hernández, Soudea Forbes, Liz Gabbard, Diana Ghazzawi, Lisa Giddens-White, Laurie Gonsoulin, Adam Green, Sagal Hassan, Kristen Hayes, Tim Heppner, Marcela Hernandez, Sary Hernandez, Abbi Hoerst, Elizabeth Jacobsen, Ashley Kelley, Sonia Khaleel, Lisa King, Sarah Kopec, Drew Krepp, Jenny Loomis, Antonia López, Stephanie Maldonado, Christina Martire, Siena Mazero, Thomas McNeely, Cindy Medici, Ivonne Mercado, Sandra Mercado, Brian Methe, Sara Miller, Mary-Lise Nazaire, Corinne Newbegin, Tara O’Hare, Max Oosterbaan, Tamara Otto, Christine Palmtag, Laura Parker, Toy Parrish, Katie Prince, Neha Priya, Jeff Robinson, Nate Robinson, Gilbert Rodriguez, Todd Rogers, Karen Rollhauser, Neela Roy, Gina Schenck, Aaron Shields, Madhu Singh, Leigh Sterten, Mary Sudul, Lisa Sweeney, Tracy Vigliotti, Bruce Vogel, Charmaine Whitman, Glenda Wisenburn-Burke, Samantha Wofford, Howard Yaffe, Dani Zamora

Exponencialmente mejor

Conocimientos2 Siguiendo con la tradición de ayudar a los maestros y las maestras con todo lo que necesiten para que sus estudiantes desarrollen un conocimiento profundo y coherente de las matemáticas, Eureka Math2 ofrece colecciones de videos y recomendaciones hechas a medida de los y las profesionales con más y con menos experiencia.

Digital2 A través de una experiencia digital perfectamente integrada, Eureka Math2 incluye cientos de imágenes inteligentes, videos cautivadores y actividades digitales interactivas que encienden la chispa de la conversación y el asombro en su salón de clases.

Accesible2 Siempre con nuestros lectores y lectoras en mente, Eureka Math2 se ha diseñado cuidadosamente para que quienes tengan dificultades con la lectura puedan acceder a las lecciones, los problemas verbales, ¡y más!

Sonrisas2 Con Eureka Math2, usted y sus estudiantes se enamorarán de las matemáticas, o recordarán qué fue lo que les hizo enamorarse de ellas.

¿Qué tiene que ver esta pintura con las matemáticas?

El tema de esta pintura impresionista de perspectiva aérea es una intersección en París durante un día gris y lluvioso. En esta escena, Gustave Caillebotte crea una sensación de profundidad al usar la perspectiva y la proporción de diversas formas, por ejemplo, ubicando figuras grandes en primer plano y figuras más pequeñas a lo lejos. Imagina que hay un plano de coordenadas en el edificio del fondo.

¿Cómo podrías determinar la distancia desde el frente del edificio hasta el fondo usando el plano de coordenadas?

En la portada

Paris Street; Rainy Day, 1877

Gustave Caillebotte, French, 1848–1894

Oil on canvas

The Art Institute of Chicago, Chicago, IL, USA

Gustave Caillebotte (1848–1894). Paris Street; Rainy Day, 1877. Oil on canvas, 212.2 × 276.2 cm (83½ × 108¾ in).

Charles H. and Mary F. S. Worcester Collection (1964.336).

The Art Institute of Chicago, Chicago, IL, USA. Photo Credit: The Art Institute of Chicago/Art Resource, NY

Módulo 1

Razones, tasas y porcentajes

Módulo 2

Operaciones con fracciones y números de varios dígitos

Módulo 3

Números racionales

Módulo 4

Expresiones y ecuaciones de un paso

Módulo 5

Área, área de la superficie y volumen

Módulo 6

Estadística