A Story of Units®
Part–Part–Total
LEARN ▸ Counting and Cardinality

Student K
Module 1
What does this painting have to do with math?
Piet Mondrian reduced his subjects to colorful geometric shapes. In this painting, bold, black horizontal and vertical lines frame the colorful squares and rectangles in red, black, yellow, and more. Do any of the shapes seem similar? Do you notice that the smaller shapes are added together to create bigger shapes? How many shapes
do you see in total?
On the cover
Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921
Piet Mondrian, Dutch, 1872–1944
Oil on canvas
Kunstmuseum Den Haag, The Hague, Netherlands
Piet Mondrian (1872–1944), Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921. Oil on canvas. Kunstmuseum Den Haag, The Hague, Netherlands. Image copyright © Kunstmuseum
Den Haag. Image credit: Bridgeman Images

Great Minds® is the creator of Eureka Math® , Wit & Wisdom® , Alexandria Plan™, and PhD Science®
Published by Great Minds PBC. greatminds.org
© 2025 Great Minds PBC. All rights reserved. No part of this work may be reproduced or used in any form or by any means—graphic, electronic, or mechanical, including photocopying or information storage and retrieval systems—without written permission from the copyright holder.
ISBN 979-8-89012-107-3
A-Print
2 3 4 5 6 7 8 9 10
29 28 27 26 25
Printed in the USA
1
XXX
A Story of Units®
K LEARN Module 1 Module 2 Module 3 Module 4 Module 5 Module 6 Counting and Cardinality
Shapes Comparison Composition and Decomposition Addition and Subtraction Place Value Foundations
Part–Part–Total ▸
Two- and Three-Dimensional
Topic B
a set shown in a picture.
Lesson 17
This lesson appears only in the Teach book.
Lesson 18
This lesson appears only in the Teach book.
© Great Minds PBC 2 K ▸ M1 EUREKA MATH2 New York Next Gen Contents
and Cardinality
A 5 Classify to Make Categories and Count Lesson 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 Compare objects based on their attributes. Lesson 2 This lesson appears only in the Teach book. Lesson 3 This lesson appears only in the Teach book. Lesson 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 Classify objects into three categories and count. Lesson 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 Classify objects into three categories, count, and match to a numeral.
Counting
Topic
13
How Many Questions with
to 5 Objects Lesson 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 Organize, count, and represent a collection of objects. Lesson 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 Practice counting accurately. Lesson 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 Count sets in linear, array, and scattered configurations. Lesson 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Answer
Up
Conserve number regardless of the arrangement of objects.
31 Write Numerals and Create Sets of Up to 5 Objects Lesson 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 Count out a group of objects to match a numeral. Lesson 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 Write numerals 1–3 to answer how many questions. Lesson 12 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 Write numerals 4 and 5 to answer how many questions. Lesson 13 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 Count out enough objects and write the numeral. Topic D 45 Decompose Numbers Lesson 14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 Understand the meaning of zero and write the numeral. Lesson 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53 Sort the same group of
in
than
Lesson 16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 Decompose
Topic C
objects
more
one way and count.
This lesson appears only in the Teach book.
3 EUREKA MATH2 New York Next Gen K ▸ M1 © Great Minds PBC Topic E . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 Answer How Many Questions with Up to 10 Objects Lesson 19 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61 Organize, count, and represent a collection of objects. Lesson 20 65 Count objects in 5-group and array configurations and match to a numeral. Lesson 21 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67 Count sets in circular configurations and match to a numeral.
22
Lesson
Lesson 23 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 Conserve number
which objects
Topic F . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73 Write Numerals and Create Sets of Up to 10 Objects Lesson 24 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75 Count out a group of objects to match a numeral. Lesson 25 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 Write numerals 6 and 7. Lesson 26 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81 Write numeral 8. Lesson 27 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85 Write numerals 9 and 10. Lesson 28 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91 Order numerals 1–10 and reason about an unknown number in the number sequence. Topic G . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93 Analyze the Count Sequence Lesson 29 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 Model the pattern of 1 more in the forward count sequence. Lesson 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101 Build number stairs to show the pattern of 1 more in the forward count sequence. Lesson 31 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103 Use ordinal numbers to describe the position and magnitude of whole numbers. Lesson 32 This lesson appears only in the Teach book Lesson 33 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105 Build number stairs to show the pattern of 1 less in the backward count sequence. Lesson 34 107 Organize, count, and represent a collection of objects. Resources Credits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 Acknowledgments . . . . . . . . . . . . . . . . . . . . . . . 110
regardless of the order in
are counted.
FAMILY MATH Classify to Make Categories and Count

Dear Family,
This newsletter will keep you up to date on what we are learning during math time. Use what you read to help your family talk about math and to practice math at home. You can expect a Family Math newsletter to come home every time our class begins a new topic.
To begin the year, students are learning to sort objects into groups by color, type, shape, or size. After they sort, they count the objects in each group and tell how many.

Words We Are Learning
A student sorts by size and then counts how many in each group.
At-Home Activities
Activity Idea 1 Whisper and Shout
A student sorts by type and then matches a number to each group.
Count together from 1 to 10 by using a whisper voice. Then count again in a loud voice. Count to 10 a few more times. Vary the counting by using silly voices, taking turns, using gestures as cues to start and stop, or by counting while marching, hopping, or doing jumping jacks. As your child is ready, count to 20 or beyond.
Activity Idea 2 Sort
Sorting is a way for students to organize their world by thinking about how things are alike and different. Give your child a set of household items that can be sorted into different categories. Kitchen utensils, laundry, or food make good choices. Let your child decide how to sort the objects. They might sort by color, shape, size. Or, they might use categories that are more personal, such as foods they like and foods they don’t like.
© Great Minds PBC 5 Module 1 Topic A
sort count number
After they sort ask questions, such as:
• How did you sort?
• Why did you sort this way?
• How many are there in this group? Can you show me how you figured that out?
Sample Sorts
Sorting Socks by Size
My Socks
Other Socks
Sorting Utensils by Use or Type
Spoons
Forks
Knives
© Great Minds PBC 6 FAMILY MATH ▸ Module 1 ▸ Topic A K ▸ M1 ▸ TA EUREKA MATH2 New York Next Gen
© Great Minds PBC 7 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TA ▸ Two-Hands Mat
Name
Draw your groups to show how you sorted.
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TA ▸ Lesson 4 © Great Minds PBC 9
4
Name
Draw your groups to show how you sorted.
© Great Minds PBC 11 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TA ▸ Lesson 5
5
FAMILY MATH
Answer How Many Questions with Up to 5 Objects
Dear Family,
Students are learning to count groups of up to 5 objects. Counting each object only once can be a challenge, especially when objects are not lined up neatly. Students are using three strategies (touch and count, move and count, and mark and count) to help them organize and count accurately. Students are learning to use these strategies to determine whether they have enough when passing out classroom materials.

At-Home Activities

Activity Idea 1 Number Match
Cut out the dot cards and number cards. Set aside the cards for 6–10 to use later. Hold up a dot card. Ask your child to tell how many dots. Then ask your child to find and hold up the matching number card. Have some fun with the number: Ask your child to stand up and hop, clap, or touch their toes the same number of times. (You can do it, too!) When cards 0–5 become easy for your child, move to cards 6–10.
CHALLENGE: Show the dot card for only two seconds. Can your child recognize how many without counting?

Activity Idea 2 Are There Enough?
As part of everyday activities we often ask the question, “Are there enough?” Children may ask themselves this question as they set the table, have a tea party with stuffed animals, or share with siblings or friends. As your child participates in everyday tasks, have them practice counting out enough by using the strategies they learned in class.
© Great Minds PBC 13
strategy enough line
Words We Are Learning
Mark and count A student puts a mark on each white flower to show it has been counted. Move and count A student picks up each sticker and moves it to the mat as they count.
Touch and count A student touches each object as they count.
Module 1 Topic B
Strategies to Count
Students learn three counting strategies to help them count accurately and find how many are in a group.
Touch and Count

Say the number while touching the object. This strategy works best when objects and pictures are in a line.


Move and Count
Say the number while moving the object away from the ones that are not yet counted.
This strategy is good for tracking objects that can be moved, especially when they are scattered.
Mark and Count
Say the number while crossing off each object. This strategy is good for tracking which objects have been counted, especially when objects are not neatly lined up and cannot be moved.
© Great Minds PBC 14 FAMILY MATH ▸ Module 1 ▸ Topic B K ▸ M1 ▸ TB EUREKA MATH2 New York Next Gen
“1, 2, 3, 4, 5"
“1” “1”
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB © Great Minds PBC 15 Module 1 ▸ Topic B ▸ FAMILY MATH 0 1 2 3 4 5 6 7 8 9 10
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB © Great Minds PBC 17 Module 1 ▸ Topic B ▸ FAMILY MATH
Draw your collection to show how you counted.
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lesson 6 © Great Minds PBC 19
6
Name
© Great Minds PBC 21 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lesson 7 ▸ Bear Game Board
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Number Path © Great Minds PBC 23 5
4 3 2 1
K ▸ M1 ▸ TB ▸ Number Path EUREKA MATH2 New York Next Gen © Great Minds PBC 24 10 9 8 7 6
Count the animals. Circle the number that tells how many.
© Great Minds PBC 25 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lesson 8
8
1 2 3 4 5 1 2 3 4 5
Name
K ▸ M1 ▸ TB ▸ Lesson 8 EUREKA MATH2 New York Next Gen © Great Minds PBC 26 PROBLEM SET 1 2 3 4 5 1 2 3 4 5
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lesson 8 © Great Minds PBC 27 PROBLEM SET 1 2 3 4 5 1 2 3 4 5
Place the cubes and count. Circle the number. Move the cubes to make a different design. Then circle the number.
© Great Minds PBC 29 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lesson 9
9 Name 3 4 5
4 5 3 4 5 3 4 5
3
K ▸ M1 ▸ TB ▸ Lesson 9 EUREKA MATH2 New York Next Gen © Great Minds PBC 30 PROBLEM SET
3 4 5 3 4
3 4 5
3 4 5
5
FAMILY MATH
Write Numerals and Create Sets of Up to 5 Objects


Dear Family,
Students are learning to count out up to 5 objects from a larger group. This is harder than it seems! It can be hard to stop counting at a specific number and not keep counting the entire group!
Students are also learning to write numbers 1 through 5 by using writing rectangles and practicing rhymes. Look for more information about this important skill on the back of this page.
Students count out to match
Students count out 3 cubes from a larger group to match the number.
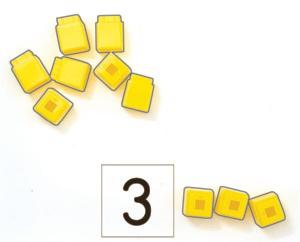

At-Home Activities
Students know there are enough cubes because each dot gets a cube.
Students know there are enough cubes because each dot gets a
Activity Idea 1 Count Out a Group
Students show 4 by using drawings and numbers.
by using
Give your child a container of household items such as pasta, beans, or pennies. Show a number from 1 to 5 and ask your child to count out the same number of items. When groups of 5 become easy for your child, count out groups up to 10.
Tip: Use the number cards from the set sent home with Family Math, module 1 topic B, or write the numbers 1–10 on index cards or sticky notes.
Activity Idea 2 Trace Numbers
Practice writing numbers 1 through 5 by asking your child to trace each number with their finger. Use the rhymes on the back of this page to remind them how to write each number. Then make it a game by asking your child to trace a number on your back. See whether you can guess the number your child traced. Once your child has had time to practice each number, trade places and see whether your child can guess the number you traced.
© Great Minds PBC 31 Module 1 Topic C
Writing Rectangle



The writing rectangle is a guide to help children correctly write numbers. The dot at the top of each writing rectangle gives children a place to start. Children are less likely to reverse their numbers when they start from the dot and keep their writing inside the rectangle. Eventually, they will be able to write numbers without the writing rectangle, but this tool provides them with structure to form numbers correctly from the start.
It is normal and developmentally appropriate for kindergartners to occasionally reverse numbers, or write them backward. Reversal of numbers should not be cause for concern. Instead, simply remind your child to begin at the dot and use the writing rectangle, while repeating the number rhyme (see below), to help write the number.
Starting numbers and letters from the top is an important habit for your child to build in kindergarten. It will help them write quickly and neatly when writing demands increase in later grades. A dot reminds children to start their numbers at the top.
Number Writing Rhymes
1 “Top to bottom, and then I am done. I just wrote the number 1.”
2 “Half a moon, there’s more to do. Slide to the right. I wrote a 2.”
3 “To the right and around the tree. Around again to make a 3.”
4 “A little line down, to the right some more. Now a big line down to make a 4.”
5 “Down the side, around a hive. Give it a hat. I wrote a 5.”
© Great Minds PBC 32 FAMILY MATH ▸ Module 1 ▸ Topic C K ▸ M1 ▸ TC EUREKA MATH2 New York Next Gen
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Two-Hands Mat © Great Minds PBC 33
Name
3 a pp le s
Sh o p p in g L i s t
2 s t r aw b e rri e s
1 ba n a n a ca r r ot s
5
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lesson 10 © Great Minds PBC 35 10
Name
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lesson 11 © Great Minds PBC 37 11
Name
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lesson 12 © Great Minds PBC 39 12
© Great Minds PBC 41 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lesson 12
12
Count and write how many.
Name
K ▸ M1 ▸ TC ▸ Lesson 12 EUREKA MATH2 New York Next Gen © Great Minds PBC 42 PROBLEM SET



EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lesson 13 © Great Minds PBC 43 13
Tacos Apples Pretzels
Menu Name



© Great Minds PBC 44 K ▸ M1 ▸ TC ▸ Lesson 13 EUREKA MATH2 New York Next Gen LESSON Order Tacos Apples Pretzels
FAMILY MATH Decompose Numbers
Dear Family,
Your child is learning about the relationship between numbers by sorting objects in more than one way. You might be thinking, Why are we still sorting? Sorting is a way to see how numbers can be broken into parts. For example, 5 bears can be sorted into 4 yellow bears and 1 red bear. The number sentence 5 is 4 and 1 represents this situation. 5 bears can also be sorted into 3 big bears and 2 small bears. Your child might say, “5 is 3 and 2” to represent this sort.


Invite your child to show you counting the math way—a new way they are learning to count on their fingers.
Words We Are Learning
At-Home Activities Activity Idea 1 Sorting Different Ways
Give your child a group of 4 or 5 items, such as toys, markers, or coins, that they can sort into different categories by color, shape, or size. Let your child decide how to sort. Then ask the following questions to help your child think about the total number of objects and the number in each group.
• How many ______ are there?
• How many groups did you make?
• How many are in this group?
Put the objects back into a pile. Ask your child to sort in a different way, and then ask the same questions. Did this sort result in the same number of groups?
© Great Minds PBC 45 Module 1 Topic D
number sentence
Sorting by color—5 is 4 and 1.
Sorting by size—5 is 3 and 2.
Activity Idea 2 Nature Hunt
Ask your child to find ways to sort or count objects while taking a walk or driving. For example, “I see 4 trees. 3 are big, and 1 is small.” If possible, collect objects like leaves, pine cones, or rocks for sorting and re-sorting later.
Counting the Math Way
Using fingers for math is not babyish. In fact, young children who are able to represent numbers or problems on their fingers do better with counting, comparing numbers, and estimating in later years. Early work with fingers builds a part of the brain that is used for arithmetic. Students learn to “see” a representation of fingers in their brains even when they don’t use their fingers to solve problems.
Your child is learning to count from 1 to 5 the math way, starting with their left pinkie finger and lifting one finger at a time until they reach their thumb.














In counting the math way, students can see and feel the number of fingers increase as they count from 1 to 10, moving from the left pinkie to the right pinkie without interruption. This left-to-right movement will be familiar when children begin to use tools such as the number path and, in later grades, the number line. Think of this work as push-ups for the brain!

© Great Minds PBC 46 FAMILY MATH ▸ Module 1 ▸ Topic D K ▸ M1 ▸ TD EUREKA MATH2 New York Next Gen
1 2 3 4 5 6 7 8 9 10
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lesson 14 ▸ Two-Hands Mat © Great Minds PBC 47
Name
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lesson 14 © Great Minds PBC 49 14
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lesson 14 © Great Minds PBC 51
14
Count and write how many.
Name
How many apples are in each tree?
How many cats are in the trees?
K ▸ M1 ▸ TD ▸ Lesson 14 EUREKA MATH2 New York Next Gen © Great Minds PBC 52 PROBLEM SET
Name
Create a stick of 5 cubes.
Break the stick to fit the puzzles. Write the partners of 5.
© Great Minds PBC 53 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lesson 15 15
1 2 3 4 5 6 7 8 9 10
Create a stick of 4 cubes.
Break the stick to fit the puzzles. Write the partners of 4.
K ▸ M1 ▸ TD ▸ Lesson 15 EUREKA MATH2 New York Next Gen © Great Minds PBC 54 PROBLEM SET
1 2 3 4 5 6 7 8 9 10
Name
Draw Kia’s 4 crayons .
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lesson 16 © Great Minds PBC 55
is and . 16
Count and write how many in all.
© Great Minds PBC 57 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lesson 16
Color 1.
16
Color 2.
Name
FAMILY MATH
Answer How Many Questions with Up to 10 Objects
Dear Family,
Students are learning to count groups of up to 10 objects. It is harder to keep track of the count in these larger groups, especially when objects are scattered or in a circle. Students are practicing the three counting strategies (touch and count, move and count, and mark and count) to keep track of objects already counted.
COUNTING CONFIGURATIONS













At-Home Activities
Activity Idea 1 Beep Number Game
Play Beep Number by saying a few numbers in order, replacing one of the numbers with the word beep. For example, if you say, “2, 3, beep, 5,” your child should respond, “4.” Use the number cards (sent home with topic B) in order as an extra support so your child can touch each number as you count. When your child is ready, invite them to say the numbers, while you guess the beep number.
Activity Idea 2 Count Toys
















Use toys or other household objects to make different counting configurations like the ones shown above. Encourage your child to touch and count or move and count the toys to find out how many there are.

© Great Minds PBC 59 Module 1 Topic E
Linear 5-Group Array Circular Scattered
5-Group Formations
Why do we use 5-groups? You may have noticed that the dot cards (sent home with topic B) show 5 dots in a line. Groups of 5 help children visualize numbers 6 through 10 (5 and 1, 5 and 2, etc.). The dots make it easy to see each number as 5 dots plus some more dots. 10 9 8 7 6
Dots are not the only way to show 5-groups. Using fingers to count the math way emphasizes the relationship between 5 and the numbers 6 through 10 (5 fingers on one hand and some on the other). Organizing objects and drawings in groups of 5 can help children see this important relationship.
Fingers to count the math way 5 and 1

Pictures 5 and 5
Cubes with a color change at 5 5 and 2
© Great Minds PBC 60 FAMILY MATH ▸ Module 1 ▸ Topic E K ▸ M1 ▸ TE EUREKA MATH2 New York Next Gen
Blue Orange
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ 5-Group Mat © Great Minds PBC 61
Name
Draw your collection to show how you counted.
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lesson 19 © Great Minds PBC 63 19
Name
Circle a group of five in all the pictures. Then count and circle how many in all.
© Great Minds PBC 65 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lesson 20
20 5 6 7 7 8 9 7 8 9 8 9 10

K ▸ M1 ▸ TE ▸ Lesson 20 EUREKA MATH2 New York Next Gen © Great Minds PBC 66 PROBLEM SET 5 6 7 5 6 7 5 6 7 8 9 10
Name Count. Circle how many on the number path.
© Great Minds PBC 67 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lesson 21 21
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10

K ▸ M1 ▸ TE ▸ Lesson 21 EUREKA MATH2 New York Next Gen © Great Minds PBC 68 PROBLEM SET 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
Count. Circle to show how many.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lesson 21 © Great Minds PBC 69 PROBLEM SET 1 2 3 4 5 6 7 8 9 10
8 9 10 8 9 10
Name
Color the first object. Count and circle how many on the number path.
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lesson 23 © Great Minds PBC 71 23
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
K ▸ M1 ▸ TE ▸ Lesson 23 EUREKA MATH2 New York Next Gen © Great Minds PBC 72 PROBLEM SET 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 1
FAMILY MATH
Write Numerals and Create Sets of Up to 10 Objects
Dear Family,
Students are learning to count out up to 10 objects from a larger group. Just as with counting out a smaller group, it can be hard to stop counting at a specific number. Some students will want to keep counting the entire group! Students are also learning to write numbers 6 through 10 by using writing rectangles and practicing rhymes. Ask your child to share some reasons why we write numbers and share some reasons of your own!
Why Do We Write Numbers?
- play restaurant
- remember the count
- make grocery list

- share your phone number
- faster than drawing
- make a calendar
- room numbers
- keep score
- play a game
- make a birthday card
Students count out a group by drawing and by circling objects in a picture.
At-Home Activities
Activity Idea 1 Hunt and Count
Students answer the question, “Why do we write numbers?” Students see their ideas recorded on a chart.
Show a number card from 1 to 10 (sent home in topic B), and ask your child to find that many blocks, spoons, pennies (or any other fun item) in your home. When the hunt is over, have some fun with the number: Ask your child to hop, clap, or touch their toes the same number of times. (You can do it too!) When this becomes easy for your child, increase the numbers to 12, 15, and then 20.
Activity Idea 2 Write Numbers
Practice writing numbers 0 through 10. Use the rhymes on the back of this page to remind your child how to write each number. Then make it a game by asking them to write the number in a rectangle of shaving cream (spread on a baking tray or the side of a bathtub). Make a dot at the top, using your finger or a bead, to help your child get started.
© Great Minds PBC 73 Module 1 Topic F
Writing Rectangle
The writing rectangle is an important tool for learning to write numbers. The dot at the top of each writing rectangle gives children a place to start and helps to prevent reversals.
Number Writing Rhymes
0 “I start at the top, and around I go. I come back up to make 0.”
1 “Top to bottom, and then I am done. I just wrote the number 1.”
2 “Half a moon, there’s more to do. Slide to the right. I wrote a 2.”
3 “To the right and around the tree. Around again to make a 3.”
4 “A little line down, to the right some more. Now a big line down to make a 4.”
5 “Down the side, around a hive. Give it a hat. I wrote a 5.”
6 “Down the side, and then a curl. The 6 makes a little swirl.”
7 “Across the sky, then drop a line. I make a 7 every time.”
8 “Make an S and do not stop. I see an 8 when I close the top.”
9 “Draw a loop and drop a line. That is the way I make a 9.”
© Great Minds PBC 74 FAMILY MATH ▸ Module 1 ▸ Topic F K ▸ M1 ▸ TF EUREKA MATH2 New York Next Gen
© Great Minds PBC 75 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ 5-Group Mat
7 carrots
Shopping List
6 strawberries
8 mushrooms
10 blueberries
9 peas
© Great Minds PBC 77 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lesson 24 24
Name
K ▸ M1 ▸ TF ▸ Lesson 24 EUREKA MATH2 New York Next Gen © Great Minds PBC 78 PROBLEM SET
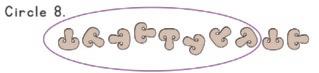
Circle 7. Circle 6. Circle 8. Circle 10. Circle 9.
Name
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lesson 25 © Great Minds PBC 79
25
Name
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lesson 26 © Great Minds PBC 81
26
Name
Count the arms and legs. Write how many.
© Great Minds PBC 83 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lesson 26 26
© Great Minds PBC 85 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lesson 27 ▸ Scoreboard Scoreboard
Name
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lesson 27 © Great Minds PBC 87 27
© Great Minds PBC 89 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lesson 27
the numbers for the I Can Count chart. 27 Name
Write
© Great Minds PBC 91 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lesson 28
28
Write the numbers in order. Draw 5-group dots to match.
Name
FAMILY MATH Analyze the Count Sequence
Dear Family,
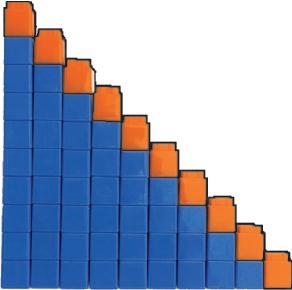
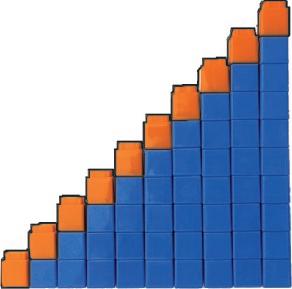
Students are exploring the sequence of numbers from 1 through 10. The number stairs make it easy to see that the next number in the count sequence is 1 more: “1; 1 more is 2.” Then “2; 1 more is 3 …” As they count back, students see the opposite, that each number is 1 less.
At-Home Activities Activity Idea 1 Number Detective
1. Use the number cards from topic B or cut out the number cards included with this letter. Mix up the cards and have your child place them in order from 0 through 10.
2. Once the cards are in order, flip a few cards so some numbers are hidden. Point to a flipped card and have your child use the numbers shown to figure out the hidden number.
Activity Idea 2 Number Match Game
Mix the number cards and dot cards (included with this letter) together, and then lay 6 cards face up. Take turns matching cards that show the same number. Replace the matched cards with cards from the deck. Play until all cards are matched. Challenge your child to put the matched cards in order from 0 through 10.
© Great Minds PBC 93
1-more number stairs
1-less number stairs
6 4 5 2 3 8 10 7 9 1
10 8 6 4 2
Module 1 Topic G
Number Stairs
In class, students build number stairs from 0 to 10 and find that the next number in the count sequence is 1 more. Number stairs allow students to visualize, or see, the pattern of 1 more in the forward counting sequence. They will also build number stairs from 10 to 0 to see that when counting back, each number is 1 less. We call this the 1-less pattern. Students also use the number stairs to see the relationship among ordinal numbers (first, second, third, … , tenth) and magnitude, or how many. They notice that the fourth stair has 4 cubes and the sixth stair has 6 cubes.
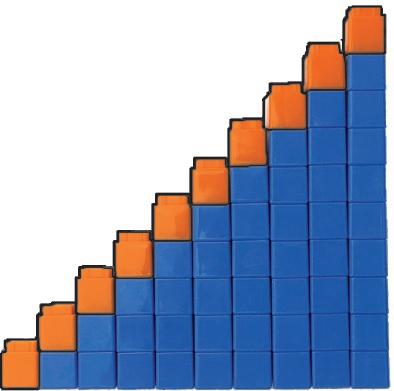
Why do children need to understand the pattern in the forward and backward count sequences? This understanding helps them know how many objects are in a group when they add 1 or take away 1. Without that understanding, a child might add a penny to a group of 24 and then count the whole group from 1.
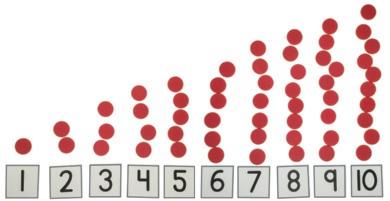
Students will see the number sequence represented on a number path and, in future grades, on the number line.
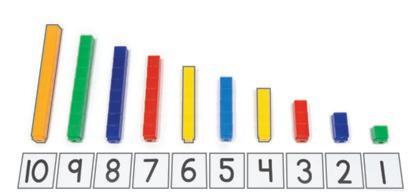
© Great Minds PBC 94 FAMILY MATH ▸ Module 1 ▸ Topic G K ▸ M1 ▸ TG EUREKA MATH2 New York Next Gen
1 3 4 5 6 7 8 9 1 0 2 1 2 3 4 5 6 7 8 9 10 K K and 1 2 number stairs number path number line
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG © Great Minds PBC 95 Module 1 ▸ Topic G ▸ FAMILY MATH 0 1 2 3 4 5 6 7 8 9 10
EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG © Great Minds PBC 97 Module 1 ▸ Topic G ▸ FAMILY MATH
© Great Minds PBC 99 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG ▸ Two-Hands Mat
© Great Minds PBC 101 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG ▸ Lesson 30 30
the numbers in order. Color the number stairs to match.
Name Write
Write the numbers in order. Color the fifth stair. Color the eighth stair.
103 © Great Minds PBC EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG ▸ Lesson 31 31
Name
© Great Minds PBC 105 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG ▸ Lesson 33 33
the numbers in order from 10 to 1. Color the number stairs to match.
Name Write
Name
Draw your collection to show how you counted.
© Great Minds PBC 107 EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG ▸ Lesson 34
34
Credits
Great Minds® has made every effort to obtain permission for the reprinting of all copyrighted material. If any owner of copyrighted material is not acknowledged herein, please contact Great Minds for proper acknowledgment in all future editions and reprints of this module.
Cover, Piet Mondrian (1872–1944), Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921. Oil on canvas. Kunstmuseum Den Haag, The Hague, Netherlands. Image copyright ©Kunstmuseum Den Haag. Image credit: Bridgeman Images; page 13, Henri Rousseau, The Flamingos, 1907. Photo credit: Dennis Hallinan/Alamy Stock Photo; pages 43, 44, (composite image) julie deshaies/ Shutterstock.com, Khumthong/Shutterstock.com, Hong Vo/Shutterstock.com; page 68, loskutnikov/ Shutterstock.com; All other images are the property of Great Minds.
For a complete list of credits, visit http://eurmath.link/media-credits.
109 © Great Minds PBC EUREKA MATH2 New York Next Gen K ▸ M1
Acknowledgments
Beth Barnes, Lauren Brown, Melissa Brown, Dawn Burns, Stella Chen, Mary Christensen-Cooper, Cheri DeBusk, Stephanie DeGiulio, Jill Diniz, Brittany duPont, Lacy Endo-Peery, Ryan Galloway, Krysta Gibbs, Melanie Gutierrez, Karen Hall, Eddie Hampton, Rachel Hylton, Travis Jones, Kelly Kagamas Tomkies, Alison Kenyon, Emily Koesters, Liz Krisher, Alicia Machuca, Ben McCarty, Kate McGill Austin, Cristina Metcalf, Ashley Meyer, Melissa Mink, Katie Moore, Bruce Myers, Marya Myers, Maximilian Peiler-Burrows, Shelley Petre, John Reynolds, Meri Robie-Craven, Robyn Sorenson, Julie Stoehr, James Tanton, Julia Tessler, DesLey V. Plaisance, Philippa Walker, MaryJo Wieland
Trevor Barnes, Brianna Bemel, Lisa Buckley, Adam Cardais, Christina Cooper, Natasha Curtis, Jessica Dahl, Brandon Dawley, Delsena Draper, Sandy Engelman, Tamara Estrada, Soudea Forbes, Jen Forbus, Reba Frederics, Liz Gabbard, Diana Ghazzawi, Lisa Giddens-White, Laurie Gonsoulin, Nathan Hall, Cassie Hart, Marcela Hernandez, Rachel Hirsh, Abbi Hoerst, Libby Howard, Amy Kanjuka, Ashley Kelley, Lisa King, Sarah Kopec, Drew Krepp, Crystal Love, Maya Márquez, Siena Mazero, Cindy Medici, Ivonne Mercado, Sandra Mercado, Brian Methe, Patricia Mickelberry, Mary-Lise Nazaire, Corinne Newbegin, Max Oosterbaan, Tamara Otto, Christine Palmtag, Andy Peterson, Lizette Porras, Karen Rollhauser, Neela Roy, Gina Schenck, Amy Schoon, Aaron Shields, Leigh Sterten, Mary Sudul, Lisa Sweeney, Samuel Weyand, Dave White, Charmaine Whitman, Nicole Williams, Glenda Wisenburn-Burke, Howard Yaffe
K ▸ M1 EUREKA MATH2 New York Next Gen © Great Minds PBC 110
Talking Tool
I Can Share My Thinking
My drawing shows . . . .
I did it this way because . . . .
I think because . . . .
I Can Agree or Disagree
I agree because . . . .
I disagree because . . . .
I did it a different way. I . . . .
I Can Ask Questions
How did you . . . ?
Why did you . . . ?
Can you explain . . . ?
I Can Say It Again
I heard you say . . . . said . . . .
Can you say it another way?
©
Great Minds PBC
MATH IS EVERYWHERE
Do you want to compare how fast you and your friends can run?
Or estimate how many bees are in a hive?
Or calculate your batting average?
Math lies behind so many of life’s wonders, puzzles, and plans. From ancient times to today, we have used math to construct pyramids, sail the seas, build skyscrapers—and even send spacecraft to Mars.
Fueled by your curiosity to understand the world, math will propel you down any path you choose.
Ready to get started?
ISBN 979-8-89012-107-3 9 798890
Module 1
Counting and Cardinality
Module 2
Two- and Three-Dimensional Shapes
Module 3
Comparison
Module 4
Composition and Decomposition
Module 5
Addition and Subtraction
Module 6
Place Value Foundations
What does this painting have to do with math?
Piet Mondrian reduced his subjects into colorful geometric shapes. In this painting bold, black horizontal and vertical lines frame the colorful squares and rectangles in red, black, yellow, and more. Do any of the shapes seem similar? Do you notice that the smaller shapes are added together to create the bigger shape? How many shapes do you see in total?
On the cover
Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921 Piet Mondrian, Dutch, 1872–1944 Oil on canvas
Kunstmuseum Den Haag, The Hague, Netherlands
Piet Mondrian, Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921, Kunstmuseum Den Haag, The Hague, Netherlands. Image credit: Bridgeman Images

121073
A














































