
AUTORIDADES DE LA UNIVERSIDAD
PRIVADA DEL VALLE
Gonzalo Vicente Ruiz Ostria, M.Sc.
Rector Nacional
Diego Alonso Villegas Zamora, Ph.D.
Vicerrector Académico Nacional
Sandra Marcela Ruiz Ostria, M.Sc.
Vicerrectora Interacción Social y Difusión
Cultural
Lic. Daniela Zambrana Grandy
Secretaria General
Antonio Carvalho Suarez, M.Sc.
Vicerrector Sede Académica Santa Cruz
Carlos Torricos, M.B.A.
Vicerrector Sede Académica Sucre
Franklin Nestor Rada, M.Sc.
Vicerrector Sede Académica La Paz
Lic. René Monje Morant
Vicerrector Sede Académica Trinidad
Jorge Carlos Ruiz De la Quintana, M.Sc.
Director Nacional de Investigación
EQUIPO DE INVESTIGACIÓN:
Claude Le Noir, (Investigador principal)
Nahúm Cayo Chileno
Alejandra Araoz Campos , Mauricio Veliz
Andrés Cardoso
Rodrigo Fuentes
Marcelo Coria
Joaquin Humberto Aquino Rocha
EDICIÓN:
Paola Andrea Antezana Pérez
Luis Marco Fernández Sandoval
Cuidado de edición:
Nahúm Cayo Chileno
COMITÉ EDITORIAL
Mgr. María Elena sahonero Saravia
Ing. Erick Muñoz Vásquez
Ing. Ricardo Vargas Bustillo
FOTOGRAFÍA:
Claude Le Noir
Esta obra está protegida bajo la Ley N° 1322 de Derechos de Autor y está prohibida la reproducción bajo cualquier medio sea digital, analógico, magnético y óptico, de cualquiera de sus páginas sin previa autorización escrita del autor.
Versión digital en Bolivia, 2022
Depósito Legal: 2-1-3572-2022
Código de Registro ISBN: 978-9917-620-02-0

Dirección: Av. América No. 165
Teléfono: (591) 4 - 318800 www.univalle.edu
ÍNDICE
PRÓLOGO
M.Sc. Ing. Nathalie Le Noir....................................................................................................3 RESUMEN..............................................................................................................................4
1. INTRODUCCIÓN..............................................................................................................5
2. MATERIALES Y MÉTODOS............................................................................................6
2.1 Área de Estudio.................................................................................................................6
2.2 Datos de precipitación de las (ex) estaciones climatológicas de la cuenca.......................8
2.3 Series de precipitación remota satelital.............................................................................9
2.4 Criterios de bondad de ajuste para verificar el desempeño de una ecuación de regresión............................................................................................................................10
2.5 Determinación de precipitaciones conforme periodo de retorno......................................12
2.6 Determinación de los caudales máximos para periodos de retorno..................................12
3. RESULTADOS...................................................................................................................17
3.1 Selección del proveedor de servicios satelitales...............................................................17
3.2 Regresiones para las precipitaciones mensuales periodo 1993-2003...............................18
3.3 Series extendidas en tiempo de precipitaciones mensuales de 1993-2003 a 1981-2019..22
3.4 Análisis periodo de retorno de las series extendidas en tiempo de precipitaciones mensuales de 1993-2003 a 1981 a 2019...................................................................................................24
3.5 Regresiones para las precipitaciones diarias periodo 1993-2003.....................................25
3.6 Regresiones para la precipitación diaria máxima anual periodo 1993 a 2003
3.6.1 Manteniendo cronología en el periodo de datos comunes.............................................27
3.6.2 No-manteniendo la cronología en el periodo de datos comunes...................................29
3.7 Series extendidas en el tiempo de la precipitación máxima diaria anual de 1993-2003 a 1981-2019.............................................................................................................................34
3.8 Análisis del periodo de retorno de las series de la precipitación máxima diaria anual extendidas de 1993-2003 a 1981 a 2019.......................................................................36
3.9 Determinación de los caudales máximos conforme periodos de retorno..........................37
3.10 Resultados de la simulación HEC-HMS para un periodo de retorno T=100 años.............................................................................................................................39
3.11 Resultados de la simulación HEC-HMS para periodos de retorno T=2, 10, 20, 30, 50, 100, 150, 200, 250 y 300 años........................................................................43
3.12 Comparación de los caudales con el Manejo Integral Cuenca Taquiña........................44
PRÓLOGO
En las gestiones 2018 y 2020, la comunidad de Tiquipaya, Cochabamba – Bolivia, se vio afectada por un evento extremo tipo aluvión hiperconcentrado conocido como “flujo de mazamorra”, el cual lamentablemente provocó una serie de pérdidas económicas e incluso de vidas humanas.
Ante la falta de estudios e información actualizada sobre este tipo de problemática de interés público, la Universidad Privada del Valle, organizó el Foro Técnico Científico “Tiquipaya Zona 0”. A través de esta actividad, se logró difundir el trabajo de investigación realizado por el M.Sc. Ing. Claude Le Noir (docente de las materias hidrología e hidráulica I y II en la Universidad Privada del Valle) junto a profesionales del área, donde se logró definir la problemática existente en la Cuenca Taquiña y el modo en la que esta afecta a la comunidad de Tiquipaya.
Si bien la problemática de la Cuenta Taquiña tiene un carácter natural también se intensificó a causa de la interacción humana, debido al crecimiento de la mancha urbana a tal punto de que la cuenca pierde el cono de deyección, además dentro del margen restrictivo del río Taquiña se encuentran construidas varias viviendas.
Asimismo, los profesionales del Foro Técnico Científico señalan la falta de datos de precipitación dentro de la cuenca como un punto crítico dentro del análisis de la problemática. Es por ello que, el M. Sc. Claude Le Noir desarrolla el presente libro, demostrando la importancia de una correcta evaluación sobre el uso de datos de precipitación registrados por sensores remotos de satélites. El presente libro permite al lector comprender la importancia de respetar la naturaleza de un cauce y asimismo la necesidad de tener datos de precipitación dentro la cuenca. En los últimos años la cuenca Taquiña no tuvo el monitoreo adecuado y sin duda alguna no debe ser un caso único a nivel nacional. Es por ello que se espera que los análisis efectuados en este libro sean replicados para casos similares evitando desastres naturales.

M.Sc. Ing. Nathalie Le Noir
Evaluación dE la factibilidad dEl uso dE datos satElitalEs En la ExtEnsión dE las sEriEs cortas dE prEcipitación para las EstacionEs tErrEstrEs En El contExto dE la cuEnca dEl río taquiña - cochabamba, bolivia
Evaluation of the feasibility of using satellite data in the extension of short series of precipitation for ground stations in the context of the River Taquiña Catchment - Cochabamba, Bolivia
Claude Le Noir1, Nahúm Cayo2, Alejandra Araoz3, Mauricio Veliz4, Andrés Cardoso5, Rodrigo Fuentes6, Marcelo Coria7 y Joaquin Humberto Aquino Rocha8
1 Universidad del Valle, Tiquipaya, Bolivia, lenoirclaude10@gmail.com
2 Universidad del Valle, Tiquipaya, Bolivia, nahum.cayo.chileno@gmail.com
3 Universidad del Valle, Tiquipaya, Bolivia, aca1008864@est.univalle.edu
4 Universidad del Valle, Tiquipaya, Bolivia, vjm2015180@est.univalle.edu
5 Universidad del Valle, Tiquipaya, Bolivia, cva2018106@est.univalle.edu
6 Universidad del Valle, Tiquipaya, Bolivia, fsr0022236@est.univalle.edu
7 Universidad del Valle, Tiquipaya, Bolivia, cgm0021858@est.univalle.edu
8 Universidad Federal do Rio de Janeiro, Rio de Janeiro, Brasil, joaquinaquinorocha@gmail.com
RESUMEN
El objetivo de la presente investigación es evaluar la factibilidad del uso de datos de precipitación registrada por sensores remotos de satélites, a fin de extender en tiempo las series cortas de precipitación registradas en las estaciones de la superficie de la Cuenca del río TaquiñaCochabamba, Bolivia. Inicialmente se realizó un análisis multicriterio, se determinó que, para este caso, el proveedor de servicios satelitales CHIRPS (Climate Hazards Group InfraRed Precipitation with Station data) es la mejor opción de ocho proveedores previamente considerados (CFSR, CHIRPS, ERAS, GRIDMET, PRISMA, MERRA2, TERRACLIMATE y TRMM/GPM). CHIRPS trabaja con datos diarios, cubre a la Cuenca del río Taquiña, tiene una resolución espacial alta de 4.8 x 4.8 km, está basado en ajustes con datos de estaciones terrestres y cubre un periodo considerable de datos (1981 a la fecha). Luego se calibraron fórmulas de regresión para las series de precipitación mensual, diaria y diaria máxima anual, todas en base al periodo común de datos (1993 a 2003) y considerando datos registrados en superficie y datos satelitales. Se verificaron los criterios de bondad de ajuste del coeficiente de determinación (R2), coeficiente de Nash-Sutcliffe (NSE), PBIAS y RSR. Las regresiones presentaron un buen ajuste para la serie de precipitación mensual (R2>0.82 y NSE>0.72), a diferencia de la precipitación diaria y máxima diaria anual como series sincrónicas. Ya para la máxima precipitación diaria, como serie ordenada asincrónica,
se obtuvo un mejor ajuste (R2>0.64 y NSE>0.64), permitiendo la extensión de la serie de 11 a 39 años. Finalmente se calcularon los caudales máximos con el programa HEC-HMS en base a las series extendidas en el tiempo de la máxima precipitación diaria anual. Se encontró una buena correspondencia con los caudales máximos del estudio del Servicio Departamental de Cuencas (2020), quienes usaron métodos hidrológicos diferentes.
Palabras clave: Criterios de bondad de ajuste – Ecuaciones de regresión – Extensión de una serie - Precipitación medida en superficie de la tierra - Precipitación satelital
ABSTRACT
The objective of the present investigation is to evaluate the feasibility of the use of precipitation data registered by remote satellite sensors, in order to extend in time the short series of precipitation registered in the surface stations of the Taquiña-Cochabamba River Catchment, Bolivia. Initially, a multi-criteria analysis was carried out, it was determined that, for this case, the satellite service provider CHIRPS (Climate Hazards Group InfraRed Precipitation with Station data) is the best option out of eight previously selected providers (CFSR, CHIRPS, ERAS, GRIDMET, PRISM, MERRA2, TERRACLIMATE and TRMM/GPM). CHIRPS work with daily data, covers the Taquiña River Basin, has a high spatial resolution of 4.8 x 4.8 km, is based on adjustments with data from ground stations, and covers a considerable period of data (1981 to date). Then, regression formulas were calibrated for the monthly, daily and annual maximum daily precipitation series, based on the common data period (1993 to 2003) considering data recorded on the surface and satellite data. The goodness-of-fit criteria for the coefficient of determination (R2), Nash-Sutcliffe coefficient (NSE), PBIAS and RSR were verified. The regressions presented a good fit for the monthly precipitation series (R2>0.82 and NSE>0.72), unlike the daily and maximum annual daily precipitation as synchronous series. For the maximum annual daily precipitation, as an asynchronous ordered series, a better fit was obtained (R2>0.64 and NSE>0.64), allowing the extension of the series from 11 to 39 years. The maximum discharges were calculated using the program HEC-HMS based on the series extended in time of the maximum annual daily precipitation. A good correspondence was found with the maximum discharges calculated in the study from Departmental Basin Service (2020), which used different hydrological methods.
Keywords: Extension of series - Goodness of fit criteria – Precipitation measured on the earth surface - regression equations - Satellite precipitation
1. INTRODUCCIÓN
La precipitación es parte fundamental del ciclo hidrológico; por tanto, una estimación precisa de este fenómeno permite una comprensión adecuada de los sistemas de recursos hídricos. Sin embargo, en varias partes del mundo, la cobertura en espacio y tiempo es deficiente (Aksu y Akgül, 2020). En este sentido, las estimaciones de precipitación basadas en satélites pueden ser una alternativa para este problema, especialmente en regiones donde no se cuentan con datos en espacio y tiempo (Toté et al., 2015; Dinku et al., 2018).
Diversos estudios concluyeron que las estimaciones de precipitación provenientes de datos de precipitación satelital: TRMM (Tropical Rainfall Measuring Mission), CHIRPS (Climate Hazards Group InfraRed Precipitation with Station data), MSWEP (Multi-source weighted-Ensemble
Precipitation), entre otros, constituyen una alternativa aceptable para ser incluidas en modelos hidrológicos de áreas donde no se disponga de una adecuada distribución espacial de estaciones meteorológicas (Ouma et al., 2012; Mantas, et al., 2015; Laura et al., 2015; Vallejos et al., 2016; Liu et al., 2019; Delgadillo, 2019; Quispe, 2020). Entre algunos ejemplos, Kizza et al. (2012) utilizaron datos satelitales TRMM para estimar las precipitaciones para la cuenca del lago Victoria (zona centro-oriental de África), información necesaria para la evaluación de recursos hídricos.
Otros estudios también han utilizado los datos de precipitación del producto satelital TRMM en estudios hidrológicos del lago Poyang, China (Li et al., 2012; Li et al., 2014). Bai et al. (2018) estudiaron la precisión de la precipitación del producto satelital CHIRPS en China. Aksu y Akgül (2020) evaluaron el rendimiento de las estimaciones de precipitación mediante datos CHIRPS en Turquía. Cavalcante et al. (2020) analizaron índices de precipitaciones extremas a partir de la estimación de datos CHIRPS en la amazonia brasileña.
A pesar de las investigaciones y avances en el área, los productos satélites deben ser evaluados para conocer su precisión en las diferentes regiones y, dependiendo de la aplicación, seleccionar el producto más apropiado (Toté et al., 2015).
Por otro lado, debido a los flujos de Mazamorra (aluviones con detritos) de 2018 y 2020 ocurridos en el municipio de Tiquipaya, Bolivia (Cuenca del río Taquiña), se ha demostrado que, para los estudios del fenómeno y el diseño de intervenciones, existe una falencia de datos básicos en el campo de la topografía, geología, geomorfología, geotécnica, hidrología, hidráulica, uso de suelos y forestales (Le Noir et al., 2019; Bolívar Vallejo, 2020, Univalle, 2022). En este sentido, la Cuenca del río Taquiña requiere estudios hidrológicos, hidráulicos, morfológicos, urbanísticos, forestales y de los flujos de la mazamorra, los cuales se encuentran dificultados por la falta de registros continuos de la precipitación de suficiente longitud en tiempo.
Las estaciones ubicadas dentro de la cuenca: Janamayu, Linkupata y Laguna Taquiña, presentan un registro de datos de precipitación diaria desde agosto de 1992 a 2003. Si bien la estación Linkupata fue rehabilitada en noviembre de 2018, los 11 años de datos no permiten extrapolar estadísticamente las precipitaciones para periodos de retorno comprendidos de 50 a 300 años. Esta información es esencial para diseñar y construir a corto plazo obras de infraestructura y defensa contra los flujos de mazamorra, inundaciones, entre otros (Read y Vogel, 2015; Dettinger et al., 2016; Watson, 2017).
Por tanto, la presente investigación tiene como objetivo analizar la factibilidad de extender en tiempo las series cortas de precipitación (mensual, diaria y máxima diaria anual) de las tres estaciones de la Cuenca del río Taquiña en base a series de precipitación registradas de forma satelital-remota. Se definieron siete pasos para alcanzar el objetivo: (1) determinar el proveedor de datos de precipitación satelital más apropiado; (2) calibrar las regresiones entre los datos de precipitación satelital y la precipitación en superficie de la tierra; (3) verificar la bondad de ajuste de las diferentes fórmulas de regresión; (4) ampliar las series de precipitación; (5) realizar el análisis de periodo de retorno sobre las series extendidas; (6) calcular los caudales máximos a la salida de la cuenca con las series extendidas de máximas precipitaciones diarias anuales, y (7) comparar los caudales máximos obtenidos con otros autores.
2. MATERIALES Y MÉTODOS
2.1 Área de Estudio
La Cuenca del río Taquiña está ubicada dentro de la región Hidrográfica del río Rocha en el Valle Bajo del Departamento de Cochabamba – Bolivia. La Cuenca del río Taquiña pertenece a tres Municipios (Tiquipaya, Cochabamba y Sacaba). El río Taquiña es una de las cincuenta y ocho torrenteras del Valle de Cochabamba (Figura 1)
Figura 1: Ubicación Cuenca del río Taquiña – Cuencas Valle Alto / Valle Sacaba / Valle Central / Valle Bajo– Departamento de Cochabamba – Bolivia.

Fuente: Le Noir et al., 2019
La cuenca se encuentra entre las coordenadas UTM (WGS84, zona 19 Sur): Este 805037 – 798853 m, Norte 8082143 – 8089494 m y tiene una altitud comprendida entre 2942 y 4631 m.s.n.m. El área hasta el punto del cono de deyección es: 19.28 km2. El límite de la cuenca se ha determinado con la plataforma ArcMap de ArcGis 10.5 y el uso de modelos digitales de elevación (MDE) ALOS PALSAR de alta resolución 12.5 x 12.5 m y de tipo corregido para el terreno, obtenido de ASF (Alaska Satellite Facility) (Figura 2).
Figura 2: Cuenca del río Taquiña, red de ríos, curvas de nivel y estaciones meteorológicas

Fuente: Elaboración propia, 2022
2.2 Datos de precipitación de las (ex) estaciones climatológicas de la cuenca
Adicionalmente, la Figura 2 muestra la ubicación de las tres estaciones meteorológicas: Janamayu, Linkupata y Laguna Taquiña, las cuales fueron operadas por el extinto Programa de Manejo Integral de Cuencas (PROMIC) y el Laboratorio de Hidráulica de Universidad Mayor de San Simón (LHUMSS) en el periodo de agosto 1992 a diciembre de 2003. De 2004 hasta la fecha, las mediciones fueron y continúan suspendidas. Posterior al evento del primer flujo de la mazamorra en febrero del 2018, el Servicio Nacional de Meteorología e Hidrología (SENAMHI), instaló una nueva estación denominada Linkupata 2018 (Figura 2), que está en funcionamiento desde noviembre de 2018 hasta la fecha.
En la Tabla 1 se detalla por estación: las coordenadas geográficas, altitud, resumen de las variables registradas, tipo de estación, operador y periodo de registro. En la Tabla 2 se analiza la disponibilidad de los datos de precipitación. Las estaciones que funcionaron de 1993 a 2003, presentaron ciertos periodos de interrupción. En Janamayu faltan 93 de los 4017 datos diarios o 2.3 %, Linkupata 7.7 % y Laguna Taquiña 7.0 %. Por parte de la estación Linkupata 2018, desde el momento de su operación, presenta una serie de datos completos.
Tabla 1: Datos generales de las estaciones meteorológicas
Fuente: Elaboración propia, 2022
Tabla 2: Diagrama de barras de datos de precipitación diaria disponible en las estaciones terrestres
Estación meteorológica
X Año en que faltan X datos de precipitaciones
Año con datos diarios completos
Año que no se tienen datos de precipitación
Fuente: Elaboración propia, 2022
El periodo de registro de la nueva estación Linkupata 2018 es corto (dos años) y se encuentra 750 m desplazada de la primera estación Linkupata; por tanto, el presente estudio no consideró esta nueva estación.
La presente investigación ha adoptado las series rellenadas por el LHUMSS, entidad encargada de las series de precipitación diaria de las estaciones estudiadas, de 1992 a 2003, verificando que no existan valores fuera de rango en los valores registrados y rellenados, y que las series obtenidas sean homogéneas y consistentes. Sin embargo, estos 11 años no son suficientes para estudios hidrológicos a largo plazo, por lo que el objeto de la presente investigación es extender los 11 años de datos a un mayor número de años, mediante el uso de precipitaciones satelitales registradas de forma remota.
2.3 Series de precipitación remota satelital
Se han estudiado varios productos de precipitación remota ofrecidos en el mercado libre, disponibles en GOOGLE CLIMATE ENGINE® (Google Developers, 2022), entre ellos: CFSR (Climate Forecast System Reanalysis dataset), CHIRPS, ERA5 (ECMWF Reanalysis v5), GridMET (4-km daily Gridded Surface Meteorological for USA), MERRA2 (Modern-Era Retrospective analysis for Research and Applications V2), PRISM (Prism Climate Group – Oregon State University) y TerraClimate (Climate & climate water balance dataset for terrestrial surfaces WorldClim).
GOOGLE CLIMATE ENGINE® (Google Developers, 2022) ofrece un fácil acceso a los datos generales de los productos de datos satelitales climatológicos y también permite descargar los datos requeridos de forma sencilla.
Mediante GIOVANNI NASA’s (Earthdata NASA, 2022) se tiene acceso al producto TRMM (Tropical Rainfall Measuring Mission) de datos generales y datos climatológicos. Es una misión conjunta entre la NASA y JAXA (Japan Aerospace Exploration Agency), la cual permite estudiar las precipitaciones tropicales y la investigación meteorológica y climática. TRMM ha funcionado en el periodo de 1997 a 2015, desde entonces se ha sustituido TRMM por GPM (Global Precipitation Mission), que tiene un alcance a nivel mundial (Asurza et al., 2018).
En el análisis multicriterio para determinar el producto que se ajuste a los requerimientos del presente estudio, se consideraron seis criterios. 1) Ser gratuito. 2) Proveer valores diarios, necesarios para estudiar eventos extremos. 3) Cubrir el área de proyecto. 4) Tener una resolución de píxel pequeño, a fin de evitar cubrir áreas mayores y, por tanto, terrestres. 5) Permitir una calibración de las fórmulas de regresión con los datos que fueron registrados en la cuenca y, a su vez, debe permitir extender los registros de una forma aceptable para estimar eventos extremos con periodos de retorno. El producto debe tener datos de 1993 a 2003 para permitir la calibración. Para extender las series debe tener datos de 2004 a la fecha y preferentemente también datos antes 1993. 6) Incluir un ajuste de los datos satelitales con los datos de una red de estaciones terrestres.
2.4 Criterios de bondad de ajuste para verificar el desempeño de una ecuación de regresión
Los indicadores de desempeño o de bondad de ajuste de una ecuación de regresión (o de un modelo) describen que tan adecuado es el ajuste del conjunto de los valores calculados al de los valores observados. En general, las medidas de bondad de ajuste permiten resumir la discrepancia entre los valores estimados con la ecuación o modelo en estudio y los valores observados. En hidrología se usan normalmente los siguientes criterios de bondad de ajuste (Golmohammadi et al., 2014; Nash y Sutcliffe, 1970):
a) Eficiencia de Nash-Sutcliffe (NSE)
La eficiencia de Nash-Sutcliffe (NSE) (Ecuación 1) determina cuánto de la variabilidad de las observaciones (datos medidos) es explicada por la simulación. Si la simulación es perfecta, NSE=1; si se intentase ajustar las observaciones con el valor promedio, entonces NSE=0. El rango de posibles valores es de −∞ < NSE ≤ 1.0, los valores observados entre 0.0 y 1.0 son considerados niveles aceptables de desempeño, pero cuando los valores de NSE son menores a 0.0, indica que el promedio de valores observados es un mejor predictor que los valores simulados, lo cual es inaceptable. El criterio de Nash Sutcliffe es uno de los más usados en hidrología (Gupta y Kling, 2011; Brown et al., 2022).
Donde:
yi = valor de la altura de precipitación observada en día i
y = valor medio de las alturas de precipitación observadas durante el tiempo total
ysim,i = valor de la altura de precipitación simulada para el día i
Algunos valores sugeridos para la toma de decisiones son resumidos en la Tabla 3.
Tabla 3: Valores referenciales del Criterio de Nash-Sutcliffe
E Ajuste
<0.2 Insuficiente
0.2 - 0.4 Satisfactorio
0.4 - 0.6 Bueno
0.6 - 0.8 Muy bueno
>0.8 Excelente
Fuente: Molnar, 2011
b) Coeficiente de correlación de Pearson (RPearson)
El coeficiente de correlación de Pearson (RPearson) describe el grado de relación lineal entre los datos simulados y los datos observados. El coeficiente de correlación oscila entre −1 a 1 y se calcula mediante la Ecuación 2. Si RPearson = 0, no existe relación lineal, si RPearson = 1 o −1, existe una perfecta relación lineal positiva o negativa.

c) Porcentaje BIAS (PBIAS)
El porcentaje de BIAS (PBIAS) mide la tendencia promedia que los datos simulados sean mayores o menores que los datos observados y se calcula mediante la Ecuación 3. El valor óptimo es 0.0 y valores de baja magnitud significan una simulación precisa. Valores positivos implican una subestimación del BIAS, y valores negativos indican una sobre estimación del BIAS.
d) Relación de la desviación estándar de observaciones Y RMSE (RSR)
Para calcular el RSR, se necesita la raíz del error cuadrático medio (RSME) y la desviación estándar de los valores observados (STDEVobs), utilizando las Ecuaciones 4 y 5 respectivamente.

Un valor RMSE = 0 es un ajuste completo. RMSE<0.5*STDEVobs (Desviación estándar de cada modelo observado) o un valor RSR (Relación de la desviación estándar de observaciones y RMSE)
< 0.5 se considera bajo e indicativo de una predicción buena del modelo. Finalmente, el RSR se calcula por la Ecuación 6.
2.5 Determinación de precipitaciones conforme periodo de retorno
Para determinar la magnitud para un periodo de retorno T de una serie observada de precipitación, en primer lugar, se calcula la frecuencia de cada valor registrado en la serie. Mediante la distribución de Weibull se normalizan estas frecuencias a probabilidades empíricas. Con estas probabilidades se construye la función acumulada de probabilidad de no-excedencias de la distribución empírica de la serie de precipitaciones observadas.
Para proyectar la serie observada de precipitaciones a diferentes periodos de retorno T, se precisa conocer la distribución teórica que mejor representa a la distribución empírica. Para determinar esta distribución teórica se debe ir probando y realizar controles de bondad de ajuste tipo visual y/o analítico (Chi-cuadrado y/o Smirnov-Kolomogrov).
Para determinar las precipitaciones que corresponden a periodos de retorno T, en la presente investigación se ha usado la plataforma de software hidrológico HidroEsta 2 (Villón Béjar, 2014).
Esta plataforma permite evaluar las distribuciones comunes en hidrología: normal, log-normal de 2 y 3 parámetros, gama de 2 y 3 parámetros, log-Pearson tipo III, Gumbel y log-Gumbel.
2.6 Determinación de los caudales máximos para periodos de retorno
Los caudales máximos se calcularon con la plataforma HEC-HMS v.4.7.1 en base a las series extendidas en el tiempo de las precipitaciones máximas diarias anuales. HEC-HMS es una plataforma para modelado hidrológico con varias opciones. HEC-HMS fue desarrollado por el Centro de Ingeniería Hidrológica del Cuerpo de Ingenieros del Ejército de los Estados Unidos.
El modelo HEC HMS de la Cuenca del río Taquiña fue construido mediante la extensión HECgeoHMS v.05 de ArcGis v.10.05. El modelo fue subdividido en 4 subcuencas: Norte, Este, Oeste y Sur, Figura 3. El punto de salida de la Subcuenca Norte coincide con la Presa Taquiña. Se trata de una subcuenca regulada. El punto de salida de la Cuenca Taquiña es elegido en el cono de deyección del río Taquiña. Las coordenadas UTM de este punto de salida se presentan en la Tabla 4.
Tabla 4: Coordenadas UTM (zona 19S) de la salida de la Cuenca Taquiña en el modelo HECHMS
Punto de salida de la cuenca UTM Este (m) UTM Norte (m) Nivel (m.s.n.m.)
Ubicado en el cono de deyección 799288 8082168 2941
Fuente: Elaboración propia, 2022
Figura 3: El modelo HEC-HMS de la Cuenca Taquiña se compone de cuatro subcuencas

Fuente: Elaboración propia, 2022
En la Tabla 5 se presentan datos necesarios para el modelo como ser el área y el perímetro de las cuatro subcuencas.
Tabla 5: Parámetros morfométricos para el modelo
Cuenca
Subcuenca
Fuente: Elaboración propia, 2022
Para la estimación de la escorrentía directa de la cuenca se activó la opción del modelo (de infiltración) del SCS (NRCS) con el número de la curva CN. El mapa con los valores CNII (Figura 4) fue determinado con HEC-geoHMS en base a los mapas de suelos y de uso de suelos de la Cuenca del río Taquiña presentados por el CLAS UMSS (2011). En Tabla 5 se presentan los valores CNIII de las subcuencas que corresponden a una condición antecedente de varios días de lluvia con suelos saturados para simular las crecidas máximas.
Para transformar la precipitación en exceso en escorrentía se usa el método del hidrograma unitario sintético del SCS, que requiere del tiempo de retardo entre los centros de gravedad del hietograma y del hidrograma. En condiciones normales el tiempo de retardo es igual a 0.6 veces el tiempo de concentración de la cuenca. Para el tiempo de concentración se utilizaron las fórmulas de Peláez (2003), Williams (1922), Kirpich (1940), Californian Culvert, SCS (1986), Piligrim y McDermott (1981), Dooge (1973), Pizarro et al. (1993) y Pasini. Se ha promediado un valor después de eliminar el valor máximo (Piligrim y McDermott, 1981) y mínimo Pasini (Tabla 5).
El modelo HEC-HMS de la cuenca se esquematiza en la Figura 5. El escurrimiento de la Subcuenca Norte entra a la laguna Taquiña, la cual está simulada como un reservorio con vertedero. El caudal laminado de la laguna Taquiña luego transita por el curso del Río_2 de la Subcuenca Este. El caudal laminado por una laguna es varias veces inferior al caudal de entrada a la laguna, situación notoria en la Subcuenca Este. Aparentemente, el Río_2 tiene una pendiente muy fuerte, pero con caudales de crecida (regulados) bajos. A la unión U_1, llegan los hidrogramas de las Subcuencas Este y Oeste y el hidrograma laminado de la laguna Taquiña transitado desde la Cuenca Norte. La suma de estos tres hidrogramas transita por el Río_1 hasta la salida de la cuenca, donde se adiciona el aporte de la Cuenca Sur.
Para el tránsito de los hidrogramas de crecida por Río_1 y Río_2 se aplicó el método cinemático con los parámetros indicados en la Tabla 6. El método es justificado porque en las cuencas de alta montaña no existe casi nada de almacenamiento de las aguas de las crecidas en el lecho de los ríos y, por ende, no existe atenuación de los caudales picos de las crecidas.
Tabla 6: Parámetros para el tránsito de los caudales en los ríos 2 y 1 del modelo HEC-HMS (método cinemático)
Cuenca
Río Sprom áreas iguales Longitud (l) Manning
Coeficiente corrección Manning Manning corregido
Ancho sección rectangular adoptado (-) (m/m) (m) (m-1/3s) (-) (m-1/3s) (m)
Subcuenca Este Río_2 20.46% 3520 0.045 1.33 0.06 10
Subcuenca Sur Río_1
0.045 1.78 0.08 20
Fuente: Elaboración propia, 2022
4: Mapa de valores CN de la Cuenca Taquiña

Fuente: Elaboración propia, 2022
Figura 5: Modelo esquemático HEC-HMS de la Cuenca del río Taquiña

Fuente: Elaboración propia, 2022
El modelo meteorológico del modelo HEC-HMS de la Cuenca del río Taquiña consistió en las tres estaciones: Janamayu, Linkupata y Laguna Taquiña.
Para las tres estaciones, partiendo de las precipitaciones máximas diarias anuales conforme los periodos de retorno, mediante el método de los coeficientes de desagregación se determinaron las
curvas PDF e IDF para la Cuenca del río Taquiña (LHUMSS). En base a estas curvas, mediante el método de los bloques alternos del USBR, se elaboraron las tormentas críticas para cada periodo de retorno y para cada una de las estaciones.
Para determinar la precipitación sobre las subcuencas se utilizó el método de los polígonos de Thyssen (método del vecino próximo), Figura 6 y Tabla 7.
Figura 6: Polígonos de Thiessen para las cuatro subcuencas del modelo HEC-HMS

Fuente: Elaboración propia, 2022
Tabla 7: Ponderadores Thiessen para las cuatro subcuencas
Subcuenca
Estación pluviométrica
Laguna Taquiña Linkupata Janamayu
Fuente: Elaboración propia, 2022
3. RESULTADOS
3.1 Selección del proveedor de servicios satelitales
El producto CHIRPS cumple con todos los criterios establecidos en la metodología; por tanto, resulta la mejor opción para el presente estudio: permite datos diarios; cubre a la Cuenca del río Taquiña; tiene una resolución espacial muy alta, es decir, un pixelado muy pequeño de 4.8 km; está basado en ajustes con datos de estaciones terrestres, y cubre un periodo con datos diarios de 1981 a la fecha, Tabla 8.
Tabla 8: análisis multicriterio para determinar la mejor opción para el proveedor de datos de precipitación satelital para la Cuenca Taquiña
Producto de precipitación remota
CFSR
Gratuito Precipitación a nivel diario
Cubre el área de proyecto
Resolución espacial grande
Km desde de 2011
Periodo de disponibilidad de datos
Km antes de 2011 1979-2021
1979-2021
Ajuste con estaciones terrestres
Fuente: Elaboración propia, 2022
En la Tabla 9 se tiene la comparación de los registros de las estaciones de la cuenca con los registros del producto CHIRPS en función del tiempo. El periodo común de datos sirve para calibrar y eventualmente validar fórmulas de regresión para extender las series de precipitación. Con precipitaciones diarias (4017 datos) se podrá realizar calibración y validación. Con precipitaciones mensuales (132 datos) y máximas diarias anuales (11 datos) se podrá realizar la calibración, pero no la validación. Luego los datos CHIRPS de 1981 a 1992 y de 2004 a 2019 servirán para extender las series.
Tabla 9: Datos de precipitación diaria disponible en las estaciones terrestres y en el producto CHIRPS
Estación
X Estación convencional - año con X datos rellenados
Estación convencional - año completo
Estación satelital - año completo Año
Fuente: Elaboración propia, 2022
3.2 Regresiones para las precipitaciones mensuales periodo 1993-2003
Las ecuaciones de regresión para las precipitaciones mensuales se determinan para el periodo común de datos de 1993 a 2003 entre las estaciones terrestres (convencionales) y las series de precipitación satelital CHIRPS.
Figura 7: Análisis nube de puntos precipitación mensual entre Janamayu CHIRPS y Janamayu convencional

Fuente: Elaboración propia, 2022
En primera instancia, se presentan los resultados para la estación Janamayu. En la Figura 7 se tiene el gráfico de nube de puntos. La variable independiente (x) es la precipitación mensual satelital CHIRPS en la localidad de Janamayu y la variable dependiente (y) es la precipitación mensual registrada en la estación convencional.
La mayoría de los puntos están encima de la recta de homogeneidad, y = x. Implica que, de una forma casi general, las precipitaciones mensuales registradas de forma convencional son mayores a las precipitaciones registradas de forma remota con CHIRPS. Existe también una importante dispersión de los puntos demostrando que una regresión de ajuste perfecto no es posible.
En la Figura 8 se tiene el gráfico de análisis doble masa series precipitación mensual Janamayu CHIRPS y Janamayu convencional. Se observan que los puntos en comportamiento general se ajustan bien a una línea. Esto implica que las dos series son consistentes y que se pueden usar los datos CHIRPS para simular los datos convencionales.
Figura 8: Análisis doble masa precipitación mensual entre Janamayu CHIRPS y Janamayu convencional

Fuente: Elaboración propia, 2022
La Figura 9 compara las funciones acumuladas de la precipitación mensual registrado por CHIRPS y por la estación convencional para Janamayu. Las dos funciones demuestran muy buena similitud, salvo que los valores acumulados de CHIRPS siempre son inferiores a los valores acumulados de la estación convencional, demostrando que se precisa de una función de regresión para simular mediante valores CHIRPS a los valores registrados por la estación convencional.
Figura 9: Análisis precipitación mensual acumulada Janamayu CHIRPS y Janamayu convencional en función del tiempo

Fuente: Elaboración propia, 2022
La Figura 10 muestra la precipitación mensual promedio anual calculada con los registros CHIRPS y los convencionales. Durante 10 meses (incluyendo la época de lluvias), el promedio anual de la precipitación mensual sobre la base de datos convencionales supera o iguala al promedio anual de la precipitación mensual sobre la base de datos CHIRPS. Los dos otros meses en época seca el promedio anual de la precipitación mensual con datos CHIRPS es superior al promedio anual de la precipitación mensual con datos convencionales.
La ecuación de la recta de regresión que mejor se ajusta a la nube de puntos es y = 1.5512x, con un coeficiente de determinación R2 = 0.8214 y un coeficiente de correlación de Pearson, RPearson = 0.9063. Una función de segundo grado mejora el coeficiente de determinación, pero solamente en el tercer digito, por simplicidad se maneja la ecuación lineal.
Figura 10: Comparación precipitación mensual promedio anual entre Janamayu CHIRPS y Janamayu Convencional

Fuente: Elaboración propia, 2022
En la Figura 11 se comparan, para la estación de Janamayu, los valores de precipitación mensual registradas de forma convencional con los valores calculados partiendo de los datos CHIRPS, a la cual se ha aplicado la ecuación de regresión para el periodo 1992 a 2003. La correspondencia entre los valores registrados y calculados mediante la fórmula de regresión es significativamente buena. Los trazos de las series presentan valores muy similares con periodos de lluvia y secos que reflejan un mismo fenómeno natural, aunque no todos los valores máximos y mínimos coinciden perfectamente para ambas series. Los resultados para la precipitación mensual de las estaciones Linkupata y Laguna Taquiña son similares a las descritas para la estación de Janamayu.
En la Tabla 10 y Tabla 11 se tienen las fórmulas de calibración para la precipitación mensual de las tres estaciones y el resultado de las pruebas de bondad del ajuste.
Figura 11: Comparación entre precipitación mensual Janamayu convencional y Janamayu CHIRPS calibrado

Fuente: Elaboración propia, 2022
Tabla 10: Precipitación mensual: fórmulas de calibración y cálculos intermedios para las pruebas de bondad de ajuste y = ax+b
Janamayu
Laguna Taquiña
Linkupata y (Observación terrestre) x (Satelital CHIRPS
Fuente: Elaboración propia, 2022

Tabla 11: Precipitación mensual: resultados pruebas de bondad de ajuste para NSE, RPearson, PBIAS y RSR (mm/mes) Ajuste (mm/mes) Correlación
Janamayu
Laguna Taquiña
Bueno x (Satelital CHIRPS y (Observación terrestre)
Linkupata NSE RPearson PBIAS RSR
Fuente: Elaboración propia, 2022
• La Eficiencia de Nash-Sutcliffe (NSE) para Janamayu, Linkupata y Laguna Taquiña es de 0.82, 0.77 y 0.77, calificándose como “excelente”, “muy bueno” y “muy bueno”, respectivamente.
• El coeficiente de correlación de Pearson (RPearson) para Janamayu, Linkupata y Laguna Taquiña es de 0.91, 0.88 y 0.88, calificándose como “muy alta”, “alta” y “alta”, respectivamente.
• Los valores PBIAS para Janamayu, Laguna Taquiña y Linkupata son: 0.7 %, 5.8 % y 2.2 %, respectivamente, calificándose como “muy buenos”, ya que son inferiores a 25 % y cercanos a 0.
• Los valores RSR son: 0.42, 0.47 y 0.48, los cuales son inferiores al valor límite de 0.5, indicando cumplimiento al criterio RSR.
3.3 Series extendidas en tiempo de precipitaciones mensuales de 1993-2003 a 1981-2019
En las Figura 12, 13 y 14 se presentan las series extendidas de la precipitación mensual de 19932003 a 1981-2019 para las estaciones Janamayu, Linkupata y Laguna Taquiña, respectivamente. El comportamiento general de cada serie es similar; no obstante, el comportamiento a detalle es diferente, mostrando que la precipitación en la Cuenca del río Taquiña no es uniforme, pero es espacialmente distribuida, a pesar de ser una cuenca pequeña de 19.3 km2 y de las pequeñas distancias entre las estaciones 1.2, 3.3 y 3.7 km. Esta no uniformidad se debe a las diferentes altitudes de ubicación de las estaciones y a una orografía diferente en cada estación respecto a las direcciones predominantes del viento.
Figura 12: Janamayu precipitación mensual – serie extendida con CHIRPS de 1981 - 2019

Fuente: Elaboración propia, 2022
Figura 13: Linkupata precipitación mensual – serie extendida con CHIRPS de 1981 - 2019

Fuente: Elaboración propia, 2022
Figura 14: Laguna Taquiña precipitación mensual – serie extendida con CHIRPS de 19812019

Fuente: Elaboración propia, 2022
3.4 Análisis periodo de retorno de las series extendidas en tiempo de precipitaciones mensuales de 1993-2003 a 1981 a 2019
En las Figura 15, 16 y 17 se presentan los análisis de periodo de retorno T a la serie extendida de la precipitación mensual a 1981-2019 para las estaciones Janamayu, Linkupata y Laguna Taquiña, respectivamente. El comportamiento general de cada serie es similar; sin embargo, el comportamiento a detalle es diferente, verificando que la precipitación en la Cuenca del río Taquiña no es uniforme, pero es espacialmente distribuida.
De las figuras anteriormente indicadas se observa que la Cuenca del río Taquiña presenta una temporada de lluvias fuerte de noviembre a marzo y una temporada de lluvias bajas de abril a octubre.
Figura 15: Linkupata precipitación mensual serie extendida con CHIRPS 1981 a 2019 análisis de periodo de retorno

Fuente: Elaboración propia, 2022
Figura 16: Janamayu precipitación mensual serie extendida con CHIRPS 1981 a 2019 análisis de periodo de retorno

Fuente: Elaboración propia, 2022
Figura 17: Laguna Taquiña precipitación mensual serie extendida con CHIRPS 1981 a 2019 análisis de periodo de retorno

Fuente: Elaboración propia, 2022
3.5 Regresiones para las precipitaciones diarias periodo 1993-2003
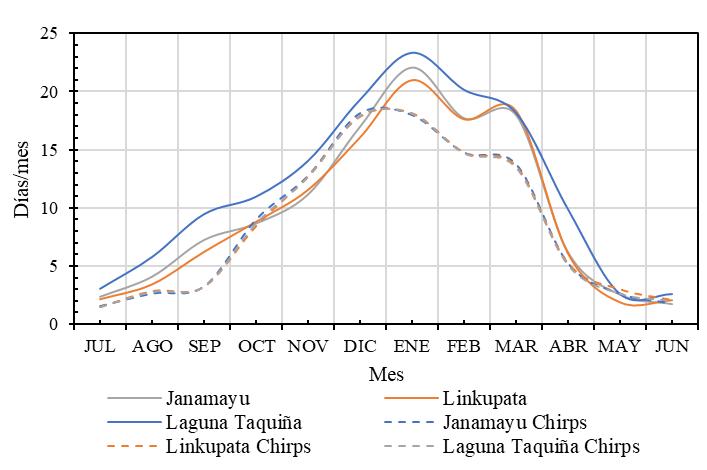
En la Figura 18 se presenta el promedio anual de los días de precipitación al mes, conforme registros observados y registros CHIRPS. La diferencia en los meses julio, agosto, octubre, noviembre, mayo y junio son de uno (1) a dos (2) días, en el mes de abril es de cinco (5) días y en los meses enero, febrero y marzo alcanza a seis (6) días. Estas diferencias en días de precipitación al mes demuestran inconsistencias a nivel de registros diarios entre los datos observados y los datos levantados de forma remota.
El análisis de nube de puntos de la precipitación diaria para las tres estaciones (Figuras 19, 20 y 21) y los 11 años (1993 y 2003) presentan bajos coeficientes de determinación (R2) para la regresión lineal, 0.1386, 0.0748 y 0.1352 para Janamayu, Laguna Taquiña y Linkupata, respectivamente. Según criterio de Nash-Sutcliffe (NSE < 0.2), un valor de NSE inferior a 0.2 es insuficiente para aspectos hidrológicos. Otros tipos de regresión no mejoran sustancialmente el R2. Existen varios puntos sobre la abscisa (días con 0 precipitación registrada en Tierra, pero sí con registro CHIRPS) y sobre la ordenada (días con 0 precipitación CHIRPS, pero si con precipitación registrada). La excesiva cantidad de estos puntos no es correcta, demostrando problemas con el registro de forma remota. Estos puntos influyen de manera negativa en la determinación de una adecuada regresión.
Figura 18: días por mes de precipitación observada y satelital cuenca Taquiña
Fuente: Elaboración propia, 2022
Figura 19: Janamayu precipitación diaria – nube de puntos entre observaciones en tierra y datos CHIRPS 1993 a 2003

Fuente: Elaboración propia, 2022
Figura 20: Laguna Taquiña precipitación diaria – nube de puntos entre observaciones en tierra y datos CHIRPS 1993 a 2003

Fuente: Elaboración propia, 2022
Figura 21: Linkupata precipitación diaria – nube de puntos entre observaciones en tierra y datos CHIRPS 1993 a 2003

Fuente: Elaboración propia, 2022
3.6 Regresiones para la precipitación diaria máxima anual periodo 1993 a 2003
3.6.1 Manteniendo cronología en el periodo de datos comunes
En la Tabla 12, se tienen las dos series cronológicas de precipitación diaria máxima anual para Janamayu, la primera serie son datos satelitales CHIRPS de 1981 a 2019 y la segunda serie son datos de la estación convencional para el periodo de registro 1993 a 2003.
En la Figura 22 se presenta la nube de puntos con su respectiva regresión lineal. El valor de R2 es -0.032. Para una regresión lineal, el coeficiente de Nash-Sutcliffe (NSE) es igual al coeficiente de determinación (R2). En el presente caso, la línea de regresión por la nube de puntos tiene un valor NSE de -0.032. Conforme la Tabla 3, el valor de NSE se clasifica como “insuficiente”; por tanto, la regresión lineal no puede ser usada. Se obtienen resultados similares para las estaciones de Linkupata y Laguna Taquiña.
Figura 22: Janamayu precipitación diaria máxima anual observaciones en función datos CHIRPS

Fuente: Elaboración propia, 2022
Tabla 12: Janamayu precipitación máximo diario anual – datos satelitales CHIRPS y datos estación convencional.
Fuente: Elaboración propia, 2022
3.6.2 No-manteniendo la cronología en el periodo de datos comunes
En la Tabla 13 tiene la información de las dos series para los años de registros simultáneos, las precipitaciones fueron ordenadas de mayor a menor para la estación de Janamayu. En la Figura 23 presenta el diagrama de dispersión de los datos y la línea de regresión. Adicionalmente, en la Tabla 13 se han anotado los valores simulados con la fórmula de la regresión lineal en función de los datos CHIRPS. Existe una buena correspondencia visual entre los puntos de dispersión y la línea de regresión. Por tratarse de una línea de regresión, el valor de la eficiencia de Nash-Sutcliffe (NSE) es igual al valor del coeficiente de determinación, R2= 0.674 = NSE. La regresión según criterio de Nash-Sutcliffe NSE se clasifica como “muy buena” (Tabla 3).
Tabla 13: Janamayu precipitación máximo diario anual - datos comunes 1993 – 2003 ordenados - CHIRPS vs. estación convencional
Fuente: Elaboración propia, 2022
Figura 23: Janamayu gráficos precipitación diaria máximo anual, datos comunes 1993 – 2003 ordenados - estación convencional vs. CHIRPS: a) con regresión lineal y b) gráfico valores de precipitación en función de las precipitaciones ordenadas.


Fuente: Elaboración propia, 2022
Se repitieron los cálculos para la estación de Linkupata, tanto el diagrama de dispersión y regresión lineal (Figura 24a) como el gráfico de línea de los valores de precipitación CHIRPS-Linkupata, todas ordenadas de mayor a menor (Figura 24b). Para la estación Taquiña, estos gráficos pueden
ser vistos en la Figura 25a y Figura 25b. Las regresiones (lineales) obtenidas para las estaciones Linkupata y Laguna Taquiña de forma visual se ajustan mejor que la regresión obtenida para la estación Janamayu. Se llega a la misma conclusión con el análisis de los coeficientes de determinación (Tabla 10).
Figura 24: Linkupata gráfico precipitación diaria máximo anual, datos comunes 1993 a 2003 ordenados - estación convencional vs. CHIRPS: a) con regresión lineal y b) gráfico valores de precipitación en función de la posición de las precipitaciones ordenadas.


Fuente: Elaboración propia, 2022
Figura 25: Laguna Taquiña - gráfico precipitación diaria máximo anual - datos comunes 1993 –2003 ordenados - estación convencional vs. CHIRPS: a) con regresión lineal y b) gráfico valores de precipitación en función de la posición de las precipitaciones ordenadas.


b)
Fuente: Elaboración propia, 2022
Tabla 14: Ecuaciones de regresión precipitación máximo diario anual y criterios bondad ajuste
Coeficientes
Muy bueno
(x) y (y) en mm/dia. xJanamayu = xLinkupata ≠ xLaguna Taquiña (X=precipitación CHIRPS)
Fuente: Elaboración propia, 2022
En la Tabla 14 se resumen todas las ecuaciones de regresión de la precipitación máxima diaria anual y los criterios de bondad de ajuste aplicados.
3.7 Series extendidas en el tiempo de la precipitación máxima diaria anual de 1993-2003 a 1981-2019
La Tabla 15 y la Figura 26 presenta las series extendidas de la máxima precipitación diaria anual de las tres estaciones de 11 (1993 a 2003) a 39 años (1981 a 2019). Se observa que los resultados para las tres estaciones son similares, pero no idénticos.
Tabla 15: Series extendidas de máxima precipitación diaria anual de 11 (1993 a 2003) a 39 años (1981 a 2019) de las 3 estaciones
Fuente: Elaboración propia, 2022
Figura 26: Series extendidas de máxima precipitación diaria anual de 11 (1993 a 2003) a 39 años (1981 a 2019) de las 3 estaciones

Fuente: Elaboración propia, 2022
3.8 Análisis del periodo de retorno de las series de la precipitación máxima diaria anual extendidas de 1993-2003 a 1981 a 2019
El resumen del análisis del tipo periodo de retorno de la serie extendida de precipitaciones máximas diarias anuales de 11 a 39 años para las tres estaciones de la cuenca es presentado en la Tabla 16. Se analizaron periodos de retorno de 2 a 300 años.
Tabla 16: Precipitaciones máximas diarias anuales en función periodo de retorno – 3 estaciones de la cuenca Taquiña según funciones de distribución ajustadas para las series extendidas de 1992-2003 a 1981-2019
Periodo de retorno (años)
Linkupata Laguna Taquiña
Distribución
Gamma 3P = Pearson T III
Gamma 3P = Pearson T III LogPearson TIII
Fuente: Elaboración propia, 2022
3.9 Determinación de los caudales máximos conforme periodos de retorno.
En la Figura 27 se tiene los hietogramas de las tormentas de diseño elaboradas conforme las series de precipitación máxima diaria anual extendidas de 1981 a 2019 en función del periodo de retorno para las tres estaciones de la cuenca. A nivel general existe correspondencia entre las precipitaciones de las tormentas de las estaciones Janamayu y Linkupata. No así entre estas dos estaciones y la estación Laguna Taquiña. En esta estación se anotan precipitaciones máximas inferiores a las precipitaciones correspondientes en las estaciones Janamayu y Linkupata.
Figura 27: Hietogramas de Tormentas Críticas para Periodos de Retorno de las tres estaciones de la cuenca, en base a las series de precipitación máxima diaria anual extendida: a) Estación Janamayu b) Estación Linkupata y c) Estación Laguna Taquiña

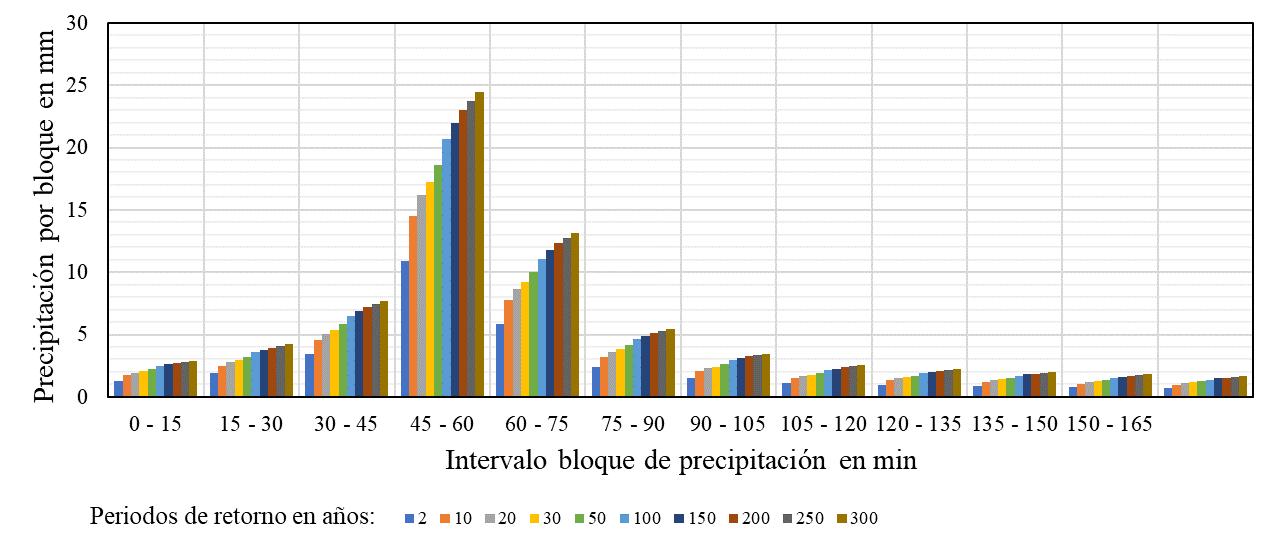

3.10 Resultados de la simulación HEC-HMS para un periodo de retorno T=100 años
El resumen de los caudales pico y sus tiempos para los diferentes elementos del esquema de cálculo HEC-HMS se muestra en la Tabla 17. Por ejemplo, el caudal pico en la salida de la cuenca es 69.1 m3/s y se produce a 1h30 desde el inicio de la tormenta (01h00) y el caudal pico en la unión U1 es de 43.6 m3/s y se produce a 1h25.
Tabla 17: Resumen global cálculo HEC-HMS para T = 100 años

Fuente: Elaboración propia, 2022
Figura 28: Hidrogramas en la salida de la cuenca para T = 100 años

Fuente: Elaboración propia, 2022
En la Figura 28 se presenta el hidrograma transitado por el Río_1 de la Subcuenca Sur de la suma de los hidrogramas de las Subcuencas Oeste, Este y Norte (valor pico 43.4 m3/s). Siendo el hidrograma de la Subcuenca Norte aguas arriba del Río_1 ya transitado por la laguna Taquiña y
la Subcuenca Este (Río_2). El otro hidrograma corresponde a la Subcuenca Sur, considerando la infiltración y el escurrimiento directo (valor pico 26.7 m3/s). La suma de los dos hidrogramas se constituye en el hidrograma saliente de la cuenca (valor pico 69.1 m3/s)
En las Figuras 29, 30 y 31 se presentan los hidrogramas y hietogramas generados a las salidas de las Subcuencas Oeste (25.7 m3/s), Este (18.0 m3/s) y Sur (26.7 m3/s), respectivamente. En la parte superior de las figuras se tiene el hietograma de la tormenta considerada sobre el área de la subcuenca. La parte roja en el hietograma refleja la parte del hietograma que infiltra y la parte azul es la precipitación neta que se convierte en escurrimiento directo según el hidrograma calculado en la parte inferior de la figura.
Figura 29: Hietograma de la precipitación total, infiltrada y en exceso e hidrograma de la Subcuenca Oeste T=100 años

Fuente: Elaboración propia, 2022
En la Figura 32 se presentan las gráficas que corresponden al elemento “reservorio con vertedero” que simula a la laguna Taquiña. En la parte superior se tiene la curva de almacenamiento que llega a un máximo de 77400 m3 con una altura de 0.70 m sobre la cresta a 3h30 desde el inicio de la tormenta. En la parte inferior se muestra el hidrograma de entrada que corresponde a la Subcuenca Norte con un pico de 19.7 m3/s a 1h35 y el hidrograma de salida de la laguna Taquiña que tiene un máximo de 2.2 m3/s a 3h30. Se tiene una laminación de los caudales en la laguna Taquiña que llega a 88% de eficiencia o al 12% del caudal de entrada.
Figura 30: Hietograma de la precipitación total, infiltrada y en exceso e hidrograma de la Subcuenca Este T=100 años

Fuente: Elaboración propia, 2022
Figura 31: Hietograma de la precipitación total, infiltrada y en exceso e hidrograma de la Subcuenca Sur T=100 años

Fuente: Elaboración propia, 2022
Las Figuras 33 y 34 muestran los hidrogramas a la entrada y salida de Río_2 (Subcuenca Este) y Rio_1 (Subcuenca Sur). No existe atenuación de los picos de los hidrogramas. El caudal pico en el Río_2 es de 2.2 m3/s y toma un tiempo de 25 minutos para llegar del inicio al final del Río_2. El caudal pico en el Río_1 es de 43.6 m3/s y tarda 10 minutos para llegar del inicio al final del Río_1.
En el elemento unión U_1 se unen los ríos de las Subcuencas Oeste y Este y continúan como el Río_1 en la Subcuenca Sur. Las Subcuencas Oeste y Este aportan con su hidrograma de la escorrentía directa en 25.7 y 18 m3/s, respectivamente. Además, el Río_2 de la Subcuenca Este aporta con el hidrograma transitado del hidrograma a la salida del embalse 2.2 m3/s (Figura 33).
La suma de estos tres hidrogramas es el hidrograma que sale de la unión U_1 con caudal máximo
de 43.6 m3/s.
Figura 32: Hidrograma a la entrada y salida de la laguna Taquiña y curva de variación de nivel en la laguna Taquiña T=100 años

Fuente: Elaboración propia, 2022
Figura 33: Hidrogramas a la entrada y salida de Río_2 Subcuenca Este T=100 años

Fuente: Elaboración propia, 2022
Figura 34: Hidrogramas a la entrada y salida de Río_1 Subcuenca Sur T=100 años

Fuente: Elaboración propia, 2022
Figura 35: Hidrogramas de entrada y salida de la unión U_2 T=100 años

Fuente: Elaboración propia, 2022
3.11 Resultados de la simulación HEC-HMS para periodos de retorno T=2, 10, 20, 30, 50, 100, 150, 200, 250 y 300 años
En la Tabla 18 se han resumido los caudales líquidos pico para los periodos de retorno T = 2, 10, 20, 30, 50, 100, 150, 200, 250 y 300 años en los diferentes lugares del esquema de la Cuenca Taquiña (Figura 5).
Tabla 18: Caudales líquidos pico para los periodos de retorno T = 2, 10, 20, 30, 50, 100, 150, 200, 250 y 300 años en los diferentes lugares del esquema de la Cuenca Taquiña.
Fuente: Elaboración propia, 2022
3.12 Comparación de los caudales con el Manejo Integral Cuenca Taquiña
Se puede comparar los resultados obtenidos con el estudio hidrológico del Manejo Integral Cuenca Taquiña (SDC, 2020) (Tabla 19). En términos hidrológicos para grandes periodos de retorno los resultados obtenidos son coincidentes con los resultados del Servicio Departamental de Cuencas (2020): para T = 100 y 200 años, la diferencia es de 13.52% y 7.25 %, respectivamente; para menores periodos de retorno, los resultados siguen coincidentes, pero con mayor diferencia (T=10 años 31.97 %).
Tabla 19: Comparación de caudales con el MIC-Taquiña
Los seis principales criterios que difieren entre los dos estudios para el cálculo de los eventos extremos se presentan en la Tabla 20.
Tabla 20: Diferentes criterios entre el presente estudio y el MIC-Taquiña
Criterio MIC-Taquiña (SDC, 2020)
1 Periodo de registro considerado
2 Distribución precipitación sobre la cuenca
11 años de las 3 estaciones de la cuenca (Janamayu, Linkupata y Laguna Taquiña) de 1993 a 2003 + 36 años de la estación Violeta de 1980 a 2016
Mediante ponderadores hipsométricas
Presente estudio
11 años de las 3 estaciones de la cuenca (Janamayu, Linkupata y Laguna Taquiña) de 1993 a 2003 extendidas a 39 años mediante correlación con datos satelitales CHIRPS de 1981 a 1992 y de 2004 a 2019.
Mediante ponderadores Thyssen
3 Transformación lluvia neta a caudal Hidrograma sintético de Clark Hidrograma sintético de la UCS
4 Modelo de tránsito de las crecidas en los ríos.
Método del Lag
5 Método de infiltración Método de la curva CN del SGS (CN ARC III = 91)
6 Mapas temáticos de suelos y uso de suelos
Levantados en el campo por el Servicio Departamental de Cuencas en 2020
Método de la onda cinemática
Método de la curva CN del SGS (CN ARC III=78)
Elaborados en 2011 por el CLAS UMSS
DISCUSIÓN
La metodología elaborada para la presente investigación aplicada a las ex estaciones climatológicas de la cuenca Taquiña permite concluir los siguientes aspectos:
1. El producto de precipitación satelital CHIRPS resulta la mejor opción para los objetivos de la presente investigación, una vez que proporciona datos diarios, incluye a la Cuenca del río Taquiña, tiene una resolución espacial alta con un pixelado pequeño de 4.8 km (en comparación a los otros proveedores analizados), está basado en ajustes con datos de estaciones terrestres y cubre un periodo de 1981 a la fecha, logrando extender las series cortas de precipitación de 1993-2003 de 11 años al periodo 1981-2019 de 39 años. Estas series nuevas de 39 años de datos de precipitación permiten un análisis de periodo de retorno con una confiabilidad aceptable.
2. A pesar de que los registros de datos de precipitación satelital CHIRPS presentan una mejor opción para la investigación, es prudente realizar futuras investigaciones que presenten un ajuste más próximo a los datos de estaciones convencionales ya que estos últimos se encuentran por encima de los datos de CHIRPS.
3. Las pruebas de bondad de ajuste para:
• La regresión de las precipitaciones mensuales presenta un ajuste de “muy bueno” a “excelente”, según el criterio de Nash-Shutliffe. En este sentido, se pueden usar los datos de precipitación satelital CHIRPS para extender las series de precipitación mensual de las tres estaciones analizadas (Janamayu, Linkupata y Laguna Taquiña). Por ejemplo, para efectuar estudios de disponibilidad o del potencial del recurso hídrico.
• La regresión de las precipitaciones diarias resulta en valores inferiores a 0.2 para el criterio de Nash-Scutliffe. Esto implica ineficiencia de las regresiones y, por consecuencia, no se pueden usar los datos de precipitación satelital CHIRPS para extender las series de precipitación diaria de las estaciones Janamayu, Linkupata y Laguna Taquiña.
• La regresión de la precipitación diaria máxima anual, manteniendo el orden cronológico del registro de los valores observados y de los valores CHIRPS, da un valor NSE de -0.032. Existe insuficiencia con está regresión basado en datos cronológicos y, por tanto, no se puede usar esta regresión con los datos de precipitación satelital CHIRPS para extender las series de precipitación diaria máxima anual de las tres estaciones.
• La regresión de la precipitación diaria máxima anual, ordenando el registro de los valores observados y CHIRPS de mayor a menor, para Janamayu, Linkupata y Laguna Taquiña, proporciona valores NSE de 0.67, 0.87 y 0.89 que se califican como ajustes “muy bueno”, “excelente” y “excelente”, respectivamente. Existe suficiencia con las regresiones basadas en datos no cronológicos y por consecuencia se puede usar esta regresión con los datos de precipitación satelital CHIRPS para extender las series de precipitación diaria máxima anual de las tres estaciones y realizar sobre las series extendidas un análisis de periodo de retorno para determinar eventos extremos.
• Ordenar los valores de la precipitación diaria máxima anual de máximo a mínimo está basado en el trabajo que se efectúa con las series de precipitación diaria máxima anual de las estaciones pluviométricas de una cuenca, donde se realiza un análisis estadístico
para la determinación de la distribución de probabilidades que mejor se ajusta. En el momento de la preparación de los datos, la serie de cada estación se ordena de mayor a menor conforme las precipitaciones y se pierde simultaneidad entre los valores de las series.
4. No existen aforos de caudales tipo evento extremo en la Cuenca Taquiña. Por ende, no es posible controlar la efectividad del modelo HEC-HMS, desarrollado en el presente documento, sobre la base de las series de máxima precipitación diaria anual extendidas en el tiempo mediante ecuaciones de regresión que se aplican a las precipitaciones satelitales CHIRPS.
Los resultados se pueden verificar con caudales modelados por otros autores, como el estudio hidrológico del estudio MIC-Taquiña, realizado por el Servicio Departamental de Cuencas (2020). A pesar de que el MIC-Taquiña ha usado 6 criterios hidrológicos diferentes, los caudales de evento extremo de las dos investigaciones son similares dentro de términos hidrológicos. Los estudios que requieren de caudales de evento extremo pueden usar los caudales del MIC-Taquiña o los determinados en el presente trabajo.
5. Transferencia de los resultados a otras regiones:
Para el caso estudiado no se puede utilizar directamente la precipitación satelital CHIRPS como representativa para la precipitación en la Cuenca del río Taquiña.
− Mediante ecuaciones de regresión lineal entre registros satelitales CHIRPS y registros en tierra si se puede simular relativamente bien las precipitaciones mensuales para la Cuenca del río Taquiña. De la misma forma, la precipitación máxima diaria anual se simula relativamente bien, considerando datos ordenados de valor máximo a mínimo.
− No es posible encontrar ecuación de regresión eficiente para simular los valores de precipitación diaria.
Los resultados presentados no pueden ser transferidos a cuencas que no cuentan con datos. En caso, de cuencas con datos de precipitación, previo se debe calcular las ecuaciones de regresión que correspondan y realizar los análisis de bondad de ajuste sobre las ecuaciones de regresión calculadas.
Los autores agradecen:
AGRADECIMIENTOS
− Al Laboratorio de Hidráulica de la Universidad Mayor de San Simón de Cochabamba (LHUMSS) por poner a disposición de la investigación a los datos diarios de precipitación de las tres (ex) estaciones de la cuenca Taquiña correspondientes al periodo 1992 a 2003.
−
A la Oficina Regional del Servicio Nacional de Meteorología e Hidrología (SENAMHI) por proporcionar a la investigación a la serie de datos diarios de precipitación de la nueva estación de la cuenca Taquiña correspondiente al periodo nov. 2018 a 2000.
−
Al Centro de Levantamientos Aero Espaciales de la Universidad Mayor de San Simón de Cochabamba (CLAS UMSS) por poner a disposición de la investigación sus mapas temáticos de suelos y uso de suelos de la Cuenca Taquiña elaborados en 2011.
−
Al M.Sc. Ing. Mauricio Restrepo, para su apoyo con la programación avanzada en la plataforma Excel para el procesamiento de los datos básicos.
REFERENCIAS BIBLIOGRÁFICAS
Aksu, H., & Akgül, M. A. (2020). Performance evaluation of CHIRPS satellite precipitation estimates over Turkey. Theoretical and Applied Climatology, 142(1), 71-84. https://doi. org/10.1016/j.jhydrol.20
Asurza Véliz, F. A., Ramos Taipe, C. L., & Lavado Casimiro, W. S. (2018). Evaluación de los productos Tropical Rainfall Measuring Mission (TRMM) y Global Precipitation Measurement (GPM) en el modelamiento hidrológico de la cuenca del río Huancané, Perú. Scientia Agropecuaria, 9(1), 53-62. http://dx.doi.org/10.17268/sci.agropecu.2018.01.06
Bai, L., Shi, C., Li, L., Yang, Y., & Wu, J. (2018). Accuracy of CHIRPS satellite-rainfall products over mainland China. Remote Sensing, 10(3), 362. https://doi.org/10.3390/rs10030362
Bolívar Vallejo, H. (2020). Informalidad urbanística sobre franjas de seguridad en la metrópoli Kanata: deslizamiento y desborde en Chilimarca en febrero de 2018 (Cochabamba-Bolivia). In XII Seminario Internacional de Investigación en Urbanismo, São Paulo-Lisboa, 2020. Faculdade de Arquitetura da Universidade de Lisboa. https://doi.org/10.5821/siiu.9993
Brown, I. W., McDougall, K., Alam, M. J., Chowdhury, R., & Chadalavada, S. (2022). Calibration of a continuous hydrologic simulation model in the urban Gowrie Creek catchment in Toowoomba, Australia. Journal of Hydrology: Regional Studies, 40, 101021. https://doi.org/10.1016/j. ejrh.2022.101021
Cavalcante, R. B. L., da Silva Ferreira, D. B., Pontes, P. R. M., Tedeschi, R. G., da Costa, C. P. W., & de Souza, E. B. (2020). Evaluation of extreme rainfall indices from CHIRPS precipitation estimates over the Brazilian Amazonia. Atmospheric Research, 238, 104879. https://doi. org/10.1016/j.atmosres.2020.104879
Centro de Levantamientos Aeroespaciales y Aplicaciones SIG (CLAS UMSS) (2011). Desarrollo para la gestion integral del Parque Nacional Tunari. Cochabamba, Bolivia: Universidad Mayor de San Simón
Delgadillo Montaño, F. (2019). Evaluación de la precipitación mediante distintas fuentes de información satelital y análisis de sensibilidad en modelo lluvia escurrimiento (caso de estudio cuenca del Piraí, Santa Cruz). Proyecto de grado, para optar al Diploma Académico de Licenciatura en Ingeniería Civil, Universidad Mayor de San Simón, 2019.
Dettinger, M., Anderson, J., Anderson, M., Brown, L. R., Cayan, D., & Maurer, E. (2016). Climate change and the Delta. San Francisco Estuary and Watershed Science, 14(3). https://doi. org/10.15447/sfews.2016v14iss3art5
Dinku, T., Funk, C., Peterson, P., Maidment, R., Tadesse, T., Gadain, H., & Ceccato, P. (2018). Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Quarterly Journal of the Royal Meteorological Society, 144, 292-312. https://doi.org/10.1002/qj.3244
Dooge, J. (1973). Linear theory of hydrologic systems (No. 1468). Agricultural Research Service, US Department of Agriculture.
Earthdata NASA (2022). “Giovanni”, v. 4.36 [Online]. Recuperado de: https://giovanni.gsfc.nasa. gov/giovanni/. Consultado el 06 de Febrero de 2022.
Golmohammadi, G., Prasher, S., Madani, A. y Rudra R. (2014). Evaluating Three Hydrological Distributed Watershed Models: MIKE-SHE, APEX y SWAT. Hydrology; I, 20-39. https://doi. org/10.3390/hydrology1010020
Google Developers (2022). Climate Engine. Recuperado de https://climateengine.com/. Consultado el 06 de Febrero de 2022.
Gupta, H. V., & Kling, H. (2011). On typical range, sensitivity, and normalization of Mean Squared Error and Nash‐Sutcliffe Efficiency type metrics. Water Resources Research, 47(10). https://doi. org/10.1029/2011WR010962
Kirpich, Z. P. (1940). Time of concentration of small agricultural watersheds. Civil engineering, 10(6), 362.
Kizza, M., Westerberg, I., Rodhe, A. y Ntale, H. L. (2012). Estimating areal rainfall over Lake Victoria and its basin using ground-base and satellite data. Journal of Hydrology; 464, 401-411. https://doi.org/10.1016/j.jhydrol.2012.07.024
Laura, E. L., Obando, O. G. F., Laura, A. L., Quispe Aragón, J.P. (2015). Validación de la precipitación estimada por satélite TRMM y su aplicación en la modelación hidrológica del rio Ramis Puno Perú. Revista Investigación Altoandino, 17 №2, 221-228.
Le Noir, C., Cayo, N. Sánchez, H., Arrázola, A., Terán, J., Zampieri, J. (2019). Análisis del flujo de la mazamorra de Tiquipaya–Bolivia 2018: identificación de causas, riesgos y acciones. Journal Boliviano de Ciencias, (46), 46-61.
Li, X. H., Zhang, Q., y Xu, C. Y. (2012). Suitability of theTRMM satellite rainfalls in driving a distributed hydrological model for water balance computations in the Xinjiang catchment, Poyang lake basin. Journal of Hydrology, 426-427, 28-38. https://doi.org/10.1016/j.jhydrol.2012.01.013
Li, X., Zhang, Q., y Xu, C., (2014). Assessing the performance of satellite-based precipitation products and its dependence on topography over Poyang Lake basin. Theoretical and Applied Climatology, 115, 713–729. https://doi.org/10.1007/s00704-013-0917-x
Liu, J., Shangguan, D., Liu, S., Ding, Y., Wang, S., & Wang, X. (2019). Evaluation and comparison of CHIRPS and MSWEP daily-precipitation products in the Qinghai-Tibet Plateau during the period of 1981–2015. Atmospheric Research, 230, 104634. https://doi.org/10.1016/j. atmosres.2019.104634
Mantas, V. M., Liu, Z., Caro, C., y Pereira, A.J.S.C. (2015). Validation of TRMM multi-satellite precipitation analysis (TMPA) products in the Peruvian Andes. Atmospheric Research, 163, 132145. https://doi.org/10.1016/j.atmosres.2014.11.012
Molnar, P. (2011). Calibration Watershedmodelling, SS 2011. Institute of Environmental Engineering, Chair of Hydrology and Water Resources Management, ETH Zurich, Switzerland.
Nash J. E., & Sutcliffe J. V., (1970). River flow forecasting through conceptual models Part I: A discussion of principles, J. HYDROL, 10, 282-290
Ouma, Y. O., Owiti, T., Kiporir, E., Kibiiy, J., y Tateishi R. (2012). Multitemporal comparative analysis of TRMM-3B42 satellite-estimated rainfall with surface gauge data at basin scales: daily, decadal and monthly evaluations. International Journal of Remote Sensing, 33(24), 7662-7684. https://doi.org/10.1080/01431161.2012.701347
Peláez, J. R. T. (2003). Facetas del cálculo hidrometeorológico y estadístico de máximos caudales. Revista de Obras Públicas: Organo profesional de los ingenieros de caminos, canales y puertos, (3430), 47-51.
Pilgrim, D. H., & McDermott, G. E. (1981, January). Design floods for small rural catchments in eastern New South Wales. In First National Local Government Engineering Conference 1981: Reprints of Papers: Reprints of Papers (pp. 138-142). Canberra: Institution of Engineers, Australia.
Pizarro, R; Gonzáles, P; Wittersheim, M; Saavedra, J.; Soto, C. (1993). Elementos Técnicos de Hidrología III. Proyecto Regional Mayor sobre uso y conservación de recursos hídricos en áreas de America Latina y el Caríbe. UNESCO-ORCYT. Editorial Universidad de Talca. Talca, Chile.
Quispe Rivas M (2020). Análisis del desempeño conceptual de Modelo Hidrológico SWAT. Proyecto de grado, para optar al Diploma Académico de Licenciatura en Ingeniería Civil, 122125, 177-201.
Read, L. K., & Vogel, R. M. (2015). Reliability, return periods, and risk under nonstationarity. Water Resources Research, 51(8), 6381-6398. https://doi.org/10.1002/2015WR017089
Servicio Departamental de Cuencas (2020). Manejo integral de la Cuenca Taquiña. Cochabamba, Bolivia: Gobierno Autónomo Departamental de Cochabamba.
Toté, C., Patricio, D., Boogaard, H., Van der Wijngaart, R., Tarnavsky, E., & Funk, C. (2015). Evaluation of satellite rainfall estimates for drought and flood monitoring in Mozambique. Remote Sensing, 7(2), 1758-1776. https://doi.org/10.3390/rs70201758
Universidad del Valle UNIVALLE (2022). Conclusiones del Foro técnico científico “Tiquipaya Zona 0” [Online]. Recuperado de: http://www.univalle.edu/. Consultado el 12 de Agosto de 2022.
Usda, S. C. S. (1986). Urban hydrology for small watersheds. Technical release, 55, 2-6.
Vallejos, A., Saavedra, O., Escalera, A. C. (2016), Análisis de la precipitación aérea de las cuencas clave de Cochabamba, basado en tecnología satelital. Investigación & Desarrollo, 16(1), 25 – 38.
Villón Béjar, M. (2014). HidroEsta, software para cálculos hidrológicos y estadísticos aplicados a la Hidrología. Revista Digital: Matemática, Educación E Internet, 12(2). https://doi.org/10.18845/ rdmei.v12i2.1678
Watson, I., & Burnett, A. D. (2017). Hydrology: An environmental approach. Routledge. https:// doi.org/10.1201/9780203751442
Williams, G. B. (1922). Flood discharges and the dimensions of spillways in India. Engineering (London), 134(9), 321-322.

