DE DOORBRAAK

DE DOORBRAAK: PYTHAGORAS

RUIMTELIJKE BETEGELING

DE DOORBRAAK IS EEN 13 KILOMETER LANGE KUNSTMATIGE BEEK IN DE NEDERLANDSE PROVINCIE OVERIJSSEL, AANGELEGD TER VERBETERING VAN DE WATERHUISHOUDING TUSSEN ALMELO EN YPELO. TER MARKERING VAN DEZE BEEK KREEG DE IN HENGELO WOONACHTIGE KUNSTENAAR RINUS ROELOFS DE OPDRACHT EEN SERIE KUNSTWERKEN TE ONTWERPEN. ELK VAN DIE KUNSTWERKEN IS OPGEBOUWD UIT EVEN GROTE GELIJKVORMIGE VEELHOEKEN. PER KUNSTWERK IS STEEDS EEN ANDERE SERIE VAN DEZELFDE VEELHOEKEN TOEGEPAST. HIERBOVEN ZIE JE EEN DETAIL VAN EEN VAN DE BEELDEN. DAARIN IS TE ZIEN DAT HET IS OPGEBOUWD UIT DEZELFDE ONREGELMATIGE ZESHOEKEN DIE KEURIG NETJES ZONDER OVERLAP OF OPENINGEN OP ELKAAR AANSLUITEN. HOE KREEG RINUS ROELOFS DAT VOOR ELKAAR?

KLAAS LAKEMAN, ARS ET MATHESIS

BETEGELING Een vlakvulling of betegeling is een opvulling van een oppervlak veelal door veelhoeken die allemaal dezelfde vorm en grootte hebben zonder overlap of openingen. Meestal gaat men er stilzwijgend van uit dat de stempels of tegels een plat vlak moeten bedekken. Maar dat hoeft niet. Je kunt ook zeggen dat een betegeling een patroon is, gemaakt van identieke vormen (tegels) die zonder gaten of overlap in elkaar passen. Met bijvoorbeeld identieke L-vormige tegels kun je een betegeling maken zoals in figuur 1. De tegels vullen keurig een plat vlak op. Maar het kan ook anders, zoals in figuur 2. Daar zie je met dezelfde L-vormige tegels een nietvlakke betegeling zonder overlap of gaten. Dat geldt ook wanneer we

de tegels combineren zoals in figuur 3. Het resultaat is een cilindrische betegeling. Hier eveneens geen overlap of gaten.

Figuur 1. Traditionele vlakke betegeling Figuur 2. Niet-vlakke betegeling Figuur 3. Cilindrische betegeling RUIMTELIJKE BETEGELING Vierkante tegels zijn de meest voor de hand liggende vormen om platte vlakken op te vullen. Maar je kunt er ook een niet-vlakke betegeling mee maken zoals in figuur 4. Ook hier is er weer een structuur zonder overlap of gaten. De meest eenvoudige manier om met vierkanten een ruimtelijke betegeling te maken is door ze te combineren tot een kubus (figuur 5). Doorgaans zijn we echter niet geneigd dit als een betegeling op te vatten. Net als de kubus kunnen ook de andere regelmatige veelvlakken worden opgevat als ruimtelijke betegelingen (figuur 6). Merk daarbij op dat een regelmatige vijfhoek gebruikt kan worden voor een ruimtelijke betegeling (het regelmatig twaalfvlak) maar niet voor een vlakke betegeling!

Figuur 5. Figuur 6.

Figuur 4.

ELEVATIE: VERHOOGDE VEELVLAKKEN Het zogenaamde elevatieproces dat Leonardo da Vinci toepaste op regelmatige veelvlakken levert achteraf beschouwd een opmerkelijke uitbreiding in de richting van ruimtelijke betegelingen. Het komt erop neer dat hij bijvoorbeeld op alle vier zijvlakken van een regelmatig viervlak eenzelfde regelmatig viervlak zette (figuur 7). In het algemeen kan dit elevatieproces van een veelvlak als volgt worden beschreven: Neem het middelpunt van een zijvlak van het veelvlak. Til het dan bij wijze van spreken loodrecht op het vlak omhoog tot de afstand van dit punt

tot elk van de hoekpunten van dit betreffende zijvlak gelijk is aan de lengte van een zijde van dat regelmatig zijvlak. Doe dit voor elk zijvlak van het regelmatig veelvlak. Zo zien we in figuur 8 nog twee tekeningen van Leonardo da Vinci met een verhoogd regelmatig twaalfvlak of verhoogde dodecaëder (figuur 8a) en een verhoogd regelmatig twintigvlak of verhoogde icosaëder (figuur 8b). Omdat de nieuwe zijvlakken allemaal gelijkzijdige driehoeken worden, is het duidelijk dat dit proces alleen maar werkt op driehoekige, vierkante en vijfhoekige zijvlakken.

Figuur 7. Verhoogd viervlak

DRAAIING Behalve voor het regelmatig twaalfvlak, hebben we voorbeelden van ruimtelijke en niet-vlakke betegelingen gezien waarvan de tegels ook gebruikt kunnen worden

Figuur 8a. Verhoogd twaalfvlak Figuur 8b. Verhoogd twintigvlak

voor vlakke betegelingen. Zou het mogelijk zijn om andere vormen van tegels te vinden die alleen kunnen worden gebruikt voor niet-vlakke of ruimtelijke betegelingen? Voor het

Figuur 9. Figuur 10.

antwoord bekijken we nogmaals de tekening met de verhoogde icosaëder van Leonardo da Vinci (figuur 8b). Deze kan worden gezien als een samenstelling van twintig driehoekige piramides met in totaal zestig (twintig keer drie) zijvlakken. Nu veranderen we de vorm van de tegels door elke piramide over eenzelfde hoek om zijn eigen as te draaien. We krijgen dan een nieuw object zoals in de figuren 9 en 10. In elke fase of tussenstand van de draaiing is de vorm van elk van de zestig tegels veranderd van een gelijkzijdige driehoek in een niet-convexe vijfhoek. In elke fase

is de vorm van de tegels hetzelfde. Het object in figuur 10 kan worden herkend als een vervlechting van vijf tetraëders, maar hier is het gewoon een set van zestig gelijkvormige tegels die een niet-vlakke betegeling vormen.

SPIRAALCILINDERS De beschreven methoden van elevatie en draaiing en combinaties daarvan leveren veel inzicht in ruimtelijke betegelingen. Ze zijn echter ontoereikend om te komen tot de kunstwerken van Rinus Roelofs langs de Doorbraak. Daar heeft hij een andere aanpak voor ontwikkeld waarmee nieuwe vormen van tegels voor cilindrische betegelingen worden verkregen. Eerst wordt een normale spiraalcurve getekend. Deze wordt onderverdeeld in gelijke stukken. Daarna wordt een rechte lijn getrokken van het startpunt aan de onderkant van de spiraal naar het startpunt van het volgende stuk, enzovoort. Deze rechte lijnen worden vervolgens naar beneden samengedrukt (geëxtrudeerd) naar de as van de spiraal (figuur 11). Een tweede spiraalachtige vorm zoals in figuur 11 wordt ondersteboven gedraaid en toegevoegd aan de oorspronkelijke (figuur 12) waarbij de assen samenvallen. Deze spiraalvormen kruisen elkaar en van de snijlijnen is de uiteindelijke vorm van de tegels af te leiden. De vorm van de voltooide tegel is in het afgebeelde voorbeeld een niet-convexe zeshoek (figuur 13). Deze kan niet worden gebruikt om een plat vlak te betegelen.

Figuur 11.

VARIATIES Uitgaande van eenzelfde spiraal laat deze methode veel variaties toe zoals de afstand tussen de punten op de spiraal, de hoek waaronder de extrusie plaats vindt en de positie van de tweede spiraalvorm waarbij zowel de hoogte als de rotatiehoek kan varieren. Elke reeks waarden levert een andere tegelvorm op. De figuren 14, 15 en 16 zijn enkele mogelijkheden. Deze spiraalvormige cilinders kunnen zelfs worden uitgerold tot een eenvoudige strook tegels die vervolgens als een soort bouwplaat weer in elkaar kan worden gerold, te vergelijken met de uitslag van een regelmatig veelvlak. Als voorbeeld is in figuur 17 het object van figuur 16 afgerold.

DE PRAKTIJK Het tekenen en verder bewerken van de spiraal waarmee wordt begonnen, wordt met behulp van aparte software op de computer

Figuur 12. Figuur 13.

gedaan. Daarmee kunnen snel allerlei variaties worden uitgevoerd om te komen tot aantrekkelijke resultaten zoals de figuren 13 tot en met 16. De zeven beelden langs

Figuur 14.

Figuur 15.

Figuur 16.

Figuur 17. Stukje strook voor de cilindrische betegeling van figuur 16 en aanzet tot in elkaar draaien.

Figuur 18.

De papieren modellen voor de zeven beelden langs de Doorbraak.

Figuur 19.

DE ZEVEN KUNSTWERKEN de Doorbraak vormen dan ook een selectie uit de grote hoeveelheid mogelijkheden. Met dezelfde software kan het gekozen resultaat ook worden uitgerold. Dat levert dan stroken op zoals in figuur 17. Die kunnen op stevig papier worden uitgeprint en uitgesneden. Daarna kan met zo’n strook een papieren model van de betreffende cilindrische spiraal in elkaar worden gedraaid. Zo’n strook is dus in feite niets anders dan een bouwplaat (figuur 18).

Het papieren model kan vervolgens dienen als voorbeeld en als uitgangspunt voor de schaalvergroting die moet plaatsvinden. Voor elk beeld moet een serie grote ijzeren tegels worden uitgesneden die vervolgens aan elkaar gelast worden (figuur 19).

Doorbraak 1. Doorbraak 2. Doorbraak 3. Doorbraak 4.

Zelf knutselen aan de Doorbraak? Bij Ars et Mathesis kun je een bouwplaat van een van de kunstwerken bestellen. Neem contact op met Klaas Lakeman (nt.lakeman@ hccnet.nl).

DE POPULARITEIT VAN MOD-97

SAMENVATTING DE VOORBIJE ZOMERWEKEN KON JE IN DE STANDAARD BIJDRAGEN LEZEN IN DE REEKS “DE SUCCESFORMULE”. WE PIKKEN HIER GRAAG EVEN IN OP DE BIJDRAGE IN DE KRANT VAN 3 AUGUSTUS EN GAAN EEN TIKKELTJE DIEPER IN OP HET WISKUNDIGE ASPECT. IN DIE BIJDRAGE HAD MEN HET OVER EEN BESCHERMING TEGEN FOUTJES VAN ONZE BANKREKENINGNUMMERS MET EEN MOD-97-CONTROLEGETAL. WELNU, OOK DE INTERNATIONALE IBAN STANDAARD IS EEN MOD-97-GEBRUIKER, EN VOOR BELGEN ZELFS EEN MOD-97TOEPASSING OP DE REEDS MOD-97-GECODEERDE REKENINGNUMMERS.

PAUL IGODT - KU LEUVEN CAMPUS KULAK, KORTRIJK STIJN SYMENS - UNIVERSITEIT ANTWERPEN HILDE VAN DEN EYNDE - JOURNALIST DE STANDAARD

Als geld eenmaal naar andermans rekening is overgeschreven, kan een bank het niet meer terugstorten. Ook niet als het bedrag per vergissing naar de verkeerde titu- laris werd overgemaakt, bijvoorbeeld doordat de betalende partij een fout cijfer ingaf in het rekeningnummer van de bestemmeling. Dergelijke onbedoelde verkeerde overschrijvingen gebeuren in België zo goed als nooit, leert navraag bij de branchevereniging Febelfin. Dat komt niet doordat wij Belgen zo’n oplettende onlinebankiers zijn, maar omdat de Belgische banken in elk rekeningnummer een slimme alarmbel hebben ingebouwd. Als iemand per vergissing een of meer verkeerde cijfers intoetst bij het ingeven van een betalingsopdracht, gaat die alarmbel af en verhindert de bank dat de verrichting wordt uitgevoerd. De kans dat iemand geld overmaakt naar een verkeerd rekeningnummer, wordt daarmee de facto onbestaande, aldus Febelfin.

Het veiligheidsnet dat door de banken wordt gespannen, mikt op de frequentst gemaakte fouten bij het online ingeven van een rekeningnummer. Wiskunde, en meer bepaald getaltheorie, wordt ingeschakeld om dergelijke fouten op te sporen. Dergelijke methodes geven vervolgens een alarmsignaal als er iets niet kan kloppen: we spreken van een “Error detection method”. Studies (zie [1]) hebben uitgewezen wat de vaakst optredende foutjes zijn bij het manipuleren van een identificatie. We hebben het dan in het algemeen over cijfer-letter combinaties. Een overzichtje helpt.

Type Fout

Een enkelvoudige fout

Transpositie van naast elkaar staande tekens

Fonetische fout

Tweeling fout

Voorbeeld

3 wordt 8, “k” wordt “h”

38 wordt 83, “an” wordt “na”

“14” wordt “40”, “50” wordt “15” “pp” wordt “dd”

Frequentie

79.1 %

10.2 %

0.5 %

0.5 %

Een overzicht van enkele meermaals optredende fouten

Zeker in de Germaanse talen, zoals het Nederlands, waar getallen als 13 en 30, 14 en 40, enzovoorts, qua uitspraak erg op elkaar lijken, kan hieruit een bepaald type dubbele fout optreden.

Niet alleen banken wapenen zicht tegen dergelijke verschrijvingen. Nagenoeg elke identificatie, of ze nu bestaat uit cijfers, letters of een combinatie van beiden, tracht zich op een of andere manier te wapenen door een foutenopsporingscontrole in te bouwen.

Reeds meer dan 10 jaar wordt voor Belgische rekeningnummers het IBAN-formaat gebruikt: startend met BE en dan gevolgd door 14 cijfers. De laatste twaalf cijfers vormen de klassieke Belgische bankrekeningnummers, typische opgedeeld in 3 delen:

Het eerste deel (a) bepaalt bij welke bank de rekening geopend werd, het tweede deel (b) is het nummer binnen deze bank en de laatste twee cijfers (c) zijn controlecijfers die schrijffouten moeten ontdekken door de zgn. mod-97-test.

Mod-97 slaat natuurlijk op het “modulo”-rekenen. En dat 97 een priemgetal is, zelfs het grootste priemgetal bestaande uit twee cijfers, heeft hierbij ook een voordeel. Je rekent “modulo ” indien je elk natuurlijk getal vervangt door de rest ervan bij deling door ; die rest noteren we mod . Wiskundigen schrijven ook mod . Zo geldt natuurlijk dat mod ; meer algemeen zijn alle even natuurlijke getallen, modulo 2 gerekend, gelijk aan . Modulo 2 rekenen verdeelt de verzameling van de natuurlijke getallen in twee disjuncte klassen: de even getallen en de oneven getallen. Je rekent nu ook meteen na dat mod , maar dat ook mod . Modulo 6 rekenen is dus niet krachtig genoeg om zelfs maar een enkelvoudige schrijffout te ontdekken.

De Belgische banken hadden aan 10 cijfers genoeg om voldoende bankrekeningnummers te kunnen aanmaken. Toch hebben ze er bij de aanvang van dat systeem voor gekozen om te werken met 12 cijfers. Als het rekeningnummer was, dan werd dat nummer uitgebreid met de rest bij deling van het getal door 97, geschreven als een 2-cijferig getal. Wanneer , werd afgesproken om niet toe te voegen, maar wel 97.

Dit systeem wordt overigens ook gehanteerd voor de nummers van de Belgische identiteitskaarten. Als de identiteitskaart van een Belg volledig bekend zou zijn door het nummer ( cijfers), dan staat er op die kaart het nummer omdat . Inderdaad: . Het getal noemen we in het nummer van deze identiteitskaart het controlegetal. De functie ervan is die van een alarmbelletje of, zo je

dat verkiest, een rood licht. Controleer je even je eigen identiteitskaart? En je eigen bankrekeningnummers (in niet IBAN-formaat)?

Deze 97-proef haalt zeer veel regelmatig voorkomende tikfouten uit een betaalopdracht. Kijken we even naar het geval van een enkelvoudige fout. Als we in het getal één cijfer vervangen door dan is (de absolute waarde van) het verschil tussen die beide getallen • ofwel een getal uit de verzameling (als we vervingen door een ) • ofwel een getal uit de verzameling (als we vervangen hebben door een ) • of in het algemeen een getal uit de verzameling vermenigvuldigd met een macht van 10.

Door slechts één cijfer te veranderen, verandert dus nooit in een getal dat een veelvoud van 97 van verschilt. Enkel getallen die een veelvoud van 97 van elkaar verschillen hebben hetzelfde controlegetal. Mocht de fout gemaakt worden in één van de twee cijfers van het controlegetal, dan wordt de fout uiteraard ook ontdekt. Het mod-97-controlegetal geeft dus een alarm bij alle enkelvoudige fouten.

Wat gebeurt er bij een transpositiefout van twee naast elkaar staande cijfers? Stel dat je bvb. het nummer overschrijft maar je maakt er van. In het algemeen gaat het dus over een situatie waarbij vervangen wordt door . Zo een transpositie zou hetzelfde controlegetal opleveren als het verschil tussen beide nummers een veelvoud van 97 wordt. Laat ons dat even onderzoeken. In het nummer is de getalwaarde van gelijk aan . Na omwisseling van beide ontstaat de getalwaarde . Het verschil tussen beide is dus gelijk aan

Beide getallen zouden hetzelfde controlegetal opleveren indien dit verschil een veelvoud is van 97. Omdat 97 een priemgetal is zou dit moeten betekenen dat ofwel 9, ofwel , ofwel een 97-voud is; wat natuurlijk niet kan. Het mod-97-controlegetal zal dus een alarm geven bij elke transpositiefout van twee naast elkaar staande cijfers.

Toch ontdekt de mod-97-test niet alle dubbele fouten. Dit kun je uitmaken door vast te stellen dat en , dit terwijl 1067 en 1164 slechts op 2 plaatsen een verschillend cijfer staan hebben. Sommige rekeningnummers werden ook opzettelijk erg verkort weergegeven. Dit geldt in het bijzonder wel voor meerdere humanitaire organisaties. Zo is het nummer 12-12 een wel heel kort en dus eenvoudig te onthouden nummer. In werkelijkheid staat het voor het nummer dan evenzeer gevat is in het mod-97-model ( ). Een ongelukkige (maar 4-voudige) schrijffout tot het nummer 21-21, zal natuurlijk ook niet ontdekt worden.

Door mod 97 te werken, verdelen we alle natuurlijke getallen in 97 disjuncte deelverzamelingen. Kiezen voor een groter priemgetal, dat dan wel minstens 3 cijfers zal tellen, zou weliswaar een groter onderscheidend vermogen hebben, maar maakt ook alles een tikkeltje meer ingewikkeld. Tegenover de grotere baat staat dan dus ook een grotere kost.

In 2006 werden de Europese banken verplicht om voor internationale betalingen in de eurozone over te schakelen op een overkoepelend systeem om bankrekeningnummers weer te geven: het IBAN systeem (International Bank Account Number). De talrijke verschillende nationale systemen werden vanaf dan gevat door dit internationaal aanvaard model. Niet in alle Europese landen bestonden bankrekeningnummers op dat ogenblik enkel uit cijfers; in sommige landen konden ook letters gebruikt worden om een bankrekening weer te geven. Dit verklaart waarom de huidige IBAN nummers best wel wat in lengte kunnen verschillen, afhankelijk van het land waarop ze betrekking hebben.

We leggen even uit hoe het IBAN systeem werkt.

Veronderstellen we even dat er in Nederland een (lokaal) bankrekeningnummer “RABO 1234 1234 00” zou bestaan, en dat we dit in het IBAN formaat moeten brengen.

Om te beginnen kreeg elk land een landcode bestaande uit twee letters. Voor Nederland is dat “NL” (voor ons land “BE”). In eerste instantie zullen we de letters omzetten in getallen. We gebruiken hiervoor de alfabetische rangschikking, en beginnen met . Elke letter wordt nu weergegeven door een getal bestaande uit 2 cijfers.

Nu vormen we het lokale rekeningnummer om tot één groot getal, en we voegen daar achteraan de landcode aan toe (voor Nederland is dat 2321 en het getal 00. Bovenstaand nummer wordt dus als volgt behandeld

Lokaal rekeningnummer

RABO 1234 1234 00 27 10 11 24 1234 1234 00

landcode

NL

23 21

00

00 00

We verkrijgen zo dus het (grote) getal . Van dit getal bepalen we de rest bij deling door 97: . En om het helemaal spannend te maken, trekken we dit resultaat af van 98: we vinden het nieuwe controlegetal . Het IBAN formaat voor het lokaal nummer hierboven wordt dan

NL75 RABO 1234 1234 00.

Het Europees Comité voor Bank Standaarden (ECBS) dat het IBAN systeem aannam, opteerde dus ook voor een mod-97-controlemechanisme. De kracht ervan was hen dus ook niet ontgaan.

We kunnen nu opmerken dat een IBAN-nummer voor een voorheen (lokaal) Belgisch rekeningnummer in feite een dubbel mod-97-controlemechanisme in zich draagt. Het is een vernuftige illustratie van een samengestelde codering, waarbij eerst een lokaal mod-97-controlegetal wordt berekend, en daarna voor het nummer met dat controlegetal nog een tweede mod-97-controlegetal. Het eerder weergegeven (fictieve) rekeningnummer 123 — 4567890 — 02 zou in het IBAN formaat dus voorgesteld worden als

BE32 1234 5678 9002

omdat

en (De landcode van België is 1114).

Vóór de invoering van het IBAN systeem werden bankrekeningnummers in Nederland tegen foutjes beschermd door de elfproef. Dat systeem werd ook gehanteerd in het vroegere systeem van ISBN nummers, die aan elke officiële publicatie (bvb. een boek) worden toegekend.

Een 9-cijferig (lokaal) Nederlands rekeningnummer, zoals bvb moet dan voldoen aan de controlevoorwaarde

Mod-97-controlegetallen leveren een beter onderscheidend vermogen dan het elfproefcontrolemechanisme, zonder dat de inspanning nodig om dit allemaal te implementeren onredelijk groot is. Het is een voorbeeld van een verstandige kosten-batenanalyse, die elke dag voor ons aan het werk is.

Wat de controleberekening niet kan verhinderen, is dat u per vergissing geld overmaakt naar het correcte rekeningnummer van partij B (laat ons zeggen uw waterleverancier), terwijl het geld voor partij A (het gas- en elektriciteitsbedrijf) was bedoeld. In zo’n geval contacteert u het best meteen uw bank. Zij is niet gemachtigd om het geld op uw rekening terug te storten, maar kan wel helpen bij het terugvorderen van het verkeerd overgemaakte bedrag bij de foutieve bestemmeling.

We eindigen graag met enkele oefeningen en een paar weetjes.

1.

2. Leg nu zelf uit: Belgische bankrekeningnummers eindigen nooit met een controlegetal 98 of 99. Controleer zelf even of het mod-97-controlegetal alle typische Nederlandse fonetische fouten (13

3.

4. wordt 30, 14 wordt 40, 15 wordt 50, 16 wordt 60, 17 wordt 70, 18 wordt 80, 19 wordt 90) ontdekt. Je rijksregisternummer bestaat uit 11 cijfers, en gebruikt een versie van de mod-97-proef. Zoek uit bij de rijksregisternummers van je gezinsleden hoe de laatste 2 cijfers berekend worden. Laat ook zien dat het omwisselen van twee niet naburige cijfers van een (klassiek) Belgisch rekeningnummer steeds ontdekt wordt aan de hand van de mod-97-proef.

WEETJE In Frankrijk heeft elke burger een uniek “Numéro de Sécurité Sociale”. Ook dat nummer wordt door een mod-97-controlegetal tegen fouten beschermd. WEETJE Misschien verrassend, maar de Belgische Douane die toeziet op de in- en uitvoer van auto’s, kent aan elk chassisnummer van een auto ook een mod-97controlegetal toe.

REFERENTIES 1. Joseph A. Gallian, Error detection methods, ACM Computing Surveys, Volume 28, No.3, pp. 504-517 2. Hilde Van Den Eynde, Hoe groot is de kans dat u geld overmaakt naar de verkeerde rekening, De Standaard, 3 augustus 2020

FINALE VWO 2019-20

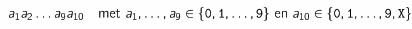
In elk officieel uitgegeven boek stond vroeger een ISBN-code (Internationaal Standaard BoekNummer) die bestond uit 10 symbolen. Zo’n code zag er als volgt uit:

Het symbool stond hierbij voor het getal 10. Bij een geldige ISBN-code was

een veelvoud van 11. Bewijs de volgende uitspraken.

(a) Als er in een geldige ISBN-code één symbool veranderd wordt, dan is het resultaat geen geldige ISBN-code. (b) Als er in een geldige ISBN-code twee verschillende symbolen van plaats verwisseld worden, dan is het resultaat geen geldige ISBN-code.