KASTANJES UITDELEN

aantallen kastanjes klinkt nogal moeilijk. Laten we dus de vraag versimpelen, en doen alsof er geen honderd kabouters zijn, maar veel minder, zeg zes.

Om het zo eenvoudig mogelijk te houden, laten we ook zeggen dat een van de kabouters, zeg kabouter 1, precies 1 kastanje heeft. Haar linkerbuurvrouw, kabouter 2, zal haar aantal kastanjes delen door dat van kabouter 1. Maar delen door 1 levert nooit een rest, en dus zal kabouter 2 zeker het getal 0 opschrijven op haar groene briefje. Alle kabouters hebben een verschillend aantal kastanjes, dus in het eenvoudigste geval heeft kabouter 2 precies 2 kastanjes. Laten we vanaf nu proberen altijd het getal 0 op de groene briefjes te krijgen. Dit betekent dat het aantal kastanjes van elke kabouter een veelvoud moet zijn van dat van haar rechterbuur. We kiezen bijvoorbeeld dat kabouter 3 precies 4 kastanjes heeft, en dat kabouter 4 bijvoorbeeld 8 kastanjes heeft. Als we zo doorgaan, vinden we dat als kabouter 5 precies 16 kastanjes heeft en kabouter 6 precies 32 kastanjes heeft, bijna alle kabouters het getal 0 op hun groene briefje hebben. Alleen kabouter 1 doet iets anders; als ze haar ene kastanje door de 32 kastanjes van kabouter 6 deelt, houdt ze natuurlijk gewoon weer 1 als rest over. In dit geval komen er dus in totaal twee verschillende getallen voor op de groene briefjes, namelijk 0 en 1. Dit is dus een situatie die voldoet aan het verhaaltje in de opgave, ware het dan met zes kabouters, in plaats van honderd.

Maar hoe zit het nu met de getallen op de rode briefjes? Kabouter 1 deelt haar aantal kastanjes door dat van kabouter 2. Maar 1 delen door 2 geeft gewoon rest 1. Net zo deelt kabouter 2 het getal 2 door 4, maar dit geeft ook gewoon rest 2. Net zo schrijven kabouters 3, 4 en 5 precies hun eigen aantal kastanjes op. Alleen bij kabouter 6 gebeurt er iets anders, want zij deelt haar aantal van 32 kastanjes door 1, en dit geeft natuurlijk rest 0. Uiteindelijk vinden we dus dat alle resten op de rode briefjes in dit geval verschillend waren; dit geeft 6 resten totaal.

Het bovenstaande zou kunnen worden opgevat als een mislukte poging. Ons wordt gevraagd om de laagst mogelijke waarde te vinden van het aantal verschillende getallen op de rode briefjes, en bovenstaand voorbeeld toont enkel aan dat het slechtst mogelijke geval, namelijk zes verschillende resten met zes kabouters, mogelijk is. Het lijkt alsof we nu helemaal niets zijn opgeschoten, maar niets is minder waar.

Wat we bemerkten bij het beschouwen van de rode briefjes is cruciaal. Als we een klein getal nemen en het delen door een groter getal, dan is de rest simpelweg gelijk aan het kleine getal. Dus stel dat een kabouter a kastanjes heeft en de kabouter daar rechts van heeft er b, waar a < b, dan is de rest van a bij deling door b simpelweg gelijk aan a, en zo weten we zeker dat het getal a op een groen briefje terecht komt. Er mogen echter maar twee verschillende getallen op de groene briefjes terecht komen, en dus kan deze situatie zich slechts hooguit twee keer voordoen. Dus de rechterbuurvrouw van een kabouter heeft altijd minder kastanjes dan zijzelf, op maximaal twee kabouters na. Dit is al enorm veel informatie! We zijn er echter nog niet volledig. In ons voorbeeld was het zo dat de rechterbuur altijd minder kastanjes had, op slechts één kabouter na. Het zou echter nog kunnen dat er twee kabouters bestaan met, zeg, a en b kastanjes waar a < b, zodat voor alle kabouters behalve deze twee, de rechterbuur altijd minder kastanjes heeft. De twee resten die voorkomen op de groene briefjes moeten dus wel a en b zijn. Beschouw nu echter de kabouter links van de kabouter met a kastanjes. Het getal op haar groene briefje wordt berekend door haar aantal kastanjes te delen door a en dan de rest op te schrijven. Deze rest is altijd kleiner dan a, maar dat is gek! Namelijk, a en b waren de enige getallen die voorkwamen op de groene briefjes, dus er is niet ook nog ruimte voor een getal nog kleiner dan a. Dit kan dus niet gebeuren en we concluderen dat de enige mogelijkheid is dat de rechterbuur van elke kabouter minder kastanjes heeft, op slechts één kabouter na.

Maar nu zijn we er eigenlijk. Namelijk, we bevinden ons weer precies in de situatie van ons voorbeeld. Elke kabouter behalve de rechterbuur van de kabouter met het minste aantal kastanjes zal haar eigen aantal op het rode briefje schrijven. De laatste kabouter schrijft een getal op dat kleiner is dan al die getallen, omdat zij de rest opschrijft bij deling door het kleinste voorkomende aantal kastanjes, en dat is altijd nóg kleiner. Dit zijn dus altijd 100 verschillende getallen en daarom moeten er op de rode briefjes altijd 100 verschillende getallen voorkomen.

Het bovenstaande is een voorbeeld van een opgave die erg moeilijk op te lossen is, tot je het probleem versimpelt en probeert om een situatie te vinden waar de opgave over spreekt. Dan is het direct veel minder abstract, en blijkt veel van de vrijheid die je op het eerste gezicht lijkt te hebben, direct te verdwijnen als sneeuw voor de zon. De structuur van de situatie

wordt dan veel duidelijker en dan is het nog slechts een bescheiden stap naar het juiste antwoord. Een echte doordenker, zoals het op de olympiade ook hoort.

INLEVERTERMIJN PRIJSVRAAG VERLENGD

In Vector 7 kon je lezen over de Pythagoras Vlakvullingen Prijsvraag. Vanwege de sluiting van de scholen wegens het Coronavirus heeft de redactie van Pythagoras besloten om de inlevertermijn van de prijsvraag over vlakvullingen te verlengen. Doe mee met de hele klas en win een uitstapje naar het Escher museum! Individueel zijn er ook leuke afdrukken van je ontwerp te winnen. Info over de prijsvraag zie Vector 7 of https://pyth.eu/prijsvraagvlakvullingen. Je kunt je oplossingen en ontwerpen inzenden tot uiterlijk 1 januari 2021 naar prijsvraag@pyth.eu.

COVID-19 EN EPIDEMIEMODELLEN

WISKUNDE & ONDERWIJS

EIND 2019 WERD ER IN DE CHINESE STAD WUHAN VOOR HET EERST MELDING GEMAAKT VAN EEN ERNSTIG VERLOPENDE LUCHTWEGENINFECTIE, WAARVAN DE OORZAAK ONBEKEND WAS. OP 7 JANUARI 2020 WERD DOOR CHINESE WETENSCHAPPERS VASTGESTELD DAT EEN NIEUW VIRUS, DAT VOORLOPIG '2019-NCOV' WERD GENOEMD, AAN DE BASIS LAG VAN DEZE UITBRAAK. EÉN MAAND LATER WORDEN OOK DE EERSTE GEVALLEN IN EUROPA GEMELD EN KONDIGT DE WHO DE WERELDWIJDE NOODSITUATIE AF. HET NOORDEN VAN ITALIË WORDT VANAF FEBRUARI UITERMATE ZWAAR GETROFFEN. OP 7 MAART PLAATST ITALIË LOMBARDIJE EN BIJ UITBREIDING HET HELE LAND ONDER QUARANTAINE. EÉN WEEK LATER WORDEN OOK IN BELGIË EN NEDERLAND STRENGE BEPERKENDE MAATREGELEN GENOMEN.

TIJDSCHRIFT VLAAMSE VERENIGING WISKUNDELAARS WWW.VVWL.BE IVAN DE WINNE IS VOORZITTER VAN DE VLAAMSE VERENIGING WISKUNDELERAARS (VVWL). DAARNAAST IS HIJ AUTEUR VAN ALLERHANDE INTERACTIEF LESMATERIAAL MET GEOGEBRA. OOK IS HIJ BEHEERDER VAN DE ELEKTRONISCHE LEEROMGEVING VOOR WISKUNDE WWW.MATHELO.NET. E-MAIL: IVAN.DEWINNE@TELENET.BE

WISKUNDIGE MODELLEN VOOR DE VERSPREIDING VAN INFECTIEZIEKTEN Het idee dat de verspreiding van infectieziekten met wiskundige formules kan beschreven worden, is al oud. In 1766 publiceerde Daniël Bernoulli een artikel waarin hij de effecten analyseerde van de pokkeninfectie op de levensverwachting. Het duurt nog tot de twintigste eeuw vooraleer de dynamiek van de verspreiding van infectieziekten werd begrepen en de eerste wiskundige modellen werden uitgewerkt.

Vandaag de dag is de epidemiologische modellering vergevorderd. Met gesofisticeerde modellen kunnen wetenschappers het verdere verloop van de verspreiding van COVID-19 of andere virussen vrij nauwkeurig simuleren. Denken we bijvoorbeeld aan het werk van het team van prof. Niel Hens (UAntwerpen en UHasselt).

In deze tekst beperken we ons tot een aantal vereenvoudigde modellen. Die laten ons toe enkele sleutelbegrippen te leren kennen en ze verschaffen ons inzicht in de dynamiek van de verspreiding van een infectieziekte.

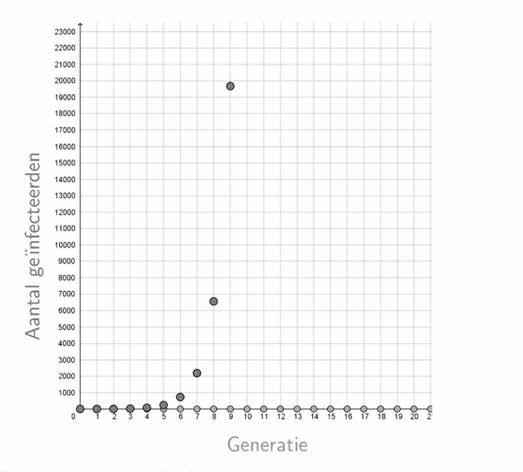
EPIDEMIEMODEL IN GENERATIES Een infectieziekte verspreidt zich door de contacten van geïnfecteerde personen met vatbare personen waarbij het virus wordt overgedragen. Met dit eerste eenvoudig model geven wij een beschrijving van de verspreiding in generaties van een infectieziekte zoals COVID-19.

Voor het coronavirus (SARS-cov-2) lag hoogstwaarschijnlijk een handvol personen aan de bron van de verdere verspreiding. Het aantal geïnfecteerde personen bij het begin van de epidemie stellen wij voor door . Wij noemen het aantal geïnfecteerde personen in de eerste generatie , in de tweede generatie , enzovoort.

Bij het opstellen van dit eerste model gaan wij uit van een aantal veronderstellingen.

Het aantal besmettingen in de k-de generatie hangt af van onder andere: • het aantal besmettingen in de voorafgaande generatie

het aantal vatbare personen die nog niet besmet zijn de periode van de infectie en hoelang geïnfecteerde personen andere vatbare personen kunnen besmetten, hoe besmettelijk de ziekte is en de manier van overdracht. HET REPRODUCTIEGETAL R In de epidemiologie maakt men gebruik van het zogenaamde (effectieve) reproductiegetal , dat aangeeft hoeveel mensen door één persoon gemiddeld besmet worden gedurende de volledige periode dat deze persoon besmettelijk is. Voor het geval van Covid-19 neemt men aan dat deze besmettelijke periode tot 14 dagen kan duren. Het reproductiegetal kan veranderen tijdens het verloop van de epidemie.

Bij het begin van een epidemie spreekt men over het basaal reproductiegetal . Dit getal geeft aan hoeveel secundaire besmettingen gemiddeld veroorzaakt worden door één geïnfecteerde persoon. Hierbij wordt ervan uitgegaan dat de volledige populatie vatbaar is voor de besmetting en er geen preventieve maatregelen zoals social distancing genomen zijn. Het basaal reproductiegetal voor Covid-19 is ongeveer .

EXPONENTIËLE GROEI Bij een nieuw virus zal bij de uitbraak van een epidemie de volledige populatie vatbaar zijn voor besmetting en is het aantal geïnfecteerde personen zeer klein zijn. Indien het reproductiegetal dan zal iedere geïnfecteerde persoon gemiddeld 2 andere vatbare personen besmetten. Het aantal nieuwe besmettingen in de k-de generatie is dan )

Algemeen geldt er dat (recursief voorschrift) Indien gekend is en het aantal besmettingen bij het begin van de epidemie, dan kan men het aantal (nieuwe) besmettingen in de k-de generatie berekenen.

Algemene formule:

Verloop van de epidemie met (links) en

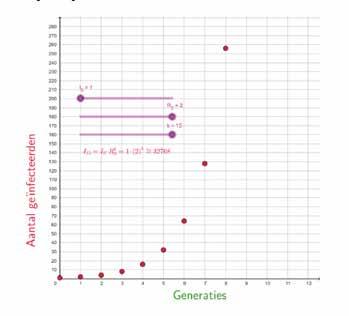
(rechts)

DREMPELWAARDE VAN HET (EFFECTIEVE) REPRODUCTIEGETAL R Bij het opstellen van dit eerste epidemiemodel werd verondersteld dat het aantal vatbare personen constant blijft. Bovendien geeft de generatie de infectie door aan de -de generatie en zijn er geen herhaalde besmettingen van de voorafgaande generaties. Na verloop van tijd zal de groep van vatbare personen erg klein worden. De waarde van het reproductiegetal zal tijdens het verdere verloop van de epidemie voortdurend wijzigen.

Indien wij dit model zouden toepassen op de verspreiding van mazelen met dan zou het aantal nieuwe besmettingen sterk oplopen en wordt dit model in de praktijk al snel onbruikbaar. Na 5 generaties zou immers gelden: . Na 10 generaties: .

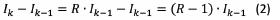
Om het effect van de grootte van te begrijpen, berekenen wij het verschil van de aantallen tussen twee opeenvolgende generaties. We zien dus:

: afname van het aantal besmettingen.

: aantal besmettingen blijft constant.

: toename van het aantal besmettingen.

Een epidemie stoppen vereist dat het gemiddeld aantal nieuwe mensen dat elke geïnfecteerde besmet kleiner is dan één. Dit kan gebeuren wanneer mensen immuun worden, een vaccinatie krijgen of hun gedrag aanpassen om overdracht te voorkomen.

OPSTELLEN FORMULE VOOR HET REPRODUCTIEGETAL Het reproductiegetal kan men berekenen met het aantal contacten, de kans op overdracht van de besmetting, de infectieuze periode en de grootte van de groep vatbare personen. Aangezien Covid-19 wordt veroorzaakt door een onbekend nieuw virus kan dit enkel door analyse van de data en schattingen. Daarom gebruiken wij bij het opstellen van de formule voor het reproductiegetal de bekende gegevens van een “gewone” seizoensgriep.

Voor de seizoensgriep is de periode van infectie gemiddeld 5 dagen. Stel dat het aantal contacten per dag gemiddeld 10 is en laat ons aannemen dat bij elk van deze contacten er = 4 % kans op besmetting is.

Het totaal aantal besmettelijke contacten dat iedere geïnfecteerde persoon heeft, is dan gelijk aan .

Voor de seizoensgriep laat een gedeelte q (60 %) van de bevolking zich vaccineren waardoor het percentage vatbare personen in de populatie kleiner wordt:

Het aantal “succesvolle” contacten die iedere geïnfecteerde in dit geval heeft, is gelijk aan: .

Indien het percentage vatbare personen kleiner wordt dan zal het reproductiegetal ook kleiner worden.

BASAAL REPRODUCTIEGETAL R 0 Indien , dan is de volledige populatie nog vatbaar voor de besmetting. In dit geval spreekt men over het basaal reproductiegetal met als notatie : Deze situatie doet zich voor bij het begin van de epidemie. Omdat er bij het coronavirus voorlopig nog geen vaccin bestaat, is de enige mogelijkheid om te verkrijgen de beperking van het aantal contacten .

DE TRANSMISSIEPARAMETER Voor onbekende virussen is het in de praktijk erg moeilijk om een onderscheid te maken tussen en . Uit de analyse van data is het iets eenvoudiger om een waarde voor het product te vinden.

Men noemt dit product de transmissieparameter

Rekening houdende met (3) krijgt men:

is een getal dat aangeeft hoeveel personen door één persoon gemiddeld besmet worden per tijdseenheid. Voor het Covid-19, met periode van besmettelijkheid (dagen), vinden we

VACCINATIE EN R 0 Stel dat een deel van de bevolking zich laat vaccineren. Het reproductiegetal is dan

De ziekte zal uitdoven indien . Hiermee kunnen wij het percentage van de bevolking berekenen dat

minimaal moet gevaccineerd worden.

Met vaccinatie (links) en

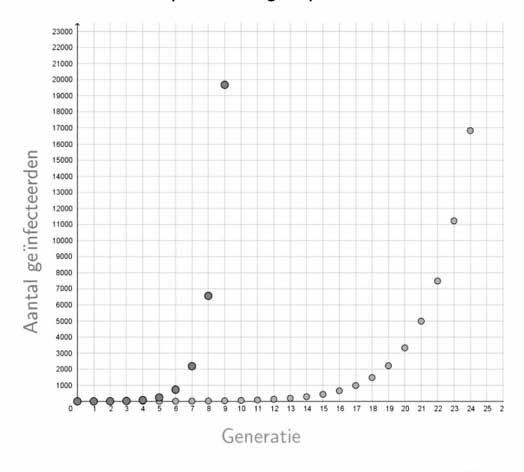
(rechts)

Dit betekent voor het coronavirus (indien ) minstens van de bevolking moet gevaccineerd worden. Er is dan sprake van groepsimmuniteit.

EPIDEMIEMODEL IN DE TIJD In het epidemiemodel dat wij tot nu toe hebben besproken, werd de verspreiding van de infectieziekte bekeken in generaties. Hierbij zijn de geïnfecteerde personen in generatie verschillend van en . Dit model geeft ons wel heel wat inzicht in de dynamiek van de verspreiding van de ziekte. Door het nemen van de nodige quarantainemaatregelen en social distancing zal het aantal contacten tussen vatbare personen en geïnfecteerde personen sterk gereduceerd kunnen worden en het reproductiegetal kleiner worden. Dit model stelt ons ook in staat om te berekenen welk gedeelte van de populatie men minstens moet vaccineren om de verdere verspreiding te voorkomen.

Dit epidemiemodel is echter moeilijk te verbinden met de dagelijkse data waarbij het aantal besmettingen worden weergegeven in de tijd. In een tweede model bestuderen wij de verandering van het aantal geïnfecteerde personen in functie van de tijd . VERANDERING VAN VOOR EEN CONSTANTE Voor dit model veronderstellen wij dat het percentage vatbare personen s constant blijft omdat de verhouding van het aantal geïnfecteerde personen tot de totale populatie bij het begin van de epidemie klein is. In een tijdsinterval komen er geïnfecteerde personen bij door besmetting en gaan er ook af door herstel (of sterfgeval). Noem de transmissieparameter en de herstelsnelheid . Dan is:

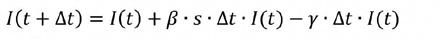
Na limietovergang voor

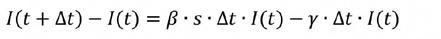
, vinden de dan dat

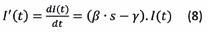
De formule voor het aantal geïnfecteerde personen in functie van de tijd (waarbij constant blijft) is:

Men noemt de groeisnelheid. Voor een volledig vatbare populatie waarbij groeisnelheid , is de

Data België maart 2020 (www.who.int)

VERBAND TUSSEN R 0, EN

Uit volgt dat . Daarom is

HET SIR-MODEL Een ander vaak gebruikt model om de verspreiding van besmettelijke ziekten te beschrijven is het zogenaamde SIR-model.

Het SIR-model is verdeelt de populatie in drie compartimenten met een verschillende infectiestatus: - S (Susceptable) aantal personen die vatbaar zijn voor de ziekte. - IR (Infected) aantal personen die besmettelijk zijn. - S (Recovered) aantal personen die genezen zijn (of overleden).

Bij aanvang van een epidemie met een nieuw virus is iedereen vatbaar voor het virus. Een beperkt aantal personen is besmettelijk. Doordat geïnfecteerde personen andere vatbare personen besmetten, zal het aantal personen binnen elke groep voortdurend wijzigen.

Omdat een besmette persoon uit groep I andere personen uit groep S besmet zal de groep S kleiner worden en de groep I groter. Daarnaast zijn er ook personen uit groep I die genezen (of overlijden) en immuniteit voor de ziekte opbouwen en uiteindelijk in groep R terecht komen.

Het SIR-model bestaat uit 3 differentiaalvergelijkingen die de veranderingen van de aantallen in elke groep beschrijven in functie van de tijd. Deze vergelijkingen zijn met elkaar verbonden.

Uit formule (8) volgt:

Hierbij is het constante vatbare deel van de populatie, de transmissiesnelheid (het gemiddeld aantal besmettingen dat één geïnfecteerd persoon per dag kan veroorzaken) enγ de herstelsnelheid (de fractie van geïnfecteerde personen die gemiddeld per dag zal herstellen).

In werkelijkheid verandert de groep van de vatbare personen bij de overgang van naar en is ook een functie van de tijd . Stel met de grootte van de populatie. De vergelijking die de verandering van het aantal geïnfecteerde personen weergeeft wordt dan: .

Men kan een stelsel van 3 differentiaalvergelijkingen opstellen die de veranderingen van de aantallen in elk van de drie groepen weergeven in functie van de tijd: .

Bovendien geldt:

Wij nemen ook aan dat de omvang van de populatie niet verandert, omdat er geen rekening wordt gehouden met geboorten, overlijdens of migratie. Dus: Het aantal vatbare personen zal kleiner worden en dus is . Het aantal herstelde personen zal toenemen en dus is . Het aantal geïnfecteerde personen zal in het begin toenemen indien . Het aantal geïnfecteerde personen zal een maximum bereiken indien . Het aantal vatbare personen is dan . Dit SIR-model kan nog verder worden gesofisticeerd door te werken met meer compartimenten. DYNAMISCHE SIMULATIE MET GEOGEBRA Voor het rekenwerk en het tekenen van de bijhorende grafieken voor S, I en R kan men handig gebruik maken van ICT-tools zoals GeoGebra. Start GeoGebra en activeer het algebravenster voor het ingeven van de formules en ook het tekenvenster voor het weergeven van de grafieken.

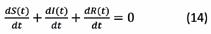
Om het stelsel (12) op te lossen moeten , de beginwaarden en ook de waarden voor de parameters en gekend zijn.

Wij definiëren vooreerst een aantal variabelen en gaan uit van een aantal veronderstellingen. • (populatie Belgische bevolking) • Wij nemen aan bij het begin slechts 1 persoon besmet is: . • Het aantal vatbare personen is dan: . • Bij het begin zijn er nog geen mensen die genezen zijn: .

Wij maken ook twee schuifknoppen en voor de overgangssnelheden en een schuifknop voor de maximale tijd dat het model zal lopen: • schuifknop tussen 0 en 0,5 met stapgrootte 0,01 • schuifknop tussen 0 en 0,25 met stapgrootte 0,01. • schuifknop tussen 0 en 500 met stapgrootte 1.

Vervolgens geven wij in het algebravenster de drie dif-

ferentiaalvergelijkingen in. GeoGebra beschikt over een commando om deze differentiaalvergelijkingen numeriek op te lossen en de bijhorende grafieken voor , en weer te geven.

ODE staat voor Ordinary Differential Equation.

LOCKDOWN EN “FLATTENING THE CURVE” VOOR COVID-19 De enige mogelijkheid om de epidemie af te remmen is het verkleinen van de waarde voor (en dus ook ). Hierdoor wordt de grafiek van het aantal besmettingen afgevlakt.

Wij onderzoeken dit voor een aantal waarden van de parameter .

Geval 1: en

Geval 3: strengere lockdown maatregelen .

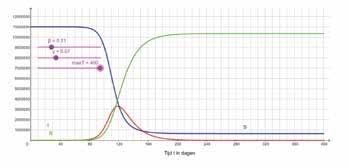
Geval 2: beperkte lockdown

en COLLECTIE GEOGEBRA BESTANDEN https://www.geogebra.org/m/nxhtkuz6

BIBLIOGRAFIE en

Dries De Smet, Krant De Standaard, 28 maart 2020 Swier Garst en Don Klinkenberg, Besmettelijke ziekten, Epsilon uitgaven deel 58 Niel Hens, Voordracht proclamatie VWO www.facebook.com/ vlaamsewiskundeolympiade/videos/876767442791237/ Ad Meskens, COVID-19 in de klas, Wiskunde en Onderwijs 182 (2020), p. 3-8 David Smith en Lang Moore, The Sir-model, Mathematical Association of America, april 2020 Simon Telen en Andreas Van Barel, The mathematics of “Flattening the curve”, maart 2020 Leo Van Echelpoel, Covidsimulatie, april 2020 https://www.facebook.com/groups/231795661356774/ World Health Organisation, www.who.int/emergencies/ diseases/novel-coronavirus-2019

HET VERBORGEN RUIMTELICHAAM, EEN SPELVORM VOOR IN DE KLAS

UITWISKELING

MICHEL ROELENS REDACTIE UITWISKELING

IN DIT ARTIKEL BESCHRIJF IK EEN INTERESSANTE WERKVORM, OF MOET IK ZEGGEN ‘SPELVORM’, DIE JE KUNT GEBRUIKEN IN LESSEN OVER RUIMTEMEETKUNDE IN DE TWEEDE OF DERDE GRAAD EN, MITS AANPASSINGEN, OOK IN DE EERSTE GRAAD.

IK LEERDE DEZE WERKVORM KENNEN TIJDENS EEN WORKSHOP OVER RUIMTEMEETKUNDE OP EEN BIJEENKOMST MET COLLEGA’S VAN DE GEM (GROUPE D’ENSEIGNEMENT MATHÉMATIQUE) VAN LOUVAIN-LA-NEUVE EN DE IREM (INSTITUT DE RECHERCHE SUR L’ENSEIGNEMENT DES MATHÉMATIQUES) VAN LILLE. DE WORKSHOP WERD GEGEVEN DOOR LOUIS ROYE (IREM) EN WE SPEELDEN HET SPEL TOEN MET EEN GROEPJE COLLEGA’S WISKUNDIGEN.

DE SPELREGELS Een ruimtelichaam zit verstopt in een doos. De deelnemers zijn ingedeeld in groepjes van vier. Eén groepje kent het verborgen lichaam. De leerlingen van dit groepje hebben het lichaam vooraf mogen bekijken, betasten, opmeten… of eventueel hebben zij het vooraf zelf gemaakt. De andere groepjes moeten proberen te achterhalen welk lichaam het is. Op het einde moeten ze in staat zijn er een vlakke ontwikkeling van te maken die uitgeknipt, gevouwen en geplakt wordt om te verifiëren dat het hetzelfde lichaam is. Om er achter te komen welk lichaam in de doos zit, stelt elke groep om de beurt luidop een vraag aan de groep die het lichaam kent. Het moeten vragen zijn die beantwoord kunnen worden met ‘ja’, ‘neen’ of een getal. Andere vragen worden niet beantwoord. De groepjes kunnen zowel de antwoorden op de eigen vragen als de antwoorden op de vragen van de andere groepjes als informatie benutten. De leraar-spelleider controleert dat de antwoorden juist zijn en noteert in telegramstijl de gestelde vragen en de antwoorden op het bord. Af en toe kan de leraar een onderbreking voorzien om de groepjes toe te laten alles op een rij te zetten.

Bij de competitieve versie wint de groep die als eerste het juiste lichaam gemaakt heeft; groepjes die een fout lichaam ‘indienen’ worden uitgeschakeld. Bij een minder competitieve variant vraagt de leraar na een tijd ‘denk je dat je nu genoeg informatie hebt?’. Groepjes die menen genoeg te weten, maken het

lichaam. Groepjes die nog vastzitten, mogen een afgevaardigde sturen die enkele seconden in de doos mag kijken en dan in zijn groepje verslag uitbrengt over wat hij gezien heeft. Bij deze variant is het de bedoeling dat zoveel mogelijk groepjes het juiste lichaam kunnen maken.

Belangrijk is ook de nabespreking. ‘Waarom kon een bepaalde vraag niet beantwoord worden? Waren alle gestelde vragen nodig of werden ook zaken gevraagd die uit de vorige antwoorden konden worden afgeleid? Indien een fout lichaam werd gemaakt, heeft die groep met bepaalde informatie geen rekening gehouden of was er te weinig informatie om het lichaam eenduidig vast te leggen?’

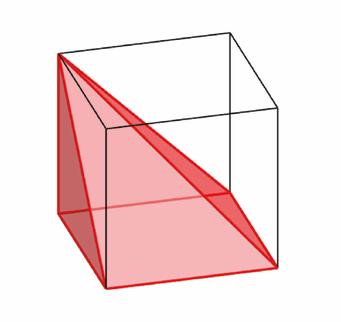
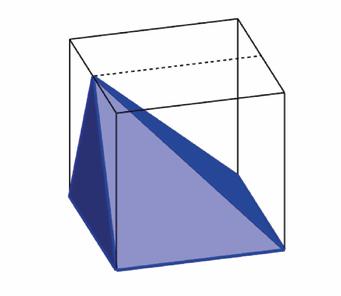
HET LICHAAM DAT WIJ MOESTEN VINDEN EN HOE WE ER LEKKER NAAST ZATEN… Toen wij aan de workshop deelnamen, was het lichaam dat in de doos zat een piramide met vierkant grondvlak, met top recht boven één hoekpunt van dit vierkant en met als hoogte de zijde van dit vierkant. Anders gezegd: het was de piramide die je krijgt als je in een kubus de hoekpunten van het grondvlak verbindt met één hoekpunt van het bovenvlak (zie figuur hieronder).

Ik probeer de vragen en antwoorden te reconstrueren.

Is het een veelvlak? Ja.

Convex? Ja.

Zijn sommige zijvlakken driehoeken? Ja.

Hoeveel zijvlakken zijn driehoeken? Vier. (Merk op dat de vorige vraag overbodig was.)

Hoeveel zijvlakken zijn vierhoeken? Eén.

Zijn er nog andere zijvlakken? Neen. (Als het antwoord ‘ja’ was geweest, hadden we met deze vraag niet zoveel geweten. We hadden bv. beter gevraagd hoeveel andere zijvlakken er nog waren.)

Hoeveel hoekpunten zijn er? Vijf. (Merk op dat we nu niet meer hoefden te vragen naar het aantal ribben. Een convex veelvlak voldoet immers aan de stelling van Euler ‘het aantal hoekpunten min het aantal ribben plus het aantal zijvlakken is 2’. Het aantal ribben is dus 5 + 5 - 2 = 8. Deze ‘geleerde’ beschouwingen gaven ons het gevoel dat we goed bezig waren…)

Is het een piramide? Ja.

Is het een rechte piramide (top recht boven het midden van het grondvlak)? Neen.

Hoeveel cm meet de zijde van het vierkante zijvlak? Zes.

Hoeveel cm is de hoogte van de piramide? Zes.

Hoeveel driehoekige zijvlakken zijn gelijkbenig? Twee.

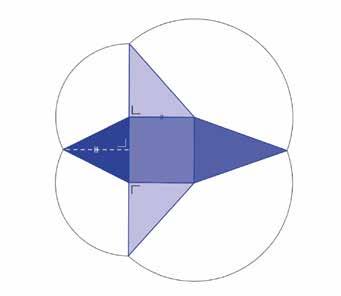
Is het veelvlak vlaksymmetrisch? Ja. Intussen zat ons groepje op een verkeerd spoor: we dachten aan een piramide met vierkant grondvlak en met de top recht boven een punt van een middellijn, maar niet boven het middelpunt (zie figuur hieronder, voor de duidelijkheid weer in een kubus getekend). We hadden er niet aan gedacht dat de gelijkbenige driehoeken ook naaste buren konden zijn (met een

gemeenschappelijke zijde) en dat de gelijke ‘benen’ van deze driehoeken niet noodzakelijk opstaande ribben van de piramide hoeven te zijn… Zijn de niet-gelijkbenige driehoeken rechthoekig? Ja. (Dat de driehoeken in werkelijkheid alle vier rechthoekig zijn, konden we met deze vraag niet achterhalen.) Op dit moment dachten we dat we het gevonden hadden: de top moest recht boven het midden van een zijde van het grondvlak staan (zie figuur hieronder).

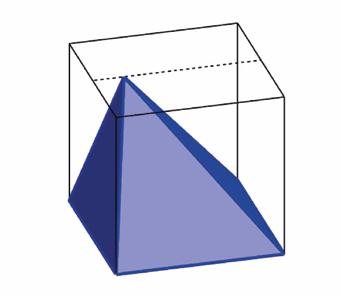
We maakten een ontwikkeling van ‘onze’ piramide (zie

figuur hieronder).

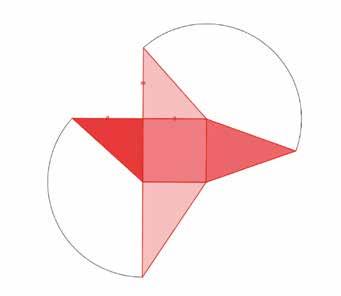
Een ander groepje had wel het juiste lichaam gemaakt. Je ziet hun ontwikkeling hieronder.

Voor jongere leerlingen kan misschien best een ‘bekender’ lichaam genomen worden, zeker de eerste keer.

Nadien probeerde ik deze workshop uit in een vierde jaar (4 uur wiskunde). Twee groepjes vonden het lichaam dat ik had gekozen. Hun strategie bleek efficiënt: ze slaagden erin te achterhalen hoe de zijvlakken waren, knipten die afzonderlijk uit en probeerden die aan elkaar te plakken, zonder zich veel zorgen te maken over een vlakke ontwikkeling uit één stuk.

Het groepje dat het lichaam kende

Dit artikel verscheen in Uitwiskeling 25/3. Benieuwd naar meer? Op www.uitwiskeling.be vind je alle info.

Het lichaam van de winnende groep, met daarnaast het origineel

OEFENING 1

VLAAMSE WISKUNDE OLYMPIADE VZW, EERSTE RONDE VWO 2020, VRAAG 9

Kobe tekent een scherpe hoek in een kwartcirkel zoals in de figuur. Hij projecteert het lijnstuk [OP] loodrecht op de stralen die de kwartcirkel begrenzen. Hij construeert twee vierkanten met die projecties als zijde. Voor welke hoek(en) is de som van hun oppervlaktes het grootst?

A

15° en 75°

B

20° en 70°

C

30° en 60°

D

45°

E

De som is steeds even groot.

HANDS-ON: DE MODELLEERWEEK AAN DE UHASSELT

SAMENVATTING RECENT HEBBEN WIJ BINNEN DE BACHELOROPLEIDING WISKUNDE AAN DE UHASSELT EEN NIEUWE ONDERWIJSVORM GEÏMPLEMENTEERD. UITDAGENDE OPDRACHTEN, AANGELEVERD DOOR VLAAMSE BEDRIJVEN, WORDEN GEDURENDE EEN HELE WEEK DOOR STUDENTEN BESTUDEERD EN "BEWERKT". IN DIT ARTIKEL BESCHRIJVEN WIJ HET VERHAAL KORT, KIEZEN WE TWEE OPDRACHTEN MET BIJBEHORENDE OPLOSSINGEN GEVONDEN DOOR DE STUDENTEN, EN GEVEN WE EEN KORTE SCHETS VAN DE ACHTERLIGGENDE WISKUNDE.

ROEL SCHROOTEN EN JOCHEN SCHÜTZ, UHASSELT, 9 SEPTEMBER 2020

1. INLEIDING De missieverklaring van het Platform Wiskunde Vlaanderen [7] formuleert het uiterst duidelijk:

Al onze maatschappelijke en technologische vooruitgang heeft op een of andere manier een wiskundige component nodig. [...] Toch blijft de enorme impact van wiskunde meestal goed verborgen. [...]

Er valt weinig aan dit, en aan de rest van deze missieverklaring, toe te voegen, behalve wellicht nog dat zelfs toekomstige wiskundigen - studenten, maar ook scholieren met een liefde voor wiskunde - het vaak moeilijk vinden om precies en begrijpelijk te kunnen vertellen waar wiskunde in de maatschappij aan bod komt. Binnen de bacheloropleiding wiskunde aan de UHasselt is er ruime aandacht voor de toegepaste wiskunde, meerdere modelleervakken staan verplicht in het curriculum. Toepassingen van de wiskunde worden besproken, maar omwille van didactische redenen zijn deze natuurlijk vaak afgezwakt. Implicaties zijn dat • de opdrachten volledig haalbaar zijn voor de student, • de docent de oplossing volledig kent en kan uitleggen, • de opdrachten iets van hun realisme verliezen.

Hiertegenover staat de aanzet die we voor de nieuwe modelleerweek gekozen hebben: we willen bewust de opdrachten niet versoepelen. Samen met industriële partners hebben wij realistische taken bedacht (op een

selectie ervan gaan we in het volgende wat dieper in), die we tijdens een intensieve week buiten de instelling aan de studenten hebben voorgelegd. Zij moesten dan ‘hands-on’, dus zonder inleidend hoorcollege of dergelijke, oplossingen zoeken. In tegenstelling tot de 'gewone' vakken is het evident dat:

wij niet kunnen/mogen verwachten dat de studenten de opdrachten volledig afmaken, de docent de oplossing niet volledig kent, en enkel steun kan geven tijdens de uitvoering, de opdrachten toch een zeer goed beeld geven van wat van een wiskundige in zijn beroepsleven verwacht zou kunnen worden.

We hebben ervoor gekozen om een volledige week in het tweede semester van het eerste jaar aan de bewerking van de opdrachten te besteden; we waren dan ook vijf dagen op stap, om de studenten de mogelijkheid te geven om buiten hun gewoon dagelijks leven zo hard mogelijk naar oplossingen te zoeken. Als bijproduct verstrengt dit ook de zo jobrelevante soft-skills, zoals groepswerk, frustratievermogen en dergelijke meer.

Het concept, ook al nieuw aan de UHasselt, bestaat aan sommige universiteiten in het buitenland al langer, in verschillende formaten. Voorbeelden die ons geïnspireerd hebben, zijn het CAMMP-initiatief aan de RWTH Aachen en de Karlsruhe Institute of Technology (Duitsland) (zie [3] met ook een aantal – meestal Duitstalige – publicaties) en de Modeling Week aan de TU Eindhoven [6]. Ook het European Consortium for Mathematics in Industrie (ECMI) organiseert sinds 1988 regelmatig modeling weeks [4].

In deze publicatie hebben wij het in detail over enkele van de taken en mogelijke oplossingsstrategieën. Vanaf 2020/21 wordt het concept uitgebreid naar excellente leerlingen uit het secundair onderwijs. We hopen met dit artikel de interesse van leerlingen en leerkrachten te wekken om er eventueel aan mee te doen. Maar ook voor mensen die niet per se geïnteresseerd zijn in de modelleerweek bieden de cases interessante voorbeelden van praktische toepassingen van wiskunde. 2. GESELECTEERDE VOORBEELDEN In dit hoofdstuk beschouwen we twee geselecteerde voorbeelden in detail. Wij bespreken de probleemstellingen, de door de studenten gevonden oplossingen en zetten dit in een bredere wiskundige context. Voor meer informatie over modelleren, in het bijzonder voor leerlingen uit het secundair onderwijs, verwijzen wij naar [1].

2.1 Voorspelling bestellingen

Van een groot logistiek bedrijf mochten wij data uit de jaren 2018 en 2019 ontvangen. Deze data hadden, onder andere, als inhoud het aantal vervoerde goederen (inclusief massa en volumes van een dergelijk goed) per dag. Het spreekt voor zich dat het bestuur van het bedrijf grote interesse heeft voor een precieze voorspelling van hoeveel goederen te verwachten zijn op een zekere dag, omdat dit implicaties op werkbezetting, aanwerving van subondernemers en dergelijke meer heeft. Het gaat hier om massaal veel data die verwerkt moeten worden. De studenten hebben zelfstandig besloten om enkel de dagelijkse ritten te bekijken. Complexiteitsreductie is, zeker voor een wiskundige, een uiterst belangrijke vaardigheid; enkel een goede doordachte hiërarchie van problemen (van 'makkelijk' naar 'moeilijk') levert typisch gezien een tevredenstellend antwoord. Complexiteitsreductie kwam bij alle oplossingen aan bod, uiteraard ook gezien het feit dat wij met de studenten enkel een week konden bezig zijn.

Terug naar het probleem: wiskundig gezien hadden de studenten dus 2x365 = 730 waarden van het aantal ritten, we noemen deze . De eerste 365 waarden, behorende tot de ritten van 2018, hebben ze gebruikt als 'trainingsdata', de laatste 365 waarden, behorende tot de ritten van 2019, als 'testdata', om de kwaliteit van hun voorspellingsmodel te analyseren.

Aan het einde van de week hebben zij twee potentiële oplossingen gevonden: 1. Eerst realiseerden zij zich dat de totale aantallen van jaar tot jaar er toch soms behoorlijk anders uitzien, dus op het eerste gezicht was er weinig verband tussen en , dus de dag één jaar later. Wat er wel relatief stabiel is, is het aantal verschillen van dag op dag, dus voor de differentie is er wel het verband

zichtbaar. (Dit moet nog gezuiverd worden van het effect van weekends, wat de studenten ook gedaan hebben door een clustering van weken te maken. Voor het gemak gaan we hier niet dieper op in, omdat het enkel de notatie moeilijker maakt.) Een eerste schatter voor het jaar 2019 hebben zij dan gevonden als

Dit levert al relatief goede resultaten, zeker de trends worden goed begrepen. Het is interessant om te zien dat de studenten de zogenaamde Euler-methode uitgevonden hebben. Deze speelt eigenlijk een rol in de behandeling van gewone differentiaalvergelijkingen. Gewone differentiaalvergelijkingen (van eerste orde, om precies te zijn) zijn vergelijkingen waar er een voorschrift is om de afgeleide van een functie te berekenen, met een gegeven functie die van de tijd en ook van de functie zelf mag afhangen. Uitgaande van een beginconditie , ook weer met gegeven, is het in vele gevallen mogelijk om , en zij het enkel numeriek, te bepalen. De Euler-methode is nu zo een numerieke methode, en ze behoort tot de simpelste methoden ter oplossing van gewone differentiaalvergelijkingen. Uitgaande van schat ze , voor een 'kleine' waarde , door zijn raaklijn. Dit is succesvol omdat er een expliciet voorschrift is voor de afgeleide, we kunnen dus benaderen: Eenmaal dat er een benadering aan bekend is, kan op dezelfde manier berekend worden: In de numerieke analyse houdt men zich bezig met het analyseren van het convergentiegedrag van dit soort algoritmes [2]. Terug naar het probleem van het logistiekbedrijf. Als men het gevonden model (1) als

Euler-methode gaat interpreteren, dan is de toebehorende 'continue' differentiaalvergelijking gegeven door

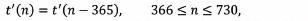
wat in feite zelfs een (toegegeven, zeer simpele) geretardeerde differentiaalvergelijking is omwille van het tijdsverschil. Het vinden van dit soort continue modellen is in vele toepassingen cruciaal om meer informatie uit het model te kunnen halen.

2. Het is aan te nemen dat er bij dit soort verhalen een periodieke structuur te herkennen is. Dit viel één van de studenten wel op, en hij kon dan ook een verband trekken met de sinus- en cosinusfuncties. Op navraag konden wij als begeleiders hem dus alert maken op de discrete Fourier-transformatie, die dan ook in

Matlab geïmplementeerd is. De Fourier-transformatie tracht een verband tussen een periodieke functie en

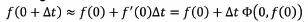
sinus- en cosinusfuncties via

te vinden. De discrete Fourier-transformatie mikt precies op hetzelfde, maar dan wel met discrete waarden zoals degene aangeleverd door . De Fourier-transformatie wordt in veel verschillende plaatsen ingezet, bv. voor het denoising van muziek, maar heeft ook haar nut hier. Ook die aanzet leverde bruikbare resultaten op met een wat betere kwaliteit wat de grote trends betreft, en wat slechtere wat de details betreft.

Uiteraard hebben beide aanzetten voor zichzelf genomen het probleem niet opgelost. Het was ook niet te verwachten dat de studenten in één week dingen gingen oplossen waar business-intelligenceunits jarenlang mee bezig zijn. Maar het is toch verbazingwekkend hoeveel wiskunde 'in de praktijk' de studenten in één week tijd uitgevonden hebben. Verdere ideeën die in het gesprek met de studenten naar voren kwamen, maar die niet getest werden, waren het koppelen van de voorspellingsmodellen aan economische waarden, het beter filteren van

vakantiedagen (in het binnen- en buitenland) en dergelijke meer. Sommige van deze extra's eisen uiteraard een interdisciplinaire aanpak.

2.2 Verdeling personeel

Een grote Vlaamse infrastructuurbeheerder is van plan om zijn personeel beter op verschillende stations te verdelen; dit met het oog op het minimaliseren van totale reistijden. Uiteraard moet hierbij met verschillende neveneffecten rekening gehouden worden: eisen van de stations betreffende het minimale/maximale aantal van personeelsleden, eisen betreffende de opleiding van zekere personeelsleden en dergelijke meer. Ook hier hebben de studenten snel besloten om het probleem te versimpelen en zo 'oplosbaarder' te maken, zo zijn ze bijvoorbeeld overgegaan van de echte reistijd te minimaliseren naar het aantal kilometers in vogelvlucht te minimaliseren. Ook de eisen betreffende de opleiding van personeelsleden hebben zij versoepeld, zonder ze volledig overboord te gooien.

Figuur 1. Een gewone sudoku kan met behulp van backtracking opgelost worden. Nadat ze enkele technische moeilijkheden opgelost hadden, zijn de studenten begonnen met een backtrackingmethode [5] te implementeren. Backtracking werd in een ander college (Computerpractica voor wiskunde) al besproken, het concept is echter relatief gemakkelijk te begrijpen en te implementeren, en relatief machtig. Gecombineerd met meer kennis van het probleem is het ook niet enkel een brute-forcemethode. Voor deze publicatie leggen wij het uit aan de hand van een bekend raadsel, nl. de sudoku. Er zijn tal van mogelijkheden om de sudoku op te lossen, voor gemakkelijke versies uit de krant is het meestal voldoende om voor elke cel te kijken welke waarden er ingevuld mogen worden. Soms is het wel zo dat dit niet tot de volledige oplossing leidt, en moeten er waarden gegokt worden. De gok kan goed zijn – dan leidt het tot de oplossing van de sudoku – of kan slecht zijn, en dan leidt het tot een raadsel dat niet meer oplosbaar is, omdat bv. in een cel geen enkel cijfer ingevuld mag worden. In het laatste geval gaat men terug (``backtracking'') en gokt men een ander cijfer. Uiteraard kunnen verschillende 'gokken' ook met elkaar gecombineerd worden, dat ligt aan de basis van het backtrackingalgoritme.

Uiteraard kan de methode ook hier gebruikt worden. In plaats van cijfers te gokken worden personeelsbezettingen voorgesteld en dan via backtracking geleidelijk beter gemaakt. Het idee hierbij is dat, in theorie, elke werknemer bij de tien dichtsbijzijnde stations kan terechtkomen. Als eerste gok krijgt iedereen het dichtsbijzijnde station toegewezen - dit leidt uiteraard tot een overbezetting van vele stations, en een onderbezetting van vele andere. Via backtracking worden dan mensen die 'te veel' bij stations zijn op andere stations geplaatst, totdat er een goede oplossing naar voren komt. Het algoritme was moeilijk om te implementeren, en ook de looptijd was vrij lang, maar uiteindelijk leidde dit tot een vermindering van de (theoretisch geschatte) dagelijkse reistijd tot grofweg de helft. De industriële partner gaf aan dat hij dit soort oplossing nog niet bedacht had en hij deze in de toekomst verder wou bekijken, wat voor de studenten uiteraard extra lof was.

3. CONCLUSIE Geen enkele groep heeft haar taak perfect opgelost, maar dit is ook niet de bedoeling geweest. Ze zijn wel in aanraking gekomen met echte problemen vanuit de bedrijfswereld, en ze hebben ook allemaal oplossingsmethoden gevonden. Het was de moeite waard om ze uit te dagen, de oplossingen hebben aangetoond dat zij in staat zijn om reeds verworven kennis van wiskunde te kunnen gebruiken op een zeer creatieve manier. De week is geëindigd met een slotpresentatie, de studenten hebben dus ook moeten vertellen over wat ze gedaan hebben, in een taal die begrijpelijk is voor niet-wiskundigen. Figuur 2. Studenten die hun resultaten presenteren tijdens de

Het is evident dat, hoe meer kennis van wiskunde men heeft, des te betere methoden men kan bedenken om problemen op te lossen. De week toont echter ook aan dat al relatief weinig kennis van wiskunde voldoende is om, althans simpele, oplossingsstrategieën voor dit singen wordt het concept daarom volgend jaar in een eerste testrit ook aangeboden voor bovengemiddelde leerlingen uit het middelbaar/secundair onderwijs. We twijfelen er geen seconde aan dat dit mogelijk is!

Met al dit hopen wij om wiskunde in de maatschappij weer meer in de kijker te zetten, of, om weer een citaat van het Platform Wiskunde Vlaanderen [7] te gebruiken, de leerlingen en studenten als ambassadeurs voor de wiskunde op te leiden, die dan de volgende doelstelling realiseren:

soort problemen te ontwikkelen. Met kleine aanpasslotpresentatie

Het uitdragen en benadrukken van het belang van de wiskunde voor de maatschappij in het algemeen, en voor innovatie in het bijzonder.

REFERENTIE 1 K. Bliss, K. Fowler, B. Galuzzo, Math Modeling, SIAM, 2014 2 A. Bultheel, Inleiding tot de numerieke wiskunde, Uitgeverij Acco, 2006 3 Computational and Mathematical Modeling Program (CAMMP), https://www.cammp.online 4 ECMI Modelling weeks, https://ecmiindmath.org/education/ modelling-weeks/ 5 V. Fack, Algoritmen en datastructuren, Uitgeverij Acco, 2014 6 Modeling Week, TU Eindhoven, https://www.win.tue.nl/~pop/ Modeling/index.html 7 Platform Wiskunde Vlaanderen, Missieverklaring, http://www.platformwiskunde.be/missieverklaring/

OEFENING 2

VLAAMSE WISKUNDE OLYMPIADE VZW, EERSTE RONDE JWO 2020, VRAAG 3

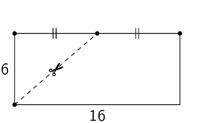
Van een rechthoek met zijden 6 en 16 snijden we een stuk af zoals in de figuur. De twee stukken die zo ontstaan, worden herschikt tot een driehoek. Hoe lang is de kortste zijde van die driehoek?

A

8

B

10

C

12

D

14

E

16