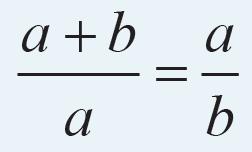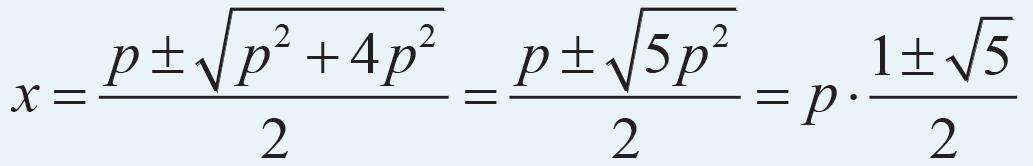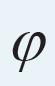VECTOR

MEI 2023 - nummer 17

TIJDSCHRIFT voor wiskundeonderwijs
BORROMEAANS, GLOBAAL, LOKAAL 3
HET KOEKJESPROBLEEM 16
BOMEN EN DOOLHOVEN 30
Met medewerking van Uitwiskeling, VVWL (Vlaamse Vereniging van Wiskundeleraars), GeoGebra Instituut, Vlaamse Wiskunde Olympiade, Ars et Mathesis en Pythagoras
VECTOR
3 BORROMEAANS: GLOBAAL, LOKAAL
HET DRIEDEURENPROBLEEM 2.0 11
16 HET KOEKJESPROBLEEM
TIENHOEK IN BURGOS 18
26 EBOLA: CONCRETE DATA
GEBRUIKEN IN DE KLAS
BOMEN EN DOOLHOVEN 30
37 GEORG CANTOR: BEDWINGER
VAN HET ONEINDIGE
VECTOR
6e jaargang - nummer 17
REDACTIE Nicolas Ruys, Tom Harteel, Anke Oderij, Ellemijn Van Puymbroeck, Karel Sierens - die Keure, Kleine Pathoekeweg 3, 8000 Brugge, educatief@diekeure.be
EXTERNE AUTEURS die occasioneel of op geregelde basis een bijdrage willen leveren, kunnen contact opnemen met educatief@diekeure.be.
VECTOR Vector is gratis voor alle leerkrachten wiskunde in België.
VERANTWOORDELIJKE UITGEVER die Keure, Kleine Pathoekeweg 3, 8000 Brugge
VORMGEVING EN DRUK Isabelle Tilleman - die Keure, Brugge REACTIES Al je reacties, suggesties en opmerkingen zijn welkom op educatief@diekeure.be
2
INHOUD
BORROMEAANS: GLOBAAL, LOKAAL
HIER ZIE JE TWEE
KOLOMMEN DIE ZIJN ONTWORPEN DOOR DE NEDERLANDSE BEEL-
DEND KUNSTENAAR
RINUS ROELOFS. DE LINKER KOLOM IS IN HET VOORJAAR VAN
2020 GEPLAATST IN HET CREMATORIUM USSELO IN ENSCHEDE EN
MAAKT DEEL UIT VAN
EEN BEELDENGROEP. DE RECHTER KOLOM STAAT
SINDS 2022 BIJ DE AFDELING WISKUNDE
VAN DE KU LEUVEN IN KORTRIJK. ZO OP HET
EERSTE GEZICHT LIJKEN
BEIDE ONTWERPEN


HETZELFDE, BEHALVE
DAN DAT DIE IN KORTRIJK HOGER IS, MAAR DIE STAAT DAN OOK IN DE BUITENRUIMTE. AAN BEIDE ONTWERPEN LIGT WELISWAAR DEZELFDE
BAKERMAT TEN GRONDSLAG, MAAR ZE VERSCHILLEN ALS BROER EN ZUS
WEL DEGELIJK VAN ELKAAR. BEIDE ZIJN IN METAAL UITGEVOERD DOOR
STROBOS METAAL UIT HENGELO.
KLAAS LAKEMAN, ARS ET MATHESIS
ARS ET MATHESIS
3
BORROMEAANSE RINGEN


Borromeaanse ringen zijn drie met elkaar verstrengelde ringen en wel zo dat als je om het even welke van de drie ringen zou doorknippen en wegnemen de twee overgebleven ringen volledig vrij komen te liggen. Het motief kwam in de 15e eeuw voor in de drie ringen uit het familiewapen van de Noord-Italiaanse familie Borromeo (figuur 1). Vandaar de naam voor deze verstrengeling.
NIET MET PLATTE RINGEN
Wat op een tekening als figuur 2A eenvoudig lijkt, is in de werkelijkheid niet altijd te realiseren. In 1987 bewezen Michael Friedman en Richard Skora dat met drie gewone platte stijve cirkelvormige ringen geen Borromeaanse combinatie is te maken. Platte cirkelvormige ringen moeten altijd worden vervormd en aangepast om tot een Borromeaanse constellatie te komen. Zoals bijvoorbeeld in het logo van de IMU, International Mathematical Union (figuur 2C). Daaruit is gemakkelijk af te leiden dat met drie rechthoeken zoals in figuur 2B of drie platte ellipsen wel een ruimtelijke Borromeaanse verstrengeling is te maken. Dat is bijvoorbeeld simpel te controleren met drie (grote) paperclips (figuur 3A).

VAN NETWERK NAAR LAGEN
Vanuit het basismotief van de drie gekoppelde ringen zijn verschillende Borromeaanse structuren te ontwikkelen. Neem bijvoorbeeld de ellipsvormige ringen uit figuur 4A. Die kunnen worden uitgebreid door aan elk uiteinde op precies dezelfde manier twee andere langwerpige ringen
op Borromeaanse wijze te koppelen (figuur 4B). En op de uiteinden daarvan ook weer. Je krijgt dan wat je een Borromeaans netwerk zou kunnen noemen. Evenzo is figuur 3B ook uit te breiden tot een Borromeaans netwerk van paperclips.
 Figuur 1
Figuur 2
Figuur 3
Figuur 1
Figuur 2
Figuur 3
4
Figuur 4
Vanuit zo’n netwerk is het een kleine stap naar zo te noemen Borromeaanse lagen. Die krijg je door in figuur 4B alle langwerpige ringen van dezelfde kleur met elkaar te verbinden. Dat levert een golvend patroon op van drie met elkaar verweven lagen zoals in figuur 4C en iets dichter gevlochten en afgesneden in figuur 5. Elke laag met een eigen kleur, maar alle drie wel met dezelfde vorm.
Door om het even welke laag in figuur 5 overal door te knippen en te verwijderen, blijven de overgebleven lagen als twee los van elkaar en op elkaar liggende tapijtjes over die nergens met elkaar zijn verbonden (figuur 6). Dit zijn dus inderdaad Borromeaanse lagen.
Je kunt het ook omdraaien. Uitgaande van twee op elkaar liggende gelijkvormige gatenmatjes zoals in figuur 6 moet er (al is het
maar in gedachten) een derde gatenmat in stukjes doorheen worden gevlochten en aan elkaar worden vastgemaakt om zo’n Borromeaanse drielagenmat te krijgen als in figuur 5.
BAKERMAT


Om tot het ontwerp van de in het begin getoonde kolommen te komen dient de Borromeaanse drielagenmat van figuur 5 als uitgangspunt. Die mat is als het ware op te vatten als de bakermat van beide verwante kolommen. Ga er in

gedachten even van uit dat de Borromeaanse lagen van figuur 5 zich inderdaad kunnen gedragen als een soepel drielaags tapijt. Dan is die op te rollen tot een cilinder- of kokervormige structuur (figuur 7). De gekleurde uiteinden aan de randen die naar elkaar worden gerold, sluiten keurig op elkaar aan. Ga maar na.
Het resultaat is een Borromeaanse kolom of koker (figuur 8). Het is echter niet een enkele kolom, maar het zijn drie met elkaar verstrengelde kolommen. Als om het even van
Figuur 5
Figuur 7
5
Figuur 6
welke kolom de verbindingen worden doorgeknipt zodat de betreffende kolom er aan stukjes tussen uit kan worden gehaald, dan zijn de overblijvende twee kolommen niet met elkaar verweven. De ene kolom zit als het ware om de andere heen. Net als bij de voorbeelden van Borromeaanse ringen hebben alle drie de kolommen afzonderlijk precies dezelfde vorm. Figuur 8 vormt het basisontwerp van de kolom(men) in het Enschedese crematorium.


ANDERE RICHTING
Zoals aangegeven in figuur 9 kan de afgesneden drielagenmat uit figuur 5 ook in een andere richting worden opgerold. De gekleurde uiteinden aan de randen die dan naar elkaar worden gerold, sluiten niet meer kleur aan kleur op elkaar aan (figuur 10A). Het levert een volledige versmelting van de drie lagen tot één enkele laag. Dat kan worden versterkt door vanuit de samengesmolten randen verder te gaan met één kleur. Dat maakt dat het hele object uiteindelijk overal
dezelfde kleur krijgt (figuur 10B). Figuur 10B vormt het basisontwerp van de kolom in Kortrijk. Omdat bij deze koker toch nog een schijnbare Borromeaanse structuur bestaat, is het een mooie tegenhanger van de koker uit figuur 8.


DE BEELDENGROEP
De beeldengroep in crematorium Usselo is op te vatten als een drieluik. Dat drieluik wordt gevormd door de drie verstrengelde kolommen binnen en twee elkaar omhullende kolom-
Figuur 8
Figuur 9
6
Figuur 10
men en een afzonderlijke ‘losgemaakte’ kolom buiten (figuur 11A, B en C). De drie verstrengelde kolommen in figuur 11A, de twee elkaar omhullende kolommen in figuur 11B en de afzonderlijke kolom uit figuur 11C hebben alle zes precies dezelfde vorm.

Ondanks plaatsing van een deel van de groep binnen en twee delen van de groep buiten kan er niet aan worden getwijfeld dat die delen bij elkaar horen, zoals de foto van de opstelling toont (figuur 12). Binnen is het nog met elkaar verstrengeld zijn, maar buiten is het los laten – laten gaan. Dat is ook de titel die aan deze beeldengroep is toebedacht.
OPBOUW
Het is natuurlijk niet zo dat voor de kolommen in het crematorium eerst
 Figuur 12 De opstelling buiten het crematorium.
Figuur 12 De opstelling buiten het crematorium.
7
Figuur 11
een soort metalen frame is gemaakt dat daarna tot een koker of kolom is omgebogen zoals uit figuur 13 zou kunnen worden opgemaakt.



Eerst zijn door Strobos Metaal alle losse delen met behulp van een laser uitgesneden (figuur 14). Een aantal daarvan is vervolgens aan elkaar gelast tot ‘niet platte ringen’ (figuur 15) waarmee de kolommen zijn opgebouwd. Zoals in figuur 11C is te zien bestaat elke kolom uit zes van die ‘ringen’, twee aan voor- en achterzijde en een aan beide zijkanten. Voor elk van de drie delen van het drieluik wordt begonnen met één zo’n kolom. Daarna worden twee van die enkele kolommen omhuld met een tweede kolom. In figuur 11B is dat de groengekleurde kolom. Dat kan nog door de vooraf gemaakte
ringen uit figuur 15 op een handige manier om de eerste kolom heen samen te stellen.
Dan komt het moeilijkste werk want bij een tweetal van die twee elkaar omhullende kolommen moet met de losse onderdelen uit figuur 14 de derde kolom worden opgebouwd. Dat moet zo gebeuren dat steeds drie ringen van drie verschillende kolommen op dezelfde manier worden verstrengeld zodat ze Borromeaanse ringen vormen. Het resultaat daarvan staat binnen in het crematorium (figuur 16).
Na las- en slijpwerk zijn de kolommen gestraald en met een kleur afgewerkt.
Figuur 13
Figuur 14
8
Figuur 15
LOKAAL BORROMEAANS
De opbouw van de kolom in Kortrijk (figuur 17) is te vergelijken met de kolommen in het Enschedese crematorium. De losse metalen onderdelen met een laser uitsnijden, enzovoort. Zoals eerder gemeld, vertoont deze kolom een schijnbare Borromeaanse structuur. Eigenlijk kan je beter spreken van plaatselijk of lokaal Borromeaans. Als je er namelijk
een stuk uit zou halen, bijvoorbeeld het op de voorzijde van de omslag ingezoomde stuk, dan heeft dat stuk weer de Borromeaanse verweving (figuur 18).

FOTO’S EN ILLUSTRATIES: figuur 2B: Klaas Lakeman, figuur 3: Emiel Kaper, alle andere foto’s en illustraties: Rinus Roelofs
 Figuur 16 In het crematorium.
Figuur 16 In het crematorium.
9
Figuur 17 De kolom in Kortrijk.
Hasse betaalt bij de bakker met haar bankkaart. Bij het intoetsen van haar viercijferige code kan de bakker zien dat ze het eerste cijfer kiest uit de eerste kolom van het toetsenbord, het tweede cijfer uit de tweede kolom en de laatste twee cijfers uit de laatste kolom. Wat is het aantal codes dat daaraan voldoet als het toetsenbord eruitziet zoals in de figuur?
OEFENING 1
Jos doet boodschappen. Hij ziet dat de appels vandaag afgeprijsd zijn: 25% korting per kilo, en daarbovenop krijgt hij bij aankoop van 2 kg appels nog 1 kg gratis. Hoeveel procent betaalt Jos vandaag minder dan vóór de afprijzing als hij drie kilo appels mee naar huis neemt?
25% 40% 50% 75%
A 12


B 54
C 72
D 81
E 108
Figuur 18 Borromeaans lokaal
OEFENING
© Junior Wiskunde Olympiade vzwTweede Ronde JWO 2022-23, vraag 2
2
© Junior Wiskunde
Tweede Ronde JWO 2022-23, vraag 3 A B C D E
10
Olympiade vzw
10%
HET DRIEDEURENPROBLEEM 2.0
HET DRIEDEURENPROBLEEM IS, ZO VERMOED IK, BIJ DE MEESTE
MENSEN WEL BEKEND, EN IK ZAL DIE KLASSIEKER HIER NIET
HERHALEN. ALS JE HET NIET KENT, KUN JE HET LEZEN IN HET ARTIKEL
“NEE HEB JE, JA KUN JE NOG KRIJGEN” IN PYTHAGORAS 57-5/6. IN
DEZE BIJDRAGE GA IK IN OP EEN VERRASSENDE VARIANT VAN DIT PROBLEEM. EERST MAAR EENS DE PRECIEZE SITUATIE SCHETSEN.
RONALD MEESTER
Aafje en Boaz hebben een quiz gewonnen, en ze krijgen nu de kans om een auto te winnen. De quizmaster laat Aafje en Boaz drie gesloten deuren zien, genummerd 1, 2 en 3. De quizmaster vertelt Aafje en Boaz dat achter één van de deuren een auto staat, achter een andere deur de sleutels van de auto, en achter weer een andere deur een geit. De regels van het spel zijn nu als volgt. Allereerst gaat Boaz weg, en mag Aafje twee deuren openmaken, zonder dat Boaz het ziet. Aafje mag twee deuren tegelijk openmaken, maar ze mag het ook één voor één doen, en daarbij de keuze van de tweede deur laten afhangen van wat er achter de eerste deur stond. De deuren worden weer gesloten, Aafje verlaat het toneel, en Boaz wordt opgehaald. Boaz mag nu ook twee deuren openmaken, net als Aafje, en volgens dezelfde regels. In het geval dat Aafje de deur met de auto heeft opengemaakt, en Boaz de deur met de sleutels, hebben ze de auto (met sleutels) gewonnen. Andersom is dus niet goed: als Boaz de auto en Aafje de sleutels heeft geopend gaan ze met lege handen naar huis.
Aafje en Boaz mogen elkaar natuurlijk niet vertellen over wat ze achter welke deur hebben gezien, maar
de quizmaster geeft hen wel de gelegenheid om van tevoren gezamenlijk een strategie af te spreken. Welke strategie kunnen ze het beste hanteren om de kans op auto plus sleutels zo groot mogelijk te maken?
Laten we allereerst eens kijken wat er gebeurt als ze helemaal geen strategie afspreken, en de deuren dus lukraak openen.
We beginnen met Aafje. Wat Aafje ook doet, de kans dat zij de auto treft is 2/3, ook als ze de uitkomst van de eerste geopende deur zou gebruiken voor de keuze van de tweede deur. Immers, met kans 1/3 kiest ze in één keer goed, maar mocht ze verkeerd kiezen dan geeft de prijs achter de eerst gekozen deur natuurlijk geen enkele informatie over welke van de twee overgebleven deuren de auto bevat. De kans om het daarna bij de keuze van de tweede deur dan goed te doen is 1/2, en zo komen we uit op kans 1/3 + 2/3 × 1/2 = 2/3. Evenzo is de kans op een specieke combinatie, bijvoorbeeld sleutel en geit, voor Aafje gelijk aan 1/3. Er zijn immers drie combinaties die allemaal dezelfde kans moeten hebben.
PYTHAGORAS 11
Dit geldt allemaal ook voor Boaz: in het bijzonder is de kans dat Boaz de sleutels kiest ook gelijk aan 2/3, en dat maakt de kans dat ze bij lukraak deuren openen met de prijs naar huis gaan gelijk aan 2/3 × 2/3 = 4/9. De vraag is dus of ze het beter kunnen doen dan deze 4/9, en zo ja hoeveel beter.
Het feit dat Aafje de auto vindt met kans 2/3 betekent automatisch dat de kans om met de prijs naar huis te gaan nooit groter kan worden dan 2/3. Deze 2/3 kans is dus een bovengrens: beter kan het zeker niet. Het aardige is nu dat er een strategie bestaat waarbij de kans om te winnen precies gelijk is aan 2/3! Dat had je misschien niet verwacht, en ik ga nu uitleggen hoe dit werkt.
We gaan het probleem eerst iets anders beschrijven. Aafje en Boaz kiezen allebei twee deuren en er zijn dan drie mogelijkheden voor wat ze hebben gevonden, als we tenminste even niet op de volgorde letten. Die mogelijkheden zijn {A, S}, {A,G} en {S,G}, waarbij A staat voor “auto”, S voor “sleutels”en G voor “geit”. We kunnen alle opties dan opschrijven in een drie-bij-drie tabel, waarbij de eerste kolom de keuze van Aafje weergeeft, en de eerste rij de keuze van Boaz:
We zien inderdaad bevestigd dat bij lukraak kiezen vier van de negen opties tot winst leiden, met een totale kans van 4/9; dat wisten we natuurlijk al. We willen nu echter een strategie vinden die aan de hokjes met een een in totaal zo groot mogelijke kans toekent.
Een dergelijke kanstabel heet een gezamenlijke kansverdeling van de keuzes van Aafje en Boaz. De getallen in deze kansverdeling hangen af van de strategie die Aafje en Boaz kiezen. Als ze bijvoorbeeld afspreken dat Aafje altijd de deuren met nummers 1 en 2 opent, en Boaz die met nummers 1 en 3, dan ziet de gezamenlijke kansverdeling er als volgt uit, zoals je zelf na kunt gaan:
We hebben een lachebekje gezet bij die combinaties waarbij Aafje en Boaz met de auto naar huis gaan, check maar even dat dit inderdaad klopt.
Als Aafje en Boaz lukraak kiezen, dan heeft elke combinatie dezelfde kans 1/9, en krijgen we de volgende kanstabel:
De kans om nu te winnen is 3/6 = 1/2, dus deze strategie is iets verstandiger dan lukraak gokken, waarbij de kans op winst immers 4/9 was. Ik merk wel op dat wanneer je de kansen per rij of per kolom optelt, het antwoord altijd 1/3 moet zijn, welke strategie je ook gebruikt. Immers, de eerste rij, bijvoorbeeld, geeft alle uitkomsten waarbij Aafje de auto en de sleutels kiest, en die kans moet altijd 1/3 zijn zoals we al hadden gezien, en hetzelfde geldt voor de andere rijen en alle kolommen.
Als Aafje en Boaz afspreken dat ze allebei gewoon deuren 1 en 2 openen, dan krijgen we deze tabel, met een winstkans van slechts 1/3:
Ik ga nu een strategie beschrijven die de volgende kanstabel zal opleveren, en waarbij de kans om te winnen dus gelijk is aan 2/3! Hoe kan dat?
{A,S} {A,G} {S,G} {A,S} {A,G} {S,G}
{A,S} {A,G} {S,G} {A,S} 1/9 1/9 1/9 {A,G} 1/9 1/9 1/9 {S,G} 1/9 1/9 1/9
{A,S} {A,G} {S,G} {A,S} 0 1/6 1/6 {A,G} 1/6 0 1/6 {S,G} 1/6 1/6 0
{A,S} {A,G} {S,G} {A,S} 1/3 0 0 {A,G} 0 1/3
{S,G} 0 0 1/3
0
12
Hier komt ie: Aafje en Boaz spreken af dat Aafje begint met het openen van deur 1. Als daar de auto of de sleutels liggen, dan opent zij deur 2; zo niet dan opent zij deur 3. Boaz maakt als eerste deur 2 open. Als daar de auto of de sleutels liggen, dan opent hij vervolgens deur 1; zo niet dan opent hij deur 3.
Waarom leidt die strategie tot de gezamenlijke kansverdeling hierboven? Het makkelijkste is waarschijnlijk om gewoon de mogelijkheden even na te gaan:
deur 1 deur 2 deur 3
Welnu, laten we dat eens proberen te onderzoeken. Natuurlijk is er een andere kanstabel te vinden waarbij de kans op succes 2/3 blijft, bijvoorbeeld deze:
We zien inderdaad dat deze strategie de gegeven gezamenlijke kansverdeling oplevert, de lachebekjes in de tabel corresponderen met de lachebekjes van dezelfde kleur in de laatste kanstabel. Hiermee hebben we dus een optimale strategie gegeven voor Aafje en Boaz. Met deze buitengewoon slimme strategie is het dus zo dat als Aafje de auto kiest, Boaz altijd de sleutels vindt. Klinkt bizar, maar het kan dus echt.
Dat betekent niet dat er geen vragen meer overblijven. Bestaat er bijvoorbeeld nog een ándere optimale strategie? Ik bedoel met een andere strategie echt een ander idee, en niet bijvoorbeeld een strategie waarbij de rollen van de deuren verwisseld worden maar waarbij verder alles hetzelfde gaat.
Maar de vraag is of er wel een strategie te bedenken is die deze tabel oplevert. Een bewijs dat er geen écht andere strategie bestaat is misschien helemaal nog niet zo makkelijk te geven, maar misschien word je door het volgende argument al wel overtuigd.
We zagen al dat de kans dat Aafje de deur met de auto opent gelijk is aan 2/3. Dat betekent dat we daarna helemaal niets meer mogen verliezen, en dat Boaz in die gevallen altijd de sleutel moet openen. Immers, we willen een kans van 2/3 op uiteindelijk succes, en de 1/3 die we mogen kwijtraken zijn we al kwijt aan een mogelijk verkeerde keuze van Aafje: de kans dat ze de auto niet opent.
Als Aafje de auto en de sleutels heeft geopend, dan moeten we dus veiligstellen dat Boaz zeker de sleutels opent. Aangezien Aafje en Boaz van tevoren natuurlijk niet weten welke keuze van Aafje in dat geval de auto en welke de sleutels gaf, kan dit alleen maar goed gaan als Boaz in dat geval dezelfde deuren als Aafje opent. Met andere woorden, dit moet van tevoren worden afgesproken: áls Aafje de auto en de sleutels opent, dan kan dat alleen maar bij deur 1 en 2 zijn (of natuurlijk een andere keuze maar dat is niet echt een wezenlijk andere strategie). Dus kan het niet anders gaan dan bij deze strategie het geval is.
Misschien ben je hierdoor niet overtuigd, en wil je het verder gaan uitzoeken. Het is dan misschien allereerst interessant om te onderzoeken welke kanstabellen überhaupt te verkrijgen zijn door een van tevoren afgesproken strategie. Of misschien vind je wel een andere manier om naar dit probleem te kijken, want soms levert een ander gezichtspunt zomaar een vruchtbaardere manier van kijken op.
{A,S} {A,G} {S,G} {A,S} 1/3 0 0 {A,G} 0 0 1/3 {S,G} 0 1/3 0
keuze Aafje keuze Boaz auto sleutels geit {A,S} {A,S} auto geit sleutels {A,G} {S,G} sleutels auto geit {A,S} {A,S} sleutels geit auto {S,G} {A,G} geit auto sleutels {S,G} {S,S} geit sleutels auto {A,G} {S,G}
{A,S} {A,G} {S,G} {A,S} 1/6 0 1/6 {A,G} 1/6 0 1/6 {S,G} 0 1/3 0
13
OEFENING 3
Bij een kaartspel worden symboolkaarten en puntenkaarten gebruikt. Florian heeft de volgende symboolkaarten in zijn hand:
In de figuur zien we zes regelmatige zeshoeken die elk oppervlakte 12 hebben. Wat is de oppervlakte van de blauwe ster?

Puntenkaarten leveren punten op voor het afgeven van symboolkaarten. De puntenkaart hiernaast bijvoorbeeld levert Florian 7 punten op: 2 punten voor elke braambes die hij afgeeft en 3 punten voor elke combinatie appel & citroen die hij afgeeft.





Welke van de volgende puntenkaarten levert Florian het meeste punten op?
A 18



B C 21 D
E 24

© Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2022-2023, vraag 1
OEFENING
4
A
B C D E © Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2022-2023, vraag 2 14
OEFENING 5
Anika schrijft de getallen 1 tot en met 8 in de cirkels van onderstaand diagram, zodat geen twee rechtstreeks verbonden cirkels opeenvolgende getallen bevatten. Hoeveel bedraagt de som van de twee getallen in de gekleurde cirkels?

OEFENING 6
De Meidoornstraat, de Lindenlaan, de Eikendreef en de Sparrenweg zijn straten met een dubbele bocht zoals in de figuur. Als voetganger wandel je enkel op de voetpaden (weergegeven door de dikke blauwe randen) of steek je een zebrapad recht over. In welke van die straten loopt de kortste weg van A naar B over minstens één zebrapad?
A In geen van die straten
B In de Meidoornstraat
C In de Meidoornstraat en de Lindenlaan
D In de Meidoornstraat, de Lindenlaan en de Eikendreef
E In de Meidoornstraat, de Lindenlaan, de Eikendreef en de Sparrenweg

© Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2022-2023,
vraag 10
© Vlaamse Wiskunde Olympiade vzwTweede Ronde VWO 2022-2023,
A 3 B 5 C 7 D 9 E 11
vraag 16
15
UITWISKELING
Het koekjesprobleem
Regi Op de Beeck, redactie Uitwiskeling
HET KOEKJESPROBLEEM
Herhalingscombinaties vormen een lastig telprobleem. Hoe tel je het aantal herhalingscombinaties? In dit artikel beschrijf ik hoe ik dit aan mijn 6u-leerlingen van het zesde jaar uitleg met behulp van koekjes.
HERHALINGSCOMBINATIES VORMEN EEN LASTIG TELPROBLEEM.
HOE TEL JE HET AANTAL COMBINATIES? IN DIT ARTIKEL BESCHRIJF IK
Het koekjesprobleem
HOE IK DIT AAN MIJN 6U-LEERLINGEN VAN HET ZESDE JAAR UITLEG
MET BEHULP VAN KOEKJES.
REGI OP DE BEECK, REDACTIE UITWISKELING
Regi Op de Beeck, redactie Uitwiskeling
Herhalingscombinaties vormen een lastig telprobleem. Hoe tel je het aantal herhalingscombinaties? In dit artikel beschrijf ik hoe ik dit aan mijn 6u-leerlingen van het zesde jaar uitleg met behulp van koekjes.
koekjesprobleem
Beeck, redactie Uitwiskeling
de volgorde niet belangrijk is (keuze 2, 7, 10, 25, 28, 39 = keuze 2, 10, 28, 7, 25, 39). Op dat moment kunnen we starten met een systematische bespreking van (herhalings)variaties, permutaties en combinaties, waarbij ik regelmatig verwijs naar de inleidende typevoorbeelden uit het groepswerk. Zo is het lottoprobleem een typisch voorbeeld voor een combinatie: een keuze waarbij de volgorde niet belangrijk en herhaling niet toegelaten is. We noteren het aantal keuzemogelijkheden als

Ik start de lessenreeks over telproblemen bij mijn 6u-leerlingen meestal met een klein groepswerk, waarbij ze enkele typische telproblemen voorgeschoteld krijgen: aantal mogelijkheden voor de pincodes van een gsm, aantal mogelijke autonummerplaten bestaande uit drie letters en drie cijfers, aantal anagrammen van ‘les’ en van ‘wiskunde’, aantal verschillende lottoformulieren waarbij zes getallen tussen 1 en 42 moeten gekozen worden... Aan de hand van deze voorbeelden kunnen we ontdekken dat de aanpak varieert, omdat de problemen verschillend zijn. Bij sommige problemen mag je meermaals een zelfde getal of letter kiezen (pincodes en nummerplaten), bij andere is herhaling niet toegelaten (bij de voorgestelde anagrammen en bij de lotto). Anderzijds is bij een pincode de volgorde van de gekozen cijfers belangrijk (pincode 1234 ≠ pincode 1324), terwijl bij de lotto de volgorde niet belangrijk is (keuze 2, 7, 10, 25, 28, 39 = keuze 2, 10, 28, 7, 25, 39). Op dat moment kunnen we starten met een systematische bespreking van (herhalings)variaties, permutaties en combinaties, waarbij ik regelmatig verwijs naar de inleidende typevoorbeelden uit het groepswerk. Zo is het lottoprobleem een typisch voorbeeld voor een combinatie: een keuze waarbij de volgorde niet belangrijk en herhaling niet toegelaten is. We noteren het aantal keuzemogelijkheden als ����!" # , het aantal combinaties van 6 uit 45
Ik start de lessenreeks over telproblemen bij mijn 6u-leerlingen meestal met een klein groepswerk, waarbij ze enkele typische telproblemen voorgeschoteld krijgen: aantal mogelijkheden voor de pincodes van een gsm, aantal mogelijke autonummerplaten bestaande uit drie letters en drie cijfers, aantal anagrammen van ‘les’ en van ‘wiskunde’, aantal verschillende lottoformulieren waarbij zes getallen tussen 1 en 42 moeten gekozen worden... Aan de hand van deze voorbeelden kunnen we ontdekken dat de aanpak varieert, omdat de problemen verschillend zijn. Bij sommige problemen mag je meermaals een zelfde getal of letter kiezen (pincodes en nummerplaten), bij andere is herhaling niet toegelaten (bij de voorgestelde anagrammen en bij de lotto). Anderzijds is bij een pincode de volgorde van de gekozen cijfers belangrijk (pincode 1234 ≠ pincode 1324), terwijl bij de lotto de volgorde niet belangrijk is (keuze 2, 7, 10, 25, 28, 39 = keuze 2, 10, 28, 7, 25, 39). Op dat moment kunnen we starten met een systematische bespreking van (herhalings)variaties, permutaties en combinaties, waarbij ik regelmatig verwijs naar de inleidende typevoorbeelden uit het groepswerk. Zo is het lottoprobleem een typisch voorbeeld voor een combinatie: een keuze waarbij de volgorde niet belangrijk en herhaling niet toegelaten is. We noteren het aantal keuzemogelijkheden als ���� aantal combinaties van 6 uit 45
de handboeken eerder saai vond, bedacht ik hier een lekkere variant: het koekjesprobleem.
Herhalingspermutaties kun je nog mooi aanbrengen via anagrammen van woorden waarbij één of meerdere letters meermaals voorkomen; de inleidende anagrammen uit het groepswerk bevatten bewust woorden met verschillende letters. Omdat herhalingscombinaties echter een lastiger telprobleem vormen en ik de voorbeelden uit de handboeken eerder saai vond, bedacht ik hier een lekkere variant: het koekjesprobleem.
Ik vertel mijn leerlingen dat ik 10 identieke koekjes heb en die wil verdelen over 4 leerlingen. Hoeveel mogelijke verdelingen zijn zo mogelijk?
, het aantal combinaties van 6 uit 45.


Ik vertel mijn leerlingen dat ik 10 identieke koekjes heb en deze wil verdelen over 4 leerlingen. Hoeveel mogelijke verdelingen zijn zo mogelijk?
Herhalingscombinaties vormen een lastig telprobleem. Hoe tel je het aantal herhalingscombinaties? In dit artikel beschrijf ik hoe ik dit aan mijn 6u-leerlingen van het zesde met behulp van koekjes.






Herhalingspermutaties kun je nog mooi aanbrengen via anagrammen van woorden waarbij één of meerdere letters meermaals voorkomen; de inleidende anagrammen uit het groepswerk bevatten bewust woorden met verschillende letters. Omdat herhalingscombinaties echter een lastiger telprobleem vormen en ik de voorbeelden uit de handboeken eerder saai vond, bedacht ik hier een lekkere variant: het koekjesprobleem.
Ik start de lessenreeks over telproblemen bij mijn 6u-leerlingen meestal met een klein groepswerk, waarbij ze enkele typische telproblemen voorgeschoteld krijgen: aantal mogelijkheden voor de pincodes van een gsm, aantal mogelijke autonummerplaten bestaande uit drie letters en drie cijfers, aantal anagrammen van ‘les’ en van ‘wiskunde’, aantal verschillende lottoformulieren waarbij zes getallen tussen 1 en 42 gekozen moeten worden... Aan de hand van deze voorbeelden kunnen we ontdekken dat de aanpak varieert, omdat de problemen verschillend zijn. Bij sommige problemen mag je meermaals eenzelfde getal of letter kiezen (pincodes en nummerplaten), bij andere is herhaling niet toegelaten (bij de voorgestelde anagrammen en bij de lotto). Anderzijds is bij een pincode de volgorde van de gekozen cijfers belangrijk (pincode 1234
Ik vertel mijn leerlingen dat ik 10 identieke koekjes heb en deze wil verdelen over 4 leerlingen. Hoeveel mogelijke verdelingen zijn zo mogelijk?
pincode 1324), terwijl bij de lotto


Herhalingspermutaties kun je nog mooi aanbrengen via anagrammen van woorden waarbij één of meerdere letters meermaals voorkomen; de inleidende anagrammen uit het groepswerk bevatten bewust woorden met verschillende letters. Omdat herhalingscombinaties echter een lastiger telprobleem vormen en ik de voorbeelden uit
Ik start de lessenreeks over telproblemen bij mijn 6u-leerlingen meestal met een klein groepswerk, waarbij ze enkele typische telproblemen voorgeschoteld krijgen: aantal mogelijkheden voor de pincodes van een gsm, aantal mogelijke autonummerplaten bestaande uit drie letters en drie cijfers, aantal anagrammen van ‘les’ en van ‘wiskunde’, aantal verschillende lottoformulieren waarbij zes getallen tussen 1 en 42 moeten gekozen worden... Aan de hand van deze voorbeelden kunnen we ontdekken dat de aanpak varieert, omdat de problemen verschillend zijn. Bij sommige problemen mag je meermaals een zelfde getal of letter kiezen (pincodes en nummerplaten), bij andere is herhaling niet toegelaten (bij de voorgestelde anagrammen en bij de lotto). Anderzijds is bij een pincode de volgorde van de gekozen cijfers belangrijk (pincode 1234 ≠ pincode 1324), terwijl bij de lotto de volgorde niet belangrijk is (keuze 2, 7, 10, 25, 28, 39 = keuze 2, 10, 28, 7, 25, 39). Op dat moment kunnen we starten met een systematische bespreking van (herhalings)variaties, permutaties en combinaties, waarbij ik regelmatig verwijs naar de inleidende typevoorbeelden uit het groepswerk. Zo is het lottoprobleem een typisch voorbeeld voor een combinatie: een keuze waarbij de volgorde niet belangrijk en herhaling niet toegelaten is. We noteren het aantal keuzemogelijkheden als ����!" # , het aantal combinaties van 6 uit 45
Het gaat hier om een telprobleem waarbij de volgorde van het verdelen over de leerlingen niet belangrijk is (omdat de koekjes identiek zijn) en herhaling
Het gaat hier om een telprobleem waarbij de volgorde van het verdelen over de leerlingen niet belangrijk is (omdat de koekjes identiek zijn) en herhaling toegelaten is (in dit geval zelfs nodig: er zijn meer koekjes dan leerlingen, dus zal je bij de verdeling in herhaling moeten vallen).
Dergelijk telprobleem noemen we een herhalingscombinatie en het aantal mogelijkheden noteren we in dit geval als
Het gaat hier om een telprobleem waarbij de volgorde van het verdelen over de leerlingen niet belangrijk is (omdat de koekjes identiek zijn) en herhaling toegelaten is (in dit geval zelfs nodig: er zijn meer koekjes dan leerlingen, dus zal je bij de verdeling in herhaling moeten vallen). Dergelijk telprobleem noemen we een herhalingscombinatie en het aantal mogelijkheden noteren we in dit geval als ����! $% . Ik laat de leerlingen dan allen naar mijn bureau komen en haal effectief 10 identieke koekjes uit mijn boekentas. Omdat mijn bureau een . Ik laat de leerlingen dan allen naar mijn bureau komen en haal effectief 10 identieke koekjes uit mijn boekentas. Omdat mijn bureau een beetje stoffig is, heb ik ook
16
Herhalingspermutaties kun je nog mooi
Uitwiskeling
PYTHAGORAS
TIENHOEK IN BURGOS
IN OUDE KERKEN KAN HEEL WAT WISKUNDE VERSTOPT ZIJN. SOMS
WORDT DIE WISKUNDE ER MET DE HAREN BIJGESLEEPT. THRILLERAUTEURS
ALS DAN BROWN WILLEN JE DOEN GELOVEN DAT ER MYSTIEKE SYMBOLEN
IN VERWERKT ZIJN MET DIEPE BETEKENISSEN DIE GEWONE MENSEN ONTGAAN. DIE OVERDRIJVING ONTNEEMT HET ZICHT OP WAT ER ZICH
WERKELIJK AFSPEELDE IN DE LATE MIDDELEEUWEN. ER IS SPRAKE
VAN EEN FASCINERENDE VOORUITGANG IN AMBACHT, KENNIS EN TECHNIEK. VANAF DE DERTIENDE EEUW GROEIT HET AANTAL MENSEN
DAT EEN UITGEBREIDE KENNIS HEEFT VAN WISKUNDE, EN DAN VOORAL
VAN DE MEETKUNDE VAN EUCLIDES EN DE ANDERE GROOTHEDEN UIT
DE GRIEKS-ROMEINSE TIJD. DE MEESTERS VAN DIE TIJD VERDIENEN
MIJN OPRECHTE BEWONDERING. NA HET TIJDVAK VAN DE ROBUUSTE
ROMAANSE ARCHITECTUUR, WORDT DE GOTISCHE BOUWKUNST
VERFIJNDER EN LEVENDIGER. ARCHITECTEN EN HUN OPDRACHTGEVERS
ZAGEN IEDERE KEER NIEUWE MOGELIJKHEDEN OM GEDURFDE
ONTWERPEN TEN UITVOER TE BRENGEN. OOK HET VAKMANSCHAP VAN
AANNEMERS EN STEENHOUWERS ONTWIKKELDE ZICH VERDER. HET BOEK “ARCHITECT EN AANNEMER, DE OPKOMST VAN DE BOUWMARKT IN DE NEDERLANDEN, 1350-1530” SCHETST DIE ONTWIKKELINGEN NAUWGEZET, ONDERBOUWD MET VELE VOORBEELDEN OP BASIS VAN GEDETAILLEERD BRONNENONDERZOEK. KENMERK VOOR DE ROMAANSE STIJL IS DE DRIEHOEK, DE VIERHOEK EN DE ZESHOEK. PAS IN DE LATERE GOTIEK VERSCHENEN VIJFHOEKEN, ZEVENHOEKEN, TIENHOEKEN OF ZELFS ELFHOEKEN.
HENK HIETBRINK
18
De kathedraal van Burgos in NoordSpanje is een voorbeeld van rijk uitgevoerde gotiek met veel variatie in de vormentaal. In 2021 verscheen in Spanje een boek met de titel "Tesoros Matematicos de la Catedral de Burgos". Het is geschreven door wiskundigen en uitgegeven door de vereniging Miguel de Guzman, een actieve groep van wiskunde docenten. Het boek is zo goed geschreven dat ik zonder enige kennis van de Spaanse taal toch begrijp waar het over gaat. De foto's en illustraties geven een goed beeld en bovendien zien wiskundige formules er in alle talen hetzelfde uit. (Figuur 1)
OPDRACHT -1: Internet staat vol met foto’s en video’s van deze kathedraal. Wanneer je de Nederlandse wikipedia pagina bezoekt, kijk dan ook eens op de Engelstalige of Spaanse pagina. Ook als je geen Spaans kent, is de trailer op de website https://cienciaycatedral. ubuinvestiga.es/ beslist de moeite waard.
In figuur 2 worden de onderdelen van de kathedraal benoemd. In deze bijdrage gaat het om de tienhoek rond de kooromgang en de apsis.
In figuur 3 zijn drie tienhoeken getekend. De eerste is om de apsis, de tweede om de kooromgang en de derde om de uiteinden van de straalkapellen. Binnen de tienhoeken zijn op de diagonalen tienpuntige sterren getekend. Het bijzondere van die tienpuntige ster is dat het één enkele zelfdoorsnijdende figuur is.
Category:Exterior_of_the_Cathedral_of_Burgos#/media/File:Burgos_-_Catedral_199.jpg

By Zarateman - Own work, CC0, https://commons.wikimedia.org/w/ index.php?curid=22952832
De tienhoeken zijn met elkaar verbonden door hun diagonalen. Iedere zijde van een binnenste tienhoek ligt op de diagonaal van de buitenste
tienhoek, om precies te zijn, tussen het eerste en het vierde hoekpunt. Bijzonder is dat je met deze constructie zowel van buiten naar
19
Figuur 1 https://commons.wikimedia.org/wiki/
binnen kunt werken als van binnen naar buiten. Deze constructie gaat ons een meetkundige rij van lengtes van zijden bezorgen. Multatuli, bekend van de literatuurlijst Nederlands, noemt het geometrische progressie.


OPDRACHT 0:

Lees op de website dbnl.org de brief van Multatuli aan Busken Huet, datum 15 augustus 1866 over gokken, kansrekening en de geometrische reeks.




De verhouding tussen de lengte van de zijde van een buitenste tienhoek en een binnenste tienhoek is een speciale verhouding, het is namelijk de gulden snede verhouding. In de volgende opdrachten ontdek je wat de gulden snede precies is, daarna ontdek je waar de gulden snede in een vijfhoek zit en tot slot bewijs je dat de constructie van opeenvolgende tienhoeken inderdaad opeenvolgende lengte van zijden oplevert in de gulden snede verhouding.
De gulden snede kun je zien als het snijden van een lijnstuk in twee delen met een scherp mes.
Een lijnstuk met lengte is verdeeld in de gulden snede verhouding wanneer het zodanig wordt verdeeld in een langste deel met lengte en een kortste deel met lengte dat .
Figuur 2: schematische plattegrond van een kerkgebouw. Bron: vrij naar wikipedia
20
Figuur 3: schematische plattegrond van de apsis en de kooromgang en de straalkapellen
OPDRACHT 1: Stel dat een getal is en dat die de onbekende is, die je meestal noemt. Stel dat . Vul deze waarde van in de vergelijking in en toon aan dat .
Met algebra kun je aantonen dat dit waar is voor iedere waarde van door de vergelijking te herleiden tot




Dit is een kwadratische vergelijking met onbekende met als oplossing zodat

Uiteraard kun je deze uitdrukking ook zien als een kwadratische vergelijking met onbekende met dezelfde oplossing .
Omdat de verhouding tussen twee lengtes een positief getal is, kun je de oplossing met het minteken verwerpen omdat deze een negatief getal oplevert. Tot zover de algebra.









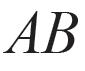













Nu verder met meetkunde. In figuur 5 zie je regelmatige vijfhoek
met middelpunt en zijde en diagonaal . Met het laatste geven we alleen maar aan dat zijde een stukje langer is dan zijde
OPDRACHT 2:
Toon aan dat de grootte van alle hoeken van de driehoeken , , , en veelvouden van 18° zijn.
OPDRACHT 3: Onderzoek welke driehoeken gelijkbenig zijn.
OPDRACHT 4: Onderzoek welke driehoeken een vergroting zijn van elkaar.
OPDRACHT 5:








Toon aan dat de lengte van de zijden van de driehoeken en zich verhouden in de gulden snede verhouding met .
Idem voor de driehoeken , en .
Figuur 5: regelmatige vijfhoek met diagonalen en snijpunten
21
Figuur 4: een lijnstuk is verdeeld in de gulden snede verhouding.
OPDRACHT 6: Toon aan dat de oplossing is van de vergelijking .
OPDRACHT 7:
Teken met Geogebra een vijfhoek. Teken ook de diagonalen. Bepaal de lengte van de verschillende lijnstukken en stel vast dat de verhouding tussen de lengtes ongeveer is



driehoek met tophoek 36° de lengte van de benen zich verhouden tot de basis in de gulden snede verhouding. Evenzo verhoudt zich in een gelijkbenige driehoek met tophoek 108° de lengte van de basis zich tot de lengte van de benen in de gulden snede verhouding. Deze driehoeken noemen we daarom gulden snede driehoeken.
de binnenste tienhoek ligt op de diagonaal van de buitenste tienhoek. Te bewijzen is dat de verhouding tussen de lengte van de zijde van de buitenste tienhoek en die van de binnenste tienhoek de gulden snede verhouding is.
OPDRACHT 8:

Benoem in figuur 6 alle gulden snede driehoeken.
In figuur 7 zie je een opeenvolging van tienhoeken die allen op dezelfde manier geconstrueerd zijn. Geometrische progressie is een oud woord dat vandaag de dag niet meer genoemd wordt in de wiskundeboeken, maar Multatuli gebruikte dit woord nog. Vandaag zeggen we "meetkundige rij".

Een bijzondere meetkundige rij is die met de gulden snede als reden (factor).
OPDRACHT 9:
Bewijs dat de lengte van de zijdes van opeenvolgende tienhoeken een meetkundige rij is met als rede de gulden snede verhouding.
Resultaat tot zover is dat je bewezen hebt dat in een gelijkbenige
Tot zover de inleiding met de vijfhoeken. Terug naar de tienhoek rond de apsis van Burgos. In figuur 6 zijn twee opeenvolgende tienhoeken getekend waarbij Iedere zijde van
Dit voorbeeld van de tienhoek rond de apsis is slechts één voorbeeld van de wiskunde in de kathedraal van Burgos. Andere voorbeelden betreffen vier cirkels in een vierkant, een achthoekig plafond en een gulden snede verhouding in een trapconstructie.
22
Figuur 6: twee regelmatige tienhoeken met diagonalen en snijpunten
LITERATUUR
Multatuli, Volledige werken. Deel 5. Millioenenstudiën. Divagatiën over zeker soort van liberalismus. Nog eens: vrye arbeid in Nederlands-Indië. Duizend-enenige hoofdstukken over specialiteiten. Brief aan den Koning, Delft, Waltman, 1872 (DBNL: https://www.dbnl.org/ tekst/mult001gstu08_01/ mult001gstu08_01_0013.php)
Multatuli, Brieven. Deel 7. Multatuli-Busken Huet 1866, brief van 15 augustus 1866 (DBNL: https://www.dbnl. org/tekst/mult001mdou09_01/ mult001mdou09_01_0027.php)
Merlijn Hurx, Architect en aannemer, de opkomst van de bouwmarkt in de Nederlanden, 1350-1530, Nijmegen, Vantilt, 2012
Constantino de la Fuente Martínez, Tesoros Matematicos de la Catedral de Burgos, Sociedad Castellano Leonesa De Educación Matematica Miguel De Guzmán, Burgos, 2021
Nemo Kennislink: https://www. nemokennislink.nl/publicaties/ het-geheim-van-de-gulden-snede/ La Ciencia que esconde la Catedral de Burgos: https://cienciaycatedral. ubuinvestiga.es/

Asociación Castellana y Leonesa de Educación Matemática"Miguel de Guzmán": https://www.socylem.es/sitio/ Animaties bij deze opdracht: https://www.geogebra.org/m/ y4ck2x6e#material/epexrpbx
 Figuur 7: opeenvolging van regelmatige tienhoeken in geometrische progressie.
Figuur 7: opeenvolging van regelmatige tienhoeken in geometrische progressie.
23
Figuur 8: octagon in de koepel van de “Capilla del Condestable” in de kathedraal van Burgos. Bron: wikipedia Commons
UITWERKING OPDRACHT 1
Het getal invullen in de vergelijking geeft
. Kruislings vermenigvuldigen geeft met als oplossing . Omdat geldt dat
UITWERKING OPDRACHT 4
Onderstaande tabel toont de vergrotingen


Basishoek Driehoek Basis Benen


UITWERKING OPDRACHT 2
Neem middelpunt zodat en .
In gelijkbenige driehoek met is de tophoek en zijn de basishoeken . Omdat is driehoek gelijkbenig met tophoek en de basishoeken zijn
In driehoek is de tophoek en de basishoeken . Zodoende is deze driehoek gelijkbenig met zijde Driehoek is gelijkbenig vanwege de gelijke basishoeken en dus is de tophoek
In driehoek zijn de basishoeken en is de tophoek en dus is ook deze driehoek gelijkbenig. Conclusie is dat in de driehoeken , , , en alle hoeken een veelvoud van 18° zijn.
UITWERKING OPDRACHT 3
Alle genoemde driehoeken zijn gelijkbenig.
Vergrotingen van elkaar zijn dus de driehoeken , en met tophoek 36° en de driehoeken en met tophoek 108°.
UITWERKING OPDRACHT 5
Driehoek is een vergroting van driehoek , dus
. Omdat en omdat , daarom , oftewel , dus





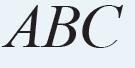
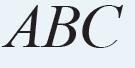

























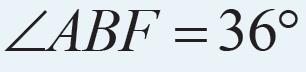




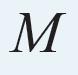
Driehoek is een vergroting van driehoek , dus
. Omdat en omdat , daarom





















.













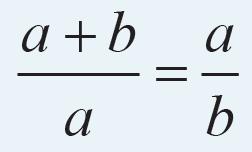
Driehoek is een vergroting van driehoek , dus
. Omdat en omdat , daarom . Na kruislings vermenigvuldigen krijg
je in beide gevallen dezelfde vergelijking
72° 54° 108° 36° 36° 72° 108° 36° 36° 72° 36° 72°
Tophoek
24
UITWERKING OPDRACHT 6
De oplossing van de vergelijking is de oplossing van de kwadratische vergelijking
. Omdat en al in de formule staan, kan toepassen van de abc-formule ondoorzichtig worden. De vergelijking doet al meer vertrouwd aan.





Nu is waardoor
. Terug naar en levert , hetgeen te bewijzen was.
UITWERKING OPDRACHT 7
In GeoGebra kun je met het commando “Regelmatige veelhoek” een vijfhoek tekenen. Alternatief is om met een geodriehoek vanuit het midden vijf lijnen met hoeken van 72° te trekken en dan met een passer de snijpunten te markeren van een cirkel met die vijf lijnen.









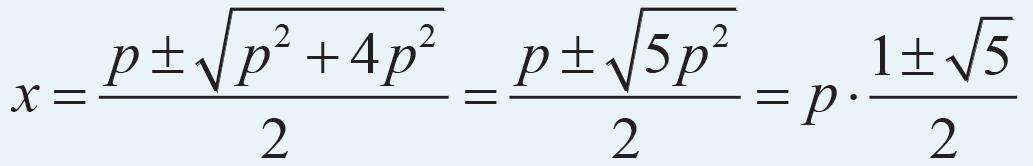


UITWERKING OPDRACHT 8
In de tienhoek is de middelpuntshoek 36°. Driehoeken , en zijn dus gulden snede driehoeken. Verder rekenen met overstaande hoeken, F-hoeken en Z-hoeken levert nog meer gelijkbenige driehoeken op met een tophoek van 36°, bijvoorbeeld de driehoeken en . Gelijkbenige driehoeken met een tophoek van 108° zijn bijvoorbeeld de driehoeken en , maar ook de driehoeken en . Ook dat zijn gulden snede driehoeken.
UITWERKING OPDRACHT 9
Stel en . Omdat driehoek een gulden
snede driehoek is met tophoek 36°, dan is . Driehoek is ook een gulden snede driehoek met tophoek 36°. Omdat , daarom is en dus . De verhouding tussen twee opeenvolgende tienhoeken is nu . Conclusie is dus dat

de lengtes van de zijden van opeenvolgende tienhoeken een meetkundige rij vormen met reden
In 2023 wordt Piet 25 jaar en Hortense 52 jaar. Hoe oud wordt Piet in het jaar dat Hortense 26 wordt?
A 36
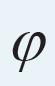
B 43








C 49

D 57


71
In de figuur staan drie cirkels en van twee ervan is de diameter gekend. De oppervlakte van het blauwe gebied is gelijk aan de oppervlakte van het rode gebied. Wat is de diameter van de derde cirkel?

OEFENING
7
E
© Junior Wiskunde Olympiade vzwTweede Ronde JWO 2022-2023, vraag 7
OEFENING
©
25
8 A 16 cm B 18 cm C 20 cm D 22 cm E 24 cm
Junior Wiskunde Olympiade vzwTweede Ronde JWO 2022-2023, vraag 13
EBOLA: CONCRETE DATA
GEBRUIKEN IN DE KLAS
IN 2014 BRAK ER IN WEST-AFRIKA EEN GROTE EBOLA-EPIDEMIE UIT. HET WAS DE ERGSTE EBOLA-EPIDEMIE DIE OOIT BESCHREVEN IS, GEZIEN HET HOGE AANTAL GEVALLEN EN OVERLIJDENS, MAAR OOK DOOR DE GEOGRAFISCHE SPREIDING VAN DE GEVALLEN. VOORAL SIERRA LEONE, LIBERIA EN GUINÉE WERDEN HARD GETROFFEN.
OOK IN DE VS EN IN EUROPA WERDEN VERSCHILLENDE BESMETTE PERSONEN NA MEDISCHE EVACUATIE BEHANDELD. ZOWEL IN DE VS ALS IN SPANJE WERDEN ENKELE GEZONDHEIDSWERKERS
ZIEK NADAT ZE DEZE ZEER BESMETTELIJKE PATIËNTEN HADDEN VERZORGD. DE HOSPITALEN VERBETERDEN NAAR AANLEIDING VAN DEZE BESMETTINGEN HUN VEILIGHEIDSPROCEDURES.
GERD HAUTEKIET, REDACTIE UITWISKELING
Op internet kun je veel informatie vinden: over het virus, het aantal slachtoffers, de veiligheidsmaatregelen, vaccins… Via Wikipedia vind je interessante grafieken die mogelijkheden bieden om in de wiskundeles aan de slag te gaan. Ze kunnen gebruikt worden bij verschillende leerstofonderdelen: aflezen van grafieken, groei, gemiddelde en ogenblikkelijke groeisnelheid, het gebruik van lineaire en logaritmische schalen voor exponentiële functies, de logistische groeicurve…
Je kunt wat we hieronder doen gemakkelijk toepassen op andere epidemieën of contexten.
AFLEZEN VAN GRAFIEKEN, DIFFERENTIEQUOTIËNT, GROEISNELHEID
Ik stelde bij de proefwerken van de kerstperiode in 2014 in het vijfde jaar de onderstaande vragen bij de grafiek in figuur 1. Nogmaals bleek dat het meer dan nodig blijft aan deze wiskundige vaardigheden van leerlingen te werken. Ook bij de eenvoudige en schijnbaar triviale vragen, kreeg ik foutieve antwoorden.
26
UITWISKELING 26
De bovenste lijn op de grafiek van figuur 1 geeft voor de ebola-epidemie van 2014 het totaal aantal gerapporteerde gevallen weer in functie van de tijd, bijgehouden tot 18 november 2014.

1. Hoeveel mensen waren er op 29 augustus 2014 al getroffen door de epidemie?




2. Hoeveel zieken kwamen er bij van 29 augustus tot 28 oktober?
3. Wat is de gemiddelde toename per dag (=gemiddelde groeisnelheid per dag) van het aantal slachtoffers in deze periode?

4. De internationale hulp is na een tijd op gang gekomen. In oktober was die op kruissnelheid. Is de situatie verbeterd? Motiveer je antwoord door de gemiddelde groeisnelheden per dag van september en oktober te vergelijken.
5. Wat is de ogenblikkelijke groeisnelheid van de epidemie op 28 oktober? Leg uit hoe je te werk gaat om dit te bepalen.

We zijn ondertussen een aantal maanden verder en vinden grafieken met informatie tot begin februari 2015.
6. Bekijk aandachtig figuur 2. Wat is de betekenis van de percentages op de verticale as?



7. Vergelijk figuur 2 en figuur 3. Welk land is het ergst getroffen door de epidemie: Sierra Leone of Liberia? Motiveer je antwoord.



8. Bekijk figuur 4. Op 26 oktober 2014 zien we een piek in de grafiek. Wat betekent deze piek?
9. In welk land werden in de laatste twee weken de meeste gevallen gerapporteerd? In welk land werden in februari minder gevallen gerapporteerd dan in de laatste week van januari?
27
Figuur 1
Figuur 2
Figuur 3
LOGISTISCHE GROEICURVE
De grafiek van figuur 3 lijkt de vorm te krijgen van een logistische groeicurve. Dit kun je aangrijpen om leerlingen meer te vertellen over de typische S-kromme, een kromme die ook in de biologieles aan bod komt. Je kunt je beperken tot de algemene vorm, het verzadigingsniveau met de asymptoot en de belangrijke ligging van het buigpunt. Deze ligt op de helft van het verzadigingsniveau. Zie figuur 5. In Uitwiskeling 22/2 werd een volledige loep aan logistische groei gewijd.
Je kunt de leerlingen de betekenis van de verschillende parameters in de formule laten ontdekken met een applet. (Figuur 6). Je kunt ze eventueel een formule laten opstellen om het verloop van het aantal slachtoffers te beschrijven.














Ook kan de link gelegd worden met differentiaalvergelijkingen. Het aantal zieken groeit logistisch met verzadigingsniveau als de groeisnelheid evenredig is met het aantal zieken en het aantal dat er nog bij kan, dit is :

met een evenredigheidsconstante.

Wiskundig sterkere leerlingen kun je laten kennis maken met de vergelijking van dit groeiproces:
LINEAIRE SCHAAL, LOGARITMISCHE SCHAAL
De grafieken van figuur 7 en 8 stellen dezelfde gegevens voor. Bij figuur 7 wordt een lineaire schaal gebruikt op de verticale as, bij figuur 8 wordt een logaritmische schaal gebruikt.

Bij zuiver exponentiële functies is de grafiek een rechte in zo’n assenstelsel. Als je dus kijkt waar de grafiek lineair verloopt, zie je waar de epidemie exponentieel verloopt. Door de helling te bepalen van het lineaire stuk in de grafiek, kun je de groeifactor bepalen van de exponentiële functies.

28
Figuur 4
Figuur 5
Figuur 6
BRONNEN
Deprez, J. en Verbeeck, G. Logistische groei. Uitwiskeling 22(2), 14-48.
Ebola, informatie voor burgers en gezondheidsprofessionals in België http://www.info-ebola.be/nl. Geraadpleegd op 19/02/2015. Elemans, J. (2013). Applet logistische groeicurve. https://www. geogebra.org/m/Zbxueu4r



Hofstede, H. Logistische groei. http://hhofstede.nl/modules/ logistischegroei.htm.

Van Ravestijn, W. (2007). Lesbrief analyse 1-3, Differentiaalvergelijkingen. http://www.wiskundeleraar.nl
Dit artikel verscheen in Uitwiskeling 31/2. Op www.uitwiskeling.be vind je alle info.

29
Figuur 9
Figuur 7: lineaire schaal
Figuur 8: logaritmische schaal
WISKUNDE & ONDERWIJS
BOMEN EN DOOLHOVEN
HET MAKEN VAN DOOLHOVEN IS IETS WAT SOMMIGE LEERLINGEN
AANSPREEKT. DE MEESTEN HEBBEN DIT REEDS UIT ZICHZELF OP
PAPIER GEDAAN. MAAR EEN ECHTE METHODIEK IS MEESTAL AFWEZIG.
WIJ ZULLEN HIER EEN ALGORITMISCHE METHODE UIT DE DOEKEN
DOEN DIE CONCEPTEN GEBRUIKT UIT DE GRAFENTHEORIE EN UIT

HET COMPUTATIONEEL DENKEN. WE ZULLEN IMMERS EEN DOOLHOF GENEREREN AAN DE HAND VAN EEN GERANDOMISEERDE VERSIE VAN
HET ALGORITME VAN PRIM DOOR HET ZOEKEN NAAR EEN OPSPANNENDE BOOM IN EEN GRIDGRAAF. GEEN PANIEK, WE BEGINNEN BIJ HET BEGIN.
DR. DIDIER DESES IS LERAAR WISKUNDE AAN HET KA KOEKELBERG EN VERBONDEN AAN DE VUB WAAR HIJ EEN SEMINARIE MATLAB DOCEERT. HIJ IS OOK LID VAN T 3-VLAANDEREN, DAT ICT BINNEN DE LESSEN WISKUNDE PROMOOT. DAARNAAST GEEFT HIJ NASCHOLINGEN VOOR LEERKRACHTEN EN HEEFT HIJ DE AFGELOPEN JAREN OOK VEELVULDIG GEPUBLICEERD IN WISKUNDE EN ONDERWIJS, WAAR HIJ OOK LID IS VAN DE REDACTIERAAD. E-MAIL: DIDDESEN@GMAIL.COM.
GRAFEN EN GRIDGRAFEN
We starten met het begrip ongerichte graaf waarbij we geen lussen toelaten. Een ongerichte graaf bestaat uit een verzameling van knopen (vertices en een verzameling van bogen (edges) tussen twee verschillende knopen van :
richte graaf genoemd. Een knoop die verbonden is met een andere, noemt men een buur van die knoop. Een pad is een rij na elkaar aansluitende knopen via bogen, waarbij alle knopen verschillend zijn. Een cykel is een gesloten pad. Een graaf heet samenhangend als er tussen elke twee knopen een pad bestaat.
We merken hier op dat de terminologie in de grafentheorie niet standaard is, vandaar dat we de definities geven die wij zullen hanteren. Soms wordt dit type graaf ook een simpele onge-



Een gridgraaf is een voorbeeld van een graaf, die als volgt kan worden voorgesteld: de knopen worden op een raster geplaatst en de bogen verbinden horizontaal of verticaal twee aangrenzende knopen.
Deze gridgraaf is een voorbeeld van een samenhangende graaf, waarbij

30
30
Figuur 1
0, 1, 4, 5, 8 een pad is van de knoop 0 naar de knoop 8. De gridgraaf bezit een aantal cykels waaronder 1, 4, 5, 2, 1. (figuur 1)




BOMEN EN OPSPANNENDE BOMEN
Een boom is een samenhangende graaf zonder cykels. Een bekende stelling over bomen zegt dat er in een boom tussen elke twee verschillende knopen altijd een uniek pad is. De omgekeerde stelling is ook geldig: elke graaf waarbij tussen elke twee verschillende knopen een uniek pad bestaat, is een boom. In een boom noemen we een knoop met slechts één boog een blad
Een opspannende boom van een graaf is een boom die bestaat uit bogen van de graaf en die alle knopen van de graaf bereikt. Elke samenhangende graaf bezit een opspannende boom. Die is echter niet uniek.
Bovenstaand voorbeeld van een gridgraaf is geen boom, het beschreven pad van 0 naar 8 is niet uniek en er bestaan cykels in de gridgraaf. We kunnen wel een opspannende boom vinden. (figuur 2)
Eén manier om een opspannende boom te vinden is het algoritme van Prim. Je vertrekt vanuit een willekeurige knoop en bouwt van daaruit een opspannende boom door telkens willekeurige buren toe te voegen, op zodanige wijze dat er geen cykels ontstaan. (figuur 3)
We werken het algoritme van Prim stapsgewijs uit op onze gridgraaf om zo een opspannende boom te vinden. In elke stap wordt het reeds gevonden deel van de boom getoond, de gekleurde bolletjes zijn de toegankelijke buren, in het rood wordt er telkens willekeurig een buur gekozen om toe te voegen in de volgende stap. (figuur 4)
Merk op dat dit een opspannende boom geeft voor onze gridgraaf, die verschillend is van de opspannende boom die we als eerder voorbeeld hebben gegeven. Dat toont dat opspannende bomen niet uniek zijn. (figuur 5)
DOOLHOVEN
De opspannende boom van een grotere gridgraaf kan gezien worden als een doolhof. Je vertrekt vanuit een blad en zoekt de weg naar een ander
31
Figuur 2
Figuur 3
Figuur 4
Figuur 5
blad door op de bogen te wandelen. Leerlingen kunnen volgende oefening maken.
Bepaal met het algoritme van Prim voor de gridgraaf hieronder een opspannende boom. Kleur hierna een willekeurig blad groen (begin) en een ander rood (einde). Laat een vriend het unieke pad zoeken tussen beide doorheen dat doolhof! (figuur 6)
Wanneer we dit algoritme toepassen op een nog grotere gridgraaf, krijgen we een ingewikkeld doolhof. Tussen elke twee knopen van deze doolhof is er een uniek pad (want het is een boom). Probeer zelf maar de weg te vinden tussen de twee aangeduide punten. Je kan ook de weg zoeken van linksboven naar rechtsonder, of
nog van linksonder naar rechtsboven, of nog … (figuur 7)
HET PROGRAMMA IN PYTHON





Onderstaand doolhof is gemaakt met een eenvoudig Python-programma. Dat maakt gebruik van het setdatatype dat verzamelingen in Python implementeert. Met a={1,2,3} maak je een verzameling aan. De doorsnede tussen twee verzamelingen a en b wordt bepaald door a | b, de unie door a|b en het verschil door a-b. Het programma ziet er als volgt uit:




32
Figuur 6
Figuur 7
• Eerst laden we de modules random en graphics. Deze laatste is een kleine module om op eenvoudige wijze grafieken te maken. Je kan ze downloaden en in dezelfde map zetten als het programma. (J. M. Zelle, graphics.py, https:// mcsp.wartburg.edu/zelle/python/)





• De variabele bepaalt de grootte van een -gridgraaf. De knopen worden genummerd van tot zoals in het voorbeeld uit de eerste paragraaf en worden in de verzameling geplaatst. Daarna wordt een grafisch venster win met relatieve coördinaten linksonder en rechtsboven gemaakt.


































• De gridgraaf wordt voorgesteld door een procedure die de buren van de knoop teruggeeft. Het resultaat bevat aanvankelijk de knopen (linker-, rechter-, onder- en boven-
buur). Door de doorsnede te nemen met sluiten we boven- en onderburen uit van de bovenste resp. onderste rij knopen. Wanneer modulo nul is, en dus in de eerst kolom knopen zit, halen we de linkerbuur weg. Indien in de laatste kolom knopen zit ( modulo ), halen we de rechterbuur weg.
• Hierna volgen twee procedures om het tekenen te vereenvoudigen: plotv voor een knoop en plote voor een boog tussen twee knopen. De coördinaten van knoop zijn waarbij de gehele deling door is en de rest bij deling door . De eerste procedure tekent een cirkeltje met straal 0,3 rond het punt met deze coördinaten en kleurt het zwart. De tweede procedure trekt een lijntje tussen de twee opgegeven knopen.
• Het eigenlijke algoritme begint nu. Er wordt een willekeurig knoop
gekozen en de voorlopige boom bestaat uit deze knoop. De toegankelijke buren van de boom bestaan uit nb(u). Verder tekenen we de gekozen knoop
• We starten nu een while-lus zolang er bereikbare buren van zijn. Telkens kiezen we willekeurig een toegankelijke buur uit en een hechtingspunt uit onze voorlopige boom.
• De boog wordt getekend en wordt met een unie toegevoegd aan . De buren van worden bij de toegankelijke buren gevoegd, maar knopen die reeds in zitten, worden afgetrokken.
• Wanneer de lus afgelopen is en dus alle knopen bereikt zijn, is een opspannende boom. We duiden nu de laatst toegevoegde knoop aan.
We krijgen zo een doolhof met aangeduid begin- (de eerst gekozen
33
knoop) en eindpunt (de laatst toegevoegde knoop). Natuurlijk kunnen elke twee knopen gebruikt worden. Die doolhoven zijn relatief gemakkelijk op te lossen. Om moeilijkere doolhoven te maken kan je het algoritme ietwat aanpassen. Vervang de regel u=choice(list(B)) in de while-lus door
Nu wordt de voorkeur gegeven aan een buur van de laatst toegevoegde knoop. Dat zorgt voor langere gangen in de doolhof. Om het verschil te zien, laat je de computer voor een grote beide methoden gebruiken en kijk je op welke manier de doolhoven groeien.
LEGO

We kunnen dat toepassen om een doolhof van Lego te bouwen. Begin met een grid te maken op een



basisplaat (32×32 of 48×48). Gebruik dan het algoritme om willekeurige verbindingen te maken (groen) en zorg dat je geen lussen hebt (rood mag niet). Versier ten slotte een aantal bladeren van de boom met een boot, huisjes, een toren … Vind dan de weg van het huis met zwart dak naar de toren of van de boot naar de boom. Met een dobbelsteen en een aantal Lego-pionnen maak je er een gezelschapsspel van! (figuur 8)


8
Figuur
34
Kom naar de vakantiecursus voor wiskundeleraren
(VC 2023)
“Priemgetallen”
Zoals elk jaar organiseert Platform Wiskunde Nederland ook in 2023 weer een vakantiecursus voor wiskundeleraren (maar ook voor aankomend wiskundeleraren en andere belangstellenden), om even ‘’bij te tanken’’ en met collega’s uit het hele land gezellig te lunchen en dineren. Dit jaar is de hoofddocent Frits Beukers. Gastdocenten zijn Roland van der Veen en Benne de Weger.


Deze cursus is geheel gewijd aan de wereld van de priemgetallen, waarvan we hier de eerste 50 opschrijven:
vraag of ieder even getal ≥ 4 te schrijven is als de som van twee priemgetallen (Goldbach vermoeden).
Antwerpen 25-26 augustus
Amsterdam 1-2 september
inspiratie geweest voor de titel van het meeslepend geschreven boek ’Music of the Primes’ van Marcus du Sautoy.
....
Door de eeuwen heen heeft deze oneindig doorlopende rij de nieuwsgierigheid gewekt van wiskundigen, zowel professioneel als liefhebber, die geprobeerd hebben om er patronen in te ontdekken. Helaas tevergeefs. Ook andere klassieke vragen zijn tot nu toe onopgelost. Zoals de
Of de vraag of er oneindig veel paren priemgetallen van de vorm n, n + 2 bestaan (priemtweeling vermoeden). Ondanks deze weerbarstigheid van het onderwerp priemgetallen is er de afgelopen tweehonderd jaar toch langzaam maar zeker vooruitgang geboekt in onze kennis. Zeker de afgelopen twee decennia zijn we getuige geweest van ontwikkelingen die we lange tijd niet voor mogelijk hadden gehouden. Zoals het werk van Yitang Zhang uit 2014 dat een heel eind richting priemtweeling vermoeden gaat, of het werk van Terence Tao en Ben Green uit 2004 dat aantoont dat de rij priemgetallen rekenkundige rijen van willekeurige lengte bevat.

Een bijzondere ontwikkeling uit 1859 is de vondst van Bernhard Riemann dat de globale verdeling van de priemgetallen gedicteerd wordt door de nulpunten van een complexe functie, de zogenaamde Riemann zeta-functie. Deze vondst is de
In deze cursus geven we een overzicht van wat de grote vragen op priemgetalgebied zijn en wat de belangrijke resultaten zijn. Veel recente resultaten vereisen geavanceerde technieken waar wij niet op in zullen gaan. Wel besteden we expliciet aandacht aan resultaten die met middelbare schoolmethoden aangepakt kunnen worden. En we kijken naar vragen zoals ’Wat is het grootst bekende priemgetal?’ of ’Hoe test je of een gegeven getal van 1000 cijfers een priemgetal is of niet?’. Tenslotte gaan we in op die geheimzinnige zeta-functie van Riemann die de globale verdeling van de priemgetallen beheerst.
Wij nodigen u van harte uit om deel te nemen aan de VC 2023. Aanmelden is mogelijk via www. platformwiskunde.nl/vakantiecursus, voor additionele vragen kunt u een mail sturen naar vakantiecursus@platformwiskunde.nl


2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229,
35
PUZZEL 1
PUZZEL 2
Verdeel deze figuren volgens de lijntjes in 2 delen die samen een vierkant vormen.
Bron: mathsjam.com 1 2 3 4 5. 6. 7 8. 9. 11. 10. 1 2 3 4 5 6 7 9 8 10 11
Verdeel deze figuren in 2 congruente (dus identieke) delen met behulp van een gebroken lijn.
1. 2. 3. 5. 1 2 4 3 5 6 36
GEORG CANTOR (1845-1918): BEDWINGER VAN HET ONEINDIGE

LIGGEN ER MEER PUNTEN OP EEN LIJN DAN OP EEN VLAK? LANG
GOLD DIT ALS EEN ONZINNIGE VRAAG, TOTDAT CANTOR ONTDEKTE
DAT ER MEER DAN ÉÉN SOORT ONEINDIGHEID IS – ONTELBAAR
VEEL ZELFS. IN HET BEGIN WAREN ER WISKUNDIGEN DIE HEM GEK VERKLAARDEN, WAT HIJ LATER IN ZIJN LEVEN INDERDAAD WERD.
MAAR TEGENWOORDIG GELDT DE VERZAMELINGENLEER DIE HIJ
ONTWIKKELDE ALS HET FUNDAMENT VAN DE WISKUNDE, ‘EEN PARADIJS WAAR NIEMAND ONS UIT KAN VERDRIJVEN’.
Georg Cantor werd in 1845 in Sint-Petersburg geboren. Zijn vader was een welvarend koopman en zijn moeder kwam uit een artistieke familie; Cantor zelf was later een verdienstelijk violist. In 1856 verhuisde de familie, om gezondheidsredenen, naar Frankfurt am Main. Cantor was op school een goede leerling die al snel wist dat hij later Wiskunde wilde gaan studeren, maar zijn vader vond een ingenieursopleiding beter voor zijn zoon.
Na drie jaar in Darmstadt te hebben gestudeerd, kreeg Cantor alsnog toestemming van zijn vader om wiskunde te gaan studeren en in 1862 ging hij daarvoor naar Zürich. In 1863 stierf zijn vader en trok Cantor naar Berlijn waar hij college kreeg van de beste wiskundigen van die tijd: Kummer, Weierstraß en Kronecker. Aan het later werk van Cantor is te zien dat de invloed van Weierstraß op Cantor het grootst geweest is. Het proefschrift waarop Cantor in 1867 promoveerde ging over kwadratische vergelijkingen
K.P. HART - REDACTIELID PYTHAGORAS
37 PYTHAGORAS
en een van de bijgevoegde stellingen luidde: In re mathematica ars proponendi quaestionem pluris facienda est quam solvendi – In de wiskunde is de kunst van het stellen van vragen waardevoller dan die van oplossen ervan. Je zou kunnen zeggen dat Cantor die stelling gedurende zijn werk steeds beter onderbouwd heeft: de vragen die hij zich daarbij stelde leveren nog steeds stof tot nadenken.



















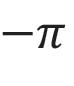












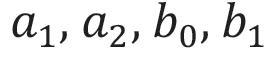
EENDUIDIGHEID
In 1869 werd Cantor in Halle aangesteld; de wiskundige Eduard Heine die daar hoogleraar was daagde Cantor uit de eenduidigheidsstelling voor trigonometrische reeksen (ook wel Fourierreeksen genoemd) te bewijzen.
Om te kijken wat die stelling zegt, bekijken we eerst een eenvoudig geval. Neem vijf getallen en en bekijk de functie gegeven door
Omdat de nulfunctie is, volgt meteen dat . Door ook met de andere functies te vermenigvuldigen, zie je dat de andere getallen nul moeten zijn.
Deze methode werkt ongeacht het aantal functies van de vorm en dat je neemt maar niet automatisch als je dit met al die functies, voor alle , doet. Bij de oneindige sommen die je dan krijgt, moet je heel goed oppassen. Hoe dan ook, Cantor slaagde erin te bewijzen dat de stelling ook voor die oneindige sommen opgaat: als de som voor alle x nul is moeten alle getallen en gelijk aan nul zijn.
Stel dat je weet dat voor alle in het interval ; wat betekent dat voor de gegeven getallen? Het klink nogal flauw: die moeten nul zijn. Dat kun je nagaan door een paar geschikte waarden voor in te vullen en de vergelijkingen die zo ontstaan op te lossen. Vul je achtereenvolgens ontstaan en in, dan krijg je het stelsel
In ons voorbeeld hadden we bij de invulmethode maar vijf (goedgekozen) punten nodig waar de functie nul was en de integratiemethode lukt als in een aantal punten geldt. Cantor begon zich af te vragen hoe dat zat bij de oneindige sommen: voor hoeveel punten mag je de eis laten vallen terwijl je toch kunt bewijzen dat de getallen en gelijk aan 0 zijn? Die vraag leidde hem tot de verzamelingenleer.
PUNTEN OP EEN LIJNSTUK
Het gebeurt niet vaak dat één persoon een heel vakgebied van de grond tilt, maar aan het eind van de 19de eeuw deed Cantor precies dat met de verzamelingenleer. De vraag die hij zich hierboven stelde riep een andere vraag op; één die al vaker gesteld was, maar waar Cantor op een geheel nieuwe manier naar keek. In 1872 had hij kennis gemaakt met Richard Dedekind en in hun briefwisseling kunnen we zien hoe hij met die vraag omging.
Na wat elimineren vind je dat ; vul je dan nog in, dan zie je dat ook .
Het kan ook handiger en dat is wat in die tijd ook al bekend was: integreer van tot . Met wat volharding zul je zien dat er weinig overblijft:

De vraag is: hoeveel punten liggen er op een lijnstuk? Het antwoord ‘oneindig veel’ bevredigde Cantor niet. In een brief aan Dedekind vroeg hij zich af of er niet meer soorten ‘oneindig’ bestaan. Heel concreet: zijn er evenveel natuurlijke als reële getallen? Cantor formuleerde duidelijk wat hij met ‘evenveel’ bedoelde:
Man nehme den Inbegriff aller positiven ganzzahligen Individuen n und bezeichne ihn mit ; ferner denke man sich etwa den Inbegriff aller positiven reellen Zahlgrössen und bezeichne ihn mit ; so ist die Frage einfach die, ob sich dem so zuordenen lasse, dass zu jedem
38
Individuum des einen Inbegriffes ein und nur eines des andern gehört?




Bestaat er een functie die zó is dat er voor elk reëel getal precies één natuurlijk getal bestaat met ? Dat is precies de manier waarop je twee verzamelingen kunt vergelijken: om te zien of er in twee emmers even veel appels en peren zitten neem je telkens uit beide emmers een appel en een peer, tot een emmer leeg is. Dan weet je of er meer appels dan peren waren (of minder of evenveel), en dat zonder echt te tellen.
Cantor bedacht dat je dat vergelijken ook kon doen zonder daadwerkelijk stap voor stap beide verzamelingen leeg te maken. Zo heeft een lijnstuk van lengte 1 evenveel punten als een lijnstuk van lengte 2. Onderstaande figuur laat zien hoe je, in één keer, voor elk punt op de korte lijn een beeldpunt op de lange lijn kunt vinden zodat elk punt op de lange lijn bij precies één punt op de korte hoort.
breuken liggen oneindig veel andere breuken. Cantor liet echter zien dat er wél evenveel natuurlijke getallen als breuken bestaan.
Cantor toonde aan dat je alle paren , met en natuurlijke getallen, in een lijst kunt zetten, zonder dat er een paar wordt overgeslagen. Daarmee is meteen duidelijk dat je de verzameling van positieve breuken in een lijst kunt zetten, want een breuk kun je zien als een paar gehele getallen: een teller en een noemer. Rangschik alle breuken zoals in het onderstaande plaatje.
Op dezelfde manier kun je inzien dat het interval en de hele verzameling evenveel punten hebben: neem de functie maar.
Wat misschien niet zo duidelijk is, is dat en evenveel punten hebben. Op het eerste gezicht zou je misschien denken dat er meer breuken zijn, want tussen elk tweetal
De pijltjes geven aan hoe je heen-en-weer slingerend door alle positieve breuken wandelt, waarbij je telkens van ‘zuidwest’ naar ‘noordoost’ loopt. Zo krijg je de volgende opsomming van alle breuken:
Hiermee hebben we nog geen bijectie tussen en de verzameling positieve breuken, want sommige breuken komen vaker voor; zo zijn 1/1, 2/2, 3/3, ... allemaal gelijk aan 1. Sla de dubbelgangers gewoon over en je krijgt wél een bijectie: bij elk natuurlijk getal (1, 2, 3, 4, 5, ...) hoort precies één positief rationaal getal (1, 2, 1/2, 3, 1/3, ...), en omgekeerd.


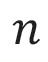






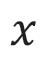
Kun je zelf bedenken hoe je visueel duidelijk kunt maken dat er evenveel rationale getallen (positief én negatief) als natuurlijke getallen zijn?

39
Cantor was niet zo visueel ingesteld; zijn bewijs dat en evenveel elementen hebben, schreef hij als volgt op: Schrijf elk rationaal getal als een vereenvoudigde breuk en maak hieruit het getal . Elk getal hoort bij eindig veel rationale getallen. Het getal hoort bij geen ; het getal hoort alleen bij ; het getal hoort bij en
het getal hoort bij en , enzovoort. We kunnen een functie construeren door de rationale getallen eerst te sorteren door middel van en dan door hun volgorde binnen . Dus




Cantor kwam op het verbluffend eenvoudige idee om naar de oneindige rij cijfers op de diagonaal te kijken (de rode cijfers). Maak een nieuw getal door de diagonaal langs te lopen en elk cijfer te veranderen; zo krijg je bijvoorbeeld het getal dat onderaan de figuur vet staat gedrukt (daar is elk cijfer met 1 vermeerderd; een 9 wordt een 0). Dat getal is verschillend van elk getal in de lijst! Immers, de waarde van de k-de decimaal van het ‘nieuwe’ getal verschilt van de k-de decimaal van het k-de getal in de lijst. Hiermee is bewezen dat er géén bijectie tussen en bestaat. En dan bestaat er natuurlijk ook geen bijectie tussen en , want [0,1] is een deelverzameling van .
Dat bewijs wordt tegenwoordig het diagonaalargument van Cantor genoemd. In deze vorm heeft Cantor het zelf echter nooit opgeschreven. Cantor deed het algemener; hierover kun je lezen in de volgende paragraaf.






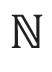




DIAGONAALARGUMENT
























Maar goed, hoe zat het dan met en ? Cantor bewees dat de situatie daar anders ligt: wat voor functie je ook neemt, er zijn altijd punten die bij geen natuurlijk getal horen. Hoe bewijs je zoiets? We laten zien dat er een getal uit is dat verschillend is van alle Onderstaande figuur geeft een beeld van hoe de lijst ... eruit zou kunnen zien. De figuur geeft slechts een voorbeeld; de volgorde van de getallen zou anders kunnen zijn, maar dat doet er niet toe.
HOEVEEL ONEINDIGHEDEN
Cantor had dus twee verschillende oneindigheden ontdekt: die van , die hij aftelbaar noemde, en die van Toen Cantor zijn theorieën hierover publiceerde, stuitte hij aanvankelijk op nogal wat scepsis bij sommige collega’s. Het idee dat je over het oneindige überhaupt iets zinnnigs kon zeggen, was zo vreemd dat velen Cantor eerst niet serieus namen. Toch hield Cantor vol; hij geloofde zelf heilig in de door hem ontwikkelde theorie. De vraag ‘of er qua grootte nog iets tussen en in de door hem ontwikkelde theorie. De vraag ‘of er qua in zit’, zou Cantor voor de rest van zijn leven bezighouden. Zelf dacht hij van niet en hij probeerde heel hard de volgende uitspraak te bewijzen: als een willekeurige oneindige verzameling reële getallen is, dan bestaat er een bijectieve afbeelding
óf een bijectieve afbeelding . Deze uitspraak heet nu de Continuümhypothese. In 1940 toonde Gödel aan dat het tegendeel niet te bewijzen is en in 1963 deed Cohen hetzelfde voor de Continuümhypothese zelf. Dit betekent dat met de uitgangspunten (de axioma’s) van de gangbare wiskunde, de Continuümhypothese niet waar of onwaar is, maar onbeslisbaar. In 1890 bewees Cantor dat er geen grootste oneindigheid is. Het bewijs heeft hetzelfde stramien als het hierboven beschreven diagonaalargument, wat in feite een speciaal geval is van Cantors veel algemenere stelling dat er geen grootste oneindigheid bestaat. Cantors bewijs hiervan gaat als volgt:
40
Neem eens een willekeurige verzameling en bekijk de familie van alle deelverzamelingen van . Die familie is ten minste zo groot als , want laat zien dat een kopie van bevat. Maar is er ook een bijectieve afbeelding ? Het antwoord is: nee. Neem een willekeurige afbeelding ; we maken een in met voor alle . Die is eenvoudig op te schrijven:
Neem nu een willekeurige ; als , dan dus , en als , dan dus weer . Dit idee is zo krachtig dat het op veel gebieden toepasbaar is. Het ligt ten grondslag aan de onvolledigheidsstellingen van Gödel, aan de oplossing van het stop-probleem (er is geen computerprogramma dat van andere programma’s kan controleren of ze zullen stoppen) en nog veel meer.
Het keerde zich bijna nog tegen Cantors eigen verzamelingenleer. Cantor had een ruime opvatting van verzameling; in het kort vond hij dat elke collectie dingen die we in gedachten bijeen kunnen brengen een verzameling is. In 1905 liet Bertrand Russell zien, na bestudering van Cantors algemene diagonaalargument, dat die opvatting te ruim was. Neem maar eens , de verzameling van alle verzamelingen, en vorm daaruit de verzameling , de verzameling van alle verzamelingen die niet zichzelf bevatten. Dan geldt voor zelf dat dan en slechts dan als . Deze redenering staat nu bekend als de paradox van Russell. Je kunt hem ook als raadseltje formuleren: ‘De kapper scheert iedereen die niet zichzelf scheert. Wie scheert de kapper?’
Dat was een onwelkome conclusie, want de verzamelingenleer was ondertussen een belangrijk stuk gereedschap voor wiskundigen geworden. De oplossing was om iets voorzichtiger met het begrip ‘verzameling’ om te gaan. Ernst Zermelo stelde in 1908 axioma’s voor de verzamelingenleer op waarmee de paradox van Russell vermeden kon worden, maar die ‘rijk’ genoeg waren om de resultaten van Cantor en zijn navolgers overeind te houden. De verzamelingenleer zit overal in de wiskunde; als een nieuwe structuur gedefinieerd wordt, dan luiden de eerste woorden meestal: ‘een verzameling met ...’ . David Hilbert onderstreepte het belang van Cantors werk
met de volgende uitspraak: Aus den Paradies, das Cantor uns geschaffen hat, soll uns niemand vertreiben können. (‘Uit het paradijs dat Cantor voor ons geschapen heeft, zal niemand ons kunnen verdrijven.’) In zijn colleges illustreerde Hilbert de verschillende ordes van oneindigheid aan zijn studenten aan de hand van een fictief hotel, waarover enkele jaren geleden een artikel in Pythagoras stond: ‘Hilbert Hotel volgeboekt’, jaargang 46 nr. 4 (februari 2007).
GEKTE






















In de tweede helft van zijn leven leed Cantor aan een depressie, waardoor zijn productiviteit verminderde en hij regelmatig moest worden opgenomen. Hij raakte soms het spoor volledig bijster. Zo gaf hij een verificatie van het Vermoeden van Goldbach (‘elk even getal groter dan 2 is de som van twee priemgetallen’) voor alle gehele getallen onder de 1000, terwijl enkele decennia eerder reeds een verificatie voor de getallen tot 10.000 was gepubliceerd. Hij begon zich bezig te houden met literatuur en probeerde te bewijzen dat Francis Bacon de werkelijke auteur was van de werken van Shakespeare. Hij publiceerde over religie en ontwikkelde zijn concept van het ‘absoluut oneindige’ dat hij gelijkstelde aan God. Aan het eind van de Eerste Wereldoorlog stierf hij in een psychiatrische instelling in Halle, Duitsland. We zullen nooit weten of zijn werk aan ‘het oneindige’ heeft bijgedragen aan zijn psychiatrische ziekte, maar een verband met zijn geniale obsessies valt niet uit te sluiten.
VERDER LEZEN
Het Zebraboekje Blik op oneindig van Leon van den Broek en Arnoud van Rooij biedt een mooie inleiding in het wiskundige werken met ‘oneindig’.
AANVULLING – DE CANTORVERZAMELING








Een van de bekendste deelverzamelingen van het interval is de Cantorverzameling. Haal uit het interval het open interval het middelste derde deel dus, weg. Haal vervolgens het middelste derde deel weg van de twee overgebleven stukken links en rechts. Herhaal deze procedure voor alle stukken die dan nog over zijn, en doe dit oneindig vaak. Wat je overhoudt, heet de Cantorverzameling. Maar wat is het precies?

41
Je denkt misschien eerst dat er niets overblijft, maar je ziet heel makkelijk in dat bijvoorbeeld de punten en in de verzameling zitten, en ook het punt . Sterker nog: de Cantorverzameling bevat evenveel punten als het oorspronkelijke lijnstuk (‘evenveel’ in de zin die Cantor bedoelde)! Anderzijds haal je met iedere stap een derde van de overgebleven lengte weg, dus uiteindelijk hou je een verzameling met lengte 0 over.
Cantor beschreef zijn verzameling niet op een meetkundige manier zoals hierboven. Hij deed het als volgt.
Als ein Beispiel einer perfekten Punktmenge, die in keinem noch so kleinen Intervall überall dicht ist, führe ich den Inbegriff aller reellen Zahlen an, die in der Formel enthalten sind, wo die Koeffizienten cv nach Belieben die beiden Werte 0 und 2 anzunehmen haben und die Reihe sowohl aus einer endlichen, wie aus einer unendlichen Anzahl von Gliedern bestehen kann.


De Cantorverzameling is dus de verzameling van alle getallen die in het drietallig stelsel met alleen nullen en tweeën te beschrijven zijn.
De Cantorverzameling, en variaties er op, komt in de hele wiskunde voor: in de analyse, in de theorie (en praktijk) van dynamische systemen, ... Heel vaak kom je een kopie van Cantors verzameling tegen als een belangrijke bouwsteen.


42
Beste vrienden van de wiskunde,
Op 17 september 2023 nemen we afscheid van de tentoonstelling Imaginary, die de voorbije maanden, na een reis door Nederland en Vlaanderen, de wiskunde gevisualiseerd heeft voor het brede publiek, met bekende maar ook verrassende toepassingen (https://www.imaginarymaths.be/).
We sluiten dit succesvolle initiatief af met het wiskundefestival MathFest, op de laatste locatie van Imaginary: het mooie bezoekerscentrum van de volkssterrenwacht van Brugge in het natuurdomein Beisbroek.
We mikken op mensen die een band hebben met wiskunde, of er ooit in aanraking mee kwamen, of gewoon nieuwsgierig zijn. Jong en oud, leerlingen en ouders,
gezinnen met kinderen, puzzelaars en knutselaars, ...
Dit is een oproep voor activiteiten om die dag vorm te geven: workshops, kampioenschappen, een recordverbreking, speelse experimenten, theater, dans, kunst, presentaties, … die jullie kunnen/ willen aanbieden aan een breed publiek. Stuur deze oproep gerust ook door naar personen, groepen, organisaties waarvan je weet dat ze iets te bieden hebben dat in het kader past.
De voorstellen worden verwacht ten laatste op maandag 5 juni om 23u59.
Volg alle updates en ander festivalnieuws op www.platformvoorwiskunde.be



43
Uitgevers Marie en Katinka over de nieuwe eindtermen
Er is eindelijk een consensus bereikt over de minimumdoelen tussen de verschillende onderwijsverstrekkers voor de basisvorming. Geen dag te vroeg als je het ons vraagt, maar uiteraard zijn we blij dat we eindelijk met concrete doelen aan de slag kunnen. Nieuw voor ons is dat we niet langer spreken over eindtermen, maar voortaan over minimumdoelen. En voor de basisvorming kunnen we alvast het nodige beginnen doen.
Wat betekent dat precies voor die Keure als uitgeverij?
Uiteraard hebben wij al die tijd niet stil gezeten in de verdere ontwikkeling van onze materialen. Ondertussen ligt de volledige tweede graad op de schoolbanken op basis van de vernietigde eindtermen. En op basis van die eindtermen zijn wij verder gegaan met de ontwikkeling en de leerlijnen van de derde graad. We hebben dus al heel wat materiaal voor het vijfde jaar ontwikkeld.
Hoe gaat dat nu precies in z’n werk?
We starten met een grondige studie van de minimumdoelen en ontwerpleerplannen van de onderwijsverstrekkers en bekijken al onze methodes om ze aan te passen waar nodig. Waar we te veel diepgang in de methodes hebben verwerkt, zullen we opnieuw aanpassen zodat ons materiaal dat in september op de schoolbanken ligt wel degelijk voldoet aan de nieuwe minimumdoelen/leerplannen. Omgekeerd, geldt dat uiteraard ook. Als blijkt dat er iets ontbreekt in de derde graad, omdat het is doorgeschoven vanuit de tweede graad, dan vullen we dit aan. Aangezien ook de minimumdoelen van de tweede graad aangepast werden, verandert daar ook het een en ander. Dat betekent dat er hier en daar wel iets te veel aangebracht zal worden in de uitgaven van de tweede graad. Concreet voor


volgend schooljaar kunnen leraren wel aan de slag met onze huidige materialen. De aanpassingen van de tweede graad voeren we aansluitend uit.
Zal het materiaal tijdig klaar zijn?
Wij hebben veel geluk dat wij het volledige uitgeeftraject in handen hebben. Een wit blad met een idee wordt een manuscript bij de auteur.
Eenmaal het binnenkomt bij ons op de uitgeverij maken wij er een consequente methode van die klaar wordt gemaakt om te drukken of om gepubliceerd te worden op ons online leerplatform.

Aangezien wij ook het drukproces helemaal in huis hebben, kunnen wij hier nu snel schakelen en ook de nodige aanpassingen nog uitvoeren voor de zomervakantie. We zetten dus alles op alles om het materiaal tijdig in de scholen te krijgen.

Kleine Pathoekeweg 3, B-8000 Brugge – 050 47 12 62 – so@diekeure.be – www.diekeure.be www.secundair.diekeure.be LEES HET VOLLEDIGE INTERVIEW OP ONZE WEBSITE www.facebook.com/DieKeureEducatief / www.instagram.com/diekeureeducatief / www.pinterest.com/diekeure
Bekijk hier het gewijzigd pakket van Nando naar aanleiding van de nieuwe eindtermen.








 Figuur 1
Figuur 2
Figuur 3
Figuur 1
Figuur 2
Figuur 3








 Figuur 12 De opstelling buiten het crematorium.
Figuur 12 De opstelling buiten het crematorium.




 Figuur 16 In het crematorium.
Figuur 16 In het crematorium.










































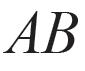




















 Figuur 7: opeenvolging van regelmatige tienhoeken in geometrische progressie.
Figuur 7: opeenvolging van regelmatige tienhoeken in geometrische progressie.