Issuu

MIJN WISKUNDE

PORTFOLIO VAARDIGHEDEN ICT

EERSTE JAAR

Hoe werkt dit portfolioschrift?

ICT kan ingeschakeld worden om berekeningen uit te voeren, maar ook om graﬁsche voorstellingen te maken en eigenschappen te analyseren.

Kennismaken met GeoGebra - GGB

Van pagina 4 tot en met 13 kan je een inleiding tot GeoGebra (GGB) terugvinden. GeoGebra is een online, dynamisch, wiskundig platform. Het omvat o.a. een tekenprogramma (2D en ook 3D), een rekenblad, een rekenmachine (CAS) en veel meer. We zullen met GeoGebra Klassiek leren hoe de basisbegrippen weergegeven en geanalyseerd kunnen worden.

Computationeel denken

Vanaf pagina 14 leer je doelgericht algoritmes begrijpen en maken volgens de principes van computationeel denken. Je maakt kennis met verschillende bouwstenen en legt de link met de geziene leerstofonderdelen uit de lessen wiskunde.

We werken met de programmeertaal Scratch. Die vind je terug via https://scratch.mit.edu.

Bebras Challenge

Als extraatje vind je drie opgaven terug van de Bebraswedstrijd, waarin leerlingen uitgedaagd worden tot computationeel en probleemoplossend denken.

Evalueer jezelf

Op de achterﬂap vind je een overzicht van de verschillende onderwerpen en vaardigheden. Evalueer jezelf. Dit doe je door jezelf minimaal één en maximaal vijf sterren te geven. Ook je leerkracht kan je werk beoordelen. In de laatste kolom komt dan de eindbeoordeling door het correcte duimpje in te kleuren.

Auteurs

Björn Carreyn

Filip Geeurickx

Roger Van Nieuwenhuyze

Portfolio bij het leerwerkboek VBTL 1 Meetkunde

Eerste editie

Verantwoordelijke uitgever die Keure

Niets uit deze uitgave mag verveelvoudigd en / of in het openbaar gemaakt worden door middel van druk, fotokopie, microﬁlm of op welke wijze dan ook zonder voorafgaande schriftelijke toestemming van de uitgever. No part of this book may be reproduced in any form by print, microﬁlm of any other means without written permission from the publisher.

ook verkrijgbaar voor het eerste jaar

1 GGB Basisbegrippen van de meetkunde

Punten tekenen

Opdracht

Icoontje op de werkbalk

Hoe uitvoeren?

Punten tekenen Klik in het tekenvenster.

Opdracht 1:

• Teken deze drie punten in het vlak: A(5, 2), B(5, -1) en C(-1, -1).

Als je weet dat ABCD een rechthoek is, wat zal dan de coördinaat van D zijn?

Wis het scherm. Dat kan op twee manieren:

• Kies voor het laatste icoontje in de werkbalk en kies de optie Verwijderen. Met dit gommetje kan je weggommen.

• Kies rechtsboven de knop met de drie streepjes . Kies Nieuw. Je hoeft niets op te slaan.

Rechten, halfrechten en lijnstukken tekenen

Opdracht

Rechte tekenen

Halfrechte tekenen

Lijnstuk tekenen

Opdracht 2:

Icoontje op de werkbalk

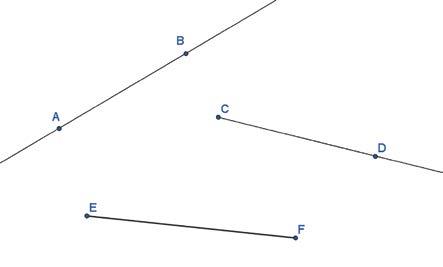
• Teken een rechte AB, een halfrechte [ CD en een lijnstuk [ EF].

Hoe uitvoeren?

Klik tweemaal in het tekenvenster.

Veelhoeken tekenen

Opdracht

Veelhoeken tekenen

Regelmatige veelhoek tekenen

Icoontje op de werkbalk Hoe uitvoeren?

Als je bijvoorbeeld een vierhoek wil tekenen, klik je viermaal in het tekenvenster. Klik ten slotte opnieuw op het eerst getekende punt.

Klik tweemaal in het tekenvenster. Vul in het venster het aantal hoekpunten in (bv. 6 als je een regelmatige zeshoek wil tekenen).

Als je een getekende rechte (of lijnstuk, of punt, of …) een andere kleur wil geven, ga je naar de rechte en klik je op de rechte met de rechtermuisknop. Kies bij Instellingen voor Kleur. Kijk ook bij Stijl en Naam wat je allemaal kan wijzigen.

Opdracht 3:

• Teken een vierhoek ABCD. Kleur de vierhoek geel.

• Teken een regelmatige zeshoek EFGHIJ. Kleur de zeshoek lichtblauw en zet Ondoorschijnend op 100.

Opdracht 4:

• Teken een punt A met coördinaat (3, 5).

• Teken een punt B met coördinaat (3, 3).

• Teken nu een groot plusteken ABCDEFGHIJKL waarvan de afstand tussen twee opeenvolgende punten steeds 2 is.

• Kleur de figuur rood in. Verwijder de figuur niet.

Opdracht 5:

• Werk verder op het plusteken uit opdracht 4.

• Voorzie het plusteken van een 3D-effect door vier parallellogrammen te tekenen en twee rechthoekige trapezia zoals in de figuur hiernaast.

• Maak onnodige labels onzichtbaar. Dat kan je doen door in het algebravenster het gekleurde cirkeltje wit te maken. Of door met de rechtermuisknop te klikken op datgene wat je onzichtbaar wil maken. Vink dan de optie Label tonen uit.

2 GGB Rechten

Middelloodlijn van een lijnstuk

Opdracht

Icoontje op de werkbalk

Hoe uitvoeren?

Teken een lijnstuk. Klik tweemaal in het tekenvenster.

Teken de middelloodlijn van dit lijnstuk. Klik op het lijnstuk.

Opdracht 1:

• Teken een lijnstuk [ AB]. Teken hiervan de middelloodlijn. Kleur deze rechte rood.

• Kies een willekeurig punt P op deze middelloodlijn.

• Teken de lijnstukken die P verbinden met de grenspunten A en B van het lijnstuk.

In het algebravenster zie je de lengten van deze twee lijnstukken. Je kan deze lengte ook zien door bij het icoontje te kiezen voor Afstand of lengte en daarna te klikken op het lijnstuk. Je krijgt de lengte te zien zonder eenheid. GeoGebra gebruikt als eenheid de gebruikte ijk op de assen.

• Verplaats nu je punt P door te klikken op en daarna P te verslepen.

Kijk na elke verschuiving naar de twee lengtes. Wat merk je op?

Afstand van een punt tot een rechte

Opdracht

Teken een rechte AB.

Teken een punt C dat niet op de rechte ligt.

Teken de loodlijn b door het punt C op de rechte AB.

Duid het snijpunt D aan van AB en b.

Icoontje op de werkbalk

Hoe uitvoeren?

Klik tweemaal in het tekenvenster.

Klik in het tekenvenster maar niet op de getekende rechte.

Klik op C en nadien op AB.

Klik op AB en op b.

Teken het lijnstuk [ CD] Verbind C met D.

Opdracht 2:

Voer de opdrachten uit de tabel op de vorige pagina uit. Maak volgende aanpassingen:

• Teken het lijnstuk [ CD] in dik rood. Bepaal de lengte van dit lijnstuk.

Deze lengte is de afstand van het punt C tot de rechte AB.

• Teken door C een andere rechte die AB snijdt. Zoek ook hier het snijpunt E met de rechte AB.

• Teken het lijnstuk [ CE] in dik oranje.

• Bepaal de lengte van het lijnstuk [ CE]

Is de lengte van [ CE] groter dan de lengte van [ CD]?

• Versleep het punt E.

Blijft de lengte van [ CE] steeds groter dan de lengte van [ CD]?

Opdracht 3:

• Teken twee lijnstukken [ AB] en [ CD]

• Teken een punt P dat even ver ligt van A als B, maar ook even ver ligt van C en D.

Hoe heb je dat punt gevonden?

Wanneer kan je dit punt P niet bepalen?

Opdracht 4:

• Teken twee verschillende punten.

• Teken een rechte door deze twee punten.

Hoeveel rechten kan je tekenen?

Bestaat er een mogelijke ligging van deze punten zodat er geen rechte kan getekend worden?

Je illustreerde hier één van de vijf axioma’s van Euclides, waarmee hij de basis legde van de meetkunde. Ga online op zoek naar de vier andere axioma’s.

3 GGB Hoeken

Hoeken tekenen

Opdracht

Teken een hoek.

Teken een hoek met gegeven grootte.

Icoontje op de werkbalk

Hoe uitvoeren?

Klik driemaal in het tekenvenster. Het tweede punt is het hoekpunt.

Klik tweemaal in het tekenvenster.

Het tweede punt is het hoekpunt.

Vul de gevraagde hoekgrootte in het scherm in.

Een hoek bestaat uit twee halfrechten met hetzelfde grenspunt. Maak elke hoek die je tekende af door vanuit het hoekpunt een halfrechte te tekenen door het andere punt. Merk op dat een hoek als naam een Griekse letter krijgt (alfa, bèta …).

Een rechte hoek wordt weergegeven als een vierkantje. Je kan dit symbool als volgt wijzigen:

• Klik met de rechtermuisknop ergens op het tekenvenster en kies voor Tekenvenster.

• Helemaal onderaan zie je Stijl voor rechte hoek. Je kiest er de onderste optie.

Wil je de kleur (of stijl, of dikte, of markering …) van een hoek wijzigen?

• Klik met de rechtermuisknop op het ingekleurde deeltje van de hoek.

• Kies bij Instellingen voor Kleur of Stijl.

Opdracht 1:

• Teken een willekeurige hoek B. Kleur deze hoek lichtoranje.

• Teken ook de twee benen van deze hoek en kleur deze ook oranje.

• Teken een tweede hoek die exact 70° is. Teken ook hier de benen.

Even grote hoeken tekenen

Opdracht Icoontje op de werkbalk Hoe uitvoeren?

Teken een hoek.

Teken een hoek met dezelfde grootte als de hoek die je eerst tekende.

Klik driemaal in het tekenvenster. Het tweede punt is het hoekpunt.

Klik tweemaal in het tekenvenster. In het pop-upvenster klik je vervolgens rechts op het klaviertje.

Zet dat klavier op Griekse symbolen en klik op het juiste symbool.

Opdracht 2:

• Teken een willekeurige hoek B en teken hiervan de bissectrice. Hiervoor kies je het icoon

Je kan de bissectrice op twee manieren tekenen:

• Klik op de hoek door op drie punten te klikken. Let op de volgorde: klik steeds het hoekpunt als tweede punt aan.

• Klik op de ene halfrechte en daarna op de andere halfrechte.

Teken de bissectrice op beide manieren. Wat is het verschil tussen beide methodes?

Opdracht 3:

• Teken een willekeurige stompe hoek alsook de twee benen van deze hoek.

• Verdeel de hoek in vier even grote hoeken.

• Geef elk van deze vier hoeken een andere kleur.

• Laat ook de grootte van deze vier hoeken verschijnen. Dit doe je door elke hoek te tekenen: de grootte verschijnt dan automatisch.

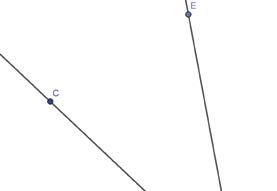
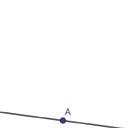
Opdracht 4:

Nevenhoeken zijn twee hoeken die één been gemeenschappelijk hebben en samen 180° vormen.

• Teken twee nevenhoeken.

• Teken bij elke hoek de bissectrice en kleur beide bissectrices rood.

Wat kan je besluiten in verband met de ligging van deze twee bissectrices?

4 GGB Driehoeken

Merkwaardige lijnen in een driehoek

Opdracht

Teken een driehoek.

Teken de hoogtelijnen in de driehoek.

Icoontje op de werkbalk Hoe uitvoeren?

Klik driemaal in het tekenvenster. Klik ten slotte opnieuw op het eerste punt.

Klik op een hoekpunt en op de zijde tegenover het hoekpunt. Doe dit voor elk hoekpunt.

Wat merk je als je de drie hoogtelijnen tekent in een driehoek?

Noem het snijpunt van de hoogtelijnen H. Versleep vervolgens een hoekpunt van de driehoek.

Blijven de hoogtelijnen steeds door één punt gaan?

Opdracht 1:

• Teken de driehoek ABC. Teken de drie middelloodlijnen van deze driehoek. Gebruik Middelloodlijn

• Versleep een hoekpunt van de driehoek. Formuleer de gevonden eigenschap.

Opdracht 2:

• Teken de driehoek DEF. Teken de drie bissectrices van deze driehoek. Gebruik Bissectrice.

• Versleep een hoekpunt van de driehoek. Formuleer de gevonden eigenschap.

Opdracht 3:

• Teken een driehoek GHI. Teken de drie zwaartelijnen van de driehoek. Gebruik Midden of middelpunt om de middens van de zijden aan te klikken. Formuleer de gevonden eigenschap.

Soorten driehoeken

Hoe teken je een gelijkbenige driehoek?

• Teken een Lijnstuk [AB]. Het lijnstuk verschijnt, alsook een kleine letter f die staat voor de lengte.

• Teken een Lijnstuk met gegeven lengte. Klik op A en geef als lengte de letter f in.

• Ga nu met Veelhoek over A, B, C en terug naar A. Je gelijkbenige driehoek is klaar.

Een gelijkzijdige driehoek teken je via Regelmatige veelhoek. Klik op twee punten en vul bij hoekpunten in het pop-upvenster 3 in.

Opdracht 4:

• Teken een rechthoekige driehoek. Kleur deze driehoek geel in.

• Teken een gelijkzijdige driehoek. Kleur deze driehoek rood in.

• Teken een stomphoekige, gelijkbenige driehoek. Kleur deze driehoek groen in.

• Teken een driehoek waarbij een hoek 80° is en een andere hoek 60° is. Gebruik het icoontje Hoek gegeven grootte. Kleur deze driehoek blauw in.

Omtrek en oppervlakte van een driehoek

Opdracht

Teken een willekeurige driehoek.

Bepaal de omtrek van de driehoek.

Bepaal de oppervlakte van de driehoek.

Opdracht 5:

Icoontje op de werkbalk Hoe uitvoeren?

Klik driemaal in het tekenvenster. Klik ten slotte opnieuw op het eerste punt.

Klik binnen de driehoek.

• Teken een gelijkzijdige driehoek en verdeel deze in vier even grote driehoeken.

• Zet elke driehoek in een andere kleur.

Opdracht 6:

• Teken (en kleur) deze gevarendriehoek.

5 GGB Vierhoeken

Een parallellogram tekenen

Opdracht

Teken een lijnstuk [ AB] en een lijnstuk [ BC], niet evenwijdig met [ AB].

Teken door C een evenwijdige rechte met [ AB].

Teken door A een evenwijdige rechte met [ BC].

Bepaal het snijpunt van deze twee rechten.

Teken het parallellogram ABCD.

Maak de twee getekende rechten onzichtbaar.

Opdracht 1:

• Teken een parallellogram ABCD dat geen rechthoek en ook geen ruit is.

Icoontje op de werkbalk

• Teken op elke zijde de middelloodlijn. Bepaal telkens het snijpunt van twee middelloodlijnen.

• Kleur de figuur die deze vier snijpunten bepalen ondoorschijnend geel in.

Welke figuur bepalen de vier middelloodlijnen in je parallellogram?

Een rechthoek tekenen

Opdracht

Teken een lijnstuk [ AB]

Teken een loodlijn in B op [ AB]

Kies een willekeurig punt C op de getekende loodlijn.

Teken door C een evenwijdige rechte met [ AB]

Teken een loodlijn in A op [ AB]

Bepaal het snijpunt D van deze loodlijn met de rechte door C evenwijdig aan [ AB].

Teken de vierhoek ABCD.

Maak de twee getekende rechten onzichtbaar.

Icoontje op de werkbalk

Opdracht 2:

• Teken een rechthoek ABCD. Teken in elke hoek de bissectrice.

• Kleur de figuur die je bekomt ondoorschijnend geel in.

Welke figuur bepalen de vier bissectrices in je parallellogram?

Opdracht 3:

• Teken een willekeurige vierhoek ABCD.

• Bepaal de middens van de zijden. Het midden van [ AB] noem je M, het midden van [ BC] noem je N, het midden van [ CD] noem je P en het midden van [ DA] noem je Q.

Welke figuur is MNPQ?

Wanneer wordt deze figuur een vierkant?

Opdracht 4:

• Teken een ruit. Verbind de opeenvolgende middens.

Welke figuur verkrijg je?

Wat weet je over de oppervlakte van deze nieuwe figuur?

Opdracht 5:

• Teken volgende vierhoeken. Start met de diagonalen die je steeds in blauw weergeeft.

a loodrecht op elkaar staan, elkaar middendoor delen en niet even lang zijn.

b niet loodrecht op elkaar staan, elkaar middendoor delen en niet even lang zijn.

c niet loodrecht op elkaar staan, elkaar middendoor delen en even lang zijn.

6 SCRATCH Commando’s en bewerkingen uitvoeren

In Scratch werken we met verschillende kleuren van blokken.

• De lichtgele blokken zijn gebeurtenissen. Aan een gebeurtenis kun je verschillende commando’s hangen. Als je op het groene vlaggetje klikt, dan worden deze commando’s uitgevoerd.

• De donkeroranje blokken dienen om variabelen te gebruiken. Voor je deze kan gebruiken, moet je ze aanmaken.

• De groene blokken zijn functies. In volgend voorbeeld werd een tekst samengevoegd met een berekende waarde.

a Voer deze code uit in Scratch.

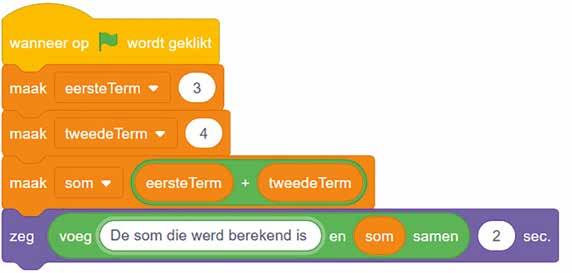
b Pas de code uit vraag a aan zodat het duidelijk wordt welke som er berekend is.

d Schrijf nieuwe code om het product van twee natuurlijke getallen te berekenen.

c Schrijf nieuwe code om het verschil van twee natuurlijke getallen te berekenen.

e Schrijf nieuwe code om het quotiënt van twee natuurlijke getallen te berekenen.

7 SCRATCH Inzicht in getallen

Bekijk aandachtig deze Scratch code:

a Voer de code een aantal keer uit. Wat doet ‘modulo’?

Tip: Wijzig de ‘4’ in de code door 2, door 3, door 5 … en bekijk telkens wat er gebeurt.

b Schrijf zelf code om de klok altijd weer te geven in een 12-delige notatie. Zo wordt 17 uur bijvoorbeeld weergegeven als 5 uur.

Er zijn ook nog andere functies zoals ‘afgerond’, ‘absoluut’ en ‘wortel’.

c Schrijf code voor het volgende probleem:

Een leerling voert zijn behaalde punten in, alsook het maximaal aantal te behalen punten.

Een programma berekent het percentage en rondt af op 1 cijfer.

In deze code wordt er een voorwaardelijke structuur gebruikt. Bekijk aandachtig de code.

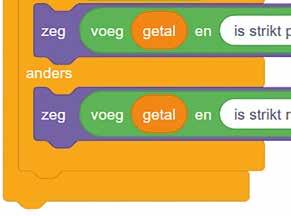
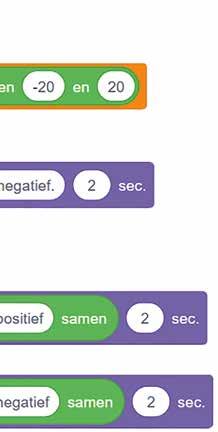
d Leg uit wat deze voorwaardelijke structuur doet.

e Schrijf code die de absolute waarde berekent van negatieve getallen.

Bij positieve getallen krijg je de melding dat de absolute waarde gelijk is aan het getal zelf.

8 SCRATCH Coördinaten

In Scratch kun je objecten laten verschijnen op een exacte positie. Hiervoor gebruik je coördinaten.

a Wijzig de code zodat het object in het derde kwadrant ligt.

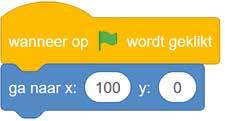
b Wijzig de code zodat het object in het tweede kwadrant ligt en ook zegt dat het in het tweede kwadrant geplaatst is.

Activeer de uitbreiding ‘Pen’.

c Wat doet deze code precies?

d Schrijf code zodat het object in het tweede kwadrant start en horizontaal 5 eenheden verder eindigt op dezelfde hoogte.

e Schrijf code zodat het object start op een punt op de eerste bissectrice van het assenstelsel en eindigt op een ander punt van diezelfde bissectrice waarbij elk coördinaatgetal negatief is.

9 SCRATCH Driehoeken en vierhoeken

Bekijk aandachtig deze code.

b Schrijf code voor het tekenen van een gelijkzijdige driehoek.

a Schrijf nu zelf nieuwe code voor het tekenen van een rechthoek waarvan de lengte drie keer zo lang is als de breedte.

c Schrijf code om deze figuur te tekenen:

10 SCRATCH Patronen en regelmaat

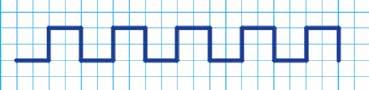
a Wat doet deze code?

b Schrijf code die past bij deze tabel.

11 EXTRA Drie Bebras-opgaven

Bebras is een internationale denkwedstrijd voor jongeren die het computationeel denken bevordert. Bebras is Litouws voor bever. De universiteit van Vilnius (die aan de oorsprong lag van Bebras) koos voor de bever vanwege de ijver en het probleemoplossend vermogen van dit dier. In België ligt de coördinatie van de wedstrijd bij de Universiteit Gent. Via bebras.be vind je meer info.

Ricca’s

Evren probeert te leren hoe een Ricca eruitziet. Evren bestudeert de volgende vijf foto’s van Ricca’s en maakt een aantal aantekeningen die nauwkeurig beschrijven wat ze ziet.

Evren krijgt dan deze zesde foto van een Ricca te zien en realiseert zich dat een van haar notities absoluut niet klopt.

Welke opmerking van Evren over Ricca’s is zeker fout?

A Ricca’s hebben altijd tanden.

B Ricca’s hebben soms vleugels.

C Ricca’s hebben hoorns of drie ogen, maar niet allebei.

D Als Ricca’s precies twee armen hebben, dan hebben ze ook precies twee benen.

Auteur tekst en tekeningen: Sarah Chan (Canada)

Vertaling: Kris Coolsaet (België)

Fotowandeling

Bever Inga gaat elke dag langs dezelfde weg op wandel. Ze neemt een camera mee.

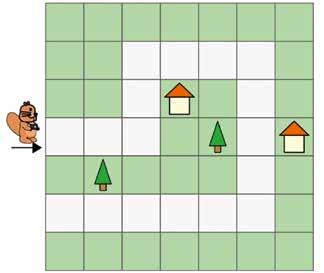
Tijdens de wandeling noteert ze de volgende symbolen om te tonen welke weg ze heeft genomen en waar ze foto’s heeft genomen op die dag.

Elke foto toont het 3 x 3 rooster vóór Inga.

Op zekere dag noteerde Inga het volgende:

Wat zijn de drie foto’s die Inga die dag heeft genomen?

Auteurs tekst: Yukio Idosaka (Japan)

Yoshiaki Matsuzawa (Japan)

Auteur tekeningen: Maiko Shimabuku (Japan)

Vertaling: Kris Coolsaet (België)

Verzegelde brieven

De Republiek Beaveria heeft een kast vol geheime brieven. Van de 16 brieven in deze kast, genummerd van 1 tot 16, waren er 10 geopend, terwijl de andere 6 nog verzegeld waren in hun enveloppen.

Op een avond sloop een vijandelijke spion naar binnen en opende een van de verzegelde brieven. Hij vergat echter de brief weer te verzegelen.

De volgende ochtend stelt de Republiek Beaveria een onderzoek in nadat ze merkt dat er nu 11 geopende brieven zijn, zoals hieronder te zien is:

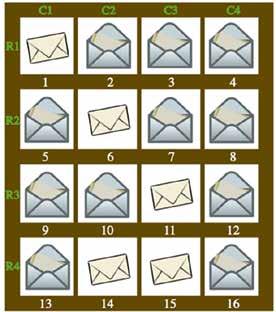
De bewaker van de Republiek herinnert zich niet alle details, maar hij weet zeker dat voordat de vijandelijke spion naar binnen sloop:

• Het aantal geopende brieven in de kolommen C2 en C4 samen even was.

• Het aantal geopende brieven in de kolommen C3 en C4 samen even was.

• Het aantal geopende brieven in de rijen R2 en R4 samen even was.

• Het aantal geopende brieven in de rijen R3 en R4 samen even was.

Welke brief werd er door de vijandelijke spion geopend?

A 5

B 9

C 10

D 13

Auteurs tekst: Mark Edward M. Gonzales (Filipijnen) Luis Fernando Cáceres Duque (Griekenland)

Auteurs tekeningen: Mark Edward M. Gonzales (Filipijnen) Ágnes Németh (Hongarije)

Vertaling: Kris Coolsaet (België)

MIJN WISKUNDE

PORTFOLIO VAARDIGHEDEN ICT

EERSTE JAAR

1GGB Basisbegrippen van de meetkunde

2GGB Rechten

3GGB Hoeken

4GGB Driehoeken

5GGB Vierhoeken

6SCRATCH Commando’s en bewerkingen uitvoeren

7SCRATCH Inzicht in getallen

8SCRATCH Coördinaten

Vaardigheid Mijn evaluatie Oordeel leerkracht Gekend of niet?

– P

9SCRATCH Driehoeken en vierhoeken C – P

10 SCRATCH Patronen en regelmaat C – P

11 Drie BEBRAS-opgaven

Vaardigheden

– P

C = Computationeel denken – P = Probleem oplossende vaardigheid

Die Keure wil het milieu beschermen. Daarom kiezen wij bewust voor papier dat het keurmerk van de Forest Stewardship Council® (FSC®) draagt. Dit product is gemaakt van materiaal afkomstig uit goed beheerde, FSC®-gecertiﬁceerde bossen en andere gecontroleerde bronnen.