LEERBOEK
Analyse 1a i Reële functies deel 1
D-finaliteit gevorderde wiskunde
Philip Bogaert
Filip Geeurickx
Marc Muylaert
Roger Van Nieuwenhuyze
Erik Willockx
CARTOONS
Dave Vanroye
Dit boek bevat zes hoofdstukken.
Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting.
Definities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.
Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt.

1 Algebraïsch rekenen 1.1 De euclidische deling 1.2 Deelbaarheid in 19 2 Veeltermfuncties Inleiding 2.2 Veeltermfuncties 38 Toepassingen 2.4 Bespreken van een aantal kenmerken 2.5 Een functievoorschrift opstellen 53 Vraagstukken 2.7 Differentiequotiënt 57 3 Rationale functies 3.1 Definitie 73 Inleidend voorbeeld 3.3 Homografische functies 75 Rationale functies benaderen door Asymptoten van grafieken van Verloop van een rationale functie Toepassingen Rationale vergelijkingen en ongelijkheden 4 Irrationale functies 4.1 Domein van een irrationale functie 101 Nulwaarden van een irrationale functie irrationale vergelijkingen 101 Irrationale functies bespreken 4.4 Toepassing 109 5 Bewerkingen met functies Rekenen met functies 6 Enkele bijzondere functies 6.2 De G-functie of functie van Legendre (entierfunctie) 6.3 Een zaagtandfunctie: 6.4 De signfunctie (of signumfunctie) 152 Functies met meervoudig voorschrift Oplossingen Trefwoordenregister 167 Analyse 1a i Reële functies deel 1
2Algoritme van Horner We proberen op een andere manier de getalwaarde van een veelterm te bepalen. Voorbeeld – –Om het aantal bewerkingen te beperken, herschrijven we eerst de veelterm – – – –– –door vervangen, krijgen we [( – –– –5 coëfficiënten getalwaarde want A 4 2 – 2 – 21 2 2 Op de bovenste rij noteren we de coëfficiënten, gerangschikt naar dalende machten van Ontbrekende coëfficiënten worden door 0 vervangen. Op de onderste rij komt de som van elke kolom. Deze praktische schikking noemen we het algoritme van Horner – – ––201 –– – ––1428 – 106 –William George Horner (1786–1837) William Horner werd geboren in 1786 in Bristol, Engeland. Daar was hij student aan de Kingswood School. Ongelooflijk maar waar: op 14-jarige leeftijd werd hij aan de school ‘assistant master’ en jaar later zelfs ‘headmaster’. Enkele jaren later verliet Horner Bristol en vestigde hij zich in Bath. Daar stichtte hij een school; hij stierf er op 22 september 1837. lossen (met daarbij horend de methodes bij de studie van veeltermen die zijn naam dragen en waarmee we in dit hoofdstuk kennismaken). Enkele jaren eerder had de Italiaan Ruffini al een vergelijkbare methode beschreven, maar beiden werden ruim 500 jaar voorafgegaan door de Chinees Chu Shih-Chieh 朱世杰 ). Dat de naam van Horner toch bekend gebleven is, is vooral te danken aan De Morgan, die in tal van artikels Horners naam aan die methode bleef geven.
1 Algebraïsch rekenen 1.2 Deelbaarheid in r [x] 1Definitie eenvoudiger te kunnen voorstellen, maken we gebruik van deze symbolen. (lees: “deelt” of “is een deler van”) (lees: “deelt niet” of “is geen deler van”) Voorbeelden 3 want 6 10 25 want 25 10 5 deelbaarheid in als en slechts als de rest van de euclidische deling van A ) 2Reststelling bij deling door x – a Bepaal het quotiënt en de rest bij de euclidische deling van A – – –Na euclidische deling vinden we: Q Bepaal nu de getalwaarde van A – –reststelling Bij de euclidische deling van een veelterm door – (met R is de rest van de deling gelijk aan de getalwaarde van het deeltal voor –Te bewijzen Bij deling van door – is R Bewijs A )= D Q )+ R )=( Q )+ ))= )= )= )=( Q )+ )= Voorbeeld De rest bij deling van door – ) 2 –3 – 8 –3 Praktisch – A –– – –––
VBTL?
Hoe gebruik je
1 2 *
De nummers van de oefeningen hebben een gele kleur.
Een sterretje duidt op een extra uitdaging.
Maak ook kennis met voorbeeldvragen uit ijkingstoetsen en toelatingsexamens.
Achteraan in dit boek vind je de oplossingen
ICT is een ideaal hulpmiddel.
Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets. Die vind je terug via www.polpo.be.



Wat moet je kennen en kunnen?
Op het einde van elk hoofdstuk zie je een handig overzicht van wat je moet kennen en kunnen
WAT MOET JE KENNEN EN KUNNEN moet leren pagina ken het oké voor ❒ ❒ ❒ Ik kan irrationale vergelijkingen algebraïsch oplossen. 101 ❒ ❒ Ik kan de grafiek van een irrationale functie tekenen met ICT. ❒ ❒ het voorschrift al dan niet met functioneel gebruik van ICT. ❒ Ik kan toepassingen en vraagstukken oplossen met behulp van een irrationale functie. Irrationale functies 4
Uit b leiden we de volgende tabel af. ( ( Het aantal konijnen dat er de zesde maand is bijgekomen, bedraagt ) – –We tekenen de rechte met vergelijking 135 op de grafiek. Die rechte snijdt de grafiek van de functie als 21. Na de 21e maand zijn er 135 konijnen.
leiding wil weten hoeveel toestellen er per uur geproduceerd moeten worden om winst te maken in de huidige situatie. Het verband tussen de winst en de productie wordt gegeven door de functie met voorschrift )= 24 72 Voor welke waarden van heeft het voorschrift geen betekenis Schets de grafiek van de winstfunctie Bepaal algebraïsch bij welke productie winst en bij welke productie verlies wordt gemaakt. Controleer je antwoord aan de hand van de grafiek van Bepaal met behulp van ICT bij welke productie de winst groter is dan 108 euro. Teken de grafieken van de functies met onderstaande voorschriften en lees er de volgende kenmerken van af domein, bereik, snijpunten met de assen, nulwaarden, tekenverloop, stijgen/dalen, extrema, symmetrie en gedrag op oneindig. Controleer met ICT. ––) –d ) –)= ) 0,05 0,3 – 1,15 ) –0,02 3 – 10 – 30 63 h ) 64 – 16 1 Stel telkens het gevraagde voorschrift op. Een veeltermfunctie van de derde graad met nulwaarden –3, en 2 en waarvan de grafiek gaat door het punt –– –Een veeltermfunctie van de vierde graad (of lager) waarvan de grafiek gaat door de punten P –3, 28 Q –1, R 0, S 1, en T 3,130 d Een veeltermfunctie van de vierde graad met dubbele nulwaarde 3, waarvan de grafiek gaat door de oorsprong en de punten P 2, 6 en Q 4,28 Maak een schets van de grafiek van de veeltermfuncties die aan volgende voorwaarden voldoen. is van de vierde graad –6 en zijn nulwaarden van –is een relatief maximum voor –is een relatief maximum voor is van de derde graad – g ligt op de grafiek van is van de derde graad ––12 13
Wiskunde in de derde graad wordt een boeiende verkenningstocht langs matrices, statistiek, goniometrie en (zoals je zult merken in dit boek) heel veel functies. De analyse van de reële functies vormt een stevige basis voor de verdere studie van de theoretische en toegepaste wiskunde. In dit boek worden heel wat aspecten van functies belicht zonder gebruik te maken van afgeleiden en integralen. Van bij het begin speelt het grafische element een grote rol.
Je kunt trouwens ontelbaar veel zaken met een functie beschrijven. Neem nu dit reuzenrad. Het is het derde grootste ter wereld en staat in Singapore. Op het hoogste punt (165 m) kun je bij helder weer 45 km ver kijken en heb je een uitzicht op Indonesië en Maleisië. Als je je in een van de 28 capsules bevindt en je drukt de hoogte van de capsule uit in functie van de tijd, dan bekom je een goniometrische functie, een soort functie die je in een van de volgende boeken zult tegenkomen.
De auteurs wensen je veel plezier met dit eerste boek analyse.


Inhoud
Algebraïsch rekenen 1.1 De euclidische deling 9 1.2 Deelbaarheid in r [ x ] 19
Veeltermfuncties 2.1 Inleiding 35 2.2 Veeltermfuncties 38 2.3 Toepassingen 45 2.4 Bespreken van een aantal kenmerken van een veeltermfunctie 49 2.5 Een functievoorschrift opstellen 53 2.6 Vraagstukken 55 2.7 Differentiequotiënt 57 3 Rationale functies 3.1 Definitie 73 3.2 Inleidend voorbeeld 73 3.3 Homografische functies 75 3.4 Rationale functies benaderen door veeltermfuncties 78 3.5 Asymptoten van grafieken van rationale functies 79 3.6 Verloop van een rationale functie 82 3.7 Toepassingen 84 3.8 Rationale vergelijkingen en ongelijkheden 86 4 Irrationale functies 4.1 Domein van een irrationale functie 101 4.2 Nulwaarden van een irrationale functie – irrationale vergelijkingen 101 4.3 Irrationale functies bespreken 103 4.4 Toepassing 109
Bewerkingen
functies 5.1 Functies transformeren 119 5.2 Rekenen met functies 129 5.3 Inverse functies 132 6 Enkele bijzondere functies 6.1 De absolutewaardefunctie 149 6.2 De G-functie of functie van Legendre (entierfunctie) 150 6.3 Een zaagtandfunctie : de mantissefunctie 151 6.4 De signfunctie (of signumfunctie) 152 6.5 Functies met meervoudig voorschrift 153 Oplossingen 158 Trefwoordenregister 167 Analyse
I Reële functies deel
1
2
5
met
1a
1


Algebraïsch rekenen 1
Algebra is een verzamelwoord voor alles wat in de wiskunde betrekking heeft op letterrekenen. We stellen getallen voor door letters en laten daar alle bewerkingen op los. Het woord zelf kent zijn oorsprong 1200 jaar geleden.
De wiskundige Al-Chwarizmi voerde de Arabische cijfers in, corrigeerde het werk van Ptolemaeus, liet een wereldkaart tekenen en schreef het boek Hisab al-jabr wa al-muqabala waarin je de term ‘algebra’ misschien herkent.


Algebraïsch rekenen
8
1.1 De euclidische deling 1 De verzameling r [x] 9 2 Algoritme van Horner 10 3 Gelijke veeltermen 11 4 Bewerkingen met veeltermen 12 5 De euclidische deling 13 6 Algoritme van de euclidische deling 14 7 Uitvoerbaarheid en eenduidigheid bij de euclidische deling 15 8 Samenvatting 15 9 Oefeningen 16 1.2 Deelbaarheid in r [x] 1 Definitie 19 2 Reststelling bij deling door x – a 19 3 Quotiënt bij deling door x – a 20 4 Kenmerk van deelbaarheid door x – a 21 5 Bepalen van de delers van de vorm x – a 21 6 Kenmerk van deelbaarheid door (x – a) ⋅ (x – b) 23 7 De veelterm xn – an 25 8 De veelterm xn + an 26 9 Ontbinden in factoren 27 10 Samenvatting 28 11 Oefeningen 29 Wat moet je kennen en kunnen? 32 1
1.1 De euclidische deling
1De verzameling r [x]
veelterm
Een veelterm is een som van eentermen.
Zozijn 2 x 2 + 3 x 1en6 x 3 4 3 x 2 + 1 2 x √7veeltermenmetéénveranderlijke x enmetreëlecoëfficiënten.
We kunnen een veelterm met één veranderlijke x ook noteren als : n i = 0 a i
Veeltermen in de veranderlijke x noteren we als A( x ), B( x ), C( x )
De verzameling van al die veeltermen noemen we R[ x ]
graad
De graad van een veelterm in x is de hoogst voorkomende exponent van x in die veelterm.
Voorbeelden :
gr ( 2x 3 – 4x + 1) = 3
gr ( 3x – 5) = 1
gr ( 9) = gr ( 9x 0 ) = 0
Opmerking :
De graad van de constante veelterm 0 ( ook de nulveelterm genoemd ) is niet gedefinieerd, want0 = 0x = 0x 2 = 0x 3 = 0x 4 =…
getalwaarde
De getalwaarde van een veelterm A( x ) voor een gegeven getal α is het reële getal dat je bekomt door in de veelterm de veranderlijke x te vervangen door α.
Notatie: A( α)
Voorbeelden :
Als A( x ) = 3x 2 – 4x + 1dan is A( 2) = 3 2 2 – 4 2 + 1 = 5
Als B( x ) = 6x 3 – 2x 2 + x – 5dan is B( 1) = 6 ( –1)3 – 2 ( –1)2 + ( –1) – 5 = –14
nulwaarde
α is een nulwaarde van een veelterm A( x ) ⟺ A( α) = 0
Voorbeelden :
5 is een nulwaarde van A( x ) = x – 5want A( 5) = 5 – 5 = 0
4 en –2 zijn nulwaarden van B( x ) = x 2 – 2x – 8
wantB(4) = 42 – 2 4 – 8 = 16 – 8 – 8 = 0 en B( –2) = ( –2)2 – 2 ⋅ ( –2) – 8 = 4 + 4 – 8 = 0
9 1 Algebraïsch rekenen
i = a n x n + a n 1 x n 1 + a n 2 x n 2 + ... + a 2 x 2 + a 1 x + a 0
x
2Algoritme van Horner
We proberen op een andere manier de getalwaarde van een veelterm te bepalen.
Voorbeeld 1 :
A( x ) = 4x 3 – 2x 2 + x – 5
Bereken A( 2)
Om het aantal bewerkingen te beperken, herschrijven we eerst de veelterm :
4x 3 – 2x 2 + x – 5 = ( 4x 2 – 2x + 1) x – 5 = [( 4x – 2) x + 1] x – 5
Als we nu x door 2 vervangen, krijgen we [( 4 2 – 2) 2 + 1] 2 – 5 = 21. Schematisch kunnen we dit als volgt voorstellen :
4 –21 –5 coëfficiënten +++
waarde van x 2
8 1226
·2 = ·2 = ·2 =
46 1321 getalwaarde want A( 2) = 4 23 – 2 22 + 2 – 5 = 21
Op de bovenste rij noteren we de coëfficiënten, gerangschikt naar dalende machten van x . Ontbrekende coëfficiënten worden door 0 vervangen. Op de onderste rij komt de som van elke kolom.
Deze praktische schikking noemen we het algoritme van Horner of het rekenschema van Horner
Voorbeeld 2 :
Bepaal A( –2) als A( x ) = 6x 4 – 2x 3 + x – 4
6 –201 – 4
–2 –12 28 – 56110
6 –1428 – 55 106
Antwoord : A( –2) = 106
William George Horner (1786–1837)
William Horner werd geboren in 1786 in Bristol, Engeland. Daar was hij student aan de Kingswood School. Ongelooflijk maar waar: op 14-jarige leeftijd werd hij aan de school ‘assistant master’ en 4 jaar later zelfs ‘headmaster’. Enkele jaren later verliet Horner Bristol en vestigde hij zich in Bath. Daar stichtte hij een school; hij stierf er op 22 september 1837.
Horners enige belangrijke bijdrage tot de wiskunde is zijn methode om algebraïsche vergelijkingen op te lossen (met daarbij horend de methodes bij de studie van veeltermen die zijn naam dragen en waarmee we in dit hoofdstuk kennismaken). Enkele jaren eerder had de Italiaan Ruffini al een vergelijkbare methode beschreven, maar beiden werden ruim 500 jaar voorafgegaan door de Chinees Chu Shih-Chieh ( 朱世杰 ). Dat de naam van Horner toch bekend gebleven is, is vooral te danken aan De Morgan, die in tal van artikels Horners naam aan die methode bleef geven.

10
3Gelijke veeltermen
gelijke veeltermen
Gelijke veeltermen zijn veeltermen waarbij de coëfficiënten van hun gelijksoortige termen gelijk zijn.
Voorbeeld :
Bepaaldereëlegetallen a , b , c en d zodat:
ax 3 4 x 2 + bx + 2 = 5 x 3 cx 2 + 2ax d
a = 5
4 = c
b = 2a
2 = d
a = 5
b = 10
c = 4
d = 2
Deze methode noemen we de methode van de onbepaalde coëfficiënten
Hierbij worden de coëfficiënten van de gevraagde termen door letters voorgesteld. Door de definitie van gelijke veeltermen toe te passen, bekomen we een stelsel vergelijkingen met de gevraagde onbekenden.
Algoritme
Een algoritme is een systematische rekenmethode voor het uitvoeren van rekenkundige bewerkingen in een bepaalde volgorde. Naast het algoritme van Horner is onder meer ook het algoritme van Euclides voor de deling bekend (in het basisonderwijs werd dit de staartdeling genoemd).
De benaming algoritme is afgeleid uit de latinisering van de naam Al-Chwarizmi (ﻲﻣزراﻮﺨﻟا), de grondlegger van de algebra. Deze Perzische geleerde uit de negende eeuw was de auteur van het boek ‘Hisab al-jabr wa al-muqabala’ (ﺔﻠﺑﺎﻘﳌا و ﱪﺠﻟا بﺎﺴﺣ), het basiswerk waaruit de algebra ontstond. Nu nog gebruiken we het woord ‘algorist’ om een rekenwonder aan te duiden, iemand die uit het hoofd en met grote snelheid bewerkingen kan uitvoeren waarvoor ieder ander mens een computer zou nodig hebben.
11 1 Algebraïsch rekenen
4Bewerkingen met veeltermen
Als :A( x ) = 3x 3 + 2x 2 – x + 4
B( x ) = 6x 3 – x 2 + 2
C( x ) =–3x 3 – 2x 2 + x – 4
D( x ) = 3x 2
E( x ) = 4x 6 – 2x 4 + 3x 3
Dan is :A( x ) + B( x ) = ( 3x 3 + 2x 2 – x + 4) + ( 6x 3 – x 2 + 2)
= 9x 3 + x 2 – x + 6
A( x ) + C( x ) = ( 3x 3 + 2x 2 – x + 4) + ( –3x 3 – 2x 2 + x – 4)
= 0
A( x ) B( x ) = ( 3x 3 + 2x 2 – x + 4) ( 6x 3 – x 2 + 2)
= 18x 6 – 3x 5 + 6x 3 + 12x 5 – 2x 4 + 4x 2 – 6x 4 + x 3 – 2x + 24x 3 – 4x 2 + 8
= 18x 6 + 9x 5 – 8x 4 + 31x 3 – 2x + 8
A( x ) ⋅ 0 = 0
[ B( x )]2 = ( 6x 3 – x 2 + 2)2
= ( 6x 3 – x 2 + 2) ⋅ ( 6x 3 – x 2 + 2)
= 36x 6 – 6x 5 + 12x 3 – 6x 5 + x 4 – 2x 2 + 12x 3 – 2x 2 + 4
= 36x 6 – 12x 5 + x 4 + 24x 3 – 4x 2 + 4
E ( x )
D ( x ) =

Uit die zes voorbeelden kunnen we de volgende eigenschappen afleiden :
–Als de som van twee veeltermen niet de nulveelterm is, dan is de graad van de som kleiner dan of gelijk aan de hoogste van de graden van de veeltermen.
–Als het product van twee veeltermen niet de nulveelterm is, dan is de graad van het product de som van de graden van de veeltermen.
–Bij het quotiënt van een veelterm door een eenterm ( ≠ 0) is de graad van het quotiënt gelijk aan het verschil van de graad van de veelterm en de graad van de eenterm ( hierbij wordt verondersteld dat de graad van de eenterm kleiner dan of gelijk is aan de laagst voorkomende graad van de verschillende termen in de veelterm)
12
4
6 2 x 4 + 3 x 3 3 x 2 = 4 3 x 4 2 3 x 2 + x
x
5De euclidische deling
In N werd de deling als volgt gedefinieerd :
∀ a ∈ N, ∀ d ∈ N0 : ∃ q , r ∈ N : a = dq + r met0 ⩽ r < d
In de uitdrukking a = dq + r is a het deeltal, d de deler, q het quotiënt en r de rest
Voorbeeld : 1254 = 23 54 + 12
125423
–11554
104
–92 12
Op analoge wijze definiëren we de deling van de veeltermen in R[ x ]
Beschouwen we nu de veeltermen x 2 + 7x + 8 en x + 1.
Omdat x 2 + 7x + 8 = (x + 1) (x + 6) + 2 noemen we x + 6 het quotiënt
deeltaldelerquotiëntrest
en 2 de rest van de euclidische deling van x 2 + 7x + 8 door x + 1.
A( x ) D( x ) Q( x ) R( x ) =⇒
Merk op dat de graad van de rest ( 2) gelijk is aan 0. Dat is kleiner dan de graad van de deler.
euclidische deling
A( x ), D( x ), Q( x ), R( x ) ∈ R[ x ] en D( x ) ≠ 0
A ( x ) = D ( x ) Q ( x ) + R ( x )
gr (R ( x )) < gr (D ( x )) ofR ( x ) = 0
De euclidische deling van A( x ) door D( x ) noteer je als A( x ) = D( x ) Q( x ) + R( x ) metgr ( R( x )) < gr ( D( x )) of R( x ) = 0. Hierbij is Q( x ) het quotiënt en R( x ) de rest.
Opmerkingen :
– De deling van twee veeltermen met quotiënt en rest noemen we een euclidische deling.
–A( x ) noemen we het deeltal, D( x ) noemen we de deler.
– Als R( x ) = 0, dan spreken we van een opgaande deling en dan is A( x ) = D( x ) Q( x )
– Als R( x ) ≠ 0, dan spreken we van een niet-opgaande deling
– Als de graad van het deeltal strikt kleiner is dan de graad van de deler, dan is het quotiënt de nulveelterm en dan is de rest gelijk aan het deeltal.
gr (A ( x )) < gr (D ( x )) =⇒ Q ( x ) = 0enR ( x ) = A ( x )
Verklaring : A( x ) = D( x ) 0 + A( x ) metgr ( A( x )) < gr ( D( x ))
Q ( x )= 0enR ( x )= A ( x )
Voorbeeld : Het quotiënt en de rest van A( x ) = 2x 3en D( x ) = x 2 4x + 2 zijn : Q( x ) = 0en R( x ) = 2x 3
want 2x 3 = ( x 2 4
13 1 Algebraïsch rekenen
+ (
x + 2) 0
2x 3) engr ( 2x 3) < gr ( x 2 4x + 2)
6Algoritme van de euclidische deling
Om het quotiënt en de rest te bepalen bij deling van twee veeltermen, gebruiken we de volgende werkwijze (algoritme) :
Voorbeeld : A( x ) = 2x 4 – 9x 2 – x – 4 D( x ) = –2x 2 + 4x – 3
Rangschik deeltal en deler naar dalende machten van x en vul bij het deeltal de ontbrekende termen aan met coëfficiënt nul.
Deel de term met de hoogste macht van het deeltal door de term met de hoogste macht van de deler. Dit geeft je de eerste term van Q(x ).
Vermenigvuldig de eerste term van Q(x ) met de deler en trek het bekomen product af van het deeltal. Je krijgt nu een partiële rest.
–
x 4 + 0x 3 – 9x 2 – x – 4 –2x 2 + 4x – 3 –x 2
Deel de term met de hoogste macht van de partiële rest door de term met de hoogste macht van de deler.
Vermenigvuldig de bekomen term met de deler en trek dit product van de partiële rest af. Herhaal die werkwijze. De partiële rest waarvan de graad kleiner is dan de graad van de deler is de gevraagde rest.
–
2x 4 + 0x 3 – 9x 2 – x – 4 –2x 2 + 4x – 3
2x 4 – 4x 3 + 3x 2 –x 2
4x 3 – 12x 2 – x – 4
2x 4 + 0x 3 – 9x 2 – x – 4 –2x 2 + 4x – 3
2x 4 – 4x 3 + 3x 2 –x 2 – 2x
4x 3 – 12x 2 – x – 4
4x 3 – 8x 2 + 6x
–
– 4x 2 – 7x – 4
2x 4 + 0x 3 – 9x 2 – x – 4 –2x 2 + 4x – 3
–2x 4 – 4x 3 + 3x 2 –x 2 – 2x + 2 = Q( x )
4x 3 – 12x 2 – x – 4
–
4x 3 – 8x 2 + 6x –
– 4x 2 – 7x – 4
– 4x 2 + 8x – 6 – 15x + 2 = R(x )
Besluit:
14
2
9x 2 – x – 4 = ( – 2x 2 + 4x – 3)( – x 2 – 2x + 2) + ( – 15x + 2) = ( – 2x 2 + 4x – 3)( – x 2 – 2x + 2) – 15x + 2
x 4 –
2
2
x 4 + 0x 3 – 9x 2 – x – 4 –2x 2 + 4x – 3
7Uitvoerbaarheid en eenduidigheid bij de euclidische deling
Bij de euclidische deling zijn het quotiënt en de rest enig.
Gegeven : A( x ), D( x ) ∈ R[ x ], D( x ) ≠ 0
Q( x ) en R( x ) zijn het quotiënt en de rest bij de euclidische deling van A( x ) door D( x ).
Te bewijzen : Q( x ) en R( x ) zijn enig
Bewijs :
1) Q( x ) en R( x ) bestaan
Uit het algoritme van de euclidische deling kunnen we afleiden dat het quotiënt en de rest steeds bestaan.
2) Q( x ) en R( x ) zijn enig
Stel dat er naast Q( x ) en R( x ) nog een quotiënt Q′( x ) en een rest R′( x ) bestaan met
Q( x ) ≠ Q′( x ).
Er geldt dan :
A( x ) = D( x ) Q( x ) + R( x ) met gr ( R( x )) < gr ( D( x )) of R( x ) = 0 (1)
A( x ) = D( x ) Q′( x ) + R′( x ) met gr ( R′( x )) < gr ( D( x )) of R′( x ) = 0 (2)
Er geldt dus: D( x ) Q( x ) + R( x ) = D( x ) Q′( x ) + R′( x ) of ook :R( x ) – R′( x ) = D( x ) · Q′( x ) – D( x ) · Q( x ) of : R( x ) – R′( x ) = D( x ) [ Q′( x ) – Q( x )]
Indien R( x ) en R′( x ) niet beide 0 zijn, leiden we uit (1) en (2) af : gr R ( x ) R ( x ) < gr (D ( x )) =⇒ gr D ( x ) Q ( x ) Q ( x ) < gr (D ( x ))
=⇒ gr (D ( x )) + gr Q ( x ) Q ( x ) < gr (D ( x ))
=⇒ gr Q ( x ) Q ( x ) < 0
Vermits een negatieve graad bij veeltermen niet bestaat, is de veronderstelling Q ( x ) ≠ Q ′( x ) vals. Dus is Q( x ) = Q′( x ). Bijgevolg is ook R( x ) = R′( x )
Taak : toon aan dat de stelling ook geldt indien R( x ) = R′( x ) = 0.
8Samenvatting
• Je weet wat een veelterm is, je kunt de graad in een letter bepalen en kent de betekenis van een nulwaarde van een veelterm.
• Je kent de definitie van de euclidische deling van twee veeltermen.
A( x ), D( x ), Q( x ), R( x ) ∈ R[ x ] en D( x ) ≠ 0
De euclidische deling van A( x ) door D( x ) noteer je als
A( x ) = D( x ) · Q( x ) + R( x ) met gr ( R( x )) < gr ( D( x )) of R( x ) = 0.
Hierbij is Q( x ) het quotiënt en R( x ) de rest.
• Je kunt het quotiënt en de rest bepalen bij de euclidische deling van twee veeltermen. Je weet dat dit quotiënt en de rest enig zijn en je kunt dit ook bewijzen.
• Je kent de definitie van een veelterm en je kunt de graad van een veelterm in een veranderlijke bepalen. Een veelterm is een som van eentermen. De graad van een veelterm in x is de hoogst voorkomende exponent van x in die veelterm.
• Je kunt de getalwaarde van een veelterm bepalen voor een gegeven waarde. De getalwaarde van een veelterm A( x ) voor een gegeven getal α is het reële getal dat je bekomt door in de veelterm de veranderlijke x te vervangen door α
• Je kunt de getalwaarde van een veelterm in één veranderlijke bepalen voor een gegeven getal door het algoritme van Horner toe te passen.
15 1 Algebraïsch rekenen
2 3 4 5
9Oefeningen
Gegeven : A ( x )= x 2 + 2 x 4
B ( x )= 3 x 2 x + 1
C ( x )= 2 x 6
D ( x )= x 3 x 2 + x
Gevraagd : Bepaal het resultaat van onderstaande bewerkingen en bepaal ook de graad van dit resultaat.
a A ( x )+ B ( x )
b A ( x ) C ( x )
c 5A ( x ) 2B ( x )
dA ( x )+ C ( x ) D ( x )
Gegeven : A ( x )= x 3 2 x 2 + x 1
B ( x )= 2 x 4 + 3 x 3 4 x 2 + 2 x 3
C ( x )= x 4 + x 2 4
Gevraagd : Zoek met het rekenschema van Horner :
aA (1)
b A ( 1)
c B ( 1)
d B ( 2)
Vervolledig onderstaand schema van Horner. …50……
–3
2…… –1 –6
eC ( x ) · D ( x )
f3A ( x ) B ( x ) 7 2 C ( x )
gD ( x ) x · A ( x )
h2D ( x ) A ( x ) · C ( x )
eC ( 2)
fC (√2)
gA 1 2
hB 1 2
Bepaal een veelterm A( x ) van de tweede graad waarvoor geldt :
aA (0)= 2;A ( 1)= 3;A (1)= 0
bA (1)= 5;A ( 1)= 1;A ( 2)= 8
Gegeven : gr ( A( x )) = 4 ; gr ( B( x )) = 2 ; gr ( C( x )) = 1
Gevraagd : Bepaal telkens gr ( P( x )) als :
aP( x ) = A( x ) + B( x ) + C( x )
bP( x ) = A( x ) – B( x ) 2C( x )
cP( x ) = A( x ) B( x ) C( x )
dA( x ) = P( x ) B( x )
eA( x ) = P( x ) B( x ) + C( x )
fB( x ) = A( x ) + P( x )
gA( x ) = P( x ) [ B( x ) + C( x )]
hC( x ) = A( x ) + B( x ) + P( x )
16
1
8
Bepaal de reële getallen a , b , c , d en e zodat de volgende uitspraken juist zijn.
a8x 3 2x 2 + x 5 = 2ax 3 4bx 2 + cx d
b3x 4 2ax 3 + ( a + 1)x 2 x + b = ax 4 + bx 3 cx 2 dx + e
c a ( 2x + 5) b ( x 1) = 3x + 4
d a (x 1) + b ( x 2) ( x + 3) c ( x 1)2 = x ( x 1)
e a ( x 2 1) + b ( x 1) + c = x 2 + x + 1
Bepaal voor elke opgave het quotiënt en de rest.
a 6x 4 2x 3 + x 2 3x 2
b 12x 6 6x 5 + x 4 2x 3
c 4x 3 + 2x 2 x x
d √2 x 3 √3 x 2 x √6 x
Voer de volgende delingen uit in R[ x ].
aA ( x ) = 3 x 3 4 x 2 5 x + 1D ( x ) = x + 5
bA ( x ) = 3 x 3 8 x 2 + 17 x 3D ( x ) = 3 x 2
cA ( x ) = 2 x 4 x 3 + 17 x 3D ( x ) = 2 x 2 + 3 x
dA ( x ) = 2 x 3 5 x 2 + 6 x 2D ( x ) = x 2 2 x + 2
eA ( x ) = 2 x 4 7 x 3 + x 2 + 7 x 3D ( x ) = x 2 1
fA ( x ) = 3 x 4 + 5 x 3 + 6 x 2 + 24 D ( x ) = 3 x 2 + 8 x 1
gA ( x ) = x 7 4 x 6 + 2 x 5 + x 4 3 x 3 + 9 x 3D ( x ) = x 4 3
hA ( x ) = x 7 3 x 6 + x 5 + 12 x 4D ( x ) = x 3 2 x + 4
iA ( x ) = x 3 27 D ( x ) = x 3
jA ( x ) = x 3 D ( x ) = x 2 x + 1
kA ( x ) = 4 x 2 x + 1D ( x ) = x 3 + 1
9 10 11 12 *
Bij de deling van de veelterm A( x ) door 6x 2 2x + 1 is het quotiënt x 1 en de rest is 2x 4. Bepaal A( x ). Controleer met ICT.
Zoek de deler van de euclidische deling als het deeltal 6x 3 + 13x 2 3x 4 is, het quotiënt 3x + 5 en de rest x + 11 is. Controleer met ICT.
Bij de deling van A( x ) = 3x 4 x 3 + ax 2 + x + 7 door x 2 + x is de rest 6x + 7. Bepaal a
Bij de deling van A( x ) = 2x 3 + ax 2 + bx + 6 door x 2 3x + 2 is de rest 0. Bepaal a en b .
1 17 Algebraïsch rekenen
DEELTAL DELER
6
7
13
Gegeven : Als je de veelterm A( x ) = 4x 3 + ax 2 + 18x + b deelt door D( x ) = x 2 2x + 3, dan is het quotiënt Q( x ) het dubbel van de rest R( x )
Gevraagd : Bepaal a en b . Noteer ook het quotiënt Q( x ) en de rest R( x ) Los dit ook op met ICT.
14 *
Bij de deling van A( x ) = 2x 3 + ax 2 + bx 2 door x 2 + 1 is de rest 4x + 3. Bepaal a en b .
De veelterm P( x ) = 6x 4 + 2x 3 + ax 2 + bx + c met a , b en c reële constanten is deelbaar door x 3 – x 2 + x – 1. Door welke van onderstaande veeltermen is P( x ) eveneens deelbaar ?
16
IJkingstoets burgerlijk ingenieur september 2018, oefening 22
Voor een veelterm P( x ) van graad 3 geldt: de hoogstegraadscoëfficiënt is 1, x = 1 is een nulpunt (nulwaarde) en de rest van de deling van P(x ) door x 2 + 4x + 5 is 3x + 7.
Bepaal de constante term van de veelterm P( x )
(A) –3 (B) –2 (C) 2 (D) 1
18
(A)
(B) 3
(C)
(D)
3x 2 + x + 4
x 2 + x – 4
3x 2 – x + 2
3x 2 – x – 2
IJkingstoets burgerlijk ingenieur juli 2017, oefening 25 *
15
1.2 Deelbaarheid
in r [x]
1Definitie
Om het begrip deelbaarheid te definiëren en om de eigenschappen en oefeningen hieromtrent eenvoudiger te kunnen voorstellen, maken we gebruik van deze symbolen.
Notatie : ∣ (lees: “deelt” of “is een deler van”)
∤ (lees: “deelt niet” of “is geen deler van”)
Voorbeelden : 3 ∣ 6 want 6 = 3 2
10 ∤ 25 want 25 = 10 · 2 + 5
deelbaarheid in r [ x]
A( x ) D( x )
Q( x ) 0
⟺ A( x ) is deelbaar door D( x )
A( x ) is deelbaar door D( x ) als en slechts als de rest van de euclidische deling van A( x ) door D( x ) nul is. D( x ) | A( x ) ⟺∃! Q( x ) ∈ R[ x ]: A( x ) = D( x ) Q( x ) ⟺ R( x ) = 0
Voorbeelden : 2x + 3 ∣ 2x 3 + 5x 2 + 5x + 3 want 2x 3 + 5x 2 + 5x + 3 = ( 2x + 3) ( x 2 + x + 1)
2x + 2 ∤ 6x 3 + 8x 2 + 4x + 20 want 6x 3 + 8x 2 + 4x + 20 = ( 2x + 2 ) ( 3x 2 + x + 1) + 18
2Reststelling bij deling door x – a
Voorbeeld : Bepaal het quotiënt en de rest bij de euclidische deling van A ( x ) = x 3 – 2x 2 + 3x – 1 door x – 2.
Na euclidische deling vinden we: Q ( x ) = x 2 + 3 en R ( x ) = 5.
Bepaal nu de getalwaarde van A ( x ) voor x = 2.
We vinden: A ( 2) = 23 – 2 22 + 3 2 – 1 = 5
reststelling
Bij de euclidische deling van een veelterm door x – a (met a ∈ R), is de rest van de deling gelijk aan de getalwaarde van het deeltal voor x = a
Gegeven : A( x ) ∈ R[ x ]
D( x ) = x – a ( a ∈ R)
Te bewijzen : Bij deling van A( x ) door x – a is R( x ) = A( a )
Bewijs : A ( x )= D ( x ) Q ( x )+ R ( x ) metgr (R ( x )) < gr (D ( x )) ofR ( x )= 0
=⇒ A ( x )=( x a ) Q ( x )+ R ( x ) metgr (R ( x ))= 0ofR ( x )= 0 (dus:R ( x )= r )
=⇒ A (a )=(a a ) · Q (a )+ r
=⇒ A (a )= r
Voorbeeld : De rest bij deling van A( x ) = 2x 3 + 9x 2 + 8x + 1 door x + 3 is A( –3) = 2 ( –3)3 + 9 ( –3)2 + 8 ( –3) + 1 = 4.
Praktisch : deler rest
– 3 A( 3)
A( x ) x – a
Q( x )
r = A( a )
2981
–3 –6 –9 3
23 –1 4
19 1 Algebraïsch rekenen
x
x + 3
x 1 2 A 1 2
A( –3)
3Quotiënt bij deling door x – a
We hernemen hetzelfde voorbeeld.
De reststelling geeft ons de rest van de deling van een veelterm A( x ) door x a Om het quotiënt te bepalen, gebruiken we het algoritme van de euclidische deling.
Als we het rekenschema van Horner ernaast plaatsen, dan kunnen we het volgende vaststellen.
Voor het quotiënt blijken de coëfficiënten van Q( x ) de reële getallen te zijn die voorkomen op de laatste lijn in het rekenschema van Horner.
We kunnen deze vaststelling gebruiken om het quotiënt bij een euclidische deling van veeltermen sneller te bepalen.
Voorbeeld :
Bepaal Q( x ) en R( x ) als A( x ) = x 3 2x 2 + 3x + 6en D( x ) = x + 2
Het deeltal is van de derde graad en de deler is van de eerste graad. Het quotiënt is bijgevolg van de tweede graad en de graad van de rest is 0.
Q( x ) = x 2 4x + 11en R( x ) = 16

20
x 3 + 9x 2 + 8x + 1 x + 3 2981
x 3 + 6x 2 2x 2 + 3x
x 2
8
2
9
+
x
4
2
2
1 3 6 93 3
+
x + 1 2 3 1 4 3x
+
x x
1
3
1
28 22 1 4
16
236 2
11
4Kenmerk van deelbaarheid door x – a
De veelterm A( x ) is deelbaar door x – a als en slechts als de getalwaarde voor x = a gelijk is aan 0. in symbolen: x – a ∣ A( x ) ⟺ A( a ) = 0
Bewijs : x a | A ( x )
definitiedeelbaarheid
derestbijdeeuclidischedelingvanA ( x ) door x a is0
reststelling
A (a ) = 0
Voorbeeld : x – 2 ∣ A( x ) = 3x 2 – 4x – 4 want A( 2) = 3 22 – 4 2 – 4 = 0
A ( x ) isdeelbaar door x a
A (a )= 0
x + 3 ∤ B( x ) = x 3 – 2x 2 + x – 1 want B( –3) = ( –3)3 – 2 ( –3)2 + ( –3) – 1 = –49 ≠ 0
Opmerking : Als A ( x ) deelbaar is door x – a , dan noemen we a een nulwaarde van de veelterm A ( x )
5Bepalen van de delers van de vorm x – a
Voorbeeld : We proberen de delers van de vorm x – a te bepalen van de veelterm A ( x ) = x 3 – 4x 2 + x + 6.
Volgens het kenmerk van deelbaarheid geldt: x – a ∣ A( x ) ⟺ A( a ) = 0
Zo weten we dat x + 1 ∣ A( x ) want A( –1) = ( –1)3 – 4 ( –1)2 + ( –1) + 6 = 0
x – 2 ∣ A( x ) want A( 2) = 23 – 4 22 + 2 + 6 = 0
x – 3 ∣ A( x ) want A( 3) = 33 – 4 32 + 3 + 6 = 0
Opvallend hierbij is dat zowel –1, 2 en 3 delers zijn van 6.
Opdat een veelterm deelbaar zou zijn door x – a , is het nodig dat de constante term van die veelterm deelbaar is door a in symbolen: x – a ∣ a n x n + a n– 1x n– 1 + + a 1x + a 0 ⟹ a ∣ a 0
Gegeven : A( x ) = an x n + a n 1x n 1 +…+ a1x + a 0 ∈ R[ x ] an , a n 1, , a1, a 0 ∈ R x a | A( x ) a ∈ R
Te bewijzen : a | a0
Bewijs :
x a | a n x n + + a 0 a | a 0 x a | a n x n
21 1 Algebraïsch rekenen
a n
x n
+ ... + a 2 x 2 + a 1 x + a 0 A
)
n + a n 1 a n 1 + + a 2 a 2 + a 1 a + a 0 = 0 a a n a n 1 + a n 1 a n 2 + ... + a 2 a + a 1 + a 0 = 0 a · a n a n 1 + a n 1 a n 2 + + a 2 a + a 1 = a 0 a
n 1 a n 1 a n 2 a 2 a a 1 = a 0 a | a 0
+
1
1
(a
= 0 a n a
a n a
Opmerking : Opdat x a | A( x ) is het nodig dat a | a 0. Dit is echter geen voldoende voorwaarde. De omgekeerde eigenschap geldt dus niet altijd !
Voorbeeld : x 2 ∤ x 2 3x + 4want A( 2) ≠ 0, nochtans : 2 | 4 Anderzijds kan x + 3 onmogelijk een deler zijn van x 2 3x + 4want –3 ∤ 4.
Praktische werkwijze voor het bepalen van een deler van de vorm x – a met a ∈ Z
We zoeken de eventuele delers van de vorm x – a ( a ∈ Z) als volgt : – bepaal de delers van de constante term a 0 ; – bepaal de getalwaarde van de veelterm voor die delers.
Voorbeelden : A (x )= x 3 + 3x 2 x 3 del ( 3)= {1, 1,3, 3}
A (1)= 0 =⇒ x 1 | A ( x )
A ( 1)= 0 =⇒ x + 1 | A ( x )
A (3) = 0 =⇒ x 3 A ( x )
A ( 3)= 0 =⇒ x + 3 | A ( x )
Dezeveeltermheeftdus3delersvandevorm x a ,nl.: x 1, x + 1en x + 3.
B (x )= x 2 3x + 5 del5 = {1, 1,5, 5}
B (1) = 0 =⇒ x 1 B ( x )
B ( 1) = 0 =⇒ x + 1 B ( x )
B (5) = 0 =⇒ x 5 B ( x )
B ( 5) = 0 =⇒ x + 5 B ( x )
Dezeveeltermheeftdusgeendelersvandevorm x a . (a ∈ Z )
Het bepalen van de delers van de vorm x – a met a ∉ Z gebeurt met behulp van ICT.

22
6Kenmerk van deelbaarheid
door (x – a) · (x – b)
eigenschap
∀ a,b ∈ R :
( x a ) ( x b ) | A ( x )
x a | A ( x ) en x b | A ( x )
Gegeven : A( x ) ∈ R[ x ] ; a , b ∈ R ; a ≠ b
( x a ) ( x b ) | A( x )
Te bewijzen : x a | A( x ) en x b | A( x )
Bewijs :
( x a ) · ( x b ) | A ( x )
definitiedeelbaarheidin R [ x ]
∃ !Q ( x ) ∈ R [ x ] : ( x a ) · ( x b ) · Q ( x ) = A ( x )
rekenenin R [ x ]
( x a ) [( x b ) Q ( x )] = A ( x ) en ( x b ) [( x a ) Q ( x )] = A ( x )
definitiedeelbaarheidin R [ x ]
x a | A ( x ) en x b | A ( x )
omgekeerde eigenschap
∀ a,b ∈ R : x a | A ( x ) en x b | A ( x ) met a = b
( x a ) · ( x b ) | A ( x )
Gegeven : A( x ) ∈ R[ x ] ; a , b ∈ R ; a ≠ b
x a | A( x ) en x b | A( x )
Te bewijzen : ( x a ) ( x b ) | A( x )
Bewijs :
x a | A ( x )
definitiedeelbaarheidin R [ x ]
∃ !Q ( x ) ∈ R [ x ] : ( x a ) Q ( x ) = A ( x ) (1)
A ( b ) = ( b a ) · Q ( b )
x b | A ( x ) =⇒ A ( b ) = 0
0 = ( b a ) · Q ( b )
b a = 0,dusisQ ( b ) = 0
Q ( b ) = 0
kenmerkvandeelbaarheiddoor x b
x b | Q ( x )
∃ !Q ( x ) ∈ R [ x ] :Q ( x ) = Q ( x ) · ( x b ) (2)
Uit (1) en (2) volgt :
A ( x ) = ( x a ) ( x b ) Q ( x )
rekenenin R [ x ]
A ( x ) = [( x a ) ( x b )] Q ( x )
definitiedeelbaarheidin R [ x ]
( x a ) ( x b ) | A ( x )
Besluit :
∀ a,b ∈ R : x a | A ( x ) en x b | A ( x ) met a = b
( x a ) ( x b ) | A ( x )
23 1 Algebraïsch rekenen
Opmerking :
Deze stelling kunnen we uitbreiden voor elk eindig aantal factoren waarvan er geen twee gelijk zijn.
( x a ) · ( x b ) · ( x c ) · ( x d ) · | A ( x )
x a | A ( x ) en x b | A ( x ) en x c | A ( x ) en x d | A ( x ) en...
Voorbeeld :
A ( x ) = 3 x 5 + 6 x 4 2 x 3 4 x 2 x 2
del ( 2) = {1, 1,2, 2}
A (1) = 0
A ( 1) = 0
A (2) = 0
A ( 2) = 0
BijgevolgisA ( x ) deelbaardoor ( x 1) ( x + 1) ( x
3010
We vinden :A( x ) = ( x 1) ( x + 1) ( x + 2) ( 3x 2 + 1)
Een veelterm van de n-de graad heeft hoogstens n verschillende nulwaarden.
Gevolg : Heefteenveeltermvande n -degraad n verschillendenulwaarden (α1 tot αn ),dankanhij geschrevenwordenals: a n x n + a
24
4
39732
A( x ) = ( x 1)( 3x 4 + 9x 3 + 7x 2 + 3x + 2)
36120 A( x ) = ( x 1)( x + 1)( 3x 3 + 6x 2 + x + 2)
+ 2) 36 2
1 2 1
397320
1 3 6 1 2
2 60 2
1 x n 1 + + a 2 x 2 + a 1 x + a 0 = a n ( x α1 ) ( x α2 ) ( x α3 ) ( x αn )
n
7De veelterm xn – an
De veelterm x 3 – a 3
Voorbeelden :
Uit voorgaande voorbeelden blijkt dat x a | x 3 a 3. We bepalen nu het quotiënt :
We passen deze formule toe op de voorbeelden :
De veelterm x n – a n ( n ∈ N0)
Voorbeelden :
x 2 | x 2 4want22 4 = 0 x 3 | x 3 27want33 27 = 0 x 5 | x 4 625want54 625 = 0
eigenschap in woorden:
Het verschil van twee gelijknamige machten is steeds deelbaar door het verschil van de grondtallen. in symbolen:
x a | x n a n ( n ∈ N0)
Bewijs : x a | x n a n wantA (a ) = a n a n = 0
Met het schema van Horner bepalen we het quotiënt : 100
Besluit :
x n a n = ( x a ) ( x n 1 + ax n 2
Voorbeelden :
x 3 125 =
25 1 Algebraïsch rekenen
x 2 | x 3 8want23 8 = 0 x 1 | x 3 1want13 1 = 0 x 4 | x 3 64want43 64 = 0
a aa 2
1 aa 2
100 a 3
a 3
0
x 3 a 3 = ( x a )( x 2 + ax + a 2)
a aa 2 a n −1 a n 1 aa 2 a n– 1 0
0 a n
2x
+…+
+ a
n 3
a n 2x + a n 1)
x
+ x
+ x 2 + x +
5 1 = ( x 1) x 4
3
1
x
· x 2 + 5 x + 25
+
2 + x +
+
(
5)
x 3 8 = ( x 2) x 2 + 2 x
4 x 3 1 = ( x 1) x
1 x 3 64 = ( x 4) x 2 + 4 x
16
x
x 17
1 |
1want117 1 = 0
8De veelterm xn + an
De veelterm x 3 + a 3
Voorbeelden :
x + 2 | x 3 + 8want ( 2)3 + 8 = 0
x + 1 | x 3 + 1want ( 1)3 + 1 = 0
x + 4 | x 3 + 64want ( 4)
Uit voorgaande voorbeelden blijkt dat x + a | x 3 + a 3. We bepalen nu het quotiënt : 100 a 3 a aa 2 a 3 1 aa 2 0
x 3 + a 3 = ( x + a )( x 2 ax + a 2)
We passen deze formule toe op de voorbeelden : x 3 + 8 = ( x + 2) x 2 2 x + 4 x 3 + 1 = ( x + 1) x 2
De veelterm x n + a n ( n ∈ 2N + 1)
Voorbeelden : x + 1 | x 5 + 1want ( 1)5 + 1 = 0
x + 2 | x 3 + 8want ( 2)3 + 8 = 0
x + 3 | x 7 + 2187want ( 3)7 + 2187 = 0
eigenschap
in woorden:
De som van twee oneven gelijknamige machten is steeds deelbaar door de som van de grondtallen. in symbolen:
x + a | x n + a n (n ∈ 2N + 1)
Bewijs : x + a | x n + a n wantA ( a ) = ( a )n + a n = 0
Met het schema van Horner bepalen we het quotiënt :
Besluit :
Voorbeelden : x 5 + 32 = x 5 + 25 = ( x + 2) x 4 2 x 3 + 4 x 2 8 x + 16
43
x
26
+
x +
x
1 x 3 + 64 = ( x + 4) x 2 4
16
100 0 a n
aa 2 a n 1 a n 1 aa 2 a n 1 0
a
x
x
ax n 2 + a 2x n 3 a n 2x + a n
n + a n = ( x + a ) (
n 1
1) met n ∈ 2N + 1
3 + 64 = x 3 +
= ( x + 4) x 2 4 x + 16
3 + 64 = 0
9Ontbinden in factoren
Om veeltermen te ontbinden in factoren kennen we al enkele mogelijkheden :
– afzonderen van een gemeenschappelijke factor :
12x 4 8x 3 + 4x 2 = 4x 2 ( 3x 2 2x + 1)
– merkwaardige producten :
4x 2 9 = ( 2x 3) ( 2x + 3)
9x 2 6x + 1 = ( 3x 1)2
– som- en productmethode :
x 2 6 x + 5
S = 6
P = 5 x = 5of x = 1
x 2 6 x + 5 =( x 5)( x 1)
– discriminantmethode :
2 x 2 + 5 x 3
D = 52 4 2 ( 3)
= 25 + 24
= 49 x 1 = 5 √49
2 · 2 = 5 7
4 = 3
2 x 2 + 5 x 3 = 2( x + 3) x 1 2
=( x + 3)(2 x 1)
– samennemen van termen :
x 2 = 5 + √49
2 · 2 = 5 + 7 4 = 1 2
x 3 + x 2 + x + 1 = x 2 ( x + 1) + x + 1 = ( x + 1) ( x 2 + 1)
– de formules voor x n a n ( n ∈ N0) en x n + a n ( n ∈ 2N + 1)
x 3 125 = ( x 5) ( x 2 + 5x + 25)
x 3 + 125 = ( x + 5) ( x 2 5x + 25)
Ook de euclidische deling van een veelterm door x a kan ons helpen bij het ontbinden in factoren.
Voorbeeld :
Om de veelterm A( x ) = x 3 2x 2 5x + 6 te ontbinden, bepalen we de delers van de vorm x a .
A (1) = 0 ⇐⇒ x 1 | A ( x )
1 2 56
1 1 1 6
1 1 60
x 3 2 x 2 5 x + 6 = ( x 1) · x 2 x 6
= ( x 1) ( x 3) ( x + 2) som-enproductmethode
27 1 Algebraïsch rekenen
10Samenvatting
• Je kent de definitie van deelbaarheid in R[ x ].
A( x ) is deelbaar door D( x ) als en slechts als de rest van de euclidische deling van A( x ) door D( x ) nul is.
D ( x ) | A ( x ) ⇐⇒∃!Q ( x ) ∈ R [ x ] :A ( x ) = D ( x ) · Q ( x ) ⇐⇒ R ( x ) = 0
• Je weet dat bij de euclidische deling van een veelterm door x – a de rest van de deling gelijk is aan de getalwaarde van het deeltal voor x = a en je kunt dit ook bewijzen.
• Je kunt bij een euclidische deling van een veelterm door x – a het quotiënt en de rest bepalen door het rekenschema van Horner te gebruiken.
• Je kent het kenmerk van de deelbaarheid van een veelterm door x – a en je kunt dit ook bewijzen. De veelterm A( x ) is deelbaar door x a als en slechts als de getalwaarde voor x = a gelijk is aan 0.
x a | A ( x ) ⇐⇒ A (a ) = 0
• Je kent de nodige voorwaarden om delers van de vorm x a te bepalen en je kunt die ook bewijzen en toepassen.
Opdat een veelterm deelbaar zou zijn door x a is het nodig dat de constante term van die veelterm deelbaar is door a
x a | a n x n + a n 1 x n 1 + ... + a 1 x + a 0 =⇒ a | a 0
• Je kent de volgende formules :
x 3 – a 3 = ( x – a ) ( x 2 + ax + a 2)
xn – an = ( x – a ) ( xn –1 + ax n –2 + a 2x n –3 + … + an –2x + an –1) n ∈ N0
x 3 + a 3 = ( x + a ) ( x 2 – ax + a 2)
xn + an = ( x + a ) ⋅ ( x n –1 – axn–2 + a 2xn –3 – –an –2x + an –1) n ∈ 2N + 1
• Je kent verschillende mogelijkheden om een veelterm te ontbinden in factoren.
28
11 Oefeningen
Bepaal het quotiënt en de rest bij deling van A( x ) door D( x )
aA ( x )= 3 x 3 x 2 + 2 x 1D ( x )= x + 1
bA ( x )= 4 x 4 3 x 3 + 2 x 2 3D ( x )= x 3
cA ( x )= 27 x 3 24 x 2 + 9 x 1D ( x )= x 1
dA ( x )= 6 x 3 x 2 + x 1D ( x )= x + 2
eA ( x )= x 3 + 12 x 2 + 47 x + 60D ( x )= x + 4
fA ( x )= x 5 x 3 x + 5D ( x )= x 1
gA ( x )= x 4 6 x 2 + 7 x 6D ( x )= x 2
hA ( x )= 9 x 3 + 53 x 2 9 x 18D ( x )= x + 6
Bepaal de delers van de vorm x – a van de volgende veeltermen ( a ∈ Z).
a x 3 3 x 2 10 x + 24 e x 4 2 x 3 + x 2
b x 3 + 2 x 2 5 x 6 f4 x 3 4 x 2 x + 1
c x 4 10 x 2 + 9 g12 x 4 8 x 3 25 x 2 13 x 2
d x 3 9 x 2 11 x + 21 h x 4 + x 3 10 x 2 4 x + 24
Bepaal k ∈ R zodat bij de euclidische deling van A( x ) door D( x ) de rest gelijk zou zijn aan r.
Toon aan dat de volgende delingen opgaan en bepaal daarna het quotiënt. A( x ) D( x )
a
c
Werk de volgende creatieve opdrachten uit.
a Zoek een veelterm van de vierde graad die deelbaar is door x – 2, x + 2 en x – 1.
b Zoek een veelterm van de vierde graad die geen enkele reële nulwaarde heeft. Controleer je antwoord grafisch.
c Noteer 5 willekeurige veeltermen van de derde graad. Controleer grafisch of elke gekozen veelterm minstens één reële nulwaarde heeft.
1 29 Algebraïsch rekenen
A( x
D( x ) r a 4x 3 – kx 2 + 2x – 1 x – 2 – 1 b –4x 4 – 6x 3 + 2x + k x + 1 0 c 3kx 2 1 2 kx + 5 4 x 1 2 3 4 d x 3 + kx + 2√3 x + √3 3√3 e 5x 3 + ( k + 1)x 2 – 31x + 3 + k x + 3 k f ( k 2 + 1)x 4 + 3x 3 + 2kx 2 – 1 x + 1 0
)
5a 3 + 4a 2 – 31a + 6 a – 2
– 1 x + 1
b 2x 4 + 3x 3 + 2x 2
6x 5 + 19x 4 + 8x 3 + 16x 2 + 2x – 3 x +
x 3 – 3ax 2 + 4a 3 x – 2
3 d
a
1 2
4 5
3
11
Bij deling van A( x ) = 2x 3 x 2 + ax b door x 1 en door x + 3 is de rest telkens 4. Bepaal a en b
Een veelterm A( x ) wordt gedeeld door x 3 en door x + 2.
De respectievelijke resten zijn 10 en 0.
Wat is de rest bij de deling van A( x ) door ( x 3) ( x + 2)?
Een veelterm A( x ) geeft bij deling door x + 1, x 1, x 2 de resten 2, 4 en 8.
Wat is de rest bij deling van A( x ) door ( x + 1) ( x 1) ( x 2)?
Bepaal a , b en c zodat 5x 3 + ax 2 + bx + c deelbaar is door x 1 en x + 1 en bij deling door x 2 de rest 36 is. Controleer dit met ICT.
De veelterm 2x 3 + x 2 + ax + b geeft bij deling door x 2 1 de rest 3x + 5. Bepaal a en b.
Ontbind de volgende veeltermen in factoren. Controleer je antwoord met ICT.
a x 2 8 x + 12 i3 x 3 x 2 59 x 55
b 6 x 2 + 13 x + 5 j2 x 3 + 5 x 2 4 x 3
c 5 x 2 8 x + 13 k x 4 2 x 2 + 1
d x 2 4 x + 1l x 4 4
e x 2 + 7 x 6 m6 x 4 + 13 x 3 13 x 6
f8 x 2 22 x + 15 n6 x 4 + 4 x 3 26 x 2 16 x + 8
g2 x 3 + x 2 22 x + 24 o6 x 4 43 x 3 + 77 x 2 + 2 x 24 h2 x 3 3 x 2 2 x + 3p
De veelterm P( x ) van graad 10 heeft als nulwaarden de getallen
en 1 7 .Waaraanis P (2) P 1 2 gelijk?
(A)
VWO 2021 eerste ronde, vraag 23 © Vlaamse Wiskunde Olympiade vzw
De rest van x 2023 bij deling door x 2 – 1 is gelijk aan :
.Waaraanis P (2) P 1 2 gelijk?
(A) 1 (B) x (C) x – 1 (D) x + 1 (E)1 – x
VWO 2023 eerste ronde, vraag 22 © Vlaamse Wiskunde Olympiade vzw
In de vijfdegraadsveelterm P( x ) zijn de zes coëfficiënten ofwel –1 ofwel 1. Je weet dat P( 2) = 15. Hoe groot is P( 1)?
(A) –4 (B) –2 (C) 0 (D) 2 (E) 5
VWO 2020 tweede ronde, vraag 19 © Vlaamse Wiskunde Olympiade vzw
30
x 5 + 3 x 4 16 x 48
1 3 , 1 4 , 1 5 , 1 6
7
1 4 , 1 5 , 1 6
3,4,5,6,7,
en 1
22
25
27
210
214
(B)
(C)
(D)
(E)
6 7
*
*
12 13 14
* 8
9 * 10
Voor P( x ) = x 3 + a 2x 2 + a 1x + a 0 met a 2, a 1, a 0 ∈ R geldt dat P( 1) = 1, P( 2) = 4 en P( 3) = 9. Waaraan is P( 4) gelijk ?
(A) 6 (B)10 (C)16 (D)22 (E)30
VWO 2022 tweede ronde, vraag 26 © Vlaamse Wiskunde Olympiade vzw
De veelterm P( x ) = 8x 3 + 8 is deelbaar door x + a , met a ∈ R. Hoeveel is de rest van de deling van P( x ) door x + 2a ?
(A) –60 (B) –56 (C) –52 (D) –50
Toelatingsexamen arts 2019, vraag 7
Voor een veelterm P( x ) van graad 2 geldt: de hoogstegraadscoëfficiënt is 1, x = 2 is een nulpunt en P( 1) = 3. Wat is de coëfficiënt bij de eerstegraadsterm ?
(A) –6 (B) –4 (C) 4 (D) 6
IJkingstoets burgerlijk ingenieur juli 2019, oefening 2
Beschouw de veelterm P( x ) = x 3 + ax 2 – b2x + a 3 waarbij a, b reële getallen zijn en a ≠ 0. Er is gegeven dat P( x ) deelbaar is door x – a . Bepaal de rest bij deling van P( x ) door x – b
(A) 3a 3 (B) 4a 3 (C) –4a 3 (D) –3a 3
IJkingstoets burgerlijk ingenieur augustus 2021, oefening 11
Gegeven de veelterm P( x ) = 2x 5 + ax 4 + bx 3 + cx 2 + dx – 36 met a , b , c , d ∈ R en nulwaarden 1, –1, 3 en –3. Bepaal de vijfde nulwaarde van deze veelterm.
(A) –4 (B) –2 (C) 2 (D) 4
IJkingstoets burgerlijk ingenieur juli 2021, oefening 8
Beschouw de veelterm P( x ) = 4x 5 – 4x 4 + ax 3 + bx 2 + 4x + 24. De parameters a en b zijn zodanig gekozen dat deze veelterm deelbaar is door 4( x – 3)( x + 2)
Welke van de volgende uitspraken is geldig ?
( A) P( –2) < P( 0) < P( 3)( B) P( –2) > P( 0) > P( 3)( C) P( –2) = P( 3) > P( 0)( D) P( –2) = P( 3) < P( 0)
IJkingstoets basiskennis wiskunde handelsingenieur 2020, vraag 12
Voor een bepaald reëel getal k is de veelterm P( x ) = x 3 + kx 2 – 5x + 8 – k deelbaar door x + k Deze veelterm is dan ook nog deelbaar door
(A) x + √2 (B) x + √3 (C) x + √5 (D) x + √6
Toelatingsexamen arts 2021, vraag 5
1 31 Algebraïsch rekenen
15 16 17 18 19 20 21
Algebraïsch rekenen 1
32 WAT MOET JE KENNEN EN KUNNEN ?
pagina Ik weet wat een veelterm is, kan de graad bepalen en ken de betekenis van de getalwaarde en een nulwaarde. 9 Ik ken het algoritme van Horner. 10 Ik kan bewerkingen met veeltermen uitvoeren. 12 Ik kan de euclidische deling uitvoeren van veeltermen met reële coëfficiënten in één onbekende. 13 Ik ken het algoritme van de euclidische deling. 14 Ik kan bewijzen dat de rest en het quotiënt bij een euclidische deling enig zijn. 15 Ik ken de reststelling bij deling door x – a 19 Ik kan het quotiënt en de rest bepalen bij deling door x – a met behulp van het algoritme van Horner. 20 Ik ken het kenmerk van deelbaarheid door x – a 21 Ik kan de delers van de vorm x – a met a ∈ Z bij een veelterm bepalen. 21 Ik ken het kenmerk van deelbaarheid door ( x – a ) ⋅ ( x – b ). 23 Ik kan een veelterm ontbinden in factoren d.m.v. deling door x – a 25 Ik kan de tweetermen x 3 – a 3 en x 3 + a 3 ontbinden in factoren. 25 Ik kan de tweetermen xn – an en xn + an ontbinden in factoren. 25 Ik kan veeltermen ontbinden in factoren door een gegeven heuristiek toe te passen. 27


Veeltermfuncties 2
Wiskunde is overal aanwezig. Ook als je nabij Brugge meevliegt met een luchtballon. De vlucht kan beschreven worden door een veeltermfunctie. Die laat je toe om heel wat toepassingen te achterhalen. Hoelang werd er gevlogen ?
Welke hoogte hebben we als we boven de kerktoren vliegen?
Kom het allemaal te weten in de studie van de veeltermfuncties.


Veeltermfuncties
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
34
Inleiding 1 Definities 35 2 Algebraïsche functies 36 3 Niet-algebraïsche functies of transcendente functies 37
Veeltermfuncties 1 Voorbeelden 38 2 Herhaling van de belangrijkste kenmerken van constante, eersteen tweedegraadsfuncties 38 3 Hogeregraadsfuncties 41 4 Oplossen van veeltermongelijkheden 44
Toepassingen 1 De vlucht met de luchtballon 45 2 Vuurpijlen schieten 48
Bespreken
kenmerken
een veeltermfunctie 1 Voorbeeld 1 49 2 Voorbeeld 2 51
van een aantal
van
1 Voorbeeld 1 53 2 Voorbeeld 2 54
Een functievoorschrift opstellen
Vraagstukken 1 Voorbeeld 1 55 2 Voorbeeld 2 56
Differentiequotiënt 1 Productiekosten beperken 57 2 Hoe snel reed Sofie ? 58
Samenvatting en oefeningen 1 Samenvatting 60 2 Oefeningen 61 Wat moet je kennen en kunnen? 70 2
2.1 Inleiding
1Definities
functie
Een functie is een verband tussen twee variabelen x en y waarbij voor elke x -waarde hoogstens één y -waarde bestaat.
x is de onafhankelijke variabele.
y is de afhankelijke variabele.
Er zijn verschillende representaties van een functie: verwoording, tabel, letterformule (voorschrift) en grafiek.
Wanneer de twee veranderlijken reële getallen zijn, spreken we van reële functies. Voor reële functies gebruiken we de letters f , g , h … of f 1, f 2, f 3 … De formule die de functie bepaalt, is het functievoorschrift. Zo spreken we dus over de functie f met voorschrift f ( x ). De y -waarden worden ook de functiewaarden of beelden genoemd.
Voorbeeld : een reëel getal en zijn kwadraat
Verwoording : Het verband tussen een reëel getal en zijn kwadraat is een functie, want elk reëel getal heeft juist één kwadraat. We stellen deze functie voor door de letter f .
Letterformule : f ( x ) = x 2 of y = x 2
Enkele functiewaarden (of beelden) :
f ( 3)= 9
f (0)= 0
f (√2)= 2
Grafiek :
Omdat elk element van R een beeld heeft, noemen we R het domein van de functie f Notatie: dom f = R
De verzameling van de functiewaarden
noemen we het bereik van de functie f . Notatie : ber f = R+
domein en bereik van een functie
Het domein van een functie f is de verzameling van de x -waarden waarvoor de functiewaarde bestaat.
Notatie: dom f
Het bereik (beeld) van een functie f is de verzameling van de y -waarden waarvoor er een x -waarde bestaat zodat y = f ( x )
8
6
4
y 2
10 0 0
f ( x )= x 2
• • • • • • •
x 6 4 2 2 4 6 2
35 2 Veeltermfuncties
x –3 5 2 √2 –1 0 √2 2 1 7 3 3 x 2 9 25 4 210 1 2 1 49 9 9
Tabel :
Notatie: ber f
Grafisch onderzoek: elke verticale snijdt de grafiek hoogstens één keer.
2Algebraïsche functies
algebraïsche functie
Een algebraïsche functie is een reële functie waarbij in het functievoorschrift enkel de bewerkingen optellen, aftrekken, vermenigvuldigen, delen en n-demachtsworteltrekking voorkomen.
Deze functies worden in drie klassen onderverdeeld : veeltermfunctie
Een veeltermfunctie van de n -de graad is een functie waarvan het functievoorschrift een veelterm is van de n -de graad in x
f ( x )= a n x n + a n 1 x n 1 + ... + a 2 x 2 + a 1 x + a 0
= i = n i = 0 a i x i met a i ∈ R en a n = 0
Voorbeelden :
Een veeltermfunctie van de derde graad met voorschrift: f ( x ) = x 3 – 4x + 8.
Een veeltermfunctie van de vijfde graad met voorschrift: f ( x ) = x 5 – x 3
In de voorbije jaren heb je al enkele veeltermfuncties bestudeerd :
– de constante functies met voorschrift :
f ( x ) = b – de eerstegraadsfuncties met voorschrift :
f ( x ) = ax + b met a ∈ R0 en b ∈ R – de tweedegraadsfuncties (kwadratische functies) met voorschrift :
f ( x ) = ax 2 + bx + c met a ∈ R0 en b, c ∈ R
rationale functie
Een rationale functie f is een functie met voorschrift f ( x )= g ( x ) h ( x ) waarbij g en h veeltermfuncties zijn en h( x ) niet de nulveelterm is.
Voorbeelden :
De rationale functie f met voorschrift: f ( x )= x 3 8 x 2 + 4 x + 3
De rationale functie f met voorschrift: f ( x )= 2 x 1 x 2 + x + 6 .
irrationale functie
Een irrationale functie is een algebraïsche functie die verschillend is van een rationale functie. Dit betekent dat in het functievoorschrift (na vereenvoudiging) de variabele x voorkomt onder een of meerdere worteltekens.
Voorbeelden :
De functies f en g met voorschriften f ( x )= √ x 2 4en g ( x )= 3 √ x + 1 x 1
36
3Niet-algebraïsche functies of transcendente functies
Het woord ‘transcendent’ betekende oorspronkelijk ‘wat het vermogen van de algebra te boven gaat’. Het is afkomstig van de Duitse wiskundige Leibniz die het in de 17e eeuw invoerde.
Voorbeelden :
FUNCTIE
FUNCTIEVOORSCHRIFT
exponentiële functies f ( x )= a x met a ∈ R + 0 \{1}
logaritmische functies f ( x )= loga x met a ∈ R + 0 \{1}
goniometrische functies f ( x )= sin x
f ( x )= G ( x )= x
G-functie
signfunctie
f ( x )= sgn ( x )
x iseengeheelgetal zodat x x < x + 1
x > 0:sgn ( x )= 1
x < 0:sgn ( x )= 1
x = 0:sgn ( x )= 0


Functies
Het woord ‘functie’ werd voor het eerst gebruikt door de Duitse wiskundige Leibniz (1646-1716), die het begrip koppelde aan gelijk welke grootheid, verbonden met een kromme. In 1718 was er de Zwitserse wiskundige Johann Bernoulli (1667-1748) die een functie definieerde als een willekeurige uitdrukking bestaande uit een veranderlijke en verschillende constanten. Zijn landgenoot Euler (1707-1783) voerde de notatie f(x) in. Het is de Duitser Dirichlet (1805-1859) die de uiteindelijke definitie vastlegde en ook begrippen zoals ‘definitiegebied’ (domein) en ‘bereik’ omschreef.
37 2 Veeltermfuncties
Bernoulli Leibniz
2.2 Veeltermfuncties
1Voorbeelden
• f met f ( x ) = –x 3 + 2x + 1 is een veeltermfunctie van de derde graad.
• f met f ( x ) = x 4 + 4x 2 + 3 is een veeltermfunctie van de vierde graad.
• f met f ( x ) = x 2 + 1 x is geen veeltermfunctie want x 2 + 1 x is geen veelterm.
Overzicht : a ≠ 0 en a n ≠ 0
VOORSCHRIFT VAN EEN …
f ( x ) = a constante functie
f ( x ) = ax + b eerstegraadsfunctie
f ( x ) = ax 2 + bx + c tweedegraadsfunctie
f ( x ) = ax 3 + bx 2 + cx + d derdegraadsfunctie
f ( x ) = ax 4 + bx 3 + cx 2 + dx + e vierdegraadsfunctie
f ( x )= a n x n + a n 1 x n 1 + ... + a 2 x 2 + a 1 x + a 0 = i = n i = 0 a i x i n -degraadsfunctie
Opmerkingen :
– Als de graad hoger is dan twee, dan spreken we van een hogeregraadsfunctie.
– Aangezien eerste- en tweedegraadsfuncties ook veeltermfuncties zijn, kunnen we verwachten dat sommige aspecten ervan ook terug te vinden zijn bij andere veeltermfuncties. Daarom een korte herhaling.
2 Herhaling van de belangrijkste kenmerken van constante, eerste- en tweedegraadsfuncties
aConstante functies
Voorschrift : f ( x ) = a a ∈ R
De grafiek is een rechte, evenwijdig met de x -as en door het punt met coördinaat ( 0, a )
( 0, a ) O
y x
f ( x ) = a
38
bEerstegraadsfuncties
Voorschrift : f ( x ) = ax + b a ∈ R0 en b ∈ R
nulwaarde: b a
Grafiek en tekentabel :
a < 0
De grafiek is een dalende rechte.
> 0
De grafiek is een stijgende rechte.
b a ,0 b a ,0
a wordt de richtingscoëfficiënt van de grafiek genoemd.
b ≠ 0grafiek is een rechte niet door O
b = 0grafiek is een rechte door O
cTweedegraadsfuncties
Voorschrift : f ( x ) = ax 2 + bx + c a ∈ R0 en b , c ∈ R
– De grafiek is een parabool met vergelijking y = ax 2 + bx + c waarvan de as evenwijdig is met de y -as.
– TopT b 2a , b 2 + 4ac 4a ofT b 2a , f b 2a
– De as: x = b 2a a > 0: dalparabool ; f b 2a is het minimum a < 0: bergparabool ; f b 2a is het maximum
– Nulwaarden: oplossingen van ax 2 + bx + c = 0
Omdetweedegraadsvergelijking ax 2 + bx + c = 0optelossen,berekenenwedediscriminant
D = b 2 4ac
D < 0 ⇐⇒ ax 2 + bx + c = 0heeftgeenreëlewortels
D = 0 ⇐⇒ ax 2 + bx + c = 0heefttweegelijkewortels
D > 0 ⇐⇒ ax 2 + bx + c = 0heefttweeverschillendewortels
V = ∅
V = b 2a
V = { x 1 , x 2 } met x 1 = b √D 2a en x 2 = b + √D 2a
Dieformulenoemenwede wortelformule ofde abc -formule
39 2 Veeltermfuncties
a
y
x ( 0, b
y
x ( 0, b ) x –∞ b a +∞ x –∞ b a +∞ f ( x ) + 0 – f ( x ) – 0 +
O
)
O
40 – Tekenverloop y x y x O O x y x O O x –∞ +∞ f ( x ) teken van a y x y x O O y x y x O O x –∞ x 1 = x 2 = b 2a +∞ f ( x ) teken van a 0 teken van a y x y x O O y x y x O O x –∞ x 1 x 2 +∞ f ( x ) teken van a 0 tegengesteld teken van a 0 teken van a a < 0 a < 0 a < 0 a > 0 a > 0 a > 0 x 1 = x 2 x 1 = x 2 x 1 x 2 x 1 x 2 D < 0 D = 0 D > 0
3Hogeregraadsfuncties
– Om de nulwaarden van een veeltermfunctie met graad hoger dan 2 algebraïsch te bepalen, ontbinden we de veelterm uit het functievoorschrift, indien mogelijk, in factoren van de eerste en/of tweede graad. Elke x-waarde waarbij een van de factoren nul wordt, is dan een nulwaarde van de veeltermfunctie.
– Om de tekentabel te maken, onderzoeken we eerst het teken van de factoren en daarna het teken van het product.
Voorbeeld 1 :
Bepaal de nulwaarden en de tekentabel van de veeltermfunctie f met als voorschrift
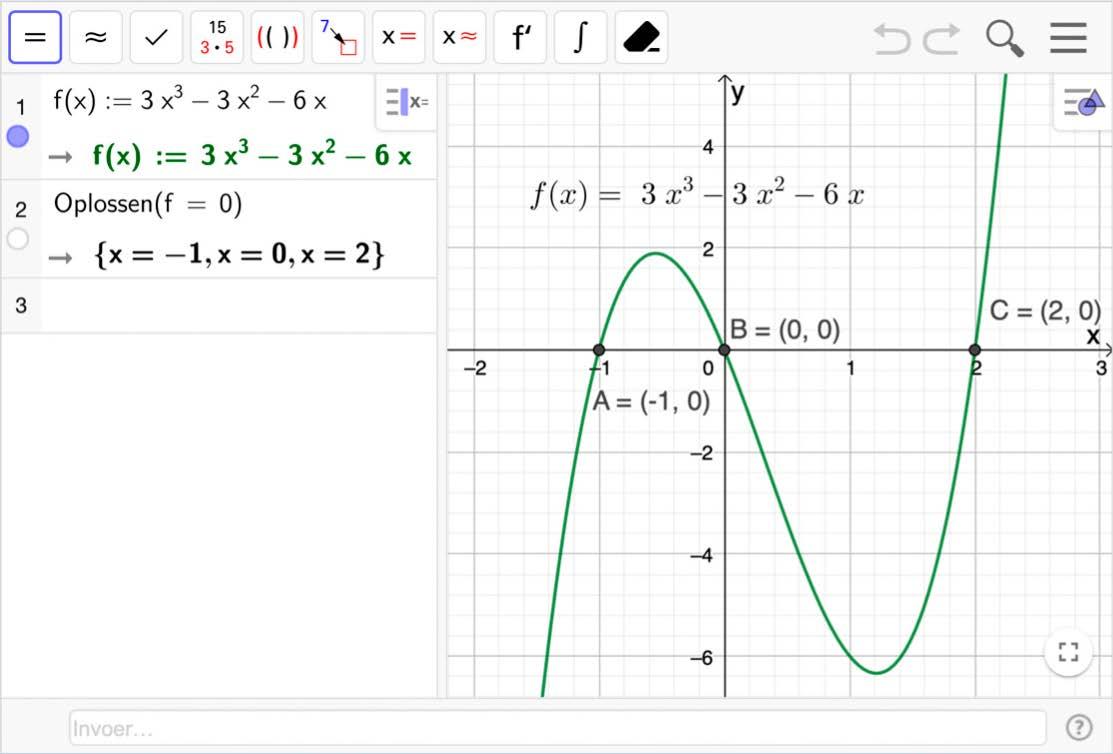
f ( x ) = 3x 3 – 3x 2 – 6x
Om de nulwaarden te vinden van de functie f ( x ) lossen we de veeltermvergelijking f ( x ) = 0 op. We ontbinden f ( x ) in factoren door de gemeenschappelijke factor af te zonderen :
f ( x ) = 3x ( x 2 – x – 2)
f ( x )= 0
3 x ( x 2 x 2)= 0
3 x = 0 of x 2 x 2 = 0
De functie f heeft 3 nulwaarden: –1, 0 en 2.
Tekentabel :
a iseennulwaarde vandeveeltermfunctie f
f (a )= 0
a b = 0
a = 0of b = 0
41 2 Veeltermfuncties
∗ x
* x 2 x 2 = 0 D = 1 + 8 = 9 > 0 x 1 = 1 √9 2 = 1 3 2 = 1 x 2 = 1 + √9 2 = 1 + 3 2 = 2
= 0 of x = 1 of x = 2
x –∞ –1 0 2 +∞ 3x x 2 – x – 2 –+ –0 ––0 –+ –+ 0 + + f ( x ) = 3x ( x 2 – x –2) – 0 + 0 – 0 +
Voorbeeld 2 :
Bepaal de nulwaarden en stel de tekentabel op van f met f ( x ) = 15x 3 – 44x 2 – 5x + 6. We ontbinden f ( x ) in factoren door een deler van de vorm x – a te zoeken. We schrijven daarna f ( x ) als een product van deler en quotiënt.
deelbaar door x – a
Opdat een veelterm deelbaar zou zijn door x – a is het nodig dat de constante term van die veelterm deelbaar is door a
x a | a n x n + a n 1 x n 1 + ... + a 1 x + a 0 =⇒ a | a 0
De veelterm A( x ) is deelbaar door x – a als en slechts als de getalwaarde voor x = a gelijk is aan 0.
x a | A ( x ) ⇐⇒ A (a )= 0 a , a 1 , a 2 ,..., a n ∈ Z
De gehele delers van 6 zijn
1, –1, 2, –2, 3, –3, 6 en –6.
f ( 1) = –28
f ( –1) = –48
f ( 2) = –60
f ( –2) = –280
f ( 3) = 0
f ( –3) = –780
f ( 6) = 1632
f ( –6) = –4788
Omdat f ( 3) = 0, is x – 3 een deler van f ( x )
Het quotiënt van de deling van f ( x ) door x – 3 bepalen we met het rekenschema van Horner :
15 –44 –5 6
3 3 45
15 1 –2 0
Dus : Q( x )= 15 x 2 + x 2 =⇒ f ( x )=( x 3)(15 x 2 + x 2)
f ( x )= 0
( x 3)(15 x 2 + x 2)= 0
De functie f heeft 3 nulwaarden: 2 5 , 1 3 en 3.
Tekentabel :
42
3
3 –6
3
x
15 x 2 + x 2 = 0 ∗ x = 3 of x = 2 5 of x = 1 3 * 15 x 2 + x 2 = 0 D = 1 + 120 = 121 > 0 x 1 = 1 √121 30 = 12 30 = 2 5 x 2 = 1 + √121 30 = 10 30 = 1 3
3 = 0 of
x –∞ 2 5 1 3 3 +∞ x – 3
+ x – 2 –+ –
–
0 –+ 0 + + +
( x ) –
+ 0 – 0 +
15x 2
0 –
–
f
0
Opmerking :
Heel wat voorschriften van veeltermfuncties kunnen we niet in factoren ontbinden. Met behulp van ICT kunnen we toch de nulwaarden en de tekentabel van die functies bepalen.
Voorbeeld :
Beschouw de functie f met f ( x ) = 4x 4 + 8x 3 – 13x 2 – 16x + 10.
We tekenen de grafiek van de functie f en leiden hieruit af dat de functie vier nulwaarden heeft.
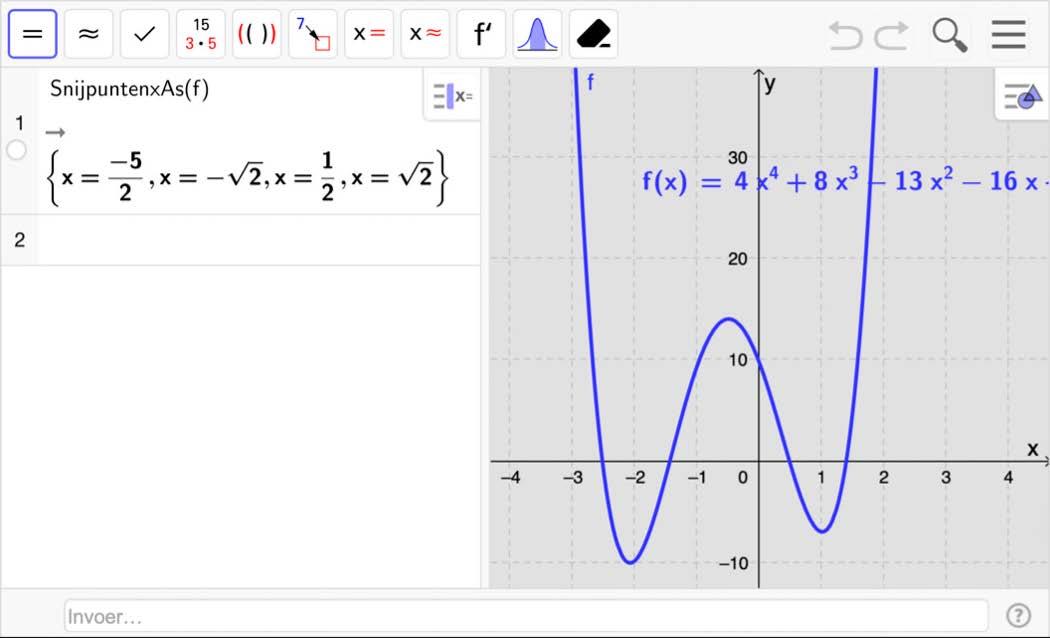
Denulwaardenzijn: 5 2 ; √2 ≈−1,4142; 1 2 ; √2 ≈ 1,4142
Aan de hand van de grafiek kunnen we nu ook de tekentabel van de functie bepalen.


43 2 Veeltermfuncties
x –∞ 5 2 √2 1 2 √2 +∞ f ( x ) + 0 – 0 + 0 – 0 +
4Oplossen van veeltermongelijkheden
Ongelijkheden waarvan de graad hoger is dan twee noemen we veeltermongelijkheden of hogeregraadsongelijkheden . Om een hogeregraadsongelijkheid op te lossen, herleiden we de ongelijkheid op nul en stellen we een tekentabel op van de functie, bepaald door die ongelijkheid.
Voorbeeld:
Los de veeltermongelijkheid op: x 3 + 3 x 2 ⩾ 4
– Eerst herleiden we de veeltermongelijkheid op nul.
x 3 + 3 x 2 – 4 ⩾ 0
– We bepalen de nulwaarden van f met f ( x ) = x 3 + 3 x 2 – 4.
We ontbinden f ( x ) in factoren :
f ( x )=( x 1)( x 2 + 4 x + 4)
of
f ( x )=( x 1)( x + 2)2
f ( x )= 0 ⇐⇒ ( x 1)( x + 2)2 = 0
⇐⇒ x 1 = 0of x + 2 = 0
⇐⇒ x = 1of x = 2
Denulwaardenzijn: 2en1.
Opmerking :
130 –4 1
Omdat de nulwaarde – 2 twee keer voorkomt, noemen we deze een tweevoudige nulwaarde van de functie f De grafiek raakt aan de x -as in ( – 2, 0 )
– Tekentabel van f ( x ) = x 3 + 3x 2 – 4 = ( x – 1)( x + 2)2
2)2
In de tekentabel kunnen we ten slotte aflezen voor welke x -waarden geldt: f ( x ) ⩾ 0 .
Dit is voor x ⩾ 1 of x = –2.
De oplossingenverzameling is V = [ 1, +∞[ ∪ { –2}
– Grafische controle
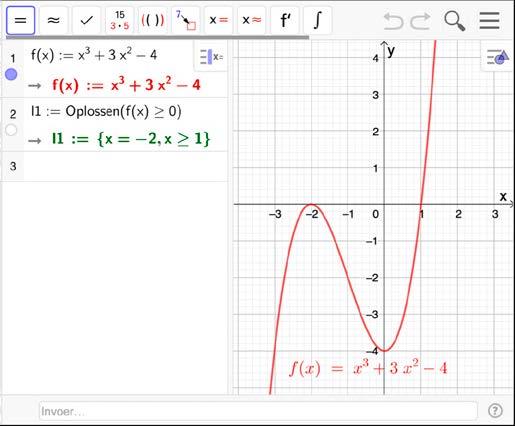
44
144 1440
– 2
+∞ x
–+ –0 –+
+ + + f ( x ) – 0 – 0 + –
x –∞
1
–1 ( x +
0
2.3 Toepassingen
1De vlucht met de luchtballon
We maken een vlucht met een luchtballon die beschreven kan worden door de veeltermfunctie h met voorschrift :
h ( t )= 24 2 t + 1 18 t 3 1 216 t 4
met h( t ): hoogte in tientallen meters
t : tijd in uren
t = 0 is het tijdstip waarop we boven de kerktoren vliegen
Gevraagd :
a Schets de grafiek van h (maak gebruik van ICT).
b Hoelang duurt de vlucht? Werk op 1 minuut nauwkeurig.
c Hoelang zijn we al in de lucht op het ogenblik dat we boven de kerktoren vliegen? Werk op 1 minuut nauwkeurig.

d Hoe hoog zijn we op het ogenblik dat we boven de kerktoren vliegen? Werk op 1 meter nauwkeurig.
e Hoelang vliegen we hoger dan 180 meter? Werk op 1 uur nauwkeurig.
Oplossing :
a We plaatsen de tijd op de x -as en de hoogte op de y -as.
b We berekenen eerst de nulwaarden van deze veeltermfunctie van de vierde graad. Op de grafiek zien we dat er twee nulwaarden zijn. Na berekening (met behulp van ICT) vinden we :
Nulwaarden: – 7,5595 en 12
Als we veronderstellen dat de luchtballon opstijgt bij de eerste nulwaarde en uiteindelijk landt bij de tweede, dan duurt de vlucht [ 12 – ( – 7,5595)] uur = 19,5595 uur = 19 uur en 34 minuten.
c Op het tijdstip t = 0 zijn we al [ 0 – ( – 7,5595)] uur = 7 uur en 34 minuten in de lucht.
45 2 Veeltermfuncties
t (inuren) h ( t ) (· 10m) 10 5 5 10 15 20 10 20 30 0 h ( t )= 24 2 t + 1 18 t 3 1 216 t 4 • ( 6,18) • (6,18)
A ( 7,5595;0) • B (12,0)
•
d De hoogte op het tijdstip t = 0 wordt gegeven door h ( 0) = 24.
Op het ogenblik dat we boven de kerktoren vliegen, bevindt de luchtballon zich op een hoogte van 24 10 meter = 240 meter.
e Willen we weten hoelang we boven 180 meter vliegen, dan moeten we de oplossingen berekenen van de ongelijkheid h( t ) > 18 :
h ( t ) > 18
24 2 t + 1 18 t 3 1 216 t 4 > 18
t 4 12 t 3 + 432 t 1296 < 0
Tekentabel van t 4 – 12t 3 + 432t – 1296 :
t –∞ – 6 6 +∞
t 4 – 12t 3 + 432t – 1296 + 0 – 0 +
Dus : V = ] –6, 6[
Antwoord : de luchtballon vliegt gedurende [ 6 – ( –6)] uur = 12 uur hoger dan 180 meter.
Terminologie :
a Domein
Het domein van een functie is de verzameling van de x -waarden (hier t -waarden) waarvoor de functie gedefinieerd is. Grafisch vinden we het domein door de grafiek van de functie loodrecht te projecteren op de x-as. Het domein van de functie h is R. We noteren: dom h = R
b Praktisch domein
Het praktisch of realistisch domein van een functie in een concreet gestelde opgave is de verzameling van de x -waarden waarvoor het beeld van de functie bestaat en in die opgave zinvol is. Omdat we gerust mogen veronderstellen dat de luchtballon zich steeds boven de grond bevindt, is h ( t ) steeds positief en dus is het praktisch domein van de functie h gelijk aan [ –7,5595; 12]
c Nulwaarden
De nulwaarden van een functie zijn de x -waarden waarvoor de functiewaarde nul wordt, m.a.w. de nulwaarden van h zijn de oplossingen van de vergelijking h ( t ) = 0. Hier hebben we twee nulwaarden, nl. –7,5595 en 12.
d Bereik
Het bereik (of beeld) van een functie is de verzameling van y -waarden (hier h -waarden) waarvoor er een x -waarde bestaat zodat y = f ( x ). Grafisch vinden we het bereik door de grafiek loodrecht te projecteren op de y -as.
Het bereik van de functie h is ]–∞, α] met α de maximaal bereikte hoogte van de luchtballon. We noteren: ber h = ]–∞, α]. Bereken met ICT de waarde van α.
e Praktisch bereik
Het praktisch of realistisch bereik van een functie in een concreet gestelde opgave is de verzameling van de y -waarden die de functie binnen de gestelde opgave effectief aanneemt. Omdat h ( t ) steeds positief verondersteld is, is het praktisch bereik hier gelijk aan [ 0, α].
46
f Relatief maximum en minimum
Wanneer er een open interval ] a , b [ rond c bestaat waar geldt dat :
∀ x ∈ ] a , b [ \ { c }: f ( x ) < f ( c )
zeggen we dat de functie f een relatief maximum bereikt in c .
Wanneer er een open interval ] a , b [ rond c bestaat waar geldt dat :
∀ x ∈ ] a , b [ \ { c }: f ( x ) > f ( c )
zeggen we dat de functie f een relatief minimum bereikt in c .
g Absoluut maximum en minimum
Wanneer er een x -waarde c bestaat waarvoor geldt dat :
∀ x ∈ dom f : f ( x ) ⩽ f ( c )
zeggen we dat de functie f een absoluut maximum bereikt in c . Het absoluut maximum hoort dus bij het hoogste punt van de grafiek.
Wanneer er een x -waarde c bestaat waarvoor geldt dat :
∀ x ∈ dom f : f ( x ) ⩾ f ( c )
zeggen we dat de functie f een absoluut minimum bereikt in c . Het absoluut minimum hoort dus bij het laagste punt van de grafiek.
Maxima en minima heten extreme waarden. Merk op dat een extreme waarde een functiewaarde is en geen x -waarde.
Illustratie :
∀ x ∈ ] a , c [ \ { b }: f ( x ) > f ( b ) , maar f ( e ) < f ( b ) zodat f ( b ) niet kleiner is dan om het even welke f ( x ) met x ∈ dom f , voor x = b bereikt de functie dus een relatief minimum.
∀ x ∈ dom f : f ( x ) ⩾ f ( g ) , voor x = g bereikt de functie een absoluut minimum.
Ga na dat voor x = d de functie een relatief maximum bereikt en dat er geen absoluut maximum voor de functie bestaat.
Opmerking :
Later zullen we een algebraïsche methode ontwikkelen om de extrema van een functie te bepalen m.b.v. afgeleiden.
47 2 Veeltermfuncties
x
6 4 2 2 4 6 4 2 2 0 a • • b • • c • • d • • e • • g • • h • •
y
2Vuurpijlen schieten
Kasper heeft na zijn verjaardagsparty nog een vuurpijl over.
Hij vuurt die af vanuit zijn slaapkamer. De pijl vliegt eerst wat naar beneden maar gaat uiteindelijk toch de lucht in om na 5 seconden te ontploffen. De hoogte wordt beschreven door :
h ( t ) = t 3 – 4t 2 + 2t + 8met h ( t ): de hoogte in meter t : de tijd in seconden
Gevraagd :
– Hoeveel meter is de vuurpijl gestegen of gedaald na elke seconde ?
– Op welke hoogte ontploft de vuurpijl ?
– Wanneer is de vuurpijl op zijn laagste punt ?
Oplossing

– Merk op dat de x -as en de y -as loodrecht op elkaar staan, maar de eenheid op de x -as veel groter is dan de eenheid op de y -as. M.a.w. het assenstelsel waarin de grafiek van de functie getekend is, is wel orthogonaal maar niet georthonormeerd.
– Bepalen we eerst de hoogte h( t ) en de toename of afname ∆h( t ) na elke seconde. Om veranderingen aan te geven wordt vaak het symbool ∆ (‘delta’) gebruikt.
– De vuurpijl ontploft na 5 seconden. Dit is op een hoogte van 43 meter.
– Wanneer de vuurpijl op zijn laagste punt is, kunnen we nu (nog) niet exact berekenen. Vanuit de grafiek vermoeden we dat dit ongeveer na twee en een halve seconde moet zijn.
48
t (ins) h ( t ) (inm) 1 2 3 4 5 6 10 20 30 40 0 0 h ( t )= t 3 4 t 2 + 2 t + 8
:
t 0 1 2 3 4 5 h ( t ) 8 7 4 5 16 43 ∆h ( t ) –1 –3 1 11 27

























