Isaac-fysica D 5 - LB Kracht en Veld H1

KRACHT EN VELD

Aan de slag met ISAAC

ISAAC-fysica 5 is een methode fysica voor het vijfde jaar D-finaliteit van het secundair onderwijs voor de richtingen wetenschappen, Latijn-wiskunde, Grieks-wiskunde en economiewiskunde. De wetenschappelijke richtingen moeten meer leerstof zien, deze extra leerstof wordt aangeduid met een specifiek icoon (zie Legende pictogrammen). De methode kenmerkt zich door de sterke didactische aanpak en cursorische leerlijn. Met ISAAC-fysica verwerf je betrouwbare feitelijke kennis. Aan de hand van vele concrete voorbeelden uit de hedendaagse leefwereld en de duidelijke structuur draagt ISAAC bij tot een gemotiveerd en efficiënt leerproces.

Opbouw en aanpak

ISAAC-fysica 5 - Kracht en veld bestaat uit drie delen. In elk deel wordt de leerstof aangebracht via een gevarieerd aanbod aan thema’s. Elk deel behandelt een bepaald veld: gravitatieveld, elektrisch veld en magnetisch veld en de bijhorende kracht: gravitatiekracht, coulombkracht en lorentzkracht. Er worden regelmatig linken tussen de verschillende delen gelegd en gelijkenissen en verschillen worden telkens uitgelicht.

3 delen

Doorheen het leerboek vind je het diabolomodel van die Keure terug.

1Intro

Tijdens het ISAAC-moment , intro, maak je kennis met het thema. Nieuwsgierigheid en verwondering staan hierbij centraal.

2Midden

Tijdens de instructieweken verwerk je de leerstof via impressie en verwondering, instructie en inoefening. Elk deel wordt afgesloten met een onderdeel 'Verder oefenen?' waar de leerstof ingeoefend wordt. Daarna volgt ook telkens een studiewijzer zodat de leerlingen weten wat ze moeten kennen en kunnen na elk deel.

Volgende onderwerpen komen aan bod:

• Gravitatiekracht en gravitatieveld

• Coulombkracht en elektrisch veld

• Lorentzkracht en magnetisch veld

3Outro

De laatste lessen van het leerboek zijn voorbehouden voor de transferopdracht of de ISAAC-actie . Dat is een concrete en functionele opdracht die het leerboek afsluit.

Oefeningen

De theorie van elk deel wordt afgesloten met een reeks ‘Verder oefenen?’. De oefeningen werden opgedeeld in drie rubrieken:

• Begrijpen

Deze oefeningen helpen je om de leerstof beter onder de knie te krijgen en te begrijpen.

• Toepassen

Dit zijn concrete toepassingen uit het dagelijkse leven waarbij je leerstof verwerkt door ze toe te passen in een context. Deze oefeningen kregen een moeilijkheidsgraad:

makkelijk

gemiddeld

moeilijk

• Analyseren

Bij deze oefeningen ga je verder op zoek naar verbanden en relaties gerelateerd aan het onderwerp. Hier vallen vaak experimenten onder of uitgebreide oefeningen in een bepaalde context.

ISAAC digitaal

Doorheen het boek vind je QR-codes. Via die QR-codes kom je op de miniwebsite terecht. Daar vind je heel wat extra bronnenmateriaal.

Op POLPO vind je de uitgewerkte versie van het ISAAC-moment en de ISAAC-actie die in het leerboek opgenomen zijn. Daarnaast worden er ook extra ISAAC-momenten en -acties aangeboden. Indien relevant worden er ook blanco verslagbladen of experimentenfiches voorzien.

Legende pictogrammen

Deze pictogrammen vind je in het leerboek.

doe de test

Dit icoon duidt een experiment volgens de wetenschappelijke methode aan.

vastzettingskader

verwijskader

tip

besluit

WIST-JE-DAT wist-je-dat

uitbreiding wetenschappen

Dit duidt een vastzettingskader aan. Hier worden belangrijke en te kennen theorie/ formules in samengebald.

Een verwijskader verwijst naar een module of leerboek waar bepaalde theorie reeds gegeven werd of gegeven zal worden.

Dit lampje geeft een tip weer of geeft wat extra informatie.

Een besluitkader omvat een besluit of een conclusie, vaak na een experiment volgens de wetenschappelijke methode.

Een wist-je-dat is een leuk en interessant weetje, vaak komt hier ook wat extra informatie bij de theorie aan bod.

Dit icoon duidt leerstof aan die te kennen is voor de wetenschappelijke richtingen, maar niet voor de Latijn-wiskunde, Grieks-wiskunde en economie-wiskunde. Deze leerstof kan natuurlijk wel optioneel aan bod komen in deze richtingen.

Akkerbouw in de fysica

Nee, we gaan geen aardappelen, lavendel of maïs telen, maar de fysica zit toch vol velden. Enkele van deze velden zal je verder in dit boek voor het eerst tegenkomen, maar laten we eerst eens kijken wat deze velden in de fysica nu precies betekenen.

Scan de QR-code en bekijk de filmpjes.

Inleiding

Op de cover prijkt een gesimuleerde afbeelding van een zwart gat. Van zwarte gaten heb je waarschijnlijk wel al gehoord, maar heb je ook al van een accretieschijf gehoord? Dat is de lichtgevende schijf die je rond het zwarte gat ziet. Dergelijke accretieschijf ontstaat wanneer materie richting een sterk gravitationeel veld, zoals een massieve ster of een zwart gat, valt. Hoe dichter de invallende materie bij de ster of het zwarte gat komt, hoe sneller ze rond de ster of het zwarte gat begint te draaien. Daarnaast neemt de dichtheid aan deeltjes ook toe nabij het centrum, hierdoor neemt het aantal botsingen tussen de deeltjes toe en als gevolg daarvan warmt de invallende materie op en zendt ze x-stralen uit. Deze x-stralen kunnen dan waargenomen worden en gebruikt worden om zwarte gaten te lokaliseren, want, onthoud, een zwart gat zelf kunnen we niet direct waarnemen.

Op de coverafbeelding kan je trouwens nog een interessant fenomeen waarnemen. Naast de accretieschijf zie je ook een kegelvormige ‘stroom’ langsheen de draai-as van het zwarte gat. Dit noemen we een jet. Over het ontstaan van jets wordt nog wat gediscussieerd, maar dat ook jets uiterst interessante fenomenen zijn, staat buiten kijf.

Een kracht kunnen we niet zien, niet ruiken, niet vastpakken … Het enige wat we wel kunnen waarnemen, is het effect van een kracht.

Als we de uitwerking van een kracht bekijken, dan zijn er twee mogelijkheden:

Een kracht kan een vervorming veroorzaken. We spreken dan van de statische werking van een kracht.

Een andere mogelijkheid is dat de kracht een verandering van bewegingstoestand tot gevolg heeft, in dat geval heeft de kracht een dynamisch effect. We spreken dan van de dynamische werking van een kracht.

Dit vertaalt zich ook in de definitie van kracht:

Een kracht is een natuurkundige grootheid die ofwel een vervorming, ofwel een verandering van bewegingstoestand tot gevolg heeft.

Een kracht kan dus een statische of dynamische uitwerking hebben.

De eenheid van kracht is newton (N). De eenheid N (newton) dankt zijn naam aan de Engelse wetenschapper Sir Isaac Newton, ook wel de vader van de zwaartekracht genoemd.

Kracht is een vectoriële grootheid.

De krachtvector stellen we voor door het symbool #–F

De grootte van de kracht stellen we voor door F

Een kracht kan steeds trekken of duwen, bijvoorbeeld bij deze steen.

Voorbeeld

De grootte van de kracht geeft weer hoe hard de persoon duwt of trekt aan de steen. Als hij niet hard genoeg duwt of trekt, dan komt er geen beweging in de steen.

Om de grootte van een kracht te meten gebruiken we een dynamometer of een krachtsensor Daarop lezen we de grootte van de uitgeoefende kracht af in newton.

Als je aan een dynamometer trekt met een kracht van 1 N, voel je dat dit een kleine kracht is.

dynamometer

krachtsensor

© courtesy of PASCO scientific

De lijn is de richting waarin de kracht trekt of duwt.

De zin van de kracht geeft weer welke kant de kracht, en dus in het vorige voorbeeld de steen, uitgaat.

Het aangrijpingspunt van de kracht is de plaats waar de kracht aangrijpt, de plaats waar hij trekt of duwt.

In de fysica wordt een lichaam vaak voorgesteld door een punt, een puntmassa. Deze puntmassa ligt dan in het massamiddelpunt en bevat alle massa van het volledige lichaam. In dat geval grijpt de kracht natuurlijk aan in die puntmassa en is dat dus het aangrijpingspunt van de kracht.

We kennen heel wat verschillende krachten. De mens heeft dan ook heel wat namen gegeven aan die krachten.

Soms is die naam gekozen naar de werking die de kracht op een voorwerp heeft, zoals drukkracht, trekkracht of dwarskracht.

Vaak wordt de kracht echter vernoemd naar de oorzaak van de kracht, denk maar aan spierkracht, zwaartekracht, wrijvingskracht of veerkracht.

We noteren bij het symbool #–F dan ook meestal een subscript om duidelijk te maken over welke kracht het gaat. Zo wordt de veerkracht met #–Fv aangeduid.

Eigenlijk zijn alle krachten in de natuur terug te brengen tot slechts vier fundamentele krachten. Zij beheersen alles wat er in het universum gebeurt:

• gravitatiekracht

• zwakke kernkracht

• elektromagnetische kracht

• sterke kernkracht

Los van dit alles kunnen we krachten nog op een andere manier indelen:

Een kracht maakt soms rechtstreeks contact met het voorwerp, bijvoorbeeld als je een steen wegschopt of een skateboard in beweging brengt. We spreken dan van een contactkracht

Soms is er geen rechtstreeks contact tussen kracht en voorwerp nodig, de kracht werkt dan ‘vanop afstand’, zoals bij de zwaartekracht. In dat geval spreken we van een veldkracht.

Bij een contactkracht is er rechtstreeks contact met het voorwerp.

Bij een veldkracht is er geen rechtstreeks contact met het voorwerp.

Hier gaan we dieper in op de veldkrachten en de velden die aan de oorzaak liggen van deze veldkrachten.

We bestuderen de velden die ontstaan rond massa’s, ladingen en magneten. Zoals we zullen zien, vertonen deze velden gelijkenissen, maar ook verschillen. Daarnaast gaan we ook de krachtwerking in deze velden bekijken.

Veld

Een veld is eigenlijk een ruimte waar aan elke plaats in die ruimte een eigenschap toegekend is.

Neem bijvoorbeeld deze kaart van België.

Met elk punt wordt een temperatuur geassocieerd, dit is dus een temperatuurveld, wat een scalair veld is (temperatuur is immers een scalaire grootheid).

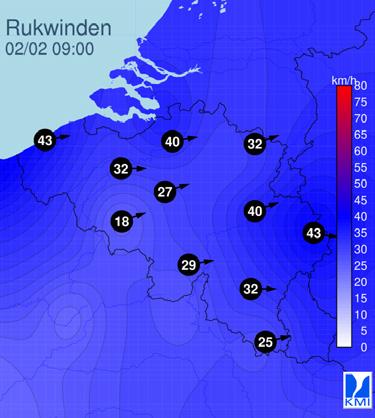
Er kan echter ook een andere eigenschap aan het veld gekoppeld zijn, zoals vochtigheid, bevolkingsdichtheid, gemiddelde leeftijd, druk …

Een veld kan ook vectorveld zijn. In dat geval is aan elke plaats een vector gekoppeld.

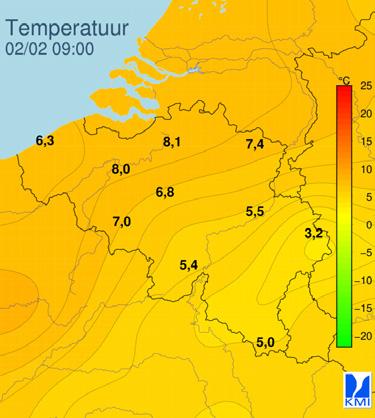
Neem bijvoorbeeld volgende kaart van België.

In dit veld wordt in elk punt de windrichting samen met de windsterkte weergegeven. Dit is een vectorveld, de windsnelheid is namelijk een vectoriële grootheid. In dit geval bezit elk punt naast een grootte ook een richting en zin.

De velden die wij gaan bestuderen zijn vectorvelden.

Scalaire en vectorvelden zijn trouwens niet de enige velden die bestaan, zo heb je ook spinorvelden of velden waar aan elk punt een functie of een toestand is geassocieerd.

1.1Geschiedenis van de gravitatie

De aarde, de hemellichamen, de sterren en het heelal intrigeren de mens al sinds mensenheugenis.

Tal van wetenschappers hebben doorheen de geschiedenis het heelal bestudeerd en beschreven. Ze ontwikkelden modellen die, in hun ogen, een correcte beschrijving gaven van het hoe en waarom van de bewegingen van hemellichamen. Het is fascinerend om te zien hoe deze modellen in de loop van de geschiedenis veranderden en aangepast werden tot wat wij, op dit moment, als het ‘correcte’ model beschouwen.

Het lijkt misschien onwaarschijnlijk, maar tot de vierde eeuw voor Christus was het idee van een platte aarde een heel normale opvatting. De beroemde filosoof Aristoteles (384 – 322 v.Chr.) ging daar tegenin en creëerde een geocentrisch model voor het zonnestelsel. In het midden van dit geocentrisch model staat dus de aarde die rond is. Planeten, sterren en andere hemellichamen zouden vastzitten op concentrische bollen die om de aarde heen draaien. De maan zou vastzitten op de bol het dichtst bij de aarde en de sterren op de buitenste bol. Alle planeten zouden aan een constante snelheid op bollen rond de aarde bewegen. Dit model kon echter niet de waargenomen bewegingen van de planeten verklaren.

Bekijk via de QR-code een korte animatie van Aristoteles’ geocentrisch wereldbeeld.

Het model van Aristoteles kon bijvoorbeeld niet de retrograde beweging (schijnbaar terugwaartse beweging) van de planeten verklaren.

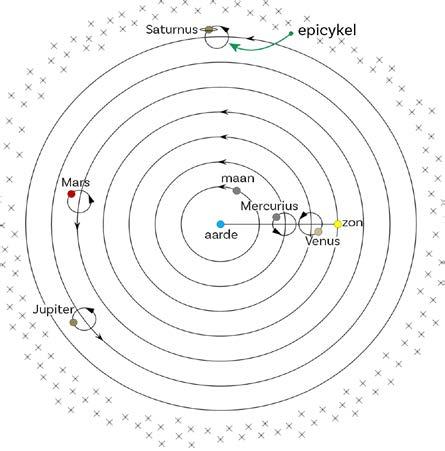
Claudius Ptolemaeus (87-150) loste dit in de tweede eeuw na Christus op door de planeten op een epicykel (hulpcirkel) te laten bewegen in hun baan om de aarde.

Via de QR-code kan je zien hoe hij op deze manier de retrograde beweging van planeten kon verklaren.

Ptolemaeus schreef zijn definitieve geocentrisch model en astronomische kennis neer in zijn Almagest dat tot in de 16e eeuw het belangrijkste sterrenkundige werk bleef.

Dat het geocentrisch model zo lang stand hield, ligt aan het feit dat de mens de aarde niet voelt bewegen en ogenschijnlijk lijken de zon en de hemellichamen nu eenmaal rond de aarde te draaien.

het geocentrisch model van Ptolemaeus

het geocentrisch model van Aristoteles

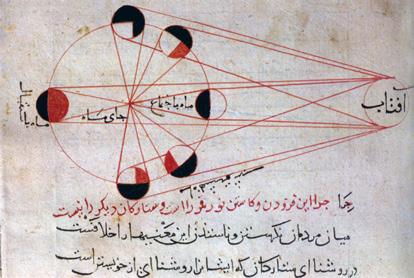
Toch was er rond 1000 na Christus al een vooruitstrevend genie Abu Reyhan AlBiruni (973 – 1048). Al-Biruni slaagde erin (bij benadering) de straal van de aarde te bepalen aan de hand van driehoeksmeetkunde. Hij dacht ook na over de mogelijkheid dat de aarde rond de zon zou draaien en beschreef op basis daarvan de zons- en maansverduistering die hij gedurende zijn leven ook waarnam.

Het was Nicolaas Copernicus (1473 – 1543) die in de 16e eeuw een nieuw theoretisch model vooropstelde, een model met de zon als centrum van het zonnestelsel, een heliocentrisch model. Copernicus plaatst de planeten hierbij opnieuw op ideale cirkels waarop de planeten een eenparig cirkelvormige beweging beschrijven.

De wetenschappelijke wereld kwam zo in de copernicaanse revolutie waarin klassiekreligieuze ideeën plaatsmaakten voor modernwetenschappelijke ideeën. In 1629 kon Galileo Galilei met behulp van een verbeterde sterrenkijker, door middel van waarnemingen, de theorie van Copernicus bevestigen.

Het is Johannes Kepler (1571 – 1630) die het copernicaanse model een eeuw later verfijnt met de introductie van ellipsvormige banen in plaats van cirkelvormige planeetbanen.

Wetten van Kepler

In het begin van de 17e eeuw schreef Johannes Kepler zijn drie wetten van Kepler. Deze wetten droegen bij tot de aanvaarding van het heliocentrisch wereldbeeld van Copernicus en verworpen het idee dat planeten altijd in cirkels rond de zon bewegen.

Eerste wet

De eerste wet van Kepler zegt dat alle planeten rond de zon bewegen in ellipsvormige banen. De zon bevindt zich daarbij in één van de brandpunten van de ellips.

Tweede wet

De tweede wet van Kepler wordt ook wel de perkenwet genoemd en zegt dat een planeet in gelijke tijdseenheden, gelijke oppervlakken doorloopt. De snelheid van de planeet verandert dus gedurende haar omloop rond de zon.

Derde wet

De derde wet van Kepler of de harmonische wet zegt dat het kwadraat van de omlooptijd T van een planeet evenredig is met de derde macht van haar halve lange as r:

= constant

Ook Isaac Newton (1643 – 1727) was een leidend figuur in de wetenschappelijke revolutie van de 17e eeuw. Newton bracht met zijn wetten van Newton en zijn algemene gravitatiewet een andere kijk op de wereld. Hij nam onder meer waar dat een lichaam met een zeer grote massa een merkbare zwaartekracht uitoefent op een lichaam met een veel kleinere massa, maar Newton realiseerde zich ook dat andere objecten in de buurt van de aarde, zoals de zon, de maan en de planeten, onderling een aantrekkingskracht op elkaar moeten uitoefenen, een onderlinge kracht die buitengewoon groot moet zijn, zelfs over grote afstand.

Normaal zouden hemellichamen in een rechte lijn bewegen, tenzij de aantrekkingskracht tussen hemellichamen deze banen afbuigt. Newton stelde dat deze kracht het lichaam met de minste massa in een baan rond het lichaam met de grootste massa zou trekken. Hij werkte een wiskundige vergelijking uit om deze bewegingen te kunnen beschrijven en onderzocht in hoeverre deze vergelijking op objecten in ons zonnestelsel van toepassing was. De omloopbanen van de planeten Mars, Jupiter en Saturnus kwamen precies overeen met de waargenomen posities.

Alle planetaire bewegingen, die reeds proefondervindelijk waren beschreven door de drie wetten van Kepler, konden nu worden afgeleid uit één fundamentele wet: de algemene gravitatiewet.

1.2Gravitatieveld

Elke massa m1 creëert rondom zich een gravitatieveld. Als een tweede massa m2 in dat gravitatieveld geplaatst wordt, ondervindt deze massa m2 een kracht, een gravitatiekracht.

Voor de meeste massa’s merken we niet veel van dit gravitatieveld of van deze gravitatiekracht. Enkel bij zeer grote massa’s, zoals planeten, wordt deze kracht waarneembaar. De reden wordt duidelijk als we de formule erbij nemen.

Elke massa creëert dus rondom zich een gravitatieveld. Dergelijk gravitatieveld is er dus ook rond de aarde. We kunnen dit veld niet zien, ruiken of voelen, maar we kennen dit gravitatieveld natuurlijk wel uit ervaring.

Door het gravitatieveld van de aarde vallen voorwerpen op aarde naar beneden en draait de maan rond de aarde. Andere massa’s hebben echter ook een gravitatieveld, het gravitatieveld van de maan merken we bijvoorbeeld aan de getijden.

Laten we dus eerst het gravitatieveld rondom één massa bekijken.

Het gravitatieveld rondom een bronmassa m1 koppelt aan elk punt in de ruimte een gravitatieveldsterkte. Deze gravitatieveldsterkte #–Eg is een vector, het gravitatieveld is dus een vectorveld.

De grootte van de gravitatieveldsterkte kunnen we berekenen met de formule:

Eg = G m1 r2

met:

G = 6,673 ⋅ 10 11 N ⋅ m2 kg2

m1 = de massa die het gravitatieveld veroorzaakt = bronmassa

r = de afstand tot het middelpunt van massa m1

Eg is een maat voor de sterkte van het gravitatieveld op een afstand r van het middelpunt van massa m1 en noemen we daarom de gravitatieveldsterkte.

GROOTHEID EENHEID NAAM SYMBOOLNAAMSYMBOOL

gravitatieveldsterkte Eg

De eenheid van gravitatieveldsterkte is N kg , wat overeenkomt met m s2

We merken hierbij op dat de gravitatieconstante G heel klein is, het gravitatieveld is daardoor slechts merkbaar voor een grote massa m1

De sterkte van het veld neemt ook kwadratisch af met de afstand tot het middelpunt van de massa (hier als een bol voorgesteld). De figuur hiernaast geeft dat effect duidelijk weer.

newton kilogram N kg = m s2

De gravitatieveldsterkte is een vectoriële grootheid en stellen we dus voor door een vector: #–Eg

#–Eg heeft naast een grootte dus ook een richting, zin en aangrijpingspunt.

Het gravitatieveld wordt vaak voorgesteld door gravitatieveldlijnen, zoals hiernaast weergegeven rondom de aarde. De pijl op de lijn geeft de zin van de gravitatieveldlijn aan.

De concentratie van de veldlijnen is een maat voor de sterkte van het veld. Hoe verder we van de aarde verwijderd zijn, hoe zwakker het veld wordt (de veldlijnen liggen namelijk steeds verder van elkaar als we verder van de aarde weg bewegen).

Een gravitatieveldlijn is een lijn die in elk punt de richting en zin van het gravitatieveld op die plaats weergeeft.

De gravitatieveldsterkte in een punt rondom de aarde heeft dezelfde richting en zin als de gravitatieveldlijn door dat punt. De grootte van de gravitatieveldsterkte berekenen we met de eerder gegeven formule.

Hoe verder van de aarde, hoe kleiner de vector #–Eg wordt. Op gelijke afstand van de aarde is de gravitatieveldsterkte dus even groot (we gaan er hierbij van uit dat de aarde een homogene sfeer is).

Dat de gravitatieveldsterkte afneemt als de afstand tot de bronmassa toeneemt, kunnen we als volgt uitleggen.

Kwadratenwet

Een belangrijke wet in de natuurkunde is de kwadratenwet, ook wel omgekeerde kwadratenwet genoemd. Deze wet geeft aan dat een grootheid omgekeerd evenredig is met het kwadraat van de afstand tot de bron van die grootheid. De kwadratenwet is zo belangrijk omdat dit verband voorkomt in tal van domeinen van de fysica, zoals hier bij het gravitatieveld, maar bijvoorbeeld ook bij ioniserende straling, elektrostatica, optica en akoestiek.

We bekijken dit even naderbij en beschouwen de veldlijnen van het gravitatieveld van een bronmassa (puntmassa of bol) (een analoge redenering geldt natuurlijk ook voor de andere domeinen van de fysica).

Beschouwen we de gravitatieveldlijnen die vertrekken uit de bronmassa, dan merken we dat, als we twee keer verder van de bron verwijderd zijn, we viermaal minder veldlijnen per oppervlakteeenheid waarnemen. Drie keer verder van de bron, nemen we negenmaal minder veldlijnen per oppervlakte-eenheid waar, enzovoort. Dit zien we duidelijk op onderstaande figuur.

Hoe groter de bronmassa, hoe meer gravitatieveldlijnen vertrekken uit de bron. Hoe groter de dichtheid van deze veldlijnen (= aantal veldlijnen per oppervlakte-eenheid), hoe sterker het gravitatieveld. We zien dat de dichtheid van de gravitatieveldlijnen omgekeerd evenredig is met het kwadraat van de afstand tot de bronmassa. Het oppervlak van de denkbeeldige bol rond de bronmassa neemt immers toe met het kwadraat van de afstand en de gravitatieveldlijnen uit de bron verdelen zich over dit oppervlak. De gravitatieveldsterkte is dus omgekeerd evenredig met het kwadraat van de afstand tot de bronmassa.

Bekijken we de aarde van dichterbij, dan zien we duidelijk dat de gravitatieveldlijnen naar het centrum van de aarde gaan. Dit is een radiaal veld. Voor iemand op het aardoppervlak lijkt het zelfs alsof de gravitatieveldlijnen evenwijdig zijn. We spreken dan van een homogeen veld

In het universum bevinden zich echter nog andere massa’s. Het veldlijnenpatroon voor een gravitatieveld dat uit meerdere massa’s bestaat, ziet er al snel veel complexer uit.

Als we de maan toevoegen aan het plaatje, krijgen we het veldlijnenpatroon zoals in de figuur hiernaast.

Ook in dergelijk veldlijnenpatroon kunnen we de gravitatieveldsterktes #–Eg tekenen. De richting en zin van #–Eg volgen ook hier de gravitatieveldlijn. Voor de grootte van #–Eg moeten we de verschillende componenten ten gevolge van de verschillende massa’s vectorieel bij elkaar optellen.

CC-SA 4 0 by MikeRun via Wikimedia Commons

Zodra er twee massa’s aanwezig zijn, speelt er ook een krachtwerking tussen deze massa’s. Deze krachtwerking noemen we de gravitatiekracht. Laten we dit even van naderbij bekijken.

1.3Gravitatiekracht

Twee massa’s m1 en m2 oefenen door hun massa een aantrekkingskracht op elkaar

uit: de gravitatiekracht #–Fg .

Voor de grootte van deze kracht geldt:

Fg = G ⋅ m1 ⋅ m2 r2

met:

r = de afstand tussen de middelpunten van de twee massa’s

G = de (universele) gravitatieconstante; G = 6,673 10 11 N ⋅ m2 kg2

Dit is de algemene gravitatiewet.

Isaac Newton beschreef deze kracht voor het eerst in 1687. Deze gravitatiewet maakt deel uit van de klassieke mechanica en werd voor het eerst geformuleerd in Newtons werk Philosophiae Naturalis Principia Mathematica dat hij op 5 juli 1687 publiceerde.

Aangezien we in de fysica massa’s vaak voorstellen door puntmassa’s, wordt de wet:

Elke puntmassa oefent een kracht uit op elke andere puntmassa.

Deze kracht is gericht langs de lijn die beide punten verbindt en is evenredig met het product van de massa’s en omgekeerd evenredig met het kwadraat van de afstand tussen beide massa’s.

Bovendien dient opgemerkt te worden dat deze kracht steeds een aantrekkende kracht is.

gravitatiekracht Fg newton N = kg m s2

De eenheid van gravitatiekracht is newton (N).

We kunnen de formule voor de grootte van de gravitatiekracht ook schrijven in functie van de gravitatieveldsterkte: F

We zien dus dat de gravitatiekracht de kracht is die massa m2 ondervindt in het gravitatieveld van massa m1. Dit is natuurlijk ook de kracht die massa m1 ondervindt in het gravitatieveld van massa m2:

De gravitatiekracht is de zwakste van de vier fundamentele krachten. De andere fundamentele krachten, namelijk de zwakke kernkracht, elektromagnetische kracht en sterke kernkracht zijn, in die volgorde, sterker. De gravitatiekracht heeft echter, net als de elektromagnetische kracht, een oneindig bereik (volgens de newtoniaanse zwaartekrachttheorie). De zwakke en sterke kernkracht hebben daarentegen een zeer kort bereik: buiten de atoomkern worden deze krachten zeer snel nul. Het grote bereik van de zwaartekracht is één van de redenen dat dit de dominante kracht is op astronomische schalen.

Volgende tabel geeft een idee van de relatieve sterktes van de fundamentele krachten en hun reikwijdte.

We merken hierbij nogmaals op dat de gravitatieconstante G heel klein is. De gravitatiekracht tussen voorwerpen is daardoor slechts merkbaar als minstens één van beide voorwerpen een grote massa heeft. We bekijken in wat volgt een paar voorbeelden.

1.3.1Gravitatiekracht tussen kleine massa’s op aarde

We berekenen de grootte van de gravitatiekracht tussen Arne (m1 = 15,3 kg) en Sofie (m2 = 13,8 kg) als ze zich 1,00 m van elkaar bevinden.

De grootte van de gravitatiekracht is:

Deze kracht is zo klein dat de kinderen er niets van merken.

WIST-JE-DAT

Zelfs als we de kinderen zouden vervangen door volwassen personen, zou deze kracht nog steeds minuscuul en niet waarneembaar zijn.

1.3.2Gravitatiekracht tussen de aarde en een persoon op aarde

We berekenen de grootte van de gravitatiekracht tussen de aarde (m1 = maarde = 5,976 1024 kg) en Jef (m2 = mJef = 81,4 kg). Als r gebruiken we de straal van de aarde, Jef bevindt zich immers op het aardoppervlak (r = 6371 km)

De grootte van de gravitatiekracht is:

= 799,7N = 800N

In dit geval is de gravitatiekracht wel waarneembaar. De massa van de aarde is dan ook aanzienlijk.

Als gevolg van deze gravitatiekracht wordt een persoon op aarde aangetrokken tot de aarde. Dit merken we bijvoorbeeld als we vanop een hoogte naar beneden springen: de aarde trekt ons daarbij eigenlijk naar beneden.

1.3.3Gravitatiekracht tussen de zon en de aarde

De gravitatiekracht is natuurlijk ook werkzaam tussen planeten en tussen de zon en planeten. We berekenen de grootte van de gravitatiekracht tussen de zon (m1 = mzon = 1,989 1030 kg) en de aarde (m2 = maarde = 5,976 1024 kg). De afstand tussen de aarde en de zon bedraagt 149,6 109 m

De grootte van de gravitatiekracht is:

We zien dat de gravitatiekracht tussen de aarde en de zon een aanzienlijke grootte heeft. Dit is ook het geval tussen andere hemellichamen in het universum.

WIST-JE-DAT

Planeten draaien in een baan rond de zon. Manen bewegen in een baan rond planeten. Wij, mensen, hebben satellieten de ruimte ingestuurd die rond de aarde draaien. Bij deze bewegingen speelt de gravitatiekracht een centrale rol.

Bekijken we bijvoorbeeld de beweging van de planeten rond de zon. Zowel de planeten als de zon hebben een aanzienlijke massa en oefenen dus een grote aantrekkingskracht uit op elkaar. Toch bewegen ze niet naar elkaar toe; hun gravitatiekracht zorgt immers niet voor een aantrekking (in de zin dat ze richting elkaar bewegen), maar zorgt voor een verandering van de bewegingstoestand van de planeten in hun baan rond de zon, meer bepaald voor de richtingsverandering van die beweging.

De gravitatiekracht neemt hier de functie van centripetale kracht.

Een centripetale kracht is de kracht die zorgt voor de richtingsverandering bij een eenparig cirkelvormige beweging.

In dit geval is het dus de gravitatiekracht die dient als centripetale kracht en die er dus voor zorgt dat de aarde in een ellipsvormige baan rond de zon beweegt. Het is ook net door de snelheid van de aarde dat de aarde niet naar de zon valt.

Intermezzo: de eenparig cirkelvormige beweging

We geven hier kort de theorie en de formules horende bij de eenparig cirkelvormige beweging. Deze zal je namelijk nodig hebben voor de oefeningen. In het zesde jaar wordt in ‘Kracht en verandering van beweging’ de eenparig cirkelvormige beweging of ECB uitvoerig behandeld.

Een eenparig cirkelvormige beweging of ECB is een eenparige beweging langs een cirkelvormige baan. De grootte van de snelheid is daarbij constant.

De ECB is dus eigenlijk net zoals de ERB, die je in de tweede graad leerde kennen, maar dan langs een cirkelvormige baan.

Het lichaam maakt zo een periodieke beweging, het volgt immers telkens opnieuw de baan van de cirkel. Ook de maan of een satelliet rond de aarde, of planeten rond de zon maken dus dergelijke periodieke beweging.

Bij periodieke bewegingen, en dus ook bij deze eenparig cirkelvormige beweging, definiëren we een periode en een frequentie:

De periode T is de duur van één cyclus (in seconden, s).

De frequentie f is het aantal cycli per tijdseenheid (in hertz, Hz) 1Hz = 1 s .

Hierbij geldt:

T = 1 f

Bij een ECB kunnen we twee snelheden definiëren:

De baansnelheid #–v : dit is de snelheid die we reeds kennen en in voorgaande figuren hebben voorgesteld. In het geval van een ECB raakt deze aan de cirkelvormige baan en is constant in grootte:

v = 2 π r T = 2 ⋅ π ⋅ r ⋅ f

waarbij:

r = de straal van de cirkel

T = de periode

f = de frequentie

De baansnelheid is een vectoriële grootheid die steeds rakend is aan de baan en waarvan de richting en zin dus steeds veranderen. De grootte van de snelheidsvector blijft echter constant gedurende heel de beweging.

De hoeksnelheid of pulsatie ω (Griekse letter omega): de hoeksnelheid geeft het verband tussen de doorlopen hoek en de tijd. Ze geeft weer welke hoek per tijdseenheid doorlopen wordt:

ω = 2 π T = 2 π f

waarbij:

T = de periode

f = de frequentie

De hoeksnelheid wordt uitgedrukt in graden seconden of radialen seconden ° s of rad s

De hoeksnelheid is een scalaire grootheid.

Er bestaat een eenvoudig verband tussen de baansnelheid en de hoeksnelheid:

v = ω r

Hoewel deze beweging eenparig (met andere woorden de grootte van de baansnelheid is constant) is, is er toch een kracht en dus ook een versnelling nodig om de richting van de beweging (en dus ook van de snelheid) bij te sturen. Zonder die kracht zou het lichaam zich voortbewegen volgens de raaklijn aan de cirkel en dus een eenparig rechtlijnige beweging, ERB, volgen. Dit is een gevolg van de eerste wet van Newton. Deze kracht noemen we de centripetale kracht.

De versnelling bij een ECB is steeds naar het middelpunt van de cirkel gericht en staat loodrecht op de snelheidsvector. De richting en zin van de versnellingsvector veranderen dus voortdurend, de grootte blijft echter wel constant en wordt gegeven door:

a = ω2 r = v2 r

Deze versnelling wordt de centripetale versnelling genoemd.

Een satelliet die met een constante snelheid rond de aarde cirkelt, ondervindt op elk moment deze centripetale versnelling. Dit houdt de satelliet in haar baan rond de aarde, maar heeft geen invloed op de snelheid van de satelliet.

De centripetale kracht bij een ECB wordt gegeven door:

Fcent = m ω2 r = m ⋅ v2 r

Ook de centripetale kracht is steeds naar het middelpunt van de cirkel gericht en staat loodrecht op de snelheidsvector. Net als bij de versnelling veranderen zijn richting en zin voortdurend, maar blijft de grootte wel constant.

Via de QR-code kan je een applet gebruiken waarin je een simulatie van de beweging van de aarde rond de zon kan bekijken. Door de ‘gravitatiekracht’ aan te vinken krijg je de gravitatiekracht die werkt op de aarde en de zon te zien.

WIST-JE-DAT

De AE of astronomische eenheid is een afstandsmaat die vrijwel gelijk is aan de gemiddelde afstand tussen de aarde en de zon. Deze afstandsmaat wordt in de astronomie gebruikt om afstanden in de ruimte aan te duiden. Sinds september 2012 is de AE gedefinieerd als exact 149597870700meter, bij benadering dus 149,6 109 m

1.3.4Gravitatiekracht tussen de aarde en de maan

We berekenen de grootte van de gravitatiekracht tussen de aarde (m1 = maarde = 5,976 ⋅ 1024 kg) en de maan (m2 = mmaan = 7,342 ⋅ 1022 kg). De afstand tussen de aarde en de maan bedraagt 384400 km

De grootte van de gravitatiekracht is:

Ook hier zorgt de gravitatiekracht ervoor dat de maan in zijn baan rond de aarde blijft. De gravitatiekracht dient hier ook als centripetale kracht.

Doordat de maan enerzijds een snelheid heeft en anderzijds naar de aarde wordt toegetrokken door de gravitatiekracht, valt de maan niet op de aarde en kan ze ook niet ontsnappen. Ze blijft dus mooi op haar baan rond de aarde.

Getijden op aarde

De gravitatiekracht die de maan op de aarde uitoefent, is grotendeels verantwoordelijk voor de getijden die we waarnemen in zeeën en oceanen (de zon levert een kleinere bijdrage aan deze getijden). Over hoe deze getijden precies ontstaan, bestaan er echter veel misvattingen.

Scan de QR-code om een correcte uitleg over het ontstaan van de getijden op aarde te weten te komen.

1.4Zwaartekracht en zwaarteveldsterkte

In de buurt van een planeet wordt de gravitatiekracht zwaartekracht genoemd, zoals wij ook gedaan hebben in de tweede graad. De term zwaartekracht beperkt zich niet tot de aarde, maar wordt ook voor andere planeten of manen gebruikt. Zo spreken we bijvoorbeeld ook van de zwaartekracht op Mars of op de maan.

De term zwaartekracht wordt wel enkel in de nabije omgeving van de planeet gebruikt.

De formule voor zwaartekracht wordt meestal als volgt geschreven:

Fz = m g

We weten ondertussen dat deze ook anders kan geschreven worden (als voorbeeld nemen we de formule voor de zwaartekracht op aarde):

Fz = Fg,aarde

m g = G ⋅ maarde ⋅ m r2

g = G maarde r2

Waarbij de massa m zich in de buurt van de aarde bevindt en met:

g = zwaarteveldsterkte in N kg

G = de (universele) gravitatieconstante; G = 6,673 ⋅ 10 11 N m2 kg2

maarde = de massa van de aarde; maarde = 5,976 1024 kg

r = de straal van de aarde (6371 km)

De grootheid g is een maat voor de ‘sterkte’ van het zwaarteveld van de aarde, vandaar de naam zwaarteveldsterkte.

We zien dat we in de formule voor de zwaarteveldsterkte, de formule voor de gravitatieveldsterkte terugvinden, maar dan met m1 = maarde

Aangezien de aarde niet perfect rond is (en de straal r van de aarde dus varieert), is de zwaarteveldsterkte op aarde niet overal even groot:

in België is g gelijk aan 9,81 N kg

aan de noordpool is g gelijk aan 9,83 N kg

aan de evenaar is g gelijk aan 9,78 N kg

Hoe verder van het middelpunt van de aarde verwijderd, hoe kleiner de zwaarteveldsterkte g

De zwaarteveldsterkte is een vector, we stellen #–g dan ook voor met een pijl die naar het middelpunt van de aarde gericht is.

Naast de afstand tot het middelpunt van de aarde, spelen eigenlijk nog tal van andere factoren een rol in de grootte van de zwaarteveldsterkte, zoals de aardrotatie en de samenstelling van de aarde. De NASA heeft op basis van een onderzoek (GRACE mission) de sterkte van het zwaarteveld weergegeven in een computermodel van de aarde.

In de afbeelding hiernaast hebben de blauwe gebieden een zwakker zwaarteveld terwijl de rode gebieden een sterker zwaarteveld kennen. We kunnen dus duidelijk de verschillen in de zwaarteveldsterkte op aarde zien.

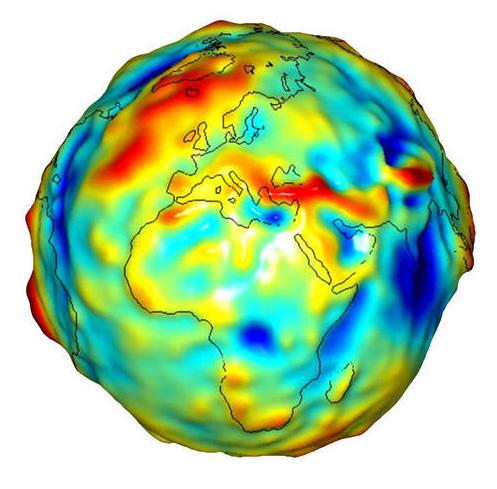
Wil je meer lezen over de GRACE mission of zwaartekracht in het algemeen? Breng dan eens een bezoekje aan de NASA website.

Met de formule:

g = G ⋅ maarde r2

kunnen we de zwaarteveldsterkte berekenen op elke gewenste hoogte.

Voor een voorwerp op een hoogte h boven het aardoppervlak wordt de formule dus:

g = G maarde r2

= G maarde (ra + h)2

WIST-JE-DAT

met:

ra = de straal van de aarde (6371 km)

h = de hoogte boven het aardoppervlak

De zwaartekracht laat voorwerpen op aarde vallen.

Een eeuwenoud verhaal vertelt hoe de beroemde natuurkundige Isaac Newton op een dag mijmerend onder een appelboom zit en plots een appel op zijn hoofd krijgt, wat Newton aan het denken zet. Volgens de legende zou dit voorval uiteindelijk geleid hebben tot Newtons algemene gravitatiewet.

De val van voorwerpen op aarde zette niet alleen Newton aan het denken. Het is een mysterieus gegeven waar heel wat wetenschappers in de loop van de geschiedenis van wakker gelegen hebben. Heel wat valproeven werden uitgevoerd, in het echt of als gedachtenexperiment, met de bedoeling om de val van voorwerpen te doorgronden. We overlopen de belangrijkste.

Aristoteles beweerde dat zware voorwerpen sneller vallen dan lichte voorwerpen.

Giambattista Benedetti weerlegde de valwet van Aristoteles op basis van een gedachtenexperiment in 1585. In gedachten liet hij twee gelijkvormige, congruente voorwerpen van dezelfde stof, die verbonden zijn door een verbinding van verwaarloosbare massa, naast elkaar vallen. Het zo verkregen voorwerp met een dubbele massa zou volgens Aristoteles tweemaal sneller moeten vallen dan de voorwerpen los van elkaar, zonder verbinding. Zonder verbinding vallen ze naast elkaar naar beneden met een bepaalde snelheid, met verbinding zouden ze dus naast elkaar vallen met een dubbel zo grote snelheid. De verbinding heeft echter een verwaarloosbare massa en is het enige verschil tussen de twee situaties, dit kan dus niet verklaren waarom de twee voorwerpen in het ene geval dubbel zo snel zouden vallen. Hieruit concludeerde Benedetti dat Aristoteles fout zat en dat de valsnelheid van voorwerpen met dezelfde dichtheid niet evenredig kan zijn met hun massa.

Rond 1590 zou de Italiaanse wetenschapper Galileo Galilei twee bollen van hetzelfde volume, maar met verschillende massa’s van de scheve toren van Pisa hebben laten vallen om aan te tonen dat hun valtijd onafhankelijk van hun massa is. Volgens het verhaal ontdekte Galileo door dit experiment dat alle objecten met dezelfde versnelling vallen.

Een soortgelijk experiment werd uitgevoerd in Delft door de wiskundige en natuurkundige Simon Stevin en Jan Cornets de Groot. De wetenschappers lieten twee loden bollen, de ene tien keer groter en zwaarder dan de andere, van 30 voet hoog vallen. Ze constateerden dat beide bollen gelijktijdig op de grond vielen. Dit experiment zou ten laatste in 1586 uitgevoerd zijn.

Zoals vaker in die tijd, was het eigenlijk niet helemaal duidelijk welke wetenschapper als eerste de valproef uitvoerde en daar de correcte conclusies uit trok. Toch wordt de valproef steeds toegeschreven aan Galileo Galilei.

Ook in de recente geschiedenis blijft de valbeweging iets dat wetenschappers boeit.

Ondertussen weten we ook waarom de valversnelling onafhankelijk is van de massa van het voorwerp. Als we de formule voor de valversnelling bekijken:

dan zien we dat de massa van het voorwerp hier niet in voorkomt.

1.5Massa en gewicht

Laten we ook nog even de grootheid gewicht bekijken.

We behandelden de grootheid gewicht reeds in de tweede graad in de module ‘Kracht en veld’.

In de volksmond worden de termen massa en gewicht regelmatig met elkaar verward. Dit zagen we al in de tweede graad toen opa het gewicht van oma wou weten. Eigenlijk wou opa dan haar massa te weten komen, maar dat bleef een diep bewaard geheim.

De zwaartekracht trekt elk voorwerp op aarde naar de aarde toe. Hierdoor oefent een voorwerp dat ondersteund wordt een kracht uit op zijn steun. Deze kracht noemen we het gewicht #–FG .

Als het voorwerp opgehangen is, dan oefent het een gewicht uit op zijn ophangpunt.

In de afbeelding zien jullie het gewicht van de jas en van de bloempot.

Als de steun of het ophangpunt een weegschaal of een dynamometer is, kan je de grootte van het gewicht onmiddellijk aflezen.

Bij een dynamometer lees je het gewicht in newton af, wat de correcte eenheid voor gewicht is.

Op de weegschaal wordt de newton omgerekend naar kilogram, waardoor we daar een massa aflezen.

Massa en gewicht zijn dus twee verschillende grootheden.

#–FG

#–FG

#–FG

#–FG

De massa m van een voorwerp is een maat voor de hoeveelheid materie en wordt uitgedrukt in kilogram (kg).

Het gewicht #–FG van een voorwerp is de kracht die het voorwerp door zijn zwaartekracht uitoefent op zijn steun.

Het symbool voor gewicht is #–FG

De grootte van het gewicht wordt aangeduid met #–FG

De eenheid van gewicht is de newton (N).

De aarde op de weegschaal

Als wij onze massa willen weten, gaan we gewoon op de weegschaal staan. De massa van de aarde bepalen, is daarentegen niet zo eenvoudig. Gelukkig hebben we de algemene gravitatiewet waarmee we de massa van de aarde kunnen bepalen. Ook Newton was benieuwd naar deze massa, maar in zijn tijd was de waarde van de gravitatieconstante G nog niet gekend. Newton zou Newton echter niet zijn als hij ook daarvoor geen ingenieus idee had.

Hoe Newton uiteindelijk de massa van de aarde bepaalde, kom je te weten in ‘Verder oefenen?’ bij ‘Analyseren’.

Een vallend lichaam is niet onderhevig aan een ondersteuning of ophanging en is dus gewichtloos

Gewichtloosheid

De toestand van gewichtloosheid doet zich voor in situaties waarin een lichaam geen gewicht ervaart, het lichaam heeft dus geen punt van ondersteuning of ophanging.

Dit doet zich voor tijdens een vrije val. Alhoewel de zwaartekracht op dat moment wel werkt op het lichaam, voel het lichaam de gevolgen van die zwaartekracht niet. Aangezien dit een heel bijzonder gevoel is, willen heel wat mensen dergelijke vrije val ervaren. Ze gaan bungeejumpen, doen een parachutesprong of maken een paraboolvlucht. Pretparkbouwers spelen hier ook op in door ‘vrije val’-attracties te bouwen.

Ook in de ruimte ervaren we deze gewichtloze toestand. Buiten de dampkring ervaren astronauten gewichtloosheid wanneer er geen raketmotor meer aanstaat; hun versnelling is op dat moment dezelfde als die van het ruimtetuig. Ondanks wat je misschien zou verwachten, ervaren ze daar wel nog de zwaartekracht, deze is maar een fractie kleiner dan op aarde. Het ruimtetuig en de astronauten zijn eigenlijk in vrije val, de enige kracht die op hen inwerkt, is de zwaartekracht en er is geen punt van ophanging of ondersteuning. Toch vallen het ruimtetuig en de astronauten niet naar de aarde: door hun grote snelheid bewegen ze op een cirkelvormige baan rond de aarde. De zwaartekracht is hier opnieuw een centripetale kracht.

Dat gewichtloosheid in is, bewijst ook de Amerikaanse rockband ‘ok go’. Deze band nam immers hun videoclip op in gewichtloosheid. Benieuwd? Scan dan de QR-code.

WIST-JE-DAT

Paraboolvluchten

Vroeger was het ervaren van gewichtloosheid in een paraboolvlucht enkel weggelegd voor astronauten en wetenschappers, maar sinds 2013 zijn deze zelfs in Europa toegankelijk voor het brede publiek. Bij dergelijke uitstap hoort wel een prijskaartje van enkele duizenden euro’s.

Tijdens een paraboolvlucht vliegen vliegtuigen in een paraboolbaan, waardoor ze gedurende zo’n 20 seconden een toestand van gewichtloosheid creëren, ook wel micrograviteit, microzwaartekracht of zero-g genoemd. De passagiers ervaren op die manier hetzelfde gevoel als astronauten in de ruimte.

Door de motoren tijdelijk uit te schakelen komt het vliegtuig in het parabolisch gedeelte in een toestand van vrije val. De zwaartekracht is daarbij zo goed als 0 g en de passagiers worden gewichtloos.

Net voor en net na de gewichtloosheid ervaren de passagiers ook een hyper-zwaartekracht, waardoor ze zich bijna twee keer zo zwaar voelen als normaal.

Een vlucht met een paraboolvliegtuig beperkt zich niet tot een eenmalige ervaring van gewichtloosheid. Tijdens dergelijke vlucht worden meestal dertig parabolen gevlogen, die elk zo’n 20 seconden duren.

1.6Einsteins gravitatie

Albert Einstein staat bekend om zijn baanbrekende theorieën. Wat hem echter echt bijzonder maakte, is dat hij op een totaal andere manier dan de meeste wetenschappers zijn theorieën opbouwde. Hij hield bijvoorbeeld niet van ingewikkelde wiskundige afleidingen, maar was meer fan van zogenaamde gedachtenexperimenten. Hierbij stelde hij zich experimenten visueel voor in zijn hoofd en werkte ze zo uit. Dit visueel denkproces zie je bijvoorbeeld in een filmfragment uit ‘genius’.

Alhoewel Einstein in zijn relativiteitstheorie de gekste dingen voorspelt, blijkt zijn in 1905 gepubliceerde artikel over de relativiteitstheorie goed leesbaar en begrijpbaar zonder te veel moeilijke wiskunde.

Voor wat gravitatie betreft, interpreteert de relativiteitstheorie deze geometrisch in tegenstelling tot de newtoniaanse interpretatie die gravitatie als krachtvectoren ziet. De algemene relativiteitstheorie verschilt op heel wat punten van newtoniaanse zwaartekracht. De relativiteitstheorie zegt bijvoorbeeld dat niks sneller dan het licht kan gaan en dat de snelheid van het licht constant is, dit in tegenstelling tot Newton die dacht dat ‘informatie’ een oneindige snelheid had. Als je bijvoorbeeld de zon zou wegnemen uit ons zonnestelsel, dan zou Newton zeggen dat we dit onmiddellijk zouden merken. Einstein zegt daarentegen dat we dit pas na een achttal minuten zullen merken, zo lang duurt het namelijk voordat het licht van de zon ons bereikt; verder zegt Newton dat massa de oorzaak is van gravitatie, volgens Einstein moet dit energie zijn: hierdoor zijn ook de massaloze fotonen onderhevig aan de zwaartekracht.

CC-SA 4.0 by MikeRun via Wikimedia Commons

De algemene relativiteitstheorie van Einstein verklaart heel wat zaken in het universum die de gravitatietheorie van Newton niet of slecht beschrijft. Zo voorspelt de relativiteitstheorie het bestaan van zwarte gaten en beschrijft ze de satelliet- en planeetbanen in ons zonnestelsel veel nauwkeuriger. Daar waar de gravitatiewet van Newton het laat afweten, bieden de Einsteinvergelijkingen wel een oplossing. Dit wil echter niet zeggen dat we Newton met het badwater moeten weggieten: voor de meeste ‘normale’ situaties biedt de gravitatiewet van Newton een correct antwoord, bovendien is het rekenwerk dat eraan verbonden is veel eenvoudiger dan bij de Einsteinvergelijkingen.

1.6.1Einsteinvergelijkingen

Het model ontwikkeld door Newton houdt dus stand voor de meeste ‘normale’ situaties, maar bij zeer zware objecten en bij sommige planetaire bewegingen klopt zijn model niet meer. Einstein ontwikkelde een nieuw model dat wel klopt in deze uitzonderlijke gevallen.

Het model van Einstein wordt tegenwoordig als het meest accurate model voor gravitatie beschouwd, maar misschien dat toekomstig onderzoek ook hier verandering in brengt. De toekomst zal dat moeten uitwijzen.

De afbeelding toont trouwens de Einsteinvergelijking op een muur in de Nederlandse stad Leiden.

De grootheid die hier helemaal rechts staat (Tμν), is de energie-momentumtensor. Deze zegt hoeveel massa en energie er op een bepaalde plaats in de ruimte aanwezig is. Het object links, namelijk:

Rμν 1 2 Rgμν

wordt ook wel als Gμν genoteerd. Dit noemen we de Einsteintensor.

Als deze Gμν niet nul is, dan wil dat zeggen dat de ruimte gekromd is. In de ruimte waar zich zware objecten bevinden (zoals sterren) is veel massa en energie aanwezig. Volgens de Einsteinvergelijking is de kromming op die plaatsen groot. Hierdoor is de baan van objecten (zoals de aarde) niet meer rechtdoor, maar afgebogen. Ook licht beweegt rond deze zware objecten niet meer rechtlijnig, maar wordt afgebogen volgens de kromming van de ruimte. Deze afbuiging van licht werd in 1919 voor het eerst waargenomen tijdens een zonne-eclips en werd beschouwd als een experimentele bevestiging van Einsteins theorie.

De essentie van Einsteins algemene relativiteitstheorie is simpel: Einsteins theorie zegt dat de aanwezigheid van een massa of energie de structuur van de ruimtetijd vervormt. Hoe groter de massa, hoe groter de kromming. Hoe dichter je de massa nadert, hoe groter de kromming wordt. Een veelgemaakte analogie is om je een trampoline voor te stellen waarop je een zware bal in het midden legt. De trampoline zal door de massa doorbuigen.

CC-SA 4.0 by Vysotsky via Wikimedia Commons

In het zonnestelsel staat Mercurius het dichtst bij de zon. Mercurius ervaart dus ook het meest de kromming in de ruimtetijd als gevolg van de massa van de zon. Hierdoor kon de baan van Mercurius niet volledig verklaard worden door Newtons gravitatiewet. Men had de Einsteinvergelijkingen nodig om de geobserveerde baan van Mercurius te beschrijven, aangezien hierin de afwijkingen in de ruimtetijd in rekening werden gebracht.

De legende doet de ronde dat Einstein van puur geluk dagenlang niet in staat was om te werken toen hij erin slaagde om de geobserveerde baan van Mercurius perfect te voorspellen. Ook dit was immers een experimentele bevestiging van zijn theorie.

Wil je meer te weten komen over hoe Einstein gravitatie interpreteert versus Newtons interpretatie? Bekijk dan het filmpje via de QR-code.

1.6.2Zwaartekrachtgolven

Op basis van zijn algemene relativiteitstheorie voorspelde Einstein in 1916 het bestaan van zwaartekrachtgolven. Hij zag deze als een fluctuatie in de kromming van de ruimtetijd. Zoals een golf plant deze fluctuatie zich vanuit de bron voort (aan de lichtsnelheid).

Het bestaan van deze zwaartekrachtgolven werd ongeveer een eeuw later, op basis van directe waarnemingen op 14 september 2015 door het LIGO-project, bevestigd.

In 2017 ontvingen de Amerikanen Rainer Weiss, Barry Barish en Kip Thorne de Nobelprijs voor de waarneming van zwaartekrachtgolven.

Dergelijke zwaartekrachtgolven treden onder andere op bij supernova’s of als twee heel zware hemellichamen op korte afstand om elkaar heen draaien, zoals bij dubbelsterren of zwarte gaten.

In 2015 werden zwaartekrachtgolven waargenomen die uitgezonden werden door twee zwarte gaten die heel snel (met een snelheid met een grootteorde gelijk aan de helft van de lichtsnelheid) om elkaar draaiden. De zwaartekrachtgolven werden ook sterker naarmate de draaibeweging sneller werd. Uiteindelijk gingen de twee zwarte gaten steeds dichter langs elkaar bewegen en ten slotte versmolten ze tot één groter zwart gat. De totale massa van dit nieuw zwart gat was niet gelijk aan de som van de massa’s van de twee oorspronkelijke zwarte gaten, een deel van de massa werd immers omgezet in energie die via de zwaartekrachtgolven werd weggedragen.

Tijdens de waarneming van de zwaartekrachtgolf in 2015 was deze trouwens ook hoorbaar, vandaar de titel van de uiteenzetting ‘Wat hoorden we voor het eerst knetterhard uit het heelal op 14 september 2015?’ die je via de QR-code kan bekijken en beluisteren.

Via de QR-code kan je ook een simulatie bekijken van het samensmelten van twee zwarte gaten en de bijhorende zwaartekrachtgolven.

Ondertussen wordt verder onderzoek gedaan. Daaruit zal moeten blijken of het model dat Einstein in 1916 ontwikkelde, zal standhouden bij nieuwe waarnemingen van zwaartekrachtgolven of dat het nog bijgestuurd moet worden.

Duidelijk is dat de fysica niet stilstaat, het blijft altijd spannend welke theoretische modellen standhouden bij nieuwe waarnemingen en welke tekortschieten.

Wil je graag een op Einstein gebaseerd uitstapje doen? In Leiden kan je een fietstocht maken langs de muurschilderingen met de Einsteinvergelijkingen, daarnaast kan je ook het Lorentzhuis bezoeken en een Einsteinmenu bestellen.

Meer lezen over het Leiden van Einstein? Scan dan de QR-code.

1.7Gravitatiepotentiaal

Een massa in het gravitatieveld van een andere massa (bronmassa) ondervindt een gravitatiekracht en zal als gevolg daarvan naar de bronmassa willen bewegen. Dit vereist energie, een massa in een gravitatieveld bezit dus de mogelijkheid om arbeid te verrichten; de massa bezit gravitatie-energie (dit is een potentiële energie). De gravitatiepotentiaal drukt uit hoeveel gravitatie-energie een eenheidsmassa (een massa van 1 kg) in een bepaald punt van het gravitatieveld bezit. Deze geeft dus een indicatie van hoe graag een massa van 1 kg naar de bronmassa wil bewegen om zo zijn gravitatiepotentiaal te verlagen.

Alle punten, even ver van een bolvormige massa gelegen, hebben dezelfde gravitatiepotentiaal Vg

Al deze punten met dezelfde gravitatiepotentiaal liggen op equipotentiaallijnen. Rond een bolvormige massa zijn deze equipotentiaallijnen dus concentrische cirkels. In onderstaande figuur worden deze voorgesteld door stippellijnen.

equipotentiaallijn

De gravitatiepotentiaal Vg in een punt P van het gravitatieveld wordt gedefinieerd als de arbeid die nodig is om een eenheidsmassa vanop oneindig in dat punt P te plaatsen.

Deze arbeid is negatief, want de bronmassa trekt de eenheidsmassa aan. De gravitatiepotentiaal is dus een energie per eenheid van massa.

De gravitatiepotentiaal wordt gegeven door de formule:

Vg = G ⋅ m1 r

met:

G = de (universele) gravitatieconstante; G = 6,673 ⋅ 10 11

N m2 kg2

m1 = de massa die het gravitatieveld veroorzaakt = de bronmassa

r = de afstand van het middelpunt van de bronmassa tot het punt waarin we de gravitatiepotentiaal berekenen

Het punt op oneindig heeft een gravitatiepotentiaal van 0 J kg , we nemen dat punt als referentiepunt.

Een potentiaal bereken je altijd ten opzichte van een referentiepunt. Enkel potentiaalverschillen hebben namelijk een fysische betekenis.

gravitatiepotentiaal Vg

De eenheid van gravitatiepotentiaal is J kg

De gravitatiepotentiaal is een scalaire grootheid.

De verandering in gravitatiepotentiaal ΔVg geeft de arbeid weer die moet geleverd worden om een eenheidsmassa te verplaatsen van een punt naar een ander punt in het gravitatieveld. Als deze arbeid nul is, dan liggen de twee punten op eenzelfde equipotentiaallijn.

Rond de aarde zijn de equipotentiaallijnen cirkels, er moet dus geen arbeid geleverd worden om een massa te verplaatsen langsheen die cirkel. De equipotentiaallijnen zijn hieronder weergegeven door middel van stippellijnen. Rondom een andere bolvormige massa krijg je een analoog beeld.

gravitatieveldlijn

equipotentiaallijn

1.8Gravitatie-energie

Op een analoge manier kunnen we ook de gravitatie-energie definiëren.

De gravitatie-energie is de arbeid die nodig is om een massa m2 vanop oneindig naar een punt P in het gravitatieveld te brengen:

Egrav = G ⋅ m1 ⋅ m2 r

waarbij:

G = de (universele) gravitatieconstante; G = 6,673 ⋅ 10 11 N ⋅ m2 kg2

m1 = de bronmassa

m2 = de massa die vanop oneindig naar een punt P in het gravitatieveld wordt gebracht

r = de afstand van het middelpunt van de bronmassa tot het punt waarin we de gravitatie-energie berekenen

We zien dus dat:

Egrav = Vg m2

Het punt op oneindig heeft een gravitatie-energie gelijk aan 0 J, we nemen dat punt als referentiepunt.

De eenheid van gravitatie-energie is J

Gravitatie-energie is een scalaire grootheid.

De gravitatie-energie is steeds negatief, dat zien we aan de formule.

Als we de gravitatie-energie van een voorwerp op het aardoppervlak berekenen, dan vinden we een negatief getal. Naarmate we het voorwerp verder van het aardoppervlak verwijderen, wordt deze waarde groter (kleiner negatief getal) om ten slotte op oneindig 0 J te worden.

Als we een massa m2 verplaatsen in het gravitatieveld van m1, dan moeten we arbeid leveren.

Deze arbeid is positief als een lichaam met massa m2 , over een afstand h, van het lichaam met massa m1 verwijderd wordt:

W = m2 ⋅ g ⋅ h

En deze arbeid is negatief als het lichaam met massa m2, over een afstand h, naar het lichaam met massa m1 toe beweegt (bijvoorbeeld vanop een hoogte h boven het aardoppervlak naar het aardoppervlak):

W =–m2 g h

We kunnen de formule voor deze arbeid als volgt afleiden. Stel dat we een massa m2 vanaf het aardoppervlak naar een hoogte h boven het aardoppervlak brengen. De geleverde arbeid is het verschil in gravitatie-energie tussen deze twee punten. We stellen de straal van de aarde voor met rA en de massa van de aarde noteren we als mA. We hebben dan: W

In de overgang van lijn 9 naar lijn 10 in voorgaande afleiding gebruiken we volgende benadering: 1 + h rA

1 = 1 h rA

Dit is geldig als: h r

Dergelijke vereenvoudigingen worden zeer vaak gebruikt in de fysica. Deze komen trouwens niet uit de lucht vallen, maar zijn wiskundig onderbouwd. We noemen dit ook wel een eerste orde Taylorbenadering.

Ben je benieuwd naar de wiskundige motivatie hierachter? Google dan zeker eens op Taylorreeksen of binomium van Newton.

We vinden op deze manier dus de formule terug voor de zwaarte-energie die we in de tweede graad reeds definieerden. Nu begrijpen jullie ook de herkomst van deze formule.

De term zwaarte-energie gebruiken we enkel in de nabijheid van planeten (in dit geval de aarde), analoog aan de term zwaartekracht en zwaarteveldsterkte. Gravitatie-energie wordt algemeen gebruikt. h m

Scan de QR-code en leer meer over gravitatie-energie.

WIST-JE-DAT

Opmerking

Deze formule voor de arbeid in een gravitatieveld is enkel geldig in de buurt van het betreffende hemellichaam, meer bepaald als de hoogte h klein is in vergelijking met de straal van het hemellichaam. Dit zagen we ook al in de afleiding van deze formule waar we de Taylorbenadering gebruikten die enkel geldig is als h ≪ rA

Als we ons niet in de buurt van het hemellichaam bevinden, moeten we een algemenere formule voor arbeid gebruiken.

In het vierde jaar bespraken we in module 1 ‘Energieomzettingen’ al arbeid.

In de tweede graad definieerden we arbeid als de energie die nodig is om een voorwerp met een bepaalde kracht over een bepaalde afstand te bewegen. We beperkten ons daarbij tot een constante kracht. Wel bekeken we de mogelijkheid dat kracht en verplaatsing niet op dezelfde werklijn liggen, wat ons volgende formule gaf:

W = F Δx cos α

Als de kracht en de verplaatsing dezelfde richting en zin hebben, wordt dit:

W = F Δx

In een F(x)-grafiek kon de arbeid dan bepaald worden als de oppervlakte onder de F(x)-curve.

In het gravitatieveld hebben we echter geen constante kracht. De gravitatiekracht is namelijk omgekeerd evenredig met het kwadraat van de afstand tot de bronmassa. De F(x)-curve is dan geen horizontale rechte meer, maar de arbeid kan nog steeds bepaald worden als de oppervlakte onder de F(x)-curve. We berekenen de arbeid dan met behulp van een integraal. In het zesde jaar zal je in de wiskunde leren dat een integraal van een bepaalde functie de oppervlakte onder die functie weergeeft en zal je leren hoe je deze integralen moet uitrekenen. Hier doen we het rekenwerk voor jou.

We berekenen de arbeid die een ruimtetuig moet leveren om te ontsnappen uit het gravitatieveld van de aarde. We moeten dus de oppervlakte onder de Fg(r)-grafiek bepalen tussen rA (de straal van de aarde, vanwaar het ruimtetuig vertrekt) en oneindig (∞, daar wordt het gravitatieveld van de aarde nul).

Deze algemene formule voor arbeid waarbij we met behulp van een integraal de oppervlakte onder een willekeurige F(x)-curve berekenen, kunnen we trouwens ook gebruiken om de eerder afgeleide formule W = m2 g h af te leiden.

Om deze formule te bekomen maakten we de veronderstelling dat de hoogte h veel kleiner is dan de straal r van het hemellichaam. Een andere interpretatie hiervan is dat we de zwaarteveldsterkte g als constant kunnen beschouwen. Dit kunnen we zien als volgt. Op het oppervlak van het hemellichaam is:

g = G ⋅ m

r2

met:

m = de massa van het hemellichaam

r = de straal van het hemellichaam

Op een hoogte h boven het hemellichaam hebben we:

g = G m (r + h)2

Als h echter veel kleiner is dan r, kunnen we h verwaarlozen in deze formule voor g; de zwaarteveldsterkte op het oppervlak en op een hoogte h zijn dan nagenoeg dezelfde en we kunnen g dus als constant beschouwen. De arbeid wordt dan:

W = r+h

r Fg dr =

r+h

G m m2

r2 dr = r+h r m2 ⋅ g ⋅ dr

r

= m2 g

g=cte

r+h r dr

= m2 g [r]r+h r

= m2 ⋅ g ⋅ ((r + h) r)

= m2 g h

met:

m = de massa van het hemellichaam

m2 = de massa van het te verplaatsen object

g = de zwaarteveldsterkte

r = de straal van het hemellichaam

Grafisch bepalen we dus de oppervlakte onder de Fg(r)-curve tussen r en r + h

De benadering die we hier maken dat g, en dus ook de gravitatiekracht, constant zijn, kunnen we grafisch als volgt weergeven:

We benaderen het groene deel van de Fg(r)-curve als een constante functie tussen r en r + h. Dit wordt weergegeven door de rode horizontale streep. Vervolgens berekenen we de oppervlakte onder deze rode horizontale streep (= de oppervlakte van de rode rechthoek = m2 ⋅ g ⋅ h). De fout die we met deze benadering maken, is gelijk aan de oppervlakte van het gearceerde deel boven

de Fg(r)-curve. Alhoewel deze grafiek niet op schaal is en deze fout (oppervlakte) in werkelijkheid nog kleiner is, zien we ook hier al dat dit gearceerde oppervlak maar een klein deel van de totale rode rechthoek is. Hierdoor kunnen we goed inzien dat dit een redelijke benadering is.

In deze grafiek kunnen we ook makkelijk zien dat deze benadering enkel geldt voor kleine h. Hoe groter we h maken, hoe groter het gearceerde oppervlak wordt en hoe groter dus onze afwijking ten opzichte van de werkelijke waarde voor de arbeid.

Op p. 17 bespraken we al dat, voor een waarnemer in de buurt van het aardoppervlak, het lijkt alsof de veldlijnen van het gravitatieveld evenwijdig lopen. Daarnaast weten we ook dat de dichtheid aan gravitatieveldlijnen een maat is voor de sterkte van het gravitatieveld. Als de veldlijnen evenwijdig lopen, is de dichtheid constant en is dus ook de gravitatieveldsterkte constant. We kunnen het gravitatieveld dan als een homogeen veld beschouwen. Ook via deze weg komen we dus tot de conclusie dat we in de buurt van een hemellichaam het gravitatieveld als constant mogen beschouwen.

Ontsnappingssnelheid

De gravitatie-energie laat toe om de ontsnappingssnelheid te berekenen. Dit is de minimale snelheid die een lichaam nodig heeft om te kunnen ontsnappen uit het gravitatieveld van de aarde. Het lichaam (massa m2) moet immers net voldoende kinetische energie meekrijgen om uit het gravitatieveld van de aarde te kunnen ontsnappen.

We leiden eerst de formule af, deze is geldig voor alle planeten (dus niet enkel voor de aarde):

Ek,begin + Egrav,begin = Ek,einde + Egrav,einde

⟺ Ek,begin + Egrav,begin = 0 + 0

Hierbij stellen we de twee termen in het rechterlid gelijk aan nul aangezien we de minimale snelheid willen berekenen om uit het gravitatieveld te ontsnappen. Daaruit is dus duidelijk dat de gravitatie-energie in de eindtoestand nul is (het lichaam bevindt zich namelijk buiten het gravitatieveld) en ook de kinetische energie in de eindtoestand wordt nul, want anders zouden we niet de minimale snelheid berekenen.

Als we de formules invullen, dan vinden we (let op het minteken van de gravitatie-energie):

1 2 m2 v2 begin G ⋅ m1 ⋅ m2 rbegin = 0

⟺ 1 2 ✟✟ m2 v2 begin = G m1 ✟✟ m2 rbegin

⟺ v2 begin = 2 ⋅ G ⋅ m1 rbegin

⟺ vbegin =   2 G m1 rbegin

De ontsnappingssnelheid is dus:

vontsnapping =   2 G m1 rbegin

Als we de ontsnappingssnelheid vanop aarde berekenen, dan vinden we:

vontsnapping =   2 G maarde raarde =

11,19 km s

waarbij:

G = 6,673 10 11 N ⋅ m2 kg2

maarde = 5,972 1024 kg

raarde = 6,371 106 m

Voor de aarde bedraagt de ontsnappingssnelheid dus ongeveer 11 km s

We kunnen de ontsnappingssnelheid ook berekenen uit de arbeid die bijvoorbeeld een ruimtetuig moet leveren om uit het gravitatieveld van de aarde te ontsnappen. We vonden voor deze arbeid:

W = 6,25 ⋅ 107 ⋅ m ⋅ J kg

met:

m = de massa van het ruimtetuig

Uit het arbeid-energietheorema hebben we dan:

ΔEk = W

⟺ Ek,begin Ek,eind = W

⟺ 1 2 ✚ ✚ m v2 begin = 6,25 107 ✚ ✚ m J kg want veind = 0 m s

⟺ v2 begin = 125 106 m2 s2

⟺ vbegin = 11183 m s = 11,2 km s

In werkelijkheid moet de snelheid nog groter zijn, want we hebben hier geen rekening gehouden met de luchtwrijving.

1.9Kort samengevat

Tot slot geven we nog een kort overzicht met alle grootheden uit dit deel. VECTOR

gravitatieveldsterkte

Eg = G m1 r2

zwaarteveldsterkte (= valversnelling)

geldig rondom een planeet g = G m1 r2

Eenheid: N kg = m s2

gravitatiekracht

Fg = G m1 m2 r2

zwaartekracht

Fz = m2 g = m g

Eenheid: N

gravitatiepotentiaal

Vg = G m1 r

ΔVg

Eenheid: J kg

gravitatie-energie

Egrav = G m1 m2 r

zwaarte-energie

ΔEz = m g h

Eenheid: J

1.10Verder oefenen?

Begrijpen

In welke twee eenheden kan de gravitatieveldsterkte uitgedrukt worden? Noteer.

Het gravitatieveld neemt kwadratisch af met de afstand. Schets dit in een grafiek voor een bolvormige, massieve massa met straal r

Is de gravitatieveldsterkte een vectoriële of scalaire grootheid? Noteer en geef ook het symbool van deze grootheid.

Schets de gravitatieveldlijnen rondom de aarde.

Geef de algemene gravitatiewet.

Geef de formule waarmee we de sterkte van een gravitatieveld op een afstand r van een lichaam met massa m kunnen berekenen.

Wat is de eenheid van de gravitatieveldsterkte? Toon dit aan met behulp van de formule.

De aarde is afgeplat. De diameter aan de evenaar bedraagt 12756 km en aan de polen 12 714 km. Welke impact heeft dit op de gravitatieveldsterkte op aarde? Verklaar.

Teken het gravitatieveld met behulp van gravitatieveldlijnen rondom de aarde en rondom de maan. Hou rekening met de sterkte van het veld bij het tekenen (de sterkte van het veld kan je weergeven door de dichtheid van de gravitatieveldlijnen).

Onderstaande afbeelding geeft de gravitatieveldlijnen op een bepaalde plaats op het Marsoppervlak weer.

Duid het juiste antwoord aan. Hieruit kunnen we besluiten dat het object net onder het Marsoppervlak:

een heel grote dichtheid heeft

een heel grote lading heeft

een heel kleine massa heeft

een lege ruimte is

Duid de grafiek aan die het best het verband tussen de grootte van de gravitatiekracht Fg en de afstand tot het middelpunt van de aarde weergeeft. Je mag ervan uitgaan dat de aarde bolvormig is en dat de massa homogeen verdeeld is.

Duid het juiste antwoord aan. De massa is hier de massa waarop de zwaartekracht werkt.

Zwaartekracht en massa zijn recht evenredig.

Zwaartekracht en massa zijn omgekeerd evenredig.

Zwaarteveldsterkte en massa zijn recht evenredig. Zwaarteveldsterkte en massa zijn omgekeerd evenredig.

Wat is het verband tussen zwaartekracht en gravitatiekracht? Duid het juiste antwoord aan.

Zwaartekracht is een speciaal geval van gravitatiekracht: één van de twee massa’s is de aarde en de gravitatieveldsterkte is constant.

Zwaartekracht is een speciaal geval van gravitatiekracht: één van de twee massa’s is de aarde.

Zwaartekracht is een speciaal geval van gravitatiekracht: één van de twee massa’s is die van een planeet en de andere massa bevindt zich op een afstand die klein is ten opzichte van de straal van die planeet.

Gravitatiekracht is een speciaal geval van zwaartekracht: voor grote afstanden en grote massa’s.

Je laat drie verschillende voorwerpen (met een verschillende massa) vanop dezelfde hoogte gelijktijdig naar beneden vallen. Welke uitspraak is dan correct? Duid het juiste antwoord aan. Ga ervan uit dat de luchtwrijving geen rol speelt.

Het lichtste voorwerp zal als eerste de grond bereiken. Het zwaarste voorwerp zal als eerste de grond bereiken. De drie voorwerpen bereiken tegelijkertijd de grond. Geen van bovenstaande uitspraken is correct.

Een bal met massa m wordt op een hoogte van 2,0 m boven het aardoppervlak losgelaten. Daarna laten we een bal met een massa gelijk aan 4m vanop dezelfde hoogte naar beneden vallen. We verwaarlozen de luchtwrijving. Duid het juiste antwoord aan. De tweede bal valt naar beneden:

met een snelheid die vier keer groter is. met een versnelling die vier keer groter is. in een tijd die vier keer groter is. door een kracht die vier keer groter is.

Een astronaut houdt op aarde een zak appelen vast. Hij oefent hierbij een kracht van 200 N uit. Stel nu dat de astronaut dezelfde zak appelen vasthoudt op de maan. De kracht die hij daarvoor moet uitoefenen, bedraagt slechts 33 N. Duid de juiste verklaring aan.

De massa van de zak appelen is kleiner op de maan dan op de aarde. Er is geen atmosfeer op de maan. De zwaarteveldsterkte op de maan is groter dan op de aarde. De zwaarteveldsterkte op de maan is kleiner dan op de aarde.

Teken het gravitatieveld rondom de aarde:

gezien vanop grote afstand van de aarde gezien vanop het aardoppervlak

De formule voor gravitatiekracht rond een bolvormige massa bevat 1 r2 . Verklaar waarom de gravitatiekracht afneemt met het kwadraat van de afstand tot het middelpunt van de bol.

Wat is een radiaal veld? Is het gravitatieveld een radiaal veld? Bespreek.

Waarom kunnen we het gravitatieveld soms zien als een radiaal veld en soms als een homogeen veld? Leg uit.

Leg uit hoe je gewichtloos kan zijn in het zwaarteveld.

Geef de definitie van gewicht. Baseer je daarop om het begrip gewichtloosheid uit te leggen.

Noteer. Wat is het teken van de gravitatie-energie:

op 5,0 m onder het aardoppervlak?

op het aardoppervlak?

op 50 m boven het aardoppervlak?

Toepassen

Bereken de zwaarteveldsterkte op Mars. Formuleer de zwaartekracht op Mars, welke impact zou die hebben op onze beweging op Mars (vergelijk met de aarde). De massa van Mars bedraagt 6,42 1023 kg en de diameter (aan de evenaar) bedraagt 6794 km

Bereken de grootte van het zwaarteveld op het aardoppervlak aan de Noordpool. De diameter van de aarde tussen de polen bedraagt 12714 km en de massa van de aarde is 5,97 1024 kg

Bereken de grootte van het gravitatieveld die een persoon van 60 kg veroorzaakt op 2,0 m van zichzelf.

Bereken de grootte van het zwaarteveld op het aardoppervlak aan de evenaar. De diameter van de aarde aan de evenaar bedraagt 12756 km en de massa van de aarde is 5,97 ⋅ 1024 kg.

De maan heeft een zwaarteveldsterkte die ongeveer zes keer kleiner is dan die op aarde. Welke massa heeft dan het grootste gewicht? Duid het juiste antwoord aan.

40 kg op de aarde

5 kg op de aarde

120 kg op de maan

100 kg op de maan

Bereken hoe groot het gravitatieveld van de aarde op … van het centrum van de aarde is (gebruik als massa de totale aardmassa).

6 ⋅ 104 m

2 ⋅ 105 m

Bereken. Hoe groot is de gravitatiekracht tussen twee massa’s van … op … van elkaar?

200 kg en 3000 kg op 45 mm van elkaar

2000 kg en 800 kg op 25 m van elkaar

1,5 1012 kg en 3 1027 kg op 45 109 m van elkaar

Bereken de minimale snelheid die nodig is om uit het gravitatieveld van de aarde te ontsnappen.

Bereken de zwaarteveldsterkte op de maan.

mmaan = 7,35 1022 kg

rmaan = 1738 km

Bereken de zwaarteveldsterkte op Mars.

mMars = 6,39 1023 kg

rMars = 3390 km

Geef de algemene gravitatiewet. Leid hieruit de formule voor de zwaarteveldsterkte af.

Met welke kracht trekken de zon en Mars elkaar aan? Teken de kracht en bereken ze.

mzon = 1,99 1030 kg

mMars = 6,42 1023 kg

rzon-Mars = 2,28 ⋅ 1011 m

Bereken de ontsnappingssnelheid voor een object op:

de maan (m = 7,34 ⋅ 1022 kg, r = 1737 km)

Mars (m = 6,42 1023 kg, r = 3390 km)

Vergelijk de gravitatiekracht tussen volgende lichamen. De gegeven afstanden zijn de afstanden tussen de middelpunten van de lichamen.

Een puntmassa van 2,0 kg en een puntmassa van 6,4 kg op 2,0 m van elkaar.

Twee neutronen op 2,5 nm van elkaar verwijderd. De massa van een neutron bedraagt 1,67 ⋅ 10–27 kg.

De aarde en de maan (maarde = 5,97 1024 kg, mmaan = 7,35 1022 kg, raarde-maan = 384400km).

Geef de waarde van G die wij gebruiken. Henry Cavendish bepaalde eind 18e eeuw deze G voor het eerst experimenteel. Hij deed dat door een lichte loden bol van 0,73 kg en een zware loden bol van 158 kg op een afstand van 23 cm (tussen de middelpunten) van elkaar te plaatsen. Hij mat een gravitatiekracht van 1,45 10–7 N. Welke waarde voor G bekwam hij zo? Bereken. Deze constante wordt ook wel de ‘constante van Cavendish’ genoemd. Welke waarde voor G vind je op het internet? Noteer de meest nauwkeurige en geef ook de fout op deze waarde.

De valversnelling aan het aardoppervlak is g = 9,81 m s2 .

De massa van de aarde bedraagt 5,9742 ⋅ 1024 kg

Bereken aan de hand van deze gegevens en de algemene gravitatiewet de straal van de aarde.

We kunnen de gravitatiewet ook voor andere planeten gebruiken:

• voor Jupiter is: r = 71,40 ⋅ 106 m en g = 24,9 m s2

• voor Venus is: r = 6,05 106 m en m = 4,87 1024 kg

Bereken hiermee de massa van Jupiter. Bereken de valversnelling aan het oppervlak van Venus.

Onderstaande grafiek geeft het verband tussen de grootte van de gravitatiekracht die inwerkt op een lichaam op een bepaalde plaats en de massa van dat lichaam weer.

Bevindt het lichaam zich op het aardoppervlak? Verklaar. Wat is de gravitatieveldsterkte/valversnelling? Waar bevindt het lichaam zich volgens jou? Noteer.

De zwaarteveldsterkte op het aardoppervlak (dus op een afstand rA van het middelpunt van de aarde, waarbij rA de straal van de aarde is) bedraagt ongeveer 10 N kg .

Wat is de zwaarteveldsterkte dan op een afstand van:

Twee peuters met massa’s 15,3 kg en 13,8 kg trekken elkaar aan met een kracht van 1,41 ⋅ 10

8 N. Hoe ver bevinden ze zich van elkaar? Bereken.

Henk ondervindt op het aardoppervlak een aantrekkingskracht van 800 N vanwege de aarde. Bereken de straal van de aarde op die plaats als je weet dat Henk een massa van 81,4 kg heeft.

mA = 5,976 ⋅ 1024 kg

Bereken de afstand tussen de aarde en de zon als je weet dat de aarde en de zon een kracht van 3,544 ⋅ 1022 N op elkaar uitoefenen. De massa van de zon bedraagt 1,989 ⋅ 1030 kg en de massa van de aarde bedraagt 5,976 ⋅ 1024 kg

Een sinaasappel van 200 g ligt op het aardoppervlak. De doorsnede van de sinaasappel bedraagt 10 cm.

Bereken de gravitatiekracht die de aarde op de sinaasappel uitoefent. Stel dat een astronaut deze sinaasappel meeneemt naar het ISS (408 km boven het aardoppervlak). Welke gravitatiekracht werkt dan op de sinaasappel? Bereken. Op welke afstand van de aarde moet de sinaasappel zich bevinden om geen gravitatiekracht van de aarde meer te ondervinden? Verklaar.

Bereken de aantrekkingskracht tussen de aarde en Pluto. We gaan er hierbij van uit dat zowel de aarde als Pluto een cirkelvormige baan om de zon beschrijven en dat op een zeker moment de aarde op de verbindingslijn zon-Pluto ligt.

G = 6,673 10 11 N ⋅ m2 kg2

mPluto = 0,013 1024 kg

maarde = 5,97 1024 kg

rzon-aarde = 0,15 ⋅ 1012 m

rzon-Pluto = 5,91 1012 m

Een satelliet met massa 120 kg bevindt zich in een baan om de aarde op 6000 km boven het aardoppervlak. Bereken de aantrekkingskracht die de aarde uitoefent op de satelliet (maarde = 5,97 1024 kg, raarde = 6371 km).

Twee identieke massa’s bevinden zich op 4,0 m van elkaar. De gravitatiekracht tussen deze massa’s bedraagt 9,0 ⋅ 10–11 N

De massa’s worden nu dichter bij elkaar gebracht tot op een afstand van 2,0 m van elkaar. Bereken de grootte van de gravitatiekracht.

Een meteoriet van 10,0 kg wordt, vanop een afstand van 10000 km van de maan, door de maan aangetrokken. Uiteindelijk stort de meteoriet neer op het maanoppervlak. Bereken de eindsnelheid van de meteoriet.

Gegeven:

• de universele gravitatieconstante: G = 6,673 10 11 N ⋅ m2 kg2

• afstand van de aarde tot de zon: raarde-zon = 1,5 ⋅ 1011 m

• periode van de aardrotatie rond de zon: Taarde = 1 jaar = 365 dagen

• afstand van Jupiter tot de zon: rJupiter-zon = 7,8 1011 m

• periode van de maanrotatie rond de aarde: Tmaan = 27,3 dagen

• afstand van de aarde tot de maan: raarde-maan = 3,8 ⋅ 108 m

• massa van de zon: mzon = 2 1030 kg

• straal van de aarde: raarde = 6,4 106 m

• massa van Uranus: mUranus = 8,67 ⋅ 1025 kg

• straal van de Uranus: rUranus = 25,4 ⋅ 106 m

• afstand van Uranus tot de zon: rUranus-zon = 2,87 1012 m

Gebruik bovenstaande gegevens om:

de massa van de aarde te bepalen

de zwaarteveldsterkte op Uranus te berekenen

de baansnelheid van de aarde in haar baan rond de zon te bepalen in m s enin km h

de baansnelheid van Jupiter in zijn baan rond de zon te bepalen in m s enin km h

de baansnelheid van Uranus in zijn baan rond de zon te bepalen in m s enin km h

de baansnelheid van de maan in haar baan rond de aarde te bepalen in m s enin km h

Een satelliet heeft een baansnelheid van 7,658 km s in zijn baan rond de aarde. Bereken op welke hoogte boven het aardoppervlak de satelliet zich bevindt. Neem als straal van de aarde 6,371 106 m.

Twee identieke massa’s bevinden zich op 4,0 m van elkaar. De gravitatiekracht tussen deze massa’s bedraagt 9,0 10–11 N. Bereken de grootte van elke massa.

Analyseren

Maak gebruik van het internet om onderstaande opgave op te lossen.

Leg uit wat de bijdrage van onderstaande wetenschappers in de ontwikkeling van de gravitatietheorie is:

Tycho Brahe

Johannes Kepler

Galileo Galilei

Isaac Newton

Gravitatiekracht: onderzoek

Open de applet via de QR-code. Met deze applet kan je de gravitatiekracht tussen twee massa’s bestuderen. Test zowel de invloed van de afstand tussen de massa’s als de invloed van de grootte van de massa’s op de grootte van gravitatiekracht. Noteer je bevindingen in een verslag. Blanco verslagbladen vind je op POLPO.

De aarde op de weegschaal

Als wij onze massa willen weten, gaan we simpelweg op een balans of weegschaal staan. We zien dan onze massa in kg verschijnen, maar wij wetenschappers weten natuurlijk dat de weegschaal eigenlijk ons gewicht meet en dit dan omrekent naar een massa in kg

Voor de bepaling van de massa van de aarde kunnen we deze techniek niet toepassen. Wel kunnen we Newtons gravitatiewet gebruiken. Newton publiceerde deze wet in 1687 in zijn meesterwerk, de Philosophiae Naturalis Principia Mathematica, beter bekend als de Principia:

Newton was natuurlijk ook benieuwd naar de massa van de aarde. In Newtons tijd was G echter nog niet gekend, dus het berekenen van de gravitatiekracht lukte in die tijd nog niet.

Gelukkig had Newton een idee. Hij bedacht een experiment gebaseerd op zijn veronderstelling dat een slinger die dicht bij een berg hangt, door de zwaartekracht die de berg op de slinger uitoefent, een kleine afwijking zou hebben.

Zelf voerde Newton het experiment nooit uit, hij dacht namelijk dat het onuitvoerbaar was. Bijna een eeuw na zijn dood werd dit experiment toch uitgevoerd, wat resulteerde in een eerste schatting van G en zo van de massa van de aarde.

Wetenschappers waren echter niet tevreden met het resultaat. Ze wilden de massa nauwkeuriger berekenen. Daarom bedachten ze eerst een experiment om de waarde van G nauwkeuriger te bepalen. Dit lukte in 1798 dankzij de torsiebalans van Cavendish.

Dankzij deze gekende waarde van G kon nu via de gravitatiewet de massa van de aarde berekend worden. Als massa’s die elkaar aantrekken, werden de massa van de aarde en de maan genomen. Aangezien de maan rond de aarde draait, is de gravitatiekracht gelijk aan de centripetale kracht. Dat geeft ons:

waarbij:

G = de gravitatieconstante

mM = de massa van de maan

mA = de massa van de aarde

r = de afstand tussen het middelpunt van de aarde en het middelpunt van de maan

vM = de baansnelheid van de maan

a

b

Bereken nu zelf even de massa van de aarde. Zoek hiervoor de nodige constanten en waarden op.

Er zijn natuurlijk ook planeten die geen maan hebben. Heb jij een idee hoe men in dat geval toch de massa zou kunnen berekenen? Noteer.

STUDIEWIJZER

Ik kan het verband tussen de grootte van de gravitatiekracht tussen twee massa’s en de grootte van de twee massa’s analyseren.

Ik kan het verband tussen de grootte van de gravitatiekracht tussen twee massa’s en de afstand tussen de twee massa’s analyseren.

Ik kan de algemene gravitatiewet historisch duiden als de zoektocht van de mens naar het hoe en het waarom van de beweging van hemellichamen. Ik kan hierbij de bijdrage van Aristoteles, Ptolemaeus, Al-Biruni, Copernicus, Kepler en Newton bespreken.

Ik kan het omgekeerd kwadratisch verband tussen de grootte van het gravitatieveld en de afstand in verband brengen met de oppervlakte van een bol die kwadratisch toeneemt met de straal.

Ik weet dat het gravitatieveld van een puntmassa of van een bolvormige massa een radiaal veld is.

Ik weet dat we het gravitatieveld in de buurt van het oppervlak van een hemellichaam lokaal als een homogeen veld kunnen benaderen waarbij we de zwaarteveldsterkte lokaal als constant beschouwen.

Ik kan uit de algemene gravitatiewet de formule voor de valversnelling (zwaarteveldsterkte) afleiden. Ik kan hieruit het verband tussen de grootte van de zwaarteveldsterkte en de hoogte afleiden.

Ik zie in dat massa geen invloed heeft op de valversnelling.

Ik kan bespreken hoe je in een zwaarteveld toch gewichtloos kan zijn.

Ik begrijp dat de gravitatiewet van Newton een ‘onmiddellijke krachtwerking op afstand’ veronderstelt en dat dit volgens de relativiteitstheorie onmogelijk is; ik kan hierbij heel kort de link met zwaartekrachtgolven leggen.

Ik kan kort uitleggen dat de gravitatiekracht de rol van centripetale kracht op zich neemt bij onder andere de beweging van de aarde rond de zon. Ik kan uitleggen dat de aarde hierdoor rond de zon beweegt.

Ik kan het verband leggen tussen de gravitatiekracht en de centripetale versnelling van een satelliet.

Ik kan de arbeid bepalen die nodig is om te ontsnappen aan het gravitatieveld.

paginanummer

p. 19-25, p. 52

p. 19-25, p. 52

p. 13-15

p. 17

p. 16-17

p. 17,

p. 43

p. 26-28

p. 28

p. 30-31

p. 31-33

p. 21-25

p. 24

p. 37-45