3.4.2. Tình huống 2

DẠY KÈM QUY NHƠN OFFICIAL 29 Kiến thức cho phép thực hiện chiến lược: đƣờng thẳng vuông góc với mặt phẳng, hai đƣờng thẳng phân biệt cùng vuông góc với một mặt phẳng sẽ song song nhau, góc giữa hai đƣờng thẳng. 3.4.2. Tình huống 2 Mục đích của tình huống: Chúng tôi sẽ phân tích mục đích của từng nhiệm vụ trong tình huống này: Pha 1: - Nhiệm vụ 3: HS thực hiện đo góc giữa 02 đƣờng thẳng trong 02 mặt phẳng, tuy nhiên 2 đƣờng thẳng này không cùng vuông góc với giao tuyến. Từ đó, mỗi một cặp đƣờng thẳng mà HS chọn sẽ cho một số đo góc khác nhau và có thể khác với góc giữa hai mặt phẳng nhƣ ở tình huống 1. Chúng tôi chọn lại hai mặt phẳng ở tình huống 1 bởi lí do: HS đã biết số đo góc giữa hai mặt phẳng trên, và GV đã công bố trƣớc toàn thể lớp học, nhƣ vậy HS sẽ không mất thời gian trong việc đo lại góc giữa hai mặt phẳng, và tránh đƣợc tình huống mỗi HS có số đo góc giữa hai mặt phẳng là khác nhau. - Nhiệm vụ 4: Chuẩn bị lại cho HS 02 mặt phẳng nhƣ ở pha 1. Yêu cầu HS chọn 2 đƣờng thẳng trong 02 mặt phẳng cùng vuông góc với giao tuyến. Xác định góc giữa hai đƣờng thẳng này. Yêu cầu HS so sánh với số đo góc giữa hai mặt phẳng. HS thực hiện đo góc giữa 2 đƣờng thẳng trong 2 mặt phẳng cùng vuông góc với giao tuyến. Từ các kết quả của HS và việc so sánh với số đo góc giữa hai mặt phẳng, HS có thể nhận thấy góc giữa hai mặt phẳng với góc giữa hai đƣờng thẳng cùng vuông góc với giao tuyến lần lƣợt nằm trong hai mặt phẳng này là bằng nhau. Pha 2: Ở pha này, chúng tôi hƣớng đến việc HS tiếp nhận kiến thức vừa học nhƣ thế nào. Ngoài ra chúng tôi chọn hai mặt phẳng có tính “hai mép” của hai mặt phẳng không vuông góc với nhau để kiểm chứng rằng HS không mặc định góc giữa “hai mép” của hai mặt phẳng là góc giữa hai mặt phẳng. Có thể trong quá trình đo đạc ở pha 1, HS vô tình chọn hai đƣờng thẳng chính là “hai mép” của hai mặt phẳng và từ đó mặc định góc giữa “hai mép” ấy là góc giữa hai mặt phẳng. Pha 3:

Ở pha này, chúng tôi hƣớng đến việc HS vận dụng góc giữa hai mặt phẳng để giải DẠY KÈM QUY NHƠN OFFICIAL 30 quyết một tình huống thực tiễn. HS phải tạo dựng một con súc sắc 8 mặt tƣơng ứng với việc HS phải ghép một bát diện đều với 8 mặt đã cho là 8 tam giác đều. Tuy nhiên việc ghép này sẽ khó khăn nếu nhƣ HS không sử dụng kiến thức góc giữa hai mặt phẳng. Giai đoạn 1: Trải nghiệm cụ thể Giai đoạn này đƣợc diễn ra ở nhiệm vụ 3 và 4 của pha 1, mục đích cho HS trải nghiệm đo góc giữa hai đƣờng thẳng bất kì, đo góc giữa hai đƣờng thẳng vuông góc với giao tuyến nằm trong hai mặt phẳng đó. Giai đoạn 2: Phản ánh qua quan sát Giai đoạn này đƣợc diễn ra ở pha 1, từ những kết quả ở giai đoạn 1, qua hệ thống câu hỏi của GV cho HS nhận thấy rằng: Góc giữa hai đƣờng thẳng bất kì trong hai mặt phẳng thì thay đổi. Tuy nhiên, góc giữa hai đƣờng thẳng trong hai mặt phẳng lần lƣợt vuông góc với giao tuyến thì không đổi và chính bằng góc giữa hai mặt phẳng. Giai đoạn 3: Khái quát hóa trừu tƣợng Giai đoạn này đƣợc diễn ra ở việc GV thể chế hóa cho HS cách xác định góc giữa hai mặt phẳng, và giới thiệu cho HS đây có thể coi là một định nghĩa khác cho khái niệm góc giữa hai mặt phẳng. Giai đoạn 4: Thử nghiệm tích cực Giai đoạn này đƣợc chúng tôi xây dựng thông qua hai pha: Pha 2: Cho HS xác định góc giữa hai mặt phẳng có tính chất “hai mép” của hai mặt phẳng không vuông góc với nhau. Pha này đòi hỏi HS vận dụng những kiến thức vừa khám phá ở trên (định nghĩa, tính chất của góc giữa hai mặt phẳng) để tìm góc giữa hai mặt phẳng cho trƣớc. Ở pha trƣớc chúng tôi có chuẩn bị hai mặt phẳng có hai mép vuông góc với nhau. Vì thế chúng tôi muốn kiểm tra rằng đối với những mặt phẳng khác, không có tính chất nhƣ trên thì HS có xác định góc giữa hai mép của mặt phẳng hay không. Để giải quyết bài toán, HS phải nắm vững định nghĩa góc giữa 2 mặt phẳng. Pha 3: Chúng tôi cho HS tiến hành làm con Súc sắc 8 mặt bởi vì chúng tôi muốn HS ứng dụng việc xác định góc giữa hai mặt phẳng để xác định góc giữa các mặt phẳng của con súc sắc. Từ số đo góc đó, HS có thể tạo dựng nên một con Súc sắc mà không phải “thử sai”. Chúng tôi dự kiến các chiến lƣợc có thể xuất hiện ở HS nhƣ sau: Nhiệm vụ 3: Đo góc giữa hai đƣờng thẳng không cùng vuông góc với giao tuyến + Chiến lƣợc 1: HS dựng hai đƣờng thẳng chéo nhau nằm trong hai mặt phẳng và không cùng vuông góc với giao tuyến bằng các xiên que đặt lên mặt phẳng.

DẠY KÈM QUY NHƠN OFFICIAL 31 HS có thể cố định các đƣờng thẳng này bằng băng dính. Sau đó xác định góc giữa hai đƣờng thẳng này bằng cách dời hai đƣờng thẳng này về hai đƣờng thẳng song song với chúng và cắt nhau. Từ các kết quả đo đƣợc, HS kết luận góc này không bằng với góc giữa hai mặt phẳng. Kiến thức cho phép thực hiện chiến lược: Góc giữa hai đƣờng thẳng. + Chiến lƣợc 2: HS dựng hai đƣờng thẳng cắt nhau nằm trong hai mặt phẳng và không cùng vuông góc với giao tuyến bằng các xiên que đặt lên mặt phẳng và cố định bằng băng dính. Sau đó xác định góc giữa hai đƣờng thẳng này và kết luận góc này không bằng với góc giữa hai mặt phẳng. Kiến thức cho phép thực hiện chiến lƣợc: Góc giữa hai đƣờng thẳng. Chiến lược 2 là chiến lược tối ưu. Nhiệm vụ 4: HS thực hiện đo góc giữa hai đƣờng thẳng nằm trong hai mặt phẳng cùng vuông góc với giao tuyến. Chiến lƣợc 1: Dựng hai đƣờng thẳng vuông góc với giao tuyến. HS dựng hai đƣờng thẳng cắt nhau và vuông góc với giao tuyến bằng các xiên que đặt lên mặt phẳng và cố định bằng băng dính.

DẠY KÈM QUY NHƠN OFFICIAL 32 Sau đó HS thực hiện đo góc giữa hai đƣờng thẳng trên. Từ những kết quả của các HS, HS kết luận đƣợc góc giữa hai mặt phẳng bằng với góc giữa hai đƣờng thẳng nằm trong hai mặt phẳng cùng vuông góc với giao tuyến. Kiến thức cho phép thực hiện chiến lược: Góc giữa hai đƣờng thẳng. Chiến lƣợc này là chiến lƣợc tối ƣu. Chiến lƣợc 2: Dựng hai đƣờng thẳng chéo nhau và vuông góc với giao tuyến

HS dựng hai đƣờng thẳng chéo nhau và vuông góc với giao tuyến bằng các xiên que DẠY KÈM QUY NHƠN OFFICIAL 33 đặt lên mặt phẳng và cố định bằng băng dính. Tuy nhiên, vì là hai đƣờng thẳng chéo nhau nên HS phải thực hiện dời một, hay cả hai đƣờng thẳng về hai đƣờng thẳng cắt nhau sau đó tiến hành đo góc nhƣ chiến lƣợc 1. Kiến thức cho phép thực hiện chiến lược: Góc giữa hai đƣờng thẳng. Pha 2: Mục đích buộc HS phải suy nghĩ đến những cách làm ở nhiệm vụ 2 của pha 1 và liên hệ đƣợc để thực hiện pha này. Chiến lƣợc 1: HS đo góc giữa “hai mép của mặt phẳng” Chiến lƣợc này là chiến lƣợc sai, chiến lƣợc này chỉ đúng khi “hai mép” của mặt phẳng vuông góc với giao tuyến. Có thể học sinh nhầm lẫn do ở pha 2 học sinh thực hiện đo góc giữa “hai mép” của mặt phẳng và thấy bằng nhau và bằng với góc giữa hai mặt phẳng. Từ đó HS dễ dàng đƣa ra một kết luận sai. Chiến lƣợc 2: HS đo góc giữa hai đƣờng thẳng nằm trong hai mặt phẳng, cùng vuông góc với giao tuyến. HS dựng hai đƣờng thẳng nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến. Từ đó HS đo góc giữa hai đƣờng thẳng trên. Và góc này cũng chính bằng góc giữa hai mặt phẳng cần tìm.

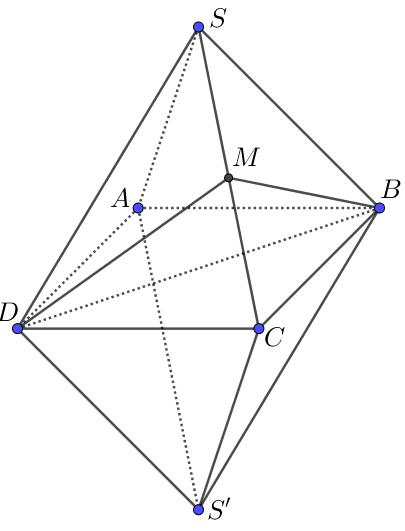
DẠY KÈM QUY NHƠN OFFICIAL 34 Kiến thức cho phép thực hiện chiến lược: Góc giữa hai mặt phẳng, góc giữa hai đƣờng thẳng. Pha 3: Mục đích buộc HS phải dùng kiến thức góc giữa hai mặt phẳng để thực hiện. Chiến lƣợc 1: HS thử ghép các mặt phẳng với nhau cho khớp. Với 8 mặt là 8 tam giác đều, HS không thể ghép lại cho khớp với nhau. Bởi vì một khi ghép, HS phải cố định nó lại. Và nếu góc giữa các mặt phẳng không đúng số đo thì những mảnh sau sẽ không khớp lại với nhau. Chiến lƣợc 2: Góc giữa hai mặt phẳng. Ở chiến lƣợc này, HS tính đƣợc góc giữa các mặt phẳng là gần bằng . Cách tính: Gọi là trung điểm của . và đều nên: . Xét hai mặt phẳng và có: [ ] Ta có:

DẠY KÈM QUY NHƠN OFFICIAL 35

√ Áp dụng định lí Cô-sin vào tam giác có: [ ] Tuy nhiên nếu dùng con số này thì HS không thể ghép lại đƣợc. Trong thực tế, góc giữa các mặt của con súc sắc này là góc nhị diện (một phần không gian bị giới hạn bởi hai nửa mặt phẳng). Và góc nhị diện trong trƣờng hợp này là góc tù. Mặt khác, số đo của góc giữa hai mặt phẳng là góc nhọn. Do đó,

chiến lƣợc dùng góc giữa hai mặt phẳng ta không thể ghép các mặt lại với nhau DẠY KÈM QUY NHƠN OFFICIAL 36 đƣợc. Chiến lƣợc 3: Phần bù của góc giữa hai mặt phẳng (Góc nhị diện) Ở chiến lƣợc này, HS nhận ra rằng góc cần tạo thành là góc tù, đó chính là phần bù của góc giữa hai mặt phẳng mà HS đã xác định ở chiến lƣợc 2. Nói cách khác, góc cần tạo thành để ghép lúc này chính là góc giữa hai nửa mặt phẳng (Góc nhị diện) và là góc tù. Do đó HS sẽ tạo thành các góc gần bằng và ghép lại với nhau.

DẠY KÈM QUY NHƠN OFFICIAL 37 Chiến lƣợc này là chiến lƣợc tối ƣu. Tóm tắt các chiến lƣợc cho tình huống 2: Pha 1 Pha 2 Pha 3Nhiệm vụ 3 Nhiệm vụ 4 Chiến lƣợc 1: HS dựng hai đƣờng thẳng chéo nhau nằm trong hai mặt phẳng và không cùng vuông góc với giao tuyến bằng các xiên que đặt lên mặt phẳng. Chiến lƣợc 2: HS dựng hai đƣờng thẳng cắt nhau nằm trong hai mặt phẳng và không cùng vuông góc với giao tuyến bằng các xiên que đặt lên mặt phẳng và cố định bằng băng dính. Chiến lược 2 là chiến lược tối ưu.

Chiến lƣợc 1:

Dựng hai đƣờng thẳng vuông góc với giao tuyến. Chiến lƣợc này là chiến lƣợc tối ƣu.

Chiến lƣợc 2:

Dựng hai đƣờng thẳng chéo nhau và vuông góc với giao tuyến. Chiến lƣợc 1: HS đo góc giữa “hai mép của mặt phẳng” Chiến lƣợc 2: HS đo góc giữa hai đƣờng thẳng nằm trong hai mặt phẳng, cùng vuông góc với giao tuyến. Chiến lƣợc 1: HS thử ghép các mặt phẳng với nhau cho khớp.

Chiến lƣợc 2:

Góc giữa hai mặt phẳng.

Chiến lƣợc 3:

Phần bù của góc giữa hai mặt phẳng (Góc nhị diện) Chiến lƣợc này là chiến lƣợc tối ƣu.