49 minute read
DẠY KÈM QUY NHƠN OFFICIAL
3.4.2. Tình huống 2......................................................................................................29 DẠY KÈM QUY NHƠN OFFICIAL 4 3.5. Kết luận.....................................................................................................................38 KẾT LUẬN.............................................................................................................................39 TÀI LIỆU THAM KHẢO.....................................................................................................41 PHỤ LỤC: KẾ HOẠCH DẠY HỌC BÀI HAI MẶT PHẲNG VUÔNG GÓC...............43 2. Phiếu học tập số 1........................................................................................................47 3. Phiếu học tập số 2........................................................................................................48 4. Phiếu học tập số 3........................................................................................................49
DANH MỤC CÁC TỪ VIẾT TẮT
Advertisement
DẠY KÈM QUY NHƠN OFFICIAL 5 Sách giáo khoa SGK Hoạt động trải nghiệm HĐTN Học sinh HS Giáo viên GV Nhà xuất bản NXB
MỞ ĐẦU
DẠY KÈM QUY NHƠN OFFICIAL 6 1. Lí do chọn đề tài Từ xa xƣa, khi nói về phƣơng pháp học tập hiệu quả, ông cha ta đã đúc kết qua câu tục ngữ “Học đi đôi với hành”. Tức là việc học tập lí thuyết phải gắn liền với việc thực hành lí thuyết đó ra sao. Song song với việc chúng ta tiếp thu tri thức thì còn cần phải trải nghiệm những vấn đề trong thực tiễn để hiểu đƣợc những ứng dụng của lí thuyết vào cuộc sống. Hầu hết những lí thuyết mà con ngƣời tìm hiều và nghiên cứu đều hƣớng đến mục tiêu vận dụng nó vào cuộc sống. Chủ tịch Hồ Chí Minh cũng đã từng nói rằng “Học để hành, học và hành phải đi đôi. Học mà không hành thì học vô ích, hành mà không học thì hành không trôi chảy”. Nhƣ vậy việc học tập lí thuyết và việc thực hành trải nghiệm là hai hoạt động đi đôi với nhau trong quá trình học tập. Hiện nay, Giáo dục Việt Nam đang chuyển từ dạy học tiếp cận nội dung sang tiếp cận năng lực. Trƣớc đây, trong việc dạy và học đơn thuần chỉ là việc giáo viên cung cấp kiến thức cho học sinh và học sinh lắng nghe, tiếp nhận kiến thức và dùng nó để giải quyết các bài toán thuần túy toán học. Tuy nhiên việc áp dụng lí thuyết đã đƣợc học để giải quyết, liên hệ đến các vấn đề trong thực tiễn là một yếu tố rất cần thiết và quan trọng. Ngoài việc củng cố lí thuyết, việc dạy học tiếp cận năng lực còn giúp ngƣời học rèn luyện đƣợc nhiều kĩ năng cần thiết. Đã và đang có rất nhiều những đề tài nghiên cứu để gắn “Toán học” vào các tình huống thực tiễn, giúp cho việc học môn Toán dễ dàng và thú vị hơn. Từ đó, học sinh hình thành đƣợc các kĩ năng then chốt, tạo cơ hội cho học sinh đƣợc thực hành, trải nghiệm, kết nối giữa Toán học vào thực tiễn. Dạy học theo định hƣớng giáo dục STEM, hay hoạt động trải nghiệm trong dạy học Toán đều đem lại cho học sinh nhiều kĩ năng, năng lực và giúp học sinh nhận thấy vai trò của Toán học trong thực tiễn. Chƣơng trình Giáo dục phổ thông tổng thể mới đã đƣợc ban hành vào tháng 12/2018. Trong Chƣơng trình Giáo dục phổ thông tổng thể mới, Bộ Giáo dục và Đào tạo đặc biệt quan tâm đến các “Hoạt động trải nghiệm” từ cấp Tiểu học đến cấp Trung học phổ thông. Đây là hoạt động bắt buộc thực hiện từ lớp 1 đến lớp 12. Hoạt động trải nghiệm phải hình thành và phát triển ở học sinh năng lực thích ứng với cuộc sống, hình thành và phát triển nhiều phẩm chất và năng lực. Việc dạy Toán hiện nay ngoài việc cung cấp các nội dung toán học thuần túy cho học sinh còn phải đảm bảo rằng học sinh biết đƣợc tính ứng dụng của kiến thức toán vào trong thực tiễn. Do đó, trong nội dung chƣơng trình môn toán, hoạt động thực hành, trải nghiệm là những hoạt động đƣợc chú trọng, nhấn mạnh và đƣợc đƣa vào tƣờng minh sau khi chƣơng trình đề cập đến các nội dung toán học. Chƣơng trình môn Toán đƣợc ban hành vào tháng 12 năm 2018 có đề cập về tính cần thiết của hoạt động trải nghiệm: “Ngoài ra, chương trình môn Toán ở từng cấp cũng dành thời lượng thích đáng để tiến hành các hoạt động thực hành và trải nghiệm cho học sinh chẳng hạn như: Tiến hành các đề tài, dự án học tập về Toán, đặc biệt là các đề tài và các dự án về ứng dụng toán học trong thực tiễn; tổ chức các trò chơi học toán, câu lạc bộ toán học, diễn đàn, hội thảo, cuộc thi về Toán; ra báo tường (hoặc nội san) về Toán; tham quan các cơ sở đào tạo và nghiên cứu toán học, giao lưu với học sinh có khả năng và yêu thích môn Toán,... Những hoạt động đó sẽ
giúp học sinh vận dụng những tri thức, kiến thức, kĩ năng, thái độ đã được tích DẠY KÈM QUY NHƠN OFFICIAL 7 luỹ từ giáo dục toán học và những kinh nghiệm của bản thân vào thực tiễn cuộc sống một cách sáng tạo; phát triển cho học sinh năng lực tổ chức và quản lí hoạt động, năng lực tự nhận thức và tích cực hoá bản thân; giúp học sinh bước đầu xác định được năng lực, sở trường của bản thân nhằm định hướng và lựa chọn nghề nghiệp; tạo lập một số năng lực cơ bản cho người lao động tương lai và người công dân có trách nhiệm.” Góc giữa hai mặt phẳng là một nội dung kiến thức không mới, có những ứng dụng vào thực tiễn. Tuy nhiên, Sách giáo khoa lớp 11 lại không trình bày về các ứng dụng mà chỉ trình bày nội dung này một cách thuần túy toán học. Với cách trình bày của sách giáo khoa hiện hành, khó có thể cho học sinh biết đƣợc ứng dụng của góc giữa hai mặt phẳng trong thực tiễn. Ngoài ra, câu hỏi “học góc giữa hai mặt phẳng để làm gì?” sẽ không đƣợc trả lời nếu nhƣ giáo viên cho HS tiếp cận thuần túy toán học nhƣ hiện tại. Với những lí do trên, chúng tôi nhận thấy sự cần thiết để thực hiện đề tài nghiên cứu: “Xây dựng hoạt động trải nghiệm dạy học chủ đề góc giữa hai mặt phẳng”. 2. Mục tiêu nghiên cứu Chúng tôi sẽ nghiên cứu, tìm hiểu lí thuyết học tập trải nghiệm và thực hành xây dựng hoạt động dạy học tri thức “Góc giữa hai mặt phẳng” bằng hoạt động trải nghiệm. 3. Câu hỏi nghiên cứu Dựa trên mục tiêu nghiên cứu, chúng tôi đặt ra những câu hỏi sau: Hoạt động trải nghiệm là gì? Hoạt động trải nghiệm trong môn Toán đƣợc thực hiện nhƣ thế nào? Có những mô hình hoạt động trải nghiệm phổ biến nào? Tri thức “Góc giữa hai mặt phẳng” đƣợc trình bày nhƣ thế nào trong chƣơng trình hiện hành và SGK? Việc trình bày tri thức này trong chƣơng trình hiện hành đã đáp ứng đƣợc những yêu cầu nào của mô hình học tập trải nghiệm? Làm thế nào để xây dựng một tình huống dạy học tri thức “Góc giữa hai mặt phẳng” bằng hoạt động trải nghiệm? 4. Phƣơng pháp nghiên cứu Phƣơng pháp phân tích và tổng hợp lí thuyết: Chúng tôi tổng hợp những công trình nghiên cứu và các tài liệu trình bày về hoạt động trải nghiệm sáng tạo để làm rõ cơ sở lí thuyết. Phƣơng pháp thực nghiệm: Xây dựng tình huống, giáo án bài dạy, sau đó thực nghiệm trên học sinh phổ thông và phân tích kết quả thực nghiệm. 5. Nội dung nghiên cứu Nội dung nghiên cứu gồm các phần sau:
Trong phần mở đầu, chúng tôi trình bày lí do chọn đề tài nghiên cứu, mục DẠY KÈM QUY NHƠN OFFICIAL 8 đích, phƣơng pháp nghiên cứu, nội dung nghiên cứu. Trong chƣơng I, chúng tôi nghiên cứu các tài liệu, luận văn liên quan đến nội dung lý thuyết học tập trải nghiệm. Trong chƣơng II, chúng tôi nghiên cứu, phân tích cách trình bày nội dung “Góc giữa hai mặt phẳng” ở Sách giáo khoa Việt Nam để làm cơ sở lí thuyết cho việc thiết kế hoạt động ở chƣơng III. Trong chƣơng III, chúng tôi sẽ xây dựng hoạt động trải nghiệm để dạy học nội dung “Góc giữa hai mặt phẳng” và tiến hành thực nghiệm ở trƣờng phổ thông để đánh giá tính khả thi của tình huống.
CHƢƠNG 1: LÍ THUYẾT HỌC TẬP TRẢI NGHIỆM
DẠY KÈM QUY NHƠN OFFICIAL 9 1.1. Hoạt động trải nghiệm là gì? 1.1.1. Khái niệm trải nghiệm Theo từ điển tiếng Việt, “Trải nghiệm là trải qua, kinh qua”; nhƣ vậy trải nghiệm có nghĩa là quá trình chủ thể trực tiếp đƣợc tham gia vào các hoạt động và từ đó rút ra đƣợc những kinh nghiệm cho bản thân mình. Theo từ điển Bách khoa Việt Nam, “trải nghiệm” đƣợc diễn giải theo hai nghĩa. “Trải nghiệm” theo nghĩa chung nhất “là bất kì một trạng thái có màu sắc, cảm xúc nào đƣợc chủ thể cảm nhận, trải qua, đọng lại thành bộ phận (cùng với tri thức, ý thức,…) trong đời sống tâm lí của con ngƣời”. Theo nghĩa hẹp, “trải nghiệm là những tín hiệu bên trong, nhờ đó các sự kiện diễn ra đối với cá nhân đƣợc ý thức chuyển thành ý kiến cá nhân, góp phần lựa chọn tự giác các động cơ cần thiết, điều chỉnh hành vi của cá nhân”. Theo Bách khoa toàn thƣ Wikipedia, trải nghiệm hay kinh nghiệm là tổng quan khái niệm bao gồm tri thức, kĩ năng trong quan sát sự vật hoặc sự kiện đạt đƣợc thông qua tham gia vào hoặc tiếp xúc đến sự vật, sự kiện đó. Nhƣ vậy, trải nghiệm đạt đƣợc thƣờng thông qua thực hành, thử nghiệm để đi đến một tri thức về sự hiểu biết về sự vật, hiện tƣợng, sự kiện. Theo Nguyễn Phƣơng Trang (2017), lí luận giáo dục đã khẳng định bản chất của giáo dục là trải nghiệm. Muốn giáo dục học sinh, ta phải tổ chức các hoạt động phù hợp, không thể bằng con đƣờng lí thuyết suông. Trên thực tế hiện nay, nền giáo dục đang chuyển từ việc tiếp cận kiến thức sang tiếp cận các năng lực. Con ngƣời không chỉ học từ sách vở, nhà trƣờng mà còn từ thực tế cuộc sống, tích lũy cho bản thân những kinh nghiệm, biết gắn liền tri thức với thực tiễn, học đi đôi với hành. Quá trình “trải nghiệm” sẽ chứa yếu tố “thử” và “sai”. Sự trải nghiệm sẽ mang lại cho con ngƣời những kinh nghiệm phong phú. Quá trình trải nghiệm là quá trình tích lũy kinh nghiệm, giúp con ngƣời hình thành vốn kinh nghiệm, vốn sống, hình thành phẩm chất và năng lực. Tác giả Nguyễn Phƣơng Trang (2017) cũng đã chỉ ra rằng có rất nhiều dạng trải nghiệm nhƣ: - Căn cứ vào phạm vi diễn ra hoạt động của học sinh: trải nghiệm trên lớp học, trải nghiệm ngoài trời… - Căn cứ vào các cơ quan tham gia hoạt động: trải nghiệm trong đầu, trải nghiệm bằng các thao tác tay chân, trải nghiệm các giác quan… - Căn cứ vào các quá trình tâm lý: + Trải nghiệm cảm giác bên ngoài + Trải nghiệm về tri giác + Trải nghiệm tƣ duy và tƣởng tƣợng
+ Trải nghiệm về ghi nhớ DẠY KÈM QUY NHƠN OFFICIAL 10 + Trải nghiệm các cung bậc cảm xúc 1.1.2. Khái niệm hoạt động trải nghiệm Theo Tƣởng Duy Hải và các cộng sự (2017), hoạt động học tập trải nghiệm là quá trình ngƣời học tham gia vào việc xây dựng kiến thức, hình thành kĩ năng, năng lực qua các thao tác, hoạt động, hành động của cá nhân đối với môi trƣờng xã hội, môi trƣờng sống, môi trƣờng tự nhiên bằng sự nhận thức và cảm xúc của chính mình. Hoạt động này dựa trên sự dịch chuyển từ những kinh nghiệm sống của bản thân thành các kiến thức của cá nhân. Theo tác giả Quách Thị Phƣơng (2016), hoạt động trải nghiệm (HĐTN) trong nhà trƣờng cần đƣợc hiểu là hoạt động có động cơ, có đối tƣợng chiếm lĩnh, đƣợc tổ chức bằng các việc làm cụ thể của học sinh, đƣợc thực hiện trong thực tế, đƣợc sự định hƣớng, hƣớng dẫn của nhà trƣờng. Đối tƣợng để trải nghiệm nằm trong thực tiễn. Qua trải nghiệm thực tiễn, ngƣời học có kiến thức, kĩ năng, tình cảm và ý chí nhất định. Sự sáng tạo sẽ có đƣợc khi giải quyết các nhiệm vụ thực tiễn phải vận dụng kiến thức, kĩ năng đã có để giải quyết vấn đề, ứng dụng trong tình huống mới, không theo chuẩn đã có, hoặc nhận biết đƣợc vấn đề trong các tình huống tƣơng tự, độc lập nhận ra chức năng mới của đối tƣợng, tìm kiếm và phân tích đƣợc các yếu tố của đối tƣợng trong các mối tƣơng quan của nó, hay độc lập tìm kiếm giải pháp thay thế và kết hợp đƣợc các phƣơng pháp đã biết để đƣa ra hƣớng giải quyết mới cho một vấn đề. 1.1.3. Bản chất của hoạt động trải nghiệm Theo Nguyễn Thị Liên và các cộng sự (2016), Bản chất của hoạt động trải nghiệm là hoạt động giáo dục đƣợc tổ chức theo con đƣờng gắn lý thuyết với thực tiễn, tạo nên sự thống nhất giữa nhận thức và hành động; hình thành và phát triển cho HS niềm tin, tình cảm, những năng lực cần có của HS trong tƣơng lai. HĐTN có những đặc trƣng dƣới đây: - Tính tham gia trực tiếp của HS vào từng hoạt động. - Tính tự chủ của HS trong kế hoạch và hành động của cá nhân. - Tính tập thể của HS. - Tính tiếp cận với môi trƣờng sống trong và ngoài môi trƣờng. - Tính sáng tạo để thích ứng và tạo ra cái mới, giá trị mới cho bản thân. - Tính trọn vẹn của hoạt động thực tiễn. - Tính công dân có trách nhiệm khi đặt ngƣời học vào các tình huống mới. - HS đƣợc khẳng định giá trị bản thân qua huy động kinh nghiệm và năng lực của mình. - HS hình thành các ý thức, phẩm chất cùng chung sống và sống có trách nhiệm với bản thân, gia đình và xã hội. - HS đƣợc tiếp cận với các giá trị cuộc sống trong các tình huống thực tiễn. 1.2. Hoạt động trải nghiệm trong môn Toán Theo tác giả Nguyễn Hữu Tuyến (2018), Tổ chức HĐTN trong môn Toán là quá trình giáo viên (GV) tạo môi trƣờng trải nghiệm, thiết kế các HĐTN, giao nhiệm vụ, hƣớng dẫn và đánh giá học sinh (HS) học tập môn Toán thông qua HĐTN. Trong
quá trình đó, GV phải đặt HS trong trạng thái trải nghiệm bởi sự đa dạng các giác DẠY KÈM QUY NHƠN OFFICIAL 11 quan từ cảm giác, đến tri giác, và cảm xúc của cá nhân đó. Từ đó, HS phải đƣợc trình bày và biểu hiện đa dạng các kinh nghiệm sống và vốn hiểu biết của mình, đồng thời phải trao cho HS cơ hội thể hiện khả năng của họ đối với ngƣời khác, với GV, chuyên gia hoặc ngƣời hiểu biết hơn về sự lựa chọn quan điểm của mình. Trong quá trình trải nghiệm, HS đóng vai trò là nhà nghiên cứu khoa học mà mục đích chính là xây dựng kiến thức một cách khách quan, theo cách “tự nhiên” đƣợc rút ra từ chính thực tế sinh động mà ngƣời học đang trải nghiệm. Kết quả thu đƣợc của HS chính là sự thích ứng mới và sự thích nghi với môi trƣờng thực tiễn đang trải nghiệm. Chƣơng trình giáo dục phổ thông môn Toán 2018 cực kì chú trọng vào hoạt động trải nghiệm ở từng môn học, kể cả môn Toán. Chƣơng trình đã cấp một thời lƣợng thích đáng để giáo viên tiến hành tổ chức cho học sinh đƣợc tham gia các hoạt động thực hành và trải nghiệm toán học nhƣ: Tiến hành các đề tài, dự án học tập, đặc biệt là các đề tài có ứng dụng trong thực tiễn; tổ chức các trò chơi, câu lạc bộ toán học, các diễn đàn, hội thảo hay các cuộc thi về toán; tham gia các cơ sở đào tạo và nghiên cứu toán, giao lƣu với các học sinh có khả năng và yêu thích môn toán. Chƣơng trình giáo dục phổ thông môn Toán 2018 cũng nêu rõ Môn Toán ở trƣờng phổ thông góp phần tạo cơ hội cho học sinh đƣợc trải nghiệm, vận dụng toán học vào thực tiễn. Chƣơng trình môn Toán ở trƣờng phổ thông cần đảm bảo sự cân đối giữa “học” kiến thức và “vận dụng” kiến thức vào giải quyết vấn đề cụ thể. Tác giả Phạm Thị Hoàng Yến (2019) đã nêu ra hoạt động trải nghiệm trong môn Toán là một điểm mới và là một vấn đề cần đƣợc nghiên cứu, triển khai trong chƣơng trình môn Toán. Mục tiêu của hoạt động này gắn chặt với mục tiêu trong chƣơng trình môn Toán, đó là: - Hình thành và phát triển năng lực toán học bao gồm các thành tố cốt lõi sau: năng lực tƣ duy và lập luận toán học; năng lực giao tiếp toán học; năng lực sử dụng công cụ, phƣơng tiện học toán. - Góp phần hình thành và phát triển ở học sinh các phẩm chất chủ yếu và năng lực chung theo các mức độ phù hợp với môn học, cấp học đƣợc quy định tại Chƣơng trình tổng thể. - Có kiến thức, kĩ năng toán học phổ thông, cơ bản, thiết yếu; phát triển khả năng giải quyết vấn đề có tính tích hợp liên môn giữa môn Toán và các môn học khác nhƣ: Vật lí, Hóa học, Sinh học, Địa lí, Tin học, Công nghệ, Lịch sử, nghệ thuật,…; tạo cơ hội để học sinh đƣợc trải nghiệm, áp dụng toán học vào thực tiễn. - Có hiểu biết tƣơng đối tổng quát về sự hữu ích của toán học đối với từng ngành nghề liên quan để làm cơ sở định hƣớng nghề nghiệp, cũng nhƣ có đủ năng lực tối thiểu để tự tìm hiểu những vấn đề liên quan đến toán học trong suốt cuộc đời. 1.3. Mô hình học tập bằng trải nghiệm Lí thuyết học tập trải nghiệm đã đƣợc nghiên cứu sâu và ngày càng phát triển. Học tập trải nghiệm là lí thuyết đƣợc ứng dụng rộng rãi trên nhiều Quốc gia trên thế giới hiện nay. Đã có rất nhiều nhà nghiên cứu về lí thuyết này, tuy nhiên lí thuyết học tập theo kinh nghiệm và chu trình học của Kolb đƣợc biết đến rộng rãi trong giáo dục hiện đại. Lí thuyết của ông đƣợc xây dựng, kế thừa từ ba mô hình học tập kinh nghiệm sau: Mô hình học tập trải nghiệm nghiên cứu hành động và phòng thí
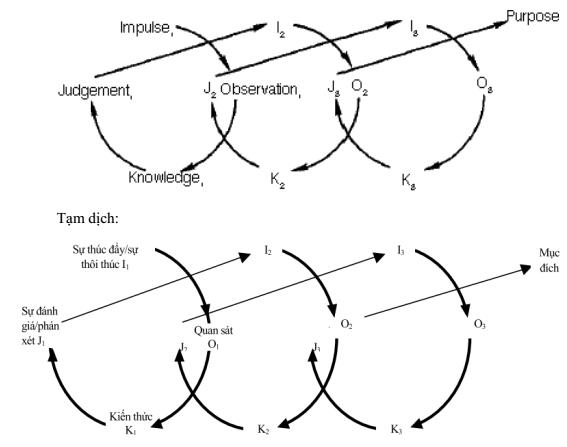
nghiệm của Lewin, mô hình học từ kinh nghiệm của John Dewey, mô hình học tập DẠY KÈM QUY NHƠN OFFICIAL 12 và phát triển nhận thức của Jean Piaget. Tác giả Hoàng Thị Thu Thảo (2019) đã giới thiệu một số mô hình học tập trải nghiệm đƣợc trình bày dƣới đây: 1.3.1. Mô hình hoạt động học tập trải nghiệm nghiên cứu hành động và phƣơng pháp phòng thí nghiệm của Lewin (The Lewinian Model of Action Research and Laboratory Training) Năm 1946, Zadek Kurt Lewin (1980 – 1947), ngƣời sáng lập của tâm lí học xã hội Mỹ, và ủng hộ tâm lí học Gestalt. Lewin đã chỉ ra đƣợc việc học tập đạt hiệu quả tối đa khi có sự xung đột biện chứng giữa kinh nghiệm cá nhân với việc phân tích giải quyết nhiệm vụ học tập. Theo ông, sự xung đột này có ý nghĩa quan trọng với việc thay đổi và giúp con ngƣời tiến bộ hơn. Và việc học đƣợc xem nhƣ là một chu trình gồm 4 giai đoạn đƣợc thể hiện trong hình vẽ 1.1. Hình vẽ 1.1. Mô hình học tập rải nghiệm của Kurt Lewin 1.3.2. Mô hình học tập trải nghiệm của Dewey John Deway (1859 – 1952) cho rằng sự học chỉ có nghĩa khi con ngƣời huy động các kinh nghiệm cụ thể của bản thân một cách tích cực và có suy nghĩ đến những kinh nghiệm này đối với mục tiêu muốn đạt đƣợc qua các hành động cụ thể. Giáo dục tốt nhất phải là sự học tập trong cuộc sống. Ông chủ trƣơng trẻ em phải học tập trong chính cuộc sống xã hội. Nhu cầu học chỉ nổi lên từ những kinh nghiệm sống hàng ngày và từ những kiến thức đã thu đƣợc theo một chuỗi các hoạt động tái hiện, đầu tƣ, vận dụng kiến thức trong các hành động của các nhân ngƣời học để tiếp tục tiến xa hơn, hiểu biết sâu hơn trong sự trải nghiệm của bản thân. Do đó, chƣơng trình dạy học và việc dạy học phải là quá trình xâu chuỗi các thành tố trong kinh nghiệm cũ và mới của trẻ; quá trình học của trẻ phải bao gồm có Xung (Impulse),
Quan sát (Observation), Kiến thức (Knowledge) và Phán xét (Judgment) sắp xếp DẠY KÈM QUY NHƠN OFFICIAL 13 trong một chu trình kéo dài cho đến khi ngƣời học đạt đƣợc mục đích học tập. Mô hình học tập của Dewey đƣợc thể hình trong hình 2. Hình vẽ 1.2: Mô hình học tập dựa trên kinh nghiệm của Deway (Deway’s Model of Experiential Learning) 1.3.3. Mô hình học tập và phát triển nhận thức của Piaget (Piaget’s Model of Learning and Cognitive Development) Jean Piaget là nhà tâm lí học phát triển và nhà triết học nổi tiếng Thụy Sĩ. Lí thuyết nhận thức của Piaget là một lí thuyết toàn diện về bản chất và phát triển của trí tuệ con ngƣời, nội dung của nó đề cập đến bản chất của bản thân kiến thức và cách thức con ngƣời dần tiếp cận, kiến tạo và sử dụng nó. Ông đặc biệt tập trung vào quá trình đồng hóa (Assimilation) và điều tiết (Accomodation) để giải thích con đƣờng phát triển nhận thức. Theo ông, trẻ em xây dựng sự hiểu biết về thế giới xung quanh, sau đó trải nghiệm sự khác biệt giữa những gì chúng khám phá trong môi trƣờng xung quanh. Mô hình học tập của ông đƣợc thể hiện trong hình vẽ 1.3:
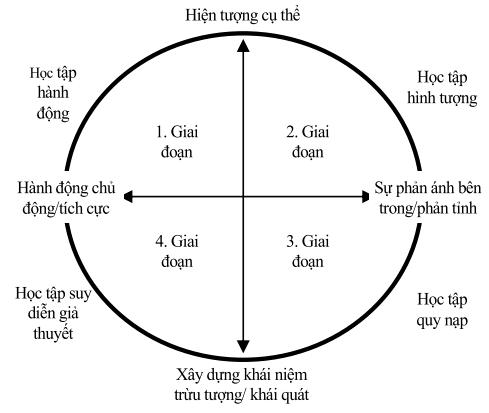
DẠY KÈM QUY NHƠN OFFICIAL 14 Tạm dịch: Hình vẽ 1.3: Mô hình học tập và phát triển nhận thức của Piaget (Piaget’s Model of Learning and Cognitive Development) 1.3.4. Mô hình học tập bằng trải nghiệm của Kolb (Kolb’s Model of Experiential Learning) Đây là mô hình học tập trải nghiệm đƣợc sử dụng phổ biến trên thế giới, nó kế thừa và phát triển từ các lí thuyết học tập của Deway, Lewin và Piaget. Và mô hình học tập trải nghiệm của Kolb là quy trình chúng tôi chọn để xây dựng hoạt động trải nghiệm cho trƣờng hợp: Góc giữa hai mặt phẳng. Năm 1984, David Kolb (nhà lí luận giáo dục ngƣời Mỹ) đã có công trình: Học tập trải nghiệm: Kinh nghiệm là tài nguyên học tập và phát triển ( Experiential Learning: Experience As the Source Of Learning And Development). Kolb tin rằng, phong cách học tập của mỗi ngƣời là kết quả từ một tƣơng tác giữa đặc điểm bên trong một cá nhân và môi trƣờng, hoàn cảnh bên ngoài của họ nhằm thu nhận và xử
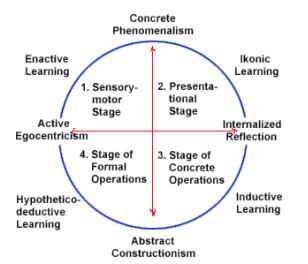
lí thông tin trong các tình huống học tập. Đây chính là nền tảng tƣ tƣởng để ông DẠY KÈM QUY NHƠN OFFICIAL 15 phát triển một mô hình học tập dựa vào trải nghiệm (Experiential learning, thƣờng đƣợc biết đến với cái tên “Chu trình học tập của Kolb”) nhằm “qui trình hóa” việc học với các giai đoạn và thao tác đƣợc định nghĩa rõ ràng. Mô hình học tập của Kolb bao gồm bốn giai đoạn nhấn mạnh sự quan tâm đến quá trình nhận thức bên trong của ngƣời học. Theo đó, ông cho rằng: “Học tập là quá trình mà kiến thức được tạo ra thông qua việc chuyển đổi kinh nghiệm. Kết quả của kiến thức là sự kết hợp giữa nắm bắt kinh nghiệm và chuyển đổi nó thành kinh nghiệm của bản thân”. Đây là một trong số những mô hình đƣợc sử dụng rộng rãi nhất trong việc thiết kế chƣơng trình học, thiết kế bài giảng, trong việc giảng dạy và hƣớng dẫn học tập cho học sinh. Theo quan điểm của Kolb, hoạt động trải nghiệm dựa trên hai tƣơng tác giữa các kiến thức và sự trải nghiệm. Kiến thức đƣợc rút ra từ chính sự trải nghiệm của ngƣời học và giá trị, ý nghĩa của kiến thức đƣợc xác nhận qua sự trải nghiệm của ngƣời học. Vì vậy, Kolb cho rằng, quá trình này tạo nên một vòng lặp giữa kiến thức và sự trải nghiệm và tuân theo một trật tự của chu trình nhƣng không nhất thiết phải khởi đầu từ một bƣớc cố định nào trong mô hình. Mô hình học tập trải nghiệm của Kolb (1984) đƣợc mô tả theo chu trình học nhƣ hình dƣới đây: Tạm dịch:
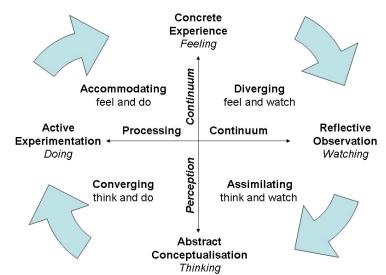
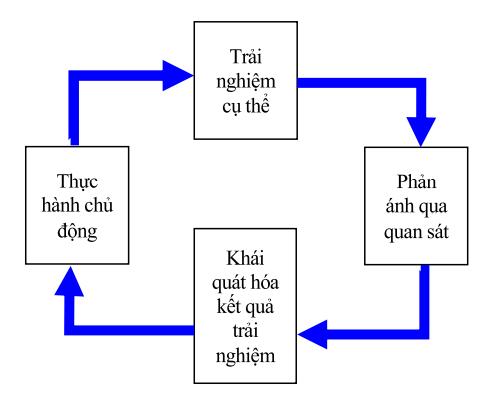
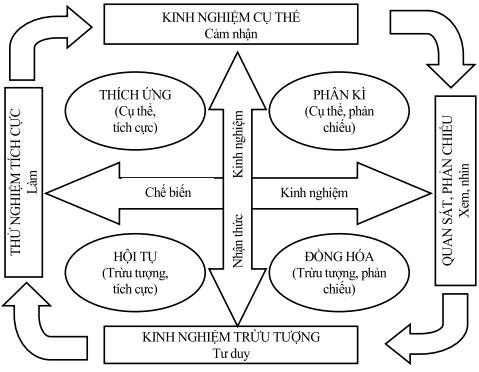
DẠY KÈM QUY NHƠN OFFICIAL 16 Hình vẽ 1.4: Mô hình học tập bằng trải nghiệm của Kolb (Kolb’s Model of Experiential Learning) Sơ đồ này đƣợc trình bày lại nhƣ sau: Trải nghiệm cụ thể là giai đoạn học tập nhờ vào cảm nhận từ những kinh nghiệm đã có trƣớc đó của ngƣời học. Ví dụ: Ngƣời học có thể đã đọc một số tài liệu, xem một số video trên Internet về chủ đề đang học tập… Tất cả những yếu tố đó sẽ tạo ra các kinh nghiệm nhất định cho ngƣời học. Tuy vậy, kinh nghiệm quan trọng nhất
là những kinh nghiệm mà các giác quan của con ngƣời có thể cảm nhận rõ ràng DẠY KÈM QUY NHƠN OFFICIAL 17 đƣợc. Phản ánh qua quan sát là giai đoạn học tập dựa trên sự xem xét kĩ lƣỡng một vấn đề nào đó. Ngƣời học cần phân tích, đánh giá các sự kiện và các kinh nghiệm đã có. Sự xem xét, đánh giá này cần mang yếu tố “phản ánh”, tức là tự mình suy tƣởng về các kinh nghiệm đó, xem mình cảm thấy thế nào, có hiểu đƣợc hay không, có thấy hợp lí không, có đúng hay cảm thấy “có cái gì đó không ổn”, có quan điểm nào đi ngƣợc với các kinh nghiệm đã có trƣớc đó không…Ví dụ quan sát phản ánh nhằm kích thích học tập, xem xét các vấn đề từ khía cạnh và hoàn cảnh hoàn toàn khác nhau. Khái quát hóa trừu tượng là giai đoạn học tập nhờ vào sự tƣ duy bao gồm: phân tích những ý tƣởng một cách hợp lí, khái quát công việc để tìm ra ý tƣởng hoặc lí thuyết mới. Bƣớc này chính là bƣớc quan trọng để các “kinh nghiệm” chuyển đổi thành “tri thức” và bắt đầu lƣu giữ trong não bộ. Không có bƣớc này, các kinh nghiệm đó sẽ không đƣợc nâng cấp hợp thức hóa để sử dụng mà chỉ là các trải nghiệm vụn vặt thu đƣợc trong quá trình học tập. Thử nghiệm tích cực là giai đoạn học tập thông qua thực hành tích cực để chuyển hóa nội dung học tập thành kinh nghiệm của bản thân, bao gồm: kiểm nghiệm các ý tƣởng mới thông qua thực hành và ứng dụng cho những vấn đề khác, giải quyết vấn đề thông qua hành động. Chu kì học tập dựa vào trải nghiệm diễn ra từ giai đoạn 1 đến giai đoạn 4 và tạo thành một vòng tròn khép kín. Quá trình học luôn diễn ra một cách liên tục và nhịp nhàng trên cơ sở những thành tựu, kết quả đã thu đƣợc. 1.4. Tổng kết chƣơng 1 Từ việc nghiên cứu những tài liệu về hoạt động trải nghiệm đã có, chúng tôi rút ra đƣợc một số nhận xét sau: - Mô hình học tập trải nghiệm của Kolb là lí thuyết học tập trải nghiệm đƣợc sử dụng phổ biến trên thế giới. Mô hình của ông kế thừa và phát triển từ các lí thuyết học tập trải nghiệm của các tác giả lớn nhƣ Dewey, Lewin và Piaget. Mô hình học tập trải nghiệm của Kolb gồm bốn giai đoạn: Trải nghiệm cụ thể, Phản ánh qua quan sát, khái quát hóa trừu tƣợng và thử nghiệm tích cực. Trong mô hình của ông, có thể bắt đầu từ một giai đoạn bất kì trong bốn giai đoạn nêu trên, tuy nhiên các giai đoạn phải đƣợc thực hiện liên tiếp theo chu trình của mình. - Hoạt động trải nghiệm trong môn Toán đƣợc thực hiện nhằm mục tiêu phát triển toàn diện các năng lực, phẩm chất cần thiết của HS; giúp HS gắn kết các kiến thức, kĩ năng và trải nghiệm bản thân để giải quyết tình huống cụ thể. Từ đó, hình thành và phát triển ở HS các năng lực toán học và các năng lực khác cần thiết. - Hoạt động trải nghiệm phù hợp với yêu cầu của việc đổi mới phƣơng pháp dạy học theo hƣớng phát triển năng lực học sinh, lấy ngƣời học làm trung tâm. - Giáo viên đóng vai trò quan trọng trong việc thiết kế tình huống thực hành cho HS, phải thiết kế những tình huống học tập dựa trên môi trƣờng, những tình huống để học sinh tích lũy đƣợc kinh nghiệm thông qua việc giải quyết tình huống. Ngƣời giáo viên phải hiểu rõ học sinh của mình để đƣa ra những tình huống phù hợp, giúp học sinh phát huy tối đa các năng lực của bản thân, và thông qua tình huống giúp học sinh trả lời đƣợc câu hỏi “Tại sao ta phải học kiến thức này?”
CHƢƠNG 2:
DẠY KÈM QUY NHƠN OFFICIAL 18 GÓC GIỮA HAI MẶT PHẲNG TRONG SÁCH GIÁO KHOA HÌNH HỌC 11 Trong chƣơng này, chúng tôi sẽ phân tích hai bộ sách giáo khoa hiện hành và hai bộ sách giáo viên tƣơng ứng nhƣ sau: - SGK 1: Trần Văn Hạo và các tác giả (2006), Hình học 11, Nhà xuất bản Giáo Dục - SGK2: Đoàn Quỳnh và các tác giả (2006), Hình học 11 nâng cao, Nhà xuất bản giáo dục - SGV1: Trần Văn Hạo và các tác giả (2006), Hình học 11 Sách giáo viên, NXB Giáo dục. - SGV2: Đoàn Quỳnh và các tác giả (2006), Hình học 11 nâng cao Sách giáo viên, NXB Giáo dục. Chúng tôi sẽ phân tích nội dung “Góc giữa hai mặt phẳng” đƣợc trình bày trong Chƣơng III- VECTO TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN. Bài 4: HAI MẶT PHẲNG VUÔNG GÓC 2.1. Sách giáo khoa Hình học 11 Ở nội dung này, mục tiêu cần đạt đƣợc nêu ra trong SGV nhƣ sau: “ - Nắm được định nghĩa góc giữa hai mặt phẳng, từ đó nắm được định nghĩa hai mặt phẳng vuông góc. - Nắm được điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau và định lí về giao tuyến của hai mặt phẳng cắt nhau cùng vuông góc với một mặt phẳng thứ ba để vận dụng làm các bài toán hình học không gian. - Nắm được định nghĩa hình lăng trụ đứng, chiều cao của hình lăng trụ đứng và các tính chất của hình lăng trụ đứng. - Nắm được định nghĩa hình chóp đều, hình chóp cụt đều và các tính chất của các hình đó.” Chúng tôi có thể thấy rằng, ở nội dung bài học này, trọng tâm của SGK1 là nội dung hai mặt phẳng vuông góc. Các mục đích của SGV1 đề cập đến tất cả đều hƣớng đến kiến thức hai mặt phẳng vuông góc. Ngoài ra, trong SGV1 còn có đề cập: “Trước khi trình bày định nghĩa hai mặt phẳng vuông góc chúng ta cần phải giới thiệu về định nghĩa góc giữa hai mặt phẳng. Trong SGK định nghĩa góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó. Sau đó, SGK có trình bày cách xác định góc giữa hai mặt phẳng cắt nhau mà về thực chất có thể coi đây là một định nghĩa khác về góc giữa hai mặt phẳng và dễ thấy rằng hai định nghĩa trên là tương đương”. Có thể thấy rằng kiến thức ở bài này xoay quanh nội dung hai mặt phẳng vuông góc. Nội dung góc giữa hai mặt phẳng chỉ là đƣợc giới thiệu qua, không đƣợc trình bày chi tiết. Nhƣ vậy, cụ thể góc giữa hai mặt phẳng đƣợc trình bày nhƣ thế nào trong SGK hiện hành? Và chiếu theo mô hình học tập trải nghiệm của Kolb thì SGK hiện hành có những hoạt động nào thể hiện đƣợc qua điểm dạy học bằng hoạt động trải nghiệm? Sách giáo khoa mở đầu bằng hình ảnh cánh cửa: “Hình ảnh của một cánh cửa chuyển động và hình ảnh của bề mặt bức tường cho ta thấy được sự thay đổi của góc giữa hai mặt phẳng.”
Nhƣ vậy góc giữa hai mặt phẳng đƣợc SGK1 giới thiệu qua một hình ảnh thực tiễn, DẠY KÈM QUY NHƠN OFFICIAL 19 cho HS cái nhìn ban đầu về góc giữa hai mặt phẳng. Sau đó SGK1 đƣa ra định nghĩa góc giữa hai mặt phẳng: “Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.” SGK1 cũng chú ý góc giữa hai mặt phẳng song song hoặc trùng nhau: “Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói rằng góc giữa hai mặt phẳng đó bằng .” SGK chỉ dừng lại ở mức độ “giới thiệu” hình ảnh trên và không có bất cứ hoạt động nào tìm hiểu về hình ảnh này. Với định nghĩa trên, việc xác định góc giữa hai mặt phẳng trong một số trƣờng hợp sẽ gặp rất nhiều khó khăn, HS phải tìm đƣợc hai đƣờng thẳng vuông góc với hai mặt phẳng và xác định góc giữa hai đƣờng thẳng này. Chƣa kể nếu hai đƣờng thẳng này chéo nhau, việc xác định góc giữa chúng lại càng khó khăn. Có lẽ, vì thế SGK1 cung cấp cách xác định góc giữa hai mặt phẳng cắt nhau, và cũng có thể coi đây là định nghĩa khác của góc giữa hai măt phẳng: “Giả sử hai mặt phẳng và cắt nhau theo giao tuyến . Từ một điểm bất kỳ trên ta dựng trong đường thẳng vuông góc với và dựng trong đường thẳng vuông góc với . Người ta chứng minh được góc giữa hai mặt phẳng và là góc tạo bởi hai đường thẳng và . (h3.31)” Nhƣ vậy ở định nghĩa này SGK1 cũng chỉ dừng lại với việc cung cấp cho HS lý thuyết mà thôi. Sau khi đƣa ra định nghĩa góc giữa hai mặt phẳng SGK1 đã đƣa ra tính chất không chứng minh liên quan đến diện tích hình chiếu của một đa giác: “Cho đa giác nằm trong mặt phẳng có diện tích và là hình chiếu vuông góc của trên mặt phẳng . Khi đó diện tích của được tính theo công thức:
với là góc giữa và .” Ở tính chất này ta thấy muốn tính đƣợc diện tích hình chiếu của đa giác thì điều kiện cần là tình đƣợc góc giữa hai mặt phẳng (góc ). Tiếp đó SGK đƣa ra bài toán áp dụng để tính góc giữa hai mặt phẳng, sau đó tính diện tích tam giác khi biết diện tích hình chiếu và góc tạo bởi mặt phẳng chứa tam giác và mặt phẳng chiếu: “Ví dụ: Cho hình chóp có đáy là tam giác đều cạnh , cạnh bên vuông góc với mặt phẳng và . a) Tính góc giữa hai mặt phẳng và . b) Tính diện tích tam giác .” Tiếp tục SGK đã đi vào một trƣờng hợp cụ thể của góc giữa hai mặt phẳng là hai mặt phẳng vuông góc, và chúng tôi cho rằng đây là nội dung trọng tâm trong bài này: “Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng là góc vuông. Nếu hai mặt phẳng và vuông góc với nhau ta ký hiệu .” Ở đây SGK định nghĩa hai mặt phẳng vuông góc nếu góc giữa hai mặt phẳng là góc vuông. Nghĩa là muốn chứng minh hai mặt phẳng vuông góc dựa theo định nghĩa ta
cần phải tìm đƣợc góc giữa hai mặt phẳng và chứng minh góc này là góc vuông. DẠY KÈM QUY NHƠN OFFICIAL 20 Ngoài ra, để thuận tiện hơn khi làm bài sau này, SGK trình bày các định lý liên quan đến hai mặt phẳng vuông góc nhằm giúp học sinh có nhiều cách chứng minh hai mặt phẳng vuông góc ngoài cách dùng đến góc giữa hai mặt phẳng. Nhƣ vậy ở phần lý thuyết SGK1 đã đƣa ra đƣợc hình ảnh góc giữa hai mặt phẳng sau đó đi vào định nghĩa góc giữa hai mặt phẳng, cách xác định góc giữa hai mặt phẳng, diện tích hình chiếu của đa giác, hai mặt phẳng vuông góc nhƣng trên phƣơng diện lý thuyết và chƣa có những hoạt động thực tế. Phân tích các bài tập liên quan đến góc giữa hai mặt phẳng Chỉ có duy nhất 1 dạng bài tập liên quan đến góc giữa hai mặt phẳng. Dạng: Tìm và tính góc giữa hai mặt phẳng Cách giải 1: - Tìm hai đƣờng thẳng lần lƣợt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng. - Góc giữa hai đƣờng thẳng này là góc giữa hai mặt phẳng. Cách giải 2: - Tìm góc giữa hai mặt phẳng. - Dùng hệ thức lƣợng trong tam giác tính góc giữa hai mặt phẳng. Căn cứ: Góc giữa hai mặt phẳng. Thông qua việc phân tích các bài tập, chúng tôi thấy rằng SGK1 đƣa ra các bài tập phân thành nhiều dạng, nội dung “Góc giữa hai mặt phẳng” xuất hiện khá ít và chỉ dừng lại ở việc tính toán thuần túy chƣa có bài tập áp dụng thực tiễn. Phần lớn các bài tập tập trung ở phần “Tính độ dài đoạn thẳng” dựa trên các hệ quả định lý ở phần “Hai mặt phẳng vuông góc” và phần “Chứng minh hai mặt phẳng vuông góc”. Góc giữa hai mặt phẳng là công cụ để chứng minh định lí liên quan đến hai mặt phẳng vuông góc; từ đó, hầu nhƣ bài tập chứng minh hai mặt phẳng vuông góc đều dùng định lý chứ ít khi dùng kĩ thuật tính góc. Tóm lại: - Ở phần lí thuyết có đề cập đến nhiều nội dung trong đó có nội dung “Góc giữa hai mặt phẳng” nhƣng chƣa có một tình huống thực tiễn minh họa cho lý thuyết, tất cả hầu nhƣ dựa trên hình vẽ. - Góc giữa hai mặt phẳng là công cụ để chứng minh các định lí về hai mặt phẳng vuông góc. Các dạng bài tập chủ yếu tập trung ở nội dung hai mặt phẳng vuông góc và đƣợc giải bằng cách căn cứ vào các định lí đã đƣợc chứng minh. - Nội dung “Góc giữa hai mặt phẳng” xuất hiện khá ít và chỉ dừng lại ở việc tính toán thuần túy chƣa có bài tập áp dụng thực tiễn. Nhƣ vậy liên quan đến nội dung góc giữa 2 mặt phẳng, đối chiếu theo chu trình học tập trải nghiệm của Kolb, chúng ta thấy rằng bƣớc 1 (trải nghiệm cụ thể) và bƣớc 2 (phản ánh) không xuất hiện. HS đƣợc trình bày trực tiếp định nghĩa, định lý (khái quát hóa trừu tƣợng) tức là bƣớc 3 của chu trình của Kolb. Bƣớc 4 (thử nghiệm tích cực) có xuất hiện thông qua một vài bài tập vận dụng định nghĩa, định lý để tính góc giữa hai mặt phẳng nhƣng số lƣợng rất ít. Hơn nữa, đó là những bài toán áp dụng thuần túy toán học mà chƣa cho phép HS ứng dụng vào những tình huống thực tiễn. 2.2. Sách giáo khoa Hình học 11 nâng cao (SGK2) Mục tiêu ở bài này trong SGV2 đƣợc đề ra có sự khác biệt so với SGV1, cụ thể nhƣ sau:
DẠY KÈM QUY NHƠN OFFICIAL 21
“Làm cho học sinh: - Biết cách tính góc giữa hai mặt phẳng - Nắm được điều kiện để hai mặt phẳng vuông góc và các tính chất liên quan; biết vận dụng chúng vào việc giải toán. - Nắm được định nghĩa của các hình lăng trụ đặc biệt, hình chóp đều và hình chóp cụt đều.” Ở nội dung góc giữa hai mặt phẳng, SGV2 yêu cầu HS phải tính đƣợc góc, thay vì SGV1 chỉ yêu cầu HS nắm đƣợc định nghĩa. Nhƣ vậy để tính đƣợc góc, HS cần phải nắm đƣợc định nghĩa và nắm đƣợc kĩ thuật xác định góc. Phần đầu tiên của SGK2 là định nghĩa góc giữa hai mặt phẳng giống với SGK1. “Góc giữa hai mặt phẳng là góc giữa hai đường thẳng vuông góc với hai mặt phẳng đó.” Riêng phần cách tìm góc của hai mặt phẳng SGK2 trình bày bằng cách khác với SGK1: “Khi hai mặt phẳng và cắt nhau theo giao tuyến , để tính góc giữa chúng, ta chỉ cần xét một mặt phẳng vuông góc với , lần lượt cắt và theo các giao tuyến và . Lúc đó, góc giữa và bằng góc giữa hai đường thẳng , .” Về bản chất hai cách viết ở hai sách giáo khoa là giống nhau. Ở đây việc lấy một mặt phẳng vuông góc với giao tuyến thì tƣơng tự nhƣ việc ta lấy hai đƣờng thẳng vuông góc với giao tuyến và giao nhau tại một điểm trên giao tuyến. Tức là hai đƣờng thẳng và mà ở SGK1 đã lấy chính là hai đƣờng thẳng và mà ở SGK2 đã đề cập. Sau đó SGK2 đã đƣa ra ví dụ để dẫn đến tính chất diện tích hình chiếu của một đa giác: “Gọi là diện tích của đa giác trong mặt phẳng và là diện tích hình chiếu của trên mặt phẳng thì , trong đó là góc giữa hai mặt phẳng và . ” Sang phần 2 SGK2 đã nêu định nghĩa hai mặt phẳng vuông góc và các hệ quả, định lý nhƣ SGK1: “2. Hai mặt phẳng vuông góc Định nghĩa 2: Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng ” Sau khi đƣa ra định nghĩa SGK2 đã đƣa ra một ví dụ áp dụng định nghĩa: “Cho hình tứ diện có đôi một vuông góc. Hãy chỉ ra các đường thẳng lần lượt vuông góc với các mặt phẳng và từ đó suy ra các mặt phẳng ấy đôi một vuông góc.” Tiếp theo các hệ quả định lý về hai mặt phẳng vuông góc đƣợc SGK2 nêu ra. Nhƣ vậy ở phần lý thuyết, SGK2 cũng tƣơng tự SGK CƠ BẢN các lý thuyết đƣợc đƣa ra dƣới dạng chữ, hình vẽ và chƣa có tình huống thực tiễn minh họa cho lý thuyết. Ở đây nếu chiếu theo mô hình học tập trải nghiệm của Kolb thì SGK nâng cao đã trình bày định nghĩa góc giữa hai mặt phẳng chỉ ở bƣớc khái quát hóa trừu tƣợng và không xuất hiện ba bƣớc còn lại. Về phần bài tập, chỉ có duy nhất 1 dạng bài tập liên quan đến góc giữa hai mặt phẳng.
Dạng : Tìm độ dài một cạnh của hình chóp biết góc giữa hai mặt phẳng
Cách giải: DẠY KÈM QUY NHƠN OFFICIAL 22 - Dựa vào góc giữa hai mặt phẳng tìm biểu thức liên hệ giữa và . - Tính theo . Căn cứ: Góc giữa hai mặt phẳng. Từ việc phân tích bài tập, chúng tôi thấy rằng SGK2 phân bố đều tất cả các dạng. Nội dung “Góc giữa hai mặt phẳng” đóng vai trò là công cụ chứ chƣa có bài tập cụ thể về tính góc giữa hai mặt phẳng. Ngoài ra SGK2 vẫn chƣa có các bài tập áp dụng góc giữa hai mặt phẳng vào thực tiễn. Tóm lại: Ở phần lí thuyết, tƣơng tự nhƣ SGK1 thì SGK2 cũng trình bày nhiều nội dung trong đó phần “Góc giữa hai mặt phẳng” trình bày định nghĩa góc giữa hai mặt phẳng và cách tìm góc giữa hai mặt phẳng cắt nhau dƣới dạng chữ, hình vẽ chƣa có tình huống thực tiễn minh họa cho lý thuyết. Còn về phần bài tập, nội dung “Góc giữa hai mặt phẳng” đóng vai trò là công cụ giải quyết các bài tập chứng minh hai mặt phẳng vuông góc và chƣa có bài toán áp dụng thực tiễn. Nhƣ vậy tƣơng tự nhƣ SGK1 liên quan đến nội dung góc giữa 2 mặt phẳng, đối chiếu theo chu trình học tập trải nghiệm của Kolb, chúng ta thấy rằng bƣớc 1 (trải nghiệm cụ thể) và bƣớc 2 (phản ánh) không xuất hiện. HS đƣợc trình bày trực tiếp định nghĩa, định lý (khái quát hóa trừu tƣợng) tức là bƣớc 3 của chu trình của Kolb. Bƣớc 4 (thử nghiệm tích cực) có xuất hiện thông qua một vài bài tập vận dụng định nghĩa, định lý để tính góc giữa hai mặt phẳng nhƣng số lƣợng rất ít. Hơn nữa, đó là những bài toán áp dụng thuần túy toán học mà chƣa cho phép HS ứng dụng vào những tình huống thực tiễn. 2.3. Tổng kết chƣơng SGK1 và SGK2 đều công bố tri thức góc giữa hai mặt phẳng mà không thông qua một hoạt động hay hệ thống câu hỏi nào để HS tìm hiểu về nó. Tiếp sau đó là những phần bài tập vận dụng kiến thức vừa học và không có một bài tập nào gắn với thực tế, hoạt động trải nghiệm thực tiễn. SGK1 có cung cấp cho HS một hình ảnh thực tế: “Hình ảnh của một cánh cửa chuyển động và hình ảnh của bề mặt bức tường cho ta thấy được sự thay đổi của góc giữa hai mặt phẳng.” Tuy nhiên SGK1 không cho HS tìm hiểu, phân tích hình ảnh này. Nếu đi sâu phân tích về hình ảnh này thì tiến trình này sẽ xuất hiện giai đoạn trải nghiệm cụ thể trong mô hình học tập trải nghiệm của Kolb. Nhƣ vậy cả hai sách giáo khoa, trong tiến trình dạy học khái niệm góc giữa hai mặt phẳng thiếu vắng đi ba giai đoạn: Trải nghiệm cụ thể, phản ánh qua quan sát và thực hành chủ động mà chỉ có duy nhất bƣớc khái niệm hóa trừu tƣợng để đƣa khái niệm góc giữa hai mặt phẳng và các định lí liên quan. Thực ra bƣớc 4 có nhƣng mờ nhạt và không thể hiện đúng ý nghĩa của bƣớc 4 trong chu trình của Kolb mà chỉ đơn thuần là bài tập áp dụng thuần túy toán học. Chúng tôi nhận thấy rằng ở nội dung này, có thể xây dựng cho HS tình huống hoạt động trải nghiệm để học tập kiến thức này. Tình huống mà chúng tôi xây dựng sẽ đƣợc trình bày ở chƣơng 3.
CHƢƠNG 3: NGHIÊN CỨU THỰC NGHIỆM
DẠY KÈM QUY NHƠN OFFICIAL 23 3.1. Mục đích thực nghiệm Nhƣ những phân tích trƣớc, nội dung góc giữa hai mặt phẳng hoàn toàn thiếu vắng các hoạt động, nhiệm vụ thực tiễn cho HS. Ở chƣơng này, chúng tôi muốn tạo ra tình huống để HS có cơ hội hoạt động trải nghiệm cá nhân, qua đó, HS có thể nhận thấy đƣợc một số ứng dụng của góc giữa hai mặt phẳng trong thực tiễn. HS có thể gắn kết bài học với đời sống và kiến thức HS học đƣợc càng nhớ lâu hơn. Ngoài ra, tình huống còn giúp HS rèn luyện năng lực tƣ duy, giải quyết vấn đề toán học. 3.2. Đối tƣợng và hình thức thực nghiệm - Thực nghiệm trên HS lớp 11, chƣa học Góc giữa hai mặt phẳng. - HS làm việc theo nhóm (4-6HS/nhóm). 3.3. Giới thiệu tình huống thực nghiệm 3.3.1. Tình huống 1: GV chuẩn bị dụng cụ cho mỗi nhóm nhƣ sau: Hai mặt phẳng cắt nhau theo giao tuyến , và 2 mặt phẳng tạo với nhau một góc ? (02 mặt phẳng này có thể là bìa, giấy foam đƣợc ghép với nhau). Những que nhựa dài, cứng, thƣớc đo góc, thƣớc ê-ke, kéo, giấy . Riêng thƣớc đo góc, ở đây chúng tôi sử dụng thƣớc đã bị cắt một phần để thuận tiện đo góc trong quá trình thực hiện của HS.

DẠY KÈM QUY NHƠN OFFICIAL 24 Nhiệm vụ 1: Yêu cầu HS dựng 02 đƣờng thẳng sao cho: đƣờng thẳng thứ nhất cắt mặt phẳng thứ nhất, đƣờng thẳng thứ hai cắt mặt phẳng thứ hai. Các đƣờng thẳng này không đƣợc vuông góc với các mặt phẳng. Sau đó xác định số đo góc giữa hai đƣờng thẳng này. Nhiệm vụ 2: Yêu cầu học sinh dựng 02 đƣờng thẳng sao cho: đƣờng thẳng thứ nhất vuông góc với mặt phẳng thứ nhất, đƣờng thẳng thứ hai vuông góc với mặt phẳng thứ hai. Sau đó xác định số đo góc giữa hai đƣờng thẳng này. Yêu cầu học sinh so sánh kết quả với nhau. Sau đó rút ra kết luận. Đi vào định nghĩa góc giữa hai mặt phẳng. Tóm tắt tình huống bằng bảng: Dụng cụ chuẩn bị Nhiệm vụ Nhiệm vụ 1 Nhiệm vụ 2 Hai mặt phẳng cắt nhau theo giao tuyến , và 2 mặt phẳng tạo với nhau một góc ; que nhựa dài, cứng; thƣớc đo góc, thƣớc ê-ke, kéo, giấy .

Dựng 2 đƣờng thẳng lần lƣợt cắt hai mặt phẳng sao cho không vuông góc với các mặt phẳng đó. Xác định số đo góc giữa hai đƣờng thẳng. Dựng 2 đƣờng thẳng lần lƣợt vuông góc với hai mặt phẳng. Xác định số đo góc giữa hai đƣờng thẳng.
3.3.2. Tình huống 2: Pha 1:
Nhiệm vụ 3: Chuẩn bị lại cho HS 02 mặt phẳng nhƣ ở tình huống 1. Yêu cầu HS chọn 2 đƣờng thẳng trong 02 mặt phẳng không cùng vuông góc với giao tuyến.
DẠY KÈM QUY NHƠN OFFICIAL 25 Xác định góc giữa hai đƣờng thẳng này. Yêu cầu HS so sánh với số đo góc giữa hai mặt phẳng. Nhiệm vụ 4: Chuẩn bị lại cho HS 02 mặt phẳng nhƣ ở tình huống 1. Yêu cầu HS chọn 2 đƣờng thẳng trong 02 mặt phẳng cùng vuông góc với giao tuyến. Xác định góc giữa hai đƣờng thẳng này. Yêu cầu HS so sánh với số đo góc giữa hai mặt phẳng. Từ hai nhiệm vụ trên, cho HS rút ra nhận xét về mối quan hệ của góc giữa hai mặt phẳng với góc giữa hai đƣờng thẳng cùng vuông góc với giao tuyến lần lƣợt nằm trong hai mặt phẳng này. Pha 2: Nhiệm vụ: Chuẩn bị cho HS 02 mặt phẳng có tính chất “hai mép” của hai mặt phẳng không vuông góc với nhau, góc giữa 2 mặt phẳng .


DẠY KÈM QUY NHƠN OFFICIAL 26 Khi đó yêu cầu HS không dựng đƣờng vuông góc với mặt phẳng hãy xác định góc giữa hai mặt phẳng này, giải thích cách làm. Pha 3: Tiến hành làm con súc sắc 8 mặt dựa trên tình huống sau: Hiện nay, Các trò chơi Boargame đang thu hút rất là nhiều giới trẻ. Những trò chơi này vừa kết hợp yếu tố ngẫu nhiên (may mắn) và trí tuệ của mỗi ngƣời. Có một số trò chơi mang yếu tố may mắn cần những con súc sắc, đặc biệt hơn, những con súc sắc này không chỉ đơn thuần là con súc sắc 6 mặt nhƣ chúng ta đã biết. Những con súc sắc này có thể là 4 mặt, 8 mặt, 12 mặt hay 20 mặt. Bây giờ, thầy (cô) muốn mô phỏng một trò chơi cho cả lớp mà cần đến con súc sắc 8 mặt, nhƣng ở ngoài thị trƣờng thì con súc sắc này rất nhỏ không thể sử dụng đƣợc. Các em hãy thử thiết kế một con súc sắc 8 mặt nhƣ vậy, biết rằng, các mặt của con súc sắc là các tam giác đều, và bây giờ thầy (cô) sẽ cung cấp 8 tam giác đều bằng nhau và dụng cụ cần thiết cho các em. Tóm tắt tình huống 2 bằng bảng:

DẠY KÈM QUY NHƠN OFFICIAL 27 Pha 1 Pha 2 Pha 3
Nhiệm vụ 3 Nhiệm vụ 4
Chuẩn bị lại cho HS 2 mặt phẳng nhƣ ở tình huống 1. - Yêu cầu chọn hai đƣờng thẳng trong hai mặt phẳng không vuông góc với giao tuyến. - Xác định số đo góc giữa hai đƣờng thẳng. - So sánh với góc giữa hai đƣờng thẳng. Chuẩn bị lại cho HS 2 mặt phẳng nhƣ ở tình huống 1. - Yêu cầu chọn hai đƣờng thẳng trong hai mặt phẳng cùng vuông góc với giao tuyến. - Xác định số đo góc giữa hai đƣờng thẳng. - So sánh với góc giữa hai đƣờng thẳng. Chuẩn bị cho HS 02 mặt phẳng có tính chất “hai mép” của hai mặt phẳng không vuông góc với nhau, góc giữa 2 mặt phẳng . Yêu cầu HS không dựng đƣờng vuông góc với mặt phẳng hãy xác định góc giữa hai mặt phẳng và giải thích cách làm. Chuẩn bị cho học sinh 8 tam giác đều bằng nhau và các dụng cụ cần thiết. Yêu cầu thiết kế một con súc sắc 8 mặt.
3.4. Phân tích tiên nghiệm tình huống 3.4.1. Tình huống 1:
Mục đích của tình huống: Chúng tôi sẽ phân tích mục đích của từng nhiệm vụ trong tình huống này: - Nhiệm vụ 1: Thông qua nhiệm vụ này, HS phát hiện đƣợc góc giữa hai đƣờng thẳng bất kì không vuông góc với hai mặt phẳng đã cho sẽ có số đo thay đổi tùy thuộc vào mỗi trƣờng hợp HS chọn đƣờng thẳng. - Nhiệm vụ 2: Giúp HS phát hiện rằng: góc giữa hai đƣờng thẳng lần lƣợt vuông góc với hai mặt phẳng có số đo không đổi (số đo của các nhóm thu đƣợc gần nhƣ nhau). Từ đó GV đi đến định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đƣờng thẳng vuông góc với hai mặt phẳng đó.
Giai đoạn 1: Trải nghiệm cụ thể
Ở giai đoạn này, mục đích cho HS trải nghiệm việc đo góc giữa hai đƣờng thẳng bất kì và hai đƣờng thẳng vuông góc với mặt phẳng.
Giai đoạn 2: Phản ánh qua quan sát
Từ những kết quả ở giai đoạn 1, thông qua hệ thống câu hỏi của GV cho HS nhận thấy rằng: Góc giữa hai đƣờng thẳng bất kì vuông góc với hai mặt phẳng luôn không đổi, góc giữa hai đƣờng thẳng bất kì cắt hai mặt phẳng có kết quả thay đổi tùy theo vị trí của đƣờng thẳng.
Giai đoạn 3: Khái quát hóa trừu tƣợng
Từ giai đoạn 2, HS nhận biết đƣợc góc giữa hai đƣờng thẳng bất kì vuông góc với hai mặt phẳng luôn không đổi, GV khái quát cho HS về khái niệm góc giữa hai mặt phẳng: “Góc giữa hai mặt phẳng là góc giữa hai đƣờng thẳng lần lƣợt vuông góc với hai mặt phẳng đó”.
Giai đoạn 4: Không có
Các chiến lƣợc HS có thể thực hiện trong tình huống này:
+ Chiến lƣợc 1: Tạo ra những đƣờng thẳng cắt nhau DẠY KÈM QUY NHƠN OFFICIAL 28 Ở chiến lƣợc này, HS sẽ tạo ra những đƣờng thẳng cắt nhau. Ở nhiệm vụ 1: HS dựng hai đƣờng thẳng cắt nhau và không vuông góc với mặt phẳng. Ở nhiệm vụ 2: HS dựng hai đƣờng thẳng cắt nhau và vuông góc với mặt phẳng. HS có thể dùng kéo đâm xuyên mặt hai mặt phẳng để tạo ra 2 lỗ tròn có thể ghim các que nhựa lên sao cho 02 que nhựa có thể cắt nhau. Từ đó HS có thể dễ dàng đo đƣợc góc của hai đƣờng thẳng này. Kiến thức cho phép thực hiện chiến lược này: Đƣờng thẳng vuông góc với mặt phẳng, Góc giữa hai đƣờng thẳng. Chiến lƣợc này là chiến lƣợc tối ƣu. + Chiến lƣợc 2: Tạo ra những đƣờng thẳng chéo nhau Ở chiến lƣợc này, sau khi HS dựng hai đƣờng thẳng vuông góc với hai mặt phẳng thì chúng không cắt nhau. Nhƣ vậy HS sẽ khó khăn trong việc phải dời 1 đƣờng thẳng khác sang 1 đƣờng thẳng song song với nó và cắt đƣờng thẳng còn lại để dễ dàng trong việc thực hiện đo góc. Và sau khi dời nhƣ vậy thì HS sẽ quay lại với chiến lƣợc 1. Chiến lƣợc này gây mất thời gian cho HS.




