Conteúdo
1Análiselinearenãolineardesistemasestruturaisvibratórios 15 1.1Analogiaentresistemasmecânicoseelétricos................18 1.2Transdutores..................................19
1.2.1Localizaçãodemodos........................23
1.3Modosnormaisnãolineares(NNM).....................24 1.4TeoriadeShawePierre,paramodosnormaisnãolinearesdevibrações.28 1.5Transportadoresvibracionaiscomexcitadores.................30
1.6Comentáriossobreressonância........................35 1.7Métododamédia...............................36 1.8Métododobalançoharmônico........................38
1.9MétododeLindstedt-Poincaré........................38 1.10SobreateoriadeTakens...........................43 Referências......................................44
2Identificaçãoporsubespaçosdesistemasdinâmicos 49 2.1Introdução...................................49
2.1.1Tiposdemodelagemdesistemasdinâmicos............51
2.1.2Identificaçãoparaprojetodecontrole................53
2.2Métodosdesubespaços............................54
2.2.1Formulaçãodoproblemadeidentificaçãoporsubespaços.....55
2.2.2AlgoritmoDSR_e..........................58
2.3Aplicações...................................63
2.3.1Identificaçãodeumaerofóliocomdoisgrausdeliberdade....64
2.3.2 Identificaçãodeumsistemamassa-molacomdoisgrausdeliberdade 72
2.4Conclusão...................................80
3Fundamentosdadinâmicadocálculofracionário 87
3.1Introdução...................................87
3.2Funçõesespeciais...............................89
3.2.1FunçãoGamma............................89
3.2.2FunçãodeMittag-Leffler.......................89
3.3TransformadasdeLaplace..........................91
3.4OperadoresdederivadafracionáriaesuastransformadasdeLaplace...92
3.4.1OperadordeRiemann-Lioville....................92
3.4.2OperadordeCaputo.........................94
3.4.3OperadordeGrunwald-Letnikov..................95
3.4.4OperadordeRiesz..........................95
3.4.5OperadordeFeller..........................97
3.5TransformadasdeLaplacedosoperadoresdederivadafracionária....98
3.6TransformadasdeFourierdosoperadores..................99
3.7Métodonumérico–integradorfracionário..................99
3.7.1MétodonuméricoparaooperadordeRiemann-Lioville......100
3.8Exemplosdeaplicaçõesdederivadasfracionárias..............101
3.8.1Aplicaçãoemumaequaçãodiferencialsimples...........101
3.8.2Exemplofísico............................104
3.8.3Aplicaçõesemsistemaseletromecânicos..............106
4Integridadedinâmica 115
4.1Introdução...................................115
4.1.1Caracterizaçãodeproblemassobaóticadaintegridadedinâmica116
4.2Robusteznoespaçodefase..........................118
4.2.1Baciasegura..............................118
4.2.2Medidasdeintegridadedinâmica..................120
4.3Robusteznoespaçodecontrole........................121
4.3.1Perfildeerosão............................121
4.3.2Bifurcaçõeshomoclínicaseoprocessodeerosão..........122
4.3.3MétododeMelnikov.........................124
4.4Aplicações...................................126
4.4.1OsciladordeHelmholtz.......................126
4.4.2OsciladordeDuffing.........................131
5Espaçodeparâmetros
5.1Introdução...................................137
5.2Esqueletodejanelasperiódicascomplexas.................141
5.3Espaçosdeparâmetrosemmapas......................143
5.4EspaçosdeparâmetrosemEDO.......................146
5.5AlgoritmoparaconstruçãodeEspaçodeParâmetrosnoMATLAB....150
6 Buscadesoluçõesanalíticasaproximadaseexistênciadeestabilidade deórbitasperiódicasdesistemasvibratóriosnãoideais(RNIS)153
6.1EfeitoSommerfeld...............................153
6.2 Aplicaçãodométododamédianosistemadeumabsorvedoreletromecânico 168
6.3Buscadesoluçãonaregiãoderessonânciainterna1:1...........168
6.4Buscadesoluçãonaregiãoderessonânciainterna1:3...........173
7 Sistemasmicroeletromecânicos(MEMS)enanoeletromecânicos(NEMS): microscopiadeforçaatômica 177
7.1Sistemasmicroeletromecânicos(MEMs)...................177
7.2Modelomatemáticodosistema........................177
7.3 Controledocomportamentocaóticoutilizandoocontroleporrealimentação comatrasodetempo(timedelayfeedbackcontrol ).............181
7.4Nanoeletromecânicos(NEMs):microscopiadeforçaatômica.......182
7.5Modelomatemáticoparaomodointermitente...............184
8Abordagemgeométricadesistemasdinâmicoselinearização porrealimentaçãodinâmicazero
195
8.1Introduçãoàabordagemgeométrica.....................195
8.2Aplicaçõesentreespaçoseuclidianos.....................196
8.3Variedadesdiferenciáveis...........................198
8.4Sistemasdinâmicos:abordagemgeométrica.................205
8.5DerivadasdeLie................................212
8.6Exemplo:pênduloinvertido.........................219
8.7Introduçãoàlinearizaçãoporrealimentação................221
8.8Sistemasdecontrolenãolineares.......................222
8.9Folheações,fibradosedistribuições.....................223
8.9.1TeoremadeFrobenius........................228
8.9.2Existênciadesistemadecoordenadas................230
8.10Controlabilidadedesistemas.........................232
8.11Linearizaçãoentrada-estado.........................234
8.12Exemplodelinearizaçãoentrada-estado...................237
8.13Linearizaçãoentrada-saída..........................240
8.13.1Dinâmicazero.............................243
8.14Exemplodelinearizaçãoentrada-saída....................243
9Programaçãodinâmicaecontroleótimo
9.1PrincípiodaOtimalidadedeBellman....................249
9.1.1Problemaderoteamentoótimo...................251
9.1.2Controleótimoutilizandoprogramaçãodinâmica.........253
9.1.3Programaçãodinâmicaparasistemasdecontrole.........255
9.1.4 Algumasconsideraçõessobreaimplementaçãocomputacionalda programaçãodinâmica........................259
9.1.5Oreguladorlineardiscreto......................261
9.2AEquaçãodeHamilton-Jacobi-Bellman...................268
10 Métodosdeanálisetempo-frequênciaemaplicaçõesdedinâmicanão linear 273
10.1Representaçãotempo-frequência.......................275
10.1.1TransformadadeFourierjanelada..................275
10.1.2Transformada wavelet ........................276
10.1.3DistribuiçãodeWigner-Ville.....................276
10.2Métodosbaseadosemmododedecomposiçãoempírica..........276
10.2.1TransformadadeHilbert-Huang(HHT)..............276
10.3 Synchrosqueezedtransform ..........................279
10.3.1Transformada waveletsynchrosqueezing ..............279
10.4Estudodecasos................................280
10.5Observaçõesfinais..............................289
10.6Apêndice....................................290
11 Materiaisinteligentesaplicadosaocontroledevibraçãodeestruturas flexíveisemmovimentoderastreamento 293
11.1Introdução...................................293
11.2Modelagemdevigasflexíveis.........................294
11.3ModelagemdomotorCC...........................296
11.4AcoplamentodavigacomomotorCC...................297
11.5Modelagemdaligacommemóriadeforma.................298
11.6ModelagemdoacoplamentoentrevigaeLMF...............299
11.7Controledeposiçãoevibraçãodaestruturaflexível............302
11.7.1Projetodecontrole..........................302
11.7.2Projetodocontroledeposiçãoangular...............303
11.7.3Projetodocontroledevibração...................305
12Controledemulticópterospormodosdeslizantes 311
12.1Introdução...................................311
12.2Notação.....................................312
12.3Equaçõesdemovimento............................313
12.3.1Movimentorotacional........................313
12.3.2Movimentotranslacional.......................314
12.3.3Modelagemdosatuadores......................315
12.3.4Esforçosdecontroleresultantes...................316
12.4Controlepormodosdeslizantes........................317
12.5Controledevoo................................320
12.5.1Arquiteturahierárquicadecontrole.................320
12.5.2Controladordeatitude........................322
12.5.3Controladordeposição........................323
12.5.4CálculodoComandodeAtitude..................324
12.5.5AlocaçãodeControle.........................325
12.6Exemplonumérico...............................326
12.7Conclusão...................................329
13Controlepassivodevibraçõesusandoneutralizadoresviscoelásticos333
13.1Introdução...................................333
13.2Neutralizadoresdinâmicosviscoelásticos..................334
13.2.1Modeloparamateriaisviscoelásticosviaderivadafracionária..334
13.2.2Modeloclássicodeneutralizadoresdinâmicosviscoelásticos...335
13.2.3Modeloviaparâmetrosequivalentesgeneralizados.........336
13.3Sistemanãolinearcúbicocomumgraudeliberdade............337
13.3.1Modelodesistemaprimário.....................337
13.3.2Modelodesistemacomposto....................339
13.3.3Identificaçãodeparâmetros.....................340
13.4Projetoótimodeneutralizadoremsistemanãolinearcúbico.......342
13.5Dessintonizaçãoportemperatura.......................343
13.6Aplicaçãonumérico-experimental.......................343
13.6.1Sistemanãolinearcúbico......................343
13.6.2Controlepassivoótimo........................347
13.7Conclusão...................................351
14Cinemáticanarobóticamóvel 355
14.1Rotação,translaçãoetransformaçãohomogênea..............355
14.1.1Conceitosdecinemática.......................358
14.1.2Cinemáticaderobôsmóveiscomrodas...............360
14.1.3Cinemáticaderobôdiferencial...................360
14.2Dinâmicaerestriçõesdemovimento.....................362
14.2.1Restriçõesholonômicos........................362
14.2.2Sistemasnãoholonômicos......................364
14.2.3Dinâmicadorobôdiferencial....................365
14.3Eventosnãodeterminísticosemrobóticamóvel...............370
14.3.1FiltrodeBayes............................371
14.3.2FiltrodeKalman...........................372
14.3.3ExtendedKalmanFilter.......................379
15Controlebioinspirado:controlebaseadonalógica fuzzy 383 15.1Teoriadosconjuntos fuzzy ..........................383
15.1.1Funçõesdepertinência fuzzy ....................383
15.1.2Fuzzificação..............................388
15.1.3Defuzzificação.............................388
15.2Controladores fuzzy ..............................391
15.2.1Tabelaoumapaderegras fuzzy ...................393 15.3Propostadecontroledevibraçãodeummodelodequartodecarro...395
15.3.1ProjetodecontroleconsiderandoomodelodeMandani......397
15.3.2ProjetodecontroleconsiderandoomodelodeTakagi-Sugeno..399
16 Sistemadeconversãodeenergiaeólicaapartirdefolhaspendulares oscilantesbioinspiradas 403 16.1Sistemadeconversãodeenergiaeólica....................403 16.1.1Introdução...............................403
16.2Materialemétodos..............................406
16.2.1Descriçãodosmodelos:FTI,FLT&FAI..............406 16.2.2Configuraçãoexperimental......................408 16.3Resultadosediscussão............................410
16.3.1Avaliaçãodevelocidadesobtidaspeloventiladoreletrodoméstico410 16.3.2Avaliaçãodedesempenhoepotênciaobtida............411 16.4Conclusão...................................415
17Análisedainfluênciadoacoplamentopiezoelétricoemdispositivode captaçãodeenergia(energyharvesting ) 419 17.1Comportamentodinâmicodeumdispositivodecaptaçãodeenergia (energyharvesting )..............................419
17.2Casolinear–coeficientedeacoplamentonãolinearcomvalor=0,00..424 17.3Casonãolinear–coeficientedeacoplamentolinearcomvalor=0,4...427 17.4Conclusão...................................430
18 Modelagemdinâmicaaplicadaaomonitoramentoediagnósticode falhasemmotoresdeinduçãotrifásicos 433
18.1Falhasemmotoresdeinduçãoesuasconsequências............434
18.1.1Origemelétrica............................435
18.1.2Origemmecânica...........................436
18.2Modelagemdinâmicadefalhas........................438
18.2.1Modelagemdevibraçõesmecânicas.................438
18.2.2Barrasquebradas...........................439
18.2.3Modelagemdascorrentesdefalhas.................440
18.3Aplicaçõesdesensoresparadetecçãodefalhasemmotoresdeindução..443
18.3.1Sensoresdevibração.........................443
18.3.2Sensoresdecorrente.........................444
18.3.3Demaissensores............................447
18.4Técnicasdeprocessamentodesinaisparadiagnósticosdefalhas.....447
18.4.1Análiseemfrequência........................448
18.4.2Análisetempo-frequência......................448
18.4.3Métodosdereconhecimentodepadrão...............449
18.5Exemploseaplicações.............................458
18.5.1Exemplosdeanáliseemmodelosdefrequênciaetempo-frequência459 18.5.2 Exemplosdediagnósticodefalhasportécnicasdereconhecimento
19Modelagemdeestruturasunidimensionaiscomparâmetros distribuídoseconcentrados 467
19.1Introdução...................................468
19.2Modelagemmatemática............................469
19.2.1Modelagemcomparâmetrosdistribuídos..............469
19.2.2Modelagemcomparâmetrosdiscretos...............470
19.2.3Princípiosdeenergia.........................471
19.3Modelomatemáticodeestruturascomparâmetrosdistribuídos......473
19.3.1Barrascomcarregamentoaxial...................473
19.3.2Eixosdetransmissãosujeitosatorques...............476
19.3.3Vigassujeitasacarregamentostransversais............476
19.4Modelagemconjuntadeparâmetroscontínuoseconcentrados.......478 19.4.1Exemplo:asaretangularplanafixadanafuselagem........481
19.5Soluçãobaseadaemtécnicavariacional...................484
19.5.1Exemplo:vigacomengasteelásticoelastro............485
19.5.2QuocientedeRayleigh........................486
19.6MétododeRayleigh-Ritz...........................489
19.6.1Exemplo:asadeaeronavecomafilamento.............491
19.7Métododeelementosfinitos.........................493
19.7.1Modelagemmatemática.......................494
19.7.2Funçõesdeinterpolação.......................497
19.7.3Elementosfinitosunidimensionaislineares.............497
19.7.4Transformaçãodecoordenadalocalparaglobal..........505
19.7.5Exemplo:MEFaplicadoavigauniforme..............506
19.8Conclusão...................................510
SobreosAutores 513
Capítulo1
Análiselinearenãolinearde sistemasestruturaisvibratórios
Asoscilações(vibrações)mecânicasestãopresentesemnossavidanasmaisdiversas situações,tendocomoexemplos,entremuitosoutrosemengenharia,osseguintes casos(Craig,1994;Inman,2019etc.):omovimentooscilantedasuspensãodeum carro,omovimentodosolopelapassagemdeumônibusnasproximidadesea propagaçãodosomdeumamúsicaassociadaàsvibraçõesacústicas.Todasessas situações,quenotamosintuitivamente,sãofenômenosfísicosnosquaisocorrem transferênciadeenergiamecânicadeumanaturezaparaoutra.
Osexemploscitadosanteriormenteapresentamasseguintesnaturezasdeenergia: nasuspensãodocarro,amolaéoelementorelacionadoàenergiapotencialelástica dedeformaçãodomaterialeoamortecedoréoelementodissipador(transformador) deenergiamecânicaparaenergiatérmica,oqueéverificadopeloaquecimento doóleodoamortecedor;asrodasdoônibus,emmovimentosobreopavimento, transmitemenergiapotencialelásticaparaosolo;amúsicaéatransmissãode ondasdepressãonoar(pressãoacústica),quesãopercebidasatravésdenosso sistemaauditivoetc.
Emalgunsproblemasdeengenharia,asoscilações(vibrações)mecânicasdevemser controladasousuprimidas.Algunsexemplosdecasosdenecessidadedecontrole deoscilações(vibrações)mecânicassão:oproblemadaestabilidadedosveículos,o problemadaemissãoderuídoemsistemasmecânicoseoproblemadasoscilações (vibrações)induzidasporatritoemmáquinas.
Comoseviulogoacima,temumaimportânciamuitograndenaengenhariaatual enãoháexageroaoafirmarqueéimprovávelaexistênciadequalquerramoda engenharianoqualelasnãoexerçampapelimportante.Asequaçõesdiferenciaisdo
movimentodesistemasdinâmicosmecânicossãocomumenteequaçõesdiferenciais aderivadasparciaisemsuascoordenadasgeneralizadasespaciaisetemporais.No casoemqueasvariáveisdoproblemanãosãodotiposeparáveis,entãoousode métodosclássicospossibilitaaeliminaçãodasvariáveisgeneralizadasespaciais, obtendo-se,destaforma,umconjuntodeequaçõesordináriasnavariáveltemporal, quersejamnaformacomcoeficientesconstantesoudependentesdotempo.
Édesumaimportânciaaanálisedaestabilidadedassoluçõesdasequaçõesdo movimento,obtidas.Normalmente,adota-seadefiniçãodeestabilidadesegundo Liapunov.Diz-sequeumpontodeequilíbriodosistemadinâmicoéestávelse, qualquerquesejaaperturbaçãoimpostaaoestadodeequilíbrio,osistemapermanecesuficientementepróximoaesseestado;nocasooposto,tem-seinstabilidade. Seosistemaperturbadotenderaoestadodeequilíbrioinicialcomopassardo tempo,diz-sequeosistemaéassintoticamenteestável.
Ascondiçõesdeestabilidade-instabilidadedinâmicasãocomumenteexpressasemteoriadevibraçõesmecânicasemtermosdecertasrelaçõesexistentesentreasfrequênciasdasexcitaçõesexternaseasfrequênciasnaturaisdosistema,denominadasderelaçõesdefrequências,cujofenômenomecânicoassociadoéchamadoderessonância.
Atransmissãodasvibraçõesparaocorpohumanopodecausardiversosprejuízos, taiscomo:dor,desconforto,perdadeeficiênciaeconcentraçãonotrabalho,tontura, náusea,turvamentodavisão,perturbaçãodafala,fadiga,perturbaçõesneurológicas oumusculares,lesõesosteoarticulares,patologiasnaregiãolombareatémesmo lesõesdacolunavertebral.Aspartesdocorpohumanoapresentamsensibilidade àfrequênciadevibraçãoemdiferentesfaixas(valores):nacabeçaemtornode 25Hz;nosglobosoculares30-60Hz;nacaixatorácica60Hz;nacolunavertebral 10-12Hz;nobraço16-30Hz;namão50-150Hz;namassapélvicaenádegas4-8Hz; naspernas2-20Hz.
Oriscodeexposiçãoàvibraçãodependedaamplitude,frequência,direção,tempo deexposiçãoecomportamentodavibraçãoaolongodotempo(contínua,intermitenteoutransitória).
Esseassuntodaexposiçãohumanaàvibraçãoétãoimportantequeexistemvárias normasinternacionaisquetratamdessatemática.Porexemplo,anormaISO2631-1 (1997)trazosrequisitosgeraisarespeitodaexposiçãohumanaàvibraçãodecorpo inteiro,abrangendométodosdemedição,severidadedevibraçãoeconfortohumano epossíveisefeitossobreasaúde.AnormaISO2631-2(2003)apresentaumguiapara aplicaçãodaISO2631-1sobrearespostahumanasobaaçãodevibraçãodeprédios.
Noambienteindustrial,existeminúmerasfontesdevibração:máquinasrotativas, máquinasalternativas,processoscomimpacto,transportadores,veículos,máquinas ferramenta,dentreoutras.Valedestacaralgunsresultadosdasvibraçõesno ambienteindustrial:ruídoexcessivo,desgasteprematuro,trincas,afrouxamentode
Capítulo2
Identificaçãoporsubespaçosde sistemasdinâmicos
Estecapítuloestáorganizadoconformedescritoaseguir.ASeção2.1apresenta umarevisãobibliográficasobreaidentificaçãodesistemasdinâmicos,distinguindo, demaneirageral,ostiposdemodelagemdesistemaseasváriasformasde representaçãonodomíniodotempo.Ênfaseédadanaidentificaçãoaplicadaao projetodecontrole.Porsuavez,aSeção2.2temcomoobjetivoapresentara formulaçãodeidentificaçãoporsubespaçosdesistemas,destacandoasprincipais ferramentasdeálgebralinearusadasnosalgoritmos,emespecialoalgoritmoDSR_e.Porfim,aSeção2.3apresentaaidentificaçãodeumaerofólioeaidentificaçãode umsistemamassa-molausando,respectivamente,dadossimuladoseexperimentais.
2.1Introdução
Atualmente,diversastécnicasdemodelagemdesistemasvêmsendoempregadasno intuitodeproverummodelomatemáticoquerepresentebemassuascaracterísticas dinâmicas.Em[13]éapresentadaaidentificaçãodeummodeloaeroelásticodoX56AMUTT(Multi-UtilityTechnologyTestbed ),umaaeronaveflexívelemsubescala daNASA(NationalAdvisoryCommitteeforAeronautics ),usandooOEM(Output ErrorMethod )[56].Otrabalhoapresentaosesforçosnatarefadeidentificação paradeterminaçãodasderivadasdeestabilidadeecontroledaaeronave.Além disso,discutealgunsaspectospráticosdeanálisesedesafiosnaáreadeidentificação deaeronavesflexíveis.
Em[12]éapresentadaaidentificaçãodeumacolunadeumdesbutanizador industrialapartirdemodelosNLARX(NonLinearAutoRegressivewitheXogenous input ).Aplantadedestilaçãoéumsistemamultivariávelaltamentecomplexo,
alémdeserumproblemapornaturezamal-condicionado,oquetornaatarefade identificaçãoaindamaisdifícil.
Porsuavez,em[10]éapresentadaaidentificaçãoecontroledeummanipulador robóticousandooalgoritmoFADE(FuzzyAdaptiveDifferentialEvolution ).Osresultadosobtidosmostramqueoalgoritmoadaptativobaseadoemlógica fuzzy possuidesempenhomelhorqueométodoOLS(OrdinaryLeastSquare )eométodopadrãoDE(DifferentialEvolution ),alémdepossuirgrandeeficiênciacomputacional.
Nessesentido,observa-sequeécrescenteousodeferramentascomputacionais paraauxiliaratarefadeobtençãodemodelosmatemáticosdesistemascomplexos. Seguindoessaperspectiva,nasúltimasdécadas,maisespecificamenteapartirdo trabalhode[4],umaoutraclassedemétodosdeidentificação,conhecidacomo métodosdesubespaços,passouaserexploradaedifundidadentrodoambiente acadêmico.
Recentemente,[9]apresentaaidentificaçãoumaplantapetroquímicausando diferentestécnicasparaobtençãodeummodelodinâmicobaseadoemdados.Um estudocomparativoentreaidentificaçãoporsubespaçoseaidentificaçãoporredes neuraisartificiaisfoirealizadousandodadossimuladosdeumdivisordeetileno industrial.
Otrabalhode[11]apresentaummétododeidentificaçãoporsubespaçosmodificado, nodomíniodotempo,baseadonaestratégiaconhecidacomo nonlinearseparation. Osresultadosobtidos,apartirdedadossimulados,demonstramefetividadedonovo métododesenvolvido,secomparadocomotradicionalalgoritmodeidentificação porsubespaçosnãolinear.
Em[58],érealizadaaidentificaçãodeumsistemadelaminaçãotandemoperando emmalhaabertaeemmalhafechadausandoosmétodosN4SID(Numerical algorithmsforSubspaceStateSpaceSystemIDentification )eSSARX(StateSpace ARX).
Dadossimuladosedadosexperimentaisforamutilizadosparaverificaraeficiência dosmétodosSIM(SubspaceIdentificationMethod )eavaliaraqualidadedos dadosusadosparaidentificação.Omodeloem[14]foiusadoparagerarosdados simulados.OsistemaéMIMO(Multi-Input,Multi-Output )10 × 14,com30 variáveisdeestadoescolhidasadequadamente.
Jáem[59]foirealizadaaidentificaçãodeumatubeiramóveldoVLS(Satellite LauncherVehicle )tambémusandoumalgoritmodesubespaços.Osistemaconsiste emumatuadoreletro-hidráulicoquemoveumdivergente,resultandoemum deslocamentoangular.OalgoritmoDSR_eapresentouestimativasparamétricas consistentesecombaixoerrodeprediçãodemodelo.
Capítulo3 Fundamentosdadinâmicado cálculofracionário
3.1Introdução
Ocálculofracionárioéumalinhadamatemáticaquepossuiaintençãodegeneralizarmodelosmatemáticos,noentanto,essageneralizaçãodessesmodelospermite fazeranalogiascomfenômenoscommovimentosanômalos,ouseja,movimentos quepossuemumacertainconstâncianasuaexecução.Exemplodessemovimento anômaloéadifusãodepartículasdeumasubstânciaquímicaque,dependendodo meioemqueestãoinseridas,podemounãodifundirem-semaisrápido.Exemploé adifusãodeumaamostradeperfumequepodesedifundirlentaourapidamente peloambientedeumasala.Essapropagaçãopermitequealgumaspessoassintam ocheirodeumperfumedeformamaisrápidaoulentadependendodocomposto químicoqueconstituioperfume[1,2,3].
Osentidodaexpressão,cálculofracionário,ouordeminteiraounãointeiraéum equívoco,poisasgeneralizaçõesqueeleoferececorrespondemaosoperadoresde ordensreaisoucomplexas.Nessecapítuloiremosabordarsomenteosoperadores deordemreal,maisprecisamenteosprincipaisoperadoresfracionários.
Emumcontextohistórico,ocálculofracionárioteveorigempormeadosde1695com estudosdeLeibnizqueprocuravaentenderosignificadodeumaderivadadeordem igualameio.EssesestudosdeLeibnizmostraramqueesseferramentalestáde possedascaracterísticas∗ queconsideravamamemóriadosistema.Essamemória podepodeteracontribuiçãodafractalidadeemqueosistemaestáinserido.
∗ Exemplodecaracterísticaéomeioqueapartículasepropaga.
Inúmerospesquisadorescontribuíramecontribuemparaasaplicaçõesdocálculo fracionário,tantodeformaanalítica† comodeformanumérica‡ .Nasrefs.[4, 5, 6, 7], sãoexploradossistemasbiológicos,sistemasmecânicos,sistemaselétricos,sistemas físicos,sistemassociais,etc.
Exemplosmaisespecíficosparaaplicaçãodocálculofracionáriosãoaanálisedo comportamentodadifusãodepartículasemreaçõesquímicas,trabalhoscomo[13], queanalisamaequaçãodedifusãoemordemfracionária,ecomoresultadotiveram osregimesdepropagaçãoatribuídosaoparâmetrodaderivadafracionária.
Outrostrabalhoscomo[10, 11]atribuemocomportamentodoíndicederefraçãoem sistemasvítroscomabaseemTealureto.Osautores,obtiveramcomoresultadoa correspondênciaentreaconcentraçãodoíondopantecomoparâmetrodooperador dederivadafracionária.
Noentanto,nasaplicaçõesemsistemaseletromecânicosdestacam-seostrabalhos de[15]queanalisamocomportamentodadinâmicadosistemaconsiderandoo operadordeRiemann-Lioville.Osautoresanalisamocomportamentodadinâmica nãolinearepropõemtécnicasdecontroleparasuprimirocomportamentocaótico quepossivelmenteomodelomatemáticopossui.Osautoresanalisamocomportamentodadinâmicanãolinearfracionáriadossistemaseletromecânicoscomo Teste0–1eassimanalisamaexistênciadecaos.
Portanto,nestecapítuloiremosabordaralgumasfunçõesespeciaiscomoafunção
Gamma Γ( ),queéumaextensãodafunçãofatorialeestáligadaaocomprimento damemóriaadotadaparaoscálculosdasequaçõesdiferenciaisfracionárias.Outra funçãoexploradaéafunçãodeMittag-Leffler,quedescreveumaclassedefunções complexasequeestãoligadasàssoluçõesanalíticasdealgumasequaçõesdiferenciais fracionárias.
TambémiremosdescreverumaintroduçãodastransformadasdeFouriereLaplace paradeterminarassoluçõesdasequaçõesdiferenciaisfracionárias.Outroaspecto abordadoéométodonuméricoapresentadoporPetrásecolaboradoresparasolução numéricadesistemasnãolineares.E,porfim,trêsexemplos:oprimeiroéum equaçãodiferencialsimplesparaaplicaçãodooperadordederivadafracionária propostoporCaputopelométododetransformadasdeLaplaceeosegundoexemplo éaplicaçãonafamosaequaçãodeSchrodingerparaobtençãodaequaçãodeonda comoscoeficientesfracionáriosdoestadosdeenergia.E,porfim,aaplicaçãono modelomatemáticonãolineardemicroscopiadeforçaAtômica,eassimpodemos verocomportamentodassériestemporais.
† Cálculodeformaalgébricadasequações,assimdeterminandoaformafuncionaldoproblema.
‡ Cálculoutilizandorotinascomputacionaisemétodosdediscretizaçãodosoperadoresaplicados aosistema.
Capítulo4
Integridadedinâmica
Nestecapítuloabordaremosoconceitodeintegridadedinâmicaesuasimplicações emsistemasdinâmicoscomaplicaçõesnaengenharia.Existemalgunspontos fundamentaisaseremconsideradosparaumainvestigaçãoprecisadaintegridadede umdeterminadosistemadinâmico,dentreosquaisdestacam-se:baciadeatração ebaciasegura,medidasdeintegridade,reduçãodeintegridade,operfildeerosão dabaciaseguraeosmecanismosresponsáveispelodesencadeamentodefenômenos deerosãodebacias.Estespontosserãodiscutidosaqui.
4.1Introdução
Estabilidadeéumdosconceitosmaisimportantesnoestudodesistemasdinâmicos. AdefiniçãodeestabilidadelocaldeLyapunov(feitanofinaldoséculoXIX)dizque, seosistemadinâmicoésubmetidoamudançasinfinitesimaisemsuascondições iniciais,então,suarespostanãoserásignificativamentealterada.Adefinição deestabilidadesegundoLyapunovéformuladaconsiderandoasensibilidadedo sistemaàpequenasmudançasnascondiçõesiniciaisdosistemadinâmico.
Comointuitodecontribuirparaosproblemasdomundoreal,JohnMichaelTutill Thompson[1, 2],nofinaldosanos1980,propõequeumsistemadinâmiconão estásuscetívelapenasaperturbaçõesnassuascondiçõesiniciais,mastambéma imperfeiçõesdemodelo.Nestecontexto,Thompsonelaboraumaquestãocentrale aindaatualparaoestudodaestabilidade:quãopequenasdevemserasmagnitudes dasperturbações?PelateoriadeLyapunovtalmagnitudepodesertãopequena quantosequeira,logo,nãoéimportantesaberamagnitudedasperturbações,por exemplo, 10 10 podeseraceitável,porém,dopontodevistaprático,Thompson percebeuqueessasmagnitudestêmumpapelfundamental[3].Assim,eleconcluiu
queoestudodaestabilidadeteóricalocalemsistemasreaisporsisónãoésuficiente paraasaplicaçõespráticas,énecessárioalgomais.
Ademais,Thompsonrecomendaqueparacompreenderasoluçãodesistemas dinâmicosnomundoreal,alémdaanáliseclássicadeestabilidadelocaldeLypaunov, deve-setambémverificarseosistemaécapazdesuportarpequenas(finitas) mudançasnascondiçõesiniciais.Dessaforma,Thompsonpassoudoestudoda estabilidade“teórica”paraaestabilidade“prática”,outambém,comoficou conhecidaessaabordagem,de“robustez”[3].Emboraemumprimeiromomento estaideiapossaparecersimples,suaimplementaçãopráticaélongedesertrivial. Logo,estareflexãodeThompsondáorigemaocampodepesquisaconhecidocomo integridadedinâmica[3].
Comoprimeiropassoparaaconstruçãodestanovateoria,Thompsondizque“se abaciadeatraçãodeumadadosistemadinâmiconãoforgrandeecompactao suficiente,assoluçõesdomesmonãopoderãoservistasnomundoreal”[4].Para entendermelhoresseconceito,equaléaimportânciadaintegridadedinâmica, veremosnaseçãoaseguiracaracterizaçãodeproblemasemdinâmicanãolineare comoaintegridadedinâmicanosauxiliaránesteproblema.
4.1.1 Caracterizaçãodeproblemassobaóticadaintegridade dinâmica
Sistemasdinâmicosdissipativospodemapresentar,paraummesmoparâmetro decontrole,aexistênciasimultâneademaisdeumatrator,podendoincluir,por exemplo,pontosdeequilíbrios,oscilaçõesperiódicasequaseperiódicas,alémde atratorescaóticos,ondecadaatratorencontra-seemseuprópriodomíniooubacia deatração.Comavariaçãodesteparâmetrodecontrole,essesatratoresirão semoverdemaneiraquebifurcaçõespossamacontecer,e,portanto,suasbacias podemsofreralterações[2].Essaspossíveismudançasquepodemocorrerestão relacionadasaotamanhoeaformadabacia,podendosercontínuasoudescontínuas, porexemplo,quandoumatratordesaparece,simultaneamentecomsuabaciade atraçãoemumabifurcaçãodotiposela-nó.Outramudançaquepodeafetaras baciasdeatraçãoéafractalizaçãodoslimitesdabacia,ouseja,oslimitesdabacia podemmudaranaturezadesuaveparafractal;esseacontecimentoestárelacionado aoemaranhamentohomoclínicodasvariedadesinvariantesdeumpontodesela[5].
Nessecenário,podemosdizerqueaintegridadedinâmicabaseia-senaanálisecontínuadaestruturaecomoocorreaevoluçãodasbaciasquandoosistemadinâmico ésubmetidoavariaçõesparamétricas.Taismudançaspodemserdesencadeadas porumasériedecomplexosfenômenosdinâmicos,demodoqueaintegridadedinâmicadeumsistemanãopodesercaracterizadopelasimplesmedidadamagnitude dabacia[3].
Capítulo5 Espaçodeparâmetros
Nestecapítuloabordaremosoconceitodeestruturasdebifurcaçãoemsistemas dinâmicosnãolinearesemumespaçodedoisparâmetrosdecontrole,comumente conhecidoscomocamarões(shrimps ).Paraessaabordagemfaremosumestudo geométricodessasestruturas,jáqueessesespaçosdeparâmetrosnãopossuemum construçãoteóricaaxiomatizada.
5.1Introdução
Estabilidadeéumdosconceitosfundamentaisnoestudodesistemasdinâmicos.O conceitoclássicodeestabilidadedeLyapunovdizqueosistemaéestávelse,sob pequenaspertubações,arespostadosistemanãosealterasubstancialmente.
Figura5.1 DuastrajetóriasdiferentesnoespaçodefasesdeumosciladordotipoDuffing;tais osciladoreseaequaçãodiferencialdeumDuffingserãotratadosmaisparaafrente.Afigura daesquerdarepresentaumfluxoemqueocomportamentodosistemaDuffingéperiódico;os valoresdeparâmetrosutilizadosaquiforam β =10.800639152526855e c=0.240742176771164. Nafiguradadireitaobteve-seumcomportamentocaóticodosistemavariandosimultaneamente essesdoisparâmetros,aqui β =10.791227340698242e c=0.248832285404205.
Percebe-senaFigura5.1queosistemaésensívelàmudançadessesparâmetros tratados,umapequenavariaçãonosdoisparâmetrosimplicouemumamudançade estabilidadedosistema,e,consequentemente,osistemapassoudeumaoscilação periódicaparaumaoscilaçãocaótica.
Nosfinaldosanos80,J.M.T.Thompson[1, 2]retomouesseconceitodeestabilidade deLyapunov,observandoqueasperturbaçõesconsideradassãoinfinitesimais, enquantonomundorealatéasmenoresperturbaçõestêmumaamplitudefinita.
Assim,surgeaprimeiraquestãocentralabordadaporThompson:quãopequena deveserumaperturbação?Dopontodevistamatemático,amagnitudedessas perturbaçõesnãoéimportante,masdopontodevistapráticoéimportante,umavez queemnossomundorealasimperfeiçõestêmumamagnitudefinitaemensurável.
Paraaanálisedesistemasdinâmicosmultidimensionaissãoutilizadosfrequentementemétodosnuméricoseferramentascomputacionais,devidoàgrandedificuldadeparaaobtençãoderesultadosanalíticosquepossamidentificarpossíveisalteraçõesnaestabilidadedosistemaenaevoluçãodosistemacomotempo.Entre ossistemasanalisadosencontram-sesistemascaóticos,osquaisapresentamgrande sensibilidadeàscondiçõesiniciaiseperturbações[3].
Usualmente,adependênciadossistemasdinâmicosemrelaçãoaosparâmetros tambéméexploradaemdiagramasbidimensionais,chamadosespaçodeparâmetros. Nessesdiagramaségeradaumagradebidimensionaldeparâmetrosdecontrole igualmenteespaçadoseparacadaelementonagradeavalia-seadinâmicapormeio deumaferramentadediagnóstico,aqualpodeser,porexemplo,omaiorexpoente deLyapunov,acontagemdeperíodos,osnúmerosderotação,dentreoutros.
Osplanosdeparâmetrospodemserutilizadosparaanalisarocomportamento dinâmicodeumsistema,observandoavariaçãodamagnitudedessesparâmetros dediagnóstico,juntocomasvariaçõesdedoisparâmetrosdosistema.Ouseja, sãoestabelecidosdoisparâmetrosdecontroleemquesequerestudaradinâmica dosistema,eparacadapardessesparâmetrosdentrodeumamalhafixaobtém-se ovalordoparâmetrodediagnóstico,oqualseráusadoparaconstruiroespaçode parâmetros.
Assim,podemosdefiniroplanodeparâmetroscomosendoumgráficotridimensional,querepresentabidimensionalmenteavariaçãodequaisquerdoisparâmetros quecompõemosistema,associadosaumterceirovalordeinteresse,oqualéo parâmetrodediagnóstico.
OparâmetrodediagnósticonormalmenteadotadoéomaiorexpoentedeLyapunov. Graficamente,éutilizadoumgradientedecorespararepresentarovalordomaior expoentedeLyapunovcomrelaçãoaopardeparâmetrosescolhidos.Assimé possívelverificarondeosistemaapresentaregiõesdeequilíbrio,regiõesperiódicas (λ< 0),regiõesquasi-periódicas(λ ≈ 0)eregiõescaóticas(λ> 0),poisparacada
Capítulo6
vibratóriosnãoideais(RNIS)
Nestecapítulo,apresentam-seosresultadosanalíticosenuméricossobreodesenvolvimentoperiódicoequaseperiódicodosistemanãolinearRayleigh-Duffingnão ideal.Emprimeirolugar,atravésdométododamédiaeexpoentesdeLyapunov, investigam-seasexistênciasderespostasperiódicasequaseperiódicascomapresençaadoefeitodeSommerfeld.Emsegundolugar,seguindocomomesmomodelomencionadoacima,determinam-seosintervalosdaexistênciaeestabilidade deórbitasperiódicasseguindooprocedimentoteóricoemcasosdeimportância.
6.1EfeitoSommerfeld
Nesteitem,apresentam-seanálisededetecçãodoefeitodeSommerfeldemsistemas (RNIS)edaexistênciaeestabilidadedeórbitasperiódicasequaseperiódicas atravésdométododamédia(verCapítulo1)edocálculodeexpoentesdeLyapunov (vervolume1).
Considera-seumavigaengastadanoextremoesquerdoesuportandonoextremo livreummotorelétricodepotêncialimitadaedesbalanceado(verFigura3.1).A equaçãogovernantedemovimento,obtidaatravésdaformulaçãodeLagrangepara
osistemacomdoisgrausdeliberdade,estárepresentadapelascoordenadasgeneralizadas x (deslocamentodaviga)e φ (deslocamentoangulardorotordesbalanceado).
Aenergiacinética T ,aenergiapotencial V ,afunçãoamortecimentodaviga GB e otorqueexercidopelomotor Γ( ˙ φ) sãoexpressaspor
onde L(φ) (quedependedatensão U (t))éotorquee H (φ) éotorquederesistência.
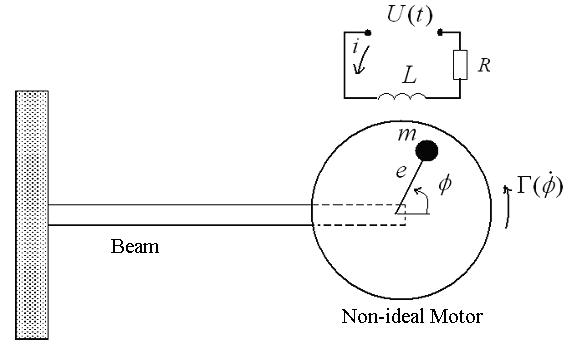
Figura6.1 Esquemadeproblema(RNIS).
Então,aequaçãodemovimentodo(RNIS)podeserescritacomo
ondeseadota ˙ X = dX dτ ,sendo τ otempoadimensional;assume-seotorquedo motorcomosendoumafunçãolineardesuavelocidadeangular Γ( ˙ φ)= Vm Cm ˙ φ, Vm sendoconsideradocomooparâmetrodecontrol,eepoderáseralteradoseuvalor deacordocomavoltagemaplicadaaomotorelétrico, Cm sendoaconstantepara cadamodeloconsideradodeummotorelétrico, α éocoeficientedeamortecimento linear, β éoamortecimentonãolinear, γ éocoeficientederigideznãolinear, q1 e q2 sãooscoeficientesdeinteraçãoentreomotordesbalanceadoeaviga,a frequêncianaturaldavalorum, X éacoordenadadomovimentooscilatórioda vigae φ éavelocidadeangulardomotor.
7.1Sistemasmicroeletromecânicos(MEMs)
Sistemasmicroeletromecânicos(MEMs)sãodispositivosemescalasmicroquecombinamcomponenteselétricosemecânicos.ExistemváriosdispositivosdeMEMs queforamutilizadoscomsucessoemdiversasáreasdaengenharia,comoacelerômetros,unidadesdenavegaçãoinercial,processamentodesinais,microturbinas, detectoresdemovimento,filtrosmecânicosparatelecomunicações.NaFigura7.1 podemosobservarumexemplodeumsistemaMEMs.
OdispositivoapresentadopelaFigura7.1(b)éconstituídoporduasplacasfixase umaplacamóvelentreelasdemassa(m ),comdeslocamentolateral(x(t)),àqual éaplicadaumatensão V (t) queécompostadeumatensãodepolarização(DC) Vp etensãoalternada(AC) Vi sin(ωt).
7.2Modelomatemáticodosistema
Aequaçãodomovimentodasplacasédadapor:
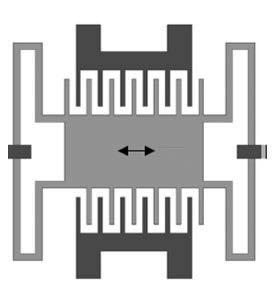
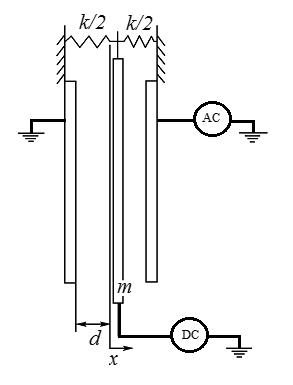
Figura7.1 SistemaMEMs:(a)dispositivodedetecçãodemovimento;(b)representação físicadosistemadedetecçãodemovimento.
Sendo Fk aforçarestauradoradamola, Fc aforçadeamortecimentoe Fe aforça elétrica,obtidasdasequações(7.2),(7.3)e(7.4).
onde: C0 representaacapacitância.
Substituindo(7.2),(7.3)e(7.4)em(7.1),obtemosaequaçãodomovimento:
Considerandoqueaamplitudedatensãodeacionamento(CA)sejamuitomenor doqueatensãodepolarização(DC),osistemaadimensionalpodeserrepresentado pelaequação(7.6):
Sendo: Ω=
Abordagemgeométricade sistemasdinâmicose linearizaçãoporrealimentação dinâmicazero
8.1Introduçãoàabordagemgeométrica
Nestecapítulo,apresenta-sea abordagemgeométrica desistemasdinâmicos,istoé, sistemasdinâmicoscujosespaçosdeestadosnãosãoeuclidianos,massimhipersuperfícies.Serávistoquealgunssistemasseencaixammelhornestaabordagem.Será necessáriointroduziralgumasdefiniçõesmatemáticasnovas,queserãoutilizadasna abordagemgeométrica,aomesmotempoqueseapresentamexemplosqueclareiam estaabordagem.NaSeção8.2,apresentam-sealgunsconceitosdecálculodiferencial paraaplicaçõesentre Rn e Rm .NaSeção8.3,apresentam-seosconceitosdevariedadesdiferenciáveis,curvas,camposvetoriaisemvariedadesdiferenciáveisefibradostangentes.NaSeção8.4,apartirdosconceitosdaseçãoanterior,apresentamseasdefiniçõesrelativasasistemasdinâmicos,comofluxosdecamposvetoriais, curvasintegraislocaisemáximas,sistemasautônomos,singularidadesedão-sealgunsexemplos.NaSeção8.5,apresentam-seosimportantesconceitosdederivadas deLiedefunçõesreaisedecamposvetoriais,essaúltimatambémconhecidacomo colchetedeLie.Essasferramentassãoimportantesparacaracterizargrandezas emsistemasdinâmicosquesãoconstantesaolongodotempo,comoaenergiaem umsistemaconservativo,mastambémparaestudaraestabilidadedeumponto deequilíbrioatravésdasfunçõesdeLyapunoveacontrolabilidadedeumsistema. Finalmente,apresenta-seumexemplonaSeção8.6.
8.2Aplicaçõesentreespaçoseuclidianos
Umsistemadinâmiconãolineardetempocontínuoéumsistemadeequações diferenciaisordináriasnãolinearesdadopor[3]:
x = F(x, u) (8.1)
onde x éovetordeestados,comcomponentes x1 ,x2 , ··· ,xn e u éovetorde entradas,comcomponentes u1 ,u2 , ··· ,um .Nocasodeessesistemaserumaplanta asercontrolada,tambémécomumhaveruma aplicaçãodesaída y = H(x, u),que relacionaaleituradossensoresdasvariáveiscontroladascomosestados. F e H sãoaplicaçõesentreespaçoseuclidianos,e,nocasodaprimeira,precisasatisfazer condiçõesdeLipschitzparatersoluçãoúnica[5].Alémdisso,essasaplicaçõessão essenciaisparaaabordagemgeométricaqueseráfeitaaqui,demodoquevalea penaapresentaralgunsconceitosfundamentais,quepodemserencontradosem[6].
Asdefiniçõesaseguirsãogeneralizaçõesdocálculodiferencialparaespaçoseuclidianosdedimensãoqualquer.Posteriormente,serãogeneralizadosparahipersuperfíciesdedimensãoqualquer,quesãoaschamadasvariedadesdiferenciáveis.Qualqueraplicaçãodestetipo F : U ⊂ Rn → Rm semprepoderáserescritaemuma formavetorial,ouseja,comoumvetorcoluna F(x)=[F1 (x) F2 (x) ··· Fm (x)]T .
Definição8.2.1 (Aplicaçãodiferenciávelentreespaçoseuclidianos). Dadauma aplicação F : U ⊂ Rn → Rm ,onde U éumabertode Rn ,diz-sequeestaé diferenciável numponto p ∈ U seexistirumaaplicaçãolinear (F∗ )p : Rn → Rm associadaàquelepontotalque F(x) podeserescritaem U como F(x)= F(p)+ (F∗ )p .(x p)+ O (|x|2 ) etalque,quando x tendepara p,ostermosdegraumaior ouigualadois,representadospor O (|x|2 ),tendemazeromaisrapidamenteque x p (segundoalgumanorma).Talaplicaçãolinearéconhecidacomo derivada de F noponto p eéúnica.
Diz-sequequandoexisteaderivadaemtodoponto p ∈ U ,entãoaaplicaçãoé diferenciável em U ,eficaentãonaturalmentedefinida.
Definição8.2.2 (Aplicaçãoderivada). Dadaumaaplicação F : U ⊂ Rn → Rm diferenciávelem U ,aaplicação F∗ : Rn → L(Rn , Rm ),talque (F∗ )(p)=(F∗ )p (definidaacima)éconhecidacomo aplicaçãoderivada de F.
Oespaçovetorial L(Rn , Rm ) éoespaçodasaplicaçõeslinearesentre Rn e Rm ,de modoquearepresentaçãomatricialéconhecidacomo matrizjacobiana [∂Fj /∂xi ], onde j éoíndicedaslinhase i éoíndicedascolunas.Essamatrizéevidentemente m × n.Pode-sepensarqueaaplicaçãoderivadaéumcampodematrizes,que associaacadapontode Rn umamatriz n × m.
Capítulo9
Programaçãodinâmicae controleótimo
Oproblemadecontroleótimoestárelacionadocomadeterminaçãodeumalei decontroleparaumsistemadinâmicominimizandoumíndicededesempenho.
Parasistemasdecontroledemalhafechadaaabordagemporrealimentaçãode estadostemtidograndeimportâncianasúltimasdécadas,empartedevidoaos desenvolvimentodeestratégiasbaseadasemimplementaçãocomputacionaldiscreta.
Aprogramaçãodinâmica,baseadanoPrincípiodaOtimalidadedeBellman, tambémcompartilhadavocaçãocaracterísticaparaimplementaçãocomputacional discreta,emboraesseprincípionãoestejarestritoasistemasdiscretos,comoserá mostradomaisadiante,naobtençãodaEquaçãodeHamilton-Jacobi-Bellman.
EstetextoapresentaumaintroduçãoaoPrincípiodaOtimalidadedeBellman esuaimplementaçãocomputacionalnaformadaprogramaçãodinâmica,tendo comoobjetivosuautilizaçãoemproblemasdecontroleótimo.
9.1PrincípiodaOtimalidadedeBellman
Em1962BellmanestabeleceuoPrincípiodaOtimalidadeemumprocessodecisório multiestágio.Umprocessodecisóriomultiestágioótimopodeserentendidocomo umalgoritmoiterativoparatomadadedecisões,oudeterminaçãodeumalei decontroleótima.OPrincípiodaOtimalidadedeBellmanestabelecequeuma estratégiaótimatemaseguintepropriedade:
‘Quaisquerquesejamoestadoeadecisão∗ emumestágio, asdecisõesdosestágiosseguintescorrespondemaumaestratégiaótimacomrelaçãoaoestadoresultantedadecisão anterior.’
Essaestratégiapodeserconsiderada,porexemplo,paraadeterminaçãodeum caminhoótimo A E ,entre A e E ,comoodaFigura9.1.Noexemplomostrado existemtrêscaminhospossíveis,cadaumcomseurespectivocusto,
A B E , JAE = JABE = JAB + JBE , A C E , JAE = JACE = JAC + JCE , A C B E , JAE = JACBE = JAC + JCB + JBE
JBE
Figura9.1 Processodecisóriomultiestágio.
Vamossuporquenaprimeiradecisão,tomadaem A,determinou-sequeocaminho ótimopassapelosegmento A C ,enadecisãoseguintepelosegmento C E . Assim,ocustoótimoparatodoocaminho A E = A C E consisteem
∗ AE = JAC + JCE (9.1)
Comisso,seocaminhoótimo A C temcustoótimo JAC emtodoocaminho ótimo A E ,então JCE éocustoótimodocaminho C E .Emoutraspalavras, se A C éumcaminhoótimodopercurso A E ,então C E ,comcusto JCE , tambéméumcaminhoótimo.
Pode-seentãodividirocaminhoótimoemsegmentosmenoresquesãoelespróprios ótimos.Damesmaforma,apartirdoscustosótimosdossegmentosmenores pode-sedeterminarocustoótimototal.Dessaforma,estabelecidooPrincípioda OtimalidadedeBellman,ademonstraçãodeque JCE éumcustoótimopodeser feitaporcontradição.
Provaporcontradição: Seja A C E ocaminhoótimode A até E .Considerandoque
CBE <JCE (9.2) tem-seentãoque
AC + JCBE <JAC + JCE = J ∗ AE (9.3)
Arelaçãomostradaem (9.3) sópodesersatisfeitaviolandoa condiçãodeque A C E éocaminhoótimode A até E .Com isso,estádemonstradoque J ∗ CE éótimo.
∗ Nocasodesistemasdecontroleótimoadecisãocorrespondeaumaaçãodecontrole.
J
Capítulo10
Métodosdeanálise
tempo-frequênciaemaplicações dedinâmicanãolinear
Introdução
Aanáliseespectral,baseadanatransformadadeFourier,atravésdaFFTmostraseeficienteparaanálisedesinaiscomcaracterísticasestacionárias,porém,muitos processosapresentadosemsistemasmecânicossãodenaturezanãoestacionaria, fazendocomquehajavariaçãodasfrequênciasemfunçãodotempo.Dessaformao sinalperdeacaracterísticaperiódica,premissabásicaparaousodatransformadade Fourier[1, 2].Diversossinaisprovenientesdemáquinasecomponentesmecânicos possuemcaracterísticatransiente.Ossinaisdeparadaepartidademotores elétricossãoparticularmenteinteressantes,poisguardamoespectrodefrequências maisrico,earmazenamtodaainformaçãoespectraldosinal.Nessescasos,técnicas baseadasnatransformadadeFouriernãosãoadequadasparaarepresentaçãodo sinalnodomíniodafrequência.Emoperaçõesnãoestacionárias,émaisdifícil determinaraamplitudeouafrequênciadosinal,umavezqueessasgrandezas podemvariaraolongodotempo,porissoéútilintroduziroconceitodeamplitude efrequênciainstantâneas.Essesconceitossãoamplamenteutilizadosatravésda transformadadeHilbert[1].
Paralidarcomessasquestões,geralmentecombinam-semétodosderepresentação nodomíniodotempoedafrequência,emumaúnicarepresentação,naqualse apresentacomooconteúdoespectraldeumsinalevoluicomotempoesemostra umaferramentamaisapropriadaparaanálisedesinaisnãoestacionários.Os métodoslinearesincluemnotadamenteoSTFTeoCWT,enquantoosmétodos
quadráticosincluem,porexemplo,oespectrograma,oescalogramaeoWVD, atravésdadensidadeespectralassociadaaosinal.
Umadastécnicasmaisutilizadasnaanálisedesinaisnãoestacionárioséa transformadadeFourierdetempocurto(STFT).Nessecasocoloca-seosinalem duasdimensões,tempoefrequência.Existeumcompromissoentretempoea frequência.Naanálisedosinalobtém-seainformaçãodequandoequaisfrequências variamaolongodotempo.Contudo,essasinformaçõesestãolimitadasaotamanho dajanela,que,umavezfixado,seráomesmoparatodasasfrequências.Outra técnicamuitoutilizadaparaaanálisedesinaisemoperaçõesnãoestacionarias eemregimetransienteéadistribuiçãodeWigner-Ville(WVD),quefazparte deumgrupodetransformadasintegraisdenominadasbilineares.Estatécnicafoi aprimeiratentativadeserealizarumaanáliseconjuntaemtempoefrequência. AdistribuiçãodeWigner-Villebilinearconseguemelhorresoluçãonodomínio conjuntodotempo-frequênciacomparativamentecomqualquertransformadalinear. Noentantosofredeumproblemadeinterferênciadetermoscruzados,quenão representaqualquerinformaçãodosinal,ouseja,aWVDdedoissinaisnãoéa somadassuasWVDindividuais.
Atransformada wavelet,quefoipropostacomointuitodesuperaralimitação dajanelaexistentenaformulaçãoSTFT,comrelaçãoàdistribuiçãoWigner-Ville, superaproblemasdeinterferênciaedeficiênciasdeoutrosmétodosbaseadosem transformadasintegrais.Umacaracterísticaimportantedatransformadaéque aresoluçãodafrequênciavarianaproporçãodavariaçãodafrequênciacentral. Nasúltimasduasdécadas,atransformadatemsidoutilizadacomsucessonas maisdiversasáreasdoconhecimentocientífico,e,emespecial,nasaplicaçõesaem sistemasmecânicos,alémdemuitosoutroscamposdaengenharia,comcomprovado sucessonaanálisedesinaisnãoestacionários.
Outratécnicaemergenteparaanálisetempo-frequênciacomlargaaplicaçãoem sistemasmecânicoséatransformadaHilbert-Huang(HHT).Essatécnicaéuma maneiradedecomporumsinalnaschamadasfunçõesdomodointrínseco,junto comumatendência,eobterdadosdefrequênciainstantânea.Eleéprojetado parafuncionarbemcomdadosnãoestacionáriosenãolineares.Emcontraste comoutrastransformaçõescomuns,comoatransformadadeFourier,aHHTé maisparecidacomumalgoritmo,possuiumaabordagemempírica,quepodeser aplicadaaumconjuntodedados,emvezdeumaferramentateórica.AHHTéum métododeanáliseempírica.Suabasedeexpansãoéadaptativa,demodoquepossa produzirresultadosfisicamentesignificativosnaanálisedesinaisnãolinearesenão estacionários.Nosúltimosanos,novastécnicasdeanálisetempo-frequênciavêm sendopropostas.Umatécnicaemergenteéa synchrosqueezedtransform.Limitações conhecidas,comotrocasentrearesoluçãodetempoefrequência,podemser
Materiaisinteligentesaplicados aocontroledevibraçãode estruturasflexíveisem movimentoderastreamento
11.1Introdução
Estruturasemmovimentoderastreamentosãoconsideradasaquelasquesemovem emtornodeumpontofixoouarticulado,sendoqueomovimentotambémpodeser encontradopeladenominaçãoderotação,giroou slewing.Essetipodeestrutura podeserencontradoemdiversossetoresdeaplicação,porexemplo,emrobôs industriais,robôsespaciais,apêndicesdesatélites,antenasentreoutros.
Muitostrabalhostêmsidodesenvolvidosnasúltimasduasdécadas,comointuito deanalisarocomportamentodinâmicodeestruturasderastreamentoflexíveis,e proporformasparacontrolaravibraçãodasmesmas.Dentreelespodemoscitar ostrabalhosde[18,17,6,10,9]EPHRAHIMeINMAN,(1990).
Segundo[18],doisdosfatoresquedificultamocontroledesistemasderastreamento flexíveissão:otorqueparaocontrolepodeapenasseraplicadonajunta,eapenas umnúmerolimitadodesensorespodeseracopladoàestruturaflexível.
Váriostrabalhosnasúltimasdécadastêmsidoapresentadoscomointuitode controlarosefeitosnegativoscausadospeloaumentodaflexibilidadenossistemas emquestão.[7]propuseramemseutrabalhoocontroleativodeumaestrutura flexívelemmovimentoderastreamentoutilizando-sedeatuadoresdecerâmica piezoelétrica(PZT).
Outrostiposdemateriaisinteligentesjáforamestudadoscomointuitodecontrolar avibraçãoedeestruturasflexíveis,comoapresentadonostrabalhosde[10, 7].Essestrabalhosapresentamaaplicaçãodeligascommemóriadeforma(LMF)como atuadoresparaocontroledevibraçãoemestruturasflexíveis.Essesatuadoresapresentamaltacapacidadedeamortecimentoedealteraçãodosmodosnaturais[19].
Váriastécnicasdecontroletêmsidoaplicadasparaocontroledeatuadoresde ligadememóriadeforma,comotécnicasdecontroleclássicocomoPIDesuas variantesapresentadoem[9],econtroladoresnãolinearescomoapresentadopor [4].Emseutrabalho[11]apresentaramaaplicaçãodeumcontrolenãolinear conhecidocomoSDRE(StateDedendentRiccatiEquations )paraocontroletanto doposicionamentoquantodavibraçãodeumsistemaderastreamentoflexível utilizandoatuadoresdeLMF.
Estecapítuloserádedicadoaapresentaramodelagemdeumaestruturaflexível emmovimentoderastreamentocujavibraçãoécontroladaatravésdaaplicaçãode atuadoresdeLMFnaestrutura.
11.2Modelagemdevigasflexíveis
Nestetópicoaestruturaderastreamentoémodeladaconsiderando-seestacomo umavigaengastadalivre(cantilever ),sendooengastenoeixoderotaçãodeum motorCC.ParaobtençãodasequaçõesdemovimentodavigaateoriadeEulerBernoullidevigasfoiutilizada.AFigura11.1apresentaumdesenhoesquemático dosistema.
Figura11.1 Desenhoesquemáticodosistemaderastreamentodeumaestruturaflexível.
OdeslocamentodavigaflexívelapresentadanaFigura11.1podeserrepresentado comosendoosomatóriodacomponenterígidaedacomponenteflexíveldaviga comoapresentadonaequação11.1[18].
Capítulo12
Controledemulticópterospor modosdeslizantes
12.1Introdução
Ocontrolepormodosdeslizantes(SMC– SlidingModeControl )éumatécnica consolidadadeprojetodecontroladoresrobustosadiscrepânciascasadasentre aplantaeoseumodelodinâmico.Pordiscrepânciascasadas,entendem-seos distúrbios,bemcomoasincertezasdeparâmetrosedemodeloquepoderiam sercanceladospelosinaldecontrole,casofossemexatamenteconhecidos.O SMCfoiinventadonaRússia,nadécadade1950,porEmelyanov[3]eseus colaboradores,dentreosquaisUtkin[21, 20],quefoiumdosmaioresresponsáveis pelasuapopularizaçãointernacional.Aindamaisresponsáveispelointeresse internacionalpeloscontroladorespormodosdeslizantessão,semdúvida,sua simplicidade,efetividadeeversatilidade(podemseraplicadosasistemasnão lineares,multivariáveis,estocásticos,descentralizados,etc.).Adesvantagem dessescontroladoresestánapossibilidadedegeraçãode chattering nasvariáveis deestadoemdecorrênciadeumaimplementaçãoemtemporealquenãopossa empregarumataxadeamostragemsuficientementegrande.Essefenômenoé aindaagravadopelapresençadedinâmicasdeatuadoresquenãotenhamsido consideradasnoprojetoequeagemcomoumfiltropassa-baixadosinaldecontrole dealtafrequência.Aolongodasúltimasdécadas,essatécnicavemganhando aprimoramentos,comoosobservadoresecontroladorescommodosdeslizantes deordemsuperior[9],aadaptaçãodeganhodechaveamento[22],projetosde controladorescontínuosesuaves[17]eumagrandequantidadedeaplicações, incluindosistemasmecatrônicoseaeroespaciais[6, 19].Emparticular,podemos encontrarumagrandequantidadedeartigosrecentessobrecontroledevoode
multicópteros(principalmentequadricópteros)subatuados,usandoalgumatécnica decontrolepormodosdeslizantes[18,13,14,4,7,8,15,12].
Estecapítuloapresentaumaintroduçãoaoprojetodecontroladorespormodos deslizantesparamulticópterossubatuados,usandoumaformulaçãosimplesde primeiraordememultivariável.Otextorestanteestáorganizadodaseguinte maneira.ASeção12.2defineanotaçãoaseradotada.ASeção12.3formulaas equaçõesdemovimento(derotaçãoetranslação)emodelaosatuadores,bem comoosesforçosresultantesdecontrole.ASeção12.4apresentaumprojetodelei decontrolemultivariávelpormodosdeslizantesdeprimeiraordem,apropriado parasistemasrepresentadosemespaçodeestadosnaformaregular.ASeção 12.5apresentaumaestruturahierárquicadecontroledeatitudeeposiçãopara multicópterosdaclasseemquestão.Emparticular,asleisdecontroledeatitude eposiçãosãoprojetadasseparadamenteusandoaestratégiaelaboradanaSeção 12.4.ASeção12.6ilustranumericamenteométodoapresentado.Porfim,aSeção 12.7apresentaasconclusões.
12.2Notação
ConsidereumsistemadecoordenadasCartesianas(SCC)descritopor Sg {G;ˆ xg , ˆ yg , ˆ zg },fixoaosoloemumpontoconhecido G,comoeixo ˆ zg apontado verticalmenteparacima.Paraosnossospropósitos,queenvolvemvooscurtos, Sg podeserconsideradoumreferencialinercial.ConsideretambémumSCCdocorpo Sb {B ;ˆ xb , ˆ yb , ˆ zb },fixoàestruturadoveículo,emseucentrodemassa B ,como eixo ˆ xb apontandoparaafrente,oeixo ˆ yb apontandoparaaesquerdaeoeixo ˆ zb apontandoparacima,nadireçãonormalàestrutura.
Denoteogrupomatricialortogonalespecialpor SO(3) {D ∈ R3×3 : DT D = I3 }. Anotaçãovetorialadotadaaquiconsideradoisdiferentestiposdevetores:vetores físicos(geométricos)evetoresalgébricos(vetorescolunas).Vetoresfísicossão denotadosporletrasminúsculasemitálicocomumasetasobrescrita, e.g., a.Por outrolado,ovetoralgébricoresultantedaprojeçãode a sobreumSCCarbitrário Sr édenotadopelamesmaletra,masnoformatoregulareemnegrito,comum subscrito r , i.e., ar ∈ R3 .Matrizessãodenotadasporletrasmaiúsculasemnegrito. Anorma2deumvetoralgébricooudeumamatrizédenotadapor . .Denote aesfera2por S2 {n ∈ R3 : n =1}.Anotação A 0 éadotadaparadizer que A ∈ Rn×n épositivadefinida.Seja a umvetorfísicoarbitrário.Arelação entresuasrepresentações ar e as é ar = Dr/s as ,onde Dr/s ∈ SO(3) éamatriz deatitudede Sr comrelaçãoa Ss .Ainversade Dr/s (quecoincidecomsua transposta)éàsvezesdenotadapor Ds/r .Representepor a r/s umagrandeza físicarelativade Sr comrelaçãoa Ss , e.g., r b/g denotaaposiçãorelativade Sb comrelaçãoa Sg .Osímbolo ei denotaumvetorunitário n-dimensionalpadrãodo
Controlepassivodevibrações usandoneutralizadores viscoelásticos
13.1Introdução
Neutralizadoresdinâmicosdevibração(NDs),tambémconhecidoscomoabsorvedoresdinâmicosdevibração,sãodispositivosamplamenteutilizadosnocontrole passivodevibrações[13].OsNDs,quandoconvenientementeprojetadosefixados empontosestratégicosdeumaestruturaousistemamecânicoquesedesejacontrolar,reduzemosníveisdevibraçãoeruídoirradiadodeformaefetiva,emuma faixadefrequênciapreviamentedefinida.Essafaixadefrequênciapoderásermais estritaoumaislargaemfunçãodoamortecimentopresentenosdispositivos.
Umaformasimpleseeficazdeseconstruirneutralizadoresdinâmicosamortecidos épelousodemateriaisviscoelásticos.Essesmateriaispossuem,deformaintrínsecaesimultânea,característicaselásticasedissipativas.Nosneutralizadoresdinâmicosviscoelásticos(NDVs),oselementosviscoelásticossubstituem,combaixo custoepraticidade,oselementosdemolaeamortecedorviscoso,presentesem neutralizadoresclássicosdotipomassa,molaeamortecedorviscoso.
UmateoriageralparaaotimizaçãodeNDsdeváriasgeometrias,aplicadosaestruturasesistemasmecânicosgenéricos,comqualquerdistribuiçãodeamortecimento, éapresentadaem[9].Essateoriasebaseianoconceitode“parâmetrosequivalentes generalizados”(PEGs).Atravésdessesparâmetros,épossíveldescreveradinâmica dosistemaacontrolar(sistemaprimário)jácomosNDsacoplados(sistemassecundários)usandoapenasascoordenadasgeneralizadas(grausdeliberdade)dosistema
acontrolar.Issoéalcançadoapesardosgrausdeliberdadeadicionaisqueosistema composto(sistemaprimáriocomNDs)possuidevidoaoacoplamentodoNDs.
Ateoriaoramencionadatemsidoaplicadacomsucesso,comorelatadoem[6],[7], [8]e[3].Napresenteexposição,visa-seabordarousodeNDVsparacontrolede vibraçõesemsistemasnãolinearescomrigidezcúbica.Paratanto,sãocontemplados,nasequência,modelospertinentesaosdispositivosdeinteresse.
13.2Neutralizadoresdinâmicosviscoelásticos
Nestaseção,aborda-seinicialmenteamodelagemdemateriaisviscoelásticosvia derivadasfracionárias.Apartirdessamodelagem,aborda-seentãoamodelagem dosNDVscomessesmateriaiseasuarepresentaçãoequivalenteporPEGs.
13.2.1Modeloparamateriaisviscoelásticosvia derivadafracionária
Ascaracterísticaselásticasedissipativasdemateriaisviscoelásticospodemser convenientementedescritasemtermosdemódulosdeelasticidadecomplexos[17]. Ummodelobastantefidedignoparaarepresentaçãodinâmicadessesmódulos,que variamdeformaexpressivacomafrequênciaeatemperatura[15],éomodelode derivadasfracionáriascom[15]quatroparâmetros([1]e[2];[16]).
Poressamodelagem,omódulocomplexodecisalhamento G(Ω,T ) domaterial viscoelásticodeinteressepodeserexpressopor[14].
(Ω,T )= G0 + G∞ ϕ0 [iαT (T )Ω]
onde Ω éafrequência(emrad/s), T éatemperatura(em K ), G0 e G∞ são, respectivamente,asassíntotasinferioresuperior(emPa)daparterealdomódulo complexo, ϕ0 éumparâmetroassociadoaotempoderelaxamentodomaterial viscoelástico, β éaordemfracionáriadaderivadafracionáriaempregadanaequação diferencialconstitutivadomaterialviscoelástico,e αT (T ) éofatordedeslocamento.
Emmateriaisviscoelásticosditostermoreologicamentesimples,queéocasoda maioriadosmateriaisempregadosemcontrolepassivodevibrações,asdependências emfrequênciaetemperaturasãoqualitativamenteinversas[15].Assimsendo, oefeitodeumacertavariaçãoemtemperaturapodeserrepresentadoporuma variaçãoequivalenteeinversaemfrequência,evice-versa.Ofatordedeslocamento, naequação(13.1),buscadescreveressainfluênciaequivalentedatemperatura sobreafrequência,constituindo,assim,umavariávelcompostaditafrequência reduzida[15].
G
Capítulo14
Cinemáticanarobóticamóvel
Nestecapítulo,primeiramente,serãoapresentadosconceitossobreadescriçãodas coordenadasdosistemarobótico.
Nasequênciaserádemonstradaametodologiaparamodelagemcinemáticados sistemas,modeloscinemáticosestãorelacionadasacomoasvelocidadesdoselementosdorobô.
Porfim,seráapresentadoumexemplodemodelagemcinemáticadeumrobô diferencial.
14.1Rotação,translaçãoetransformaçãohomogênea
Pararepresentaçãodeposicionamentoeorientaçãodeumsistemadecoordenadas faz-senecessárioseguirametodologiadosistemauniversaldecoordenadas.
Deacordocom[1],umavezestabelecidoosistemadecoordenadacomoumvetor deposição R3×1 ,compostopelascoordenadas X,Y e Z ,podemosentãorepresentar osoperadoresderotação,translaçãoetransformaçãohomogêneacomooperações matriciais.Destaforma,umponto A P representaadistânciaaolongodoseixosdo plano {A}.Oselementosindividuaisde A P podemservistopelaEquação(14.1).
Arepresentaçãográficade A P podeservistanaFigura(14.1).
A ZA XA P {A}
Figura14.1 Vetoremrelaçãoaoplano {A}.
Alémdadefiniçãodascoordenadasdeumvetor,torna-senecessáriodefinira orientaçãodeumcorponoespaço.Ovetordefinidopor A P podeserrotacionado pelooperadorderotação R ,demostradonaEquação(14.2). B A R =
r11 r11 r11 r21 r21 r21 r31 r31 r31
(14.2)
NaFigura(14.2),aposiçãode A P (sistemadereferênciaglobal)emrelaçãoa B P éencontradoatravésdamultiplicaçãodamatrizde A B R (θ ) (lê-serotaçãodo sistemadereferência B em A)pelaposiçãode B P
Figura14.2 Rotaçãonoplano {A}
Arotaçãopodeacontecertantoem x,y ou z ,conformeémostradonaEquação (14.3).
Capítulo15
Controlebioinspirado:controle baseadonalógica fuzzy
15.1Teoriadosconjuntos fuzzy
Ateoriadosconjuntos fuzzy foidesenvolvidaapartirde1965comostrabalhosde LotfiZadeh,professornaUniversidadedaCalifórniaemBerkeley.Apartirdalógica fuzzy,deriva-seocontrole fuzzy,queéumatécnicamodernadecontroleemquenão énecessáriooconhecimentoprecisodosmodelosmatemáticos.Osdoisprincipais componentesdeumsistema fuzzy sãosuaestruturaeasfunçõesdepertinência.
15.1.1Funçõesdepertinência fuzzy
Asfunçõesdepertinência fuzzy representamaçõesteóricasepráticasdesistemas fuzzy,epodemserrepresentadasporfunçõesnuméricas,gráficosoutabelas utilizadasparaatribuirvaloresdepertinência fuzzy paravaloresdiscretosdeuma variável,emseuuniversodediscurso.Umfatorimportanteéograudesuperposição entreasfunçõesdepertinência,sendonormalmenteaplicadassuperposiçõesentre 25%e75%.NaFigura15.1éapresentadaumexemplodefunçãodepertinência comsuperposiçãode50%,considerandofunçõesdepertinênciatriangulares.
Figura15.1 Fuzzificaçãoporfunçãotriangularcom50%desuperposição,onde:ng(negativo grande),nm(negativomédio),ze(zero),pm(positivomédio)epg(positivogrande)sãoos valoreslinguísticos.
NaFigura15.2éapresentadaafunçãotriangulardefinidaporseulimiteinferiora, superiorbepelovalormodalm,talque a<m<b.
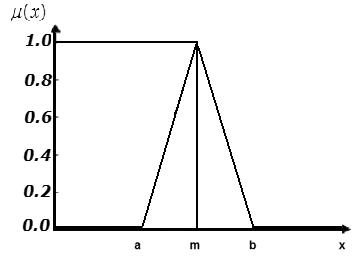
Figura15.2 Funçãotriangular.
Naequação(15.1)éapresentadaaequaçãomatemáticadafunçãotriangulardada pelaFigura15.2.
NaFigura15.3éapresentadaafunçãotrapezoidaldefinidaporseulimiteinferior a,superiorbepeloslimitesdeseusuportem(inferior)en(superior),talque a<m<n<b.
Sistemadeconversãodeenergia eólicaapartirdefolhas pendularesoscilantes bioinspiradas
16.1Sistemadeconversãodeenergiaeólica
16.1.1Introdução
Énotáveletambémmuitofácilpercebercomofatoresdeordemcultural,social, econômica,energéticaetecnológicadomeiomodernosejamtãodistintossecomparados,porexemplo,comarealidadevividaemtempospassados,principalmente aoconsiderarmososaspectoseavançosalcançadosnasáreasdaciência,saúdee tecnologia.Poroutrolado,juntocomessesprogressos,vieramtambémalgumas mudanças.Nãoobstante,aformacomopassamosautilizarenergiamudou,especialmentecomoadventodaenergiaelétrica,impactandopositivamenteomeiosocial comincrementodacapacidadeprodutiva,maiorqualidadedevida,maissaúde, confortoeacessoabensdeconsumo[3, 9].Contudo,namesmaproporção,aumentamostambémademandaenergéticacomoadventodarevoluçãoindustrial,globalização,interneteodesenvolvimentodenovosdispositivoseletrônicosmóveis,aplicativos, smarts [26,2],entreoutrosatoresquefiguramnachamada“eradigital”. Emmeioaestecenário,oconceitode“EnergyHarvesting ”apresenta-secomouma alternativamodestamentesimplese,aomesmotempo,inovadoranosuprimentode partedessademandaenergéticacrescenteapartirdefontessustentáveisdeenergia [21].Talcomoosbiocombustíveis,esseconceitotornou-setambémumaáreade
amplointeresse,sobretudonasúltimasduasdécadas,impulsionado,segundo[2], pelareduçãonoconsumodoscircuitoseletrônicosintegrados,somadoaosurgimento dedispositivosportáteis,bemcomoasinovaçõesalcançadasnossistemasde comunicaçãosemfio.
Dentreasabordagensinvestigadasnaliteratura,autilizaçãodedispositivos eletromecânicosécomumenterelatadaeamplamenteaplicadaemocasiõesonde deseja-setirarproveitosobreasvibraçõesmecânicasnaturais[11, 10, 6, 23, 18, 15].
Ousodemateriaispiezoelétricosapresentavantagemsobreumaestruturasimples,debaixocustoefácilaplicação[18].Estes,porsuavez,possuemumacaracterísticaintrínseca,resultantedeumcomportamentopoucousualdenominado “piezoeletricidade”.Este,porsuavez,consistenahabilidadedomaterialemresponderadiferentesestímulosfísicosexternosdemaneiradiretaouinversa[14]. Diretamente,omecanismodefuncionamentododispositivopartedageraçãode umsinalelétricoemrespostaaumaforçamecânicaexternaaplicadaaolongodo material(carga,flexãooutorção).Aocontráriodisso,quandosubmetidoàaplicaçãodeumacargaelétrica,omaterialéentãoflexionado([14,20]).
Inúmerasobraspropõemdiferentesformasdeconvertervibraçõesmecânicascausadaspelaaçãodoventoemeletricidade,dentreasquaiscabedestacaraconcepção arquitetônicadefolhadeárvoreartificialbioinspiradafeitaapartirdemateriais flexíveis[11, 10, 16, 24, 1, 15].Grandepartedosautoresutilizamopolímeropiezoelétricodepolifluoretodevinilideno(PVDF)emrazãodacompatibilidadedo materialcomfontesenergéticasrenovávelemfunçãodaaltaflexibilidadedomaterial,oquepoderesultaremdiversaspropostasapartirdequalquerforçamotriz queresultenomovimentodomaterial.
[11]propuseramumgeradormuitosemelhanteaumaárvorecomo harvester deenergiaeólica.Otrabalhoinvestigouosefeitosnoposicionamentodahaste piezoelétrica(caule)emrelaçãoàdireçãodofluxodear,ajustandoumdispositivo deescoamentoparaleloeoutrodeescoamentocruzadoemrelaçãoaofluxode ar.Alémdisso,osautorestambémtestaramainfluênciadediferentesformas geométricasdefolhas,porexemplo,triangular,quadrada,trapézio,entreoutras, feitasapartirdematerialflexível.Oestudorelatouaprimoramentonassaídasde potêncianodispositivodefluxocruzado,comvaloresmáximosdeaproximadamente 14µW e 3, 5µW ,respectivamente,comventosde6,5m/seumaresistênciaàcarga de 1M Ω.Estaconfiguraçãoampliaaexcitaçãododispositivoessencialmentepor causardeformaçõesporflexão,otimizandoassaídasdepotência[10].Aumentando aresistênciadacargapara 10M Ω,apotênciamáximadesaídafoielevadapara 296µW ,comvelocidadedoventodeaproximadamente8m/s.
Emumestudosimilar,propostopor[1],foramtambémanalisadasduasconfigurações,dentreasquaispropôsumanovaalternativadefluxocruzado,posicionando
17.1 Comportamentodinâmicodeumdispositivode captaçãodeenergia(energyharvesting )
OmodelomatemáticoapresentadonaFigura17.1paracapturadeenergia(energy harvesting)éumosciladormecânicoquefoiconcebidocombasenaestrutura aporticadanãolinearestudadapor[3,6,7,8,9].
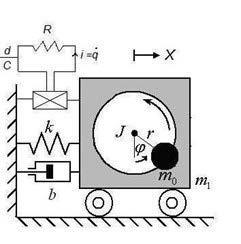
Figura17.1 Modeloesquemáticodeumsistemadecapturadeenergianãoideal.
Osistemadecapturadeenergiaconsisteemumamassadesbalanceada m0 ,a massadaestrutura m1 ,darigidezdamola k ,doamortecimentolinear b,do deslocamentohorizontaldosistema x(t),dodeslocamentoangulardorotor φ(t), domomentodeinércia J ,edaexcentricidade r ,onde k = kl x + knl x3 representa arigidezdosistema,tendo kl comoocoeficientedamolalineare knl ocoeficiente damolanãolinear(molacúbica).
Omovimentonadireçãohorizontaldaestruturaaporticadafoiconsideradocomo forçadoporumaexcitaçãonãoidealobtidapelarotaçãodoeixodeummotor elétricodecorrentecontínua(CC)comumamassadesbalanceadaacopladaque fornecepotêncialimitada.Algunsexemplosdaanálisesobreateoriadossistemas nãoideaissãoosrealizadospor[12,1,2,11].
Otorqueresistivoaplicadoaomotorérepresentadopelafunção H (φ) eotorque deacionamentodafontedeenergia(motor)érepresentadopor L(φ) segundo [1,15,16].
Asequaçõesdomovimentodosistemadinâmicoforamobtidaspormeioda aplicaçãodasequaçõesdeLagrange.Todosospassosdamanipulaçãodasequações seencontramem[10].
Asequaçõesresultantessãoapresentadasnosistemadeequações(17.1).
Afunçãoquedefineafontedeenergianãoidealécomoumafunçãolinear,que representaascurvascaracterísticasdarelaçãoentreotorqueversusvelocidadedo motordecorrentecontínua[6,1,7].
Afunçãoquedefineafontedeenergianaformalinearérepresentadapelaequação (17.2).
Onde V1 estárelacionadocomatensãoaplicadaàarmaduradomotordecorrente contínua,ouseja,umpossívelparâmetrodecontroledoproblema,e V2 éuma constanteparacadamodelodemotordecorrentecontínua(CC)considerado.As camadasdematerialpiezoelétricoaplicadassãorepresentadaspor P1 e P2 .Paraa
Modelagemdinâmicaaplicada aomonitoramentoediagnóstico defalhasemmotoresde induçãotrifásicos
Introdução
Oadventodaindústria4.0suscitoumudançasnoquecondizàsmetodologiasde controledeprocessosindustriais.Destaforma,abuscapelamáximaeficiênciade umprocessonãoseencontramaisalicerçadaplenamentenaautomação.Osnovos paradigmasqueconotamosdesafioscientíficosetecnológicosatuaissãobaseados nacapacidadedeumprocessoindustrialpossuiraltograudemonitoramentoe prediçãodefalhas.
Nestecontexto,osmotoresdeinduçãotrifásicos(MIT)sãoutilizadoscomoforça motrizdediversosprocessos,sendocomponentesprimordiaisparaacadeiaprodutiva.Estudosindicamqueessesmotoresestãoassociadosa90%dossistemascom acionamentoelétricoeconsomemmaisdedoisterçosdaenergiaelétricaproduzida globalmente.Portanto,abuscapeloconhecimentodascondiçõesdinâmicasdeoperaçãodosMITstemcrescidosignificativamentenosúltimosanos.Amotivaçãovem tantodepesquisadorescomodeváriossetoresdaindústria,umavezqueodiagnósticoincipientedeumafalhapodegerareconomiacommanutençõespontuaise programadas,conquistandoumelevadograudecontroleeplanejamentoindustrial.
Assim,amodelagemdinâmicaaplicadaaomonitoramentoediagnósticodefalhas emMITsdesempenhaumpapelfundamentalnamelhoriadaeficiênciadosprocessos
industriais,umavezqueaidentificaçãoprecocedeumanãoconformidadepode evitarfalhastotais,alémdepermitiroplanejamentodasaçõesdemanutenção. Baseadonestaproblemática,estecapítuloapresentaalgunsmodelosparaadetecção eidentificaçãodefalhasemmotoresdeinduçãotrifásicosbemcomoossensores eastécnicasdeprocessamentodedadosmaisutilizadasparaodiagnósticode avariasincipientes.
18.1Falhasemmotoresdeindução esuasconsequências
Osmotoresdeinduçãotrifásicossãoconhecidosporsuaacessibilidadeesua versatilidade.Seusaltosníveisdeeficiênciarevolucionaramosmeiosdeprodução etransformaramessesmotoresnaprincipalmatrizdeenergiamecânicapara grandepartedosequipamentosindustriais.Noentanto,apesardesuarobustez, manifestam-senosMITsdiferentestiposdefalhas,tantodeorigemelétricaquanto deorigemmecânica.Nospróximossubcapítulosserãoapresentadasalgumasdas principaisfalhasqueacometemessesdispositivos.AsanomaliasemMITsestão frequentementeconectadasdiretaouindiretamenteentresi.Contudo,asdivisões forampensadasdemodoafacilitarodetalhamentoeasconsequênciasdecadauma.
Paramelhorentendimento,éimportantereforçaralgunsconceitossimplesdo funcionamentodosmotoresdeindução:
• velocidadesíncrona(ns ):representaavelocidadedocampogiranteemRPM (rotaçõesporminuto)criadopelamáquinaepodesercalculadopor:
emque f éafrequênciadaredee p éonúmerodepolos.
• escorregamento(s):éaproporçãoentreavelocidadedorotoreavelocidade síncronaeécalculadopor:
emque nr éavelocidadedorotoremRPM.
• frequênciaderotação(fr ):éafrequênciaemHertzdorotordamáquina,é calculadacomo:
Capítulo19
Modelagemdeestruturas unidimensionaiscomparâmetros distribuídoseconcentrados
Estecapítuloestáorganizadoemdiversasseções.ASeção19.1apresentauma visãogeralsobreaanálisedinâmicadeestruturas.ASeção19.2apresentauma descriçãodosprincípiosdeenergiausadosparacompormodelosmatemáticosde estruturascomcomportamentodinâmico,destacandooprincípiovariacionalde Hamilton,utilizadocomvantagemquandoossistemasestruturaissãocontínuos, comparâmetrosdistribuídos,eométododasequaçõesdeLagrange,quepermite facilmentederivarosistemadeequaçõesdemovimentodesistemasestruturaiscom parâmetrosconcentradosediversosgrausdeliberdade.ASeção19.3apresentaos casosdemodelagemmatemáticadeestruturasunidimensionaiscomparâmetros distribuídosnocomprimento,comoéocasodasbarras,eixosevigas.ASeção 19.4apresentaainclusãodeparâmetrosconcentradosnamodelagemmatemática deestruturascontínuas.ASeção19.5apresentaaanálisedevibraçãolivrede estruturasmodeladasporparâmetrosdistribuídoseconcentrados.ASeção19.6 apresentaométodoaproximadodeRayleigh-Ritzaplicadoavibraçãodevigas contínuascomadiçãodeparâmetrosconcentrados.Porfim,aSeção19.7apresenta amodelagemdeestruturascomplexaspelométododeelementosfinitos,método estequedecorredométododeRayleigh-Ritz.Essemétodotransformaageometria complexadeumaestruturaemumconjuntodesub-regiõescujasgeometriassão descritasporfunçõesmatemáticasmaissimplesnoscálculosdedeformação,tensão edeslocamentosdaestrutura.
19.1Introdução
Aanálisedetensõesedeformaçõeséumapreocupaçãodaengenhariadeestruturas, aindamaisquandoestasestãosujeitasacarregamentosdinâmicosdiversose arbitrários.Emcertosentido,aanálisedocomportamentoestruturalperante carregamentosdinâmicoséumaextensãodaanáliseestruturaltradicional,que observaapenascarregamentosestáticos.Deformageral,ocarregamentoestático podeservistocomoumaformaparticulardecarregamentodinâmico.Noentanto, paraestruturaslineareséconvenientedistinguirentreascomponentesestáticas edinâmicasdocarregamento,duranteaanálise,eavaliarseparadamentecada respostaestrutural,paraentãosobreporasrespostasestáticasedinâmicas,como componentescalculadasdeumarespostageral.Éimportantetambémlembrarque osmétodosestáticosedinâmicosdeanáliseestruturaltêmcaracterísticasdiferentes.
Otermo“dinâmica”trazconsigoavariaçãodetempo,sejanoscarregamentos, deslocamentos,tensõesoudeformaçõesdaestrutura.Ocarregamentoédito dinâmicoquandosuamagnitude,direção,sentidoe/oupontodeaplicaçãovariam comotempo.Dessaforma,arespostaaocarregamentodinâmicopodesero deslocamentodeumdeterminadopontodaestruturaqueapresentavaloredireção variandonotempo.Outrasrespostasaoscarregamentosdinâmicos,comotensões edeformações,tambémsãovariáveisnotempo.
Édeconsensoque,seumaestruturaélevadaaresponderdinamicamente,entãoesforçosdecorrentesdasvelocidadeseaceleraçõesdoselementosestruturais surgem.Seessesesforçossãoapreciáveisemmagnitude,devemsersomadosaos carregamentosestáticos.Poroutrolado,éconsideradosuficientefazersomentea análiseestruturalestáticaquandohácertezadequeosesforçosdinâmicosprovenientesdevelocidadeseaceleraçõessãopequenosedesprezíveis.
Carregamentosdinâmicospodemserdeterminísticosoualeatórios.Ocarregamento determinísticotemcomodescriçãoumafunçãotemporalquepodeserdefinida analiticamente.Aanálisedeterminísticaéentãousadaparaobterrespostasdo sistemaestruturalemfunçãodestetipodecarregamento.Poroutrolado,sea variaçãodocarregamentonãoécompletamenteconhecida,maspodeserdefinida emumsentidoestatístico,entãoocarregamentoéconsideradocomoaleatório. Sendoassim,asrespostasestruturaisprovenientesserãotambémdenominadas aleatóriasounãodeterminísticas.
Aanáliseestruturalnoslevadiretamenteaosdeslocamentosdaestruturacomhistóricosdetempocorrespondentesaohistóricodocarregamentoprescrito;outros tiposdegrandezas,comotensões,deformações,forçasinternasetc.,sãonormalmenteobtidasapartirdosdeslocamentos,emumafasesecundáriadaanálise.
