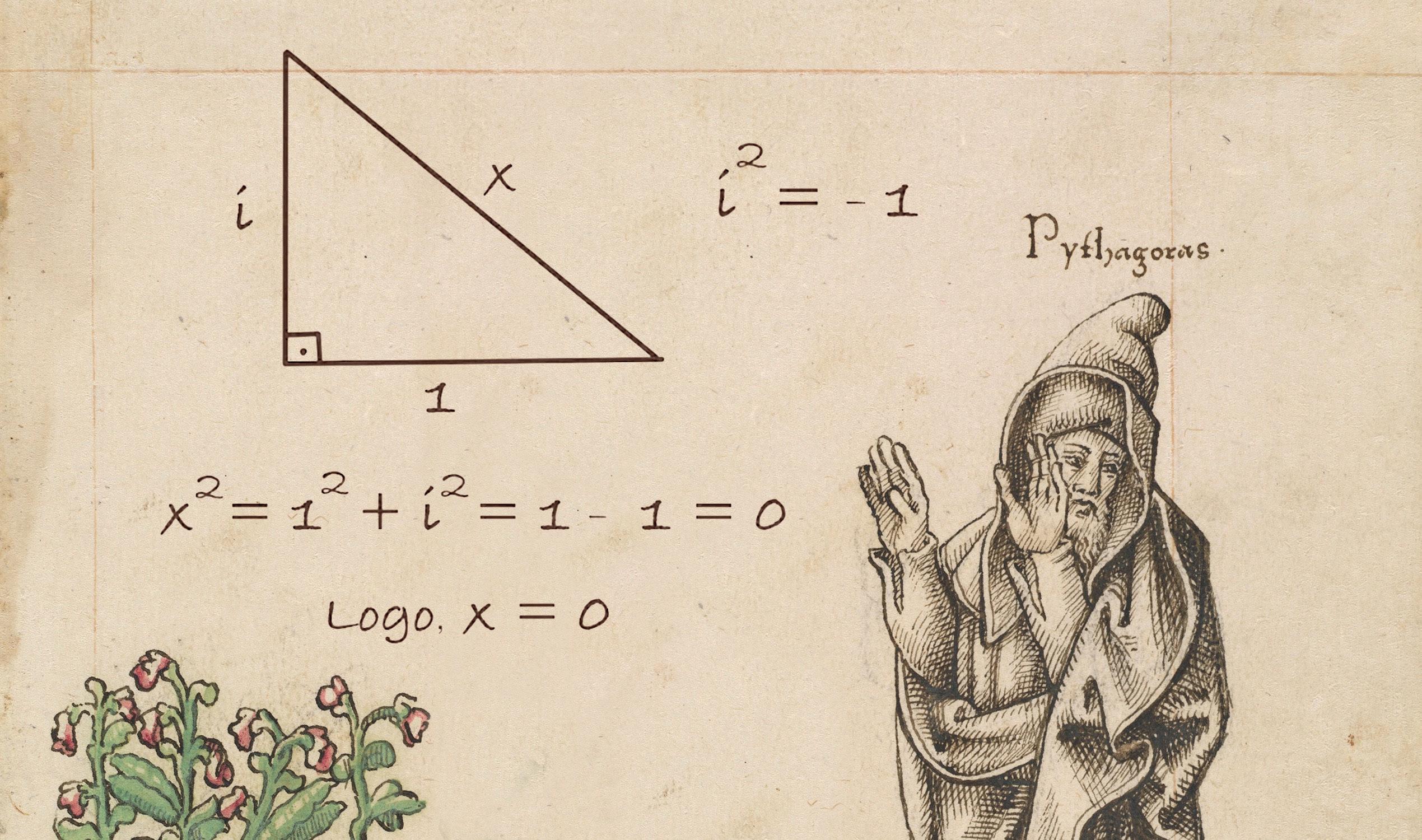
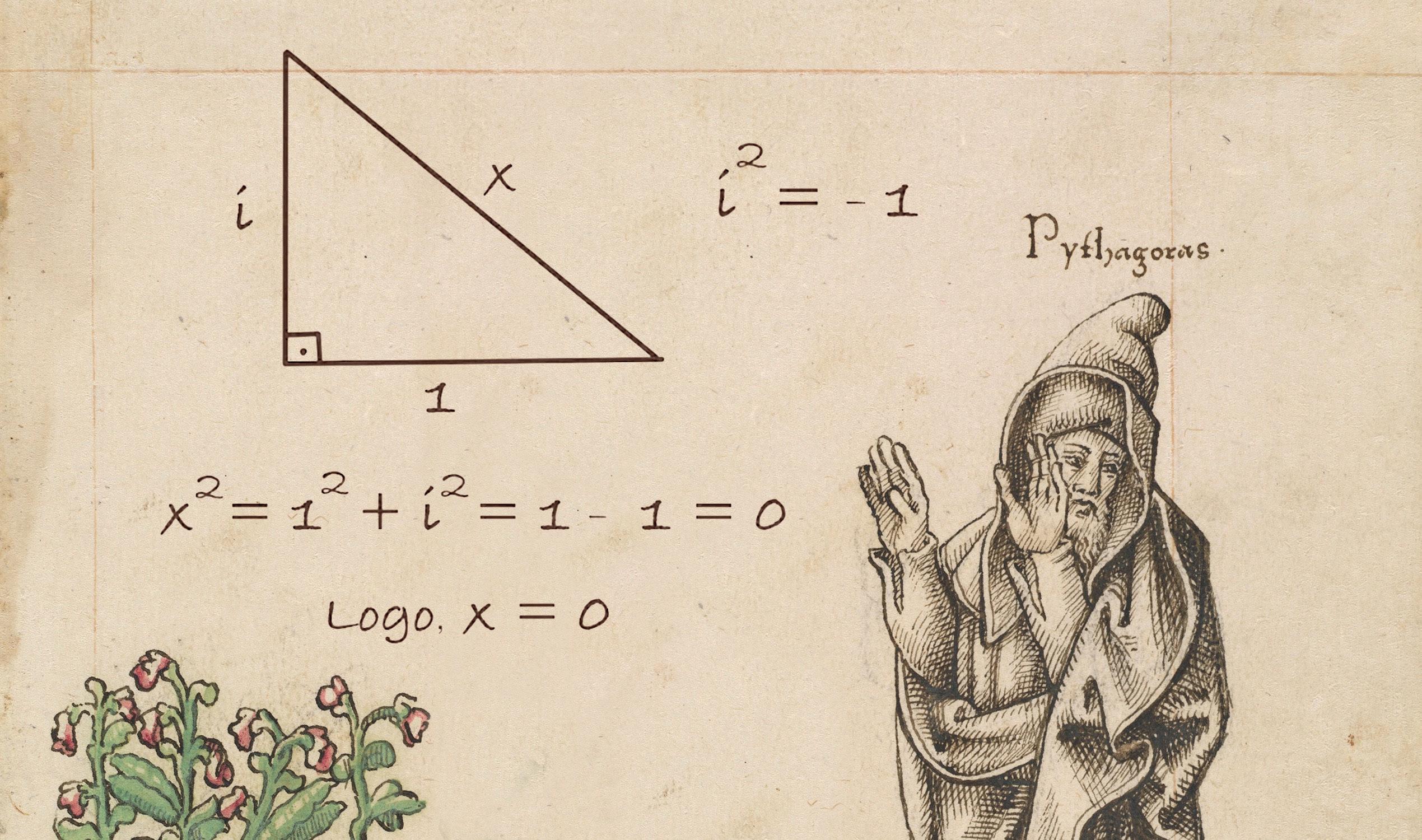
A MATEMÁTICA EM MEMES
Uma forma inusitada de estudar Matemática
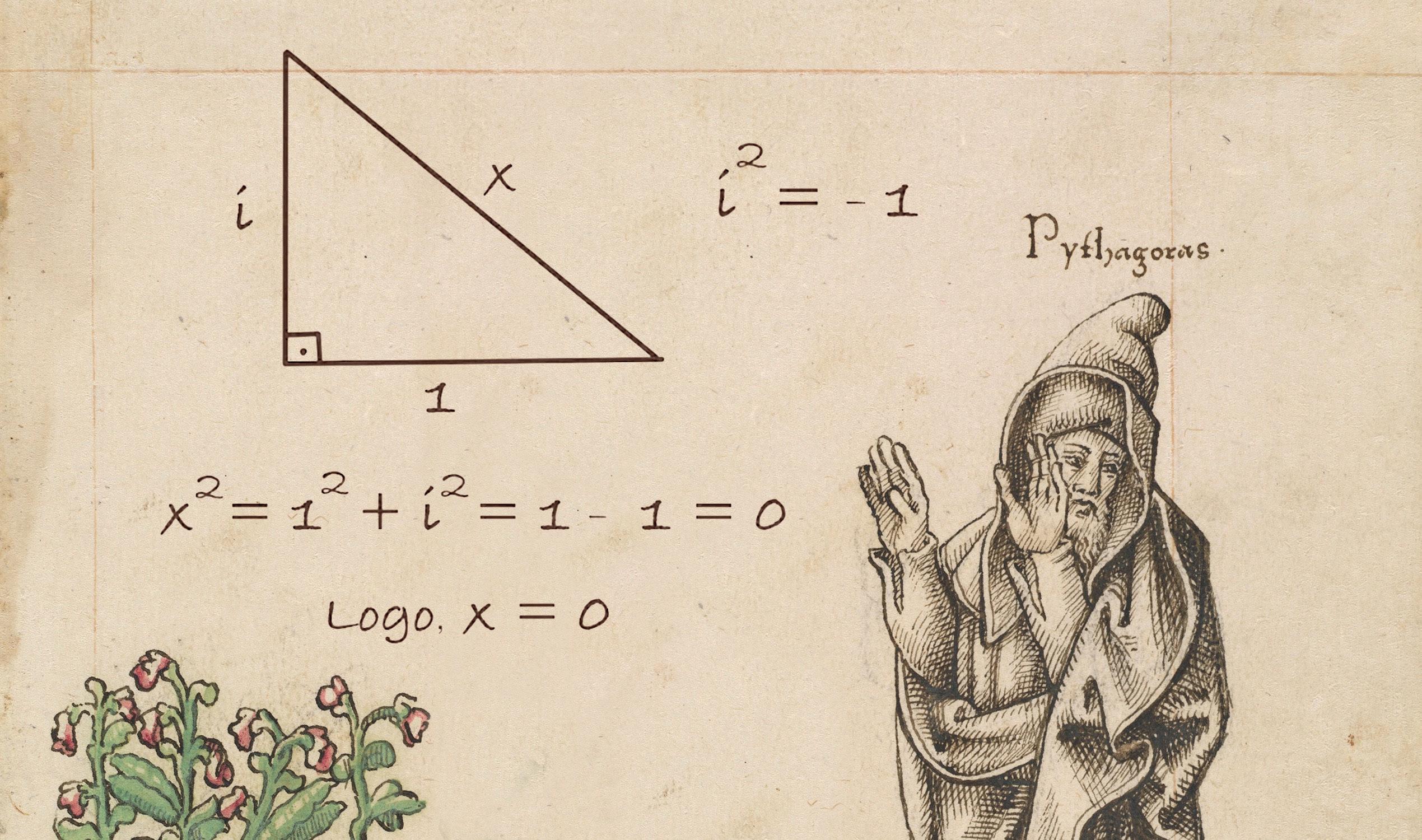

3.14“Fome”deconhecimento
3.15Nolimite(doerro!)
3.22Umaintegral,v´ariasrespostas?
Piadas“fundamentais”
1.1SOMANDOFRA¸C ˜ OES...N ˜ AO,ESPEREUMPOUCO...
Observeailustra¸c˜aoabaixocomaten¸c˜ao,extra´ıdadosite“math-fail.com”.
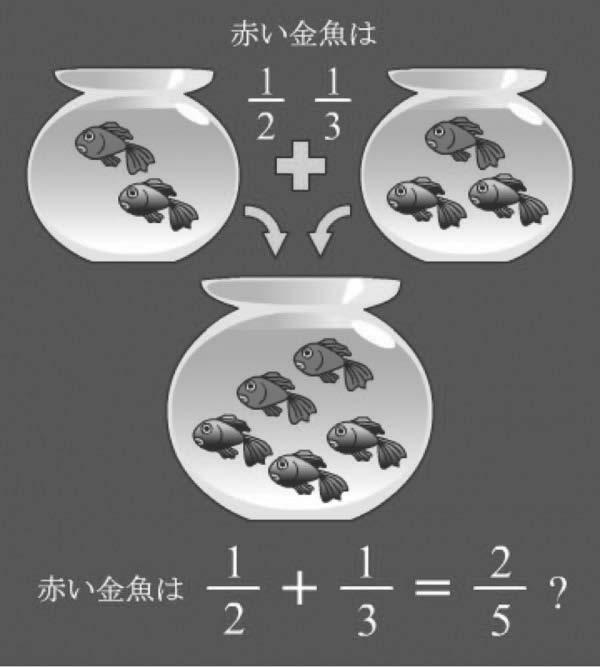
Semd´uvidaasomaacimaest´aincorreta,poisailustra¸c˜aorepresentariade fatoumasoma,masdeinteirosoudefra¸c˜oescommesmodenominador;n˜aode fra¸c˜oescomdenominadoresdiferentescomoamesma“sugere”.Pois,parasomar fra¸c˜oesdedenominadoresdiferentes,paraasfra¸c˜oespoderem“conversar”dever˜ao serconvertidasparaummesmodenominadorcomum.Comoest´anailustra¸c˜ao,o erroseriaequivalentea,porexemplo,somar1cent´ımetrocom1metroeobter2 (doisoquˆe?)Oquesedevefazer,nestecaso,´eescrever:
ouseja,convertemosmetroparacent´ımetros(porexemplo),parapoderefetuar asoma.Assim,no“exemplo”dailustra¸c˜ao,oquedeveriaserfeito(esque¸cados aqu´ariosedospeixes,elesserviramapenasparageraraconfus˜ao)parasomar
AMatem´aticaemmemes:umaformainusitadadeestudarMatem´atica
seriamultiplicarnumeradoredenominadordafra¸c˜ao 1 2 por3emultiplicarnumeradoredenominadordafra¸c˜ao 1 3 por2,poisnestecasoodenominadordeambas asfra¸c˜oesficar´a comum,nocaso6:
arespostacertaparaasoma 1 2 + 1 3 .
Umoutro“meme”quecirculabastantepelainternet,referenteaoproblema acima,´easeguinte“tenta¸c˜ao”:

Exerc´ıcios
1.Efetue:
1.2PEDINDOEMPRESTADO
Oseguintememefoiextra´ıdodosite“mundoacademy.com”,ondetemosum personagemquetemqueresolveraseguinteopera¸c˜ao:18 9,queconsisteemuma contaextremamentesimples,deresultado9,masquepodecausarcertaconfus˜ao quandooestudantevˆeissopelaprimeiraveznass´eriesiniciais.

Aideiadoproblema´eobservarque18´edecompostoem10 + 8,umadezenae oitounidades.Temosdetirar9unidades,e,semontarmosaconta,comon˜aose podesubtarir8de9,o8deve“pediremprestado”dadezenao1,que,nocaso, pedeemprestado,naverdade,10,oqual,somadocom8,resultaem18,parasubtrairde9,ouseja,o“empr´estimo”n˜aoajudouemnada,deixandoopobrepersonagememestadodedesespero.
Defato,essa´eumacontaqueoestudantedevesaberfazerdireto,sempedir “empr´estimos”dod´ıgitoseguinte.
Vejamosumoutroexemplo,ondearegrado“empr´estimo”seapliquedefato. Considerecalcular537 359.Nestecaso,semontarmosaconta, 537 359 dein´ıcio,dever´ıamossubtrair7de9,oquen˜ao´eposs´ıvel,edessaforma,como
537 = 500 + 30 + 7 e
359 = 300 + 50 + 9, aopediremprestado1do3(naverdade10de30),teremos
537 = 500 +( 20 + 10)+ 7 = 500 + 20 + 17 = 520 + 17, eent˜ao17 9 = 8unidades.
AMatem´aticaemmemes:umaformainusitadadeestudarMatem´atica
Emseguida,deveremos,olhandoosd´ıgitosdasdezenas,fazer2 5(naverdade, 20 50,poiss˜aod´ıgitosdasdezenas),oquen˜aod´aparasubtrair,eent˜ao,doque aindan˜aooperamos,temos
520 = 500 + 20 = ( 400 + 100)+ 20 = 400 + 120, eent˜aofaremos120 50 = 70,ouseja,7dezenas.
Porfim,subtraindoascentenasrestantes,
400 300 = 100, ouseja,umacentena.Dessaforma,adiferen¸ca537 359resultaem1centena,7 dezenase8unidades,ouseja,em178.Deformapr´atica,seescreve:
5 32 17 359 , 8
ouseja,7pediuemprestado1do3,efez-se17 9 = 8,paraod´ıgitodaunidade.
Depois,paraadezena,fazemos
54 127 359 78
ouseja,parasubtrairasdezenas,temos2 5,sendoqueo2pede1emprestado ao5(defato,est´apedindo100emprestadodo500,eent˜aofaz-se12 5 = 7,o que,narealidade´e120 50 = 70).
Por,fim,subtraindoascentenasrestantes,obtemos 4 127 359 178 ouseja, 537 359 178
Deformageral,umn´umerointeiropositivo 𝑎 ´edenotadopor
onde 𝑎 𝑗 ∈{ 0, 1, 2,..., 9 } s˜aoosd´ıgitosdon´umero 𝑎 .Porexemplo,setivermos 𝑎 = 5047,ent˜aotemososd´ıgitos
• 𝑎 0 = 7(unidade)
• 𝑎 1 = 4(dezena)
• 𝑎 2 = 0(centena)
• 𝑎 3 = 5(milhar)
Umn´umerointeiropositivo,dessaforma,podeserdecompostoem potˆencias debasedez,comosegue:
Assim,porexemplo,temos
Assim,paraefetuarumadiferen¸ca
escrevemos
oque,agrupandonasmesmaspotˆencias,resultaem
Noentanto,asdiferen¸casentreosparˆentesesdevemserpositivas,poisrepresentamd´ıgitosdoresultadodadiferen¸caentre 𝑎 e 𝑏 .Poressaraz˜ao,deve-seaveriguarque,paracadaposi¸c˜ao 𝑗 entre0e 𝑘 :
(i)se 𝑎 𝑗 ≥ 𝑏 𝑗 ,ent˜aofaz-serealmenteadiferen¸ca 𝑎 𝑗 𝑏 𝑗 ; (ii)se 𝑎 𝑗 <𝑏 𝑗 ,ent˜aotoma-se1 𝑎 𝑗 = 10 + 𝑎 𝑗 efaz-se1 𝑎 𝑗 𝑏 𝑗 ,enestecasood´ıgito 𝑎 𝑗 +1 torna-se 𝑎 𝑗 +1 = 𝑎 𝑗 1(ouseja,od´ıgitomais`aesquerda,que´e 𝑎 𝑗 +1 , emprestou1paraod´ıgito 𝑎 𝑗 )
Comessealgoritmo,retornemosaoexemploanterior,pararesolvˆe-lousandoa formageral:
Exerc´ıcios
1. Efetueasopera¸c˜oesabaixodeduasformas:Efetuandoadiferen¸ca montandoaconta,comofeitonoin´ıcio;edecompondoosn´umeros empotˆenciadebasedezeusandooalgoritmoestabelecidonotexto.
(a)807 349(b)6094 887(c)77777 59999
2. Umcomputadortrabalhainternamenteapenascomadi¸c˜oes.Logo, paraexecutar,porexemplo,umadiferen¸caentre 𝑎 e 𝑏 ,ouseja 𝑎 𝑏 , elesoma 𝑎 comocomplementoa de 𝑏 .Porexemplo,se 𝑎 = 74e 𝑏 = 26,ent˜ao 𝑎 𝑏 = 54 26,masocomputador“pensa”assim:
26 −→ 54 + 74 = 128, edepois“despreza”o“1”,chegandoaoresultado28.Mostregenericamentequeissodefatosempre´eposs´ıvel.
3. Sejaon´umero 𝑛 ,nosistemadebasedez,formadoporumn´umero parded´ıgitos,ealternadamenteporapenasdoisd´ıgitos,isto´e, 𝑛 = 𝑥𝑦𝑥𝑦𝑥𝑦 ··· 𝑥𝑦 .Trocandoaordem 𝑥𝑦 por 𝑦𝑥 ,formamosum novon´umero 𝑝 comamesmaquantidadeded´ıgitos,ouseja, 𝑝 = 𝑦𝑥𝑦𝑥 ··· 𝑦𝑥 .Proveque 𝑛 + 𝑝 ´em´ultiplode 𝑥 + 𝑦 edˆeexemplos.O queresulta 𝑛+ 𝑝 𝑥 + 𝑦 ?
a Ocomplementodeumn´umero´eoquantofaltaparaelechegar`aunidadedeseupeso. Porexemplo,ocomplementode30´e70,pois 30 + 70 = 100;j´aocomplementode476 ser´a524,pois 476 + 524 = 1000
CAP ´ ITULO2
Piadasde“n´ıvelm´edio”
2.1FANTASIADODIADASBRUXAS

Agra¸cadapiadaconsisteemobservarque,enquantoumdospersonagensest´a fantasiadocomacamiseta1,ooutroest´afantasiadocomacamiseta0, 9.Por´em, trata-sedamesmafantasia(omesmovalor),ouseja,vamosmostrarque
1 = 0, 9 .
Antesdetudo,recordequeumn´umerodecimal´etodon´umerodaforma 𝑎,𝑎 1 𝑎 2 𝑎 3 𝑎 4 ...,
onde 𝑎,𝑎 1 ,𝑎 2 ,𝑎 3 ,... s˜aoosd´ıgitosquepertencemaoconjunto { 0, 1, 2,..., 9 } .Por exemplo,on´umero
4, 730254933013
´eumn´umerodecimal finito ou exato,poispossuiumaquantidadefinitaded´ıgitos ap´osav´ırgula,enquantoque
1, 2347676767676767676
AMatem´aticaemmemes:umaformainusitadadeestudarMatem´atica
´eumn´umerodecimal infinito,noqual,nestecaso,osd´ıgitos7e6aparecem periodicamente,eindefinidamente.Nestecaso,podemosabreviarescrevendo 1, 23476, ondeabarrahorizontaldescreveo per´ıodo don´umerodecimal.
Claroqueexistemn´umerosdecimaisinfinitoscujapartedecimaln˜ao´eperi´odica [ser˜aoosn´umerosirracionais],porexemplo,osn´umeros 0, 101001000100001000001 ... e
= 3, 141592653 ...
Masvoltemos`anossafesta`afantasia.Noteque
ouseja,
Noteque,definindoasequˆencia ( 𝑎
temosque
∈ N, ouseja,talsequˆencia´eumaprogress˜aogeom´etrica(P.G.)deraz˜ao 𝑞 = 1 10 < 1.
Assim,oquetemosem(2.1)´easomainfinitadeumaprogress˜aogeom´etrica cujoprimeirotermo´e 𝑎 1 = 9 10 ecujaraz˜ao´e 𝑞 = 1 10
Ent˜ao,paraentenderafantasia0, 9,precisamosobteraf´ormuladasoma dosinfinitostermosdaprogress˜aogeom´etrica.Lembrandoque,dadaaP.G. ( 𝑎 1 ,𝑎 2 ,𝑎 3 ,𝑎 4 ,... ) ,cujaraz˜aoseja 𝑞< 1,temosque,comoopr´oximotermoda sequˆencia´eotermoanteriormultiplicadopelaraz˜ao,
Assim,sendo 𝑆 asomainfinita,temos
Multiplicandopor 𝑞 ,vem
Dessasduasigualdades,levandoasegundaparaaprimeira,obtemos
oque,isolando 𝑆 ,vem
dondesegueque(isso´eposs´ıveldevido`aconvergˆenciaqueir´aexistir)
Assim,voltandoaoproblema,onde
ouseja,
isto´e,a“roupa”´eamesma[ouseja,0, 99999 ... ´eoutrarepresenta¸c˜aodecimal para1].
Vamosdeixaraquialgunsexerc´ıciosparaverificaresosseguintesparesdefantasias:
Exerc´ıcios
1.Mostreque (a) 3 11 = 0, 27(b) 8 7 = 1, 142857(c) 1 12 = 0, 083
2.*Expliqueque0, 27 = 0, 269999999999 ...
2.2MATRIZESTRANSPOSTAS?

Doestudodematrizes,dadaumamatriz
com 𝑚 linhase 𝑛 colunasdaforma
asuatransposta,denotadapor 𝐴 𝑡 ,´edefinidacomosendoamatriz
, ouseja,apartirdamatriz 𝐴 ,paraobtersuatransposta,trocamoslinhaspor colunas,isto´e,alinha1de 𝐴 𝑡 ´eacoluna1de 𝐴 ,eassimpordiante.Porexemplo,se 𝐴 = 2 17 103 2 × 3 ,
ent˜aoasuatranspostaser´adadapor
Ohumorpresentenafotoconsistiuemobservarque,sendo 𝐴 a´arvoreem suaposi¸c˜aonatural,navertical,ent˜aosua“transposta”seriaamesma´arvorena horizontal,ouseja,ca´ıda,oquen˜aofazsentido;foiapenasumabrincadeiracom orealconceitodematriztranspostaesuanota¸c˜ao.
Exerc´ıcios
1.Obtenhaatranspostadecadamatriz:
2.3EMVERDADEVOSDIGO...FUN¸C ˜ OESQUADR ´ ATICAS

Aimagemacimafoiextra´ıdadosite“matematica.pt”.JesusCristoensinava seusdisc´ıpuloseseguidorespormeiode par´abolas,ques˜aonarrativasaleg´oricas quetransmitemumamensagemindireta,pormeiodecompara¸c˜aoouanalogia.
Paramontarohumordatiraacima,oautorusaacoincidˆenciadenomesdesse conceitoedoconceitodafun¸c˜aopolinomialdesegundograu,tamb´emchamada defun¸c˜aoquadr´atica, 𝑓 : R → R dadapor
cujoesbo¸cogr´aficochama-seuma par´abola,ondeaconcavidadedamesmapode servoltadaparacima,se 𝑎> 0,ouvoltadaparabaixo,se 𝑎< 0.QuandoseestudamderivadasemC´alculoissoficaperfeitamenteclaro,analisandoosinalda derivadasegundade 𝑓 .
Paradeterminaros zeros deumafun¸c˜ao,ques˜aoospontosondeelainterceptaoeixohorizontal,casoexistam,bastaverificaronde 𝑓 ( 𝑥 ) = 0.
Nocasodapar´abola,bastaresolveraequa¸c˜aodesegundograu
𝑎𝑥
e,paraisso,usamosaf´ormuladeB´askaraparaobteroszerosdestetipodefun¸c˜ao. Recordemosapenas,aqui,queoszerospara 𝑓 ( 𝑥 ) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 s˜ao 𝑥 = 𝑏 ± √Δ 2 𝑎
onde Δ= 𝑏 2 4 𝑎𝑐
Noteque,pelofatode Δ serumradicando,tiramosasseguintesconclus˜oes quanto`aan´alisedasra´ızes:
• Se Δ > 0,ent˜aoafun¸c˜aoquadr´aticapossuidoiszerosdistintos.
• Se Δ= 0,ent˜aoafun¸c˜aoquadr´aticapossuium´unicozero.
• Se Δ < 0,ent˜aoafun¸c˜aoquadr´atican˜aotemzeros.
Dadaapar´aboladeequa¸c˜ao 𝑓 ( 𝑥 ) = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 ,j´asabemosqueosseuszeros, seexistirem,s˜aodadospor
Piadasde“n´ıvelsuperior”
3.1INDU¸C ˜ AOGATEM ´ ATICA
Observeoseguintememe,extra´ıdodosite“mymathscloud.com”:

Naprimeiraimagemtemosumailustra¸c˜aodaideiadaindu¸c˜aomatem´atica: pe¸casdeumjogodedomin´oenfileiradascomoobjetivodederrubartodas, produzindoumefeitodequeda“emcascata”,ouseja,aquedadeumaproduza quedadapr´oxima[ocuriosonessailustra¸c˜ao´equeest´aaumentandootamanho dape¸ca,maspodeseroutraideiaobscura:comoderrubarinicialmenteumape¸ca diminutavai,aolongodasequˆenciadequedas,produziraquedadeumape¸ca colossal].Ailustra¸c˜aoaoladotrazdoisgatospregui¸cosos,quepoderiaservircomo umexemplode hip´oteseetesedaindu¸c˜ao:numprimeiromomentoumgato 𝑛 boceja,oque,numsegundomomento, induz ogato 𝑛 + 1abocejartamb´em.
Brincadeiras`aparte,vamosexploraragoraaquest˜aodaindu¸c˜aomatem´atica, queconsistenumassuntoextremamenteimportanteepoderosodaMatem´atica. Paraprovarpropriedadesassociadasaosn´umerosnaturais,usamosumm´etodo chamado indu¸c˜aomatem´atica,elaboradopelomatem´aticoGiuseppePeano(18581932).Normalmentetalprinc´ıpio´eestudadoemdisciplinasdeAritm´eticaouAn´alisenaReta.Essem´etodo´eusadoparaprovarpropriedadesemqueter´ıamosque testarinfinitosvaloresnaturaisparacomprovarseumadadapropriedadeenvolvendoosnaturais´everdadeiraoun˜ao.Noentanto,n˜ao´eposs´ıveltestarinfinitos valoresparacomprovarumapropriedade,apenasaindu¸c˜ao,conformedescreveremos,funcionar´a.
AMatem´aticaemmemes:umaformainusitadadeestudarMatem´atica
Proposi¸c˜ao3.1. (Primeiroprinc´ıpiodaindu¸c˜aomatem´atica) Sejam 𝑃 ( 𝑛 ) uma afirma¸c˜aoreferenteaosn´umerosnaturaise 𝑎 ∈ N taisque
(i) 𝑃 ( 𝑛 ) ´everdadeirapara 𝑛 = 𝑎 ;
(ii) se 𝑃 ( 𝑘 ) forverdadeira,ent˜ao 𝑃 ( 𝑘 + 1) tamb´em´everdadeira.
Ent˜ao, 𝑃 ( 𝑛 ) ´everdadeira, ∀ 𝑛 ≥ 𝑎 .
Observa¸c˜oes:
(a)Oitem(i)´echamadode basedaindu¸c˜ao.
(b)Noitem(ii),anecessidade “se 𝑃 ( 𝑘 ) forverdadeira...” chama-sehip´oteseda indu¸c˜ao,easuficiˆencia “...ent˜ao 𝑃 ( 𝑘 + 1) tamb´em´everdadeira” chama-setese daindu¸c˜ao,ouseja,ogato 𝑛 bocejandoeinduzindoumbocejonogato 𝑛 + 1.
(c)Asduascondi¸c˜oes(i)e(ii)devemsersatisfeitas.Paraentenderautiliza¸c˜ao desseprinc´ıpio,pensemosemumjogo“infinito”depe¸casdedomin´oenfileiradasondequeremosderrubartodasasinfinitaspe¸cas.2 Oquequeremos dizercomoprinc´ıpiodaindu¸c˜aomatem´atica´eque,sabendo-seque(i)derrubamosaprimeirape¸ca;e(ii)ocairdeumadaspe¸casproporcionar´aa quedadape¸caseguinte;conclu´ımosquetodasasinfinitaspe¸cascair˜ao.
Vamos`ademonstra¸c˜aodesseprinc´ıpio.
Demonstra¸c˜ao. Sejaoconjunto 𝐿 = { 𝑥 ∈ N : 𝑥 ≥ 𝑎 e 𝑃 ( 𝑥 ) ´efalsa } .
Precisamosmostrarque 𝐿 = ∅ .Porabsurdo,se 𝐿 ≠ ∅ ,ent˜ao 𝐿 cont´empelo menosumelemento.
Como 𝐿 ⊂ N e N possuiumelementom´ınimo,nocaso1,segueque 𝐿 tamb´em possuir´aumelementom´ınimo.
Seja 𝑚 ∈ 𝐿 talque 𝑚 = min 𝐿 ,onde min 𝐿 denotaoelementom´ınimodo conjunto 𝐿 .Ent˜ao,segueque 𝑃 ( 𝑚 ) ´efalsae 𝑚 ≥ 𝑎. (3.1)
2 Elasn˜aoprecisamtertamanhocrescentecomonaprimeirailustra¸c˜aodomeme.
Pelabasedaindu¸c˜ao(i)conclu´ımosque 𝑃 ( 𝑎 ) ´everdadeira,portanto,temos que 𝑚>𝑎
Como 𝑚 ´eom´ınimode 𝐿 ,segueque 𝑚 1 ∉ 𝐿 e,ent˜ao, 𝑃 ( 𝑚 1) ´everdadeira. Mas,por(ii),conclu´ımosque 𝑃 ( 𝑚 ) tamb´em´everdadeira,oquecontradiz(3.1). Absurdo!Logo,conclu´ımosque 𝐿 = ∅ e,ent˜ao,valeoprinc´ıpiodaindu¸c˜ao.
Apenascomoilustra¸c˜ao,apresentamosdoisexemplosdeaplica¸c˜aodesseprinc´ıpio.
Exemplo1. Proveque2 𝑛 <𝑛 !, ∀𝑛> 3.
Solu¸c˜ao.
(i)basedaindu¸c˜ao:quando 𝑛 = 4temosque
24 = 16 < 24 = 4!, logo,valeabasedaindu¸c˜ao.
(ii)Suponhaqueapropriedadesejav´alidaparaumcerto 𝑛 = 𝑘 ,i.e.,quevalea hip´otesedeindu¸c˜ao
2 𝑘 <𝑘 !,𝑘> 3 .
Precisamosmostrarquevalepara 𝑛 = 𝑘 + 1,ouseja,precisamosmostrarque 2 𝑘 +1 < ( 𝑘 + 1) !
Defato,noteque ( 𝑘 + 1) ! = ( 𝑘 + 1)· 𝑘 ! .
Comopelahip´otesedeindu¸c˜aotemosque2 𝑘 <𝑘 !,𝑘> 3,vamosencontrara estimativa ( 𝑘 + 1) ! = ( 𝑘 + 1)· 𝑘 ! > ( 𝑘 + 1)· 2 𝑘 , ecomopara 𝑘> 3tem-seque 𝑘 + 1 > 4 > 2,obteremos ( 𝑘 + 1) ! > ( 𝑘 + 1)· 2 𝑘 > 2 · 2 𝑘 ,
ouseja,obtemosatesedaindu¸c˜ao:
Logo,segue(ii).
De(i)e(ii)seguepeloprinc´ıpiodaindu¸c˜aomatem´aticaque
Exemplo2. Proveporindu¸c˜aomatem´aticaque
Solu¸c˜ao. Vamosverificarquevalem(i)e(ii). (i)Para 𝑛 = 1temosquevaleaigualdade,pois
Logo,valeabasedaindu¸c˜ao.
(ii)Suponhamosqueaigualdadevalepara 𝑛 = 𝑘 ,i.e.,que
. (3.2)
Precisamosmostrarquevalepara 𝑛 = 𝑘 + 1,ouseja,precisamosencontrar 1 1 2 + 1 2 3 + 1 3 4 + ... + 1 ( 𝑘 + 1)( 𝑘 + 2) = 𝑘 + 1 𝑘 + 2 .
Assim,adicionandootermo
( 𝑘 + 1)( 𝑘 + 2) emambososmembrosde(3.2)temos 1 1 · 2 + 1 2 · 3 + 1 3 · 4 + ... + 1 𝑘 ( 𝑘 + 1) + 1 ( 𝑘 + 1)( 𝑘 + 2) = 𝑘 𝑘 + 1 + 1 ( 𝑘 + 1)( 𝑘 + 2) = 𝑘 ( 𝑘 + 2)+ 1 ( 𝑘 + 1)( 𝑘 + 2) = 𝑘 2 + 2 𝑘 + 1 ( 𝑘 + 1)( 𝑘 + 2) = ( 𝑘 + 1) 2 ( 𝑘 + 1)( 𝑘 + 2) = 𝑘 + 1 𝑘 + 2 .
Logo,peloprinc´ıpiodaindu¸c˜aomatem´atica,conclu´ımosoexerc´ıcio.
Exerc´ıcios
1.Useaindu¸c˜aomatem´aticaparaprovarque
(a)1 + 3 + 5 + ... +( 2𝑛 + 1) = ( 𝑛 + 1) 2 , ∀𝑛 ∈ N
(
(c) 𝑛 ≥ 4 ⇒ 2 𝑛 <𝑛 !
(d)12 + 32 + +( 2𝑛 1) 2 = 𝑛 ( 2𝑛 1)( 2𝑛 + 1) 3 , ∀𝑛 ∈ N (e) 1 1
2. Proveque cos 𝜃 + cos 3 𝜃 + ... + cos ( 2𝑛 1) 𝜃 = sin2𝑛𝜃 2sin 𝜃 ,paratodo 𝑛 ≥ 1 eparatodo 𝜃 talquesin 𝜃 ≠ 0.
3. *Proveporindu¸c˜aosobre 𝑛 que ( 1 + 𝑥 ) 𝑛 ≥ 1 + 𝑛𝑥 , ∀𝑛 ∈ N e ∀𝑥 ∈ R, 𝑥 ≥ 1.(Estadesigualdade´edenominadadedesigualdadedeBernoulli.
4.Mostreque2 𝑛 <𝑛 ! <𝑛 𝑛 ,para 𝑛 ≥ 4.
3.2EXPANS ˜ AOGASEIFICADA
Observeomemeabaixo,extra´ıdodosite“knowyourmeme.com”,ondeoautor “criou”umanovateoria:
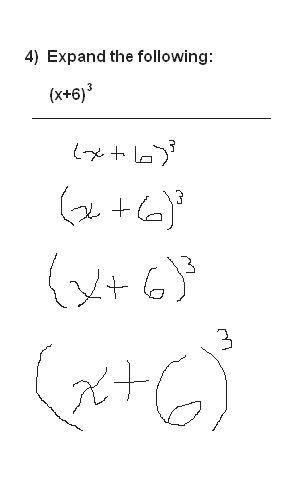
Engana-sequempensouemexpans˜aobinomial(pelomenosnacabe¸cadoindiv´ıduoqueofez).Comoelen˜aosabia,eleresolveu“criar”suapr´opriateoria,que poder´ıamosdenotarpor expans˜aobinomialgaseificada.Talvezeletenhapensado naF´ısica,emparticularnapartedeexpans˜aodegases.Este´eohumordatira. Vamosagorapassarparaumaconstru¸c˜aoparaaresolu¸c˜aomatematicamentecorretadoproblema,ouseja,semousodateoriagaseificada.
Aquest˜aoconsisteemobteraexpans˜aopara ( 𝑥 + 6) 3 (expans˜aobinomial).De modogeral,vamosobteraf´ormulaparaexpandir ( 𝑎 + 𝑏 ) 𝑛 , 𝑛 ∈ N.Repareque, desenvolvendo ( 𝑎 + 𝑏 ) 𝑛 para 𝑛 = 0, 1, 2, 3e4,vamosobter
( 𝑎 + 𝑏 ) 0 = 1 ( 𝑎 + 𝑏 ) 1 = 𝑎 + 𝑏 ( 𝑎 + 𝑏 ) 2 = 𝑎 2 + 2 𝑎𝑏 + 𝑏 2 ( 𝑎 + 𝑏 )
𝑏
( 𝑎 + 𝑏 ) 4 = 𝑎 4 + 4 𝑎 3 𝑏 + 6 𝑎 2 𝑏 2 + 4 𝑎𝑏 3 + 𝑏 4 . . .
Ent˜ao,pareceexistirumpadr˜aodecomportamento.Chamemosdelinha 𝑖 a linhadapotˆencia 𝑖 .Assim,porexemplo,alinha0´eaprimeiralinha,ondetemos
( 𝑎 + 𝑏 ) 0 = 1, j´aalinha1´easegundalinha,ondetemos ( 𝑎 + 𝑏 ) 1 = 𝑎 + 𝑏, eassimpordiante.Ent˜ao,nalinha 𝑖 h´a 𝑖 + 1aditivos.Notetamb´emquenalinha 𝑖 ,olhandoaspotˆenciasdoproduto 𝑎𝑏 ,temosqueaspotˆenciasde 𝑎 decrescemde 𝑖 at´ezero,enquantoaspotˆenciasde 𝑏 crescemde0at´e 𝑖 .Porexemplo,
𝑎 + 𝑏 ) 4 = 𝑎
Restaobservarocomportamentodoscoeficientes(asconstantesquemultiplicamosfatores 𝑎𝑏 ).Paraisso,vamos“limpar”oesquemafeitoacimaeolhar apenasoscoeficientes:
Quem já não se deparou com algum meme matemático, ao “passear pela internet”? Alguns engraçados e outros nem tanto… Mas será que, olhando com bastante atenção, não existe por trás desses memes algum aprendizado interessante, ou até surpreendente, relacionado à Matemática?
Este livro convida o leitor a explorar diversos tópicos fundamentais da Matemática – conteúdos que vão do ensino básico ao ensino superior – de forma leve, divertida e descontraída. Cada meme serve como ponto de partida para uma apresentação cuidadosa, que combina humor com elegância e rigor matemático, tornando a jornada pelo mundo dos números envolvente e instigante.

