

©VANIN
4 XL 5 uur – deel 1
©VANIN
Philippe De Crock
Dirk Taecke
Thierry Van den Ouwelant
MET MEDEWERKING VAN
Veerle Descheemaeker
Etienne Goemaere
Christophe Gryson
Eddy Magits
Tom Van der Auwera
Martine Verrelst

Via www.diddit.be heb je toegang tot het onlineleerplatform bij Pienter 4. Activeer je account aan de hand van de onderstaande code en accepteer de gebruiksvoorwaarden.
Kies je ervoor om je aan te melden met je Smartschool-account, zorg er dan zeker voor dat je e-mailadres aan dat account gekoppeld is. Zo kunnen we je optimaal ondersteunen.
Let op: activeer deze licentie pas vanaf 1 september; de licentieperiode start vanaf activatie en is slechts 365 dagen geldig.
Pienter XL 4 – 5u – deel 1
Fotokopieerapparaten zijn algemeen verspreid en vele mensen maken er haast onnadenkend gebruik van voor allerlei doeleinden. Jammer genoeg ontstaan boeken niet met hetzelfde gemak als kopieën.
Boeken samenstellen kost veel inzet, tijd en geld. De vergoeding van de auteurs en van iedereen die bij het maken en verhandelen van boeken betrokken is, komt voort uit de verkoop van die boeken.
In België beschermt de auteurswet de rechten van deze mensen. Wanneer u van boeken of van gedeelten eruit zonder toestemming kopieën maakt, buiten de uitdrukkelijk bij wet bepaalde uitzonderingen, ontneemt u hen dus een stuk van die vergoeding. Daarom vragen auteurs en uitgevers u beschermde teksten niet zonder schriftelijke toestemming te kopiëren buiten de uitdrukkelijk bij wet bepaalde uitzonderingen. Verdere informatie over kopieerrechten en de wetgeving met betrekking tot reproductie vindt u op www.reprobel.be.
Ook voor het onlinelesmateriaal gelden deze voorwaarden. De licentie die toegang verleent tot dat materiaal is persoonlijk. Bij vermoeden van misbruik kan die gedeactiveerd worden. Meer informatie over de gebruiksvoorwaarden leest u op www.diddit.be.
© Uitgeverij Van In, Wommelgem, 2024
De uitgever heeft ernaar gestreefd de relevante auteursrechten te regelen volgens de wettelijke bepalingen. Wie desondanks meent zekere rechten te kunnen doen gelden, wordt verzocht zich tot de uitgever te wenden.
Fotocredits
©VANIN
p. 244 vragen Bebras-wedstrijd © 2019 Bebras – International Challenge on Informatics and Computational Thinking; licentie: CC-BY-SA 4.0; auteurs tekst: Laura Ungureanu (RO), Corina Vint (RO), Arnheidur Gudmundsdottir (IS), Margot Phillipps (NZ), Sebastien Combefis (BE), Eslam AbdElAal (EG), Georgios Fesakis (GR), J. P. Pretti (CA), Vipul Shah (IN); vertaling Nederlands: Kris Coolsaet (BE); auteurs van de afbeeldingen: Alessandra Rădulescu (RO), Eslam AbdElAal (EG) – de Bebraswedstrijd wordt in Belgie georganiseerd door de CSITEd vzw met de steun van de Universiteit Gent – https://www.bebras. be/nl, p. 246, 247, 250 tabellen en grafieken © Cuypers K., Lebacq T., Teppers E. (eds.), voedselconsumptiepeiling 20142015 (WIV-ISP), p. 277 wereldkaart temperatuurverschil © Data source: ERA5, Copernicus Climate Change Service/ECMWF, tabel bouwgrond © Trends Vastgoedgids (lente 2020), p. 283 box-and-whiskerplot © Schlurcher / CC-BY-3.0 & GDFL 1.2, p. 290 Eliud Kipchoge © Belga Image, p. 316 Global Hunger Index © MWiemers / CC-BY-SA-4.0
Eerste druk 2024
ISBN 978-94-647-0612-3
D/2024/0078/100 Omslagontwerp: Fikfak Art. 606358/01 Tekeningen: Dirk Vandamme NUR 120 Lay-out: Crius Publishing
Inhoudsopgave
Hoe werk je met Pienter? 4
Hoofdstuk 1 Waarheidstabellen 7
Hoofdstuk 2 Tweedegraadsvergelijkingen 57
Hoofdstuk 3 Functies f (x) = c x 109
Hoofdstuk 4 Deelbaarheid bij veeltermen
©VANIN
Hoofdstuk 5 Goniometrie
Hoofdstuk 6 Beschrijvende statistiek 245
GEOGEBRA
3.3 De functie f (x) = c x
Na 1 uur is de hoogte
Na 3 uur is de hoogte
3.3.1 Het omgekeerd evenredig verband
Hoe werk je met Pienter?
Na 7 uur is de hoogte
Voorbeeld
De hoogte y (in cm) kun je uitdrukken in functie van de tijd x (in h):
Elk hoofdstuk start met een inhoudsopgave en een cartoon. Dat geeft je een eerste indruk van het hoofdstuk.
y = Vul de tabel in. Teken de punten in het assenstelsel en verbind ze.
Een fietser rijdt met een constante snelheid van Antwerpen naar Blankenberge en moet daarvoor 120 km afleggen. De afstand s (in km) die de fietser aflegt in functie van de tijd t (in h), kun je uitdrukken met de formule s = v t, waarbij v de gemiddelde snelheid voorstelt (in km/h). t (h)12345612
v (km/h)
Bij het begin van elk hoofdstuk maak je aan de hand van een realistische inleiding of een kort onderzoek kennis met het onderwerp dat aan bod zal komen.
s = v t (km)
Het product v t is constant. De grootheden v en t zijn omgekeerd evenredig
Er geldt: v =
Definitie Omgekeerd evenredig verband
3.1 Basisbegrippen over functies
Twee grootheden y en x zijn omgekeerd evenredig als het product x y constant is.
3.1.1 Inleiding
Formule
GEOGEBRA
x y = c ⇒ y = c x (met c ∈ r0 ). Je noemt c de evenredigheidsconstante
Een brandende kaars is 20 cm lang.
De hoogte y van de kaars vermindert met 2 cm per uur.
Als twee grootheden y en x omgekeerd evenredig zijn, dan is y = c x (met c ∈ r0).
Na 1 uur is de hoogte
Na 3 uur is de hoogte
Grafiek van een omgekeerd evenredig verband
Na 7 uur is de hoogte
v (km/h)
GEOGEBRA
De hoogte y (in cm) kun je uitdrukken in functie van de tijd x (in h):
y = Vul de tabel in. Teken de
Definitie Functie

Is het verband tussen y en x een functie? Verklaar je antwoord.
Teken de grafiek van het verband dat de snelheid v (in km/h) weergeeft in functie van de tijd t (in h). De grafiek is

in het assenstelsel en verbind ze.
Een functie is een verband waarbij elk argument hoogstens één beeld heeft.
PIENTER XL 4 - 5u I HOOFDSTUK
Besluit
1 O 23456789 101112 20 40 60 80 100 120 t (h)
De grafische voorstelling van een omgekeerd evenredig verband y = c x (met c ∈ r0) is een (deel van een) hyperbool.
4 - 5u HOOFDSTUK 3
Na elk stuk theorie kun je meteen oefenen. Niet alle oefeningen zijn even moeilijk. Ze zijn opgedeeld in drie reeksen:
Is het verband tussen y en x een functie? Verklaar je antwoord.
REEKS A eenvoudige toepassingen
Oefeningen
REEKS A

Stap voor stap kom je meer te weten over wiskunde in het dagelijks leven.
Je leert formuleren in definities, eigenschappen, rekenregels of besluiten.
Je leert ook eigenschappen bewijzen.
10 Vervolledig de grafieken van de functie f (x) = c x a)
REEKS B basisniveau
Definitie Functie
Een functie is een verband waarbij elk argument hoogstens één beeld heeft.
REEKS C verdiepingsniveau
Oefeningen zijn genummerd per hoofdstuk en aangeduid met een verticale streep.
Op diddit vind je extra oefeningen.
11 Met welke factor moet je de grafiek van de functie f samendrukken of uitrekken om de grafiek van de functie g te verkrijgen? Maak een schets van de grafiek van g (x).
In de marge worden soms pictogrammen gebruikt. Hieronder vind je hun betekenis.
ICT Duidt aan wanneer je een ICT-bestand op diddit terugvindt, bv. Excel of GeoGebra.
Interessante weetjes of achtergrondinformatie herken je aan een kader met vraagteken.
R Duidt aan dat je bij het onlinelesmateriaal een remediëringsoefening kunt vinden.
XL Geeft aan dat je bij het onlinelesmateriaal extra uitdagende leerstof vindt.
Je leraar zal telkens aangeven wat precies voor jou van toepassing is.
Soms is het handig dat je extra lesinformatie via GeoGebra of een videofragment zoals een instructiefilmpje zelf kunt bekijken of beluisteren op je smartphone. Als je dit icoon ziet, open dan de VAN IN Plus-app en scan de pagina. Op het einde van elk hoofdstuk vind je alles wat je moet kennen en kunnen bijeengebracht in een studiewijzer. Dat is een ideale leidraad om je samenvatting te maken.
©VANIN
STUDIEWIJZER
3.1 Basisbegrippen over functies
• Het domein van een functie is de verzameling van alle reële getallen waarvoor je een functiewaarde kunt bepalen.
Notatie: dom f
• Het praktisch domein van een functie is het deel van het domein dat de fysisch aanvaardbare argumenten bevat.
Notatie: pdom f
• Het bereik van een functie is de verzameling van alle functiewaarden.
Notatie: ber f
• Het praktisch bereik van een functie is het deel van het bereik dat de fysisch aanvaardbare beelden bevat.
Notatie: pber f Een nulwaarde van een functie f is een getal a waarvoor f (a) = 0.
KUNNEN
Het tekenschema en het verloop van een functie opstellen aan de hand van de grafiek.
Elk hoofdstuk sluit af met de rubriek ‘Pienter problemen oplossen’ of ‘Problemen uit JWO’ (Junior Wiskunde Olympiade). Het is aan jou om aan de hand van heuristieken en probleemoplossend denken de problemen op te lossen.
3.2 De functie f (x) = 1 x KENNEN
Sommige onderdelen zijn aangeduid met een groene band. Je leerkracht zal aangeven wat je wel en niet moet kennen.
f (x) = 1 x
• De y-as (x = 0) is de verticale asymptoot (VA) van de grafiek van f
• De x-as (y = 0) is de horizontale asymptoot (HA) van de grafiek van f
KUNNEN
De grafiek van de functie f (x) = 1 x herkennen.
Achteraan in het boek zitten twee bladen met een cartoon. Die kun je gebruiken als voorblad voor je eigen notities of voor afgedrukte oefeningen van Pienter remediëren en voor extra leerstof.
De grafiek van de functie f (x) = 1 x schetsen, uitgaande van een tabel met coördinaten van een aantal punten.
Met behulp van de grafiek van f (x) = 1 x onderzoek doen naar:
• het domein en het bereik;
• de eventuele nulwaarden;
• het tekenschema;
• het verloop;
• de verticale en horizontale asymptoot;
• symmetrie.


PIENTER EN DIDDIT
Het onlineleerplatform bij Pienter
Materiaal
Hier vind je het lesmateriaal en de online-oefeningen. Gebruik de filters bovenaan, de indeling aan de linkerkant of de zoekfunctie om snel je materiaal te vinden.
Lesmateriaal
Hier vind je het extra lesmateriaal bij Pienter, zoals remediëringsoefeningen en Excel-bestanden.
Oefeningen
• De leerstof kun je inoefenen op jouw niveau.
• Je kunt hier vrij oefenen.
Opdrachten
Hier vind je de opdrachten terug die de leerkracht voor jou heeft klaargezet.
Evalueren
Hier kan de leerkracht toetsen voor jou klaarzetten.
Resultaten
Wil je weten hoever je al staat met oefenen, opdrachten en evaluaties? Hier vind je een helder overzicht van je resultaten.
E-book
Het e-book is de digitale versie van het leerwerkschrift. Je kunt erin noteren, aantekeningen maken, zelf materiaal toevoegen ...


Meer info over diddit vind je op www.vanin.diddit.be/nl/leerling.
HOOFDSTUK 1 I WAARHEIDSTABELLEN

1.1 Inleiding
Stel dat je met twee vrienden een terrasje doet. Je vrienden bestellen een cola en jijzelf een fruitsapje. Als de ober bij het serveren zichzelf moeite wil besparen, vraagt hij eerst voor wie het fruitsap is. Op die manier kan hij besluiten voor wie de cola’s zijn. Logisch, toch?
Redeneren is een vorm van denken waarbij je besluiten trekt uit allerhande uitspraken. Als je, in de wiskunde of elders, een besluit (conclusie) afleidt uit een aantal gegevens (premissen), dan vormen de opeenvolgende stappen die van de gegevens tot het besluit leiden, een redeneerproces
©VANIN
Logica is het onderdeel binnen de wiskunde dat zich bezighoudt met de leer van het redeneren. Het woord ‘logica’ stamt af van het Griekse woord logos, dat ‘rede’ betekent.
Aristoteles (384 – 322 v. Chr.) was een Griekse filosoof en wetenschapper die, samen met Socrates en Plato, wordt beschouwd als een van de invloedrijkste filosofen in de westerse traditie. Hij wist de leer van de logica te systematiseren.
In zijn werk Organon, een verzameling van logische geschriften, maakte hij een onderscheid tussen de leer van de bewering, de definitie, de gevolgtrekking en het wetenschappelijk bewijs.
Centraal in zijn theorie staan de zogenaamde syllogismen, logische redeneringen waaruit je een conclusie afleidt.
Een van zijn bekendste syllogismen is het volgende: Alle mensen zijn sterfelijk. (eerste premisse) Socrates is een mens. (tweede premisse) Socrates is sterfelijk. (conclusie)

De leer van Aristoteles domineerde tweeduizend jaar lang de wetenschappelijke manier van redeneren in de westerse wereld. Zijn teksten werden, zelfs nog tot honderden jaren na zijn dood, door andere filosofen weerlegd, aangevuld, bewerkt en bediscussieerd.
Voorbeelden
Is de redenering waar of onwaar? Als ze onwaar is, geef dan een korte verklaring.
a) De afstandsbediening of de televisie werkt niet.
De televisie werkt wel, dus is het de afstandsbediening die niet werkt.
b) Het schilderij hangt niet in het museum als het gestolen is. Het schilderij hangt niet in het museum. Dus het is gestolen.
c) Ik kan in mijn jas en mijn jas kan in mijn boekentas. Ik kan dus in mijn boekentas.
waar onwaar
1.2 Proposities en connectieven
1.2.1 Proposities
Propositielogica is een tak binnen de wiskunde die zich bezighoudt met het redeneren met uitspraken die ofwel waar, ofwel onwaar zijn. Zulke uitspraken noem je proposities.
Voorbeelden van proposities
• Een gelijkbenige driehoek heeft minstens twee even grote hoeken. (waar)
• De aarde is een planeet. (waar)
• 12 – 8 = 5 (onwaar)
• De maand februari telt 30 dagen. (onwaar)
Definitie
Propositie
Een propositie is een uitspraak die ofwel waar, ofwel onwaar is.
De volgende zinnen zijn geen proposities.
• Is er leven op Saturnus? Een vraagstelling is nooit een propositie, omdat je niet kunt bepalen of ze waar of onwaar is.
• Doe de deur dicht! Een bevel of zin in de gebiedende wijs is nooit een propositie, omdat je niet kunt bepalen of hij waar of onwaar is.
• Je hebt een mooie trui aan. Een subjectieve uitspraak of mening heeft betrekking op de persoonlijke smaak en voorkeur. Subjectieve uitspraken zijn geen proposities.
• n is een priemgetal. De uitspraak ‘n is een priemgetal’ is soms waar (n = 5) en soms onwaar (n = 8). De uitspraak is geen propositie, omdat je de waarde van n niet kent.
Voorbeelden
Is de uitspraak een propositie?
Indien ja, is de propositie waar (w) of onwaar (o)?
Indien nee, geef een verklaring.
propositie geen propositie verklaring w o
a) 1 + 1 = 2
b) Het is warm vandaag.
c) De hoofdstad van Frankrijk is Parijs.
d) 3 is kleiner dan 2.
e) Is 0 het kleinste natuurlijk getal?
f) 19 is een priemgetal.
g) Anderlecht is beter dan Club Brugge.
h) Ga naar je kamer!
Het is in de omgangstaal niet altijd eenvoudig om de juiste woorden te vinden om een welbepaalde redenering weer te geven. Bovendien heeft iedereen een eigen taalgevoel.
Zo kan de ontvanger een boodschap soms anders interpreteren dan de zender bedoelde.
Stel, je belooft aan een kind het volgende:
Als je braaf bent, dan krijg je een zuurtje of een stuk chocoladecake.
Wat kan het kind precies verwachten?
Kan het, als het braaf is, een zuurtje én een stuk chocoladecake krijgen?
Mag het, als het braaf is, zelf kiezen tussen een zuurtje of een stuk chocoladecake?
Krijgt het ook iets als het niet braaf is, of is dat uitgesloten?
Wat als het een heel klein beetje niet braaf is? Hoe braaf moet het eigenlijk zijn om iets te krijgen?
©VANIN
Om dergelijke onduidelijkheden te vermijden, stel je proposities voor in symbolentaal.
Een propositie stel je voor door een kleine letter: p, q, r
Als een propositie waar is, geef je dat weer met het getal 1.
Als een propositie onwaar is, geef je dat weer met het getal 0.
Je noemt de waarde 1 of 0 de waarheidswaarde van een propositie.
Samengestelde proposities verbinden enkelvoudige proposities met een connectief
benaming connectief je leest: de negatie ¬ niet de conjunctie
en de disjunctie
of de implicatie
als … dan de equivalentie ⇔ als en slechts als
Voorbeelden
p: Je bent braaf.
q: Je krijgt een zuurtje.
r: Je krijgt een stuk chocoladecake.
Formuleer in woorden.
¬p q ˄ r q ˅ r
p ⇒ q
p ⇔ q
Voor samengestelde proposities hangt de waarheidswaarde af van de waarheidswaarde van de verschillende enkelvoudige proposities (deeluitspraken).
Die waarheidswaarde bepaal je met waarheidstabellen.
Oefeningen
REEKS A
1 Is de uitspraak een propositie?
Indien ja, is de propositie waar (w) of onwaar (o)?
Indien nee, geef een verklaring.
a) 2 is het kleinste priemgetal.
b) Je ziet er goed uit vandaag.
c) Had dan gezwegen!
d) Je wiskundeleerkracht is de beste leerkracht van de school.
e) 3 2 + 4 2 = 5 2
f) Een schildpad is een amfibie.
g) Is Einstein geboren in de 20e eeuw?
h) Ik ben getrouwd met het mooiste meisje van de wereld.
i) De Duitse vlag bestaat uit de kleuren zwart, geel en blauw.
j) Een jachtluipaard is het snelste landdier ter wereld.
k) Een parallellogram heeft juist één paar evenwijdige zijden.
l) Houd je mond!
m) Een oneven macht van een negatief grondtal is altijd negatief.
n) Hoe oud is jouw broer?
o) Ik vind cola het lekkerst.
p) De zon is groter dan de maan.
q) Elke mens is sterfelijk.
r) 9 is een deler van 378.
s) n is een even getal.
t) (–7)–1 = 7
propositie geen propositie verklaring w o
1.2.2 Negatie van een propositie
p: Pieter speelt voetbal.
q: Pieter speelt geen voetbal.
Beide uitspraken kunnen niet tegelijkertijd waar of onwaar zijn. Als de eerste propositie waar is, is de tweede propositie onwaar. Als de eerste propositie onwaar is, is de tweede propositie waar.
Je zegt dat q de negatie is van p
Notatie: ¬p
Je leest: niet p
Het teken ¬ noem je het negatieteken.
©VANIN
Het negatieteken ¬ gaat, anders dan in de gewone omgangstaal, vooraf aan de uitspraak waarop het betrekking heeft. De propositie ‘Pieter speelt geen voetbal’ noteer je dus als volgt: ¬p
De negatie is eigenlijk een speciaal connectief.
Bij een negatie zijn er geen twee deeluitspraken, maar maak je van één propositie een iets complexere propositie. In de meeste naslagwerken over logica wordt de negatie wel als een connectief beschouwd.
De formule ¬p is waar als p onwaar is, en omgekeerd.
Je kunt dat samenvatten in een waarheidstabel:
Definitie Negatie
De negatie van een propositie p is een uitspraak die enkel waar is als en slechts als p onwaar is.
Voorbeelden
Formuleer de volgende proposities in woorden.
p: 9 is een oneven getal. ¬p:
q: De deur staat open. ¬q:
r: Ik neem een paraplu mee naar buiten. ¬r:
s: De hoofdstad van Spanje is Barcelona. ¬s:
1.2.3
Conjunctie van twee proposities
p: Jules eet graag frietjes.
q: Marie eet graag stoofvlees.
Je voegt de twee proposities samen tot een nieuwe, samengestelde propositie:
Jules eet graag frietjes en Marie eet graag stoofvlees. Je noemt die nieuwe uitspraak de conjunctie van p en q
Notatie: p ˄ q
Je leest: p en q
Het teken ˄ noem je het conjunctieteken.
Voor de conjunctie heb je een grotere waarheidstabel nodig. Er zijn namelijk vier mogelijke combinaties voor de waarheidswaarden van twee proposities p en q
De propositie ‘Jules eet graag frietjes en Marie eet graag stoofvlees’ kan enkel waar zijn als beide deeluitspraken p en q waar zijn.
Je kunt dat samenvatten in een waarheidstabel:
Definitie Conjunctie
De conjunctie van twee proposities p en q is een uitspraak die enkel waar is als en slechts als p en q waar zijn.
©VANIN
De propositielogica brengt enkele beperkingen met zich mee en kan niet alle nuances uit de omgangstaal weergeven. De zin ‘Jules en Marie gaan op reis’ kun je opsplitsen in ‘Jules gaat op reis’ en ‘Marie gaat op reis’. Daaruit blijkt niet of ze samen op reis gaan.
Zo zit er ook een beperking in de weergave van de chronologie. In de spreektaal geeft ‘en’ vaak een tijdsvolgorde aan. Uit de zin ‘Jules kwam binnen en deed het licht aan’ kun je afleiden dat Jules binnenkwam alvorens hij het licht aandeed. Als er staat ‘Jules deed het licht aan en kwam binnen’, krijgt de zin een andere betekenis.
Dat soort bijzonderheden kun je moeilijk uitdrukken in de propositielogica.

1.2.4 Disjunctie van twee proposities
p: Wassim gaat met de fiets naar school.
q: Nikolay gaat met de bus naar school.
Je voegt de twee proposities samen tot een nieuwe, samengestelde propositie:
Wassim gaat met de fiets naar school of Nikolay gaat met de bus naar school.
Je noemt die nieuwe uitspraak de disjunctie van p en q
Notatie: p ˅ q
Je leest: p of q
Het teken ˅ noem je het disjunctieteken.
Definitie
De propositie ‘Wassim gaat met de fiets naar school of Nikolay gaat met de bus naar school’ kan enkel onwaar zijn als beide deeluitspraken p en q onwaar zijn.
Je kunt dat samenvatten in een waarheidstabel:
Disjunctie
De disjunctie van twee proposities p en q is een uitspraak die enkel onwaar is als en slechts als p en q onwaar zijn.
Een waarheidstabel van een enkelvoudige propositie p bevat twee mogelijke
waarheidswaarden: 1 of 0.
Een waarheidstabel van twee proposities p en q bevat vier mogelijkheden.
Beide proposities kunnen waar of onwaar zijn, p kan waar zijn en q onwaar, of omgekeerd.
Een waarheidstabel met drie proposities p, q en r bevat acht mogelijkheden.
Een waarheidstabel met vier proposities p, q, r en s bevat zestien mogelijkheden.
©VANIN
Algemeen wordt het aantal mogelijkheden in een waarheidstabel met n proposities bepaald door de formule 2 n
Besluit
Inclusieve disjunctie
• Personen die behoren tot de leeftijdscategorie 65+ of die behoren tot een van de risicogroepen, krijgen voorrang bij de inenting tegen COVID-19 en tegen de griep.
Zal een persoon met diabetes uit de leeftijdscategorie 65+ ook voorrang krijgen?
• Personen uit de leeftijdscategorie 60+ of personen met een beperking krijgen korting bij de aankoop van een inkomticket voor de Efteling.
Krijgt een man van 64 jaar met een beperking ook korting?
‘Of’ betekent in deze voorbeelden ofwel het ene, ofwel het andere, ofwel allebei.
Je noemt die ‘of’ de inclusieve of
©VANIN
In de logica gebruik je de inclusieve of ‘Of’ betekent dan ofwel het ene, ofwel het andere, ofwel allebei.
Exclusieve disjunctie
In de omgangstaal heeft het woord ‘of’ vaak een andere betekenis.
Een leerkracht laat zijn leerlingen de keuze:
De toets gaat maandag door of de toets gaat dinsdag door.
Geen enkele leerling verwacht de toets op zowel maandag als dinsdag.
‘Of’ betekent hier ofwel het ene, ofwel het andere, maar niet allebei.
Je noemt die ‘of’ de exclusieve of
Notatie: p ˅ q
Je leest: ofwel p, ofwel q
Een andere notatie voor de exclusieve of is: p ⊕ q.
Je kunt dat samenvatten in een waarheidstabel:
Voorbeelden
Welke ‘of’ wordt gebruikt? Vul in met ‘inclusief’ of ‘exclusief’.
a) 2 is een rationaal getal of een irrationaal getal.
b) Mensen met een hond of een kat moeten hun huisdieren binnenhouden bij oudjaar.
c) Je kunt kiezen tussen de studierichtingen wetenschappen of economie.
d) Wil je melk of suiker bij jouw koffie?
1.2.5 Implicatie van twee proposities
p: Het regent.
q: De straten worden nat.
GEOGEBRA
Je voegt de twee proposities samen tot een nieuwe, samengestelde propositie: als het regent, dan worden de straten nat.
• ‘Het regent’ noem je het antecedens
• ‘De straten worden nat’ noem je het consequens
Je noemt die nieuwe uitspraak een implicatie
Notatie: p ⇒ q
Je leest: als p, dan q Het teken ⇒ noem je het implicatieteken.
De uitspraak is waar als het regent en de straten nat worden. De uitspraak is onwaar als het regent en de straten niet nat worden.
Maar wat als het niet regent? De straten kunnen dan nog altijd nat worden, omdat het bijvoorbeeld sneeuwt of hagelt. Ook in dat geval is de uitspraak dus waar.
Je kunt dat samenvatten in een waarheidstabel:
Definitie Implicatie
De implicatie van twee proposities p en q is een uitspraak die enkel onwaar is als en slechts als p waar en q onwaar is.
Opmerking
Bij een implicatie mag je de twee proposities niet zomaar van plaats wisselen.
©VANIN
De uitspraak ‘als je jarig bent, dan krijg je een ruiker bloemen’ heeft een andere betekenis dan ‘als je een ruiker bloemen krijgt, dan ben je jarig’.
Voorbeeld
p: Julia snijdt uien. q: Julia moet huilen.
a) Formuleer de propositie in woorden.
p ⇒ q:
b) Wanneer is die uitspraak waar? Leg uit.
1.2.6 Equivalentie van twee proposities
p: Een driehoek is gelijkzijdig.
q: Een driehoek heeft drie even grote hoeken.
Je voegt de twee proposities samen tot een nieuwe, samengestelde propositie: een driehoek is gelijkzijdig als en slechts als de driehoek drie even grote hoeken heeft. Je noemt die nieuwe uitspraak een equivalentie
Notatie: p ⇔ q
Je leest: p als en slechts als q Het teken ⇔ noem je het equivalentieteken.
De uitspraak is waar als de driehoek gelijkzijdig is en drie even grote hoeken heeft. De uitspraak is ook waar als de driehoek niet gelijkzijdig is en geen drie even grote hoeken heeft (denk aan een willekeurige driehoek met hoeken van 50º, 60º en 70º).
Je kunt dat samenvatten in een waarheidstabel:
Definitie
Equivalentie
De equivalentie van twee proposities p en q is een uitspraak die enkel waar is als en slechts als p en q waar zijn, of beide onwaar zijn.
Een equivalentie wordt ook weleens een bi-implicatie genoemd, omdat de implicatie in beide richtingen geldt.
De uitspraak ‘als er vrede is, dan is er geen oorlog’ (⇒) geldt ook in de andere richting: ‘als er geen oorlog is, dan is er vrede’ (⇐).
Je kunt dus stellen dat p ⇔ q
1.2.7 Overzicht
Vul de waarheidstabel bij de verschillende connectieven aan.
1.2.8 Volgorde van de connectieven
Net als bij de volgorde van de bewerkingen, interpreteer je eerst de connectieven binnen de haakjes. Daarna geldt een afnemende prioriteit van de connectieven: ¬, ˄, ˅, ⇒, ⇔
Dat wil zeggen dat je ¬ altijd eerst interpreteert, daarna ˄ enzovoort.
Algemeen Bij een combinatie van connectieven gelden de volgende voorrangsregels (van links naar rechts): ( ) , ¬ , ˄ , ˅ , ⇒⁄⇐ , ⇔
Voorbeeld
Als Veerle een blauwe broek draagt, dan draagt Nathalie geen rood T-shirt, en Sigrid draagt gele sokken als en slechts als Nathalie een rood T-shirt draagt.
a) Noteer de uitspraak in symbolen.
enkelvoudige proposities samengestelde propositie
p: q: In symbolen: r: Je interpreteert de twee deeluitspraken binnen de haakjes elk afzonderlijk.
In de deeluitspraak (p ⇒ ¬q) interpreteer je eerst ¬q, omdat ¬ voorrang heeft op ⇒.
b) Vul de waarheidstabel aan.
c) Wanneer is de uitspraak waar?
Oefeningen
REEKS A
2 Formuleer de samengestelde proposities in woorden.
p: Het regent.
q: De zon schijnt.
a) p ˄ q
b) q ˅ r
c) p ⇒ r
d) ¬p ⇒ q
REEKS B
r: Ik neem een paraplu mee naar buiten.
3 Formuleer de samengestelde proposities in woorden.
p: Dieter is ziek.
r: Dieter gaat naar school.
q: Dieter maakt zijn huiswerk. s: Mama gaat werken.
a) ¬p ⇒ r
b) r ⇔ s
c) ¬q ⇒ ¬r
d) ¬p ˄ q ⇒ r
e) ¬s ˄ ¬q ⇒ p
4 Formuleer de samengestelde proposities in woorden.
p: Kevin geeft een pass aan Romelu. s: Dries trapt een hoekschop.
q: Romelu maakt een doelpunt. t: De scheidsrechter fluit af.
r: Thibaut trapt de bal uit.
a) s ˄ p ⇒ q
b) r ⇒ t
c) ¬p ⇒ ¬q
d) ¬t ˄ r ⇒ q
e) s ˅ r ⇒ ¬t
5 Formuleer de enkelvoudige proposities in woorden. Noteer vervolgens de samengestelde propositie in symbolen.
a) Katleen of Mario komt naar het feest.
p:
q:
b) Jaouad speelt piano, maar Bart niet.
p:
q:
In symbolen:
In symbolen:
c) De zon schijnt en er is veel wind, maar het regent niet.
p:
q: r:
In symbolen:
d) Amina speelt graag badminton, maar traint niet graag.
p:
q:
e) Gianni kent Engels noch Duits.
p:
q:
In symbolen:
In symbolen:
f) Als An niet slaagt voor haar rijexamen, komt ze niet met de auto naar school.
p:
q:
In symbolen:
g) Als Iwan blij is, is Sofia dat niet en als Iwan niet blij is, is Sofia dat wel.
p:
q:
In symbolen:
6 Noteer de samengestelde proposities in symbolen.
p: Je slaagt voor het proefwerk wiskunde.
q: Je maakt elke oefening in de cursus.
r: Je maakt elke extra oefening in de elektronische leeromgeving. in symbolen
a) Je maakt elke extra oefening in de elektronische leeromgeving, maar je maakt niet elke oefening in de cursus.
b) Je behaalt een onvoldoende op het proefwerk wiskunde als je niet elke oefening in de cursus maakt.
c) Elke oefening in de cursus of elke extra oefening in de elektronische leeromgeving maken, volstaat om te slagen voor het proefwerk wiskunde.
d) Het is niet waar dat je een onvoldoende behaalt voor het proefwerk wiskunde als je niet elke oefening in de elektronische leeromgeving maakt.
7 Noteer de samengestelde proposities in symbolen.
p: Jef speelt piano.
q: Myra speelt harp.
r: Hanneke speelt dwarsfluit.
s: Layla speelt klarinet. in symbolen
a) Als Jef geen piano speelt en Myra geen harp speelt, dan speelt Hanneke dwarsfluit.
b) Als Layla klarinet speelt of als Hanneke dwarsfluit speelt, dan speelt Myra geen harp.
c) Hanneke speelt geen dwarsfluit als en slechts als Layla geen klarinet speelt.
d) Layla speelt klarinet als Myra geen harp speelt.
e) Jef speelt geen piano en Myra speelt geen harp als Hanneke geen dwarsfluit speelt.

8 Zijn de uitspraken waar of onwaar? Verklaar met een waarheidstabel.
a) Als de maan van kaas is, dan dansen er muizen op de maan.
p:
q: p q
b) 5 is een priemgetal of 5 is een even getal.
p:
q: p q
c) Het is niet waar dat (–2)2 = 4.
p:
q: p
d) Als 3² = 9, dan 6 – 2 = 3.
p:
q: p q
In symbolen:
De uitspraak is
In symbolen:
De uitspraak is
In symbolen:
De uitspraak is
In symbolen:
De uitspraak is
e) Als het niet waar is dat de zon groter is dan de aarde, dan is elke smurf geel.
p:
q: p q
f) 2 = 5 als en slechts als 1 = –13.
p:
q: p q
In symbolen:
De uitspraak is
In symbolen:
De uitspraak is
9 Zijn de uitspraken waar of onwaar? Verklaar met een waarheidstabel.
p: 7 > 18 r: 11 0 = 1
q: 18 is een even getal.
a) p ⇒ q
De uitspraak is
b) ¬r ˄ q
De uitspraak is
c) s ⇔ p
De uitspraak is
d) (p ⇒ s) ˅ (s ⇒ p)
De uitspraak is
e) (p ⇔ q) ˄ ¬r
De uitspraak is
f) (p ˄ ¬q) ˅ r
s: 3 ∈ q
De uitspraak is
10 Stel de waarheidstabel van de samengestelde proposities op.
a) ¬p ˄ q
d) p ⇒ ¬q
b) p ˅ ¬q
©VANIN
c) ¬(p ˅ q)
e) ¬(p ⇒ q)
f) ¬p ⇔ q
11 Stel de waarheidstabel van de samengestelde proposities op.
a) ¬(p ˄ ¬q)
b) (p ⇒ q) ˅ ¬q
12 De ouders van Yassine doen vlak voor de proefwerken de volgende ware uitspraak: ‘Als je slaagt voor wiskunde, dan krijg je een nieuwe smartphone.’
Yassine krijgt na de proefwerken een nieuwe smartphone. Kun je daaruit besluiten dat hij geslaagd was voor wiskunde?
p:
q:
In symbolen:

13 In een rechtszaak doet een rechter de volgende uitspraak:
‘De eerste getuige spreekt de waarheid of de tweede getuige spreekt de waarheid niet.’
Een advocaat is het niet eens met de rechter. Wat moet hij dan aantonen?
p:
q:

In symbolen:
14
Een leerkracht wiskunde zegt tegen zijn leerlingen: ‘Het is niet waar dat iemand in de klas een onvoldoende heeft, of het is wél waar dat er gespiekt werd tijdens de toets.’ Achteraf zegt de leerkracht dat hij een leugen vertelde. Wat kunnen de leerlingen daaruit besluiten?
p:
q:
In symbolen:
©VANIN

REEKS C
15 Als het in Knokke minstens 27 ºC én zonnig is, dan zit het strand overvol.
Op 21 juli 2014 zat het strand niet overvol. Wat kun je dan besluiten over het weer op die dag?
A) Als het minstens 27 ºC was, dan was het zonnig.
B) Als het minder dan 27 ºC was, dan was het zonnig.
C) Als het minder dan 27 ºC was, dan was het niet zonnig.
D) Het was minder dan 27 ºC en het was niet zonnig.
E) Het was minder dan 27 ºC of het was niet zonnig.
JWO, editie 2015, tweede ronde
16 Als het niet waar is dat Cercle Brugge de beker of de competitie wint, dan wint Cercle Brugge de Europa League.
a) Vul aan.
p: q:
r: In symbolen:
b) Vul de waarheidstabel aan.
c) Wanneer is die uitspraak waar?
17 Als Elise en Noa de waarheid niet spreken, dan is het niet waar dat Louiz liegt.
a) Vul aan.
p: q: In symbolen:
r:
b) Vul de waarheidstabel aan.
c) Wanneer is die uitspraak waar?

18 Als het niet waar is dat Eliane een hond of Wesley een cavia heeft, dan heeft Hendrik geen kat.
a) Vul aan.
p: q: In symbolen:
r:
b) Vul de waarheidstabel aan.
©VANIN
c) Wanneer is die uitspraak waar?
19 Het is niet waar dat het niet waar is dat het vierkant rood of de driehoek groen is, als en slechts als het niet waar is dat de cirkel blauw of het vierkant rood is.
a) Vul aan.
p:
q: In symbolen:
r:
b) Vul de waarheidstabel aan.
c) Wanneer is die uitspraak waar?
1.3 Logische raadsels
Drie vrienden zouden graag naar Schoolrock Festival gaan, maar twijfelen een beetje. ‘Flor gaat zeker naar Schoolrock als Anaïs gaat, en Seppe gaat alleen als en slechts als Flor niet gaat.’ Wie gaat er naar Schoolrock?
Mogelijkheid 1: • Nummer de verschillende uitspraken.
• Zet alle mogelijkheden in een tabel.
• Schrap de mogelijkheden die strijdig zijn met het gegeven.
Flor gaat zeker naar Schoolrock als Anaïs gaat. (1) Seppe gaat alleen als en slechts als Flor niet gaat. (2)
Flor Anaïs Seppe
gaat gaat gaat
gaat gaat gaat niet
gaat gaat niet gaat
gaat gaat niet gaat niet
gaat niet gaat gaat
gaat niet gaat gaat niet
gaat niet gaat niet gaat
gaat niet gaat niet gaat niet
Mogelijkheid 2: • Zet de uitspraak om naar een propositie in symbolen.
p: Flor gaat.
q: Anaïs gaat.
r: Seppe gaat.
• Stel een waarheidstabel op.
In symbolen: (q ⇒ p) ˄ (r ⇔ ¬p)
Oefeningen
REEKS B
20 Als Stijn vanavond televisie mag kijken, dan mag Thibe geen televisie kijken. Oscar mag enkel televisie kijken als en slechts als Thibe geen televisie mag kijken. Wie mag er vanavond televisie kijken? Los op met een waarheidstabel.
©VANIN
21 Van drie beweringen A, B en C weet je het volgende:
• Als A waar is, dan zijn B en C waar.
• Als B waar is, dan is er van A en C ten minste één waar.
• Als C waar is, dan is A waar en B onwaar.
Welke van de beweringen A, B en C zijn waar?
Lijst de verschillende mogelijkheden op in een tabel.
22 Sommige aliens hebben groene tenen. De andere hebben paarse tenen.
Aliens met groene tenen komen alleen op Mars voor.
Welke van de volgende groepen bestaat zeker uit leugenaars?
A) De aliens met paarse tenen die zeggen dat ze van Mars komen.
B) De aliens met groene tenen die zeggen dat ze van Mars komen.
C) De aliens met paarse tenen die zeggen dat ze van Venus komen.
D) De aliens van Mars die zeggen dat ze paarse tenen hebben.
E) De aliens van Venus die zeggen dat ze groene tenen hebben.
JWO, editie 2020, tweede ronde
©VANIN
23 Vijf vrienden spelen een spel. Een van hen is de mol en liegt altijd.
De anderen spreken altijd de waarheid.
• Wout zegt: ‘Maarten of Jens is de mol.’
• Lisa antwoordt: ‘De mol is een man.’
• Jens zegt: ‘Lisa is de mol niet en ik ook niet.’
• Maarten stelt: ‘De mol is een vrouw.’
• Inneke beweert: ‘Ik ben de mol niet.’
Wie is de mol?
A) Wout B) Lisa C) Jens D) Maarten E) Inneke
JWO, editie 2020, tweede ronde
24 Een van drie broers Kwik, Kwek en Kwak heeft geld gestolen uit de spaarpot van zijn ouders. Nadat de ouders hun zonen confronteren met de feiten, besluiten ze dat Kwik en Kwek de hoofdverdachten zijn. De drie broers doen de volgende uitspraken:
• Kwik: ‘Kwek is schuldig en Kwak is onschuldig.’
• Kwek: ‘Als Kwik schuldig is, dan is Kwak ook schuldig.’
• Kwak: ‘Ik ben onschuldig, maar minstens een van de anderen is schuldig.’ Stel dat de onschuldige broers de waarheid spraken en de schuldige loog, wie heeft er dan geld gestolen uit de spaarpot van zijn ouders?
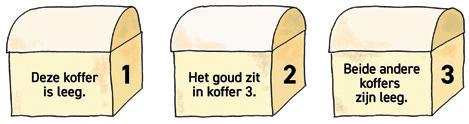
25 Een ridder moet kiezen tussen drie koffers. Hij weet dat er goud in juist één koffer zit en dat op maar één koffer een ware uitspraak staat. In welke koffer zit het goud?
26 In een bos wonen drie kabouters: Smul, Smal en Boemel. Kabouter Smul staat erom bekend om altijd de waarheid te spreken, en kabouter Smal om altijd te liegen.
Kabouter Boemel is een twijfelaar: hij liegt soms en spreekt soms de waarheid.
Tijdens een mooie wandeltocht door het bos kom je hen tegen en stel je de volgende vraag: ‘Wie van jullie is de oprechte kabouter, wie de leugenaar en wie de twijfelaar?’
De linkse kabouter wijst naar de middelste en zegt: ‘Hij is de oprechte.’
De rechtse kabouter wijst naar de linkse kabouter en zegt: ‘Hij is de oprechte.’
De middelste zwijgt. Wie is wie?
©VANIN
27 Voor je liggen vier kaarten: een 5, een 8, een blauwe kaart en een groene kaart. Boven de kaarten staat: ‘Als een kaart een even getal heeft op één kant, dan is de andere kant van die kaart blauw.’
Welke kaart(en) moet je omdraaien om na te gaan of die uitspraak correct is?
Bron: www.nieuwsblad.be
1.4 Tautologieën en contradicties
1.4.1 Begripsvorming
Logische equivalentie
GEOGEBRA
Twee (enkelvoudige of samengestelde) proposities p en q zijn gelijkwaardig als en slechts als ze voor alle gevallen dezelfde waarheidswaarde hebben.
Je noemt de proposities logisch equivalent
Als je een equivalentieteken tussen twee gelijkwaardige proposities plaatst, verkrijg je altijd een ware uitspraak.
Notatie: p ⇔ q
Je leest: p is gelijkwaardig met q
Tautologie
Als een getal oneven en een priemgetal is, dan is het getal oneven.
p: Een getal is oneven.
In symbolen: q: Een getal is een priemgetal.
Vul de waarheidstabel aan.
De samengestelde propositie is voor alle waarden van de enkelvoudige proposities
Je noemt die propositie een tautologie
Definitie Tautologie
Een tautologie is een samengestelde propositie die altijd waar is.
Contradictie
Een reëel getal is rationaal en irrationaal.
p: Een reëel getal is rationaal.
Vul de waarheidstabel aan.
In symbolen:
De samengestelde propositie is voor alle waarden van de enkelvoudige proposities
Je noemt die propositie een contradictie
Definitie Contradictie
Een contradictie is een samengestelde propositie die altijd onwaar is.
1.4.2 De wet van de uitgesloten derde
‘Elk getal is even of oneven’ is altijd een ware uitspraak. Er is geen derde mogelijkheid. p: Elk getal is even.
te bewijzen p ˅ ¬p is een tautologie.
bewijs
0
Besluit Wet van de uitgesloten derde
1.4.3 De wet van de dubbele negatie
‘De zon schijnt’ is gelijkwaardig met ‘het is niet waar dat de zon niet schijnt’. p: De zon schijnt.
te bewijzen p ⇔ ¬(¬p) bewijs
Besluit Wet van de dubbele negatie
1.4.4 Een implicatie noteren als een disjunctie
‘Als je slaagt voor wiskunde, dan krijg je een nieuwe smartphone’ is gelijkwaardig met ‘je slaagt niet voor wiskunde of je krijgt een nieuwe smartphone’. p: Je slaagt voor wiskunde. q: Je krijgt een nieuwe smartphone. te bewijzen p ⇒
©VANIN
Besluit Een implicatie noteren als een disjunctie
1.4.5 Een equivalentie noteren als een conjunctie
‘Een driehoek is gelijkzijdig als en slechts als de driehoek drie even grote hoeken heeft’ is gelijkwaardig met
‘als een driehoek gelijkzijdig is, dan zijn alle hoeken even groot en als alle hoeken in een driehoek even groot zijn, dan is de driehoek gelijkzijdig’.
p: Een driehoek is gelijkzijdig. q: Een driehoek heeft drie even grote hoeken. te bewijzen
Besluit Een equivalentie noteren als een conjunctie
1.4.6 De wet van de contrapositie
‘Als het regent, dan worden de straten nat’ is gelijkwaardig met ‘als de straten niet nat worden, dan regent het niet’.
p: Het regent. q: De straten worden nat.
bewijzen
Besluit Wet van de contrapositie
Opmerking
Een veelgemaakte fout is om te stellen dat p ⇒ q gelijkwaardig is met ¬p ⇒ ¬q
Voorbeeld
p: n is een viervoud. q: n is een even getal.
a) Formuleer de proposities in woorden.
p ⇒ q: ¬p ⇒ ¬q:
b) Zijn die uitspraken waar of onwaar?
Algemeen
Toon aan dat de propositie p ⇒ q niet dezelfde waarheidswaarden oplevert als ¬p ⇒ ¬q
De twee uitspraken leveren niet dezelfde waarheidswaarden op. Je kunt dus besluiten dat p ⇒ q niet gelijkwaardig is met ¬p ⇒ ¬q.
In de omgangstaal betekent ‘als … dan …’ soms meer dan wat je strikt genomen zegt.
Als je vader zegt ‘Als je slaagt voor al je examens, dan krijg je een Nintendo Switch’, dan bedoelt hij (wellicht) impliciet ook ‘Als je niet slaagt voor al je examens, dan krijg je geen Nintendo Switch’.
Stel p: Je slaagt voor al je examens en q: Je krijgt een Nintendo Switch. Dan zegt je vader p ⇒ q, maar bedoelt hij stilzwijgend eigenlijk ook ¬p ⇒ ¬q en zelfs q ⇒ p
©VANIN
In de wiskunde kun je jezelf dergelijk slordig en dubbelzinnig taalgebruik niet veroorloven en houd je je aan de regels van de logica.
1.4.7 De wetten van De Morgan
Voorbeeld 1
‘Het is niet waar dat Jef piano speelt en dat Marie harp speelt’ is gelijkwaardig met ‘Jef speelt geen piano of Marie speelt geen harp’.
p: Jef speelt piano. q: Marie speelt harp.
bewijs
1 1 1 0
0 1
0 0
Je kunt besluiten dat de negatie van een conjunctie gelijk is aan de disjunctie van de negaties
Voorbeeld 2
‘Het is niet waar dat Jef piano speelt of dat Marie harp speelt’ is gelijkwaardig met ‘Jef speelt geen piano en Marie speelt geen harp’.
p: Jef speelt piano. q: Marie speelt harp. te bewijzen ¬(
bewijs
1 0
0 1
0 0
Je kunt besluiten dat de negatie van een disjunctie gelijk is aan de conjunctie van de negaties
Besluit De wetten van De Morgan
Oefeningen
REEKS A
28 Vul de tabel aan.
implicatie contrapositie
a) Als ik ga werken, dan neem ik altijd de fiets.
b)
©VANIN
Als de zon niet schijnt, dan is het donker.
c) Als ik geslaagd ben voor mijn examen, dan geef ik een feestje.
d) Als ik niet volledig ontspannen ben, dan ben ik niet op vakantie.
e) Als Melissa mij een zoen geeft, dan krijg ik kriebels in mijn buik.
29 Gegeven: ‘Als de lift niet werkt, dan neem ik de trap.’
a) Stel dat die propositie waar is en ik de trap neem. Wil dat dan zeggen dat de lift kapot is?
p:
In symbolen: q: p q
b) Formuleer de contrapositie van die uitspraak in woorden.
30 Gebruik de wetten van De Morgan om de uitspraken om te vormen.
a) Het is niet waar dat Ariane tennis en basketbal speelt.
b) Het is niet waar dat Geert bruine of blauwe schoenen draagt.
c) Ik wil geen bruine suiker of geen siroop op mijn pannenkoek.
d) Maandag staat er geen toets gepland en dinsdag ook niet.
REEKS B
31 Bewijs met een waarheidstabel dat de proposities tautologieën zijn.
a) p ⇒ (p ˅ q)
b) (p ˄ q) ˅ p ⇔ p
(p ˄ ¬p) ⇒ q
e) ¬p ⇒ (p ⇒ q)
©VANIN
p ˄ q ⇔ q ˄ p
f) (p ⇒ q) ˅ (q ⇒ p)
(p ⇔ q) ⇔ (q ⇔ p)
p ˄ (p ⇔ q) ⇒ q
c)
g)
d)
h)
32 Bewijs met een waarheidstabel dat de proposities contradicties zijn.
a) (p ⇒ q) ⇔ (p ˄ ¬q)
b) (p ˄ q) ˄ (¬p ˅ ¬q)
©VANIN
33 Noteer de uitspraak eenvoudiger. Formuleer de wet waarop je steunt.
a) Het is niet waar dat jij geen leugenaar bent.
b) Als de elektriciteitsrekening niet betaald wordt vóór 31 maart, dan kunnen we geen televisie meer kijken.
c) Als ik niet mee kan op schoolreis, dan werden mijn kleren niet op tijd gewassen.
d) Het is niet waar dat het getal 2 niet het kleinste priemgetal is.
e) Als je naar de stad vertrekt met de auto, dan neem ik de bus, en als ik de bus neem, dan vertrek jij met de auto naar de stad.
f) Het is niet waar dat het niet waar is dat, als ik de weddenschap niet win, Club Brugge geen kampioen speelt.
34 Bewijs met een waarheidstabel dat de proposities tautologieën zijn.
a) (p ⇒ r) ˄ (q ⇒ r) ⇔ (p ˅ q ⇒ r)
©VANIN
b) p ˅ (q ˄ r) ⇔ (p ˅ q) ˄ (p ˅ r)
Net zoals je steunt op de eigenschappen van de bewerkingen in de getallenleer (commutatief, associatief …), gebruik je die eigenschappen ook in de propositielogica. Je kunt ze stuk voor stuk bewijzen met behulp van waarheidstabellen.
Enkele voorbeelden:
• De conjunctie is commutatief: p ˄ q ⇔ q ˄ p
• De equivalentie is associatief: [(p ⇔ q) ⇔ r] ⇔ [p ⇔ (q ⇔ r)].
• De disjunctie is distributief ten opzichte van de conjunctie: p ˅ (q ˄ r) ⇔ (p ˅ q) ˄ (p ˅ r).
Het bewijs van die laatste eigenschap vind je in de voorgaande oefening.
1.5 Bewijstechnieken
1.5.1 Nodige en voldoende voorwaarde
Eigenschap
Als een vierhoek een ruit is, dan staan de diagonalen loodrecht op elkaar.
p: Een vierhoek is een ruit.
q: De diagonalen staan loodrecht op elkaar.
In symbolen: p ⇒ q
Het is voldoende dat een vierhoek een ruit is opdat de diagonalen loodrecht op elkaar staan, maar niet nodig, want er bestaan ook andere vierhoeken waarvan de diagonalen loodrecht op elkaar staan (bv. een vlieger).
Het loodrecht op elkaar staan van de diagonalen is nodig opdat de vierhoek een ruit zou kunnen zijn.
Bij een ware implicatie p ⇒ q noem je p de voldoende voorwaarde voor q
Bij een ware implicatie p ⇒ q noem je q de nodige voorwaarde voor p
Besluit Om een eigenschap te bewijzen, bewijs je de implicatie p ⇒ q. Je neemt p als ‘gegeven’ en q als ‘te bewijzen’.
©VANIN
Kenmerk
Een driehoek is gelijkbenig als en slechts als de driehoek minstens twee even grote hoeken heeft. p: Een driehoek is gelijkbenig. In symbolen: p ⇔ q q: Een driehoek heeft minstens twee even grote hoeken.
Minstens twee even grote hoeken in een driehoek is een nodige (p ⇒ q) en een voldoende (p ⇐ q) voorwaarde voor gelijkbenigheid. Een gelijkbenige driehoek heeft altijd minstens twee gelijke hoeken, en omgekeerd zul je geen driehoek vinden met minstens twee gelijke hoeken die niet gelijkbenig is. Een eigenschap waarvan ook de omgekeerde eigenschap geldt, noem je een kenmerk of een (alternatieve) definitie.
Besluit Om een kenmerk te bewijzen, bewijs je de equivalentie p ⇔ q Je bewijs bestaat uit twee stappen: je bewijst p ⇒ q en q ⇒ p
Oefeningen
REEKS B
35 Vul in met ‘voldoende’, ‘nodig(e)’ of ‘nodig(e) en voldoende’.
a) Opdat een driehoek gelijkzijdig is, is het dat hij gelijkbenig is.
b) Opdat een driehoek rechthoekig is, is het dat de stelling van Pythagoras geldt.
c) Opdat een punt op de middelloodlijn van een lijnstuk ligt, is het dat het punt even ver ligt van de grenspunten van dat lijnstuk.
d) Opdat een vierhoek een vierkant is, is het dat de vierhoek een parallellogram is.
e) Opdat twee driehoeken gelijkvormig zijn, is het dat de drie paar overeenkomstige zijden evenredig zijn.
f) Het middendoor snijden van de diagonalen is een voorwaarde opdat een vierhoek een vierkant is.
g) Opdat een lijnstuk een middenparallel is van een driehoek, is het om te stellen dat het lijnstuk evenwijdig is met en half zo lang is als de derde zijde.
h) Opdat een getal deelbaar is door 3, is het dat het getal deelbaar is door 9.
i) Dat een getal deelbaar is door 2 en ook door 3, is een voorwaarde opdat het getal deelbaar is door 6.
j) Opdat a en b snijdende rechten zijn, is het dat a en b loodrecht op elkaar staan.
©VANIN
36 Vul de best passende pijl in. Kies uit: ⇒, ⇐, ⇔.
a) Een getal is deelbaar door 3. Een getal is deelbaar door 6.
b) Twee driehoeken zijn congruent. Twee driehoeken hebben dezelfde oppervlakte.
c) Een driehoek is gelijkzijdig. Een driehoek heeft drie even grote hoeken.
d) x + 2 = 4 x = 4 – 2
e) Een getal is een natuurlijk getal. Een getal is een geheel getal.
f) x ∈ r + x 2 ∈ r +
g) |PQ | = |QR | Q is het midden van [PR].
h) Een vierhoek is een rechthoek. Een vierhoek is een trapezium.
i) a is een irrationaal getal. a is een reëel getal.
j) De rechten a en b zijn evenwijdig. a = b
1.5.2 Rechtstreeks bewijs
Om een implicatie p ⇒ q te bewijzen, gebruik je in veel gevallen een rechtstreeks bewijs. Je vertrekt van het gegeven en steunt op definities, axioma’s en al bewezen eigenschappen om uit te komen bij wat je wilt bewijzen.
Definitie Rechtstreeks bewijs
Een rechtstreeks bewijs is een bewijs waarbij je een uitspraak bewijst door te steunen op definities, axioma’s en al bewezen eigenschappen.
Voorbeeld 1
©VANIN
gegeven
a < b met a, b ∈ r0 + te bewijzen
a 2 < b 2 bewijs
a < b a < b beide leden vermenigvuldigen met a ∈ r0 + beide leden vermenigvuldigen met b ∈ r0 +
a 2 < ab (1) ab < b 2 (2)
volgt uit (1) en (2) a 2 < ab < b 2 a 2 < b 2
besluit
Voorbeeld 2
Bewijs de volgende eigenschap: als drie natuurlijke getallen opeenvolgend zijn, dan is de som van die getallen altijd een drievoud.
gegeven
drie opeenvolgende getallen met n ∈ n te bewijzen bewijs
besluit
1.5.3 Bewijs door tegenvoorbeeld
‘Alle kanaries zijn geel.’
Die uitspraak stelt dat een bepaalde eigenschap (geel)
geldt voor alle kanaries. Als je één kanarie vindt die niet geel is, dan is die bewering ontkracht.
Elke rode kanarie zou dus een tegenvoorbeeld zijn van de bewering ‘alle kanaries zijn geel’.

Met een voorbeeld kun je een bepaalde bewering illustreren. Met een tegenvoorbeeld kun je een bepaalde bewering ontkrachten.
Definitie Tegenvoorbeeld
Een tegenvoorbeeld is een uitzondering op een vooropgestelde regel.
©VANIN
Een tegenvoorbeeld is een specifiek geval van de falsificatie (= het vinden van een tegenbewijs) van de universele kwantor
Notatie: ∀
Je leest: voor alle
Naast de universele kwantor bestaan ook deze kwantoren:
• de existentiële kwantor
Notatie: ∃
Je leest: er bestaat
• de uniciteitskwantor
Notatie: ∃!
Je leest: er bestaat juist één
Voorbeelden
• ∀ x ∈ r : x 2 – 9 = 0 is een onware uitspraak, omdat 2 een reëel getal is waarvoor geldt: 2 2 – 9 ≠ 0.
• ∃ x ∈ r : x 2 – 9 = 0 is een ware uitspraak, omdat 3 een reëel getal is waarvoor geldt: 3 2 – 9 = 0.
• ∀ a ∈ z, ∃! (–a) ∈ z : is een ware uitspraak, omdat elk geheel getal a + (–a) = –a + a = 0 juist één symmetrisch element voor de optelling heeft, namelijk zijn tegengestelde.
Zijn de volgende uitspraken waar of onwaar?
Geef een tegenvoorbeeld als de uitspraak onwaar is.
a) Als de diagonalen van een vierhoek loodrecht op elkaar staan, dan is de vierhoek een vierkant.
b) Elk priemgetal is oneven.
c) Alle vierkantswortels zijn irrationale getallen.
d) Alle getallen die deelbaar zijn door 4, zijn ook deelbaar door 2.
1.5.4 Bewijs uit het ongerijmde
Stel dat je voor een splitsing staat en weet dat een van de twee paden naar je vakantiebestemming leidt.
Je besluit het linkse pad te nemen, dat jammer genoeg na een tijd doodloopt.
Je keert terug en weet nu zeker dat het rechtse pad naar je bestemming leidt.
In het derde jaar bewees je dat 2 een irrationaal getal is.
Daarvoor ging je uit van de veronderstelling dat als 2 een rationaal getal was, je het kon schrijven als een onvereenvoudigbare breuk a b
In het bewijs toonde je echter aan dat a en b even getallen zijn.
Als a en b even getallen zijn, kun je de breuk a b wél vereenvoudigen.
Je verkreeg een contradictie. Je kon daaruit besluiten dat je veronderstelling fout was.
Definitie
Bewijs uit het ongerijmde
Een bewijs uit het ongerijmde is een bewijs waarbij je de negatie van het ‘te bewijzen’ neemt en die toevoegt aan de gegevens.
Je redeneert logisch verder tot je een contradictie verkrijgt.
Voorbeeld
Bewijs uit het ongerijmde dat er geen gehele getallen a en b bestaan waarvoor geldt dat 8a – 6b = 101.
gegeven
a, b ∈ z
te bewijzen
8a – 6b ≠ 101 bewijs
Veronderstel dat er wél gehele getallen a en b bestaan waarvoor geldt dat 8a – 6b = 101.
Stap 1: 101 is een oneven getal.
Uit de gelijkheid 8a – 6b = 101 volgt dat 8a – 6b ook een oneven getal is. (1)
Stap 2: 8a – 6b = 2 (4a – 3b) de distributieve eigenschap
Je kunt concluderen dat 8a – 6b een even getal is. (2)
Uitspraak (2) is in tegenspraak met uitspraak (1). De veronderstelling moet dus fout zijn.
besluit
Er bestaan geen gehele getallen a en b waarvoor geldt dat 8a – 6b = 101.
Verklaring
De tegenspraak is hier van de vorm p ˄ ¬p en bijgevolg een contradictie p: 8a – 6b is een oneven getal. ¬p: 8a – 6b is een even getal.
1.6 Logische poorten
1.6.1 Logische poorten
Logische poorten zijn schakelingen of bouwstenen van elektronica. Ze zijn voornamelijk opgebouwd uit elektronische componenten, zoals transistors, weerstanden en dioden.
Het belangrijkste kenmerk van logische poorten is dat ze meer dan één ingang kunnen bevatten, maar slechts één uitgang.
De verschillende poorten leveren lage of hoge spanningssignalen aan die uitgang. Die spanningssignalen stel je voor met 0 of 1.
Er zijn drie elementaire poorten
©VANIN
Een NIET-poort is een digitale elektronische schakeling met één ingang en één uitgang.
De logische toestand van de uitgang is uitsluitend 1 als en slechts als de ingang 0 is.
Een andere naam voor een NIET-poort is ‘inverter’.
Een OF-poort is een digitale elektronische schakeling met twee (of meerdere) ingangen en één uitgang. De logische toestand van de uitgang is uitsluitend 1 als en slechts als minstens een van de ingangen 1 is.
Een EN-poort is een digitale elektronische schakeling met twee (of meerdere) ingangen en één uitgang. De logische toestand van de uitgang is uitsluitend 1 als en slechts als alle ingangen 1 zijn.
Er bestaan verschillende systemen om poorten weer te geven:
• het ANSI-systeem (American National Standard of Industry), dat het meest gebruikt wordt;
• het IEC-systeem (International Electrotechnical Commission);
• het DIN-systeem (Deutsche Institut für Normung).
Met de drie elementaire poorten kun je nog andere poorten bouwen.
poort ANSI-symbool waarheidstabel verband met propositielogica
1.6.2 Modeloefening 1
Een schakelaar en een drukknop werden verbonden met een lampje.
Wanneer zal het lampje branden?
Het lampje zal branden als
Het lampje zal branden als
negatie van de conjunctie ¬(A ˄ B) = U
1.6.3 Modeloefening 2
Vul de waarheidstabel van de logische schakelingen aan. Beantwoord de bijbehorende vragen.
• Zal het lampje branden als schakelaars A en B uit staan en drukknop C niet is ingedrukt?
• Zal het lampje branden als schakelaars A en B aan staan en drukknop C niet wordt ingedrukt?
• Zal het lampje branden als schakelaar A aan staat, B uit staat en drukknop C niet wordt ingedrukt?
• Zal het lampje branden als schakelaar A aan staat en drukknoppen B en C worden ingedrukt?
• Zal het lampje branden als schakelaar A uit staat en drukknoppen B en C niet worden ingedrukt?
• Zal het lampje branden als schakelaar A uit staat, drukknop B wordt ingedrukt en drukknop C niet wordt ingedrukt?
Oefeningen
REEKS A
37 Onderzoek of het lampje zal branden.
Het lampje zal wel/niet branden.
Het lampje zal wel/niet branden.
Het lampje zal wel/niet branden.
38 Vul de waarheidstabel van de logische schakelingen aan. Beantwoord de bijbehorende vragen.
©VANIN
• Zal het lampje branden als schakelaar A uit staat en drukknoppen B en C worden ingedrukt?
• Zal het lampje branden als schakelaar A aan staat, drukknop B wordt ingedrukt en drukknop C niet wordt ingedrukt?
• Zal het lampje branden als schakelaars A en C uit staan en drukknop B wordt ingedrukt?
• Zal het lampje branden als schakelaars A en C aan staan en drukknop B niet wordt ingedrukt?
39 Vul de waarheidstabel van de logische schakelingen aan.
1.1 Inleiding
1.2 Proposities en connectieven

Een propositie is een uitspraak die ofwel waar, ofwel onwaar is.
De negatie van een propositie p is een uitspraak die enkel waar is als en slechts als p onwaar is.
Notatie: ¬p
Je leest: niet p
©VANIN
De conjunctie van twee proposities p en q is een uitspraak die enkel waar is als en slechts als p en q waar zijn.
Notatie: p ˄ q
Je leest: p en q
De disjunctie van twee proposities p en q is een uitspraak die enkel onwaar is als en slechts als p en q onwaar zijn.
Notatie: p ˅ q
Je leest: p of q
In de logica gebruik je meestal de inclusieve of.
‘Of’ betekent dan ofwel het ene, ofwel het andere, ofwel allebei.
De exclusieve of betekent ofwel het ene, ofwel het andere, maar niet allebei.
Notatie: p ˅ q
Je leest: ofwel p, ofwel q
De implicatie van twee proposities p en q is een uitspraak die enkel onwaar is als en slechts als p waar en q onwaar is.
Notatie: p ⇒ q
Je leest: als p, dan q
De equivalentie van twee proposities p en q is een uitspraak die enkel waar is als en slechts als p en q waar zijn, of beide onwaar zijn.
Notatie: p ⇔ q
Je leest: p als en slechts als q
Bij een combinatie van connectieven gelden de volgende voorrangsregels: ( ), ¬,

Een (enkelvoudige of samengestelde) propositie in symbolen noteren.
Een (enkelvoudige of samengestelde) propositie in woorden formuleren.
De waarheidswaarde van een (enkelvoudige of samengestelde) propositie bepalen met behulp van een waarheidstabel.
Vraagstukken oplossen met behulp van een waarheidstabel.
1.3 Logische raadsels

KUNNEN
Logische raadsels oplossen met behulp van een waarheidstabel.
Logische raadsels oplossen door een oplijsting te maken van de verschillende mogelijkheden.
1.4 Tautologieën en contradicties


KENNEN
Een tautologie is een samengestelde propositie die altijd waar is.
Een contradictie is een samengestelde propositie die altijd onwaar is.
Je kent de volgende logische wetten:
• de wet van de uitgesloten derde: p ˅ ¬p
• de wet van de dubbele negatie: p ⇔ ¬(¬p)
• de wet van de contrapositie: p ⇒ q ⇔ ¬q ⇒ ¬p
• de wetten van De Morgan: ¬(p ˄ q) ⇔ ¬p ˅ ¬q ¬(p ˅ q) ⇔ ¬p ˄ ¬q
©VANIN
KUNNEN
De logische wetten gebruiken om proposities te herformuleren en/of eenvoudiger te schrijven.
Bewijzen met een waarheidstabel dat een welbepaalde samengestelde propositie een tautologie is.
Bewijzen met een waarheidstabel dat een welbepaalde samengestelde propositie een contradictie is.
Een implicatie noteren als een disjunctie en omgekeerd: p ⇒ q ⇔ ¬p ˅ q
Een equivalentie noteren als een conjunctie en omgekeerd: (p ⇔ q) ⇔ (p ⇒ q) ˄ (q ⇒ p)
1.5 Bewijstechnieken

Bij een ware implicatie p ⇒ q noem je p de voldoende voorwaarde voor q; q noem je de nodige voorwaarde voor p
Een rechtstreeks bewijs is een bewijs waarbij je een uitspraak bewijst door te steunen op definities, axioma’s en al bewezen eigenschappen.
Een tegenvoorbeeld is een uitzondering op een vooropgestelde regel.
Als je een uitspraak wilt bewijzen uit het ongerijmde, dan neem je de negatie van het ‘te bewijzen’ en voeg je die toe aan de gegevens. Je redeneert logisch verder tot je een contradictie verkrijgt.
1.6 Logische poorten

Een NIET-poort is een digitale elektronische schakeling met één ingang en één uitgang.
De logische toestand van de uitgang is uitsluitend 1 als en slechts als de ingang 0 is.
Een OF-poort is een digitale elektronische schakeling met twee (of meerdere) ingangen en één uitgang. De logische toestand van de uitgang is uitsluitend 1 als en slechts als minstens een van de ingangen 1 is.
Een EN-poort is een digitale elektronische schakeling met twee (of meerdere) ingangen en één uitgang. De logische toestand van de uitgang is uitsluitend 1 als en slechts als alle ingangen 1 zijn.

De waarheidswaarde bepalen van de uitgang (lamp) door de theorie van de logische poorten toe te passen.
De waarheidstabel van een logische schakeling opstellen.
De waarheidstabel van de verschillende logische poorten opstellen: NIET, OF, EN, XOF, NOF, NEN.
KENNEN
KUNNEN
1. De volgende uitspraak is onwaar: ‘Als de som van de cijfers van een natuurlijk getal n deelbaar is door 6, dan is n deelbaar door 6.’ Welk van de volgende waarden van n toont dat aan?

JWO, editie 2016, eerste ronde
©VANIN
2. Een papierstrook wordt geplooid zodat er een hoek van 40º ontstaat, zoals op de figuur. Hoe groot is a?

JWO, editie 2020, eerste ronde
3. Voor alle positieve getallen x geldt dat 2 + 42x + 4x – 2 gelijk is aan …

JWO, editie 2018, eerste ronde
HOOFDSTUK 2 I TWEEDEGRAADSVERGELIJKINGEN
2.1 Vergelijkingen van de tweede graad in één onbekende 58
2.2 Onvolledige tweedegraadsvergelijkingen oplossen 61
2.3 Tweedegraadsvergelijkingen oplossen: algemeen 71
2.4 Som en product van de wortels van een tweedegraadsvergelijking 84
2.5 Vraagstukken 90
2.6 Vergelijkingen herleidbaar tot tweedegraadsvergelijkingen 102

2.1 Vergelijkingen van de tweede graad in één onbekende
2.1.1 Inleiding

Oplossing
Boer Jelle bakent een rechthoekig stuk weiland af met een lint van 134 meter.
©VANIN
Bereken de afmetingen van dat stuk weiland, als je weet dat de lengte 7 meter groter is dan de breedte.
• Keuze van de onbekende: Stel: de breedte is x.
De lengte is dan
• Opstellen van de vergelijking:
• Antwoord:
• Controle:
Een aantal probleemstellingen kun je oplossen met behulp van een vergelijking van de eerste graad in één onbekende. Die techniek leerde je al in het tweede en derde jaar.
Werkwijze Om een eerstegraadsvergelijking in één onbekende op te lossen, ga je als volgt te werk:
• Werk, indien nodig, eerst de haakjes uit.
• Plaats alle termen met de onbekende in het ene lid en alle andere termen in het andere lid.
• Werk beide leden uit.
• Deel beide leden door de coëfficiënt van de onbekende, als die niet nul is.
Van een rechthoekige driehoek is de ene rechthoekszijde dubbel zo lang als de andere.
Bereken de lengte van de twee rechthoekszijden, als je weet dat de oppervlakte 144 cm2 bedraagt.
De bovenstaande probleemstelling kun je niet oplossen met een vergelijking van de eerste graad in één onbekende. Je stelt een vergelijking van de tweede graad in één onbekende op.
Oplossing
• Keuze van de onbekende: Stel: de kortste rechthoekszijde is x.
De langste rechthoekszijde is dan
• Opstellen van de vergelijking:
• Antwoord:
• Controle:
Aangezien een lengte een positief getal is, is slechts een van de verkregen oplossingen logisch, namelijk
2.1.3 Tweedegraadsvergelijkingen
Definitie Tweedegraadsvergelijking
Een tweedegraadsvergelijking is een vergelijking van de vorm ax 2 + bx + c = 0, met a ∈ r0 en b, c ∈ r.
Andere benamingen zijn vierkantsvergelijking of kwadratische vergelijking.
Waarom mag a niet gelijk zijn aan 0?
De coëfficiënten b en c mogen wel 0 zijn.
In dat geval spreek je van een onvolledige tweedegraadsvergelijking
Voorbeelden
a) Plaats een vinkje bij de tweedegraadsvergelijkingen.
b) Noteer bij elke tweedegraadsvergelijking de coëfficiënten a, b en c
c) Duid met een kruisje aan welke tweedegraadsvergelijkingen volledig of onvolledig zijn.
b c volledig onvolledig
2.2.1 Vergelijkingen van de vorm ax 2 + bx = 0 (met b ≠ 0 en c = 0)
Inleiding
van een product naar een som van een som naar een product 2x ? (x + 1) =
(–x + 3) =
x ? (–10 + x) =
©VANIN
De distributieve eigenschap laat je toe om een gemeenschappelijke factor buiten de haakjes te plaatsen. Die methode kun je gebruiken om onvolledige tweedegraadsvergelijkingen op te lossen.
Voorbeeld 1
Voorbeeld 2 2x 2 – 7x = 0
x ? (2x – 7) = 0 Een product is nul als een van de factoren nul is.
x = 0 of 2x – 7 = 0
x = 0 of 2x = 7
x = 0 of x = 7 2 V = 0, 7 2 {}
Let op! Wat is er verkeerd aan de volgende methode?
2x 2 – 7x = 0
Algemeen Om een onvolledige tweedegraadsvergelijking van de vorm ax 2 + bx = 0 (met b ≠ 0 en c = 0) op te lossen, kun je de gemeenschappelijke factor x afzonderen en elk van de factoren gelijkstellen aan nul.
2.2.2 Vergelijkingen van de vorm ax 2 + c = 0 (met b = 0 en c ≠ 0)
Inleiding
van een product naar een som van een som naar een product
(x + 1) ? (x – 1) = x 2 – 9 =
(x – 6) ? (x + 6) = 16 – x 2 =
(–4 – x) (–x + 4) = –25 + x 2 =
Het merkwaardig product (a + b) ? (a – b) = a 2 – b 2 laat je toe om het verschil van twee kwadraten te schrijven als een product.
Ook die methode kun je gebruiken om onvolledige tweedegraadsvergelijkingen op te lossen.
Voorbeeld 1
9x 2 – 16 = 0
methode 1
(3x + 4) (3x – 4) = 0
methode 2
3x + 4 = 0 of 3x – 4 = 0 3x = – 4 of 3x = 4 x = –4 3 of x = 4 3 V = –4 3 , 4 3 {} 9x 2 = 16 x 2 = 16 9 x = –16 9 of x = 16 9 x = –4 3 of x = 4 3
Voorbeeld 2
3x 2 – 12 = 0
methode 1
methode 2 3 x + 12 () 3 x – 12 () = 0
3 x + 12 = 0 of 3 x – 12 = 0 3 x = –12 of 3 x = 12 x = –12 3 of x = 12 3 x = –2 of x = 2 V = {–2, 2} 3x 2 = 12 x 2 = 4 x = –4 of x = 4 x = –2 of x = 2 V = {–2, 2}
Voorbeeld 3
–2x 2 – 8 = 0
methode 1
–2x 2 – 8 = 0
Het linkerlid is geen verschil van twee kwadraten en dus niet ontbindbaar volgens deze methode.
V = [
methode 2
–2x 2 = 8
x 2 = –4
Deze vergelijking heeft geen reële oplossingen.
V = [
Algemeen Om een onvolledige tweedegraadsvergelijking van de vorm ax 2 + c = 0 (met b = 0 en c ≠ 0) op te lossen, kun je gebruikmaken van de volgende methodes:
• de formule van het verschil van twee kwadraten: a 2 – b 2 = (a + b) ? (a – b);
• de definitie van een vierkantswortel.
2.2.3 Vergelijkingen van de vorm ax 2 = 0 (met b = 0 en c = 0)
Voorbeeld
–2x 2 = 0
x 2 = 0
x = 0 V = {0}
Algemeen Om een onvolledige tweedegraadsvergelijking van de vorm ax 2 = 0 (met b = 0 en c = 0) op te lossen, kun je gebruikmaken van de definitie van een vierkantswortel. Er is telkens maar één oplossing: 0.
Een veelterm schrijven als het product van twee of meerdere factoren, noem je ontbinden in factoren
De veelterm 3x 2 + 5x kun je ontbinden in twee factoren en noteren als 3x 2 + 5x = x ? (3x + 5). Je noemt die veelterm ontbindbaar

REEKS A
1 Los de onvolledige vergelijkingen op door een gemeenschappelijke factor af te zonderen.
a) 15x 2 – 3x = 0
b) 5x 2 – 8x = 0
c) 3x 2 + 4x = 0
e) 4x – 12x 2 = 0
©VANIN
d) –10x 2 + 6x = 0
f) –12x 2 – 15x = 0
g) 81x 2 + 27x = 0
h) –25x 2 – 12x = 0
2 Los de onvolledige tweedegraadsvergelijkingen op. verschil van twee kwadraten
a) 4x 2 – 9 = 0
definitie vierkantswortel
b) x 2 – 16 = 0
©VANIN
c) 36x 2 – 25 = 0
–1 + 49x 2 = 0
e) 4 + 81x 2 = 0
d)
3 Los de onvolledige tweedegraadsvergelijkingen
a) 3x 2 – 9x = 0
g) –16x 2 = 4
©VANIN
b) 5x 2 – 20 = 0 h) 2x 2 = 9x
c) 2x 2 + 16 = 0
i) –16x 2 = –9
d) 12x 2 + 4x = 0
j) –4 – 3x 2 = 0
e) –2x 2 + 5x = 0 k) 3x = –8x 2
f) –25x 2 + 9 = 0
l) –16x 2 = 4x
a) 2x 2 –1 2 = 0
b) 3 4 x 2 + 1 2 x = 0
c) –5 6 x 2 + 2 3 x = 0
d) –1 5 x 2 – 4 = 0
f) 2 7 x 2 = 4x
©VANIN
e) –5 3 x 2 = 0
g) –9 8 + 1 2 x 2 = 0
h) 5 4 x 2 = –1 7 x 2
i) –8 3 x 2 = 3 16
j) –11 5 x 2 = 1 3 x
5 De lengte van een rechthoekig stuk land is driemaal de breedte.
De oppervlakte is 1 875 m2
Bereken de afmetingen van dat stuk land.
©VANIN
6 Een projectiel wordt vanaf de grond verticaal omhooggeschoten.
De hoogte h (in m) die het bereikt na t seconden wordt gegeven door de formule h = 90t − 5t 2 .
Na hoeveel seconden zal het projectiel opnieuw op de grond vallen?

7 Als je de zijde van een vierkant verdubbelt, dan wordt de oppervlakte 243 m2 groter.
Bereken de zijde van het oorspronkelijke vierkant.
8 Los de tweedegraadsvergelijkingen op.
x–3=–5ofx–3=5
x=–2ofx=8 V=–2,8 {}
a) (x – 3) 2 = 25 c) –5 (x – 2) 2 – 20 = 0 b) 4 ? (x + 5) 2 – 25 = 0
9 Los de tweedegraadsvergelijkingen op.
a) (x + 1) 2 – 2 ? (x + 1) = 0
(x+1) ? [(x+1)–2] =0
(x+1) ? (x–1)=0
x+1=0ofx–1=0
x=–1ofx=1
–3 ? (5x – 4) 2 + 12 = 0
V=–1,1 {}
–3 ? (2 – 3x) 2 = 7 ? (2 – 3x) b) 3 ? (2x – 1) = 2 ? (2x – 1) 2
8 ? (6 – 3x) 2 = –5 ? (3x – 6)
De Babyloniërs hebben ongeveer 4 000 jaar geleden een methode ontwikkeld om twee getallen te bepalen waarvan de som en het product gegeven zijn.

Voorbeeld: van twee getallen is de som 10 en het product 21. De getallen werden voorgesteld als 5 – x en 5 + x (twee getallen die even ver van 5 liggen), zodat geldt: (5 – x) (5 + x) = 21.
Na uitwerking verkrijg je: 25 – x 2 = 21 of x 2 = 4.
Vermits de Babyloniërs nog geen negatieve getallen kenden, vonden ze: x = 2.
De twee gevraagde getallen zijn dus 3 en 7.
10 Los op met de methode van de Babyloniërs.
a) Bereken twee getallen waarvan de som 22 en het product 112 is.
b) Bereken twee getallen waarvan de som 100 en het product 2 331 is.
2.3 Tweedegraadsvergelijkingen oplossen:
2.3.1
De methode van de kwadraatafsplitsing
Inleiding
Werk uit.
Schrijf als het kwadraat van een tweeterm.
(x + 4) 2 = x 2 + 6x + 9 = = =
©VANIN
(x – 6) 2 = 16 – 8x + x 2 = = =
(5 + x) 2 = 4x 2 + 4x + 1 = = =
Het merkwaardig product (a + b) 2 = a 2 + 2ab + b 2 laat je toe om sommige drietermen te schrijven als een kwadraat van een tweeterm
Die methode kun je gebruiken om tweedegraadsvergelijkingen op te lossen.
Voorbeeld 1
x 2 – 4x + 4 = 0
x 2 + 2 x (–2) + (–2) 2 = 0
(x – 2) 2 = 0
x – 2 = 0
Je noteert het linkerlid als een kwadraat van een tweeterm.
x = 2 V = {2}
Voorbeeld 2
x 2 + 8x + 7 = 0
x 2 + 8x = –7
x 2 + 2 x 4 + 4 2 = –7 + 4 2
(x + 4) 2 = 9
x + 4 = –3 of x + 4 = 3
Je verandert de constante term van lid.
Je vermeerdert beide leden met 4 2
Je noteert het linkerlid als een kwadraat van een tweeterm.
x = –7 of x = –1 V = {–7, –1}
REEKS B
11 Los de tweedegraadsvergelijkingen op met behulp van kwadraatafsplitsing.
a) x 2 + 10x + 25 = 0
b) x 2 – 6x + 9 = 0
c) 16x 2 + 8x + 1 = 0
e) x 2 + 6x + 8 = 0
©VANIN
d) 9x 2 – 6x + 1 = 0
f) x 2 – 2x – 35 = 0
g) 3x 2 + 24x – 27 = 0
h) 2x 2 – 20x + 68 = 0
2.3.2 De formules opstellen
ax 2 + bx + c = 0
x 2 + b a x + c a = 0
x 2 + b a x = –c a
x 2 + 2 b 2a x = –c a
x 2 + 2 b 2a x + b 2a 2 = –c a + b 2a 2
x + b 2a 2 = –c a + b 2 4a 2
met a ∈ r0 en b, c ∈ r
Je deelt beide leden door a
Je verandert de constante term van lid.
Je maakt het dubbel product zichtbaar.
©VANIN
Je vermeerdert beide leden met b 2a 2
Je schrijft het linkerlid als een kwadraat van een tweeterm.
Je werkt het rechterlid verder uit. x + b 2a 2 = b 2 – 4ac 4a 2
Stel: D = b 2 – 4ac. x + b 2a 2 = D 4a 2
Het linkerlid is een kwadraat en dus positief. Ook de noemer van het rechterlid is positief.
Daarom is de teller van het rechterlid (b 2 – 4ac) bepalend voor het aantal oplossingen.
Je noemt D = b 2 – 4ac de discriminant van de vergelijking
geval:
De vergelijking heeft geen oplossingen, want het linkerlid is positief en het rechterlid is strikt negatief.
2.3.3
Overzicht
Om de tweedegraadsvergelijking ax 2 + bx + c = 0 op te lossen, bereken je eerst de discriminant D = b 2 – 4ac
> 0
twee verschillende oplossingen: één oplossing (of twee samenvallende oplossingen): geen reële oplossingen
2.3.4
©VANIN
Als je in de eerste formules D vervangt door 0, dan verkrijg je twee keer hetzelfde resultaat. Als D = 0, spreek je daarom van twee samenvallende oplossingen (x1 = x2).
De oplossingen van een tweedegraadsvergelijking noem je wortels
De formules die je in staat stellen om die wortels te berekenen, noem je wortelformules
Voorbeelden
GEOGEBRA
Stroomdiagram en Nassi-Shneiderman diagram
Oefeningen
REEKS A
12 Los de tweedegraadsvergelijkingen op met behulp van de discriminant.
a) x 2 + 2x – 3 = 0
b) x 2 + 3x – 10 = 0
c) x 2 – x + 2 = 0
d) x 2 – 10x + 25 = 0
f) –x 2 + x + 6 = 0
©VANIN
e) –x 2 + 3x – 2 = 0
g) x 2 – 4x – 5 = 0
h) x 2 + 28x + 196 = 0
i) x 2 – 12x + 40 = 0
j) –x 2 + 16x – 64 = 0
13 Los de tweedegraadsvergelijkingen op met behulp van de discriminant.
a) 2x 2 – 5x – 3 = 0
b) 25x 2 + 70x + 49 = 0
f) 14x 2 – 3x – 5 = 0
g) –3x 2 + 6x – 4 = 0
©VANIN
c) 3x 2 – 13x + 12 = 0
h) –64x 2 + 48x – 9 = 0
d) 5x 2 + 15x + 17 = 0 i) –12x 2 + 43x – 21 = 0
e) 6x 2 + x – 1 = 0
j) –9x 2 – 6x – 1 = 0
Los de tweedegraadsvergelijkingen
a) x 2 + x – 4 = 0
e) 12x (x + 4) = 24x (2 – x) – 5
©VANIN
b) –4x 2 + 11x – 1 = 0
f) 3x 2 – 4 3 x + 4 = 0
c) 28x = –49 – 4x 2
g) x 2 – 3x + 9 4 = 0
d) (4x – 1) 2 – 64 = 0 h) 3 8 x 2 –5 4 x + 15 2 = 0
a) 3x + x ? (x – 2) = 0
e) (–3x + 6) 2 – 16 = 0
b) –121x 2 + 4 = 0
©VANIN
c) x ? (11x – 3) = 5
f) 36x 2 – 96x + 64 = 0
g) –x 2 – 1 = 0
d) 3x (x – 1) = 4 – 3x h) –10x 2 + 15x – 10 = 0
a) x 2 –1 5 31 2 x + 7 = 0
b) –1 2 –1 3 x + 4 + x 2 = 0
c) –x –1 3 x + 4 –1 9 x = 0
d) 2x 2 – (x + 2) ? (x – 3) = 6
e) 14 (x – 4) – (x + 2) = (x + 2) (x – 4)
f) (2x – 3) 2 + 17x (x – 1) = 9
©VANIN
a) (x + 3) 2 – (2x – 1) 2 = 0
c) (3x – 5) 2 – (x – 4) 2 = 0
©VANIN
b) (2x – 1) 2 – 16 (2 – 3x) 2 = 0
d) 4 (–5x – 1) 2 – 9 (1 + x) 2 = 0
18 Bepaal de parameter m zodat aan de gegeven voorwaarde voldaan is.
a) x 2 + 6x – m = 0 heeft geen reële oplossingen.
e) 2x 2 + 3x – m – 3 = 0 heeft twee verschillende oplossingen.
©VANIN
b) x 2 – 3x + 4m = 0 heeft twee verschillende oplossingen.
f) –3mx 2 – 4x + 5 = 0 heeft geen reële oplossingen.
c) x 2 + mx + 4 = 0 heeft één oplossing.
g) 8mx 2 + 2mx – 2 = 0 heeft één oplossing.
d) mx 2 – x + 3m = 0 heeft één oplossing.
h) (m – 2)x 2 + (2m – 1)x + m + 2 = 0 heeft geen reële oplossingen.
19 Los op naar x (a en b zijn strikt positieve reële parameters). a) x 2 + 7ax + 12a 2 = 0 d) x 2 – 4bx + 4b 2 – 25 = 0
b) x 2 + ax + a 2 = 0
x 2 + bx –3 4 b 2 = 0
x 2 – ax + a – 1 = 0 (a > 2)
©VANIN
3x 2 – bx – 2b – 12 = 0 (b > –12)
c)
20 Los op naar x (a en b zijn strikt positieve reële parameters).
a) x 2 + ax – b 2 + ab = 0 (a > 2b)
c) x 2 + ax – bx – ab = 0
©VANIN
b) 4x 2 – 8ax – 9b 2 + 12ab = 0 (8a > 12b)
d) abx 2 + a 2 x – b 2 x – ab = 0
2.4 Som en product van de wortels van een tweedegraadsvergelijking
2.4.1
De formules opstellen
De tweedegraadsvergelijking ax
Besluit Als de tweedegraadsvergelijking ax
2.4.2
Voorbeelden
Door gebruik te maken van S en P, is het mogelijk sommige eenvoudige tweedegraadsvergelijkingen ‘uit het hoofd’ op te lossen.
Opmerkingen
• Als D < 0, dan kunnen de getallen S en P wel berekend worden, maar hebben ze geen reële betekenis.
• De som- en productmethode is vooral handig als de coëfficiënt van x 2 gelijk is aan 1 of –1.
• Als je niet onmiddellijk de oplossingen vindt, gebruik je beter de wortelformules.
2.4.3 Het omgekeerde vraagstuk
Gegeven: de som S en het product P van de reële getallen x 1 en x 2
Gevraagd: bepaal x 1 en x 2
Oplossing:
x 1 + x 2 = S en x 1 x 2 = P
⇓
⇓ je vervangt x 2 door S – x 1
x 2 = S – x 1 x 1 (S – x 1) = P
⇓ de vermenigvuldiging is distributief t.o.v. de optelling
x 1 ? S – x 1 2 = P
⇓ eigenschap gelijkheden
x 1 2 – S ? x 1 + P = 0
x 1 is dus een oplossing van de tweedegraadsvergelijking x 2 – Sx + P = 0.
Analoog kun je aantonen dat ook x 2 een oplossing is van dezelfde vergelijking.
Besluit
©VANIN
Als S = x 1 + x 2 en P = x 1 ? x 2 gegeven zijn, dan zijn x 1 en x 2 de oplossingen van de tweedegraadsvergelijking x 2 − Sx + P = 0.
Voorbeeld
De som van twee getallen is 1 9 en hun product is – 2 27 . Bepaal die getallen.
Oplossing:
De getallen zijn de oplossingen van
Wegwerken van de noemers:
D = x 1 = x 2 =
De gevraagde getallen zijn en
De discriminantformule afleiden via de eigenschap van de som en het product van de twee wortels
REEKS A
21 Los op met de som- en productmethode.
a) x 2 – 8x + 7 = 0
b) x 2 – 12x + 20 = 0
c) x 2 + 2x – 15 = 0
d) x 2 + 3x – 28 = 0
g) x 2 – 4x – 96 = 0
©VANIN
e) x 2 – 3x – 18 = 0
h) x 2 + 13x + 36 = 0
i) x 2 + 14x + 40 = 0
j) –x 2 – 17x + 18 = 0
k) –x 2 + 9x + 70 = 0
f) x 2 + 4x – 12 = 0
l) –x 2 – 2x + 35 = 0
22 Bepaal twee getallen waarvan de som S en het product P gegeven zijn.
a) S = –9 en P = 3 2
De gevraagde getallen zijn
b) S = 6 en P = 0
d) S = –1 12 en P = –1 12
©VANIN
De gevraagde getallen zijn en en
e) S = 1 36 en P = –5 72
De gevraagde getallen zijn
De gevraagde getallen zijn en en
c) S = –1 en P = –3
f) S = – 0,5 en P = – 0,84
De gevraagde getallen zijn
De gevraagde getallen zijn en en
23 Van de tweedegraadsvergelijkingen is telkens één oplossing gegeven. Bereken de andere oplossing zonder gebruik te maken van de discriminant.
24 Bepaal een tweedegraadsvergelijking met de gegeven oplossingen. Werk de noemers weg. a) 5 en – 4
25 Bepaal de parameter m zodat aan de gegeven voorwaarde voldaan is.
a) x 2 – 3x + m = 0
–1 is een oplossing.
1) D ⩾ 0: 2)
b) –3x 2 + mx – 6 = 0
2 is een oplossing.
1) D ⩾ 0: 2)
c) x 2 + 2mx – 5 = 0
De som van de wortels is 8.
1) D ⩾ 0: 2)
e) 3x 2 + 5mx – 9 = 0
Er zijn twee tegengestelde oplossingen.
©VANIN
d) –4x 2 – 3mx + 1 = 0
De som van de wortels is 2.
1) D ⩾ 0: 2)
f) –5x 2 + 6x – 8m = 0
Het product van de wortels is 16.
g) x 2 – 8x + 2m = 0
Het product van de wortels is 6.
h) 2x 2 – 7x – 3m = 0
De twee wortels zijn elkaars omgekeerde.
2.5 Vraagstukken
2.5.1 Voorbeeld 1
Het product van twee opeenvolgende natuurlijke getallen is gelijk aan 342. Bepaal die getallen.
Stel: x is het kleinste getal. Het grootste getal is dan
• Opstellen van de vergelijking:
• Oplossen van de vergelijking:
De enige aanvaardbare oplossing is
Antwoord:
Controle:
2.5.2 Voorbeeld 2
Een kader is 20 cm lang en 12 cm hoog.
De foto is 84 cm 2 groot.
Bereken de breedte van het frame, als je weet dat het overal even breed is.
Stel: x is de breedte van het frame.

De afmetingen van de foto: de lengte is en de hoogte is
• Opstellen van de vergelijking:
• Oplossen van de vergelijking:
De enige aanvaardbare oplossing is
Antwoord:
Controle:
2.5.3 Voorbeeld 3
a) Verdeel het lijnstuk [AB ] in twee deellijnstukken [AC ] en [CB ], A x 1 CB zodat het langste stuk zich verhoudt tot het kortste stuk zoals de volledige lengte van het lijnstuk zich verhoudt tot het langste stuk.
Stel: het kortste stuk = | CB | = 1; het langste stuk = | AC | = x
• Opstellen van de vergelijking: x 1 = x + 1 x
Een gelijkheid van twee verhoudingen noem je een evenredigheid. Het product van de uitersten is dan gelijk aan het product van de middelsten.
Je verkrijgt de volgende vergelijking:
• Oplossen van de vergelijking:
De enige aanvaardbare oplossing is (op acht cijfers na de komma).
• Controle:
b) Bereken een positief reëel getal waarvan het kwadraat gelijk is aan dat getal vermeerderd met 1 en het omgekeerde gelijk aan dat getal verminderd met 1.
Stel: x is het gevraagde getal.
• Opstellen van de vergelijkingen:
Vergelijking 1: Vergelijking 2:
• Oplossen van de vergelijkingen:
Vergelijking 1: Vergelijking 2:
Beide vergelijkingen leveren dezelfde tweedegraadsvergelijking op, die je ook bij de verdeling van het lijnstuk verkreeg.
Die vergelijking heeft als oplossingen:
x 1 = x2 =
De enige aanvaardbare oplossing is (op acht cijfers na de komma).
• Controle:
Het getal ϕ = 1 + 5 2 (‘phi’) noem je de gulden snede of goddelijke verhouding
Die verhouding werd voor het eerst wiskundig bepaald door Euclides, in de derde eeuw vóór Christus. Het getal duikt echter al veel vroeger op in de architectuur.
In de klassieke architectuur, en ook later, werd die verhouding gezien als de meest esthetische.
Enkele beroemde voorbeelden:
• De grote piramide van Cheops: de hellingshoek van de schuine vlakken is 51º 50
De cosinus van die hoek is het omgekeerde van ϕ (of dus ook ϕ – 1).
• In het Parthenon, de oude Griekse tempel op de Akropolis in Athene, zijn bepaalde verhoudingen van afmetingen gelijk aan de gulden snede (zie figuur 1).
• Het ‘geheim’ van de goede akoestiek in de Griekse theaters is de gulden snede.
De verhouding tussen de hoger en lager gelegen tribunes is gelijk aan ϕ
©VANIN
• Vele gotische kathedralen, met als beroemdste voorbeeld de kathedraal van Laon in Frankrijk, vertonen, zowel in de torens als in de voorgevel, verhoudingen gelijk aan de gulden snede.
1
Ook in de kunst speelt de gulden snede een belangrijke rol. Vooral in de renaissance werd de gulden snede gezien als een universeel schoonheidsideaal. De naam ‘goddelijke verhouding’ dateert dan ook uit die periode. Voorbeelden van het gebruik van de gulden snede zijn onder andere te vinden in de volgende beroemde werken:
• de Mona Lisa (zie figuur 2);
• de renaissancetuinen in Frankrijk;
• de meeste beeldhouwwerken van Rodin;
• de vierkanten van Mondriaan.
Niet alleen in de wiskunde, de architectuur en de kunst speelt de gulden snede een belangrijke rol. Ook de natuur zelf levert haar bijdrage:
• de hoeken die waarneembaar zijn bij de spiralen die worden gevormd door de pitten van een zonnebloem of bij madeliefjes, zijn gelijk aan 360º/ϕ of 360º – 360º/ϕ;
• de verhoudingen van de volumes in de opeenvolgende kamers van schelpen (zie figuur 3);
• de verhoudingen bij het menselijk lichaam (zie figuur 4).


figuur 2 figuur 3
4
Oefeningen
REEKS
A
26 Los de vraagstukken op.
a) Het product van twee opeenvolgende natuurlijke getallen is 1 482. Bereken die getallen.
c) De som van de kwadraten van twee opeenvolgende natuurlijke getallen is 421. Bereken die getallen.
©VANIN
Controle:
b) De som van een getal en zijn kwadraat is het vijfvoud van dat getal. Bereken dat getal.
Controle:
d) Van een natuurlijk getal is het kwadraat 552 meer dan het getal zelf. Bereken dat getal.
Controle:
Controle:
27 Het aantal judopartijen dat gespeeld wordt in een competitie met n spelers, is gelijk aan n (n – 1) 2 .
a) Hoeveel partijen moeten er worden gespeeld in een competitie met tien spelers?
b) Hoeveel spelers hebben meegedaan aan een competitie waarin 496 partijen werden gespeeld?

Controle:
28 Het aantal diagonalen van een veelhoek wordt bepaald door de formule N = k (k – 3) 2 . Daarbij is k het aantal zijden van de veelhoek en N het aantal diagonalen.
a) Hoeveel diagonalen heeft een zeshoek?
b) Een veelhoek heeft 77 diagonalen. Hoeveel zijden heeft die veelhoek?
Controle:
29 De ene rechthoekszijde van een rechthoekige driehoek is 2 cm langer dan de andere. De schuine zijde is 10 cm. Bereken de rechthoekszijden.
Controle:
30 Als je de zijde van een vierkant verdrievoudigt, dan wordt de oppervlakte 5 832 m2 groter. Bereken de zijde van het oorspronkelijke vierkant.
Controle:
31 Het verschil van twee natuurlijke getallen is 21. Hun product is 1 296. Bereken die getallen.
Controle:
32 De afgelegde weg s (in m) van een bewegend voorwerp wordt gegeven door de formule s = v 0 ? t + 1 2 ? a ? t 2. Daarbij is v0 de beginsnelheid (in m/s) en a de versnelling (in m/s2).
Een voorwerp beweegt met een beginsnelheid van 10 m/s. De versnelling is 3 m/s2.
a) Na hoeveel tijd heeft het voorwerp 100 m afgelegd? Rond af op 0,001 s.
Controle:
b) Bereken de gemiddelde snelheid in dat tijdsinterval. Rond af op 0,01 m/s.
33 De oppervlakte van een cilinder wordt gegeven door de formule A = 2 r 2 + 2 r h.
Daarin is h de hoogte en r de straal van het grondvlak.
Bereken de straal van het grondvlak als de hoogte 12 cm en de oppervlakte 680 cm2 is. Rond af op 1 mm nauwkeurig. h r
Controle:
34 Een stuk land bestaat uit twee aaneengesloten vierkante stukken. De zijde van het grote vierkant is 2 m langer dan het dubbel van de zijde van het kleine vierkant. De totale oppervlakte van beide vierkanten is 2 377 m2. Bereken de zijden van de vierkanten.
Controle:
35 Op een trouwfeest wordt een champagnetoren gestapeld. Nadat de gasten aangekomen zijn, wordt er van bovenaf champagne gegoten, totdat alle glazen gevuld zijn. Het aantal glazen per laag in die toren kun je berekenen met deze formule: aantal glazen per laag = 1 2 n 2 + 1 2 n (daarbij is n het nummer van de laag van bovenaf geteld). Bereken in welke laag 45 glazen staan.
laag 2 laag 1
laag 3

Controle:
36 Oma heeft een lappendeken gemaakt met 315 gelijke vierkante lapjes. Als ze vierkante lapjes had genomen met een zijde die 6 cm groter is, dan zou ze maar 140 lapjes nodig gehad hebben voor een even groot deken.
Wat is de oppervlakte van elk lapje en van het lappendeken?
Controle:
37 De beroemde schrijver H. Gentemans heeft een nieuwe roman geschreven.
Een boekenwinkel bestelt een aantal boeken en betaalt daarvoor 930 euro.
Bij aankomst van de bestelling blijken er twee boeken meer te zijn dan er besteld waren. De totale prijs blijft hetzelfde, zodat de prijs per boek daalt met 0,50 euro.
Hoeveel boeken werden er besteld en wat was de oorspronkelijke prijs?

Controle:
38 In een fabriek moeten 1 650 balpennen in dozen worden ingepakt. Als er in elke doos vijf balpennen meer konden, zouden er drie dozen minder nodig zijn. Bereken het aantal balpennen dat oorspronkelijk in één doos kon.

©VANIN
Controle:
39 In een getal van twee cijfers is het cijfer van de eenheden vier meer dan het cijfer van de tientallen. Een tweede getal verkrijg je door in het eerste getal de cijfers van plaats te wisselen. Het product van die twee getallen is gelijk aan 5 605. Bepaal die getallen.
Controle:
40 De snelheid van de boot van Tom in stilstaand water is 15 km/h. Hij vaart in een rivier 40 km stroomopwaarts en 40 km stroomafwaarts in 6 h.
Bereken de stroomsnelheid van het water in die rivier.

©VANIN
Controle:
41 ABCD is een rechthoek met lengte 10 cm en breedte 3 cm.
Bereken x zodat ∆BCP een rechthoekige driehoek is met ^ P = 90º.
Controle:
2.6 Vergelijkingen herleidbaar tot tweedegraadsvergelijkingen
2.6.1 Bikwadratische vergelijkingen
Definitie Bikwadratische vergelijking
Een bikwadratische vergelijking is een vergelijking van de vorm ax 4 + bx 2 + c = 0, met a ∈ r0 en b, c ∈ r
Voorbeeld 1
x 4 – 5x 2 + 4 = 0
t 2 – 5t + 4 = 0
D = (–5) 2 – 4 ? 1 ? 4 = 9
Stel: x 2 = t
©VANIN
t 1 = 5 – 3 2 1 = 1 en t 2 = 5 + 3 2 1 = 4
x 2 = 1 of x 2 = 4
x = –1 of x = 1 of x = –2 of x = 2
V = {–2, –1, 1, 2}
Voorbeeld 2
x 4 – x 2 – 12 = 0
Stel:
Algemeen Om een bikwadratische vergelijking op te lossen, ga je als volgt te werk:
• Stel: x 2 = t.
• Bepaal de oplossingen t 1 en t 2 van de verkregen tweedegraadsvergelijking in t
• Los de vergelijkingen x 2 = t 1 en x 2 = t 2 op.
2.6.2 Vergelijkingen van de vorm a [f (x)] 2 + b [f (x)] + c = 0
Voorbeeld 1
8x 6 + 7x 3 – 1 = 0 Stel: x 3 = t
= t 1 = en t 2 = x 3 = of x 3 =
Voorbeeld 2
(x 2 – 2x) 2 + 2 ? (x 2 – 2x) – 3 = 0 Stel: D = t 1 = en t 2 = = of =
Je krijgt twee tweedegraadsvergelijkingen:
Algemeen Om een vergelijking van de vorm
• Stel: f (x) = t
+ b[f (x)] + c = 0 op te lossen, ga je als volgt te werk:
• Bepaal de oplossingen t 1 en t 2 van de verkregen tweedegraadsvergelijking in t
• Los de vergelijkingen f (x) = t 1 en f (x) = t 2 op.
Opmerking
Een bikwadratische vergelijking kan beschouwd worden als een speciaal geval van de vergelijking a[f(x)]² + b[f(x)] + c = 0.
REEKS B
42 Los de vergelijkingen op.
a) x 4 – 5x 2 + 4 = 0
c) x 6 – 28x 3 + 27 = 0
©VANIN
b) 4x 4 – 29x 2 + 45 = 0
d) x 4 – 2x 2 – 8 = 0
(3x – 1) 2 – 3 ? (3x – 1) + 2 = 0
©VANIN
2.7 Een drieterm van de vorm ax² + bx + c ontbinden in factoren
STUDIEWIJZER Tweedegraadsvergelijkingen
2.1 Vergelijkingen van de tweede graad in één onbekende voor de leerling voor de

Een tweedegraadsvergelijking is een vergelijking van de vorm ax 2 + bx + c = 0, met a ∈ r 0 en b, c ∈ r
2.2 Onvolledige tweedegraadsvergelijkingen oplossen

KENNEN
• ax 2 + bx = 0 (met b ≠ 0 en c = 0) methode: een gemeenschappelijke factor afzonderen
• ax 2 + c = 0 (met b = 0 en c ≠ 0) methode 1: a 2 – b 2 = (a + b) ? (a - b) methode 2: definitie vierkantswortel
• ax 2 = 0 (met b = 0 en c = 0) Er is één oplossing: 0.

©VANIN
KUNNEN
Een onvolledige tweedegraadsvergelijking oplossen.
2.3 Tweedegraadsvergelijkingen oplossen: algemeen

D (discriminant) = b 2 − 4ac
• D > 0: twee verschillende oplossingen
x 1 = –b
D 2
en x 2 = –b +
KENNEN
• D = 0: één oplossing (of twee samenvallende oplossingen)
x 1 = x 2 = –b 2a
• D < 0: geen reële oplossingen

KUNNEN
Een tweedegraadsvergelijking herkennen en oplossen
• door kwadraatafsplitsing;
• met de wortelformules;
• door ontbinding in factoren.
De best passende methode gebruiken.
De wortelformules om een tweedegraadsvergelijking op te lossen, bewijzen.
Een tweedegraadsvergelijking oplossen met ICT.
Een tweedegraadsvergelijking vereenvoudigen en in de standaardvorm brengen, indien nodig.
Een tweedegraadsvergelijking met lettercoëfficiënten oplossen.
Parameterwaarden berekenen zodat aan bepaalde voorwaarden voldaan is.
2.4 Som en product van de wortels van een tweedegraadsvergelijking voor de leerling voor de leerkracht

KENNEN –
Als de tweedegraadsvergelijking ax 2 + bx + c = 0 oplossingen x 1 en x 2 heeft,
dan is S = x 1 + x 2 = –b a en P = x 1 x 2 = c a
Als S = x 1 + x 2 en P = x 1 ? x 2 gegeven zijn, dan zijn x 1 en x 2 de oplossingen van de tweedegraadsvergelijking x 2 − Sx + P = 0.

KUNNEN
Een tweedegraadsvergelijking oplossen door de som en het product van de wortels te gebruiken.
Twee getallen bepalen als de som en het product van die getallen gegeven zijn.
Een tweedegraadsvergelijking opstellen waarvan de oplossingen gegeven zijn.
2.5 Vraagstukken

©VANIN
KUNNEN
Vraagstukken oplossen die aanleiding geven tot een tweedegraadsvergelijking.
2.6 Vergelijkingen herleidbaar tot tweedegraadsvergelijkingen

KENNEN
Een bikwadratische vergelijking is een vergelijking van de vorm ax 4 + bx 2 + c = 0 met a ∈ r 0 en b, c ∈ r
Een bikwadratische vergelijking kan beschouwd worden als een speciaal geval van de vergelijking a[f(x)]² + b[f(x)] + c = 0.

KUNNEN
Vergelijkingen oplossen die herleidbaar zijn tot een tweedegraadsvergelijking.
1. Twee vierkanten liggen in een groot vierkant, zoals op de figuur. Wat is de verhouding van de oppervlaktes van vierkant I en II?
JWO, editie 2022, eerste ronde
2. Wat is de oppervlakte van het vierkant op de figuur? 4 1

©VANIN

JWO, editie 2012, tweede ronde
3. Amira is de code van oma’s huis vergeten. Ze weet nog dat de code uit vijf cijfers bestaat. Ze ziet dat op het klavier de toetsen 1 en 3 precies evenveel afgesleten zijn en dat de toets 7 nóg meer is afgesleten. De andere toetsen zijn blijkbaar nog nooit gebruikt. Als Amira het slim aanpakt, hoeveel codes moet ze dan hoogstens intikken om de deur te openen?
JWO, editie 2020, eerste ronde

©VANIN

3.1 Basisbegrippen over functies
3.1.1 Inleiding
Een brandende kaars is 20 cm lang.
De hoogte y van de kaars vermindert met 2 cm per uur.
GEOGEBRA
Na 1 uur is de hoogte
Na 3 uur is de hoogte
Na 7 uur is de hoogte
De hoogte y (in cm) kun je uitdrukken in functie van de tijd x (in h):
y =
Vul de tabel in.
Teken de punten in het assenstelsel en verbind ze. x (h) y (cm)

Is het verband tussen y en x een functie? Verklaar je antwoord.
Definitie Functie
Een functie is een verband waarbij elk argument hoogstens één beeld heeft.
3.1.2 Domein en bereik
Gegeven: de grafiek van de functie f (x) = –2x + 20
• Als je de grafiek loodrecht projecteert op de x-as, kun je het domein van de functie aflezen.
dom f =
• Als je de grafiek loodrecht projecteert op de y-as,
kun je het bereik van de functie aflezen.
Definitie Domein
Het domein van een functie is de verzameling van alle reële getallen waarvoor je een functiewaarde kunt bepalen.
In symbolen
dom f = {x ∈ r | f (x) ∈ r}
Definitie Bereik
Het bereik van een functie is de verzameling van alle functiewaarden.
In symbolen
ber f = {f (x) | x ∈ dom f }
Praktisch domein en bereik
Als je rekening houdt met de context van de brandende kaars, kun je enkel argumenten kiezen die gelijk zijn aan of groter zijn dan en kleiner zijn dan of gelijk zijn aan .
Het praktisch domein van f is
Notatie: pdom f
Je kunt binnen diezelfde context ook enkel functiewaarden bereiken die gelijk zijn aan of groter zijn dan en kleiner zijn dan of gelijk zijn aan
Het praktisch bereik van f is
Notatie: pber f
3.1.3 Nulwaarde van een functie
Voor welke waarde van de tijd x is de hoogte van de kaars nul?
Die waarde noem je de nulwaarde van de functie f
Hoe lees je de nulwaarde van de functie f af op de grafiek?
Definitie Nulwaarde
Een nulwaarde van een functie f is een getal a waarvoor f (a) = 0.
Voorbeeld
Bepaal de nulwaarde(n).
f (x) = 20 – 2x f (x) = x 2 – 9
3.1.4 Tekenschema en verloop van een functie
Gegeven is de grafiek van de functie f (x) = –2x + 20
• Voor welke waarden van x is f (x) > 0?
Voor welke waarden van x is f (x) = 0?
Voor welke waarden van x is f (x) < 0?
Je kunt dat voorstellen in een tekenschema van f (x).
tekenschema van f (x) tekenschema binnen de context van de kaars
• Nemen de functiewaarden toe of nemen ze af als het argument x toeneemt?
De functie is stijgend / dalend.
Je kunt het verloop van de functie f schematisch voorstellen.
verloop van f verloop binnen de context van de kaars
Algemeen Tekenschema en verloop van een functie
• tekenschema
verloop
3.1.5 Voorbeeld
Teken de grafiek van f (x) = 3x – 2.
Bepaal het domein, het bereik, de nulwaarde, het tekenschema en het verloop van de functie.
x f (x)
• dom f = ber f =
• nulwaarde: • tekenschema
Oefeningen
REEKS A
1 Bepaal het tekenschema en het verloop van de functies waarvan de grafiek getekend is. a)
tekenschema
(x) • verloop
• tekenschema x f (x) • verloop x f
• tekenschema x f (x)
• verloop x f
2 Bepaal het tekenschema en het verloop van de functies waarvan de grafiek getekend is. a)
• tekenschema
f (x) • verloop x f
©VANIN
• verloop x f
3 Bepaal de nulwaarde(n).
a) f (x) = 5 – 2x 3 c) f (x) = 3x 2 – 6
b) f (x) = (x + 2) 2 d) f (x) = 3x + 1 2
3.2.1 Kenmerken
x f (x) – 8 – 0,125 – 4 – 0,25 – 2 – 0,5 – 1 – 1
©VANIN
Je noemt de grafiek een (orthogonale) hyperbool. Een hyperbool bestaat uit twee hyperbooltakken.
• dom f = ber f =
• nulwaarde: Heeft de grafiek een snijpunt met de x-as?
• nulwaarde: Is er een nulwaarde voor de functie?
• tekenschema:
• verloop:
f (x)
De functiewaarde van 0 bestaat niet. Je duidt dat aan met een verticale streep.
• symmetrie:
De twee takken van de grafiek liggen symmetrisch ten opzichte van
De grafiek van f is een kromme.
Het symmetriemiddelpunt is de ( , ).
3.2.2 Asymptoten
Verticale asymptoot
De grafiek van f (x) = 1 x vertoont een onderbreking voor x = 0 omdat 0 niet tot het domein behoort.
Je bekijkt nu het gedrag van de functie in de omgeving van 0.
Je kiest argumenten die naderen tot 0, zonder 0 te bereiken, en berekent de functiewaarden.
Notatie: x → 0
Je leest: x nadert tot 0.
Als x tot 0 nadert, dan wordt f (x) groter in absolute waarde.
De grafiek komt dichter en dichter tot de y-as, zonder die ooit te raken of te snijden.
Je noemt de y-as een verticale asymptoot. De vergelijking van die asymptoot is
Horizontale asymptoot
Je bekijkt nu het gedrag van de functie in de omgeving van – ∞ en + ∞.
Je kiest argumenten die heel groot en heel klein zijn en je berekent de functiewaarden.
Als x groter wordt in absolute waarde, dan nadert f (x) tot 0.
De grafiek nadert dichter en dichter tot de x-as, zonder die ooit te raken of te snijden.
Je noemt de x-as een horizontale asymptoot. De vergelijking van die asymptoot is
3.2.3 Voorbeeld
Oom Jan is overleden. Hij laat een erfenis na die gelijk verdeeld moet worden onder zijn vijf kinderen. Elk van zijn kinderen krijgt een vijfde van de erfenis.
Verdeel je de erfenis onder x personen, dan kun je het deel y dat elke persoon krijgt, bepalen met de formule y = 1 x
Waarom is het verband tussen y en x een functie?
©VANIN
Je noteert: f (x) = 1 x .
dom f = ber f = pdom f = pber f =
Vul de tabel in en teken de grafiek. Rond, indien nodig, af op 0,001.
Waarom mag je de punten niet verbinden?
3.3.1 Het omgekeerd evenredig verband
Voorbeeld
Een fietser rijdt met een constante snelheid van Antwerpen naar Blankenberge en moet daarvoor 120 km afleggen. De afstand s (in km) die de fietser aflegt in functie van de tijd t (in h), kun je uitdrukken met de formule s = v ? t, waarbij v de gemiddelde snelheid voorstelt (in km/h). t (h) 1 2 3 4 5 6 12
v (km/h)
s = v t (km)
Het product v t is constant. De grootheden v en t zijn omgekeerd evenredig
Er geldt: v =
Definitie Omgekeerd evenredig verband
Twee grootheden y en x zijn omgekeerd evenredig als het product x y constant is.
x y = c ⇒ y = c x (met c ∈ r0 ). Je noemt c de evenredigheidsconstante
Formule
Als twee grootheden y en x omgekeerd evenredig zijn, dan is y = c x (met c ∈ r0).
Grafiek van een omgekeerd evenredig verband
v (km/h)
GEOGEBRA
©VANIN
Teken de grafiek van het verband dat de snelheid v (in km/h) weergeeft in functie van de tijd t (in h).
De grafiek is
Besluit
De grafische voorstelling van een omgekeerd evenredig verband y = c x (met c ∈ r0) is een (deel van een) hyperbool.
Oefeningen
REEKS A
4 Stellen de tabellen omgekeerd evenredige verbanden voor?
©VANIN
REEKS B
5 Hoe hoger een verkeersdrempel, hoe trager de auto’s erover rijden. In een stad zijn er verkeersdrempels met vier verschillende hoogten. De politie heeft de resultaten opgemeten voor het verband tussen de gemiddelde snelheid v (in km/h) van de voorbijrijdende auto’s en de hoogte h (in cm) van de drempel.
h (cm) 4 5 6 8
v (km/h) 60 48 40 30

a) Toon aan dat het verband tussen v en h omgekeerd evenredig is.
b) Geef de formule van het verband:
c) Volgens de wet spreek je van een verkeersdrempel vanaf 2 cm en mag die niet hoger zijn dan 12 cm. Bepaal daaruit het praktisch domein en bereik van de functie v pdom v = pber v =
d) Hoe hoog (op 1 mm) moet een drempel zijn om de gemiddelde snelheid tot 50 km/h te beperken?
6 Eén keer per jaar, op kerstavond, speelt Stijn mee met een loterij. Een pot van 2 000 000 euro wordt dan gelijk verdeeld onder de winnaars in rang 1. De tabel toont de winst y per persoon (in euro) in functie van het aantal winnaars x.
a) Vul de tabel aan. b) Teken de grafiek. x y (euro) 1 2 4 5 8 10
(euro)
c) Mag je de punten van de grafiek verbinden? Verklaar.
d) Zijn de grootheden y en x omgekeerd evenredig? Verklaar.
e) Hoeveel bedraagt de winst per persoon als er zes winnaars zijn in rang 1? Rond af op 1 euro.
7 Om een nieuwe asfaltlaag in een drukke winkelstraat te leggen, hebben 35 arbeiders 8 dagen nodig. Hoeveel dagen hebben 20 arbeiders nodig?
8 Boer Tom zet elke dag een aantal koeien uit op zijn weiland. 8 koeien kunnen grazen gedurende 24 dagen. 12 koeien kunnen grazen gedurende 16 dagen.
a) Toon aan dat het verband tussen het aantal dagen y en het aantal koeien x omgekeerd evenredig is.
b) Geef de formule van het verband:
c) Vul de tabel aan. x 2 4 8 12 24 y 24 16
d) In hoeveel dagen grazen 6 koeien het weiland af?
©VANIN
REEKS C
Een hijskraan is een werktuig waarmee je zware lasten kunt hijsen en horizontaal verplaatsen. De last hangt aan een katrol die kan bewegen langs de arm van de kraan. De massa die een kraan kan tillen, hangt af van de plaats waar de katrol aan de arm van de kraan hangt. Hangt een massa te ver van de kraan, dan bestaat de kans dat de kraan omvalt.
De afstand van de plaats waaronder de katrol hangt, tot het steunpunt van de draaiarm noem je de armlengte. De grootste massa m max (in kg) die een kraan kan tillen, hangt af van de armlengte a (in m).
9 Een aannemer huurt voor enkele weken een hijskraan om een nieuwbouwproject te verwezenlijken.
Voor die kraan geldt: m max = 120 000 a
a) Zijn de grootheden m max en a omgekeerd evenredig? Verklaar.
b) Mag een massa van 7 500 kg op een armlengte van 15 m hangen?

c) Bereken bij deze kraan de maximale armlengte waarop een massa van 6 ton kan hangen.
3.3.2 Grafische betekenis van c in f (x) = c x
Voorbeelden
GEOGEBRA
©VANIN
Om de grafiek van de functie g (x) = 4 x te verkrijgen, moet je de y-coördinaat van elk punt van de grafiek van f (x) = 1 x vermenigvuldigen met 4.
Je zegt dat de grafiek van f (x) = 1 x verticaal is uitgerekt met factor 4.
Om de grafiek van de functie g (x) = 1 4x te verkrijgen, moet je de y-coördinaat van elk punt van de grafiek van f (x) = 1 x vermenigvuldigen met 1 4
Je zegt dat de grafiek van f (x) = 1 x verticaal is samengedrukt met factor 4. Verticaal samendrukken met factor 4 is hetzelfde als verticaal uitrekken met factor 1 4
<
x f (x) = 1 x g (x) = –1 x
4 – 0,25 0,25
2 – 0,5 0,5 0 | | 2 0,5 –0,5 4 0,25 –0,25 (– 1)
| |
Om de grafiek van de functie g (x) = –1 x
te verkrijgen, moet je de y-coördinaat van elk punt van de grafiek van f (x) = 1 x vermenigvuldigen met –1.
De grafiek van f (x) = 1 x is gespiegeld ten opzichte van de x-as
Algemeen
Om de grafiek van de functie g (x) = –5 x
te verkrijgen, moet je de y-coördinaat van elk punt van de grafiek van f (x) = 1 x vermenigvuldigen met –5.
©VANIN
De grafiek van f (x) = 1 x is achtereenvolgens:
• verticaal uitgerekt met factor 5;
• gespiegeld ten opzichte van de x-as
De grafiek van de functie g (x) = c x , met c ∈ r0, ontstaat door de grafiek van de functie f (x) = 1 x uit te rekken of samen te drukken.
• Voor | c | > 1 wordt de grafiek van f verticaal uitgerekt met factor | c |.
• Voor | c | < 1 wordt de grafiek van f verticaal samengedrukt met factor 1 | c | .
Als c < 0, wordt de grafiek ook gespiegeld ten opzichte van de x-as.
Oefeningen
REEKS A
10 Vervolledig de grafieken van de functie f (x) = c x .
11 Met welke factor moet je de grafiek van de functie f samendrukken of uitrekken om de grafiek van de functie g te verkrijgen? Maak een schets van de grafiek van g (x).
a) g (x) = 3 x c) g (x) = 1 4x
b) g (x) = 1 2x d) g (x) = 5 x verticale met factor verticale met factor
12 Bepaal het functievoorschrift van elke functie f .
REEKS B
13 Bepaal het functievoorschrift van de vorm f (x) = c x (met c ∈ r0), als je weet dat:
a) het punt A (2, 5) tot de grafiek van de functie behoort.
c) het punt A (– 3, 7) tot de grafiek van de functie behoort.
f (x) = f (x) =
b) het punt A –2, 2 3 tot de grafiek van de functie behoort.
d) het punt A 4 7 , 14 3 tot de grafiek van de functie behoort.
f (x) = f (x) =
14 Bepaal het functievoorschrift, het domein, het bereik, het tekenschema en het verloop van elke functie f
• f (x) =
• dom f = ber f =
• tekenschema
• f (x) =
• dom f = ber f =
• tekenschema
x f (x) x f (x)
• verloop
• verloop x f x f
• f (x) =
• dom f = ber f =
• tekenschema
• f (x) =
• dom f = ber f =
• tekenschema
x f (x) x f (x)
• verloop
• verloop x f x f
15 Maak gebruik van de grafieken van de functies f en g om de vergelijkingen op te lossen.
a) gegeven:
(x) = 1 x en g (x) = x
vergelijking:
1 x = x
b) gegeven:
f (x) = 1 x en g (x) = x 3
vergelijking:
1 x = x 3
c) gegeven:
f (x) = 1 x en g (x) = 2x + 1
vergelijking:
1 x = 2x + 1
d) gegeven:
f (x) = 1 x en g (x) = – 3x
vergelijking:
1 x = – 3x
16 De getekende grafieken van de functie g zijn ontstaan door de grafieken van de functie f (x) = 1 x te spiegelen en/of te verschuiven. Bepaal het domein, het bereik, het tekenschema, het verloop en de vergelijking van de asymptoten van elke functie g.
©VANIN
tekenschema
• verloop
tekenschema
verloop
• VA: HA: • VA: HA:
17 Bij de aankoop van een nieuwe smartphone is het belangrijk om kritisch naar de batterijduur te kijken. De stand-bytijd van een smartphone is de maximale tijd die de smartphone kan aanstaan zonder gebruikt te worden. Die is afhankelijk van het type toestel. Het spanningsverloop U (in V) van een batterij van een smartphone wordt gegeven door de functie U (t ) = 3,60 + 20 t – 50 Daarbij is t de tijd (in h) na het opladen.
a) Teken met ICT de grafiek van de functie U, zonder rekening te houden met de werkelijkheid.
b) Bepaal de spanning van de batterij onmiddellijk na het opladen.
c) Met hoeveel procent neemt de spanning af tijdens de eerste dag na het herladen? Rond af op 0,01 %.
d) Geef het praktisch domein en bereik van de functie U
pdom U = pber U =
18 Een achtbaan is een constructie uit hout of staal waarover karretjes een parcours afleggen met hoge snelheid. Een karretje begint omhoog te rijden volgens de functie f en vervolgt daarna zijn weg volgens de functie g.
Het voorschrift van f is f (x) = –0,68 ∙ (x – 4,37)2 + 13.
Het voorschrift van g is g (x) = 17 x – 4, 4 + 2 , met x de horizontale verplaatsing (in m) en f (x) en g (x) de verticale verplaatsing (in m).
a) Op welke hoogte bevindt het karretje zich in
• het punt A?
• het punt B?
b) Welke horizontale verplaatsing heeft het karretje gemaakt als het zich op een hoogte van 3 m bevindt?
Het karretje gaat omhoog: Het karretje gaat omlaag:
3.3.3 Een trendlijn tekenen met behulp van ICT
Een leerkracht fysica demonstreert haar leerlingen de wet van Boyle. Hiervoor vult ze een injectiespuit van 20 ml met een gas en koppelt ze die spuit aan een druksensor.
Terwijl een leerling uit de klas de spuit elke keer een beetje meer indrukt en het volume V (in ml) dus verkleint, leest een andere leerling telkens de gemiddelde druk p (in kPa) op de druksensor.
Dat levert de volgende meetresultaten op:
©VANIN
Je kunt de gegevens voorstellen met een spreidingsdiagram of puntenwolk
De punten liggen, bij benadering, op een hyperbooltak. Het verband tussen p en V is dus waarschijnlijk een omgekeerd evenredig verband.
Om dat verband te vinden, teken je met ICT een trendlijn (regressielijn) door de punten.
a) Bepaal het verband tussen de gemiddelde druk p (in kPa) en het volume V (in ml).
b) Hoeveel bedraagt de druk als je het gas samendrukt tot een volume van 4 ml?
c) Bij welk volume verkrijg je een gemiddelde druk van 140 kPa? Rond af op 0,1 ml. GEOGEBRA
Oefeningen
REEKS B
19 Een computerbedrijf beraadt zich over de kostprijs p (in euro) van een nieuwe laptop, die het binnen enkele weken op de markt wil brengen. Om de vooropgestelde omzet te behalen, moet het bedrijf minstens q laptops verkopen. In de tabel staan enkele voorstellen, uitgewerkt door een van de directieleden.
a) Bepaal via regressie het verband tussen de minimumhoeveelheid te verkopen laptops q en de kostprijs p (in euro).
b) Hoeveel laptops moet het bedrijf minstens verkopen om dezelfde omzet te behalen, als het de verkoopprijs vastlegt op 750 euro?
c) Hoeveel zou de kostprijs van een laptop bedragen, als men zeker is van een minimale verkoop van 5 000 laptops? Rond af op 1 euro.
d) Geef de economische betekenis van de verticale asymptoot van de grafiek van het verband.
20 Elektrische weerstand of resistantie is de elektrische eigenschap van materialen om de doorgang van elektrische stroom te bemoeilijken. Hoe hoger de weerstand R (in V), hoe lager de stroomsterkte I (in A) door een geleider bij een gelijke spanning U (in V). Hieronder staan enkele meetresultaten bij een welbepaalde geleider.
a) Bepaal via regressie het verband tussen de stroomsterkte I (in A) en de weerstand R (in V).
(V) I (A)
4,60
1 000 0,23
b) Vanaf welke weerstand is de stroomsterkte minder dan 0,50 A?
Als een duiker zich onder water bevindt, ademt hij de lucht in onder een grotere druk dan normaal.
Daardoor ontstaat meer stikstofgas in het bloed. Als de duiker te lang onder water blijft of te snel terug naar het oppervlak stijgt, kan de stikstof belletjes doen ontstaan in het bloed.
De duiker krijgt last van hoofdpijn, spierpijn en duizeligheid. In ernstige gevallen kan hij buiten bewustzijn raken of zelfs sterven. Dat verschijnsel noem je de Caissonziekte

21 De tabel toont de maximale tijd t (in min) die een duiker onder water mag blijven als hij zich op een diepte d (in m) bevindt.
a) Vul de tabel aan. d (m) d 2 (m2) t (min)
b) Bepaal via regressie het verband tussen t en d 2
c) Hoelang mag een duiker onder water blijven, als hij zich op een diepte van 60 m bevindt? Rond af op 1 minuut.
d) Hoe diep mag een duiker gaan, als hij zuurstof heeft voor 1 h 30 min? Rond af op 0,1 m.
3.1 Basisbegrippen over functies

KENNEN
• Het domein van een functie is de verzameling van alle reële getallen waarvoor je een functiewaarde kunt bepalen.
Notatie: dom f
• Het praktisch domein van een functie is het deel van het domein dat de fysisch aanvaardbare argumenten bevat.
Notatie: pdom f
• Het bereik van een functie is de verzameling van alle functiewaarden.
Notatie: ber f
• Het praktisch bereik van een functie is het deel van het bereik dat de fysisch aanvaardbare beelden bevat.
Notatie: pber f
Een nulwaarde van een functie f is een getal a waarvoor f (a) = 0.

©VANIN
KUNNEN
Het tekenschema en het verloop van een functie opstellen aan de hand van de grafiek.
3.2 De functie f (x) = 1 x

f (x) = 1 x
• De y-as (x = 0) is de verticale asymptoot (VA) van de grafiek van f
• De x-as (y = 0) is de horizontale asymptoot (HA) van de grafiek van f

KUNNEN
De grafiek van de functie f (x) = 1 x herkennen.
De grafiek van de functie f (x) = 1 x schetsen, uitgaande van een tabel met coördinaten van een aantal punten.
Met behulp van de grafiek van f (x) = 1 x onderzoek doen naar:
• het domein en het bereik;
• de eventuele nulwaarden;
• het tekenschema;
• het verloop;
• de verticale en horizontale asymptoot;
• symmetrie.
3.3 De functie f (x) = c x voor de leerling voor

KENNEN
Twee grootheden y en x zijn omgekeerd evenredig als het product x y constant is.
De grafische voorstelling van een omgekeerd evenredig verband y = c x is een (deel van een) hyperbool.
De grafiek van de functie g (x) = c x , met c ∈ r0, ontstaat door de grafiek van de functie f (x) = 1 x uit te rekken of samen te drukken.
• Voor | c | > 1 wordt de grafiek van f verticaal uitgerekt met factor | c |.
• Voor | c | < 1 wordt de grafiek van f verticaal samengedrukt met factor 1 | c |
Als c < 0, wordt de grafiek ook gespiegeld ten opzichte van de x-as.

©VANIN
KUNNEN
Omgekeerd evenredige verbanden herkennen in tabellen en de vergelijking ervan opstellen. Vraagstukken met gegeven omgekeerd evenredige verbanden oplossen.
De grafiek van de functie f (x) = c x herkennen.
De grafiek van de functie f (x) = c x tekenen met en zonder ICT.
Met behulp van de grafiek van f (x) = c x onderzoek doen naar:
• het functievoorschrift;
• het domein en het bereik;
• de eventuele nulwaarden;
• het tekenschema;
• het verloop;
• de verticale en horizontale asymptoot;
• symmetrie.
Het verband tussen twee numerieke grootheden in een dataset onderzoeken met ICT en daarbij:
• een spreidingsdiagram of puntenwolk opstellen en interpreteren;
• een trendlijn met bijbehorend voorschrift bepalen en interpreteren.
1. Op de figuur hieronder is van zes vierkanten de oppervlakte gegeven. Wat is de oppervlakte van het zevende vierkant?

?
©VANIN
JWO, editie 2020, tweede ronde
2. Drie buren leggen de oogst van hun moestuin samen.
• Annelies heeft drie tomaten en x paprika’s.
• Boudewijn heeft y tomaten en drie wortels.
• Claudia heeft vier tomaten, vijf paprika’s en z wortels.
Nadat ze de oogst verdeeld hebben, heeft iedereen drie tomaten, twee paprika’s en vier wortels. Er is geen overschot.
Waaraan is x + y + z gelijk?
JWO, editie 2016, eerste ronde
3. Hoeveel kleuren heb je minimaal nodig om de onderstaande landkaart met zeventien landen in te kleuren? Daarbij mogen twee landen die aan elkaar grenzen, niet dezelfde kleur hebben.


JWO, editie 2021, eerste ronde
HOOFDSTUK 4 I DEELBAARHEID BIJ VEELTERMEN
©VANIN
4.1 Veeltermen in één veranderlijke 138
4.2 De euclidische deling van twee veeltermen 142
4.3 Deling door x – a 153
4.4 Tweetermen van de vorm a 3 – b 3 en a 3 + b 3 ontbinden in factoren 167
Studiewijzer 169
Pienter problemen oplossen 170

5.1 Veeltermeninéénveranderlijke
4.1 Veeltermen in één veranderlijke
5.1 Veeltermeninéénveranderlijke
5.1 Veeltermeninéénveranderlijke
5.1.1
4.1.1 Veelterm
5.1 Veeltermeninéénveranderlijke
Veelterm
5.1.1 Veelterm
Definitie Veelterm
5.1.1 Veelterm
5.1.1 Veelterm
Definitie Veelterm
Eenveeltermiseensomvaneentermen.
Definitie Veelterm
Definitie Veelterm
Eenveeltermiseensomvaneentermen.
Eenveeltermiseensomvaneentermen.
Eenveeltermiseensomvaneentermen.
Deveelterm5 a + 6 b 5iseendrietermindeonbekende(n)
Deveelterm6 x 3 + 5 x 2 + 3 x 7iseenviertermindeonbekende(n)
Deveelterm5 a + 6 b 5iseendrietermindeonbekende(n)
Deveelterm5 a + 6 b 5iseendrietermindeonbekende(n)
Indithoofdstukwerkjemetveeltermeninéénveranderlijke.
Deveelterm5 a + 6 b 5iseendrietermindeonbekende(n)
In dit hoofdstuk werk je met veeltermen in één veranderlijke of onbekende.
Deveelterm6 x 3 + 5 x 2 + 3 x 7iseenviertermindeonbekende(n)
Deveelterm6 x 3 + 5 x 2 + 3 x 7iseenviertermindeonbekende(n)
Jenoteertzo’nveeltermmeteenletter,gevolgddoordeonbekendetussenhaakjes.
Deveelterm6 x 3 + 5 x 2 + 3 x 7iseenviertermindeonbekende(n)
Je noteert zo’n veelterm met een letter, gevolgd door de onbekende tussen haakjes.
Voorbeeld: v (x) = −2 x 2 + 5 x iseenveelterminéénveranderlijke x.
Indithoofdstukwerkjemetveeltermeninéénveranderlijke. Jenoteertzo’nveeltermmeteenletter,gevolgddoordeonbekendetussenhaakjes.
Voorbeeld
Indithoofdstukwerkjemetveeltermeninéénveranderlijke. Jenoteertzo’nveeltermmeteenletter,gevolgddoordeonbekendetussenhaakjes.
Voorbeeld: v (x) = −2 x 2 + 5 x iseenveelterminéénveranderlijke x.
Indithoofdstukwerkjemetveeltermeninéénveranderlijke. Jenoteertzo’nveeltermmeteenletter,gevolgddoordeonbekendetussenhaakjes.
Voorbeeld: v (x) = −2 x 2 + 5 x iseenveelterminéénveranderlijke x.
v (x) = – 2 x 2 + 5 x is een veelterm in één veranderlijke x.
Voorbeeld: v (x) = −2 x 2 + 5 x iseenveelterminéénveranderlijke x.
5.1.2 Herleidenenrangschikkenvanveeltermen
5.1.2 Herleidenenrangschikkenvanveeltermen
4.1.2 Herleiden en rangschikken van een veelterm
5.1.2
5.1.2
Neemdeveelterm
Herleidenenrangschikkenvanveeltermen
Neemdeveelterm g (x) = 4 x + 6 x 2 8 x 3 + 7 x 5 x 2 + x 3 8
• Eenveelterm herleiden,betekentdatjedegelijksoortigeeentermenoptelt.
Herleidenenrangschikkenvanveeltermen
Neemdeveelterm g (x) = 4 x + 6 x 2 8 x 3 + 7 x 5 x 2 + x 3
Neemdeveelterm g (x) = 4 x + 6 x 2 8 x 3 + 7 x 5 x 2 + x 3 8
Herleiddegegevenveelterm:
• Een veelterm betekent dat je de gelijksoortige eentermen optelt.
• Eenveelterm herleiden,betekentdatjedegelijksoortigeeentermenoptelt.
• Eenveelterm herleiden,betekentdatjedegelijksoortigeeentermenoptelt. Herleiddegegevenveelterm:
• Eenveelterm rangschikken,betekentdatjedeveeltermherschrijft naardalende(ofstijgende)machtenvandeveranderlijke.
• Eenveelterm herleiden,betekentdatjedegelijksoortigeeentermenoptelt.
Herleiddegegevenveelterm:
Herleiddegegevenveelterm:
• Een veelterm rangschikken betekent dat je de veelterm herschrijft naar dalende (of stijgende) machten van de veranderlijke.
• Eenveelterm rangschikken,betekentdatjedeveeltermherschrijft naardalende(ofstijgende)machtenvandeveranderlijke.
Rangschikdeveeltermnaardalendemachtenvan x :
• Eenveelterm rangschikken,betekentdatjedeveeltermherschrijft naardalende(ofstijgende)machtenvandeveranderlijke.
• Eenveelterm rangschikken,betekentdatjedeveeltermherschrijft naardalende(ofstijgende)machtenvandeveranderlijke.
Rangschikdeveeltermnaardalendemachtenvan x :
Rangschikdeveeltermnaardalendemachtenvan x :
Rangschikdeveeltermnaardalendemachtenvan x :
Eenveeltermwaarinalleopeenvolgendemachtenvandeonbekendevoorkomen,noemje volledig Isdegegevenveelterm g (x)volledig?
Eenveeltermwaarinalleopeenvolgendemachtenvandeonbekendevoorkomen,noemje volledig Isdegegevenveelterm g (x)volledig?
Eenveeltermwaarinalleopeenvolgendemachtenvandeonbekendevoorkomen,noemje volledig Isdegegevenveelterm g (x)volledig?
5.1.3 Getalwaardevaneenveelterm
Eenveeltermwaarinalleopeenvolgendemachtenvandeonbekendevoorkomen,noemje volledig Isdegegevenveelterm g (x)volledig?
4.1.3 Getalwaarde van een veelterm
5.1.3 Getalwaardevaneenveelterm
5.1.3
5.1.3
Getalwaardevaneenveelterm
Getalwaardevaneenveelterm
Degetalwaardevaneenveeltermvoor x = a, ishetgetaldatjeverkrijgtdoordeonbekende x tevervangendoor a Degetalwaardevan f (x) = 2 x 2 + 7 x 9voor x = a schrijfjekortwegals f (a). f (−2) = f (4) =
f (– 2) =
Degetalwaardevaneenveeltermvoor x = a, ishetgetaldatjeverkrijgtdoordeonbekende x tevervangendoor a Degetalwaardevan f (x) = 2 x 2 + 7 x 9voor x = a schrijfjekortwegals f (a). f (−2) = f (4) =
Degetalwaardevaneenveeltermvoor x = a, ishetgetaldatjeverkrijgtdoordeonbekende x tevervangendoor a Degetalwaardevan f (x) = 2 x 2 + 7 x 9voor x = a schrijfjekortwegals f (a). f (−2) = f (4) =
Degetalwaardevaneenveeltermvoor x = a, ishetgetaldatjeverkrijgtdoordeonbekende x tevervangendoor a Degetalwaardevan f (x) = 2 x 2 + 7 x 9voor x = a schrijfjekortwegals f (a). f (−2) = f (4) =
5.1.4 Graadvaneenveelterm
f (4) = ©VANIN
5.1.4 Graadvaneenveelterm
Definitie Graadvaneenveelterm
5.1.4 Graadvaneenveelterm
5.1.4 Graadvaneenveelterm
4.1.4 Graad van een veelterm
Definitie Graadvaneenveelterm
Degraadvaneenveeltermin x isdehoogsteexponentvandeonbekende x indieveelterm.
Definitie Graadvaneenveelterm
Definitie Graadvaneenveelterm
Degraadvaneenveeltermin x isdehoogsteexponentvandeonbekende x indieveelterm.
Notatie:gr ( f (x))
Degraadvaneenveeltermin x isdehoogsteexponentvandeonbekende x indieveelterm.
Degraadvaneenveeltermin x isdehoogsteexponentvandeonbekende x indieveelterm.
Notatie:gr ( f (x))
Notatie:gr ( f (x))
Notatie:gr ( f (x))
(x) = 5 x
(x)) =
(x)) =
(x) = 7 x 6 + 8 x 5 gr (p(
)) =
5.1.5 Coëfficiëntenrij
4.1.5 Coëfficiëntenrij
Gegeven: f (x) = −2 x 3 x 4 + 6 x 3 + 6
Jerangschiktdeveelterm: f (x) = −3 x 4 + 6 x 3 2 x + 6
Jemaaktdeveeltermvolledig: f (x) = −3 x 4 + 6 x 3 + 0 x 2 2 x + 6
Derijgetallen−3,6,0,−2,6noemjede coëfficiëntenrij vandezeveelterm.
Noteerdecoëfficiëntenrijvan g (x) = x 5 + 8 x 3 + x 2 x 2 :
4.1.6
Bewerkingen met veeltermen
5.1.6 Bewerkingenmetveeltermen
Optellenenaftrekkenvanveeltermen
Werkwijze • Werkdehaakjesuit.
• Herleiddeverkregensom.
Herleid de verkregen veelterm naar dalende machten van x
(7 x 2 5 x + 4) + (3 x 6) (3 x 3 5) (2 x 4 5 x 3 x) = 7 x 2 5 x + 4 + 3 x 6 = = =
Vermenigvuldigenvaneeneentermeneenveelterm
Werkwijze
• Vermenigvuldigdeeentermmetelketermvandeveelterm.
Vermenigvuldig de eenterm met elke term van de veelterm (distributieve eigenschap).
• Teldeverkregenproductenop.
2 x (x 2 2 x + 3) −3 x 2 (2 x 4 5 x 3 + 3)
= 2 x x 2 + 2 x (−2 x) + 2 x 3=
Werkwijze
Vermenigvuldigenvanveeltermen
• Vermenigvuldigelketermvandeeneveeltermmetelketermvandeandereveelterm.
• Teldeverkregenproductenopenherleidhetresultaat.
Tel de verkregen producten op en herleid het resultaat, indien mogelijk.
(2 x + 3) (x 3 5) (− x 3 3) (2 x 2 x + 7)
= 2 x x 3 + 2 x (−5) + 3 x 3 + 3 (−5)
Oefeningen
REEKSA
1 Herleidenrangschiknaardalendemachtenvandeonbekende.
a)3 x + 5 x 4 7 x 2 4 x =
b)−8 5a 3 + 2a 3a 3 + 6a 2 =
c)7 x 4 3 x 2 + 9 x 7x 2 2 x 3 5 =
©VANIN
d)− t 3 + 4 t 6 t 2 5 t 3 + t 9 t 2 =
2 Berekendegetalwaarden.
Bereken de getalwaarde.
a) f (x) = 2 x 2 + 3 x 5 f (−3) = f (2) =
b) g (b) = b 3 + 4 b 2 3 g (−2) = g (3) =
c) h (y) = y 4 2 y 2 4 h (3) = h (−1) =
3 Bepaaldegraad.
a)gr(6 x 3 + 7 x 11) =
f (– 3) = g (3) = h (– 1) = i (– 2) =
d) i (x) = x 5 + 2 x 3 i (−2) = i (2) =
e)gr (x (x 3 5)) =
b)gr(−8 x 2 + 9 x 3 7 x 2) = f)gr ((x + 2) (x 3)) =
c)gr(5 + 3 x 2 7 x 4) = g)gr((x 7) (x 2 + x)) =
x x g h = g)gr
d)gr(x 4 5 x 3 3 x 4 + 9) = h)gr (x 2 (x 3 + 2) x) =
4 Bepaaldecoëfficiëntenrij.
Bepaal de coëfficiëntenrij. Herleid en rangschik de veelterm eerst indien nodig.
a)−8 x 6 + x 5 3 x 4 + 2 x 3 6 x 2 + 7 x 3
b)2 x 5 4 x 3 + 6 x 2 x + 5
c)3 x 7 + 6 x 4 3 x 2 + 5 x 4 + 8 x 9
R5 Werkuit,herleid,rangschikenbepaaldegraad.
5 Werk uit. Herleid en rangschik de verkregen veelterm. Bepaal de graad van die veelterm.
(−2
a)(x 2) (−2 x 2 3 x + 4)
c)(3 x x 2) (2 x 3 5)
©VANIN
b)(7 x 8) (−3 x 2 + 5x)
d) x 2 (x 5 x 2) x 3
6 Werkuit,herleid,rangschikenbepaaldegraad.
Werk uit. Herleid en rangschik de verkregen veelterm. Bepaal de graad van die veelterm.
a)(2 x 2 x + 3) (x 3 2 x 2 4)
b)(x + 3 x 2) (2 x x 3) (−5 x 2)
4.2 De euclidische deling van twee veeltermen
4.2.1 Inleiding
gehele getallen
• Bepaal x ∈ ℤ zodat
4 x = 28
Oplossing: x = 7
JOBNAME:Pienter.4TSO.lwsPAGE:6SESS:689OUTPUT:FriMar3009:11:462018
7 noem je het quotiënt van de deling van het deeltal 28 door de deler 4.
• Bepaal x ∈ ℤ zodat
4 x = 31
Er is geen geheel getal x te vinden dat aan de vergelijking voldoet.
Je zegt dat 31 niet deelbaar is door 4 in de verzameling van de gehele getallen.
• Er geldt: 4 7 + 3 = 31
7 noem je het quotiënt q van de deling van het deeltal D = 31
door de deler d = 4.
De rest r van de deling is 3.
veeltermen in één veranderlijke
• Bepaal een veelterm f (x) zodat
2x f (x) = 6 x 2 + 4 x
Oplossing: f (x) = 3 x + 2
3x + 2 noem je het quotiënt van de deling van het deeltal 6 x 2 + 4 x door de deler 2x
• Bepaal een veelterm f (x) zodat
2x f (x) = 6 x 2 + 4 x + 3
Er is geen veelterm f (x) te vinden die aan de vergelijking voldoet.
Je zegt dat 6 x 2 + 4 x + 3 niet deelbaar is door 2x in de verzameling van de veeltermen.
• Er geldt: 2x (3x + 2) + 3 = 6 x 2 + 4 x + 3
3x + 2 is het quotiënt q (x) van de deling van het deeltal D (x) = 6 x 2 + 4 x + 3
door de deler d (x) = 2x
5.2 Deeuclidischedelingvantweeveeltermen
De rest r (x) van de deling is 3.
4.2.2 De staartdeling van een veelterm door een eenterm
5.2.1 Destaartdeling
©VANIN
delingvannatuurlijkegetallen
deling van gehele getallen
5.2.2 Opgaandedeling Eenopgaandedelingiseendelingwaarbijde
delingvaneenveeltermdooreeneenterm
5.2.3 Destaartdelingbijdedelingvantweeveeltermen
4.2.3 De staartdeling bij de deling van twee veeltermen
OmD(x) = 5 x 4 3 x 3 + 7 x 9tedelendoor d (x) = x 2,kunjeookeenstaartdelinggebruiken.
Om D (x) = 5x 4 – 3x 3 + 7x – 9 te delen door d (x) = x –2, kun je ook een staartdeling gebruiken.
Je rangschikt het deeltal en de deler naar dalende machten van x
• Jerangschikthetdeeltalnaardalendemachtenvan x Bijonvolledigeveeltermenschrijfjedeontbrekendemachtenvan x meteencoëfficiënt0.
• Jedeeltdeeerstetermvanhetdeeltal(5 x 4)doordeeerstetermvandedeler(x).
Hetresultaatisdeeerstetermvanhetquotiënt.
©VANIN
• Jevermenigvuldigtdeeerstetermvanhetquotiënt(5 x 3)metdedeler(x 2).
Deverkregenveelterm(5 x 4 10 x 3)trekjeafvanhetdeeltal.
• Jedeeltopnieuwdeeersteterm(7 x 3)doordeeerstetermvandedeler.
Hetresultaat(7 x 2)isdetweedetermvanhetquotiënt.
• Jeblijftdezewerkwijzeherhalentotdegraadvanderestkleinerisdandegraadvandedeler.
q (x) =
r (x) =
d (x) q (x) + r (x) =
5.2
enwashetsamenmetdeBijbeleenvandemeestgedrukteboeken. In DeElementen behandeldehijonderandere:
enwashetsamenmetdeBijbeleenvandemeestgedrukteboeken. In DeElementen behandeldehijonderandere:
• detheorievandeelbaarheid;
• detheorievandeelbaarheid;
dieindietijdbeschikbaarwasin13boeken: Daarinwerdvanuitvijfaxioma’sallewiskundesystematischafgeleid. 2000jaarlangwasditeenvandebelangrijkstewiskundewerken enwashetsamenmetdeBijbeleenvandemeestgedrukteboeken. In DeElementen behandeldehijonderandere:
enwashetsamenmetdeBijbeleenvandemeestgedrukteboeken. In DeElementen
• degrootstegemenedelereneenalgoritmeomdieteberekenen;
Deeuclidischedelingvantweeveeltermen
Algemeen De euclidische deling van de veelterm D (x) door de veelterm d (x), waarbij d (x) ≠ 0, heeft als quotiënt de veelterm q (x) en als rest de veelterm r (x)
• degrootstegemenedelereneenalgoritmeomdieteberekenen;
q + r
)noemjedaneendelervanD(x). D(x) delingvannatuurlijkegetallen
• eenbewijsdateroneindigveelpriemgetallenzijn.
• detheorievandeelbaarheid;
Deeuclidischedelingvantweeveeltermen
• eenbewijsdateroneindigveelpriemgetallenzijn.
• detheorievandeelbaarheid; • degrootstegemenedelereneenalgoritmeomdieteberekenen; • eenbewijsdateroneindigveelpriemgetallenzijn.
• degrootstegemenedelereneenalgoritmeomdieteberekenen;
Voorbeelden
5.2.1 Destaartdeling
• eenbewijsdateroneindigveelpriemgetallenzijn.
Voorbeelden
Voerdedelingenuit.
D (x) = d (x) ⋅q (x) + r (x) waarbij gr (r (x)) < gr (d (x)) of r (x) = 0 Als r (x) = 0, dan spreek je van een opgaande deling.
Voorbeelden Voerdedelingenuit.
Voerdedelingenuit.
Voorbeelden Voerdedelingenuit.
delingvaneenveeltermdooreeneenterm
Voorbeelden
delingvannatuurlijkegetallen
delingvaneenveeltermdooreeneenterm
Opmerking
Opmerking
Opmerking
gr (q (x)) = gr (D(x)) gr (d (x))
gr (q (x)) = gr(D (x)) – gr(d (x))
Opmerking
gr (q (x)) = gr (D(x)) gr (d (x))
5.2.2 Opgaandedeling
Stelling Bij de deling van een veelterm D (x) door de veelterm d (x), waarbij d (x) ≠ 0, bestaat er juist één quotiënt q (x) en juist één rest r (x)
Eenopgaandedelingiseendelingwaarbijde
Bewijs
Eenopgaandedelingiseendelingwaarbijde
D(x)isdeelbaardoor d (x) ⇔ D(x) = d (x) q (x)
©VANIN
Eenstaartdelingiseenalgoritmeomeendelinguittevoeren.
Eenstaartdelingiseenalgoritmeomeendelinguittevoeren. HetwoordalgoritmeiseenverbasteringvanhetOudengelsewoord algorism,datvanhetLatijnsewoordalgorismuskomt.
Criterium D(x)isdeelbaardoor
d (x)noemjedaneendelervanD(x).
Notatie: d (x) D(x)
HetwoordalgoritmeiseenverbasteringvanhetOudengelsewoord algorism,datvanhetLatijnsewoordalgorismuskomt.
Bewijs uit het ongerijmde: als je kunt aantonen dat het onmogelijk is dat er twee verschillende quotiënten zijn en twee verschillende resten, dan is er juist één quotiënt en juist één rest.
Stel: er bestaan twee quotiënten q 1 (x) en q
Eenstaartdelingiseenalgoritmeomeendelinguittevoeren. HetwoordalgoritmeiseenverbasteringvanhetOudengelsewoord algorism,datvanhetLatijnsewoordalgorismuskomt. Hetwoord‘algorisme’verweesoorspronkelijkalleennaarderegelsvoor hetrekenenmetArabischecijfers,maarevolueerdeinde18eeeuw naar‘algoritme’.Hetwoordalgoritmewordtnugebruiktvooralle eindigeproceduresomproblemenoptelossenoftakenuittevoeren.
Eenstaartdelingiseenalgoritmeomeendelinguittevoeren. HetwoordalgoritmeiseenverbasteringvanhetOudengelsewoord algorism,datvanhetLatijnsewoordalgorismuskomt. Hetwoord‘algorisme’verweesoorspronkelijkalleennaarderegelsvoor hetrekenenmetArabischecijfers,maarevolueerdeinde18eeeuw naar‘algoritme’.Hetwoordalgoritmewordtnugebruiktvooralle eindigeproceduresomproblemenoptelossenoftakenuittevoeren. Heteerstealgoritmevooreencomputer,geschrevenin1842, istevindenindenotitiesvanAdaByron.
Voorbeeld
Hetwoord‘algorisme’verweesoorspronkelijkalleennaarderegelsvoor hetrekenenmetArabischecijfers,maarevolueerdeinde18eeeuw naar‘algoritme’.Hetwoordalgoritmewordtnugebruiktvooralle eindigeproceduresomproblemenoptelossenoftakenuittevoeren. Heteerstealgoritmevooreencomputer,geschrevenin1842, istevindenindenotitiesvanAdaByron. Zijwordtdaarombeschouwdalsdeeerstecomputerprogrammeur.
Hetwoord‘algorisme’verweesoorspronkelijkalleennaarderegelsvoor hetrekenenmetArabischecijfers,maarevolueerdeinde18eeeuw naar‘algoritme’.Hetwoordalgoritmewordtnugebruiktvooralle eindigeproceduresomproblemenoptelossenoftakenuittevoeren.
Heteerstealgoritmevooreencomputer,geschrevenin1842, istevindenindenotitiesvanAdaByron.
(x) en twee resten r
(x) en r 2 (x)
Zijwordtdaarombeschouwdalsdeeerstecomputerprogrammeur.
Zijwordtdaarombeschouwdalsdeeerstecomputerprogrammeur.
Dan: D (x) = d (x) q 1 (x) + r 1 (x) met gr (
Heteerstealgoritmevooreencomputer,geschrevenin1842, istevindenindenotitiesvanAdaByron.
) =
Zijwordtdaarombeschouwdalsdeeerstecomputerprogrammeur.
I ALGEBRAÏSCHREKENEN
= 0 alle termen naar het linkerlid
⇔ d (x) [q 1 (x) – q 2 (x)] + r 1 (x) – r 2 (x) = 0 de factor d (x) afzonderen
Omdat gr (r 1 (x) – r 2 (x)) < gr (d (x)) of r 1 (x) – r 2 (x) = 0 kunnen d (x) [q 1 (x) – q 2 (x)] en r 1 (x) – r 2 (x) niet tegengesteld zijn
⇒ d (x) [q 1 (x) – q 2 (x)] = 0 en r 1 (x) – r 2 (x) = 0
⇒ q 1 (x) – q 2 (x) = 0 en r 1 (x) – r 2 (x) = 0
Besluit: er bestaat juist één quotiënt q (x) en juist één rest r (x) d (x) ≠ 0
⇔ q 1 (x) = q 2 (x) en r 1 (x) = r 2 (x)
5.2.2 Opgaandedeling
4.2.4 Opgaande deling
Kenmerk
Eenopgaandedelingiseendelingwaarbijde
Een opgaande deling is een deling waarbij
D (x) is deelbaar door d (x) ⇔ D (x) = d (x) q (x)
Criterium D(x)isdeelbaardoor d (x) ⇔ D(x) = d (x) q (x)
d (x)noemjedaneendelervanD(x).
Notatie: d (x) D(x)
Voorbeeld
Voorbeeld
Toon aan dat D (x) = 2x 3 –
Een veelterm ontbinden in factoren
I ALGEBRAÏSCHREKENEN
©VANIN
(x) = ⇒ D (x) is deelbaar door d (x)
Controle: d (x) ⋅ q (x) = D (x)
Een veelterm ontbinden in factoren betekent dat je de veelterm schrijft als een product van veeltermen en eentermen die een lagere graad hebben dan de oorspronkelijke veelterm. Als de veelterm D (x) deelbaar is door de veelterm d (x), dan kan je D (x) schrijven als een product d (x) q (x). Dit product is een ontbinding in factoren van D (x)
• Ontbind D (x) = 6x 2 + 4x in factoren.
D (x) is deelbaar door 2x (zie § 4.2.1). Het quotiënt is
⇒ 6x 2 + 4x =
De veelterm 6x 2 + 4x is ontbonden in de factoren en
• Werk het product van de toegevoegde tweetermen uit:
(3x – 4) (3x + 4) =
De verkregen veelterm D (x) = kan je ontbinden in de factoren 3x – 4 en 3x + 4 en is dus deelbaar door 3x – 4 en door 3x + 4
• Bepaal het quotiënt van de deling van D (x) = 9x 2 – 25 door d (x) = 3x + 5
9x 2 – 25 = (3x + 5) ⇒ q (x) =
Oefeningen
Oefeningen
REEKSA
7 Berekenhetquotiëntzonderstaartdeling. deeltal
a)8 x 5 + 6 x 3 + 24 2
b)7x 4 + 5x 2 + x x
c)12 x 5 72 x 2 + 9 x 3x d)−2 x 4 3 x 3 + x 2 x 2
x
8 BerekenhetquotiëntenderestvandedelingvanD(x)door d (x).
Bereken het quotiënt en de rest van de deling van D (x) door d (x).
a)D(x)=4x 2 8 d (x)=2 x c)D(x)=2 x 4 3 x 2 d(x)=4x 3 q (x) = en r(x) = q (x) = en r (x) =
D (x) D (x) D (x) D (x)
b)D(x)=−2 x 3 +3 x 2 +5 d (x)=6 x 2 d)D(x)=4 x 3 −10 x 2 +7 xd (x)=−2 x q (x) = en r (x) =
Bepaalhetdeeltal.
a) deeltal:
©VANIN
b) deeltal:
c) deeltal: d) deeltal: e) deeltal:
R 10 Berekenhetquotiëntenderestvandedelingvan D (x)door d (x).
Bereken het quotiënt en de rest van de deling van (x) door d (x).
a)D(x)=28 x 2 +53 x +31 d (x)=4x +3
D (x)
q (x) =
r (x) =
D (x)
d)D(x)=6 x 2 +3x −8 d (x)=2 x −4
D (x)
q (x) =
r (x) =
b)D(x)=6 x 3 + 16 x 2 x −6 d (x)=3 x +2e)D(x)=−4 x 3 + 7 x 2 +7 x +4 d (x)=− x + 2
q (x) =
r (x) =
D (x)
q (x) =
r (x) =
D (x)
D (x)
c)D(x)=6 x 2 + 5 x + 8 d (x)= x +4f)D(x)=−4 x 2 + 2 x −5 d (x)= x 2 1
q (x) =
r (x) =
q (x) =
r (x) =
R 11 BerekenhetquotiëntenderestvandedelingvanD(x)door d (x).Maakdeproef.
Bereken het quotiënt en de rest van de deling van D (x) door d (x). Maak de proef.
D (x)
a)D(x)=−3 x 3 14 x 2 16 x −7
d (x)= x 2 + 4 x +3
q (x) = en r (x) =
Proef:
D (x)
b)D(x)=−6 x 4 + 7 x 3 17 x 2 +11 x −8
d (x)=2 x 2 x + 1
q (x) = en r (x) =
Proef:
R 12
BerekenhetquotiëntenderestvandedelingvanD(x)door d (x).Maakdeproef.
Bereken het quotiënt en de rest van de deling van D (x) door d (x). Maak de proef.
a)D(x)= x 5 x 3 +5 d (x)= x 3 + 3
D (x)
q (x) = en r (x) =
Proef:
b)D(x)= x 4 3x 3 + xd (x)= x 2 + x +1
D (x)
q (x) = en r (x) =
Proef:
a) D (x) = x 4 + 2x 3 – 2x 2 + 7x – 2 = (x 2 + 3x - 1) ( ) b) D (x) = 4x 5 + 9x 3 + 4x 2 + 9 = (4x 2 + 9) ( )
©VANIN
14 Losop.
a)Bereken a en b zodat ax 3 + bx 2 + 3 x + 2deelbaarisdoor x 2 + x + 1. Berekenhetquotiënt.
©VANIN
Antwoord: a = en b = en q (x) =
b)Bereken a en b zodatbijdelingvan2 x 3 + ax 2 + bx + 1door2 x 2 3 x + 1derest3 x −4is. Berekenhetquotiënt.
Antwoord: a = en b = en q (x) =
5.3.1
DeregelvanHorner
4.3.1 De regel van Horner
Jebepaalthetquotiëntenderestvandedelingvan2 x 3 3 x 2 4 x + 2door x 3.
Bijhetmakenvaneenstaartdelingrekenjeeigenlijkenkelmetdecoëfficiënten.
DeregelvanHorner
Jekuntdecoëfficiëntenschikkeninhetvolgendeschema.
2−3−42
Jelaatdeeerstecoëfficiëntvanhetdeeltalzakken. 3 2
2−3−42
Jevermenigvuldigtdatgetalmet a Hetverkregenproductschrijfje onderdetweedecoëfficiëntvanhetdeeltal. 3 6 2
2− 3−42
Jeteltdecoëfficiëntenhetproducteronderop. 3 6 23
2−3−42
Jeherhaaltdezewerkwijze voorallecoëfficiëntenvanhetdeeltal. Jezeteenverticaalstreepjevóórhetlaatstegetal. 3 6915 23517
©VANIN
2−3−42
Deverkregenrijisdecoëfficiëntenrijvanquotiëntenrest. q (x) = r (x) = gr (q (x)) = gr (r (x)) = 3 6915 23517
Dit algoritme om snel het quotiënt en de rest van een deling door x – a (met a ∈ r) te berekenen, staat bekend als de regel van Horner
Ditalgoritmeomsnelhetquotiëntenderestvaneendelingdoor x a teberekenen, staatbekendals deregelvanHorner
Opmerking
Zorgeraltijdvoordathetdeeltaleenvolledigeveeltermis.
Voorbeelden
Voorbeelden
Voorbeelden
a) D(x) = 3 x 3 4 x 2 9 x + 10
D (x)
a) D(x) = 3 x 3 4 x 2 9 x + 10
d (x) = x 2
d (x) = x 2
c) D(x) = x 3 + 1
c) D(x) = x 3 + 1
D (x
d (x) = x 1
d (x) = x 1 q (x) = r (x) = b) D(x) = −2 x 2 + 5 x + 7
q (x) =
q (x) = r (x) =
r (x) =
D (x)
b) D(x) = −2 x 2 + 5 x + 7
d (x) = x + 3
d (x) = x + 3
q (x) =
q (x) =
r (x) =
r (x) =
©VANIN


q (x) =
r (x) =
D (x)
d) D(x) = x 4 x 2 + 2 x + 5
d) D(x) = x 4 x 2 + 2 x + 5
d (x) = x + 2
d (x) = x + 2
q (x) =
r (x) =
q (x) = r (x) = 3−4−910
WilliamGeorgeHorner (1786-1837)waseenBritsewiskundige. HijstudeerdeaandeKingswoodSchoolinBristol.Opzijnveertiendewerd hijdaarassistent-directeurenopzijnachttiendewerdhijerzelfsdirecteur. OpzijndrieëntwintigstestichttehijeeneigenschoolinBath. Hijisbekendomzijnschemaomveeltermentedelendoor x a, dathijpubliceerdein1830.
WilliamGeorgeHorner (1786-1837)waseenBritsewiskundige. HijstudeerdeaandeKingswoodSchoolinBristol.Opzijnveertiendewerd hijdaarassistent-directeurenopzijnachttiendewerdhijerzelfsdirecteur. OpzijndrieëntwintigstestichttehijeeneigenschoolinBath. Hijisbekendomzijnschemaomveeltermentedelendoor x a, dathijpubliceerdein1830.
de duivel) uit: met dat apparaat kon hij beelden laten bewegen (de voorloper van de film).
In1834vondhijookhet‘Daedalum’(wielvan deduivel)uit.Eenapparaatwaarmeehijbeelden konlatenbewegen(devoorlopervandefilm). Vreemdgenoegwerdzijnuitvindingvergeten. PasmeerdandertigjaarlaterwerderinAmerikaeenpatentopgenomen doorWilliamF.Lincoln.
Lincolnvervingdenaam‘Daedalum’door‘zoetrope’of‘levendwiel’.
In1834vondhijookhet‘Daedalum’(wielvan deduivel)uit.Eenapparaatwaarmeehijbeelden konlatenbewegen(devoorlopervandefilm). Vreemdgenoegwerdzijnuitvindingvergeten. PasmeerdandertigjaarlaterwerderinAmerikaeenpatentopgenomen doorWilliamF.Lincoln. Lincolnvervingdenaam‘Daedalum’door‘zoetrope’of‘levendwiel’.


Oefeningen
Oefeningen
REEKSA
15 BerekenhetquotiëntenderestvandedelingvanD(x)door d (x)metderegelvanHorner.
Bereken het quotiënt en de rest van de deling van D (x) door d (x) met de regel van Horner.
a)D(x) = 5 x 3 + 7 x 2 x + 11
D ( )
d (x) = x 2
d)D(x) = x 5 + 3 x 4 + 2 x 3 + 6 x 2 + 7 x + 21
D (x)
d (x) = x + 3
−3−30−60−21 102070
q (x) = q (x)=
r (x) = r (x)=
b)D(x) = x 4 2 x 3 + 8 x 2 16 x
d (x) = x + 2
1−28−160
−2−28−3296
1−416−4896
D (x)
c)D(x) = x 4 27
D ( ) D (x) D (x)
e)D(x) = x 3 + 9 x 2 1
d (x) = x 4
−190−1 4−42080 −152079
q (x) = q (x) =
r (x) = r (x) =
d (x) = x 3
r (x) = r (x) = 57−111 2103466 5173377
f)D(x) = 2 x 5 + 10 x 4 + x 2 + 2 x
d (x) = x + 5
2100120
−5−1000−515 2001−315
1000−27 3392781 1392754 1326721
q (x) = q (x) =
16 BerekenhetquotiëntenderestvandedelingvanD(x)door d (x)metderegelvanHorner.
a)D(x) = x 2 + 3 x 9
Bereken het quotiënt en de rest van de deling van D (x) door d (x) met de regel van Horner. D (x) D (x
d (x) = x 1 2
d)D(x)= x 3 1 2 x 2 −8 x + 3 2
d (x)= x −3
q (x) = q (x) =
r (x) = r (x) =
(x) D (x)
b)D(x)=4 x 3 −7 x +3 e)D(x) = 6 5 x 4 2 x 3 21 20 x + 9 4
d (x)= x + 3 2 d (x) = x 5 3 q (x) =
(x) =
(x) =
(x) = c)D(x) = x 3 1 3 x 2 + 4 3 x
x) = x 3 + 2x 2 + 4x + 4 2 d (x) = x + 2
17 Vervolledig het rekenschema van Horner en bepaal telkens het deeltal, de deler, het quotiënt en de rest. a) 3
D (x) = d (x) = q (x) = r (x) =
(x) =
D (x) = d (x) = q (x) = r (x) =
©VANIN
18 Bereken het quotiënt en de rest van de deling van D (x) door d (x) met de regel van Horner (a
5.3.2 Dereststelling
4.3.2 De reststelling
5.3.2 Dereststelling
Berekenderestvandedeling.
Berekenderestvandedeling.
Berekenderestvandedeling.
(−3 x 4 8 x 3 7 x 2 + 5 x + 3):(x + 2)
(−3 x 4 8 x 3 7 x 2 + 5 x + 3):(x + 2)
(−3 x 4 8 x 3 7 x 2 + 5 x + 3):(x + 2) r (x) =
−3−8−753
−3−8−753
−2646−22
−2646−22
−3−8−753
−3−2−311−19
−3−2−311−19
−2646−22
r (x) =
r (x) =
−3−2−311−19
Watsteljevast?
Wat stel je vast?
Watsteljevast?
Watsteljevast?
Stel: f (x)=−3 x 4 −8x 3 −7 x 2 +5 x +3
Stel: f (x)=−3 x 4 −8x 3 −7 x 2 +5 x +3
Berekendegetalwaarde f (−2).
Stel: f (x)=−3 x 4 −8x 3 −7 x 2 +5 x +3
Berekendegetalwaarde f (−2). f (−2) = −3 (−2) 4 8 (−2) 3 7 (−2) 2 + 5 (−2) + 3
Stel: D (x) = D (– 2). D (– 2)
Berekendegetalwaarde f (−2). f (−2) = −3 (−2) 4 8 (−2)
f (−2) = −3 (−2) 4 8 (−2) 3 7 (−2) 2 + 5 (−2) + 3 = = =
Omderestvaneendelingdoor x a teberekenen,volstaathetdusom f (a)teberekenen.
Omderestvaneendelingdoor x a teberekenen,volstaathetdusom f (a)teberekenen.
Om de rest van een deling van een veelterm D (x) door x – a te berekenen, volstaat het dus om D (a) te berekenen.
Reststelling
Omderestvaneendelingdoor x a teberekenen,volstaathetdusom f (a)teberekenen.
Reststelling
Reststelling
Reststelling
Reststelling Derestvandedelingvaneenveelterm f (x)door x a isgelijkaan f (a).
Reststelling Derestvandedelingvaneenveelterm f (x)door x a isgelijkaan f (a).
Kenmerk De rest van de deling van een veelterm D (x) door x – a (met a ∈ r) is gelijk aan D (a).
Reststelling Derestvandedelingvaneenveelterm f (x)door x a isgelijkaan f (a).
Bewijs
Bewijs
f (x) = (x a) q (x) + r (x)
f (x) = (x a) q (x) + r (x)
Bewijs
Bewijs
gr (r (x)) 1of r (x) = 0 ⇒ r (x) R
gr (r (x)) 1of r (x) = 0 ⇒ r (x) R
D (x) = (x – a) q (x) + r (x)
stel r (x) = r
stel r (x) = r
Criterium
Criterium
Criterium
⇓ gr (r (x)) < 1 of r (x) = 0 ⇒ r (x) ∈ r stel r (x) = r
f (x) = (x a) q (x) + r
f (x) = (x a) q (x) + r
f (x) = (x a) q (x) + r (x) gr (r (x)) 1of r (x) = 0 ⇒ r (x) R
f (a) = (a a) q (a) + r
f (a) = (a a) q (a) + r
stel r (x) = r
D (x) = (x – a) q (x) + r ⇓ bereken de getalwaarde D (a)
f (a) = 0 q (a) + r
f (a) = 0 q (a) + r
f (x) = (x a) q (x) + r
f (a) = r
f (a) = r
f (a) = (a a) q (a) + r
f (a) = 0 q (a) + r
D (a) = (a – a) q (a) + r = 0 q (a) + r = r
Voorbeelden
f (a) = r
Voorbeelden
Bepaalderestzonderdedelinguittevoeren.
Voorbeelden
Bepaalderestzonderdedelinguittevoeren. opgave berekeningen
Bepaalderestzonderdedelinguittevoeren. opgave berekeningen
Deelbaarheidscriterium
Deelbaarheidscriterium
Eenveeltermisdeelbaardooreenandereveeltermalsderest0is.
Eenveeltermisdeelbaardooreenandereveeltermalsderest0is.
Deelbaarheidscriterium
Kenmerk van deelbaarheid door x – a
Eenveeltermisdeelbaardooreenandereveeltermalsderest0is.
Eenveelterm f (x)isdeelbaardoor x a alsenslechtsals
Eenveelterm f (x)isdeelbaardoor x a alsenslechtsals
Een veelterm is deelbaar door een andere veelterm als en slechts als de rest 0 is.
f (a) = 0.
f (a) = 0.
Kenmerk Een veelterm D (x) is deelbaar door x – a (met a ∈ r) ⇔ D (a) = 0
Eenveelterm f (x)isdeelbaardoor x a alsenslechtsals
f (a) = 0.
4.3.3 Toepassing: de methode van de onbepaalde coëfficiënten
5.3.3 Toepassing:demethodevandeonbepaaldecoëfficiënten
5.3.3 Toepassing:demethodevandeonbepaaldecoëfficiënten
5.3.3 Toepassing:demethodevandeonbepaaldecoëfficiënten
5.3.3 Toepassing:demethodevandeonbepaaldecoëfficiënten
Modeloefening1
Modeloefening 1
Modeloefening1
Modeloefening1
Modeloefening1
Bij deling van D (x)
Bijdelingvan f (x) = x 3 + ax 2 + 16 x + 21door x + 3isderest0. Bepaaldecoëfficiënt a
Bijdelingvan f (x) = x 3 + ax 2 + 16 x + 21door x + 3isderest0. Bepaaldecoëfficiënt a
Bijdelingvan f (x) = x 3 + ax 2 + 16 x + 21door x + 3isderest0. Bepaaldecoëfficiënt a
Bijdelingvan f (x) = x 3 + ax 2 + 16 x + 21door x + 3isderest0. Bepaaldecoëfficiënt a
Jegebruiktdereststelling:
Jegebruiktdereststelling:
Jegebruiktdereststelling:
Jegebruiktdereststelling:
D (– 3)
(−3) = (−3) 3
= (−3) 3
Modeloefening2
Modeloefening 2
Modeloefening2
Modeloefening2
Modeloefening2
Bij deling van D (x)
Bijdelingvan f (x) = ax
Bijdelingvan
Bijdelingvan f (x) = ax 3 + bx 2 + 2x + 1door x 2isderest1enbijdelingdoor x 3isderest4. Bepaaldecoëfficiënten a en b
Bepaaldecoëfficiënten
x 2isderest1enbijdelingdoor x 3isderest4. Bepaaldecoëfficiënten a en b
Bijdelingvan f (x) = ax 3 + bx 2 + 2x + 1door x 2isderest1enbijdelingdoor x 3isderest4. Bepaaldecoëfficiënten a en b
Jegebruiktdereststelling:
Jegebruiktdereststelling:
Jegebruiktdereststelling:
Jegebruiktdereststelling:
D (2)
D (3)
Jeverkrijgthetstelsel
Je verkrijgt het stelsel S
Jeverkrijgthetstelsel
Je lost dit stelsel op om de waarde van a en b te vinden.
Modeloefening3
Modeloefening3
Modeloefening3
Modeloefening3
Bijdelingvan f (x)door x 2isderest3enbijdelingdoor x 4isderest5. Berekenderestvandedelingvan f (x)door(x 2) (x 4).
Bijdelingvan f (x)door x 2isderest3enbijdelingdoor x 4isderest5.
Bijdelingvan f (x)door x 2isderest3enbijdelingdoor x 4isderest5.
Berekenderestvandedelingvan f (x)door(x 2) (x 4).
f (x) = q (x) d (x) + r (x)
f (x) = q
Berekenderestvandedelingvan f (x)door(x 2) (x 4). f (x) = q (x) d (
) + r (x) f (x) = q (x) (x 2) (x 4) + r (x)
Bijdelingvan f (x)door x 2isderest3enbijdelingdoor x 4isderest5. Berekenderestvandedelingvan f (x)door(x 2) (x 4). f (x) = q (x) d (x) + r (x) f (x) = q (x) (x 2) (x 4) + r (x)
Aangeziengr(d (x)) = 2isgr (r (x)) 1. r (x)isdusvandevorm ax + b
Aangeziengr(d (x)) = 2isgr (r (x)) 1. r (x)isdusvandevorm ax + b
Aangeziengr(d (x)) = 2isgr (r (x)) 1. r (x)isdusvandevorm ax + b
Aangeziengr(d (x)) = 2isgr (r (x)) 1. r (x)isdusvandevorm ax + b
f (x) = q (x) (x 2) (x 4) + (ax + b)
f (x) = q (x) (x 2) (x 4) + (ax + b)
f (x) = q (x) (x 2) (x 4) + (ax + b)
f (x) = q (x) (x 2) (x 4) + (ax + b)
Uithetgegevenhaalje: f (2) = 3en f (4) = 5. f (2) = q (2) (2 2) (2 4) + (2 a +
Uithetgegevenhaalje: f (2) = 3en f (4) = 5.
Uithetgegevenhaalje: f (2) = 3en f (4) = 5.
Dus: a = b =
Uithetgegevenhaalje: f (2) = 3en f (4) = 5. f (2) = q (2)
f (2) = q (2) (2 2) (2 4) + (2 a + b) = q (2) 0 + (2 a
= 2
+ b = 3 f (4) = q (4) (4 2) (4 4) + (4 b = 5
(4
Jeverkrijgthetstelsel
(4) = q (4) (4 2) (4 4) + (4 = 5
Jeverkrijgthetstelsel 2 a + b 4 a + b
Jeverkrijgthetstelsel 2 a + b = 4 a
Jeverkrijgthetstelsel 2 a + b 4 a + b =
Antwoord:derestvandedelingvan
Antwoord:derestvandedelingvan +
Antwoord:derestvandedelingvan 1.
Antwoord:derestvandedelingvan 1.

4.3.4 Deling van een veelterm door (x – a) (x – b)
Inleiding
Bij deling van een getal door 3 is de rest 2 en bij deling van dat getal door 5 is de rest 3. Als je dat getal deelt door 15 (= 3 5), dan is de rest altijd gelijk aan 8. Je ziet drie voorbeelden.
Voor een veelterm D (x) kun je de rest bij deling door (x – a) (x – b) bepalen aan de hand van de resten bij deling door x – a en door x – b.
Modeloefening
Bij deling van D (x) door x – 2 is de rest 3 en bij deling door x – 4 is de rest 5.
Bereken de rest van de deling van D (x) door (x – 2) (x – 4).
D (x) = d (x) q (x) + r (x)
D (x) = (x – 2) (x – 4) q (x) + r (x) ⇓ gr (r (x)) < gr (d
D (x) = (x – 2) (x – 4) q (x) + ax + b
De rest van de deling van D (x) door x – 2 is 3 ⇒ D (2) = 3 (reststelling)
D (2) = (2 – 2) (2 – 4) q (2) + a 2 + b = 3 ⇔ 0 (– 2) q (2) + 2
De rest van de deling van D (x) door x – 4 is 5 ⇒
D (4) = (4 – 2) (4 – 4) q (4) + a 4 + b = 5 ⇔ 2 0 q (4) + 4a + b = 5 ⇔ 4a + b = 5
Je lost het stelsel S 2a + b = 3 4a + b = 5 op.
(4) = 5
Dus: de rest van de deling van D (x) door (x – 2) (x – 4) is
Kenmerk van deelbaarheid door (x – a) (x – b)
Gegeven is de veelterm D (x) = 2x 4 – x 3 – 16x 2 – 3x + 18
• x + 2 is een deler van D (x) want
x – 3 is een deler van D (x) want
• (x + 2) (x – 3) = x 2 – x – 6
Bereken het quotiënt en de rest van de deling van D (x) door x 2 – x – 6
q (x) = r (x) =
Besluit:
Kenmerk Een veelterm D (x) is deelbaar door (x – a) (x – b), met a ≠ b ⇔ D (x) is deelbaar door x – a en door x – b
Bewijs
©VANIN
D (x) is deelbaar door (x – a) (x – b) ⇓ eigenschap deelbaarheid
D (x) = (x – a) (x – b) q (x)
Stel: q 1 (x) = (x – b) q (x)
Dan: D (x) = (x – a) q 1 (x)
Stel: q 2 (x) = (x – a) q (x)
Dan: D (x) = (x – b) q 2 (x)
⇒ D (x) is deelbaar door x – a en door x – b
D (x) is deelbaar door x – a ⇓ eigenschap deelbaarheid
D (x) = (x – a) q 1 (x) (1)
D (x) is deelbaar door x – b ⇕ kenmerk van deelbaarheid
D (b) = 0 ⇔ (b – a) q 1 (b) = 0 ⇔ q 1 (b) = 0 b – a ≠ 0
⇒ q 1 (x) is deelbaar door x – b
⇒ q 1 (x) = (x – b) q (x) (2)
Uit (1) en (2) ⇒ D (x) = (x – a) (x – b) ⋅ q (x)
⇒ D (x) is deelbaar door (x – a) (x – b)
Oefeningen
Oefeningen
REEKSA
17 Berekenderestzonderdedelinguittevoeren. deeltal
a)2 x 3 + 8 x 2 + 5 x 17 x 1
©VANIN
b) x 5 1 x 1 c) x 4 + 2 x 3 + x 24 x 2
18 Kleurdehokjeswaarineenveeltermstaatdiedeelbaarisdoor x 1.
Watsteljevastbijdecoëfficiëntenvandeveeltermendiedeelbaarzijndoor x 1?
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
21 Bepaal de waarde van d (x) een deler is van D (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x).
f (x) d (x) berekeningen p
f (x) d (x) berekeningen p
f (x) d (x) berekeningen p
f (x) d (x) berekeningen p
f (x) d (x) berekeningen p
f (x) d (x) berekeningen p
f (x) d (x) berekeningen p
f (x) d (x) berekeningen p
f (x) d (x) berekeningen p
D ( )
f (x) d (x) berekeningen p
a) x 3 + 5 x 2 px x 2
f (x) d (x) berekeningen p
a) x 3 + 5 x 2 px x 2
a) x 3 + 5 x 2 px x 2
a) x 3 + 5 x 2 px x 2
a) x 3 + 5 x 2 px x 2
a) x 3 + 5 x 2 px x 2
a) x 3 + 5 x 2 px x 2
a) x 3 + 5 x 2 px x 2
a) x 3 + 5 x 2 px x 2
a) x 3 + 5 x 2 px x 2
a) x 3 + 5 x 2 px x 2
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
b) x 4 + px 3 3 x 15 x + 3
JOBNAME:Pienter.4TSO.lwsPAGE:23SESS:682OUTPUT:FriMar3009:11:462018
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
c)2 x 4 5 x 2 8 x 3 + px x 4
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
d)7 x 3 + 33 x 2 + px x + 5
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
22 Bepaal de waarde van zodat de rest van de deling van D (x) door d (x) gelijk is aan r.
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r
20 Bepaaldewaardevan p zodatderestvandedelingvan f (x)door d (x)gelijkisaan r.
f (x) d (x) r berekeningen p
f (x) d (x) r berekeningen p
f (x) d (x) r berekeningen p
19 Bepaaldewaardevan p zodat d (x)eendelerisvan f (x). f (x) d (x) berekeningen p
f (x) d (x) r berekeningen p
f (x) d (x) r berekeningen p
f (x) d (x) r berekeningen p
f (x) d (x) r berekeningen p
f (x) d (x) r berekeningen p
f (x) d (x) r berekeningen p
f (x) d (x) r berekeningen p
D (x
f (x) d (x) r berekeningen p
a) x 3 + 8 x 2 + 7 x + px + 16
a) x 3 + 8 x 2 + 7 + px + 16
a) x 3 + 8 x 2 + 7 + px + 16
a) x 3 + 8 x 2 + 7 x + px + 16
a) x 3 + 8 x 2 + 7 x + px + 16
a) x 3 + 8 x 2 + 7 x + px + 16
a) x 3 + 8 x 2 + 7 x + px + 16
a) x 3 + 8 x 2 + 7 x + px + 16
a) x 3 + 8 x 2 + 7 x + px + 16
a) x 3 + 8 x 2 + 7 x + px + 16
a) x 3 + 8 x 2 + 7 x + px + 16
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
b)2 x 4 2 x 3 + px 2 x 10 x 1−8
a) x 3 + 5 x 2 px x 2 b) x 4 + px 3 3 x 15 x + 3
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)4x 3 + 8x 2 + px 3 x + 211
c)2 x 4 5 x 2 8 x 3 + px x 4
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d) px 4 + 4 x 3 + 3 x 2 6 x 9 x 29
d)7 x 3 + 33 x 2 + px x + 5
23 Bepaal de coëfficiënten a en b.
a) De veelterm x 3 + ax 2 + bx – 12 is deelbaar door x + 2 en x – 2
©VANIN
Antwoord: a = b =
b) Bij deling van x 3 + ax 2 + 11x + b door x – 1 en x – 2 is de rest telkens 5.
Antwoord: a = b =
c) Bij deling van x 3 + ax 2 – bx – 5 door x + 2 en x + 3 is de rest telkens 7.
Antwoord: a = b =
d) Bij deling van ax 3 + bx 2 + 4x – 3 door x – 2 is de rest -7 en bij deling door x + 1 is de rest -4.
Antwoord: a = b =
24 Bepaal de rest van de deling.
a) Bij deling van D (x) door x + 1 is de rest 2 en bij deling door x – 2 is de rest 5.
Bepaal de rest bij deling van D (x) door (x + 1) ⋅ (x – 2)
©VANIN
b) Bij deling van D (x) door x + 2 is de rest 3 en bij deling door x + 3 is de rest 2.
Bepaal de rest bij deling van D (x) door (x + 2) (x + 3)
25 Gegeven zijn de veeltermen D (x) = 3x 3 – 2x 2 – 19x – 6 en d (x) = x 2 – x – 6.
a) Toon aan dat d (x) deelbaar is door x + 2.
b) Ontbind d (x) in factoren.
©VANIN
c) Toon aan dat D (x) deelbaar is door d (x), zonder de deling uit te voeren.
26 Toon aan dat D (x) = 3x 4 – 23x 2 – 36 deelbaar is door d (x) = x 2 – 9, zonder de deling uit te voeren.
27 Bepaal de rest van de deling van D (x) = – 4x 3 + 3x 2 – 7x + 5 door d (x) = x 2 + 2x, zonder de deling uit te voeren.
4.4 Tweetermen van de vorm a 3 – b 3 en a 3 + b 3 ontbinden in factoren
Tweetermen van de vorm a 3 – b 3
voorbeeld algemeen
Gegeven is de veelterm D (x) = x 3 – 8
D (x) is deelbaar door x – 2
want D (2) = 2 3 – 8 = 8 – 8 = 0
Je deelt x 3 – 8 door x – 2 :
Gegeven is de veelterm D (a) = a 3 – b 3
D (a) is deelbaar door a – b
want D (b) = b 3 – b 3 = 0
Je deelt a 3 – b 3 door a – b :
8
Formule a 3 – b 3 = (a – b) (a 2 + ab + b 2)
Tweetermen van de vorm a 3 + b 3 voorbeeld algemeen
Gegeven is de veelterm D (x) = x 3 + 8
D (x) is deelbaar door
want
Je deelt x 3 + 8 door :
©VANIN
q (x) = x 3 + 8 =
Formule a 3 + b 3 = (a + b) (a 2 - ab + b 2)
Voorbeelden
Gegeven is de veelterm D (a) = a 3 + b 3
D (a) is deelbaar door
want
Je deelt a 3 + b 3 door :
q (a) = a 3 + b 3 =
x 3 + 64 = x 3 + 4 3 = 8x 3 – 1 =
Oefeningen
REEKS B
28 Ontbind in factoren.
a) 1 – x 3 =
b) 125 + x 3 =
©VANIN
c) 27x 3 – 8 =
d) 343x 3 + y 3 =
e) 1 8 x 3 + 1 27 =
f) – x 3 + 64y 3 =
g) 216x 3 –1 8 =
h) –8 27 x 3 + 1 64 =
REEKS C
29 Ontbind in factoren.
a) 8x 4 – 27x =
b) – x 3 – 27y 3 =
c) 27x 7 – 64xy 3 = =
d) x 6 + y 6 =
e) x 6 – y 6 = =
STUDIEWIJZER Deelbaarheid bij veeltermen
4.1 Veeltermen in één veranderlijke

Een veelterm is een som van eentermen.
KENNEN

De graad van een veelterm in x is de hoogste exponent van de onbekende x in die veelterm.
KUNNEN
Veeltermen optellen, aftrekken en vermenigvuldigen.
©VANIN
4.2 De euclidische deling van twee veeltermen


KENNEN
D (x) is deelbaar door d (x) ⇔ D (x) = d (x) q (x).
De euclidische deling van de veelterm D (x) door de veelterm d (x), waarbij d (x) ≠ 0, heeft als quotiënt de veelterm q (x) en als rest de veelterm r (x) als en slechts als
D (x) = d (x) q (x) + r (x) waarbij gr (r (x)) < gr (d (x)) of r (x) = 0.
Bij de deling van een veelterm D (x) door de veelterm d (x), waarbij d (x) ≠ 0, bestaat er juist één quotiënt q (x) en juist één rest r (x).
KUNNEN
De euclidische deling van veeltermen in één veranderlijke uitvoeren.
De uniciteit bewijzen van quotiënt en rest bij een euclidische deling van veeltermen.
4.3 Deling door x – a

De rest van de deling van een veelterm D (x) door x – a (met a ∈ r) is gelijk aan D (a).
Een veelterm D (x) is deelbaar door x – a (met a

D (a) = 0.
Een veelterm D (x) is deelbaar door (x – a) (x – b) , met a ≠ b ⇔ D (x) is deelbaar door x – a en door x – b
KUNNEN
De deling van een veelterm door x – a uitvoeren met de regel van Horner.
De reststelling bewijzen en toepassen.
Oefeningen oplossen met de methode van de onbepaalde coëfficiënten.
De rest bepalen bij deling van een veelterm door (x – a) (x – b) door gebruik te maken van de resten bij deling door x – a en door x – b
4.4 Tweetermen van de vorm a 3 – b 3 en a 3 + b 3 ontbinden in factoren

KENNEN

Tweetermen van de vorm a 3 + b 3 en a 3 – b 3 ontbinden in factoren.

Welke heuristiek(en) gebruik je om de onderstaande problemen op te lossen?
❑ concreet materiaal
❑ schets
❑ schema/tabel
❑ vereenvoudig
❑ gok verstandig
❑ filter
❑ patroon
❑ kennis
❑ logisch nadenken
❑ ...
©VANIN
1. Een getal heeft zeven cijfers. Het eerste cijfer is gelijk aan het aantal nullen in het getal, het tweede gelijk aan het aantal enen, het derde gelijk aan het aantal tweeën, enzovoort, tot aan het zevende cijfer, dat gelijk is aan het aantal zessen. Bepaal dat getal.
2. In de figuur staan drie cirkels en van twee ervan is de diameter gekend.
De oppervlakte van het blauwe gebied is gelijk aan de oppervlakte van het lichtrode gebied. Wat is de diameter van de derde cirkel? (JWO, tweede ronde 2023)
3. Je koopt een broek en krijgt 25 % korting. Als trouwe klant van de winkel krijg je daarbovenop nog een extra korting van 15 %. Hoeveel procent korting krijg je in totaal?
HOOFDSTUK 5 I GONIOMETRIE
5.1 Goniometrische getallen in een rechthoekige driehoek
5.2 Georiënteerde hoeken
5.3 De goniometrische cirkel
5.4 Goniometrische getallen van een hoek
5.5 Goniometrische getallen van verwante hoeken
5.6 Relaties tussen de goniometrische getallen van een hoek
5.7 Willekeurige driehoeken oplossen
Studiewijzer
Pienter problemen oplossen
©VANIN

5.1 Goniometrische getallen in een rechthoekige driehoek
Definitie Sinus Cosinus Tangens
De sinus (sin) van een scherpe hoek in een rechthoekige driehoek is de verhouding overstaande rechthoekszijde schuinezijde
De cosinus (cos) van een scherpe hoek in een rechthoekige driehoek is de verhouding aanliggenderechthoekszijde schuinezijde
De tangens (tan) van een scherpe hoek in een rechthoekige driehoek is de verhouding overstaanderechthoekszijde aanliggenderechthoekszijde
De verhoudingen van de zijden in een rechthoekige driehoek zijn afhankelijk van de scherpe hoek. Je noemt die verhoudingen goniometrische getallen van de scherpe hoek.
Bij het oplossen van rechthoekige driehoeken gebruik je de volgende formules.
som van de scherpe hoeken
stelling van Pythagoras
Goniometrische getallen in een rechthoekige driehoek met GeoGebra

Oefeningen
REEKS A
1 De volgende dakconstructie is gegeven.

aan tot een ware uitspraak.
2 Bereken op 0,000 01 nauwkeurig.
a) sin 69º 11 12 ≈ c) tan 16º 17 18 ≈ b) cos 12º 7 ≈ d) cos 84º 56 ≈
3 Bereken op 1 nauwkeurig.
a) sin a = 0,4 ⇒ a = c) cos a = 0,83 ⇒ a = b) tan a = 0,35 ⇒ a = d) tan a = 1,3 ⇒ a =
4 Bereken het gevraagde in de rechthoekige driehoek. Rond, indien nodig, de hoeken af op 1 en de zijden op 0,01.
5 De structuur van een watermolecule is een gelijkbenige driehoek met het zuurstofatoom als tophoek en twee waterstofatomen. Tussen elk waterstofatoom en zuurstofatoom bestaat een covalente binding. De sinus van een basishoek is 0,612 217 28. Bereken de grootte van een basishoek en van de tophoek. Rond af op 1 nauwkeurig.
6 In de chemieles breng je een vloeistof over met een pipet in een erlenmeyer. De lengte van de pipet is 35 cm. De erlenmeyer heeft een hoogte van 15 cm. De hoogte | CE | = 39,8 cm.
Om de vloeistof te laten uitlopen, houd je de pipet schuin, maar onder welke hoekgrootte met het horizontale oppervlak?

7 Tijdens de voetbaltraining neemt de Britse sterspeler Canshotwell een ongelofelijke strafschop. De bal vertrekt van de penaltystip op 11 m van het midden van het doel en belandt keihard in de rechterbovenhoek. De bal raakt nog net de binnenkant van de paal. Het doel is 2,44 m hoog en 7,32 m breed. In totaal legde de bal 11,8 m af tot hij de paal raakte. Bereken de hoek waaronder de bal vertrok.
7,32


5.2 Georiënteerde hoeken
Inleiding
• Bij de omschakeling van wintertijd naar zomertijd, in het voorjaar, van winter- naar zomertijd moet je de klok een uur vooruitdraaien. De kleine wijzer beweegt dan over een hoek van 30º.
• Bij de omschakeling van zomertijd naar wintertijd, in het najaar, van zomer- naar wintertijd moet je de klok een uur terugdraaien. De kleine wijzer beweegt dan over een hoek van 30º.
Een ezelsbruggetje:
in het voorjaar zet je de klok vooruit en in het najaar zet je de klok achteruit.
In beide gevallen meet de hoek tussen de begin- en eindpositie van de kleine wijzer 30º.
Om de twee situaties te onderscheiden, oriënteer je de hoek. De oriëntatie gebeurt met de zin van de wijzers mee of tegen de zin van de wijzers in. Vermits je in de natuur meestal te maken hebt met de tegenwijzerzin (bijvoorbeeld bij de beweging van de planeten), kies je die zin als positief. Zo wordt de overgang van zomer- naar wintertijd gekenmerkt door een georiënteerde hoek van 30º en de overgang van winter- naar zomertijd door een georiënteerde hoek van –30º.
Geef zelf twee voorbeelden van situaties waarin de oriëntatie van een hoek noodzakelijk is.
Definitie
Georiënteerde hoek
Een georiënteerde hoek is een hoek waarbij een pijl het beginbeen en het eindbeen van de hoek aanduidt.
Notatie: A ^ OB
Je spreekt over de georiënteerde hoek A ^ OB met de halfrechte [OA als beginbeen en de halfrechte [OB als eindbeen.
• Is de hoek georiënteerd in tegenwijzerzin, dan noem je de hoek positief.
• Is de hoek georiënteerd in wijzerzin, dan noem je de hoek negatief.
Hieronder zie je twee voorstellingen van dezelfde georiënteerde hoek, want het begin- en eindbeen zijn hetzelfde.
positieve oriëntatie negatieve oriëntatie
A beginbeen eindbeen
A beginbeen eindbeen
Georiënteerde hoeken duid je meestal aan met kleine Griekse letters: a, b, g, d, « Het Griekse
Oefeningen
REEKS A
8 Zijn de hoeken positief of negatief georiënteerd?
oriëntatie
©VANIN
9 Josse staat voor een deur. Zijn de hoeken om de deur te openen positief of negatief georiënteerd?

❒ negatief
❒ positief

❒ negatief
❒ positief
10 Zie jij de danseres draaien volgens een hoek die positief of negatief georiënteerd is?
❒ positief ❒ negatief
5.3 De goniometrische cirkel
5.3.1 Begrippen
Je voorziet het vlak van een loodrecht assenstelsel met gelijke eenheden: een orthonormaal assenstelsel.
De punten E x en E y duiden de eenheid op de assen aan.
Je noemt ze eenheidspunten
In een orthonormaal assenstelsel kan de eenheid willekeurig gekozen worden. Een straal gelijk aan 1 betekent dus niet dat die 1 cm lang moet zijn.
Definitie Goniometrische cirkel
De goniometrische cirkel is de cirkel met middelpunt O en straal 1.
Het assenstelsel verdeelt het vlak in vier kwadranten
Je nummert ze met Romeinse cijfers, zoals op de figuur hiernaast. De assen zelf behoren niet tot een kwadrant.
Elke georiënteerde hoek kun je voorstellen
op de goniometrische cirkel:
• Het hoekpunt is altijd het middelpunt van de cirkel.
• Het beginbeen valt samen met de positieve x-as.
• Het snijpunt A van het eindbeen van de georiënteerde hoek en de goniometrische cirkel noem je het beeldpunt van de hoek a
Noteer het juiste begrip in het kadertje.
5.3.2 De zestigdelige graad
Om de hoekgrootte van de georiënteerde hoek a
te bepalen, plaats je de getallen 0 en 360 bij E x Verder verdeel je de cirkel in 360 gelijke delen: graden (º).
met het beeldpunt A van de hoek a komt juist één getal van het interval [0, 360[ overeen.
Dat getal noem je het maatgetal van a Het maatgetal van a is gelijk aan 22.
Je noteert: a = 22º.
Roteer je de halfrechte [OA verder in tegenwijzerzin,
dan kun je de hoekgrootte 382º (22º + 360º), 742º (22º + 2 360º) … toekennen aan a Als je in wijzerzin roteert, dan komt met A ook een hoekgrootte –338º (22º – 360º), –698º (22º – 2 ? 360º) … overeen.
De georiënteerde hoek a heeft oneindig veel hoekgroottes die 360º van elkaar verschillen bij een of meerdere omwentelingen.
Elke georiënteerde hoek heeft juist één beeldpunt op de goniometrische cirkel. met elk punt op de goniometrische cirkel komt juist één georiënteerde hoek overeen.
Algemeen
Bij elk punt van de goniometrische cirkel kun je oneindig veel hoekgroottes plaatsen. Als a een van die hoekgroottes is, dan zijn de andere van de vorm a + k ? 360º (k ∈ Z).
Voorbeelden
• b =
• Het beeldpunt van b is
• Het beeldpunt van b ligt in kwadrant
• g =
• Het beeldpunt van g is
• Het beeldpunt van g ligt in kwadrant
5.3.3 Georiënteerde hoeken en omwentelingshoeken
Voorbeeld
Joran gaat naar de kermis en neemt plaats op de draaimolen. De carrousel draait één volledige ronde in twintig seconden.
Over welke hoek heeft hij in totaal gedraaid in twee minuten?
• aantal afgelegde rondes:
• draaihoek:
©VANIN

De verkregen hoek heeft hetzelfde beeldpunt op de goniometrische cirkel als de nulhoek. maar 2 160º gelijkstellen aan 0º zou betekenen dat Joran niet bewogen heeft.
Daarom maak je een onderscheid tussen twee soorten hoeken.
georiënteerde hoeken omwentelingshoeken
Een georiënteerde hoek wordt volledig bepaald door zijn beeldpunt op de goniometrische cirkel.
De georiënteerde hoeken
a = –500º en b = –140º zijn gelijk, want ze hebben hetzelfde beeldpunt.
In meetkundevraagstukken werk je met georiënteerde hoeken.
Er zijn twee mogelijkheden om te werken met een representant:
• a ∈ [0º, 360º[
• a ∈ ]–180º, 180º]
Deze laatste noem je de hoofdwaarde van de georiënteerde hoek.
Voorbeeld
Een omwentelingshoek wordt volledig bepaald door zijn maatgetal.
De omwentelingshoeken
a = –500º en b = –140º zijn verschillend, want hun maatgetal is niet gelijk.
Om fysische verschijnselen met een periodiek karakter te beschrijven, werk je met omwentelingshoeken.
Kim neemt plaats op dezelfde draaimolen. Het is druk en Kim maakt een ritje van 1 minuut en 35 seconden.
Bepaal:
• het aantal afgelegde rondes:
• de draaihoek:
• de representant van de draaihoek in [0º, 360º[:
• de hoofdwaarde van de draaihoek:
Oefeningen
REEKS A
11 Teken het beeldpunt A van de gevraagde hoek op de goniometrische cirkel.
12 In welk kwadrant ligt de gegeven hoek?
13 Bepaal van de georiënteerde hoeken de representant in [0º, 360º[.
a) 888º d) –3 600º 5
b) –69º e) 3 600º 5
c) –720º 5 f) 4 444º 44 44
©VANIN
14 Bepaal van de georiënteerde hoeken de hoofdwaarde en hun kwadrant.
a) 245º f) –2 212º
b) 523º 20 g) 2 140º 14
c) 930º h) –2 140º 6 15
d) –740º 20 i) 2 240º 23 56
e) 11 425º j) –4 420º 46 37
15 Een fietswiel heeft een diameter van 68 cm.
Over welke hoek is het wiel gedraaid als je de fiets 2 m verplaatst?
16 Een satelliet draait 3 000 km boven het aardoppervlak en maakt één omwenteling rond de aarde in 360 minuten. De straal van de aarde is 6 400 km.
a) Welke afstand heeft de satelliet afgelegd in 1 dag? Rond af op 1 m nauwkeurig.
b) Over welke hoek heeft de satelliet in totaal gedraaid?
5.4 Goniometrische getallen van een hoek
5.4.1 Cosinus van een hoek
Gegeven: een hoek a uit het eerste kwadrant met beeldpunt A
Is het punt A x de loodrechte projectie van A op x, dan geldt in de rechthoekige driehoek OAA x
De cosinus van een hoek is het eerste coördinaatgetal van het beeldpunt van de hoek op de goniometrische cirkel.
Duid op elke goniometrische cirkel de cosinus van de gegeven hoek aan.
Vul het besluit aan met de afgelezen waarde, een plusteken of een minteken.
5.4.2 Sinus van een hoek
Gegeven: een hoek a uit het eerste kwadrant met beeldpunt A
Is het punt A y de loodrechte projectie van A op y,
dan geldt in de rechthoekige driehoek OAA x
sin a = = =
Definitie Sinus
De sinus van een hoek is het tweede coördinaatgetal van het beeldpunt van de hoek op de goniometrische cirkel.
Duid op elke goniometrische cirkel de sinus van de gegeven hoek aan. Vul het besluit aan met de afgelezen waarde, een plusteken of een minteken.
5.4.3 Tangens van een hoek
Definitie Tangens
tan a = sin a cos a als cos a ≠ 0
Gevolgen van de definitie
• Voor welke hoeken is de tangens niet gedefinieerd?
• De waarde van de tangens kan elk reëel getal zijn.
Meetkundige betekenis van de tangens
Je bepaalt de vergelijking van de rechte OA door O (0, 0) en A (cos a, sin a):
Besluit
Je vult de coördinaat van het punt T (1, yT) in: yT = sin a cos a 1 = sin a
De tangens van een hoek is het tweede coördinaatgetal van het snijpunt van de raaklijn in het punt E
(1, 0) aan de goniometrische cirkel en het eindbeen van de hoek.
Duid op elke goniometrische cirkel de tangens van de gegeven hoek aan. Vul het besluit aan met de afgelezen waarde, een plusteken of een minteken.
5.4.4 Cotangens van een hoek
Definitie Cotangens
cot a = cos a sin a als sin a ≠ 0
Gevolg cot a = 1 tan a als tan a ≠ 0
• Voor welke hoeken is de cotangens niet gedefinieerd?
• De waarde van de cotangens kan elk reëel getal zijn.
Meetkundige betekenis van de cotangens
Je bepaalt de vergelijking van de rechte OA door O (0, 0) en A (cos a, sin a):
Je vult de coördinaat van het punt T (xT, 1) in:
1 = sin a cos a xT ⇔ cos a sin a =
Besluit De cotangens van een hoek is het eerste coördinaatgetal van het snijpunt van de raaklijn in het punt E y (0, 1) aan de goniometrische cirkel en het eindbeen van de hoek.
Duid op elke goniometrische cirkel de cotangens van de gegeven hoek aan.
Vul het besluit aan met de afgelezen waarde, een plusteken of een minteken.
Besluit
5.4.5 Verband tussen hellingshoek en richtingscoëfficiënt
Definitie Hellingshoek
De hellingshoek a van een rechte is de georiënteerde hoek tussen die rechte en de x-as.
• Teken de rechte a met vergelijking y = 2x.
Wat is de richtingscoëfficiënt van de rechte a?
• Teken de hellingshoek a van de rechte a.
• Lees de coördinaat af van het snijpunt
van de rechten a en t:
Wat is de tangens van de hoek a?
• Teken de rechte b met vergelijking y = 2x + 3.
Wat is de richtingscoëfficiënt van de rechte b?
• Teken de hellingshoek a van de rechte b.
Besluit:
Eigenschap
©VANIN
In een orthonormaal assenstelsel is de tangens van de hellingshoek van een rechte gelijk aan de richtingscoëfficiënt van die rechte.
Voorbeeld 1
Bereken de hellingshoek a van de rechte met vergelijking y = 2x + 3.
Voorbeeld 2
Bepaal de vergelijking van de rechte r die door A (3, –1) gaat en een hoek a van 135º maakt met de x-as.
Oefeningen
REEKS A
17 Teken het beeldpunt van de hoek op de goniometrische cirkel. Schat de goniometrische getallen op 0,1 nauwkeurig.
a) a = 45º met beeldpunt A
cos a ≈
©VANIN
sin a ≈
tan a ≈
b) b = –90º met beeldpunt B
cos b ≈
sin b ≈
tan b ≈
c) g = 120º met beeldpunt C
cos g ≈
sin g ≈
tan g ≈
d) d = –130º met beeldpunt D
cos d ≈
sin d ≈
tan d ≈
e) « = –210º met beeldpunt E
cos « ≈
sin « ≈
tan « ≈
f) w = 315º met beeldpunt F
cos w ≈
sin w ≈
tan w ≈
18 Teken op de goniometrische cirkel de beeldpunten A 1 en A 2 van de hoek a .
a) sin a = 3 4
e) sin a = –2 5
©VANIN
b) cos a = –1 2
f) cos a = 0,6
c) tan a = 1,5
g) tan a = –0,8
d) cot a = –3 5 h) cot a = 0,8
19 Bepaal het teken van de goniometrische getallen. a cos a sin a tan a cot a
a) 100o
b) –50o
c) 250o
d) 50o
e) –220o
20 Bereken, op 0,01 nauwkeurig, de coördinaatgetallen van de hoekpunten van de regelmatige negenhoek ingeschreven in de goniometrische cirkel.
21 Bereken de hellingshoek van de rechten met de onderstaande vergelijking.
richtingscoëfficiënt hellingshoek
a) y = 2x – 3
b) y = 3x + 4
c) y = –x + 6
d) y = 5 – 4x
e) y = –3 x
f) y = 3 5 x + 2
22 Langs de weg zie je een verkeersbord staan dat aangeeft dat de weg 10 % stijgt. Wat is de hellingshoek die het wegdek maakt met de horizontale? Bepaal je antwoord op 1 nauwkeurig.
23 In een mijn zitten na het instorten van de verticale schacht een aantal mijnwerkers 150 m onder de grond vast. Om ze te bevrijden, moeten de reddingswerkers een nieuwe schacht boren. Onder welke hoek moet de nieuwe schacht gegraven worden, als ze op 500 m van de oude verticale schacht de graafwerken beginnen? Bepaal je antwoord op 1 nauwkeurig.
24 Bepaal de vergelijking van de rechte. Rond de richtingscoëfficiënt af op een eenheid.
a) Van een rechte r zijn de hellingshoek a = 83º 39 35 en een punt P (3, –1) gegeven.
b) Van een rechte s zijn de hellingshoek a = –63º 26 6 en een punt P (1, 2) gegeven.
REEKS C
25 Bepaal zonder rekenmachine of de uitdrukkingen juist of fout zijn. juist fout juist fout
a) sin 30º < cos 30º
b) –432º behoort tot kwadrant II
c) tan 45º = 1
d) tan (–45º) < tan (–60º)
e) sin (30º + 60º) = sin 30º + sin 60º
f) cos 30º < cos 60º
g) sin 30º < sin 60º
h) sin (180º – 30º) = sin 30º
i) cos (1 980º – 60º) = cos 60º
j) cos (–230º) > 0
5.5 Goniometrische getallen van verwante hoeken
5.5.1 Inleiding
Teken de beeldpunten van de hoeken en geef de hoekgrootte.
1 1 O y x beeldpunt hoek
a) a1 in I met sin a1 = 0,50 A 1
b) a2 in II met sin a2 = 0,50 A 2
c) b1 in I met cos b1 = 0,50 B 1
d) b2 in IV met cos b2 = 0,50 B 2
verband tussen de hoeken benaming
b1 en b2
a1 en a2
a1 en b1
5.5.2 Gelijke hoeken
Definitie Gelijke hoeken
Twee georiënteerde hoeken zijn gelijk als en slechts als hun maatgetallen, op een veelvoud van 360 na, aan elkaar gelijk zijn.
GEOGEBRA
In symbolen
a = b ⇔ b = a + k ? 360º (k ∈ Z)
Gelijke hoeken hebben hetzelfde beeldpunt op de goniometrische cirkel.
Besluit cos (a + k ? 360º) = cos a sin (a + k ? 360º) = sin a tan (a + k ? 360º) = tan a cot (a + k ? 360º) = cot a
5.5.3 Tegengestelde hoeken
Definitie Tegengestelde hoeken
Twee georiënteerde hoeken zijn tegengesteld als en slechts als hun som de nulhoek is.
In symbolen
a en b zijn tegengesteld ⇔ a + b = 0º + k 360º = k 360º (k ∈ Z) of ook
b is het tegengestelde van a ⇔ b = –a + k 360º (k ∈ Z)
Voorbeelden (geef telkens drie verschillende hoekgroottes)
–30º is een tegengestelde van
45º is een tegengestelde van
Noem A en A de beeldpunten van de tegengestelde hoeken a en –a.
Wat stel je vast in verband met de coördinaatgetallen van A en A?
Besluit
©VANIN
Besluit
De beeldpunten van tegengestelde hoeken liggen symmetrisch ten opzichte van de x-as.
Goniometrische getallen van tegengestelde hoeken
5.5.4 Supplementaire hoeken
Definitie Supplementaire hoeken
Twee georiënteerde hoeken zijn supplementair als en slechts als hun som de gestrekte hoek is.
In symbolen
a en b zijn supplementair ⇔ a + b = 180º + k 360º (k ∈ Z) of ook
b is het supplement van a ⇔ b = 180º – a + k 360º (k ∈ Z)
Voorbeelden (geef telkens drie verschillende hoekgroottes)
30º is een supplement van
135º is een supplement van Noem A en A de beeldpunten van de supplementaire hoeken a en 180º – a.
Wat stel je vast in verband met de coördinaatgetallen van A en A?
Besluit
©VANIN
De beeldpunten van supplementaire hoeken liggen symmetrisch ten opzichte van de y-as.
Goniometrische getallen van supplementaire hoeken
5.5.5 Antisupplementaire hoeken
Definitie Antisupplementaire hoeken
Twee georiënteerde hoeken zijn antisupplementair als en slechts als hun verschil de gestrekte hoek is.
In symbolen
a en b zijn antisupplementair ⇔ b – a = 180º + k 360º (k ∈ Z) of ook
GEOGEBRA
b is het antisupplement van a ⇔ b = 180º + a + k 360º (k ∈ Z)
Voorbeelden (geef telkens drie verschillende hoekgroottes)
30º is een antisupplement van
–45º is een antisupplement van
Noem A en A de beeldpunten van de antisupplementaire hoeken a en 180º + a.
Wat stel je vast in verband met de coördinaatgetallen van A en A?
Besluit De beeldpunten van antisupplementaire hoeken liggen symmetrisch ten opzichte van de oorsprong.
Goniometrische getallen van antisupplementaire hoeken
Besluit cos (180º + a) = –cos a sin (180º + a) = –sin a
(180º + a) = tan a cot (180º + a) = cot a
5.5.6 Complementaire hoeken
Definitie Complementaire hoeken
Twee georiënteerde hoeken zijn complementair als en slechts als hun som de rechte hoek is.
In symbolen
a en b zijn complementair ⇔ a + b = 90º + k 360º (k ∈ Z) of ook
b is het complement van a ⇔ b = 90º – a + k 360º (k ∈ Z)
Noem A en A de beeldpunten van de complementaire hoeken a en 90º – a
Wat stel je vast in verband met de coördinaatgetallen van A en A?
Besluit De beeldpunten van complementaire hoeken liggen symmetrisch ten opzichte van de bissectrice van het eerste kwadrant.
Goniometrische getallen van complementaire hoeken
©VANIN
Besluit
5.5.7 Anticomplementaire hoeken
Definitie Anticomplementaire hoeken
Twee georiënteerde hoeken zijn anticomplementair als en slechts als hun verschil de rechte hoek is.
In symbolen
a en b zijn anticomplementair ⇔ b – a = 90º + k 360º (k ∈ Z) of ook
b is het anticomplement van a ⇔ b = 90º + a + k 360º (k ∈ Z)
Besluit
Noem A en A de beeldpunten van de anticomplementaire hoeken a en 90º + a
Wat stel je vast in verband met de coördinaatgetallen van A en A?
(90º + a) = –cot a cot (90º + a) = –tan a GEOGEBRA
©VANIN
De beeldpunten van anticomplementaire hoeken vind je door ze te spiegelen ten opzichte van de bissectrice van het eerste kwadrant en ze daarna te spiegelen ten opzichte van de y-as.
Goniometrische getallen van anticomplementaire hoeken
Besluit cos (90º + a) = –sin a
(90º + a) = cos a
Samenvatting Gelijke hoeken
Tegengestelde hoeken
cos (a + k 360º) = cos a
sin (a + k 360º) = sin a
tan (a + k ? 360º) = tan a
cot (a + k ? 360º) = cot a
©VANIN
De beeldpunten van tegengestelde hoeken liggen symmetrisch ten opzichte van de x-as.
cos (–a) = cos a
sin (–a) = – sin a
tan (–a) = – tan a
cot (–a) = – cot a
Supplementaire hoeken
De beeldpunten van supplementaire hoeken liggen symmetrisch ten opzichte van de y-as.
cos (180º – a) = – cos a
sin (180º – a) = sin a
tan (180º – a) = – tan a
cot (180º – a) = – cot a
Antisupplementaire hoeken
Complementaire hoeken
De beeldpunten van antisupplementaire hoeken liggen symmetrisch ten opzichte van de oorsprong.
cos (180º + a) = – cos a
sin (180º + a) = – sin a
tan (180º + a) = tan a
cot (180º + a) = cot a
©VANIN
De beeldpunten van complementaire hoeken liggen symmetrisch ten opzichte van de bissectrice van het eerste kwadrant.
cos (90º – a) = sin a
sin (90º – a) = cos a
tan (90º – a) = cot a
cot (90º – a) = tan a
Anticomplementaire hoeken
De beeldpunten van anticomplementaire hoeken vind je door ze te spiegelen ten opzichte van de bissectrice van het eerste kwadrant en ze daarna te spiegelen ten opzichte van de y-as.
cos (90º + a) = – sin a
sin (90º + a) = cos a
tan (90º + a) = – cot a
cot (90º + a) = – tan a
5.5.8 Alle hoeken vanuit een goniometrisch getal berekenen
Voorbeelden
• cos a = –0,25
Tegengestelde hoeken hebben dezelfde cosinus.
Vind je één oplossing, dan is de tegengestelde hoek ook een oplossing.
Je vindt alle oplossingen door een willekeurig veelvoud van 360º op te tellen.

• sin a = 0,4
dus a = 26º 33 54 + k 360º (k ∈ Z) of a = –153º 26 6 + k ? 360º (k ∈ Z). 1 –1 1 –1 y x O t GEOGEBRA
Een tegengestelde van 104º 28 39 is –104º 28 39
dus a = 104º 28 39 + k ? 360º (k ∈ Z) of a = –104º 28 39 + k ? 360º (k ∈ Z).
Supplementaire hoeken hebben dezelfde sinus.
Vind je één oplossing, dan is de supplementaire hoek ook een oplossing.
Je vindt alle oplossingen door een willekeurig veelvoud van 360º op te tellen.

• tan a = 4
©VANIN
Een supplement van 23º 34 41 is 180º – 23º 34 41 = 156º 25 19
dus a = 23º 34 41 + k 360º (k ∈ Z) of
= 156º 25 19 + k ? 360º (k ∈ Z).
Antisupplementaire hoeken hebben dezelfde tangens.
Vind je één oplossing, dan is de antisupplementaire hoek ook een oplossing.
Je vindt alle oplossingen door een willekeurig veelvoud van 360º op te tellen.

• cot a = 2
Een antisupplement van 75º 57 50 is 180º + 75º 57 50 = 255º 57 50 hoofdwaarde: –104º 2 10
dus a = 75º 57 50 + k 360º (k ∈ Z) of a = –104º 2 10 + k ? 360º (k ∈ Z).
Je vormt de opgave met de cotangens om naar een opgave met de tangens. De verdere werkwijze is hetzelfde als bij het vorige voorbeeld.
Als cot a = 2, dan is tan a = 1 2

Een antisupplement van 26º 33 54 is 180º + 26º 33 54 = 206º 33 54 hoofdwaarde: –153º 26 6
Oefeningen
REEKS A
26 Geef van elke hoek de hoofdwaarde van de hoek die de gevraagde verwantschap oplevert. hoek tegengesteld supplementair antisupplementair complementair anticomplementair
a) 25º
b) –75º
c) –110º
d) 240º
e) 305º
f) –355º
©VANIN
27 Wat is de verwantschap tussen de gegeven hoeken?
a) 25º en –295º zijn g) –25º en 65º zijn
b) –25º en –205º zijn h) 35º en 685º zijn
c) 105º en 75º zijn i) 50º en 490º zijn
d) 30º en –690º zijn j) 470º en 380º zijn
e) 30º en –150º zijn k) 256º en –284º zijn
f) –330º en 420º zijn l) 170º en 190º zijn
Transformaties en coördinaten
• Bij een spiegeling ten opzichte van de x-as blijft het eerste coördinaatgetal gelijk en verandert het tweede coördinaatgetal van teken.
• Bij een spiegeling ten opzichte van de y-as verandert het eerste coördinaatgetal van teken en blijft het tweede coördinaatgetal gelijk.
• Bij een spiegeling ten opzichte van de bissectrice van het eerste kwadrant worden de coördinaatgetallen van plaats verwisseld.
• Bij een spiegeling ten opzichte van de oorsprong veranderen beide coördinaatgetallen van teken.
28 Bepaal de hoek a op 1 nauwkeurig. Geef alle oplossingen.
Vereenvoudig door de formules van verwante hoeken te gebruiken.
a) tan (180º – a) cos a
f) sin (180º – a) cot (180º – a)
b) cos (90º – a) cos (180º – a)
©VANIN
c) cot (180º + a) cot (90º – a)
g) sin (180º + a) tan (180º + a)
h) sin (90º – a) cot (90º + a)
d) tan (90º – a) cos (–a)
i) cot (– a) + tan (90º + a)
e)
cos (90º + a) sin (90º + a) sin (–a)
j) tan (– a) ? cos (180º + a)
31 Vereenvoudig door de formules van verwante hoeken te gebruiken.
a) sin a cos (180º – a) + cos a sin (180º – a)
b) sin (90º – a) + sin (180º – a) + sin (360º + a) + sin (180º + a)
c) tan (90º + a) tan (180º + a) + cot (–a)
32 Bepaal de georiënteerde hoek die de laserstraal met de x-as maakt.


5.6 Relaties tussen de goniometrische getallen van een hoek
5.6.1 Afgeleide formules uit de definitie
van tangens
Je noteert de afgeleide formules voor de sinus en de cosinus van een hoek uit de definitie van de tangens, als de tangens bestaat:
tan a = sin a cos a als cos a ≠ 0
Formules
sin a = cos a tan a
5.6.2 De grondformule
GEOGEBRA
cos a = sin a tan a als tan a ≠ 0
tekening A y x α O Ay Ax gegeven
een hoek a met beeldpunt A op de goniometrische cirkel
te bewijzen
cos 2 a + sin 2 a = 1
bewijs
Stel: px (A) = A x en py (A) = A y
In de rechthoekige driehoek OAA x geldt de stelling van Pythagoras:
| OA x |2 + | AA x |2 = | OA |2
| AA x | = | OA y |
| OA x |2 + | OA y |2 = | OA |2
definitie sinus en cosinus en straal goniometrische cirkel
| cos a |2 + | sin a |2 = 12
(cos a)2 + (sin a)2 = 12
cos 2 a + sin 2 a = 1
besluit
cos 2 a + sin 2 a = 1
een kwadraat is altijd positief
notatie
Die formule noem je de grondformule van de goniometrie.
5.6.3 Toepassingen
Identiteiten bewijzen
Voorbeeld 1 Toon
Voorbeeld 2

Goniometrische getallen berekenen vanuit het gegeven goniometrisch getal en het gegeven kwadrant
Voorbeeld 1
Gegeven: sin a = 1 4 en a ligt in het tweede kwadrant.
Bereken
Voorbeeld 2
Gegeven: tan a = 2 en a ligt in het derde kwadrant.
Bereken
Formularium
Oefeningen
REEKS A
cos 2 a + sin 2 a = 1 tan a = sin a cos a
cos 2 a = 1 – sin 2 a cot a = cos a sin a
sin 2 a = 1 – cos 2 a 1 + tan2 a = 1 cos 2 a
©VANIN
33 Vereenvoudig.
a) tan a ? cot a b) 1 cos a sin a
c) tan a ? cos a
d) sin a cos a tan a
e) sin 2 a ? cot 2 a f) cos 2 a – 1
g) 2 – cos 2 a – sin 2 a
a) 1 cos 2 a – tan2 a
b) 1 sin2 – cot 2
©VANIN
c) 1 + cos 2 a sin2 a
d) (sin 2 a – 1) ? tan 2 a
e) 1 – sin2 a cos a sin a 1 – cos 2 a
f) tan2 a 1 + tan2 a
a) 1 – cos 2 a sin a + 1 – sin2 a cos a = sin a + cos a
b) tan a 1 + tan2 a = sin a ? cos a
©VANIN
(cos a – sin a) 2 = 1 – 2 ? cos a ? sin a
d) (cos a + sin a) 2 + (cos a – sin a) 2 = 2
e) tan a + cot a = 1 sin a cos a
c)
Bereken, zonder rekenmachine, de ontbrekende goniometrische getallen voor de hoek in het gegeven kwadrant.
a) cos a = 1 3 en a ∈ IV
c) sin a = 0,25 en a ∈ I
©VANIN
b) tan a = –4 3 en a ∈ II
d) cot a = –1 en a ∈ IV
37 Bereken, zonder rekenmachine, de ontbrekende goniometrische getallen voor de hoek in het gegeven kwadrant.
a) sin a = –2 2 en a ∈ IV
c) cos a = 3 2 en a ∈ IV
©VANIN
b) tan a = –1 en a ∈ II
d) cot a = 3 en a ∈ III
5.7 Willekeurige driehoeken oplossen
Als je de top van de toren van Pisa vanuit twee punten observeert, dan zijn de hoeken waaronder je de top ziet respectievelijk 47º 43 35 en 28º 48 39
De hellingshoek van de toren zelf bedraagt 81º.
Wat is de hoogte x van de toren als de observatiepunten, die in een lijn liggen met de toren, 50 m uit elkaar liggen?
Toren van Pisa
De (scheve) toren van Pisa is de vrijstaande klokkentoren (een campanile) bij de kathedraal van Pisa (Duomo di Pisa). De toren is een van de onderdelen van het Campo dei miracoli.
©VANIN
De bedoeling was een verticale toren te bouwen, maar het overhellen begon kort na het begin van de bouw in augustus 1173. Bouwmeesters waren Gugilmo en Buonanno.
De toren is 55 meter hoog en de massa wordt geschat op 14 453 ton.
De huidige helling is ongeveer 10 %. De toren heeft 297 treden.
Naar verluidt liet Galilei voorwerpen van de toren naar beneden vallen om de valeigenschappen te bestuderen. Dat wordt als een mythe beschouwd.
Op 27 februari 1964 vroeg de Italiaanse regering om hulp om te zorgen dat de toren niet zou omvallen. Op 7 januari 1990 werd de toren gesloten uit veiligheidsoverwegingen.
Vervolgens werd hij gerestaureerd om de helling te verminderen.
Na ruim tien jaar werk werd de toren weer voor het publiek geopend op 15 december 2001. In augustus 2004 heeft een evaluatie van experts uitgewezen dat de toren de eerstvolgende drie eeuwen niet zal instorten. De toren is opnieuw in veiligheid, stelde professor Carlo Viggiani van de universiteit van Napels in de Italiaanse media.
Professor michele Jamiolkowski, de ingenieur die de renovatiewerken leidde, voegde eraan toe dat de 800 jaar oude toren sinds september 2003 opnieuw stabiel is.
Gedurende de laatste fase van de renovatie, die 28 miljoen euro kostte, hebben de experts de fundamenten van het gebouw versterkt en de toren 44 centimeter rechtop getrokken.
De overhelling bedraagt nu iets meer dan vier meter.
Er werd beslist de toren niet opnieuw recht te zetten, want dat zou het toerisme geen goed doen. De toren heeft opnieuw dezelfde inclinatie als in het jaar 1800.
5.7.1 De sinusregel
Bereken de verhoudingen op een eenheid nauwkeurig.
GEOGEBRA
De verhouding van een zijde op de sinus van de overstaande hoek is constant.
Bewijs van de sinusregel
Eerste geval: driehoek ABC is rechthoekig
tekening
GEOGEBRA
bewijs
In een rechthoekige driehoek ABC geldt:
gegeven een rechthoekige driehoek ABC met g = 90º te bewijzen
besluit
Tweede geval: driehoek ABC is scherphoekig
tekening
GEOGEBRA
gegeven een scherphoekige driehoek ABC te bewijzen a sin a = b sin b = c sin g
©VANIN
bewijs
In een scherphoekige driehoek ABC met hoogte [ BD ] op AC geldt:
ABD is rechthoekig
BCD is rechthoekig
sin a = | BD | c sin g = | BD | a c sin a = | BD | a sin g = | BD |
c sin a = a sin g a sin a = c sin g
Analoog kun je aantonen dat a sin a = b sin b
besluit
a sin a = b sin b = c sin g

Derde geval: driehoek ABC is stomphoekig
tekening
GEOGEBRA
gegeven een stomphoekige driehoek ABC met b > 90º te bewijzen a sin a = b sin b = c sin g
©VANIN
bewijs
In een stomphoekige driehoek ABC met hoogte [ CD ] op AD geldt:
CBD isrechthoekig CAD isrechthoekig
sin(180º – b)= | DC | a sin a = | DC | b supplementairehoeken
sin sin b = = | DC | a b b sin a =| DC | | DC | a sin b = b sin a a sin a = b sin b
Analoog kun je aantonen dat a sin a = c sin g .
besluit
a sin a = b sin b = c sin g
5.7.2 De cosinusregel
Teken de hoogtelijn uit B op AC en noem het snijpunt D
In de rechthoekige driehoek BDC geldt:
GEOGEBRA
Cosinusregel
Het kwadraat van een zijde is gelijk aan de som van de kwadraten van de andere zijden, verminderd met het dubbelproduct van de andere zijden maal de cosinus van de overstaande hoek.
Bewijs van de cosinusregel
Eerste geval: driehoek ABC is rechthoekig
tekening A
GEOGEBRA
©VANIN
bewijs
In een rechthoekige driehoek met g = 90º geldt:
c 2 = a 2 + b 2 – 2 a b cos g
⇔ c 2 = a 2 + b 2 – 2 a b cos 90º
⇔ c 2 = a 2 + b 2 – 2 ? a ? b ? 0
gegeven een rechthoekige driehoek ABC met g = 90º te bewijzen
c 2 = a 2 + b 2 – 2 a b cos g
⇔ c 2 = a 2 + b 2 Dit is de stelling van Pythagoras. De stelling van Pythagoras is een bijzonder geval van de cosinusregel.
besluit
c 2 = a 2 + b 2 – 2 a b cos g
Tweede geval: driehoek ABC is scherphoekig
tekening
B bC ca D α γ β gegeven een scherphoekige driehoek ABC te bewijzen
bewijs
©VANIN
In een scherphoekige driehoek ABC met hoogte [ BD ] op AC geldt de stelling van Pythagoras:
merkwaardig product
stelling van Pythagoras
besluit

GEOGEBRA
Derde geval: driehoek ABC is stomphoekig
tekening A
bewijs
gegeven een stomphoekige driehoek ABC met b > 90º te bewijzen b 2 =
©VANIN
In een stomphoekige driehoek ABC met hoogte [ CD ] op AB geldt de stelling van Pythagoras:
merkwaardig product
besluit
stelling
Pythagoras
Gevolgen
5.7.3 Willekeurige driehoeken oplossen
Formularium
©VANIN
De som van de hoeken in een driehoek is 180º.
Sinusregel
Cosinusregel
Eén zijde en twee hoeken zijn gegeven
gegeven
In een driehoek ABC zijn
c = 12,5 cm
a = 25º b = 45º
gevraagd de zijden a en b op 0,1 cm nauwkeurig en de hoek g op 1º nauwkeurig oplossing
• g = 180º – (a + b ) = 180º – (25º + 45º) = 180º – 70º = 110º
• a sin = c sin ⇔ a = c sin a sin g = 12,5 sin 25º sin 110º ≈ 5,6 (cm)
• b sin = c sin ⇔ b = c sin b sin g = 12,5 sin 45º sin 110º ≈ 9,4 (cm)
Opmerking
Gebruik bij voorkeur enkel de gegeven zijden.
Wat is daarvoor de reden?
Twee zijden en een ingesloten hoek zijn gegeven
gegeven
In een driehoek ABC zijn
b = 8 cm
c = 5 cm a = 40º
gevraagd
©VANIN
zijde a op 0,1 cm nauwkeurig en de hoeken b en g op 1 nauwkeurig oplossing
• a = b 2 + c 2 – 2 b c cos a
≈ 82 + 52 – 2 8 5 cos 40º ≈ 5,3 (cm)
• De sinusregel is niet aan te raden om hoeken te berekenen, omdat sin (180º – b) = sin b b sin b = a sin a ⇔ sin b = b sin a a ⇔ sin b = 8 sin 40º a ≈ 0,976 76 ⇒ b = 77º 37 26 of b = 102º 22 34
Je verkrijgt dus een dubbele oplossing.
Bij de cosinusregel doet dat probleem zich niet voor, vermits alle hoeken van een driehoek tussen 0º en 180º liggen.
• b 2 = a 2 + c 2 – 2 ? a ? c ? cos b
⇔ 2 a c cos b = a 2 + c 2 – b 2
⇔ cos b = a 2 + c 2 – b 2 2 a c = a 2 + 52 – 82 2 a 5
≈ –0,214 33
⇒ b = 102º 22 34
• g = 180º – (a + b ) = 180º – (40º + 102º 22 34) = 37º 37 26
Drie zijden zijn gegeven
gegeven
In een driehoek ABC zijn
a = 4 cm
b = 7 cm
c = 5 cm
gevraagd de hoeken a, b en g op 1 nauwkeurig
©VANIN
oplossing
• cos a = cos a = b 2 + c 2 – a 2 2 b c = 49 + 25 – 16 2 7 5
cos a ≈ 0,828 57
⇒ a = 34º 2 52
• cos b = cos b = a 2 + c 2 – b 2 2 a c = 16 + 25 – 49 2 4 5
cos b = –0,2
⇒ b = 101º 32 13
• g = 180º – (a + b ) = 44º 24 55
De som van de hoeken van een driehoek is 180º. Aan die eigenschap twijfelt wellicht niemand. Je bent immers bezig met euclidische meetkunde en in die meetkunde ga je ervan uit dat door een punt buiten een rechte juist één rechte kan worden bepaald die evenwijdig is met de gegeven rechte.

maar is dat wel zo? Je ziet immers de wereld anders dan hij is. De eerste bekende wiskundige die de euclidische meetkunde in twijfel trok, was Carl Friedrich Gauss (1777-1855), toen hij de meetkunde van de gekromde oppervlakten ontdekte bij het bestuderen van de geografie van het koninkrijk Hannover. Hij publiceerde echter nooit zijn theorieën. Uit de bevindingen van Gauss

Riemann ontstond de hyperbolische meetkunde (Lobachevski en Bolyai), waarin werd uitgegaan van het axioma dat er oneindig veel rechten kunnen worden bepaald die door een punt gaan en evenwijdig zijn met een gegeven rechte. Een gevolg daarvan is dat de som van de hoeken van een driehoek kleiner is dan 180º.
Bekender echter is de elliptische meetkunde van Riemann. Hij ging ervan uit dat door een punt geen enkele rechte te vinden is die evenwijdig is aan een gegeven rechte (denk hier bijvoorbeeld aan het bepalen van rechten op een bol). In die meetkunde is de som van de hoeken van een driehoek groter dan 180º. Het is die Riemann-meetkunde die Einstein later gebruikte in de wiskundige ontwikkeling van de relativiteitstheorie.
Twee zijden en een niet-ingesloten hoek zijn gegeven
gegeven
In een driehoek ABC zijn
a = 5 cm
b = 4 cm
b = 30º
gevraagd de zijde c op 0,01 cm nauwkeurig en de hoeken a en g op 1 nauwkeurig oplossing
©VANIN
Als je de situatie via een tekening bekijkt, merk je dat er twee oplossingen mogelijk zijn.
Dat vind je ook terug bij het oplossen van de driehoek.
Bij elk van die waarden voor a horen ook waarden voor g en c
Opmerking
Uit een situatieschets voor een willekeurige driehoek ABC waar a = 5 cm en b = 30º kun je achterhalen dat naargelang de afmetingen van b
• er juist één oplossing is als b = 2,5 cm
©VANIN
• er geen oplossingen zijn als b < 2,5 cm.
Let wel dat het bovenstaande geen regel is, maar samengaat met de gegeven a en b
Drie hoeken zijn gegeven
Twee driehoeken met gelijke hoeken zijn wel gelijkvormig, maar niet noodzakelijk congruent.
Er zijn dus oneindig veel driehoeken mogelijk bij drie gegeven hoeken.
Opmerking
Wanneer het gegeven overeenkomt met een congruentiekenmerk HZH, ZHZ of ZZZ, dan is er voor de driehoek slechts één oplossing.
Samenvatting gegeven 1 zijde + 2 hoeken 2 zijden 3 zijden + niet-ingesloten hoek + ingesloten hoek oplossen met sinusregel cosinusregel
REEKS A
38 Los de driehoek ABC op. Bereken de zijden op 0,1 en de hoeken op 1 nauwkeurig.
a) a = 57 b = 21º g = 34º
©VANIN
b) b = 57 c = 21 a = 34º
c) a = 17 b = 19 c = 6
39 Los de driehoek ABC op. Bereken de zijden op 0,1 en de hoeken op 1 nauwkeurig.
a) a = 17 b = 39º g = 61º
b) b = 37 c = 21 a = 144º
c) b = 63 c = 120 g = 134º
40 Los de driehoek ABC op. Bereken de zijden op 0,01 en de hoeken op 1 nauwkeurig.
a) a = 27,5 b = 43º 19 g = 51º 27
©VANIN
b) b = 25 c = 20 a = 64º 5 23
b = 4,5 c = 6 b = 40º
c)
41 Los de driehoek XYZ op. Bereken de zijden op 0,001 en de hoeken op 1 nauwkeurig.
a) x = 275 y = 300 z = 100
b) x = 175 z = 101 ^ X = 105º
c) x = 75 z = 31 ^ Z = 50º
Toepassingen
Toepassing uit de topografie x
gegeven
^ A = 81º
D1 = 47º 43 35
gevraagd x oplossing ^ D 1 + ^ D 2 = 180º (nevenhoeken)
D 2 = 180º – 47º 43 35 = 132º 16 25
Je observeert de toren van Pisa vanuit twee punten. Je ziet de top vanuit een hoek van 47º 43 35 en vanuit een hoek van 28º 48 39. De hellingshoek van de toren bedraagt 81º. Wat is de hoogte x van de toren, als de observatiepunten, die in één lijn liggen met de toren, 50 m uit elkaar liggen? Bepaal je antwoord op 1 cm nauwkeurig.
©VANIN
Sinusregel in n BCD
Sinusregel in n ABD
De toren is 55,69 m hoog.
Krachten samenstellen
gegeven
de krachten F1 en F2 die een hoek a insluiten (zie figuur)
gevraagd
©VANIN
• de grootte van de resultante FR op 1 N nauwkeurig
• de hoek tussen F1 en FR op 1 nauwkeurig
oplossing
• Je noteert het maatgetal van de grootte van de twee krachten als F1 en F2
Je past de cosinusregel toe in de driehoek ABC met | AC | = F1 , | BC | = F2 en | AB | = FR
FR = F 1 2 + F 2 2 – 2 F 1 F 2 cos (180º – a) cos (180º – a) = –cosa
FR = F 1 2 + F 2 2 + 2 F 1 F 2 cos a
Die cosinusregel voor de resultante van twee krachten verschilt dus qua vorm met die uit de wiskunde.
• Om ∅ te berekenen, pas je nogmaals de cosinusregel toe. cos ∅ = F 1 2 + F R 2 – F 2 2 2 F 1 F R ⇒ ∅
Voorbeeld
F1 en F2 hebben hetzelfde aangrijpingspunt en maken een hoek van 60º.
F1 is 600 N en F2 is 500 N.
Hoe groot is dan de resultante en welke hoek maakt die met de krachten?
Oplossing
FR maakt een hoek van met F1
FR maakt een hoek van met F2
Oefeningen
REEKS A
42 Om een brug te bouwen tussen twee plaatsen (A en B)
langs een rivier, moet de ingenieur de afstand
tussen beide punten kennen.
Daarvoor gaat hij aan één oever van plaats A naar plaats C.
De afstand tussen A en C is 20 m.
De hoek waaronder B gezien wordt vanuit A ten opzichte van de rechte AC, is 155º 23 .
De hoek waaronder B gezien wordt vanuit C ten opzichte van de rechte AC, is 20º 51
Bepaal, op 1 cm nauwkeurig, de afstand tussen A en B.
B
©VANIN
43 Twee auto’s, die in radiocontact staan met elkaar, volgen in een vlak landschap
een onbemande weerballon.
Op een gegeven ogenblik gaan beide auto’s aan de kant staan zodat ze in hetzelfde horizontale vlak 2,5 km van elkaar verwijderd zijn.
De bestuurders, Philippe en Laurent, meten de hoek naar de onderkant van de mand.
Philippe meet een hoek van 40º en Laurent een hoek van 30º.
Hoe hoog bevindt de weerballon zich boven de grond? Bepaal je antwoord op 1 m nauwkeurig.
20 m
AC
km
De knoop is een eenheid van snelheid die veel gebruikt wordt in de zeevaart.
Eén knoop is één zeemijl per uur.
Eén zeemijl is gedefinieerd als precies 1 852 meter.
Een knoop is dus een snelheid van 1,852 km/h of 0,514 4... m/s.

©VANIN
Een zeemijl was ooit gedefinieerd als de lengte van een boogminuut van een grootcirkel van de aarde. Door de afplatting van de aarde was die zeemijl echter niet overal even lang.
De doorsnede van een bol met een vlak is een cirkel.
Gaat het vlak door het middelpunt van de bol, dan spreek je van een grootcirkel.
Zo zijn alle meridianen van onze aardbol in feite grootcirkels.
De breedtecirkels of parallellen noem je – afgezien van de evenaar –kleincirkels.
44 Een schip vaart met een snelheid van 15 knopen. De stuurman ziet een vuurtoren eerst onder een hoek van 13º 35 7 en 20 minuten later onder een hoek van 29º 15 40 met zijn vaarrichting. Hoe ver is hij in beide gevallen van de vuurtoren verwijderd?
Bepaal je antwoord op 1 m nauwkeurig.
= 13° 35 7
29° 15 40
45 De diagonalen van een parallellogram meten 64 mm en 100 mm. Ze snijden elkaar onder een hoek van 50º.
Bereken de zijden van dat parallellogram op 0,1 mm en de hoeken op 1 .
46 Bereken de grootte, op 1 N, en de richting, op 1, van de resultante van twee krachten, 500 N en 700 N groot, als de richtingen van beide krachten een hoek vormen van 36º 25 17 .
N
N
25 17
47 Bereken de grootte, op 1 N, en de richting, op 1 , van de resultante van twee krachten, 1 500 N en 925 N groot, als de richtingen van beide krachten een hoek vormen van 125º 34
48
Gegeven:
K het midden van [ BC ] L het midden van [ EH ]
Gevraagd:
Bereken de hoek a op 1 nauwkeurig.
49 Vanaf de top van een mast van 24 m hoog worden twee metalen kabels, die onderling een hoek van 32º maken, naar de grond gespannen.
De ene kabel komt in de grond op 10 m van de mast, de andere op 8 m van de mast.
Waar de kabels in de grond komen, wordt telkens een verstraler gezet.
Bereken de afstand tussen de twee verstralers.
Bepaal je antwoord op 0,01 m nauwkeurig.
50
Een piramide ingeschreven in een kubus heeft een vierkant grondvlak met zijde 30 cm.
Bereken:
a) de hoek a tussen twee opstaande ribben;
b) de hoek b tussen de gronddiagonaal en een opstaande ribbe.
Rond de hoeken af op 1 nauwkeurig.

AB
30 cm
51 Bereken de oppervlakte van de driehoek ABC.
Bepaal je antwoord op 0,01 cm2 nauwkeurig.
52 Bereken de lengte van de zwaartelijnen in de driehoek ABC als | BC | = 25 cm, ^ B = 48º en ^ C = 55º. Bepaal je antwoord op 0,1 cm nauwkeurig.
53 Twee werklieden proberen een zware kist langs een hellend vlak naar binnen te trekken. Bereken de grootte van de resultante FR . Bepaal je antwoord op 1 N nauwkeurig.
Bereken de hoek tussen F2 en FR . Bepaal je antwoord op 1 nauwkeurig.
©VANIN
54 Hieronder zie je een schematische voorstelling van een kruk- en drijfstangmechanisme.

Bereken de lengte van het uitgeschoven gedeelte [CB ] van de drijfstang bij een hoek van 60º. Bepaal je antwoord op 0,1 cm nauwkeurig.
55 Vanuit twee punten A en B zie je aan de overzijde van een rivier twee torens D en C
Bereken de afstand tussen de twee torens met de meetgegevens op de figuur. Bepaal je antwoord op 1 cm nauwkeurig.
©VANIN
56 Gegeven: een piramide met een vierkant grondvlak met zijde 20 cm en opstaande ribben van 45 cm. Bereken de hoeken van de driehoek ABC
Bepaal je antwoord op 1 nauwkeurig.
57 De evenwijdige zijden van een trapezium meten 12 cm en 16 cm. De opstaande zijden zijn 4,5 cm en 5 cm lang. Bereken van dat trapezium de grootte van de hoeken op 1 nauwkeurig en de lengte van de diagonalen op 1 mm nauwkeurig.
©VANIN
STUDIEWIJZER Goniometrie
5.1 Goniometrische getallen in een rechthoekige driehoek

De sinus (sin) van een scherpe hoek in een rechthoekige driehoek is de verhouding overstaande rechthoekszijde schuine zijde .
De cosinus (cos) van een scherpe hoek in een rechthoekige driehoek is de verhouding aanliggende rechthoekszijde schuine zijde
De tangens (tan) van een scherpe hoek in een rechthoekige driehoek is de verhouding overstaande rechthoekszijde aanliggende rechthoekszijde
5.2 Georiënteerde hoeken

Een georiënteerde hoek is een hoek waarbij een pijl het beginbeen en het eindbeen van de hoek aanduidt.
5.3 De goniometrische cirkel


©VANIN
KENNEN
De goniometrische cirkel is de cirkel met middelpunt O en straal 1.
KUNNEN
Een georiënteerde hoek voorstellen door zijn beeldpunt op de goniometrische cirkel. De hoofdwaarde van een hoek bepalen.
5.4 Goniometrische getallen van een hoek

KENNEN
De cosinus van een hoek is het eerste coördinaatgetal van het beeldpunt van de hoek op de goniometrische cirkel.
De sinus van een hoek is het tweede coördinaatgetal van het beeldpunt van de hoek op de goniometrische cirkel.
Voor een willekeurige hoek a definieer je: tan = sin cos als cos a ≠ 0
De tangens van een hoek is het tweede coördinaatgetal van het snijpunt van de raaklijn in het punt E x (1, 0) aan de goniometrische cirkel en het eindbeen van de hoek.
Voor een willekeurige hoek a definieer je: cot = cos sin als sin a ≠ 0
Gevolg: cot = 1 tan als tan a ≠ 0.
De cotangens van een hoek is het eerste coördinaatgetal van het snijpunt van de raaklijn in het punt E y (0, 1) aan de goniometrische cirkel en het eindbeen van de hoek.
De hellingshoek a van een rechte is de georiënteerde hoek tussen die rechte en de x-as.
In een orthonormaal assenstelsel is de tangens van de hellingshoek van een rechte gelijk aan de richtingscoëfficiënt van die rechte.

KUNNEN
met ICT de goniometrische getallen van een hoek berekenen.
Een hoek tekenen aan de hand van een goniometrisch getal.
De goniometrische getallen schatten bij een getekende hoek.
De hellingshoek van een rechte bepalen.
5.5 Goniometrische getallen van verwante hoeken

KENNEN
Twee georiënteerde hoeken zijn gelijk als en slechts als hun maatgetallen, op een veelvoud van 360 na, aan elkaar gelijk zijn.
Gelijke hoeken hebben gelijke goniometrische getallen.
Twee georiënteerde hoeken zijn tegengesteld als en slechts als hun som de nulhoek is.
cos (–a) = cos a sin (–a) = –sin a
©VANIN
tan (–a) = –tan a cot (–a) = –cot a
Twee georiënteerde hoeken zijn supplementair als en slechts als hun som de gestrekte hoek is.
cos (180o – a) = –cos a sin (180o – a) = sin a
tan (180o – a) = –tan a cot (180o – a) = –cot a
Twee georiënteerde hoeken zijn antisupplementair als en slechts als hun verschil de gestrekte hoek is.
cos (180o + a) = –cos a sin (180o + a) = –sin a
tan (180o + a) = tan a cot (180o + a) = cot a
Twee georiënteerde hoeken zijn complementair als en slechts als hun som de rechte hoek is.
cos (90o – a) = sin a sin (90o – a) = cos a
tan (90o – a) = cot a cot (90o – a) = tan a
Twee georiënteerde hoeken zijn anticomplementair als en slechts als hun verschil de rechte hoek is.
cos (90o + a) = –sin a
sin (90o + a) = cos a

tan (90o + a) = –cot a cot (90o + a) = –tan a
Een verwantschap tussen twee hoeken herkennen.
De relaties tussen de goniometrische getallen van een hoek onderling en tussen die van verwante hoeken gebruiken.
met ICT hoeken terugzoeken waarvan een goniometrisch getal gegeven is.
5.6 Relaties tussen de goniometrische getallen van een hoek

Afgeleide formules uit tan a = sin cos (als cos a ≠ 0): sin a = tan a cos a cos a = sin tan (als tan a bestaat en verschillend is van 0)
Grondformule: cos 2 a + sin 2 a = 1
Afgeleide formules:
cos 2 a = 1 – sin 2 a sin 2 a = 1 – cos 2 a 1 + tan 2 a = 1 cos2

KUNNEN
Uit een goniometrisch getal van een hoek de andere goniometrische getallen afleiden.
De grondformule en de afgeleide formules gebruiken om goniometrische uitdrukkingen te vereenvoudigen of identiteiten te bewijzen.
5.7 Willekeurige driehoeken oplossen

De sinusregel bewijzen
a sin = b sin = c sin
De cosinusregel bewijzen a

KENNEN
©VANIN
KUNNEN
De sinusregel en cosinusregel gebruiken bij het oplossen van willekeurige driehoeken.
Bij realistische opgaven de oplossing interpreteren.
Pienter problemen oplossen

Welke heuristiek(en) gebruik je om de onderstaande problemen op te lossen?
❑ concreet materiaal
❑ schets
❑ schema/tabel
❑ vereenvoudig
❑ gok verstandig
1. De directrice vindt glas recycleren belangrijk in haar school.
Het glas is ofwel wit, ofwel gekleurd. Ze krijgt drie verschillende glastransformatoren. Twee van de glastransformatoren kunnen elk twee stuks recycleerbaar glas verwerken. De derde transformator kan één stuk recycleerbaar glas verwerken.
Deze machine produceert enkel wit glas als er twee witte stukken glas in gelegd worden. Elke andere combinatie levert gekleurd glas op.
Deze machine produceert enkel gekleurd glas als er twee gekleurde stukken glas in gelegd worden. Elke andere combinatie levert wit glas op. Deze machine transformeert gekleurd glas in wit glas en wit glas in gekleurd glas.
❑ filter
❑ patroon
❑ kennis
❑ logisch nadenken
❑
©VANIN
De directrice bedacht het volgende systeem:
X Y Z T
Welk soort glas moet de directrice in de machine leggen op de punten X, Y, Z en T, zodat er enkel nog wit glas uitkomt?
X Y Z T
A wit wit gekleurd wit B gekleurd gekleurd gekleurd wit C wit gekleurd gekleurd wit D gekleurd gekleurd wit gekleurd
Bron: Bebras-wedstrijd, niveau Padawan, 2019
2. Een luchtvaartmaatschappij biedt vluchten aan tussen verschillende wereldsteden, zoals afgebeeld in dit schema.
D.C.

Om haar CO2-uitstoot te verminderen en op die manier een steentje bij te dragen aan het klimaat, wil de maatschappij enkele van haar routes schrappen, maar op zo’n manier dat haar klanten nog altijd naar dezelfde steden kunnen vliegen.
(Als ze bijvoorbeeld de route tussen San Francisco en Washington schrapt, kunnen klanten nog altijd van San Francisco naar Washington vliegen via New York.) Hoeveel routes kan de maatschappij schrappen? A) 6
7
Bron: Bebras-wedstrijd, niveau Padawan, 2019
8
9
Washington,
San Francisco
New York
Londen
Parijs
Moskou
Caïro
Kuala Lumpur
HOOFDSTUK 6 I BESCHRIJVENDE STATISTIEK
6.1 Categorische en niet-gegroepeerde numerieke gegevens
6.2 Gegroepeerde numerieke gegevens
6.3 Centrummaten bij gegroepeerde gegevens
6.4 Spreidingsmaten
6.5 Symmetrische en scheve verdelingen
Tweedimensionale statistiek
problemen oplossen
©VANIN

6.1 Categorische en niet-gegroepeerde numerieke gegevens
6.1.1 Gegevens
verzamelen
In 2014-2015 werd, in opdracht van de FOD volksgezondheid, een Belgische nationale voedselpeiling gehouden. Het doel van die peiling was om de voedingsinname en -gewoontes van de Belgische bevolking te onderzoeken.
3 200 personen
1 600 mannen1 600 vrouwen
3-5 jaar6-9 jaar10-17 jaar18-39 jaar 40-64 jaar 500 kleuters 500 kinderen 1 000 adolescenten 600 jongvolwassenen 600 volwassenen
De populatie bij dat onderzoek was de volledige Belgische bevolking. Omdat het niet realistisch is om de volledige populatie te ondervragen, werd een steekproef getrokken.
Over welk soort steekproef gaat het hier?
De ondervraagde personen (de respondenten) zijn de elementen van de steekproef. geslacht
man vrouw
Daarvoor werden 3 200 personen geselecteerd en onderverdeeld in 64 groepen van 50 personen, verdeeld over alle provincies in België.
Een van de kenmerken die men onderzocht, was de houding ten opzichte van het persoonlijke lichaamsgewicht.
Dat kenmerk leverde niet-geordende categorische gegevens op.
Het resultaat van de enquête vind je in de frequentietabel hiernaast.
©VANIN
Het staafdiagram toont hoeveel procent van de ondervraagden minstens vijf dagen per week ontbijt. Welk soort gegevens zijn hier verwerkt?
Een andere vraag was hoeveel tijd men besteedt aan het ontbijt.
Welk soort gegevens levert dat kenmerk op?
minstens vijf dagen ontbijt per week

6.1.2 Categorische gegevens verwerken
Een frequentietabel opstellen
Een van de onderwerpen van de voedselconsumptiepeiling was het onderzoek naar de reden waarom mensen biologische producten kopen.
reden aankoop biologische producten
De producten zijn gezonder. 53 %
De smaak van de producten is beter. 38 %
De kwaliteit van de producten is beter. 38 %
De producten zijn beter voor het milieu. 31 %
Wat valt er op als je de percentages bekijkt?
Hoe komt dat?

aan 60 mensen die in de supermarkt bioproducten kochten, werd gevraagd wat de belangrijkste reden was voor hun aankoop.
GZ = de gezondheid; SM = de smaak; KW = de kwaliteit; MI = het milieu.
Stel een frequentietabel op.
KW GZ SM MI GZ KW
SM KW MI GZ SM MI
KW SM GZ SM MI GZ
GZ MI GZ KW KW SM
KW GZ SM GZ GZ MI
GZ MI KW SM GZ KW
KW SM MI GZ MI GZ
KW GZ GZ KW SM KW
SM GZ SM KW GZ KW
KW SM MI GZ KW MI
reden ni fi
GZ SM KW MI
• Hoeveel mensen die bioproducten kopen, doen dat niet vanwege het milieu?
• Hoeveel procent van de klanten koopt bio vanwege de smaak of de kwaliteit?
staafdiagram
belangrijkste reden tot aankoop van bioproducten bij 60 mensen
cirkeldiagram
belangrijkste reden tot aankoop van bioproducten bij 60 mensen
= gezondheid; SM = smaak; KW = kwaliteit; MI = milieu

GZ = gezondheid; SM = smaak; KW = kwaliteit; MI = milieu
GZ
Oefeningen
REEKS B
1 Op de site van Brussels Airport in Zaventem werken meer dan 20 000 mensen. Aan 80 van hen wordt gevraagd uit welk landsgedeelte ze afkomstig zijn.
VL = Vlaamse Gemeenschap; FR = Franse Gemeenschap; DU = Duitstalige Gemeenschap; BR = Brussel. FR vL vL BR FR vL DU FR vL BR
vL FR vL vL FR FR vL BR BR vL BR vL FR FR vL BR FR vL vL vL FR FR vL BR vL FR vL vL BR FR vL vL FR vL DU BR FR FR vL BR BR FR vL FR FR vL FR vL vL FR vL FR FR vL FR BR vL DU FR vL DU FR vL BR vL vL FR FR BR vL
a) Stel een frequentietabel op. regio n i f i vL FR DU BR

b) Teken met IcT een staafdiagram voor de absolute frequentie.
c) Teken met IcT een cirkeldiagram voor de relatieve frequentie.
d) Hoeveel van de 80 respondenten zijn afkomstig uit de vlaamse Gemeenschap of Brussel?
e) Hoeveel procent is niet afkomstig uit de Franse Gemeenschap?
f) Op 1 december 2021 werkten 28 836 mensen op de site. Hoeveel daarvan zouden, volgens de steekproef, uit de Duitstalige Gemeenschap komen?
g) Druk het verschil uit tussen het aantal werknemers uit de vlaamse Gemeenschap en het aantal werknemers uit de Franse Gemeenschap.
• in procentpunt:
• in procent:
6.1.3 Niet-gegroepeerde numerieke gegevens verwerken
Een frequentietabel opstellen
Groenten en fruit horen bij een gezonde levensstijl.
• De aanbevolen consumptie van fruit bedraagt twee stukken per dag.
• Slechts 9 % van de bevolking (3-64 jaar) voldoet aan de aanbeveling.
• Twee op de drie (64 %) jonge kinderen (3-5 jaar) halen wel de richtlijn voor fruit.

aan 48 leerlingen van een vierde jaar wordt gevraagd hoeveel stukken fruit ze gisteren hebben gegeten.
Stel een frequentietabel op.
• Welk deel van de leerlingen at gisteren twee stukken fruit?
• Hoeveel leerlingen aten gisteren drie of vier stukken fruit?
• Geef de betekenis van de cumulatieve relatieve frequentie van het waarnemingsgetal 3.
• Hoeveel procent van de ondervraagde leerlingen at gisteren minstens één stuk fruit?
• Is de steekproef die hier is uitgevoerd, een goede steekproef? Waarom (niet)?
staafdiagram
fruitconsumptie bij 48 vierdejaars
©VANIN
aantal stukken fruit per dag
lijndiagram
fruitconsumptie bij 48 vierdejaars
aantal leerlingen
aantal stukken fruit per dag
cumulatief staaf- en lijndiagram
%
fruitconsumptie bij 48 vierdejaars aantal stukken fruit per dag
Oefeningen
REEKS B
Een vegetariër eet geen vlees en geen vis.
Iemand die wel vis eet, maar geen vlees, is een pescotariër
Veganisten bannen alle dierlijke producten (dus ook melk, eieren, lederwaren …) uit hun leven.
Mensen die, vanwege hun gezondheid of uit zorg voor het milieu, op sommige dagen geen vlees of vis eten, noem je flexitariërs

2 Aan 110 Vlaamse gezinnen wordt gevraagd hoeveel dagen van de week ze helemaal geen vlees of vis eten.
a) Stel een frequentietabel op.
b) Hoeveel procent van de gezinnen is vegetarisch?
c) Geef de betekenis van de cumulatieve relatieve frequentie van 2.
d) Hoeveel gezinnen eten meer dan de helft van de dagen geen vlees of vis?
Centrummaten bij niet-gegroepeerde numerieke gegevens
(rekenkundig) gemiddelde mediaan modus
Het gemiddelde x van een rij getallen x 1, x 2, ..., x n is de som van die getallen gedeeld door het aantal getallen:
x = x i i = 1 n n
De mediaan Me van een gerangschikte rij met n getallen, is het getal met rangorde n + 1 2
De modus Mo is het gegeven met de grootste frequentie.
je rondt het gemiddelde af op één cijfer meer na de komma dan de oorspronkelijke gegevens.
Welke centrummaten worden gebruikt in deze vier voorbeelden?

In vergelijking met 2010 is de consumptie van brood in 2020 afgenomen. De consumptie van fruit is gelijk gebleven.
©VANIN
Eenpersoonshuishoudens zijn het meest voorkomende huistype.

De helft van de tieners in Limburg leest minstens twee boeken per maand.
vruchtbaarheidsgraad wereldwijd
Bron: data.worldbank.org
2019: vruchtbaarheidsgraad wereldwijd gehalveerd tot 2,4 (als het getal onder 2,1 zakt, begint de bevolking te krimpen)
Centrummaten uit een niet-gegroepeerde frequentietabel bepalen
Een leerkracht Nederlands geeft aan het begin van het schooljaar een woorddictee met tien moeilijke woorden. De frequentietabel toont het aantal gemaakte fouten.
vul de frequentietabel aan.
7 1 10
9
14
8
11 6 8 7 6

• Om het gemiddelde te berekenen, gebruik je de formule x = n i x i i = 1 k n
Daarbij is k het aantal verschillende gegevens.
x =
Schat het totale aantal gemaakte fouten, als er 150 leerlingen het dictee maken.
• De mediaan bepaal je met behulp van de cumulatieve frequentieverdeling.
Geef de betekenis van de mediaan.
• Wat is het meest voorkomende aantal fouten?
• De leerkracht trekt één punt af per gemaakte fout. Bereken het klasgemiddelde op 10.
• Welke centrummaat wordt beïnvloed als een van de leerlingen die zeven fouten maakte, tien fouten had gemaakt?
Oefeningen
REEKS B
3 Juist of fout? Duid aan met een vinkje en verklaar je antwoord.
a) De mediaan is niet vatbaar voor uitschieters.
b) als de leerkracht na een toets zegt dat je bij de betere helft van de klas hoort, dan ligt je score boven het gemiddelde.
juist fout
©VANIN
c) als je de punten van twee klassen van dezelfde richting voor een proefwerk wilt vergelijken, gebruik je de mediaan.
d) als je wilt aantonen dat een bepaald gegeven het meest voorkomt, gebruik je de modus.
e) Het is mogelijk dat alle gegevens, op één na, kleiner zijn dan het gemiddelde.
4 Welke centrummaat werd gebruikt bij de onderstaande onderzoeksresultaten?
a) Kinderen ontbijten vaker dan tieners.
b) De helft van de mensen heeft minstens drie cOvID-19-zelftesten gedaan in 2021.
c) Nederlanders zijn groter dan Belgen.
5 In een bedrijf wordt op een dag bij alle bedienden geregistreerd hoeveel koppen koffie ze die dag hebben gedronken.
©VANIN
a) vul de frequentietabel aan.
b) De helft van de bedienden dronk minstens koppen.
c) In een ander bedrijf werken 95 bedienden.
Schat hoeveel koppen koffie men daar per dag moet voorzien.

6 Het cirkeldiagram toont de grootte van de huishoudens in Vlaanderen in 2021. Het aantal huishoudens met meer dan zes personen werd niet opgenomen in het onderzoek.
aantal personen per huishouden in Vlaanderen
a) Bepaal de modus.
b) Geef de betekenis van de modus.
e) Geef de betekenis van de mediaan.
c) Hoe groot is het gemiddelde huishouden in vlaanderen?
d) Bepaal de mediaan.
6.2 Gegroepeerde numerieke gegevens
6.2.1 Gegroepeerde frequentietabel
Onderzoek naar de massa (in kg) van de zesdejaars in een school leverde de volgende resultaten op.
©VANIN
massa zesdejaars aantal leerlingen
Op het staafdiagram zie je dat er maar liefst 33 verschillende waarden zijn, elk met een absolute frequentie gelijk aan 1, 2 of 3.
Daarom is het overzichtelijker om de gegevens in klassen te groeperen
• Een klasse is een interval dat gesloten is in zijn ondergrens en open in zijn bovengrens.
Bijvoorbeeld: de klasse [45, 50[.
De grenzen van de klasse noem je de klassengrenzen
• Het klassenmidden mi is het gemiddelde van de klassengrenzen van de i-de klasse.
Bijvoorbeeld: het midden van de klasse [45, 50[ is 45 + 50 2 = 47,5.
• De klassenbreedte is het verschil tussen de bovengrens en de ondergrens van de klasse. je kiest voor alle klassen een gelijke klassenbreedte.
Bijvoorbeeld: de breedte van de klasse [45, 50[ is 50 – 45 = 5.
• Het aantal klassen is minimaal 5 en maximaal 15.
• Het kleinste gegeven behoort tot de eerste klasse en het grootste gegeven tot de laatste klasse.
als je de resultaten onderbrengt in een gegroepeerde frequentietabel, zie je alleen nog dat er bijvoorbeeld zes gegevens tot de klasse [50, 55[ behoren. Wat die gegevens zijn, is niet meer zichtbaar. Dat houdt een verlies aan informatie in.
• Hoeveel leerlingen wegen tussen 65 kg en 70 kg?
• Geef de betekenis van de relatieve frequentie van de derde klasse.
©VANIN
• Hoeveel procent van de leerlingen weegt tussen 70 kg en 80 kg?
• Geef de betekenis van de cumulatieve absolute frequentie van de derde klasse.
• Hoeveel procent van de leerlingen weegt minstens 85 kg?
6.2.2 Grafische voorstellingen
Histogram
De frequentie bij de gegroepeerde gegevens over de massa van de zesdejaars stel je voor door een histogram
Een histogram is een staafdiagram met aaneengesloten staven dat gebruikt wordt bij gegroepeerde gegevens.
Op de horizontale as plaats je de klassen en op de verticale as de frequentie.
©VANIN
massa zesdejaars
aantal leerlingen 10 12 8 4 2 6 0
[45, 50[[50, 55[[55, 60[[60, 65[[65, 70[[70, 75[[75, 80[[80, 85[[85, 90[[90, 95[
massa (kg)
Frequentiepolygoon
Een frequentiepolygoon is een type lijndiagram dat gebruikt wordt bij gegroepeerde gegevens en dat de roosterpunten (mi , ni ) of (mi , fi ) verbindt.
De frequentiepolygoon sluit aan op de horizontale as in de punten (a, 0) en (b, 0).
Daarbij is a het klassenmidden van de klasse die de eerste klasse van de steekproef voorafgaat, en b het klassenmidden van de klasse die op de laatste klasse van de steekproef volgt.
Op die manier ontstaat een veelhoek of polygoon.
massa zesdejaars
aantal leerlingen
(kg)
Een ogief is een type cumulatief lijndiagram dat gebruikt wordt bij gegroepeerde gegevens en dat de roosterpunten (a1 , 0) en (bi , cfi ) of (bi , cni ) met elkaar verbindt.
Bij die grafische voorstelling wordt de cumulatieve frequentie van elke klasse toegekend aan de klassenbovengrens bi van de klasse, wat logisch is, gelet op de betekenis van de cumulatieve frequenties.
De klassenondergrens a1 van de eerste klasse is de klassenbovengrens van de klasse voorafgaand aan de eerste klasse van de steekproef. Die klasse geef je de cumulatieve frequentie 0 of 0 %.
massa zesdejaars
(kg)
Los de vragen op met behulp van het ogief.
• Hoeveel procent van de leerlingen weegt minder dan 68 kg?
• Hoeveel leerlingen wegen tussen 76 kg en 85 kg?
• vanaf welke massa behoort een leerling tot het zwaarste kwart?

Frequentietabel
Om de klassenfrequenties te bepalen, gebruik je de functie INTERvaL(gegevensmatrix;interval_verw).
Die functie telt van een geselecteerd gebied (de gegevensmatrix) hoeveel elementen in een interval ]a, b] liggen, waarbij a en b twee opeenvolgende getallen zijn van de intervalverwijzing.
©VANIN
Omdat je in de statistiek met intervallen van de vorm [a, b[ werkt, moet je een hulpkolom gebruiken: per klasse voer je de werkelijke klassenbovengrenzen in.
Open het bestand ‘massa.xlsx’ en ga als volgt te werk.
• Geef de werkelijke klassenbovengrenzen (w.k.b.) in de G-kolom in.
• Selecteer in één keer alle cellen waarin het resultaat van de telling moet komen (dat noem je een matrix). je selecteert dus de cellen c12 tot en met c21.
• Formule: =INTERvaL(a1:j7;G12:G21).
• Druk Shift + Ctrl + Enter om de matrix te verwerken.
• Het resultaat van de telling komt in de geselecteerde cellen.
• Werk de frequentietabel verder af.


Histogram
Open het bestand ‘massa.frequentietabel.xlsx’ en ga als volgt te werk.
• Selecteer de cellen met de absolute freqenties en voeg een staafdiagram in.
• Om de staven tegen elkaar te plaatsen:
■ rechtermuisklik op een van de staven;
■ gegevensreeks opmaken;
■ breedte tussenruimte: 0 %.
• Kies voor een randkleur met een ononderbroken streep.
Frequentiepolygoon
Open het bestand ‘massa.frequentietabel.xlsx’ en ga als volgt te werk.
klasse mi ni fi
[40,45[42,500,00%
[45,50[47,534,41%
[50,55[52,568,82%
[55,60[57,5710,29%
[60,65[62,568,82%
[65,70[67,51014,71%
[70,75[72,545,88%
[75,80[77,51116,18%
[80,85[82,5913,24%
[85,90[87,5811,76%
[90,95[92,545,88%
[95,100[97,500,00%
©VANIN
• voeg boven rij 12 en onder rij 21 een nieuwe rij in en verwijder de opmaak.
• voer een nieuwe fictieve eerste klasse [40,45[ in met klassenmidden 42,5 en een nieuwe fictieve laatste klasse [95,100[ met klassenmidden 97,5.
• je geeft deze twee extra klassen een frequentie 0 (0 %).
• Selecteer de cellen met de relatieve frequenties en voeg een lijndiagram met markeringen in.
• Selecteer voor de horizontale as de klassenmiddens.
• vink alle rasterlijnen aan.
• Zet de aspositie op de maatstreepjes.
• De verdere opmaak doe je naar eigen voorkeur.
• Sla het bestand op om verder te gebruiken bij het ogief.
Ogief
Open het bestand dat je verkregen hebt na de frequentiepolygoon en ga als volgt te werk.
• Geef de fictieve eerste klasse [40,45[ de cumulatieve frequentie 0 (0 %).
• Maak een extra kolom aan met de klassenbovengrenzen (k.b.). De bovengrens van de eerste klasse is 45, van de laatste klasse 95.
• Selecteer de cellen met de cumulatieve relatieve frequenties en voeg een lijndiagram in.
• Selecteer voor de horizontale as de klassenbovengrenzen.
• De verdere afwerking is analoog als bij de frequentiepolygoon.
• Pas het maximum van de verticale as aan: 1,0 i.p.v. 1,2 en kies 0,1 als primaire eenheid en 0,05 als secundaire eenheid.
GEOGEBRA
Oefeningen
REEKS A
7 Aan 100 jongeren werd gevraagd hoeveel zakgeld (in euro) ze per maand krijgen. zakgeld per maand aantal
©VANIN

a) Welke klasse telt het grootste aantal jongeren?
b) Hoeveel jongeren krijgen tussen 30 en 40 euro zakgeld?
c) Hoeveel procent van de jongeren krijgt minder dan 10 euro zakgeld?
8 Tijdens het medisch onderzoek meet de verpleegster de lichaamslengte. De frequentiepolygoon toont de lichaamslengte (in cm) van een groep jongens.
lichaamslengte jongens
b) Hoeveel jongens werden tijdens het onderzoek gemeten?
c) Hoeveel jongens zijn kleiner dan 170 cm?
d) Hoeveel procent van de jongens meet 190 cm of meer?
a) Maak een frequentietabel. lengte (cm) ni cni
9 In een postkantoor houdt men de wachttijden aan het loket bij. Het diagram geeft een overzicht van die wachttijden (in min).
wachttijden aan het loket
a) Hoe noem je deze grafische voorstelling?
b) Hoeveel procent van de mensen moet minder dan vijf minuten wachten aan het loket?
cumulatief
©VANIN
c) Hoeveel procent van de mensen moet acht minuten of meer wachten aan het loket?
wachttijd (min)
d) voor hoeveel procent van de mensen bedraagt de wachttijd drie tot zes minuten?
10 Aan alle leerlingen van het vierde jaar van een school werd gevraagd op hoeveel kilometer ze van school wonen.
afstand tot school

afstand (km)
a) Hoeveel leerlingen zitten er in die school in het vierde jaar?
b) Hoeveel leerlingen wonen op 10 km of minder van school?
c) Hoeveel leerlingen wonen op 12 km of verder van school?
d) Hoeveel leerlingen wonen op een afstand van 6 tot 10 km van school?
e) Hoeveel procent van de leerlingen woont op minder dan 4 km van school?
f) De veertig leerlingen van het vierde jaar die het dichtst bij school wonen, wordt gevraagd deel te nemen aan een enquête. In die enquête vraagt men ook hoe ver de leerlingen van school wonen. Tot welke klasse behoort dan de leerling die het verst van school woont?
11 Gedurende een aantal dagen werd het aantal bezoekers van een website bijgehouden.
a) vervolledig de frequentietabel.
b) Gedurende hoeveel dagen werd het bezoekersaantal bijgehouden?
c) Teken met IcT een histogram voor de absolute frequentie.
d) Gedurende hoeveel dagen telde men tussen 100 en 250 bezoekers?
e) Hoeveel dagen werden er 200 of meer bezoekers geteld?
f) Teken met IcT het ogief voor de cumulatieve relatieve frequentie.
g) Hoeveel procent van de dagen tel je tussen 125 en 225 bezoekers?
12 Aan de bezoekers van een film in een bioscoop wordt de leeftijd (in jaren) gevraagd.

a) Maak een frequentietabel. Breng de gegevens onder in klassen met klassenbreedte 10. leeftijd mi
[10, 20[
©VANIN
b) Uit welke leeftijdsklasse komen de meeste filmbezoekers?
c) Hoeveel mensen tussen 40 en 60 jaar wonen de film bij?
d) Hoeveel procent van de bezoekers is jonger dan 40 jaar?
e) Bij een soortgelijke film zijn er 88 mensen aanwezig.
Schat hoeveel daarvan minstens 50 jaar zijn.
f) Teken met IcT een histogram voor de absolute frequentie.
g) Teken met IcT een frequentiepolygoon voor de relatieve frequentie.
h) Teken met IcT een ogief voor de cumulatieve relatieve frequentie.
i) Hoeveel procent van de filmbezoekers is jonger dan 22 jaar?
j) Hoe oud zijn de 25 % oudste filmbezoekers?
k) Hoeveel procent meer 20- tot 30-jarigen waren er dan 10- tot 20-jarigen? Rond af op 0,1 %.
13 Op een examen wiskunde op 140 werden de volgende punten behaald.
a) Maak een frequentietabel. Breng de gegevens onder in klassen met klassenbreedte 10.
punten
b) Hoeveel leerlingen behaalden tussen 100 en 130?
c) Hoeveel leerlingen slaagden?
d) Teken met IcT een frequentiepolygoon voor de relatieve frequentie.
e) Teken met IcT een ogief voor de cumulatieve relatieve frequentie.
f) Hoeveel procent van de leerlingen behaalde minder dan 75?
14 Een aardappelverwerkingsbedrijf heeft van 96 willekeurig gekozen aardappelen de massa (in g) bepaald.
a) Maak een frequentietabel. De benedengrens van de eerste klasse is 30 en de klassenbreedte is 15.
b) Hoeveel procent van de aardappelen weegt minder dan 90 g?
c) Hoeveel aardappelen wegen 120 g of meer?
d) Teken met IcT een histogram voor de absolute frequentie.
e) Teken met IcT een frequentiepolygoon voor de absolute frequentie.
f) Teken met IcT het ogief voor de cumulatieve relatieve frequentie.
g) Hoeveel aardappelen wegen minder dan 100 g?
15 In de tabel staan de snelheden (in km/h) die tijdens een snelheidscontrole in de bebouwde kom werden opgetekend.
a) Maak een frequentietabel. Breng de gegevens onder in klassen met klassenbreedte 5. snelheid
b) Hoeveel auto’s werden gecontroleerd?
c) Hoeveel van de gecontroleerde voertuigen reden minstens 70 km/h?
d) Hoeveel procent reed minder dan 50 km/h?
e) Hoeveel auto’s reden 30 tot 45 km/h?
f) Teken met IcT een frequentiepolygoon voor de relatieve frequentie.
g) Teken met IcT een ogief voor de cumulatieve relatieve frequentie.
h) Hoeveel procent van de auto’s reed minder dan 62 km/h?
Uit een onderzoek van het Wetenschappelijk Instituut voor volksgezondheid in België blijkt dat 55 % van de adolescenten op een weekdag de aanbevolen limiet van twee uur schermtijd op de smartphone overschrijdt. Op een weekenddag loopt dat percentage op tot 84 %.

16 Je voert een onderzoek naar het dagelijkse aantal minuten schermtijd van de leerlingen van je klas of jaar.
Iedere leerling kijkt op zijn smartphone naar de schermtijd van de vorige dag. Je noteert de gegevens in een tabel met ruwe gegevens.
a) Maak een frequentietabel. Breng de gegevens onder in klassen met breedte 20.
schermtijd (min) mi
b) Hoeveel procent van de leerlingen is minder dan een uur per dag bezig met de smartphone?
c) Hoeveel leerlingen zijn langer dan twee uur per dag bezig?
d) Hoeveel procent is tussen een uur en twee uur bezig?
e) Teken met IcT:
• een histogram voor de relatieve frequentie;
• een frequentiepolygoon voor de absolute frequentie;
• een ogief voor de cumulatieve relatieve frequentie.
f) Schat bij hoeveel leerlingen de schermtijd hoogstens anderhalf uur is.
g) Wat is de schermtijd van de 20 % leerlingen die het langst met hun toestel bezig zijn?
6.3 Centrummaten bij gegroepeerde gegevens
6.3.1 Het gemiddelde
aan 83 leerkrachten van een school is gevraagd op hoeveel kilometer ze van school wonen.

Bereken het gemiddelde met IcT:
Het gemiddelde uit een gegroepeerde frequentietabel benaderen
Formule
©VANIN
Stel dat je niet over de tabel met ruwe gegevens beschikt, maar enkel over een frequentietabel. Om het gemiddelde te bepalen vanuit een gegroepeerde frequentietabel, vertegenwoordig je alle gegevens van een klasse door hun klassenmidden.
k frequentietabel met klassenbreedte 5 frequentietabel met klassenbreedte 10 klasse mi ni ni mi
[0, 5[ 2,5 15 37,5
[5, 10[ 7,5 18 135
[10, 15[ 12,5 16 200
[15, 20[ 17,5 10 175
[20, 25[ 22,5 8 180
[25, 30[ 27,5 6 165
[30, 35[ 32,5 4 130
[35, 40[ 37,5 4 150
[40, 45[ 42,5 2 85
Wat stel je vast als je de gemiddelden vergelijkt?
klasse mi ni ni mi
[0, 10[ 5 33
[10, 20[ 15 26
[20, 30[ 25 14
[30, 40[ 35 8
[40, 50[ 45 2 83
6.3.2 De mediaan
Bereken voor de tabel met ruwe gegevens van de vorige pagina de mediaan met IcT:
De mediaan uit een gegroepeerde frequentietabel benaderen
Stel dat je niet over de tabel met ruwe gegevens beschikt, maar enkel over een frequentietabel. je bepaalt dan eerst de klasse waarin het getal met rangorde n + 1 2 (de 50%-grens) is gelegen.
Die klasse noem je de mediaanklasse
frequentietabel met klassenbreedte 5 frequentietabel met klassenbreedte 10 klasse mi ni cni cfi
[0, 5[ 2,5 15 15 18,07 %
[5, 10[ 7,5 18 33 39,76 %
[10, 15[ 12,5 16 49 59,04 %
[15, 20[ 17,5 10 59 71,08 %
[20, 25[ 22,5 8 67 80,72 %
[25, 30[ 27,5 6 73 87,95 %
[30, 35[ 32,5 4 77 92,77 %
[35, 40[ 37,5 4 81 97,59 %
[40, 45[ 42,5 2 83 100,00 %
klasse mi ni cni cfi
[0, 10[ 5 33
[10, 20[ 15 26
[20, 30[ 25 14
[30, 40[ 35 8
[40, 50[ 45 2
De mediaan kun je benaderen door het klassenmidden te nemen van de mediaanklasse.
Me ≈ Me ≈
Ook nu zie je een mogelijk verlies aan nauwkeurigheid als de klassenbreedte groter wordt.
De mediaan uit het ogief benaderen
je kunt de mediaan ook schatten via het ogief, door gebruik te maken van de 50%-rechte.
Lineaire benadering van de mediaan
[5, 10[ 33 39,76 % 10
[10, 15[ 49 59,04 % 15
33 gegevens zijn kleiner dan 10 en 49 gegevens zijn kleiner dan 15. De mediaan is het getal met rangorde 84 2 = 42 en ligt dus tussen 10 en 15.
Om de mediaan te bepalen, gebruik je lineaire interpolatie:
6.3.3 De modale klasse
Definitie
©VANIN
Modale klasse
De modale klasse is de klasse met de grootste frequentie.
Voorbeeld
Bepaal de modale klasse bij de afstand van huis naar school:
Oefeningen
REEKS A
17 Een aardappelverwerkingsbedrijf heeft van 96 willekeurig gekozen aardappelen de massa (in g) bepaald (zie oefening 14).
a) Hoeveel weegt de zwaarste helft van de aardappelen?
b) je neemt 500 willekeurige aardappelen. Schat de totale massa op 1 g nauwkeurig.
c) vergelijk het gemiddelde en de mediaan. Wat kun je daaruit besluiten?
18 In de tabel staan de snelheden (in km/h) die tijdens een snelheidscontrole in de bebouwde kom werden opgetekend. De maximale toegelaten snelheid is er 50 km/h (zie oefening 15).
a) Welke centrummaat gebruik je om te illustreren wat de snelheidsbeperking is?
Bereken die centrummaat.
b) Klopt de bewering dat meer dan de helft van de auto’s te snel reed?
ICT
19 In een drukke winkelstraat werd aan 200 vrouwen gevraagd welk budget (in euro) ze elke maand aan kleding besteden.
De resultaten worden weergegeven in de frequentietabel.
budget (euro) ni
[0, 100[ 15
[100, 200[ 73
[200, 300[ 38
[300, 400[ 26
[400, 500[ 19
[500, 600[ 14
[600, 700[ 8
[700, 800[ 4
[800, 900[ 2
[900, 1 000[ 1
a) Bereken het gemiddelde.
b) Geef de betekenis van het gemiddelde.
c) Bepaal de mediaan.
d) Geef de betekenis van de mediaan.
e) Welke bedragen worden het meest besteed?
20 In de tabel zie je de leeftijdsverdeling van de Belgische bevolking op 1 januari 2023.
leeftijd (jaren) ni
[0, 10[ 1 240 172
[10, 20[ 1 358 845
[20, 30[ 1 404 025
[30, 40[ 1 533 931
[40, 50[ 1 510 095
[50, 60[ 1 583 282
[60, 70[ 1 413 090
[70, 80[ 1 012 409
[80, 90[ 512 632
[90, 100[ 126 343
[100, 110[ 2 733
a) vul de frequentietabel aan met IcT.
b) Bereken de gemiddelde leeftijd in België.
c) Bepaal de mediaan.
d) Geef de betekenis van de mediaan.
e) Wat is de modale klasse?
f) Hoeveel procent van de bevolking behoort tot die modale klasse?
ICT
21 Je voert een onderzoek naar het dagelijkse aantal minuten schermtijd van de leerlingen van je klas of jaar.
Iedere leerling kijkt op zijn smartphone naar de schermtijd van de vorige dag. Gebruik de verwerking van oefening 16 en beantwoord de volgende vragen.
a) Geef een schatting van het totale aantal uren schermtijd per dag van de leerlingen van jouw klas (of jaar).
b) De helft van de leerlingen van de klas (of het jaar) is minstens minuten per dag bezig met de smartphone.
©VANIN
c) Welke centrummaat zou je gebruiken om het aantal minuten schermtijd van leerlingen van verschillende leeftijden te vergelijken?
d) Welke centrummaat gebruik je het best om je eigen schermtijd te vergelijken met de schermtijd van de ondervraagde leerlingen?
REEKS C
De as van een wiel wordt bevestigd in een kogellager. Een lager is een asblok waarin de as kan draaien en heeft als belangrijkste taak het verlagen van de wrijving tussen de verschillende onderdelen. Een kogellager bestaat uit een binnen- en een buitenring, met daartussen een rij bolvormige kogels. Bij de draaibeweging draaien de kogels mee, waardoor veel wrijving wordt voorkomen.

22 Een bedrijf maakt kogellagers die een diameter van 20,5 mm moeten hebben. Als controle wordt er een steekproef uitgevoerd bij 160 willekeurig gekozen kogellagers.
diameter (mm) ni
[20,0; 20,1[ 9
[20,1; 20,2[ 13
[20,2; 20,3[ 17
[20,3; 20,4[ 26
[20,4; 20,5[ 34
[20,5; 20,6[ 23
[20,6; 20,7[ 16
[20,7; 20,8[ 12
[20,8; 20,9[ 9
[20,9; 21,0[ 1
a) vul de frequentietabel aan met IcT.
b) Is de machine die de kogellagers maakt, goed afgesteld?
c) Bepaal de mediaan door lineaire interpolatie.
6.4.1 Inleiding
temperatuurverschil 1981-2010 en 2020


Bron: climate.copernicus.eu, 2020
Tussen 1981-2010 en 2020 is de gemiddelde jaartemperatuur op aarde met 0,8 ºc toegenomen.

Mannen zijn gemiddeld 16 cm groter dan vrouwen. De grootste Belgische vrouw is 204 cm groot.
Haar man is 14 cm kleiner.
overgewicht volwassenen
verdeling beroepsbevolking Vlaams Gewest naar maandelijks inkomen en geslacht
©VANIN
Bron: RIVM, 2019
De helft van de Nederlanders heeft een BMI die groter is dan 25 en is dus, volgens de norm, te zwaar.
Statbel, 2021
Het gemiddelde netto maandelijkse inkomen in vlaanderen in 2020 bedroeg 1 903 euro.

Katten worden gemiddeld 14 jaar.
Een kwart wordt echter niet ouder dan 9 jaar en een kwart wordt zelfs ouder dan 17 jaar.
gemeenten met duurste bouwgrond
1 antwerpen
2 Leuven
3 Koksijde
4 Gent
5 asse
6 Grimbergen
7 Ranst
8 Bornem
9 Middelkerke
10 Knokke-Heist
11 Opwijk
Bron: Trends, 2020
De gemiddelde prijs voor bouwgrond in vlaanderen is 263,70 euro per m2
De mediaanprijs is 224 euro per m2
De bovenstaande voorbeelden tonen dat de centrummaten geen totaalbeeld geven.
Er moeten ook getallen bepaald worden die de spreiding weergeven ten opzichte van die centrummaten.
euro/m2
euro/m2
euro/m2
euro/m2
euro/m2
euro/m2
Bron:
6.4.2 De variatiebreedte
Voorbeeld 1
De leerlingen van twee klassen van het vierde jaar hebben het voorbije weekend auto’s gewassen voor het goede doel.
Per gewassen auto kregen ze 10 euro.
De opbrengst voor beide klassen zie je in de tabel.
KLaS a

opbrengst (euro) 10 20 30 40 50 60 70 80 90 100 Me =
aantal leerlingen 3 6 3 3 1
KLaS B opbrengst (euro) 10 20 30 40 50 60 70 80 90 100 Me =
leerlingen 1 3 1 3 3
De twee klassen hebben dezelfde mediaan en ongeveer hetzelfde gemiddelde.
Waarin verschillen de gegevensrijen dan wel?
Definitie Variatiebreedte
De variatiebreedte R is het verschil tussen het grootste en het kleinste waarnemingsgetal.
In het voorbeeld is
• de variatiebreedte voor klas a:
• de variatiebreedte voor klas B:
Dat geeft aan dat voor klas B de gegevens sterker gespreid zijn.
Een voordeel van de variatiebreedte is dat ze gemakkelijk te berekenen is.
Een nadeel is dat er slechts rekening gehouden wordt met de twee uiterste waarden en niet met de frequenties.
Voorbeeld 2
©VANIN
De histogrammen tonen rapportresultaten met dezelfde variatiebreedte R = wiskunderapport klas A
Leg uit waarin de ligging van de gegevens ten opzichte van het centrum van elkaar verschilt.
6.4.3 Kwartielen
aan 15 gezinnen werd gevraagd hoeveel smartphones er binnen het gezin zijn. je kunt de gegevensrij verdelen in vier delen met elk evenveel waarnemingsgetallen.
Definitie Kwartielen
Van een geordende rij met n gegevens is:
middelste50%
©VANIN
het eerste kwartiel Q1 het getal met rangorde n + 1 4 (25%-grens); het tweede kwartiel Q2 het getal met rangorde n + 1 2 (50%-grens); het derde kwartiel Q3 het getal met rangorde 3 n + 1 4 (75%-grens).
Merk op: Q2 = Me
In het voorbeeld: rangorde waarde betekenis
Q1 n + 1 4 = 4 2
Q2 n + 1 2 = 8 4
Q3 3 n + 1 4 = 12 5
25 % van de gezinnen heeft hoogstens 2 smartphones. 75 % van de gezinnen heeft minstens 2 smartphones.
50 % van de gezinnen heeft hoogstens 4 smartphones. 50 % van de gezinnen heeft minstens 4 smartphones.
75 % van de gezinnen heeft hoogstens 5 smartphones. 25 % van de gezinnen heeft minstens 5 smartphones.
Kwartielen uit een niet-gegroepeerde frequentietabel bepalen je bepaalt de 25%-grens, de 50%-grens en de 75%-grens.
Op een analoge manier kun je een rij verdelen in 10 of 100 delen. je spreekt dan van decielen en percentielen
Kwartielen uit een tabel met ruwe gegevens berekenen
aan 83 leerkrachten van een school is gevraagd op hoeveel kilometer ze van school wonen.
Bereken de kwartielen met IcT: Q1 = Me = Q3 =
Geef de betekenis van het eerste en derde kwartiel.
Kwartielen met Excel

Kwartielen met GeoGebra
Kwartielen uit het ogief benaderen
je gebruikt de Excelfunctie ‘KWaRTIEL(matrix;kwartiel)’of 'KWaRTIEL.INc(matrix;kwartiel)'.
Selecteer de cellen waarin de gegevens staan waarvan je het eerste of derde kwartiel wilt berekenen.
Druk op enter.
analoog aan de mediaan kun je de klasse bepalen waarin het eerste en derde kwartiel liggen, en daarvan het midden gebruiken om de kwartielen te benaderen.
Door gebruik te maken van het ogief, kun je nauwkeuriger werken.
6.4.4 De interkwartielafstand
Definitie Interkwartielafstand
De interkwartielafstand is het verschil tussen het derde en het eerste kwartiel.
Notatie
IQR
Voorbeelden
• Het aantal smartphones binnen een gezin (zie 6.4.3): IQR =
• De afstand van thuis naar school (zie 6.4.3): IQR =
Het nadeel van de interkwartielafstand is dat alleen de spreiding van de middelste helft van de gegevens wordt bekeken.
je houdt geen rekening met de 25 % kleinste en de 25 % grootste gegevens.
6.4.5 De boxplot
De kwartielen vormen samen met het kleinste en het grootste waarnemingsgetal de vijfgetallensamenvatting
De boxplot is een grafische voorstelling van de vijfgetallensamenvatting die bestaat uit:
• een rechthoek (de box) die als basis de interkwartielafstand heeft;
• een verticale lijn in de box die de plaats van de mediaan weergeeft;
• vanaf de box getekende lijnen (de whiskers) naar het minimum en het maximum.
Een boxplot verdeelt de gegevens in vier gebieden die elk een vierde (25 %) van de waarnemingsgetallen bevatten.
Opmerking
je kunt het gemiddelde via de boxplot schatten door het midden van de box te bepalen.

Voorbeeld 1
Uit een grootschalig onderzoek naar het eten van fruit bij vijftien- tot achttienjarigen in vlaanderen is gebleken dat een kwart van de ondervraagden hoogstens één stuk fruit per dag eet. De helft van de respondenten eet minstens twee stukken fruit en een kwart eet minstens vier stukken fruit per dag. Niemand eet meer dan zes stukken fruit per dag.
Bespreking:

• De mediaan ligt links in de box en is dus op het eerste gezicht kleiner dan het gemiddelde.
• je ziet de grootste spreiding bij het derde en vierde kwart, en de kleinste spreiding bij het eerste en tweede kwart.
Voorbeeld 2
aan 83 leerkrachten van een school is gevraagd op hoeveel kilometer ze van school wonen (zie 6.4.3). Teken de boxplot met IcT en beantwoord de vragen.
• Schat het gemiddelde en controleer.
• Het werkelijke gemiddelde is 14,7 (zie 6.3.1).
• verklaar het verschil tussen je schatting en het werkelijke gemiddelde.



• Zet alle gegevens in één kolom.
• Selecteer de gegevens.
• Invoegen: Box en Whisker.
• voeg ‘Gegevenslabels’ toe.
• Pas de lay-out aan naar eigen voorkeur.
Boxplot met Excel
GEOGEBRA
Uitschieters
De hematocrietwaarde van menselijk bloed is de verhouding van het volume rode bloedcellen ten opzichte van het totale volume van het bloed. De hematocrietwaarde wordt uitgedrukt in procent.
Rode bloedcellen zorgen voor het transport van zuurstof in het bloed, zodat een hoge hematocrietwaarde een belangrijk voordeel betekent voor duursporters.
van twaalf wielrenners is de hematocrietwaarde gemeten: 45 47 44 45 49 43 46 56 45 43 44 48
Bereken het gemiddelde en de mediaan: x ≈ Me =
Het is duidelijk dat het gegeven 56 het gemiddelde sterk beïnvloedt.
verwijder de ‘uitschieter’ 56 uit de gegevensrij en bereken opnieuw het gemiddelde: x ≈
Een handige methode om na te gaan of een gegeven een uitschieter is, is het IQR-criterium.
Het IQR-criterium voor uitschieters
Een waarnemingsgetal is een uitschieter als het minstens 1,5 keer de interkwartielafstand boven het derde kwartiel of onder het eerste kwartiel gelegen is.
Toon aan dat het gegeven 56 volgens het criterium een uitschieter is.
©VANIN
Voorbeeld
Zijn er uitschieters bij de gegevens over de afstand van thuis naar school? (zie 6.4.3) tijd


25 % – 75

De box-and-whiskerplot werd voor het eerst gebruikt in 1977 door de amerikaanse statisticus john Tukey.
In het oorspronkelijke ontwerp strekten de horizontale lijnen (de ‘whiskers’) zich uit tot maximaal 1,5 keer de interkwartielafstand onder het eerste of boven het derde kwartiel.
De ‘zwakke uitschieters’ werden met kleine kringetjes op de tekening aangebracht en de ‘sterke uitschieters’ (meer dan 3 keer de interkwartielafstand onder Q 1 of boven Q 3 ) met kruisjes.
REEKS A
23 Op een dag in de soldenperiode wordt op straat aan een aantal mensen gevraagd naar het aantal gekochte kledingstukken.
a) Bereken de variatiebreedte en geef de betekenis.
b) Bereken het eerste en het derde kwartiel en geef de betekenis.
c) Bereken de interkwartielafstand en geef de betekenis.
d) Teken met IcT de boxplot en bespreek.
24 Een aardappelverwerkingsbedrijf heeft van 96 willekeurig gekozen aardappelen de massa (in g) bepaald (zie oefeningen 14 en 17).
a) Wat is het verschil tussen de zwaarste en de lichtste aardappel?
b) Hoeveel weegt het zwaarste kwart van de aardappelen?
c) Zijn er uitschieters bij de gegevens?
d) Teken de boxplot met IcT en bespreek.
e) ‘Er wegen meer aardappelen tussen 31 g en 93,75 g, dan tussen 117 g en 144 g.’ Klopt die bewering?
25 De boxplot toont de resultaten voor een toets wiskunde (op 20 punten).
a) Wat was beste score?
b) Bepaal de variatiebreedte.
c) vul in:
• De helft van de leerlingen behaalde hoogstens
• Een kwart van de leerlingen behaalde minstens
d) Geef een schatting van het klasgemiddelde.
26 Een onderzoek naar de leeftijd waarop vrouwen in België hun eerste kind krijgen, levert de volgende boxplot op.
©VANIN
a) Bepaal de mediaan en geef de betekenis.
b) Bepaal het eerste kwartiel en geef de betekenis.
c) In de vS is er een vrouw die haar eerste kind kreeg op de leeftijd van 52 jaar. Is ze voor het onderzoek in België dan een uitschieter?

27 De punten op tien voor een toets worden voorgesteld in een cumulatief lijndiagram. punten op 10
a) Een kwart van de leerlingen behaalde minstens
b) Geef de betekenis van de mediaan.
c) Bereken de interkwartielafstand en geef de betekenis.
©VANIN
28 Aan de schoolpoort werd de snelheid (in km/h) van de bromfietsen door de politie gecontroleerd. De resultaten worden weergegeven in het ogief.
snelheid (km/h)
a) De helft van de bromfietsen rijdt minstens
b) 25 % van de bromfietsen rijdt hoogstens ; een kwart minstens
29 Een leerkracht Nederlands geeft aan het begin van het schooljaar een woorddictee met tien moeilijke woorden. De frequentietabel toont het aantal gemaakte fouten (zie 6.1.4).
xi ni
0 7 1 10 2 9 3 14 4 8 5 11 6 8 7 6 73 d) Teken met IcT de boxplot en bespreek.
a) Wat is de variatiebreedte?
b) Bepaal het eerste en derde kwartiel en geef de betekenis.
c) Wat is de spreiding van de middelste helft van de leerlingen?
30 In een bedrijf wordt op een dag bij alle bedienden geregistreerd hoeveel koppen koffie ze die dag hebben gedronken (zie oefening 5).
xi ni a) Zijn er uitschieters bij de gegevens?
b) Me = 3 < x = 3,3 verklaar. 0 5 1 6
2
31 In een drukke winkelstraat werd aan 200 vrouwen gevraagd welk budget (in euro) ze elke maand aan kleding besteden (zie oefening 19).
budget ni a) vul in (maak gebruik van het ogief):
[0, 100[ 15
[100, 200[ 73
[200, 300[ 38
[300, 400[ 26
[400, 500[ 19
[500, 600[ 14
[600, 700[ 8
[700, 800[ 4
[800, 900[ 2
[900, 1 000[ 1
• Een kwart van de vrouwen besteedt minstens per maand.
• Een kwart van de vrouwen besteedt hoogstens per maand.
b) Welke voorstelling zou je gebruiken om te verduidelijken
waarom het gemiddelde groter is dan de mediaan?
c) Teken die voorstelling met IcT en bespreek.
32 In de tabel zie je de leeftijdsverdeling van de Belgische bevolking op 1 januari 2023 (zie oefening 20). leeftijd (jaren) ni
[0, 10[ 1 240 172
[10, 20[ 1 358 845
[20, 30[ 1 404 025
[30, 40[ 1 533 931
[40, 50[ 1 510 095
[50, 60[ 1 583 282
[60, 70[ 1 413 090
[70, 80[ 1 012 409
[80, 90[ 512 632
[90, 100[ 126 343
[100, 110[ 2 733
a) Bepaal het eerste en derde kwartiel en geef de betekenis.
b) Rosa is 107 jaar. Kun je haar leeftijd als uitschieter beschouwen?
33 Je voert een onderzoek naar het dagelijkse aantal minuten schermtijd van de leerlingen van je klas of jaar.
Iedere leerling kijkt op zijn smartphone naar de schermtijd van de vorige dag. Gebruik de verwerking van oefeningen 16 en 21 en beantwoord de vragen.
a) Bereken de variatiebreedte en geef de betekenis.

©VANIN
b) Een kwart van de leerlingen is hoogstens minuten per dag bezig met de smartphone.
c) Een kwart van de leerlingen is minstens minuten per dag bezig met de smartphone.
d) Teken de boxplot met IcT en bespreek.
Uitschieters verwijderen uit een rij waarnemingsgetallen is niet altijd een goede statistische methode.
• Uitschieters die ontstaan zijn door een meetfout of een verkeerde omzetting van eenheden, bijvoorbeeld van inches naar cm, verwijder je het best.
• Uitschieters die werkelijk afwijken van de andere gegevens, zoals een topprestatie in de sport, verwijder je beter niet.

34 Is het een goede statistische methode om de uitschieter te verwijderen in de volgende gevallen? ja nee
a) De lengte (in cm) wordt bepaald van 150 volwassen Belgische vrouwen. van één vrouw wordt een lengte van 204 cm genoteerd.
b) Men meet de temperatuur (in ºc) in de 55 klaslokalen van een school. In lokaal a104 wordt een temperatuur van 85 ºc gemeten.
c) Bij metingen van het ozongehalte in de zomer aan de kust liggen alle waarden tussen 62 en 184 µg/m3, behalve in Oostende, waar 265 µg/m3 wordt gemeten.
d) Bij een toets wiskunde heeft iedereen minstens 8 op 20. Leopold heeft gespiekt en heeft 0 op 20 gekregen.
6.4.7 Variantie en standaardafwijking
In een klas werd een toets gehouden. De resultaten zie je in de frequentietabel. je kunt voor elk resultaat kijken hoe ver het zich van het gemiddelde bevindt. voor elke x i verkrijg je zo de afwijking ten opzichte van het gemiddelde: xi − x
Het gemiddelde van die afwijkingen is nul omdat de afwijkingen ten opzichte van het gemiddelde zowel positief als negatief zijn. De positieve en negatieve afwijkingen neutraliseren elkaar.
Daarom kwadrateer je die afwijkingen en bereken je de gemiddelde kwadratische afwijking:
i = 1 k n
n i (x i – x )2
je noemt die gemiddelde kwadratische afwijking ook de variantie, genoteerd s 2
De afwijkingen t.o.v. het gemiddelde worden zo groter gemaakt dan ze in werkelijkheid zijn. Een ander probleem is dat het resultaat niet meer dezelfde eenheid heeft als de waarnemingsgetallen zelf.
Een spreidingsmaat in dezelfde eenheid als de waarnemingsgetallen is de positieve vierkantswortel uit de variantie. Dat getal noem je de standaardafwijking.
Definitie Variantie en standaardafwijking
©VANIN
De variantie s 2 van een rij gegevens is gelijk aan de gemiddelde kwadratische afwijking ten opzichte van het gemiddelde. De standaardafwijking s van een rij gegevens is gelijk aan de positieve vierkantswortel uit de variantie.
Opmerkingen
• je rondt de standaardafwijking af op twee cijfers meer dan de gegevens.
• De enige betekenis die je voorlopig kunt geven aan de standaardafwijking, is dat het een soort ‘gemiddelde afwijking ten opzichte van het gemiddelde’ weergeeft.
De standaardafwijking uit een tabel met ruwe gegevens berekenen
aan 83 leerkrachten van een school is gevraagd op hoeveel kilometer ze van school wonen.
x ≈ 14,7 (zie 6.3.1) Bereken de standaardafwijking met IcT: s ≈
Standaardafwijking met Excel

Standaardafwijking met GeoGebra
je gebruikt de Excelfunctie ‘STDEvP’. Selecteer de cellen waarin de gegevens staan waarvan je de standaardafwijking wilt berekenen. Druk op enter en rond af op twee cijfers meer dan de gegevens.
De standaardafwijking uit een gegroepeerde frequentietabel benaderen
je gebruikt de formule s =
klasse mi ni
[0, 5[ 2,5 15
[5, 10[ 7,5 18
[10, 15[ 12,5 16
[15, 20[ 17,5 10
[20, 25[ 22,5 8
[25, 30[ 27,5 6
[30, 35[ 32,5 4
[35, 40[ 37,5 4
[40, 45[ 42,5 2
Voorbeeld 1
Op een toets wiskunde behaalden de elf leerlingen van de klas de volgende punten op twintig:
voor een toets Frans op vijftig waren de punten als volgt:
De standaardafwijking is voor beide gegevensrijen hetzelfde. Toch is het duidelijk dat de relatieve spreiding ten opzichte van het gemiddelde in de tweede rij kleiner is dan in de eerste. je maakt de spreiding relatief door de standaardafwijking te delen door het gemiddelde.
Definitie Variatiecoëfficiënt
De variatiecoëfficiënt V = s x
De variatiecoëfficiënt is een maat voor de relatieve spreiding van de waarnemingsgetallen ten opzichte van het gemiddelde. je drukt V meestal uit in procent.
Bereken de variatiecoëfficiënt in de bovenstaande voorbeelden. V1 ≈ V2 ≈
Gebruik van de variatiecoëfficiënt
• De variatiecoëfficiënt is vooral nuttig om het variëren van gegevensrijen te vergelijken waarbij verschillende eenheden zijn gebruikt. Denk bijvoorbeeld aan centimeter en inch.
• Bij wetenschappelijk onderzoek wordt het resultaat van een studie betrouwbaar genoemd als V < 5 % en altijd verworpen als V > 30 %.
• Bij machines die nauwkeurig werk moeten verrichten, wordt een variatiecoëfficiënt van maximaal 5 % toegestaan.
Voorbeeld 2
©VANIN
In een onderzoek naar de invloed van de luchtweerstand op de snelheid waarmee een voorwerp valt, laat men 30 keer een bal van op een hoogte van 5 m vallen. je ziet de tijd (in s) die nodig is om de grond te bereiken. Levert het experiment betrouwbare informatie op?

6.4.9 De standaardscore
Voorbeeld
De gemiddelde schoenmaat van vrouwen in België is 39,0. De standaardafwijking is 1,62. In de verenigde Staten gebruiken ze andere maten. Daar is de gemiddelde schoenmaat bij vrouwen 6,78 met een standaardafwijking 0,873.
De Belgische Kristina heeft maat 41. Haar amerikaanse vriendin jennifer heeft maat 7,5. Wie heeft relatief gezien de grootste maat?

Om die vraag te beantwoorden, moet je de gegevens onafhankelijk maken van de meeteenheid. Dat doe je door de standaardscore of z-score te berekenen.
Definitie Standaardscore
De standaardscore of z-score van een waarnemingsgetal xi is het getal z i = x i – x s
De standaardscore drukt het verschil uit van een waarnemingsgetal ten opzichte van het gemiddelde in verhouding tot de standaardafwijking.
Beantwoord nu de vraag wie relatief de grootste schoenmaat heeft.
zK = zJ =
©VANIN
Gebruik van de standaardscore standaardscore betekenis
z < –2
Meer dan 2 keer de standaardafwijking onder het gemiddelde: uitzonderlijk laag.
–2 < z < –1 Laag.
–1 < z < 1
Minder dan 1 keer de standaardafwijking verwijderd van het gemiddelde: behorend tot de standaardgroep x – s, x + s []
1 < z < 2 Hoog.
z > 2
Meer dan 2 keer de standaardafwijking boven het gemiddelde: uitzonderlijk hoog.
Oefeningen
REEKS A
35 In een jeugdbeweging werd de hemdsmaat van een aantal jongens genoteerd.
©VANIN
a) Bereken het gemiddelde en de standaardafwijking.
b) Yassin heeft maat 44. Bereken de standaardscore.
c) Geef de betekenis van die standaardscore.
36 Een aardappelverwerkingsbedrijf heeft van 96 willekeurig gekozen aardappelen de massa (in g) bepaald (zie oefeningen 14, 17 en 24).
a) Bereken het gemiddelde en de standaardafwijking:
b) Hoe uitzonderlijk is een aardappel met een massa die meer dan twee keer de standaardafwijking afwijkt van het gemiddelde?
37 Een leerkracht Nederlands geeft aan het begin van het schooljaar een woorddictee met tien moeilijke woorden.
De frequentietabel toont het aantal gemaakte fouten (zie oefening 29).
xi ni
0 7 1 10 2 9 3 14 4 8 5 11
6 8 7 6 73
a) vul de frequentietabel aan.
b) Het gemiddelde aantal fouten is 3,4. Bereken de standaardafwijking.
c) Heeft iemand met zeven fouten een uitzonderlijk slecht dictee gemaakt?
38 Bepaalde doosjes met punaises zouden volgens het etiket 120 punaises bevatten. De fabrikant doet een steekproef bij 95 willekeurige doosjes punaises. Het resultaat zie je in de frequentietabel.
xi ni
115 2 116 5 117 7 118 10 119 12
18
13
12
6
6
3
1
a) vul de frequentietabel aan.

b) Is de vulmachine goed afgesteld?
c) Werkt de machine voldoende nauwkeurig?
39 In de tabel zie je de leeftijdsverdeling van de Belgische bevolking op 1 januari 2023 (zie oefeningen 20 en 32).
klasse mi ni
[0, 10[ 5 1 240 172
[10, 20[ 15 1 358 845
[20, 30[ 25 1 404 025
[30, 40[ 35 1 533 931
[40, 50[ 45 1 510 095
[50, 60[ 55 1 583 282
[60, 70[ 65 1 413 090
[70, 80[ 75 1 012 409
[80, 90[ 85 512 632
[90, 100[ 95 126 343
[100, 110[ 105 2 733 11 697 557
a) vul de frequentietabel aan.
b) De gemiddelde Belg is 42,2 jaar. Bereken de standaardafwijking.
©VANIN
c) Hoe oud moet je zijn om uitzonderlijk oud te zijn?
d) Zara heeft een standaardscore van 1,85. Bereken haar leeftijd.
40 Je voert een onderzoek naar het dagelijkse aantal minuten schermtijd van de leerlingen van je klas of jaar. Iedere leerling kijkt op zijn smartphone naar de schermtijd van de vorige dag. Gebruik de verwerking van oefeningen 16, 21 en 33 en beantwoord de vragen.
a) Bereken de standaardafwijking.
b) Bereken de variatiecoëfficiënt en geef de betekenis.
c) Hoeveel procent van de gegevens ligt minder dan één keer de standaardafwijking van het gemiddelde verwijderd?
d) je bent dagelijks gemiddeld drie uur met je smartphone bezig. Bereken je standaardscore en geef de betekenis.
41 Een fabrikant maakt conservenblikken met gepelde tomaten. Op het etiket staat dat de inhoud 1 l is. Van een aantal blikken werd de inhoud (in ml) nagegaan.
inhoud (ml) mi ni fi cni cfi
[970, 980[ 46
[980, 990[ 97
[990, 1 000[ 127
[1 000, 1 010[ 98
[1 010, 1 020[ 63
[1 020, 1 030[ 19
[1 030, 1 040[ 10
a) vul de frequentietabel aan.
b) Teken met IcT het ogief.
c) Bepaal de mediaan en geef de betekenis.
d) Bepaal het eerste en het derde kwartiel en geef de betekenis.

e) Zijn er uitschieters bij de gegevens?
f) Staat de vulmachine goed ingesteld?
g) voorspel, zonder de boxplot te tekenen, waar de mediaan zal liggen in de box.
h) Werkt de vulmachine voldoende nauwkeurig?
i) Een blik tomaten heeft een standaardscore van –0,8. Bereken de inhoud.
42 De enige constante in de natuurkunde is de lichtsnelheid in het luchtledige. In 1882 verrichtten Michelson en Newcomb de eerste redelijk nauwkeurige metingen van die lichtsnelheid.
Daarvoor maten ze de tijd (in µs) die een lichtstraal nodig had om een afstand van 7 443,37 m te overbruggen. Dat was de afstand van hun laboratorium tot een spiegel aan het Washington-monument en terug. Je ziet hun resultaten in het histogram.
[16, 20[[20, 24[[24, 28[[28, 32[[32, 36[[36, 40[
(ms)
a) Bereken het gemiddelde.
b) Bereken vanuit het gemiddelde een benadering voor de lichtsnelheid c in m/s.
c) Teken met IcT de boxplot en bespreek.
d) Bereken de standaardafwijking.
6.5 Symmetrische en scheve verdelingen
6.5.1 Symmetrische verdelingen
Voorbeeld 1
veel zitten is niet gezond. Dat weet iedereen.
De Nationale Gezondheidsraad adviseert aan jongeren om minstens één uur per dag matig tot intensief te bewegen.
Matig intensieve lichamelijke activiteit, zoals wandelen, fietsen of paardrijden, zorgt voor een verhoogde hartslag en een versnelde ademhaling.
Zwaar intensieve lichamelijke activiteit zorgt ervoor dat je gaat zweten en soms buiten adem raakt.
©VANIN

Een aantal jaar geleden werd een onderzoek gedaan bij 570 jongeren tussen 12 en 18 jaar naar het aantal minuten matig tot zwaar intensieve lichamelijke activiteit.
matig tot zwaar intensief bewegen bij adolescenten
5,00
0,00 %
De mediaan ligt perfect in het midden van de box en is gelijk aan het gemiddelde.
Beide centrummaten liggen ook in de modale klasse.
De spreiding bij het eerste en vierde kwart is helemaal gelijk.
je kunt daarom spreken van een symmetrische verdeling.
Voorbeeld 2
je gooit 60 keer met twee dobbelstenen en telt de som van het aantal ogen.
60 worpen met twee dobbelstenen
Het lijndiagram vertoont geen symmetrie. Dat wordt ook bevestigd door de centrummaten.
x ≈ 7,2 Me = 7 Mo = 6
Op het eerste gezicht zou je dus kunnen besluiten dat het experiment geen symmetrische verdeling oplevert.
ICT ©VANIN
2345678 9101112
som van de ogen
Met IcT kun je een experiment uitvoeren waarbij 6 000 worpen worden gesimuleerd.

je krijgt dan het volgende lijndiagram te zien.
6 000 worpen met twee dobbelstenen
je gebruikt de Excelfunctie ‘aSELEcTTUSSEN’. als laagste getal geef je 1 in en als hoogste getal 6. je kan daarna zowel naar rechts als naar onder doorvoeren, tot je 6 000 cellen hebt.
Dit experiment levert dus wel de verwachte symmetrie.
je ziet meteen dat het gemiddelde, de mediaan en de modus aan elkaar gelijk zijn, namelijk
som van de ogen
vooraleer te besluiten of een verdeling wel of niet symmetrisch is, is het dus belangrijk dat de steekproef voldoende groot is.
Besluit Als een verdeling symmetrisch is, dan zijn de mediaan, het gemiddelde en de modus aan elkaar gelijk (Mo = Me = x). Omgekeerd is dat niet altijd het geval. Bij gegroepeerde gegevens liggen de mediaan en het gemiddelde dan in het midden van de modale klasse.
6.5.2 De normale verdeling
Een bijzondere symmetrische verdeling is de normale verdeling
veel natuurlijke kenmerken, zoals de lengte van een mens, de inhoud van een fles melk of de massa van eieren, kunnen beschreven worden door een symmetrische verdeling met een klokvormige kromme als grafische voorstelling.
Die grafiek noemt men soms ook de gausscurve, naar de Duitse wiskundige carl Friedrich Gauss, ook wel de prins van de wiskunde genoemd.
©VANIN
De gausscurve bezit een aantal opmerkelijke eigenschappen.
68 % van de gegevens ligt binnen het interval [x – s, x + s]. je noemt dat interval de standaardgroep
De 16 % van de gegevens die meer dan een standaardafwijking verwijderd zijn van het gemiddelde, noem je betrekkelijk hoog of laag
95 % van de gegevens ligt binnen het interval [x – 2s, x + 2s].
De 5 % van de gegevens die meer dan twee standaardafwijkingen verwijderd zijn van het gemiddelde, noem je uitzonderlijk
99,7 % van de gegevens ligt binnen het interval [x − 3s, x + 3s].
De 0,3 % van de gegevens die meer dan drie standaardafwijkingen verwijderd zijn van het gemiddelde, noem je zeer uitzonderlijk
6.5.3 Rechtsscheve verdelingen
België telt ongeveer 50 000 dokters, 150 000 verpleegkundigen en 110 000 zorgkundigen.
Een zorgkundige is iemand die opgeleid is om verpleegkundigen bij te staan.
Bij de dokters is het aantal mannen en vrouwen ongeveer gelijk verdeeld.
Bij de verpleegkundigen en zorgkundigen is de overgrote meerderheid een vrouw.
Het histogram toont de leeftijdsverdeling bij de zorgkundigen.

©VANIN
Besluit
leeftijd van de zorgkundigen in België relatief aantal zorgkundigen
leeftijd (jaren)
Bron: statbel.fgov.be (kerncijfers 2021)
vertrek je van de ruwe data van het onderzoek, dan vind je de volgende centrummaten:
x ≈ 38,8 Me = 37 modale klasse = [25, 35[
De mediaan is kleiner dan het gemiddelde en beide centrummaten liggen boven de modale klasse. Er is dus een ‘staart naar rechts’.
Een dergelijke verdeling noem je rechtsscheef
Als een verdeling rechtsscheef is, dan liggen de mediaan en het gemiddelde bij gegroepeerde gegevens meestal boven de modale klasse.
Opmerking
Bij niet-gegroepeerde gegevens geldt: Mo < Me < x
6.5.4
Linksscheve verdelingen
De frequentiepolygoon toont de geboortemassa (in g) van alle kinderen die vorig jaar in een bepaald vlaams ziekenhuis zijn geboren.
geboortemassa van 467 baby's
massa (g)
vertrek je van de ruwe data van het onderzoek, dan vind je de volgende centrummaten:
De mediaan is groter dan het gemiddelde en beide centrummaten liggen onder de modale klasse. Er is dus een ‘staart naar links’.
Een dergelijke verdeling noem je linksscheef.
Besluit
Als een verdeling linksscheef is, dan liggen de mediaan en het gemiddelde bij gegroepeerde gegevens meestal onder de modale klasse.
Opmerkingen
• Bij niet-gegroepeerde gegevens geldt: x < Me < Mo.
• Een boxplot is een handig instrument om een staart te illustreren.
Oefeningen
REEKS A
43 Van enkele voldoende grote steekproeven krijg je telkens het gemiddelde, de mediaan en de modus of modale klasse. Is de verdeling symmetrisch (S), linksscheef (L), rechtsscheef (R) of geen van de drie (G)?
a) x = 1 683 Me = 1 630 Mo klasse = [1 500, 1 600[
b) x = 54,3 Me = 54,5 Mo = 54
c) x = 1,7 Me = 2 Mo = 1
d) x = 39,3 Me = 38,5 Mo klasse = [36, 38[
e) x = 78,1 Me = 78 Mo klasse = [75, 80[
44 Tot welk soort verdeling zullen de volgende statistische onderzoeken leiden? Kies uit een symmetrische verdeling (S), een linksscheve verdeling (L) en een rechtsscheve verdeling (R).
a) De inkomstenverdeling (in euro per maand) van de 18- tot 25-jarigen in vlaanderen.
b) De duur (in weken) van een zwangerschap.
c) Het intelligentiequotiënt (IQ) van 12-jarigen.
d) De spanwijdte (in cm) van de vleugels van vlinders.
e) Het aantal gemaakte doelpunten per match in de eerste klasse van het Belgisch voetbal.
f) De leeftijd waarop een Belgische vrouw sterft.
g) De inhoud (in cl) van een bekertje koffie dat door een automatische vulmachine wordt gevuld.
45 Aan een aantal Vlaamse gezinnen wordt gevraagd hoeveel dagen van de week ze helemaal geen vlees of vis eten (zie oefening 2).
aantal dagen in de week zonder vlees of vis relatief aantal gezinnen
a) Met welk soort verdeling heb je hier te maken?
aantal dagen
b) Toon aan, zonder te berekenen, dat het gemiddelde groter is dan 1.
46 Je ziet vier boxplots die de verdeling van de leeftijden van de bewoners van vier verschillende appartementsblokken weergeeft. Welk soort verdeling hoort bij elk van die boxplots?
47 Van 90 kippeneieren wordt de massa (in g) bepaald. Toon aan dat aan de nodige voorwaarde voor een symmetrische verdeling is voldaan.
massa (g) ni
[45, 50[ 2
[50, 55[ 12
[55, 60[ 22
[60, 65[ 33
[65, 70[ 9
[70, 75[ 7
[75, 80[ 5
REEKS C

48 Bij een onderzoek naar de levensduur van ledverlichting werd bij 80 ledlampen nagegaan hoelang (in h) ze ononderbroken kunnen blijven branden. Het resultaat van het onderzoek zie je in de frequentietabel.
levensduur (h) ni
[20 000, 24 000[ 5
[24 000, 28 000[ 7
[28 000, 32 000[ 9
[32 000, 36 000[ 12
[36 000, 40 000[ 14
[40 000, 44 000[ 12
[44 000, 48 000[ 7
[48 000, 52 000[ 8
[52 000, 56 000[ 6
• Toon aan dat aan de nodige voorwaarde voor een symmetrische verdeling is voldaan.
• voldoet de verdeling aan de voorwaarden voor een normale verdeling?
6.6.1 Spreidingsdiagram en trendlijn
Inleiding

af en toe online gamen verbetert de schoolresultaten van vijftienjarigen. Maar activiteiten op sociale media hebben een averechts effect.

Regelmatige lichaamsbeweging bevordert het geheugen.
©VANIN
De toename van de gemiddelde temperatuur kan alleen verklaard worden door de menselijke invloed in rekening te brengen.
Tot nu toe heb je in dit hoofdstuk enkel met één statistische veranderlijke gewerkt. In dat geval spreek je van eendimensionale of univariate statistiek.
In de tweedimensionale of bivariate statistiek behandel je de mogelijke samenhang tussen twee veranderlijken. De ene veranderlijke kan de andere beïnvloeden, en omgekeerd. Ook de sterkte van het verband is belangrijk.
Om een benaderende formule te vinden voor het verband tussen de twee gemeten veranderlijken, gebruik je regressie je maakte daar al kennis mee in de hoofdstukken over eerstegraadsfuncties en functies van de vorm f (x ) = c x
Regressie met



Rechter muisklik op één van de punten –trendlijn toevoegen.




Voorbeeld 1
aan 17 vrouwen werd de lengte en de schoenmaat gevraagd. Gebruik lineaire regressie om het verband te bepalen tussen de schoenmaat y en de lengte x (in cm).
schoenmaat
verband tussen lichaamslengte en schoenmaat bij 17 vrouwen
• De vergelijking van de trendlijn is
(cm)
Voorbeeld 2
• Schat de schoenmaat van een vrouw van 175 cm.
• Schat de lengte van een vrouw met schoenmaat 42. Rond af op 1 cm.
Het risico op een verkeersongeval is, volgens een studie van het Instituut voor Mobiliteit van de universiteit Hasselt, even groot voor mannen als voor vrouwen.
De kans op een ongeval met doden of gewonden is wel afhankelijk van het geslacht.
De tabel toont de kans op een ziekenhuisopname bij een ongeval bij mannen.
Bepaal, via machtsregressie, het omgekeerd evenredig verband tussen de kans (in procent) en de leeftijd (in jaren).
leeftijd mi kans (%)
[15, 25[ 20 1,9
[25, 35[ 30 1,1
[35, 45[ 40 0,82
©VANIN
[45, 55[ 50 0,68
[55, 65[ 60 0,52
[65, 75[ 70 0,51
kans op een ziekenhuisopname bij een verkeersongeval bij mannen
leeftijd (jaren)
als x de leeftijd (in jaren) is en y de kans (in procent) op een ziekenhuisopname bij een ongeval, dan geldt: y ≈
6.6.2 Lineaire regressie
Covariantie
Een puntenwolk is een grafische voorstelling van puntenkoppels (x, y). Daarbij is x de onafhankelijke veranderlijke en y de afhankelijke veranderlijke.

als bij een toenemende waarde van x over het algemeen een toenemende waarde van y hoort, dan spreek je van een positieve covariantie
©VANIN

als bij een toenemende waarde van x over het algemeen een afnemende waarde van y hoort, dan spreek je van een negatieve covariantie
Lineaire regressie
Bij lineaire regressie zoek je een rechte als trendlijn bij een puntenwolk. Die rechte past zo goed mogelijk bij de puntenkoppels.



Het verband tussen y en x noem je sterk als de punten, over het algemeen, vrij dicht bij de regressierechte liggen. als de punten vrij ver van de regressierechte verwijderd liggen, spreek je van een zwak verband.
De wiskundige methode om bij een dataset de best passende regressielijn te bepalen, is afkomstig van carl Friedrich Gauss. In 1801 stelde hij voor om de som van de kwadraten van de verticale afwijkingen ten opzichte van de trendlijn (de zogenaamde ‘residuen’) te minimaliseren. y voorspelde waarde residu waargenomen waarde x Die methode (‘de kleinste-kwadratenmethode’) stelde astronomen in staat om heel nauwkeurig de baan van hemellichamen te bepalen.
6.6.3 De correlatiecoëfficiënt bij lineaire regressie
als je in het woordenboek de betekenis van het woord ‘correlatie’ opzoekt, dan vind je als uitleg: ‘de manier waarop iets samenhangt met iets anders’.
In de statistiek gebruikt men de correlatiecoëfficiënt r om de sterkte van die samenhang te bepalen. Er zijn meerdere definities van dat begrip, maar de meest gebruikte is de correlatiecoëfficiënt van Pearson (een Engelse statisticus die leefde van 1857 tot 1936).
De correlatiecoëfficiënt berekenen met ICT
Bereken de correlatiecoëfficiënt bij het verband tussen de schoenmaat en de lichaamslengte van zeventien vrouwen (voorbeeld 1 uit 6.6.1).
Correlatiecoëfficiënt met Excel
Open het bestand ‘lengte en schoenmaat.xlsx’.
Om de correlatiecoëfficiënt te berekenen, gebruik je de functie ‘cORRELaTIE(matrix1;matrix2)’.


Betekenis van de correlatiecoëfficiënt
De correlatiecoëfficiënt is een getal tussen –1 en 1. als r > 0, dan is er een positief verband. als r < 0, dan is er een negatief verband.

©VANIN

geen enkel verband sterk positief verband


zeer zwak positief verband zeer sterk negatief verband


zwak negatief verband uitzonderlijk sterk positief verband


matig positief verband perfecte negatieve correlatie
Oefeningen
REEKS B
49 Een kleine steekproef die zocht naar het verband tussen de lichaamslengte y (in cm) van een volwassen zoon en de lichaamslengte x (in cm) van zijn vader, leverde de volgende data op.
©VANIN
a) Bepaal via lineaire regressie het verband tussen y en x.
b) Bereken de correlatiecoëfficiënt en geef de betekenis.
c) Schat de lengte van een zoon waarvan de vader 175 cm is. Rond af op 1 cm.
d) vergelijk die geschatte waarde met de gemeten waarde(n).
e) Schat de lengte van een vader van wie de zoon 190 cm groot is. Rond af op 1 cm.
f) Waarom is dat resultaat verrassend?
g) De vader van Ilan is 5 cm groter dan de vader van Millau. Schat hoeveel groter Ilan zal worden dan Millau. Rond af op 0,1 cm.

50 Hoe hoger de temperatuur, hoe meer dorst je hebt.
In de tabel zie je de gemiddelde dagtemperatuur x (in ºC) en het aantal liter water y dat in een warenhuis op die dag werd verkocht.
a) Bepaal via lineaire regressie het verband tussen y en x
b) Bereken de correlatiecoëfficiënt en geef de betekenis.
c) Schat de verkochte hoeveelheid water als het 32 ºc is. Rond af op 1 l.
d) Geef de betekenis van de richtingscoëfficiënt van het lineaire verband.
e) Geef de betekenis van het snijpunt met de y-as van de grafiek van het lineaire verband.
f) Op een kille dag heeft het warenhuis maar 500 liter water verkocht. Hoeveel graden was het die dag? Rond af op 0,1 ºc
g) Bij welke gemiddelde dagtemperatuur verkoopt het warenhuis minstens 1 000 l water?

51 Op een toets moesten de leerlingen invullen hoeveel minuten ze hadden gestudeerd voor de toets. Ze moesten ook een score van 1 (heel eenvoudig) tot 5 (heel moeilijk) geven over de moeilijkheidsgraad van de toets. In de tabel is x het aantal minuten studie, y de moeilijkheidsgraad en z de punten op 20 voor de toets.
(min)
(op 20)
a) Bepaal via lineaire regressie het verband tussen
z en x:
y en x:
z en y:

b) Noa heeft drie kwartier gestudeerd voor de toets. Schat hoeveel punten ze zal behalen.
c) Lars gaf een score 2 voor de moeilijkheidsgraad van de toets. Schat hoeveel minuten hij heeft gestudeerd. Rond af op 1 min.
d) Geef de betekenis van de richtingscoëfficiënt van het lineaire verband tussen z en y
e) Tussen welke veranderlijken is het verband het sterkst?
52 Het percentage mensen dat aan ondervoeding lijdt, daalt wereldwijd. Tegelijk stijgt het percentage meisjes dat onderwijs kan genieten. De tabel toont de evolutie van het aantal meisjes x (in procent) dat op de basisschoolleeftijd naar school gaat en het aantal mensen y (in procent) dat ondervoed is.
a) Druk de toename van het aantal schoolgaande meisjes tussen 1970 en 2019 uit
• in procentpunt:
• in procent:
b) Bepaal via lineaire regressie het verband tussen y en x
c) Geef de betekenis van de richtingscoëfficiënt van de trendlijn.
d) Hoeveel procent van de meisjes zou naar de lagere school moeten gaan opdat ondervoeding volledig de wereld uit zou zijn?
e) Bereken de sterkte van het verband tussen y en x.
Hunger Index (2019)

Zeer hoog (⩾ 50,0)
Hoog (35,0 - 49,9)
Redelijk hoog (20,0 - 34,9)
Redelijk laag (10,0 - 19,9)
Laag (⩽ 9,9)
Onvolledige gegevens, zorgwekkend
Geen of onvolledige gegevens
Global
STUDIEWIJZER Beschrijvende statistiek
6.1 Categorische en niet-gegroepeerde numerieke gegevens

Het gemiddelde x van een rij getallen x 1, x 2, ..., x n is de som van die getallen gedeeld door het aantal getallen:
x = x i i = 1 n n
De mediaan Me van een gerangschikte rij met n getallen is het getal met rangorde n + 1 2
©VANIN

De modus Mo is het gegeven met de grootste frequentie.
KUNNEN
Statistische terminologie in verband met het verzamelen van gegevens beheersen. categorische gegevens verwerken (frequentietabel, grafische voorstellingen).
Niet-gegroepeerde numerieke gegevens verwerken (frequentietabel, grafische voorstellingen).
De centrummaten gemiddelde, mediaan en modus bepalen met IcT en vanuit een gegeven frequentietabel.
De centrummaten interpreteren in een context.
6.2 Gegroepeerde numerieke gegevens


KENNEN
Een klasse is een interval dat gesloten is in zijn ondergrens en open is in zijn bovengrens.
Een histogram is een staafdiagram met aaneengesloten staven.
Een frequentiepolygoon is een gebroken lijn die de roosterpunten (mi , ni ) of (mi , fi ) verbindt en die aansluit op de horizontale as in de punten (a, 0) en (b, 0).
Daarbij is a het klassenmidden van de klasse die de eerste klasse voorafgaat, en b het klassenmidden van de klasse die op de laatste klasse van de steekproef volgt. Een ogief is een gebroken lijn die de roosterpunten (a1, 0) en (bi , cfi ) of (bi , cni ) met elkaar verbindt.
KUNNEN
Gegroepeerde numerieke gegevens verwerken (frequentietabel, grafische voorstellingen) en vragen beantwoorden vanuit de frequentietabel of een grafische voorstelling.
6.3 Centrummaten bij gegroepeerde gegevens


, met k het aantal verschillende klassen en
De mediaanklasse is de klasse waarin het getal met rangorde n + 1 2 (de 50%-grens) is gelegen.
De modale klasse is de klasse met de grootste frequentie.
©VANIN
KUNNEN
Het gemiddelde berekenen met IcT en vanuit een gegroepeerde frequentietabel.
De mediaan berekenen met IcT en vanuit een gegroepeerde frequentietabel (met behulp van het ogief).
De mediaan benaderen via lineaire interpolatie.
De modale klasse bepalen vanuit een gegroepeerde frequentietabel.
De centrummaten interpreteren in een context.
6.4 Spreidingsmaten

De variatiebreedte R is het verschil tussen het grootste en het kleinste waarnemingsgetal.
van een geordende rij met n gegevens is:
het eerste kwartiel Q1 het getal met rangorde n + 1 4 (25%-grens);
het tweede kwartiel Q2 het getal met rangorde n + 1 2 (50%-grens);
het derde kwartiel Q3 het getal met rangorde 3 ? n + 1 4 (75%-grens).
Het tweede kwartiel is dus gelijk aan de mediaan.
De interkwartielafstand IQR is het verschil tussen het derde en eerste kwartiel.
De boxplot is een grafische voorstelling van de vijfgetallensamenvatting die bestaat uit:
• een rechthoek die als basis de interkwartielafstand heeft;
• een verticale lijn in de box die de plaats van de mediaan weergeeft;
• een vanaf de box getekende lijn naar het minimum en maximum.
Een waarnemingsgetal is een uitschieter als het minstens 1,5 keer de interkwartielafstand boven het derde kwartiel of onder het eerste kwartiel gelegen is.
De variantie s 2 van een rij gegevens is gelijk aan de gemiddelde kwadratische afwijking ten opzichte van het gemiddelde.
De standaardafwijking s van een rij gegevens is gelijk aan de positieve vierkantswortel uit de variantie. s = n i (x i – x )2 i = 1 k n of s ≈ n i (m i –i = 1 k n x )2
De variatiecoëfficiënt V = s x
De standaardscore of z-score van een waarnemingsgetal xi is het getal zi = x i – x s
KENNEN

De variatiebreedte, de kwartielen en de interkwartielafstand berekenen met IcT en vanuit een frequentietabel (met behulp van een ogief bij gegroepeerde gegevens) en interpreteren in een context.
Een boxplot met IcT tekenen en interpreteren.
Bepalen of een waarnemingsgetal een uitschieter is.
De standaardafwijkingen berekenen met IcT en vanuit een frequentietabel.
De variatiecoëfficiënt berekenen en interpreteren in functie van de variabiliteit van de gegevens.
De standaardscore berekenen en interpreteren.
©VANIN
6.5 Symmetrische en scheve verdelingen

als een verdeling symmetrisch is, dan zijn de mediaan, het gemiddelde en de modus aan elkaar gelijk (Mo = Me = x). Omgekeerd is dat niet altijd het geval.
Bij gegroepeerde gegevens liggen de mediaan en het gemiddelde dan in het midden van de modale klasse.
als een verdeling rechtsscheef is, dan is de mediaan kleiner dan het gemiddelde en zijn beide groter dan de modus (Mo < Me < x).
Bij gegroepeerde gegevens liggen de mediaan en het gemiddelde meestal boven de modale klasse.
als een verdeling linksscheef is, dan is de mediaan groter dan het gemiddelde en zijn beide kleiner dan de modus (x < Me < Mo).
Bij gegroepeerde gegevens liggen de mediaan en het gemiddelde onder de modale klasse.

Bepalen of een verdeling symmetrisch (in het bijzonder normaal verdeeld), rechtsscheef of linksscheef is.
6.6 Tweedimensionale statistiek

Een puntenwolk is een grafische voorstelling van puntenkoppels (x, y).
Daarbij is x de onafhankelijke veranderlijke en y de afhankelijke veranderlijke.
Bij lineaire regressie zoek je een rechte als trendlijn bij een puntenwolk. Die rechte past zo goed mogelijk bij de puntenkoppels.
De correlatiecoëfficiënt geeft de sterkte weer van het verband dat bij een lineaire regressie hoort.

Regressie gebruiken om bij een puntenwolk de best passende (lineaire) trendlijn te bepalen.
De correlatiecoëfficiënt met IcT berekenen en daarmee de sterkte van een lineair verband weergeven.
Pienter problemen oplossen

Welke heuristiek(en) gebruik je om de onderstaande problemen op te lossen?
❑ concreet materiaal
❑ schets
❑ schema/tabel
❑ vereenvoudig
❑ gok verstandig
1. Wat is het eerste cijfer na de komma dat verschilt van nul in de decimale ontwikkeling van 10 5010 ? a) 1 B) 2 c) 4 D) 5 E) 9
JWO, editie 2021, eerste ronde
❑ filter
❑ patroon
❑ kennis
❑ logisch nadenken
❑ ...
©VANIN
2. In een rechthoek met breedte 2 cm teken je een (rood) lijnstuk van 2,5 cm en een (groen) lijnstuk van 2,9 cm. Bereken de aangeduide afstand x
3. Sep vertrekt met de fiets naar school.
Op de klok thuis is het dan 8.15 uur, maar die klok loopt een beetje achter. als hij op school komt, ziet hij op de schoolklok, die perfect werkt, dat het 8.40 uur is.
Sep fietst na school even snel als ’s morgens naar huis.
Hij vertrekt als het op de schoolklok 16.04 uur is. Bij zijn thuiskomst toont de klok thuis 16.17 uur.
Hoeveel loopt de thuisklok achter?

PIENTER REMEDIËREN
©VANIN

EXTRA LEERSTOF
©VANIN

Overzicht Extra Leerstof (deel 1)
Stroomdiagram en Nassi-Shneiderman diagram
De discriminantformule afleiden via de eigenschap van de som en het product van de twee wortels
2.7 Een drieterm van de vorm ax² + bx + c ontbinden in factoren
