04 Computationeel denken in de praktijk
Hoe computationeel denken in je lessen naar voren halen?
De basisconcepten vormen het vertrekpunt om computationeel denken in de klas te introduceren. Maar in de praktijk komen er veel meer concepten en praktijken bij kijken. Je zal leerlingen via eenvoudige problemen computationeel denken aanleren, om hen nadien geleidelijk aan in staat te stellen om complexe problemen aan te pakken.
1.1
Computationeel denken in vertrouwde lesinhouden
Misschien zie je ertegen op om computationeel denken aan te brengen bovenop een al overvol programma, of denk je dat het veel voorbereidingstijd zal vragen. Het is daarom nuttig dat je nagaat waar computationeel denken al in het vertrouwde deel van het curriculum aanwezig is. 1
Computationeel denken komt namelijk vast al aan bod in je lessen. Je moet je lessen dus niet volledig omgooien om rond computationeel denken te werken. Kleine aanpassingen, zoals bepaalde redeneringen en denkpatronen meer expliciet maken, kunnen al volstaan. Dat betekent ook dat computationeel denken in jouw lessen niet noodzakelijk een grote tijdsinvestering vraagt.
HOUT
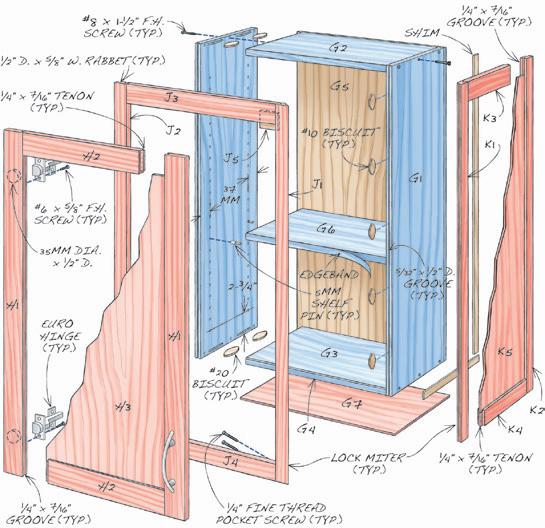
Decompositie pas je toe in de les hout als je een kastje ontwerpt (figuur 1). Daarbij moet je heel wat keuzes maken. Uit welk materiaal zal je het kastje maken? Wat zijn de afmetingen van het corpus? Welke methode kies je om de achterwand te bevestigen? Met welke verbindingen werk je? Welke scharnieren zijn het meest geschikt?
Je past ook abstractie toe, bijvoorbeeld als je de software efficiënt inzet door variabelen te gebruiken, zodat de afmetingen van een ontwerp automatisch worden aangepast en herrekend, zoals bij een kast op maat binnen een gegeven ruimte. Het voordeel van zo’n abstractie wordt extra duidelijk als de afmetingen van de te zagen planken automatisch worden berekend op basis van gewenste hoogte, lengte en diepte van het kastje.
1 Hennessey et al. (2017).
Uit: www.popularwoodworking.com, geraadpleegd op 1 september 2025
Figuur 1 Decompositie en abstractie: ontwerp houten kastje (Kitchen Cabinet Essentials, 9 april 2020)
WISKUNDE
Abstractie pas je toe in de wiskundeles als je uit een vraagstuk de gegevens en het gevraagde haalt (figuur 2). gegeven gevraagd
Uit: Pienter 5-6 D/A – reële functies en algebra (leerwerkboek), p. 21 (VAN IN)
Figuur 2 Abstractie: gegeven en gevraagd
BIOLOGIE
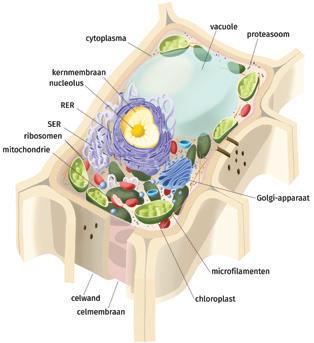
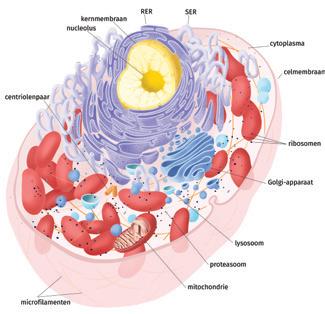
Patroonherkenning pas je toe in de biologieles als je je kennis over een plantencel moet transfereren naar een dierlijke cel. In figuur 3 zie je dat er redelijk wat overeenkomsten zijn.
Uit: Genie Biologie 5, pp. 18-19 (VAN IN)
Figuur 3 Patroonherkenning: plantencel versus dierlijke cel
NEDERLANDS
Algoritmisch denken pas je toe in de Nederlandse taal als je met de regel van ‘t kofschip beslist of een voltooid deelwoord van een regelmatig werkwoord met d of t wordt geschreven. Op dat moment voer je een algoritme uit, zoals figuur 4 illustreert.
BEGIN
NEEM de stam van het werkwoord
NEEM de laatste letter van de stam
ALS de laatste letter IN tkofschip DAN het voltooid deelwoord eindigt op t ANDERS het voltooid deelwoord eindigt op d
EINDE
Figuur 4 Regel van ‘t kofschip
Het is dus zinvol om na te gaan waar je al aan computationeel denken werkt in je lessen.
1.2 Lesvoorbereiding: schema basisconcepten
Denk je dat een van je bestaande lessen in aanmerking komt om met computationeel denken aan de slag te gaan? Schematiseer dan eerst hoe de vier basisconcepten van computationeel denken in een lesonderdeel aan bod komen of kunnen komen (figuur 5). Nadien beslis je waarop je wil focussen in je eigenlijke les en welke wijzigingen je hiervoor moet aanbrengen in je lesvoorbereiding.
probleemstelling
decompositie patroonherkenning
abstractie algoritmisch denken
programma
Figuur 5 Schema basisconcepten
Dit schema is vooral bedoeld om je lessen computationeel denken voor te bereiden. 2 Als je wil, kan je ook je leerlingen zo’n schema laten invullen. In het kader van het minimumdoel van de tweede graad over de impact van digitale systemen is dat zelfs aangewezen.
In figuur 6 vind je een uitgewerkt voorbeeld dat je onder andere in studierichtingen met arbeidsmarktfinaliteit zou kunnen gebruiken. Ook in de volgende hoofdstukken zal je dit schema nog vaak tegenkomen. Het schema invullen is geen zwart-witverhaal. Je ervaring en kennis bepalen hoe je het invult: meer of minder gedetailleerd, met andere accenten of invalshoeken.
2 Het is fijn om te lezen dat volgens Dong et al. (2019) hun soortgelijk model leerkrachten stimuleert om verbanden te leggen tussen computationeel denken en lesinhouden.
CASESTUDY – DE TREIN NEMEN
De leerlingen hebben al geleerd hoe ze een uitstap met de bus plannen. In deze activiteit moeten ze het geleerde toepassen, nu voor een uitstap met de trein. Ze zullen bijvoorbeeld herkennen dat er gelijkenissen zijn tussen de bus nemen en de trein nemen.
probleemstelling
Je hebt al geleerd hoe je de bus neemt. Volgende week staat er een uitstap naar Brussel op het programma met de trein.
Zoek uit waar en wanneer je moet vertrekken om op tijd in Brussel aan te komen.
decompositie
• Wat is het dichtstbijzijnde station? – Zijn daar rechtstreekse treinen naar Brussel of zullen we moeten overstappen?
– Hoe geraken we in het station? Te voet, met de fiets, met de bus?
• Waar moeten we zijn in Brussel? In welk station moeten we uitstappen?
• Op welke tijdstippen vertrekt er een trein richting Brussel?
– Waar vinden we de treinuren?
– Om hoe laat moeten we dan naar het station vertrekken?
• Op welk perron moeten we opstappen?
• Zijn er vertragingen of is er een staking aangekondigd?
• patroonherkenning
abstractie
• Het perron wordt geabstraheerd tot een getal, het perronnummer.
• De reis wordt geabstraheerd tot de te volgen route: een opeenvolging van plaatsen (huis, school, stations …).
• Een reis met de bus of met de trein plannen gebeurt op een gelijksoortige manier. Voor beide kan eventueel een app worden gebruikt. Zowel de perrons als de bushaltes worden op een abstracte manier aangeduid, met een naam of een nummer.
algoritmisch denken
• De te volgen route: een lijst van de opeenvolgende tijdstippen en overeenkomstige plaatsen.
Dit is een voorbeeld waarbij niet moet worden geprogrammeerd.
Figuur 6 Schema basisconcepten – probleemstelling: de trein nemen
Hoe computationeel denken bij je leerlingen introduceren?
2.1 Oriënteren en voorkennis activeren
• Welke digitale toestellen heb je in huis?
• Welke AI-toepassingen gebruik je regelmatig?
• Welke digitale toepassingen gebruik je op een doordeweekse dag, vanaf het moment dat je wakker wordt tot je aankomt op school?
Door voorbeelden te geven van computationeel denken in het dagelijkse leven, zorg je ervoor dat je leerlingen snel vertrouwd raken met de nieuwe terminologie. Computationeel denken krijgt zo een persoonlijke betekenis en de alomtegenwoordigheid ervan in het dagelijkse leven wordt duidelijk.3 Je countert op die manier ook de misvatting dat algoritmen ‘enkel dienen om wiskundige problemen op te lossen en niet toepasbaar zouden zijn in andere domeinen’ (Yadav et al., 2017b).4
ONTBIJT
MAKEN
Onbewust gebruik je computationeel denken elk dag, bijvoorbeeld als je het ontbijt klaarmaakt. Als dat ontbijt bestaat uit een boterham met confituur en een zachtgekookt eitje, en je daarbij ook nog wil genieten van een kop thee, dan moet je meerdere taken tot een goed einde brengen (figuur 7). Bovendien vergt het wat planning om alles ongeveer op hetzelfde moment klaar te hebben. In de praktijk zal je bekijken hoe je de verschillende deeltaken (boterham, ei, thee) kan uitvoeren en hoeveel tijd elk van deze taken in beslag neemt. Misschien zet je je huisgenoten wel mee aan het werk? Je zet hen dan wellicht op weg met korte instructies, zonder in te gaan op alle details. Het is vast niet nodig om elke actie te specifiëren ...
© Dwengo vzw
Figuur 7 Een ontbijt maken: deeltaken en stappenplan
3 Voogt et al. (2015).
4 Ook Papert (1980) zei al dat alledaagse gebeurtenissen als voorbeeld kunnen dienen voor computerprogramma’s.
Hoofdstuk 4 Computationeel denken in de praktijk
Via dit voorbeeld geef je een concrete invulling aan elk van de vier basisconcepten van computationeel denken: decompositie, abstractie, patroonherkenning en algoritmisch denken.
Via www.mijnstudiemateriaal.be kan je een filmpje bekijken dat met hetzelfde voorbeeld illustreert wat computationeel denken kan betekenen in ons dagelijkse leven.
Er zijn nog heel wat andere momenten waarop leerlingen in contact komen met computationeel denken.
COMPUTATIONEEL DENKEN IN HET DAGELIJKSE LEVEN VAN LEERLINGEN
• Je denkt na of het efficiënt en wenselijk is om voor een schooltaak een Altoepassing te gebruiken. Je verdiept je daarvoor in de werking van dat systeem.
• Je vraagt aan Siri of Alexa om het licht aan te doen. Hoe zit het dan met het energieverbruik in vergelijking met wanneer je zelf de lichtschakelaar bedient? Welke stappen voert de app uit?
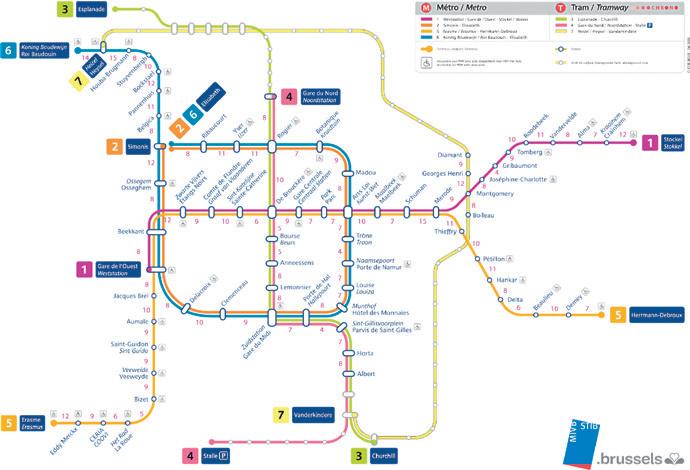
• Je komt in Brussel en wil de metro nemen. Hiervoor bekijk je het metroplan. Zo’n metroplan is een abstractie van alle lijnen en aansluitingen (figuur 8).
Uit: www.mivbstories.be, geraadpleegd op 1 september 2025
Figuur 8 Metroplan van Brussel
Je kan de ‘ontbijtoefening’ dus gemakkelijk herhalen met andere situaties en toepassingen waarmee de leerlingen dagelijks worden geconfronteerd. Ook de voorbeelden bij de definities van de vier basisconcepten kunnen hierbij als inspiratiebron dienen (zie de paragraaf ‘Voorbeelden uit het leven gegrepen’ in het hoofdstuk ‘Computationeel denken: definitie en basisconcepten’).
2.2 Aandachtspunten oriëntatiefase
In een probleemoplossend proces moet je de basisconcepten van computationeel denken op een doordachte manier toepassen. Niet alle vormen van decompositie leiden bijvoorbeeld tot een oplossing van een probleem. 5
B OODSCHAPPENLIJST 6
Je moet naar de winkel met een lange boodschappenlijst. Om gemakkelijker te kunnen controleren of je niets bent vergeten, groepeer je de producten op de lijst. Het is een optie om ze op te kleur te groeperen: eerst alle ‘rode’ producten, zoals rode bieten en producten in een rode verpakking, dan de ‘groene’ enzovoort. Het is duidelijk dat dit geen goede manier is om het probleem op te splitsen. Jij pakt het vast anders aan!
Decompositie is dus niet alleen het probleem in delen opsplitsen, je gebruikt het ook om een probleem te herformuleren. Belangrijk is dat je de juiste manier kiest om dit te doen. Bij het oplossen van een probleem kan je decompositie op meerdere manieren toepassen. Je kan bijvoorbeeld alle onderdelen van een fiets opsommen (structurele decompositie). Een andere mogelijkheid is dat je alles opsomt dat je moet weten om een trip met de bus te ondernemen (functionele decompositie). Je kan gaan kijken in welke volgorde de onderdelen van een proces na elkaar moeten komen (sequentiële decompositie). Of misschien breng je in kaart welke deelproblemen afhankelijk zijn van welke andere deelproblemen (afhankelijkheidsdecompositie).7 Merk bovendien op dat decompositie vaak als een iteratief proces voorkomt, zoals bij het ontbijtvoorbeeld: de drie deelproblemen werden nog eens opgedeeld.
5 Neutens (2022).
6 Ibid.
7 Rich et al. (2019).
Kenmerkend voor abstractie in een context van computationeel denken en computerwetenschappen is dat het op verschillende niveaus voorkomt.8 Computerwetenschappers spreken over problemen aanpakken op ‘hoog’ of ‘laag’ niveau. Daarmee bedoelen ze een hoog of laag abstractieniveau. Het ontbijtprobleem, bijvoorbeeld, wordt eerst opgesplitst in drie deeltaken. In principe is het probleem dan aangepakt op een hoog abstractieniveau. Ga je voor elke deeltaak heel gedetailleerde instructies geven, dan heb je het probleem aangepakt op een laag abstractieniveau
Als je het recept van een kersentaart omvormt zodat het algemeen kan worden ingezet voor een fruittaart, dan ben je aan het generaliseren, met andere woorden je gaat dan over naar een hoger abstractieniveau. Als je beseft dat een aardbeientaart een fruittaart is, dan kan je via patroonherkenning het recept van een fruittaart aanpassen naar een aardbeientaart. Deze vorm van patroonherkenning komt overeen met het aanpassen van een oplossing voor een verwant probleem. In het ontbijtvoorbeeld komt er een andere vorm van patroonherkenning naar voren. Zowel om thee te zetten als om een ei te koken, moet je water koken.
Gezien het belang van algoritmen kan het nuttig zijn om wat langer stil te staan bij algoritmisch denken. Algoritmisch denken gaat volgens de definitie over het duidelijk formuleren van instructies. Via de activiteiten ‘Programmeer eens een mens’ en ‘Sandwich BOT’ kan je je leerlingen laten ondervinden hoe belangrijk het is om een computer nauwkeurige en ondubbelzinnige opdrachten te geven. 9
Als je een geheel van eenduidige instructies stapsgewijs uitvoert om een probleem op te lossen, maak je zoals een computer gebruik van een algoritme. Om vaardig te zijn in algoritmisch denken, het denkproces om zelf een algoritme op te stellen, moet je eerst weten wat een algoritme is en in staat zijn om een algoritme uit te voeren. Vandaar dat een algoritme uitvoeren ook vaak wordt beschouwd als een deelaspect van algoritmisch denken. In de praktijk komt algoritmisch denken dus op verschillende beheersingsniveaus aan bod in de klas.
Hetzelfde is waar voor abstractie. 10 Om te kunnen abstraheren moet je eerst gegeven abstracties kunnen begrijpen.
8 Statter & Armoni (2020).
9 Je kan deze activiteiten ook doen in een les Engels of Frans. Tegelijk oefen je dan op spreekvaardigheid en woordenschat.
10 Böttcher et al. (2016). algoritme uitvoeren vs algoritmisch denken abstractie begrijpen vs abstractie bedenken
Bebraswedstrijd
Hoofdstuk 4 Computationeel denken in de
PROGRAMMEER EENS EEN MENS
Een leerling geeft instructies aan de rest van de klas om een tekening na te maken, zonder dat de andere leerlingen deze tekening hebben gezien.
Fracis wyffels
Figuur 9 Dwengo-project ‘Udavi’ in India
Via www.mijnstudiemateriaal.be vind je meer uitleg bij deze activiteit.
Blijf je liever in de ontbijtsfeer, dan kan je de alternatieve versie ‘Sandwich BOT’ gebruiken.
SANDWICH BOT
De leerkracht/robot smeert een boterham met jam door de instructies van de leerlingen letterlijk te volgen.
Via www.mijnstudiemateriaal.be kan je een filmpje over deze opdracht bekijken.
Bij deze leuke opdrachten wordt vaak wat afgelachen, maar het mag daar niet bij blijven. Een nabespreking bij deze activiteiten mag zeker niet ontbreken om leerlingen te doen begrijpen wat de link is met digitale systemen en computationeel denken.
2.3 De vier basisconcepten aanbrengen
Om bij je leerlingen helder te krijgen waarover computationeel denken gaat, kan je gebruikmaken van de vragen van de Bebraswedstrijd. Deze internationale wedstrijd wil mensen warm maken voor informatica. De deelnemers krijgen problemen voorgeschoteld die gelinkt zijn aan concepten uit de computerwetenschappen11, en tegelijk hun computationeel denken testen.
11 In de minimumdoelen wordt de term informaticawetenschappen gebruikt, dat is een synoniem van computerwetenschappen.
©
In de vragen van de Bebraswedstrijd komt vaak maar een basisconcept aan bod. De vragen worden ook op een zeer toegankelijke en aantrekkelijke manier geformuleerd. De wedstijd wordt bovendien ingericht voor leerlingen van verschillende leeftijden, van basisonderwijs tot secundair onderwijs, en met vragen van verschillende moeilijkheidsgraden (figuur 10 en figuur 11). Hierdoor is de Bebraswedstrijd uitermate geschikt om de basisconcepten bij je leerlingen aan te brengen.
IJSMACHINE
Een ijsmachine produceert op een systematische manier gekleurde bollen ijs.
Voor elk hoorntje worden vier bollen geschept. De figuur hieronder toont hoe de laatste drie ijsjes eruitzagen.
Naar: Bebras (tekst: Opráné Vecsei Éva, Zsuzsa Pluhár, Sébastien Combéfis; afbeelding: onbekend; vertaling: Kris Coolsaet)
Figuur 10 Bebras 2013-HU-01. Patroonherkenning – eerste graad
Hoe ziet het volgende ijsje eruit dat de machine zal maken?
Bespreking
In deze opgave wordt expliciet gevraagd om een patroon te herkennen en te extrapoleren. Deze opgave is bedoeld voor jonge kinderen en is dus voor iedereen gemakkelijk te begrijpen.
De ijsmachine produceert bollen ijs in vier verschillende kleuren die altijd in dezelfde volgorde voorkomen. De onderste bol van een ijsje heeft daarom altijd dezelfde kleur als de bovenste bol van het vorige ijsje.
De kleuren van de bollen bij de laatste drie ijsjes waren: groen – rood – paars –blauw, blauw – groen – rood – paars, paars – blauw – groen – rood. De vaste volgorde is ‘groen – rood – paars – blauw’ en de laatste bol van het vorige ijsje was rood. Het ijsje moet dus eerst een rode bol krijgen en daarna een paarse, een blauwe en een groene.
laagdrempelig
STORMBESTENDIG NETWERK
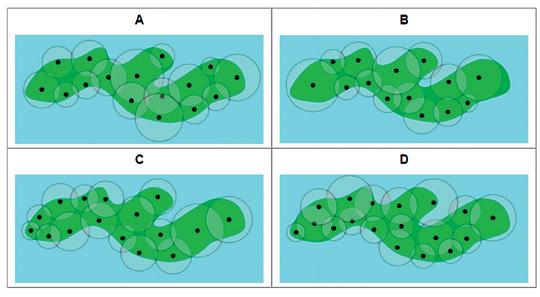
De gsm-maatschappij Bever Telecom wil gsm-masten plaatsen op Windeneiland. Het dekkingsgebied van een mast wordt weergegeven door een cirkel, waarbij de mast het middelpunt is van de cirkel. Twee masten heten verbonden met elkaar als hun dekkingsgebieden overlappen. Twee masten kunnen met elkaar communiceren als er een rij tussenliggende masten bestaat waarbij elke mast met een volgende mast is verbonden. Door de sterke wind op het eiland gebeurt het af en toe dat een mast breekt. Ook als er een mast niet meer functioneert, willen we dat eender welke twee overblijvende masten met elkaar kunnen blijven communiceren.
Naar: Bebras (tekst: Zoltán Molnár, Zsuzsa Pluhár; afbeeldingen: Iva Blöchliger; vertaling: Kris Coolsaet)
Figuur 11 Bebras 2014-HU-02. Abstractie – derde graad
Welke van de opstellingen A, B, C, D moet je gebruiken?
Een bespreking van dit voorbeeld en meer informatie over de internationale Bebraswedstrijd vind je via www.mijnstudiemateriaal.be.
Je kiest best voor vragen die de nieuwe begrippen niet al te overweldigend laten binnenkomen bij je leerlingen. Zo kan je je leerlingen op een laagdrempelige manier voeling laten krijgen met de basisconcepten van computationeel denken. In een nabespreking kan je de link met computerwetenschappen verduidelijken.
3
Computationeel denken koppelen aan andere 21e-eeuwse competenties
Er is een kloof tussen het belang dat wordt gehecht aan de 21e-eeuwse competenties en de manier waarop er in de praktijk vaak mee wordt omgegaan in scholen. Er wordt weinig tijd aan besteed, de leerstof wordt niet aangeboden binnen reallife contexten, de doelstellingen worden verengd tot alleen het gebruik van software en de kansen die digitale technologie biedt om te leren, blijven vaak onbenut.12
Er zijn nochtans opportuniteiten. De 21e-eeuwse competenties kunnen, net zoals computationeel denken, aan bod komen binnen je vertrouwde lesinhouden.13 Bovendien kan computationeel denken competenties zoals mediawijsheid, kritisch denken, cultureel bewustzijn en creativiteit versterken. 14 Benut de samenhang tussen de 21e-eeuwse competenties (zie het hoofdstuk ‘Computationeel denken, een basiscompetentie’). Informatiegeletterdheid sluit bijvoorbeeld aan bij patroonherkenning en abstractie, als je grafieken interpreteert of er zelf gaat maken. Je kan in de les dus tegelijk werken aan programmeren en creativiteit, of computationeel denken en informatiegeletterdheid. Je kan computationeel denken samen met andere 21e-eeuwse competenties integreren in het bestaande curriculum en spreiden over verschillende vakgebieden. Je kan opteren om er vakoverstijgend aan te werken. 15
3.1 Creativiteit
EEN DEFINITIE VAN CREATIVITEIT
Creativiteit is het vermogen om ideeën of artefacten te bedenken die nieuw en doelgericht zijn.16
Het is zinvol om na te denken over hoe je computationeel denken een plaats kan geven in het curriculum om creativiteit, ook in de betekenis van creatief denken, bij leerlingen te bevorderen. 17 Creatief denken, of – zoals Mariano en Chiappe (2021)
12 Voogt et al. (2013); Struyve et al. (2024).
13 Voogt et al. (2013); Goldberg et al. (2013).
14 Gretter & Yadav (2016) en (Voogt et al. (2013, 2015).
15 Volgens Struyve et al. (2024) correleren de prestaties van leerlingen op computationeel denken met de mate waarin leerkrachten nascholingen volgen en samenwerken met collega’s rond ICT.
16 Toivonen (2024); Sternberg & Lubart (1998).
17 Voogt et al. (2015). opportuniteiten samenhang
het zeggen – ‘creative non-routine thinking’, gaat over een elegante (wiskundige) oplossing of mooie schakeling bedenken, leerstof uit verschillende disciplines in verband kunnen brengen, een probleem benaderen vanuit een onverwachte invalshoek ... Volgens sommige onderzoekers kan computationeel denken gebruikers omvormen tot makers: menselijke creativiteit kan naar een hoger niveau worden getild door computationeel denken, met name door automatisering en algoritmisch denken te gebruiken. 18
De computer biedt nieuwe mogelijkheden tot expressie en creatief denken.19 Je leerlingen kunnen bijvoorbeeld een originele oplossing voor een probleem implementeren in de computer, of op een creatieve manier een digitaal systeem creëren. Programmeren biedt hun een eigentijdse manier om zich creatief te uiten. Dankzij digitale tools kunnen ze creatieve oplossingen verwezenlijken die zonder computer onmogelijk waren.
CREATIEF ZIJN MET DE COMPUTER
• Jonge leerlingen kunnen een open opdracht uitvoeren binnen een blokgebaseerde programmeeromgeving met een simulator, of een fysieke robot bouwen.
• Leerlingen kunnen data verzamelen via het internet of metingen doen met een microcontrollerplatform, zoals de Dwenguino.
• Oudere leerlingen kunnen digitale muziek creëren, al dan niet met gebruik van AI, of een logo ontwerpen in Python.
• Leerlingen kunnen creatief zijn met digitale foto's of video's, of hun creatieve ideeën uitwerken met generatieve AI.
3.2
Media- en informatiegeletterdheid
Media- en informatiegeletterdheid zijn complementair met computationeel denken en overlappen er deels mee. 20 Deze competenties gaan over het ‘belang van digitaal vaardig zijn, bekeken vanuit de bredere, sociale impact van het internet’ (Gretter & Yadav, 2016). Tabel 1 toont wat dit concreet kan betekenen.
18 Mishra & Yadav (2013).
19 Papert (1980); Voogt et al. (2015).
20 In de paragraaf ‘Informatiegeletterdheid’ van het hoofdstuk ‘Computationeel denken als leerdoel’ las je al dat er samenhang is tussen de minimumdoelen over informatiegeletterdheid, mediawijsheid en computationeel denken.
Link met aspecten van computationeel denken uit de minimumdoelen
Decompositie en abstractie
Hoofdstuk 4 Computationeel denken in de praktijk
Concepten en praktijken van computationeel denken
Abstractie
Algoritmisch denken, patroonherkenning, abstractie, mediawijsheid, impact op de maatschappij
Algoritmisch denken
Algoritmen
Elementen van media- en informatiegeletterdheid
Informatie synthetiseren om te focussen op kernideeën
Leren begrijpen hoe algoritmen worden gebruikt om online content af te leveren
Programmeren
Decompositie, patroonherkenning, abstractie en algoritmisch denken
Mediawijsheid, impact op de maatschappij
Bouwstenen van digitale systemen, mediawijsheid
Informatiegeletterdheid
Creativiteit
Globale impact
Het internet
Data en informatie
Naar: Gretter & Yadav (2016)
Programma’s achter de mediaplatformen leren begrijpen
Computationele artefacten ontwikkelen, media inbegrepen
Toegang tot media en informatie promoten om gebruikers te versterken
Privacykwesties begrijpen om veilig met anderen te communiceren
Toegang verkrijgen tot informatie en die evalueren om nieuwe inzichten te ontwikkelen
Tabel 1 Complementariteit van bepaalde concepten en praktijken van computationeel denken en bepaalde elementen van media- en informatiegeletterdheid vanuit 21e-eeuwse competenties en burgerschap volgens Gretter & Yadav (2016), en door ons gekoppeld aan aspecten van computationeel denken uit de Vlaamse minimumdoelen
3.3 Sociale en culturele dimensie van computationele geletterdheid
Ook de ‘sociale en culturele vaardigheden’ staan niet los van computationeel denken. Wing (2006) noemt ‘understanding human behavior ’ als een aspect van computationeel denken. Lowe en Brophy (2017) benadrukken dat bijna elk digitaal systeem deel is van een groter systeem waarin de mens centraal staat (zie figuur 12 verderop). Computationeel denken draait dus rond mensen. De digitale toepassingen worden namelijk door en voor mensen gemaakt. 21 Soms zijn er ook onbedoelde gevolgen. Neem het wagenpark: moderne auto’s zitten vol elektronica, zoals rijhulpsystemen die de verkeersveiligheid verhogen. Tegelijkertijd verdwijnen de auto’s waaraan autoliefhebbers onder de motorkap kunnen sleutelen, stilaan uit het straatbeeld.
Laat je leerlingen daarom ondervinden dat het bij werken met computers niet alleen gaat om technische vaardigheden, algoritmen, informatie verwerken of kunnen programmeren. Computers gebruiken houdt ook in dat je rekening houdt met de impact ervan op de samenleving.
IMPACT COMPUTERS OP DE SAMENLEVING
• Omgaan met culturele bias in computersystemen (zie het hoofdstuk ‘Computationeel denken en mediawijsheid’).
• Je kan de impact van algoritmen op de maatschappij bespreken (zie het hoofdstuk ‘Computationeel denken en mediawijsheid’).
Ook Kafai en Proctor (2022) beschouwen aan de slag gaan met computers als een sociale activiteit, waarbij cultuur, burgerzin, kritisch gebruik, persoonlijke expressie en connecteren met anderen een belangrijke rol spelen. Pogingen om het sollicitatieproces te objectiveren met computers hebben al geleid tot de uitsluiting van bepaalde groepen, als gevolg van de vooringenomenheid in de gebruikte AIsystemen. Het gebruik van een hologram van een overledene tijdens een uitvaart roept terechte vragen op over culturele aanvaardbaarheid en respect. Bied concepten en praktijken van computationeel denken daarom niet aan zonder context en beperk je niet tot de typische STEM-contexten, zoals fysica, maar neem een context die de doelgroep aanspreekt. Je kan bijvoorbeeld ook kiezen voor biologie of taaltechnologie, in het kader van een maatschappelijk relevant probleem.
21 Curzon & McOwan (2017).
De unplugged activiteit 'Locked-in' in het hoofdstuk 'Computationeel denken in de humanities en arts' sluit aan bij deze sociale dimensie van computationeel denken.
Waarom rijden autonome taxi’s vandaag alleen in afgebakende zones en niet over het volledige grondgebied van een stad?
3.4 STEM-leeromgevingen
Ook STEM-leeromgevingen22 zijn geschikt om computationeel denken en andere 21e-eeuwse competenties te ontwikkelen. In STEM-lessen moedig je leerlingen aan om creatieve oplossingen voor maatschappelijk relevante problemen te bedenken. Vaak moeten ze daarvoor een beroep doen op hun digitale competenties. Mariano en Chiappe (2021) geven enkele voorbeelden.
COMPUTATIONEEL DENKEN IN STEM-LEEROMGEVINGEN
• Via project-based learning kan je bijvoorbeeld samenwerken, kritisch denken en probleemoplossend denken aan bod laten komen.
• Via de E-discipline wordt creatief denken aangemoedigd.
• Ook via kunst- en taaldisciplines kan je inzetten op creativiteit en innovatie, bijvoorbeeld digitale kunst en taaltechnologie.
• Via de S-, T- en E-disciplines kan je ingaan op systemen en computationeel denken.
• De T zelf kan je associëren met het ontwikkelen van digitale geletterdheid.
• De S en T kunnen ten dienste staan van informatiegeletterdheid en cultureel bewustzijn. Ook via kunst- en taaldisciplines kan je daaraan werken.23
De kunst is om 21e-eeuwse competenties, STEM-onderwijs, onderwijs in nietSTEM-vakken en het bestaande curriculum met elkaar te verweven24 (zie meer hierover in het hoofdstuk ‘Computationeel denken in de humanities en arts').
digitale competenties
22 STEM staat voor Science, Technology, Engineering, Mathematics. Soms voegt men ook Arts toe, dan spreekt men van STEAM. Arts mag je in deze context ruim interpreteren: het kan ook over de humanities gaan. Hoewel wij zelf het acroniem STEM gebruiken, juichen we de samenwerking met niet-STEM-vakken voor STEM-onderwijs toe.
23 Deze voorbeelden zijn ontleend aan Mariano & Chiappe (2021).
24 Mariano & Chiappe (2021).
Je kan de digitale vaardigheden samen met andere competenties aan bod laten komen in de klas. Als je computationeel denken vakoverstijgend aanbiedt in relevante reallife contexten, is het gemakkelijk om andere 21e-eeuwse competenties daarin mee te nemen.25
4 Algemene aandachtspunten
Computationeel denken biedt je een houvast om een complex probleem aan te pakken. Je bedenkt een manier om met behulp van de computer tot een oplossing voor dat probleem te komen. Soms helpt computationeel denken om het probleem efficiënt aan te pakken, soms leidt het ertoe dat je de computer makkelijker kan inzetten.
Als je beslist om een probleem via computationeel denken te benaderen, is het belangrijk om enkele zaken in het achterhoofd te houden.
• Doordacht
In een probleemoplossend proces moet je de basisconcepten van computationeel denken op een doordachte manier toepassen. Decompositie is bijvoorbeeld niet alleen het probleem in delen opsplitsen (zie de paragraaf 'Aandachtspunten oriëntatiefase' in dit hoofdstuk; in dezelfde paragraaf las je ook dat decompositie, abstractie, patroonherkenning en algoritmisch denken op verschillende manieren aan bod kunnen komen). Laat ook je leerlingen ervaren dat het belangrijk is dat je de juiste manier kiest om dit te doen.
• Verweven
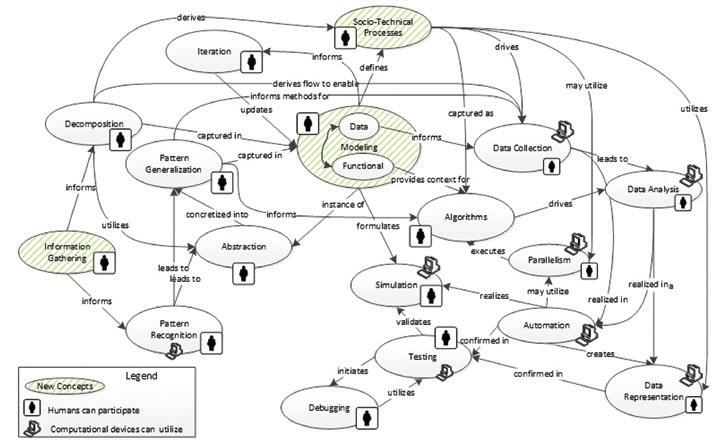
Het is belangrijk dat je leerlingen ondervinden dat de concepten van computationeel denken in de praktijk met elkaar verweven zijn (zie de paragraaf ‘Voorbeelden uit het leven gegrepen' in het hoofdstuk 'Computationeel denken: definitie en basisconcepten'). Het framework van Lowe en Brophy (2017) in figuur 12 brengt concepten en praktijken van computationeel denken in kaart, toont hoe ze tot elkaar in relatie staan, en of een mens of een computer de uitvoerder is van een bepaalde taak. Het kader zet bijvoorbeeld ook in de verf dat data iets anders is dan informatie en dat bij modelleren decompositie, abstractie en patroonherkenning worden gebruikt.
25 Grover & Pea (2017).
houvast
Figuur 12 Geoperationaliseerde conceptmap
• Van eenvoudig naar complex
Als je met computationeel denken aan de slag gaat op school, begin je best met eenvoudige problemen. Finaal is het wel de bedoeling dat je leerlingen een complex probleem oplossen met de computer. De complexiteit van dat probleem hangt uiteraard af van de studierichting en de leeftijd van de leerlingen.
• Unplugged
Computationeel denken houdt in dat je het op te lossen probleem goed begrijpt en formuleert, dat je een oplossing bedenkt, een algoritme opstelt en (indien gewenst) implementeert in de computer. De oplossing van een probleem kan je formuleren zonder computer, zelfs als je ervoor kiest om de oplossing toch door een computer te laten uitvoeren. 26 Je kan ervoor kiezen dat de leerlingen niet programmeren, maar de oplossing beschrijven in woorden of een algoritme formuleren in pseudocode. Bovendien zijn er veel manieren om zonder computer, ‘unplugged’, aan computationeel denken te werken (zie paragraaf ‘Voorbeelden uit het leven gegrepen’, dit hoofdstuk en het hoofdstuk ‘Computationeel denken unplugged’). Het is alleen niet de bedoeling dat je je tot unplugged-benaderingen beperkt. Die maken ingewikkelde concepten weliswaar vaak toegankelijker, maar zijn niet toereikend om computationeel te leren denken.
26 Hemmendinger (2010); Barr & Stephenson (2011); Grover & Pea (2017).
Uit: Lowe & Brophy (2017)
• Met programmeren
Combineer unplugged met ‘plugged’ activiteiten. Je wil namelijk niet dat leerlingen abstractie kunnen uitleggen bij een alledaags voorbeeld, maar het niet kunnen toepassen als ze een complex probleem moeten oplossen met de computer. Om digitale systemen ten volle te begrijpen, zal er bijvoorbeeld ook programmeren aan te pas moeten komen27 (zie het hoofdstuk ‘Inspiratie en misvattingen’). Let wel, dat moet niet tekstueel programmeren zijn. Je leerlingen een eenvoudig programma laten schrijven in een blokgebaseerde programmeeromgeving (in de volgende hoofdstukken vind je voorbeelden) of een toestel programmeren met de software voorzien door de fabrikant, kan volstaan.
• Breed spectrum
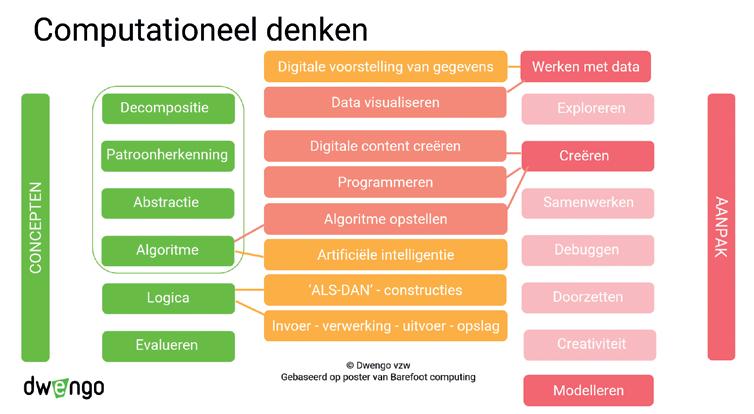
Computationeel denken is een competentie waarvoor leerlingen de nodige kennis en vaardigheden moeten verwerven. Computationeel denken is bovendien niet beperkt tot de basisconcepten. Het framework in figuur 12, het schema in figuur 13 en de voorbeelden in de paragraaf ‘Media- en informatiegeletterdheid’ illustreren hoe gevarieerd computationeel denken aan bod kan komen in de klas. Zoals besproken in het hoofdstuk ‘Computationeel denken als leerdoel’ vind je ook minimumdoelen over computationeel denken in andere sleutelcompetenties dan die over ‘Digitale competentie en mediawijsheid’.
Bij de voorbereiding van een les in jouw vak kan je vertrekken van de vier basisconcepten, maar benut zeker ook andere concepten en praktijken van computationeel denken als deze al vervat zijn in je lessen. Praktijken zoals het werken met data, modelleren, simuleren en debuggen komen voor in de minimumdoelen (zie kader achteraan in dit hoofdstuk).
• Terminologie
Moeten je leerlingen ook overweg kunnen met de terminologie zoals gedefinieerd in het hoofdstuk ‘Computationeel denken: definitie en basisconcepten’?
Vanuit de minimumdoelen is het niet verplicht dat leerlingen deze terminologie kennen. Je kan gerust spreken over ‘op zoek gaan naar deelproblemen’ in plaats van de term decompositie te gebruiken. Maar we durven er toch voor pleiten om je leerlingen de terminologie aan te leren. Dat maakt het gemakkelijker (en transparanter voor de leerlingen) om vakoverstijgend, met verschillende leerkrachten, aan computationeel denken te werken en daar over de jaren
27 Bell & Lodi (2019).
heen een verticale leerlijn rond op te bouwen. Je kan dan helder over nieuwe concepten communiceren.
Dezelfde woorden en vakterminologie gebruiken binnen verschillende vakken, is dus zeker een pluspunt. Niet voor niets bevat de sleutelcompetentie over leercompetenties het minimumdoel 'De leerlingen gebruiken school- en vaktaal'. Dat wil niet zeggen dat je leerlingen op een toets moet vragen om een definitie van patroonherkenning te geven, maar eerder dat je nagaat of ze patronen kunnen herkennen in een gegeven concrete situatie.
Houd er ook rekening mee dat eenzelfde term soms verschillende ladingen kan dekken. Evalueren binnen computationeel denken slaat op de evaluatie van de uiteindelijke oplossing, niet op (zelf)evaluatie van een leerling. Abstractie komt ook voor in wiskunde en in de beeldende kunsten, maar wel met een eigen doel. Je kan hier even op ingaan in de klas.
• Klemtoon
Door te werken met complexe problemen binnen reallife contexten worden leerlingen geconfronteerd met dubbelzinnigheid. Omdat het nu eenmaal inherent is aan het schrijven van een computerprogramma dat het vaak niet meteen werkt, zou programmeren de angst om fouten te maken bij leerlingen kunnen verminderen. Ze voelen zich gesterkt bij het leren van nieuwe dingen. Ze zijn ook meer betrokken en worden aangezet tot zelfreflectie. Tot slot zijn ze geneigd met elkaar te delen wat ze gemaakt hebben en erover te communiceren. 28
In lessen rond computationeel denken komen dus ook skills zoals doorzettingsvermogen, zelfregulering, helder communiceren, kunnen samenwerken en kunnen omgaan met complexiteit en dubbelzinnigheid aan bod. Let op dat de focus van de les niet naar deze vaardigheden verschuift, want dan zou je wel eens uit het oog kunnen verliezen dat er eigenlijk moet worden gewerkt aan de skill van computationeel denken zelf. 29
28 Papert (1980).
29 Voogt et al. (2015); Yadav et al. (2017a).
© Dwengo vzw, op basis van de poster van Barefoot computing (www.barefootcomputing.org)
Figuur 13 Concepten en praktijken van computationeel denken (niet exhaustief)
ANDERE CONCEPTEN VAN COMPUTATIONEEL DENKEN IN DE MINIMUMDOELEN30
• Tweede graad, doorstroomfinaliteit: ‘De leerlingen bepalen de waarheidswaarde van logische uitspraken met behulp van waarheidstabellen.’
• Tweede graad, cesuurdoel: ‘De leerlingen beoordelen de onderzoekbaarheid van een historische vraag.’
• Derde graad, doorstroomfinaliteit en dubbele finaliteit: ‘De leerlingen gebruiken de normale verdeling als continu model bij gegeven data.’
• Derde graad, doorstroomfinaliteit en dubbele finaliteit: ‘De leerlingen gebruiken modellen voor exponentiële groei.’
• Derde graad, doorstroomfinaliteit en dubbele finaliteit: ‘De leerlingen reflecteren over mogelijke maatregelen met betrekking tot klimaatverandering.’
De toelichting vermeldt ‘op basis van IPCC-modellen’.
• Derde graad, specifiek minimumdoel: ‘De leerlingen gebruiken matrixmodellen om evoluties te beschrijven.’
Met als onderliggend (kennis)element: ‘Matrixvoorstelling van een graaf’.
• Derde graad, specifiek minimumdoel: ‘De leerlingen gaan kritisch en doelgericht om met taaltechnologische hulpmiddelen.’
Met in de toelichting o.a. ‘culturele en seksistische bias’.
30 AHOVOKS (2020).